Update 第五章 卷积神经网络（CNN）.md

ch05_卷积神经网络(CNN)/第五章 卷积神经网络（CNN）.md

@@ -376,6 +376,49 @@ Softmax: 4030维。
 （2）不共享的卷积核并不增加inference时特征的计算量，仅会增加训练时的计算量。
 使用不共享的卷积核，由于需要训练的参数量大大增加，因此往往需要通过其他方法增加数据量。
 
+## 5.22 NetVLAD池化    （贡献者：熊楚原-中国人民大学）
+
+NetVLAD是论文\[15\]提出的一个局部特征聚合的方法。
+
+在传统的网络里面，例如VGG啊，最后一层卷积层输出的特征都是类似于Batchsize x 3 x 3 x 512的这种东西，然后会经过FC聚合，或者进行一个Global Average Pooling（NIN里的做法），或者怎么样，变成一个向量型的特征，然后进行Softmax or 其他的Loss。
+
+这种方法说简单点也就是输入一个图片或者什么的结构性数据，然后经过特征提取得到一个长度固定的向量，之后可以用度量的方法去进行后续的操作，比如分类啊，检索啊，相似度对比等等。
+
+那么NetVLAD考虑的主要是最后一层卷积层输出的特征这里，我们不想直接进行欠采样或者全局映射得到特征，对于最后一层输出的W x H x D，设计一个新的池化，去聚合一个“局部特征“，这即是NetVLAD的作用。
+
+NetVLAD的一个输入是一个W x H x D的图像特征，例如VGG-Net最后的3 x 3 x 512这样的矩阵，在网络中还需加一个维度为Batchsize。
+
+NetVLAD还需要另输入一个标量K即表示VLAD的聚类中心数量，它主要是来构成一个矩阵C，是通过原数据算出来的每一个$W \times H$特征的聚类中心，C的shape即$C: K \times D$，然后根据三个输入，VLAD是计算下式的V:
+
+$$V(j, k) = \sum_{i=1}^{N}{a_k(x_i)(x_i(j) - c_k(j))}$$
+
+其中j表示维度，从1到D，可以看到V的j是和输入与c对应的，对每个类别k，都对所有的x进行了计算，如果$x_i$属于当前类别k，$a_k=1$，否则$a_k=0$，计算每一个x和它聚类中心的残差，然后把残差加起来，即是每个类别k的结果，最后分别L2正则后拉成一个长向量后再做L2正则，正则非常的重要，因为这样才能统一所有聚类算出来的值，而残差和的目的主要是消减不同聚类上的分布不均，两者共同作用才能得到最后正常的输出。
+
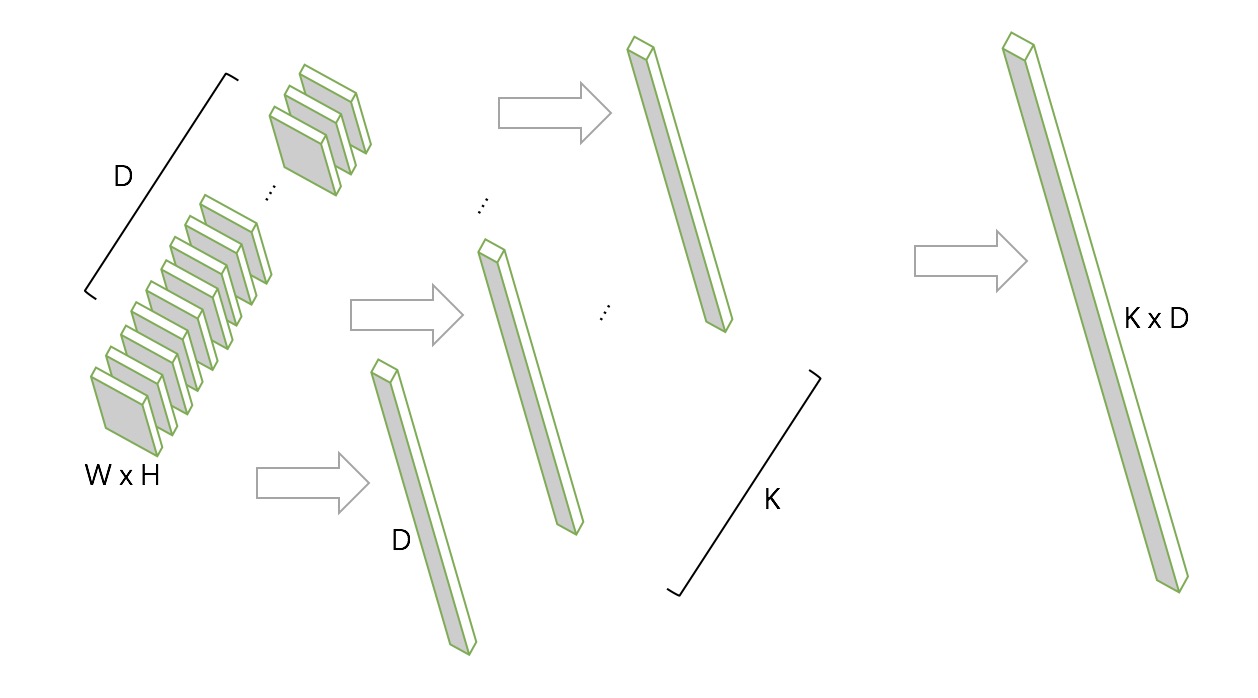
+输入与输出如下图所示：
+
+![image](http://www.ecohnoch.cn/img/netvlad.jpeg)
+
+中间得到的K个D维向量即是对D个x都进行了与聚类中心计算残差和的过程，最终把K个D维向量合起来后进行即得到最终输出的$K \times D$长度的一维向量。
+
+而VLAD本身是不可微的，因为上面的a要么是0要么是1，表示要么当前描述x是当前聚类，要么不是，是个离散的，NetVLAD为了能够在深度卷积网络里使用反向传播进行训练，对a进行了修正。
+
+那么问题就是如何重构一个a，使其能够评估当前的这个x和各个聚类的关联程度？用softmax来得到：
+
+$$a_k = \frac{e^{W_k^T x_i + b_k}}{e^{W_{k'}^T x_i + b_{k'}}}$$
+
+将这个把上面的a替换后，即是NetVLAD的公式，可以进行反向传播更新参数。
+
+所以一共有三个可训练参数，上式a中的$W: K \times D$，上式a中的$b: K \times 1$，聚类中心$c: K \times D$，而原始VLAD只有一个参数c。
+
+最终池化得到的输出是一个恒定的K x D的一维向量（经过了L2正则），如果带Batchsize，输出即为Batchsize x (K x D)的二维矩阵。
+
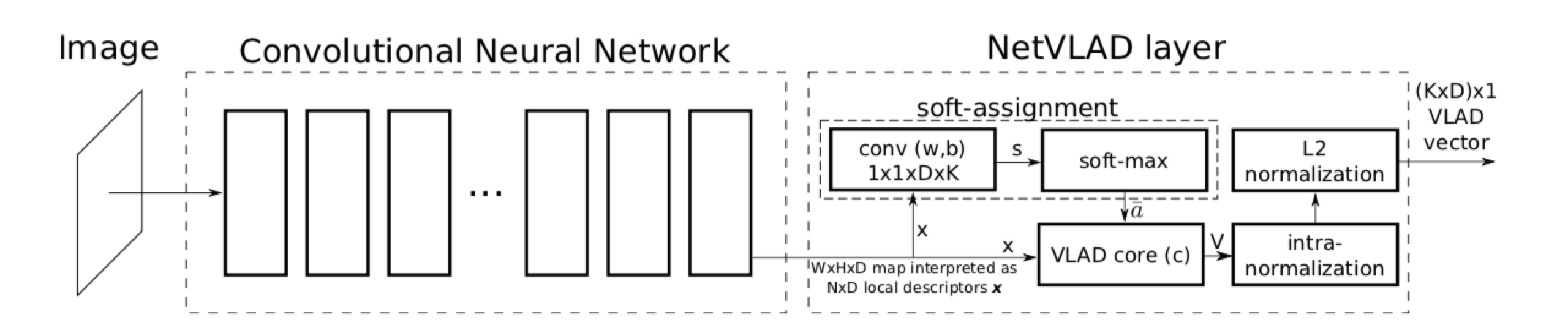
+NetVLAD作为池化层嵌入CNN网络即如下图所示，
+
+![image](http://www.ecohnoch.cn/img/netvlad_emb.png)
+
+原论文中采用将传统图像检索方法VLAD进行改进后应用在CNN的池化部分作为一种另类的局部特征池化，在场景检索上取得了很好的效果。
+
+后续相继又提出了ActionVLAD、ghostVLAD等改进。
 
 
 ## 参考文献
@@ -408,5 +451,6 @@ Softmax: 4030维。
 
 [14]  Jianxin W U ,  Gao B B ,  Wei X S , et al. Resource-constrained deep learning: challenges and practices[J]. Scientia Sinica(Informationis), 2018.
 
+[15] Arandjelovic R , Gronat P , Torii A , et al. [IEEE 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) - Las Vegas, NV, USA (2016.6.27-2016.6.30)] 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) - NetVLAD: CNN Architecture for Weakly Supervised Place Recognition[C]// 2016:5297-5307.