同步网站新增功能及文章
This commit is contained in:
parent
c8fb370905
commit
68d6053bc4
290
README.md
290
README.md
|
|
@ -78,183 +78,173 @@ Gitee Pages 地址:https://labuladong.gitee.io/algo/
|
|||
|
||||
# 目录
|
||||
|
||||
### 第零章、必读文章
|
||||
<!-- table start -->
|
||||
|
||||
* [学习算法和刷题的框架思维](https://labuladong.github.io/article/wx.html?wx=ZYaXOSVM3YBIeRWm7E_jcQ)
|
||||
* [我的刷题心得](https://labuladong.github.io/article/wx.html?wx=_XhcgHrI15PsPp-Ie87p3w)
|
||||
* [动态规划解题套路框架](https://labuladong.github.io/article/?qno=509)
|
||||
* [回溯算法解题套路框架](https://labuladong.github.io/article/?qno=51)
|
||||
* [BFS 算法解题套路框架](https://labuladong.github.io/article/?qno=111)
|
||||
* [手把手带你刷二叉树(纲领篇)](https://labuladong.github.io/article/?qno=104)
|
||||
* [一文搞懂单链表的六大解题套路](https://labuladong.github.io/article/?qno=21)
|
||||
* [一文秒杀所有岛屿题目](https://labuladong.github.io/article/?qno=200)
|
||||
* [我写了首诗,让你闭着眼睛也能写对二分搜索](https://labuladong.github.io/article/?qno=704)
|
||||
* [我写了首诗,把滑动窗口算法算法变成了默写题](https://labuladong.github.io/article/?qno=76)
|
||||
* [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.github.io/article/?qno=121)
|
||||
* [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.github.io/article/?qno=198)
|
||||
* [一个方法团灭 nSum 问题](https://labuladong.github.io/article/?qno=15)
|
||||
* [提高刷题幸福感的小技巧](https://labuladong.github.io/article/wx.html?wx=ucGZavJVKNCJ5j7T15voZA)
|
||||
### [第零章、核心框架汇总](https://labuladong.github.io/algo/)
|
||||
* [学习算法和刷题的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法)
|
||||
* [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
* [双指针技巧秒杀七道链表题目](https://labuladong.github.io/article/fname.html?fname=链表技巧)
|
||||
* [双指针技巧秒杀七道数组题目](https://labuladong.github.io/article/fname.html?fname=双指针技巧)
|
||||
* [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结)
|
||||
* [动态规划解题套路框架](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)
|
||||
* [回溯算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版)
|
||||
* [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.github.io/article/fname.html?fname=子集排列组合)
|
||||
* [BFS 算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=BFS框架)
|
||||
* [我写了首诗,把二分搜索算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=二分查找详解)
|
||||
* [我写了首诗,把滑动窗口算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=滑动窗口技巧进阶)
|
||||
* [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.github.io/article/fname.html?fname=团灭股票问题)
|
||||
* [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.github.io/article/fname.html?fname=抢房子)
|
||||
* [一个方法团灭 nSum 问题](https://labuladong.github.io/article/fname.html?fname=nSum)
|
||||
* [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度)
|
||||
* [算法笔试「骗分」套路](https://labuladong.github.io/article/fname.html?fname=刷题技巧)
|
||||
|
||||
|
||||
### 第一章、手把手刷数据结构
|
||||
### [第一章、手把手刷数据结构](https://labuladong.github.io/algo/)
|
||||
* [手把手刷链表算法](https://labuladong.github.io/algo/)
|
||||
* [双指针技巧秒杀七道链表题目](https://labuladong.github.io/article/fname.html?fname=链表技巧)
|
||||
* [递归魔法:反转单链表](https://labuladong.github.io/article/fname.html?fname=递归反转链表的一部分)
|
||||
* [如何 K 个一组反转链表](https://labuladong.github.io/article/fname.html?fname=k个一组反转链表)
|
||||
* [如何判断回文链表](https://labuladong.github.io/article/fname.html?fname=判断回文链表)
|
||||
|
||||
* [手把手刷链表题目](https://labuladong.github.io/algo/)
|
||||
* [一文搞懂单链表的六大解题套路](https://labuladong.github.io/article/?qno=21)
|
||||
* [递归反转链表的一部分](https://labuladong.github.io/article/?qno=206)
|
||||
* [如何 K 个一组反转链表](https://labuladong.github.io/article/?qno=25)
|
||||
* [如何判断回文链表](https://labuladong.github.io/article/?qno=234)
|
||||
* [手把手刷数组算法](https://labuladong.github.io/algo/)
|
||||
* [双指针技巧秒杀七道数组题目](https://labuladong.github.io/article/fname.html?fname=双指针技巧)
|
||||
* [小而美的算法技巧:前缀和数组](https://labuladong.github.io/article/fname.html?fname=前缀和技巧)
|
||||
* [小而美的算法技巧:差分数组](https://labuladong.github.io/article/fname.html?fname=差分技巧)
|
||||
* [二维数组的花式遍历技巧](https://labuladong.github.io/article/fname.html?fname=花式遍历)
|
||||
* [我写了首诗,把滑动窗口算法算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=滑动窗口技巧进阶)
|
||||
* [滑动窗口算法延伸:Rabin Karp 字符匹配算法](https://labuladong.github.io/article/fname.html?fname=rabinkarp)
|
||||
* [我写了首诗,让你闭着眼睛也能写对二分搜索](https://labuladong.github.io/article/fname.html?fname=二分查找详解)
|
||||
* [带权重的随机选择算法](https://labuladong.github.io/article/fname.html?fname=随机权重)
|
||||
* [二分搜索怎么用?我又总结了套路](https://labuladong.github.io/article/fname.html?fname=二分运用)
|
||||
* [田忌赛马背后的算法决策](https://labuladong.github.io/article/fname.html?fname=田忌赛马)
|
||||
* [常数时间删除/查找数组中的任意元素](https://labuladong.github.io/article/fname.html?fname=随机集合)
|
||||
* [一道数组去重的算法题把我整不会了](https://labuladong.github.io/article/fname.html?fname=单调栈去重)
|
||||
|
||||
* [手把手刷二叉树](https://labuladong.github.io/algo/)
|
||||
* [手把手带你刷二叉树(纲领篇)](https://labuladong.github.io/article/?qno=104)
|
||||
* [手把手带你刷二叉树(第一期)](https://labuladong.github.io/article/?qno=226)
|
||||
* [手把手带你刷二叉树(第二期)](https://labuladong.github.io/article/?qno=654)
|
||||
* [手把手带你刷二叉树(第三期)](https://labuladong.github.io/article/?qno=652)
|
||||
* [手把手带你刷二叉搜索树(第一期)](https://labuladong.github.io/article/?qno=230)
|
||||
* [手把手带你刷二叉搜索树(第二期)](https://labuladong.github.io/article/?qno=450)
|
||||
* [手把手带你刷二叉搜索树(第三期)](https://labuladong.github.io/article/?qno=96)
|
||||
* [美团面试官:你对后序遍历一无所知](https://labuladong.github.io/article/?qno=1373)
|
||||
* [二叉树的序列化,就那几个框架,枯燥至极](https://labuladong.github.io/article/?qno=297)
|
||||
* [题目不让我干什么,我偏要干什么](https://labuladong.github.io/article/?qno=341)
|
||||
* [Git原理之最近公共祖先](https://labuladong.github.io/article/?qno=236)
|
||||
* [如何计算完全二叉树的节点数](https://labuladong.github.io/article/?qno=222)
|
||||
* [二叉树八股文:递归改迭代](https://labuladong.github.io/article/wx.html?wx=jI8_-E6rx2HVBOmuQOTgHg)
|
||||
* [手把手刷二叉树算法](https://labuladong.github.io/algo/)
|
||||
* [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结)
|
||||
* [东哥带你刷二叉树(思路篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列1)
|
||||
* [东哥带你刷二叉树(构造篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列2)
|
||||
* [东哥带你刷二叉树(序列化篇)](https://labuladong.github.io/article/fname.html?fname=二叉树的序列化)
|
||||
* [东哥带你刷二叉树(后序篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列3)
|
||||
* [归并排序详解及应用](https://labuladong.github.io/article/fname.html?fname=归并排序)
|
||||
* [东哥带你刷二叉搜索树(特性篇)](https://labuladong.github.io/article/fname.html?fname=BST1)
|
||||
* [东哥带你刷二叉搜索树(基操篇)](https://labuladong.github.io/article/fname.html?fname=BST2)
|
||||
* [东哥带你刷二叉搜索树(构造篇)](https://labuladong.github.io/article/fname.html?fname=BST3)
|
||||
* [快速排序详解及应用](https://labuladong.github.io/article/fname.html?fname=快速排序)
|
||||
* [题目不让我干什么,我偏要干什么](https://labuladong.github.io/article/fname.html?fname=nestInteger)
|
||||
* [Git原理之最近公共祖先](https://labuladong.github.io/article/fname.html?fname=公共祖先)
|
||||
* [如何计算完全二叉树的节点数](https://labuladong.github.io/article/fname.html?fname=完全二叉树节点数)
|
||||
|
||||
* [手把手刷图算法](https://labuladong.github.io/algo/)
|
||||
* [图论基础](https://labuladong.github.io/article/?qno=797)
|
||||
* [拓扑排序详解及运用](https://labuladong.github.io/article/?qno=207)
|
||||
* [二分图判定](https://labuladong.github.io/article/?qno=785)
|
||||
* [Union-Find算法详解](https://labuladong.github.io/article/?qno=323)
|
||||
* [Union-Find算法应用](https://labuladong.github.io/article/?qno=130)
|
||||
* [Kruskal 最小生成树算法](https://labuladong.github.io/article/?qno=261)
|
||||
* [Prim 最小生成树算法](https://labuladong.github.io/article/wx.html?wx=bvi0wGdbtB4nkYye0yzmqg)
|
||||
* [众里寻他千百度:名流问题](https://labuladong.github.io/article/?qno=277)
|
||||
* [我写了一个模板,把 Dijkstra 算法变成了默写题](https://labuladong.github.io/article/?qno=743)
|
||||
* [图论基础及遍历算法](https://labuladong.github.io/article/fname.html?fname=图)
|
||||
* [环检测及拓扑排序算法](https://labuladong.github.io/article/fname.html?fname=拓扑排序)
|
||||
* [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
|
||||
* [并查集(Union-Find)算法](https://labuladong.github.io/article/fname.html?fname=UnionFind算法详解)
|
||||
* [Kruskal 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=kruskal)
|
||||
* [Prim 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=prim算法)
|
||||
* [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
* [众里寻他千百度:名流问题](https://labuladong.github.io/article/fname.html?fname=名人问题)
|
||||
|
||||
* [手把手设计数据结构](https://labuladong.github.io/algo/)
|
||||
* [算法就像搭乐高:带你手撸 LRU 算法](https://labuladong.github.io/article/?qno=146)
|
||||
* [算法就像搭乐高:带你手撸 LFU 算法](https://labuladong.github.io/article/?qno=460)
|
||||
* [前缀树算法模板秒杀五道算法题](https://labuladong.github.io/article/?qno=208)
|
||||
* [数据结构设计:最大栈](https://labuladong.github.io/article/?qno=895)
|
||||
* [一道求中位数的算法题把我整不会了](https://labuladong.github.io/article/?qno=295)
|
||||
* [设计朋友圈时间线功能](https://labuladong.github.io/article/?qno=355)
|
||||
* [单调栈结构解决三道算法题](https://labuladong.github.io/article/?qno=496)
|
||||
* [单调队列结构解决滑动窗口问题](https://labuladong.github.io/article/?qno=239)
|
||||
* [二叉堆详解实现优先级队列](https://labuladong.github.io/article/wx.html?wx=o7tdyLiYm668dpUWd-x7Lg)
|
||||
* [队列实现栈以及栈实现队列](https://labuladong.github.io/article/?qno=232)
|
||||
|
||||
* [手把手刷数组题目](https://labuladong.github.io/algo/)
|
||||
* [小而美的算法技巧:前缀和数组](https://labuladong.github.io/article/?qno=303)
|
||||
* [小而美的算法技巧:差分数组](https://labuladong.github.io/article/?qno=370)
|
||||
* [二维数组的花式遍历技巧](https://labuladong.github.io/article/?qno=48)
|
||||
* [双指针技巧总结](https://labuladong.github.io/article/?qno=167)
|
||||
* [我写了首诗,把滑动窗口算法算法变成了默写题](https://labuladong.github.io/article/?qno=76)
|
||||
* [我写了首诗,让你闭着眼睛也能写对二分搜索](https://labuladong.github.io/article/?qno=704)
|
||||
* [二分搜索怎么用?我又总结了套路](https://labuladong.github.io/article/?qno=875)
|
||||
* [我和快手面试官对二分搜索进行了深度探讨](https://labuladong.github.io/article/?qno=410)
|
||||
* [田忌赛马背后的算法决策](https://labuladong.github.io/article/?qno=870)
|
||||
* [给我常数时间,我可以删除/查找数组中的任意元素](https://labuladong.github.io/article/?qno=380)
|
||||
* [带权重的随机选择算法](https://labuladong.github.io/article/?qno=528)
|
||||
* [一道数组去重的算法题把我整不会了](https://labuladong.github.io/article/?qno=316)
|
||||
* [如何去除有序数组的重复元素](https://labuladong.github.io/article/?qno=26)
|
||||
* [twoSum问题的核心思想](https://labuladong.github.io/article/?qno=1)
|
||||
|
||||
### 第二章、手把手刷动态规划
|
||||
* [算法就像搭乐高:带你手撸 LRU 算法](https://labuladong.github.io/article/fname.html?fname=LRU算法)
|
||||
* [算法就像搭乐高:带你手撸 LFU 算法](https://labuladong.github.io/article/fname.html?fname=LFU)
|
||||
* [前缀树算法模板秒杀五道算法题](https://labuladong.github.io/article/fname.html?fname=trie)
|
||||
* [一道求中位数的算法题把我整不会了](https://labuladong.github.io/article/fname.html?fname=数据流中位数)
|
||||
* [单调栈结构解决三道算法题](https://labuladong.github.io/article/fname.html?fname=单调栈)
|
||||
* [单调队列结构解决滑动窗口问题](https://labuladong.github.io/article/fname.html?fname=单调队列)
|
||||
* [二叉堆详解实现优先级队列](https://labuladong.github.io/article/fname.html?fname=二叉堆详解实现优先级队列)
|
||||
* [队列实现栈以及栈实现队列](https://labuladong.github.io/article/fname.html?fname=队列实现栈栈实现队列)
|
||||
* [设计朋友圈时间线功能](https://labuladong.github.io/article/fname.html?fname=设计Twitter)
|
||||
|
||||
### [第二章、手把手刷动态规划](https://labuladong.github.io/algo/)
|
||||
* [动态规划基本技巧](https://labuladong.github.io/algo/)
|
||||
* [动态规划解题核心框架](https://labuladong.github.io/article/?qno=509)
|
||||
* [动态规划设计:最长递增子序列](https://labuladong.github.io/article/?qno=300)
|
||||
* [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/wx.html?wx=qvlfyKBiXVX7CCwWFR-XKg)
|
||||
* [base case 和备忘录的初始值怎么定?](https://labuladong.github.io/article/?qno=931)
|
||||
* [对动态规划进行降维打击](https://labuladong.github.io/article/wx.html?wx=SnyN1Gn6DTLm0uJyp5l6CQ)
|
||||
* [动态规划和回溯算法到底谁是谁爹?](https://labuladong.github.io/article/?qno=494)
|
||||
* [动态规划解题套路框架](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)
|
||||
* [动态规划设计:最长递增子序列](https://labuladong.github.io/article/fname.html?fname=动态规划设计:最长递增子序列)
|
||||
* [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
* [base case 和备忘录的初始值怎么定?](https://labuladong.github.io/article/fname.html?fname=备忘录等基础)
|
||||
* [对动态规划进行降维打击](https://labuladong.github.io/article/fname.html?fname=状态压缩技巧)
|
||||
|
||||
* [子序列类型问题](https://labuladong.github.io/algo/)
|
||||
* [经典动态规划:编辑距离](https://labuladong.github.io/article/?qno=72)
|
||||
* [动态规划设计:最长递增子序列](https://labuladong.github.io/article/?qno=300)
|
||||
* [二维递增子序列:信封嵌套问题](https://labuladong.github.io/article/?qno=354)
|
||||
* [动态规划设计:最大子数组](https://labuladong.github.io/article/?qno=53)
|
||||
* [经典动态规划:最长公共子序列](https://labuladong.github.io/article/?qno=1143)
|
||||
* [动态规划之子序列问题解题模板](https://labuladong.github.io/article/?qno=516)
|
||||
* [经典动态规划:编辑距离](https://labuladong.github.io/article/fname.html?fname=编辑距离)
|
||||
* [动态规划设计:最长递增子序列](https://labuladong.github.io/article/fname.html?fname=动态规划设计:最长递增子序列)
|
||||
* [动态规划设计:最大子数组](https://labuladong.github.io/article/fname.html?fname=最大子数组)
|
||||
* [经典动态规划:最长公共子序列](https://labuladong.github.io/article/fname.html?fname=LCS)
|
||||
* [动态规划之子序列问题解题模板](https://labuladong.github.io/article/fname.html?fname=子序列问题模板)
|
||||
|
||||
* [背包类型问题](https://labuladong.github.io/algo/)
|
||||
* [经典动态规划:0-1 背包问题](https://labuladong.github.io/article/wx.html?wx=RXfnhSpVBmVneQjDSUSAVQ)
|
||||
* [经典动态规划:子集背包问题](https://labuladong.github.io/article/?qno=416)
|
||||
* [经典动态规划:完全背包问题](https://labuladong.github.io/article/?qno=518)
|
||||
* [经典动态规划:0-1 背包问题](https://labuladong.github.io/article/fname.html?fname=背包问题)
|
||||
* [经典动态规划:子集背包问题](https://labuladong.github.io/article/fname.html?fname=背包子集)
|
||||
* [经典动态规划:完全背包问题](https://labuladong.github.io/article/fname.html?fname=背包零钱)
|
||||
* [动态规划和回溯算法到底谁是谁爹?](https://labuladong.github.io/article/fname.html?fname=targetSum)
|
||||
|
||||
* [用动态规划玩游戏](https://labuladong.github.io/algo/)
|
||||
* [动态规划之最小路径和](https://labuladong.github.io/article/?qno=64)
|
||||
* [动态规划帮我通关了《魔塔》](https://labuladong.github.io/article/?qno=174)
|
||||
* [动态规划帮我通关了《辐射4》](https://labuladong.github.io/article/?qno=514)
|
||||
* [旅游省钱大法:加权最短路径](https://labuladong.github.io/article/?qno=787)
|
||||
* [经典动态规划:正则表达式](https://labuladong.github.io/article/?qno=10)
|
||||
* [经典动态规划:高楼扔鸡蛋](https://labuladong.github.io/article/wx.html?wx=xn4LjWfaKTPQeCXR0qDqZg)
|
||||
* [经典动态规划:高楼扔鸡蛋(进阶)](https://labuladong.github.io/article/wx.html?wx=7XPGKe7bMkwovH95cnhang)
|
||||
* [经典动态规划:戳气球](https://labuladong.github.io/article/?qno=312)
|
||||
* [经典动态规划:博弈问题](https://labuladong.github.io/article/wx.html?wx=xTeOzqNiGJwbwIpS3ySZqw)
|
||||
* [经典动态规划:四键键盘](https://labuladong.github.io/article/?qno=651)
|
||||
* [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.github.io/article/?qno=198)
|
||||
* [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.github.io/article/?qno=121)
|
||||
* [有限状态机之 KMP 字符匹配算法](https://labuladong.github.io/article/?qno=28)
|
||||
* [构造回文的最小插入次数](https://labuladong.github.io/article/?qno=1312)
|
||||
* [动态规划之最小路径和](https://labuladong.github.io/article/fname.html?fname=最小路径和)
|
||||
* [动态规划帮我通关了《魔塔》](https://labuladong.github.io/article/fname.html?fname=魔塔)
|
||||
* [动态规划帮我通关了《辐射4》](https://labuladong.github.io/article/fname.html?fname=转盘)
|
||||
* [旅游省钱大法:加权最短路径](https://labuladong.github.io/article/fname.html?fname=旅行最短路径)
|
||||
* [经典动态规划:正则表达式](https://labuladong.github.io/article/fname.html?fname=动态规划之正则表达)
|
||||
* [经典动态规划:高楼扔鸡蛋](https://labuladong.github.io/article/fname.html?fname=高楼扔鸡蛋问题)
|
||||
* [经典动态规划:戳气球](https://labuladong.github.io/article/fname.html?fname=扎气球)
|
||||
* [经典动态规划:博弈问题](https://labuladong.github.io/article/fname.html?fname=动态规划之博弈问题)
|
||||
* [经典动态规划:四键键盘](https://labuladong.github.io/article/fname.html?fname=动态规划之四键键盘)
|
||||
* [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.github.io/article/fname.html?fname=抢房子)
|
||||
* [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.github.io/article/fname.html?fname=团灭股票问题)
|
||||
* [有限状态机之 KMP 字符匹配算法](https://labuladong.github.io/article/fname.html?fname=动态规划之KMP字符匹配算法)
|
||||
|
||||
* [贪心类型问题](https://labuladong.github.io/algo/)
|
||||
* [贪心算法之区间调度问题](https://labuladong.github.io/article/?qno=435)
|
||||
* [扫描线技巧:安排会议室](https://labuladong.github.io/article/?qno=253)
|
||||
* [剪视频剪出一个贪心算法](https://labuladong.github.io/article/?qno=1024)
|
||||
* [如何运用贪心思想玩跳跃游戏](https://labuladong.github.io/article/?qno=55)
|
||||
* [当老司机学会了贪心算法](https://labuladong.github.io/article/?qno=134)
|
||||
|
||||
### 第三章、必知必会算法技巧
|
||||
* [贪心算法之区间调度问题](https://labuladong.github.io/article/fname.html?fname=贪心算法之区间调度问题)
|
||||
* [扫描线技巧:安排会议室](https://labuladong.github.io/article/fname.html?fname=安排会议室)
|
||||
* [剪视频剪出一个贪心算法](https://labuladong.github.io/article/fname.html?fname=剪视频)
|
||||
* [如何运用贪心思想玩跳跃游戏](https://labuladong.github.io/article/fname.html?fname=跳跃游戏)
|
||||
* [当老司机学会了贪心算法](https://labuladong.github.io/article/fname.html?fname=老司机)
|
||||
|
||||
### [第三章、必知必会算法技巧](https://labuladong.github.io/algo/)
|
||||
* [暴力搜索算法](https://labuladong.github.io/algo/)
|
||||
* [回溯算法解题套路框架](https://labuladong.github.io/article/?qno=51)
|
||||
* [经典回溯算法:集合划分问题](https://labuladong.github.io/article/?qno=698)
|
||||
* [回溯算法团灭子集、排列、组合问题](https://labuladong.github.io/article/?qno=78)
|
||||
* [回溯算法最佳实践:解数独](https://labuladong.github.io/article/?qno=37)
|
||||
* [回溯算法最佳实践:括号生成](https://labuladong.github.io/article/?qno=22)
|
||||
* [BFS 算法解题套路框架](https://labuladong.github.io/article/?qno=111)
|
||||
* [如何用 BFS 算法秒杀各种智力题](https://labuladong.github.io/article/?qno=773)
|
||||
* [回溯算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版)
|
||||
* [经典回溯算法:集合划分问题](https://labuladong.github.io/article/fname.html?fname=集合划分)
|
||||
* [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.github.io/article/fname.html?fname=子集排列组合)
|
||||
* [一文秒杀所有岛屿题目](https://labuladong.github.io/article/fname.html?fname=岛屿题目)
|
||||
* [回溯算法最佳实践:解数独](https://labuladong.github.io/article/fname.html?fname=sudoku)
|
||||
* [回溯算法最佳实践:括号生成](https://labuladong.github.io/article/fname.html?fname=合法括号生成)
|
||||
* [BFS 算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=BFS框架)
|
||||
* [如何用 BFS 算法秒杀各种智力题](https://labuladong.github.io/article/fname.html?fname=BFS解决滑动拼图)
|
||||
|
||||
* [数学运算技巧](https://labuladong.github.io/algo/)
|
||||
* [常用的位操作](https://labuladong.github.io/article/?qno=191)
|
||||
* [讲两道常考的阶乘算法题](https://labuladong.github.io/article/?qno=172)
|
||||
* [如何高效寻找素数](https://labuladong.github.io/article/?qno=204)
|
||||
* [如何高效进行模幂运算](https://labuladong.github.io/article/?qno=372)
|
||||
* [如何寻找缺失的元素](https://labuladong.github.io/article/?qno=268)
|
||||
* [如何同时寻找缺失和重复的元素](https://labuladong.github.io/article/?qno=645)
|
||||
* [如何在无限序列中随机抽取元素](https://labuladong.github.io/article/?qno=382)
|
||||
* [一行代码就能解决的算法题](https://labuladong.github.io/article/?qno=292)
|
||||
* [几个反直觉的概率问题](https://labuladong.github.io/article/wx.html?wx=eCgxtBpsrZjJQ9KmhKrEJw)
|
||||
|
||||
* [其他算法技巧](https://labuladong.github.io/algo/)
|
||||
* [快速排序亲兄弟:快速选择算法](https://labuladong.github.io/article/?qno=215)
|
||||
* [分治算法详解:运算优先级](https://labuladong.github.io/article/?qno=241)
|
||||
* [一个方法解决三道区间问题](https://labuladong.github.io/article/?qno=1288)
|
||||
* [常用的位操作](https://labuladong.github.io/article/fname.html?fname=常用的位操作)
|
||||
* [讲两道常考的阶乘算法题](https://labuladong.github.io/article/fname.html?fname=阶乘题目)
|
||||
* [如何高效寻找素数](https://labuladong.github.io/article/fname.html?fname=打印素数)
|
||||
* [如何高效进行模幂运算](https://labuladong.github.io/article/fname.html?fname=superPower)
|
||||
* [如何同时寻找缺失和重复的元素](https://labuladong.github.io/article/fname.html?fname=缺失和重复的元素)
|
||||
* [如何在无限序列中随机抽取元素](https://labuladong.github.io/article/fname.html?fname=水塘抽样)
|
||||
* [一行代码就能解决的算法题](https://labuladong.github.io/article/fname.html?fname=一行代码解决的智力题)
|
||||
* [几个反直觉的概率问题](https://labuladong.github.io/article/fname.html?fname=几个反直觉的概率问题)
|
||||
|
||||
* [经典面试题](https://labuladong.github.io/algo/)
|
||||
* [谁能想到,斗地主也能玩出算法](https://labuladong.github.io/article/?qno=659)
|
||||
* [东哥吃葡萄时竟然吃出一道算法题!](https://labuladong.github.io/article/wx.html?wx=3VjL7Gud1bQQrbjedzEhMQ)
|
||||
* [烧饼排序算法](https://labuladong.github.io/article/?qno=969)
|
||||
* [字符串乘法计算](https://labuladong.github.io/article/?qno=43)
|
||||
* [如何实现一个计算器](https://labuladong.github.io/article/?qno=224)
|
||||
* [如何高效解决接雨水问题](https://labuladong.github.io/article/?qno=42)
|
||||
* [如何寻找最长回文子串](https://labuladong.github.io/article/?qno=5)
|
||||
* [如何解决括号相关的问题](https://labuladong.github.io/article/?qno=20)
|
||||
* [如何判定完美矩形](https://labuladong.github.io/article/?qno=391)
|
||||
* [如何调度考生的座位](https://labuladong.github.io/article/?qno=855)
|
||||
* [二分查找高效判定子序列](https://labuladong.github.io/article/?qno=392)
|
||||
* [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
* [一个方法解决三道区间问题](https://labuladong.github.io/article/fname.html?fname=区间问题合集)
|
||||
* [谁能想到,斗地主也能玩出算法](https://labuladong.github.io/article/fname.html?fname=斗地主)
|
||||
* [烧饼排序算法](https://labuladong.github.io/article/fname.html?fname=烧饼排序)
|
||||
* [字符串乘法计算](https://labuladong.github.io/article/fname.html?fname=字符串乘法)
|
||||
* [如何实现一个计算器](https://labuladong.github.io/article/fname.html?fname=实现计算器)
|
||||
* [如何高效解决接雨水问题](https://labuladong.github.io/article/fname.html?fname=接雨水)
|
||||
* [如何解决括号相关的问题](https://labuladong.github.io/article/fname.html?fname=括号插入)
|
||||
* [如何判定完美矩形](https://labuladong.github.io/article/fname.html?fname=完美矩形)
|
||||
* [如何调度考生的座位](https://labuladong.github.io/article/fname.html?fname=座位调度)
|
||||
* [二分查找高效判定子序列](https://labuladong.github.io/article/fname.html?fname=二分查找判定子序列)
|
||||
|
||||
### 第四章、通用计算机技术
|
||||
|
||||
* [Linux 文件系统都是什么鬼](https://labuladong.github.io/article/wx.html?wx=kJx07mbQQExV3JUGJo4nYw)
|
||||
* [Linux 的进程、线程、文件描述符是什么](https://labuladong.github.io/article/wx.html?wx=USb5e2Zoc0LRgRShRpTYfg)
|
||||
* [关于 Linux shell 你必须知道的](https://labuladong.github.io/article/wx.html?wx=h3SXmZ2yMtOKEKdACUx1Ew)
|
||||
* [Linux shell 的实用小技巧](https://labuladong.github.io/article/wx.html?wx=vCtu4lkcoixJELH2t9r7pg)
|
||||
* [Linux 管道符原理大揭秘](https://labuladong.github.io/article/wx.html?wx=p3rwjoCWN2WnH4xxtwDiyQ)
|
||||
* [一文看懂 session 和 cookie](https://labuladong.github.io/article/wx.html?wx=lEAFW9ZSiqHJOfMnznPPHA)
|
||||
* [加密算法的前身今世](https://labuladong.github.io/article/wx.html?wx=HvZsBiNn9tPcq11fmWgcLQ)
|
||||
* [我用四个命令概括了 Git 的所有套路](https://labuladong.github.io/article/wx.html?wx=VdeQpFCL3GGsfOKrIRW6Hw)
|
||||
* [Git/SQL/正则表达式的在线练习平台](https://labuladong.github.io/article/wx.html?wx=rSc4b-mdZSLuqBmvPWF8Vw)
|
||||
### [第四章、通用计算机技术](https://labuladong.github.io/algo/)
|
||||
* [Linux 文件系统都是什么鬼](https://labuladong.github.io/article/fname.html?fname=linux文件系统)
|
||||
* [Linux 的进程/线程/文件描述符是什么](https://labuladong.github.io/article/fname.html?fname=linux进程)
|
||||
* [关于 Linux shell 你必须知道的](https://labuladong.github.io/article/fname.html?fname=linuxshell)
|
||||
* [Linux shell 的实用小技巧](https://labuladong.github.io/article/fname.html?fname=linuxshell技巧)
|
||||
* [Linux 管道符原理大揭秘](https://labuladong.github.io/article/fname.html?fname=linux技巧3)
|
||||
* [一文看懂 session 和 cookie](https://labuladong.github.io/article/fname.html?fname=session和cookie)
|
||||
* [加密算法的前身今世](https://labuladong.github.io/article/fname.html?fname=密码技术)
|
||||
* [我用四个命令概括了 Git 的所有套路](https://labuladong.github.io/article/fname.html?fname=git常用命令)
|
||||
* [Git/SQL/正则表达式的在线练习平台](https://labuladong.github.io/article/fname.html?fname=在线练习平台)
|
||||
|
||||
<!-- table end -->
|
||||
|
||||
# 感谢如下大佬参与翻译
|
||||
|
||||
|
|
|
|||
|
|
@ -0,0 +1,84 @@
|
|||
# 详解最长公共子序列问题,秒杀三道动态规划题目
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [1143. Longest Common Subsequence](https://leetcode.com/problems/longest-common-subsequence/) | [1143. 最长公共子序列](https://leetcode.cn/problems/longest-common-subsequence/) | 🟠
|
||||
| [583. Delete Operation for Two Strings](https://leetcode.com/problems/delete-operation-for-two-strings/) | [583. 两个字符串的删除操作](https://leetcode.cn/problems/delete-operation-for-two-strings/) | 🟠
|
||||
| [712. Minimum ASCII Delete Sum for Two Strings](https://leetcode.com/problems/minimum-ascii-delete-sum-for-two-strings/) | [712. 两个字符串的最小ASCII删除和](https://leetcode.cn/problems/minimum-ascii-delete-sum-for-two-strings/) | 🟠
|
||||
| - | [剑指 Offer II 095. 最长公共子序列](https://leetcode.cn/problems/qJnOS7/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
不知道大家做算法题有什么感觉,**我总结出来做算法题的技巧就是,把大的问题细化到一个点,先研究在这个小的点上如何解决问题,然后再通过递归/迭代的方式扩展到整个问题**。
|
||||
|
||||
比如说我们前文 [手把手带你刷二叉树第三期](https://labuladong.github.io/article/fname.html?fname=二叉树系列3),解决二叉树的题目,我们就会把整个问题细化到某一个节点上,想象自己站在某个节点上,需要做什么,然后套二叉树递归框架就行了。
|
||||
|
||||
动态规划系列问题也是一样,尤其是子序列相关的问题。**本文从「最长公共子序列问题」展开,总结三道子序列问题**,解这道题仔细讲讲这种子序列问题的套路,你就能感受到这种思维方式了。
|
||||
|
||||
### 最长公共子序列
|
||||
|
||||
计算最长公共子序列(Longest Common Subsequence,简称 LCS)是一道经典的动态规划题目,力扣第 1143 题「最长公共子序列」就是这个问题:
|
||||
|
||||
给你输入两个字符串 `s1` 和 `s2`,请你找出他们俩的最长公共子序列,返回这个子序列的长度。函数签名如下:
|
||||
|
||||
```java
|
||||
int longestCommonSubsequence(String s1, String s2);
|
||||
```
|
||||
|
||||
比如说输入 `s1 = "zabcde", s2 = "acez"`,它俩的最长公共子序列是 `lcs = "ace"`,长度为 3,所以算法返回 3。
|
||||
|
||||
如果没有做过这道题,一个最简单的暴力算法就是,把 `s1` 和 `s2` 的所有子序列都穷举出来,然后看看有没有公共的,然后在所有公共子序列里面再寻找一个长度最大的。
|
||||
|
||||
显然,这种思路的复杂度非常高,你要穷举出所有子序列,这个复杂度就是指数级的,肯定不实际。
|
||||
|
||||
正确的思路是不要考虑整个字符串,而是细化到 `s1` 和 `s2` 的每个字符。前文 [子序列解题模板](https://labuladong.github.io/article/fname.html?fname=子序列问题模板) 中总结的一个规律:
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [动态规划之子序列问题解题模板](https://labuladong.github.io/article/fname.html?fname=子序列问题模板)
|
||||
- [经典动态规划:编辑距离](https://labuladong.github.io/article/fname.html?fname=编辑距离)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [97. Interleaving String](https://leetcode.com/problems/interleaving-string/?show=1) | [97. 交错字符串](https://leetcode.cn/problems/interleaving-string/?show=1) |
|
||||
| - | [剑指 Offer II 095. 最长公共子序列](https://leetcode.cn/problems/qJnOS7/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
应合作方要求,本文不便在此发布,请扫码关注回复关键词「LCS」或 [点这里](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_6298793ae4b09dda12708be8/1) 查看:
|
||||
|
||||

|
||||
|
|
@ -1,23 +1,28 @@
|
|||
# 动态规划之KMP字符匹配算法
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[28.实现 strStr()](https://leetcode-cn.com/problems/implement-strstr)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [28. Implement strStr()](https://leetcode.com/problems/implement-strstr/) | [28. 实现 strStr()](https://leetcode.cn/problems/implement-strstr/) | 🟢
|
||||
|
||||
**-----------**
|
||||
|
||||
> 阅读本文之前,建议你先学习一下另一种字符串匹配算法:[Rabin Karp 字符匹配算法](https://labuladong.github.io/article/fname.html?fname=rabinkarp)。
|
||||
|
||||
KMP 算法(Knuth-Morris-Pratt 算法)是一个著名的字符串匹配算法,效率很高,但是确实有点复杂。
|
||||
|
||||
很多读者抱怨 KMP 算法无法理解,这很正常,想到大学教材上关于 KMP 算法的讲解,也不知道有多少未来的 Knuth、Morris、Pratt 被提前劝退了。有一些优秀的同学通过手推 KMP 算法的过程来辅助理解该算法,这是一种办法,不过本文要从逻辑层面帮助读者理解算法的原理。十行代码之间,KMP 灰飞烟灭。
|
||||
|
|
@ -28,13 +33,13 @@ KMP 算法(Knuth-Morris-Pratt 算法)是一个著名的字符串匹配算法
|
|||
|
||||
读者见过的 KMP 算法应该是,一波诡异的操作处理 `pat` 后形成一个一维的数组 `next`,然后根据这个数组经过又一波复杂操作去匹配 `txt`。时间复杂度 O(N),空间复杂度 O(M)。其实它这个 `next` 数组就相当于 `dp` 数组,其中元素的含义跟 `pat` 的前缀和后缀有关,判定规则比较复杂,不好理解。**本文则用一个二维的 `dp` 数组(但空间复杂度还是 O(M)),重新定义其中元素的含义,使得代码长度大大减少,可解释性大大提高**。
|
||||
|
||||
PS:本文的代码参考《算法4》,原代码使用的数组名称是 `dfa`(确定有限状态机),因为我们的公众号之前有一系列动态规划的文章,就不说这么高大上的名词了,我对书中代码进行了一点修改,并沿用 `dp` 数组的名称。
|
||||
> PS:本文的代码参考《算法4》,原代码使用的数组名称是 `dfa`(确定有限状态机),因为我们的公众号之前有一系列动态规划的文章,就不说这么高大上的名词了,我对书中代码进行了一点修改,并沿用 `dp` 数组的名称。
|
||||
|
||||
### 一、KMP 算法概述
|
||||
|
||||
首先还是简单介绍一下 KMP 算法和暴力匹配算法的不同在哪里,难点在哪里,和动态规划有啥关系。
|
||||
|
||||
暴力的字符串匹配算法很容易写,看一下它的运行逻辑:
|
||||
力扣第 28 题「实现 strStr」就是字符串匹配问题,暴力的字符串匹配算法很容易写,看一下它的运行逻辑:
|
||||
|
||||
```java
|
||||
// 暴力匹配(伪码)
|
||||
|
|
@ -57,19 +62,19 @@ int search(String pat, String txt) {
|
|||
|
||||
对于暴力算法,如果出现不匹配字符,同时回退 `txt` 和 `pat` 的指针,嵌套 for 循环,时间复杂度 `O(MN)`,空间复杂度`O(1)`。最主要的问题是,如果字符串中重复的字符比较多,该算法就显得很蠢。
|
||||
|
||||
比如 txt = "aaacaaab" pat = "aaab":
|
||||
比如 `txt = "aaacaaab", pat = "aaab"`:
|
||||
|
||||

|
||||

|
||||
|
||||
很明显,`pat` 中根本没有字符 c,根本没必要回退指针 `i`,暴力解法明显多做了很多不必要的操作。
|
||||
|
||||
KMP 算法的不同之处在于,它会花费空间来记录一些信息,在上述情况中就会显得很聪明:
|
||||
|
||||

|
||||

|
||||
|
||||
再比如类似的 txt = "aaaaaaab" pat = "aaab",暴力解法还会和上面那个例子一样蠢蠢地回退指针 `i`,而 KMP 算法又会耍聪明:
|
||||
再比如类似的 `txt = "aaaaaaab", pat = "aaab"`,暴力解法还会和上面那个例子一样蠢蠢地回退指针 `i`,而 KMP 算法又会耍聪明:
|
||||
|
||||

|
||||

|
||||
|
||||
因为 KMP 算法知道字符 b 之前的字符 a 都是匹配的,所以每次只需要比较字符 b 是否被匹配就行了。
|
||||
|
||||
|
|
@ -92,21 +97,21 @@ pat = "aaab"
|
|||
|
||||
只不过对于 `txt1` 的下面这个即将出现的未匹配情况:
|
||||
|
||||

|
||||

|
||||
|
||||
`dp` 数组指示 `pat` 这样移动:
|
||||
|
||||

|
||||

|
||||
|
||||
PS:这个`j` 不要理解为索引,它的含义更准确地说应该是**状态**(state),所以它会出现这个奇怪的位置,后文会详述。
|
||||
> PS:这个`j` 不要理解为索引,它的含义更准确地说应该是**状态**(state),所以它会出现这个奇怪的位置,后文会详述。
|
||||
|
||||
而对于 `txt2` 的下面这个即将出现的未匹配情况:
|
||||
|
||||

|
||||

|
||||
|
||||
`dp` 数组指示 `pat` 这样移动:
|
||||
|
||||

|
||||

|
||||
|
||||
明白了 `dp` 数组只和 `pat` 有关,那么我们这样设计 KMP 算法就会比较漂亮:
|
||||
|
||||
|
|
@ -140,46 +145,45 @@ int pos2 = kmp.search("aaaaaaab"); //4
|
|||
|
||||
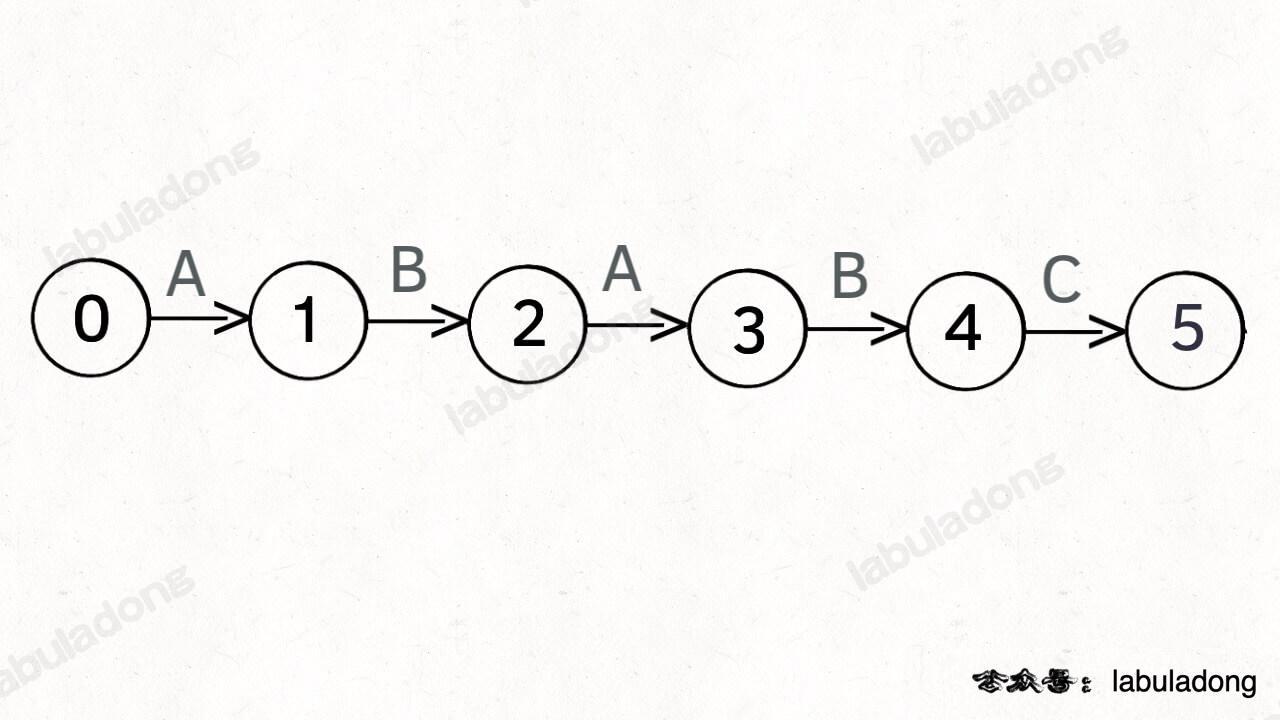
为什么说 KMP 算法和状态机有关呢?是这样的,我们可以认为 `pat` 的匹配就是状态的转移。比如当 pat = "ABABC":
|
||||
|
||||

|
||||
|
||||
|
||||
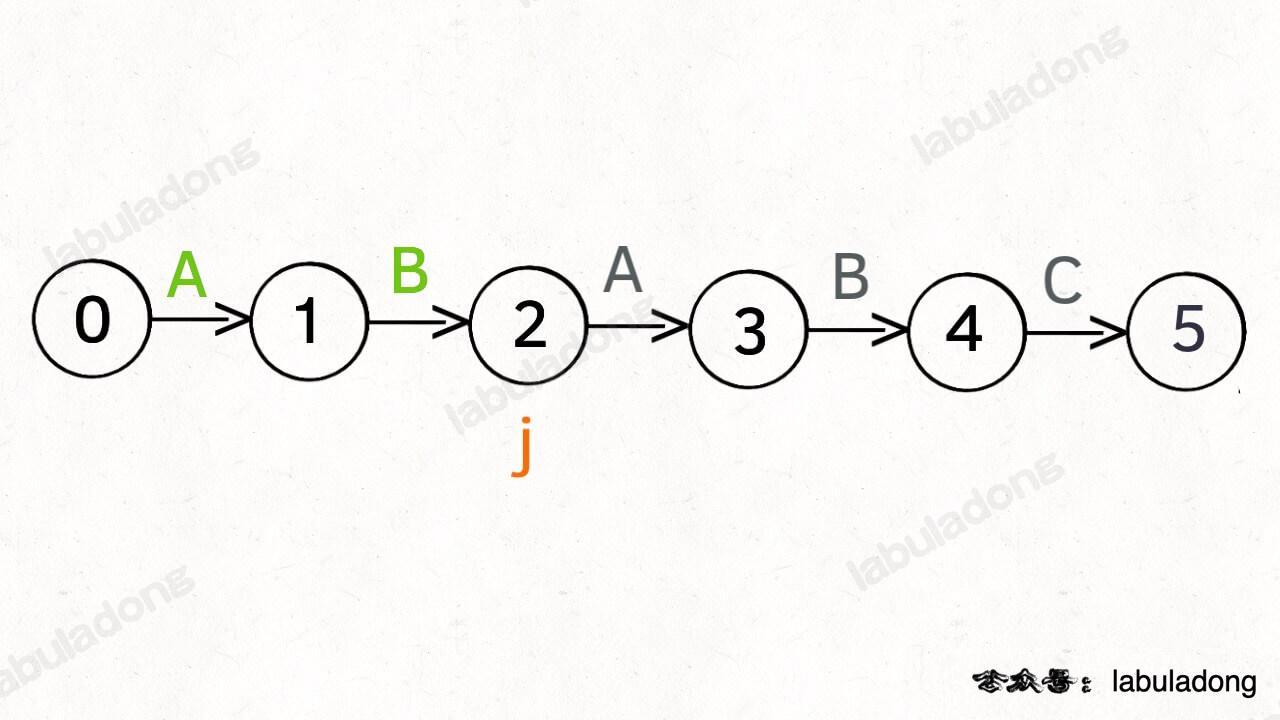
如上图,圆圈内的数字就是状态,状态 0 是起始状态,状态 5(`pat.length`)是终止状态。开始匹配时 `pat` 处于起始状态,一旦转移到终止状态,就说明在 `txt` 中找到了 `pat`。比如说当前处于状态 2,就说明字符 "AB" 被匹配:
|
||||
|
||||

|
||||
|
||||
|
||||
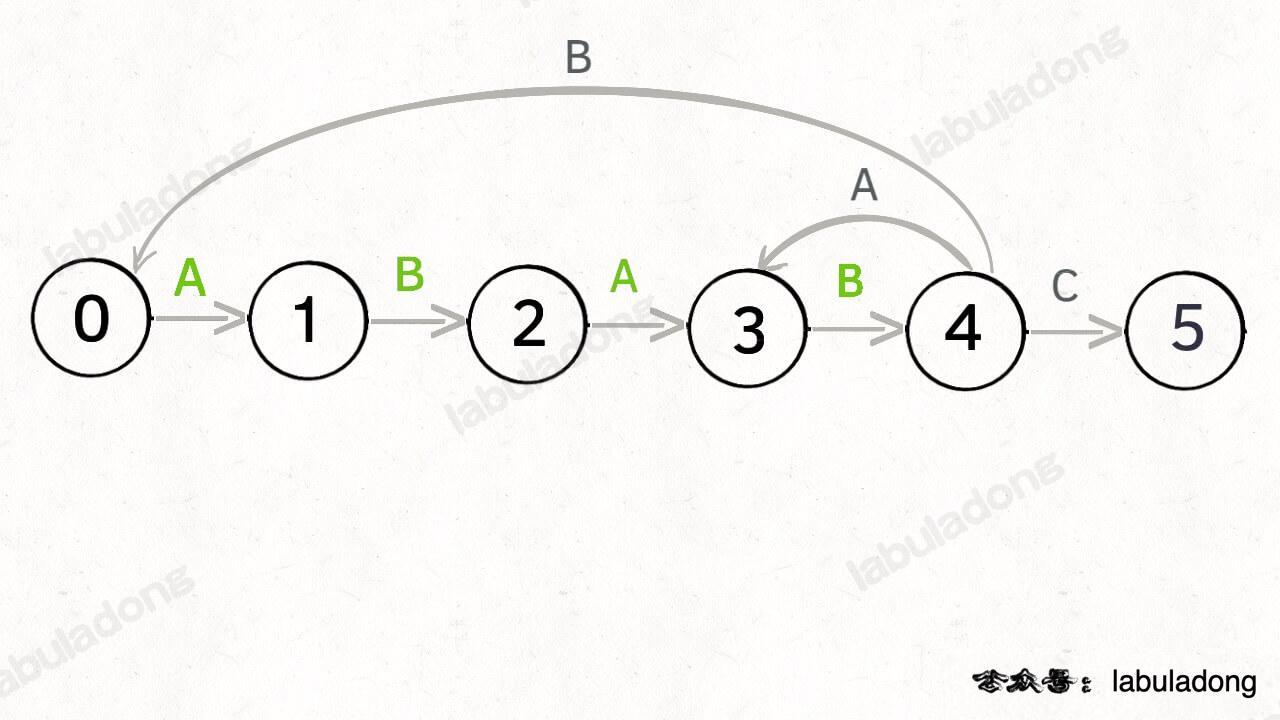
另外,处于不同状态时,`pat` 状态转移的行为也不同。比如说假设现在匹配到了状态 4,如果遇到字符 A 就应该转移到状态 3,遇到字符 C 就应该转移到状态 5,如果遇到字符 B 就应该转移到状态 0:
|
||||
|
||||

|
||||
|
||||
|
||||
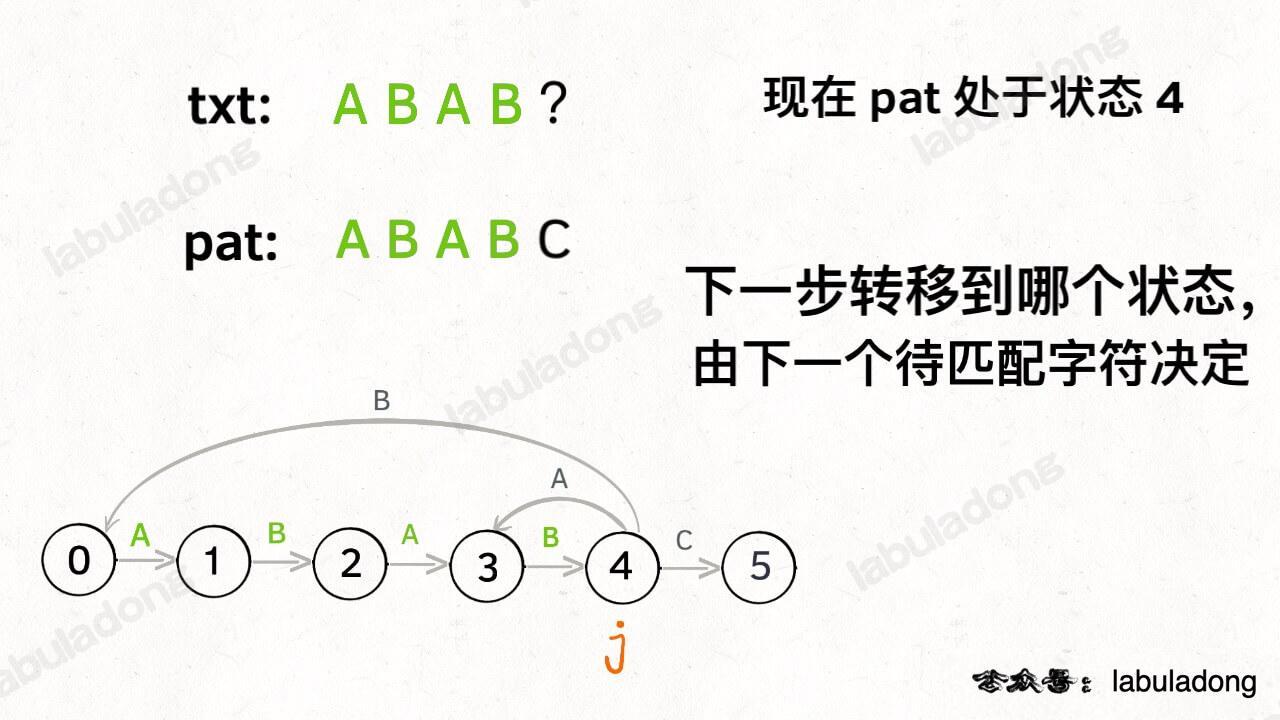
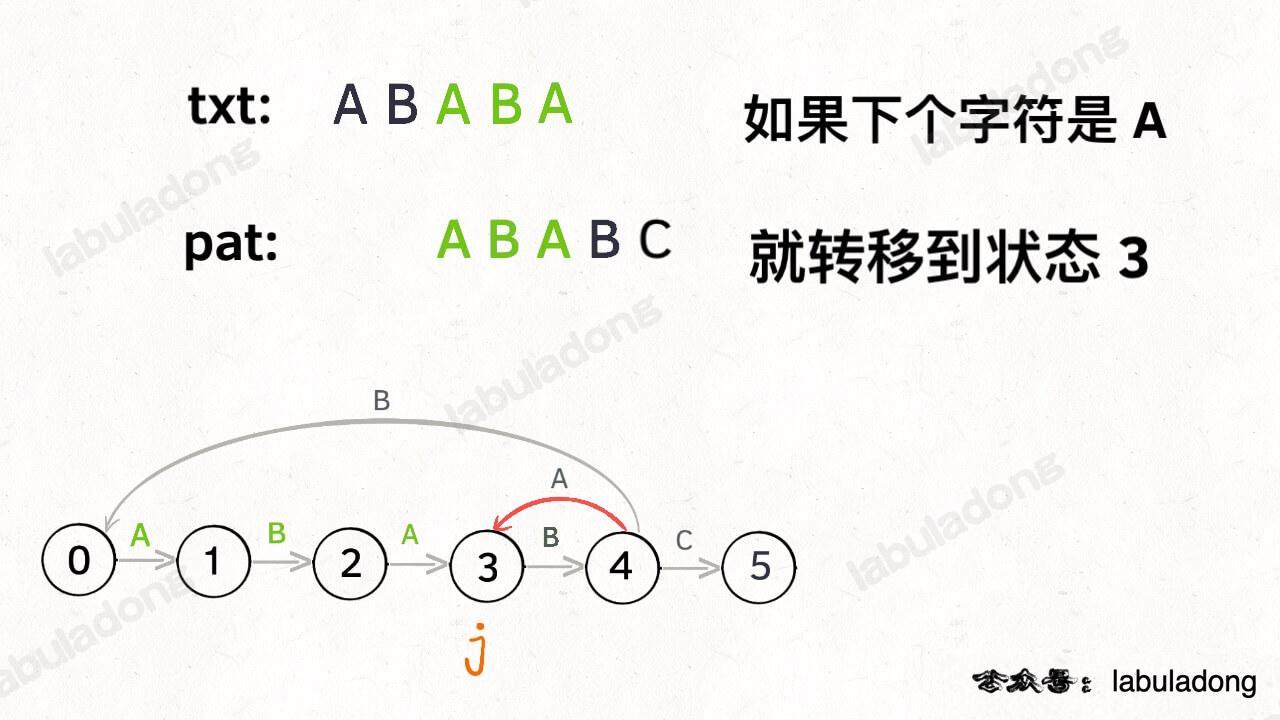
具体什么意思呢,我们来一个个举例看看。用变量 `j` 表示指向当前状态的指针,当前 `pat` 匹配到了状态 4:
|
||||
|
||||

|
||||
|
||||
|
||||
如果遇到了字符 "A",根据箭头指示,转移到状态 3 是最聪明的:
|
||||
|
||||

|
||||
|
||||
|
||||
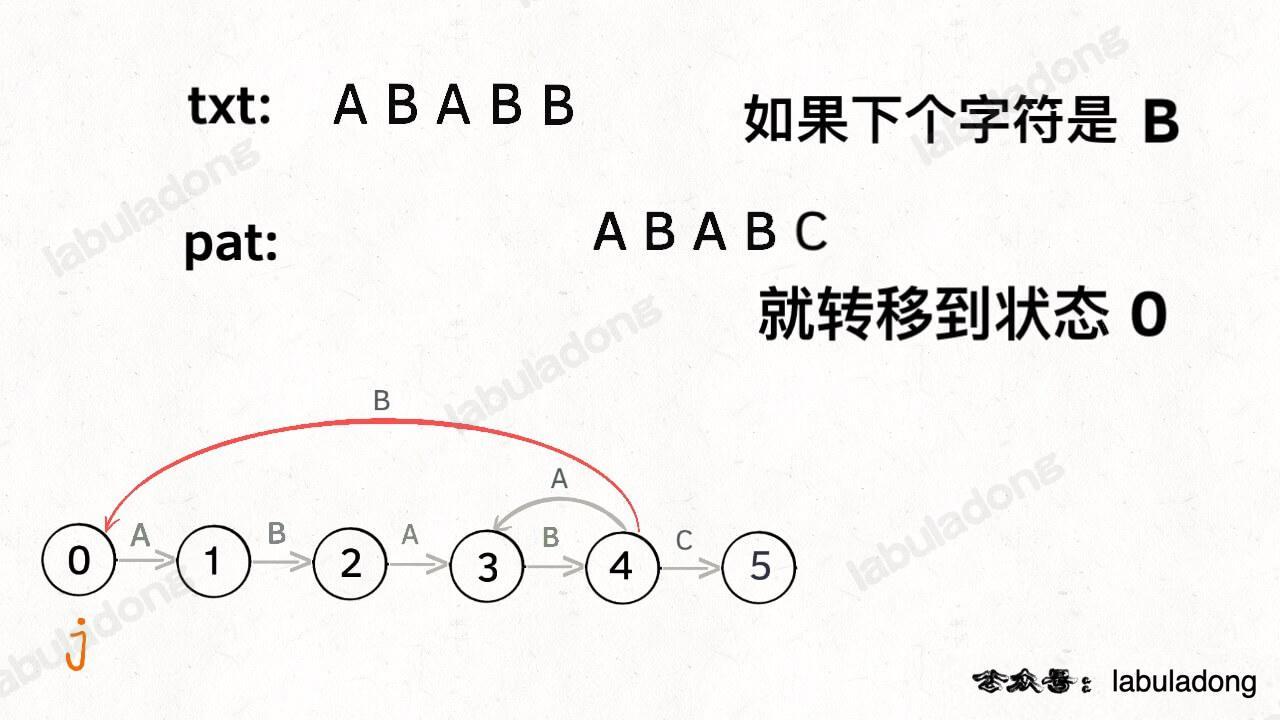
如果遇到了字符 "B",根据箭头指示,只能转移到状态 0(一夜回到解放前):
|
||||
|
||||

|
||||
|
||||
|
||||
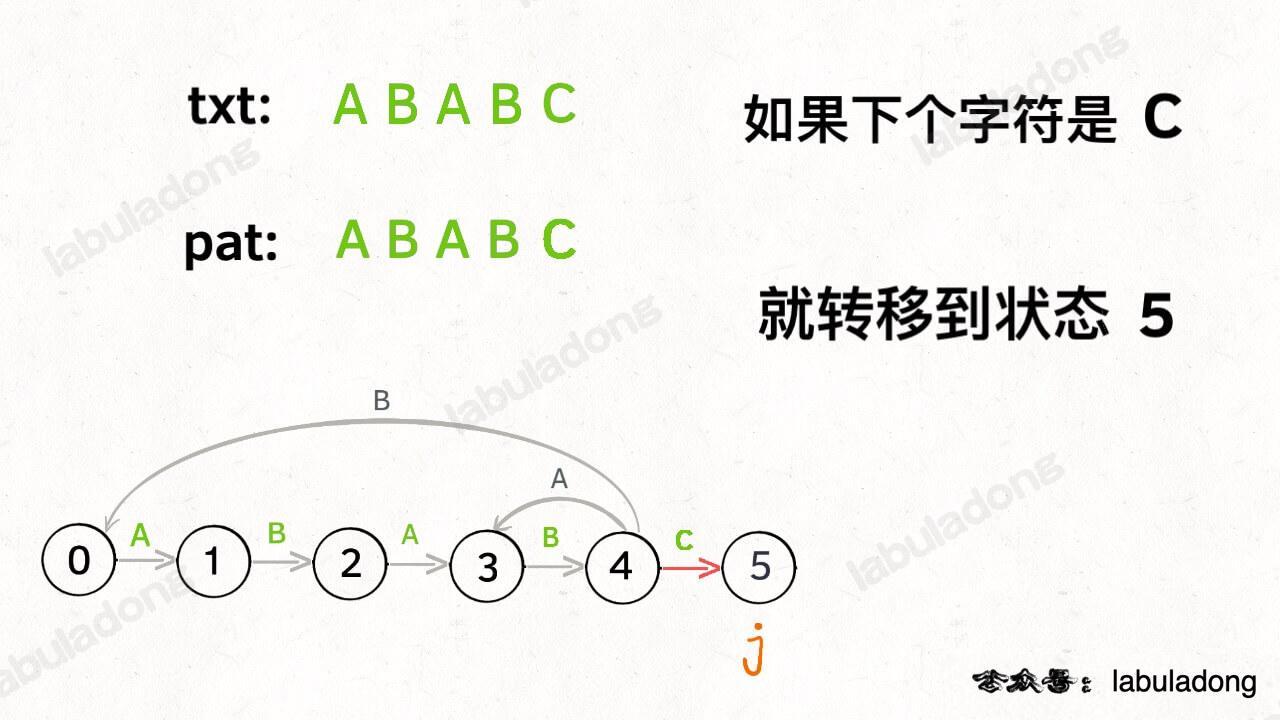
如果遇到了字符 "C",根据箭头指示,应该转移到终止状态 5,这也就意味着匹配完成:
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
当然了,还可能遇到其他字符,比如 Z,但是显然应该转移到起始状态 0,因为 `pat` 中根本都没有字符 Z:
|
||||
|
||||

|
||||
|
||||
|
||||
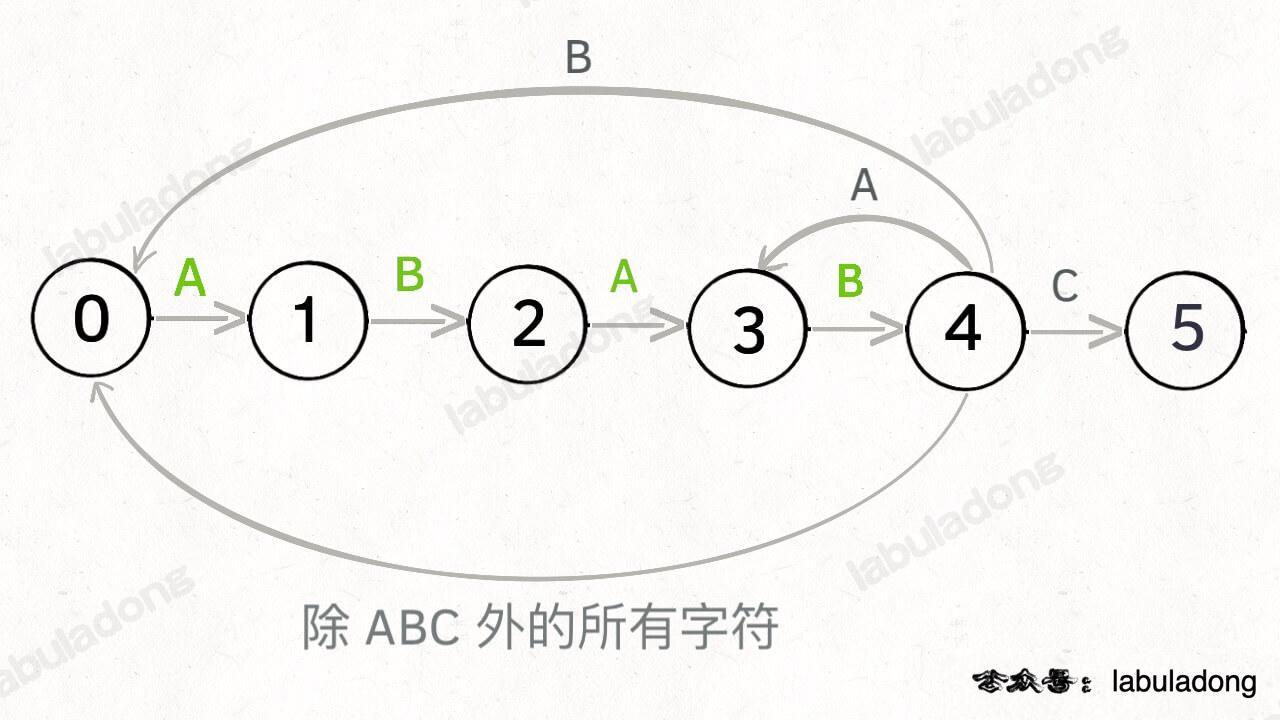
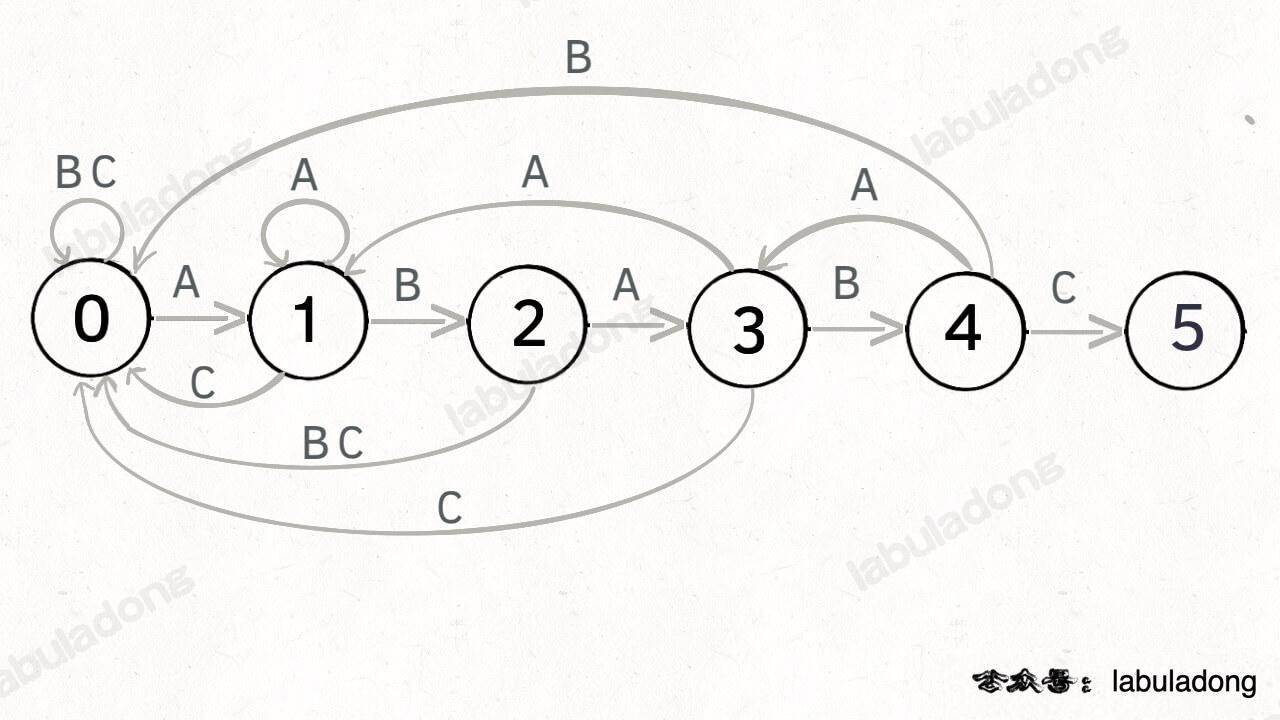
这里为了清晰起见,我们画状态图时就把其他字符转移到状态 0 的箭头省略,只画 `pat` 中出现的字符的状态转移:
|
||||
|
||||

|
||||
|
||||
|
||||
KMP 算法最关键的步骤就是构造这个状态转移图。**要确定状态转移的行为,得明确两个变量,一个是当前的匹配状态,另一个是遇到的字符**;确定了这两个变量后,就可以知道这个情况下应该转移到哪个状态。
|
||||
|
||||
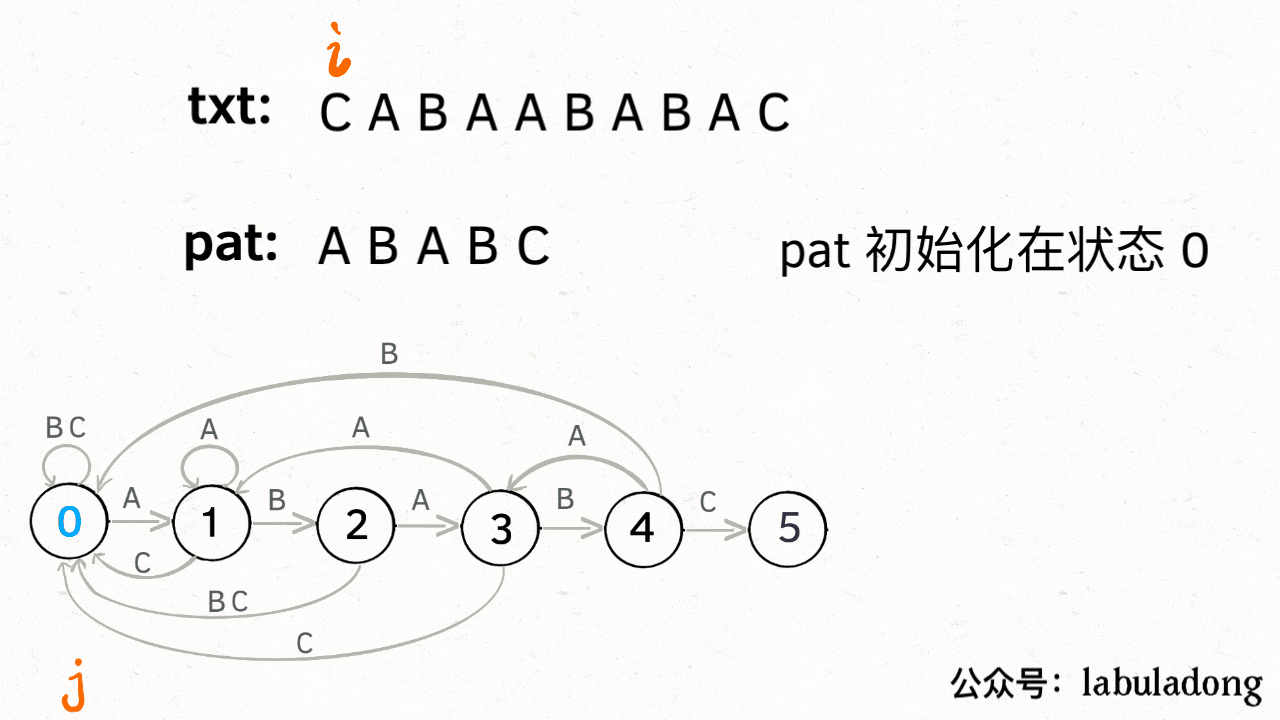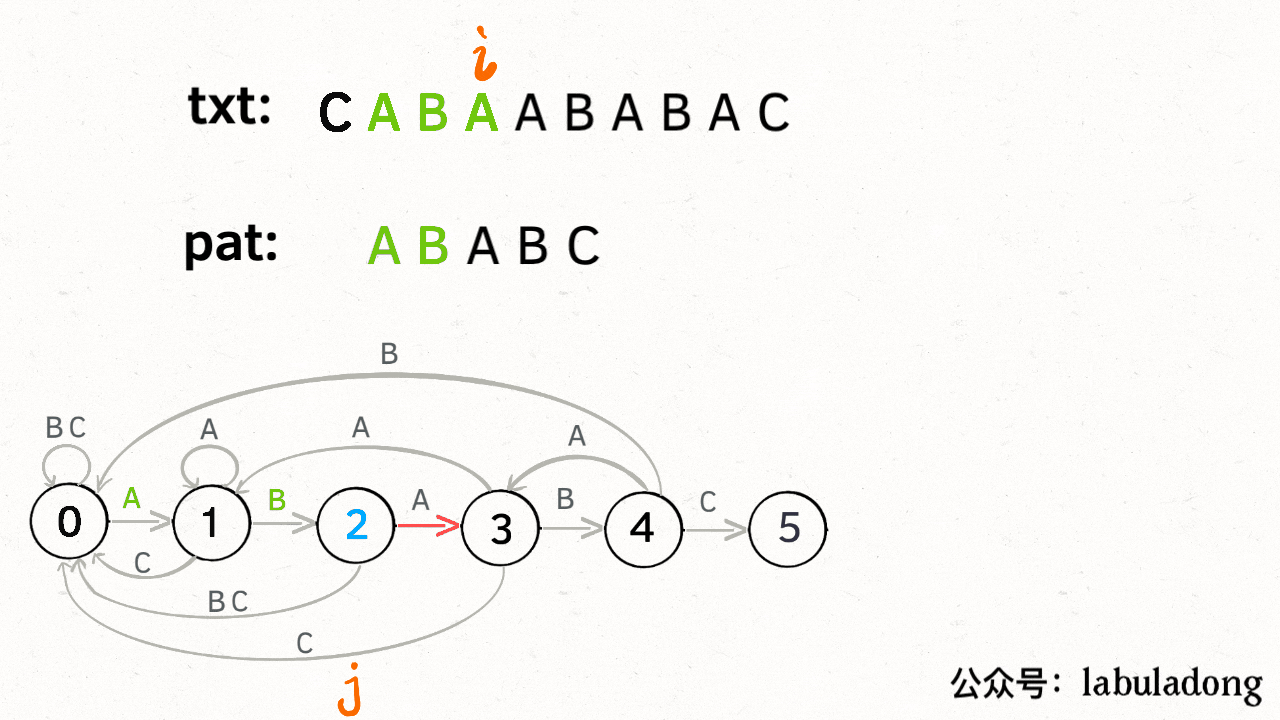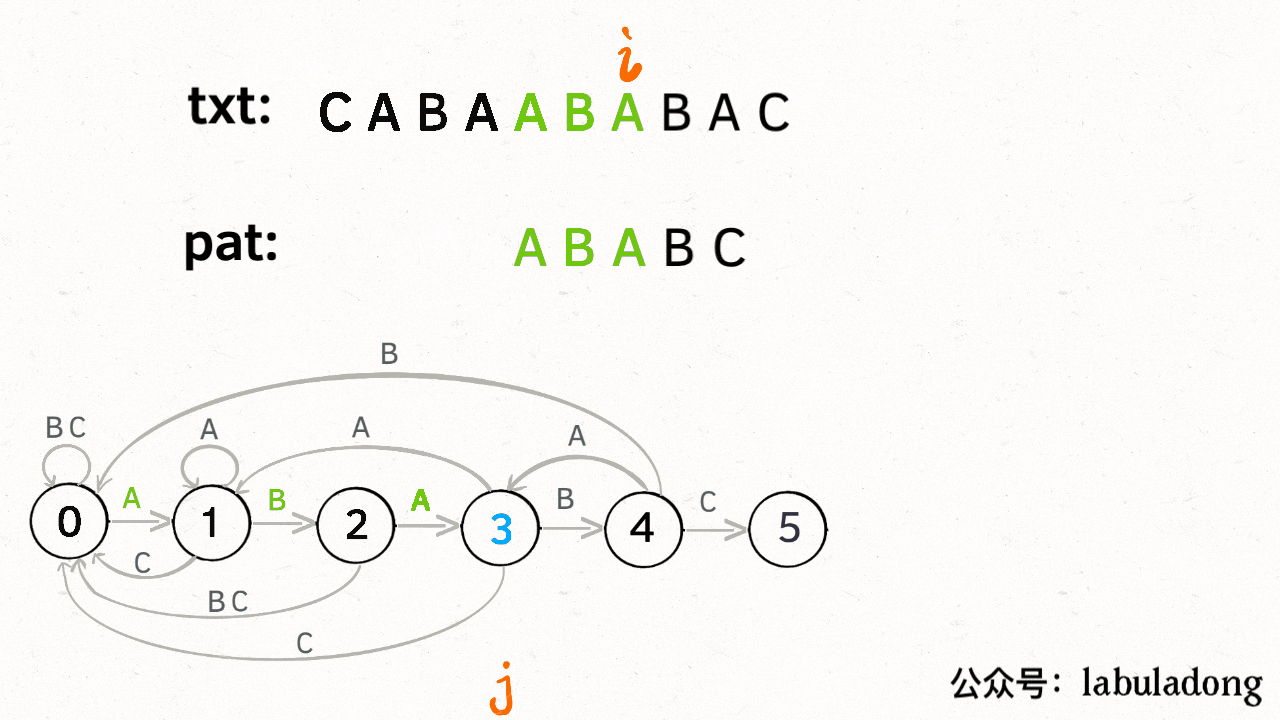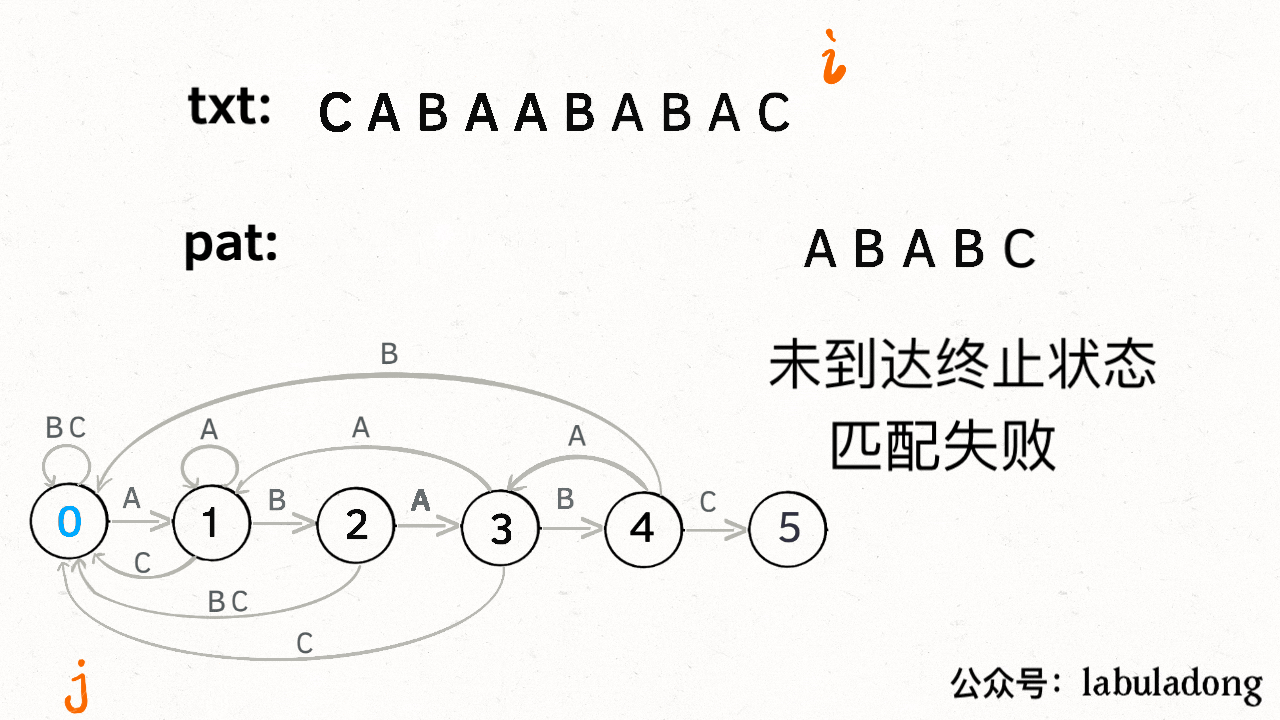
下面看一下 KMP 算法根据这幅状态转移图匹配字符串 `txt` 的过程:
|
||||
|
||||

|
||||
|
||||
|
||||
**请记住这个 GIF 的匹配过程,这就是 KMP 算法的核心逻辑**!
|
||||
|
||||
|
|
@ -234,29 +238,29 @@ for 0 <= j < M: # 状态
|
|||
|
||||
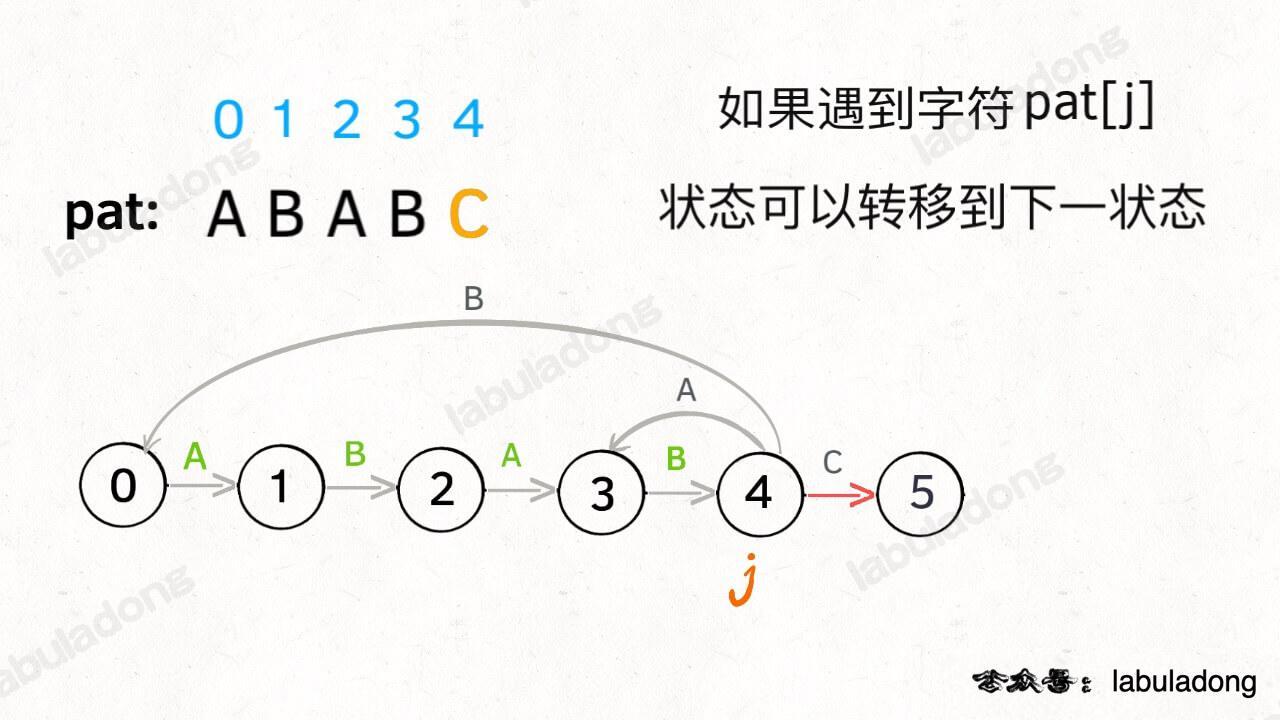
这个 next 状态应该怎么求呢?显然,**如果遇到的字符 `c` 和 `pat[j]` 匹配的话**,状态就应该向前推进一个,也就是说 `next = j + 1`,我们不妨称这种情况为**状态推进**:
|
||||
|
||||

|
||||
|
||||
|
||||
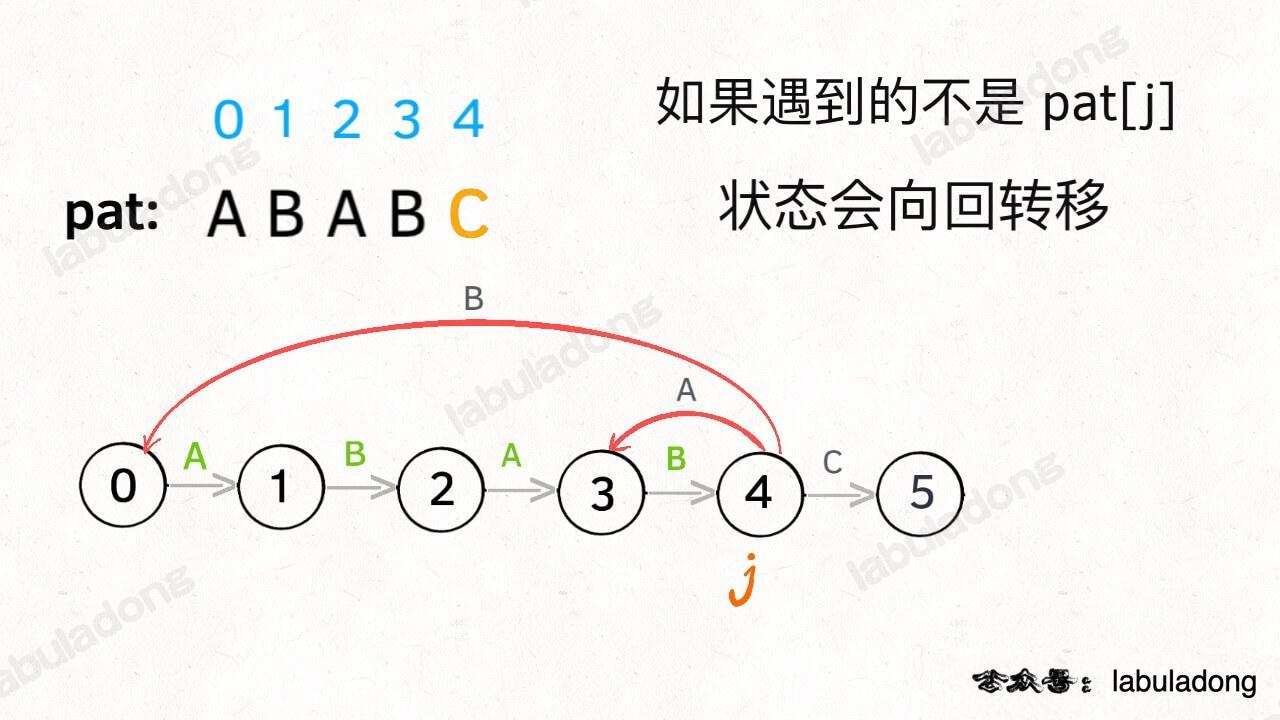
**如果字符 `c` 和 `pat[j]` 不匹配的话**,状态就要回退(或者原地不动),我们不妨称这种情况为**状态重启**:
|
||||
|
||||

|
||||
|
||||
|
||||
那么,如何得知在哪个状态重启呢?解答这个问题之前,我们再定义一个名字:**影子状态**(我编的名字),用变量 `X` 表示。**所谓影子状态,就是和当前状态具有相同的前缀**。比如下面这种情况:
|
||||
|
||||

|
||||
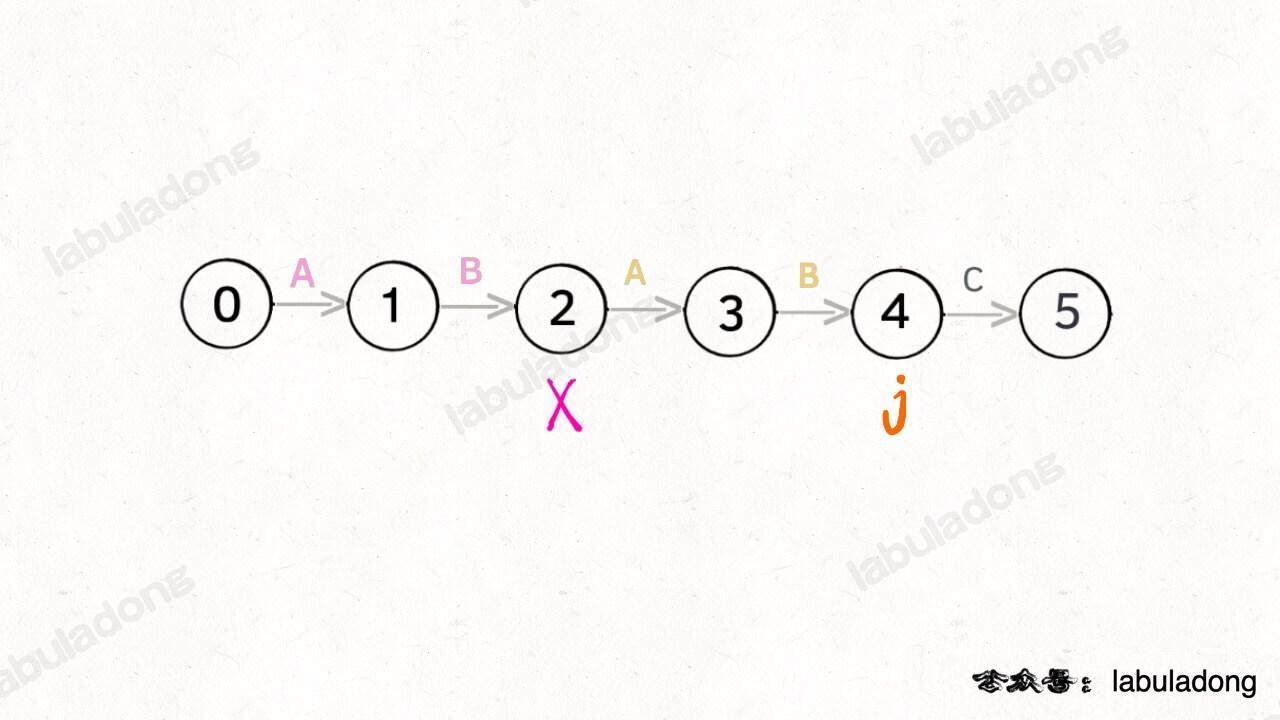
|
||||
|
||||
当前状态 `j = 4`,其影子状态为 `X = 2`,它们都有相同的前缀 "AB"。因为状态 `X` 和状态 `j` 存在相同的前缀,所以当状态 `j` 准备进行状态重启的时候(遇到的字符 `c` 和 `pat[j]` 不匹配),可以通过 `X` 的状态转移图来获得**最近的重启位置**。
|
||||
|
||||
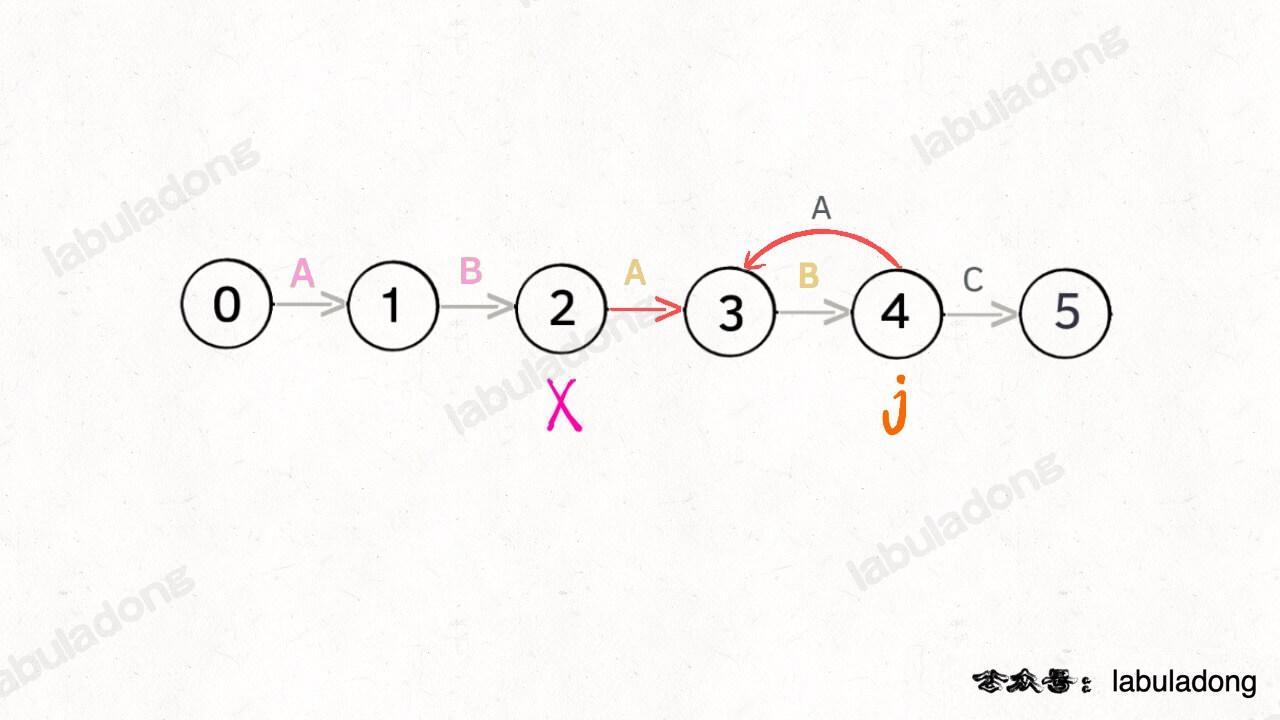
比如说刚才的情况,如果状态 `j` 遇到一个字符 "A",应该转移到哪里呢?首先只有遇到 "C" 才能推进状态,遇到 "A" 显然只能进行状态重启。**状态 `j` 会把这个字符委托给状态 `X` 处理,也就是 `dp[j]['A'] = dp[X]['A']`**:
|
||||
|
||||

|
||||
|
||||
|
||||
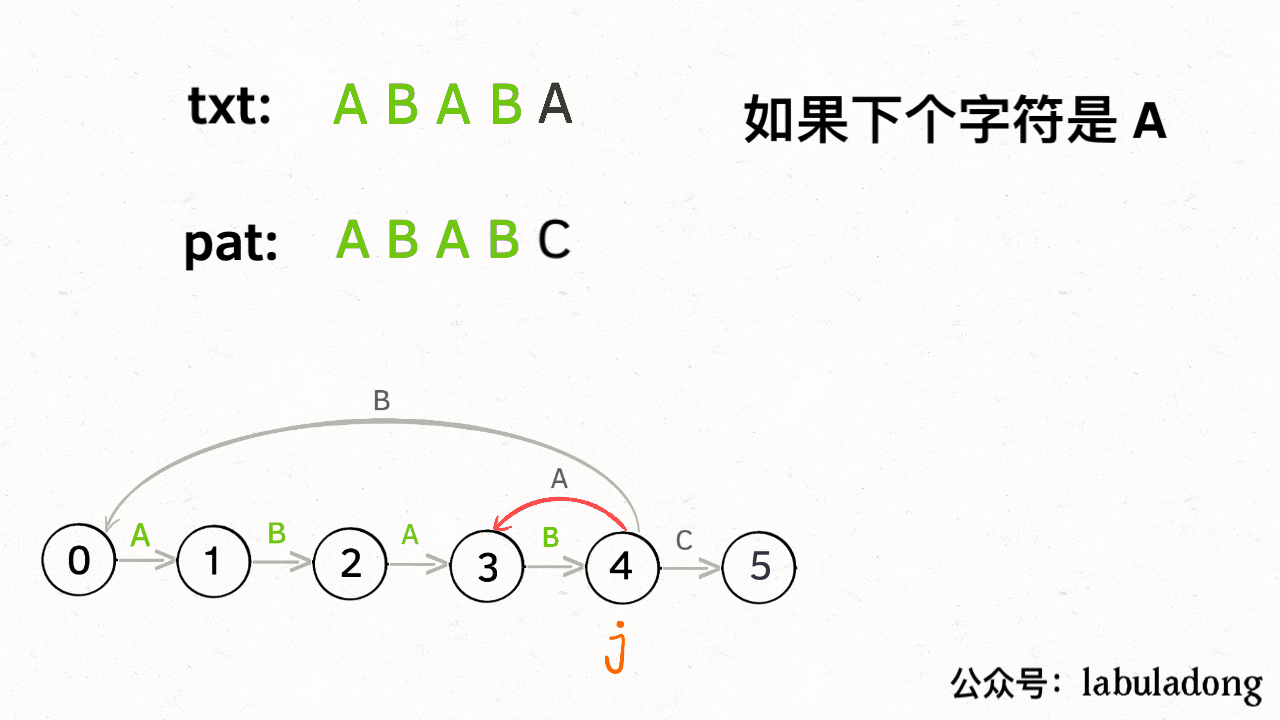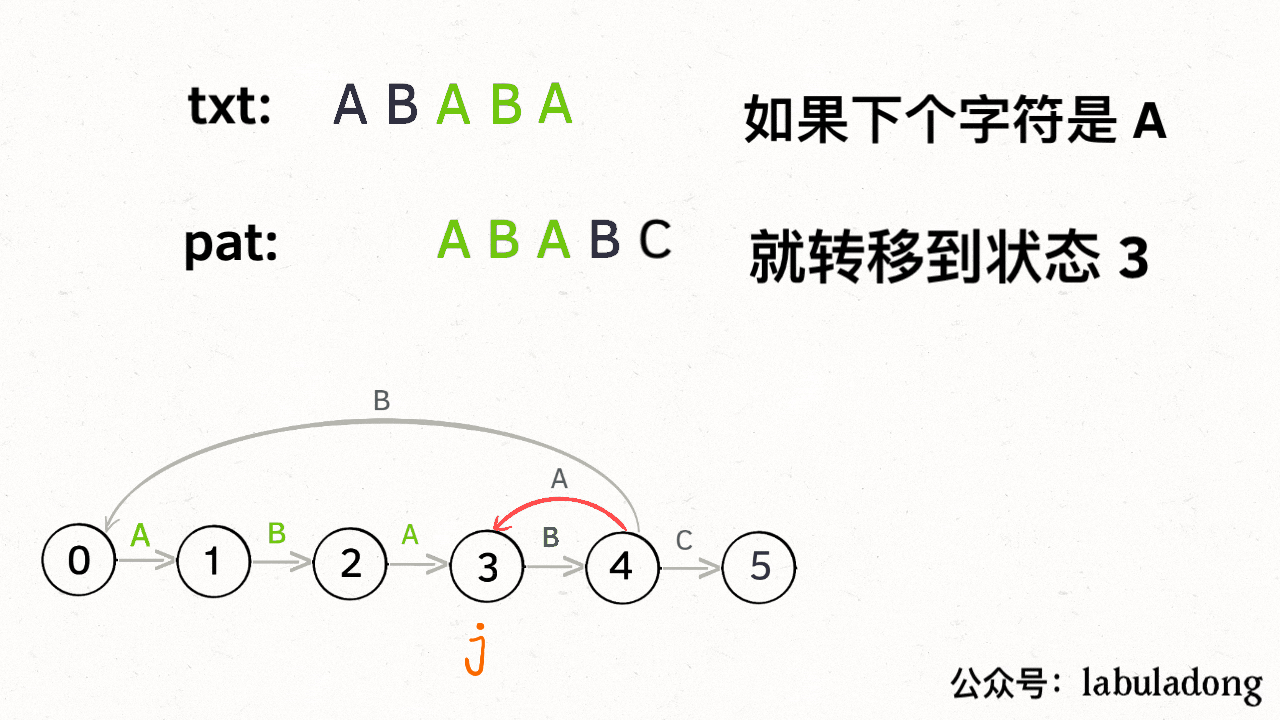
为什么这样可以呢?因为:既然 `j` 这边已经确定字符 "A" 无法推进状态,**只能回退**,而且 KMP 就是要**尽可能少的回退**,以免多余的计算。那么 `j` 就可以去问问和自己具有相同前缀的 `X`,如果 `X` 遇见 "A" 可以进行「状态推进」,那就转移过去,因为这样回退最少。
|
||||
|
||||

|
||||
|
||||
|
||||
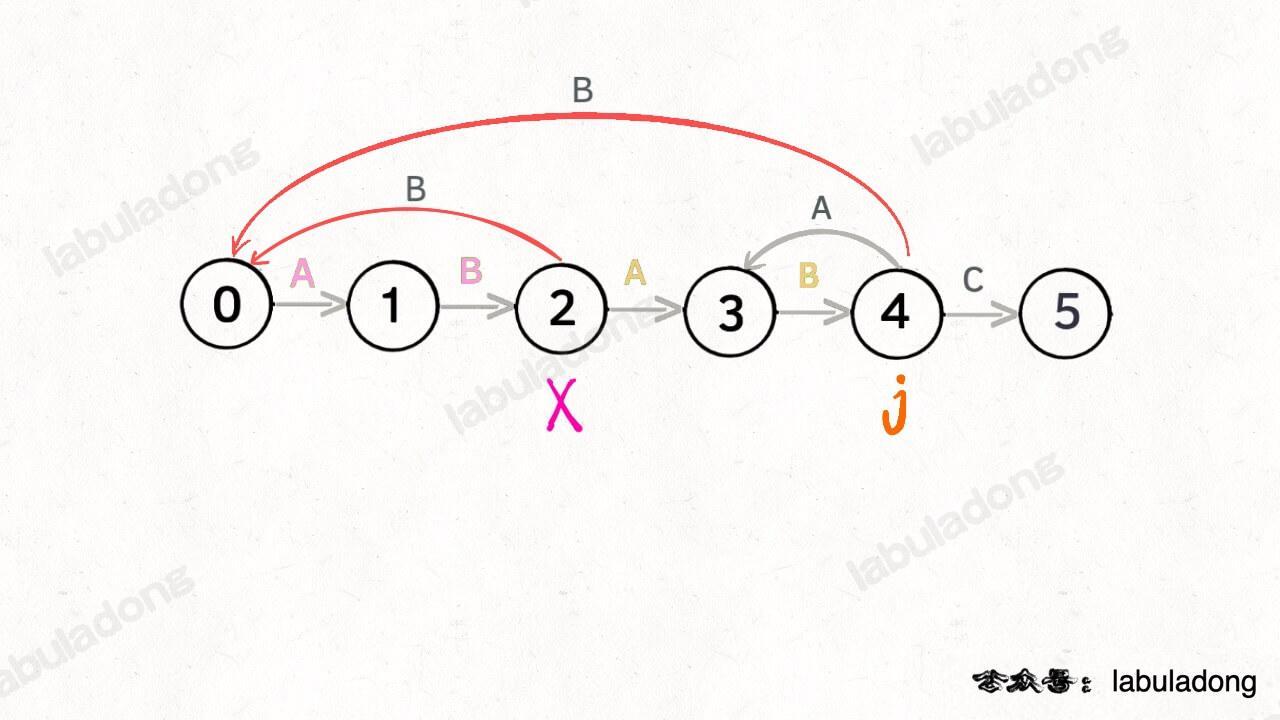
当然,如果遇到的字符是 "B",状态 `X` 也不能进行「状态推进」,只能回退,`j` 只要跟着 `X` 指引的方向回退就行了:
|
||||
|
||||

|
||||
|
||||
|
||||
你也许会问,这个 `X` 怎么知道遇到字符 "B" 要回退到状态 0 呢?因为 `X` 永远跟在 `j` 的身后,状态 `X` 如何转移,在之前就已经算出来了。动态规划算法不就是利用过去的结果解决现在的问题吗?
|
||||
|
||||
|
|
@ -350,7 +354,7 @@ for (int i = 0; i < N; i++) {
|
|||
|
||||
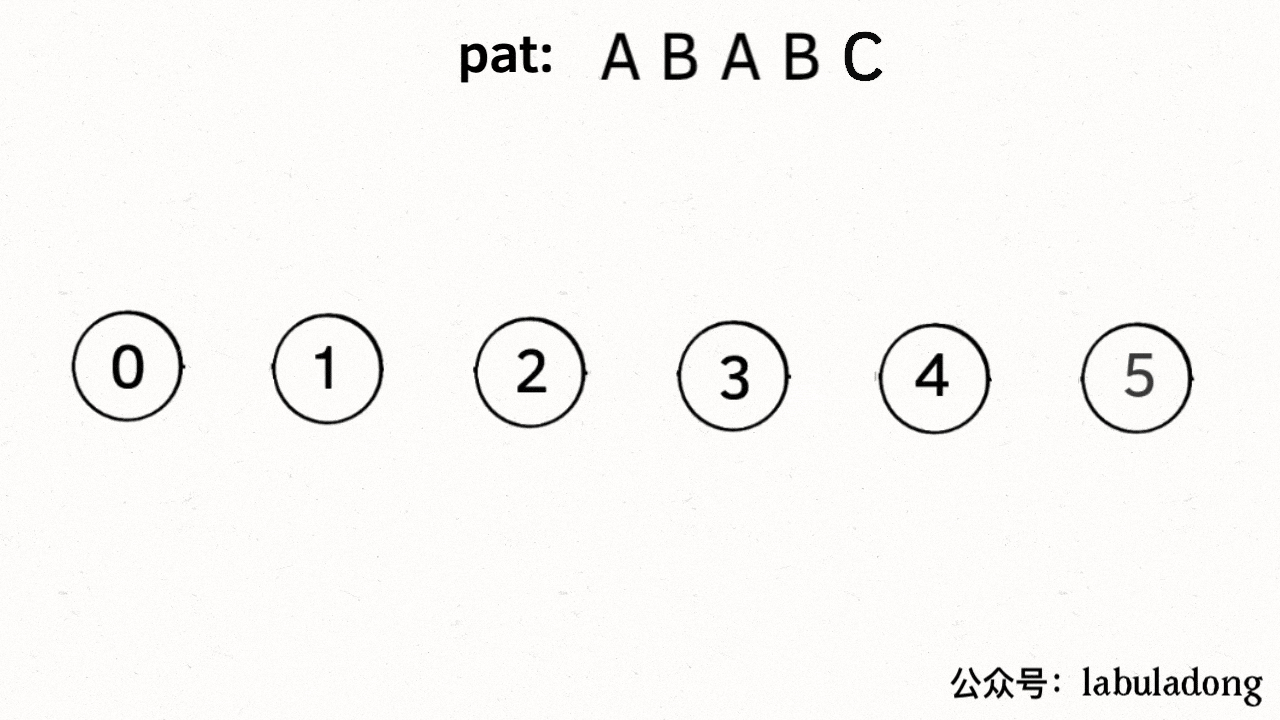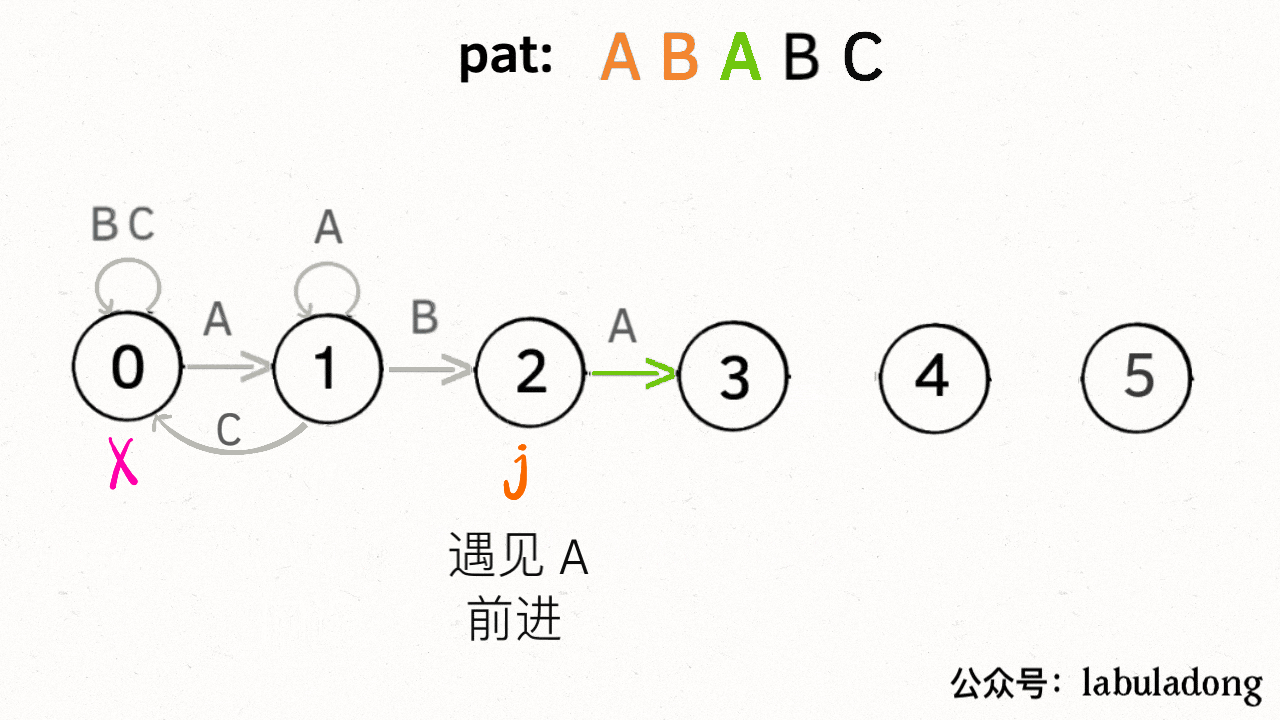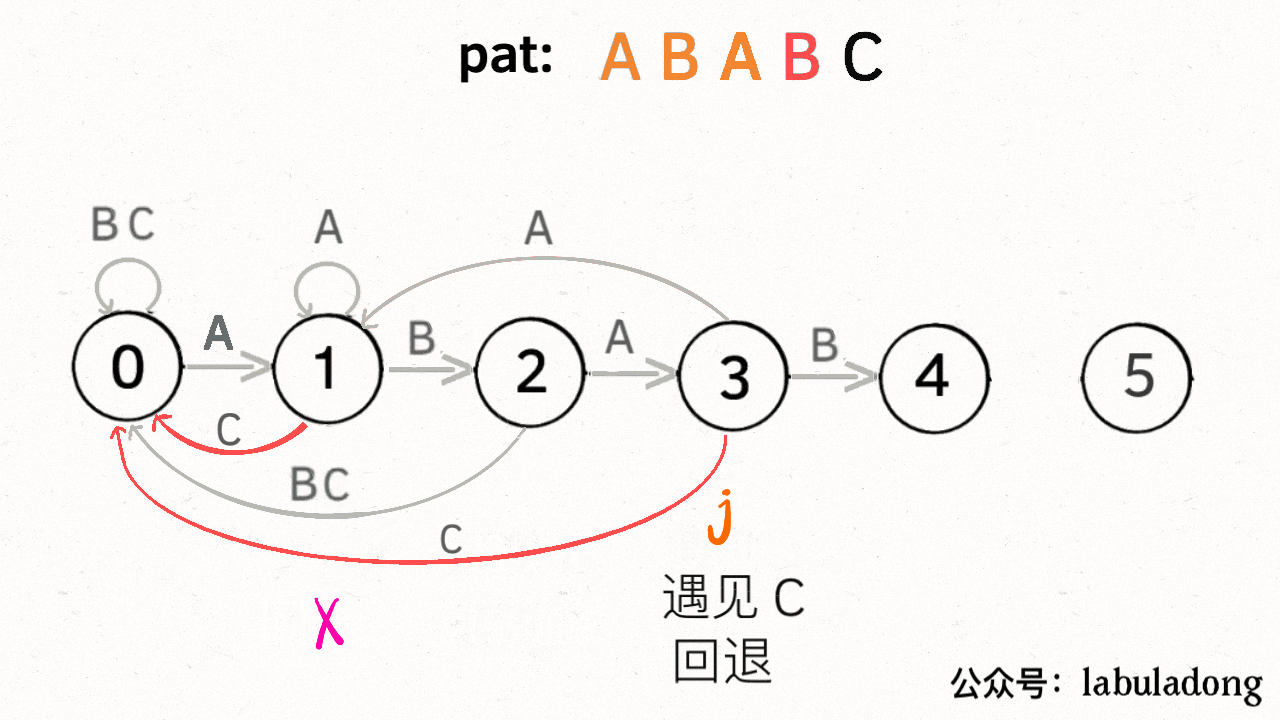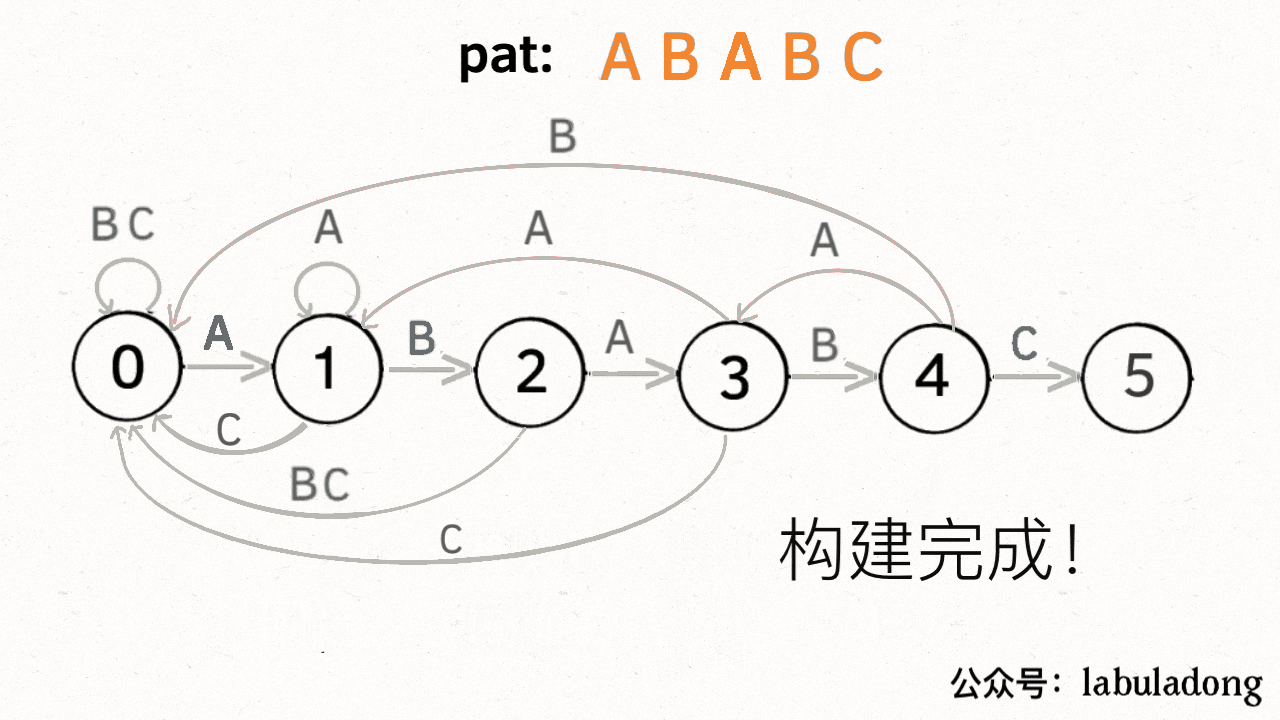
下面来看一下状态转移图的完整构造过程,你就能理解状态 `X` 作用之精妙了:
|
||||
|
||||

|
||||
|
||||
|
||||
至此,KMP 算法的核心终于写完啦啦啦啦!看下 KMP 算法的完整代码吧:
|
||||
|
||||
|
|
@ -419,15 +423,26 @@ KMP 算法也就是动态规划那点事,我们的公众号文章目录有一
|
|||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [滑动窗口算法延伸:Rabin Karp 字符匹配算法](https://labuladong.github.io/article/fname.html?fname=rabinkarp)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[28.实现 strStr()](https://leetcode-cn.com/problems/implement-strstr)
|
||||
|
|
|
|||
|
|
@ -1,50 +1,71 @@
|
|||
# 动态规划之博弈问题
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[877.石子游戏](https://leetcode-cn.com/problems/stone-game)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [486. Predict the Winner](https://leetcode.com/problems/predict-the-winner/) | [486. 预测赢家](https://leetcode.cn/problems/predict-the-winner/) | 🟠
|
||||
| [877. Stone Game](https://leetcode.com/problems/stone-game/) | [877. 石子游戏](https://leetcode.cn/problems/stone-game/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
上一篇文章 [几道智力题](https://labuladong.gitee.io/algo/) 中讨论到一个有趣的「石头游戏」,通过题目的限制条件,这个游戏是先手必胜的。但是智力题终究是智力题,真正的算法问题肯定不会是投机取巧能搞定的。所以,本文就借石头游戏来讲讲「假设两个人都足够聪明,最后谁会获胜」这一类问题该如何用动态规划算法解决。
|
||||
上一篇文章 [几道智力题](https://labuladong.github.io/article/fname.html?fname=一行代码解决的智力题) 中讨论到一个有趣的「石头游戏」,通过题目的限制条件,这个游戏是先手必胜的。但是智力题终究是智力题,真正的算法问题肯定不会是投机取巧能搞定的。所以,本文就借石头游戏来讲讲「假设两个人都足够聪明,最后谁会获胜」这一类问题该如何用动态规划算法解决。
|
||||
|
||||
博弈类问题的套路都差不多,下文参考 [这个 YouTube 视频](https://www.youtube.com/watch?v=WxpIHvsu1RI) 的思路讲解,其核心思路是在二维 dp 的基础上使用元组分别存储两个人的博弈结果。掌握了这个技巧以后,别人再问你什么俩海盗分宝石,俩人拿硬币的问题,你就告诉别人:我懒得想,直接给你写个算法算一下得了。
|
||||
|
||||
我们「石头游戏」改的更具有一般性:
|
||||
我们把力扣第 877 题「石头游戏」改的更具有一般性:
|
||||
|
||||
你和你的朋友面前有一排石头堆,用一个数组 piles 表示,piles[i] 表示第 i 堆石子有多少个。你们轮流拿石头,一次拿一堆,但是只能拿走最左边或者最右边的石头堆。所有石头被拿完后,谁拥有的石头多,谁获胜。
|
||||
你和你的朋友面前有一排石头堆,用一个数组 `piles` 表示,`piles[i]` 表示第 `i` 堆石子有多少个。你们轮流拿石头,一次拿一堆,但是只能拿走最左边或者最右边的石头堆。所有石头被拿完后,谁拥有的石头多,谁获胜。
|
||||
|
||||
石头的堆数可以是任意正整数,石头的总数也可以是任意正整数,这样就能打破先手必胜的局面了。比如有三堆石头 `piles = [1, 100, 3]`,先手不管拿 1 还是 3,能够决定胜负的 100 都会被后手拿走,后手会获胜。
|
||||
|
||||
**假设两人都很聪明**,请你设计一个算法,返回先手和后手的最后得分(石头总数)之差。比如上面那个例子,先手能获得 4 分,后手会获得 100 分,你的算法应该返回 -96。
|
||||
**假设两人都很聪明**,请你写一个 `stoneGame` 函数,返回先手和后手的最后得分(石头总数)之差。比如上面那个例子,先手能获得 4 分,后手会获得 100 分,你的算法应该返回 -96。
|
||||
|
||||
这样推广之后,这个问题算是一道 Hard 的动态规划问题了。**博弈问题的难点在于,两个人要轮流进行选择,而且都贼精明,应该如何编程表示这个过程呢?**
|
||||
这样推广之后就变成了一道难度比较高的动态规划问题了,力扣第 486 题「预测赢家」就是一道类似的问题:
|
||||
|
||||
还是强调多次的套路,首先明确 dp 数组的含义,然后和股票买卖系列问题类似,只要找到「状态」和「选择」,一切就水到渠成了。
|
||||

|
||||
|
||||
### 一、定义 dp 数组的含义
|
||||
函数签名如下:
|
||||
|
||||
定义 dp 数组的含义是很有技术含量的,同一问题可能有多种定义方法,不同的定义会引出不同的状态转移方程,不过只要逻辑没有问题,最终都能得到相同的答案。
|
||||
```java
|
||||
boolean PredictTheWinner(int[] nums);
|
||||
```
|
||||
|
||||
那么如果有了一个计算先手和后手分差的 `stoneGame` 函数,这道题的解法就直接出来了:
|
||||
|
||||
```java
|
||||
public boolean PredictTheWinner(int[] nums) {
|
||||
// 先手的分数大于等于后手,则能赢
|
||||
return stoneGame(nums) >= 0;
|
||||
}
|
||||
```
|
||||
|
||||
这个 `stoneGame` 函数怎么写呢?博弈问题的难点在于,两个人要轮流进行选择,而且都贼精明,应该如何编程表示这个过程呢?其实不难,还是按照 [动态规划核心框架](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 中强调多次的套路,首先明确 `dp` 数组的含义,然后只要找到「状态」和「选择」,一切就水到渠成了。
|
||||
|
||||
### 一、定义 `dp` 数组的含义
|
||||
|
||||
定义 `dp` 数组的含义是很有技术含量的,同一问题可能有多种定义方法,不同的定义会引出不同的状态转移方程,不过只要逻辑没有问题,最终都能得到相同的答案。
|
||||
|
||||
我建议不要迷恋那些看起来很牛逼,代码很短小的奇技淫巧,最好是稳一点,采取可解释性最好,最容易推广的设计思路。本文就给出一种博弈问题的通用设计框架。
|
||||
|
||||
介绍 dp 数组的含义之前,我们先看一下 dp 数组最终的样子:
|
||||
介绍 `dp` 数组的含义之前,我们先看一下 `dp` 数组最终的样子:
|
||||
|
||||

|
||||

|
||||
|
||||
下文讲解时,认为元组是包含 first 和 second 属性的一个类,而且为了节省篇幅,将这两个属性简写为 fir 和 sec。比如按上图的数据,我们说 `dp[1][3].fir = 10`,`dp[0][1].sec = 3`。
|
||||
下文讲解时,认为元组是包含 `first` 和 `second` 属性的一个类,而且为了节省篇幅,将这两个属性简写为 `fir` 和 `sec`。比如按上图的数据,我们说 `dp[1][3].fir = 11`,`dp[0][1].sec = 2`。
|
||||
|
||||
先回答几个读者可能提出的问题:
|
||||
|
||||
|
|
@ -52,22 +73,21 @@
|
|||
|
||||
**以下是对 dp 数组含义的解释:**
|
||||
|
||||
```python
|
||||
dp[i][j].fir 表示,对于 piles[i...j] 这部分石头堆,先手能获得的最高分数。
|
||||
dp[i][j].sec 表示,对于 piles[i...j] 这部分石头堆,后手能获得的最高分数。
|
||||
`dp[i][j].fir = x` 表示,对于 `piles[i...j]` 这部分石头堆,先手能获得的最高分数为 `x`。
|
||||
|
||||
举例理解一下,假设 piles = [3, 9, 1, 2],索引从 0 开始
|
||||
dp[0][1].fir = 9 意味着:面对石头堆 [3, 9],先手最终能够获得 9 分。
|
||||
dp[1][3].sec = 2 意味着:面对石头堆 [9, 1, 2],后手最终能够获得 2 分。
|
||||
```
|
||||
`dp[i][j].sec = y` 表示,对于 `piles[i...j]` 这部分石头堆,后手能获得的最高分数为 `y`。
|
||||
|
||||
我们想求的答案是先手和后手最终分数之差,按照这个定义也就是 `dp[0][n-1].fir - dp[0][n-1].sec`,即面对整个 piles,先手的最优得分和后手的最优得分之差。
|
||||
举例理解一下,假设 `piles = [2, 8, 3, 5]`,索引从 0 开始,那么:
|
||||
|
||||
`dp[0][1].fir = 8` 意味着:面对石头堆 `[2, 8]`,先手最多能够获得 8 分;`dp[1][3].sec = 5` 意味着:面对石头堆 `[8, 3, 5]`,后手最多能够获得 5 分。
|
||||
|
||||
我们想求的答案是先手和后手最终分数之差,按照这个定义也就是 `dp[0][n-1].fir - dp[0][n-1].sec`,即面对整个 `piles`,先手的最优得分和后手的最优得分之差。
|
||||
|
||||
### 二、状态转移方程
|
||||
|
||||
写状态转移方程很简单,首先要找到所有「状态」和每个状态可以做的「选择」,然后择优。
|
||||
|
||||
根据前面对 dp 数组的定义,**状态显然有三个:开始的索引 i,结束的索引 j,当前轮到的人。**
|
||||
根据前面对 `dp` 数组的定义,**状态显然有三个:开始的索引 `i`,结束的索引 `j`,当前轮到的人。**
|
||||
|
||||
```python
|
||||
dp[i][j][fir or sec]
|
||||
|
|
@ -84,16 +104,15 @@ for 0 <= i < n:
|
|||
for j <= i < n:
|
||||
for who in {fir, sec}:
|
||||
dp[i][j][who] = max(left, right)
|
||||
|
||||
```
|
||||
|
||||
上面的伪码是动态规划的一个大致的框架,股票系列问题中也有类似的伪码。这道题的难点在于,两人是交替进行选择的,也就是说先手的选择会对后手有影响,这怎么表达出来呢?
|
||||
上面的伪码是动态规划的一个大致的框架,这道题的难点在于,两人足够聪明,而且是交替进行选择的,也就是说先手的选择会对后手有影响,这怎么表达出来呢?
|
||||
|
||||
根据我们对 dp 数组的定义,很容易解决这个难点,**写出状态转移方程:**
|
||||
根据我们对 `dp` 数组的定义,很容易解决这个难点,**写出状态转移方程:**
|
||||
|
||||
```python
|
||||
dp[i][j].fir = max(piles[i] + dp[i+1][j].sec, piles[j] + dp[i][j-1].sec)
|
||||
dp[i][j].fir = max( 选择最左边的石头堆 , 选择最右边的石头堆 )
|
||||
dp[i][j].fir = max( 选择最左边的石头堆 , 选择最右边的石头堆 )
|
||||
# 解释:我作为先手,面对 piles[i...j] 时,有两种选择:
|
||||
# 要么我选择最左边的那一堆石头,然后面对 piles[i+1...j]
|
||||
# 但是此时轮到对方,相当于我变成了后手;
|
||||
|
|
@ -122,18 +141,23 @@ dp[i][j].sec = 0
|
|||
# 后手没有石头拿了,得分为 0
|
||||
```
|
||||
|
||||

|
||||

|
||||
|
||||
这里需要注意一点,我们发现 base case 是斜着的,而且我们推算 dp[i][j] 时需要用到 dp[i+1][j] 和 dp[i][j-1]:
|
||||
这里需要注意一点,我们发现 base case 是斜着的,而且我们推算 `dp[i][j]` 时需要用到 `dp[i+1][j]` 和 `dp[i][j-1]`:
|
||||
|
||||

|
||||

|
||||
|
||||
所以说算法不能简单的一行一行遍历 dp 数组,**而要斜着遍历数组:**
|
||||
根据前文 [动态规划答疑篇](https://labuladong.github.io/article/fname.html?fname=最优子结构) 判断 `dp` 数组遍历方向的原则,算法应该倒着遍历 `dp` 数组:
|
||||
|
||||

|
||||
|
||||
说实话,斜着遍历二维数组说起来容易,你还真不一定能想出来怎么实现,不信你思考一下?这么巧妙的状态转移方程都列出来了,要是不会写代码实现,那真的很尴尬了。
|
||||
```java
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
dp[i][j] = ...
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
|
||||
### 三、代码实现
|
||||
|
||||
|
|
@ -149,7 +173,7 @@ class Pair {
|
|||
}
|
||||
```
|
||||
|
||||
然后直接把我们的状态转移方程翻译成代码即可,可以注意一下斜着遍历数组的技巧:
|
||||
然后直接把我们的状态转移方程翻译成代码即可,注意我们要倒着遍历数组:
|
||||
|
||||
```java
|
||||
/* 返回游戏最后先手和后手的得分之差 */
|
||||
|
|
@ -165,14 +189,15 @@ int stoneGame(int[] piles) {
|
|||
dp[i][i].fir = piles[i];
|
||||
dp[i][i].sec = 0;
|
||||
}
|
||||
// 斜着遍历数组
|
||||
for (int l = 2; l <= n; l++) {
|
||||
for (int i = 0; i <= n - l; i++) {
|
||||
int j = l + i - 1;
|
||||
|
||||
// 倒着遍历数组
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
// 先手选择最左边或最右边的分数
|
||||
int left = piles[i] + dp[i+1][j].sec;
|
||||
int right = piles[j] + dp[i][j-1].sec;
|
||||
// 套用状态转移方程
|
||||
// 先手肯定会选择更大的结果,后手的选择随之改变
|
||||
if (left > right) {
|
||||
dp[i][j].fir = left;
|
||||
dp[i][j].sec = dp[i+1][j].fir;
|
||||
|
|
@ -189,29 +214,37 @@ int stoneGame(int[] piles) {
|
|||
|
||||
动态规划解法,如果没有状态转移方程指导,绝对是一头雾水,但是根据前面的详细解释,读者应该可以清晰理解这一大段代码的含义。
|
||||
|
||||
而且,注意到计算 `dp[i][j]` 只依赖其左边和下边的元素,所以说肯定有优化空间,转换成一维 dp,想象一下把二维平面压扁,也就是投影到一维。但是,一维 dp 比较复杂,可解释性很差,大家就不必浪费这个时间去理解了。
|
||||
而且,注意到计算 `dp[i][j]` 只依赖其左边和下边的元素,所以说肯定有优化空间,转换成一维 dp,想象一下把二维平面压扁,也就是投影到一维。但是,一维 `dp` 比较复杂,可解释性比较差,大家就不必浪费这个时间去理解了。
|
||||
|
||||
### 四、最后总结
|
||||
|
||||
本文给出了解决博弈问题的动态规划解法。博弈问题的前提一般都是在两个聪明人之间进行,编程描述这种游戏的一般方法是二维 dp 数组,数组中通过元组分别表示两人的最优决策。
|
||||
|
||||
之所以这样设计,是因为先手在做出选择之后,就成了后手,后手在对方做完选择后,就变成了先手。这种角色转换使得我们可以重用之前的结果,典型的动态规划标志。
|
||||
之所以这样设计,是因为先手在做出选择之后,就成了后手,后手在对方做完选择后,就变成了先手。**这种角色转换使得我们可以重用之前的结果,典型的动态规划标志**。
|
||||
|
||||
读到这里的朋友应该能理解算法解决博弈问题的套路了。学习算法,一定要注重算法的模板框架,而不是一些看起来牛逼的思路,也不要奢求上来就写一个最优的解法。不要舍不得多用空间,不要过早尝试优化,不要惧怕多维数组。`dp` 数组就是存储信息避免重复计算的,随便用,直到咱满意为止。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [贪心算法之区间调度问题](https://labuladong.github.io/article/fname.html?fname=贪心算法之区间调度问题)
|
||||
|
||||
</details><hr>
|
||||
|
||||
读到这里的朋友应该能理解算法解决博弈问题的套路了。学习算法,一定要注重算法的模板框架,而不是一些看起来牛逼的思路,也不要奢求上来就写一个最优的解法。不要舍不得多用空间,不要过早尝试优化,不要惧怕多维数组。dp 数组就是存储信息避免重复计算的,随便用,直到咱满意为止。
|
||||
|
||||
希望本文对你有帮助。
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
### python
|
||||
|
|
|
|||
|
|
@ -1,32 +1,57 @@
|
|||
# 动态规划之四键键盘
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[651.四键键盘](https://leetcode-cn.com/problems/4-keys-keyboard)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [651. 4 Keys Keyboard](https://leetcode.com/problems/4-keys-keyboard/)🔒 | [651. 4键键盘](https://leetcode.cn/problems/4-keys-keyboard/)🔒 | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
PS:现在这到题好想变成会员题目了?我当时做的时候还是免费的。
|
||||
|
||||
四键键盘问题很有意思,而且可以明显感受到:对 dp 数组的不同定义需要完全不同的逻辑,从而产生完全不同的解法。
|
||||
力扣第 651 题「四键键盘」很有意思,而且可以明显感受到:对 `dp` 数组的不同定义需要完全不同的逻辑,从而产生完全不同的解法。
|
||||
|
||||
首先看一下题目:
|
||||
|
||||

|
||||
假设你有一个特殊的键盘,上面只有四个键,它们分别是:
|
||||
|
||||
如何在 N 次敲击按钮后得到最多的 A?我们穷举呗,每次有对于每次按键,我们可以穷举四种可能,很明显就是一个动态规划问题。
|
||||
1、`A` 键:在屏幕上打印一个 `A`。
|
||||
|
||||
2、`Ctrl-A` 键:选中整个屏幕。
|
||||
|
||||
3、`Ctrl-C` 键:复制选中的区域到缓冲区。
|
||||
|
||||
4、`Ctrl-V` 键:将缓冲区的内容输入到光标所在的屏幕上。
|
||||
|
||||
这就和我们平时使用的全选复制粘贴功能完全相同嘛,只不过题目把 `Ctrl` 的组合键视为了一个键。现在要求你只能进行 `N` 次操作,请你计算屏幕上最多能显示多少个 `A`?
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int maxA(int N);
|
||||
```
|
||||
|
||||
比如说输入 `N = 3`,算法返回 3,因为连按 3 次 `A` 键是最优的方案。
|
||||
|
||||
如果输入是 `N = 7`,则算法返回 9,最优的操作序列如下:
|
||||
|
||||
`A`, `A`, `A`, `Ctrl-A`, `Ctrl-C`, `Ctrl-V`, `Ctrl-V`
|
||||
|
||||
可以得到 9 个 `A`。
|
||||
|
||||
如何在 `N` 次敲击按钮后得到最多的 `A`?我们穷举呗,每次有对于每次按键,我们可以穷举四种可能,很明显就是一个动态规划问题。
|
||||
|
||||
### 第一种思路
|
||||
|
||||
|
|
@ -107,7 +132,7 @@ dp[n][a_num][copy]
|
|||
# 状态的总数(时空复杂度)就是这个三维数组的体积
|
||||
```
|
||||
|
||||
我们知道变量 `n` 最多为 `N`,但是 `a_num` 和 `copy` 最多为多少我们很难计算,复杂度起码也有 O(N^3) 把。所以这个算法并不好,复杂度太高,且已经无法优化了。
|
||||
我们知道变量 `n` 最多为 `N`,但是 `a_num` 和 `copy` 最多为多少我们很难计算,复杂度起码也有 O(N^3) 吧。所以这个算法并不好,复杂度太高,且已经无法优化了。
|
||||
|
||||
这也就说明,我们这样定义「状态」是不太优秀的,下面我们换一种定义 dp 的思路。
|
||||
|
||||
|
|
@ -165,7 +190,7 @@ public int maxA(int N) {
|
|||
|
||||
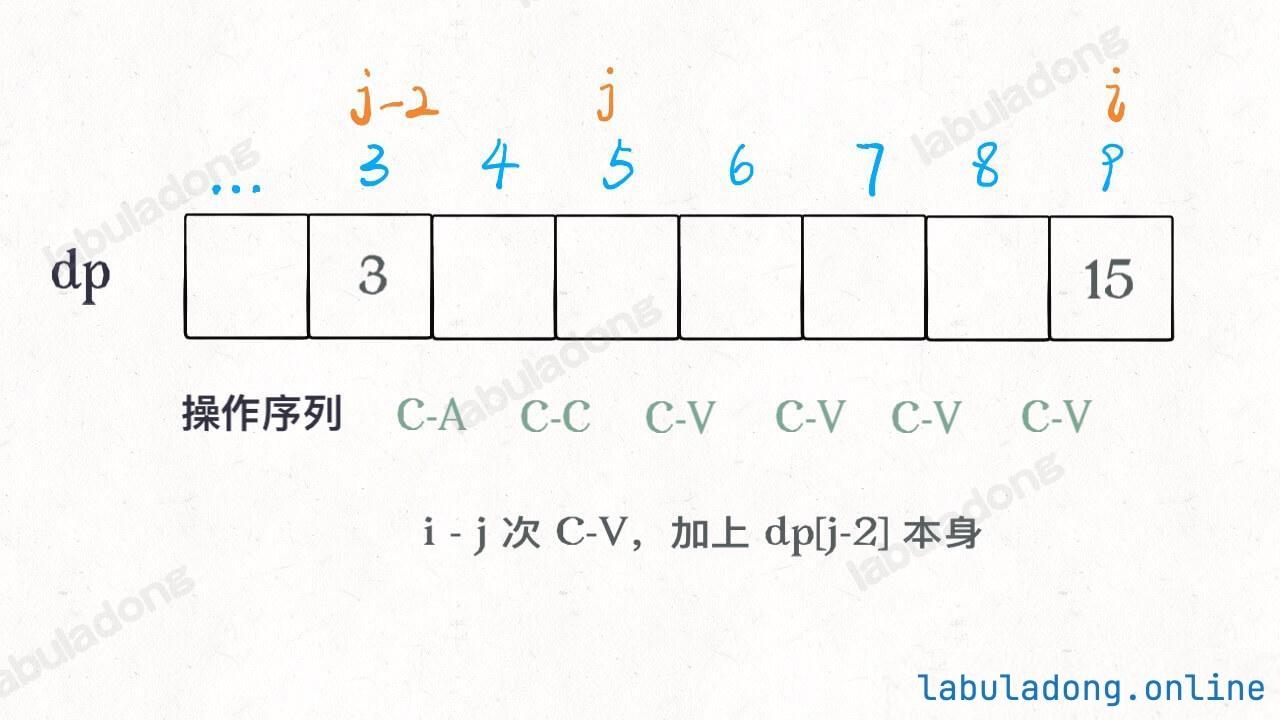
其中 `j` 变量减 2 是给 `C-A C-C` 留下操作数,看个图就明白了:
|
||||
|
||||

|
||||
|
||||
|
||||
这样,此算法就完成了,时间复杂度 O(N^2),空间复杂度 O(N),这种解法应该是比较高效的了。
|
||||
|
||||
|
|
@ -188,15 +213,27 @@ def dp(n, a_num, copy):
|
|||
|
||||
根据这个事实,我们重新定义了状态,重新寻找了状态转移,从逻辑上减少了无效的子问题个数,从而提高了算法的效率。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.github.io/article/fname.html?fname=抢房子)
|
||||
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||

|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
|
|
|
|||
|
|
@ -2,18 +2,23 @@
|
|||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[10.正则表达式匹配](https://leetcode-cn.com/problems/regular-expression-matching/)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [10. Regular Expression Matching](https://leetcode.com/problems/regular-expression-matching/) | [10. 正则表达式匹配](https://leetcode.cn/problems/regular-expression-matching/) | 🔴
|
||||
| - | [剑指 Offer 19. 正则表达式匹配](https://leetcode.cn/problems/zheng-ze-biao-da-shi-pi-pei-lcof/) | 🔴
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -108,190 +113,40 @@ if (s[i] == p[j] || p[j] == '.') {
|
|||
bool dp(string& s, int i, string& p, int j);
|
||||
```
|
||||
|
||||
`dp` 函数的定义如下:
|
||||
|
||||
**若 `dp(s, i, p, j) = true`,则表示 `s[i..]` 可以匹配 `p[j..]`;若 `dp(s, i, p, j) = false`,则表示 `s[i..]` 无法匹配 `p[j..]`**。
|
||||
|
||||
根据这个定义,我们想要的答案就是 `i = 0, j = 0` 时 `dp` 函数的结果,所以可以这样使用这个 `dp` 函数:
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
```cpp
|
||||
bool isMatch(string s, string p) {
|
||||
// 指针 i,j 从索引 0 开始移动
|
||||
return dp(s, 0, p, 0);
|
||||
```
|
||||
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
- [经典动态规划:编辑距离](https://labuladong.github.io/article/fname.html?fname=编辑距离)
|
||||
|
||||
可以根据之前的代码写出 `dp` 函数的主要逻辑:
|
||||
</details><hr>
|
||||
|
||||
```cpp
|
||||
bool dp(string& s, int i, string& p, int j) {
|
||||
if (s[i] == p[j] || p[j] == '.') {
|
||||
// 匹配
|
||||
if (j < p.size() - 1 && p[j + 1] == '*') {
|
||||
// 1.1 通配符匹配 0 次或多次
|
||||
return dp(s, i, p, j + 2)
|
||||
|| dp(s, i + 1, p, j);
|
||||
} else {
|
||||
// 1.2 常规匹配 1 次
|
||||
return dp(s, i + 1, p, j + 1);
|
||||
}
|
||||
} else {
|
||||
// 不匹配
|
||||
if (j < p.size() - 1 && p[j + 1] == '*') {
|
||||
// 2.1 通配符匹配 0 次
|
||||
return dp(s, i, p, j + 2);
|
||||
} else {
|
||||
// 2.2 无法继续匹配
|
||||
return false;
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**根据 `dp` 函数的定义**,这几种情况都很好解释:
|
||||
|
||||
1.1 通配符匹配 0 次或多次
|
||||
|
||||
将 `j` 加 2,`i` 不变,含义就是直接跳过 `p[j]` 和之后的通配符,即通配符匹配 0 次:
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||

|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
将 `i` 加 1,`j` 不变,含义就是 `p[j]` 匹配了 `s[i]`,但 `p[j]` 还可以继续匹配,即通配符匹配多次的情况:
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer 19. 正则表达式匹配](https://leetcode.cn/problems/zheng-ze-biao-da-shi-pi-pei-lcof/?show=1) |
|
||||
|
||||

|
||||
</details>
|
||||
|
||||
两种情况只要有一种可以完成匹配即可,所以对上面两种情况求或运算。
|
||||
|
||||
1.2 常规匹配 1 次
|
||||
|
||||
由于这个条件分支是无 `*` 的常规匹配,那么如果 `s[i] == p[j]`,就是 `i` 和 `j` 分别加一:
|
||||
|
||||

|
||||
|
||||
2.1 通配符匹配 0 次
|
||||
|
||||
类似情况 1.1,将 `j` 加 2,`i` 不变:
|
||||
|
||||

|
||||
|
||||
2.2 如果没有 `*` 通配符,也无法匹配,那只能说明匹配失败了:
|
||||
|
||||

|
||||
|
||||
看图理解应该很容易了,现在可以思考一下 `dp` 函数的 base case:
|
||||
|
||||
**一个 base case 是 `j == p.size()` 时**,按照 `dp` 函数的定义,这意味着模式串 `p` 已经被匹配完了,那么应该看看文本串 `s` 匹配到哪里了,如果 `s` 也恰好被匹配完,则说明匹配成功:
|
||||
|
||||
```cpp
|
||||
if (j == p.size()) {
|
||||
return i == s.size();
|
||||
}
|
||||
```
|
||||
|
||||
**另一个 base case 是 `i == s.size()` 时**,按照 `dp` 函数的定义,这种情况意味着文本串 `s` 已经全部被匹配了,那么是不是只要简单地检查一下 `p` 是否也匹配完就行了呢?
|
||||
|
||||
```cpp
|
||||
if (i == s.size()) {
|
||||
// 这样行吗?
|
||||
return j == p.size();
|
||||
}
|
||||
```
|
||||
|
||||
**这是不正确的,此时并不能根据 `j` 是否等于 `p.size()` 来判断是否完成匹配,只要 `p[j..]` 能够匹配空串,就可以算完成匹配**。比如说 `s = "a", p = "ab*c*"`,当 `i` 走到 `s` 末尾的时候,`j` 并没有走到 `p` 的末尾,但是 `p` 依然可以匹配 `s`。
|
||||
|
||||
所以我们可以写出如下代码:
|
||||
|
||||
```cpp
|
||||
int m = s.size(), n = p.size();
|
||||
|
||||
if (i == s.size()) {
|
||||
// 如果能匹配空串,一定是字符和 * 成对儿出现
|
||||
if ((n - j) % 2 == 1) {
|
||||
return false;
|
||||
}
|
||||
// 检查是否为 x*y*z* 这种形式
|
||||
for (; j + 1 < p.size(); j += 2) {
|
||||
if (p[j + 1] != '*') {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
根据以上思路,就可以写出完整的代码:
|
||||
|
||||
```cpp
|
||||
/* 计算 p[j..] 是否匹配 s[i..] */
|
||||
bool dp(string& s, int i, string& p, int j) {
|
||||
int m = s.size(), n = p.size();
|
||||
// base case
|
||||
if (j == n) {
|
||||
return i == m;
|
||||
}
|
||||
if (i == m) {
|
||||
if ((n - j) % 2 == 1) {
|
||||
return false;
|
||||
}
|
||||
for (; j + 1 < n; j += 2) {
|
||||
if (p[j + 1] != '*') {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
// 记录状态 (i, j),消除重叠子问题
|
||||
string key = to_string(i) + "," + to_string(j);
|
||||
if (memo.count(key)) return memo[key];
|
||||
|
||||
bool res = false;
|
||||
|
||||
if (s[i] == p[j] || p[j] == '.') {
|
||||
if (j < n - 1 && p[j + 1] == '*') {
|
||||
res = dp(s, i, p, j + 2)
|
||||
|| dp(s, i + 1, p, j);
|
||||
} else {
|
||||
res = dp(s, i + 1, p, j + 1);
|
||||
}
|
||||
} else {
|
||||
if (j < n - 1 && p[j + 1] == '*') {
|
||||
res = dp(s, i, p, j + 2);
|
||||
} else {
|
||||
res = false;
|
||||
}
|
||||
}
|
||||
// 将当前结果记入备忘录
|
||||
memo[key] = res;
|
||||
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
代码中用了一个哈希表 `memo` 消除重叠子问题,因为正则表达算法的递归框架如下:
|
||||
|
||||
```cpp
|
||||
bool dp(string& s, int i, string& p, int j) {
|
||||
dp(s, i, p, j + 2); // 1
|
||||
dp(s, i + 1, p, j); // 2
|
||||
dp(s, i + 1, p, j + 1); // 3
|
||||
}
|
||||
```
|
||||
|
||||
那么,如果让你从 `dp(s, i, p, j)` 得到 `dp(s, i+2, p, j+2)`,至少有两条路径:`1 -> 2 -> 2` 和 `3 -> 3`,那么就说明 `(i+2, j+2)` 这个状态存在重复,这就说明存在重叠子问题。
|
||||
|
||||
动态规划的时间复杂度为「状态的总数」*「每次递归花费的时间」,本题中状态的总数当然就是 `i` 和 `j` 的组合,也就是 `M * N`(`M` 为 `s` 的长度,`N` 为 `p` 的长度);递归函数 `dp` 中没有循环(base case 中的不考虑,因为 base case 的触发次数有限),所以一次递归花费的时间为常数。二者相乘,总的时间复杂度为 `O(MN)`。
|
||||
|
||||
空间复杂度很简单,就是备忘录 `memo` 的大小,即 `O(MN)`。
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
应合作方要求,本文不便在此发布,请扫码关注回复关键词「正则」或 [点这里](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_6298796ae4b01a4852072fb9/1) 查看:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||

|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
### javascript
|
||||
|
|
|
|||
|
|
@ -2,30 +2,41 @@
|
|||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[300.最长上升子序列](https://leetcode-cn.com/problems/longest-increasing-subsequence)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/) | [300. 最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/) | 🟠
|
||||
| [354. Russian Doll Envelopes](https://leetcode.com/problems/russian-doll-envelopes/) | [354. 俄罗斯套娃信封问题](https://leetcode.cn/problems/russian-doll-envelopes/) | 🔴
|
||||
|
||||
**-----------**
|
||||
|
||||
也许有读者看了前文 [动态规划详解](https://labuladong.gitee.io/algo/),学会了动态规划的套路:找到了问题的「状态」,明确了 `dp` 数组/函数的含义,定义了 base case;但是不知道如何确定「选择」,也就是不到状态转移的关系,依然写不出动态规划解法,怎么办?
|
||||
也许有读者看了前文 [动态规划详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶),学会了动态规划的套路:找到了问题的「状态」,明确了 `dp` 数组/函数的含义,定义了 base case;但是不知道如何确定「选择」,也就是找不到状态转移的关系,依然写不出动态规划解法,怎么办?
|
||||
|
||||
不要担心,动态规划的难点本来就在于寻找正确的状态转移方程,本文就借助经典的「最长递增子序列问题」来讲一讲设计动态规划的通用技巧:**数学归纳思想**。
|
||||
|
||||
最长递增子序列(Longest Increasing Subsequence,简写 LIS)是非常经典的一个算法问题,比较容易想到的是动态规划解法,时间复杂度 O(N^2),我们借这个问题来由浅入深讲解如何找状态转移方程,如何写出动态规划解法。比较难想到的是利用二分查找,时间复杂度是 O(NlogN),我们通过一种简单的纸牌游戏来辅助理解这种巧妙的解法。
|
||||
|
||||
先看一下题目,很容易理解:
|
||||
力扣第 300 题「最长递增子序列」就是这个问题:
|
||||
|
||||

|
||||
输入一个无序的整数数组,请你找到其中最长的严格递增子序列的长度,函数签名如下:
|
||||
|
||||
```java
|
||||
int lengthOfLIS(int[] nums);
|
||||
```
|
||||
|
||||
比如说输入 `nums=[10,9,2,5,3,7,101,18]`,其中最长的递增子序列是 `[2,3,7,101]`,所以算法的输出应该是 4。
|
||||
|
||||
注意「子序列」和「子串」这两个名词的区别,子串一定是连续的,而子序列不一定是连续的。下面先来设计动态规划算法解决这个问题。
|
||||
|
||||
|
|
@ -33,34 +44,31 @@
|
|||
|
||||
动态规划的核心设计思想是数学归纳法。
|
||||
|
||||
相信大家对数学归纳法都不陌生,高中就学过,而且思路很简单。比如我们想证明一个数学结论,那么**我们先假设这个结论在 `k<n` 时成立,然后根据这个假设,想办法推导证明出 `k=n` 的时候此结论也成立**。如果能够证明出来,那么就说明这个结论对于 `k` 等于任何数都成立。
|
||||
相信大家对数学归纳法都不陌生,高中就学过,而且思路很简单。比如我们想证明一个数学结论,那么**我们先假设这个结论在 `k < n` 时成立,然后根据这个假设,想办法推导证明出 `k = n` 的时候此结论也成立**。如果能够证明出来,那么就说明这个结论对于 `k` 等于任何数都成立。
|
||||
|
||||
类似的,我们设计动态规划算法,不是需要一个 dp 数组吗?我们可以假设 `dp[0...i-1]` 都已经被算出来了,然后问自己:怎么通过这些结果算出 `dp[i]`?
|
||||
|
||||
直接拿最长递增子序列这个问题举例你就明白了。不过,首先要定义清楚 dp 数组的含义,即 `dp[i]` 的值到底代表着什么?
|
||||
|
||||
**我们的定义是这样的:`dp[i]` 表示以 `nums[i]` 这个数结尾的最长递增子序列的长度。**
|
||||
**我们的定义是这样的:`dp[i]` 表示以 `nums[i]` 这个数结尾的最长递增子序列的长度**。
|
||||
|
||||
PS:为什么这样定义呢?这是解决子序列问题的一个套路,后文[动态规划之子序列问题解题模板](https://labuladong.gitee.io/algo/) 总结了几种常见套路。你读完本章所有的动态规划问题,就会发现 `dp` 数组的定义方法也就那几种。
|
||||
> PS:为什么这样定义呢?这是解决子序列问题的一个套路,后文 [动态规划之子序列问题解题模板](https://labuladong.github.io/article/fname.html?fname=子序列问题模板) 总结了几种常见套路。你读完本章所有的动态规划问题,就会发现 `dp` 数组的定义方法也就那几种。
|
||||
|
||||
根据这个定义,我们就可以推出 base case:`dp[i]` 初始值为 1,因为以 `nums[i]` 结尾的最长递增子序列起码要包含它自己。
|
||||
|
||||
举两个例子:
|
||||
|
||||

|
||||

|
||||
|
||||
这个 GIF 展示了算法演进的过程:
|
||||
|
||||

|
||||
|
||||
算法演进的过程是这样的,:
|
||||
|
||||

|
||||

|
||||
|
||||
根据这个定义,我们的最终结果(子序列的最大长度)应该是 dp 数组中的最大值。
|
||||
|
||||
```java
|
||||
int res = 0;
|
||||
for (int i = 0; i < dp.size(); i++) {
|
||||
for (int i = 0; i < dp.length; i++) {
|
||||
res = Math.max(res, dp[i]);
|
||||
}
|
||||
return res;
|
||||
|
|
@ -68,24 +76,29 @@ return res;
|
|||
|
||||
读者也许会问,刚才的算法演进过程中每个 `dp[i]` 的结果是我们肉眼看出来的,我们应该怎么设计算法逻辑来正确计算每个 `dp[i]` 呢?
|
||||
|
||||
这就是动态规划的重头戏了,要思考如何设计算法逻辑进行状态转移,才能正确运行呢?这里就可以使用数学归纳的思想:
|
||||
这就是动态规划的重头戏,如何设计算法逻辑进行状态转移,才能正确运行呢?这里需要使用数学归纳的思想:
|
||||
|
||||
**假设我们已经知道了 `dp[0..4]` 的所有结果,我们如何通过这些已知结果推出 `dp[5]` 呢**?
|
||||
|
||||

|
||||

|
||||
|
||||
根据刚才我们对 `dp` 数组的定义,现在想求 `dp[5]` 的值,也就是想求以 `nums[5]` 为结尾的最长递增子序列。
|
||||
|
||||
**`nums[5] = 3`,既然是递增子序列,我们只要找到前面那些结尾比 3 小的子序列,然后把 3 接到最后,就可以形成一个新的递增子序列,而且这个新的子序列长度加一**。
|
||||
**`nums[5] = 3`,既然是递增子序列,我们只要找到前面那些结尾比 3 小的子序列,然后把 3 接到这些子序列末尾,就可以形成一个新的递增子序列,而且这个新的子序列长度加一**。
|
||||
|
||||
显然,可能形成很多种新的子序列,但是我们只选择最长的那一个,把最长子序列的长度作为 `dp[5]` 的值即可。
|
||||
`nums[5]` 前面有哪些元素小于 `nums[5]`?这个好算,用 for 循环比较一波就能把这些元素找出来。
|
||||
|
||||

|
||||
以这些元素为结尾的最长递增子序列的长度是多少?回顾一下我们对 `dp` 数组的定义,它记录的正是以每个元素为末尾的最长递增子序列的长度。
|
||||
|
||||
以我们举的例子来说,`nums[0]` 和 `nums[4]` 都是小于 `nums[5]` 的,然后对比 `dp[0]` 和 `dp[4]` 的值,我们让 `nums[5]` 和更长的递增子序列结合,得出 `dp[5] = 3`:
|
||||
|
||||

|
||||
|
||||
```java
|
||||
for (int j = 0; j < i; j++) {
|
||||
if (nums[i] > nums[j])
|
||||
if (nums[i] > nums[j]) {
|
||||
dp[i] = Math.max(dp[i], dp[j] + 1);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -96,8 +109,12 @@ for (int j = 0; j < i; j++) {
|
|||
```java
|
||||
for (int i = 0; i < nums.length; i++) {
|
||||
for (int j = 0; j < i; j++) {
|
||||
if (nums[i] > nums[j])
|
||||
// 寻找 nums[0..j-1] 中比 nums[i] 小的元素
|
||||
if (nums[i] > nums[j]) {
|
||||
// 把 nums[i] 接在后面,即可形成长度为 dp[j] + 1,
|
||||
// 且以 nums[i] 为结尾的递增子序列
|
||||
dp[i] = Math.max(dp[i], dp[j] + 1);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
|
@ -105,7 +122,8 @@ for (int i = 0; i < nums.length; i++) {
|
|||
结合我们刚才说的 base case,下面我们看一下完整代码:
|
||||
|
||||
```java
|
||||
public int lengthOfLIS(int[] nums) {
|
||||
int lengthOfLIS(int[] nums) {
|
||||
// 定义:dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
|
||||
int[] dp = new int[nums.length];
|
||||
// base case:dp 数组全都初始化为 1
|
||||
Arrays.fill(dp, 1);
|
||||
|
|
@ -124,17 +142,19 @@ public int lengthOfLIS(int[] nums) {
|
|||
}
|
||||
```
|
||||
|
||||
至此,这道题就解决了,时间复杂度 O(N^2)。总结一下如何找到动态规划的状态转移关系:
|
||||
至此,这道题就解决了,时间复杂度 `O(N^2)`。总结一下如何找到动态规划的状态转移关系:
|
||||
|
||||
1、明确 `dp` 数组所存数据的含义。这一步对于任何动态规划问题都很重要,如果不得当或者不够清晰,会阻碍之后的步骤。
|
||||
1、明确 `dp` 数组的定义。这一步对于任何动态规划问题都很重要,如果不得当或者不够清晰,会阻碍之后的步骤。
|
||||
|
||||
2、根据 `dp` 数组的定义,运用数学归纳法的思想,假设 `dp[0...i-1]` 都已知,想办法求出 `dp[i]`,一旦这一步完成,整个题目基本就解决了。
|
||||
|
||||
但如果无法完成这一步,很可能就是 `dp` 数组的定义不够恰当,需要重新定义 `dp` 数组的含义;或者可能是 `dp` 数组存储的信息还不够,不足以推出下一步的答案,需要把 `dp` 数组扩大成二维数组甚至三维数组。
|
||||
|
||||
目前的解法是标准的动态规划,但对最长递增子序列问题来说,这个解法不是最优的,可能无法通过所有测试用例了,下面讲讲更高效的解法。
|
||||
|
||||
### 二、二分查找解法
|
||||
|
||||
这个解法的时间复杂度为 O(NlogN),但是说实话,正常人基本想不到这种解法(也许玩过某些纸牌游戏的人可以想出来)。所以大家了解一下就好,正常情况下能够给出动态规划解法就已经很不错了。
|
||||
这个解法的时间复杂度为 `O(NlogN)`,但是说实话,正常人基本想不到这种解法(也许玩过某些纸牌游戏的人可以想出来)。所以大家了解一下就好,正常情况下能够给出动态规划解法就已经很不错了。
|
||||
|
||||
根据题目的意思,我都很难想象这个问题竟然能和二分查找扯上关系。其实最长递增子序列和一种叫做 patience game 的纸牌游戏有关,甚至有一种排序方法就叫做 patience sorting(耐心排序)。
|
||||
|
||||
|
|
@ -142,7 +162,7 @@ public int lengthOfLIS(int[] nums) {
|
|||
|
||||
首先,给你一排扑克牌,我们像遍历数组那样从左到右一张一张处理这些扑克牌,最终要把这些牌分成若干堆。
|
||||
|
||||

|
||||

|
||||
|
||||
**处理这些扑克牌要遵循以下规则**:
|
||||
|
||||
|
|
@ -150,22 +170,22 @@ public int lengthOfLIS(int[] nums) {
|
|||
|
||||
比如说上述的扑克牌最终会被分成这样 5 堆(我们认为纸牌 A 的牌面是最大的,纸牌 2 的牌面是最小的)。
|
||||
|
||||

|
||||

|
||||
|
||||
为什么遇到多个可选择堆的时候要放到最左边的堆上呢?因为这样可以保证牌堆顶的牌有序(2, 4, 7, 8, Q),证明略。
|
||||
|
||||

|
||||

|
||||
|
||||
按照上述规则执行,可以算出最长递增子序列,牌的堆数就是最长递增子序列的长度,证明略。
|
||||
|
||||

|
||||

|
||||
|
||||
我们只要把处理扑克牌的过程编程写出来即可。每次处理一张扑克牌不是要找一个合适的牌堆顶来放吗,牌堆顶的牌不是**有序**吗,这就能用到二分查找了:用二分查找来搜索当前牌应放置的位置。
|
||||
|
||||
PS:旧文[二分查找算法详解](https://labuladong.gitee.io/algo/)详细介绍了二分查找的细节及变体,这里就完美应用上了,如果没读过强烈建议阅读。
|
||||
> PS:前文 [二分查找算法详解](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 详细介绍了二分查找的细节及变体,这里就完美应用上了,如果没读过强烈建议阅读。
|
||||
|
||||
```java
|
||||
public int lengthOfLIS(int[] nums) {
|
||||
int lengthOfLIS(int[] nums) {
|
||||
int[] top = new int[nums.length];
|
||||
// 牌堆数初始化为 0
|
||||
int piles = 0;
|
||||
|
|
@ -203,15 +223,115 @@ public int lengthOfLIS(int[] nums) {
|
|||
|
||||
所以,这个方法作为思维拓展好了。但动态规划的设计方法应该完全理解:假设之前的答案已知,利用数学归纳的思想正确进行状态的推演转移,最终得到答案。
|
||||
|
||||
### 三、拓展到二维
|
||||
|
||||
我们看一个经常出现在生活中的有趣问题,力扣第 354 题「俄罗斯套娃信封问题」,先看下题目:
|
||||
|
||||

|
||||
|
||||
**这道题目其实是最长递增子序列的一个变种,因为每次合法的嵌套是大的套小的,相当于在二维平面中找一个最长递增的子序列,其长度就是最多能嵌套的信封个数**。
|
||||
|
||||
前面说的标准 LIS 算法只能在一维数组中寻找最长子序列,而我们的信封是由 `(w, h)` 这样的二维数对形式表示的,如何把 LIS 算法运用过来呢?
|
||||
|
||||

|
||||
|
||||
读者也许会想,通过 `w × h` 计算面积,然后对面积进行标准的 LIS 算法。但是稍加思考就会发现这样不行,比如 `1 × 10` 大于 `3 × 3`,但是显然这样的两个信封是无法互相嵌套的。
|
||||
|
||||
这道题的解法比较巧妙:
|
||||
|
||||
**先对宽度 `w` 进行升序排序,如果遇到 `w` 相同的情况,则按照高度 `h` 降序排序;之后把所有的 `h` 作为一个数组,在这个数组上计算 LIS 的长度就是答案**。
|
||||
|
||||
画个图理解一下,先对这些数对进行排序:
|
||||
|
||||

|
||||
|
||||
然后在 `h` 上寻找最长递增子序列,这个子序列就是最优的嵌套方案:
|
||||
|
||||

|
||||
|
||||
为什么呢?稍微思考一下就明白了:
|
||||
|
||||
首先,对宽度 `w` 从小到大排序,确保了 `w` 这个维度可以互相嵌套,所以我们只需要专注高度 `h` 这个维度能够互相嵌套即可。
|
||||
|
||||
其次,两个 `w` 相同的信封不能相互包含,所以对于宽度 `w` 相同的信封,对高度 `h` 进行降序排序,保证 LIS 中不存在多个 `w` 相同的信封(因为题目说了长宽相同也无法嵌套)。
|
||||
|
||||
下面看解法代码:
|
||||
|
||||
```java
|
||||
// envelopes = [[w, h], [w, h]...]
|
||||
public int maxEnvelopes(int[][] envelopes) {
|
||||
int n = envelopes.length;
|
||||
// 按宽度升序排列,如果宽度一样,则按高度降序排列
|
||||
Arrays.sort(envelopes, new Comparator<int[]>()
|
||||
{
|
||||
public int compare(int[] a, int[] b) {
|
||||
return a[0] == b[0] ?
|
||||
b[1] - a[1] : a[0] - b[0];
|
||||
}
|
||||
});
|
||||
// 对高度数组寻找 LIS
|
||||
int[] height = new int[n];
|
||||
for (int i = 0; i < n; i++)
|
||||
height[i] = envelopes[i][1];
|
||||
|
||||
return lengthOfLIS(height);
|
||||
}
|
||||
|
||||
int lengthOfLIS(int[] nums) {
|
||||
// 见前文
|
||||
}
|
||||
```
|
||||
|
||||
为了清晰,我将代码分为了两个函数, 你也可以合并,这样可以节省下 `height` 数组的空间。
|
||||
|
||||
由于增加了测试用例,这里必须使用二分搜索版的 `lengthOfLIS` 函数才能通过所有测试用例。这样的话算法的时间复杂度为 `O(NlogN)`,因为排序和计算 LIS 各需要 `O(NlogN)` 的时间,加到一起还是 `O(NlogN)`;空间复杂度为 `O(N)`,因为计算 LIS 的函数中需要一个 `top` 数组。
|
||||
|
||||
接下来可阅读:
|
||||
|
||||
* [动态规划之最大子数组](https://labuladong.github.io/article/fname.html?fname=最大子数组)
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [二分查找高效判定子序列](https://labuladong.github.io/article/fname.html?fname=二分查找判定子序列)
|
||||
- [动态规划之子序列问题解题模板](https://labuladong.github.io/article/fname.html?fname=子序列问题模板)
|
||||
- [动态规划解题套路框架](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)
|
||||
- [动态规划设计:最大子数组](https://labuladong.github.io/article/fname.html?fname=最大子数组)
|
||||
- [动态规划问题的两种穷举视角](https://labuladong.github.io/article/fname.html?fname=动归两种视角)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1425. Constrained Subsequence Sum](https://leetcode.com/problems/constrained-subsequence-sum/?show=1) | [1425. 带限制的子序列和](https://leetcode.cn/problems/constrained-subsequence-sum/?show=1) |
|
||||
| [256. Paint House](https://leetcode.com/problems/paint-house/?show=1)🔒 | [256. 粉刷房子](https://leetcode.cn/problems/paint-house/?show=1)🔒 |
|
||||
| - | [剑指 Offer II 091. 粉刷房子](https://leetcode.cn/problems/JEj789/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
### javascript
|
||||
|
|
|
|||
|
|
@ -1,54 +1,65 @@
|
|||
# 动态规划详解
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[509.斐波那契数](https://leetcode-cn.com/problems/fibonacci-number)
|
||||
|
||||
[322.零钱兑换](https://leetcode-cn.com/problems/coin-change)
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [322. Coin Change](https://leetcode.com/problems/coin-change/) | [322. 零钱兑换](https://leetcode.cn/problems/coin-change/) | 🟠
|
||||
| [509. Fibonacci Number](https://leetcode.com/problems/fibonacci-number/) | [509. 斐波那契数](https://leetcode.cn/problems/fibonacci-number/) | 🟢
|
||||
| - | [剑指 Offer II 103. 最少的硬币数目](https://leetcode.cn/problems/gaM7Ch/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
本文有视频版:[动态规划框架套路详解](https://www.bilibili.com/video/BV1XV411Y7oE)
|
||||
> 本文有视频版:[动态规划框架套路详解](https://www.bilibili.com/video/BV1XV411Y7oE)
|
||||
|
||||
这篇文章是我们公众号半年前一篇 200 多赞赏的成名之作 [动态规划详解](https://mp.weixin.qq.com/s/1V3aHVonWBEXlNUvK3S28w) 的进阶版。由于账号迁移的原因,旧文无法被搜索到,所以我润色了本文,并添加了更多干货内容,希望本文成为解决动态规划的一部「指导方针」。
|
||||
|
||||
动态规划问题(Dynamic Programming)应该是很多读者头疼的,不过这类问题也是最具有技巧性,最有意思的。本书使用了整整一个章节专门来写这个算法,动态规划的重要性也可见一斑。
|
||||
|
||||
刷题刷多了就会发现,算法技巧就那几个套路,**我们后续的动态规划系列章节,都在使用本文的解题框架思维**,如果你心里有数,就会轻松很多。所以本文放在第一章,来扒一扒动态规划的裤子,形成一套解决这类问题的思维框架,希望能够成为解决动态规划问题的一部指导方针。本文就来讲解该算法的基本套路框架,下面上干货。
|
||||
本文解决几个问题:
|
||||
|
||||
**首先,动态规划问题的一般形式就是求最值**。动态规划其实是运筹学的一种最优化方法,只不过在计算机问题上应用比较多,比如说让你求**最长**递增子序列呀,**最小**编辑距离呀等等。
|
||||
动态规划是什么?解决动态规划问题有什么技巧?如何学习动态规划?
|
||||
|
||||
刷题刷多了就会发现,算法技巧就那几个套路,我们后续的动态规划系列章节,都在使用本文的解题框架思维,如果你心里有数,就会轻松很多。所以本文放在第一章,来扒一扒动态规划的裤子,形成一套解决这类问题的思维框架,希望能够成为解决动态规划问题的一部指导方针。本文就来讲解该算法的基本套路框架,下面上干货。
|
||||
|
||||
首先,**动态规划问题的一般形式就是求最值**。动态规划其实是运筹学的一种最优化方法,只不过在计算机问题上应用比较多,比如说让你求最长递增子序列呀,最小编辑距离呀等等。
|
||||
|
||||
既然是要求最值,核心问题是什么呢?**求解动态规划的核心问题是穷举**。因为要求最值,肯定要把所有可行的答案穷举出来,然后在其中找最值呗。
|
||||
|
||||
动态规划这么简单,就是穷举就完事了?我看到的动态规划问题都很难啊!
|
||||
|
||||
首先,动态规划的穷举有点特别,因为这类问题**存在「重叠子问题」**,如果暴力穷举的话效率会极其低下,所以需要「备忘录」或者「DP table」来优化穷举过程,避免不必要的计算。
|
||||
首先,虽然动态规划的核心思想就是穷举求最值,但是问题可以千变万化,穷举所有可行解其实并不是一件容易的事,需要你熟练掌握递归思维,只有列出**正确的「状态转移方程」**,才能正确地穷举。而且,你需要判断算法问题是否**具备「最优子结构」**,是否能够通过子问题的最值得到原问题的最值。另外,动态规划问题**存在「重叠子问题」**,如果暴力穷举的话效率会很低,所以需要你使用「备忘录」或者「DP table」来优化穷举过程,避免不必要的计算。
|
||||
|
||||
而且,动态规划问题一定会**具备「最优子结构」**,才能通过子问题的最值得到原问题的最值。
|
||||
以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解,但是在实际的算法问题中,写出状态转移方程是最困难的,这也就是为什么很多朋友觉得动态规划问题困难的原因,我来提供我总结的一个思维框架,辅助你思考状态转移方程:
|
||||
|
||||
另外,虽然动态规划的核心思想就是穷举求最值,但是问题可以千变万化,穷举所有可行解其实并不是一件容易的事,只有列出**正确的「状态转移方程」**才能正确地穷举。
|
||||
**明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 `dp` 数组/函数的含义**。
|
||||
|
||||
以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解,但是在实际的算法问题中,**写出状态转移方程是最困难的**,这也就是为什么很多朋友觉得动态规划问题困难的原因,我来提供我研究出来的一个思维框架,辅助你思考状态转移方程:
|
||||
|
||||
**明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义**。
|
||||
|
||||
按上面的套路走,最后的结果就可以套这个框架:
|
||||
按上面的套路走,最后的解法代码就会是如下的框架:
|
||||
|
||||
```python
|
||||
# 自顶向下递归的动态规划
|
||||
def dp(状态1, 状态2, ...):
|
||||
for 选择 in 所有可能的选择:
|
||||
# 此时的状态已经因为做了选择而改变
|
||||
result = 求最值(result, dp(状态1, 状态2, ...))
|
||||
return result
|
||||
|
||||
# 自底向上迭代的动态规划
|
||||
# 初始化 base case
|
||||
dp[0][0][...] = base
|
||||
dp[0][0][...] = base case
|
||||
# 进行状态转移
|
||||
for 状态1 in 状态1的所有取值:
|
||||
for 状态2 in 状态2的所有取值:
|
||||
|
|
@ -60,13 +71,13 @@ for 状态1 in 状态1的所有取值:
|
|||
|
||||
### 一、斐波那契数列
|
||||
|
||||
请读者不要嫌弃这个例子简单,**只有简单的例子才能让你把精力充分集中在算法背后的通用思想和技巧上,而不会被那些隐晦的细节问题搞的莫名其妙**。想要困难的例子,历史文章里有的是。
|
||||
力扣第 509 题「斐波那契数」就是这个问题,请读者不要嫌弃这个例子简单,**只有简单的例子才能让你把精力充分集中在算法背后的通用思想和技巧上,而不会被那些隐晦的细节问题搞的莫名其妙**。想要困难的例子,接下来的动态规划系列里有的是。
|
||||
|
||||
**1、暴力递归**
|
||||
|
||||
斐波那契数列的数学形式就是递归的,写成代码就是这样:
|
||||
|
||||
```cpp
|
||||
```java
|
||||
int fib(int N) {
|
||||
if (N == 1 || N == 2) return 1;
|
||||
return fib(N - 1) + fib(N - 2);
|
||||
|
|
@ -75,13 +86,13 @@ int fib(int N) {
|
|||
|
||||
这个不用多说了,学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂,但是十分低效,低效在哪里?假设 n = 20,请画出递归树:
|
||||
|
||||

|
||||

|
||||
|
||||
PS:但凡遇到需要递归的问题,最好都画出递归树,这对你分析算法的复杂度,寻找算法低效的原因都有巨大帮助。
|
||||
> PS:但凡遇到需要递归的问题,最好都画出递归树,这对你分析算法的复杂度,寻找算法低效的原因都有巨大帮助。
|
||||
|
||||
这个递归树怎么理解?就是说想要计算原问题 `f(20)`,我就得先计算出子问题 `f(19)` 和 `f(18)`,然后要计算 `f(19)`,我就要先算出子问题 `f(18)` 和 `f(17)`,以此类推。最后遇到 `f(1)` 或者 `f(2)` 的时候,结果已知,就能直接返回结果,递归树不再向下生长了。
|
||||
|
||||
**递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间。**
|
||||
**递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间**。
|
||||
|
||||
首先计算子问题个数,即递归树中节点的总数。显然二叉树节点总数为指数级别,所以子问题个数为 O(2^n)。
|
||||
|
||||
|
|
@ -99,19 +110,18 @@ PS:但凡遇到需要递归的问题,最好都画出递归树,这对你分
|
|||
|
||||
一般使用一个数组充当这个「备忘录」,当然你也可以使用哈希表(字典),思想都是一样的。
|
||||
|
||||
```cpp
|
||||
```java
|
||||
int fib(int N) {
|
||||
if (N < 1) return 0;
|
||||
// 备忘录全初始化为 0
|
||||
vector<int> memo(N + 1, 0);
|
||||
int[] memo = new int[N + 1];
|
||||
// 进行带备忘录的递归
|
||||
return helper(memo, N);
|
||||
}
|
||||
|
||||
int helper(vector<int>& memo, int n) {
|
||||
// base case
|
||||
if (n == 1 || n == 2) return 1;
|
||||
// 已经计算过
|
||||
|
||||
int helper(int[] memo, int n) {
|
||||
// base case
|
||||
if (n == 0 || n == 1) return n;
|
||||
// 已经计算过,不用再计算了
|
||||
if (memo[n] != 0) return memo[n];
|
||||
memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
|
||||
return memo[n];
|
||||
|
|
@ -120,80 +130,101 @@ int helper(vector<int>& memo, int n) {
|
|||
|
||||
现在,画出递归树,你就知道「备忘录」到底做了什么。
|
||||
|
||||

|
||||

|
||||
|
||||
实际上,带「备忘录」的递归算法,把一棵存在巨量冗余的递归树通过「剪枝」,改造成了一幅不存在冗余的递归图,极大减少了子问题(即递归图中节点)的个数。
|
||||
|
||||

|
||||

|
||||
|
||||
**递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间。**
|
||||
**递归算法的时间复杂度怎么计算?就是用子问题个数乘以解决一个子问题需要的时间**。
|
||||
|
||||
子问题个数,即图中节点的总数,由于本算法不存在冗余计算,子问题就是 `f(1)`, `f(2)`, `f(3)` ... `f(20)`,数量和输入规模 n = 20 成正比,所以子问题个数为 O(n)。
|
||||
|
||||
解决一个子问题的时间,同上,没有什么循环,时间为 O(1)。
|
||||
|
||||
所以,本算法的时间复杂度是 O(n)。比起暴力算法,是降维打击。
|
||||
所以,本算法的时间复杂度是 O(n),比起暴力算法,是降维打击。
|
||||
|
||||
至此,带备忘录的递归解法的效率已经和迭代的动态规划解法一样了。实际上,这种解法和迭代的动态规划已经差不多了,只不过这种方法叫做「自顶向下」,动态规划叫做「自底向上」。
|
||||
至此,带备忘录的递归解法的效率已经和迭代的动态规划解法一样了。实际上,这种解法和常见的动态规划解法已经差不多了,只不过这种解法是「自顶向下」进行「递归」求解,我们更常见的动态规划代码是「自底向上」进行「递推」求解。
|
||||
|
||||
啥叫「自顶向下」?注意我们刚才画的递归树(或者说图),是从上向下延伸,都是从一个规模较大的原问题比如说 `f(20)`,向下逐渐分解规模,直到 `f(1)` 和 `f(2)` 这两个 base case,然后逐层返回答案,这就叫「自顶向下」。
|
||||
|
||||
啥叫「自底向上」?反过来,我们直接从最底下,最简单,问题规模最小的 `f(1)` 和 `f(2)` 开始往上推,直到推到我们想要的答案 `f(20)`,这就是动态规划的思路,这也是为什么动态规划一般都脱离了递归,而是由循环迭代完成计算。
|
||||
啥叫「自底向上」?反过来,我们直接从最底下、最简单、问题规模最小、已知结果的 `f(1)` 和 `f(2)`(base case)开始往上推,直到推到我们想要的答案 `f(20)`。这就是「递推」的思路,这也是动态规划一般都脱离了递归,而是由循环迭代完成计算的原因。
|
||||
|
||||
**3、dp 数组的迭代解法**
|
||||
**3、`dp` 数组的迭代(递推)解法**
|
||||
|
||||
有了上一步「备忘录」的启发,我们可以把这个「备忘录」独立出来成为一张表,就叫做 DP table 吧,在这张表上完成「自底向上」的推算岂不美哉!
|
||||
有了上一步「备忘录」的启发,我们可以把这个「备忘录」独立出来成为一张表,通常叫做 DP table,在这张表上完成「自底向上」的推算岂不美哉!
|
||||
|
||||
```cpp
|
||||
```java
|
||||
int fib(int N) {
|
||||
if (N == 0) return 0;
|
||||
if (N == 1) return 1;
|
||||
vector<int> dp(N + 1, 0);
|
||||
int[] dp = new int[N + 1];
|
||||
// base case
|
||||
dp[1] = dp[2] = 1;
|
||||
for (int i = 3; i <= N; i++)
|
||||
dp[0] = 0; dp[1] = 1;
|
||||
// 状态转移
|
||||
for (int i = 2; i <= N; i++) {
|
||||
dp[i] = dp[i - 1] + dp[i - 2];
|
||||
}
|
||||
|
||||
return dp[N];
|
||||
}
|
||||
```
|
||||
|
||||

|
||||

|
||||
|
||||
画个图就很好理解了,而且你发现这个 DP table 特别像之前那个「剪枝」后的结果,只是反过来算而已。实际上,带备忘录的递归解法中的「备忘录」,最终完成后就是这个 DP table,所以说这两种解法其实是差不多的,大部分情况下,效率也基本相同。
|
||||
|
||||
这里,引出「状态转移方程」这个名词,实际上就是描述问题结构的数学形式:
|
||||
|
||||

|
||||

|
||||
|
||||
为啥叫「状态转移方程」?其实就是为了听起来高端。你把 `f(n)` 想做一个状态 `n`,这个状态 `n` 是由状态 `n - 1` 和状态 `n - 2` 相加转移而来,这就叫状态转移,仅此而已。
|
||||
为啥叫「状态转移方程」?其实就是为了听起来高端。
|
||||
|
||||
你会发现,上面的几种解法中的所有操作,例如 `return f(n - 1) + f(n - 2)`,`dp[i] = dp[i - 1] + dp[i - 2]`,以及对备忘录或 DP table 的初始化操作,都是围绕这个方程式的不同表现形式。可见列出「状态转移方程」的重要性,它是解决问题的核心。而且很容易发现,其实状态转移方程直接代表着暴力解法。
|
||||
`f(n)` 的函数参数会不断变化,所以你把参数 `n` 想做一个状态,这个状态 `n` 是由状态 `n - 1` 和状态 `n - 2` 转移(相加)而来,这就叫状态转移,仅此而已。
|
||||
|
||||
**千万不要看不起暴力解,动态规划问题最困难的就是写出这个暴力解,即状态转移方程**。只要写出暴力解,优化方法无非是用备忘录或者 DP table,再无奥妙可言。
|
||||
你会发现,上面的几种解法中的所有操作,例如 `return f(n - 1) + f(n - 2)`,`dp[i] = dp[i - 1] + dp[i - 2]`,以及对备忘录或 DP table 的初始化操作,都是围绕这个方程式的不同表现形式。
|
||||
|
||||
这个例子的最后,讲一个细节优化。细心的读者会发现,根据斐波那契数列的状态转移方程,当前状态只和之前的两个状态有关,其实并不需要那么长的一个 DP table 来存储所有的状态,只要想办法存储之前的两个状态就行了。所以,可以进一步优化,把空间复杂度降为 O(1):
|
||||
可见列出「状态转移方程」的重要性,它是解决问题的核心,而且很容易发现,其实状态转移方程直接代表着暴力解法。
|
||||
|
||||
```cpp
|
||||
**千万不要看不起暴力解,动态规划问题最困难的就是写出这个暴力解,即状态转移方程**。
|
||||
|
||||
只要写出暴力解,优化方法无非是用备忘录或者 DP table,再无奥妙可言。
|
||||
|
||||
这个例子的最后,讲一个细节优化。
|
||||
|
||||
细心的读者会发现,根据斐波那契数列的状态转移方程,当前状态只和之前的两个状态有关,其实并不需要那么长的一个 DP table 来存储所有的状态,只要想办法存储之前的两个状态就行了。
|
||||
|
||||
所以,可以进一步优化,把空间复杂度降为 O(1)。这也就是我们最常见的计算斐波那契数的算法:
|
||||
|
||||
```java
|
||||
int fib(int n) {
|
||||
if (n == 2 || n == 1)
|
||||
return 1;
|
||||
int prev = 1, curr = 1;
|
||||
for (int i = 3; i <= n; i++) {
|
||||
int sum = prev + curr;
|
||||
prev = curr;
|
||||
curr = sum;
|
||||
if (n == 0 || n == 1) {
|
||||
// base case
|
||||
return n;
|
||||
}
|
||||
return curr;
|
||||
// 分别代表 dp[i - 1] 和 dp[i - 2]
|
||||
int dp_i_1 = 1, dp_i_2 = 0;
|
||||
for (int i = 2; i <= n; i++) {
|
||||
// dp[i] = dp[i - 1] + dp[i - 2];
|
||||
int dp_i = dp_i_1 + dp_i_2;
|
||||
// 滚动更新
|
||||
dp_i_2 = dp_i_1;
|
||||
dp_i_1 = dp_i;
|
||||
}
|
||||
return dp_i_1;
|
||||
}
|
||||
```
|
||||
|
||||
这个技巧就是所谓的「**状态压缩**」,如果我们发现每次状态转移只需要 DP table 中的一部分,那么可以尝试用状态压缩来缩小 DP table 的大小,只记录必要的数据,上述例子就相当于把DP table 的大小从 `n` 缩小到 2。后续的动态规划章节中我们还会看到这样的例子,一般来说是把一个二维的 DP table 压缩成一维,即把空间复杂度从 O(n^2) 压缩到 O(n)。
|
||||
这一般是动态规划问题的最后一步优化,如果我们发现每次状态转移只需要 DP table 中的一部分,那么可以尝试缩小 DP table 的大小,只记录必要的数据,从而降低空间复杂度。
|
||||
|
||||
上述例子就相当于把DP table 的大小从 `n` 缩小到 2。后续的动态规划章节中我们还会看到这样的例子,一般来说是把一个二维的 DP table 压缩成一维,即把空间复杂度从 O(n^2) 压缩到 O(n)。
|
||||
|
||||
有人会问,动态规划的另一个重要特性「最优子结构」,怎么没有涉及?下面会涉及。斐波那契数列的例子严格来说不算动态规划,因为没有涉及求最值,以上旨在说明重叠子问题的消除方法,演示得到最优解法逐步求精的过程。下面,看第二个例子,凑零钱问题。
|
||||
|
||||
### 二、凑零钱问题
|
||||
|
||||
先看下题目:给你 `k` 种面值的硬币,面值分别为 `c1, c2 ... ck`,每种硬币的数量无限,再给一个总金额 `amount`,问你**最少**需要几枚硬币凑出这个金额,如果不可能凑出,算法返回 -1 。算法的函数签名如下:
|
||||
这是力扣第 322 题「零钱兑换」:
|
||||
|
||||
给你 `k` 种面值的硬币,面值分别为 `c1, c2 ... ck`,每种硬币的数量无限,再给一个总金额 `amount`,问你**最少**需要几枚硬币凑出这个金额,如果不可能凑出,算法返回 -1 。算法的函数签名如下:
|
||||
|
||||
```java
|
||||
// coins 中是可选硬币面值,amount 是目标金额
|
||||
|
|
@ -210,105 +241,133 @@ int coinChange(int[] coins, int amount);
|
|||
|
||||
比如说,假设你考试,每门科目的成绩都是互相独立的。你的原问题是考出最高的总成绩,那么你的子问题就是要把语文考到最高,数学考到最高…… 为了每门课考到最高,你要把每门课相应的选择题分数拿到最高,填空题分数拿到最高…… 当然,最终就是你每门课都是满分,这就是最高的总成绩。
|
||||
|
||||
得到了正确的结果:最高的总成绩就是总分。因为这个过程符合最优子结构,“每门科目考到最高”这些子问题是互相独立,互不干扰的。
|
||||
得到了正确的结果:最高的总成绩就是总分。因为这个过程符合最优子结构,「每门科目考到最高」这些子问题是互相独立,互不干扰的。
|
||||
|
||||
但是,如果加一个条件:你的语文成绩和数学成绩会互相制约,数学分数高,语文分数就会降低,反之亦然。这样的话,显然你能考到的最高总成绩就达不到总分了,按刚才那个思路就会得到错误的结果。因为子问题并不独立,语文数学成绩无法同时最优,所以最优子结构被破坏。
|
||||
但是,如果加一个条件:你的语文成绩和数学成绩会互相制约,不能同时达到满分,数学分数高,语文分数就会降低,反之亦然。
|
||||
|
||||
回到凑零钱问题,为什么说它符合最优子结构呢?比如你想求 `amount = 11` 时的最少硬币数(原问题),如果你知道凑出 `amount = 10` 的最少硬币数(子问题),你只需要把子问题的答案加一(再选一枚面值为 1 的硬币)就是原问题的答案。因为硬币的数量是没有限制的,所以子问题之间没有相互制,是互相独立的。
|
||||
这样的话,显然你能考到的最高总成绩就达不到总分了,按刚才那个思路就会得到错误的结果。因为「每门科目考到最高」的子问题并不独立,语文数学成绩户互相影响,无法同时最优,所以最优子结构被破坏。
|
||||
|
||||
PS:关于最优子结构的问题,后文[动态规划答疑篇](https://labuladong.gitee.io/algo/) 还会再举例探讨。
|
||||
回到凑零钱问题,为什么说它符合最优子结构呢?假设你有面值为 `1, 2, 5` 的硬币,你想求 `amount = 11` 时的最少硬币数(原问题),如果你知道凑出 `amount = 10, 9, 6` 的最少硬币数(子问题),你只需要把子问题的答案加一(再选一枚面值为 `1, 2, 5` 的硬币),求个最小值,就是原问题的答案。因为硬币的数量是没有限制的,所以子问题之间没有相互制,是互相独立的。
|
||||
|
||||
那么,既然知道了这是个动态规划问题,就要思考**如何列出正确的状态转移方程**?
|
||||
> PS:关于最优子结构的问题,后文 [动态规划答疑篇](https://labuladong.github.io/article/fname.html?fname=最优子结构) 还会再举例探讨。
|
||||
|
||||
1、**确定 base case**,这个很简单,显然目标金额 `amount` 为 0 时算法返回 0,因为不需要任何硬币就已经凑出目标金额了。
|
||||
那么,既然知道了这是个动态规划问题,就要思考如何列出正确的状态转移方程?
|
||||
|
||||
2、**确定「状态」,也就是原问题和子问题中会变化的变量**。由于硬币数量无限,硬币的面额也是题目给定的,只有目标金额会不断地向 base case 靠近,所以唯一的「状态」就是目标金额 `amount`。
|
||||
**1、确定 base case**,这个很简单,显然目标金额 `amount` 为 0 时算法返回 0,因为不需要任何硬币就已经凑出目标金额了。
|
||||
|
||||
3、**确定「选择」,也就是导致「状态」产生变化的行为**。目标金额为什么变化呢,因为你在选择硬币,你每选择一枚硬币,就相当于减少了目标金额。所以说所有硬币的面值,就是你的「选择」。
|
||||
**2、确定「状态」,也就是原问题和子问题中会变化的变量**。由于硬币数量无限,硬币的面额也是题目给定的,只有目标金额会不断地向 base case 靠近,所以唯一的「状态」就是目标金额 `amount`。
|
||||
|
||||
4、**明确 `dp` 函数/数组的定义**。我们这里讲的是自顶向下的解法,所以会有一个递归的 `dp` 函数,一般来说函数的参数就是状态转移中会变化的量,也就是上面说到的「状态」;函数的返回值就是题目要求我们计算的量。就本题来说,状态只有一个,即「目标金额」,题目要求我们计算凑出目标金额所需的最少硬币数量。所以我们可以这样定义 `dp` 函数:
|
||||
**3、确定「选择」,也就是导致「状态」产生变化的行为**。目标金额为什么变化呢,因为你在选择硬币,你每选择一枚硬币,就相当于减少了目标金额。所以说所有硬币的面值,就是你的「选择」。
|
||||
|
||||
`dp(n)` 的定义:输入一个目标金额 `n`,返回凑出目标金额 `n` 的最少硬币数量。
|
||||
**4、明确 `dp` 函数/数组的定义**。我们这里讲的是自顶向下的解法,所以会有一个递归的 `dp` 函数,一般来说函数的参数就是状态转移中会变化的量,也就是上面说到的「状态」;函数的返回值就是题目要求我们计算的量。就本题来说,状态只有一个,即「目标金额」,题目要求我们计算凑出目标金额所需的最少硬币数量。
|
||||
|
||||
**所以我们可以这样定义 `dp` 函数:`dp(n)` 表示,输入一个目标金额 `n`,返回凑出目标金额 `n` 所需的最少硬币数量**。
|
||||
|
||||
搞清楚上面这几个关键点,解法的伪码就可以写出来了:
|
||||
|
||||
```python
|
||||
# 伪码框架
|
||||
def coinChange(coins: List[int], amount: int):
|
||||
```java
|
||||
// 伪码框架
|
||||
int coinChange(int[] coins, int amount) {
|
||||
// 题目要求的最终结果是 dp(amount)
|
||||
return dp(coins, amount)
|
||||
}
|
||||
|
||||
# 定义:要凑出金额 n,至少要 dp(n) 个硬币
|
||||
def dp(n):
|
||||
# 做选择,选择需要硬币最少的那个结果
|
||||
for coin in coins:
|
||||
res = min(res, 1 + dp(n - coin))
|
||||
return res
|
||||
|
||||
# 题目要求的最终结果是 dp(amount)
|
||||
return dp(amount)
|
||||
// 定义:要凑出金额 n,至少要 dp(coins, n) 个硬币
|
||||
int dp(int[] coins, int n) {
|
||||
// 做选择,选择需要硬币最少的那个结果
|
||||
for (int coin : coins) {
|
||||
res = min(res, 1 + dp(n - coin))
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
根据伪码,我们加上 base case 即可得到最终的答案。显然目标金额为 0 时,所需硬币数量为 0;当目标金额小于 0 时,无解,返回 -1:
|
||||
|
||||
```python
|
||||
def coinChange(coins: List[int], amount: int):
|
||||
```java
|
||||
int coinChange(int[] coins, int amount) {
|
||||
// 题目要求的最终结果是 dp(amount)
|
||||
return dp(coins, amount)
|
||||
}
|
||||
|
||||
def dp(n):
|
||||
# base case
|
||||
if n == 0: return 0
|
||||
if n < 0: return -1
|
||||
# 求最小值,所以初始化为正无穷
|
||||
res = float('INF')
|
||||
for coin in coins:
|
||||
subproblem = dp(n - coin)
|
||||
# 子问题无解,跳过
|
||||
if subproblem == -1: continue
|
||||
res = min(res, 1 + subproblem)
|
||||
// 定义:要凑出金额 n,至少要 dp(coins, n) 个硬币
|
||||
int dp(int[] coins, int amount) {
|
||||
// base case
|
||||
if (amount == 0) return 0;
|
||||
if (amount < 0) return -1;
|
||||
|
||||
return res if res != float('INF') else -1
|
||||
|
||||
return dp(amount)
|
||||
int res = Integer.MAX_VALUE;
|
||||
for (int coin : coins) {
|
||||
// 计算子问题的结果
|
||||
int subProblem = dp(coins, amount - coin);
|
||||
// 子问题无解则跳过
|
||||
if (subProblem == -1) continue;
|
||||
// 在子问题中选择最优解,然后加一
|
||||
res = Math.min(res, subProblem + 1);
|
||||
}
|
||||
|
||||
return res == Integer.MAX_VALUE ? -1 : res;
|
||||
}
|
||||
```
|
||||
|
||||
> PS:这里 `coinChange` 和 `dp` 函数的签名完全一样,所以理论上不需要额外写一个 `dp` 函数。但为了后文讲解方便,这里还是另写一个 `dp` 函数来实现主要逻辑。
|
||||
|
||||
> 另外,我经常看到有人问,子问题的结果为什么要加 1(`subProblem + 1`),而不是加硬币金额之类的。我这里统一提示一下,动态规划问题的关键是 `dp` 函数/数组的定义,你这个函数的返回值代表什么?你回过头去搞清楚这一点,然后就知道为什么要给子问题的返回值加 1 了。
|
||||
|
||||
至此,状态转移方程其实已经完成了,以上算法已经是暴力解法了,以上代码的数学形式就是状态转移方程:
|
||||
|
||||

|
||||

|
||||
|
||||
至此,这个问题其实就解决了,只不过需要消除一下重叠子问题,比如 `amount = 11, coins = {1,2,5}` 时画出递归树看看:
|
||||
|
||||

|
||||

|
||||
|
||||
**递归算法的时间复杂度分析:子问题总数 x 每个子问题的时间**。
|
||||
**递归算法的时间复杂度分析:子问题总数 x 解决每个子问题所需的时间**。
|
||||
|
||||
子问题总数为递归树节点个数,这个比较难看出来,是 O(n^k),总之是指数级别的。每个子问题中含有一个 for 循环,复杂度为 O(k)。所以总时间复杂度为 O(k * n^k),指数级别。
|
||||
子问题总数为递归树的节点个数,但算法会进行剪枝,剪枝的时机和题目给定的具体硬币面额有关,所以可以想象,这棵树生长的并不规则,确切算出树上有多少节点是比较困难的。对于这种情况,我们一般的做法是按照最坏的情况估算一个时间复杂度的上界。
|
||||
|
||||
假设目标金额为 `n`,给定的硬币个数为 `k`,那么递归树最坏情况下高度为 `n`(全用面额为 1 的硬币),然后再假设这是一棵满 `k` 叉树,则节点的总数在 `k^n` 这个数量级。
|
||||
|
||||
接下来看每个子问题的复杂度,由于每次递归包含一个 for 循环,复杂度为 `O(k)`,相乘得到总时间复杂度为 `O(k^n)`,指数级别。
|
||||
|
||||
**2、带备忘录的递归**
|
||||
|
||||
类似之前斐波那契数列的例子,只需要稍加修改,就可以通过备忘录消除子问题:
|
||||
|
||||
```python
|
||||
def coinChange(coins: List[int], amount: int):
|
||||
# 备忘录
|
||||
memo = dict()
|
||||
def dp(n):
|
||||
# 查备忘录,避免重复计算
|
||||
if n in memo: return memo[n]
|
||||
# base case
|
||||
if n == 0: return 0
|
||||
if n < 0: return -1
|
||||
res = float('INF')
|
||||
for coin in coins:
|
||||
subproblem = dp(n - coin)
|
||||
if subproblem == -1: continue
|
||||
res = min(res, 1 + subproblem)
|
||||
|
||||
# 记入备忘录
|
||||
memo[n] = res if res != float('INF') else -1
|
||||
return memo[n]
|
||||
|
||||
return dp(amount)
|
||||
```java
|
||||
int[] memo;
|
||||
|
||||
int coinChange(int[] coins, int amount) {
|
||||
memo = new int[amount + 1];
|
||||
// 备忘录初始化为一个不会被取到的特殊值,代表还未被计算
|
||||
Arrays.fill(memo, -666);
|
||||
|
||||
return dp(coins, amount);
|
||||
}
|
||||
|
||||
int dp(int[] coins, int amount) {
|
||||
if (amount == 0) return 0;
|
||||
if (amount < 0) return -1;
|
||||
// 查备忘录,防止重复计算
|
||||
if (memo[amount] != -666)
|
||||
return memo[amount];
|
||||
|
||||
int res = Integer.MAX_VALUE;
|
||||
for (int coin : coins) {
|
||||
// 计算子问题的结果
|
||||
int subProblem = dp(coins, amount - coin);
|
||||
// 子问题无解则跳过
|
||||
if (subProblem == -1) continue;
|
||||
// 在子问题中选择最优解,然后加一
|
||||
res = Math.min(res, subProblem + 1);
|
||||
}
|
||||
// 把计算结果存入备忘录
|
||||
memo[amount] = (res == Integer.MAX_VALUE) ? -1 : res;
|
||||
return memo[amount];
|
||||
}
|
||||
```
|
||||
|
||||
不画图了,很显然「备忘录」大大减小了子问题数目,完全消除了子问题的冗余,所以子问题总数不会超过金额数 `n`,即子问题数目为 O(n)。处理一个子问题的时间不变,仍是 O(k),所以总的时间复杂度是 O(kn)。
|
||||
不画图了,很显然「备忘录」大大减小了子问题数目,完全消除了子问题的冗余,所以子问题总数不会超过金额数 `n`,即子问题数目为 `O(n)`。处理一个子问题的时间不变,仍是 `O(k)`,所以总的时间复杂度是 `O(kn)`。
|
||||
|
||||
**3、dp 数组的迭代解法**
|
||||
|
||||
|
|
@ -318,28 +377,32 @@ def coinChange(coins: List[int], amount: int):
|
|||
|
||||
根据我们文章开头给出的动态规划代码框架可以写出如下解法:
|
||||
|
||||
```cpp
|
||||
int coinChange(vector<int>& coins, int amount) {
|
||||
```java
|
||||
int coinChange(int[] coins, int amount) {
|
||||
int[] dp = new int[amount + 1];
|
||||
// 数组大小为 amount + 1,初始值也为 amount + 1
|
||||
vector<int> dp(amount + 1, amount + 1);
|
||||
Arrays.fill(dp, amount + 1);
|
||||
|
||||
// base case
|
||||
dp[0] = 0;
|
||||
// 外层 for 循环在遍历所有状态的所有取值
|
||||
for (int i = 0; i < dp.size(); i++) {
|
||||
for (int i = 0; i < dp.length; i++) {
|
||||
// 内层 for 循环在求所有选择的最小值
|
||||
for (int coin : coins) {
|
||||
// 子问题无解,跳过
|
||||
if (i - coin < 0) continue;
|
||||
dp[i] = min(dp[i], 1 + dp[i - coin]);
|
||||
if (i - coin < 0) {
|
||||
continue;
|
||||
}
|
||||
dp[i] = Math.min(dp[i], 1 + dp[i - coin]);
|
||||
}
|
||||
}
|
||||
return (dp[amount] == amount + 1) ? -1 : dp[amount];
|
||||
}
|
||||
```
|
||||
|
||||

|
||||

|
||||
|
||||
PS:为啥 `dp` 数组初始化为 `amount + 1` 呢,因为凑成 `amount` 金额的硬币数最多只可能等于 `amount`(全用 1 元面值的硬币),所以初始化为 `amount + 1` 就相当于初始化为正无穷,便于后续取最小值。
|
||||
> PS:为啥 `dp` 数组中的值都初始化为 `amount + 1` 呢,因为凑成 `amount` 金额的硬币数最多只可能等于 `amount`(全用 1 元面值的硬币),所以初始化为 `amount + 1` 就相当于初始化为正无穷,便于后续取最小值。为啥不直接初始化为 int 型的最大值 `Integer.MAX_VALUE` 呢?因为后面有 `dp[i - coin] + 1`,这就会导致整型溢出。
|
||||
|
||||
### 三、最后总结
|
||||
|
||||
|
|
@ -351,22 +414,93 @@ PS:为啥 `dp` 数组初始化为 `amount + 1` 呢,因为凑成 `amount` 金
|
|||
|
||||
**计算机解决问题其实没有任何奇技淫巧,它唯一的解决办法就是穷举**,穷举所有可能性。算法设计无非就是先思考“如何穷举”,然后再追求“如何聪明地穷举”。
|
||||
|
||||
列出动态转移方程,就是在解决“如何穷举”的问题。之所以说它难,一是因为很多穷举需要递归实现,二是因为有的问题本身的解空间复杂,不那么容易穷举完整。
|
||||
列出状态转移方程,就是在解决“如何穷举”的问题。之所以说它难,一是因为很多穷举需要递归实现,二是因为有的问题本身的解空间复杂,不那么容易穷举完整。
|
||||
|
||||
备忘录、DP table 就是在追求“如何聪明地穷举”。用空间换时间的思路,是降低时间复杂度的不二法门,除此之外,试问,还能玩出啥花活?
|
||||
|
||||
之后我们会有一章专门讲解动态规划问题,如果有任何问题都可以随时回来重读本文,希望读者在阅读每个题目和解法时,多往「状态」和「选择」上靠,才能对这套框架产生自己的理解,运用自如。
|
||||
|
||||
接下来可阅读:
|
||||
|
||||
* [动态规划设计:最长递增子序列](https://labuladong.github.io/article/fname.html?fname=动态规划设计:最长递增子序列)
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [base case 和备忘录的初始值怎么定?](https://labuladong.github.io/article/fname.html?fname=备忘录等基础)
|
||||
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.github.io/article/fname.html?fname=抢房子)
|
||||
- [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.github.io/article/fname.html?fname=团灭股票问题)
|
||||
- [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结)
|
||||
- [两种思路解决单词拼接问题](https://labuladong.github.io/article/fname.html?fname=单词拼接)
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [动态规划帮我通关了《辐射4》](https://labuladong.github.io/article/fname.html?fname=转盘)
|
||||
- [动态规划帮我通关了《魔塔》](https://labuladong.github.io/article/fname.html?fname=魔塔)
|
||||
- [动态规划设计:最长递增子序列](https://labuladong.github.io/article/fname.html?fname=动态规划设计:最长递增子序列)
|
||||
- [动态规划问题的两种穷举视角](https://labuladong.github.io/article/fname.html?fname=动归两种视角)
|
||||
- [如何运用贪心思想玩跳跃游戏](https://labuladong.github.io/article/fname.html?fname=跳跃游戏)
|
||||
- [学习算法和刷题的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法)
|
||||
- [对动态规划进行降维打击](https://labuladong.github.io/article/fname.html?fname=状态压缩技巧)
|
||||
- [归并排序详解及应用](https://labuladong.github.io/article/fname.html?fname=归并排序)
|
||||
- [当老司机学会了贪心算法](https://labuladong.github.io/article/fname.html?fname=老司机)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [旅游省钱大法:加权最短路径](https://labuladong.github.io/article/fname.html?fname=旅行最短路径)
|
||||
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
- [算法学习和心流体验](https://labuladong.github.io/article/fname.html?fname=心流)
|
||||
- [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度)
|
||||
- [算法笔试「骗分」套路](https://labuladong.github.io/article/fname.html?fname=刷题技巧)
|
||||
- [经典动态规划:0-1 背包问题](https://labuladong.github.io/article/fname.html?fname=背包问题)
|
||||
- [经典动态规划:博弈问题](https://labuladong.github.io/article/fname.html?fname=动态规划之博弈问题)
|
||||
- [经典动态规划:完全背包问题](https://labuladong.github.io/article/fname.html?fname=背包零钱)
|
||||
- [经典动态规划:戳气球](https://labuladong.github.io/article/fname.html?fname=扎气球)
|
||||
- [经典动态规划:最长公共子序列](https://labuladong.github.io/article/fname.html?fname=LCS)
|
||||
- [经典动态规划:编辑距离](https://labuladong.github.io/article/fname.html?fname=编辑距离)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [112. Path Sum](https://leetcode.com/problems/path-sum/?show=1) | [112. 路径总和](https://leetcode.cn/problems/path-sum/?show=1) |
|
||||
| [115. Distinct Subsequences](https://leetcode.com/problems/distinct-subsequences/?show=1) | [115. 不同的子序列](https://leetcode.cn/problems/distinct-subsequences/?show=1) |
|
||||
| [139. Word Break](https://leetcode.com/problems/word-break/?show=1) | [139. 单词拆分](https://leetcode.cn/problems/word-break/?show=1) |
|
||||
| [1696. Jump Game VI](https://leetcode.com/problems/jump-game-vi/?show=1) | [1696. 跳跃游戏 VI](https://leetcode.cn/problems/jump-game-vi/?show=1) |
|
||||
| [221. Maximal Square](https://leetcode.com/problems/maximal-square/?show=1) | [221. 最大正方形](https://leetcode.cn/problems/maximal-square/?show=1) |
|
||||
| [240. Search a 2D Matrix II](https://leetcode.com/problems/search-a-2d-matrix-ii/?show=1) | [240. 搜索二维矩阵 II](https://leetcode.cn/problems/search-a-2d-matrix-ii/?show=1) |
|
||||
| [256. Paint House](https://leetcode.com/problems/paint-house/?show=1)🔒 | [256. 粉刷房子](https://leetcode.cn/problems/paint-house/?show=1)🔒 |
|
||||
| [62. Unique Paths](https://leetcode.com/problems/unique-paths/?show=1) | [62. 不同路径](https://leetcode.cn/problems/unique-paths/?show=1) |
|
||||
| [63. Unique Paths II](https://leetcode.com/problems/unique-paths-ii/?show=1) | [63. 不同路径 II](https://leetcode.cn/problems/unique-paths-ii/?show=1) |
|
||||
| [70. Climbing Stairs](https://leetcode.com/problems/climbing-stairs/?show=1) | [70. 爬楼梯](https://leetcode.cn/problems/climbing-stairs/?show=1) |
|
||||
| [91. Decode Ways](https://leetcode.com/problems/decode-ways/?show=1) | [91. 解码方法](https://leetcode.cn/problems/decode-ways/?show=1) |
|
||||
| - | [剑指 Offer 04. 二维数组中的查找](https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/?show=1) |
|
||||
| - | [剑指 Offer 10- II. 青蛙跳台阶问题](https://leetcode.cn/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 091. 粉刷房子](https://leetcode.cn/problems/JEj789/?show=1) |
|
||||
| - | [剑指 Offer II 097. 子序列的数目](https://leetcode.cn/problems/21dk04/?show=1) |
|
||||
| - | [剑指 Offer II 098. 路径的数目](https://leetcode.cn/problems/2AoeFn/?show=1) |
|
||||
| - | [剑指 Offer II 103. 最少的硬币数目](https://leetcode.cn/problems/gaM7Ch/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
### python
|
||||
|
|
|
|||
|
|
@ -0,0 +1,450 @@
|
|||
# 两种思路解决单词拼接问题
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [139. Word Break](https://leetcode.com/problems/word-break/) | [139. 单词拆分](https://leetcode.cn/problems/word-break/) | 🟠
|
||||
| [140. Word Break II](https://leetcode.com/problems/word-break-ii/) | [140. 单词拆分 II](https://leetcode.cn/problems/word-break-ii/) | 🔴
|
||||
|
||||
**-----------**
|
||||
|
||||
之前 [手把手带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结) 把递归穷举划分为「遍历」和「分解问题」两种思路,其中「遍历」的思路扩展延伸一下就是回溯算法,「分解问题」的思路可以扩展成动态规划算法。
|
||||
|
||||
我在 [手把手带你刷二叉树(思路篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列1) 对一些二叉树问题进行举例,同时给出「遍历」和「分解问题」两种思路的解法,帮大家借助二叉树理解更高级的算法设计思想。
|
||||
|
||||
当然,这种思维转换不止局限于二叉树相关的算法,本文就跳出二叉树类型问题,来看看实际算法题中如何把问题抽象成树形结构,从而进行「遍历」和「分解问题」的思维转换,从 [回溯算法](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 顺滑地切换到 [动态规划算法](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)。
|
||||
|
||||
先说句题外话,前文 [动态规划核心框架详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 说,**标准的动态规划问题一定是求最值的**,因为动态规划类型问题有一个性质叫做「最优子结构」,即从子问题的最优解推导出原问题的最优解。
|
||||
|
||||
但在我们平常的语境中,就算不是求最值的题目,只要看见使用备忘录消除重叠子问题,我们一般都称它为动态规划算法。严格来讲这是不符合动态规划问题的定义的,说这种解法叫做「带备忘录的 DFS 算法」可能更准确些。不过咱也不用太纠结这种名词层面的细节,既然大家叫的顺口,就叫它动态规划也无妨。
|
||||
|
||||
本文讲解的两道题目也不是求最值的,但依然会把他们的解法称为动态规划解法,这里提前跟大家说下这里面的细节,免得细心的读者疑惑。其他不多说了,直接看题目吧。
|
||||
|
||||
### 单词拆分 I
|
||||
|
||||
首先看下力扣第 139 题「单词拆分」:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
boolean wordBreak(String s, List<String> wordDict);
|
||||
```
|
||||
|
||||
这是一道非常高频的面试题,我们来思考下如何通过「遍历」和「分解问题」的思路来解决它。
|
||||
|
||||
**先说说「遍历」的思路,也就是用回溯算法解决本题**。回溯算法最经典的应用就是排列组合相关的问题了,不难发现这道题换个说法也可以变成一个排列问题:
|
||||
|
||||
现在给你一个不包含重复单词的单词列表 `wordDict` 和一个字符串 `s`,请你判断是否可以从 `wordDict` 中选出若干单词的排列(可以重复挑选)构成字符串 `s`。
|
||||
|
||||
这就是前文 [回溯算法秒杀排列组合问题的九种变体](https://labuladong.github.io/article/fname.html?fname=子集排列组合) 中讲到的最后一种变体:元素无重可复选的排列问题,前文我写了一个 `permuteRepeat` 函数,代码如下:
|
||||
|
||||
```java
|
||||
List<List<Integer>> res = new LinkedList<>();
|
||||
LinkedList<Integer> track = new LinkedList<>();
|
||||
|
||||
// 元素无重可复选的全排列
|
||||
public List<List<Integer>> permuteRepeat(int[] nums) {
|
||||
backtrack(nums);
|
||||
return res;
|
||||
}
|
||||
|
||||
// 回溯算法核心函数
|
||||
void backtrack(int[] nums) {
|
||||
// base case,到达叶子节点
|
||||
if (track.size() == nums.length) {
|
||||
// 收集根到叶子节点路径上的值
|
||||
res.add(new LinkedList(track));
|
||||
return;
|
||||
}
|
||||
|
||||
// 回溯算法标准框架
|
||||
for (int i = 0; i < nums.length; i++) {
|
||||
// 做选择
|
||||
track.add(nums[i]);
|
||||
// 进入下一层回溯树
|
||||
backtrack(nums);
|
||||
// 取消选择
|
||||
track.removeLast();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
给这个函数输入 `nums = [1,2,3]`,输出是 3^3 = 27 种可能的组合:
|
||||
|
||||
```java
|
||||
[
|
||||
[1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],
|
||||
[2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],
|
||||
[3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]
|
||||
]
|
||||
```
|
||||
|
||||
这段代码实际上就是遍历一棵高度为 `N + 1` 的满 `N` 叉树(`N` 为 `nums` 的长度),其中根到叶子的每条路径上的元素就是一个排列结果:
|
||||
|
||||

|
||||
|
||||
类比一下,本文讲的这道题也有异曲同工之妙,假设 `wordDict = ["a", "aa", "ab"], s = "aaab"`,想用 `wordDict` 中的单词拼出 `s`,其实也面对着类似的一棵 `M` 叉树,`M` 为 `wordDict` 中单词的个数,**你需要做的就是站在回溯树的每个节点上,看看哪个单词能够匹配 `s[i..]` 的前缀,从而判断应该往哪条树枝上走**:
|
||||
|
||||

|
||||
|
||||
然后,按照前文 [回溯算法框架详解](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 所说,你把 `backtrack` 函数理解成在回溯树上游走的一个指针,维护每个节点上的变量 `i`,即可遍历整棵回溯树,寻找出匹配 `s` 的组合。
|
||||
|
||||
回溯算法解法代码如下:
|
||||
|
||||
```java
|
||||
List<String> wordDict;
|
||||
// 记录是否找到一个合法的答案
|
||||
boolean found = false;
|
||||
// 记录回溯算法的路径
|
||||
LinkedList<String> track = new LinkedList<>();
|
||||
|
||||
// 主函数
|
||||
public boolean wordBreak(String s, List<String> wordDict) {
|
||||
this.wordDict = wordDict;
|
||||
// 执行回溯算法穷举所有可能的组合
|
||||
backtrack(s, 0);
|
||||
return found;
|
||||
}
|
||||
|
||||
// 回溯算法框架
|
||||
void backtrack(String s, int i) {
|
||||
// base case
|
||||
if (found) {
|
||||
// 如果已经找到答案,就不要再递归搜索了
|
||||
return;
|
||||
}
|
||||
if (i == s.length()) {
|
||||
// 整个 s 都被匹配完成,找到一个合法答案
|
||||
found = true;
|
||||
return;
|
||||
}
|
||||
|
||||
// 回溯算法框架
|
||||
for (String word : wordDict) {
|
||||
// 看看哪个单词能够匹配 s[i..] 的前缀
|
||||
int len = word.length();
|
||||
if (i + len <= s.length()
|
||||
&& s.substring(i, i + len).equals(word)) {
|
||||
// 找到一个单词匹配 s[i..i+len)
|
||||
// 做选择
|
||||
track.addLast(word);
|
||||
// 进入回溯树的下一层,继续匹配 s[i+len..]
|
||||
backtrack(s, i + len);
|
||||
// 撤销选择
|
||||
track.removeLast();
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这段代码就是严格按照回溯算法框架写出来的,应该不难理解,但这段代码无法通过所有测试用例,我们按照之前 [算法时空复杂度使用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度) 中讲到的方法来分析一下它的时间复杂度。
|
||||
|
||||
递归函数的时间复杂度的粗略估算方法就是用递归函数调用次数(递归树的节点数) x 递归函数本身的复杂度。对于这道题来说,递归树的每个节点其实就是对 `s` 进行的一次切割,那么最坏情况下 `s` 能有多少种切割呢?长度为 `N` 的字符串 `s` 中共有 `N - 1` 个「缝隙」可供切割,每个缝隙可以选择「切」或者「不切」,所以 `s` 最多有 `O(2^N)` 种切割方式,即递归树上最多有 `O(2^N)` 个节点。
|
||||
|
||||
当然,实际情况可定会好一些,毕竟存在剪枝逻辑,但从最坏复杂度的角度来看,递归树的节点个数确实是指数级别的。
|
||||
|
||||
那么 `backtrack` 函数本身的时间复杂度是多少呢?主要的时间消耗是遍历 `wordDict` 寻找匹配 `s[i..]` 的前缀的单词:
|
||||
|
||||
```java
|
||||
// 遍历 wordDict 的所有单词
|
||||
for (String word : wordDict) {
|
||||
// 看看哪个单词能够匹配 s[i..] 的前缀
|
||||
int len = word.length();
|
||||
if (i + len <= s.length()
|
||||
&& s.substring(i, i + len).equals(word)) {
|
||||
// 找到一个单词匹配 s[i..i+len)
|
||||
// ...
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
设 `wordDict` 的长度为 `M`,字符串 `s` 的长度为 `N`,那么这段代码的最坏时间复杂度是 `O(MN)`(for 循环 `O(M)`,Java 的 `substring` 方法 `O(N)`),所以总的时间复杂度是 `O(2^N * MN)`。
|
||||
|
||||
这里顺便说一个细节优化,其实你也可以反过来,通过穷举 `s[i..]` 的前缀去判断 `wordDict` 中是否有对应的单词:
|
||||
|
||||
```java
|
||||
// 注意,要转化成哈希集合,提高 contains 方法的效率
|
||||
HashSet<String> wordDict = new HashSet<>(wordDict);
|
||||
|
||||
// 遍历 s[i..] 的所有前缀
|
||||
for (int len = 1; i + len <= s.length(); len++) {
|
||||
// 看看 wordDict 中是否有单词能匹配 s[i..] 的前缀
|
||||
String prefix = s.substring(i, i + len);
|
||||
if (wordDict.contains(prefix)) {
|
||||
// 找到一个单词匹配 s[i..i+len)
|
||||
// ...
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这段代码和刚才那段代码的结果是一样的,但这段代码的时间复杂度变成了 `O(N^2)`,和刚才的代码不同。
|
||||
|
||||
到底哪样子好呢?这要看题目给的数据范围。本题说了 `1 <= s.length <= 300, 1 <= wordDict.length <= 1000`,所以 `O(N^2)` 的结果较小,这段代码的实际运行效率应该稍微高一些,这个是一个细节的优化,你可以自己做一下,我就不写了。
|
||||
|
||||
不过即便你优化这段代码,总的时间复杂度依然是指数级的 `O(2^N * N^2)`,是无法通过所有测试用例的,那么问题出在哪里呢?
|
||||
|
||||
比如输入 `wordDict = ["a", "aa"], s = "aaab"`,算法无法找到一个可行的组合,所以一定会遍历整棵回溯树,但你注意这里面会存在重复的情况:
|
||||
|
||||

|
||||
|
||||
图中标红的这两部分,虽然经历了不同的切分,但是切分得出的结果是相同的,所以这两个节点下面的子树也是重复的,即存在冗余计算,极端情况下会消耗大量时间。
|
||||
|
||||
**如何消除冗余计算呢?这就要稍微转变一下思维模式,用「分解问题」的思维模式来考虑这道题**。
|
||||
|
||||
我们刚才以排列组合的视角思考这个问题,现在我们换一种视角,思考一下是否能够把原问题分解成规模更小,结构相同的子问题,然后通过子问题的结果计算原问题的结果。
|
||||
|
||||
对于输入的字符串 `s`,如果我能够从单词列表 `wordDict` 中找到一个单词匹配 `s` 的前缀 `s[0..k]`,那么只要我能拼出 `s[k+1..]`,就一定能拼出整个 `s`。换句话说,我把规模较大的原问题 `wordBreak(s[0..])` 分解成了规模较小的子问题 `wordBreak(s[k+1..])`,然后通过子问题的解反推出原问题的解。
|
||||
|
||||
有了这个思路就可以定义一个 `dp` 函数,并给出该函数的定义:
|
||||
|
||||
```java
|
||||
// 定义:返回 s[i..] 是否能够被拼出
|
||||
int dp(String s, int i);
|
||||
|
||||
// 计算整个 s 是否能被拼出,调用 dp(s, 0)
|
||||
```
|
||||
|
||||
有了这个函数定义,就可以把刚才的逻辑大致翻译成伪码:
|
||||
|
||||
```java
|
||||
List<String> wordDict;
|
||||
|
||||
// 定义:返回 s[i..] 是否能够被拼出
|
||||
int dp(String s, int i) {
|
||||
// base case,s[i..] 是空串
|
||||
if (i == s.length()) {
|
||||
return true;
|
||||
}
|
||||
// 遍历 wordDict,看看哪些单词是 s[i..] 的前缀
|
||||
for (Strnig word : wordDict) {
|
||||
if word 是 s[i..] 的前缀 {
|
||||
int len = word.length();
|
||||
// 只要 s[i+len..] 可以被拼出,s[i..] 就能被拼出
|
||||
if (dp(s, i + len) == true) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
}
|
||||
// 所有单词都尝试过,无法拼出整个 s
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
类似之前讲的回溯算法,`dp` 函数中的 for 循环也可以优化一下:
|
||||
|
||||
```java
|
||||
// 注意,用哈希集合快速判断元素是否存在
|
||||
HashSet<String> wordDict;
|
||||
|
||||
// 定义:返回 s[i..] 是否能够被拼出
|
||||
int dp(String s, int i) {
|
||||
// base case,s[i..] 是空串
|
||||
if (i == s.length()) {
|
||||
return true;
|
||||
}
|
||||
|
||||
// 遍历 s[i..] 的所有前缀,看看哪些前缀存在 wordDict 中
|
||||
for (int len = 1; i + len <= s.length(); len++) {
|
||||
if wordDict 中存在 s[i..len) {
|
||||
// 只要 s[i+len..] 可以被拼出,s[i..] 就能被拼出
|
||||
if (dp(s, i + len) == true) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
}
|
||||
// 所有单词都尝试过,无法拼出整个 s
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
对于这个 `dp` 函数,指针 `i` 的位置就是「状态」,所以我们可以通过添加备忘录的方式优化效率,避免对相同的子问题进行冗余计算。最终的解法代码如下:
|
||||
|
||||
```java
|
||||
// 用哈希集合方便快速判断是否存在
|
||||
HashSet<String> wordDict;
|
||||
// 备忘录,-1 代表未计算,0 代表无法凑出,1 代表可以凑出
|
||||
int[] memo;
|
||||
|
||||
// 主函数
|
||||
public boolean wordBreak(String s, List<String> wordDict) {
|
||||
// 转化为哈希集合,快速判断元素是否存在
|
||||
this.wordDict = new HashSet<>(wordDict);
|
||||
// 备忘录初始化为 -1
|
||||
this.memo = new int[s.length()];
|
||||
Arrays.fill(memo, -1);
|
||||
return dp(s, 0);
|
||||
}
|
||||
|
||||
// 定义:s[i..] 是否能够被拼出
|
||||
boolean dp(String s, int i) {
|
||||
// base case
|
||||
if (i == s.length()) {
|
||||
return true;
|
||||
}
|
||||
// 防止冗余计算
|
||||
if (memo[i] != -1) {
|
||||
return memo[i] == 0 ? false : true;
|
||||
}
|
||||
|
||||
// 遍历 s[i..] 的所有前缀
|
||||
for (int len = 1; i + len <= s.length(); len++) {
|
||||
// 看看哪些前缀存在 wordDict 中
|
||||
String prefix = s.substring(i, i + len);
|
||||
if (wordDict.contains(prefix)) {
|
||||
// 找到一个单词匹配 s[i..i+len)
|
||||
// 只要 s[i+len..] 可以被拼出,s[i..] 就能被拼出
|
||||
boolean subProblem = dp(s, i + len);
|
||||
if (subProblem == true) {
|
||||
memo[i] = 1;
|
||||
return true;
|
||||
}
|
||||
}
|
||||
}
|
||||
// s[i..] 无法被拼出
|
||||
memo[i] = 0;
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
这个解法能够通过所有测试用例,我们根据 [算法时空复杂度使用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度) 来算一下它的时间复杂度:
|
||||
|
||||
因为有备忘录的辅助,消除了递归树上的重复节点,使得递归函数的调用次数从指数级别降低为状态的个数 `O(N)`,函数本身的复杂度还是 `O(N^2)`,所以总的时间复杂度是 `O(N^3)`,相较回溯算法的效率有大幅提升。
|
||||
|
||||
### 单词拆分 II
|
||||
|
||||
有了上一道题的铺垫,力扣第 140 题「单词拆分 II」就容易多了,先看下题目:
|
||||
|
||||

|
||||
|
||||
相较上一题,这道题不是单单问你 `s` 是否能被拼出,还要问你是怎么拼的,其实只要把之前的解法稍微改一改就可以解决这道题。
|
||||
|
||||
上一道题的回溯算法维护一个 `found` 变量,只要找到一种拼接方案就提前结束遍历回溯树,那么在这道题中我们不要提前结束遍历,并把所有可行的拼接方案收集起来就能得到答案:
|
||||
|
||||
```java
|
||||
// 记录结果
|
||||
List<String> res = new LinkedList<>();
|
||||
// 记录回溯算法的路径
|
||||
LinkedList<String> track = new LinkedList<>();
|
||||
List<String> wordDict;
|
||||
|
||||
// 主函数
|
||||
public List<String> wordBreak(String s, List<String> wordDict) {
|
||||
this.wordDict = wordDict;
|
||||
// 执行回溯算法穷举所有可能的组合
|
||||
backtrack(s, 0);
|
||||
return res;
|
||||
}
|
||||
|
||||
// 回溯算法框架
|
||||
void backtrack(String s, int i) {
|
||||
// base case
|
||||
if (i == s.length()) {
|
||||
// 找到一个合法组合拼出整个 s,转化成字符串
|
||||
res.add(String.join(" ", track));
|
||||
return;
|
||||
}
|
||||
|
||||
// 回溯算法框架
|
||||
for (String word : wordDict) {
|
||||
// 看看哪个单词能够匹配 s[i..] 的前缀
|
||||
int len = word.length();
|
||||
if (i + len <= s.length()
|
||||
&& s.substring(i, i + len).equals(word)) {
|
||||
// 找到一个单词匹配 s[i..i+len)
|
||||
// 做选择
|
||||
track.addLast(word);
|
||||
// 进入回溯树的下一层,继续匹配 s[i+len..]
|
||||
backtrack(s, i + len);
|
||||
// 撤销选择
|
||||
track.removeLast();
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这个解法的时间复杂度和前一道题类似,依然是 `O(2^N * MN)`,但由于这道题给的数据规模较小,所以可以通过所有测试用例。
|
||||
|
||||
类似的,这个问题也可以用分解问题的思维解决,把上一道题的 `dp` 函数稍作修改即可:
|
||||
|
||||
```java
|
||||
HashSet<String> wordDict;
|
||||
// 备忘录
|
||||
List<String>[] memo;
|
||||
|
||||
public List<String> wordBreak(String s, List<String> wordDict) {
|
||||
this.wordDict = new HashSet<>(wordDict);
|
||||
memo = new List[s.length()];
|
||||
return dp(s, 0);
|
||||
}
|
||||
|
||||
|
||||
|
||||
// 定义:返回用 wordDict 构成 s[i..] 的所有可能
|
||||
List<String> dp(String s, int i) {
|
||||
List<String> res = new LinkedList<>();
|
||||
if (i == s.length()) {
|
||||
res.add("");
|
||||
return res;
|
||||
}
|
||||
// 防止冗余计算
|
||||
if (memo[i] != null) {
|
||||
return memo[i];
|
||||
}
|
||||
|
||||
// 遍历 s[i..] 的所有前缀
|
||||
for (int len = 1; i + len <= s.length(); len++) {
|
||||
// 看看哪些前缀存在 wordDict 中
|
||||
String prefix = s.substring(i, i + len);
|
||||
if (wordDict.contains(prefix)) {
|
||||
// 找到一个单词匹配 s[i..i+len)
|
||||
List<String> subProblem = dp(s, i + len);
|
||||
// 构成 s[i+len..] 的所有组合加上 prefix
|
||||
// 就是构成构成 s[i] 的所有组合
|
||||
for (String sub : subProblem) {
|
||||
if (sub.isEmpty()) {
|
||||
// 防止多余的空格
|
||||
res.add(prefix);
|
||||
} else {
|
||||
res.add(prefix + " " + sub);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
// 存入备忘录
|
||||
memo[i] = res;
|
||||
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
这个解法依然用备忘录消除了重叠子问题,所以 `dp` 函数递归调用的次数减少为 `O(N)`,但 `dp` 函数本身的时间复杂度上升了,因为 `subProblem` 是一个子集列表,它的长度是指数级的。再加上 Java 中用 `+` 拼接字符串的效率并不高,且还要消耗备忘录去存储所有子问题的结果,所以这个算法的时间复杂度并不比回溯算法低,依然是指数级别。
|
||||
|
||||
综上,我们处理排列组合问题时一般使用回溯算法去「遍历」回溯树,而不用「分解问题」的思路去处理,因为存储子问题的结果就需要大量的时间和空间,除非重叠子问题的数量较多的极端情况,否则得不偿失。
|
||||
|
||||
以上就是本文的全部内容,希望你能对回溯思路和分解问题的思路有更深刻的理解。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
227
动态规划系列/团灭股票问题.md
227
动态规划系列/团灭股票问题.md
|
|
@ -1,35 +1,33 @@
|
|||
# 团灭 LeetCode 股票买卖问题
|
||||
|
||||
<!-- [团灭 LeetCode 股票买卖问题](https://mp.weixin.qq.com/s/4nqJMIyCKQD7IJ-HI6S3Vg) -->
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://gitee.com/labuladong/upic/raw/master/2021_04_23/21_28_41.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[121. 买卖股票的最佳时机(简单)](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/)
|
||||
|
||||
[122. 买卖股票的最佳时机 II(简单)](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/)
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
[123. 买卖股票的最佳时机 III(困难)](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/)
|
||||
|
||||
[188. 买卖股票的最佳时机 IV(困难)](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/)
|
||||
|
||||
[309. 最佳买卖股票时机含冷冻期(中等)](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/)
|
||||
|
||||
[714. 买卖股票的最佳时机含手续费(中等)](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/)
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [121. Best Time to Buy and Sell Stock](https://leetcode.com/problems/best-time-to-buy-and-sell-stock/) | [121. 买卖股票的最佳时机](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/) | 🟢
|
||||
| [122. Best Time to Buy and Sell Stock II](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-ii/) | [122. 买卖股票的最佳时机 II](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/) | 🟠
|
||||
| [123. Best Time to Buy and Sell Stock III](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iii/) | [123. 买卖股票的最佳时机 III](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/) | 🔴
|
||||
| [188. Best Time to Buy and Sell Stock IV](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-iv/) | [188. 买卖股票的最佳时机 IV](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/) | 🔴
|
||||
| [309. Best Time to Buy and Sell Stock with Cooldown](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/) | [309. 最佳买卖股票时机含冷冻期](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/) | 🟠
|
||||
| [714. Best Time to Buy and Sell Stock with Transaction Fee](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/) | [714. 买卖股票的最佳时机含手续费](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/) | 🟠
|
||||
| - | [剑指 Offer 63. 股票的最大利润](https://leetcode.cn/problems/gu-piao-de-zui-da-li-run-lcof/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
很多读者抱怨 LeetCode 的股票系列问题奇技淫巧太多,如果面试真的遇到这类问题,基本不会想到那些巧妙的办法,怎么办?**所以本文拒绝奇技淫巧,而是稳扎稳打,只用一种通用方法解决所用问题,以不变应万变**。
|
||||
很多读者抱怨力扣上的股票系列问题奇技淫巧太多,如果面试真的遇到这类问题,基本不会想到那些巧妙的办法,怎么办?**所以本文拒绝奇技淫巧,而是稳扎稳打,只用一种通用方法解决所用问题,以不变应万变**。
|
||||
|
||||
这篇文章参考 [英文版高赞题解](https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/discuss/108870/Most-consistent-ways-of-dealing-with-the-series-of-stock-problems) 的思路,用状态机的技巧来解决,可以全部提交通过。不要觉得这个名词高大上,文学词汇而已,实际上就是 DP table,看一眼就明白了。
|
||||
|
||||
|
|
@ -54,19 +52,19 @@ int maxProfit(vector<int>& prices) {
|
|||
|
||||
本文就来告诉你这个框架,然后带着你一道一道秒杀。这篇文章用状态机的技巧来解决,可以全部提交通过。不要觉得这个名词高大上,文学词汇而已,实际上就是 DP table,看一眼就明白了。
|
||||
|
||||
这 6 道题目是有共性的,我就抽出来第 4 道题目,因为这道题是一个最泛化的形式,其他的问题都是这个形式的简化,看下题目:
|
||||
这 6 道题目是有共性的,我们只需要抽出来力扣第 188 题「买卖股票的最佳时机 IV」进行研究,因为这道题是最泛化的形式,其他的问题都是这个形式的简化,看下题目:
|
||||
|
||||

|
||||

|
||||
|
||||
第一题是只进行一次交易,相当于 `k = 1`;第二题是不限交易次数,相当于 `k = +infinity`(正无穷);第三题是只进行 2 次交易,相当于 `k = 2`;剩下两道也是不限次数,但是加了交易「冷冻期」和「手续费」的额外条件,其实就是第二题的变种,都很容易处理。
|
||||
|
||||
如果你还不熟悉题目,可以去 LeetCode 查看这些题目的内容,本文为了节省篇幅,就不列举这些题目的具体内容了。下面言归正传,开始解题。
|
||||
下面言归正传,开始解题。
|
||||
|
||||
### 一、穷举框架
|
||||
|
||||
首先,还是一样的思路:如何穷举?
|
||||
|
||||
[动态规划核心套路](../动态规划系列/动态规划详解进阶.md) 说过,动态规划算法本质上就是穷举「状态」,然后在「选择」中选择最优解。
|
||||
[动态规划核心套路](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 说过,动态规划算法本质上就是穷举「状态」,然后在「选择」中选择最优解。
|
||||
|
||||
那么对于这道题,我们具体到每一天,看看总共有几种可能的「状态」,再找出每个「状态」对应的「选择」。我们要穷举所有「状态」,穷举的目的是根据对应的「选择」更新状态。听起来抽象,你只要记住「状态」和「选择」两个词就行,下面实操一下就很容易明白了。
|
||||
|
||||
|
|
@ -111,7 +109,7 @@ for 0 <= i < n:
|
|||
|
||||
只看「持有状态」,可以画个状态转移图:
|
||||
|
||||

|
||||

|
||||
|
||||
通过这个图可以很清楚地看到,每种状态(0 和 1)是如何转移而来的。根据这个图,我们来写一下状态转移方程:
|
||||
|
||||
|
|
@ -137,13 +135,13 @@ dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
|
|||
|
||||
2、我昨天本没有持有,且截至昨天最大交易次数限制为 `k - 1`;但今天我选择 `buy`,所以今天我就持有股票了,最大交易次数限制为 `k`。
|
||||
|
||||
> 这里着重提醒一下,时刻牢记「状态」的定义,`k` 的定义并不是「已进行的交易次数」,而是「最大交易次数的上限限制」。如果确定今天进行一次交易,且要保证截至今天最大交易次数上限为 `k`,那么昨天的最大交易次数上限必须是 `k - 1`。
|
||||
> 这里着重提醒一下,**时刻牢记「状态」的定义**,状态 `k` 的定义并不是「已进行的交易次数」,而是「最大交易次数的上限限制」。如果确定今天进行一次交易,且要保证截至今天最大交易次数上限为 `k`,那么昨天的最大交易次数上限必须是 `k - 1`。
|
||||
|
||||
这个解释应该很清楚了,如果 `buy`,就要从利润中减去 `prices[i]`,如果 `sell`,就要给利润增加 `prices[i]`。今天的最大利润就是这两种可能选择中较大的那个。
|
||||
|
||||
注意 `k` 的限制,在选择 `buy` 的时候相当于开启了一次交易,那么对于昨天来说,交易次数的上限 `k` 应该减小 1。
|
||||
|
||||
> 修正:以前我以为在 `sell` 的时候给 `k` 减小 1 和在 `buy` 的时候给 `k` 减小 1 是等效的,但细心的读者向我提出质疑,经过深入思考我发现前者确实是错误的,因为交易是从 `buy` 开始,如果 `buy` 的选择不改变交易次数 `k` 的约束,会出现交易次数超出限制的的错误。
|
||||
> 修正:以前我以为在 `sell` 的时候给 `k` 减小 1 和在 `buy` 的时候给 `k` 减小 1 是等效的,但细心的读者向我提出质疑,经过深入思考我发现前者确实是错误的,因为交易是从 `buy` 开始,如果 `buy` 的选择不改变交易次数 `k` 的话,会出现交易次数超出限制的的错误。
|
||||
|
||||
现在,我们已经完成了动态规划中最困难的一步:状态转移方程。**如果之前的内容你都可以理解,那么你已经可以秒杀所有问题了,只要套这个框架就行了**。不过还差最后一点点,就是定义 base case,即最简单的情况。
|
||||
|
||||
|
|
@ -179,7 +177,9 @@ dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
|
|||
|
||||
### 三、秒杀题目
|
||||
|
||||
**第一题,k = 1**
|
||||
**第一题,先说力扣第 121 题「买卖股票的最佳时机」,相当于 `k = 1` 的情况**:
|
||||
|
||||

|
||||
|
||||
直接套状态转移方程,根据 base case,可以做一些化简:
|
||||
|
||||
|
|
@ -227,7 +227,7 @@ if (i - 1 == -1) {
|
|||
}
|
||||
```
|
||||
|
||||
第一题就解决了,但是这样处理 base case 很麻烦,而且注意一下状态转移方程,新状态只和相邻的一个状态有关,其实不用整个 `dp` 数组,只需要一个变量储存相邻的那个状态就足够了,这样可以把空间复杂度降到 O(1):
|
||||
第一题就解决了,但是这样处理 base case 很麻烦,而且注意一下状态转移方程,新状态只和相邻的一个状态有关,所以可以用前文 [动态规划的降维打击:空间压缩技巧](https://labuladong.github.io/article/fname.html?fname=状态压缩技巧),不需要用整个 `dp` 数组,只需要一个变量储存相邻的那个状态就足够了,这样可以把空间复杂度降到 O(1):
|
||||
|
||||
```java
|
||||
// 原始版本
|
||||
|
|
@ -264,7 +264,11 @@ int maxProfit_k_1(int[] prices) {
|
|||
|
||||
两种方式都是一样的,不过这种编程方法简洁很多,但是如果没有前面状态转移方程的引导,是肯定看不懂的。后续的题目,你可以对比一下如何把 `dp` 数组的空间优化掉。
|
||||
|
||||
**第二题,k = +infinity**
|
||||
**第二题,看一下力扣第 122 题「买卖股票的最佳时机 II」,也就是 `k` 为正无穷的情况**:
|
||||
|
||||

|
||||
|
||||
题目还专门强调可以在同一天出售,但我觉得这个条件纯属多余,如果当天买当天卖,那利润当然就是 0,这不是和没有进行交易是一样的吗?这道题的特点在于没有给出交易总数 `k` 的限制,也就相当于 `k` 为正无穷。
|
||||
|
||||
如果 `k` 为正无穷,那么就可以认为 `k` 和 `k - 1` 是一样的。可以这样改写框架:
|
||||
|
||||
|
|
@ -311,9 +315,11 @@ int maxProfit_k_inf(int[] prices) {
|
|||
}
|
||||
```
|
||||
|
||||
**第三题,k = +infinity with cooldown**
|
||||
**第三题,看力扣第 309 题「最佳买卖股票时机含冷冻期」,也就是 `k` 为正无穷,但含有交易冷冻期的情况**:
|
||||
|
||||
每次 `sell` 之后要等一天才能继续交易。只要把这个特点融入上一题的状态转移方程即可:
|
||||

|
||||
|
||||
和上一道题一样的,只不过每次 `sell` 之后要等一天才能继续交易,只要把这个特点融入上一题的状态转移方程即可:
|
||||
|
||||
```python
|
||||
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
|
||||
|
|
@ -367,9 +373,11 @@ int maxProfit_with_cool(int[] prices) {
|
|||
}
|
||||
```
|
||||
|
||||
**第四题,k = +infinity with fee**
|
||||
**第四题,看力扣第 714 题「买卖股票的最佳时机含手续费」,也就是 `k` 为正无穷且考虑交易手续费的情况**:
|
||||
|
||||
每次交易要支付手续费,只要把手续费从利润中减去即可。改写方程:
|
||||

|
||||
|
||||
每次交易要支付手续费,只要把手续费从利润中减去即可,改写方程:
|
||||
|
||||
```python
|
||||
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
|
||||
|
|
@ -378,7 +386,7 @@ dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
|
|||
在第一个式子里减也是一样的,相当于卖出股票的价格减小了。
|
||||
```
|
||||
|
||||
> 如果直接把 `fee` 放在第一个式子里减,会有测试用例无法通过,错误原因是整型溢出而不是思路问题。一种解决方案是把代码中的 `int` 类型都改成 `long` 类型,避免 `int` 的整型溢出。
|
||||
> 如果直接把 `fee` 放在第一个式子里减,会有一些测试用例无法通过,错误原因是整型溢出而不是思路问题。一种解决方案是把代码中的 `int` 类型都改成 `long` 类型,避免 `int` 的整型溢出。
|
||||
|
||||
直接翻译成代码,注意状态转移方程改变后 base case 也要做出对应改变:
|
||||
|
||||
|
|
@ -418,11 +426,13 @@ int maxProfit_with_fee(int[] prices, int fee) {
|
|||
}
|
||||
```
|
||||
|
||||
**第五题,k = 2**
|
||||
**第五题,看力扣第 123 题「买卖股票的最佳时机 III」,也就是 `k = 2` 的情况**:
|
||||
|
||||
`k = 2` 和前面题目的情况稍微不同,因为上面的情况都和 `k` 的关系不太大。要么 `k` 是正无穷,状态转移和 `k` 没关系了;要么 `k = 1`,跟 `k = 0` 这个 base case 挨得近,最后也没有存在感。
|
||||

|
||||
|
||||
这道题 `k = 2` 和后面要讲的 `k` 是任意正整数的情况中,对 `k` 的处理就凸显出来了。我们直接写代码,边写边分析原因。
|
||||
`k = 2` 和前面题目的情况稍微不同,因为上面的情况都和 `k` 的关系不太大:要么 `k` 是正无穷,状态转移和 `k` 没关系了;要么 `k = 1`,跟 `k = 0` 这个 base case 挨得近,最后也没有存在感。
|
||||
|
||||
这道题 `k = 2` 和后面要讲的 `k` 是任意正整数的情况中,对 `k` 的处理就凸显出来了,我们直接写代码,边写边分析原因。
|
||||
|
||||
```java
|
||||
原始的状态转移方程,没有可化简的地方
|
||||
|
|
@ -490,15 +500,15 @@ int maxProfit_k_2(int[] prices) {
|
|||
|
||||
> **PS:这里肯定会有读者疑惑,`k` 的 base case 是 0,按理说应该从 `k = 1, k++` 这样穷举状态 `k` 才对?而且如果你真的这样从小到大遍历 `k`,提交发现也是可以的**。
|
||||
|
||||
这个疑问很正确,因为我们前文 [动态规划答疑篇](../动态规划系列/最优子结构.md) 有介绍 `dp` 数组的遍历顺序是怎么确定的,主要是根据 base case,以 base case 为起点,逐步向结果靠近。
|
||||
这个疑问很正确,因为我们前文 [动态规划答疑篇](https://labuladong.github.io/article/fname.html?fname=最优子结构) 有介绍 `dp` 数组的遍历顺序是怎么确定的,主要是根据 base case,以 base case 为起点,逐步向结果靠近。
|
||||
|
||||
但为什么我从大到小遍历 `k` 也可以正确提交呢?因为你注意看,`dp[i][k]` 不会依赖 `dp[i][k - 1]`,而是依赖 `dp[i - 1][k - 1]`,对于 `dp[i - 1][...]`,都是已经计算出来的。所以不管你是 `k = max_k, k--`,还是 `k = 1, k++`,都是可以得出正确答案的。
|
||||
但为什么我从大到小遍历 `k` 也可以正确提交呢?因为你注意看,`dp[i][k][..]` 不会依赖 `dp[i][k - 1][..]`,而是依赖 `dp[i - 1][k - 1][..]`,而 `dp[i - 1][..][..]`,都是已经计算出来的,所以不管你是 `k = max_k, k--`,还是 `k = 1, k++`,都是可以得出正确答案的。
|
||||
|
||||
那为什么我使用 `k = max_k, k--` 的方式呢?因为这样符合语义。
|
||||
那为什么我使用 `k = max_k, k--` 的方式呢?因为这样符合语义:
|
||||
|
||||
你买股票,初始的「状态」是什么?应该是从第 0 天开始,而且还没有进行过买卖,所以最大交易次数限制 `k` 应该是 `max_k`;而随着「状态」的推移,你会进行交易,那么交易次数上限 `k` 应该不断减少,这样一想,`k = max_k, k--` 的方式是比较合乎实际场景的。
|
||||
|
||||
当然,这里 `k` 取值范围比较小,所以可以不用 for 循环,直接把 k = 1 和 2 的情况全部列举出来也可以:
|
||||
当然,这里 `k` 取值范围比较小,所以也可以不用 for 循环,直接把 k = 1 和 2 的情况全部列举出来也可以:
|
||||
|
||||
```java
|
||||
// 状态转移方程:
|
||||
|
|
@ -524,13 +534,17 @@ int maxProfit_k_2(int[] prices) {
|
|||
|
||||
有状态转移方程和含义明确的变量名指导,相信你很容易看懂。其实我们可以故弄玄虚,把上述四个变量换成 `a, b, c, d`。这样当别人看到你的代码时就会大惊失色,对你肃然起敬。
|
||||
|
||||
**第六题,k = any integer**
|
||||
**第六题,看力扣第 188 题「买卖股票的最佳时机 IV」,即 `k` 可以是题目给定的任何数的情况**:
|
||||
|
||||
有了上一题 `k = 2` 的铺垫,这题应该和上一题的第一个解法没啥区别。但是出现了一个超内存的错误,原来是传入的 `k` 值会非常大,`dp` 数组太大了。现在想想,交易次数 `k` 最多有多大呢?
|
||||

|
||||
|
||||
一次交易由买入和卖出构成,至少需要两天。所以说有效的限制 `k` 应该不超过 `n/2`,如果超过,就没有约束作用了,相当于 `k = +infinity`。这种情况是之前解决过的。
|
||||
有了上一题 `k = 2` 的铺垫,这题应该和上一题的第一个解法没啥区别,你把上一题的 `k = 2` 换成题目输入的 `k` 就行了。
|
||||
|
||||
直接把之前的代码重用:
|
||||
但试一下发现会出一个内存超限的错误,原来是传入的 `k` 值会非常大,`dp` 数组太大了。那么现在想想,交易次数 `k` 最多有多大呢?
|
||||
|
||||
一次交易由买入和卖出构成,至少需要两天。所以说有效的限制 `k` 应该不超过 `n/2`,如果超过,就没有约束作用了,相当于 `k` 没有限制的情况,而这种情况是之前解决过的。
|
||||
|
||||
所以我们可以直接把之前的代码重用:
|
||||
|
||||
```java
|
||||
int maxProfit_k_any(int max_k, int[] prices) {
|
||||
|
|
@ -539,7 +553,7 @@ int maxProfit_k_any(int max_k, int[] prices) {
|
|||
return 0;
|
||||
}
|
||||
if (max_k > n / 2) {
|
||||
// 交易次数 k 没有限制的情况
|
||||
// 复用之前交易次数 k 没有限制的情况
|
||||
return maxProfit_k_inf(prices);
|
||||
}
|
||||
|
||||
|
|
@ -570,20 +584,131 @@ int maxProfit_k_any(int max_k, int[] prices) {
|
|||
|
||||
至此,6 道题目通过一个状态转移方程全部解决。
|
||||
|
||||
**四、最后总结**
|
||||
### 万法归一
|
||||
|
||||
本文给大家讲了如何通过状态转移的方法解决复杂的问题,用一个状态转移方程秒杀了 6 道股票买卖问题,现在想想,其实也不算难对吧?这已经属于动态规划问题中较困难的了。
|
||||
如果你能看到这里,已经可以给你鼓掌了,初次理解如此复杂的动态规划问题想必消耗了你不少的脑细胞,不过这是值得的,股票系列问题已经属于动态规划问题中较困难的了,如果这些题你都能搞懂,试问,其他那些虾兵蟹将又何足道哉?
|
||||
|
||||
**现在你已经过了九九八十一难中的前八十难,最后我还要再难为你一下,请你实现如下函数**:
|
||||
|
||||
```java
|
||||
int maxProfit_all_in_one(int max_k, int[] prices, int cooldown, int fee);
|
||||
```
|
||||
|
||||
输入股票价格数组 `prices`,你最多进行 `max_k` 次交易,每次交易需要额外消耗 `fee` 的手续费,而且每次交易之后需要经过 `cooldown` 天的冷冻期才能进行下一次交易,请你计算并返回可以获得的最大利润。
|
||||
|
||||
怎么样,有没有被吓到?如果你直接给别人出一道这样的题目,估计对方要当场吐血,不过我们这样一步步做过来,你应该很容易发现这道题目就是之前我们探讨的几种情况的组合体嘛。
|
||||
|
||||
所以,我们只要把之前实现的几种代码掺和到一块,**在 base case 和状态转移方程中同时加上 `cooldown` 和 `fee` 的约束就行了**:
|
||||
|
||||
```java
|
||||
// 同时考虑交易次数的限制、冷冻期和手续费
|
||||
int maxProfit_all_in_one(int max_k, int[] prices, int cooldown, int fee) {
|
||||
int n = prices.length;
|
||||
if (n <= 0) {
|
||||
return 0;
|
||||
}
|
||||
if (max_k > n / 2) {
|
||||
// 交易次数 k 没有限制的情况
|
||||
return maxProfit_k_inf(prices, cooldown, fee);
|
||||
}
|
||||
|
||||
int[][][] dp = new int[n][max_k + 1][2];
|
||||
// k = 0 时的 base case
|
||||
for (int i = 0; i < n; i++) {
|
||||
dp[i][0][1] = Integer.MIN_VALUE;
|
||||
dp[i][0][0] = 0;
|
||||
}
|
||||
|
||||
for (int i = 0; i < n; i++)
|
||||
for (int k = max_k; k >= 1; k--) {
|
||||
if (i - 1 == -1) {
|
||||
// base case 1
|
||||
dp[i][k][0] = 0;
|
||||
dp[i][k][1] = -prices[i] - fee;
|
||||
continue;
|
||||
}
|
||||
|
||||
// 包含 cooldown 的 base case
|
||||
if (i - cooldown - 1 < 0) {
|
||||
// base case 2
|
||||
dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
|
||||
// 别忘了减 fee
|
||||
dp[i][k][1] = Math.max(dp[i-1][k][1], -prices[i] - fee);
|
||||
continue;
|
||||
}
|
||||
dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
|
||||
// 同时考虑 cooldown 和 fee
|
||||
dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-cooldown-1][k-1][0] - prices[i] - fee);
|
||||
}
|
||||
return dp[n - 1][max_k][0];
|
||||
}
|
||||
|
||||
// k 无限制,包含手续费和冷冻期
|
||||
int maxProfit_k_inf(int[] prices, int cooldown, int fee) {
|
||||
int n = prices.length;
|
||||
int[][] dp = new int[n][2];
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (i - 1 == -1) {
|
||||
// base case 1
|
||||
dp[i][0] = 0;
|
||||
dp[i][1] = -prices[i] - fee;
|
||||
continue;
|
||||
}
|
||||
|
||||
// 包含 cooldown 的 base case
|
||||
if (i - cooldown - 1 < 0) {
|
||||
// base case 2
|
||||
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
|
||||
// 别忘了减 fee
|
||||
dp[i][1] = Math.max(dp[i-1][1], -prices[i] - fee);
|
||||
continue;
|
||||
}
|
||||
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
|
||||
// 同时考虑 cooldown 和 fee
|
||||
dp[i][1] = Math.max(dp[i - 1][1], dp[i - cooldown - 1][0] - prices[i] - fee);
|
||||
}
|
||||
return dp[n - 1][0];
|
||||
}
|
||||
```
|
||||
|
||||
你可以用这个 `maxProfit_all_in_one` 函数去完成之前讲的 6 道题目,因为我们无法对 `dp` 数组进行优化,所以执行效率上不是最优的,但正确性上肯定是没有问题的。
|
||||
|
||||
最后总结一下吧,本文给大家讲了如何通过状态转移的方法解决复杂的问题,用一个状态转移方程秒杀了 6 道股票买卖问题,现在回头去看,其实也不算那么可怕对吧?
|
||||
|
||||
关键就在于列举出所有可能的「状态」,然后想想怎么穷举更新这些「状态」。一般用一个多维 `dp` 数组储存这些状态,从 base case 开始向后推进,推进到最后的状态,就是我们想要的答案。想想这个过程,你是不是有点理解「动态规划」这个名词的意义了呢?
|
||||
|
||||
具体到股票买卖问题,我们发现了三个状态,使用了一个三维数组,无非还是穷举 + 更新,不过我们可以说的高大上一点,这叫「三维 DP」,怕不怕?这个大实话一说,立刻显得你高人一等,名利双收有没有,所以给个在看/分享吧,鼓励一下我。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
- [经典动态规划:0-1 背包问题](https://labuladong.github.io/article/fname.html?fname=背包问题)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer 63. 股票的最大利润](https://leetcode.cn/problems/gu-piao-de-zui-da-li-run-lcof/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||

|
||||
|
|
@ -1,21 +1,24 @@
|
|||
# 动态规划之子序列问题解题模板
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[516.最长回文子序列](https://leetcode-cn.com/problems/longest-palindromic-subsequence)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [1312. Minimum Insertion Steps to Make a String Palindrome](https://leetcode.com/problems/minimum-insertion-steps-to-make-a-string-palindrome/) | [1312. 让字符串成为回文串的最少插入次数](https://leetcode.cn/problems/minimum-insertion-steps-to-make-a-string-palindrome/) | 🔴
|
||||
| [516. Longest Palindromic Subsequence](https://leetcode.com/problems/longest-palindromic-subsequence/) | [516. 最长回文子序列](https://leetcode.cn/problems/longest-palindromic-subsequence/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -23,154 +26,39 @@
|
|||
|
||||
首先,子序列问题本身就相对子串、子数组更困难一些,因为前者是不连续的序列,而后两者是连续的,就算穷举你都不一定会,更别说求解相关的算法问题了。
|
||||
|
||||
而且,子序列问题很可能涉及到两个字符串,比如前文「最长公共子序列」,如果没有一定的处理经验,真的不容易想出来。所以本文就来扒一扒子序列问题的套路,其实就有两种模板,相关问题只要往这两种思路上想,十拿九稳。
|
||||
而且,子序列问题很可能涉及到两个字符串,比如前文 [最长公共子序列](https://labuladong.github.io/article/fname.html?fname=LCS),如果没有一定的处理经验,真的不容易想出来。所以本文就来扒一扒子序列问题的套路,其实就有两种模板,相关问题只要往这两种思路上想,十拿九稳。
|
||||
|
||||
一般来说,这类问题都是让你求一个**最长子序列**,因为最短子序列就是一个字符嘛,没啥可问的。一旦涉及到子序列和最值,那几乎可以肯定,**考察的是动态规划技巧,时间复杂度一般都是 O(n^2)**。
|
||||
|
||||
原因很简单,你想想一个字符串,它的子序列有多少种可能?起码是指数级的吧,这种情况下,不用动态规划技巧,还想怎么着?
|
||||
|
||||
既然要用动态规划,那就要定义 dp 数组,找状态转移关系。我们说的两种思路模板,就是 dp 数组的定义思路。不同的问题可能需要不同的 dp 数组定义来解决。
|
||||
既然要用动态规划,那就要定义 `dp` 数组,找状态转移关系。我们说的两种思路模板,就是 `dp` 数组的定义思路。不同的问题可能需要不同的 `dp` 数组定义来解决。
|
||||
|
||||
### 一、两种思路
|
||||
|
||||
**1、第一种思路模板是一个一维的 dp 数组**:
|
||||
|
||||
```java
|
||||
int n = array.length;
|
||||
int[] dp = new int[n];
|
||||
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j < i; j++) {
|
||||
dp[i] = 最值(dp[i], dp[j] + ...)
|
||||
}
|
||||
}
|
||||
```
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
举个我们写过的例子「最长递增子序列」,在这个思路中 dp 数组的定义是:
|
||||
- [动态规划设计:最长递增子序列](https://labuladong.github.io/article/fname.html?fname=动态规划设计:最长递增子序列)
|
||||
- [如何判断回文链表](https://labuladong.github.io/article/fname.html?fname=判断回文链表)
|
||||
- [对动态规划进行降维打击](https://labuladong.github.io/article/fname.html?fname=状态压缩技巧)
|
||||
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
- [经典动态规划:最长公共子序列](https://labuladong.github.io/article/fname.html?fname=LCS)
|
||||
|
||||
**在子数组 `array[0..i]` 中,我们要求的子序列(最长递增子序列)的长度是 `dp[i]`**。
|
||||
</details><hr>
|
||||
|
||||
为啥最长递增子序列需要这种思路呢?前文说得很清楚了,因为这样符合归纳法,可以找到状态转移的关系,这里就不具体展开了。
|
||||
|
||||
**2、第二种思路模板是一个二维的 dp 数组**:
|
||||
|
||||
```java
|
||||
int n = arr.length;
|
||||
int[][] dp = new dp[n][n];
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (arr[i] == arr[j])
|
||||
dp[i][j] = dp[i][j] + ...
|
||||
else
|
||||
dp[i][j] = 最值(...)
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这种思路运用相对更多一些,尤其是涉及两个字符串/数组的子序列,比如前文讲的「最长公共子序列」。本思路中 dp 数组含义又分为「只涉及一个字符串」和「涉及两个字符串」两种情况。
|
||||
|
||||
**2.1 涉及两个字符串/数组时**(比如最长公共子序列),dp 数组的含义如下:
|
||||
|
||||
**在子数组 `arr1[0..i]` 和子数组 `arr2[0..j]` 中,我们要求的子序列(最长公共子序列)长度为 `dp[i][j]`**。
|
||||
|
||||
**2.2 只涉及一个字符串/数组时**(比如本文要讲的最长回文子序列),dp 数组的含义如下:
|
||||
|
||||
**在子数组 `array[i..j]` 中,我们要求的子序列(最长回文子序列)的长度为 `dp[i][j]`**。
|
||||
|
||||
第一种情况可以参考这两篇旧文:「编辑距离」「公共子序列」
|
||||
|
||||
下面就借最长回文子序列这个问题,详解一下第二种情况下如何使用动态规划。
|
||||
|
||||
### 二、最长回文子序列
|
||||
|
||||
之前解决了「最长回文子串」的问题,这次提升难度,求最长回文子序列的长度:
|
||||
|
||||

|
||||
|
||||
我们说这个问题对 dp 数组的定义是:**在子串 `s[i..j]` 中,最长回文子序列的长度为 `dp[i][j]`**。一定要记住这个定义才能理解算法。
|
||||
|
||||
为啥这个问题要这样定义二维的 dp 数组呢?我们前文多次提到,**找状态转移需要归纳思维,说白了就是如何从已知的结果推出未知的部分**,这样定义容易归纳,容易发现状态转移关系。
|
||||
|
||||
具体来说,如果我们想求 `dp[i][j]`,假设你知道了子问题 `dp[i+1][j-1]` 的结果(`s[i+1..j-1]` 中最长回文子序列的长度),你是否能想办法算出 `dp[i][j]` 的值(`s[i..j]` 中,最长回文子序列的长度)呢?
|
||||
|
||||

|
||||
|
||||
可以!这取决于 `s[i]` 和 `s[j]` 的字符:
|
||||
|
||||
**如果它俩相等**,那么它俩加上 `s[i+1..j-1]` 中的最长回文子序列就是 `s[i..j]` 的最长回文子序列:
|
||||
|
||||

|
||||
|
||||
**如果它俩不相等**,说明它俩**不可能同时**出现在 `s[i..j]` 的最长回文子序列中,那么把它俩**分别**加入 `s[i+1..j-1]` 中,看看哪个子串产生的回文子序列更长即可:
|
||||
|
||||

|
||||
|
||||
以上两种情况写成代码就是这样:
|
||||
|
||||
```java
|
||||
if (s[i] == s[j])
|
||||
// 它俩一定在最长回文子序列中
|
||||
dp[i][j] = dp[i + 1][j - 1] + 2;
|
||||
else
|
||||
// s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长?
|
||||
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
|
||||
```
|
||||
|
||||
至此,状态转移方程就写出来了,根据 dp 数组的定义,我们要求的就是 `dp[0][n - 1]`,也就是整个 `s` 的最长回文子序列的长度。
|
||||
|
||||
### 三、代码实现
|
||||
|
||||
首先明确一下 base case,如果只有一个字符,显然最长回文子序列长度是 1,也就是 `dp[i][j] = 1 (i == j)`。
|
||||
|
||||
因为 `i` 肯定小于等于 `j`,所以对于那些 `i > j` 的位置,根本不存在什么子序列,应该初始化为 0。
|
||||
|
||||
另外,看看刚才写的状态转移方程,想求 `dp[i][j]` 需要知道 `dp[i+1][j-1]`,`dp[i+1][j]`,`dp[i][j-1]` 这三个位置;再看看我们确定的 base case,填入 dp 数组之后是这样:
|
||||
|
||||

|
||||
|
||||
**为了保证每次计算 `dp[i][j]`,左下右方向的位置已经被计算出来,只能斜着遍历或者反着遍历**:
|
||||
|
||||

|
||||
|
||||
我选择反着遍历,代码如下:
|
||||
|
||||
```cpp
|
||||
int longestPalindromeSubseq(string s) {
|
||||
int n = s.size();
|
||||
// dp 数组全部初始化为 0
|
||||
vector<vector<int>> dp(n, vector<int>(n, 0));
|
||||
// base case
|
||||
for (int i = 0; i < n; i++)
|
||||
dp[i][i] = 1;
|
||||
// 反着遍历保证正确的状态转移
|
||||
for (int i = n - 1; i >= 0; i--) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
// 状态转移方程
|
||||
if (s[i] == s[j])
|
||||
dp[i][j] = dp[i + 1][j - 1] + 2;
|
||||
else
|
||||
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
|
||||
}
|
||||
}
|
||||
// 整个 s 的最长回文子串长度
|
||||
return dp[0][n - 1];
|
||||
}
|
||||
```
|
||||
|
||||
至此,最长回文子序列的问题就解决了。
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
应合作方要求,本文不便在此发布,请扫码关注回复关键词「子序列」或 [点这里](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62987943e4b01c509ab8b6aa/1) 查看:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,labuladong 带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||

|
||||
|
||||
======其他语言代码======
|
||||
|
||||
|
|
|
|||
246
动态规划系列/抢房子.md
246
动态规划系列/抢房子.md
|
|
@ -2,22 +2,26 @@
|
|||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[198.打家劫舍](https://leetcode-cn.com/problems/house-robber)
|
||||
|
||||
[213.打家劫舍II](https://leetcode-cn.com/problems/house-robber-ii)
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
[337.打家劫舍III](https://leetcode-cn.com/problems/house-robber-iii)
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [198. House Robber](https://leetcode.com/problems/house-robber/) | [198. 打家劫舍](https://leetcode.cn/problems/house-robber/) | 🟠
|
||||
| [213. House Robber II](https://leetcode.com/problems/house-robber-ii/) | [213. 打家劫舍 II](https://leetcode.cn/problems/house-robber-ii/) | 🟠
|
||||
| [337. House Robber III](https://leetcode.com/problems/house-robber-iii/) | [337. 打家劫舍 III](https://leetcode.cn/problems/house-robber-iii/) | 🟠
|
||||
| - | [剑指 Offer II 089. 房屋偷盗](https://leetcode.cn/problems/Gu0c2T/) | 🟠
|
||||
| - | [剑指 Offer II 090. 环形房屋偷盗](https://leetcode.cn/problems/PzWKhm/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -27,234 +31,46 @@
|
|||
|
||||
下面,我们从第一道开始分析。
|
||||
|
||||
### House Robber I
|
||||
### 打家劫舍 I
|
||||
|
||||

|
||||
力扣第 198 题「打家劫舍」的题目如下:
|
||||
|
||||
街上有一排房屋,用一个包含非负整数的数组 `nums` 表示,每个元素 `nums[i]` 代表第 `i` 间房子中的现金数额。现在你是一名专业小偷,你希望**尽可能多**的盗窃这些房子中的现金,但是,**相邻的房子不能被同时盗窃**,否则会触发报警器,你就凉凉了。
|
||||
|
||||
请你写一个算法,计算在不触动报警器的前提下,最多能够盗窃多少现金呢?函数签名如下:
|
||||
|
||||
```java
|
||||
public int rob(int[] nums);
|
||||
int rob(int[] nums);
|
||||
```
|
||||
|
||||
题目很容易理解,而且动态规划的特征很明显。我们前文「动态规划详解」做过总结,**解决动态规划问题就是找「状态」和「选择」,仅此而已**。
|
||||
比如说输入 `nums=[2,1,7,9,3,1]`,算法返回 12,小偷可以盗窃 `nums[0], nums[3], nums[5]` 三个房屋,得到的现金之和为 2 + 9 + 1 = 12,是最优的选择。
|
||||
|
||||
假想你就是这个专业强盗,从左到右走过这一排房子,在每间房子前都有两种**选择**:抢或者不抢。
|
||||
题目很容易理解,而且动态规划的特征很明显。我们前文 [动态规划详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 做过总结,**解决动态规划问题就是找「状态」和「选择」,仅此而已**。
|
||||
|
||||
如果你抢了这间房子,那么你**肯定**不能抢相邻的下一间房子了,只能从下下间房子开始做选择。
|
||||
|
||||
如果你不抢这件房子,那么你可以走到下一间房子前,继续做选择。
|
||||
|
||||
当你走过了最后一间房子后,你就没得抢了,能抢到的钱显然是 0(**base case**)。
|
||||
|
||||
以上的逻辑很简单吧,其实已经明确了「状态」和「选择」:**你面前房子的索引就是状态,抢和不抢就是选择**。
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||

|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
在两个选择中,每次都选更大的结果,最后得到的就是最多能抢到的 money:
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer II 089. 房屋偷盗](https://leetcode.cn/problems/Gu0c2T/?show=1) |
|
||||
| - | [剑指 Offer II 090. 环形房屋偷盗](https://leetcode.cn/problems/PzWKhm/?show=1) |
|
||||
|
||||
```java
|
||||
// 主函数
|
||||
public int rob(int[] nums) {
|
||||
return dp(nums, 0);
|
||||
}
|
||||
// 返回 nums[start..] 能抢到的最大值
|
||||
private int dp(int[] nums, int start) {
|
||||
if (start >= nums.length) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
int res = Math.max(
|
||||
// 不抢,去下家
|
||||
dp(nums, start + 1),
|
||||
// 抢,去下下家
|
||||
nums[start] + dp(nums, start + 2)
|
||||
);
|
||||
return res;
|
||||
}
|
||||
```
|
||||
</details>
|
||||
|
||||
明确了状态转移,就可以发现对于同一 `start` 位置,是存在重叠子问题的,比如下图:
|
||||
|
||||

|
||||
|
||||
盗贼有多种选择可以走到这个位置,如果每次到这都进入递归,岂不是浪费时间?所以说存在重叠子问题,可以用备忘录进行优化:
|
||||
|
||||
```java
|
||||
private int[] memo;
|
||||
// 主函数
|
||||
public int rob(int[] nums) {
|
||||
// 初始化备忘录
|
||||
memo = new int[nums.length];
|
||||
Arrays.fill(memo, -1);
|
||||
// 强盗从第 0 间房子开始抢劫
|
||||
return dp(nums, 0);
|
||||
}
|
||||
|
||||
// 返回 dp[start..] 能抢到的最大值
|
||||
private int dp(int[] nums, int start) {
|
||||
if (start >= nums.length) {
|
||||
return 0;
|
||||
}
|
||||
// 避免重复计算
|
||||
if (memo[start] != -1) return memo[start];
|
||||
|
||||
int res = Math.max(dp(nums, start + 1),
|
||||
nums[start] + dp(nums, start + 2));
|
||||
// 记入备忘录
|
||||
memo[start] = res;
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
这就是自顶向下的动态规划解法,我们也可以略作修改,写出**自底向上**的解法:
|
||||
|
||||
```java
|
||||
int rob(int[] nums) {
|
||||
int n = nums.length;
|
||||
// dp[i] = x 表示:
|
||||
// 从第 i 间房子开始抢劫,最多能抢到的钱为 x
|
||||
// base case: dp[n] = 0
|
||||
int[] dp = new int[n + 2];
|
||||
for (int i = n - 1; i >= 0; i--) {
|
||||
dp[i] = Math.max(dp[i + 1], nums[i] + dp[i + 2]);
|
||||
}
|
||||
return dp[0];
|
||||
}
|
||||
```
|
||||
|
||||
我们又发现状态转移只和 `dp[i]` 最近的两个状态有关,所以可以进一步优化,将空间复杂度降低到 O(1)。
|
||||
|
||||
```java
|
||||
int rob(int[] nums) {
|
||||
int n = nums.length;
|
||||
// 记录 dp[i+1] 和 dp[i+2]
|
||||
int dp_i_1 = 0, dp_i_2 = 0;
|
||||
// 记录 dp[i]
|
||||
int dp_i = 0;
|
||||
for (int i = n - 1; i >= 0; i--) {
|
||||
dp_i = Math.max(dp_i_1, nums[i] + dp_i_2);
|
||||
dp_i_2 = dp_i_1;
|
||||
dp_i_1 = dp_i;
|
||||
}
|
||||
return dp_i;
|
||||
}
|
||||
```
|
||||
|
||||
以上的流程,在我们「动态规划详解」中详细解释过,相信大家都能手到擒来了。我认为很有意思的是这个问题的 follow up,需要基于我们现在的思路做一些巧妙的应变。
|
||||
|
||||
### House Robber II
|
||||
|
||||
这道题目和第一道描述基本一样,强盗依然不能抢劫相邻的房子,输入依然是一个数组,但是告诉你**这些房子不是一排,而是围成了一个圈**。
|
||||
|
||||
也就是说,现在第一间房子和最后一间房子也相当于是相邻的,不能同时抢。比如说输入数组 `nums=[2,3,2]`,算法返回的结果应该是 3 而不是 4,因为开头和结尾不能同时被抢。
|
||||
|
||||
这个约束条件看起来应该不难解决,我们前文「单调栈解决 Next Greater Number」说过一种解决环形数组的方案,那么在这个问题上怎么处理呢?
|
||||
|
||||
首先,首尾房间不能同时被抢,那么只可能有三种不同情况:要么都不被抢;要么第一间房子被抢最后一间不抢;要么最后一间房子被抢第一间不抢。
|
||||
|
||||

|
||||
|
||||
那就简单了啊,这三种情况,那种的结果最大,就是最终答案呗!不过,其实我们不需要比较三种情况,只要比较情况二和情况三就行了,**因为这两种情况对于房子的选择余地比情况一大呀,房子里的钱数都是非负数,所以选择余地大,最优决策结果肯定不会小**。
|
||||
|
||||
所以只需对之前的解法稍作修改即可:
|
||||
|
||||
```java
|
||||
public int rob(int[] nums) {
|
||||
int n = nums.length;
|
||||
if (n == 1) return nums[0];
|
||||
return Math.max(robRange(nums, 0, n - 2),
|
||||
robRange(nums, 1, n - 1));
|
||||
}
|
||||
|
||||
// 仅计算闭区间 [start,end] 的最优结果
|
||||
int robRange(int[] nums, int start, int end) {
|
||||
int n = nums.length;
|
||||
int dp_i_1 = 0, dp_i_2 = 0;
|
||||
int dp_i = 0;
|
||||
for (int i = end; i >= start; i--) {
|
||||
dp_i = Math.max(dp_i_1, nums[i] + dp_i_2);
|
||||
dp_i_2 = dp_i_1;
|
||||
dp_i_1 = dp_i;
|
||||
}
|
||||
return dp_i;
|
||||
}
|
||||
```
|
||||
|
||||
至此,第二问也解决了。
|
||||
|
||||
### House Robber III
|
||||
|
||||
第三题又想法设法地变花样了,此强盗发现现在面对的房子不是一排,不是一圈,而是一棵二叉树!房子在二叉树的节点上,相连的两个房子不能同时被抢劫,果然是传说中的高智商犯罪:
|
||||
|
||||

|
||||
|
||||
整体的思路完全没变,还是做抢或者不抢的选择,去收益较大的选择。甚至我们可以直接按这个套路写出代码:
|
||||
|
||||
```java
|
||||
Map<TreeNode, Integer> memo = new HashMap<>();
|
||||
public int rob(TreeNode root) {
|
||||
if (root == null) return 0;
|
||||
// 利用备忘录消除重叠子问题
|
||||
if (memo.containsKey(root))
|
||||
return memo.get(root);
|
||||
// 抢,然后去下下家
|
||||
int do_it = root.val
|
||||
+ (root.left == null ?
|
||||
0 : rob(root.left.left) + rob(root.left.right))
|
||||
+ (root.right == null ?
|
||||
0 : rob(root.right.left) + rob(root.right.right));
|
||||
// 不抢,然后去下家
|
||||
int not_do = rob(root.left) + rob(root.right);
|
||||
|
||||
int res = Math.max(do_it, not_do);
|
||||
memo.put(root, res);
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
这道题就解决了,时间复杂度 O(N),`N` 为数的节点数。
|
||||
|
||||
但是这道题让我觉得巧妙的点在于,还有更漂亮的解法。比如下面是我在评论区看到的一个解法:
|
||||
|
||||
```java
|
||||
int rob(TreeNode root) {
|
||||
int[] res = dp(root);
|
||||
return Math.max(res[0], res[1]);
|
||||
}
|
||||
|
||||
/* 返回一个大小为 2 的数组 arr
|
||||
arr[0] 表示不抢 root 的话,得到的最大钱数
|
||||
arr[1] 表示抢 root 的话,得到的最大钱数 */
|
||||
int[] dp(TreeNode root) {
|
||||
if (root == null)
|
||||
return new int[]{0, 0};
|
||||
int[] left = dp(root.left);
|
||||
int[] right = dp(root.right);
|
||||
// 抢,下家就不能抢了
|
||||
int rob = root.val + left[0] + right[0];
|
||||
// 不抢,下家可抢可不抢,取决于收益大小
|
||||
int not_rob = Math.max(left[0], left[1])
|
||||
+ Math.max(right[0], right[1]);
|
||||
|
||||
return new int[]{not_rob, rob};
|
||||
}
|
||||
```
|
||||
|
||||
时间复杂度 O(N),空间复杂度只有递归函数堆栈所需的空间,不需要备忘录的额外空间。
|
||||
|
||||
你看他和我们的思路不一样,修改了递归函数的定义,略微修改了思路,使得逻辑自洽,依然得到了正确的答案,而且代码更漂亮。这就是我们前文「不同定义产生不同解法」所说过的动态规划问题的一个特性。
|
||||
|
||||
实际上,这个解法比我们的解法运行时间要快得多,虽然算法分析层面时间复杂度是相同的。原因在于此解法没有使用额外的备忘录,减少了数据操作的复杂性,所以实际运行效率会快。
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
应合作方要求,本文不便在此发布,请扫码关注回复关键词「抢房子」或 [点这里](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62987952e4b09dda12708bf8/1) 查看:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||

|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[198.打家劫舍](https://leetcode-cn.com/problems/house-robber)
|
||||
|
|
|
|||
279
动态规划系列/最优子结构.md
279
动态规划系列/最优子结构.md
|
|
@ -1,25 +1,33 @@
|
|||
# 动态规划答疑篇
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
这篇文章就给你讲明白两个问题:
|
||||
> 本文有视频版:[动态规划详解进阶](https://www.bilibili.com/video/BV1uv411W73P/)
|
||||
|
||||
本文是两年前发的 [动态规划答疑篇](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 之后的一篇全面答疑文章。以下是正文。
|
||||
|
||||
这篇文章就给你讲明白以下几个问题:
|
||||
|
||||
1、到底什么才叫「最优子结构」,和动态规划什么关系。
|
||||
|
||||
2、为什么动态规划遍历 `dp` 数组的方式五花八门,有的正着遍历,有的倒着遍历,有的斜着遍历。
|
||||
2、如何判断一个问题是动态规划问题,即如何看出是否存在重叠子问题。
|
||||
|
||||
3、为什么经常看到将 `dp` 数组的大小设置为 `n + 1` 而不是 `n`。
|
||||
|
||||
4、为什么动态规划遍历 `dp` 数组的方式五花八门,有的正着遍历,有的倒着遍历,有的斜着遍历。
|
||||
|
||||
### 一、最优子结构详解
|
||||
|
||||
|
|
@ -33,7 +41,7 @@
|
|||
|
||||
再举个例子:假设你们学校有 10 个班,你已知每个班的最大分数差(最高分和最低分的差值)。那么现在我让你计算全校学生中的最大分数差,你会不会算?可以想办法算,但是肯定不能通过已知的这 10 个班的最大分数差推到出来。因为这 10 个班的最大分数差不一定就包含全校学生的最大分数差,比如全校的最大分数差可能是 3 班的最高分和 6 班的最低分之差。
|
||||
|
||||
这次我给你提出的问题就**不符合最优子结构**,因为你没办通过每个班的最优值推出全校的最优值,没办法通过子问题的最优值推出规模更大的问题的最优值。前文「动态规划详解」说过,想满足最优子结构,子问题之间必须互相独立。全校的最大分数差可能出现在两个班之间,显然子问题不独立,所以这个问题本身不符合最优子结构。
|
||||
这次我给你提出的问题就**不符合最优子结构**,因为你没办通过每个班的最优值推出全校的最优值,没办法通过子问题的最优值推出规模更大的问题的最优值。前文 [动态规划详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 说过,想满足最优子结,子问题之间必须互相独立。全校的最大分数差可能出现在两个班之间,显然子问题不独立,所以这个问题本身不符合最优子结构。
|
||||
|
||||
**那么遇到这种最优子结构失效情况,怎么办?策略是:改造问题**。对于最大分数差这个问题,我们不是没办法利用已知的每个班的分数差吗,那我只能这样写一段暴力代码:
|
||||
|
||||
|
|
@ -52,7 +60,7 @@ return result;
|
|||
|
||||
当然,上面这个例子太简单了,不过请读者回顾一下,我们做动态规划问题,是不是一直在求各种最值,本质跟我们举的例子没啥区别,无非需要处理一下重叠子问题。
|
||||
|
||||
前文不[同定义不同解法](https://labuladong.gitee.io/algo/) 和 [高楼扔鸡蛋进阶](https://labuladong.gitee.io/algo/) 就展示了如何改造问题,不同的最优子结构,可能导致不同的解法和效率。
|
||||
前文不 [同定义不同解法](https://labuladong.github.io/article/fname.html?fname=动态规划之四键键盘) 和 [高楼扔鸡蛋问题](https://labuladong.github.io/article/fname.html?fname=高楼扔鸡蛋问题) 就展示了如何改造问题,不同的最优子结构,可能导致不同的解法和效率。
|
||||
|
||||
再举个常见但也十分简单的例子,求一棵二叉树的最大值,不难吧(简单起见,假设节点中的值都是非负数):
|
||||
|
||||
|
|
@ -72,11 +80,196 @@ int maxVal(TreeNode root) {
|
|||
|
||||
动态规划不就是从最简单的 base case 往后推导吗,可以想象成一个链式反应,以小博大。但只有符合最优子结构的问题,才有发生这种链式反应的性质。
|
||||
|
||||
找最优子结构的过程,其实就是证明状态转移方程正确性的过程,方程符合最优子结构就可以写暴力解了,写出暴力解就可以看出有没有重叠子问题了,有则优化,无则 OK。这也是套路,经常刷题的朋友应该能体会。
|
||||
找最优子结构的过程,其实就是证明状态转移方程正确性的过程,方程符合最优子结构就可以写暴力解了,写出暴力解就可以看出有没有重叠子问题了,有则优化,无则 OK。这也是套路,经常刷题的读者应该能体会。
|
||||
|
||||
这里就不举那些正宗动态规划的例子了,读者可以翻翻历史文章,看看状态转移是如何遵循最优子结构的,这个话题就聊到这,下面再来看另外个动态规划迷惑行为。
|
||||
这里就不举那些正宗动态规划的例子了,读者可以翻翻历史文章,看看状态转移是如何遵循最优子结构的,这个话题就聊到这,下面再来看其他的动态规划迷惑行为。
|
||||
|
||||
### 二、dp 数组的遍历方向
|
||||
### 二、如何一眼看出重叠子问题
|
||||
|
||||
经常有读者说:
|
||||
|
||||
看了前文 [动态规划核心套路](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶),我知道了如何一步步优化动态规划问题;
|
||||
|
||||
看了前文 [动态规划设计:数学归纳法](https://labuladong.github.io/article/fname.html?fname=动态规划设计:最长递增子序列),我知道了利用数学归纳法写出暴力解(状态转移方程)。
|
||||
|
||||
**但就算我写出了暴力解,我很难判断这个解法是否存在重叠子问题**,从而无法确定是否可以运用备忘录等方法去优化算法效率。
|
||||
|
||||
对于这个问题,其实我在动态规划系列的文章中写过几次,在这里再统一总结一下吧。
|
||||
|
||||
**首先,最简单粗暴的方式就是画图,把递归树画出来,看看有没有重复的节点**。
|
||||
|
||||
比如最简单的例子,[动态规划核心套路](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 中斐波那契数列的递归树:
|
||||
|
||||

|
||||
|
||||
这棵递归树很明显存在重复的节点,所以我们可以通过备忘录避免冗余计算。
|
||||
|
||||
但毕竟斐波那契数列问题太简单了,实际的动态规划问题比较复杂,比如二维甚至三维的动态规划,当然也可以画递归树,但不免有些复杂。
|
||||
|
||||
比如在 [最小路径和问题](https://labuladong.github.io/article/fname.html?fname=最小路径和) 中,我们写出了这样一个暴力解法:
|
||||
|
||||
```java
|
||||
int dp(int[][] grid, int i, int j) {
|
||||
if (i == 0 && j == 0) {
|
||||
return grid[0][0];
|
||||
}
|
||||
if (i < 0 || j < 0) {
|
||||
return Integer.MAX_VALUE;
|
||||
}
|
||||
|
||||
return Math.min(
|
||||
dp(grid, i - 1, j),
|
||||
dp(grid, i, j - 1)
|
||||
) + grid[i][j];
|
||||
}
|
||||
```
|
||||
|
||||
你不需要读过前文,光看这个函数代码就能看出来,该函数递归过程中参数 `i, j` 在不断变化,即「状态」是 `(i, j)` 的值,你是否可以判断这个解法是否存在重叠子问题呢?
|
||||
|
||||
假设输入的 `i = 8, j = 7`,二维状态的递归树如下图,显然出现了重叠子问题:
|
||||
|
||||

|
||||
|
||||
**但稍加思考就可以知道,其实根本没必要画图,可以通过递归框架直接判断是否存在重叠子问题**。
|
||||
|
||||
具体操作就是直接删掉代码细节,抽象出该解法的递归框架:
|
||||
|
||||
```java
|
||||
int dp(int[][] grid, int i, int j) {
|
||||
dp(grid, i - 1, j), // #1
|
||||
dp(grid, i, j - 1) // #2
|
||||
}
|
||||
```
|
||||
|
||||
可以看到 `i, j` 的值在不断减小,那么我问你一个问题:如果我想从状态 `(i, j)` 转移到 `(i-1, j-1)`,有几种路径?
|
||||
|
||||
显然有两种路径,可以是 `(i, j) -> #1 -> #2` 或者 `(i, j) -> #2 -> #1`,不止一种,说明 `(i-1, j-1)` 会被多次计算,所以一定存在重叠子问题。
|
||||
|
||||
再举个稍微复杂的例子,前文 [正则表达式问题](https://labuladong.github.io/article/fname.html?fname=动态规划之正则表达) 的暴力解代码:
|
||||
|
||||
```cpp
|
||||
bool dp(string& s, int i, string& p, int j) {
|
||||
int m = s.size(), n = p.size();
|
||||
if (j == n) return i == m;
|
||||
if (i == m) {
|
||||
if ((n - j) % 2 == 1) return false;
|
||||
for (; j + 1 < n; j += 2) {
|
||||
if (p[j + 1] != '*') return false;
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
if (s[i] == p[j] || p[j] == '.') {
|
||||
if (j < n - 1 && p[j + 1] == '*') {
|
||||
return dp(s, i, p, j + 2)
|
||||
|| dp(s, i + 1, p, j);
|
||||
} else {
|
||||
return dp(s, i + 1, p, j + 1);
|
||||
}
|
||||
} else if (j < n - 1 && p[j + 1] == '*') {
|
||||
return dp(s, i, p, j + 2);
|
||||
}
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
代码有些复杂对吧,如果画图的话有些麻烦,但我们不画图,直接忽略所有细节代码和条件分支,只抽象出递归框架:
|
||||
|
||||
```cpp
|
||||
bool dp(string& s, int i, string& p, int j) {
|
||||
dp(s, i, p, j + 2); // #1
|
||||
dp(s, i + 1, p, j); // #2
|
||||
dp(s, i + 1, p, j + 1); // #3
|
||||
dp(s, i, p, j + 2); // #4
|
||||
}
|
||||
```
|
||||
|
||||
和上一题一样,这个解法的「状态」也是 `(i, j)` 的值,那么我继续问你问题:如果我想从状态 `(i, j)` 转移到 `(i+2, j+2)`,有几种路径?
|
||||
|
||||
显然,至少有两条路径:`(i, j) -> #1 -> #4` 和 `(i, j) -> #3 -> #3`。
|
||||
|
||||
所以,不用画图就知道这个解法也存在重叠子问题,需要用备忘录技巧去优化。
|
||||
|
||||
### 三、dp 数组的大小设置
|
||||
|
||||
比如说前文 [编辑距离问题](https://labuladong.github.io/article/fname.html?fname=编辑距离),我首先讲的是自顶向下的递归解法,实现了这样一个 `dp` 函数:
|
||||
|
||||
```java
|
||||
int minDistance(String s1, String s2) {
|
||||
int m = s1.length(), n = s2.length();
|
||||
// 按照 dp 函数的定义,计算 s1 和 s2 的最小编辑距离
|
||||
return dp(s1, m - 1, s2, n - 1);
|
||||
}
|
||||
|
||||
// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp(s1, i, s2, j)
|
||||
int dp(String s1, int i, String s2, int j) {
|
||||
// 处理 base case
|
||||
if (i == -1) {
|
||||
return j + 1;
|
||||
}
|
||||
if (j == -1) {
|
||||
return i + 1;
|
||||
}
|
||||
|
||||
// 进行状态转移
|
||||
if (s1.charAt(i) == s2.charAt(j)) {
|
||||
return dp(s1, i - 1, s2, j - 1);
|
||||
} else {
|
||||
return min(
|
||||
dp(s1, i, s2, j - 1) + 1,
|
||||
dp(s1, i - 1, s2, j) + 1,
|
||||
dp(s1, i - 1, s2, j - 1) + 1
|
||||
);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
然后改造成了自底向上的迭代解法:
|
||||
|
||||
```java
|
||||
int minDistance(String s1, String s2) {
|
||||
int m = s1.length(), n = s2.length();
|
||||
// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp[i+1][j+1]
|
||||
int[][] dp = new int[m + 1][n + 1];
|
||||
// 初始化 base case
|
||||
for (int i = 1; i <= m; i++)
|
||||
dp[i][0] = i;
|
||||
for (int j = 1; j <= n; j++)
|
||||
dp[0][j] = j;
|
||||
|
||||
// 自底向上求解
|
||||
for (int i = 1; i <= m; i++) {
|
||||
for (int j = 1; j <= n; j++) {
|
||||
// 进行状态转移
|
||||
if (s1.charAt(i-1) == s2.charAt(j-1)) {
|
||||
dp[i][j] = dp[i - 1][j - 1];
|
||||
} else {
|
||||
dp[i][j] = min(
|
||||
dp[i - 1][j] + 1,
|
||||
dp[i][j - 1] + 1,
|
||||
dp[i - 1][j - 1] + 1
|
||||
);
|
||||
}
|
||||
}
|
||||
}
|
||||
// 按照 dp 数组的定义,存储 s1 和 s2 的最小编辑距离
|
||||
return dp[m][n];
|
||||
}
|
||||
```
|
||||
|
||||
这两种解法思路是完全相同的,但就有读者提问,为什么迭代解法中的 `dp` 数组初始化大小要设置为 `int[m+1][n+1]`?为什么 `s1[0..i]` 和 `s2[0..j]` 的最小编辑距离要存储在 `dp[i+1][j+1]` 中,有一位索引偏移?
|
||||
|
||||
能不能模仿 `dp` 函数的定义,把 `dp` 数组初始化为 `int[m][n]`,然后让 `s1[0..i]` 和 `s2[0..j]` 的最小编辑距离要存储在 `dp[i][j]` 中?
|
||||
|
||||
**理论上,你怎么定义都可以,只要根据定义处理好 base case 就可以**。
|
||||
|
||||
你看 `dp` 函数的定义,`dp(s1, i, s2, j)` 计算 `s1[0..i]` 和 `s2[0..j]` 的编辑距离,那么 `i, j` 等于 -1 时代表空串的 base case,所以函数开头处理了这两种特殊情况。
|
||||
|
||||
再看 `dp` 数组,你当然也可以定义 `dp[i][j]` 存储 `s1[0..i]` 和 `s2[0..j]` 的编辑距离,但问题是 base case 怎么搞?索引怎么能是 -1 呢?
|
||||
|
||||
所以我们把 `dp` 数组初始化为 `int[m+1][n+1]`,让索引整体偏移一位,把索引 0 留出来作为 base case 表示空串,然后定义 `dp[i+1][j+1]` 存储 `s1[0..i]` 和 `s2[0..j]` 的编辑距离。
|
||||
|
||||
### 四、dp 数组的遍历方向
|
||||
|
||||
我相信读者做动态规问题时,肯定会对 `dp` 数组的遍历顺序有些头疼。我们拿二维 `dp` 数组来举例,有时候我们是正向遍历:
|
||||
|
||||
|
|
@ -107,19 +300,19 @@ for (int l = 2; l <= n; l++) {
|
|||
}
|
||||
```
|
||||
|
||||
甚至更让人迷惑的是,有时候发现正向反向遍历都可以得到正确答案,比如我们在「团灭股票问题」中有的地方就正反皆可。
|
||||
甚至更让人迷惑的是,有时候发现正向反向遍历都可以得到正确答案,比如我们在 [团灭股票问题](https://labuladong.github.io/article/fname.html?fname=团灭股票问题) 中有的地方就正反皆可。
|
||||
|
||||
那么,如果仔细观察的话可以发现其中的原因的。你只要把住两点就行了:
|
||||
如果仔细观察的话可以发现其中的原因,你只要把住两点就行了:
|
||||
|
||||
**1、遍历的过程中,所需的状态必须是已经计算出来的**。
|
||||
|
||||
**2、遍历的终点必须是存储结果的那个位置**。
|
||||
**2、遍历结束后,存储结果的那个位置必须已经被计算出来**。
|
||||
|
||||
下面来距离解释上面两个原则是什么意思。
|
||||
下面来具体解释上面两个原则是什么意思。
|
||||
|
||||
比如编辑距离这个经典的问题,详解见前文「编辑距离详解」,我们通过对 `dp` 数组的定义,确定了 base case 是 `dp[..][0]` 和 `dp[0][..]`,最终答案是 `dp[m][n]`;而且我们通过状态转移方程知道 `dp[i][j]` 需要从 `dp[i-1][j]`, `dp[i][j-1]`, `dp[i-1][j-1]` 转移而来,如下图:
|
||||
比如编辑距离这个经典的问题,详解见前文 [编辑距离详解](https://labuladong.github.io/article/fname.html?fname=编辑距离),我们通过对 `dp` 数组的定义,确定了 base case 是 `dp[..][0]` 和 `dp[0][..]`,最终答案是 `dp[m][n]`;而且我们通过状态转移方程知道 `dp[i][j]` 需要从 `dp[i-1][j]`, `dp[i][j-1]`, `dp[i-1][j-1]` 转移而来,如下图:
|
||||
|
||||

|
||||

|
||||
|
||||
那么,参考刚才说的两条原则,你该怎么遍历 `dp` 数组?肯定是正向遍历:
|
||||
|
||||
|
|
@ -132,28 +325,62 @@ for (int i = 1; i < m; i++)
|
|||
|
||||
因为,这样每一步迭代的左边、上边、左上边的位置都是 base case 或者之前计算过的,而且最终结束在我们想要的答案 `dp[m][n]`。
|
||||
|
||||
再举一例,回文子序列问题,详见前文「子序列问题模板」,我们通过过对 `dp` 数组的定义,确定了 base case 处在中间的对角线,`dp[i][j]` 需要从 `dp[i+1][j]`, `dp[i][j-1]`, `dp[i+1][j-1]` 转移而来,想要求的最终答案是 `dp[0][n-1]`,如下图:
|
||||
再举一例,回文子序列问题,详见前文 [子序列问题模板](https://labuladong.github.io/article/fname.html?fname=子序列问题模板),我们通过过对 `dp` 数组的定义,确定了 base case 处在中间的对角线,`dp[i][j]` 需要从 `dp[i+1][j]`, `dp[i][j-1]`, `dp[i+1][j-1]` 转移而来,想要求的最终答案是 `dp[0][n-1]`,如下图:
|
||||
|
||||

|
||||

|
||||
|
||||
这种情况根据刚才的两个原则,就可以有两种正确的遍历方式:
|
||||
|
||||

|
||||

|
||||
|
||||
要么从左至右斜着遍历,要么从下向上从左到右遍历,这样才能保证每次 `dp[i][j]` 的左边、下边、左下边已经计算完毕,得到正确结果。
|
||||
|
||||
现在,你应该理解了这两个原则,主要就是看 base case 和最终结果的存储位置,保证遍历过程中使用的数据都是计算完毕的就行,有时候确实存在多种方法可以得到正确答案,可根据个人口味自行选择。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.github.io/article/fname.html?fname=团灭股票问题)
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [动态规划解题套路框架](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)
|
||||
- [经典动态规划:博弈问题](https://labuladong.github.io/article/fname.html?fname=动态规划之博弈问题)
|
||||
- [经典动态规划:戳气球](https://labuladong.github.io/article/fname.html?fname=扎气球)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [115. Distinct Subsequences](https://leetcode.com/problems/distinct-subsequences/?show=1) | [115. 不同的子序列](https://leetcode.cn/problems/distinct-subsequences/?show=1) |
|
||||
| [139. Word Break](https://leetcode.com/problems/word-break/?show=1) | [139. 单词拆分](https://leetcode.cn/problems/word-break/?show=1) |
|
||||
| [221. Maximal Square](https://leetcode.com/problems/maximal-square/?show=1) | [221. 最大正方形](https://leetcode.cn/problems/maximal-square/?show=1) |
|
||||
| [256. Paint House](https://leetcode.com/problems/paint-house/?show=1)🔒 | [256. 粉刷房子](https://leetcode.cn/problems/paint-house/?show=1)🔒 |
|
||||
| [63. Unique Paths II](https://leetcode.com/problems/unique-paths-ii/?show=1) | [63. 不同路径 II](https://leetcode.cn/problems/unique-paths-ii/?show=1) |
|
||||
| [91. Decode Ways](https://leetcode.com/problems/decode-ways/?show=1) | [91. 解码方法](https://leetcode.cn/problems/decode-ways/?show=1) |
|
||||
| - | [剑指 Offer II 091. 粉刷房子](https://leetcode.cn/problems/JEj789/?show=1) |
|
||||
| - | [剑指 Offer II 097. 子序列的数目](https://leetcode.cn/problems/21dk04/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||

|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
### javascript
|
||||
|
|
|
|||
|
|
@ -1,338 +0,0 @@
|
|||
# 最长公共子序列
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[1143.最长公共子序列](https://leetcode-cn.com/problems/longest-common-subsequence)
|
||||
|
||||
**-----------**
|
||||
|
||||
最长公共子序列(Longest Common Subsequence,简称 LCS)是一道非常经典的面试题目,因为它的解法是典型的二维动态规划,大部分比较困难的字符串问题都和这个问题一个套路,比如说编辑距离。而且,这个算法稍加改造就可以用于解决其他问题,所以说 LCS 算法是值得掌握的。
|
||||
|
||||
题目就是让我们求两个字符串的 LCS 长度:
|
||||
|
||||
```
|
||||
输入: str1 = "abcde", str2 = "ace"
|
||||
输出: 3
|
||||
解释: 最长公共子序列是 "ace",它的长度是 3
|
||||
```
|
||||
|
||||
肯定有读者会问,为啥这个问题就是动态规划来解决呢?因为子序列类型的问题,穷举出所有可能的结果都不容易,而动态规划算法做的就是穷举 + 剪枝,它俩天生一对儿。所以可以说只要涉及子序列问题,十有八九都需要动态规划来解决,往这方面考虑就对了。
|
||||
|
||||
下面就来手把手分析一下,这道题目如何用动态规划技巧解决。
|
||||
|
||||
### 一、动态规划思路
|
||||
|
||||
**第一步,一定要明确 `dp` 数组的含义**。对于两个字符串的动态规划问题,套路是通用的。
|
||||
|
||||
比如说对于字符串 `s1` 和 `s2`,一般来说都要构造一个这样的 DP table:
|
||||
|
||||

|
||||
|
||||
为了方便理解此表,我们暂时认为索引是从 1 开始的,待会的代码中只要稍作调整即可。其中,`dp[i][j]` 的含义是:对于 `s1[1..i]` 和 `s2[1..j]`,它们的 LCS 长度是 `dp[i][j]`。
|
||||
|
||||
比如上图的例子,d[2][4] 的含义就是:对于 `"ac"` 和 `"babc"`,它们的 LCS 长度是 2。我们最终想得到的答案应该是 `dp[3][6]`。
|
||||
|
||||
**第二步,定义 base case。**
|
||||
|
||||
我们专门让索引为 0 的行和列表示空串,`dp[0][..]` 和 `dp[..][0]` 都应该初始化为 0,这就是 base case。
|
||||
|
||||
比如说,按照刚才 dp 数组的定义,`dp[0][3]=0` 的含义是:对于字符串 `""` 和 `"bab"`,其 LCS 的长度为 0。因为有一个字符串是空串,它们的最长公共子序列的长度显然应该是 0。
|
||||
|
||||
**第三步,找状态转移方程。**
|
||||
|
||||
这是动态规划最难的一步,不过好在这种字符串问题的套路都差不多,权且借这道题来聊聊处理这类问题的思路。
|
||||
|
||||
状态转移说简单些就是做选择,比如说这个问题,是求 `s1` 和 `s2` 的最长公共子序列,不妨称这个子序列为 `lcs`。那么对于 `s1` 和 `s2` 中的每个字符,有什么选择?很简单,两种选择,要么在 `lcs` 中,要么不在。
|
||||
|
||||

|
||||
|
||||
这个「在」和「不在」就是选择,关键是,应该如何选择呢?这个需要动点脑筋:如果某个字符应该在 `lcs` 中,那么这个字符肯定同时存在于 `s1` 和 `s2` 中,因为 `lcs` 是最长**公共**子序列嘛。所以本题的思路是这样:
|
||||
|
||||
用两个指针 `i` 和 `j` 从后往前遍历 `s1` 和 `s2`,如果 `s1[i]==s2[j]`,那么这个字符**一定在 `lcs` 中**;否则的话,`s1[i]` 和 `s2[j]` 这两个字符**至少有一个不在 `lcs` 中**,需要丢弃一个。先看一下递归解法,比较容易理解:
|
||||
|
||||
```python
|
||||
def longestCommonSubsequence(str1, str2) -> int:
|
||||
def dp(i, j):
|
||||
# 空串的 base case
|
||||
if i == -1 or j == -1:
|
||||
return 0
|
||||
if str1[i] == str2[j]:
|
||||
# 这边找到一个 lcs 的元素,继续往前找
|
||||
return dp(i - 1, j - 1) + 1
|
||||
else:
|
||||
# 谁能让 lcs 最长,就听谁的
|
||||
return max(dp(i-1, j), dp(i, j-1))
|
||||
|
||||
# i 和 j 初始化为最后一个索引
|
||||
return dp(len(str1)-1, len(str2)-1)
|
||||
```
|
||||
|
||||
对于第一种情况,找到一个 `lcs` 中的字符,同时将 `i` `j` 向前移动一位,并给 `lcs` 的长度加一;对于后者,则尝试两种情况,取更大的结果。
|
||||
|
||||
其实这段代码就是暴力解法,我们可以通过备忘录或者 DP table 来优化时间复杂度,比如通过前文描述的 DP table 来解决:
|
||||
|
||||
```python
|
||||
def longestCommonSubsequence(str1, str2) -> int:
|
||||
m, n = len(str1), len(str2)
|
||||
# 构建 DP table 和 base case
|
||||
dp = [[0] * (n + 1) for _ in range(m + 1)]
|
||||
# 进行状态转移
|
||||
for i in range(1, m + 1):
|
||||
for j in range(1, n + 1):
|
||||
if str1[i - 1] == str2[j - 1]:
|
||||
# 找到一个 lcs 中的字符
|
||||
dp[i][j] = 1 + dp[i-1][j-1]
|
||||
else:
|
||||
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
|
||||
|
||||
return dp[-1][-1]
|
||||
```
|
||||
|
||||
### 二、疑难解答
|
||||
|
||||
对于 `s1[i]` 和 `s2[j]` 不相等的情况,**至少有一个**字符不在 `lcs` 中,会不会两个字符都不在呢?比如下面这种情况:
|
||||
|
||||

|
||||
|
||||
所以代码是不是应该考虑这种情况,改成这样:
|
||||
|
||||
```python
|
||||
if str1[i - 1] == str2[j - 1]:
|
||||
# ...
|
||||
else:
|
||||
dp[i][j] = max(dp[i-1][j],
|
||||
dp[i][j-1],
|
||||
dp[i-1][j-1])
|
||||
```
|
||||
|
||||
我一开始也有这种怀疑,其实可以这样改,也能得到正确答案,但是多此一举,因为 `dp[i-1][j-1]` 永远是三者中最小的,max 根本不可能取到它。
|
||||
|
||||
原因在于我们对 dp 数组的定义:对于 `s1[1..i]` 和 `s2[1..j]`,它们的 LCS 长度是 `dp[i][j]`。
|
||||
|
||||

|
||||
|
||||
这样一看,显然 `dp[i-1][j-1]` 对应的 `lcs` 长度不可能比前两种情况大,所以没有必要参与比较。
|
||||
|
||||
### 三、总结
|
||||
|
||||
对于两个字符串的动态规划问题,一般来说都是像本文一样定义 DP table,因为这样定义有一个好处,就是容易写出状态转移方程,`dp[i][j]` 的状态可以通过之前的状态推导出来:
|
||||
|
||||

|
||||
|
||||
找状态转移方程的方法是,思考每个状态有哪些「选择」,只要我们能用正确的逻辑做出正确的选择,算法就能够正确运行。
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[1143.最长公共子序列](https://leetcode-cn.com/problems/longest-common-subsequence)
|
||||
|
||||
### c++
|
||||
|
||||
[Edwenc](https://github.com/Edwenc) 提供 C++ 代码:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int longestCommonSubsequence(string text1, string text2) {
|
||||
// 先计算两条字符串的长度
|
||||
int m = text1.size();
|
||||
int n = text2.size();
|
||||
|
||||
// 构建dp矩阵 默认初始值0
|
||||
// 这里会多扩建一边和一列
|
||||
// 因为dp[i][j]的含义是:对于 s1[1..i] 和 s2[1..j],它们的LCS长度是 dp[i][j]。
|
||||
// 所以当i或者j为零时 LCS的长度默认为0
|
||||
vector< vector<int> > dp ( m+1 , vector<int> ( n+1 , 0 ) );
|
||||
|
||||
// 状态转移
|
||||
// i、j都从1开始遍历 因为下面的操作中都会-1 相当于从0开始
|
||||
for ( int i=1 ; i<m+1 ; i++ ){
|
||||
for ( int j=1 ; j<n+1 ; j++ ){
|
||||
// 如果text1和text2相同
|
||||
// 就在它们的前一位基础上加一
|
||||
// 如果不同 只能在之前的两者中去最大
|
||||
dp[i][j] = (text1[i-1] == text2[j-1]) ? dp[i-1][j-1] + 1 : max( dp[i-1][j] , dp[i][j-1] );
|
||||
}
|
||||
}
|
||||
|
||||
// 返回最终右下角的值
|
||||
return dp[m][n];
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
### java
|
||||
|
||||
[Shawn](https://github.com/Shawn-Hx) 提供 Java 代码:
|
||||
|
||||
```java
|
||||
public int longestCommonSubsequence(String text1, String text2) {
|
||||
// 字符串转为char数组以加快访问速度
|
||||
char[] str1 = text1.toCharArray();
|
||||
char[] str2 = text2.toCharArray();
|
||||
|
||||
int m = str1.length, n = str2.length;
|
||||
// 构建dp table,初始值默认为0
|
||||
int[][] dp = new int[m + 1][n + 1];
|
||||
// 状态转移
|
||||
for (int i = 1; i <= m; i++)
|
||||
for (int j = 1; j <= n; j++)
|
||||
if (str1[i - 1] == str2[j - 1])
|
||||
// 找到LCS中的字符
|
||||
dp[i][j] = dp[i-1][j-1] + 1;
|
||||
else
|
||||
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
|
||||
|
||||
return dp[m][n];
|
||||
}
|
||||
```
|
||||
|
||||
### python
|
||||
|
||||
[lo-tp](http://blog.lotp.xyz/) 提供 Python 代码:
|
||||
|
||||
```python
|
||||
class Solution(object):
|
||||
def longestCommonSubsequence(self, text1, text2):
|
||||
# calculate the size of the first and second string
|
||||
sz1, sz2 = len(text1), len(text2)
|
||||
# since to calculate dp(i,j) we only need dp(i-1,j-1), dp(i-1,j), dp(i,j-1)
|
||||
# we don't have to save data before i-1
|
||||
# we use dp to save dp(i-1, 0), dp(i-1, 1)....dp(i-1, sz2)
|
||||
# we use tmp to save dp(i, 0), dp(i,1)....(dpi-1, sz2)
|
||||
tmp, dp = [0]*(sz2+1), [0]*(sz2+1)
|
||||
for i in range(0, sz1):
|
||||
for j in range(0, sz2):
|
||||
tmp[j+1] = dp[j] + \
|
||||
1 if text1[i] == text2[j] else max(tmp[j], dp[j+1])
|
||||
# In the next iteration, we will calculate dp(i+1,0),dp(i+1, 1)....dp(i+1,sz2)
|
||||
# So we exchange dp and tmp
|
||||
tmp, dp = dp, tmp
|
||||
return dp[-1]
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
**暴力解法**
|
||||
|
||||
```js
|
||||
var longestCommonSubsequence = function (text1, text2) {
|
||||
let s1 = text1.length;
|
||||
let s2 = text2.length;
|
||||
let dp = function (i, j) {
|
||||
// 空串的base case
|
||||
if (i === -1 || j === -1) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
if (text1[i] === text2[j]) {
|
||||
// 这边找到一个 lcs 的元素,继续往前找
|
||||
return dp(i - 1, j - 1) + 1
|
||||
} else {
|
||||
// 谁能让lcs最长,就听谁的
|
||||
return Math.max(dp(i - 1, j), dp(i, j - 1))
|
||||
}
|
||||
}
|
||||
// i 和 j 初始化为最后一个索引
|
||||
return dp(s1 - 1, s2 - 1)
|
||||
};
|
||||
```
|
||||
|
||||
**暴力解法+备忘录优化**
|
||||
|
||||
```js
|
||||
var longestCommonSubsequence = function (text1, text2) {
|
||||
let s1 = text1.length;
|
||||
let s2 = text2.length;
|
||||
let memo = new Map();
|
||||
|
||||
let dp = function (i, j) {
|
||||
// 空串的base case
|
||||
if (i === -1 || j === -1) {
|
||||
return 0;
|
||||
}
|
||||
|
||||
// 查询一下备忘录,防止重复计算
|
||||
let key = i + "," + j
|
||||
if (memo.has(key)) {
|
||||
return memo.get(key)
|
||||
}
|
||||
|
||||
let res;
|
||||
if (text1[i] === text2[j]) {
|
||||
// 这边找到一个 lcs 的元素,继续往前找
|
||||
// 记入备忘录
|
||||
res = dp(i - 1, j - 1) + 1
|
||||
memo.set(key, res)
|
||||
} else {
|
||||
// 谁能让lcs最长,就听谁的
|
||||
res = Math.max(dp(i - 1, j), dp(i, j - 1))
|
||||
memo.set(key, res)
|
||||
}
|
||||
return res;
|
||||
}
|
||||
// i 和 j 初始化为最后一个索引
|
||||
return dp(s1 - 1, s2 - 1)
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
**DPtable优化**
|
||||
|
||||
```js
|
||||
var longestCommonSubsequence = function (text1, text2) {
|
||||
let s1 = text1.length;
|
||||
let s2 = text2.length;
|
||||
|
||||
// 构建 DP table 和 base case
|
||||
// 初始化一个 (s1+1)*(s2+1)的dp表
|
||||
let dp = new Array(s1 + 1);
|
||||
for (let i = 0; i < s1 + 1; i++) {
|
||||
dp[i] = new Array(s2 + 1);
|
||||
dp[i].fill(0, 0, s2 + 1)
|
||||
}
|
||||
|
||||
// 进行状态转移
|
||||
for (let i = 1; i < s1 + 1; i++) {
|
||||
for (let j = 1; j < s2 + 1; j++) {
|
||||
if (text1[i - 1] === text2[j - 1]) {
|
||||
// 找到一个lcs中的字符
|
||||
dp[i][j] = 1 + dp[i - 1][j - 1]
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// i 和 j 初始化为最后一个索引
|
||||
return dp[s1][s2]
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
|
|
@ -0,0 +1,250 @@
|
|||
# 对动态规划发动降维打击
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
**-----------**
|
||||
|
||||
我们号之前写过十几篇动态规划文章,可以说动态规划技巧对于算法效率的提升非常可观,一般来说都能把指数级和阶乘级时间复杂度的算法优化成 O(N^2),堪称算法界的二向箔,把各路魑魅魍魉统统打成二次元。
|
||||
|
||||
但是,动态规划求解的过程中也是可以进行阶段性优化的,如果你认真观察某些动态规划问题的状态转移方程,就能够把它们解法的空间复杂度进一步降低,由 O(N^2) 降低到 O(N)。
|
||||
|
||||
> PS:之前我在本文中误用了「状态压缩」这个词,有读者指出「状态压缩」这个词的含义是把多个状态通过二进制运算用一个整数表示出来,从而减少 `dp` 数组的维度。而本文描述的优化方式是通过观察状态转移方程的依赖关系,从而减少 `dp` 数组的维度,确实和「状态压缩」有所区别。所以严谨起见,我把原来文章中的「状态压缩」都改为了「空间压缩」,避免名词的误用。
|
||||
|
||||
能够使用空间压缩技巧的动态规划都是二维 `dp` 问题,**你看它的状态转移方程,如果计算状态 `dp[i][j]` 需要的都是 `dp[i][j]` 相邻的状态,那么就可以使用空间压缩技巧**,将二维的 `dp` 数组转化成一维,将空间复杂度从 O(N^2) 降低到 O(N)。
|
||||
|
||||
什么叫「和 `dp[i][j]` 相邻的状态」呢,比如前文 [最长回文子序列](https://labuladong.github.io/article/fname.html?fname=子序列问题模板) 中,最终的代码如下:
|
||||
|
||||
```cpp
|
||||
int longestPalindromeSubseq(string s) {
|
||||
int n = s.size();
|
||||
// dp 数组全部初始化为 0
|
||||
vector<vector<int>> dp(n, vector<int>(n, 0));
|
||||
// base case
|
||||
for (int i = 0; i < n; i++)
|
||||
dp[i][i] = 1;
|
||||
// 反着遍历保证正确的状态转移
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
// 状态转移方程
|
||||
if (s[i] == s[j])
|
||||
dp[i][j] = dp[i + 1][j - 1] + 2;
|
||||
else
|
||||
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
|
||||
}
|
||||
}
|
||||
// 整个 s 的最长回文子串长度
|
||||
return dp[0][n - 1];
|
||||
}
|
||||
```
|
||||
|
||||
> PS:我们本文不探讨如何推状态转移方程,只探讨对二维 DP 问题进行空间压缩的技巧。技巧都是通用的,所以如果你没看过前文,不明白这段代码的逻辑也无妨,完全不会阻碍你学会空间压缩。
|
||||
|
||||
你看我们对 `dp[i][j]` 的更新,其实只依赖于 `dp[i+1][j-1], dp[i][j-1], dp[i+1][j]` 这三个状态:
|
||||
|
||||

|
||||
|
||||
这就叫和 `dp[i][j]` 相邻,反正你计算 `dp[i][j]` 只需要这三个相邻状态,其实根本不需要那么大一个二维的 dp table 对不对?**空间压缩的核心思路就是,将二维数组「投影」到一维数组**:
|
||||
|
||||

|
||||
|
||||
思路很直观,但是也有一个明显的问题,图中 `dp[i][j-1]` 和 `dp[i+1][j-1]` 这两个状态处在同一列,而一维数组中只能容下一个,那么当我计算 `dp[i][j]` 时,他俩必然有一个会被另一个覆盖掉,怎么办?
|
||||
|
||||
这就是空间压缩的难点,下面就来分析解决这个问题,还是拿「最长回文子序列」问题举例,它的状态转移方程主要逻辑就是如下这段代码:
|
||||
|
||||
```cpp
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
// 状态转移方程
|
||||
if (s[i] == s[j])
|
||||
dp[i][j] = dp[i + 1][j - 1] + 2;
|
||||
else
|
||||
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
想把二维 `dp` 数组压缩成一维,一般来说是把第一个维度,也就是 `i` 这个维度去掉,只剩下 `j` 这个维度。**压缩后的一维 `dp` 数组就是之前二维 `dp` 数组的 `dp[i][..]` 那一行**。
|
||||
|
||||
我们先将上述代码进行改造,直接无脑去掉 `i` 这个维度,把 `dp` 数组变成一维:
|
||||
|
||||
```cpp
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
// 在这里,一维 dp 数组中的数是什么?
|
||||
if (s[i] == s[j])
|
||||
dp[j] = dp[j - 1] + 2;
|
||||
else
|
||||
dp[j] = max(dp[j], dp[j - 1]);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
上述代码的一维 `dp` 数组只能表示二维 `dp` 数组的一行 `dp[i][..]`,那我怎么才能得到 `dp[i+1][j-1], dp[i][j-1], dp[i+1][j]` 这几个必要的的值,进行状态转移呢?
|
||||
|
||||
在代码中注释的位置,将要进行状态转移,更新 `dp[j]`,那么我们要来思考两个问题:
|
||||
|
||||
1、在对 `dp[j]` 赋新值之前,`dp[j]` 对应着二维 `dp` 数组中的什么位置?
|
||||
|
||||
2、`dp[j-1]` 对应着二维 `dp` 数组中的什么位置?
|
||||
|
||||
**对于问题 1,在对 `dp[j]` 赋新值之前,`dp[j]` 的值就是外层 for 循环上一次迭代算出来的值,也就是对应二维 `dp` 数组中 `dp[i+1][j]` 的位置**。
|
||||
|
||||
**对于问题 2,`dp[j-1]` 的值就是内层 for 循环上一次迭代算出来的值,也就是对应二维 `dp` 数组中 `dp[i][j-1]` 的位置**。
|
||||
|
||||
那么问题已经解决了一大半了,只剩下二维 `dp` 数组中的 `dp[i+1][j-1]` 这个状态我们不能直接从一维 `dp` 数组中得到:
|
||||
|
||||
```cpp
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
if (s[i] == s[j])
|
||||
// dp[i][j] = dp[i+1][j-1] + 2;
|
||||
dp[j] = ?? + 2;
|
||||
else
|
||||
// dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
|
||||
dp[j] = max(dp[j], dp[j - 1]);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
因为 for 循环遍历 `i` 和 `j` 的顺序为从左向右,从下向上,所以可以发现,在更新一维 `dp` 数组的时候,`dp[i+1][j-1]` 会被 `dp[i][j-1]` 覆盖掉,图中标出了这四个位置被遍历到的次序:
|
||||
|
||||

|
||||
|
||||
**那么如果我们想得到 `dp[i+1][j-1]`,就必须在它被覆盖之前用一个临时变量 `temp` 把它存起来,并把这个变量的值保留到计算 `dp[i][j]` 的时候**。为了达到这个目的,结合上图,我们可以这样写代码:
|
||||
|
||||
```cpp
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
// 存储 dp[i+1][j-1] 的变量
|
||||
int pre = 0;
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
int temp = dp[j];
|
||||
if (s[i] == s[j])
|
||||
// dp[i][j] = dp[i+1][j-1] + 2;
|
||||
dp[j] = pre + 2;
|
||||
else
|
||||
dp[j] = max(dp[j], dp[j - 1]);
|
||||
// 到下一轮循环,pre 就是 dp[i+1][j-1] 了
|
||||
pre = temp;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
别小看这段代码,这是一维 `dp` 最精妙的地方,会者不难,难者不会。为了清晰起见,我用具体的数值来拆解这个逻辑:
|
||||
|
||||
假设现在 `i = 5, j = 7` 且 `s[5] == s[7]`,那么现在会进入下面这个逻辑对吧:
|
||||
|
||||
```cpp
|
||||
if (s[5] == s[7])
|
||||
// dp[5][7] = dp[i+1][j-1] + 2;
|
||||
dp[7] = pre + 2;
|
||||
```
|
||||
|
||||
我问你这个 `pre` 变量是什么?是内层 for 循环上一次迭代的 `temp` 值。
|
||||
|
||||
那我再问你内层 for 循环上一次迭代的 `temp` 值是什么?是 `dp[j-1]` 也就是 `dp[6]`,但这是外层 for 循环上一次迭代对应的 `dp[6]`,也就是二维 `dp` 数组中的 `dp[i+1][6] = dp[6][6]`。
|
||||
|
||||
也就是说,`pre` 变量就是 `dp[i+1][j-1] = dp[6][6]`,也就是我们想要的结果。
|
||||
|
||||
那么现在我们成功对状态转移方程进行了降维打击,算是最硬的的骨头啃掉了,但注意到我们还有 base case 要处理呀:
|
||||
|
||||
```cpp
|
||||
// dp 数组全部初始化为 0
|
||||
vector<vector<int>> dp(n, vector<int>(n, 0));
|
||||
// base case
|
||||
for (int i = 0; i < n; i++)
|
||||
dp[i][i] = 1;
|
||||
```
|
||||
|
||||
如何把 base case 也打成一维呢?很简单,记住空间压缩就是投影,我们把 base case 投影到一维看看:
|
||||
|
||||

|
||||
|
||||
二维 `dp` 数组中的 base case 全都落入了一维 `dp` 数组,不存在冲突和覆盖,所以说我们直接这样写代码就行了:
|
||||
|
||||
```cpp
|
||||
// 一维 dp 数组全部初始化为 1
|
||||
vector<int> dp(n, 1);
|
||||
```
|
||||
|
||||
至此,我们把 base case 和状态转移方程都进行了降维,实际上已经写出完整代码了:
|
||||
|
||||
```cpp
|
||||
int longestPalindromeSubseq(string s) {
|
||||
int n = s.size();
|
||||
// base case:一维 dp 数组全部初始化为 0
|
||||
vector<int> dp(n, 1);
|
||||
|
||||
for (int i = n - 2; i >= 0; i--) {
|
||||
int pre = 0;
|
||||
for (int j = i + 1; j < n; j++) {
|
||||
int temp = dp[j];
|
||||
// 状态转移方程
|
||||
if (s[i] == s[j])
|
||||
dp[j] = pre + 2;
|
||||
else
|
||||
dp[j] = max(dp[j], dp[j - 1]);
|
||||
pre = temp;
|
||||
}
|
||||
}
|
||||
return dp[n - 1];
|
||||
}
|
||||
```
|
||||
|
||||
本文就结束了,不过空间压缩技巧再牛逼,也是基于常规动态规划思路之上的。
|
||||
|
||||
你也看到了,使用空间压缩技巧对二维 `dp` 数组进行降维打击之后,解法代码的可读性变得非常差了,如果直接看这种解法,任何人都是一脸懵逼的。算法的优化就是这么一个过程,先写出可读性很好的暴力递归算法,然后尝试运用动态规划技巧优化重叠子问题,最后尝试用空间压缩技巧优化空间复杂度。
|
||||
|
||||
也就是说,你最起码能够熟练运用我们前文 [动态规划框架套路详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 的套路找出状态转移方程,写出一个正确的动态规划解法,然后才有可能观察状态转移的情况,分析是否可能使用空间压缩技巧来优化。
|
||||
|
||||
希望读者能够稳扎稳打,层层递进,对于这种比较极限的优化,不做也罢。毕竟套路存于心,走遍天下都不怕!
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [一个方法团灭 LeetCode 股票买卖问题](https://labuladong.github.io/article/fname.html?fname=团灭股票问题)
|
||||
- [动态规划之最小路径和](https://labuladong.github.io/article/fname.html?fname=最小路径和)
|
||||
- [动态规划设计:最大子数组](https://labuladong.github.io/article/fname.html?fname=最大子数组)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [经典动态规划:子集背包问题](https://labuladong.github.io/article/fname.html?fname=背包子集)
|
||||
- [经典动态规划:完全背包问题](https://labuladong.github.io/article/fname.html?fname=背包零钱)
|
||||
- [经典动态规划:最长公共子序列](https://labuladong.github.io/article/fname.html?fname=LCS)
|
||||
- [经典动态规划:高楼扔鸡蛋](https://labuladong.github.io/article/fname.html?fname=高楼扔鸡蛋问题)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [63. Unique Paths II](https://leetcode.com/problems/unique-paths-ii/?show=1) | [63. 不同路径 II](https://leetcode.cn/problems/unique-paths-ii/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
255
动态规划系列/编辑距离.md
255
动态规划系列/编辑距离.md
|
|
@ -1,28 +1,41 @@
|
|||
# 编辑距离
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[72.编辑距离](https://leetcode-cn.com/problems/edit-distance)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [72. Edit Distance](https://leetcode.com/problems/edit-distance/) | [72. 编辑距离](https://leetcode.cn/problems/edit-distance/) | 🔴
|
||||
|
||||
**-----------**
|
||||
|
||||
前几天看了一份鹅场的面试题,算法部分大半是动态规划,最后一题就是写一个计算编辑距离的函数,今天就专门写一篇文章来探讨一下这个问题。
|
||||
> 本文有视频版:[编辑距离详解动态规划](https://www.bilibili.com/video/BV1uv411W73P/)
|
||||
|
||||
我个人很喜欢编辑距离这个问题,因为它看起来十分困难,解法却出奇得简单漂亮,而且它是少有的比较实用的算法(是的,我承认很多算法问题都不太实用)。下面先来看下题目:
|
||||
前几天看了一份鹅厂的面试题,算法部分大半是动态规划,最后一题就是写一个计算编辑距离的函数,今天就专门写一篇文章来探讨一下这个问题。
|
||||
|
||||

|
||||
我个人很喜欢编辑距离这个问题,因为它看起来十分困难,解法却出奇得简单漂亮,而且它是少有的比较实用的算法(我承认很多算法问题都不太实用)。
|
||||
|
||||
力扣第 72 题「编辑距离」就是这个问题,先看下题目:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int minDistance(String s1, String s2)
|
||||
```
|
||||
|
||||
为什么说这个问题难呢,因为显而易见,它就是难,让人手足无措,望而生畏。
|
||||
|
||||
|
|
@ -36,25 +49,27 @@
|
|||
|
||||
编辑距离问题就是给我们两个字符串 `s1` 和 `s2`,只能用三种操作,让我们把 `s1` 变成 `s2`,求最少的操作数。需要明确的是,不管是把 `s1` 变成 `s2` 还是反过来,结果都是一样的,所以后文就以 `s1` 变成 `s2` 举例。
|
||||
|
||||
前文「最长公共子序列」说过,**解决两个字符串的动态规划问题,一般都是用两个指针 `i,j` 分别指向两个字符串的最后,然后一步步往前走,缩小问题的规模**。
|
||||
前文 [最长公共子序列](https://labuladong.github.io/article/fname.html?fname=LCS) 说过,**解决两个字符串的动态规划问题,一般都是用两个指针 `i, j` 分别指向两个字符串的最后,然后一步步往前移动,缩小问题的规模**。
|
||||
|
||||
设两个字符串分别为 "rad" 和 "apple",为了把 `s1` 变成 `s2`,算法会这样进行:
|
||||
> PS:其实让 `i, j` 从前往后移动也可以,改一下 `dp` 函数/数组的定义即可,思路是完全一样的。
|
||||
|
||||

|
||||
设两个字符串分别为 `"rad"` 和 `"apple"`,为了把 `s1` 变成 `s2`,算法会这样进行:
|
||||
|
||||

|
||||

|
||||
|
||||
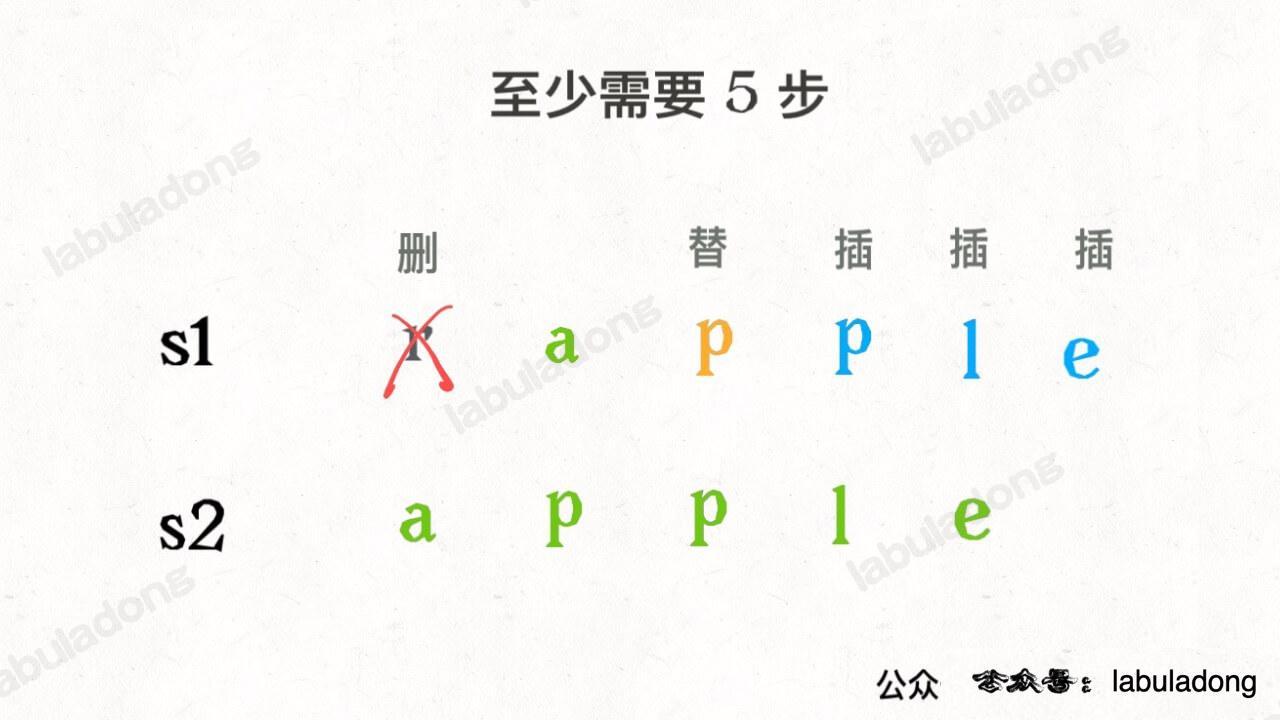
|
||||
|
||||
请记住这个 GIF 过程,这样就能算出编辑距离。关键在于如何做出正确的操作,稍后会讲。
|
||||
|
||||
根据上面的 GIF,可以发现操作不只有三个,其实还有第四个操作,就是什么都不要做(skip)。比如这个情况:
|
||||
|
||||

|
||||
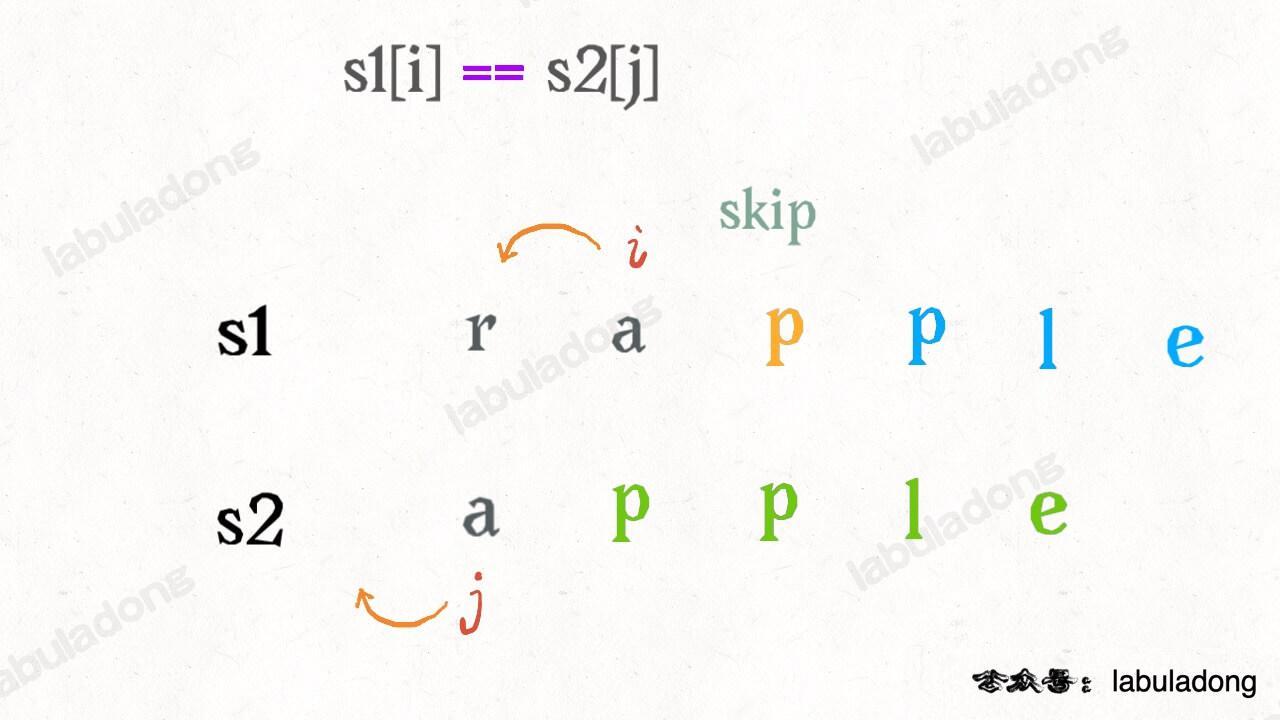
|
||||
|
||||
因为这两个字符本来就相同,为了使编辑距离最小,显然不应该对它们有任何操作,直接往前移动 `i,j` 即可。
|
||||
因为这两个字符本来就相同,为了使编辑距离最小,显然不应该对它们有任何操作,直接往前移动 `i, j` 即可。
|
||||
|
||||
还有一个很容易处理的情况,就是 `j` 走完 `s2` 时,如果 `i` 还没走完 `s1`,那么只能用删除操作把 `s1` 缩短为 `s2`。比如这个情况:
|
||||
|
||||

|
||||
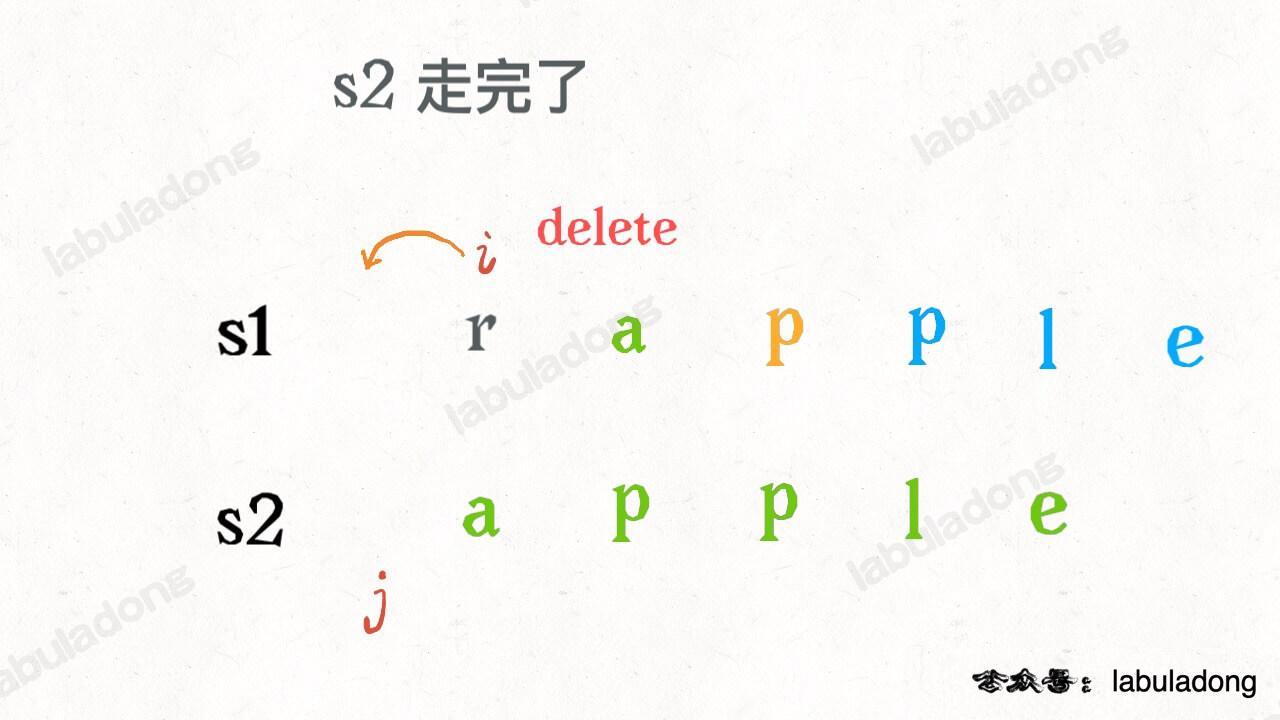
|
||||
|
||||
类似的,如果 `i` 走完 `s1` 时 `j` 还没走完了 `s2`,那就只能用插入操作把 `s2` 剩下的字符全部插入 `s1`。等会会看到,这两种情况就是算法的 **base case**。
|
||||
|
||||
|
|
@ -79,43 +94,50 @@ else:
|
|||
替换(replace)
|
||||
```
|
||||
|
||||
有这个框架,问题就已经解决了。读者也许会问,这个「三选一」到底该怎么选择呢?很简单,全试一遍,哪个操作最后得到的编辑距离最小,就选谁。这里需要递归技巧,理解需要点技巧,先看下代码:
|
||||
有这个框架,问题就已经解决了。读者也许会问,这个「三选一」到底该怎么选择呢?很简单,全试一遍,哪个操作最后得到的编辑距离最小,就选谁。这里需要递归技巧,先看下暴力解法代码:
|
||||
|
||||
```python
|
||||
def minDistance(s1, s2) -> int:
|
||||
```java
|
||||
int minDistance(String s1, String s2) {
|
||||
int m = s1.length(), n = s2.length();
|
||||
// i,j 初始化指向最后一个索引
|
||||
return dp(s1, m - 1, s2, n - 1);
|
||||
}
|
||||
|
||||
def dp(i, j):
|
||||
# base case
|
||||
if i == -1: return j + 1
|
||||
if j == -1: return i + 1
|
||||
|
||||
if s1[i] == s2[j]:
|
||||
return dp(i - 1, j - 1) # 啥都不做
|
||||
else:
|
||||
return min(
|
||||
dp(i, j - 1) + 1, # 插入
|
||||
dp(i - 1, j) + 1, # 删除
|
||||
dp(i - 1, j - 1) + 1 # 替换
|
||||
)
|
||||
|
||||
# i,j 初始化指向最后一个索引
|
||||
return dp(len(s1) - 1, len(s2) - 1)
|
||||
// 定义:返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
|
||||
int dp(String s1, int i, String s2, int j) {
|
||||
// base case
|
||||
if (i == -1) return j + 1;
|
||||
if (j == -1) return i + 1;
|
||||
|
||||
if (s1.charAt(i) == s2.charAt(j)) {
|
||||
return dp(s1, i - 1, s2, j - 1); // 啥都不做
|
||||
}
|
||||
return min(
|
||||
dp(s1, i, s2, j - 1) + 1, // 插入
|
||||
dp(s1, i - 1, s2, j) + 1, // 删除
|
||||
dp(s1, i - 1, s2, j - 1) + 1 // 替换
|
||||
);
|
||||
}
|
||||
|
||||
int min(int a, int b, int c) {
|
||||
return Math.min(a, Math.min(b, c));
|
||||
}
|
||||
```
|
||||
|
||||
下面来详细解释一下这段递归代码,base case 应该不用解释了,主要解释一下递归部分。
|
||||
|
||||
都说递归代码的可解释性很好,这是有道理的,只要理解函数的定义,就能很清楚地理解算法的逻辑。我们这里 dp(i, j) 函数的定义是这样的:
|
||||
都说递归代码的可解释性很好,这是有道理的,只要理解函数的定义,就能很清楚地理解算法的逻辑。我们这里 `dp` 函数的定义是这样的:
|
||||
|
||||
```python
|
||||
def dp(i, j) -> int
|
||||
# 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
|
||||
```java
|
||||
// 定义:返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
|
||||
int dp(String s1, int i, String s2, int j) {
|
||||
```
|
||||
|
||||
**记住这个定义**之后,先来看这段代码:
|
||||
|
||||
```python
|
||||
if s1[i] == s2[j]:
|
||||
return dp(i - 1, j - 1) # 啥都不做
|
||||
return dp(s1, i - 1, s2, j - 1); # 啥都不做
|
||||
# 解释:
|
||||
# 本来就相等,不需要任何操作
|
||||
# s1[0..i] 和 s2[0..j] 的最小编辑距离等于
|
||||
|
|
@ -123,98 +145,121 @@ if s1[i] == s2[j]:
|
|||
# 也就是说 dp(i, j) 等于 dp(i-1, j-1)
|
||||
```
|
||||
|
||||
如果 `s1[i]!=s2[j]`,就要对三个操作递归了,稍微需要点思考:
|
||||
如果 `s1[i] != s2[j]`,就要对三个操作递归了,稍微需要点思考:
|
||||
|
||||
```python
|
||||
dp(i, j - 1) + 1, # 插入
|
||||
dp(s1, i, s2, j - 1) + 1, # 插入
|
||||
# 解释:
|
||||
# 我直接在 s1[i] 插入一个和 s2[j] 一样的字符
|
||||
# 那么 s2[j] 就被匹配了,前移 j,继续跟 i 对比
|
||||
# 别忘了操作数加一
|
||||
```
|
||||
|
||||

|
||||

|
||||
|
||||
```python
|
||||
dp(i - 1, j) + 1, # 删除
|
||||
dp(s1, i - 1, s2, j) + 1, # 删除
|
||||
# 解释:
|
||||
# 我直接把 s[i] 这个字符删掉
|
||||
# 前移 i,继续跟 j 对比
|
||||
# 操作数加一
|
||||
```
|
||||
|
||||

|
||||

|
||||
|
||||
```python
|
||||
dp(i - 1, j - 1) + 1 # 替换
|
||||
dp(s1, i - 1, s2, j - 1) + 1 # 替换
|
||||
# 解释:
|
||||
# 我直接把 s1[i] 替换成 s2[j],这样它俩就匹配了
|
||||
# 同时前移 i,j 继续对比
|
||||
# 操作数加一
|
||||
```
|
||||
|
||||

|
||||

|
||||
|
||||
现在,你应该完全理解这段短小精悍的代码了。还有点小问题就是,这个解法是暴力解法,存在重叠子问题,需要用动态规划技巧来优化。
|
||||
|
||||
**怎么能一眼看出存在重叠子问题呢**?前文「动态规划之正则表达式」有提过,这里再简单提一下,需要抽象出本文算法的递归框架:
|
||||
**怎么能一眼看出存在重叠子问题呢**?前文 [动态规划之正则表达式](https://labuladong.github.io/article/fname.html?fname=动态规划之正则表达) 有提过,这里再简单提一下,需要抽象出本文算法的递归框架:
|
||||
|
||||
```python
|
||||
def dp(i, j):
|
||||
dp(i - 1, j - 1) #1
|
||||
dp(i, j - 1) #2
|
||||
dp(i - 1, j) #3
|
||||
```java
|
||||
int dp(i, j) {
|
||||
dp(i - 1, j - 1); // #1
|
||||
dp(i, j - 1); // #2
|
||||
dp(i - 1, j); // #3
|
||||
}
|
||||
```
|
||||
|
||||
对于子问题 `dp(i-1, j-1)`,如何通过原问题 `dp(i, j)` 得到呢?有不止一条路径,比如 `dp(i, j) -> #1` 和 `dp(i, j) -> #2 -> #3`。一旦发现一条重复路径,就说明存在巨量重复路径,也就是重叠子问题。
|
||||
|
||||
### 三、动态规划优化
|
||||
|
||||
对于重叠子问题呢,前文「动态规划详解」详细介绍过,优化方法无非是备忘录或者 DP table。
|
||||
对于重叠子问题呢,前文 [动态规划详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 详细介绍过,优化方法无非是备忘录或者 DP table。
|
||||
|
||||
备忘录很好加,原来的代码稍加修改即可:
|
||||
|
||||
```python
|
||||
def minDistance(s1, s2) -> int:
|
||||
|
||||
memo = dict() # 备忘录
|
||||
def dp(i, j):
|
||||
if (i, j) in memo:
|
||||
return memo[(i, j)]
|
||||
...
|
||||
|
||||
if s1[i] == s2[j]:
|
||||
memo[(i, j)] = ...
|
||||
else:
|
||||
memo[(i, j)] = ...
|
||||
return memo[(i, j)]
|
||||
```java
|
||||
// 备忘录
|
||||
int[][] memo;
|
||||
|
||||
return dp(len(s1) - 1, len(s2) - 1)
|
||||
public int minDistance(String s1, String s2) {
|
||||
int m = s1.length(), n = s2.length();
|
||||
// 备忘录初始化为特殊值,代表还未计算
|
||||
memo = new int[m][n];
|
||||
for (int[] row : memo) {
|
||||
Arrays.fill(row, -1);
|
||||
}
|
||||
return dp(s1, m - 1, s2, n - 1);
|
||||
}
|
||||
|
||||
int dp(String s1, int i, String s2, int j) {
|
||||
if (i == -1) return j + 1;
|
||||
if (j == -1) return i + 1;
|
||||
// 查备忘录,避免重叠子问题
|
||||
if (memo[i][j] != -1) {
|
||||
return memo[i][j];
|
||||
}
|
||||
// 状态转移,结果存入备忘录
|
||||
if (s1.charAt(i) == s2.charAt(j)) {
|
||||
memo[i][j] = dp(s1, i - 1, s2, j - 1);
|
||||
} else {
|
||||
memo[i][j] = min(
|
||||
dp(s1, i, s2, j - 1) + 1,
|
||||
dp(s1, i - 1, s2, j) + 1,
|
||||
dp(s1, i - 1, s2, j - 1) + 1
|
||||
);
|
||||
}
|
||||
return memo[i][j];
|
||||
}
|
||||
|
||||
int min(int a, int b, int c) {
|
||||
return Math.min(a, Math.min(b, c));
|
||||
}
|
||||
```
|
||||
|
||||
**主要说下 DP table 的解法**:
|
||||
|
||||
首先明确 dp 数组的含义,dp 数组是一个二维数组,长这样:
|
||||
首先明确 `dp` 数组的含义,`dp` 数组是一个二维数组,长这样:
|
||||
|
||||

|
||||
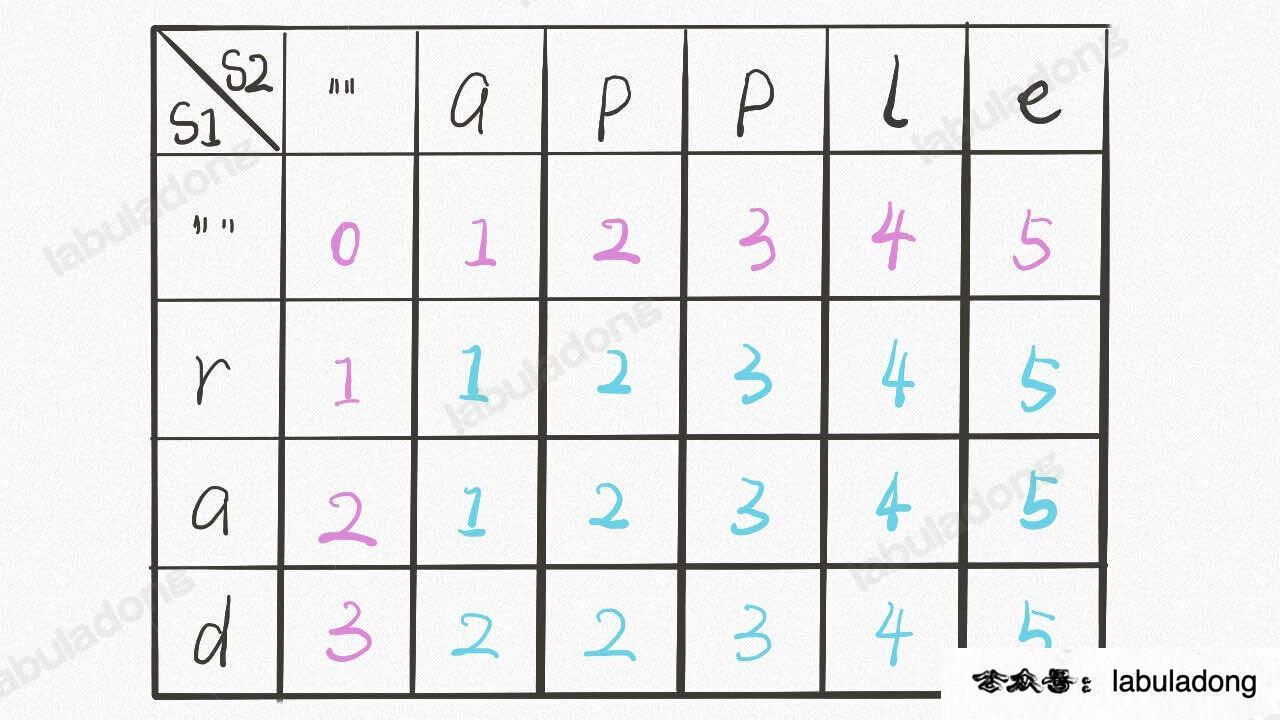
|
||||
|
||||
有了之前递归解法的铺垫,应该很容易理解。`dp[..][0]` 和 `dp[0][..]` 对应 base case,`dp[i][j]` 的含义和之前的 dp 函数类似:
|
||||
有了之前递归解法的铺垫,应该很容易理解。`dp[..][0]` 和 `dp[0][..]` 对应 base case,`dp[i][j]` 的含义和之前的 `dp` 函数类似:
|
||||
|
||||
```python
|
||||
def dp(i, j) -> int
|
||||
# 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
|
||||
```java
|
||||
int dp(String s1, int i, String s2, int j)
|
||||
// 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
|
||||
|
||||
dp[i-1][j-1]
|
||||
# 存储 s1[0..i] 和 s2[0..j] 的最小编辑距离
|
||||
// 存储 s1[0..i] 和 s2[0..j] 的最小编辑距离
|
||||
```
|
||||
|
||||
dp 函数的 base case 是 `i,j` 等于 -1,而数组索引至少是 0,所以 dp 数组会偏移一位。
|
||||
`dp` 函数的 base case 是 `i, j` 等于 -1,而数组索引至少是 0,所以 `dp` 数组会偏移一位。
|
||||
|
||||
既然 dp 数组和递归 dp 函数含义一样,也就可以直接套用之前的思路写代码,**唯一不同的是,DP table 是自底向上求解,递归解法是自顶向下求解**:
|
||||
既然 `dp` 数组和递归 `dp` 函数含义一样,也就可以直接套用之前的思路写代码,**唯一不同的是,DP table 是自底向上求解,递归解法是自顶向下求解**:
|
||||
|
||||
```java
|
||||
int minDistance(String s1, String s2) {
|
||||
int m = s1.length(), n = s2.length();
|
||||
// 定义:s1[0..i] 和 s2[0..j] 的最小编辑距离是 dp[i+1][j+1]
|
||||
int[][] dp = new int[m + 1][n + 1];
|
||||
// base case
|
||||
for (int i = 1; i <= m; i++)
|
||||
|
|
@ -222,16 +267,19 @@ int minDistance(String s1, String s2) {
|
|||
for (int j = 1; j <= n; j++)
|
||||
dp[0][j] = j;
|
||||
// 自底向上求解
|
||||
for (int i = 1; i <= m; i++)
|
||||
for (int j = 1; j <= n; j++)
|
||||
if (s1.charAt(i-1) == s2.charAt(j-1))
|
||||
for (int i = 1; i <= m; i++) {
|
||||
for (int j = 1; j <= n; j++) {
|
||||
if (s1.charAt(i-1) == s2.charAt(j-1)) {
|
||||
dp[i][j] = dp[i - 1][j - 1];
|
||||
else
|
||||
} else {
|
||||
dp[i][j] = min(
|
||||
dp[i - 1][j] + 1,
|
||||
dp[i][j - 1] + 1,
|
||||
dp[i-1][j-1] + 1
|
||||
dp[i - 1][j - 1] + 1
|
||||
);
|
||||
}
|
||||
}
|
||||
}
|
||||
// 储存着整个 s1 和 s2 的最小编辑距离
|
||||
return dp[m][n];
|
||||
}
|
||||
|
|
@ -245,7 +293,7 @@ int min(int a, int b, int c) {
|
|||
|
||||
一般来说,处理两个字符串的动态规划问题,都是按本文的思路处理,建立 DP table。为什么呢,因为易于找出状态转移的关系,比如编辑距离的 DP table:
|
||||
|
||||

|
||||
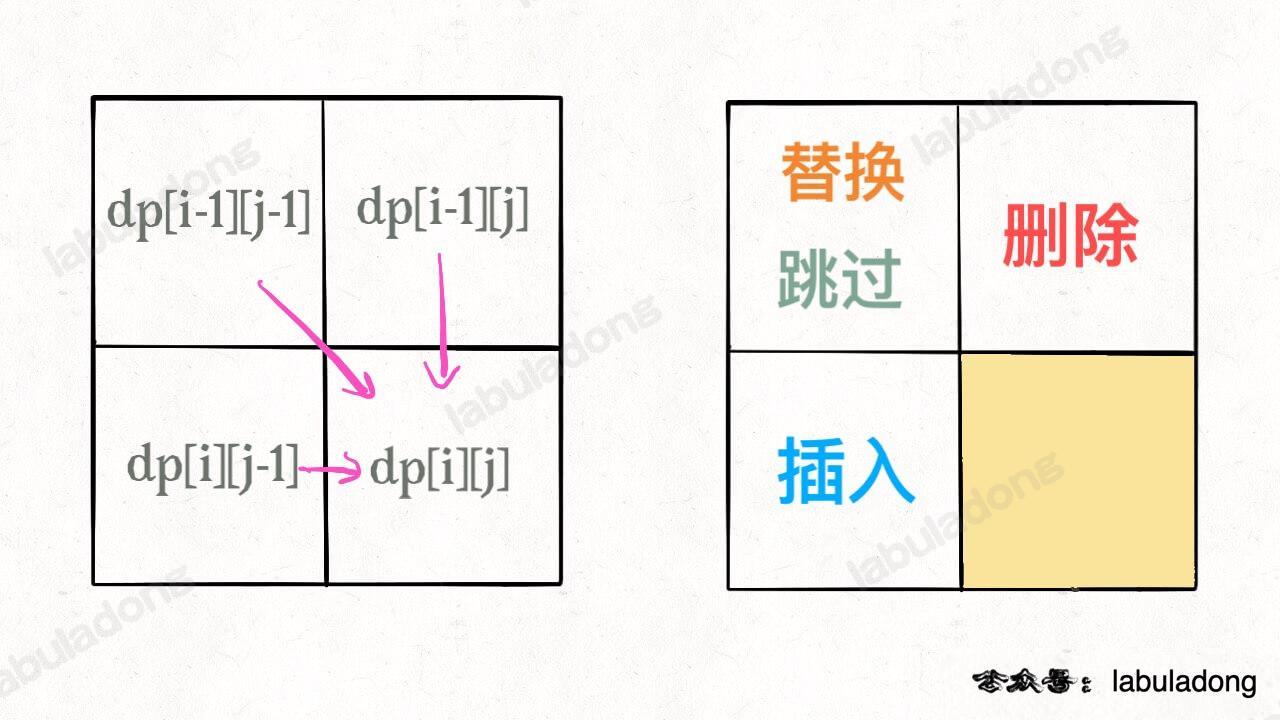
|
||||
|
||||
还有一个细节,既然每个 `dp[i][j]` 只和它附近的三个状态有关,空间复杂度是可以压缩成 `O(min(M, N))` 的(M,N 是两个字符串的长度)。不难,但是可解释性大大降低,读者可以自己尝试优化一下。
|
||||
|
||||
|
|
@ -271,23 +319,48 @@ class Node {
|
|||
|
||||
我们的最终结果不是 `dp[m][n]` 吗,这里的 `val` 存着最小编辑距离,`choice` 存着最后一个操作,比如说是插入操作,那么就可以左移一格:
|
||||
|
||||

|
||||
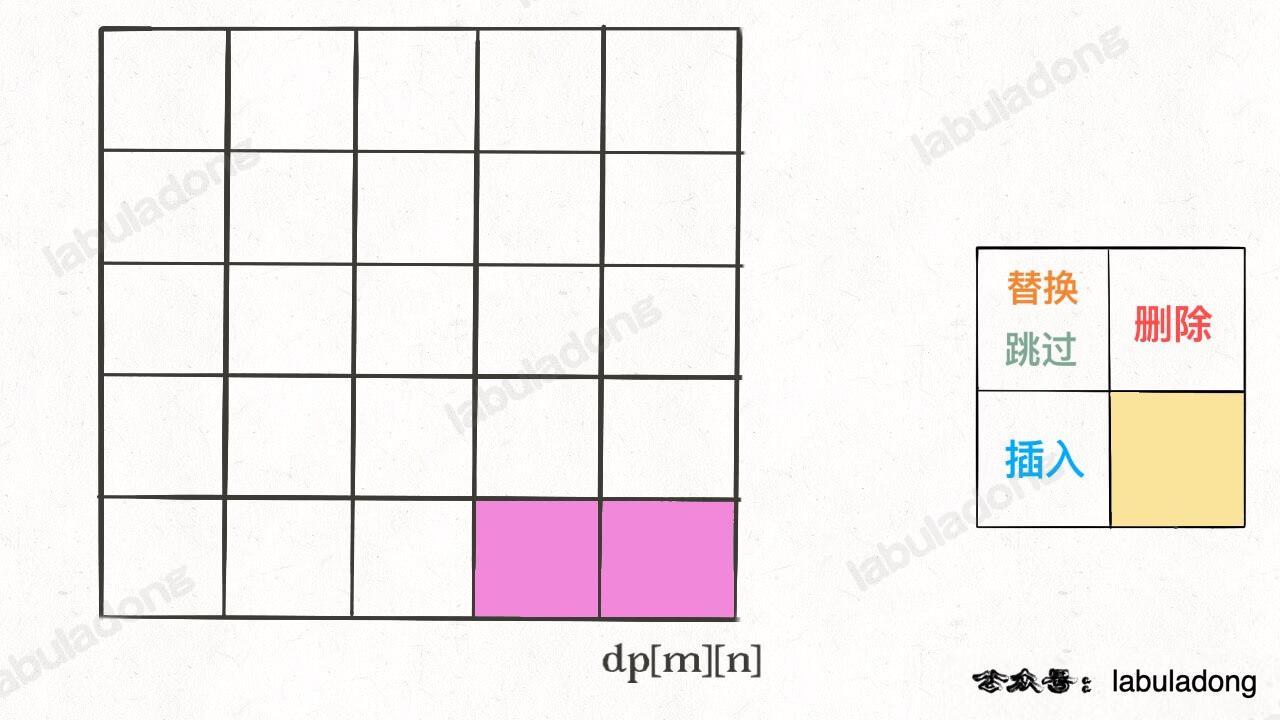
|
||||
|
||||
重复此过程,可以一步步回到起点 `dp[0][0]`,形成一条路径,按这条路径上的操作进行编辑,就是最佳方案。
|
||||
|
||||

|
||||
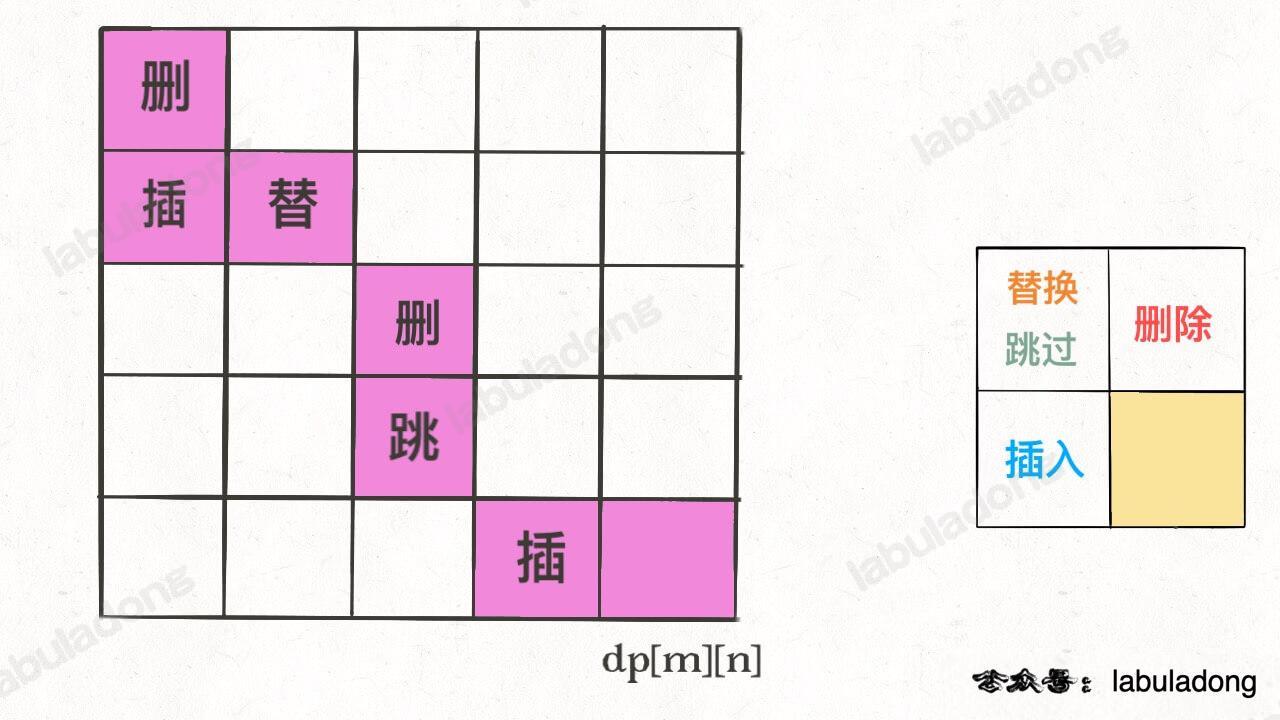
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [动态规划之子序列问题解题模板](https://labuladong.github.io/article/fname.html?fname=子序列问题模板)
|
||||
- [动态规划和回溯算法到底谁是谁爹?](https://labuladong.github.io/article/fname.html?fname=targetSum)
|
||||
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [97. Interleaving String](https://leetcode.com/problems/interleaving-string/?show=1) | [97. 交错字符串](https://leetcode.cn/problems/interleaving-string/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
### python
|
||||
|
|
|
|||
|
|
@ -1,20 +1,21 @@
|
|||
# 动态规划之背包问题
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
本文有视频版:[0-1背包问题详解](https://www.bilibili.com/video/BV15B4y1P7X7/)
|
||||
> 本文有视频版:[0-1背包问题详解](https://www.bilibili.com/video/BV15B4y1P7X7/)
|
||||
|
||||
后台天天有人问背包问题,这个问题其实不难啊,如果我们号动态规划系列的十几篇文章你都看过,借助框架,遇到背包问题可以说是手到擒来好吧。无非就是状态 + 选择,也没啥特别之处嘛。
|
||||
|
||||
|
|
@ -22,6 +23,8 @@
|
|||
|
||||
给你一个可装载重量为 `W` 的背包和 `N` 个物品,每个物品有重量和价值两个属性。其中第 `i` 个物品的重量为 `wt[i]`,价值为 `val[i]`,现在让你用这个背包装物品,最多能装的价值是多少?
|
||||
|
||||

|
||||
|
||||
举个简单的例子,输入如下:
|
||||
|
||||
```
|
||||
|
|
@ -34,11 +37,11 @@ val = [4, 2, 3]
|
|||
|
||||
题目就是这么简单,一个典型的动态规划问题。这个题目中的物品不可以分割,要么装进包里,要么不装,不能说切成两块装一半。这就是 0-1 背包这个名词的来历。
|
||||
|
||||
解决这个问题没有什么排序之类巧妙的方法,只能穷举所有可能,根据我们 [动态规划详解](https://labuladong.gitee.io/algo/) 中的套路,直接走流程就行了。
|
||||
解决这个问题没有什么排序之类巧妙的方法,只能穷举所有可能,根据我们 [动态规划详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 中的套路,直接走流程就行了。
|
||||
|
||||
### 动规标准套路
|
||||
|
||||
看来我得每篇动态规划文章都得重复一遍套路,历史文章中的动态规划问题都是按照下面的套路来的。
|
||||
看来每篇动态规划文章都得重复一遍套路,历史文章中的动态规划问题都是按照下面的套路来的。
|
||||
|
||||
**第一步要明确两点,「状态」和「选择」**。
|
||||
|
||||
|
|
@ -55,7 +58,7 @@ for 状态1 in 状态1的所有取值:
|
|||
dp[状态1][状态2][...] = 择优(选择1,选择2...)
|
||||
```
|
||||
|
||||
PS:此框架出自历史文章 [团灭 LeetCode 股票问题](https://labuladong.gitee.io/algo/)。
|
||||
> PS:此框架出自历史文章 [团灭 LeetCode 股票问题](https://labuladong.github.io/article/fname.html?fname=团灭股票问题)。
|
||||
|
||||
**第二步要明确 `dp` 数组的定义**。
|
||||
|
||||
|
|
@ -65,7 +68,7 @@ PS:此框架出自历史文章 [团灭 LeetCode 股票问题](https://labulado
|
|||
|
||||
比如说,如果 `dp[3][5] = 6`,其含义为:对于给定的一系列物品中,若只对前 3 个物品进行选择,当背包容量为 5 时,最多可以装下的价值为 6。
|
||||
|
||||
PS:为什么要这么定义?便于状态转移,或者说这就是套路,记下来就行了。建议看一下我们的动态规划系列文章,几种套路都被扒得清清楚楚了。
|
||||
> PS:为什么要这么定义?便于状态转移,或者说这就是套路,记下来就行了。建议看一下我们的动态规划系列文章,几种套路都被扒得清清楚楚了。
|
||||
|
||||
根据这个定义,我们想求的最终答案就是 `dp[N][W]`。base case 就是 `dp[0][..] = dp[..][0] = 0`,因为没有物品或者背包没有空间的时候,能装的最大价值就是 0。
|
||||
|
||||
|
|
@ -93,15 +96,15 @@ return dp[N][W]
|
|||
|
||||
先重申一下刚才我们的 `dp` 数组的定义:
|
||||
|
||||
`dp[i][w]` 表示:对于前 `i` 个物品,当前背包的容量为 `w` 时,这种情况下可以装下的最大价值是 `dp[i][w]`。
|
||||
`dp[i][w]` 表示:对于前 `i` 个物品(从 1 开始计数),当前背包的容量为 `w` 时,这种情况下可以装下的最大价值是 `dp[i][w]`。
|
||||
|
||||
**如果你没有把这第 `i` 个物品装入背包**,那么很显然,最大价值 `dp[i][w]` 应该等于 `dp[i-1][w]`,继承之前的结果。
|
||||
|
||||
**如果你把这第 `i` 个物品装入了背包**,那么 `dp[i][w]` 应该等于 `dp[i-1][w - wt[i-1]] + val[i-1]`。
|
||||
**如果你把这第 `i` 个物品装入了背包**,那么 `dp[i][w]` 应该等于 `val[i-1] + dp[i-1][w - wt[i-1]]`。
|
||||
|
||||
首先,由于 `i` 是从 1 开始的,所以 `val` 和 `wt` 的索引是 `i-1` 时表示第 `i` 个物品的价值和重量。
|
||||
首先,由于数组索引从 0 开始,而我们定义中的 `i` 是从 1 开始计数的,所以 `val[i-1]` 和 `wt[i-1]` 表示第 `i` 个物品的价值和重量。
|
||||
|
||||
而 `dp[i-1][w - wt[i-1]]` 也很好理解:你如果装了第 `i` 个物品,就要寻求剩余重量 `w - wt[i-1]` 限制下的最大价值,加上第 `i` 个物品的价值 `val[i-1]`。
|
||||
你如果选择将第 `i` 个物品装进背包,那么第 `i` 个物品的价值 `val[i-1]` 肯定就到手了,接下来你就要在剩余容量 `w - wt[i-1]` 的限制下,在前 `i - 1` 个物品中挑选,求最大价值,即 `dp[i-1][w - wt[i-1]]`。
|
||||
|
||||
综上就是两种选择,我们都已经分析完毕,也就是写出来了状态转移方程,可以进一步细化代码:
|
||||
|
||||
|
|
@ -117,21 +120,23 @@ return dp[N][W]
|
|||
|
||||
**最后一步,把伪码翻译成代码,处理一些边界情况**。
|
||||
|
||||
我用 C++ 写的代码,把上面的思路完全翻译了一遍,并且处理了 `w - wt[i-1]` 可能小于 0 导致数组索引越界的问题:
|
||||
我用 Java 写的代码,把上面的思路完全翻译了一遍,并且处理了 `w - wt[i-1]` 可能小于 0 导致数组索引越界的问题:
|
||||
|
||||
```cpp
|
||||
int knapsack(int W, int N, vector<int>& wt, vector<int>& val) {
|
||||
```java
|
||||
int knapsack(int W, int N, int[] wt, int[] val) {
|
||||
// base case 已初始化
|
||||
vector<vector<int>> dp(N + 1, vector<int>(W + 1, 0));
|
||||
int[][] dp = new int[N + 1][W + 1];
|
||||
for (int i = 1; i <= N; i++) {
|
||||
for (int w = 1; w <= W; w++) {
|
||||
if (w - wt[i-1] < 0) {
|
||||
if (w - wt[i - 1] < 0) {
|
||||
// 这种情况下只能选择不装入背包
|
||||
dp[i][w] = dp[i - 1][w];
|
||||
} else {
|
||||
// 装入或者不装入背包,择优
|
||||
dp[i][w] = max(dp[i - 1][w - wt[i-1]] + val[i-1],
|
||||
dp[i - 1][w]);
|
||||
dp[i][w] = Math.max(
|
||||
dp[i - 1][w - wt[i-1]] + val[i-1],
|
||||
dp[i - 1][w]
|
||||
);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
|
@ -142,17 +147,30 @@ int knapsack(int W, int N, vector<int>& wt, vector<int>& val) {
|
|||
|
||||
至此,背包问题就解决了,相比而言,我觉得这是比较简单的动态规划问题,因为状态转移的推导比较自然,基本上你明确了 `dp` 数组的定义,就可以理所当然地确定状态转移了。
|
||||
|
||||
接下来请阅读:
|
||||
接下来可阅读:
|
||||
|
||||
* [完全背包问题之零钱兑换](https://labuladong.github.io/article/fname.html?fname=背包零钱)
|
||||
* [背包问题变体之子集分割](https://labuladong.github.io/article/fname.html?fname=背包子集)
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [扫描线技巧:安排会议室](https://labuladong.github.io/article/fname.html?fname=安排会议室)
|
||||
- [经典动态规划:子集背包问题](https://labuladong.github.io/article/fname.html?fname=背包子集)
|
||||
- [经典动态规划:完全背包问题](https://labuladong.github.io/article/fname.html?fname=背包零钱)
|
||||
- [经典回溯算法:集合划分问题](https://labuladong.github.io/article/fname.html?fname=集合划分)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
* [背包问题变体之子集分割](https://labuladong.gitee.io/algo/)
|
||||
* [完全背包问题之零钱兑换](https://labuladong.gitee.io/algo/)
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||

|
||||
|
|
|
|||
|
|
@ -1,22 +1,24 @@
|
|||
# 贪心算法之区间调度问题
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[435. 无重叠区间](https://leetcode-cn.com/problems/non-overlapping-intervals/)
|
||||
|
||||
[452.用最少数量的箭引爆气球](https://leetcode-cn.com/problems/minimum-number-of-arrows-to-burst-balloons)
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [435. Non-overlapping Intervals](https://leetcode.com/problems/non-overlapping-intervals/) | [435. 无重叠区间](https://leetcode.cn/problems/non-overlapping-intervals/) | 🟠
|
||||
| [452. Minimum Number of Arrows to Burst Balloons](https://leetcode.com/problems/minimum-number-of-arrows-to-burst-balloons/) | [452. 用最少数量的箭引爆气球](https://leetcode.cn/problems/minimum-number-of-arrows-to-burst-balloons/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -28,19 +30,21 @@
|
|||
|
||||
比如你面前放着 100 张人民币,你只能拿十张,怎么才能拿最多的面额?显然每次选择剩下钞票中面值最大的一张,最后你的选择一定是最优的。
|
||||
|
||||
然而,大部分问题明显不具有贪心选择性质。比如打斗地主,对手出对儿三,按照贪心策略,你应该出尽可能小的牌刚好压制住对方,但现实情况我们甚至可能会出王炸。这种情况就不能用贪心算法,而得使用动态规划解决,参见前文「动态规划解决博弈问题」。
|
||||
然而,大部分问题明显不具有贪心选择性质。比如打斗地主,对手出对儿三,按照贪心策略,你应该出尽可能小的牌刚好压制住对方,但现实情况我们甚至可能会出王炸。这种情况就不能用贪心算法,而得使用动态规划解决,参见前文 [动态规划解决博弈问题](https://labuladong.github.io/article/fname.html?fname=动态规划之博弈问题)。
|
||||
|
||||
### 一、问题概述
|
||||
|
||||
言归正传,本文解决一个很经典的贪心算法问题 Interval Scheduling(区间调度问题)。给你很多形如 `[start, end]` 的闭区间,请你设计一个算法,**算出这些区间中最多有几个互不相交的区间**。
|
||||
言归正传,本文解决一个很经典的贪心算法问题 Interval Scheduling(区间调度问题),也就是力扣第 435 题「无重叠区间」:
|
||||
|
||||
给你很多形如 `[start, end]` 的闭区间,请你设计一个算法,**算出这些区间中最多有几个互不相交的区间**。
|
||||
|
||||
```java
|
||||
int intervalSchedule(int[][] intvs) {}
|
||||
int intervalSchedule(int[][] intvs);
|
||||
```
|
||||
|
||||
举个例子,`intvs = [[1,3], [2,4], [3,6]]`,这些区间最多有 2 个区间互不相交,即 `[[1,3], [3,6]]`,你的算法应该返回 2。注意边界相同并不算相交。
|
||||
|
||||
这个问题在生活中的应用广泛,比如你今天有好几个活动,每个活动都可以用区间 `[start, end]` 表示开始和结束的时间,请问你今天**最多能参加几个活动呢?**显然你一个人不能同时参加两个活动,所以说这个问题就是求这些时间区间的最大不相交子集。
|
||||
这个问题在生活中的应用广泛,比如你今天有好几个活动,每个活动都可以用区间 `[start, end]` 表示开始和结束的时间,请问你今天**最多能参加几个活动呢**?显然你一个人不能同时参加两个活动,所以说这个问题就是求这些时间区间的最大不相交子集。
|
||||
|
||||
### 二、贪心解法
|
||||
|
||||
|
|
@ -50,19 +54,21 @@ int intervalSchedule(int[][] intvs) {}
|
|||
|
||||
正确的思路其实很简单,可以分为以下三步:
|
||||
|
||||
1. 从区间集合 intvs 中选择一个区间 x,这个 x 是在当前所有区间中**结束最早的**(end 最小)。
|
||||
2. 把所有与 x 区间相交的区间从区间集合 intvs 中删除。
|
||||
3. 重复步骤 1 和 2,直到 intvs 为空为止。之前选出的那些 x 就是最大不相交子集。
|
||||
1、从区间集合 `intvs` 中选择一个区间 `x`,这个 `x` 是在当前所有区间中**结束最早的**(`end` 最小)。
|
||||
|
||||
把这个思路实现成算法的话,可以按每个区间的 `end` 数值升序排序,因为这样处理之后实现步骤 1 和步骤 2 都方便很多:
|
||||
2、把所有与 `x` 区间相交的区间从区间集合 `intvs` 中删除。
|
||||
|
||||

|
||||
3、重复步骤 1 和 2,直到 `intvs` 为空为止。之前选出的那些 `x` 就是最大不相交子集。
|
||||
|
||||
现在来实现算法,对于步骤 1,由于我们预先按照 `end` 排了序,所以选择 x 是很容易的。关键在于,如何去除与 x 相交的区间,选择下一轮循环的 x 呢?
|
||||
把这个思路实现成算法的话,可以按每个区间的 `end` 数值升序排序,因为这样处理之后实现步骤 1 和步骤 2 都方便很多,如下 GIF 所示:
|
||||
|
||||
**由于我们事先排了序**,不难发现所有与 x 相交的区间必然会与 x 的 `end` 相交;如果一个区间不想与 x 的 `end` 相交,它的 `start` 必须要大于(或等于)x 的 `end`:
|
||||
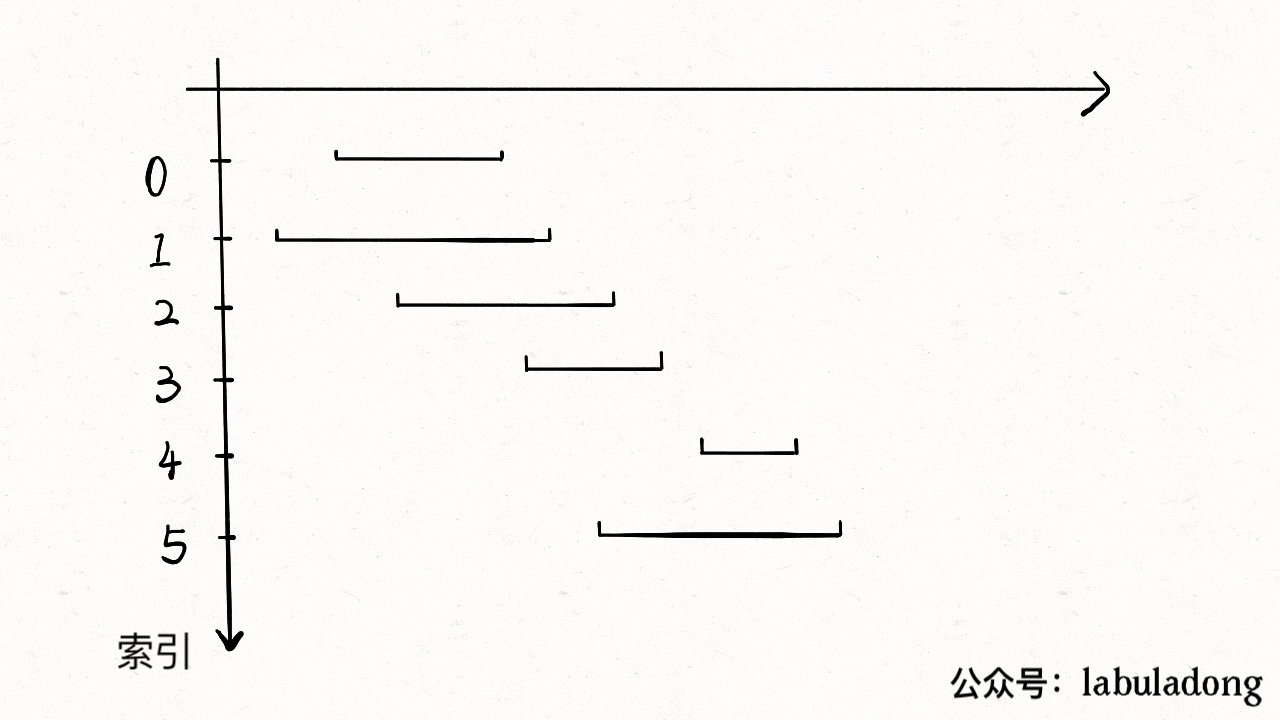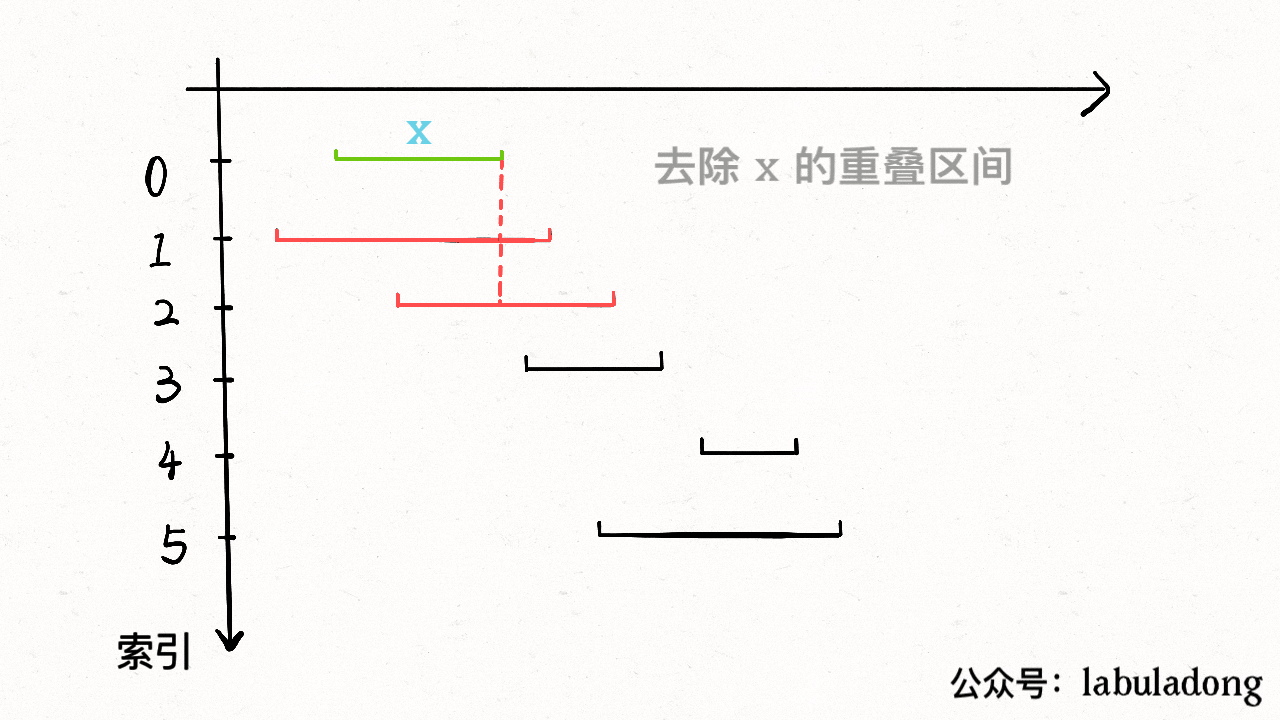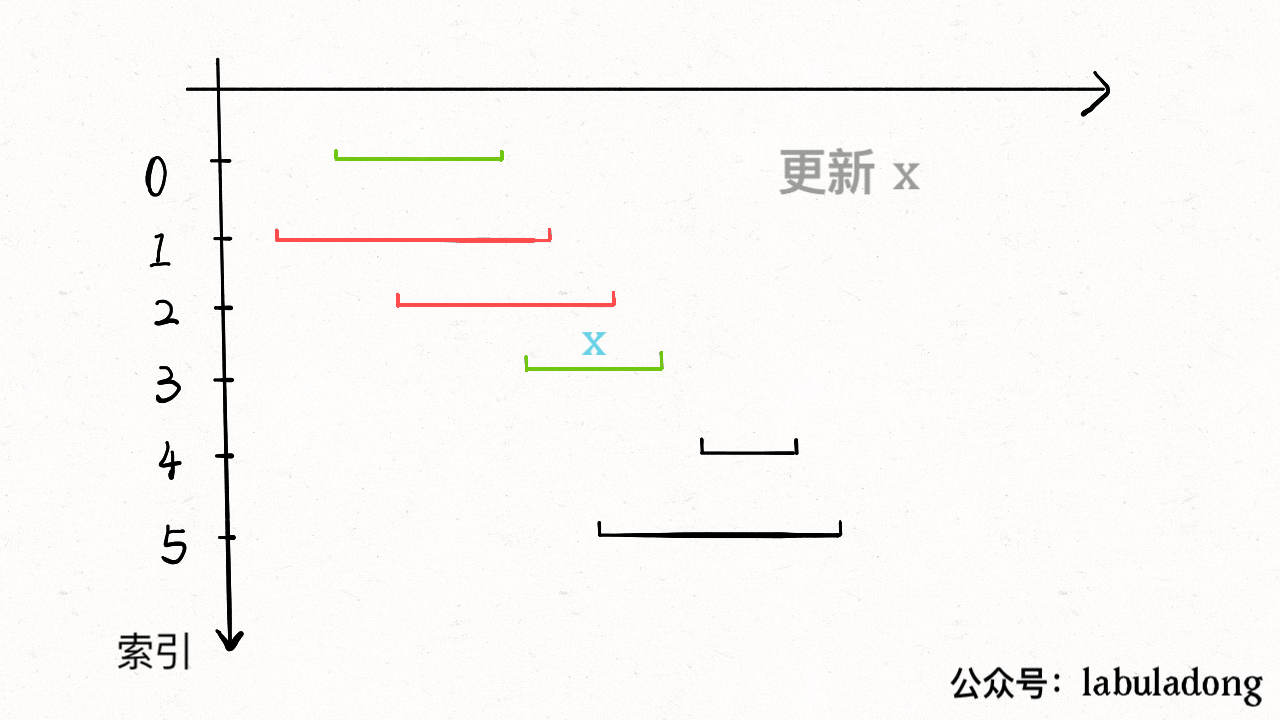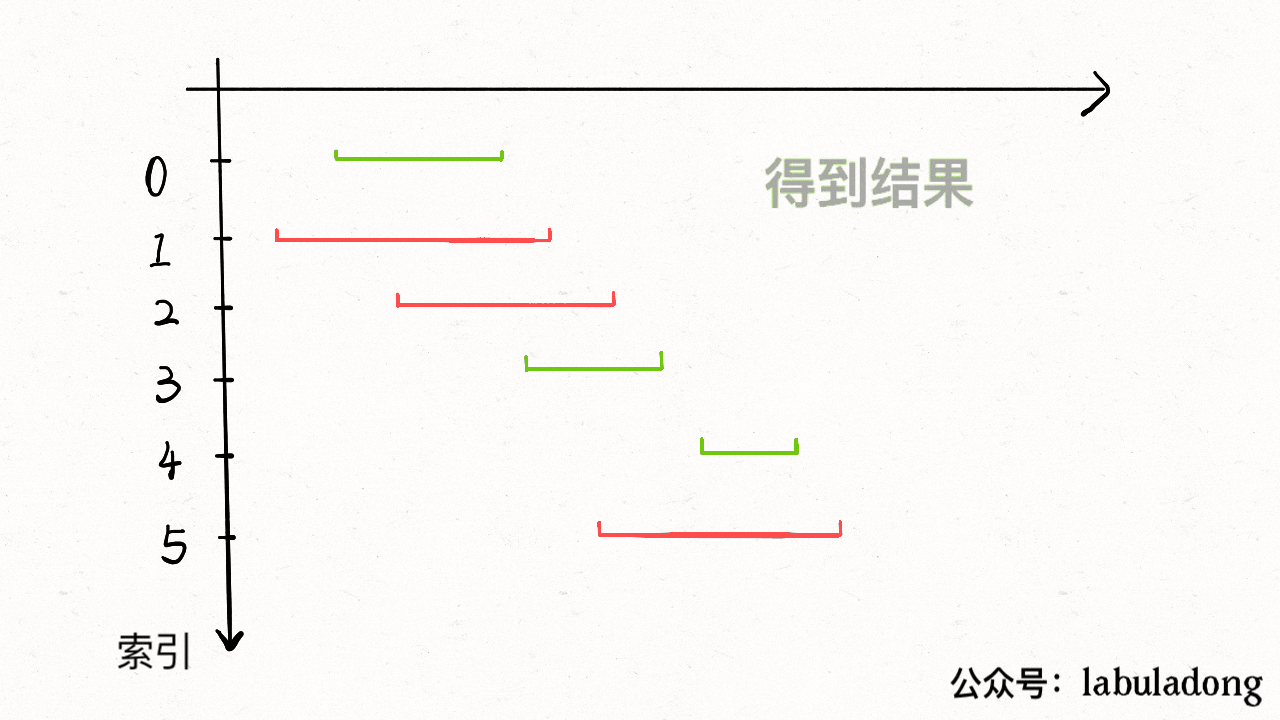
|
||||
|
||||

|
||||
现在来实现算法,对于步骤 1,由于我们预先按照 `end` 排了序,所以选择 `x` 是很容易的。关键在于,如何去除与 `x` 相交的区间,选择下一轮循环的 `x` 呢?
|
||||
|
||||
**由于我们事先排了序**,不难发现所有与 `x` 相交的区间必然会与 `x` 的 `end` 相交;如果一个区间不想与 `x` 的 `end` 相交,它的 `start` 必须要大于(或等于)`x` 的 `end`:
|
||||
|
||||
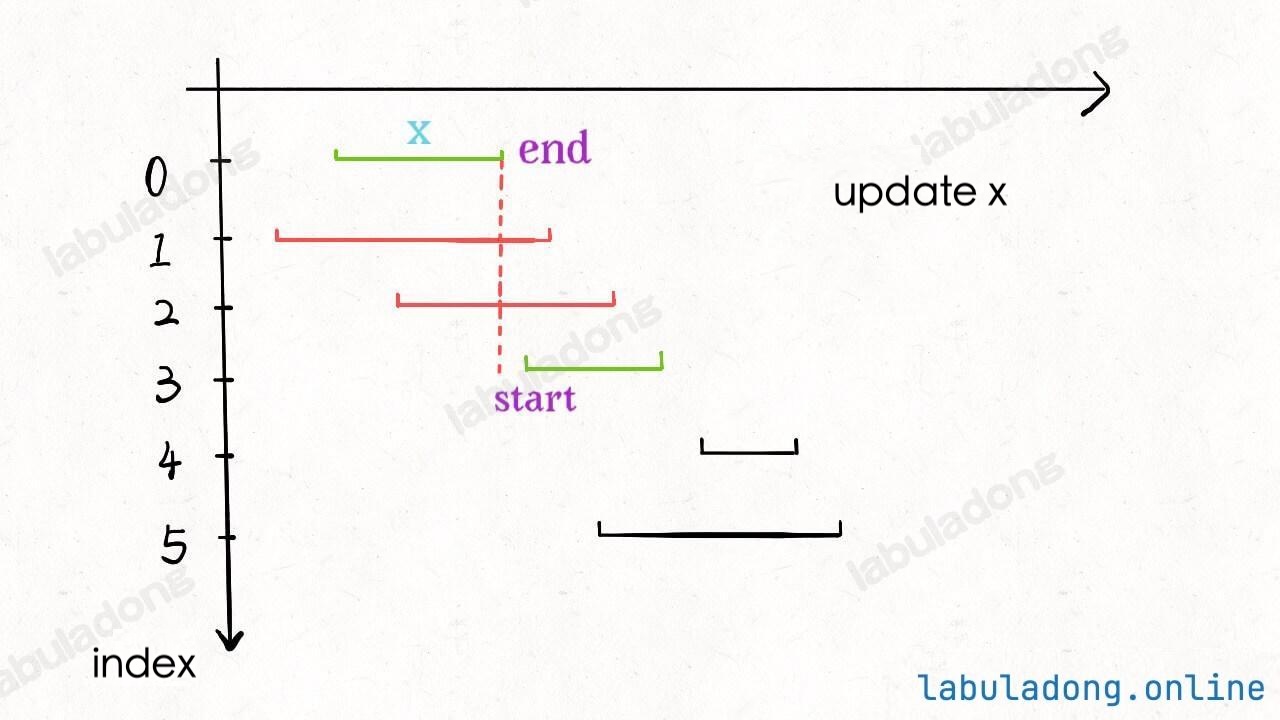
|
||||
|
||||
看下代码:
|
||||
|
||||
|
|
@ -71,14 +77,8 @@ public int intervalSchedule(int[][] intvs) {
|
|||
if (intvs.length == 0) return 0;
|
||||
// 按 end 升序排序
|
||||
Arrays.sort(intvs, new Comparator<int[]>() {
|
||||
@Override
|
||||
public int compare(int[] a, int[] b) {
|
||||
// 这里不能使用 a[1] - b[1],要注意溢出问题
|
||||
if (a[1] < b[1])
|
||||
return -1;
|
||||
else if (a[1] > b[1])
|
||||
return 1;
|
||||
else return 0;
|
||||
return a[1] - b[1];
|
||||
}
|
||||
});
|
||||
// 至少有一个区间不相交
|
||||
|
|
@ -99,11 +99,19 @@ public int intervalSchedule(int[][] intvs) {
|
|||
|
||||
### 三、应用举例
|
||||
|
||||
下面举例几道 LeetCode 题目应用一下区间调度算法。
|
||||
下面再举例几道具体的题目应用一下区间调度算法。
|
||||
|
||||
第 435 题,无重叠区间:
|
||||
首先是力扣第 435 题「无重叠区间」问题:
|
||||
|
||||

|
||||
输入一个区间的集合,请你计算,要想使其中的区间都互不重叠,至少需要移除几个区间?函数签名如下:
|
||||
|
||||
```java
|
||||
int eraseOverlapIntervals(int[][] intvs);
|
||||
```
|
||||
|
||||
其中,可以假设输入的区间的终点总是大于起点,另外边界相等的区间只算接触,但并不算相互重叠。
|
||||
|
||||
比如说输入是 `intvs = [[1,2],[2,3],[3,4],[1,3]]`,算法返回 1,因为只要移除 `[1,3]` 后,剩下的区间就没有重叠了。
|
||||
|
||||
我们已经会求最多有几个区间不会重叠了,那么剩下的不就是至少需要去除的区间吗?
|
||||
|
||||
|
|
@ -114,17 +122,25 @@ int eraseOverlapIntervals(int[][] intervals) {
|
|||
}
|
||||
```
|
||||
|
||||
第 452 题,用最少的箭头射爆气球:
|
||||
再说说力扣第 452 题「用最少的箭头射爆气球」,我来描述一下题目:
|
||||
|
||||

|
||||
假设在二维平面上有很多圆形的气球,这些圆形投影到 x 轴上会形成一个个区间对吧。那么给你输入这些区间,你沿着 x 轴前进,可以垂直向上射箭,请问你至少要射几箭才能把这些气球全部射爆呢?
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int findMinArrowShots(int[][] intvs);
|
||||
```
|
||||
|
||||
比如说输入为 `[[10,16],[2,8],[1,6],[7,12]]`,算法应该返回 2,因为我们可以在 `x` 为 6 的地方射一箭,射爆 `[2,8]` 和 `[1,6]` 两个气球,然后在 `x` 为 10,11 或 12 的地方射一箭,射爆 `[10,16]` 和 `[7,12]` 两个气球。
|
||||
|
||||
其实稍微思考一下,这个问题和区间调度算法一模一样!如果最多有 `n` 个不重叠的区间,那么就至少需要 `n` 个箭头穿透所有区间:
|
||||
|
||||

|
||||
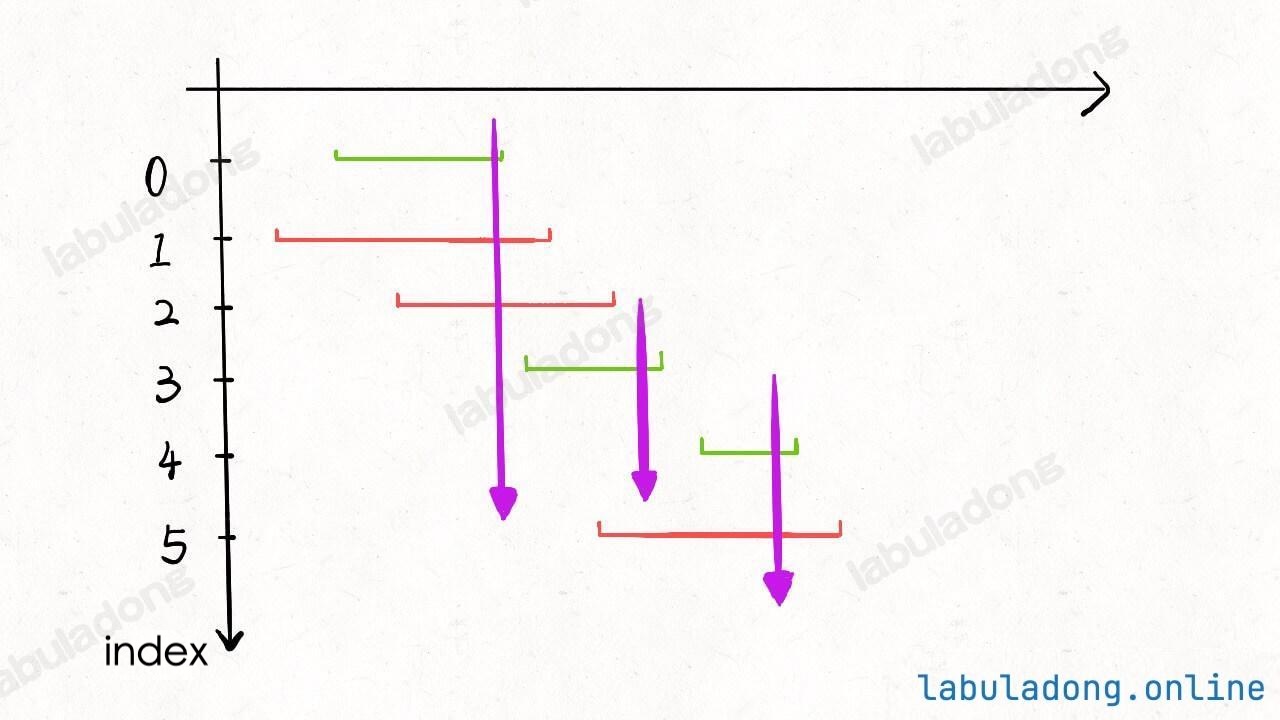
|
||||
|
||||
只是有一点不一样,在 `intervalSchedule` 算法中,如果两个区间的边界触碰,不算重叠;而按照这道题目的描述,箭头如果碰到气球的边界气球也会爆炸,所以说相当于区间的边界触碰也算重叠:
|
||||
|
||||

|
||||
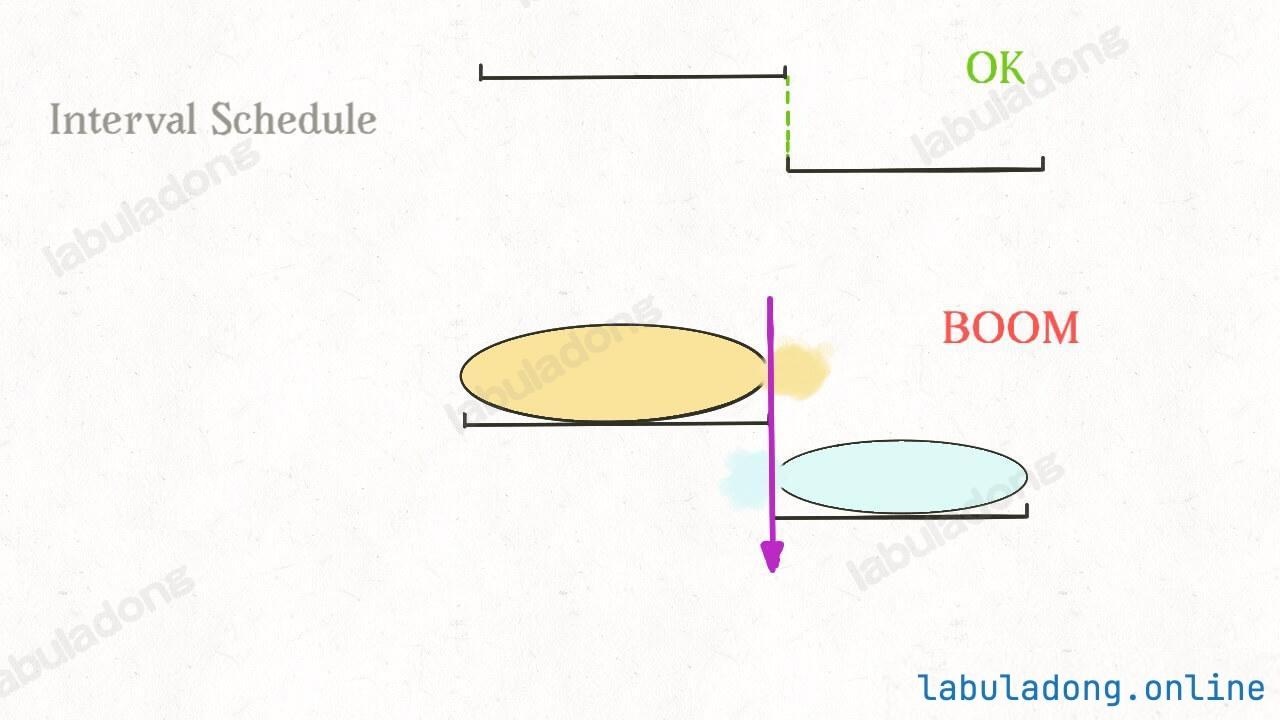
|
||||
|
||||
所以只要将之前的算法稍作修改,就是这道题目的答案:
|
||||
|
||||
|
|
@ -144,17 +160,35 @@ int findMinArrowShots(int[][] intvs) {
|
|||
}
|
||||
```
|
||||
|
||||
接下来可阅读:
|
||||
|
||||
* [贪心算法之跳跃游戏](https://labuladong.github.io/article/fname.html?fname=跳跃游戏)
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [一个方法解决三道区间问题](https://labuladong.github.io/article/fname.html?fname=区间问题合集)
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [剪视频剪出一个贪心算法](https://labuladong.github.io/article/fname.html?fname=剪视频)
|
||||
- [如何运用贪心思想玩跳跃游戏](https://labuladong.github.io/article/fname.html?fname=跳跃游戏)
|
||||
- [扫描线技巧:安排会议室](https://labuladong.github.io/article/fname.html?fname=安排会议室)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[435. 无重叠区间](https://leetcode-cn.com/problems/non-overlapping-intervals/)
|
||||
|
|
|
|||
|
|
@ -1,332 +0,0 @@
|
|||
# 经典动态规划问题:高楼扔鸡蛋(进阶)
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[887.鸡蛋掉落](https://leetcode-cn.com/problems/super-egg-drop/)
|
||||
|
||||
**-----------**
|
||||
|
||||
上篇文章聊了高楼扔鸡蛋问题,讲了一种效率不是很高,但是较为容易理解的动态规划解法。后台很多读者问如何更高效地解决这个问题,今天就谈两种思路,来优化一下这个问题,分别是二分查找优化和重新定义状态转移。
|
||||
|
||||
如果还不知道高楼扔鸡蛋问题的读者可以看下「经典动态规划:高楼扔鸡蛋」,那篇文章详解了题目的含义和基本的动态规划解题思路,请确保理解前文,因为今天的优化都是基于这个基本解法的。
|
||||
|
||||
二分搜索的优化思路也许是我们可以尽力尝试写出的,而修改状态转移的解法可能是不容易想到的,可以借此见识一下动态规划算法设计的玄妙,当做思维拓展。
|
||||
|
||||
### 二分搜索优化
|
||||
|
||||
之前提到过这个解法,核心是因为状态转移方程的单调性,这里可以具体展开看看。
|
||||
|
||||
首先简述一下原始动态规划的思路:
|
||||
|
||||
1、暴力穷举尝试在所有楼层 `1 <= i <= N` 扔鸡蛋,每次选择尝试次数**最少**的那一层;
|
||||
|
||||
2、每次扔鸡蛋有两种可能,要么碎,要么没碎;
|
||||
|
||||
3、如果鸡蛋碎了,`F` 应该在第 `i` 层下面,否则,`F` 应该在第 `i` 层上面;
|
||||
|
||||
4、鸡蛋是碎了还是没碎,取决于哪种情况下尝试次数**更多**,因为我们想求的是最坏情况下的结果。
|
||||
|
||||
核心的状态转移代码是这段:
|
||||
|
||||
```python
|
||||
# 当前状态为 K 个鸡蛋,面对 N 层楼
|
||||
# 返回这个状态下的最优结果
|
||||
def dp(K, N):
|
||||
for 1 <= i <= N:
|
||||
# 最坏情况下的最少扔鸡蛋次数
|
||||
res = min(res,
|
||||
max(
|
||||
dp(K - 1, i - 1), # 碎
|
||||
dp(K, N - i) # 没碎
|
||||
) + 1 # 在第 i 楼扔了一次
|
||||
)
|
||||
return res
|
||||
```
|
||||
|
||||
这个 for 循环就是下面这个状态转移方程的具体代码实现:
|
||||
|
||||
<!-- $$ dp(K, N) = \min_{0 <= i <= N}\{\max\{dp(K - 1, i - 1), dp(K, N - i)\} + 1\}$$ -->
|
||||
|
||||

|
||||
|
||||
如果能够理解这个状态转移方程,那么就很容易理解二分查找的优化思路。
|
||||
|
||||
首先我们根据 `dp(K, N)` 数组的定义(有 `K` 个鸡蛋面对 `N` 层楼,最少需要扔几次),**很容易知道 `K` 固定时,这个函数随着 `N` 的增加一定是单调递增的**,无论你策略多聪明,楼层增加测试次数一定要增加。
|
||||
|
||||
那么注意 `dp(K - 1, i - 1)` 和 `dp(K, N - i)` 这两个函数,其中 `i` 是从 1 到 `N` 单增的,如果我们固定 `K` 和 `N`,**把这两个函数看做关于 `i` 的函数,前者随着 `i` 的增加应该也是单调递增的,而后者随着 `i` 的增加应该是单调递减的**:
|
||||
|
||||

|
||||
|
||||
这时候求二者的较大值,再求这些最大值之中的最小值,其实就是求这两条直线交点,也就是红色折线的最低点嘛。
|
||||
|
||||
我们前文「二分查找只能用来查找元素吗」讲过,二分查找的运用很广泛,形如下面这种形式的 for 循环代码:
|
||||
|
||||
```java
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (isOK(i))
|
||||
return i;
|
||||
}
|
||||
```
|
||||
|
||||
都很有可能可以运用二分查找来优化线性搜索的复杂度,回顾这两个 `dp` 函数的曲线,我们要找的最低点其实就是这种情况:
|
||||
|
||||
```java
|
||||
for (int i = 1; i <= N; i++) {
|
||||
if (dp(K - 1, i - 1) == dp(K, N - i))
|
||||
return dp(K, N - i);
|
||||
}
|
||||
```
|
||||
|
||||
熟悉二分搜索的同学肯定敏感地想到了,这不就是相当于求 Valley(山谷)值嘛,可以用二分查找来快速寻找这个点的,直接看代码吧,整体的思路还是一样,只是加快了搜索速度:
|
||||
|
||||
```python
|
||||
def superEggDrop(self, K: int, N: int) -> int:
|
||||
|
||||
memo = dict()
|
||||
def dp(K, N):
|
||||
if K == 1: return N
|
||||
if N == 0: return 0
|
||||
if (K, N) in memo:
|
||||
return memo[(K, N)]
|
||||
|
||||
# for 1 <= i <= N:
|
||||
# res = min(res,
|
||||
# max(
|
||||
# dp(K - 1, i - 1),
|
||||
# dp(K, N - i)
|
||||
# ) + 1
|
||||
# )
|
||||
|
||||
res = float('INF')
|
||||
# 用二分搜索代替线性搜索
|
||||
lo, hi = 1, N
|
||||
while lo <= hi:
|
||||
mid = (lo + hi) // 2
|
||||
broken = dp(K - 1, mid - 1) # 碎
|
||||
not_broken = dp(K, N - mid) # 没碎
|
||||
# res = min(max(碎,没碎) + 1)
|
||||
if broken > not_broken:
|
||||
hi = mid - 1
|
||||
res = min(res, broken + 1)
|
||||
else:
|
||||
lo = mid + 1
|
||||
res = min(res, not_broken + 1)
|
||||
|
||||
memo[(K, N)] = res
|
||||
return res
|
||||
|
||||
return dp(K, N)
|
||||
```
|
||||
|
||||
这个算法的时间复杂度是多少呢?**动态规划算法的时间复杂度就是子问题个数 × 函数本身的复杂度**。
|
||||
|
||||
函数本身的复杂度就是忽略递归部分的复杂度,这里 `dp` 函数中用了一个二分搜索,所以函数本身的复杂度是 O(logN)。
|
||||
|
||||
子问题个数也就是不同状态组合的总数,显然是两个状态的乘积,也就是 O(KN)。
|
||||
|
||||
所以算法的总时间复杂度是 O(K\*N\*logN), 空间复杂度 O(KN)。效率上比之前的算法 O(KN^2) 要高效一些。
|
||||
|
||||
### 重新定义状态转移
|
||||
|
||||
前文「不同定义有不同解法」就提过,找动态规划的状态转移本就是见仁见智,比较玄学的事情,不同的状态定义可以衍生出不同的解法,其解法和复杂程度都可能有巨大差异。这里就是一个很好的例子。
|
||||
|
||||
再回顾一下我们之前定义的 `dp` 数组含义:
|
||||
|
||||
```python
|
||||
def dp(k, n) -> int
|
||||
# 当前状态为 k 个鸡蛋,面对 n 层楼
|
||||
# 返回这个状态下最少的扔鸡蛋次数
|
||||
```
|
||||
|
||||
用 dp 数组表示的话也是一样的:
|
||||
|
||||
```python
|
||||
dp[k][n] = m
|
||||
# 当前状态为 k 个鸡蛋,面对 n 层楼
|
||||
# 这个状态下最少的扔鸡蛋次数为 m
|
||||
```
|
||||
|
||||
按照这个定义,就是**确定当前的鸡蛋个数和面对的楼层数,就知道最小扔鸡蛋次数**。最终我们想要的答案就是 `dp(K, N)` 的结果。
|
||||
|
||||
这种思路下,肯定要穷举所有可能的扔法的,用二分搜索优化也只是做了「剪枝」,减小了搜索空间,但本质思路没有变,还是穷举。
|
||||
|
||||
现在,我们稍微修改 `dp` 数组的定义,**确定当前的鸡蛋个数和最多允许的扔鸡蛋次数,就知道能够确定 `F` 的最高楼层数**。具体来说是这个意思:
|
||||
|
||||
```python
|
||||
dp[k][m] = n
|
||||
# 当前有 k 个鸡蛋,可以尝试扔 m 次鸡蛋
|
||||
# 这个状态下,最坏情况下最多能确切测试一栋 n 层的楼
|
||||
|
||||
# 比如说 dp[1][7] = 7 表示:
|
||||
# 现在有 1 个鸡蛋,允许你扔 7 次;
|
||||
# 这个状态下最多给你 7 层楼,
|
||||
# 使得你可以确定楼层 F 使得鸡蛋恰好摔不碎
|
||||
# (一层一层线性探查嘛)
|
||||
```
|
||||
|
||||
这其实就是我们原始思路的一个「反向」版本,我们先不管这种思路的状态转移怎么写,先来思考一下这种定义之下,最终想求的答案是什么?
|
||||
|
||||
我们最终要求的其实是扔鸡蛋次数 `m`,但是这时候 `m` 在状态之中而不是 `dp` 数组的结果,可以这样处理:
|
||||
|
||||
```java
|
||||
int superEggDrop(int K, int N) {
|
||||
|
||||
int m = 0;
|
||||
while (dp[K][m] < N) {
|
||||
m++;
|
||||
// 状态转移...
|
||||
}
|
||||
return m;
|
||||
}
|
||||
```
|
||||
|
||||
题目不是**给你 `K` 鸡蛋,`N` 层楼,让你求最坏情况下最少的测试次数 `m`** 吗?`while` 循环结束的条件是 `dp[K][m] == N`,也就是**给你 `K` 个鸡蛋,测试 `m` 次,最坏情况下最多能测试 `N` 层楼**。
|
||||
|
||||
注意看这两段描述,是完全一样的!所以说这样组织代码是正确的,关键就是状态转移方程怎么找呢?还得从我们原始的思路开始讲。之前的解法配了这样图帮助大家理解状态转移思路:
|
||||
|
||||

|
||||
|
||||
这个图描述的仅仅是某一个楼层 `i`,原始解法还得线性或者二分扫描所有楼层,要求最大值、最小值。但是现在这种 `dp` 定义根本不需要这些了,基于下面两个事实:
|
||||
|
||||
**1、无论你在哪层楼扔鸡蛋,鸡蛋只可能摔碎或者没摔碎,碎了的话就测楼下,没碎的话就测楼上**。
|
||||
|
||||
**2、无论你上楼还是下楼,总的楼层数 = 楼上的楼层数 + 楼下的楼层数 + 1(当前这层楼)**。
|
||||
|
||||
根据这个特点,可以写出下面的状态转移方程:
|
||||
|
||||
`dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1`
|
||||
|
||||
**`dp[k][m - 1]` 就是楼上的楼层数**,因为鸡蛋个数 `k` 不变,也就是鸡蛋没碎,扔鸡蛋次数 `m` 减一;
|
||||
|
||||
**`dp[k - 1][m - 1]` 就是楼下的楼层数**,因为鸡蛋个数 `k` 减一,也就是鸡蛋碎了,同时扔鸡蛋次数 `m` 减一。
|
||||
|
||||
PS:这个 `m` 为什么要减一而不是加一?之前定义得很清楚,这个 `m` 是一个允许的次数上界,而不是扔了几次。
|
||||
|
||||

|
||||
|
||||
至此,整个思路就完成了,只要把状态转移方程填进框架即可:
|
||||
|
||||
```java
|
||||
int superEggDrop(int K, int N) {
|
||||
// m 最多不会超过 N 次(线性扫描)
|
||||
int[][] dp = new int[K + 1][N + 1];
|
||||
// base case:
|
||||
// dp[0][..] = 0
|
||||
// dp[..][0] = 0
|
||||
// Java 默认初始化数组都为 0
|
||||
int m = 0;
|
||||
while (dp[K][m] < N) {
|
||||
m++;
|
||||
for (int k = 1; k <= K; k++)
|
||||
dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1;
|
||||
}
|
||||
return m;
|
||||
}
|
||||
```
|
||||
|
||||
如果你还觉得这段代码有点难以理解,其实它就等同于这样写:
|
||||
|
||||
```java
|
||||
for (int m = 1; dp[K][m] < N; m++)
|
||||
for (int k = 1; k <= K; k++)
|
||||
dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1;
|
||||
```
|
||||
|
||||
看到这种代码形式就熟悉多了吧,因为我们要求的不是 `dp` 数组里的值,而是某个符合条件的索引 `m`,所以用 `while` 循环来找到这个 `m` 而已。
|
||||
|
||||
这个算法的时间复杂度是多少?很明显就是两个嵌套循环的复杂度 O(KN)。
|
||||
|
||||
另外注意到 `dp[m][k]` 转移只和左边和左上的两个状态有关,所以很容易优化成一维 `dp` 数组,这里就不写了。
|
||||
|
||||
### 还可以再优化
|
||||
|
||||
再往下就要用一些数学方法了,不具体展开,就简单提一下思路吧。
|
||||
|
||||
在刚才的思路之上,**注意函数 `dp(m, k)` 是随着 `m` 单增的,因为鸡蛋个数 `k` 不变时,允许的测试次数越多,可测试的楼层就越高**。
|
||||
|
||||
这里又可以借助二分搜索算法快速逼近 `dp[K][m] == N` 这个终止条件,时间复杂度进一步下降为 O(KlogN),我们可以设 `g(k, m) =`……
|
||||
|
||||
算了算了,打住吧。我觉得我们能够写出 O(K\*N\*logN) 的二分优化算法就行了,后面的这些解法呢,听个响鼓个掌就行了,把欲望限制在能力的范围之内才能拥有快乐!
|
||||
|
||||
不过可以肯定的是,根据二分搜索代替线性扫描 `m` 的取值,代码的大致框架肯定是修改穷举 `m` 的 for 循环:
|
||||
|
||||
```java
|
||||
// 把线性搜索改成二分搜索
|
||||
// for (int m = 1; dp[K][m] < N; m++)
|
||||
int lo = 1, hi = N;
|
||||
while (lo < hi) {
|
||||
int mid = (lo + hi) / 2;
|
||||
if (... < N) {
|
||||
lo = ...
|
||||
} else {
|
||||
hi = ...
|
||||
}
|
||||
|
||||
for (int k = 1; k <= K; k++)
|
||||
// 状态转移方程
|
||||
}
|
||||
```
|
||||
|
||||
简单总结一下吧,第一个二分优化是利用了 `dp` 函数的单调性,用二分查找技巧快速搜索答案;第二种优化是巧妙地修改了状态转移方程,简化了求解了流程,但相应的,解题逻辑比较难以想到;后续还可以用一些数学方法和二分搜索进一步优化第二种解法,不过看了看镜子中的发量,算了。
|
||||
|
||||
本文终,希望对你有一点启发。
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
[887.鸡蛋掉落](https://leetcode-cn.com/problems/super-egg-drop/)
|
||||
|
||||
### javascript
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number} K
|
||||
* @param {number} N
|
||||
* @return {number}
|
||||
*/
|
||||
var superEggDrop = function (K, N) {
|
||||
// m 最多不会超过 N 次(线性扫描)
|
||||
// 初始化一个 (K+1)(N+1) 的矩阵
|
||||
let dp = new Array(K + 1);
|
||||
|
||||
// base case:
|
||||
// dp[0][..] = 0
|
||||
// dp[..][0] = 0
|
||||
// 初始化数组都为 0
|
||||
for (let i = 0; i < K + 1; i++) {
|
||||
dp[i] = new Array(N + 1);
|
||||
dp[i].fill(0, 0, N + 1);
|
||||
}
|
||||
|
||||
let m = 0;
|
||||
while (dp[K][m] < N) {
|
||||
m++;
|
||||
for (let k = 1; k <= K; k++) {
|
||||
dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1;
|
||||
}
|
||||
}
|
||||
return m;
|
||||
};
|
||||
```
|
||||
|
||||
|
|
@ -1,33 +1,37 @@
|
|||
# 经典动态规划问题:高楼扔鸡蛋
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[887.鸡蛋掉落](https://leetcode-cn.com/problems/super-egg-drop/)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [887. Super Egg Drop](https://leetcode.com/problems/super-egg-drop/) | [887. 鸡蛋掉落](https://leetcode.cn/problems/super-egg-drop/) | 🔴
|
||||
|
||||
**-----------**
|
||||
|
||||
今天要聊一个很经典的算法问题,若干层楼,若干个鸡蛋,让你算出最少的尝试次数,找到鸡蛋恰好摔不碎的那层楼。国内大厂以及谷歌脸书面试都经常考察这道题,只不过他们觉得扔鸡蛋太浪费,改成扔杯子,扔破碗什么的。
|
||||
本文要聊一个很经典的算法问题,若干层楼,若干个鸡蛋,让你算出最少的尝试次数,找到鸡蛋恰好摔不碎的那层楼。国内大厂以及谷歌脸书面试都经常考察这道题,只不过他们觉得扔鸡蛋太浪费,改成扔杯子,扔破碗什么的。
|
||||
|
||||
具体的问题等会再说,但是这道题的解法技巧很多,光动态规划就好几种效率不同的思路,最后还有一种极其高效数学解法。秉承咱们号一贯的作风,拒绝奇技淫巧,拒绝过于诡异的技巧,因为这些技巧无法举一反三,学了也不划算。
|
||||
具体的问题等会再说,但是这道题的解法技巧很多,光动态规划就好几种效率不同的思路,最后还有一种极其高效数学解法。秉承本书一贯的作风,拒绝过于诡异的技巧,因为这些技巧无法举一反三,学了也不划算。
|
||||
|
||||
下面就来用我们一直强调的动态规划通用思路来研究一下这道题。
|
||||
|
||||
### 一、解析题目
|
||||
|
||||
题目是这样:你面前有一栋从 1 到 `N` 共 `N` 层的楼,然后给你 `K` 个鸡蛋(`K` 至少为 1)。现在确定这栋楼存在楼层 `0 <= F <= N`,在这层楼将鸡蛋扔下去,鸡蛋**恰好没摔碎**(高于 `F` 的楼层都会碎,低于 `F` 的楼层都不会碎)。现在问你,**最坏**情况下,你**至少**要扔几次鸡蛋,才能**确定**这个楼层 `F` 呢?
|
||||
这是力扣第 887 题「鸡蛋掉落」,我描述一下题目:
|
||||
|
||||
你面前有一栋从 1 到 `N` 共 `N` 层的楼,然后给你 `K` 个鸡蛋(`K` 至少为 1)。现在确定这栋楼存在楼层 `0 <= F <= N`,在这层楼将鸡蛋扔下去,鸡蛋**恰好没摔碎**(高于 `F` 的楼层都会碎,低于 `F` 的楼层都不会碎)。现在问你,**最坏**情况下,你**至少**要扔几次鸡蛋,才能**确定**这个楼层 `F` 呢?
|
||||
|
||||
也就是让你找摔不碎鸡蛋的最高楼层 `F`,但什么叫「最坏情况」下「至少」要扔几次呢?我们分别举个例子就明白了。
|
||||
|
||||
|
|
@ -49,8 +53,6 @@
|
|||
|
||||
以这种策略,**最坏**情况应该是试到第 7 层鸡蛋还没碎(`F = 7`),或者鸡蛋一直碎到第 1 层(`F = 0`)。然而无论那种最坏情况,只需要试 `log7` 向上取整等于 3 次,比刚才尝试 7 次要少,这就是所谓的**至少**要扔几次。
|
||||
|
||||
PS:这有点像 Big O 表示法计算算法的复杂度。
|
||||
|
||||
实际上,如果不限制鸡蛋个数的话,二分思路显然可以得到最少尝试的次数,但问题是,**现在给你了鸡蛋个数的限制 `K`,直接使用二分思路就不行了**。
|
||||
|
||||
比如说只给你 1 个鸡蛋,7 层楼,你敢用二分吗?你直接去第 4 层扔一下,如果鸡蛋没碎还好,但如果碎了你就没有鸡蛋继续测试了,无法确定鸡蛋恰好摔不碎的楼层 `F` 了。这种情况下只能用线性扫描的方法,算法返回结果应该是 7。
|
||||
|
|
@ -59,205 +61,33 @@ PS:这有点像 Big O 表示法计算算法的复杂度。
|
|||
|
||||
很遗憾,并不是,比如说把楼层变高一些,100 层,给你 2 个鸡蛋,你在 50 层扔一下,碎了,那就只能线性扫描 1~49 层了,最坏情况下要扔 50 次。
|
||||
|
||||
如果不要「二分」,变成「五分」「十分」都会大幅减少最坏情况下的尝试次数。比方说第一个鸡蛋每隔十层楼扔,在哪里碎了第二个鸡蛋一个个线性扫描,总共不会超过 20 次。
|
||||
|
||||
最优解其实是 14 次。最优策略非常多,而且并没有什么规律可言。
|
||||
如果不要「二分」,变成「五分」「十分」都会大幅减少最坏情况下的尝试次数。比方说第一个鸡蛋每隔十层楼扔,在哪里碎了第二个鸡蛋一个个线性扫描,总共不会超过 20 次。最优解其实是 14 次。最优策略非常多,而且并没有什么规律可言。
|
||||
|
||||
说了这么多废话,就是确保大家理解了题目的意思,而且认识到这个题目确实复杂,就连我们手算都不容易,如何用算法解决呢?
|
||||
|
||||
### 二、思路分析
|
||||
|
||||
对动态规划问题,直接套我们以前多次强调的框架即可:这个问题有什么「状态」,有什么「选择」,然后穷举。
|
||||
|
||||
**「状态」很明显,就是当前拥有的鸡蛋数 `K` 和需要测试的楼层数 `N`**。随着测试的进行,鸡蛋个数可能减少,楼层的搜索范围会减小,这就是状态的变化。
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
**「选择」其实就是去选择哪层楼扔鸡蛋**。回顾刚才的线性扫描和二分思路,二分查找每次选择到楼层区间的中间去扔鸡蛋,而线性扫描选择一层层向上测试。不同的选择会造成状态的转移。
|
||||
- [二分搜索怎么用?我又总结了套路](https://labuladong.github.io/article/fname.html?fname=二分运用)
|
||||
- [二分搜索怎么用?我和快手面试官进行了深度探讨](https://labuladong.github.io/article/fname.html?fname=二分分割子数组)
|
||||
- [动态规划问题的两种穷举视角](https://labuladong.github.io/article/fname.html?fname=动归两种视角)
|
||||
- [最优子结构原理和 dp 数组遍历方向](https://labuladong.github.io/article/fname.html?fname=最优子结构)
|
||||
- [经典动态规划:戳气球](https://labuladong.github.io/article/fname.html?fname=扎气球)
|
||||
|
||||
现在明确了「状态」和「选择」,**动态规划的基本思路就形成了**:肯定是个二维的 `dp` 数组或者带有两个状态参数的 `dp` 函数来表示状态转移;外加一个 for 循环来遍历所有选择,择最优的选择更新状态:
|
||||
</details><hr>
|
||||
|
||||
```python
|
||||
# 当前状态为 K 个鸡蛋,面对 N 层楼
|
||||
# 返回这个状态下的最优结果
|
||||
def dp(K, N):
|
||||
int res
|
||||
for 1 <= i <= N:
|
||||
res = min(res, 这次在第 i 层楼扔鸡蛋)
|
||||
return res
|
||||
```
|
||||
|
||||
这段伪码还没有展示递归和状态转移,不过大致的算法框架已经完成了。
|
||||
|
||||
我们选择在第 `i` 层楼扔了鸡蛋之后,可能出现两种情况:鸡蛋碎了,鸡蛋没碎。**注意,这时候状态转移就来了**:
|
||||
|
||||
**如果鸡蛋碎了**,那么鸡蛋的个数 `K` 应该减一,搜索的楼层区间应该从 `[1..N]` 变为 `[1..i-1]` 共 `i-1` 层楼;
|
||||
|
||||
**如果鸡蛋没碎**,那么鸡蛋的个数 `K` 不变,搜索的楼层区间应该从 `[1..N]` 变为 `[i+1..N]` 共 `N-i` 层楼。
|
||||
|
||||

|
||||
|
||||
PS:细心的读者可能会问,在第i层楼扔鸡蛋如果没碎,楼层的搜索区间缩小至上面的楼层,是不是应该包含第i层楼呀?不必,因为已经包含了。开头说了 F 是可以等于 0 的,向上递归后,第i层楼其实就相当于第 0 层,可以被取到,所以说并没有错误。
|
||||
|
||||
因为我们要求的是**最坏情况**下扔鸡蛋的次数,所以鸡蛋在第 `i` 层楼碎没碎,取决于那种情况的结果**更大**:
|
||||
|
||||
```python
|
||||
def dp(K, N):
|
||||
for 1 <= i <= N:
|
||||
# 最坏情况下的最少扔鸡蛋次数
|
||||
res = min(res,
|
||||
max(
|
||||
dp(K - 1, i - 1), # 碎
|
||||
dp(K, N - i) # 没碎
|
||||
) + 1 # 在第 i 楼扔了一次
|
||||
)
|
||||
return res
|
||||
```
|
||||
|
||||
递归的 base case 很容易理解:当楼层数 `N` 等于 0 时,显然不需要扔鸡蛋;当鸡蛋数 `K` 为 1 时,显然只能线性扫描所有楼层:
|
||||
|
||||
```python
|
||||
def dp(K, N):
|
||||
if K == 1: return N
|
||||
if N == 0: return 0
|
||||
...
|
||||
```
|
||||
|
||||
至此,其实这道题就解决了!只要添加一个备忘录消除重叠子问题即可:
|
||||
|
||||
```python
|
||||
def superEggDrop(K: int, N: int):
|
||||
|
||||
memo = dict()
|
||||
def dp(K, N) -> int:
|
||||
# base case
|
||||
if K == 1: return N
|
||||
if N == 0: return 0
|
||||
# 避免重复计算
|
||||
if (K, N) in memo:
|
||||
return memo[(K, N)]
|
||||
|
||||
res = float('INF')
|
||||
# 穷举所有可能的选择
|
||||
for i in range(1, N + 1):
|
||||
res = min(res,
|
||||
max(
|
||||
dp(K, N - i),
|
||||
dp(K - 1, i - 1)
|
||||
) + 1
|
||||
)
|
||||
# 记入备忘录
|
||||
memo[(K, N)] = res
|
||||
return res
|
||||
|
||||
return dp(K, N)
|
||||
```
|
||||
|
||||
这个算法的时间复杂度是多少呢?**动态规划算法的时间复杂度就是子问题个数 × 函数本身的复杂度**。
|
||||
|
||||
函数本身的复杂度就是忽略递归部分的复杂度,这里 `dp` 函数中有一个 for 循环,所以函数本身的复杂度是 O(N)。
|
||||
|
||||
子问题个数也就是不同状态组合的总数,显然是两个状态的乘积,也就是 O(KN)。
|
||||
|
||||
所以算法的总时间复杂度是 O(K*N^2), 空间复杂度 O(KN)。
|
||||
|
||||
### 三、疑难解答
|
||||
|
||||
这个问题很复杂,但是算法代码却十分简洁,这就是动态规划的特性,穷举加备忘录/DP table 优化,真的没啥新意。
|
||||
|
||||
首先,有读者可能不理解代码中为什么用一个 for 循环遍历楼层 `[1..N]`,也许会把这个逻辑和之前探讨的线性扫描混为一谈。其实不是的,**这只是在做一次「选择」**。
|
||||
|
||||
比方说你有 2 个鸡蛋,面对 10 层楼,你**这次**选择去哪一层楼扔呢?不知道,那就把这 10 层楼全试一遍。至于下次怎么选择不用你操心,有正确的状态转移,递归会算出每个选择的代价,我们取最优的那个就是最优解。
|
||||
|
||||
另外,这个问题还有更好的解法,比如修改代码中的 for 循环为二分搜索,可以将时间复杂度降为 O(K\*N\*logN);再改进动态规划解法可以进一步降为 O(KN);使用数学方法解决,时间复杂度达到最优 O(K*logN),空间复杂度达到 O(1)。
|
||||
|
||||
二分的解法也有点误导性,你很可能以为它跟我们之前讨论的二分思路扔鸡蛋有关系,实际上没有半毛钱关系。能用二分搜索是因为状态转移方程的函数图像具有单调性,可以快速找到最值。
|
||||
|
||||
简单介绍一下二分查找的优化吧,其实只是在优化这段代码:
|
||||
|
||||
```python
|
||||
def dp(K, N):
|
||||
for 1 <= i <= N:
|
||||
# 最坏情况下的最少扔鸡蛋次数
|
||||
res = min(res,
|
||||
max(
|
||||
dp(K - 1, i - 1), # 碎
|
||||
dp(K, N - i) # 没碎
|
||||
) + 1 # 在第 i 楼扔了一次
|
||||
)
|
||||
return res
|
||||
```
|
||||
|
||||
这个 for 循环就是下面这个状态转移方程的具体代码实现:
|
||||
|
||||
<!-- $$ dp(K, N) = \min_{0 <= i <= N}\{\max\{dp(K - 1, i - 1), dp(K, N - i)\} + 1\}$$ -->
|
||||
|
||||

|
||||
|
||||
首先我们根据 `dp(K, N)` 数组的定义(有 `K` 个鸡蛋面对 `N` 层楼,最少需要扔几次),**很容易知道 `K` 固定时,这个函数一定是单调递增的**,无论你策略多聪明,楼层增加测试次数一定要增加。
|
||||
|
||||
那么注意 `dp(K - 1, i - 1)` 和 `dp(K, N - i)` 这两个函数,其中 `i` 是从 1 到 `N` 单增的,如果我们固定 `K` 和 `N`,**把这两个函数看做关于 `i` 的函数,前者随着 `i` 的增加应该也是单调递增的,而后者随着 `i` 的增加应该是单调递减的**:
|
||||
|
||||

|
||||
|
||||
这时候求二者的较大值,再求这些最大值之中的最小值,其实就是求这个交点嘛,熟悉二分搜索的同学肯定敏感地想到了,这不就是相当于求 Valley(山谷)值嘛,可以用二分查找来快速寻找这个点的。
|
||||
|
||||
直接贴一下代码吧,思路还是完全一样的:
|
||||
|
||||
```python
|
||||
def superEggDrop(self, K: int, N: int) -> int:
|
||||
|
||||
memo = dict()
|
||||
def dp(K, N):
|
||||
if K == 1: return N
|
||||
if N == 0: return 0
|
||||
if (K, N) in memo:
|
||||
return memo[(K, N)]
|
||||
|
||||
# for 1 <= i <= N:
|
||||
# res = min(res,
|
||||
# max(
|
||||
# dp(K - 1, i - 1),
|
||||
# dp(K, N - i)
|
||||
# ) + 1
|
||||
# )
|
||||
|
||||
res = float('INF')
|
||||
# 用二分搜索代替线性搜索
|
||||
lo, hi = 1, N
|
||||
while lo <= hi:
|
||||
mid = (lo + hi) // 2
|
||||
broken = dp(K - 1, mid - 1) # 碎
|
||||
not_broken = dp(K, N - mid) # 没碎
|
||||
# res = min(max(碎,没碎) + 1)
|
||||
if broken > not_broken:
|
||||
hi = mid - 1
|
||||
res = min(res, broken + 1)
|
||||
else:
|
||||
lo = mid + 1
|
||||
res = min(res, not_broken + 1)
|
||||
|
||||
memo[(K, N)] = res
|
||||
return res
|
||||
|
||||
return dp(K, N)
|
||||
```
|
||||
|
||||
这里就不展开其他解法了,留在下一篇文章 [高楼扔鸡蛋进阶](https://labuladong.gitee.io/algo/)
|
||||
|
||||
我觉得吧,我们这种解法就够了:找状态,做选择,足够清晰易懂,可流程化,可举一反三。掌握这套框架学有余力的话,再去考虑那些奇技淫巧也不迟。
|
||||
|
||||
最后预告一下,《动态规划详解(修订版)》和《回溯算法详解(修订版)》已经动笔了,教大家用模板的力量来对抗变化无穷的算法题,敬请期待。
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
应合作方要求,本文不便在此发布,请扫码关注回复关键词「鸡蛋」或 [点这里](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_6298795de4b01a4852072fa7/1) 查看:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||

|
||||
|
||||
======其他语言代码======
|
||||
|
||||
|
|
|
|||
|
|
@ -0,0 +1,254 @@
|
|||
# 动态规划算法通关魔塔
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [174. Dungeon Game](https://leetcode.com/problems/dungeon-game/) | [174. 地下城游戏](https://leetcode.cn/problems/dungeon-game/) | 🔴
|
||||
|
||||
**-----------**
|
||||
|
||||
「魔塔」是一款经典的地牢类游戏,碰怪物要掉血,吃血瓶能加血,你要收集钥匙,一层一层上楼,最后救出美丽的公主。
|
||||
|
||||
现在手机上仍然可以玩这个游戏:
|
||||
|
||||

|
||||
|
||||
嗯,相信这款游戏承包了不少人的童年回忆,记得小时候,一个人拿着游戏机玩,两三个人围在左右指手画脚,这导致玩游戏的人体验极差,而左右的人异常快乐 😂
|
||||
|
||||
力扣第 174 题「地下城游戏」是一道类似的题目,我简单描述一下:
|
||||
|
||||
输入一个存储着整数的二维数组 `grid`,如果 `grid[i][j] > 0`,说明这个格子装着血瓶,经过它可以增加对应的生命值;如果 `grid[i][j] == 0`,则这是一个空格子,经过它不会发生任何事情;如果 `grid[i][j] < 0`,说明这个格子有怪物,经过它会损失对应的生命值。
|
||||
|
||||
现在你是一名骑士,将会出现在最上角,公主被困在最右下角,你只能向右和向下移动,请问你初始至少需要多少生命值才能成功救出公主?
|
||||
|
||||
**换句话说,就是问你至少需要多少初始生命值,能够让骑士从最左上角移动到最右下角,且任何时候生命值都要大于 0**。
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int calculateMinimumHP(int[][] grid);
|
||||
```
|
||||
|
||||
比如题目给我们举的例子,输入如下一个二维数组 `grid`,用 `K` 表示骑士,用 `P` 表示公主:
|
||||
|
||||

|
||||
|
||||
算法应该返回 7,也就是说骑士的初始生命值**至少**为 7 时才能成功救出公主,行进路线如图中的箭头所示。
|
||||
|
||||
上篇文章 [最小路径和](https://labuladong.github.io/article/fname.html?fname=最小路径和) 写过类似的问题,问你从左上角到右下角的最小路径和是多少。
|
||||
|
||||
我们做算法题一定要尝试举一反三,感觉今天这道题和最小路径和有点关系对吧?
|
||||
|
||||
想要最小化骑士的初始生命值,是不是意味着要最大化骑士行进路线上的血瓶?是不是相当于求「最大路径和」?是不是可以直接套用计算「最小路径和」的思路?
|
||||
|
||||
但是稍加思考,发现这个推论并不成立,吃到最多的血瓶,并不一定就能获得最小的初始生命值。
|
||||
|
||||
比如如下这种情况,如果想要吃到最多的血瓶获得「最大路径和」,应该按照下图箭头所示的路径,初始生命值需要 11:
|
||||
|
||||

|
||||
|
||||
但也很容易看到,正确的答案应该是下图箭头所示的路径,初始生命值只需要 1:
|
||||
|
||||

|
||||
|
||||
**所以,关键不在于吃最多的血瓶,而是在于如何损失最少的生命值**。
|
||||
|
||||
这类求最值的问题,肯定要借助动态规划技巧,要合理设计 `dp` 数组/函数的定义。类比前文 [最小路径和问题](https://labuladong.github.io/article/fname.html?fname=最小路径和),`dp` 函数签名肯定长这样:
|
||||
|
||||
```java
|
||||
int dp(int[][] grid, int i, int j);
|
||||
```
|
||||
|
||||
但是这道题对 `dp` 函数的定义比较有意思,按照常理,这个 `dp` 函数的定义应该是:
|
||||
|
||||
**从左上角(`grid[0][0]`)走到 `grid[i][j]` 至少需要 `dp(grid, i, j)` 的生命值**。
|
||||
|
||||
这样定义的话,base case 就是 `i, j` 都等于 0 的时候,我们可以这样写代码:
|
||||
|
||||
```java
|
||||
int calculateMinimumHP(int[][] grid) {
|
||||
int m = grid.length;
|
||||
int n = grid[0].length;
|
||||
// 我们想计算左上角到右下角所需的最小生命值
|
||||
return dp(grid, m - 1, n - 1);
|
||||
}
|
||||
|
||||
int dp(int[][] grid, int i, int j) {
|
||||
// base case
|
||||
if (i == 0 && j == 0) {
|
||||
// 保证骑士落地不死就行了
|
||||
return gird[i][j] > 0 ? 1 : -grid[i][j] + 1;
|
||||
}
|
||||
...
|
||||
}
|
||||
```
|
||||
|
||||
> **PS:为了简洁,之后 `dp(grid, i, j)` 就简写为 `dp(i, j)`,大家理解就好**。
|
||||
|
||||
接下来我们需要找状态转移了,还记得如何找状态转移方程吗?我们这样定义 `dp` 函数能否正确进行状态转移呢?
|
||||
|
||||
我们希望 `dp(i, j)` 能够通过 `dp(i-1, j)` 和 `dp(i, j-1)` 推导出来,这样就能不断逼近 base case,也就能够正确进行状态转移。
|
||||
|
||||
具体来说,「到达 `A` 的最小生命值」应该能够由「到达 `B` 的最小生命值」和「到达 `C` 的最小生命值」推导出来:
|
||||
|
||||

|
||||
|
||||
**但问题是,能推出来么?实际上是不能的**。
|
||||
|
||||
因为按照 `dp` 函数的定义,你只知道「能够从左上角到达 `B` 的最小生命值」,但并不知道「到达 `B` 时的生命值」。
|
||||
|
||||
「到达 `B` 时的生命值」是进行状态转移的必要参考,我给你举个例子你就明白了,假设下图这种情况:
|
||||
|
||||

|
||||
|
||||
你说这种情况下,骑士救公主的最优路线是什么?
|
||||
|
||||
显然是按照图中蓝色的线走到 `B`,最后走到 `A` 对吧,这样初始血量只需要 1 就可以;如果走黄色箭头这条路,先走到 `C` 然后走到 `A`,初始血量至少需要 6。
|
||||
|
||||
为什么会这样呢?骑士走到 `B` 和 `C` 的最少初始血量都是 1,为什么最后是从 `B` 走到 `A`,而不是从 `C` 走到 `A` 呢?
|
||||
|
||||
因为骑士走到 `B` 的时候生命值为 11,而走到 `C` 的时候生命值依然是 1。
|
||||
|
||||
如果骑士执意要通过 `C` 走到 `A`,那么初始血量必须加到 6 点才行;而如果通过 `B` 走到 `A`,初始血量为 1 就够了,因为路上吃到血瓶了,生命值足够抗 `A` 上面怪物的伤害。
|
||||
|
||||
这下应该说的很清楚了,再回顾我们对 `dp` 函数的定义,上图的情况,算法只知道 `dp(1, 2) = dp(2, 1) = 1`,都是一样的,怎么做出正确的决策,计算出 `dp(2, 2)` 呢?
|
||||
|
||||
**所以说,我们之前对 `dp` 数组的定义是错误的,信息量不足,算法无法做出正确的状态转移**。
|
||||
|
||||
正确的做法需要反向思考,依然是如下的 `dp` 函数:
|
||||
|
||||
```java
|
||||
int dp(int[][] grid, int i, int j);
|
||||
```
|
||||
|
||||
但是我们要修改 `dp` 函数的定义:
|
||||
|
||||
**从 `grid[i][j]` 到达终点(右下角)所需的最少生命值是 `dp(grid, i, j)`**。
|
||||
|
||||
那么可以这样写代码:
|
||||
|
||||
```java
|
||||
int calculateMinimumHP(int[][] grid) {
|
||||
// 我们想计算左上角到右下角所需的最小生命值
|
||||
return dp(grid, 0, 0);
|
||||
}
|
||||
|
||||
int dp(int[][] grid, int i, int j) {
|
||||
int m = grid.length;
|
||||
int n = grid[0].length;
|
||||
// base case
|
||||
if (i == m - 1 && j == n - 1) {
|
||||
return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
|
||||
}
|
||||
...
|
||||
}
|
||||
```
|
||||
|
||||
根据新的 `dp` 函数定义和 base case,我们想求 `dp(0, 0)`,那就应该试图通过 `dp(i, j+1)` 和 `dp(i+1, j)` 推导出 `dp(i, j)`,这样才能不断逼近 base case,正确进行状态转移。
|
||||
|
||||
具体来说,「从 `A` 到达右下角的最少生命值」应该由「从 `B` 到达右下角的最少生命值」和「从 `C` 到达右下角的最少生命值」推导出来:
|
||||
|
||||

|
||||
|
||||
能不能推导出来呢?这次是可以的,假设 `dp(0, 1) = 5, dp(1, 0) = 4`,那么可以肯定要从 `A` 走向 `C`,因为 4 小于 5 嘛。
|
||||
|
||||
那么怎么推出 `dp(0, 0)` 是多少呢?
|
||||
|
||||
假设 `A` 的值为 1,既然知道下一步要往 `C` 走,且 `dp(1, 0) = 4` 意味着走到 `grid[1][0]` 的时候至少要有 4 点生命值,那么就可以确定骑士出现在 `A` 点时需要 4 - 1 = 3 点初始生命值,对吧。
|
||||
|
||||
那如果 `A` 的值为 10,落地就能捡到一个大血瓶,超出了后续需求,4 - 10 = -6 意味着骑士的初始生命值为负数,这显然不可以,骑士的生命值小于 1 就挂了,所以这种情况下骑士的初始生命值应该是 1。
|
||||
|
||||
综上,状态转移方程已经推出来了:
|
||||
|
||||
```java
|
||||
int res = min(
|
||||
dp(i + 1, j),
|
||||
dp(i, j + 1)
|
||||
) - grid[i][j];
|
||||
|
||||
dp(i, j) = res <= 0 ? 1 : res;
|
||||
```
|
||||
|
||||
根据这个核心逻辑,加一个备忘录消除重叠子问题,就可以直接写出最终的代码了:
|
||||
|
||||
```java
|
||||
/* 主函数 */
|
||||
int calculateMinimumHP(int[][] grid) {
|
||||
int m = grid.length;
|
||||
int n = grid[0].length;
|
||||
// 备忘录中都初始化为 -1
|
||||
memo = new int[m][n];
|
||||
for (int[] row : memo) {
|
||||
Arrays.fill(row, -1);
|
||||
}
|
||||
|
||||
return dp(grid, 0, 0);
|
||||
}
|
||||
|
||||
// 备忘录,消除重叠子问题
|
||||
int[][] memo;
|
||||
|
||||
/* 定义:从 (i, j) 到达右下角,需要的初始血量至少是多少 */
|
||||
int dp(int[][] grid, int i, int j) {
|
||||
int m = grid.length;
|
||||
int n = grid[0].length;
|
||||
// base case
|
||||
if (i == m - 1 && j == n - 1) {
|
||||
return grid[i][j] >= 0 ? 1 : -grid[i][j] + 1;
|
||||
}
|
||||
if (i == m || j == n) {
|
||||
return Integer.MAX_VALUE;
|
||||
}
|
||||
// 避免重复计算
|
||||
if (memo[i][j] != -1) {
|
||||
return memo[i][j];
|
||||
}
|
||||
// 状态转移逻辑
|
||||
int res = Math.min(
|
||||
dp(grid, i, j + 1),
|
||||
dp(grid, i + 1, j)
|
||||
) - grid[i][j];
|
||||
// 骑士的生命值至少为 1
|
||||
memo[i][j] = res <= 0 ? 1 : res;
|
||||
|
||||
return memo[i][j];
|
||||
}
|
||||
```
|
||||
|
||||
这就是自顶向下带备忘录的动态规划解法,参考前文 [动态规划套路详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 很容易就可以改写成 `dp` 数组的迭代解法,这里就不写了,读者可以尝试自己写一写。
|
||||
|
||||
这道题的核心是定义 `dp` 函数,找到正确的状态转移方程,从而计算出正确的答案。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [base case 和备忘录的初始值怎么定?](https://labuladong.github.io/article/fname.html?fname=备忘录等基础)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -0,0 +1,156 @@
|
|||
# 合法括号生成算法
|
||||
|
||||
<!-- [回溯算法最佳实践:合法括号生成](https://mp.weixin.qq.com/s/XVnoX-lBzColVvVXNkGc5g) -->
|
||||
|
||||
<!-- number: 861 -->
|
||||
|
||||
{{ config article_header_icon }}
|
||||
|
||||

|
||||
|
||||
{{ config article_header_ad }}
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
[22. 括号生成(中等)](https://leetcode.cn/problems/generate-parentheses)
|
||||
|
||||
**-----------**
|
||||
|
||||
括号问题可以简单分成两类,一类是前文写过的 [括号的合法性判断](../高频面试系列/括号插入.md) ,一类是合法括号的生成。对于括号合法性的判断,主要是借助「栈」这种数据结构,而对于括号的生成,一般都要利用回溯递归的思想。
|
||||
|
||||
关于回溯算法,我们前文写过一篇 [回溯算法套路框架详解](../算法思维系列/回溯算法详解修订版.md) 反响非常好,读本文前应该读过那篇文章,这样你就能够进一步了解回溯算法的框架使用方法了。
|
||||
|
||||
回到正题,看下力扣第 22 题「括号生成」,要求如下:
|
||||
|
||||
请你写一个算法,输入是一个正整数 `n`,输出是 `n` 对儿括号的所有合法组合,函数签名如下:
|
||||
|
||||
```cpp
|
||||
vector<string> generateParenthesis(int n);
|
||||
```
|
||||
|
||||
比如说,输入 `n=3`,输出为如下 5 个字符串:
|
||||
|
||||
```shell
|
||||
"((()))",
|
||||
"(()())",
|
||||
"(())()",
|
||||
"()(())",
|
||||
"()()()"
|
||||
```
|
||||
|
||||
有关括号问题,你只要记住以下性质,思路就很容易想出来:
|
||||
|
||||
**1、一个「合法」括号组合的左括号数量一定等于右括号数量,这个很好理解**。
|
||||
|
||||
**2、对于一个「合法」的括号字符串组合 `p`,必然对于任何 ` 0 <= i < len(p)` 都有:子串 `p[0..i]` 中左括号的数量都大于或等于右括号的数量**。
|
||||
|
||||
如果不跟你说这个性质,可能不太容易发现,但是稍微想一下,其实很容易理解,因为从左往右算的话,肯定是左括号多嘛,到最后左右括号数量相等,说明这个括号组合是合法的。
|
||||
|
||||
反之,比如这个括号组合 `))((`,前几个子串都是右括号多于左括号,显然不是合法的括号组合。
|
||||
|
||||
下面就来手把手实践一下回溯算法框架。
|
||||
|
||||
### 回溯思路
|
||||
|
||||
明白了合法括号的性质,如何把这道题和回溯算法扯上关系呢?
|
||||
|
||||
算法输入一个整数 `n`,让你计算 **`n` 对儿括号**能组成几种合法的括号组合,可以改写成如下问题:
|
||||
|
||||
**现在有 `2n` 个位置,每个位置可以放置字符 `(` 或者 `)`,组成的所有括号组合中,有多少个是合法的**?
|
||||
|
||||
这个命题和题目的意思完全是一样的对吧,那么我们先想想如何得到全部 `2^(2n)` 种组合,然后再根据我们刚才总结出的合法括号组合的性质筛选出合法的组合,不就完事儿了?
|
||||
|
||||
如何得到所有的组合呢?这就是标准的暴力穷举回溯框架啊,我们前文 [回溯算法套路框架详解](../算法思维系列/回溯算法详解修订版.md) 都总结过了:
|
||||
|
||||
```python
|
||||
result = []
|
||||
def backtrack(路径, 选择列表):
|
||||
if 满足结束条件:
|
||||
result.add(路径)
|
||||
return
|
||||
|
||||
for 选择 in 选择列表:
|
||||
做选择
|
||||
backtrack(路径, 选择列表)
|
||||
撤销选择
|
||||
```
|
||||
|
||||
那么对于我们的需求,如何打印所有括号组合呢?套一下框架就出来了,伪码如下:
|
||||
|
||||
```cpp
|
||||
void backtrack(int n, int i, string& track) {
|
||||
// i 代表当前的位置,共 2n 个位置
|
||||
// 穷举到最后一个位置了,得到一个长度为 2n 组合
|
||||
if (i == 2 * n) {
|
||||
print(track);
|
||||
return;
|
||||
}
|
||||
|
||||
// 对于每个位置可以是左括号或者右括号两种选择
|
||||
for choice in ['(', ')'] {
|
||||
track.push(choice); // 做选择
|
||||
// 穷举下一个位置
|
||||
backtrack(n, i + 1, track);
|
||||
track.pop(choice); // 撤销选择
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
那么,现在能够打印所有括号组合了,如何从它们中筛选出合法的括号组合呢?很简单,加几个条件进行「剪枝」就行了。
|
||||
|
||||
对于 `2n` 个位置,必然有 `n` 个左括号,`n` 个右括号,所以我们不是简单的记录穷举位置 `i`,而是**用 `left` 记录还可以使用多少个左括号,用 `right` 记录还可以使用多少个右括号**,这样就可以通过刚才总结的合法括号规律进行筛选了:
|
||||
|
||||
```cpp
|
||||
vector<string> generateParenthesis(int n) {
|
||||
if (n == 0) return {};
|
||||
// 记录所有合法的括号组合
|
||||
vector<string> res;
|
||||
// 回溯过程中的路径
|
||||
string track;
|
||||
// 可用的左括号和右括号数量初始化为 n
|
||||
backtrack(n, n, track, res);
|
||||
return res;
|
||||
}
|
||||
|
||||
// 可用的左括号数量为 left 个,可用的右括号数量为 rgiht 个
|
||||
void backtrack(int left, int right,
|
||||
string& track, vector<string>& res) {
|
||||
// 若左括号剩下的多,说明不合法
|
||||
if (right < left) return;
|
||||
// 数量小于 0 肯定是不合法的
|
||||
if (left < 0 || right < 0) return;
|
||||
// 当所有括号都恰好用完时,得到一个合法的括号组合
|
||||
if (left == 0 && right == 0) {
|
||||
res.push_back(track);
|
||||
return;
|
||||
}
|
||||
|
||||
// 尝试放一个左括号
|
||||
track.push_back('('); // 选择
|
||||
backtrack(left - 1, right, track, res);
|
||||
track.pop_back(); // 撤消选择
|
||||
|
||||
// 尝试放一个右括号
|
||||
track.push_back(')'); // 选择
|
||||
backtrack(left, right - 1, track, res);
|
||||
track.pop_back(); // 撤消选择
|
||||
}
|
||||
```
|
||||
|
||||
这样,我们的算法就完成了,算法的复杂度是多少呢?这个比较难分析,**对于递归相关的算法,时间复杂度这样计算(递归次数)*(递归函数本身的时间复杂度)**。
|
||||
|
||||
`backtrack` 就是我们的递归函数,其中没有任何 for 循环代码,所以递归函数本身的时间复杂度是 O(1),但关键是这个函数的递归次数是多少?换句话说,给定一个 `n`,`backtrack` 函数递归被调用了多少次?
|
||||
|
||||
我们前面怎么分析动态规划算法的递归次数的?主要是看「状态」的个数对吧。其实回溯算法和动态规划的本质都是穷举,只不过动态规划存在「重叠子问题」可以优化,而回溯算法不存在而已。
|
||||
|
||||
所以说这里也可以用「状态」这个概念,**对于 `backtrack` 函数,状态有三个,分别是 `left, right, track`**,这三个变量的所有组合个数就是 `backtrack` 函数的状态个数(调用次数)。
|
||||
|
||||
`left` 和 `right` 的组合好办,他俩取值就是 0~n 嘛,组合起来也就 `n^2` 种而已;这个 `track` 的长度虽然取在 0~2n,但对于每一个长度,它还有指数级的括号组合,这个是不好算的。
|
||||
|
||||
说了这么多,就是想让大家知道这个算法的复杂度是指数级,而且不好算,这里就不具体展开了,是 `4^n / sqrt(n)`,有兴趣的读者可以搜索一下「卡特兰数」相关的知识了解一下这个复杂度是怎么算的。
|
||||
|
||||
**_____________**
|
||||
|
||||
{{ config article_tail_ad }}
|
||||
|
||||

|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 关于 Linux shell 你必须知道的技巧
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -150,6 +146,20 @@ $ where connect.sh
|
|||
$ sudo /home/fdl/bin/connect.sh
|
||||
```
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Linux 管道符原理大揭秘](https://labuladong.github.io/article/fname.html?fname=linux技巧3)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,16 +1,17 @@
|
|||
# Linux的进程、线程、文件描述符是什么
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -22,7 +23,7 @@ Linux 中的进程就是一个数据结构,看明白就可以理解文件描
|
|||
|
||||
首先,抽象地来说,我们的计算机就是这个东西:
|
||||
|
||||

|
||||
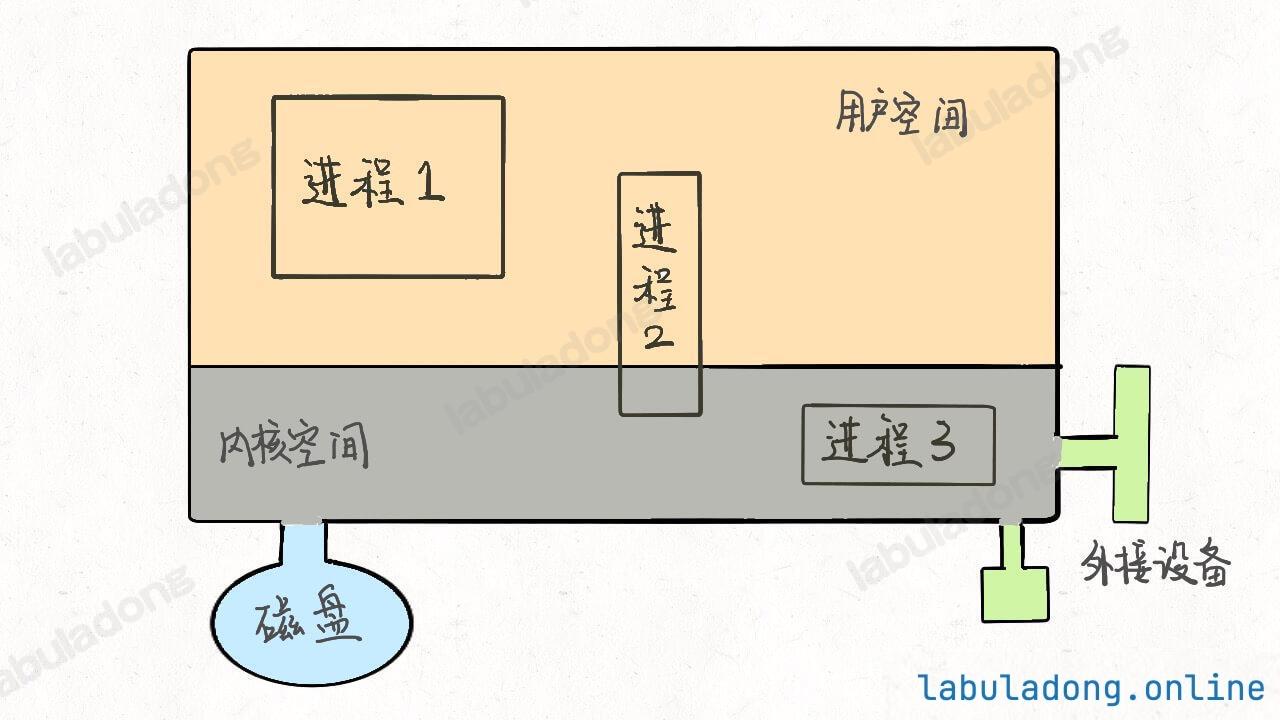
|
||||
|
||||
这个大的矩形表示计算机的**内存空间**,其中的小矩形代表**进程**,左下角的圆形表示**磁盘**,右下角的图形表示一些**输入输出设备**,比如鼠标键盘显示器等等。另外,注意到内存空间被划分为了两块,上半部分表示**用户空间**,下半部分表示**内核空间**。
|
||||
|
||||
|
|
@ -53,45 +54,45 @@ struct task_struct {
|
|||
};
|
||||
```
|
||||
|
||||
`task_struct`就是 Linux 内核对于一个进程的描述,也可以称为「进程描述符」。源码比较复杂,我这里就截取了一小部分比较常见的。
|
||||
`task_struct` 就是 Linux 内核对于一个进程的描述,也可以称为「进程描述符」。源码比较复杂,我这里就截取了一小部分比较常见的。
|
||||
|
||||
其中比较有意思的是`mm`指针和`files`指针。`mm`指向的是进程的虚拟内存,也就是载入资源和可执行文件的地方;`files`指针指向一个数组,这个数组里装着所有该进程打开的文件的指针。
|
||||
其中比较有意思的是 `mm` 指针和 `files` 指针。`mm` 指向的是进程的虚拟内存,也就是载入资源和可执行文件的地方;`files` 指针指向一个数组,这个数组里装着所有该进程打开的文件的指针。
|
||||
|
||||
### 二、文件描述符是什么
|
||||
|
||||
先说`files`,它是一个文件指针数组。一般来说,一个进程会从`files[0]`读取输入,将输出写入`files[1]`,将错误信息写入`files[2]`。
|
||||
先说 `files`,它是一个文件指针数组。一般来说,一个进程会从 `files[0]` 读取输入,将输出写入 `files[1]`,将错误信息写入 `files[2]`。
|
||||
|
||||
举个例子,以我们的角度 C 语言的`printf`函数是向命令行打印字符,但是从进程的角度来看,就是向`files[1]`写入数据;同理,`scanf`函数就是进程试图从`files[0]`这个文件中读取数据。
|
||||
举个例子,以我们的角度 C 语言的 `printf` 函数是向命令行打印字符,但是从进程的角度来看,就是向 `files[1]` 写入数据;同理,`scanf` 函数就是进程试图从 `files[0]` 这个文件中读取数据。
|
||||
|
||||
**每个进程被创建时,`files`的前三位被填入默认值,分别指向标准输入流、标准输出流、标准错误流。我们常说的「文件描述符」就是指这个文件指针数组的索引**,所以程序的文件描述符默认情况下 0 是输入,1 是输出,2 是错误。
|
||||
**每个进程被创建时,`files` 的前三位被填入默认值,分别指向标准输入流、标准输出流、标准错误流。我们常说的「文件描述符」就是指这个文件指针数组的索引**,所以程序的文件描述符默认情况下 0 是输入,1 是输出,2 是错误。
|
||||
|
||||
我们可以重新画一幅图:
|
||||
|
||||

|
||||
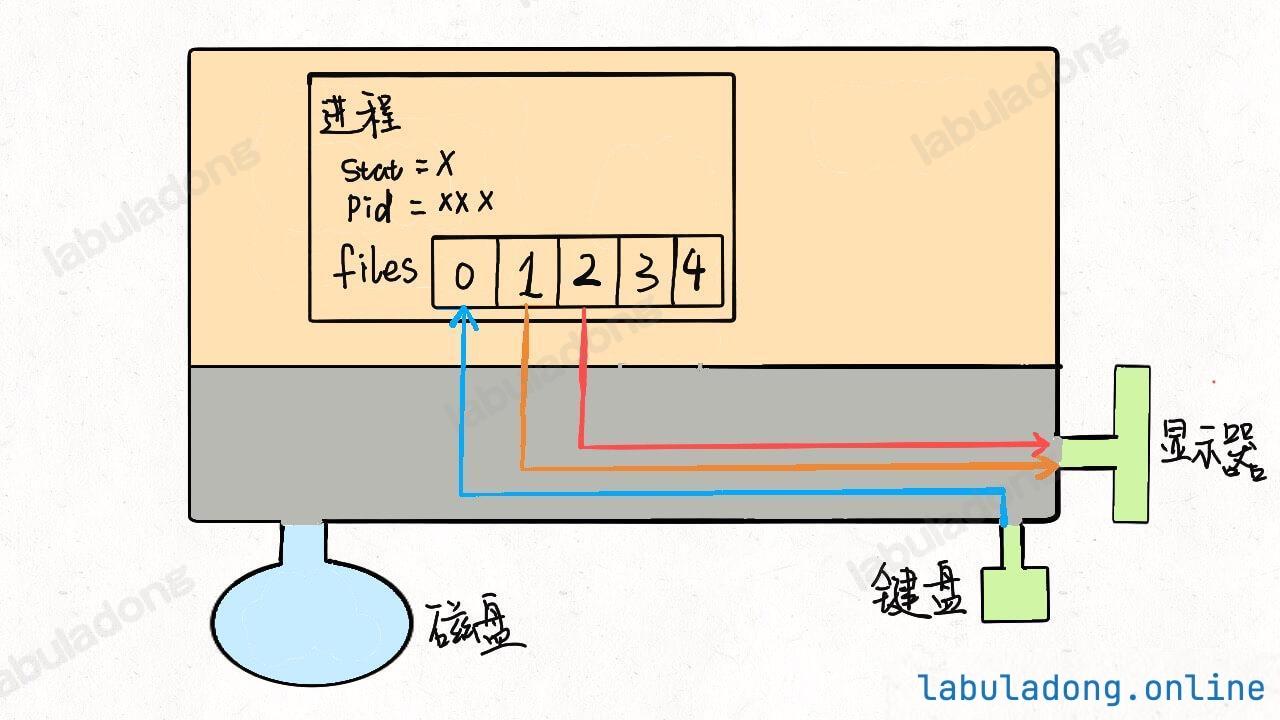
|
||||
|
||||
对于一般的计算机,输入流是键盘,输出流是显示器,错误流也是显示器,所以现在这个进程和内核连了三根线。因为硬件都是由内核管理的,我们的进程需要通过「系统调用」让内核进程访问硬件资源。
|
||||
|
||||
PS:不要忘了,Linux 中一切都被抽象成文件,设备也是文件,可以进行读和写。
|
||||
> PS:不要忘了,Linux 中一切都被抽象成文件,设备也是文件,可以进行读和写。
|
||||
|
||||
如果我们写的程序需要其他资源,比如打开一个文件进行读写,这也很简单,进行系统调用,让内核把文件打开,这个文件就会被放到`files`的第 4 个位置:
|
||||
如果我们写的程序需要其他资源,比如打开一个文件进行读写,这也很简单,进行系统调用,让内核把文件打开,这个文件就会被放到 `files` 的第 4 个位置:
|
||||
|
||||

|
||||
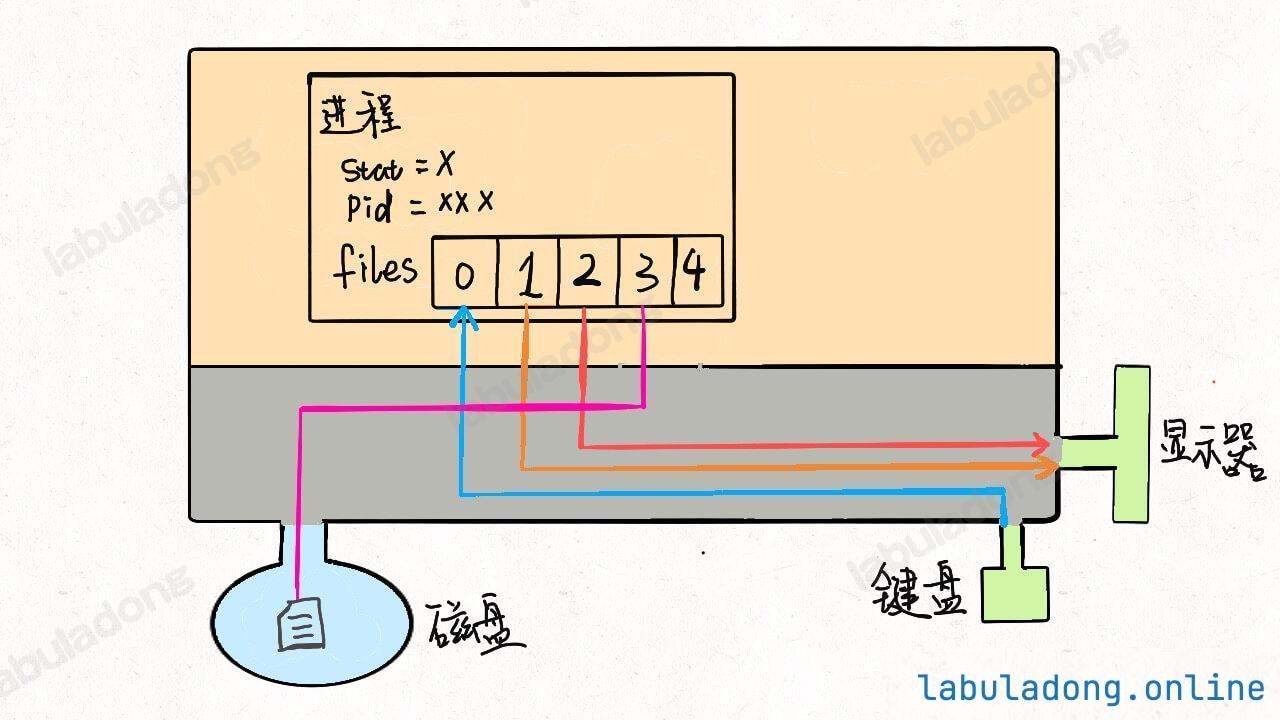
|
||||
|
||||
明白了这个原理,**输入重定向**就很好理解了,程序想读取数据的时候就会去`files[0]`读取,所以我们只要把`files[0]`指向一个文件,那么程序就会从这个文件中读取数据,而不是从键盘:
|
||||
明白了这个原理,**输入重定向**就很好理解了,程序想读取数据的时候就会去 `files[0]` 读取,所以我们只要把 `files[0]` 指向一个文件,那么程序就会从这个文件中读取数据,而不是从键盘:
|
||||
|
||||
```shell
|
||||
$ command < file.txt
|
||||
```
|
||||
|
||||

|
||||
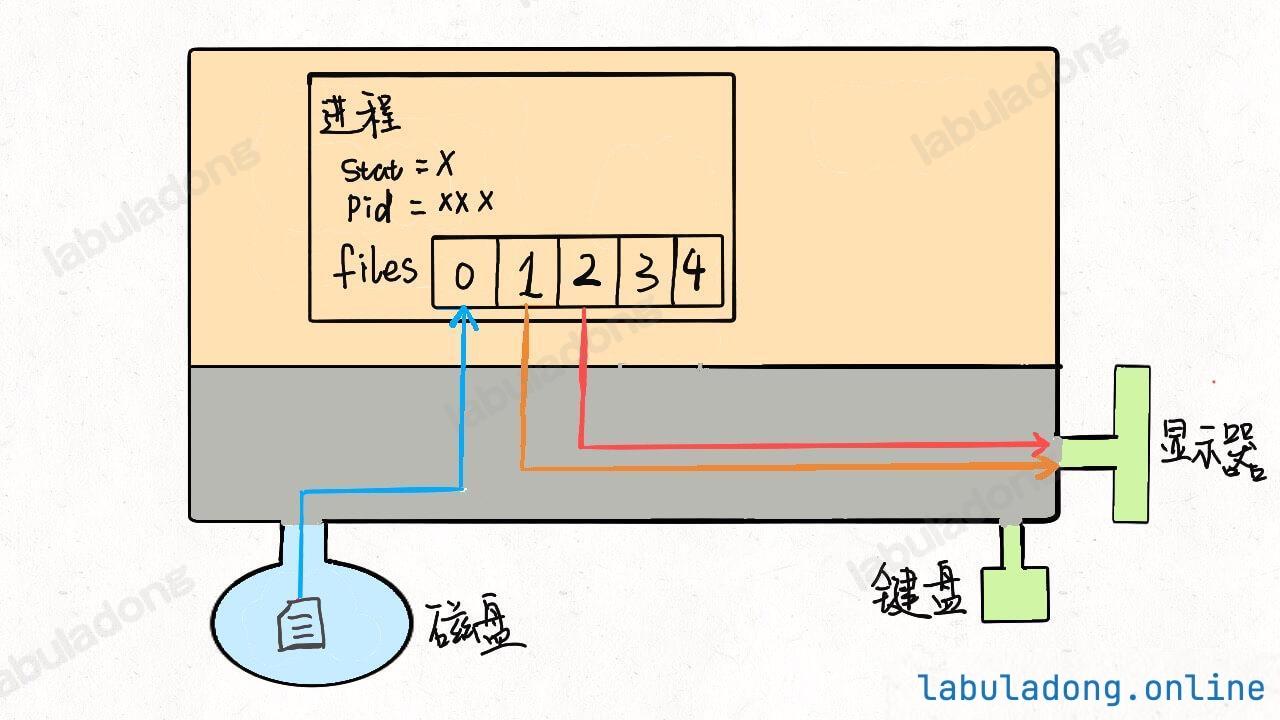
|
||||
|
||||
同理,**输出重定向**就是把`files[1]`指向一个文件,那么程序的输出就不会写入到显示器,而是写入到这个文件中:
|
||||
同理,**输出重定向**就是把 `files[1]` 指向一个文件,那么程序的输出就不会写入到显示器,而是写入到这个文件中:
|
||||
|
||||
```shell
|
||||
$ command > file.txt
|
||||
```
|
||||
|
||||

|
||||
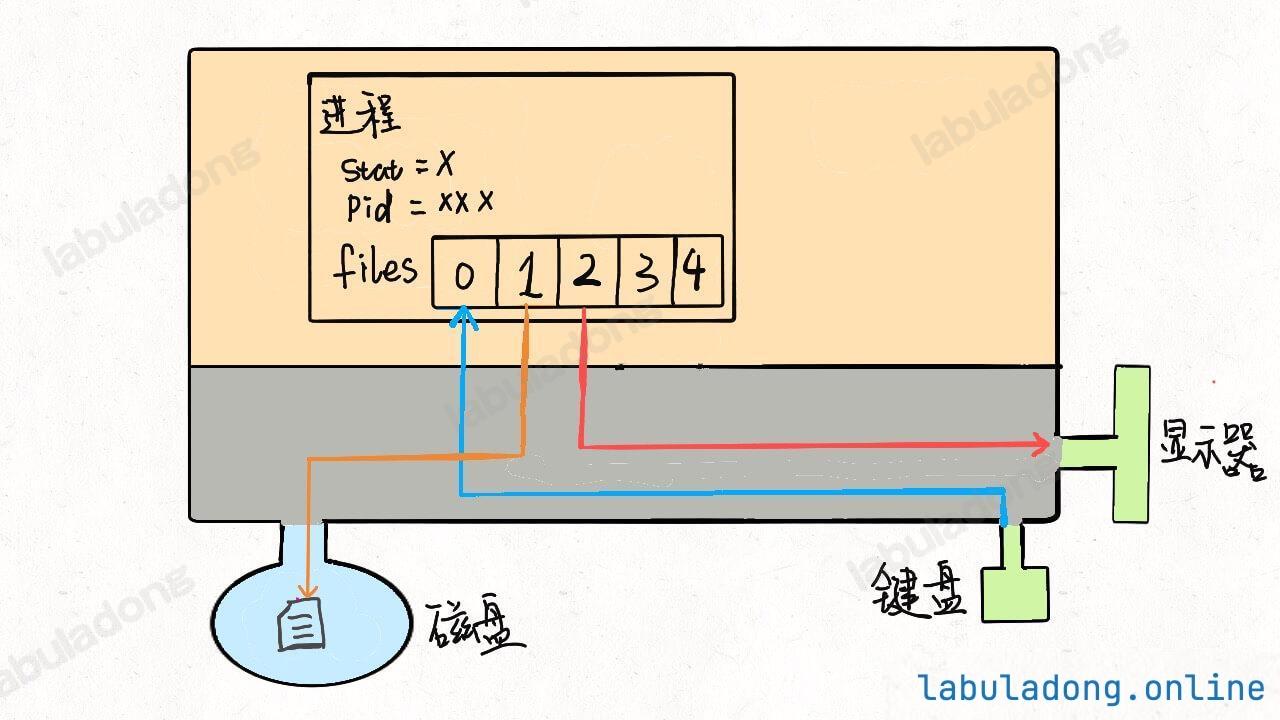
|
||||
|
||||
错误重定向也是一样的,就不再赘述。
|
||||
|
||||
|
|
@ -101,9 +102,9 @@ $ command > file.txt
|
|||
$ cmd1 | cmd2 | cmd3
|
||||
```
|
||||
|
||||

|
||||
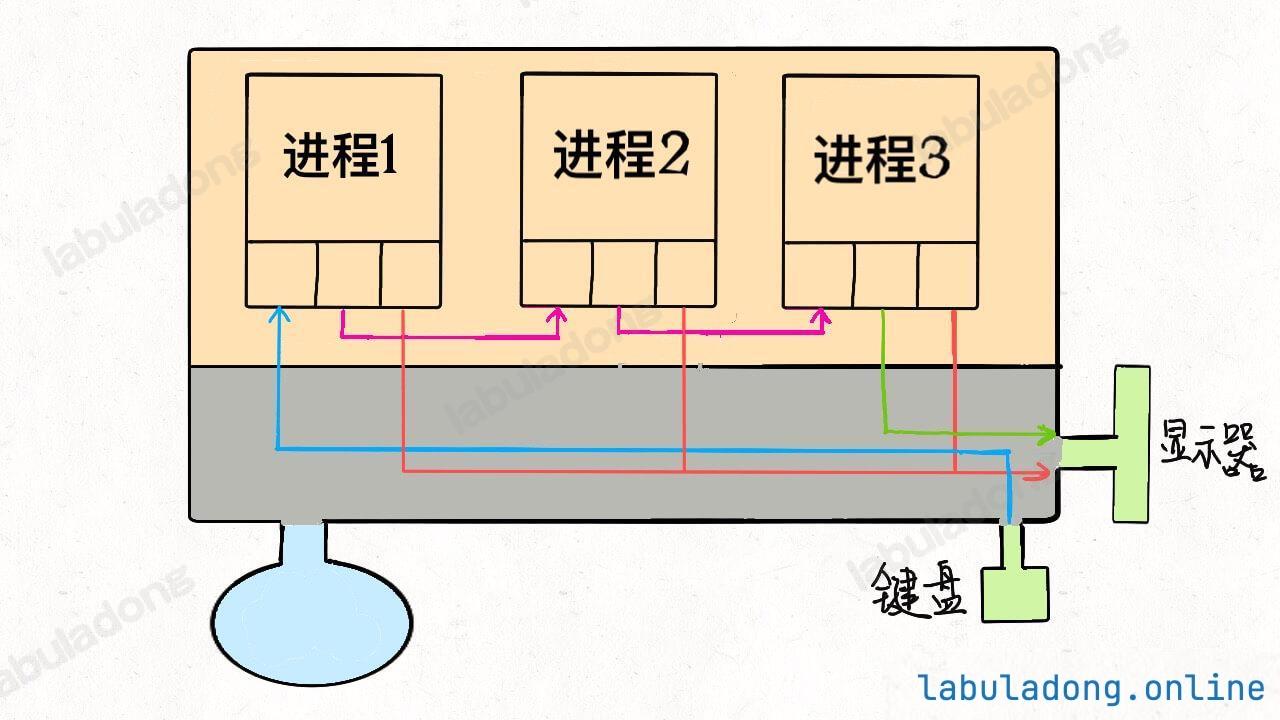
|
||||
|
||||
到这里,你可能也看出「Linux 中一切皆文件」设计思路的高明了,不管是设备、另一个进程、socket 套接字还是真正的文件,全部都可以读写,统一装进一个简单的`files`数组,进程通过简单的文件描述符访问相应资源,具体细节交于操作系统,有效解耦,优美高效。
|
||||
到这里,你可能也看出「Linux 中一切皆文件」设计思路的高明了,不管是设备、另一个进程、socket 套接字还是真正的文件,全部都可以读写,统一装进一个简单的 `files` 数组,进程通过简单的文件描述符访问相应资源,具体细节交于操作系统,有效解耦,优美高效。
|
||||
|
||||
### 三、线程是什么
|
||||
|
||||
|
|
@ -111,13 +112,13 @@ $ cmd1 | cmd2 | cmd3
|
|||
|
||||
为什么说 Linux 中线程和进程基本没有区别呢,因为从 Linux 内核的角度来看,并没有把线程和进程区别对待。
|
||||
|
||||
我们知道系统调用`fork()`可以新建一个子进程,函数`pthread()`可以新建一个线程。**但无论线程还是进程,都是用`task_struct`结构表示的,唯一的区别就是共享的数据区域不同**。
|
||||
我们知道系统调用 `fork()` 可以新建一个子进程,函数 `pthread()` 可以新建一个线程。**但无论线程还是进程,都是用 `task_struct` 结构表示的,唯一的区别就是共享的数据区域不同**。
|
||||
|
||||
换句话说,线程看起来跟进程没有区别,只是线程的某些数据区域和其父进程是共享的,而子进程是拷贝副本,而不是共享。就比如说,`mm`结构和`files`结构在线程中都是共享的,我画两张图你就明白了:
|
||||
换句话说,线程看起来跟进程没有区别,只是线程的某些数据区域和其父进程是共享的,而子进程是拷贝副本,而不是共享。就比如说,`mm` 结构和 `files` 结构在线程中都是共享的,我画两张图你就明白了:
|
||||
|
||||

|
||||
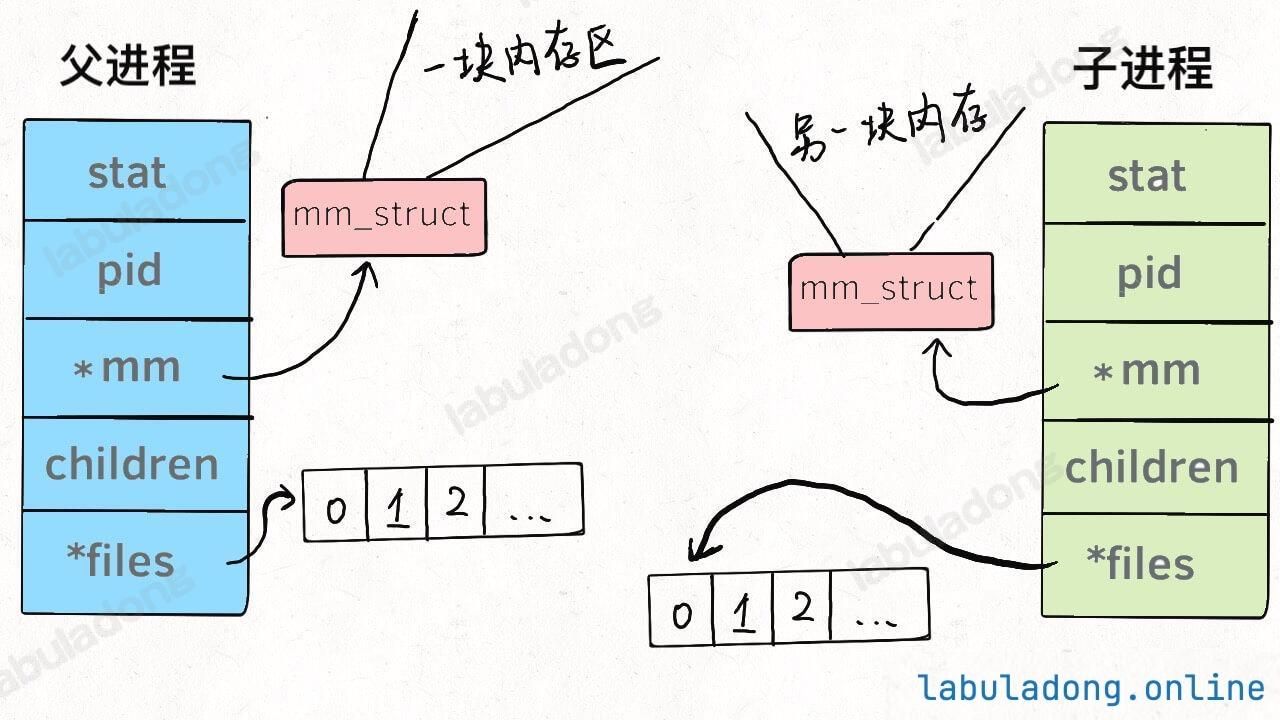
|
||||
|
||||

|
||||
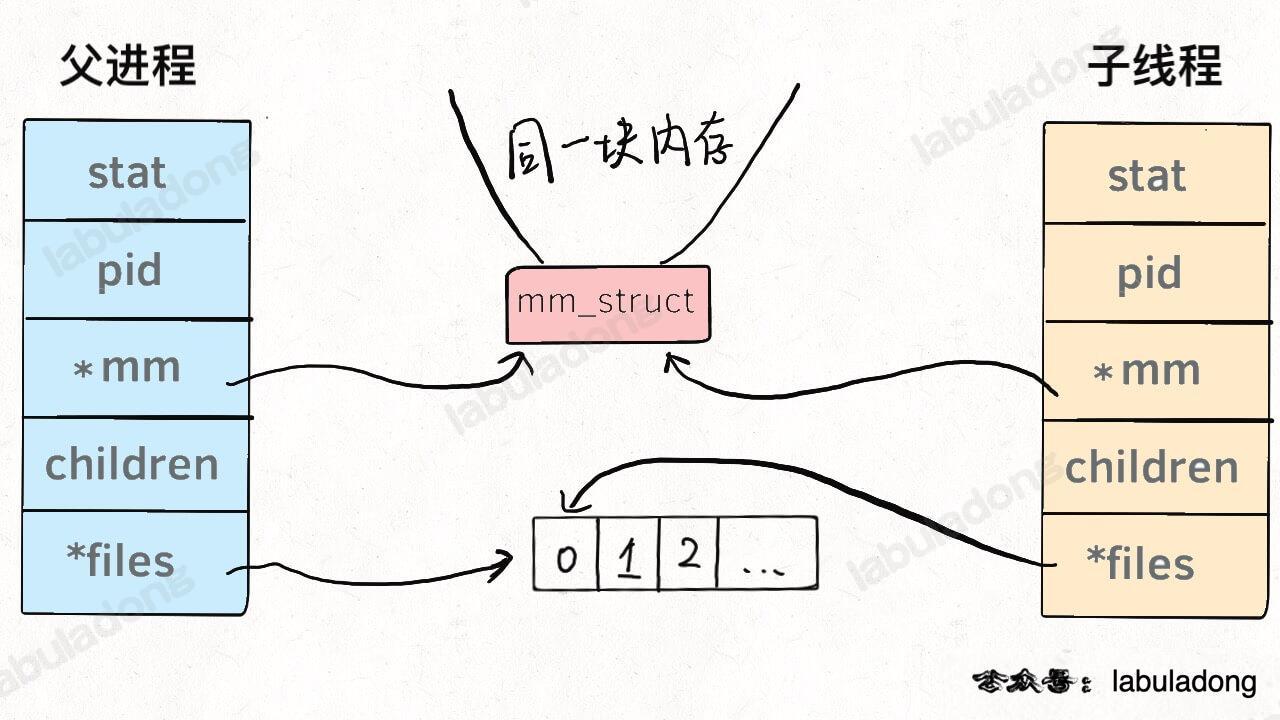
|
||||
|
||||
所以说,我们的多线程程序要利用锁机制,避免多个线程同时往同一区域写入数据,否则可能造成数据错乱。
|
||||
|
||||
|
|
@ -129,14 +130,27 @@ $ cmd1 | cmd2 | cmd3
|
|||
|
||||
在 Linux 中新建线程和进程的效率都是很高的,对于新建进程时内存区域拷贝的问题,Linux 采用了 copy-on-write 的策略优化,也就是并不真正复制父进程的内存空间,而是等到需要写操作时才去复制。**所以 Linux 中新建进程和新建线程都是很迅速的**。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Linux shell 的实用小技巧](https://labuladong.github.io/article/fname.html?fname=linuxshell技巧)
|
||||
- [Linux 管道符原理大揭秘](https://labuladong.github.io/article/fname.html?fname=linux技巧3)
|
||||
- [关于 Linux shell 你必须知道的](https://labuladong.github.io/article/fname.html?fname=linuxshell)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||

|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
|
@ -1,16 +1,17 @@
|
|||
# Redis 入侵
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -20,7 +21,7 @@
|
|||
|
||||
经过一番攀谈交心了解到,他跑了一个比较古老已经停止维护的开源项目,安装的旧版本的 Redis,而且他对 Linux 的使用不是很熟练。我就知道,他的服务器已经被攻陷了,想到也许还会有不少像我这位朋友的人,不重视操作系统的权限、防火墙的设置和数据库的保护,我就写一篇文章简单看看这种情况出现的原因,以及如何防范。
|
||||
|
||||
PS:这种手法现在已经行不通了,因为新版本 Redis 都增加了 protect mode,增加了安全性,我们只能在本地简单模拟一下,就别乱试了。
|
||||
> PS:这种手法现在已经行不通了,因为新版本 Redis 都增加了 protect mode,增加了安全性,我们只能在本地简单模拟一下,就别乱试了。
|
||||
|
||||
### 事件经过
|
||||
|
||||
|
|
@ -46,29 +47,29 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
|
|||
|
||||
除了密码登录之外,还可以使用 RSA 密钥对登录,但是必须要把我的公钥存到 root 的家目录中 `/root/.ssh/authored_keys`。我们知道 `/root` 目录的权限设置是不允许任何其他用户闯入读写的:
|
||||
|
||||

|
||||

|
||||
|
||||
但是,我发现自己竟然可以直接访问 Redis:
|
||||
|
||||

|
||||

|
||||
|
||||
如果 Redis 是以 root 的身份运行的,那么我就可以通过操作 Redis,让它把我的公钥写到 root 的家目录中。Redis 有一种持久化方式是生成 RDB 文件,其中会包含原始数据。
|
||||
|
||||
我露出了邪恶的微笑,先把 Redis 中的数据全部清空,然后把我的 RSA 公钥写到数据库里,这里在开头和结尾加换行符目的是避免 RDB 文件生成过程中损坏到公钥字符串:
|
||||
|
||||

|
||||

|
||||
|
||||
命令 Redis 把生成的数据文件保存到 `/root/.ssh/` 中的 `authored_keys` 文件中:
|
||||
|
||||

|
||||

|
||||
|
||||
现在,root 的家目录中已经包含了我们的 RSA 公钥,我们现在可以通过密钥对登录进 root 了:
|
||||
|
||||

|
||||

|
||||
|
||||
看一下刚才写入 root 家的公钥:
|
||||
|
||||

|
||||

|
||||
|
||||
乱码是 GDB 文件的某种编码吧,但是中间的公钥被完整保存了,而且 ssh 登录程序竟然也识别了这段被乱码包围的公钥!
|
||||
|
||||
|
|
@ -94,14 +95,14 @@ Redis 监听的默认端口是 6379,我们设置它接收网卡 127.0.0.1 的
|
|||
|
||||
3、利用 rename 功能伪装 flushall 这种危险命令,以防被删库,丢失数据。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||

|
||||
|
||||
======其他语言代码======
|
||||
|
|
@ -1,16 +1,17 @@
|
|||
# 一文读懂 session 和 cookie
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -45,11 +46,11 @@ func cookie(w http.ResponseWriter, r *http.Request) {
|
|||
|
||||
当浏览器访问对应网址时,通过浏览器的开发者工具查看此次 HTTP 通信的细节,可以看见服务器的回应发出了两次 `SetCookie` 命令:
|
||||
|
||||

|
||||
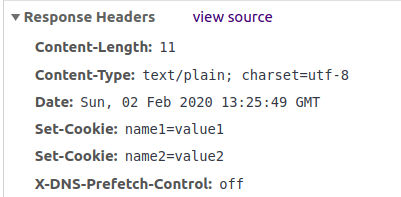
|
||||
|
||||
在这之后,浏览器的请求中的 `Cookie` 字段就带上了这两个 cookie:
|
||||
|
||||

|
||||
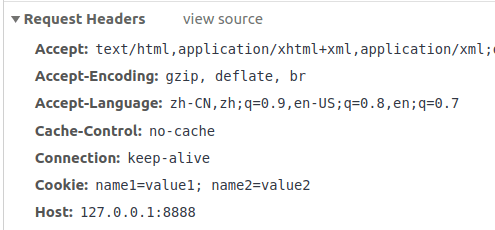
|
||||
|
||||
**cookie 的作用其实就是这么简单,无非就是服务器给每个客户端(浏览器)打的标签**,方便服务器辨认而已。当然,HTTP 还有很多参数可以设置 cookie,比如过期时间,或者让某个 cookie 只有某个特定路径才能使用等等。
|
||||
|
||||
|
|
@ -69,7 +70,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
|
|||
|
||||
那如果我不让浏览器发送 cookie,每次都伪装成一个第一次来试用的小萌新,不就可以不断白嫖了么?浏览器会把网站的 cookie 以文件的形式存在某些地方(不同的浏览器配置不同),你把他们找到然后删除就行了。但是对于 Firefox 和 Chrome 浏览器,有很多插件可以直接编辑 cookie,比如我的 Chrome 浏览器就用的一款叫做 EditThisCookie 的插件,这是他们官网:
|
||||
|
||||

|
||||
|
||||
|
||||
这类插件可以读取浏览器在当前网页的 cookie,点开插件可以任意编辑和删除 cookie。**当然,偶尔白嫖一两次还行,不鼓励高频率白嫖,想常用还是掏钱吧,否则网站赚不到钱,就只能取消免费试用这个机制了**。
|
||||
|
||||
|
|
@ -79,7 +80,7 @@ session 就可以配合 cookie 解决这一问题,比如说一个 cookie 存
|
|||
|
||||
session 的原理不难,但是具体实现它可是很有技巧的,一般需要三个组件配合完成,它们分别是 `Manager`、`Provider` 和 `Session` 三个类(接口)。
|
||||
|
||||

|
||||
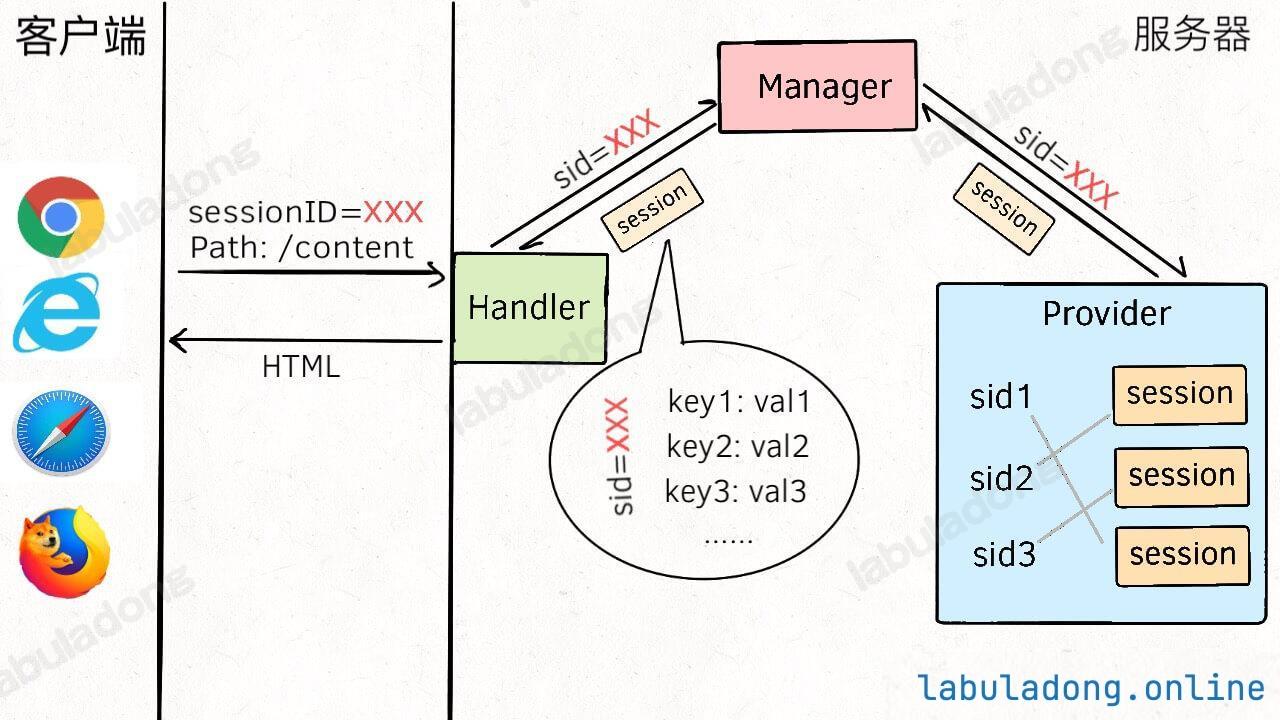
|
||||
|
||||
1、浏览器通过 HTTP 协议向服务器请求路径 `/content` 的网页资源,对应路径上有一个 Handler 函数接收请求,解析 HTTP header 中的 cookie,得到其中存储的 sessionID,然后把这个 ID 发给 `Manager`。
|
||||
|
||||
|
|
@ -93,7 +94,6 @@ session 的原理不难,但是具体实现它可是很有技巧的,一般需
|
|||
|
||||
**这就是设计层面的技巧了**,下面就来说说,为什么分成 `Manager`、`Provider` 和 `Session`。
|
||||
|
||||
|
||||
先从最底层的 `Session` 说。既然 session 就是键值对,为啥不直接用哈希表,而是要抽象出这么一个数据结构呢?
|
||||
|
||||
第一,因为 `Session` 结构可能不止存储了一个哈希表,还可以存储一些辅助数据,比如 `sid`,访问次数,过期时间或者最后一次的访问时间,这样便于实现想 LRU、LFU 这样的算法。
|
||||
|
|
@ -115,7 +115,7 @@ type Session interface {
|
|||
|
||||
再说 `Provider` 为啥要抽象出来。我们上面那个图的 `Provider` 就是一个散列表,保存 `sid` 到 `Session` 的映射,但是实际中肯定会更加复杂。我们不是要时不时删除一些 session 吗,除了设置存活时间之外,还可以采用一些其他策略,比如 LRU 缓存淘汰算法,这样就需要 `Provider` 内部使用哈希链表这种数据结构来存储 session。
|
||||
|
||||
PS:关于 LRU 算法的奥妙,参见前文「LRU 算法详解」。
|
||||
> PS:关于 LRU 算法的奥妙,参见前文 [LRU 算法详解](https://labuladong.github.io/article/fname.html?fname=LRU算法)。
|
||||
|
||||
因此,`Provider` 作为一个容器,就是要屏蔽算法细节,以合理的数据结构和算法组织 `sid` 和 `Session` 的映射关系,只需要实现下面这几个方法实现对 session 的增删查改:
|
||||
|
||||
|
|
@ -134,7 +134,6 @@ type Provider interface {
|
|||
}
|
||||
```
|
||||
|
||||
|
||||
最后说 `Manager`,大部分具体工作都委托给 `Session` 和 `Provider` 承担了,`Manager` 主要就是一个参数集合,比如 session 的存活时间,清理过期 session 的策略,以及 session 的可用存储方式。`Manager` 屏蔽了操作的具体细节,我们可以通过 `Manager` 灵活地配置 session 机制。
|
||||
|
||||
综上,session 机制分成几部分的最主要原因就是解耦,实现定制化。我在 Github 上看过几个 Go 语言实现的 session 服务,源码都很简单,有兴趣的朋友可以学习学习:
|
||||
|
|
@ -143,14 +142,14 @@ https://github.com/alexedwards/scs
|
|||
|
||||
https://github.com/astaxie/build-web-application-with-golang
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||

|
||||
|
||||
======其他语言代码======
|
||||
167
技术/刷题技巧.md
167
技术/刷题技巧.md
|
|
@ -1,22 +1,21 @@
|
|||
# 刷题小技巧
|
||||
|
||||
# 算法笔试骗分套路
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
相信每个人都有过被代码的小 bug 搞得心态爆炸的经历,本文分享一个我最常用的简单技巧,可以大幅提升刷题的幸福感。
|
||||
|
||||
在这之前,首先回答一个问题,刷力扣题是直接在网页上刷比较好还是在本地 IDE 上刷比较好?
|
||||
首先回答一个问题,刷力扣题是直接在网页上刷比较好还是在本地 IDE 上刷比较好?
|
||||
|
||||
如果是牛客网笔试那种自己处理输入输出的判题形式,一定要在 IDE 上写,这个没啥说的,但**像力扣这种判题形式,我个人偏好直接在网页上刷**,原因有二:
|
||||
|
||||
|
|
@ -34,15 +33,121 @@
|
|||
|
||||
如果平时练习的时候就习惯没有 IDE 的自动补全,习惯手写代码大脑编译,到时候面试的时候写代码就能更快更从容。
|
||||
|
||||
之前我面快手的时候,有个面试官让我 [实现 LRU 算法](https://labuladong.gitee.io/algo/),我直接把双链表的实现、哈希链表的实现,在网页上全写出来了,而且一次无 bug 跑通,可以看到面试官惊讶的表情😂
|
||||
之前我面快手的时候,有个面试官让我 [实现 LRU 算法](https://labuladong.github.io/article/fname.html?fname=LRU算法),我直接把双链表的实现、哈希链表的实现,在网页上全写出来了,而且一次无 bug 跑通,可以看到面试官惊讶的表情😂
|
||||
|
||||
我秋招能当 offer 收割机,很大程度上就是因为手写算法这一关超出面试官的预期,其实都是因为之前在网页上刷题练出来的。
|
||||
|
||||
接下来分享我觉得最常实用的干货技巧。
|
||||
当然,实在不想在网页上刷,也可以用我的 vscode 刷题插件或者 JetBrains 刷题插件,插件和我的网站内容都有完美的融合:
|
||||
|
||||

|
||||
|
||||
### 避实就虚
|
||||
|
||||
大家也知道,大部分笔试题目都需要你自己来处理输入数据,然后让程序打印输出。判题的底层原理是,把你程序的输出用 Linux 重定向符 `>` 写到文件里面,然后比较你的输出和正确答案是否相同。
|
||||
|
||||
那么有的问题难点就变得形同虚设,我们可以偷工减料,举个简化的例子,假设题目说给你输入一串用空格分隔的字符,告诉你这代表一个单链表,请你把这个单链表翻转,并且强调,一定要把输入的数字转化成单链表之后再翻转哦!
|
||||
|
||||
那你怎么做?真就自己定义一个 `ListNode` 单链表节点类,然后再写代码把输入转化成一个单链表,然后再用让人头晕的指针操作去老老实实翻转单链表?
|
||||
|
||||
搞清楚我们是来 AC 题目的,不是来学习算法思维的。正确的做法是直接把输入存到数组里,然后用 [双指针技巧](https://labuladong.github.io/article/fname.html?fname=双指针技巧) 几行代码给它翻转了,然后打印出来完事儿。
|
||||
|
||||
我就见过不少这种题目,比如题目说输入的是一个单链表,让我分组翻转链表,而且还特别强调要用递归实现,就是我们前文 [K 个一组翻转链表](https://labuladong.github.io/article/fname.html?fname=k个一组反转链表) 的算法。嗯,如果用数组进行翻转,两分钟就写出来了,嘿嘿。
|
||||
|
||||
还有我们前文 [扁平化嵌套列表](https://labuladong.github.io/article/fname.html?fname=nestInteger) 讲到的题目,思路很巧妙,但是在笔试中遇到时,输入是一个形如 `[1,[4,[6]]]` 的字符串,那直接用正则表达式把数字抽出来,就是一个扁平化的列表了……
|
||||
|
||||
### 巧用随机数
|
||||
|
||||
再说一个鸡贼的技巧,注意那些输出为「二值」的题目,二值就是类似布尔值,或者 0 和 1 这种组合有限的。
|
||||
|
||||
比如说很多题目是这样,巴拉巴拉给你说一堆条件,然后问你输入的数据能不能达成这些条件,如果能的话请输出 `YES`,不能的话输出 `NO`。
|
||||
|
||||
如果你会做当然好,如果不会做怎么办?
|
||||
|
||||
首先这样提交一下:
|
||||
|
||||
```java
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
System.out.println("YES");
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
看下 case 通过率,假设是 60%,那么说明结果为 `YES` 有 60% 的概率,所以可以这样写代码:
|
||||
|
||||
```java
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
// 60% 的概率输出 YES,40% 的概率输出 NO
|
||||
System.out.println((new Random().nextInt() % 100) < 60 ? "YES" : "NO");
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
嘿嘿,这题你可以不会,但是一定要在力所能及的范围内做到极致!
|
||||
|
||||
### 编程语言的选择
|
||||
|
||||
仅从做算法题的角度来说,我个人比较建议使用 Java 作为笔试的编程语言。因为 JetBrain 家的 IntelliJ 实在是太香了,相比其他语言的编辑器,不仅有 `psvm` 和 `sout` 这样的快捷命令(你要是连这都不知道,赶紧面壁去),而且可以帮你检查出很多笔误,比如说 `while` 循环里面忘记递增变量,或者 `return` 语句错写到循环里这种由于疏忽所导致的问题。
|
||||
|
||||
C++ 也还行,但是我觉得没有 Java 好用。我印象中 C++ 连个分割字符串的 `split` 函数都没有,光这点我就不想用 C++ 了……
|
||||
|
||||
还有一点,C++ 代码对时间的限制高,别的语言时间限制 4000ms,C++ 限制 2000ms,我觉得挺吃亏的。怪不得看别人用 C++ 写算法,为了提高速度,都不用标准库的 `vector` 容器,非要用原始的 `int[]` 数组,我看着都头疼。
|
||||
|
||||
Python 的话我刷题用的比较少,因为我不太喜欢用动态语言,不好调试。不过这个语言的奇技淫巧太多,如果你深谙 Python 的套路,可以在某些时候投机取巧。比如说我们前文写到的 [表达式求值算法](https://labuladong.github.io/article/fname.html?fname=实现计算器) 是一个困难级别的算法,但如果用 Python 内置的 `exec` 函数,直接就能算出答案。
|
||||
|
||||
这个在笔试里肯定是很占便宜的,因为之前说了,我们要的是结果,没人在乎你是怎么得到结果的。
|
||||
|
||||
### 解法代码分层
|
||||
|
||||
代码分层应该算是一种比较好的习惯,可以增加写代码的速度和降低调试的难度。
|
||||
|
||||
简单说就是,不要把所有代码都写在 `main` 函数里面,我一直使用的套路是,`main` 函数负责接收数据,加一个 `solution` 函数负责统一处理数据和输出答案,然后再用诸如 `backtrack` 这样一个函数处理具体的算法逻辑。
|
||||
|
||||
举个例子,比如说一道题,我决定用带备忘录的动态规划求解,代码的大致结构是这样:
|
||||
|
||||
```java
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
// 主要负责接收数据
|
||||
int N = scanner.nextInt();
|
||||
int[][] orders = new int[N][2];
|
||||
for (int i = 0; i < N; i++) {
|
||||
orders[i][0] = scanner.nextInt();
|
||||
orders[i][1] = scanner.nextInt();
|
||||
}
|
||||
// 委托 solution 进行求解
|
||||
solution(orders);
|
||||
}
|
||||
|
||||
static void solution(int[][] orders) {
|
||||
// 排除一些基本的边界情况
|
||||
if (orders.length == 0) {
|
||||
System.out.println("None");
|
||||
return;
|
||||
}
|
||||
// 委托 dp 函数执行具体的算法逻辑
|
||||
int res = dp(orders, 0);
|
||||
// 负责输出结果
|
||||
System.out.println(res);
|
||||
}
|
||||
|
||||
// 备忘录
|
||||
static HashMap<String, Integer> memo = new HashMap<>();
|
||||
static int dp(int[][] orders, int start) {
|
||||
// 具体的算法逻辑
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
你看这样分层是不是很清楚,每个函数都有自己主要负责的任务,如果哪里出了问题,你也容易 debug。
|
||||
|
||||
倒不是说要把代码写得多规范,至于 `private` 这种约束免了也无妨,变量用拼音命名也 OK,关键是别把代码直接全写到 `main` 函数里面,真的乱,不出错也罢,一旦出错,估计要花一番功夫调试了,找不到问题乱了阵脚,那是要尽量避免的。
|
||||
|
||||
### 如何给算法 debug
|
||||
|
||||
代码的错误时无法避免的,有时候可能整个思路都错了,有时候可能是某些细节问题,比如 `i` 和 `j` 写反了,这种问题怎么排查?
|
||||
代码的错误是无法避免的,有时候可能整个思路都错了,有时候可能是某些细节问题,比如 `i` 和 `j` 写反了,这种问题怎么排查?
|
||||
|
||||
我想一般的算法问题肯定不难排查,肉眼检查应该都没啥问题,再不济 `print` 打印一些关键变量的值,总能发现问题。
|
||||
|
||||
|
|
@ -76,7 +181,7 @@ void printIndent(int n) {
|
|||
|
||||
**在递归函数的开头,调用 `printIndent(count++)` 并打印关键变量;然后在所有 `return` 语句之前调用 `printIndent(--count)` 并打印返回值**。
|
||||
|
||||
举个具体的例子,比如说上篇文章 [练琴时悟出的一个动态规划算法](https://labuladong.gitee.io/algo/) 中实现了一个递归的 `dp` 函数,大致的结构如下:
|
||||
举个具体的例子,比如说上篇文章 [练琴时悟出的一个动态规划算法](https://labuladong.github.io/article/fname.html?fname=转盘) 中实现了一个递归的 `dp` 函数,大致的结构如下:
|
||||
|
||||
```cpp
|
||||
int dp(string& ring, int i, string& key, int j) {
|
||||
|
|
@ -130,24 +235,48 @@ int dp(string& ring, int i, string& key, int j) {
|
|||
|
||||
如果去掉注释,执行一个测试用例,输出如下:
|
||||
|
||||

|
||||

|
||||
|
||||
这样,我们通过对比对应的缩进就能知道每次递归时输入的关键参数 `i, j` 的值,以及每次递归调用返回的结果是多少。
|
||||
|
||||
**最重要的是,这样可以比较直观地看出递归过程,你有没有发现这就是一棵递归树**?
|
||||
|
||||

|
||||

|
||||
|
||||
前文 [动态规划套路详解](https://labuladong.gitee.io/algo/) 说过,理解递归函数最重要的就是画出递归树,这样打印一下,连递归树都不用自己画了,而且还能清晰地看出每次递归的返回值。
|
||||
前文 [动态规划套路详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 说过,理解递归函数最重要的就是画出递归树,这样打印一下,连递归树都不用自己画了,而且还能清晰地看出每次递归的返回值。
|
||||
|
||||
**可以说,这是对刷题「幸福感」提升最大的一个小技巧,比 IDE 打断点要高效**。
|
||||
|
||||
好了,本文分享就到这里,马上快过年了,估计大家都无心学习了,不过刷题还是要坚持的,这就叫弯道超车,顺便实践一下这个技巧。
|
||||
### 考前复习策略
|
||||
|
||||
考前就别和某一道算法题死磕了,不划算。
|
||||
|
||||
应该尽可能多的看各种各样的题目,思考五分钟,想不出来解法的话直接看别人的答案。看懂思路就行了,甚至自己写一遍都没必要,因为比较浪费时间。
|
||||
|
||||
笔试的时候最怕的是没思路,所以把各种题型都过目一下,起码心里不会慌,只要有思路,平均一道题二三十分钟搞定还是不难的。
|
||||
|
||||
前面不是说了么,没有什么问题是暴力穷举解决不了的,直接用 [回溯算法套路框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 硬上,大不了加个备忘录,不就成 [动态规划套路框架](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 了么,再大不了这题我不做了么,暴力过上 60% 的 case 也挺 OK 的。
|
||||
|
||||
别的不多说了,套路这个东西,说来简单,一点就透,但问题是不点就不透。本文我简单介绍了几个笔试算法的技巧,各位好好品味~
|
||||
|
||||
最后,请秋招的同学多向身边的朋友推荐 labuladong 公众号。算法真的没那么难,这一切只是手段而已,过算法笔试拿 offer 才是目的。为了达到目的,套路是必须的,可以少走很多弯路,你的朋友会感谢你的,我也会感谢你的😏
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [带权重的随机选择算法](https://labuladong.github.io/article/fname.html?fname=随机权重)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
如果本文对你有帮助,点个在看,就会被推荐更多相似文章。
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号「labuladong」查看详情;后台回复关键词「进群」可加入算法群,回复题号获取对应的文章**:
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||

|
||||
|
|
|
|||
52
技术/在线练习平台.md
52
技术/在线练习平台.md
|
|
@ -1,16 +1,17 @@
|
|||
# 在线刷题学习平台
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -22,7 +23,7 @@
|
|||
|
||||
这是个叫做 Learning Git Branching 的项目,是我一定要推荐的:
|
||||
|
||||

|
||||
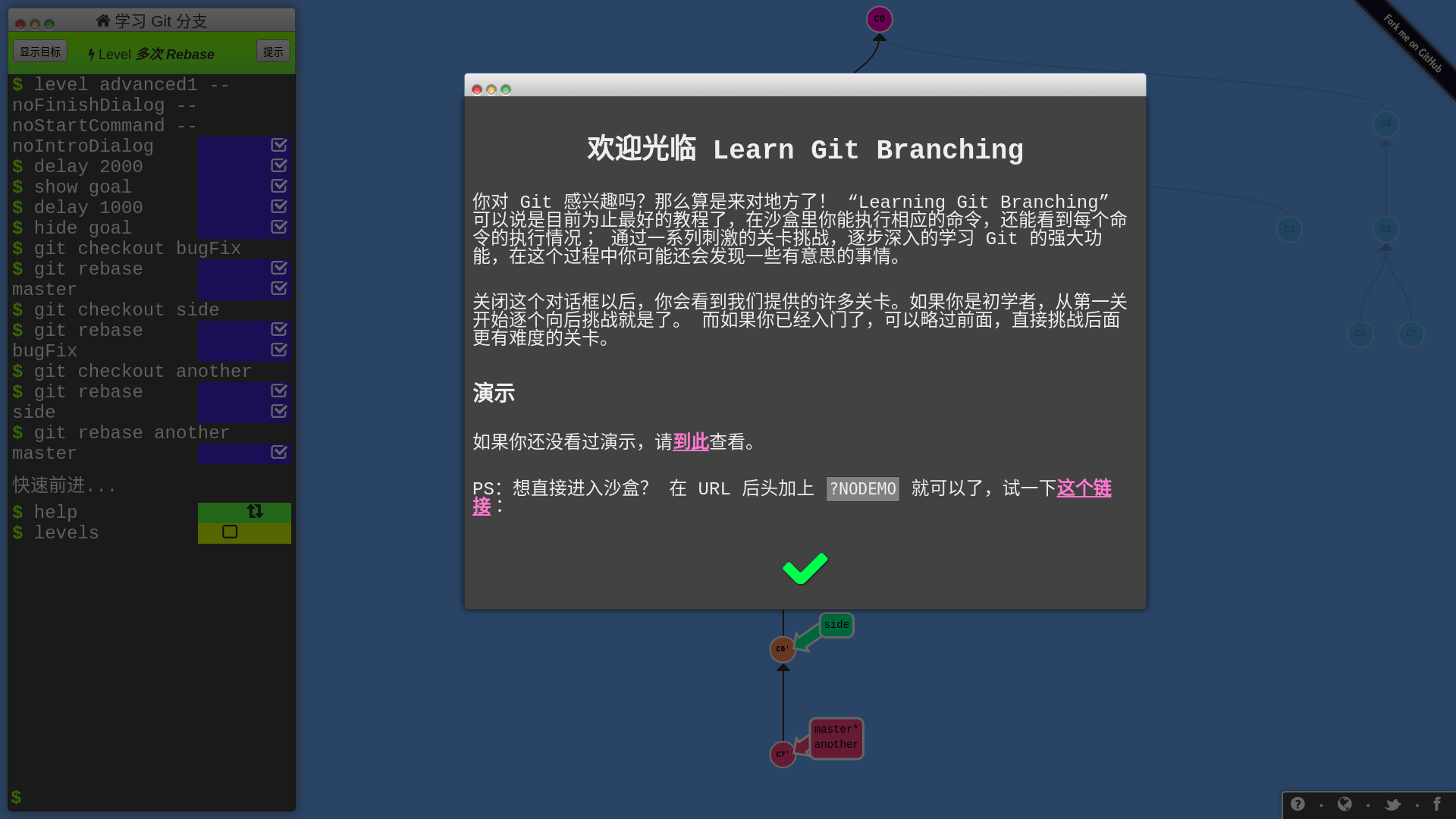
|
||||
|
||||
正如对话框中的自我介绍,这确实也是我至今发现的**最好**的 Git 动画教程,没有之一。
|
||||
|
||||
|
|
@ -30,21 +31,21 @@
|
|||
|
||||
这个网站的教程不是给你举那种修改文件的细节例子,而是将每次 `commit` 都抽象成树的节点,**用动画闯关的形式**,让你自由使用 Git 命令完成目标:
|
||||
|
||||

|
||||
|
||||
|
||||
所有 Git 分支都被可视化了,你只要在左侧的命令行输入 Git 命令,分支会进行相应的变化,只要达成任务目标,你就过关啦!网站还会记录你的命令数,试试能不能以最少的命令数过关!
|
||||
|
||||

|
||||
|
||||
|
||||
我一开始以为这个教程只包含本地 Git 仓库的版本管理,**后来我惊奇地发现它还有远程仓库的操作教程**!
|
||||
|
||||

|
||||

|
||||
|
||||

|
||||
|
||||
|
||||
真的跟玩游戏一样,难度设计合理,流畅度很好,我一玩都停不下来了,几小时就打通了,哈哈哈!
|
||||
|
||||

|
||||
|
||||
|
||||
总之,这个教程很适合初学和进阶,如果你觉得自己对 Git 的掌握还不太好,用 Git 命令还是靠碰运气,就可以玩玩这个教程,相信能够让你更熟练地使用 Git。
|
||||
|
||||
|
|
@ -64,13 +65,13 @@ https://learngitbranching.js.org
|
|||
|
||||
先说练习平台,叫做 RegexOne:
|
||||
|
||||

|
||||
|
||||
|
||||
前面有基本教程,后面有一些常见的正则表达式题目,比如判断邮箱、URL、电话号,或者抽取日志的关键信息等等。
|
||||
|
||||
只要写出符合要求的正则表达式,就可以进入下一个问题,关键是每道题还有标准答案,可以点击下面的 solution 按钮查看:
|
||||
|
||||

|
||||
|
||||
|
||||
RegexOne 网址:
|
||||
|
||||
|
|
@ -78,7 +79,7 @@ https://regexone.com/
|
|||
|
||||
再说测试工具,是个叫做 RegExr 的 Github 项目,这是它的网站:
|
||||
|
||||

|
||||
|
||||
|
||||
可以看见,输入文本和正则模式串后,**网站会给正则表达式添加好看且容易辨认的样式,自动在文本中搜索模式串,高亮显示匹配的字符串,并且还会显示每个分组捕获的字符串**。
|
||||
|
||||
|
|
@ -92,13 +93,13 @@ https://regexr.com/
|
|||
|
||||
这是一个叫做 SQLZOO 的网站,左侧是所有的练习内容:
|
||||
|
||||

|
||||
|
||||
|
||||
SQLZOO 是一款很好用的 SQL 练习平台,英文不难理解,可以直接看英文版,但是也可以切换繁体中文,比较友好。
|
||||
|
||||
这里都是比较常用的 SQL 命令,给你一个需求,你写 SQL 语句实现正确的查询结果。**最重要的是,这里不仅对每个命令的用法有详细解释,每个专题后面还有选择题(quiz),而且有判题系统,甚至有的比较难的题目还有视频讲解**:
|
||||
|
||||

|
||||
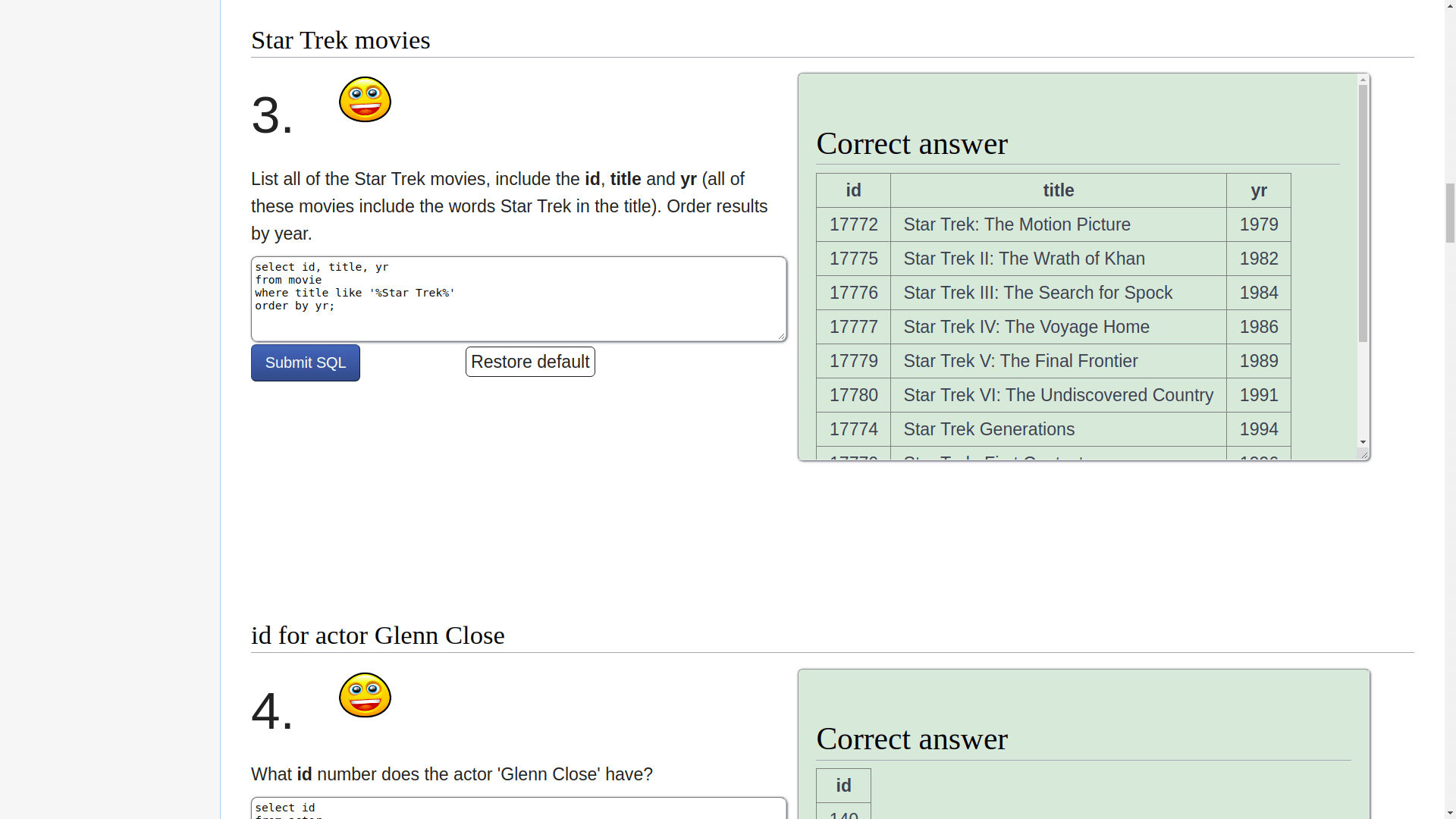
|
||||
|
||||
至于难度,循序渐进,即便对新手也很友好,靠后的问题确实比较有技巧性,相信这是热爱思维挑战的人喜欢的!LeetCode 也有 SQL 相关的题目,不过难度一般比较大,我觉得 SQLZOO 刷完基础 SQL 命令再去 LeetCode 刷比较合适。
|
||||
|
||||
|
|
@ -107,14 +108,23 @@ SQLZOO 是一款很好用的 SQL 练习平台,英文不难理解,可以直
|
|||
https://sqlzoo.net/
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [我用四个命令概括了 Git 的所有套路](https://labuladong.github.io/article/fname.html?fname=git常用命令)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||

|
||||
|
||||
======其他语言代码======
|
||||
36
技术/密码技术.md
36
技术/密码技术.md
|
|
@ -1,16 +1,17 @@
|
|||
# 密码算法的前世今生
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
|
|
@ -58,19 +59,19 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
|
|||
|
||||
首先,Alice 和 Bob 协商出两个数字 `N` 和 `G` 作为生成元,当然协商过程可以被窃听者 Hack 窃取,所以我把这两个数画到中间,代表三方都知道:
|
||||
|
||||

|
||||

|
||||
|
||||
现在 Alice 和 Bob **心中**各自想一个数字出来,分别称为 `A` 和 `B` 吧:
|
||||
|
||||

|
||||

|
||||
|
||||
现在 Alice 将自己心里的这个数字 `A` 和 `G` 通过某些运算得出一个数 `AG`,然后发给 Bob;Bob 将自己心里的数 `B` 和 `G` 通过相同的运算得出一个数 `BG`,然后发给 Alice:
|
||||
|
||||

|
||||

|
||||
|
||||
现在的情况变成这样了:
|
||||
|
||||

|
||||

|
||||
|
||||
注意,类似刚才举的散列函数的例子,知道 `AG` 和 `G`,并不能反推出 `A` 是多少,`BG` 同理。
|
||||
|
||||
|
|
@ -78,7 +79,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
|
|||
|
||||
而对于 Hack,可以窃取传输过程中的 `G`,`AG`,`BG`,但是由于计算不可逆,怎么都无法结合出 `ABG` 这个数字。
|
||||
|
||||

|
||||

|
||||
|
||||
以上就是基本流程,至于具体的数字取值是有讲究的,运算方法在百度上很容易找到,限于篇幅我就不具体写了。
|
||||
|
||||
|
|
@ -86,7 +87,7 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
|
|||
|
||||
对于该算法,Hack 又想到一种破解方法,不是窃听 Alice 和 Bob 的通信数据,而是直接同时冒充 Alice 和 Bob 的身份,也就是我们说的「**中间人攻击**」:
|
||||
|
||||

|
||||

|
||||
|
||||
这样,双方根本无法察觉在和 Hack 共享秘密,后果就是 Hack 可以解密甚至修改数据。
|
||||
|
||||
|
|
@ -158,9 +159,9 @@ Diffie-Hellman 密钥交换算法可以做到。**准确的说,该算法并不
|
|||
|
||||
4、Alice 通过这个公钥加密数据,开始和 Bob 通信。
|
||||
|
||||

|
||||
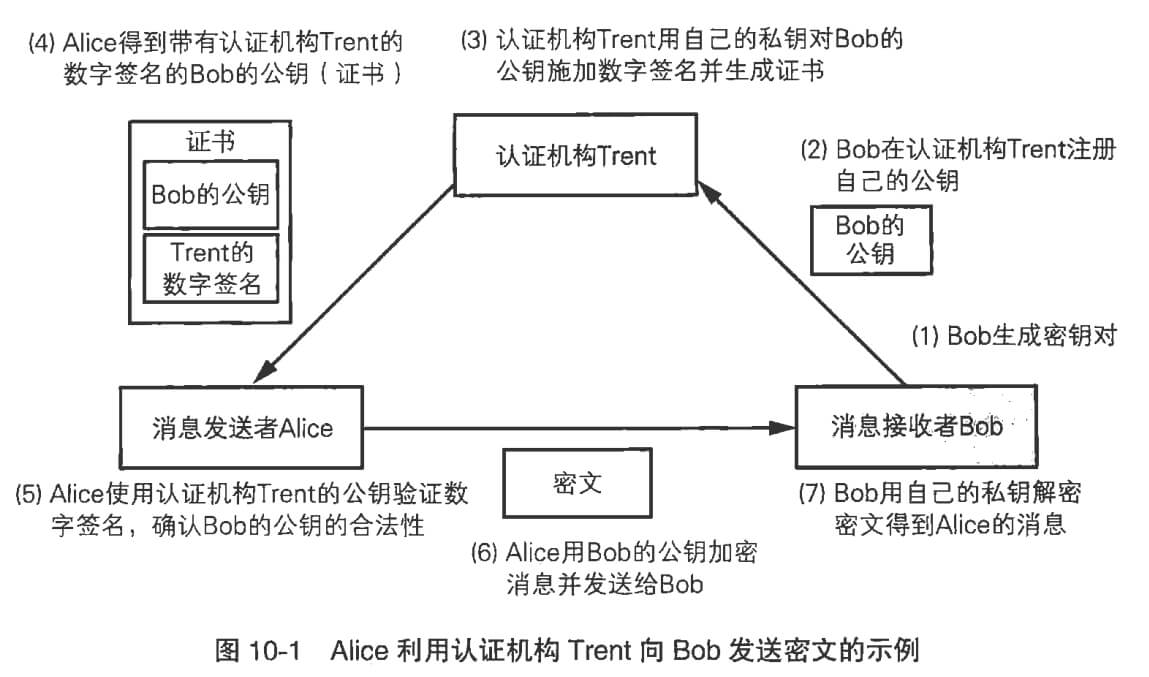
|
||||
|
||||
PS:以上只是为了说明,证书只需要安装一次,并不需要每次都向认证机构请求;一般是服务器直接给客户端发送证书,而不是认证机构。
|
||||
> PS:以上只是为了说明,证书只需要安装一次,并不需要每次都向认证机构请求;一般是服务器直接给客户端发送证书,而不是认证机构。
|
||||
|
||||
也许有人问,Alice 要想通过数字签名确定证书的有效性,前提是要有该机构的(认证)公钥,这不是又回到刚才的死循环了吗?
|
||||
|
||||
|
|
@ -190,14 +191,15 @@ HTTPS 协议中的 SSL/TLS 安全层会组合使用以上几种加密方式,**
|
|||
|
||||
密码技术只是安全的一小部分,即便是通过正规机构认证的 HTTPS 站点,也不意味着可信任,只能说明其数据传输是安全的。技术永远不可能真正保护你,最重要的还是得提高个人的安全防范意识,多留心眼儿,谨慎处理敏感数据。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||

|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
|
@ -0,0 +1,253 @@
|
|||
# 手把手带你刷二叉搜索树(第一期)
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [1038. Binary Search Tree to Greater Sum Tree](https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/) | [1038. 把二叉搜索树转换为累加树](https://leetcode.cn/problems/binary-search-tree-to-greater-sum-tree/) | 🟠
|
||||
| [230. Kth Smallest Element in a BST](https://leetcode.com/problems/kth-smallest-element-in-a-bst/) | [230. 二叉搜索树中第K小的元素](https://leetcode.cn/problems/kth-smallest-element-in-a-bst/) | 🟠
|
||||
| [538. Convert BST to Greater Tree](https://leetcode.com/problems/convert-bst-to-greater-tree/) | [538. 把二叉搜索树转换为累加树](https://leetcode.cn/problems/convert-bst-to-greater-tree/) | 🟠
|
||||
| - | [剑指 Offer II 054. 所有大于等于节点的值之和](https://leetcode.cn/problems/w6cpku/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
PS:[刷题插件](https://mp.weixin.qq.com/s/OE1zPVPj0V2o82N4HtLQbw) 集成了手把手刷二叉树功能,按照公式和套路讲解了 150 道二叉树题目,可手把手带你刷完二叉树分类的题目,迅速掌握递归思维。
|
||||
|
||||
前文手把手带你刷二叉树已经写了 [第一期](https://labuladong.github.io/article/fname.html?fname=二叉树系列1),[第二期](https://labuladong.github.io/article/fname.html?fname=二叉树系列2) 和 [第三期](https://labuladong.github.io/article/fname.html?fname=二叉树系列3),今天写一篇二叉搜索树(Binary Search Tree,后文简写 BST)相关的文章,手把手带你刷 BST。
|
||||
|
||||
首先,BST 的特性大家应该都很熟悉了:
|
||||
|
||||
1、对于 BST 的每一个节点 `node`,左子树节点的值都比 `node` 的值要小,右子树节点的值都比 `node` 的值大。
|
||||
|
||||
2、对于 BST 的每一个节点 `node`,它的左侧子树和右侧子树都是 BST。
|
||||
|
||||
二叉搜索树并不算复杂,但我觉得它可以算是数据结构领域的半壁江山,直接基于 BST 的数据结构有 AVL 树,红黑树等等,拥有了自平衡性质,可以提供 logN 级别的增删查改效率;还有 B+ 树,线段树等结构都是基于 BST 的思想来设计的。
|
||||
|
||||
**从做算法题的角度来看 BST,除了它的定义,还有一个重要的性质:BST 的中序遍历结果是有序的(升序)**。
|
||||
|
||||
也就是说,如果输入一棵 BST,以下代码可以将 BST 中每个节点的值升序打印出来:
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) return;
|
||||
traverse(root.left);
|
||||
// 中序遍历代码位置
|
||||
print(root.val);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
那么根据这个性质,我们来做两道算法题。
|
||||
|
||||
### 寻找第 K 小的元素
|
||||
|
||||
这是力扣第 230 题「二叉搜索树中第 K 小的元素」,看下题目:
|
||||
|
||||

|
||||
|
||||
这个需求很常见吧,一个直接的思路就是升序排序,然后找第 `k` 个元素呗。BST 的中序遍历其实就是升序排序的结果,找第 `k` 个元素肯定不是什么难事。
|
||||
|
||||
按照这个思路,可以直接写出代码:
|
||||
|
||||
```java
|
||||
int kthSmallest(TreeNode root, int k) {
|
||||
// 利用 BST 的中序遍历特性
|
||||
traverse(root, k);
|
||||
return res;
|
||||
}
|
||||
|
||||
// 记录结果
|
||||
int res = 0;
|
||||
// 记录当前元素的排名
|
||||
int rank = 0;
|
||||
void traverse(TreeNode root, int k) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
traverse(root.left, k);
|
||||
/* 中序遍历代码位置 */
|
||||
rank++;
|
||||
if (k == rank) {
|
||||
// 找到第 k 小的元素
|
||||
res = root.val;
|
||||
return;
|
||||
}
|
||||
/*****************/
|
||||
traverse(root.right, k);
|
||||
}
|
||||
```
|
||||
|
||||
这道题就做完了,不过呢,还是要多说几句,因为这个解法并不是最高效的解法,而是仅仅适用于这道题。
|
||||
|
||||
我们前文 [高效计算数据流的中位数](https://labuladong.github.io/article/fname.html?fname=数据流中位数) 中就提过今天的这个问题:
|
||||
|
||||
> 如果让你实现一个在二叉搜索树中通过排名计算对应元素的方法 `select(int k)`,你会怎么设计?
|
||||
|
||||
如果按照我们刚才说的方法,利用「BST 中序遍历就是升序排序结果」这个性质,每次寻找第 `k` 小的元素都要中序遍历一次,最坏的时间复杂度是 `O(N)`,`N` 是 BST 的节点个数。
|
||||
|
||||
要知道 BST 性质是非常牛逼的,像红黑树这种改良的自平衡 BST,增删查改都是 `O(logN)` 的复杂度,让你算一个第 `k` 小元素,时间复杂度竟然要 `O(N)`,有点低效了。
|
||||
|
||||
所以说,计算第 `k` 小元素,最好的算法肯定也是对数级别的复杂度,不过这个依赖于 BST 节点记录的信息有多少。
|
||||
|
||||
我们想一下 BST 的操作为什么这么高效?就拿搜索某一个元素来说,BST 能够在对数时间找到该元素的根本原因还是在 BST 的定义里,左子树小右子树大嘛,所以每个节点都可以通过对比自身的值判断去左子树还是右子树搜索目标值,从而避免了全树遍历,达到对数级复杂度。
|
||||
|
||||
那么回到这个问题,想找到第 `k` 小的元素,或者说找到排名为 `k` 的元素,如果想达到对数级复杂度,关键也在于每个节点得知道他自己排第几。
|
||||
|
||||
比如说你让我查找排名为 `k` 的元素,当前节点知道自己排名第 `m`,那么我可以比较 `m` 和 `k` 的大小:
|
||||
|
||||
1、如果 `m == k`,显然就是找到了第 `k` 个元素,返回当前节点就行了。
|
||||
|
||||
2、如果 `k < m`,那说明排名第 `k` 的元素在左子树,所以可以去左子树搜索第 `k` 个元素。
|
||||
|
||||
3、如果 `k > m`,那说明排名第 `k` 的元素在右子树,所以可以去右子树搜索第 `k - m - 1` 个元素。
|
||||
|
||||
这样就可以将时间复杂度降到 `O(logN)` 了。
|
||||
|
||||
那么,如何让每一个节点知道自己的排名呢?
|
||||
|
||||
这就是我们之前说的,需要在二叉树节点中维护额外信息。**每个节点需要记录,以自己为根的这棵二叉树有多少个节点**。
|
||||
|
||||
也就是说,我们 `TreeNode` 中的字段应该如下:
|
||||
|
||||
```java
|
||||
class TreeNode {
|
||||
int val;
|
||||
// 以该节点为根的树的节点总数
|
||||
int size;
|
||||
TreeNode left;
|
||||
TreeNode right;
|
||||
}
|
||||
```
|
||||
|
||||
有了 `size` 字段,外加 BST 节点左小右大的性质,对于每个节点 `node` 就可以通过 `node.left` 推导出 `node` 的排名,从而做到我们刚才说到的对数级算法。
|
||||
|
||||
当然,`size` 字段需要在增删元素的时候需要被正确维护,力扣提供的 `TreeNode` 是没有 `size` 这个字段的,所以我们这道题就只能利用 BST 中序遍历的特性实现了,但是我们上面说到的优化思路是 BST 的常见操作,还是有必要理解的。
|
||||
|
||||
### BST 转化累加树
|
||||
|
||||
力扣第 538 题和 1038 题都是这道题,完全一样,你可以把它们一块做掉。看下题目:
|
||||
|
||||
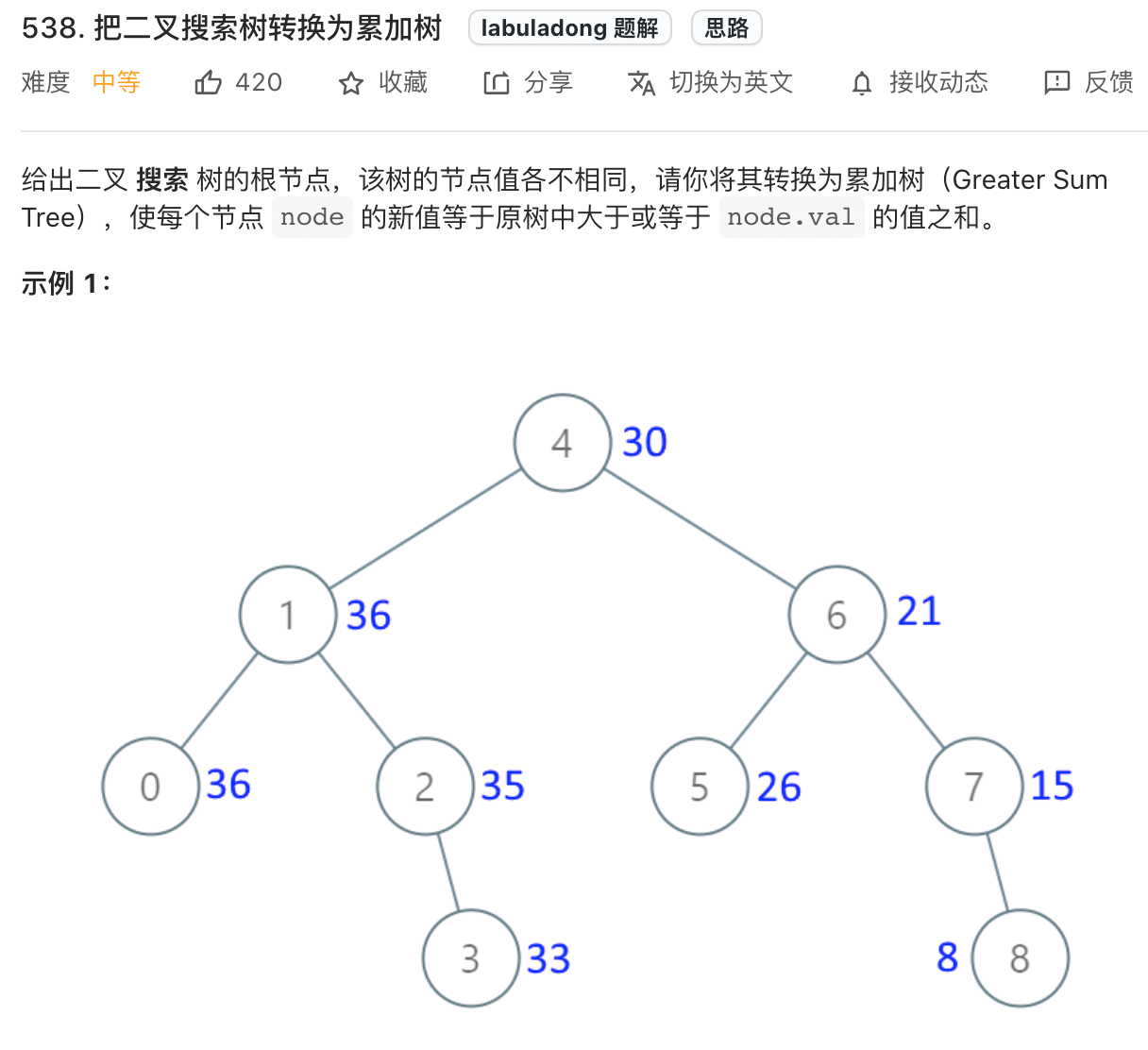
|
||||
|
||||
题目应该不难理解,比如图中的节点 5,转化成累加树的话,比 5 大的节点有 6,7,8,加上 5 本身,所以累加树上这个节点的值应该是 5+6+7+8=26。
|
||||
|
||||
我们需要把 BST 转化成累加树,函数签名如下:
|
||||
|
||||
```java
|
||||
TreeNode convertBST(TreeNode root)
|
||||
```
|
||||
|
||||
按照二叉树的通用思路,需要思考每个节点应该做什么,但是这道题上很难想到什么思路。
|
||||
|
||||
BST 的每个节点左小右大,这似乎是一个有用的信息,既然累加和是计算大于等于当前值的所有元素之和,那么每个节点都去计算右子树的和,不就行了吗?
|
||||
|
||||
这是不行的。对于一个节点来说,确实右子树都是比它大的元素,但问题是它的父节点也可能是比它大的元素呀?这个没法确定的,我们又没有触达父节点的指针,所以二叉树的通用思路在这里用不了。
|
||||
|
||||
**其实,正确的解法很简单,还是利用 BST 的中序遍历特性**。
|
||||
|
||||
刚才我们说了 BST 的中序遍历代码可以升序打印节点的值:
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) return;
|
||||
traverse(root.left);
|
||||
// 中序遍历代码位置
|
||||
print(root.val);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
那如果我想降序打印节点的值怎么办?
|
||||
|
||||
很简单,只要把递归顺序改一下就行了:
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) return;
|
||||
// 先递归遍历右子树
|
||||
traverse(root.right);
|
||||
// 中序遍历代码位置
|
||||
print(root.val);
|
||||
// 后递归遍历左子树
|
||||
traverse(root.left);
|
||||
}
|
||||
```
|
||||
|
||||
**这段代码可以降序打印 BST 节点的值,如果维护一个外部累加变量 `sum`,然后把 `sum` 赋值给 BST 中的每一个节点,不就将 BST 转化成累加树了吗**?
|
||||
|
||||
看下代码就明白了:
|
||||
|
||||
```java
|
||||
TreeNode convertBST(TreeNode root) {
|
||||
traverse(root);
|
||||
return root;
|
||||
}
|
||||
|
||||
// 记录累加和
|
||||
int sum = 0;
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
traverse(root.right);
|
||||
// 维护累加和
|
||||
sum += root.val;
|
||||
// 将 BST 转化成累加树
|
||||
root.val = sum;
|
||||
traverse(root.left);
|
||||
}
|
||||
```
|
||||
|
||||
这道题就解决了,核心还是 BST 的中序遍历特性,只不过我们修改了递归顺序,降序遍历 BST 的元素值,从而契合题目累加树的要求。
|
||||
|
||||
简单总结下吧,BST 相关的问题,要么利用 BST 左小右大的特性提升算法效率,要么利用中序遍历的特性满足题目的要求,也就这么些事儿吧。
|
||||
|
||||
最后调查下,经过这几篇二叉树相关的系列文章,大家刷题有没有点感觉了?可以留言和我交流。本文对你有帮助的话,请三连~
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [东哥带你刷二叉搜索树(基操篇)](https://labuladong.github.io/article/fname.html?fname=BST2)
|
||||
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.github.io/article/fname.html?fname=BST3)
|
||||
- [二叉树的递归转迭代的代码框架](https://labuladong.github.io/article/fname.html?fname=迭代遍历二叉树)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer II 054. 所有大于等于节点的值之和](https://leetcode.cn/problems/w6cpku/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -0,0 +1,316 @@
|
|||
# 手把手带你刷二叉搜索树(第二期)
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [450. Delete Node in a BST](https://leetcode.com/problems/delete-node-in-a-bst/) | [450. 删除二叉搜索树中的节点](https://leetcode.cn/problems/delete-node-in-a-bst/) | 🟠
|
||||
| [700. Search in a Binary Search Tree](https://leetcode.com/problems/search-in-a-binary-search-tree/) | [700. 二叉搜索树中的搜索](https://leetcode.cn/problems/search-in-a-binary-search-tree/) | 🟢
|
||||
| [701. Insert into a Binary Search Tree](https://leetcode.com/problems/insert-into-a-binary-search-tree/) | [701. 二叉搜索树中的插入操作](https://leetcode.cn/problems/insert-into-a-binary-search-tree/) | 🟠
|
||||
| [98. Validate Binary Search Tree](https://leetcode.com/problems/validate-binary-search-tree/) | [98. 验证二叉搜索树](https://leetcode.cn/problems/validate-binary-search-tree/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
PS:[刷题插件](https://mp.weixin.qq.com/s/OE1zPVPj0V2o82N4HtLQbw) 集成了手把手刷二叉树功能,按照公式和套路讲解了 150 道二叉树题目,可手把手带你刷完二叉树分类的题目,迅速掌握递归思维。
|
||||
|
||||
我们前文 [东哥带你刷二叉搜索树(特性篇)](https://labuladong.github.io/article/fname.html?fname=BST1) 介绍了 BST 的基本特性,还利用二叉搜索树「中序遍历有序」的特性来解决了几道题目,本文来实现 BST 的基础操作:判断 BST 的合法性、增、删、查。其中「删」和「判断合法性」略微复杂。
|
||||
|
||||
BST 的基础操作主要依赖「左小右大」的特性,可以在二叉树中做类似二分搜索的操作,寻找一个元素的效率很高。比如下面这就是一棵合法的二叉树:
|
||||
|
||||
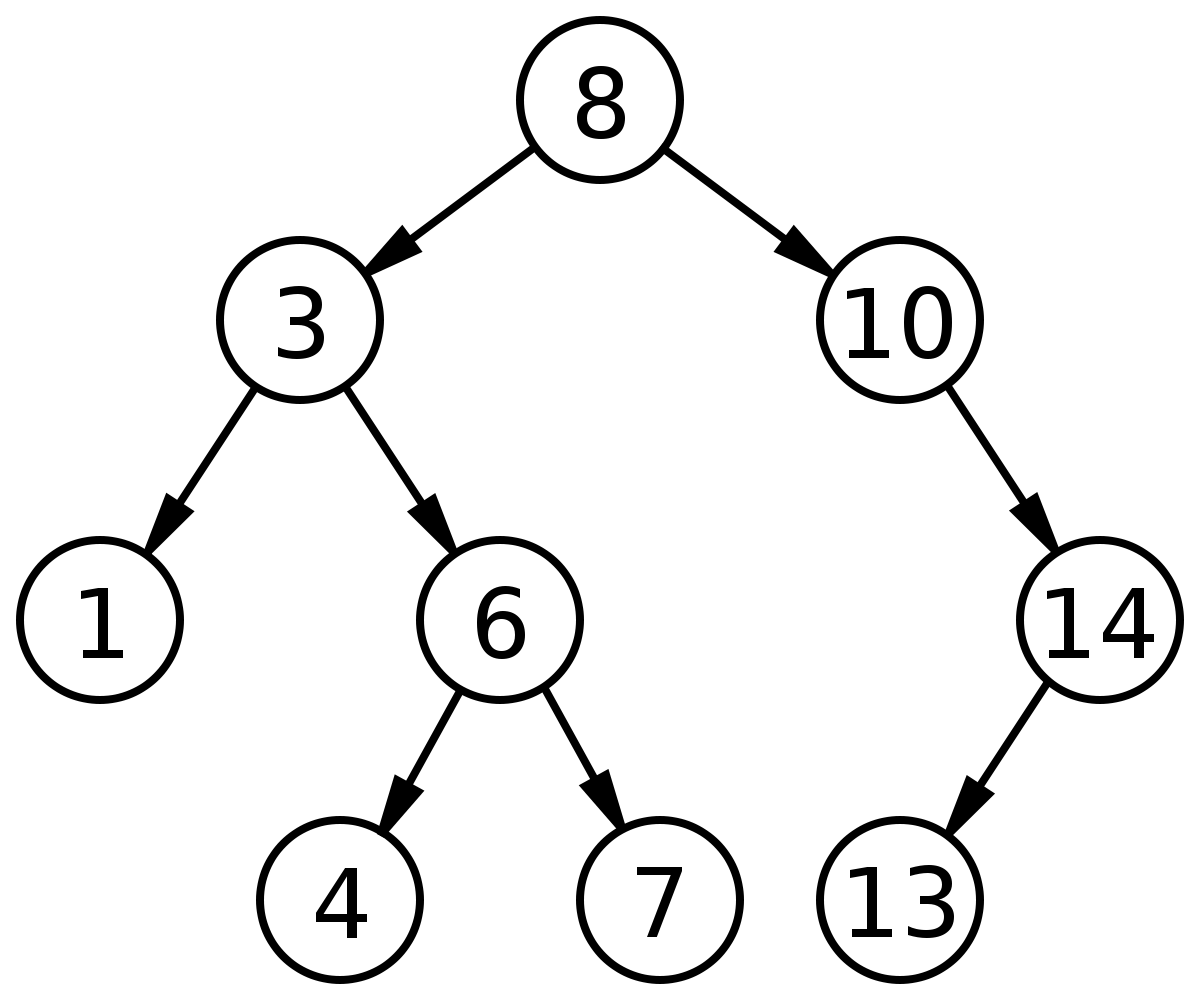
|
||||
|
||||
对于 BST 相关的问题,你可能会经常看到类似下面这样的代码逻辑:
|
||||
|
||||
```java
|
||||
void BST(TreeNode root, int target) {
|
||||
if (root.val == target)
|
||||
// 找到目标,做点什么
|
||||
if (root.val < target)
|
||||
BST(root.right, target);
|
||||
if (root.val > target)
|
||||
BST(root.left, target);
|
||||
}
|
||||
```
|
||||
|
||||
这个代码框架其实和二叉树的遍历框架差不多,无非就是利用了 BST 左小右大的特性而已。接下来看下 BST 这种结构的基础操作是如何实现的。
|
||||
|
||||
### 一、判断 BST 的合法性
|
||||
|
||||
力扣第 98 题「验证二叉搜索树」就是让你判断输入的 BST 是否合法。注意,这里是有坑的哦,按照 BST 左小右大的特性,每个节点想要判断自己是否是合法的 BST 节点,要做的事不就是比较自己和左右孩子吗?感觉应该这样写代码:
|
||||
|
||||
```java
|
||||
boolean isValidBST(TreeNode root) {
|
||||
if (root == null) return true;
|
||||
// root 的左边应该更小
|
||||
if (root.left != null && root.left.val >= root.val)
|
||||
return false;
|
||||
// root 的右边应该更大
|
||||
if (root.right != null && root.right.val <= root.val)
|
||||
return false;
|
||||
|
||||
return isValidBST(root.left)
|
||||
&& isValidBST(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
但是这个算法出现了错误,BST 的每个节点应该要小于右边子树的**所有**节点,下面这个二叉树显然不是 BST,因为节点 10 的右子树中有一个节点 6,但是我们的算法会把它判定为合法 BST:
|
||||
|
||||

|
||||
|
||||
**出现问题的原因在于,对于每一个节点 `root`,代码值检查了它的左右孩子节点是否符合左小右大的原则;但是根据 BST 的定义,`root` 的整个左子树都要小于 `root.val`,整个右子树都要大于 `root.val`**。
|
||||
|
||||
问题是,对于某一个节点 `root`,他只能管得了自己的左右子节点,怎么把 `root` 的约束传递给左右子树呢?请看正确的代码:
|
||||
|
||||
```java
|
||||
boolean isValidBST(TreeNode root) {
|
||||
return isValidBST(root, null, null);
|
||||
}
|
||||
|
||||
/* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
|
||||
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
|
||||
// base case
|
||||
if (root == null) return true;
|
||||
// 若 root.val 不符合 max 和 min 的限制,说明不是合法 BST
|
||||
if (min != null && root.val <= min.val) return false;
|
||||
if (max != null && root.val >= max.val) return false;
|
||||
// 限定左子树的最大值是 root.val,右子树的最小值是 root.val
|
||||
return isValidBST(root.left, min, root)
|
||||
&& isValidBST(root.right, root, max);
|
||||
}
|
||||
```
|
||||
|
||||
我们通过使用辅助函数,增加函数参数列表,在参数中携带额外信息,将这种约束传递给子树的所有节点,这也是二叉树算法的一个小技巧吧。
|
||||
|
||||
### 在 BST 中搜索元素
|
||||
|
||||
力扣第 700 题「二叉搜索树中的搜索」就是让你在 BST 中搜索值为 `target` 的节点,函数签名如下:
|
||||
|
||||
```java
|
||||
TreeNode searchBST(TreeNode root, int target);
|
||||
```
|
||||
|
||||
如果是在一棵普通的二叉树中寻找,可以这样写代码:
|
||||
|
||||
```java
|
||||
TreeNode searchBST(TreeNode root, int target);
|
||||
if (root == null) return null;
|
||||
if (root.val == target) return root;
|
||||
// 当前节点没找到就递归地去左右子树寻找
|
||||
TreeNode left = searchBST(root.left, target);
|
||||
TreeNode right = searchBST(root.right, target);
|
||||
|
||||
return left != null ? left : right;
|
||||
}
|
||||
```
|
||||
|
||||
这样写完全正确,但这段代码相当于穷举了所有节点,适用于所有二叉树。那么应该如何充分利用 BST 的特殊性,把「左小右大」的特性用上?
|
||||
|
||||
很简单,其实不需要递归地搜索两边,类似二分查找思想,根据 `target` 和 `root.val` 的大小比较,就能排除一边。我们把上面的思路稍稍改动:
|
||||
|
||||
```java
|
||||
TreeNode searchBST(TreeNode root, int target) {
|
||||
if (root == null) {
|
||||
return null;
|
||||
}
|
||||
// 去左子树搜索
|
||||
if (root.val > target) {
|
||||
return searchBST(root.left, target);
|
||||
}
|
||||
// 去右子树搜索
|
||||
if (root.val < target) {
|
||||
return searchBST(root.right, target);
|
||||
}
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
### 在 BST 中插入一个数
|
||||
|
||||
对数据结构的操作无非遍历 + 访问,遍历就是「找」,访问就是「改」。具体到这个问题,插入一个数,就是先找到插入位置,然后进行插入操作。
|
||||
|
||||
上一个问题,我们总结了 BST 中的遍历框架,就是「找」的问题。直接套框架,加上「改」的操作即可。**一旦涉及「改」,就类似二叉树的构造问题,函数要返回 `TreeNode` 类型,并且要对递归调用的返回值进行接收**。
|
||||
|
||||
```java
|
||||
TreeNode insertIntoBST(TreeNode root, int val) {
|
||||
// 找到空位置插入新节点
|
||||
if (root == null) return new TreeNode(val);
|
||||
// if (root.val == val)
|
||||
// BST 中一般不会插入已存在元素
|
||||
if (root.val < val)
|
||||
root.right = insertIntoBST(root.right, val);
|
||||
if (root.val > val)
|
||||
root.left = insertIntoBST(root.left, val);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
### 三、在 BST 中删除一个数
|
||||
|
||||
这个问题稍微复杂,跟插入操作类似,先「找」再「改」,先把框架写出来再说:
|
||||
|
||||
```java
|
||||
TreeNode deleteNode(TreeNode root, int key) {
|
||||
if (root.val == key) {
|
||||
// 找到啦,进行删除
|
||||
} else if (root.val > key) {
|
||||
// 去左子树找
|
||||
root.left = deleteNode(root.left, key);
|
||||
} else if (root.val < key) {
|
||||
// 去右子树找
|
||||
root.right = deleteNode(root.right, key);
|
||||
}
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
找到目标节点了,比方说是节点 `A`,如何删除这个节点,这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况,用图片来说明。
|
||||
|
||||
**情况 1**:`A` 恰好是末端节点,两个子节点都为空,那么它可以当场去世了。
|
||||
|
||||
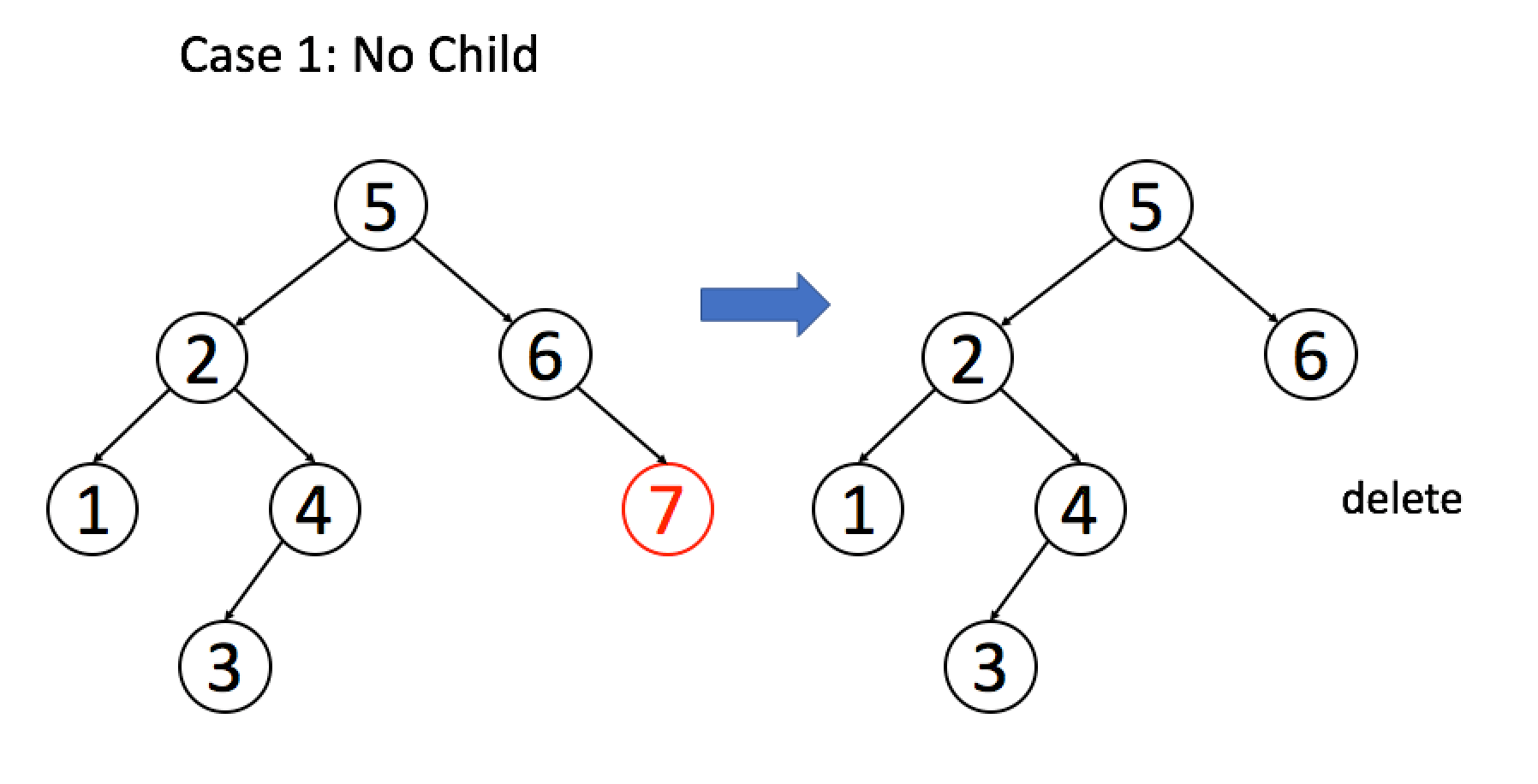
|
||||
|
||||
```java
|
||||
if (root.left == null && root.right == null)
|
||||
return null;
|
||||
```
|
||||
|
||||
**情况 2**:`A` 只有一个非空子节点,那么它要让这个孩子接替自己的位置。
|
||||
|
||||
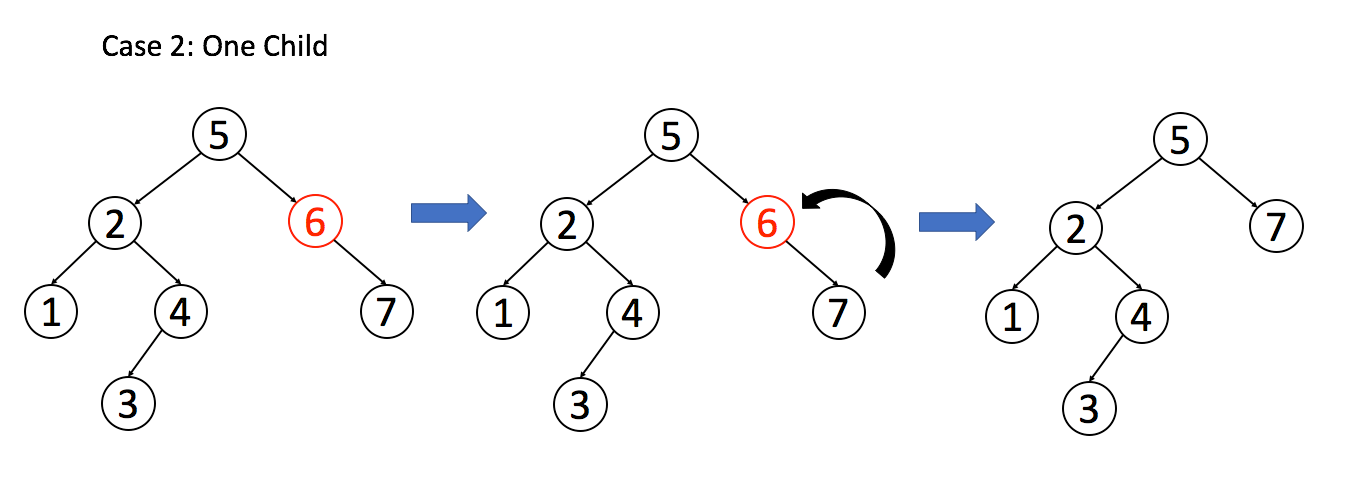
|
||||
|
||||
```java
|
||||
// 排除了情况 1 之后
|
||||
if (root.left == null) return root.right;
|
||||
if (root.right == null) return root.left;
|
||||
```
|
||||
|
||||
**情况 3**:`A` 有两个子节点,麻烦了,为了不破坏 BST 的性质,`A` 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。
|
||||
|
||||
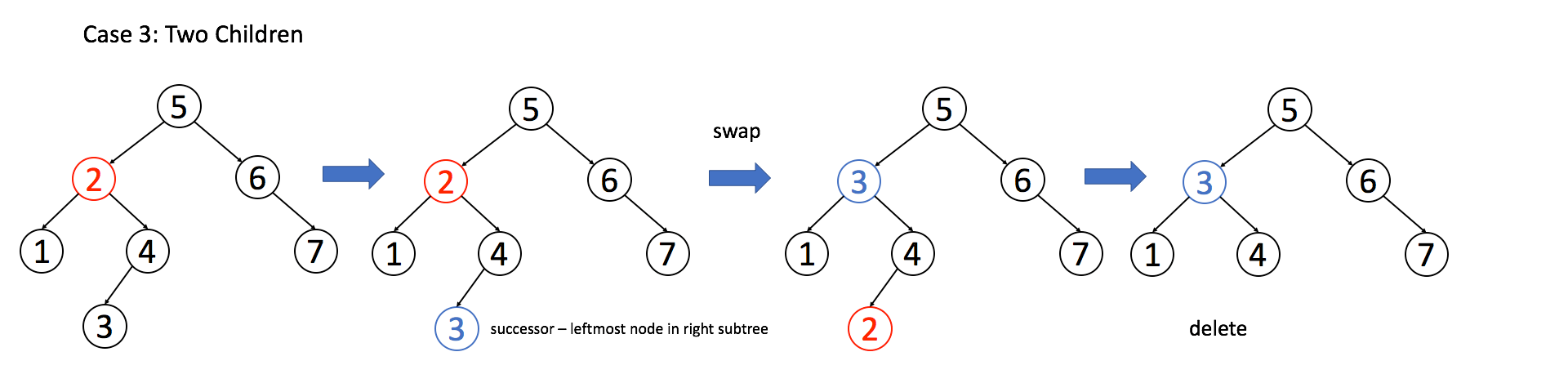
|
||||
|
||||
```java
|
||||
if (root.left != null && root.right != null) {
|
||||
// 找到右子树的最小节点
|
||||
TreeNode minNode = getMin(root.right);
|
||||
// 把 root 改成 minNode
|
||||
root.val = minNode.val;
|
||||
// 转而去删除 minNode
|
||||
root.right = deleteNode(root.right, minNode.val);
|
||||
}
|
||||
```
|
||||
|
||||
三种情况分析完毕,填入框架,简化一下代码:
|
||||
|
||||
```java
|
||||
TreeNode deleteNode(TreeNode root, int key) {
|
||||
if (root == null) return null;
|
||||
if (root.val == key) {
|
||||
// 这两个 if 把情况 1 和 2 都正确处理了
|
||||
if (root.left == null) return root.right;
|
||||
if (root.right == null) return root.left;
|
||||
// 处理情况 3
|
||||
// 获得右子树最小的节点
|
||||
TreeNode minNode = getMin(root.right);
|
||||
// 删除右子树最小的节点
|
||||
root.right = deleteNode(root.right, minNode.val);
|
||||
// 用右子树最小的节点替换 root 节点
|
||||
minNode.left = root.left;
|
||||
minNode.right = root.right;
|
||||
root = minNode;
|
||||
} else if (root.val > key) {
|
||||
root.left = deleteNode(root.left, key);
|
||||
} else if (root.val < key) {
|
||||
root.right = deleteNode(root.right, key);
|
||||
}
|
||||
return root;
|
||||
}
|
||||
|
||||
TreeNode getMin(TreeNode node) {
|
||||
// BST 最左边的就是最小的
|
||||
while (node.left != null) node = node.left;
|
||||
return node;
|
||||
}
|
||||
```
|
||||
|
||||
这样,删除操作就完成了。注意一下,上述代码在处理情况 3 时通过一系列略微复杂的链表操作交换 `root` 和 `minNode` 两个节点:
|
||||
|
||||
```java
|
||||
// 处理情况 3
|
||||
// 获得右子树最小的节点
|
||||
TreeNode minNode = getMin(root.right);
|
||||
// 删除右子树最小的节点
|
||||
root.right = deleteNode(root.right, minNode.val);
|
||||
// 用右子树最小的节点替换 root 节点
|
||||
minNode.left = root.left;
|
||||
minNode.right = root.right;
|
||||
root = minNode;
|
||||
```
|
||||
|
||||
有的读者可能会疑惑,替换 `root` 节点为什么这么麻烦,直接改 `val` 字段不就行了?看起来还更简洁易懂:
|
||||
|
||||
```java
|
||||
// 处理情况 3
|
||||
// 获得右子树最小的节点
|
||||
TreeNode minNode = getMin(root.right);
|
||||
// 删除右子树最小的节点
|
||||
root.right = deleteNode(root.right, minNode.val);
|
||||
// 用右子树最小的节点替换 root 节点
|
||||
root.val = minNode.val;
|
||||
```
|
||||
|
||||
仅对于这道算法题来说是可以的,但这样操作并不完美,我们一般不会通过修改节点内部的值来交换节点。因为在实际应用中,BST 节点内部的数据域是用户自定义的,可以非常复杂,而 BST 作为数据结构(一个工具人),其操作应该和内部存储的数据域解耦,所以我们更倾向于使用指针操作来交换节点,根本没必要关心内部数据。
|
||||
|
||||
最后总结一下吧,通过这篇文章,我们总结出了如下几个技巧:
|
||||
|
||||
1、如果当前节点会对下面的子节点有整体影响,可以通过辅助函数增长参数列表,借助参数传递信息。
|
||||
|
||||
2、在二叉树递归框架之上,扩展出一套 BST 代码框架:
|
||||
|
||||
```java
|
||||
void BST(TreeNode root, int target) {
|
||||
if (root.val == target)
|
||||
// 找到目标,做点什么
|
||||
if (root.val < target)
|
||||
BST(root.right, target);
|
||||
if (root.val > target)
|
||||
BST(root.left, target);
|
||||
}
|
||||
```
|
||||
|
||||
3、根据代码框架掌握了 BST 的增删查改操作。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.github.io/article/fname.html?fname=BST3)
|
||||
- [二叉树的递归转迭代的代码框架](https://labuladong.github.io/article/fname.html?fname=迭代遍历二叉树)
|
||||
- [前缀树算法模板秒杀五道算法题](https://labuladong.github.io/article/fname.html?fname=trie)
|
||||
- [后序遍历的妙用](https://labuladong.github.io/article/fname.html?fname=后序遍历)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -0,0 +1,869 @@
|
|||
# 我写了一个模板,把 Dijkstra 算法变成了默写题
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [1514. Path with Maximum Probability](https://leetcode.com/problems/path-with-maximum-probability/) | [1514. 概率最大的路径](https://leetcode.cn/problems/path-with-maximum-probability/) | 🟠
|
||||
| [1631. Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/) | [1631. 最小体力消耗路径](https://leetcode.cn/problems/path-with-minimum-effort/) | 🟠
|
||||
| [743. Network Delay Time](https://leetcode.com/problems/network-delay-time/) | [743. 网络延迟时间](https://leetcode.cn/problems/network-delay-time/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
其实,很多算法的底层原理异常简单,无非就是一步一步延伸,变得**看起来**好像特别复杂,特别牛逼。
|
||||
|
||||
但如果你看过历史文章,应该可以对算法形成自己的理解,就会发现很多算法都是换汤不换药,毫无新意,非常枯燥。
|
||||
|
||||
比如,[东哥手把手带你刷二叉树(总纲)](https://labuladong.github.io/article/fname.html?fname=二叉树总结) 中说二叉树非常重要,你把这个结构掌握了,就会发现 [动态规划](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶),[分治算法](https://labuladong.github.io/article/fname.html?fname=分治算法),[回溯(DFS)算法](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版),[BFS 算法框架](https://labuladong.github.io/article/fname.html?fname=BFS框架),[Union-Find 并查集算法](https://labuladong.github.io/article/fname.html?fname=UnionFind算法详解),[二叉堆实现优先级队列](https://labuladong.github.io/article/fname.html?fname=二叉堆详解实现优先级队列) 就是把二叉树翻来覆去的运用。
|
||||
|
||||
那么本文又要告诉你,Dijkstra 算法(一般音译成迪杰斯特拉算法)无非就是一个 BFS 算法的加强版,它们都是从二叉树的层序遍历衍生出来的。
|
||||
|
||||
这也是为什么我在 [学习数据结构和算法的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法) 中这么强调二叉树的原因。
|
||||
|
||||
**下面我们由浅入深,从二叉树的层序遍历聊到 Dijkstra 算法,给出 Dijkstra 算法的代码框架,顺手秒杀几道运用 Dijkstra 算法的题目**。
|
||||
|
||||
### 图的抽象
|
||||
|
||||
前文 [图论第一期:遍历基础](https://labuladong.github.io/article/fname.html?fname=图) 说过「图」这种数据结构的基本实现,图中的节点一般就抽象成一个数字(索引),图的具体实现一般是「邻接矩阵」或者「邻接表」。
|
||||
|
||||

|
||||
|
||||
比如上图这幅图用邻接表和邻接矩阵的存储方式如下:
|
||||
|
||||

|
||||
|
||||
前文 [图论第二期:拓扑排序](https://labuladong.github.io/article/fname.html?fname=拓扑排序) 告诉你,我们用邻接表的场景更多,结合上图,一幅图可以用如下 Java 代码表示:
|
||||
|
||||
```java
|
||||
// graph[s] 存储节点 s 指向的节点(出度)
|
||||
List<Integer>[] graph;
|
||||
```
|
||||
|
||||
**如果你想把一个问题抽象成「图」的问题,那么首先要实现一个 API `adj`**:
|
||||
|
||||
```java
|
||||
// 输入节点 s 返回 s 的相邻节点
|
||||
List<Integer> adj(int s);
|
||||
```
|
||||
|
||||
类似多叉树节点中的 `children` 字段记录当前节点的所有子节点,`adj(s)` 就是计算一个节点 `s` 的相邻节点。
|
||||
|
||||
比如上面说的用邻接表表示「图」的方式,`adj` 函数就可以这样表示:
|
||||
|
||||
```java
|
||||
List<Integer>[] graph;
|
||||
|
||||
// 输入节点 s,返回 s 的相邻节点
|
||||
List<Integer> adj(int s) {
|
||||
return graph[s];
|
||||
}
|
||||
```
|
||||
|
||||
当然,对于「加权图」,我们需要知道两个节点之间的边权重是多少,所以还可以抽象出一个 `weight` 方法:
|
||||
|
||||
```java
|
||||
// 返回节点 from 到节点 to 之间的边的权重
|
||||
int weight(int from, int to);
|
||||
```
|
||||
|
||||
这个 `weight` 方法可以根据实际情况而定,因为不同的算法题,题目给的「权重」含义可能不一样,我们存储权重的方式也不一样。
|
||||
|
||||
有了上述基础知识,就可以搞定 Dijkstra 算法了,下面我给你从二叉树的层序遍历开始推演出 Dijkstra 算法的实现。
|
||||
|
||||
### 二叉树层级遍历和 BFS 算法
|
||||
|
||||
我们之前说过二叉树的层级遍历框架:
|
||||
|
||||
```java
|
||||
// 输入一棵二叉树的根节点,层序遍历这棵二叉树
|
||||
void levelTraverse(TreeNode root) {
|
||||
if (root == null) return 0;
|
||||
Queue<TreeNode> q = new LinkedList<>();
|
||||
q.offer(root);
|
||||
|
||||
int depth = 1;
|
||||
// 从上到下遍历二叉树的每一层
|
||||
while (!q.isEmpty()) {
|
||||
int sz = q.size();
|
||||
// 从左到右遍历每一层的每个节点
|
||||
for (int i = 0; i < sz; i++) {
|
||||
TreeNode cur = q.poll();
|
||||
printf("节点 %s 在第 %s 层", cur, depth);
|
||||
|
||||
// 将下一层节点放入队列
|
||||
if (cur.left != null) {
|
||||
q.offer(cur.left);
|
||||
}
|
||||
if (cur.right != null) {
|
||||
q.offer(cur.right);
|
||||
}
|
||||
}
|
||||
depth++;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
我们先来思考一个问题,注意二叉树的层级遍历 `while` 循环里面还套了个 `for` 循环,为什么要这样?
|
||||
|
||||
`while` 循环和 `for` 循环的配合正是这个遍历框架设计的巧妙之处:
|
||||
|
||||
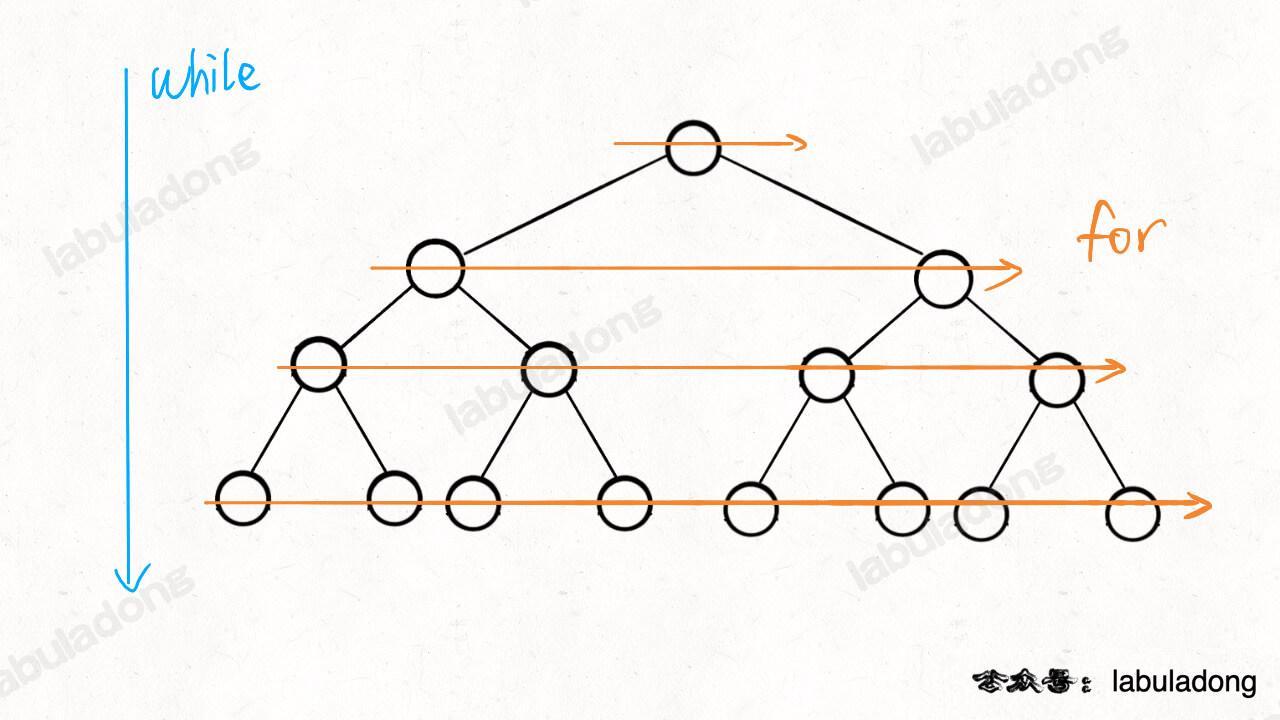
|
||||
|
||||
**`while` 循环控制一层一层往下走,`for` 循环利用 `sz` 变量控制从左到右遍历每一层二叉树节点**。
|
||||
|
||||
注意我们代码框架中的 `depth` 变量,其实就记录了当前遍历到的层数。换句话说,每当我们遍历到一个节点 `cur`,都知道这个节点属于第几层。
|
||||
|
||||
算法题经常会问二叉树的最大深度呀,最小深度呀,层序遍历结果呀,等等问题,所以记录下来这个深度 `depth` 是有必要的。
|
||||
|
||||
基于二叉树的遍历框架,我们又可以扩展出多叉树的层序遍历框架:
|
||||
|
||||
```java
|
||||
// 输入一棵多叉树的根节点,层序遍历这棵多叉树
|
||||
void levelTraverse(TreeNode root) {
|
||||
if (root == null) return;
|
||||
Queue<TreeNode> q = new LinkedList<>();
|
||||
q.offer(root);
|
||||
|
||||
int depth = 1;
|
||||
// 从上到下遍历多叉树的每一层
|
||||
while (!q.isEmpty()) {
|
||||
int sz = q.size();
|
||||
// 从左到右遍历每一层的每个节点
|
||||
for (int i = 0; i < sz; i++) {
|
||||
TreeNode cur = q.poll();
|
||||
printf("节点 %s 在第 %s 层", cur, depth);
|
||||
|
||||
// 将下一层节点放入队列
|
||||
for (TreeNode child : cur.children) {
|
||||
q.offer(child);
|
||||
}
|
||||
}
|
||||
depth++;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
基于多叉树的遍历框架,我们又可以扩展出 BFS(广度优先搜索)的算法框架:
|
||||
|
||||
```java
|
||||
// 输入起点,进行 BFS 搜索
|
||||
int BFS(Node start) {
|
||||
Queue<Node> q; // 核心数据结构
|
||||
Set<Node> visited; // 避免走回头路
|
||||
|
||||
q.offer(start); // 将起点加入队列
|
||||
visited.add(start);
|
||||
|
||||
int step = 0; // 记录搜索的步数
|
||||
while (q not empty) {
|
||||
int sz = q.size();
|
||||
/* 将当前队列中的所有节点向四周扩散一步 */
|
||||
for (int i = 0; i < sz; i++) {
|
||||
Node cur = q.poll();
|
||||
printf("从 %s 到 %s 的最短距离是 %s", start, cur, step);
|
||||
|
||||
/* 将 cur 的相邻节点加入队列 */
|
||||
for (Node x : cur.adj()) {
|
||||
if (x not in visited) {
|
||||
q.offer(x);
|
||||
visited.add(x);
|
||||
}
|
||||
}
|
||||
}
|
||||
step++;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
如果对 BFS 算法不熟悉,可以看前文 [BFS 算法框架](https://labuladong.github.io/article/fname.html?fname=BFS框架),这里只是为了让你做个对比,所谓 BFS 算法,就是把算法问题抽象成一幅「无权图」,然后继续玩二叉树层级遍历那一套罢了。
|
||||
|
||||
**注意,我们的 BFS 算法框架也是 `while` 循环嵌套 `for` 循环的形式,也用了一个 `step` 变量记录 `for` 循环执行的次数,无非就是多用了一个 `visited` 集合记录走过的节点,防止走回头路罢了**。
|
||||
|
||||
为什么这样呢?
|
||||
|
||||
所谓「无权图」,与其说每条「边」没有权重,不如说每条「边」的权重都是 1,从起点 `start` 到任意一个节点之间的路径权重就是它们之间「边」的条数,那可不就是 `step` 变量记录的值么?
|
||||
|
||||
再加上 BFS 算法利用 `for` 循环一层一层向外扩散的逻辑和 `visited` 集合防止走回头路的逻辑,当你每次从队列中拿出节点 `cur` 的时候,从 `start` 到 `cur` 的最短权重就是 `step` 记录的步数。
|
||||
|
||||
但是,到了「加权图」的场景,事情就没有这么简单了,因为你不能默认每条边的「权重」都是 1 了,这个权重可以是任意正数(Dijkstra 算法要求不能存在负权重边),比如下图的例子:
|
||||
|
||||
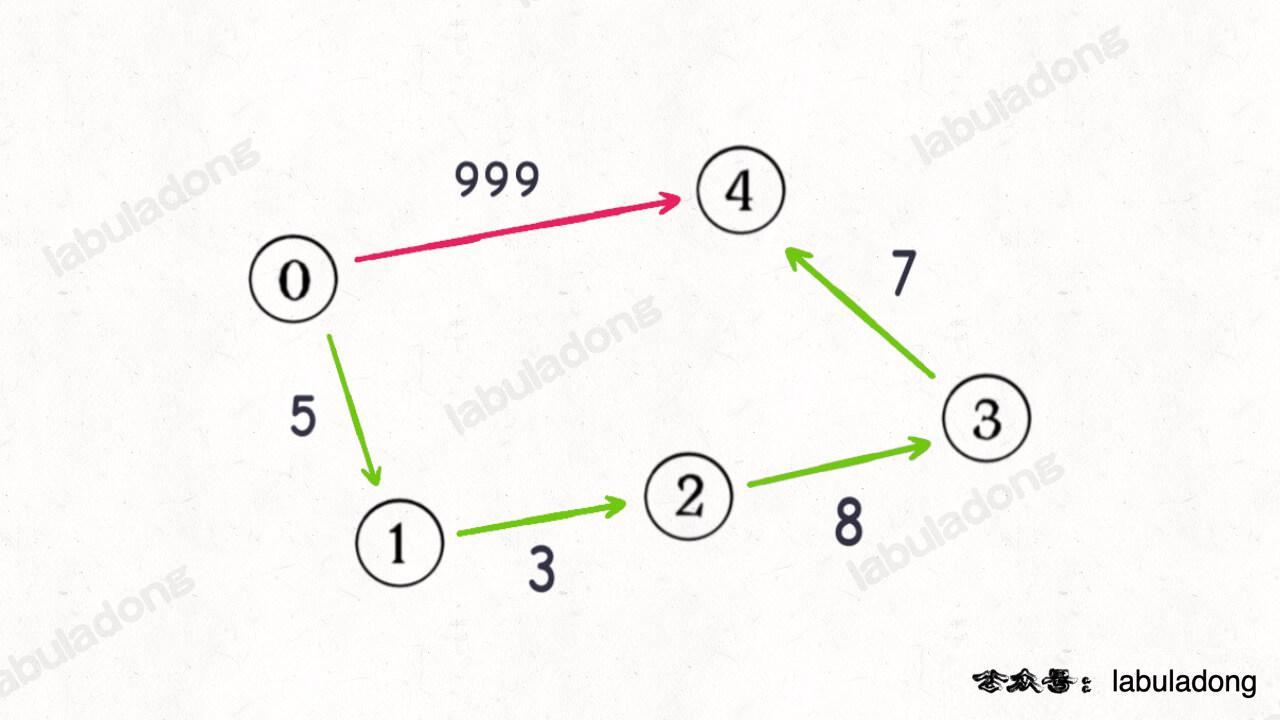
|
||||
|
||||
如果沿用 BFS 算法中的 `step` 变量记录「步数」,显然红色路径一步就可以走到终点,但是这一步的权重很大;正确的最小权重路径应该是绿色的路径,虽然需要走很多步,但是路径权重依然很小。
|
||||
|
||||
其实 Dijkstra 和 BFS 算法差不多,不过在讲解 Dijkstra 算法框架之前,我们首先需要对之前的框架进行如下改造:
|
||||
|
||||
**想办法去掉 `while` 循环里面的 `for` 循环**。
|
||||
|
||||
为什么?有了刚才的铺垫,这个不难理解,刚才说 `for` 循环是干什么用的来着?
|
||||
|
||||
是为了让二叉树一层一层往下遍历,让 BFS 算法一步一步向外扩散,因为这个层数 `depth`,或者这个步数 `step`,在之前的场景中有用。
|
||||
|
||||
但现在我们想解决「加权图」中的最短路径问题,「步数」已经没有参考意义了,「路径的权重之和」才有意义,所以这个 `for` 循环可以被去掉。
|
||||
|
||||
怎么去掉?就拿二叉树的层级遍历来说,其实你可以直接去掉 `for` 循环相关的代码:
|
||||
|
||||
```java
|
||||
// 输入一棵二叉树的根节点,遍历这棵二叉树所有节点
|
||||
void levelTraverse(TreeNode root) {
|
||||
if (root == null) return 0;
|
||||
Queue<TreeNode> q = new LinkedList<>();
|
||||
q.offer(root);
|
||||
|
||||
// 遍历二叉树的每一个节点
|
||||
while (!q.isEmpty()) {
|
||||
TreeNode cur = q.poll();
|
||||
printf("我不知道节点 %s 在第几层", cur);
|
||||
|
||||
// 将子节点放入队列
|
||||
if (cur.left != null) {
|
||||
q.offer(cur.left);
|
||||
}
|
||||
if (cur.right != null) {
|
||||
q.offer(cur.right);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
但问题是,没有 `for` 循环,你也没办法维护 `depth` 变量了。
|
||||
|
||||
如果你想同时维护 `depth` 变量,让每个节点 `cur` 知道自己在第几层,可以想其他办法,比如新建一个 `State` 类,记录每个节点所在的层数:
|
||||
|
||||
```java
|
||||
class State {
|
||||
// 记录 node 节点的深度
|
||||
int depth;
|
||||
TreeNode node;
|
||||
|
||||
State(TreeNode node, int depth) {
|
||||
this.depth = depth;
|
||||
this.node = node;
|
||||
}
|
||||
}
|
||||
|
||||
// 输入一棵二叉树的根节点,遍历这棵二叉树所有节点
|
||||
void levelTraverse(TreeNode root) {
|
||||
if (root == null) return 0;
|
||||
Queue<State> q = new LinkedList<>();
|
||||
q.offer(new State(root, 1));
|
||||
|
||||
// 遍历二叉树的每一个节点
|
||||
while (!q.isEmpty()) {
|
||||
State cur = q.poll();
|
||||
TreeNode cur_node = cur.node;
|
||||
int cur_depth = cur.depth;
|
||||
printf("节点 %s 在第 %s 层", cur_node, cur_depth);
|
||||
|
||||
// 将子节点放入队列
|
||||
if (cur_node.left != null) {
|
||||
q.offer(new State(cur_node.left, cur_depth + 1));
|
||||
}
|
||||
if (cur_node.right != null) {
|
||||
q.offer(new State(cur_node.right, cur_depth + 1));
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这样,我们就可以不使用 `for` 循环也确切地知道每个二叉树节点的深度了。
|
||||
|
||||
**如果你能够理解上面这段代码,我们就可以来看 Dijkstra 算法的代码框架了**。
|
||||
|
||||
### Dijkstra 算法框架
|
||||
|
||||
**首先,我们先看一下 Dijkstra 算法的签名**:
|
||||
|
||||
```java
|
||||
// 输入一幅图和一个起点 start,计算 start 到其他节点的最短距离
|
||||
int[] dijkstra(int start, List<Integer>[] graph);
|
||||
```
|
||||
|
||||
输入是一幅图 `graph` 和一个起点 `start`,返回是一个记录最短路径权重的数组。
|
||||
|
||||
比方说,输入起点 `start = 3`,函数返回一个 `int[]` 数组,假设赋值给 `distTo` 变量,那么从起点 `3` 到节点 `6` 的最短路径权重的值就是 `distTo[6]`。
|
||||
|
||||
是的,标准的 Dijkstra 算法会把从起点 `start` 到所有其他节点的最短路径都算出来。
|
||||
|
||||
当然,如果你的需求只是计算从起点 `start` 到某一个终点 `end` 的最短路径,那么在标准 Dijkstra 算法上稍作修改就可以更高效地完成这个需求,这个我们后面再说。
|
||||
|
||||
**其次,我们也需要一个 `State` 类来辅助算法的运行**:
|
||||
|
||||
```java
|
||||
class State {
|
||||
// 图节点的 id
|
||||
int id;
|
||||
// 从 start 节点到当前节点的距离
|
||||
int distFromStart;
|
||||
|
||||
State(int id, int distFromStart) {
|
||||
this.id = id;
|
||||
this.distFromStart = distFromStart;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
类似刚才二叉树的层序遍历,我们也需要用 `State` 类记录一些额外信息,也就是使用 `distFromStart` 变量记录从起点 `start` 到当前这个节点的距离。
|
||||
|
||||
刚才说普通 BFS 算法中,根据 BFS 的逻辑和无权图的特点,第一次遇到某个节点所走的步数就是最短距离,所以用一个 `visited` 数组防止走回头路,每个节点只会经过一次。
|
||||
|
||||
加权图中的 Dijkstra 算法和无权图中的普通 BFS 算法不同,在 Dijkstra 算法中,你第一次经过某个节点时的路径权重,不见得就是最小的,所以对于同一个节点,我们可能会经过多次,而且每次的 `distFromStart` 可能都不一样,比如下图:
|
||||
|
||||
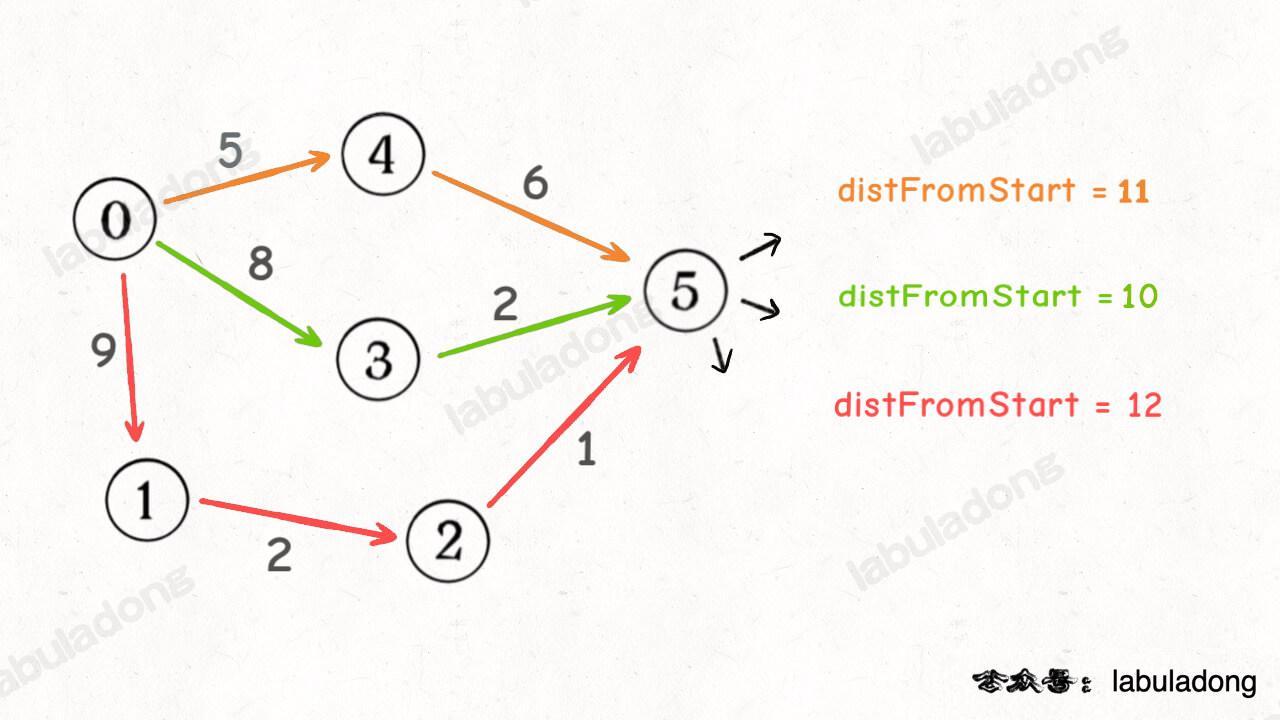
|
||||
|
||||
我会经过节点 `5` 三次,每次的 `distFromStart` 值都不一样,那我取 `distFromStart` 最小的那次,不就是从起点 `start` 到节点 `5` 的最短路径权重了么?
|
||||
|
||||
好了,明白上面的几点,我们可以来看看 Dijkstra 算法的代码模板。
|
||||
|
||||
**其实,Dijkstra 可以理解成一个带 dp table(或者说备忘录)的 BFS 算法,伪码如下**:
|
||||
|
||||
```java
|
||||
// 返回节点 from 到节点 to 之间的边的权重
|
||||
int weight(int from, int to);
|
||||
|
||||
// 输入节点 s 返回 s 的相邻节点
|
||||
List<Integer> adj(int s);
|
||||
|
||||
// 输入一幅图和一个起点 start,计算 start 到其他节点的最短距离
|
||||
int[] dijkstra(int start, List<Integer>[] graph) {
|
||||
// 图中节点的个数
|
||||
int V = graph.length;
|
||||
// 记录最短路径的权重,你可以理解为 dp table
|
||||
// 定义:distTo[i] 的值就是节点 start 到达节点 i 的最短路径权重
|
||||
int[] distTo = new int[V];
|
||||
// 求最小值,所以 dp table 初始化为正无穷
|
||||
Arrays.fill(distTo, Integer.MAX_VALUE);
|
||||
// base case,start 到 start 的最短距离就是 0
|
||||
distTo[start] = 0;
|
||||
|
||||
// 优先级队列,distFromStart 较小的排在前面
|
||||
Queue<State> pq = new PriorityQueue<>((a, b) -> {
|
||||
return a.distFromStart - b.distFromStart;
|
||||
});
|
||||
|
||||
// 从起点 start 开始进行 BFS
|
||||
pq.offer(new State(start, 0));
|
||||
|
||||
while (!pq.isEmpty()) {
|
||||
State curState = pq.poll();
|
||||
int curNodeID = curState.id;
|
||||
int curDistFromStart = curState.distFromStart;
|
||||
|
||||
if (curDistFromStart > distTo[curNodeID]) {
|
||||
// 已经有一条更短的路径到达 curNode 节点了
|
||||
continue;
|
||||
}
|
||||
// 将 curNode 的相邻节点装入队列
|
||||
for (int nextNodeID : adj(curNodeID)) {
|
||||
// 看看从 curNode 达到 nextNode 的距离是否会更短
|
||||
int distToNextNode = distTo[curNodeID] + weight(curNodeID, nextNodeID);
|
||||
if (distTo[nextNodeID] > distToNextNode) {
|
||||
// 更新 dp table
|
||||
distTo[nextNodeID] = distToNextNode;
|
||||
// 将这个节点以及距离放入队列
|
||||
pq.offer(new State(nextNodeID, distToNextNode));
|
||||
}
|
||||
}
|
||||
}
|
||||
return distTo;
|
||||
}
|
||||
```
|
||||
|
||||
**对比普通的 BFS 算法,你可能会有以下疑问**:
|
||||
|
||||
**1、没有 `visited` 集合记录已访问的节点,所以一个节点会被访问多次,会被多次加入队列,那会不会导致队列永远不为空,造成死循环**?
|
||||
|
||||
**2、为什么用优先级队列 `PriorityQueue` 而不是 `LinkedList` 实现的普通队列?为什么要按照 `distFromStart` 的值来排序**?
|
||||
|
||||
**3、如果我只想计算起点 `start` 到某一个终点 `end` 的最短路径,是否可以修改算法,提升一些效率**?
|
||||
|
||||
我们先回答第一个问题,为什么这个算法不用 `visited` 集合也不会死循环。
|
||||
|
||||
对于这类问题,我教你一个思考方法:
|
||||
|
||||
循环结束的条件是队列为空,那么你就要注意看什么时候往队列里放元素(调用 `offer`)方法,再注意看什么时候从队列往外拿元素(调用 `poll` 方法)。
|
||||
|
||||
`while` 循环每执行一次,都会往外拿一个元素,但想往队列里放元素,可就有很多限制了,必须满足下面这个条件:
|
||||
|
||||
```java
|
||||
// 看看从 curNode 达到 nextNode 的距离是否会更短
|
||||
if (distTo[nextNodeID] > distToNextNode) {
|
||||
// 更新 dp table
|
||||
distTo[nextNodeID] = distToNextNode;
|
||||
pq.offer(new State(nextNodeID, distToNextNode));
|
||||
}
|
||||
```
|
||||
|
||||
这也是为什么我说 `distTo` 数组可以理解成我们熟悉的 dp table,因为这个算法逻辑就是在不断的最小化 `distTo` 数组中的元素:
|
||||
|
||||
如果你能让到达 `nextNodeID` 的距离更短,那就更新 `distTo[nextNodeID]` 的值,让你入队,否则的话对不起,不让入队。
|
||||
|
||||
**因为两个节点之间的最短距离(路径权重)肯定是一个确定的值,不可能无限减小下去,所以队列一定会空,队列空了之后,`distTo` 数组中记录的就是从 `start` 到其他节点的最短距离**。
|
||||
|
||||
接下来解答第二个问题,为什么要用 `PriorityQueue` 而不是 `LinkedList` 实现的普通队列?
|
||||
|
||||
如果你非要用普通队列,其实也没问题的,你可以直接把 `PriorityQueue` 改成 `LinkedList`,也能得到正确答案,但是效率会低很多。
|
||||
|
||||
**Dijkstra 算法使用优先级队列,主要是为了效率上的优化,类似一种贪心算法的思路**。
|
||||
|
||||
为什么说是一种贪心思路呢,比如说下面这种情况,你想计算从起点 `start` 到终点 `end` 的最短路径权重:
|
||||
|
||||
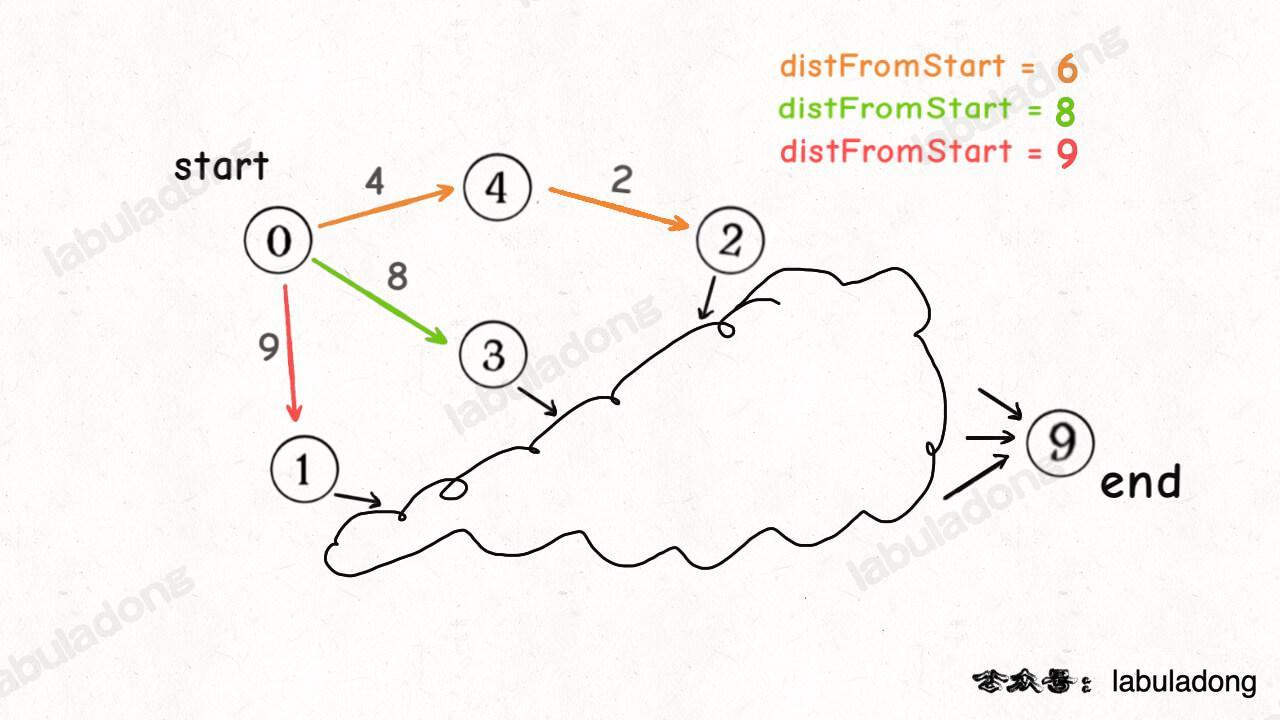
|
||||
|
||||
假设你当前只遍历了图中的这几个节点,那么你下一步准备遍历那个节点?这三条路径都可能成为最短路径的一部分,**但你觉得哪条路径更有「潜力」成为最短路径中的一部分**?
|
||||
|
||||
从目前的情况来看,显然橙色路径的可能性更大嘛,所以我们希望节点 `2` 排在队列靠前的位置,优先被拿出来向后遍历。
|
||||
|
||||
所以我们使用 `PriorityQueue` 作为队列,让 `distFromStart` 的值较小的节点排在前面,这就类似我们之前讲 [贪心算法](https://labuladong.github.io/article/fname.html?fname=跳跃游戏) 说到的贪心思路,可以很大程度上优化算法的效率。
|
||||
|
||||
大家应该听过 Bellman-Ford 算法,这个算法是一种更通用的最短路径算法,因为它可以处理带有负权重边的图,Bellman-Ford 算法逻辑和 Dijkstra 算法非常类似,用到的就是普通队列,本文就提一句,后面有空再具体写。
|
||||
|
||||
接下来说第三个问题,如果只关心起点 `start` 到某一个终点 `end` 的最短路径,是否可以修改代码提升算法效率。
|
||||
|
||||
肯定可以的,因为我们标准 Dijkstra 算法会算出 `start` 到所有其他节点的最短路径,你只想计算到 `end` 的最短路径,相当于减少计算量,当然可以提升效率。
|
||||
|
||||
需要在代码中做的修改也非常少,只要改改函数签名,再加个 if 判断就行了:
|
||||
|
||||
```java
|
||||
// 输入起点 start 和终点 end,计算起点到终点的最短距离
|
||||
int dijkstra(int start, int end, List<Integer>[] graph) {
|
||||
|
||||
// ...
|
||||
|
||||
while (!pq.isEmpty()) {
|
||||
State curState = pq.poll();
|
||||
int curNodeID = curState.id;
|
||||
int curDistFromStart = curState.distFromStart;
|
||||
|
||||
// 在这里加一个判断就行了,其他代码不用改
|
||||
if (curNodeID == end) {
|
||||
return curDistFromStart;
|
||||
}
|
||||
|
||||
if (curDistFromStart > distTo[curNodeID]) {
|
||||
continue;
|
||||
}
|
||||
|
||||
// ...
|
||||
}
|
||||
|
||||
// 如果运行到这里,说明从 start 无法走到 end
|
||||
return Integer.MAX_VALUE;
|
||||
}
|
||||
```
|
||||
|
||||
因为优先级队列自动排序的性质,**每次**从队列里面拿出来的都是 `distFromStart` 值最小的,所以当你**第一次**从队列中拿出终点 `end` 时,此时的 `distFromStart` 对应的值就是从 `start` 到 `end` 的最短距离。
|
||||
|
||||
这个算法较之前的实现提前 return 了,所以效率有一定的提高。
|
||||
|
||||
### 时间复杂度分析
|
||||
|
||||
Dijkstra 算法的时间复杂度是多少?你去网上查,可能会告诉你是 `O(ElogV)`,其中 `E` 代表图中边的条数,`V` 代表图中节点的个数。
|
||||
|
||||
因为理想情况下优先级队列中最多装 `V` 个节点,对优先级队列的操作次数和 `E` 成正比,所以整体的时间复杂度就是 `O(ElogV)`。
|
||||
|
||||
不过这是理想情况,Dijkstra 算法的代码实现有很多版本,不同编程语言或者不同数据结构 API 都会导致算法的时间复杂度发生一些改变。
|
||||
|
||||
比如本文实现的 Dijkstra 算法,使用了 Java 的 `PriorityQueue` 这个数据结构,这个容器类底层使用二叉堆实现,但没有提供通过索引操作队列中元素的 API,所以队列中会有重复的节点,最多可能有 `E` 个节点存在队列中。
|
||||
|
||||
所以本文实现的 Dijkstra 算法复杂度并不是理想情况下的 `O(ElogV)`,而是 `O(ElogE)`,可能会略大一些,因为图中边的条数一般是大于节点的个数的。
|
||||
|
||||
不过就对数函数来说,就算真数大一些,对数函数的结果也大不了多少,所以这个算法实现的实际运行效率也是很高的,以上只是理论层面的时间复杂度分析,供大家参考。
|
||||
|
||||
### 秒杀三道题目
|
||||
|
||||
以上说了 Dijkstra 算法的框架,下面我们套用这个框架做几道题,实践出真知。
|
||||
|
||||
第一题是力扣第 743 题「网络延迟时间」,题目如下:
|
||||
|
||||
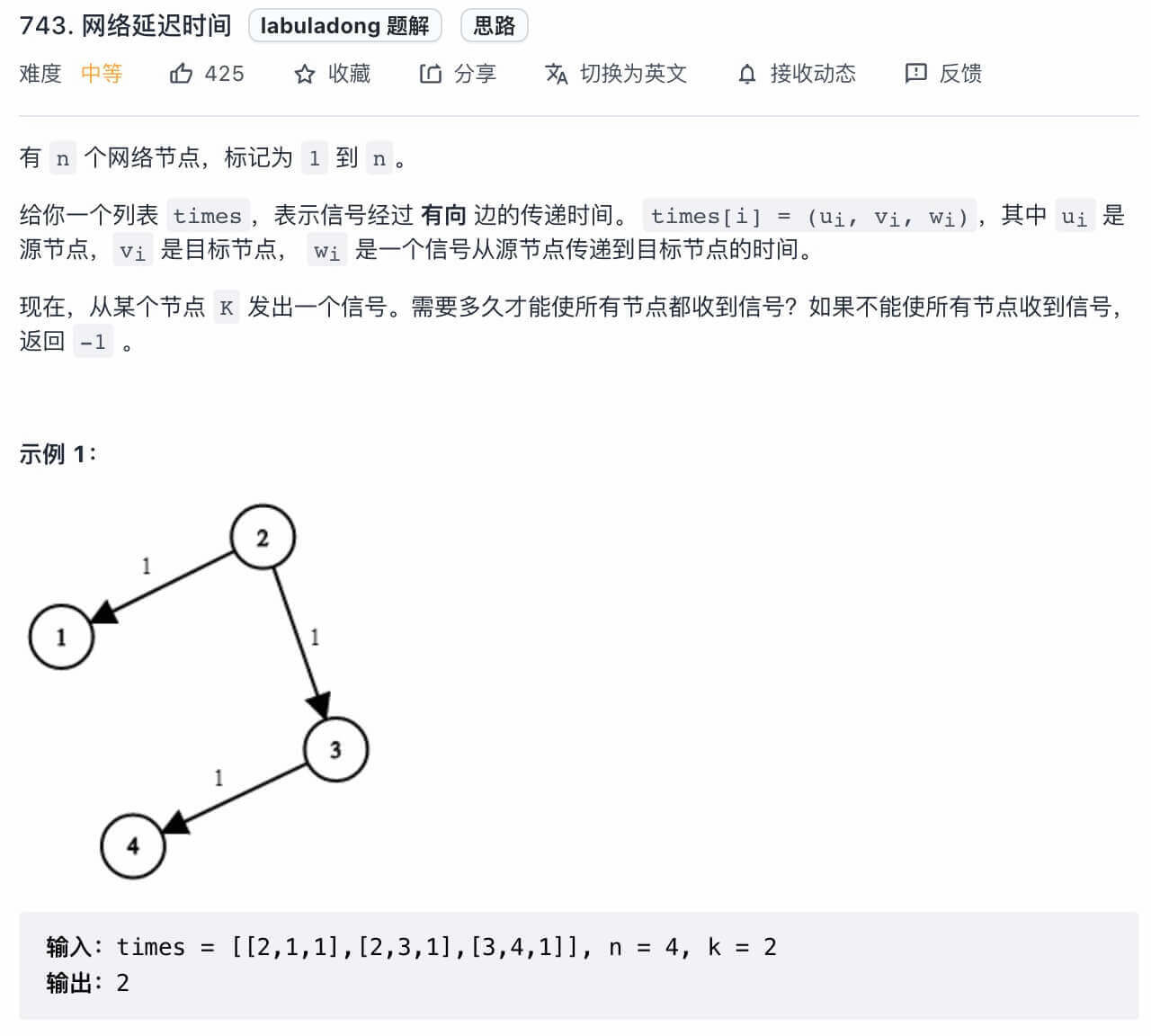
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
// times 记录边和权重,n 为节点个数(从 1 开始),k 为起点
|
||||
// 计算从 k 发出的信号至少需要多久传遍整幅图
|
||||
int networkDelayTime(int[][] times, int n, int k)
|
||||
```
|
||||
|
||||
让你求所有节点都收到信号的时间,你把所谓的传递时间看做距离,实际上就是问你「从节点 `k` 到其他所有节点的最短路径中,最长的那条最短路径距离是多少」,说白了就是让你算从节点 `k` 出发到其他所有节点的最短路径,就是标准的 Dijkstra 算法。
|
||||
|
||||
在用 Dijkstra 之前,别忘了要满足一些条件,加权有向图,没有负权重边,OK,可以用 Dijkstra 算法计算最短路径。
|
||||
|
||||
根据我们之前 Dijkstra 算法的框架,我们可以写出下面代码:
|
||||
|
||||
```java
|
||||
int networkDelayTime(int[][] times, int n, int k) {
|
||||
// 节点编号是从 1 开始的,所以要一个大小为 n + 1 的邻接表
|
||||
List<int[]>[] graph = new LinkedList[n + 1];
|
||||
for (int i = 1; i <= n; i++) {
|
||||
graph[i] = new LinkedList<>();
|
||||
}
|
||||
// 构造图
|
||||
for (int[] edge : times) {
|
||||
int from = edge[0];
|
||||
int to = edge[1];
|
||||
int weight = edge[2];
|
||||
// from -> List<(to, weight)>
|
||||
// 邻接表存储图结构,同时存储权重信息
|
||||
graph[from].add(new int[]{to, weight});
|
||||
}
|
||||
// 启动 dijkstra 算法计算以节点 k 为起点到其他节点的最短路径
|
||||
int[] distTo = dijkstra(k, graph);
|
||||
|
||||
// 找到最长的那一条最短路径
|
||||
int res = 0;
|
||||
for (int i = 1; i < distTo.length; i++) {
|
||||
if (distTo[i] == Integer.MAX_VALUE) {
|
||||
// 有节点不可达,返回 -1
|
||||
return -1;
|
||||
}
|
||||
res = Math.max(res, distTo[i]);
|
||||
}
|
||||
return res;
|
||||
}
|
||||
|
||||
// 输入一个起点 start,计算从 start 到其他节点的最短距离
|
||||
int[] dijkstra(int start, List<int[]>[] graph) {}
|
||||
```
|
||||
|
||||
上述代码首先利用题目输入的数据转化成邻接表表示一幅图,接下来我们可以直接套用 Dijkstra 算法的框架:
|
||||
|
||||
```java
|
||||
class State {
|
||||
// 图节点的 id
|
||||
int id;
|
||||
// 从 start 节点到当前节点的距离
|
||||
int distFromStart;
|
||||
|
||||
State(int id, int distFromStart) {
|
||||
this.id = id;
|
||||
this.distFromStart = distFromStart;
|
||||
}
|
||||
}
|
||||
|
||||
// 输入一个起点 start,计算从 start 到其他节点的最短距离
|
||||
int[] dijkstra(int start, List<int[]>[] graph) {
|
||||
// 定义:distTo[i] 的值就是起点 start 到达节点 i 的最短路径权重
|
||||
int[] distTo = new int[graph.length];
|
||||
Arrays.fill(distTo, Integer.MAX_VALUE);
|
||||
// base case,start 到 start 的最短距离就是 0
|
||||
distTo[start] = 0;
|
||||
|
||||
// 优先级队列,distFromStart 较小的排在前面
|
||||
Queue<State> pq = new PriorityQueue<>((a, b) -> {
|
||||
return a.distFromStart - b.distFromStart;
|
||||
});
|
||||
// 从起点 start 开始进行 BFS
|
||||
pq.offer(new State(start, 0));
|
||||
|
||||
while (!pq.isEmpty()) {
|
||||
State curState = pq.poll();
|
||||
int curNodeID = curState.id;
|
||||
int curDistFromStart = curState.distFromStart;
|
||||
|
||||
if (curDistFromStart > distTo[curNodeID]) {
|
||||
continue;
|
||||
}
|
||||
|
||||
// 将 curNode 的相邻节点装入队列
|
||||
for (int[] neighbor : graph[curNodeID]) {
|
||||
int nextNodeID = neighbor[0];
|
||||
int distToNextNode = distTo[curNodeID] + neighbor[1];
|
||||
// 更新 dp table
|
||||
if (distTo[nextNodeID] > distToNextNode) {
|
||||
distTo[nextNodeID] = distToNextNode;
|
||||
pq.offer(new State(nextNodeID, distToNextNode));
|
||||
}
|
||||
}
|
||||
}
|
||||
return distTo;
|
||||
}
|
||||
```
|
||||
|
||||
你对比之前说的代码框架,只要稍稍修改,就可以把这道题目解决了。
|
||||
|
||||
感觉这道题完全没有难度,下面我们再看一道题目,力扣第 1631 题「最小体力消耗路径」:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
// 输入一个二维矩阵,计算从左上角到右下角的最小体力消耗
|
||||
int minimumEffortPath(int[][] heights);
|
||||
```
|
||||
|
||||
我们常见的二维矩阵题目,如果让你从左上角走到右下角,比较简单的题一般都会限制你只能向右或向下走,但这道题可没有限制哦,你可以上下左右随便走,只要路径的「体力消耗」最小就行。
|
||||
|
||||
如果你把二维数组中每个 `(x, y)` 坐标看做一个节点,它的上下左右坐标就是相邻节点,它对应的值和相邻坐标对应的值之差的绝对值就是题目说的「体力消耗」,你就可以理解为边的权重。
|
||||
|
||||
这样一想,是不是就在让你以左上角坐标为起点,以右下角坐标为终点,计算起点到终点的最短路径?Dijkstra 算法是不是可以做到?
|
||||
|
||||
```java
|
||||
// 输入起点 start 和终点 end,计算起点到终点的最短距离
|
||||
int dijkstra(int start, int end, List<Integer>[] graph)
|
||||
```
|
||||
|
||||
**只不过,这道题中评判一条路径是长还是短的标准不再是路径经过的权重总和,而是路径经过的权重最大值**。
|
||||
|
||||
明白这一点,再想一下使用 Dijkstra 算法的前提,加权有向图,没有负权重边,求最短路径,OK,可以使用,咱们来套框架。
|
||||
|
||||
二维矩阵抽象成图,我们先实现一下图的 `adj` 方法,之后的主要逻辑会清晰一些:
|
||||
|
||||
```java
|
||||
// 方向数组,上下左右的坐标偏移量
|
||||
int[][] dirs = new int[][]{{0,1}, {1,0}, {0,-1}, {-1,0}};
|
||||
|
||||
// 返回坐标 (x, y) 的上下左右相邻坐标
|
||||
List<int[]> adj(int[][] matrix, int x, int y) {
|
||||
int m = matrix.length, n = matrix[0].length;
|
||||
// 存储相邻节点
|
||||
List<int[]> neighbors = new ArrayList<>();
|
||||
for (int[] dir : dirs) {
|
||||
int nx = x + dir[0];
|
||||
int ny = y + dir[1];
|
||||
if (nx >= m || nx < 0 || ny >= n || ny < 0) {
|
||||
// 索引越界
|
||||
continue;
|
||||
}
|
||||
neighbors.add(new int[]{nx, ny});
|
||||
}
|
||||
return neighbors;
|
||||
}
|
||||
```
|
||||
|
||||
类似的,我们现在认为一个二维坐标 `(x, y)` 是图中的一个节点,所以这个 `State` 类也需要修改一下:
|
||||
|
||||
```java
|
||||
class State {
|
||||
// 矩阵中的一个位置
|
||||
int x, y;
|
||||
// 从起点 (0, 0) 到当前位置的最小体力消耗(距离)
|
||||
int effortFromStart;
|
||||
|
||||
State(int x, int y, int effortFromStart) {
|
||||
this.x = x;
|
||||
this.y = y;
|
||||
this.effortFromStart = effortFromStart;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
接下来,就可以套用 Dijkstra 算法的代码模板了:
|
||||
|
||||
```java
|
||||
// Dijkstra 算法,计算 (0, 0) 到 (m - 1, n - 1) 的最小体力消耗
|
||||
int minimumEffortPath(int[][] heights) {
|
||||
int m = heights.length, n = heights[0].length;
|
||||
// 定义:从 (0, 0) 到 (i, j) 的最小体力消耗是 effortTo[i][j]
|
||||
int[][] effortTo = new int[m][n];
|
||||
// dp table 初始化为正无穷
|
||||
for (int i = 0; i < m; i++) {
|
||||
Arrays.fill(effortTo[i], Integer.MAX_VALUE);
|
||||
}
|
||||
// base case,起点到起点的最小消耗就是 0
|
||||
effortTo[0][0] = 0;
|
||||
|
||||
// 优先级队列,effortFromStart 较小的排在前面
|
||||
Queue<State> pq = new PriorityQueue<>((a, b) -> {
|
||||
return a.effortFromStart - b.effortFromStart;
|
||||
});
|
||||
|
||||
// 从起点 (0, 0) 开始进行 BFS
|
||||
pq.offer(new State(0, 0, 0));
|
||||
|
||||
while (!pq.isEmpty()) {
|
||||
State curState = pq.poll();
|
||||
int curX = curState.x;
|
||||
int curY = curState.y;
|
||||
int curEffortFromStart = curState.effortFromStart;
|
||||
|
||||
// 到达终点提前结束
|
||||
if (curX == m - 1 && curY == n - 1) {
|
||||
return curEffortFromStart;
|
||||
}
|
||||
|
||||
if (curEffortFromStart > effortTo[curX][curY]) {
|
||||
continue;
|
||||
}
|
||||
// 将 (curX, curY) 的相邻坐标装入队列
|
||||
for (int[] neighbor : adj(heights, curX, curY)) {
|
||||
int nextX = neighbor[0];
|
||||
int nextY = neighbor[1];
|
||||
// 计算从 (curX, curY) 达到 (nextX, nextY) 的消耗
|
||||
int effortToNextNode = Math.max(
|
||||
effortTo[curX][curY],
|
||||
Math.abs(heights[curX][curY] - heights[nextX][nextY])
|
||||
);
|
||||
// 更新 dp table
|
||||
if (effortTo[nextX][nextY] > effortToNextNode) {
|
||||
effortTo[nextX][nextY] = effortToNextNode;
|
||||
pq.offer(new State(nextX, nextY, effortToNextNode));
|
||||
}
|
||||
}
|
||||
}
|
||||
// 正常情况不会达到这个 return
|
||||
return -1;
|
||||
}
|
||||
```
|
||||
|
||||
你看,稍微改一改代码模板,这道题就解决了。
|
||||
|
||||
最后看一道题吧,力扣第 1514 题「概率最大的路径」,看下题目:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
// 输入一幅无向图,边上的权重代表概率,返回从 start 到达 end 最大的概率
|
||||
double maxProbability(int n, int[][] edges, double[] succProb, int start, int end)
|
||||
```
|
||||
|
||||
我说这题一看就是 Dijkstra 算法,但聪明的你肯定会反驳我:
|
||||
|
||||
**1、这题给的是无向图,也可以用 Dijkstra 算法吗**?
|
||||
|
||||
**2、更重要的是,Dijkstra 算法计算的是最短路径,计算的是最小值,这题让你计算最大概率是一个最大值,怎么可能用 Dijkstra 算法呢**?
|
||||
|
||||
问得好!
|
||||
|
||||
首先关于有向图和无向图,前文 [图算法基础](https://labuladong.github.io/article/fname.html?fname=图) 说过,无向图本质上可以认为是「双向图」,从而转化成有向图。
|
||||
|
||||
重点说说最大值和最小值这个问题,其实 Dijkstra 和很多最优化算法一样,计算的是「最优值」,这个最优值可能是最大值,也可能是最小值。
|
||||
|
||||
标准 Dijkstra 算法是计算最短路径的,但你有想过为什么 Dijkstra 算法不允许存在负权重边么?
|
||||
|
||||
**因为 Dijkstra 计算最短路径的正确性依赖一个前提:路径中每增加一条边,路径的总权重就会增加**。
|
||||
|
||||
这个前提的数学证明大家有兴趣可以自己搜索一下,我这里只说结论,其实你把这个结论反过来也是 OK 的:
|
||||
|
||||
如果你想计算最长路径,路径中每增加一条边,路径的总权重就会减少,要是能够满足这个条件,也可以用 Dijkstra 算法。
|
||||
|
||||
你看这道题是不是符合这个条件?边和边之间是乘法关系,每条边的概率都是小于 1 的,所以肯定会越乘越小。
|
||||
|
||||
只不过,这道题的解法要把优先级队列的排序顺序反过来,一些 if 大小判断也要反过来,我们直接看解法代码吧:
|
||||
|
||||
```java
|
||||
double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
|
||||
List<double[]>[] graph = new LinkedList[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
graph[i] = new LinkedList<>();
|
||||
}
|
||||
// 构造邻接表结构表示图
|
||||
for (int i = 0; i < edges.length; i++) {
|
||||
int from = edges[i][0];
|
||||
int to = edges[i][1];
|
||||
double weight = succProb[i];
|
||||
// 无向图就是双向图;先把 int 统一转成 double,待会再转回来
|
||||
graph[from].add(new double[]{(double)to, weight});
|
||||
graph[to].add(new double[]{(double)from, weight});
|
||||
}
|
||||
|
||||
return dijkstra(start, end, graph);
|
||||
}
|
||||
|
||||
class State {
|
||||
// 图节点的 id
|
||||
int id;
|
||||
// 从 start 节点到达当前节点的概率
|
||||
double probFromStart;
|
||||
|
||||
State(int id, double probFromStart) {
|
||||
this.id = id;
|
||||
this.probFromStart = probFromStart;
|
||||
}
|
||||
}
|
||||
|
||||
double dijkstra(int start, int end, List<double[]>[] graph) {
|
||||
// 定义:probTo[i] 的值就是节点 start 到达节点 i 的最大概率
|
||||
double[] probTo = new double[graph.length];
|
||||
// dp table 初始化为一个取不到的最小值
|
||||
Arrays.fill(probTo, -1);
|
||||
// base case,start 到 start 的概率就是 1
|
||||
probTo[start] = 1;
|
||||
|
||||
// 优先级队列,probFromStart 较大的排在前面
|
||||
Queue<State> pq = new PriorityQueue<>((a, b) -> {
|
||||
return Double.compare(b.probFromStart, a.probFromStart);
|
||||
});
|
||||
// 从起点 start 开始进行 BFS
|
||||
pq.offer(new State(start, 1));
|
||||
|
||||
while (!pq.isEmpty()) {
|
||||
State curState = pq.poll();
|
||||
int curNodeID = curState.id;
|
||||
double curProbFromStart = curState.probFromStart;
|
||||
|
||||
// 遇到终点提前返回
|
||||
if (curNodeID == end) {
|
||||
return curProbFromStart;
|
||||
}
|
||||
|
||||
if (curProbFromStart < probTo[curNodeID]) {
|
||||
// 已经有一条概率更大的路径到达 curNode 节点了
|
||||
continue;
|
||||
}
|
||||
// 将 curNode 的相邻节点装入队列
|
||||
for (double[] neighbor : graph[curNodeID]) {
|
||||
int nextNodeID = (int)neighbor[0];
|
||||
// 看看从 curNode 达到 nextNode 的概率是否会更大
|
||||
double probToNextNode = probTo[curNodeID] * neighbor[1];
|
||||
if (probTo[nextNodeID] < probToNextNode) {
|
||||
probTo[nextNodeID] = probToNextNode;
|
||||
pq.offer(new State(nextNodeID, probToNextNode));
|
||||
}
|
||||
}
|
||||
}
|
||||
// 如果到达这里,说明从 start 开始无法到达 end,返回 0
|
||||
return 0.0;
|
||||
}
|
||||
```
|
||||
|
||||
好了,到这里本文就结束了,总共 6000 多字,这三道例题都是比较困难的,如果你能够看到这里,真得给你鼓掌。
|
||||
|
||||
其实前文 [毕业旅行省钱算法](https://labuladong.github.io/article/fname.html?fname=旅行最短路径) 中讲过限制之下的最小路径问题,当时是使用动态规划思路解决的,但文末也给了 Dijkstra 算法代码,仅仅在本文模板的基础上做了一些变换,你理解本文后可以对照着去看看那道题目。
|
||||
|
||||
最后还是那句话,做题在质不在量,希望大家能够透彻理解最基本的数据结构,以不变应万变。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [BFS 算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=BFS框架)
|
||||
- [Kruskal 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=kruskal)
|
||||
- [Prim 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=prim算法)
|
||||
- [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结)
|
||||
- [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
|
||||
- [图论基础及遍历算法](https://labuladong.github.io/article/fname.html?fname=图)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [旅游省钱大法:加权最短路径](https://labuladong.github.io/article/fname.html?fname=旅行最短路径)
|
||||
- [环检测及拓扑排序算法](https://labuladong.github.io/article/fname.html?fname=拓扑排序)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 二叉堆详解实现优先级队列
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -230,6 +226,42 @@ public Key delMax() {
|
|||
|
||||
> 最后打个广告,我亲自制作了一门 [数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO),以视频课为主,手把手带你实现常用的数据结构及相关算法,旨在帮助算法基础较为薄弱的读者深入理解常用数据结构的底层原理,在算法学习中少走弯路。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [双指针技巧秒杀七道链表题目](https://labuladong.github.io/article/fname.html?fname=链表技巧)
|
||||
- [如何调度考生的座位](https://labuladong.github.io/article/fname.html?fname=座位调度)
|
||||
- [快速排序详解及应用](https://labuladong.github.io/article/fname.html?fname=快速排序)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1104. Path In Zigzag Labelled Binary Tree](https://leetcode.com/problems/path-in-zigzag-labelled-binary-tree/?show=1) | [1104. 二叉树寻路](https://leetcode.cn/problems/path-in-zigzag-labelled-binary-tree/?show=1) |
|
||||
| [1845. Seat Reservation Manager](https://leetcode.com/problems/seat-reservation-manager/?show=1) | [1845. 座位预约管理系统](https://leetcode.cn/problems/seat-reservation-manager/?show=1) |
|
||||
| [23. Merge k Sorted Lists](https://leetcode.com/problems/merge-k-sorted-lists/?show=1) | [23. 合并K个升序链表](https://leetcode.cn/problems/merge-k-sorted-lists/?show=1) |
|
||||
| [662. Maximum Width of Binary Tree](https://leetcode.com/problems/maximum-width-of-binary-tree/?show=1) | [662. 二叉树最大宽度](https://leetcode.cn/problems/maximum-width-of-binary-tree/?show=1) |
|
||||
| [703. Kth Largest Element in a Stream](https://leetcode.com/problems/kth-largest-element-in-a-stream/?show=1) | [703. 数据流中的第 K 大元素](https://leetcode.cn/problems/kth-largest-element-in-a-stream/?show=1) |
|
||||
| - | [剑指 Offer II 059. 数据流的第 K 大数值](https://leetcode.cn/problems/jBjn9C/?show=1) |
|
||||
| - | [剑指 Offer II 078. 合并排序链表](https://leetcode.cn/problems/vvXgSW/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,718 +0,0 @@
|
|||
# 二叉搜索树操作集锦
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[100.相同的树](https://leetcode-cn.com/problems/same-tree)
|
||||
|
||||
[450.删除二叉搜索树中的节点](https://leetcode-cn.com/problems/delete-node-in-a-bst)
|
||||
|
||||
[701.二叉搜索树中的插入操作](https://leetcode-cn.com/problems/insert-into-a-binary-search-tree)
|
||||
|
||||
[700.二叉搜索树中的搜索](https://leetcode-cn.com/problems/search-in-a-binary-search-tree)
|
||||
|
||||
[98.验证二叉搜索树](https://leetcode-cn.com/problems/validate-binary-search-tree)
|
||||
|
||||
**-----------**
|
||||
|
||||
通过之前的文章[框架思维](https://labuladong.gitee.io/algo/),二叉树的遍历框架应该已经印到你的脑子里了,这篇文章就来实操一下,看看框架思维是怎么灵活运用,秒杀一切二叉树问题的。
|
||||
|
||||
二叉树算法的设计的总路线:明确一个节点要做的事情,然后剩下的事抛给框架。
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
// root 需要做什么?在这做。
|
||||
// 其他的不用 root 操心,抛给框架
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
举两个简单的例子体会一下这个思路,热热身。
|
||||
|
||||
**1. 如何把二叉树所有的节点中的值加一?**
|
||||
|
||||
```java
|
||||
void plusOne(TreeNode root) {
|
||||
if (root == null) return;
|
||||
root.val += 1;
|
||||
|
||||
plusOne(root.left);
|
||||
plusOne(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
**2. 如何判断两棵二叉树是否完全相同?**
|
||||
|
||||
```java
|
||||
boolean isSameTree(TreeNode root1, TreeNode root2) {
|
||||
// 都为空的话,显然相同
|
||||
if (root1 == null && root2 == null) return true;
|
||||
// 一个为空,一个非空,显然不同
|
||||
if (root1 == null || root2 == null) return false;
|
||||
// 两个都非空,但 val 不一样也不行
|
||||
if (root1.val != root2.val) return false;
|
||||
|
||||
// root1 和 root2 该比的都比完了
|
||||
return isSameTree(root1.left, root2.left)
|
||||
&& isSameTree(root1.right, root2.right);
|
||||
}
|
||||
```
|
||||
|
||||
借助框架,上面这两个例子不难理解吧?如果可以理解,那么所有二叉树算法你都能解决。
|
||||
|
||||
|
||||
|
||||
二叉搜索树(Binary Search Tree,简称 BST)是一种很常用的的二叉树。它的定义是:一个二叉树中,任意节点的值要大于等于左子树所有节点的值,且要小于等于右边子树的所有节点的值。
|
||||
|
||||
如下就是一个符合定义的 BST:
|
||||
|
||||

|
||||
|
||||
|
||||
下面实现 BST 的基础操作:判断 BST 的合法性、增、删、查。其中“删”和“判断合法性”略微复杂。
|
||||
|
||||
**零、判断 BST 的合法性**
|
||||
|
||||
这里是有坑的哦,我们按照刚才的思路,每个节点自己要做的事不就是比较自己和左右孩子吗?看起来应该这样写代码:
|
||||
```java
|
||||
boolean isValidBST(TreeNode root) {
|
||||
if (root == null) return true;
|
||||
if (root.left != null && root.val <= root.left.val) return false;
|
||||
if (root.right != null && root.val >= root.right.val) return false;
|
||||
|
||||
return isValidBST(root.left)
|
||||
&& isValidBST(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
但是这个算法出现了错误,BST 的每个节点应该要小于右边子树的所有节点,下面这个二叉树显然不是 BST,但是我们的算法会把它判定为 BST。
|
||||
|
||||

|
||||
|
||||
出现错误,不要慌张,框架没有错,一定是某个细节问题没注意到。我们重新看一下 BST 的定义,root 需要做的不只是和左右子节点比较,而是要整个左子树和右子树所有节点比较。怎么办,鞭长莫及啊!
|
||||
|
||||
这种情况,我们可以使用辅助函数,增加函数参数列表,在参数中携带额外信息,请看正确的代码:
|
||||
|
||||
```java
|
||||
boolean isValidBST(TreeNode root) {
|
||||
return isValidBST(root, null, null);
|
||||
}
|
||||
|
||||
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {
|
||||
if (root == null) return true;
|
||||
if (min != null && root.val <= min.val) return false;
|
||||
if (max != null && root.val >= max.val) return false;
|
||||
return isValidBST(root.left, min, root)
|
||||
&& isValidBST(root.right, root, max);
|
||||
}
|
||||
```
|
||||
|
||||
**一、在 BST 中查找一个数是否存在**
|
||||
|
||||
根据我们的指导思想,可以这样写代码:
|
||||
|
||||
```java
|
||||
boolean isInBST(TreeNode root, int target) {
|
||||
if (root == null) return false;
|
||||
if (root.val == target) return true;
|
||||
|
||||
return isInBST(root.left, target)
|
||||
|| isInBST(root.right, target);
|
||||
}
|
||||
```
|
||||
|
||||
这样写完全正确,充分证明了你的框架性思维已经养成。现在你可以考虑一点细节问题了:如何充分利用信息,把 BST 这个“左小右大”的特性用上?
|
||||
|
||||
很简单,其实不需要递归地搜索两边,类似二分查找思想,根据 target 和 root.val 的大小比较,就能排除一边。我们把上面的思路稍稍改动:
|
||||
|
||||
```java
|
||||
boolean isInBST(TreeNode root, int target) {
|
||||
if (root == null) return false;
|
||||
if (root.val == target)
|
||||
return true;
|
||||
if (root.val < target)
|
||||
return isInBST(root.right, target);
|
||||
if (root.val > target)
|
||||
return isInBST(root.left, target);
|
||||
// root 该做的事做完了,顺带把框架也完成了,妙
|
||||
}
|
||||
```
|
||||
|
||||
于是,我们对原始框架进行改造,抽象出一套**针对 BST 的遍历框架**:
|
||||
|
||||
```java
|
||||
void BST(TreeNode root, int target) {
|
||||
if (root.val == target)
|
||||
// 找到目标,做点什么
|
||||
if (root.val < target)
|
||||
BST(root.right, target);
|
||||
if (root.val > target)
|
||||
BST(root.left, target);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
**二、在 BST 中插入一个数**
|
||||
|
||||
对数据结构的操作无非遍历 + 访问,遍历就是“找”,访问就是“改”。具体到这个问题,插入一个数,就是先找到插入位置,然后进行插入操作。
|
||||
|
||||
上一个问题,我们总结了 BST 中的遍历框架,就是“找”的问题。直接套框架,加上“改”的操作即可。一旦涉及“改”,函数就要返回 TreeNode 类型,并且对递归调用的返回值进行接收。
|
||||
|
||||
```java
|
||||
TreeNode insertIntoBST(TreeNode root, int val) {
|
||||
// 找到空位置插入新节点
|
||||
if (root == null) return new TreeNode(val);
|
||||
// if (root.val == val)
|
||||
// BST 中一般不会插入已存在元素
|
||||
if (root.val < val)
|
||||
root.right = insertIntoBST(root.right, val);
|
||||
if (root.val > val)
|
||||
root.left = insertIntoBST(root.left, val);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
**三、在 BST 中删除一个数**
|
||||
|
||||
这个问题稍微复杂,不过你有框架指导,难不住你。跟插入操作类似,先“找”再“改”,先把框架写出来再说:
|
||||
|
||||
```java
|
||||
TreeNode deleteNode(TreeNode root, int key) {
|
||||
if (root.val == key) {
|
||||
// 找到啦,进行删除
|
||||
} else if (root.val > key) {
|
||||
root.left = deleteNode(root.left, key);
|
||||
} else if (root.val < key) {
|
||||
root.right = deleteNode(root.right, key);
|
||||
}
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
找到目标节点了,比方说是节点 A,如何删除这个节点,这是难点。因为删除节点的同时不能破坏 BST 的性质。有三种情况,用图片来说明。
|
||||
|
||||
情况 1:A 恰好是末端节点,两个子节点都为空,那么它可以当场去世了。
|
||||
|
||||
图片来自 LeetCode
|
||||

|
||||
|
||||
```java
|
||||
if (root.left == null && root.right == null)
|
||||
return null;
|
||||
```
|
||||
|
||||
情况 2:A 只有一个非空子节点,那么它要让这个孩子接替自己的位置。
|
||||
|
||||
图片来自 LeetCode
|
||||

|
||||
|
||||
```java
|
||||
// 排除了情况 1 之后
|
||||
if (root.left == null) return root.right;
|
||||
if (root.right == null) return root.left;
|
||||
```
|
||||
|
||||
情况 3:A 有两个子节点,麻烦了,为了不破坏 BST 的性质,A 必须找到左子树中最大的那个节点,或者右子树中最小的那个节点来接替自己。我们以第二种方式讲解。
|
||||
|
||||
图片来自 LeetCode
|
||||

|
||||
|
||||
```java
|
||||
if (root.left != null && root.right != null) {
|
||||
// 找到右子树的最小节点
|
||||
TreeNode minNode = getMin(root.right);
|
||||
// 把 root 改成 minNode
|
||||
root.val = minNode.val;
|
||||
// 转而去删除 minNode
|
||||
root.right = deleteNode(root.right, minNode.val);
|
||||
}
|
||||
```
|
||||
|
||||
三种情况分析完毕,填入框架,简化一下代码:
|
||||
|
||||
```java
|
||||
TreeNode deleteNode(TreeNode root, int key) {
|
||||
if (root == null) return null;
|
||||
if (root.val == key) {
|
||||
// 这两个 if 把情况 1 和 2 都正确处理了
|
||||
if (root.left == null) return root.right;
|
||||
if (root.right == null) return root.left;
|
||||
// 处理情况 3
|
||||
TreeNode minNode = getMin(root.right);
|
||||
root.val = minNode.val;
|
||||
root.right = deleteNode(root.right, minNode.val);
|
||||
} else if (root.val > key) {
|
||||
root.left = deleteNode(root.left, key);
|
||||
} else if (root.val < key) {
|
||||
root.right = deleteNode(root.right, key);
|
||||
}
|
||||
return root;
|
||||
}
|
||||
|
||||
TreeNode getMin(TreeNode node) {
|
||||
// BST 最左边的就是最小的
|
||||
while (node.left != null) node = node.left;
|
||||
return node;
|
||||
}
|
||||
```
|
||||
|
||||
删除操作就完成了。注意一下,这个删除操作并不完美,因为我们一般不会通过 root.val = minNode.val 修改节点内部的值来交换节点,而是通过一系列略微复杂的链表操作交换 root 和 minNode 两个节点。因为具体应用中,val 域可能会很大,修改起来很耗时,而链表操作无非改一改指针,而不会去碰内部数据。
|
||||
|
||||
但这里忽略这个细节,旨在突出 BST 基本操作的共性,以及借助框架逐层细化问题的思维方式。
|
||||
|
||||
**四、最后总结**
|
||||
|
||||
通过这篇文章,你学会了如下几个技巧:
|
||||
|
||||
1. 二叉树算法设计的总路线:把当前节点要做的事做好,其他的交给递归框架,不用当前节点操心。
|
||||
|
||||
2. 如果当前节点会对下面的子节点有整体影响,可以通过辅助函数增长参数列表,借助参数传递信息。
|
||||
|
||||
3. 在二叉树框架之上,扩展出一套 BST 遍历框架:
|
||||
```java
|
||||
void BST(TreeNode root, int target) {
|
||||
if (root.val == target)
|
||||
// 找到目标,做点什么
|
||||
if (root.val < target)
|
||||
BST(root.right, target);
|
||||
if (root.val > target)
|
||||
BST(root.left, target);
|
||||
}
|
||||
```
|
||||
|
||||
4. 掌握了 BST 的基本操作。
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
[100.相同的树](https://leetcode-cn.com/problems/same-tree)
|
||||
|
||||
[450.删除二叉搜索树中的节点](https://leetcode-cn.com/problems/delete-node-in-a-bst)
|
||||
|
||||
[701.二叉搜索树中的插入操作](https://leetcode-cn.com/problems/insert-into-a-binary-search-tree)
|
||||
|
||||
[700.二叉搜索树中的搜索](https://leetcode-cn.com/problems/search-in-a-binary-search-tree)
|
||||
|
||||
[98.验证二叉搜索树](https://leetcode-cn.com/problems/validate-binary-search-tree)
|
||||
|
||||
### c++
|
||||
|
||||
[dekunma](https://www.linkedin.com/in/dekun-ma-036a9b198/)提供第98题C++代码:
|
||||
|
||||
```c++
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* struct TreeNode {
|
||||
* int val;
|
||||
* TreeNode *left;
|
||||
* TreeNode *right;
|
||||
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
|
||||
* };
|
||||
*/
|
||||
class Solution {
|
||||
public:
|
||||
bool isValidBST(TreeNode* root) {
|
||||
// 用helper method求解
|
||||
return isValidBST(root, nullptr, nullptr);
|
||||
}
|
||||
|
||||
bool isValidBST(TreeNode* root, TreeNode* min, TreeNode* max) {
|
||||
// base case, root为nullptr
|
||||
if (!root) return true;
|
||||
|
||||
// 不符合BST的条件
|
||||
if (min && root->val <= min->val) return false;
|
||||
if (max && root->val >= max->val) return false;
|
||||
|
||||
// 向左右子树分别递归求解
|
||||
return isValidBST(root->left, min, root)
|
||||
&& isValidBST(root->right, root, max);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
[yanggg1997](https://github.com/yanggg1997)提供第100题C++代码:
|
||||
|
||||
``` c++
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* struct TreeNode {
|
||||
* int val;
|
||||
* TreeNode *left;
|
||||
* TreeNode *right;
|
||||
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
|
||||
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
|
||||
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
|
||||
* };
|
||||
*/
|
||||
class Solution {
|
||||
public:
|
||||
bool isSameTree(TreeNode* p, TreeNode* q) {
|
||||
// 若当前节点均为空,则此处相同
|
||||
if(!p && !q) return true;
|
||||
// 若当前节点在一棵树上有而另一棵树上为空,则两棵树不同
|
||||
if(!p && q) return false;
|
||||
if(p && !q) return false;
|
||||
// 若当前节点在两棵树上均存在。
|
||||
if(p->val != q->val)
|
||||
{
|
||||
return false;
|
||||
}
|
||||
else
|
||||
{
|
||||
// 向左右子树分别递归判断
|
||||
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
|
||||
}
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
### python
|
||||
|
||||
[ChenjieXu](https://github.com/ChenjieXu)提供第98题Python3代码:
|
||||
|
||||
```python
|
||||
def isValidBST(self, root):
|
||||
# 递归函数
|
||||
def helper(node, lower = float('-inf'), upper = float('inf')):
|
||||
if not node:
|
||||
return True
|
||||
|
||||
val = node.val
|
||||
if val <= lower or val >= upper:
|
||||
return False
|
||||
# 右节点
|
||||
if not helper(node.right, val, upper):
|
||||
return False
|
||||
# 左节点
|
||||
if not helper(node.left, lower, val):
|
||||
return False
|
||||
return True
|
||||
|
||||
return helper(root)
|
||||
|
||||
```
|
||||
|
||||
[lixiandea](https://github.com/lixiandea)提供第100题Python3代码:
|
||||
|
||||
```python
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
class Solution:
|
||||
def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
|
||||
'''
|
||||
当前节点值相等且树的子树相等,则树相等。
|
||||
递归退出条件:两个节点存在一个节点为空
|
||||
'''
|
||||
if p == None:
|
||||
if q == None:
|
||||
return True
|
||||
else:
|
||||
return False
|
||||
if q == None:
|
||||
return False
|
||||
# 当前节点相同且左子树和右子树分别相同
|
||||
return p.val==q.val and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)
|
||||
```
|
||||
|
||||
|
||||
[Edwenc](https://github.com/Edwenc) 提供 leetcode第450题的python3 代码:
|
||||
|
||||
```python
|
||||
# Definition for a binary tree node.
|
||||
# class TreeNode:
|
||||
# def __init__(self, val=0, left=None, right=None):
|
||||
# self.val = val
|
||||
# self.left = left
|
||||
# self.right = right
|
||||
|
||||
class Solution:
|
||||
def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
|
||||
# 如果没有树 直接返回None
|
||||
if root == None:
|
||||
return None
|
||||
|
||||
# 如果要删除的结点 就是当前结点
|
||||
if root.val == key:
|
||||
# 左子树为空 只有右子树需要被更新 直接返回
|
||||
if root.left == None:
|
||||
return root.right
|
||||
# 右子树为空 只有左子树需要被更新 直接返回
|
||||
if root.right== None:
|
||||
return root.left
|
||||
|
||||
# 找出此结点左子树的最大值
|
||||
# 用这个最大值 来代替当前结点
|
||||
# 再在左子树中递归地删除这个最大值结点
|
||||
big = self.getMax( root.left )
|
||||
root.val = big.val
|
||||
root.left = self.deleteNode( root.left , big.val )
|
||||
|
||||
# 当前结点较大 它的左子树中需要删除节点 递归到左子树
|
||||
elif root.val > key:
|
||||
root.left = self.deleteNode( root.left , key)
|
||||
# 当前结点较小 它的右子树中需要删除节点 递归到右子树
|
||||
else:
|
||||
root.right= self.deleteNode( root.right, key)
|
||||
|
||||
return root
|
||||
|
||||
# 辅助函数
|
||||
# 功能是找出此二叉搜索树中最大元素的结点 并返回此结点
|
||||
def getMax( self , node ):
|
||||
# 一直找它的右子树 直到为空
|
||||
while node.right:
|
||||
node = node.right
|
||||
return node
|
||||
```
|
||||
|
||||
### java
|
||||
```
|
||||
/**
|
||||
* 第【98】题的扩展解法:
|
||||
* 对于BST,有一个重要的性质,即“BST的中序遍历是单调递增的”。抓住这个性质,我们可以通过中序遍历来判断该二叉树是不是BST。
|
||||
* 我们定义preNode节点表示上一个遍历的节点,在中序遍历的时候,比较当前节点和preNode节点的大小,一旦有节点小于或等于前一个节点,则不满足BST的规则,直接返回false,否则遍历结束,返回true。
|
||||
*/
|
||||
TreeNode preNode = null;
|
||||
public boolean isValidBST(TreeNode root) {
|
||||
if (root == null) return true;
|
||||
|
||||
boolean leftRes = isValidBST(root.left);
|
||||
|
||||
if (preNode != null && root.val <= preNode.val) {
|
||||
return false;
|
||||
}
|
||||
preNode = root;
|
||||
|
||||
boolean rightRes = isValidBST(root.right);
|
||||
|
||||
return leftRes && rightRes;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
1. 如何把二叉树所有的节点中的值加一?
|
||||
|
||||
热热身,体会体会二叉树的递归思想。
|
||||
|
||||
```js
|
||||
let plusOne = function(root) {
|
||||
if (root == null) return;
|
||||
root.val += 1;
|
||||
|
||||
plusOne(root.left);
|
||||
plusOne(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
2. 如何判断两棵二叉树是否完全相同?
|
||||
|
||||
[100.相同的树](https://leetcode-cn.com/problems/same-tree)
|
||||
|
||||
```js
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* function TreeNode(val) {
|
||||
* this.val = val;
|
||||
* this.left = this.right = null;
|
||||
* }
|
||||
*/
|
||||
/**
|
||||
* @param {TreeNode} p
|
||||
* @param {TreeNode} q
|
||||
* @return {boolean}
|
||||
*/
|
||||
var isSameTree = function(p, q) {
|
||||
if(p == null && q == null)
|
||||
return true;
|
||||
if(p == null || q == null)
|
||||
return false;
|
||||
if(p.val != q.val)
|
||||
return false;
|
||||
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
零、判断 BST 的合法性
|
||||
|
||||
[98. 验证二叉搜索树](https://leetcode-cn.com/problems/validate-binary-search-tree/)
|
||||
|
||||
```js
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* function TreeNode(val, left, right) {
|
||||
* this.val = (val===undefined ? 0 : val)
|
||||
* this.left = (left===undefined ? null : left)
|
||||
* this.right = (right===undefined ? null : right)
|
||||
* }
|
||||
*/
|
||||
/**
|
||||
* @param {TreeNode} root
|
||||
* @return {boolean}
|
||||
*/
|
||||
var isValidBST = function (root) {
|
||||
return helper(root, null, null);
|
||||
};
|
||||
|
||||
var helper = function (root, min, max) {
|
||||
if (root == null) return true;
|
||||
if (min != null && root.val <= min.val) return false;
|
||||
if (max != null && root.val >= max.val) return false;
|
||||
return helper(root.left, min, root)
|
||||
&& helper(root.right, root, max);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
一、在BST 中查找一个数是否存在
|
||||
|
||||
[700.二叉搜索树中的搜索](https://leetcode-cn.com/problems/search-in-a-binary-search-tree)
|
||||
|
||||
```js
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* function TreeNode(val, left, right) {
|
||||
* this.val = (val===undefined ? 0 : val)
|
||||
* this.left = (left===undefined ? null : left)
|
||||
* this.right = (right===undefined ? null : right)
|
||||
* }
|
||||
*/
|
||||
/**
|
||||
* @param {TreeNode} root
|
||||
* @param {number} val
|
||||
* @return {TreeNode}
|
||||
*/
|
||||
var searchBST = function(root, target) {
|
||||
if (root == null) return null;
|
||||
if (root.val === target)
|
||||
return root;
|
||||
if (root.val < target)
|
||||
return searchBST(root.right, target);
|
||||
if (root.val > target)
|
||||
return searchBST(root.left, target);
|
||||
// root 该做的事做完了,顺带把框架也完成了,妙
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
二、在 BST 中插入一个数
|
||||
|
||||
[701.二叉搜索树中的插入操作](https://leetcode-cn.com/problems/insert-into-a-binary-search-tree)
|
||||
|
||||
```js
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* function TreeNode(val, left, right) {
|
||||
* this.val = (val===undefined ? 0 : val)
|
||||
* this.left = (left===undefined ? null : left)
|
||||
* this.right = (right===undefined ? null : right)
|
||||
* }
|
||||
*/
|
||||
/**
|
||||
* @param {TreeNode} root
|
||||
* @param {number} val
|
||||
* @return {TreeNode}
|
||||
*/
|
||||
var insertIntoBST = function(root, val) {
|
||||
// 找到空位置插入新节点
|
||||
if (root == null) return new TreeNode(val);
|
||||
// if (root.val == val)
|
||||
// BST 中一般不会插入已存在元素
|
||||
if (root.val < val)
|
||||
root.right = insertIntoBST(root.right, val);
|
||||
if (root.val > val)
|
||||
root.left = insertIntoBST(root.left, val);
|
||||
return root;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
三、在 BST 中删除一个数
|
||||
|
||||
[450.删除二叉搜索树中的节点](https://leetcode-cn.com/problems/delete-node-in-a-bst)
|
||||
|
||||
```js
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* function TreeNode(val, left, right) {
|
||||
* this.val = (val===undefined ? 0 : val)
|
||||
* this.left = (left===undefined ? null : left)
|
||||
* this.right = (right===undefined ? null : right)
|
||||
* }
|
||||
*/
|
||||
/**
|
||||
* @param {TreeNode} root
|
||||
* @param {number} key
|
||||
* @return {TreeNode}
|
||||
*/
|
||||
var deleteNode = function(root, key) {
|
||||
if (!root) return null
|
||||
// if key > root.val, delete node in root.right. Otherwise delete node in root.left.
|
||||
if (key > root.val) {
|
||||
const rightNode = deleteNode(root.right, key)
|
||||
root.right = rightNode
|
||||
return root
|
||||
} else if (key < root.val) {
|
||||
const leftNode = deleteNode(root.left, key)
|
||||
root.left = leftNode
|
||||
return root
|
||||
} else {
|
||||
// now root.val === key
|
||||
if (!root.left) {
|
||||
return root.right
|
||||
}
|
||||
if (!root.right) {
|
||||
return root.left
|
||||
}
|
||||
// 将删除元素的左下方元素替代删除元素;
|
||||
// 将左下方元素的右侧最下方子元素衔接删除元素的右下方子元素;
|
||||
const rightChild = root.right
|
||||
let newRightChild = root.left
|
||||
while (newRightChild.right) {
|
||||
newRightChild = newRightChild.right
|
||||
}
|
||||
newRightChild.right = rightChild
|
||||
return root.left
|
||||
}
|
||||
};
|
||||
```
|
||||
|
|
@ -0,0 +1,796 @@
|
|||
# 东哥手把手带你刷二叉树(纲领篇)
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [104. Maximum Depth of Binary Tree](https://leetcode.com/problems/maximum-depth-of-binary-tree/) | [104. 二叉树的最大深度](https://leetcode.cn/problems/maximum-depth-of-binary-tree/) | 🟢
|
||||
| [144. Binary Tree Preorder Traversal](https://leetcode.com/problems/binary-tree-preorder-traversal/) | [144. 二叉树的前序遍历](https://leetcode.cn/problems/binary-tree-preorder-traversal/) | 🟢
|
||||
| [543. Diameter of Binary Tree](https://leetcode.com/problems/diameter-of-binary-tree/) | [543. 二叉树的直径](https://leetcode.cn/problems/diameter-of-binary-tree/) | 🟢
|
||||
| - | [剑指 Offer 55 - I. 二叉树的深度](https://leetcode.cn/problems/er-cha-shu-de-shen-du-lcof/) | 🟢
|
||||
|
||||
**-----------**
|
||||
|
||||
> 本文有视频版:[二叉树/递归的框架思维(纲领篇)](https://www.bilibili.com/video/BV1nG411x77H/)
|
||||
|
||||
PS:[刷题插件](https://mp.weixin.qq.com/s/OE1zPVPj0V2o82N4HtLQbw) 集成了手把手刷二叉树功能,按照公式和套路讲解了 150 道二叉树题目,可手把手带你刷完二叉树分类的题目,迅速掌握递归思维。
|
||||
|
||||
公众号历史文章的整个脉络都是按照 [学习数据结构和算法的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法) 提出的框架来构建的,其中着重强调了二叉树题目的重要性,所以把本文放在第一篇。
|
||||
|
||||
我刷了这么多年题,浓缩出二叉树算法的一个总纲放在这里,也许用词不是特别专业化,也没有什么教材会收录我的这些经验总结,但目前各个刷题平台的题库,没有一道二叉树题目能跳出本文划定的框架。如果你能发现一道题目和本文给出的框架不兼容,请留言告知我。
|
||||
|
||||
先在开头总结一下,二叉树解题的思维模式分两类:
|
||||
|
||||
**1、是否可以通过遍历一遍二叉树得到答案**?如果可以,用一个 `traverse` 函数配合外部变量来实现,这叫「遍历」的思维模式。
|
||||
|
||||
**2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案**?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
|
||||
|
||||
无论使用哪种思维模式,你都需要思考:
|
||||
|
||||
**如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做**?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
|
||||
|
||||
本文中会用题目来举例,但都是最最简单的题目,所以不用担心自己看不懂,我可以帮你从最简单的问题中提炼出所有二叉树题目的共性,并将二叉树中蕴含的思维进行升华,反手用到 [动态规划](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶),[回溯算法](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版),[分治算法](https://labuladong.github.io/article/fname.html?fname=分治算法),[图论算法](https://labuladong.github.io/article/fname.html?fname=图) 中去,这也是我一直强调框架思维的原因。希望你在学习了上述高级算法后,也能回头再来看看本文,会对它们有更深刻的认识。
|
||||
|
||||
首先,我还是要不厌其烦地强调一下二叉树这种数据结构及相关算法的重要性。
|
||||
|
||||
### 二叉树的重要性
|
||||
|
||||
举个例子,比如两个经典排序算法 [快速排序](https://labuladong.github.io/article/fname.html?fname=快速排序) 和 [归并排序](https://labuladong.github.io/article/fname.html?fname=归并排序),对于它俩,你有什么理解?
|
||||
|
||||
**如果你告诉我,快速排序就是个二叉树的前序遍历,归并排序就是个二叉树的后序遍历,那么我就知道你是个算法高手了**。
|
||||
|
||||
为什么快速排序和归并排序能和二叉树扯上关系?我们来简单分析一下他们的算法思想和代码框架:
|
||||
|
||||
快速排序的逻辑是,若要对 `nums[lo..hi]` 进行排序,我们先找一个分界点 `p`,通过交换元素使得 `nums[lo..p-1]` 都小于等于 `nums[p]`,且 `nums[p+1..hi]` 都大于 `nums[p]`,然后递归地去 `nums[lo..p-1]` 和 `nums[p+1..hi]` 中寻找新的分界点,最后整个数组就被排序了。
|
||||
|
||||
快速排序的代码框架如下:
|
||||
|
||||
```java
|
||||
void sort(int[] nums, int lo, int hi) {
|
||||
/****** 前序遍历位置 ******/
|
||||
// 通过交换元素构建分界点 p
|
||||
int p = partition(nums, lo, hi);
|
||||
/************************/
|
||||
|
||||
sort(nums, lo, p - 1);
|
||||
sort(nums, p + 1, hi);
|
||||
}
|
||||
```
|
||||
|
||||
先构造分界点,然后去左右子数组构造分界点,你看这不就是一个二叉树的前序遍历吗?
|
||||
|
||||
再说说归并排序的逻辑,若要对 `nums[lo..hi]` 进行排序,我们先对 `nums[lo..mid]` 排序,再对 `nums[mid+1..hi]` 排序,最后把这两个有序的子数组合并,整个数组就排好序了。
|
||||
|
||||
归并排序的代码框架如下:
|
||||
|
||||
```java
|
||||
// 定义:排序 nums[lo..hi]
|
||||
void sort(int[] nums, int lo, int hi) {
|
||||
int mid = (lo + hi) / 2;
|
||||
// 排序 nums[lo..mid]
|
||||
sort(nums, lo, mid);
|
||||
// 排序 nums[mid+1..hi]
|
||||
sort(nums, mid + 1, hi);
|
||||
|
||||
/****** 后序位置 ******/
|
||||
// 合并 nums[lo..mid] 和 nums[mid+1..hi]
|
||||
merge(nums, lo, mid, hi);
|
||||
/*********************/
|
||||
}
|
||||
```
|
||||
|
||||
先对左右子数组排序,然后合并(类似合并有序链表的逻辑),你看这是不是二叉树的后序遍历框架?另外,这不就是传说中的分治算法嘛,不过如此呀。
|
||||
|
||||
如果你一眼就识破这些排序算法的底细,还需要背这些经典算法吗?不需要。你可以手到擒来,从二叉树遍历框架就能扩展出算法了。
|
||||
|
||||
说了这么多,旨在说明,二叉树的算法思想的运用广泛,甚至可以说,只要涉及递归,都可以抽象成二叉树的问题。
|
||||
|
||||
接下来我们从二叉树的前中后序开始讲起,让你深刻理解这种数据结构的魅力。
|
||||
|
||||
### 深入理解前中后序
|
||||
|
||||
我先甩给你几个问题,请默默思考 30 秒:
|
||||
|
||||
1、你理解的二叉树的前中后序遍历是什么,仅仅是三个顺序不同的 List 吗?
|
||||
|
||||
2、请分析,后序遍历有什么特殊之处?
|
||||
|
||||
3、请分析,为什么多叉树没有中序遍历?
|
||||
|
||||
答不上来,说明你对前中后序的理解仅仅局限于教科书,不过没关系,我用类比的方式解释一下我眼中的前中后序遍历。
|
||||
|
||||
首先,回顾一下 [学习数据结构和算法的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法) 中说到的二叉树遍历框架:
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
// 前序位置
|
||||
traverse(root.left);
|
||||
// 中序位置
|
||||
traverse(root.right);
|
||||
// 后序位置
|
||||
}
|
||||
```
|
||||
|
||||
先不管所谓前中后序,单看 `traverse` 函数,你说它在做什么事情?
|
||||
|
||||
其实它就是一个能够遍历二叉树所有节点的一个函数,和你遍历数组或者链表本质上没有区别:
|
||||
|
||||
```java
|
||||
/* 迭代遍历数组 */
|
||||
void traverse(int[] arr) {
|
||||
for (int i = 0; i < arr.length; i++) {
|
||||
|
||||
}
|
||||
}
|
||||
|
||||
/* 递归遍历数组 */
|
||||
void traverse(int[] arr, int i) {
|
||||
if (i == arr.length) {
|
||||
return;
|
||||
}
|
||||
// 前序位置
|
||||
traverse(arr, i + 1);
|
||||
// 后序位置
|
||||
}
|
||||
|
||||
/* 迭代遍历单链表 */
|
||||
void traverse(ListNode head) {
|
||||
for (ListNode p = head; p != null; p = p.next) {
|
||||
|
||||
}
|
||||
}
|
||||
|
||||
/* 递归遍历单链表 */
|
||||
void traverse(ListNode head) {
|
||||
if (head == null) {
|
||||
return;
|
||||
}
|
||||
// 前序位置
|
||||
traverse(head.next);
|
||||
// 后序位置
|
||||
}
|
||||
```
|
||||
|
||||
单链表和数组的遍历可以是迭代的,也可以是递归的,**二叉树这种结构无非就是二叉链表**,由于没办法简单改写成迭代形式,所以一般说二叉树的遍历框架都是指递归的形式。
|
||||
|
||||
你也注意到了,只要是递归形式的遍历,都可以有前序位置和后序位置,分别在递归之前和递归之后。
|
||||
|
||||
**所谓前序位置,就是刚进入一个节点(元素)的时候,后序位置就是即将离开一个节点(元素)的时候**,那么进一步,你把代码写在不同位置,代码执行的时机也不同:
|
||||
|
||||

|
||||
|
||||
比如说,如果让你**倒序打印**一条单链表上所有节点的值,你怎么搞?
|
||||
|
||||
实现方式当然有很多,但如果你对递归的理解足够透彻,可以利用后序位置来操作:
|
||||
|
||||
```java
|
||||
/* 递归遍历单链表,倒序打印链表元素 */
|
||||
void traverse(ListNode head) {
|
||||
if (head == null) {
|
||||
return;
|
||||
}
|
||||
traverse(head.next);
|
||||
// 后序位置
|
||||
print(head.val);
|
||||
}
|
||||
```
|
||||
|
||||
结合上面那张图,你应该知道为什么这段代码能够倒序打印单链表了吧,本质上是利用递归的堆栈帮你实现了倒序遍历的效果。
|
||||
|
||||
那么说回二叉树也是一样的,只不过多了一个中序位置罢了。
|
||||
|
||||
教科书里只会问你前中后序遍历结果分别是什么,所以对于一个只上过大学数据结构课程的人来说,他大概以为二叉树的前中后序只不过对应三种顺序不同的 `List<Integer>` 列表。
|
||||
|
||||
但是我想说,**前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点**,绝不仅仅是三个顺序不同的 List:
|
||||
|
||||
前序位置的代码在刚刚进入一个二叉树节点的时候执行;
|
||||
|
||||
后序位置的代码在将要离开一个二叉树节点的时候执行;
|
||||
|
||||
中序位置的代码在一个二叉树节点左子树都遍历完,即将开始遍历右子树的时候执行。
|
||||
|
||||
你注意本文的用词,我一直说前中后序「位置」,就是要和大家常说的前中后序「遍历」有所区别:你可以在前序位置写代码往一个 List 里面塞元素,那最后得到的就是前序遍历结果;但并不是说你就不可以写更复杂的代码做更复杂的事。
|
||||
|
||||
画成图,前中后序三个位置在二叉树上是这样:
|
||||
|
||||

|
||||
|
||||
**你可以发现每个节点都有「唯一」属于自己的前中后序位置**,所以我说前中后序遍历是遍历二叉树过程中处理每一个节点的三个特殊时间点。
|
||||
|
||||
这里你也可以理解为什么多叉树没有中序位置,因为二叉树的每个节点只会进行唯一一次左子树切换右子树,而多叉树节点可能有很多子节点,会多次切换子树去遍历,所以多叉树节点没有「唯一」的中序遍历位置。
|
||||
|
||||
说了这么多基础的,就是要帮你对二叉树建立正确的认识,然后你会发现:
|
||||
|
||||
**二叉树的所有问题,就是让你在前中后序位置注入巧妙的代码逻辑,去达到自己的目的,你只需要单独思考每一个节点应该做什么,其他的不用你管,抛给二叉树遍历框架,递归会在所有节点上做相同的操作**。
|
||||
|
||||
你也可以看到,[图论算法基础](https://labuladong.github.io/article/fname.html?fname=图) 把二叉树的遍历框架扩展到了图,并以遍历为基础实现了图论的各种经典算法,不过这是后话,本文就不多说了。
|
||||
|
||||
### 两种解题思路
|
||||
|
||||
前文 [我的算法学习心得](https://labuladong.github.io/article/fname.html?fname=算法心得) 说过:
|
||||
|
||||
**二叉树题目的递归解法可以分两类思路,第一类是遍历一遍二叉树得出答案,第二类是通过分解问题计算出答案,这两类思路分别对应着 [回溯算法核心框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 和 [动态规划核心框架](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)**。
|
||||
|
||||
当时我是用二叉树的最大深度这个问题来举例,重点在于把这两种思路和动态规划和回溯算法进行对比,而本文的重点在于分析这两种思路如何解决二叉树的题目。
|
||||
|
||||
力扣第 104 题「二叉树的最大深度」就是最大深度的题目,所谓最大深度就是根节点到「最远」叶子节点的最长路径上的节点数,比如输入这棵二叉树,算法应该返回 3:
|
||||
|
||||

|
||||
|
||||
你做这题的思路是什么?显然遍历一遍二叉树,用一个外部变量记录每个节点所在的深度,取最大值就可以得到最大深度,**这就是遍历二叉树计算答案的思路**。
|
||||
|
||||
解法代码如下:
|
||||
|
||||
```java
|
||||
// 记录最大深度
|
||||
int res = 0;
|
||||
// 记录遍历到的节点的深度
|
||||
int depth = 0;
|
||||
|
||||
// 主函数
|
||||
int maxDepth(TreeNode root) {
|
||||
traverse(root);
|
||||
return res;
|
||||
}
|
||||
|
||||
// 二叉树遍历框架
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
// 前序位置
|
||||
depth++;
|
||||
if (root.left == null && root.right == null) {
|
||||
// 到达叶子节点,更新最大深度
|
||||
res = Math.max(res, depth);
|
||||
}
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
// 后序位置
|
||||
depth--;
|
||||
}
|
||||
```
|
||||
|
||||
这个解法应该很好理解,但为什么需要在前序位置增加 `depth`,在后序位置减小 `depth`?
|
||||
|
||||
因为前面说了,前序位置是进入一个节点的时候,后序位置是离开一个节点的时候,`depth` 记录当前递归到的节点深度,你把 `traverse` 理解成在二叉树上游走的一个指针,所以当然要这样维护。
|
||||
|
||||
至于对 `res` 的更新,你放到前中后序位置都可以,只要保证在进入节点之后,离开节点之前(即 `depth` 自增之后,自减之前)就行了。
|
||||
|
||||
当然,你也很容易发现一棵二叉树的最大深度可以通过子树的最大深度推导出来,**这就是分解问题计算答案的思路**。
|
||||
|
||||
解法代码如下:
|
||||
|
||||
```java
|
||||
// 定义:输入根节点,返回这棵二叉树的最大深度
|
||||
int maxDepth(TreeNode root) {
|
||||
if (root == null) {
|
||||
return 0;
|
||||
}
|
||||
// 利用定义,计算左右子树的最大深度
|
||||
int leftMax = maxDepth(root.left);
|
||||
int rightMax = maxDepth(root.right);
|
||||
// 整棵树的最大深度等于左右子树的最大深度取最大值,
|
||||
// 然后再加上根节点自己
|
||||
int res = Math.max(leftMax, rightMax) + 1;
|
||||
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
只要明确递归函数的定义,这个解法也不难理解,但为什么主要的代码逻辑集中在后序位置?
|
||||
|
||||
因为这个思路正确的核心在于,你确实可以通过子树的最大深度推导出原树的深度,所以当然要首先利用递归函数的定义算出左右子树的最大深度,然后推出原树的最大深度,主要逻辑自然放在后序位置。
|
||||
|
||||
如果你理解了最大深度这个问题的两种思路,**那么我们再回头看看最基本的二叉树前中后序遍历**,就比如算前序遍历结果吧。
|
||||
|
||||
我们熟悉的解法就是用「遍历」的思路,我想应该没什么好说的:
|
||||
|
||||
```java
|
||||
List<Integer> res = new LinkedList<>();
|
||||
|
||||
// 返回前序遍历结果
|
||||
List<Integer> preorderTraverse(TreeNode root) {
|
||||
traverse(root);
|
||||
return res;
|
||||
}
|
||||
|
||||
// 二叉树遍历函数
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
// 前序位置
|
||||
res.add(root.val);
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
但你是否能够用「分解问题」的思路,来计算前序遍历的结果?
|
||||
|
||||
换句话说,不要用像 `traverse` 这样的辅助函数和任何外部变量,单纯用题目给的 `preorderTraverse` 函数递归解题,你会不会?
|
||||
|
||||
我们知道前序遍历的特点是,根节点的值排在首位,接着是左子树的前序遍历结果,最后是右子树的前序遍历结果:
|
||||
|
||||

|
||||
|
||||
那这不就可以分解问题了么,**一棵二叉树的前序遍历结果 = 根节点 + 左子树的前序遍历结果 + 右子树的前序遍历结果**。
|
||||
|
||||
所以,你可以这样实现前序遍历算法:
|
||||
|
||||
```java
|
||||
// 定义:输入一棵二叉树的根节点,返回这棵树的前序遍历结果
|
||||
List<Integer> preorderTraverse(TreeNode root) {
|
||||
List<Integer> res = new LinkedList<>();
|
||||
if (root == null) {
|
||||
return res;
|
||||
}
|
||||
// 前序遍历的结果,root.val 在第一个
|
||||
res.add(root.val);
|
||||
// 利用函数定义,后面接着左子树的前序遍历结果
|
||||
res.addAll(preorderTraverse(root.left));
|
||||
// 利用函数定义,最后接着右子树的前序遍历结果
|
||||
res.addAll(preorderTraverse(root.right));
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
中序和后序遍历也是类似的,只要把 `add(root.val)` 放到中序和后序对应的位置就行了。
|
||||
|
||||
这个解法短小精干,但为什么不常见呢?
|
||||
|
||||
一个原因是**这个算法的复杂度不好把控**,比较依赖语言特性。
|
||||
|
||||
Java 的话无论 ArrayList 还是 LinkedList,`addAll` 方法的复杂度都是 O(N),所以总体的最坏时间复杂度会达到 O(N^2),除非你自己实现一个复杂度为 O(1) 的 `addAll` 方法,底层用链表的话并不是不可能。
|
||||
|
||||
当然,最主要的原因还是因为教科书上从来没有这么教过……
|
||||
|
||||
上文举了两个简单的例子,但还有不少二叉树的题目是可以同时使用两种思路来思考和求解的,这就要靠你自己多去练习和思考,不要仅仅满足于一种熟悉的解法思路。
|
||||
|
||||
综上,遇到一道二叉树的题目时的通用思考过程是:
|
||||
|
||||
**1、是否可以通过遍历一遍二叉树得到答案**?如果可以,用一个 `traverse` 函数配合外部变量来实现。
|
||||
|
||||
**2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案**?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值。
|
||||
|
||||
**3、无论使用哪一种思维模式,你都要明白二叉树的每一个节点需要做什么,需要在什么时候(前中后序)做**。
|
||||
|
||||
**[我的刷题插件](https://mp.weixin.qq.com/s/uOubir_nLzQtp_fWHL73JA) 更新了所有值得一做的二叉树题目思路,全部归类为上述两种思路**,你如果按照插件提供的思路解法过一遍二叉树的所有题目,不仅可以完全掌握递归思维,而且可以更容易理解高级的算法:
|
||||
|
||||

|
||||
|
||||
### 后序位置的特殊之处
|
||||
|
||||
说后序位置之前,先简单说下中序和前序。
|
||||
|
||||
中序位置主要用在 BST 场景中,你完全可以把 BST 的中序遍历认为是遍历有序数组。
|
||||
|
||||
前序位置本身其实没有什么特别的性质,之所以你发现好像很多题都是在前序位置写代码,实际上是因为我们习惯把那些对前中后序位置不敏感的代码写在前序位置罢了。
|
||||
|
||||
你可以发现,前序位置的代码执行是自顶向下的,而后序位置的代码执行是自底向上的:
|
||||
|
||||

|
||||
|
||||
这不奇怪,因为本文开头就说了前序位置是刚刚进入节点的时刻,后序位置是即将离开节点的时刻。
|
||||
|
||||
**但这里面大有玄妙,意味着前序位置的代码只能从函数参数中获取父节点传递来的数据,而后序位置的代码不仅可以获取参数数据,还可以获取到子树通过函数返回值传递回来的数据**。
|
||||
|
||||
举具体的例子,现在给你一棵二叉树,我问你两个简单的问题:
|
||||
|
||||
1、如果把根节点看做第 1 层,如何打印出每一个节点所在的层数?
|
||||
|
||||
2、如何打印出每个节点的左右子树各有多少节点?
|
||||
|
||||
第一个问题可以这样写代码:
|
||||
|
||||
```java
|
||||
// 二叉树遍历函数
|
||||
void traverse(TreeNode root, int level) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
// 前序位置
|
||||
printf("节点 %s 在第 %d 层", root, level);
|
||||
traverse(root.left, level + 1);
|
||||
traverse(root.right, level + 1);
|
||||
}
|
||||
|
||||
// 这样调用
|
||||
traverse(root, 1);
|
||||
```
|
||||
|
||||
第二个问题可以这样写代码:
|
||||
|
||||
```java
|
||||
// 定义:输入一棵二叉树,返回这棵二叉树的节点总数
|
||||
int count(TreeNode root) {
|
||||
if (root == null) {
|
||||
return 0;
|
||||
}
|
||||
int leftCount = count(root.left);
|
||||
int rightCount = count(root.right);
|
||||
// 后序位置
|
||||
printf("节点 %s 的左子树有 %d 个节点,右子树有 %d 个节点",
|
||||
root, leftCount, rightCount);
|
||||
|
||||
return leftCount + rightCount + 1;
|
||||
}
|
||||
```
|
||||
|
||||
这两个问题的根本区别在于:一个节点在第几层,你从根节点遍历过来的过程就能顺带记录;而以一个节点为根的整棵子树有多少个节点,你需要遍历完子树之后才能数清楚。
|
||||
|
||||
结合这两个简单的问题,你品味一下后序位置的特点,只有后序位置才能通过返回值获取子树的信息。
|
||||
|
||||
**那么换句话说,一旦你发现题目和子树有关,那大概率要给函数设置合理的定义和返回值,在后序位置写代码了**。
|
||||
|
||||
接下来看下后序位置是如何在实际的题目中发挥作用的,简单聊下力扣第 543 题「二叉树的直径」,让你计算一棵二叉树的最长直径长度。
|
||||
|
||||
所谓二叉树的「直径」长度,就是任意两个结点之间的路径长度。最长「直径」并不一定要穿过根结点,比如下面这棵二叉树:
|
||||
|
||||

|
||||
|
||||
它的最长直径是 3,即 `[4,2,1,3]`,`[4,2,1,9]` 或者 `[5,2,1,3]` 这几条「直径」的长度。
|
||||
|
||||
解决这题的关键在于,**每一条二叉树的「直径」长度,就是一个节点的左右子树的最大深度之和**。
|
||||
|
||||
现在让我求整棵树中的最长「直径」,那直截了当的思路就是遍历整棵树中的每个节点,然后通过每个节点的左右子树的最大深度算出每个节点的「直径」,最后把所有「直径」求个最大值即可。
|
||||
|
||||
最大深度的算法我们刚才实现过了,上述思路就可以写出以下代码:
|
||||
|
||||
```java
|
||||
// 记录最大直径的长度
|
||||
int maxDiameter = 0;
|
||||
|
||||
public int diameterOfBinaryTree(TreeNode root) {
|
||||
// 对每个节点计算直径,求最大直径
|
||||
traverse(root);
|
||||
return maxDiameter;
|
||||
}
|
||||
|
||||
// 遍历二叉树
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
// 对每个节点计算直径
|
||||
int leftMax = maxDepth(root.left);
|
||||
int rightMax = maxDepth(root.right);
|
||||
int myDiameter = leftMax + rightMax;
|
||||
// 更新全局最大直径
|
||||
maxDiameter = Math.max(maxDiameter, myDiameter);
|
||||
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
|
||||
// 计算二叉树的最大深度
|
||||
int maxDepth(TreeNode root) {
|
||||
if (root == null) {
|
||||
return 0;
|
||||
}
|
||||
int leftMax = maxDepth(root.left);
|
||||
int rightMax = maxDepth(root.right);
|
||||
return 1 + Math.max(leftMax, rightMax);
|
||||
}
|
||||
```
|
||||
|
||||
这个解法是正确的,但是运行时间很长,原因也很明显,`traverse` 遍历每个节点的时候还会调用递归函数 `maxDepth`,而 `maxDepth` 是要遍历子树的所有节点的,所以最坏时间复杂度是 O(N^2)。
|
||||
|
||||
这就出现了刚才探讨的情况,**前序位置无法获取子树信息,所以只能让每个节点调用 `maxDepth` 函数去算子树的深度**。
|
||||
|
||||
那如何优化?我们应该把计算「直径」的逻辑放在后序位置,准确说应该是放在 `maxDepth` 的后序位置,因为 `maxDepth` 的后序位置是知道左右子树的最大深度的。
|
||||
|
||||
所以,稍微改一下代码逻辑即可得到更好的解法:
|
||||
|
||||
```java
|
||||
// 记录最大直径的长度
|
||||
int maxDiameter = 0;
|
||||
|
||||
public int diameterOfBinaryTree(TreeNode root) {
|
||||
maxDepth(root);
|
||||
return maxDiameter;
|
||||
}
|
||||
|
||||
int maxDepth(TreeNode root) {
|
||||
if (root == null) {
|
||||
return 0;
|
||||
}
|
||||
int leftMax = maxDepth(root.left);
|
||||
int rightMax = maxDepth(root.right);
|
||||
// 后序位置,顺便计算最大直径
|
||||
int myDiameter = leftMax + rightMax;
|
||||
maxDiameter = Math.max(maxDiameter, myDiameter);
|
||||
|
||||
return 1 + Math.max(leftMax, rightMax);
|
||||
}
|
||||
```
|
||||
|
||||
这下时间复杂度只有 `maxDepth` 函数的 O(N) 了。
|
||||
|
||||
讲到这里,照应一下前文:遇到子树问题,首先想到的是给函数设置返回值,然后在后序位置做文章。
|
||||
|
||||
> 思考题:请你思考一下,运用后序遍历的题目使用的是「遍历」的思路还是「分解问题」的思路?我会在文末给出答案。
|
||||
|
||||
反过来,如果你写出了类似一开始的那种递归套递归的解法,大概率也需要反思是不是可以通过后序遍历优化了。
|
||||
|
||||
**[我的刷题插件](https://mp.weixin.qq.com/s/uOubir_nLzQtp_fWHL73JA)对于这类考察后序遍历的题目也有特殊的说明**,并且会给出前置题目,帮助你由浅入深理解这类题目:
|
||||
|
||||

|
||||
|
||||
### 层序遍历
|
||||
|
||||
二叉树题型主要是用来培养递归思维的,而层序遍历属于迭代遍历,也比较简单,这里就过一下代码框架吧:
|
||||
|
||||
```java
|
||||
// 输入一棵二叉树的根节点,层序遍历这棵二叉树
|
||||
void levelTraverse(TreeNode root) {
|
||||
if (root == null) return;
|
||||
Queue<TreeNode> q = new LinkedList<>();
|
||||
q.offer(root);
|
||||
|
||||
// 从上到下遍历二叉树的每一层
|
||||
while (!q.isEmpty()) {
|
||||
int sz = q.size();
|
||||
// 从左到右遍历每一层的每个节点
|
||||
for (int i = 0; i < sz; i++) {
|
||||
TreeNode cur = q.poll();
|
||||
// 将下一层节点放入队列
|
||||
if (cur.left != null) {
|
||||
q.offer(cur.left);
|
||||
}
|
||||
if (cur.right != null) {
|
||||
q.offer(cur.right);
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这里面 while 循环和 for 循环分管从上到下和从左到右的遍历:
|
||||
|
||||

|
||||
|
||||
前文 [BFS 算法框架](https://labuladong.github.io/article/fname.html?fname=BFS框架) 就是从二叉树的层序遍历扩展出来的,常用于求无权图的**最短路径**问题。
|
||||
|
||||
当然这个框架还可以灵活修改,题目不需要记录层数(步数)时可以去掉上述框架中的 for 循环,比如前文 [Dijkstra 算法](https://labuladong.github.io/article/fname.html?fname=dijkstra算法) 中计算加权图的最短路径问题,详细探讨了 BFS 算法的扩展。
|
||||
|
||||
值得一提的是,有些很明显需要用层序遍历技巧的二叉树的题目,也可以用递归遍历的方式去解决,而且技巧性会更强,非常考察你对前中后序的把控。
|
||||
|
||||
对于这类问题,[我的刷题插件](https://mp.weixin.qq.com/s/uOubir_nLzQtp_fWHL73JA)也会同时提供递归遍历和层序遍历的解法代码:
|
||||
|
||||

|
||||
|
||||
好了,本文已经够长了,围绕前中后序位置算是把二叉树题目里的各种套路给讲透了,真正能运用出来多少,就需要你亲自刷题实践和思考了。
|
||||
|
||||
希望大家能探索尽可能多的解法,只要参透二叉树这种基本数据结构的原理,那么就很容易在学习其他高级算法的道路上找到抓手,打通回路,形成闭环(手动狗头)。
|
||||
|
||||
最后,我在不断完善刷题插件对二叉树系列题目的支持,在公众号后台回复关键词「**插件**」即可下载。
|
||||
|
||||
**2022/5/12 更新**:
|
||||
|
||||
关于层序遍历(以及其扩展出的 [BFS 算法框架](https://labuladong.github.io/article/fname.html?fname=BFS框架)),我在最后多说几句。
|
||||
|
||||
如果你对二叉树足够熟悉,可以想到很多方式通过递归函数得到层序遍历结果,比如下面这种写法:
|
||||
|
||||
```java
|
||||
List<List<Integer>> res = new ArrayList<>();
|
||||
|
||||
List<List<Integer>> levelTraverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return res;
|
||||
}
|
||||
// root 视为第 0 层
|
||||
traverse(root, 0);
|
||||
return res;
|
||||
}
|
||||
|
||||
void traverse(TreeNode root, int depth) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
// 前序位置,看看是否已经存储 depth 层的节点了
|
||||
if (res.size() <= depth) {
|
||||
// 第一次进入 depth 层
|
||||
res.add(new LinkedList<>());
|
||||
}
|
||||
// 前序位置,在 depth 层添加 root 节点的值
|
||||
res.get(depth).add(root.val);
|
||||
traverse(root.left, depth + 1);
|
||||
traverse(root.right, depth + 1);
|
||||
}
|
||||
```
|
||||
|
||||
这种思路从结果上说确实可以得到层序遍历结果,但其本质还是二叉树的前序遍历,或者说 DFS 的思路,而不是层序遍历,或者说 BFS 的思路。因为这个解法是依赖前序遍历自顶向下、自左向右的顺序特点得到了正确的结果。
|
||||
|
||||
**抽象点说,这个解法更像是从左到右的「列序遍历」,而不是自顶向下的「层序遍历」**。所以对于计算最小距离的场景,这个解法完全等同于 DFS 算法,没有 BFS 算法的性能的优势。
|
||||
|
||||
还有优秀读者评论了这样一种递归进行层序遍历的思路:
|
||||
|
||||
```java
|
||||
List<List<Integer>> res = new LinkedList<>();
|
||||
|
||||
List<List<Integer>> levelTraverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return res;
|
||||
}
|
||||
List<TreeNode> nodes = new LinkedList<>();
|
||||
nodes.add(root);
|
||||
traverse(nodes);
|
||||
return res;
|
||||
}
|
||||
|
||||
void traverse(List<TreeNode> curLevelNodes) {
|
||||
// base case
|
||||
if (curLevelNodes.isEmpty()) {
|
||||
return;
|
||||
}
|
||||
// 前序位置,计算当前层的值和下一层的节点列表
|
||||
List<Integer> nodeValues = new LinkedList<>();
|
||||
List<TreeNode> nextLevelNodes = new LinkedList<>();
|
||||
for (TreeNode node : curLevelNodes) {
|
||||
nodeValues.add(node.val);
|
||||
if (node.left != null) {
|
||||
nextLevelNodes.add(node.left);
|
||||
}
|
||||
if (node.right != null) {
|
||||
nextLevelNodes.add(node.right);
|
||||
}
|
||||
}
|
||||
// 前序位置添加结果,可以得到自顶向下的层序遍历
|
||||
res.add(nodeValues);
|
||||
traverse(nextLevelNodes);
|
||||
// 后序位置添加结果,可以得到自底向上的层序遍历结果
|
||||
// res.add(nodeValues);
|
||||
}
|
||||
```
|
||||
|
||||
这个 `traverse` 函数很像递归遍历单链表的函数,其实就是把二叉树的每一层抽象理解成单链表的一个节点进行遍历。
|
||||
|
||||
相较上一个递归解法,这个递归解法是自顶向下的「层序遍历」,更接近 BFS 的奥义,可以作为 BFS 算法的递归实现扩展一下思维。
|
||||
|
||||
> 思考题答案:文中后序遍历的例题使用了「分解问题」的思路。因为当前节点接收并利用了子树返回的信息,这就意味着你把原问题分解成了当前节点 + 左右子树的子问题。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [Git原理之最近公共祖先](https://labuladong.github.io/article/fname.html?fname=公共祖先)
|
||||
- [东哥带你刷二叉树(后序篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列3)
|
||||
- [东哥带你刷二叉树(序列化篇)](https://labuladong.github.io/article/fname.html?fname=二叉树的序列化)
|
||||
- [东哥带你刷二叉树(思路篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列1)
|
||||
- [东哥带你刷二叉树(构造篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列2)
|
||||
- [两种思路解决单词拼接问题](https://labuladong.github.io/article/fname.html?fname=单词拼接)
|
||||
- [前缀树算法模板秒杀五道算法题](https://labuladong.github.io/article/fname.html?fname=trie)
|
||||
- [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.github.io/article/fname.html?fname=子集排列组合)
|
||||
- [回溯算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版)
|
||||
- [归并排序详解及应用](https://labuladong.github.io/article/fname.html?fname=归并排序)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [算法学习和心流体验](https://labuladong.github.io/article/fname.html?fname=心流)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1008. Construct Binary Search Tree from Preorder Traversal](https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/?show=1) | [1008. 前序遍历构造二叉搜索树](https://leetcode.cn/problems/construct-binary-search-tree-from-preorder-traversal/?show=1) |
|
||||
| [1022. Sum of Root To Leaf Binary Numbers](https://leetcode.com/problems/sum-of-root-to-leaf-binary-numbers/?show=1) | [1022. 从根到叶的二进制数之和](https://leetcode.cn/problems/sum-of-root-to-leaf-binary-numbers/?show=1) |
|
||||
| [1026. Maximum Difference Between Node and Ancestor](https://leetcode.com/problems/maximum-difference-between-node-and-ancestor/?show=1) | [1026. 节点与其祖先之间的最大差值](https://leetcode.cn/problems/maximum-difference-between-node-and-ancestor/?show=1) |
|
||||
| [1080. Insufficient Nodes in Root to Leaf Paths](https://leetcode.com/problems/insufficient-nodes-in-root-to-leaf-paths/?show=1) | [1080. 根到叶路径上的不足节点](https://leetcode.cn/problems/insufficient-nodes-in-root-to-leaf-paths/?show=1) |
|
||||
| [110. Balanced Binary Tree](https://leetcode.com/problems/balanced-binary-tree/?show=1) | [110. 平衡二叉树](https://leetcode.cn/problems/balanced-binary-tree/?show=1) |
|
||||
| [1110. Delete Nodes And Return Forest](https://leetcode.com/problems/delete-nodes-and-return-forest/?show=1) | [1110. 删点成林](https://leetcode.cn/problems/delete-nodes-and-return-forest/?show=1) |
|
||||
| [1120. Maximum Average Subtree](https://leetcode.com/problems/maximum-average-subtree/?show=1)🔒 | [1120. 子树的最大平均值](https://leetcode.cn/problems/maximum-average-subtree/?show=1)🔒 |
|
||||
| [113. Path Sum II](https://leetcode.com/problems/path-sum-ii/?show=1) | [113. 路径总和 II](https://leetcode.cn/problems/path-sum-ii/?show=1) |
|
||||
| [114. Flatten Binary Tree to Linked List](https://leetcode.com/problems/flatten-binary-tree-to-linked-list/?show=1) | [114. 二叉树展开为链表](https://leetcode.cn/problems/flatten-binary-tree-to-linked-list/?show=1) |
|
||||
| [116. Populating Next Right Pointers in Each Node](https://leetcode.com/problems/populating-next-right-pointers-in-each-node/?show=1) | [116. 填充每个节点的下一个右侧节点指针](https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/?show=1) |
|
||||
| [124. Binary Tree Maximum Path Sum](https://leetcode.com/problems/binary-tree-maximum-path-sum/?show=1) | [124. 二叉树中的最大路径和](https://leetcode.cn/problems/binary-tree-maximum-path-sum/?show=1) |
|
||||
| [1261. Find Elements in a Contaminated Binary Tree](https://leetcode.com/problems/find-elements-in-a-contaminated-binary-tree/?show=1) | [1261. 在受污染的二叉树中查找元素](https://leetcode.cn/problems/find-elements-in-a-contaminated-binary-tree/?show=1) |
|
||||
| [129. Sum Root to Leaf Numbers](https://leetcode.com/problems/sum-root-to-leaf-numbers/?show=1) | [129. 求根节点到叶节点数字之和](https://leetcode.cn/problems/sum-root-to-leaf-numbers/?show=1) |
|
||||
| [1315. Sum of Nodes with Even-Valued Grandparent](https://leetcode.com/problems/sum-of-nodes-with-even-valued-grandparent/?show=1) | [1315. 祖父节点值为偶数的节点和](https://leetcode.cn/problems/sum-of-nodes-with-even-valued-grandparent/?show=1) |
|
||||
| [1325. Delete Leaves With a Given Value](https://leetcode.com/problems/delete-leaves-with-a-given-value/?show=1) | [1325. 删除给定值的叶子节点](https://leetcode.cn/problems/delete-leaves-with-a-given-value/?show=1) |
|
||||
| [1339. Maximum Product of Splitted Binary Tree](https://leetcode.com/problems/maximum-product-of-splitted-binary-tree/?show=1) | [1339. 分裂二叉树的最大乘积](https://leetcode.cn/problems/maximum-product-of-splitted-binary-tree/?show=1) |
|
||||
| [1367. Linked List in Binary Tree](https://leetcode.com/problems/linked-list-in-binary-tree/?show=1) | [1367. 二叉树中的列表](https://leetcode.cn/problems/linked-list-in-binary-tree/?show=1) |
|
||||
| [1372. Longest ZigZag Path in a Binary Tree](https://leetcode.com/problems/longest-zigzag-path-in-a-binary-tree/?show=1) | [1372. 二叉树中的最长交错路径](https://leetcode.cn/problems/longest-zigzag-path-in-a-binary-tree/?show=1) |
|
||||
| [1373. Maximum Sum BST in Binary Tree](https://leetcode.com/problems/maximum-sum-bst-in-binary-tree/?show=1) | [1373. 二叉搜索子树的最大键值和](https://leetcode.cn/problems/maximum-sum-bst-in-binary-tree/?show=1) |
|
||||
| [1379. Find a Corresponding Node of a Binary Tree in a Clone of That Tree](https://leetcode.com/problems/find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree/?show=1) | [1379. 找出克隆二叉树中的相同节点](https://leetcode.cn/problems/find-a-corresponding-node-of-a-binary-tree-in-a-clone-of-that-tree/?show=1) |
|
||||
| [1430. Check If a String Is a Valid Sequence from Root to Leaves Path in a Binary Tree](https://leetcode.com/problems/check-if-a-string-is-a-valid-sequence-from-root-to-leaves-path-in-a-binary-tree/?show=1)🔒 | [1430. 判断给定的序列是否是二叉树从根到叶的路径](https://leetcode.cn/problems/check-if-a-string-is-a-valid-sequence-from-root-to-leaves-path-in-a-binary-tree/?show=1)🔒 |
|
||||
| [1448. Count Good Nodes in Binary Tree](https://leetcode.com/problems/count-good-nodes-in-binary-tree/?show=1) | [1448. 统计二叉树中好节点的数目](https://leetcode.cn/problems/count-good-nodes-in-binary-tree/?show=1) |
|
||||
| [145. Binary Tree Postorder Traversal](https://leetcode.com/problems/binary-tree-postorder-traversal/?show=1) | [145. 二叉树的后序遍历](https://leetcode.cn/problems/binary-tree-postorder-traversal/?show=1) |
|
||||
| [1457. Pseudo-Palindromic Paths in a Binary Tree](https://leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/?show=1) | [1457. 二叉树中的伪回文路径](https://leetcode.cn/problems/pseudo-palindromic-paths-in-a-binary-tree/?show=1) |
|
||||
| [1469. Find All The Lonely Nodes](https://leetcode.com/problems/find-all-the-lonely-nodes/?show=1)🔒 | [1469. 寻找所有的独生节点](https://leetcode.cn/problems/find-all-the-lonely-nodes/?show=1)🔒 |
|
||||
| [1485. Group Sold Products By The Date](https://leetcode.com/problems/group-sold-products-by-the-date/?show=1)🔒 | [1485. 按日期分组销售产品](https://leetcode.cn/problems/group-sold-products-by-the-date/?show=1)🔒 |
|
||||
| [1490. Clone N-ary Tree](https://leetcode.com/problems/clone-n-ary-tree/?show=1)🔒 | [1490. 克隆 N 叉树](https://leetcode.cn/problems/clone-n-ary-tree/?show=1)🔒 |
|
||||
| [1602. Find Nearest Right Node in Binary Tree](https://leetcode.com/problems/find-nearest-right-node-in-binary-tree/?show=1)🔒 | [1602. 找到二叉树中最近的右侧节点](https://leetcode.cn/problems/find-nearest-right-node-in-binary-tree/?show=1)🔒 |
|
||||
| [1612. Check If Two Expression Trees are Equivalent](https://leetcode.com/problems/check-if-two-expression-trees-are-equivalent/?show=1)🔒 | [1612. 检查两棵二叉表达式树是否等价](https://leetcode.cn/problems/check-if-two-expression-trees-are-equivalent/?show=1)🔒 |
|
||||
| [2049. Count Nodes With the Highest Score](https://leetcode.com/problems/count-nodes-with-the-highest-score/?show=1) | [2049. 统计最高分的节点数目](https://leetcode.cn/problems/count-nodes-with-the-highest-score/?show=1) |
|
||||
| [226. Invert Binary Tree](https://leetcode.com/problems/invert-binary-tree/?show=1) | [226. 翻转二叉树](https://leetcode.cn/problems/invert-binary-tree/?show=1) |
|
||||
| [250. Count Univalue Subtrees](https://leetcode.com/problems/count-univalue-subtrees/?show=1)🔒 | [250. 统计同值子树](https://leetcode.cn/problems/count-univalue-subtrees/?show=1)🔒 |
|
||||
| [257. Binary Tree Paths](https://leetcode.com/problems/binary-tree-paths/?show=1) | [257. 二叉树的所有路径](https://leetcode.cn/problems/binary-tree-paths/?show=1) |
|
||||
| [270. Closest Binary Search Tree Value](https://leetcode.com/problems/closest-binary-search-tree-value/?show=1)🔒 | [270. 最接近的二叉搜索树值](https://leetcode.cn/problems/closest-binary-search-tree-value/?show=1)🔒 |
|
||||
| [298. Binary Tree Longest Consecutive Sequence](https://leetcode.com/problems/binary-tree-longest-consecutive-sequence/?show=1)🔒 | [298. 二叉树最长连续序列](https://leetcode.cn/problems/binary-tree-longest-consecutive-sequence/?show=1)🔒 |
|
||||
| [333. Largest BST Subtree](https://leetcode.com/problems/largest-bst-subtree/?show=1)🔒 | [333. 最大 BST 子树](https://leetcode.cn/problems/largest-bst-subtree/?show=1)🔒 |
|
||||
| [366. Find Leaves of Binary Tree](https://leetcode.com/problems/find-leaves-of-binary-tree/?show=1)🔒 | [366. 寻找二叉树的叶子节点](https://leetcode.cn/problems/find-leaves-of-binary-tree/?show=1)🔒 |
|
||||
| [404. Sum of Left Leaves](https://leetcode.com/problems/sum-of-left-leaves/?show=1) | [404. 左叶子之和](https://leetcode.cn/problems/sum-of-left-leaves/?show=1) |
|
||||
| [426. Convert Binary Search Tree to Sorted Doubly Linked List](https://leetcode.com/problems/convert-binary-search-tree-to-sorted-doubly-linked-list/?show=1)🔒 | [426. 将二叉搜索树转化为排序的双向链表](https://leetcode.cn/problems/convert-binary-search-tree-to-sorted-doubly-linked-list/?show=1)🔒 |
|
||||
| [501. Find Mode in Binary Search Tree](https://leetcode.com/problems/find-mode-in-binary-search-tree/?show=1) | [501. 二叉搜索树中的众数](https://leetcode.cn/problems/find-mode-in-binary-search-tree/?show=1) |
|
||||
| [508. Most Frequent Subtree Sum](https://leetcode.com/problems/most-frequent-subtree-sum/?show=1) | [508. 出现次数最多的子树元素和](https://leetcode.cn/problems/most-frequent-subtree-sum/?show=1) |
|
||||
| [513. Find Bottom Left Tree Value](https://leetcode.com/problems/find-bottom-left-tree-value/?show=1) | [513. 找树左下角的值](https://leetcode.cn/problems/find-bottom-left-tree-value/?show=1) |
|
||||
| [515. Find Largest Value in Each Tree Row](https://leetcode.com/problems/find-largest-value-in-each-tree-row/?show=1) | [515. 在每个树行中找最大值](https://leetcode.cn/problems/find-largest-value-in-each-tree-row/?show=1) |
|
||||
| [530. Minimum Absolute Difference in BST](https://leetcode.com/problems/minimum-absolute-difference-in-bst/?show=1) | [530. 二叉搜索树的最小绝对差](https://leetcode.cn/problems/minimum-absolute-difference-in-bst/?show=1) |
|
||||
| [538. Convert BST to Greater Tree](https://leetcode.com/problems/convert-bst-to-greater-tree/?show=1) | [538. 把二叉搜索树转换为累加树](https://leetcode.cn/problems/convert-bst-to-greater-tree/?show=1) |
|
||||
| [549. Binary Tree Longest Consecutive Sequence II](https://leetcode.com/problems/binary-tree-longest-consecutive-sequence-ii/?show=1)🔒 | [549. 二叉树中最长的连续序列](https://leetcode.cn/problems/binary-tree-longest-consecutive-sequence-ii/?show=1)🔒 |
|
||||
| [559. Maximum Depth of N-ary Tree](https://leetcode.com/problems/maximum-depth-of-n-ary-tree/?show=1) | [559. N 叉树的最大深度](https://leetcode.cn/problems/maximum-depth-of-n-ary-tree/?show=1) |
|
||||
| [563. Binary Tree Tilt](https://leetcode.com/problems/binary-tree-tilt/?show=1) | [563. 二叉树的坡度](https://leetcode.cn/problems/binary-tree-tilt/?show=1) |
|
||||
| [572. Subtree of Another Tree](https://leetcode.com/problems/subtree-of-another-tree/?show=1) | [572. 另一棵树的子树](https://leetcode.cn/problems/subtree-of-another-tree/?show=1) |
|
||||
| [606. Construct String from Binary Tree](https://leetcode.com/problems/construct-string-from-binary-tree/?show=1) | [606. 根据二叉树创建字符串](https://leetcode.cn/problems/construct-string-from-binary-tree/?show=1) |
|
||||
| [617. Merge Two Binary Trees](https://leetcode.com/problems/merge-two-binary-trees/?show=1) | [617. 合并二叉树](https://leetcode.cn/problems/merge-two-binary-trees/?show=1) |
|
||||
| [623. Add One Row to Tree](https://leetcode.com/problems/add-one-row-to-tree/?show=1) | [623. 在二叉树中增加一行](https://leetcode.cn/problems/add-one-row-to-tree/?show=1) |
|
||||
| [654. Maximum Binary Tree](https://leetcode.com/problems/maximum-binary-tree/?show=1) | [654. 最大二叉树](https://leetcode.cn/problems/maximum-binary-tree/?show=1) |
|
||||
| [663. Equal Tree Partition](https://leetcode.com/problems/equal-tree-partition/?show=1)🔒 | [663. 均匀树划分](https://leetcode.cn/problems/equal-tree-partition/?show=1)🔒 |
|
||||
| [666. Path Sum IV](https://leetcode.com/problems/path-sum-iv/?show=1)🔒 | [666. 路径总和 IV](https://leetcode.cn/problems/path-sum-iv/?show=1)🔒 |
|
||||
| [669. Trim a Binary Search Tree](https://leetcode.com/problems/trim-a-binary-search-tree/?show=1) | [669. 修剪二叉搜索树](https://leetcode.cn/problems/trim-a-binary-search-tree/?show=1) |
|
||||
| [671. Second Minimum Node In a Binary Tree](https://leetcode.com/problems/second-minimum-node-in-a-binary-tree/?show=1) | [671. 二叉树中第二小的节点](https://leetcode.cn/problems/second-minimum-node-in-a-binary-tree/?show=1) |
|
||||
| [687. Longest Univalue Path](https://leetcode.com/problems/longest-univalue-path/?show=1) | [687. 最长同值路径](https://leetcode.cn/problems/longest-univalue-path/?show=1) |
|
||||
| [776. Split BST](https://leetcode.com/problems/split-bst/?show=1)🔒 | [776. 拆分二叉搜索树](https://leetcode.cn/problems/split-bst/?show=1)🔒 |
|
||||
| [865. Smallest Subtree with all the Deepest Nodes](https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/?show=1) | [865. 具有所有最深节点的最小子树](https://leetcode.cn/problems/smallest-subtree-with-all-the-deepest-nodes/?show=1) |
|
||||
| [894. All Possible Full Binary Trees](https://leetcode.com/problems/all-possible-full-binary-trees/?show=1) | [894. 所有可能的满二叉树](https://leetcode.cn/problems/all-possible-full-binary-trees/?show=1) |
|
||||
| [897. Increasing Order Search Tree](https://leetcode.com/problems/increasing-order-search-tree/?show=1) | [897. 递增顺序搜索树](https://leetcode.cn/problems/increasing-order-search-tree/?show=1) |
|
||||
| [938. Range Sum of BST](https://leetcode.com/problems/range-sum-of-bst/?show=1) | [938. 二叉搜索树的范围和](https://leetcode.cn/problems/range-sum-of-bst/?show=1) |
|
||||
| [951. Flip Equivalent Binary Trees](https://leetcode.com/problems/flip-equivalent-binary-trees/?show=1) | [951. 翻转等价二叉树](https://leetcode.cn/problems/flip-equivalent-binary-trees/?show=1) |
|
||||
| [965. Univalued Binary Tree](https://leetcode.com/problems/univalued-binary-tree/?show=1) | [965. 单值二叉树](https://leetcode.cn/problems/univalued-binary-tree/?show=1) |
|
||||
| [968. Binary Tree Cameras](https://leetcode.com/problems/binary-tree-cameras/?show=1) | [968. 监控二叉树](https://leetcode.cn/problems/binary-tree-cameras/?show=1) |
|
||||
| [971. Flip Binary Tree To Match Preorder Traversal](https://leetcode.com/problems/flip-binary-tree-to-match-preorder-traversal/?show=1) | [971. 翻转二叉树以匹配先序遍历](https://leetcode.cn/problems/flip-binary-tree-to-match-preorder-traversal/?show=1) |
|
||||
| [979. Distribute Coins in Binary Tree](https://leetcode.com/problems/distribute-coins-in-binary-tree/?show=1) | [979. 在二叉树中分配硬币](https://leetcode.cn/problems/distribute-coins-in-binary-tree/?show=1) |
|
||||
| [987. Vertical Order Traversal of a Binary Tree](https://leetcode.com/problems/vertical-order-traversal-of-a-binary-tree/?show=1) | [987. 二叉树的垂序遍历](https://leetcode.cn/problems/vertical-order-traversal-of-a-binary-tree/?show=1) |
|
||||
| [988. Smallest String Starting From Leaf](https://leetcode.com/problems/smallest-string-starting-from-leaf/?show=1) | [988. 从叶结点开始的最小字符串](https://leetcode.cn/problems/smallest-string-starting-from-leaf/?show=1) |
|
||||
| [993. Cousins in Binary Tree](https://leetcode.com/problems/cousins-in-binary-tree/?show=1) | [993. 二叉树的堂兄弟节点](https://leetcode.cn/problems/cousins-in-binary-tree/?show=1) |
|
||||
| [998. Maximum Binary Tree II](https://leetcode.com/problems/maximum-binary-tree-ii/?show=1) | [998. 最大二叉树 II](https://leetcode.cn/problems/maximum-binary-tree-ii/?show=1) |
|
||||
| - | [剑指 Offer 06. 从尾到头打印链表](https://leetcode.cn/problems/cong-wei-dao-tou-da-yin-lian-biao-lcof/?show=1) |
|
||||
| - | [剑指 Offer 26. 树的子结构](https://leetcode.cn/problems/shu-de-zi-jie-gou-lcof/?show=1) |
|
||||
| - | [剑指 Offer 27. 二叉树的镜像](https://leetcode.cn/problems/er-cha-shu-de-jing-xiang-lcof/?show=1) |
|
||||
| - | [剑指 Offer 34. 二叉树中和为某一值的路径](https://leetcode.cn/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof/?show=1) |
|
||||
| - | [剑指 Offer 36. 二叉搜索树与双向链表](https://leetcode.cn/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/?show=1) |
|
||||
| - | [剑指 Offer 55 - I. 二叉树的深度](https://leetcode.cn/problems/er-cha-shu-de-shen-du-lcof/?show=1) |
|
||||
| - | [剑指 Offer 55 - II. 平衡二叉树](https://leetcode.cn/problems/ping-heng-er-cha-shu-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 045. 二叉树最底层最左边的值](https://leetcode.cn/problems/LwUNpT/?show=1) |
|
||||
| - | [剑指 Offer II 049. 从根节点到叶节点的路径数字之和](https://leetcode.cn/problems/3Etpl5/?show=1) |
|
||||
| - | [剑指 Offer II 051. 节点之和最大的路径](https://leetcode.cn/problems/jC7MId/?show=1) |
|
||||
| - | [剑指 Offer II 052. 展平二叉搜索树](https://leetcode.cn/problems/NYBBNL/?show=1) |
|
||||
| - | [剑指 Offer II 054. 所有大于等于节点的值之和](https://leetcode.cn/problems/w6cpku/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
397
数据结构系列/二叉树系列1.md
397
数据结构系列/二叉树系列1.md
|
|
@ -1,118 +1,48 @@
|
|||
# 东哥手把手带你刷二叉树(第一期)
|
||||
|
||||
# 东哥手把手带你刷二叉树(思维篇)
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[226.翻转二叉树(简单)](https://leetcode-cn.com/problems/invert-binary-tree)
|
||||
|
||||
[114.二叉树展开为链表(中等)](https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list)
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
[116.填充每个节点的下一个右侧节点指针(中等)](https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node)
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [114. Flatten Binary Tree to Linked List](https://leetcode.com/problems/flatten-binary-tree-to-linked-list/) | [114. 二叉树展开为链表](https://leetcode.cn/problems/flatten-binary-tree-to-linked-list/) | 🟠
|
||||
| [116. Populating Next Right Pointers in Each Node](https://leetcode.com/problems/populating-next-right-pointers-in-each-node/) | [116. 填充每个节点的下一个右侧节点指针](https://leetcode.cn/problems/populating-next-right-pointers-in-each-node/) | 🟠
|
||||
| [226. Invert Binary Tree](https://leetcode.com/problems/invert-binary-tree/) | [226. 翻转二叉树](https://leetcode.cn/problems/invert-binary-tree/) | 🟢
|
||||
| - | [剑指 Offer 27. 二叉树的镜像](https://leetcode.cn/problems/er-cha-shu-de-jing-xiang-lcof/) | 🟢
|
||||
|
||||
**-----------**
|
||||
|
||||
我们公众号的成名之作 [学习数据结构和算法的框架思维](https://labuladong.gitee.io/algo/) 中多次强调,先刷二叉树的题目,先刷二叉树的题目,先刷二叉树的题目,因为很多经典算法,以及我们前文讲过的所有回溯、动归、分治算法,其实都是树的问题,而树的问题就永远逃不开树的递归遍历框架这几行破代码:
|
||||
> 本文有视频版:[二叉树/递归的框架思维(纲领篇)](https://www.bilibili.com/video/BV1nG411x77H/)
|
||||
|
||||
```java
|
||||
/* 二叉树遍历框架 */
|
||||
void traverse(TreeNode root) {
|
||||
// 前序遍历
|
||||
traverse(root.left)
|
||||
// 中序遍历
|
||||
traverse(root.right)
|
||||
// 后序遍历
|
||||
}
|
||||
```
|
||||
PS:[刷题插件](https://mp.weixin.qq.com/s/OE1zPVPj0V2o82N4HtLQbw) 集成了手把手刷二叉树功能,按照公式和套路讲解了 150 道二叉树题目,可手把手带你刷完二叉树分类的题目,迅速掌握递归思维。
|
||||
|
||||
上篇公众号文章让读者留言说说对什么问题还有疑惑,我接下来可以重点写一写相关的文章。结果还有很多读者说觉得「递归」非常难以理解,说实话,递归解法应该是最简单,最容易理解的才对,行云流水地写递归代码是学好算法的基本功,而二叉树相关的题目就是最练习递归基本功,最练习框架思维的。
|
||||
本文承接 [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结),先复述一下前文总结的二叉树解题总纲:
|
||||
|
||||
我先花一些篇幅说明二叉树算法的重要性。
|
||||
> 二叉树解题的思维模式分两类:
|
||||
>
|
||||
> **1、是否可以通过遍历一遍二叉树得到答案**?如果可以,用一个 `traverse` 函数配合外部变量来实现,这叫「遍历」的思维模式。
|
||||
>
|
||||
> **2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案**?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
|
||||
>
|
||||
> 无论使用哪种思维模式,你都需要思考:
|
||||
>
|
||||
> **如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做**?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
|
||||
|
||||
### 一、二叉树的重要性
|
||||
本文就以几道比较简单的题目为例,带你实践运用这几条总纲,理解「遍历」的思维和「分解问题」的思维有何区别和联系。
|
||||
|
||||
举个例子,比如说我们的经典算法「快速排序」和「归并排序」,对于这两个算法,你有什么理解?**如果你告诉我,快速排序就是个二叉树的前序遍历,归并排序就是个二叉树的后序遍历,那么我就知道你是个算法高手了**。
|
||||
|
||||
为什么快速排序和归并排序能和二叉树扯上关系?我们来简单分析一下他们的算法思想和代码框架:
|
||||
|
||||
快速排序的逻辑是,若要对 `nums[lo..hi]` 进行排序,我们先找一个分界点 `p`,通过交换元素使得 `nums[lo..p-1]` 都小于等于 `nums[p]`,且 `nums[p+1..hi]` 都大于 `nums[p]`,然后递归地去 `nums[lo..p-1]` 和 `nums[p+1..hi]` 中寻找新的分界点,最后整个数组就被排序了。
|
||||
|
||||
快速排序的代码框架如下:
|
||||
|
||||
```java
|
||||
void sort(int[] nums, int lo, int hi) {
|
||||
/****** 前序遍历位置 ******/
|
||||
// 通过交换元素构建分界点 p
|
||||
int p = partition(nums, lo, hi);
|
||||
/************************/
|
||||
|
||||
sort(nums, lo, p - 1);
|
||||
sort(nums, p + 1, hi);
|
||||
}
|
||||
```
|
||||
|
||||
先构造分界点,然后去左右子数组构造分界点,你看这不就是一个二叉树的前序遍历吗?
|
||||
|
||||
再说说归并排序的逻辑,若要对 `nums[lo..hi]` 进行排序,我们先对 `nums[lo..mid]` 排序,再对 `nums[mid+1..hi]` 排序,最后把这两个有序的子数组合并,整个数组就排好序了。
|
||||
|
||||
归并排序的代码框架如下:
|
||||
|
||||
```java
|
||||
void sort(int[] nums, int lo, int hi) {
|
||||
int mid = (lo + hi) / 2;
|
||||
sort(nums, lo, mid);
|
||||
sort(nums, mid + 1, hi);
|
||||
|
||||
/****** 后序遍历位置 ******/
|
||||
// 合并两个排好序的子数组
|
||||
merge(nums, lo, mid, hi);
|
||||
/************************/
|
||||
}
|
||||
```
|
||||
|
||||
先对左右子数组排序,然后合并(类似合并有序链表的逻辑),你看这是不是二叉树的后序遍历框架?另外,这不就是传说中的分治算法嘛,不过如此呀。
|
||||
|
||||
如果你一眼就识破这些排序算法的底细,还需要背这些算法代码吗?这不是手到擒来,从框架慢慢扩展就能写出算法了。
|
||||
|
||||
说了这么多,旨在说明,二叉树的算法思想的运用广泛,甚至可以说,只要涉及递归,都可以抽象成二叉树的问题,**所以本文和后续的 [手把手带你刷二叉树(第二期)](https://labuladong.gitee.io/algo/) 以及 [手把手刷二叉树(第三期)](https://labuladong.gitee.io/algo/),我们直接上几道比较有意思,且能体现出递归算法精妙的二叉树题目,东哥手把手教你怎么用算法框架搞定它们**。
|
||||
|
||||
### 二、写递归算法的秘诀
|
||||
|
||||
我们前文 [二叉树的最近公共祖先](https://labuladong.gitee.io/algo/) 写过,**写递归算法的关键是要明确函数的「定义」是什么,然后相信这个定义,利用这个定义推导最终结果,绝不要跳入递归的细节**。
|
||||
|
||||
怎么理解呢,我们用一个具体的例子来说,比如说让你计算一棵二叉树共有几个节点:
|
||||
|
||||
```java
|
||||
// 定义:count(root) 返回以 root 为根的树有多少节点
|
||||
int count(TreeNode root) {
|
||||
// base case
|
||||
if (root == null) return 0;
|
||||
// 自己加上子树的节点数就是整棵树的节点数
|
||||
return 1 + count(root.left) + count(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
这个问题非常简单,大家应该都会写这段代码,`root` 本身就是一个节点,加上左右子树的节点数就是以 `root` 为根的树的节点总数。
|
||||
|
||||
左右子树的节点数怎么算?其实就是计算根为 `root.left` 和 `root.right` 两棵树的节点数呗,按照定义,递归调用 `count` 函数即可算出来。
|
||||
|
||||
**写树相关的算法,简单说就是,先搞清楚当前 `root` 节点该做什么,然后根据函数定义递归调用子节点**,递归调用会让孩子节点做相同的事情。
|
||||
|
||||
我们接下来看几道算法题目实操一下。
|
||||
|
||||
### 三、算法实践
|
||||
|
||||
**第一题、翻转二叉树**
|
||||
### 一、翻转二叉树
|
||||
|
||||
我们先从简单的题开始,看看力扣第 226 题「翻转二叉树」,输入一个二叉树根节点 `root`,让你把整棵树镜像翻转,比如输入的二叉树如下:
|
||||
|
||||
|
|
@ -134,45 +64,95 @@ int count(TreeNode root) {
|
|||
9 6 3 1
|
||||
```
|
||||
|
||||
通过观察,**我们发现只要把二叉树上的每一个节点的左右子节点进行交换,最后的结果就是完全翻转之后的二叉树**。
|
||||
不难发现,只要把二叉树上的每一个节点的左右子节点进行交换,最后的结果就是完全翻转之后的二叉树。
|
||||
|
||||
可以直接写出解法代码:
|
||||
那么现在开始在心中默念二叉树解题总纲:
|
||||
|
||||
**1、这题能不能用「遍历」的思维模式解决**?
|
||||
|
||||
可以,我写一个 `traverse` 函数遍历每个节点,让每个节点的左右子节点颠倒过来就行了。
|
||||
|
||||
单独抽出一个节点,需要让它做什么?让它把自己的左右子节点交换一下。
|
||||
|
||||
需要在什么时候做?好像前中后序位置都可以。
|
||||
|
||||
综上,可以写出如下解法代码:
|
||||
|
||||
```java
|
||||
// 将整棵树的节点翻转
|
||||
// 主函数
|
||||
TreeNode invertTree(TreeNode root) {
|
||||
// base case
|
||||
// 遍历二叉树,交换每个节点的子节点
|
||||
traverse(root);
|
||||
return root;
|
||||
}
|
||||
|
||||
// 二叉树遍历函数
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return null;
|
||||
return;
|
||||
}
|
||||
|
||||
/**** 前序遍历位置 ****/
|
||||
// root 节点需要交换它的左右子节点
|
||||
/**** 前序位置 ****/
|
||||
// 每一个节点需要做的事就是交换它的左右子节点
|
||||
TreeNode tmp = root.left;
|
||||
root.left = root.right;
|
||||
root.right = tmp;
|
||||
|
||||
// 让左右子节点继续翻转它们的子节点
|
||||
invertTree(root.left);
|
||||
invertTree(root.right);
|
||||
|
||||
// 遍历框架,去遍历左右子树的节点
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
你把前序位置的代码移到后序位置也可以,但是直接移到中序位置是不行的,需要稍作修改,这应该很容易看出来吧,我就不说了。
|
||||
|
||||
按理说,这道题已经解决了,不过为了对比,我们再继续思考下去。
|
||||
|
||||
**2、这题能不能用「分解问题」的思维模式解决**?
|
||||
|
||||
我们尝试给 `invertTree` 函数赋予一个定义:
|
||||
|
||||
```java
|
||||
// 定义:将以 root 为根的这棵二叉树翻转,返回翻转后的二叉树的根节点
|
||||
TreeNode invertTree(TreeNode root);
|
||||
```
|
||||
|
||||
然后思考,对于某一个二叉树节点 `x` 执行 `invertTree(x)`,你能利用这个递归函数的定义做点啥?
|
||||
|
||||
我可以用 `invertTree(x.left)` 先把 `x` 的左子树翻转,再用 `invertTree(x.right)` 把 `x` 的右子树翻转,最后把 `x` 的左右子树交换,这恰好完成了以 `x` 为根的整棵二叉树的翻转,即完成了 `invertTree(x)` 的定义。
|
||||
|
||||
直接写出解法代码:
|
||||
|
||||
```java
|
||||
// 定义:将以 root 为根的这棵二叉树翻转,返回翻转后的二叉树的根节点
|
||||
TreeNode invertTree(TreeNode root) {
|
||||
if (root == null) {
|
||||
return null;
|
||||
}
|
||||
// 利用函数定义,先翻转左右子树
|
||||
TreeNode left = invertTree(root.left);
|
||||
TreeNode right = invertTree(root.right);
|
||||
|
||||
// 然后交换左右子节点
|
||||
root.left = right;
|
||||
root.right = left;
|
||||
|
||||
// 和定义逻辑自恰:以 root 为根的这棵二叉树已经被翻转,返回 root
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
这道题目比较简单,关键思路在于我们发现翻转整棵树就是交换每个节点的左右子节点,于是我们把交换左右子节点的代码放在了前序遍历的位置。
|
||||
这种「分解问题」的思路,核心在于你要给递归函数一个合适的定义,然后用函数的定义来解释你的代码;如果你的逻辑成功自恰,那么说明你这个算法是正确的。
|
||||
|
||||
值得一提的是,如果把交换左右子节点的代码放在后序遍历的位置也是可以的,但是放在中序遍历的位置是不行的,请你想一想为什么?这个应该不难想到,我会把答案置顶在公众号留言区。
|
||||
好了,这道题就分析到这,「遍历」和「分解问题」的思路都可以解决,看下一道题。
|
||||
|
||||
首先讲这道题目是想告诉你,**二叉树题目的一个难点就是,如何把题目的要求细化成每个节点需要做的事情**。
|
||||
### 第二题、填充节点的右侧指针
|
||||
|
||||
这种洞察力需要多刷题训练,我们看下一道题。
|
||||
这是力扣第 116 题「填充每个二叉树节点的右侧指针」,看下题目:
|
||||
|
||||
**第二题、填充二叉树节点的右侧指针**
|
||||

|
||||
|
||||
这是力扣第 116 题,看下题目:
|
||||
|
||||

|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
Node connect(Node root);
|
||||
|
|
@ -180,71 +160,87 @@ Node connect(Node root);
|
|||
|
||||
题目的意思就是把二叉树的每一层节点都用 `next` 指针连接起来:
|
||||
|
||||

|
||||

|
||||
|
||||
而且题目说了,输入是一棵「完美二叉树」,形象地说整棵二叉树是一个正三角形,除了最右侧的节点 `next` 指针会指向 `null`,其他节点的右侧一定有相邻的节点。
|
||||
|
||||
这道题怎么做呢?把每一层的节点穿起来,是不是只要把每个节点的左右子节点都穿起来就行了?
|
||||
这道题怎么做呢?来默念二叉树解题总纲:
|
||||
|
||||
我们可以模仿上一道题,写出如下代码:
|
||||
**1、这题能不能用「遍历」的思维模式解决**?
|
||||
|
||||
很显然,一定可以。
|
||||
|
||||
每个节点要做的事也很简单,把自己的 `next` 指针指向右侧节点就行了。
|
||||
|
||||
也许你会模仿上一道题,直接写出如下代码:
|
||||
|
||||
```java
|
||||
Node connect(Node root) {
|
||||
// 二叉树遍历函数
|
||||
void traverse(Node root) {
|
||||
if (root == null || root.left == null) {
|
||||
return root;
|
||||
return;
|
||||
}
|
||||
|
||||
// 把左子节点的 next 指针指向右子节点
|
||||
root.left.next = root.right;
|
||||
|
||||
connect(root.left);
|
||||
connect(root.right);
|
||||
|
||||
return root;
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
这样其实有很大问题,再看看这张图:
|
||||
但是,这段代码其实有很大问题,因为它只能把相同父节点的两个节点穿起来,再看看这张图:
|
||||
|
||||

|
||||

|
||||
|
||||
节点 5 和节点 6 不属于同一个父节点,那么按照这段代码的逻辑,它俩就没办法被穿起来,这是不符合题意的。
|
||||
节点 5 和节点 6 不属于同一个父节点,那么按照这段代码的逻辑,它俩就没办法被穿起来,这是不符合题意的,但是问题出在哪里?
|
||||
|
||||
回想刚才说的,**二叉树的问题难点在于,如何把题目的要求细化成每个节点需要做的事情**,但是如果只依赖一个节点的话,肯定是没办法连接「跨父节点」的两个相邻节点的。
|
||||
**传统的 `traverse` 函数是遍历二叉树的所有节点,但现在我们想遍历的其实是两个相邻节点之间的「空隙」**。
|
||||
|
||||
那么,我们的做法就是增加函数参数,一个节点做不到,我们就给他安排两个节点,「将每一层二叉树节点连接起来」可以细化成「将每两个相邻节点都连接起来」:
|
||||
所以我们可以在二叉树的基础上进行抽象,你把图中的每一个方框看做一个节点:
|
||||
|
||||

|
||||
|
||||
**这样,一棵二叉树被抽象成了一棵三叉树,三叉树上的每个节点就是原先二叉树的两个相邻节点**。
|
||||
|
||||
现在,我们只要实现一个 `traverse` 函数来遍历这棵三叉树,每个「三叉树节点」需要做的事就是把自己内部的两个二叉树节点穿起来:
|
||||
|
||||
```java
|
||||
// 主函数
|
||||
Node connect(Node root) {
|
||||
if (root == null) return null;
|
||||
connectTwoNode(root.left, root.right);
|
||||
// 遍历「三叉树」,连接相邻节点
|
||||
traverse(root.left, root.right);
|
||||
return root;
|
||||
}
|
||||
|
||||
// 辅助函数
|
||||
void connectTwoNode(Node node1, Node node2) {
|
||||
// 三叉树遍历框架
|
||||
void traverse(Node node1, Node node2) {
|
||||
if (node1 == null || node2 == null) {
|
||||
return;
|
||||
}
|
||||
/**** 前序遍历位置 ****/
|
||||
// 将传入的两个节点连接
|
||||
/**** 前序位置 ****/
|
||||
// 将传入的两个节点穿起来
|
||||
node1.next = node2;
|
||||
|
||||
// 连接相同父节点的两个子节点
|
||||
connectTwoNode(node1.left, node1.right);
|
||||
connectTwoNode(node2.left, node2.right);
|
||||
traverse(node1.left, node1.right);
|
||||
traverse(node2.left, node2.right);
|
||||
// 连接跨越父节点的两个子节点
|
||||
connectTwoNode(node1.right, node2.left);
|
||||
traverse(node1.right, node2.left);
|
||||
}
|
||||
```
|
||||
|
||||
这样,`connectTwoNode` 函数不断递归,可以无死角覆盖整棵二叉树,将所有相邻节点都连接起来,也就避免了我们之前出现的问题,这道题就解决了。
|
||||
这样,`traverse` 函数遍历整棵「三叉树」,将所有相邻节的二叉树节点都连接起来,也就避免了我们之前出现的问题,把这道题完美解决。
|
||||
|
||||
**第三题、将二叉树展开为链表**
|
||||
**2、这题能不能用「分解问题」的思维模式解决**?
|
||||
|
||||
这是力扣第 114 题,看下题目:
|
||||
嗯,好像没有什么特别好的思路,所以这道题无法使用「分解问题」的思维来解决。
|
||||
|
||||

|
||||
### 第三题、将二叉树展开为链表
|
||||
|
||||
这是力扣第 114 题「将二叉树展开为链表」,看下题目:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
|
|
@ -252,19 +248,55 @@ void connectTwoNode(Node node1, Node node2) {
|
|||
void flatten(TreeNode root);
|
||||
```
|
||||
|
||||
我们尝试给出这个函数的定义:
|
||||
**1、这题能不能用「遍历」的思维模式解决**?
|
||||
|
||||
**给 `flatten` 函数输入一个节点 `root`,那么以 `root` 为根的二叉树就会被拉平为一条链表**。
|
||||
乍一看感觉是可以的:对整棵树进行前序遍历,一边遍历一边构造出一条「链表」就行了:
|
||||
|
||||
我们再梳理一下,如何按题目要求把一棵树拉平成一条链表?很简单,以下流程:
|
||||
```java
|
||||
// 虚拟头节点,dummy.right 就是结果
|
||||
TreeNode dummy = new TreeNode(-1);
|
||||
// 用来构建链表的指针
|
||||
TreeNode p = dummy;
|
||||
|
||||
1、将 `root` 的左子树和右子树拉平。
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
// 前序位置
|
||||
p.right = new TreeNode(root.val);
|
||||
p = p.right;
|
||||
|
||||
2、将 `root` 的右子树接到左子树下方,然后将整个左子树作为右子树。
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
但是注意 `flatten` 函数的签名,返回类型为 `void`,也就是说题目希望我们在原地把二叉树拉平成链表。
|
||||
|
||||
上面三步看起来最难的应该是第一步对吧,如何把 `root` 的左右子树拉平?其实很简单,按照 `flatten` 函数的定义,对 `root` 的左右子树递归调用 `flatten` 函数即可:
|
||||
这样一来,没办法通过简单的二叉树遍历来解决这道题了。
|
||||
|
||||
**2、这题能不能用「分解问题」的思维模式解决**?
|
||||
|
||||
我们尝试给出 `flatten` 函数的定义:
|
||||
|
||||
```java
|
||||
// 定义:输入节点 root,然后 root 为根的二叉树就会被拉平为一条链表
|
||||
void flatten(TreeNode root);
|
||||
```
|
||||
|
||||
有了这个函数定义,如何按题目要求把一棵树拉平成一条链表?
|
||||
|
||||
对于一个节点 `x`,可以执行以下流程:
|
||||
|
||||
1、先利用 `flatten(x.left)` 和 `flatten(x.right)` 将 `x` 的左右子树拉平。
|
||||
|
||||
2、将 `x` 的右子树接到左子树下方,然后将整个左子树作为右子树。
|
||||
|
||||

|
||||
|
||||
这样,以 `x` 为根的整棵二叉树就被拉平了,恰好完成了 `flatten(x)` 的定义。
|
||||
|
||||
直接看代码实现:
|
||||
|
||||
```java
|
||||
// 定义:将以 root 为根的树拉平为链表
|
||||
|
|
@ -272,6 +304,7 @@ void flatten(TreeNode root) {
|
|||
// base case
|
||||
if (root == null) return;
|
||||
|
||||
// 利用定义,把左右子树拉平
|
||||
flatten(root.left);
|
||||
flatten(root.right);
|
||||
|
||||
|
|
@ -293,35 +326,71 @@ void flatten(TreeNode root) {
|
|||
}
|
||||
```
|
||||
|
||||
你看,这就是递归的魅力,你说 `flatten` 函数是怎么把左右子树拉平的?说不清楚,但是只要知道 `flatten` 的定义如此,相信这个定义,让 `root` 做它该做的事情,然后 `flatten` 函数就会按照定义工作。另外注意递归框架是后序遍历,因为我们要先拉平左右子树才能进行后续操作。
|
||||
你看,这就是递归的魅力,你说 `flatten` 函数是怎么把左右子树拉平的?
|
||||
|
||||
至此,这道题也解决了,我们旧文 [k个一组翻转链表](https://labuladong.gitee.io/algo/) 的递归思路和本题也有一些类似。
|
||||
不容易说清楚,但是只要知道 `flatten` 的定义如此并利用这个定义,让每一个节点做它该做的事情,然后 `flatten` 函数就会按照定义工作。
|
||||
|
||||
### 四、最后总结
|
||||
至此,这道题也解决了,我们前文 [k个一组翻转链表](https://labuladong.github.io/article/fname.html?fname=k个一组反转链表) 的递归思路和本题也有一些类似。
|
||||
|
||||
递归算法的关键要明确函数的定义,相信这个定义,而不要跳进递归细节。
|
||||
最后,首尾呼应,再次默写二叉树解题总纲。
|
||||
|
||||
写二叉树的算法题,都是基于递归框架的,我们先要搞清楚 `root` 节点它自己要做什么,然后根据题目要求选择使用前序,中序,后续的递归框架。
|
||||
二叉树解题的思维模式分两类:
|
||||
|
||||
二叉树题目的难点在于如何通过题目的要求思考出每一个节点需要做什么,这个只能通过多刷题进行练习了。
|
||||
**1、是否可以通过遍历一遍二叉树得到答案**?如果可以,用一个 `traverse` 函数配合外部变量来实现,这叫「遍历」的思维模式。
|
||||
|
||||
如果本文讲的三道题对你有一些启发,请三连,数据好的话东哥下次再来一波手把手刷题文,你会发现二叉树的题真的是越刷越顺手,欲罢不能,恨不得一口气把二叉树的题刷通。
|
||||
**2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案**?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
|
||||
|
||||
接下来请阅读:
|
||||
无论使用哪种思维模式,你都需要思考:
|
||||
|
||||
**如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做**?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
|
||||
|
||||
希望你能仔细体会,并运用到所有二叉树题目上。
|
||||
|
||||
接下来可阅读:
|
||||
|
||||
* [手把手刷二叉树(第二期)](https://labuladong.github.io/article/fname.html?fname=二叉树系列2)
|
||||
* [手把手刷二叉树(第三期)](https://labuladong.github.io/article/fname.html?fname=二叉树系列3)
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [东哥带你刷二叉搜索树(构造篇)](https://labuladong.github.io/article/fname.html?fname=BST3)
|
||||
- [东哥带你刷二叉搜索树(特性篇)](https://labuladong.github.io/article/fname.html?fname=BST1)
|
||||
- [东哥带你刷二叉树(构造篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列2)
|
||||
- [两种思路解决单词拼接问题](https://labuladong.github.io/article/fname.html?fname=单词拼接)
|
||||
- [二叉树的递归转迭代的代码框架](https://labuladong.github.io/article/fname.html?fname=迭代遍历二叉树)
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [后序遍历的妙用](https://labuladong.github.io/article/fname.html?fname=后序遍历)
|
||||
- [归并排序详解及应用](https://labuladong.github.io/article/fname.html?fname=归并排序)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer 26. 树的子结构](https://leetcode.cn/problems/shu-de-zi-jie-gou-lcof/?show=1) |
|
||||
| - | [剑指 Offer 27. 二叉树的镜像](https://leetcode.cn/problems/er-cha-shu-de-jing-xiang-lcof/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
* [手把手刷二叉树(第二期)](https://labuladong.gitee.io/algo/)
|
||||
* [手把手刷二叉树(第三期)](https://labuladong.gitee.io/algo/)
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||

|
||||
|
||||
|
||||
======其他语言代码======
|
||||
|
|
@ -0,0 +1,588 @@
|
|||
# 东哥手把手带你刷二叉树(构造篇)
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [105. Construct Binary Tree from Preorder and Inorder Traversal](https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/) | [105. 从前序与中序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/) | 🟠
|
||||
| [106. Construct Binary Tree from Inorder and Postorder Traversal](https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/) | [106. 从中序与后序遍历序列构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/) | 🟠
|
||||
| [654. Maximum Binary Tree](https://leetcode.com/problems/maximum-binary-tree/) | [654. 最大二叉树](https://leetcode.cn/problems/maximum-binary-tree/) | 🟠
|
||||
| [889. Construct Binary Tree from Preorder and Postorder Traversal](https://leetcode.com/problems/construct-binary-tree-from-preorder-and-postorder-traversal/) | [889. 根据前序和后序遍历构造二叉树](https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-postorder-traversal/) | 🟠
|
||||
| - | [剑指 Offer 07. 重建二叉树](https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
PS:[刷题插件](https://mp.weixin.qq.com/s/OE1zPVPj0V2o82N4HtLQbw) 集成了手把手刷二叉树功能,按照公式和套路讲解了 150 道二叉树题目,可手把手带你刷完二叉树分类的题目,迅速掌握递归思维。
|
||||
|
||||
本文是承接 [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结) 的第二篇文章,先复述一下前文总结的二叉树解题总纲:
|
||||
|
||||
> 二叉树解题的思维模式分两类:
|
||||
>
|
||||
> **1、是否可以通过遍历一遍二叉树得到答案**?如果可以,用一个 `traverse` 函数配合外部变量来实现,这叫「遍历」的思维模式。
|
||||
>
|
||||
> **2、是否可以定义一个递归函数,通过子问题(子树)的答案推导出原问题的答案**?如果可以,写出这个递归函数的定义,并充分利用这个函数的返回值,这叫「分解问题」的思维模式。
|
||||
>
|
||||
> 无论使用哪种思维模式,你都需要思考:
|
||||
>
|
||||
> **如果单独抽出一个二叉树节点,它需要做什么事情?需要在什么时候(前/中/后序位置)做**?其他的节点不用你操心,递归函数会帮你在所有节点上执行相同的操作。
|
||||
|
||||
第一篇文章 [东哥带你刷二叉树(思维篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列1) 讲了「遍历」和「分解问题」两种思维方式,本文讲二叉树的构造类问题。
|
||||
|
||||
**二叉树的构造问题一般都是使用「分解问题」的思路:构造整棵树 = 根节点 + 构造左子树 + 构造右子树**。
|
||||
|
||||
接下来直接看题。
|
||||
|
||||
### 构造最大二叉树
|
||||
|
||||
先来道简单的,这是力扣第 654 题「最大二叉树」,题目如下:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
TreeNode constructMaximumBinaryTree(int[] nums);
|
||||
```
|
||||
|
||||
每个二叉树节点都可以认为是一棵子树的根节点,对于根节点,首先要做的当然是把想办法把自己先构造出来,然后想办法构造自己的左右子树。
|
||||
|
||||
所以,我们要遍历数组把找到最大值 `maxVal`,从而把根节点 `root` 做出来,然后对 `maxVal` 左边的数组和右边的数组进行递归构建,作为 `root` 的左右子树。
|
||||
|
||||
按照题目给出的例子,输入的数组为 `[3,2,1,6,0,5]`,对于整棵树的根节点来说,其实在做这件事:
|
||||
|
||||
```java
|
||||
TreeNode constructMaximumBinaryTree([3,2,1,6,0,5]) {
|
||||
// 找到数组中的最大值
|
||||
TreeNode root = new TreeNode(6);
|
||||
// 递归调用构造左右子树
|
||||
root.left = constructMaximumBinaryTree([3,2,1]);
|
||||
root.right = constructMaximumBinaryTree([0,5]);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
再详细一点,就是如下伪码:
|
||||
|
||||
```java
|
||||
TreeNode constructMaximumBinaryTree(int[] nums) {
|
||||
if (nums is empty) return null;
|
||||
// 找到数组中的最大值
|
||||
int maxVal = Integer.MIN_VALUE;
|
||||
int index = 0;
|
||||
for (int i = 0; i < nums.length; i++) {
|
||||
if (nums[i] > maxVal) {
|
||||
maxVal = nums[i];
|
||||
index = i;
|
||||
}
|
||||
}
|
||||
|
||||
TreeNode root = new TreeNode(maxVal);
|
||||
// 递归调用构造左右子树
|
||||
root.left = constructMaximumBinaryTree(nums[0..index-1]);
|
||||
root.right = constructMaximumBinaryTree(nums[index+1..nums.length-1]);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
**当前 `nums` 中的最大值就是根节点,然后根据索引递归调用左右数组构造左右子树即可**。
|
||||
|
||||
明确了思路,我们可以重新写一个辅助函数 `build`,来控制 `nums` 的索引:
|
||||
|
||||
```java
|
||||
/* 主函数 */
|
||||
TreeNode constructMaximumBinaryTree(int[] nums) {
|
||||
return build(nums, 0, nums.length - 1);
|
||||
}
|
||||
|
||||
// 定义:将 nums[lo..hi] 构造成符合条件的树,返回根节点
|
||||
TreeNode build(int[] nums, int lo, int hi) {
|
||||
// base case
|
||||
if (lo > hi) {
|
||||
return null;
|
||||
}
|
||||
|
||||
// 找到数组中的最大值和对应的索引
|
||||
int index = -1, maxVal = Integer.MIN_VALUE;
|
||||
for (int i = lo; i <= hi; i++) {
|
||||
if (maxVal < nums[i]) {
|
||||
index = i;
|
||||
maxVal = nums[i];
|
||||
}
|
||||
}
|
||||
|
||||
// 先构造出根节点
|
||||
TreeNode root = new TreeNode(maxVal);
|
||||
// 递归调用构造左右子树
|
||||
root.left = build(nums, lo, index - 1);
|
||||
root.right = build(nums, index + 1, hi);
|
||||
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
至此,这道题就做完了,还是挺简单的对吧,下面看两道更困难一些的。
|
||||
|
||||
### 通过前序和中序遍历结果构造二叉树
|
||||
|
||||
力扣第 105 题「从前序和中序遍历序列构造二叉树」就是这道经典题目,面试笔试中常考:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
TreeNode buildTree(int[] preorder, int[] inorder);
|
||||
```
|
||||
|
||||
废话不多说,直接来想思路,首先思考,根节点应该做什么。
|
||||
|
||||
**类似上一题,我们肯定要想办法确定根节点的值,把根节点做出来,然后递归构造左右子树即可**。
|
||||
|
||||
我们先来回顾一下,前序遍历和中序遍历的结果有什么特点?
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
// 前序遍历
|
||||
preorder.add(root.val);
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
|
||||
void traverse(TreeNode root) {
|
||||
traverse(root.left);
|
||||
// 中序遍历
|
||||
inorder.add(root.val);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
前文 [二叉树就那几个框架](https://labuladong.github.io/article/fname.html?fname=nestInteger) 写过,这样的遍历顺序差异,导致了 `preorder` 和 `inorder` 数组中的元素分布有如下特点:
|
||||
|
||||

|
||||
|
||||
找到根节点是很简单的,前序遍历的第一个值 `preorder[0]` 就是根节点的值。
|
||||
|
||||
关键在于如何通过根节点的值,将 `preorder` 和 `postorder` 数组划分成两半,构造根节点的左右子树?
|
||||
|
||||
换句话说,对于以下代码中的 `?` 部分应该填入什么:
|
||||
|
||||
```java
|
||||
/* 主函数 */
|
||||
public TreeNode buildTree(int[] preorder, int[] inorder) {
|
||||
// 根据函数定义,用 preorder 和 inorder 构造二叉树
|
||||
return build(preorder, 0, preorder.length - 1,
|
||||
inorder, 0, inorder.length - 1);
|
||||
}
|
||||
|
||||
/*
|
||||
build 函数的定义:
|
||||
若前序遍历数组为 preorder[preStart..preEnd],
|
||||
中序遍历数组为 inorder[inStart..inEnd],
|
||||
构造二叉树,返回该二叉树的根节点
|
||||
*/
|
||||
TreeNode build(int[] preorder, int preStart, int preEnd,
|
||||
int[] inorder, int inStart, int inEnd) {
|
||||
// root 节点对应的值就是前序遍历数组的第一个元素
|
||||
int rootVal = preorder[preStart];
|
||||
// rootVal 在中序遍历数组中的索引
|
||||
int index = 0;
|
||||
for (int i = inStart; i <= inEnd; i++) {
|
||||
if (inorder[i] == rootVal) {
|
||||
index = i;
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
TreeNode root = new TreeNode(rootVal);
|
||||
// 递归构造左右子树
|
||||
root.left = build(preorder, ?, ?,
|
||||
inorder, ?, ?);
|
||||
|
||||
root.right = build(preorder, ?, ?,
|
||||
inorder, ?, ?);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
对于代码中的 `rootVal` 和 `index` 变量,就是下图这种情况:
|
||||
|
||||

|
||||
|
||||
另外,也有读者注意到,通过 for 循环遍历的方式去确定 `index` 效率不算高,可以进一步优化。
|
||||
|
||||
因为题目说二叉树节点的值不存在重复,所以可以使用一个 HashMap 存储元素到索引的映射,这样就可以直接通过 HashMap 查到 `rootVal` 对应的 `index`:
|
||||
|
||||
```java
|
||||
// 存储 inorder 中值到索引的映射
|
||||
HashMap<Integer, Integer> valToIndex = new HashMap<>();
|
||||
|
||||
public TreeNode buildTree(int[] preorder, int[] inorder) {
|
||||
for (int i = 0; i < inorder.length; i++) {
|
||||
valToIndex.put(inorder[i], i);
|
||||
}
|
||||
return build(preorder, 0, preorder.length - 1,
|
||||
inorder, 0, inorder.length - 1);
|
||||
}
|
||||
|
||||
|
||||
TreeNode build(int[] preorder, int preStart, int preEnd,
|
||||
int[] inorder, int inStart, int inEnd) {
|
||||
int rootVal = preorder[preStart];
|
||||
// 避免 for 循环寻找 rootVal
|
||||
int index = valToIndex.get(rootVal);
|
||||
// ...
|
||||
}
|
||||
```
|
||||
|
||||
现在我们来看图做填空题,下面这几个问号处应该填什么:
|
||||
|
||||
```java
|
||||
root.left = build(preorder, ?, ?,
|
||||
inorder, ?, ?);
|
||||
|
||||
root.right = build(preorder, ?, ?,
|
||||
inorder, ?, ?);
|
||||
```
|
||||
|
||||
对于左右子树对应的 `inorder` 数组的起始索引和终止索引比较容易确定:
|
||||
|
||||

|
||||
|
||||
```java
|
||||
root.left = build(preorder, ?, ?,
|
||||
inorder, inStart, index - 1);
|
||||
|
||||
root.right = build(preorder, ?, ?,
|
||||
inorder, index + 1, inEnd);
|
||||
```
|
||||
|
||||
对于 `preorder` 数组呢?如何确定左右数组对应的起始索引和终止索引?
|
||||
|
||||
这个可以通过左子树的节点数推导出来,假设左子树的节点数为 `leftSize`,那么 `preorder` 数组上的索引情况是这样的:
|
||||
|
||||

|
||||
|
||||
看着这个图就可以把 `preorder` 对应的索引写进去了:
|
||||
|
||||
```java
|
||||
int leftSize = index - inStart;
|
||||
|
||||
root.left = build(preorder, preStart + 1, preStart + leftSize,
|
||||
inorder, inStart, index - 1);
|
||||
|
||||
root.right = build(preorder, preStart + leftSize + 1, preEnd,
|
||||
inorder, index + 1, inEnd);
|
||||
```
|
||||
|
||||
至此,整个算法思路就完成了,我们再补一补 base case 即可写出解法代码:
|
||||
|
||||
```java
|
||||
TreeNode build(int[] preorder, int preStart, int preEnd,
|
||||
int[] inorder, int inStart, int inEnd) {
|
||||
|
||||
if (preStart > preEnd) {
|
||||
return null;
|
||||
}
|
||||
|
||||
// root 节点对应的值就是前序遍历数组的第一个元素
|
||||
int rootVal = preorder[preStart];
|
||||
// rootVal 在中序遍历数组中的索引
|
||||
int index = valToIndex.get(rootVal);
|
||||
|
||||
int leftSize = index - inStart;
|
||||
|
||||
// 先构造出当前根节点
|
||||
TreeNode root = new TreeNode(rootVal);
|
||||
// 递归构造左右子树
|
||||
root.left = build(preorder, preStart + 1, preStart + leftSize,
|
||||
inorder, inStart, index - 1);
|
||||
|
||||
root.right = build(preorder, preStart + leftSize + 1, preEnd,
|
||||
inorder, index + 1, inEnd);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
我们的主函数只要调用 `build` 函数即可,你看着函数这么多参数,解法这么多代码,似乎比我们上面讲的那道题难很多,让人望而生畏,实际上呢,这些参数无非就是控制数组起止位置的,画个图就能解决了。
|
||||
|
||||
### 通过后序和中序遍历结果构造二叉树
|
||||
|
||||
类似上一题,这次我们利用**后序**和**中序**遍历的结果数组来还原二叉树,这是力扣第 106 题「从后序和中序遍历序列构造二叉树」:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
TreeNode buildTree(int[] inorder, int[] postorder);
|
||||
```
|
||||
|
||||
类似的,看下后序和中序遍历的特点:
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
// 后序遍历
|
||||
postorder.add(root.val);
|
||||
}
|
||||
|
||||
void traverse(TreeNode root) {
|
||||
traverse(root.left);
|
||||
// 中序遍历
|
||||
inorder.add(root.val);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
这样的遍历顺序差异,导致了 `postorder` 和 `inorder` 数组中的元素分布有如下特点:
|
||||
|
||||

|
||||
|
||||
这道题和上一题的关键区别是,后序遍历和前序遍历相反,根节点对应的值为 `postorder` 的最后一个元素。
|
||||
|
||||
整体的算法框架和上一题非常类似,我们依然写一个辅助函数 `build`:
|
||||
|
||||
```java
|
||||
// 存储 inorder 中值到索引的映射
|
||||
HashMap<Integer, Integer> valToIndex = new HashMap<>();
|
||||
|
||||
TreeNode buildTree(int[] inorder, int[] postorder) {
|
||||
for (int i = 0; i < inorder.length; i++) {
|
||||
valToIndex.put(inorder[i], i);
|
||||
}
|
||||
return build(inorder, 0, inorder.length - 1,
|
||||
postorder, 0, postorder.length - 1);
|
||||
}
|
||||
|
||||
/*
|
||||
build 函数的定义:
|
||||
后序遍历数组为 postorder[postStart..postEnd],
|
||||
中序遍历数组为 inorder[inStart..inEnd],
|
||||
构造二叉树,返回该二叉树的根节点
|
||||
*/
|
||||
TreeNode build(int[] inorder, int inStart, int inEnd,
|
||||
int[] postorder, int postStart, int postEnd) {
|
||||
// root 节点对应的值就是后序遍历数组的最后一个元素
|
||||
int rootVal = postorder[postEnd];
|
||||
// rootVal 在中序遍历数组中的索引
|
||||
int index = valToIndex.get(rootVal);
|
||||
|
||||
TreeNode root = new TreeNode(rootVal);
|
||||
// 递归构造左右子树
|
||||
root.left = build(preorder, ?, ?,
|
||||
inorder, ?, ?);
|
||||
|
||||
root.right = build(preorder, ?, ?,
|
||||
inorder, ?, ?);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
现在 `postoder` 和 `inorder` 对应的状态如下:
|
||||
|
||||
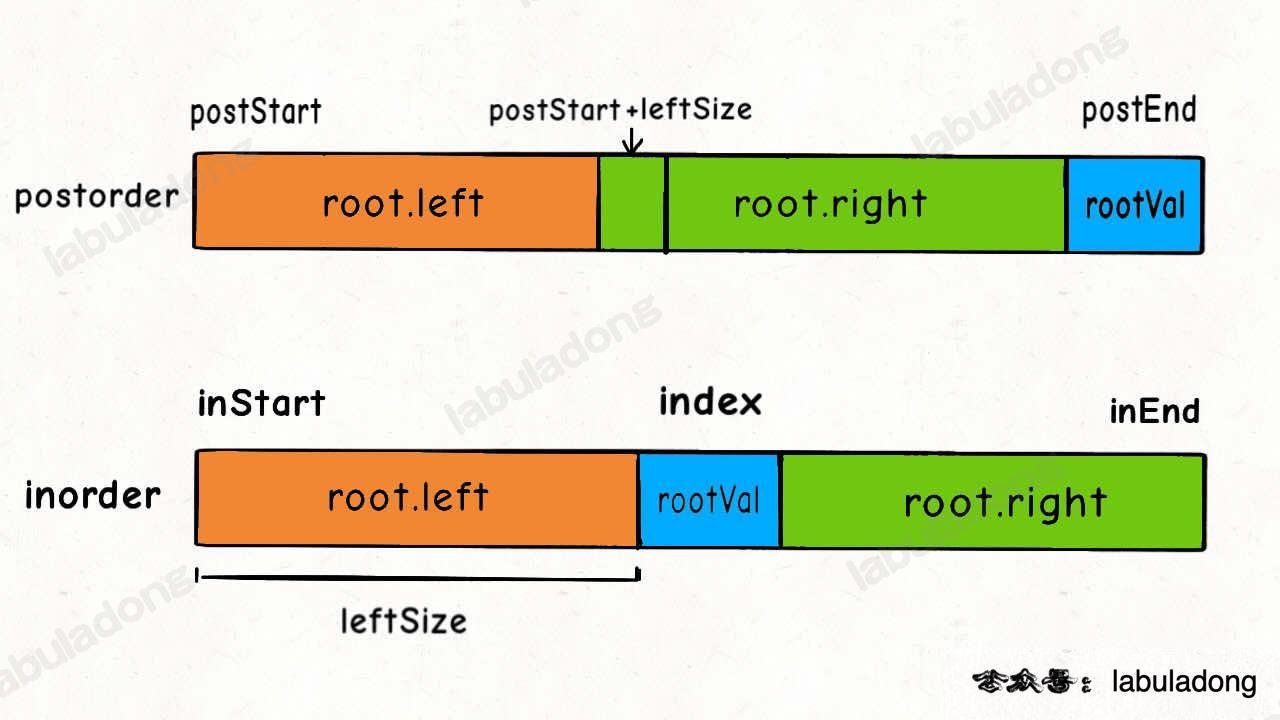
|
||||
|
||||
我们可以按照上图将问号处的索引正确填入:
|
||||
|
||||
```java
|
||||
int leftSize = index - inStart;
|
||||
|
||||
root.left = build(inorder, inStart, index - 1,
|
||||
postorder, postStart, postStart + leftSize - 1);
|
||||
|
||||
root.right = build(inorder, index + 1, inEnd,
|
||||
postorder, postStart + leftSize, postEnd - 1);
|
||||
```
|
||||
|
||||
综上,可以写出完整的解法代码:
|
||||
|
||||
```java
|
||||
TreeNode build(int[] inorder, int inStart, int inEnd,
|
||||
int[] postorder, int postStart, int postEnd) {
|
||||
|
||||
if (inStart > inEnd) {
|
||||
return null;
|
||||
}
|
||||
// root 节点对应的值就是后序遍历数组的最后一个元素
|
||||
int rootVal = postorder[postEnd];
|
||||
// rootVal 在中序遍历数组中的索引
|
||||
int index = valToIndex.get(rootVal);
|
||||
// 左子树的节点个数
|
||||
int leftSize = index - inStart;
|
||||
TreeNode root = new TreeNode(rootVal);
|
||||
// 递归构造左右子树
|
||||
root.left = build(inorder, inStart, index - 1,
|
||||
postorder, postStart, postStart + leftSize - 1);
|
||||
|
||||
root.right = build(inorder, index + 1, inEnd,
|
||||
postorder, postStart + leftSize, postEnd - 1);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
有了前一题的铺垫,这道题很快就解决了,无非就是 `rootVal` 变成了最后一个元素,再改改递归函数的参数而已,只要明白二叉树的特性,也不难写出来。
|
||||
|
||||
### 通过后序和前序遍历结果构造二叉树
|
||||
|
||||
这是力扣第 889 题「根据前序和后序遍历构造二叉树」,给你输入二叉树的前序和后序遍历结果,让你还原二叉树的结构。
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
TreeNode constructFromPrePost(int[] preorder, int[] postorder);
|
||||
```
|
||||
|
||||
这道题和前两道题有一个本质的区别:
|
||||
|
||||
**通过前序中序,或者后序中序遍历结果可以确定唯一一棵原始二叉树,但是通过前序后序遍历结果无法确定唯一的原始二叉树**。
|
||||
|
||||
题目也说了,如果有多种可能的还原结果,你可以返回任意一种。
|
||||
|
||||
为什么呢?我们说过,构建二叉树的套路很简单,先找到根节点,然后找到并递归构造左右子树即可。
|
||||
|
||||
前两道题,可以通过前序或者后序遍历结果找到根节点,然后根据中序遍历结果确定左右子树(题目说了树中没有 `val` 相同的节点)。
|
||||
|
||||
这道题,你可以确定根节点,但是无法确切的知道左右子树有哪些节点。
|
||||
|
||||
举个例子,比如给你这个输入:
|
||||
|
||||
```
|
||||
preorder = [1,2,3], postorder = [3,2,1]
|
||||
```
|
||||
|
||||
下面这两棵树都是符合条件的,但显然它们的结构不同:
|
||||
|
||||

|
||||
|
||||
不过话说回来,用后序遍历和前序遍历结果还原二叉树,解法逻辑上和前两道题差别不大,也是通过控制左右子树的索引来构建:
|
||||
|
||||
**1、首先把前序遍历结果的第一个元素或者后序遍历结果的最后一个元素确定为根节点的值**。
|
||||
|
||||
**2、然后把前序遍历结果的第二个元素作为左子树的根节点的值**。
|
||||
|
||||
**3、在后序遍历结果中寻找左子树根节点的值,从而确定了左子树的索引边界,进而确定右子树的索引边界,递归构造左右子树即可**。
|
||||
|
||||

|
||||
|
||||
详情见代码。
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
// 存储 postorder 中值到索引的映射
|
||||
HashMap<Integer, Integer> valToIndex = new HashMap<>();
|
||||
|
||||
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
|
||||
for (int i = 0; i < postorder.length; i++) {
|
||||
valToIndex.put(postorder[i], i);
|
||||
}
|
||||
return build(preorder, 0, preorder.length - 1,
|
||||
postorder, 0, postorder.length - 1);
|
||||
}
|
||||
|
||||
// 定义:根据 preorder[preStart..preEnd] 和 postorder[postStart..postEnd]
|
||||
// 构建二叉树,并返回根节点。
|
||||
TreeNode build(int[] preorder, int preStart, int preEnd,
|
||||
int[] postorder, int postStart, int postEnd) {
|
||||
if (preStart > preEnd) {
|
||||
return null;
|
||||
}
|
||||
if (preStart == preEnd) {
|
||||
return new TreeNode(preorder[preStart]);
|
||||
}
|
||||
|
||||
// root 节点对应的值就是前序遍历数组的第一个元素
|
||||
int rootVal = preorder[preStart];
|
||||
// root.left 的值是前序遍历第二个元素
|
||||
// 通过前序和后序遍历构造二叉树的关键在于通过左子树的根节点
|
||||
// 确定 preorder 和 postorder 中左右子树的元素区间
|
||||
int leftRootVal = preorder[preStart + 1];
|
||||
// leftRootVal 在后序遍历数组中的索引
|
||||
int index = valToIndex.get(leftRootVal);
|
||||
// 左子树的元素个数
|
||||
int leftSize = index - postStart + 1;
|
||||
|
||||
// 先构造出当前根节点
|
||||
TreeNode root = new TreeNode(rootVal);
|
||||
// 递归构造左右子树
|
||||
// 根据左子树的根节点索引和元素个数推导左右子树的索引边界
|
||||
root.left = build(preorder, preStart + 1, preStart + leftSize,
|
||||
postorder, postStart, index);
|
||||
root.right = build(preorder, preStart + leftSize + 1, preEnd,
|
||||
postorder, index + 1, postEnd - 1);
|
||||
|
||||
return root;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
代码和前两道题非常类似,我们可以看着代码思考一下,为什么通过前序遍历和后序遍历结果还原的二叉树可能不唯一呢?
|
||||
|
||||
关键在这一句:
|
||||
|
||||
```java
|
||||
int leftRootVal = preorder[preStart + 1];
|
||||
```
|
||||
|
||||
我们假设前序遍历的第二个元素是左子树的根节点,但实际上左子树有可能是空指针,那么这个元素就应该是右子树的根节点。由于这里无法确切进行判断,所以导致了最终答案的不唯一。
|
||||
|
||||
至此,通过前序和后序遍历结果还原二叉树的问题也解决了。
|
||||
|
||||
最后呼应下前文,**二叉树的构造问题一般都是使用「分解问题」的思路:构造整棵树 = 根节点 + 构造左子树 + 构造右子树**。先找出根节点,然后根据根节点的值找到左右子树的元素,进而递归构建出左右子树。
|
||||
|
||||
现在你是否明白其中的玄妙了呢?
|
||||
|
||||
接下来可阅读:
|
||||
|
||||
* [手把手刷二叉树(第三期)](https://labuladong.github.io/article/fname.html?fname=二叉树系列3)
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [东哥带你刷二叉搜索树(特性篇)](https://labuladong.github.io/article/fname.html?fname=BST1)
|
||||
- [东哥带你刷二叉树(序列化篇)](https://labuladong.github.io/article/fname.html?fname=二叉树的序列化)
|
||||
- [东哥带你刷二叉树(思路篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列1)
|
||||
- [二叉树的递归转迭代的代码框架](https://labuladong.github.io/article/fname.html?fname=迭代遍历二叉树)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1008. Construct Binary Search Tree from Preorder Traversal](https://leetcode.com/problems/construct-binary-search-tree-from-preorder-traversal/?show=1) | [1008. 前序遍历构造二叉搜索树](https://leetcode.cn/problems/construct-binary-search-tree-from-preorder-traversal/?show=1) |
|
||||
| - | [剑指 Offer 07. 重建二叉树](https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,11 +1,5 @@
|
|||
# 特殊数据结构:单调栈
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -15,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -203,6 +197,43 @@ int[] nextGreaterElements(int[] nums) {
|
|||
|
||||
我会在 [单调栈的几种变体](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_628dc1ace4b09dda126cf793/1) 对比单调栈的几种其他形式,并在 [单调栈的运用](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_628dc2d7e4b0cedf38b67734/1) 中给出单调栈的经典例题。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [一个方法团灭 LeetCode 打家劫舍问题](https://labuladong.github.io/article/fname.html?fname=抢房子)
|
||||
- [一道数组去重的算法题把我整不会了](https://labuladong.github.io/article/fname.html?fname=单调栈去重)
|
||||
- [单调栈代码模板的几种变体](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_628dc1ace4b09dda126cf793/1)
|
||||
- [单调队列的通用实现及经典习题](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62a692efe4b01a48520b9b9b/1)
|
||||
- [单调队列结构解决滑动窗口问题](https://labuladong.github.io/article/fname.html?fname=单调队列)
|
||||
- [数据结构设计:最大栈](https://labuladong.github.io/article/fname.html?fname=最大栈)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1019. Next Greater Node In Linked List](https://leetcode.com/problems/next-greater-node-in-linked-list/?show=1) | [1019. 链表中的下一个更大节点](https://leetcode.cn/problems/next-greater-node-in-linked-list/?show=1) |
|
||||
| [1944. Number of Visible People in a Queue](https://leetcode.com/problems/number-of-visible-people-in-a-queue/?show=1) | [1944. 队列中可以看到的人数](https://leetcode.cn/problems/number-of-visible-people-in-a-queue/?show=1) |
|
||||
| [402. Remove K Digits](https://leetcode.com/problems/remove-k-digits/?show=1) | [402. 移掉 K 位数字](https://leetcode.cn/problems/remove-k-digits/?show=1) |
|
||||
| [42. Trapping Rain Water](https://leetcode.com/problems/trapping-rain-water/?show=1) | [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/?show=1) |
|
||||
| [901. Online Stock Span](https://leetcode.com/problems/online-stock-span/?show=1) | [901. 股票价格跨度](https://leetcode.cn/problems/online-stock-span/?show=1) |
|
||||
| [918. Maximum Sum Circular Subarray](https://leetcode.com/problems/maximum-sum-circular-subarray/?show=1) | [918. 环形子数组的最大和](https://leetcode.cn/problems/maximum-sum-circular-subarray/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,11 +1,5 @@
|
|||
# 特殊数据结构:单调队列
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -15,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -270,6 +264,38 @@ class MonotonicQueue<E extends Comparable<E>> {
|
|||
|
||||
我将在 [单调队列通用实现及应用](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62a692efe4b01a48520b9b9b/1) 中给出单调队列的通用实现和经典习题。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [数据结构设计:最大栈](https://labuladong.github.io/article/fname.html?fname=最大栈)
|
||||
- [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1425. Constrained Subsequence Sum](https://leetcode.com/problems/constrained-subsequence-sum/?show=1) | [1425. 带限制的子序列和](https://leetcode.cn/problems/constrained-subsequence-sum/?show=1) |
|
||||
| [1696. Jump Game VI](https://leetcode.com/problems/jump-game-vi/?show=1) | [1696. 跳跃游戏 VI](https://leetcode.cn/problems/jump-game-vi/?show=1) |
|
||||
| [862. Shortest Subarray with Sum at Least K](https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k/?show=1) | [862. 和至少为 K 的最短子数组](https://leetcode.cn/problems/shortest-subarray-with-sum-at-least-k/?show=1) |
|
||||
| [918. Maximum Sum Circular Subarray](https://leetcode.com/problems/maximum-sum-circular-subarray/?show=1) | [918. 环形子数组的最大和](https://leetcode.cn/problems/maximum-sum-circular-subarray/?show=1) |
|
||||
| - | [剑指 Offer 59 - I. 滑动窗口的最大值](https://leetcode.cn/problems/hua-dong-chuang-kou-de-zui-da-zhi-lcof/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -0,0 +1,359 @@
|
|||
# 图论算法基础
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [797. All Paths From Source to Target](https://leetcode.com/problems/all-paths-from-source-to-target/) | [797. 所有可能的路径](https://leetcode.cn/problems/all-paths-from-source-to-target/) | 🟠
|
||||
| - | [剑指 Offer II 110. 所有路径](https://leetcode.cn/problems/bP4bmD/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
> 本文有视频版:[图论基础及遍历算法](https://www.bilibili.com/video/BV19G41187cL/)
|
||||
|
||||
经常有读者问我「图」这种数据结构,其实我在 [学习数据结构和算法的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法) 中说过,虽然图可以玩出更多的算法,解决更复杂的问题,但本质上图可以认为是多叉树的延伸。
|
||||
|
||||
面试笔试很少出现图相关的问题,就算有,大多也是简单的遍历问题,基本上可以完全照搬多叉树的遍历。
|
||||
|
||||
那么,本文依然秉持我们号的风格,只讲「图」最实用的,离我们最近的部分,让你心里对图有个直观的认识,文末我给出了其他经典图论算法,理解本文后应该都可以拿下的。
|
||||
|
||||
### 图的逻辑结构和具体实现
|
||||
|
||||
一幅图是由**节点**和**边**构成的,逻辑结构如下:
|
||||
|
||||

|
||||
|
||||
**什么叫「逻辑结构」?就是说为了方便研究,我们把图抽象成这个样子**。
|
||||
|
||||
根据这个逻辑结构,我们可以认为每个节点的实现如下:
|
||||
|
||||
```java
|
||||
/* 图节点的逻辑结构 */
|
||||
class Vertex {
|
||||
int id;
|
||||
Vertex[] neighbors;
|
||||
}
|
||||
```
|
||||
|
||||
看到这个实现,你有没有很熟悉?它和我们之前说的多叉树节点几乎完全一样:
|
||||
|
||||
```java
|
||||
/* 基本的 N 叉树节点 */
|
||||
class TreeNode {
|
||||
int val;
|
||||
TreeNode[] children;
|
||||
}
|
||||
```
|
||||
|
||||
所以说,图真的没啥高深的,本质上就是个高级点的多叉树而已,适用于树的 DFS/BFS 遍历算法,全部适用于图。
|
||||
|
||||
不过呢,上面的这种实现是「逻辑上的」,实际上我们很少用这个 `Vertex` 类实现图,而是用常说的**邻接表和邻接矩阵**来实现。
|
||||
|
||||
比如还是刚才那幅图:
|
||||
|
||||

|
||||
|
||||
用邻接表和邻接矩阵的存储方式如下:
|
||||
|
||||

|
||||
|
||||
邻接表很直观,我把每个节点 `x` 的邻居都存到一个列表里,然后把 `x` 和这个列表关联起来,这样就可以通过一个节点 `x` 找到它的所有相邻节点。
|
||||
|
||||
邻接矩阵则是一个二维布尔数组,我们权且称为 `matrix`,如果节点 `x` 和 `y` 是相连的,那么就把 `matrix[x][y]` 设为 `true`(上图中绿色的方格代表 `true`)。如果想找节点 `x` 的邻居,去扫一圈 `matrix[x][..]` 就行了。
|
||||
|
||||
如果用代码的形式来表现,邻接表和邻接矩阵大概长这样:
|
||||
|
||||
```java
|
||||
// 邻接表
|
||||
// graph[x] 存储 x 的所有邻居节点
|
||||
List<Integer>[] graph;
|
||||
|
||||
// 邻接矩阵
|
||||
// matrix[x][y] 记录 x 是否有一条指向 y 的边
|
||||
boolean[][] matrix;
|
||||
```
|
||||
|
||||
**那么,为什么有这两种存储图的方式呢?肯定是因为他们各有优劣**。
|
||||
|
||||
对于邻接表,好处是占用的空间少。
|
||||
|
||||
你看邻接矩阵里面空着那么多位置,肯定需要更多的存储空间。
|
||||
|
||||
但是,邻接表无法快速判断两个节点是否相邻。
|
||||
|
||||
比如说我想判断节点 `1` 是否和节点 `3` 相邻,我要去邻接表里 `1` 对应的邻居列表里查找 `3` 是否存在。但对于邻接矩阵就简单了,只要看看 `matrix[1][3]` 就知道了,效率高。
|
||||
|
||||
所以说,使用哪一种方式实现图,要看具体情况。
|
||||
|
||||
> PS:在常规的算法题中,邻接表的使用会更频繁一些,主要是因为操作起来较为简单,但这不意味着邻接矩阵应该被轻视。矩阵是一个强有力的数学工具,图的一些隐晦性质可以借助精妙的矩阵运算展现出来。不过本文不准备引入数学内容,所以有兴趣的读者可以自行搜索学习。
|
||||
|
||||
最后,我们再明确一个图论中特有的**度**(degree)的概念,在无向图中,「度」就是每个节点相连的边的条数。
|
||||
|
||||
由于有向图的边有方向,所以有向图中每个节点「度」被细分为**入度**(indegree)和**出度**(outdegree),比如下图:
|
||||
|
||||

|
||||
|
||||
其中节点 `3` 的入度为 3(有三条边指向它),出度为 1(它有 1 条边指向别的节点)。
|
||||
|
||||
好了,对于「图」这种数据结构,能看懂上面这些就绰绰够用了。
|
||||
|
||||
那你可能会问,我们上面说的这个图的模型仅仅是「有向无权图」,不是还有什么加权图,无向图,等等……
|
||||
|
||||
**其实,这些更复杂的模型都是基于这个最简单的图衍生出来的**。
|
||||
|
||||
**有向加权图怎么实现**?很简单呀:
|
||||
|
||||
如果是邻接表,我们不仅仅存储某个节点 `x` 的所有邻居节点,还存储 `x` 到每个邻居的权重,不就实现加权有向图了吗?
|
||||
|
||||
如果是邻接矩阵,`matrix[x][y]` 不再是布尔值,而是一个 int 值,0 表示没有连接,其他值表示权重,不就变成加权有向图了吗?
|
||||
|
||||
如果用代码的形式来表现,大概长这样:
|
||||
|
||||
```java
|
||||
// 邻接表
|
||||
// graph[x] 存储 x 的所有邻居节点以及对应的权重
|
||||
List<int[]>[] graph;
|
||||
|
||||
// 邻接矩阵
|
||||
// matrix[x][y] 记录 x 指向 y 的边的权重,0 表示不相邻
|
||||
int[][] matrix;
|
||||
```
|
||||
|
||||
**无向图怎么实现**?也很简单,所谓的「无向」,是不是等同于「双向」?
|
||||
|
||||

|
||||
|
||||
如果连接无向图中的节点 `x` 和 `y`,把 `matrix[x][y]` 和 `matrix[y][x]` 都变成 `true` 不就行了;邻接表也是类似的操作,在 `x` 的邻居列表里添加 `y`,同时在 `y` 的邻居列表里添加 `x`。
|
||||
|
||||
把上面的技巧合起来,就变成了无向加权图……
|
||||
|
||||
好了,关于图的基本介绍就到这里,现在不管来什么乱七八糟的图,你心里应该都有底了。
|
||||
|
||||
下面来看看所有数据结构都逃不过的问题:遍历。
|
||||
|
||||
### 图的遍历
|
||||
|
||||
**[学习数据结构和算法的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法) 说过,各种数据结构被发明出来无非就是为了遍历和访问,所以「遍历」是所有数据结构的基础**。
|
||||
|
||||
图怎么遍历?还是那句话,参考多叉树,多叉树的 DFS 遍历框架如下:
|
||||
|
||||
```java
|
||||
/* 多叉树遍历框架 */
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) return;
|
||||
// 前序位置
|
||||
for (TreeNode child : root.children) {
|
||||
traverse(child);
|
||||
}
|
||||
// 后序位置
|
||||
}
|
||||
```
|
||||
|
||||
图和多叉树最大的区别是,图是可能包含环的,你从图的某一个节点开始遍历,有可能走了一圈又回到这个节点,而树不会出现这种情况,从某个节点出发必然走到叶子节点,绝不可能回到它自身。
|
||||
|
||||
所以,如果图包含环,遍历框架就要一个 `visited` 数组进行辅助:
|
||||
|
||||
```java
|
||||
// 记录被遍历过的节点
|
||||
boolean[] visited;
|
||||
// 记录从起点到当前节点的路径
|
||||
boolean[] onPath;
|
||||
|
||||
/* 图遍历框架 */
|
||||
void traverse(Graph graph, int s) {
|
||||
if (visited[s]) return;
|
||||
// 经过节点 s,标记为已遍历
|
||||
visited[s] = true;
|
||||
// 做选择:标记节点 s 在路径上
|
||||
onPath[s] = true;
|
||||
for (int neighbor : graph.neighbors(s)) {
|
||||
traverse(graph, neighbor);
|
||||
}
|
||||
// 撤销选择:节点 s 离开路径
|
||||
onPath[s] = false;
|
||||
}
|
||||
```
|
||||
|
||||
注意 `visited` 数组和 `onPath` 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
|
||||
|
||||

|
||||
|
||||
**上述 GIF 描述了递归遍历二叉树的过程,在 `visited` 中被标记为 true 的节点用灰色表示,在 `onPath` 中被标记为 true 的节点用绿色表示**,类比贪吃蛇游戏,`visited` 记录蛇经过过的格子,而 `onPath` 仅仅记录蛇身。在图的遍历过程中,`onPath` 用于判断是否成环,类比当贪吃蛇自己咬到自己(成环)的场景,这下你可以理解它们二者的区别了吧。
|
||||
|
||||
如果让你处理路径相关的问题,这个 `onPath` 变量是肯定会被用到的,比如 [拓扑排序](https://labuladong.github.io/article/fname.html?fname=拓扑排序) 中就有运用。
|
||||
|
||||
另外,你应该注意到了,这个 `onPath` 数组的操作很像前文 [回溯算法核心套路](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 中做「做选择」和「撤销选择」,区别在于位置:回溯算法的「做选择」和「撤销选择」在 for 循环里面,而对 `onPath` 数组的操作在 for 循环外面。
|
||||
|
||||
为什么有这个区别呢?这就是前文 [回溯算法核心套路](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 中讲到的回溯算法和 DFS 算法的区别所在:回溯算法关注的不是节点,而是树枝。不信你看前文画的回溯树,我们需要在「树枝」上做选择和撤销选择:
|
||||
|
||||
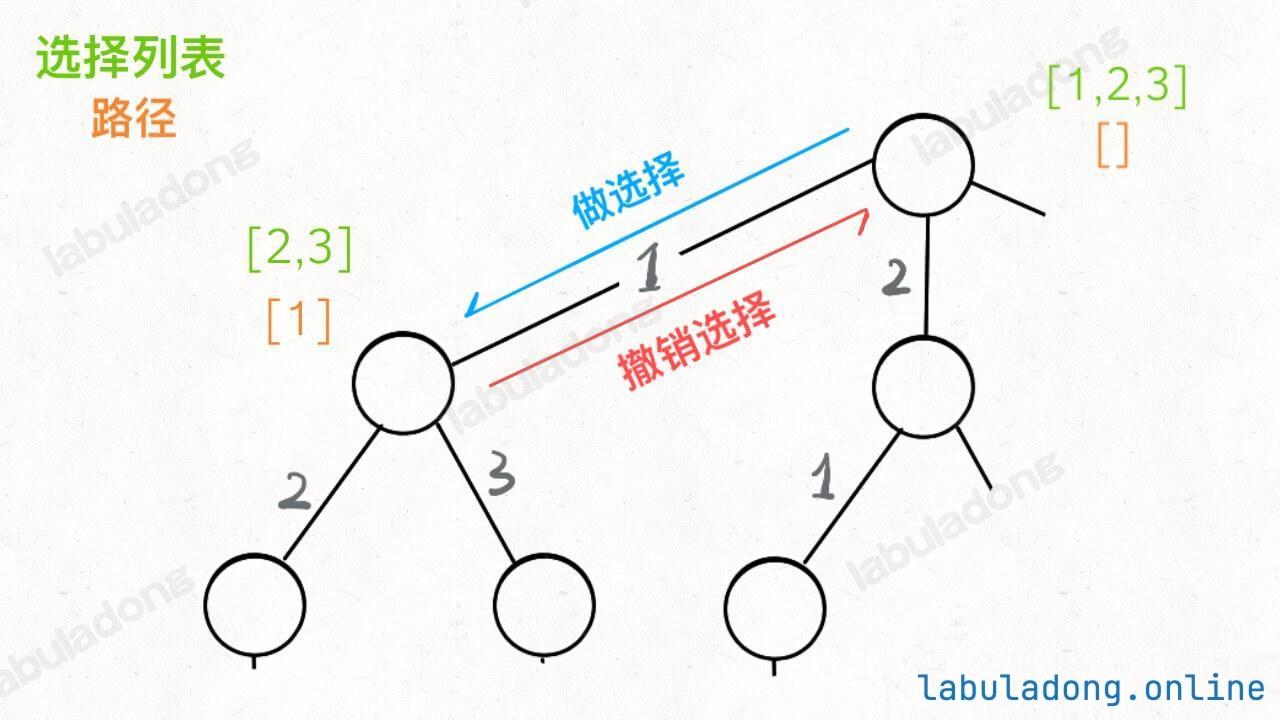
|
||||
|
||||
他们的区别可以这样反应到代码上:
|
||||
|
||||
```java
|
||||
// DFS 算法,关注点在节点
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) return;
|
||||
printf("进入节点 %s", root);
|
||||
for (TreeNode child : root.children) {
|
||||
traverse(child);
|
||||
}
|
||||
printf("离开节点 %s", root);
|
||||
}
|
||||
|
||||
// 回溯算法,关注点在树枝
|
||||
void backtrack(TreeNode root) {
|
||||
if (root == null) return;
|
||||
for (TreeNode child : root.children) {
|
||||
// 做选择
|
||||
printf("从 %s 到 %s", root, child);
|
||||
backtrack(child);
|
||||
// 撤销选择
|
||||
printf("从 %s 到 %s", child, root);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
如果执行这段代码,你会发现根节点被漏掉了:
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
if (root == null) return;
|
||||
for (TreeNode child : root.children) {
|
||||
printf("进入节点 %s", child);
|
||||
traverse(child);
|
||||
printf("离开节点 %s", child);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
所以对于这里「图」的遍历,我们应该用 DFS 算法,即把 `onPath` 的操作放到 for 循环外面,否则会漏掉记录起始点的遍历。
|
||||
|
||||
说了这么多 `onPath` 数组,再说下 `visited` 数组,其目的很明显了,由于图可能含有环,`visited` 数组就是防止递归重复遍历同一个节点进入死循环的。
|
||||
|
||||
当然,如果题目告诉你图中不含环,可以把 `visited` 数组都省掉,基本就是多叉树的遍历。
|
||||
|
||||
### 题目实践
|
||||
|
||||
下面我们来看力扣第 797 题「所有可能路径」,函数签名如下:
|
||||
|
||||
```java
|
||||
List<List<Integer>> allPathsSourceTarget(int[][] graph);
|
||||
```
|
||||
|
||||
题目输入一幅**有向无环图**,这个图包含 `n` 个节点,标号为 `0, 1, 2,..., n - 1`,请你计算所有从节点 `0` 到节点 `n - 1` 的路径。
|
||||
|
||||
输入的这个 `graph` 其实就是「邻接表」表示的一幅图,`graph[i]` 存储这节点 `i` 的所有邻居节点。
|
||||
|
||||
比如输入 `graph = [[1,2],[3],[3],[]]`,就代表下面这幅图:
|
||||
|
||||

|
||||
|
||||
算法应该返回 `[[0,1,3],[0,2,3]]`,即 `0` 到 `3` 的所有路径。
|
||||
|
||||
**解法很简单,以 `0` 为起点遍历图,同时记录遍历过的路径,当遍历到终点时将路径记录下来即可**。
|
||||
|
||||
既然输入的图是无环的,我们就不需要 `visited` 数组辅助了,直接套用图的遍历框架:
|
||||
|
||||
```java
|
||||
// 记录所有路径
|
||||
List<List<Integer>> res = new LinkedList<>();
|
||||
|
||||
public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
|
||||
// 维护递归过程中经过的路径
|
||||
LinkedList<Integer> path = new LinkedList<>();
|
||||
traverse(graph, 0, path);
|
||||
return res;
|
||||
}
|
||||
|
||||
/* 图的遍历框架 */
|
||||
void traverse(int[][] graph, int s, LinkedList<Integer> path) {
|
||||
// 添加节点 s 到路径
|
||||
path.addLast(s);
|
||||
|
||||
int n = graph.length;
|
||||
if (s == n - 1) {
|
||||
// 到达终点
|
||||
res.add(new LinkedList<>(path));
|
||||
// 可以在这直接 return,但要 removeLast 正确维护 path
|
||||
// path.removeLast();
|
||||
// return;
|
||||
// 不 return 也可以,因为图中不包含环,不会出现无限递归
|
||||
}
|
||||
|
||||
// 递归每个相邻节点
|
||||
for (int v : graph[s]) {
|
||||
traverse(graph, v, path);
|
||||
}
|
||||
|
||||
// 从路径移出节点 s
|
||||
path.removeLast();
|
||||
}
|
||||
```
|
||||
|
||||
这道题就这样解决了,注意 Java 的语言特性,因为 Java 函数参数传的是对象引用,所以向 `res` 中添加 `path` 时需要拷贝一个新的列表,否则最终 `res` 中的列表都是空的。
|
||||
|
||||
最后总结一下,图的存储方式主要有邻接表和邻接矩阵,无论什么花里胡哨的图,都可以用这两种方式存储。
|
||||
|
||||
在笔试中,最常考的算法是图的遍历,和多叉树的遍历框架是非常类似的。
|
||||
|
||||
当然,图还会有很多其他的有趣算法,比如 [二分图判定](https://labuladong.github.io/article/fname.html?fname=二分图),[环检测和拓扑排序](https://labuladong.github.io/article/fname.html?fname=拓扑排序)(编译器循环引用检测就是类似的算法),[最小生成树](https://labuladong.github.io/article/fname.html?fname=kruskal),[Dijkstra 最短路径算法](https://labuladong.github.io/article/fname.html?fname=dijkstra算法) 等等,有兴趣的读者可以去看看,本文就到这了。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [Prim 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=prim算法)
|
||||
- [一文秒杀所有岛屿题目](https://labuladong.github.io/article/fname.html?fname=岛屿题目)
|
||||
- [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结)
|
||||
- [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
|
||||
- [众里寻他千百度:名流问题](https://labuladong.github.io/article/fname.html?fname=名人问题)
|
||||
- [前缀树算法模板秒杀五道算法题](https://labuladong.github.io/article/fname.html?fname=trie)
|
||||
- [回溯算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [环检测及拓扑排序算法](https://labuladong.github.io/article/fname.html?fname=拓扑排序)
|
||||
- [算法学习和心流体验](https://labuladong.github.io/article/fname.html?fname=心流)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [133. Clone Graph](https://leetcode.com/problems/clone-graph/?show=1) | [133. 克隆图](https://leetcode.cn/problems/clone-graph/?show=1) |
|
||||
| [200. Number of Islands](https://leetcode.com/problems/number-of-islands/?show=1) | [200. 岛屿数量](https://leetcode.cn/problems/number-of-islands/?show=1) |
|
||||
| [2049. Count Nodes With the Highest Score](https://leetcode.com/problems/count-nodes-with-the-highest-score/?show=1) | [2049. 统计最高分的节点数目](https://leetcode.cn/problems/count-nodes-with-the-highest-score/?show=1) |
|
||||
| - | [剑指 Offer II 110. 所有路径](https://leetcode.cn/problems/bP4bmD/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 拆解复杂问题:实现计算器
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -309,6 +305,20 @@ def calculate(s: str) -> int:
|
|||
|
||||
**退而求其次是一种很聪明策略**。你想想啊,假设这是一道考试题,你不会实现这个计算器,但是你写了字符串转整数的算法并指出了容易溢出的陷阱,那起码可以得 20 分吧;如果你能够处理加减法,那可以得 40 分吧;如果你能处理加减乘除四则运算,那起码够 70 分了;再加上处理空格字符,80 有了吧。我就是不会处理括号,那就算了,80 已经很 OK 了好不好。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [算法笔试「骗分」套路](https://labuladong.github.io/article/fname.html?fname=刷题技巧)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -0,0 +1,607 @@
|
|||
# 拓扑排序详解及运用
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [207. Course Schedule](https://leetcode.com/problems/course-schedule/) | [207. 课程表](https://leetcode.cn/problems/course-schedule/) | 🟠
|
||||
| [210. Course Schedule II](https://leetcode.com/problems/course-schedule-ii/) | [210. 课程表 II](https://leetcode.cn/problems/course-schedule-ii/) | 🟠
|
||||
| - | [剑指 Offer II 113. 课程顺序](https://leetcode.cn/problems/QA2IGt/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
> 本文有视频版:[拓扑排序详解及应用](https://www.bilibili.com/video/BV1kW4y1y7Ew/)
|
||||
|
||||
图这种数据结构有一些比较特殊的算法,比如二分图判断,有环图无环图的判断,拓扑排序,以及最经典的最小生成树,单源最短路径问题,更难的就是类似网络流这样的问题。
|
||||
|
||||
不过以我的经验呢,像网络流这种问题,你又不是打竞赛的,没时间的话就没必要学了;像 [最小生成树](https://labuladong.github.io/article/fname.html?fname=prim算法) 和 [最短路径问题](https://labuladong.github.io/article/fname.html?fname=dijkstra算法),虽然从刷题的角度用到的不多,但它们属于经典算法,学有余力可以掌握一下;像 [二分图判定](https://labuladong.github.io/article/fname.html?fname=二分图)、拓扑排序这一类,属于比较基本且有用的算法,应该比较熟练地掌握。
|
||||
|
||||
**那么本文就结合具体的算法题,来说两个图论算法:有向图的环检测、拓扑排序算法**。
|
||||
|
||||
这两个算法既可以用 DFS 思路解决,也可以用 BFS 思路解决,相对而言 BFS 解法从代码实现上看更简洁一些,但 DFS 解法有助于你进一步理解递归遍历数据结构的奥义,所以本文中我先讲 DFS 遍历的思路,再讲 BFS 遍历的思路。
|
||||
|
||||
### 环检测算法(DFS 版本)
|
||||
|
||||
先来看看力扣第 207 题「课程表」:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
boolean canFinish(int numCourses, int[][] prerequisites);
|
||||
```
|
||||
|
||||
题目应该不难理解,什么时候无法修完所有课程?当存在循环依赖的时候。
|
||||
|
||||
其实这种场景在现实生活中也十分常见,比如我们写代码 import 包也是一个例子,必须合理设计代码目录结构,否则会出现循环依赖,编译器会报错,所以编译器实际上也使用了类似算法来判断你的代码是否能够成功编译。
|
||||
|
||||
**看到依赖问题,首先想到的就是把问题转化成「有向图」这种数据结构,只要图中存在环,那就说明存在循环依赖**。
|
||||
|
||||
具体来说,我们首先可以把课程看成「有向图」中的节点,节点编号分别是 `0, 1, ..., numCourses-1`,把课程之间的依赖关系看做节点之间的有向边。
|
||||
|
||||
比如说必须修完课程 `1` 才能去修课程 `3`,那么就有一条有向边从节点 `1` 指向 `3`。
|
||||
|
||||
所以我们可以根据题目输入的 `prerequisites` 数组生成一幅类似这样的图:
|
||||
|
||||

|
||||
|
||||
**如果发现这幅有向图中存在环,那就说明课程之间存在循环依赖,肯定没办法全部上完;反之,如果没有环,那么肯定能上完全部课程**。
|
||||
|
||||
好,那么想解决这个问题,首先我们要把题目的输入转化成一幅有向图,然后再判断图中是否存在环。
|
||||
|
||||
如何转换成图呢?我们前文 [图论基础](https://labuladong.github.io/article/fname.html?fname=图) 写过图的两种存储形式,邻接矩阵和邻接表。
|
||||
|
||||
以我刷题的经验,常见的存储方式是使用邻接表,比如下面这种结构:
|
||||
|
||||
```java
|
||||
List<Integer>[] graph;
|
||||
```
|
||||
|
||||
**`graph[s]` 是一个列表,存储着节点 `s` 所指向的节点**。
|
||||
|
||||
所以我们首先可以写一个建图函数:
|
||||
|
||||
```java
|
||||
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
|
||||
// 图中共有 numCourses 个节点
|
||||
List<Integer>[] graph = new LinkedList[numCourses];
|
||||
for (int i = 0; i < numCourses; i++) {
|
||||
graph[i] = new LinkedList<>();
|
||||
}
|
||||
for (int[] edge : prerequisites) {
|
||||
int from = edge[1], to = edge[0];
|
||||
// 添加一条从 from 指向 to 的有向边
|
||||
// 边的方向是「被依赖」关系,即修完课程 from 才能修课程 to
|
||||
graph[from].add(to);
|
||||
}
|
||||
return graph;
|
||||
}
|
||||
```
|
||||
|
||||
图建出来了,怎么判断图中有没有环呢?
|
||||
|
||||
**先不要急,我们先来思考如何遍历这幅图,只要会遍历,就可以判断图中是否存在环了**。
|
||||
|
||||
前文 [图论基础](https://labuladong.github.io/article/fname.html?fname=图) 写了 DFS 算法遍历图的框架,无非就是从多叉树遍历框架扩展出来的,加了个 `visited` 数组罢了:
|
||||
|
||||
```java
|
||||
// 防止重复遍历同一个节点
|
||||
boolean[] visited;
|
||||
// 从节点 s 开始 DFS 遍历,将遍历过的节点标记为 true
|
||||
void traverse(List<Integer>[] graph, int s) {
|
||||
if (visited[s]) {
|
||||
return;
|
||||
}
|
||||
/* 前序遍历代码位置 */
|
||||
// 将当前节点标记为已遍历
|
||||
visited[s] = true;
|
||||
for (int t : graph[s]) {
|
||||
traverse(graph, t);
|
||||
}
|
||||
/* 后序遍历代码位置 */
|
||||
}
|
||||
```
|
||||
|
||||
那么我们就可以直接套用这个遍历代码:
|
||||
|
||||
```java
|
||||
// 防止重复遍历同一个节点
|
||||
boolean[] visited;
|
||||
|
||||
boolean canFinish(int numCourses, int[][] prerequisites) {
|
||||
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
|
||||
|
||||
visited = new boolean[numCourses];
|
||||
for (int i = 0; i < numCourses; i++) {
|
||||
traverse(graph, i);
|
||||
}
|
||||
}
|
||||
|
||||
void traverse(List<Integer>[] graph, int s) {
|
||||
// 代码见上文
|
||||
}
|
||||
```
|
||||
|
||||
注意图中并不是所有节点都相连,所以要用一个 for 循环将所有节点都作为起点调用一次 DFS 搜索算法。
|
||||
|
||||
这样,就能遍历这幅图中的所有节点了,你打印一下 `visited` 数组,应该全是 true。
|
||||
|
||||
前文 [学习数据结构和算法的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法) 说过,图的遍历和遍历多叉树差不多,所以到这里你应该都能很容易理解。
|
||||
|
||||
现在可以思考如何判断这幅图中是否存在环。
|
||||
|
||||
我们前文 [回溯算法核心套路详解](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 说过,你可以把递归函数看成一个在递归树上游走的指针,这里也是类似的:
|
||||
|
||||
你也可以把 `traverse` 看做在图中节点上游走的指针,只需要再添加一个布尔数组 `onPath` 记录当前 `traverse` 经过的路径:
|
||||
|
||||
```java
|
||||
boolean[] onPath;
|
||||
boolean[] visited;
|
||||
|
||||
boolean hasCycle = false;
|
||||
|
||||
void traverse(List<Integer>[] graph, int s) {
|
||||
if (onPath[s]) {
|
||||
// 发现环!!!
|
||||
hasCycle = true;
|
||||
}
|
||||
if (visited[s] || hasCycle) {
|
||||
return;
|
||||
}
|
||||
// 将节点 s 标记为已遍历
|
||||
visited[s] = true;
|
||||
// 开始遍历节点 s
|
||||
onPath[s] = true;
|
||||
for (int t : graph[s]) {
|
||||
traverse(graph, t);
|
||||
}
|
||||
// 节点 s 遍历完成
|
||||
onPath[s] = false;
|
||||
}
|
||||
```
|
||||
|
||||
这里就有点回溯算法的味道了,在进入节点 `s` 的时候将 `onPath[s]` 标记为 true,离开时标记回 false,如果发现 `onPath[s]` 已经被标记,说明出现了环。
|
||||
|
||||
注意 `visited` 数组和 `onPath` 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
|
||||
|
||||

|
||||
|
||||
**上述 GIF 描述了递归遍历二叉树的过程,在 `visited` 中被标记为 true 的节点用灰色表示,在 `onPath` 中被标记为 true 的节点用绿色表示**。
|
||||
|
||||
> PS:类比贪吃蛇游戏,`visited` 记录蛇经过过的格子,而 `onPath` 仅仅记录蛇身。`onPath` 用于判断是否成环,类比当贪吃蛇自己咬到自己(成环)的场景。
|
||||
|
||||
这样,就可以在遍历图的过程中顺便判断是否存在环了,完整代码如下:
|
||||
|
||||
```java
|
||||
// 记录一次递归堆栈中的节点
|
||||
boolean[] onPath;
|
||||
// 记录遍历过的节点,防止走回头路
|
||||
boolean[] visited;
|
||||
// 记录图中是否有环
|
||||
boolean hasCycle = false;
|
||||
|
||||
boolean canFinish(int numCourses, int[][] prerequisites) {
|
||||
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
|
||||
|
||||
visited = new boolean[numCourses];
|
||||
onPath = new boolean[numCourses];
|
||||
|
||||
for (int i = 0; i < numCourses; i++) {
|
||||
// 遍历图中的所有节点
|
||||
traverse(graph, i);
|
||||
}
|
||||
// 只要没有循环依赖可以完成所有课程
|
||||
return !hasCycle;
|
||||
}
|
||||
|
||||
void traverse(List<Integer>[] graph, int s) {
|
||||
if (onPath[s]) {
|
||||
// 出现环
|
||||
hasCycle = true;
|
||||
}
|
||||
|
||||
if (visited[s] || hasCycle) {
|
||||
// 如果已经找到了环,也不用再遍历了
|
||||
return;
|
||||
}
|
||||
// 前序代码位置
|
||||
visited[s] = true;
|
||||
onPath[s] = true;
|
||||
for (int t : graph[s]) {
|
||||
traverse(graph, t);
|
||||
}
|
||||
// 后序代码位置
|
||||
onPath[s] = false;
|
||||
}
|
||||
|
||||
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
|
||||
// 代码见前文
|
||||
}
|
||||
```
|
||||
|
||||
这道题就解决了,核心就是判断一幅有向图中是否存在环。
|
||||
|
||||
不过如果出题人继续恶心你,让你不仅要判断是否存在环,还要返回这个环具体有哪些节点,怎么办?
|
||||
|
||||
你可能说,`onPath` 里面为 true 的索引,不就是组成环的节点编号吗?
|
||||
|
||||
不是的,假设下图中绿色的节点是递归的路径,它们在 `onPath` 中的值都是 true,但显然成环的节点只是其中的一部分:
|
||||
|
||||

|
||||
|
||||
这个问题留给大家思考,我会在公众号留言区置顶正确的答案。
|
||||
|
||||
**那么接下来,我们来再讲一个经典的图算法:拓扑排序**。
|
||||
|
||||
### 拓扑排序算法(DFS 版本)
|
||||
|
||||
看下力扣第 210 题「课程表 II」:
|
||||
|
||||

|
||||
|
||||
这道题就是上道题的进阶版,不是仅仅让你判断是否可以完成所有课程,而是进一步让你返回一个合理的上课顺序,保证开始修每个课程时,前置的课程都已经修完。
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int[] findOrder(int numCourses, int[][] prerequisites);
|
||||
```
|
||||
|
||||
这里我先说一下拓扑排序(Topological Sorting)这个名词,网上搜出来的定义很数学,这里干脆用百度百科的一幅图来让你直观地感受下:
|
||||
|
||||

|
||||
|
||||
> PS:图片中拓扑排序的结果有误,`C7->C8->C6` 应该改为 `C6->C7->C8`。
|
||||
|
||||
**直观地说就是,让你把一幅图「拉平」,而且这个「拉平」的图里面,所有箭头方向都是一致的**,比如上图所有箭头都是朝右的。
|
||||
|
||||
很显然,如果一幅有向图中存在环,是无法进行拓扑排序的,因为肯定做不到所有箭头方向一致;反过来,如果一幅图是「有向无环图」,那么一定可以进行拓扑排序。
|
||||
|
||||
但是我们这道题和拓扑排序有什么关系呢?
|
||||
|
||||
**其实也不难看出来,如果把课程抽象成节点,课程之间的依赖关系抽象成有向边,那么这幅图的拓扑排序结果就是上课顺序**。
|
||||
|
||||
首先,我们先判断一下题目输入的课程依赖是否成环,成环的话是无法进行拓扑排序的,所以我们可以复用上一道题的主函数:
|
||||
|
||||
```java
|
||||
public int[] findOrder(int numCourses, int[][] prerequisites) {
|
||||
if (!canFinish(numCourses, prerequisites)) {
|
||||
// 不可能完成所有课程
|
||||
return new int[]{};
|
||||
}
|
||||
// ...
|
||||
}
|
||||
```
|
||||
|
||||
那么关键问题来了,如何进行拓扑排序?是不是又要秀什么高大上的技巧了?
|
||||
|
||||
**其实特别简单,将后序遍历的结果进行反转,就是拓扑排序的结果**。
|
||||
|
||||
> PS:有的读者提到,他在网上看到的拓扑排序算法不用对后序遍历结果进行反转,这是为什么呢?
|
||||
|
||||
你确实可以看到这样的解法,原因是他建图的时候对边的定义和我不同。我建的图中箭头方向是「被依赖」关系,比如节点 `1` 指向 `2`,含义是节点 `1` 被节点 `2` 依赖,即做完 `1` 才能去做 `2`,
|
||||
|
||||
如果你反过来,把有向边定义为「依赖」关系,那么整幅图中边全部反转,就可以不对后序遍历结果反转。具体来说,就是把我的解法代码中 `graph[from].add(to);` 改成 `graph[to].add(from);` 就可以不反转了。
|
||||
|
||||
**不过呢,现实中一般都是从初级任务指向进阶任务,所以像我这样把边定义为「被依赖」关系可能比较符合我们的认知习惯**。
|
||||
|
||||
直接看解法代码吧,在上一题环检测的代码基础上添加了记录后序遍历结果的逻辑:
|
||||
|
||||
```java
|
||||
// 记录后序遍历结果
|
||||
List<Integer> postorder = new ArrayList<>();
|
||||
// 记录是否存在环
|
||||
boolean hasCycle = false;
|
||||
boolean[] visited, onPath;
|
||||
|
||||
// 主函数
|
||||
public int[] findOrder(int numCourses, int[][] prerequisites) {
|
||||
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
|
||||
visited = new boolean[numCourses];
|
||||
onPath = new boolean[numCourses];
|
||||
// 遍历图
|
||||
for (int i = 0; i < numCourses; i++) {
|
||||
traverse(graph, i);
|
||||
}
|
||||
// 有环图无法进行拓扑排序
|
||||
if (hasCycle) {
|
||||
return new int[]{};
|
||||
}
|
||||
// 逆后序遍历结果即为拓扑排序结果
|
||||
Collections.reverse(postorder);
|
||||
int[] res = new int[numCourses];
|
||||
for (int i = 0; i < numCourses; i++) {
|
||||
res[i] = postorder.get(i);
|
||||
}
|
||||
return res;
|
||||
}
|
||||
|
||||
// 图遍历函数
|
||||
void traverse(List<Integer>[] graph, int s) {
|
||||
if (onPath[s]) {
|
||||
// 发现环
|
||||
hasCycle = true;
|
||||
}
|
||||
if (visited[s] || hasCycle) {
|
||||
return;
|
||||
}
|
||||
// 前序遍历位置
|
||||
onPath[s] = true;
|
||||
visited[s] = true;
|
||||
for (int t : graph[s]) {
|
||||
traverse(graph, t);
|
||||
}
|
||||
// 后序遍历位置
|
||||
postorder.add(s);
|
||||
onPath[s] = false;
|
||||
}
|
||||
|
||||
// 建图函数
|
||||
List<Integer>[] buildGraph(int numCourses, int[][] prerequisites) {
|
||||
// 代码见前文
|
||||
}
|
||||
```
|
||||
|
||||
代码虽然看起来多,但是逻辑应该是很清楚的,只要图中无环,那么我们就调用 `traverse` 函数对图进行 DFS 遍历,记录后序遍历结果,最后把后序遍历结果反转,作为最终的答案。
|
||||
|
||||
**那么为什么后序遍历的反转结果就是拓扑排序呢**?
|
||||
|
||||
我这里也避免数学证明,用一个直观地例子来解释,我们就说二叉树,这是我们说过很多次的二叉树遍历框架:
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
// 前序遍历代码位置
|
||||
traverse(root.left)
|
||||
// 中序遍历代码位置
|
||||
traverse(root.right)
|
||||
// 后序遍历代码位置
|
||||
}
|
||||
```
|
||||
|
||||
二叉树的后序遍历是什么时候?遍历完左右子树之后才会执行后序遍历位置的代码。换句话说,当左右子树的节点都被装到结果列表里面了,根节点才会被装进去。
|
||||
|
||||
**后序遍历的这一特点很重要,之所以拓扑排序的基础是后序遍历,是因为一个任务必须等到它依赖的所有任务都完成之后才能开始开始执行**。
|
||||
|
||||
你把二叉树理解成一幅有向图,边的方向是由父节点指向子节点,那么就是下图这样:
|
||||
|
||||

|
||||
|
||||
按照我们的定义,边的含义是「被依赖」关系,那么上图的拓扑排序应该首先是节点 `1`,然后是 `2, 3`,以此类推。
|
||||
|
||||
但显然标准的后序遍历结果不满足拓扑排序,而如果把后序遍历结果反转,就是拓扑排序结果了:
|
||||
|
||||

|
||||
|
||||
以上,我直观解释了一下为什么「拓扑排序的结果就是反转之后的后序遍历结果」,当然,我的解释并没有严格的数学证明,有兴趣的读者可以自己查一下。
|
||||
|
||||
### 环检测算法(BFS 版本)
|
||||
|
||||
刚才讲了用 DFS 算法利用 `onPath` 数组判断是否存在环;也讲了用 DFS 算法利用逆后序遍历进行拓扑排序。
|
||||
|
||||
其实 BFS 算法借助 `indegree` 数组记录每个节点的「入度」,也可以实现这两个算法。不熟悉 BFS 算法的读者可阅读前文 [BFS 算法核心框架](https://labuladong.github.io/article/fname.html?fname=BFS框架)。
|
||||
|
||||
所谓「出度」和「入度」是「有向图」中的概念,很直观:如果一个节点 `x` 有 `a` 条边指向别的节点,同时被 `b` 条边所指,则称节点 `x` 的出度为 `a`,入度为 `b`。
|
||||
|
||||
先说环检测算法,直接看 BFS 的解法代码:
|
||||
|
||||
```java
|
||||
// 主函数
|
||||
public boolean canFinish(int numCourses, int[][] prerequisites) {
|
||||
// 建图,有向边代表「被依赖」关系
|
||||
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
|
||||
// 构建入度数组
|
||||
int[] indegree = new int[numCourses];
|
||||
for (int[] edge : prerequisites) {
|
||||
int from = edge[1], to = edge[0];
|
||||
// 节点 to 的入度加一
|
||||
indegree[to]++;
|
||||
}
|
||||
|
||||
// 根据入度初始化队列中的节点
|
||||
Queue<Integer> q = new LinkedList<>();
|
||||
for (int i = 0; i < numCourses; i++) {
|
||||
if (indegree[i] == 0) {
|
||||
// 节点 i 没有入度,即没有依赖的节点
|
||||
// 可以作为拓扑排序的起点,加入队列
|
||||
q.offer(i);
|
||||
}
|
||||
}
|
||||
|
||||
// 记录遍历的节点个数
|
||||
int count = 0;
|
||||
// 开始执行 BFS 循环
|
||||
while (!q.isEmpty()) {
|
||||
// 弹出节点 cur,并将它指向的节点的入度减一
|
||||
int cur = q.poll();
|
||||
count++;
|
||||
for (int next : graph[cur]) {
|
||||
indegree[next]--;
|
||||
if (indegree[next] == 0) {
|
||||
// 如果入度变为 0,说明 next 依赖的节点都已被遍历
|
||||
q.offer(next);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 如果所有节点都被遍历过,说明不成环
|
||||
return count == numCourses;
|
||||
}
|
||||
|
||||
|
||||
// 建图函数
|
||||
List<Integer>[] buildGraph(int n, int[][] edges) {
|
||||
// 见前文
|
||||
}
|
||||
```
|
||||
|
||||
我先总结下这段 BFS 算法的思路:
|
||||
|
||||
1、构建邻接表,和之前一样,边的方向表示「被依赖」关系。
|
||||
|
||||
2、构建一个 `indegree` 数组记录每个节点的入度,即 `indegree[i]` 记录节点 `i` 的入度。
|
||||
|
||||
3、对 BFS 队列进行初始化,将入度为 0 的节点首先装入队列。
|
||||
|
||||
**4、开始执行 BFS 循环,不断弹出队列中的节点,减少相邻节点的入度,并将入度变为 0 的节点加入队列**。
|
||||
|
||||
**5、如果最终所有节点都被遍历过(`count` 等于节点数),则说明不存在环,反之则说明存在环**。
|
||||
|
||||
我画个图你就容易理解了,比如下面这幅图,节点中的数字代表该节点的入度:
|
||||
|
||||

|
||||
|
||||
队列进行初始化后,入度为 0 的节点首先被加入队列:
|
||||
|
||||

|
||||
|
||||
开始执行 BFS 循环,从队列中弹出一个节点,减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
|
||||
|
||||

|
||||
|
||||
继续从队列弹出节点,并减少相邻节点的入度,这一次没有新产生的入度为 0 的节点:
|
||||
|
||||

|
||||
|
||||
继续从队列弹出节点,并减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
|
||||
|
||||

|
||||
|
||||
继续弹出节点,直到队列为空:
|
||||
|
||||

|
||||
|
||||
这时候,所有节点都被遍历过一遍,也就说明图中不存在环。
|
||||
|
||||
反过来说,如果按照上述逻辑执行 BFS 算法,存在节点没有被遍历,则说明成环。
|
||||
|
||||
比如下面这种情况,队列中最初只有一个入度为 0 的节点:
|
||||
|
||||

|
||||
|
||||
当弹出这个节点并减小相邻节点的入度之后队列为空,但并没有产生新的入度为 0 的节点加入队列,所以 BFS 算法终止:
|
||||
|
||||

|
||||
|
||||
你看到了,如果存在节点没有被遍历,那么说明图中存在环,现在回头去看 BFS 的代码,你应该就很容易理解其中的逻辑了。
|
||||
|
||||
### 拓扑排序算法(BFS 版本)
|
||||
|
||||
**如果你能看懂 BFS 版本的环检测算法,那么就很容易得到 BFS 版本的拓扑排序算法,因为节点的遍历顺序就是拓扑排序的结果**。
|
||||
|
||||
比如刚才举的第一个例子,下图每个节点中的值即入队的顺序:
|
||||
|
||||

|
||||
|
||||
显然,这个顺序就是一个可行的拓扑排序结果。
|
||||
|
||||
所以,我们稍微修改一下 BFS 版本的环检测算法,记录节点的遍历顺序即可得到拓扑排序的结果:
|
||||
|
||||
```java
|
||||
// 主函数
|
||||
public int[] findOrder(int numCourses, int[][] prerequisites) {
|
||||
// 建图,和环检测算法相同
|
||||
List<Integer>[] graph = buildGraph(numCourses, prerequisites);
|
||||
// 计算入度,和环检测算法相同
|
||||
int[] indegree = new int[numCourses];
|
||||
for (int[] edge : prerequisites) {
|
||||
int from = edge[1], to = edge[0];
|
||||
indegree[to]++;
|
||||
}
|
||||
|
||||
// 根据入度初始化队列中的节点,和环检测算法相同
|
||||
Queue<Integer> q = new LinkedList<>();
|
||||
for (int i = 0; i < numCourses; i++) {
|
||||
if (indegree[i] == 0) {
|
||||
q.offer(i);
|
||||
}
|
||||
}
|
||||
|
||||
// 记录拓扑排序结果
|
||||
int[] res = new int[numCourses];
|
||||
// 记录遍历节点的顺序(索引)
|
||||
int count = 0;
|
||||
// 开始执行 BFS 算法
|
||||
while (!q.isEmpty()) {
|
||||
int cur = q.poll();
|
||||
// 弹出节点的顺序即为拓扑排序结果
|
||||
res[count] = cur;
|
||||
count++;
|
||||
for (int next : graph[cur]) {
|
||||
indegree[next]--;
|
||||
if (indegree[next] == 0) {
|
||||
q.offer(next);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
if (count != numCourses) {
|
||||
// 存在环,拓扑排序不存在
|
||||
return new int[]{};
|
||||
}
|
||||
|
||||
return res;
|
||||
}
|
||||
|
||||
// 建图函数
|
||||
List<Integer>[] buildGraph(int n, int[][] edges) {
|
||||
// 见前文
|
||||
}
|
||||
```
|
||||
|
||||
按道理,[图的遍历](https://labuladong.github.io/article/fname.html?fname=图) 都需要 `visited` 数组防止走回头路,这里的 BFS 算法其实是通过 `indegree` 数组实现的 `visited` 数组的作用,只有入度为 0 的节点才能入队,从而保证不会出现死循环。
|
||||
|
||||
好了,到这里环检测算法、拓扑排序算法的 BFS 实现也讲完了,继续留一个思考题:
|
||||
|
||||
对于 BFS 的环检测算法,如果问你形成环的节点具体是哪些,你应该如何实现呢?
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [Kruskal 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=kruskal)
|
||||
- [Prim 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=prim算法)
|
||||
- [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
|
||||
- [图论基础及遍历算法](https://labuladong.github.io/article/fname.html?fname=图)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer II 113. 课程顺序](https://leetcode.cn/problems/QA2IGt/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 设计Twitter
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -294,6 +290,20 @@ public List<Integer> getNewsFeed(int userId) {
|
|||
|
||||
最后,Github 上有一个优秀的开源项目,专门收集了很多大型系统设计的案例和解析,而且有中文版本,上面这个图也出自该项目。对系统设计感兴趣的读者可以点击 [这里](https://github.com/donnemartin/system-design-primer) 查看。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [数据结构设计:最大栈](https://labuladong.github.io/article/fname.html?fname=最大栈)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,9 +1,5 @@
|
|||
# 递归反转链表的一部分
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -225,6 +221,35 @@ ListNode reverseBetween(ListNode head, int m, int n) {
|
|||
|
||||
> 最后打个广告,我亲自制作了一门 [数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO),以视频课为主,手把手带你实现常用的数据结构及相关算法,旨在帮助算法基础较为薄弱的读者深入理解常用数据结构的底层原理,在算法学习中少走弯路。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [如何判断回文链表](https://labuladong.github.io/article/fname.html?fname=判断回文链表)
|
||||
- [烧饼排序算法](https://labuladong.github.io/article/fname.html?fname=烧饼排序)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer 24. 反转链表](https://leetcode.cn/problems/fan-zhuan-lian-biao-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 024. 反转链表](https://leetcode.cn/problems/UHnkqh/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,9 +1,5 @@
|
|||
# 队列实现栈|栈实现队列
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -227,6 +223,23 @@ public boolean empty() {
|
|||
|
||||
希望本文对你有帮助。
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer 09. 用两个栈实现队列](https://leetcode.cn/problems/yong-liang-ge-zhan-shi-xian-dui-lie-lcof/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -0,0 +1,429 @@
|
|||
# BFS 算法框架套路详解
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [111. Minimum Depth of Binary Tree](https://leetcode.com/problems/minimum-depth-of-binary-tree/) | [111. 二叉树的最小深度](https://leetcode.cn/problems/minimum-depth-of-binary-tree/) | 🟢
|
||||
| [752. Open the Lock](https://leetcode.com/problems/open-the-lock/) | [752. 打开转盘锁](https://leetcode.cn/problems/open-the-lock/) | 🟠
|
||||
| - | [剑指 Offer II 109. 开密码锁](https://leetcode.cn/problems/zlDJc7/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
> 本文有视频版:[BFS 算法核心框架套路](https://www.bilibili.com/video/BV1oT411u7Vn/)
|
||||
|
||||
后台有很多人问起 BFS 和 DFS 的框架,今天就来说说吧。
|
||||
|
||||
首先,你要说我没写过 BFS 框架,这话没错,今天写个框架你背住就完事儿了。但要是说没写过 DFS 框架,那你还真是说错了,**其实 DFS 算法就是回溯算法**,我们前文 [回溯算法框架套路详解](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 就写过了,而且写得不是一般得好,建议好好复习,嘿嘿嘿~
|
||||
|
||||
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
|
||||
|
||||
BFS 相对 DFS 的最主要的区别是:**BFS 找到的路径一定是最短的,但代价就是空间复杂度可能比 DFS 大很多**,至于为什么,我们后面介绍了框架就很容易看出来了。
|
||||
|
||||
本文就由浅入深写两道 BFS 的典型题目,分别是「二叉树的最小高度」和「打开密码锁的最少步数」,手把手教你怎么写 BFS 算法。
|
||||
|
||||
## 一、算法框架
|
||||
|
||||
要说框架的话,我们先举例一下 BFS 出现的常见场景好吧,**问题的本质就是让你在一幅「图」中找到从起点 `start` 到终点 `target` 的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿**,把枯燥的本质搞清楚了,再去欣赏各种问题的包装才能胸有成竹嘛。
|
||||
|
||||
这个广义的描述可以有各种变体,比如走迷宫,有的格子是围墙不能走,从起点到终点的最短距离是多少?如果这个迷宫带「传送门」可以瞬间传送呢?
|
||||
|
||||
再比如说两个单词,要求你通过某些替换,把其中一个变成另一个,每次只能替换一个字符,最少要替换几次?
|
||||
|
||||
再比如说连连看游戏,两个方块消除的条件不仅仅是图案相同,还得保证两个方块之间的最短连线不能多于两个拐点。你玩连连看,点击两个坐标,游戏是如何判断它俩的最短连线有几个拐点的?
|
||||
|
||||
再比如……
|
||||
|
||||
净整些花里胡哨的,这些问题都没啥奇技淫巧,本质上就是一幅「图」,让你从一个起点,走到终点,问最短路径。这就是 BFS 的本质,框架搞清楚了直接默写就好。
|
||||
|
||||

|
||||
|
||||
记住下面这个框架就 OK 了:
|
||||
|
||||
```java
|
||||
// 计算从起点 start 到终点 target 的最近距离
|
||||
int BFS(Node start, Node target) {
|
||||
Queue<Node> q; // 核心数据结构
|
||||
Set<Node> visited; // 避免走回头路
|
||||
|
||||
q.offer(start); // 将起点加入队列
|
||||
visited.add(start);
|
||||
int step = 0; // 记录扩散的步数
|
||||
|
||||
while (q not empty) {
|
||||
int sz = q.size();
|
||||
/* 将当前队列中的所有节点向四周扩散 */
|
||||
for (int i = 0; i < sz; i++) {
|
||||
Node cur = q.poll();
|
||||
/* 划重点:这里判断是否到达终点 */
|
||||
if (cur is target)
|
||||
return step;
|
||||
/* 将 cur 的相邻节点加入队列 */
|
||||
for (Node x : cur.adj()) {
|
||||
if (x not in visited) {
|
||||
q.offer(x);
|
||||
visited.add(x);
|
||||
}
|
||||
}
|
||||
}
|
||||
/* 划重点:更新步数在这里 */
|
||||
step++;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
队列 `q` 就不说了,BFS 的核心数据结构;`cur.adj()` 泛指 `cur` 相邻的节点,比如说二维数组中,`cur` 上下左右四面的位置就是相邻节点;`visited` 的主要作用是防止走回头路,大部分时候都是必须的,但是像一般的二叉树结构,没有子节点到父节点的指针,不会走回头路就不需要 `visited`。
|
||||
|
||||
### 二、二叉树的最小高度
|
||||
|
||||
先来个简单的问题实践一下 BFS 框架吧,判断一棵二叉树的**最小**高度,这也是力扣第 111 题「二叉树的最小深度」:
|
||||
|
||||

|
||||
|
||||
怎么套到 BFS 的框架里呢?首先明确一下起点 `start` 和终点 `target` 是什么,怎么判断到达了终点?
|
||||
|
||||
**显然起点就是 `root` 根节点,终点就是最靠近根节点的那个「叶子节点」嘛**,叶子节点就是两个子节点都是 `null` 的节点:
|
||||
|
||||
```java
|
||||
if (cur.left == null && cur.right == null)
|
||||
// 到达叶子节点
|
||||
```
|
||||
|
||||
那么,按照我们上述的框架稍加改造来写解法即可:
|
||||
|
||||
```java
|
||||
int minDepth(TreeNode root) {
|
||||
if (root == null) return 0;
|
||||
Queue<TreeNode> q = new LinkedList<>();
|
||||
q.offer(root);
|
||||
// root 本身就是一层,depth 初始化为 1
|
||||
int depth = 1;
|
||||
|
||||
while (!q.isEmpty()) {
|
||||
int sz = q.size();
|
||||
/* 将当前队列中的所有节点向四周扩散 */
|
||||
for (int i = 0; i < sz; i++) {
|
||||
TreeNode cur = q.poll();
|
||||
/* 判断是否到达终点 */
|
||||
if (cur.left == null && cur.right == null)
|
||||
return depth;
|
||||
/* 将 cur 的相邻节点加入队列 */
|
||||
if (cur.left != null)
|
||||
q.offer(cur.left);
|
||||
if (cur.right != null)
|
||||
q.offer(cur.right);
|
||||
}
|
||||
/* 这里增加步数 */
|
||||
depth++;
|
||||
}
|
||||
return depth;
|
||||
}
|
||||
```
|
||||
|
||||
这里注意这个 `while` 循环和 `for` 循环的配合,**`while` 循环控制一层一层往下走,`for` 循环利用 `sz` 变量控制从左到右遍历每一层二叉树节点**:
|
||||
|
||||

|
||||
|
||||
这一点很重要,这个形式在普通 BFS 问题中都很常见,但是在 [Dijkstra 算法模板框架](https://labuladong.github.io/article/fname.html?fname=dijkstra算法) 中我们修改了这种代码模式,读完并理解本文后你可以去看看 BFS 算法是如何演变成 Dijkstra 算法在加权图中寻找最短路径的。
|
||||
|
||||
话说回来,二叉树本身是很简单的数据结构,我想上述代码你应该可以理解的,其实其他复杂问题都是这个框架的变形,再探讨复杂问题之前,我们解答两个问题:
|
||||
|
||||
**1、为什么 BFS 可以找到最短距离,DFS 不行吗**?
|
||||
|
||||
首先,你看 BFS 的逻辑,`depth` 每增加一次,队列中的所有节点都向前迈一步,这保证了第一次到达终点的时候,走的步数是最少的。
|
||||
|
||||
DFS 不能找最短路径吗?其实也是可以的,但是时间复杂度相对高很多。你想啊,DFS 实际上是靠递归的堆栈记录走过的路径,你要找到最短路径,肯定得把二叉树中所有树杈都探索完才能对比出最短的路径有多长对不对?而 BFS 借助队列做到一次一步「齐头并进」,是可以在不遍历完整棵树的条件下找到最短距离的。
|
||||
|
||||
形象点说,DFS 是线,BFS 是面;DFS 是单打独斗,BFS 是集体行动。这个应该比较容易理解吧。
|
||||
|
||||
**2、既然 BFS 那么好,为啥 DFS 还要存在**?
|
||||
|
||||
BFS 可以找到最短距离,但是空间复杂度高,而 DFS 的空间复杂度较低。
|
||||
|
||||
还是拿刚才我们处理二叉树问题的例子,假设给你的这个二叉树是满二叉树,节点数为 `N`,对于 DFS 算法来说,空间复杂度无非就是递归堆栈,最坏情况下顶多就是树的高度,也就是 `O(logN)`。
|
||||
|
||||
但是你想想 BFS 算法,队列中每次都会储存着二叉树一层的节点,这样的话最坏情况下空间复杂度应该是树的最底层节点的数量,也就是 `N/2`,用 Big O 表示的话也就是 `O(N)`。
|
||||
|
||||
由此观之,BFS 还是有代价的,一般来说在找最短路径的时候使用 BFS,其他时候还是 DFS 使用得多一些(主要是递归代码好写)。
|
||||
|
||||
好了,现在你对 BFS 了解得足够多了,下面来一道难一点的题目,深化一下框架的理解吧。
|
||||
|
||||
### 三、解开密码锁的最少次数
|
||||
|
||||
这是力扣第 752 题「打开转盘锁」,比较有意思:
|
||||
|
||||

|
||||
|
||||
题目中描述的就是我们生活中常见的那种密码锁,如果没有任何约束,最少的拨动次数很好算,就像我们平时开密码锁那样直奔密码拨就行了。
|
||||
|
||||
但现在的难点就在于,不能出现 `deadends`,应该如何计算出最少的转动次数呢?
|
||||
|
||||
**第一步,我们不管所有的限制条件,不管 `deadends` 和 `target` 的限制,就思考一个问题:如果让你设计一个算法,穷举所有可能的密码组合,你怎么做**?
|
||||
|
||||
穷举呗,再简单一点,如果你只转一下锁,有几种可能?总共有 4 个位置,每个位置可以向上转,也可以向下转,也就是有 8 种可能对吧。
|
||||
|
||||
比如说从 `"0000"` 开始,转一次,可以穷举出 `"1000", "9000", "0100", "0900"...` 共 8 种密码。然后,再以这 8 种密码作为基础,对每个密码再转一下,穷举出所有可能...
|
||||
|
||||
**仔细想想,这就可以抽象成一幅图,每个节点有 8 个相邻的节点**,又让你求最短距离,这不就是典型的 BFS 嘛,框架就可以派上用场了,先写出一个「简陋」的 BFS 框架代码再说别的:
|
||||
|
||||
```java
|
||||
// 将 s[j] 向上拨动一次
|
||||
String plusOne(String s, int j) {
|
||||
char[] ch = s.toCharArray();
|
||||
if (ch[j] == '9')
|
||||
ch[j] = '0';
|
||||
else
|
||||
ch[j] += 1;
|
||||
return new String(ch);
|
||||
}
|
||||
// 将 s[i] 向下拨动一次
|
||||
String minusOne(String s, int j) {
|
||||
char[] ch = s.toCharArray();
|
||||
if (ch[j] == '0')
|
||||
ch[j] = '9';
|
||||
else
|
||||
ch[j] -= 1;
|
||||
return new String(ch);
|
||||
}
|
||||
|
||||
// BFS 框架,打印出所有可能的密码
|
||||
void BFS(String target) {
|
||||
Queue<String> q = new LinkedList<>();
|
||||
q.offer("0000");
|
||||
|
||||
while (!q.isEmpty()) {
|
||||
int sz = q.size();
|
||||
/* 将当前队列中的所有节点向周围扩散 */
|
||||
for (int i = 0; i < sz; i++) {
|
||||
String cur = q.poll();
|
||||
/* 判断是否到达终点 */
|
||||
System.out.println(cur);
|
||||
|
||||
/* 将一个节点的相邻节点加入队列 */
|
||||
for (int j = 0; j < 4; j++) {
|
||||
String up = plusOne(cur, j);
|
||||
String down = minusOne(cur, j);
|
||||
q.offer(up);
|
||||
q.offer(down);
|
||||
}
|
||||
}
|
||||
/* 在这里增加步数 */
|
||||
}
|
||||
return;
|
||||
}
|
||||
```
|
||||
|
||||
> PS:这段代码当然有很多问题,但是我们做算法题肯定不是一蹴而就的,而是从简陋到完美的。不要完美主义,咱要慢慢来,好不。
|
||||
|
||||
**这段 BFS 代码已经能够穷举所有可能的密码组合了,但是显然不能完成题目,有如下问题需要解决**:
|
||||
|
||||
1、会走回头路。比如说我们从 `"0000"` 拨到 `"1000"`,但是等从队列拿出 `"1000"` 时,还会拨出一个 `"0000"`,这样的话会产生死循环。
|
||||
|
||||
2、没有终止条件,按照题目要求,我们找到 `target` 就应该结束并返回拨动的次数。
|
||||
|
||||
3、没有对 `deadends` 的处理,按道理这些「死亡密码」是不能出现的,也就是说你遇到这些密码的时候需要跳过。
|
||||
|
||||
如果你能够看懂上面那段代码,真得给你鼓掌,只要按照 BFS 框架在对应的位置稍作修改即可修复这些问题:
|
||||
|
||||
```java
|
||||
int openLock(String[] deadends, String target) {
|
||||
// 记录需要跳过的死亡密码
|
||||
Set<String> deads = new HashSet<>();
|
||||
for (String s : deadends) deads.add(s);
|
||||
// 记录已经穷举过的密码,防止走回头路
|
||||
Set<String> visited = new HashSet<>();
|
||||
Queue<String> q = new LinkedList<>();
|
||||
// 从起点开始启动广度优先搜索
|
||||
int step = 0;
|
||||
q.offer("0000");
|
||||
visited.add("0000");
|
||||
|
||||
while (!q.isEmpty()) {
|
||||
int sz = q.size();
|
||||
/* 将当前队列中的所有节点向周围扩散 */
|
||||
for (int i = 0; i < sz; i++) {
|
||||
String cur = q.poll();
|
||||
|
||||
/* 判断是否到达终点 */
|
||||
if (deads.contains(cur))
|
||||
continue;
|
||||
if (cur.equals(target))
|
||||
return step;
|
||||
|
||||
/* 将一个节点的未遍历相邻节点加入队列 */
|
||||
for (int j = 0; j < 4; j++) {
|
||||
String up = plusOne(cur, j);
|
||||
if (!visited.contains(up)) {
|
||||
q.offer(up);
|
||||
visited.add(up);
|
||||
}
|
||||
String down = minusOne(cur, j);
|
||||
if (!visited.contains(down)) {
|
||||
q.offer(down);
|
||||
visited.add(down);
|
||||
}
|
||||
}
|
||||
}
|
||||
/* 在这里增加步数 */
|
||||
step++;
|
||||
}
|
||||
// 如果穷举完都没找到目标密码,那就是找不到了
|
||||
return -1;
|
||||
}
|
||||
```
|
||||
|
||||
至此,我们就解决这道题目了。有一个比较小的优化:可以不需要 `dead` 这个哈希集合,可以直接将这些元素初始化到 `visited` 集合中,效果是一样的,可能更加优雅一些。
|
||||
|
||||
### 四、双向 BFS 优化
|
||||
|
||||
你以为到这里 BFS 算法就结束了?恰恰相反。BFS 算法还有一种稍微高级一点的优化思路:**双向 BFS**,可以进一步提高算法的效率。
|
||||
|
||||
篇幅所限,这里就提一下区别:**传统的 BFS 框架就是从起点开始向四周扩散,遇到终点时停止;而双向 BFS 则是从起点和终点同时开始扩散,当两边有交集的时候停止**。
|
||||
|
||||
为什么这样能够能够提升效率呢?其实从 Big O 表示法分析算法复杂度的话,它俩的最坏复杂度都是 `O(N)`,但是实际上双向 BFS 确实会快一些,我给你画两张图看一眼就明白了:
|
||||
|
||||
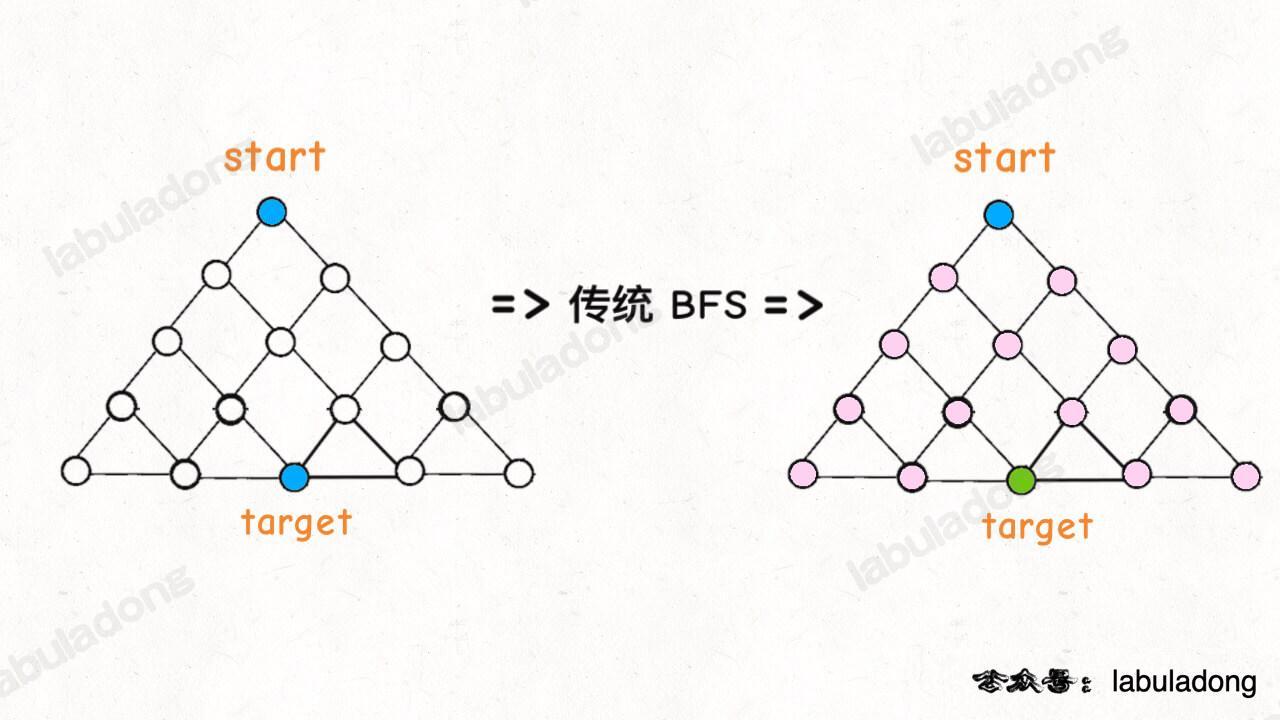
|
||||
|
||||
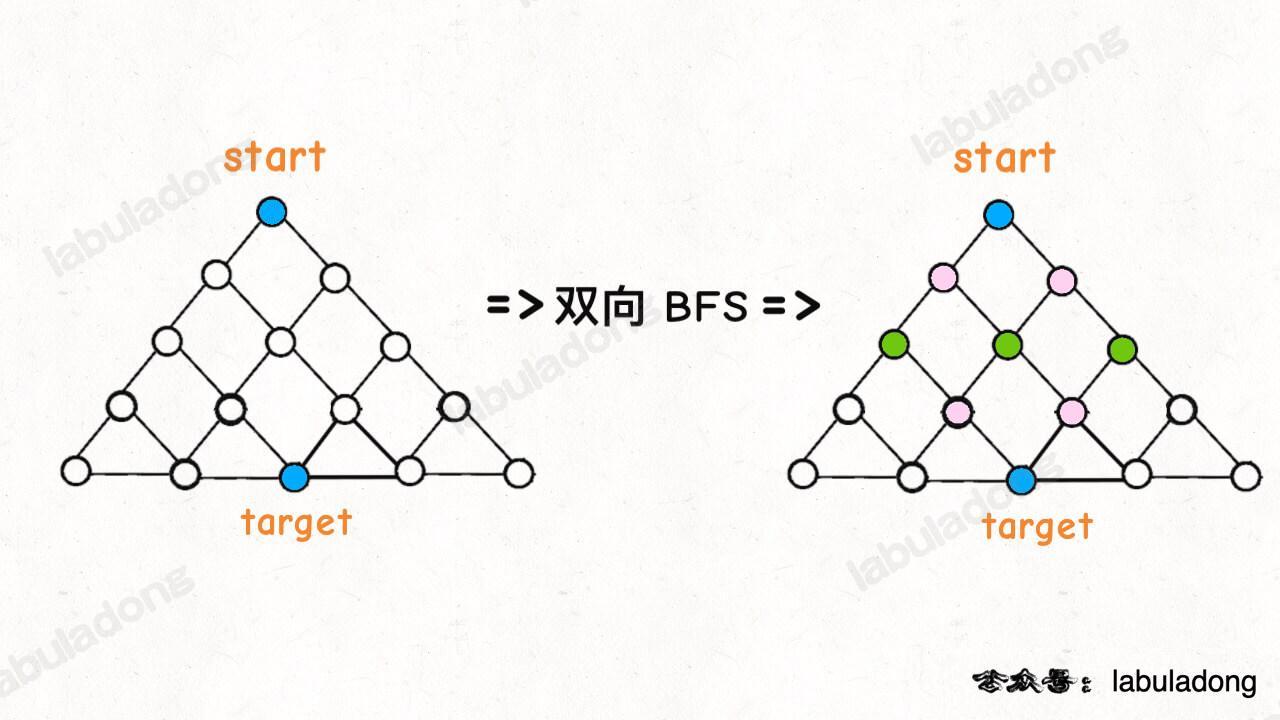
|
||||
|
||||
图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到 `target`;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。从这个例子可以直观地感受到,双向 BFS 是要比传统 BFS 高效的。
|
||||
|
||||
**不过,双向 BFS 也有局限,因为你必须知道终点在哪里**。比如我们刚才讨论的二叉树最小高度的问题,你一开始根本就不知道终点在哪里,也就无法使用双向 BFS;但是第二个密码锁的问题,是可以使用双向 BFS 算法来提高效率的,代码稍加修改即可:
|
||||
|
||||
```java
|
||||
int openLock(String[] deadends, String target) {
|
||||
Set<String> deads = new HashSet<>();
|
||||
for (String s : deadends) deads.add(s);
|
||||
// 用集合不用队列,可以快速判断元素是否存在
|
||||
Set<String> q1 = new HashSet<>();
|
||||
Set<String> q2 = new HashSet<>();
|
||||
Set<String> visited = new HashSet<>();
|
||||
|
||||
int step = 0;
|
||||
q1.add("0000");
|
||||
q2.add(target);
|
||||
|
||||
while (!q1.isEmpty() && !q2.isEmpty()) {
|
||||
// 哈希集合在遍历的过程中不能修改,用 temp 存储扩散结果
|
||||
Set<String> temp = new HashSet<>();
|
||||
|
||||
/* 将 q1 中的所有节点向周围扩散 */
|
||||
for (String cur : q1) {
|
||||
/* 判断是否到达终点 */
|
||||
if (deads.contains(cur))
|
||||
continue;
|
||||
if (q2.contains(cur))
|
||||
return step;
|
||||
|
||||
visited.add(cur);
|
||||
|
||||
/* 将一个节点的未遍历相邻节点加入集合 */
|
||||
for (int j = 0; j < 4; j++) {
|
||||
String up = plusOne(cur, j);
|
||||
if (!visited.contains(up))
|
||||
temp.add(up);
|
||||
String down = minusOne(cur, j);
|
||||
if (!visited.contains(down))
|
||||
temp.add(down);
|
||||
}
|
||||
}
|
||||
/* 在这里增加步数 */
|
||||
step++;
|
||||
// temp 相当于 q1
|
||||
// 这里交换 q1 q2,下一轮 while 就是扩散 q2
|
||||
q1 = q2;
|
||||
q2 = temp;
|
||||
}
|
||||
return -1;
|
||||
}
|
||||
```
|
||||
|
||||
双向 BFS 还是遵循 BFS 算法框架的,只是**不再使用队列,而是使用 HashSet 方便快速判断两个集合是否有交集**。
|
||||
|
||||
另外的一个技巧点就是 **while 循环的最后交换 `q1` 和 `q2` 的内容**,所以只要默认扩散 `q1` 就相当于轮流扩散 `q1` 和 `q2`。
|
||||
|
||||
其实双向 BFS 还有一个优化,就是在 while 循环开始时做一个判断:
|
||||
|
||||
```java
|
||||
// ...
|
||||
while (!q1.isEmpty() && !q2.isEmpty()) {
|
||||
if (q1.size() > q2.size()) {
|
||||
// 交换 q1 和 q2
|
||||
temp = q1;
|
||||
q1 = q2;
|
||||
q2 = temp;
|
||||
}
|
||||
// ...
|
||||
```
|
||||
|
||||
为什么这是一个优化呢?
|
||||
|
||||
因为按照 BFS 的逻辑,队列(集合)中的元素越多,扩散之后新的队列(集合)中的元素就越多;在双向 BFS 算法中,如果我们每次都选择一个较小的集合进行扩散,那么占用的空间增长速度就会慢一些,效率就会高一些。
|
||||
|
||||
不过话说回来,**无论传统 BFS 还是双向 BFS,无论做不做优化,从 Big O 衡量标准来看,时间复杂度都是一样的**,只能说双向 BFS 是一种 trick,算法运行的速度会相对快一点,掌握不掌握其实都无所谓。最关键的是把 BFS 通用框架记下来,反正所有 BFS 算法都可以用它套出解法。
|
||||
|
||||
接下来可阅读:
|
||||
|
||||
* [BFS 算法如何解决智力题](https://labuladong.github.io/article/fname.html?fname=BFS解决滑动拼图)
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [Prim 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=prim算法)
|
||||
- [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结)
|
||||
- [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
|
||||
- [二叉树的递归转迭代的代码框架](https://labuladong.github.io/article/fname.html?fname=迭代遍历二叉树)
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [如何用 BFS 算法秒杀各种智力题](https://labuladong.github.io/article/fname.html?fname=BFS解决滑动拼图)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [旅游省钱大法:加权最短路径](https://labuladong.github.io/article/fname.html?fname=旅行最短路径)
|
||||
- [环检测及拓扑排序算法](https://labuladong.github.io/article/fname.html?fname=拓扑排序)
|
||||
- [算法学习和心流体验](https://labuladong.github.io/article/fname.html?fname=心流)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [102. Binary Tree Level Order Traversal](https://leetcode.com/problems/binary-tree-level-order-traversal/?show=1) | [102. 二叉树的层序遍历](https://leetcode.cn/problems/binary-tree-level-order-traversal/?show=1) |
|
||||
| [117. Populating Next Right Pointers in Each Node II](https://leetcode.com/problems/populating-next-right-pointers-in-each-node-ii/?show=1) | [117. 填充每个节点的下一个右侧节点指针 II](https://leetcode.cn/problems/populating-next-right-pointers-in-each-node-ii/?show=1) |
|
||||
| [431. Encode N-ary Tree to Binary Tree](https://leetcode.com/problems/encode-n-ary-tree-to-binary-tree/?show=1)🔒 | [431. 将 N 叉树编码为二叉树](https://leetcode.cn/problems/encode-n-ary-tree-to-binary-tree/?show=1)🔒 |
|
||||
| [773. Sliding Puzzle](https://leetcode.com/problems/sliding-puzzle/?show=1) | [773. 滑动谜题](https://leetcode.cn/problems/sliding-puzzle/?show=1) |
|
||||
| [863. All Nodes Distance K in Binary Tree](https://leetcode.com/problems/all-nodes-distance-k-in-binary-tree/?show=1) | [863. 二叉树中所有距离为 K 的结点](https://leetcode.cn/problems/all-nodes-distance-k-in-binary-tree/?show=1) |
|
||||
| - | [剑指 Offer 32 - II. 从上到下打印二叉树 II](https://leetcode.cn/problems/cong-shang-dao-xia-da-yin-er-cha-shu-ii-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 109. 开密码锁](https://leetcode.cn/problems/zlDJc7/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -0,0 +1,188 @@
|
|||
# BFS 算法秒杀各种益智游戏
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [773. Sliding Puzzle](https://leetcode.com/problems/sliding-puzzle/) | [773. 滑动谜题](https://leetcode.cn/problems/sliding-puzzle/) | 🔴
|
||||
|
||||
**-----------**
|
||||
|
||||
滑动拼图游戏大家应该都玩过,下图是一个 4x4 的滑动拼图:
|
||||
|
||||

|
||||
|
||||
拼图中有一个格子是空的,可以利用这个空着的格子移动其他数字。你需要通过移动这些数字,得到某个特定排列顺序,这样就算赢了。
|
||||
|
||||
我小时候还玩过一款叫做「华容道」的益智游戏,也和滑动拼图比较类似:
|
||||
|
||||

|
||||
|
||||
实际上,滑动拼图游戏也叫数字华容道,你看它俩挺相似的。
|
||||
|
||||
那么这种游戏怎么玩呢?我记得是有一些套路的,类似于魔方还原公式。但是我们今天不来研究让人头秃的技巧,**这些益智游戏通通可以用暴力搜索算法解决,所以今天我们就学以致用,用 BFS 算法框架来秒杀这些游戏**。
|
||||
|
||||
### 一、题目解析
|
||||
|
||||
力扣第 773 题「滑动谜题」就是这个问题,题目的要求如下:
|
||||
|
||||
给你一个 2x3 的滑动拼图,用一个 2x3 的数组 `board` 表示。拼图中有数字 0~5 六个数,其中**数字 0 就表示那个空着的格子**,你可以移动其中的数字,当 `board` 变为 `[[1,2,3],[4,5,0]]` 时,赢得游戏。
|
||||
|
||||
请你写一个算法,计算赢得游戏需要的最少移动次数,如果不能赢得游戏,返回 -1。
|
||||
|
||||
比如说输入的二维数组 `board = [[4,1,2],[5,0,3]]`,算法应该返回 5:
|
||||
|
||||
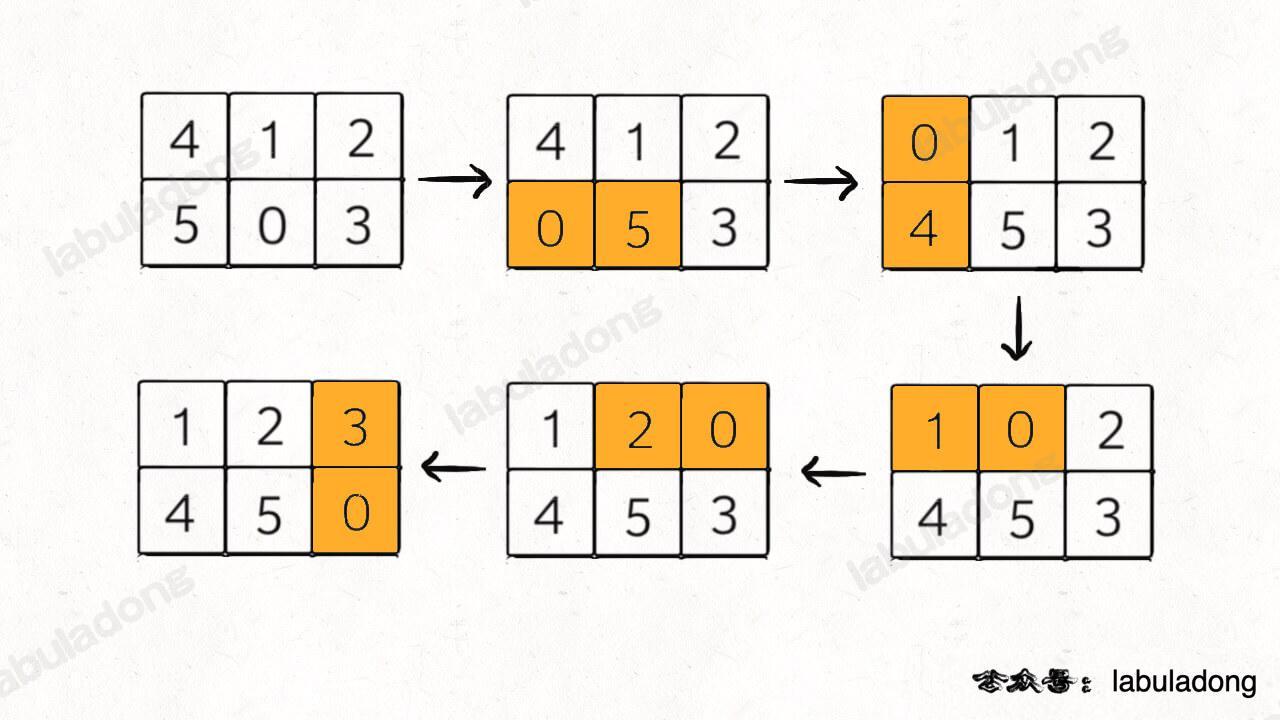
|
||||
|
||||
如果输入的是 `board = [[1,2,3],[5,4,0]]`,则算法返回 -1,因为这种局面下无论如何都不能赢得游戏。
|
||||
|
||||
### 二、思路分析
|
||||
|
||||
对于这种计算最小步数的问题,我们就要敏感地想到 BFS 算法。
|
||||
|
||||
这个题目转化成 BFS 问题是有一些技巧的,我们面临如下问题:
|
||||
|
||||
1、一般的 BFS 算法,是从一个起点 `start` 开始,向终点 `target` 进行寻路,但是拼图问题不是在寻路,而是在不断交换数字,这应该怎么转化成 BFS 算法问题呢?
|
||||
|
||||
2、即便这个问题能够转化成 BFS 问题,如何处理起点 `start` 和终点 `target`?它们都是数组哎,把数组放进队列,套 BFS 框架,想想就比较麻烦且低效。
|
||||
|
||||
首先回答第一个问题,**BFS 算法并不只是一个寻路算法,而是一种暴力搜索算法**,只要涉及暴力穷举的问题,BFS 就可以用,而且可以最快地找到答案。
|
||||
|
||||
你想想计算机怎么解决问题的?哪有那么多奇技淫巧,本质上就是把所有可行解暴力穷举出来,然后从中找到一个最优解罢了。
|
||||
|
||||
明白了这个道理,我们的问题就转化成了:**如何穷举出 `board` 当前局面下可能衍生出的所有局面**?这就简单了,看数字 0 的位置呗,和上下左右的数字进行交换就行了:
|
||||
|
||||
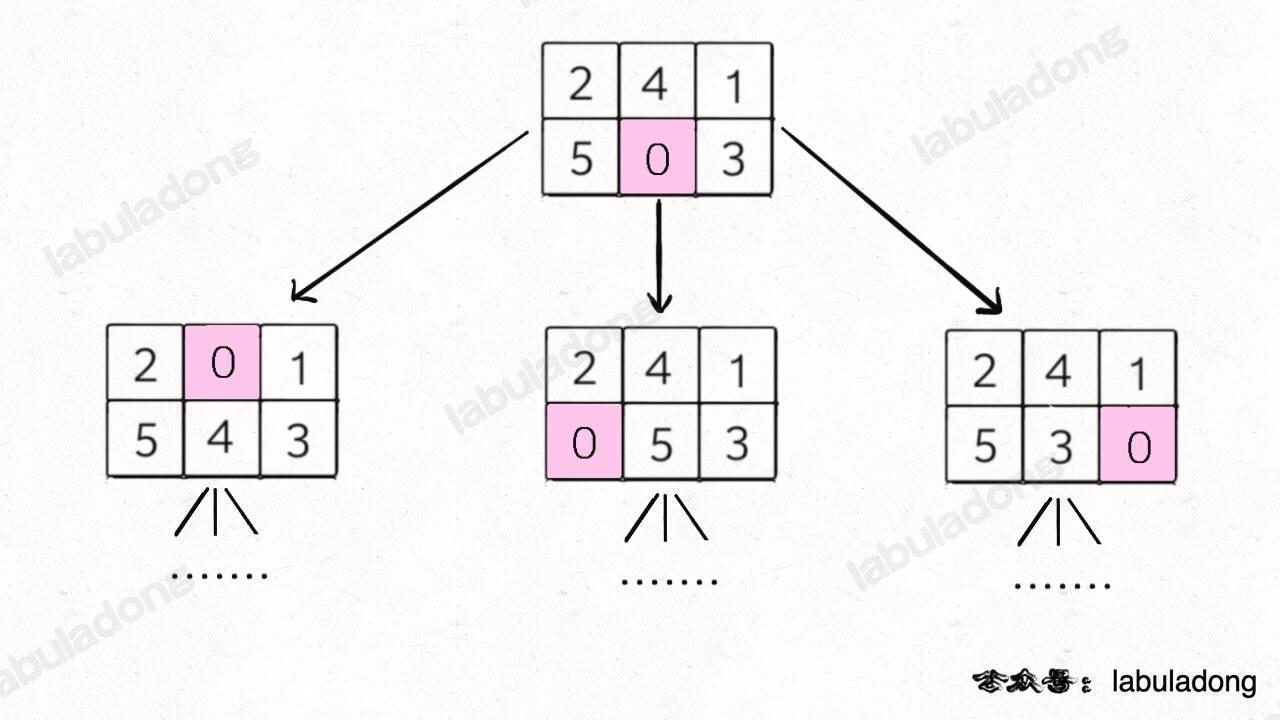
|
||||
|
||||
这样其实就是一个 BFS 问题,每次先找到数字 0,然后和周围的数字进行交换,形成新的局面加入队列…… 当第一次到达 `target` 时,就得到了赢得游戏的最少步数。
|
||||
|
||||
对于第二个问题,我们这里的 `board` 仅仅是 2x3 的二维数组,所以可以压缩成一个一维字符串。**其中比较有技巧性的点在于,二维数组有「上下左右」的概念,压缩成一维后,如何得到某一个索引上下左右的索引**?
|
||||
|
||||
对于这道题,题目说输入的数组大小都是 2 x 3,所以我们可以直接手动写出来这个映射:
|
||||
|
||||
```java
|
||||
// 记录一维字符串的相邻索引
|
||||
int[][] neighbor = new int[][]{
|
||||
{1, 3},
|
||||
{0, 4, 2},
|
||||
{1, 5},
|
||||
{0, 4},
|
||||
{3, 1, 5},
|
||||
{4, 2}
|
||||
};
|
||||
```
|
||||
|
||||
**这个含义就是,在一维字符串中,索引 `i` 在二维数组中的的相邻索引为 `neighbor[i]`**:
|
||||
|
||||
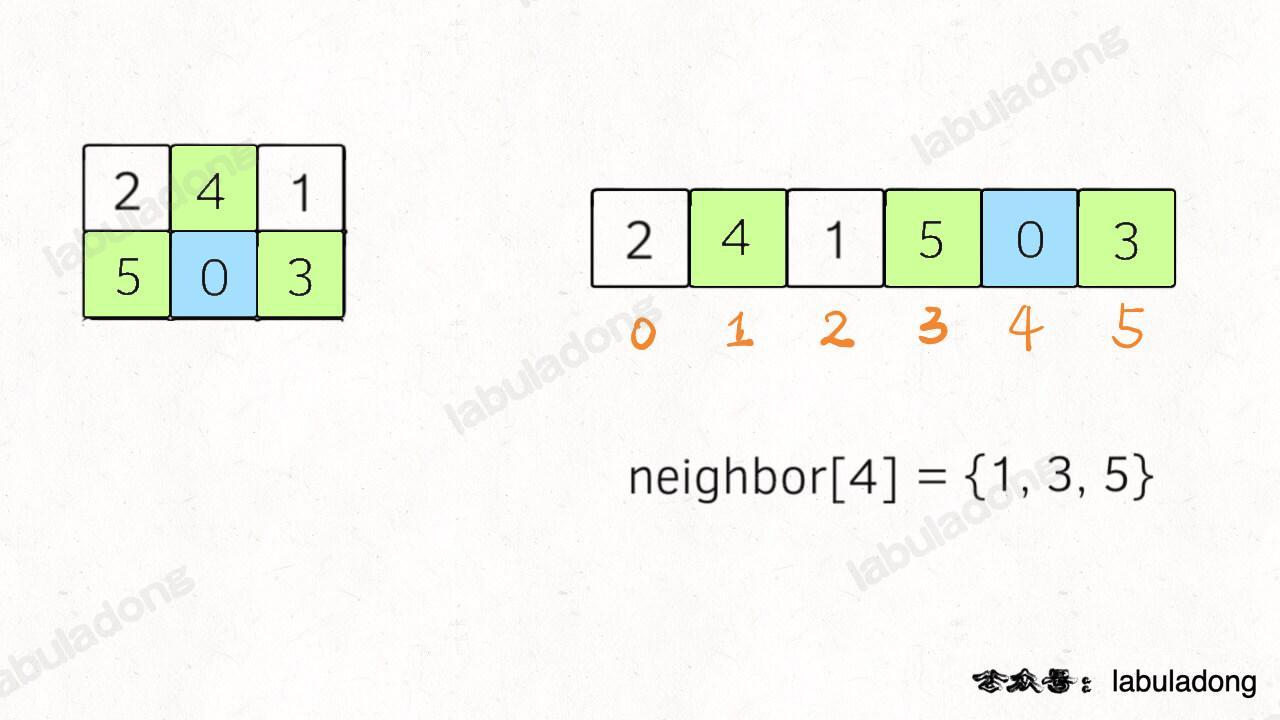
|
||||
|
||||
那么对于一个 `m x n` 的二维数组,手写它的一维索引映射肯定不现实了,如何用代码生成它的一维索引映射呢?
|
||||
|
||||
观察上图就能发现,如果二维数组中的某个元素 `e` 在一维数组中的索引为 `i`,那么 `e` 的左右相邻元素在一维数组中的索引就是 `i - 1` 和 `i + 1`,而 `e` 的上下相邻元素在一维数组中的索引就是 `i - n` 和 `i + n`,其中 `n` 为二维数组的列数。
|
||||
|
||||
这样,对于 `m x n` 的二维数组,我们可以写一个函数来生成它的 `neighbor` 索引映射,篇幅所限,我这里就不写了。
|
||||
|
||||
至此,我们就把这个问题完全转化成标准的 BFS 问题了,借助前文 [BFS 算法框架](https://labuladong.github.io/article/fname.html?fname=BFS框架) 的代码框架,直接就可以套出解法代码了:
|
||||
|
||||
```java
|
||||
public int slidingPuzzle(int[][] board) {
|
||||
int m = 2, n = 3;
|
||||
StringBuilder sb = new StringBuilder();
|
||||
String target = "123450";
|
||||
// 将 2x3 的数组转化成字符串作为 BFS 的起点
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
sb.append(board[i][j]);
|
||||
}
|
||||
}
|
||||
String start = sb.toString();
|
||||
|
||||
// 记录一维字符串的相邻索引
|
||||
int[][] neighbor = new int[][]{
|
||||
{1, 3},
|
||||
{0, 4, 2},
|
||||
{1, 5},
|
||||
{0, 4},
|
||||
{3, 1, 5},
|
||||
{4, 2}
|
||||
};
|
||||
|
||||
/******* BFS 算法框架开始 *******/
|
||||
Queue<String> q = new LinkedList<>();
|
||||
HashSet<String> visited = new HashSet<>();
|
||||
// 从起点开始 BFS 搜索
|
||||
q.offer(start);
|
||||
visited.add(start);
|
||||
|
||||
int step = 0;
|
||||
while (!q.isEmpty()) {
|
||||
int sz = q.size();
|
||||
for (int i = 0; i < sz; i++) {
|
||||
String cur = q.poll();
|
||||
// 判断是否达到目标局面
|
||||
if (target.equals(cur)) {
|
||||
return step;
|
||||
}
|
||||
// 找到数字 0 的索引
|
||||
int idx = 0;
|
||||
for (; cur.charAt(idx) != '0'; idx++) ;
|
||||
// 将数字 0 和相邻的数字交换位置
|
||||
for (int adj : neighbor[idx]) {
|
||||
String new_board = swap(cur.toCharArray(), adj, idx);
|
||||
// 防止走回头路
|
||||
if (!visited.contains(new_board)) {
|
||||
q.offer(new_board);
|
||||
visited.add(new_board);
|
||||
}
|
||||
}
|
||||
}
|
||||
step++;
|
||||
}
|
||||
/******* BFS 算法框架结束 *******/
|
||||
return -1;
|
||||
}
|
||||
|
||||
private String swap(char[] chars, int i, int j) {
|
||||
char temp = chars[i];
|
||||
chars[i] = chars[j];
|
||||
chars[j] = temp;
|
||||
return new String(chars);
|
||||
}
|
||||
```
|
||||
|
||||
至此,这道题目就解决了,其实框架完全没有变,套路都是一样的,我们只是花了比较多的时间将滑动拼图游戏转化成 BFS 算法。
|
||||
|
||||
很多益智游戏都是这样,虽然看起来特别巧妙,但都架不住暴力穷举,常用的算法就是回溯算法或者 BFS 算法。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [BFS 算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=BFS框架)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,326 +0,0 @@
|
|||
# FloodFill算法详解及应用
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [733. Flood Fill](https://leetcode.com/problems/flood-fill/) | [733. 图像渲染](https://leetcode.cn/problems/flood-fill/) | 🟢
|
||||
|
||||
**-----------**
|
||||
|
||||
啥是 FloodFill 算法呢,最直接的一个应用就是「颜色填充」,就是 Windows 绘画本中那个小油漆桶的标志,可以把一块被圈起来的区域全部染色。
|
||||
|
||||
|
||||
|
||||
这种算法思想还在许多其他地方有应用。比如说扫雷游戏,有时候你点一个方格,会一下子展开一片区域,这个展开过程,就是 FloodFill 算法实现的。
|
||||
|
||||

|
||||
|
||||
类似的,像消消乐这类游戏,相同方块积累到一定数量,就全部消除,也是 FloodFill 算法的功劳。
|
||||
|
||||
|
||||
|
||||
通过以上的几个例子,你应该对 FloodFill 算法有个概念了,现在我们要抽象问题,提取共同点。
|
||||
|
||||
### 一、构建框架
|
||||
|
||||
以上几个例子,都可以抽象成一个二维矩阵(图片其实就是像素点矩阵),然后从某个点开始向四周扩展,直到无法再扩展为止。
|
||||
|
||||
矩阵,可以抽象为一幅「图」,这就是一个图的遍历问题,也就类似一个 N 叉树遍历的问题。几行代码就能解决,直接上框架吧:
|
||||
|
||||
```java
|
||||
// (x, y) 为坐标位置
|
||||
void fill(int x, int y) {
|
||||
fill(x - 1, y); // 上
|
||||
fill(x + 1, y); // 下
|
||||
fill(x, y - 1); // 左
|
||||
fill(x, y + 1); // 右
|
||||
}
|
||||
```
|
||||
|
||||
这个框架可以解决所有在二维矩阵中遍历的问题,说得高端一点,这就叫深度优先搜索(Depth First Search,简称 DFS),说得简单一点,这就叫四叉树遍历框架。坐标 (x, y) 就是 root,四个方向就是 root 的四个子节点。
|
||||
|
||||
下面看一道 LeetCode 题目,其实就是让我们来实现一个「颜色填充」功能。
|
||||
|
||||

|
||||
|
||||
根据上篇文章,我们讲了「树」算法设计的一个总路线,今天就可以用到:
|
||||
|
||||
```java
|
||||
int[][] floodFill(int[][] image,
|
||||
int sr, int sc, int newColor) {
|
||||
|
||||
int origColor = image[sr][sc];
|
||||
fill(image, sr, sc, origColor, newColor);
|
||||
return image;
|
||||
}
|
||||
|
||||
void fill(int[][] image, int x, int y,
|
||||
int origColor, int newColor) {
|
||||
// 出界:超出边界索引
|
||||
if (!inArea(image, x, y)) return;
|
||||
// 碰壁:遇到其他颜色,超出 origColor 区域
|
||||
if (image[x][y] != origColor) return;
|
||||
image[x][y] = newColor;
|
||||
|
||||
fill(image, x, y + 1, origColor, newColor);
|
||||
fill(image, x, y - 1, origColor, newColor);
|
||||
fill(image, x - 1, y, origColor, newColor);
|
||||
fill(image, x + 1, y, origColor, newColor);
|
||||
}
|
||||
|
||||
boolean inArea(int[][] image, int x, int y) {
|
||||
return x >= 0 && x < image.length
|
||||
&& y >= 0 && y < image[0].length;
|
||||
}
|
||||
```
|
||||
|
||||
只要你能够理解这段代码,一定要给你鼓掌,给你 99 分,因为你对「框架思维」的掌控已经炉火纯青,此算法已经 cover 了 99% 的情况,仅有一个细节问题没有解决,就是当 origColor 和 newColor 相同时,会陷入无限递归。
|
||||
|
||||
### 二、研究细节
|
||||
|
||||
为什么会陷入无限递归呢,很好理解,因为每个坐标都要搜索上下左右,那么对于一个坐标,一定会被上下左右的坐标搜索。**被重复搜索时,必须保证递归函数能够能正确地退出,否则就会陷入死循环**。
|
||||
|
||||
为什么 newColor 和 origColor 不同时可以正常退出呢?把算法流程画个图理解一下:
|
||||
|
||||
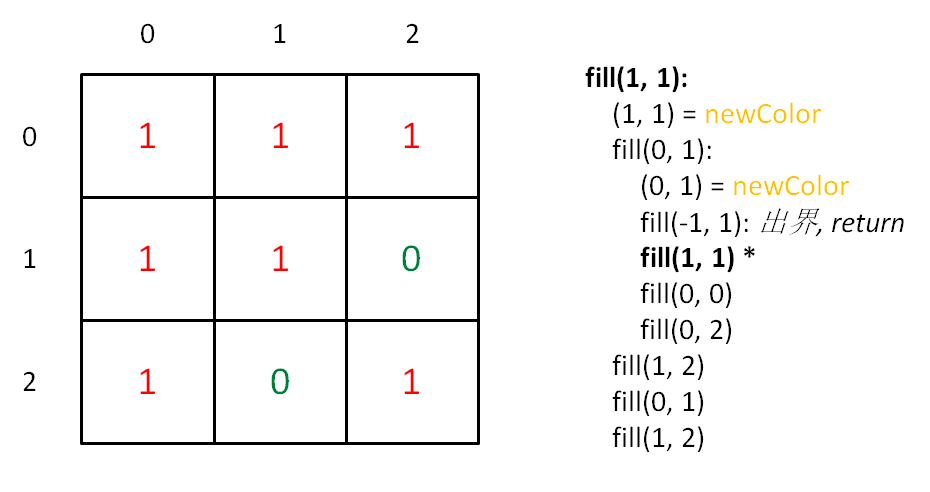
|
||||
|
||||
可以看到,fill(1, 1) 被重复搜索了,我们用 fill(1, 1)* 表示这次重复搜索。fill(1, 1)* 执行时,(1, 1) 已经被换成了 newColor,所以 fill(1, 1)* 会在这个 if 语句被怼回去,正确退出了。
|
||||
|
||||
```java
|
||||
// 碰壁:遇到其他颜色,超出 origColor 区域
|
||||
if (image[x][y] != origColor) return;
|
||||
```
|
||||
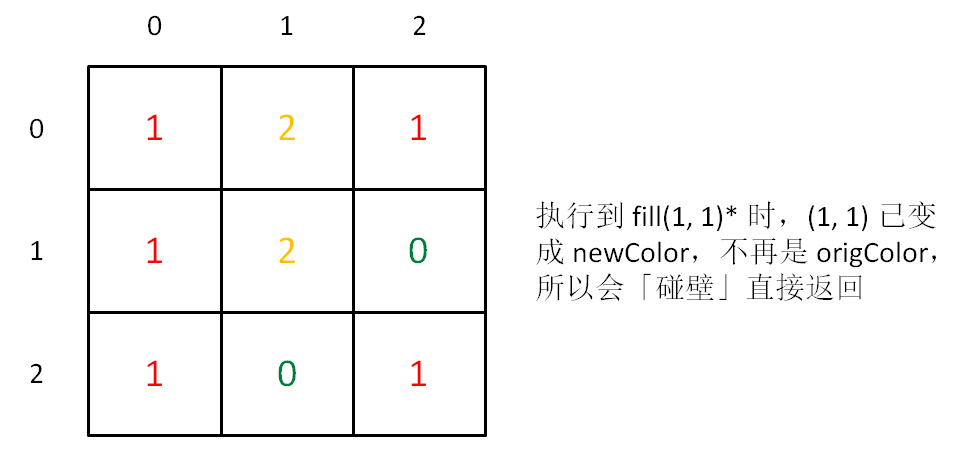
|
||||
|
||||
但是,如果说 origColor 和 newColor 一样,这个 if 语句就无法让 fill(1, 1)* 正确退出,而是开启了下面的重复递归,形成了死循环。
|
||||
|
||||
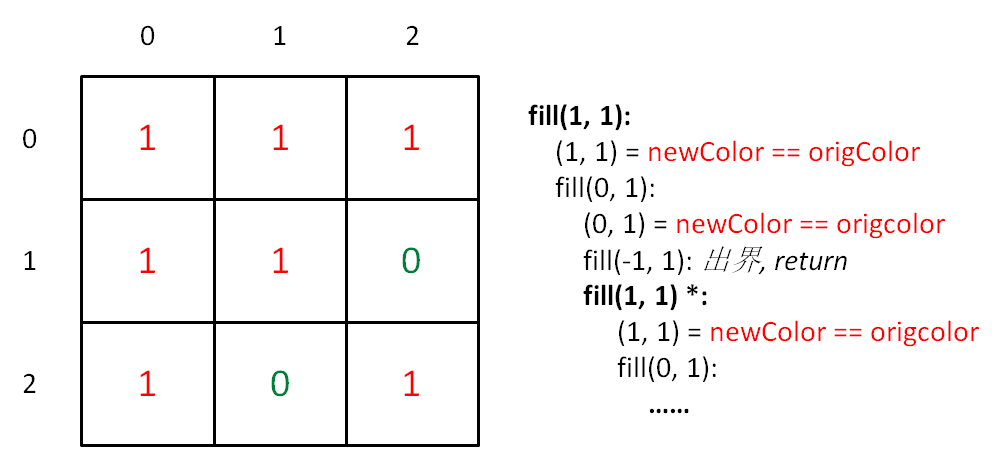
|
||||
|
||||
### 三、处理细节
|
||||
|
||||
如何避免上述问题的发生,最容易想到的就是用一个和 image 一样大小的二维 bool 数组记录走过的地方,一旦发现重复立即 return。
|
||||
|
||||
```java
|
||||
// 出界:超出边界索引
|
||||
if (!inArea(image, x, y)) return;
|
||||
// 碰壁:遇到其他颜色,超出 origColor 区域
|
||||
if (image[x][y] != origColor) return;
|
||||
// 不走回头路
|
||||
if (visited[x][y]) return;
|
||||
visited[x][y] = true;
|
||||
image[x][y] = newColor;
|
||||
```
|
||||
|
||||
完全 OK,这也是处理「图」的一种常用手段。不过对于此题,不用开数组,我们有一种更好的方法,那就是回溯算法。
|
||||
|
||||
前文 [回溯算法框架套路](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版)讲过,这里不再赘述,直接套回溯算法框架:
|
||||
|
||||
```java
|
||||
void fill(int[][] image, int x, int y,
|
||||
int origColor, int newColor) {
|
||||
// 出界:超出数组边界
|
||||
if (!inArea(image, x, y)) return;
|
||||
// 碰壁:遇到其他颜色,超出 origColor 区域
|
||||
if (image[x][y] != origColor) return;
|
||||
// 已探索过的 origColor 区域
|
||||
if (image[x][y] == -1) return;
|
||||
|
||||
// choose:打标记,以免重复
|
||||
image[x][y] = -1;
|
||||
fill(image, x, y + 1, origColor, newColor);
|
||||
fill(image, x, y - 1, origColor, newColor);
|
||||
fill(image, x - 1, y, origColor, newColor);
|
||||
fill(image, x + 1, y, origColor, newColor);
|
||||
// unchoose:将标记替换为 newColor
|
||||
image[x][y] = newColor;
|
||||
}
|
||||
```
|
||||
|
||||
这种解决方法是最常用的,相当于使用一个特殊值 -1 代替 visited 数组的作用,达到不走回头路的效果。为什么是 -1,因为题目中说了颜色取值在 0 - 65535 之间,所以 -1 足够特殊,能和颜色区分开。
|
||||
|
||||
### 四、拓展延伸:自动魔棒工具和扫雷
|
||||
|
||||
大部分图片编辑软件一定有「自动魔棒工具」这个功能:点击一个地方,帮你自动选中相近颜色的部分。如下图,我想选中老鹰,可以先用自动魔棒选中蓝天背景,然后反向选择,就选中了老鹰。我们来分析一下自动魔棒工具的原理。
|
||||
|
||||

|
||||
|
||||
显然,这个算法肯定是基于 FloodFill 算法的,但有两点不同:首先,背景色是蓝色,但不能保证都是相同的蓝色,毕竟是像素点,可能存在肉眼无法分辨的深浅差异,而我们希望能够忽略这种细微差异。第二,FloodFill 算法是「区域填充」,这里更像「边界填充」。
|
||||
|
||||
对于第一个问题,很好解决,可以设置一个阈值 threshold,在阈值范围内波动的颜色都视为 origColor:
|
||||
|
||||
```java
|
||||
if (Math.abs(image[x][y] - origColor) > threshold)
|
||||
return;
|
||||
```
|
||||
|
||||
对于第二个问题,我们首先明确问题:不要把区域内所有 origColor 的都染色,而是只给区域最外圈染色。然后,我们分析,如何才能仅给外围染色,即如何才能找到最外围坐标,最外围坐标有什么特点?
|
||||
|
||||
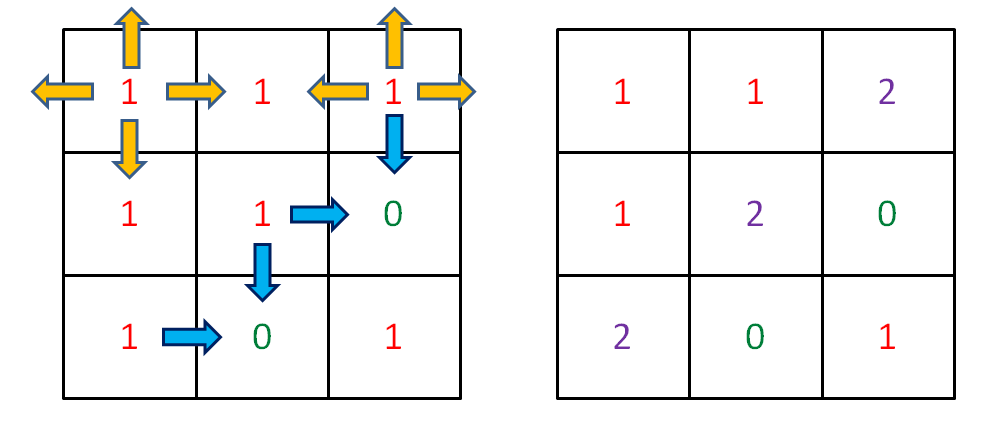
|
||||
|
||||
可以发现,区域边界上的坐标,至少有一个方向不是 origColor,而区域内部的坐标,四面都是 origColor,这就是解决问题的关键。保持框架不变,使用 visited 数组记录已搜索坐标,主要代码如下:
|
||||
|
||||
```java
|
||||
int fill(int[][] image, int x, int y,
|
||||
int origColor, int newColor) {
|
||||
// 出界:超出数组边界
|
||||
if (!inArea(image, x, y)) return 0;
|
||||
// 已探索过的 origColor 区域
|
||||
if (visited[x][y]) return 1;
|
||||
// 碰壁:遇到其他颜色,超出 origColor 区域
|
||||
if (image[x][y] != origColor) return 0;
|
||||
|
||||
visited[x][y] = true;
|
||||
|
||||
int surround =
|
||||
fill(image, x - 1, y, origColor, newColor)
|
||||
+ fill(image, x + 1, y, origColor, newColor)
|
||||
+ fill(image, x, y - 1, origColor, newColor)
|
||||
+ fill(image, x, y + 1, origColor, newColor);
|
||||
|
||||
if (surround < 4)
|
||||
image[x][y] = newColor;
|
||||
|
||||
return 1;
|
||||
}
|
||||
```
|
||||
|
||||
这样,区域内部的坐标探索四周后得到的 surround 是 4,而边界的坐标会遇到其他颜色,或超出边界索引,surround 会小于 4。如果你对这句话不理解,我们把逻辑框架抽象出来看:
|
||||
|
||||
```java
|
||||
int fill(int[][] image, int x, int y,
|
||||
int origColor, int newColor) {
|
||||
// 出界:超出数组边界
|
||||
if (!inArea(image, x, y)) return 0;
|
||||
// 已探索过的 origColor 区域
|
||||
if (visited[x][y]) return 1;
|
||||
// 碰壁:遇到其他颜色,超出 origColor 区域
|
||||
if (image[x][y] != origColor) return 0;
|
||||
// 未探索且属于 origColor 区域
|
||||
if (image[x][y] == origColor) {
|
||||
// ...
|
||||
return 1;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这 4 个 if 判断涵盖了 (x, y) 的所有可能情况,surround 的值由四个递归函数相加得到,而每个递归函数的返回值就这四种情况的一种。借助这个逻辑框架,你一定能理解上面那句话了。
|
||||
|
||||
这样就实现了仅对 origColor 区域边界坐标染色的目的,等同于完成了魔棒工具选定区域边界的功能。
|
||||
|
||||
这个算法有两个细节问题,一是必须借助 visited 来记录已探索的坐标,而无法使用回溯算法;二是开头几个 if 顺序不可打乱。读者可以思考一下原因。
|
||||
|
||||
同理,思考扫雷游戏,应用 FloodFill 算法展开空白区域的同时,也需要计算并显示边界上雷的个数,如何实现的?其实也是相同的思路,遇到雷就返回 true,这样 surround 变量存储的就是雷的个数。当然,扫雷的 FloodFill 算法不能只检查上下左右,还得加上四个斜向。
|
||||
|
||||
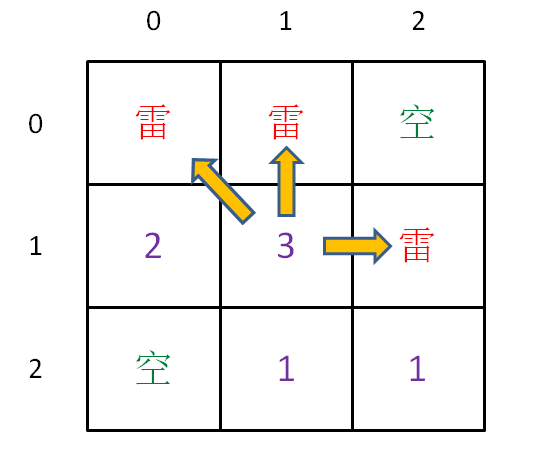
|
||||
|
||||
以上详细讲解了 FloodFill 算法的框架设计,**二维矩阵中的搜索问题,都逃不出这个算法框架**。
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
[733.图像渲染](https://leetcode-cn.com/problems/flood-fill)
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
**BFS**
|
||||
从起始像素向上下左右扩散,只要相邻的点存在并和起始点颜色相同,就染成新的颜色,并继续扩散。
|
||||
|
||||
借助一个队列去遍历节点,考察出列的节点,带出满足条件的节点入列。已经染成新色的节点不会入列,避免重复访问节点。
|
||||
|
||||
时间复杂度:O(n)。空间复杂度:O(n)
|
||||
|
||||
```js
|
||||
const floodFill = (image, sr, sc, newColor) => {
|
||||
const m = image.length;
|
||||
const n = image[0].length;
|
||||
const oldColor = image[sr][sc];
|
||||
if (oldColor == newColor) return image;
|
||||
|
||||
const fill = (i, j) => {
|
||||
if (i < 0 || i >= m || j < 0 || j >= n || image[i][j] != oldColor) {
|
||||
return;
|
||||
}
|
||||
image[i][j] = newColor;
|
||||
fill(i - 1, j);
|
||||
fill(i + 1, j);
|
||||
fill(i, j - 1);
|
||||
fill(i, j + 1);
|
||||
};
|
||||
|
||||
fill(sr, sc);
|
||||
return image;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
**DFS**
|
||||
|
||||
思路与上文相同。
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[][]} image
|
||||
* @param {number} sr
|
||||
* @param {number} sc
|
||||
* @param {number} newColor
|
||||
* @return {number[][]}
|
||||
*/
|
||||
let floodFill = function (image, sr, sc, newColor) {
|
||||
let origColor = image[sr][sc];
|
||||
fill(image, sr, sc, origColor, newColor);
|
||||
return image;
|
||||
}
|
||||
|
||||
let fill = function (image, x, y, origColor, newColor) {
|
||||
// 出界:超出边界索引
|
||||
if (!inArea(image, x, y)) return;
|
||||
|
||||
// 碰壁:遇到其他颜色,超出 origColor 区域
|
||||
if (image[x][y] !== origColor) return;
|
||||
|
||||
// 已探索过的 origColor 区域
|
||||
if (image[x][y] === -1) return;
|
||||
|
||||
// 打标记 避免重复
|
||||
image[x][y] = -1;
|
||||
|
||||
fill(image, x, y + 1, origColor, newColor);
|
||||
fill(image, x, y - 1, origColor, newColor);
|
||||
fill(image, x - 1, y, origColor, newColor);
|
||||
fill(image, x + 1, y, origColor, newColor);
|
||||
|
||||
// un choose:将标记替换为 newColor
|
||||
image[x][y] = newColor;
|
||||
}
|
||||
|
||||
let inArea = function (image, x, y) {
|
||||
return x >= 0 && x < image.length
|
||||
&& y >= 0 && y < image[0].length;
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -1,570 +0,0 @@
|
|||
# Union-Find算法应用
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[130.被围绕的区域](https://leetcode-cn.com/problems/surrounded-regions)
|
||||
|
||||
[990.等式方程的可满足性](https://leetcode-cn.com/problems/satisfiability-of-equality-equations)
|
||||
|
||||
[261.以图判树](https://leetcode-cn.com/problems/graph-valid-tree/)
|
||||
|
||||
**-----------**
|
||||
|
||||
上篇文章很多读者对于 Union-Find 算法的应用表示很感兴趣,这篇文章就拿几道 LeetCode 题目来讲讲这个算法的巧妙用法。
|
||||
|
||||
首先,复习一下,Union-Find 算法解决的是图的动态连通性问题,这个算法本身不难,能不能应用出来主要是看你抽象问题的能力,是否能够把原始问题抽象成一个有关图论的问题。
|
||||
|
||||
先复习一下上篇文章写的算法代码,回答读者提出的几个问题:
|
||||
|
||||
```java
|
||||
class UF {
|
||||
// 记录连通分量个数
|
||||
private int count;
|
||||
// 存储若干棵树
|
||||
private int[] parent;
|
||||
// 记录树的“重量”
|
||||
private int[] size;
|
||||
|
||||
public UF(int n) {
|
||||
this.count = n;
|
||||
parent = new int[n];
|
||||
size = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
parent[i] = i;
|
||||
size[i] = 1;
|
||||
}
|
||||
}
|
||||
|
||||
/* 将 p 和 q 连通 */
|
||||
public void union(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
if (rootP == rootQ)
|
||||
return;
|
||||
|
||||
// 小树接到大树下面,较平衡
|
||||
if (size[rootP] > size[rootQ]) {
|
||||
parent[rootQ] = rootP;
|
||||
size[rootP] += size[rootQ];
|
||||
} else {
|
||||
parent[rootP] = rootQ;
|
||||
size[rootQ] += size[rootP];
|
||||
}
|
||||
count--;
|
||||
}
|
||||
|
||||
/* 判断 p 和 q 是否互相连通 */
|
||||
public boolean connected(int p, int q) {
|
||||
int rootP = find(p);
|
||||
int rootQ = find(q);
|
||||
// 处于同一棵树上的节点,相互连通
|
||||
return rootP == rootQ;
|
||||
}
|
||||
|
||||
/* 返回节点 x 的根节点 */
|
||||
private int find(int x) {
|
||||
while (parent[x] != x) {
|
||||
// 进行路径压缩
|
||||
parent[x] = parent[parent[x]];
|
||||
x = parent[x];
|
||||
}
|
||||
return x;
|
||||
}
|
||||
|
||||
public int count() {
|
||||
return count;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
算法的关键点有 3 个:
|
||||
|
||||
1、用 `parent` 数组记录每个节点的父节点,相当于指向父节点的指针,所以 `parent` 数组内实际存储着一个森林(若干棵多叉树)。
|
||||
|
||||
2、用 `size` 数组记录着每棵树的重量,目的是让 `union` 后树依然拥有平衡性,而不会退化成链表,影响操作效率。
|
||||
|
||||
3、在 `find` 函数中进行路径压缩,保证任意树的高度保持在常数,使得 `union` 和 `connected` API 时间复杂度为 O(1)。
|
||||
|
||||
有的读者问,**既然有了路径压缩,`size` 数组的重量平衡还需要吗**?这个问题很有意思,因为路径压缩保证了树高为常数(不超过 3),那么树就算不平衡,高度也是常数,基本没什么影响。
|
||||
|
||||
我认为,论时间复杂度的话,确实,不需要重量平衡也是 O(1)。但是如果加上 `size` 数组辅助,效率还是略微高一些,比如下面这种情况:
|
||||
|
||||

|
||||
|
||||
如果带有重量平衡优化,一定会得到情况一,而不带重量优化,可能出现情况二。高度为 3 时才会触发路径压缩那个 `while` 循环,所以情况一根本不会触发路径压缩,而情况二会多执行很多次路径压缩,将第三层节点压缩到第二层。
|
||||
|
||||
也就是说,去掉重量平衡,虽然对于单个的 `find` 函数调用,时间复杂度依然是 O(1),但是对于 API 调用的整个过程,效率会有一定的下降。当然,好处就是减少了一些空间,不过对于 Big O 表示法来说,时空复杂度都没变。
|
||||
|
||||
下面言归正传,来看看这个算法有什么实际应用。
|
||||
|
||||
### 一、DFS 的替代方案
|
||||
|
||||
很多使用 DFS 深度优先算法解决的问题,也可以用 Union-Find 算法解决。
|
||||
|
||||
比如第 130 题,被围绕的区域:给你一个 M×N 的二维矩阵,其中包含字符 `X` 和 `O`,让你找到矩阵中**四面**被 `X` 围住的 `O`,并且把它们替换成 `X`。
|
||||
|
||||
```java
|
||||
void solve(char[][] board);
|
||||
```
|
||||
|
||||
注意哦,必须是四面被围的 `O` 才能被换成 `X`,也就是说边角上的 `O` 一定不会被围,进一步,与边角上的 `O` 相连的 `O` 也不会被 `X` 围四面,也不会被替换。
|
||||
|
||||

|
||||
|
||||
PS:这让我想起小时候玩的棋类游戏「黑白棋」,只要你用两个棋子把对方的棋子夹在中间,对方的子就被替换成你的子。可见,占据四角的棋子是无敌的,与其相连的边棋子也是无敌的(无法被夹掉)。
|
||||
|
||||
解决这个问题的传统方法也不困难,先用 for 循环遍历棋盘的**四边**,用 DFS 算法把那些与边界相连的 `O` 换成一个特殊字符,比如 `#`;然后再遍历整个棋盘,把剩下的 `O` 换成 `X`,把 `#` 恢复成 `O`。这样就能完成题目的要求,时间复杂度 O(MN)。
|
||||
|
||||
这个问题也可以用 Union-Find 算法解决,虽然实现复杂一些,甚至效率也略低,但这是使用 Union-Find 算法的通用思想,值得一学。
|
||||
|
||||
**你可以把那些不需要被替换的 `O` 看成一个拥有独门绝技的门派,它们有一个共同祖师爷叫 `dummy`,这些 `O` 和 `dummy` 互相连通,而那些需要被替换的 `O` 与 `dummy` 不连通**。
|
||||
|
||||

|
||||
|
||||
这就是 Union-Find 的核心思路,明白这个图,就很容易看懂代码了。
|
||||
|
||||
首先要解决的是,根据我们的实现,Union-Find 底层用的是一维数组,构造函数需要传入这个数组的大小,而题目给的是一个二维棋盘。
|
||||
|
||||
这个很简单,二维坐标 `(x,y)` 可以转换成 `x * n + y` 这个数(`m` 是棋盘的行数,`n` 是棋盘的列数)。敲黑板,**这是将二维坐标映射到一维的常用技巧**。
|
||||
|
||||
其次,我们之前描述的「祖师爷」是虚构的,需要给他老人家留个位置。索引 `[0.. m*n-1]` 都是棋盘内坐标的一维映射,那就让这个虚拟的 `dummy` 节点占据索引 `m * n` 好了。
|
||||
|
||||
```java
|
||||
void solve(char[][] board) {
|
||||
if (board.length == 0) return;
|
||||
|
||||
int m = board.length;
|
||||
int n = board[0].length;
|
||||
// 给 dummy 留一个额外位置
|
||||
UF uf = new UF(m * n + 1);
|
||||
int dummy = m * n;
|
||||
// 将首列和末列的 O 与 dummy 连通
|
||||
for (int i = 0; i < m; i++) {
|
||||
if (board[i][0] == 'O')
|
||||
uf.union(i * n, dummy);
|
||||
if (board[i][n - 1] == 'O')
|
||||
uf.union(i * n + n - 1, dummy);
|
||||
}
|
||||
// 将首行和末行的 O 与 dummy 连通
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (board[0][j] == 'O')
|
||||
uf.union(j, dummy);
|
||||
if (board[m - 1][j] == 'O')
|
||||
uf.union(n * (m - 1) + j, dummy);
|
||||
}
|
||||
// 方向数组 d 是上下左右搜索的常用手法
|
||||
int[][] d = new int[][]{{1,0}, {0,1}, {0,-1}, {-1,0}};
|
||||
for (int i = 1; i < m - 1; i++)
|
||||
for (int j = 1; j < n - 1; j++)
|
||||
if (board[i][j] == 'O')
|
||||
// 将此 O 与上下左右的 O 连通
|
||||
for (int k = 0; k < 4; k++) {
|
||||
int x = i + d[k][0];
|
||||
int y = j + d[k][1];
|
||||
if (board[x][y] == 'O')
|
||||
uf.union(x * n + y, i * n + j);
|
||||
}
|
||||
// 所有不和 dummy 连通的 O,都要被替换
|
||||
for (int i = 1; i < m - 1; i++)
|
||||
for (int j = 1; j < n - 1; j++)
|
||||
if (!uf.connected(dummy, i * n + j))
|
||||
board[i][j] = 'X';
|
||||
}
|
||||
```
|
||||
|
||||
这段代码很长,其实就是刚才的思路实现,只有和边界 `O` 相连的 `O` 才具有和 `dummy` 的连通性,他们不会被替换。
|
||||
|
||||
说实话,Union-Find 算法解决这个简单的问题有点杀鸡用牛刀,它可以解决更复杂,更具有技巧性的问题,**主要思路是适时增加虚拟节点,想办法让元素「分门别类」,建立动态连通关系**。
|
||||
|
||||
### 二、判定合法等式
|
||||
|
||||
这个问题用 Union-Find 算法就显得十分优美了。题目是这样:
|
||||
|
||||
给你一个数组 `equations`,装着若干字符串表示的算式。每个算式 `equations[i]` 长度都是 4,而且只有这两种情况:`a==b` 或者 `a!=b`,其中 `a,b` 可以是任意小写字母。你写一个算法,如果 `equations` 中所有算式都不会互相冲突,返回 true,否则返回 false。
|
||||
|
||||
比如说,输入 `["a==b","b!=c","c==a"]`,算法返回 false,因为这三个算式不可能同时正确。
|
||||
|
||||
再比如,输入 `["c==c","b==d","x!=z"]`,算法返回 true,因为这三个算式并不会造成逻辑冲突。
|
||||
|
||||
我们前文说过,动态连通性其实就是一种等价关系,具有「自反性」「传递性」和「对称性」,其实 `==` 关系也是一种等价关系,具有这些性质。所以这个问题用 Union-Find 算法就很自然。
|
||||
|
||||
核心思想是,**将 `equations` 中的算式根据 `==` 和 `!=` 分成两部分,先处理 `==` 算式,使得他们通过相等关系各自勾结成门派;然后处理 `!=` 算式,检查不等关系是否破坏了相等关系的连通性**。
|
||||
|
||||
```java
|
||||
boolean equationsPossible(String[] equations) {
|
||||
// 26 个英文字母
|
||||
UF uf = new UF(26);
|
||||
// 先让相等的字母形成连通分量
|
||||
for (String eq : equations) {
|
||||
if (eq.charAt(1) == '=') {
|
||||
char x = eq.charAt(0);
|
||||
char y = eq.charAt(3);
|
||||
uf.union(x - 'a', y - 'a');
|
||||
}
|
||||
}
|
||||
// 检查不等关系是否打破相等关系的连通性
|
||||
for (String eq : equations) {
|
||||
if (eq.charAt(1) == '!') {
|
||||
char x = eq.charAt(0);
|
||||
char y = eq.charAt(3);
|
||||
// 如果相等关系成立,就是逻辑冲突
|
||||
if (uf.connected(x - 'a', y - 'a'))
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
至此,这道判断算式合法性的问题就解决了,借助 Union-Find 算法,是不是很简单呢?
|
||||
|
||||
### 三、简单总结
|
||||
|
||||
使用 Union-Find 算法,主要是如何把原问题转化成图的动态连通性问题。对于算式合法性问题,可以直接利用等价关系,对于棋盘包围问题,则是利用一个虚拟节点,营造出动态连通特性。
|
||||
|
||||
另外,将二维数组映射到一维数组,利用方向数组 `d` 来简化代码量,都是在写算法时常用的一些小技巧,如果没见过可以注意一下。
|
||||
|
||||
很多更复杂的 DFS 算法问题,都可以利用 Union-Find 算法更漂亮的解决。LeetCode 上 Union-Find 相关的问题也就二十多道,有兴趣的读者可以去做一做。
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[130.被围绕的区域](https://leetcode-cn.com/problems/surrounded-regions)
|
||||
|
||||
[990.等式方程的可满足性](https://leetcode-cn.com/problems/satisfiability-of-equality-equations)
|
||||
|
||||
[261.以图判树](https://leetcode-cn.com/problems/graph-valid-tree/)
|
||||
|
||||
|
||||
|
||||
### java
|
||||
|
||||
第261题的Java代码(提供:[LEODPEN](https://github.com/LEODPEN))
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
|
||||
class DisjointSet {
|
||||
|
||||
int count; // 连通分量的总个数
|
||||
int[] parent; // 每个节点的头节点(不一定是连通分量的最终头节点)
|
||||
int[] size; // 每个连通分量的大小
|
||||
|
||||
public DisjointSet(int n) {
|
||||
parent = new int[n];
|
||||
size = new int[n];
|
||||
// 初为n个连通分量,期望最后为1
|
||||
count = n;
|
||||
for (int i = 0; i < n; i++) {
|
||||
// 初始的连通分量只有该节点本身
|
||||
parent[i] = i;
|
||||
size[i] = 1;
|
||||
}
|
||||
}
|
||||
|
||||
/**
|
||||
* @param first 节点1
|
||||
* @param second 节点2
|
||||
* @return 未连通 && 连通成功
|
||||
*/
|
||||
public boolean union(int first, int second) {
|
||||
// 分别找到包含first 和 second 的最终根节点
|
||||
int firstParent = findRootParent(first), secondParent = findRootParent(second);
|
||||
// 相等说明已经处于一个连通分量,即说明有环
|
||||
if (firstParent == secondParent) return false;
|
||||
// 将较小的连通分量融入较大的连通分量
|
||||
if (size[firstParent] >= size[secondParent]) {
|
||||
parent[secondParent] = firstParent;
|
||||
size[firstParent] += size[secondParent];
|
||||
} else {
|
||||
parent[firstParent] = secondParent;
|
||||
size[secondParent] += size[firstParent];
|
||||
}
|
||||
// 连通分量已合并,count减少
|
||||
count--;
|
||||
return true;
|
||||
}
|
||||
|
||||
/**
|
||||
* @param node 某节点
|
||||
* @return 包含该节点的连通分量的最终根节点
|
||||
*/
|
||||
private int findRootParent(int node) {
|
||||
while (node != parent[node]) {
|
||||
// 压缩路径
|
||||
parent[node] = parent[parent[node]];
|
||||
node = parent[node];
|
||||
}
|
||||
return node;
|
||||
}
|
||||
}
|
||||
|
||||
public boolean validTree(int n, int[][] edges) {
|
||||
// 树的特性:节点数 = 边数 + 1
|
||||
if (edges.length != n - 1) return false;
|
||||
DisjointSet djs = new DisjointSet(n);
|
||||
for (int[] edg : edges) {
|
||||
// 判断连通情况(如果合并的两个点在一个连通分量里,说明有环)
|
||||
if (!djs.union(edg[0], edg[1])) return false;
|
||||
}
|
||||
// 是否全部节点均已相连
|
||||
return djs.count == 1;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
[130.被围绕的区域](https://leetcode-cn.com/problems/surrounded-regions)
|
||||
|
||||
```js
|
||||
class UF {
|
||||
// 记录连通分量
|
||||
count;
|
||||
|
||||
// 节点 x 的根节点是 parent[x]
|
||||
parent;
|
||||
|
||||
// 记录树的“重量”
|
||||
size;
|
||||
|
||||
constructor(n) {
|
||||
|
||||
// 一开始互不连通
|
||||
this.count = n;
|
||||
|
||||
// 父节点指针初始指向自己
|
||||
this.parent = new Array(n);
|
||||
|
||||
this.size = new Array(n);
|
||||
|
||||
for (let i = 0; i < n; i++) {
|
||||
this.parent[i] = i;
|
||||
this.size[i] = 1;
|
||||
}
|
||||
}
|
||||
|
||||
/* 返回某个节点 x 的根节点 */
|
||||
find(x) {
|
||||
// 根节点的 parent[x] == x
|
||||
while (this.parent[x] !== x) {
|
||||
// 进行路径压缩
|
||||
this.parent[x] = this.parent[this.parent[x]];
|
||||
x = this.parent[x];
|
||||
}
|
||||
return x;
|
||||
}
|
||||
|
||||
/* 将 p 和 q 连接 */
|
||||
union(p, q) {
|
||||
// 如果某两个节点被连通,则让其中的(任意)
|
||||
// 一个节点的根节点接到另一个节点的根节点上
|
||||
let rootP = this.find(p);
|
||||
let rootQ = this.find(q);
|
||||
if (rootP === rootQ) return;
|
||||
|
||||
// 小树接到大树下面,较平衡
|
||||
if (this.size[rootP] > this.size[rootQ]) {
|
||||
this.parent[rootQ] = rootP;
|
||||
this.size[rootP] += this.size[rootQ];
|
||||
} else {
|
||||
this.parent[rootP] = rootQ;
|
||||
this.size[rootQ] += this.size[rootP];
|
||||
}
|
||||
|
||||
this.count--; // 两个分量合二为一
|
||||
}
|
||||
|
||||
/* 判断 p 和 q 是否连通 */
|
||||
connected(p, q) {
|
||||
let rootP = this.find(p);
|
||||
let rootQ = this.find(q);
|
||||
return rootP === rootQ;
|
||||
};
|
||||
|
||||
/* 返回图中有多少个连通分量 */
|
||||
getCount() {
|
||||
return this.count;
|
||||
};
|
||||
}
|
||||
|
||||
/**
|
||||
* @param {[][]} board
|
||||
* @return {void} Do not return anything, modify board in-place instead.
|
||||
*/
|
||||
let solve = function (board) {
|
||||
if (board.length === 0) return;
|
||||
|
||||
let m = board.length;
|
||||
let n = board[0].length;
|
||||
|
||||
// 给 dummy 留一个额外位置
|
||||
let uf = new UF(m * n + 1);
|
||||
let dummy = m * n;
|
||||
// 将首列和末列的 O 与 dummy 连通
|
||||
for (let i = 0; i < m; i++) {
|
||||
if (board[i][0] === 'O')
|
||||
uf.union(i * n, dummy);
|
||||
if (board[i][n - 1] === 'O')
|
||||
uf.union(i * n + n - 1, dummy);
|
||||
}
|
||||
// 将首行和末行的 O 与 dummy 连通
|
||||
for (let j = 0; j < n; j++) {
|
||||
if (board[0][j] === 'O')
|
||||
uf.union(j, dummy);
|
||||
if (board[m - 1][j] === 'O')
|
||||
uf.union(n * (m - 1) + j, dummy);
|
||||
}
|
||||
// 方向数组 d 是上下左右搜索的常用手法
|
||||
let d = [[1, 0], [0, 1], [0, -1], [-1, 0]];
|
||||
for (let i = 1; i < m - 1; i++)
|
||||
for (let j = 1; j < n - 1; j++)
|
||||
if (board[i][j] === 'O')
|
||||
// 将此 O 与上下左右的 O 连通
|
||||
for (let k = 0; k < 4; k++) {
|
||||
let x = i + d[k][0];
|
||||
let y = j + d[k][1];
|
||||
if (board[x][y] === 'O')
|
||||
uf.union(x * n + y, i * n + j);
|
||||
}
|
||||
// 所有不和 dummy 连通的 O,都要被替换
|
||||
for (let i = 1; i < m - 1; i++)
|
||||
for (let j = 1; j < n - 1; j++)
|
||||
if (!uf.connected(dummy, i * n + j))
|
||||
board[i][j] = 'X';
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
[990.等式方程的可满足性](https://leetcode-cn.com/problems/surrounded-regions)
|
||||
|
||||
需要注意的点主要为js字符与ASCII码互转。
|
||||
|
||||
在java、c这些语言中,字符串直接相减,得到的是ASCII码的差值,结果为整数;而js中`"a" - "b"`的结果为NaN,所以需要使用`charCodeAt(index)`方法来获取字符的ASCII码,index不填时,默认结果为第一个字符的ASCII码。
|
||||
|
||||
```js
|
||||
class UF {
|
||||
// 记录连通分量
|
||||
count;
|
||||
|
||||
// 节点 x 的根节点是 parent[x]
|
||||
parent;
|
||||
|
||||
// 记录树的“重量”
|
||||
size;
|
||||
|
||||
constructor(n) {
|
||||
|
||||
// 一开始互不连通
|
||||
this.count = n;
|
||||
|
||||
// 父节点指针初始指向自己
|
||||
this.parent = new Array(n);
|
||||
|
||||
this.size = new Array(n);
|
||||
|
||||
for (let i = 0; i < n; i++) {
|
||||
this.parent[i] = i;
|
||||
this.size[i] = 1;
|
||||
}
|
||||
}
|
||||
|
||||
/* 返回某个节点 x 的根节点 */
|
||||
find(x) {
|
||||
// 根节点的 parent[x] == x
|
||||
while (this.parent[x] !== x) {
|
||||
// 进行路径压缩
|
||||
this.parent[x] = this.parent[this.parent[x]];
|
||||
x = this.parent[x];
|
||||
}
|
||||
return x;
|
||||
}
|
||||
|
||||
/* 将 p 和 q 连接 */
|
||||
union(p, q) {
|
||||
// 如果某两个节点被连通,则让其中的(任意)
|
||||
// 一个节点的根节点接到另一个节点的根节点上
|
||||
let rootP = this.find(p);
|
||||
let rootQ = this.find(q);
|
||||
if (rootP === rootQ) return;
|
||||
|
||||
// 小树接到大树下面,较平衡
|
||||
if (this.size[rootP] > this.size[rootQ]) {
|
||||
this.parent[rootQ] = rootP;
|
||||
this.size[rootP] += this.size[rootQ];
|
||||
} else {
|
||||
this.parent[rootP] = rootQ;
|
||||
this.size[rootQ] += this.size[rootP];
|
||||
}
|
||||
|
||||
this.count--; // 两个分量合二为一
|
||||
}
|
||||
|
||||
/* 判断 p 和 q 是否连通 */
|
||||
connected(p, q) {
|
||||
let rootP = this.find(p);
|
||||
let rootQ = this.find(q);
|
||||
return rootP === rootQ;
|
||||
};
|
||||
|
||||
/* 返回图中有多少个连通分量 */
|
||||
getCount() {
|
||||
return this.count;
|
||||
};
|
||||
}
|
||||
/**
|
||||
* @param {string[]} equations
|
||||
* @return {boolean}
|
||||
*/
|
||||
let equationsPossible = function (equations) {
|
||||
// 26 个英文字母
|
||||
let uf = new UF(26);
|
||||
// 先让相等的字母形成连通分量
|
||||
for (let eq of equations) {
|
||||
if (eq[1] === '=') {
|
||||
let x = eq[0];
|
||||
let y = eq[3];
|
||||
|
||||
// 'a'.charCodeAt() 为 97
|
||||
uf.union(x.charCodeAt(0) - 97, y.charCodeAt(0) - 97);
|
||||
}
|
||||
}
|
||||
// 检查不等关系是否打破相等关系的连通性
|
||||
for (let eq of equations) {
|
||||
if (eq[1] === '!') {
|
||||
let x = eq[0];
|
||||
let y = eq[3];
|
||||
// 如果相等关系成立,就是逻辑冲突
|
||||
if (uf.connected(x.charCodeAt(0) - 97, y.charCodeAt(0) - 97))
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
};
|
||||
```
|
||||
|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# Union-Find 算法详解
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -527,6 +523,41 @@ class UF {
|
|||
|
||||
最后,Union-Find 算法也会在一些其他经典图论算法中用到,比如判断「图」和「树」,以及最小生成树的计算,详情见 [Kruskal 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=kruskal)。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [Kruskal 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=kruskal)
|
||||
- [Prim 最小生成树算法](https://labuladong.github.io/article/fname.html?fname=prim算法)
|
||||
- [一文秒杀所有岛屿题目](https://labuladong.github.io/article/fname.html?fname=岛屿题目)
|
||||
- [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1361. Validate Binary Tree Nodes](https://leetcode.com/problems/validate-binary-tree-nodes/?show=1) | [1361. 验证二叉树](https://leetcode.cn/problems/validate-binary-tree-nodes/?show=1) |
|
||||
| [200. Number of Islands](https://leetcode.com/problems/number-of-islands/?show=1) | [200. 岛屿数量](https://leetcode.cn/problems/number-of-islands/?show=1) |
|
||||
| [261. Graph Valid Tree](https://leetcode.com/problems/graph-valid-tree/?show=1)🔒 | [261. 以图判树](https://leetcode.cn/problems/graph-valid-tree/?show=1)🔒 |
|
||||
| [765. Couples Holding Hands](https://leetcode.com/problems/couples-holding-hands/?show=1) | [765. 情侣牵手](https://leetcode.cn/problems/couples-holding-hands/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,300 +0,0 @@
|
|||
# twoSum问题的核心思想
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[1.两数之和](https://leetcode-cn.com/problems/two-sum)
|
||||
|
||||
[170.两数之和 III - 数据结构设计](https://leetcode-cn.com/problems/two-sum-iii-data-structure-design)
|
||||
|
||||
**-----------**
|
||||
|
||||
Two Sum 系列问题在 LeetCode 上有好几道,这篇文章就挑出有代表性的几道,介绍一下这种问题怎么解决。
|
||||
|
||||
### TwoSum I
|
||||
|
||||
这个问题的**最基本形式**是这样:给你一个数组和一个整数 `target`,可以保证数组中**存在**两个数的和为 `target`,请你返回这两个数的索引。
|
||||
|
||||
比如输入 `nums = [3,1,3,6], target = 6`,算法应该返回数组 `[0,2]`,因为 3 + 3 = 6。
|
||||
|
||||
这个问题如何解决呢?首先最简单粗暴的办法当然是穷举了:
|
||||
|
||||
```java
|
||||
int[] twoSum(int[] nums, int target) {
|
||||
|
||||
for (int i = 0; i < nums.length; i++)
|
||||
for (int j = i + 1; j < nums.length; j++)
|
||||
if (nums[j] == target - nums[i])
|
||||
return new int[] { i, j };
|
||||
|
||||
// 不存在这么两个数
|
||||
return new int[] {-1, -1};
|
||||
}
|
||||
```
|
||||
|
||||
这个解法非常直接,时间复杂度 O(N^2),空间复杂度 O(1)。
|
||||
|
||||
可以通过一个哈希表减少时间复杂度:
|
||||
|
||||
```java
|
||||
int[] twoSum(int[] nums, int target) {
|
||||
int n = nums.length;
|
||||
index<Integer, Integer> index = new HashMap<>();
|
||||
// 构造一个哈希表:元素映射到相应的索引
|
||||
for (int i = 0; i < n; i++)
|
||||
index.put(nums[i], i);
|
||||
|
||||
for (int i = 0; i < n; i++) {
|
||||
int other = target - nums[i];
|
||||
// 如果 other 存在且不是 nums[i] 本身
|
||||
if (index.containsKey(other) && index.get(other) != i)
|
||||
return new int[] {i, index.get(other)};
|
||||
}
|
||||
|
||||
return new int[] {-1, -1};
|
||||
}
|
||||
```
|
||||
|
||||
这样,由于哈希表的查询时间为 O(1),算法的时间复杂度降低到 O(N),但是需要 O(N) 的空间复杂度来存储哈希表。不过综合来看,是要比暴力解法高效的。
|
||||
|
||||
**我觉得 Two Sum 系列问题就是想教我们如何使用哈希表处理问题**。我们接着往后看。
|
||||
|
||||
### TwoSum II
|
||||
|
||||
这里我们稍微修改一下上面的问题。我们设计一个类,拥有两个 API:
|
||||
|
||||
```java
|
||||
class TwoSum {
|
||||
// 向数据结构中添加一个数 number
|
||||
public void add(int number);
|
||||
// 寻找当前数据结构中是否存在两个数的和为 value
|
||||
public boolean find(int value);
|
||||
}
|
||||
```
|
||||
|
||||
如何实现这两个 API 呢,我们可以仿照上一道题目,使用一个哈希表辅助 `find` 方法:
|
||||
|
||||
```java
|
||||
class TwoSum {
|
||||
Map<Integer, Integer> freq = new HashMap<>();
|
||||
|
||||
public void add(int number) {
|
||||
// 记录 number 出现的次数
|
||||
freq.put(number, freq.getOrDefault(number, 0) + 1);
|
||||
}
|
||||
|
||||
public boolean find(int value) {
|
||||
for (Integer key : freq.keySet()) {
|
||||
int other = value - key;
|
||||
// 情况一
|
||||
if (other == key && freq.get(key) > 1)
|
||||
return true;
|
||||
// 情况二
|
||||
if (other != key && freq.containsKey(other))
|
||||
return true;
|
||||
}
|
||||
return false;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
进行 `find` 的时候有两种情况,举个例子:
|
||||
|
||||
情况一:`add` 了 `[3,3,2,5]` 之后,执行 `find(6)`,由于 3 出现了两次,3 + 3 = 6,所以返回 true。
|
||||
|
||||
情况二:`add` 了 `[3,3,2,5]` 之后,执行 `find(7)`,那么 `key` 为 2,`other` 为 5 时算法可以返回 true。
|
||||
|
||||
除了上述两种情况外,`find` 只能返回 false 了。
|
||||
|
||||
对于这个解法的时间复杂度呢,`add` 方法是 O(1),`find` 方法是 O(N),空间复杂度为 O(N),和上一道题目比较类似。
|
||||
|
||||
**但是对于 API 的设计,是需要考虑现实情况的**。比如说,我们设计的这个类,使用 `find` 方法非常频繁,那么每次都要 O(N) 的时间,岂不是很浪费费时间吗?对于这种情况,我们是否可以做些优化呢?
|
||||
|
||||
是的,对于频繁使用 `find` 方法的场景,我们可以进行优化。我们可以参考上一道题目的暴力解法,借助**哈希集合**来针对性优化 `find` 方法:
|
||||
|
||||
```java
|
||||
class TwoSum {
|
||||
Set<Integer> sum = new HashSet<>();
|
||||
List<Integer> nums = new ArrayList<>();
|
||||
|
||||
public void add(int number) {
|
||||
// 记录所有可能组成的和
|
||||
for (int n : nums)
|
||||
sum.add(n + number);
|
||||
nums.add(number);
|
||||
}
|
||||
|
||||
public boolean find(int value) {
|
||||
return sum.contains(value);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这样 `sum` 中就储存了所有加入数字可能组成的和,每次 `find` 只要花费 O(1) 的时间在集合中判断一下是否存在就行了,显然非常适合频繁使用 `find` 的场景。
|
||||
|
||||
### 三、总结
|
||||
|
||||
对于 TwoSum 问题,一个难点就是给的数组**无序**。对于一个无序的数组,我们似乎什么技巧也没有,只能暴力穷举所有可能。
|
||||
|
||||
**一般情况下,我们会首先把数组排序再考虑双指针技巧**。TwoSum 启发我们,HashMap 或者 HashSet 也可以帮助我们处理无序数组相关的简单问题。
|
||||
|
||||
另外,设计的核心在于权衡,利用不同的数据结构,可以得到一些针对性的加强。
|
||||
|
||||
最后,如果 TwoSum I 中给的数组是有序的,应该如何编写算法呢?答案很简单,前文「双指针技巧汇总」写过:
|
||||
|
||||
```java
|
||||
int[] twoSum(int[] nums, int target) {
|
||||
int left = 0, right = nums.length - 1;
|
||||
while (left < right) {
|
||||
int sum = nums[left] + nums[right];
|
||||
if (sum == target) {
|
||||
return new int[]{left, right};
|
||||
} else if (sum < target) {
|
||||
left++; // 让 sum 大一点
|
||||
} else if (sum > target) {
|
||||
right--; // 让 sum 小一点
|
||||
}
|
||||
}
|
||||
// 不存在这样两个数
|
||||
return new int[]{-1, -1};
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[1.两数之和](https://leetcode-cn.com/problems/two-sum)
|
||||
|
||||
[170.两数之和 III - 数据结构设计](https://leetcode-cn.com/problems/two-sum-iii-data-structure-design)
|
||||
|
||||
|
||||
|
||||
### python
|
||||
|
||||
由[JodyZ0203](https://github.com/JodyZ0203)提供 1. Two Sums Python3 解法代码:
|
||||
|
||||
只用一个哈希表
|
||||
|
||||
```python
|
||||
class Solution:
|
||||
def twoSum(self, nums, target):
|
||||
"""
|
||||
:type nums: List[int]
|
||||
:type target: int
|
||||
:rtype: List[int]
|
||||
"""
|
||||
# 提前构造一个哈希表
|
||||
hashTable = {}
|
||||
# 寻找两个目标数值
|
||||
for i, n in enumerate(nums):
|
||||
other_num = target - n
|
||||
# 如果存在这个余数 other_num
|
||||
if other_num in hashTable.keys():
|
||||
# 查看是否存在哈希表里,如果存在的话就返回数组
|
||||
return [i, hashTable[other_num]]
|
||||
# 如果不存在的话继续处理剩余的数
|
||||
hashTable[n] = i
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
[1.两数之和](https://leetcode-cn.com/problems/two-sum)
|
||||
|
||||
穷举
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @param {number} target
|
||||
* @return {number[]}
|
||||
*/
|
||||
var twoSum = function (nums, target) {
|
||||
for (let i = 0; i < nums.length; i++)
|
||||
for (let j = i + 1; j < nums.length; j++)
|
||||
if (nums[j] === target - nums[i])
|
||||
return [i, j];
|
||||
|
||||
// 不存在这么两个数
|
||||
return [-1, -1];
|
||||
};
|
||||
```
|
||||
|
||||
备忘录
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @param {number} target
|
||||
* @return {number[]}
|
||||
*/
|
||||
var twoSum = function (nums, target) {
|
||||
let n = nums.length;
|
||||
let index = new Map();
|
||||
// 构造一个哈希表:元素映射到相应的索引
|
||||
for (let i = 0; i < n; i++)
|
||||
index.set(nums[i], i);
|
||||
|
||||
for (let i = 0; i < n; i++) {
|
||||
let other = target - nums[i];
|
||||
// 如果 other 存在且不是 nums[i] 本身
|
||||
if (index.has(other) && index.get(other) !== i)
|
||||
return [i, index.get(other)];
|
||||
}
|
||||
|
||||
// 不存在这么两个数
|
||||
return [-1, -1];
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
[170.两数之和 III - 数据结构设计](https://leetcode-cn.com/problems/two-sum-iii-data-structure-design)
|
||||
|
||||
哈希集合优化。
|
||||
|
||||
```js
|
||||
class TwoSum {
|
||||
constructor() {
|
||||
this.sum = new Set();
|
||||
this.nums = [];
|
||||
}
|
||||
|
||||
// 向数据结构中添加一个数 number
|
||||
add(number) {
|
||||
// 记录所有可能组成的和
|
||||
for (let n of this.nums) {
|
||||
this.sum.push(n + number)
|
||||
}
|
||||
this.nums.add(number);
|
||||
}
|
||||
|
||||
// 寻找当前数据结构中是否存在两个数的和为 value
|
||||
find(value) {
|
||||
return this.sum.has(value);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -1,102 +0,0 @@
|
|||
# 为什么我推荐《算法4》
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
通知:如果本站对你学习算法有帮助,**请收藏网址,并推荐给你的朋友**。由于 **labuladong** 的算法套路太火,很多人直接拿我的 GitHub 文章去开付费专栏,价格还不便宜。我这免费写给你看,**多宣传原创作者是你唯一能做的**,谁也不希望劣币驱逐良币对吧?
|
||||
|
||||
咱们的公众号有很多硬核的算法文章,今天就聊点轻松的,就具体聊聊我非常“鼓吹”的《算法4》。这本书我在之前的文章多次推荐过,但是没有具体的介绍,今天就来正式介绍一下。。
|
||||
|
||||
我的推荐不会直接甩一大堆书目,而是会联系实际生活,讲一些书中有趣有用的知识,无论你最后会不会去看这本书,本文都会给你带来一些收获。
|
||||
|
||||
**首先这本书是适合初学者的**。总是有很多读者问,我只会 C 语言,能不能看《算法4》?学算法最好用什么语言?诸如此类的问题。
|
||||
|
||||
经常看咱们公众号的读者应该体会到了,算法其实是一种思维模式,和你用什么语言没啥关系。我们的文章也不会固定用某一种语言,而是什么语言写出来容易理解就用什么语言。再退一步说,到底适不适合你,网上找个 PDF 亲自看一下不就知道了?
|
||||
|
||||
《算法4》看起来挺厚的,但是前面几十页是教你 Java 的;每章后面还有习题,占了不少页数;每章还有一些数学证明,这些都可以忽略。这样算下来,剩下的就是基础知识和疑难解答之类的内容,含金量很高,把这些基础知识动手实践一遍,真的就可以达到不错的水平了。
|
||||
|
||||
我觉得这本书之所以能有这么高的评分,一个是因为讲解详细,还有大量配图,另一个原因就是书中把一些算法和现实生活中的使用场景联系起来,你不仅知道某个算法怎么实现,也知道它大概能运用到什么场景,下面我就来介绍两个图算法的简单应用。
|
||||
|
||||
### 一、二分图的应用
|
||||
|
||||
我想举的第一个例子是**二分图**。简单来说,二分图就是一幅拥有特殊性质的图:能够用两种颜色为所有顶点着色,使得任何一条边的两个顶点颜色不同。
|
||||
|
||||

|
||||
|
||||
明白了二分图是什么,能解决什么实际问题呢?**算法方面,常见的操作是如何判定一幅图是不是二分图**。比如说下面这道 LeetCode 题目:
|
||||
|
||||

|
||||
|
||||
你想想,如果我们把每个人视为一个顶点,边代表讨厌;相互讨厌的两个人之间连接一条边,就可以形成一幅图。那么根据刚才二分图的定义,如果这幅图是一幅二分图,就说明这些人可以被分为两组,否则的话就不行。
|
||||
|
||||
这是判定二分图算法的一个应用,**其实二分图在数据结构方面也有一些不错的特性**。
|
||||
|
||||
比如说我们需要一种数据结构来储存电影和演员之间的关系:某一部电影肯定是由多位演员出演的,且某一位演员可能会出演多部电影。你使用什么数据结构来存储这种关系呢?
|
||||
|
||||
既然是存储映射关系,最简单的不就是使用哈希表嘛,我们可以使用一个 `HashMap<String, List<String>>` 来存储电影到演员列表的映射,如果给一部电影的名字,就能快速得到出演该电影的演员。
|
||||
|
||||
但是如果给出一个演员的名字,我们想快速得到该演员演出的所有电影,怎么办呢?这就需要「反向索引」,对之前的哈希表进行一些操作,新建另一个哈希表,把演员作为键,把电影列表作为值。
|
||||
|
||||
对于上面这个例子,可以使用二分图来取代哈希表。电影和演员是具有二分图性质的:如果把电影和演员视为图中的顶点,出演关系作为边,那么与电影顶点相连的一定是演员,与演员相邻的一定是电影,不存在演员和演员相连,电影和电影相连的情况。
|
||||
|
||||
回顾二分图的定义,如果对演员和电影顶点着色,肯定就是一幅二分图:
|
||||
|
||||

|
||||
|
||||
如果这幅图构建完成,就不需要反向索引,对于演员顶点,其直接连接的顶点就是他出演的电影,对于电影顶点,其直接连接的顶点就是出演演员。
|
||||
|
||||
当然,对于这个问题,书中还提到了一些其他有趣的玩法,比如说社交网络中「间隔度数」的计算(六度空间理论应该听说过)等等,其实就是一个 BFS 广度优先搜索寻找最短路径的问题,具体代码实现这里就不展开了。
|
||||
|
||||
### 二、套汇的算法
|
||||
|
||||
如果我们说货币 A 到货币 B 的汇率是 10,意思就是 1 单位的货币 A 可以换 10 单位货币 B。如果我们把每种货币视为一幅图的顶点,货币之间的汇率视为加权有向边,那么整个汇率市场就是一幅「完全加权有向图」。
|
||||
|
||||
一旦把现实生活中的情景抽象成图,就有可能运用算法解决一些问题。比如说图中可能存在下面的情况:
|
||||
|
||||

|
||||
|
||||
图中的加权有向边代表汇率,我们可以发现如果把 100 单位的货币 A 换成 B,再换成 C,最后换回 A,就可以得到 100×0.9×0.8×1.4 = 100.8 单位的 A!如果交易的金额大一些的话,赚的钱是很可观的,这种空手套白狼的操作就是套汇。
|
||||
|
||||
现实中交易会有种种限制,而且市场瞬息万变,但是套汇的利润还是很高的,关键就在于如何**快速**找到这种套汇机会呢?
|
||||
|
||||
借助图的抽象,我们发现套汇机会其实就是一个环,且这个环上的权重之积大于 1,只要在顺着这个环交易一圈就能空手套白狼。
|
||||
|
||||
图论中有一个经典算法叫做 **Bellman-Ford 算法,可以用于寻找负权重环**。对于我们说的套汇问题,可以先把所有边的权重 w 替换成 -ln(w),这样「寻找权重乘积大于 1 的环」就转化成了「寻找权重和小于 0 的环」,就可以使用 Bellman-Ford 算法在 O(EV) 的时间内寻找负权重环,也就是寻找套汇机会。
|
||||
|
||||
《算法4》就介绍到这里,关于上面两个例子的具体内容,可以自己去看书,**公众号后台回复关键词「算法4」就有 PDF**。
|
||||
|
||||
|
||||
### 三、最后说几句
|
||||
|
||||
首先,前文说对于数学证明、章后习题可以忽略,可能有人要抬杠了:难道习题和数学证明不重要吗?
|
||||
|
||||
那我想说,就是不重要,起码对大多数人来说不重要。我觉得吧,学习就要带着目的性去学,大部分人学算法不就是巩固计算机知识,对付面试题目吗?**如果是这个目的**,那就学些基本的数据结构和经典算法,明白它们的时间复杂度,然后去刷题就好了,何必和习题、证明过不去?
|
||||
|
||||
这也是我从来不推荐《算法导论》这本书的原因。如果有人给你推荐这本书,只可能有两个原因,要么他是真大佬,要么他在装大佬。《算法导论》中充斥大量数学证明,而且很多数据结构是很少用到的,顶多当个字典用。你说你学了那些有啥用呢,饶过自己呗。
|
||||
|
||||
另外,读书在精不在多。你花时间《算法4》过个大半(最后小半部分有点困难),同时刷点题,看看咱们的公众号文章,算法这块真就够了,别对细节问题太较真。
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
|
@ -1,11 +1,5 @@
|
|||
# 二分查找算法详解
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -15,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -505,6 +499,58 @@ int right_bound(int[] nums, int target) {
|
|||
|
||||
理解本文能保证你写出正确的二分查找的代码,但实际题目中不会直接让你写二分代码,我会在 [二分查找的变体](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62a07736e4b01a485209b0b4/1) 和 [二分查找的运用](https://labuladong.github.io/article/fname.html?fname=二分运用) 中进一步讲解如何把二分思维运用到更多算法题中。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [base case 和备忘录的初始值怎么定?](https://labuladong.github.io/article/fname.html?fname=备忘录等基础)
|
||||
- [丑数系列算法详解](https://labuladong.github.io/article/fname.html?fname=丑数)
|
||||
- [二分搜索怎么用?我又总结了套路](https://labuladong.github.io/article/fname.html?fname=二分运用)
|
||||
- [二分搜索怎么用?我和快手面试官进行了深度探讨](https://labuladong.github.io/article/fname.html?fname=二分分割子数组)
|
||||
- [二分搜索算法经典题目](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62a07736e4b01a485209b0b4/1)
|
||||
- [二分查找高效判定子序列](https://labuladong.github.io/article/fname.html?fname=二分查找判定子序列)
|
||||
- [动态规划设计:最长递增子序列](https://labuladong.github.io/article/fname.html?fname=动态规划设计:最长递增子序列)
|
||||
- [双指针技巧秒杀七道数组题目](https://labuladong.github.io/article/fname.html?fname=双指针技巧)
|
||||
- [带权重的随机选择算法](https://labuladong.github.io/article/fname.html?fname=随机权重)
|
||||
- [快速排序详解及应用](https://labuladong.github.io/article/fname.html?fname=快速排序)
|
||||
- [我写了首诗,把滑动窗口算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=滑动窗口技巧进阶)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [讲两道常考的阶乘算法题](https://labuladong.github.io/article/fname.html?fname=阶乘题目)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1201. Ugly Number III](https://leetcode.com/problems/ugly-number-iii/?show=1) | [1201. 丑数 III](https://leetcode.cn/problems/ugly-number-iii/?show=1) |
|
||||
| [162. Find Peak Element](https://leetcode.com/problems/find-peak-element/?show=1) | [162. 寻找峰值](https://leetcode.cn/problems/find-peak-element/?show=1) |
|
||||
| [240. Search a 2D Matrix II](https://leetcode.com/problems/search-a-2d-matrix-ii/?show=1) | [240. 搜索二维矩阵 II](https://leetcode.cn/problems/search-a-2d-matrix-ii/?show=1) |
|
||||
| [33. Search in Rotated Sorted Array](https://leetcode.com/problems/search-in-rotated-sorted-array/?show=1) | [33. 搜索旋转排序数组](https://leetcode.cn/problems/search-in-rotated-sorted-array/?show=1) |
|
||||
| [35. Search Insert Position](https://leetcode.com/problems/search-insert-position/?show=1) | [35. 搜索插入位置](https://leetcode.cn/problems/search-insert-position/?show=1) |
|
||||
| [74. Search a 2D Matrix](https://leetcode.com/problems/search-a-2d-matrix/?show=1) | [74. 搜索二维矩阵](https://leetcode.cn/problems/search-a-2d-matrix/?show=1) |
|
||||
| [793. Preimage Size of Factorial Zeroes Function](https://leetcode.com/problems/preimage-size-of-factorial-zeroes-function/?show=1) | [793. 阶乘函数后 K 个零](https://leetcode.cn/problems/preimage-size-of-factorial-zeroes-function/?show=1) |
|
||||
| [81. Search in Rotated Sorted Array II](https://leetcode.com/problems/search-in-rotated-sorted-array-ii/?show=1) | [81. 搜索旋转排序数组 II](https://leetcode.cn/problems/search-in-rotated-sorted-array-ii/?show=1) |
|
||||
| [852. Peak Index in a Mountain Array](https://leetcode.com/problems/peak-index-in-a-mountain-array/?show=1) | [852. 山脉数组的峰顶索引](https://leetcode.cn/problems/peak-index-in-a-mountain-array/?show=1) |
|
||||
| - | [剑指 Offer 04. 二维数组中的查找](https://leetcode.cn/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/?show=1) |
|
||||
| - | [剑指 Offer 53 - I. 在排序数组中查找数字 I](https://leetcode.cn/problems/zai-pai-xu-shu-zu-zhong-cha-zhao-shu-zi-lcof/?show=1) |
|
||||
| - | [剑指 Offer 53 - II. 0~n-1中缺失的数字](https://leetcode.cn/problems/que-shi-de-shu-zi-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 068. 查找插入位置](https://leetcode.cn/problems/N6YdxV/?show=1) |
|
||||
| - | [剑指 Offer II 069. 山峰数组的顶部](https://leetcode.cn/problems/B1IidL/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
255
算法思维系列/信封嵌套问题.md
255
算法思维系列/信封嵌套问题.md
|
|
@ -1,255 +0,0 @@
|
|||
# 信封嵌套问题
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[354.俄罗斯套娃信封问题](https://leetcode-cn.com/problems/russian-doll-envelopes)
|
||||
|
||||
**-----------**
|
||||
|
||||
很多算法问题都需要排序技巧,其难点不在于排序本身,而是需要巧妙地排序进行预处理,将算法问题进行转换,为之后的操作打下基础。
|
||||
|
||||
信封嵌套问题就需要先按特定的规则排序,之后就转换为一个 [最长递增子序列问题](https://labuladong.gitee.io/algo/),可以用前文 [二分查找详解](https://labuladong.gitee.io/algo/) 的技巧来解决了。
|
||||
|
||||
### 一、题目概述
|
||||
|
||||
信封嵌套问题是个很有意思且经常出现在生活中的问题,先看下题目:
|
||||
|
||||

|
||||
|
||||
这道题目其实是最长递增子序列(Longes Increasing Subsequence,简写为 LIS)的一个变种,因为很显然,每次合法的嵌套是大的套小的,相当于找一个最长递增的子序列,其长度就是最多能嵌套的信封个数。
|
||||
|
||||
但是难点在于,标准的 LIS 算法只能在数组中寻找最长子序列,而我们的信封是由 `(w, h)` 这样的二维数对形式表示的,如何把 LIS 算法运用过来呢?
|
||||
|
||||

|
||||
|
||||
读者也许会想,通过 `w × h` 计算面积,然后对面积进行标准的 LIS 算法。但是稍加思考就会发现这样不行,比如 `1 × 10` 大于 `3 × 3`,但是显然这样的两个信封是无法互相嵌套的。
|
||||
|
||||
### 二、解法
|
||||
|
||||
这道题的解法是比较巧妙的:
|
||||
|
||||
**先对宽度 `w` 进行升序排序,如果遇到 `w` 相同的情况,则按照高度 `h` 降序排序。之后把所有的 `h` 作为一个数组,在这个数组上计算 LIS 的长度就是答案。**
|
||||
|
||||
画个图理解一下,先对这些数对进行排序:
|
||||
|
||||

|
||||
|
||||
然后在 `h` 上寻找最长递增子序列:
|
||||
|
||||

|
||||
|
||||
这个子序列就是最优的嵌套方案。
|
||||
|
||||
这个解法的关键在于,对于宽度 `w` 相同的数对,要对其高度 `h` 进行降序排序。因为两个宽度相同的信封不能相互包含的,逆序排序保证在 `w` 相同的数对中最多只选取一个。
|
||||
|
||||
下面看代码:
|
||||
|
||||
```java
|
||||
// envelopes = [[w, h], [w, h]...]
|
||||
public int maxEnvelopes(int[][] envelopes) {
|
||||
int n = envelopes.length;
|
||||
// 按宽度升序排列,如果宽度一样,则按高度降序排列
|
||||
Arrays.sort(envelopes, new Comparator<int[]>()
|
||||
{
|
||||
public int compare(int[] a, int[] b) {
|
||||
return a[0] == b[0] ?
|
||||
b[1] - a[1] : a[0] - b[0];
|
||||
}
|
||||
});
|
||||
// 对高度数组寻找 LIS
|
||||
int[] height = new int[n];
|
||||
for (int i = 0; i < n; i++)
|
||||
height[i] = envelopes[i][1];
|
||||
|
||||
return lengthOfLIS(height);
|
||||
}
|
||||
```
|
||||
|
||||
关于最长递增子序列的寻找方法,在前文中详细介绍了动态规划解法,并用扑克牌游戏解释了二分查找解法,本文就不展开了,直接套用算法模板:
|
||||
|
||||
```java
|
||||
/* 返回 nums 中 LIS 的长度 */
|
||||
public int lengthOfLIS(int[] nums) {
|
||||
int piles = 0, n = nums.length;
|
||||
int[] top = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
// 要处理的扑克牌
|
||||
int poker = nums[i];
|
||||
int left = 0, right = piles;
|
||||
// 二分查找插入位置
|
||||
while (left < right) {
|
||||
int mid = (left + right) / 2;
|
||||
if (top[mid] >= poker)
|
||||
right = mid;
|
||||
else
|
||||
left = mid + 1;
|
||||
}
|
||||
if (left == piles) piles++;
|
||||
// 把这张牌放到牌堆顶
|
||||
top[left] = poker;
|
||||
}
|
||||
// 牌堆数就是 LIS 长度
|
||||
return piles;
|
||||
}
|
||||
```
|
||||
|
||||
为了清晰,我将代码分为了两个函数, 你也可以合并,这样可以节省下 `height` 数组的空间。
|
||||
|
||||
此算法的时间复杂度为 `O(NlogN)`,因为排序和计算 LIS 各需要 `O(NlogN)` 的时间。
|
||||
|
||||
空间复杂度为 `O(N)`,因为计算 LIS 的函数中需要一个 `top` 数组。
|
||||
|
||||
### 三、总结
|
||||
|
||||
这个问题是个 Hard 级别的题目,难就难在排序,正确地排序后此问题就被转化成了一个标准的 LIS 问题,容易解决一些。
|
||||
|
||||
其实这种问题还可以拓展到三维,比如说现在不是让你嵌套信封,而是嵌套箱子,每个箱子有长宽高三个维度,请你算算最多能嵌套几个箱子?
|
||||
|
||||
我们可能会这样想,先把前两个维度(长和宽)按信封嵌套的思路求一个嵌套序列,最后在这个序列的第三个维度(高度)找一下 LIS,应该能算出答案。
|
||||
|
||||
实际上,这个思路是错误的。这类问题叫做「偏序问题」,上升到三维会使难度巨幅提升,需要借助一种高级数据结构「树状数组」,有兴趣的读者可以自行搜索。
|
||||
|
||||
有很多算法问题都需要排序后进行处理,阿东正在进行整理总结。希望本文对你有帮助。
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
[354.俄罗斯套娃信封问题](https://leetcode-cn.com/problems/russian-doll-envelopes)
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
[300. 最长递增子序列](https://leetcode-cn.com/problems/longest-increasing-subsequence/)
|
||||
|
||||
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
|
||||
|
||||
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @return {number}
|
||||
*/
|
||||
let lengthOfLIS = function(nums) {
|
||||
let top = new Array(nums.length);
|
||||
|
||||
// 牌堆数初始化为 0
|
||||
let piles = 0;
|
||||
|
||||
for (let i = 0; i < nums.length; i++) {
|
||||
// 要处理的扑克牌
|
||||
let poker = nums[i];
|
||||
|
||||
/***** 搜索左侧边界的二分查找 *****/
|
||||
let left = 0, right = piles;
|
||||
while (left < right) {
|
||||
let mid = (left + right) / 2;
|
||||
if (top[mid] > poker) {
|
||||
right = mid;
|
||||
} else if (top[mid] < poker) {
|
||||
left = mid + 1;
|
||||
} else {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
/*********************************/
|
||||
|
||||
// 没找到合适的牌堆,新建一堆
|
||||
if (left === piles) piles++;
|
||||
|
||||
// 把这张牌放到牌堆顶
|
||||
top[left] = poker;
|
||||
}
|
||||
|
||||
// 牌堆数就是 LIS 长度
|
||||
return piles;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
[354.俄罗斯套娃信封问题](https://leetcode-cn.com/problems/russian-doll-envelopes)
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @return {number}
|
||||
*/
|
||||
let lengthOfLIS = function(nums) {
|
||||
let top = new Array(nums.length);
|
||||
|
||||
// 牌堆数初始化为 0
|
||||
let piles = 0;
|
||||
|
||||
for (let i = 0; i < nums.length; i++) {
|
||||
// 要处理的扑克牌
|
||||
let poker = nums[i];
|
||||
|
||||
/***** 搜索左侧边界的二分查找 *****/
|
||||
let left = 0, right = piles;
|
||||
while (left < right) {
|
||||
let mid = Math.floor((left + right) / 2);
|
||||
if (top[mid] > poker) {
|
||||
right = mid;
|
||||
} else if (top[mid] < poker) {
|
||||
left = mid + 1;
|
||||
} else {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
/*********************************/
|
||||
|
||||
// 没找到合适的牌堆,新建一堆
|
||||
if (left === piles) piles++;
|
||||
|
||||
// 把这张牌放到牌堆顶
|
||||
top[left] = poker;
|
||||
}
|
||||
|
||||
// 牌堆数就是 LIS 长度
|
||||
return piles;
|
||||
};
|
||||
|
||||
/**
|
||||
* @param {number[][]} envelopes
|
||||
* @return {number}
|
||||
*/
|
||||
var maxEnvelopes = function (envelopes) {
|
||||
let n = envelopes.length;
|
||||
// 按宽度升序排列,如果宽度一样,则按高度降序排列
|
||||
envelopes.sort((a, b) => {
|
||||
return a[0] === b[0] ? b[1] - a[1] : a[0] - b[0];
|
||||
})
|
||||
|
||||
// 对高度数组寻找 LIS
|
||||
let height = new Array(n);
|
||||
for (let i = 0; i < n; i++)
|
||||
height[i] = envelopes[i][1];
|
||||
|
||||
return lengthOfLIS(height);
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
|
|
@ -1,20 +1,21 @@
|
|||
# 几个反直觉的概率问题
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
上篇文章 [洗牌算法详解](https://labuladong.gitee.io/algo/) 讲到了验证概率算法的蒙特卡罗方法,今天聊点轻松的内容:几个和概率相关的有趣问题。
|
||||
上篇文章 [洗牌算法详解](https://labuladong.github.io/article/fname.html?fname=洗牌算法) 讲到了验证概率算法的蒙特卡罗方法,今天聊点轻松的内容:几个和概率相关的有趣问题。
|
||||
|
||||
计算概率有下面两个最简单的原则:
|
||||
|
||||
|
|
@ -28,7 +29,6 @@
|
|||
|
||||
下面介绍几个简单却具有迷惑性的问题,分别是男孩女孩问题、生日悖论、三门问题。当然,三门问题可能是大家最耳熟的,所以就多说一些有趣的思考。
|
||||
|
||||
|
||||
### 一、男孩女孩问题
|
||||
|
||||
假设有一个家庭,有两个孩子,现在告诉你其中有一个男孩,请问另一个也是男孩的概率是多少?
|
||||
|
|
@ -51,14 +51,13 @@
|
|||
|
||||
我竟然觉得有那么一丝道理!但其实,我们只是通过年龄差异来表示两个孩子的独立性,也就是说即便两个孩子同性,也有两种可能。所以不要用双胞胎抬杠了。
|
||||
|
||||
|
||||
### 二、生日悖论
|
||||
|
||||
生日悖论是由这样一个问题引出的:一个屋子里需要有多少人,才能使得存在至少两个人生日是同一天的概率达到 50%?
|
||||
|
||||
答案是 23 个人,也就是说房子里如果有 23 个人,那么就有 50% 的概率会存在两个人生日相同。这个结论看起来不可思议,所以被称为悖论。按照直觉,要得到 50% 的概率,起码得有 183 个人吧,因为一年有 365 天呀?其实不是的,觉得这个结论不可思议主要有两个思维误区:
|
||||
|
||||
**第一个误区是误解「存在」这个词的含义。**
|
||||
**第一个误区是误解「存在」这个词的含义**。
|
||||
|
||||
读者可能认为,如果 23 个人中出现相同生日的概率就能达到 50%,是不是意味着:
|
||||
|
||||
|
|
@ -72,7 +71,7 @@
|
|||
|
||||
这样计算得到的结果是不是看起来合理多了?生日悖论计算对象的不是某一个人,而是一个整体,其中包含了所有人的排列组合,它们的概率之和当然会大得多。
|
||||
|
||||
**第二个误区是认为概率是线性变化的。**
|
||||
**第二个误区是认为概率是线性变化的**。
|
||||
|
||||
读者可能认为,如果 23 个人中出现相同生日的概率就能达到 50%,是不是意味着 46 个人的概率就能达到 100%?
|
||||
|
||||
|
|
@ -84,8 +83,7 @@
|
|||
|
||||
那为什么只要 23 个人出现相同生日的概率就能大于 50% 了呢?我们先计算 23 个人生日都唯一(不重复)的概率。只有 1 个人的时候,生日唯一的概率是 `365/365`,2 个人时,生日唯一的概率是 `365/365 × 364/365`,以此类推可知 23 人的生日都唯一的概率:
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
算出来大约是 0.493,所以存在相同生日的概率就是 0.507,差不多就是 50% 了。实际上,按照这个算法,当人数达到 70 时,存在两个人生日相同的概率就上升到了 99.9%,基本可以认为是 100% 了。所以从概率上说,一个几十人的小团体中存在生日相同的人真没啥稀奇的。
|
||||
|
||||
|
|
@ -97,13 +95,13 @@
|
|||
|
||||
你是游戏参与者,现在有门 1,2,3,假设你随机选择了门 1,然后主持人打开了门 3 告诉你那后面是山羊。现在,你是坚持你最初的选择门 1,还是选择换成门 2 呢?
|
||||
|
||||

|
||||

|
||||
|
||||
答案是应该换门,换门之后抽到跑车的概率是 2/3,不换的话是 1/3。又一次反直觉,感觉换不换的中奖概率应该都一样啊,因为最后肯定就剩两个门,一个是羊,一个是跑车,这是事实,所以不管选哪个的概率不都是 1/2 吗?
|
||||
|
||||
类似前面说的男孩女孩问题,最简单稳妥的方法就是把所有可能结果穷举出来:
|
||||
|
||||

|
||||

|
||||
|
||||
很容易看到选择换门中奖的概率是 2/3,不换的话是 1/3。
|
||||
|
||||
|
|
@ -129,14 +127,15 @@
|
|||
|
||||
当然,运用此策略蒙题的前提是你真的抓瞎,真的随机乱选答案,这样概率才能作为最后的杀手锏。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||

|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
|
@ -1,11 +1,5 @@
|
|||
# 经典数组技巧:前缀和数组
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -15,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -183,6 +177,56 @@ class NumMatrix {
|
|||
除了本文举例的基本用法,前缀和数组经常和其他数据结构或算法技巧相结合,我会在 [前缀和技巧高频习题](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_627cd61de4b0cedf38b0f3a0/1) 中举例讲解。
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [二维数组的花式遍历技巧](https://labuladong.github.io/article/fname.html?fname=花式遍历)
|
||||
- [动态规划设计:最大子数组](https://labuladong.github.io/article/fname.html?fname=最大子数组)
|
||||
- [小而美的算法技巧:差分数组](https://labuladong.github.io/article/fname.html?fname=差分技巧)
|
||||
- [带权重的随机选择算法](https://labuladong.github.io/article/fname.html?fname=随机权重)
|
||||
- [归并排序详解及应用](https://labuladong.github.io/article/fname.html?fname=归并排序)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [经典数组技巧:差分数组](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_629e0d3ae4b0812e17a32f01/1)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1314. Matrix Block Sum](https://leetcode.com/problems/matrix-block-sum/?show=1) | [1314. 矩阵区域和](https://leetcode.cn/problems/matrix-block-sum/?show=1) |
|
||||
| [1352. Product of the Last K Numbers](https://leetcode.com/problems/product-of-the-last-k-numbers/?show=1) | [1352. 最后 K 个数的乘积](https://leetcode.cn/problems/product-of-the-last-k-numbers/?show=1) |
|
||||
| [238. Product of Array Except Self](https://leetcode.com/problems/product-of-array-except-self/?show=1) | [238. 除自身以外数组的乘积](https://leetcode.cn/problems/product-of-array-except-self/?show=1) |
|
||||
| [327. Count of Range Sum](https://leetcode.com/problems/count-of-range-sum/?show=1) | [327. 区间和的个数](https://leetcode.cn/problems/count-of-range-sum/?show=1) |
|
||||
| [437. Path Sum III](https://leetcode.com/problems/path-sum-iii/?show=1) | [437. 路径总和 III](https://leetcode.cn/problems/path-sum-iii/?show=1) |
|
||||
| [523. Continuous Subarray Sum](https://leetcode.com/problems/continuous-subarray-sum/?show=1) | [523. 连续的子数组和](https://leetcode.cn/problems/continuous-subarray-sum/?show=1) |
|
||||
| [525. Contiguous Array](https://leetcode.com/problems/contiguous-array/?show=1) | [525. 连续数组](https://leetcode.cn/problems/contiguous-array/?show=1) |
|
||||
| [560. Subarray Sum Equals K](https://leetcode.com/problems/subarray-sum-equals-k/?show=1) | [560. 和为 K 的子数组](https://leetcode.cn/problems/subarray-sum-equals-k/?show=1) |
|
||||
| [724. Find Pivot Index](https://leetcode.com/problems/find-pivot-index/?show=1) | [724. 寻找数组的中心下标](https://leetcode.cn/problems/find-pivot-index/?show=1) |
|
||||
| [862. Shortest Subarray with Sum at Least K](https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k/?show=1) | [862. 和至少为 K 的最短子数组](https://leetcode.cn/problems/shortest-subarray-with-sum-at-least-k/?show=1) |
|
||||
| [918. Maximum Sum Circular Subarray](https://leetcode.com/problems/maximum-sum-circular-subarray/?show=1) | [918. 环形子数组的最大和](https://leetcode.cn/problems/maximum-sum-circular-subarray/?show=1) |
|
||||
| [974. Subarray Sums Divisible by K](https://leetcode.com/problems/subarray-sums-divisible-by-k/?show=1) | [974. 和可被 K 整除的子数组](https://leetcode.cn/problems/subarray-sums-divisible-by-k/?show=1) |
|
||||
| - | [剑指 Offer 57 - II. 和为s的连续正数序列](https://leetcode.cn/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 010. 和为 k 的子数组](https://leetcode.cn/problems/QTMn0o/?show=1) |
|
||||
| - | [剑指 Offer II 011. 0 和 1 个数相同的子数组](https://leetcode.cn/problems/A1NYOS/?show=1) |
|
||||
| - | [剑指 Offer II 012. 左右两边子数组的和相等](https://leetcode.cn/problems/tvdfij/?show=1) |
|
||||
| - | [剑指 Offer II 013. 二维子矩阵的和](https://leetcode.cn/problems/O4NDxx/?show=1) |
|
||||
| - | [剑指 Offer II 050. 向下的路径节点之和](https://leetcode.cn/problems/6eUYwP/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
206
算法思维系列/区间交集问题.md
206
算法思维系列/区间交集问题.md
|
|
@ -1,206 +0,0 @@
|
|||
# 区间交集问题
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[986.区间列表的交集](https://leetcode-cn.com/problems/interval-list-intersections)
|
||||
|
||||
**-----------**
|
||||
|
||||
本文是区间系列问题的第三篇,前两篇分别讲了区间的最大不相交子集和重叠区间的合并,今天再写一个算法,可以快速找出两组区间的交集。
|
||||
|
||||
先看下题目,LeetCode 第 986 题就是这个问题:
|
||||
|
||||

|
||||
|
||||
题目很好理解,就是让你找交集,注意区间都是闭区间。
|
||||
|
||||
### 思路
|
||||
|
||||
解决区间问题的思路一般是先排序,以便操作,不过题目说已经排好序了,那么可以用两个索引指针在 `A` 和 `B` 中游走,把交集找出来,代码大概是这样的:
|
||||
|
||||
```python
|
||||
# A, B 形如 [[0,2],[5,10]...]
|
||||
def intervalIntersection(A, B):
|
||||
i, j = 0, 0
|
||||
res = []
|
||||
while i < len(A) and j < len(B):
|
||||
# ...
|
||||
j += 1
|
||||
i += 1
|
||||
return res
|
||||
```
|
||||
|
||||
不难,我们先老老实实分析一下各种情况。
|
||||
|
||||
首先,**对于两个区间**,我们用 `[a1,a2]` 和 `[b1,b2]` 表示在 `A` 和 `B` 中的两个区间,那么什么情况下这两个区间**没有交集**呢:
|
||||
|
||||

|
||||
|
||||
只有这两种情况,写成代码的条件判断就是这样:
|
||||
|
||||
```python
|
||||
if b2 < a1 or a2 < b1:
|
||||
[a1,a2] 和 [b1,b2] 无交集
|
||||
```
|
||||
|
||||
那么,什么情况下,两个区间存在交集呢?根据命题的否定,上面逻辑的否命题就是存在交集的条件:
|
||||
|
||||
```python
|
||||
# 不等号取反,or 也要变成 and
|
||||
if b2 >= a1 and a2 >= b1:
|
||||
[a1,a2] 和 [b1,b2] 存在交集
|
||||
```
|
||||
|
||||
接下来,两个区间存在交集的情况有哪些呢?穷举出来:
|
||||
|
||||

|
||||
|
||||
这很简单吧,就这四种情况而已。那么接下来思考,这几种情况下,交集是否有什么共同点呢?
|
||||
|
||||

|
||||
|
||||
我们惊奇地发现,交集区间是有规律的!如果交集区间是 `[c1,c2]`,那么 `c1=max(a1,b1)`,`c2=min(a2,b2)`!这一点就是寻找交集的核心,我们把代码更进一步:
|
||||
|
||||
```python
|
||||
while i < len(A) and j < len(B):
|
||||
a1, a2 = A[i][0], A[i][1]
|
||||
b1, b2 = B[j][0], B[j][1]
|
||||
if b2 >= a1 and a2 >= b1:
|
||||
res.append([max(a1, b1), min(a2, b2)])
|
||||
# ...
|
||||
```
|
||||
|
||||
最后一步,我们的指针 `i` 和 `j` 肯定要前进(递增)的,什么时候应该前进呢?
|
||||
|
||||

|
||||
|
||||
结合动画示例就很好理解了,是否前进,只取决于 `a2` 和 `b2` 的大小关系:
|
||||
|
||||
```python
|
||||
while i < len(A) and j < len(B):
|
||||
# ...
|
||||
if b2 < a2:
|
||||
j += 1
|
||||
else:
|
||||
i += 1
|
||||
```
|
||||
|
||||
### 代码
|
||||
|
||||
```python
|
||||
# A, B 形如 [[0,2],[5,10]...]
|
||||
def intervalIntersection(A, B):
|
||||
i, j = 0, 0 # 双指针
|
||||
res = []
|
||||
while i < len(A) and j < len(B):
|
||||
a1, a2 = A[i][0], A[i][1]
|
||||
b1, b2 = B[j][0], B[j][1]
|
||||
# 两个区间存在交集
|
||||
if b2 >= a1 and a2 >= b1:
|
||||
# 计算出交集,加入 res
|
||||
res.append([max(a1, b1), min(a2, b2)])
|
||||
# 指针前进
|
||||
if b2 < a2: j += 1
|
||||
else: i += 1
|
||||
return res
|
||||
```
|
||||
|
||||
总结一下,区间类问题看起来都比较复杂,情况很多难以处理,但实际上通过观察各种不同情况之间的共性可以发现规律,用简洁的代码就能处理。
|
||||
|
||||
另外,区间问题没啥特别厉害的奇技淫巧,其操作也朴实无华,但其应用却十分广泛。
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[986.区间列表的交集](https://leetcode-cn.com/problems/interval-list-intersections)
|
||||
|
||||
|
||||
|
||||
### java
|
||||
|
||||
[KiraZh](https://github.com/KiraZh)提供第986题Java代码
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public int[][] intervalIntersection(int[][] A, int[][] B) {
|
||||
List<int[]> res = new ArrayList<>();
|
||||
int a = 0, b = 0;
|
||||
while(a < A.length && b < B.length) {
|
||||
// 确定左边界,两个区间左边界的最大值
|
||||
int left = Math.max(A[a][0], B[b][0]);
|
||||
// 确定右边界,两个区间右边界的最小值
|
||||
int right = Math.min(A[a][1], B[b][1]);
|
||||
// 左边界小于右边界则加入结果集
|
||||
if (left <= right)
|
||||
res.add(new int[] {left, right});
|
||||
// 右边界更大的保持不动,另一个指针移动,继续比较
|
||||
if(A[a][1] < B[b][1]) a++;
|
||||
else b++;
|
||||
}
|
||||
// 将结果转为数组
|
||||
return res.toArray(new int[0][]);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
[986.区间列表的交集](https://leetcode-cn.com/problems/interval-list-intersections)
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[][]} firstList
|
||||
* @param {number[][]} secondList
|
||||
* @return {number[][]}
|
||||
*/
|
||||
var intervalIntersection = function (firstList, secondList) {
|
||||
let i, j;
|
||||
i = j = 0;
|
||||
|
||||
let res = [];
|
||||
|
||||
while (i < firstList.length && j < secondList.length) {
|
||||
let a1 = firstList[i][0];
|
||||
let a2 = firstList[i][1];
|
||||
let b1 = secondList[j][0];
|
||||
let b2 = secondList[j][1];
|
||||
|
||||
// 两个区间存在交集
|
||||
if (b2 >= a1 && a2 >= b1) {
|
||||
// 计算出交集,加入 res
|
||||
res.push([Math.max(a1, b1), Math.min(a2, b2)])
|
||||
}
|
||||
|
||||
// 指针前进
|
||||
if (b2 < a2) {
|
||||
j += 1;
|
||||
} else {
|
||||
i += 1
|
||||
}
|
||||
}
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
|
|
@ -1,237 +0,0 @@
|
|||
# 区间调度问题之区间合并
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[56.合并区间](https://leetcode-cn.com/problems/merge-intervals)
|
||||
|
||||
**-----------**
|
||||
|
||||
上篇文章用贪心算法解决了区间调度问题:给你很多区间,让你求其中的最大不重叠子集。
|
||||
|
||||
其实对于区间相关的问题,还有很多其他类型,本文就来讲讲区间合并问题(Merge Interval)。
|
||||
|
||||
LeetCode 第 56 题就是一道相关问题,题目很好理解:
|
||||
|
||||

|
||||
|
||||
我们解决区间问题的一般思路是先排序,然后观察规律。
|
||||
|
||||
### 一、思路
|
||||
|
||||
一个区间可以表示为 `[start, end]`,前文聊的区间调度问题,需要按 `end` 排序,以便满足贪心选择性质。而对于区间合并问题,其实按 `end` 和 `start` 排序都可以,不过为了清晰起见,我们选择按 `start` 排序。
|
||||
|
||||

|
||||
|
||||
**显然,对于几个相交区间合并后的结果区间 `x`,`x.start` 一定是这些相交区间中 `start` 最小的,`x.end` 一定是这些相交区间中 `end` 最大的。**
|
||||
|
||||

|
||||
|
||||
由于已经排了序,`x.start` 很好确定,求 `x.end` 也很容易,可以类比在数组中找最大值的过程:
|
||||
|
||||
```java
|
||||
int max_ele = arr[0];
|
||||
for (int i = 1; i < arr.length; i++)
|
||||
max_ele = max(max_ele, arr[i]);
|
||||
return max_ele;
|
||||
```
|
||||
|
||||
### 二、代码
|
||||
|
||||
```python
|
||||
# intervals 形如 [[1,3],[2,6]...]
|
||||
def merge(intervals):
|
||||
if not intervals: return []
|
||||
# 按区间的 start 升序排列
|
||||
intervals.sort(key=lambda intv: intv[0])
|
||||
res = []
|
||||
res.append(intervals[0])
|
||||
|
||||
for i in range(1, len(intervals)):
|
||||
curr = intervals[i]
|
||||
# res 中最后一个元素的引用
|
||||
last = res[-1]
|
||||
if curr[0] <= last[1]:
|
||||
# 找到最大的 end
|
||||
last[1] = max(last[1], curr[1])
|
||||
else:
|
||||
# 处理下一个待合并区间
|
||||
res.append(curr)
|
||||
return res
|
||||
```
|
||||
|
||||
看下动画就一目了然了:
|
||||
|
||||

|
||||
|
||||
至此,区间合并问题就解决了。本文篇幅短小,因为区间合并只是区间问题的一个类型,后续还有一些区间问题。本想把所有问题类型都总结在一篇文章,但有读者反应,长文只会收藏不会看... 所以还是分成小短文吧,读者有什么看法可以在留言板留言交流。
|
||||
|
||||
本文终,希望对你有帮助。
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[56.合并区间](https://leetcode-cn.com/problems/merge-intervals)
|
||||
|
||||
|
||||
|
||||
### java
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
/**
|
||||
* 1. 先对区间集合进行排序(根据开始位置)
|
||||
* 2. 合并的情况一共有三种
|
||||
* a. b. c.
|
||||
* |---------| |--------| |--------|
|
||||
* |---------| |--| |--------|
|
||||
* a和b两种情况,合并取右边界大的值,c情况不合并
|
||||
*
|
||||
*/
|
||||
|
||||
private int[][] tmp;
|
||||
|
||||
public int[][] merge(int[][] intervals) {
|
||||
if(intervals == null ||intervals.length == 0)return new int[0][0];
|
||||
int length = intervals.length;
|
||||
//将列表中的区间按照左端点升序排序
|
||||
// Arrays.sort(intervals,(v1,v2) -> v1[0]-v2[0]);
|
||||
|
||||
this.tmp = new int[length][2];
|
||||
sort(intervals,0,length-1);
|
||||
|
||||
int[][] ans = new int[length][2];
|
||||
int index = -1;
|
||||
for(int[] interval:intervals){
|
||||
// 当结果数组是空是,或者当前区间的起始位置 > 结果数组中最后区间的终止位置(即上图情况c);
|
||||
// 则不合并,直接将当前区间加入结果数组。
|
||||
if(index == -1 || interval[0] > ans[index][1]){
|
||||
ans[++index] = interval;
|
||||
}else{
|
||||
// 反之将当前区间合并至结果数组的最后区间(即上图情况a,b)
|
||||
ans[index][1] = Math.max(ans[index][1],interval[1]);
|
||||
}
|
||||
}
|
||||
return Arrays.copyOf(ans, index + 1);
|
||||
}
|
||||
|
||||
//归并排序
|
||||
public void sort(int[][] intervals,int l,int r){
|
||||
if(l >= r)return;
|
||||
|
||||
int mid = l + (r-l)/2;
|
||||
sort(intervals,l,mid);
|
||||
sort(intervals,mid+1,r);
|
||||
|
||||
//合并
|
||||
int i=l,j=mid+1;
|
||||
for(int k=l;k<=r;k++){
|
||||
if(i>mid)tmp[k]=intervals[j++];
|
||||
else if(j>r)tmp[k]=intervals[i++];
|
||||
else if(intervals[i][0]>intervals[j][0])tmp[k] = intervals[j++];
|
||||
else tmp[k] = intervals[i++];
|
||||
}
|
||||
|
||||
System.arraycopy(tmp,l,intervals,l,r-l+1);
|
||||
}
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
### c++
|
||||
|
||||
[Kian](https://github.com/KianKw/) 提供第 56 题 C++ 代码
|
||||
|
||||
```c++
|
||||
class Solution {
|
||||
public:
|
||||
vector<vector<int>> merge(vector<vector<int>>& intervals) {
|
||||
// len 为 intervals 的长度
|
||||
int len = intervals.size();
|
||||
if (len < 1)
|
||||
return {};
|
||||
|
||||
// 按区间的 start 升序排列
|
||||
sort(intervals.begin(), intervals.end());
|
||||
|
||||
// 初始化 res 数组
|
||||
vector<vector<int>> res;
|
||||
res.push_back(intervals[0]);
|
||||
|
||||
for (int i = 1; i < len; i++) {
|
||||
vector<int> curr = intervals[i];
|
||||
// res.back() 为 res 中最后一个元素的索引
|
||||
if (curr[0] <= res.back()[1]) {
|
||||
// 找到最大的 end
|
||||
res.back()[1] = max(res.back()[1], curr[1]);
|
||||
} else {
|
||||
// 处理下一个待合并区间
|
||||
res.push_back(curr);
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
[56. 合并区间](https://leetcode-cn.com/problems/merge-intervals/)
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[][]} intervals
|
||||
* @return {number[][]}
|
||||
*/
|
||||
var merge = function (intervals) {
|
||||
if (intervals.length < 1) {
|
||||
return []
|
||||
}
|
||||
|
||||
// 按区间的 start 升序排列
|
||||
intervals.sort((a, b) => {
|
||||
return a[0] - b[0]
|
||||
})
|
||||
|
||||
const res = []
|
||||
res.push(intervals[0].concat())
|
||||
|
||||
for (let i = 1; i < intervals.length; i++) {
|
||||
|
||||
let curr = intervals[i]
|
||||
// res 中最后一个元素的引用
|
||||
let last = res[res.length - 1]
|
||||
|
||||
if (curr[0] <= last[1]) {
|
||||
// 找到最大的 end
|
||||
last[1] = Math.max(last[1], curr[1])
|
||||
} else {
|
||||
// 处理下一个待合并区间
|
||||
res.push(curr.concat())
|
||||
}
|
||||
}
|
||||
return res
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -1,11 +1,5 @@
|
|||
# 数组双指针技巧汇总
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -15,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -385,6 +379,49 @@ String longestPalindrome(String s) {
|
|||
|
||||
到这里,数组相关的双指针技巧就全部讲完了,这些技巧的更多扩展延伸见 [更多双指针经典高频题](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62a1dd68e4b09dda1273a5f9/1)。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [一个方法团灭 nSum 问题](https://labuladong.github.io/article/fname.html?fname=nSum)
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [动态规划之子序列问题解题模板](https://labuladong.github.io/article/fname.html?fname=子序列问题模板)
|
||||
- [双指针更多经典题目](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62a1dd68e4b09dda1273a5f9/1)
|
||||
- [如何判断回文链表](https://labuladong.github.io/article/fname.html?fname=判断回文链表)
|
||||
- [我写了首诗,把滑动窗口算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=滑动窗口技巧进阶)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [扫描线技巧:安排会议室](https://labuladong.github.io/article/fname.html?fname=安排会议室)
|
||||
- [田忌赛马背后的算法决策](https://labuladong.github.io/article/fname.html?fname=田忌赛马)
|
||||
- [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度)
|
||||
- [算法笔试「骗分」套路](https://labuladong.github.io/article/fname.html?fname=刷题技巧)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1. Two Sum](https://leetcode.com/problems/two-sum/?show=1) | [1. 两数之和](https://leetcode.cn/problems/two-sum/?show=1) |
|
||||
| [281. Zigzag Iterator](https://leetcode.com/problems/zigzag-iterator/?show=1)🔒 | [281. 锯齿迭代器](https://leetcode.cn/problems/zigzag-iterator/?show=1)🔒 |
|
||||
| [42. Trapping Rain Water](https://leetcode.com/problems/trapping-rain-water/?show=1) | [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/?show=1) |
|
||||
| [80. Remove Duplicates from Sorted Array II](https://leetcode.com/problems/remove-duplicates-from-sorted-array-ii/?show=1) | [80. 删除有序数组中的重复项 II](https://leetcode.cn/problems/remove-duplicates-from-sorted-array-ii/?show=1) |
|
||||
| [82. Remove Duplicates from Sorted List II](https://leetcode.com/problems/remove-duplicates-from-sorted-list-ii/?show=1) | [82. 删除排序链表中的重复元素 II](https://leetcode.cn/problems/remove-duplicates-from-sorted-list-ii/?show=1) |
|
||||
| - | [剑指 Offer 21. 调整数组顺序使奇数位于偶数前面](https://leetcode.cn/problems/diao-zheng-shu-zu-shun-xu-shi-qi-shu-wei-yu-ou-shu-qian-mian-lcof/?show=1) |
|
||||
| - | [剑指 Offer 57. 和为s的两个数字](https://leetcode.cn/problems/he-wei-sde-liang-ge-shu-zi-lcof/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,9 +1,5 @@
|
|||
# 回溯算法详解
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -333,6 +329,67 @@ def backtrack(...):
|
|||
|
||||
动态规划和回溯算法底层都把问题抽象成了树的结构,但这两种算法在思路上是完全不同的。在 [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结) 你将看到动态规划和回溯算法更深层次的区别和联系。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [BFS 算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=BFS框架)
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [FloodFill算法详解及应用](https://labuladong.github.io/article/fname.html?fname=FloodFill算法详解及应用)
|
||||
- [base case 和备忘录的初始值怎么定?](https://labuladong.github.io/article/fname.html?fname=备忘录等基础)
|
||||
- [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结)
|
||||
- [两种思路解决单词拼接问题](https://labuladong.github.io/article/fname.html?fname=单词拼接)
|
||||
- [二分搜索怎么用?我和快手面试官进行了深度探讨](https://labuladong.github.io/article/fname.html?fname=二分分割子数组)
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [前缀树算法模板秒杀五道算法题](https://labuladong.github.io/article/fname.html?fname=trie)
|
||||
- [动态规划和回溯算法到底谁是谁爹?](https://labuladong.github.io/article/fname.html?fname=targetSum)
|
||||
- [回溯算法最佳实践:括号生成](https://labuladong.github.io/article/fname.html?fname=合法括号生成)
|
||||
- [回溯算法最佳实践:解数独](https://labuladong.github.io/article/fname.html?fname=sudoku)
|
||||
- [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.github.io/article/fname.html?fname=子集排列组合)
|
||||
- [图论基础及遍历算法](https://labuladong.github.io/article/fname.html?fname=图)
|
||||
- [学习算法和刷题的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [环检测及拓扑排序算法](https://labuladong.github.io/article/fname.html?fname=拓扑排序)
|
||||
- [算法学习和心流体验](https://labuladong.github.io/article/fname.html?fname=心流)
|
||||
- [算法笔试「骗分」套路](https://labuladong.github.io/article/fname.html?fname=刷题技巧)
|
||||
- [经典动态规划:戳气球](https://labuladong.github.io/article/fname.html?fname=扎气球)
|
||||
- [经典回溯算法:集合划分问题](https://labuladong.github.io/article/fname.html?fname=集合划分)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [112. Path Sum](https://leetcode.com/problems/path-sum/?show=1) | [112. 路径总和](https://leetcode.cn/problems/path-sum/?show=1) |
|
||||
| [113. Path Sum II](https://leetcode.com/problems/path-sum-ii/?show=1) | [113. 路径总和 II](https://leetcode.cn/problems/path-sum-ii/?show=1) |
|
||||
| [140. Word Break II](https://leetcode.com/problems/word-break-ii/?show=1) | [140. 单词拆分 II](https://leetcode.cn/problems/word-break-ii/?show=1) |
|
||||
| [17. Letter Combinations of a Phone Number](https://leetcode.com/problems/letter-combinations-of-a-phone-number/?show=1) | [17. 电话号码的字母组合](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/?show=1) |
|
||||
| [22. Generate Parentheses](https://leetcode.com/problems/generate-parentheses/?show=1) | [22. 括号生成](https://leetcode.cn/problems/generate-parentheses/?show=1) |
|
||||
| [39. Combination Sum](https://leetcode.com/problems/combination-sum/?show=1) | [39. 组合总和](https://leetcode.cn/problems/combination-sum/?show=1) |
|
||||
| [698. Partition to K Equal Sum Subsets](https://leetcode.com/problems/partition-to-k-equal-sum-subsets/?show=1) | [698. 划分为k个相等的子集](https://leetcode.cn/problems/partition-to-k-equal-sum-subsets/?show=1) |
|
||||
| [77. Combinations](https://leetcode.com/problems/combinations/?show=1) | [77. 组合](https://leetcode.cn/problems/combinations/?show=1) |
|
||||
| [78. Subsets](https://leetcode.com/problems/subsets/?show=1) | [78. 子集](https://leetcode.cn/problems/subsets/?show=1) |
|
||||
| - | [剑指 Offer 34. 二叉树中和为某一值的路径](https://leetcode.cn/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 079. 所有子集](https://leetcode.cn/problems/TVdhkn/?show=1) |
|
||||
| - | [剑指 Offer II 080. 含有 k 个元素的组合](https://leetcode.cn/problems/uUsW3B/?show=1) |
|
||||
| - | [剑指 Offer II 081. 允许重复选择元素的组合](https://leetcode.cn/problems/Ygoe9J/?show=1) |
|
||||
| - | [剑指 Offer II 083. 没有重复元素集合的全排列](https://leetcode.cn/problems/VvJkup/?show=1) |
|
||||
| - | [剑指 Offer II 085. 生成匹配的括号](https://leetcode.cn/problems/IDBivT/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,9 +1,5 @@
|
|||
# 字符串乘法
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -98,6 +94,10 @@ string multiply(string num1, string num2) {
|
|||
|
||||
也许算法就是一种**寻找思维定式的思维**吧,希望本文对你有帮助。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,22 +1,23 @@
|
|||
# 学习算法和刷题的思路指南
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
通知:如果本站对你学习算法有帮助,**请收藏网址,并推荐给你的朋友**。由于 **labuladong** 的算法套路太火,很多人直接拿我的 GitHub 文章去开付费专栏,价格还不便宜。我这免费写给你看,**多宣传原创作者是你唯一能做的**,谁也不希望劣币驱逐良币对吧?
|
||||
> 本文有视频版:[学习数据结构和算法的框架思维](https://www.bilibili.com/video/BV1EN4y1M79p/)
|
||||
|
||||
这是好久之前的一篇文章「学习数据结构和算法的框架思维」的修订版。之前那篇文章收到广泛好评,没看过也没关系,这篇文章会涵盖之前的所有内容,并且会举很多代码的实例,教你如何使用框架思维。
|
||||
这是好久之前的一篇文章 [学习数据结构和算法的框架思维](https://mp.weixin.qq.com/s/gE-5KMi4bBvJovdsQXIKgw) 的修订版。之前那篇文章收到广泛好评,没看过也没关系,这篇文章会涵盖之前的所有内容,并且会举很多代码的实例,教你如何使用框架思维。
|
||||
|
||||
首先,这里讲的都是普通的数据结构,咱不是搞算法竞赛的,野路子出生,我只会解决常规的问题。另外,以下是我个人的经验的总结,没有哪本算法书会写这些东西,所以请读者试着理解我的角度,别纠结于细节问题,因为这篇文章就是希望对数据结构和算法建立一个框架性的认识。
|
||||
|
||||
|
|
@ -46,7 +47,6 @@
|
|||
|
||||
**链表**因为元素不连续,而是靠指针指向下一个元素的位置,所以不存在数组的扩容问题;如果知道某一元素的前驱和后驱,操作指针即可删除该元素或者插入新元素,时间复杂度 O(1)。但是正因为存储空间不连续,你无法根据一个索引算出对应元素的地址,所以不能随机访问;而且由于每个元素必须存储指向前后元素位置的指针,会消耗相对更多的储存空间。
|
||||
|
||||
|
||||
### 二、数据结构的基本操作
|
||||
|
||||
对于任何数据结构,其基本操作无非遍历 + 访问,再具体一点就是:增删查改。
|
||||
|
|
@ -84,7 +84,7 @@ void traverse(ListNode head) {
|
|||
|
||||
void traverse(ListNode head) {
|
||||
// 递归访问 head.val
|
||||
traverse(head.next)
|
||||
traverse(head.next);
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -98,8 +98,8 @@ class TreeNode {
|
|||
}
|
||||
|
||||
void traverse(TreeNode root) {
|
||||
traverse(root.left)
|
||||
traverse(root.right)
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -120,134 +120,164 @@ void traverse(TreeNode root) {
|
|||
}
|
||||
```
|
||||
|
||||
N 叉树的遍历又可以扩展为图的遍历,因为图就是好几 N 叉棵树的结合体。你说图是可能出现环的?这个很好办,用个布尔数组 visited 做标记就行了,这里就不写代码了。
|
||||
`N` 叉树的遍历又可以扩展为图的遍历,因为图就是好几 `N` 叉棵树的结合体。你说图是可能出现环的?这个很好办,用个布尔数组 `visited` 做标记就行了,这里就不写代码了。
|
||||
|
||||
**所谓框架,就是套路。不管增删查改,这些代码都是永远无法脱离的结构,你可以把这个结构作为大纲,根据具体问题在框架上添加代码就行了,下面会具体举例**。
|
||||
**所谓框架,就是套路。不管增删查改,这些代码都是永远无法脱离的结构**,你可以把这个结构作为大纲,根据具体问题在框架上添加代码就行了,下面会具体举例。
|
||||
|
||||
### 三、算法刷题指南
|
||||
|
||||
首先要明确的是,**数据结构是工具,算法是通过合适的工具解决特定问题的方法**。也就是说,学习算法之前,最起码得了解那些常用的数据结构,了解它们的特性和缺陷。
|
||||
首先要明确的是,数据结构是工具,算法是通过合适的工具解决特定问题的方法。也就是说,学习算法之前,最起码得了解那些常用的数据结构,了解它们的特性和缺陷。
|
||||
|
||||
那么该如何在 LeetCode 刷题呢?之前的文章[算法学习之路](https://labuladong.gitee.io/algo/)写过一些,什么按标签刷,坚持下去云云。现在距那篇文章已经过去将近一年了,我不说那些不痛不痒的话,直接说具体的建议:
|
||||
所以我建议的刷题顺序是:
|
||||
|
||||
**先刷二叉树,先刷二叉树,先刷二叉树**!
|
||||
**1、先学习像数组、链表这种基本数据结构的常用算法**,比如单链表翻转,前缀和数组,二分搜索等。
|
||||
|
||||
这是我这刷题一年的亲身体会,下图是去年十月份的提交截图:
|
||||
因为这些算法属于会者不难难者不会的类型,难度不大,学习它们不会花费太多时间。而且这些小而美的算法经常让你大呼精妙,能够有效培养你对算法的兴趣。
|
||||
|
||||

|
||||
**2、学会基础算法之后,不要急着上来就刷回溯算法、动态规划这类笔试常考题,而应该先刷二叉树,先刷二叉树,先刷二叉树**,重要的事情说三遍。
|
||||
|
||||
这是我这刷题多年的亲身体会,下图是我刚开始学算法的提交截图:
|
||||
|
||||
|
||||
|
||||
公众号文章的阅读数据显示,大部分人对数据结构相关的算法文章不感兴趣,而是更关心动规回溯分治等等技巧。为什么要先刷二叉树呢,**因为二叉树是最容易培养框架思维的,而且大部分算法技巧,本质上都是树的遍历问题**。
|
||||
|
||||
刷二叉树看到题目没思路?根据很多读者的问题,其实大家不是没思路,只是没有理解我们说的「框架」是什么。**不要小看这几行破代码,几乎所有二叉树的题目都是一套这个框架就出来了**。
|
||||
刷二叉树看到题目没思路?根据很多读者的问题,其实大家不是没思路,只是没有理解我们说的「框架」是什么。
|
||||
|
||||
**不要小看这几行破代码,几乎所有二叉树的题目都是一套这个框架就出来了**:
|
||||
|
||||
```java
|
||||
void traverse(TreeNode root) {
|
||||
// 前序遍历
|
||||
traverse(root.left)
|
||||
// 中序遍历
|
||||
traverse(root.right)
|
||||
// 后序遍历
|
||||
// 前序位置
|
||||
traverse(root.left);
|
||||
// 中序位置
|
||||
traverse(root.right);
|
||||
// 后序位置
|
||||
}
|
||||
```
|
||||
|
||||
比如说我随便拿几道题的解法出来,不用管具体的代码逻辑,只要看看框架在其中是如何发挥作用的就行。
|
||||
|
||||
LeetCode 124 题,难度 Hard,让你求二叉树中最大路径和,主要代码如下:
|
||||
力扣第 124 题,难度困难,让你求二叉树中最大路径和,主要代码如下:
|
||||
|
||||
```cpp
|
||||
int ans = INT_MIN;
|
||||
int oneSideMax(TreeNode* root) {
|
||||
if (root == nullptr) return 0;
|
||||
int left = max(0, oneSideMax(root->left));
|
||||
int right = max(0, oneSideMax(root->right));
|
||||
ans = max(ans, left + right + root->val);
|
||||
return max(left, right) + root->val;
|
||||
```java
|
||||
int res = Integer.MIN_VALUE;
|
||||
int oneSideMax(TreeNode root) {
|
||||
if (root == null) return 0;
|
||||
int left = max(0, oneSideMax(root.left));
|
||||
int right = max(0, oneSideMax(root.right));
|
||||
// 后序位置
|
||||
res = Math.max(res, left + right + root.val);
|
||||
return Math.max(left, right) + root.val;
|
||||
}
|
||||
```
|
||||
|
||||
你看,这就是个后序遍历嘛。
|
||||
注意递归函数的位置,这就是个后序遍历嘛,无非就是把 `traverse` 函数名字改成 `oneSideMax` 了。
|
||||
|
||||
LeetCode 105 题,难度 Medium,让你根据前序遍历和中序遍历的结果还原一棵二叉树,很经典的问题吧,主要代码如下:
|
||||
力扣第 105 题,难度中等,让你根据前序遍历和中序遍历的结果还原一棵二叉树,很经典的问题吧,主要代码如下:
|
||||
|
||||
```java
|
||||
TreeNode buildTree(int[] preorder, int preStart, int preEnd,
|
||||
int[] inorder, int inStart, int inEnd, Map<Integer, Integer> inMap) {
|
||||
TreeNode build(int[] preorder, int preStart, int preEnd,
|
||||
int[] inorder, int inStart, int inEnd) {
|
||||
// 前序位置,寻找左右子树的索引
|
||||
if (preStart > preEnd) {
|
||||
return null;
|
||||
}
|
||||
int rootVal = preorder[preStart];
|
||||
int index = 0;
|
||||
for (int i = inStart; i <= inEnd; i++) {
|
||||
if (inorder[i] == rootVal) {
|
||||
index = i;
|
||||
break;
|
||||
}
|
||||
}
|
||||
int leftSize = index - inStart;
|
||||
TreeNode root = new TreeNode(rootVal);
|
||||
|
||||
if(preStart > preEnd || inStart > inEnd) return null;
|
||||
|
||||
TreeNode root = new TreeNode(preorder[preStart]);
|
||||
int inRoot = inMap.get(root.val);
|
||||
int numsLeft = inRoot - inStart;
|
||||
|
||||
root.left = buildTree(preorder, preStart + 1, preStart + numsLeft,
|
||||
inorder, inStart, inRoot - 1, inMap);
|
||||
root.right = buildTree(preorder, preStart + numsLeft + 1, preEnd,
|
||||
inorder, inRoot + 1, inEnd, inMap);
|
||||
// 递归构造左右子树
|
||||
root.left = build(preorder, preStart + 1, preStart + leftSize,
|
||||
inorder, inStart, index - 1);
|
||||
root.right = build(preorder, preStart + leftSize + 1, preEnd,
|
||||
inorder, index + 1, inEnd);
|
||||
return root;
|
||||
}
|
||||
```
|
||||
|
||||
不要看这个函数的参数很多,只是为了控制数组索引而已,本质上该算法也就是一个前序遍历。
|
||||
不要看这个函数的参数很多,只是为了控制数组索引而已。注意找递归函数 `build` 的位置,本质上该算法也就是一个前序遍历,因为它在前序遍历的位置加了一坨代码逻辑。
|
||||
|
||||
LeetCode 99 题,难度 Hard,恢复一棵 BST,主要代码如下:
|
||||
力扣第 230 题,难度中等,寻找二叉搜索树中的第 `k` 小的元素,主要代码如下:
|
||||
|
||||
```cpp
|
||||
void traverse(TreeNode* node) {
|
||||
if (!node) return;
|
||||
traverse(node->left);
|
||||
if (node->val < prev->val) {
|
||||
s = (s == NULL) ? prev : s;
|
||||
t = node;
|
||||
```java
|
||||
int res = 0;
|
||||
int rank = 0;
|
||||
void traverse(TreeNode root, int k) {
|
||||
if (root == null) {
|
||||
return;
|
||||
}
|
||||
prev = node;
|
||||
traverse(node->right);
|
||||
traverse(root.left, k);
|
||||
/* 中序遍历代码位置 */
|
||||
rank++;
|
||||
if (k == rank) {
|
||||
res = root.val;
|
||||
return;
|
||||
}
|
||||
/*****************/
|
||||
traverse(root.right, k);
|
||||
}
|
||||
```
|
||||
|
||||
这不就是个中序遍历嘛,对于一棵 BST 中序遍历意味着什么,应该不需要解释了吧。
|
||||
|
||||
你看,Hard 难度的题目不过如此,而且还这么有规律可循,只要把框架写出来,然后往相应的位置加东西就行了,这不就是思路吗。
|
||||
你看,二叉树的题目不过如此,只要把框架写出来,然后往相应的位置加代码就行了,这不就是思路吗。
|
||||
|
||||
对于一个理解二叉树的人来说,刷一道二叉树的题目花不了多长时间。那么如果你对刷题无从下手或者有畏惧心理,不妨从二叉树下手,前 10 道也许有点难受;结合框架再做 20 道,也许你就有点自己的理解了;刷完整个专题,再去做什么回溯动规分治专题,**你就会发现只要涉及递归的问题,都是树的问题**。
|
||||
|
||||
PS:[刷题插件](https://mp.weixin.qq.com/s/OE1zPVPj0V2o82N4HtLQbw) 集成了手把手刷二叉树功能,按照公式和套路讲解了 150 道二叉树题目,可手把手带你刷完二叉树分类的题目,迅速掌握递归思维。
|
||||
|
||||
再举例吧,说几道我们之前文章写过的问题。
|
||||
|
||||
[动态规划详解](https://labuladong.gitee.io/algo/)说过凑零钱问题,暴力解法就是遍历一棵 N 叉树:
|
||||
[动态规划详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)说过凑零钱问题,暴力解法就是遍历一棵 N 叉树:
|
||||
|
||||

|
||||

|
||||
|
||||
```python
|
||||
def coinChange(coins: List[int], amount: int):
|
||||
```java
|
||||
int dp(int[] coins, int amount) {
|
||||
// base case
|
||||
if (amount == 0) return 0;
|
||||
if (amount < 0) return -1;
|
||||
|
||||
def dp(n):
|
||||
if n == 0: return 0
|
||||
if n < 0: return -1
|
||||
|
||||
res = float('INF')
|
||||
for coin in coins:
|
||||
subproblem = dp(n - coin)
|
||||
# 子问题无解,跳过
|
||||
if subproblem == -1: continue
|
||||
res = min(res, 1 + subproblem)
|
||||
return res if res != float('INF') else -1
|
||||
|
||||
return dp(amount)
|
||||
int res = Integer.MAX_VALUE;
|
||||
for (int coin : coins) {
|
||||
int subProblem = dp(coins, amount - coin);
|
||||
// 子问题无解则跳过
|
||||
if (subProblem == -1) continue;
|
||||
// 在子问题中选择最优解,然后加一
|
||||
res = Math.min(res, subProblem + 1);
|
||||
}
|
||||
return res == Integer.MAX_VALUE ? -1 : res;
|
||||
}
|
||||
```
|
||||
|
||||
这么多代码看不懂咋办?直接提取出框架,就能看出核心思路了:
|
||||
|
||||
```python
|
||||
# 不过是一个 N 叉树的遍历问题而已
|
||||
def dp(n):
|
||||
for coin in coins:
|
||||
dp(n - coin)
|
||||
int dp(int amount) {
|
||||
for (int coin : coins) {
|
||||
dp(amount - coin);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
其实很多动态规划问题就是在遍历一棵树,你如果对树的遍历操作烂熟于心,起码知道怎么把思路转化成代码,也知道如何提取别人解法的核心思路。
|
||||
|
||||
再看看回溯算法,前文[回溯算法详解](https://labuladong.gitee.io/algo/)干脆直接说了,回溯算法就是个 N 叉树的前后序遍历问题,没有例外。
|
||||
再看看回溯算法,前文 [回溯算法详解](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 干脆直接说了,回溯算法就是个 N 叉树的前后序遍历问题,没有例外。
|
||||
|
||||
比如 N 皇后问题吧,主要代码如下:
|
||||
比如全排列问题吧,本质上全排列就是在遍历下面这棵树,到叶子节点的路径就是一个全排列:
|
||||
|
||||
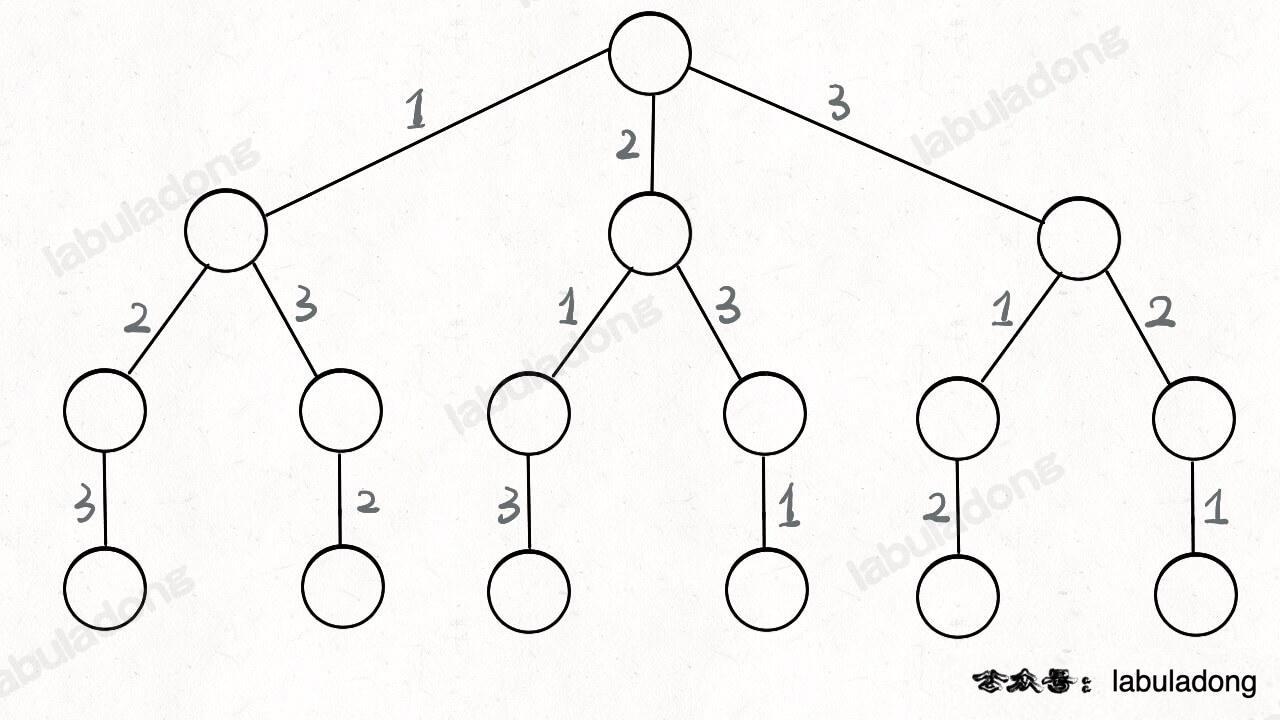
|
||||
|
||||
全排列算法的主要代码如下:
|
||||
|
||||
```java
|
||||
void backtrack(int[] nums, LinkedList<Integer> track) {
|
||||
|
|
@ -264,7 +294,12 @@ void backtrack(int[] nums, LinkedList<Integer> track) {
|
|||
backtrack(nums, track);
|
||||
track.removeLast();
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
看不懂?没关系,把其中的递归部分抽取出来:
|
||||
|
||||
```java
|
||||
/* 提取出 N 叉树遍历框架 */
|
||||
void backtrack(int[] nums, LinkedList<Integer> track) {
|
||||
for (int i = 0; i < nums.length; i++) {
|
||||
|
|
@ -272,11 +307,11 @@ void backtrack(int[] nums, LinkedList<Integer> track) {
|
|||
}
|
||||
```
|
||||
|
||||
N 叉树的遍历框架,找出来了把~你说,树这种结构重不重要?
|
||||
N 叉树的遍历框架,找出来了吧?你说,树这种结构重不重要?
|
||||
|
||||
**综上,对于畏惧算法的朋友来说,可以先刷树的相关题目,试着从框架上看问题,而不要纠结于细节问题**。
|
||||
**综上,对于畏惧算法的同学来说,可以先刷树的相关题目,试着从框架上看问题,而不要纠结于细节问题**。
|
||||
|
||||
纠结细节问题,就比如纠结 i 到底应该加到 n 还是加到 n - 1,这个数组的大小到底应该开 n 还是 n + 1 ?
|
||||
纠结细节问题,就比如纠结 `i` 到底应该加到 `n` 还是加到 `n - 1`,这个数组的大小到底应该开 `n` 还是 `n + 1`?
|
||||
|
||||
从框架上看问题,就是像我们这样基于框架进行抽取和扩展,既可以在看别人解法时快速理解核心逻辑,也有助于找到我们自己写解法时的思路方向。
|
||||
|
||||
|
|
@ -284,27 +319,71 @@ N 叉树的遍历框架,找出来了把~你说,树这种结构重不重要
|
|||
|
||||
但是,你要是心中没有框架,那么你根本无法解题,给了你答案,你也不会发现这就是个树的遍历问题。
|
||||
|
||||
这种思维是很重要的,[动态规划详解](https://labuladong.gitee.io/algo/)中总结的找状态转移方程的几步流程,有时候按照流程写出解法,说实话我自己都不知道为啥是对的,反正它就是对了。。。
|
||||
这种思维是很重要的,[动态规划详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶) 中总结的找状态转移方程的几步流程,有时候按照流程写出解法,可能自己都不知道为啥是对的,反正它就是对了。。。
|
||||
|
||||
**这就是框架的力量,能够保证你在快睡着的时候,依然能写出正确的程序;就算你啥都不会,都能比别人高一个级别。**
|
||||
**这就是框架的力量,能够保证你在快睡着的时候,依然能写出正确的程序;就算你啥都不会,都能比别人高一个级别**。
|
||||
|
||||
|
||||
### 四、总结几句
|
||||
本文最后,总结一下吧:
|
||||
|
||||
数据结构的基本存储方式就是链式和顺序两种,基本操作就是增删查改,遍历方式无非迭代和递归。
|
||||
|
||||
刷算法题建议从「树」分类开始刷,结合框架思维,把这几十道题刷完,对于树结构的理解应该就到位了。这时候去看回溯、动规、分治等算法专题,对思路的理解可能会更加深刻一些。
|
||||
学完基本算法之后,建议从「二叉树」系列问题开始刷,结合框架思维,把树结构理解到位,然后再去看回溯、动规、分治等算法专题,对思路的理解就会更加深刻。
|
||||
|
||||
> 最后打个广告,我亲自制作了一门 [数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO),以视频课为主,手把手带你实现常用的数据结构及相关算法,旨在帮助算法基础较为薄弱的读者深入理解常用数据结构的底层原理,在算法学习中少走弯路。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [Dijkstra 算法模板及应用](https://labuladong.github.io/article/fname.html?fname=dijkstra算法)
|
||||
- [一文秒杀所有岛屿题目](https://labuladong.github.io/article/fname.html?fname=岛屿题目)
|
||||
- [东哥带你刷二叉树(序列化篇)](https://labuladong.github.io/article/fname.html?fname=二叉树的序列化)
|
||||
- [东哥带你刷二叉树(纲领篇)](https://labuladong.github.io/article/fname.html?fname=二叉树总结)
|
||||
- [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
|
||||
- [二叉树的递归转迭代的代码框架](https://labuladong.github.io/article/fname.html?fname=迭代遍历二叉树)
|
||||
- [前缀树算法模板秒杀五道算法题](https://labuladong.github.io/article/fname.html?fname=trie)
|
||||
- [动态规划和回溯算法到底谁是谁爹?](https://labuladong.github.io/article/fname.html?fname=targetSum)
|
||||
- [回溯算法秒杀所有排列/组合/子集问题](https://labuladong.github.io/article/fname.html?fname=子集排列组合)
|
||||
- [回溯算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版)
|
||||
- [图论基础及遍历算法](https://labuladong.github.io/article/fname.html?fname=图)
|
||||
- [如何 K 个一组反转链表](https://labuladong.github.io/article/fname.html?fname=k个一组反转链表)
|
||||
- [如何判断回文链表](https://labuladong.github.io/article/fname.html?fname=判断回文链表)
|
||||
- [归并排序详解及应用](https://labuladong.github.io/article/fname.html?fname=归并排序)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [环检测及拓扑排序算法](https://labuladong.github.io/article/fname.html?fname=拓扑排序)
|
||||
- [算法学习和心流体验](https://labuladong.github.io/article/fname.html?fname=心流)
|
||||
- [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度)
|
||||
- [题目不让我干什么,我偏要干什么](https://labuladong.github.io/article/fname.html?fname=nestInteger)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [100. Same Tree](https://leetcode.com/problems/same-tree/?show=1) | [100. 相同的树](https://leetcode.cn/problems/same-tree/?show=1) |
|
||||
| [341. Flatten Nested List Iterator](https://leetcode.com/problems/flatten-nested-list-iterator/?show=1) | [341. 扁平化嵌套列表迭代器](https://leetcode.cn/problems/flatten-nested-list-iterator/?show=1) |
|
||||
| [589. N-ary Tree Preorder Traversal](https://leetcode.com/problems/n-ary-tree-preorder-traversal/?show=1) | [589. N 叉树的前序遍历](https://leetcode.cn/problems/n-ary-tree-preorder-traversal/?show=1) |
|
||||
| [590. N-ary Tree Postorder Traversal](https://leetcode.com/problems/n-ary-tree-postorder-traversal/?show=1) | [590. N 叉树的后序遍历](https://leetcode.cn/problems/n-ary-tree-postorder-traversal/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||

|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
|
@ -0,0 +1,300 @@
|
|||
# 那些小而美的算法技巧:前缀和/差分数组
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [1094. Car Pooling](https://leetcode.com/problems/car-pooling/) | [1094. 拼车](https://leetcode.cn/problems/car-pooling/) | 🟠
|
||||
| [1109. Corporate Flight Bookings](https://leetcode.com/problems/corporate-flight-bookings/) | [1109. 航班预订统计](https://leetcode.cn/problems/corporate-flight-bookings/) | 🟠
|
||||
| [370. Range Addition](https://leetcode.com/problems/range-addition/)🔒 | [370. 区间加法](https://leetcode.cn/problems/range-addition/)🔒 | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
前文 [前缀和技巧详解](https://labuladong.github.io/article/fname.html?fname=前缀和技巧) 写过的前缀和技巧是非常常用的算法技巧,**前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和**。
|
||||
|
||||
没看过前文没关系,这里简单介绍一下前缀和,核心代码就是下面这段:
|
||||
|
||||
```java
|
||||
class PrefixSum {
|
||||
// 前缀和数组
|
||||
private int[] prefix;
|
||||
|
||||
/* 输入一个数组,构造前缀和 */
|
||||
public PrefixSum(int[] nums) {
|
||||
prefix = new int[nums.length + 1];
|
||||
// 计算 nums 的累加和
|
||||
for (int i = 1; i < prefix.length; i++) {
|
||||
prefix[i] = prefix[i - 1] + nums[i - 1];
|
||||
}
|
||||
}
|
||||
|
||||
/* 查询闭区间 [i, j] 的累加和 */
|
||||
public int query(int i, int j) {
|
||||
return prefix[j + 1] - prefix[i];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
|
||||
`prefix[i]` 就代表着 `nums[0..i-1]` 所有元素的累加和,如果我们想求区间 `nums[i..j]` 的累加和,只要计算 `prefix[j+1] - prefix[i]` 即可,而不需要遍历整个区间求和。
|
||||
|
||||
本文讲一个和前缀和思想非常类似的算法技巧「差分数组」,**差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减**。
|
||||
|
||||
比如说,我给你输入一个数组 `nums`,然后又要求给区间 `nums[2..6]` 全部加 1,再给 `nums[3..9]` 全部减 3,再给 `nums[0..4]` 全部加 2,再给...
|
||||
|
||||
一通操作猛如虎,然后问你,最后 `nums` 数组的值是什么?
|
||||
|
||||
常规的思路很容易,你让我给区间 `nums[i..j]` 加上 `val`,那我就一个 for 循环给它们都加上呗,还能咋样?这种思路的时间复杂度是 O(N),由于这个场景下对 `nums` 的修改非常频繁,所以效率会很低下。
|
||||
|
||||
这里就需要差分数组的技巧,类似前缀和技巧构造的 `prefix` 数组,我们先对 `nums` 数组构造一个 `diff` 差分数组,**`diff[i]` 就是 `nums[i]` 和 `nums[i-1]` 之差**:
|
||||
|
||||
```java
|
||||
int[] diff = new int[nums.length];
|
||||
// 构造差分数组
|
||||
diff[0] = nums[0];
|
||||
for (int i = 1; i < nums.length; i++) {
|
||||
diff[i] = nums[i] - nums[i - 1];
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
|
||||
通过这个 `diff` 差分数组是可以反推出原始数组 `nums` 的,代码逻辑如下:
|
||||
|
||||
```java
|
||||
int[] res = new int[diff.length];
|
||||
// 根据差分数组构造结果数组
|
||||
res[0] = diff[0];
|
||||
for (int i = 1; i < diff.length; i++) {
|
||||
res[i] = res[i - 1] + diff[i];
|
||||
}
|
||||
```
|
||||
|
||||
**这样构造差分数组 `diff`,就可以快速进行区间增减的操作**,如果你想对区间 `nums[i..j]` 的元素全部加 3,那么只需要让 `diff[i] += 3`,然后再让 `diff[j+1] -= 3` 即可:
|
||||
|
||||
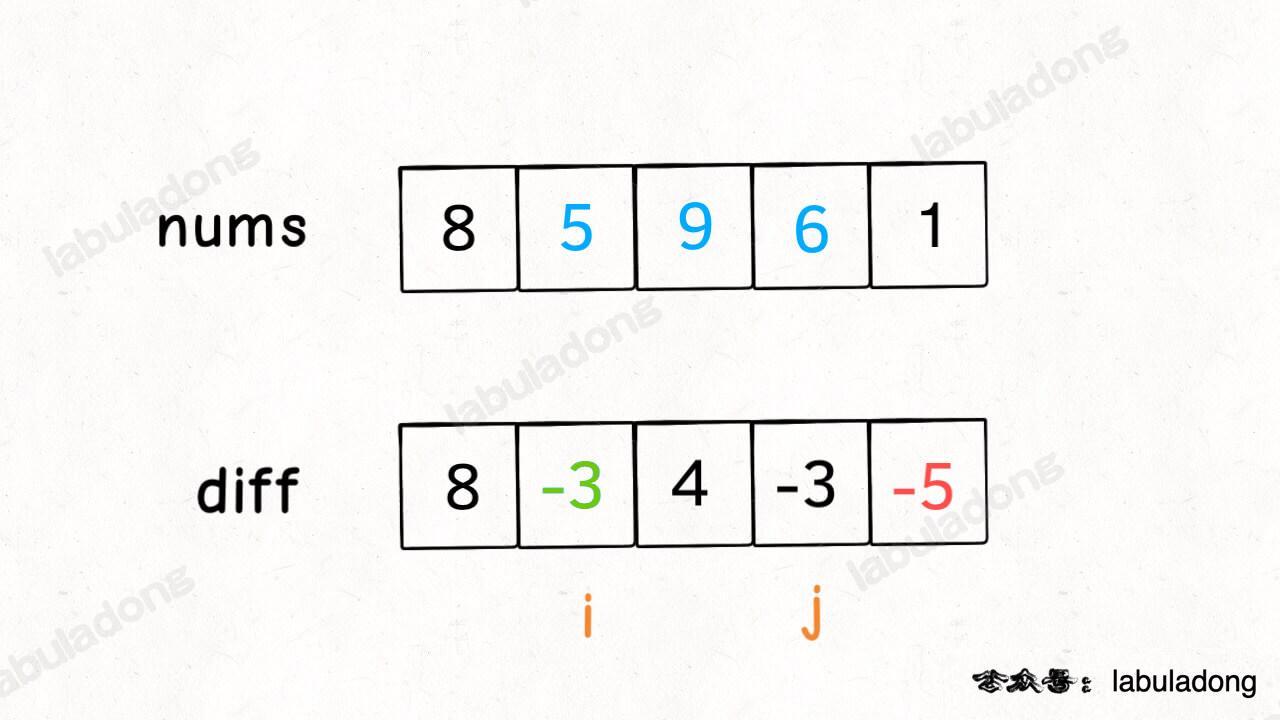
|
||||
|
||||
**原理很简单,回想 `diff` 数组反推 `nums` 数组的过程,`diff[i] += 3` 意味着给 `nums[i..]` 所有的元素都加了 3,然后 `diff[j+1] -= 3` 又意味着对于 `nums[j+1..]` 所有元素再减 3,那综合起来,是不是就是对 `nums[i..j]` 中的所有元素都加 3 了**?
|
||||
|
||||
只要花费 O(1) 的时间修改 `diff` 数组,就相当于给 `nums` 的整个区间做了修改。多次修改 `diff`,然后通过 `diff` 数组反推,即可得到 `nums` 修改后的结果。
|
||||
|
||||
现在我们把差分数组抽象成一个类,包含 `increment` 方法和 `result` 方法:
|
||||
|
||||
```java
|
||||
// 差分数组工具类
|
||||
class Difference {
|
||||
// 差分数组
|
||||
private int[] diff;
|
||||
|
||||
/* 输入一个初始数组,区间操作将在这个数组上进行 */
|
||||
public Difference(int[] nums) {
|
||||
assert nums.length > 0;
|
||||
diff = new int[nums.length];
|
||||
// 根据初始数组构造差分数组
|
||||
diff[0] = nums[0];
|
||||
for (int i = 1; i < nums.length; i++) {
|
||||
diff[i] = nums[i] - nums[i - 1];
|
||||
}
|
||||
}
|
||||
|
||||
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
|
||||
public void increment(int i, int j, int val) {
|
||||
diff[i] += val;
|
||||
if (j + 1 < diff.length) {
|
||||
diff[j + 1] -= val;
|
||||
}
|
||||
}
|
||||
|
||||
/* 返回结果数组 */
|
||||
public int[] result() {
|
||||
int[] res = new int[diff.length];
|
||||
// 根据差分数组构造结果数组
|
||||
res[0] = diff[0];
|
||||
for (int i = 1; i < diff.length; i++) {
|
||||
res[i] = res[i - 1] + diff[i];
|
||||
}
|
||||
return res;
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
这里注意一下 `increment` 方法中的 if 语句:
|
||||
|
||||
```java
|
||||
public void increment(int i, int j, int val) {
|
||||
diff[i] += val;
|
||||
if (j + 1 < diff.length) {
|
||||
diff[j + 1] -= val;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
当 `j+1 >= diff.length` 时,说明是对 `nums[i]` 及以后的整个数组都进行修改,那么就不需要再给 `diff` 数组减 `val` 了。
|
||||
|
||||
### 算法实践
|
||||
|
||||
首先,力扣第 370 题「区间加法」 就直接考察了差分数组技巧:
|
||||
|
||||

|
||||
|
||||
那么我们直接复用刚才实现的 `Difference` 类就能把这道题解决掉:
|
||||
|
||||
```java
|
||||
int[] getModifiedArray(int length, int[][] updates) {
|
||||
// nums 初始化为全 0
|
||||
int[] nums = new int[length];
|
||||
// 构造差分解法
|
||||
Difference df = new Difference(nums);
|
||||
|
||||
for (int[] update : updates) {
|
||||
int i = update[0];
|
||||
int j = update[1];
|
||||
int val = update[2];
|
||||
df.increment(i, j, val);
|
||||
}
|
||||
|
||||
return df.result();
|
||||
}
|
||||
```
|
||||
|
||||
当然,实际的算法题可能需要我们对题目进行联想和抽象,不会这么直接地让你看出来要用差分数组技巧,这里看一下力扣第 1109 题「航班预订统计」:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int[] corpFlightBookings(int[][] bookings, int n)
|
||||
```
|
||||
|
||||
这个题目就在那绕弯弯,其实它就是个差分数组的题,我给你翻译一下:
|
||||
|
||||
给你输入一个长度为 `n` 的数组 `nums`,其中所有元素都是 0。再给你输入一个 `bookings`,里面是若干三元组 `(i, j,k)`,每个三元组的含义就是要求你给 `nums` 数组的闭区间 `[i-1,j-1]` 中所有元素都加上 `k`。请你返回最后的 `nums` 数组是多少?
|
||||
|
||||
> PS:因为题目说的 `n` 是从 1 开始计数的,而数组索引从 0 开始,所以对于输入的三元组 `(i, j,k)`,数组区间应该对应 `[i-1,j-1]`。
|
||||
|
||||
这么一看,不就是一道标准的差分数组题嘛?我们可以直接复用刚才写的类:
|
||||
|
||||
```java
|
||||
int[] corpFlightBookings(int[][] bookings, int n) {
|
||||
// nums 初始化为全 0
|
||||
int[] nums = new int[n];
|
||||
// 构造差分解法
|
||||
Difference df = new Difference(nums);
|
||||
|
||||
for (int[] booking : bookings) {
|
||||
// 注意转成数组索引要减一哦
|
||||
int i = booking[0] - 1;
|
||||
int j = booking[1] - 1;
|
||||
int val = booking[2];
|
||||
// 对区间 nums[i..j] 增加 val
|
||||
df.increment(i, j, val);
|
||||
}
|
||||
// 返回最终的结果数组
|
||||
return df.result();
|
||||
}
|
||||
```
|
||||
|
||||
这道题就解决了。
|
||||
|
||||
还有一道很类似的题目是力扣第 1094 题「拼车」,我简单描述下题目:
|
||||
|
||||
你是一个开公交车的司机,公交车的最大载客量为 `capacity`,沿途要经过若干车站,给你一份乘客行程表 `int[][] trips`,其中 `trips[i] = [num, start, end]` 代表着有 `num` 个旅客要从站点 `start` 上车,到站点 `end` 下车,请你计算是否能够一次把所有旅客运送完毕(不能超过最大载客量 `capacity`)。
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
boolean carPooling(int[][] trips, int capacity);
|
||||
```
|
||||
|
||||
比如输入:
|
||||
|
||||
```shell
|
||||
trips = [[2,1,5],[3,3,7]], capacity = 4
|
||||
```
|
||||
|
||||
这就不能一次运完,因为 `trips[1]` 最多只能上 2 人,否则车就会超载。
|
||||
|
||||
相信你已经能够联想到差分数组技巧了:**`trips[i]` 代表着一组区间操作,旅客的上车和下车就相当于数组的区间加减;只要结果数组中的元素都小于 `capacity`,就说明可以不超载运输所有旅客**。
|
||||
|
||||
但问题是,差分数组的长度(车站的个数)应该是多少呢?题目没有直接给,但给出了数据取值范围:
|
||||
|
||||
```java
|
||||
0 <= trips[i][1] < trips[i][2] <= 1000
|
||||
```
|
||||
|
||||
车站编号从 0 开始,最多到 1000,也就是最多有 1001 个车站,那么我们的差分数组长度可以直接设置为 1001,这样索引刚好能够涵盖所有车站的编号:
|
||||
|
||||
```java
|
||||
boolean carPooling(int[][] trips, int capacity) {
|
||||
// 最多有 1001 个车站
|
||||
int[] nums = new int[1001];
|
||||
// 构造差分解法
|
||||
Difference df = new Difference(nums);
|
||||
|
||||
for (int[] trip : trips) {
|
||||
// 乘客数量
|
||||
int val = trip[0];
|
||||
// 第 trip[1] 站乘客上车
|
||||
int i = trip[1];
|
||||
// 第 trip[2] 站乘客已经下车,
|
||||
// 即乘客在车上的区间是 [trip[1], trip[2] - 1]
|
||||
int j = trip[2] - 1;
|
||||
// 进行区间操作
|
||||
df.increment(i, j, val);
|
||||
}
|
||||
|
||||
int[] res = df.result();
|
||||
|
||||
// 客车自始至终都不应该超载
|
||||
for (int i = 0; i < res.length; i++) {
|
||||
if (capacity < res[i]) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return true;
|
||||
}
|
||||
```
|
||||
|
||||
至此,这道题也解决了。
|
||||
|
||||
最后,差分数组和前缀和数组都是比较常见且巧妙的算法技巧,分别适用不同的场景,而且是会者不难,难者不会。所以,关于差分数组的使用,你学会了吗?
|
||||
|
||||
> 最后打个广告,我亲自制作了一门 [数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO),以视频课为主,手把手带你实现常用的数据结构及相关算法,旨在帮助算法基础较为薄弱的读者深入理解常用数据结构的底层原理,在算法学习中少走弯路。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [二维数组的花式遍历技巧](https://labuladong.github.io/article/fname.html?fname=花式遍历)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [扫描线技巧:安排会议室](https://labuladong.github.io/article/fname.html?fname=安排会议室)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 常用的位运算技巧
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -247,6 +243,35 @@ int missingNumber(int[] nums) {
|
|||
|
||||
http://graphics.stanford.edu/~seander/bithacks.html#ReverseParallel
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [丑数系列算法详解](https://labuladong.github.io/article/fname.html?fname=丑数)
|
||||
- [如何同时寻找缺失和重复的元素](https://labuladong.github.io/article/fname.html?fname=缺失和重复的元素)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [389. Find the Difference](https://leetcode.com/problems/find-the-difference/?show=1) | [389. 找不同](https://leetcode.cn/problems/find-the-difference/?show=1) |
|
||||
| - | [剑指 Offer 15. 二进制中1的个数](https://leetcode.cn/problems/er-jin-zhi-zhong-1de-ge-shu-lcof/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,7 +1,5 @@
|
|||
# 洗牌算法
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -11,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -204,6 +202,21 @@ for (int feq : count)
|
|||
|
||||
第二部分写了洗牌算法正确性的衡量标准,即每种随机结果出现的概率必须相等。如果我们不用严格的数学证明,可以通过蒙特卡罗方法大力出奇迹,粗略验证算法的正确性。蒙特卡罗方法也有不同的思路,不过要求不必太严格,因为我们只是寻求一个简单的验证。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [几个反直觉的概率问题](https://labuladong.github.io/article/fname.html?fname=几个反直觉的概率问题)
|
||||
- [快速排序详解及应用](https://labuladong.github.io/article/fname.html?fname=快速排序)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
580
算法思维系列/滑动窗口技巧.md
580
算法思维系列/滑动窗口技巧.md
|
|
@ -1,580 +0,0 @@
|
|||
# 滑动窗口算法框架
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**最新消息:关注公众号参与活动,有机会成为 [70k star 算法仓库](https://github.com/labuladong/fucking-algorithm) 的贡献者,机不可失时不再来**!
|
||||
|
||||
相关推荐:
|
||||
* [东哥吃葡萄时竟然吃出一道算法题!](https://labuladong.gitee.io/algo/)
|
||||
* [如何寻找缺失的元素](https://labuladong.gitee.io/algo/)
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[76.最小覆盖子串](https://leetcode-cn.com/problems/minimum-window-substring)
|
||||
|
||||
[567.字符串的排列](https://leetcode-cn.com/problems/permutation-in-string)
|
||||
|
||||
[438.找到字符串中所有字母异位词](https://leetcode-cn.com/problems/find-all-anagrams-in-a-string)
|
||||
|
||||
[3.无重复字符的最长子串](https://leetcode-cn.com/problems/longest-substring-without-repeating-characters)
|
||||
|
||||
**-----------**
|
||||
|
||||
本文是之前的一篇文章 [滑动窗口算法详解](https://mp.weixin.qq.com/s/nJHIxQ2BbqhDv5jZ9NgXrQ) 的修订版,添加了滑动窗口算法更详细的解释。
|
||||
|
||||
本文详解「滑动窗口」这种高级双指针技巧的算法框架,带你秒杀几道高难度的子字符串匹配问题。
|
||||
|
||||
LeetCode 上至少有 9 道题目可以用此方法高效解决。但是有几道是 VIP 题目,有几道题目虽不难但太复杂,所以本文只选择点赞最高,较为经典的,最能够讲明白的三道题来讲解。第一题为了让读者掌握算法模板,篇幅相对长,后两题就基本秒杀了。
|
||||
|
||||
本文代码为 C++ 实现,不会用到什么编程方面的奇技淫巧,但是还是简单介绍一下一些用到的数据结构,以免有的读者因为语言的细节问题阻碍对算法思想的理解:
|
||||
|
||||
`unordered_map` 就是哈希表(字典),它的一个方法 count(key) 相当于 containsKey(key) 可以判断键 key 是否存在。
|
||||
|
||||
可以使用方括号访问键对应的值 map[key]。需要注意的是,如果该 key 不存在,C++ 会自动创建这个 key,并把 map[key] 赋值为 0。
|
||||
|
||||
所以代码中多次出现的 `map[key]++` 相当于 Java 的 `map.put(key, map.getOrDefault(key, 0) + 1)`。
|
||||
|
||||
本文大部分代码都是图片形式,可以点开放大,更重要的是可以左右滑动方便对比代码。下面进入正题。
|
||||
|
||||
### 一、最小覆盖子串
|
||||
|
||||

|
||||
|
||||
题目不难理解,就是说要在 S(source) 中找到包含 T(target) 中全部字母的一个子串,顺序无所谓,但这个子串一定是所有可能子串中最短的。
|
||||
|
||||
如果我们使用暴力解法,代码大概是这样的:
|
||||
|
||||
```java
|
||||
for (int i = 0; i < s.size(); i++)
|
||||
for (int j = i + 1; j < s.size(); j++)
|
||||
if s[i:j] 包含 t 的所有字母:
|
||||
更新答案
|
||||
```
|
||||
|
||||
思路很直接吧,但是显然,这个算法的复杂度肯定大于 O(N^2) 了,不好。
|
||||
|
||||
滑动窗口算法的思路是这样:
|
||||
|
||||
1、我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引闭区间 [left, right] 称为一个「窗口」。
|
||||
|
||||
2、我们先不断地增加 right 指针扩大窗口 [left, right],直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
|
||||
|
||||
3、此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right],直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
|
||||
|
||||
4、重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
|
||||
|
||||
这个思路其实也不难,**第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解。**左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动。
|
||||
|
||||
下面画图理解一下,needs 和 window 相当于计数器,分别记录 T 中字符出现次数和窗口中的相应字符的出现次数。
|
||||
|
||||
初始状态:
|
||||
|
||||

|
||||
|
||||
增加 right,直到窗口 [left, right] 包含了 T 中所有字符:
|
||||
|
||||

|
||||
|
||||
|
||||
现在开始增加 left,缩小窗口 [left, right]。
|
||||
|
||||

|
||||
|
||||
直到窗口中的字符串不再符合要求,left 不再继续移动。
|
||||
|
||||

|
||||
|
||||
|
||||
之后重复上述过程,先移动 right,再移动 left…… 直到 right 指针到达字符串 S 的末端,算法结束。
|
||||
|
||||
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。至于如何具体到问题,如何得出此题的答案,都是编程问题,等会提供一套模板,理解一下就会了。
|
||||
|
||||
上述过程可以简单地写出如下伪码框架:
|
||||
|
||||
```cpp
|
||||
string s, t;
|
||||
// 在 s 中寻找 t 的「最小覆盖子串」
|
||||
int left = 0, right = 0;
|
||||
string res = s;
|
||||
|
||||
while(right < s.size()) {
|
||||
window.add(s[right]);
|
||||
right++;
|
||||
// 如果符合要求,移动 left 缩小窗口
|
||||
while (window 符合要求) {
|
||||
// 如果这个窗口的子串更短,则更新 res
|
||||
res = minLen(res, window);
|
||||
window.remove(s[left]);
|
||||
left++;
|
||||
}
|
||||
}
|
||||
return res;
|
||||
```
|
||||
|
||||
如果上述代码你也能够理解,那么你离解题更近了一步。现在就剩下一个比较棘手的问题:如何判断 window 即子串 s[left...right] 是否符合要求,是否包含 t 的所有字符呢?
|
||||
|
||||
可以用两个哈希表当作计数器解决。用一个哈希表 needs 记录字符串 t 中包含的字符及出现次数,用另一个哈希表 window 记录当前「窗口」中包含的字符及出现的次数,如果 window 包含所有 needs 中的键,且这些键对应的值都大于等于 needs 中的值,那么就可以知道当前「窗口」符合要求了,可以开始移动 left 指针了。
|
||||
|
||||
现在将上面的框架继续细化:
|
||||
|
||||
```cpp
|
||||
string s, t;
|
||||
// 在 s 中寻找 t 的「最小覆盖子串」
|
||||
int left = 0, right = 0;
|
||||
string res = s;
|
||||
|
||||
// 相当于两个计数器
|
||||
unordered_map<char, int> window;
|
||||
unordered_map<char, int> needs;
|
||||
for (char c : t) needs[c]++;
|
||||
|
||||
// 记录 window 中已经有多少字符符合要求了
|
||||
int match = 0;
|
||||
|
||||
while (right < s.size()) {
|
||||
char c1 = s[right];
|
||||
if (needs.count(c1)) {
|
||||
window[c1]++; // 加入 window
|
||||
if (window[c1] == needs[c1])
|
||||
// 字符 c1 的出现次数符合要求了
|
||||
match++;
|
||||
}
|
||||
right++;
|
||||
|
||||
// window 中的字符串已符合 needs 的要求了
|
||||
while (match == needs.size()) {
|
||||
// 更新结果 res
|
||||
res = minLen(res, window);
|
||||
char c2 = s[left];
|
||||
if (needs.count(c2)) {
|
||||
window[c2]--; // 移出 window
|
||||
if (window[c2] < needs[c2])
|
||||
// 字符 c2 出现次数不再符合要求
|
||||
match--;
|
||||
}
|
||||
left++;
|
||||
}
|
||||
}
|
||||
return res;
|
||||
```
|
||||
|
||||
上述代码已经具备完整的逻辑了,只有一处伪码,即更新 res 的地方,不过这个问题太好解决了,直接看解法吧!
|
||||
|
||||
```cpp
|
||||
string minWindow(string s, string t) {
|
||||
// 记录最短子串的开始位置和长度
|
||||
int start = 0, minLen = INT_MAX;
|
||||
int left = 0, right = 0;
|
||||
|
||||
unordered_map<char, int> window;
|
||||
unordered_map<char, int> needs;
|
||||
for (char c : t) needs[c]++;
|
||||
|
||||
int match = 0;
|
||||
|
||||
while (right < s.size()) {
|
||||
char c1 = s[right];
|
||||
if (needs.count(c1)) {
|
||||
window[c1]++;
|
||||
if (window[c1] == needs[c1])
|
||||
match++;
|
||||
}
|
||||
right++;
|
||||
|
||||
while (match == needs.size()) {
|
||||
if (right - left < minLen) {
|
||||
// 更新最小子串的位置和长度
|
||||
start = left;
|
||||
minLen = right - left;
|
||||
}
|
||||
char c2 = s[left];
|
||||
if (needs.count(c2)) {
|
||||
window[c2]--;
|
||||
if (window[c2] < needs[c2])
|
||||
match--;
|
||||
}
|
||||
left++;
|
||||
}
|
||||
}
|
||||
return minLen == INT_MAX ?
|
||||
"" : s.substr(start, minLen);
|
||||
}
|
||||
```
|
||||
|
||||
如果直接甩给你这么一大段代码,我想你的心态是爆炸的,但是通过之前的步步跟进,你是否能够理解这个算法的内在逻辑呢?你是否能清晰看出该算法的结构呢?
|
||||
|
||||
这个算法的时间复杂度是 O(M + N),M 和 N 分别是字符串 S 和 T 的长度。因为我们先用 for 循环遍历了字符串 T 来初始化 needs,时间 O(N),之后的两个 while 循环最多执行 2M 次,时间 O(M)。
|
||||
|
||||
读者也许认为嵌套的 while 循环复杂度应该是平方级,但是你这样想,while 执行的次数就是双指针 left 和 right 走的总路程,最多是 2M 嘛。
|
||||
|
||||
|
||||
### 二、找到字符串中所有字母异位词
|
||||
|
||||

|
||||
|
||||
这道题的难度是 Easy,但是评论区点赞最多的一条是这样:
|
||||
|
||||
`How can this problem be marked as easy???`
|
||||
|
||||
实际上,这个 Easy 是属于了解双指针技巧的人的,只要把上一道题的代码改中更新 res 部分的代码稍加修改就成了这道题的解:
|
||||
|
||||
```cpp
|
||||
vector<int> findAnagrams(string s, string t) {
|
||||
// 用数组记录答案
|
||||
vector<int> res;
|
||||
int left = 0, right = 0;
|
||||
unordered_map<char, int> needs;
|
||||
unordered_map<char, int> window;
|
||||
for (char c : t) needs[c]++;
|
||||
int match = 0;
|
||||
|
||||
while (right < s.size()) {
|
||||
char c1 = s[right];
|
||||
if (needs.count(c1)) {
|
||||
window[c1]++;
|
||||
if (window[c1] == needs[c1])
|
||||
match++;
|
||||
}
|
||||
right++;
|
||||
|
||||
while (match == needs.size()) {
|
||||
// 如果 window 的大小合适
|
||||
// 就把起始索引 left 加入结果
|
||||
if (right - left == t.size()) {
|
||||
res.push_back(left);
|
||||
}
|
||||
char c2 = s[left];
|
||||
if (needs.count(c2)) {
|
||||
window[c2]--;
|
||||
if (window[c2] < needs[c2])
|
||||
match--;
|
||||
}
|
||||
left++;
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
因为这道题和上一道的场景类似,也需要 window 中包含串 t 的所有字符,但上一道题要找长度最短的子串,这道题要找长度相同的子串,也就是「字母异位词」嘛。
|
||||
|
||||
### 三、无重复字符的最长子串
|
||||
|
||||

|
||||
|
||||
遇到子串问题,首先想到的就是滑动窗口技巧。
|
||||
|
||||
类似之前的思路,使用 window 作为计数器记录窗口中的字符出现次数,然后先向右移动 right,当 window 中出现重复字符时,开始移动 left 缩小窗口,如此往复:
|
||||
|
||||
```cpp
|
||||
int lengthOfLongestSubstring(string s) {
|
||||
int left = 0, right = 0;
|
||||
unordered_map<char, int> window;
|
||||
int res = 0; // 记录最长长度
|
||||
|
||||
while (right < s.size()) {
|
||||
char c1 = s[right];
|
||||
window[c1]++;
|
||||
right++;
|
||||
// 如果 window 中出现重复字符
|
||||
// 开始移动 left 缩小窗口
|
||||
while (window[c1] > 1) {
|
||||
char c2 = s[left];
|
||||
window[c2]--;
|
||||
left++;
|
||||
}
|
||||
res = max(res, right - left);
|
||||
}
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
需要注意的是,因为我们要求的是最长子串,所以需要在每次移动 right 增大窗口时更新 res,而不是像之前的题目在移动 left 缩小窗口时更新 res。
|
||||
|
||||
### 最后总结
|
||||
|
||||
通过上面三道题,我们可以总结出滑动窗口算法的抽象思想:
|
||||
|
||||
```java
|
||||
int left = 0, right = 0;
|
||||
|
||||
while (right < s.size()) {
|
||||
window.add(s[right]);
|
||||
right++;
|
||||
|
||||
while (valid) {
|
||||
window.remove(s[left]);
|
||||
left++;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
其中 window 的数据类型可以视具体情况而定,比如上述题目都使用哈希表充当计数器,当然你也可以用一个数组实现同样效果,因为我们只处理英文字母。
|
||||
|
||||
稍微麻烦的地方就是这个 valid 条件,为了实现这个条件的实时更新,我们可能会写很多代码。比如前两道题,看起来解法篇幅那么长,实际上思想还是很简单,只是大多数代码都在处理这个问题而已。
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
[Jiajun](https://github.com/liujiajun) 提供最小覆盖子串 Python3 代码:
|
||||
```python3
|
||||
class Solution:
|
||||
def minWindow(self, s: str, t: str) -> str:
|
||||
# 最短子串开始位置和长度
|
||||
start, min_len = 0, float('Inf')
|
||||
left, right = 0, 0
|
||||
res = s
|
||||
|
||||
# 两个计数器
|
||||
needs = Counter(t)
|
||||
window = collections.defaultdict(int)
|
||||
# defaultdict在访问的key不存在的时候返回默认值0, 可以减少一次逻辑判断
|
||||
|
||||
match = 0
|
||||
|
||||
while right < len(s):
|
||||
c1 = s[right]
|
||||
if needs[c1] > 0:
|
||||
window[c1] += 1
|
||||
if window[c1] == needs[c1]:
|
||||
match += 1
|
||||
right += 1
|
||||
|
||||
while match == len(needs):
|
||||
if right - left < min_len:
|
||||
# 更新最小子串长度
|
||||
min_len = right - left
|
||||
start = left
|
||||
c2 = s[left]
|
||||
if needs[c2] > 0:
|
||||
window[c2] -= 1
|
||||
if window[c2] < needs[c2]:
|
||||
match -= 1
|
||||
left += 1
|
||||
|
||||
return s[start:start+min_len] if min_len != float("Inf") else ""
|
||||
```
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
### python
|
||||
|
||||
第3题 Python3 代码(提供: [FaDrYL](https://github.com/FaDrYL) ):
|
||||
```python
|
||||
def lengthOfLongestSubstring(self, s: str) -> int:
|
||||
# 子字符串
|
||||
sub = ""
|
||||
largest = 0
|
||||
|
||||
# 循环字符串,将当前字符加入子字符串,并检查长度
|
||||
for i in range(len(s)):
|
||||
if s[i] not in sub:
|
||||
# 当前字符不存在于子字符串中,加入当前字符
|
||||
sub += s[i]
|
||||
else:
|
||||
# 如果当前子字符串的长度超过了之前的记录
|
||||
if len(sub) > largest:
|
||||
largest = len(sub)
|
||||
# 将子字符串从当前字符处+1切片至最后,并加入当前字符
|
||||
sub = sub[sub.find(s[i])+1:] + s[i]
|
||||
|
||||
# 如果最后的子字符串长度超过了之前的记录
|
||||
if len(sub) > largest:
|
||||
return len(sub)
|
||||
return largest
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
[76.最小覆盖子串](https://leetcode-cn.com/problems/minimum-window-substring)
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {string} s
|
||||
* @param {string} t
|
||||
* @return {string}
|
||||
*/
|
||||
const minWindow = (s, t) => {
|
||||
let minLen = s.length + 1;
|
||||
let start = s.length; // 结果子串的起始位置
|
||||
let map = {}; // 存储目标字符和对应的缺失个数
|
||||
let missingType = 0; // 当前缺失的字符种类数
|
||||
for (const c of t) { // t为baac的话,map为{a:2,b:1,c:1}
|
||||
if (!map[c]) {
|
||||
missingType++; // 需要找齐的种类数 +1
|
||||
map[c] = 1;
|
||||
} else {
|
||||
map[c]++;
|
||||
}
|
||||
}
|
||||
let l = 0, r = 0; // 左右指针
|
||||
for (; r < s.length; r++) { // 主旋律扩张窗口,超出s串就结束
|
||||
let rightChar = s[r]; // 获取right指向的新字符
|
||||
if (map[rightChar] !== undefined) map[rightChar]--; // 是目标字符,它的缺失个数-1
|
||||
if (map[rightChar] == 0) missingType--; // 它的缺失个数新变为0,缺失的种类数就-1
|
||||
while (missingType == 0) { // 当前窗口包含所有字符的前提下,尽量收缩窗口
|
||||
if (r - l + 1 < minLen) { // 窗口宽度如果比minLen小,就更新minLen
|
||||
minLen = r - l + 1;
|
||||
start = l; // 更新最小窗口的起点
|
||||
}
|
||||
let leftChar = s[l]; // 左指针要右移,左指针指向的字符要被丢弃
|
||||
if (map[leftChar] !== undefined) map[leftChar]++; // 被舍弃的是目标字符,缺失个数+1
|
||||
if (map[leftChar] > 0) missingType++; // 如果缺失个数新变为>0,缺失的种类+1
|
||||
l++; // 左指针要右移 收缩窗口
|
||||
}
|
||||
}
|
||||
if (start == s.length) return "";
|
||||
return s.substring(start, start + minLen); // 根据起点和minLen截取子串
|
||||
};
|
||||
```
|
||||
|
||||
[567.字符串的排列](https://leetcode-cn.com/problems/permutation-in-string)
|
||||
|
||||
```js
|
||||
var checkInclusion = function(s1, s2) {
|
||||
const n = s1.length, m = s2.length;
|
||||
if (n > m) {
|
||||
return false;
|
||||
}
|
||||
const cnt1 = new Array(26).fill(0);
|
||||
const cnt2 = new Array(26).fill(0);
|
||||
for (let i = 0; i < n; ++i) {
|
||||
++cnt1[s1[i].charCodeAt() - 'a'.charCodeAt()];
|
||||
++cnt2[s2[i].charCodeAt() - 'a'.charCodeAt()];
|
||||
}
|
||||
if (cnt1.toString() === cnt2.toString()) {
|
||||
return true;
|
||||
}
|
||||
for (let i = n; i < m; ++i) {
|
||||
++cnt2[s2[i].charCodeAt() - 'a'.charCodeAt()];
|
||||
--cnt2[s2[i - n].charCodeAt() - 'a'.charCodeAt()];
|
||||
if (cnt1.toString() === cnt2.toString()) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
};
|
||||
```
|
||||
|
||||
[438.找到字符串中所有字母异位词](https://leetcode-cn.com/problems/find-all-anagrams-in-a-string)
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {string} s
|
||||
* @param {string} p
|
||||
* @return {number[]}
|
||||
*/
|
||||
var findAnagrams = function(s, p) {
|
||||
// 用于保存结果
|
||||
const res = []
|
||||
// 用于统计p串所需字符
|
||||
const need = new Map()
|
||||
for(let i = 0; i < p.length; i++) {
|
||||
need.set(p[i], need.has(p[i])?need.get(p[i])+1: 1)
|
||||
}
|
||||
// 定义滑动窗口
|
||||
let left = 0, right = 0, valid = 0
|
||||
// 用于统计窗口中的字符
|
||||
const window = new Map()
|
||||
// 遍历s串
|
||||
while(right < s.length) {
|
||||
// 进入窗口的字符
|
||||
const c = s[right]
|
||||
// 扩大窗口
|
||||
right++
|
||||
// 进入窗口的字符是所需字符
|
||||
if (need.has(c)) {
|
||||
// 更新滑动窗口中的字符记录
|
||||
window.set(c, window.has(c)?window.get(c)+1:1)
|
||||
// 当窗口中的字符数和滑动窗口中的字符数一致
|
||||
if (window.get(c) === need.get(c)) {
|
||||
// 有效字符自增
|
||||
valid++
|
||||
}
|
||||
}
|
||||
// 当滑动窗口的大小超出p串长度时 收缩窗口
|
||||
while (right - left >= p.length) {
|
||||
// 有效字符和所需字符数一致 找到一条符合条件的子串
|
||||
if (valid === need.size) {
|
||||
// 保存子串的起始索引位置
|
||||
res.push(left)
|
||||
}
|
||||
// 离开窗口的字符
|
||||
const d = s[left]
|
||||
// 收缩窗口
|
||||
left++
|
||||
// 如果离开窗口字符是所需字符
|
||||
if (need.has(d)) {
|
||||
// 如果离开字符数和所需字符数一致
|
||||
if (window.get(d) === need.get(d)) {
|
||||
// 有效字符减少一个
|
||||
valid--
|
||||
}
|
||||
// 更新滑动窗口中的字符数
|
||||
window.set(d, window.get(d)-1)
|
||||
}
|
||||
}
|
||||
}
|
||||
// 返回结果
|
||||
return res
|
||||
};
|
||||
```
|
||||
|
||||
[3.无重复字符的最长子串](https://leetcode-cn.com/problems/longest-substring-without-repeating-characters)
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {string} s
|
||||
* @return {number}
|
||||
*/
|
||||
var lengthOfLongestSubstring = function(s) {
|
||||
// 哈希集合,记录每个字符是否出现过
|
||||
const occ = new Set();
|
||||
const n = s.length;
|
||||
// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动
|
||||
let rk = -1, ans = 0;
|
||||
for (let i = 0; i < n; ++i) {
|
||||
if (i != 0) {
|
||||
// 左指针向右移动一格,移除一个字符
|
||||
occ.delete(s.charAt(i - 1));
|
||||
}
|
||||
while (rk + 1 < n && !occ.has(s.charAt(rk + 1))) {
|
||||
// 不断地移动右指针
|
||||
occ.add(s.charAt(rk + 1));
|
||||
++rk;
|
||||
}
|
||||
// 第 i 到 rk 个字符是一个极长的无重复字符子串
|
||||
ans = Math.max(ans, rk - i + 1);
|
||||
}
|
||||
return ans;
|
||||
};
|
||||
```
|
||||
|
||||
|
|
@ -0,0 +1,481 @@
|
|||
# 滑动窗口算法框架
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [3. Longest Substring Without Repeating Characters](https://leetcode.com/problems/longest-substring-without-repeating-characters/) | [3. 无重复字符的最长子串](https://leetcode.cn/problems/longest-substring-without-repeating-characters/) | 🟠
|
||||
| [438. Find All Anagrams in a String](https://leetcode.com/problems/find-all-anagrams-in-a-string/) | [438. 找到字符串中所有字母异位词](https://leetcode.cn/problems/find-all-anagrams-in-a-string/) | 🟠
|
||||
| [567. Permutation in String](https://leetcode.com/problems/permutation-in-string/) | [567. 字符串的排列](https://leetcode.cn/problems/permutation-in-string/) | 🟠
|
||||
| [76. Minimum Window Substring](https://leetcode.com/problems/minimum-window-substring/) | [76. 最小覆盖子串](https://leetcode.cn/problems/minimum-window-substring/) | 🔴
|
||||
| - | [剑指 Offer 48. 最长不含重复字符的子字符串](https://leetcode.cn/problems/zui-chang-bu-han-zhong-fu-zi-fu-de-zi-zi-fu-chuan-lcof/) | 🟠
|
||||
| - | [剑指 Offer II 014. 字符串中的变位词](https://leetcode.cn/problems/MPnaiL/) | 🟠
|
||||
| - | [剑指 Offer II 015. 字符串中的所有变位词](https://leetcode.cn/problems/VabMRr/) | 🟠
|
||||
| - | [剑指 Offer II 016. 不含重复字符的最长子字符串](https://leetcode.cn/problems/wtcaE1/) | 🟠
|
||||
| - | [剑指 Offer II 017. 含有所有字符的最短字符串](https://leetcode.cn/problems/M1oyTv/) | 🔴
|
||||
|
||||
**-----------**
|
||||
|
||||
> 本文有视频版:[滑动窗口算法核心模板框架](https://www.bilibili.com/video/BV1AV4y1n7Zt/)
|
||||
|
||||
鉴于前文 [二分搜索框架详解](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 的那首《二分搜索升天词》很受好评,并在民间广为流传,成为安睡助眠的一剂良方,今天在滑动窗口算法框架中,我再次编写一首小诗来歌颂滑动窗口算法的伟大(手动狗头):
|
||||
|
||||

|
||||
|
||||
哈哈,我自己快把自己夸上天了,大家乐一乐就好,不要当真:)
|
||||
|
||||
关于双指针的快慢指针和左右指针的用法,可以参见前文 [双指针技巧汇总](https://labuladong.github.io/article/fname.html?fname=双指针技巧),本文就解决一类最难掌握的双指针技巧:滑动窗口技巧。总结出一套框架,可以保你闭着眼睛都能写出正确的解法。
|
||||
|
||||
说起滑动窗口算法,很多读者都会头疼。这个算法技巧的思路非常简单,就是维护一个窗口,不断滑动,然后更新答案么。LeetCode 上有起码 10 道运用滑动窗口算法的题目,难度都是中等和困难。该算法的大致逻辑如下:
|
||||
|
||||
```cpp
|
||||
int left = 0, right = 0;
|
||||
|
||||
while (right < s.size()) {
|
||||
// 增大窗口
|
||||
window.add(s[right]);
|
||||
right++;
|
||||
|
||||
while (window needs shrink) {
|
||||
// 缩小窗口
|
||||
window.remove(s[left]);
|
||||
left++;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
这个算法技巧的时间复杂度是 O(N),比字符串暴力算法要高效得多。
|
||||
|
||||
其实困扰大家的,不是算法的思路,而是各种细节问题。比如说如何向窗口中添加新元素,如何缩小窗口,在窗口滑动的哪个阶段更新结果。即便你明白了这些细节,也容易出 bug,找 bug 还不知道怎么找,真的挺让人心烦的。
|
||||
|
||||
**所以今天我就写一套滑动窗口算法的代码框架,我连再哪里做输出 debug 都给你写好了,以后遇到相关的问题,你就默写出来如下框架然后改三个地方就行,还不会出 bug**:
|
||||
|
||||
```cpp
|
||||
/* 滑动窗口算法框架 */
|
||||
void slidingWindow(string s) {
|
||||
unordered_map<char, int> window;
|
||||
|
||||
int left = 0, right = 0;
|
||||
while (right < s.size()) {
|
||||
// c 是将移入窗口的字符
|
||||
char c = s[right];
|
||||
// 增大窗口
|
||||
right++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
...
|
||||
|
||||
/*** debug 输出的位置 ***/
|
||||
printf("window: [%d, %d)\n", left, right);
|
||||
/********************/
|
||||
|
||||
// 判断左侧窗口是否要收缩
|
||||
while (window needs shrink) {
|
||||
// d 是将移出窗口的字符
|
||||
char d = s[left];
|
||||
// 缩小窗口
|
||||
left++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
...
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**其中两处 `...` 表示的更新窗口数据的地方,到时候你直接往里面填就行了**。
|
||||
|
||||
而且,这两个 `...` 处的操作分别是扩大和缩小窗口的更新操作,等会你会发现它们操作是完全对称的。
|
||||
|
||||
另外,虽然滑动窗口代码框架中有一个嵌套的 while 循环,但算法的时间复杂度依然是 `O(N)`,其中 `N` 是输入字符串/数组的长度。
|
||||
|
||||
为什么呢?简单说,字符串/数组中的每个元素都只会进入窗口一次,然后被移出窗口一次,不会说有某些元素多次进入和离开窗口,所以算法的时间复杂度就和字符串/数组的长度成正比。前文 [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度) 有具体讲时间复杂度的估算,这里就不展开了。
|
||||
|
||||
说句题外话,我发现很多人喜欢执着于表象,不喜欢探求问题的本质。比如说有很多人评论我这个框架,说什么散列表速度慢,不如用数组代替散列表;还有很多人喜欢把代码写得特别短小,说我这样代码太多余,影响编译速度,LeetCode 上速度不够快。
|
||||
|
||||
我的意见是,算法主要看时间复杂度,你能确保自己的时间复杂度最优就行了。至于 LeetCode 所谓的运行速度,那个都是玄学,只要不是慢的离谱就没啥问题,根本不值得你从编译层面优化,不要舍本逐末……
|
||||
|
||||
我的公众号重点在于算法思想,你把框架思维了然于心,然后随你魔改代码好吧,你高兴就好。
|
||||
|
||||
言归正传,下面就直接上**四道**力扣原题来套这个框架,其中第一道题会详细说明其原理,后面四道就直接闭眼睛秒杀了。
|
||||
|
||||
因为滑动窗口很多时候都是在处理字符串相关的问题,而 Java 处理字符串不方便,所以本文代码为 C++ 实现。不会用到什么编程语言层面的奇技淫巧,但是还是简单介绍一下一些用到的数据结构,以免有的读者因为语言的细节问题阻碍对算法思想的理解:
|
||||
|
||||
`unordered_map` 就是哈希表(字典),相当于 Java 的 `HashMap`,它的一个方法 `count(key)` 相当于 Java 的 `containsKey(key)` 可以判断键 key 是否存在。
|
||||
|
||||
可以使用方括号访问键对应的值 `map[key]`。需要注意的是,如果该 `key` 不存在,C++ 会自动创建这个 key,并把 `map[key]` 赋值为 0。所以代码中多次出现的 `map[key]++` 相当于 Java 的 `map.put(key, map.getOrDefault(key, 0) + 1)`。
|
||||
|
||||
另外,Java 中的 Integer 和 String 这种包装类不能直接用 `==` 进行相等判断,而应该使用类的 `equals` 方法,这个语言特性坑了不少读者,在代码部分我会给出具体提示。
|
||||
|
||||
### 一、最小覆盖子串
|
||||
|
||||
先来看看力扣第 76 题「最小覆盖子串」难度 Hard:
|
||||
|
||||

|
||||
|
||||
就是说要在 `S`(source) 中找到包含 `T`(target) 中全部字母的一个子串,且这个子串一定是所有可能子串中最短的。
|
||||
|
||||
如果我们使用暴力解法,代码大概是这样的:
|
||||
|
||||
```java
|
||||
for (int i = 0; i < s.size(); i++)
|
||||
for (int j = i + 1; j < s.size(); j++)
|
||||
if s[i:j] 包含 t 的所有字母:
|
||||
更新答案
|
||||
```
|
||||
|
||||
思路很直接,但是显然,这个算法的复杂度肯定大于 O(N^2) 了,不好。
|
||||
|
||||
**滑动窗口算法的思路是这样**:
|
||||
|
||||
1、我们在字符串 `S` 中使用双指针中的左右指针技巧,初始化 `left = right = 0`,把索引**左闭右开**区间 `[left, right)` 称为一个「窗口」。
|
||||
|
||||
> PS:理论上你可以设计两端都开或者两端都闭的区间,但设计为左闭右开区间是最方便处理的。因为这样初始化 `left = right = 0` 时区间 `[0, 0)` 中没有元素,但只要让 `right` 向右移动(扩大)一位,区间 `[0, 1)` 就包含一个元素 `0` 了。如果你设置为两端都开的区间,那么让 `right` 向右移动一位后开区间 `(0, 1)` 仍然没有元素;如果你设置为两端都闭的区间,那么初始区间 `[0, 0]` 就包含了一个元素。这两种情况都会给边界处理带来不必要的麻烦。
|
||||
|
||||
2、我们先不断地增加 `right` 指针扩大窗口 `[left, right)`,直到窗口中的字符串符合要求(包含了 `T` 中的所有字符)。
|
||||
|
||||
3、此时,我们停止增加 `right`,转而不断增加 `left` 指针缩小窗口 `[left, right)`,直到窗口中的字符串不再符合要求(不包含 `T` 中的所有字符了)。同时,每次增加 `left`,我们都要更新一轮结果。
|
||||
|
||||
4、重复第 2 和第 3 步,直到 `right` 到达字符串 `S` 的尽头。
|
||||
|
||||
这个思路其实也不难,**第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解**,也就是最短的覆盖子串。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动,这就是「滑动窗口」这个名字的来历。
|
||||
|
||||
下面画图理解一下,`needs` 和 `window` 相当于计数器,分别记录 `T` 中字符出现次数和「窗口」中的相应字符的出现次数。
|
||||
|
||||
初始状态:
|
||||
|
||||
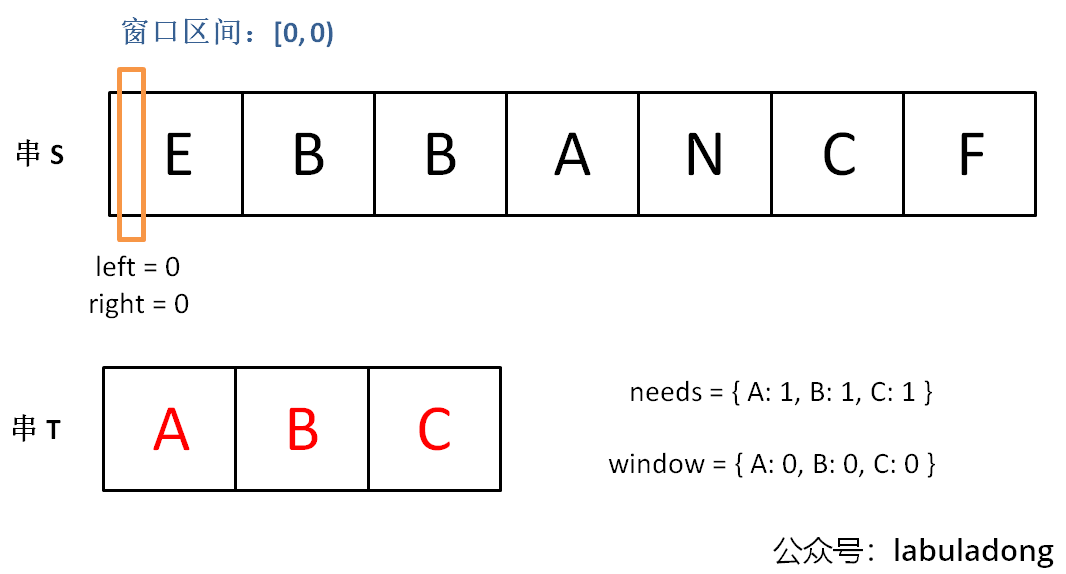
|
||||
|
||||
增加 `right`,直到窗口 `[left, right)` 包含了 `T` 中所有字符:
|
||||
|
||||
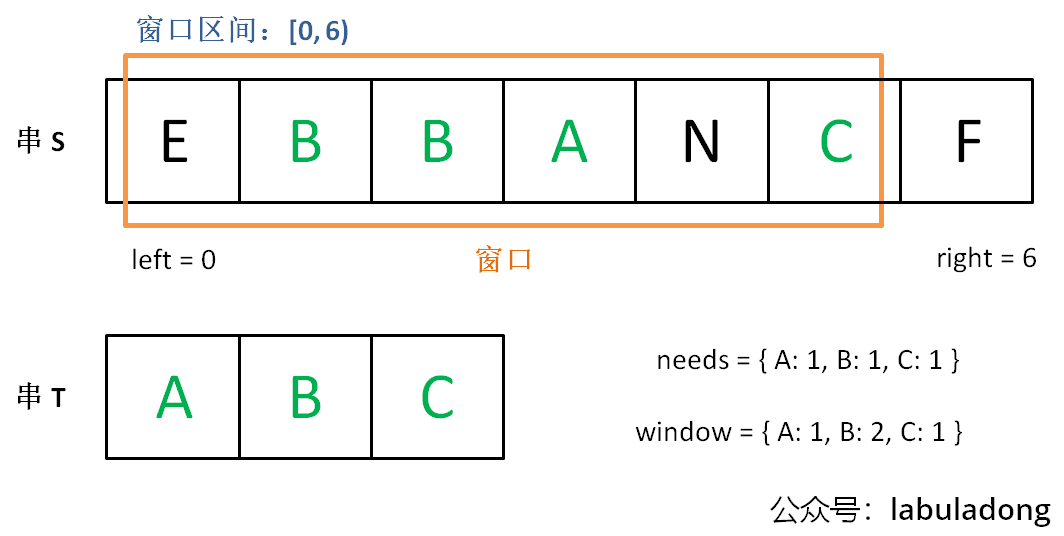
|
||||
|
||||
现在开始增加 `left`,缩小窗口 `[left, right)`:
|
||||
|
||||
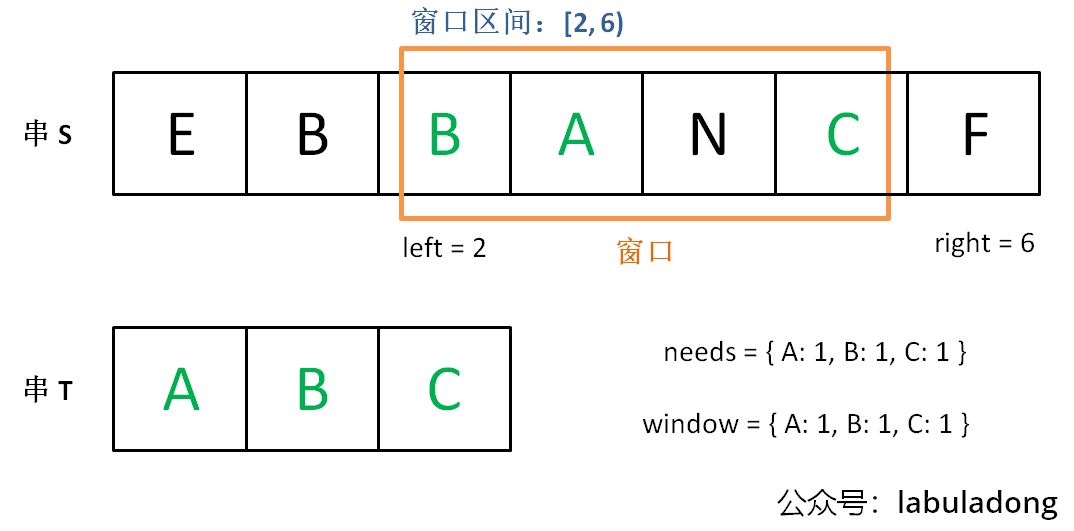
|
||||
|
||||
直到窗口中的字符串不再符合要求,`left` 不再继续移动:
|
||||
|
||||
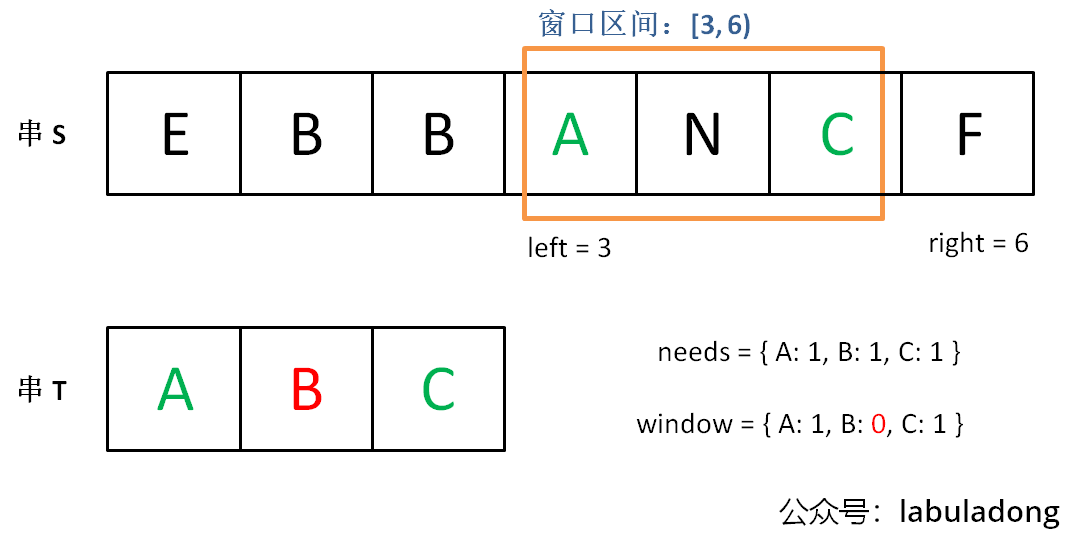
|
||||
|
||||
之后重复上述过程,先移动 `right`,再移动 `left`…… 直到 `right` 指针到达字符串 `S` 的末端,算法结束。
|
||||
|
||||
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。**现在我们来看看这个滑动窗口代码框架怎么用**:
|
||||
|
||||
首先,初始化 `window` 和 `need` 两个哈希表,记录窗口中的字符和需要凑齐的字符:
|
||||
|
||||
```cpp
|
||||
unordered_map<char, int> need, window;
|
||||
for (char c : t) need[c]++;
|
||||
```
|
||||
|
||||
然后,使用 `left` 和 `right` 变量初始化窗口的两端,不要忘了,区间 `[left, right)` 是左闭右开的,所以初始情况下窗口没有包含任何元素:
|
||||
|
||||
```cpp
|
||||
int left = 0, right = 0;
|
||||
int valid = 0;
|
||||
while (right < s.size()) {
|
||||
// 开始滑动
|
||||
}
|
||||
```
|
||||
|
||||
**其中 `valid` 变量表示窗口中满足 `need` 条件的字符个数**,如果 `valid` 和 `need.size` 的大小相同,则说明窗口已满足条件,已经完全覆盖了串 `T`。
|
||||
|
||||
**现在开始套模板,只需要思考以下几个问题**:
|
||||
|
||||
1、什么时候应该移动 `right` 扩大窗口?窗口加入字符时,应该更新哪些数据?
|
||||
|
||||
2、什么时候窗口应该暂停扩大,开始移动 `left` 缩小窗口?从窗口移出字符时,应该更新哪些数据?
|
||||
|
||||
3、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新?
|
||||
|
||||
如果一个字符进入窗口,应该增加 `window` 计数器;如果一个字符将移出窗口的时候,应该减少 `window` 计数器;当 `valid` 满足 `need` 时应该收缩窗口;应该在收缩窗口的时候更新最终结果。
|
||||
|
||||
下面是完整代码:
|
||||
|
||||
```cpp
|
||||
string minWindow(string s, string t) {
|
||||
unordered_map<char, int> need, window;
|
||||
for (char c : t) need[c]++;
|
||||
|
||||
int left = 0, right = 0;
|
||||
int valid = 0;
|
||||
// 记录最小覆盖子串的起始索引及长度
|
||||
int start = 0, len = INT_MAX;
|
||||
while (right < s.size()) {
|
||||
// c 是将移入窗口的字符
|
||||
char c = s[right];
|
||||
// 扩大窗口
|
||||
right++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
if (need.count(c)) {
|
||||
window[c]++;
|
||||
if (window[c] == need[c])
|
||||
valid++;
|
||||
}
|
||||
|
||||
// 判断左侧窗口是否要收缩
|
||||
while (valid == need.size()) {
|
||||
// 在这里更新最小覆盖子串
|
||||
if (right - left < len) {
|
||||
start = left;
|
||||
len = right - left;
|
||||
}
|
||||
// d 是将移出窗口的字符
|
||||
char d = s[left];
|
||||
// 缩小窗口
|
||||
left++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
if (need.count(d)) {
|
||||
if (window[d] == need[d])
|
||||
valid--;
|
||||
window[d]--;
|
||||
}
|
||||
}
|
||||
}
|
||||
// 返回最小覆盖子串
|
||||
return len == INT_MAX ?
|
||||
"" : s.substr(start, len);
|
||||
}
|
||||
```
|
||||
|
||||
> PS:使用 Java 的读者要尤其警惕语言特性的陷阱。Java 的 Integer,String 等类型判定相等应该用 `equals` 方法而不能直接用等号 `==`,这是 Java 包装类的一个隐晦细节。所以在缩小窗口更新数据的时候,不能直接改写为 `window.get(d) == need.get(d)`,而要用 `window.get(d).equals(need.get(d))`,之后的题目代码同理。
|
||||
|
||||
需要注意的是,当我们发现某个字符在 `window` 的数量满足了 `need` 的需要,就要更新 `valid`,表示有一个字符已经满足要求。而且,你能发现,两次对窗口内数据的更新操作是完全对称的。
|
||||
|
||||
当 `valid == need.size()` 时,说明 `T` 中所有字符已经被覆盖,已经得到一个可行的覆盖子串,现在应该开始收缩窗口了,以便得到「最小覆盖子串」。
|
||||
|
||||
移动 `left` 收缩窗口时,窗口内的字符都是可行解,所以应该在收缩窗口的阶段进行最小覆盖子串的更新,以便从可行解中找到长度最短的最终结果。
|
||||
|
||||
至此,应该可以完全理解这套框架了,滑动窗口算法又不难,就是细节问题让人烦得很。**以后遇到滑动窗口算法,你就按照这框架写代码,保准没有 bug,还省事儿**。
|
||||
|
||||
下面就直接利用这套框架秒杀几道题吧,你基本上一眼就能看出思路了。
|
||||
|
||||
### 二、字符串排列
|
||||
|
||||
这是力扣第 567 题「字符串的排列」,难度中等:
|
||||
|
||||

|
||||
|
||||
注意哦,输入的 `s1` 是可以包含重复字符的,所以这个题难度不小。
|
||||
|
||||
这种题目,是明显的滑动窗口算法,**相当给你一个 `S` 和一个 `T`,请问你 `S` 中是否存在一个子串,包含 `T` 中所有字符且不包含其他字符**?
|
||||
|
||||
首先,先复制粘贴之前的算法框架代码,然后明确刚才提出的几个问题,即可写出这道题的答案:
|
||||
|
||||
```cpp
|
||||
// 判断 s 中是否存在 t 的排列
|
||||
bool checkInclusion(string t, string s) {
|
||||
unordered_map<char, int> need, window;
|
||||
for (char c : t) need[c]++;
|
||||
|
||||
int left = 0, right = 0;
|
||||
int valid = 0;
|
||||
while (right < s.size()) {
|
||||
char c = s[right];
|
||||
right++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
if (need.count(c)) {
|
||||
window[c]++;
|
||||
if (window[c] == need[c])
|
||||
valid++;
|
||||
}
|
||||
|
||||
// 判断左侧窗口是否要收缩
|
||||
while (right - left >= t.size()) {
|
||||
// 在这里判断是否找到了合法的子串
|
||||
if (valid == need.size())
|
||||
return true;
|
||||
char d = s[left];
|
||||
left++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
if (need.count(d)) {
|
||||
if (window[d] == need[d])
|
||||
valid--;
|
||||
window[d]--;
|
||||
}
|
||||
}
|
||||
}
|
||||
// 未找到符合条件的子串
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
对于这道题的解法代码,基本上和最小覆盖子串一模一样,只需要改变几个地方:
|
||||
|
||||
1、本题移动 `left` 缩小窗口的时机是窗口大小大于 `t.size()` 时,应为排列嘛,显然长度应该是一样的。
|
||||
|
||||
2、当发现 `valid == need.size()` 时,就说明窗口中就是一个合法的排列,所以立即返回 `true`。
|
||||
|
||||
至于如何处理窗口的扩大和缩小,和最小覆盖子串完全相同。
|
||||
|
||||
> PS:由于这道题中 `[left, right)` 其实维护的是一个**定长**的窗口,窗口大小为 `t.size()`。因为定长窗口每次向前滑动时只会移出一个字符,所以可以把内层的 while 改成 if,效果是一样的。
|
||||
|
||||
### 三、找所有字母异位词
|
||||
|
||||
这是力扣第 438 题「找到字符串中所有字母异位词」,难度中等:
|
||||
|
||||

|
||||
|
||||
呵呵,这个所谓的字母异位词,不就是排列吗,搞个高端的说法就能糊弄人了吗?**相当于,输入一个串 `S`,一个串 `T`,找到 `S` 中所有 `T` 的排列,返回它们的起始索引**。
|
||||
|
||||
直接默写一下框架,明确刚才讲的 4 个问题,即可秒杀这道题:
|
||||
|
||||
```cpp
|
||||
vector<int> findAnagrams(string s, string t) {
|
||||
unordered_map<char, int> need, window;
|
||||
for (char c : t) need[c]++;
|
||||
|
||||
int left = 0, right = 0;
|
||||
int valid = 0;
|
||||
vector<int> res; // 记录结果
|
||||
while (right < s.size()) {
|
||||
char c = s[right];
|
||||
right++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
if (need.count(c)) {
|
||||
window[c]++;
|
||||
if (window[c] == need[c])
|
||||
valid++;
|
||||
}
|
||||
// 判断左侧窗口是否要收缩
|
||||
while (right - left >= t.size()) {
|
||||
// 当窗口符合条件时,把起始索引加入 res
|
||||
if (valid == need.size())
|
||||
res.push_back(left);
|
||||
char d = s[left];
|
||||
left++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
if (need.count(d)) {
|
||||
if (window[d] == need[d])
|
||||
valid--;
|
||||
window[d]--;
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
跟寻找字符串的排列一样,只是找到一个合法异位词(排列)之后将起始索引加入 `res` 即可。
|
||||
|
||||
### 四、最长无重复子串
|
||||
|
||||
这是力扣第 3 题「无重复字符的最长子串」,难度中等:
|
||||
|
||||

|
||||
|
||||
这个题终于有了点新意,不是一套框架就出答案,不过反而更简单了,稍微改一改框架就行了:
|
||||
|
||||
```cpp
|
||||
int lengthOfLongestSubstring(string s) {
|
||||
unordered_map<char, int> window;
|
||||
|
||||
int left = 0, right = 0;
|
||||
int res = 0; // 记录结果
|
||||
while (right < s.size()) {
|
||||
char c = s[right];
|
||||
right++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
window[c]++;
|
||||
// 判断左侧窗口是否要收缩
|
||||
while (window[c] > 1) {
|
||||
char d = s[left];
|
||||
left++;
|
||||
// 进行窗口内数据的一系列更新
|
||||
window[d]--;
|
||||
}
|
||||
// 在这里更新答案
|
||||
res = max(res, right - left);
|
||||
}
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
这就是变简单了,连 `need` 和 `valid` 都不需要,而且更新窗口内数据也只需要简单的更新计数器 `window` 即可。
|
||||
|
||||
当 `window[c]` 值大于 1 时,说明窗口中存在重复字符,不符合条件,就该移动 `left` 缩小窗口了嘛。
|
||||
|
||||
唯一需要注意的是,在哪里更新结果 `res` 呢?我们要的是最长无重复子串,哪一个阶段可以保证窗口中的字符串是没有重复的呢?
|
||||
|
||||
这里和之前不一样,要在收缩窗口完成后更新 `res`,因为窗口收缩的 while 条件是存在重复元素,换句话说收缩完成后一定保证窗口中没有重复嘛。
|
||||
|
||||
好了,滑动窗口算法模板就讲到这里,希望大家能理解其中的思想,记住算法模板并融会贯通。回顾一下,遇到子数组/子串相关的问题,你只要能回答出来以下几个问题,就能运用滑动窗口算法:
|
||||
|
||||
1、什么时候应该扩大窗口?
|
||||
|
||||
2、什么时候应该缩小窗口?
|
||||
|
||||
3、什么时候得到一个合法的答案?
|
||||
|
||||
我在 [滑动窗口经典习题](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62b57985e4b00a4f371dd705/1) 中使用这套思维模式列举了更多经典的习题,旨在强化你对算法的理解和记忆,以后就再也不怕子串、子数组问题了。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [动态规划设计:最大子数组](https://labuladong.github.io/article/fname.html?fname=最大子数组)
|
||||
- [单调队列的通用实现及经典习题](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62a692efe4b01a48520b9b9b/1)
|
||||
- [单调队列结构解决滑动窗口问题](https://labuladong.github.io/article/fname.html?fname=单调队列)
|
||||
- [双指针技巧秒杀七道数组题目](https://labuladong.github.io/article/fname.html?fname=双指针技巧)
|
||||
- [归并排序详解及应用](https://labuladong.github.io/article/fname.html?fname=归并排序)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [滑动窗口算法延伸:Rabin Karp 字符匹配算法](https://labuladong.github.io/article/fname.html?fname=rabinkarp)
|
||||
- [滑动窗口算法经典习题](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_62b57985e4b00a4f371dd705/1)
|
||||
- [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1004. Max Consecutive Ones III](https://leetcode.com/problems/max-consecutive-ones-iii/?show=1) | [1004. 最大连续1的个数 III](https://leetcode.cn/problems/max-consecutive-ones-iii/?show=1) |
|
||||
| [1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit](https://leetcode.com/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/?show=1) | [1438. 绝对差不超过限制的最长连续子数组](https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/?show=1) |
|
||||
| [1658. Minimum Operations to Reduce X to Zero](https://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/?show=1) | [1658. 将 x 减到 0 的最小操作数](https://leetcode.cn/problems/minimum-operations-to-reduce-x-to-zero/?show=1) |
|
||||
| [209. Minimum Size Subarray Sum](https://leetcode.com/problems/minimum-size-subarray-sum/?show=1) | [209. 长度最小的子数组](https://leetcode.cn/problems/minimum-size-subarray-sum/?show=1) |
|
||||
| [219. Contains Duplicate II](https://leetcode.com/problems/contains-duplicate-ii/?show=1) | [219. 存在重复元素 II](https://leetcode.cn/problems/contains-duplicate-ii/?show=1) |
|
||||
| [220. Contains Duplicate III](https://leetcode.com/problems/contains-duplicate-iii/?show=1) | [220. 存在重复元素 III](https://leetcode.cn/problems/contains-duplicate-iii/?show=1) |
|
||||
| [395. Longest Substring with At Least K Repeating Characters](https://leetcode.com/problems/longest-substring-with-at-least-k-repeating-characters/?show=1) | [395. 至少有 K 个重复字符的最长子串](https://leetcode.cn/problems/longest-substring-with-at-least-k-repeating-characters/?show=1) |
|
||||
| [424. Longest Repeating Character Replacement](https://leetcode.com/problems/longest-repeating-character-replacement/?show=1) | [424. 替换后的最长重复字符](https://leetcode.cn/problems/longest-repeating-character-replacement/?show=1) |
|
||||
| [713. Subarray Product Less Than K](https://leetcode.com/problems/subarray-product-less-than-k/?show=1) | [713. 乘积小于K的子数组](https://leetcode.cn/problems/subarray-product-less-than-k/?show=1) |
|
||||
| [862. Shortest Subarray with Sum at Least K](https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k/?show=1) | [862. 和至少为 K 的最短子数组](https://leetcode.cn/problems/shortest-subarray-with-sum-at-least-k/?show=1) |
|
||||
| - | [剑指 Offer 48. 最长不含重复字符的子字符串](https://leetcode.cn/problems/zui-chang-bu-han-zhong-fu-zi-fu-de-zi-zi-fu-chuan-lcof/?show=1) |
|
||||
| - | [剑指 Offer 57 - II. 和为s的连续正数序列](https://leetcode.cn/problems/he-wei-sde-lian-xu-zheng-shu-xu-lie-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 009. 乘积小于 K 的子数组](https://leetcode.cn/problems/ZVAVXX/?show=1) |
|
||||
| - | [剑指 Offer II 014. 字符串中的变位词](https://leetcode.cn/problems/MPnaiL/?show=1) |
|
||||
| - | [剑指 Offer II 015. 字符串中的所有变位词](https://leetcode.cn/problems/VabMRr/?show=1) |
|
||||
| - | [剑指 Offer II 016. 不含重复字符的最长子字符串](https://leetcode.cn/problems/wtcaE1/?show=1) |
|
||||
| - | [剑指 Offer II 017. 含有所有字符的最短字符串](https://leetcode.cn/problems/M1oyTv/?show=1) |
|
||||
| - | [剑指 Offer II 057. 值和下标之差都在给定的范围内](https://leetcode.cn/problems/7WqeDu/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 烧饼排序
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -146,6 +142,10 @@ void reverse(int[] arr, int i, int j) {
|
|||
|
||||
不妨分享一下你的思考。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
105
算法思维系列/算法学习之路.md
105
算法思维系列/算法学习之路.md
|
|
@ -1,105 +0,0 @@
|
|||
# 算法学习之路
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
之前发的那篇关于框架性思维的文章,我也发到了不少其他圈子,受到了大家的普遍好评,这一点我真的没想到,首先感谢大家的认可,我会更加努力,写出通俗易懂的算法文章。
|
||||
|
||||
有很多朋友问我数据结构和算法到底该怎么学,尤其是很多朋友说自己是「小白」,感觉这些东西好难啊,就算看了之前的「框架思维」,也感觉自己刷题乏力,希望我能聊聊我从一个非科班小白一路是怎么学过来的。
|
||||
|
||||
首先要给怀有这样疑问的朋友鼓掌,因为你现在已经「知道自己不知道」,而且开始尝试学习、刷题、寻求帮助,能做到这一点本身就是及其困难的。
|
||||
|
||||
关于「框架性思维」,对于一个小白来说,可能暂时无法完全理解(如果你能理解,说明你水平已经不错啦,不是小白啦)。就像软件工程,对于我这种没带过项目的人来说,感觉其内容枯燥乏味,全是废话,但是对于一个带过团队的人,他就会觉得软件工程里的每一句话都是精华。暂时不太理解没关系,留个印象,功夫到了很快就明白了。
|
||||
|
||||
下面写一写我一路过来的一些经验。如果你已经看过很多「如何高效刷题」「如何学习算法」的文章,却还是没有开始行动并坚持下去,本文的第五点就是写给你的。
|
||||
|
||||
我觉得之所以有时候认为自己是「小白」,是由于知识某些方面的空白造成的。具体到数据结构的学习,无非就是两个问题搞得不太清楚:**这是啥?有啥用?**
|
||||
|
||||
举个例子,比如说你看到了「栈」这个名词,老师可能会讲这些关键词:先进后出、函数堆栈等等。但是,对于初学者,这些描述属于文学词汇,没有实际价值,没有解决最基本的两个问题。如何回答这两个基本问题呢?回答「这是啥」需要看教科书,回答「有啥用」需要刷算法题。
|
||||
|
||||
**一、这是啥?**
|
||||
|
||||
这个问题最容易解决,就像一层窗户纸,你只要随便找本书看两天,自己动手实现一个「队列」「栈」之类的数据结构,就能捅破这层窗户纸。
|
||||
|
||||
这时候你就能理解「框架思维」文章中的前半部分了:数据结构无非就是数组、链表为骨架的一些特定操作而已;每个数据结构实现的功能无非增删查改罢了。
|
||||
|
||||
比如说「列队」这个数据结构,无非就是基于数组或者链表,实现 enqueue 和 dequeue 两个方法。这两个方法就是增和删呀,连查和改的方法都不需要。
|
||||
|
||||
**二、有啥用?**
|
||||
|
||||
解决这个问题,就涉及算法的设计了,是个持久战,需要经常进行抽象思考,刷算法题,培养「计算机思维」。
|
||||
|
||||
之前的文章讲了,算法就是对数据结构准确而巧妙的运用。常用算法问题也就那几大类,算法题无非就是不断变换场景,给那几个算法框架套上不同的皮。刷题,就是在锻炼你的眼力,看你能不能看穿问题表象揪出相应的解法框架。
|
||||
|
||||
比如说,让你求解一个迷宫,你要把这个问题层层抽象:迷宫 -> 图的遍历 -> N 叉树的遍历 -> 二叉树的遍历。然后让框架指导你写具体的解法。
|
||||
|
||||
抽象问题,直击本质,是刷题中你需要刻意培养的能力。
|
||||
|
||||
**三、如何看书**
|
||||
|
||||
直接推荐一本公认的好书,《算法第 4 版》,我一般简写成《算法4》。不要蜻蜓点水,这本书你能选择性的看上 50%,基本上就达到平均水平了。别怕这本书厚,因为起码有三分之一不用看,下面讲讲怎么看这本书。
|
||||
|
||||
看书仍然遵循递归的思想:自顶向下,逐步求精。
|
||||
|
||||
这本书知识结构合理,讲解也清楚,所以可以按顺序学习。**书中正文的算法代码一定要亲自敲一遍**,因为这些真的是扎实的基础,要认真理解。不要以为自己看一遍就看懂了,不动手的话理解不了的。但是,开头部分的基础可以酌情跳过;书中的数学证明,如不影响对算法本身的理解,完全可以跳过;章节最后的练习题,也可以全部跳过。这样一来,这本书就薄了很多。
|
||||
|
||||
相信读者现在已经认可了「框架性思维」的重要性,这种看书方式也是一种框架性策略,抓大放小,着重理解整体的知识架构,而忽略证明、练习题这种细节问题,即**保持自己对新知识的好奇心,避免陷入无限的细节被劝退。**
|
||||
|
||||
当然,《算法4》到后面的内容也比较难了,比如那几个著名的串算法,以及正则表达式算法。这些属于「经典算法」,看个人接受能力吧,单说刷 LeetCode 的话,基本用不上,量力而行即可。
|
||||
|
||||
**四、如何刷题**
|
||||
|
||||
首先声明一下,**算法和数学水平没关系,和编程语言也没关系**,你爱用什么语言用什么。算法,主要是培养一种新的思维方式。所谓「计算机思维」,就跟你考驾照一样,你以前骑自行车,有一套自行车的规则和技巧,现在你开汽车,就需要适应并练习开汽车的规则和技巧。
|
||||
|
||||
LeetCode 上的算法题和前面说的「经典算法」不一样,我们权且称为「解闷算法」吧,因为很多题目都比较有趣,有种在做奥数题或者脑筋急转弯的感觉。比如说,让你用队列实现一个栈,或者用栈实现一个队列,以及不用加号做加法,开脑洞吧?
|
||||
|
||||
当然,这些问题虽然看起来无厘头,实际生活中也用不到,但是想解决这些问题依然要靠数据结构以及对基础知识的理解,也许这就是很多公司面试都喜欢出这种「智力题」的原因。下面说几点技巧吧。
|
||||
|
||||
**尽量刷英文版的 LeetCode**,中文版的“力扣”是阉割版,不仅很多题目没有答案,而且连个讨论区都没有。英文版的是真的很良心了,很多问题都有官方解答,详细易懂。而且讨论区(Discuss)也沉淀了大量优质内容,甚至好过官方解答。真正能打开你思路的,很可能是讨论区各路大神的思路荟萃。
|
||||
|
||||
PS:**如果有的英文题目实在看不懂,有个小技巧**,你在题目页面的 url 里加一个 -cn,即 https://leetcode.com/xxx 改成 https://leetcode-cn.com/xxx,这样就能切换到相应的中文版页面查看。
|
||||
|
||||
对于初学者,**强烈建议从 Explore 菜单里最下面的 Learn 开始刷**,这个专题就是专门教你学习数据结构和基本算法的,教学篇和相应的练习题结合,不要太良心。
|
||||
|
||||
最近 Learn 专题里新增了一些内容,我们挑数据结构相关的内容刷就行了,像 Ruby,Machine Learning 就没必要刷了。刷完 Learn 专题的基础内容,基本就有能力去 Explore 菜单的 Interview 专题刷面试题,或者去 Problem 菜单,在真正的题海里遨游了。
|
||||
|
||||
无论刷 Explore 还是 Problems 菜单,**最好一个分类一个分类的刷,不要蜻蜓点水**。比如说这几天就刷链表,刷完链表再去连刷几天二叉树。这样做是为了帮助你提取「框架」。一旦总结出针对一类问题的框架,解决同类问题可谓是手到擒来。
|
||||
|
||||
**五、道理我都懂,还是不能坚持下去**
|
||||
|
||||
这其实无关算法了,还是老生常谈的执行力的问题。不说什么破鸡汤了,我觉得**解决办法就是「激起欲望」**,注意我说的是欲望,而不是常说的兴趣,拿我自己说说吧。
|
||||
|
||||
半年前我开始刷题,目的和大部分人都一样的,就是为毕业找工作做准备。只不过,大部分人是等到临近毕业了才开始刷,而我离毕业还有一阵子。这不是炫耀我多有觉悟,而是我承认自己的极度平凡。
|
||||
|
||||
首先,我真的想找到一份不错的工作(谁都想吧?),我想要高薪呀!否则我在朋友面前,女神面前放下的骚话,最终都会反过来啪啪地打我的脸。我也是要恰饭,要面子,要虚荣心的嘛。赚钱,虚荣心,足以激起我的欲望了。
|
||||
|
||||
但是,我不擅长 deadline 突击,我理解东西真的慢,所以干脆笨鸟先飞了。智商不够,拿时间来补,我没能力两个月突击,干脆拉长战线,打他个两年游击战,我还不信耗不死算法这个强敌。事实证明,你如果认真学习一个月,就能够取得肉眼可见的进步了。
|
||||
|
||||
现在,我依然在坚持刷题,而且为了另外一个原因,这个公众号。我没想到自己的文字竟然能够帮助到他人,甚至能得到认可。这也是虚荣心啊,我不能让读者失望啊,我想让更多的人认可(夸)我呀!
|
||||
|
||||
以上,不光是坚持刷算法题吧,很多场景都适用。执行力是要靠「欲望」支撑的,我也是一凡人,只有那些看得见摸得着的东西才能使我快乐呀。读者不妨也尝试把刷题学习和自己的切身利益联系起来,这恐怕是坚持下去最简单直白的理由了。
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
|
@ -0,0 +1,331 @@
|
|||
# 二维数组的花式遍历
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [151. Reverse Words in a String](https://leetcode.com/problems/reverse-words-in-a-string/) | [151. 翻转字符串里的单词](https://leetcode.cn/problems/reverse-words-in-a-string/) | 🟠
|
||||
| [48. Rotate Image](https://leetcode.com/problems/rotate-image/) | [48. 旋转图像](https://leetcode.cn/problems/rotate-image/) | 🟠
|
||||
| [54. Spiral Matrix](https://leetcode.com/problems/spiral-matrix/) | [54. 螺旋矩阵](https://leetcode.cn/problems/spiral-matrix/) | 🟠
|
||||
| [59. Spiral Matrix II](https://leetcode.com/problems/spiral-matrix-ii/) | [59. 螺旋矩阵 II](https://leetcode.cn/problems/spiral-matrix-ii/) | 🟠
|
||||
| - | [剑指 Offer 29. 顺时针打印矩阵](https://leetcode.cn/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/) | 🟢
|
||||
|
||||
**-----------**
|
||||
|
||||
有不少读者说,看过很多公众号历史文章之后,掌握了框架思维,可以解决大部分有套路框架可循的题目。
|
||||
|
||||
但是框架思维也不是万能的,有一些特定技巧呢,属于会者不难,难者不会的类型,只能通过多刷题进行总结和积累。
|
||||
|
||||
那么本文我分享一些巧妙的二维数组的花式操作,你只要有个印象,以后遇到类似题目就不会懵圈了。
|
||||
|
||||
### 顺/逆时针旋转矩阵
|
||||
|
||||
对二维数组进行旋转是常见的笔试题,力扣第 48 题「旋转图像」就是很经典的一道:
|
||||
|
||||

|
||||
|
||||
题目很好理解,就是让你将一个二维矩阵顺时针旋转 90 度,**难点在于要「原地」修改**,函数签名如下:
|
||||
|
||||
```java
|
||||
void rotate(int[][] matrix)
|
||||
```
|
||||
|
||||
如何「原地」旋转二维矩阵?稍想一下,感觉操作起来非常复杂,可能要设置巧妙的算法机制来「一圈一圈」旋转矩阵:
|
||||
|
||||

|
||||
|
||||
**但实际上,这道题不能走寻常路**,在讲巧妙解法之前,我们先看另一道谷歌曾经考过的算法题热热身:
|
||||
|
||||
给你一个包含若干单词和空格的字符串 `s`,请你写一个算法,**原地**反转所有单词的顺序。
|
||||
|
||||
比如说,给你输入这样一个字符串:
|
||||
|
||||
```shell
|
||||
s = "hello world labuladong"
|
||||
```
|
||||
|
||||
你的算法需要**原地**反转这个字符串中的单词顺序:
|
||||
|
||||
```shell
|
||||
s = "labuladong world hello"
|
||||
```
|
||||
|
||||
常规的方式是把 `s` 按空格 `split` 成若干单词,然后 `reverse` 这些单词的顺序,最后把这些单词 `join` 成句子。但这种方式使用了额外的空间,并不是「原地反转」单词。
|
||||
|
||||
**正确的做法是,先将整个字符串 `s` 反转**:
|
||||
|
||||
```shell
|
||||
s = "gnodalubal dlrow olleh"
|
||||
```
|
||||
|
||||
**然后将每个单词分别反转**:
|
||||
|
||||
```shell
|
||||
s = "labuladong world hello"
|
||||
```
|
||||
|
||||
这样,就实现了原地反转所有单词顺序的目的。力扣第 151 题「颠倒字符串中的单词」就是类似的问题,你可以顺便去做一下。
|
||||
|
||||
我讲这道题的目的是什么呢?
|
||||
|
||||
**旨在说明,有时候咱们拍脑袋的常规思维,在计算机看来可能并不是最优雅的;但是计算机觉得最优雅的思维,对咱们来说却不那么直观**。也许这就是算法的魅力所在吧。
|
||||
|
||||
回到之前说的顺时针旋转二维矩阵的问题,常规的思路就是去寻找原始坐标和旋转后坐标的映射规律,但我们是否可以让思维跳跃跳跃,尝试把矩阵进行反转、镜像对称等操作,可能会出现新的突破口。
|
||||
|
||||
**我们可以先将 `n x n` 矩阵 `matrix` 按照左上到右下的对角线进行镜像对称**:
|
||||
|
||||

|
||||
|
||||
**然后再对矩阵的每一行进行反转**:
|
||||
|
||||

|
||||
|
||||
**发现结果就是 `matrix` 顺时针旋转 90 度的结果**:
|
||||
|
||||

|
||||
|
||||
将上述思路翻译成代码,即可解决本题:
|
||||
|
||||
```java
|
||||
// 将二维矩阵原地顺时针旋转 90 度
|
||||
public void rotate(int[][] matrix) {
|
||||
int n = matrix.length;
|
||||
// 先沿对角线镜像对称二维矩阵
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = i; j < n; j++) {
|
||||
// swap(matrix[i][j], matrix[j][i]);
|
||||
int temp = matrix[i][j];
|
||||
matrix[i][j] = matrix[j][i];
|
||||
matrix[j][i] = temp;
|
||||
}
|
||||
}
|
||||
// 然后反转二维矩阵的每一行
|
||||
for (int[] row : matrix) {
|
||||
reverse(row);
|
||||
}
|
||||
}
|
||||
|
||||
// 反转一维数组
|
||||
void reverse(int[] arr) {
|
||||
int i = 0, j = arr.length - 1;
|
||||
while (j > i) {
|
||||
// swap(arr[i], arr[j]);
|
||||
int temp = arr[i];
|
||||
arr[i] = arr[j];
|
||||
arr[j] = temp;
|
||||
i++;
|
||||
j--;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
肯定有读者会问,如果没有做过这道题,怎么可能想到这种思路呢?
|
||||
|
||||
仔细想想,旋转二维矩阵的难点在于将「行」变成「列」,将「列」变成「行」,而只有按照对角线的对称操作是可以轻松完成这一点的,对称操作之后就很容易发现规律了。
|
||||
|
||||
**既然说道这里,我们可以发散一下,如何将矩阵逆时针旋转 90 度呢**?
|
||||
|
||||
思路是类似的,只要通过另一条对角线镜像对称矩阵,然后再反转每一行,就得到了逆时针旋转矩阵的结果:
|
||||
|
||||

|
||||
|
||||
翻译成代码如下:
|
||||
|
||||
```java
|
||||
// 将二维矩阵原地逆时针旋转 90 度
|
||||
void rotate2(int[][] matrix) {
|
||||
int n = matrix.length;
|
||||
// 沿左下到右上的对角线镜像对称二维矩阵
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < n - i; j++) {
|
||||
// swap(matrix[i][j], matrix[n-j-1][n-i-1])
|
||||
int temp = matrix[i][j];
|
||||
matrix[i][j] = matrix[n - j - 1][n - i - 1];
|
||||
matrix[n - j - 1][n - i - 1] = temp;
|
||||
}
|
||||
}
|
||||
// 然后反转二维矩阵的每一行
|
||||
for (int[] row : matrix) {
|
||||
reverse(row);
|
||||
}
|
||||
}
|
||||
|
||||
void reverse(int[] arr) { /* 见上文 */}
|
||||
```
|
||||
|
||||
至此,旋转矩阵的问题就解决了。
|
||||
|
||||
### 矩阵的螺旋遍历
|
||||
|
||||
我的公众号动态规划系列文章经常需要遍历二维 `dp` 数组,但难点在于状态转移方程而不是数组的遍历,顶多就是倒序遍历。
|
||||
|
||||
但接下来我们讲一下力扣第 54 题「螺旋矩阵」,看一看二维矩阵可以如何花式遍历:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
List<Integer> spiralOrder(int[][] matrix)
|
||||
```
|
||||
|
||||
**解题的核心思路是按照右、下、左、上的顺序遍历数组,并使用四个变量圈定未遍历元素的边界**:
|
||||
|
||||

|
||||
|
||||
随着螺旋遍历,相应的边界会收缩,直到螺旋遍历完整个数组:
|
||||
|
||||

|
||||
|
||||
只要有了这个思路,翻译出代码就很容易了:
|
||||
|
||||
```java
|
||||
List<Integer> spiralOrder(int[][] matrix) {
|
||||
int m = matrix.length, n = matrix[0].length;
|
||||
int upper_bound = 0, lower_bound = m - 1;
|
||||
int left_bound = 0, right_bound = n - 1;
|
||||
List<Integer> res = new LinkedList<>();
|
||||
// res.size() == m * n 则遍历完整个数组
|
||||
while (res.size() < m * n) {
|
||||
if (upper_bound <= lower_bound) {
|
||||
// 在顶部从左向右遍历
|
||||
for (int j = left_bound; j <= right_bound; j++) {
|
||||
res.add(matrix[upper_bound][j]);
|
||||
}
|
||||
// 上边界下移
|
||||
upper_bound++;
|
||||
}
|
||||
|
||||
if (left_bound <= right_bound) {
|
||||
// 在右侧从上向下遍历
|
||||
for (int i = upper_bound; i <= lower_bound; i++) {
|
||||
res.add(matrix[i][right_bound]);
|
||||
}
|
||||
// 右边界左移
|
||||
right_bound--;
|
||||
}
|
||||
|
||||
if (upper_bound <= lower_bound) {
|
||||
// 在底部从右向左遍历
|
||||
for (int j = right_bound; j >= left_bound; j--) {
|
||||
res.add(matrix[lower_bound][j]);
|
||||
}
|
||||
// 下边界上移
|
||||
lower_bound--;
|
||||
}
|
||||
|
||||
if (left_bound <= right_bound) {
|
||||
// 在左侧从下向上遍历
|
||||
for (int i = lower_bound; i >= upper_bound; i--) {
|
||||
res.add(matrix[i][left_bound]);
|
||||
}
|
||||
// 左边界右移
|
||||
left_bound++;
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
力扣第 59 题「螺旋矩阵 II」也是类似的题目,只不过是反过来,让你按照螺旋的顺序生成矩阵:
|
||||
|
||||

|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int[][] generateMatrix(int n)
|
||||
```
|
||||
|
||||
有了上面的铺垫,稍微改一下代码即可完成这道题:
|
||||
|
||||
```java
|
||||
int[][] generateMatrix(int n) {
|
||||
int[][] matrix = new int[n][n];
|
||||
int upper_bound = 0, lower_bound = n - 1;
|
||||
int left_bound = 0, right_bound = n - 1;
|
||||
// 需要填入矩阵的数字
|
||||
int num = 1;
|
||||
|
||||
while (num <= n * n) {
|
||||
if (upper_bound <= lower_bound) {
|
||||
// 在顶部从左向右遍历
|
||||
for (int j = left_bound; j <= right_bound; j++) {
|
||||
matrix[upper_bound][j] = num++;
|
||||
}
|
||||
// 上边界下移
|
||||
upper_bound++;
|
||||
}
|
||||
|
||||
if (left_bound <= right_bound) {
|
||||
// 在右侧从上向下遍历
|
||||
for (int i = upper_bound; i <= lower_bound; i++) {
|
||||
matrix[i][right_bound] = num++;
|
||||
}
|
||||
// 右边界左移
|
||||
right_bound--;
|
||||
}
|
||||
|
||||
if (upper_bound <= lower_bound) {
|
||||
// 在底部从右向左遍历
|
||||
for (int j = right_bound; j >= left_bound; j--) {
|
||||
matrix[lower_bound][j] = num++;
|
||||
}
|
||||
// 下边界上移
|
||||
lower_bound--;
|
||||
}
|
||||
|
||||
if (left_bound <= right_bound) {
|
||||
// 在左侧从下向上遍历
|
||||
for (int i = lower_bound; i >= upper_bound; i--) {
|
||||
matrix[i][left_bound] = num++;
|
||||
}
|
||||
// 左边界右移
|
||||
left_bound++;
|
||||
}
|
||||
}
|
||||
return matrix;
|
||||
}
|
||||
```
|
||||
|
||||
至此,两道螺旋矩阵的题目也解决了。
|
||||
|
||||
以上就是遍历二维数组的一些技巧,其他数组技巧可参见之前的文章 [前缀和数组](https://labuladong.github.io/article/fname.html?fname=前缀和技巧),[差分数组](https://labuladong.github.io/article/fname.html?fname=差分技巧),[数组双指针算法集合](https://labuladong.github.io/article/fname.html?fname=链表技巧)。
|
||||
|
||||
> 最后打个广告,我亲自制作了一门 [数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO),以视频课为主,手把手带你实现常用的数据结构及相关算法,旨在帮助算法基础较为薄弱的读者深入理解常用数据结构的底层原理,在算法学习中少走弯路。
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1260. Shift 2D Grid](https://leetcode.com/problems/shift-2d-grid/?show=1) | [1260. 二维网格迁移](https://leetcode.cn/problems/shift-2d-grid/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
351
算法思维系列/递归详解.md
351
算法思维系列/递归详解.md
|
|
@ -1,351 +0,0 @@
|
|||
# 递归详解
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
**-----------**
|
||||
|
||||
首先说明一个问题,简单阐述一下递归,分治算法,动态规划,贪心算法这几个东西的区别和联系,心里有个印象就好。
|
||||
|
||||
递归是一种编程技巧,一种解决问题的思维方式;分治算法和动态规划很大程度上是递归思想基础上的(虽然动态规划的最终版本大都不是递归了,但解题思想还是离不开递归),解决更具体问题的两类算法思想;贪心算法是动态规划算法的一个子集,可以更高效解决一部分更特殊的问题。
|
||||
|
||||
分治算法将在这节讲解,以最经典的归并排序为例,它把待排序数组不断二分为规模更小的子问题处理,这就是 “分而治之” 这个词的由来。显然,排序问题分解出的子问题是不重复的,如果有的问题分解后的子问题有重复的(重叠子问题性质),那么就交给动态规划算法去解决!
|
||||
|
||||
## 递归详解
|
||||
|
||||
介绍分治之前,首先要弄清楚递归这个概念。
|
||||
|
||||
递归的基本思想是某个函数直接或者间接地调用自身,这样就把原问题的求解转换为许多性质相同但是规模更小的子问题。我们只需要关注如何把原问题划分成符合条件的子问题,而不需要去研究这个子问题是如何被解决的。递归和枚举的区别在于:枚举是横向地把问题划分,然后依次求解子问题,而递归是把问题逐级分解,是纵向的拆分。
|
||||
|
||||
以下会举例说明我对递归的一点理解,**如果你不想看下去了,请记住这几个问题怎么回答:**
|
||||
|
||||
1. 如何给一堆数字排序? 答:分成两半,先排左半边再排右半边,最后合并就行了,至于怎么排左边和右边,请重新阅读这句话。
|
||||
2. 孙悟空身上有多少根毛? 答:一根毛加剩下的毛。
|
||||
3. 你今年几岁? 答:去年的岁数加一岁,1999 年我出生。
|
||||
|
||||
递归代码最重要的两个特征:结束条件和自我调用。自我调用是在解决子问题,而结束条件定义了最简子问题的答案。
|
||||
|
||||
```c++
|
||||
int func(你今年几岁) {
|
||||
// 最简子问题,结束条件
|
||||
if (你1999年几岁) return 我0岁;
|
||||
// 自我调用,缩小规模
|
||||
return func(你去年几岁) + 1;
|
||||
}
|
||||
```
|
||||
|
||||
其实仔细想想,**递归运用最成功的是什么?我认为是数学归纳法。**我们高中都学过数学归纳法,使用场景大概是:我们推不出来某个求和公式,但是我们试了几个比较小的数,似乎发现了一点规律,然后编了一个公式,看起来应该是正确答案。但是数学是很严谨的,你哪怕穷举了一万个数都是正确的,但是第一万零一个数正确吗?这就要数学归纳法发挥神威了,可以假设我们编的这个公式在第 k 个数时成立,如果证明在第 k + 1 时也成立,那么我们编的这个公式就是正确的。
|
||||
|
||||
那么数学归纳法和递归有什么联系?我们刚才说了,递归代码必须要有结束条件,如果没有的话就会进入无穷无尽的自我调用,直到内存耗尽。而数学证明的难度在于,你可以尝试有穷种情况,但是难以将你的结论延伸到无穷大。这里就可以看出联系了 —— 无穷。
|
||||
|
||||
递归代码的精髓在于调用自己去解决规模更小的子问题,直到到达结束条件;而数学归纳法之所以有用,就在于不断把我们的猜测向上加一,扩大结论的规模,没有结束条件,从而把结论延伸到无穷无尽,也就完成了猜测正确性的证明。
|
||||
|
||||
### 为什么要写递归
|
||||
|
||||
首先为了训练逆向思考的能力。递推的思维是正常人的思维,总是看着眼前的问题思考对策,解决问题是将来时;递归的思维,逼迫我们倒着思考,看到问题的尽头,把解决问题的过程看做过去时。
|
||||
|
||||
第二,练习分析问题的结构,当问题可以被分解成相同结构的小问题时,你能敏锐发现这个特点,进而高效解决问题。
|
||||
|
||||
第三,跳出细节,从整体上看问题。再说说归并排序,其实可以不用递归来划分左右区域的,但是代价就是代码极其难以理解,大概看一下代码(归并排序在后面讲,这里大致看懂意思就行,体会递归的妙处):
|
||||
|
||||
```java
|
||||
void sort(Comparable[] a){
|
||||
int N = a.length;
|
||||
// 这么复杂,是对排序的不尊重。我拒绝研究这样的代码。
|
||||
for (int sz = 1; sz < N; sz = sz + sz)
|
||||
for (int lo = 0; lo < N - sz; lo += sz + sz)
|
||||
merge(a, lo, lo + sz - 1, Math.min(lo + sz + sz - 1, N - 1));
|
||||
}
|
||||
|
||||
/* 我还是选择递归,简单,漂亮 */
|
||||
void sort(Comparable[] a, int lo, int hi) {
|
||||
if (lo >= hi) return;
|
||||
int mid = lo + (hi - lo) / 2;
|
||||
sort(a, lo, mid); // 排序左半边
|
||||
sort(a, mid + 1, hi); // 排序右半边
|
||||
merge(a, lo, mid, hi); // 合并两边
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
看起来简洁漂亮是一方面,关键是**可解释性很强**:把左半边排序,把右半边排序,最后合并两边。而非递归版本看起来不知所云,充斥着各种难以理解的边界计算细节,特别容易出 bug 且难以调试,人生苦短,我更倾向于递归版本。
|
||||
|
||||
显然有时候递归处理是高效的,比如归并排序,**有时候是低效的**,比如数孙悟空身上的毛,因为堆栈会消耗额外空间,而简单的递推不会消耗空间。比如这个例子,给一个链表头,计算它的长度:
|
||||
|
||||
```java
|
||||
/* 典型的递推遍历框架,需要额外空间 O(1) */
|
||||
public int size(Node head) {
|
||||
int size = 0;
|
||||
for (Node p = head; p != null; p = p.next) size++;
|
||||
return size;
|
||||
}
|
||||
/* 我偏要递归,万物皆递归,需要额外空间 O(N) */
|
||||
public int size(Node head) {
|
||||
if (head == null) return 0;
|
||||
return size(head.next) + 1;
|
||||
}
|
||||
```
|
||||
|
||||
### 写递归的技巧
|
||||
|
||||
我的一点心得是:**明白一个函数的作用并相信它能完成这个任务,千万不要试图跳进细节。**千万不要跳进这个函数里面企图探究更多细节,否则就会陷入无穷的细节无法自拔,人脑能压几个栈啊。
|
||||
|
||||
先举个最简单的例子:遍历二叉树。
|
||||
|
||||
```cpp
|
||||
void traverse(TreeNode* root) {
|
||||
if (root == nullptr) return;
|
||||
traverse(root->left);
|
||||
traverse(root->right);
|
||||
}
|
||||
```
|
||||
|
||||
这几行代码就足以扫荡任何一棵二叉树了。我想说的是,对于递归函数`traverse(root)`,我们只要相信:给它一个根节点`root`,它就能遍历这棵树,因为写这个函数不就是为了这个目的吗?所以我们只需要把这个节点的左右节点再甩给这个函数就行了,因为我相信它能完成任务的。那么遍历一棵N叉数呢?太简单了好吧,和二叉树一模一样啊。
|
||||
|
||||
```cpp
|
||||
void traverse(TreeNode* root) {
|
||||
if (root == nullptr) return;
|
||||
for (child : root->children)
|
||||
traverse(child);
|
||||
}
|
||||
```
|
||||
|
||||
至于遍历的什么前、中、后序,那都是显而易见的,对于N叉树,显然没有中序遍历。
|
||||
|
||||
|
||||
|
||||
以下**详解 LeetCode 的一道题来说明**:给一颗二叉树,和一个目标值,节点上的值有正有负,返回树中和等于目标值的路径条数,让你编写 pathSum 函数:
|
||||
|
||||
```
|
||||
/* 来源于 LeetCode PathSum III: https://leetcode.com/problems/path-sum-iii/ */
|
||||
root = [10,5,-3,3,2,null,11,3,-2,null,1],
|
||||
sum = 8
|
||||
|
||||
10
|
||||
/ \
|
||||
5 -3
|
||||
/ \ \
|
||||
3 2 11
|
||||
/ \ \
|
||||
3 -2 1
|
||||
|
||||
Return 3. The paths that sum to 8 are:
|
||||
|
||||
1. 5 -> 3
|
||||
2. 5 -> 2 -> 1
|
||||
3. -3 -> 11
|
||||
```
|
||||
|
||||
```cpp
|
||||
/* 看不懂没关系,底下有更详细的分析版本,这里突出体现递归的简洁优美 */
|
||||
int pathSum(TreeNode root, int sum) {
|
||||
if (root == null) return 0;
|
||||
return count(root, sum) +
|
||||
pathSum(root.left, sum) + pathSum(root.right, sum);
|
||||
}
|
||||
int count(TreeNode node, int sum) {
|
||||
if (node == null) return 0;
|
||||
return (node.val == sum) +
|
||||
count(node.left, sum - node.val) + count(node.right, sum - node.val);
|
||||
}
|
||||
```
|
||||
|
||||
题目看起来很复杂吧,不过代码却极其简洁,这就是递归的魅力。我来简单总结这个问题的**解决过程**:
|
||||
|
||||
首先明确,递归求解树的问题必然是要遍历整棵树的,所以**二叉树的遍历框架**(分别对左右孩子递归调用函数本身)必然要出现在主函数 pathSum 中。那么对于每个节点,他们应该干什么呢?他们应该看看,自己和脚底下的小弟们包含多少条符合条件的路径。好了,这道题就结束了。
|
||||
|
||||
按照前面说的技巧,根据刚才的分析来定义清楚每个递归函数应该做的事:
|
||||
|
||||
PathSum 函数:给他一个节点和一个目标值,他返回以这个节点为根的树中,和为目标值的路径总数。
|
||||
|
||||
count 函数:给他一个节点和一个目标值,他返回以这个节点为根的树中,能凑出几个以该节点为路径开头,和为目标值的路径总数。
|
||||
|
||||
```cpp
|
||||
/* 有了以上铺垫,详细注释一下代码 */
|
||||
int pathSum(TreeNode root, int sum) {
|
||||
if (root == null) return 0;
|
||||
int pathImLeading = count(root, sum); // 自己为开头的路径数
|
||||
int leftPathSum = pathSum(root.left, sum); // 左边路径总数(相信他能算出来)
|
||||
int rightPathSum = pathSum(root.right, sum); // 右边路径总数(相信他能算出来)
|
||||
return leftPathSum + rightPathSum + pathImLeading;
|
||||
}
|
||||
int count(TreeNode node, int sum) {
|
||||
if (node == null) return 0;
|
||||
// 我自己能不能独当一面,作为一条单独的路径呢?
|
||||
int isMe = (node.val == sum) ? 1 : 0;
|
||||
// 左边的小老弟,你那边能凑几个 sum - node.val 呀?
|
||||
int leftBrother = count(node.left, sum - node.val);
|
||||
// 右边的小老弟,你那边能凑几个 sum - node.val 呀?
|
||||
int rightBrother = count(node.right, sum - node.val);
|
||||
return isMe + leftBrother + rightBrother; // 我这能凑这么多个
|
||||
}
|
||||
```
|
||||
|
||||
还是那句话,明白每个函数能做的事,并相信他们能够完成。
|
||||
|
||||
总结下,PathSum 函数提供的二叉树遍历框架,在遍历中对每个节点调用 count 函数,看出先序遍历了吗(这道题什么序都是一样的);count 函数也是一个二叉树遍历,用于寻找以该节点开头的目标值路径。好好体会吧!
|
||||
|
||||
## 分治算法
|
||||
|
||||
**归并排序**,典型的分治算法;分治,典型的递归结构。
|
||||
|
||||
分治算法可以分三步走:分解 -> 解决 -> 合并
|
||||
|
||||
1. 分解原问题为结构相同的子问题。
|
||||
2. 分解到某个容易求解的边界之后,进行第归求解。
|
||||
3. 将子问题的解合并成原问题的解。
|
||||
|
||||
归并排序,我们就叫这个函数`merge_sort`吧,按照我们上面说的,要明确该函数的职责,即**对传入的一个数组排序**。OK,那么这个问题能不能分解呢?当然可以!给一个数组排序,不就等于给该数组的两半分别排序,然后合并就完事了。
|
||||
|
||||
```cpp
|
||||
void merge_sort(一个数组) {
|
||||
if (可以很容易处理) return;
|
||||
merge_sort(左半个数组);
|
||||
merge_sort(右半个数组);
|
||||
merge(左半个数组, 右半个数组);
|
||||
}
|
||||
```
|
||||
|
||||
好了,这个算法也就这样了,完全没有任何难度。记住之前说的,相信函数的能力,传给他半个数组,那么这半个数组就已经被排好了。而且你会发现这不就是个二叉树遍历模板吗?为什么是后序遍历?因为我们分治算法的套路是 **分解 -> 解决(触底) -> 合并(回溯)** 啊,先左右分解,再处理合并,回溯就是在退栈,就相当于后序遍历了。至于`merge`函数,参考两个有序链表的合并,简直一模一样,下面直接贴代码吧。
|
||||
|
||||
下面参考《算法4》的 Java 代码,很漂亮。由此可见,不仅算法思想思想重要,编码技巧也是挺重要的吧!多思考,多模仿。
|
||||
|
||||
```java
|
||||
public class Merge {
|
||||
// 不要在 merge 函数里构造新数组了,因为 merge 函数会被多次调用,影响性能
|
||||
// 直接一次性构造一个足够大的数组,简洁,高效
|
||||
private static Comparable[] aux;
|
||||
|
||||
public static void sort(Comparable[] a) {
|
||||
aux = new Comparable[a.length];
|
||||
sort(a, 0, a.length - 1);
|
||||
}
|
||||
|
||||
private static void sort(Comparable[] a, int lo, int hi) {
|
||||
if (lo >= hi) return;
|
||||
int mid = lo + (hi - lo) / 2;
|
||||
sort(a, lo, mid);
|
||||
sort(a, mid + 1, hi);
|
||||
merge(a, lo, mid, hi);
|
||||
}
|
||||
|
||||
private static void merge(Comparable[] a, int lo, int mid, int hi) {
|
||||
int i = lo, j = mid + 1;
|
||||
for (int k = lo; k <= hi; k++)
|
||||
aux[k] = a[k];
|
||||
for (int k = lo; k <= hi; k++) {
|
||||
if (i > mid) { a[k] = aux[j++]; }
|
||||
else if (j > hi) { a[k] = aux[i++]; }
|
||||
else if (less(aux[j], aux[i])) { a[k] = aux[j++]; }
|
||||
else { a[k] = aux[i++]; }
|
||||
}
|
||||
}
|
||||
|
||||
private static boolean less(Comparable v, Comparable w) {
|
||||
return v.compareTo(w) < 0;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
LeetCode 上有分治算法的专项练习,可复制到浏览器去做题:
|
||||
|
||||
https://leetcode.com/tag/divide-and-conquer/
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
### javascript
|
||||
|
||||
[437. 路径总和 III](https://leetcode-cn.com/problems/path-sum-iii/)
|
||||
|
||||
```js
|
||||
/**
|
||||
* Definition for a binary tree node.
|
||||
* function TreeNode(val, left, right) {
|
||||
* this.val = (val===undefined ? 0 : val)
|
||||
* this.left = (left===undefined ? null : left)
|
||||
* this.right = (right===undefined ? null : right)
|
||||
* }
|
||||
*/
|
||||
/**
|
||||
* @param {TreeNode} root
|
||||
* @param {number} sum
|
||||
* @return {number}
|
||||
*/
|
||||
var pathSum = function(root, sum) {
|
||||
// 二叉树-题目要求只能从父节点到子节点 所以用先序遍历
|
||||
|
||||
// 路径总数
|
||||
let ans = 0
|
||||
|
||||
// 存储前缀和
|
||||
let map = new Map()
|
||||
|
||||
// 先序遍历二叉树
|
||||
function dfs(presum,node) {
|
||||
if(!node)return 0 // 遍历出口
|
||||
|
||||
// 将当前前缀和添加到map
|
||||
map.set(presum,(map.get(presum) || 0) +1 )
|
||||
// 从根节点到当前节点的值
|
||||
let target = presum + node.val
|
||||
|
||||
// target-sum = 需要的前缀和长度
|
||||
// 然而前缀和之前我们都存过了 检索map里key为该前缀和的value
|
||||
// map的值相当于有多少个节点到当前节点=sum 也就是有几条路径
|
||||
ans+=(map.get(target - sum) || 0)
|
||||
|
||||
// 按顺序遍历左右节点
|
||||
dfs(target,node.left)
|
||||
dfs(target,node.right)
|
||||
|
||||
// 这层遍历完就把该层的前缀和去掉
|
||||
map.set(presum,map.get(presum) -1 )
|
||||
}
|
||||
dfs(0,root)
|
||||
return ans
|
||||
};
|
||||
```
|
||||
|
||||
归并排序
|
||||
|
||||
```js
|
||||
var sort = function (arr) {
|
||||
if (arr.length <= 1) return arr;
|
||||
|
||||
let mid = parseInt(arr.length / 2);
|
||||
// 递归调用自身,拆分的数组都是排好序的,最后传入merge合并处理
|
||||
return merge(sort(arr.slice(0, mid)), sort(arr.slice(mid)));
|
||||
}
|
||||
// 将两个排好序的数组合并成一个顺序数组
|
||||
var merge = function (left, right) {
|
||||
let res = [];
|
||||
while (left.length > 0 && right.length > 0) {
|
||||
// 不断比较left和right数组的第一项,小的取出存入res
|
||||
left[0] < right[0] ? res.push(left.shift()) : res.push(right.shift());
|
||||
}
|
||||
return res.concat(left, right);
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -0,0 +1,573 @@
|
|||
# 经典回溯算法:集合划分问题
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [698. Partition to K Equal Sum Subsets](https://leetcode.com/problems/partition-to-k-equal-sum-subsets/) | [698. 划分为k个相等的子集](https://leetcode.cn/problems/partition-to-k-equal-sum-subsets/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
之前说过回溯算法是笔试中最好用的算法,只要你没什么思路,就用回溯算法暴力求解,即便不能通过所有测试用例,多少能过一点。
|
||||
|
||||
回溯算法的技巧也不难,前文 [回溯算法框架套路](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 说过,回溯算法就是穷举一棵决策树的过程,只要在递归之前「做选择」,在递归之后「撤销选择」就行了。
|
||||
|
||||
**但是,就算暴力穷举,不同的思路也有优劣之分**。
|
||||
|
||||
本文就来看一道非常经典的回溯算法问题,力扣第 698 题「划分为k个相等的子集」。这道题可以帮你更深刻理解回溯算法的思维,得心应手地写出回溯函数。
|
||||
|
||||
题目非常简单:
|
||||
|
||||
给你输入一个数组 `nums` 和一个正整数 `k`,请你判断 `nums` 是否能够被平分为元素和相同的 `k` 个子集。
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
boolean canPartitionKSubsets(int[] nums, int k);
|
||||
```
|
||||
|
||||
我们之前 [背包问题之子集划分](https://labuladong.github.io/article/fname.html?fname=背包子集) 写过一次子集划分问题,不过那道题只需要我们把集合划分成两个相等的集合,可以转化成背包问题用动态规划技巧解决。
|
||||
|
||||
> 思考题:为什么划分成两个相等的子集可以转化成背包问题用动态规划思路解决,而划分成 `k` 个相等的子集就不可以转化成背包问题,只能用回溯算法暴力穷举?请先尝试自己思考,我会在文末给出答案。
|
||||
|
||||
但是如果划分成多个相等的集合,解法一般只能通过暴力穷举,时间复杂度爆表,是练习回溯算法和递归思维的好机会。
|
||||
|
||||
### 一、思路分析
|
||||
|
||||
首先,我们回顾一下以前学过的排列组合知识:
|
||||
|
||||
1、`P(n, k)`(也有很多书写成 `A(n, k)`)表示从 `n` 个不同元素中拿出 `k` 个元素的排列(Permutation/Arrangement);`C(n, k)` 表示从 `n` 个不同元素中拿出 `k` 个元素的组合(Combination)总数。
|
||||
|
||||
2、「排列」和「组合」的主要区别在于是否考虑顺序的差异。
|
||||
|
||||
3、排列、组合总数的计算公式:
|
||||
|
||||

|
||||
|
||||
好,现在我问一个问题,这个排列公式 `P(n, k)` 是如何推导出来的?为了搞清楚这个问题,我需要讲一点组合数学的知识。
|
||||
|
||||
排列组合问题的各种变体都可以抽象成「球盒模型」,`P(n, k)` 就可以抽象成下面这个场景:
|
||||
|
||||

|
||||
|
||||
即,将 `n` 个标记了不同序号的球(标号为了体现顺序的差异),放入 `k` 个标记了不同序号的盒子中(其中 `n >= k`,每个盒子最终都装有恰好一个球),共有 `P(n, k)` 种不同的方法。
|
||||
|
||||
现在你来,往盒子里放球,你怎么放?其实有两种视角。
|
||||
|
||||
**首先,你可以站在盒子的视角**,每个盒子必然要选择一个球。
|
||||
|
||||
这样,第一个盒子可以选择 `n` 个球中的任意一个,然后你需要让剩下 `k - 1` 个盒子在 `n - 1` 个球中选择:
|
||||
|
||||

|
||||
|
||||
**另外,你也可以站在球的视角**,因为并不是每个球都会被装进盒子,所以球的视角分两种情况:
|
||||
|
||||
1、第一个球可以不装进任何一个盒子,这样的话你就需要将剩下 `n - 1` 个球放入 `k` 个盒子。
|
||||
|
||||
2、第一个球可以装进 `k` 个盒子中的任意一个,这样的话你就需要将剩下 `n - 1` 个球放入 `k - 1` 个盒子。
|
||||
|
||||
结合上述两种情况,可以得到:
|
||||
|
||||

|
||||
|
||||
你看,两种视角得到两个不同的递归式,但这两个递归式解开的结果都是我们熟知的阶乘形式:
|
||||
|
||||

|
||||
|
||||
至于如何解递归式,涉及数学的内容比较多,这里就不做深入探讨了,有兴趣的读者可以自行学习组合数学相关知识。
|
||||
|
||||
回到正题,这道算法题让我们求子集划分,子集问题和排列组合问题有所区别,但我们可以借鉴「球盒模型」的抽象,用两种不同的视角来解决这道子集划分问题。
|
||||
|
||||
把装有 `n` 个数字的数组 `nums` 分成 `k` 个和相同的集合,你可以想象将 `n` 个数字分配到 `k` 个「桶」里,最后这 `k` 个「桶」里的数字之和要相同。
|
||||
|
||||
前文 [回溯算法框架套路](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 说过,回溯算法的关键在哪里?
|
||||
|
||||
关键是要知道怎么「做选择」,这样才能利用递归函数进行穷举。
|
||||
|
||||
那么模仿排列公式的推导思路,将 `n` 个数字分配到 `k` 个桶里,我们也可以有两种视角:
|
||||
|
||||
**视角一,如果我们切换到这 `n` 个数字的视角,每个数字都要选择进入到 `k` 个桶中的某一个**。
|
||||
|
||||

|
||||
|
||||
**视角二,如果我们切换到这 `k` 个桶的视角,对于每个桶,都要遍历 `nums` 中的 `n` 个数字,然后选择是否将当前遍历到的数字装进自己这个桶里**。
|
||||
|
||||

|
||||
|
||||
你可能问,这两种视角有什么不同?
|
||||
|
||||
**用不同的视角进行穷举,虽然结果相同,但是解法代码的逻辑完全不同,进而算法的效率也会不同;对比不同的穷举视角,可以帮你更深刻地理解回溯算法,我们慢慢道来**。
|
||||
|
||||
### 二、以数字的视角
|
||||
|
||||
用 for 循环迭代遍历 `nums` 数组大家肯定都会:
|
||||
|
||||
```java
|
||||
for (int index = 0; index < nums.length; index++) {
|
||||
System.out.println(nums[index]);
|
||||
}
|
||||
```
|
||||
|
||||
递归遍历数组你会不会?其实也很简单:
|
||||
|
||||
```java
|
||||
void traverse(int[] nums, int index) {
|
||||
if (index == nums.length) {
|
||||
return;
|
||||
}
|
||||
System.out.println(nums[index]);
|
||||
traverse(nums, index + 1);
|
||||
}
|
||||
```
|
||||
|
||||
只要调用 `traverse(nums, 0)`,和 for 循环的效果是完全一样的。
|
||||
|
||||
那么回到这道题,以数字的视角,选择 `k` 个桶,用 for 循环写出来是下面这样:
|
||||
|
||||
```java
|
||||
// k 个桶(集合),记录每个桶装的数字之和
|
||||
int[] bucket = new int[k];
|
||||
|
||||
// 穷举 nums 中的每个数字
|
||||
for (int index = 0; index < nums.length; index++) {
|
||||
// 穷举每个桶
|
||||
for (int i = 0; i < k; i++) {
|
||||
// nums[index] 选择是否要进入第 i 个桶
|
||||
// ...
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
如果改成递归的形式,就是下面这段代码逻辑:
|
||||
|
||||
```java
|
||||
// k 个桶(集合),记录每个桶装的数字之和
|
||||
int[] bucket = new int[k];
|
||||
|
||||
// 穷举 nums 中的每个数字
|
||||
void backtrack(int[] nums, int index) {
|
||||
// base case
|
||||
if (index == nums.length) {
|
||||
return;
|
||||
}
|
||||
// 穷举每个桶
|
||||
for (int i = 0; i < bucket.length; i++) {
|
||||
// 选择装进第 i 个桶
|
||||
bucket[i] += nums[index];
|
||||
// 递归穷举下一个数字的选择
|
||||
backtrack(nums, index + 1);
|
||||
// 撤销选择
|
||||
bucket[i] -= nums[index];
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
虽然上述代码仅仅是穷举逻辑,还不能解决我们的问题,但是只要略加完善即可:
|
||||
|
||||
```java
|
||||
// 主函数
|
||||
boolean canPartitionKSubsets(int[] nums, int k) {
|
||||
// 排除一些基本情况
|
||||
if (k > nums.length) return false;
|
||||
int sum = 0;
|
||||
for (int v : nums) sum += v;
|
||||
if (sum % k != 0) return false;
|
||||
|
||||
// k 个桶(集合),记录每个桶装的数字之和
|
||||
int[] bucket = new int[k];
|
||||
// 理论上每个桶(集合)中数字的和
|
||||
int target = sum / k;
|
||||
// 穷举,看看 nums 是否能划分成 k 个和为 target 的子集
|
||||
return backtrack(nums, 0, bucket, target);
|
||||
}
|
||||
|
||||
// 递归穷举 nums 中的每个数字
|
||||
boolean backtrack(
|
||||
int[] nums, int index, int[] bucket, int target) {
|
||||
|
||||
if (index == nums.length) {
|
||||
// 检查所有桶的数字之和是否都是 target
|
||||
for (int i = 0; i < bucket.length; i++) {
|
||||
if (bucket[i] != target) {
|
||||
return false;
|
||||
}
|
||||
}
|
||||
// nums 成功平分成 k 个子集
|
||||
return true;
|
||||
}
|
||||
|
||||
// 穷举 nums[index] 可能装入的桶
|
||||
for (int i = 0; i < bucket.length; i++) {
|
||||
// 剪枝,桶装装满了
|
||||
if (bucket[i] + nums[index] > target) {
|
||||
continue;
|
||||
}
|
||||
// 将 nums[index] 装入 bucket[i]
|
||||
bucket[i] += nums[index];
|
||||
// 递归穷举下一个数字的选择
|
||||
if (backtrack(nums, index + 1, bucket, target)) {
|
||||
return true;
|
||||
}
|
||||
// 撤销选择
|
||||
bucket[i] -= nums[index];
|
||||
}
|
||||
|
||||
// nums[index] 装入哪个桶都不行
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
有之前的铺垫,相信这段代码是比较容易理解的,其实我们可以再做一个优化。
|
||||
|
||||
主要看 `backtrack` 函数的递归部分:
|
||||
|
||||
```java
|
||||
for (int i = 0; i < bucket.length; i++) {
|
||||
// 剪枝
|
||||
if (bucket[i] + nums[index] > target) {
|
||||
continue;
|
||||
}
|
||||
|
||||
if (backtrack(nums, index + 1, bucket, target)) {
|
||||
return true;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
**如果我们让尽可能多的情况命中剪枝的那个 if 分支,就可以减少递归调用的次数,一定程度上减少时间复杂度**。
|
||||
|
||||
如何尽可能多的命中这个 if 分支呢?要知道我们的 `index` 参数是从 0 开始递增的,也就是递归地从 0 开始遍历 `nums` 数组。
|
||||
|
||||
如果我们提前对 `nums` 数组排序,把大的数字排在前面,那么大的数字会先被分配到 `bucket` 中,对于之后的数字,`bucket[i] + nums[index]` 会更大,更容易触发剪枝的 if 条件。
|
||||
|
||||
所以可以在之前的代码中再添加一些代码:
|
||||
|
||||
```java
|
||||
boolean canPartitionKSubsets(int[] nums, int k) {
|
||||
// 其他代码不变
|
||||
// ...
|
||||
/* 降序排序 nums 数组 */
|
||||
Arrays.sort(nums);
|
||||
for (i = 0, j = nums.length - 1; i < j; i++, j--) {
|
||||
// 交换 nums[i] 和 nums[j]
|
||||
int temp = nums[i];
|
||||
nums[i] = nums[j];
|
||||
nums[j] = temp;
|
||||
}
|
||||
/*******************/
|
||||
return backtrack(nums, 0, bucket, target);
|
||||
}
|
||||
```
|
||||
|
||||
由于 Java 的语言特性,这段代码通过先升序排序再反转,达到降序排列的目的。
|
||||
|
||||
这个解法可以得到正确答案,但耗时比较多,已经无法通过所有测试用例了,接下来看看另一种视角的解法。
|
||||
|
||||
### 三、以桶的视角
|
||||
|
||||
文章开头说了,**以桶的视角进行穷举,每个桶需要遍历 `nums` 中的所有数字,决定是否把当前数字装进桶中;当装满一个桶之后,还要装下一个桶,直到所有桶都装满为止**。
|
||||
|
||||
这个思路可以用下面这段代码表示出来:
|
||||
|
||||
```java
|
||||
// 装满所有桶为止
|
||||
while (k > 0) {
|
||||
// 记录当前桶中的数字之和
|
||||
int bucket = 0;
|
||||
for (int i = 0; i < nums.length; i++) {
|
||||
// 决定是否将 nums[i] 放入当前桶中
|
||||
if (canAdd(bucket, num[i])) {
|
||||
bucket += nums[i];
|
||||
}
|
||||
if (bucket == target) {
|
||||
// 装满了一个桶,装下一个桶
|
||||
k--;
|
||||
break;
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
那么我们也可以把这个 while 循环改写成递归函数,不过比刚才略微复杂一些,首先写一个 `backtrack` 递归函数出来:
|
||||
|
||||
```java
|
||||
boolean backtrack(int k, int bucket,
|
||||
int[] nums, int start, boolean[] used, int target);
|
||||
```
|
||||
|
||||
不要被这么多参数吓到,我会一个个解释这些参数。**如果你能够透彻理解本文,也能得心应手地写出这样的回溯函数**。
|
||||
|
||||
这个 `backtrack` 函数的参数可以这样解释:
|
||||
|
||||
现在 `k` 号桶正在思考是否应该把 `nums[start]` 这个元素装进来;目前 `k` 号桶里面已经装的数字之和为 `bucket`;`used` 标志某一个元素是否已经被装到桶中;`target` 是每个桶需要达成的目标和。
|
||||
|
||||
根据这个函数定义,可以这样调用 `backtrack` 函数:
|
||||
|
||||
```java
|
||||
boolean canPartitionKSubsets(int[] nums, int k) {
|
||||
// 排除一些基本情况
|
||||
if (k > nums.length) return false;
|
||||
int sum = 0;
|
||||
for (int v : nums) sum += v;
|
||||
if (sum % k != 0) return false;
|
||||
|
||||
boolean[] used = new boolean[nums.length];
|
||||
int target = sum / k;
|
||||
// k 号桶初始什么都没装,从 nums[0] 开始做选择
|
||||
return backtrack(k, 0, nums, 0, used, target);
|
||||
}
|
||||
```
|
||||
|
||||
实现 `backtrack` 函数的逻辑之前,再重复一遍,从桶的视角:
|
||||
|
||||
1、需要遍历 `nums` 中所有数字,决定哪些数字需要装到当前桶中。
|
||||
|
||||
2、如果当前桶装满了(桶内数字和达到 `target`),则让下一个桶开始执行第 1 步。
|
||||
|
||||
下面的代码就实现了这个逻辑:
|
||||
|
||||
```java
|
||||
boolean backtrack(int k, int bucket,
|
||||
int[] nums, int start, boolean[] used, int target) {
|
||||
// base case
|
||||
if (k == 0) {
|
||||
// 所有桶都被装满了,而且 nums 一定全部用完了
|
||||
// 因为 target == sum / k
|
||||
return true;
|
||||
}
|
||||
if (bucket == target) {
|
||||
// 装满了当前桶,递归穷举下一个桶的选择
|
||||
// 让下一个桶从 nums[0] 开始选数字
|
||||
return backtrack(k - 1, 0 ,nums, 0, used, target);
|
||||
}
|
||||
|
||||
// 从 start 开始向后探查有效的 nums[i] 装入当前桶
|
||||
for (int i = start; i < nums.length; i++) {
|
||||
// 剪枝
|
||||
if (used[i]) {
|
||||
// nums[i] 已经被装入别的桶中
|
||||
continue;
|
||||
}
|
||||
if (nums[i] + bucket > target) {
|
||||
// 当前桶装不下 nums[i]
|
||||
continue;
|
||||
}
|
||||
// 做选择,将 nums[i] 装入当前桶中
|
||||
used[i] = true;
|
||||
bucket += nums[i];
|
||||
// 递归穷举下一个数字是否装入当前桶
|
||||
if (backtrack(k, bucket, nums, i + 1, used, target)) {
|
||||
return true;
|
||||
}
|
||||
// 撤销选择
|
||||
used[i] = false;
|
||||
bucket -= nums[i];
|
||||
}
|
||||
// 穷举了所有数字,都无法装满当前桶
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
**这段代码是可以得出正确答案的,但是效率很低,我们可以思考一下是否还有优化的空间**。
|
||||
|
||||
首先,在这个解法中每个桶都可以认为是没有差异的,但是我们的回溯算法却会对它们区别对待,这里就会出现重复计算的情况。
|
||||
|
||||
什么意思呢?我们的回溯算法,说到底就是穷举所有可能的组合,然后看是否能找出和为 `target` 的 `k` 个桶(子集)。
|
||||
|
||||
那么,比如下面这种情况,`target = 5`,算法会在第一个桶里面装 `1, 4`:
|
||||
|
||||

|
||||
|
||||
现在第一个桶装满了,就开始装第二个桶,算法会装入 `2, 3`:
|
||||
|
||||

|
||||
|
||||
然后以此类推,对后面的元素进行穷举,凑出若干个和为 5 的桶(子集)。
|
||||
|
||||
但问题是,如果最后发现无法凑出和为 `target` 的 `k` 个子集,算法会怎么做?
|
||||
|
||||
回溯算法会回溯到第一个桶,重新开始穷举,现在它知道第一个桶里装 `1, 4` 是不可行的,它会尝试把 `2, 3` 装到第一个桶里:
|
||||
|
||||

|
||||
|
||||
现在第一个桶装满了,就开始装第二个桶,算法会装入 `1, 4`:
|
||||
|
||||

|
||||
|
||||
好,到这里你应该看出来问题了,这种情况其实和之前的那种情况是一样的。也就是说,到这里你其实已经知道不需要再穷举了,必然凑不出来和为 `target` 的 `k` 个子集。
|
||||
|
||||
但我们的算法还是会傻乎乎地继续穷举,因为在她看来,第一个桶和第二个桶里面装的元素不一样,那这就是两种不一样的情况呀。
|
||||
|
||||
那么我们怎么让算法的智商提高,识别出这种情况,避免冗余计算呢?
|
||||
|
||||
你注意这两种情况的 `used` 数组肯定长得一样,所以 `used` 数组可以认为是回溯过程中的「状态」。
|
||||
|
||||
**所以,我们可以用一个 `memo` 备忘录,在装满一个桶时记录当前 `used` 的状态,如果当前 `used` 的状态是曾经出现过的,那就不用再继续穷举,从而起到剪枝避免冗余计算的作用**。
|
||||
|
||||
有读者肯定会问,`used` 是一个布尔数组,怎么作为键进行存储呢?这其实是小问题,比如我们可以把数组转化成字符串,这样就可以作为哈希表的键进行存储了。
|
||||
|
||||
看下代码实现,只要稍微改一下 `backtrack` 函数即可:
|
||||
|
||||
```java
|
||||
// 备忘录,存储 used 数组的状态
|
||||
HashMap<String, Boolean> memo = new HashMap<>();
|
||||
|
||||
boolean backtrack(int k, int bucket, int[] nums, int start, boolean[] used, int target) {
|
||||
// base case
|
||||
if (k == 0) {
|
||||
return true;
|
||||
}
|
||||
// 将 used 的状态转化成形如 [true, false, ...] 的字符串
|
||||
// 便于存入 HashMap
|
||||
String state = Arrays.toString(used);
|
||||
|
||||
if (bucket == target) {
|
||||
// 装满了当前桶,递归穷举下一个桶的选择
|
||||
boolean res = backtrack(k - 1, 0, nums, 0, used, target);
|
||||
// 将当前状态和结果存入备忘录
|
||||
memo.put(state, res);
|
||||
return res;
|
||||
}
|
||||
|
||||
if (memo.containsKey(state)) {
|
||||
// 如果当前状态曾今计算过,就直接返回,不要再递归穷举了
|
||||
return memo.get(state);
|
||||
}
|
||||
|
||||
// 其他逻辑不变...
|
||||
}
|
||||
```
|
||||
|
||||
这样提交解法,发现执行效率依然比较低,这次不是因为算法逻辑上的冗余计算,而是代码实现上的问题。
|
||||
|
||||
**因为每次递归都要把 `used` 数组转化成字符串,这对于编程语言来说也是一个不小的消耗,所以我们还可以进一步优化**。
|
||||
|
||||
注意题目给的数据规模 `nums.length <= 16`,也就是说 `used` 数组最多也不会超过 16,那么我们完全可以用「位图」的技巧,用一个 int 类型的 `used` 变量来替代 `used` 数组。
|
||||
|
||||
具体来说,我们可以用整数 `used` 的第 `i` 位(`(used >> i) & 1`)的 1/0 来表示 `used[i]` 的 true/false。
|
||||
|
||||
这样一来,不仅节约了空间,而且整数 `used` 也可以直接作为键存入 HashMap,省去数组转字符串的消耗。
|
||||
|
||||
看下最终的解法代码:
|
||||
|
||||
```java
|
||||
public boolean canPartitionKSubsets(int[] nums, int k) {
|
||||
// 排除一些基本情况
|
||||
if (k > nums.length) return false;
|
||||
int sum = 0;
|
||||
for (int v : nums) sum += v;
|
||||
if (sum % k != 0) return false;
|
||||
|
||||
int used = 0; // 使用位图技巧
|
||||
int target = sum / k;
|
||||
// k 号桶初始什么都没装,从 nums[0] 开始做选择
|
||||
return backtrack(k, 0, nums, 0, used, target);
|
||||
}
|
||||
|
||||
HashMap<Integer, Boolean> memo = new HashMap<>();
|
||||
|
||||
boolean backtrack(int k, int bucket,
|
||||
int[] nums, int start, int used, int target) {
|
||||
// base case
|
||||
if (k == 0) {
|
||||
// 所有桶都被装满了,而且 nums 一定全部用完了
|
||||
return true;
|
||||
}
|
||||
if (bucket == target) {
|
||||
// 装满了当前桶,递归穷举下一个桶的选择
|
||||
// 让下一个桶从 nums[0] 开始选数字
|
||||
boolean res = backtrack(k - 1, 0, nums, 0, used, target);
|
||||
// 缓存结果
|
||||
memo.put(used, res);
|
||||
return res;
|
||||
}
|
||||
|
||||
if (memo.containsKey(used)) {
|
||||
// 避免冗余计算
|
||||
return memo.get(used);
|
||||
}
|
||||
|
||||
for (int i = start; i < nums.length; i++) {
|
||||
// 剪枝
|
||||
if (((used >> i) & 1) == 1) { // 判断第 i 位是否是 1
|
||||
// nums[i] 已经被装入别的桶中
|
||||
continue;
|
||||
}
|
||||
if (nums[i] + bucket > target) {
|
||||
continue;
|
||||
}
|
||||
// 做选择
|
||||
used |= 1 << i; // 将第 i 位置为 1
|
||||
bucket += nums[i];
|
||||
// 递归穷举下一个数字是否装入当前桶
|
||||
if (backtrack(k, bucket, nums, i + 1, used, target)) {
|
||||
return true;
|
||||
}
|
||||
// 撤销选择
|
||||
used ^= 1 << i; // 使用异或运算将第 i 位恢复 0
|
||||
bucket -= nums[i];
|
||||
}
|
||||
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
至此,这道题的第二种思路也完成了。
|
||||
|
||||
### 四、最后总结
|
||||
|
||||
本文写的这两种思路都可以算出正确答案,不过第一种解法即便经过了排序优化,也明显比第二种解法慢很多,这是为什么呢?
|
||||
|
||||
我们来分析一下这两个算法的时间复杂度,假设 `nums` 中的元素个数为 `n`。
|
||||
|
||||
先说第一个解法,也就是从数字的角度进行穷举,`n` 个数字,每个数字有 `k` 个桶可供选择,所以组合出的结果个数为 `k^n`,时间复杂度也就是 `O(k^n)`。
|
||||
|
||||
第二个解法,每个桶要遍历 `n` 个数字,对每个数字有「装入」或「不装入」两种选择,所以组合的结果有 `2^n` 种;而我们有 `k` 个桶,所以总的时间复杂度为 `O(k*2^n)`。
|
||||
|
||||
**当然,这是对最坏复杂度上界的粗略估算,实际的复杂度肯定要好很多,毕竟我们添加了这么多剪枝逻辑**。不过,从复杂度的上界已经可以看出第一种思路要慢很多了。
|
||||
|
||||
所以,谁说回溯算法没有技巧性的?虽然回溯算法就是暴力穷举,但穷举也分聪明的穷举方式和低效的穷举方式,关键看你以谁的「视角」进行穷举。
|
||||
|
||||
通俗来说,我们应该尽量「少量多次」,就是说宁可多做几次选择(乘法关系),也不要给太大的选择空间(指数关系);做 `n` 次「`k` 选一」仅重复一次(`O(k^n)`),比 `n` 次「二选一」重复 `k` 次(`O(k*2^n)`)效率低很多。
|
||||
|
||||
好了,这道题我们从两种视角进行穷举,虽然代码量看起来多,但核心逻辑都是类似的,相信你通过本文能够更深刻地理解回溯算法。
|
||||
|
||||
> 文中思考题答案:为什么划分两个相等的子集可以转化成背包问题?
|
||||
|
||||
> [0-1 背包问题](https://labuladong.github.io/article/fname.html?fname=背包问题) 的场景中,有一个背包和若干物品,每个物品有**两个选择**,分别是「装进背包」和「不装进背包」。把原集合 `S` 划分成两个相等子集 `S_1, S_2` 的场景下,`S` 中的每个元素也有**两个选择**,分别是「装进 `S_1`」和「不装进 `S_1`(装进 `S_2`)」,这时候的穷举思路其实和背包问题相同。
|
||||
|
||||
> 但如果你想把 `S` 划分成 `k` 个相等的子集,相当于 `S` 中的每个元素有 **`k` 个选择**,这和标准背包问题的场景有本质区别,是无法套用背包问题的解题思路的。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [动态规划问题的两种穷举视角](https://labuladong.github.io/article/fname.html?fname=动归两种视角)
|
||||
- [谁能想到,斗地主也能玩出算法](https://labuladong.github.io/article/fname.html?fname=斗地主)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,11 +1,5 @@
|
|||
# LRU 缓存淘汰算法设计
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -15,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -348,6 +342,37 @@ class LRUCache {
|
|||
|
||||
* [手把手带你实现 LFU 算法](https://labuladong.github.io/article/fname.html?fname=LFU)
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [一文看懂 session 和 cookie](https://labuladong.github.io/article/fname.html?fname=session和cookie)
|
||||
- [常数时间删除/查找数组中的任意元素](https://labuladong.github.io/article/fname.html?fname=随机集合)
|
||||
- [数据结构设计:最大栈](https://labuladong.github.io/article/fname.html?fname=最大栈)
|
||||
- [算法就像搭乐高:带你手撸 LFU 算法](https://labuladong.github.io/article/fname.html?fname=LFU)
|
||||
- [算法笔试「骗分」套路](https://labuladong.github.io/article/fname.html?fname=刷题技巧)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer II 031. 最近最少使用缓存](https://leetcode.cn/problems/OrIXps/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,373 +0,0 @@
|
|||
# 如何运用二分查找算法
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[875.爱吃香蕉的珂珂](https://leetcode-cn.com/problems/koko-eating-bananas)
|
||||
|
||||
[1011.在D天内送达包裹的能力](https://leetcode-cn.com/problems/capacity-to-ship-packages-within-d-days)
|
||||
|
||||
**-----------**
|
||||
|
||||
二分查找到底有能运用在哪里?
|
||||
|
||||
最常见的就是教科书上的例子,在**有序数组**中搜索给定的某个目标值的索引。再推广一点,如果目标值存在重复,修改版的二分查找可以返回目标值的左侧边界索引或者右侧边界索引。
|
||||
|
||||
PS:以上提到的三种二分查找算法形式在前文「二分查找详解」有代码详解,如果没看过强烈建议看看。
|
||||
|
||||
抛开有序数组这个枯燥的数据结构,二分查找如何运用到实际的算法问题中呢?当搜索空间有序的时候,就可以通过二分搜索「剪枝」,大幅提升效率。
|
||||
|
||||
说起来玄乎得很,本文先用一个具体的「Koko 吃香蕉」的问题来举个例子。
|
||||
|
||||
### 一、问题分析
|
||||
|
||||

|
||||
|
||||
也就是说,Koko 每小时最多吃一堆香蕉,如果吃不下的话留到下一小时再吃;如果吃完了这一堆还有胃口,也只会等到下一小时才会吃下一堆。在这个条件下,让我们确定 Koko 吃香蕉的**最小速度**(根/小时)。
|
||||
|
||||
如果直接给你这个情景,你能想到哪里能用到二分查找算法吗?如果没有见过类似的问题,恐怕是很难把这个问题和二分查找联系起来的。
|
||||
|
||||
那么我们先抛开二分查找技巧,想想如何暴力解决这个问题呢?
|
||||
|
||||
首先,算法要求的是「`H` 小时内吃完香蕉的最小速度」,我们不妨称为 `speed`,请问 `speed` 最大可能为多少,最少可能为多少呢?
|
||||
|
||||
显然最少为 1,最大为 `max(piles)`,因为一小时最多只能吃一堆香蕉。那么暴力解法就很简单了,只要从 1 开始穷举到 `max(piles)`,一旦发现发现某个值可以在 `H` 小时内吃完所有香蕉,这个值就是最小速度:
|
||||
|
||||
```java
|
||||
int minEatingSpeed(int[] piles, int H) {
|
||||
// piles 数组的最大值
|
||||
int max = getMax(piles);
|
||||
for (int speed = 1; speed < max; speed++) {
|
||||
// 以 speed 是否能在 H 小时内吃完香蕉
|
||||
if (canFinish(piles, speed, H))
|
||||
return speed;
|
||||
}
|
||||
return max;
|
||||
}
|
||||
```
|
||||
|
||||
注意这个 for 循环,就是在**连续的空间线性搜索,这就是二分查找可以发挥作用的标志**。由于我们要求的是最小速度,所以可以用一个**搜索左侧边界的二分查找**来代替线性搜索,提升效率:
|
||||
|
||||
```java
|
||||
int minEatingSpeed(int[] piles, int H) {
|
||||
// 套用搜索左侧边界的算法框架
|
||||
int left = 1, right = getMax(piles) + 1;
|
||||
while (left < right) {
|
||||
// 防止溢出
|
||||
int mid = left + (right - left) / 2;
|
||||
if (canFinish(piles, mid, H)) {
|
||||
right = mid;
|
||||
} else {
|
||||
left = mid + 1;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
}
|
||||
```
|
||||
|
||||
PS:如果对于这个二分查找算法的细节问题有疑问,建议看下前文「二分查找详解」搜索左侧边界的算法模板,这里不展开了。
|
||||
|
||||
剩下的辅助函数也很简单,可以一步步拆解实现:
|
||||
|
||||
```java
|
||||
// 时间复杂度 O(N)
|
||||
boolean canFinish(int[] piles, int speed, int H) {
|
||||
int time = 0;
|
||||
for (int n : piles) {
|
||||
time += timeOf(n, speed);
|
||||
}
|
||||
return time <= H;
|
||||
}
|
||||
|
||||
int timeOf(int n, int speed) {
|
||||
return (n / speed) + ((n % speed > 0) ? 1 : 0);
|
||||
}
|
||||
|
||||
int getMax(int[] piles) {
|
||||
int max = 0;
|
||||
for (int n : piles)
|
||||
max = Math.max(n, max);
|
||||
return max;
|
||||
}
|
||||
```
|
||||
|
||||
至此,借助二分查找技巧,算法的时间复杂度为 O(NlogN)。
|
||||
|
||||
### 二、扩展延伸
|
||||
|
||||
类似的,再看一道运输问题:
|
||||
|
||||

|
||||
|
||||
要在 `D` 天内运输完所有货物,货物不可分割,如何确定运输的最小载重呢(下文称为 `cap`)?
|
||||
|
||||
其实本质上和 Koko 吃香蕉的问题一样的,首先确定 `cap` 的最小值和最大值分别为 `max(weights)` 和 `sum(weights)`。
|
||||
|
||||
我们要求**最小载重**,所以可以用搜索左侧边界的二分查找算法优化线性搜索:
|
||||
|
||||
```java
|
||||
// 寻找左侧边界的二分查找
|
||||
int shipWithinDays(int[] weights, int D) {
|
||||
// 载重可能的最小值
|
||||
int left = getMax(weights);
|
||||
// 载重可能的最大值 + 1
|
||||
int right = getSum(weights) + 1;
|
||||
while (left < right) {
|
||||
int mid = left + (right - left) / 2;
|
||||
if (canFinish(weights, D, mid)) {
|
||||
right = mid;
|
||||
} else {
|
||||
left = mid + 1;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
}
|
||||
|
||||
// 如果载重为 cap,是否能在 D 天内运完货物?
|
||||
boolean canFinish(int[] w, int D, int cap) {
|
||||
int i = 0;
|
||||
for (int day = 0; day < D; day++) {
|
||||
int maxCap = cap;
|
||||
while ((maxCap -= w[i]) >= 0) {
|
||||
i++;
|
||||
if (i == w.length)
|
||||
return true;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
```
|
||||
|
||||
通过这两个例子,你是否明白了二分查找在实际问题中的应用?
|
||||
|
||||
```java
|
||||
for (int i = 0; i < n; i++)
|
||||
if (isOK(i))
|
||||
return ans;
|
||||
```
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[875.爱吃香蕉的珂珂](https://leetcode-cn.com/problems/koko-eating-bananas)
|
||||
|
||||
[1011.在D天内送达包裹的能力](https://leetcode-cn.com/problems/capacity-to-ship-packages-within-d-days)
|
||||
|
||||
|
||||
|
||||
### c++
|
||||
[cchroot](https://github.com/cchroot) 提供 C++ 代码:
|
||||
|
||||
```c++
|
||||
class Solution {
|
||||
public:
|
||||
int minEatingSpeed(vector<int>& piles, int H) {
|
||||
// 二分法查找最小速度
|
||||
// 初始化最小速度为 1,最大速度为题目设定的最大值 10^9
|
||||
// 这里也可以遍历 piles 数组,获取数组中的最大值,设置 right 为数组中的最大值即可(因为每堆香蕉1小时吃完是最快的)
|
||||
// log2(10^9) 约等于30,次数不多,所以这里暂时就不采取遍历获取最大值了
|
||||
int left = 1, right = pow(10, 9);
|
||||
while (left < right) { // 二分法基本的防止溢出
|
||||
int mid = left + (right - left) / 2;
|
||||
// 以 mid 的速度吃香蕉,是否能在 H 小时内吃完香蕉
|
||||
if (!canFinish(piles, mid, H))
|
||||
left = mid + 1;
|
||||
else
|
||||
right = mid;
|
||||
}
|
||||
return left;
|
||||
}
|
||||
|
||||
// 以 speed 的速度是否能把香蕉吃完
|
||||
bool canFinish(vector<int>& piles, int speed, int H) {
|
||||
int time = 0;
|
||||
// 遍历累加时间 time
|
||||
for (int p: piles)
|
||||
time += (p - 1) / speed + 1;
|
||||
return time <= H; // time 小于等于 H 说明能在 H 小时吃完返回 true, 否则返回 false
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
### python
|
||||
[tonytang731](https://https://github.com/tonytang731) 提供 Python3 代码:
|
||||
|
||||
```python
|
||||
import math
|
||||
|
||||
class Solution:
|
||||
def minEatingSpeed(self, piles, H):
|
||||
# 初始化起点和终点, 最快的速度可以一次拿完最大的一堆
|
||||
start = 1
|
||||
end = max(piles)
|
||||
|
||||
# while loop进行二分查找
|
||||
while start + 1 < end:
|
||||
mid = start + (end - start) // 2
|
||||
|
||||
# 如果中点所需时间大于H, 我们需要加速, 将起点设为中点
|
||||
if self.timeH(piles, mid) > H:
|
||||
start = mid
|
||||
# 如果中点所需时间小于H, 我们需要减速, 将终点设为中点
|
||||
else:
|
||||
end = mid
|
||||
|
||||
# 提交前确认起点是否满足条件,我们要尽量慢拿
|
||||
if self.timeH(piles, start) <= H:
|
||||
return start
|
||||
|
||||
# 若起点不符合, 则中点是答案
|
||||
return end
|
||||
|
||||
|
||||
|
||||
def timeH(self, piles, K):
|
||||
# 初始化时间
|
||||
H = 0
|
||||
|
||||
#求拿每一堆需要多长时间
|
||||
for pile in piles:
|
||||
H += math.ceil(pile / K)
|
||||
|
||||
return H
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
用js写二分的时候,一定要注意使用`Math.floor((right - left) / 2)`或者`paserInt()`将结果整数化!由于js不声明变量类型,很多时候就很难发现自己浮点数、整数使用的问题。
|
||||
|
||||
[875.爱吃香蕉的珂珂](https://leetcode-cn.com/problems/koko-eating-bananas)
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} piles
|
||||
* @param {number} H
|
||||
* @return {number}
|
||||
*/
|
||||
var minEatingSpeed = function (piles, H) {
|
||||
// 套用搜索左侧边界的算法框架
|
||||
let left = 1, right = getMax(piles) + 1;
|
||||
|
||||
while (left < right) {
|
||||
// 防止溢出
|
||||
let mid = left + Math.floor((right - left) / 2);
|
||||
if (canFinish(piles, mid, H)) {
|
||||
right = mid;
|
||||
} else {
|
||||
left = mid + 1;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
};
|
||||
|
||||
// 时间复杂度 O(N)
|
||||
let canFinish = (piles, speed, H) => {
|
||||
let time = 0;
|
||||
for (let n of piles) {
|
||||
time += timeOf(n, speed);
|
||||
}
|
||||
return time <= H;
|
||||
}
|
||||
|
||||
// 计算所需时间
|
||||
let timeOf = (n, speed) => {
|
||||
return Math.floor(
|
||||
(n / speed) + ((n % speed > 0) ? 1 : 0)
|
||||
);
|
||||
}
|
||||
|
||||
let getMax = (piles) => {
|
||||
let max = 0;
|
||||
for (let n of piles) {
|
||||
max = Math.max(n, max);
|
||||
}
|
||||
return max;
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
[传送门:1011.在D天内送达包裹的能力](https://leetcode-cn.com/problems/capacity-to-ship-packages-within-d-days)
|
||||
|
||||
```js
|
||||
// 第1011题
|
||||
/**
|
||||
* @param {number[]} weights
|
||||
* @param {number} D
|
||||
* @return {number}
|
||||
*/
|
||||
// 寻找左侧边界的二分查找
|
||||
var shipWithinDays = function (weights, D) {
|
||||
// 载重可能的最小值
|
||||
let left = getMax(weights);
|
||||
|
||||
// 载重可能的最大值 + 1
|
||||
let right = getSum(weights) + 1;
|
||||
|
||||
while (left < right) {
|
||||
let mid = left + Math.floor((right - left) / 2);
|
||||
if (canFinish(weights, D, mid)) {
|
||||
right = mid;
|
||||
} else {
|
||||
left = mid + 1;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
}
|
||||
|
||||
// 如果载重为 cap,是否能在 D 天内运完货物?
|
||||
let canFinish = (w, D, cap) => {
|
||||
let i = 0;
|
||||
for (let day = 0; day < D; day++) {
|
||||
let maxCap = cap;
|
||||
while ((maxCap -= w[i]) >= 0) {
|
||||
i++;
|
||||
if (i === w.length)
|
||||
return true;
|
||||
}
|
||||
}
|
||||
return false;
|
||||
}
|
||||
|
||||
let getMax = (piles) => {
|
||||
let max = 0;
|
||||
for (let n of piles) {
|
||||
max = Math.max(n, max);
|
||||
}
|
||||
return max;
|
||||
}
|
||||
|
||||
/**
|
||||
* @param {number[]} weights
|
||||
// 获取货物总重量
|
||||
*/
|
||||
let getSum = (weights) => {
|
||||
return weights.reduce((total, cur) => {
|
||||
total += cur;
|
||||
return total
|
||||
}, 0)
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 如何k个一组反转链表
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -155,6 +151,21 @@ ListNode reverseKGroup(ListNode head, int k) {
|
|||
|
||||
> 最后打个广告,我亲自制作了一门 [数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO),以视频课为主,手把手带你实现常用的数据结构及相关算法,旨在帮助算法基础较为薄弱的读者深入理解常用数据结构的底层原理,在算法学习中少走弯路。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [东哥带你刷二叉树(思路篇)](https://labuladong.github.io/article/fname.html?fname=二叉树系列1)
|
||||
- [算法笔试「骗分」套路](https://labuladong.github.io/article/fname.html?fname=刷题技巧)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,9 +1,5 @@
|
|||
# 一行代码就能解决的算法题
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -145,6 +141,22 @@ int bulbSwitch(int n) {
|
|||
|
||||
就算有的 `n` 平方根结果是小数,强转成 int 型,也相当于一个最大整数上界,比这个上界小的所有整数,平方后的索引都是最后亮着的灯的索引。所以说我们直接把平方根转成整数,就是这个问题的答案。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [丑数系列算法详解](https://labuladong.github.io/article/fname.html?fname=丑数)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [经典动态规划:博弈问题](https://labuladong.github.io/article/fname.html?fname=动态规划之博弈问题)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,9 +1,5 @@
|
|||
# 二分查找高效判定子序列
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -230,6 +226,10 @@ int left_bound(ArrayList<Integer> arr, int target) {
|
|||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -0,0 +1,142 @@
|
|||
# 二分查找的实际运用
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [1011. Capacity To Ship Packages Within D Days](https://leetcode.com/problems/capacity-to-ship-packages-within-d-days/) | [1011. 在 D 天内送达包裹的能力](https://leetcode.cn/problems/capacity-to-ship-packages-within-d-days/) | 🟠
|
||||
| [410. Split Array Largest Sum](https://leetcode.com/problems/split-array-largest-sum/) | [410. 分割数组的最大值](https://leetcode.cn/problems/split-array-largest-sum/) | 🔴
|
||||
| [875. Koko Eating Bananas](https://leetcode.com/problems/koko-eating-bananas/) | [875. 爱吃香蕉的珂珂](https://leetcode.cn/problems/koko-eating-bananas/) | 🟠
|
||||
| - | [剑指 Offer II 073. 狒狒吃香蕉](https://leetcode.cn/problems/nZZqjQ/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
我们前文 [我写了首诗,把二分搜索变成了默写题](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 详细介绍了二分搜索的细节问题,探讨了「搜索一个元素」,「搜索左侧边界」,「搜索右侧边界」这三个情况,教你如何写出正确无 bug 的二分搜索算法。
|
||||
|
||||
**但是前文总结的二分搜索代码框架仅仅局限于「在有序数组中搜索指定元素」这个基本场景,具体的算法问题没有这么直接,可能你都很难看出这个问题能够用到二分搜索**。
|
||||
|
||||
所以本文就来总结一套二分搜索算法运用的框架套路,帮你在遇到二分搜索算法相关的实际问题时,能够有条理地思考分析,步步为营,写出答案。
|
||||
|
||||
### 原始的二分搜索代码
|
||||
|
||||
二分搜索的原型就是在「**有序数组**」中搜索一个元素 `target`,返回该元素对应的索引。
|
||||
|
||||
如果该元素不存在,那可以返回一个什么特殊值,这种细节问题只要微调算法实现就可实现。
|
||||
|
||||
还有一个重要的问题,如果「**有序数组**」中存在多个 `target` 元素,那么这些元素肯定挨在一起,这里就涉及到算法应该返回最左侧的那个 `target` 元素的索引还是最右侧的那个 `target` 元素的索引,也就是所谓的「搜索左侧边界」和「搜索右侧边界」,这个也可以通过微调算法的代码来实现。
|
||||
|
||||
**我们前文 [我写了首诗,把二分搜索变成了默写题](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 详细探讨了上述问题,对这块还不清楚的读者建议复习前文**,已经搞清楚基本二分搜索算法的读者可以继续看下去。
|
||||
|
||||
**在具体的算法问题中,常用到的是「搜索左侧边界」和「搜索右侧边界」这两种场景**,很少有让你单独「搜索一个元素」。
|
||||
|
||||
因为算法题一般都让你求最值,比如让你求吃香蕉的「最小速度」,让你求轮船的「最低运载能力」,求最值的过程,必然是搜索一个边界的过程,所以后面我们就详细分析一下这两种搜索边界的二分算法代码。
|
||||
|
||||
「搜索左侧边界」的二分搜索算法的具体代码实现如下:
|
||||
|
||||
```java
|
||||
// 搜索左侧边界
|
||||
int left_bound(int[] nums, int target) {
|
||||
if (nums.length == 0) return -1;
|
||||
int left = 0, right = nums.length;
|
||||
|
||||
while (left < right) {
|
||||
int mid = left + (right - left) / 2;
|
||||
if (nums[mid] == target) {
|
||||
// 当找到 target 时,收缩右侧边界
|
||||
right = mid;
|
||||
} else if (nums[mid] < target) {
|
||||
left = mid + 1;
|
||||
} else if (nums[mid] > target) {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
}
|
||||
```
|
||||
|
||||
假设输入的数组 `nums = [1,2,3,3,3,5,7]`,想搜索的元素 `target = 3`,那么算法就会返回索引 2。
|
||||
|
||||
如果画一个图,就是这样:
|
||||
|
||||

|
||||
|
||||
「搜索右侧边界」的二分搜索算法的具体代码实现如下:
|
||||
|
||||
```java
|
||||
// 搜索右侧边界
|
||||
int right_bound(int[] nums, int target) {
|
||||
if (nums.length == 0) return -1;
|
||||
int left = 0, right = nums.length;
|
||||
|
||||
while (left < right) {
|
||||
int mid = left + (right - left) / 2;
|
||||
if (nums[mid] == target) {
|
||||
// 当找到 target 时,收缩左侧边界
|
||||
left = mid + 1;
|
||||
} else if (nums[mid] < target) {
|
||||
left = mid + 1;
|
||||
} else if (nums[mid] > target) {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
return left - 1;
|
||||
}
|
||||
```
|
||||
|
||||
输入同上,那么算法就会返回索引 4,如果画一个图,就是这样:
|
||||
|
||||

|
||||
|
||||
好,上述内容都属于复习,我想读到这里的读者应该都能理解。记住上述的图像,所有能够抽象出上述图像的问题,都可以使用二分搜索解决。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [丑数系列算法详解](https://labuladong.github.io/article/fname.html?fname=丑数)
|
||||
- [二分搜索怎么用?我和快手面试官进行了深度探讨](https://labuladong.github.io/article/fname.html?fname=二分分割子数组)
|
||||
- [我写了首诗,把二分搜索算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=二分查找详解)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [经典动态规划:高楼扔鸡蛋](https://labuladong.github.io/article/fname.html?fname=高楼扔鸡蛋问题)
|
||||
- [讲两道常考的阶乘算法题](https://labuladong.github.io/article/fname.html?fname=阶乘题目)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [1201. Ugly Number III](https://leetcode.com/problems/ugly-number-iii/?show=1) | [1201. 丑数 III](https://leetcode.cn/problems/ugly-number-iii/?show=1) |
|
||||
| - | [剑指 Offer II 073. 狒狒吃香蕉](https://leetcode.cn/problems/nZZqjQ/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
应合作方要求,本文不便在此发布,请扫码关注回复关键词「二分」或 [点这里](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_627cce2de4b01a4851fe0ed1/1) 查看:
|
||||
|
||||

|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 如何高效判断回文链表
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -265,6 +261,23 @@ p.next = reverse(q);
|
|||
|
||||
> 最后打个广告,我亲自制作了一门 [数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO),以视频课为主,手把手带你实现常用的数据结构及相关算法,旨在帮助算法基础较为薄弱的读者深入理解常用数据结构的底层原理,在算法学习中少走弯路。
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer II 027. 回文链表](https://leetcode.cn/problems/aMhZSa/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
202
高频面试系列/合法括号判定.md
202
高频面试系列/合法括号判定.md
|
|
@ -1,202 +0,0 @@
|
|||
# 如何判定括号合法性
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[20.有效的括号](https://leetcode-cn.com/problems/valid-parentheses)
|
||||
|
||||
**-----------**
|
||||
|
||||
对括号的合法性判断是一个很常见且实用的问题,比如说我们写的代码,编辑器和编译器都会检查括号是否正确闭合。而且我们的代码可能会包含三种括号 `[](){}`,判断起来有一点难度。
|
||||
|
||||
本文就来聊一道关于括号合法性判断的算法题,相信能加深你对**栈**这种数据结构的理解。
|
||||
|
||||
题目很简单,输入一个字符串,其中包含 `[](){}` 六种括号,请你判断这个字符串组成的括号是否合法。
|
||||
|
||||
```
|
||||
Input: "()[]{}"
|
||||
Output: true
|
||||
|
||||
Input: "([)]"
|
||||
Output: false
|
||||
|
||||
Input: "{[]}"
|
||||
Output: true
|
||||
```
|
||||
|
||||
解决这个问题之前,我们先降低难度,思考一下,**如果只有一种括号 `()`**,应该如何判断字符串组成的括号是否合法呢?
|
||||
|
||||
### 一、处理一种括号
|
||||
|
||||
字符串中只有圆括号,如果想让括号字符串合法,那么必须做到:
|
||||
|
||||
**每个右括号 `)` 的左边必须有一个左括号 `(` 和它匹配**。
|
||||
|
||||
比如说字符串 `()))((` 中,中间的两个右括号**左边**就没有左括号匹配,所以这个括号组合是不合法的。
|
||||
|
||||
那么根据这个思路,我们可以写出算法:
|
||||
|
||||
```cpp
|
||||
bool isValid(string str) {
|
||||
// 待匹配的左括号数量
|
||||
int left = 0;
|
||||
for (char c : str) {
|
||||
if (c == '(')
|
||||
left++;
|
||||
else // 遇到右括号
|
||||
left--;
|
||||
|
||||
if (left < 0)
|
||||
return false;
|
||||
}
|
||||
return left == 0;
|
||||
}
|
||||
```
|
||||
|
||||
如果只有圆括号,这样就能正确判断合法性。对于三种括号的情况,我一开始想模仿这个思路,定义三个变量 `left1`,`left2`,`left3` 分别处理每种括号,虽然要多写不少 if else 分支,但是似乎可以解决问题。
|
||||
|
||||
但实际上直接照搬这种思路是不行的,比如说只有一个括号的情况下 `(())` 是合法的,但是多种括号的情况下, `[(])` 显然是不合法的。
|
||||
|
||||
仅仅记录每种左括号出现的次数已经不能做出正确判断了,我们要加大存储的信息量,可以利用栈来模仿类似的思路。
|
||||
|
||||
### 二、处理多种括号
|
||||
|
||||
栈是一种先进后出的数据结构,处理括号问题的时候尤其有用。
|
||||
|
||||
我们这道题就用一个名为 `left` 的栈代替之前思路中的 `left` 变量,**遇到左括号就入栈,遇到右括号就去栈中寻找最近的左括号,看是否匹配**。
|
||||
|
||||
```cpp
|
||||
bool isValid(string str) {
|
||||
stack<char> left;
|
||||
for (char c : str) {
|
||||
if (c == '(' || c == '{' || c == '[')
|
||||
left.push(c);
|
||||
else // 字符 c 是右括号
|
||||
if (!left.empty() && leftOf(c) == left.top())
|
||||
left.pop();
|
||||
else
|
||||
// 和最近的左括号不匹配
|
||||
return false;
|
||||
}
|
||||
// 是否所有的左括号都被匹配了
|
||||
return left.empty();
|
||||
}
|
||||
|
||||
char leftOf(char c) {
|
||||
if (c == '}') return '{';
|
||||
if (c == ')') return '(';
|
||||
return '[';
|
||||
}
|
||||
```
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[20.有效的括号](https://leetcode-cn.com/problems/valid-parentheses)
|
||||
|
||||
### python
|
||||
```python
|
||||
def isValid(self, s: str) -> bool:
|
||||
left = []
|
||||
leftOf = {
|
||||
')':'(',
|
||||
']':'[',
|
||||
'}':'{'
|
||||
}
|
||||
for c in s:
|
||||
if c in '([{':
|
||||
left.append(c)
|
||||
elif left and leftOf[c]==left[-1]: # 右括号 + left不为空 + 和最近左括号能匹配
|
||||
left.pop()
|
||||
else: # 右括号 + (left为空 / 和堆顶括号不匹配)
|
||||
return False
|
||||
|
||||
# left中所有左括号都被匹配则return True 反之False
|
||||
return not left
|
||||
```
|
||||
|
||||
|
||||
|
||||
### java
|
||||
|
||||
```java
|
||||
//基本思想:每次遇到左括号时都将相对应的右括号')',']'或'}'推入堆栈
|
||||
//如果在字符串中出现右括号,则需要检查堆栈是否为空,以及顶部元素是否与该右括号相同。如果不是,则该字符串无效。
|
||||
//最后,我们还需要检查堆栈是否为空
|
||||
public boolean isValid(String s) {
|
||||
Deque<Character> stack = new ArrayDeque<>();
|
||||
for(char c : s.toCharArray()){
|
||||
//是左括号就将相对应的右括号入栈
|
||||
if(c=='(') {
|
||||
stack.offerLast(')');
|
||||
}else if(c=='{'){
|
||||
stack.offerLast('}');
|
||||
}else if(c=='['){
|
||||
stack.offerLast(']');
|
||||
}else if(stack.isEmpty() || stack.pollLast()!=c){//出现右括号,检查堆栈是否为空,以及顶部元素是否与该右括号相同
|
||||
return false;
|
||||
}
|
||||
}
|
||||
return stack.isEmpty();
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {string} s是
|
||||
* @return {boolean}
|
||||
*/
|
||||
var isValid = function (s) {
|
||||
let left = []
|
||||
for (let c of s) {
|
||||
if (c === '(' || c === '{' || c === '[') {
|
||||
left.push(c);
|
||||
} else {
|
||||
// 字符c是右括号
|
||||
//出现右括号,检查堆栈是否为空,以及顶部元素是否与该右括号相同
|
||||
if (left.length !== 0 && leftOf(c) === left[left.length - 1]) {
|
||||
left.pop();
|
||||
} else {
|
||||
// 和最近的左括号不匹配
|
||||
return false;
|
||||
}
|
||||
}
|
||||
}
|
||||
return left.length === 0;
|
||||
};
|
||||
|
||||
|
||||
let leftOf = function (c) {
|
||||
if (c === '}') return '{';
|
||||
if (c === ')') return '(';
|
||||
return '[';
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
|
@ -0,0 +1,274 @@
|
|||
# 众里寻他千百度:找网红算法
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [277. Find the Celebrity](https://leetcode.com/problems/find-the-celebrity/)🔒 | [277. 搜寻名人](https://leetcode.cn/problems/find-the-celebrity/)🔒 | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
今天来讨论经典的「名流问题」:
|
||||
|
||||
给你 `n` 个人的社交关系(你知道任意两个人之间是否认识),然后请你找出这些人中的「名人」。
|
||||
|
||||
所谓「名人」有两个条件:
|
||||
|
||||
1、所有其他人都认识「名人」。
|
||||
|
||||
2、「名人」不认识任何其他人。
|
||||
|
||||
这是一个图相关的算法问题,社交关系嘛,本质上就可以抽象成一幅图。
|
||||
|
||||
如果把每个人看做图中的节点,「认识」这种关系看做是节点之间的有向边,那么名人就是这幅图中一个特殊的节点:
|
||||
|
||||

|
||||
|
||||
**这个节点没有一条指向其他节点的有向边;且其他所有节点都有一条指向这个节点的有向边**。
|
||||
|
||||
或者说的专业一点,名人节点的出度为 0,入度为 `n - 1`。
|
||||
|
||||
那么,这 `n` 个人的社交关系是如何表示的呢?
|
||||
|
||||
前文 [图论算法基础](https://labuladong.github.io/article/fname.html?fname=图) 说过,图有两种存储形式,一种是邻接表,一种是邻接矩阵,邻接表的主要优势是节约存储空间;邻接矩阵的主要优势是可以迅速判断两个节点是否相邻。
|
||||
|
||||
对于名人问题,显然会经常需要判断两个人之间是否认识,也就是两个节点是否相邻,所以我们可以用邻接矩阵来表示人和人之间的社交关系。
|
||||
|
||||
那么,把名流问题描述成算法的形式就是这样的:
|
||||
|
||||
给你输入一个大小为 `n x n` 的二维数组(邻接矩阵) `graph` 表示一幅有 `n` 个节点的图,每个人都是图中的一个节点,编号为 `0` 到 `n - 1`。
|
||||
|
||||
如果 `graph[i][j] == 1` 代表第 `i` 个人认识第 `j` 个人,如果 `graph[i][j] == 0` 代表第 `i` 个人不认识第 `j` 个人。
|
||||
|
||||
有了这幅图表示人与人之间的关系,请你计算,这 `n` 个人中,是否存在「名人」?
|
||||
|
||||
如果存在,算法返回这个名人的编号,如果不存在,算法返回 -1。
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int findCelebrity(int[][] graph);
|
||||
```
|
||||
|
||||
比如输入的邻接矩阵长这样:
|
||||
|
||||

|
||||
|
||||
那么算法应该返回 2。
|
||||
|
||||
力扣第 277 题「搜寻名人」就是这个经典问题,不过并不是直接把邻接矩阵传给你,而是只告诉你总人数 `n`,同时提供一个 API `knows` 来查询人和人之间的社交关系:
|
||||
|
||||
```java
|
||||
// 可以直接调用,能够返回 i 是否认识 j
|
||||
boolean knows(int i, int j);
|
||||
|
||||
// 请你实现:返回「名人」的编号
|
||||
int findCelebrity(int n) {
|
||||
// todo
|
||||
}
|
||||
```
|
||||
|
||||
很明显,`knows` API 本质上还是在访问邻接矩阵。为了简单起见,我们后面就按力扣的题目形式来探讨一下这个经典问题。
|
||||
|
||||
### 暴力解法
|
||||
|
||||
我们拍拍脑袋就能写出一个简单粗暴的算法:
|
||||
|
||||
```java
|
||||
int findCelebrity(int n) {
|
||||
for (int cand = 0; cand < n; cand++) {
|
||||
int other;
|
||||
for (other = 0; other < n; other++) {
|
||||
if (cand == other) continue;
|
||||
// 保证其他人都认识 cand,且 cand 不认识任何其他人
|
||||
// 否则 cand 就不可能是名人
|
||||
if (knows(cand, other) || !knows(other, cand)) {
|
||||
break;
|
||||
}
|
||||
}
|
||||
if (other == n) {
|
||||
// 找到名人
|
||||
return cand;
|
||||
}
|
||||
}
|
||||
// 没有一个人符合名人特性
|
||||
return -1;
|
||||
}
|
||||
```
|
||||
|
||||
`cand` 是候选人(candidate)的缩写,我们的暴力算法就是从头开始穷举,把每个人都视为候选人,判断是否符合「名人」的条件。
|
||||
|
||||
刚才也说了,`knows` 函数底层就是在访问一个二维的邻接矩阵,一次调用的时间复杂度是 O(1),所以这个暴力解法整体的最坏时间复杂度是 O(N^2)。
|
||||
|
||||
那么,是否有其他高明的办法来优化时间复杂度呢?其实是有优化空间的,你想想,我们现在最耗时的地方在哪里?
|
||||
|
||||
对于每一个候选人 `cand`,我们都要用一个内层 for 循环去判断这个 `cand` 到底符不符合「名人」的条件。
|
||||
|
||||
这个内层 for 循环看起来就蠢,虽然判断一个人「是名人」必须用一个 for 循环,但判断一个人「不是名人」就不用这么麻烦了。
|
||||
|
||||
**因为「名人」的定义保证了「名人」的唯一性,所以我们可以利用排除法,先排除那些显然不是「名人」的人,从而避免 for 循环的嵌套,降低时间复杂度**。
|
||||
|
||||
### 优化解法
|
||||
|
||||
我再重复一遍所谓「名人」的定义:
|
||||
|
||||
1、所有其他人都认识名人。
|
||||
|
||||
2、名人不认识任何其他人。
|
||||
|
||||
这个定义就很有意思,它保证了人群中最多有一个名人。
|
||||
|
||||
这很好理解,如果有两个人同时是名人,那么这两条定义就自相矛盾了。
|
||||
|
||||
**换句话说,只要观察任意两个候选人的关系,我一定能确定其中的一个人不是名人,把他排除**。
|
||||
|
||||
至于另一个候选人是不是名人,只看两个人的关系肯定是不能确定的,但这不重要,重要的是排除掉一个必然不是名人的候选人,缩小了包围圈。
|
||||
|
||||
这是优化的核心,也是比较难理解的,所以我们先来说说为什么观察任意两个候选人的关系,就能排除掉一个。
|
||||
|
||||
你想想,两个人之间的关系可能是什么样的?
|
||||
|
||||
无非就是四种:你认识我我不认识你,我认识你你不认识我,咱俩互相认识,咱两互相不认识。
|
||||
|
||||
如果把人比作节点,红色的有向边表示不认识,绿色的有向边表示认识,那么两个人的关系无非是如下四种情况:
|
||||
|
||||

|
||||
|
||||
不妨认为这两个人的编号分别是 `cand` 和 `other`,然后我们逐一分析每种情况,看看怎么排除掉一个人。
|
||||
|
||||
对于情况一,`cand` 认识 `other`,所以 `cand` 肯定不是名人,排除。因为名人不可能认识别人。
|
||||
|
||||
对于情况二,`other` 认识 `cand`,所以 `other` 肯定不是名人,排除。
|
||||
|
||||
对于情况三,他俩互相认识,肯定都不是名人,可以随便排除一个。
|
||||
|
||||
对于情况四,他俩互不认识,肯定都不是名人,可以随便排除一个。因为名人应该被所有其他人认识。
|
||||
|
||||
综上,只要观察任意两个之间的关系,就至少能确定一个人不是名人,上述情况判断可以用如下代码表示:
|
||||
|
||||
```java
|
||||
if (knows(cand, other) || !knows(other, cand)) {
|
||||
// cand 不可能是名人
|
||||
} else {
|
||||
// other 不可能是名人
|
||||
}
|
||||
```
|
||||
|
||||
如果能够理解这一个特点,那么写出优化解法就简单了。
|
||||
|
||||
**我们可以不断从候选人中选两个出来,然后排除掉一个,直到最后只剩下一个候选人,这时候再使用一个 for 循环判断这个候选人是否是货真价实的「名人」**。
|
||||
|
||||
这个思路的完整代码如下:
|
||||
|
||||
```java
|
||||
int findCelebrity(int n) {
|
||||
if (n == 1) return 0;
|
||||
// 将所有候选人装进队列
|
||||
LinkedList<Integer> q = new LinkedList<>();
|
||||
for (int i = 0; i < n; i++) {
|
||||
q.addLast(i);
|
||||
}
|
||||
// 一直排除,直到只剩下一个候选人停止循环
|
||||
while (q.size() >= 2) {
|
||||
// 每次取出两个候选人,排除一个
|
||||
int cand = q.removeFirst();
|
||||
int other = q.removeFirst();
|
||||
if (knows(cand, other) || !knows(other, cand)) {
|
||||
// cand 不可能是名人,排除,让 other 归队
|
||||
q.addFirst(other);
|
||||
} else {
|
||||
// other 不可能是名人,排除,让 cand 归队
|
||||
q.addFirst(cand);
|
||||
}
|
||||
}
|
||||
|
||||
// 现在排除得只剩一个候选人,判断他是否真的是名人
|
||||
int cand = q.removeFirst();
|
||||
for (int other = 0; other < n; other++) {
|
||||
if (other == cand) {
|
||||
continue;
|
||||
}
|
||||
// 保证其他人都认识 cand,且 cand 不认识任何其他人
|
||||
if (!knows(other, cand) || knows(cand, other)) {
|
||||
return -1;
|
||||
}
|
||||
}
|
||||
// cand 是名人
|
||||
return cand;
|
||||
}
|
||||
```
|
||||
|
||||
这个算法避免了嵌套 for 循环,时间复杂度降为 O(N) 了,不过引入了一个队列来存储候选人集合,使用了 O(N) 的空间复杂度。
|
||||
|
||||
> PS:`LinkedList` 的作用只是充当一个容器把候选人装起来,每次找出两个进行比较和淘汰,但至于具体找出哪两个,都是无所谓的,也就是说候选人归队的顺序无所谓,我们用的是 `addFirst` 只是方便后续的优化,你完全可以用 `addLast`,结果都是一样的。
|
||||
|
||||
是否可以进一步优化,把空间复杂度也优化掉?
|
||||
|
||||
### 最终解法
|
||||
|
||||
如果你能够理解上面的优化解法,其实可以不需要额外的空间解决这个问题,代码如下:
|
||||
|
||||
```java
|
||||
int findCelebrity(int n) {
|
||||
// 先假设 cand 是名人
|
||||
int cand = 0;
|
||||
for (int other = 1; other < n; other++) {
|
||||
if (!knows(other, cand) || knows(cand, other)) {
|
||||
// cand 不可能是名人,排除
|
||||
// 假设 other 是名人
|
||||
cand = other;
|
||||
} else {
|
||||
// other 不可能是名人,排除
|
||||
// 什么都不用做,继续假设 cand 是名人
|
||||
}
|
||||
}
|
||||
|
||||
// 现在的 cand 是排除的最后结果,但不能保证一定是名人
|
||||
for (int other = 0; other < n; other++) {
|
||||
if (cand == other) continue;
|
||||
// 需要保证其他人都认识 cand,且 cand 不认识任何其他人
|
||||
if (!knows(other, cand) || knows(cand, other)) {
|
||||
return -1;
|
||||
}
|
||||
}
|
||||
|
||||
return cand;
|
||||
}
|
||||
```
|
||||
|
||||
我们之前的解法用到了 `LinkedList` 充当一个队列,用于存储候选人集合,而这个优化解法利用 `other` 和 `cand` 的交替变化,模拟了我们之前操作队列的过程,避免了使用额外的存储空间。
|
||||
|
||||
现在,解决名人问题的解法时间复杂度为 O(N),空间复杂度为 O(1),已经是最优解法了。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,190 +0,0 @@
|
|||
# 如何去除有序数组的重复元素
|
||||
|
||||
我们知道对于数组来说,在尾部插入、删除元素是比较高效的,时间复杂度是 O(1),但是如果在中间或者开头插入、删除元素,就会涉及数据的搬移,时间复杂度为 O(N),效率较低。
|
||||
|
||||
所以对于一般处理数组的算法问题,我们要尽可能只对数组尾部的元素进行操作,以避免额外的时间复杂度。
|
||||
|
||||
这篇文章讲讲如何对一个有序数组去重,先看下题目:
|
||||
|
||||

|
||||
|
||||
显然,由于数组已经排序,所以重复的元素一定连在一起,找出它们并不难,但如果毎找到一个重复元素就立即删除它,就是在数组中间进行删除操作,整个时间复杂度是会达到 O(N^2)。而且题目要求我们原地修改,也就是说不能用辅助数组,空间复杂度得是 O(1)。
|
||||
|
||||
其实,**对于数组相关的算法问题,有一个通用的技巧:要尽量避免在中间删除元素,那我就先想办法把这个元素换到最后去**。这样的话,最终待删除的元素都拖在数组尾部,一个一个 pop 掉就行了,每次操作的时间复杂度也就降低到 O(1) 了。
|
||||
|
||||
按照这个思路呢,又可以衍生出解决类似需求的通用方式:双指针技巧。具体一点说,应该是快慢指针。
|
||||
|
||||
我们让慢指针 `slow` 走左后面,快指针 `fast` 走在前面探路,找到一个不重复的元素就告诉 `slow` 并让 `slow` 前进一步。这样当 `fast` 指针遍历完整个数组 `nums` 后,**`nums[0..slow]` 就是不重复元素,之后的所有元素都是重复元素**。
|
||||
|
||||
```java
|
||||
int removeDuplicates(int[] nums) {
|
||||
int n = nums.length;
|
||||
if (n == 0) return 0;
|
||||
int slow = 0, fast = 1;
|
||||
while (fast < n) {
|
||||
if (nums[fast] != nums[slow]) {
|
||||
slow++;
|
||||
// 维护 nums[0..slow] 无重复
|
||||
nums[slow] = nums[fast];
|
||||
}
|
||||
fast++;
|
||||
}
|
||||
// 长度为索引 + 1
|
||||
return slow + 1;
|
||||
}
|
||||
```
|
||||
|
||||
看下算法执行的过程:
|
||||
|
||||

|
||||
|
||||
再简单扩展一下,如果给你一个有序链表,如何去重呢?其实和数组是一模一样的,唯一的区别是把数组赋值操作变成操作指针而已:
|
||||
|
||||
```java
|
||||
ListNode deleteDuplicates(ListNode head) {
|
||||
if (head == null) return null;
|
||||
ListNode slow = head, fast = head.next;
|
||||
while (fast != null) {
|
||||
if (fast.val != slow.val) {
|
||||
// nums[slow] = nums[fast];
|
||||
slow.next = fast;
|
||||
// slow++;
|
||||
slow = slow.next;
|
||||
}
|
||||
// fast++
|
||||
fast = fast.next;
|
||||
}
|
||||
// 断开与后面重复元素的连接
|
||||
slow.next = null;
|
||||
return head;
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
|
||||
======其他语言代码======
|
||||
|
||||
[26. 删除排序数组中的重复项](https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/)
|
||||
|
||||
[83. 删除排序链表中的重复元素](https://leetcode-cn.com/problems/remove-duplicates-from-sorted-list/)
|
||||
|
||||
### python
|
||||
|
||||
[eric wang](https://www.github.com/eric496) 提供有序数组 Python3 代码
|
||||
|
||||
```python
|
||||
def removeDuplicates(self, nums: List[int]) -> int:
|
||||
n = len(nums)
|
||||
|
||||
if n == 0:
|
||||
return 0
|
||||
|
||||
slow, fast = 0, 1
|
||||
|
||||
while fast < n:
|
||||
if nums[fast] != nums[slow]:
|
||||
slow += 1
|
||||
nums[slow] = nums[fast]
|
||||
|
||||
fast += 1
|
||||
|
||||
return slow + 1
|
||||
```
|
||||
|
||||
[eric wang](https://www.github.com/eric496) 提供有序链表 Python3 代码
|
||||
|
||||
```python
|
||||
def deleteDuplicates(self, head: ListNode) -> ListNode:
|
||||
if not head:
|
||||
return head
|
||||
|
||||
slow, fast = head, head.next
|
||||
|
||||
while fast:
|
||||
if fast.val != slow.val:
|
||||
slow.next = fast
|
||||
slow = slow.next
|
||||
|
||||
fast = fast.next
|
||||
|
||||
# 断开与后面重复元素的连接
|
||||
slow.next = None
|
||||
return head
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
[26. 删除排序数组中的重复项](https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/)
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @return {number}
|
||||
*/
|
||||
var removeDuplicates = function(nums) {
|
||||
let n = nums.length;
|
||||
if (n === 0) return 0;
|
||||
if (n === 1) return 1;
|
||||
let slow = 0, fast = 1;
|
||||
while (fast < n) {
|
||||
if (nums[fast] !== nums[slow]) {
|
||||
slow++;
|
||||
// 维护nums[0...slow]无重复
|
||||
nums[slow] = nums[fast];
|
||||
}
|
||||
fast++;
|
||||
}
|
||||
|
||||
// 长度为索引+1
|
||||
return slow + 1;
|
||||
};
|
||||
```
|
||||
|
||||
[83. 删除排序链表中的重复元素](https://leetcode-cn.com/problems/remove-duplicates-from-sorted-list/)
|
||||
|
||||
```js
|
||||
/**
|
||||
* Definition for singly-linked list.
|
||||
* function ListNode(val, next) {
|
||||
* this.val = (val===undefined ? 0 : val)
|
||||
* this.next = (next===undefined ? null : next)
|
||||
* }
|
||||
*/
|
||||
/**
|
||||
* @param {ListNode} head
|
||||
* @return {ListNode}
|
||||
*/
|
||||
var deleteDuplicates = function (head) {
|
||||
if (head == null) return null;
|
||||
let slow = head, fast = head.next;
|
||||
while (fast != null) {
|
||||
if(fast.val !== slow.val){
|
||||
// nums[slow] = nums[fast];
|
||||
slow.next = fast;
|
||||
// slow++;
|
||||
slow = slow.next;
|
||||
}
|
||||
|
||||
// fast++
|
||||
fast = fast.next;
|
||||
}
|
||||
|
||||
// 断开与后面重复元素的连接
|
||||
slow.next = null;
|
||||
return head;
|
||||
}
|
||||
```
|
||||
|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 一文秒杀所有排列组合子集问题
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -922,6 +918,43 @@ void backtrack(int[] nums) {
|
|||
|
||||
如果你能够看到这里,真得给你鼓掌,相信你以后遇到各种乱七八糟的算法题,也能一眼看透它们的本质,以不变应万变。另外,考虑到篇幅,本文并没有对这些算法进行复杂度的分析,你可以使用我在 [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度) 讲到的复杂度分析方法尝试自己分析它们的复杂度。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [两种思路解决单词拼接问题](https://labuladong.github.io/article/fname.html?fname=单词拼接)
|
||||
- [分治算法详解:运算优先级](https://labuladong.github.io/article/fname.html?fname=分治算法)
|
||||
- [回溯算法解题套路框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版)
|
||||
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
|
||||
- [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [17. Letter Combinations of a Phone Number](https://leetcode.com/problems/letter-combinations-of-a-phone-number/?show=1) | [17. 电话号码的字母组合](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/?show=1) |
|
||||
| [491. Increasing Subsequences](https://leetcode.com/problems/increasing-subsequences/?show=1) | [491. 递增子序列](https://leetcode.cn/problems/increasing-subsequences/?show=1) |
|
||||
| - | [剑指 Offer 38. 字符串的排列](https://leetcode.cn/problems/zi-fu-chuan-de-pai-lie-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 079. 所有子集](https://leetcode.cn/problems/TVdhkn/?show=1) |
|
||||
| - | [剑指 Offer II 080. 含有 k 个元素的组合](https://leetcode.cn/problems/uUsW3B/?show=1) |
|
||||
| - | [剑指 Offer II 081. 允许重复选择元素的组合](https://leetcode.cn/problems/Ygoe9J/?show=1) |
|
||||
| - | [剑指 Offer II 083. 没有重复元素集合的全排列](https://leetcode.cn/problems/VvJkup/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -0,0 +1,202 @@
|
|||
# 扫描线技巧解决会议室安排问题
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [253. Meeting Rooms II](https://leetcode.com/problems/meeting-rooms-ii/)🔒 | [253. 会议室 II](https://leetcode.cn/problems/meeting-rooms-ii/)🔒 | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
之前面试,被问到一道非常经典且非常实用的算法题目:会议室安排问题。
|
||||
|
||||
力扣上类似的问题是会员题目,你可能没办法做,但对于这种经典的算法题,掌握思路还是必要的。
|
||||
|
||||
先说下题目,力扣第 253 题「会议室 II」:
|
||||
|
||||
给你输入若干形如 `[begin, end]` 的区间,代表若干会议的开始时间和结束时间,请你计算至少需要申请多少间会议室。
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
// 返回需要申请的会议室数量
|
||||
int minMeetingRooms(int[][] meetings);
|
||||
```
|
||||
|
||||
比如给你输入 `meetings = [[0,30],[5,10],[15,20]]`,算法应该返回 2,因为后两个会议和第一个会议时间是冲突的,至少申请两个会议室才能让所有会议顺利进行。
|
||||
|
||||
如果会议之间的时间有重叠,那就得额外申请会议室来开会,想求至少需要多少间会议室,就是让你计算同一时刻最多有多少会议在同时进行。
|
||||
|
||||
换句话说,**如果把每个会议的起始时间看做一个线段区间,那么题目就是让你求最多有几个重叠区间**,仅此而已。
|
||||
|
||||
对于这种时间安排的问题,本质上讲就是区间调度问题,十有八九得排序,然后找规律来解决。
|
||||
|
||||
### 题目延伸
|
||||
|
||||
我们之前写过很多区间调度相关的文章,这里就顺便帮大家梳理一下这类问题的思路:
|
||||
|
||||
**第一个场景**,假设现在只有一个会议室,还有若干会议,你如何将尽可能多的会议安排到这个会议室里?
|
||||
|
||||
这个问题需要将这些会议(区间)按结束时间(右端点)排序,然后进行处理,详见前文 [贪心算法做时间管理](https://labuladong.github.io/article/fname.html?fname=贪心算法之区间调度问题)。
|
||||
|
||||
**第二个场景**,给你若干较短的视频片段,和一个较长的视频片段,请你从较短的片段中尽可能少地挑出一些片段,拼接出较长的这个片段。
|
||||
|
||||
这个问题需要将这些视频片段(区间)按开始时间(左端点)排序,然后进行处理,详见前文 [剪视频剪出一个贪心算法](https://labuladong.github.io/article/fname.html?fname=剪视频)。
|
||||
|
||||
**第三个场景**,给你若干区间,其中可能有些区间比较短,被其他区间完全覆盖住了,请你删除这些被覆盖的区间。
|
||||
|
||||
这个问题需要将这些区间按左端点排序,然后就能找到并删除那些被完全覆盖的区间了,详见前文 [删除覆盖区间](https://labuladong.github.io/article/fname.html?fname=区间问题合集)。
|
||||
|
||||
**第四个场景**,给你若干区间,请你将所有有重叠部分的区间进行合并。
|
||||
|
||||
这个问题需要将这些区间按左端点排序,方便找出存在重叠的区间,详见前文 [合并重叠区间](https://labuladong.github.io/article/fname.html?fname=区间问题合集)。
|
||||
|
||||
**第五个场景**,有两个部门同时预约了同一个会议室的若干时间段,请你计算会议室的冲突时段。
|
||||
|
||||
这个问题就是给你两组区间列表,请你找出这两组区间的交集,这需要你将这些区间按左端点排序,详见前文 [区间交集问题](https://labuladong.github.io/article/fname.html?fname=区间问题合集)。
|
||||
|
||||
**第六个场景**,假设现在只有一个会议室,还有若干会议,如何安排会议才能使这个会议室的闲置时间最少?
|
||||
|
||||
这个问题需要动动脑筋,说白了这就是个 0-1 背包问题的变形:
|
||||
|
||||
会议室可以看做一个背包,每个会议可以看做一个物品,物品的价值就是会议的时长,请问你如何选择物品(会议)才能最大化背包中的价值(会议室的使用时长)?
|
||||
|
||||
当然,这里背包的约束不是一个最大重量,而是各个物品(会议)不能互相冲突。把各个会议按照结束时间进行排序,然后参考前文 [0-1 背包问题详解](https://labuladong.github.io/article/fname.html?fname=背包问题) 的思路即可解决,等我以后有机会可以写一写这个问题。
|
||||
|
||||
**第七个场景**,就是本文想讲的场景,给你若干会议,让你合理申请会议室。
|
||||
|
||||
好了,举例了这么多,来看看今天的这个问题如何解决。
|
||||
|
||||
### 题目分析
|
||||
|
||||
重复一下题目的本质:
|
||||
|
||||
**给你输入若干时间区间,让你计算同一时刻「最多」有几个区间重叠**。
|
||||
|
||||
题目的关键点在于,给你任意一个时刻,你是否能够说出这个时刻有几个会议?
|
||||
|
||||
如果可以做到,那我遍历所有的时刻,找个最大值,就是需要申请的会议室数量。
|
||||
|
||||
有没有一种数据结构或者算法,给我输入若干区间,我能知道每个位置有多少个区间重叠?
|
||||
|
||||
老读者肯定可以联想到之前说过的一个算法技巧:[差分数组技巧](https://labuladong.github.io/article/fname.html?fname=差分技巧)。
|
||||
|
||||
把时间线想象成一个初始值为 0 的数组,每个时间区间 `[i, j]` 就相当于一个子数组,这个时间区间有一个会议,那我就把这个子数组中的元素都加一。
|
||||
|
||||
最后,每个时刻有几个会议我不就知道了吗?我遍历整个数组,不就知道至少需要几间会议室了吗?
|
||||
|
||||
举例来说,如果输入 `meetings = [[0,30],[5,10],[15,20]]`,那么我们就给数组中 `[0,30],[5,10],[15,20]` 这几个索引区间分别加一,最后遍历数组,求个最大值就行了。
|
||||
|
||||
还记得吗,差分数组技巧可以在 O(1) 时间对整个区间的元素进行加减,所以可以拿来解决这道题。
|
||||
|
||||
不过,这个解法的效率不算高,所以我这里不准备具体写差分数组的解法,参照 [差分数组技巧](https://labuladong.github.io/article/fname.html?fname=差分技巧) 的原理,有兴趣的读者可以自己尝试去实现。
|
||||
|
||||
**基于差分数组的思路,我们可以推导出一种更高效,更优雅的解法**。
|
||||
|
||||
我们首先把这些会议的时间区间进行投影:
|
||||
|
||||

|
||||
|
||||
红色的点代表每个会议的开始时间点,绿色的点代表每个会议的结束时间点。
|
||||
|
||||
现在假想有一条带着计数器的线,在时间线上从左至右进行扫描,每遇到红色的点,计数器 `count` 加一,每遇到绿色的点,计数器 `count` 减一:
|
||||
|
||||

|
||||
|
||||
**这样一来,每个时刻有多少个会议在同时进行,就是计数器 `count` 的值,`count` 的最大值,就是需要申请的会议室数量**。
|
||||
|
||||
对差分数组技巧熟悉的读者一眼就能看出来了,这个扫描线其实就是差分数组的遍历过程,所以我们说这是差分数组技巧衍生出来的解法。
|
||||
|
||||
### 代码实现
|
||||
|
||||
那么,如何写代码实现这个扫描的过程呢?
|
||||
|
||||
首先,对区间进行投影,就相当于对每个区间的起点和终点分别进行排序:
|
||||
|
||||

|
||||
|
||||
```java
|
||||
int minMeetingRooms(int[][] meetings) {
|
||||
int n = meetings.length;
|
||||
int[] begin = new int[n];
|
||||
int[] end = new int[n];
|
||||
// 把左端点和右端点单独拿出来
|
||||
for(int i = 0; i < n; i++) {
|
||||
begin[i] = meetings[i][0];
|
||||
end[i] = meetings[i][1];
|
||||
}
|
||||
// 排序后就是图中的红点
|
||||
Arrays.sort(begin);
|
||||
// 排序后就是图中的绿点
|
||||
Arrays.sort(end);
|
||||
|
||||
// ...
|
||||
}
|
||||
```
|
||||
|
||||
然后就简单了,扫描线从左向右前进,遇到红点就对计数器加一,遇到绿点就对计数器减一,计数器 `count` 的最大值就是答案:
|
||||
|
||||
```java
|
||||
int minMeetingRooms(int[][] meetings) {
|
||||
int n = meetings.length;
|
||||
int[] begin = new int[n];
|
||||
int[] end = new int[n];
|
||||
for(int i = 0; i < n; i++) {
|
||||
begin[i] = meetings[i][0];
|
||||
end[i] = meetings[i][1];
|
||||
}
|
||||
Arrays.sort(begin);
|
||||
Arrays.sort(end);
|
||||
|
||||
// 扫描过程中的计数器
|
||||
int count = 0;
|
||||
// 双指针技巧
|
||||
int res = 0, i = 0, j = 0;
|
||||
while (i < n && j < n) {
|
||||
if (begin[i] < end[j]) {
|
||||
// 扫描到一个红点
|
||||
count++;
|
||||
i++;
|
||||
} else {
|
||||
// 扫描到一个绿点
|
||||
count--;
|
||||
j++;
|
||||
}
|
||||
// 记录扫描过程中的最大值
|
||||
res = Math.max(res, count);
|
||||
}
|
||||
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
这里使用的是 [双指针技巧](https://labuladong.github.io/article/fname.html?fname=双指针技巧),根据 `i, j` 的相对位置模拟扫描线前进的过程。
|
||||
|
||||
至此,这道题就做完了。当然,这个题目也可以变形,比如给你若干会议,问你 `k` 个会议室够不够用,其实你套用本文的解法代码,也可以很轻松解决。
|
||||
|
||||
接下来可阅读:
|
||||
|
||||
* [区间问题系列合集](https://labuladong.github.io/article/fname.html?fname=区间问题合集)
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -0,0 +1,534 @@
|
|||
# DFS 算法秒杀岛屿系列题目
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [1020. Number of Enclaves](https://leetcode.com/problems/number-of-enclaves/) | [1020. 飞地的数量](https://leetcode.cn/problems/number-of-enclaves/) | 🟠
|
||||
| [1254. Number of Closed Islands](https://leetcode.com/problems/number-of-closed-islands/) | [1254. 统计封闭岛屿的数目](https://leetcode.cn/problems/number-of-closed-islands/) | 🟠
|
||||
| [1905. Count Sub Islands](https://leetcode.com/problems/count-sub-islands/) | [1905. 统计子岛屿](https://leetcode.cn/problems/count-sub-islands/) | 🟠
|
||||
| [200. Number of Islands](https://leetcode.com/problems/number-of-islands/) | [200. 岛屿数量](https://leetcode.cn/problems/number-of-islands/) | 🟠
|
||||
| [694. Number of Distinct Islands](https://leetcode.com/problems/number-of-distinct-islands/)🔒 | [694. 不同岛屿的数量](https://leetcode.cn/problems/number-of-distinct-islands/)🔒 | 🟠
|
||||
| [695. Max Area of Island](https://leetcode.com/problems/max-area-of-island/) | [695. 岛屿的最大面积](https://leetcode.cn/problems/max-area-of-island/) | 🟠
|
||||
| - | [剑指 Offer II 105. 岛屿的最大面积](https://leetcode.cn/problems/ZL6zAn/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
岛屿系列算法问题是经典的面试高频题,虽然基本的问题并不难,但是这类问题有一些有意思的扩展,比如求子岛屿数量,求形状不同的岛屿数量等等,本文就来把这些问题一网打尽。
|
||||
|
||||
**岛屿系列题目的核心考点就是用 DFS/BFS 算法遍历二维数组**。
|
||||
|
||||
本文主要来讲解如何用 DFS 算法来秒杀岛屿系列题目,不过用 BFS 算法的核心思路是完全一样的,无非就是把 DFS 改写成 BFS 而已。
|
||||
|
||||
那么如何在二维矩阵中使用 DFS 搜索呢?如果你把二维矩阵中的每一个位置看做一个节点,这个节点的上下左右四个位置就是相邻节点,那么整个矩阵就可以抽象成一幅网状的「图」结构。
|
||||
|
||||
根据 [学习数据结构和算法的框架思维](https://labuladong.github.io/article/fname.html?fname=学习数据结构和算法的高效方法),完全可以根据二叉树的遍历框架改写出二维矩阵的 DFS 代码框架:
|
||||
|
||||
```java
|
||||
// 二叉树遍历框架
|
||||
void traverse(TreeNode root) {
|
||||
traverse(root.left);
|
||||
traverse(root.right);
|
||||
}
|
||||
|
||||
// 二维矩阵遍历框架
|
||||
void dfs(int[][] grid, int i, int j, boolean[][] visited) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
if (i < 0 || j < 0 || i >= m || j >= n) {
|
||||
// 超出索引边界
|
||||
return;
|
||||
}
|
||||
if (visited[i][j]) {
|
||||
// 已遍历过 (i, j)
|
||||
return;
|
||||
}
|
||||
// 进入节点 (i, j)
|
||||
visited[i][j] = true;
|
||||
dfs(grid, i - 1, j, visited); // 上
|
||||
dfs(grid, i + 1, j, visited); // 下
|
||||
dfs(grid, i, j - 1, visited); // 左
|
||||
dfs(grid, i, j + 1, visited); // 右
|
||||
}
|
||||
```
|
||||
|
||||
因为二维矩阵本质上是一幅「图」,所以遍历的过程中需要一个 `visited` 布尔数组防止走回头路,如果你能理解上面这段代码,那么搞定所有岛屿系列题目都很简单。
|
||||
|
||||
这里额外说一个处理二维数组的常用小技巧,你有时会看到使用「方向数组」来处理上下左右的遍历,和前文 [图遍历框架](https://labuladong.github.io/article/fname.html?fname=图) 的代码很类似:
|
||||
|
||||
```java
|
||||
// 方向数组,分别代表上、下、左、右
|
||||
int[][] dirs = new int[][]{{-1,0}, {1,0}, {0,-1}, {0,1}};
|
||||
|
||||
void dfs(int[][] grid, int i, int j, boolean[][] visited) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
if (i < 0 || j < 0 || i >= m || j >= n) {
|
||||
// 超出索引边界
|
||||
return;
|
||||
}
|
||||
if (visited[i][j]) {
|
||||
// 已遍历过 (i, j)
|
||||
return;
|
||||
}
|
||||
|
||||
// 进入节点 (i, j)
|
||||
visited[i][j] = true;
|
||||
// 递归遍历上下左右的节点
|
||||
for (int[] d : dirs) {
|
||||
int next_i = i + d[0];
|
||||
int next_j = j + d[1];
|
||||
dfs(grid, next_i, next_j, visited);
|
||||
}
|
||||
// 离开节点 (i, j)
|
||||
}
|
||||
```
|
||||
|
||||
这种写法无非就是用 for 循环处理上下左右的遍历罢了,你可以按照个人喜好选择写法。
|
||||
|
||||
### 岛屿数量
|
||||
|
||||
这是力扣第 200 题「岛屿数量」,最简单也是最经典的一道问题,题目会输入一个二维数组 `grid`,其中只包含 `0` 或者 `1`,`0` 代表海水,`1` 代表陆地,且假设该矩阵四周都是被海水包围着的。
|
||||
|
||||
我们说连成片的陆地形成岛屿,那么请你写一个算法,计算这个矩阵 `grid` 中岛屿的个数,函数签名如下:
|
||||
|
||||
```java
|
||||
int numIslands(char[][] grid);
|
||||
```
|
||||
|
||||
比如说题目给你输入下面这个 `grid` 有四片岛屿,算法应该返回 4:
|
||||
|
||||

|
||||
|
||||
思路很简单,关键在于如何寻找并标记「岛屿」,这就要 DFS 算法发挥作用了,我们直接看解法代码:
|
||||
|
||||
```java
|
||||
// 主函数,计算岛屿数量
|
||||
int numIslands(char[][] grid) {
|
||||
int res = 0;
|
||||
int m = grid.length, n = grid[0].length;
|
||||
// 遍历 grid
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (grid[i][j] == '1') {
|
||||
// 每发现一个岛屿,岛屿数量加一
|
||||
res++;
|
||||
// 然后使用 DFS 将岛屿淹了
|
||||
dfs(grid, i, j);
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
|
||||
// 从 (i, j) 开始,将与之相邻的陆地都变成海水
|
||||
void dfs(char[][] grid, int i, int j) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
if (i < 0 || j < 0 || i >= m || j >= n) {
|
||||
// 超出索引边界
|
||||
return;
|
||||
}
|
||||
if (grid[i][j] == '0') {
|
||||
// 已经是海水了
|
||||
return;
|
||||
}
|
||||
// 将 (i, j) 变成海水
|
||||
grid[i][j] = '0';
|
||||
// 淹没上下左右的陆地
|
||||
dfs(grid, i + 1, j);
|
||||
dfs(grid, i, j + 1);
|
||||
dfs(grid, i - 1, j);
|
||||
dfs(grid, i, j - 1);
|
||||
}
|
||||
```
|
||||
|
||||
**为什么每次遇到岛屿,都要用 DFS 算法把岛屿「淹了」呢?主要是为了省事,避免维护 `visited` 数组**。
|
||||
|
||||
因为 `dfs` 函数遍历到值为 `0` 的位置会直接返回,所以只要把经过的位置都设置为 `0`,就可以起到不走回头路的作用。
|
||||
|
||||
> PS:这类 DFS 算法还有个别名叫做 [FloodFill 算法](https://labuladong.github.io/article/fname.html?fname=FloodFill算法详解及应用),现在有没有觉得 FloodFill 这个名字还挺贴切的~
|
||||
|
||||
这个最最基本的算法问题就说到这,我们来看看后面的题目有什么花样。
|
||||
|
||||
### 封闭岛屿的数量
|
||||
|
||||
上一题说二维矩阵四周可以认为也是被海水包围的,所以靠边的陆地也算作岛屿。
|
||||
|
||||
力扣第 1254 题「统计封闭岛屿的数目」和上一题有两点不同:
|
||||
|
||||
1、用 `0` 表示陆地,用 `1` 表示海水。
|
||||
|
||||
2、让你计算「封闭岛屿」的数目。所谓「封闭岛屿」就是上下左右全部被 `1` 包围的 `0`,也就是说**靠边的陆地不算作「封闭岛屿」**。
|
||||
|
||||
函数签名如下:
|
||||
|
||||
```java
|
||||
int closedIsland(int[][] grid)
|
||||
```
|
||||
|
||||
比如题目给你输入如下这个二维矩阵:
|
||||
|
||||

|
||||
|
||||
算法返回 2,只有图中灰色部分的 `0` 是四周全都被海水包围着的「封闭岛屿」。
|
||||
|
||||
**那么如何判断「封闭岛屿」呢?其实很简单,把上一题中那些靠边的岛屿排除掉,剩下的不就是「封闭岛屿」了吗**?
|
||||
|
||||
有了这个思路,就可以直接看代码了,注意这题规定 `0` 表示陆地,用 `1` 表示海水:
|
||||
|
||||
```java
|
||||
// 主函数:计算封闭岛屿的数量
|
||||
int closedIsland(int[][] grid) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
for (int j = 0; j < n; j++) {
|
||||
// 把靠上边的岛屿淹掉
|
||||
dfs(grid, 0, j);
|
||||
// 把靠下边的岛屿淹掉
|
||||
dfs(grid, m - 1, j);
|
||||
}
|
||||
for (int i = 0; i < m; i++) {
|
||||
// 把靠左边的岛屿淹掉
|
||||
dfs(grid, i, 0);
|
||||
// 把靠右边的岛屿淹掉
|
||||
dfs(grid, i, n - 1);
|
||||
}
|
||||
// 遍历 grid,剩下的岛屿都是封闭岛屿
|
||||
int res = 0;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (grid[i][j] == 0) {
|
||||
res++;
|
||||
dfs(grid, i, j);
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
|
||||
// 从 (i, j) 开始,将与之相邻的陆地都变成海水
|
||||
void dfs(int[][] grid, int i, int j) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
if (i < 0 || j < 0 || i >= m || j >= n) {
|
||||
return;
|
||||
}
|
||||
if (grid[i][j] == 1) {
|
||||
// 已经是海水了
|
||||
return;
|
||||
}
|
||||
// 将 (i, j) 变成海水
|
||||
grid[i][j] = 1;
|
||||
// 淹没上下左右的陆地
|
||||
dfs(grid, i + 1, j);
|
||||
dfs(grid, i, j + 1);
|
||||
dfs(grid, i - 1, j);
|
||||
dfs(grid, i, j - 1);
|
||||
}
|
||||
```
|
||||
|
||||
只要提前把靠边的陆地都淹掉,然后算出来的就是封闭岛屿了。
|
||||
|
||||
> PS:处理这类岛屿题目除了 DFS/BFS 算法之外,Union Find 并查集算法也是一种可选的方法,前文 [Union Find 算法运用](https://labuladong.github.io/article/fname.html?fname=UnionFind算法详解) 就用 Union Find 算法解决了一道类似的问题。
|
||||
|
||||
这道岛屿题目的解法稍微改改就可以解决力扣第 1020 题「飞地的数量」,这题不让你求封闭岛屿的数量,而是求封闭岛屿的面积总和。
|
||||
|
||||
其实思路都是一样的,先把靠边的陆地淹掉,然后去数剩下的陆地数量就行了,注意第 1020 题中 `1` 代表陆地,`0` 代表海水:
|
||||
|
||||
```java
|
||||
int numEnclaves(int[][] grid) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
// 淹掉靠边的陆地
|
||||
for (int i = 0; i < m; i++) {
|
||||
dfs(grid, i, 0);
|
||||
dfs(grid, i, n - 1);
|
||||
}
|
||||
for (int j = 0; j < n; j++) {
|
||||
dfs(grid, 0, j);
|
||||
dfs(grid, m - 1, j);
|
||||
}
|
||||
|
||||
// 数一数剩下的陆地
|
||||
int res = 0;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (grid[i][j] == 1) {
|
||||
res += 1;
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return res;
|
||||
}
|
||||
|
||||
// 和之前的实现类似
|
||||
void dfs(int[][] grid, int i, int j) {
|
||||
// ...
|
||||
}
|
||||
```
|
||||
|
||||
篇幅所限,具体代码我就不写了,我们继续看其他的岛屿题目。
|
||||
|
||||
### 岛屿的最大面积
|
||||
|
||||
这是力扣第 695 题「岛屿的最大面积」,`0` 表示海水,`1` 表示陆地,现在不让你计算岛屿的个数了,而是让你计算最大的那个岛屿的面积,函数签名如下:
|
||||
|
||||
```java
|
||||
int maxAreaOfIsland(int[][] grid)
|
||||
```
|
||||
|
||||
比如题目给你输入如下一个二维矩阵:
|
||||
|
||||

|
||||
|
||||
其中面积最大的是橘红色的岛屿,算法返回它的面积 6。
|
||||
|
||||
**这题的大体思路和之前完全一样,只不过 `dfs` 函数淹没岛屿的同时,还应该想办法记录这个岛屿的面积**。
|
||||
|
||||
我们可以给 `dfs` 函数设置返回值,记录每次淹没的陆地的个数,直接看解法吧:
|
||||
|
||||
```java
|
||||
int maxAreaOfIsland(int[][] grid) {
|
||||
// 记录岛屿的最大面积
|
||||
int res = 0;
|
||||
int m = grid.length, n = grid[0].length;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (grid[i][j] == 1) {
|
||||
// 淹没岛屿,并更新最大岛屿面积
|
||||
res = Math.max(res, dfs(grid, i, j));
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
|
||||
// 淹没与 (i, j) 相邻的陆地,并返回淹没的陆地面积
|
||||
int dfs(int[][] grid, int i, int j) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
if (i < 0 || j < 0 || i >= m || j >= n) {
|
||||
// 超出索引边界
|
||||
return 0;
|
||||
}
|
||||
if (grid[i][j] == 0) {
|
||||
// 已经是海水了
|
||||
return 0;
|
||||
}
|
||||
// 将 (i, j) 变成海水
|
||||
grid[i][j] = 0;
|
||||
|
||||
return dfs(grid, i + 1, j)
|
||||
+ dfs(grid, i, j + 1)
|
||||
+ dfs(grid, i - 1, j)
|
||||
+ dfs(grid, i, j - 1) + 1;
|
||||
}
|
||||
```
|
||||
|
||||
解法和之前相比差不多,我也不多说了,接下来的两道岛屿题目是比较有技巧性的,我们重点来看一下。
|
||||
|
||||
### 子岛屿数量
|
||||
|
||||
如果说前面的题目都是模板题,那么力扣第 1905 题「统计子岛屿」可能得动动脑子了:
|
||||
|
||||

|
||||
|
||||
**这道题的关键在于,如何快速判断子岛屿**?肯定可以借助 [Union Find 并查集算法](https://labuladong.github.io/article/fname.html?fname=UnionFind算法详解) 来判断,不过本文重点在 DFS 算法,就不展开并查集算法了。
|
||||
|
||||
什么情况下 `grid2` 中的一个岛屿 `B` 是 `grid1` 中的一个岛屿 `A` 的子岛?
|
||||
|
||||
当岛屿 `B` 中所有陆地在岛屿 `A` 中也是陆地的时候,岛屿 `B` 是岛屿 `A` 的子岛。
|
||||
|
||||
**反过来说,如果岛屿 `B` 中存在一片陆地,在岛屿 `A` 的对应位置是海水,那么岛屿 `B` 就不是岛屿 `A` 的子岛**。
|
||||
|
||||
那么,我们只要遍历 `grid2` 中的所有岛屿,把那些不可能是子岛的岛屿排除掉,剩下的就是子岛。
|
||||
|
||||
依据这个思路,可以直接写出下面的代码:
|
||||
|
||||
```java
|
||||
int countSubIslands(int[][] grid1, int[][] grid2) {
|
||||
int m = grid1.length, n = grid1[0].length;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (grid1[i][j] == 0 && grid2[i][j] == 1) {
|
||||
// 这个岛屿肯定不是子岛,淹掉
|
||||
dfs(grid2, i, j);
|
||||
}
|
||||
}
|
||||
}
|
||||
// 现在 grid2 中剩下的岛屿都是子岛,计算岛屿数量
|
||||
int res = 0;
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (grid2[i][j] == 1) {
|
||||
res++;
|
||||
dfs(grid2, i, j);
|
||||
}
|
||||
}
|
||||
}
|
||||
return res;
|
||||
}
|
||||
|
||||
// 从 (i, j) 开始,将与之相邻的陆地都变成海水
|
||||
void dfs(int[][] grid, int i, int j) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
if (i < 0 || j < 0 || i >= m || j >= n) {
|
||||
return;
|
||||
}
|
||||
if (grid[i][j] == 0) {
|
||||
return;
|
||||
}
|
||||
|
||||
grid[i][j] = 0;
|
||||
dfs(grid, i + 1, j);
|
||||
dfs(grid, i, j + 1);
|
||||
dfs(grid, i - 1, j);
|
||||
dfs(grid, i, j - 1);
|
||||
}
|
||||
```
|
||||
|
||||
这道题的思路和计算「封闭岛屿」数量的思路有些类似,只不过后者排除那些靠边的岛屿,前者排除那些不可能是子岛的岛屿。
|
||||
|
||||
### 不同的岛屿数量
|
||||
|
||||
这是本文的最后一道岛屿题目,作为压轴题,当然是最有意思的。
|
||||
|
||||
力扣第 694 题「不同的岛屿数量」,题目还是输入一个二维矩阵,`0` 表示海水,`1` 表示陆地,这次让你计算 **不同的 (distinct)** 岛屿数量,函数签名如下:
|
||||
|
||||
```java
|
||||
int numDistinctIslands(int[][] grid)
|
||||
```
|
||||
|
||||
比如题目输入下面这个二维矩阵:
|
||||
|
||||

|
||||
|
||||
其中有四个岛屿,但是左下角和右上角的岛屿形状相同,所以不同的岛屿共有三个,算法返回 3。
|
||||
|
||||
很显然我们得想办法把二维矩阵中的「岛屿」进行转化,变成比如字符串这样的类型,然后利用 HashSet 这样的数据结构去重,最终得到不同的岛屿的个数。
|
||||
|
||||
如果想把岛屿转化成字符串,说白了就是序列化,序列化说白了就是遍历嘛,前文 [二叉树的序列化和反序列化](https://labuladong.github.io/article/fname.html?fname=二叉树的序列化) 讲了二叉树和字符串互转,这里也是类似的。
|
||||
|
||||
**首先,对于形状相同的岛屿,如果从同一起点出发,`dfs` 函数遍历的顺序肯定是一样的**。
|
||||
|
||||
因为遍历顺序是写死在你的递归函数里面的,不会动态改变:
|
||||
|
||||
```java
|
||||
void dfs(int[][] grid, int i, int j) {
|
||||
// 递归顺序:
|
||||
dfs(grid, i - 1, j); // 上
|
||||
dfs(grid, i + 1, j); // 下
|
||||
dfs(grid, i, j - 1); // 左
|
||||
dfs(grid, i, j + 1); // 右
|
||||
}
|
||||
```
|
||||
|
||||
所以,遍历顺序从某种意义上说就可以用来描述岛屿的形状,比如下图这两个岛屿:
|
||||
|
||||

|
||||
|
||||
假设它们的遍历顺序是:
|
||||
|
||||
> 下,右,上,撤销上,撤销右,撤销下
|
||||
|
||||
如果我用分别用 `1, 2, 3, 4` 代表上下左右,用 `-1, -2, -3, -4` 代表上下左右的撤销,那么可以这样表示它们的遍历顺序:
|
||||
|
||||
> 2, 4, 1, -1, -4, -2
|
||||
|
||||
**你看,这就相当于是岛屿序列化的结果,只要每次使用 `dfs` 遍历岛屿的时候生成这串数字进行比较,就可以计算到底有多少个不同的岛屿了**。
|
||||
|
||||
> PS:细心的读者问到,为什么记录「撤销」操作才能唯一表示遍历顺序呢?不记录撤销操作好像也可以?实际上不是的。
|
||||
>
|
||||
> 比方说「下,右,撤销右,撤销下」和「下,撤销下,右,撤销右」显然是两个不同的遍历顺序,但如果不记录撤销操作,那么它俩都是「下,右」,成了相同的遍历顺序,显然是不对的。
|
||||
|
||||
所以我们需要稍微改造 `dfs` 函数,添加一些函数参数以便记录遍历顺序:
|
||||
|
||||
```java
|
||||
void dfs(int[][] grid, int i, int j, StringBuilder sb, int dir) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
if (i < 0 || j < 0 || i >= m || j >= n
|
||||
|| grid[i][j] == 0) {
|
||||
return;
|
||||
}
|
||||
// 前序遍历位置:进入 (i, j)
|
||||
grid[i][j] = 0;
|
||||
sb.append(dir).append(',');
|
||||
|
||||
dfs(grid, i - 1, j, sb, 1); // 上
|
||||
dfs(grid, i + 1, j, sb, 2); // 下
|
||||
dfs(grid, i, j - 1, sb, 3); // 左
|
||||
dfs(grid, i, j + 1, sb, 4); // 右
|
||||
|
||||
// 后序遍历位置:离开 (i, j)
|
||||
sb.append(-dir).append(',');
|
||||
}
|
||||
```
|
||||
|
||||
`dir` 记录方向,`dfs` 函数递归结束后,`sb` 记录着整个遍历顺序。有了这个 `dfs` 函数就好办了,我们可以直接写出最后的解法代码:
|
||||
|
||||
```java
|
||||
int numDistinctIslands(int[][] grid) {
|
||||
int m = grid.length, n = grid[0].length;
|
||||
// 记录所有岛屿的序列化结果
|
||||
HashSet<String> islands = new HashSet<>();
|
||||
for (int i = 0; i < m; i++) {
|
||||
for (int j = 0; j < n; j++) {
|
||||
if (grid[i][j] == 1) {
|
||||
// 淹掉这个岛屿,同时存储岛屿的序列化结果
|
||||
StringBuilder sb = new StringBuilder();
|
||||
// 初始的方向可以随便写,不影响正确性
|
||||
dfs(grid, i, j, sb, 666);
|
||||
islands.add(sb.toString());
|
||||
}
|
||||
}
|
||||
}
|
||||
// 不相同的岛屿数量
|
||||
return islands.size();
|
||||
}
|
||||
```
|
||||
|
||||
这样,这道题就解决了,至于为什么初始调用 `dfs` 函数时的 `dir` 参数可以随意写,这里涉及 DFS 和回溯算法的一个细微差别,前文 [图算法基础](https://labuladong.github.io/article/fname.html?fname=图) 有写,这里就不展开了。
|
||||
|
||||
以上就是全部岛屿系列题目的解题思路,也许前面的题目大部分人会做,但是最后两题还是比较巧妙的,希望本文对你有帮助。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [并查集(Union-Find)算法](https://labuladong.github.io/article/fname.html?fname=UnionFind算法详解)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| - | [剑指 Offer 13. 机器人的运动范围](https://leetcode.cn/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/?show=1) |
|
||||
| - | [剑指 Offer II 105. 岛屿的最大面积](https://leetcode.cn/problems/ZL6zAn/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 如何调度考生的座位
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -228,6 +224,10 @@ private int distance(int[] intv) {
|
|||
|
||||
希望本文对大家有帮助。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,9 +1,5 @@
|
|||
# 如何高效寻找素数
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -178,6 +174,33 @@ int countPrimes(int n) {
|
|||
|
||||
以上就是素数算法相关的全部内容。怎么样,是不是看似简单的问题却有不少细节可以打磨呀?
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [丑数系列算法详解](https://labuladong.github.io/article/fname.html?fname=丑数)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [264. Ugly Number II](https://leetcode.com/problems/ugly-number-ii/?show=1) | [264. 丑数 II](https://leetcode.cn/problems/ugly-number-ii/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -1,9 +1,7 @@
|
|||
# 接雨水问题详解
|
||||
|
||||
|
||||
<!-- [手把手搞懂接雨水问题的多种解法](https://mp.weixin.qq.com/s/8E2WHPdArs3KwSwaxFunHw) -->
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +11,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -278,6 +276,10 @@ if (height[left] < height[right]) {
|
|||
|
||||
至此,这道题也解决了。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
246
高频面试系列/最长回文子串.md
246
高频面试系列/最长回文子串.md
|
|
@ -1,246 +0,0 @@
|
|||
# 如何寻找最长回文子串
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[5.最长回文子串](https://leetcode-cn.com/problems/longest-palindromic-substring)
|
||||
|
||||
**-----------**
|
||||
|
||||
回文串是面试常常遇到的问题(虽然问题本身没啥意义),本文就告诉你回文串问题的核心思想是什么。
|
||||
|
||||
首先,明确一下什:**回文串就是正着读和反着读都一样的字符串**。
|
||||
|
||||
比如说字符串 `aba` 和 `abba` 都是回文串,因为它们对称,反过来还是和本身一样。反之,字符串 `abac` 就不是回文串。
|
||||
|
||||
可以看到回文串的的长度可能是奇数,也可能是偶数,这就添加了回文串问题的难度,解决该类问题的核心是**双指针**。下面就通过一道最长回文子串的问题来具体理解一下回文串问题:
|
||||
|
||||

|
||||
|
||||
```cpp
|
||||
string longestPalindrome(string s) {}
|
||||
```
|
||||
|
||||
### 一、思考
|
||||
|
||||
对于这个问题,我们首先应该思考的是,给一个字符串 `s`,如何在 `s` 中找到一个回文子串?
|
||||
|
||||
有一个很有趣的思路:既然回文串是一个正着反着读都一样的字符串,那么如果我们把 `s` 反转,称为 `s'`,然后在 `s` 和 `s'` 中寻找**最长公共子串**,这样应该就能找到最长回文子串。
|
||||
|
||||
比如说字符串 `abacd`,反过来是 `dcaba`,它的最长公共子串是 `aba`,也就是最长回文子串。
|
||||
|
||||
但是这个思路是错误的,比如说字符串 `aacxycaa`,反转之后是 `aacyxcaa`,最长公共子串是 `aac`,但是最长回文子串应该是 `aa`。
|
||||
|
||||
虽然这个思路不正确,但是**这种把问题转化为其他形式的思考方式是非常值得提倡的**。
|
||||
|
||||
下面,就来说一下正确的思路,如何使用双指针。
|
||||
|
||||
**寻找回文串的问题核心思想是:从中间开始向两边扩散来判断回文串**。对于最长回文子串,就是这个意思:
|
||||
|
||||
```python
|
||||
for 0 <= i < len(s):
|
||||
找到以 s[i] 为中心的回文串
|
||||
更新答案
|
||||
```
|
||||
|
||||
但是呢,我们刚才也说了,回文串的长度可能是奇数也可能是偶数,如果是 `abba`这种情况,没有一个中心字符,上面的算法就没辙了。所以我们可以修改一下:
|
||||
|
||||
```python
|
||||
for 0 <= i < len(s):
|
||||
找到以 s[i] 为中心的回文串
|
||||
找到以 s[i] 和 s[i+1] 为中心的回文串
|
||||
更新答案
|
||||
```
|
||||
|
||||
PS:读者可能发现这里的索引会越界,等会会处理。
|
||||
|
||||
### 二、代码实现
|
||||
|
||||
按照上面的思路,先要实现一个函数来寻找最长回文串,这个函数是有点技巧的:
|
||||
|
||||
```cpp
|
||||
string palindrome(string& s, int l, int r) {
|
||||
// 防止索引越界
|
||||
while (l >= 0 && r < s.size()
|
||||
&& s[l] == s[r]) {
|
||||
// 向两边展开
|
||||
l--; r++;
|
||||
}
|
||||
// 返回以 s[l] 和 s[r] 为中心的最长回文串
|
||||
return s.substr(l + 1, r - l - 1);
|
||||
}
|
||||
```
|
||||
|
||||
为什么要传入两个指针 `l` 和 `r` 呢?**因为这样实现可以同时处理回文串长度为奇数和偶数的情况**:
|
||||
|
||||
```python
|
||||
for 0 <= i < len(s):
|
||||
# 找到以 s[i] 为中心的回文串
|
||||
palindrome(s, i, i)
|
||||
# 找到以 s[i] 和 s[i+1] 为中心的回文串
|
||||
palindrome(s, i, i + 1)
|
||||
更新答案
|
||||
```
|
||||
|
||||
下面看下 `longestPalindrome` 的完整代码:
|
||||
|
||||
```cpp
|
||||
string longestPalindrome(string s) {
|
||||
string res;
|
||||
for (int i = 0; i < s.size(); i++) {
|
||||
// 以 s[i] 为中心的最长回文子串
|
||||
string s1 = palindrome(s, i, i);
|
||||
// 以 s[i] 和 s[i+1] 为中心的最长回文子串
|
||||
string s2 = palindrome(s, i, i + 1);
|
||||
// res = longest(res, s1, s2)
|
||||
res = res.size() > s1.size() ? res : s1;
|
||||
res = res.size() > s2.size() ? res : s2;
|
||||
}
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
至此,这道最长回文子串的问题就解决了,时间复杂度 O(N^2),空间复杂度 O(1)。
|
||||
|
||||
值得一提的是,这个问题可以用动态规划方法解决,时间复杂度一样,但是空间复杂度至少要 O(N^2) 来存储 DP table。这道题是少有的动态规划非最优解法的问题。
|
||||
|
||||
另外,这个问题还有一个巧妙的解法,时间复杂度只需要 O(N),不过该解法比较复杂,我个人认为没必要掌握。该算法的名字叫 Manacher's Algorithm(马拉车算法),有兴趣的读者可以自行搜索一下。
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[5.最长回文子串](https://leetcode-cn.com/problems/longest-palindromic-substring)
|
||||
|
||||
### java
|
||||
|
||||
[cchromt](https://github.com/cchroot) 提供 Java 代码:
|
||||
|
||||
```java
|
||||
// 中心扩展算法
|
||||
class Solution {
|
||||
public String longestPalindrome(String s) {
|
||||
// 如果字符串长度小于2,则直接返回其本身
|
||||
if (s.length() < 2) {
|
||||
return s;
|
||||
}
|
||||
String res = "";
|
||||
for (int i = 0; i < s.length() - 1; i++) {
|
||||
// 以 s.charAt(i) 为中心的最长回文子串
|
||||
String s1 = palindrome(s, i, i);
|
||||
// 以 s.charAt(i) 和 s.charAt(i+1) 为中心的最长回文子串
|
||||
String s2 = palindrome(s, i, i + 1);
|
||||
res = res.length() > s1.length() ? res : s1;
|
||||
res = res.length() > s2.length() ? res : s2;
|
||||
}
|
||||
return res;
|
||||
}
|
||||
|
||||
public String palindrome(String s, int left, int right) {
|
||||
// 索引未越界的情况下,s.charAt(left) == s.charAt(right) 则继续向两边拓展
|
||||
while (left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
|
||||
left--;
|
||||
right++;
|
||||
}
|
||||
// 这里要注意,跳出 while 循环时,恰好满足 s.charAt(i) != s.charAt(j),因此截取的的字符串为[left+1, right-1]
|
||||
return s.substring(left + 1, right);
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
[enrilwang](https://github.com/enrilwang) 提供 Python 代码:
|
||||
|
||||
```python
|
||||
# 中心扩展算法
|
||||
class Solution:
|
||||
def longestPalindrome(self, s: str) -> str:
|
||||
#用n来装字符串长度,res来装答案
|
||||
n = len(s)
|
||||
res = str()
|
||||
#字符串长度小于2,就返回本身
|
||||
if n < 2: return s
|
||||
for i in range(n-1):
|
||||
#oddstr是以i为中心的最长回文子串
|
||||
oddstr = self.centerExtend(s,i,i)
|
||||
#evenstr是以i和i+1为中心的最长回文子串
|
||||
evenstr = self.centerExtend(s,i,i+1)
|
||||
temp = oddstr if len(oddstr)>len(evenstr) else evenstr
|
||||
if len(temp)>len(res):res=temp
|
||||
|
||||
return res
|
||||
|
||||
def centerExtend(self,s:str,left,right)->str:
|
||||
|
||||
while left >= 0 and right < len(s) and s[left] == s[right]:
|
||||
left -= 1
|
||||
right += 1
|
||||
#这里要注意,跳出while循环时,恰好s[left] != s[right]
|
||||
return s[left+1:right]
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
做完这题,大家可以去看看 [647. 回文子串](https://leetcode-cn.com/problems/palindromic-substrings/) ,也是类似的题目
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {string} s
|
||||
* @return {string}
|
||||
*/
|
||||
var longestPalindrome = function (s) {
|
||||
let res = "";
|
||||
for (let i = 0; i < s.length; i++) {
|
||||
// 以s[i]为中心的最长回文子串
|
||||
let s1 = palindrome(s,i,i);
|
||||
|
||||
// 以 s[i] 和 s[i+1] 为中心的最长回文子串
|
||||
let s2 = palindrome(s, i, i + 1);
|
||||
|
||||
// res = longest(res, s1, s2)
|
||||
res = res.length > s1.length ? res : s1;
|
||||
res = res.length > s2.length ? res : s2;
|
||||
}
|
||||
};
|
||||
|
||||
// 寻找最长回文串
|
||||
let palindrome = (s, l, r) => {
|
||||
// 防止索引越界
|
||||
while (l >= 0 && r < s.length && s[l] === s[r]) {
|
||||
// 向两边展开
|
||||
l--;
|
||||
r++;
|
||||
}
|
||||
|
||||
// 返回以s[l]和s[r]为中心的最长回文串
|
||||
return s.substr(l + 1, r - l - 1)
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 随机算法之水塘抽样算法
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -128,6 +124,23 @@ int[] getRandom(ListNode head, int k) {
|
|||
|
||||
答案见 [我的这篇文章](https://labuladong.github.io/article/fname.html?fname=随机集合)。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [一道求中位数的算法题把我整不会了](https://labuladong.github.io/article/fname.html?fname=数据流中位数)
|
||||
- [丑数系列算法详解](https://labuladong.github.io/article/fname.html?fname=丑数)
|
||||
- [带权重的随机选择算法](https://labuladong.github.io/article/fname.html?fname=随机权重)
|
||||
- [常数时间删除/查找数组中的任意元素](https://labuladong.github.io/article/fname.html?fname=随机集合)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
293
高频面试系列/消失的元素.md
293
高频面试系列/消失的元素.md
|
|
@ -1,293 +0,0 @@
|
|||
# 如何寻找消失的元素
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://i.loli.net/2020/10/10/MhRTyUKfXZOlQYN.jpg"><img src="https://img.shields.io/badge/公众号-@labuladong-000000.svg?style=flat-square&logo=WeChat"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**《labuladong 的算法秘籍》、《labuladong 的刷题笔记》两本 PDF 和刷题插件 2.0 免费开放下载,详情见 [labuladong 的刷题三件套正式发布](https://mp.weixin.qq.com/s/yN4cHQRsFa5SWlacopHXYQ)**~
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便去 LeetCode 上拿下如下题目:
|
||||
|
||||
[448.找到所有数组中消失的数字](https://leetcode-cn.com/problems/find-all-numbers-disappeared-in-an-array)
|
||||
|
||||
**-----------**
|
||||
|
||||
之前也有文章写过几个有趣的智力题,今天再聊一道巧妙的题目。
|
||||
|
||||
题目非常简单:
|
||||
|
||||

|
||||
|
||||
给一个长度为 n 的数组,其索引应该在 `[0,n)`,但是现在你要装进去 n + 1 个元素 `[0,n]`,那么肯定有一个元素装不下嘛,请你找出这个缺失的元素。
|
||||
|
||||
这道题不难的,我们应该很容易想到,把这个数组排个序,然后遍历一遍,不就很容易找到缺失的那个元素了吗?
|
||||
|
||||
或者说,借助数据结构的特性,用一个 HashSet 把数组里出现的数字都储存下来,再遍历 `[0,n]` 之间的数字,去 HashSet 中查询,也可以很容易查出那个缺失的元素。
|
||||
|
||||
排序解法的时间复杂度是 O(NlogN),HashSet 的解法时间复杂度是 O(N),但是还需要 O(N) 的空间复杂度存储 HashSet。
|
||||
|
||||
**第三种方法是位运算**。
|
||||
|
||||
对于异或运算(`^`),我们知道它有一个特殊性质:一个数和它本身做异或运算结果为 0,一个数和 0 做异或运算还是它本身。
|
||||
|
||||
而且异或运算满足交换律和结合律,也就是说:
|
||||
|
||||
2 ^ 3 ^ 2 = 3 ^ (2 ^ 2) = 3 ^ 0 = 3
|
||||
|
||||
而这道题索就可以通过这些性质巧妙算出缺失的那个元素。比如说 `nums = [0,3,1,4]`:
|
||||
|
||||

|
||||
|
||||
|
||||
为了容易理解,我们假设先把索引补一位,然后让每个元素和自己相等的索引相对应:
|
||||
|
||||

|
||||
|
||||
|
||||
这样做了之后,就可以发现除了缺失元素之外,所有的索引和元素都组成一对儿了,现在如果把这个落单的索引 2 找出来,也就找到了缺失的那个元素。
|
||||
|
||||
如何找这个落单的数字呢,**只要把所有的元素和索引做异或运算,成对儿的数字都会消为 0,只有这个落单的元素会剩下**,也就达到了我们的目的。
|
||||
|
||||
```java
|
||||
int missingNumber(int[] nums) {
|
||||
int n = nums.length;
|
||||
int res = 0;
|
||||
// 先和新补的索引异或一下
|
||||
res ^= n;
|
||||
// 和其他的元素、索引做异或
|
||||
for (int i = 0; i < n; i++)
|
||||
res ^= i ^ nums[i];
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||

|
||||
|
||||
由于异或运算满足交换律和结合律,所以总是能把成对儿的数字消去,留下缺失的那个元素的。
|
||||
|
||||
至此,时间复杂度 O(N),空间复杂度 O(1),已经达到了最优,我们是否就应该打道回府了呢?
|
||||
|
||||
如果这样想,说明我们受算法的毒害太深,随着我们学习的知识越来越多,反而容易陷入思维定式,这个问题其实还有一个特别简单的解法:**等差数列求和公式**。
|
||||
|
||||
题目的意思可以这样理解:现在有个等差数列 0, 1, 2,..., n,其中少了某一个数字,请你把它找出来。那这个数字不就是 `sum(0,1,..n) - sum(nums)` 嘛?
|
||||
|
||||
```java
|
||||
int missingNumber(int[] nums) {
|
||||
int n = nums.length;
|
||||
// 公式:(首项 + 末项) * 项数 / 2
|
||||
int expect = (0 + n) * (n + 1) / 2;
|
||||
|
||||
int sum = 0;
|
||||
for (int x : nums)
|
||||
sum += x;
|
||||
return expect - sum;
|
||||
}
|
||||
```
|
||||
|
||||
你看,这种解法应该是最简单的,但说实话,我自己也没想到这个解法,而且我去问了几个大佬,他们也没想到这个最简单的思路。相反,如果去问一个初中生,他也许很快就能想到。
|
||||
|
||||
做到这一步了,我们是否就应该打道回府了呢?
|
||||
|
||||
如果这样想,说明我们对细节的把控还差点火候。在用求和公式计算 `expect` 时,你考虑过**整型溢出**吗?如果相乘的结果太大导致溢出,那么结果肯定是错误的。
|
||||
|
||||
刚才我们的思路是把两个和都加出来然后相减,为了避免溢出,干脆一边求和一边减算了。很类似刚才位运算解法的思路,仍然假设 `nums = [0,3,1,4]`,先补一位索引再让元素跟索引配对:
|
||||
|
||||

|
||||
|
||||
|
||||
我们让每个索引减去其对应的元素,再把相减的结果加起来,不就是那个缺失的元素吗?
|
||||
|
||||
```java
|
||||
public int missingNumber(int[] nums) {
|
||||
int n = nums.length;
|
||||
int res = 0;
|
||||
// 新补的索引
|
||||
res += n - 0;
|
||||
// 剩下索引和元素的差加起来
|
||||
for (int i = 0; i < n; i++)
|
||||
res += i - nums[i];
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
由于加减法满足交换律和结合律,所以总是能把成对儿的数字消去,留下缺失的那个元素的。
|
||||
|
||||
至此这道算法题目经历九曲十八弯,终于再也没有什么坑了。
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**刷算法,学套路,认准 labuladong,公众号和 [在线电子书](https://labuladong.gitee.io/algo/) 持续更新最新文章**。
|
||||
|
||||
**本小抄即将出版,微信扫码关注公众号,后台回复「小抄」限时免费获取,回复「进群」可进刷题群一起刷题,带你搞定 LeetCode**。
|
||||
|
||||
<p align='center'>
|
||||
<img src="../pictures/qrcode.jpg" width=200 >
|
||||
</p>
|
||||
======其他语言代码======
|
||||
|
||||
[剑指 Offer 53 - II. 0~n-1中缺失的数字](https://leetcode-cn.com/problems/que-shi-de-shu-zi-lcof/)
|
||||
|
||||
[448.找到所有数组中消失的数字](https://leetcode-cn.com/problems/find-all-numbers-disappeared-in-an-array)
|
||||
|
||||
|
||||
|
||||
### python
|
||||
|
||||
```python
|
||||
def missingNumber(self, nums: List[int]) -> int:
|
||||
#思路1,位运算
|
||||
res = len(nums)
|
||||
for i,num in enumerate(nums):
|
||||
res ^= i^num
|
||||
return res
|
||||
```
|
||||
|
||||
```python
|
||||
def missingNumber(self, nums: List[int]) -> int:
|
||||
#思路2,求和
|
||||
n = len(nums)
|
||||
return n*(n+1)//2-sum(nums)
|
||||
```
|
||||
|
||||
```python
|
||||
def missingNumber(self, nums: List[int]) -> int:
|
||||
#思路3,防止整形溢出的优化
|
||||
res = len(nums)
|
||||
for i,num in enumerate(nums):
|
||||
res+=i-num
|
||||
return res
|
||||
```
|
||||
|
||||
事实上,在python3中不存在整数溢出的问题(只要内存放得下),思路3的优化提升并不大,不过看上去有内味了哈...
|
||||
|
||||
### c++
|
||||
|
||||
[happy-yuxuan](https://github.com/happy-yuxuan) 提供 三种方法的 C++ 代码:
|
||||
|
||||
```c++
|
||||
// 方法:异或元素和索引
|
||||
int missingNumber(vector<int>& nums) {
|
||||
int n = nums.size();
|
||||
int res = 0;
|
||||
// 先和新补的索引异或一下
|
||||
res ^= n;
|
||||
// 和其他的元素、索引做异或
|
||||
for (int i = 0; i < n; i++)
|
||||
res ^= i ^ nums[i];
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
```c++
|
||||
// 方法:等差数列求和
|
||||
int missingNumber(vector<int>& nums) {
|
||||
int n = nums.size();
|
||||
// 公式:(首项 + 末项) * 项数 / 2
|
||||
int expect = (0 + n) * (n + 1) / 2;
|
||||
int sum = 0;
|
||||
for (int x : nums)
|
||||
sum += x;
|
||||
return expect - sum;
|
||||
}
|
||||
```
|
||||
|
||||
```c++
|
||||
// 方法:防止整型溢出
|
||||
int missingNumber(vector<int>& nums) {
|
||||
int n = nums.size();
|
||||
int res = 0;
|
||||
// 新补的索引
|
||||
res += n - 0;
|
||||
// 剩下索引和元素的差加起来
|
||||
for (int i = 0; i < n; i++)
|
||||
res += i - nums[i];
|
||||
return res;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
### javascript
|
||||
|
||||
[传送门:剑指 Offer 53 - II. 0~n-1中缺失的数字](https://leetcode-cn.com/problems/que-shi-de-shu-zi-lcof/)
|
||||
|
||||
**位运算**
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @return {number}
|
||||
*/
|
||||
var missingNumber = function(nums) {
|
||||
let n = nums.length;
|
||||
let res = 0;
|
||||
|
||||
// 先和新补的索引异或一下
|
||||
res ^= n;
|
||||
|
||||
// 和其它的元素、索引做异或
|
||||
for (let i = 0; i < n; i++) {
|
||||
res ^= i ^ nums[i];
|
||||
}
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
**直接相减**
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @return {number}
|
||||
*/
|
||||
var missingNumber = function(nums) {
|
||||
let n = nums.length;
|
||||
let res = 0;
|
||||
// 新补的索引
|
||||
res += n - 0;
|
||||
|
||||
// 剩下索引和元素的差加起来
|
||||
for (let i = 0; i < n; i++) {
|
||||
res += i - nums[i];
|
||||
}
|
||||
return res;
|
||||
};
|
||||
```
|
||||
|
||||
|
||||
|
||||
[传送门:448. 找到所有数组中消失的数字](https://leetcode-cn.com/problems/find-all-numbers-disappeared-in-an-array/)
|
||||
|
||||
这道题的核心思路是将访问过的元素变成负数,第二次遍历直接收集正数并加入结果集中。
|
||||
|
||||
```js
|
||||
/**
|
||||
* @param {number[]} nums
|
||||
* @return {number[]}
|
||||
*/
|
||||
var findDisappearedNumbers = function (nums) {
|
||||
for (let i = 0; i < nums.length; i++) {
|
||||
let newIndex = Math.abs(nums[i]) - 1;
|
||||
if (nums[newIndex] > 0) {
|
||||
nums[newIndex] *= -1;
|
||||
}
|
||||
}
|
||||
|
||||
let result = [];
|
||||
for (let i = 1; i <= nums.length; i++) {
|
||||
if (nums[i - 1] > 0) {
|
||||
result.push(i);
|
||||
}
|
||||
}
|
||||
return result;
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
|
|
@ -1,9 +1,5 @@
|
|||
# 如何寻找缺失和重复的元素
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
|
|
@ -13,7 +9,7 @@
|
|||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。**
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
|
|
@ -25,7 +21,7 @@
|
|||
|
||||
**-----------**
|
||||
|
||||
今天就聊一道很看起来简单却十分巧妙的问题,寻找缺失和重复的元素。之前的一篇文章 [常用的位操作](算法思维系列/常用的位操作.md) 中也写过类似的问题,不过这次的和上次的问题使用的技巧不同。
|
||||
今天就聊一道很看起来简单却十分巧妙的问题,寻找缺失和重复的元素。之前的一篇文章 [常用的位操作](https://labuladong.github.io/article/fname.html?fname=常用的位操作) 中也写过类似的问题,不过这次的和上次的问题使用的技巧不同。
|
||||
|
||||
这是力扣第 645 题「错误的集合」,我来描述一下这个题目:
|
||||
|
||||
|
|
@ -132,6 +128,24 @@ int[] findErrorNums(int[] nums) {
|
|||
|
||||
异或运算也是常用的,因为异或性质 `a ^ a = 0, a ^ 0 = a`,如果将索引和元素同时异或,就可以消除成对儿的索引和元素,留下的就是重复或者缺失的元素。可以看看前文 [常用的位运算](https://labuladong.github.io/article/fname.html?fname=常用的位操作),介绍过这种方法。
|
||||
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的题目</strong></summary>
|
||||
|
||||
<strong>安装 [我的 Chrome 刷题插件](https://mp.weixin.qq.com/s/X-fE9sR4BLi6T9pn7xP4pg) 点开下列题目可直接查看解题思路:</strong>
|
||||
|
||||
| LeetCode | 力扣 |
|
||||
| :----: | :----: |
|
||||
| [442. Find All Duplicates in an Array](https://leetcode.com/problems/find-all-duplicates-in-an-array/?show=1) | [442. 数组中重复的数据](https://leetcode.cn/problems/find-all-duplicates-in-an-array/?show=1) |
|
||||
| [448. Find All Numbers Disappeared in an Array](https://leetcode.com/problems/find-all-numbers-disappeared-in-an-array/?show=1) | [448. 找到所有数组中消失的数字](https://leetcode.cn/problems/find-all-numbers-disappeared-in-an-array/?show=1) |
|
||||
|
||||
</details>
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
|
|
|||
|
|
@ -0,0 +1,225 @@
|
|||
# 带权重的随机选择算法
|
||||
|
||||
<p align='center'>
|
||||
<a href="https://github.com/labuladong/fucking-algorithm" target="view_window"><img alt="GitHub" src="https://img.shields.io/github/stars/labuladong/fucking-algorithm?label=Stars&style=flat-square&logo=GitHub"></a>
|
||||
<a href="https://appktavsiei5995.pc.xiaoe-tech.com/index" target="_blank"><img class="my_header_icon" src="https://img.shields.io/static/v1?label=精品课程&message=查看&color=pink&style=flat"></a>
|
||||
<a href="https://www.zhihu.com/people/labuladong"><img src="https://img.shields.io/badge/%E7%9F%A5%E4%B9%8E-@labuladong-000000.svg?style=flat-square&logo=Zhihu"></a>
|
||||
<a href="https://space.bilibili.com/14089380"><img src="https://img.shields.io/badge/B站-@labuladong-000000.svg?style=flat-square&logo=Bilibili"></a>
|
||||
</p>
|
||||
|
||||

|
||||
|
||||
**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V1.9,[第 11 期刷题打卡挑战(9/19 开始)](https://mp.weixin.qq.com/s/eUG2OOzY3k_ZTz-CFvtv5Q) 开始报名。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
|
||||
|
||||
|
||||
|
||||
读完本文,你不仅学会了算法套路,还可以顺便解决如下题目:
|
||||
|
||||
| LeetCode | 力扣 | 难度 |
|
||||
| :----: | :----: | :----: |
|
||||
| [528. Random Pick with Weight](https://leetcode.com/problems/random-pick-with-weight/) | [528. 按权重随机选择](https://leetcode.cn/problems/random-pick-with-weight/) | 🟠
|
||||
| - | [剑指 Offer II 071. 按权重生成随机数](https://leetcode.cn/problems/cuyjEf/) | 🟠
|
||||
|
||||
**-----------**
|
||||
|
||||
写这篇的文章的原因是玩 LOL 手游。
|
||||
|
||||
我有个朋友抱怨说打排位匹配的队友太菜了,我就说我打排位觉得队友都挺行的啊,好像不怎么坑?
|
||||
|
||||
朋友意味深长地说了句:一般隐藏分比较高的玩家,排位如果排不到实力相当的队友,就会排到一些菜狗。
|
||||
|
||||
嗯?我想了几秒钟感觉这小伙子不对劲,他意思是说我隐藏分低,还是说我就是那条菜狗?
|
||||
|
||||
我立马要求和他开黑打一把,证明我不是菜狗,他才是菜狗。开黑结果这里不便透露,大家猜猜吧。
|
||||
|
||||
打完之后我就来发文了,因为我对游戏的匹配机制有了一点思考。
|
||||
|
||||

|
||||
|
||||
**所谓「隐藏分」我不知道是不是真的,毕竟匹配机制是所有竞技类游戏的核心环节,想必非常复杂,不是简单几个指标就能搞定的**。
|
||||
|
||||
但是如果把这个「隐藏分」机制简化,倒是一个值得思考的算法问题:系统如何以不同的随机概率进行匹配?
|
||||
|
||||
或者简单点说,如何带权重地做随机选择?
|
||||
|
||||
不要觉得这个很容易,如果给你一个长度为 `n` 的数组,让你从中等概率随机抽取一个元素,你肯定会做,random 一个 `[0, n-1]` 的数字出来作为索引就行了,每个元素被随机选到的概率都是 `1/n`。
|
||||
|
||||
但假设每个元素都有不同的权重,权重地大小代表随机选到这个元素的概率大小,你如何写算法去随机获取元素呢?
|
||||
|
||||
力扣第 528 题「按权重随机选择」就是这样一个问题:
|
||||
|
||||

|
||||
|
||||
我们就来思考一下这个问题,解决按照权重随机选择元素的问题。
|
||||
|
||||
### 解法思路
|
||||
|
||||
首先回顾一下我们和随机算法有关的历史文章:
|
||||
|
||||
前文 [设计随机删除元素的数据结构](https://labuladong.github.io/article/fname.html?fname=随机集合) 主要考察的是数据结构的使用,每次把元素移到数组尾部再删除,可以避免数据搬移。
|
||||
|
||||
前文 [无限序列中随机抽取元素](https://labuladong.github.io/article/fname.html?fname=水塘抽样) 讲的是经典的「水塘抽样算法」,运用简单的数学运算,在无限序列中等概率选取元素。
|
||||
|
||||
前文 [算法笔试技巧](https://labuladong.github.io/article/fname.html?fname=刷题技巧) 中我还分享过一个巧用概率最大化测试用例通过率的骗分技巧。
|
||||
|
||||
**不过上述旧文并不能解决本文提出的问题,反而是前文 [前缀和技巧](https://labuladong.github.io/article/fname.html?fname=前缀和技巧) 加上 [二分搜索详解](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 能够解决带权重的随机选择算法**。
|
||||
|
||||
这个随机算法和前缀和技巧和二分搜索技巧能扯上啥关系?且听我慢慢道来。
|
||||
|
||||
假设给你输入的权重数组是 `w = [1,3,2,1]`,我们想让概率符合权重,那么可以抽象一下,根据权重画出这么一条彩色的线段:
|
||||
|
||||

|
||||
|
||||
如果我在线段上面随机丢一个石子,石子落在哪个颜色上,我就选择该颜色对应的权重索引,那么每个索引被选中的概率是不是就是和权重相关联了?
|
||||
|
||||
**所以,你再仔细看看这条彩色的线段像什么?这不就是 [前缀和数组](https://labuladong.github.io/article/fname.html?fname=前缀和技巧) 嘛**:
|
||||
|
||||

|
||||
|
||||
那么接下来,如何模拟在线段上扔石子?
|
||||
|
||||
当然是随机数,比如上述前缀和数组 `preSum`,取值范围是 `[1, 7]`,那么我生成一个在这个区间的随机数 `target = 5`,就好像在这条线段中随机扔了一颗石子:
|
||||
|
||||

|
||||
|
||||
还有个问题,`preSum` 中并没有 5 这个元素,我们应该选择比 5 大的最小元素,也就是 6,即 `preSum` 数组的索引 3:
|
||||
|
||||

|
||||
|
||||
**如何快速寻找数组中大于等于目标值的最小元素?[二分搜索算法](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 就是我们想要的**。
|
||||
|
||||
到这里,这道题的核心思路就说完了,主要分几步:
|
||||
|
||||
1、根据权重数组 `w` 生成前缀和数组 `preSum`。
|
||||
|
||||
2、生成一个取值在 `preSum` 之内的随机数,用二分搜索算法寻找大于等于这个随机数的最小元素索引。
|
||||
|
||||
3、最后对这个索引减一(因为前缀和数组有一位索引偏移),就可以作为权重数组的索引,即最终答案:
|
||||
|
||||

|
||||
|
||||
### 解法代码
|
||||
|
||||
上述思路应该不难理解,但是写代码的时候坑可就多了。
|
||||
|
||||
要知道涉及开闭区间、索引偏移和二分搜索的题目,需要你对算法的细节把控非常精确,否则会出各种难以排查的 bug。
|
||||
|
||||
下面来抠细节,继续前面的例子:
|
||||
|
||||

|
||||
|
||||
就比如这个 `preSum` 数组,你觉得随机数 `target` 应该在什么范围取值?闭区间 `[0, 7]` 还是左闭右开 `[0, 7)`?
|
||||
|
||||
都不是,应该在闭区间 `[1, 7]` 中选择,**因为前缀和数组中 0 本质上是个占位符**,仔细体会一下:
|
||||
|
||||

|
||||
|
||||
所以要这样写代码:
|
||||
|
||||
```java
|
||||
int n = preSum.length;
|
||||
// target 取值范围是闭区间 [1, preSum[n - 1]]
|
||||
int target = rand.nextInt(preSum[n - 1]) + 1;
|
||||
```
|
||||
|
||||
接下来,在 `preSum` 中寻找大于等于 `target` 的最小元素索引,应该用什么品种的二分搜索?搜索左侧边界的还是搜索右侧边界的?
|
||||
|
||||
实际上应该使用搜索左侧边界的二分搜索:
|
||||
|
||||
```java
|
||||
// 搜索左侧边界的二分搜索
|
||||
int left_bound(int[] nums, int target) {
|
||||
if (nums.length == 0) return -1;
|
||||
int left = 0, right = nums.length;
|
||||
while (left < right) {
|
||||
int mid = left + (right - left) / 2;
|
||||
if (nums[mid] == target) {
|
||||
right = mid;
|
||||
} else if (nums[mid] < target) {
|
||||
left = mid + 1;
|
||||
} else if (nums[mid] > target) {
|
||||
right = mid;
|
||||
}
|
||||
}
|
||||
return left;
|
||||
}
|
||||
```
|
||||
|
||||
前文 [二分搜索详解](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 着重讲了数组中存在目标元素重复的情况,没仔细讲目标元素不存在的情况,这里补充一下。
|
||||
|
||||
**当目标元素 `target` 不存在数组 `nums` 中时,搜索左侧边界的二分搜索的返回值可以做以下几种解读**:
|
||||
|
||||
1、返回的这个值是 `nums` 中大于等于 `target` 的最小元素索引。
|
||||
|
||||
2、返回的这个值是 `target` 应该插入在 `nums` 中的索引位置。
|
||||
|
||||
3、返回的这个值是 `nums` 中小于 `target` 的元素个数。
|
||||
|
||||
比如在有序数组 `nums = [2,3,5,7]` 中搜索 `target = 4`,搜索左边界的二分算法会返回 2,你带入上面的说法,都是对的。
|
||||
|
||||
所以以上三种解读都是等价的,可以根据具体题目场景灵活运用,显然这里我们需要的是第一种。
|
||||
|
||||
综上,我们可以写出最终解法代码:
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
// 前缀和数组
|
||||
private int[] preSum;
|
||||
private Random rand = new Random();
|
||||
|
||||
public Solution(int[] w) {
|
||||
int n = w.length;
|
||||
// 构建前缀和数组,偏移一位留给 preSum[0]
|
||||
preSum = new int[n + 1];
|
||||
preSum[0] = 0;
|
||||
// preSum[i] = sum(w[0..i-1])
|
||||
for (int i = 1; i <= n; i++) {
|
||||
preSum[i] = preSum[i - 1] + w[i - 1];
|
||||
}
|
||||
}
|
||||
|
||||
public int pickIndex() {
|
||||
int n = preSum.length;
|
||||
// 在闭区间 [1, preSum[n - 1]] 中随机选择一个数字
|
||||
int target = rand.nextInt(preSum[n - 1]) + 1;
|
||||
// 获取 target 在前缀和数组 preSum 中的索引
|
||||
// 别忘了前缀和数组 preSum 和原始数组 w 有一位索引偏移
|
||||
return left_bound(preSum, target) - 1;
|
||||
}
|
||||
|
||||
// 搜索左侧边界的二分搜索
|
||||
private int left_bound(int[] nums, int target) {
|
||||
// 见上文
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
有了之前的铺垫,相信你能够完全理解上述代码,这道随机权重的题目就解决了。
|
||||
|
||||
经常有读者留言调侃,每次都是看我的文章「云刷题」,看完就会了,也不用亲自动手刷了。
|
||||
|
||||
但我想说的是,很多题目思路一说就懂,但是深入一些的话很多细节都可能有坑,本文讲的这道题就是一个例子,所以还是建议多实践,多总结。
|
||||
|
||||
后续我准备在核心读者群开展每天刷题打卡的活动,帮大家走出第一步,培养每天刷题 + 总结的习惯,有兴趣的读者在公众号后台回复关键词「核心群」加我微信。
|
||||
|
||||
> 最后打个广告,我亲自制作了一门 [数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO),以视频课为主,手把手带你实现常用的数据结构及相关算法,旨在帮助算法基础较为薄弱的读者深入理解常用数据结构的底层原理,在算法学习中少走弯路。
|
||||
|
||||
|
||||
|
||||
<hr>
|
||||
<details>
|
||||
<summary><strong>引用本文的文章</strong></summary>
|
||||
|
||||
- [如何在无限序列中随机抽取元素](https://labuladong.github.io/article/fname.html?fname=水塘抽样)
|
||||
|
||||
</details><hr>
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**_____________**
|
||||
|
||||
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「进群」可加入算法群;回复「PDF」可获取精华文章 PDF**:
|
||||
|
||||

|
||||
Loading…
Reference in New Issue