
-
+

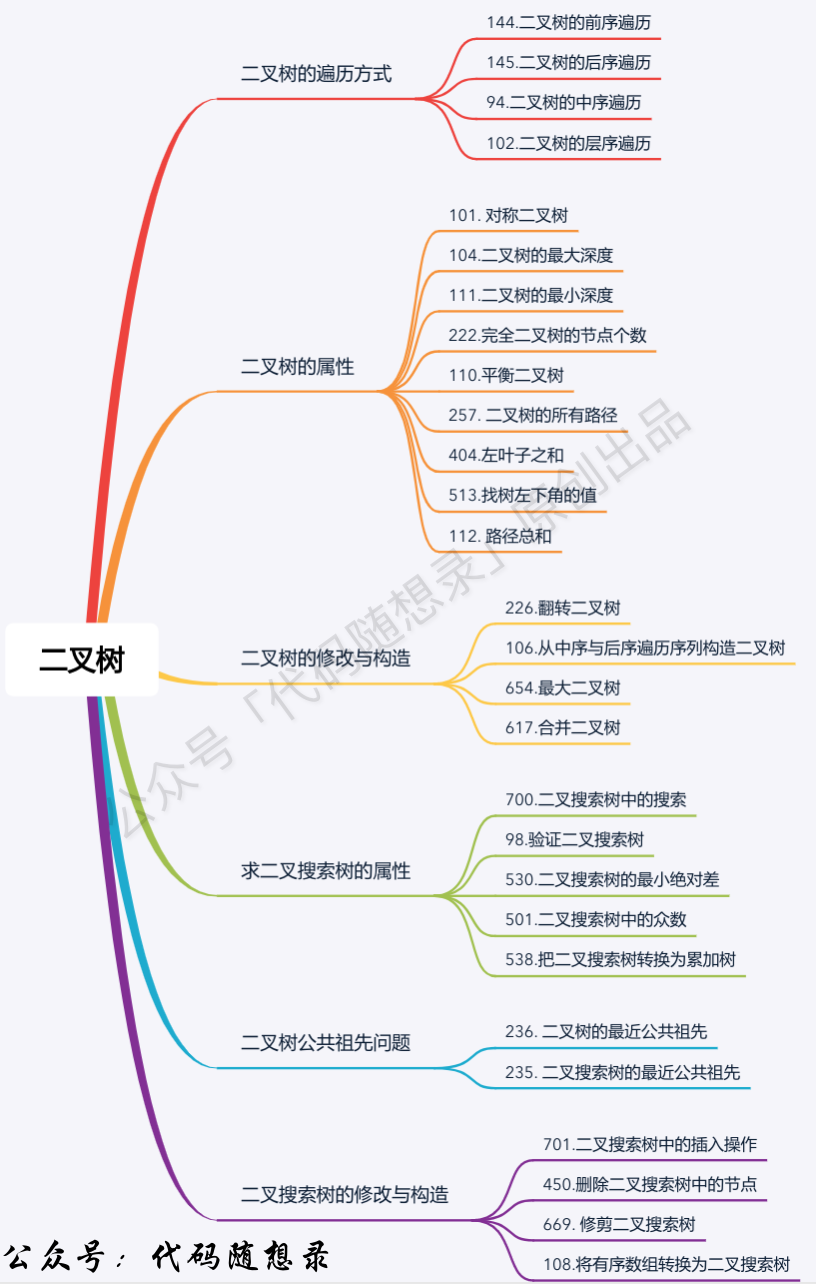 +
+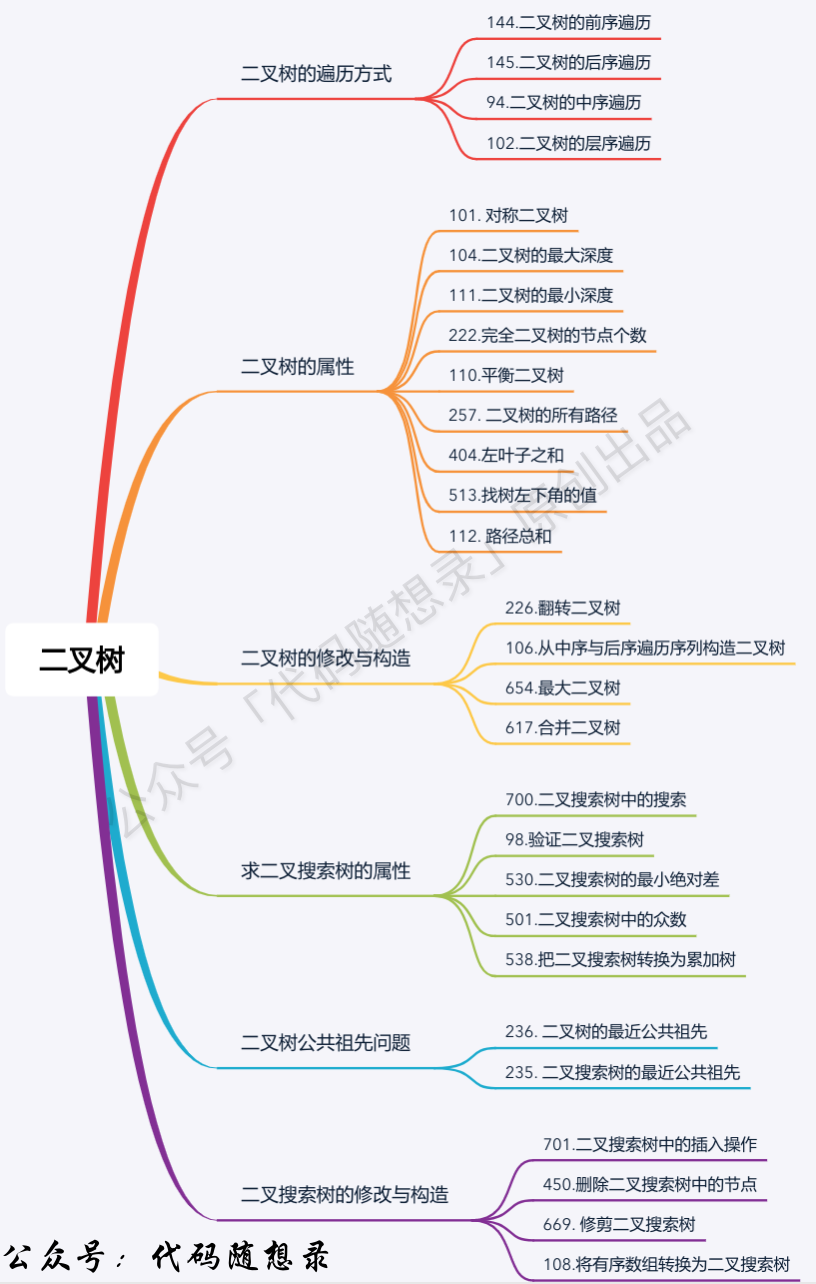 1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
@@ -233,7 +220,7 @@
题目分类大纲如下:
-
1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
@@ -233,7 +220,7 @@
题目分类大纲如下:
- +
+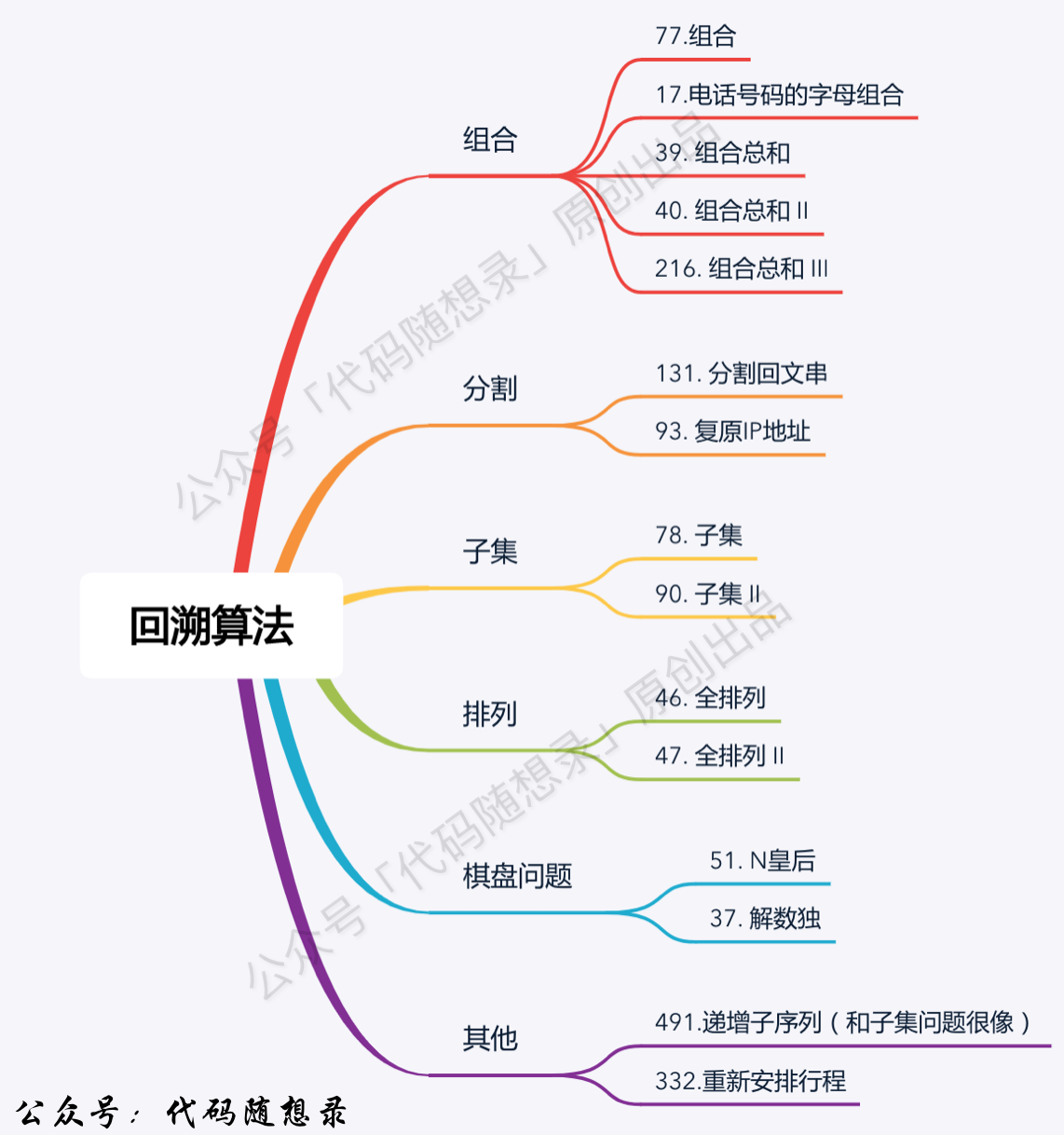 1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
2. [回溯算法:77.组合](./problems/0077.组合.md)
@@ -499,7 +486,7 @@
# 贡献者
-[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者收益于此项目。
+[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者受益于此项目。
# Star 趋势
@@ -507,24 +494,13 @@
# 关于作者
-大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术研发。对算法和C++后端技术有一定的见解,利用工作之余重新刷leetcode。
+大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术底层技术研发。
-加入「代码随想录」刷题小分队(微信群),可以扫下方二维码,加代码随想录客服微信。
+# PDF下载
-如果是已工作,备注:姓名-城市-岗位-组队刷题。如果学生,备注:姓名-学校-年级-组队刷题。**备注没有自我介绍不通过哦**
+添加如下企业微信,会自动发送给大家PDF版本,顺便可以选择是否加入刷题群。
+添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
2. [回溯算法:77.组合](./problems/0077.组合.md)
@@ -499,7 +486,7 @@
# 贡献者
-[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者收益于此项目。
+[点此这里](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢他们补充了LeetCode-Master的其他语言版本,让更多的读者受益于此项目。
# Star 趋势
@@ -507,24 +494,13 @@
# 关于作者
-大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术研发。对算法和C++后端技术有一定的见解,利用工作之余重新刷leetcode。
+大家好,我是程序员Carl,哈工大师兄,《代码随想录》作者,先后在腾讯和百度从事后端技术底层技术研发。
-加入「代码随想录」刷题小分队(微信群),可以扫下方二维码,加代码随想录客服微信。
+# PDF下载
-如果是已工作,备注:姓名-城市-岗位-组队刷题。如果学生,备注:姓名-学校-年级-组队刷题。**备注没有自我介绍不通过哦**
+添加如下企业微信,会自动发送给大家PDF版本,顺便可以选择是否加入刷题群。
+添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**


-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# 1. 两数之和 @@ -349,6 +349,7 @@ function twoSum(nums: number[], target: number): number[] { index = helperMap.get(target - nums[i]); if (index !== undefined) { resArr = [i, index]; + break; } helperMap.set(nums[i], i); } @@ -537,8 +538,8 @@ int* twoSum(int* nums, int numsSize, int target, int* returnSize){ return NULL; } ``` +
 -
diff --git a/problems/0005.最长回文子串.md b/problems/0005.最长回文子串.md
index b13f9ac3..a13daf1e 100644
--- a/problems/0005.最长回文子串.md
+++ b/problems/0005.最长回文子串.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0005.最长回文子串.md b/problems/0005.最长回文子串.md
index b13f9ac3..a13daf1e 100644
--- a/problems/0005.最长回文子串.md
+++ b/problems/0005.最长回文子串.md
@@ -1,8 +1,8 @@
-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
@@ -677,8 +677,8 @@ public class Solution { } ``` +
 -
diff --git a/problems/0015.三数之和.md b/problems/0015.三数之和.md
index bf165788..ae218385 100644
--- a/problems/0015.三数之和.md
+++ b/problems/0015.三数之和.md
@@ -1,13 +1,11 @@
-
diff --git a/problems/0015.三数之和.md b/problems/0015.三数之和.md
index bf165788..ae218385 100644
--- a/problems/0015.三数之和.md
+++ b/problems/0015.三数之和.md
@@ -1,13 +1,11 @@
-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-> 用哈希表解决了[两数之和](https://programmercarl.com/0001.两数之和.html),那么三数之和呢? - # 第15题. 三数之和 [力扣题目链接](https://leetcode.cn/problems/3sum/) @@ -938,8 +936,8 @@ object Solution { } } ``` +
 -
diff --git a/problems/0017.电话号码的字母组合.md b/problems/0017.电话号码的字母组合.md
index cbd99f8d..a06ee72d 100644
--- a/problems/0017.电话号码的字母组合.md
+++ b/problems/0017.电话号码的字母组合.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0017.电话号码的字母组合.md b/problems/0017.电话号码的字母组合.md
index cbd99f8d..a06ee72d 100644
--- a/problems/0017.电话号码的字母组合.md
+++ b/problems/0017.电话号码的字母组合.md
@@ -1,8 +1,8 @@
-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# 17.电话号码的字母组合 @@ -260,7 +260,7 @@ class Solution { } - //每次迭代获取一个字符串,所以会设计大量的字符串拼接,所以这里选择更为高效的 StringBuilder + //每次迭代获取一个字符串,所以会涉及大量的字符串拼接,所以这里选择更为高效的 StringBuilder StringBuilder temp = new StringBuilder(); //比如digits如果为"23",num 为0,则str表示2对应的 abc @@ -274,7 +274,7 @@ class Solution { String str = numString[digits.charAt(num) - '0']; for (int i = 0; i < str.length(); i++) { temp.append(str.charAt(i)); - //c + //递归,处理下一层 backTracking(digits, numString, num + 1); //剔除末尾的继续尝试 temp.deleteCharAt(temp.length() - 1); @@ -765,8 +765,8 @@ public class Solution } ``` +
 -
diff --git a/problems/0018.四数之和.md b/problems/0018.四数之和.md
index 17715b2e..89bc2a8b 100644
--- a/problems/0018.四数之和.md
+++ b/problems/0018.四数之和.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0018.四数之和.md b/problems/0018.四数之和.md
index 17715b2e..89bc2a8b 100644
--- a/problems/0018.四数之和.md
+++ b/problems/0018.四数之和.md
@@ -1,8 +1,8 @@
-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
> 一样的道理,能解决四数之和 @@ -697,8 +697,8 @@ def four_sum(nums, target) return result end ``` +
 -
diff --git a/problems/0019.删除链表的倒数第N个节点.md b/problems/0019.删除链表的倒数第N个节点.md
index c7a2cfcb..f0ef2366 100644
--- a/problems/0019.删除链表的倒数第N个节点.md
+++ b/problems/0019.删除链表的倒数第N个节点.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0019.删除链表的倒数第N个节点.md b/problems/0019.删除链表的倒数第N个节点.md
index c7a2cfcb..f0ef2366 100644
--- a/problems/0019.删除链表的倒数第N个节点.md
+++ b/problems/0019.删除链表的倒数第N个节点.md
@@ -1,8 +1,8 @@
-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
@@ -22,10 +22,12 @@ 输入:head = [1,2,3,4,5], n = 2 输出:[1,2,3,5] + 示例 2: 输入:head = [1], n = 1 输出:[] + 示例 3: 输入:head = [1,2], n = 1 @@ -98,27 +100,32 @@ public: ### Java: ```java -public ListNode removeNthFromEnd(ListNode head, int n){ - ListNode dummyNode = new ListNode(0); - dummyNode.next = head; +class Solution { + public ListNode removeNthFromEnd(ListNode head, int n) { + //新建一个虚拟头节点指向head + ListNode dummyNode = new ListNode(0); + dummyNode.next = head; + //快慢指针指向虚拟头节点 + ListNode fastIndex = dummyNode; + ListNode slowIndex = dummyNode; - ListNode fastIndex = dummyNode; - ListNode slowIndex = dummyNode; + // 只要快慢指针相差 n 个结点即可 + for (int i = 0; i <= n; i++) { + fastIndex = fastIndex.next; + } + while (fastIndex != null) { + fastIndex = fastIndex.next; + slowIndex = slowIndex.next; + } - // 只要快慢指针相差 n 个结点即可 - for (int i = 0; i < n ; i++){ - fastIndex = fastIndex.next; + // 此时 slowIndex 的位置就是待删除元素的前一个位置。 + // 具体情况可自己画一个链表长度为 3 的图来模拟代码来理解 + // 检查 slowIndex.next 是否为 null,以避免空指针异常 + if (slowIndex.next != null) { + slowIndex.next = slowIndex.next.next; + } + return dummyNode.next; } - - while (fastIndex != null){ - fastIndex = fastIndex.next; - slowIndex = slowIndex.next; - } - - //此时 slowIndex 的位置就是待删除元素的前一个位置。 - //具体情况可自己画一个链表长度为 3 的图来模拟代码来理解 - slowIndex.next = slowIndex.next.next; - return dummyNode.next; } ``` @@ -187,16 +194,18 @@ func removeNthFromEnd(head *ListNode, n int) *ListNode { * @param {number} n * @return {ListNode} */ -var removeNthFromEnd = function(head, n) { - let ret = new ListNode(0, head), - slow = fast = ret; - while(n--) fast = fast.next; - while (fast.next !== null) { - fast = fast.next; - slow = slow.next - }; - slow.next = slow.next.next; - return ret.next; +var removeNthFromEnd = function (head, n) { + // 创建哨兵节点,简化解题逻辑 + let dummyHead = new ListNode(0, head); + let fast = dummyHead; + let slow = dummyHead; + while (n--) fast = fast.next; + while (fast.next !== null) { + slow = slow.next; + fast = fast.next; + } + slow.next = slow.next.next; + return dummyHead.next; }; ``` ### TypeScript: diff --git a/problems/0020.有效的括号.md b/problems/0020.有效的括号.md index 17fbe2be..d310f415 100644 --- a/problems/0020.有效的括号.md +++ b/problems/0020.有效的括号.md @@ -1,8 +1,8 @@
-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
diff --git a/problems/0024.两两交换链表中的节点.md b/problems/0024.两两交换链表中的节点.md index b2a830a7..23dba84b 100644 --- a/problems/0024.两两交换链表中的节点.md +++ b/problems/0024.两两交换链表中的节点.md @@ -1,8 +1,8 @@
-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# 24. 两两交换链表中的节点 @@ -81,7 +81,7 @@ public: 上面的代码我第一次提交执行用时8ms,打败6.5%的用户,差点吓到我了。 -心想应该没有更好的方法了吧,也就$O(n)$的时间复杂度,重复提交几次,这样了: +心想应该没有更好的方法了吧,也就 $O(n)$ 的时间复杂度,重复提交几次,这样了:  @@ -181,6 +181,23 @@ class Solution { } ``` +```java +// 将步骤 2,3 交换顺序,这样不用定义 temp 节点 +public ListNode swapPairs(ListNode head) { + ListNode dummy = new ListNode(0, head); + ListNode cur = dummy; + while (cur.next != null && cur.next.next != null) { + ListNode node1 = cur.next;// 第 1 个节点 + ListNode node2 = cur.next.next;// 第 2 个节点 + cur.next = node2; // 步骤 1 + node1.next = node2.next;// 步骤 3 + node2.next = node1;// 步骤 2 + cur = cur.next.next; + } + return dummy.next; +} +``` + ### Python: ```python @@ -285,6 +302,21 @@ var swapPairs = function (head) { }; ``` +```javascript +// 递归版本 +var swapPairs = function (head) { + if (head == null || head.next == null) { + return head; + } + + let after = head.next; + head.next = swapPairs(after.next); + after.next = head; + + return after; +}; +``` + ### TypeScript: ```typescript diff --git a/problems/0027.移除元素.md b/problems/0027.移除元素.md index 2a2005d7..480800e9 100644 --- a/problems/0027.移除元素.md +++ b/problems/0027.移除元素.md @@ -1,8 +1,8 @@
-
+
 -
-
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
+参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# 27. 移除元素 @@ -119,35 +119,6 @@ public: * 时间复杂度:O(n) * 空间复杂度:O(1) -```CPP -/** -* 相向双指针方法,基于元素顺序可以改变的题目描述改变了元素相对位置,确保了移动最少元素 -* 时间复杂度:O(n) -* 空间复杂度:O(1) -*/ -class Solution { -public: - int removeElement(vector
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
diff --git a/problems/0188.买卖股票的最佳时机IV.md b/problems/0188.买卖股票的最佳时机IV.md
index 2521749f..def69277 100644
--- a/problems/0188.买卖股票的最佳时机IV.md
+++ b/problems/0188.买卖股票的最佳时机IV.md
@@ -1,8 +1,8 @@
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
+
+ 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
+
+
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
+
+ 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
+
+
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
+
+ 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
+
+
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
-
+
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益! 参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
 diff --git a/problems/0028.实现strStr.md b/problems/0028.实现strStr.md
index 8d0cc525..e0cb123e 100644
--- a/problems/0028.实现strStr.md
+++ b/problems/0028.实现strStr.md
@@ -1,8 +1,8 @@
diff --git a/problems/0028.实现strStr.md b/problems/0028.实现strStr.md
index 8d0cc525..e0cb123e 100644
--- a/problems/0028.实现strStr.md
+++ b/problems/0028.实现strStr.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md b/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
index 22936fef..16adcdf1 100644
--- a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
+++ b/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md b/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
index 22936fef..16adcdf1 100644
--- a/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
+++ b/problems/0034.在排序数组中查找元素的第一个和最后一个位置.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0035.搜索插入位置.md b/problems/0035.搜索插入位置.md
index 80b7e40e..b5be9a5f 100644
--- a/problems/0035.搜索插入位置.md
+++ b/problems/0035.搜索插入位置.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0035.搜索插入位置.md b/problems/0035.搜索插入位置.md
index 80b7e40e..b5be9a5f 100644
--- a/problems/0035.搜索插入位置.md
+++ b/problems/0035.搜索插入位置.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0037.解数独.md b/problems/0037.解数独.md
index d96e59df..70d52e9e 100644
--- a/problems/0037.解数独.md
+++ b/problems/0037.解数独.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0037.解数独.md b/problems/0037.解数独.md
index d96e59df..70d52e9e 100644
--- a/problems/0037.解数独.md
+++ b/problems/0037.解数独.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0039.组合总和.md b/problems/0039.组合总和.md
index 81558cc1..92c68562 100644
--- a/problems/0039.组合总和.md
+++ b/problems/0039.组合总和.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0039.组合总和.md b/problems/0039.组合总和.md
index 81558cc1..92c68562 100644
--- a/problems/0039.组合总和.md
+++ b/problems/0039.组合总和.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0040.组合总和II.md b/problems/0040.组合总和II.md
index 994b04b8..22cf726d 100644
--- a/problems/0040.组合总和II.md
+++ b/problems/0040.组合总和II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0040.组合总和II.md b/problems/0040.组合总和II.md
index 994b04b8..22cf726d 100644
--- a/problems/0040.组合总和II.md
+++ b/problems/0040.组合总和II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0042.接雨水.md b/problems/0042.接雨水.md
index 73d787b1..0484f830 100644
--- a/problems/0042.接雨水.md
+++ b/problems/0042.接雨水.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0042.接雨水.md b/problems/0042.接雨水.md
index 73d787b1..0484f830 100644
--- a/problems/0042.接雨水.md
+++ b/problems/0042.接雨水.md
@@ -1,9 +1,9 @@
-
 -
- -
- -
diff --git a/problems/0046.全排列.md b/problems/0046.全排列.md
index 15e6ae16..638a2a7c 100644
--- a/problems/0046.全排列.md
+++ b/problems/0046.全排列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0046.全排列.md b/problems/0046.全排列.md
index 15e6ae16..638a2a7c 100644
--- a/problems/0046.全排列.md
+++ b/problems/0046.全排列.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0047.全排列II.md b/problems/0047.全排列II.md
index 7f2c3638..56006a77 100644
--- a/problems/0047.全排列II.md
+++ b/problems/0047.全排列II.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0047.全排列II.md b/problems/0047.全排列II.md
index 7f2c3638..56006a77 100644
--- a/problems/0047.全排列II.md
+++ b/problems/0047.全排列II.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0051.N皇后.md b/problems/0051.N皇后.md
index 1e108540..6ced679c 100644
--- a/problems/0051.N皇后.md
+++ b/problems/0051.N皇后.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0051.N皇后.md b/problems/0051.N皇后.md
index 1e108540..6ced679c 100644
--- a/problems/0051.N皇后.md
+++ b/problems/0051.N皇后.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0052.N皇后II.md b/problems/0052.N皇后II.md
index 29c2b588..271484a4 100644
--- a/problems/0052.N皇后II.md
+++ b/problems/0052.N皇后II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0052.N皇后II.md b/problems/0052.N皇后II.md
index 29c2b588..271484a4 100644
--- a/problems/0052.N皇后II.md
+++ b/problems/0052.N皇后II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0053.最大子序和.md b/problems/0053.最大子序和.md
index 74ff2ca4..551c39bf 100644
--- a/problems/0053.最大子序和.md
+++ b/problems/0053.最大子序和.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0053.最大子序和.md b/problems/0053.最大子序和.md
index 74ff2ca4..551c39bf 100644
--- a/problems/0053.最大子序和.md
+++ b/problems/0053.最大子序和.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0054.螺旋矩阵.md b/problems/0054.螺旋矩阵.md
index 85e6a936..4d54ccd6 100644
--- a/problems/0054.螺旋矩阵.md
+++ b/problems/0054.螺旋矩阵.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0054.螺旋矩阵.md b/problems/0054.螺旋矩阵.md
index 85e6a936..4d54ccd6 100644
--- a/problems/0054.螺旋矩阵.md
+++ b/problems/0054.螺旋矩阵.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
- -
- -
diff --git a/problems/0063.不同路径II.md b/problems/0063.不同路径II.md
index 8c208ea8..6819c19f 100644
--- a/problems/0063.不同路径II.md
+++ b/problems/0063.不同路径II.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0063.不同路径II.md b/problems/0063.不同路径II.md
index 8c208ea8..6819c19f 100644
--- a/problems/0063.不同路径II.md
+++ b/problems/0063.不同路径II.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0070.爬楼梯.md b/problems/0070.爬楼梯.md
index 67bbdd7b..1d0b192f 100644
--- a/problems/0070.爬楼梯.md
+++ b/problems/0070.爬楼梯.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0070.爬楼梯.md b/problems/0070.爬楼梯.md
index 67bbdd7b..1d0b192f 100644
--- a/problems/0070.爬楼梯.md
+++ b/problems/0070.爬楼梯.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0070.爬楼梯完全背包版本.md b/problems/0070.爬楼梯完全背包版本.md
index 622b1117..07e0261e 100644
--- a/problems/0070.爬楼梯完全背包版本.md
+++ b/problems/0070.爬楼梯完全背包版本.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0070.爬楼梯完全背包版本.md b/problems/0070.爬楼梯完全背包版本.md
index 622b1117..07e0261e 100644
--- a/problems/0070.爬楼梯完全背包版本.md
+++ b/problems/0070.爬楼梯完全背包版本.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
diff --git a/problems/0077.组合优化.md b/problems/0077.组合优化.md
index 9577d65f..0fa568af 100644
--- a/problems/0077.组合优化.md
+++ b/problems/0077.组合优化.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0077.组合优化.md b/problems/0077.组合优化.md
index 9577d65f..0fa568af 100644
--- a/problems/0077.组合优化.md
+++ b/problems/0077.组合优化.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0078.子集.md b/problems/0078.子集.md
index 06547e3d..1415f2d2 100644
--- a/problems/0078.子集.md
+++ b/problems/0078.子集.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0078.子集.md b/problems/0078.子集.md
index 06547e3d..1415f2d2 100644
--- a/problems/0078.子集.md
+++ b/problems/0078.子集.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0084.柱状图中最大的矩形.md b/problems/0084.柱状图中最大的矩形.md
index b836705a..1c4d7f59 100644
--- a/problems/0084.柱状图中最大的矩形.md
+++ b/problems/0084.柱状图中最大的矩形.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0084.柱状图中最大的矩形.md b/problems/0084.柱状图中最大的矩形.md
index b836705a..1c4d7f59 100644
--- a/problems/0084.柱状图中最大的矩形.md
+++ b/problems/0084.柱状图中最大的矩形.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0090.子集II.md b/problems/0090.子集II.md
index 6d618978..03bbd1dc 100644
--- a/problems/0090.子集II.md
+++ b/problems/0090.子集II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0090.子集II.md b/problems/0090.子集II.md
index 6d618978..03bbd1dc 100644
--- a/problems/0090.子集II.md
+++ b/problems/0090.子集II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0093.复原IP地址.md b/problems/0093.复原IP地址.md
index c662957a..73d5e3c3 100644
--- a/problems/0093.复原IP地址.md
+++ b/problems/0093.复原IP地址.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0093.复原IP地址.md b/problems/0093.复原IP地址.md
index c662957a..73d5e3c3 100644
--- a/problems/0093.复原IP地址.md
+++ b/problems/0093.复原IP地址.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0096.不同的二叉搜索树.md b/problems/0096.不同的二叉搜索树.md
index 15b99083..e0e77310 100644
--- a/problems/0096.不同的二叉搜索树.md
+++ b/problems/0096.不同的二叉搜索树.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0096.不同的二叉搜索树.md b/problems/0096.不同的二叉搜索树.md
index 15b99083..e0e77310 100644
--- a/problems/0096.不同的二叉搜索树.md
+++ b/problems/0096.不同的二叉搜索树.md
@@ -1,9 +1,9 @@
-
 -
- -
- -
diff --git a/problems/0100.相同的树.md b/problems/0100.相同的树.md
index 56a6c884..7268b9f0 100644
--- a/problems/0100.相同的树.md
+++ b/problems/0100.相同的树.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0100.相同的树.md b/problems/0100.相同的树.md
index 56a6c884..7268b9f0 100644
--- a/problems/0100.相同的树.md
+++ b/problems/0100.相同的树.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0101.对称二叉树.md b/problems/0101.对称二叉树.md
index 8442f0ab..063b5429 100644
--- a/problems/0101.对称二叉树.md
+++ b/problems/0101.对称二叉树.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0101.对称二叉树.md b/problems/0101.对称二叉树.md
index 8442f0ab..063b5429 100644
--- a/problems/0101.对称二叉树.md
+++ b/problems/0101.对称二叉树.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0102.二叉树的层序遍历.md b/problems/0102.二叉树的层序遍历.md
index 4411b560..421c5dd9 100644
--- a/problems/0102.二叉树的层序遍历.md
+++ b/problems/0102.二叉树的层序遍历.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0102.二叉树的层序遍历.md b/problems/0102.二叉树的层序遍历.md
index 4411b560..421c5dd9 100644
--- a/problems/0102.二叉树的层序遍历.md
+++ b/problems/0102.二叉树的层序遍历.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0104.二叉树的最大深度.md b/problems/0104.二叉树的最大深度.md
index 1f55f197..0f93cb0f 100644
--- a/problems/0104.二叉树的最大深度.md
+++ b/problems/0104.二叉树的最大深度.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0104.二叉树的最大深度.md b/problems/0104.二叉树的最大深度.md
index 1f55f197..0f93cb0f 100644
--- a/problems/0104.二叉树的最大深度.md
+++ b/problems/0104.二叉树的最大深度.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0106.从中序与后序遍历序列构造二叉树.md b/problems/0106.从中序与后序遍历序列构造二叉树.md
index 0e0ab1d7..3518343f 100644
--- a/problems/0106.从中序与后序遍历序列构造二叉树.md
+++ b/problems/0106.从中序与后序遍历序列构造二叉树.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0106.从中序与后序遍历序列构造二叉树.md b/problems/0106.从中序与后序遍历序列构造二叉树.md
index 0e0ab1d7..3518343f 100644
--- a/problems/0106.从中序与后序遍历序列构造二叉树.md
+++ b/problems/0106.从中序与后序遍历序列构造二叉树.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0108.将有序数组转换为二叉搜索树.md b/problems/0108.将有序数组转换为二叉搜索树.md
index 9fa684cf..4804ccd3 100644
--- a/problems/0108.将有序数组转换为二叉搜索树.md
+++ b/problems/0108.将有序数组转换为二叉搜索树.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0108.将有序数组转换为二叉搜索树.md b/problems/0108.将有序数组转换为二叉搜索树.md
index 9fa684cf..4804ccd3 100644
--- a/problems/0108.将有序数组转换为二叉搜索树.md
+++ b/problems/0108.将有序数组转换为二叉搜索树.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0110.平衡二叉树.md b/problems/0110.平衡二叉树.md
index 40fdcd14..dd05bdd6 100644
--- a/problems/0110.平衡二叉树.md
+++ b/problems/0110.平衡二叉树.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0110.平衡二叉树.md b/problems/0110.平衡二叉树.md
index 40fdcd14..dd05bdd6 100644
--- a/problems/0110.平衡二叉树.md
+++ b/problems/0110.平衡二叉树.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0111.二叉树的最小深度.md b/problems/0111.二叉树的最小深度.md
index 6d1632d5..cd7096ac 100644
--- a/problems/0111.二叉树的最小深度.md
+++ b/problems/0111.二叉树的最小深度.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0111.二叉树的最小深度.md b/problems/0111.二叉树的最小深度.md
index 6d1632d5..cd7096ac 100644
--- a/problems/0111.二叉树的最小深度.md
+++ b/problems/0111.二叉树的最小深度.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0115.不同的子序列.md b/problems/0115.不同的子序列.md
index 96ab2583..8682b88d 100644
--- a/problems/0115.不同的子序列.md
+++ b/problems/0115.不同的子序列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0115.不同的子序列.md b/problems/0115.不同的子序列.md
index 96ab2583..8682b88d 100644
--- a/problems/0115.不同的子序列.md
+++ b/problems/0115.不同的子序列.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0116.填充每个节点的下一个右侧节点指针.md b/problems/0116.填充每个节点的下一个右侧节点指针.md
index 60ea9210..ca36ac6f 100644
--- a/problems/0116.填充每个节点的下一个右侧节点指针.md
+++ b/problems/0116.填充每个节点的下一个右侧节点指针.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0116.填充每个节点的下一个右侧节点指针.md b/problems/0116.填充每个节点的下一个右侧节点指针.md
index 60ea9210..ca36ac6f 100644
--- a/problems/0116.填充每个节点的下一个右侧节点指针.md
+++ b/problems/0116.填充每个节点的下一个右侧节点指针.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0121.买卖股票的最佳时机.md b/problems/0121.买卖股票的最佳时机.md
index fb548cbc..e9aea0e6 100644
--- a/problems/0121.买卖股票的最佳时机.md
+++ b/problems/0121.买卖股票的最佳时机.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0121.买卖股票的最佳时机.md b/problems/0121.买卖股票的最佳时机.md
index fb548cbc..e9aea0e6 100644
--- a/problems/0121.买卖股票的最佳时机.md
+++ b/problems/0121.买卖股票的最佳时机.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0122.买卖股票的最佳时机II(动态规划).md b/problems/0122.买卖股票的最佳时机II(动态规划).md
index 24c7f168..f0dff505 100644
--- a/problems/0122.买卖股票的最佳时机II(动态规划).md
+++ b/problems/0122.买卖股票的最佳时机II(动态规划).md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0122.买卖股票的最佳时机II(动态规划).md b/problems/0122.买卖股票的最佳时机II(动态规划).md
index 24c7f168..f0dff505 100644
--- a/problems/0122.买卖股票的最佳时机II(动态规划).md
+++ b/problems/0122.买卖股票的最佳时机II(动态规划).md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0123.买卖股票的最佳时机III.md b/problems/0123.买卖股票的最佳时机III.md
index 18f19c51..d06b4f80 100644
--- a/problems/0123.买卖股票的最佳时机III.md
+++ b/problems/0123.买卖股票的最佳时机III.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0123.买卖股票的最佳时机III.md b/problems/0123.买卖股票的最佳时机III.md
index 18f19c51..d06b4f80 100644
--- a/problems/0123.买卖股票的最佳时机III.md
+++ b/problems/0123.买卖股票的最佳时机III.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
diff --git a/problems/0130.被围绕的区域.md b/problems/0130.被围绕的区域.md
index 1ddaaa7f..8ef8d5b2 100644
--- a/problems/0130.被围绕的区域.md
+++ b/problems/0130.被围绕的区域.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0130.被围绕的区域.md b/problems/0130.被围绕的区域.md
index 1ddaaa7f..8ef8d5b2 100644
--- a/problems/0130.被围绕的区域.md
+++ b/problems/0130.被围绕的区域.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0131.分割回文串.md b/problems/0131.分割回文串.md
index ca342d4b..822d4399 100644
--- a/problems/0131.分割回文串.md
+++ b/problems/0131.分割回文串.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0131.分割回文串.md b/problems/0131.分割回文串.md
index ca342d4b..822d4399 100644
--- a/problems/0131.分割回文串.md
+++ b/problems/0131.分割回文串.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0132.分割回文串II.md b/problems/0132.分割回文串II.md
index eb91a189..85e047f2 100644
--- a/problems/0132.分割回文串II.md
+++ b/problems/0132.分割回文串II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0132.分割回文串II.md b/problems/0132.分割回文串II.md
index eb91a189..85e047f2 100644
--- a/problems/0132.分割回文串II.md
+++ b/problems/0132.分割回文串II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0134.加油站.md b/problems/0134.加油站.md
index c093023d..c88b43b1 100644
--- a/problems/0134.加油站.md
+++ b/problems/0134.加油站.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0134.加油站.md b/problems/0134.加油站.md
index c093023d..c88b43b1 100644
--- a/problems/0134.加油站.md
+++ b/problems/0134.加油站.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0135.分发糖果.md b/problems/0135.分发糖果.md
index 210f4995..6805857e 100644
--- a/problems/0135.分发糖果.md
+++ b/problems/0135.分发糖果.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0135.分发糖果.md b/problems/0135.分发糖果.md
index 210f4995..6805857e 100644
--- a/problems/0135.分发糖果.md
+++ b/problems/0135.分发糖果.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0139.单词拆分.md b/problems/0139.单词拆分.md
index a3d59ec7..816892d5 100644
--- a/problems/0139.单词拆分.md
+++ b/problems/0139.单词拆分.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0139.单词拆分.md b/problems/0139.单词拆分.md
index a3d59ec7..816892d5 100644
--- a/problems/0139.单词拆分.md
+++ b/problems/0139.单词拆分.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0142.环形链表II.md b/problems/0142.环形链表II.md
index a643fd70..d97b160b 100644
--- a/problems/0142.环形链表II.md
+++ b/problems/0142.环形链表II.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0142.环形链表II.md b/problems/0142.环形链表II.md
index a643fd70..d97b160b 100644
--- a/problems/0142.环形链表II.md
+++ b/problems/0142.环形链表II.md
@@ -1,9 +1,9 @@
-
 -
- -
- -
- -
- -
- -
- -
diff --git a/problems/0189.旋转数组.md b/problems/0189.旋转数组.md
index d60612e9..b47ee4b9 100644
--- a/problems/0189.旋转数组.md
+++ b/problems/0189.旋转数组.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0189.旋转数组.md b/problems/0189.旋转数组.md
index d60612e9..b47ee4b9 100644
--- a/problems/0189.旋转数组.md
+++ b/problems/0189.旋转数组.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0198.打家劫舍.md b/problems/0198.打家劫舍.md
index 480222ef..032204bb 100644
--- a/problems/0198.打家劫舍.md
+++ b/problems/0198.打家劫舍.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0198.打家劫舍.md b/problems/0198.打家劫舍.md
index 480222ef..032204bb 100644
--- a/problems/0198.打家劫舍.md
+++ b/problems/0198.打家劫舍.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0200.岛屿数量.广搜版.md b/problems/0200.岛屿数量.广搜版.md
index 85471f73..00e4efd8 100644
--- a/problems/0200.岛屿数量.广搜版.md
+++ b/problems/0200.岛屿数量.广搜版.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0200.岛屿数量.广搜版.md b/problems/0200.岛屿数量.广搜版.md
index 85471f73..00e4efd8 100644
--- a/problems/0200.岛屿数量.广搜版.md
+++ b/problems/0200.岛屿数量.广搜版.md
@@ -1,8 +1,8 @@
 -
- -```
-
diff --git a/problems/0200.岛屿数量.深搜版.md b/problems/0200.岛屿数量.深搜版.md
index 83d295bd..46579203 100644
--- a/problems/0200.岛屿数量.深搜版.md
+++ b/problems/0200.岛屿数量.深搜版.md
@@ -1,8 +1,8 @@
-```
-
diff --git a/problems/0200.岛屿数量.深搜版.md b/problems/0200.岛屿数量.深搜版.md
index 83d295bd..46579203 100644
--- a/problems/0200.岛屿数量.深搜版.md
+++ b/problems/0200.岛屿数量.深搜版.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0203.移除链表元素.md b/problems/0203.移除链表元素.md
index d6d7e6c2..efcc6414 100644
--- a/problems/0203.移除链表元素.md
+++ b/problems/0203.移除链表元素.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0203.移除链表元素.md b/problems/0203.移除链表元素.md
index d6d7e6c2..efcc6414 100644
--- a/problems/0203.移除链表元素.md
+++ b/problems/0203.移除链表元素.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0205.同构字符串.md b/problems/0205.同构字符串.md
index e07ab746..e416d9ce 100644
--- a/problems/0205.同构字符串.md
+++ b/problems/0205.同构字符串.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0205.同构字符串.md b/problems/0205.同构字符串.md
index e07ab746..e416d9ce 100644
--- a/problems/0205.同构字符串.md
+++ b/problems/0205.同构字符串.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0206.翻转链表.md b/problems/0206.翻转链表.md
index 5a57939a..430bebe5 100644
--- a/problems/0206.翻转链表.md
+++ b/problems/0206.翻转链表.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0206.翻转链表.md b/problems/0206.翻转链表.md
index 5a57939a..430bebe5 100644
--- a/problems/0206.翻转链表.md
+++ b/problems/0206.翻转链表.md
@@ -1,8 +1,8 @@
 -
- +
+
+
+ +
diff --git a/problems/0209.长度最小的子数组.md b/problems/0209.长度最小的子数组.md
index 5934d5e3..e399ac90 100644
--- a/problems/0209.长度最小的子数组.md
+++ b/problems/0209.长度最小的子数组.md
@@ -1,8 +1,8 @@
+
diff --git a/problems/0209.长度最小的子数组.md b/problems/0209.长度最小的子数组.md
index 5934d5e3..e399ac90 100644
--- a/problems/0209.长度最小的子数组.md
+++ b/problems/0209.长度最小的子数组.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
- -
diff --git a/problems/0225.用队列实现栈.md b/problems/0225.用队列实现栈.md
index 6900e668..c7dc52f1 100644
--- a/problems/0225.用队列实现栈.md
+++ b/problems/0225.用队列实现栈.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0225.用队列实现栈.md b/problems/0225.用队列实现栈.md
index 6900e668..c7dc52f1 100644
--- a/problems/0225.用队列实现栈.md
+++ b/problems/0225.用队列实现栈.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0226.翻转二叉树.md b/problems/0226.翻转二叉树.md
index 8691953a..824968f0 100644
--- a/problems/0226.翻转二叉树.md
+++ b/problems/0226.翻转二叉树.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0226.翻转二叉树.md b/problems/0226.翻转二叉树.md
index 8691953a..824968f0 100644
--- a/problems/0226.翻转二叉树.md
+++ b/problems/0226.翻转二叉树.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0232.用栈实现队列.md b/problems/0232.用栈实现队列.md
index 41933ca4..e8a3d2ec 100644
--- a/problems/0232.用栈实现队列.md
+++ b/problems/0232.用栈实现队列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0232.用栈实现队列.md b/problems/0232.用栈实现队列.md
index 41933ca4..e8a3d2ec 100644
--- a/problems/0232.用栈实现队列.md
+++ b/problems/0232.用栈实现队列.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0235.二叉搜索树的最近公共祖先.md b/problems/0235.二叉搜索树的最近公共祖先.md
index 2a11f9f4..597c2dff 100644
--- a/problems/0235.二叉搜索树的最近公共祖先.md
+++ b/problems/0235.二叉搜索树的最近公共祖先.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0235.二叉搜索树的最近公共祖先.md b/problems/0235.二叉搜索树的最近公共祖先.md
index 2a11f9f4..597c2dff 100644
--- a/problems/0235.二叉搜索树的最近公共祖先.md
+++ b/problems/0235.二叉搜索树的最近公共祖先.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0236.二叉树的最近公共祖先.md b/problems/0236.二叉树的最近公共祖先.md
index 049f70c7..5e80e702 100644
--- a/problems/0236.二叉树的最近公共祖先.md
+++ b/problems/0236.二叉树的最近公共祖先.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0236.二叉树的最近公共祖先.md b/problems/0236.二叉树的最近公共祖先.md
index 049f70c7..5e80e702 100644
--- a/problems/0236.二叉树的最近公共祖先.md
+++ b/problems/0236.二叉树的最近公共祖先.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0239.滑动窗口最大值.md b/problems/0239.滑动窗口最大值.md
index 19ac1261..23bf615b 100644
--- a/problems/0239.滑动窗口最大值.md
+++ b/problems/0239.滑动窗口最大值.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0239.滑动窗口最大值.md b/problems/0239.滑动窗口最大值.md
index 19ac1261..23bf615b 100644
--- a/problems/0239.滑动窗口最大值.md
+++ b/problems/0239.滑动窗口最大值.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0257.二叉树的所有路径.md b/problems/0257.二叉树的所有路径.md
index 4c6c92c5..2d9292bc 100644
--- a/problems/0257.二叉树的所有路径.md
+++ b/problems/0257.二叉树的所有路径.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0257.二叉树的所有路径.md b/problems/0257.二叉树的所有路径.md
index 4c6c92c5..2d9292bc 100644
--- a/problems/0257.二叉树的所有路径.md
+++ b/problems/0257.二叉树的所有路径.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
diff --git a/problems/0300.最长上升子序列.md b/problems/0300.最长上升子序列.md
index 6d82eae1..f256d15c 100644
--- a/problems/0300.最长上升子序列.md
+++ b/problems/0300.最长上升子序列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0300.最长上升子序列.md b/problems/0300.最长上升子序列.md
index 6d82eae1..f256d15c 100644
--- a/problems/0300.最长上升子序列.md
+++ b/problems/0300.最长上升子序列.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
- -
diff --git a/problems/0337.打家劫舍III.md b/problems/0337.打家劫舍III.md
index 61b9f99c..7aae5cbf 100644
--- a/problems/0337.打家劫舍III.md
+++ b/problems/0337.打家劫舍III.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0337.打家劫舍III.md b/problems/0337.打家劫舍III.md
index 61b9f99c..7aae5cbf 100644
--- a/problems/0337.打家劫舍III.md
+++ b/problems/0337.打家劫舍III.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0344.反转字符串.md b/problems/0344.反转字符串.md
index 44184c53..793c9af3 100644
--- a/problems/0344.反转字符串.md
+++ b/problems/0344.反转字符串.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0344.反转字符串.md b/problems/0344.反转字符串.md
index 44184c53..793c9af3 100644
--- a/problems/0344.反转字符串.md
+++ b/problems/0344.反转字符串.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0349.两个数组的交集.md b/problems/0349.两个数组的交集.md
index 9902fff8..e17e940f 100644
--- a/problems/0349.两个数组的交集.md
+++ b/problems/0349.两个数组的交集.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0349.两个数组的交集.md b/problems/0349.两个数组的交集.md
index 9902fff8..e17e940f 100644
--- a/problems/0349.两个数组的交集.md
+++ b/problems/0349.两个数组的交集.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
- -
diff --git a/problems/0392.判断子序列.md b/problems/0392.判断子序列.md
index ebd567cb..92246e4f 100644
--- a/problems/0392.判断子序列.md
+++ b/problems/0392.判断子序列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0392.判断子序列.md b/problems/0392.判断子序列.md
index ebd567cb..92246e4f 100644
--- a/problems/0392.判断子序列.md
+++ b/problems/0392.判断子序列.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0404.左叶子之和.md b/problems/0404.左叶子之和.md
index 3d0f5a8a..1ba71dc9 100644
--- a/problems/0404.左叶子之和.md
+++ b/problems/0404.左叶子之和.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0404.左叶子之和.md b/problems/0404.左叶子之和.md
index 3d0f5a8a..1ba71dc9 100644
--- a/problems/0404.左叶子之和.md
+++ b/problems/0404.左叶子之和.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0406.根据身高重建队列.md b/problems/0406.根据身高重建队列.md
index b0b02c14..b7e94543 100644
--- a/problems/0406.根据身高重建队列.md
+++ b/problems/0406.根据身高重建队列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0406.根据身高重建队列.md b/problems/0406.根据身高重建队列.md
index b0b02c14..b7e94543 100644
--- a/problems/0406.根据身高重建队列.md
+++ b/problems/0406.根据身高重建队列.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0416.分割等和子集.md b/problems/0416.分割等和子集.md
index 71e01ae3..4d2e6bf6 100644
--- a/problems/0416.分割等和子集.md
+++ b/problems/0416.分割等和子集.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0416.分割等和子集.md b/problems/0416.分割等和子集.md
index 71e01ae3..4d2e6bf6 100644
--- a/problems/0416.分割等和子集.md
+++ b/problems/0416.分割等和子集.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0417.太平洋大西洋水流问题.md b/problems/0417.太平洋大西洋水流问题.md
index 8fe0f1b4..b8448e93 100644
--- a/problems/0417.太平洋大西洋水流问题.md
+++ b/problems/0417.太平洋大西洋水流问题.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0417.太平洋大西洋水流问题.md b/problems/0417.太平洋大西洋水流问题.md
index 8fe0f1b4..b8448e93 100644
--- a/problems/0417.太平洋大西洋水流问题.md
+++ b/problems/0417.太平洋大西洋水流问题.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0450.删除二叉搜索树中的节点.md b/problems/0450.删除二叉搜索树中的节点.md
index 60dae7b9..f6057f44 100644
--- a/problems/0450.删除二叉搜索树中的节点.md
+++ b/problems/0450.删除二叉搜索树中的节点.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0450.删除二叉搜索树中的节点.md b/problems/0450.删除二叉搜索树中的节点.md
index 60dae7b9..f6057f44 100644
--- a/problems/0450.删除二叉搜索树中的节点.md
+++ b/problems/0450.删除二叉搜索树中的节点.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0452.用最少数量的箭引爆气球.md b/problems/0452.用最少数量的箭引爆气球.md
index cd57f83b..318c3035 100644
--- a/problems/0452.用最少数量的箭引爆气球.md
+++ b/problems/0452.用最少数量的箭引爆气球.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0452.用最少数量的箭引爆气球.md b/problems/0452.用最少数量的箭引爆气球.md
index cd57f83b..318c3035 100644
--- a/problems/0452.用最少数量的箭引爆气球.md
+++ b/problems/0452.用最少数量的箭引爆气球.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0455.分发饼干.md b/problems/0455.分发饼干.md
index b6f5bae5..9f59d3ad 100644
--- a/problems/0455.分发饼干.md
+++ b/problems/0455.分发饼干.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0455.分发饼干.md b/problems/0455.分发饼干.md
index b6f5bae5..9f59d3ad 100644
--- a/problems/0455.分发饼干.md
+++ b/problems/0455.分发饼干.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
diff --git a/problems/0474.一和零.md b/problems/0474.一和零.md
index af50fa5c..47b34a0f 100644
--- a/problems/0474.一和零.md
+++ b/problems/0474.一和零.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0474.一和零.md b/problems/0474.一和零.md
index af50fa5c..47b34a0f 100644
--- a/problems/0474.一和零.md
+++ b/problems/0474.一和零.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0491.递增子序列.md b/problems/0491.递增子序列.md
index 1aa69a36..8f642a5f 100644
--- a/problems/0491.递增子序列.md
+++ b/problems/0491.递增子序列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0491.递增子序列.md b/problems/0491.递增子序列.md
index 1aa69a36..8f642a5f 100644
--- a/problems/0491.递增子序列.md
+++ b/problems/0491.递增子序列.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0496.下一个更大元素I.md b/problems/0496.下一个更大元素I.md
index d97a3e84..54182d30 100644
--- a/problems/0496.下一个更大元素I.md
+++ b/problems/0496.下一个更大元素I.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0496.下一个更大元素I.md b/problems/0496.下一个更大元素I.md
index d97a3e84..54182d30 100644
--- a/problems/0496.下一个更大元素I.md
+++ b/problems/0496.下一个更大元素I.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0501.二叉搜索树中的众数.md b/problems/0501.二叉搜索树中的众数.md
index 20627d1a..93b3fb54 100644
--- a/problems/0501.二叉搜索树中的众数.md
+++ b/problems/0501.二叉搜索树中的众数.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0501.二叉搜索树中的众数.md b/problems/0501.二叉搜索树中的众数.md
index 20627d1a..93b3fb54 100644
--- a/problems/0501.二叉搜索树中的众数.md
+++ b/problems/0501.二叉搜索树中的众数.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0503.下一个更大元素II.md b/problems/0503.下一个更大元素II.md
index 6df83fb2..62066d85 100644
--- a/problems/0503.下一个更大元素II.md
+++ b/problems/0503.下一个更大元素II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0503.下一个更大元素II.md b/problems/0503.下一个更大元素II.md
index 6df83fb2..62066d85 100644
--- a/problems/0503.下一个更大元素II.md
+++ b/problems/0503.下一个更大元素II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0509.斐波那契数.md b/problems/0509.斐波那契数.md
index 71c022bd..21b07802 100644
--- a/problems/0509.斐波那契数.md
+++ b/problems/0509.斐波那契数.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0509.斐波那契数.md b/problems/0509.斐波那契数.md
index 71c022bd..21b07802 100644
--- a/problems/0509.斐波那契数.md
+++ b/problems/0509.斐波那契数.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0513.找树左下角的值.md b/problems/0513.找树左下角的值.md
index d897bba1..d69ceb6f 100644
--- a/problems/0513.找树左下角的值.md
+++ b/problems/0513.找树左下角的值.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0513.找树左下角的值.md b/problems/0513.找树左下角的值.md
index d897bba1..d69ceb6f 100644
--- a/problems/0513.找树左下角的值.md
+++ b/problems/0513.找树左下角的值.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0518.零钱兑换II.md b/problems/0518.零钱兑换II.md
index 59fdf6cd..255912d6 100644
--- a/problems/0518.零钱兑换II.md
+++ b/problems/0518.零钱兑换II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0518.零钱兑换II.md b/problems/0518.零钱兑换II.md
index 59fdf6cd..255912d6 100644
--- a/problems/0518.零钱兑换II.md
+++ b/problems/0518.零钱兑换II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0530.二叉搜索树的最小绝对差.md b/problems/0530.二叉搜索树的最小绝对差.md
index 82b3f5d4..7fe64ad2 100644
--- a/problems/0530.二叉搜索树的最小绝对差.md
+++ b/problems/0530.二叉搜索树的最小绝对差.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0530.二叉搜索树的最小绝对差.md b/problems/0530.二叉搜索树的最小绝对差.md
index 82b3f5d4..7fe64ad2 100644
--- a/problems/0530.二叉搜索树的最小绝对差.md
+++ b/problems/0530.二叉搜索树的最小绝对差.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0538.把二叉搜索树转换为累加树.md b/problems/0538.把二叉搜索树转换为累加树.md
index 7fcb5efd..b95b5854 100644
--- a/problems/0538.把二叉搜索树转换为累加树.md
+++ b/problems/0538.把二叉搜索树转换为累加树.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0538.把二叉搜索树转换为累加树.md b/problems/0538.把二叉搜索树转换为累加树.md
index 7fcb5efd..b95b5854 100644
--- a/problems/0538.把二叉搜索树转换为累加树.md
+++ b/problems/0538.把二叉搜索树转换为累加树.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0541.反转字符串II.md b/problems/0541.反转字符串II.md
index 80e662f9..3e304fab 100644
--- a/problems/0541.反转字符串II.md
+++ b/problems/0541.反转字符串II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0541.反转字符串II.md b/problems/0541.反转字符串II.md
index 80e662f9..3e304fab 100644
--- a/problems/0541.反转字符串II.md
+++ b/problems/0541.反转字符串II.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
diff --git a/problems/0647.回文子串.md b/problems/0647.回文子串.md
index 4887ff83..2011bee3 100644
--- a/problems/0647.回文子串.md
+++ b/problems/0647.回文子串.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0647.回文子串.md b/problems/0647.回文子串.md
index 4887ff83..2011bee3 100644
--- a/problems/0647.回文子串.md
+++ b/problems/0647.回文子串.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0654.最大二叉树.md b/problems/0654.最大二叉树.md
index f54558a6..fed9b2b9 100644
--- a/problems/0654.最大二叉树.md
+++ b/problems/0654.最大二叉树.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0654.最大二叉树.md b/problems/0654.最大二叉树.md
index f54558a6..fed9b2b9 100644
--- a/problems/0654.最大二叉树.md
+++ b/problems/0654.最大二叉树.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0657.机器人能否返回原点.md b/problems/0657.机器人能否返回原点.md
index ef587391..eccfef3a 100644
--- a/problems/0657.机器人能否返回原点.md
+++ b/problems/0657.机器人能否返回原点.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0657.机器人能否返回原点.md b/problems/0657.机器人能否返回原点.md
index ef587391..eccfef3a 100644
--- a/problems/0657.机器人能否返回原点.md
+++ b/problems/0657.机器人能否返回原点.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0669.修剪二叉搜索树.md b/problems/0669.修剪二叉搜索树.md
index 6824c7e2..aef84659 100644
--- a/problems/0669.修剪二叉搜索树.md
+++ b/problems/0669.修剪二叉搜索树.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0669.修剪二叉搜索树.md b/problems/0669.修剪二叉搜索树.md
index 6824c7e2..aef84659 100644
--- a/problems/0669.修剪二叉搜索树.md
+++ b/problems/0669.修剪二叉搜索树.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/0673.最长递增子序列的个数.md b/problems/0673.最长递增子序列的个数.md
index 0277f249..0366ee80 100644
--- a/problems/0673.最长递增子序列的个数.md
+++ b/problems/0673.最长递增子序列的个数.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0673.最长递增子序列的个数.md b/problems/0673.最长递增子序列的个数.md
index 0277f249..0366ee80 100644
--- a/problems/0673.最长递增子序列的个数.md
+++ b/problems/0673.最长递增子序列的个数.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0674.最长连续递增序列.md b/problems/0674.最长连续递增序列.md
index ece62944..cebb552b 100644
--- a/problems/0674.最长连续递增序列.md
+++ b/problems/0674.最长连续递增序列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0674.最长连续递增序列.md b/problems/0674.最长连续递增序列.md
index ece62944..cebb552b 100644
--- a/problems/0674.最长连续递增序列.md
+++ b/problems/0674.最长连续递增序列.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0685.冗余连接II.md b/problems/0685.冗余连接II.md
index c07dda3a..3f489d82 100644
--- a/problems/0685.冗余连接II.md
+++ b/problems/0685.冗余连接II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0685.冗余连接II.md b/problems/0685.冗余连接II.md
index c07dda3a..3f489d82 100644
--- a/problems/0685.冗余连接II.md
+++ b/problems/0685.冗余连接II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0695.岛屿的最大面积.md b/problems/0695.岛屿的最大面积.md
index 87b1b5bb..11b638d4 100644
--- a/problems/0695.岛屿的最大面积.md
+++ b/problems/0695.岛屿的最大面积.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0695.岛屿的最大面积.md b/problems/0695.岛屿的最大面积.md
index 87b1b5bb..11b638d4 100644
--- a/problems/0695.岛屿的最大面积.md
+++ b/problems/0695.岛屿的最大面积.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0700.二叉搜索树中的搜索.md b/problems/0700.二叉搜索树中的搜索.md
index 58ada3cb..9ec51524 100644
--- a/problems/0700.二叉搜索树中的搜索.md
+++ b/problems/0700.二叉搜索树中的搜索.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0700.二叉搜索树中的搜索.md b/problems/0700.二叉搜索树中的搜索.md
index 58ada3cb..9ec51524 100644
--- a/problems/0700.二叉搜索树中的搜索.md
+++ b/problems/0700.二叉搜索树中的搜索.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0701.二叉搜索树中的插入操作.md b/problems/0701.二叉搜索树中的插入操作.md
index 5cb0de99..6b9e5834 100644
--- a/problems/0701.二叉搜索树中的插入操作.md
+++ b/problems/0701.二叉搜索树中的插入操作.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0701.二叉搜索树中的插入操作.md b/problems/0701.二叉搜索树中的插入操作.md
index 5cb0de99..6b9e5834 100644
--- a/problems/0701.二叉搜索树中的插入操作.md
+++ b/problems/0701.二叉搜索树中的插入操作.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0707.设计链表.md b/problems/0707.设计链表.md
index fecdbc3c..47771d28 100644
--- a/problems/0707.设计链表.md
+++ b/problems/0707.设计链表.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0707.设计链表.md b/problems/0707.设计链表.md
index fecdbc3c..47771d28 100644
--- a/problems/0707.设计链表.md
+++ b/problems/0707.设计链表.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0714.买卖股票的最佳时机含手续费(动态规划).md b/problems/0714.买卖股票的最佳时机含手续费(动态规划).md
index 88ba9271..73714147 100644
--- a/problems/0714.买卖股票的最佳时机含手续费(动态规划).md
+++ b/problems/0714.买卖股票的最佳时机含手续费(动态规划).md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0714.买卖股票的最佳时机含手续费(动态规划).md b/problems/0714.买卖股票的最佳时机含手续费(动态规划).md
index 88ba9271..73714147 100644
--- a/problems/0714.买卖股票的最佳时机含手续费(动态规划).md
+++ b/problems/0714.买卖股票的最佳时机含手续费(动态规划).md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0718.最长重复子数组.md b/problems/0718.最长重复子数组.md
index e00b3ded..6c8e7101 100644
--- a/problems/0718.最长重复子数组.md
+++ b/problems/0718.最长重复子数组.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0718.最长重复子数组.md b/problems/0718.最长重复子数组.md
index e00b3ded..6c8e7101 100644
--- a/problems/0718.最长重复子数组.md
+++ b/problems/0718.最长重复子数组.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
- -
diff --git a/problems/0743.网络延迟时间.md b/problems/0743.网络延迟时间.md
new file mode 100644
index 00000000..e631951a
--- /dev/null
+++ b/problems/0743.网络延迟时间.md
@@ -0,0 +1,1227 @@
+
+# 743.网络延迟时间
+
+https://leetcode.cn/problems/network-delay-time/description/
+
+
+有 n 个网络节点,标记为 1 到 n。
+
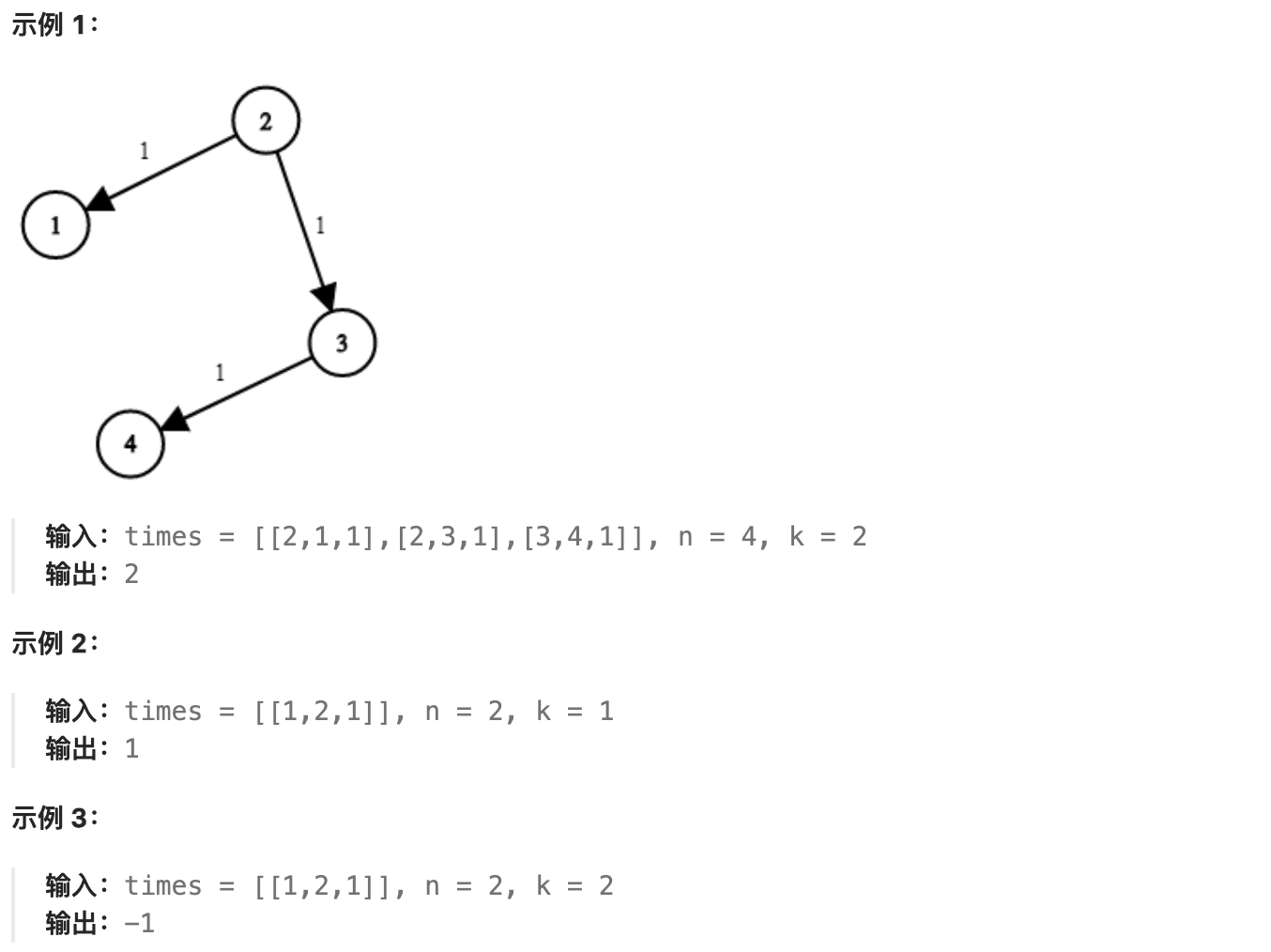
+给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
+
+现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
+
+
+
+提示:
+
+* 1 <= k <= n <= 100
+* 1 <= times.length <= 6000
+* times[i].length == 3
+* 1 <= ui, vi <= n
+* ui != vi
+* 0 <= wi <= 100
+* 所有 (ui, vi) 对都 互不相同(即,不含重复边)
+
+# dijkstra 精讲
+
+本题就是求最短路,最短路是图论中的经典问题即:给出一个有向图,一个起点,一个终点,问起点到终点的最短路径。
+
+接下来,我们来详细讲解最短路算法中的 dijkstra 算法。
+
+dijkstra算法:在有权图(权值非负数)中求从起点到其他节点的最短路径算法。
+
+需要注意两点:
+
+* dijkstra 算法可以同时求 起点到所有节点的最短路径
+* 权值不能为负数
+
+(这两点后面我们会讲到)
+
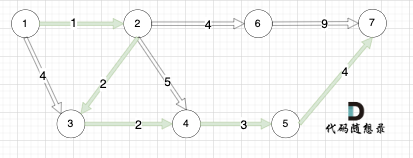
+如本题示例中的图:
+
+
+
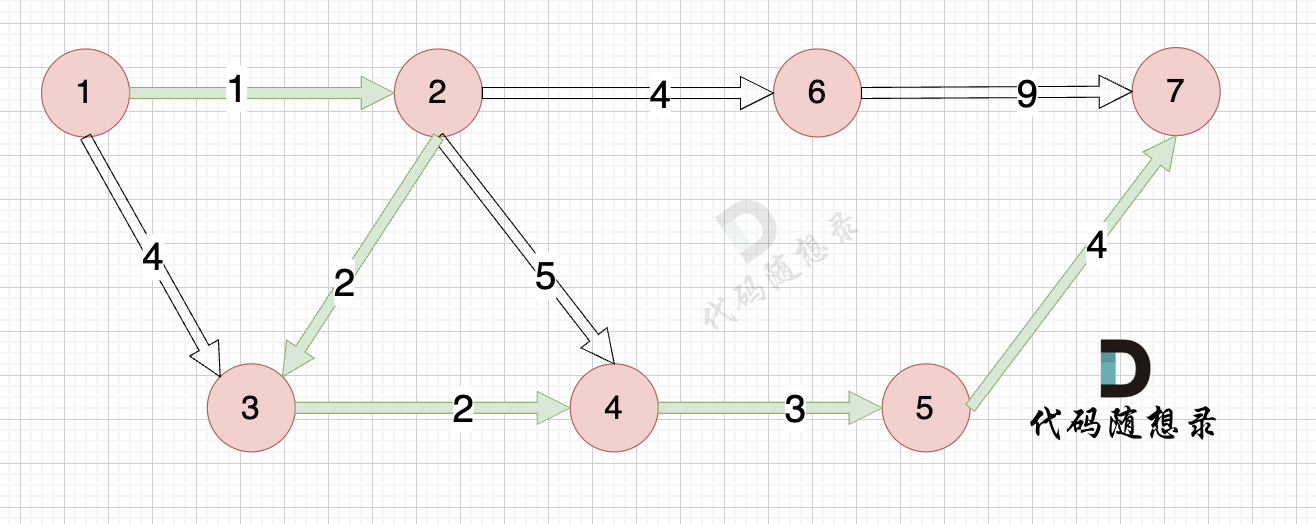
+起点(节点1)到终点(节点7) 的最短路径是 图中 标记绿线的部分。
+
+最短路径的权值为12。
+
+其实 dijkstra 算法 和 我们之前讲解的prim算法思路非常接近,如果大家认真学过[prim算法](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w),那么理解 Dijkstra 算法会相对容易很多。(这也是我要先讲prim再讲dijkstra的原因)
+
+dijkstra 算法 同样是贪心的思路,不断寻找距离 源点最近的没有访问过的节点。
+
+这里我也给出 **dijkstra三部曲**:
+
+1. 第一步,选源点到哪个节点近且该节点未被访问过
+2. 第二步,该最近节点被标记访问过
+3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
+
+大家此时已经会发现,这和prim算法 怎么这么像呢。
+
+我在[prim算法](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w)讲解中也给出了三部曲。 prim 和 dijkstra 确实很像,思路也是类似的,这一点我在后面还会详细来讲。
+
+在dijkstra算法中,同样有一个数组很重要,起名为:minDist。
+
+**minDist数组 用来记录 每一个节点距离源点的最小距离**。
+
+理解这一点很重要,也是理解 dijkstra 算法的核心所在。
+
+大家现在看着可能有点懵,不知道什么意思。
+
+没关系,先让大家有一个印象,对理解后面讲解有帮助。
+
+我们先来画图看一下 dijkstra 的工作过程,以本题示例为例: (以下为朴素版dijkstra的思路)
+
+(**示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从 1 开始计数,下标0 就不使用了,这样 下标和节点标号就可以对应上了,避免大家搞混**)
+
+## 朴素版dijkstra
+
+### 模拟过程
+
+-----------
+
+0、初始化
+
+minDist数组数值初始化为int最大值。
+
+这里在强点一下 **minDist数组的含义:记录所有节点到源点的最短路径**,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。
+
+
+
+(图中,max 表示默认值,节点0 不做处理,统一从下标1 开始计算,这样下标和节点数值统一, 方便大家理解,避免搞混)
+
+源点(节点1) 到自己的距离为0,所以 minDist[1] = 0
+
+此时所有节点都没有被访问过,所以 visited数组都为0
+
+---------------
+
+以下为dijkstra 三部曲
+
+1、选源点到哪个节点近且该节点未被访问过
+
+源点距离源点最近,距离为0,且未被访问。
+
+2、该最近节点被标记访问过
+
+标记源点访问过
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+
+更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
+
+* 源点到节点2的最短距离为1,小于原minDist[2]的数值max,更新minDist[2] = 1
+* 源点到节点3的最短距离为4,小于原minDist[3]的数值max,更新minDist[4] = 4
+
+可能有录友问:为啥和 minDist[2] 比较?
+
+再强调一下 minDist[2] 的含义,它表示源点到节点2的最短距离,那么目前我们得到了 源点到节点2的最短距离为1,小于默认值max,所以更新。 minDist[3]的更新同理
+
+
+-------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+未访问过的节点中,源点到节点2距离最近,选节点2
+
+2、该最近节点被标记访问过
+
+节点2被标记访问过
+
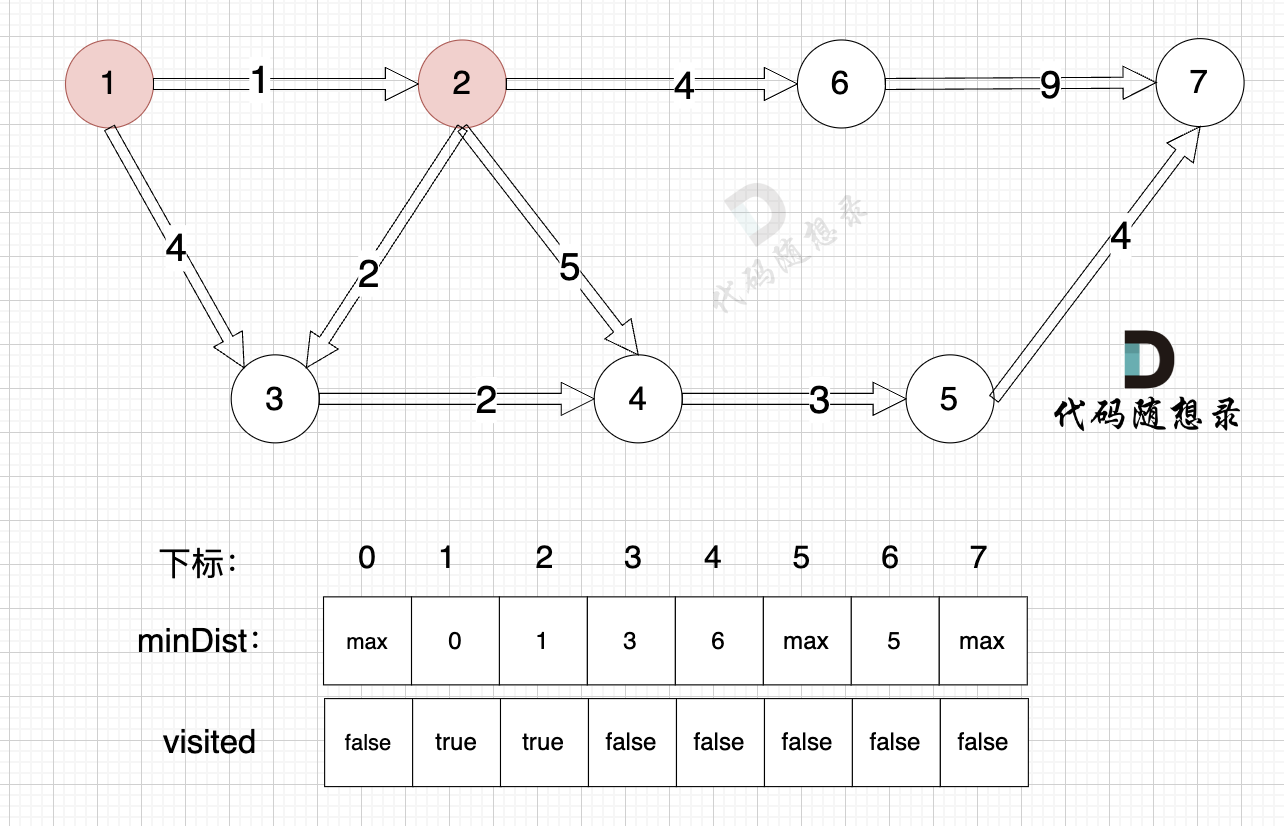
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+
+更新 minDist数组,即:源点(节点1) 到 节点6 、 节点3 和 节点4的距离。
+
+**为什么更新这些节点呢? 怎么不更新其他节点呢**?
+
+因为 源点(节点1)通过 已经计算过的节点(节点2) 可以链接到的节点 有 节点3,节点4和节点6.
+
+
+更新 minDist数组:
+
+* 源点到节点6的最短距离为5,小于原minDist[6]的数值max,更新minDist[6] = 5
+* 源点到节点3的最短距离为3,小于原minDist[3]的数值4,更新minDist[3] = 3
+* 源点到节点4的最短距离为6,小于原minDist[4]的数值max,更新minDist[4] = 6
+
+
+
+-------------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+未访问过的节点中,源点距离哪些节点最近,怎么算的?
+
+其实就是看 minDist数组里的数值,minDist 记录了 源点到所有节点的最近距离,结合visited数组筛选出未访问的节点就好。
+
+从 上面的图,或者 从minDist数组中,我们都能看出 未访问过的节点中,源点(节点1)到节点3距离最近。
+
+
+2、该最近节点被标记访问过
+
+节点3被标记访问过
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
+
+更新 minDist数组:
+
+* 源点到节点4的最短距离为5,小于原minDist[4]的数值6,更新minDist[4] = 5
+
+------------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+距离源点最近且没有被访问过的节点,有节点4 和 节点6,距离源点距离都是 5 (minDist[4] = 5,minDist[6] = 5) ,选哪个节点都可以。
+
+2、该最近节点被标记访问过
+
+节点4被标记访问过
+
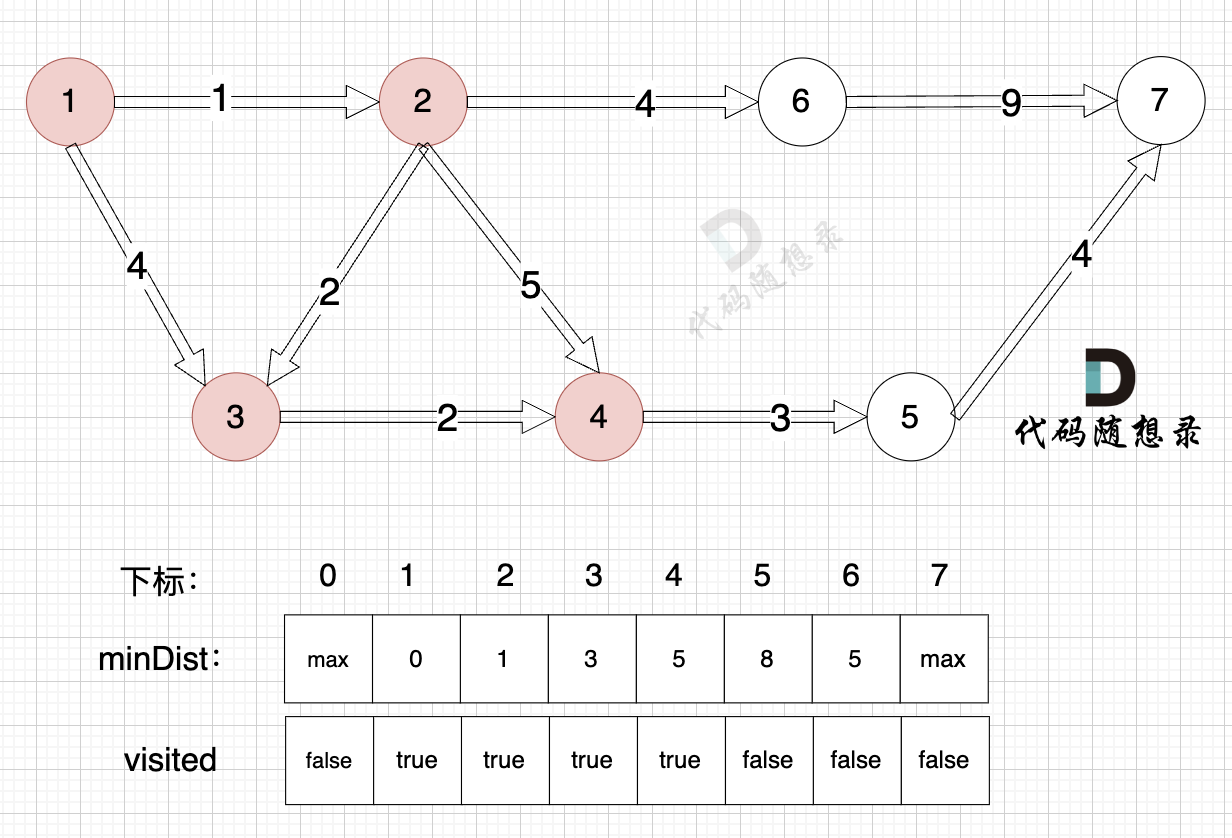
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+由于节点4的加入,那么源点可以链接到节点5 所以更新minDist数组:
+
+* 源点到节点5的最短距离为8,小于原minDist[5]的数值max,更新minDist[5] = 8
+
+--------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+距离源点最近且没有被访问过的节点,是节点6,距离源点距离是 5 (minDist[6] = 5)
+
+
+2、该最近节点被标记访问过
+
+节点6 被标记访问过
+
+
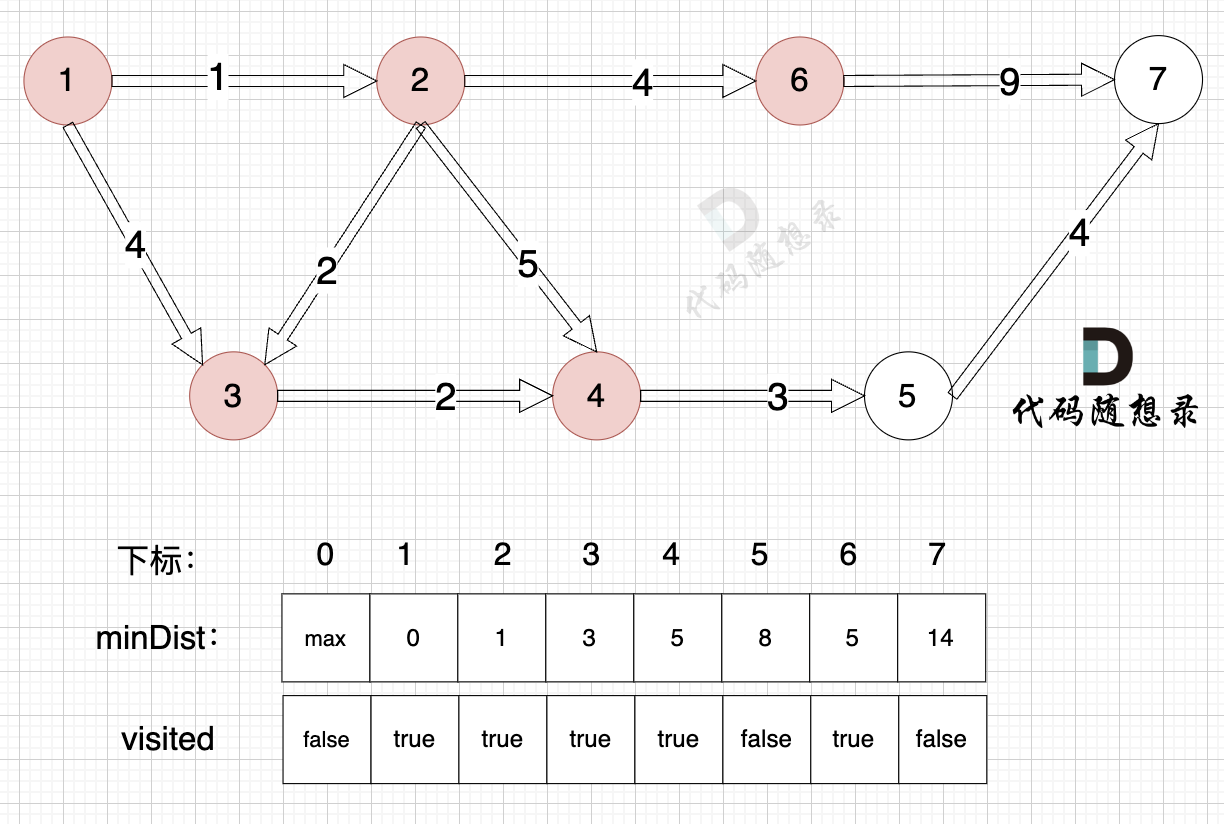
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+由于节点6的加入,那么源点可以链接到节点7 所以 更新minDist数组:
+
+* 源点到节点7的最短距离为14,小于原minDist[7]的数值max,更新minDist[7] = 14
+
+
+
+-------------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+距离源点最近且没有被访问过的节点,是节点5,距离源点距离是 8 (minDist[5] = 8)
+
+2、该最近节点被标记访问过
+
+节点5 被标记访问过
+
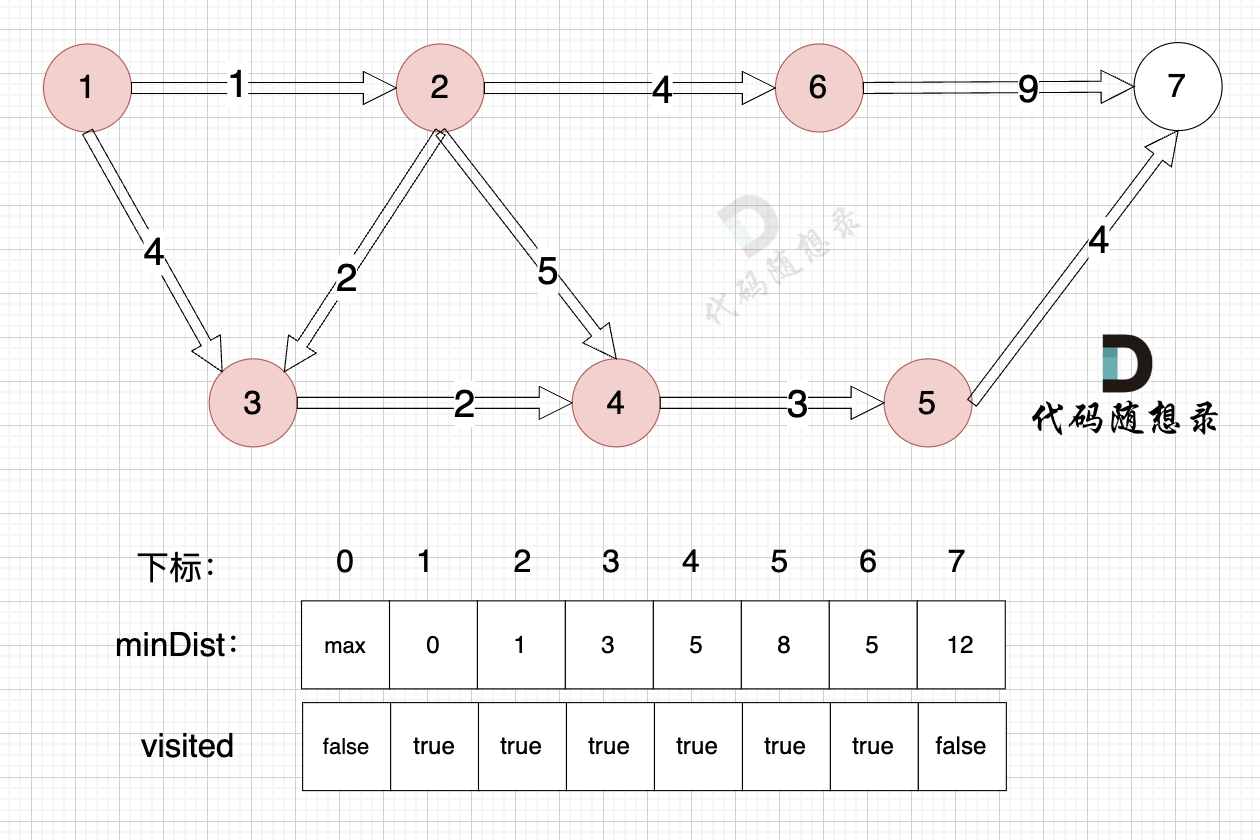
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+由于节点5的加入,那么源点有新的路径可以链接到节点7 所以 更新minDist数组:
+
+* 源点到节点7的最短距离为12,小于原minDist[7]的数值14,更新minDist[7] = 12
+
+-----------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+距离源点最近且没有被访问过的节点,是节点7(终点),距离源点距离是 12 (minDist[7] = 12)
+
+2、该最近节点被标记访问过
+
+节点7 被标记访问过
+
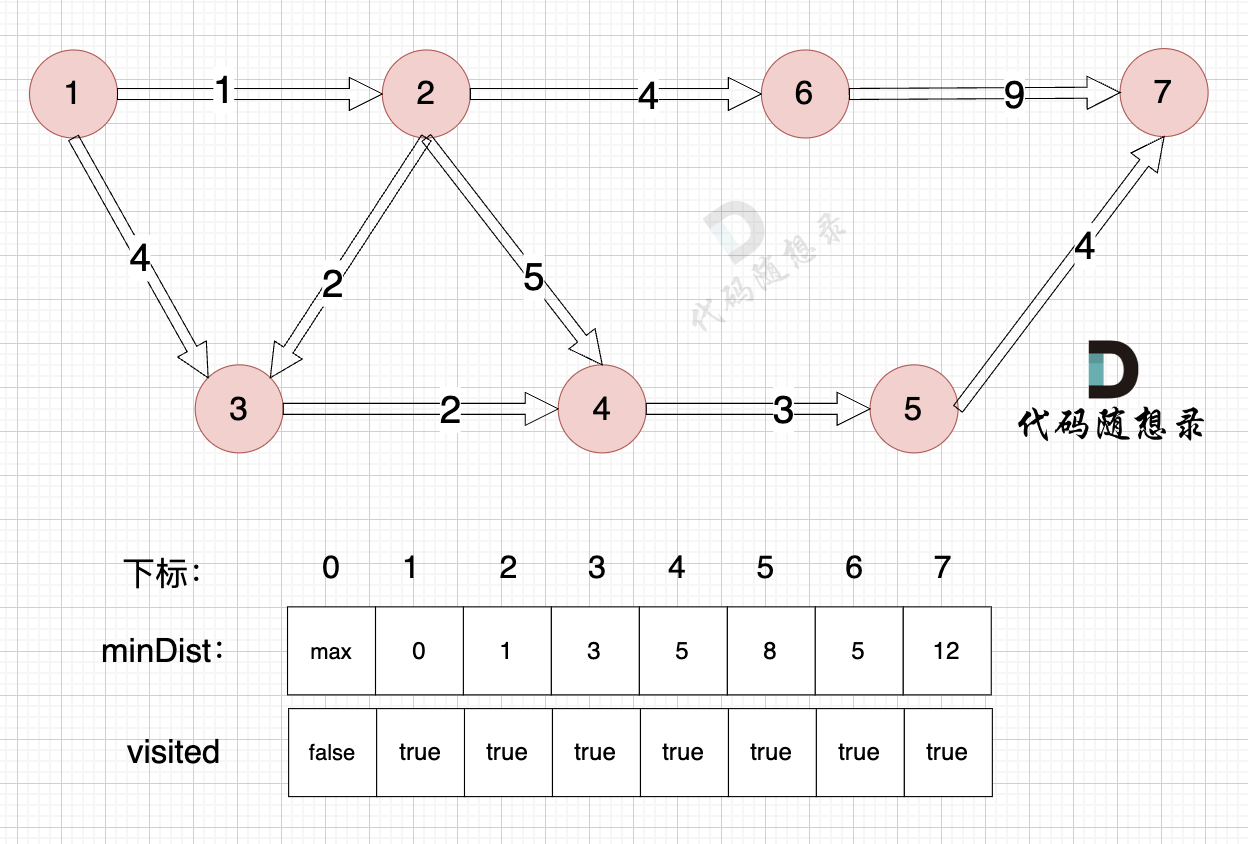
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+节点7加入,但节点7到节点7的距离为0,所以 不用更新minDist数组
+
+--------------------
+
+最后我们要求起点(节点1) 到终点 (节点7)的距离。
+
+再来回顾一下minDist数组的含义:记录 每一个节点距离源点的最小距离。
+
+那么起到(节点1)到终点(节点7)的最短距离就是 minDist[7] ,按上面举例讲解来说,minDist[7] = 12,节点1 到节点7的最短路径为 12。
+
+路径如图:
+
+
+
+在上面的讲解中,每一步 我都是按照 dijkstra 三部曲来讲解的,理解了这三部曲,代码也就好懂的。
+
+### 代码实现
+
+本题代码如下,里面的 三部曲 我都做了注释,大家按照我上面的讲解 来看如下代码:
+
+```CPP
+class Solution {
+public:
+ int networkDelayTime(vector
-
diff --git a/problems/0743.网络延迟时间.md b/problems/0743.网络延迟时间.md
new file mode 100644
index 00000000..e631951a
--- /dev/null
+++ b/problems/0743.网络延迟时间.md
@@ -0,0 +1,1227 @@
+
+# 743.网络延迟时间
+
+https://leetcode.cn/problems/network-delay-time/description/
+
+
+有 n 个网络节点,标记为 1 到 n。
+
+给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
+
+现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
+
+
+
+提示:
+
+* 1 <= k <= n <= 100
+* 1 <= times.length <= 6000
+* times[i].length == 3
+* 1 <= ui, vi <= n
+* ui != vi
+* 0 <= wi <= 100
+* 所有 (ui, vi) 对都 互不相同(即,不含重复边)
+
+# dijkstra 精讲
+
+本题就是求最短路,最短路是图论中的经典问题即:给出一个有向图,一个起点,一个终点,问起点到终点的最短路径。
+
+接下来,我们来详细讲解最短路算法中的 dijkstra 算法。
+
+dijkstra算法:在有权图(权值非负数)中求从起点到其他节点的最短路径算法。
+
+需要注意两点:
+
+* dijkstra 算法可以同时求 起点到所有节点的最短路径
+* 权值不能为负数
+
+(这两点后面我们会讲到)
+
+如本题示例中的图:
+
+
+
+起点(节点1)到终点(节点7) 的最短路径是 图中 标记绿线的部分。
+
+最短路径的权值为12。
+
+其实 dijkstra 算法 和 我们之前讲解的prim算法思路非常接近,如果大家认真学过[prim算法](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w),那么理解 Dijkstra 算法会相对容易很多。(这也是我要先讲prim再讲dijkstra的原因)
+
+dijkstra 算法 同样是贪心的思路,不断寻找距离 源点最近的没有访问过的节点。
+
+这里我也给出 **dijkstra三部曲**:
+
+1. 第一步,选源点到哪个节点近且该节点未被访问过
+2. 第二步,该最近节点被标记访问过
+3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
+
+大家此时已经会发现,这和prim算法 怎么这么像呢。
+
+我在[prim算法](https://mp.weixin.qq.com/s/yX936hHC6Z10K36Vm1Wl9w)讲解中也给出了三部曲。 prim 和 dijkstra 确实很像,思路也是类似的,这一点我在后面还会详细来讲。
+
+在dijkstra算法中,同样有一个数组很重要,起名为:minDist。
+
+**minDist数组 用来记录 每一个节点距离源点的最小距离**。
+
+理解这一点很重要,也是理解 dijkstra 算法的核心所在。
+
+大家现在看着可能有点懵,不知道什么意思。
+
+没关系,先让大家有一个印象,对理解后面讲解有帮助。
+
+我们先来画图看一下 dijkstra 的工作过程,以本题示例为例: (以下为朴素版dijkstra的思路)
+
+(**示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从 1 开始计数,下标0 就不使用了,这样 下标和节点标号就可以对应上了,避免大家搞混**)
+
+## 朴素版dijkstra
+
+### 模拟过程
+
+-----------
+
+0、初始化
+
+minDist数组数值初始化为int最大值。
+
+这里在强点一下 **minDist数组的含义:记录所有节点到源点的最短路径**,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。
+
+
+
+(图中,max 表示默认值,节点0 不做处理,统一从下标1 开始计算,这样下标和节点数值统一, 方便大家理解,避免搞混)
+
+源点(节点1) 到自己的距离为0,所以 minDist[1] = 0
+
+此时所有节点都没有被访问过,所以 visited数组都为0
+
+---------------
+
+以下为dijkstra 三部曲
+
+1、选源点到哪个节点近且该节点未被访问过
+
+源点距离源点最近,距离为0,且未被访问。
+
+2、该最近节点被标记访问过
+
+标记源点访问过
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+
+更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
+
+* 源点到节点2的最短距离为1,小于原minDist[2]的数值max,更新minDist[2] = 1
+* 源点到节点3的最短距离为4,小于原minDist[3]的数值max,更新minDist[4] = 4
+
+可能有录友问:为啥和 minDist[2] 比较?
+
+再强调一下 minDist[2] 的含义,它表示源点到节点2的最短距离,那么目前我们得到了 源点到节点2的最短距离为1,小于默认值max,所以更新。 minDist[3]的更新同理
+
+
+-------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+未访问过的节点中,源点到节点2距离最近,选节点2
+
+2、该最近节点被标记访问过
+
+节点2被标记访问过
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+
+更新 minDist数组,即:源点(节点1) 到 节点6 、 节点3 和 节点4的距离。
+
+**为什么更新这些节点呢? 怎么不更新其他节点呢**?
+
+因为 源点(节点1)通过 已经计算过的节点(节点2) 可以链接到的节点 有 节点3,节点4和节点6.
+
+
+更新 minDist数组:
+
+* 源点到节点6的最短距离为5,小于原minDist[6]的数值max,更新minDist[6] = 5
+* 源点到节点3的最短距离为3,小于原minDist[3]的数值4,更新minDist[3] = 3
+* 源点到节点4的最短距离为6,小于原minDist[4]的数值max,更新minDist[4] = 6
+
+
+
+-------------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+未访问过的节点中,源点距离哪些节点最近,怎么算的?
+
+其实就是看 minDist数组里的数值,minDist 记录了 源点到所有节点的最近距离,结合visited数组筛选出未访问的节点就好。
+
+从 上面的图,或者 从minDist数组中,我们都能看出 未访问过的节点中,源点(节点1)到节点3距离最近。
+
+
+2、该最近节点被标记访问过
+
+节点3被标记访问过
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
+
+更新 minDist数组:
+
+* 源点到节点4的最短距离为5,小于原minDist[4]的数值6,更新minDist[4] = 5
+
+------------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+距离源点最近且没有被访问过的节点,有节点4 和 节点6,距离源点距离都是 5 (minDist[4] = 5,minDist[6] = 5) ,选哪个节点都可以。
+
+2、该最近节点被标记访问过
+
+节点4被标记访问过
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+由于节点4的加入,那么源点可以链接到节点5 所以更新minDist数组:
+
+* 源点到节点5的最短距离为8,小于原minDist[5]的数值max,更新minDist[5] = 8
+
+--------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+距离源点最近且没有被访问过的节点,是节点6,距离源点距离是 5 (minDist[6] = 5)
+
+
+2、该最近节点被标记访问过
+
+节点6 被标记访问过
+
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+由于节点6的加入,那么源点可以链接到节点7 所以 更新minDist数组:
+
+* 源点到节点7的最短距离为14,小于原minDist[7]的数值max,更新minDist[7] = 14
+
+
+
+-------------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+距离源点最近且没有被访问过的节点,是节点5,距离源点距离是 8 (minDist[5] = 8)
+
+2、该最近节点被标记访问过
+
+节点5 被标记访问过
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+由于节点5的加入,那么源点有新的路径可以链接到节点7 所以 更新minDist数组:
+
+* 源点到节点7的最短距离为12,小于原minDist[7]的数值14,更新minDist[7] = 12
+
+-----------------
+
+1、选源点到哪个节点近且该节点未被访问过
+
+距离源点最近且没有被访问过的节点,是节点7(终点),距离源点距离是 12 (minDist[7] = 12)
+
+2、该最近节点被标记访问过
+
+节点7 被标记访问过
+
+3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
+
+
+
+节点7加入,但节点7到节点7的距离为0,所以 不用更新minDist数组
+
+--------------------
+
+最后我们要求起点(节点1) 到终点 (节点7)的距离。
+
+再来回顾一下minDist数组的含义:记录 每一个节点距离源点的最小距离。
+
+那么起到(节点1)到终点(节点7)的最短距离就是 minDist[7] ,按上面举例讲解来说,minDist[7] = 12,节点1 到节点7的最短路径为 12。
+
+路径如图:
+
+
+
+在上面的讲解中,每一步 我都是按照 dijkstra 三部曲来讲解的,理解了这三部曲,代码也就好懂的。
+
+### 代码实现
+
+本题代码如下,里面的 三部曲 我都做了注释,大家按照我上面的讲解 来看如下代码:
+
+```CPP
+class Solution {
+public:
+ int networkDelayTime(vector -
- -
diff --git a/problems/0763.划分字母区间.md b/problems/0763.划分字母区间.md
index 8b0ca7b8..52186927 100644
--- a/problems/0763.划分字母区间.md
+++ b/problems/0763.划分字母区间.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0763.划分字母区间.md b/problems/0763.划分字母区间.md
index 8b0ca7b8..52186927 100644
--- a/problems/0763.划分字母区间.md
+++ b/problems/0763.划分字母区间.md
@@ -1,8 +1,8 @@
 -
- +
+
+
+ +
diff --git a/problems/0797.所有可能的路径.md b/problems/0797.所有可能的路径.md
index 05b55b5b..40e1bbe7 100644
--- a/problems/0797.所有可能的路径.md
+++ b/problems/0797.所有可能的路径.md
@@ -1,8 +1,8 @@
+
diff --git a/problems/0797.所有可能的路径.md b/problems/0797.所有可能的路径.md
index 05b55b5b..40e1bbe7 100644
--- a/problems/0797.所有可能的路径.md
+++ b/problems/0797.所有可能的路径.md
@@ -1,8 +1,8 @@
 -
- -
- -
- -
- -
diff --git a/problems/0860.柠檬水找零.md b/problems/0860.柠檬水找零.md
index db70112d..804ff13c 100644
--- a/problems/0860.柠檬水找零.md
+++ b/problems/0860.柠檬水找零.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0860.柠檬水找零.md b/problems/0860.柠檬水找零.md
index db70112d..804ff13c 100644
--- a/problems/0860.柠檬水找零.md
+++ b/problems/0860.柠檬水找零.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0922.按奇偶排序数组II.md b/problems/0922.按奇偶排序数组II.md
index 72be8fa7..1ac6800c 100644
--- a/problems/0922.按奇偶排序数组II.md
+++ b/problems/0922.按奇偶排序数组II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0922.按奇偶排序数组II.md b/problems/0922.按奇偶排序数组II.md
index 72be8fa7..1ac6800c 100644
--- a/problems/0922.按奇偶排序数组II.md
+++ b/problems/0922.按奇偶排序数组II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/0925.长按键入.md b/problems/0925.长按键入.md
index 11edecd0..f4a8fa8e 100644
--- a/problems/0925.长按键入.md
+++ b/problems/0925.长按键入.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/0925.长按键入.md b/problems/0925.长按键入.md
index 11edecd0..f4a8fa8e 100644
--- a/problems/0925.长按键入.md
+++ b/problems/0925.长按键入.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/0968.监控二叉树.md b/problems/0968.监控二叉树.md
index 9743ca2b..d59496c8 100644
--- a/problems/0968.监控二叉树.md
+++ b/problems/0968.监控二叉树.md
@@ -1,9 +1,9 @@
-
-
diff --git a/problems/0968.监控二叉树.md b/problems/0968.监控二叉树.md
index 9743ca2b..d59496c8 100644
--- a/problems/0968.监控二叉树.md
+++ b/problems/0968.监控二叉树.md
@@ -1,9 +1,9 @@
-
 -
- -
- -
diff --git a/problems/1002.查找常用字符.md b/problems/1002.查找常用字符.md
index 8d81e3f8..f938c2b7 100644
--- a/problems/1002.查找常用字符.md
+++ b/problems/1002.查找常用字符.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1002.查找常用字符.md b/problems/1002.查找常用字符.md
index 8d81e3f8..f938c2b7 100644
--- a/problems/1002.查找常用字符.md
+++ b/problems/1002.查找常用字符.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/1005.K次取反后最大化的数组和.md b/problems/1005.K次取反后最大化的数组和.md
index 498015d0..fa27d3b7 100644
--- a/problems/1005.K次取反后最大化的数组和.md
+++ b/problems/1005.K次取反后最大化的数组和.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1005.K次取反后最大化的数组和.md b/problems/1005.K次取反后最大化的数组和.md
index 498015d0..fa27d3b7 100644
--- a/problems/1005.K次取反后最大化的数组和.md
+++ b/problems/1005.K次取反后最大化的数组和.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/1035.不相交的线.md b/problems/1035.不相交的线.md
index e0625a2b..8ee52c5d 100644
--- a/problems/1035.不相交的线.md
+++ b/problems/1035.不相交的线.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1035.不相交的线.md b/problems/1035.不相交的线.md
index e0625a2b..8ee52c5d 100644
--- a/problems/1035.不相交的线.md
+++ b/problems/1035.不相交的线.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/1047.删除字符串中的所有相邻重复项.md b/problems/1047.删除字符串中的所有相邻重复项.md
index ffe13530..4aa0e954 100644
--- a/problems/1047.删除字符串中的所有相邻重复项.md
+++ b/problems/1047.删除字符串中的所有相邻重复项.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1047.删除字符串中的所有相邻重复项.md b/problems/1047.删除字符串中的所有相邻重复项.md
index ffe13530..4aa0e954 100644
--- a/problems/1047.删除字符串中的所有相邻重复项.md
+++ b/problems/1047.删除字符串中的所有相邻重复项.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/1049.最后一块石头的重量II.md b/problems/1049.最后一块石头的重量II.md
index 4c3c01a0..4f2cc9e3 100644
--- a/problems/1049.最后一块石头的重量II.md
+++ b/problems/1049.最后一块石头的重量II.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1049.最后一块石头的重量II.md b/problems/1049.最后一块石头的重量II.md
index 4c3c01a0..4f2cc9e3 100644
--- a/problems/1049.最后一块石头的重量II.md
+++ b/problems/1049.最后一块石头的重量II.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/1143.最长公共子序列.md b/problems/1143.最长公共子序列.md
index 12bd90f8..7fa7bb68 100644
--- a/problems/1143.最长公共子序列.md
+++ b/problems/1143.最长公共子序列.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1143.最长公共子序列.md b/problems/1143.最长公共子序列.md
index 12bd90f8..7fa7bb68 100644
--- a/problems/1143.最长公共子序列.md
+++ b/problems/1143.最长公共子序列.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/1221.分割平衡字符串.md b/problems/1221.分割平衡字符串.md
index 2a7b0922..a32ca98f 100644
--- a/problems/1221.分割平衡字符串.md
+++ b/problems/1221.分割平衡字符串.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1221.分割平衡字符串.md b/problems/1221.分割平衡字符串.md
index 2a7b0922..a32ca98f 100644
--- a/problems/1221.分割平衡字符串.md
+++ b/problems/1221.分割平衡字符串.md
@@ -1,8 +1,8 @@
 -
- -
- -
-
diff --git a/problems/1334.阈值距离内邻居最少的城市.md b/problems/1334.阈值距离内邻居最少的城市.md
new file mode 100644
index 00000000..d8d8861f
--- /dev/null
+++ b/problems/1334.阈值距离内邻居最少的城市.md
@@ -0,0 +1,55 @@
+
-
-
diff --git a/problems/1334.阈值距离内邻居最少的城市.md b/problems/1334.阈值距离内邻居最少的城市.md
new file mode 100644
index 00000000..d8d8861f
--- /dev/null
+++ b/problems/1334.阈值距离内邻居最少的城市.md
@@ -0,0 +1,55 @@
+ +
+
+
+ +
diff --git a/problems/1356.根据数字二进制下1的数目排序.md b/problems/1356.根据数字二进制下1的数目排序.md
index c2455cf0..9cfb6743 100644
--- a/problems/1356.根据数字二进制下1的数目排序.md
+++ b/problems/1356.根据数字二进制下1的数目排序.md
@@ -1,8 +1,8 @@
+
diff --git a/problems/1356.根据数字二进制下1的数目排序.md b/problems/1356.根据数字二进制下1的数目排序.md
index c2455cf0..9cfb6743 100644
--- a/problems/1356.根据数字二进制下1的数目排序.md
+++ b/problems/1356.根据数字二进制下1的数目排序.md
@@ -1,8 +1,8 @@
 -
- -
diff --git a/problems/1365.有多少小于当前数字的数字.md b/problems/1365.有多少小于当前数字的数字.md
index c706ba21..94c1eb77 100644
--- a/problems/1365.有多少小于当前数字的数字.md
+++ b/problems/1365.有多少小于当前数字的数字.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1365.有多少小于当前数字的数字.md b/problems/1365.有多少小于当前数字的数字.md
index c706ba21..94c1eb77 100644
--- a/problems/1365.有多少小于当前数字的数字.md
+++ b/problems/1365.有多少小于当前数字的数字.md
@@ -1,8 +1,8 @@
 -
- -
- -
diff --git a/problems/1791.找出星型图的中心节点.md b/problems/1791.找出星型图的中心节点.md
index 9bcc7ef9..e3db7947 100644
--- a/problems/1791.找出星型图的中心节点.md
+++ b/problems/1791.找出星型图的中心节点.md
@@ -1,8 +1,8 @@
-
diff --git a/problems/1791.找出星型图的中心节点.md b/problems/1791.找出星型图的中心节点.md
index 9bcc7ef9..e3db7947 100644
--- a/problems/1791.找出星型图的中心节点.md
+++ b/problems/1791.找出星型图的中心节点.md
@@ -1,8 +1,8 @@
 -
- -
- diff --git a/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md b/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
index 8be48f38..a5dab942 100644
--- a/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
+++ b/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
@@ -1,9 +1,9 @@
-
diff --git a/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md b/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
index 8be48f38..a5dab942 100644
--- a/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
+++ b/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
@@ -1,9 +1,9 @@
-
 -
- -
diff --git a/problems/kamacoder/00.软件构建.md b/problems/kamacoder/00.软件构建.md
new file mode 100644
index 00000000..7229489b
--- /dev/null
+++ b/problems/kamacoder/00.软件构建.md
@@ -0,0 +1,337 @@
+
+# 拓扑排序精讲
+
+[卡码网:软件构建](https://kamacoder.com/problempage.php?pid=1191)
+
+题目描述:
+
+某个大型软件项目的构建系统拥有 N 个文件,文件编号从 0 到 N - 1,在这些文件中,某些文件依赖于其他文件的内容,这意味着如果文件 A 依赖于文件 B,则必须在处理文件 A 之前处理文件 B (0 <= A, B <= N - 1)。请编写一个算法,用于确定文件处理的顺序。
+
+输入描述:
+
+第一行输入两个正整数 M, N。表示 N 个文件之间拥有 M 条依赖关系。
+
+后续 M 行,每行两个正整数 S 和 T,表示 T 文件依赖于 S 文件。
+
+输出描述:
+
+输出共一行,如果能处理成功,则输出文件顺序,用空格隔开。
+
+如果不能成功处理(相互依赖),则输出 -1。
+
+输入示例:
+
+```
+5 4
+0 1
+0 2
+1 3
+2 4
+```
+
+输出示例:
+
+0 1 2 3 4
+
+提示信息:
+
+文件依赖关系如下:
+
+
+
+所以,文件处理的顺序除了示例中的顺序,还存在
+
+0 2 4 1 3
+
+0 2 1 3 4
+
+等等合法的顺序。
+
+数据范围:
+
+* 0 <= N <= 10 ^ 5
+* 1 <= M <= 10 ^ 9
+
+
+## 拓扑排序的背景
+
+本题是拓扑排序的经典题目。
+
+一聊到 拓扑排序,一些录友可能会想这是排序,不会想到这是图论算法。
+
+其实拓扑排序是经典的图论问题。
+
+先说说 拓扑排序的应用场景。
+
+大学排课,例如 先上A课,才能上B课,上了B课才能上C课,上了A课才能上D课,等等一系列这样的依赖顺序。 问给规划出一条 完整的上课顺序。
+
+拓扑排序在文件处理上也有应用,我们在做项目安装文件包的时候,经常发现 复杂的文件依赖关系, A依赖B,B依赖C,B依赖D,C依赖E 等等。
+
+如果给出一条线性的依赖顺序来下载这些文件呢?
+
+有录友想上面的例子都很简单啊,我一眼能给排序出来。
+
+那如果上面的依赖关系是一百对呢,一千对甚至上万个依赖关系,这些依赖关系中可能还有循环依赖,你如何发现循环依赖呢,又如果排出线性顺序呢。
+
+所以 拓扑排序就是专门解决这类问题的。
+
+概括来说,**给出一个 有向图,把这个有向图转成线性的排序 就叫拓扑排序**。
+
+当然拓扑排序也要检测这个有向图 是否有环,即存在循环依赖的情况,因为这种情况是不能做线性排序的。
+
+所以**拓扑排序也是图论中判断有向无环图的常用方法**。
+
+------------
+
+
+## 拓扑排序的思路
+
+拓扑排序指的是一种 解决问题的大体思路, 而具体算法,可能是广搜也可能是深搜。
+
+大家可能发现 各式各样的解法,纠结哪个是拓扑排序?
+
+其实只要能在把 有向无环图 进行线性排序 的算法 都可以叫做 拓扑排序。
+
+实现拓扑排序的算法有两种:卡恩算法(BFS)和DFS
+
+> 卡恩1962年提出这种解决拓扑排序的思路
+
+一般来说我们只需要掌握 BFS (广度优先搜索)就可以了,清晰易懂,如果还想多了解一些,可以再去学一下 DFS 的思路,但 DFS 不是本篇重点。
+
+接下来我们来讲解BFS的实现思路。
+
+以题目中示例为例如图:
+
+
+
+做拓扑排序的话,如果肉眼去找开头的节点,一定能找到 节点0 吧,都知道要从节点0 开始。
+
+但为什么我们能找到 节点0呢,因为我们肉眼看着 这个图就是从 节点0出发的。
+
+作为出发节点,它有什么特征?
+
+你看节点0 的入度 为0 出度为2, 也就是 没有边指向它,而它有两条边是指出去的。
+
+> 节点的入度表示 有多少条边指向它,节点的出度表示有多少条边 从该节点出发。
+
+所以当我们做拓扑排序的时候,应该优先找 入度为 0 的节点,只有入度为0,它才是出发节点。
+**理解以上内容很重要**!
+
+接下来我给出 拓扑排序的过程,其实就两步:
+
+1. 找到入度为0 的节点,加入结果集
+2. 将该节点从图中移除
+
+循环以上两步,直到 所有节点都在图中被移除了。
+
+结果集的顺序,就是我们想要的拓扑排序顺序 (结果集里顺序可能不唯一)
+
+## 模拟过程
+
+用本题的示例来模拟一下这一过程:
+
+
+1、找到入度为0 的节点,加入结果集
+
+
+
+2、将该节点从图中移除
+
+
+
+----------------
+
+1、找到入度为0 的节点,加入结果集
+
+
+
+这里大家会发现,节点1 和 节点2 入度都为0, 选哪个呢?
+
+选哪个都行,所以这也是为什么拓扑排序的结果是不唯一的。
+
+2、将该节点从图中移除
+
+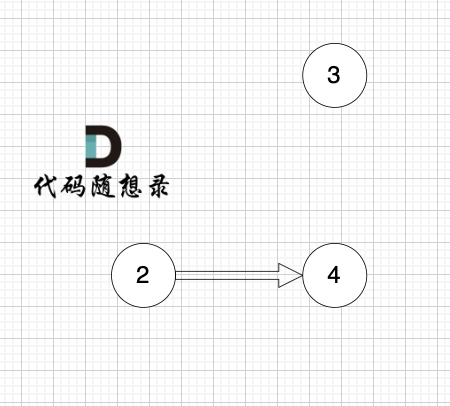
+
+---------------
+
+1、找到入度为0 的节点,加入结果集
+
+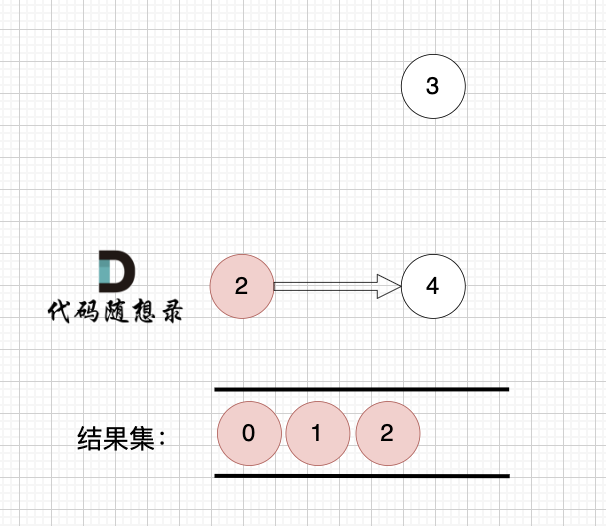
+
+节点2 和 节点3 入度都为0,选哪个都行,这里选节点2
+
+2、将该节点从图中移除
+
+
+
+--------------
+
+后面的过程一样的,节点3 和 节点4,入度都为0,选哪个都行。
+
+最后结果集为: 0 1 2 3 4 。当然结果不唯一的。
+
+## 判断有环
+
+如果有 有向环怎么办呢?例如这个图:
+
+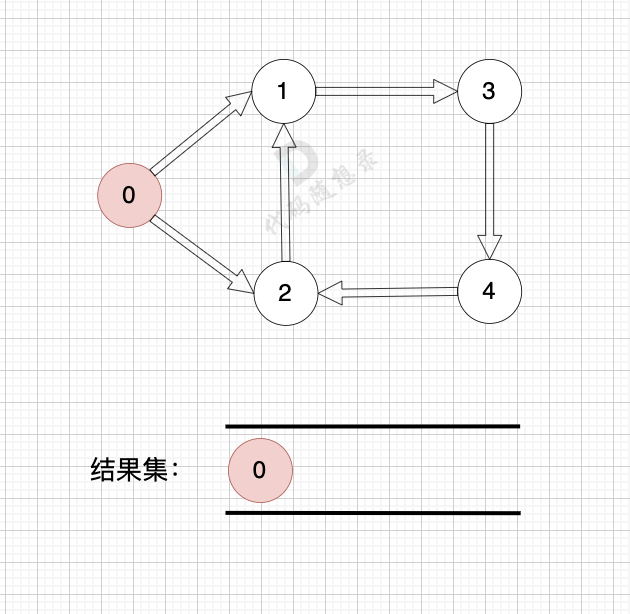
+
+这个图,我们只能将入度为0 的节点0 接入结果集。
+
+之后,节点1、2、3、4 形成了环,找不到入度为0 的节点了,所以此时结果集里只有一个元素。
+那么如果我们发现结果集元素个数 不等于 图中节点个数,我们就可以认定图中一定有 有向环!
+这也是拓扑排序判断有向环的方法。
+
+通过以上过程的模拟大家会发现这个拓扑排序好像不难,还有点简单。
+
+## 写代码
+
+理解思想后,确实不难,但代码写起来也不容易。
+
+为了每次可以找到所有节点的入度信息,我们要在初始话的时候,就把每个节点的入度 和 每个节点的依赖关系做统计。
+
+代码如下:
+
+```CPP
+cin >> n >> m;
+vector
-
diff --git a/problems/kamacoder/00.软件构建.md b/problems/kamacoder/00.软件构建.md
new file mode 100644
index 00000000..7229489b
--- /dev/null
+++ b/problems/kamacoder/00.软件构建.md
@@ -0,0 +1,337 @@
+
+# 拓扑排序精讲
+
+[卡码网:软件构建](https://kamacoder.com/problempage.php?pid=1191)
+
+题目描述:
+
+某个大型软件项目的构建系统拥有 N 个文件,文件编号从 0 到 N - 1,在这些文件中,某些文件依赖于其他文件的内容,这意味着如果文件 A 依赖于文件 B,则必须在处理文件 A 之前处理文件 B (0 <= A, B <= N - 1)。请编写一个算法,用于确定文件处理的顺序。
+
+输入描述:
+
+第一行输入两个正整数 M, N。表示 N 个文件之间拥有 M 条依赖关系。
+
+后续 M 行,每行两个正整数 S 和 T,表示 T 文件依赖于 S 文件。
+
+输出描述:
+
+输出共一行,如果能处理成功,则输出文件顺序,用空格隔开。
+
+如果不能成功处理(相互依赖),则输出 -1。
+
+输入示例:
+
+```
+5 4
+0 1
+0 2
+1 3
+2 4
+```
+
+输出示例:
+
+0 1 2 3 4
+
+提示信息:
+
+文件依赖关系如下:
+
+
+
+所以,文件处理的顺序除了示例中的顺序,还存在
+
+0 2 4 1 3
+
+0 2 1 3 4
+
+等等合法的顺序。
+
+数据范围:
+
+* 0 <= N <= 10 ^ 5
+* 1 <= M <= 10 ^ 9
+
+
+## 拓扑排序的背景
+
+本题是拓扑排序的经典题目。
+
+一聊到 拓扑排序,一些录友可能会想这是排序,不会想到这是图论算法。
+
+其实拓扑排序是经典的图论问题。
+
+先说说 拓扑排序的应用场景。
+
+大学排课,例如 先上A课,才能上B课,上了B课才能上C课,上了A课才能上D课,等等一系列这样的依赖顺序。 问给规划出一条 完整的上课顺序。
+
+拓扑排序在文件处理上也有应用,我们在做项目安装文件包的时候,经常发现 复杂的文件依赖关系, A依赖B,B依赖C,B依赖D,C依赖E 等等。
+
+如果给出一条线性的依赖顺序来下载这些文件呢?
+
+有录友想上面的例子都很简单啊,我一眼能给排序出来。
+
+那如果上面的依赖关系是一百对呢,一千对甚至上万个依赖关系,这些依赖关系中可能还有循环依赖,你如何发现循环依赖呢,又如果排出线性顺序呢。
+
+所以 拓扑排序就是专门解决这类问题的。
+
+概括来说,**给出一个 有向图,把这个有向图转成线性的排序 就叫拓扑排序**。
+
+当然拓扑排序也要检测这个有向图 是否有环,即存在循环依赖的情况,因为这种情况是不能做线性排序的。
+
+所以**拓扑排序也是图论中判断有向无环图的常用方法**。
+
+------------
+
+
+## 拓扑排序的思路
+
+拓扑排序指的是一种 解决问题的大体思路, 而具体算法,可能是广搜也可能是深搜。
+
+大家可能发现 各式各样的解法,纠结哪个是拓扑排序?
+
+其实只要能在把 有向无环图 进行线性排序 的算法 都可以叫做 拓扑排序。
+
+实现拓扑排序的算法有两种:卡恩算法(BFS)和DFS
+
+> 卡恩1962年提出这种解决拓扑排序的思路
+
+一般来说我们只需要掌握 BFS (广度优先搜索)就可以了,清晰易懂,如果还想多了解一些,可以再去学一下 DFS 的思路,但 DFS 不是本篇重点。
+
+接下来我们来讲解BFS的实现思路。
+
+以题目中示例为例如图:
+
+
+
+做拓扑排序的话,如果肉眼去找开头的节点,一定能找到 节点0 吧,都知道要从节点0 开始。
+
+但为什么我们能找到 节点0呢,因为我们肉眼看着 这个图就是从 节点0出发的。
+
+作为出发节点,它有什么特征?
+
+你看节点0 的入度 为0 出度为2, 也就是 没有边指向它,而它有两条边是指出去的。
+
+> 节点的入度表示 有多少条边指向它,节点的出度表示有多少条边 从该节点出发。
+
+所以当我们做拓扑排序的时候,应该优先找 入度为 0 的节点,只有入度为0,它才是出发节点。
+**理解以上内容很重要**!
+
+接下来我给出 拓扑排序的过程,其实就两步:
+
+1. 找到入度为0 的节点,加入结果集
+2. 将该节点从图中移除
+
+循环以上两步,直到 所有节点都在图中被移除了。
+
+结果集的顺序,就是我们想要的拓扑排序顺序 (结果集里顺序可能不唯一)
+
+## 模拟过程
+
+用本题的示例来模拟一下这一过程:
+
+
+1、找到入度为0 的节点,加入结果集
+
+
+
+2、将该节点从图中移除
+
+
+
+----------------
+
+1、找到入度为0 的节点,加入结果集
+
+
+
+这里大家会发现,节点1 和 节点2 入度都为0, 选哪个呢?
+
+选哪个都行,所以这也是为什么拓扑排序的结果是不唯一的。
+
+2、将该节点从图中移除
+
+
+
+---------------
+
+1、找到入度为0 的节点,加入结果集
+
+
+
+节点2 和 节点3 入度都为0,选哪个都行,这里选节点2
+
+2、将该节点从图中移除
+
+
+
+--------------
+
+后面的过程一样的,节点3 和 节点4,入度都为0,选哪个都行。
+
+最后结果集为: 0 1 2 3 4 。当然结果不唯一的。
+
+## 判断有环
+
+如果有 有向环怎么办呢?例如这个图:
+
+
+
+这个图,我们只能将入度为0 的节点0 接入结果集。
+
+之后,节点1、2、3、4 形成了环,找不到入度为0 的节点了,所以此时结果集里只有一个元素。
+那么如果我们发现结果集元素个数 不等于 图中节点个数,我们就可以认定图中一定有 有向环!
+这也是拓扑排序判断有向环的方法。
+
+通过以上过程的模拟大家会发现这个拓扑排序好像不难,还有点简单。
+
+## 写代码
+
+理解思想后,确实不难,但代码写起来也不容易。
+
+为了每次可以找到所有节点的入度信息,我们要在初始话的时候,就把每个节点的入度 和 每个节点的依赖关系做统计。
+
+代码如下:
+
+```CPP
+cin >> n >> m;
+vector
+#include
+#include
+#include
+#include
+#include
+#include
+#include