diff --git a/README.md b/README.md
index 2d40e2b9..06de2f5d 100644
--- a/README.md
+++ b/README.md
@@ -181,7 +181,7 @@
题目分类大纲如下:
-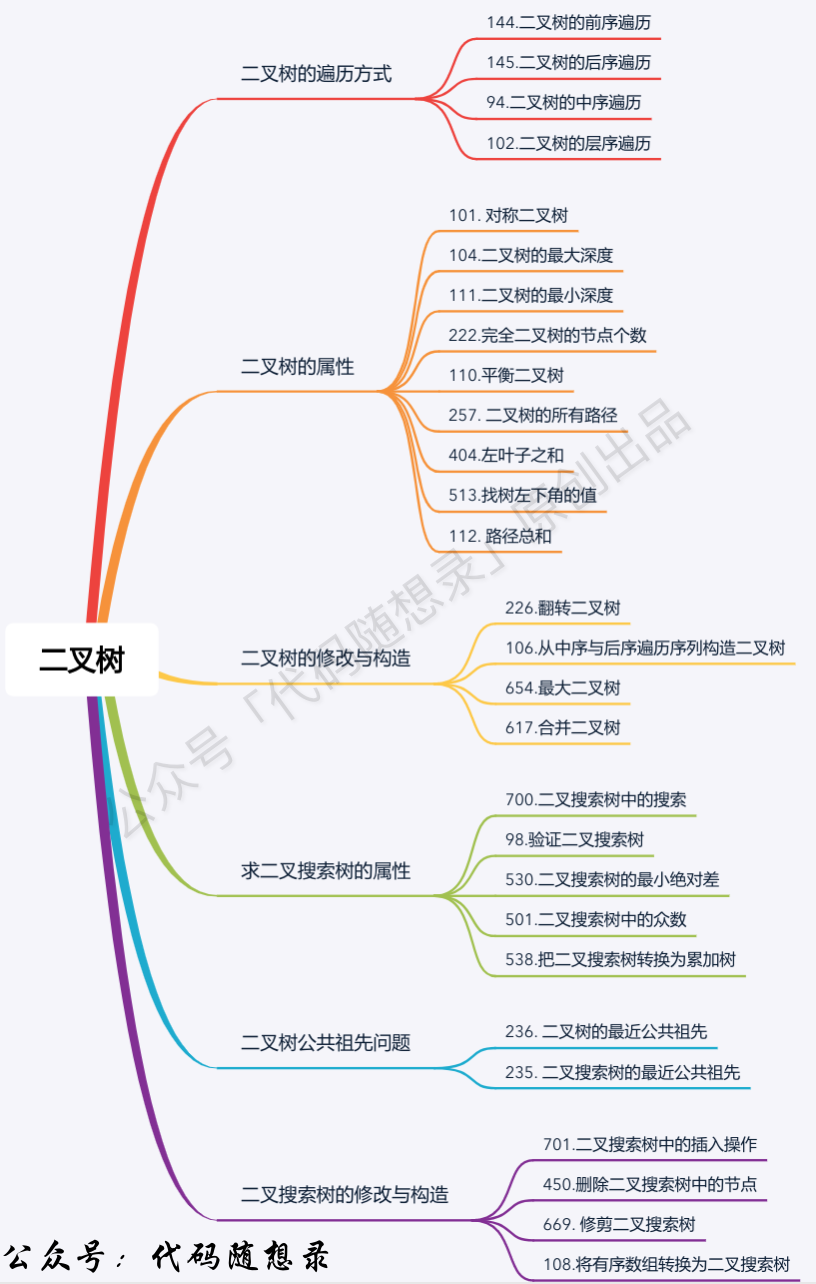 +
+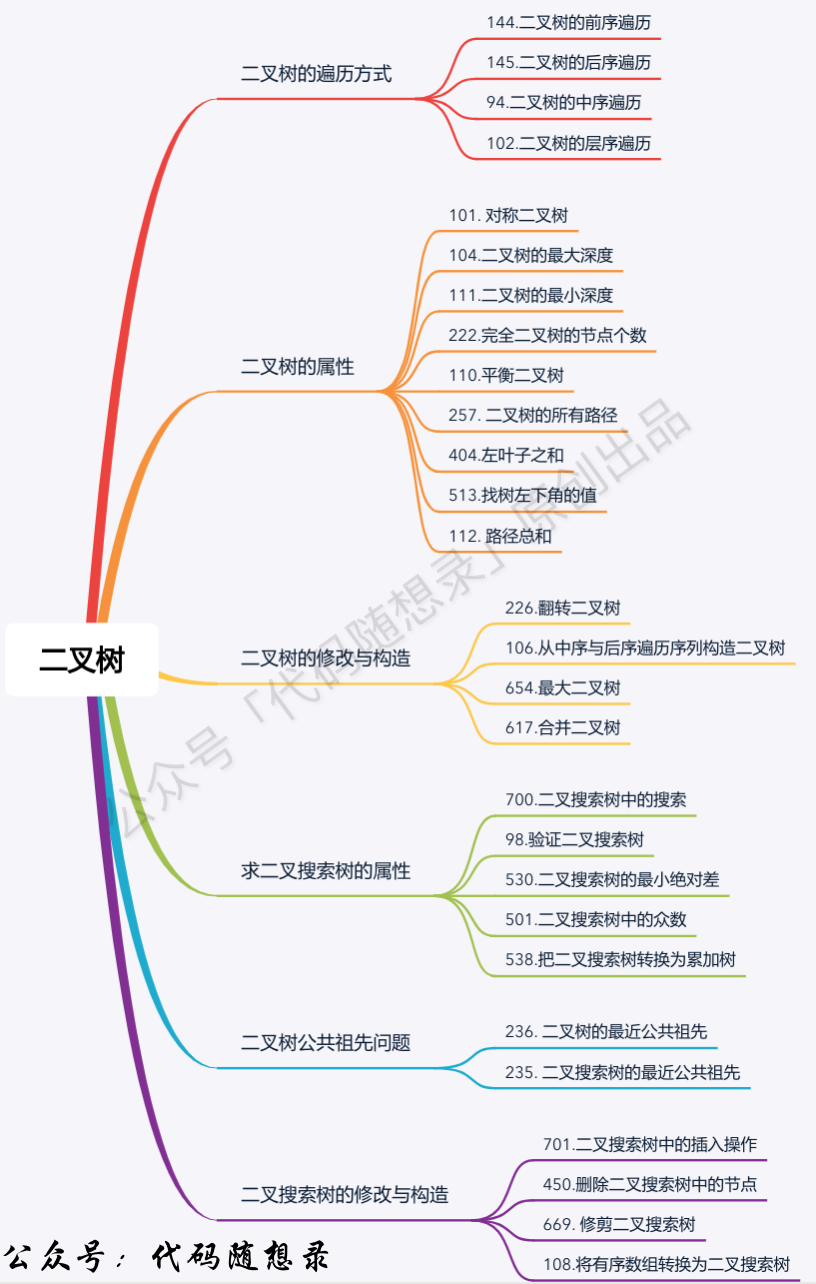 1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
@@ -222,7 +222,7 @@
题目分类大纲如下:
-
1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
@@ -222,7 +222,7 @@
题目分类大纲如下:
-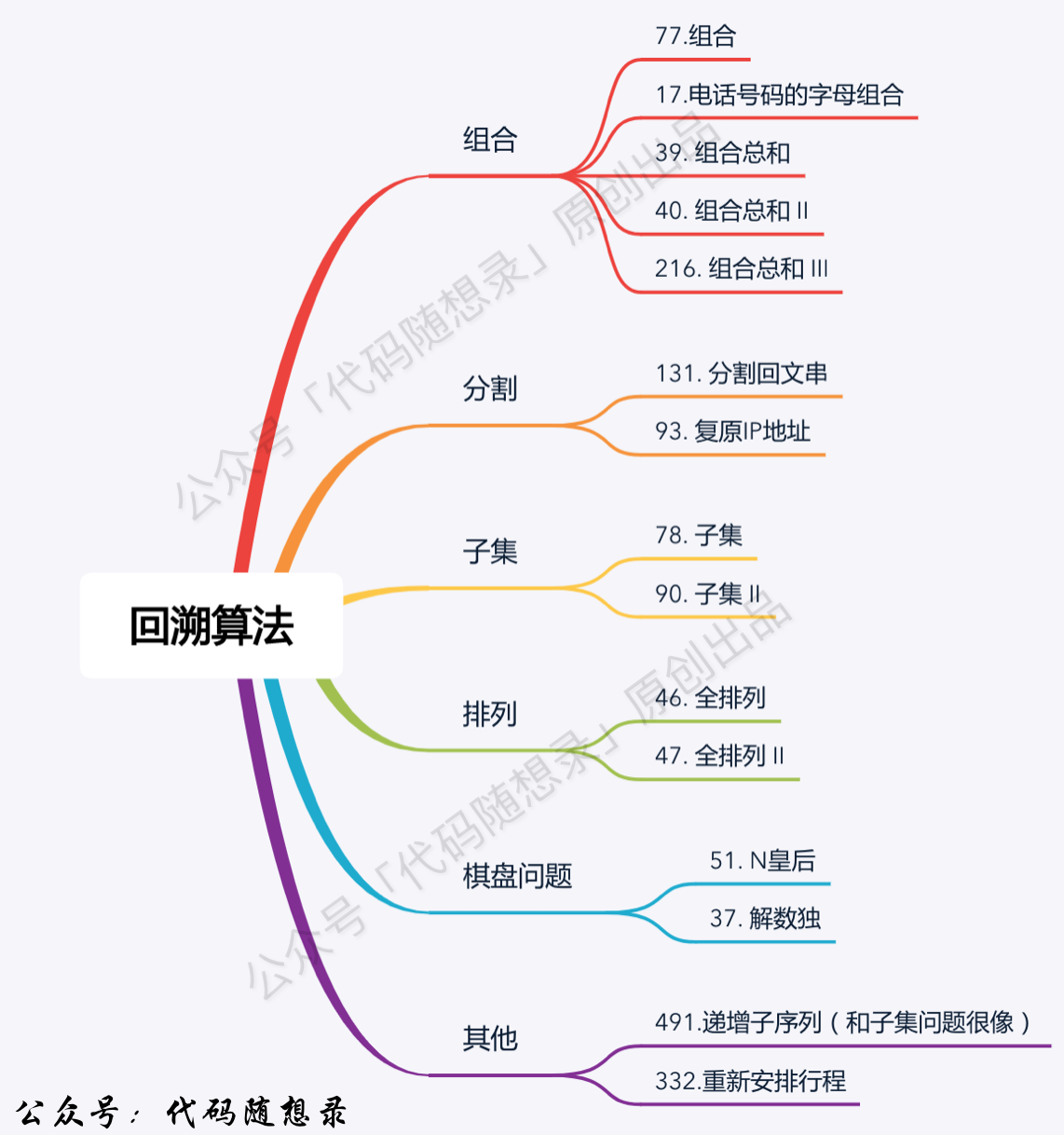 +
+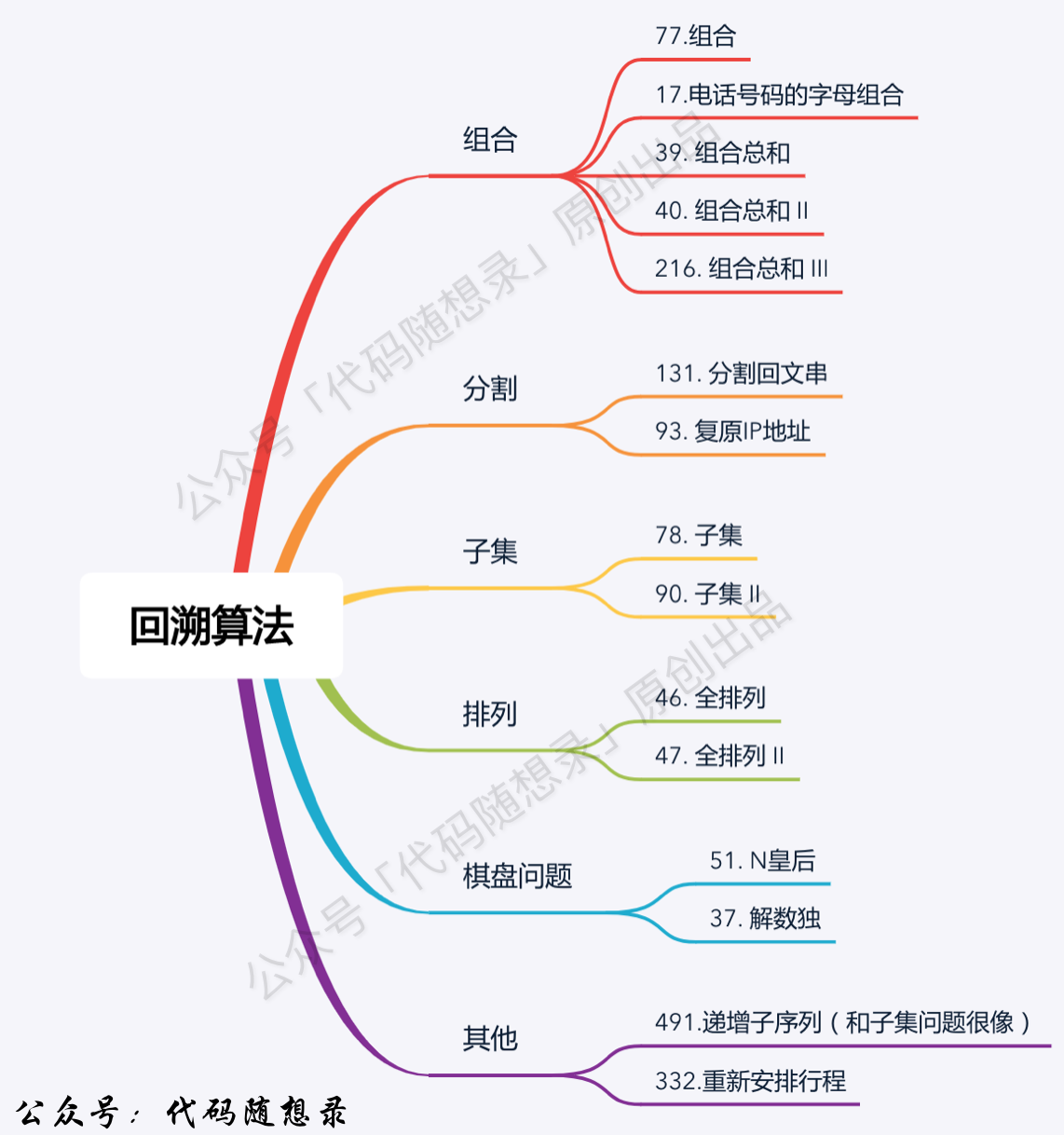 1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
2. [回溯算法:77.组合](./problems/0077.组合.md)
@@ -252,7 +252,7 @@
题目分类大纲如下:
-
1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
2. [回溯算法:77.组合](./problems/0077.组合.md)
@@ -252,7 +252,7 @@
题目分类大纲如下:
- +
+ 1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
@@ -503,5 +503,5 @@
添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
-
1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
@@ -503,5 +503,5 @@
添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
-

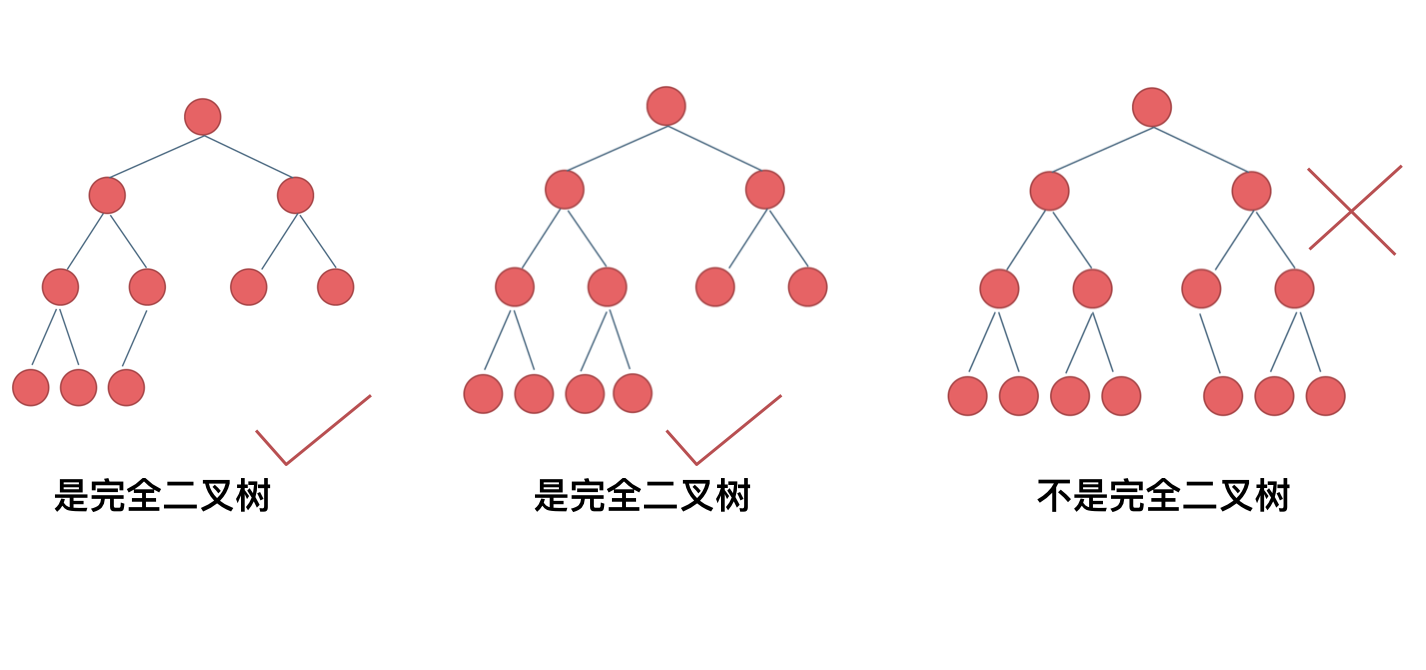 +
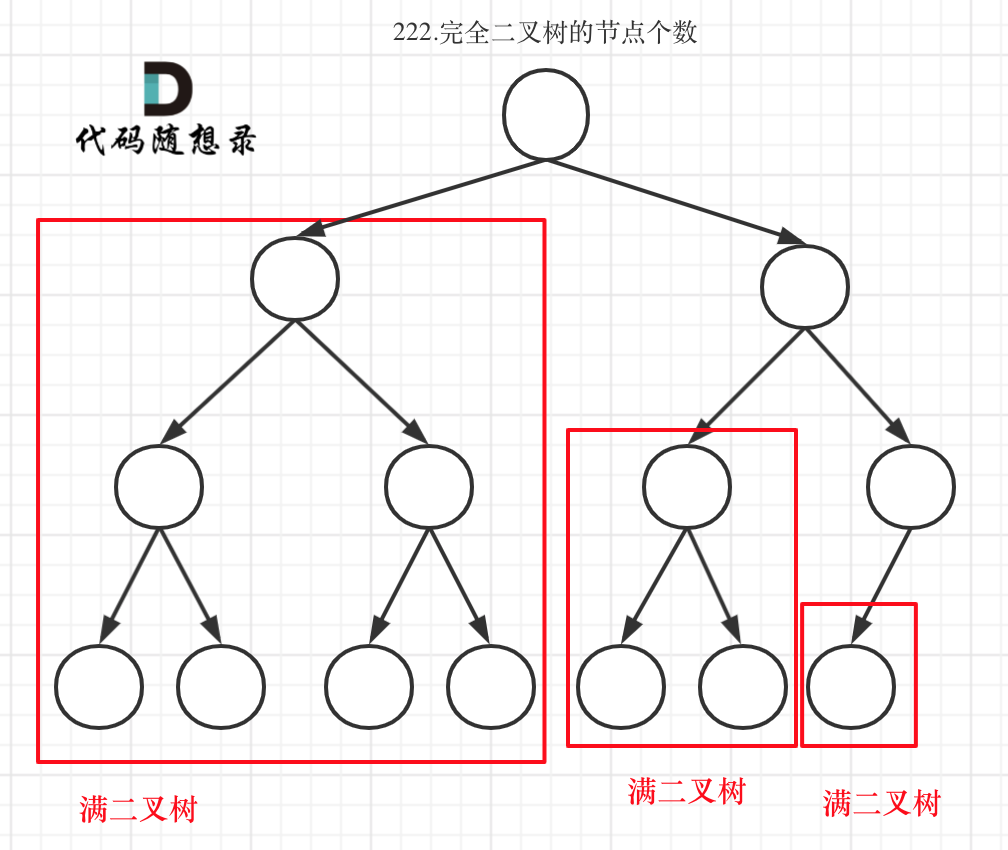
+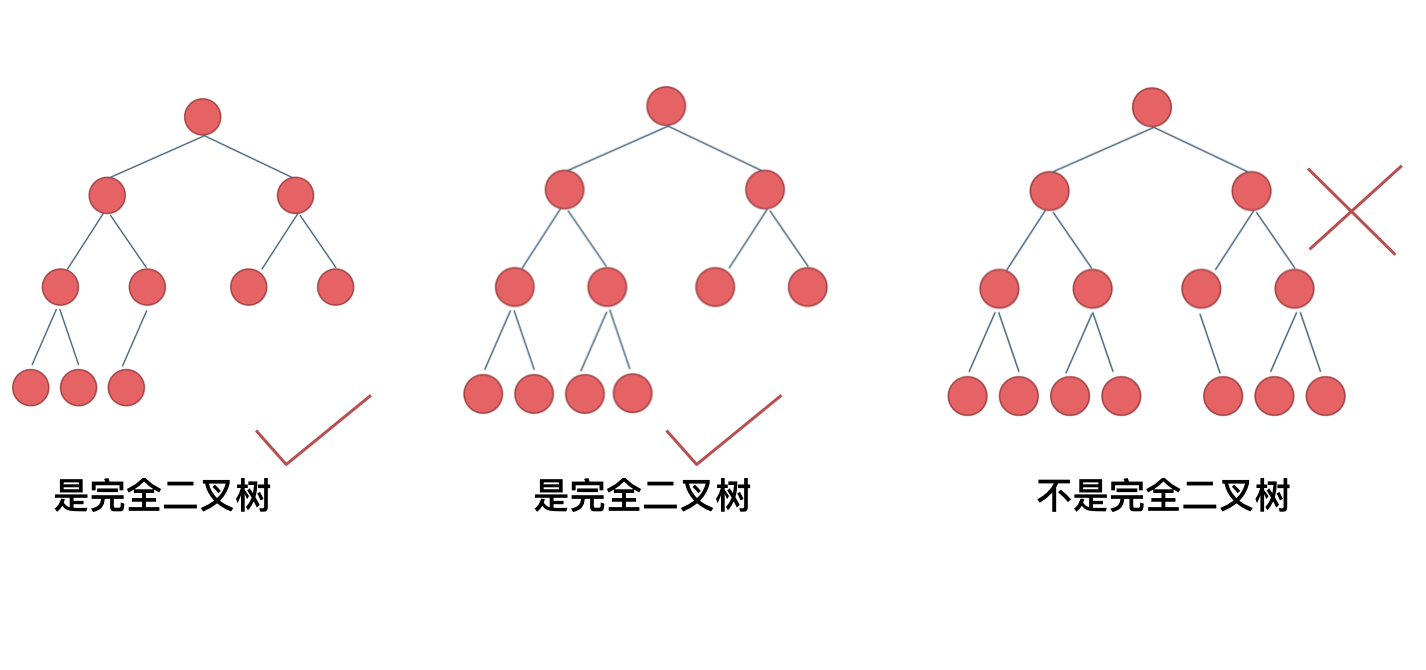 完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
@@ -162,10 +162,10 @@ public:
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
完全二叉树(一)如图:
-
+
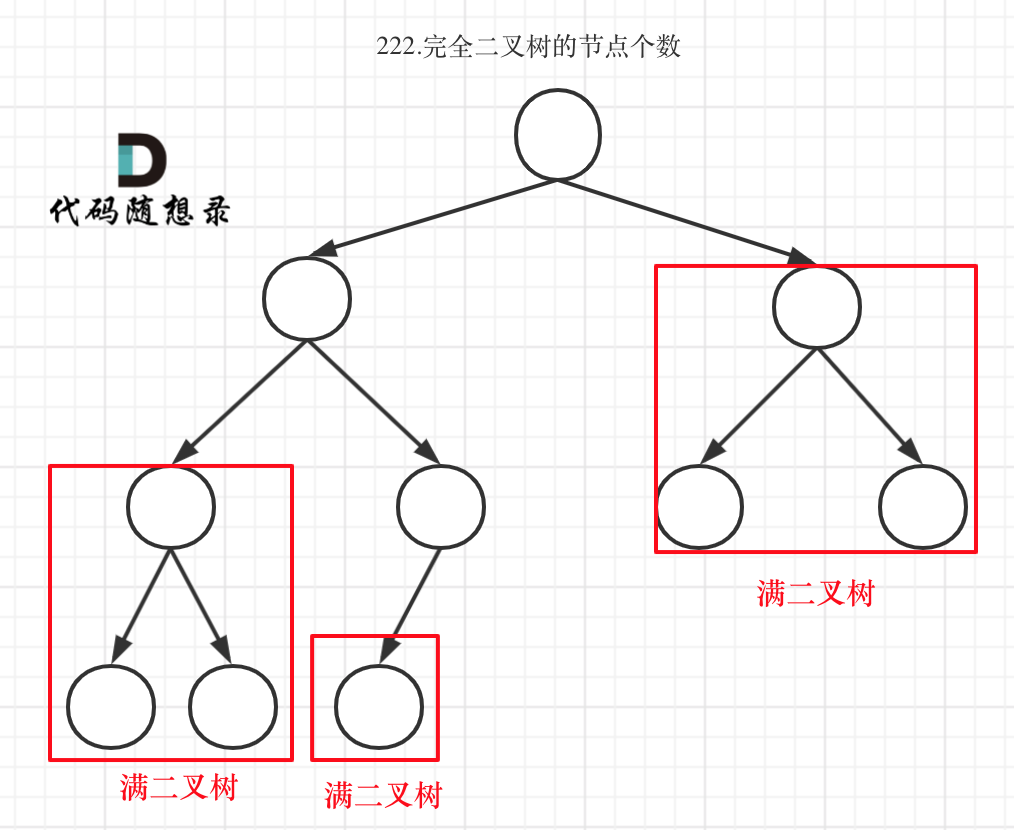
完全二叉树(二)如图:
-
+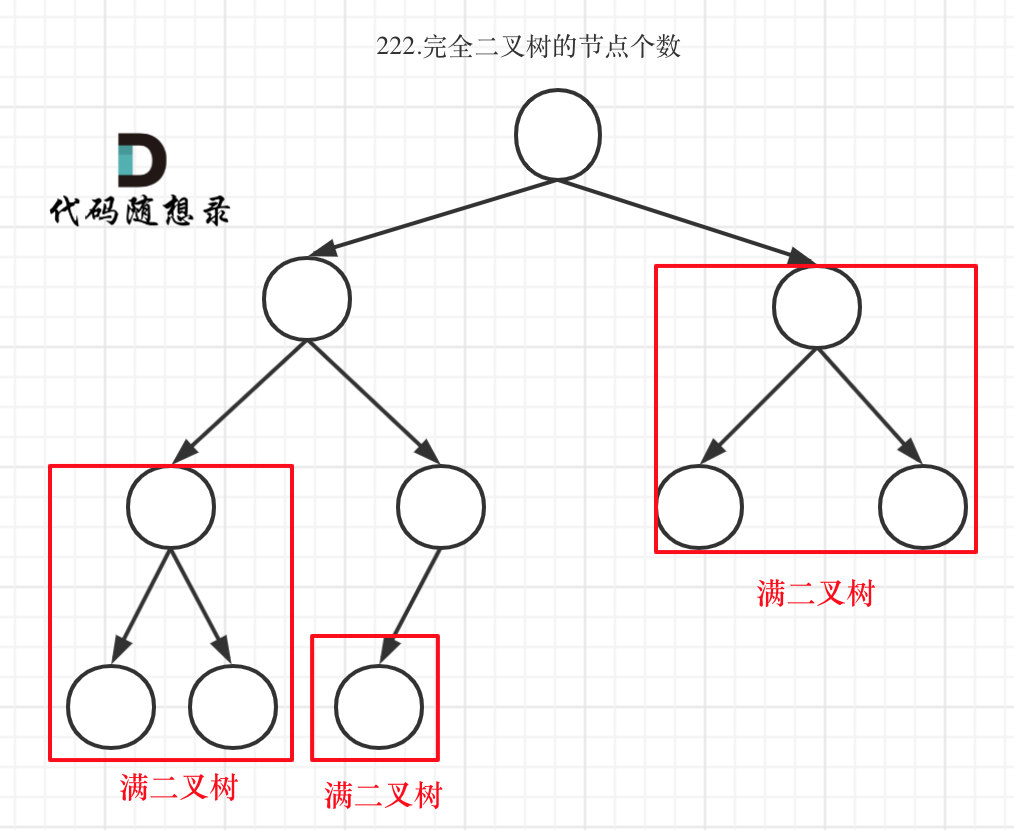
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
@@ -173,15 +173,15 @@ public:
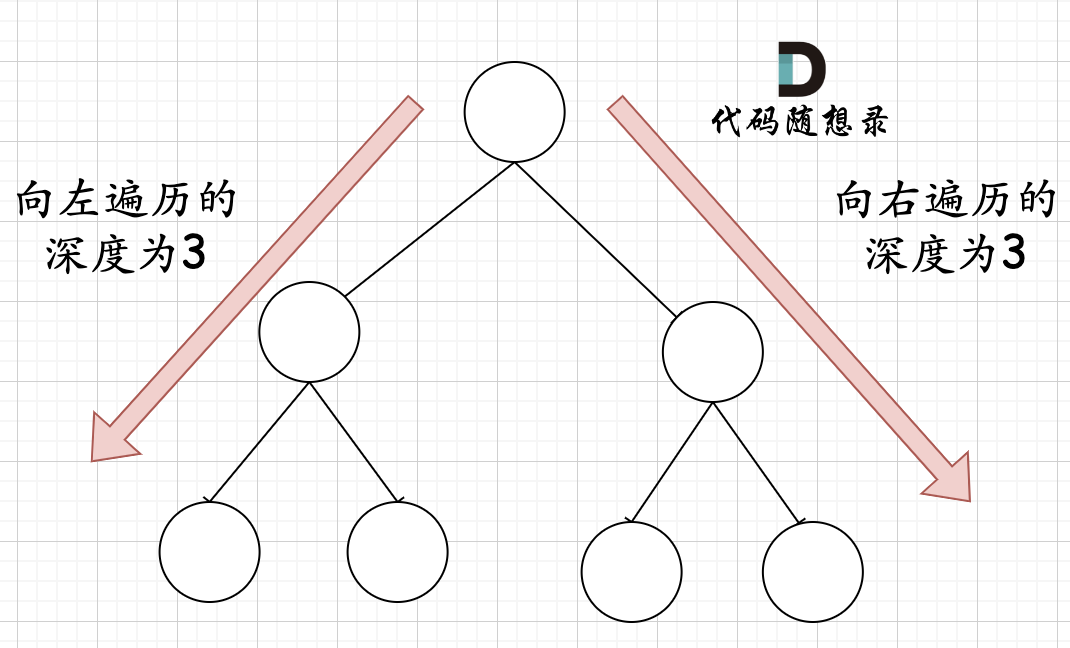
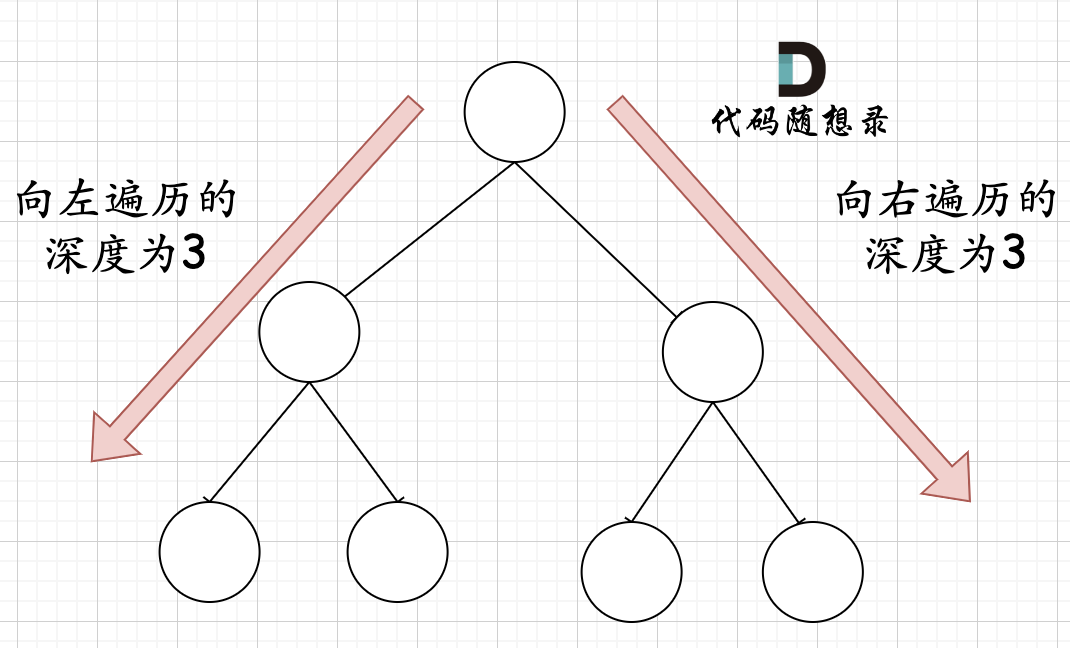
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
-
+
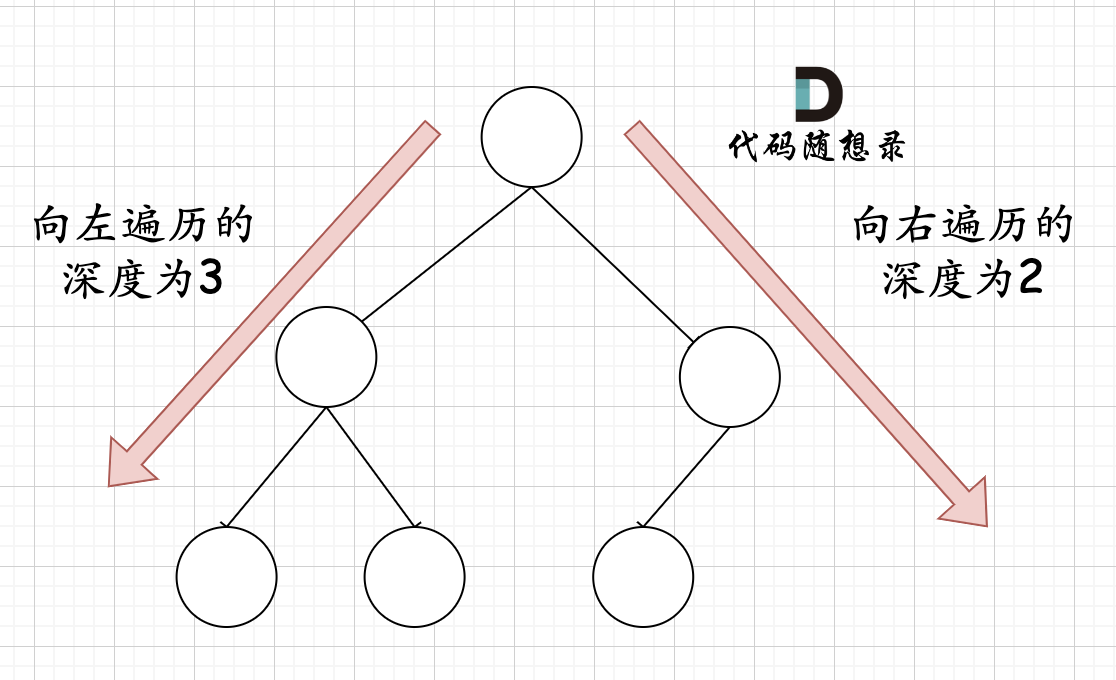
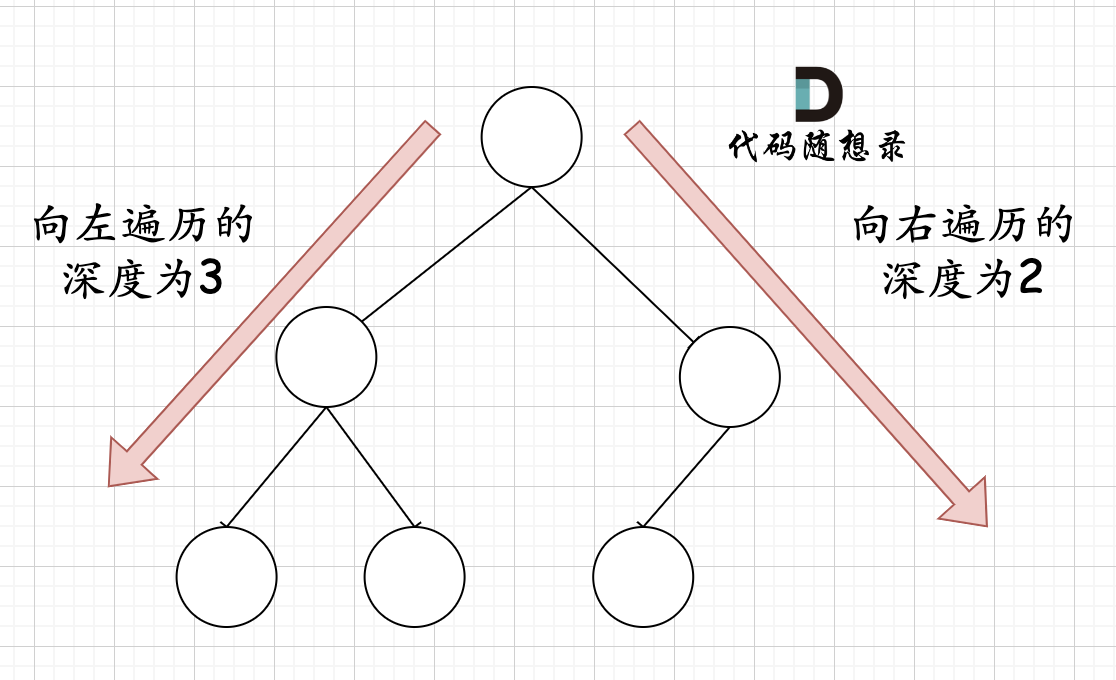
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
-
+
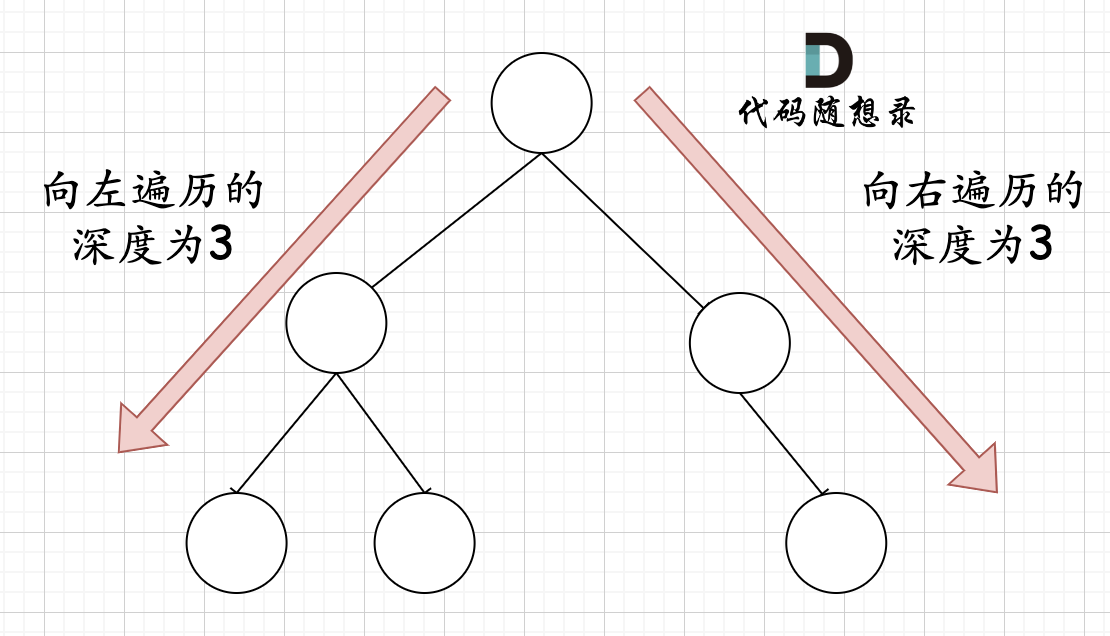
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
-
+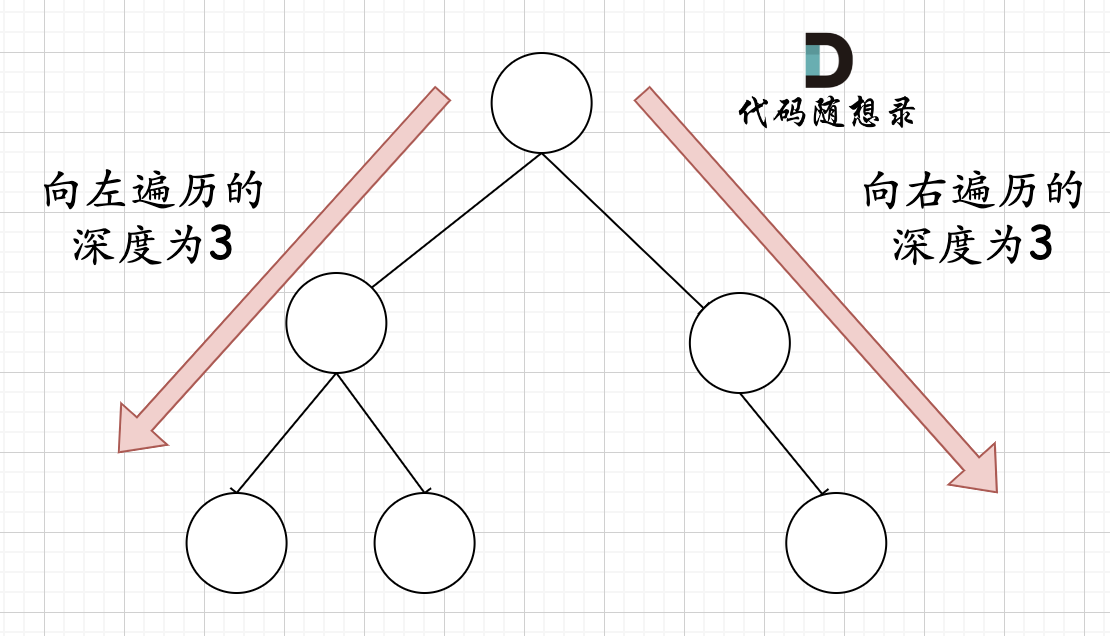
如果这么想,大家就是对 完全二叉树理解有误区了,**以上这棵二叉树,它根本就不是一个完全二叉树**!
diff --git a/problems/0226.翻转二叉树.md b/problems/0226.翻转二叉树.md
index 0980e600..248a28a4 100644
--- a/problems/0226.翻转二叉树.md
+++ b/problems/0226.翻转二叉树.md
@@ -10,7 +10,7 @@
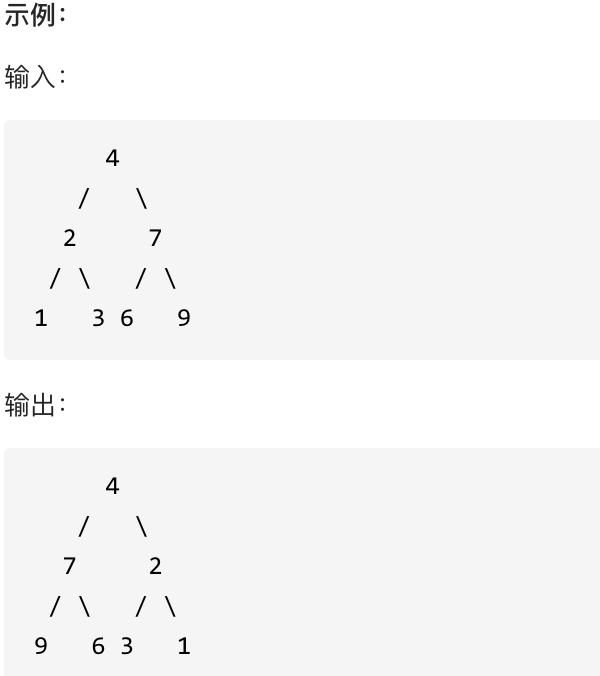
翻转一棵二叉树。
-
+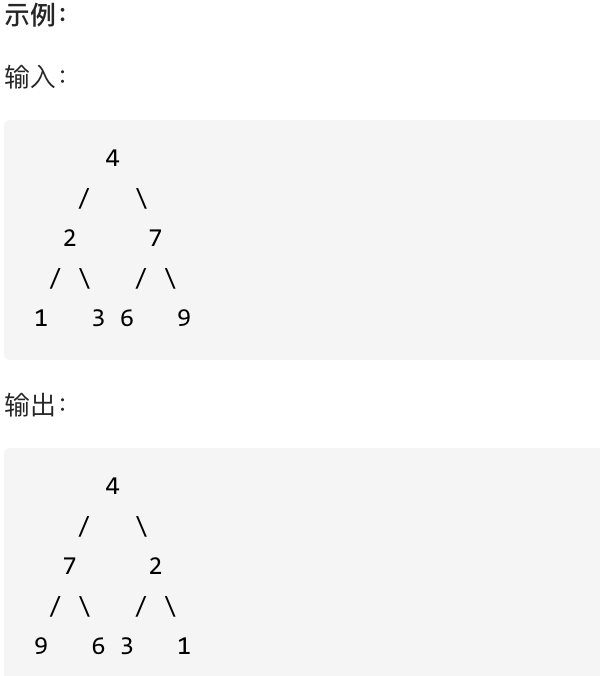
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,全当一个乐子哈)
@@ -35,7 +35,7 @@
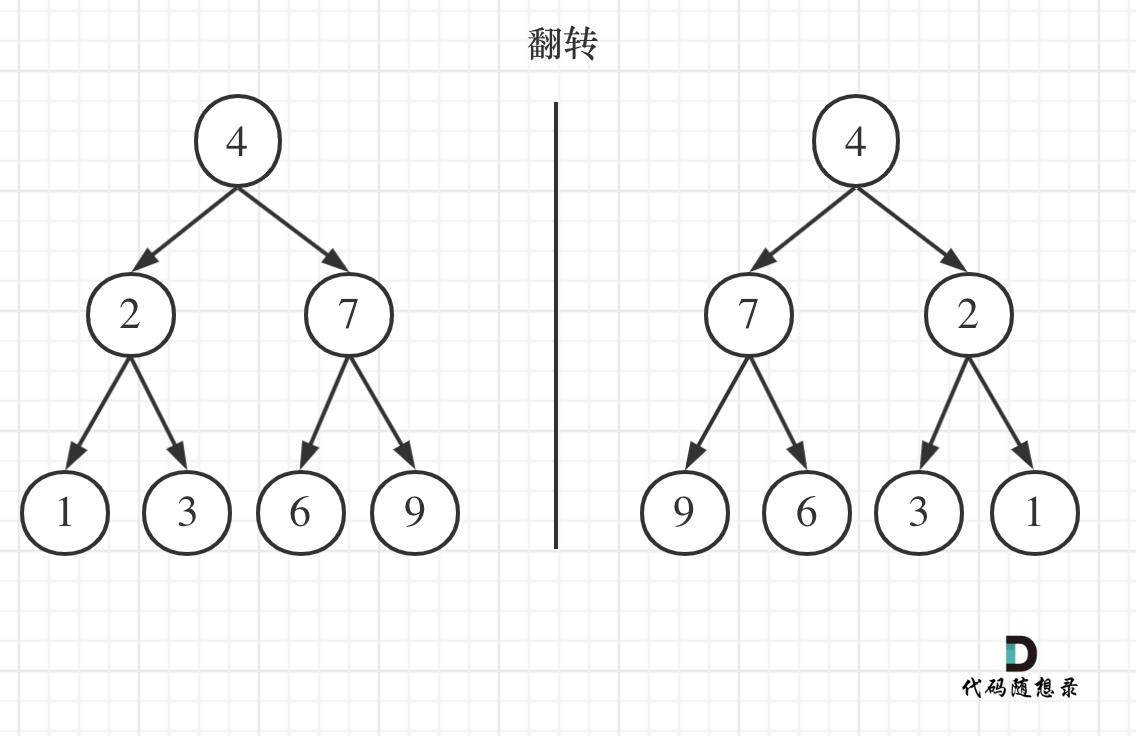
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
-
+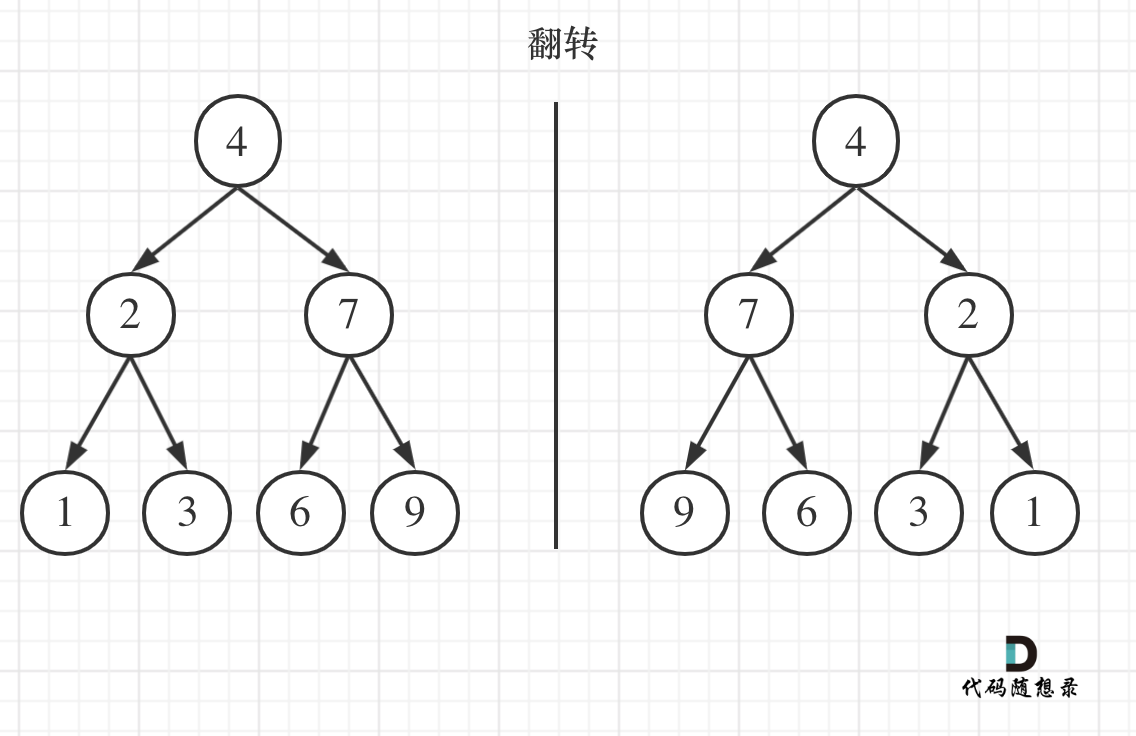
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
diff --git a/problems/0235.二叉搜索树的最近公共祖先.md b/problems/0235.二叉搜索树的最近公共祖先.md
index c5eb603a..98cc5b7d 100644
--- a/problems/0235.二叉搜索树的最近公共祖先.md
+++ b/problems/0235.二叉搜索树的最近公共祖先.md
@@ -14,7 +14,7 @@
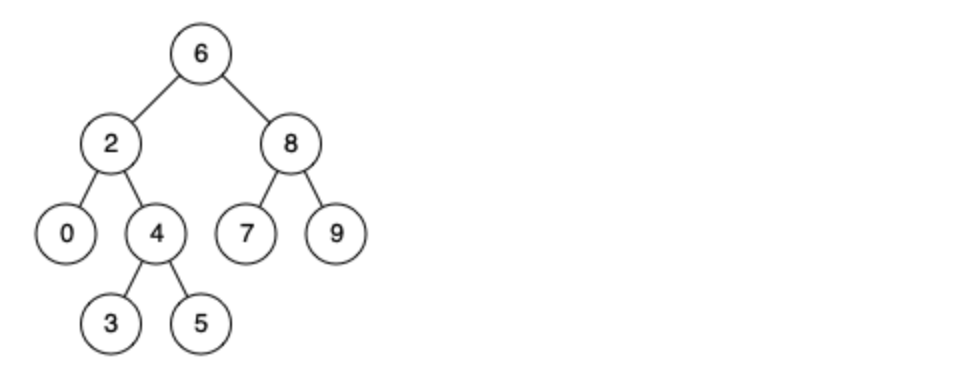
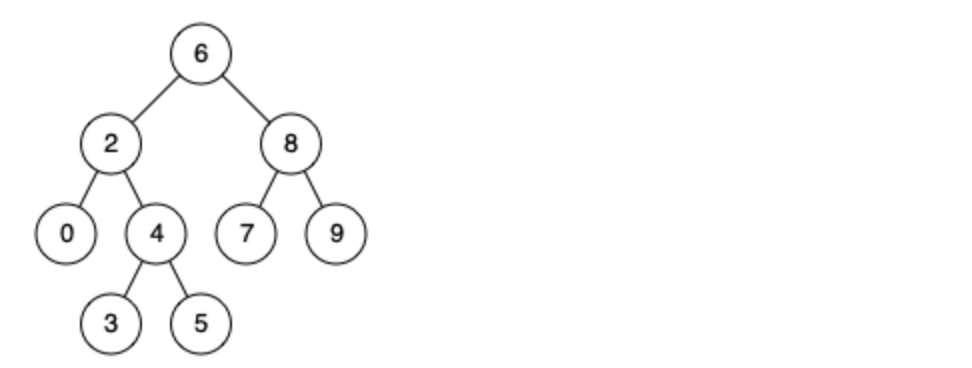
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
-
+
示例 1:
@@ -52,7 +52,7 @@
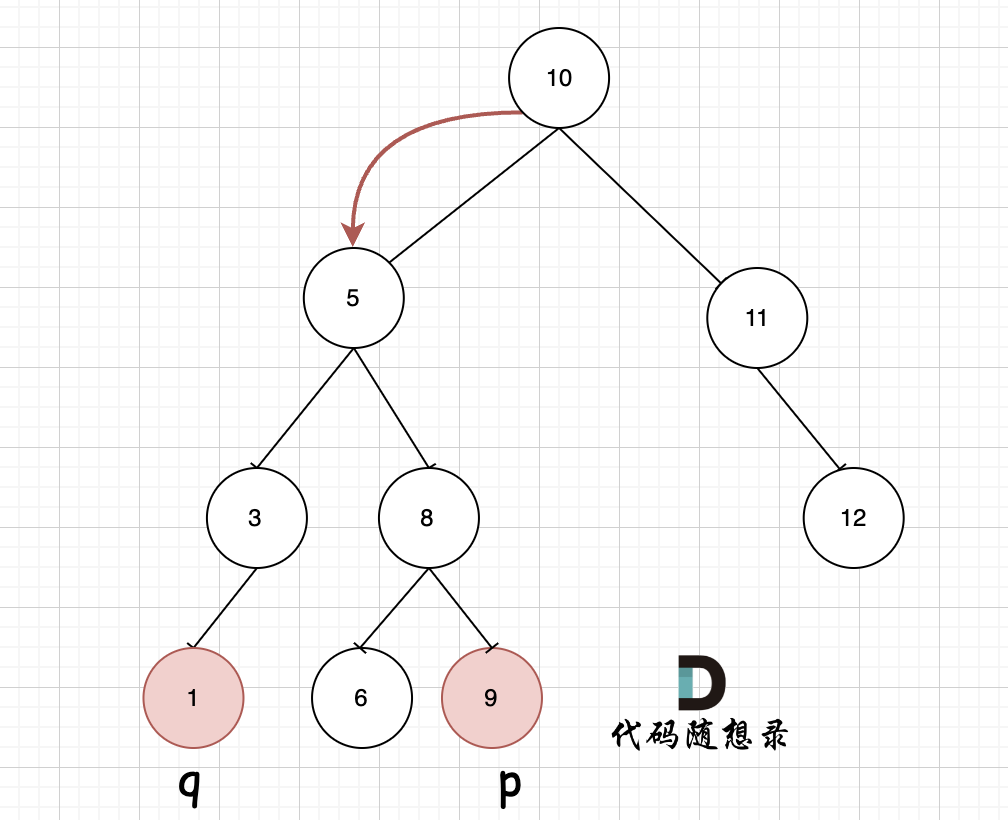
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
-
+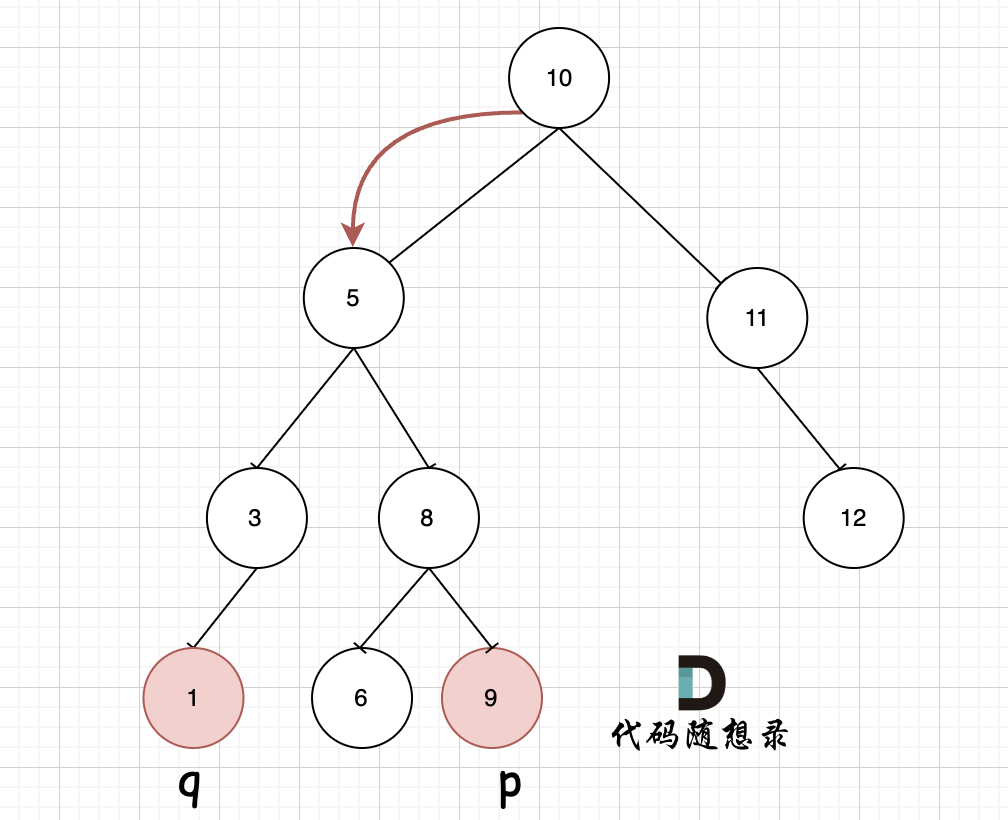
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
@@ -64,7 +64,7 @@
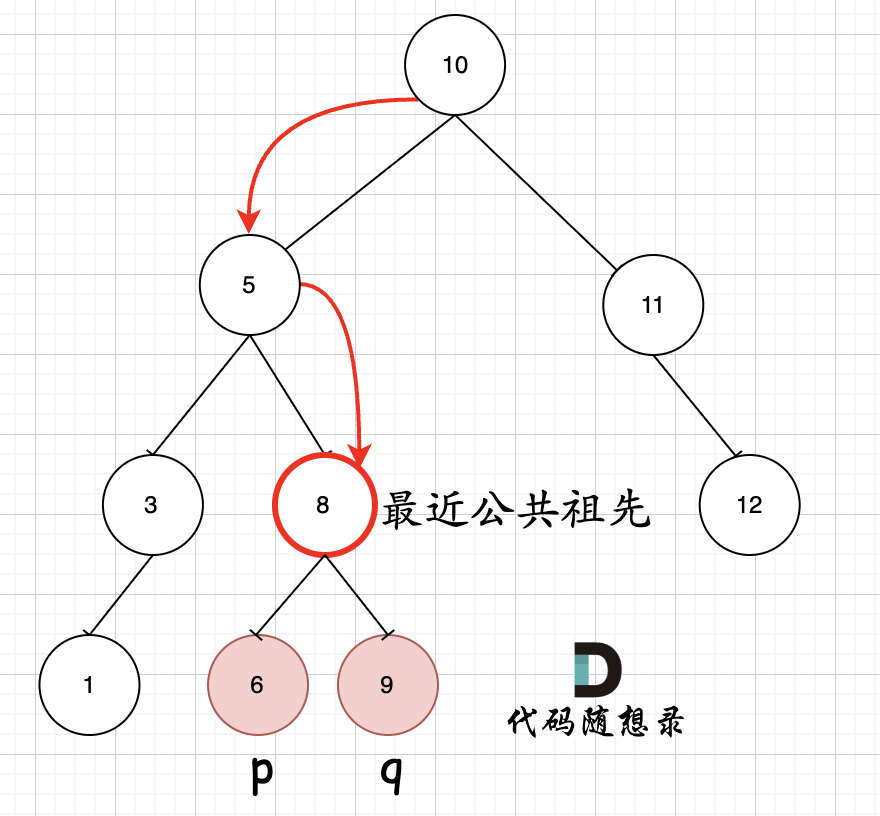
如图所示:p为节点6,q为节点9
-
+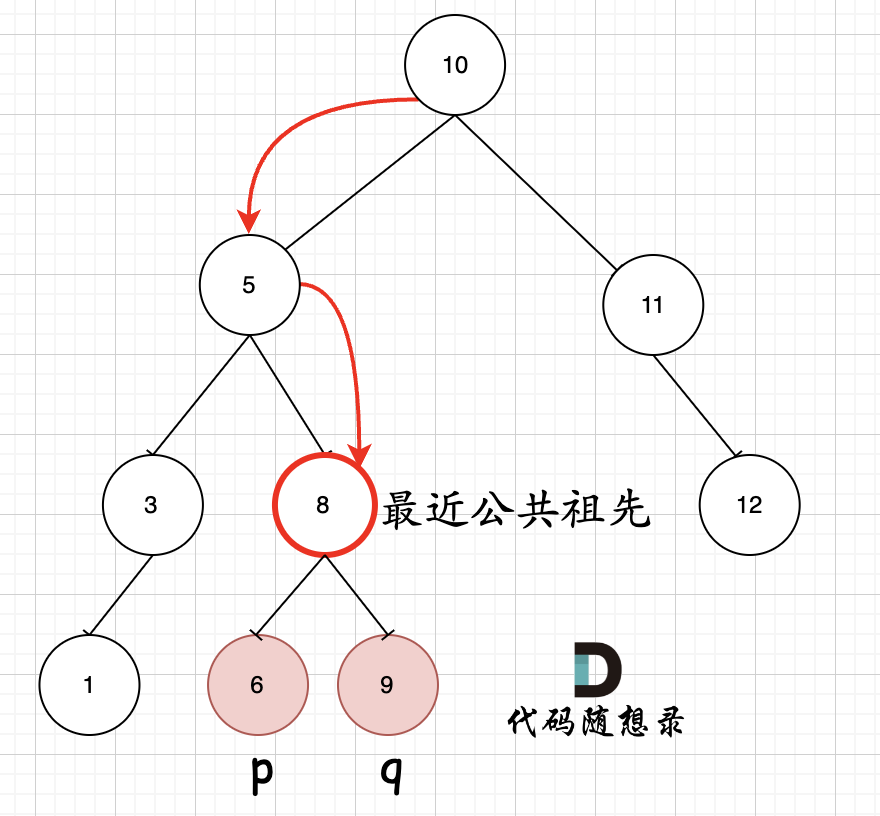
可以看出直接按照指定的方向,就可以找到节点8,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
diff --git a/problems/0236.二叉树的最近公共祖先.md b/problems/0236.二叉树的最近公共祖先.md
index f15d1cff..537d6240 100644
--- a/problems/0236.二叉树的最近公共祖先.md
+++ b/problems/0236.二叉树的最近公共祖先.md
@@ -16,7 +16,7 @@
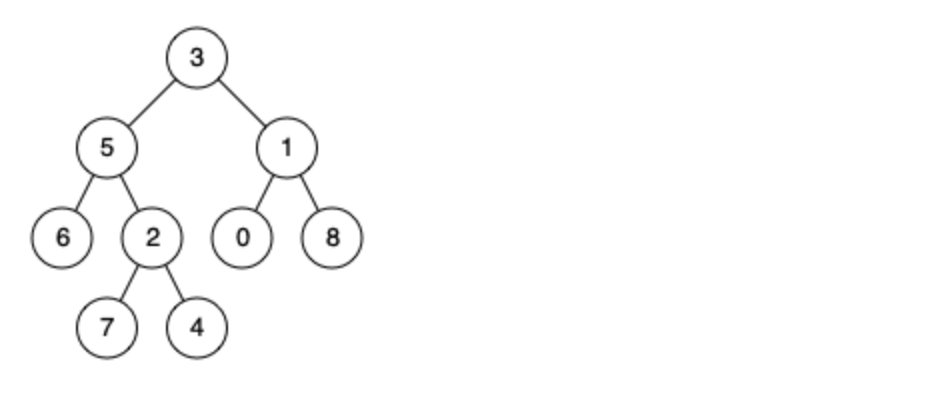
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
-
+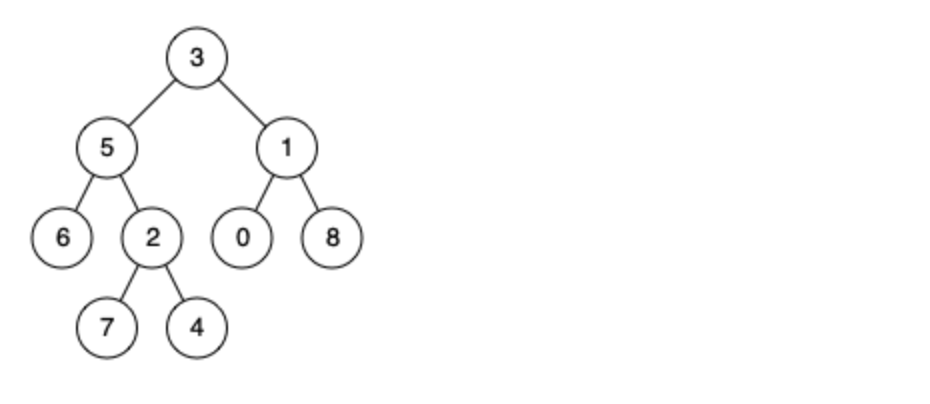
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
@@ -51,7 +51,7 @@
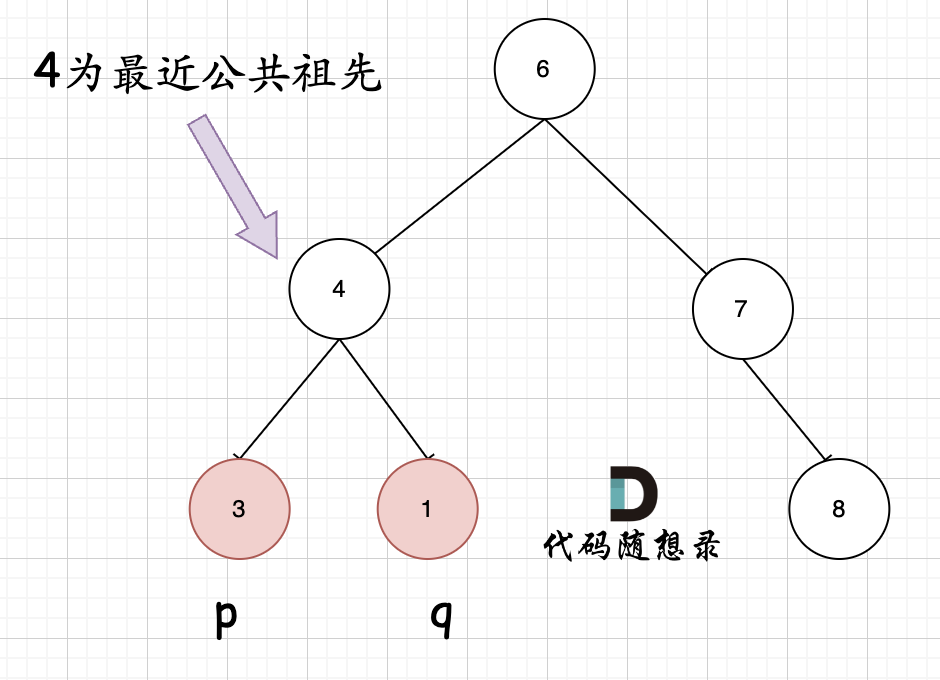
**首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。** 即情况一:
-
+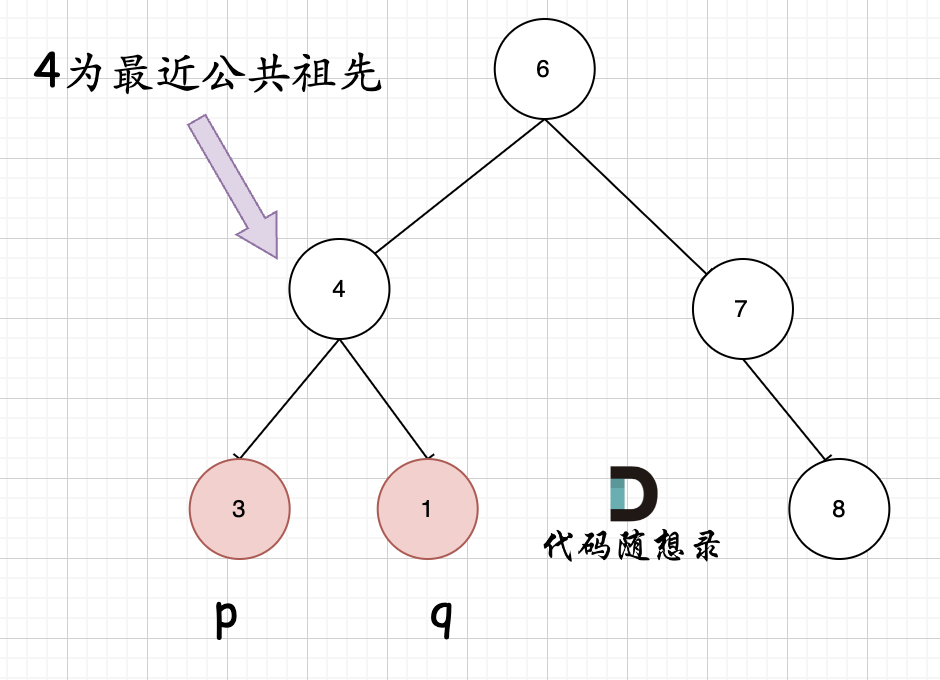
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
@@ -61,7 +61,7 @@
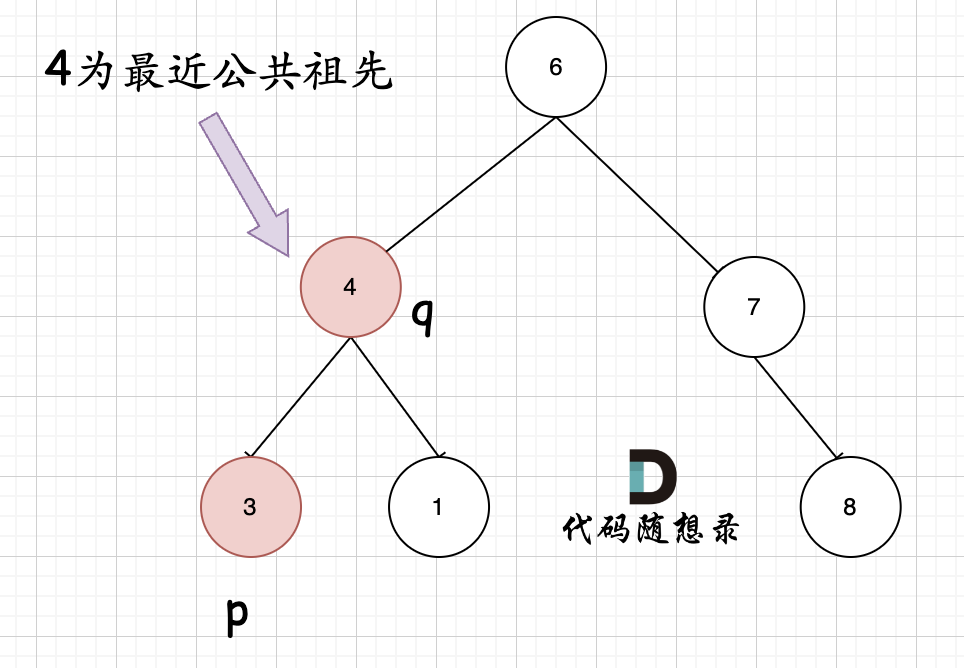
**但是很多人容易忽略一个情况,就是节点本身p(q),它拥有一个子孙节点q(p)。** 情况二:
-
+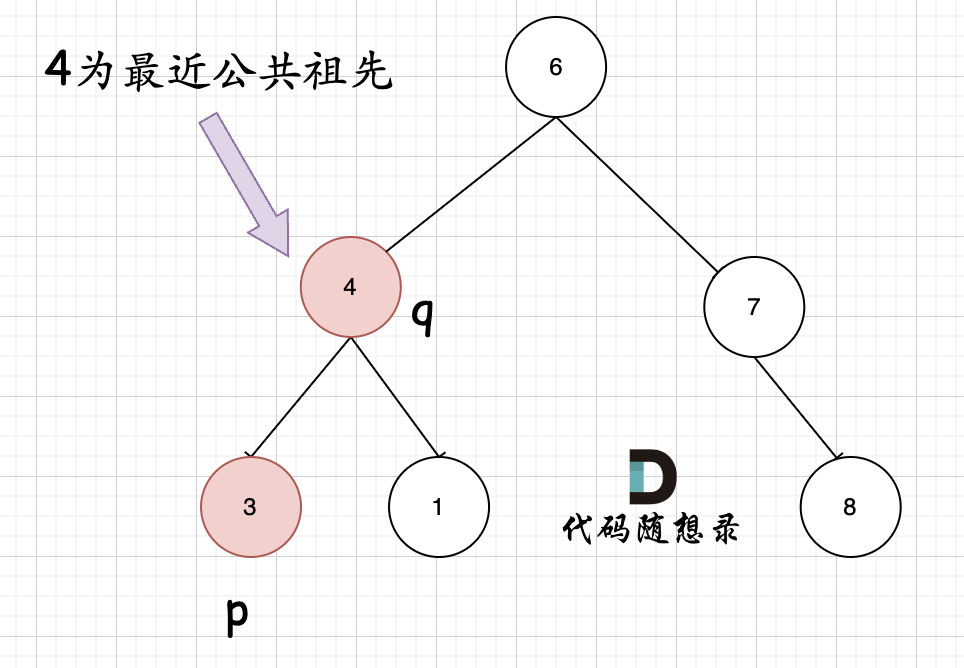
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
@@ -129,7 +129,7 @@ left与right的逻辑处理; // 中
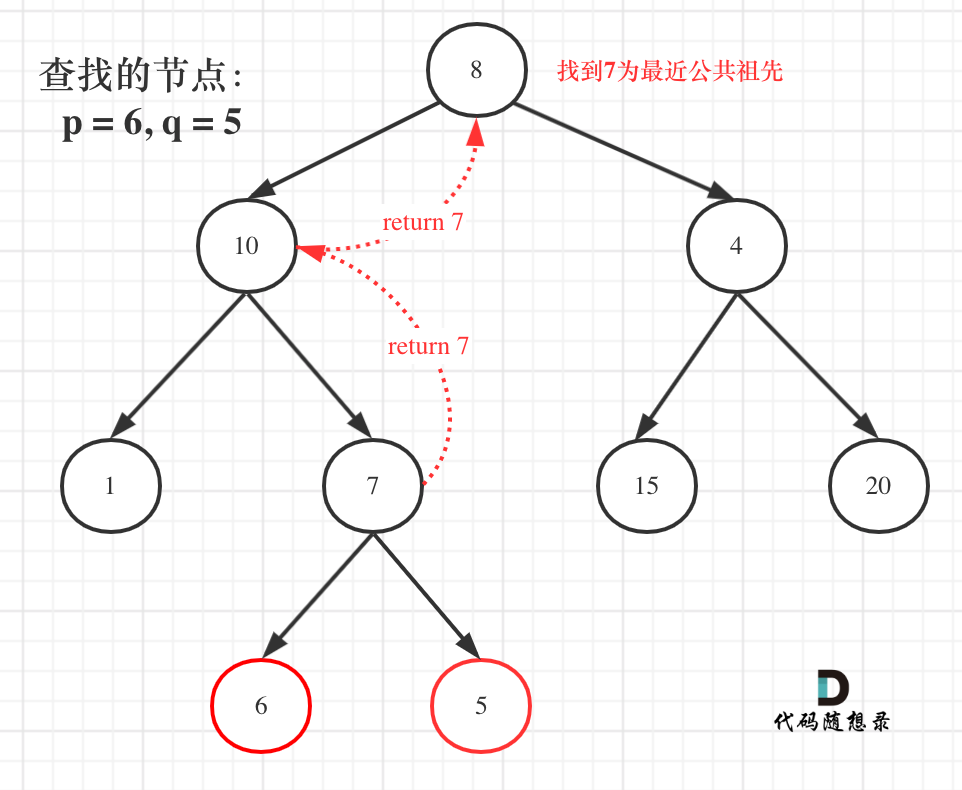
如图:
-
+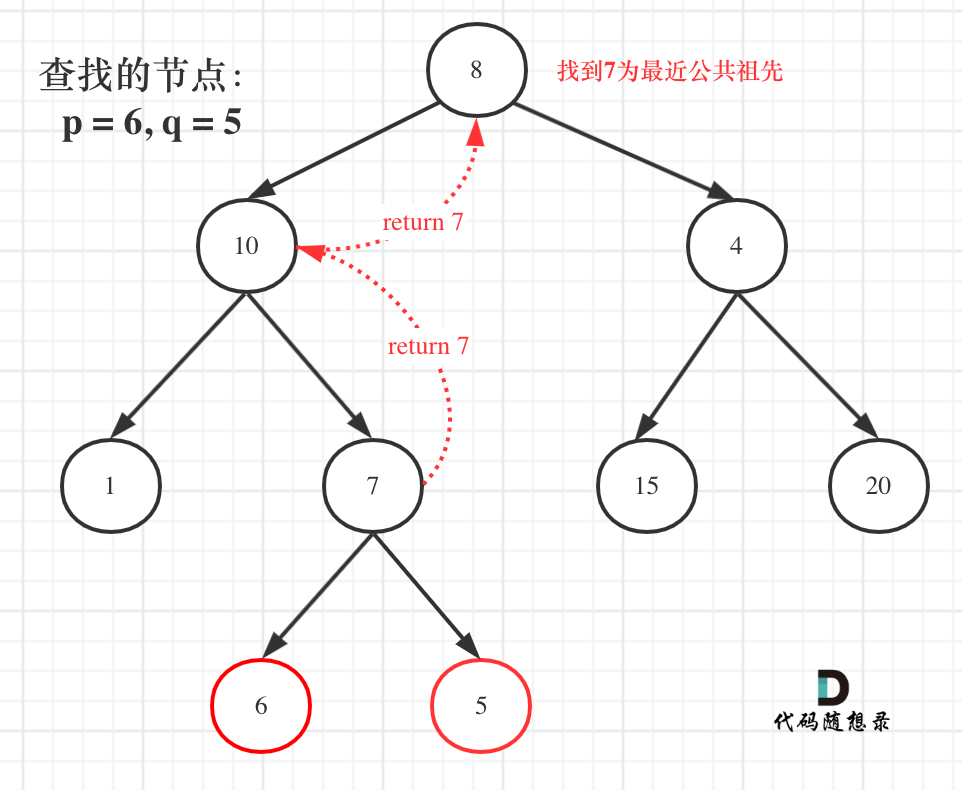
就像图中一样直接返回7。
@@ -162,7 +162,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
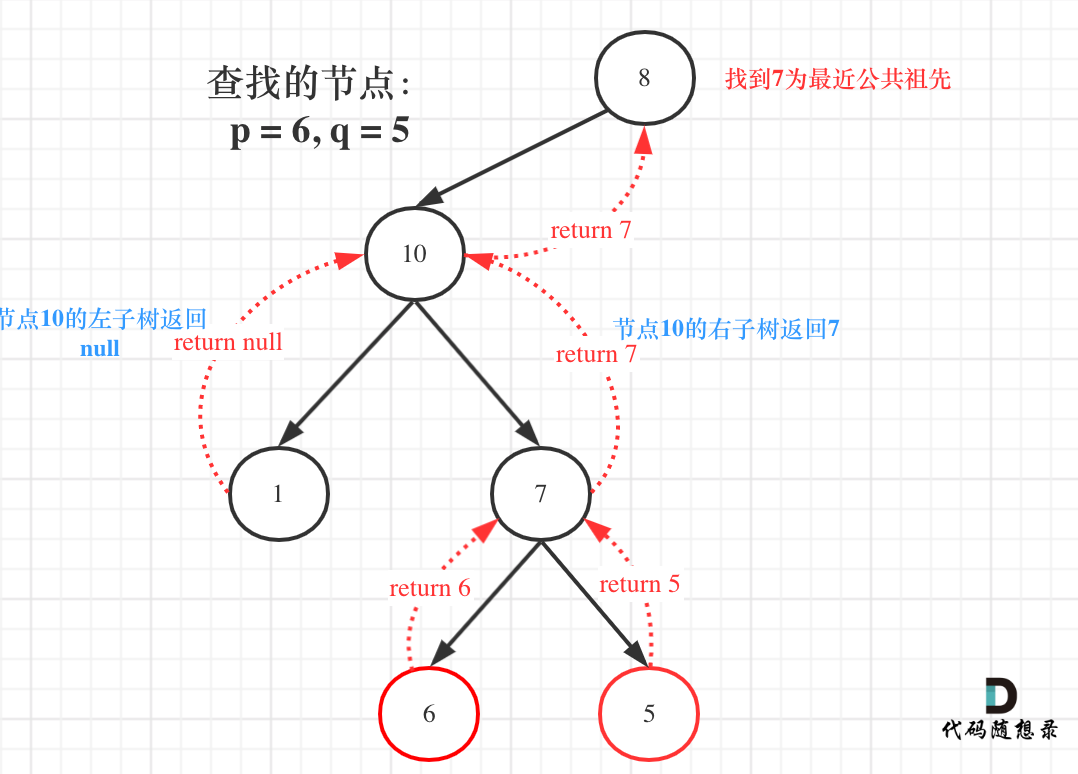
如图:
-
+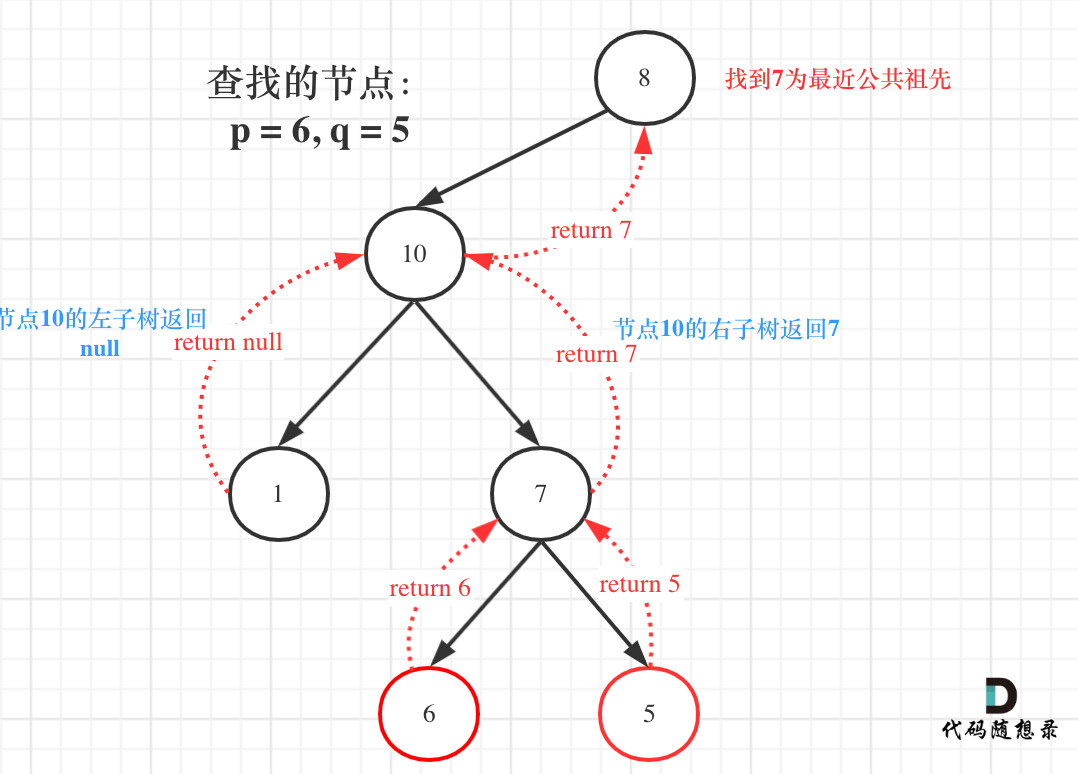
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
@@ -183,7 +183,7 @@ else { // (left == NULL && right == NULL)
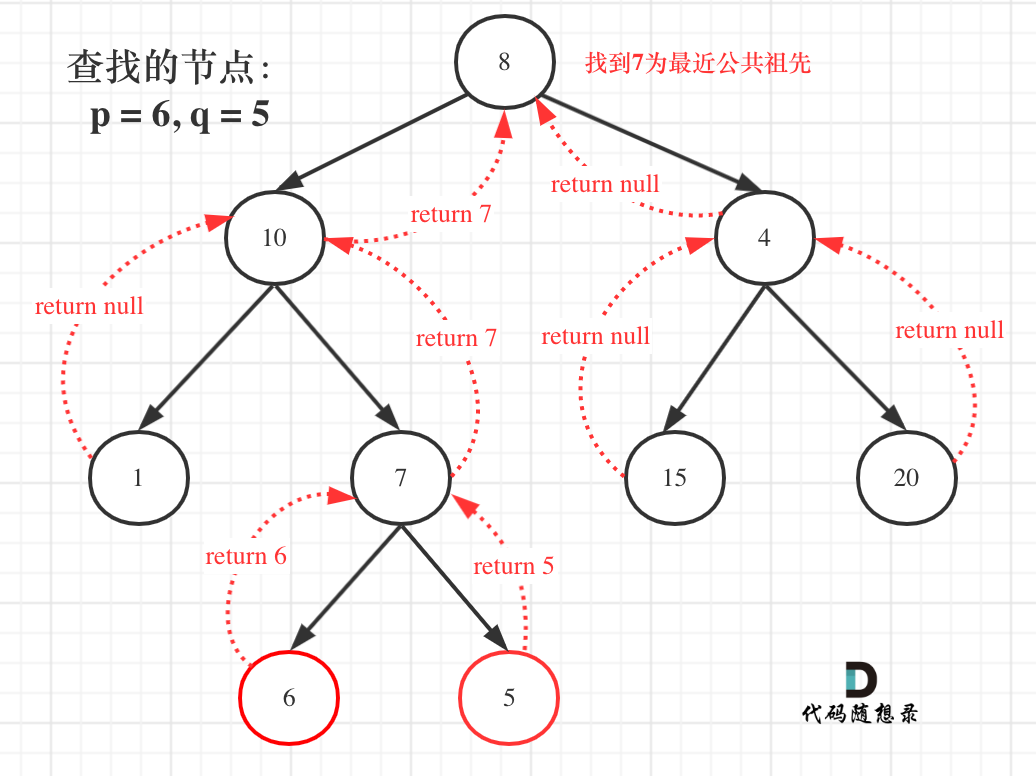
那么寻找最小公共祖先,完整流程图如下:
-
+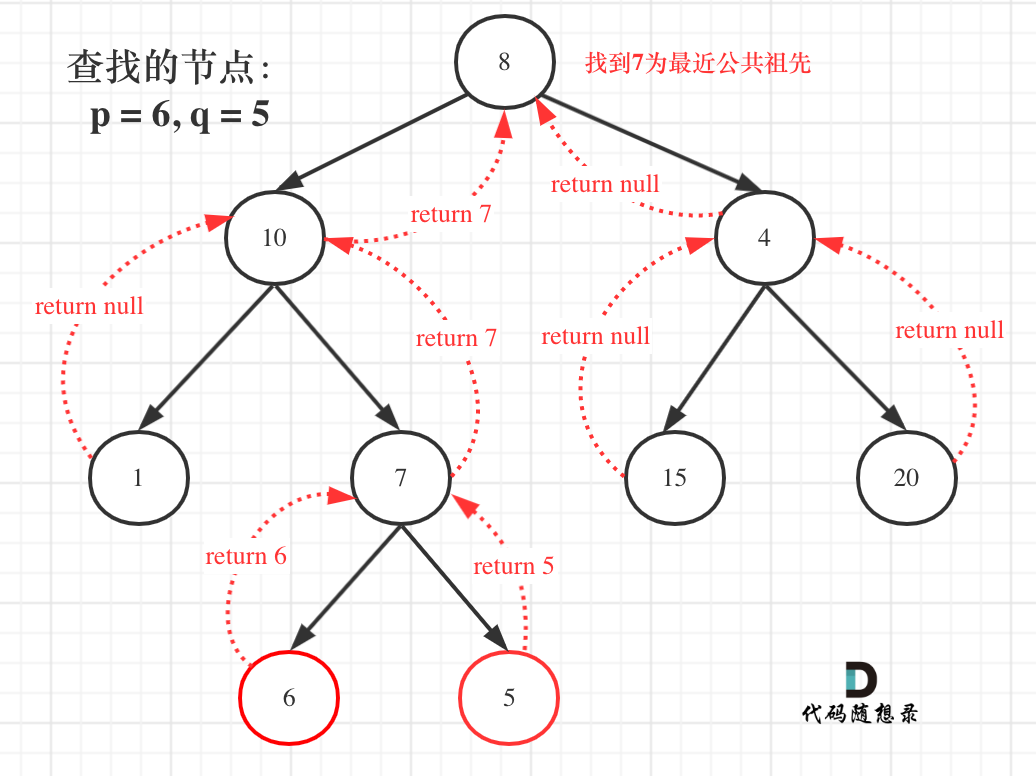
**从图中,大家可以看到,我们是如何回溯遍历整棵二叉树,将结果返回给头结点的!**
diff --git a/problems/0257.二叉树的所有路径.md b/problems/0257.二叉树的所有路径.md
index 287db209..5d713511 100644
--- a/problems/0257.二叉树的所有路径.md
+++ b/problems/0257.二叉树的所有路径.md
@@ -14,7 +14,7 @@
说明: 叶子节点是指没有子节点的节点。
示例:
-
+
## 算法公开课
@@ -28,7 +28,7 @@
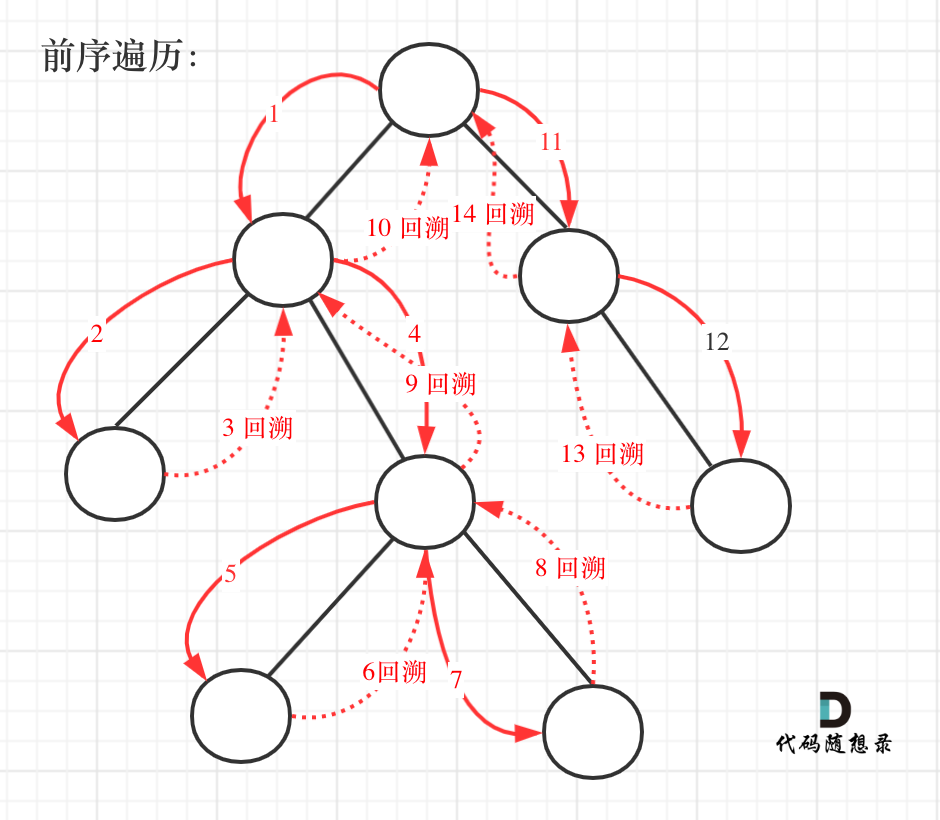
前序遍历以及回溯的过程如图:
-
+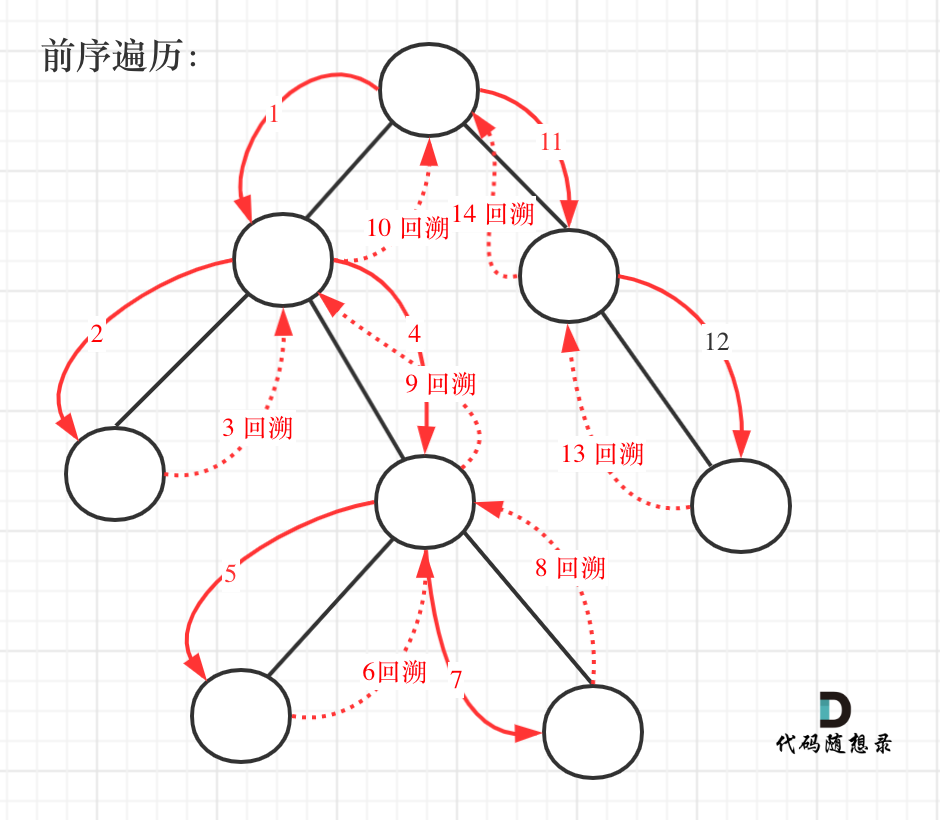
我们先使用递归的方式,来做前序遍历。**要知道递归和回溯就是一家的,本题也需要回溯。**
@@ -315,7 +315,7 @@ public:
其实关键还在于 参数,使用的是 `string path`,这里并没有加上引用`&` ,即本层递归中,path + 该节点数值,但该层递归结束,上一层path的数值并不会受到任何影响。 如图所示:
-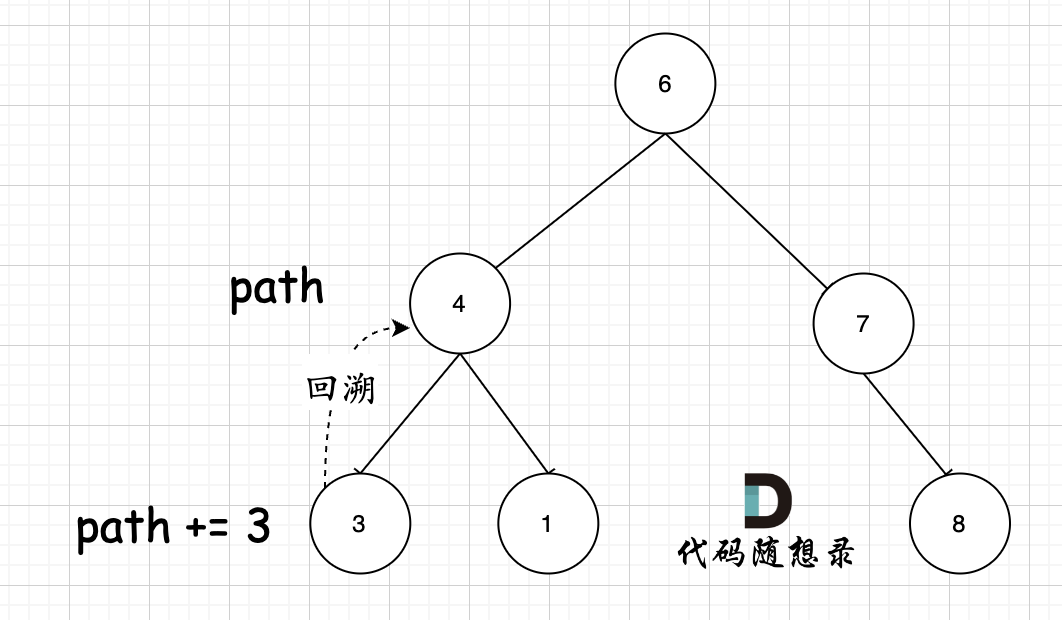
+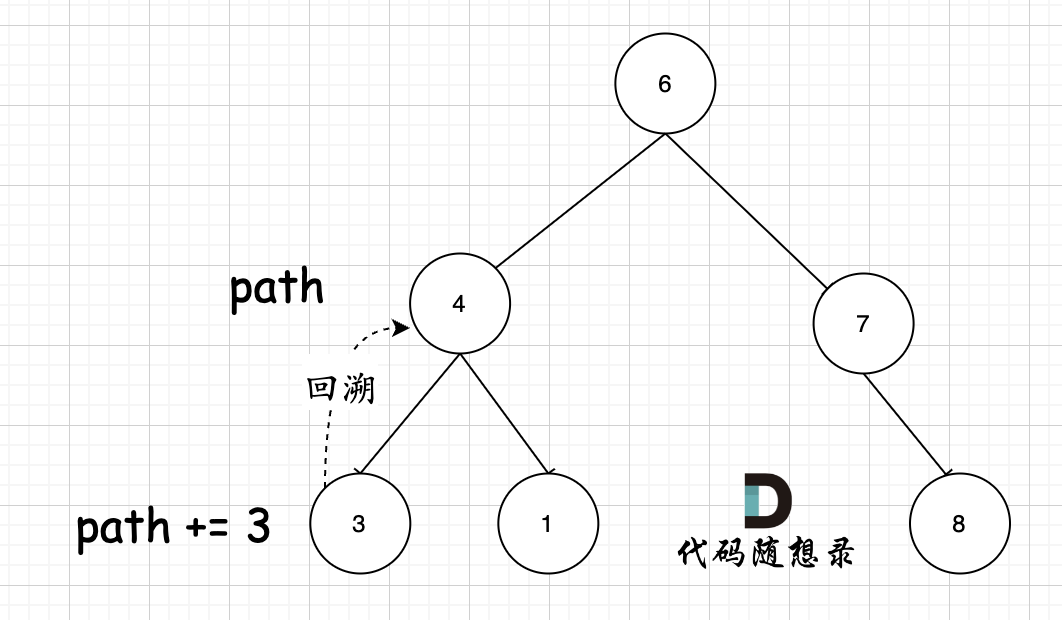
节点4 的path,在遍历到节点3,path+3,遍历节点3的递归结束之后,返回节点4(回溯的过程),path并不会把3加上。
diff --git a/problems/0279.完全平方数.md b/problems/0279.完全平方数.md
index c1077bd4..8171a409 100644
--- a/problems/0279.完全平方数.md
+++ b/problems/0279.完全平方数.md
@@ -93,7 +93,7 @@ for (int i = 0; i <= n; i++) { // 遍历背包
已输入n为5例,dp状态图如下:
-
+
dp[0] = 0
dp[1] = min(dp[0] + 1) = 1
diff --git a/problems/0300.最长上升子序列.md b/problems/0300.最长上升子序列.md
index 7d2e4886..de37ed5c 100644
--- a/problems/0300.最长上升子序列.md
+++ b/problems/0300.最长上升子序列.md
@@ -85,7 +85,7 @@ for (int i = 1; i < nums.size(); i++) {
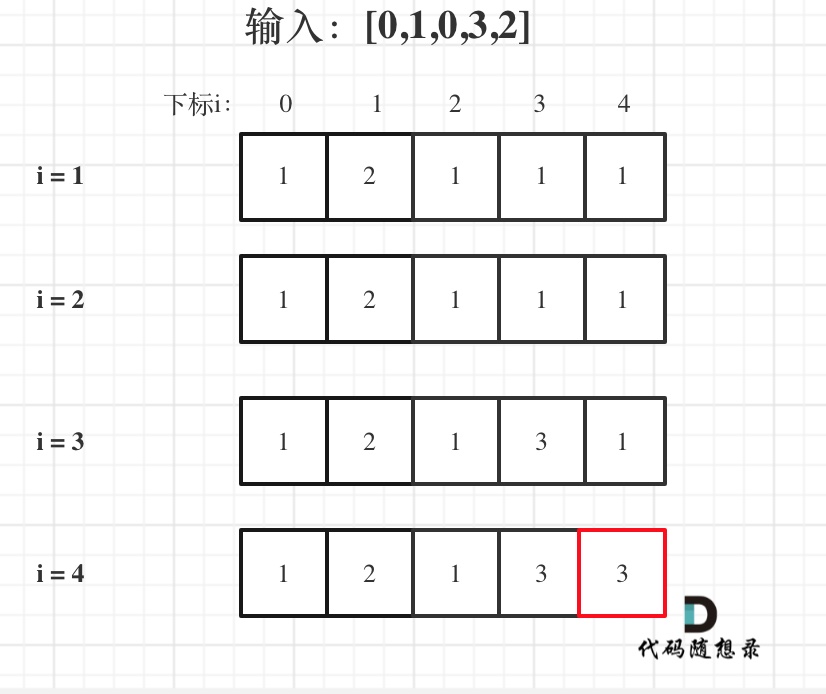
输入:[0,1,0,3,2],dp数组的变化如下:
-
+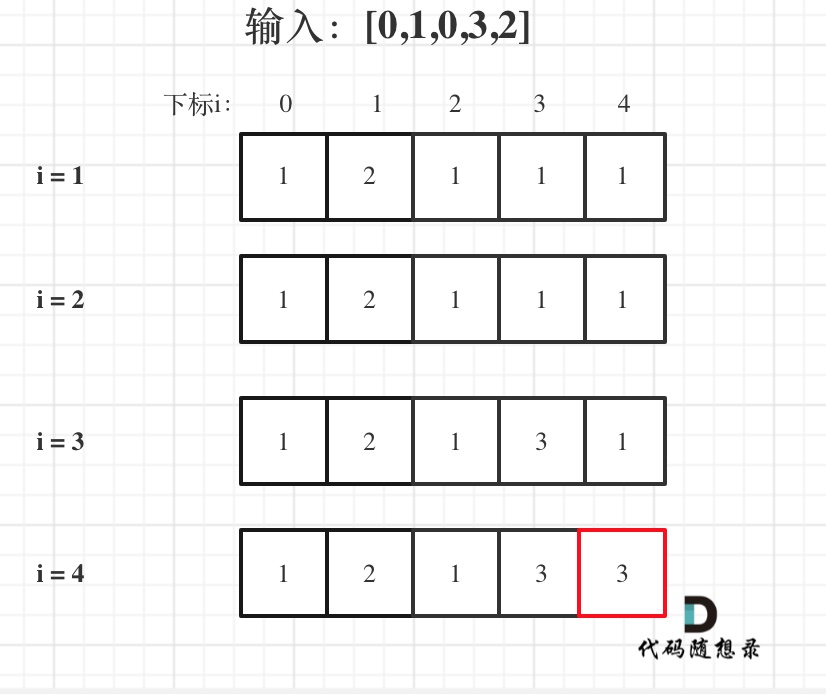
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
diff --git a/problems/0309.最佳买卖股票时机含冷冻期.md b/problems/0309.最佳买卖股票时机含冷冻期.md
index 6a819335..599a1f42 100644
--- a/problems/0309.最佳买卖股票时机含冷冻期.md
+++ b/problems/0309.最佳买卖股票时机含冷冻期.md
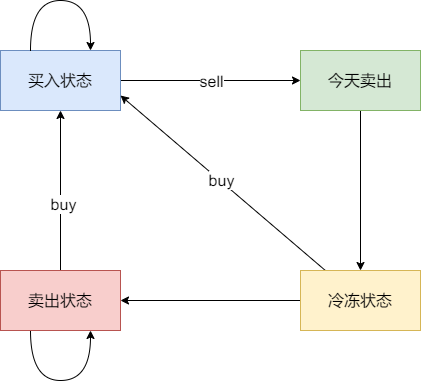
@@ -47,7 +47,7 @@ dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
* 状态三:今天卖出股票
* 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
-
+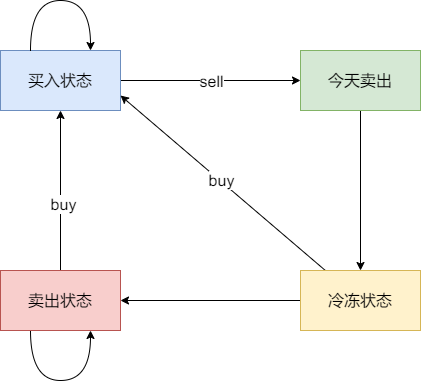
j的状态为:
@@ -136,7 +136,7 @@ dp[i][3] = dp[i - 1][2];
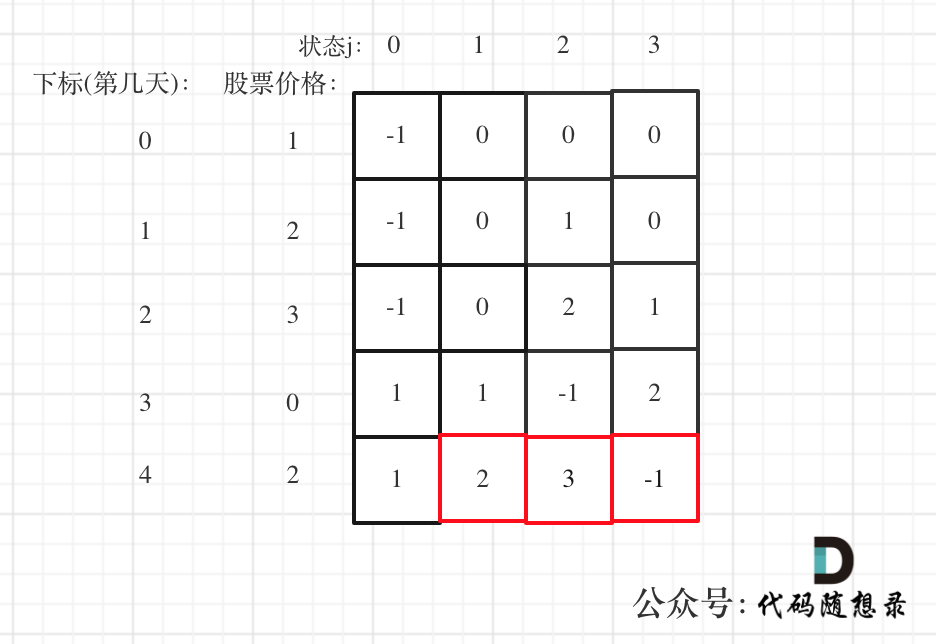
以 [1,2,3,0,2] 为例,dp数组如下:
-
+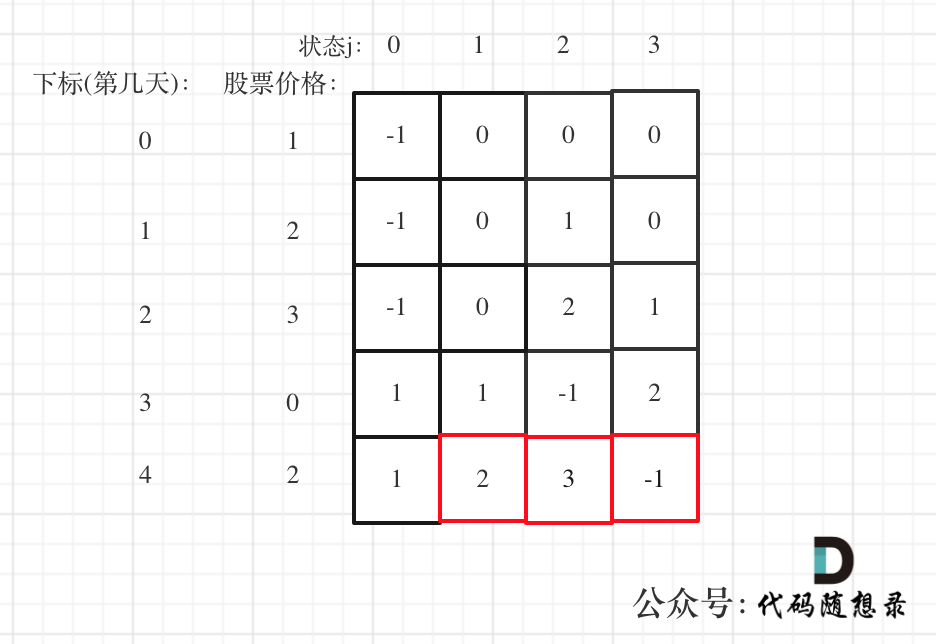
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
diff --git a/problems/0322.零钱兑换.md b/problems/0322.零钱兑换.md
index dea77a3d..7f3bc1e4 100644
--- a/problems/0322.零钱兑换.md
+++ b/problems/0322.零钱兑换.md
@@ -104,7 +104,7 @@ dp[0] = 0;
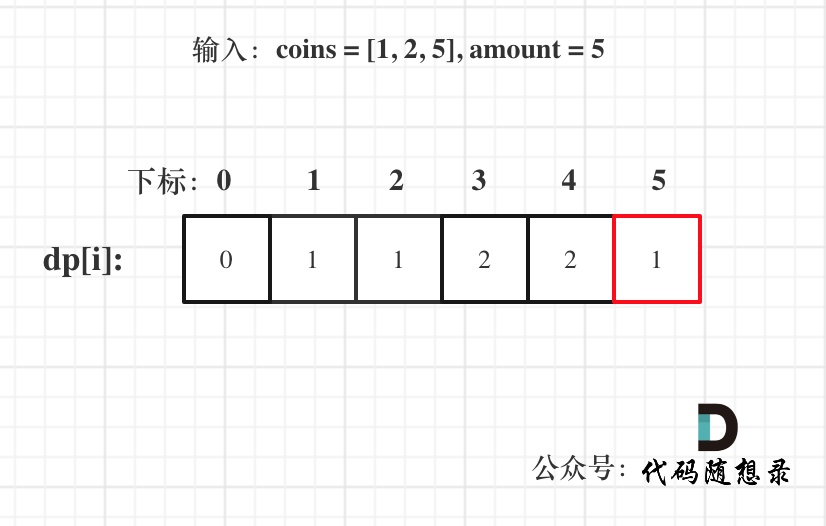
以输入:coins = [1, 2, 5], amount = 5为例
-
+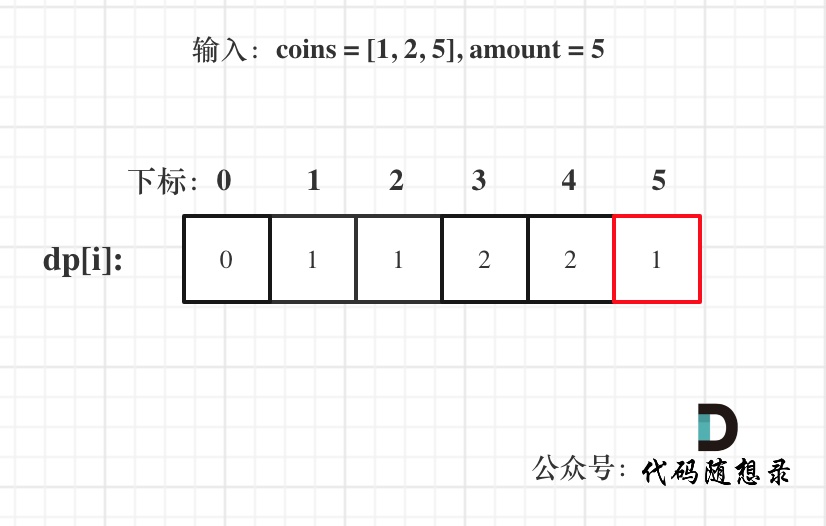
dp[amount]为最终结果。
diff --git a/problems/0332.重新安排行程.md b/problems/0332.重新安排行程.md
index f1df2522..fcdb6a33 100644
--- a/problems/0332.重新安排行程.md
+++ b/problems/0332.重新安排行程.md
@@ -57,7 +57,7 @@
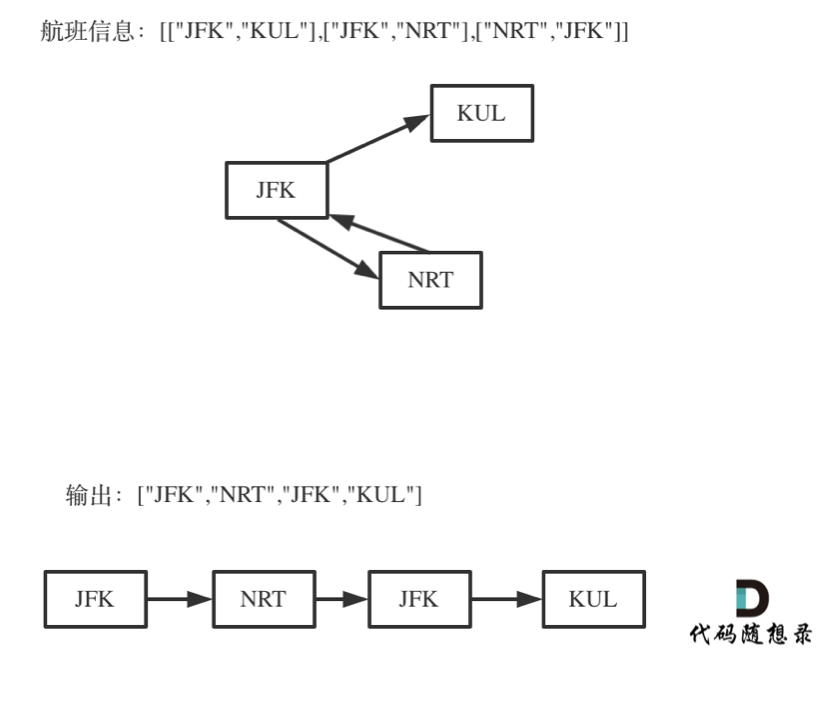
对于死循环,我来举一个有重复机场的例子:
-
+
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
@@ -111,7 +111,7 @@ void backtracking(参数) {
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
-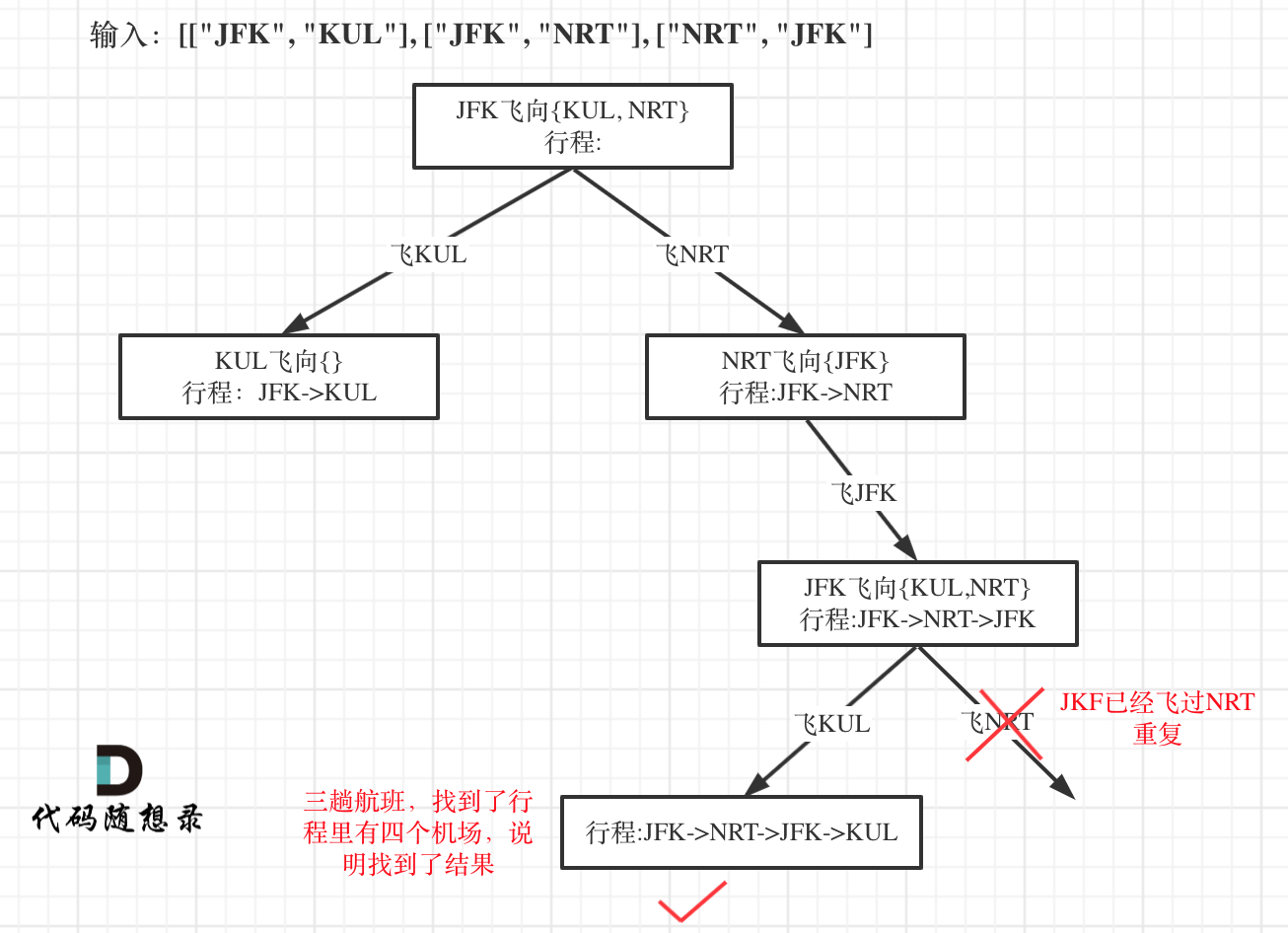
+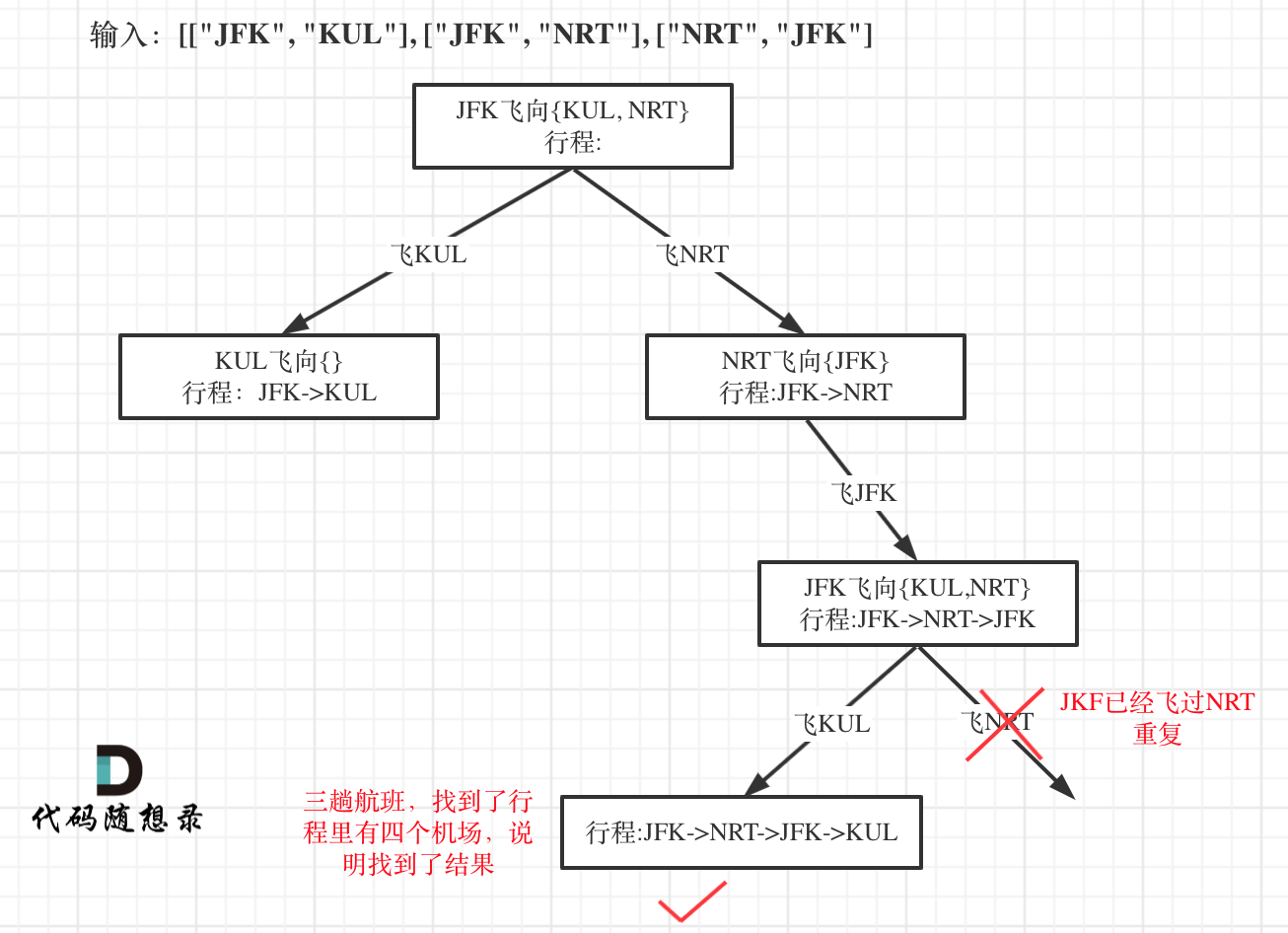
开始回溯三部曲讲解:
@@ -137,7 +137,7 @@ bool backtracking(int ticketNum, vector& result) {
因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,如图:
-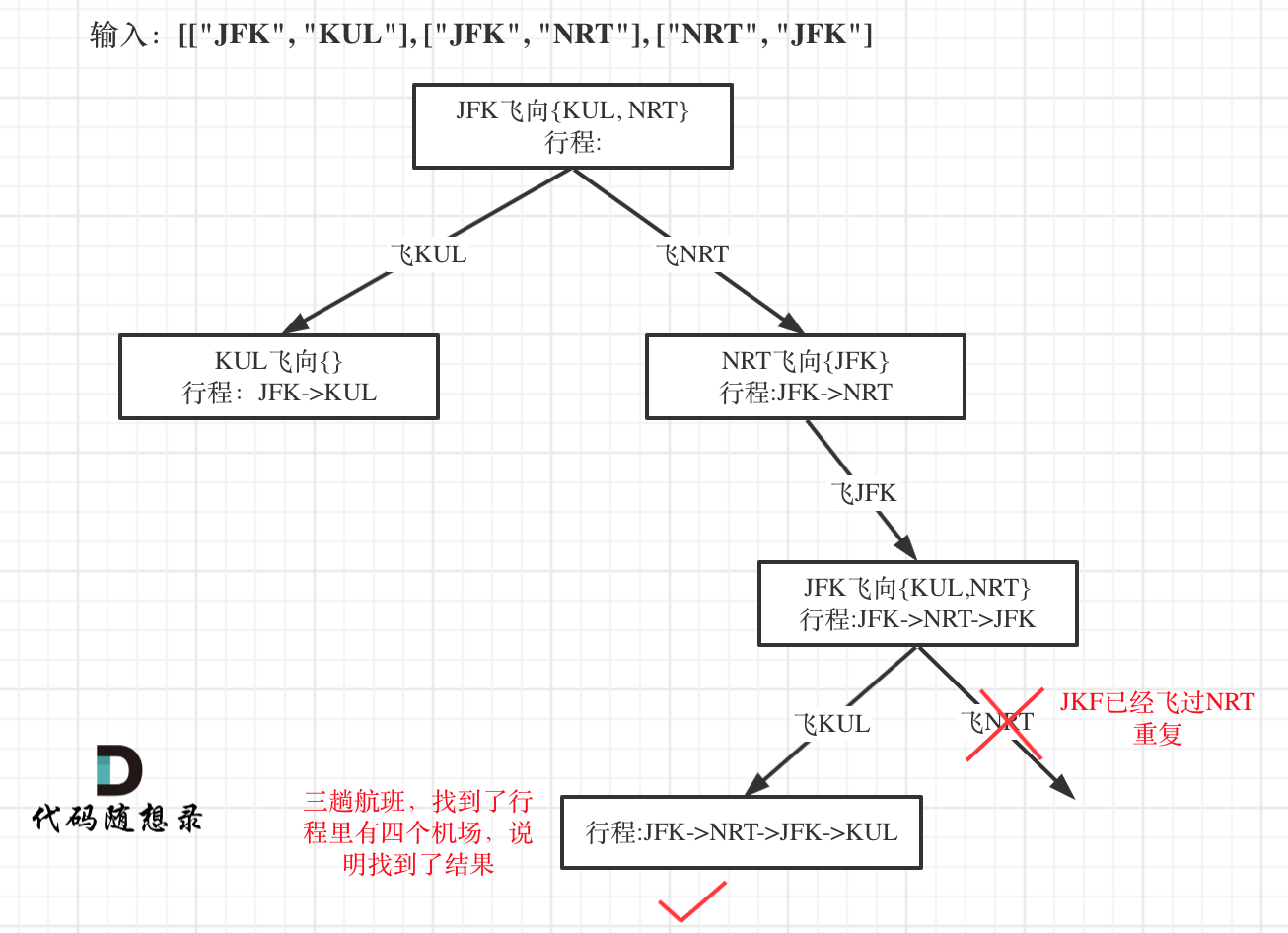
+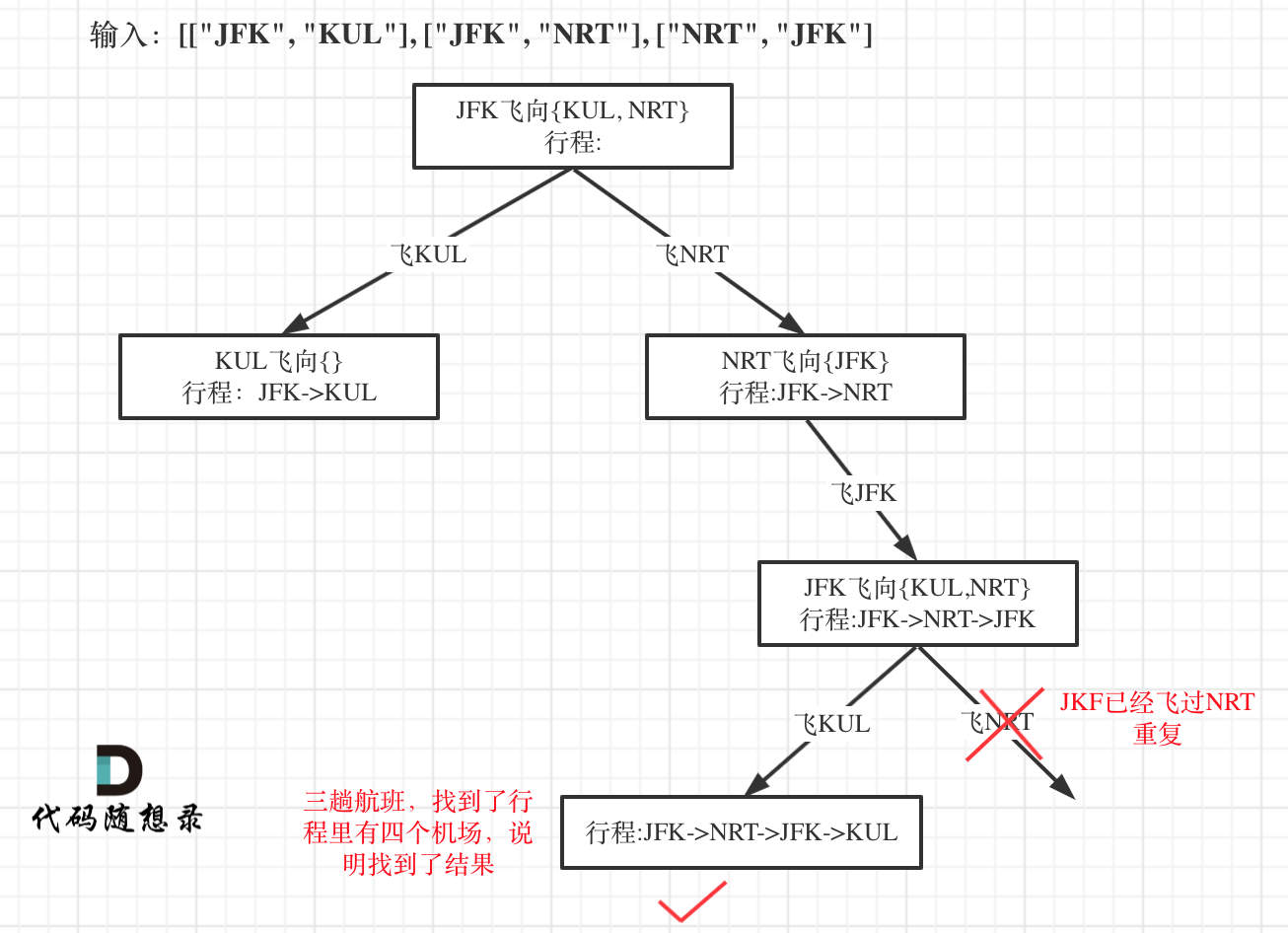
所以找到了这个叶子节点了直接返回,这个递归函数的返回值问题我们在讲解二叉树的系列的时候,在这篇[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://programmercarl.com/0112.路径总和.html)详细介绍过。
diff --git a/problems/0337.打家劫舍III.md b/problems/0337.打家劫舍III.md
index 08728e4f..4916af4c 100644
--- a/problems/0337.打家劫舍III.md
+++ b/problems/0337.打家劫舍III.md
@@ -12,7 +12,7 @@
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
-
+
## 算法公开课
@@ -177,7 +177,7 @@ return {val2, val1};
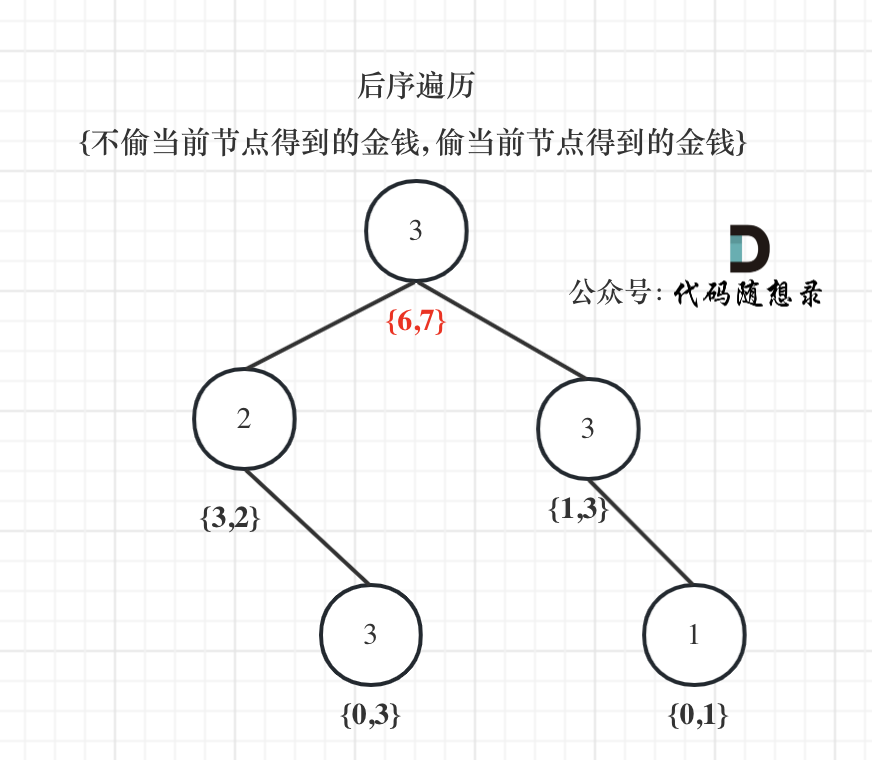
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
-
+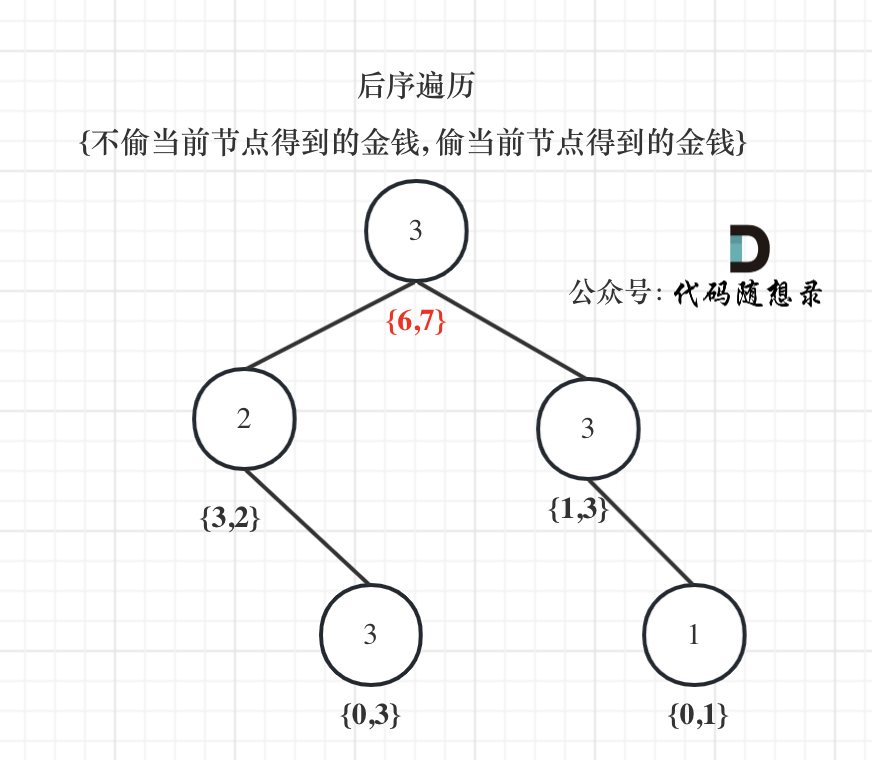
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
diff --git a/problems/0343.整数拆分.md b/problems/0343.整数拆分.md
index 06549185..203c4228 100644
--- a/problems/0343.整数拆分.md
+++ b/problems/0343.整数拆分.md
@@ -127,7 +127,7 @@ for (int i = 3; i <= n ; i++) {
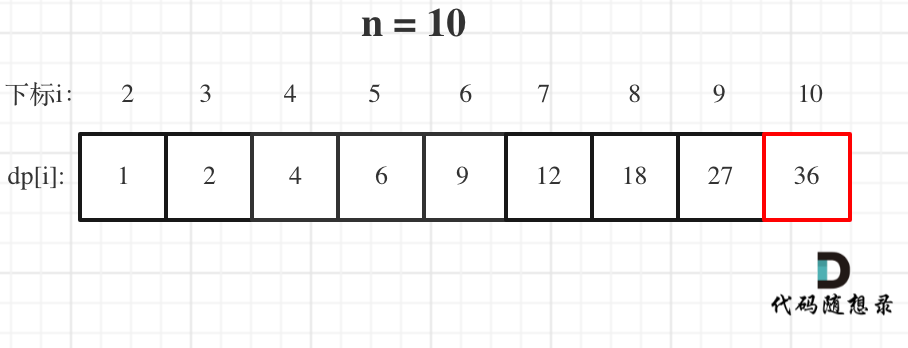
举例当n为10 的时候,dp数组里的数值,如下:
-
+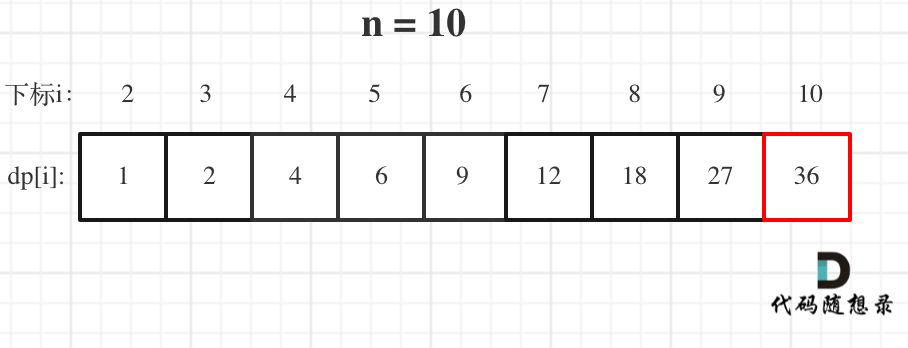
以上动规五部曲分析完毕,C++代码如下:
diff --git a/problems/0349.两个数组的交集.md b/problems/0349.两个数组的交集.md
index 5066bff1..65d22a80 100644
--- a/problems/0349.两个数组的交集.md
+++ b/problems/0349.两个数组的交集.md
@@ -14,7 +14,7 @@
题意:给定两个数组,编写一个函数来计算它们的交集。
-
+
**说明:**
输出结果中的每个元素一定是唯一的。
@@ -51,7 +51,7 @@ std::set和std::multiset底层实现都是红黑树,std::unordered_set的底
思路如图所示:
-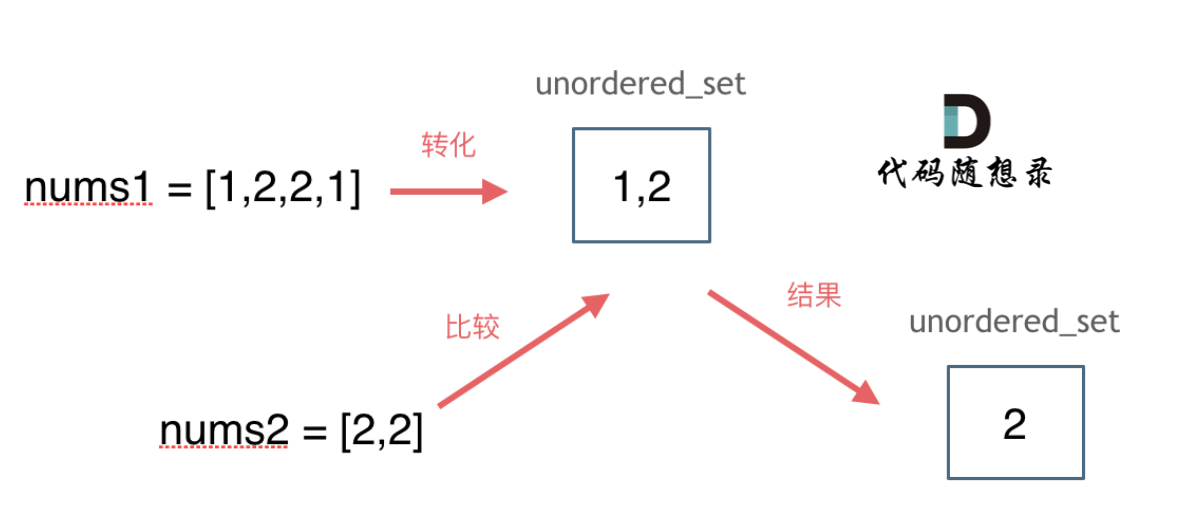
+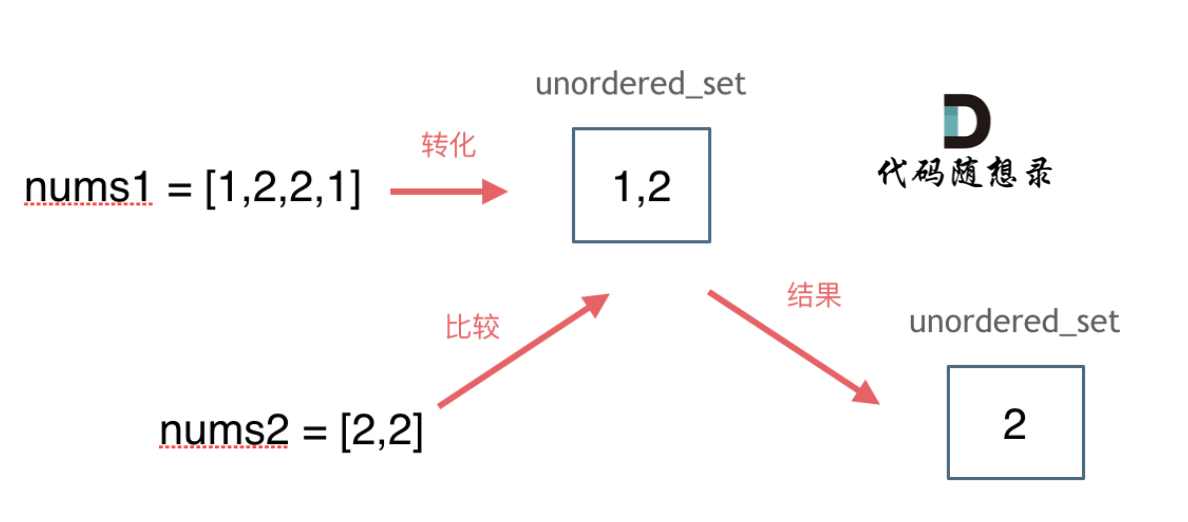
C++代码如下:
diff --git a/problems/0376.摆动序列.md b/problems/0376.摆动序列.md
index 886d86ae..50934981 100644
--- a/problems/0376.摆动序列.md
+++ b/problems/0376.摆动序列.md
@@ -46,7 +46,7 @@
用示例二来举例,如图所示:
-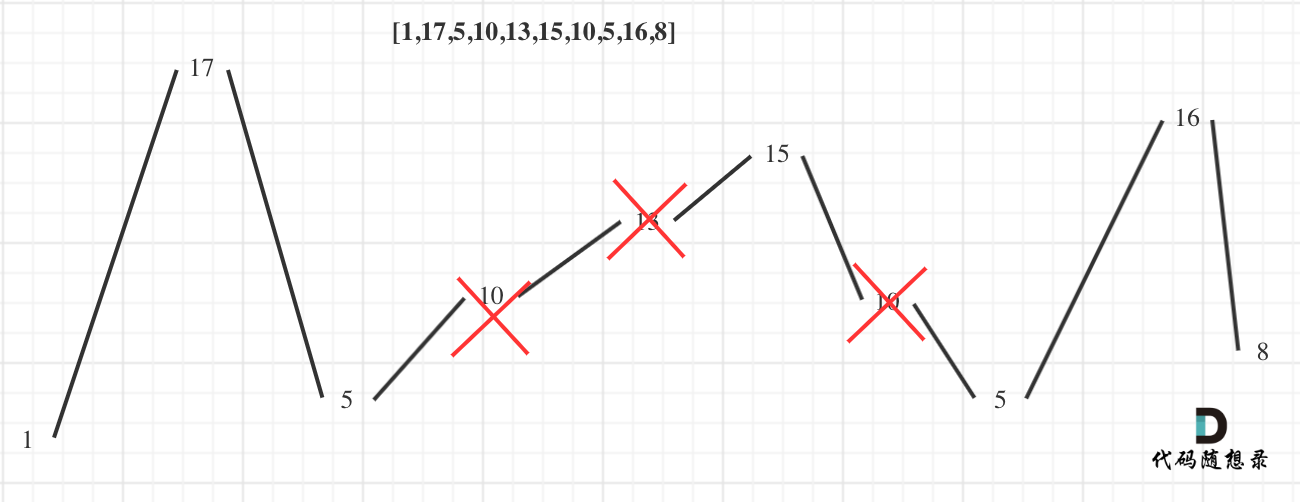
+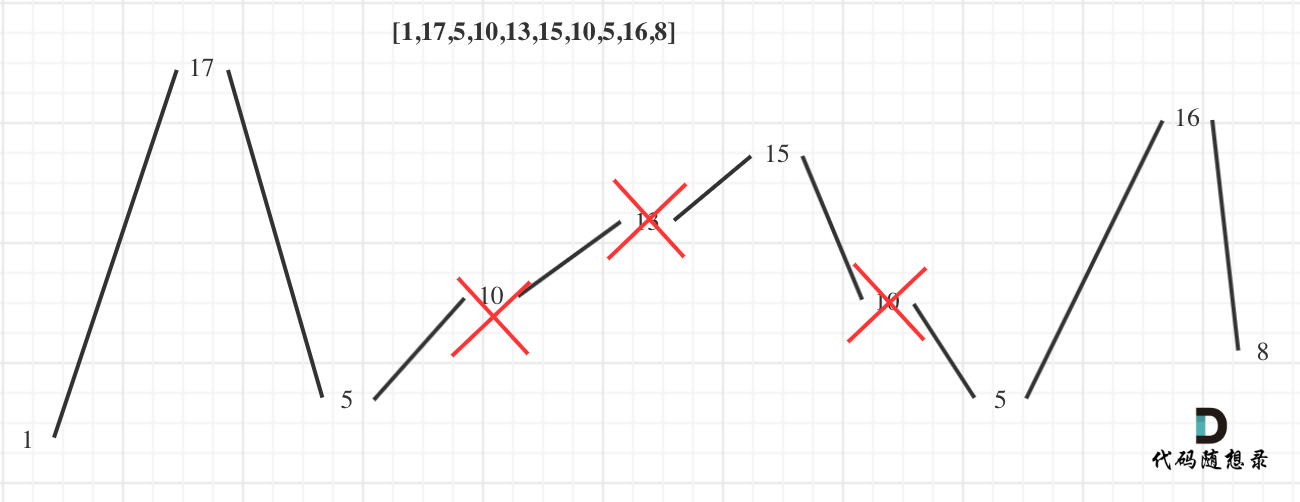
**局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值**。
@@ -72,13 +72,13 @@
例如 [1,2,2,2,2,1]这样的数组,如图:
-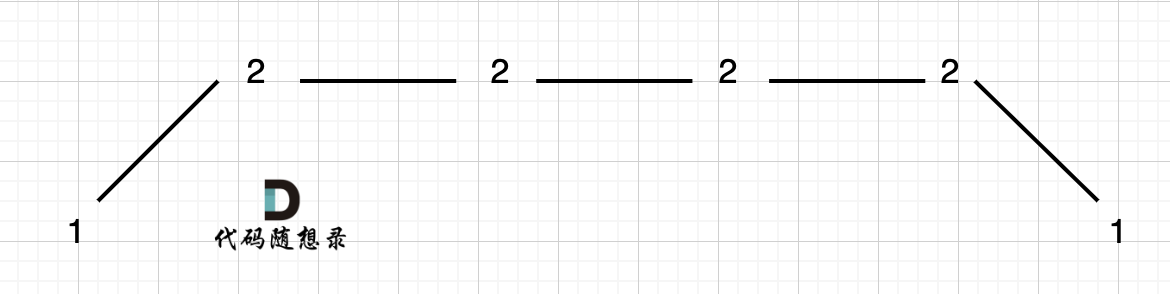
+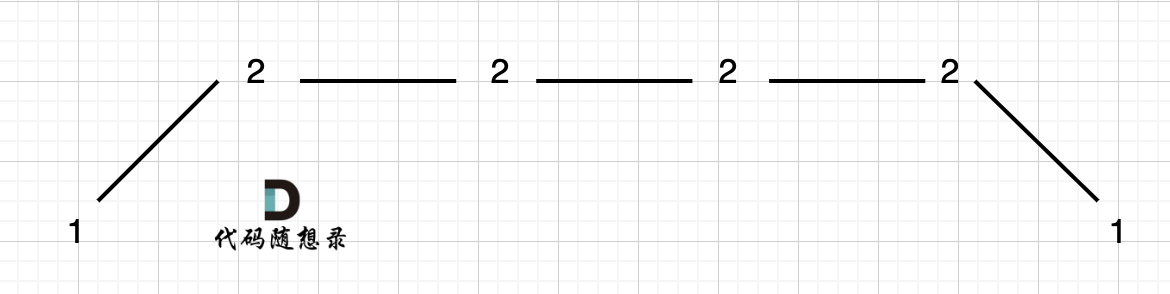
它的摇摆序列长度是多少呢? **其实是长度是 3**,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。
如图,可以统一规则,删除左边的三个 2:
-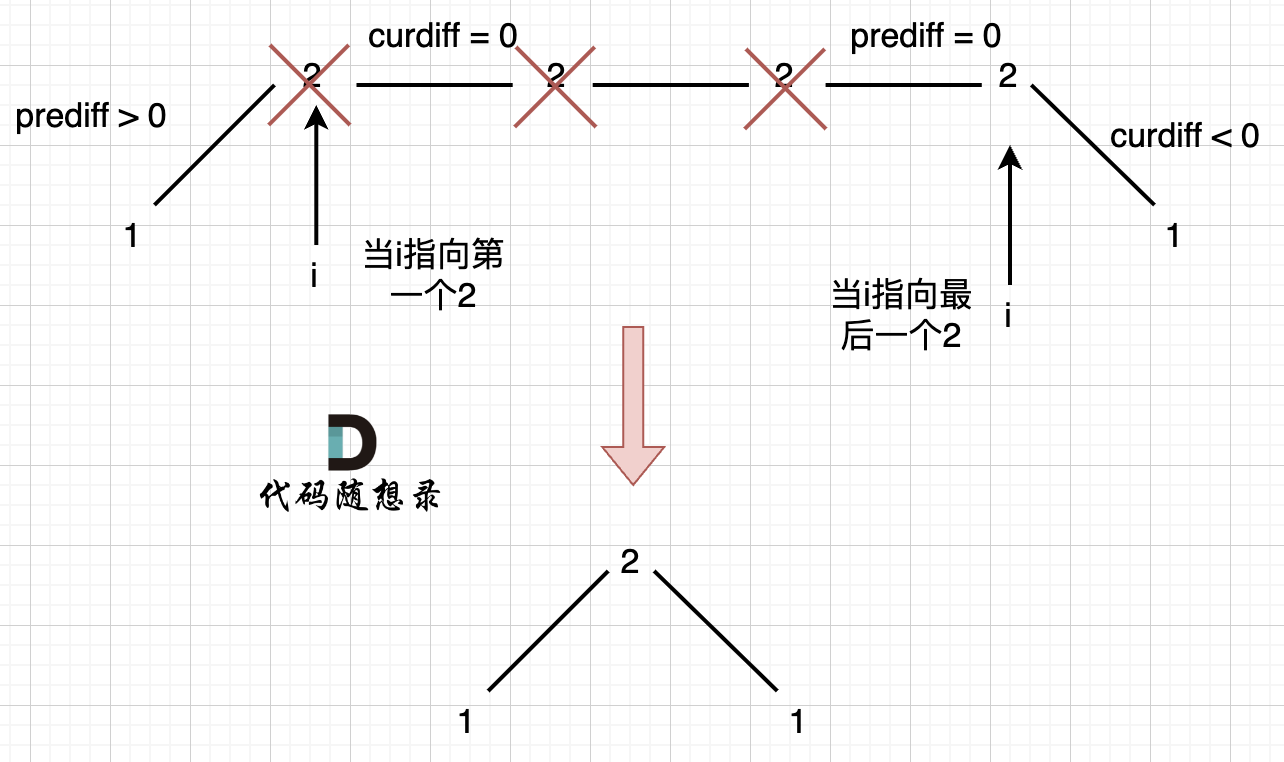
+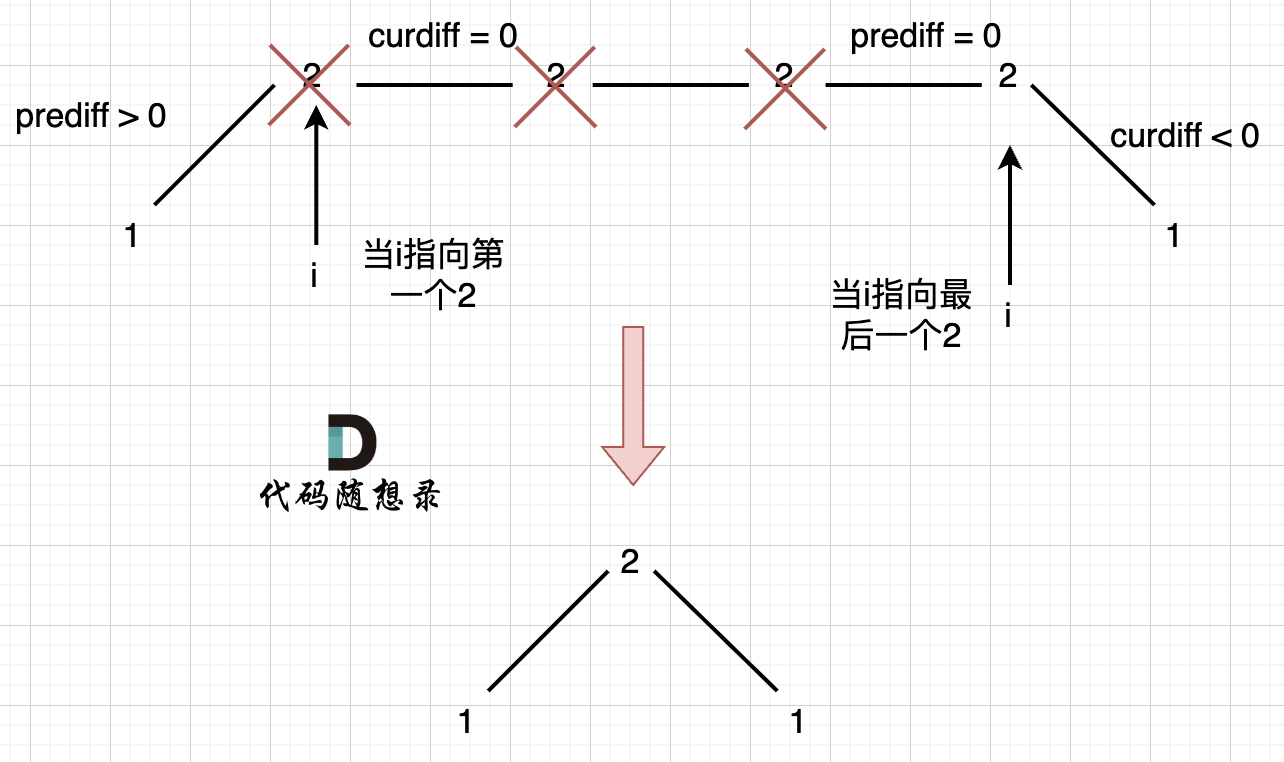
在图中,当 i 指向第一个 2 的时候,`prediff > 0 && curdiff = 0` ,当 i 指向最后一个 2 的时候 `prediff = 0 && curdiff < 0`。
@@ -106,7 +106,7 @@
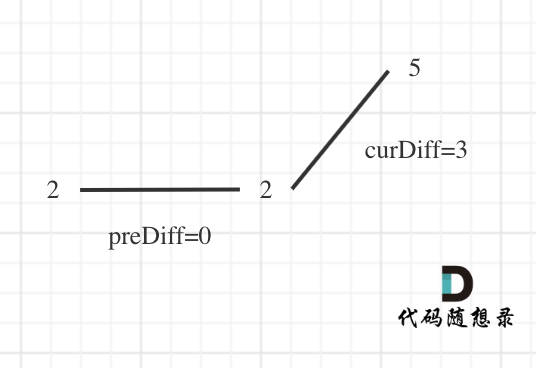
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0,如图:
-
+
针对以上情形,result 初始为 1(默认最右面有一个峰值),此时 curDiff > 0 && preDiff <= 0,那么 result++(计算了左面的峰值),最后得到的 result 就是 2(峰值个数为 2 即摆动序列长度为 2)
@@ -145,7 +145,7 @@ public:
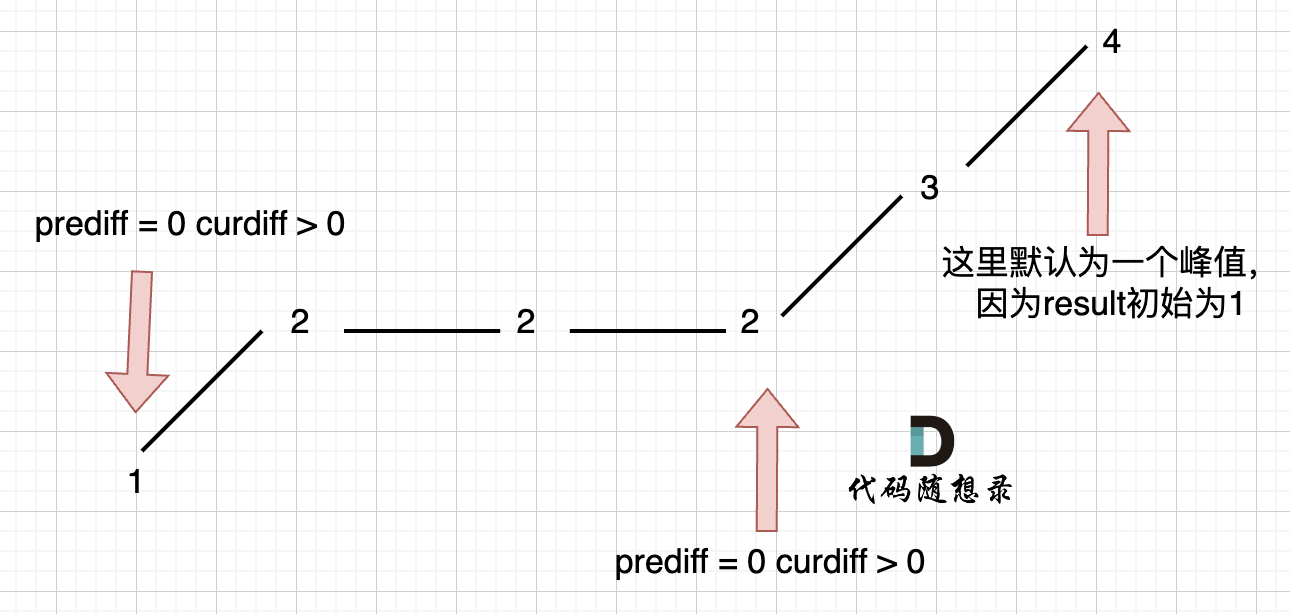
在版本一中,我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
-
+
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是 2,因为 单调中的平坡 不能算峰值(即摆动)。
@@ -184,7 +184,7 @@ public:
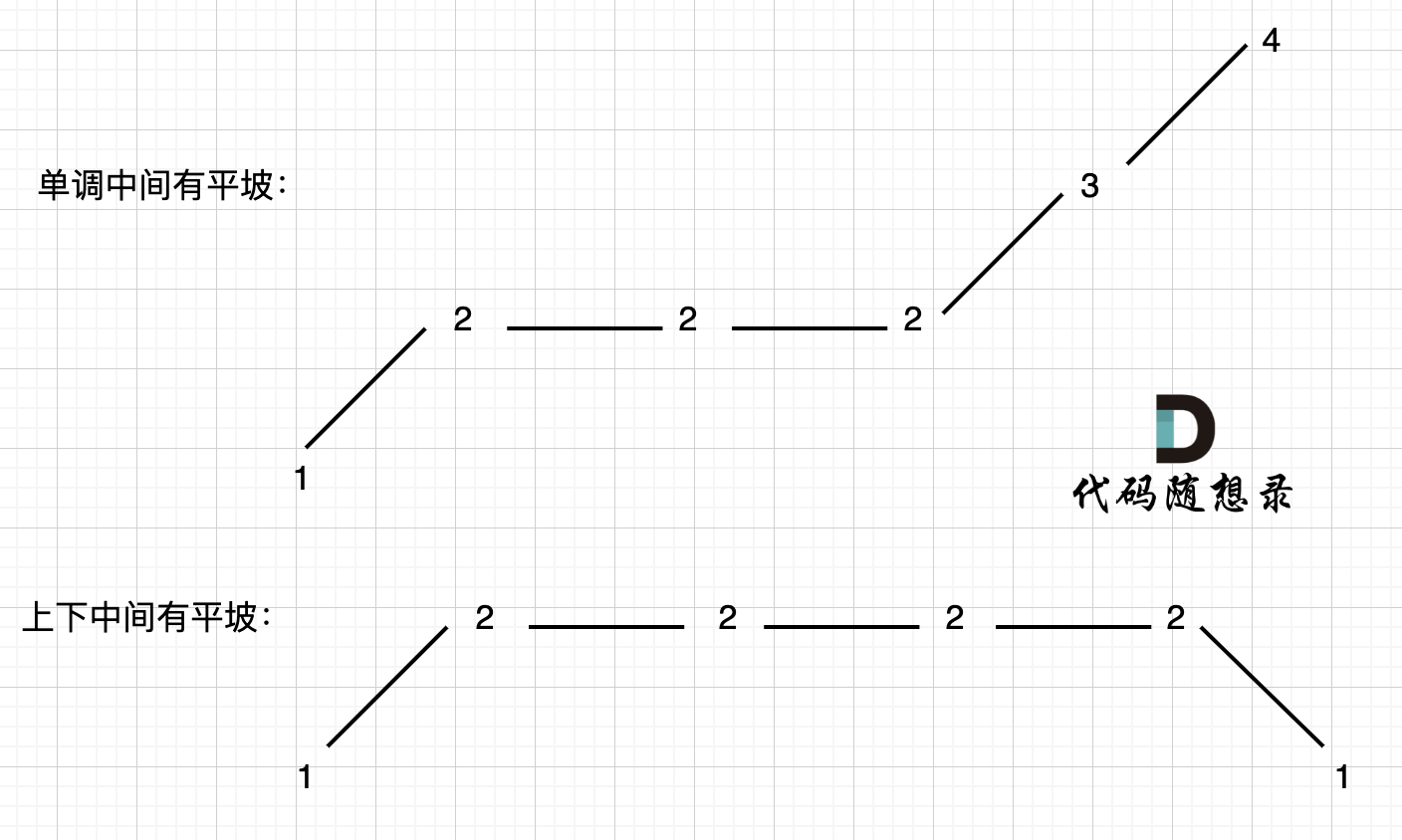
**本题异常情况的本质,就是要考虑平坡**, 平坡分两种,一个是 上下中间有平坡,一个是单调有平坡,如图:
-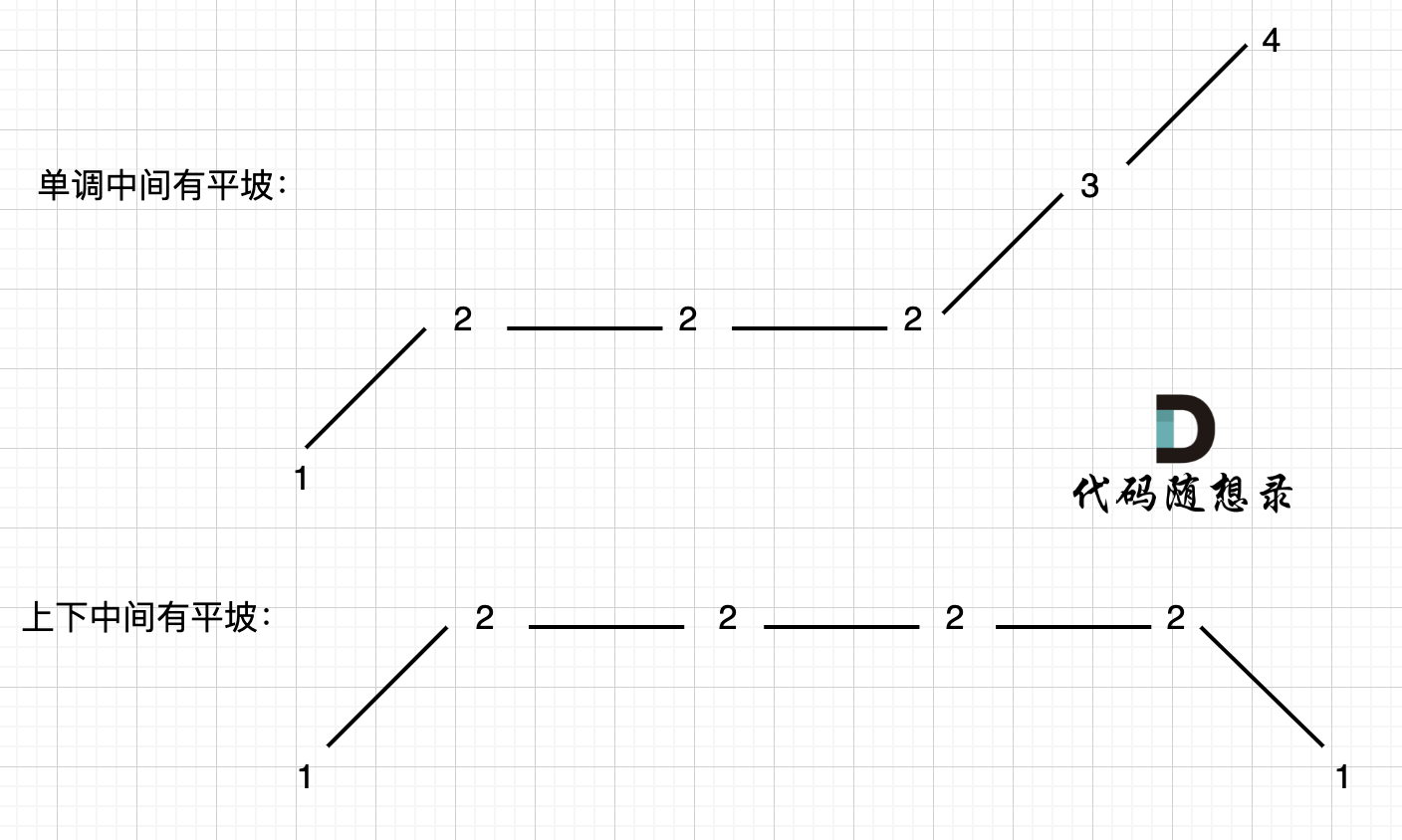
+
### 思路 2(动态规划)
diff --git a/problems/0377.组合总和Ⅳ.md b/problems/0377.组合总和Ⅳ.md
index d2feb0c5..20a94331 100644
--- a/problems/0377.组合总和Ⅳ.md
+++ b/problems/0377.组合总和Ⅳ.md
@@ -103,7 +103,7 @@ dp[i](考虑nums[j])可以由 dp[i - nums[j]](不考虑nums[j]) 推导
我们再来用示例中的例子推导一下:
-
+
如果代码运行处的结果不是想要的结果,就把dp[i]都打出来,看看和我们推导的一不一样。
diff --git a/problems/0392.判断子序列.md b/problems/0392.判断子序列.md
index 2a5be51c..d59b7bc1 100644
--- a/problems/0392.判断子序列.md
+++ b/problems/0392.判断子序列.md
@@ -80,7 +80,7 @@ if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前
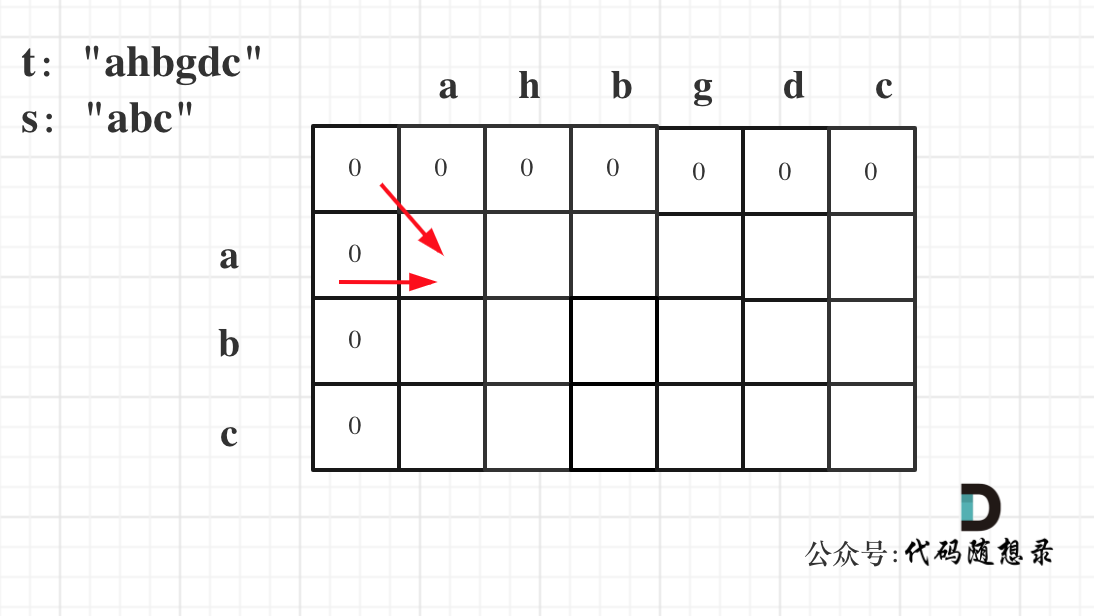
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:
-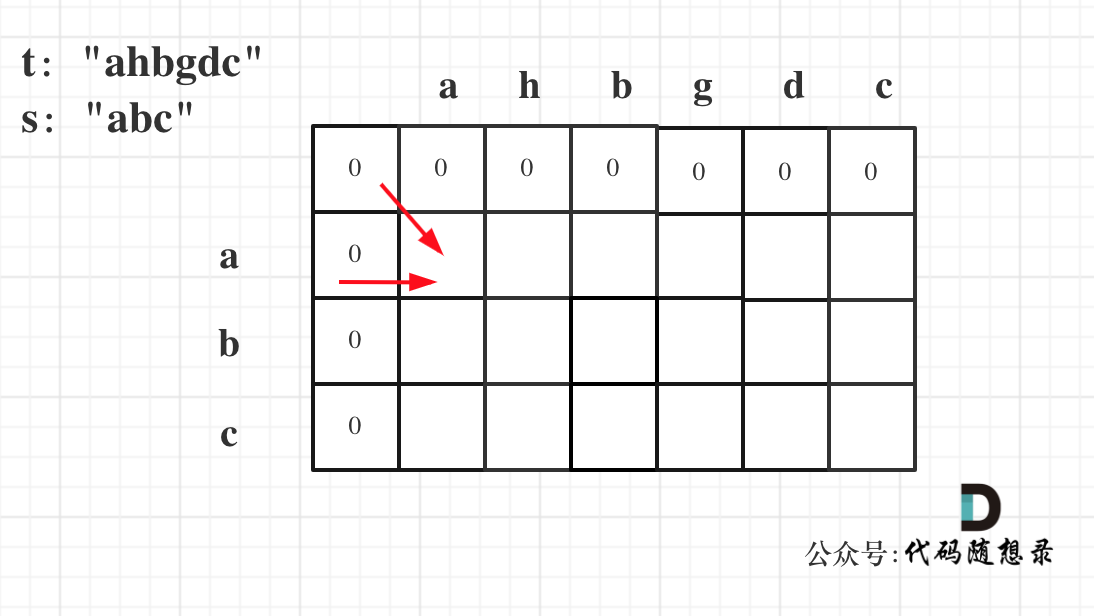
+
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
@@ -98,14 +98,14 @@ vector> dp(s.size() + 1, vector(t.size() + 1, 0));
如图所示:
-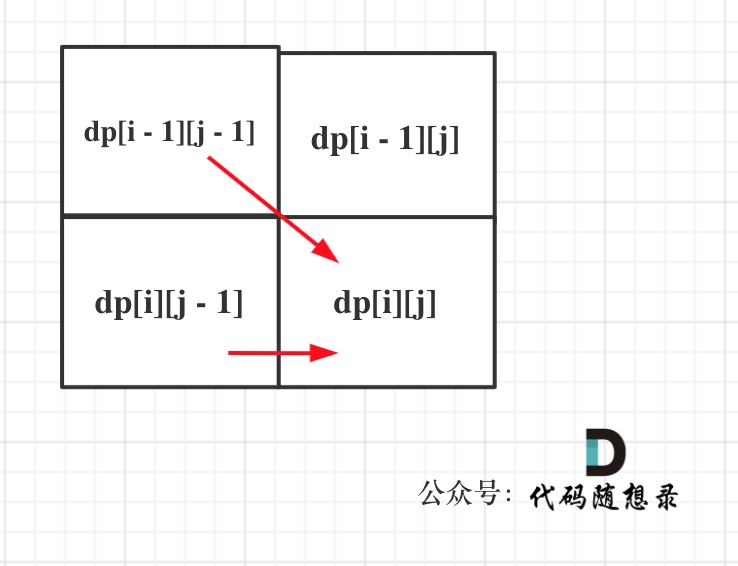
+
5. 举例推导dp数组
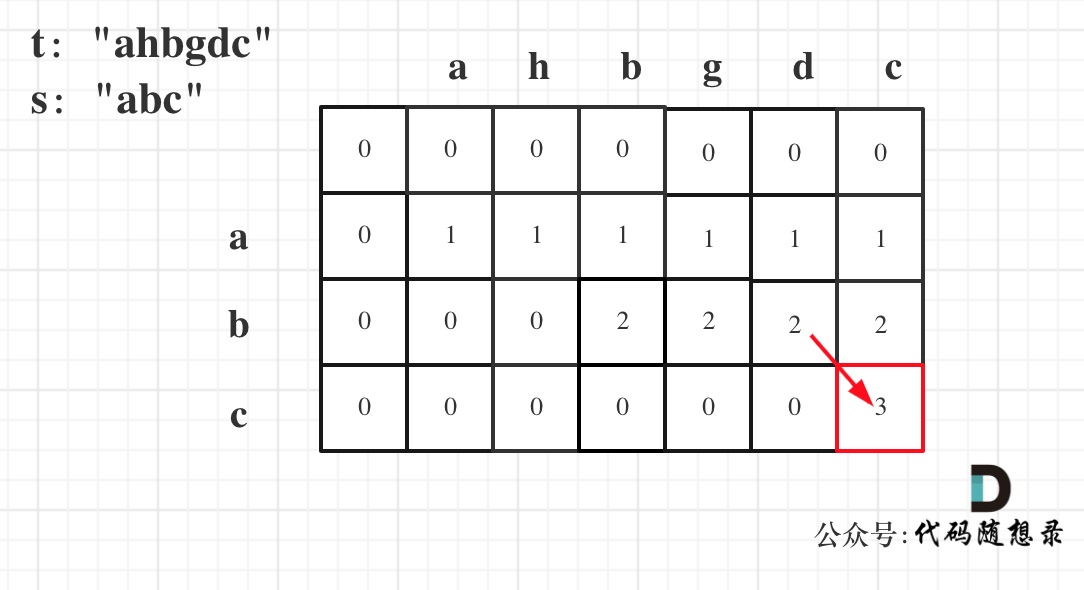
以示例一为例,输入:s = "abc", t = "ahbgdc",dp状态转移图如下:
-
+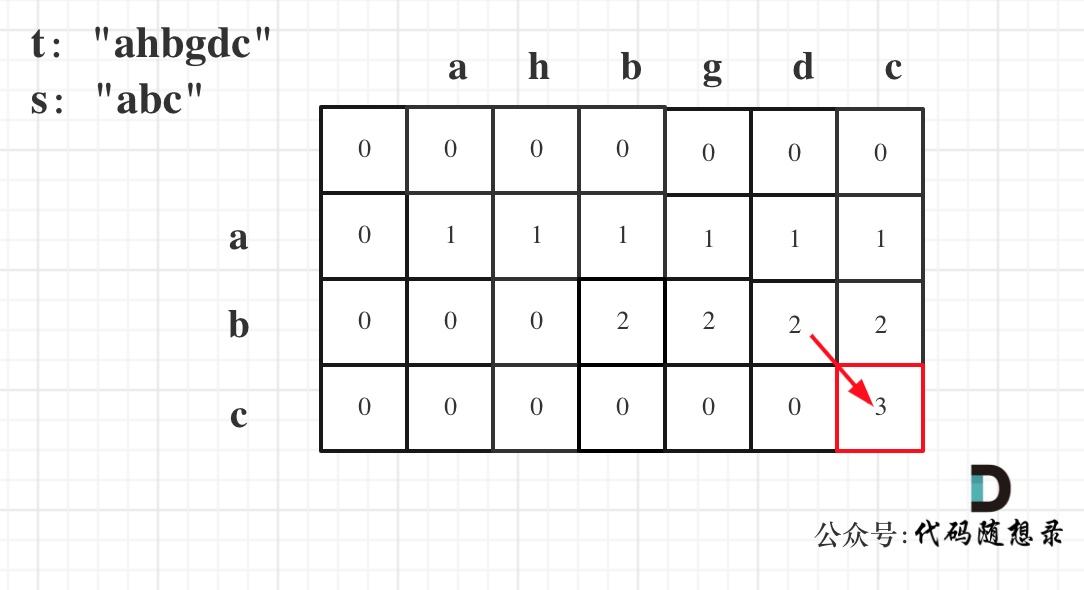
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
diff --git a/problems/0404.左叶子之和.md b/problems/0404.左叶子之和.md
index 0efdb6f6..69723815 100644
--- a/problems/0404.左叶子之和.md
+++ b/problems/0404.左叶子之和.md
@@ -12,7 +12,7 @@
示例:
-
+
## 算法公开课
@@ -26,12 +26,12 @@
大家思考一下如下图中二叉树,左叶子之和究竟是多少?
-
+
**其实是0,因为这棵树根本没有左叶子!**
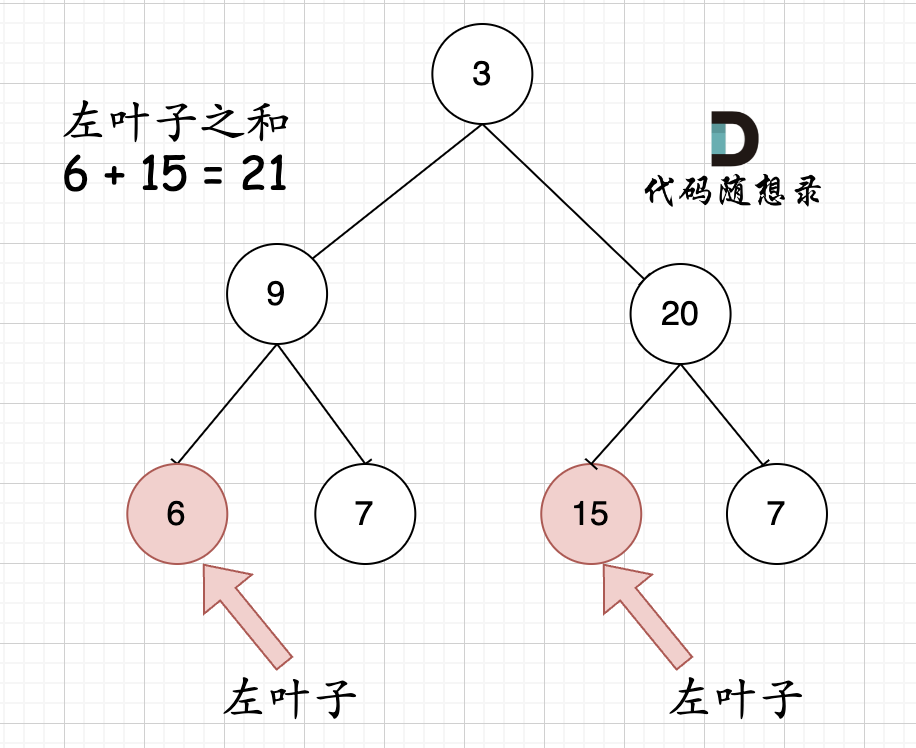
但看这个图的左叶子之和是多少?
-
+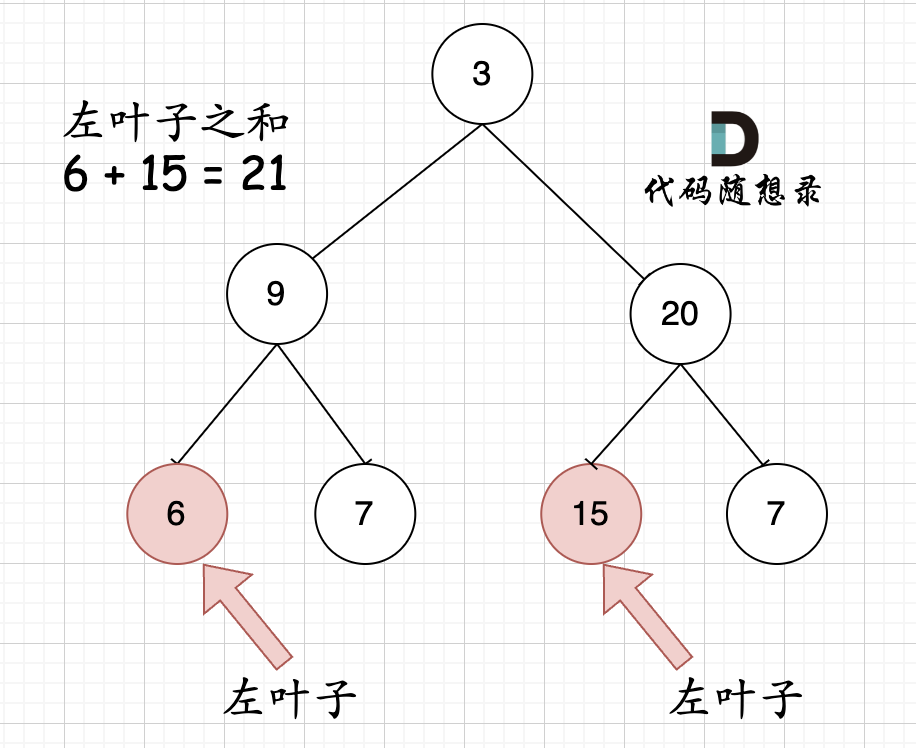
相信通过这两个图,大家对最左叶子的定义有明确理解了。
diff --git a/problems/0406.根据身高重建队列.md b/problems/0406.根据身高重建队列.md
index 11853e11..0d060ee8 100644
--- a/problems/0406.根据身高重建队列.md
+++ b/problems/0406.根据身高重建队列.md
@@ -61,7 +61,7 @@
以图中{5,2} 为例:
-
+
按照身高排序之后,优先按身高高的people的k来插入,后序插入节点也不会影响前面已经插入的节点,最终按照k的规则完成了队列。
diff --git a/problems/0416.分割等和子集.md b/problems/0416.分割等和子集.md
index 9cc6db0e..79b4d4f7 100644
--- a/problems/0416.分割等和子集.md
+++ b/problems/0416.分割等和子集.md
@@ -155,7 +155,7 @@ dp[j]的数值一定是小于等于j的。
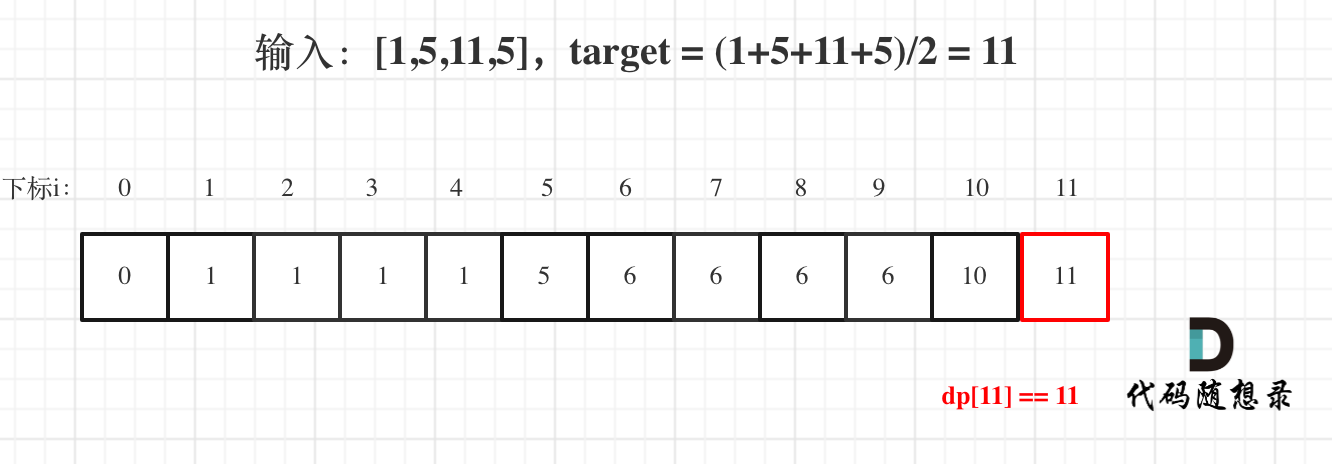
用例1,输入[1,5,11,5] 为例,如图:
-
+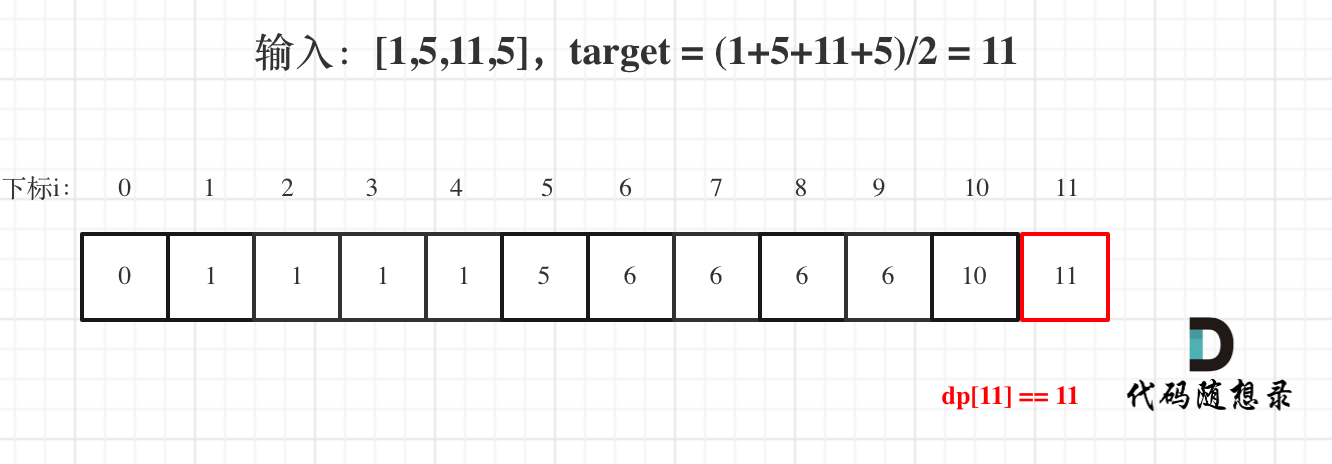
最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
diff --git a/problems/0417.太平洋大西洋水流问题.md b/problems/0417.太平洋大西洋水流问题.md
index ec87eb95..116cd08e 100644
--- a/problems/0417.太平洋大西洋水流问题.md
+++ b/problems/0417.太平洋大西洋水流问题.md
@@ -18,7 +18,7 @@
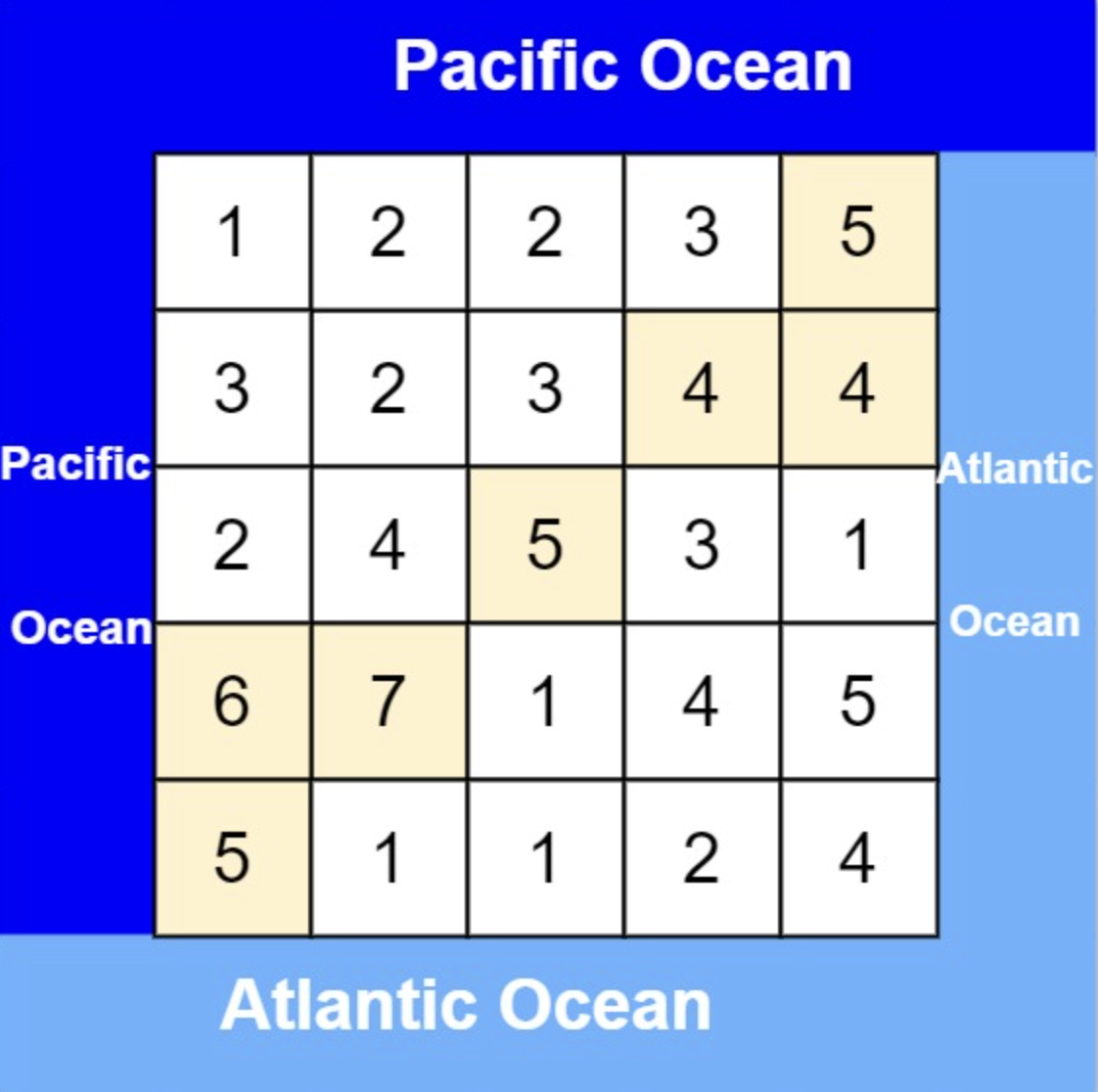
示例 1:
-
+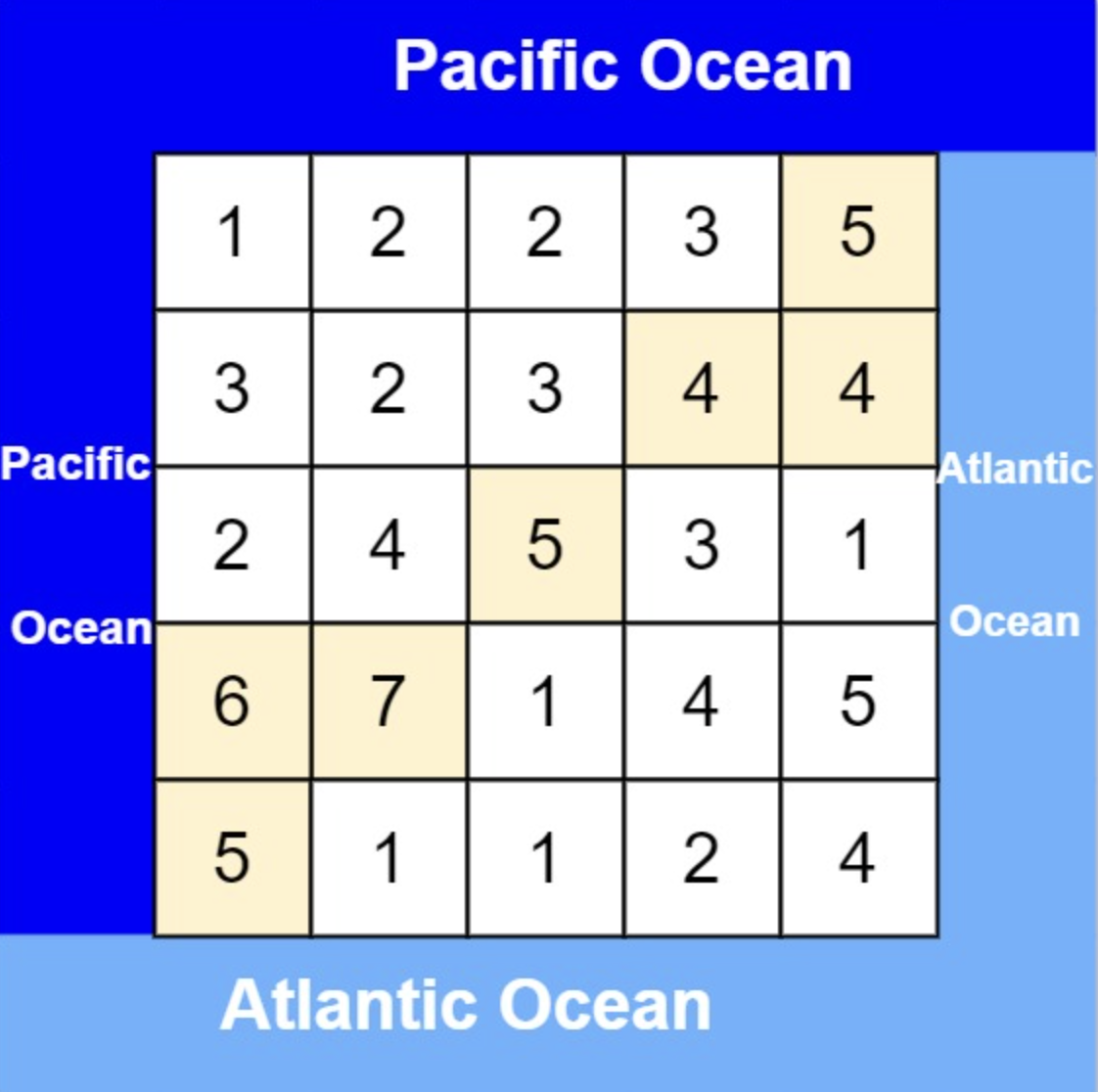
* 输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
* 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
@@ -130,11 +130,11 @@ public:
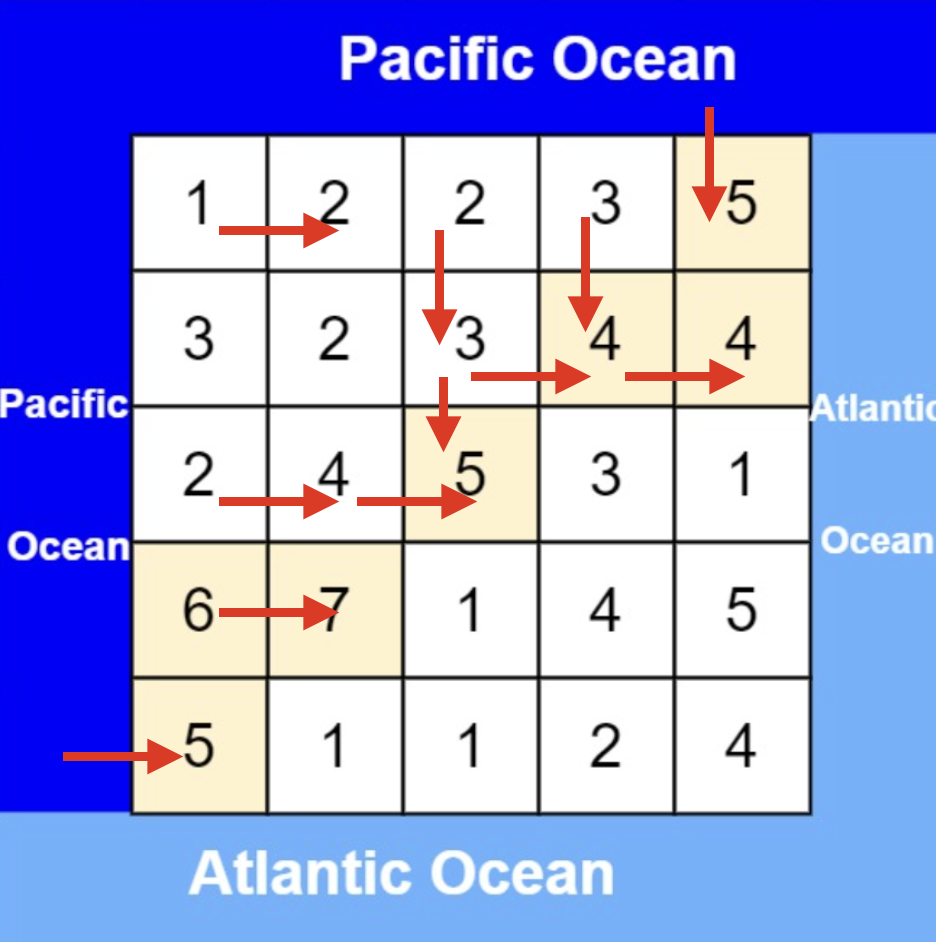
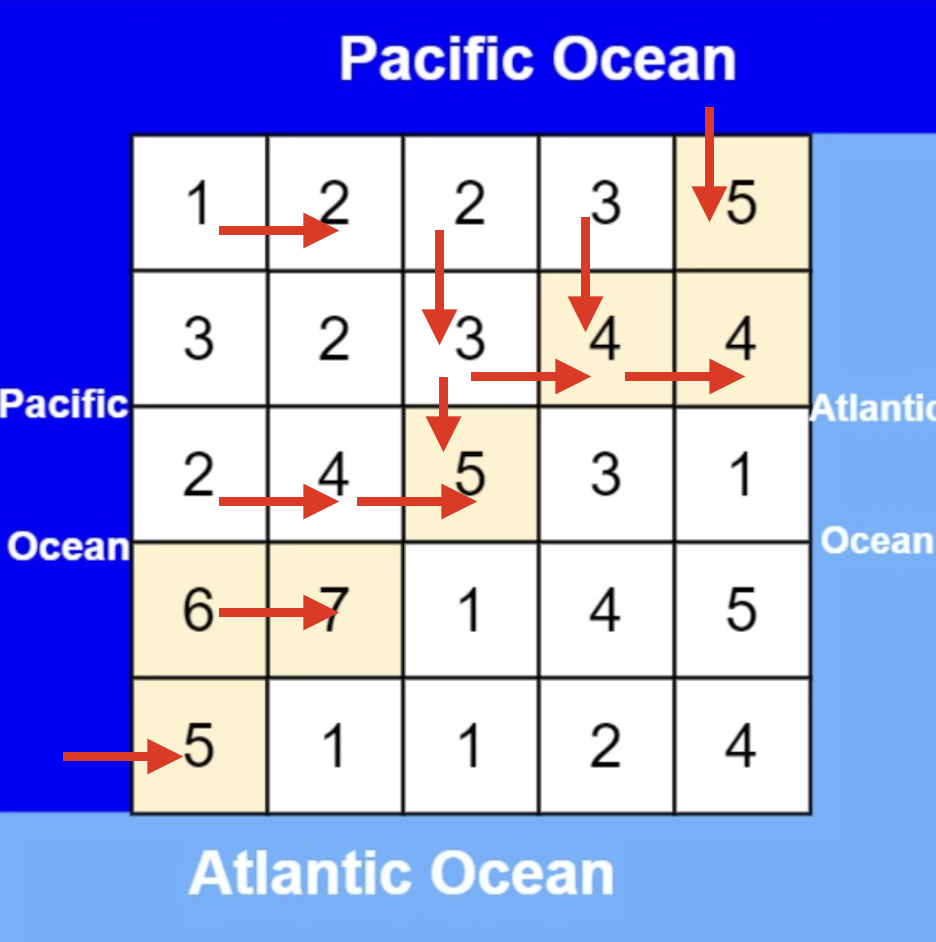
从太平洋边上节点出发,如图:
-
+
从大西洋边上节点出发,如图:
-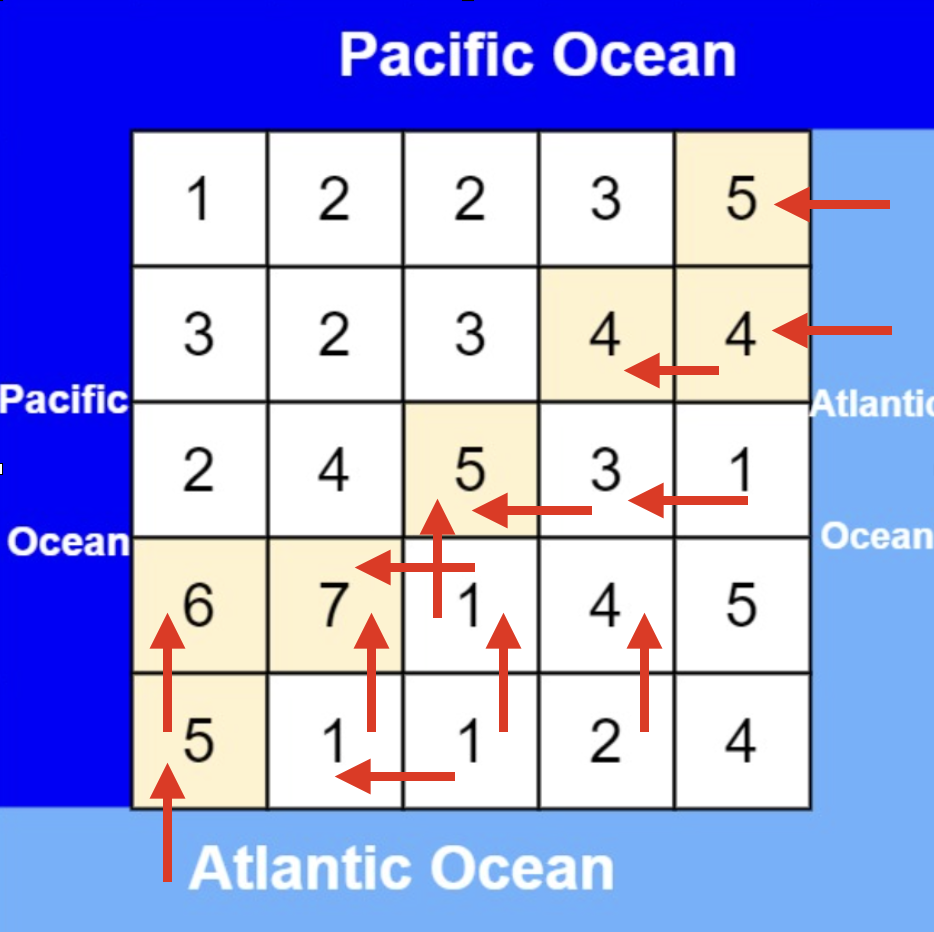
+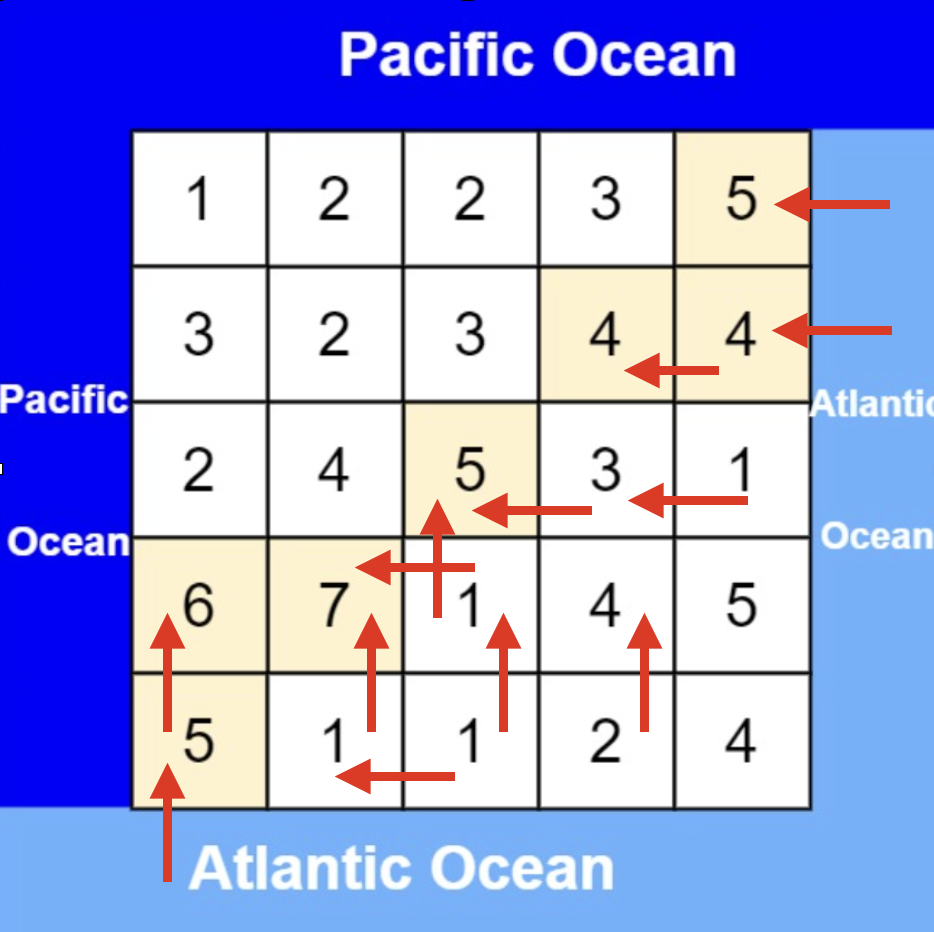
按照这样的逻辑,就可以写出如下遍历代码:(详细注释)
diff --git a/problems/0435.无重叠区间.md b/problems/0435.无重叠区间.md
index a37d1cad..04845ea7 100644
--- a/problems/0435.无重叠区间.md
+++ b/problems/0435.无重叠区间.md
@@ -44,7 +44,7 @@
这里记录非交叉区间的个数还是有技巧的,如图:
-
+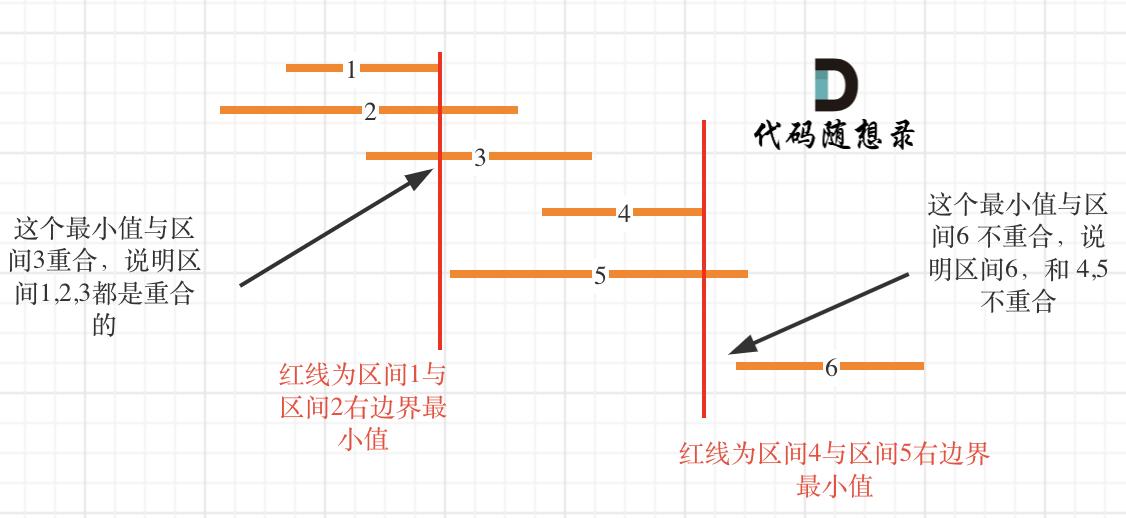
区间,1,2,3,4,5,6都按照右边界排好序。
diff --git a/problems/0450.删除二叉搜索树中的节点.md b/problems/0450.删除二叉搜索树中的节点.md
index 72809184..406116a3 100644
--- a/problems/0450.删除二叉搜索树中的节点.md
+++ b/problems/0450.删除二叉搜索树中的节点.md
@@ -20,7 +20,7 @@
示例:
-
+
## 算法公开课
diff --git a/problems/0452.用最少数量的箭引爆气球.md b/problems/0452.用最少数量的箭引爆气球.md
index 85449882..17d21cd1 100644
--- a/problems/0452.用最少数量的箭引爆气球.md
+++ b/problems/0452.用最少数量的箭引爆气球.md
@@ -76,7 +76,7 @@
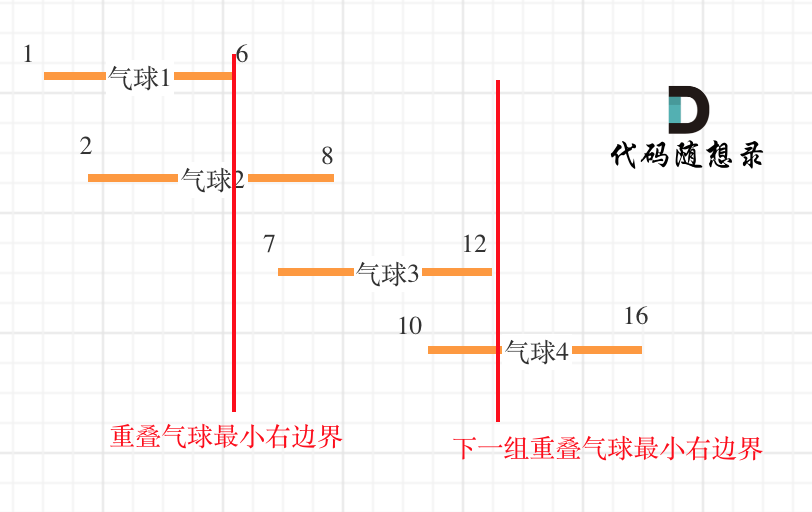
以题目示例: [[10,16],[2,8],[1,6],[7,12]]为例,如图:(方便起见,已经排序)
-
+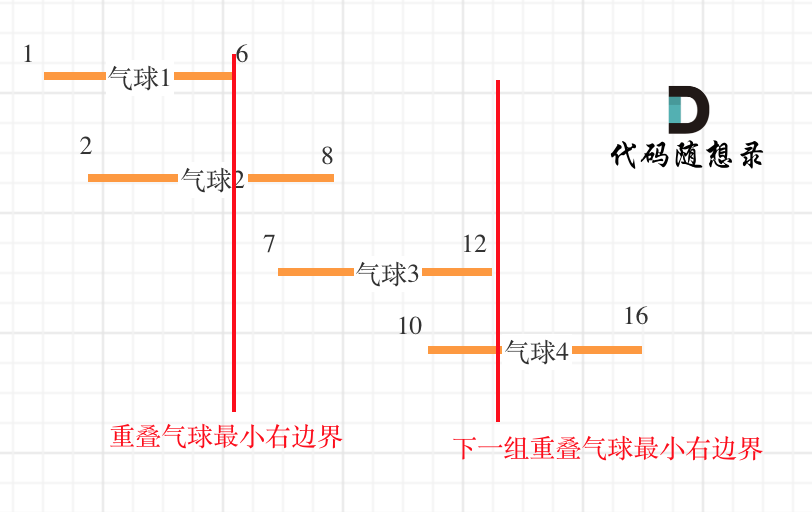
可以看出首先第一组重叠气球,一定是需要一个箭,气球3,的左边界大于了 第一组重叠气球的最小右边界,所以再需要一支箭来射气球3了。
diff --git a/problems/0455.分发饼干.md b/problems/0455.分发饼干.md
index a2a1b1f3..2a6ade1b 100644
--- a/problems/0455.分发饼干.md
+++ b/problems/0455.分发饼干.md
@@ -46,7 +46,7 @@
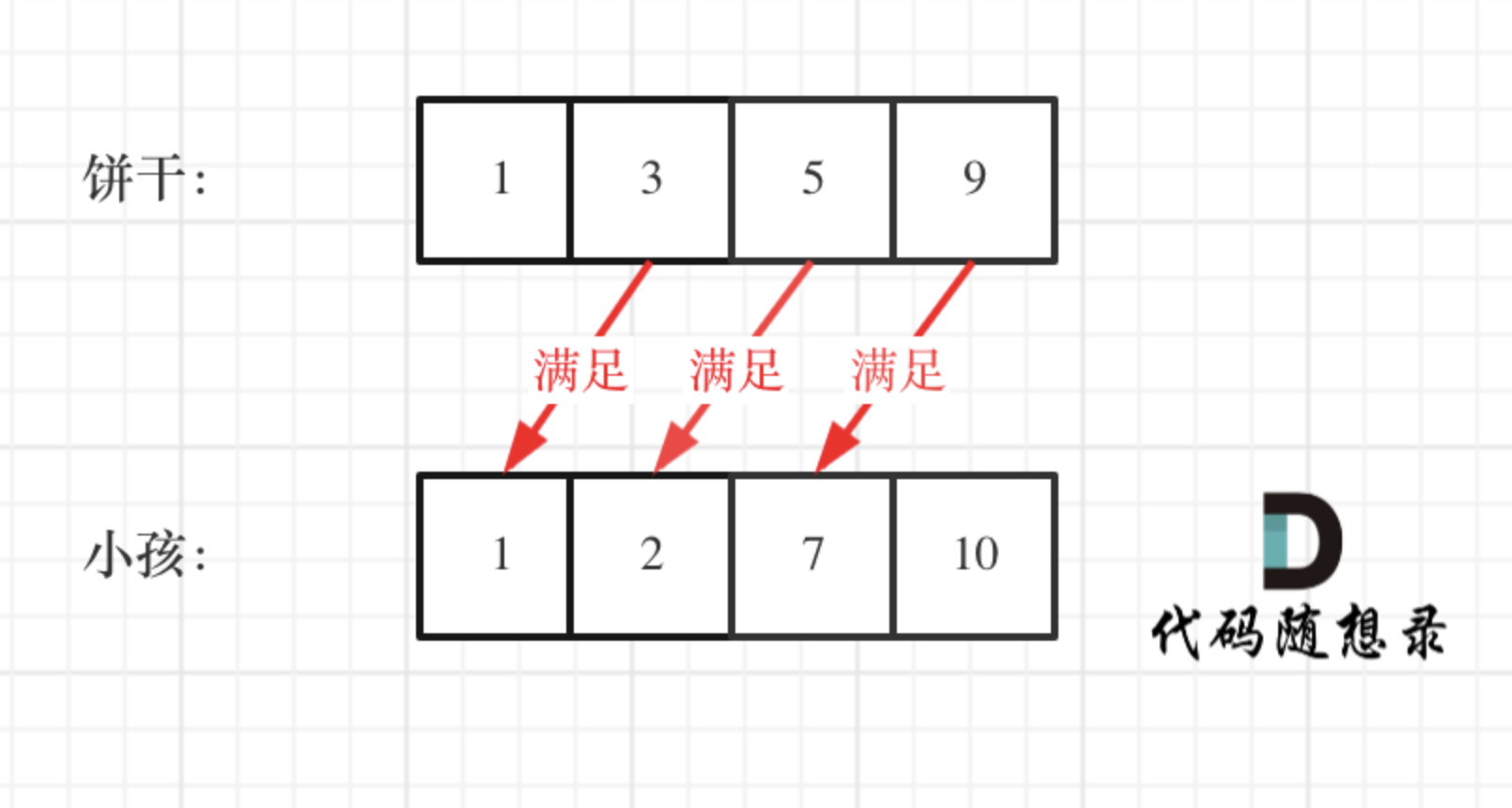
如图:
-
+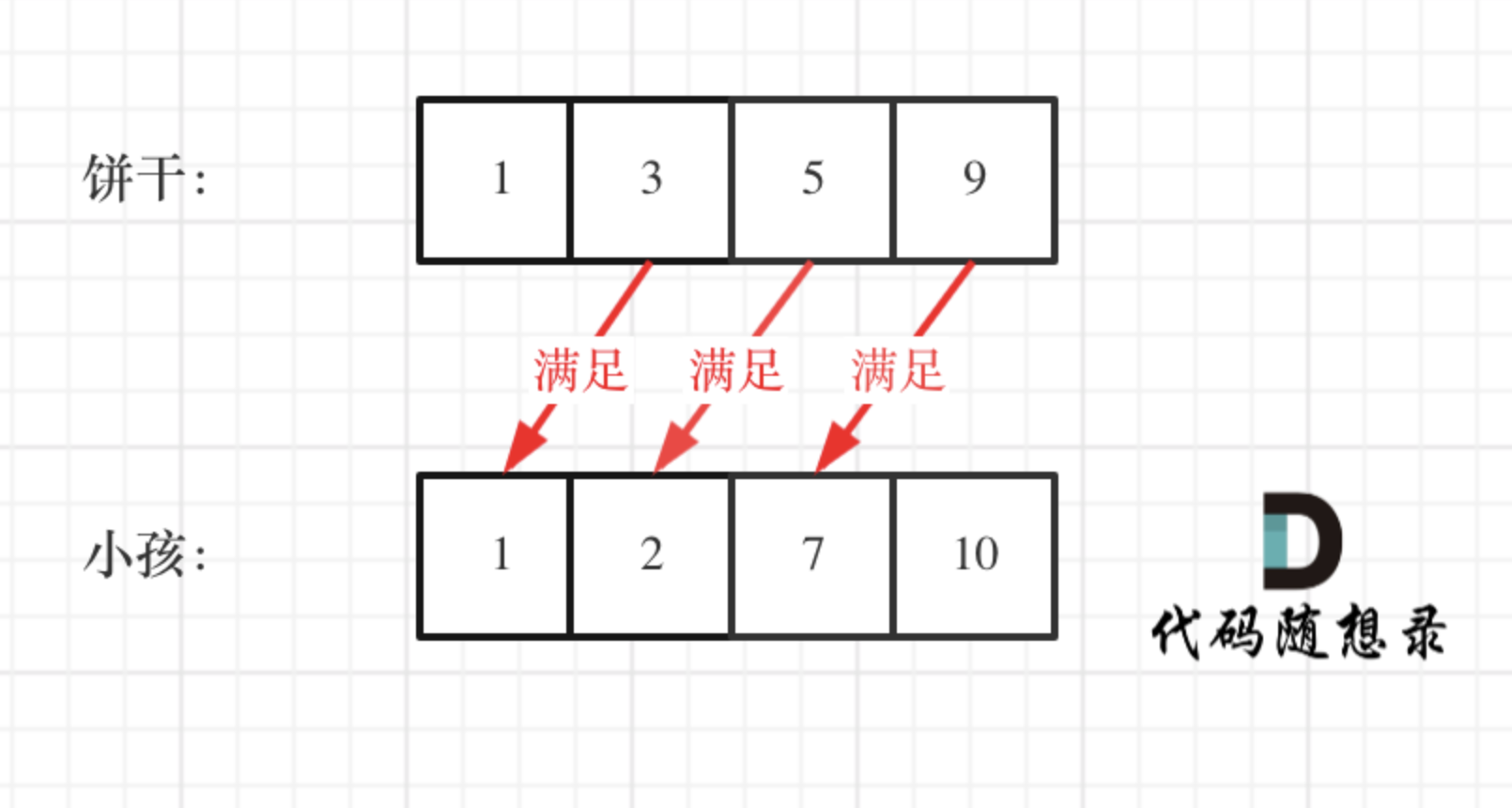
这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
@@ -89,7 +89,7 @@ public:
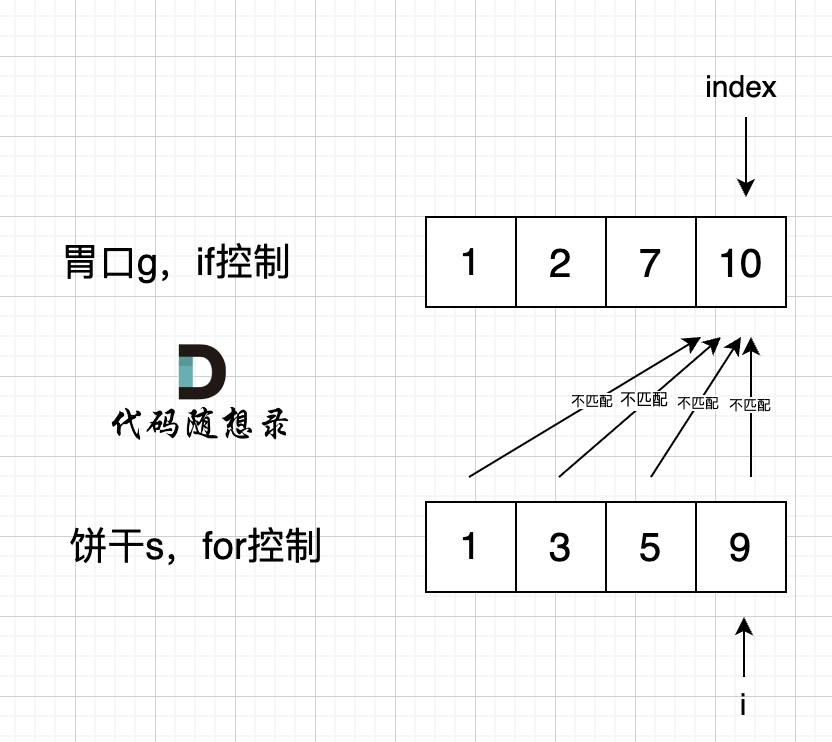
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :
-
+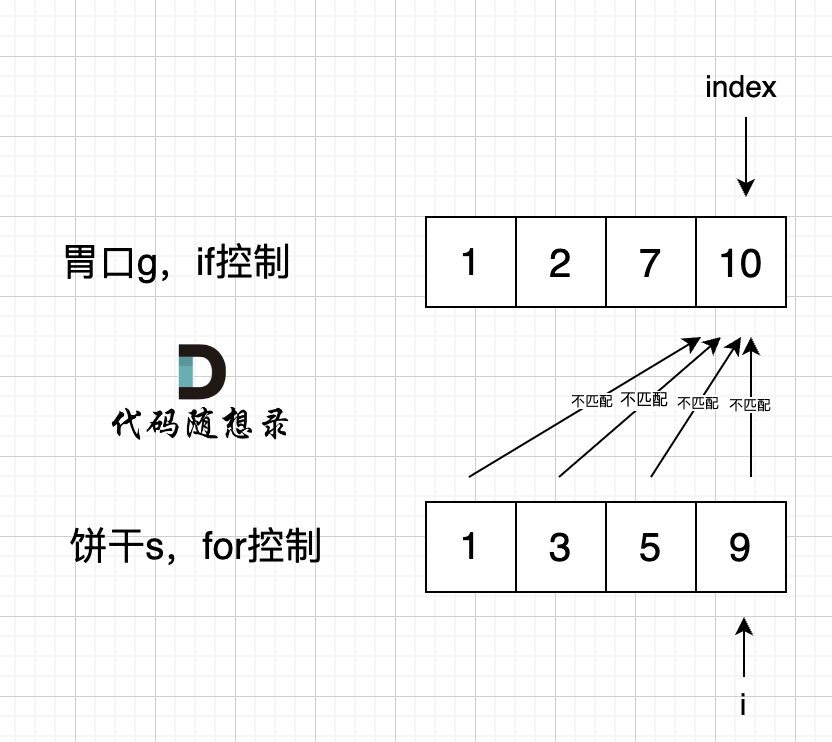
if 里的 index 指向 胃口 10, for 里的 i 指向饼干 9,因为 饼干 9 满足不了 胃口 10,所以 i 持续向前移动,而 index 走不到` s[index] >= g[i]` 的逻辑,所以 index 不会移动,那么当 i 持续向前移动,最后所有的饼干都匹配不上。
diff --git a/problems/0459.重复的子字符串.md b/problems/0459.重复的子字符串.md
index 78aad3e7..627a27a4 100644
--- a/problems/0459.重复的子字符串.md
+++ b/problems/0459.重复的子字符串.md
@@ -46,13 +46,13 @@
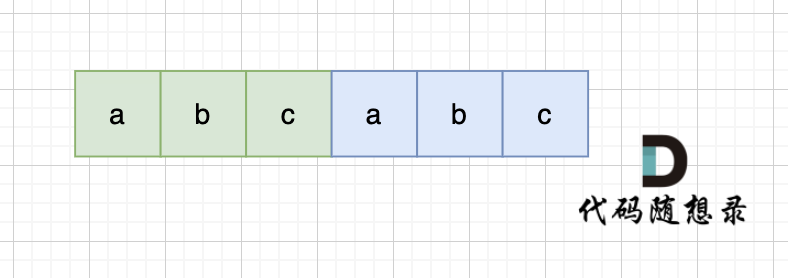
当一个字符串s:abcabc,内部由重复的子串组成,那么这个字符串的结构一定是这样的:
-
+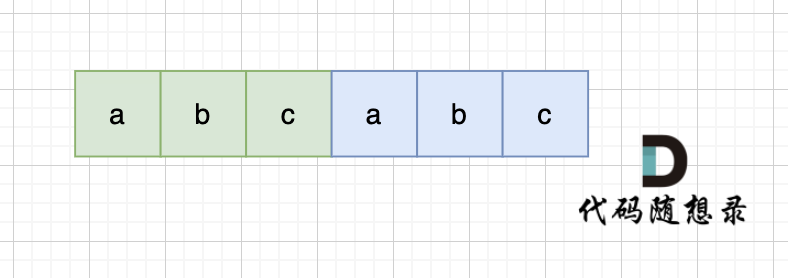
也就是由前后相同的子串组成。
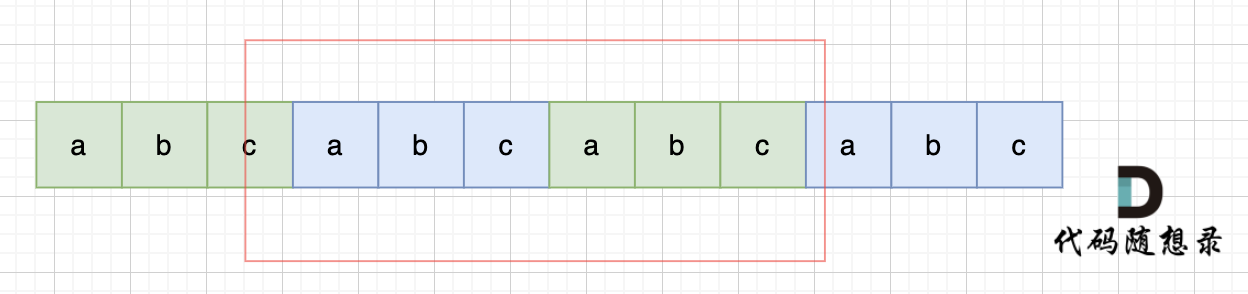
那么既然前面有相同的子串,后面有相同的子串,用 s + s,这样组成的字符串中,后面的子串做前串,前面的子串做后串,就一定还能组成一个s,如图:
-
+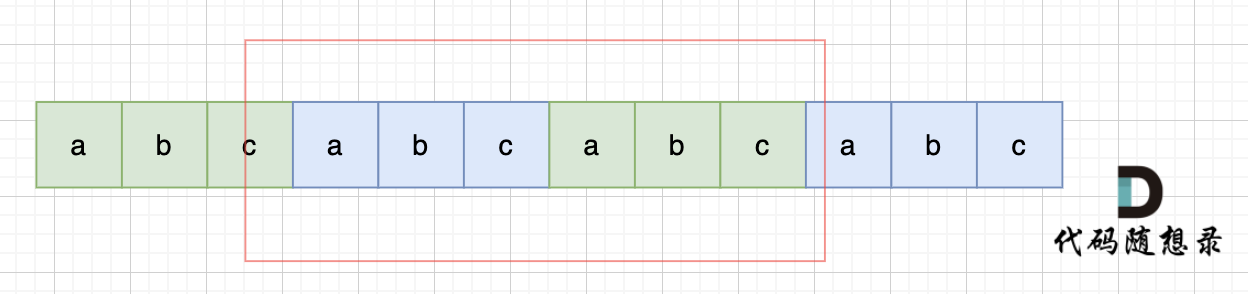
当然,我们在判断 s + s 拼接的字符串里是否出现一个s的的时候,**要刨除 s + s 的首字符和尾字符**,这样避免在s+s中搜索出原来的s,我们要搜索的是中间拼接出来的s。
@@ -64,11 +64,11 @@
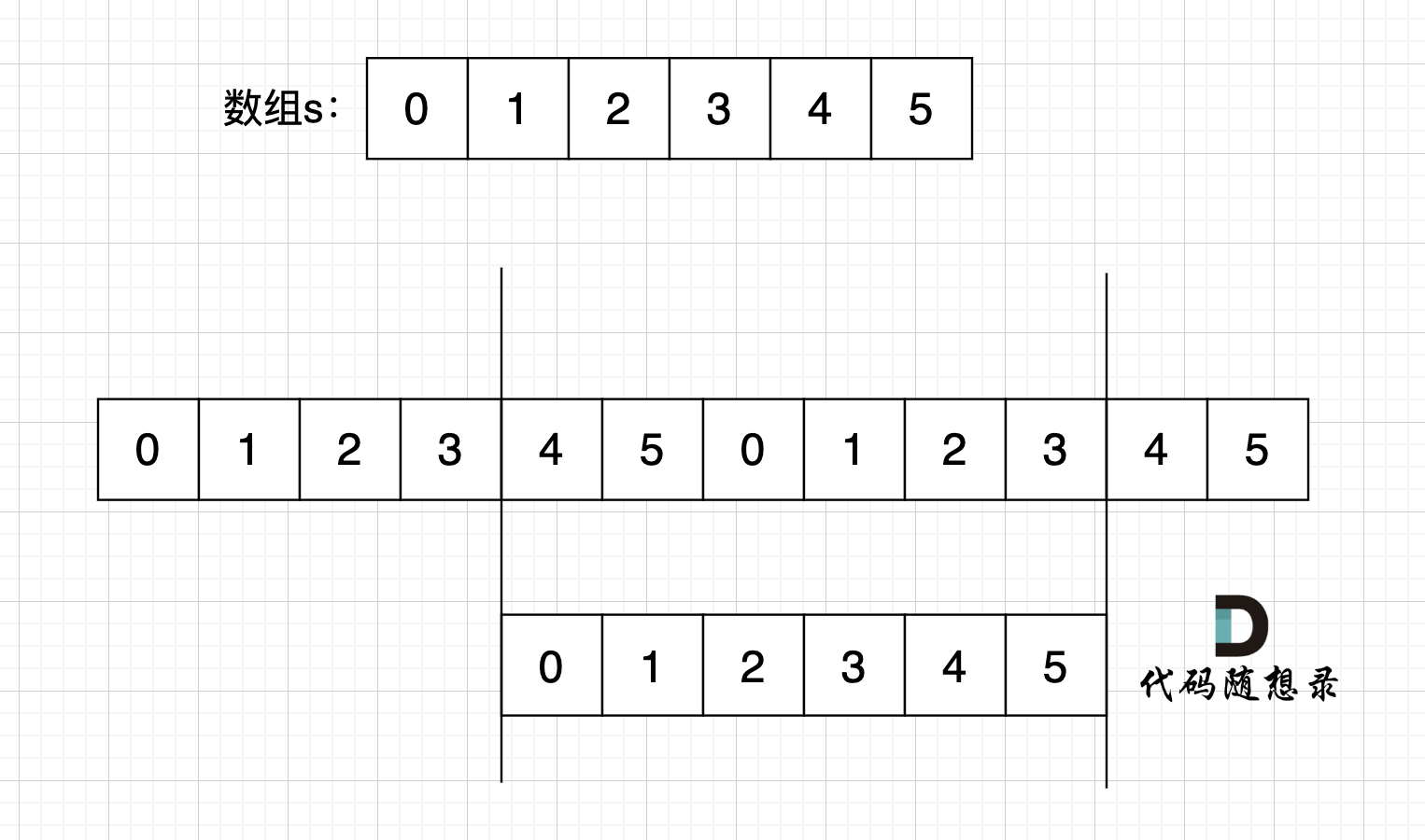
如图,字符串s,图中数字为数组下标,在 s + s 拼接后, 不算首尾字符,中间凑成s字符串。 (图中数字为数组下标)
-
+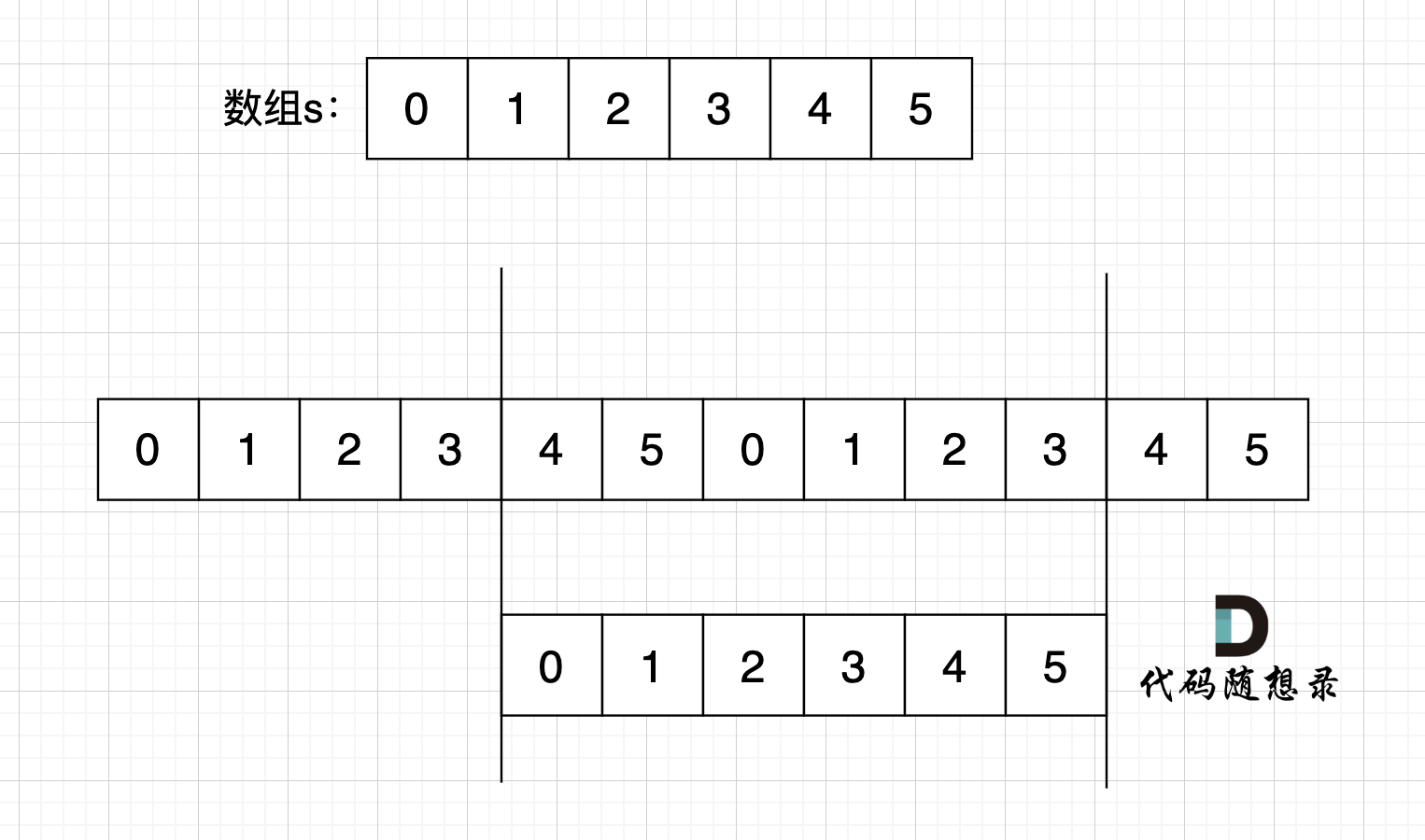
图中,因为中间拼接成了s,根据红色框 可以知道 s[4] = s[0], s[5] = s[1], s[0] = s[2], s[1] = s[3] s[2] = s[4] ,s[3] = s[5]
-
+
以上相等关系我们串联一下:
@@ -83,7 +83,7 @@ s[5] = s[1] = s[3]
这里可以有录友想,凭什么就是这样组成的s呢,我换一个方式组成s 行不行,如图:
-
+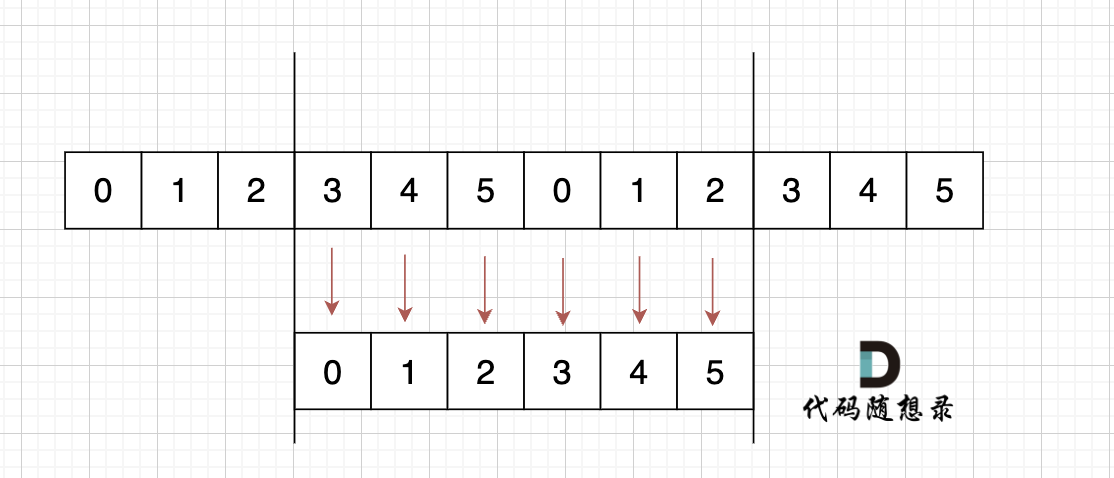
s[3] = s[0],s[4] = s[1] ,s[5] = s[2],s[0] = s[3],s[1] = s[4],s[2] = s[5]
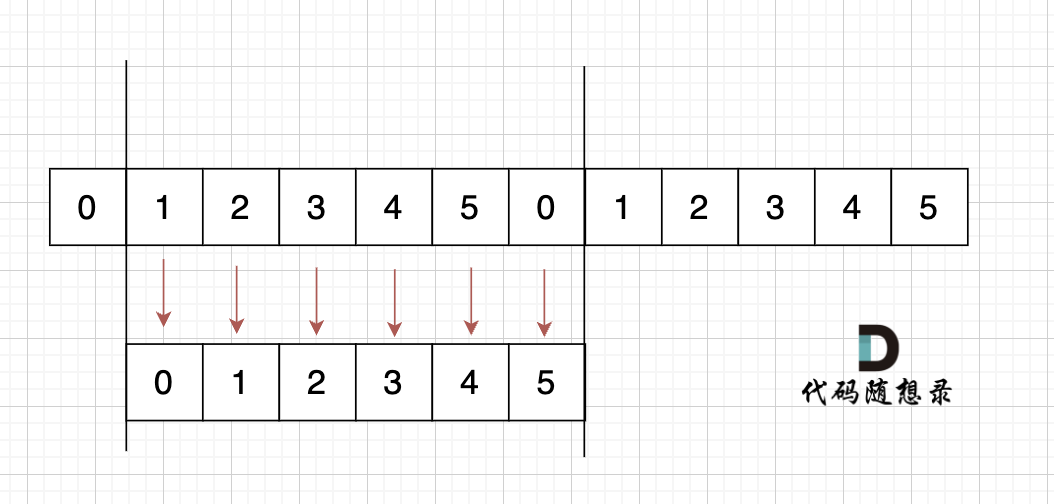
@@ -101,7 +101,7 @@ s[0] s[1] s[2] = s[3] s[4] s[5]
如果是这样的呢,如图:
-
+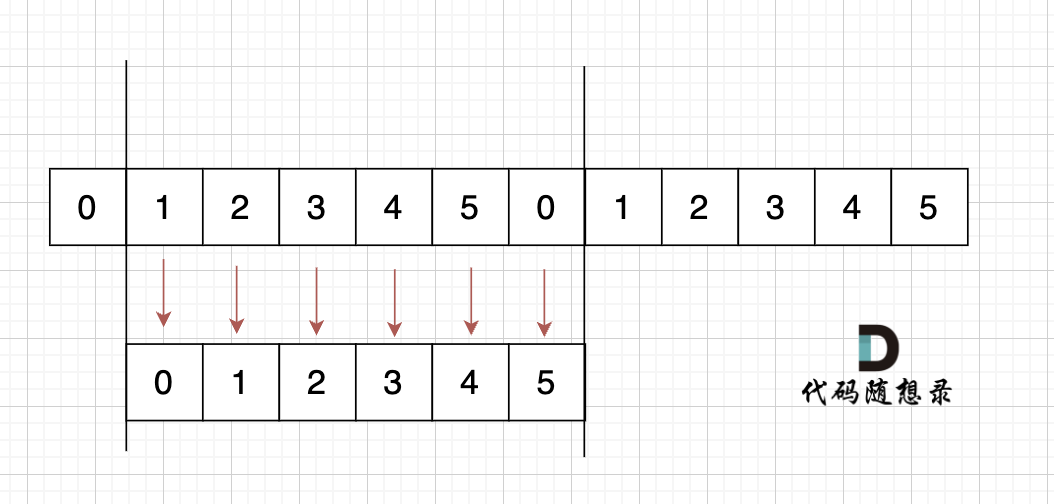
s[1] = s[0],s[2] = s[1] ,s[3] = s[2],s[4] = s[3],s[5] = s[4],s[0] = s[5]
@@ -165,23 +165,23 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
那么相同前后缀可以是这样:
-
+
也可以是这样:
-
+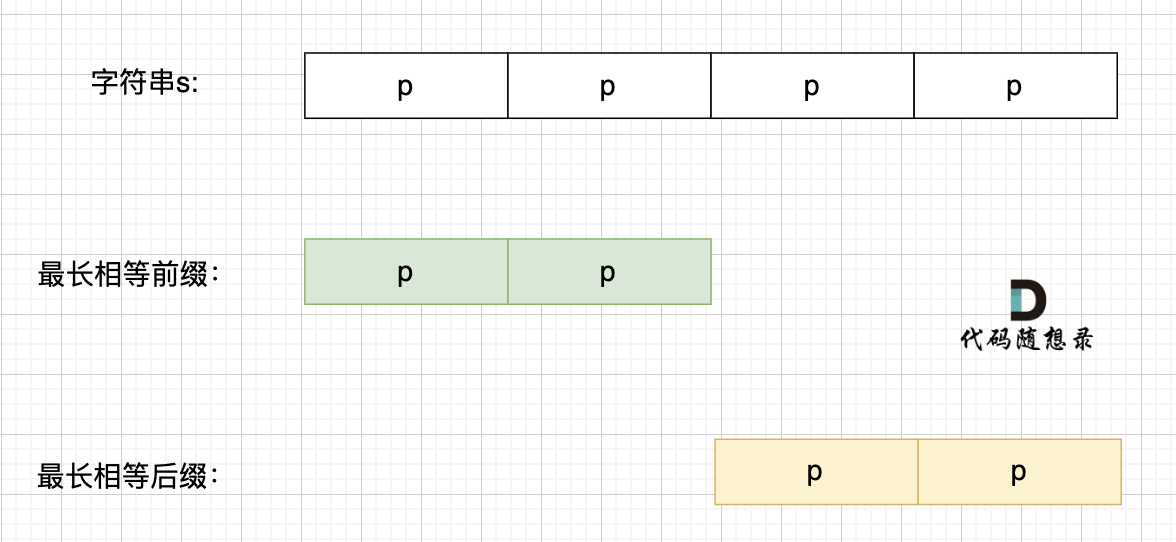
最长的相等前后缀,也就是这样:
-
+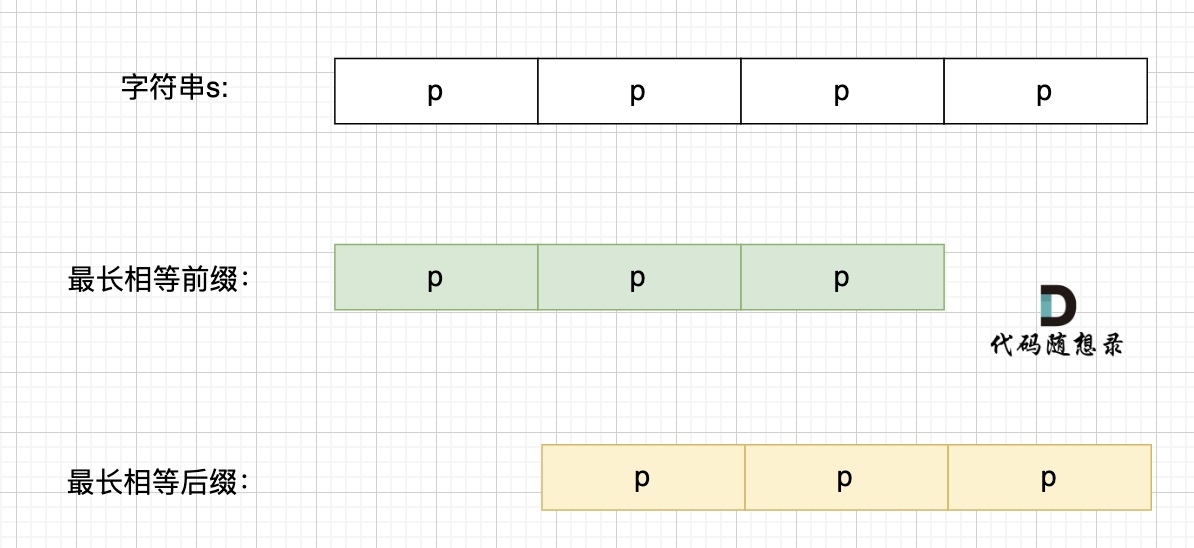
这里有录友就想:如果字符串s 是由最小重复子串p组成,最长相等前后缀就不能更长一些? 例如这样:
-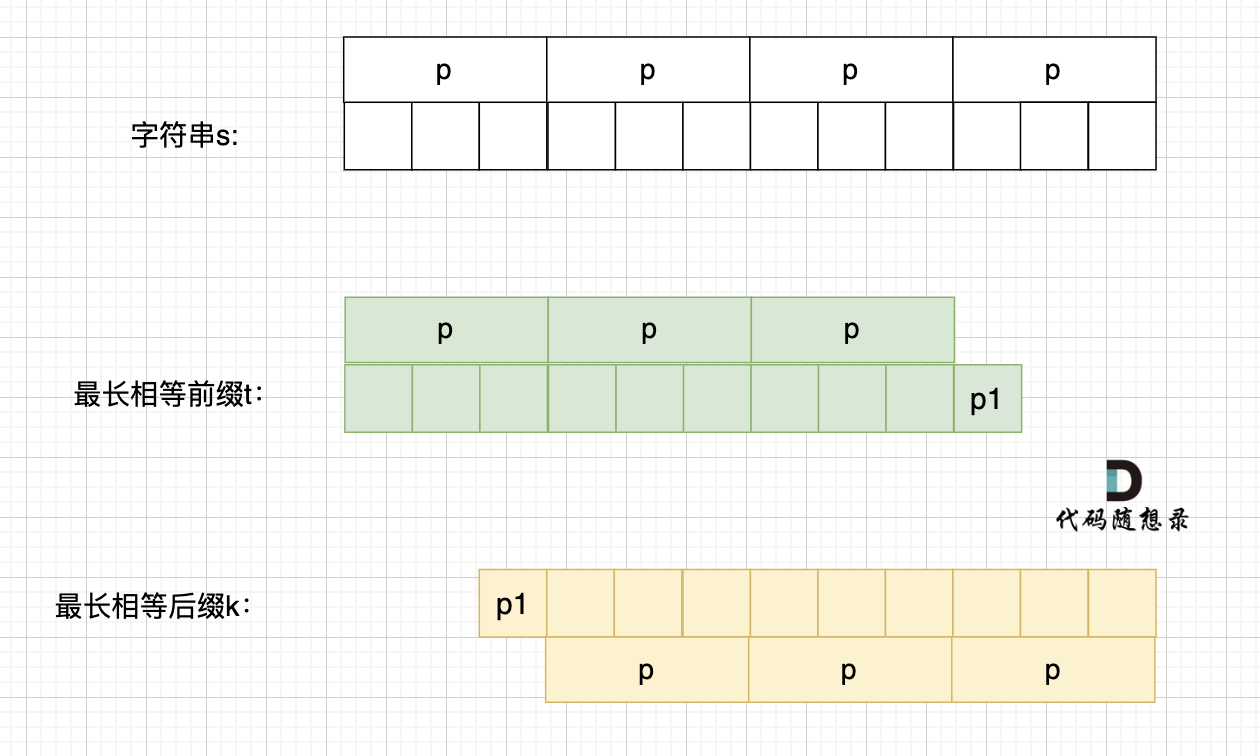
+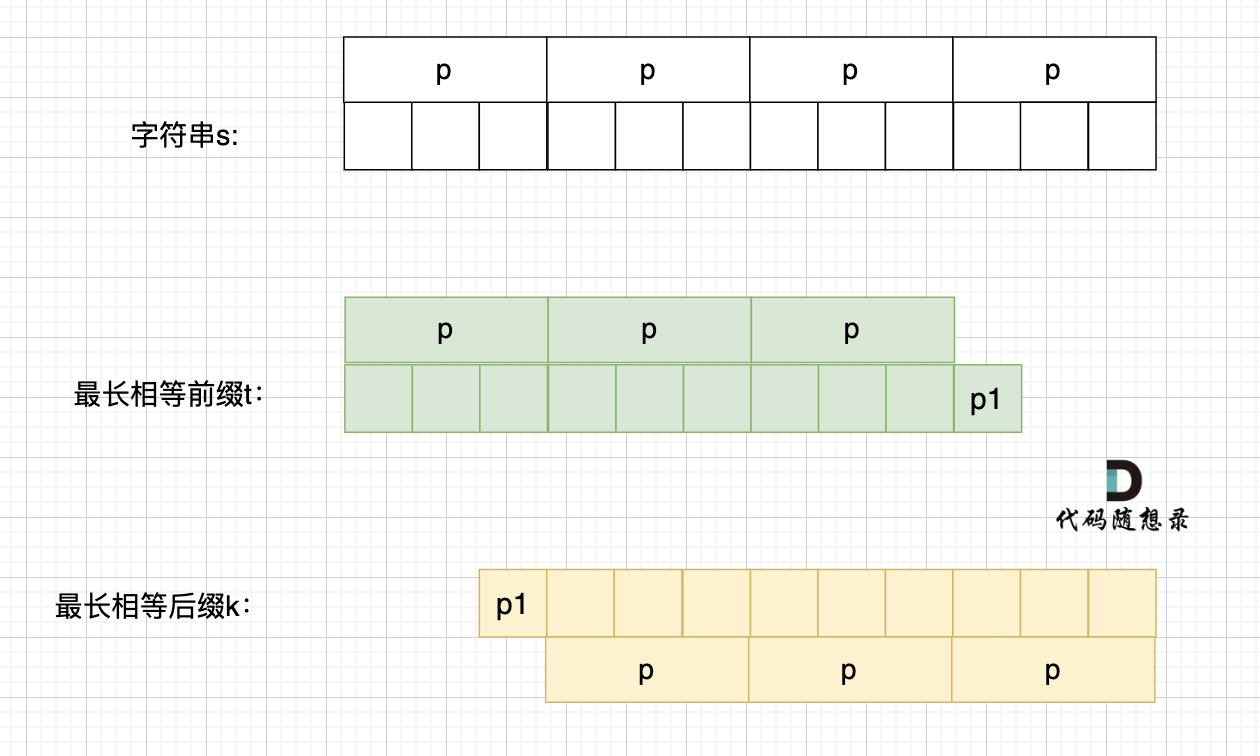
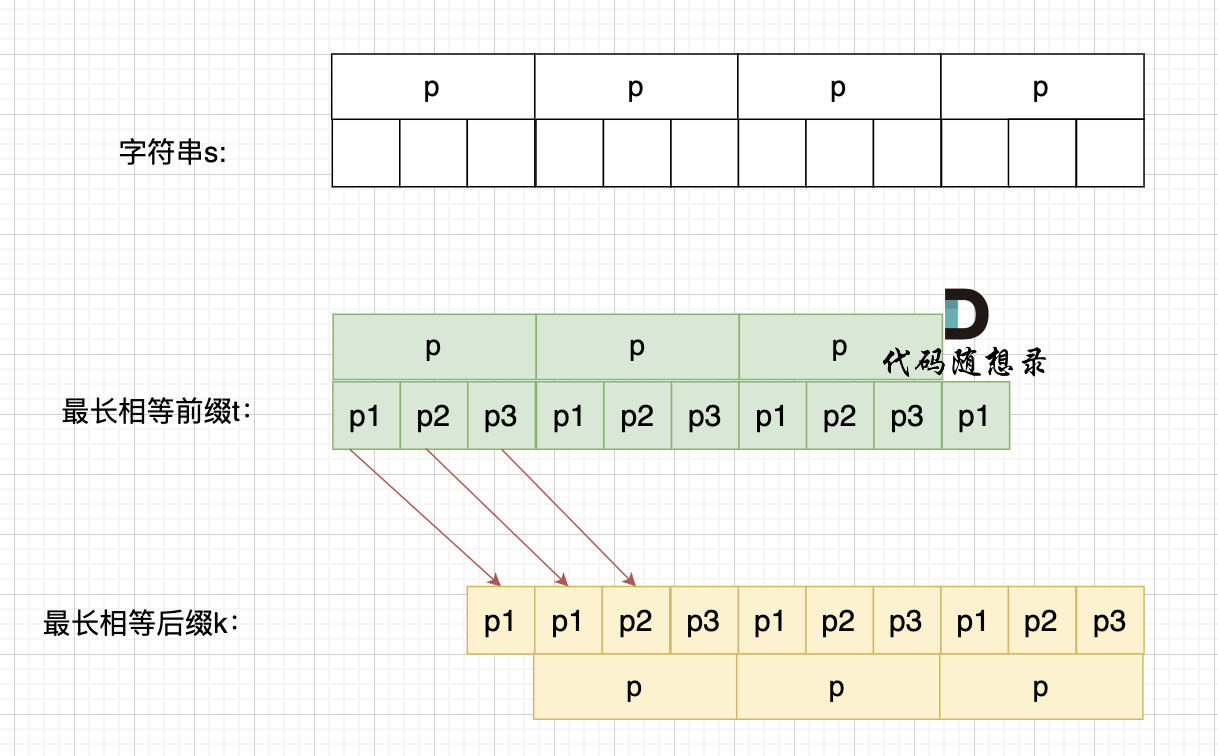
如果这样的话,因为前后缀要相同,所以 p2 = p1,p3 = p2,如图:
-
+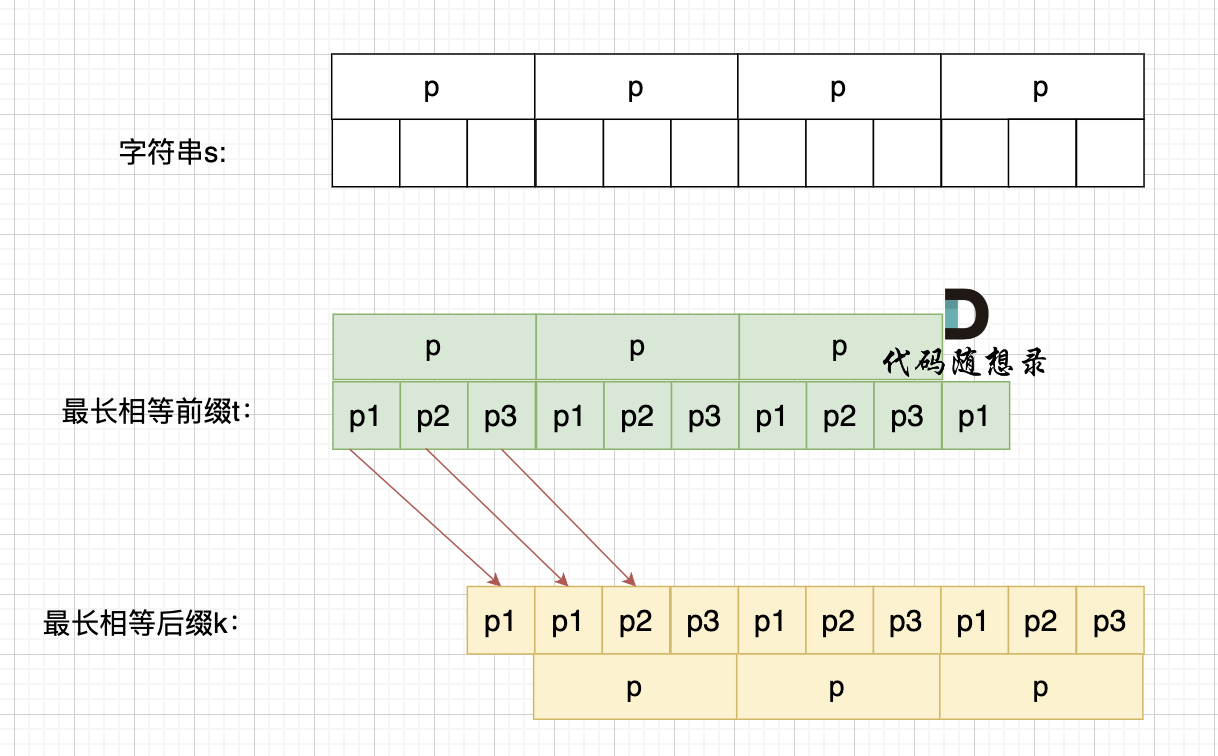
p2 = p1,p3 = p2 即: p1 = p2 = p3
@@ -203,7 +203,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
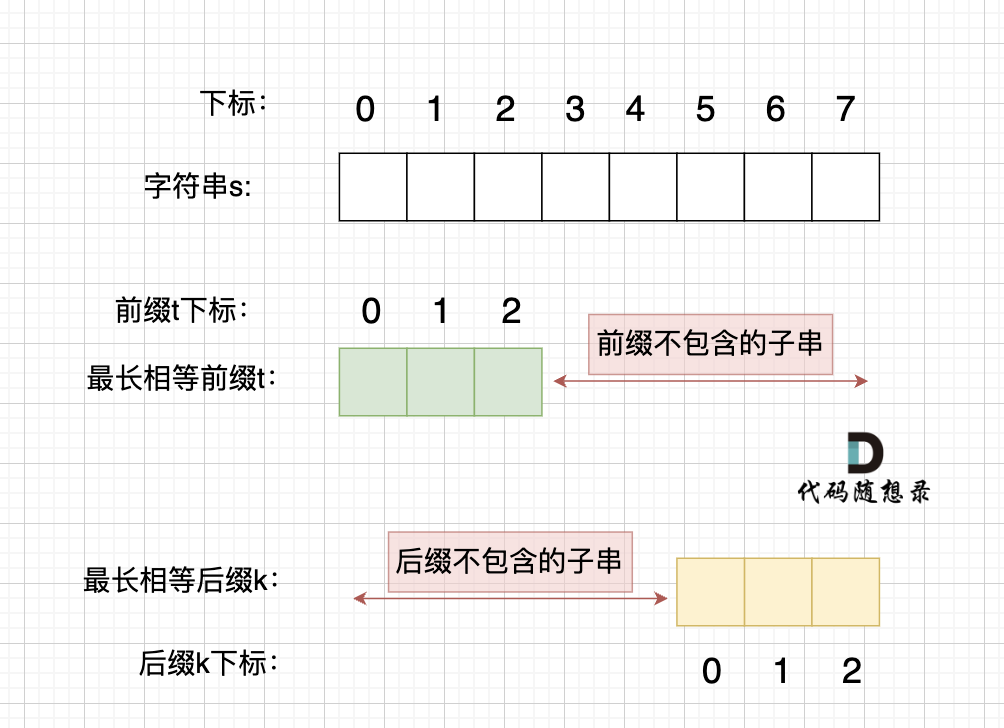
情况一, 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大,那一定不是字符串s的重复子串,如图:
-
+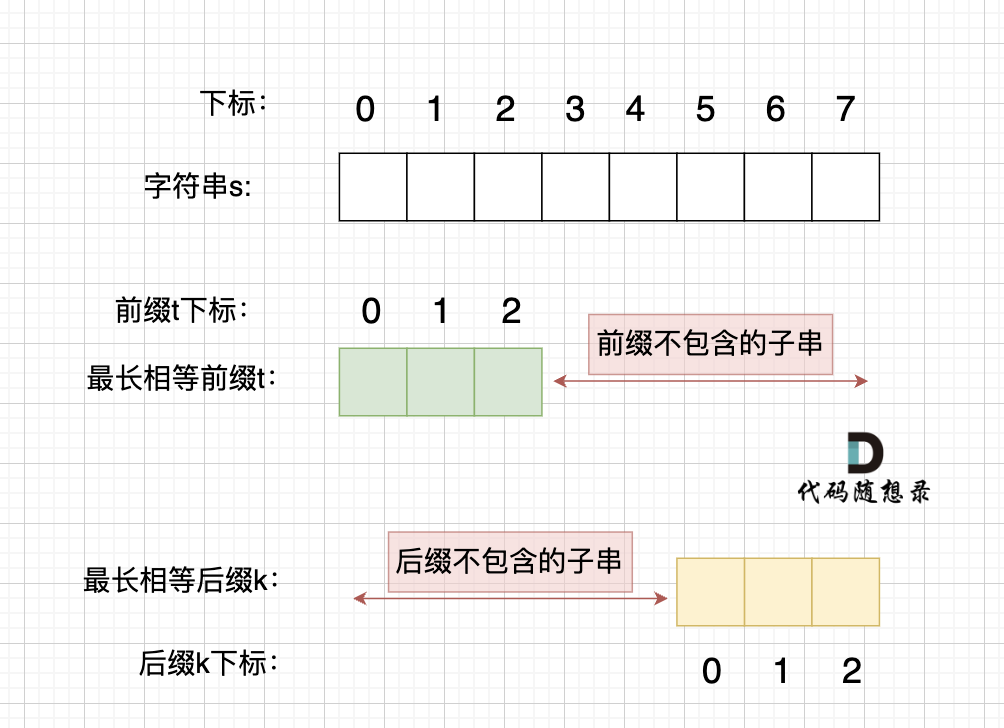
图中:前后缀不包含的子串的长度 大于 字符串s的长度的 二分之一
@@ -211,7 +211,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
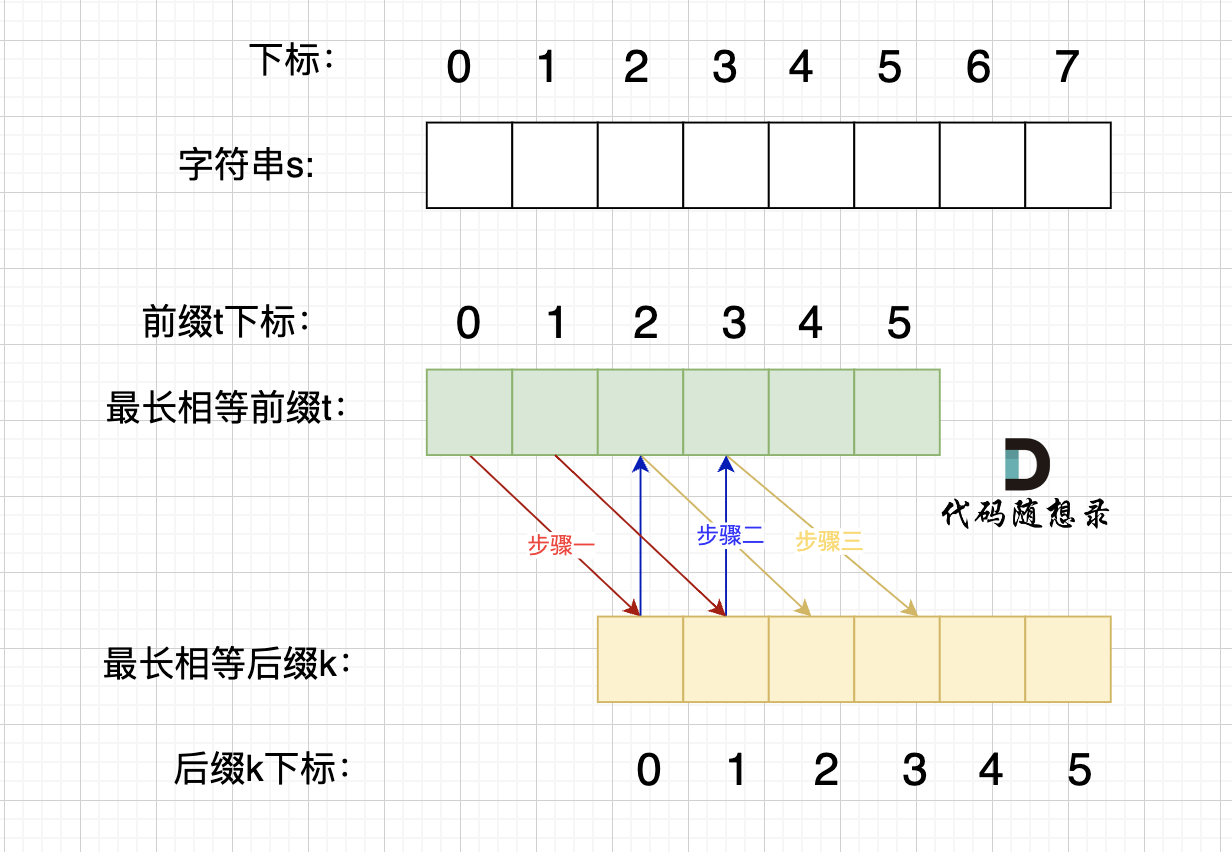
情况二,最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,如图:
-
+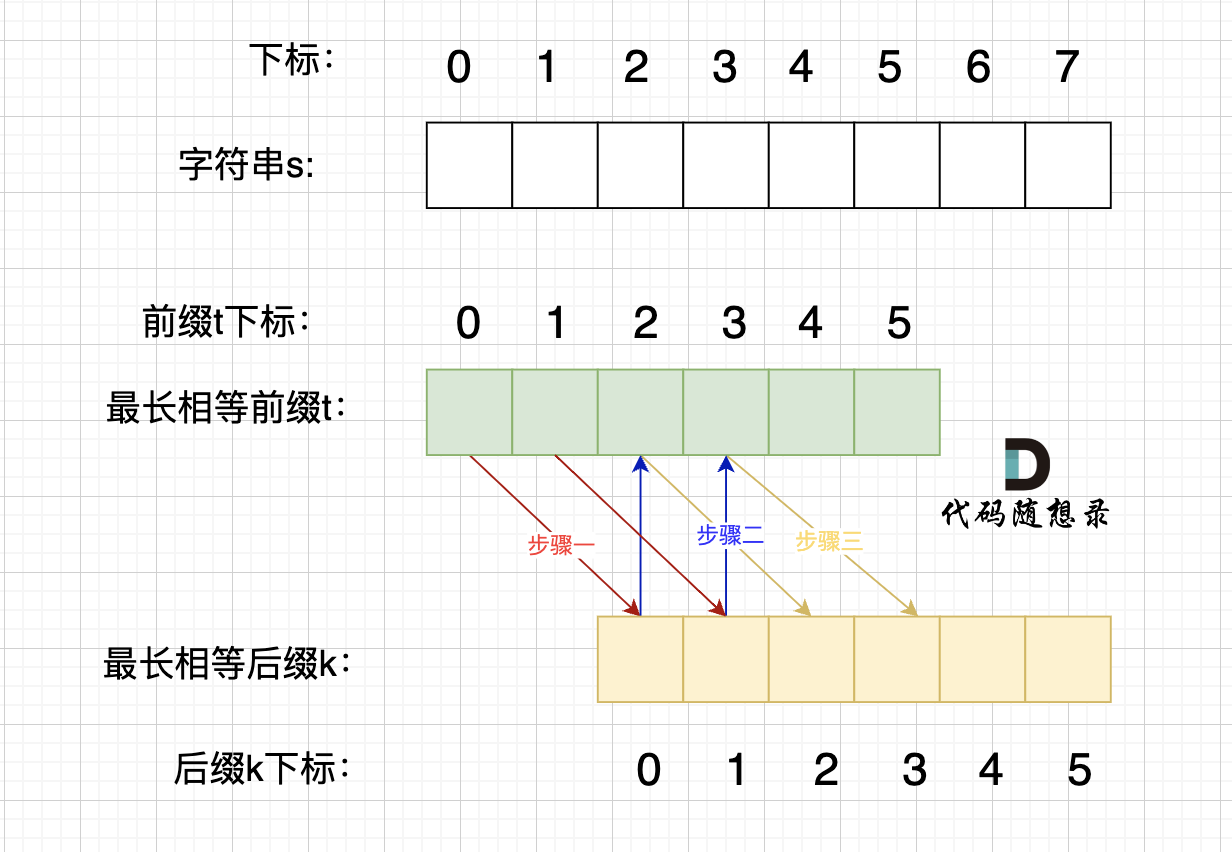
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,所以 s[0] 一定和 s[2]相同,s[1] 一定和 s[3]相同,即:,s[0]s[1]与s[2]s[3]相同 。
@@ -234,7 +234,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
那么它的最长相同前后缀,就不是上图中的前后缀,而是这样的的前后缀:
-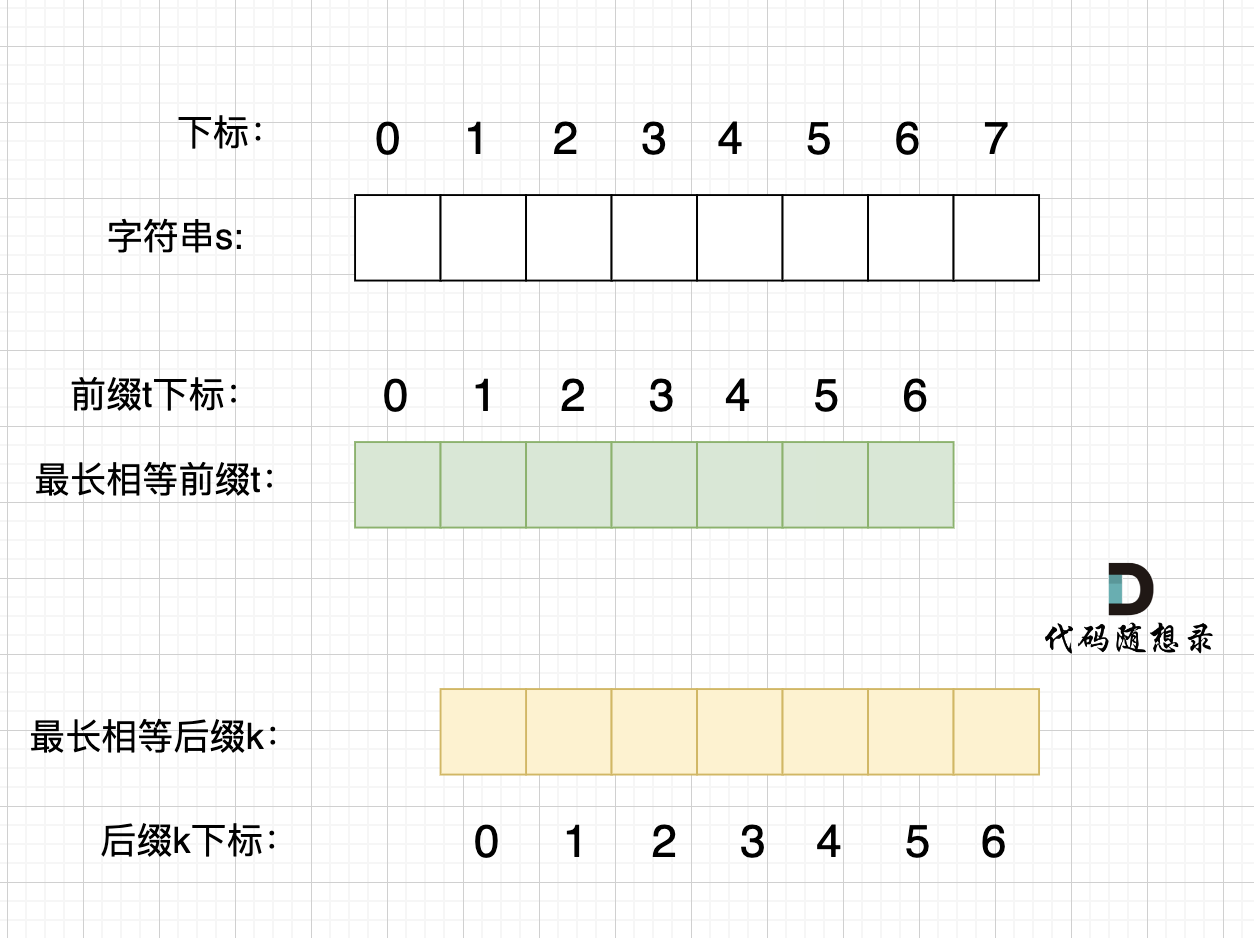
+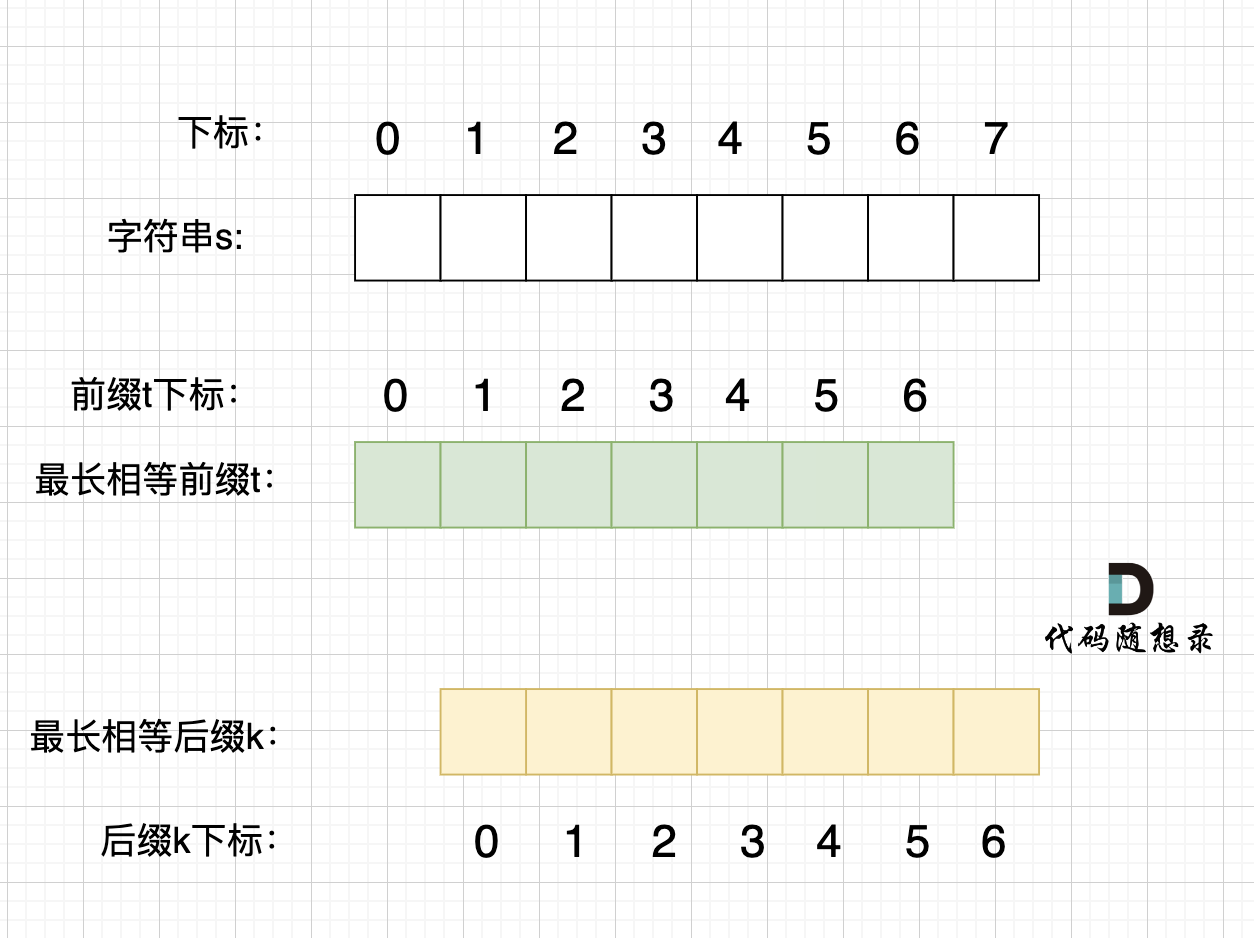
录友可能再问,由一个字符组成的字符串,最长相等前后缀凭什么就是这样的。
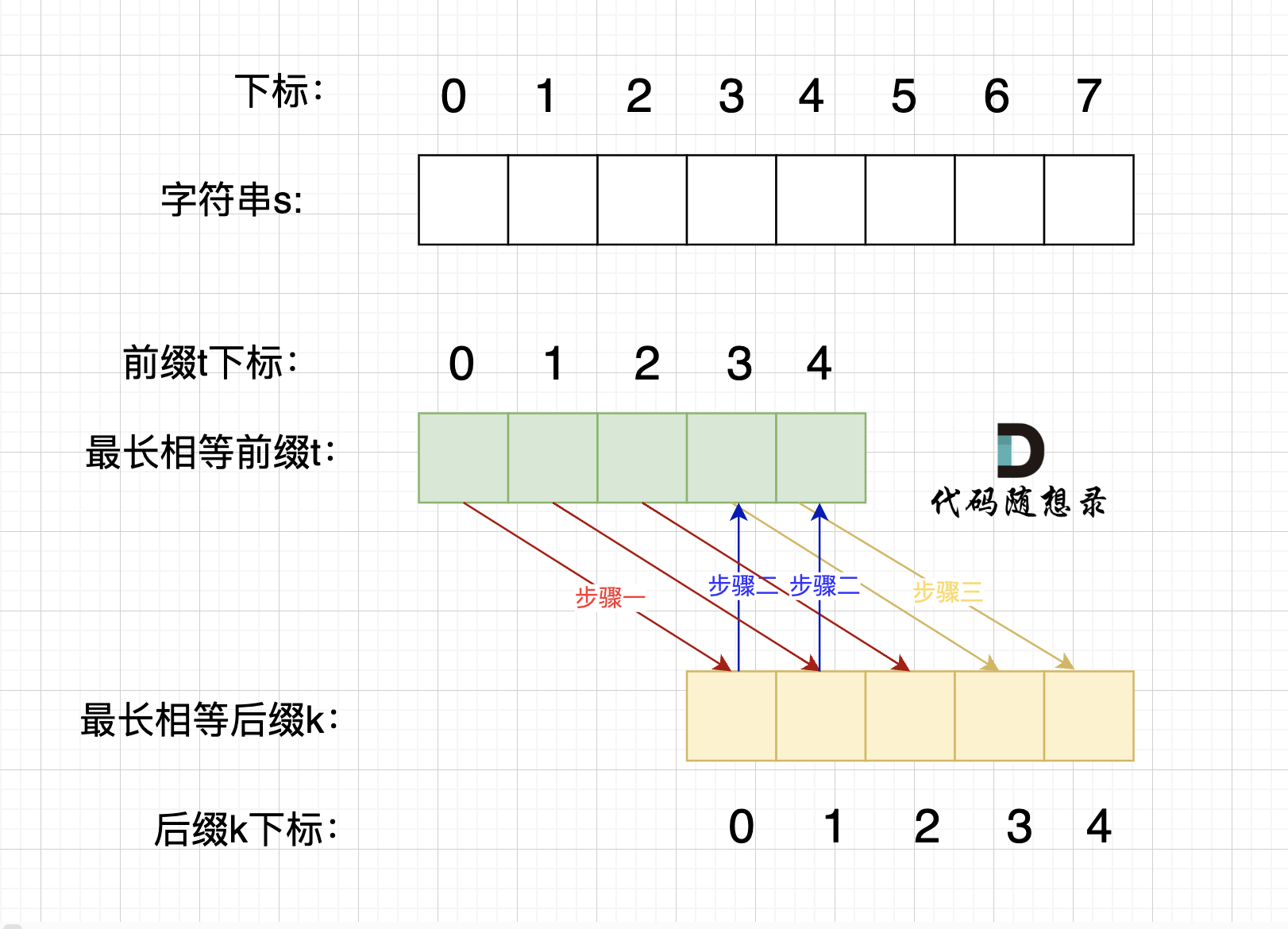
@@ -250,7 +250,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
**情况三,最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除得情况**,如图:
-
+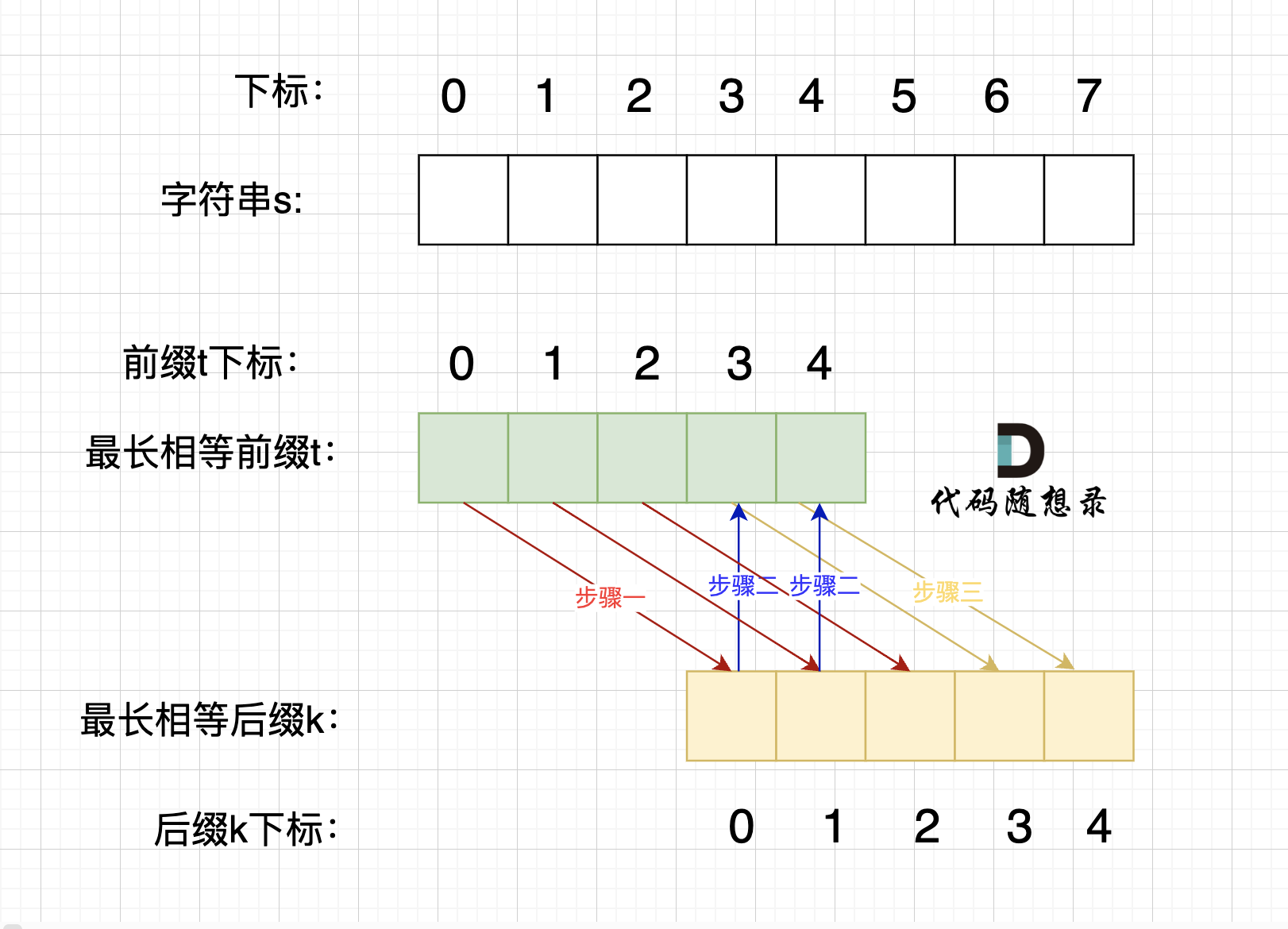
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,t[2] 与 k[2]相同。
diff --git a/problems/0463.岛屿的周长.md b/problems/0463.岛屿的周长.md
index bff619cc..40ddc57d 100644
--- a/problems/0463.岛屿的周长.md
+++ b/problems/0463.岛屿的周长.md
@@ -15,7 +15,7 @@
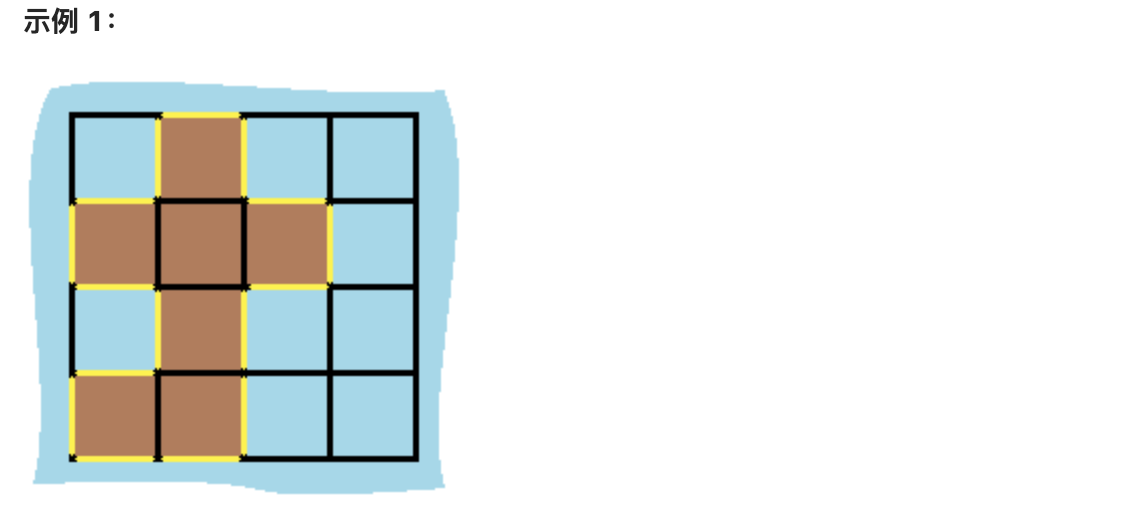
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
-
+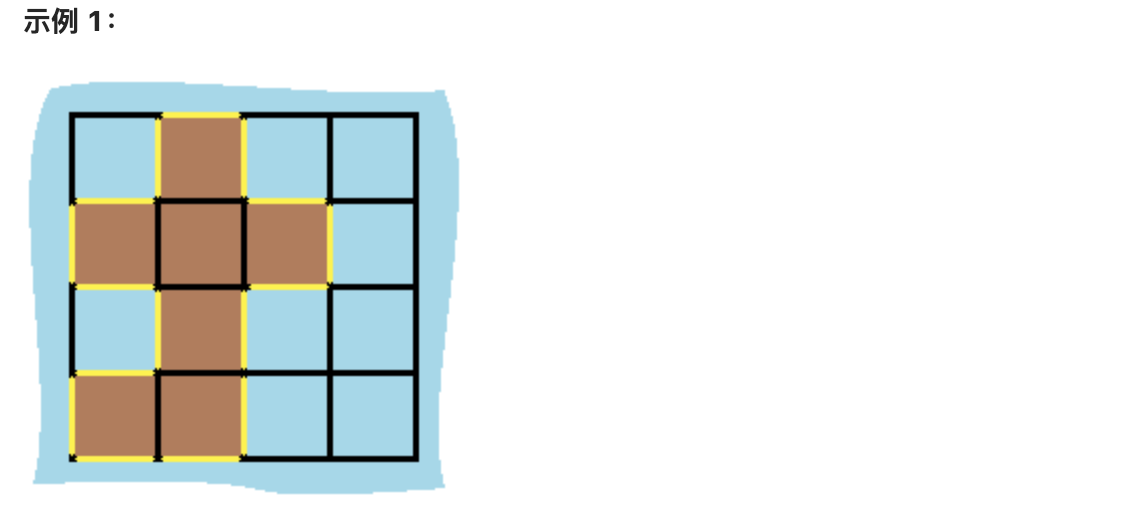
* 输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
* 输出:16
diff --git a/problems/0474.一和零.md b/problems/0474.一和零.md
index ca525ab2..8166b39a 100644
--- a/problems/0474.一和零.md
+++ b/problems/0474.一和零.md
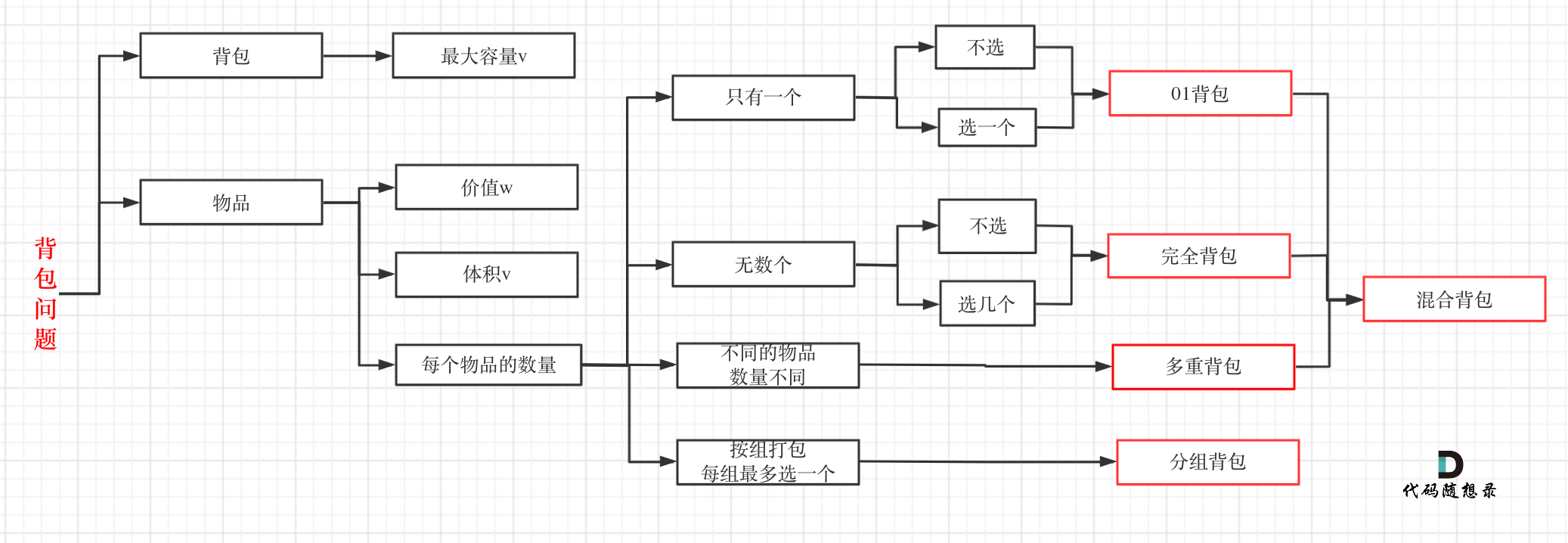
@@ -51,7 +51,7 @@
其实本题并不是多重背包,再来看一下这个图,捋清几种背包的关系
-
+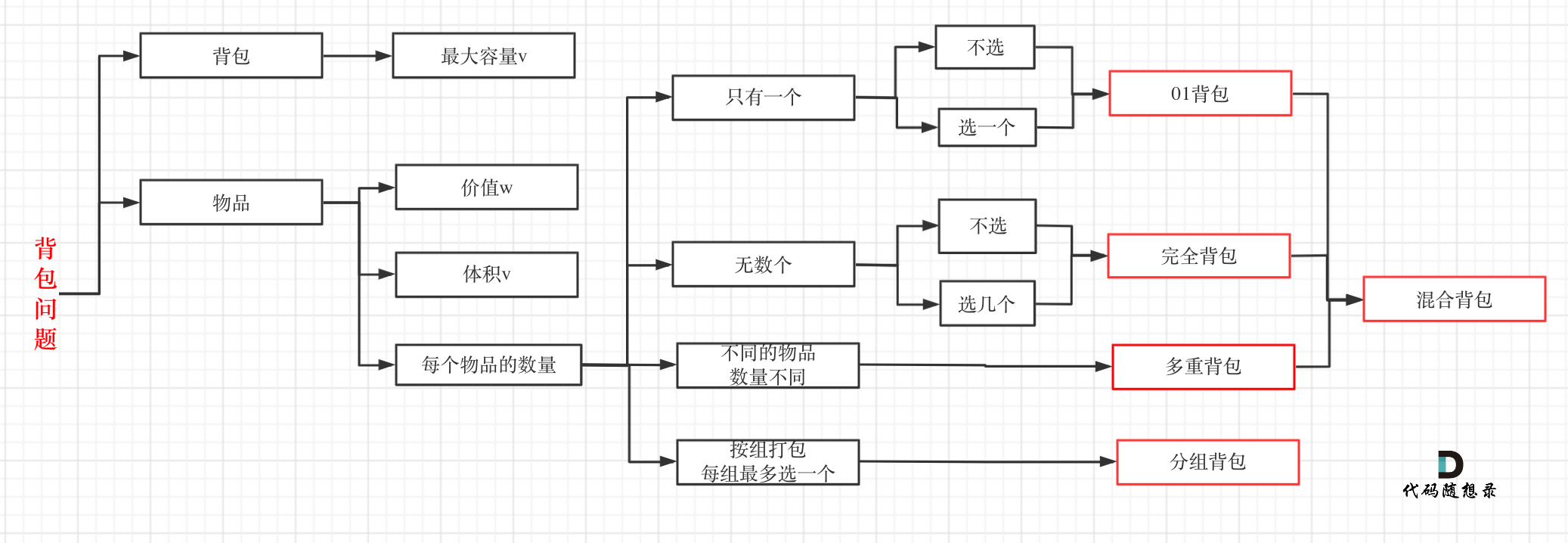
多重背包是每个物品,数量不同的情况。
@@ -127,7 +127,7 @@ for (string str : strs) { // 遍历物品
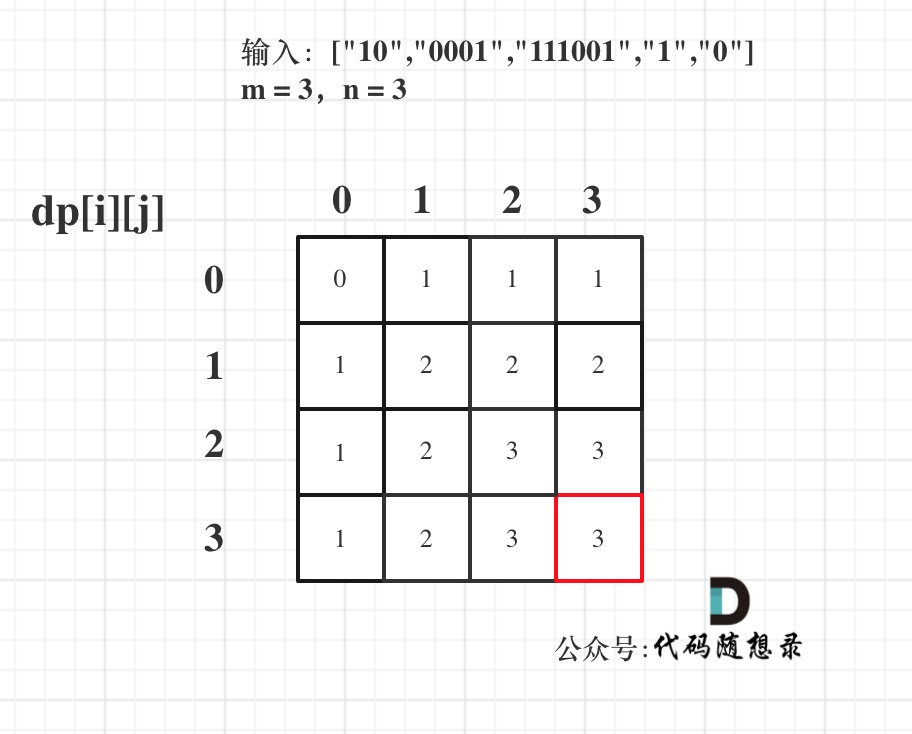
最后dp数组的状态如下所示:
-
+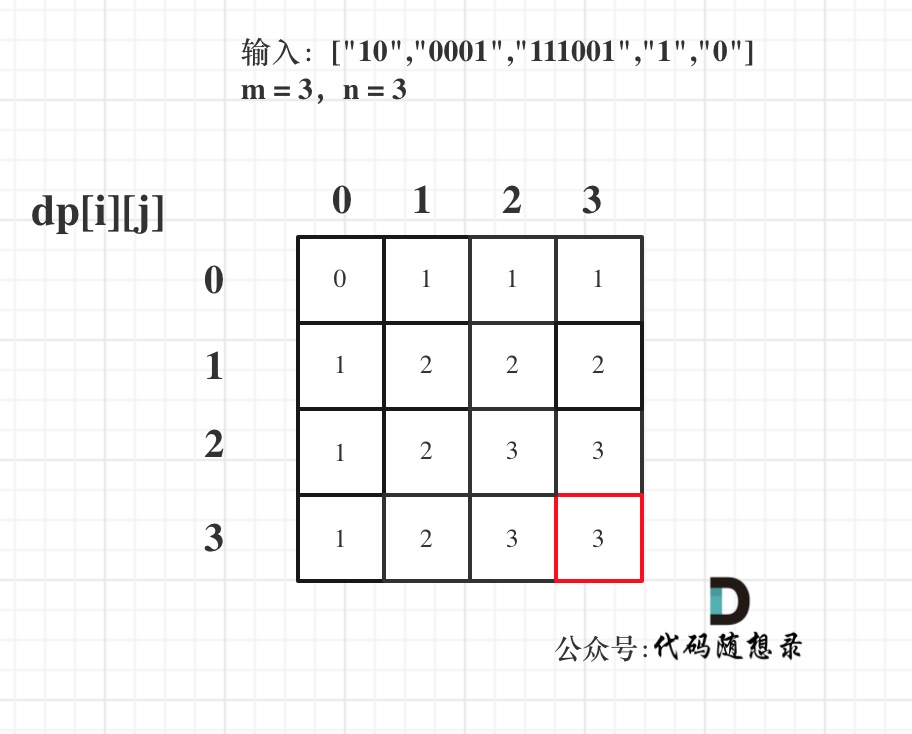
以上动规五部曲分析完毕,C++代码如下:
diff --git a/problems/0491.递增子序列.md b/problems/0491.递增子序列.md
index 1b927dd3..b3171c8a 100644
--- a/problems/0491.递增子序列.md
+++ b/problems/0491.递增子序列.md
@@ -45,7 +45,7 @@
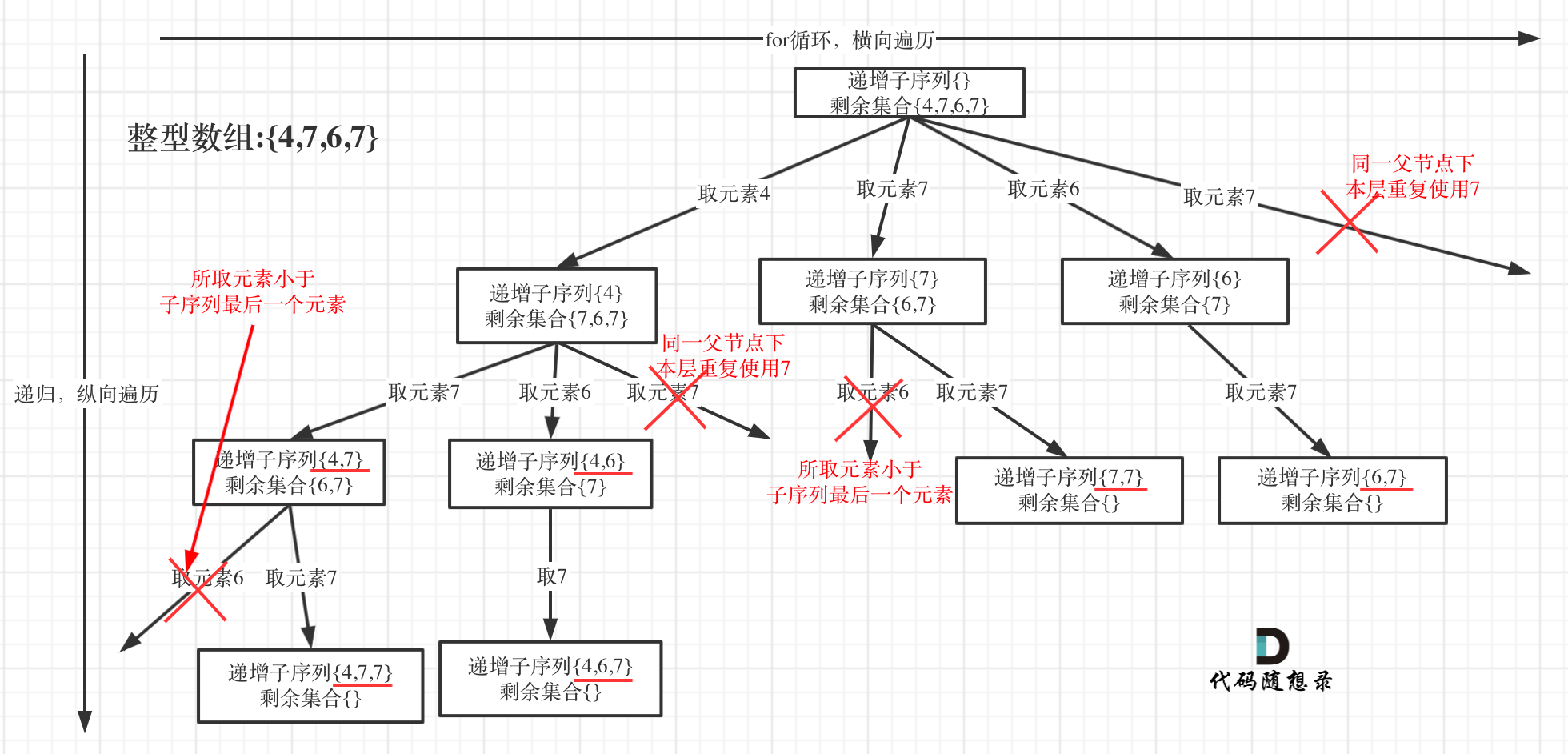
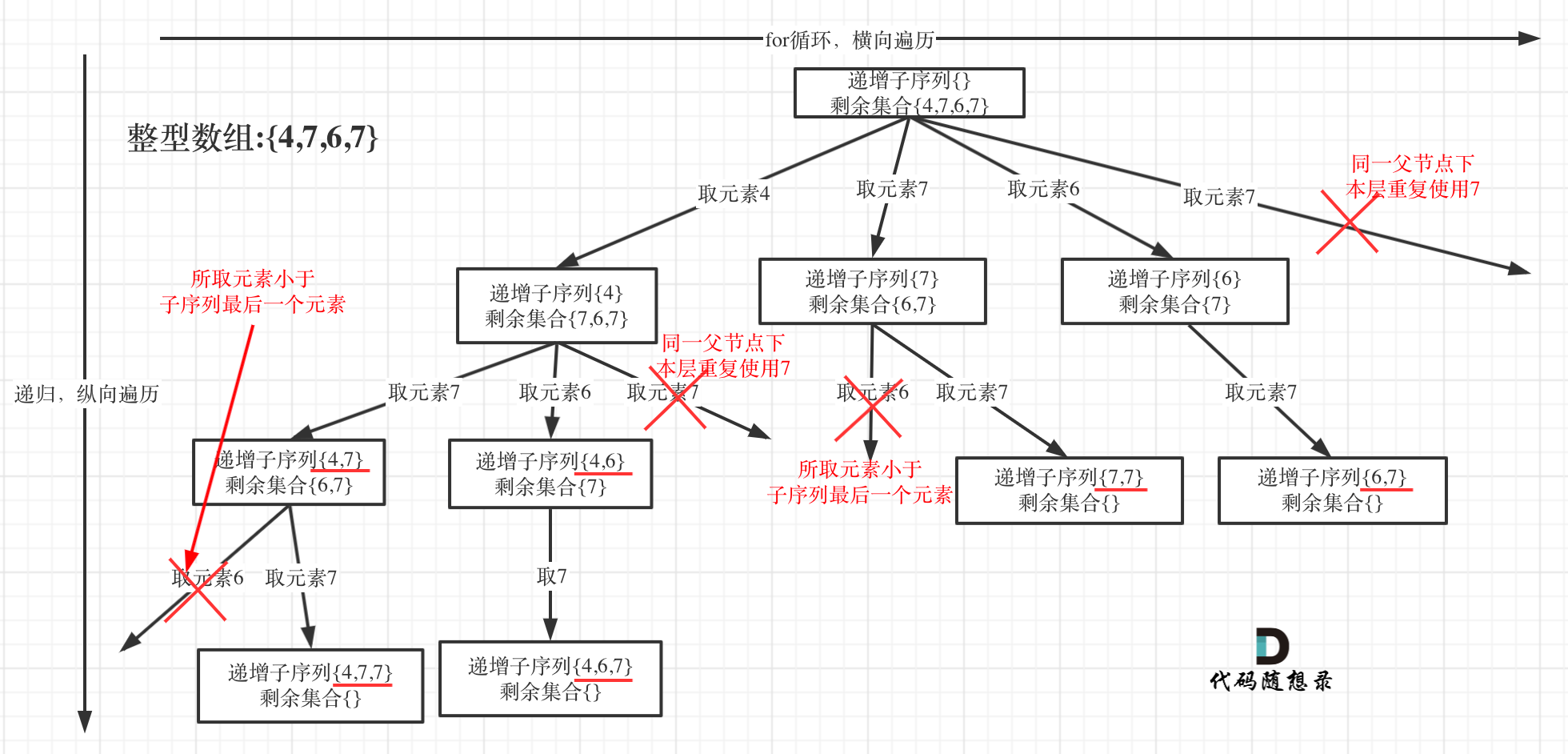
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
-
+
@@ -79,7 +79,7 @@ if (path.size() > 1) {
* 单层搜索逻辑
-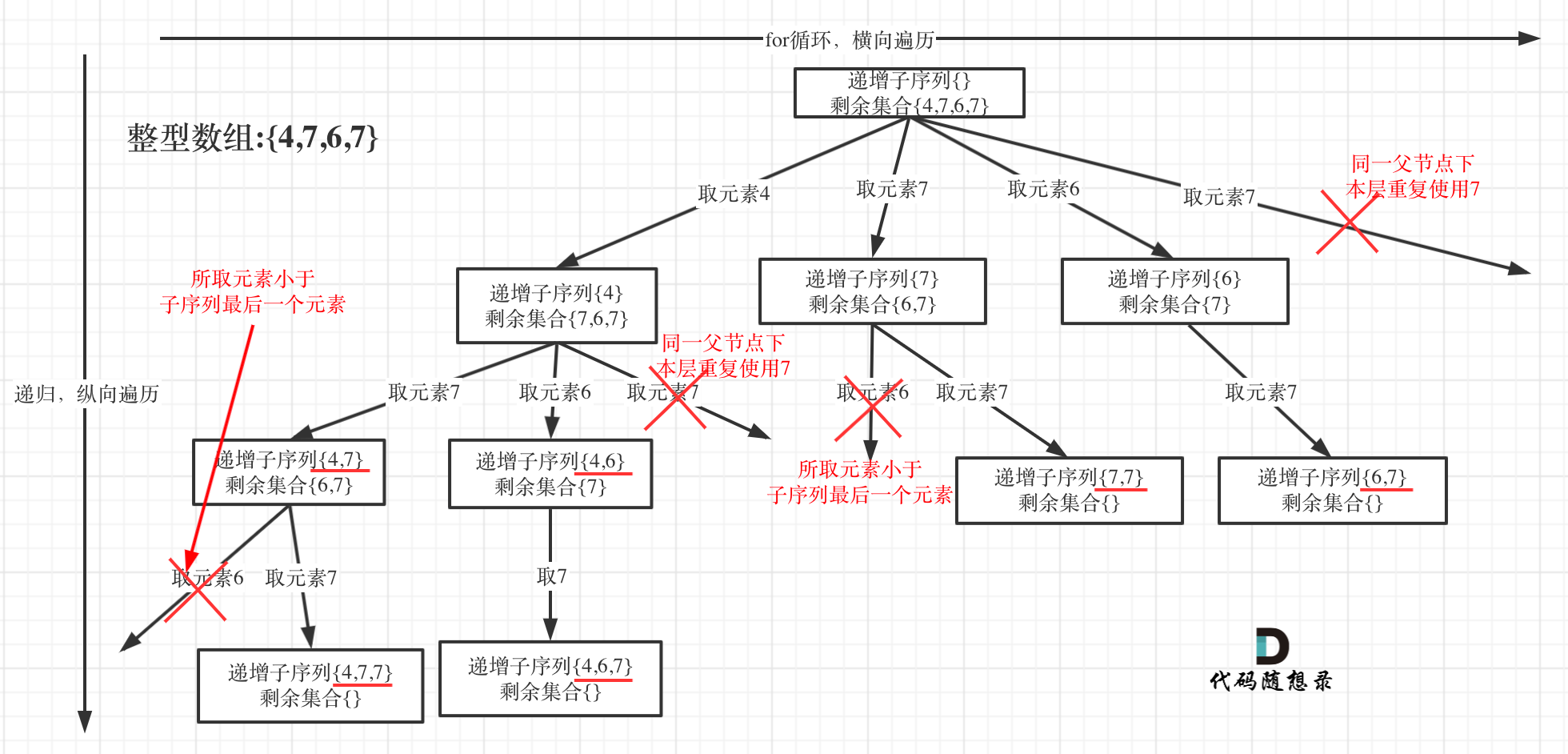
+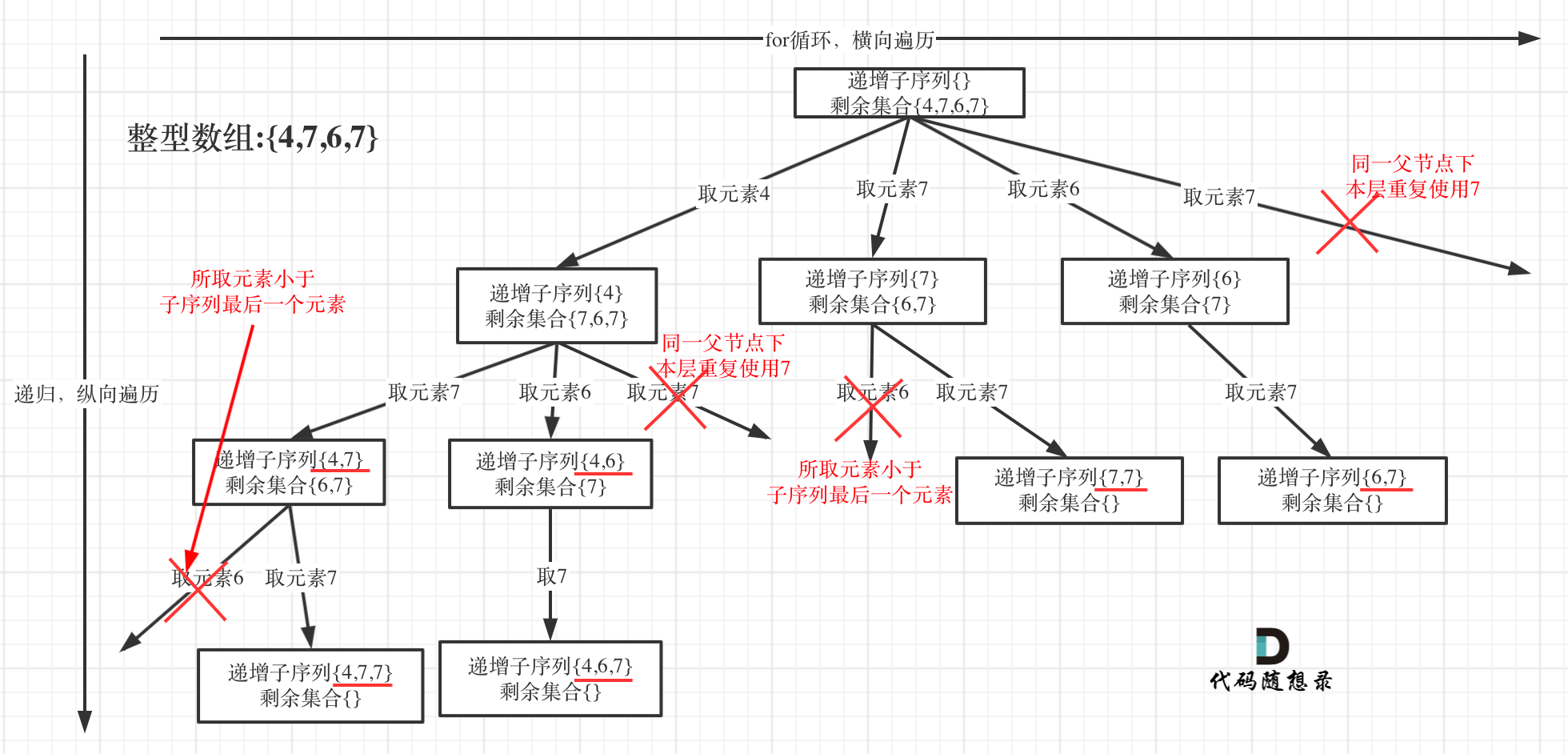
在图中可以看出,**同一父节点下的同层上使用过的元素就不能再使用了**
那么单层搜索代码如下:
diff --git a/problems/0494.目标和.md b/problems/0494.目标和.md
index bde843ea..a23e1743 100644
--- a/problems/0494.目标和.md
+++ b/problems/0494.目标和.md
@@ -163,7 +163,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
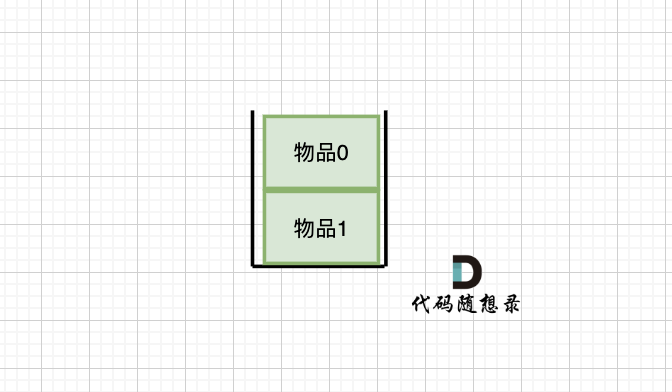
先只考虑物品0,如图:
-
+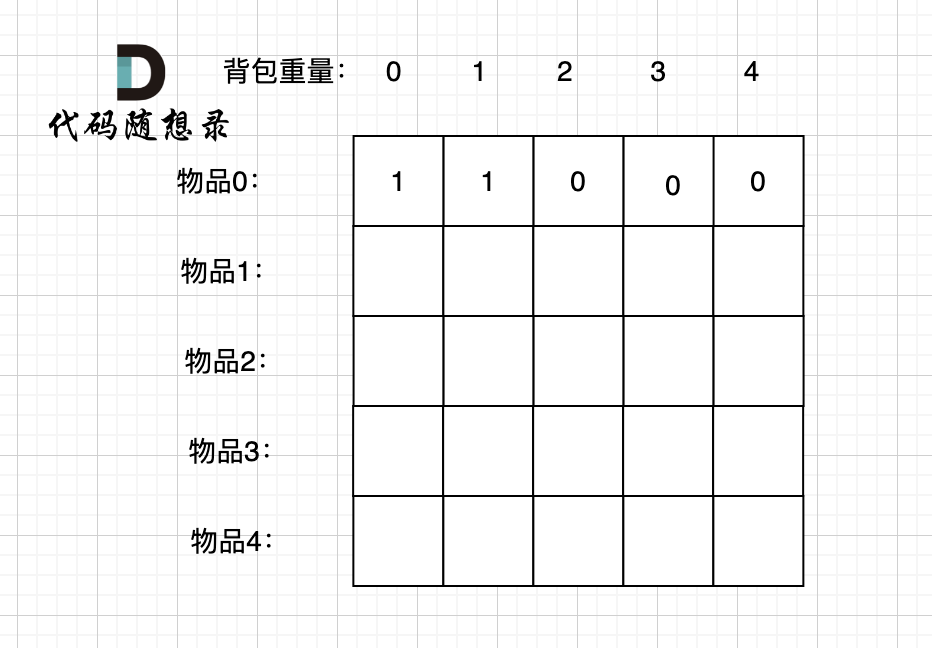
(这里的所有物品,都是题目中的数字1)。
@@ -177,7 +177,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
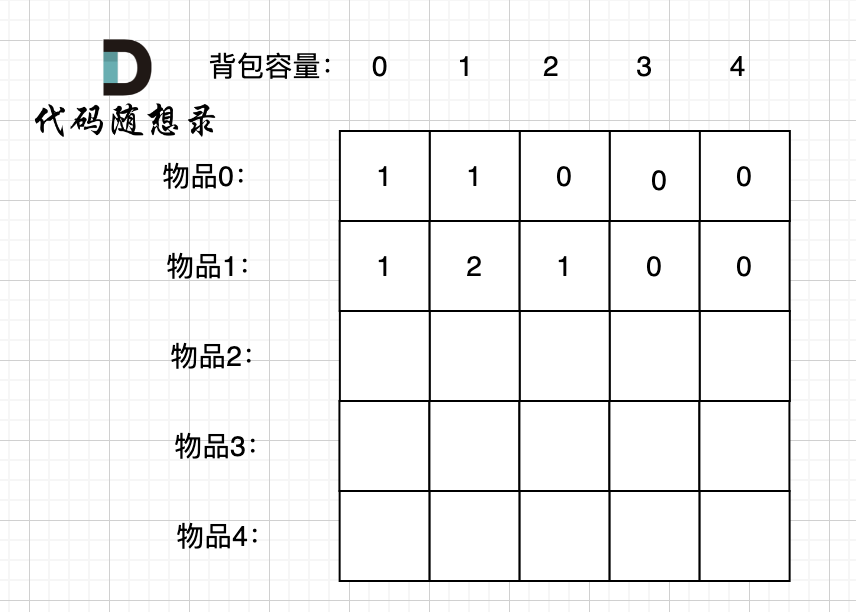
接下来 考虑 物品0 和 物品1,如图:
-
+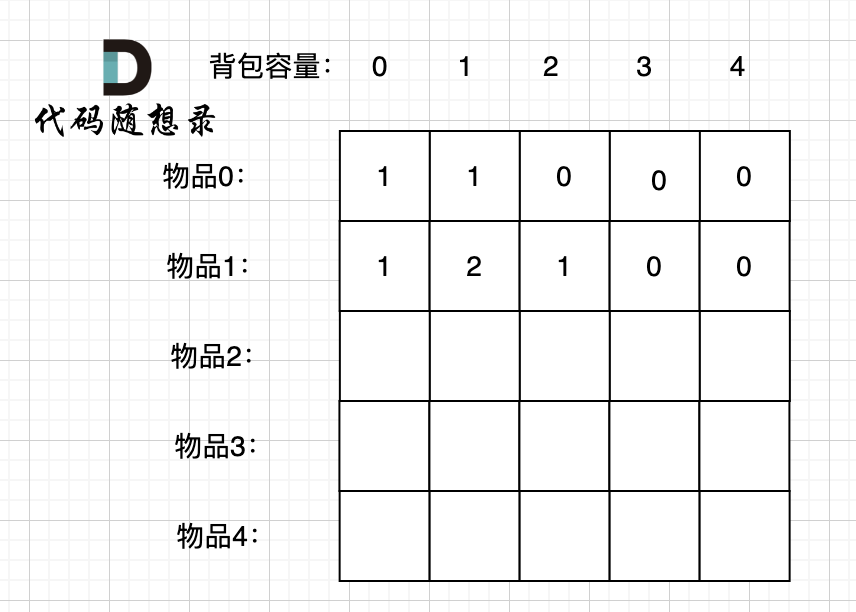
装满背包容量为0 的方法个数是1,即 放0件物品。
@@ -191,7 +191,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
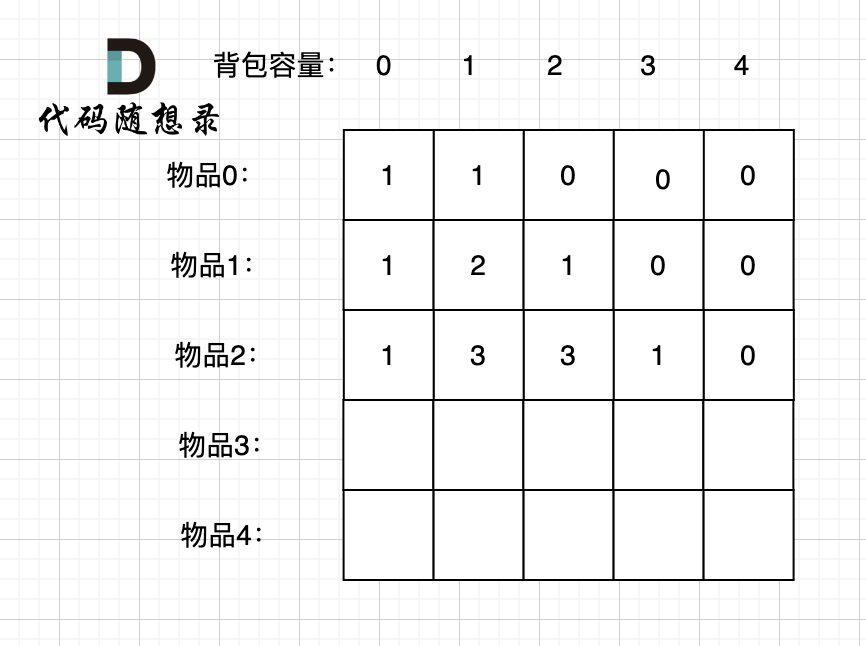
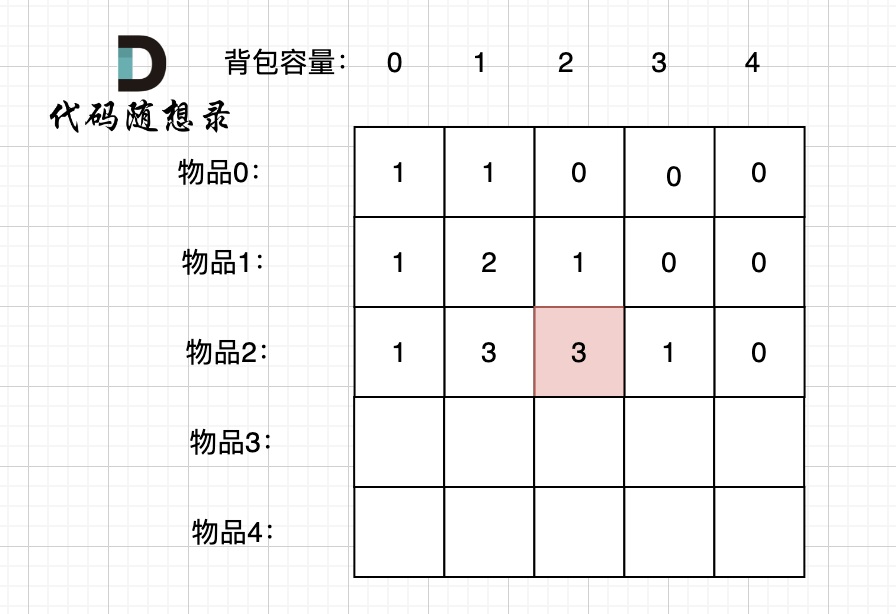
接下来 考虑 物品0 、物品1 和 物品2 ,如图:
-
+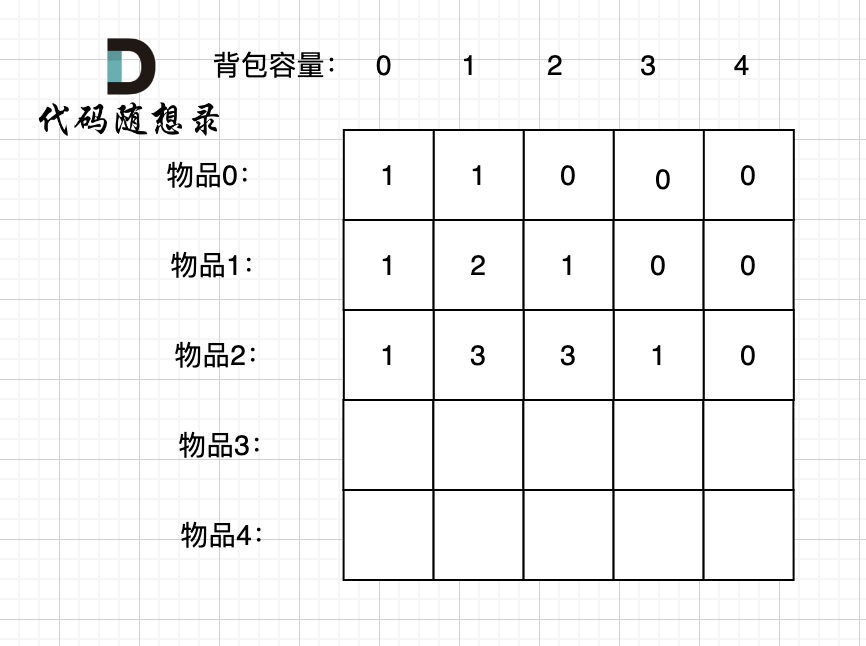
装满背包容量为0 的方法个数是1,即 放0件物品。
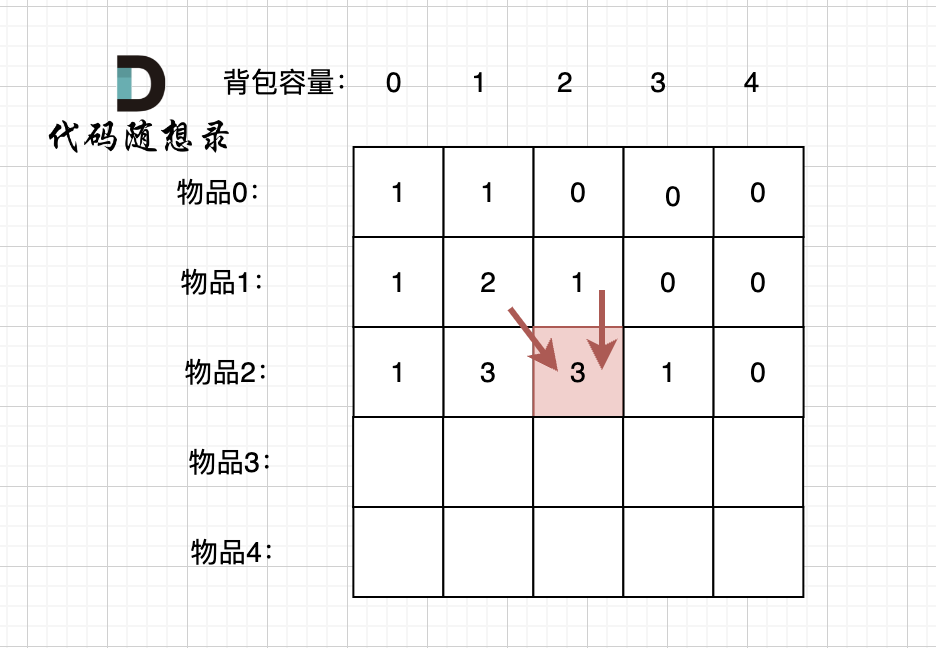
@@ -207,17 +207,17 @@ if (abs(target) > sum) return 0; // 此时没有方案
如图红色部分:
-
+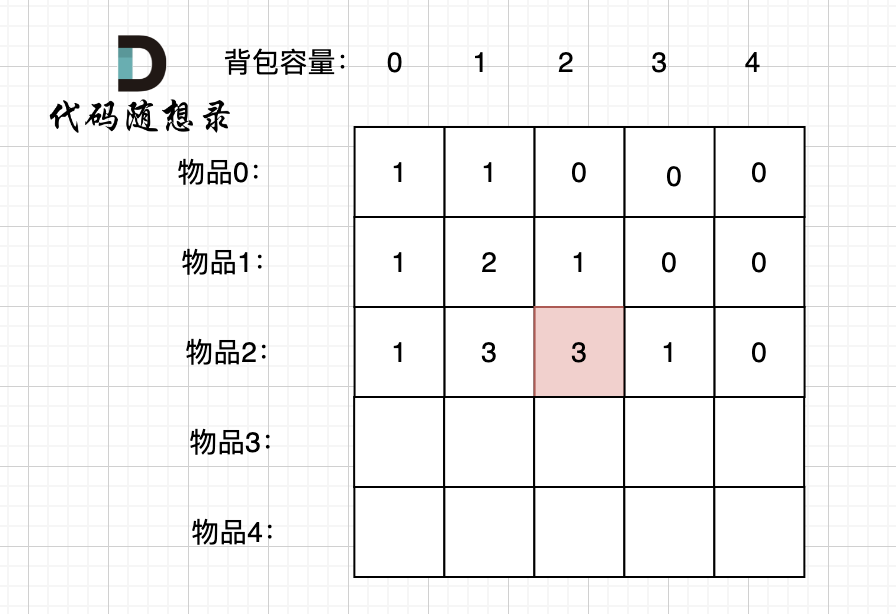
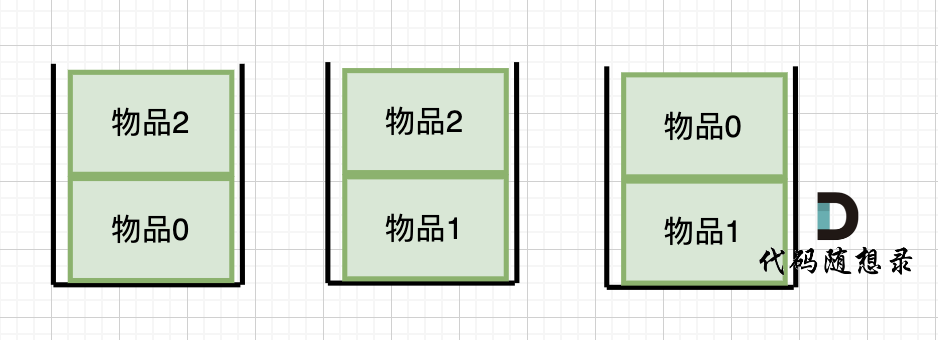
dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物品1 和 物品2, 如图所示,三种方法:
-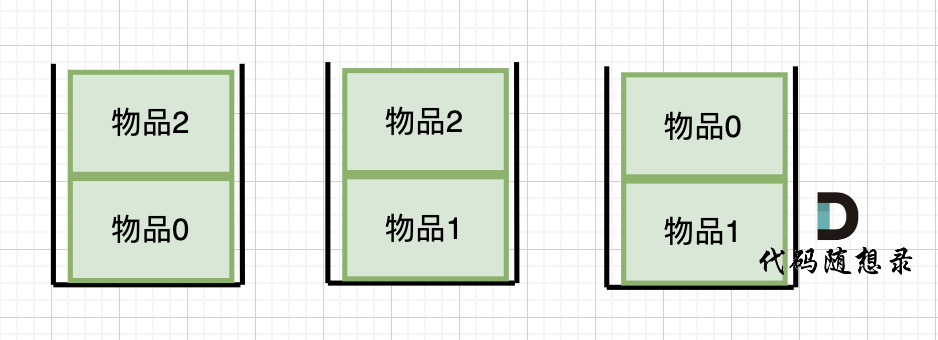
+
**容量为2 的背包,如果不放 物品2 有几种方法呢**?
有 dp[1][2] 种方法,即 背包容量为2,只考虑物品0 和 物品1 ,有 dp[1][2] 种方法,如图:
-
+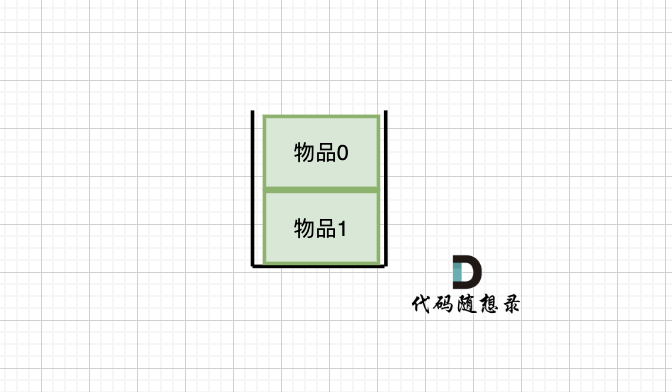
**容量为2 的背包, 如果放 物品2 有几种方法呢**?
@@ -229,7 +229,7 @@ dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物
如图:
-
+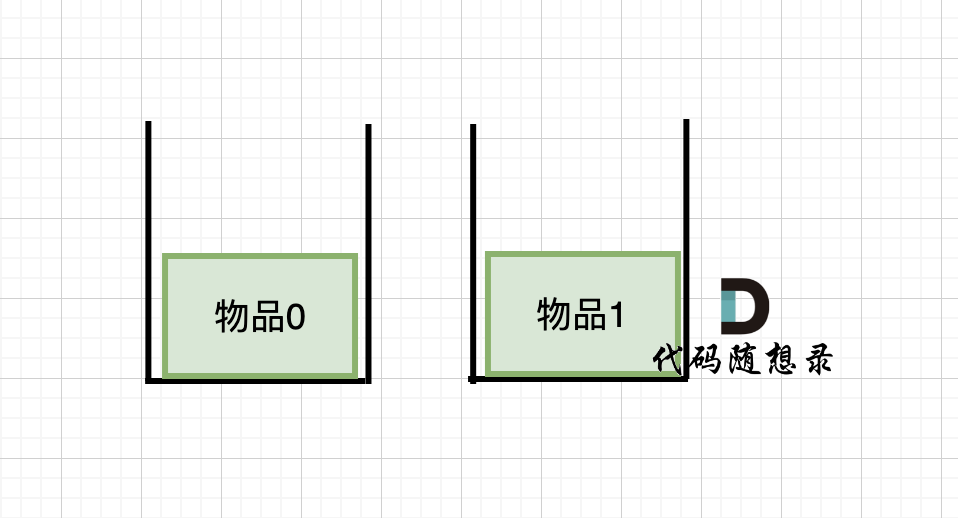
有录友可能疑惑,这里计算的是放满 容量为2的背包 有几种方法,那物品2去哪了?
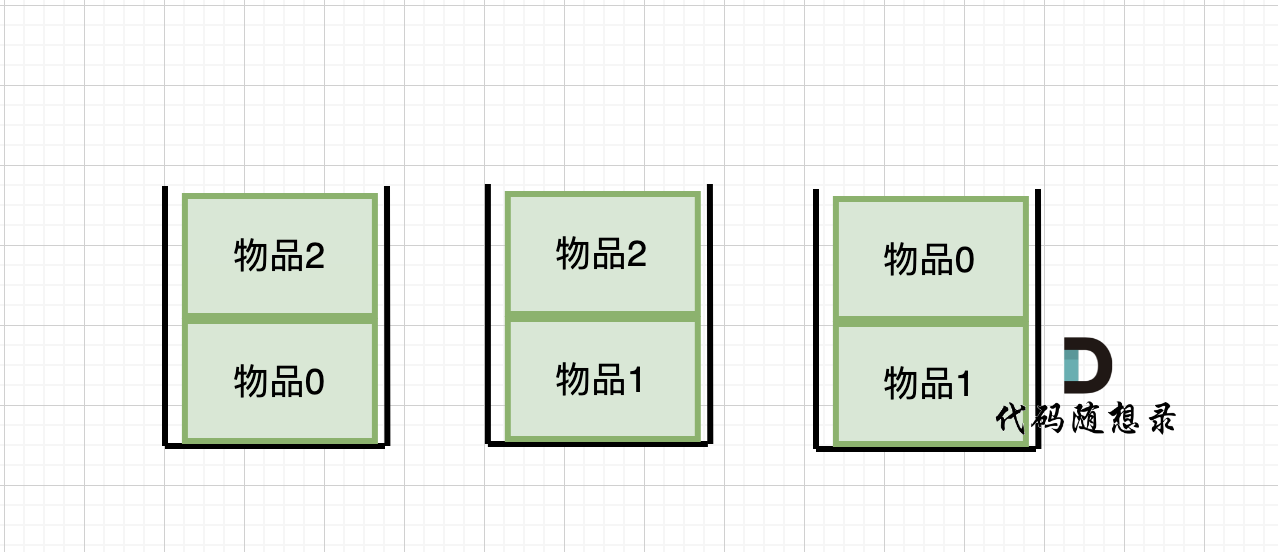
@@ -239,7 +239,7 @@ dp[2][2] = 容量为2的背包不放物品2有几种方法 + 容量为2的背包
所以 dp[2][2] = dp[1][2] + dp[1][1] ,如图:
-
+
以上过程,抽象化如下:
@@ -266,11 +266,11 @@ else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
先明确递推的方向,如图,求解 dp[2][2] 是由 上方和左上方推出。
-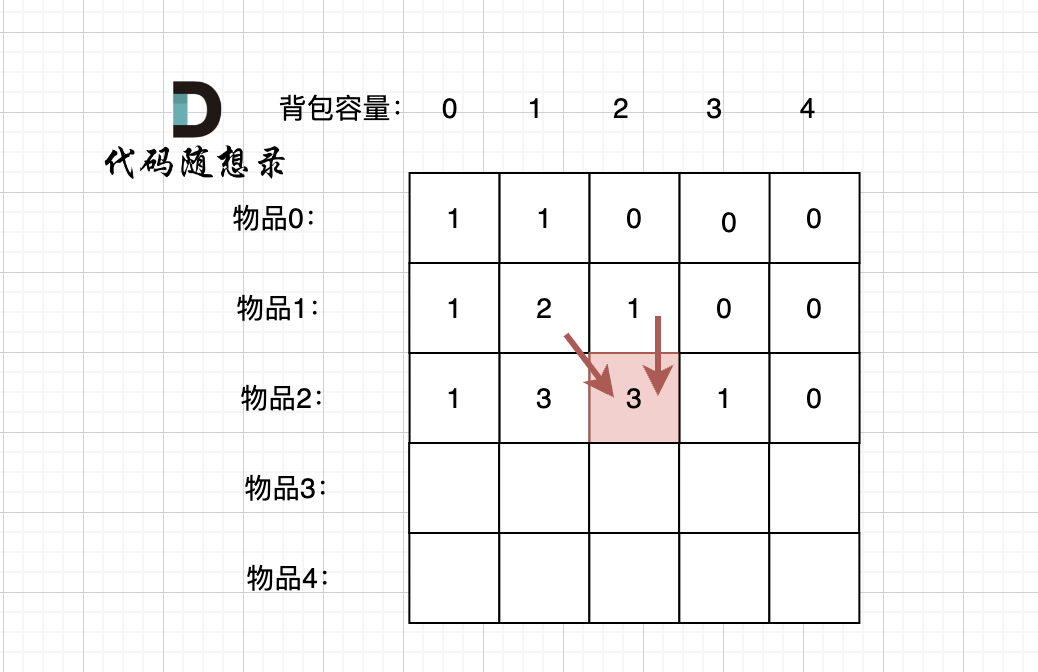
+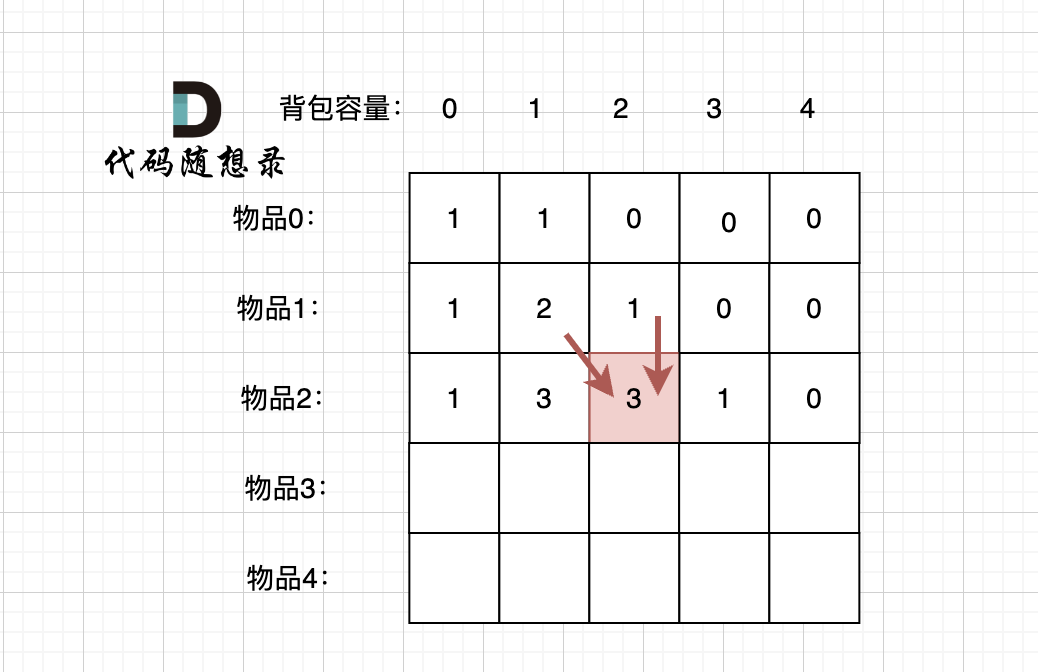
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,如图红色部分:
-
+
关于dp[0][0]的值,在上面的递推公式讲解中已经讲过,装满背包容量为0 的方法数量是1,即 放0件物品。
@@ -323,7 +323,7 @@ for (int i = 0; i < nums.size(); i++) {
例如下图,如果上方没数值,左上方没数值,就无法推出 dp[2][2]。
-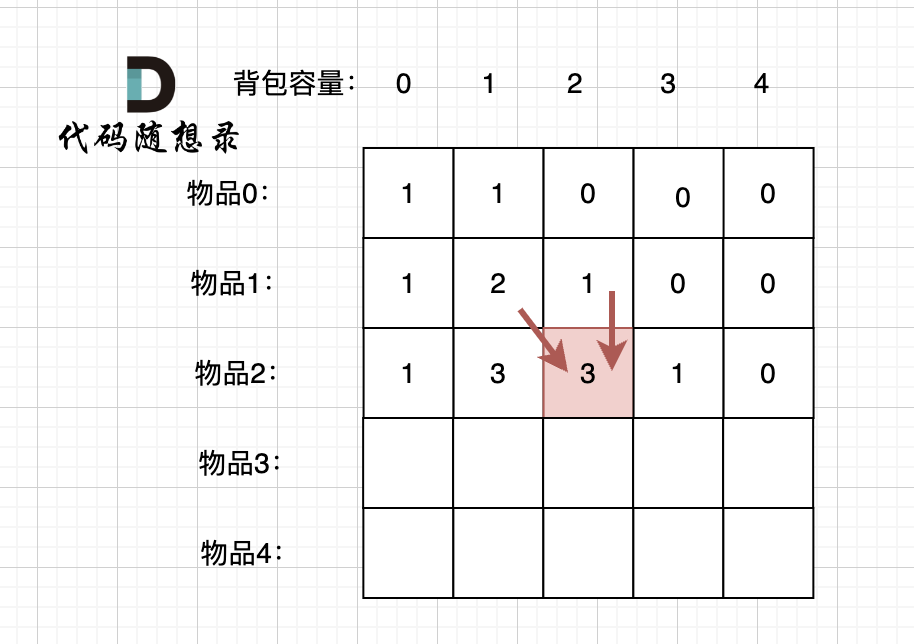
+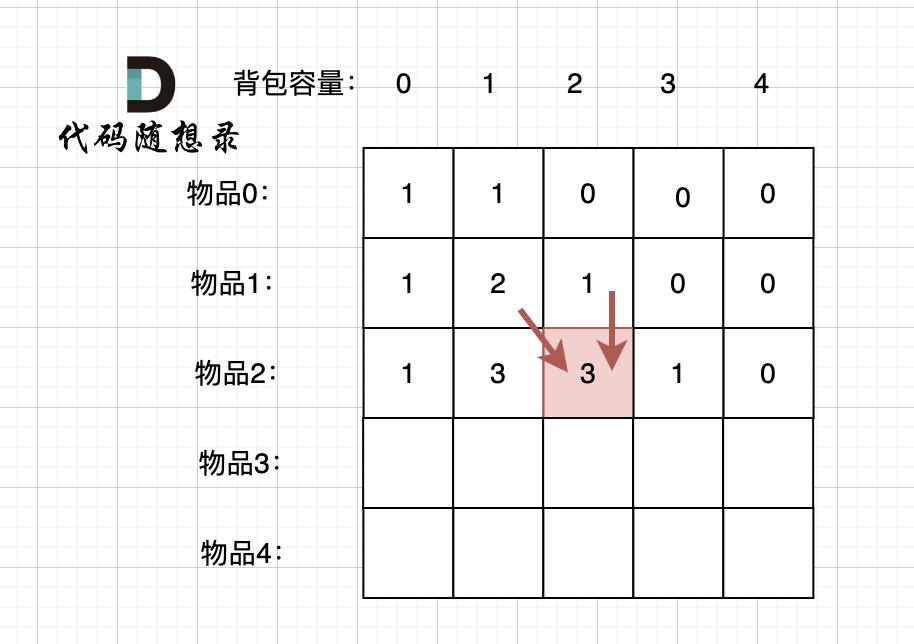
那么是先 从上到下 ,再从左到右遍历,例如这样:
@@ -349,11 +349,11 @@ for (int j = 0; j <= bagSize; j++) { // 列,遍历背包
这里我再画图讲一下,以求dp[2][2]为例,当先从上到下,再从左到右遍历,矩阵是这样:
-
+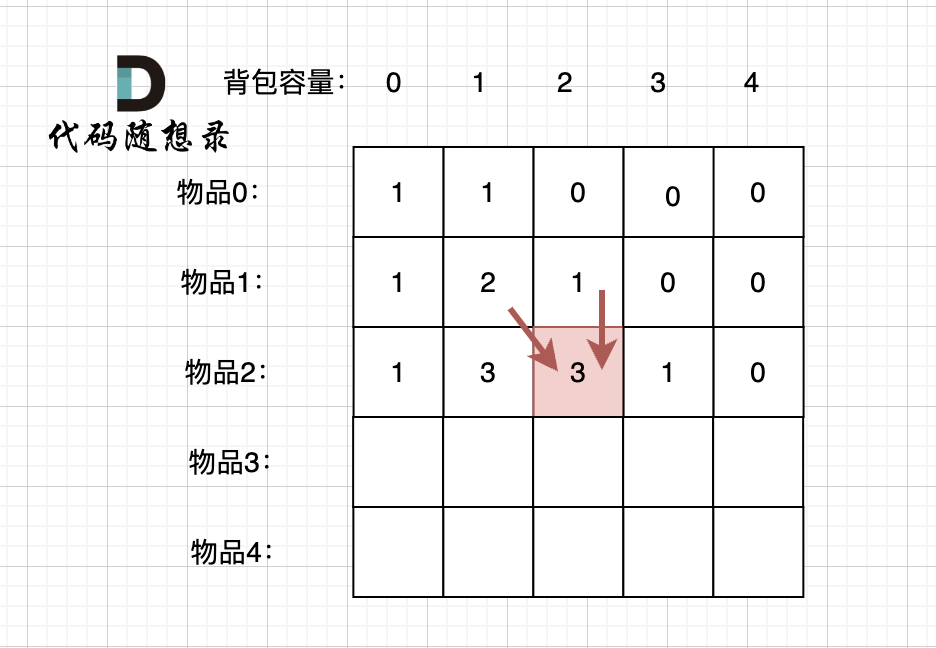
当先从左到右,再从上到下遍历,矩阵是这样:
-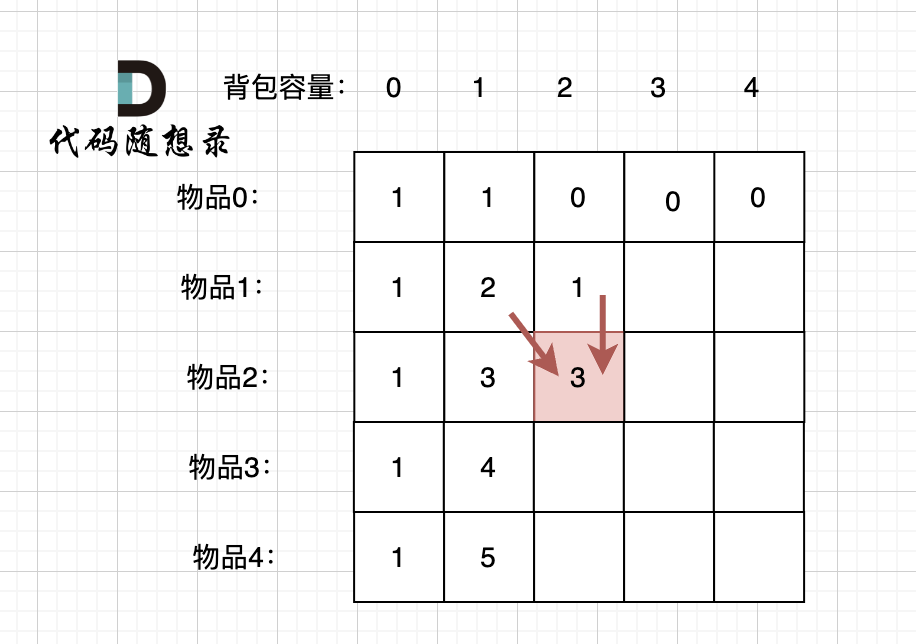
+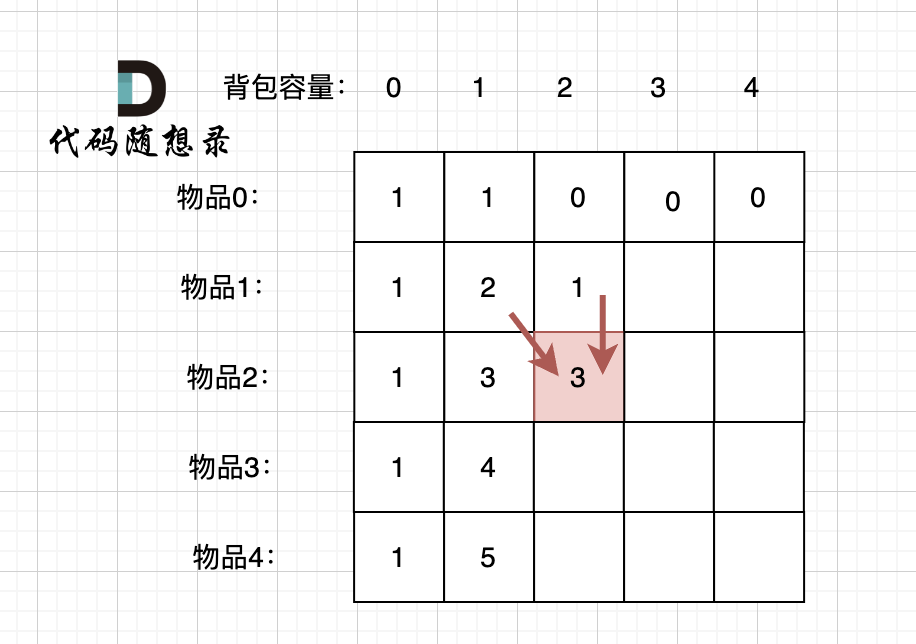
这里大家可以看出,无论是以上哪种遍历,都不影响 dp[2][2]的求值,用来 推导 dp[2][2] 的数值都在。
@@ -366,7 +366,7 @@ bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
-
+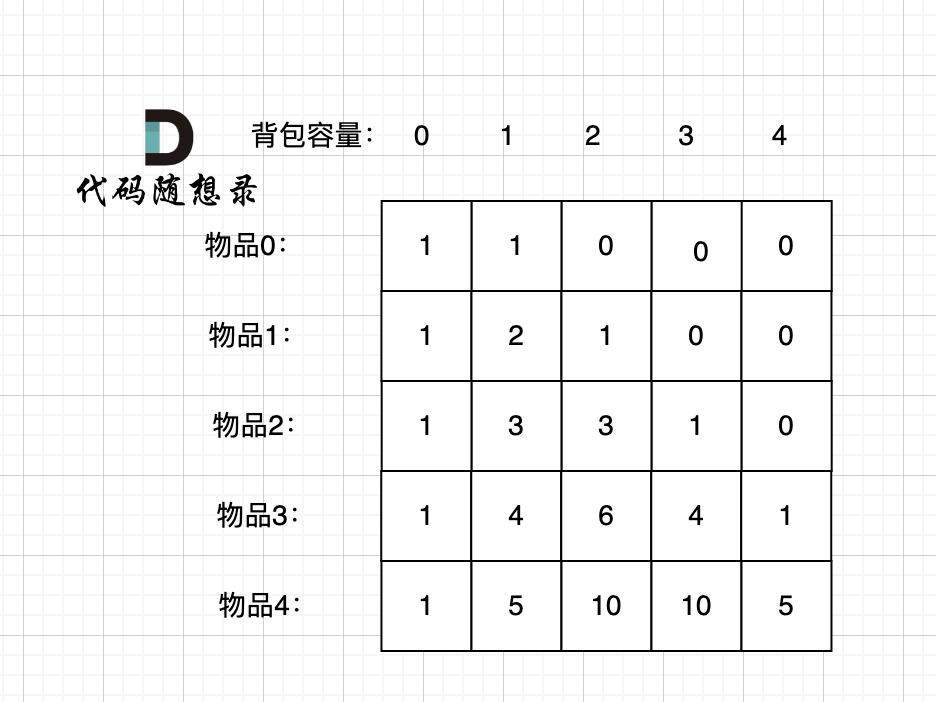
这么大的矩阵,我们是可以自己手动模拟出来的。
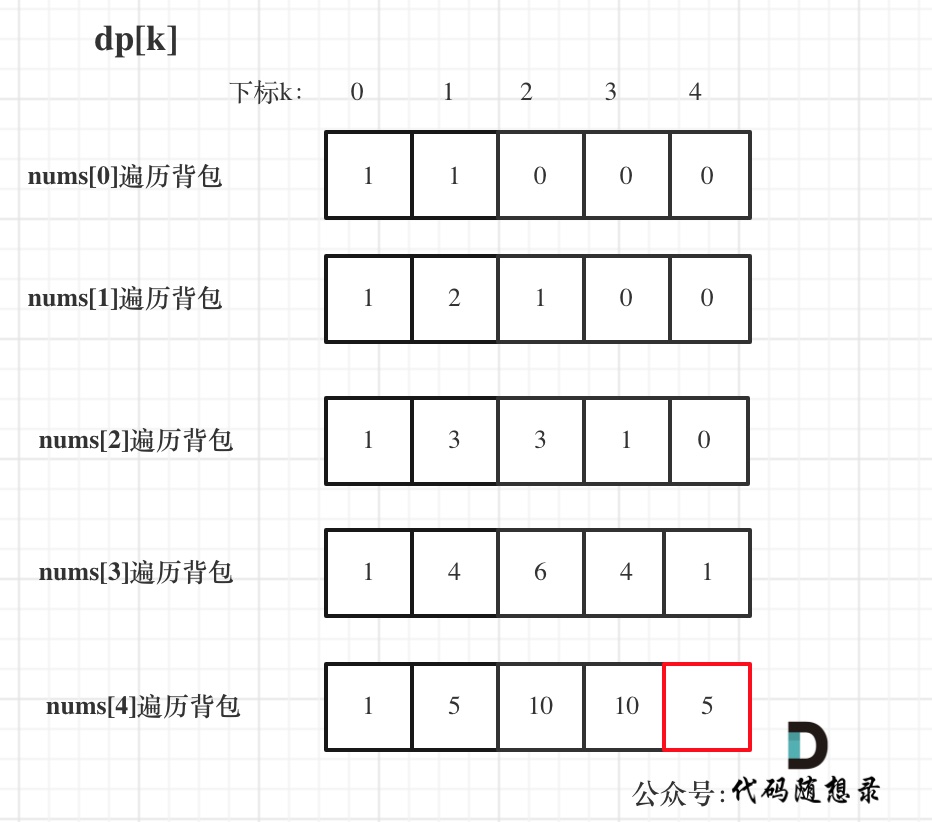
@@ -445,7 +445,7 @@ bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
-
+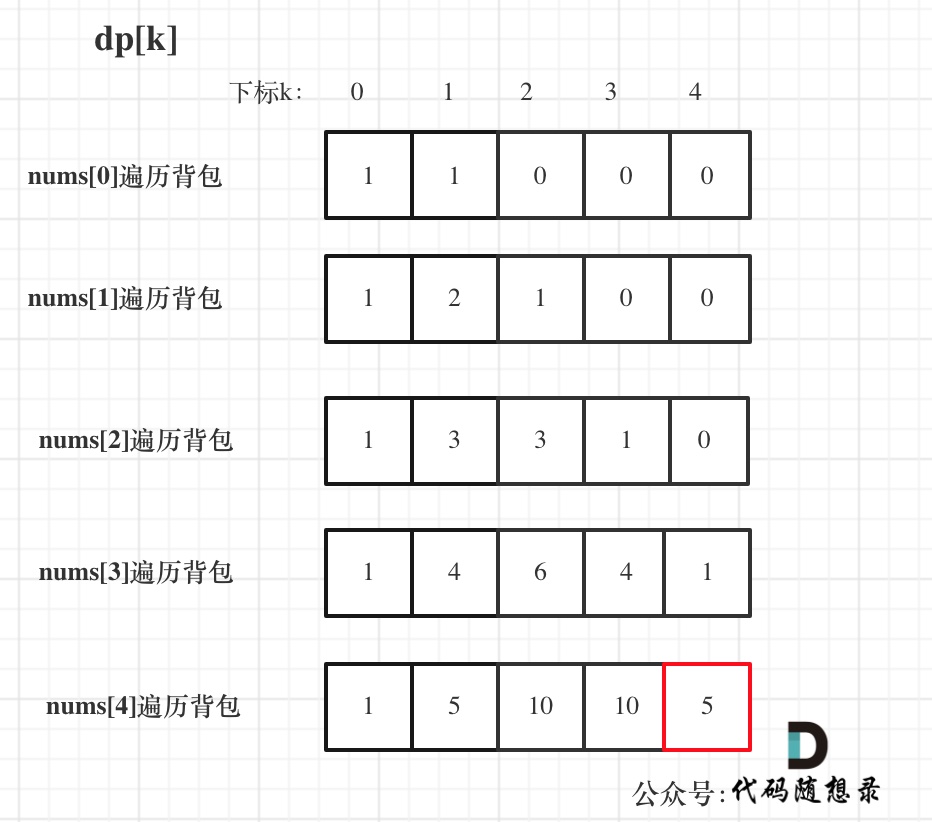
大家可以和 二维dp数组的打印结果做一下对比。
diff --git a/problems/0501.二叉搜索树中的众数.md b/problems/0501.二叉搜索树中的众数.md
index 32a89e85..8cca8e65 100644
--- a/problems/0501.二叉搜索树中的众数.md
+++ b/problems/0501.二叉搜索树中的众数.md
@@ -23,7 +23,7 @@
给定 BST [1,null,2,2],
-
+
返回[2].
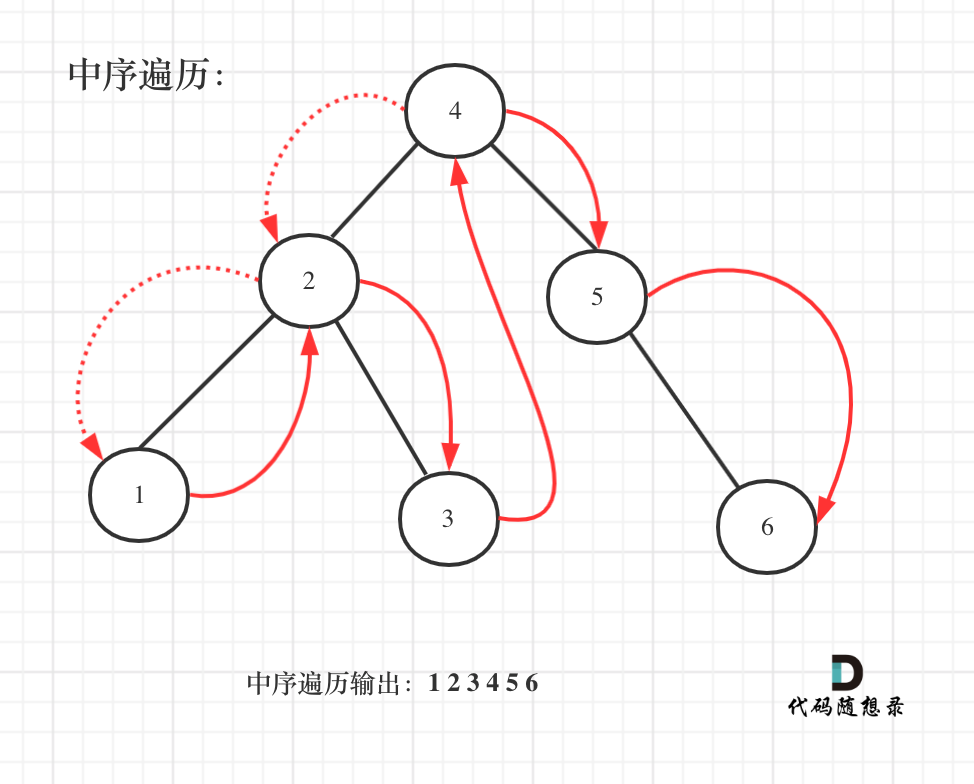
@@ -144,7 +144,7 @@ public:
如图:
-
+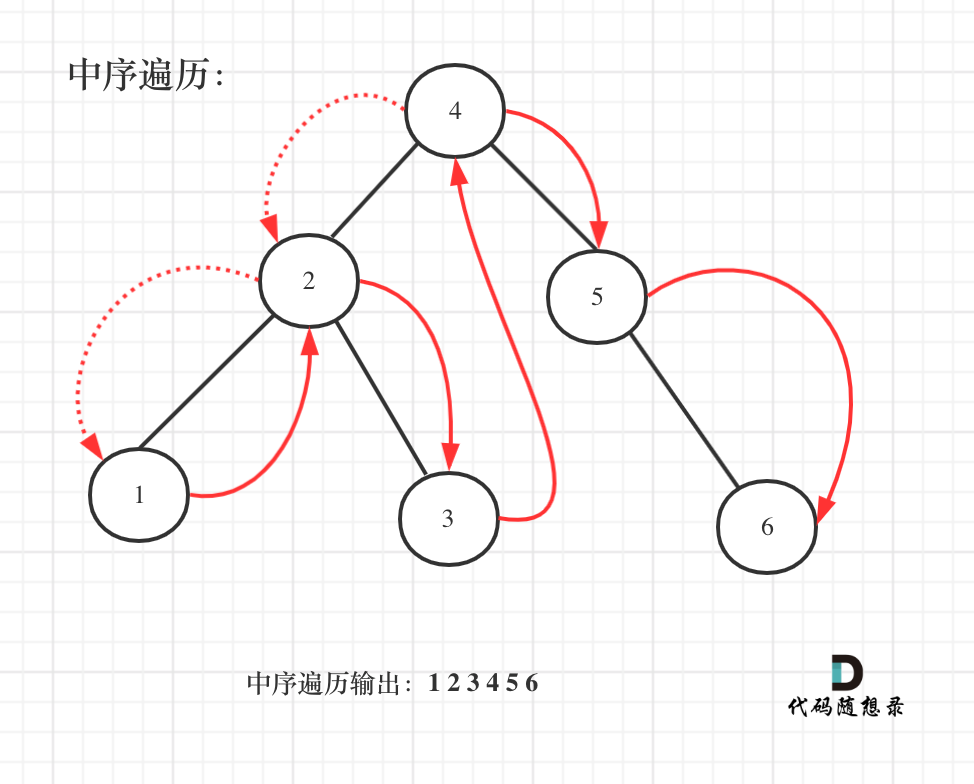
中序遍历代码如下:
diff --git a/problems/0513.找树左下角的值.md b/problems/0513.找树左下角的值.md
index da373603..4098cb7b 100644
--- a/problems/0513.找树左下角的值.md
+++ b/problems/0513.找树左下角的值.md
@@ -12,11 +12,11 @@
示例 1:
-
+
示例 2:
-
+
## 算法公开课
diff --git a/problems/0516.最长回文子序列.md b/problems/0516.最长回文子序列.md
index f0ef2f53..5e456ac9 100644
--- a/problems/0516.最长回文子序列.md
+++ b/problems/0516.最长回文子序列.md
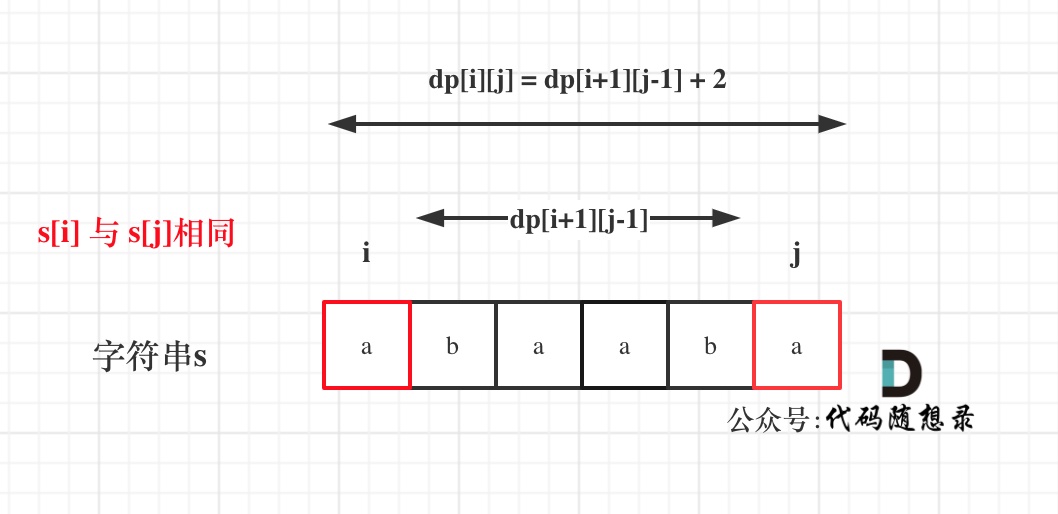
@@ -56,7 +56,7 @@
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如图:
-
+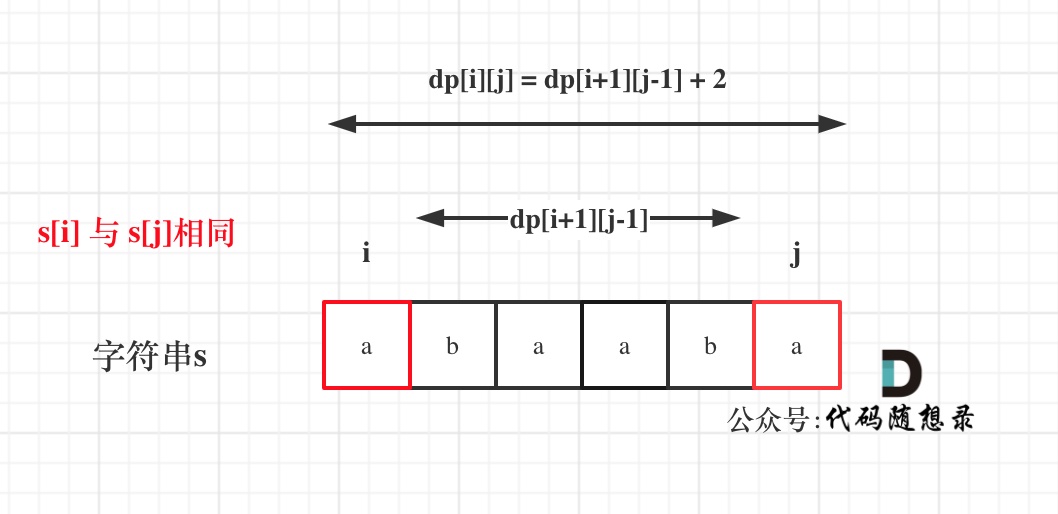
(如果这里看不懂,回忆一下dp[i][j]的定义)
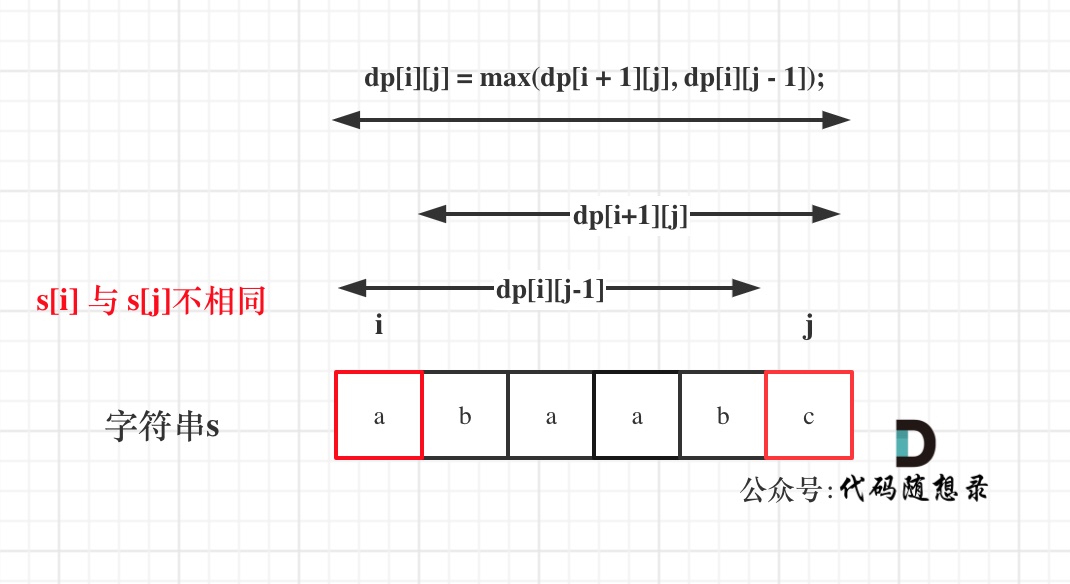
@@ -68,7 +68,7 @@
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
-
+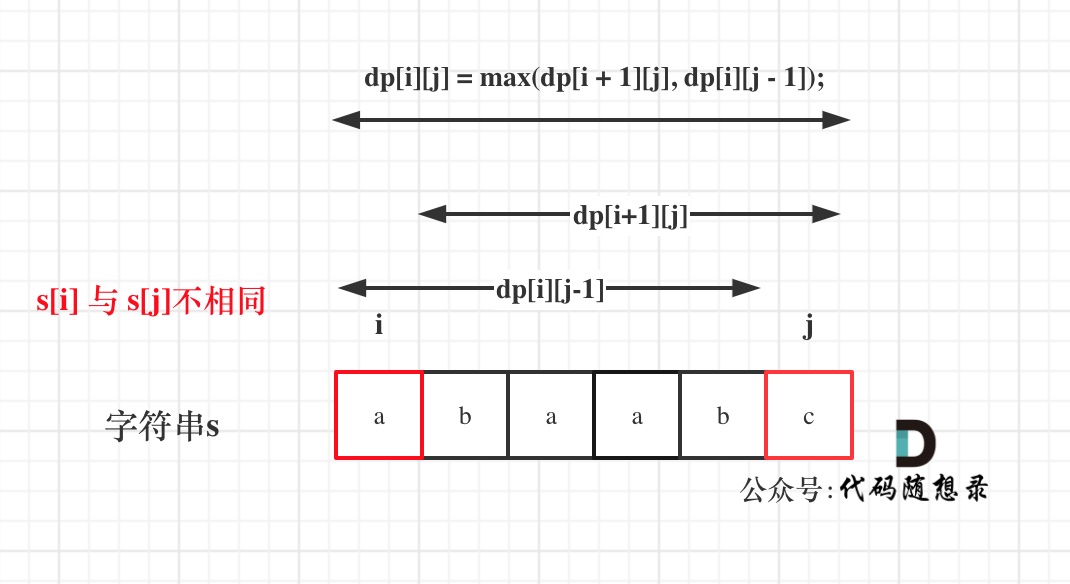
代码如下:
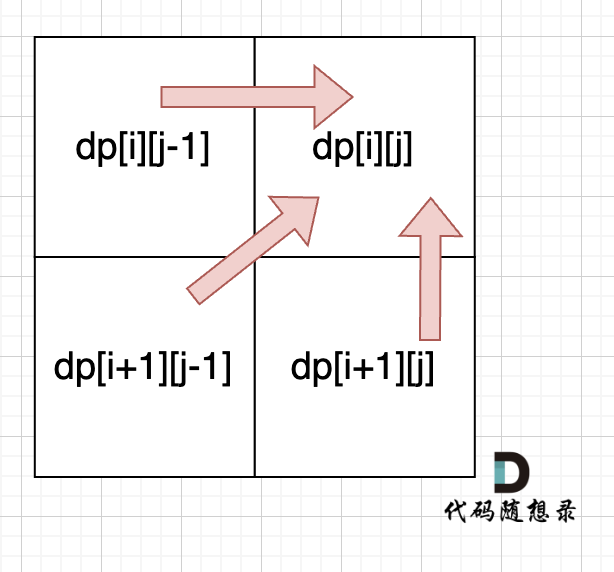
@@ -97,7 +97,7 @@ for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],如图:
-
+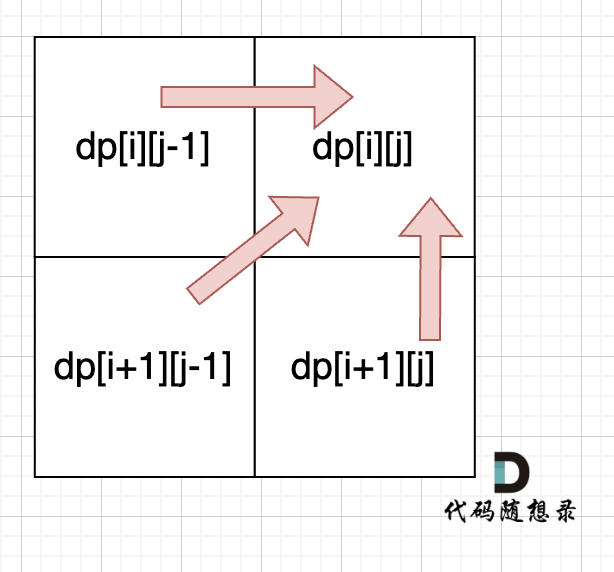
**所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的**。
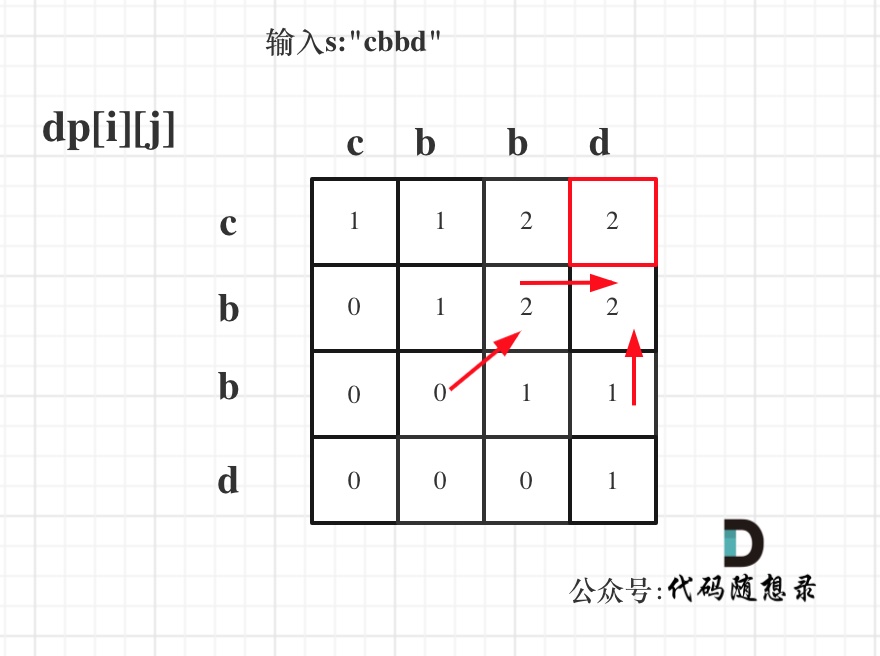
@@ -121,7 +121,7 @@ for (int i = s.size() - 1; i >= 0; i--) {
输入s:"cbbd" 为例,dp数组状态如图:
-
+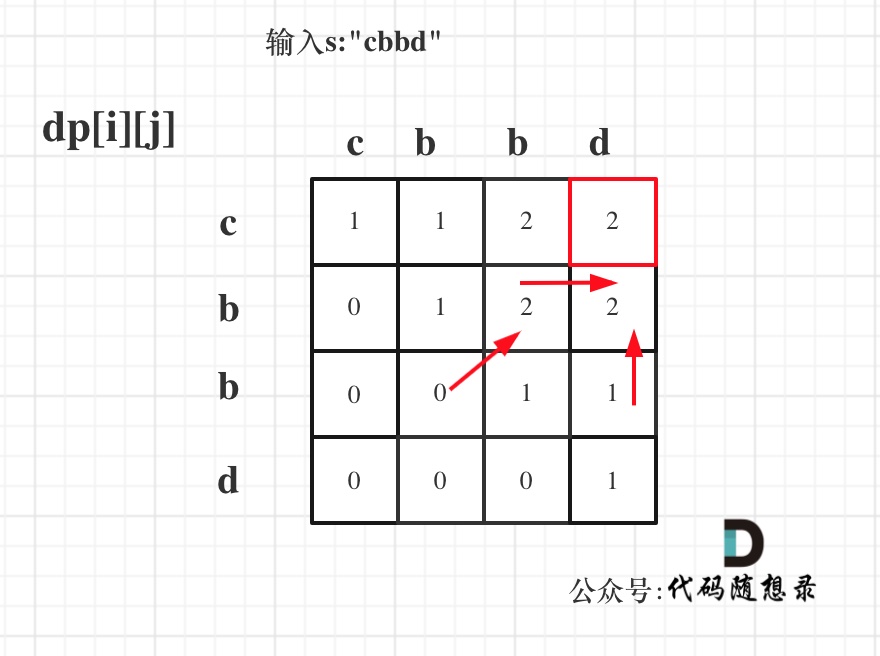
红色框即:dp[0][s.size() - 1]; 为最终结果。
diff --git a/problems/0518.零钱兑换II.md b/problems/0518.零钱兑换II.md
index 1698db98..95122a7c 100644
--- a/problems/0518.零钱兑换II.md
+++ b/problems/0518.零钱兑换II.md
@@ -136,7 +136,7 @@
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,如图红色部分:
-
+
这里首先要关注的就是 dp[0][0] 应该是多少?
@@ -296,7 +296,7 @@ for (int j = 0; j <= amount; j++) { // 遍历背包容量
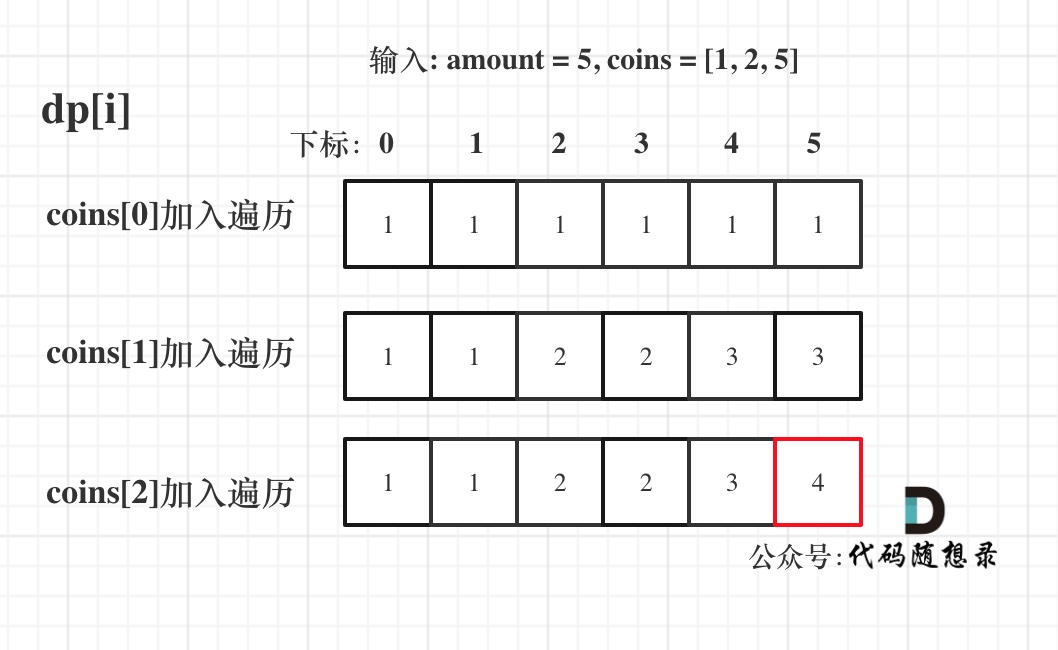
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
-
+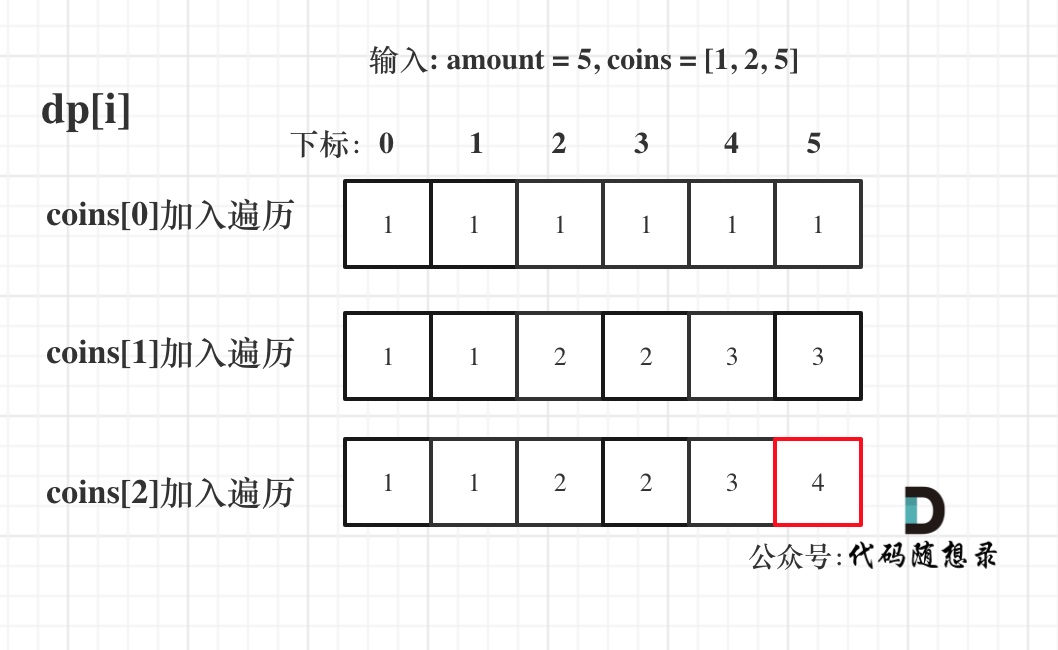
最后红色框dp[amount]为最终结果。
diff --git a/problems/0530.二叉搜索树的最小绝对差.md b/problems/0530.二叉搜索树的最小绝对差.md
index d7b0e056..466bd744 100644
--- a/problems/0530.二叉搜索树的最小绝对差.md
+++ b/problems/0530.二叉搜索树的最小绝对差.md
@@ -13,7 +13,7 @@
示例:
-
+
提示:树中至少有 2 个节点。
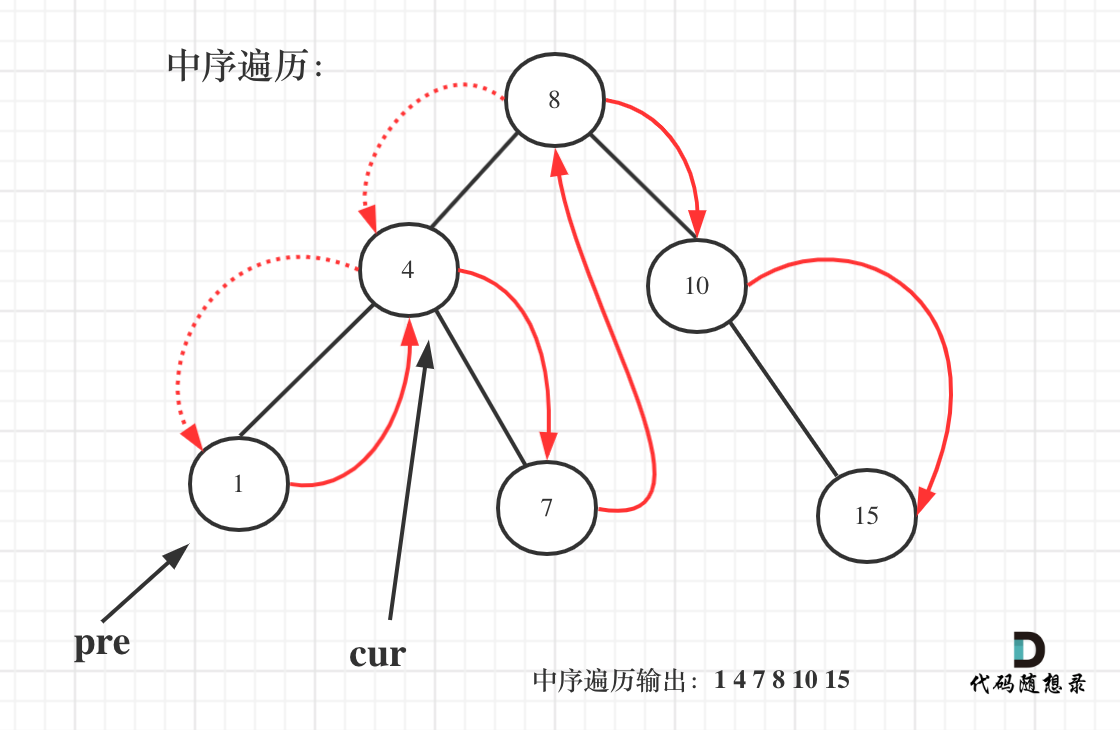
@@ -70,7 +70,7 @@ public:
如图:
-
+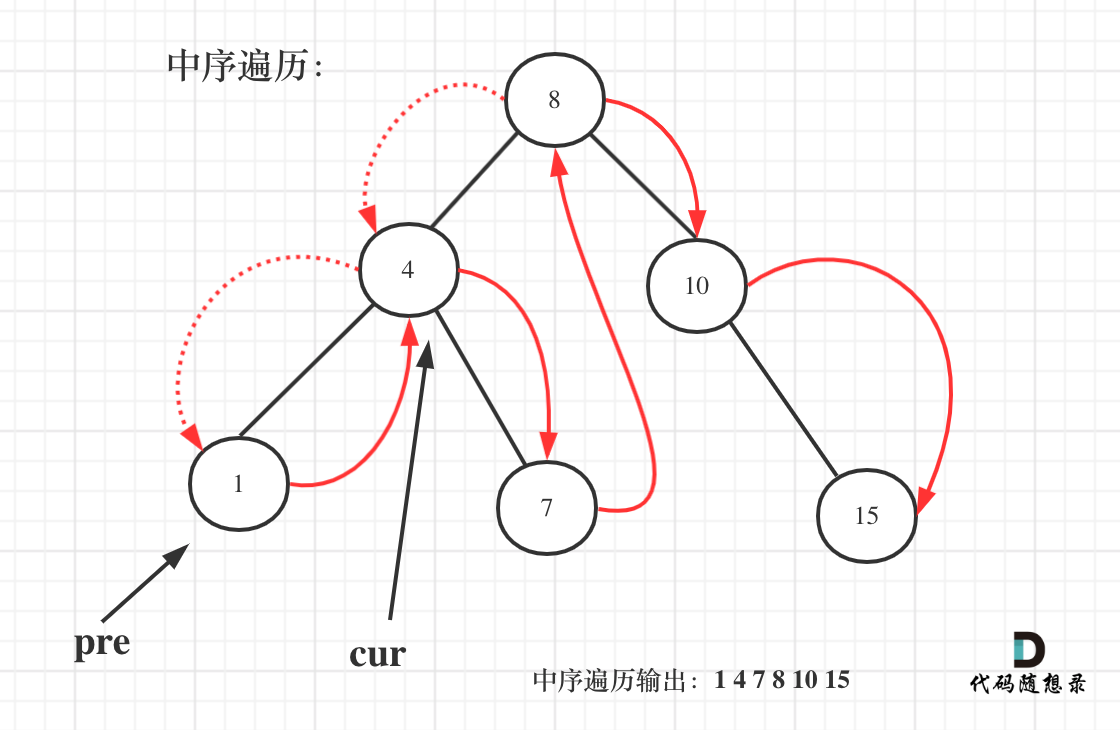
一些同学不知道在递归中如何记录前一个节点的指针,其实实现起来是很简单的,大家只要看过一次,写过一次,就掌握了。
diff --git a/problems/0538.把二叉搜索树转换为累加树.md b/problems/0538.把二叉搜索树转换为累加树.md
index 1bbbdac7..45bf1f96 100644
--- a/problems/0538.把二叉搜索树转换为累加树.md
+++ b/problems/0538.把二叉搜索树转换为累加树.md
@@ -18,7 +18,7 @@
示例 1:
-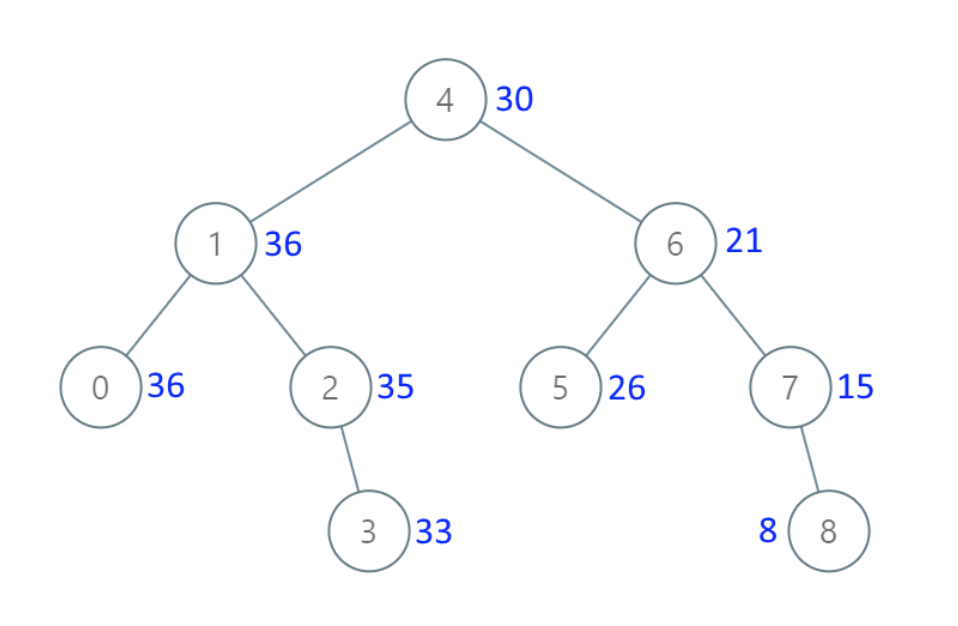
+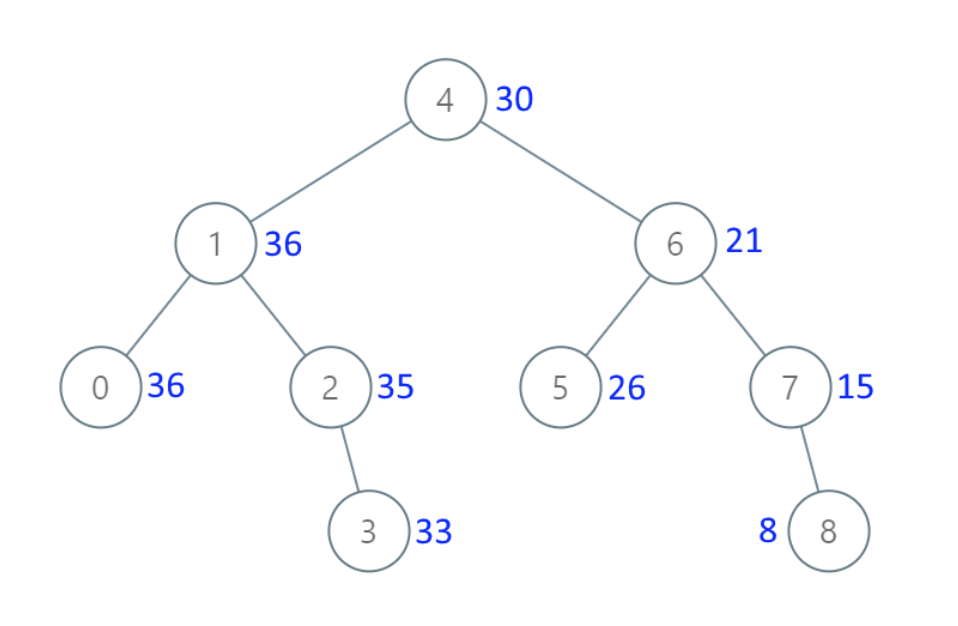
* 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
* 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
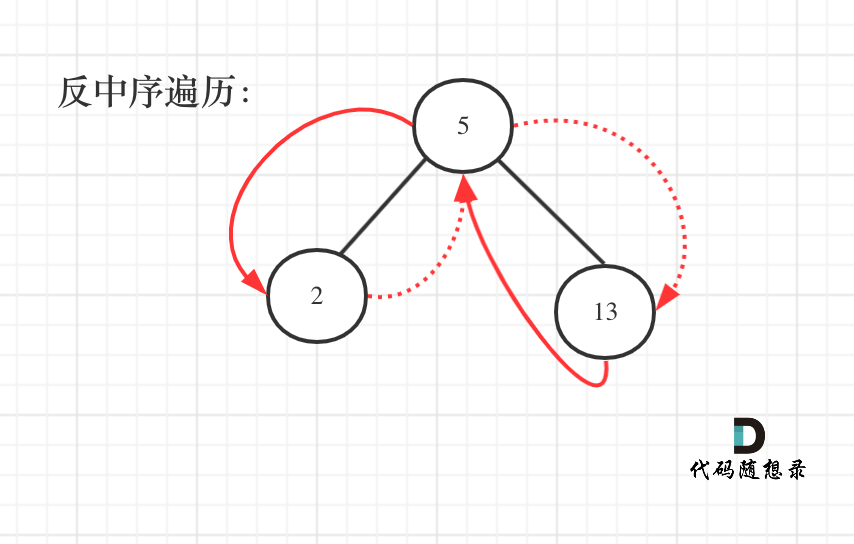
@@ -67,7 +67,7 @@
遍历顺序如图所示:
-
+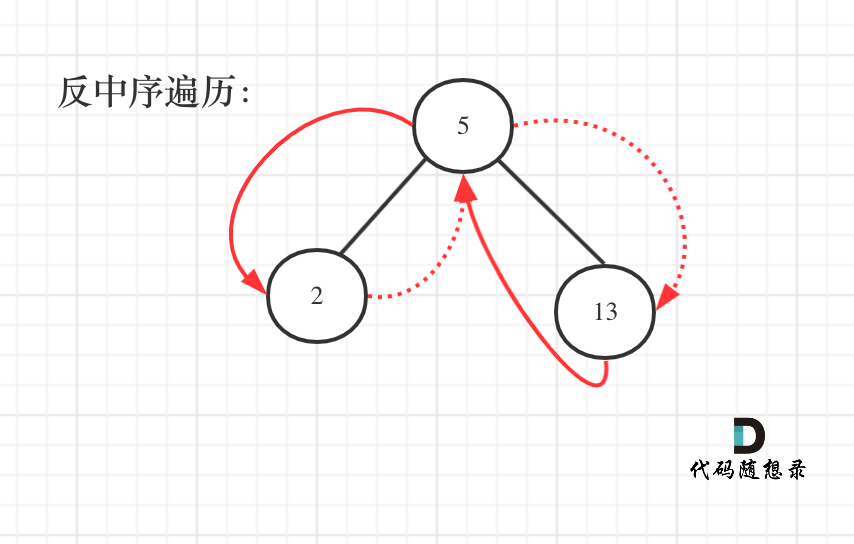
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
diff --git a/problems/0583.两个字符串的删除操作.md b/problems/0583.两个字符串的删除操作.md
index a86dfad1..7f7d30f6 100644
--- a/problems/0583.两个字符串的删除操作.md
+++ b/problems/0583.两个字符串的删除操作.md
@@ -81,7 +81,7 @@ for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
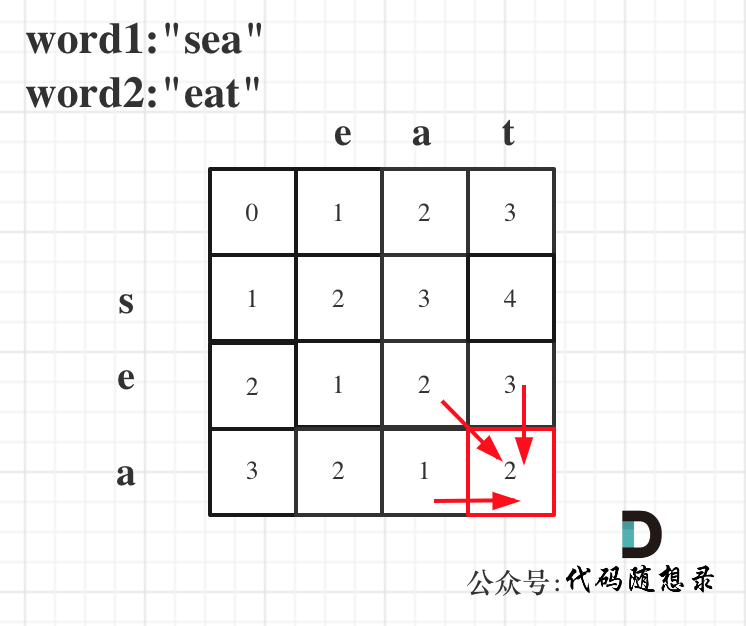
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
-
+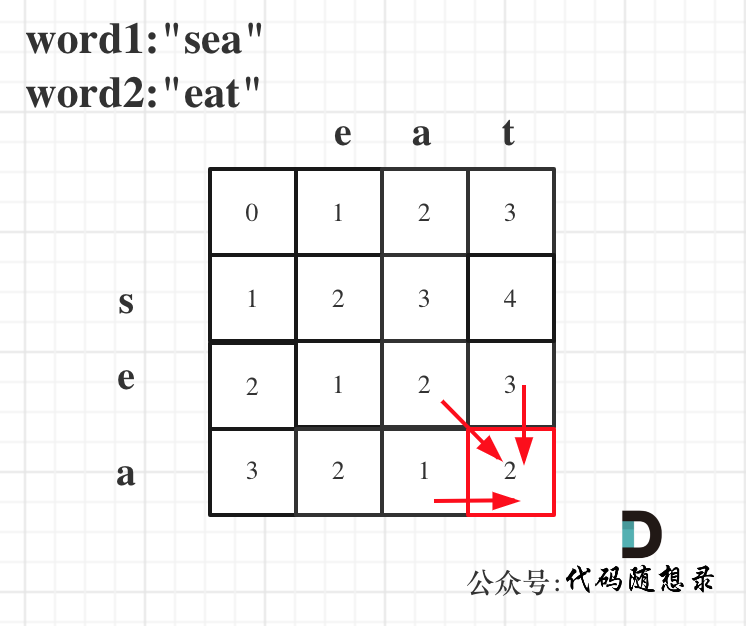
以上分析完毕,代码如下:
diff --git a/problems/0617.合并二叉树.md b/problems/0617.合并二叉树.md
index f180c4f3..755200fe 100644
--- a/problems/0617.合并二叉树.md
+++ b/problems/0617.合并二叉树.md
@@ -13,7 +13,7 @@
示例 1:
-
+
注意: 合并必须从两个树的根节点开始。
diff --git a/problems/0647.回文子串.md b/problems/0647.回文子串.md
index e2783027..72829535 100644
--- a/problems/0647.回文子串.md
+++ b/problems/0647.回文子串.md
@@ -48,7 +48,7 @@ dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
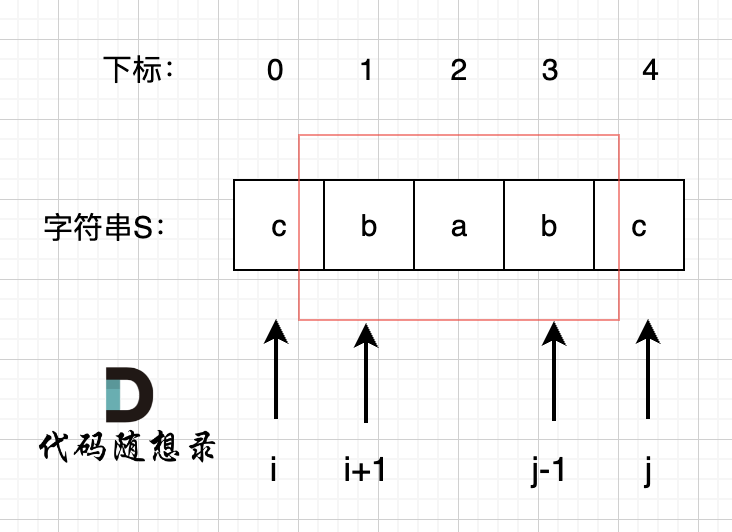
所以我们要看回文串的性质。 如图:
-
+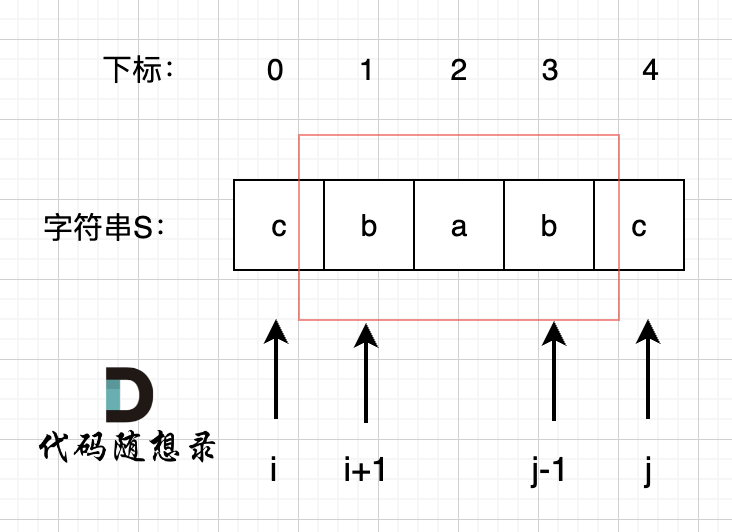
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
@@ -106,7 +106,7 @@ dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹
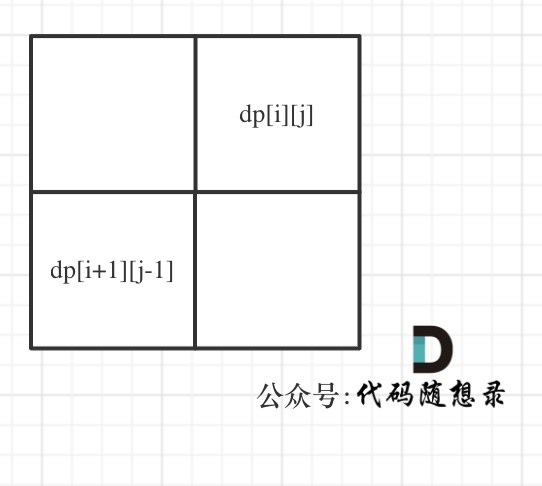
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
-
+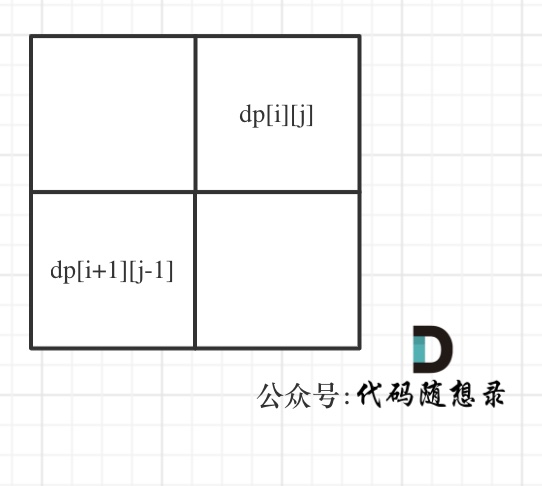
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
@@ -136,7 +136,7 @@ for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
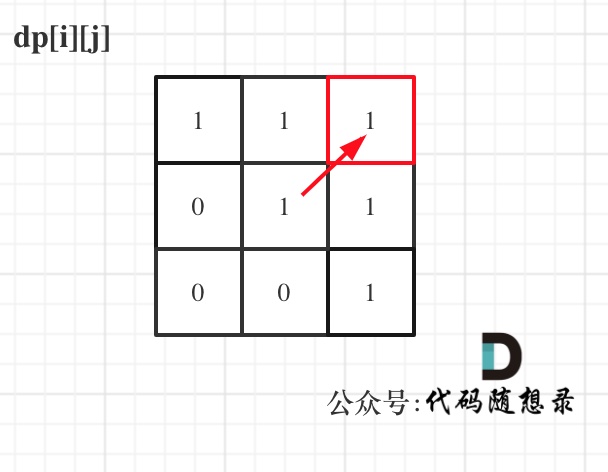
举例,输入:"aaa",dp[i][j]状态如下:
-
+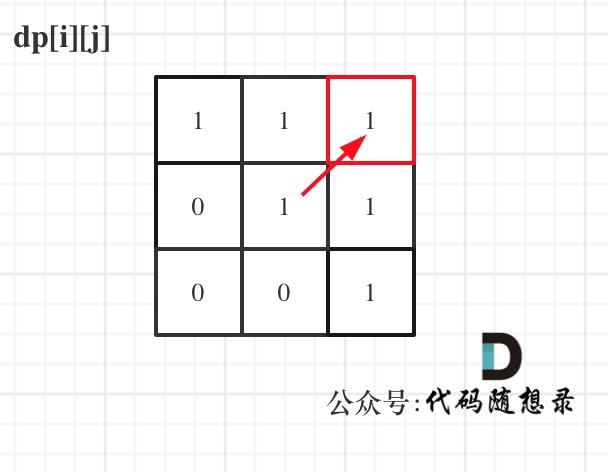
图中有6个true,所以就是有6个回文子串。
diff --git a/problems/0654.最大二叉树.md b/problems/0654.最大二叉树.md
index 9f897a75..b8841a8b 100644
--- a/problems/0654.最大二叉树.md
+++ b/problems/0654.最大二叉树.md
@@ -17,7 +17,7 @@
示例 :
-
+
提示:
diff --git a/problems/0669.修剪二叉搜索树.md b/problems/0669.修剪二叉搜索树.md
index 0a05360b..f4ded2c4 100644
--- a/problems/0669.修剪二叉搜索树.md
+++ b/problems/0669.修剪二叉搜索树.md
@@ -14,9 +14,9 @@
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
-
+
-
+
## 算法公开课
@@ -50,7 +50,7 @@ public:
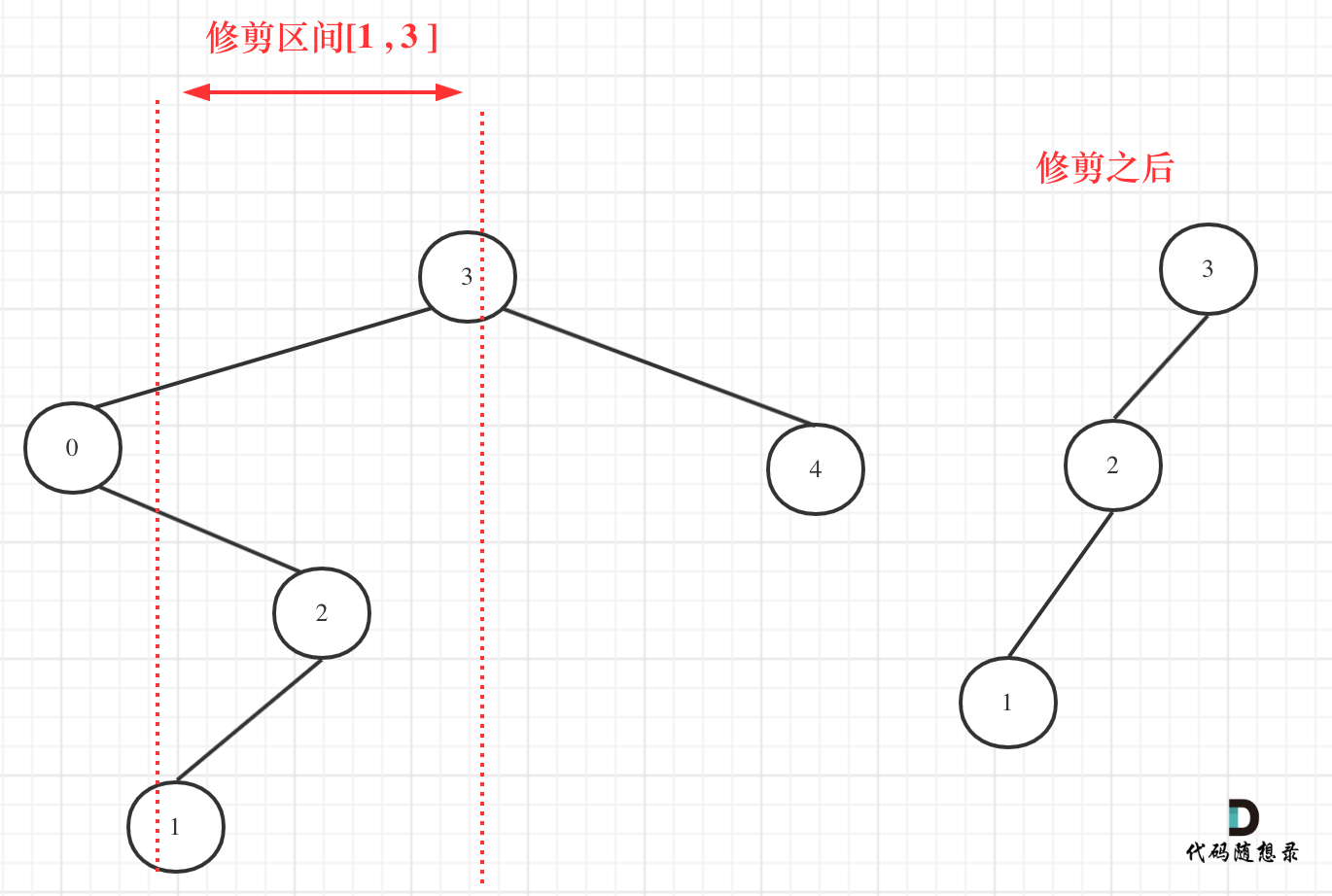
我们在重新关注一下第二个示例,如图:
-
+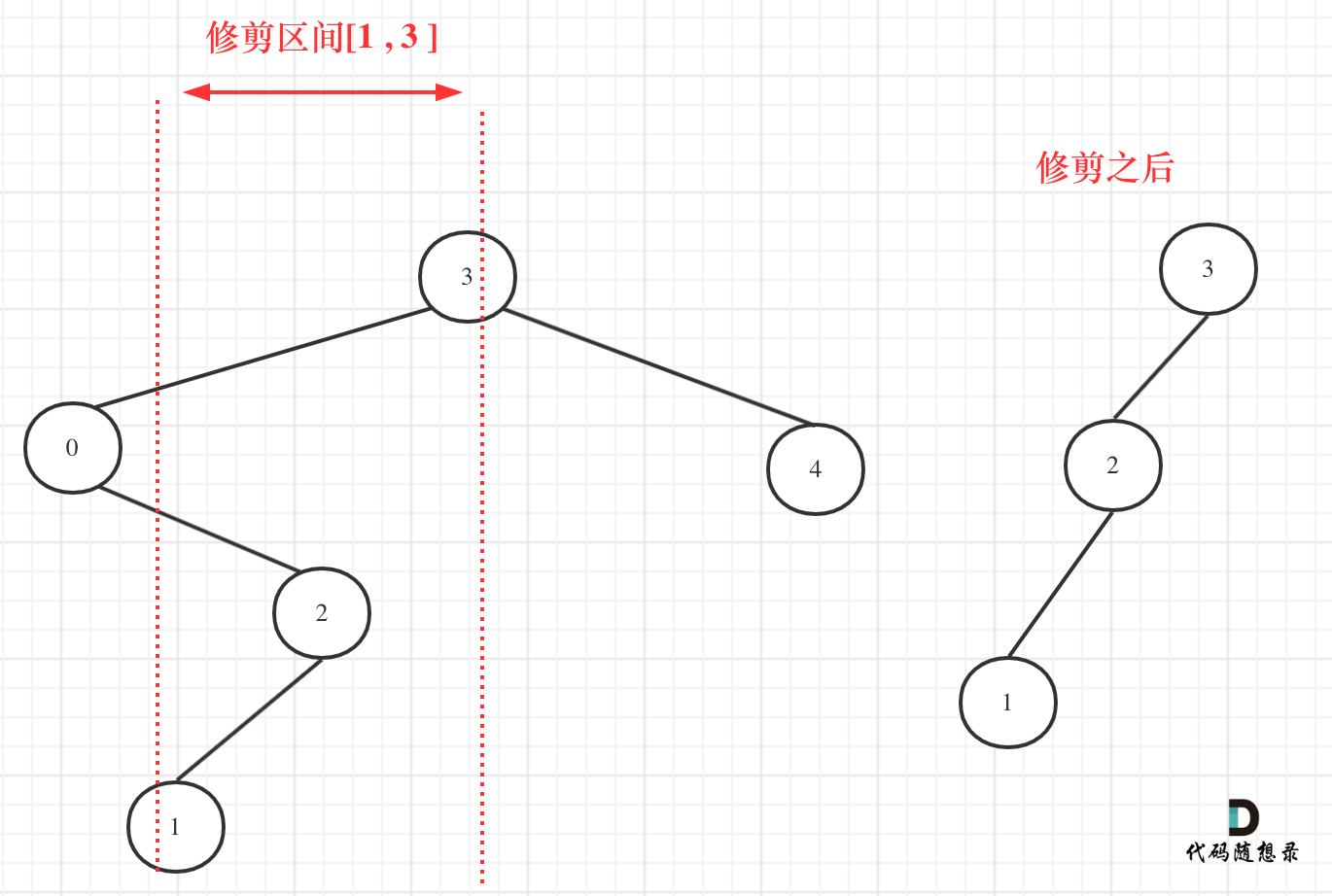
**所以以上的代码是不可行的!**
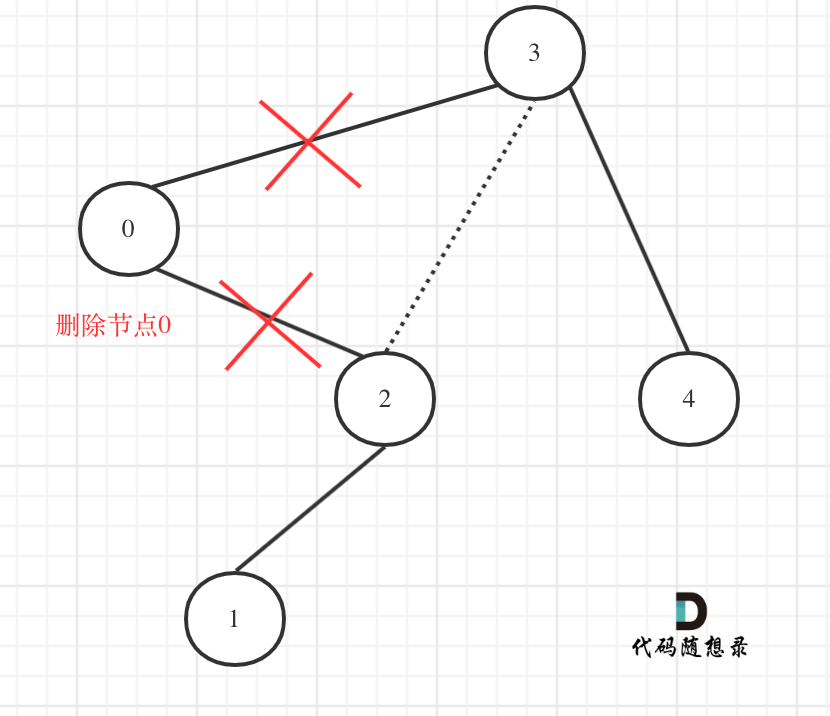
@@ -60,7 +60,7 @@ public:
在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点0从二叉树中移除),如图:
-
+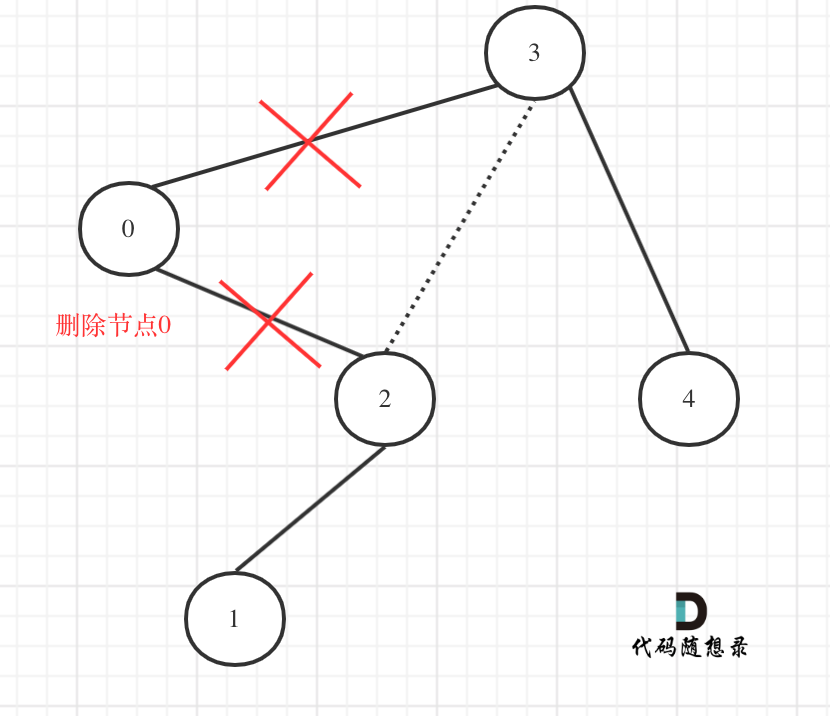
理解了最关键部分了我们再递归三部曲:
@@ -127,7 +127,7 @@ return root;
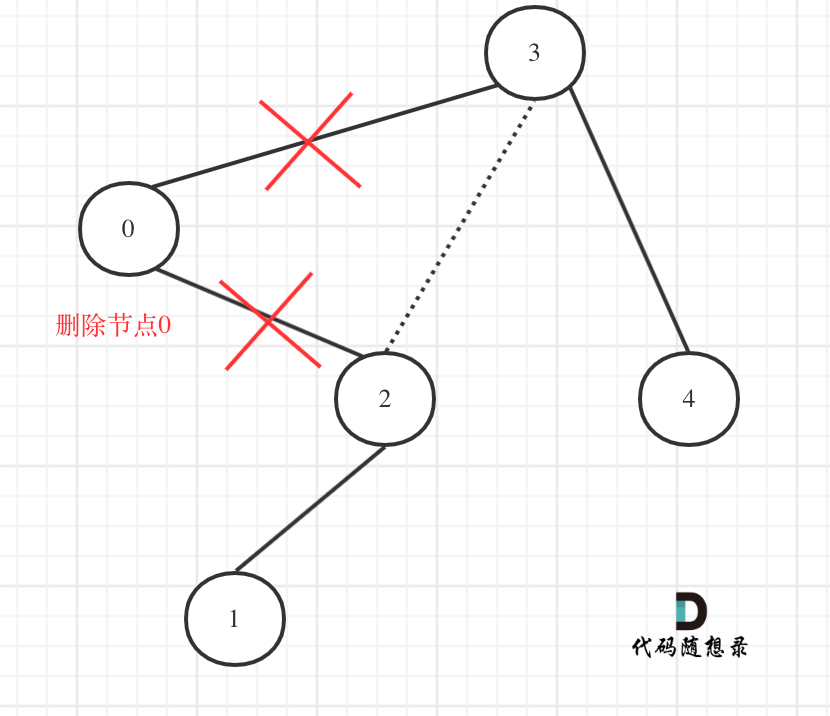
在回顾一下上面的代码,针对下图中二叉树的情况:
-
+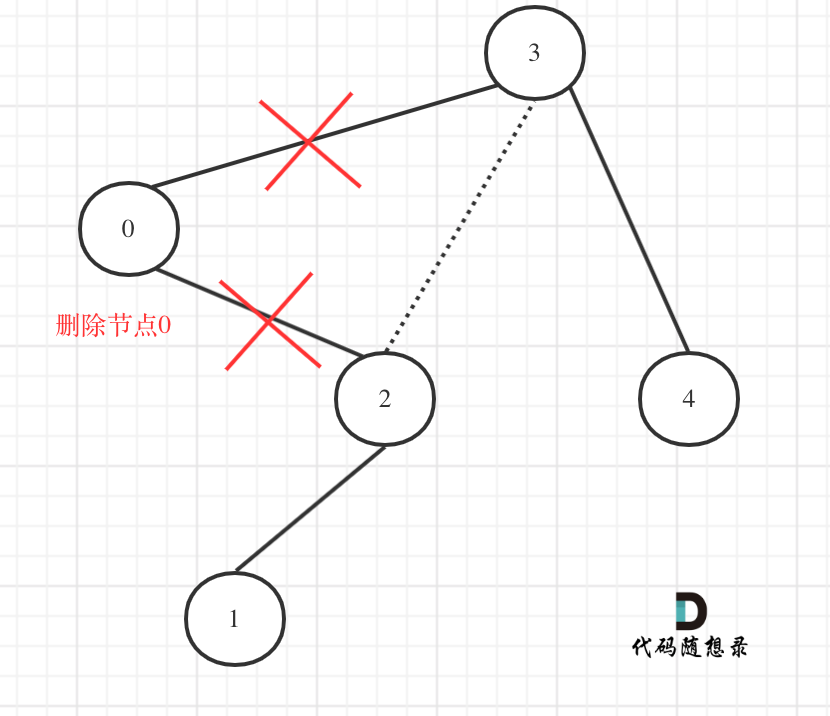
如下代码相当于把节点0的右孩子(节点2)返回给上一层,
diff --git a/problems/0673.最长递增子序列的个数.md b/problems/0673.最长递增子序列的个数.md
index 9bfa91cc..92009f5b 100644
--- a/problems/0673.最长递增子序列的个数.md
+++ b/problems/0673.最长递增子序列的个数.md
@@ -178,7 +178,7 @@ for (int i = 0; i < nums.size(); i++) {
输入:[1,3,5,4,7]
-
+
**如果代码写出来了,怎么改都通过不了,那么把dp和count打印出来看看对不对!**
diff --git a/problems/0674.最长连续递增序列.md b/problems/0674.最长连续递增序列.md
index 2c490c0c..16bb2f18 100644
--- a/problems/0674.最长连续递增序列.md
+++ b/problems/0674.最长连续递增序列.md
@@ -85,7 +85,7 @@ for (int i = 1; i < nums.size(); i++) {
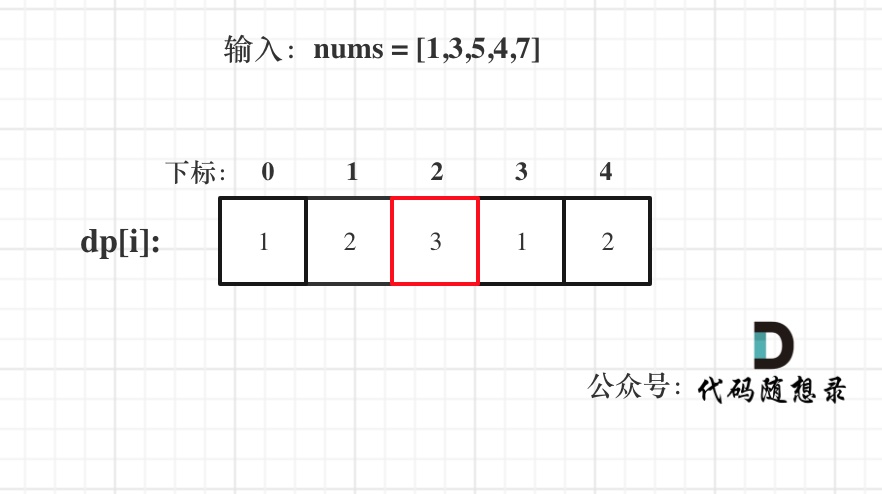
已输入nums = [1,3,5,4,7]为例,dp数组状态如下:
-
+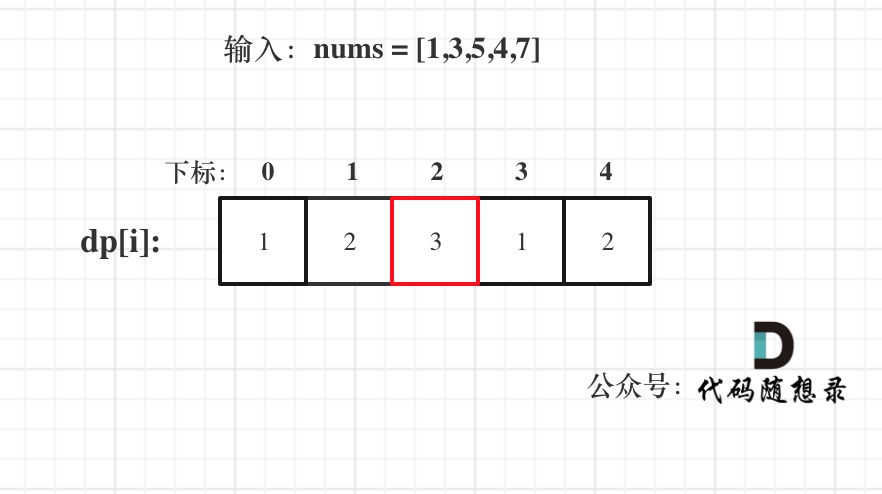
**注意这里要取dp[i]里的最大值,所以dp[2]才是结果!**
diff --git a/problems/0684.冗余连接.md b/problems/0684.冗余连接.md
index e6d2d8e5..8a7234df 100644
--- a/problems/0684.冗余连接.md
+++ b/problems/0684.冗余连接.md
@@ -12,7 +12,7 @@
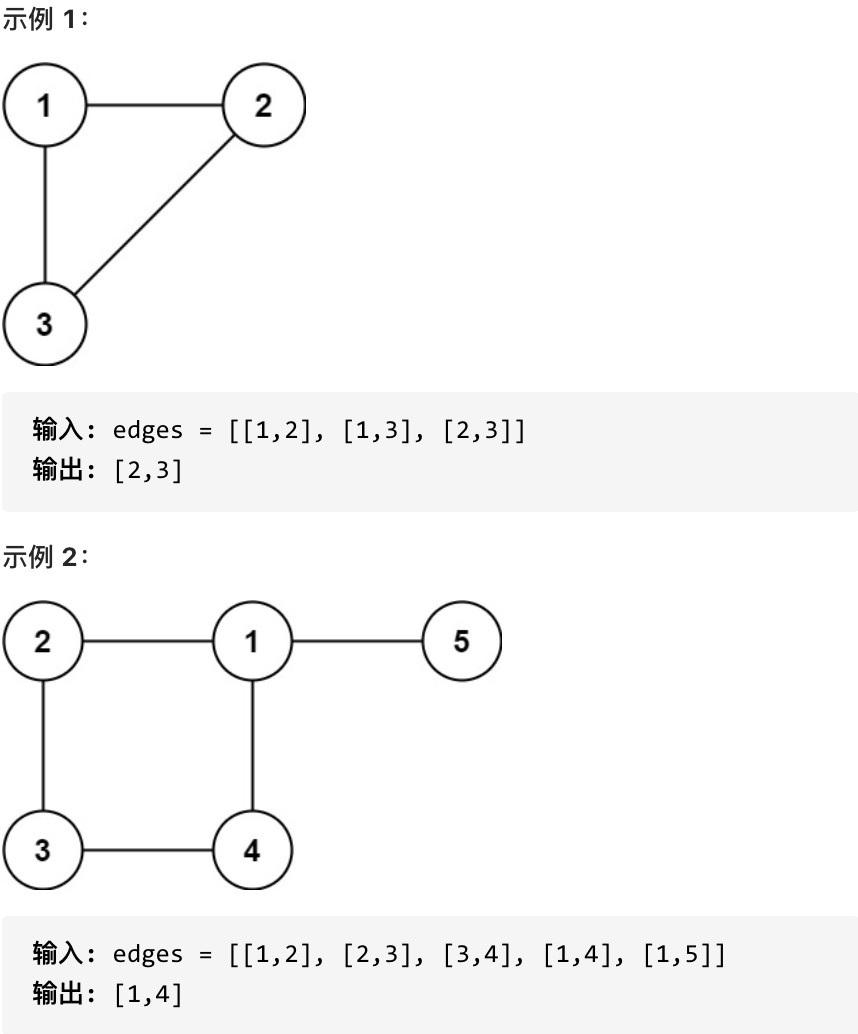
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
-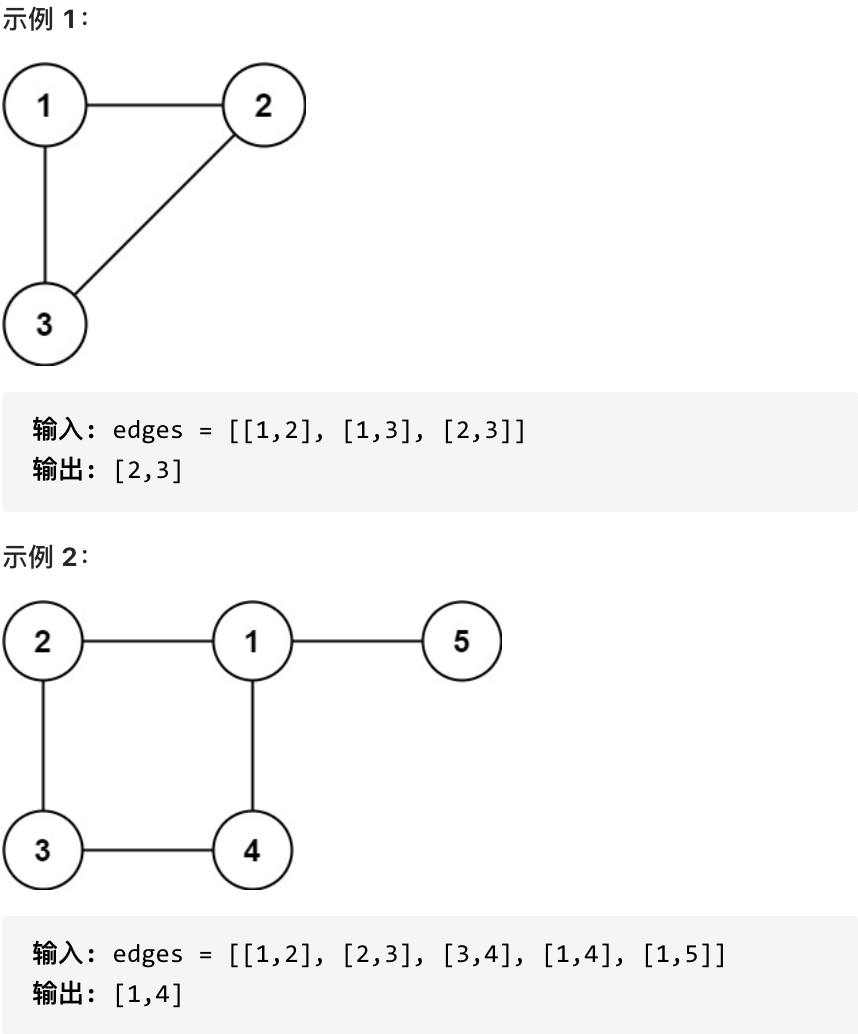
+
提示:
* n == edges.length
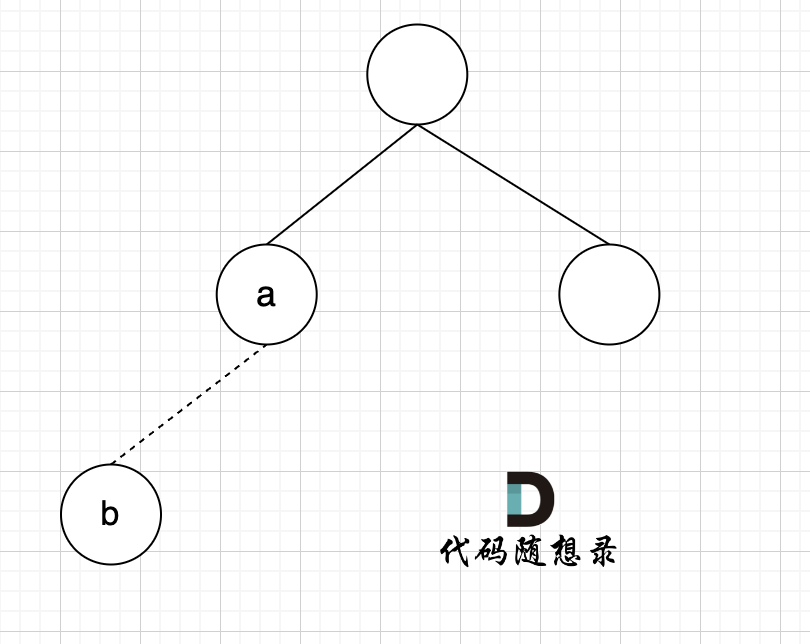
@@ -85,7 +85,7 @@ void join(int u, int v) {
如图所示:
-
+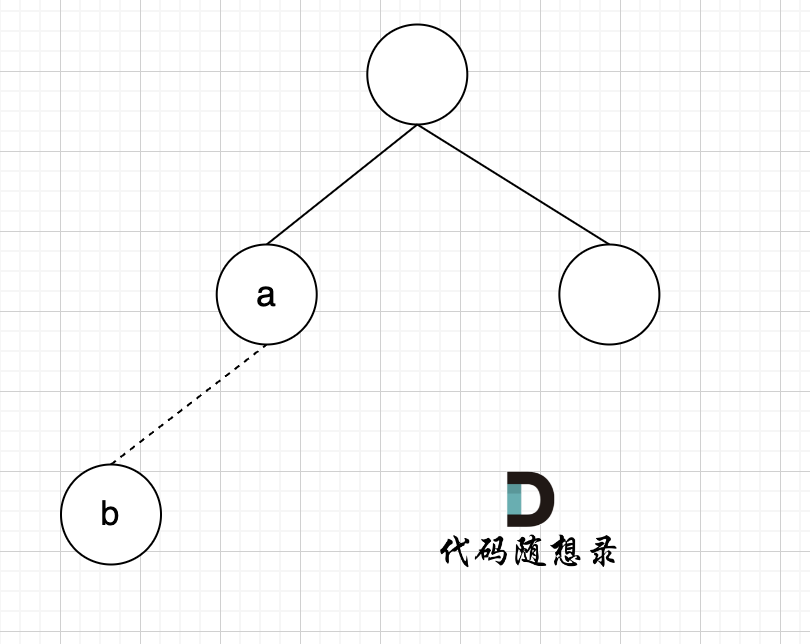
节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
@@ -95,7 +95,7 @@ void join(int u, int v) {
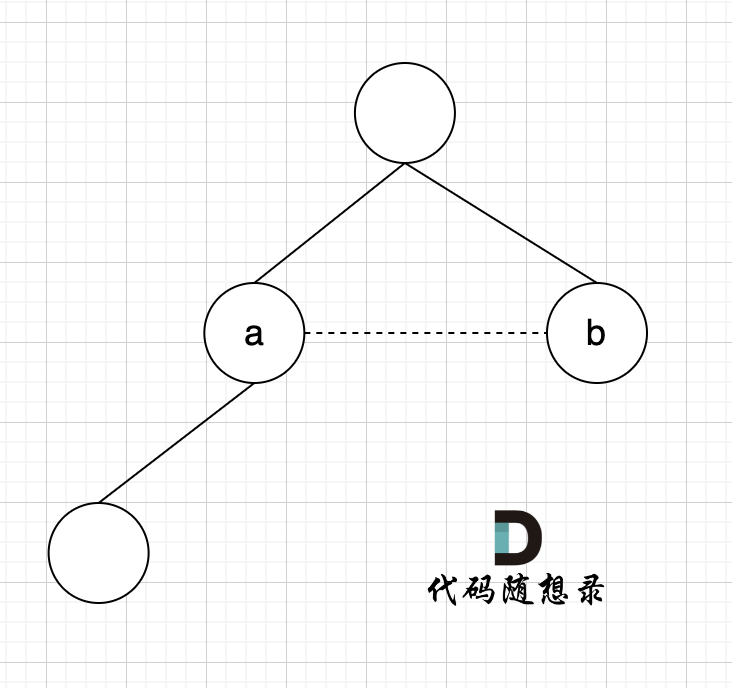
如图所示:
-
+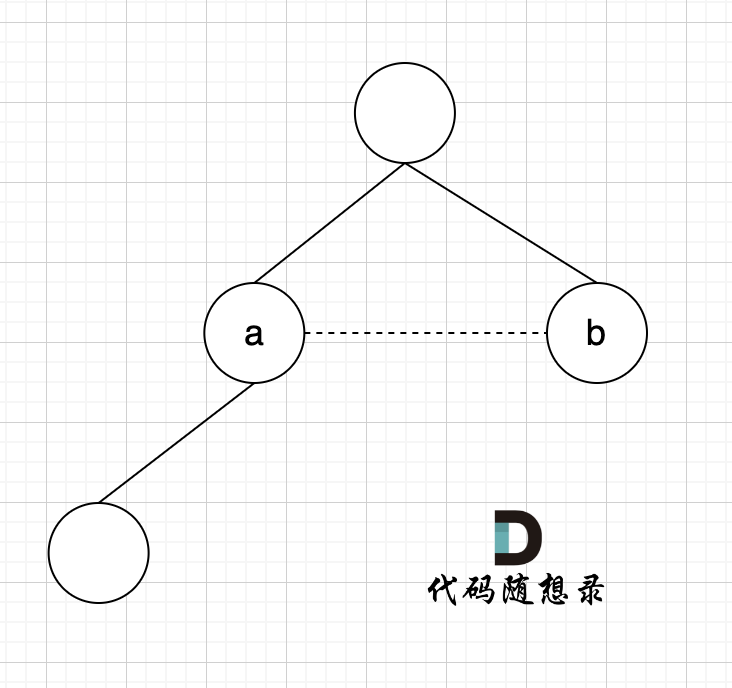
已经判断 节点A 和 节点B 在在同一个集合(同一个根),如果将 节点A 和 节点B 连在一起就一定会出现环。
diff --git a/problems/0685.冗余连接II.md b/problems/0685.冗余连接II.md
index 7b0e320c..66f7bfe1 100644
--- a/problems/0685.冗余连接II.md
+++ b/problems/0685.冗余连接II.md
@@ -16,9 +16,9 @@
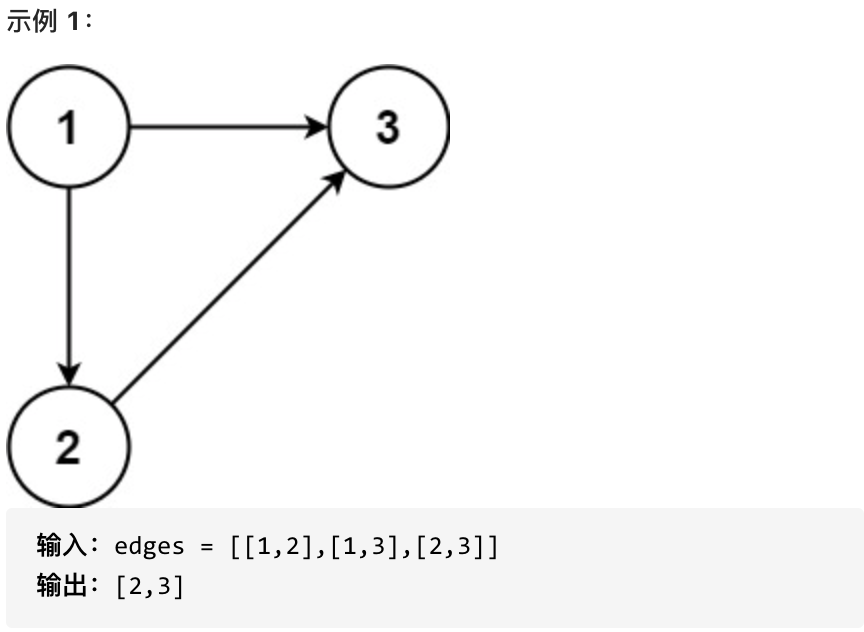
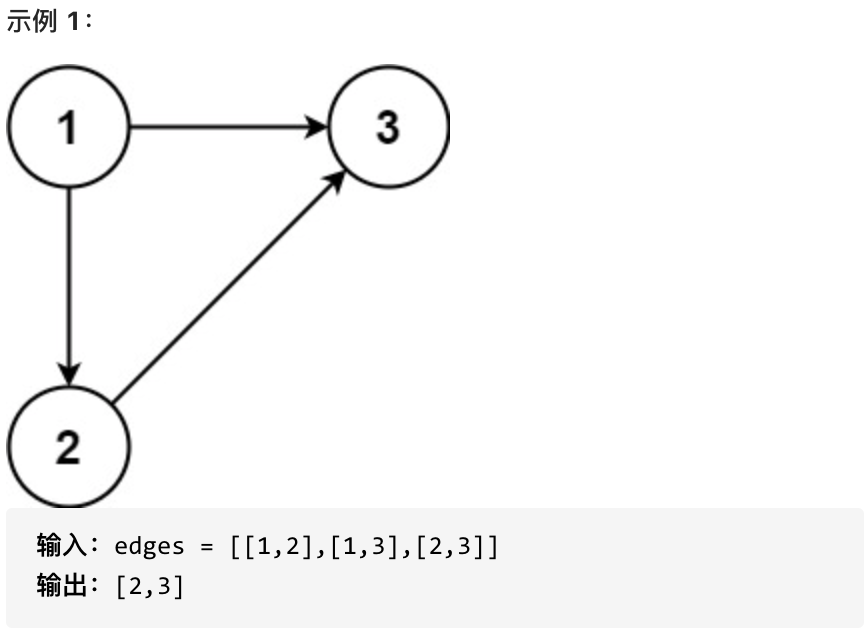
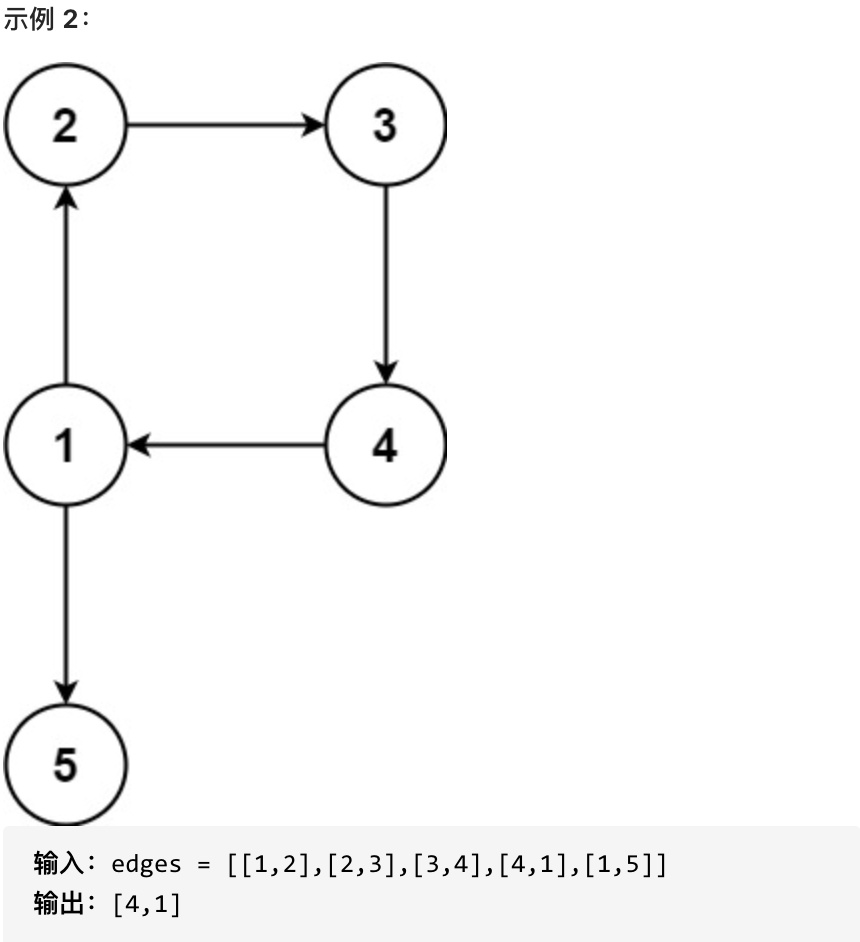
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
-
+
-
+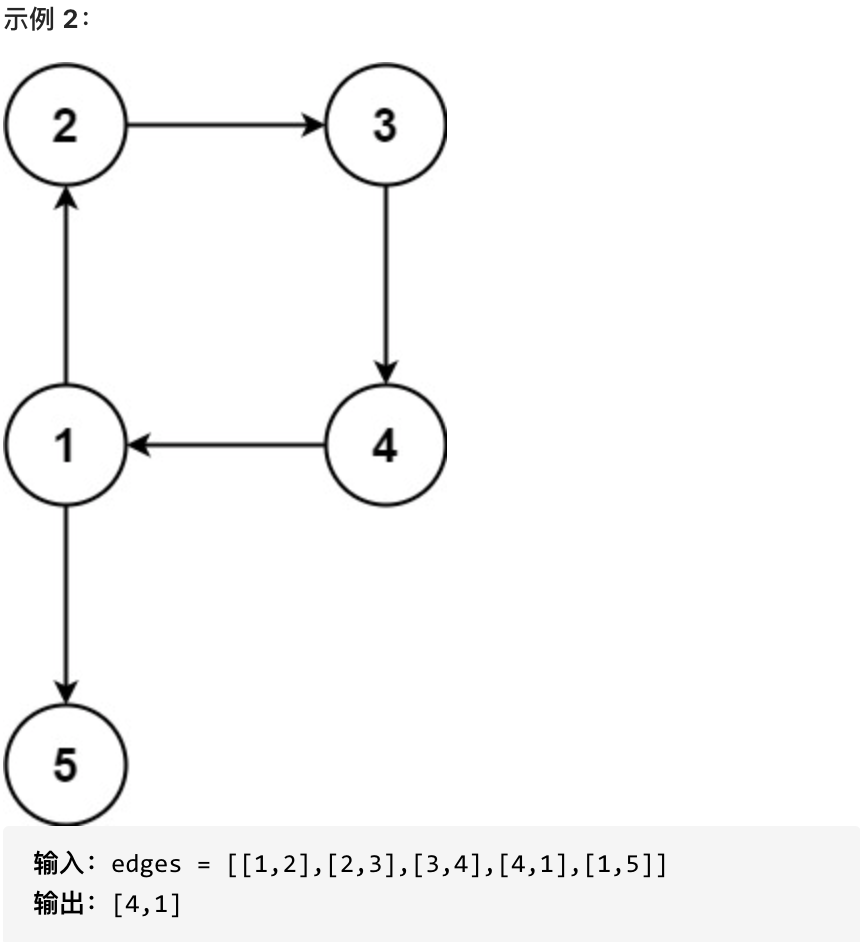
提示:
diff --git a/problems/0695.岛屿的最大面积.md b/problems/0695.岛屿的最大面积.md
index 0b84e651..972a9995 100644
--- a/problems/0695.岛屿的最大面积.md
+++ b/problems/0695.岛屿的最大面积.md
@@ -14,7 +14,7 @@
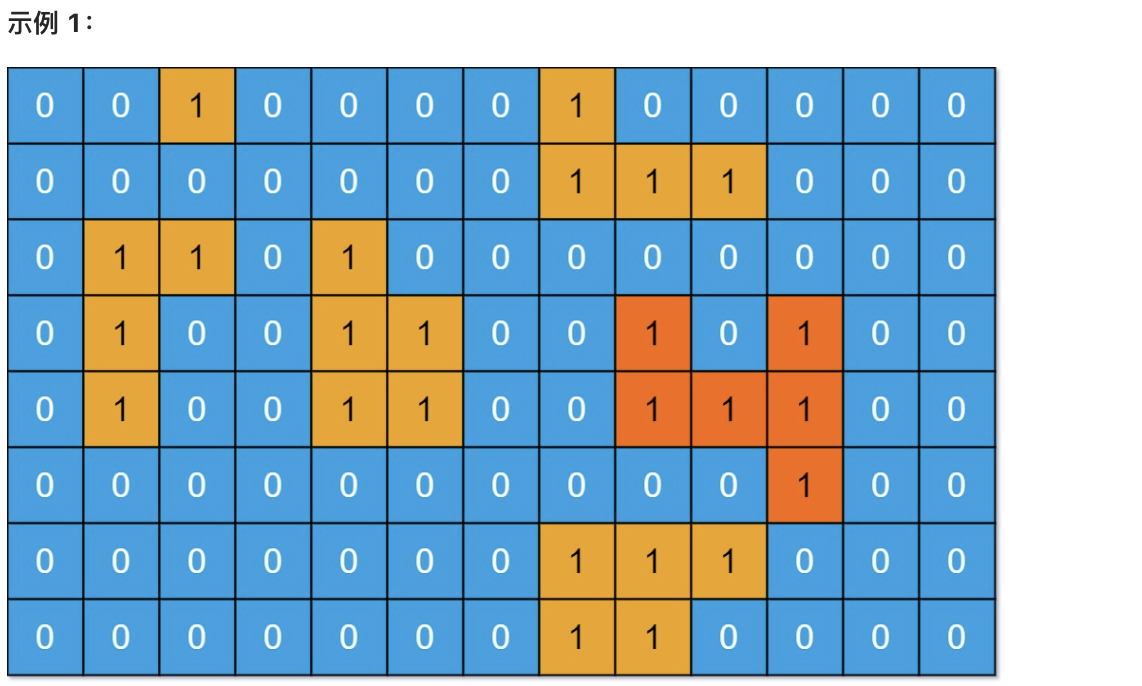
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
-
+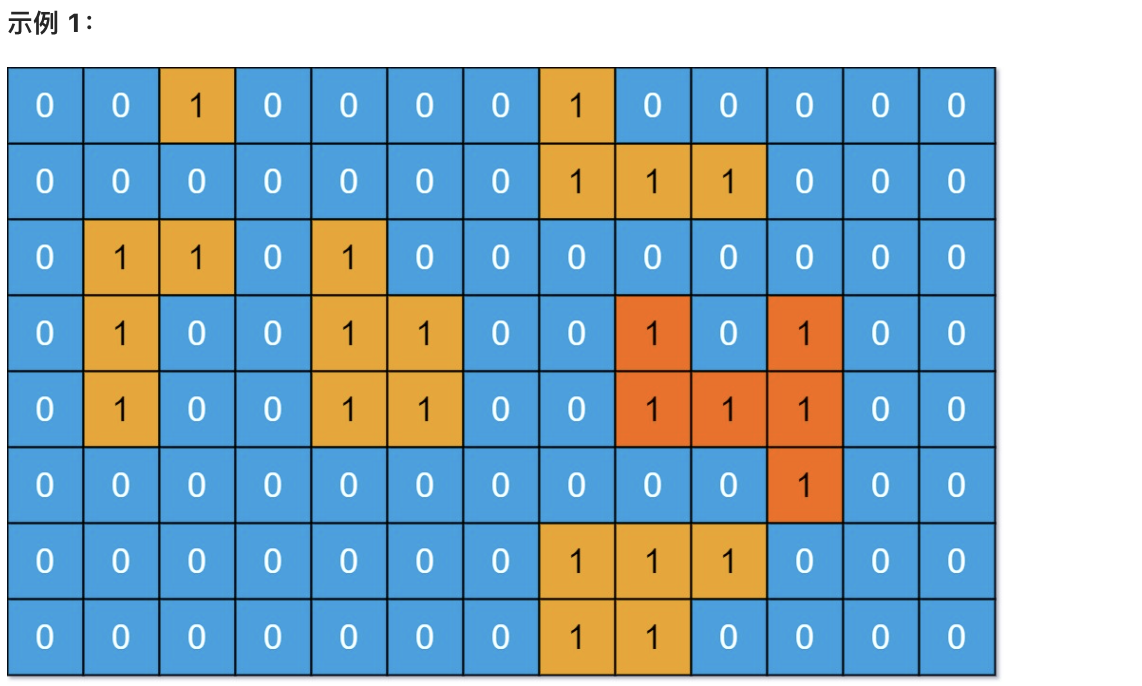
* 输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
* 输出:6
@@ -27,7 +27,7 @@
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
-
+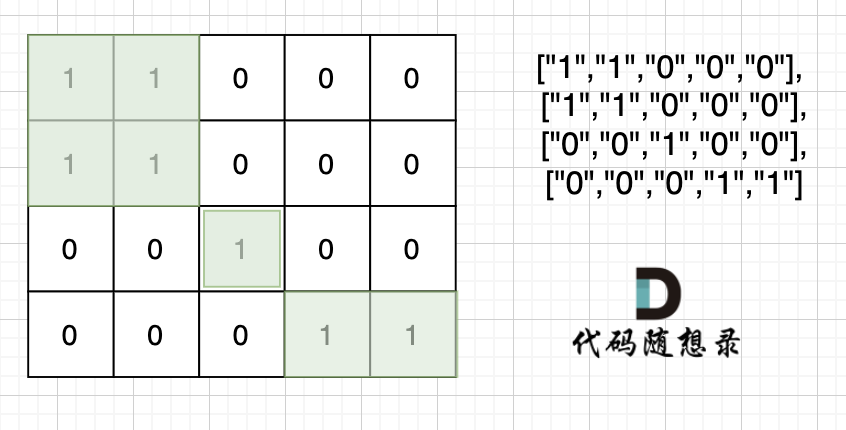
这道题目也是 dfs bfs基础类题目,就是搜索每个岛屿上“1”的数量,然后取一个最大的。
diff --git a/problems/0700.二叉搜索树中的搜索.md b/problems/0700.二叉搜索树中的搜索.md
index 4225b3fe..0c373f61 100644
--- a/problems/0700.二叉搜索树中的搜索.md
+++ b/problems/0700.二叉搜索树中的搜索.md
@@ -12,7 +12,7 @@
例如,
-
+
在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
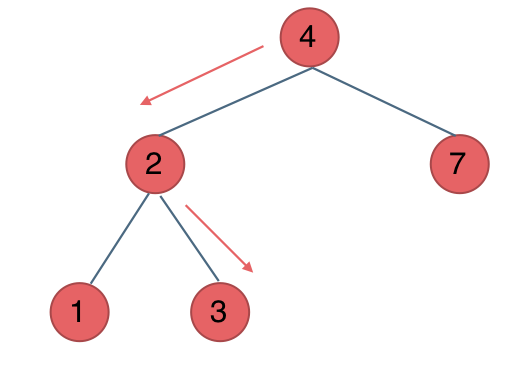
@@ -124,7 +124,7 @@ public:
中间节点如果大于3就向左走,如果小于3就向右走,如图:
-
+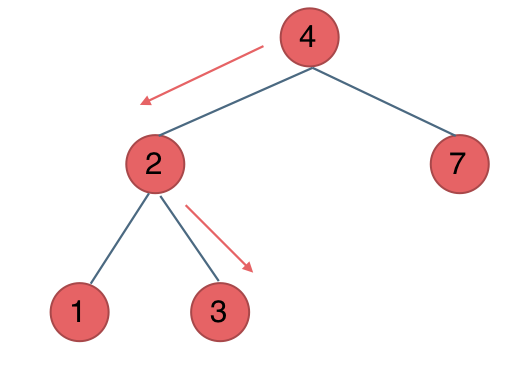
所以迭代法代码如下:
diff --git a/problems/0701.二叉搜索树中的插入操作.md b/problems/0701.二叉搜索树中的插入操作.md
index ef383faa..6ce9ef33 100644
--- a/problems/0701.二叉搜索树中的插入操作.md
+++ b/problems/0701.二叉搜索树中的插入操作.md
@@ -12,7 +12,7 @@
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。
-
+
提示:
diff --git a/problems/0704.二分查找.md b/problems/0704.二分查找.md
index 40501874..0ce2f3b8 100644
--- a/problems/0704.二分查找.md
+++ b/problems/0704.二分查找.md
@@ -59,7 +59,7 @@
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
-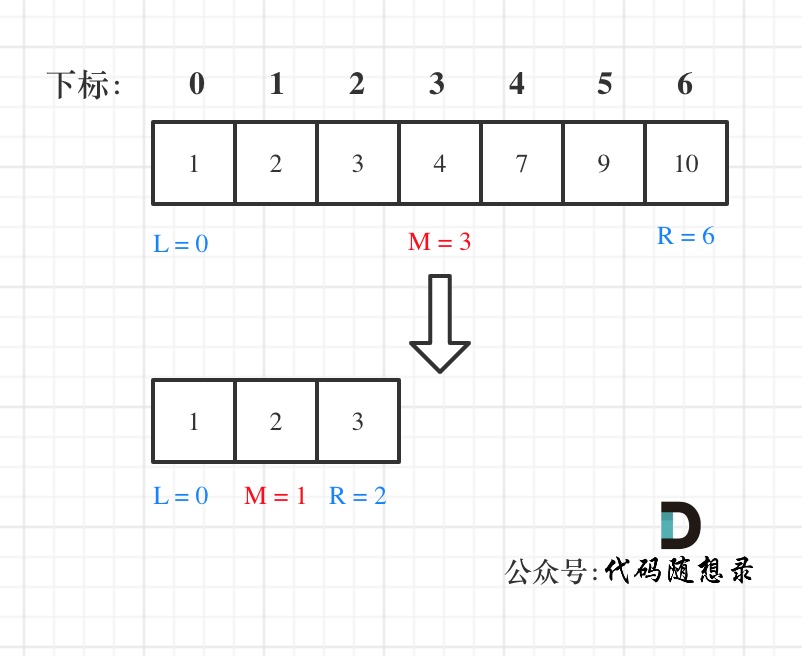
+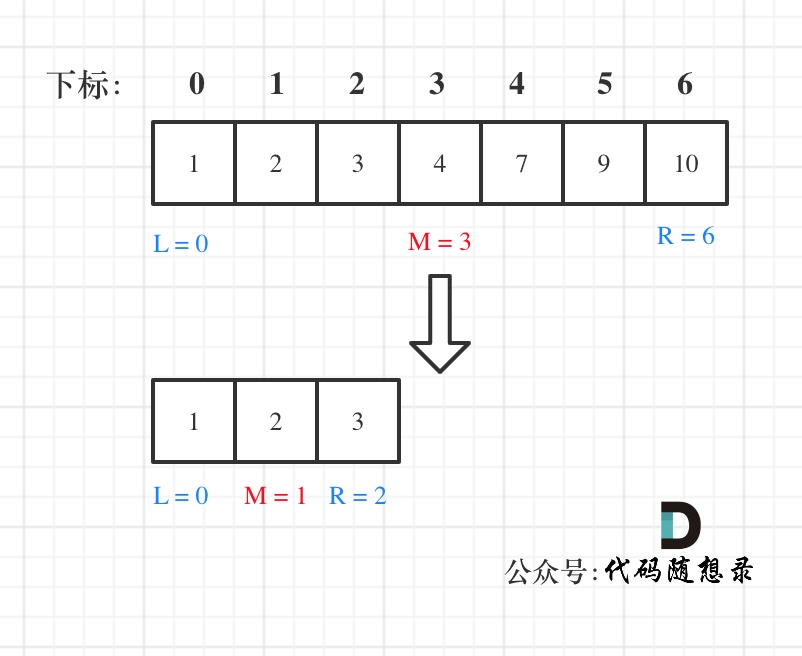
代码如下:(详细注释)
@@ -102,7 +102,7 @@ public:
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(**注意和方法一的区别**)
-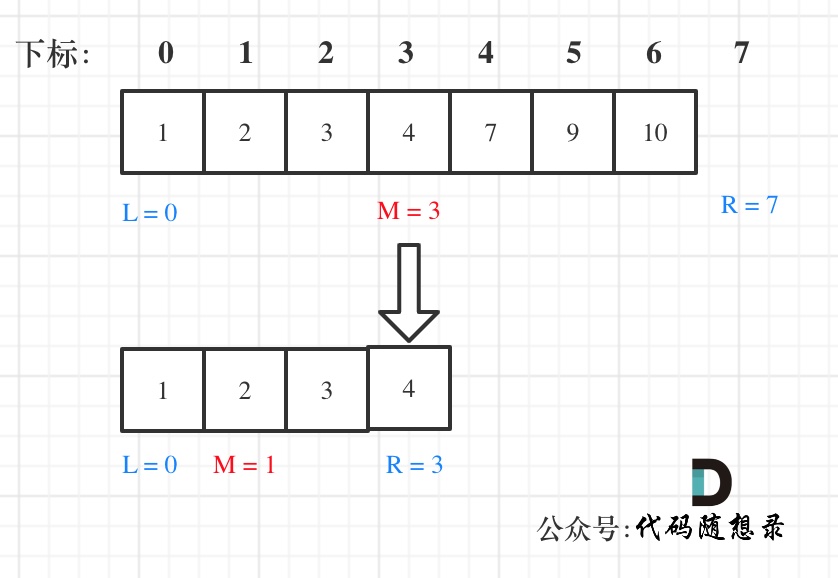
+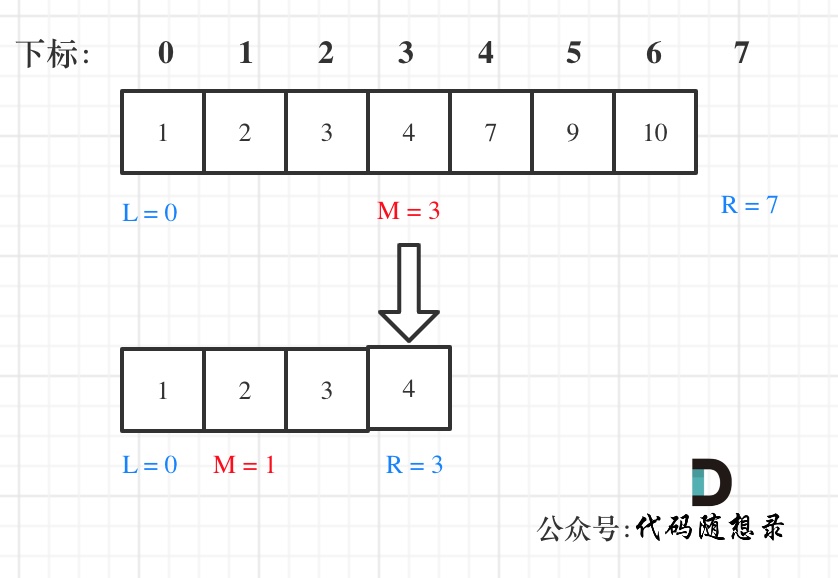
代码如下:(详细注释)
diff --git a/problems/0707.设计链表.md b/problems/0707.设计链表.md
index 7023bd90..a2b2803b 100644
--- a/problems/0707.设计链表.md
+++ b/problems/0707.设计链表.md
@@ -20,7 +20,7 @@
* deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个节点。
-
+
## 算法公开课
@@ -35,10 +35,10 @@
如果对链表的虚拟头结点不清楚,可以看这篇文章:[链表:听说用虚拟头节点会方便很多?](https://programmercarl.com/0203.移除链表元素.html)
删除链表节点:
-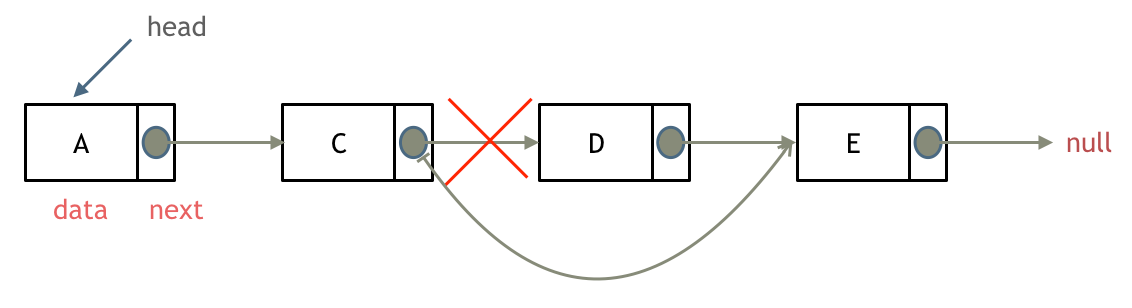
+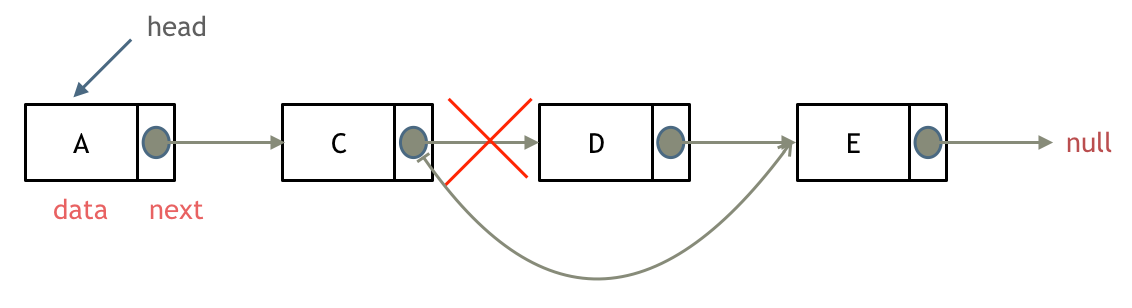
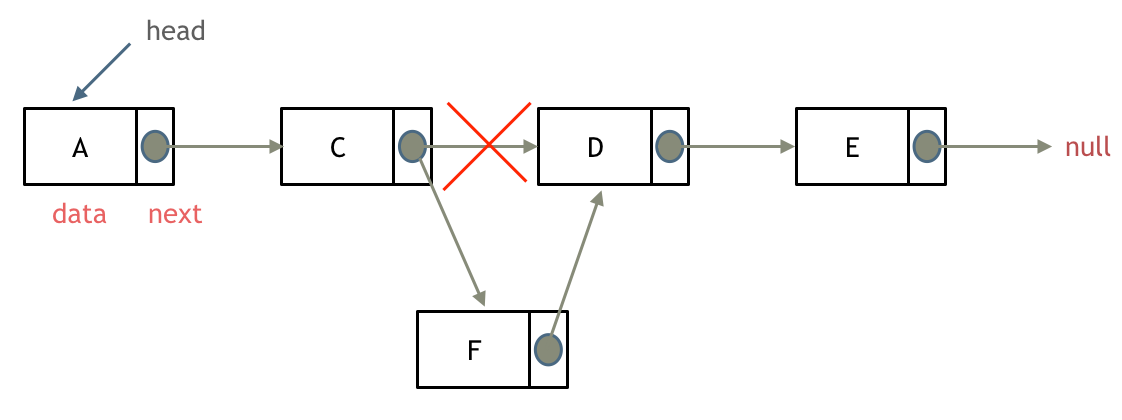
添加链表节点:
-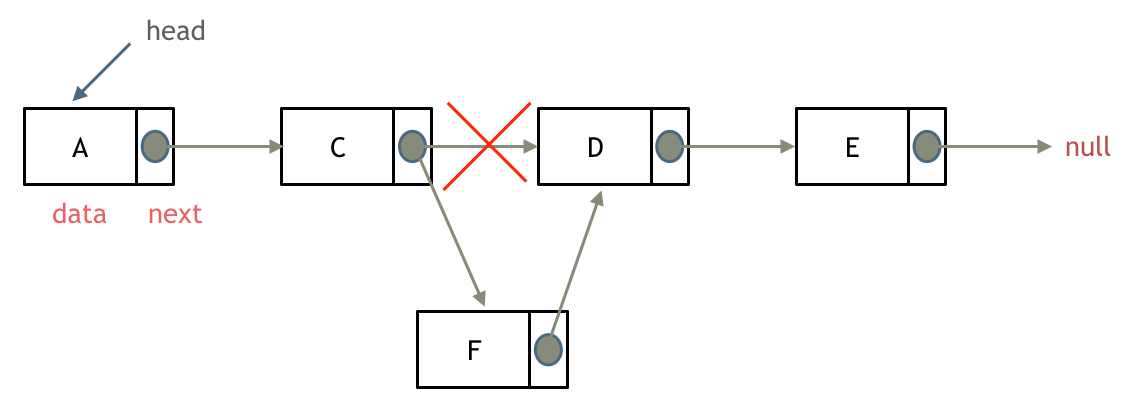
+
这道题目设计链表的五个接口:
* 获取链表第index个节点的数值
diff --git a/problems/0718.最长重复子数组.md b/problems/0718.最长重复子数组.md
index 0e4b346d..b371bd85 100644
--- a/problems/0718.最长重复子数组.md
+++ b/problems/0718.最长重复子数组.md
@@ -95,7 +95,7 @@ for (int i = 1; i <= nums1.size(); i++) {
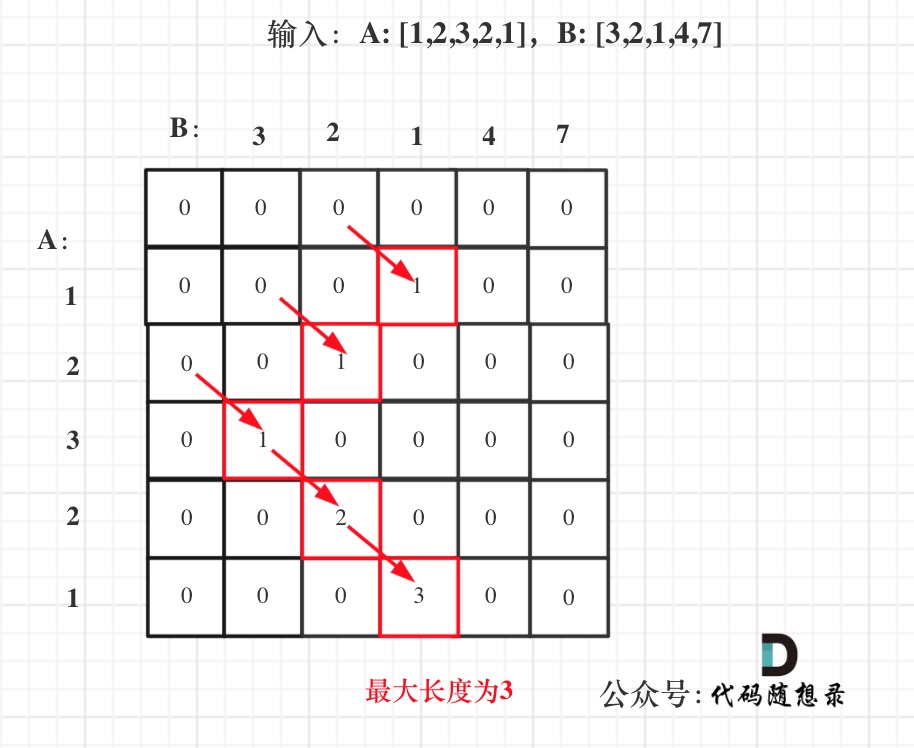
拿示例1中,A: [1,2,3,2,1],B: [3,2,1,4,7]为例,画一个dp数组的状态变化,如下:
-
+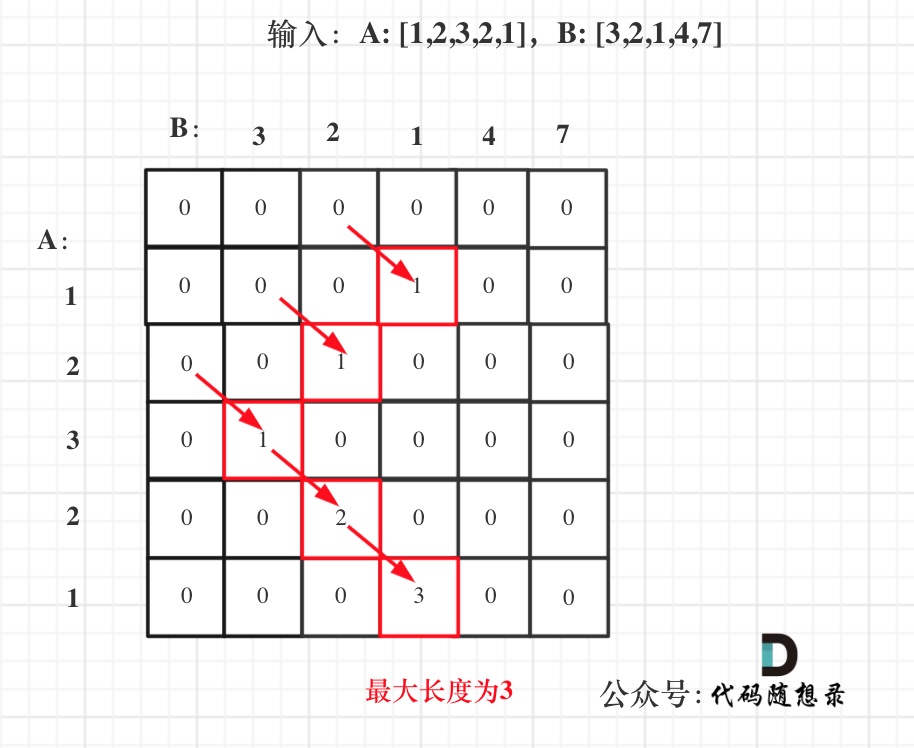
以上五部曲分析完毕,C++代码如下:
@@ -127,7 +127,7 @@ public:
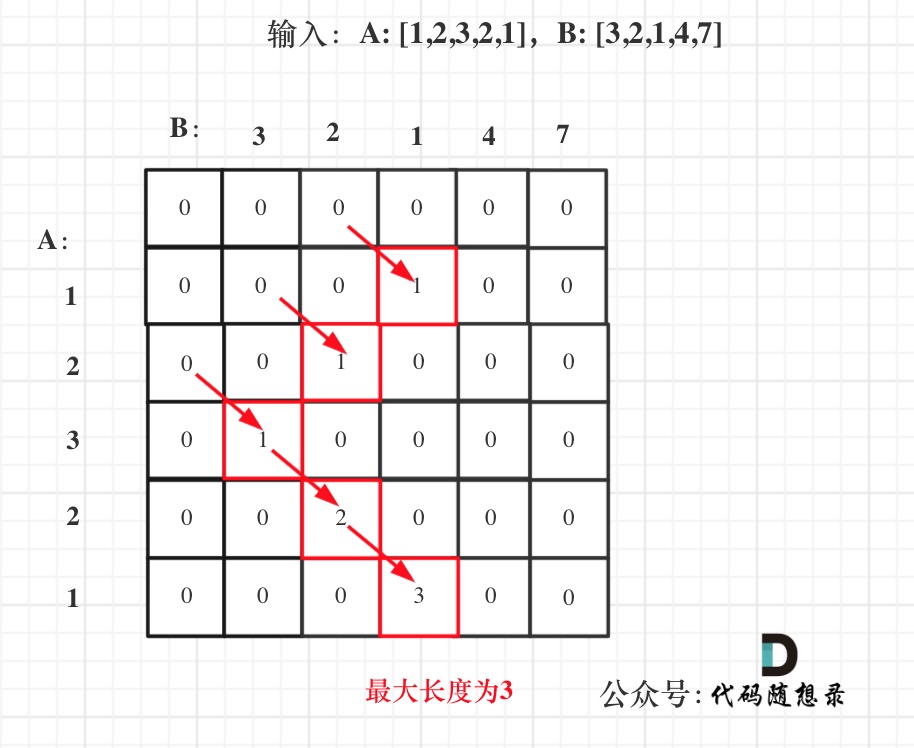
在如下图中:
-
+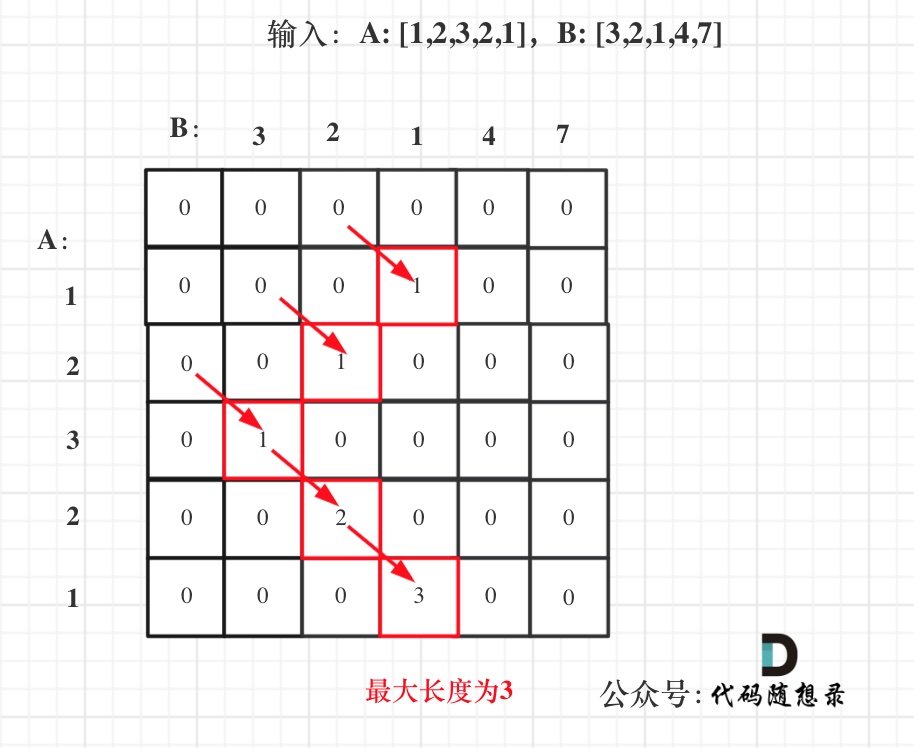
我们可以看出dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组,也就是dp[j]都是由dp[j - 1]推出。
diff --git a/problems/0739.每日温度.md b/problems/0739.每日温度.md
index 542aad29..ed43cf14 100644
--- a/problems/0739.每日温度.md
+++ b/problems/0739.每日温度.md
@@ -69,7 +69,7 @@
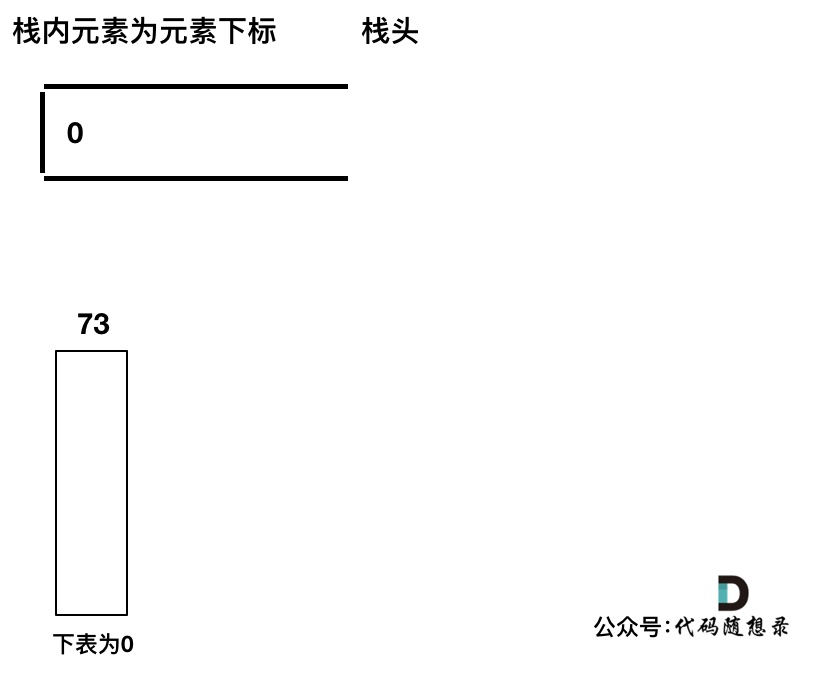
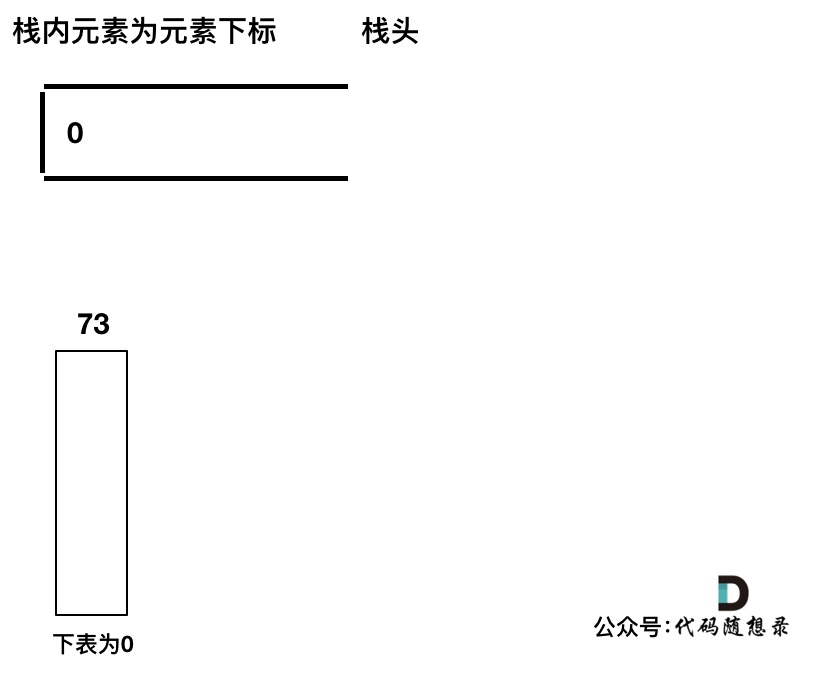
首先先将第一个遍历元素加入单调栈
-
+
---------
@@ -77,65 +77,65 @@
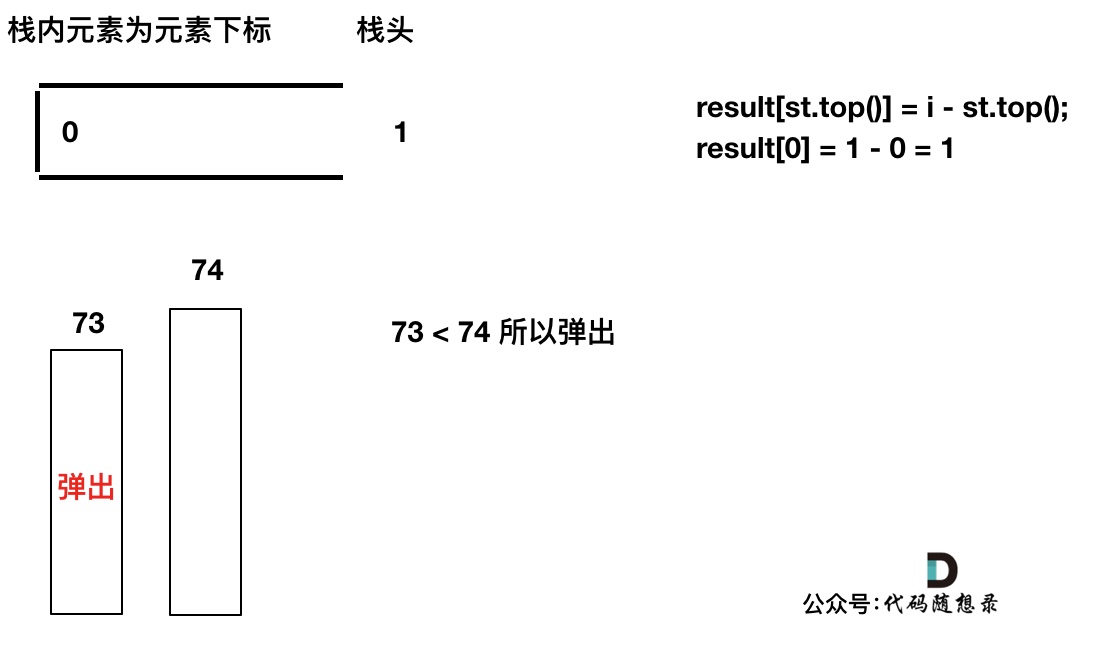
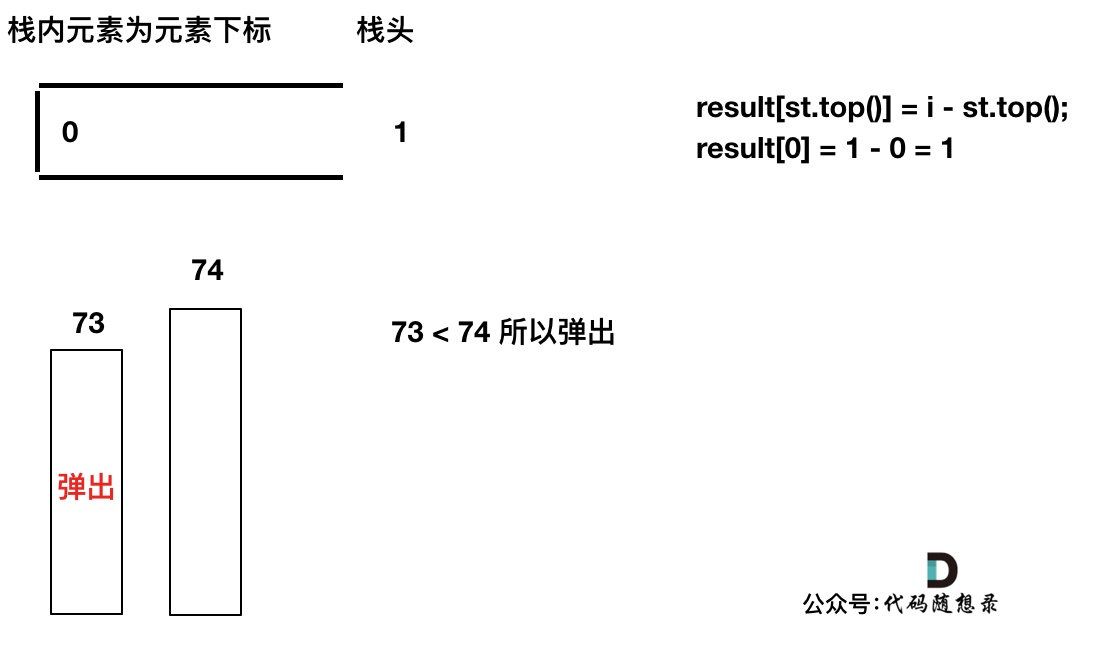
我们要保持一个递增单调栈(从栈头到栈底),所以将T[0]弹出,T[1]加入,此时result数组可以记录了,result[0] = 1,即T[0]右面第一个比T[0]大的元素是T[1]。
-
+
-----------
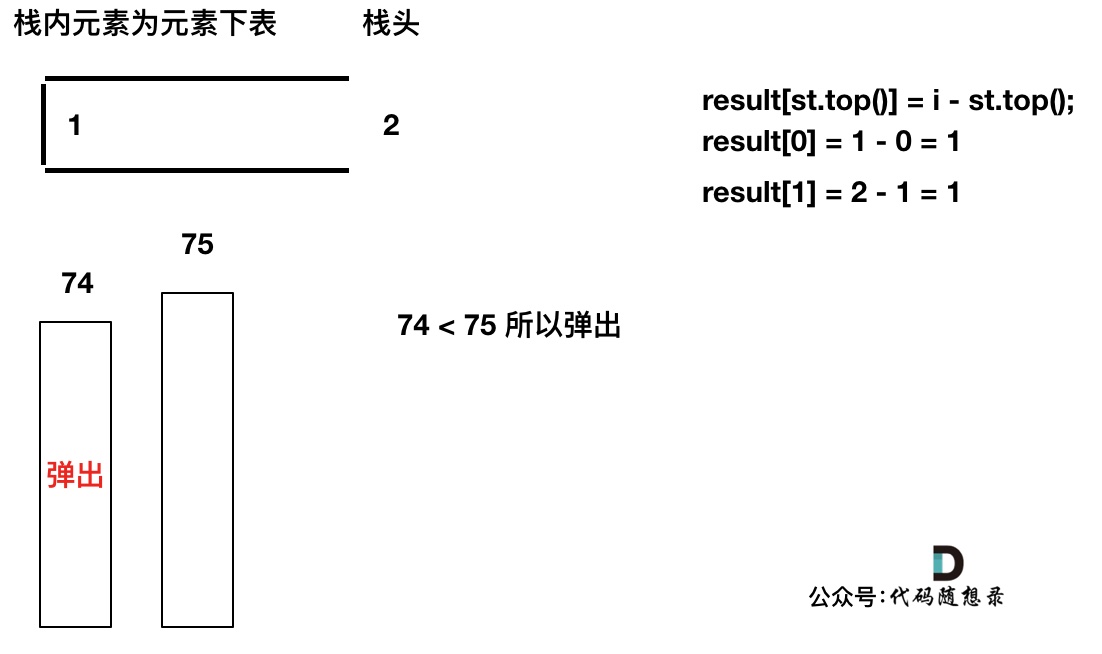
加入T[2],同理,T[1]弹出
-
+
-------
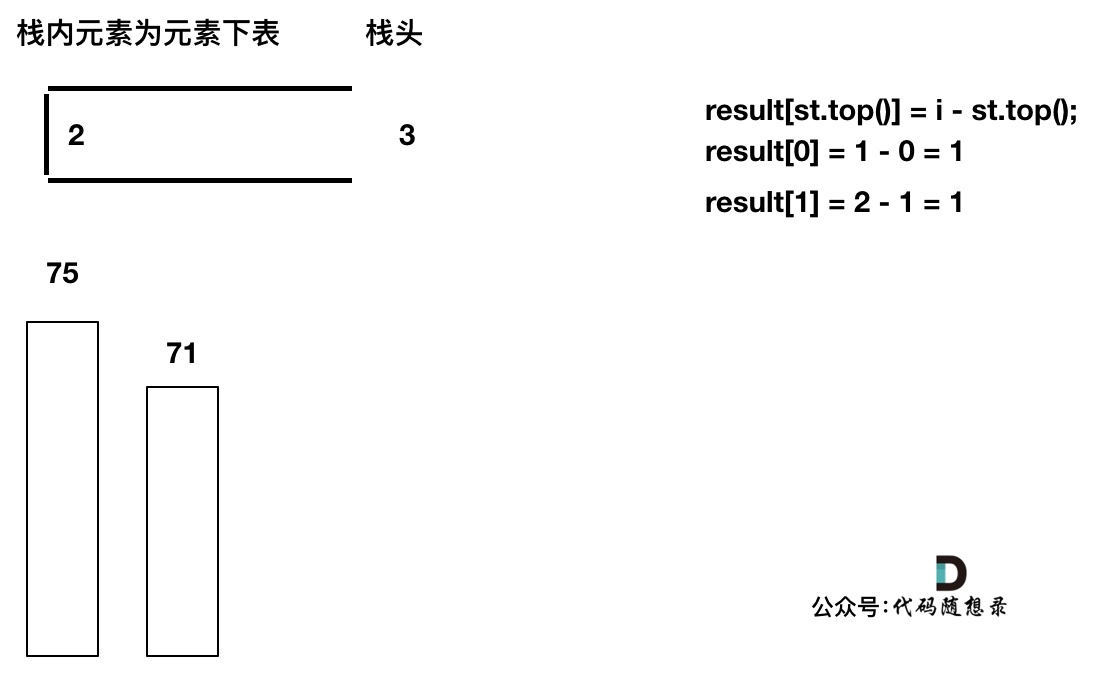
加入T[3],T[3] < T[2] (当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况),加T[3]加入单调栈。
-
+
---------
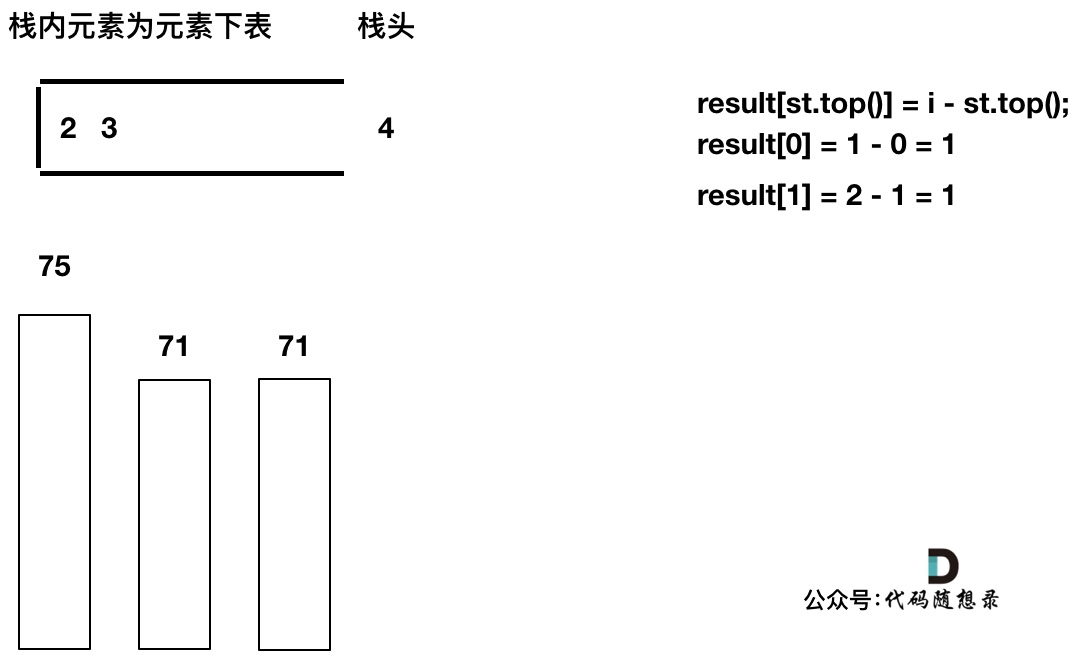
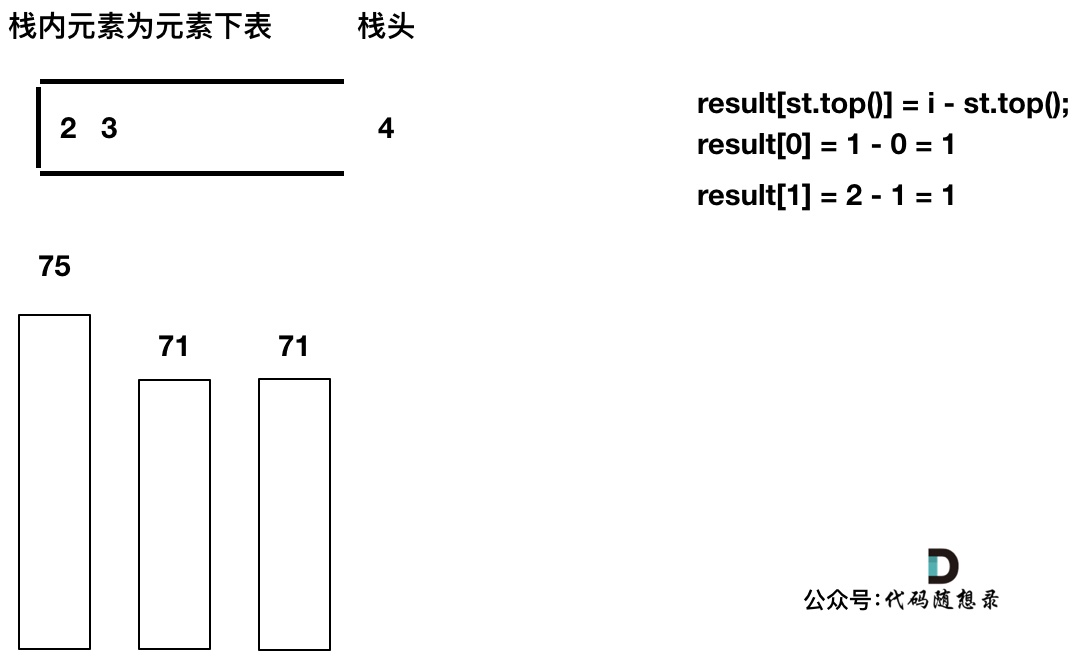
加入T[4],T[4] == T[3] (当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况),此时依然要加入栈,不用计算距离,因为我们要求的是右面第一个大于本元素的位置,而不是大于等于!
-
+
---------
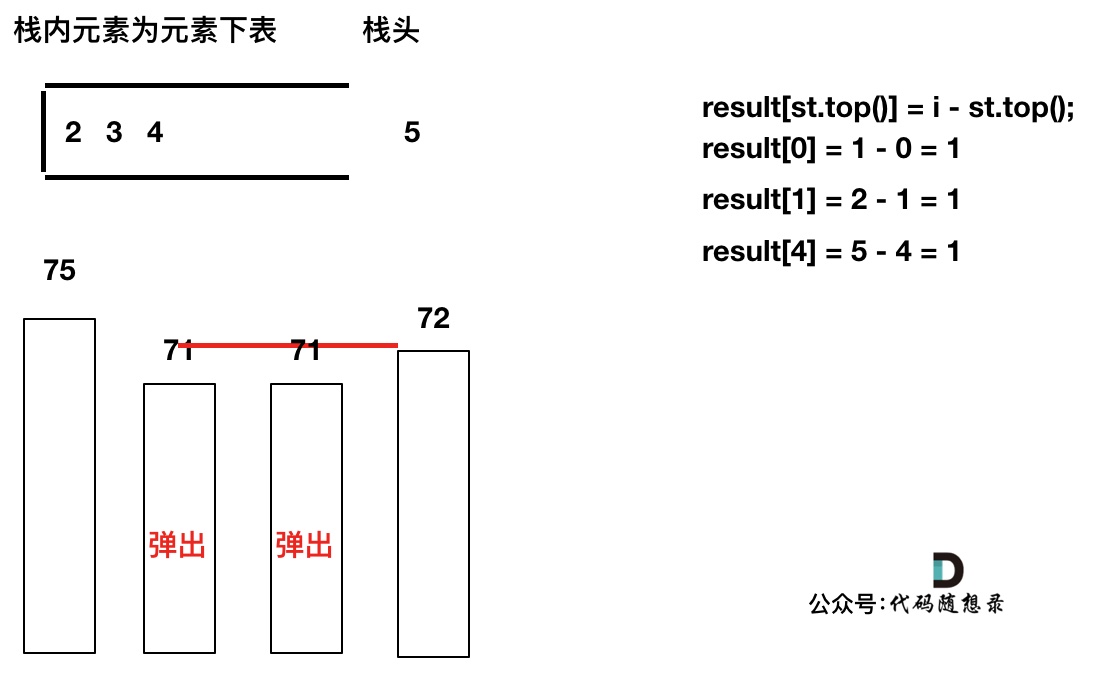
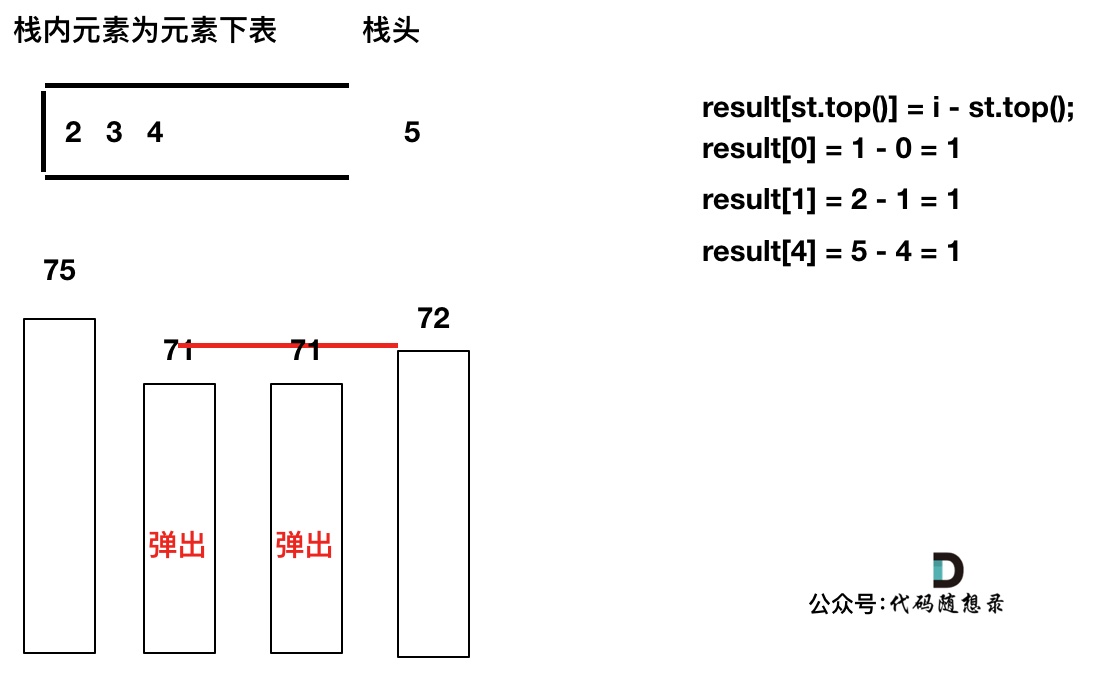
加入T[5],T[5] > T[4] (当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),将T[4]弹出,同时计算距离,更新result
-
+
----------
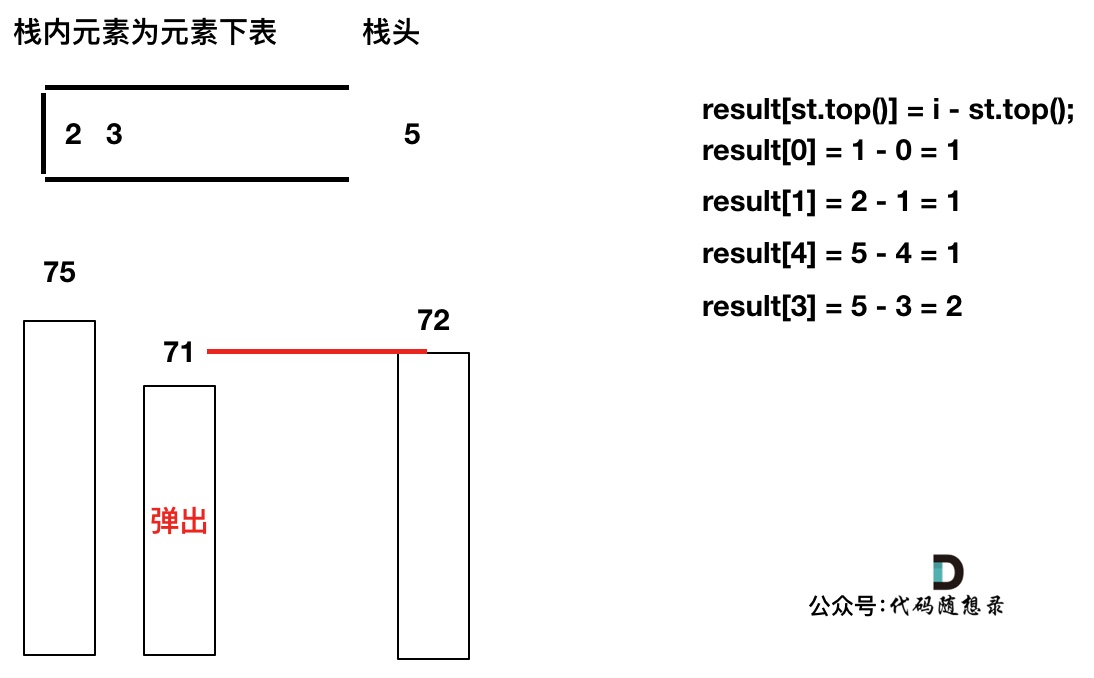
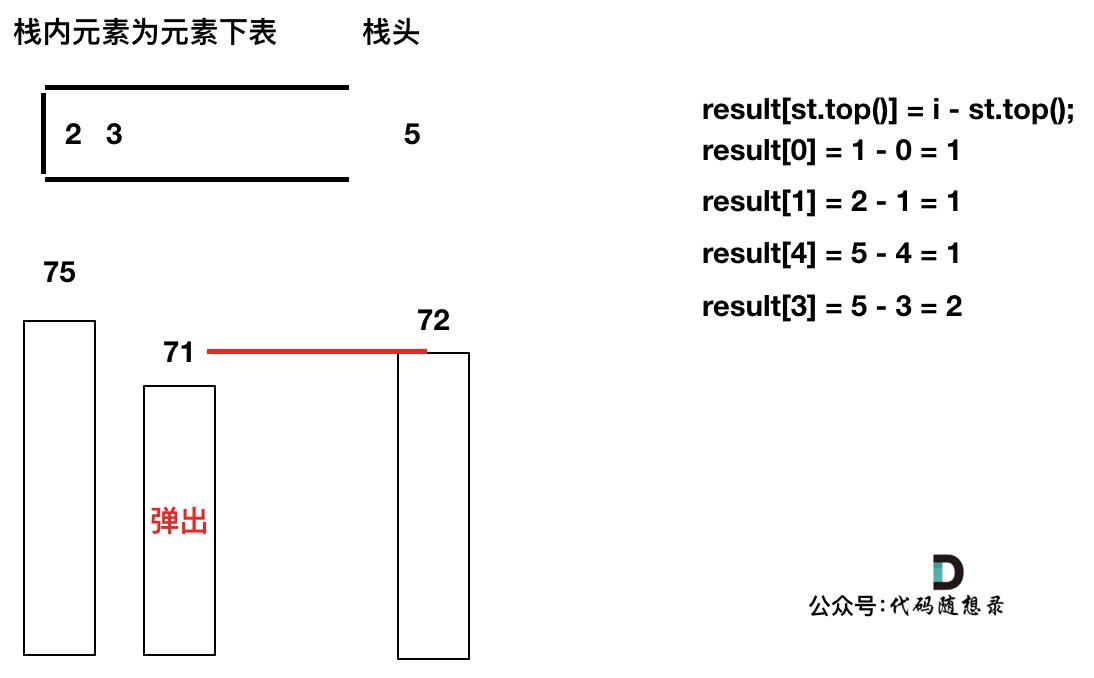
T[4]弹出之后, T[5] > T[3] (当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),将T[3]继续弹出,同时计算距离,更新result
-
+
-------
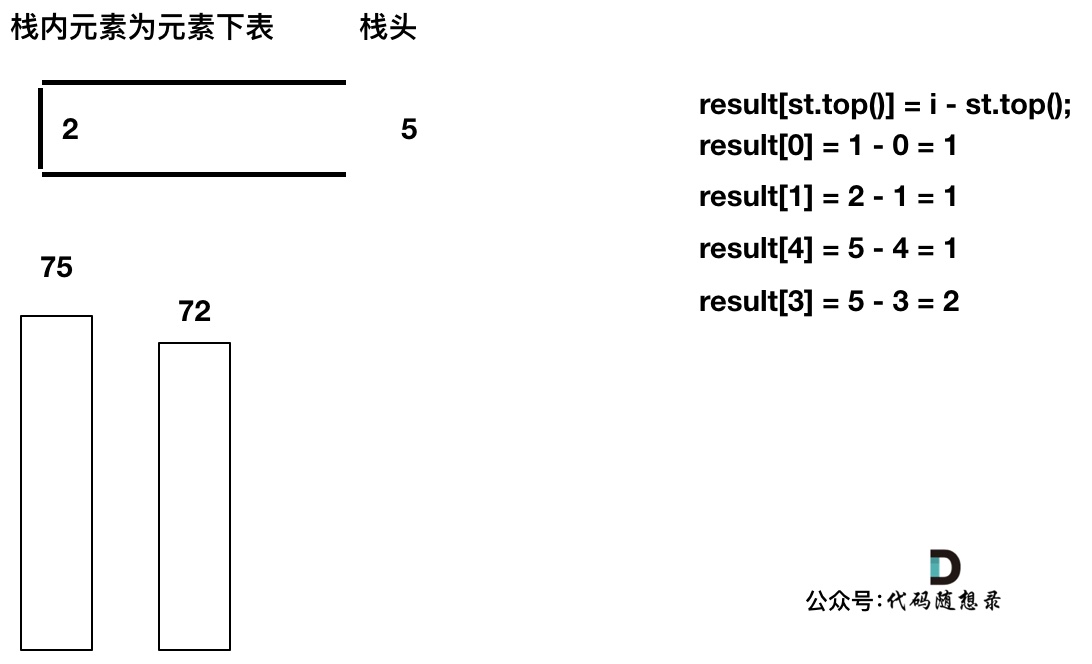
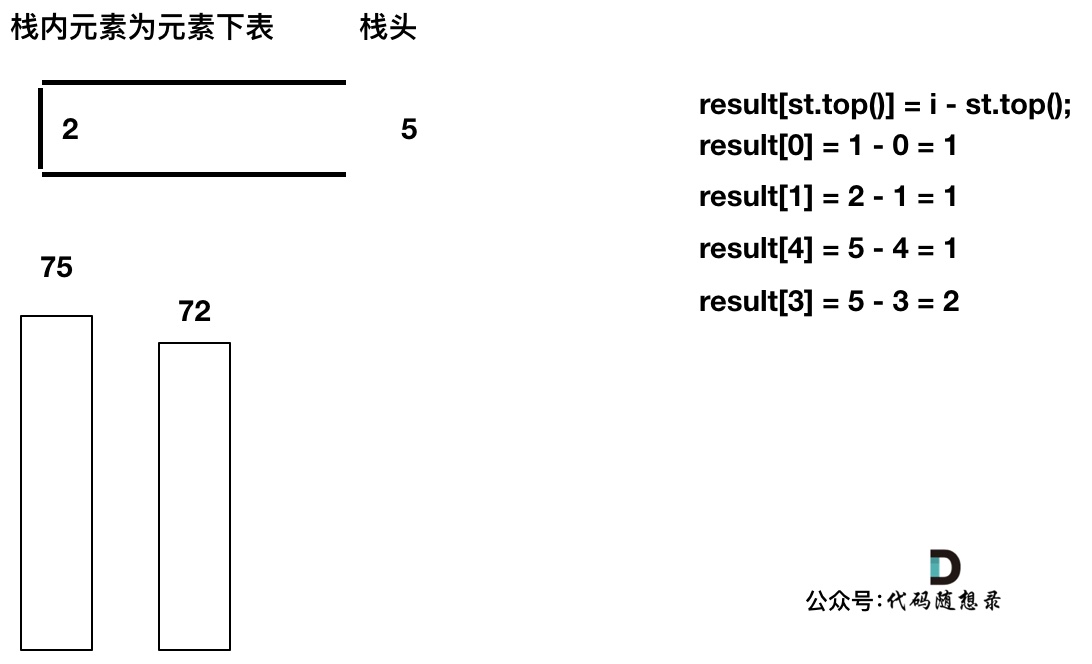
直到发现T[5]小于T[st.top()],终止弹出,将T[5]加入单调栈
-
+
-------
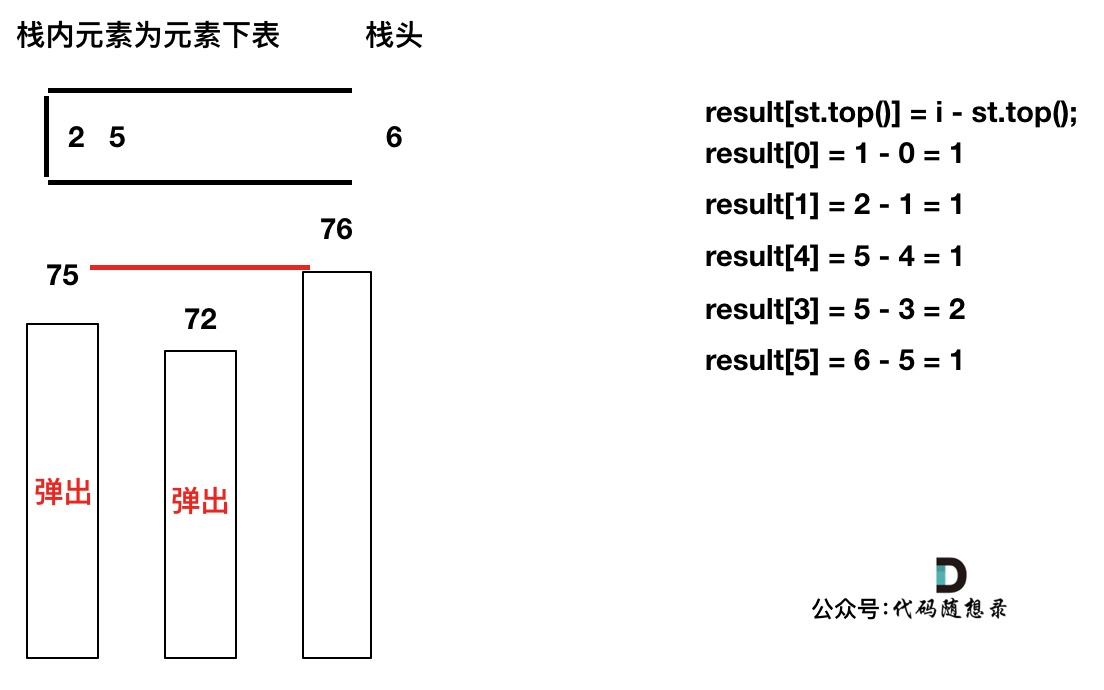
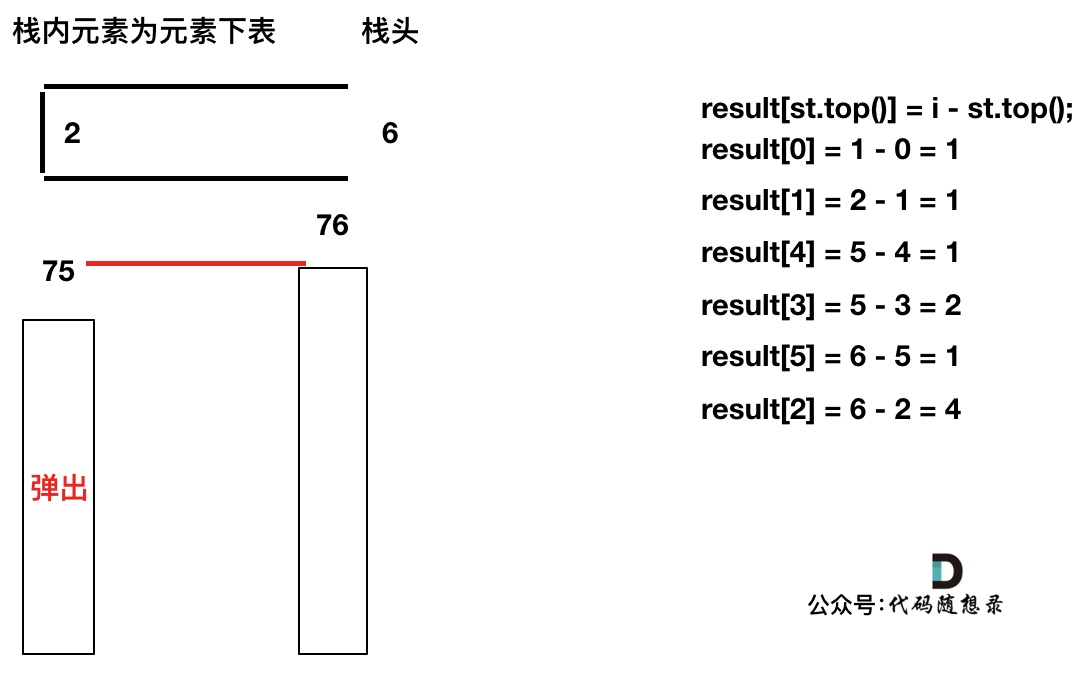
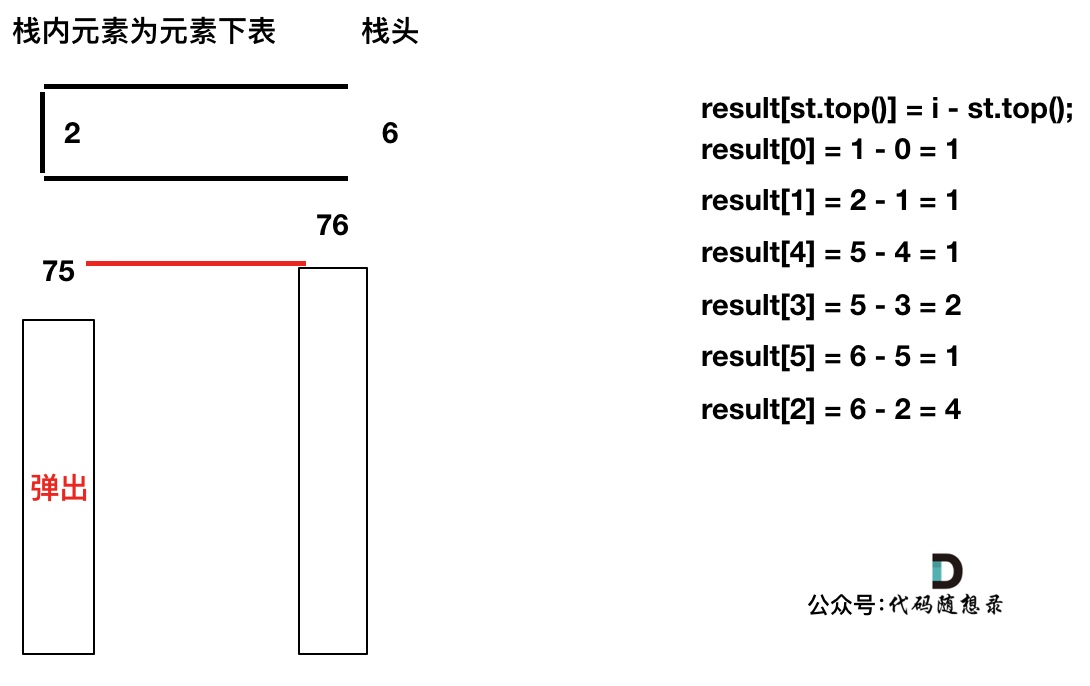
加入T[6],同理,需要将栈里的T[5],T[2]弹出
-
+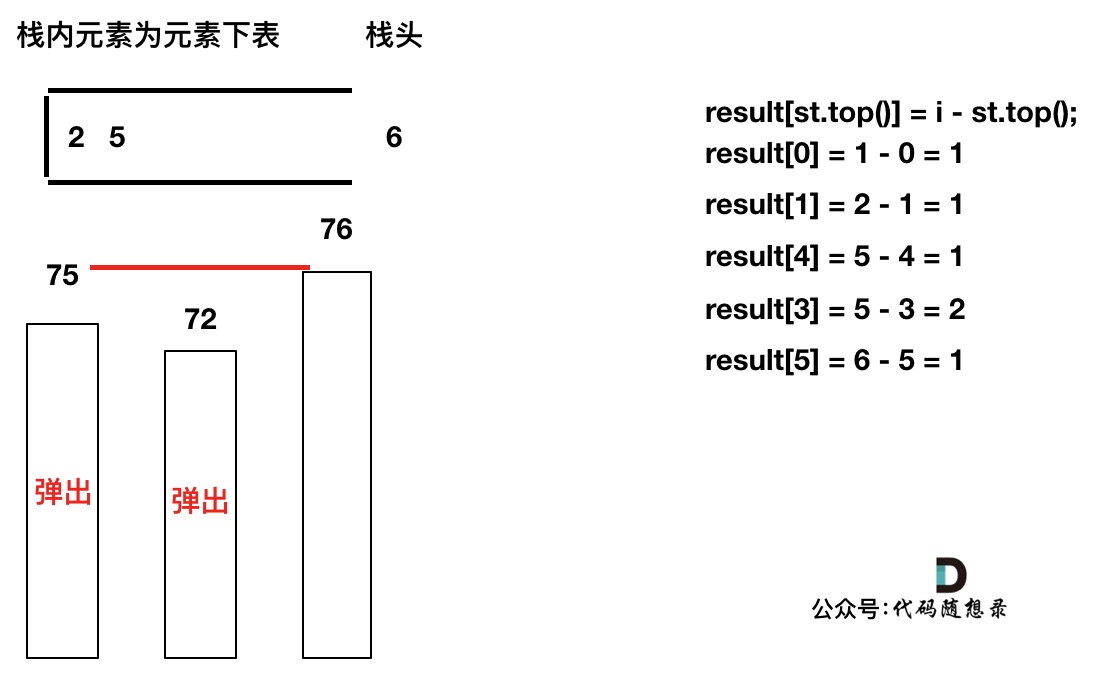
-------
同理,继续弹出
-
+
------
此时栈里只剩下了T[6]
-
+
------------
加入T[7], T[7] < T[6] 直接入栈,这就是最后的情况,result数组也更新完了。
-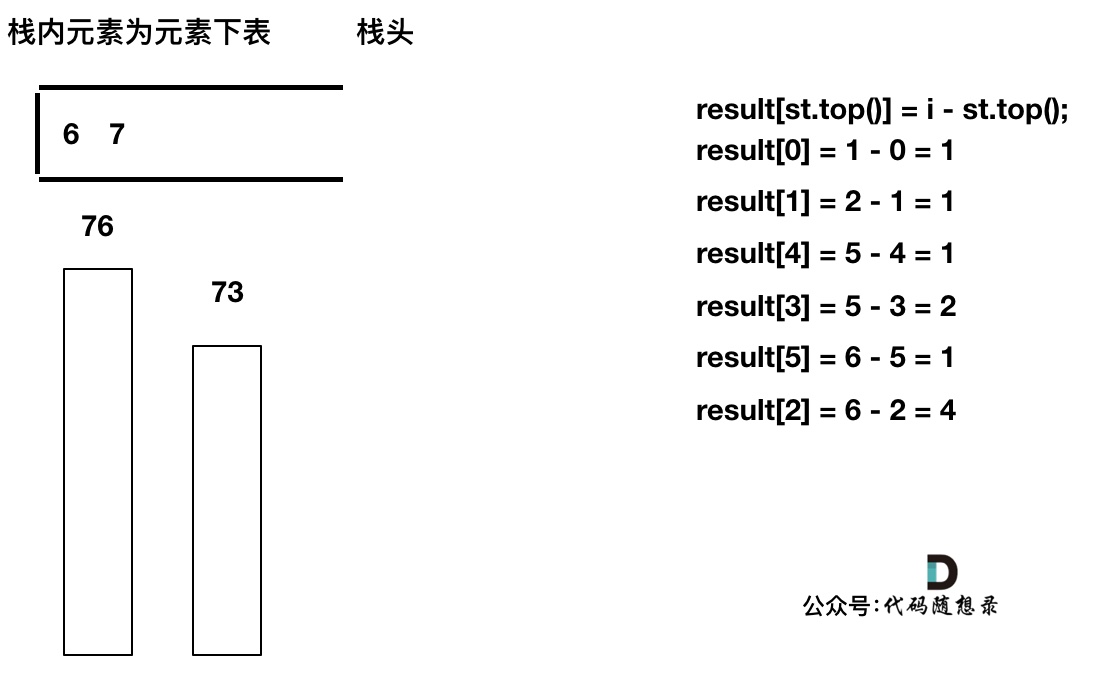
+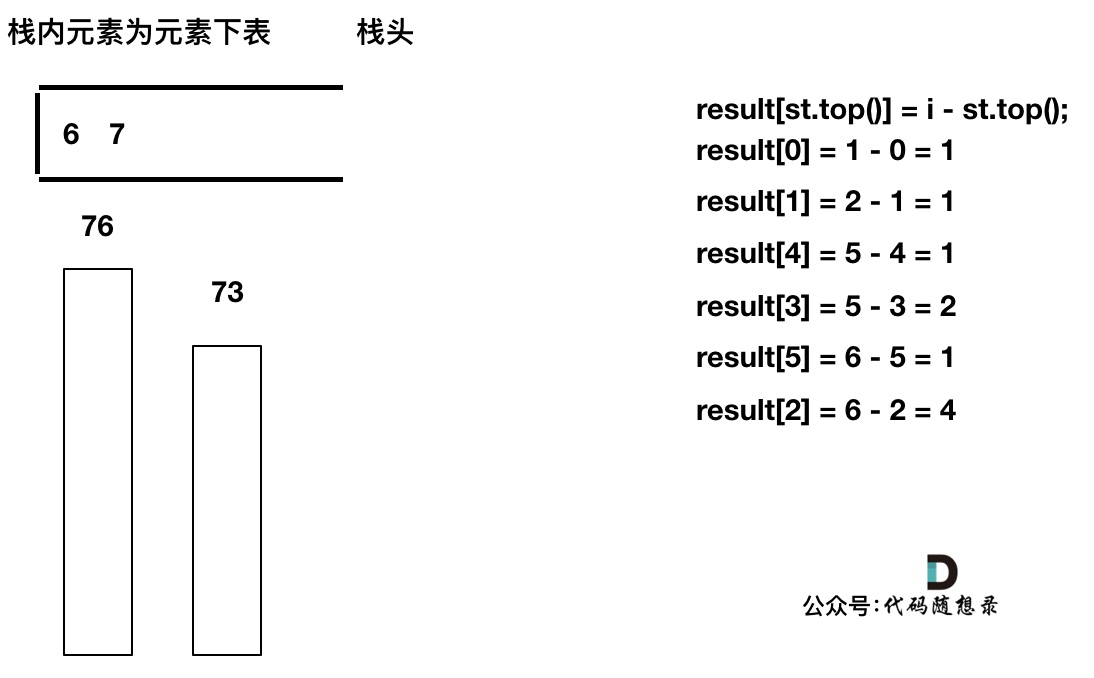
此时有同学可能就疑惑了,那result[6] , result[7]怎么没更新啊,元素也一直在栈里。
diff --git a/problems/0743.网络延迟时间.md b/problems/0743.网络延迟时间.md
index 6533a240..c8a87361 100644
--- a/problems/0743.网络延迟时间.md
+++ b/problems/0743.网络延迟时间.md
@@ -13,7 +13,7 @@ https://leetcode.cn/problems/network-delay-time/description/
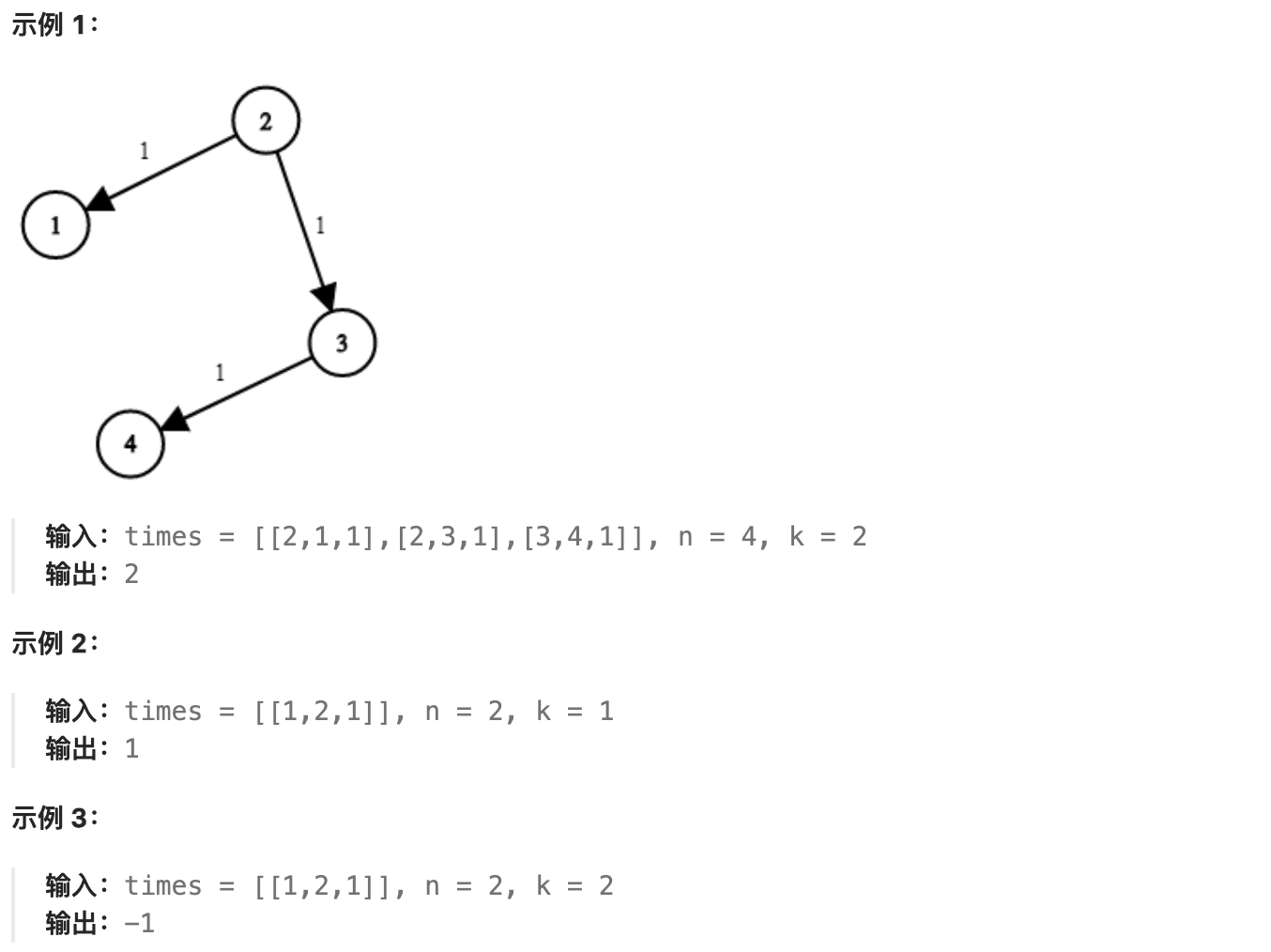
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
-
+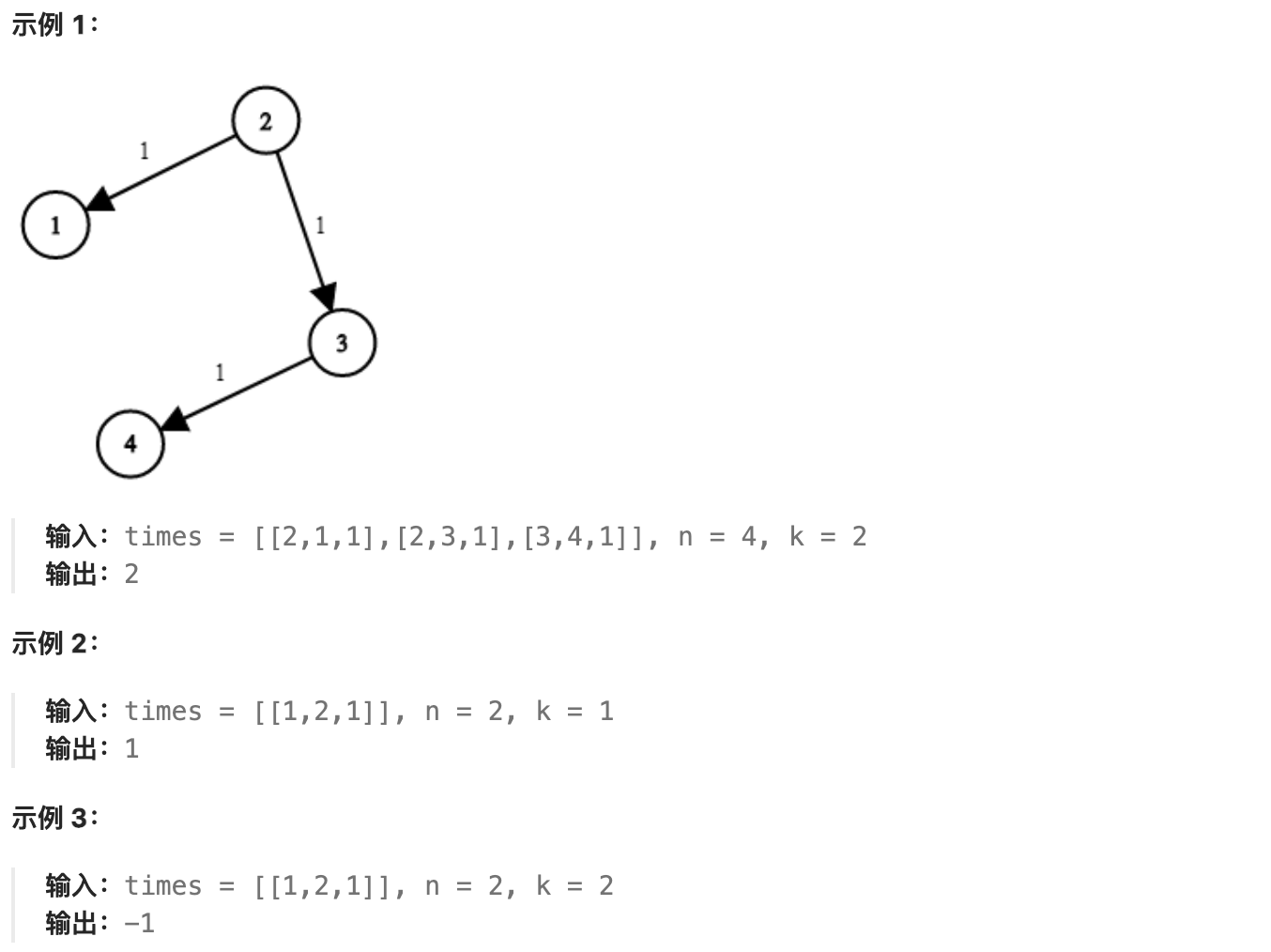
提示:
@@ -42,7 +42,7 @@ dijkstra算法:在有权图(权值非负数)中求从起点到其他节点
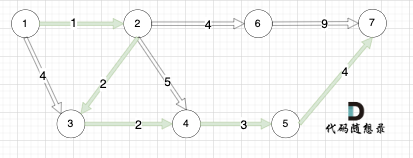
如本题示例中的图:
-
+
起点(节点1)到终点(节点7) 的最短路径是 图中 标记绿线的部分。
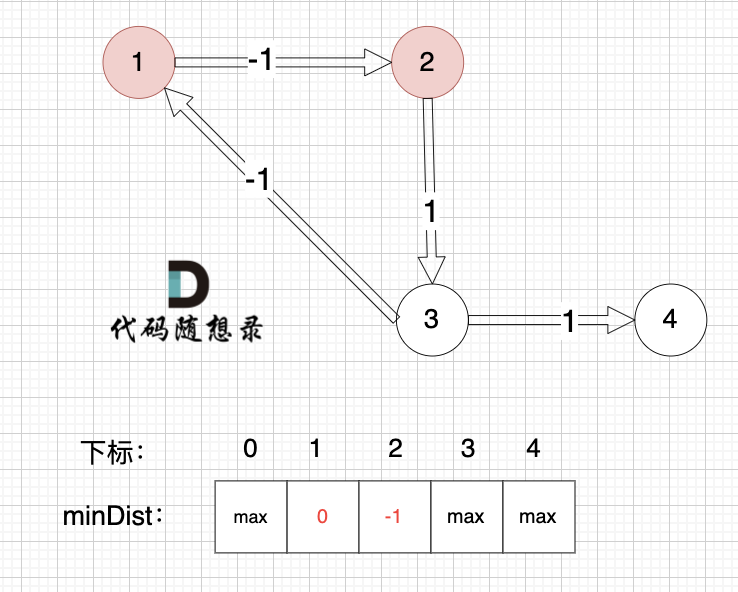
@@ -88,7 +88,7 @@ minDist数组数值初始化为int最大值。
这里在强点一下 **minDist数组的含义:记录所有节点到源点的最短路径**,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。
-
+
(图中,max 表示默认值,节点0 不做处理,统一从下标1 开始计算,这样下标和节点数值统一, 方便大家理解,避免搞混)
@@ -110,7 +110,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
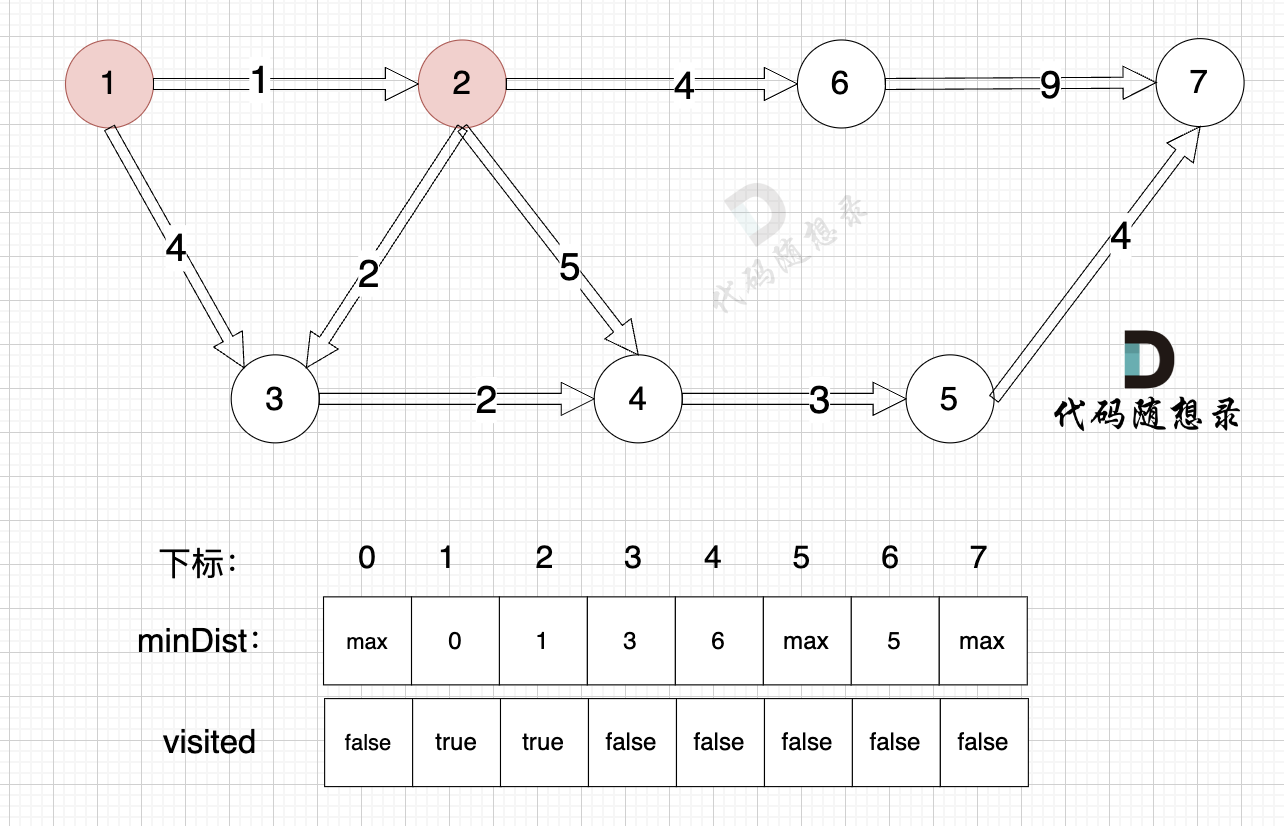
@@ -136,7 +136,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点6 、 节点3 和 节点4的距离。
@@ -170,7 +170,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
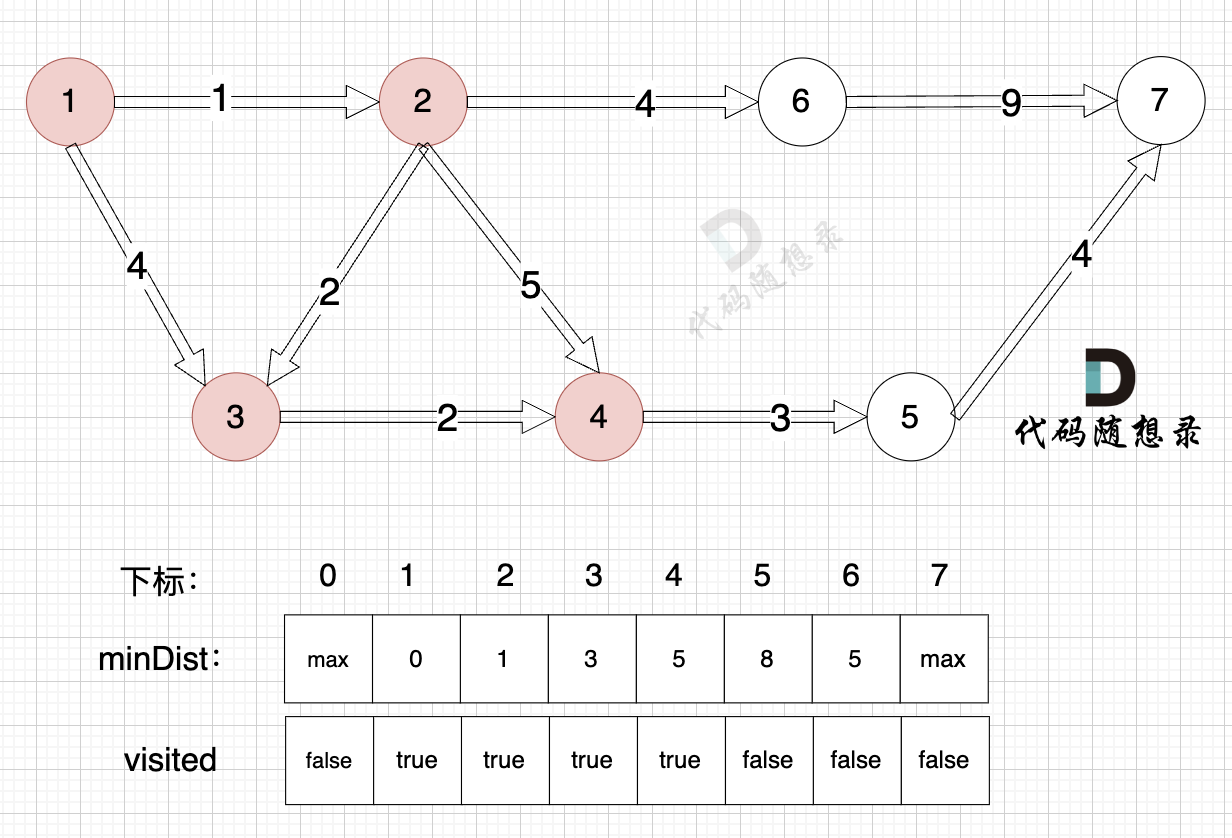
@@ -190,7 +190,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点4的加入,那么源点可以链接到节点5 所以更新minDist数组:
@@ -210,7 +210,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点6的加入,那么源点可以链接到节点7 所以 更新minDist数组:
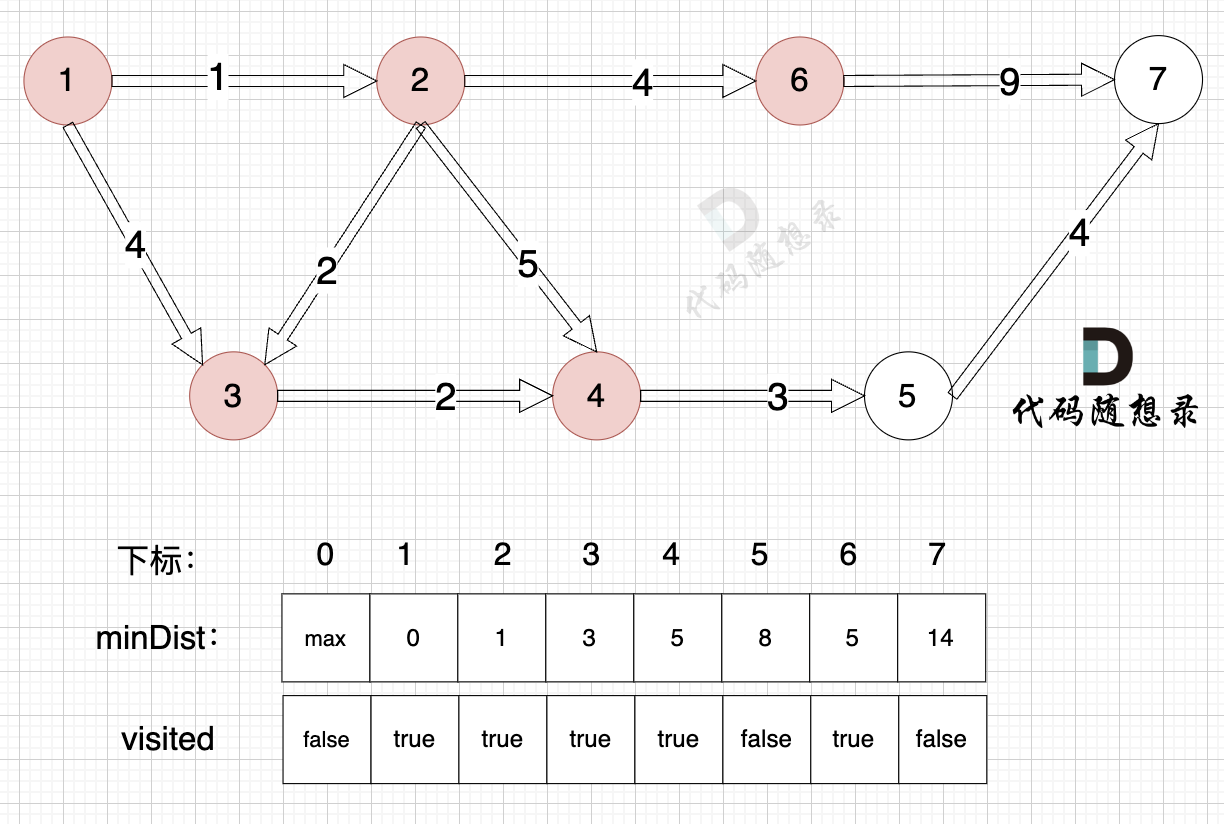
@@ -230,7 +230,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点5的加入,那么源点有新的路径可以链接到节点7 所以 更新minDist数组:
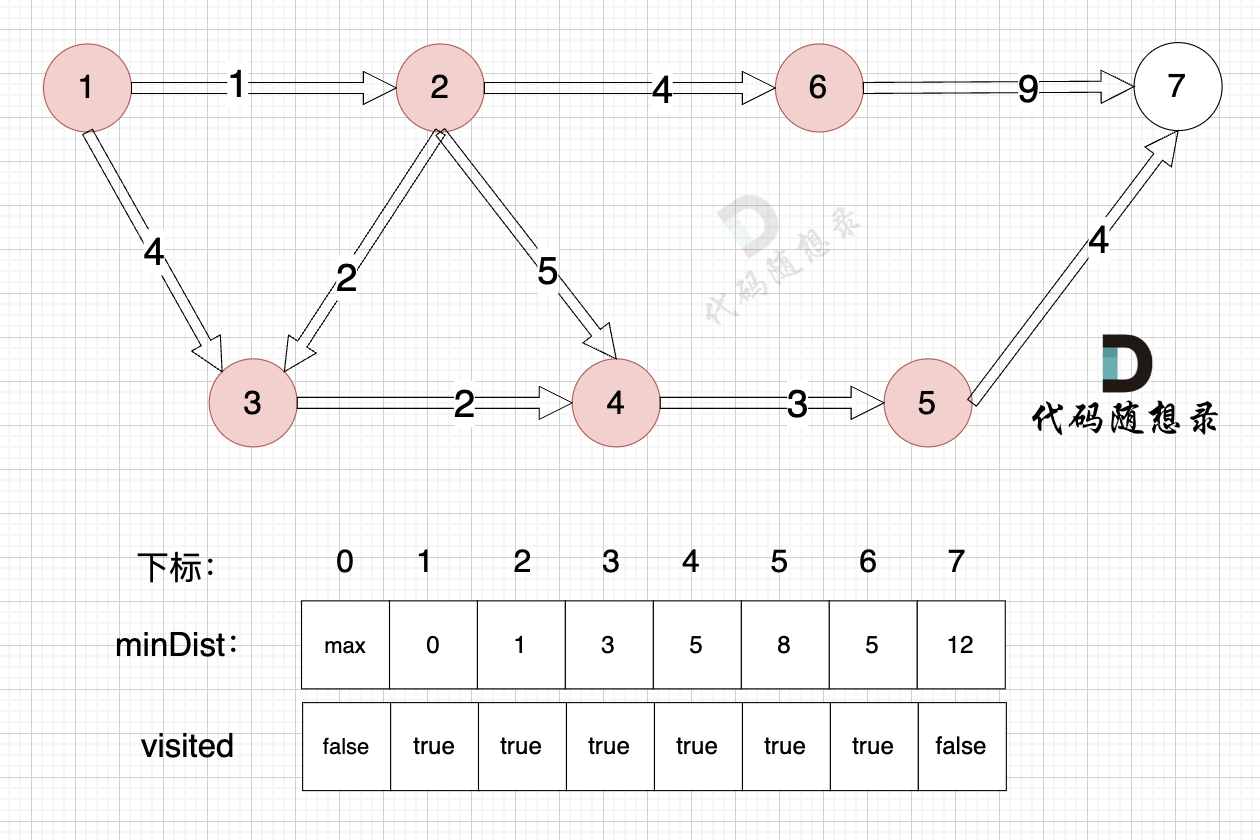
@@ -248,7 +248,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
节点7加入,但节点7到节点7的距离为0,所以 不用更新minDist数组
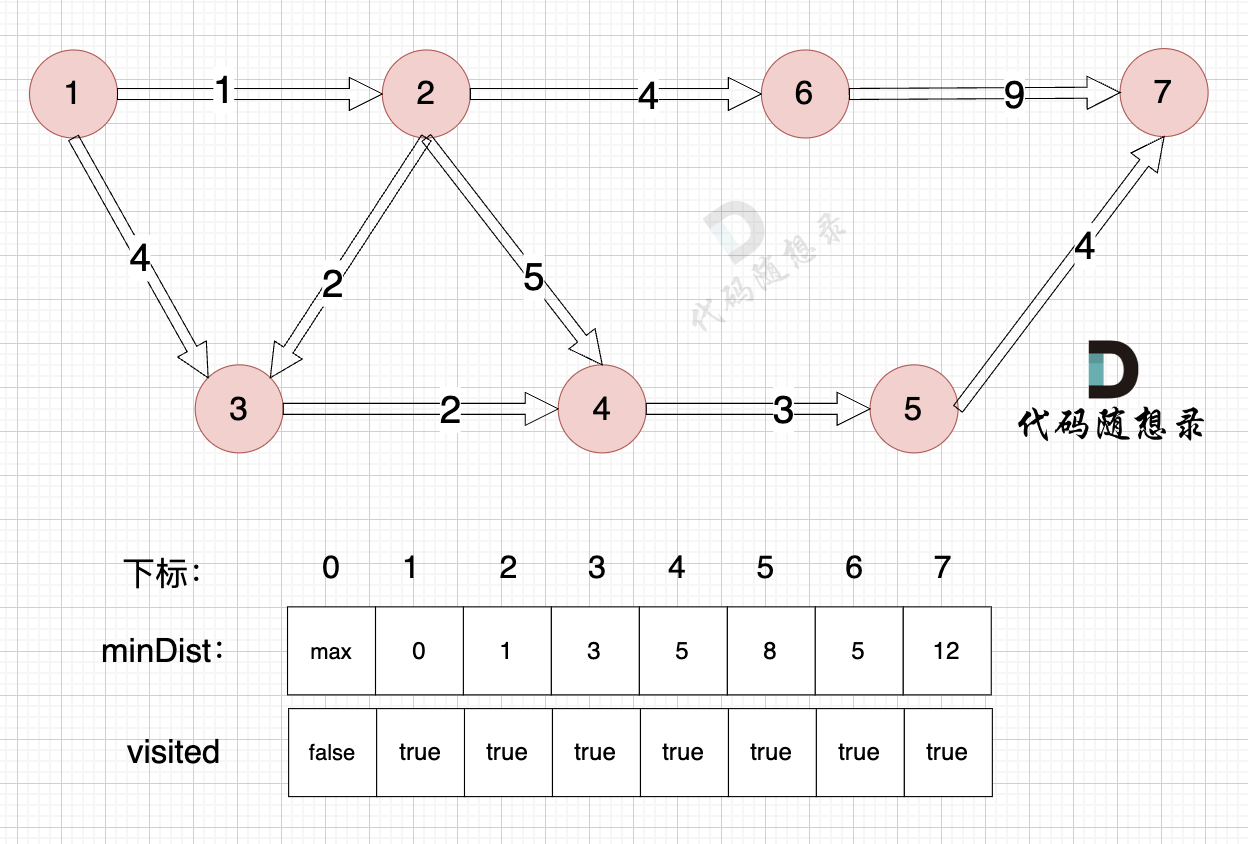
@@ -262,7 +262,7 @@ minDist数组数值初始化为int最大值。
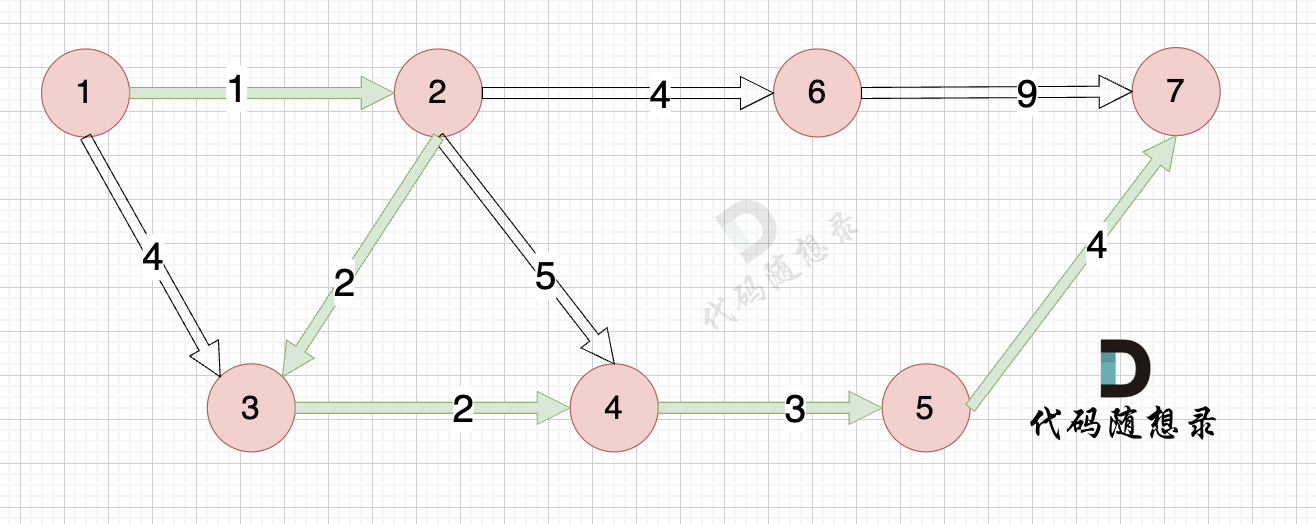
路径如图:
-
+
在上面的讲解中,每一步 我都是按照 dijkstra 三部曲来讲解的,理解了这三部曲,代码也就好懂的。
@@ -431,7 +431,7 @@ select:4
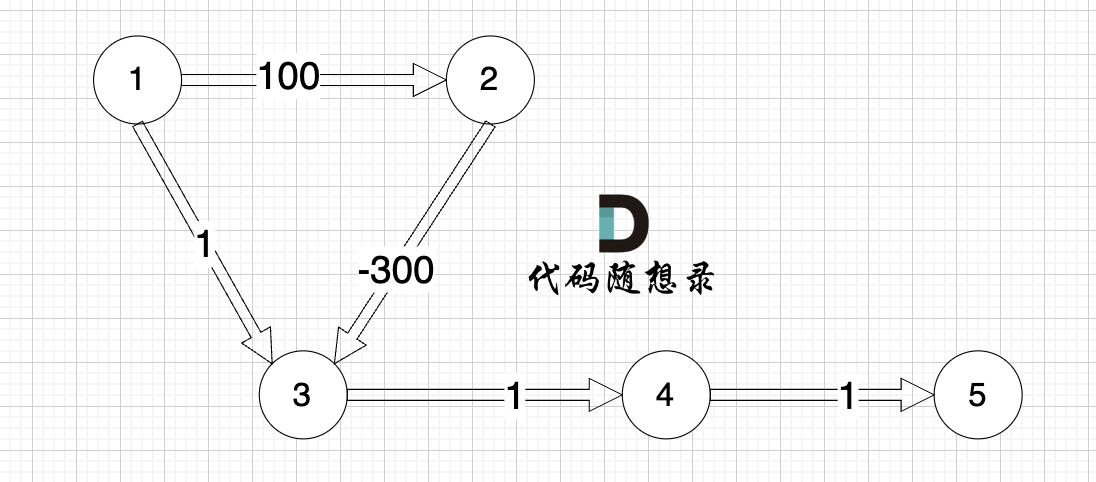
看一下这个图: (有负权值)
-
+
节点1 到 节点5 的最短路径 应该是 节点1 -> 节点2 -> 节点3 -> 节点4 -> 节点5
@@ -441,7 +441,7 @@ select:4
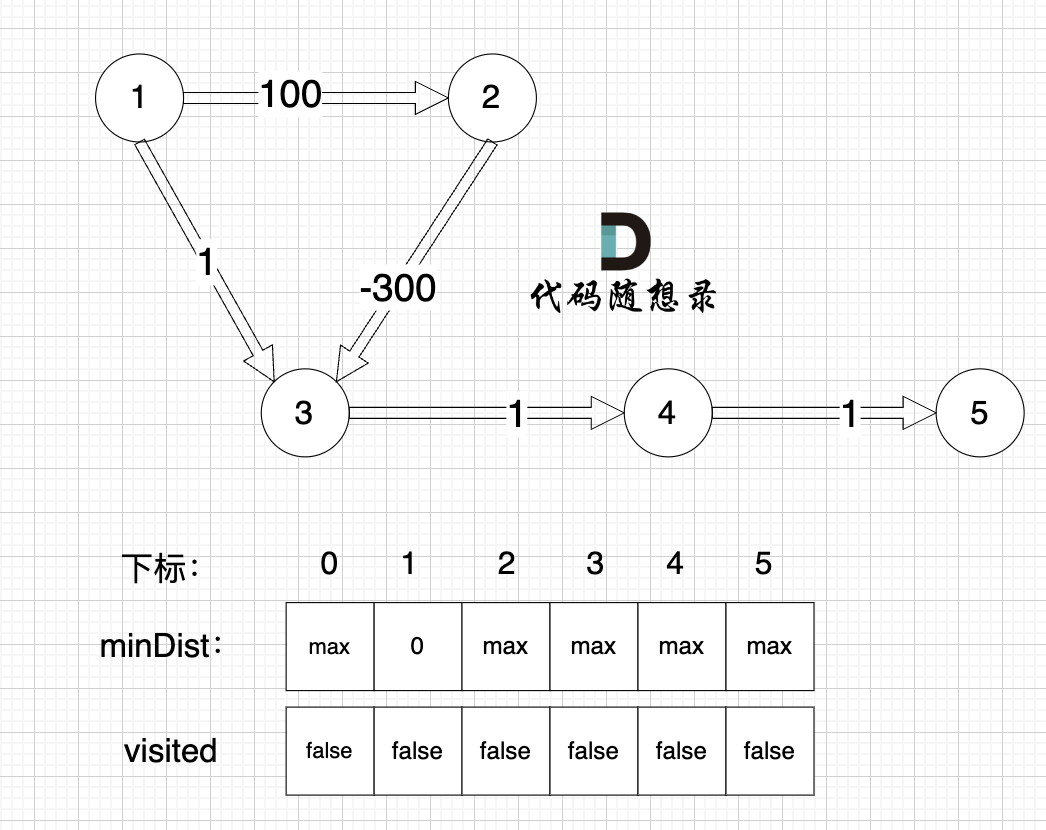
初始化:
-
+
---------------
@@ -455,7 +455,7 @@ select:4
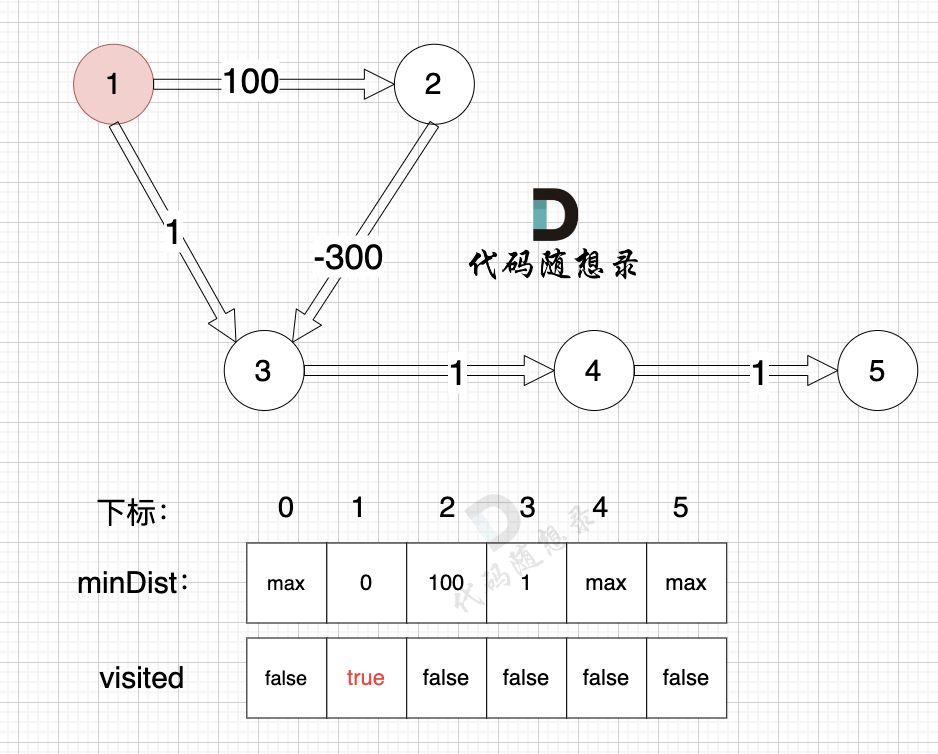
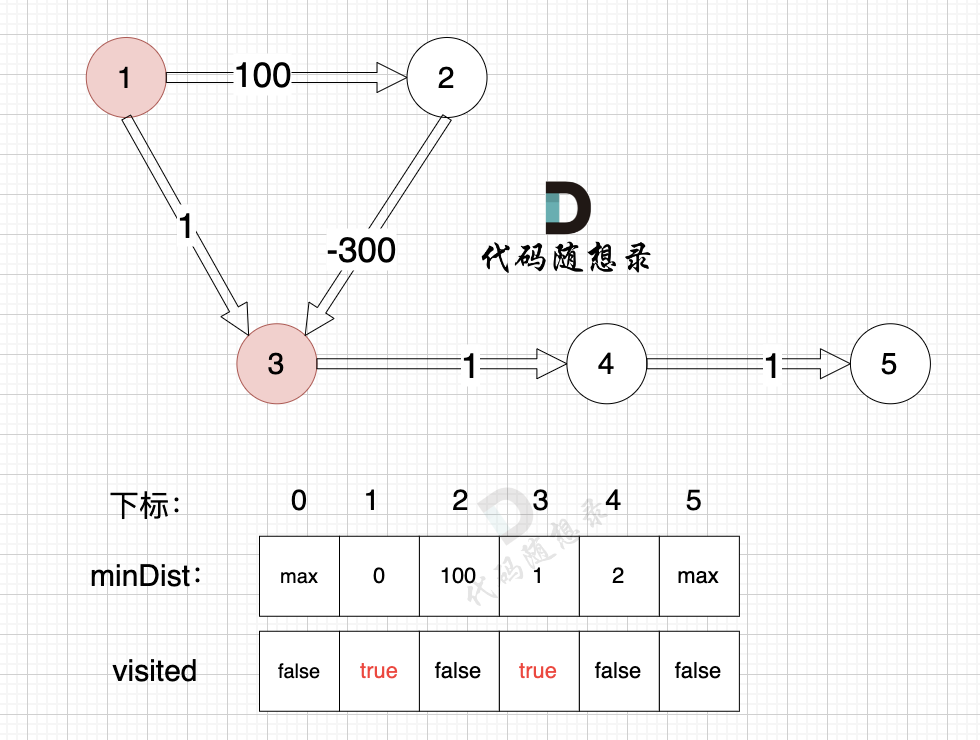
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
@@ -474,7 +474,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
@@ -492,7 +492,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-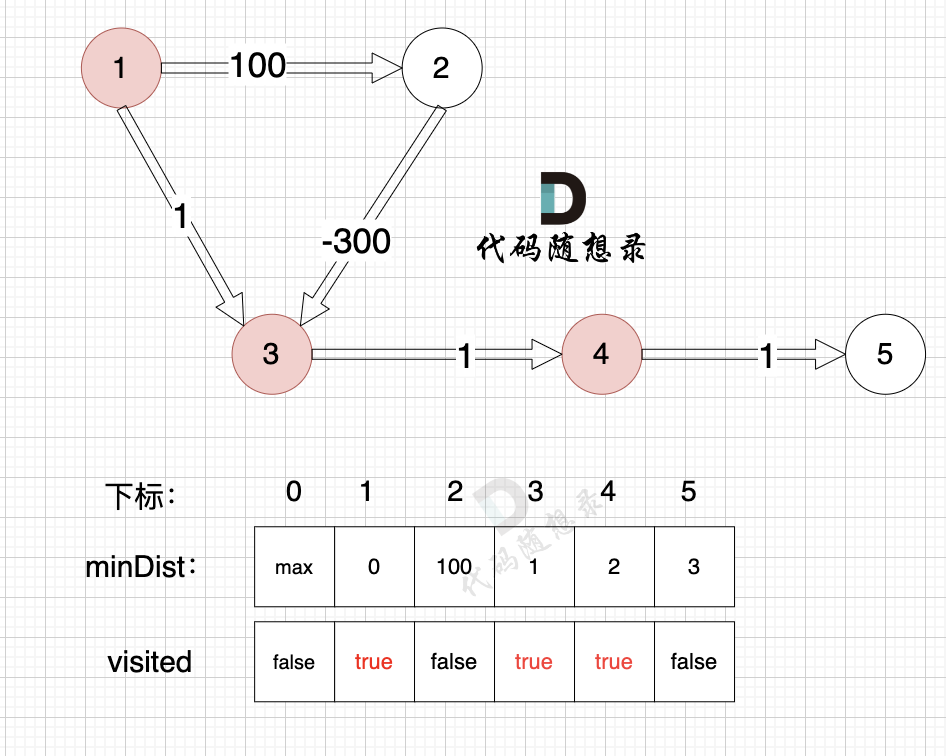
+
由于节点4的加入,那么源点可以有新的路径链接到节点5 所以更新minDist数组:
@@ -510,7 +510,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-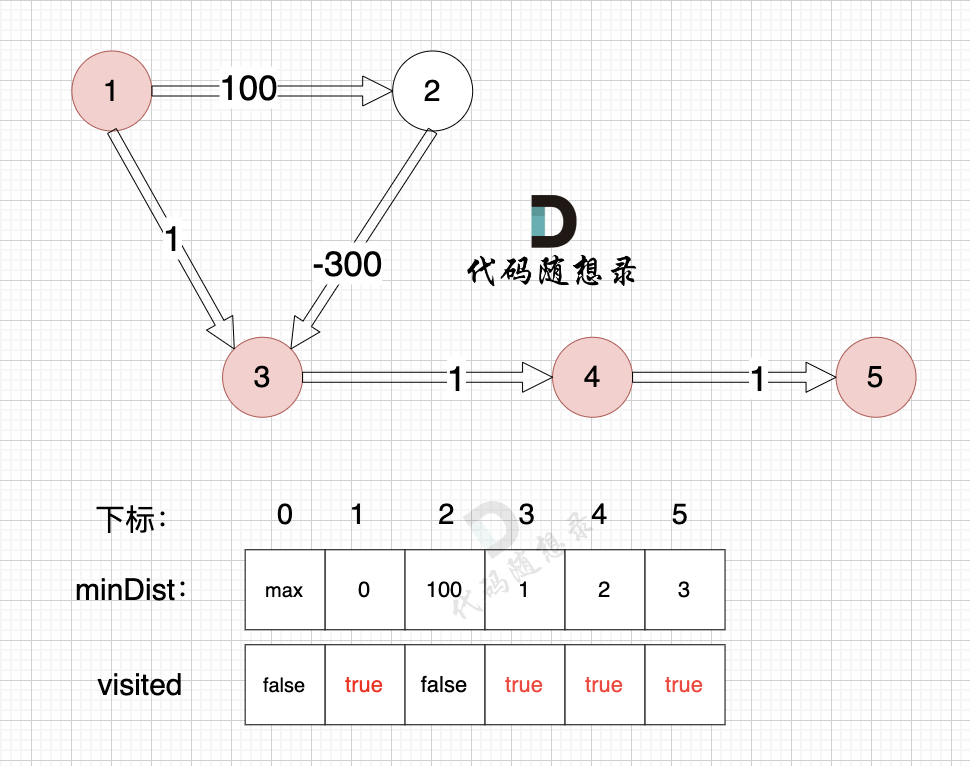
+
节点5的加入,而节点5 没有链接其他节点, 所以不用更新minDist数组,仅标记节点5被访问过了
@@ -526,7 +526,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-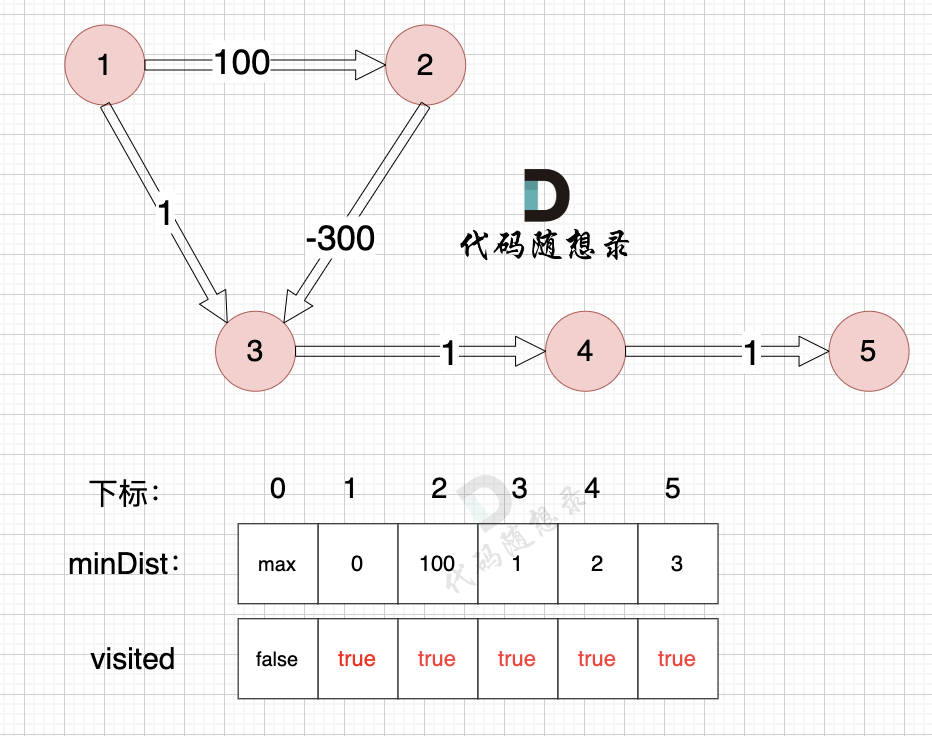
+
--------------
@@ -654,7 +654,7 @@ for (int v = 1; v <= n; v++) {
如图:
-
+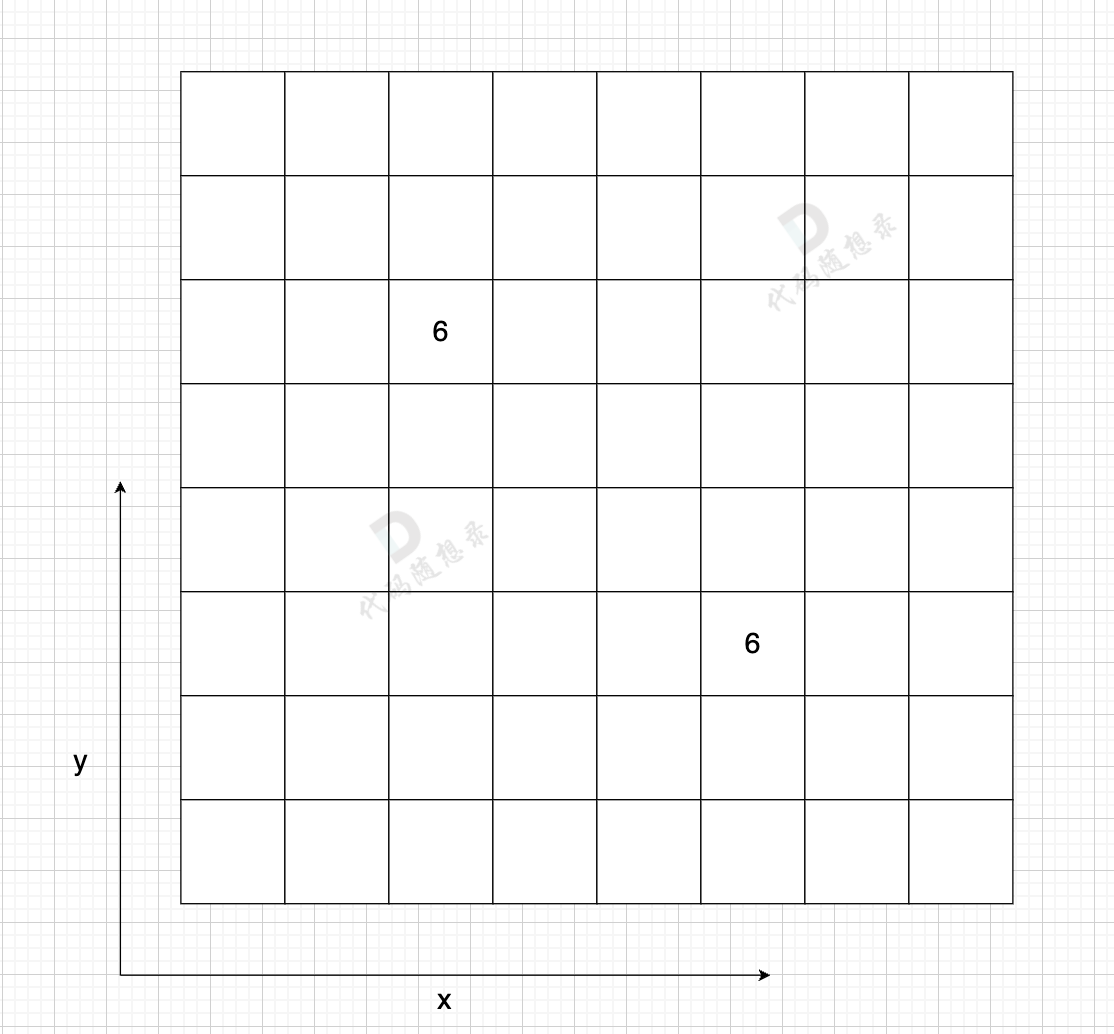
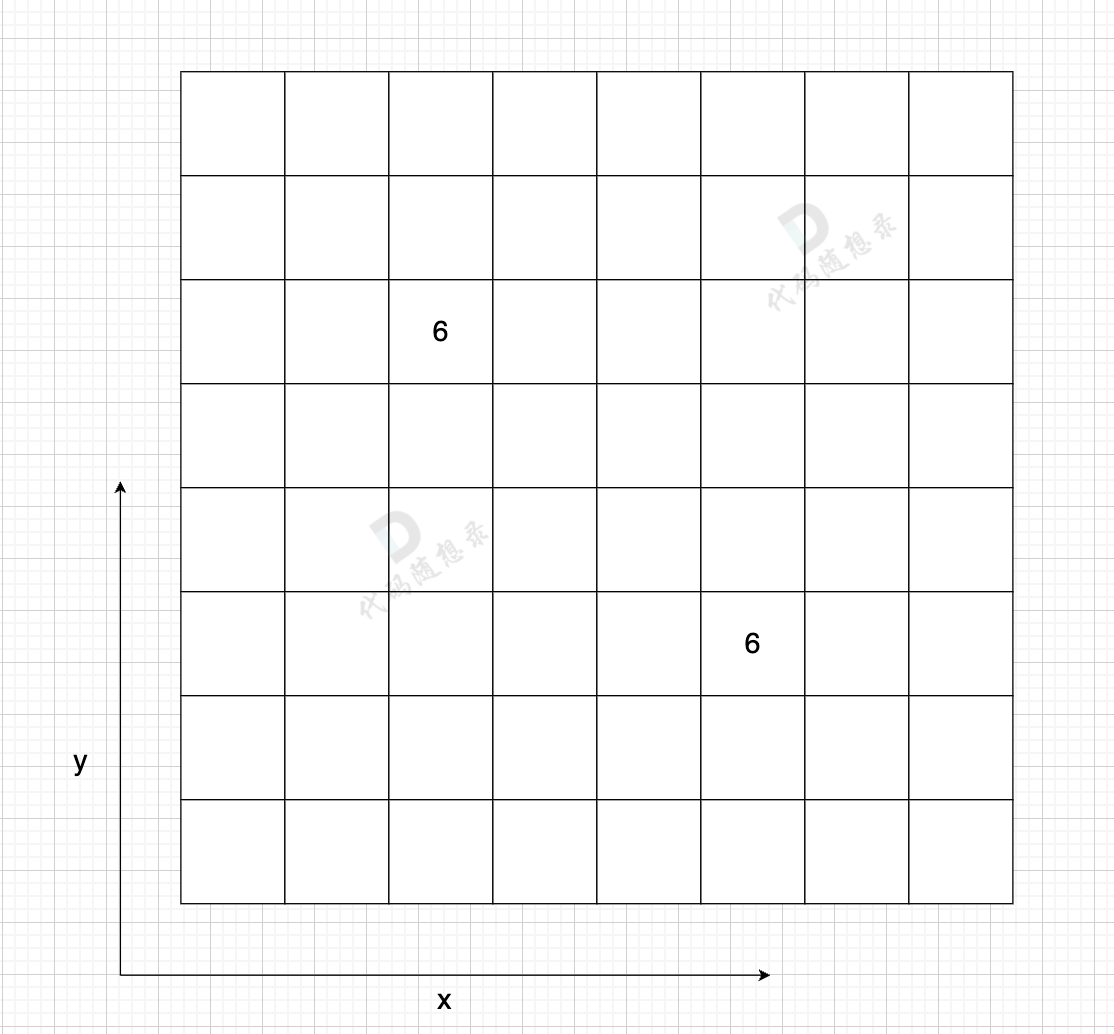
在一个 n (节点数)为8 的图中,就需要申请 8 * 8 这么大的空间,有一条双向边,即:grid[2][5] = 6,grid[5][2] = 6
@@ -678,7 +678,7 @@ for (int v = 1; v <= n; v++) {
邻接表的构造如图:
-
+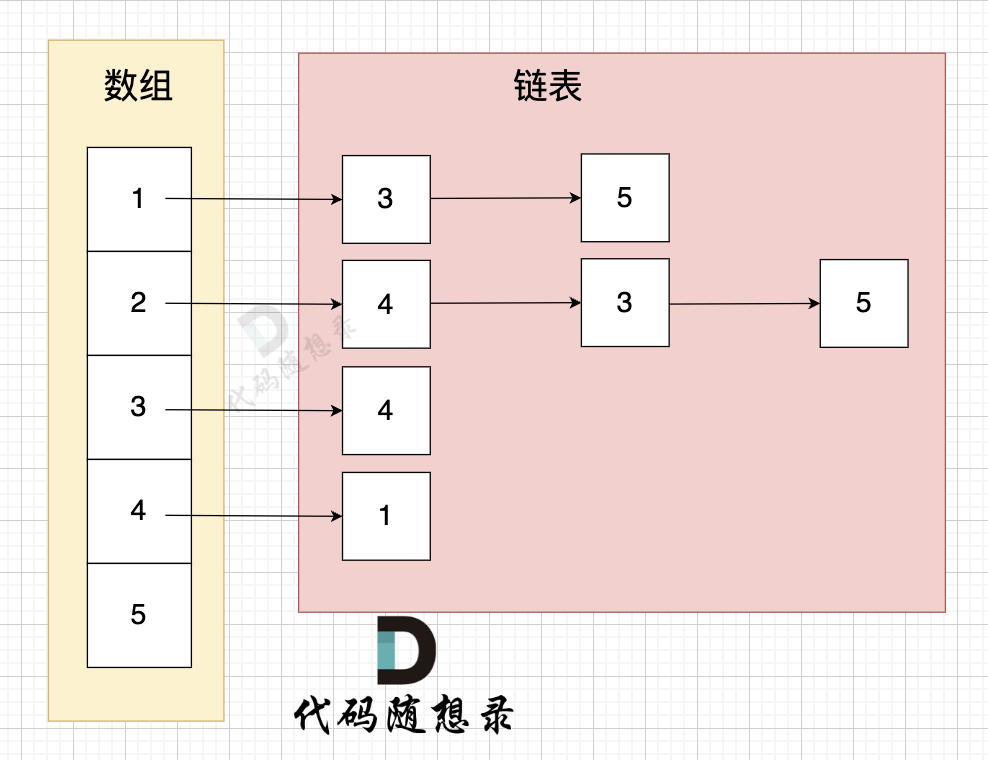
这里表达的图是:
@@ -763,7 +763,7 @@ vector> grid(n + 1);
不少录友,不知道 如何定义的数据结构,怎么表示邻接表的,我来给大家画一个图:
-
+
图中邻接表表示:
@@ -784,7 +784,7 @@ vector>> grid(n + 1);
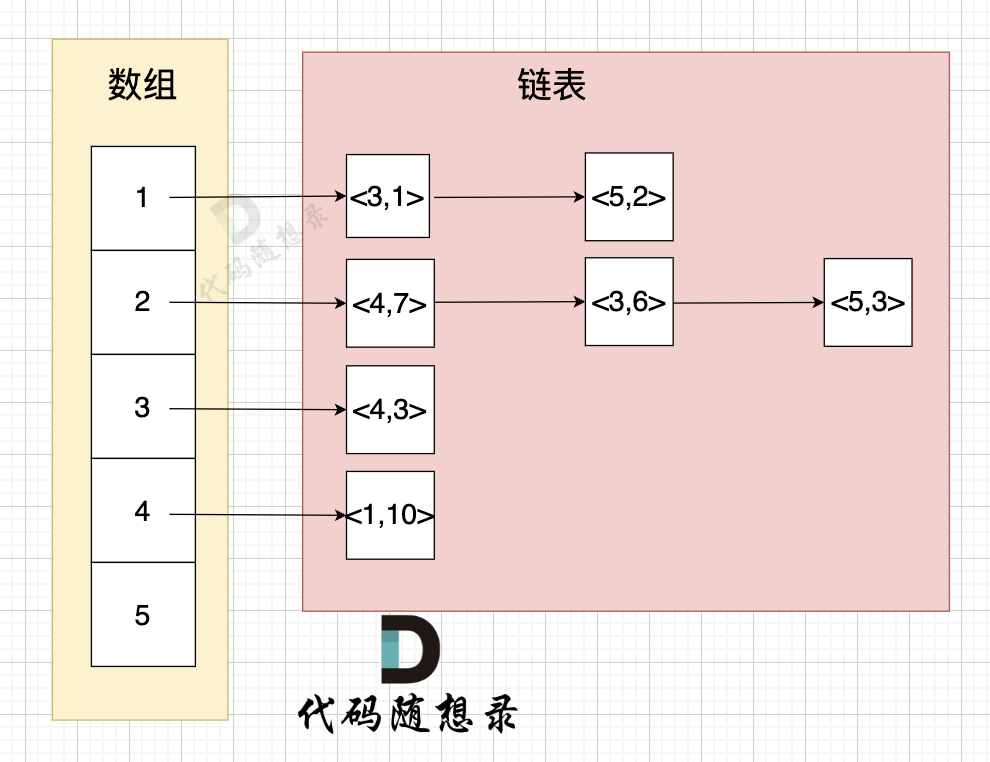
举例来给大家展示 该代码表达的数据 如下:
-
+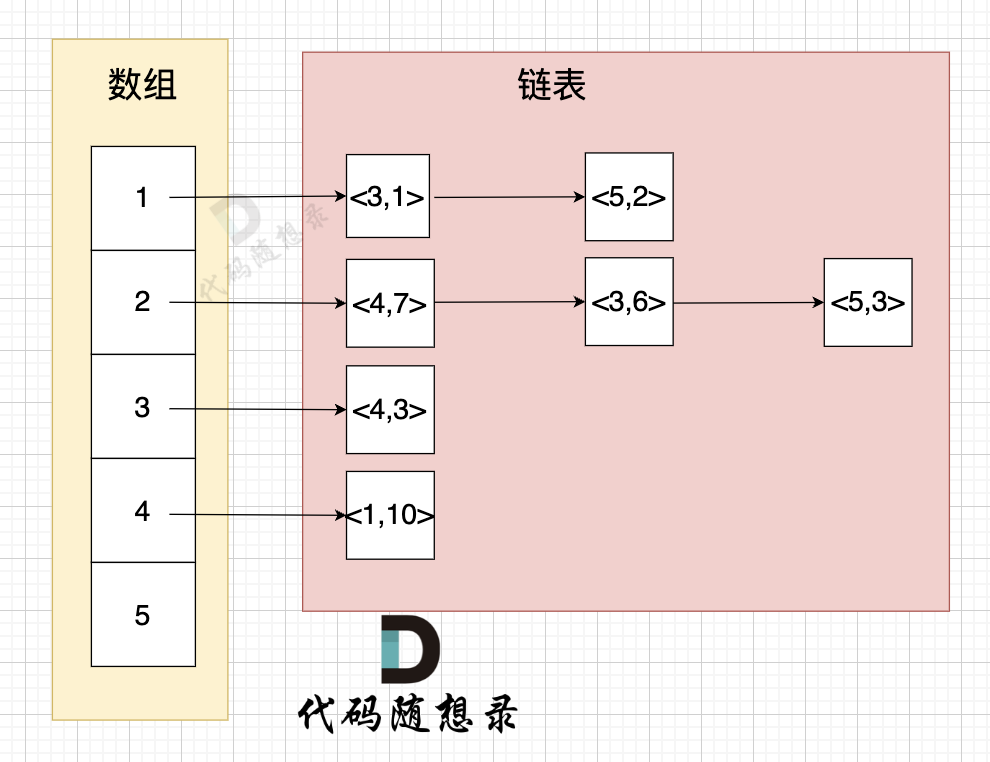
* 节点1 指向 节点3 权值为 1
* 节点1 指向 节点5 权值为 2
@@ -907,7 +907,7 @@ for (int v = 1; v <= n; v++) {
再回顾一下邻接表的构造(数组 + 链表):
-
+
假如 加入的cur 是节点 2, 那么 grid[2] 表示的就是图中第二行链表。 (grid数组的构造我们在 上面 「图的存储」中讲过)
diff --git a/problems/0746.使用最小花费爬楼梯.md b/problems/0746.使用最小花费爬楼梯.md
index 9145c7ed..147c7bfb 100644
--- a/problems/0746.使用最小花费爬楼梯.md
+++ b/problems/0746.使用最小花费爬楼梯.md
@@ -52,7 +52,7 @@
请你计算并返回达到楼梯顶部的最低花费。
-
+
## 思路
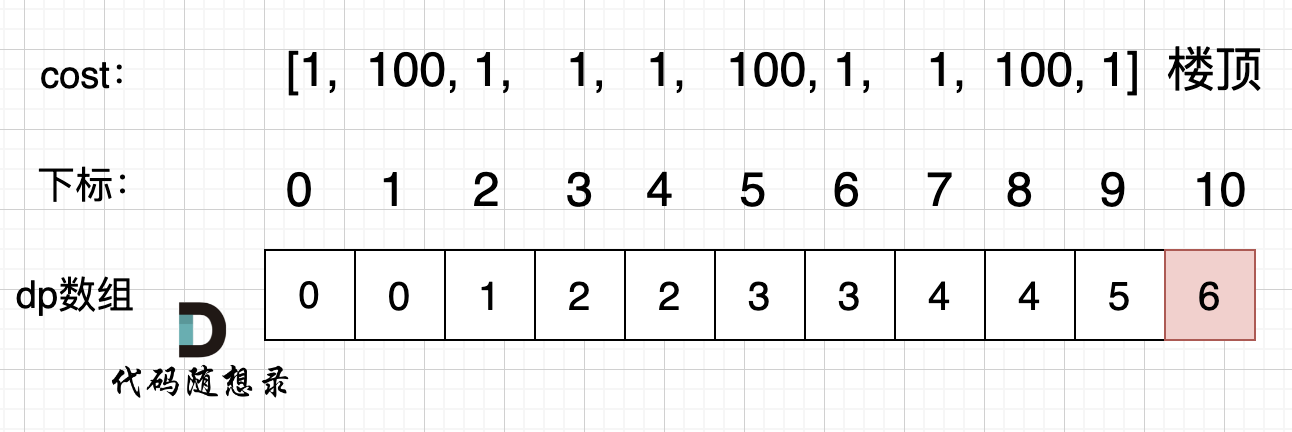
@@ -112,7 +112,7 @@ dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
-
+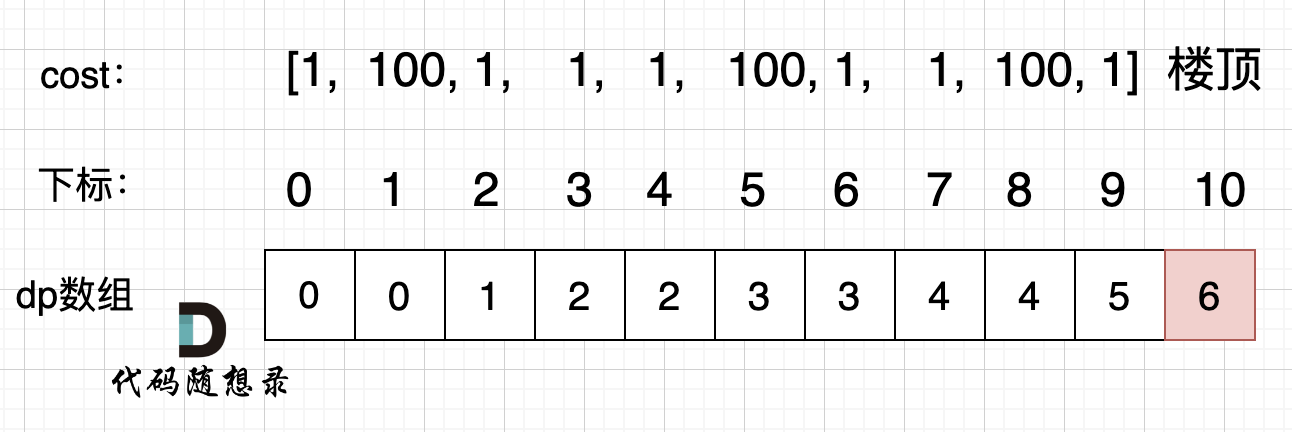
如果大家代码写出来有问题,就把dp数组打印出来,看看和如上推导的是不是一样的。
diff --git a/problems/0763.划分字母区间.md b/problems/0763.划分字母区间.md
index 70ebfe4f..daf52bea 100644
--- a/problems/0763.划分字母区间.md
+++ b/problems/0763.划分字母区间.md
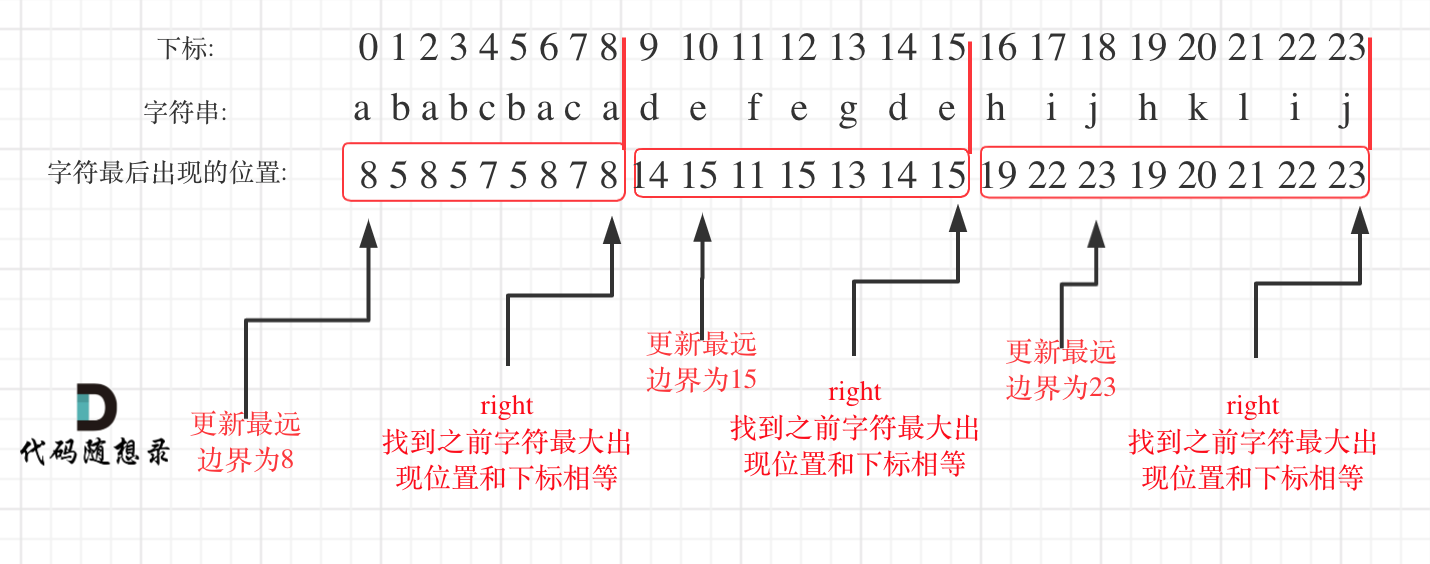
@@ -44,7 +44,7 @@
如图:
-
+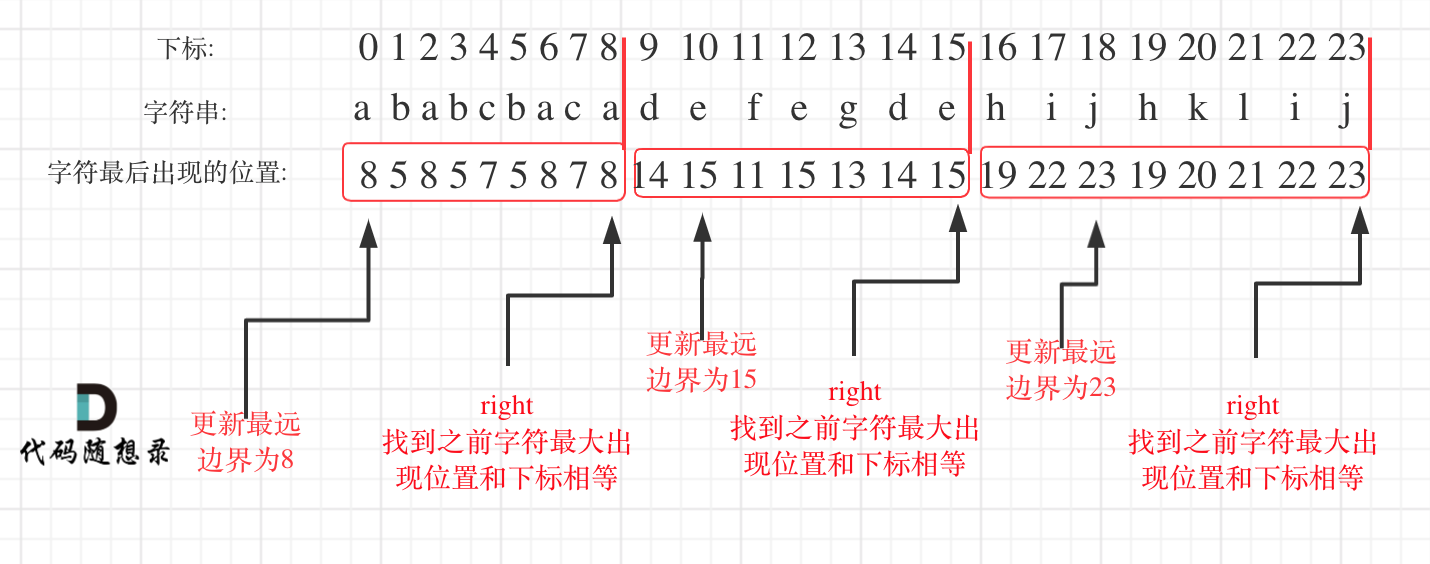
明白原理之后,代码并不复杂,如下:
diff --git a/problems/0787.K站中转内最便宜的航班.md b/problems/0787.K站中转内最便宜的航班.md
index 68d84215..6133ac77 100644
--- a/problems/0787.K站中转内最便宜的航班.md
+++ b/problems/0787.K站中转内最便宜的航班.md
@@ -9,11 +9,11 @@
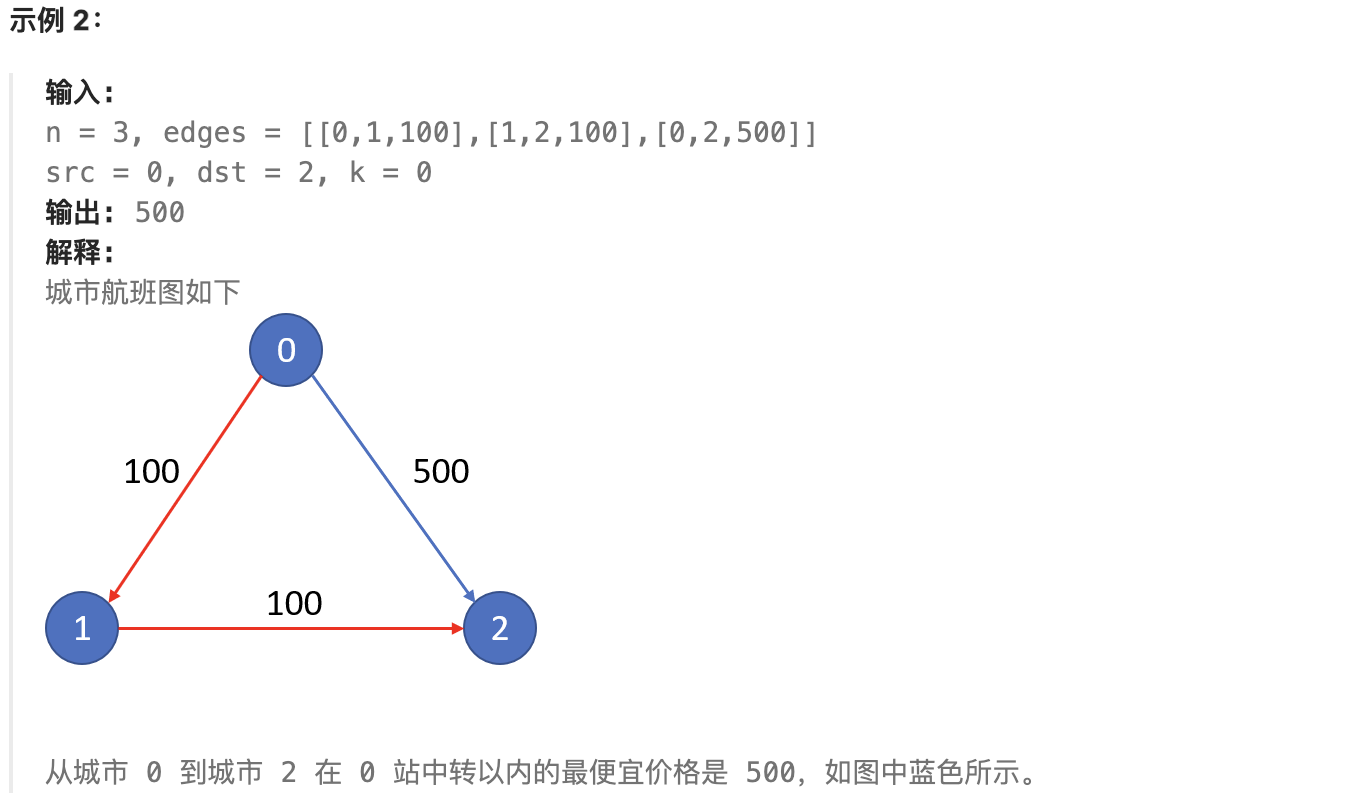
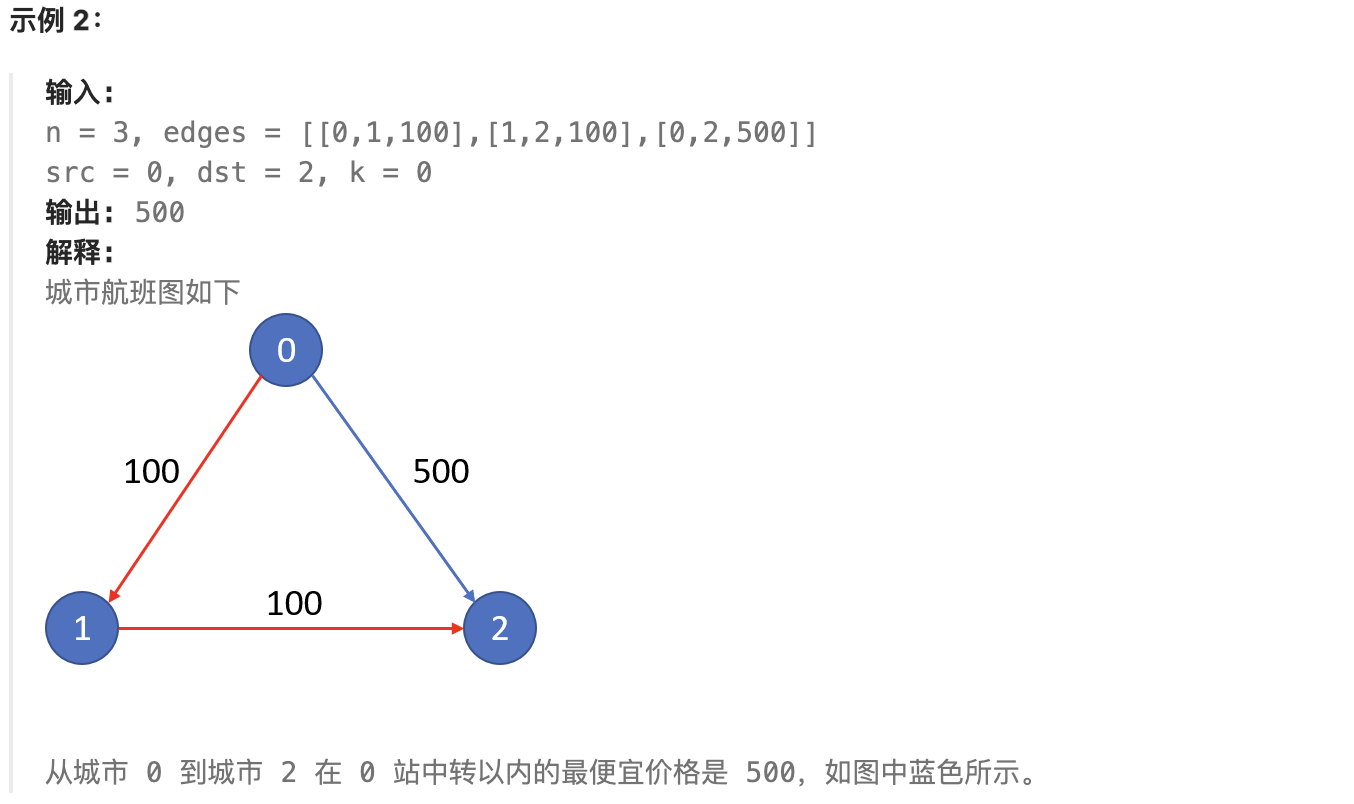
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到出一条最多经过 k 站中转的路线,使得从 src 到 dst 的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出 -1。
-
+
-
+
-
+
## 思路
diff --git a/problems/0797.所有可能的路径.md b/problems/0797.所有可能的路径.md
index a37e5c3f..639b6b2b 100644
--- a/problems/0797.所有可能的路径.md
+++ b/problems/0797.所有可能的路径.md
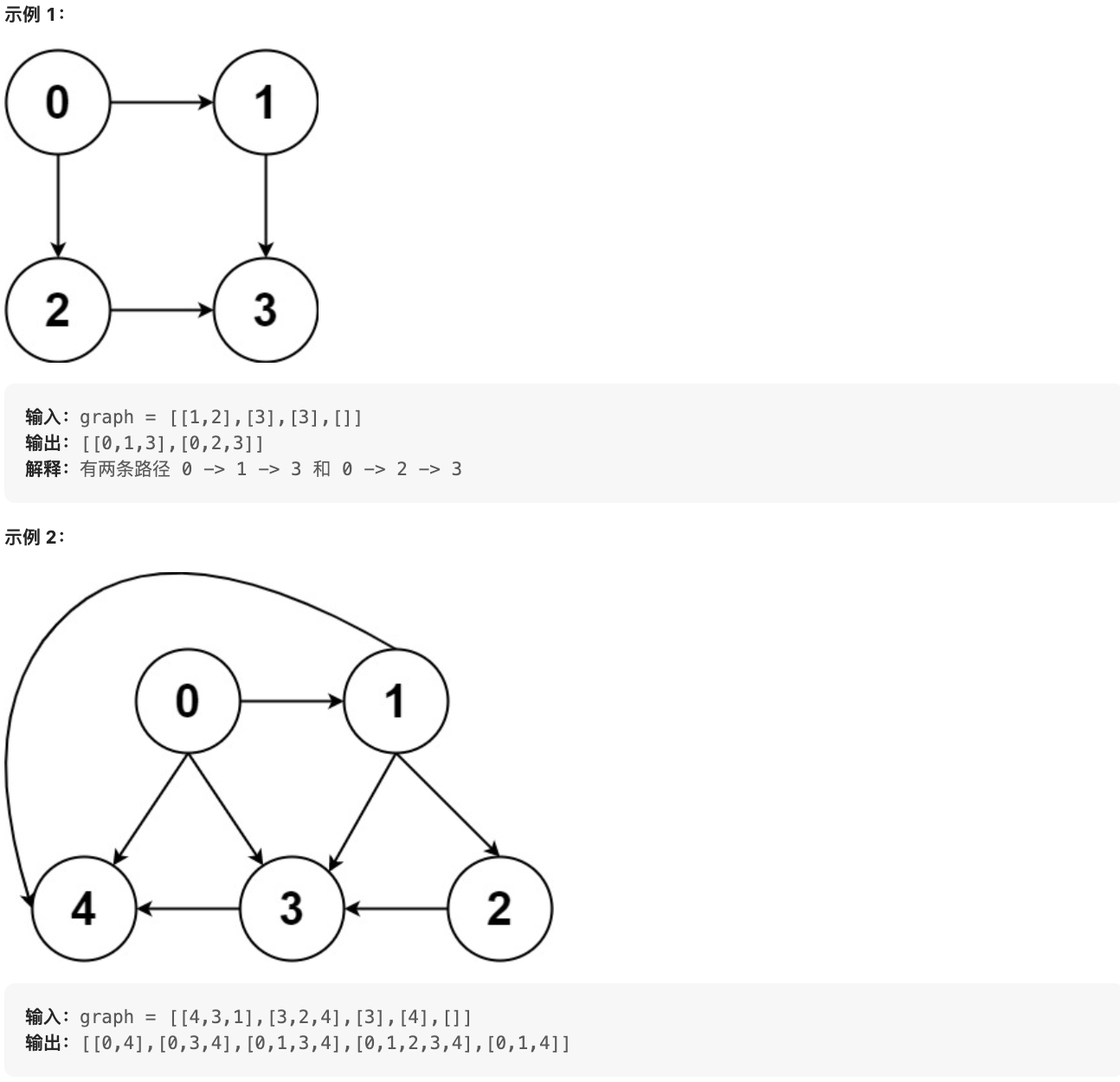
@@ -11,7 +11,7 @@
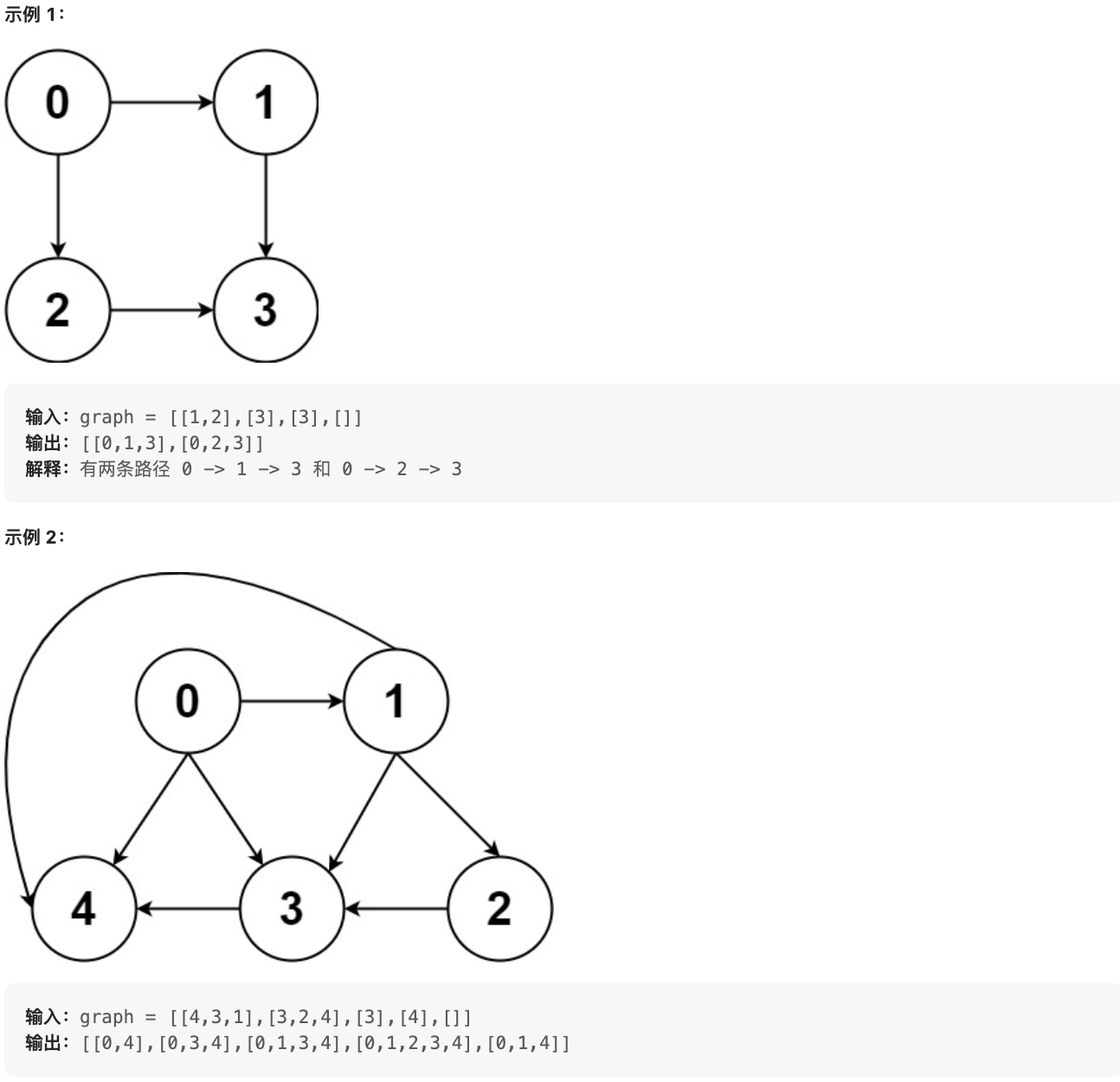
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
-
+
提示:
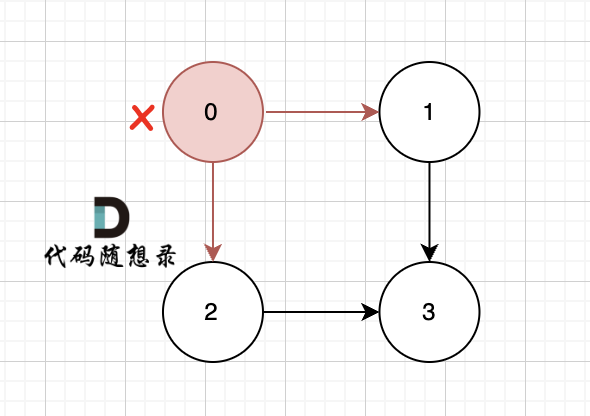
@@ -96,7 +96,7 @@ path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
一些录友可以疑惑这里如果找到x 链接的节点的,例如如果x目前是节点0,那么目前的过程就是这样的:
-
+
二维数组中,graph[x][i] 都是x链接的节点,当前遍历的节点就是 `graph[x][i]` 。
diff --git a/problems/0827.最大人工岛.md b/problems/0827.最大人工岛.md
index 0ebda252..e6aa4601 100644
--- a/problems/0827.最大人工岛.md
+++ b/problems/0827.最大人工岛.md
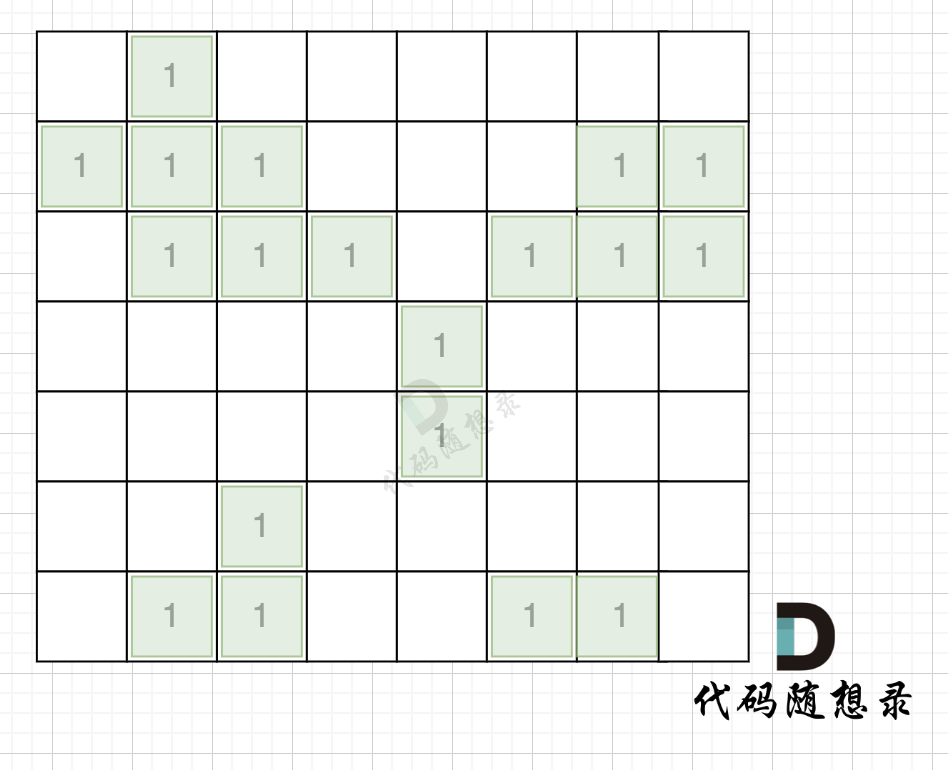
@@ -51,11 +51,11 @@
拿如下地图的岛屿情况来举例: (1为陆地)
-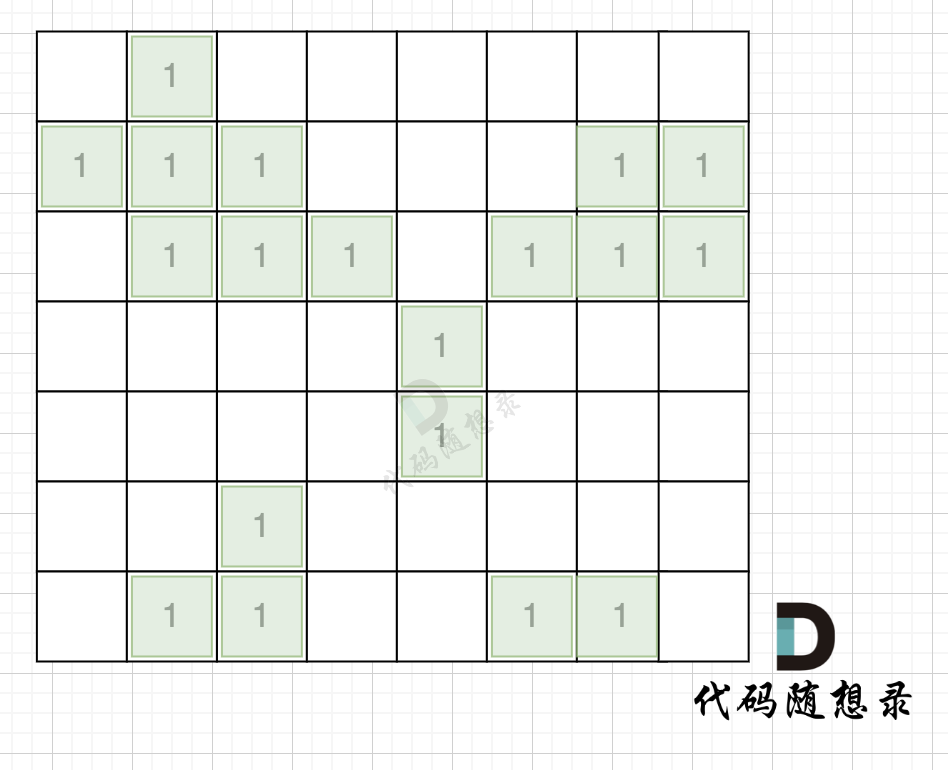
+
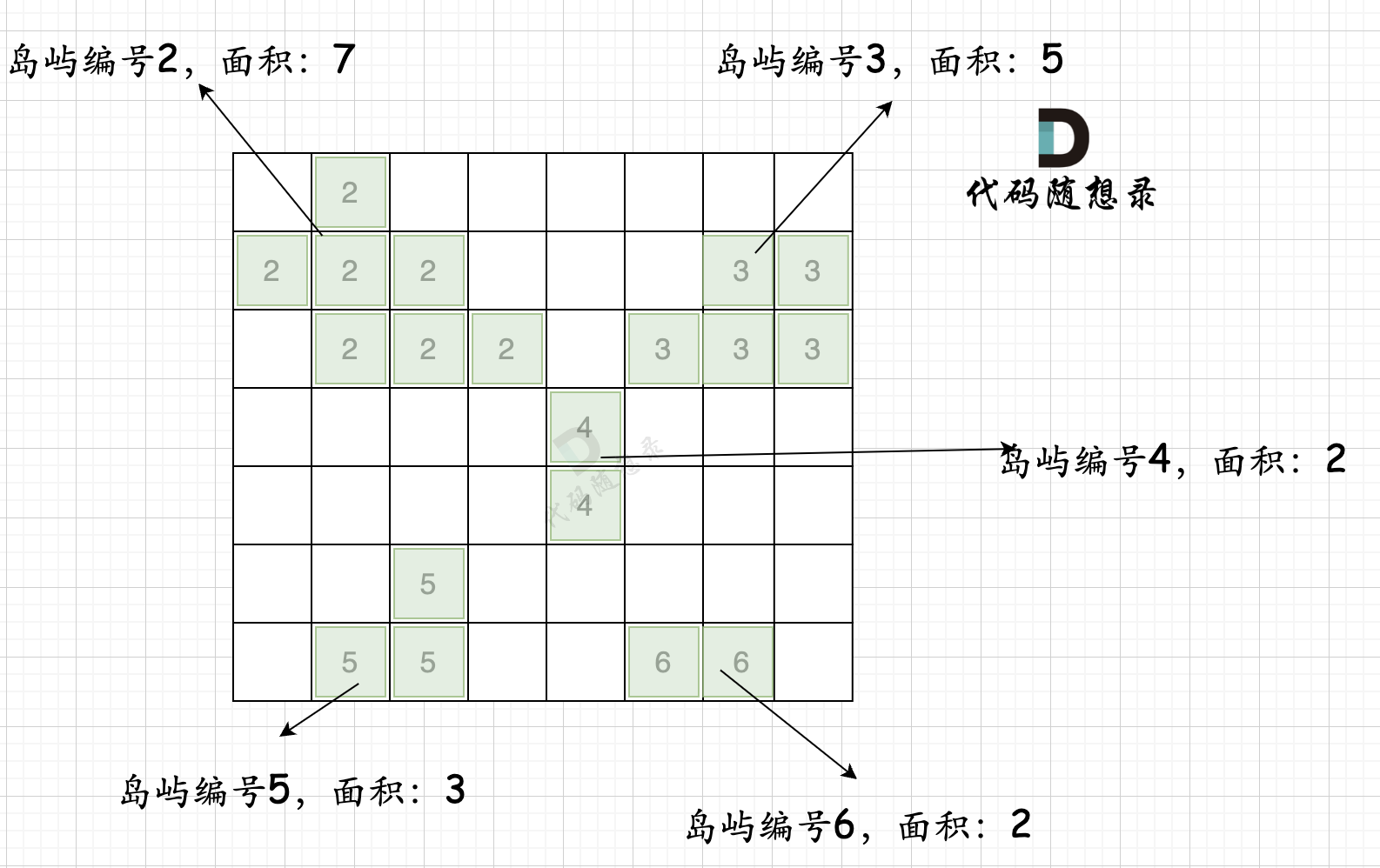
第一步,则遍历题目,并将岛屿到编号和面积上的统计,过程如图所示:
-
+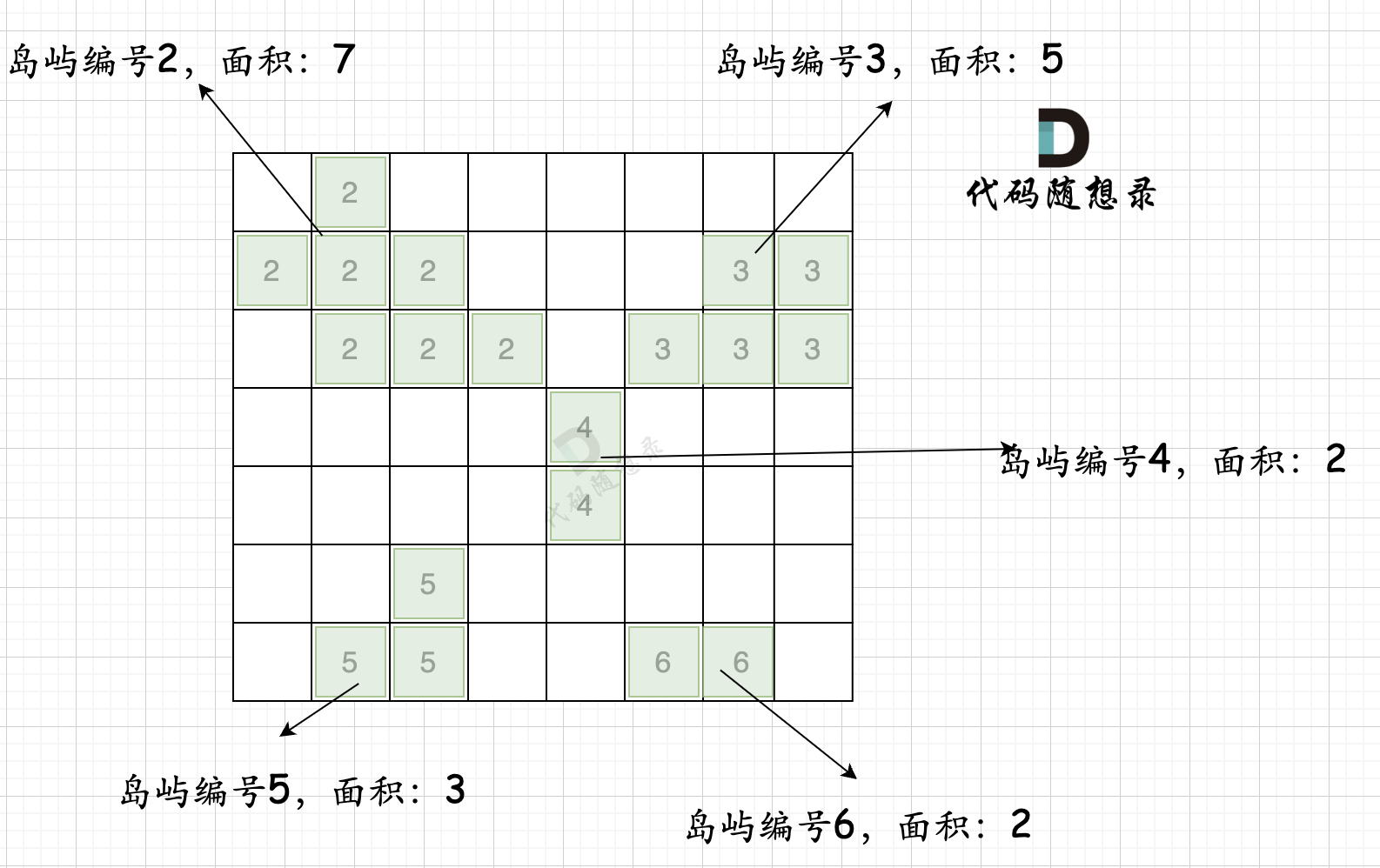
本过程代码如下:
@@ -102,7 +102,7 @@ int largestIsland(vector>& grid) {
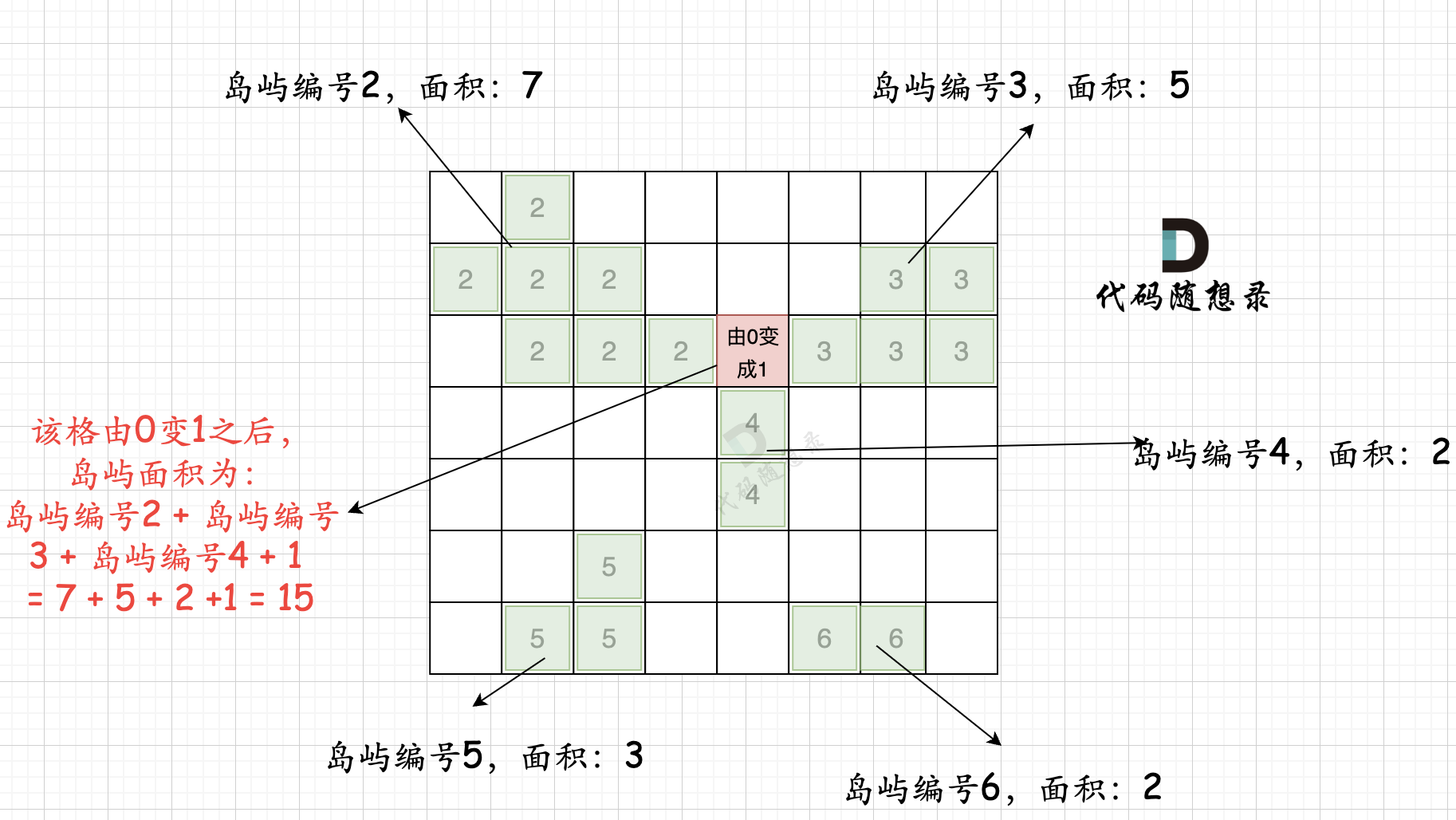
第二步过程如图所示:
-
+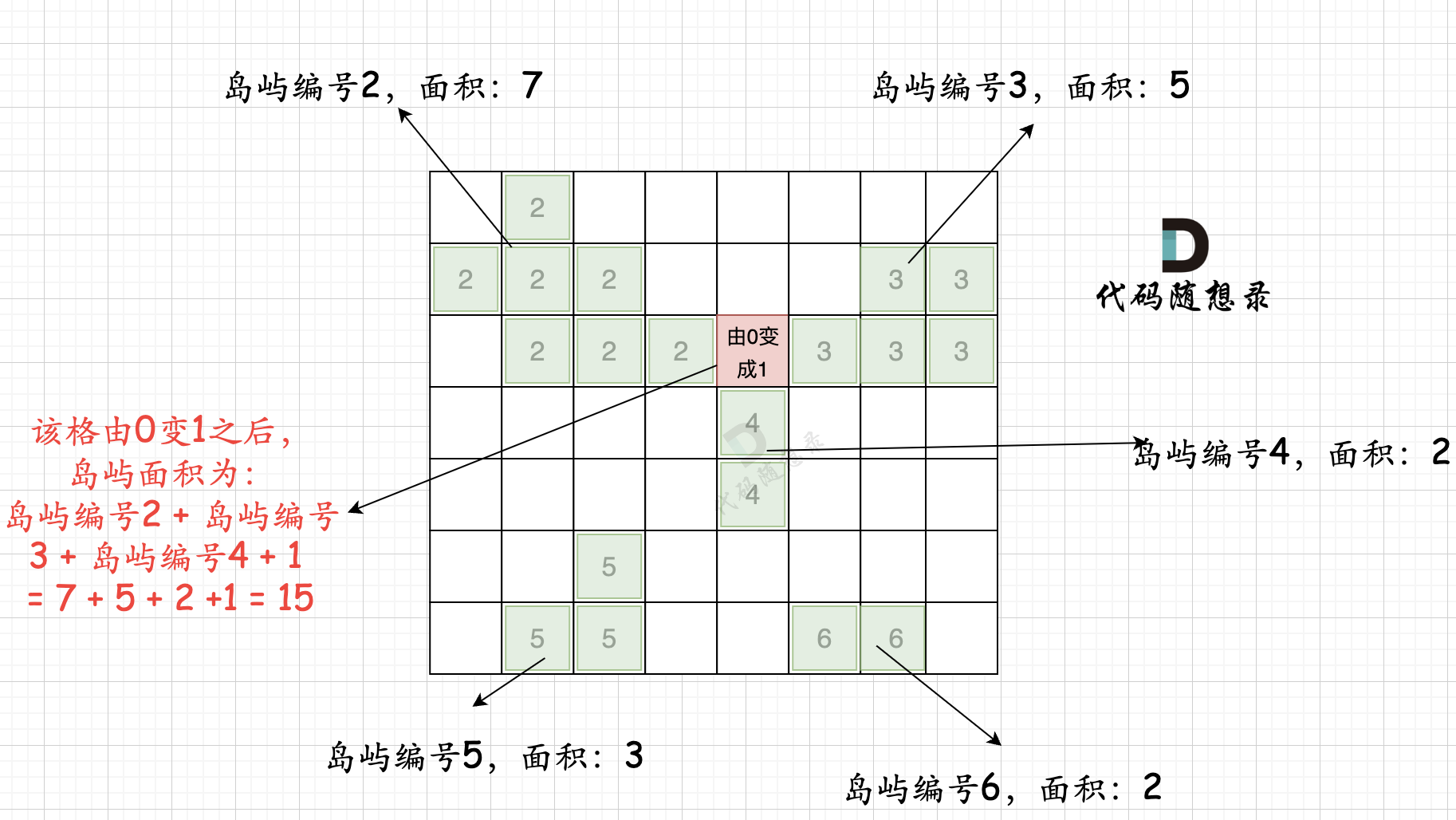
也就是遍历每一个0的方格,并统计其相邻岛屿面积,最后取一个最大值。
diff --git a/problems/0841.钥匙和房间.md b/problems/0841.钥匙和房间.md
index 4076fce5..60180d27 100644
--- a/problems/0841.钥匙和房间.md
+++ b/problems/0841.钥匙和房间.md
@@ -35,7 +35,7 @@
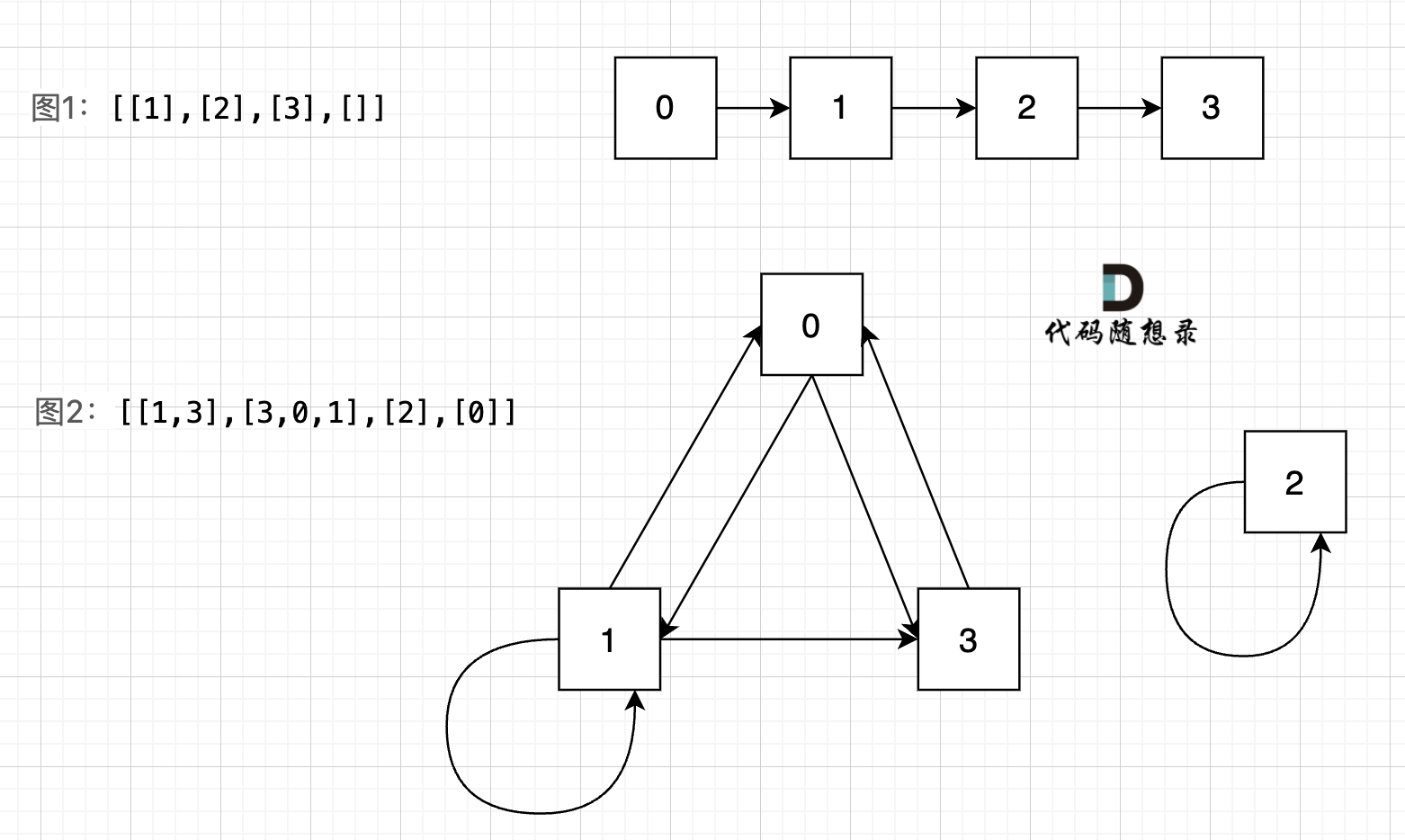
图中给我的两个示例: `[[1],[2],[3],[]]` `[[1,3],[3,0,1],[2],[0]]`,画成对应的图如下:
-
+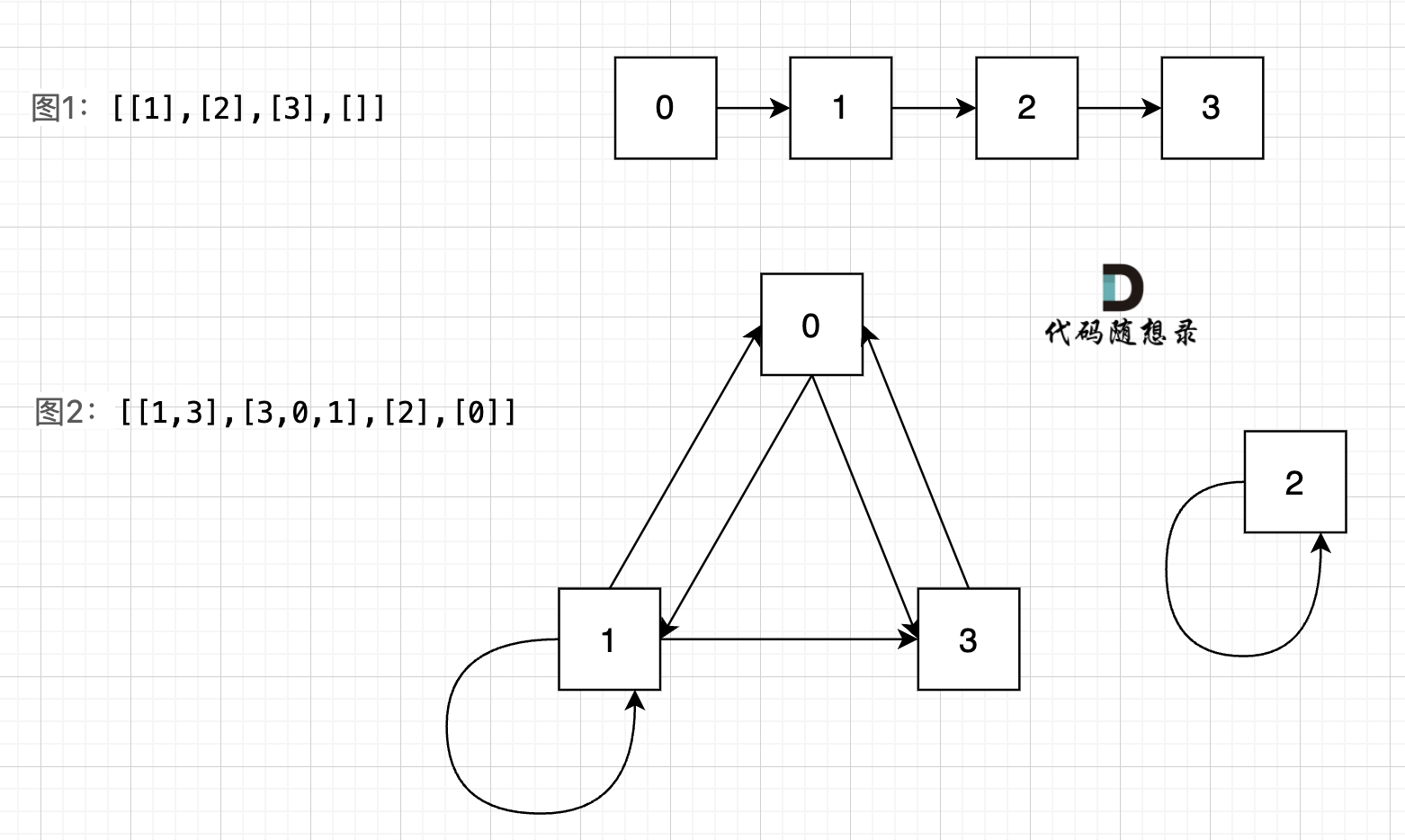
我们可以看出图1的所有节点都是链接的,而图二中,节点2 是孤立的。
@@ -48,7 +48,7 @@
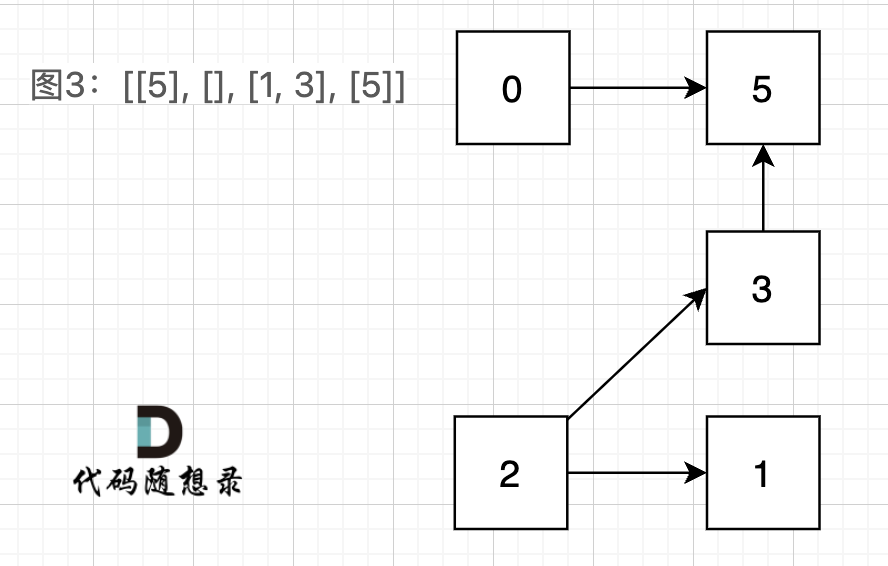
图3:[[5], [], [1, 3], [5]] ,如图:
-
+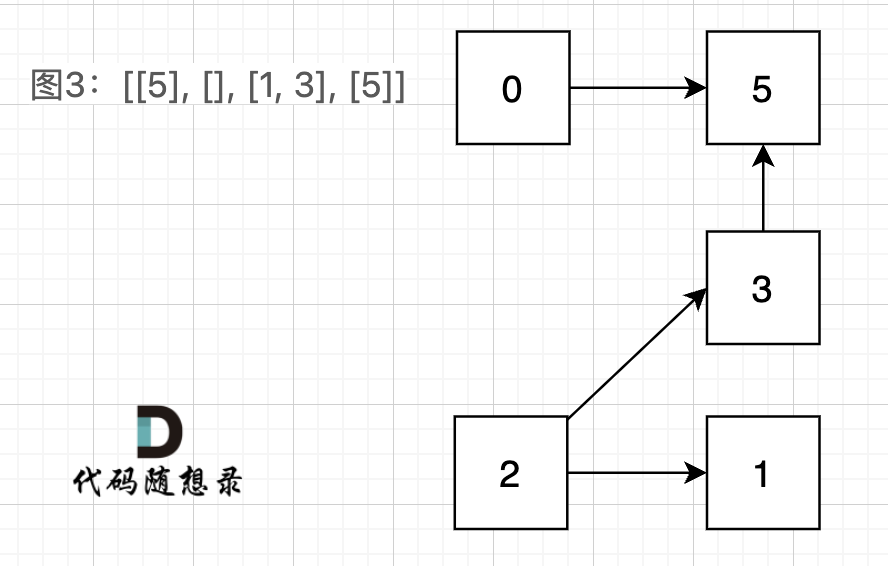
在图3中,大家可以发现,节点0只能到节点5,然后就哪也去不了了。
diff --git a/problems/0941.有效的山脉数组.md b/problems/0941.有效的山脉数组.md
index 383f6aa5..d4165f36 100644
--- a/problems/0941.有效的山脉数组.md
+++ b/problems/0941.有效的山脉数组.md
@@ -16,7 +16,7 @@
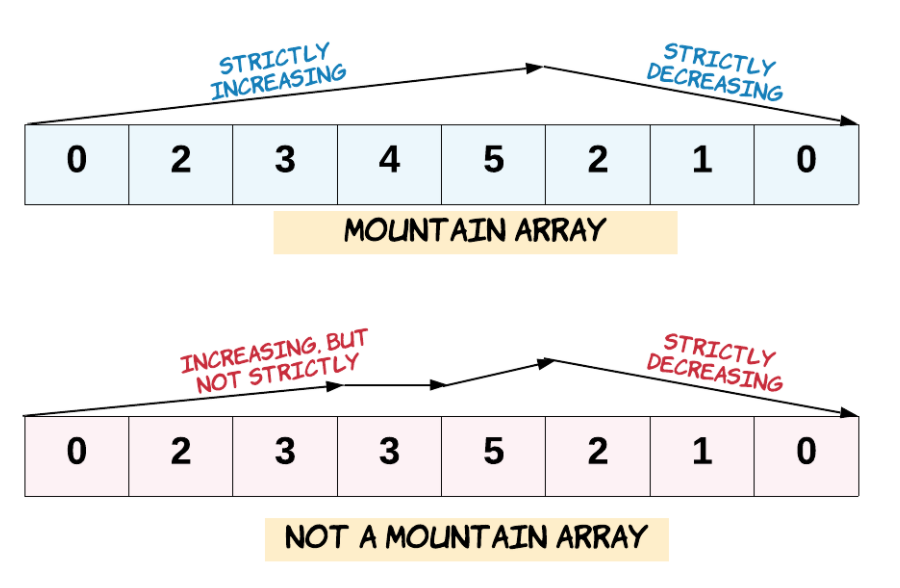
* arr[0] < arr[1] < ... arr[i-1] < arr[i]
* arr[i] > arr[i+1] > ... > arr[arr.length - 1]
-
+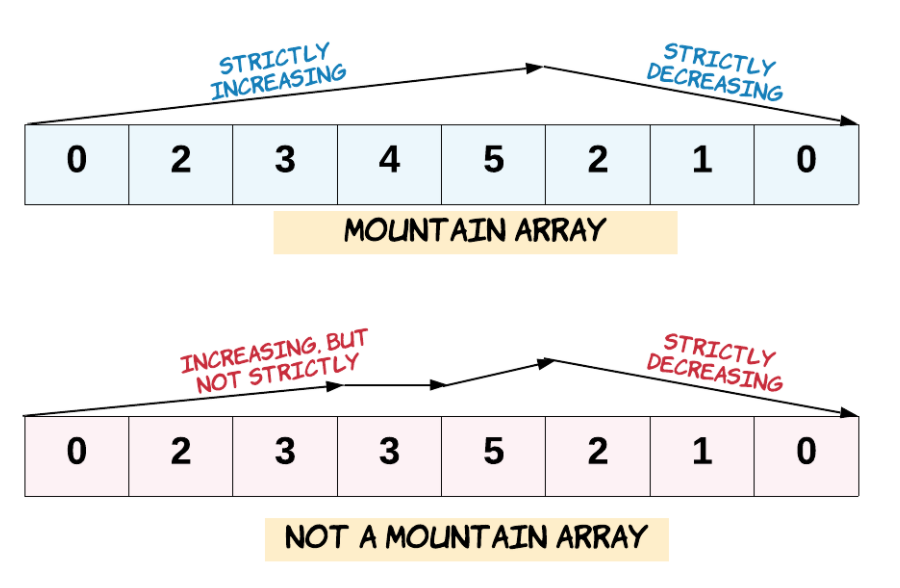
示例 1:
* 输入:arr = [2,1]
diff --git a/problems/0968.监控二叉树.md b/problems/0968.监控二叉树.md
index 0df2cc5b..d8c31ca9 100644
--- a/problems/0968.监控二叉树.md
+++ b/problems/0968.监控二叉树.md
@@ -17,7 +17,7 @@
示例 1:
-
+
* 输入:[0,0,null,0,0]
* 输出:1
@@ -25,7 +25,7 @@
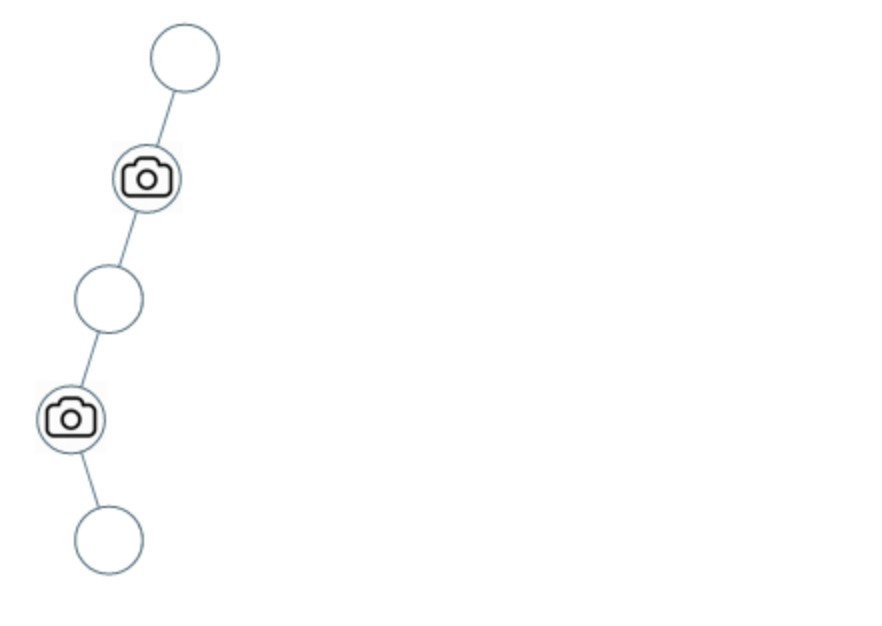
示例 2:
-
+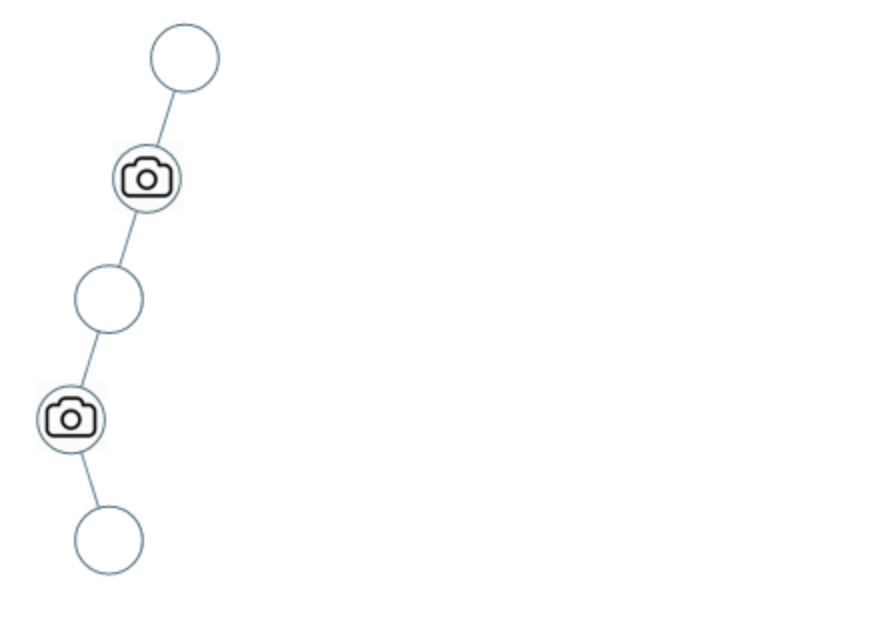
* 输入:[0,0,null,0,null,0,null,null,0]
* 输出:2
@@ -143,7 +143,7 @@ if (cur == NULL) return 2;
如图:
-
+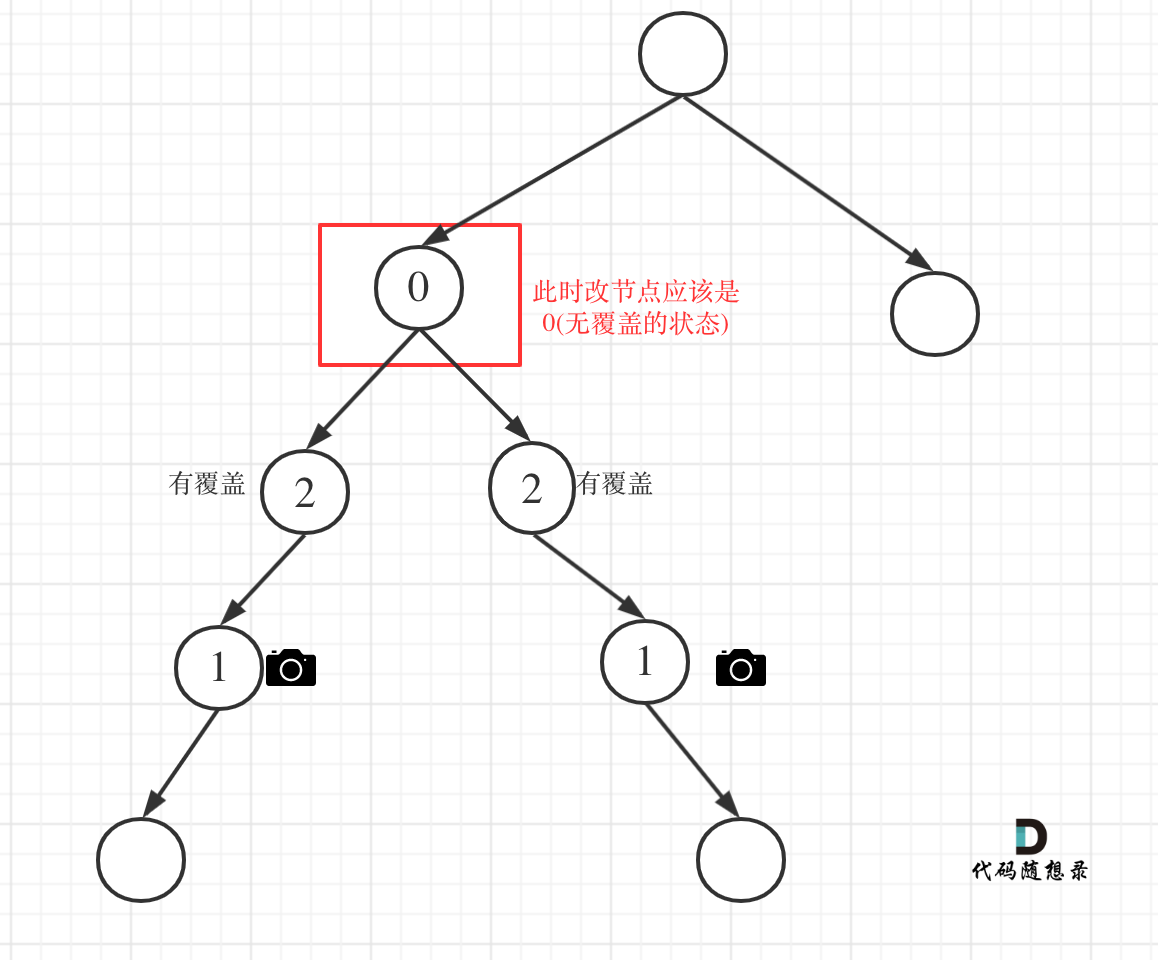
代码如下:
@@ -191,7 +191,7 @@ if (left == 1 || right == 1) return 2;
**从这个代码中,可以看出,如果left == 1, right == 0 怎么办?其实这种条件在情况2中已经判断过了**,如图:
-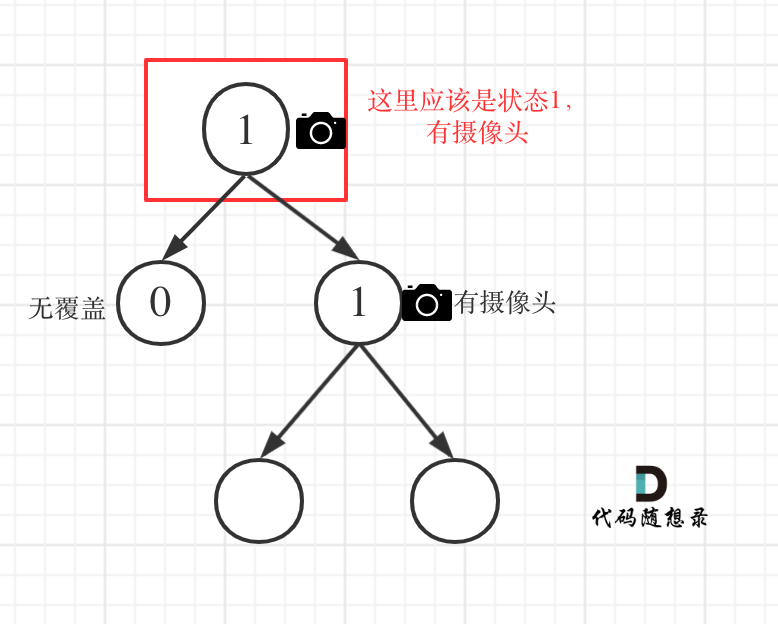
+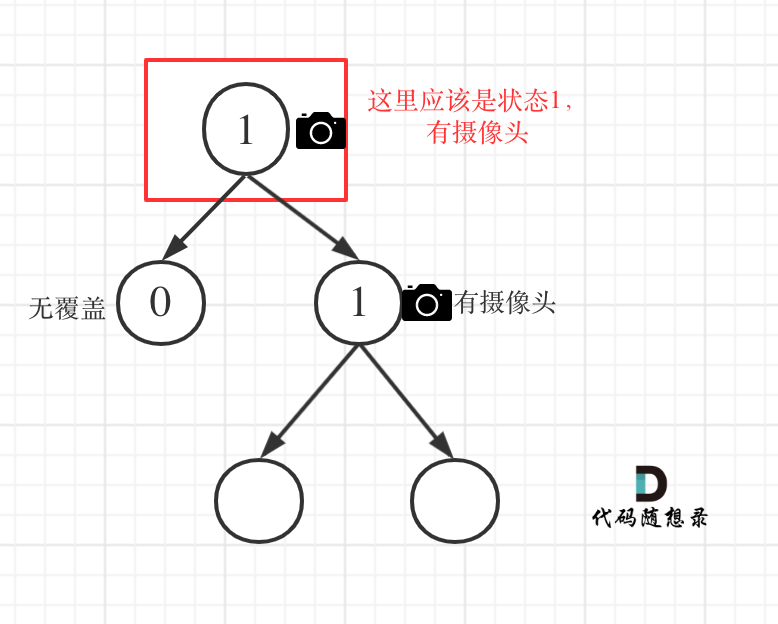
这种情况也是大多数同学容易迷惑的情况。
@@ -199,7 +199,7 @@ if (left == 1 || right == 1) return 2;
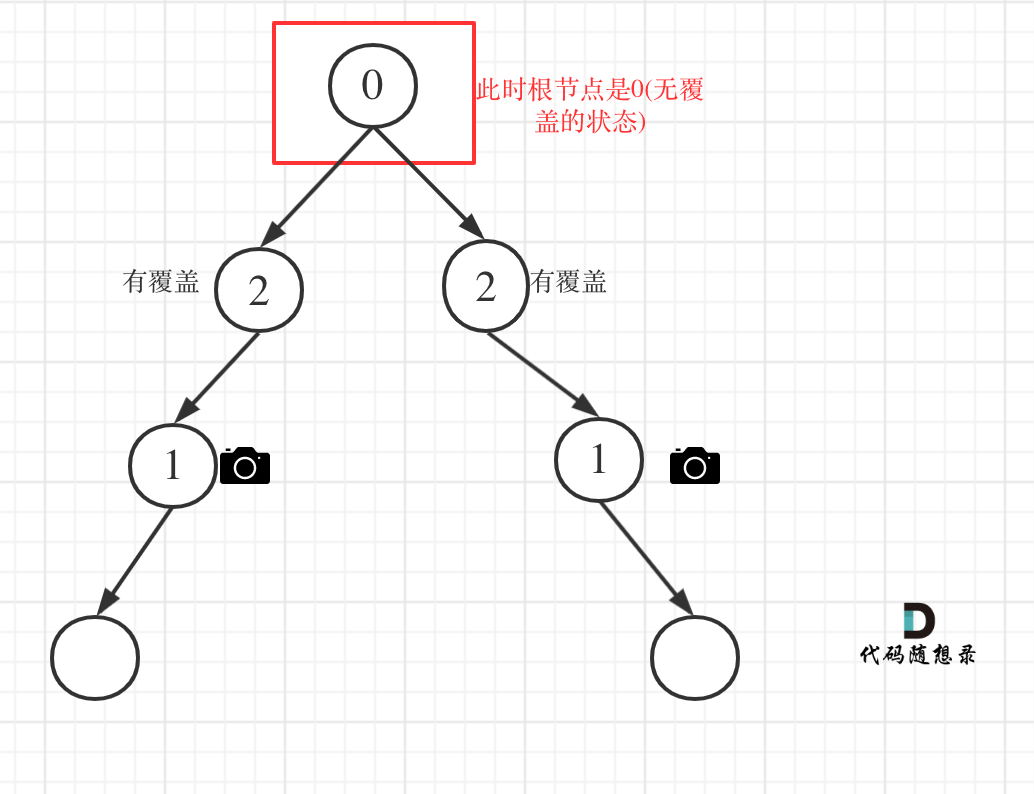
以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况,如图:
-
+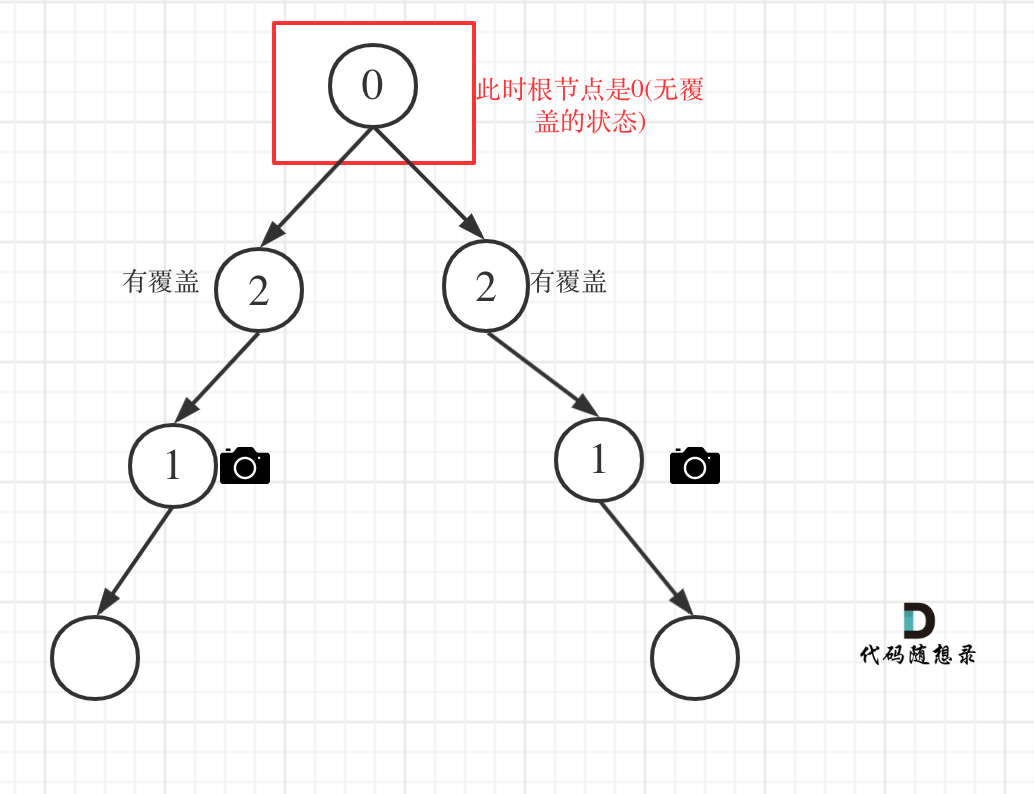
所以递归结束之后,还要判断根节点,如果没有覆盖,result++,代码如下:
diff --git a/problems/1020.飞地的数量.md b/problems/1020.飞地的数量.md
index 030d56a0..ae6b3895 100644
--- a/problems/1020.飞地的数量.md
+++ b/problems/1020.飞地的数量.md
@@ -12,13 +12,13 @@
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
-
+
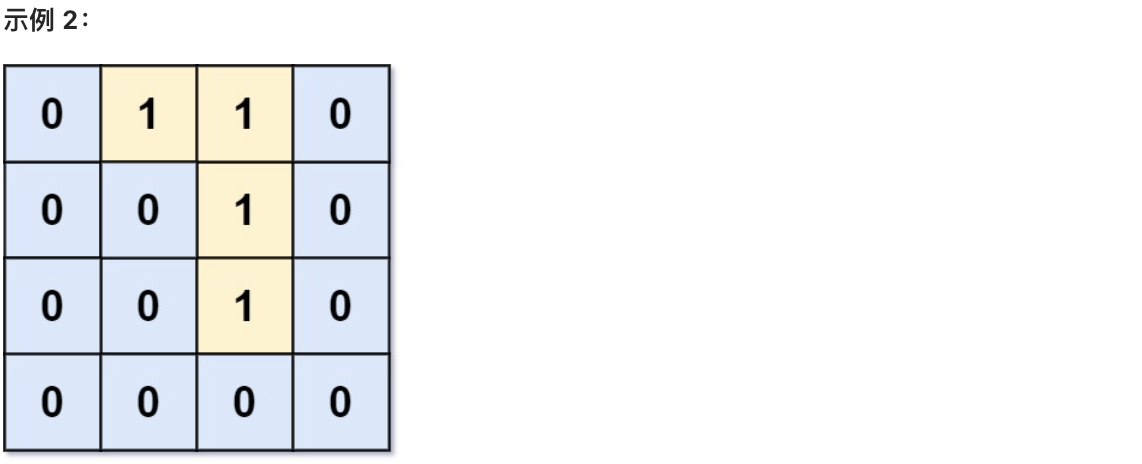
* 输入:grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
* 输出:3
* 解释:有三个 1 被 0 包围。一个 1 没有被包围,因为它在边界上。
-
+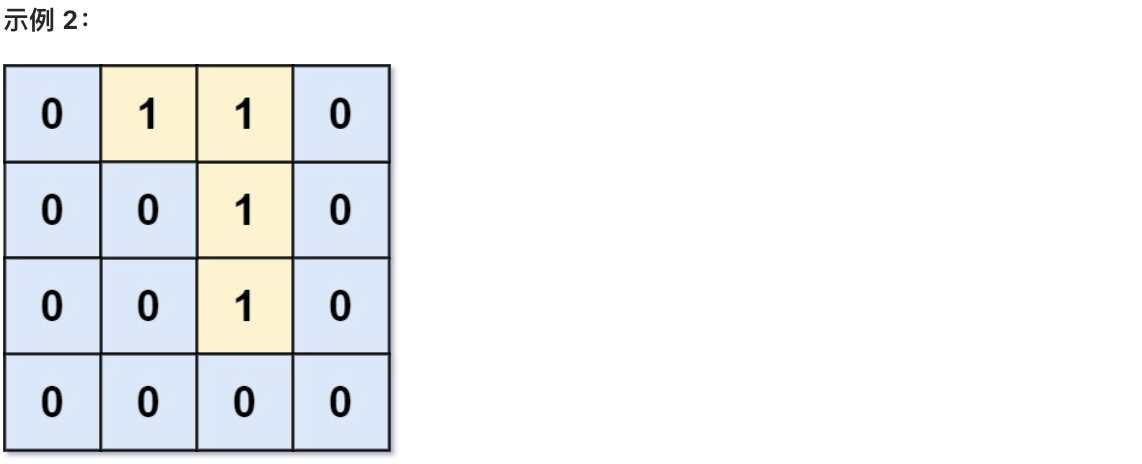
* 输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
* 输出:0
@@ -32,11 +32,11 @@
如图,在遍历地图周围四个边,靠地图四边的陆地,都为绿色,
-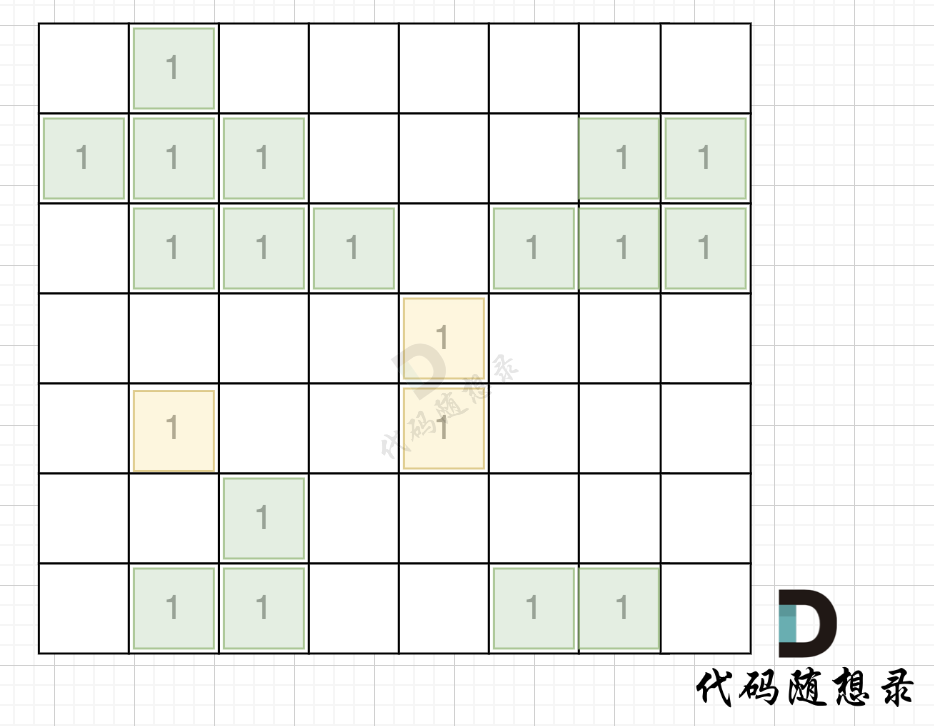
+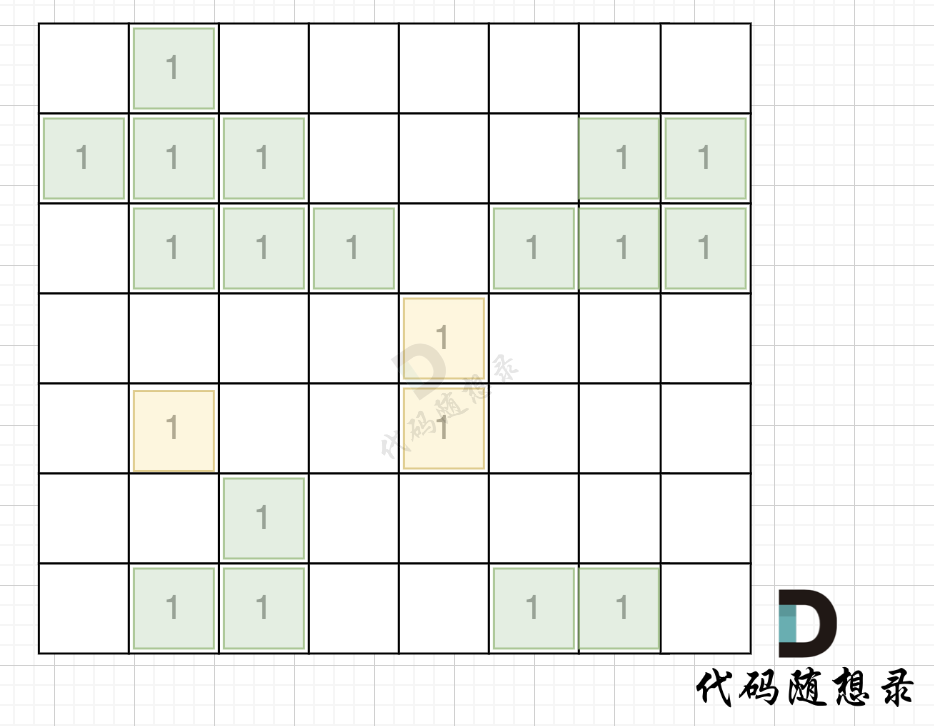
在遇到地图周边陆地的时候,将1都变为0,此时地图为这样:
-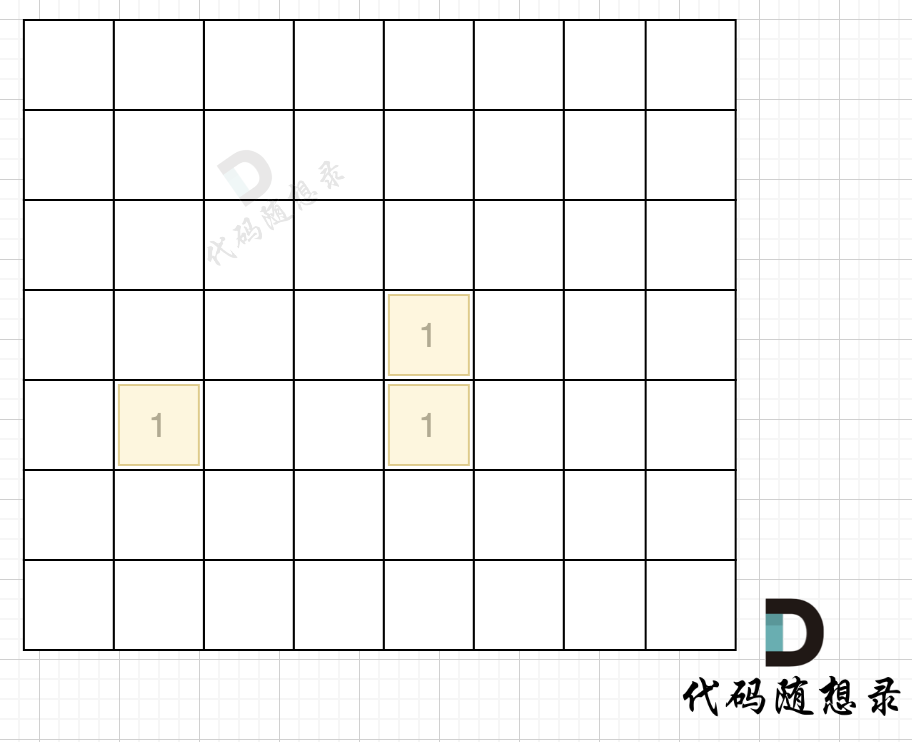
+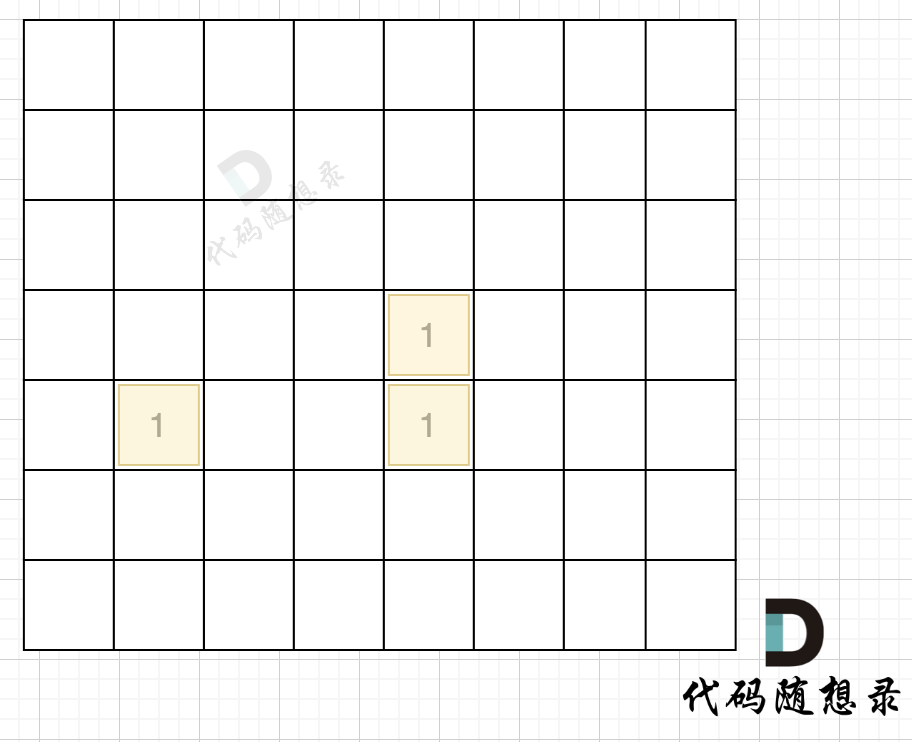
然后我们再去遍历这个地图,遇到有陆地的地方,去采用深搜或者广搜,边统计所有陆地。
diff --git a/problems/1035.不相交的线.md b/problems/1035.不相交的线.md
index 53e0f370..0119df82 100644
--- a/problems/1035.不相交的线.md
+++ b/problems/1035.不相交的线.md
@@ -18,7 +18,7 @@
以这种方法绘制线条,并返回可以绘制的最大连线数。
-
+
## 算法公开课
@@ -36,7 +36,7 @@
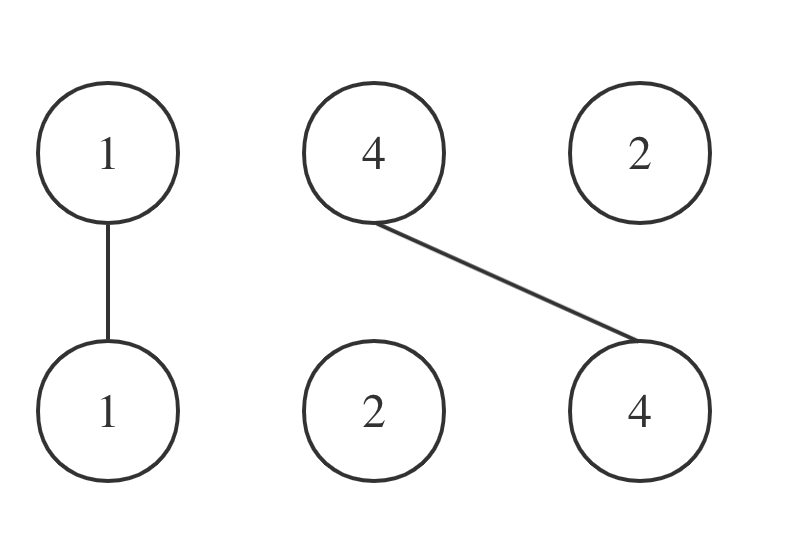
拿示例一nums1 = [1,4,2], nums2 = [1,2,4]为例,相交情况如图:
-
+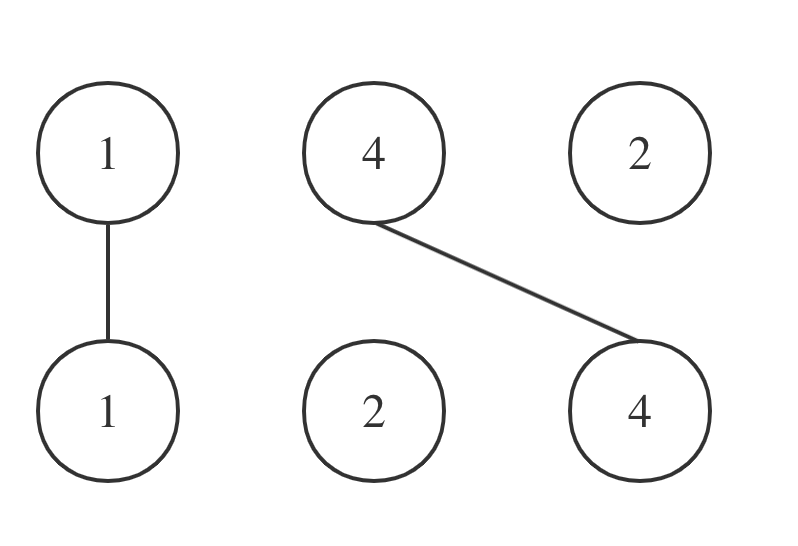
其实也就是说nums1和nums2的最长公共子序列是[1,4],长度为2。 这个公共子序列指的是相对顺序不变(即数字4在字符串nums1中数字1的后面,那么数字4也应该在字符串nums2数字1的后面)
diff --git a/problems/1049.最后一块石头的重量II.md b/problems/1049.最后一块石头的重量II.md
index 62e7d9c5..6dfba4ed 100644
--- a/problems/1049.最后一块石头的重量II.md
+++ b/problems/1049.最后一块石头的重量II.md
@@ -114,7 +114,7 @@ for (int i = 0; i < stones.size(); i++) { // 遍历物品
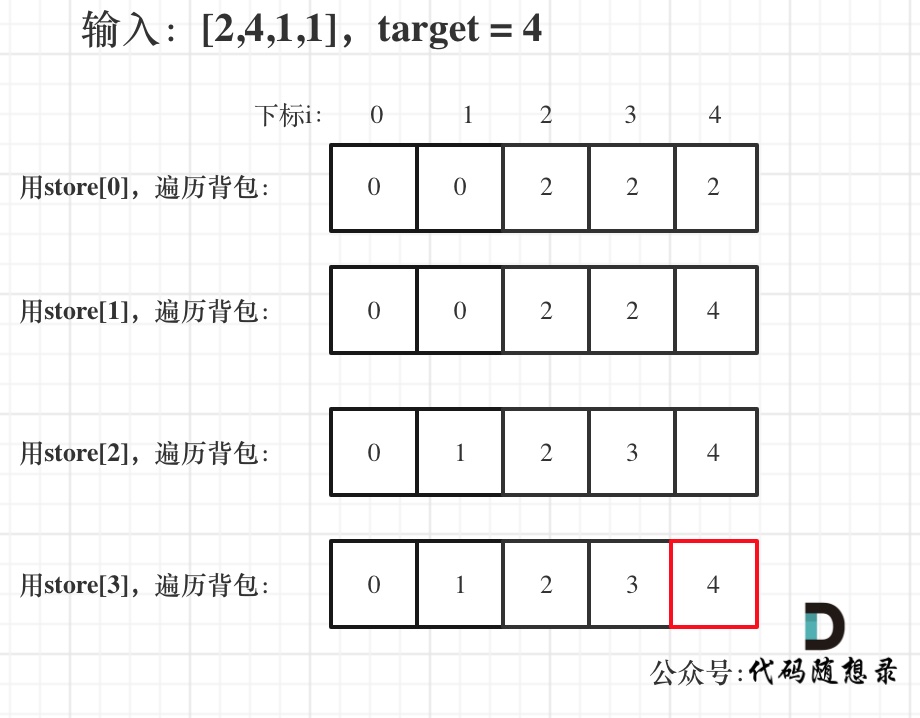
举例,输入:[2,4,1,1],此时target = (2 + 4 + 1 + 1)/2 = 4 ,dp数组状态图如下:
-
+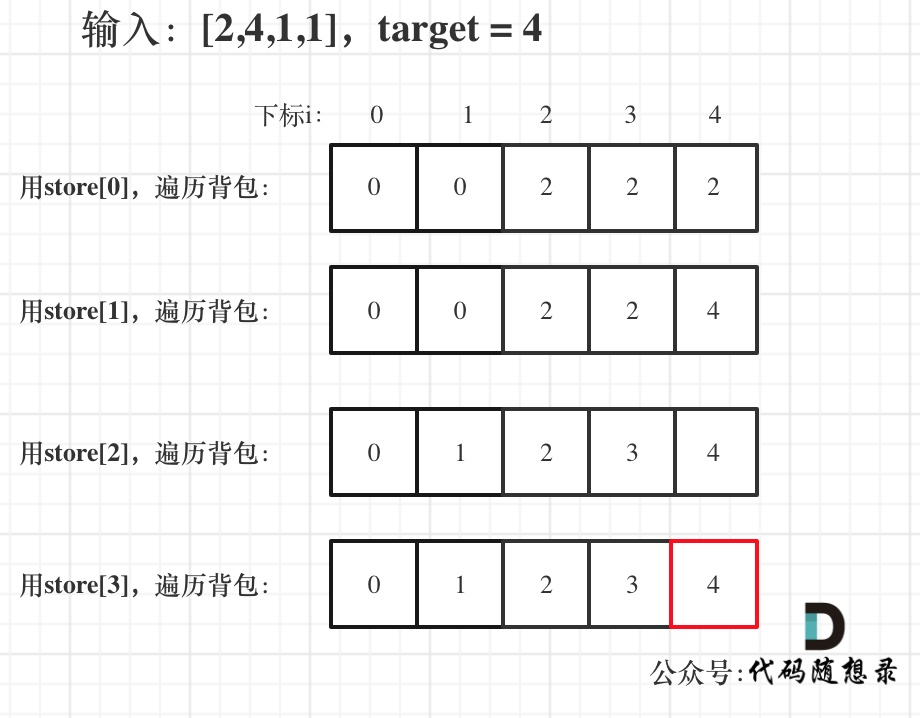
最后dp[target]里是容量为target的背包所能背的最大重量。
diff --git a/problems/1143.最长公共子序列.md b/problems/1143.最长公共子序列.md
index 821f3c42..91c29b83 100644
--- a/problems/1143.最长公共子序列.md
+++ b/problems/1143.最长公共子序列.md
@@ -94,7 +94,7 @@ vector> dp(text1.size() + 1, vector(text2.size() + 1, 0));
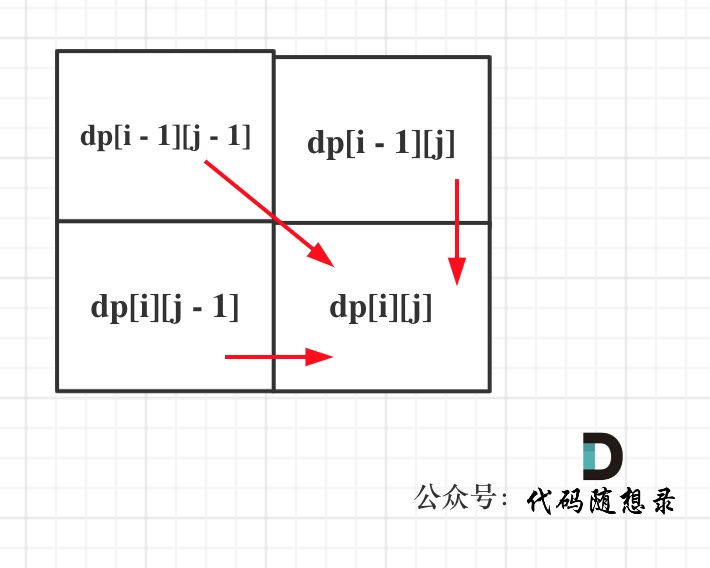
从递推公式,可以看出,有三个方向可以推出dp[i][j],如图:
-
+
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵。
@@ -103,7 +103,7 @@ vector> dp(text1.size() + 1, vector(text2.size() + 1, 0));
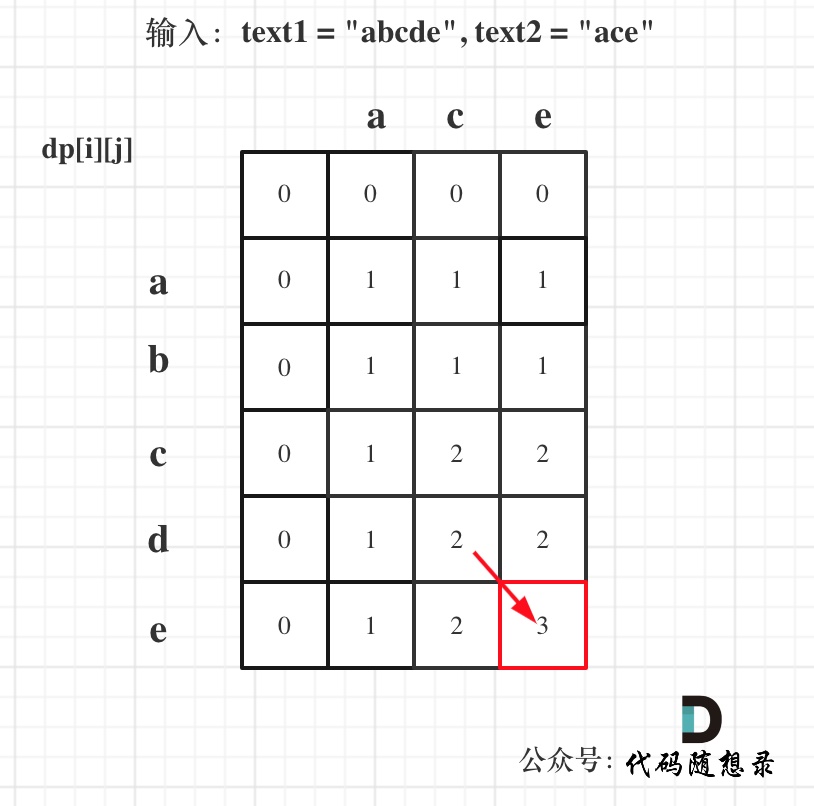
以输入:text1 = "abcde", text2 = "ace" 为例,dp状态如图:
-
+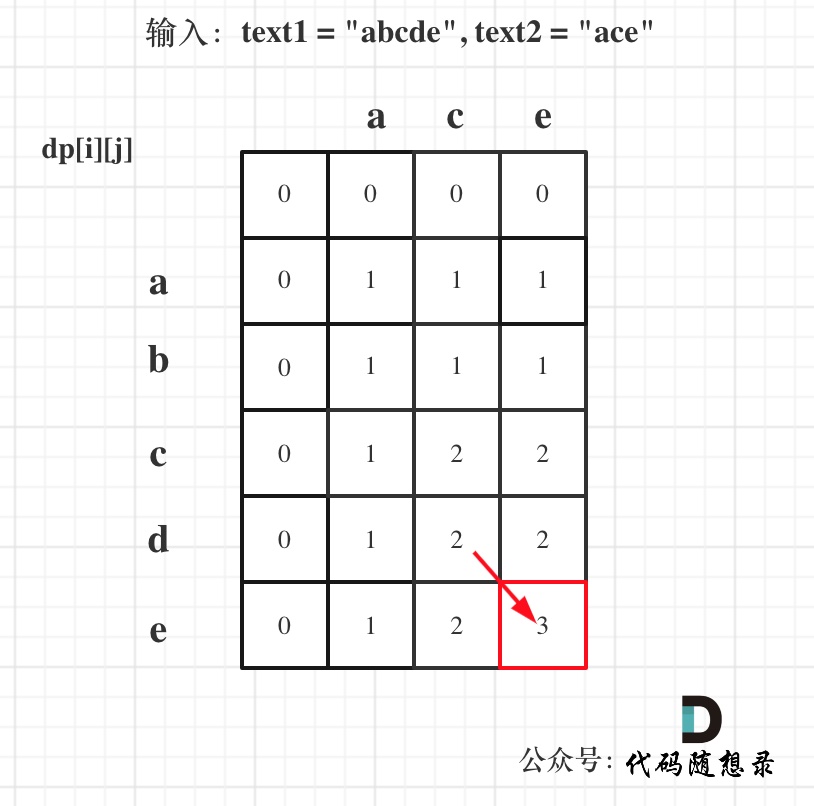
最后红框dp[text1.size()][text2.size()]为最终结果
diff --git a/problems/1254.统计封闭岛屿的数目.md b/problems/1254.统计封闭岛屿的数目.md
index 5d996709..ebea30e3 100644
--- a/problems/1254.统计封闭岛屿的数目.md
+++ b/problems/1254.统计封闭岛屿的数目.md
@@ -10,13 +10,13 @@
请返回 封闭岛屿 的数目。
-
+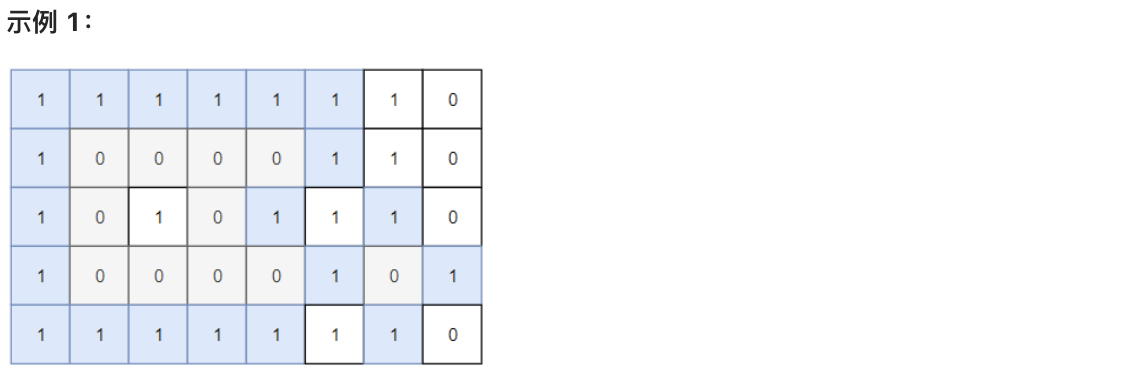
* 输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
* 输出:2
* 解释:灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)。
-
+
* 输入:grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
* 输出:1
diff --git a/problems/1382.将二叉搜索树变平衡.md b/problems/1382.将二叉搜索树变平衡.md
index 7a1a7f3c..7b0d3204 100644
--- a/problems/1382.将二叉搜索树变平衡.md
+++ b/problems/1382.将二叉搜索树变平衡.md
@@ -15,7 +15,7 @@
示例:
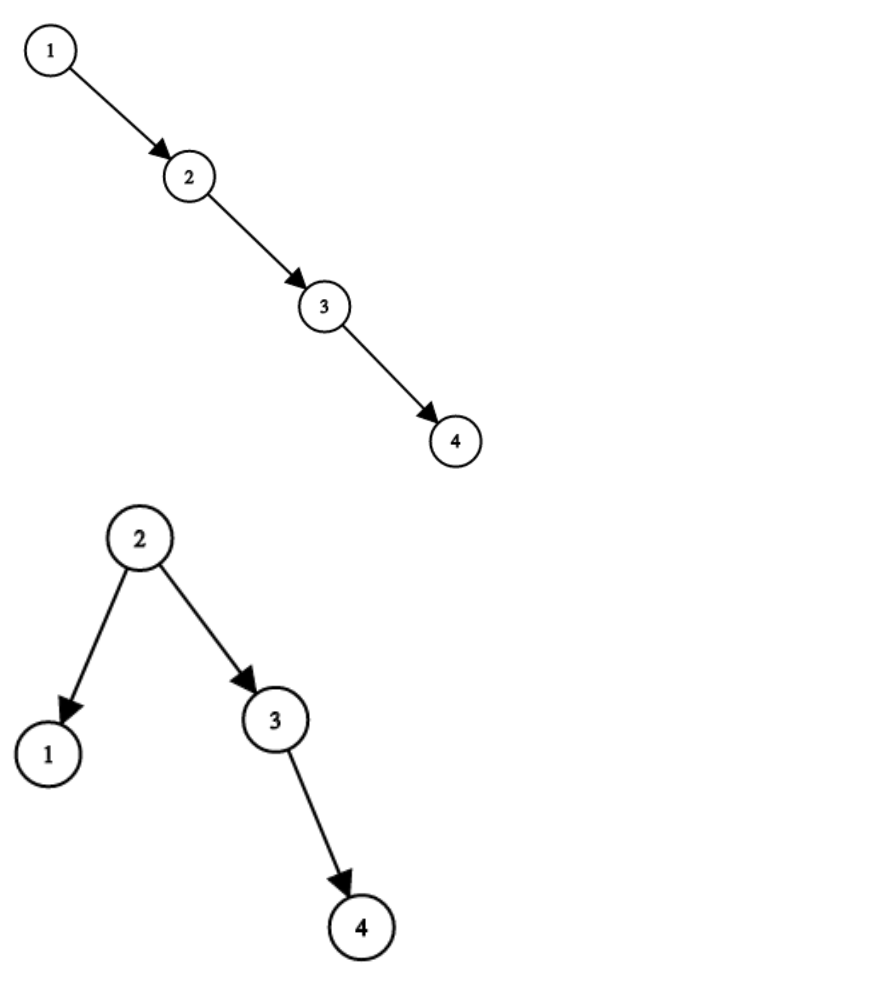
-
+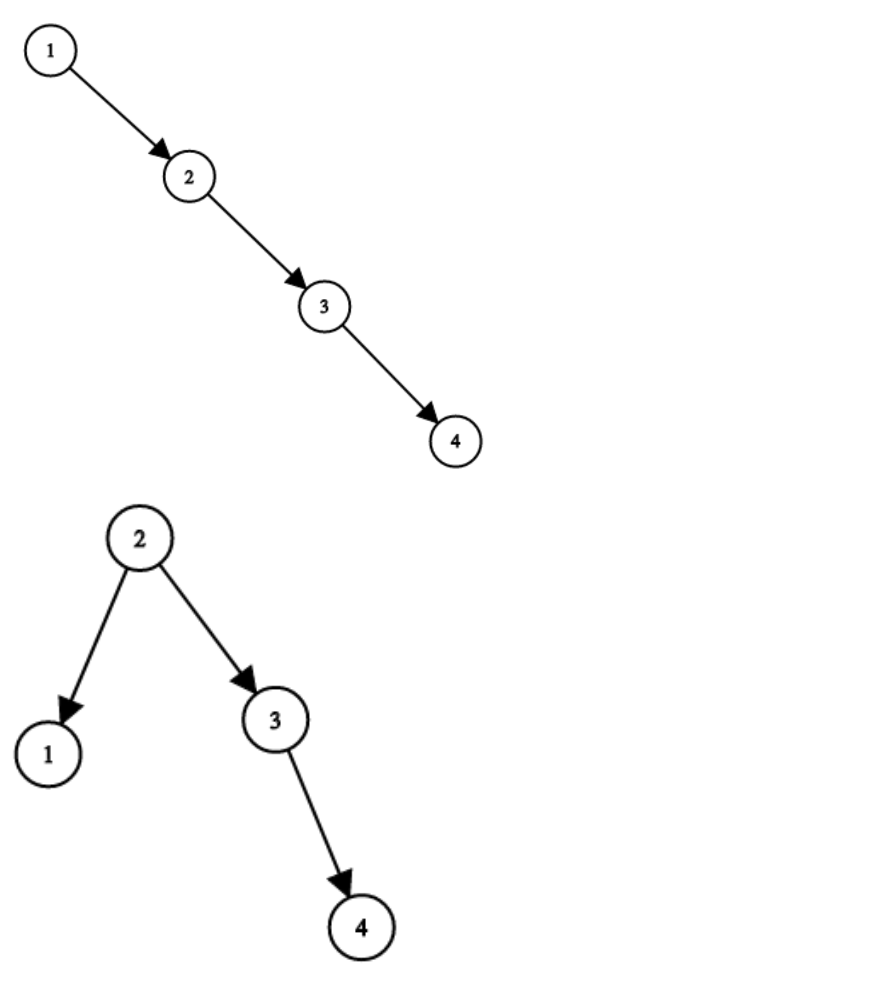
* 输入:root = [1,null,2,null,3,null,4,null,null]
* 输出:[2,1,3,null,null,null,4]
diff --git a/problems/1791.找出星型图的中心节点.md b/problems/1791.找出星型图的中心节点.md
index e9ea5f44..5dd56c65 100644
--- a/problems/1791.找出星型图的中心节点.md
+++ b/problems/1791.找出星型图的中心节点.md
@@ -10,7 +10,7 @@
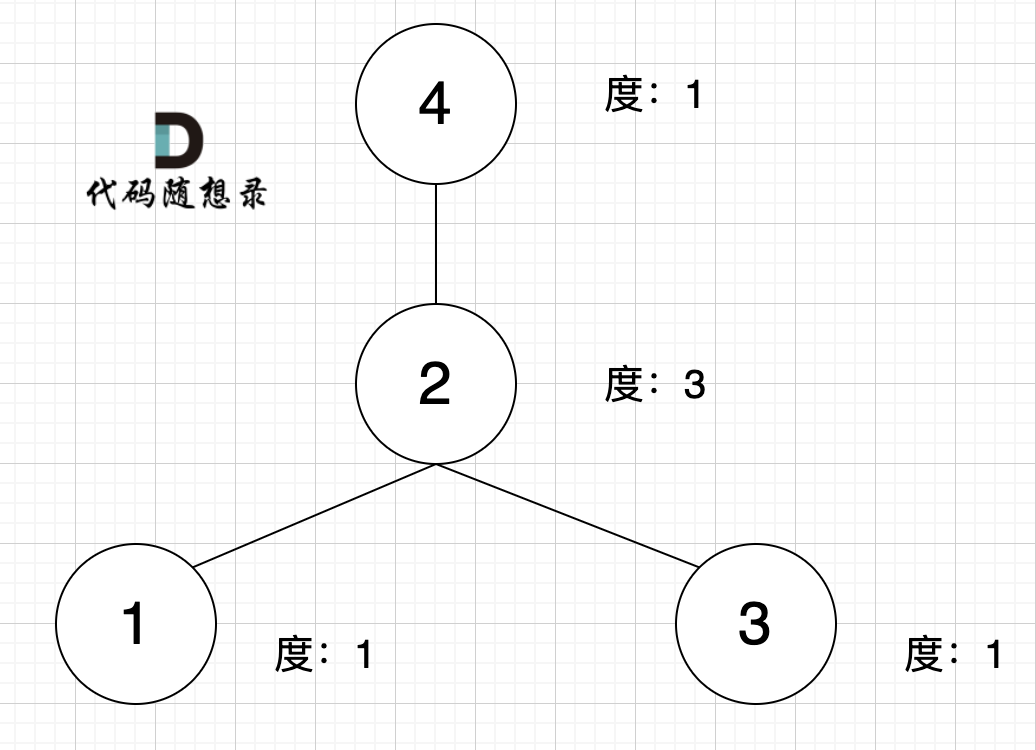
什么是度,可以理解为,链接节点的边的数量。 题目中度如图所示:
-
+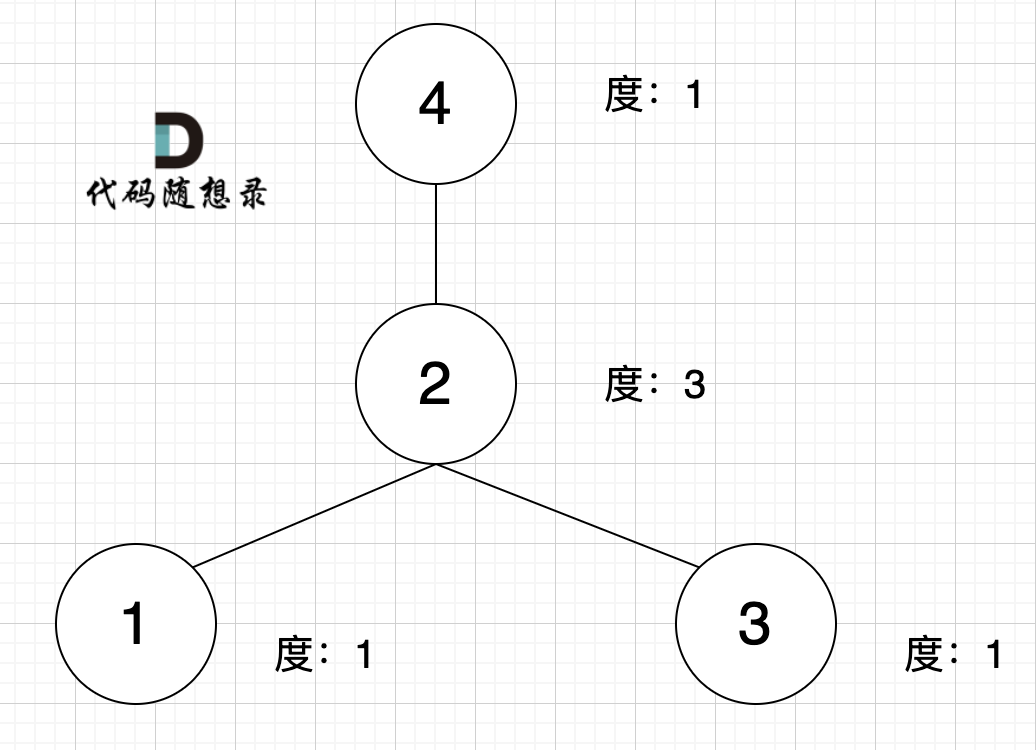
至于出度和入度,那就是在有向图里的概念了,本题是无向图。
diff --git a/problems/1971.寻找图中是否存在路径.md b/problems/1971.寻找图中是否存在路径.md
index acb54415..33b48698 100644
--- a/problems/1971.寻找图中是否存在路径.md
+++ b/problems/1971.寻找图中是否存在路径.md
@@ -12,7 +12,7 @@
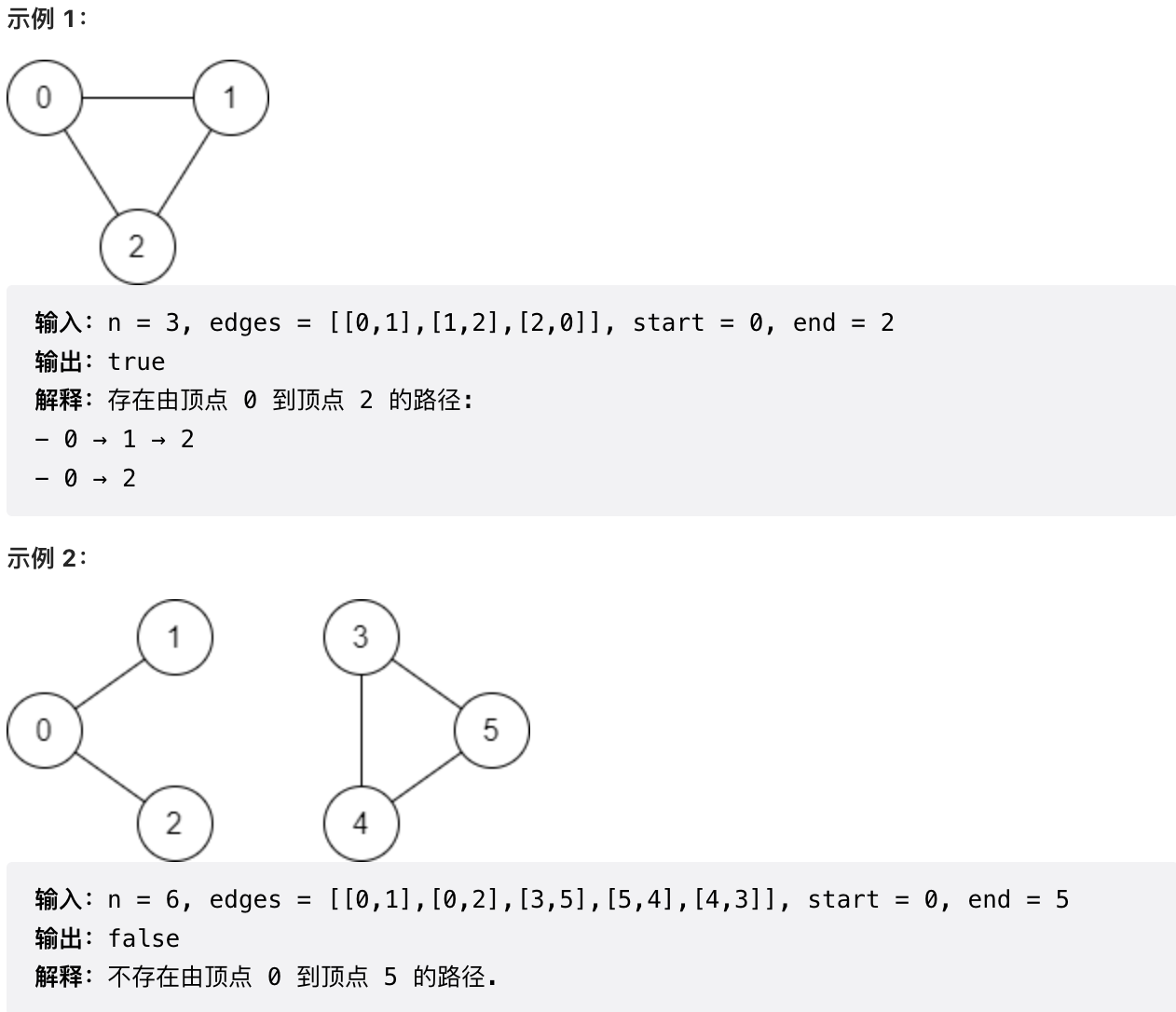
给你数组 edges 和整数 n、start 和 end,如果从 start 到 end 存在 有效路径 ,则返回 true,否则返回 false 。
-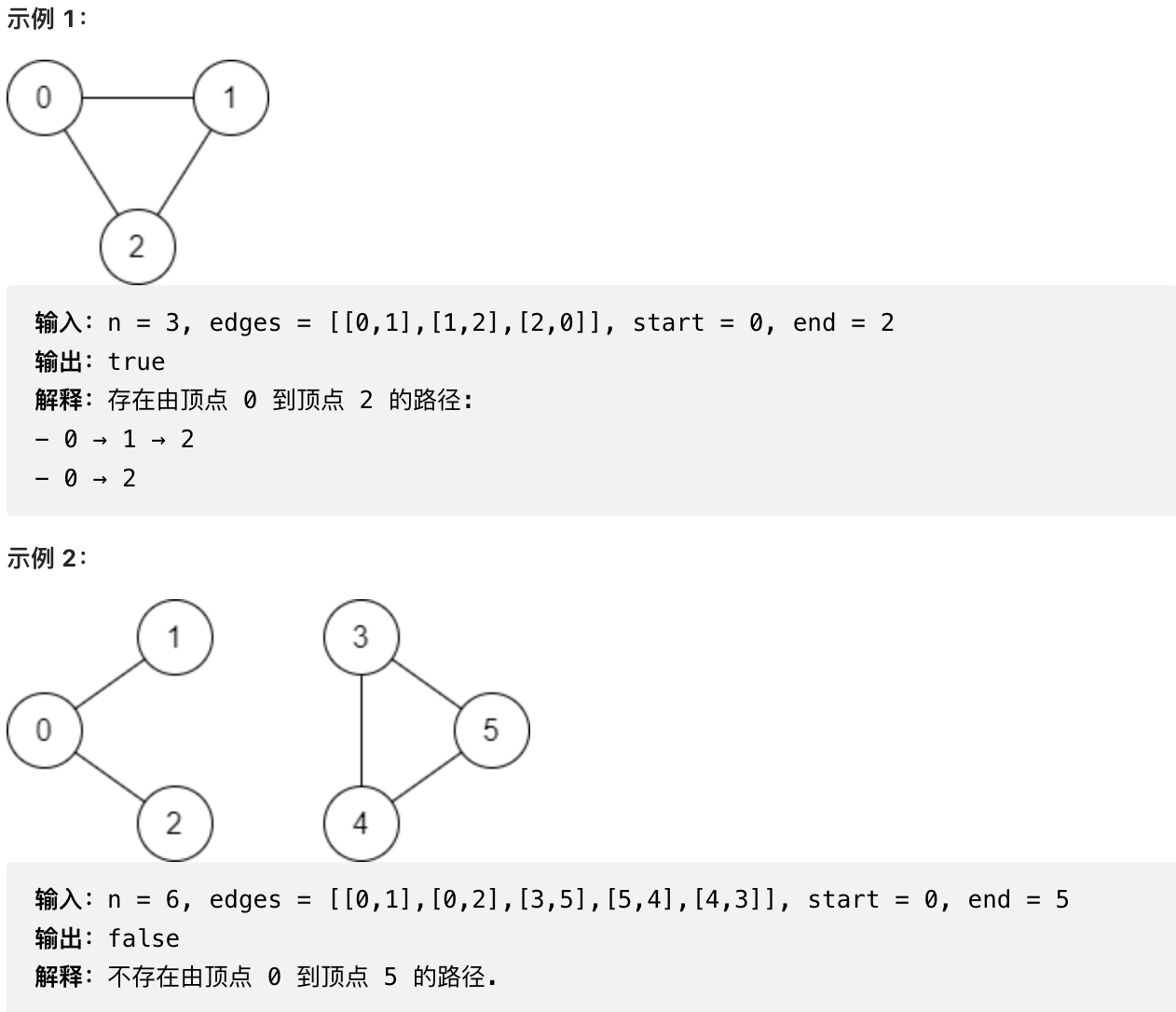
+
diff --git a/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md b/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
index 7276af53..830bba7e 100644
--- a/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
+++ b/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
@@ -13,7 +13,7 @@
## 超时是怎么回事
-
+
大家在leetcode上练习算法的时候应该都遇到过一种错误是“超时”。
@@ -129,11 +129,11 @@ int main() {
来看一下运行的效果,如下图:
-
+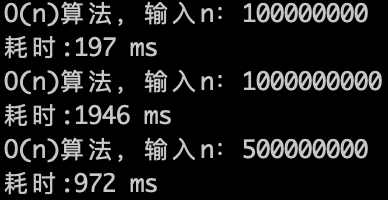
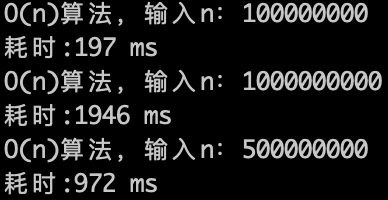
O(n)的算法,1s内大概计算机可以运行 5 * (10^8)次计算,可以推测一下O(n^2) 的算法应该1s可以处理的数量级的规模是 5 * (10^8)开根号,实验数据如下。
-
+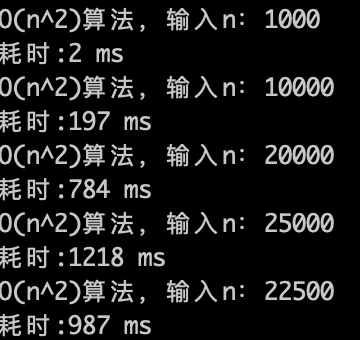
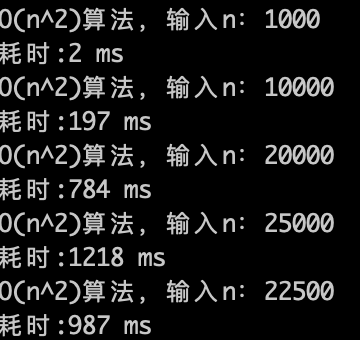
O(n^2)的算法,1s内大概计算机可以运行 22500次计算,验证了刚刚的推测。
@@ -141,7 +141,7 @@ O(n^2)的算法,1s内大概计算机可以运行 22500次计算,验证了刚
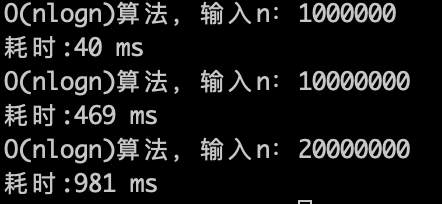
理论上应该是比 O(n)少一个数量级,因为logn的复杂度 其实是很快,看一下实验数据。
-
+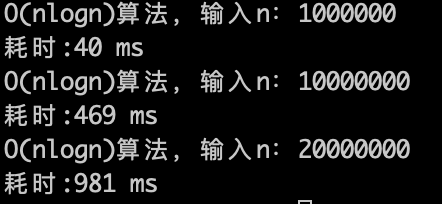
O(nlogn)的算法,1s内大概计算机可以运行 2 * (10^7)次计算,符合预期。
@@ -149,7 +149,7 @@ O(nlogn)的算法,1s内大概计算机可以运行 2 * (10^7)次计算,符
**整体测试数据整理如下:**
-
+
至于O(log n)和O(n^3) 等等这些时间复杂度在1s内可以处理的多大的数据规模,大家可以自己写一写代码去测一下了。
diff --git a/problems/kamacoder/0047.参会dijkstra堆.md b/problems/kamacoder/0047.参会dijkstra堆.md
index 75c12f8a..e361e8e0 100644
--- a/problems/kamacoder/0047.参会dijkstra堆.md
+++ b/problems/kamacoder/0047.参会dijkstra堆.md
@@ -46,13 +46,13 @@
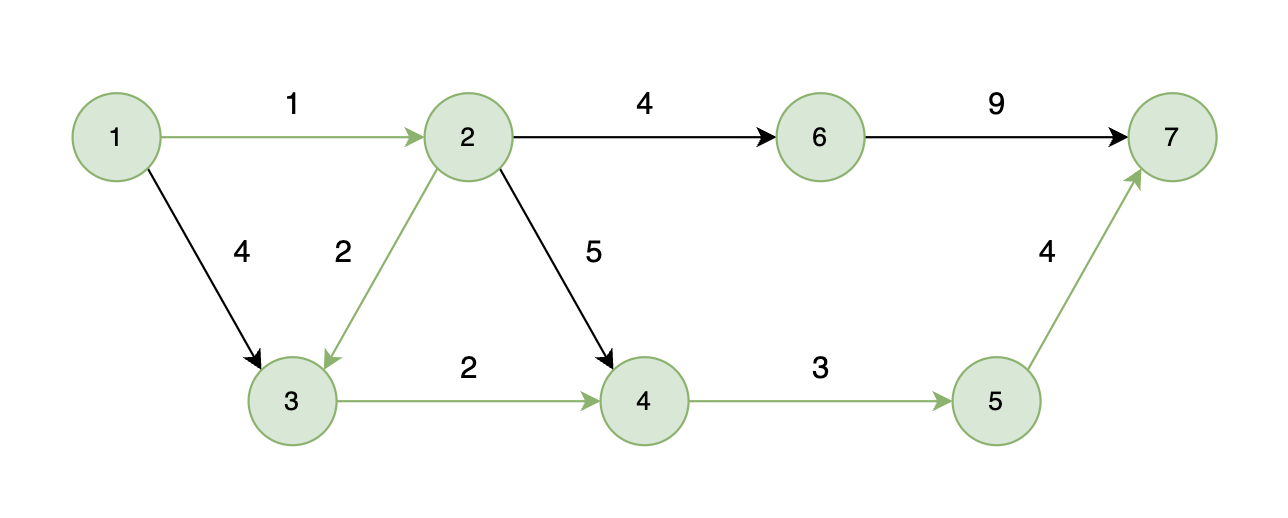
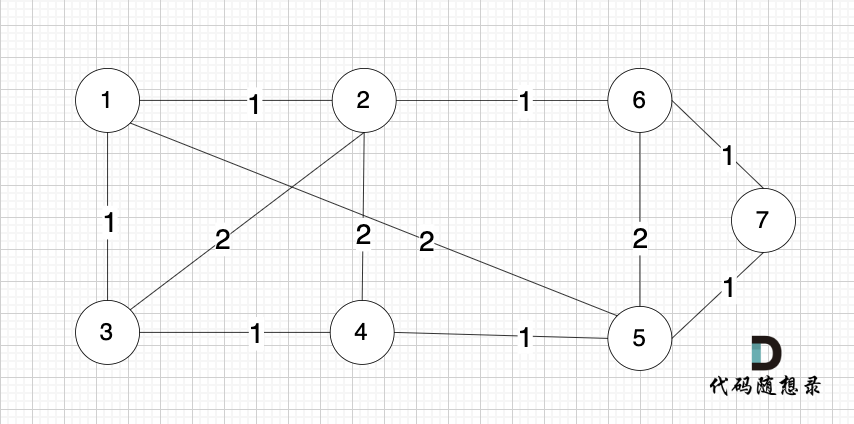
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
-
+
不能到达的情况:
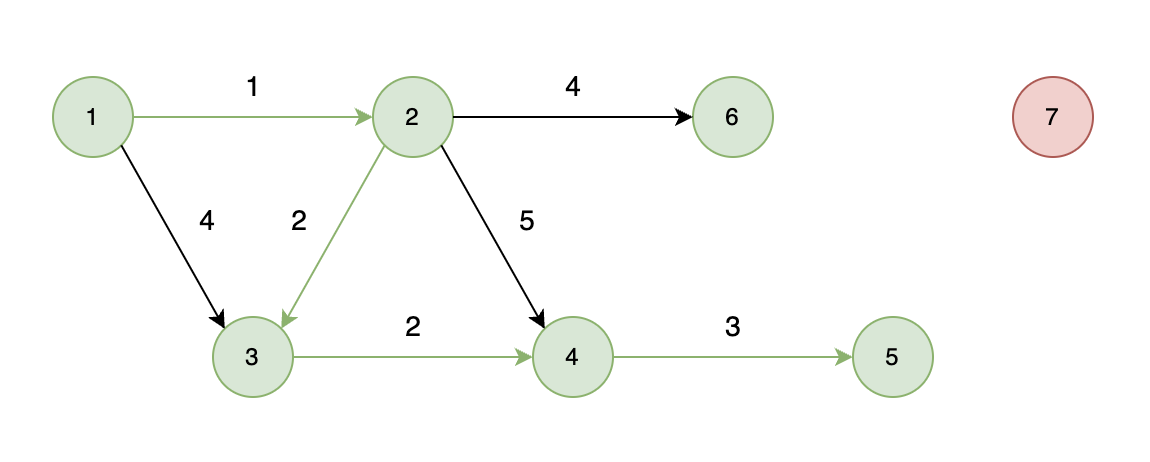
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
-
+
数据范围:
@@ -101,7 +101,7 @@
如图:
-
+
在一个 n (节点数)为8 的图中,就需要申请 8 * 8 这么大的空间,有一条双向边,即:grid[2][5] = 6,grid[5][2] = 6
@@ -125,7 +125,7 @@
邻接表的构造如图:
-
+
这里表达的图是:
@@ -210,7 +210,7 @@ vector> grid(n + 1);
不少录友,不知道 如何定义的数据结构,怎么表示邻接表的,我来给大家画一个图:
-
+
图中邻接表表示:
@@ -231,7 +231,7 @@ vector>> grid(n + 1);
举例来给大家展示 该代码表达的数据 如下:
-
+
* 节点1 指向 节点3 权值为 1
* 节点1 指向 节点5 权值为 2
@@ -354,7 +354,7 @@ for (int v = 1; v <= n; v++) {
再回顾一下邻接表的构造(数组 + 链表):
-
+
假如 加入的cur 是节点 2, 那么 grid[2] 表示的就是图中第二行链表。 (grid数组的构造我们在 上面 「图的存储」中讲过)
diff --git a/problems/kamacoder/0047.参会dijkstra朴素.md b/problems/kamacoder/0047.参会dijkstra朴素.md
index e71e9d53..1ff9f1a8 100644
--- a/problems/kamacoder/0047.参会dijkstra朴素.md
+++ b/problems/kamacoder/0047.参会dijkstra朴素.md
@@ -46,13 +46,13 @@
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
-
+
不能到达的情况:
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
-
+
数据范围:
@@ -76,7 +76,7 @@ dijkstra算法:在有权图(权值非负数)中求从起点到其他节点
如本题示例中的图:
-
+
起点(节点1)到终点(节点7) 的最短路径是 图中 标记绿线的部分。
@@ -122,7 +122,7 @@ minDist数组数值初始化为int最大值。
这里在强点一下 **minDist数组的含义:记录所有节点到源点的最短路径**,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。
-
+
(图中,max 表示默认值,节点0 不做处理,统一从下标1 开始计算,这样下标和节点数值统一, 方便大家理解,避免搞混)
@@ -144,7 +144,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
@@ -170,7 +170,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点6 、 节点3 和 节点4的距离。
@@ -204,7 +204,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
@@ -224,7 +224,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点4的加入,那么源点可以链接到节点5 所以更新minDist数组:
@@ -244,7 +244,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点6的加入,那么源点可以链接到节点7 所以 更新minDist数组:
@@ -264,7 +264,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点5的加入,那么源点有新的路径可以链接到节点7 所以 更新minDist数组:
@@ -282,7 +282,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
节点7加入,但节点7到节点7的距离为0,所以 不用更新minDist数组
@@ -296,7 +296,7 @@ minDist数组数值初始化为int最大值。
路径如图:
-
+
在上面的讲解中,每一步 我都是按照 dijkstra 三部曲来讲解的,理解了这三部曲,代码也就好懂的。
@@ -541,7 +541,7 @@ int main() {
对应如图:
-
+
### 出现负数
@@ -549,7 +549,7 @@ int main() {
看一下这个图: (有负权值)
-
+
节点1 到 节点5 的最短路径 应该是 节点1 -> 节点2 -> 节点3 -> 节点4 -> 节点5
@@ -559,7 +559,7 @@ int main() {
初始化:
-
+
---------------
@@ -573,7 +573,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
@@ -592,7 +592,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
@@ -610,7 +610,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点4的加入,那么源点可以有新的路径链接到节点5 所以更新minDist数组:
@@ -628,7 +628,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
节点5的加入,而节点5 没有链接其他节点, 所以不用更新minDist数组,仅标记节点5被访问过了
@@ -644,7 +644,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
--------------
diff --git a/problems/kamacoder/0053.寻宝-Kruskal.md b/problems/kamacoder/0053.寻宝-Kruskal.md
index 861efe68..585fa476 100644
--- a/problems/kamacoder/0053.寻宝-Kruskal.md
+++ b/problems/kamacoder/0053.寻宝-Kruskal.md
@@ -63,7 +63,7 @@ kruscal的思路:
依然以示例中,如下这个图来举例。
-
+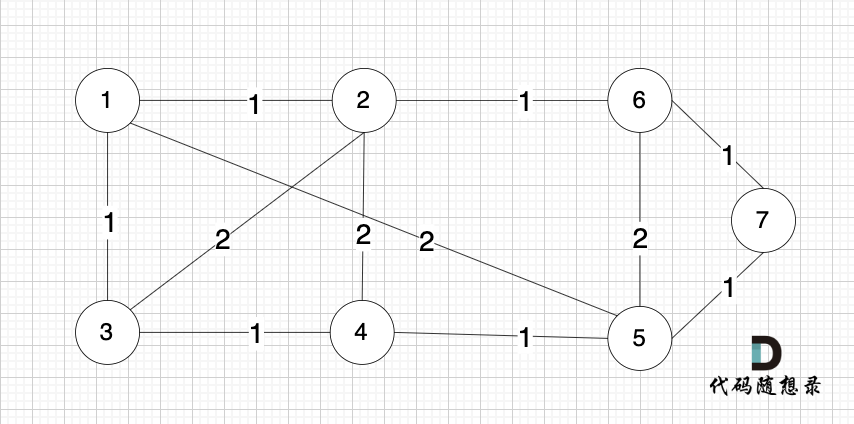
将图中的边按照权值有小到大排序,这样从贪心的角度来说,优先选 权值小的边加入到 最小生成树中。
@@ -77,13 +77,13 @@ kruscal的思路:
选边(1,2),节点1 和 节点2 不在同一个集合,所以生成树可以添加边(1,2),并将 节点1,节点2 放在同一个集合。
-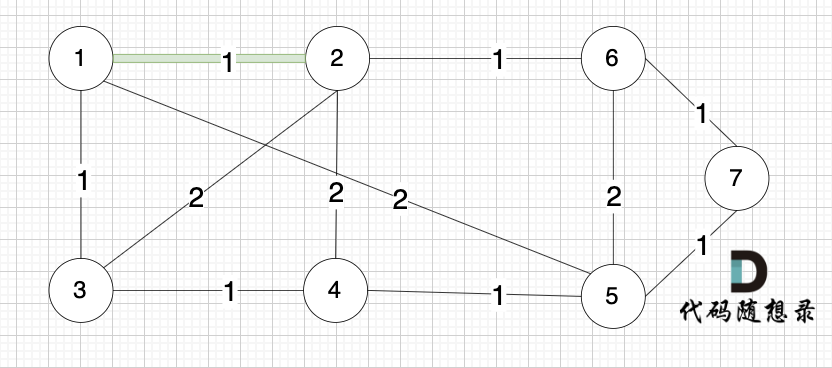
+
--------
选边(4,5),节点4 和 节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5 放到同一个集合。
-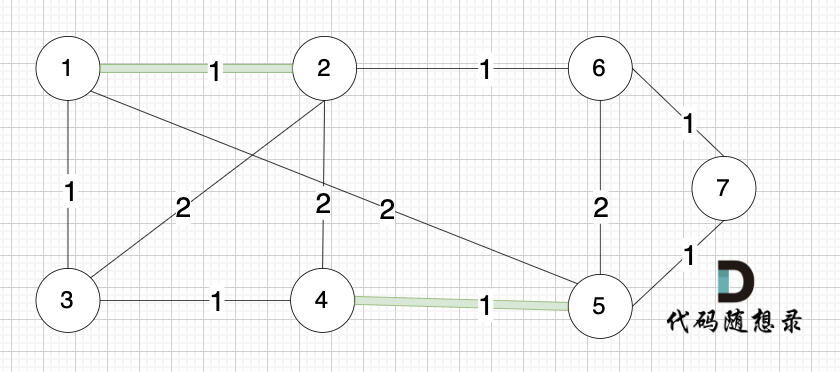
+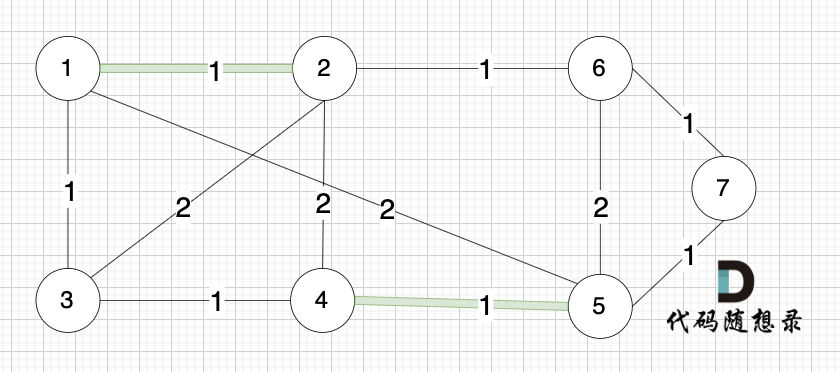
**大家判断两个节点是否在同一个集合,就看图中两个节点是否有绿色的粗线连着就行**
@@ -93,25 +93,25 @@ kruscal的思路:
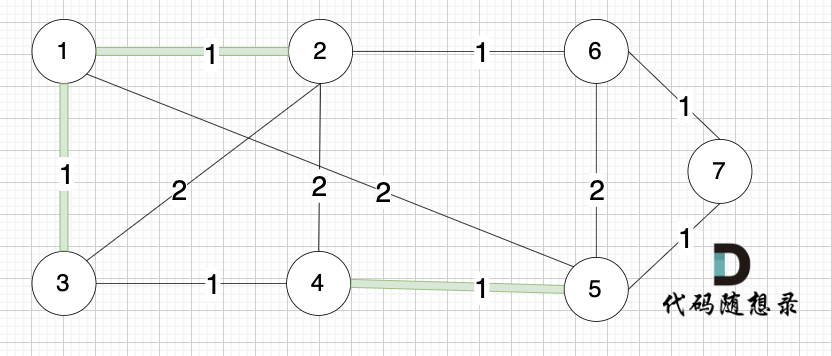
选边(1,3),节点1 和 节点3 不在同一个集合,生成树添加边(1,3),并将节点1,节点3 放到同一个集合。
-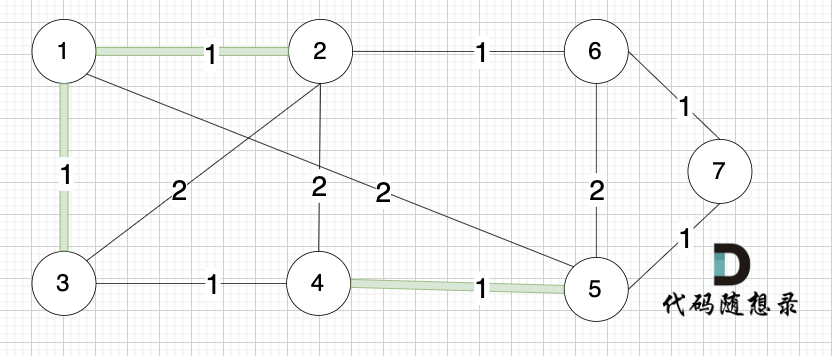
+
---------
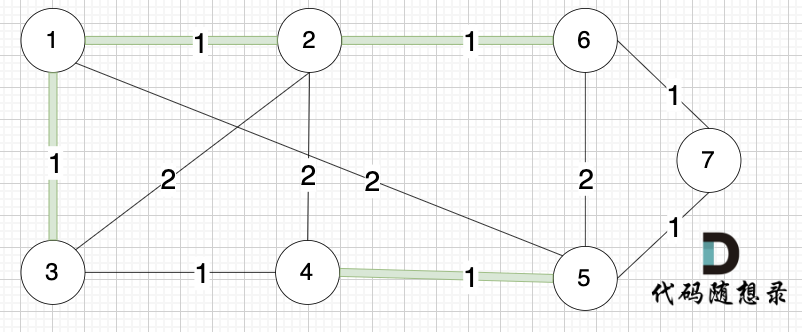
选边(2,6),节点2 和 节点6 不在同一个集合,生成树添加边(2,6),并将节点2,节点6 放到同一个集合。
-
+
--------
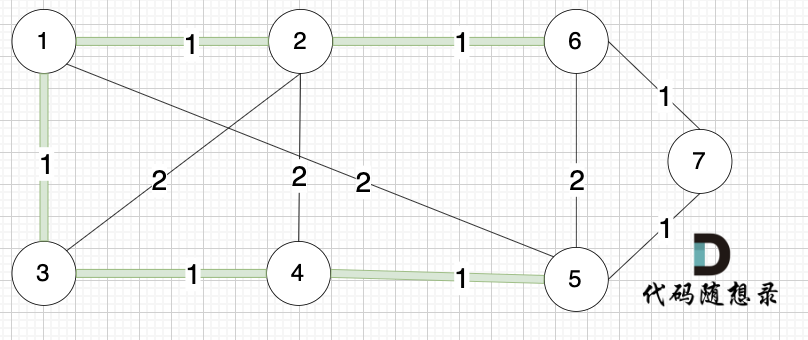
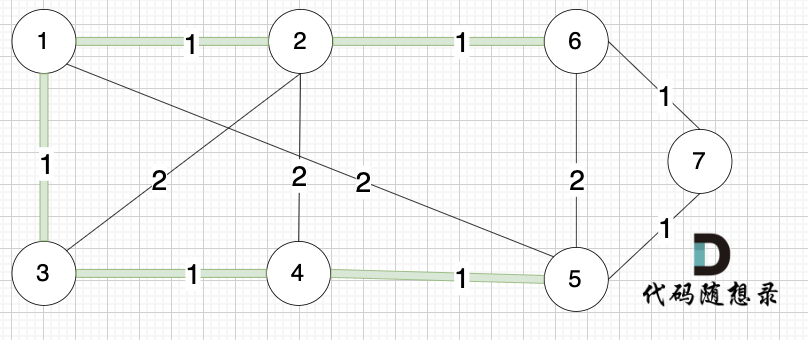
选边(3,4),节点3 和 节点4 不在同一个集合,生成树添加边(3,4),并将节点3,节点4 放到同一个集合。
-
+
----------
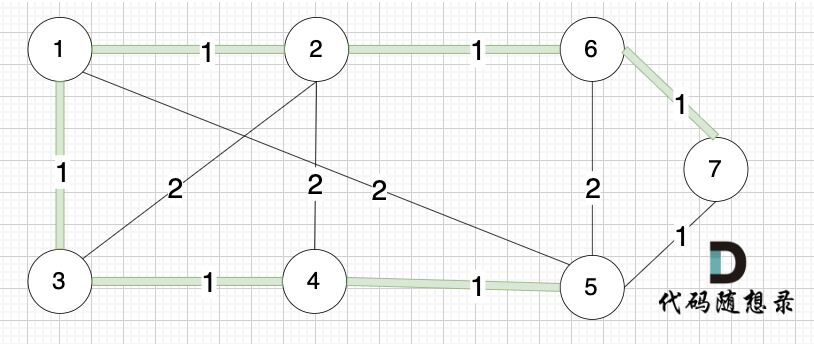
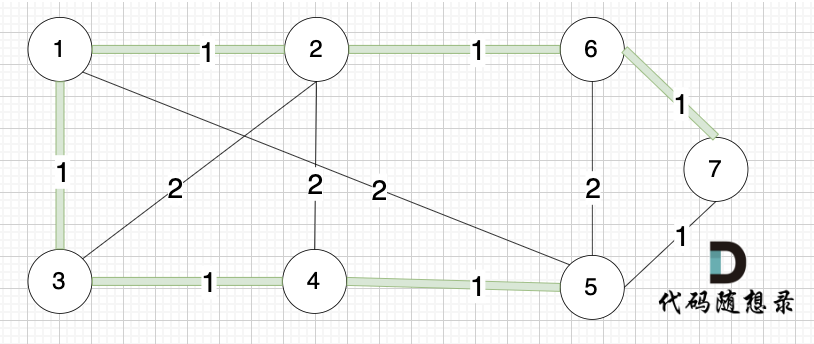
选边(6,7),节点6 和 节点7 不在同一个集合,生成树添加边(6,7),并将 节点6,节点7 放到同一个集合。
-
+
-----------
@@ -126,7 +126,7 @@ kruscal的思路:
此时 我们就已经生成了一个最小生成树,即:
-
+
在上面的讲解中,看图的话 大家知道如何判断 两个节点 是否在同一个集合(是否有绿色的线连在一起),以及如何把两个节点加入集合(就在图中把两个节点连上)
@@ -346,7 +346,7 @@ int main() {
大家可能发现 怎么和我们 模拟画的图不一样,差别在于 代码生成的最小生成树中 节点5 和 节点7相连的。
-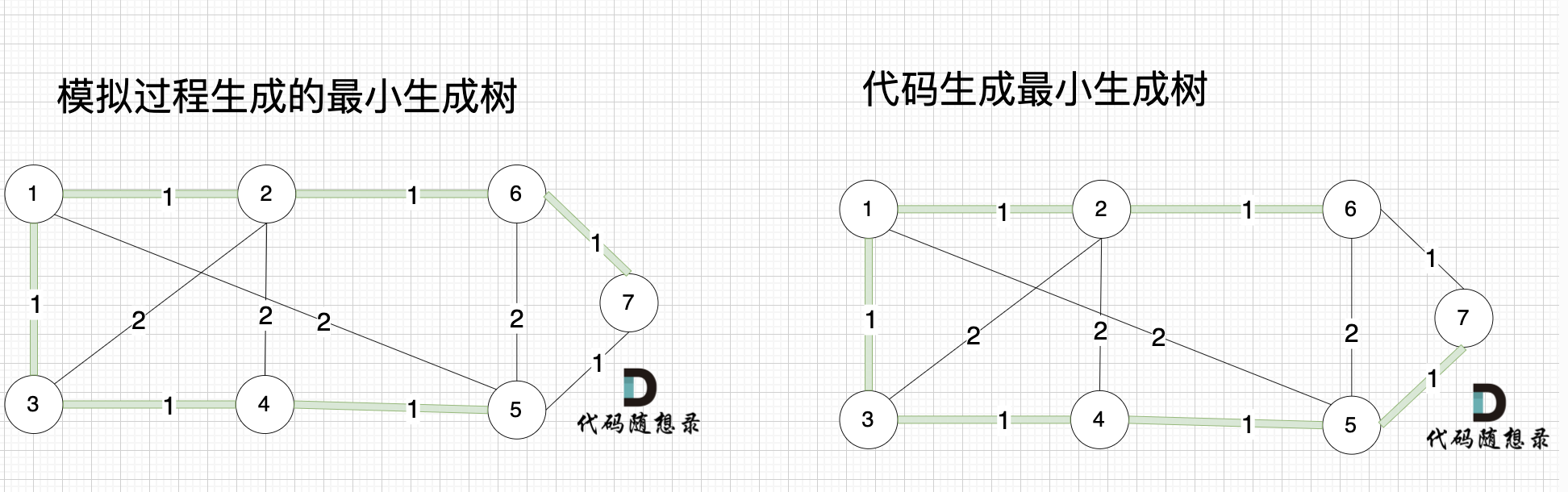
+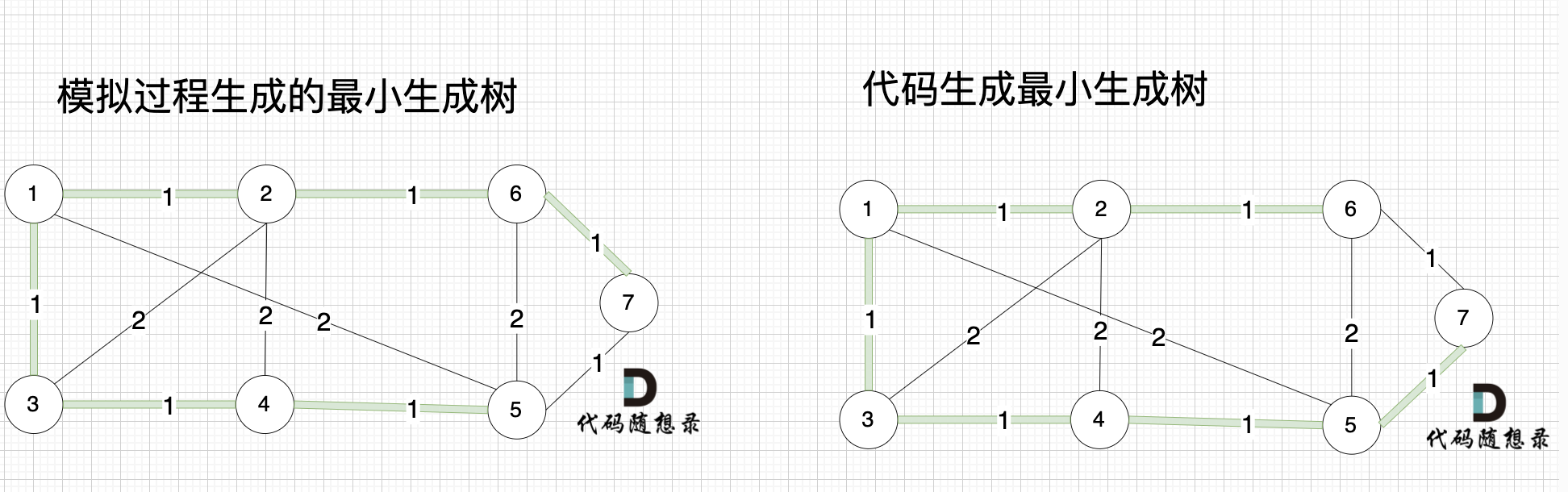
其实造成这个差别 是对边排序的时候 权值相同的边先后顺序的问题导致的,无论相同权值边的顺序是什么样的,最后都能得出最小生成树。
@@ -366,7 +366,7 @@ Kruskal 与 prim 的关键区别在于,prim维护的是节点的集合,而 K
节点未必一定要连着边那, 例如 这个图,大家能明显感受到边没有那么多对吧,但节点数量 和 上述我们讲的例子是一样的。
-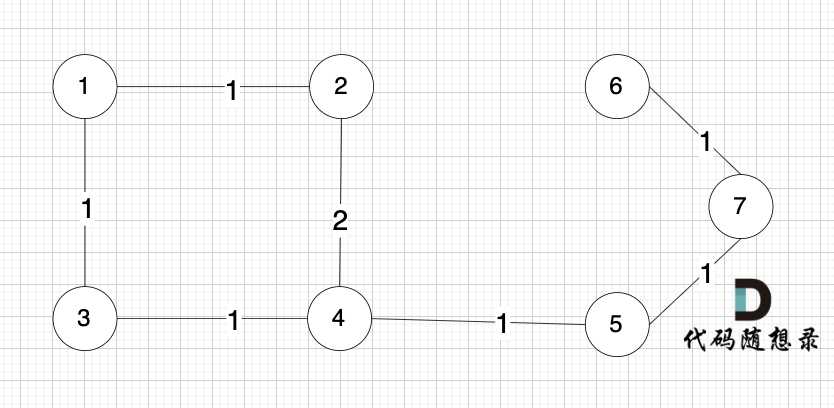
+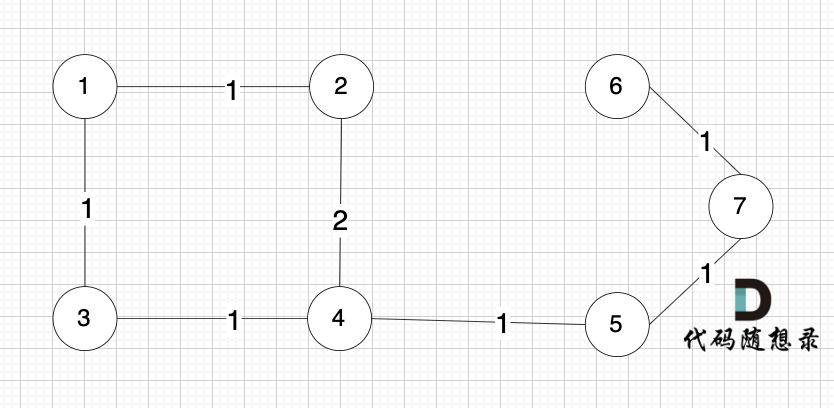
为什么边少的话,使用 Kruskal 更优呢?
diff --git a/problems/kamacoder/0053.寻宝-prim.md b/problems/kamacoder/0053.寻宝-prim.md
index 8e26bea4..a7d35841 100644
--- a/problems/kamacoder/0053.寻宝-prim.md
+++ b/problems/kamacoder/0053.寻宝-prim.md
@@ -61,7 +61,7 @@
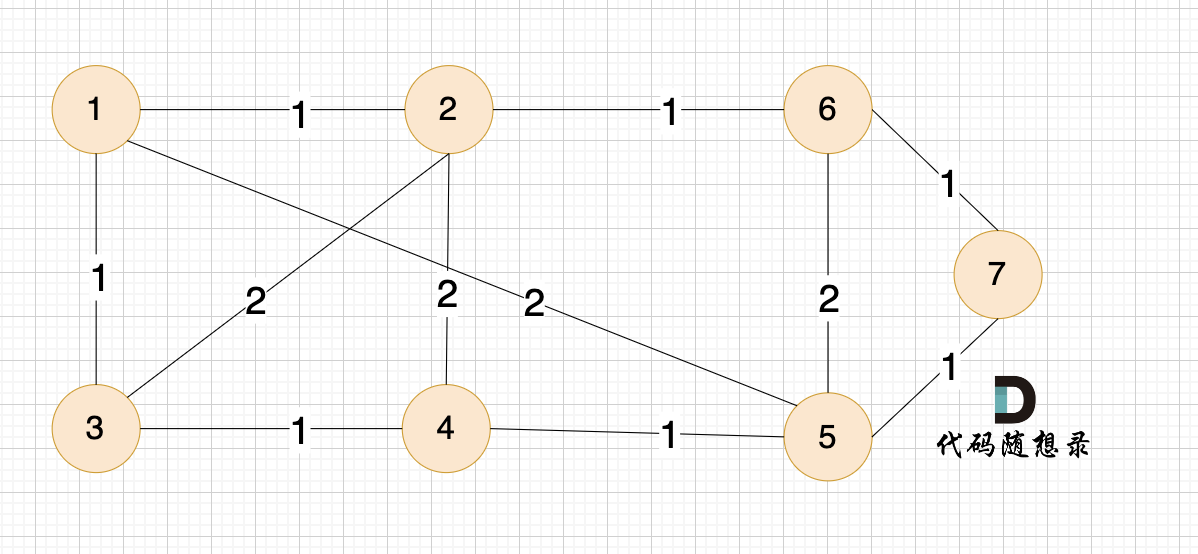
例如本题示例中的无向有权图为:
-
+
那么在这个图中,如何选取n-1条边使得图中所有节点连接到一起,并且边的权值和最小呢?
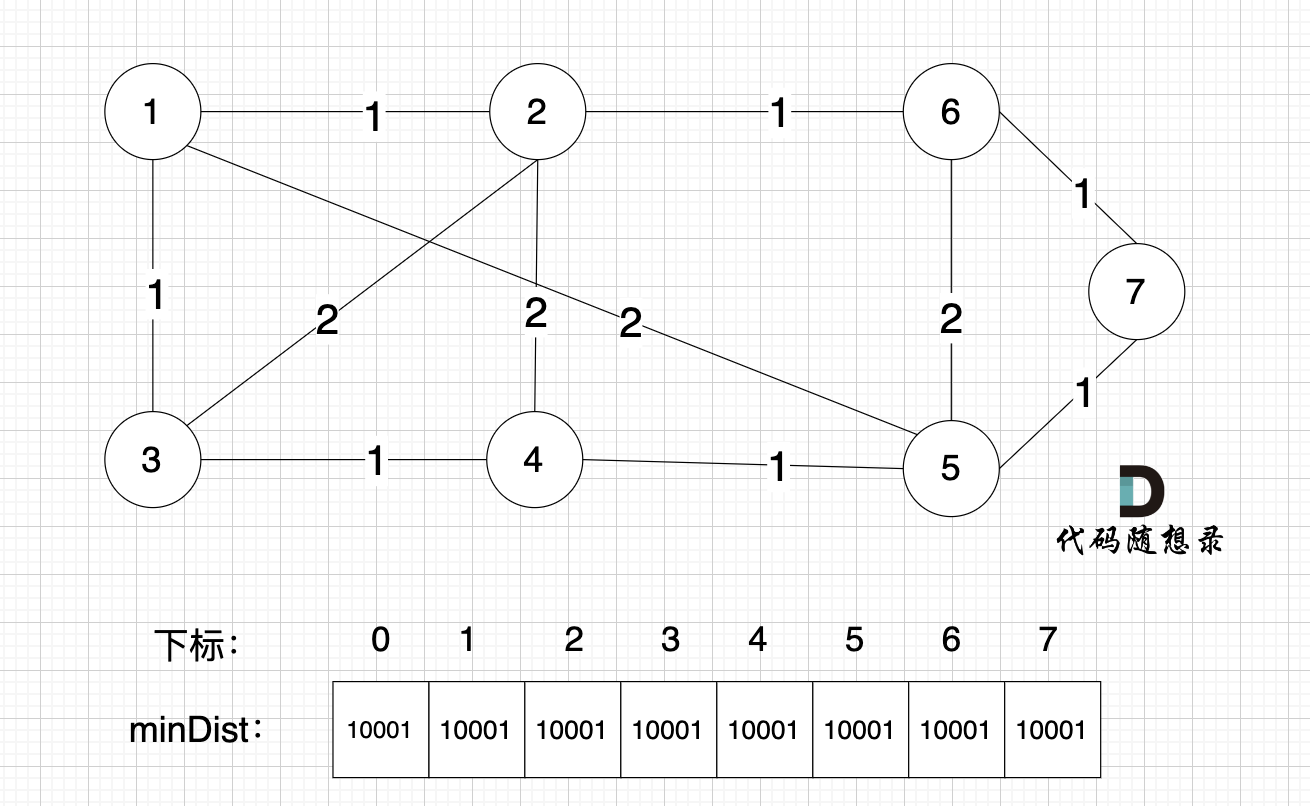
@@ -100,7 +100,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
如图:
-
+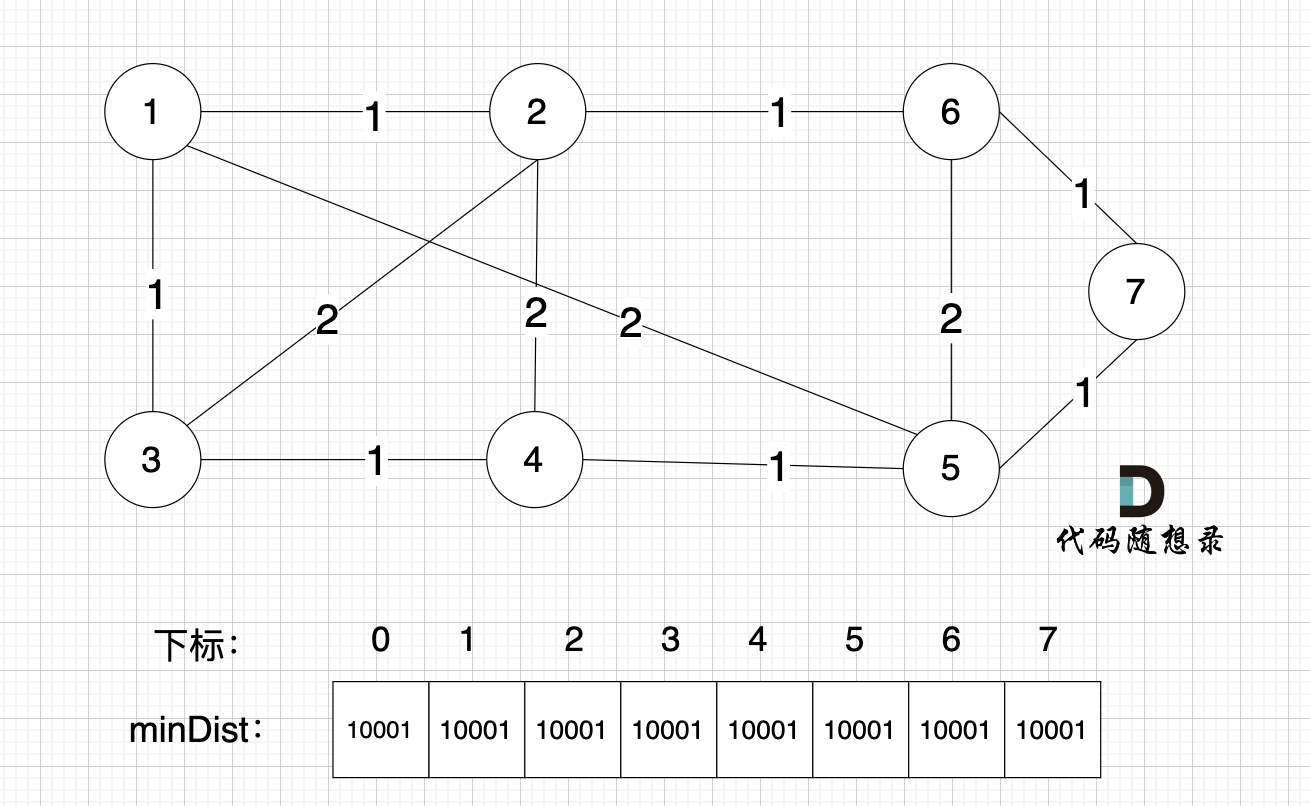
开始构造最小生成树
@@ -118,7 +118,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
接下来,我们要更新所有节点距离最小生成树的距离,如图:
-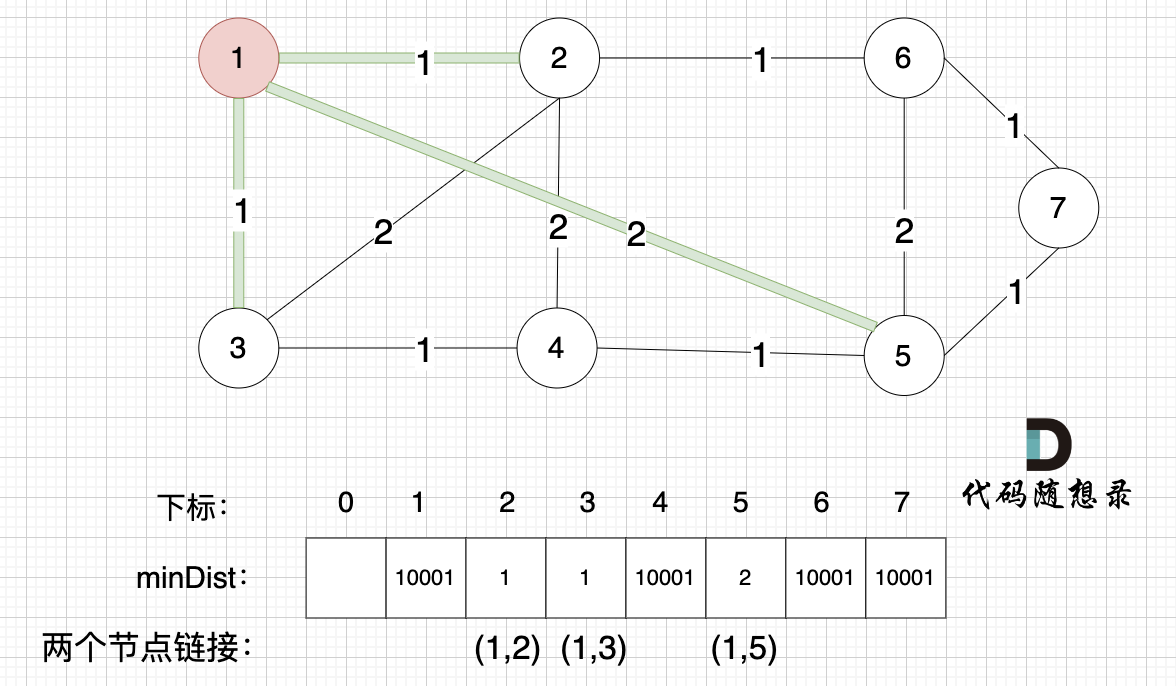
+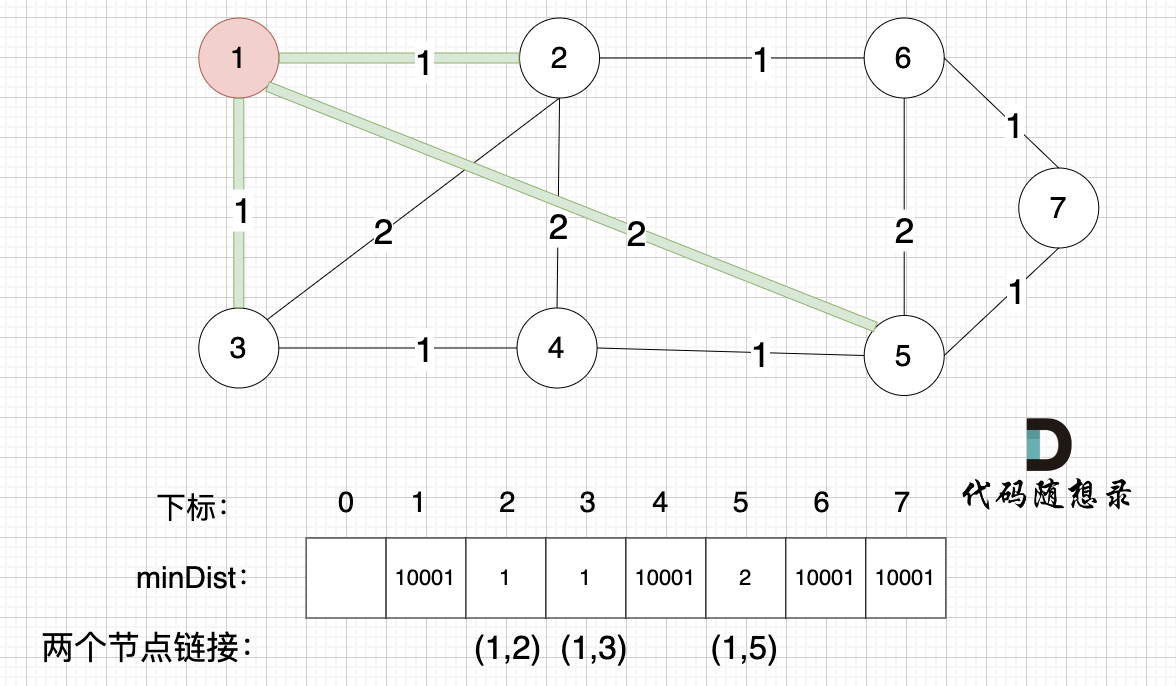
注意下标0,我们就不管它了,下标1与节点1对应,这样可以避免大家把节点搞混。
@@ -148,7 +148,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
接下来,我们要更新节点距离最小生成树的距离,如图:
-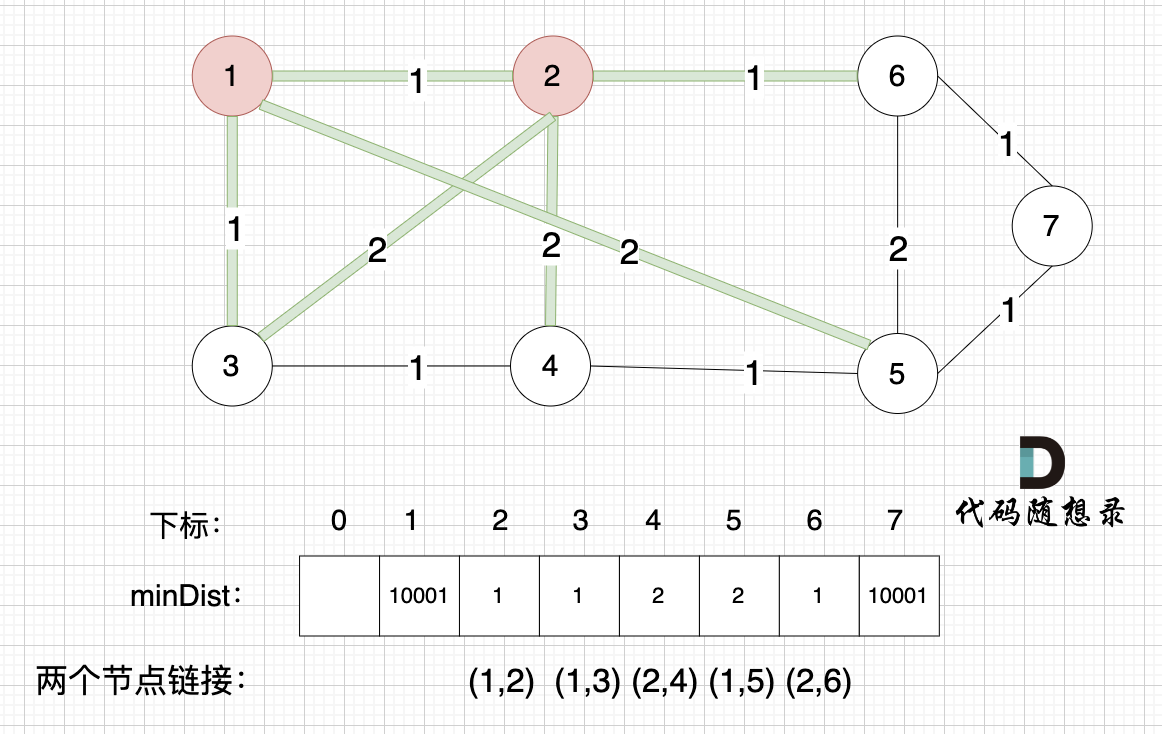
+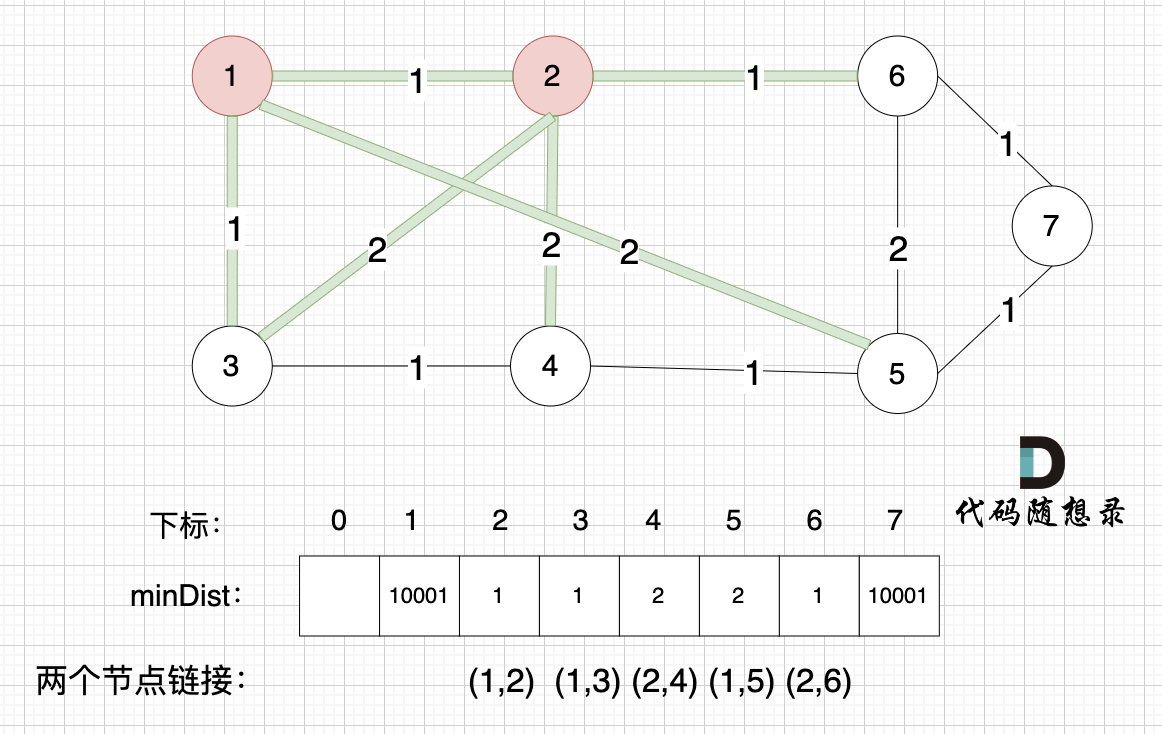
此时所有非生成树的节点距离最小生成树(节点1、节点2)的距离都已经跟新了。
@@ -172,7 +172,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
接下来更新节点距离最小生成树的距离,如图:
-
+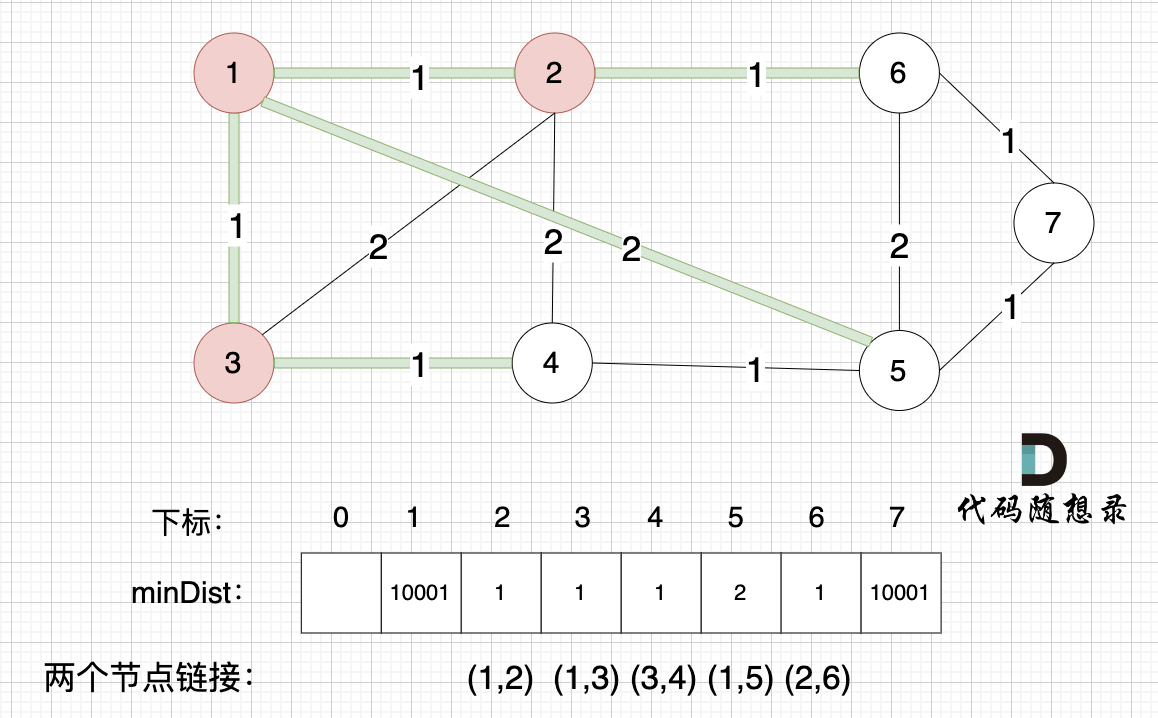
所有非生成树的节点距离最小生成树(节点1、节点2、节点3)的距离都已经跟新了。
@@ -188,7 +188,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
继续选择一个距离最小生成树(节点1、节点2、节点3)最近的非生成树里的节点,为了巩固大家对minDist数组的理解,这里我再啰嗦一遍:
-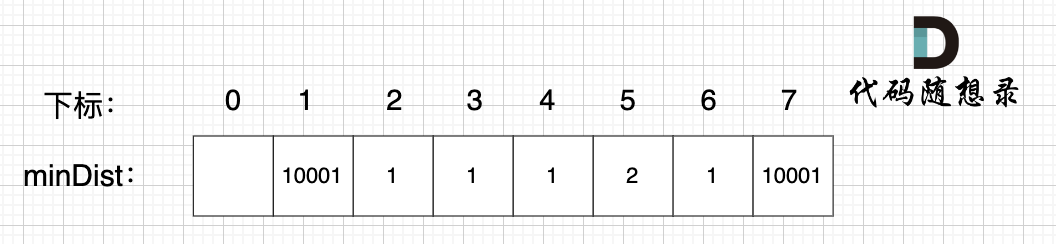
+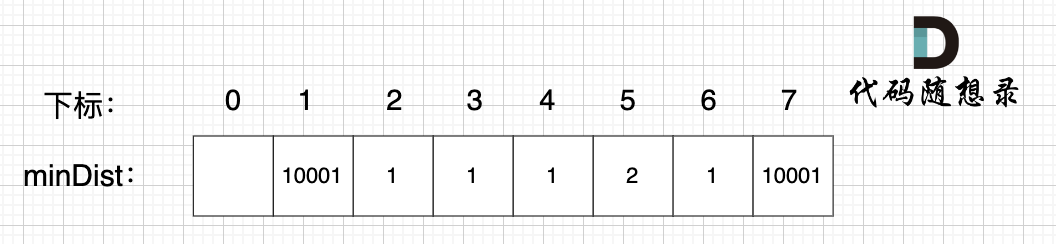
**minDist数组是记录了所有非生成树节点距离生成树的最小距离**,所以从数组里我们能看出来,非生成树节点4和节点6距离生成树最近。
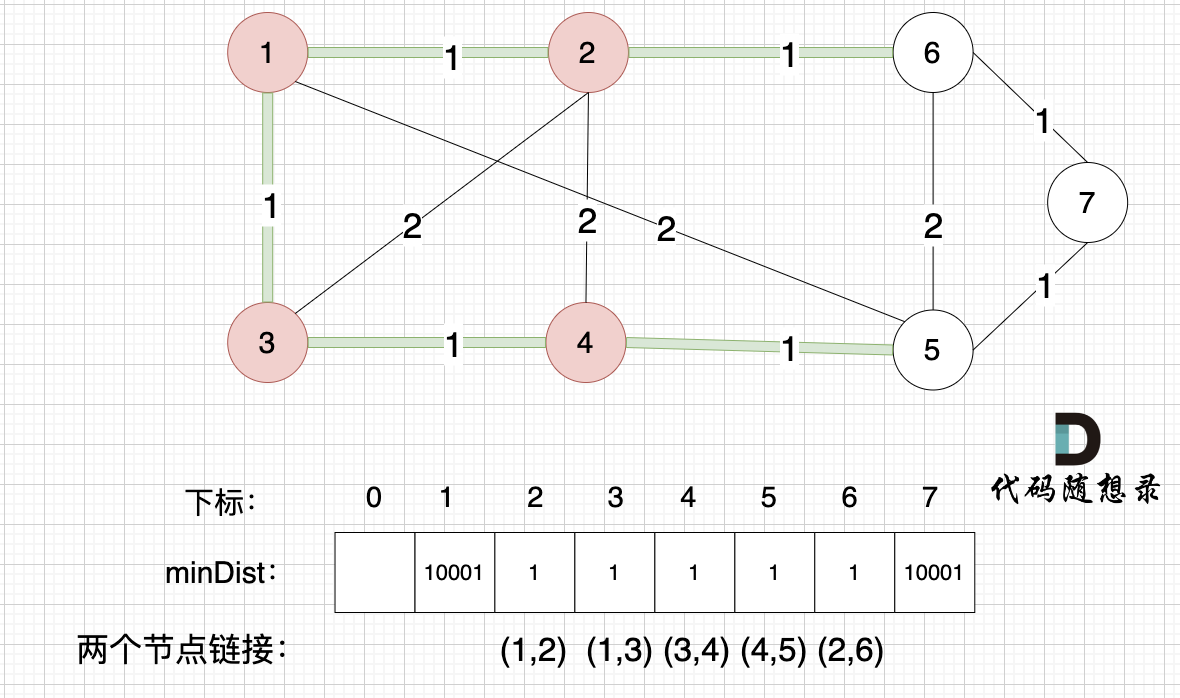
@@ -209,7 +209,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
接下来更新节点距离最小生成树的距离,如图:
-
+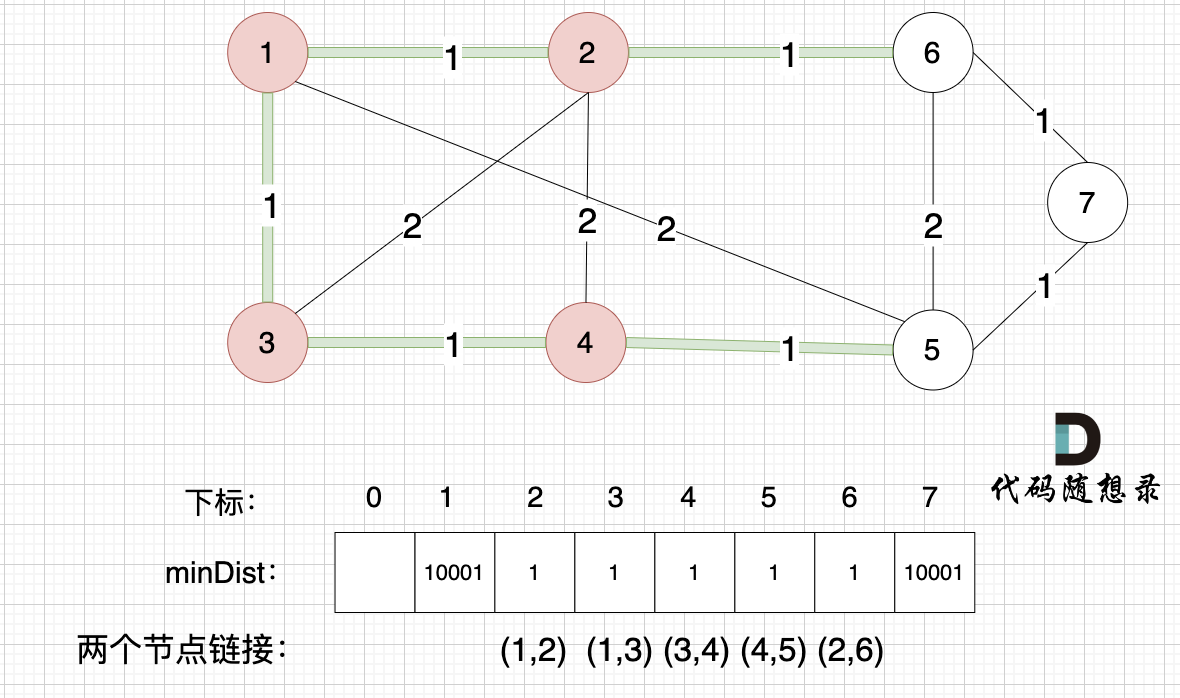
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4)的距离。
@@ -232,7 +232,7 @@ minDist数组已经更新了所有非生成树的节点距离最小生成树(
接下来更新节点距离最小生成树的距离,如图:
-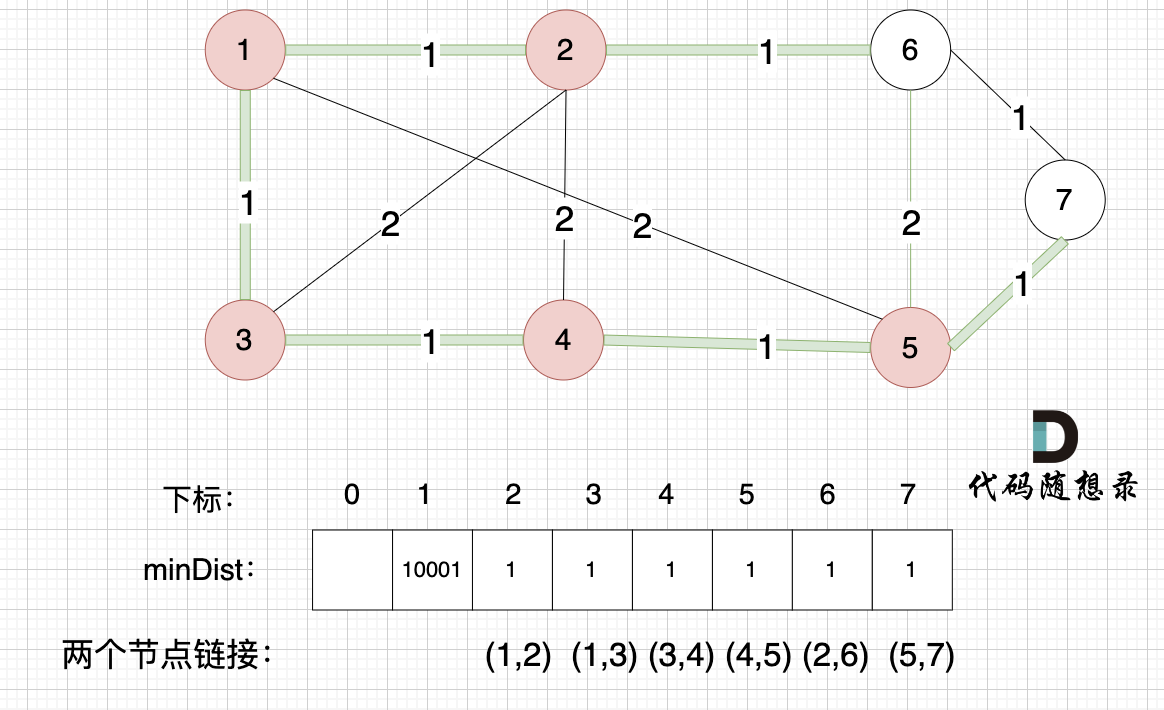
+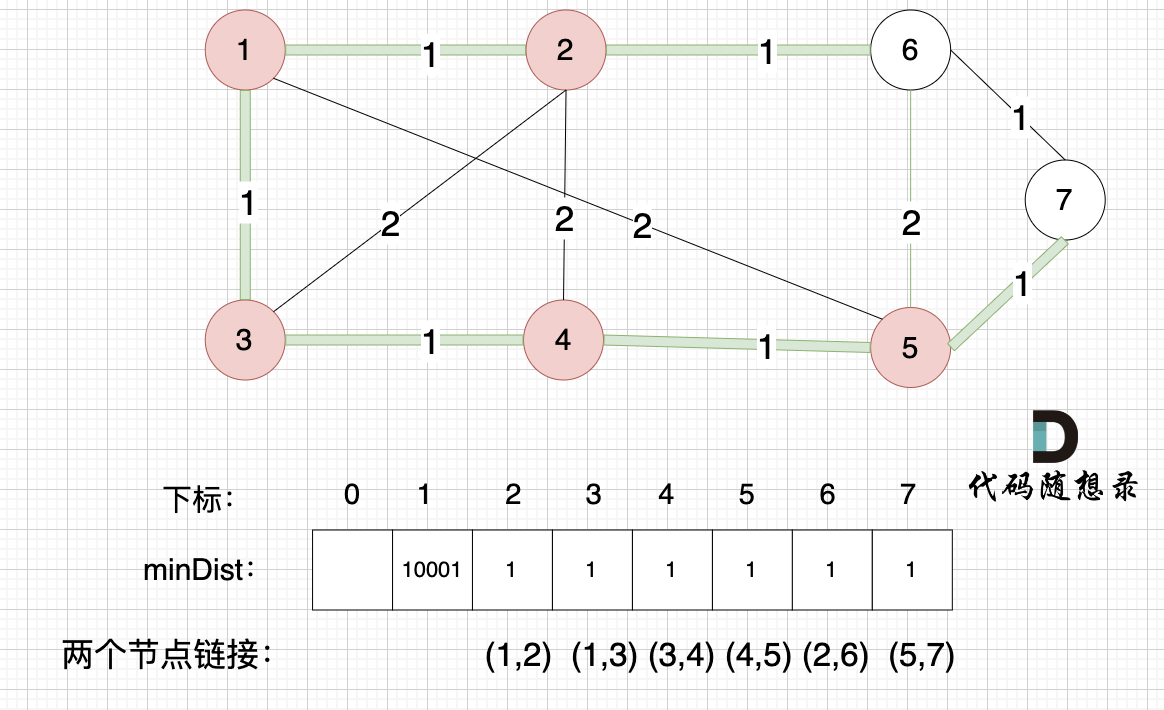
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4、节点5)的距离。
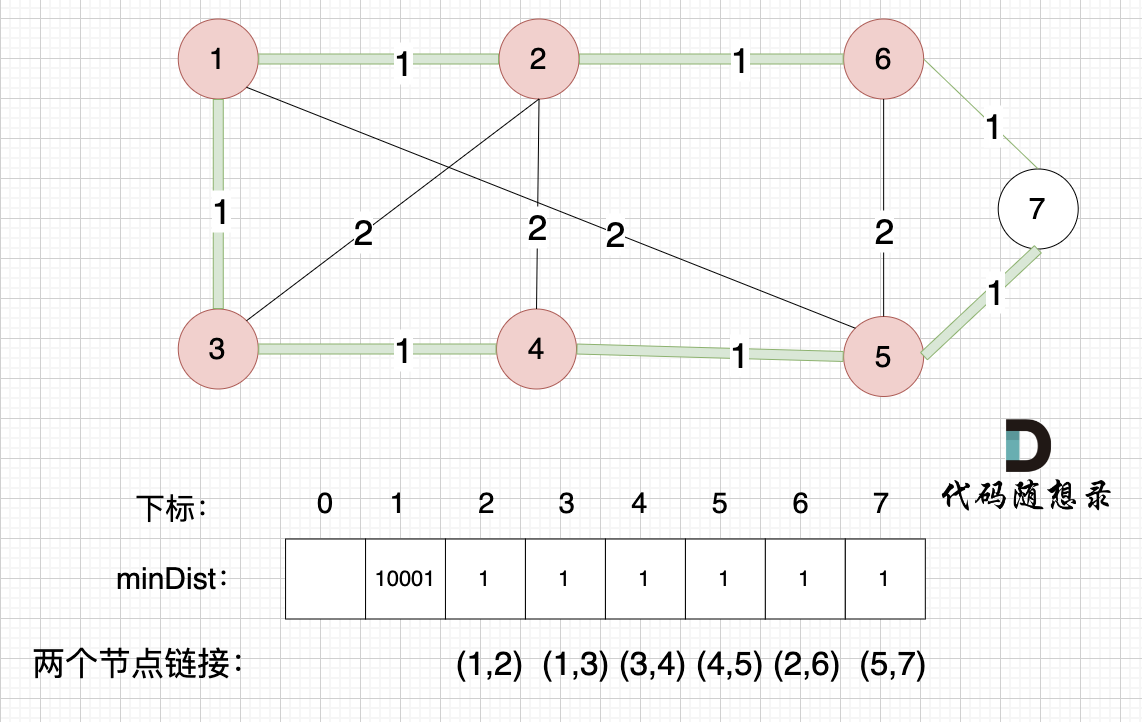
@@ -253,11 +253,11 @@ minDist数组已经更新了所有非生成树的节点距离最小生成树(
节点1、节点2、节点3、节点4、节点5、节点6算是最小生成树的节点,接下来更新节点距离最小生成树的距离,如图:
-
+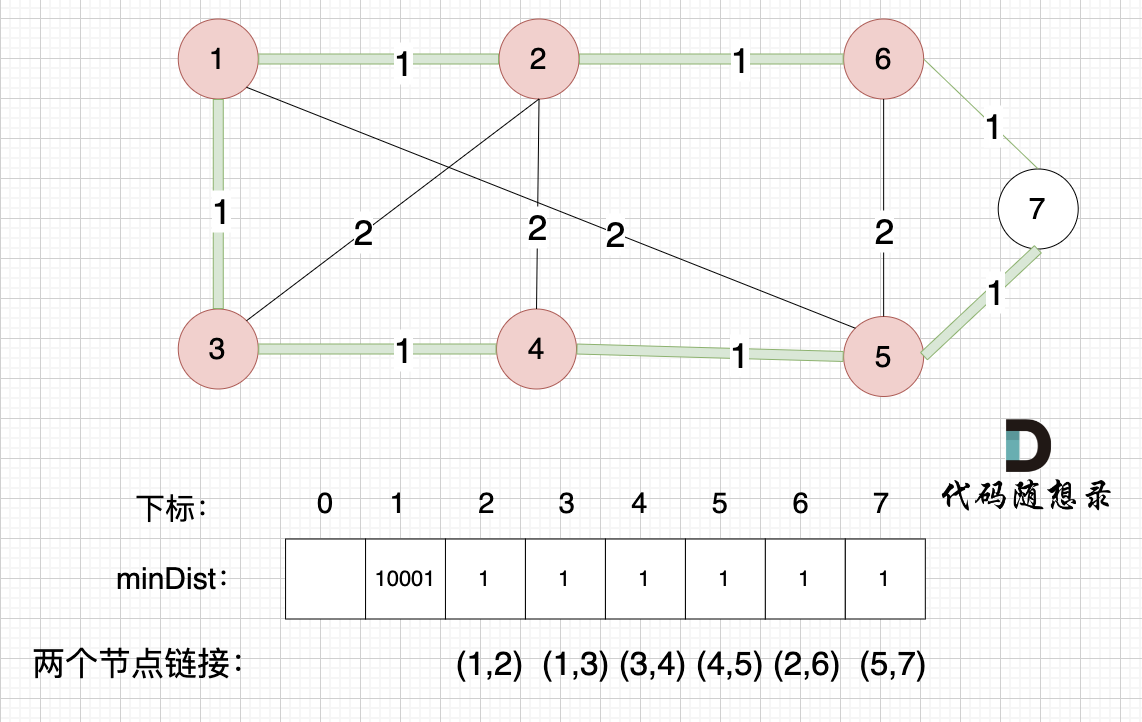
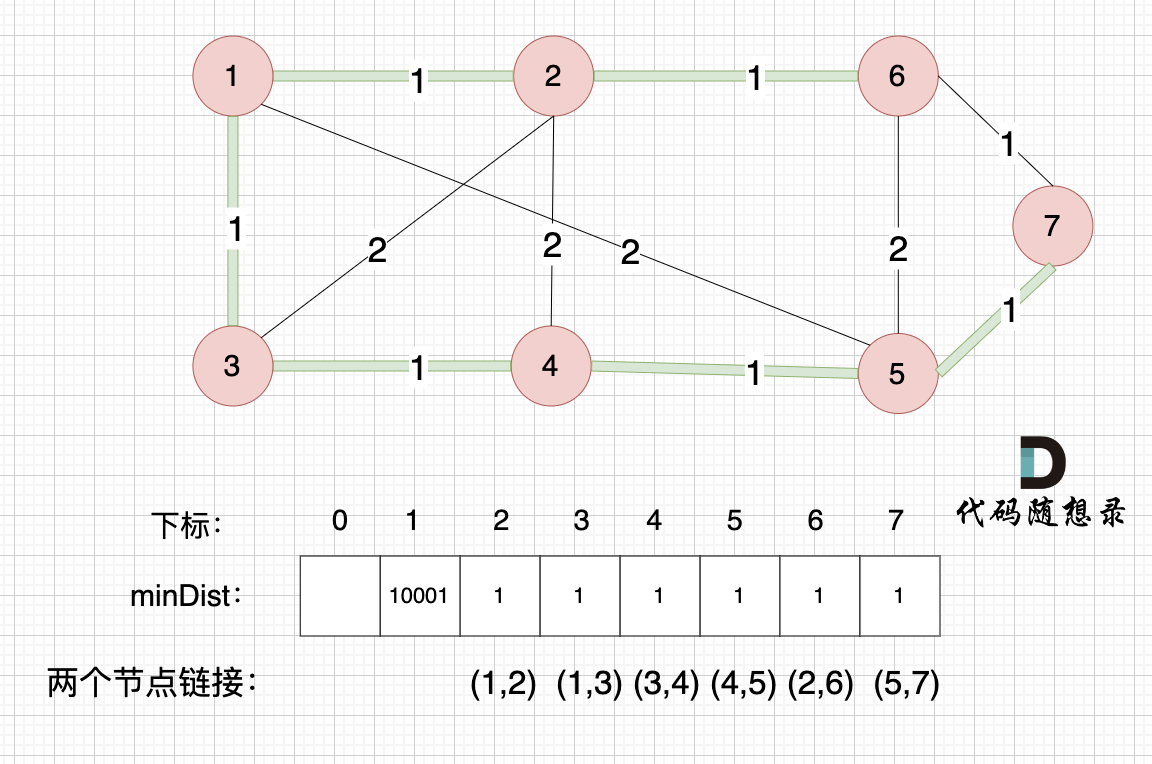
这里就不在重复描述了,大家类推,最后,节点7加入生成树,如图:
-
+
### 最后
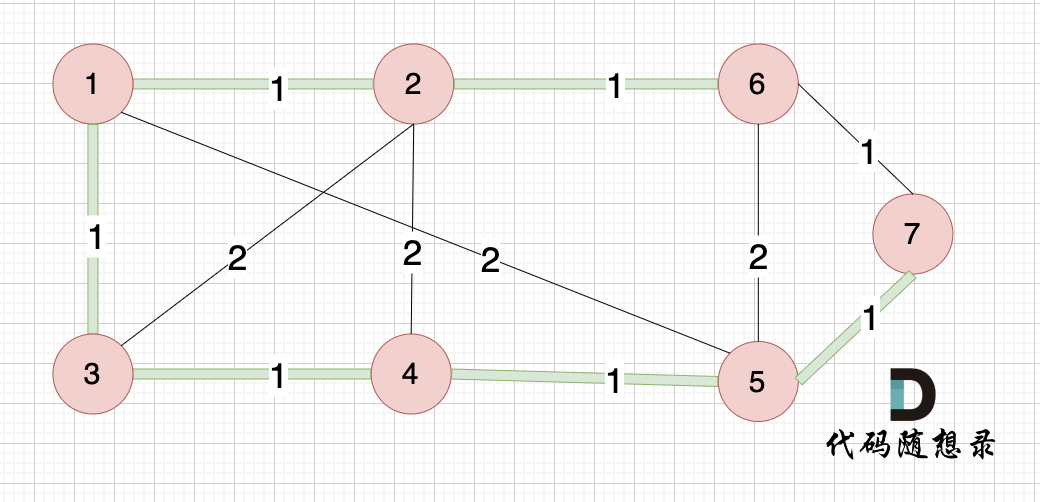
@@ -478,7 +478,7 @@ int main() {
大家可以和我们本题最后生成的最小生成树的图去对比一下边的链接情况:
-
+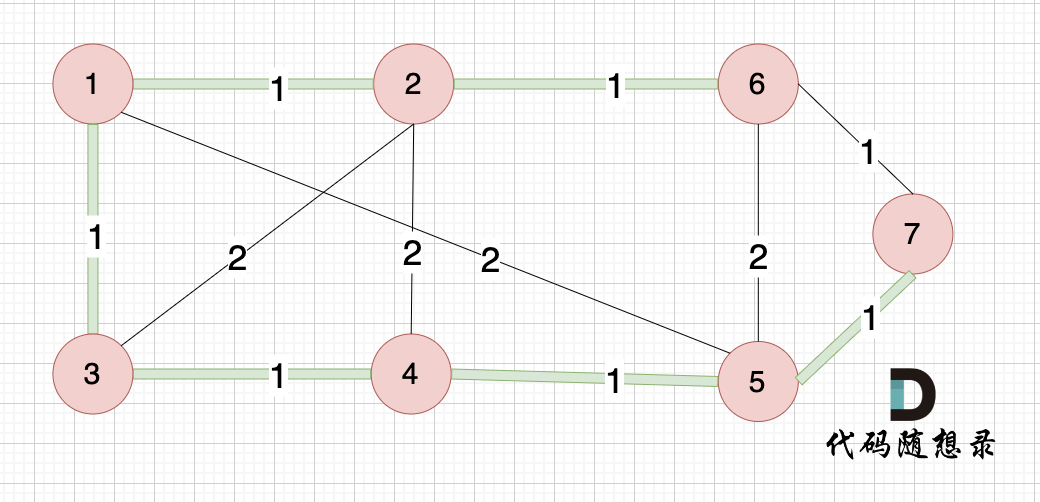
绿色的边是最小生成树,和我们的输出完全一致。
diff --git a/problems/kamacoder/0054.替换数字.md b/problems/kamacoder/0054.替换数字.md
index f788d65b..665e8ecb 100644
--- a/problems/kamacoder/0054.替换数字.md
+++ b/problems/kamacoder/0054.替换数字.md
@@ -29,11 +29,11 @@
如图:
-
+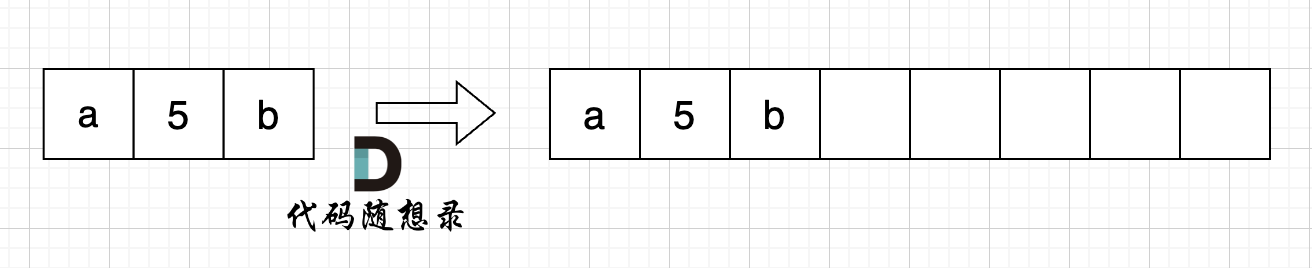
然后从后向前替换数字字符,也就是双指针法,过程如下:i指向新长度的末尾,j指向旧长度的末尾。
-
+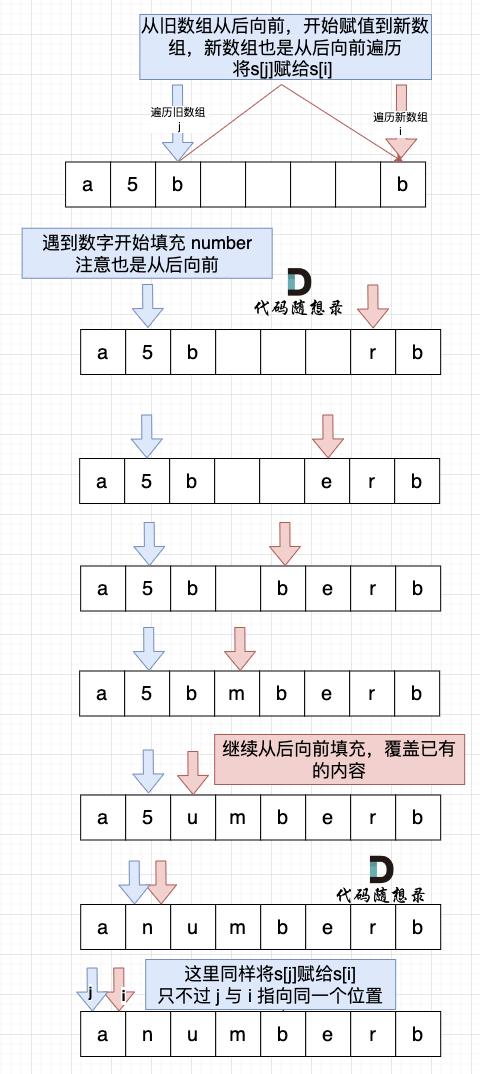
有同学问了,为什么要从后向前填充,从前向后填充不行么?
diff --git a/problems/kamacoder/0055.右旋字符串.md b/problems/kamacoder/0055.右旋字符串.md
index 2b32cb44..48150222 100644
--- a/problems/kamacoder/0055.右旋字符串.md
+++ b/problems/kamacoder/0055.右旋字符串.md
@@ -40,16 +40,16 @@ fgabcde
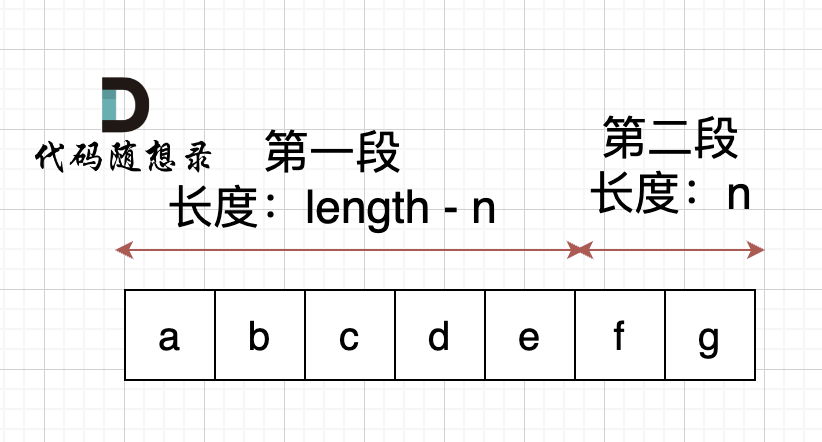
本题中,我们需要将字符串右移n位,字符串相当于分成了两个部分,如果n为2,符串相当于分成了两个部分,如图: (length为字符串长度)
-
+
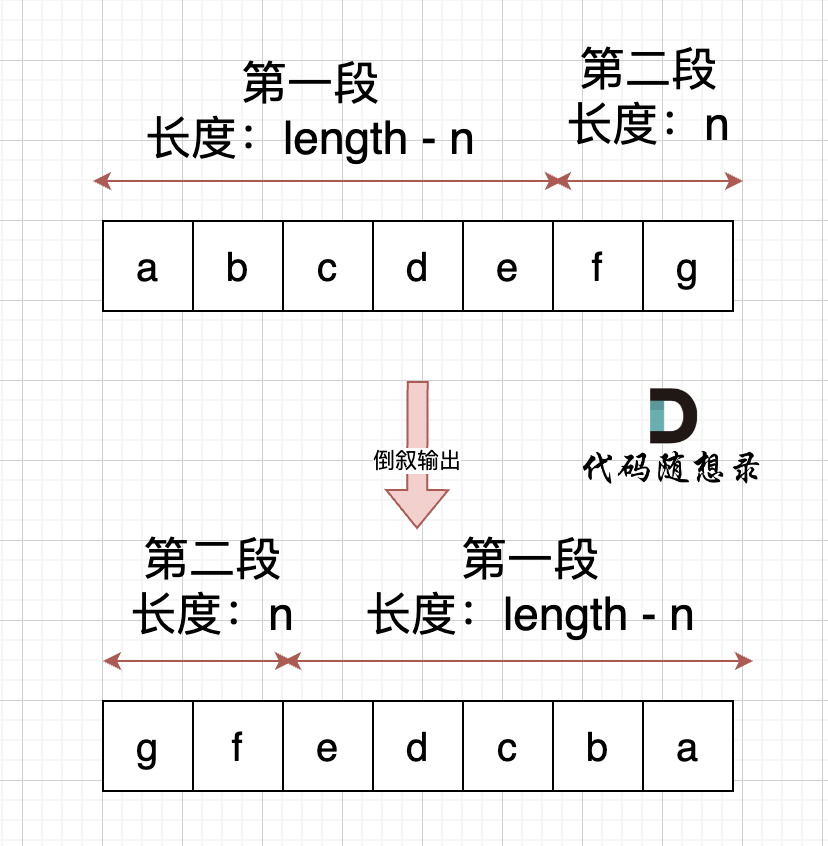
右移n位, 就是将第二段放在前面,第一段放在后面,先不考虑里面字符的顺序,是不是整体倒叙不就行了。如图:
-
+
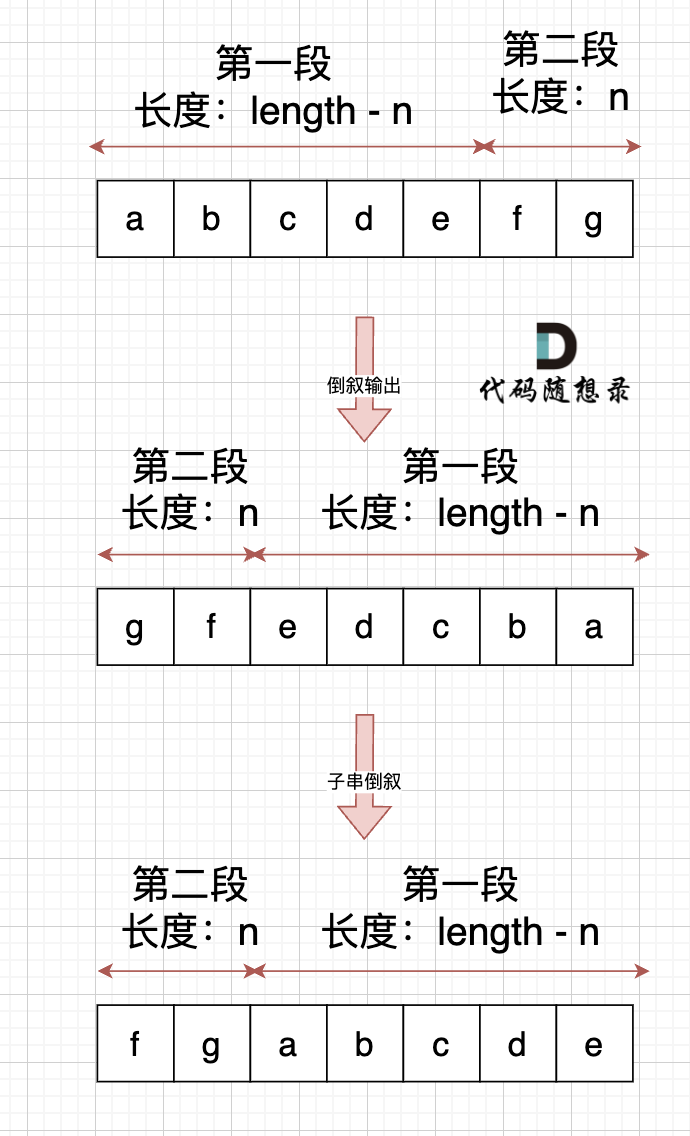
此时第一段和第二段的顺序是我们想要的,但里面的字符位置被我们倒叙,那么此时我们在把 第一段和第二段里面的字符再倒叙一把,这样字符顺序不就正确了。 如果:
-
+
其实,思路就是 通过 整体倒叙,把两段子串顺序颠倒,两个段子串里的的字符在倒叙一把,**负负得正**,这样就不影响子串里面字符的顺序了。
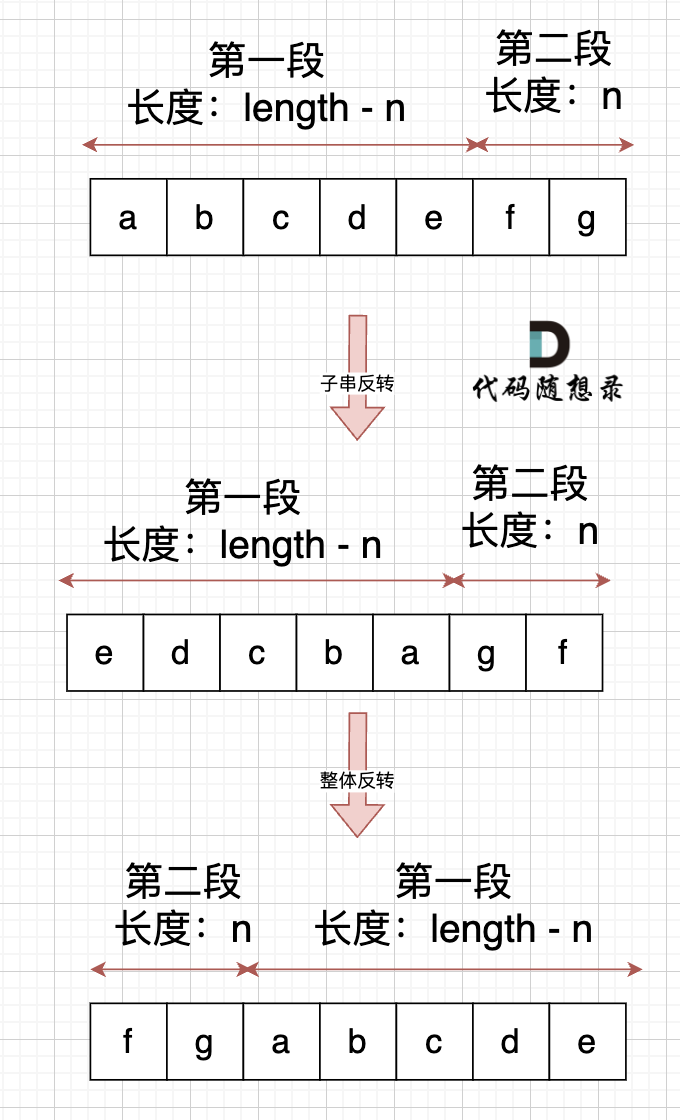
@@ -80,7 +80,7 @@ int main() {
可以的,不过,要记得 控制好 局部反转的长度,如果先局部反转,那么先反转的子串长度就是 len - n,如图:
-
+
代码如下:
diff --git a/problems/kamacoder/0058.区间和.md b/problems/kamacoder/0058.区间和.md
index 23e7189a..a6342ef8 100644
--- a/problems/kamacoder/0058.区间和.md
+++ b/problems/kamacoder/0058.区间和.md
@@ -93,7 +93,7 @@ int main() {
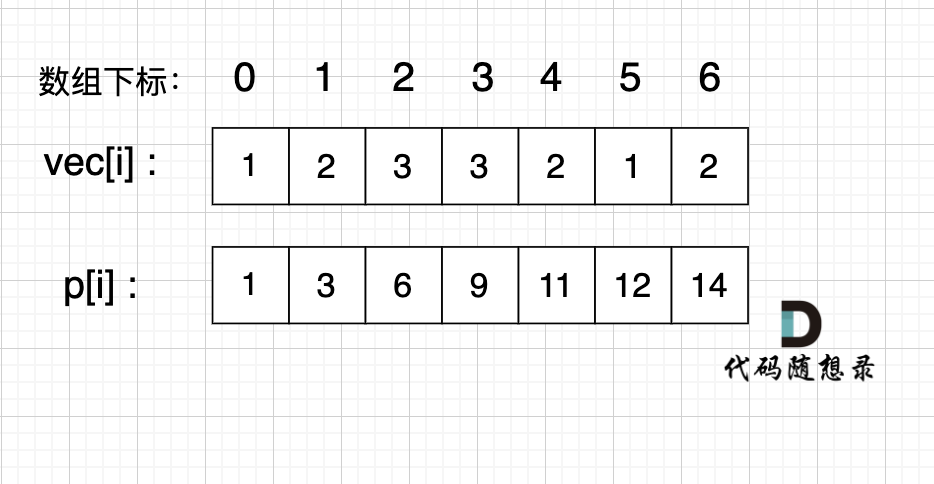
如图:
-
+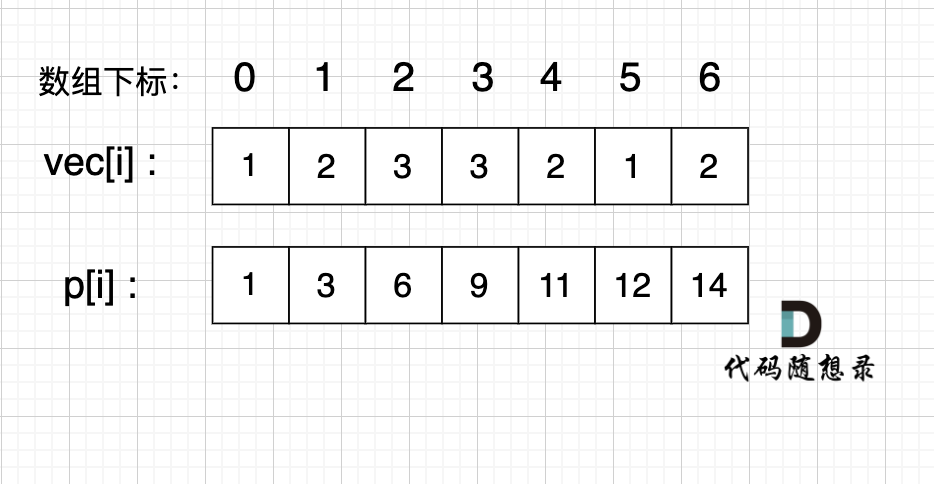
如果,我们想统计,在vec数组上 下标 2 到下标 5 之间的累加和,那是不是就用 p[5] - p[1] 就可以了。
@@ -109,7 +109,7 @@ int main() {
如图所示:
-
+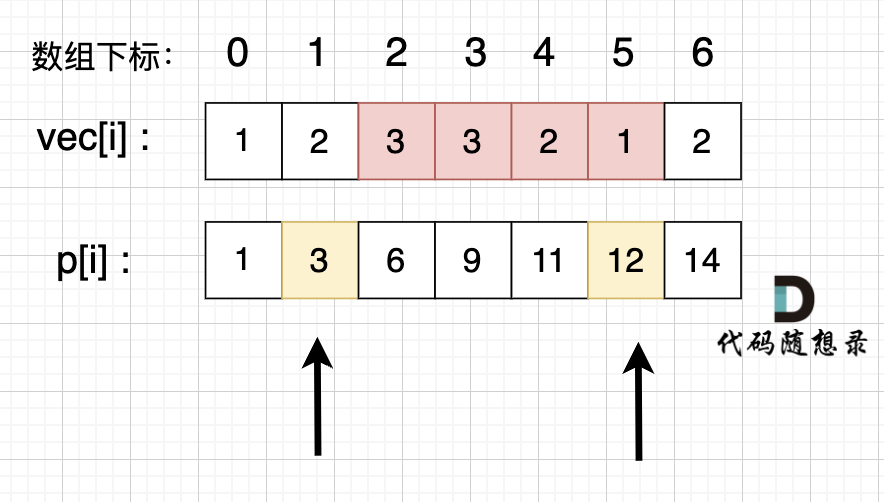
`p[5] - p[1]` 就是 红色部分的区间和。
diff --git a/problems/kamacoder/0094.城市间货物运输I-SPFA.md b/problems/kamacoder/0094.城市间货物运输I-SPFA.md
index 99986aaa..b5920292 100644
--- a/problems/kamacoder/0094.城市间货物运输I-SPFA.md
+++ b/problems/kamacoder/0094.城市间货物运输I-SPFA.md
@@ -62,7 +62,7 @@
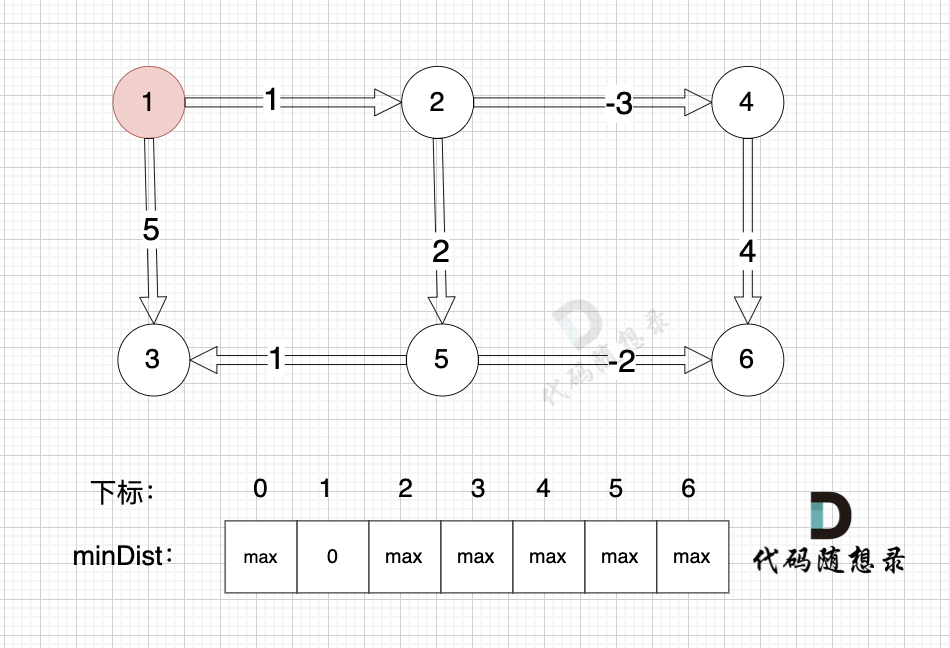
给大家举一个例子:
-
+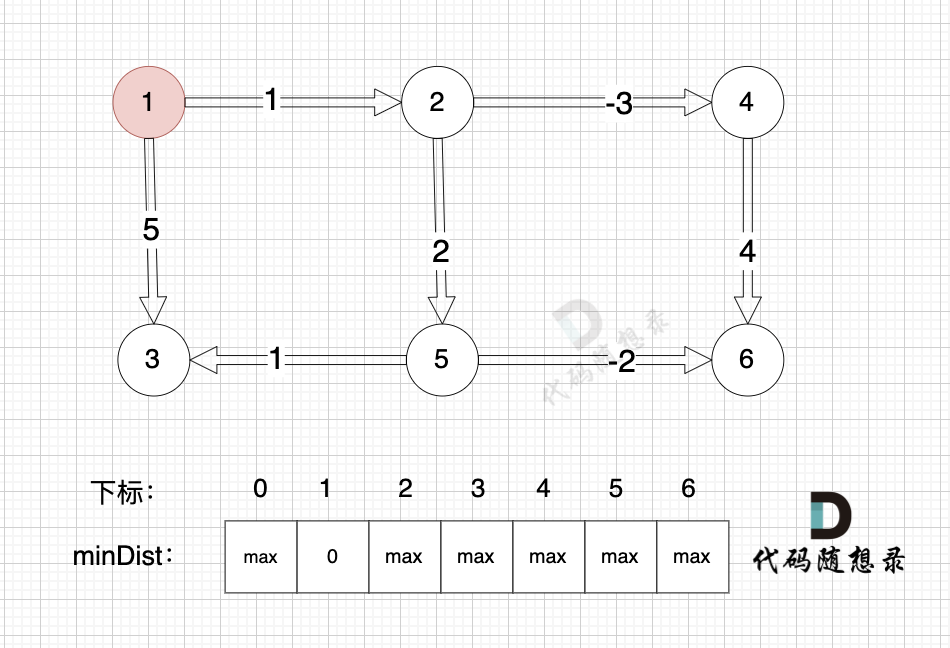
本图中,对所有边进行松弛,真正有效的松弛,只有松弛 边(节点1->节点2) 和 边(节点1->节点3) 。
@@ -97,7 +97,7 @@
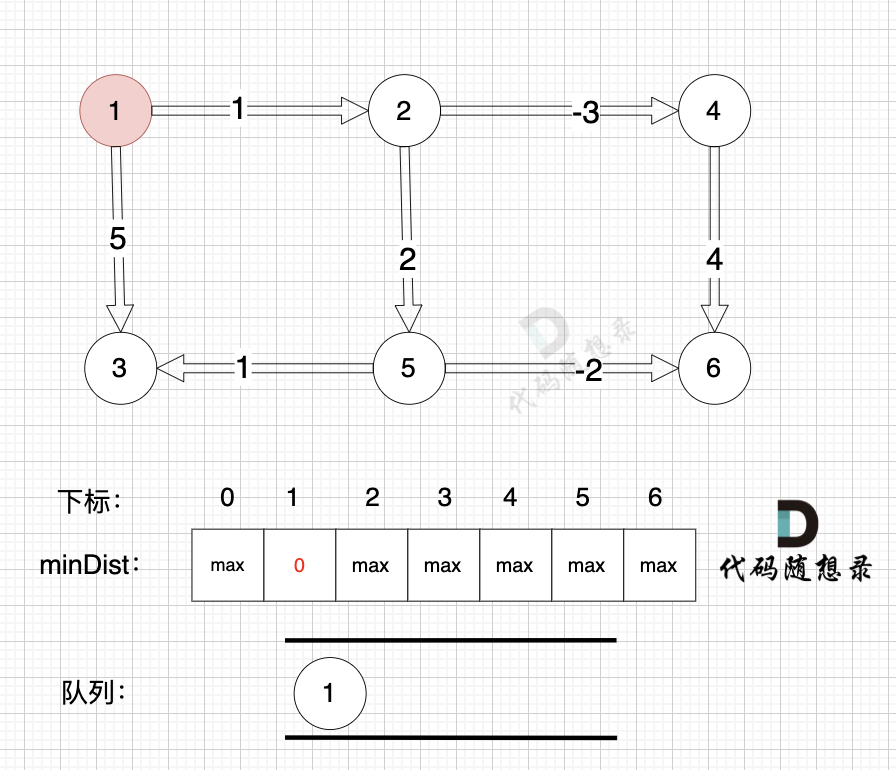
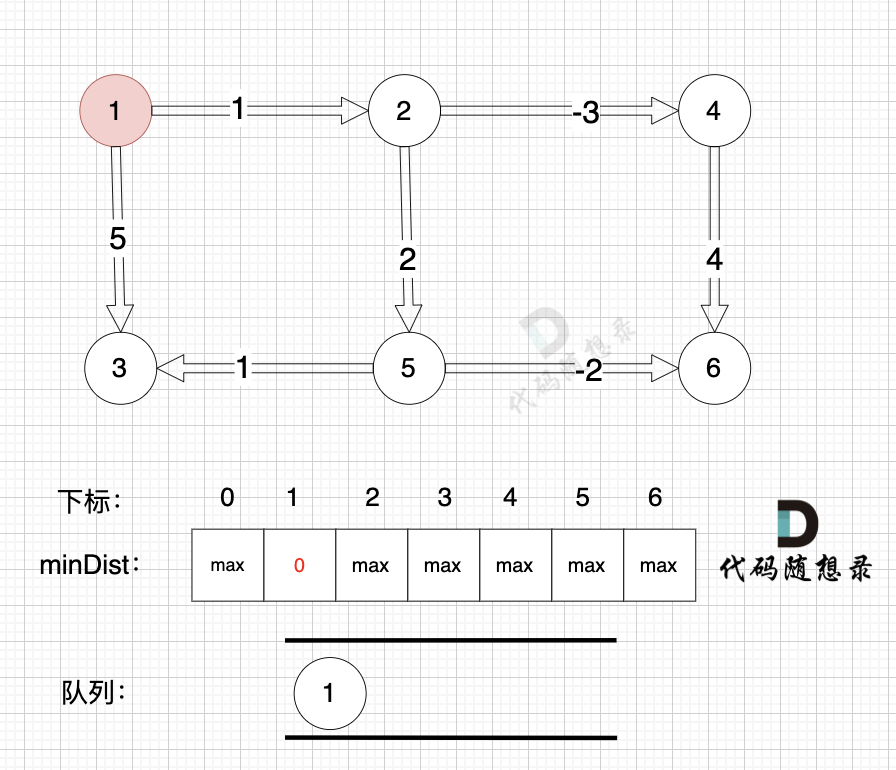
初始化,起点为节点1, 起点到起点的最短距离为0,所以minDist[1] 为 0。 将节点1 加入队列 (下次松弛从节点1开始)
-
+
------------
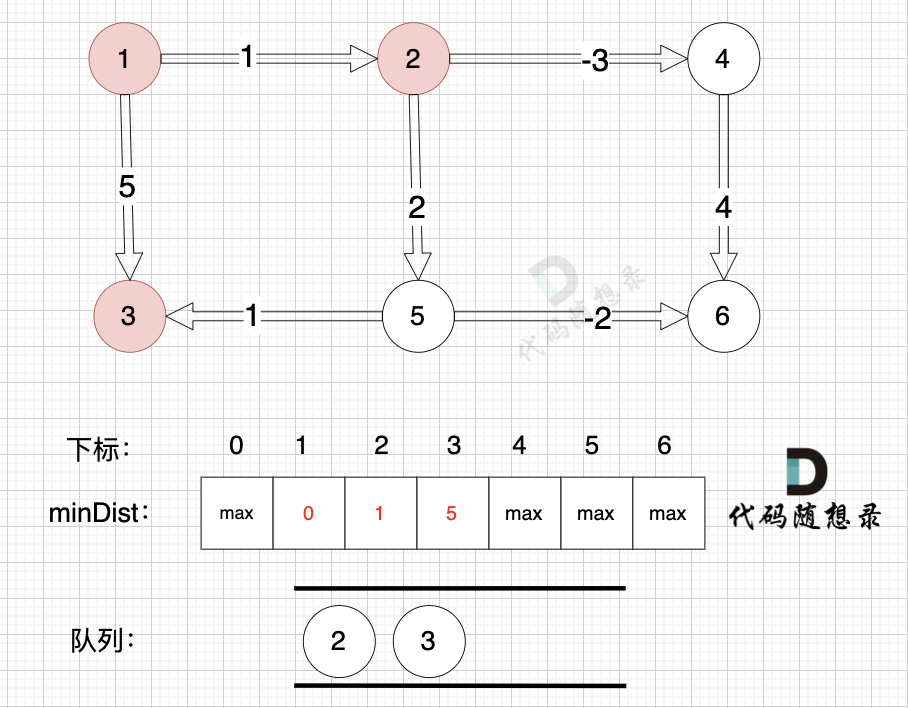
@@ -109,7 +109,7 @@
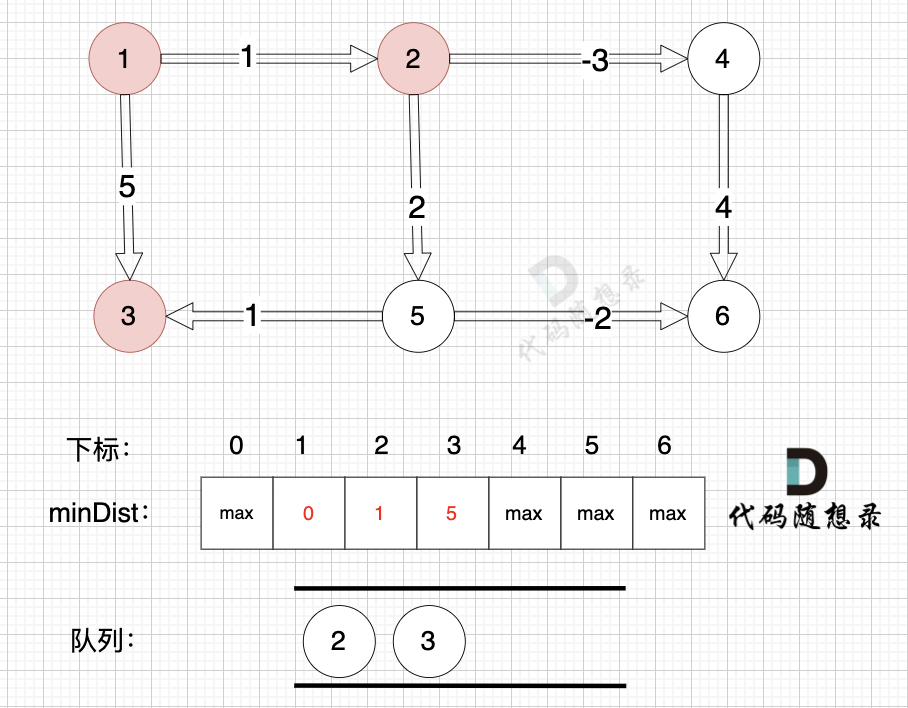
将节点2、节点3 加入队列,如图:
-
+
-----------------
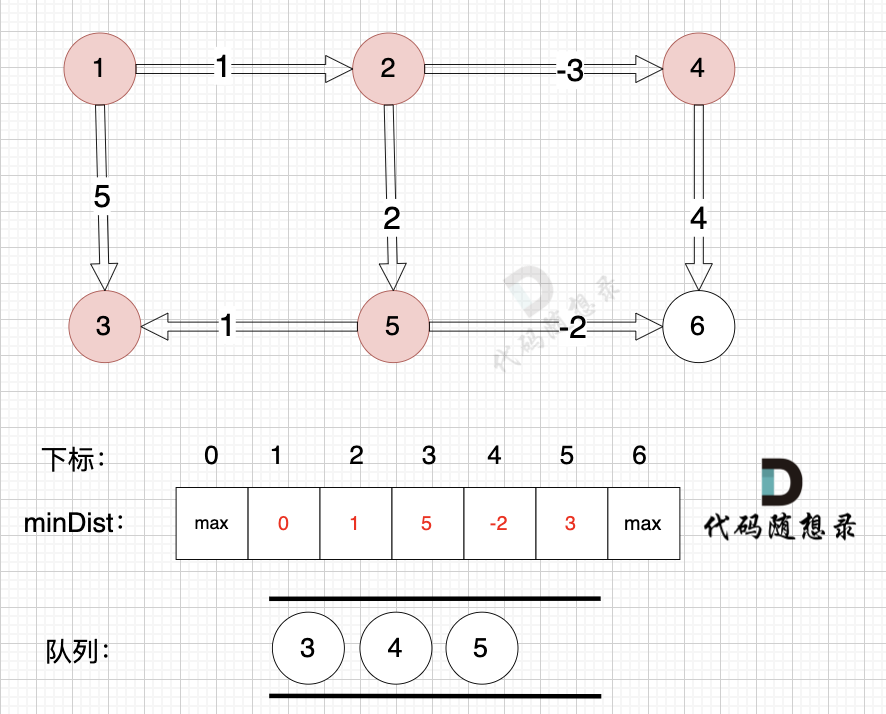
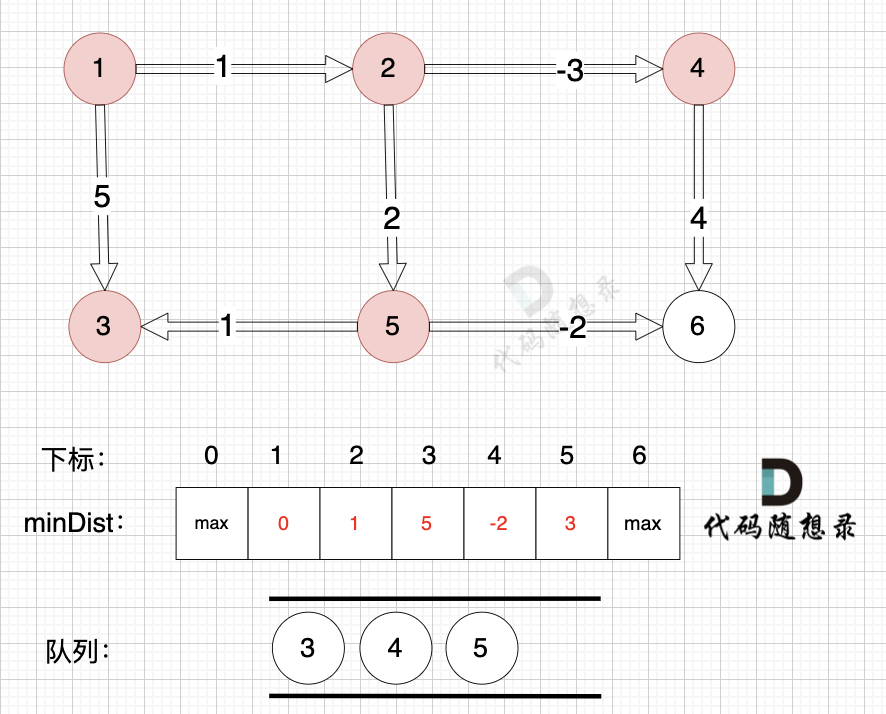
@@ -124,7 +124,7 @@
将节点4,节点5 加入队列,如图:
-
+
--------------------
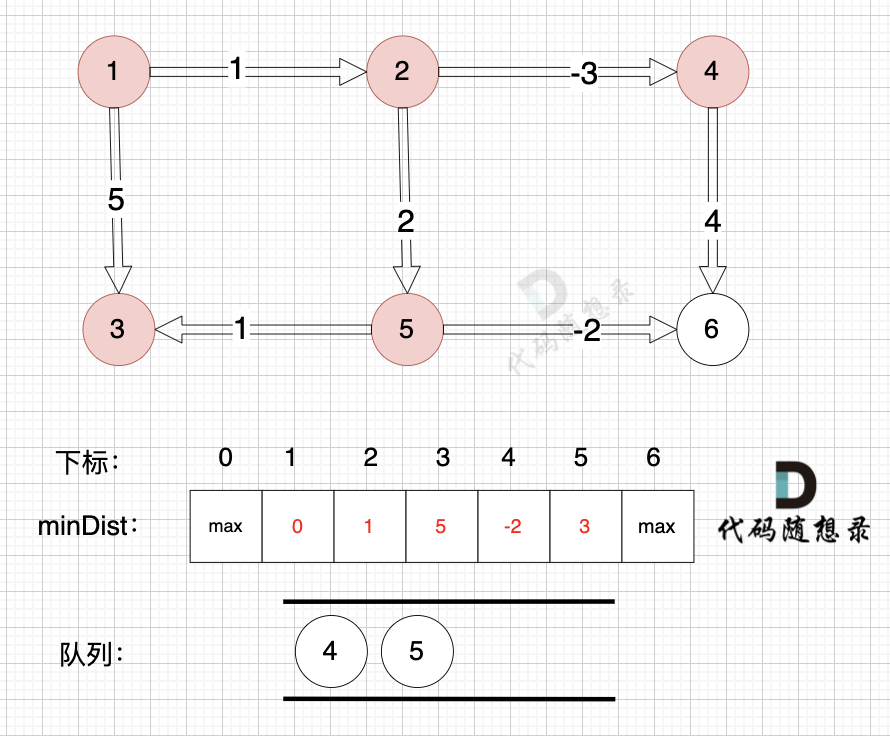
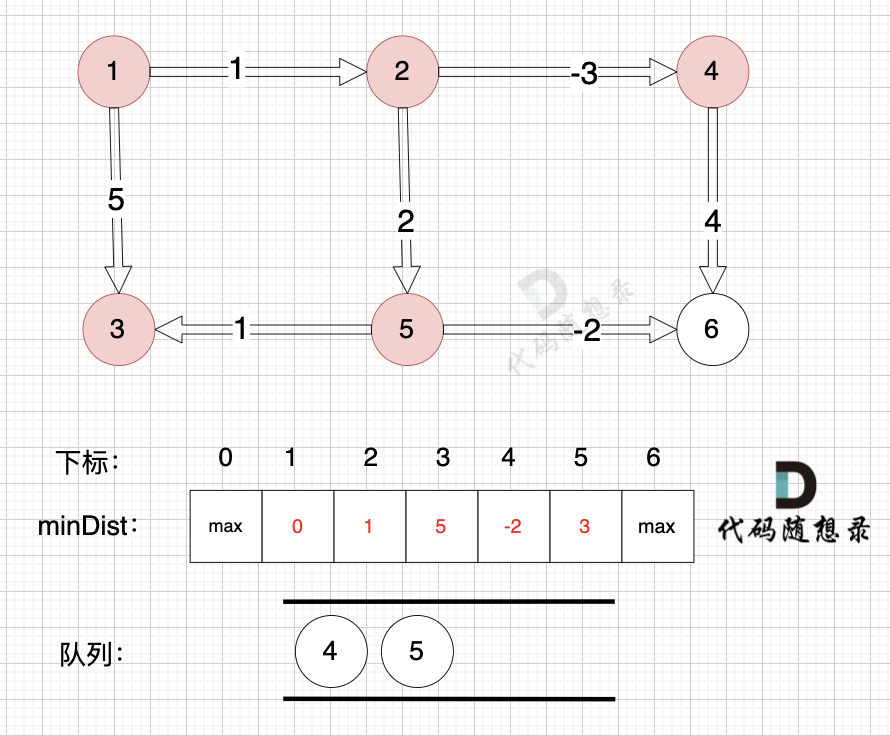
@@ -134,7 +134,7 @@
因为没有从节点3作为出发点的边,所以这里就从队列里取出节点3就好,不用做其他操作,如图:
-
+
------------
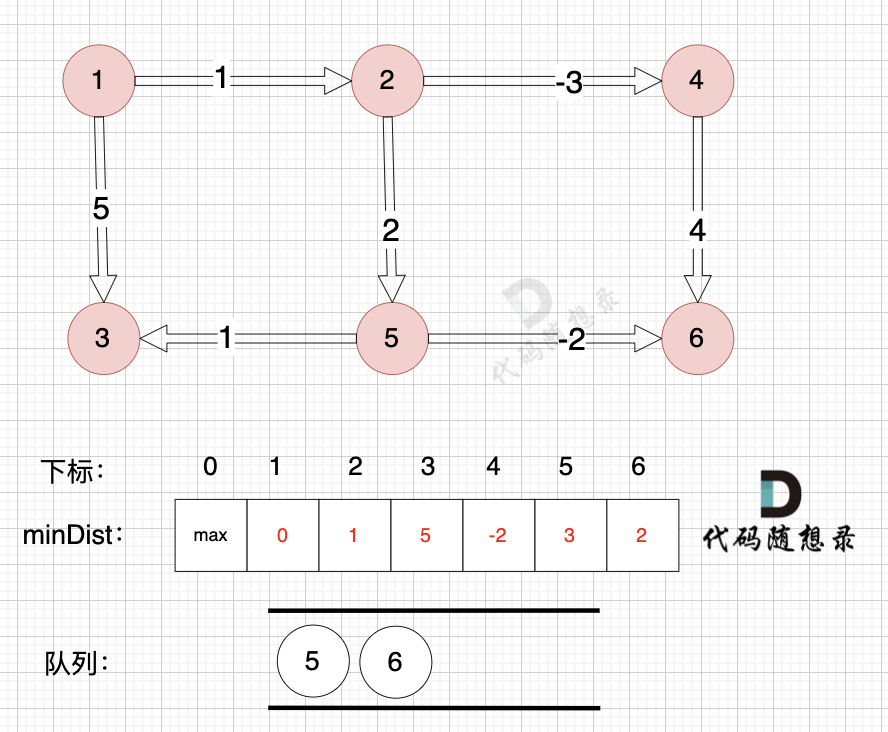
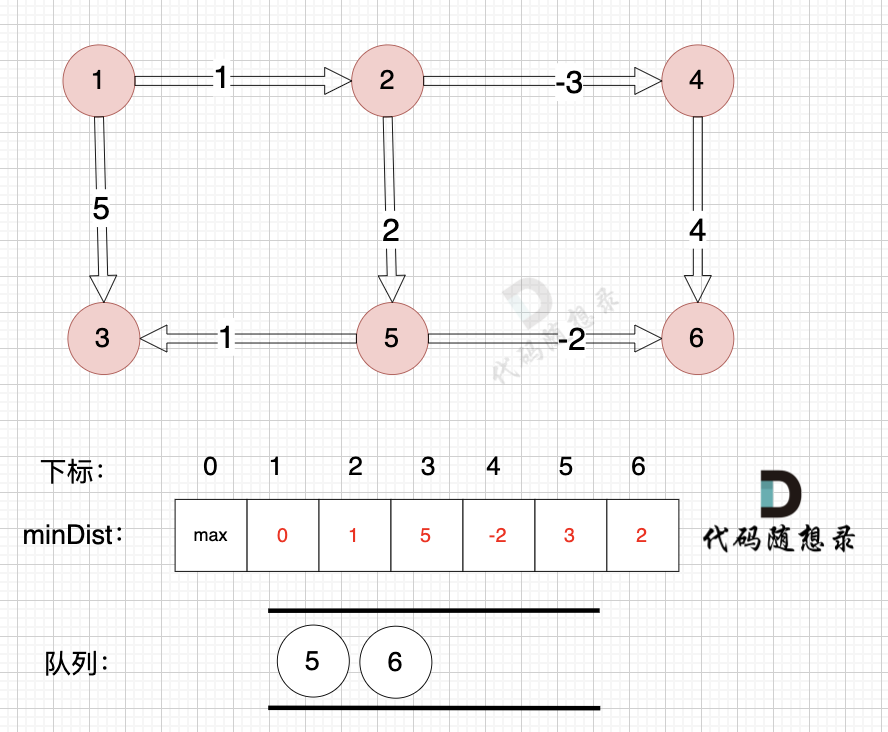
@@ -147,7 +147,7 @@
如图:
-
+
---------------
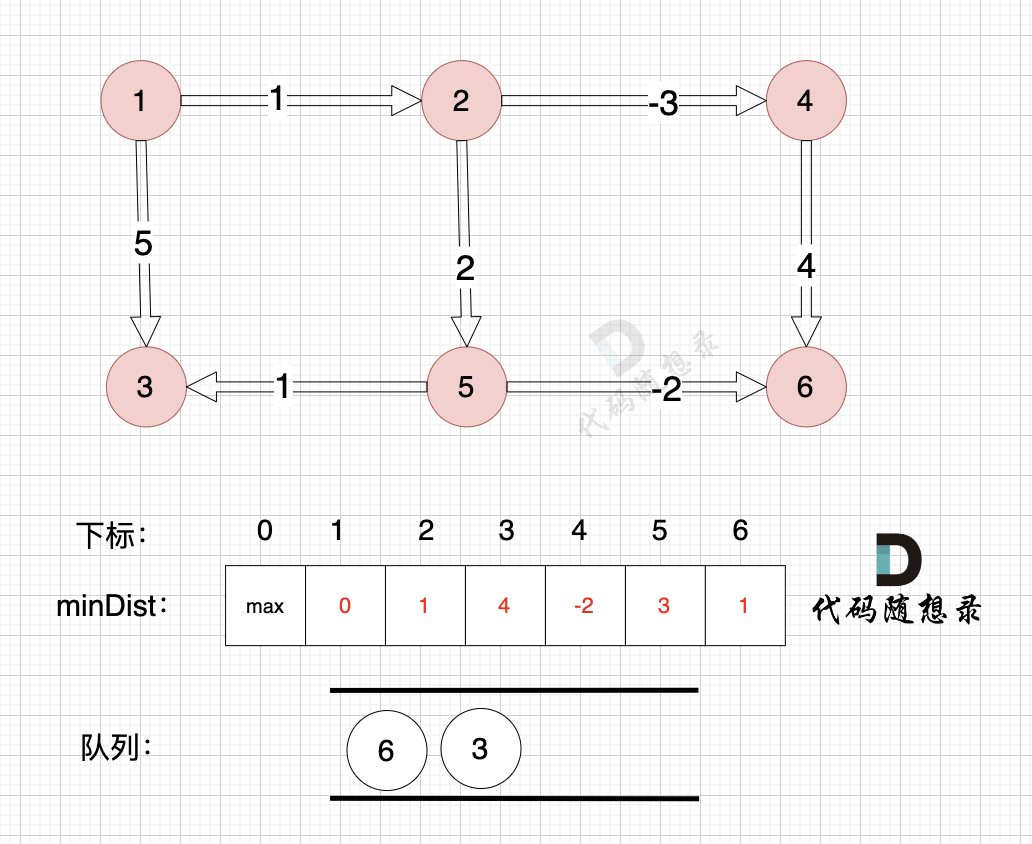
@@ -160,7 +160,7 @@
如图,将节点3加入队列,因为节点6已经在队列里,所以不用重复添加
-
+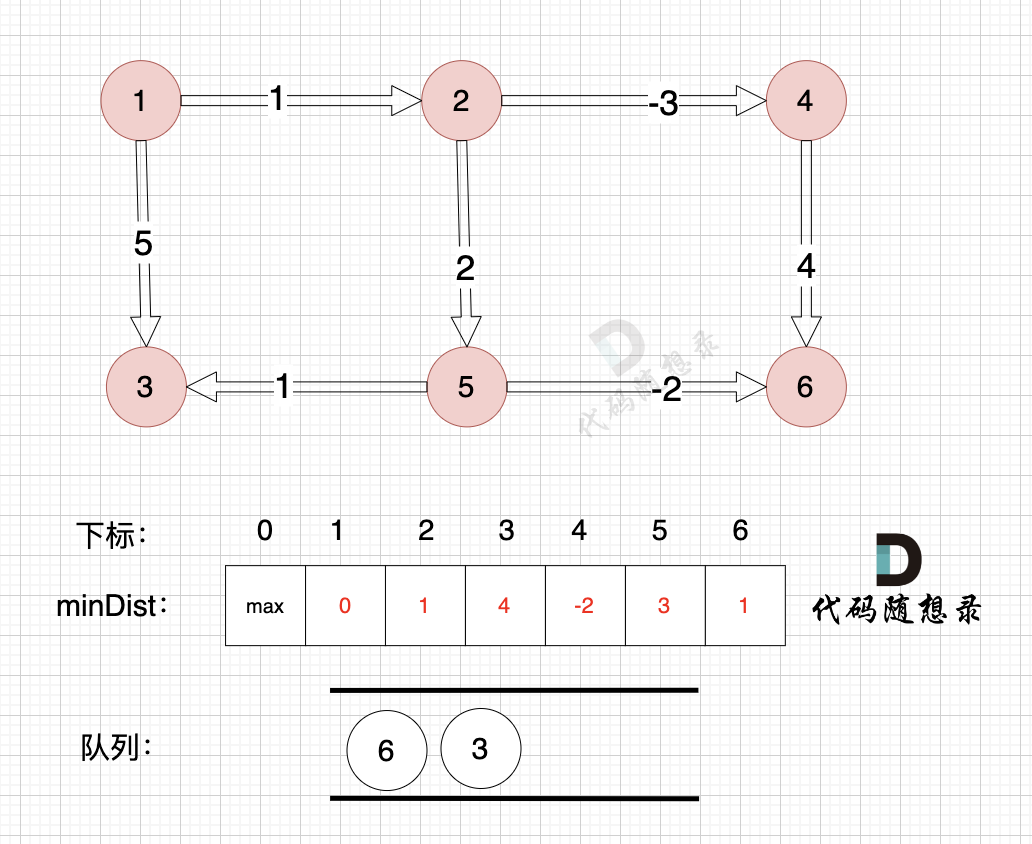
所以我们在加入队列的过程可以有一个优化,**用visited数组记录已经在队列里的元素,已经在队列的元素不用重复加入**
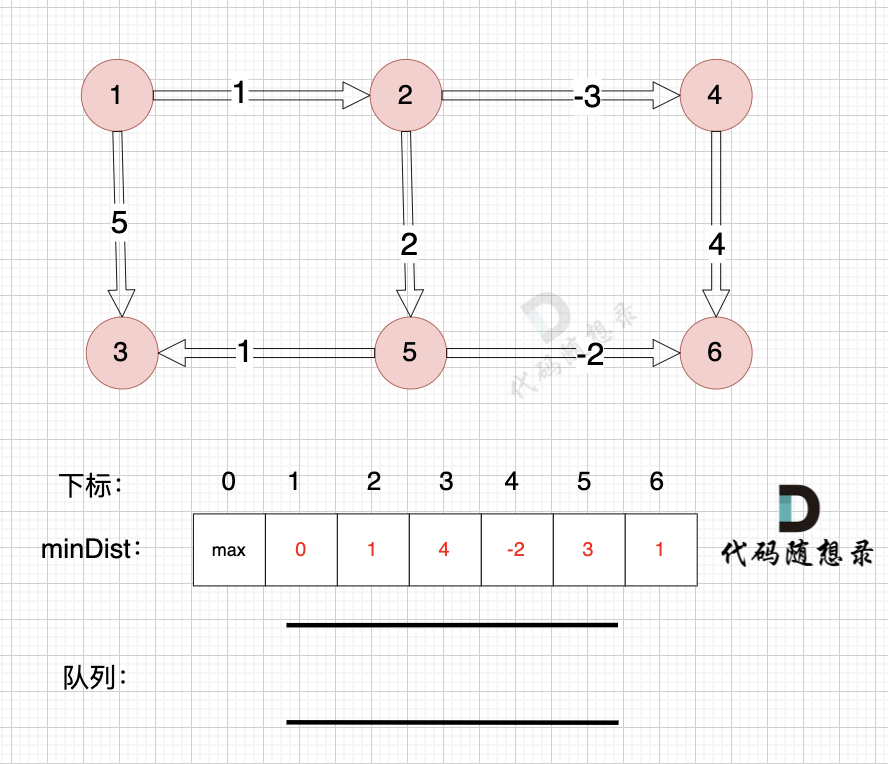
@@ -174,7 +174,7 @@
所以直接从队列中取出,如图:
-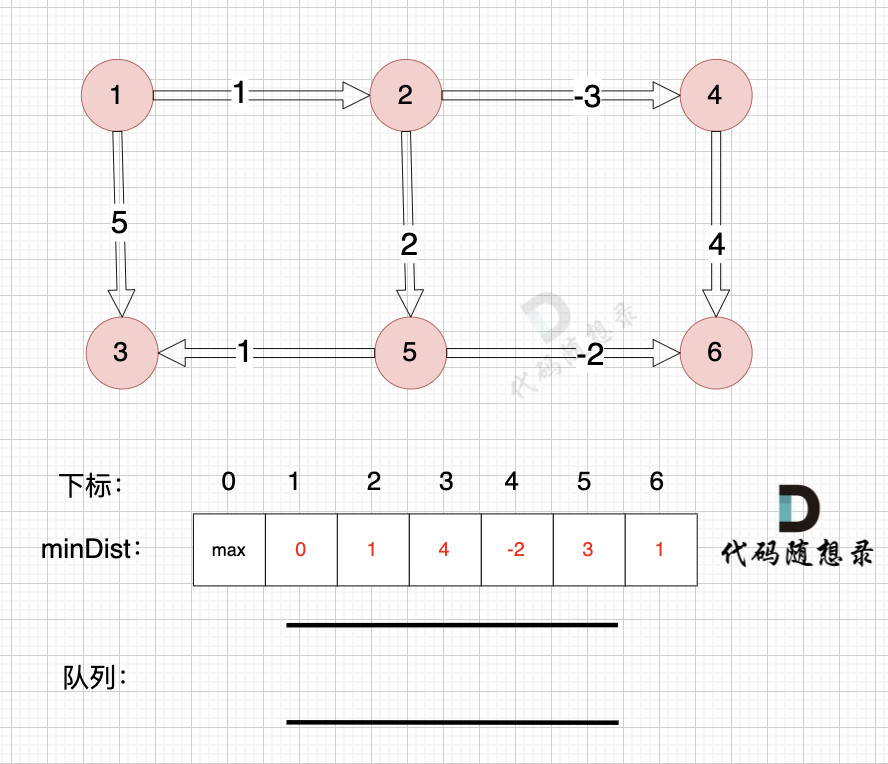
+
----------
@@ -264,7 +264,7 @@ int main() {
至于为什么 双向图且每一个节点和所有其他节点都相连的话,每个节点 都有 n-1 条指向该节点的边, 我再来举个例子,如图:
-[](https://code-thinking-1253855093.file.myqcloud.com/pics/20240416104138.png)
+[](https://file.kamacoder.com/pics/20240416104138.png)
图中 每个节点都与其他所有节点相连,节点数n 为 4,每个节点都有3条指向该节点的边,即入度为3。
@@ -329,7 +329,7 @@ SPFA(队列优化版Bellman_ford) 在理论上 时间复杂度更胜一筹
如图:
-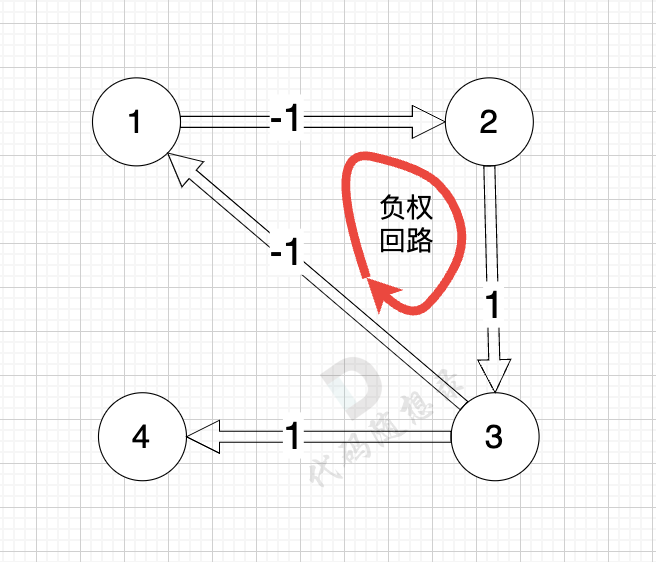
+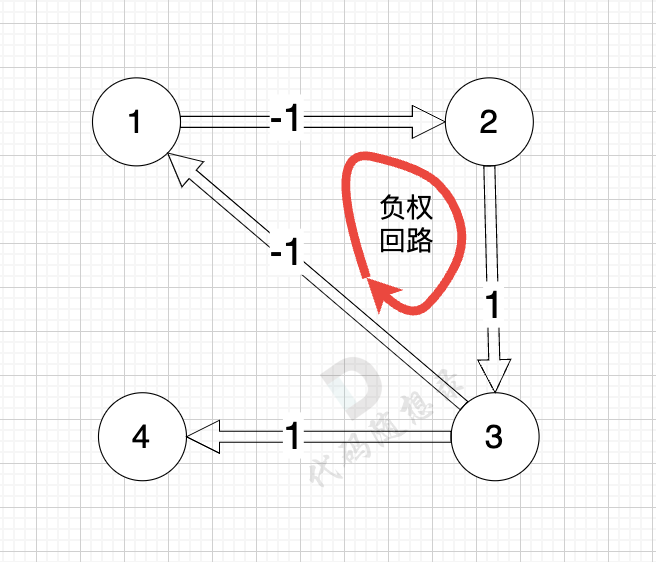
正权回路 就是有环,但环的总权值为正数。
diff --git a/problems/kamacoder/0094.城市间货物运输I.md b/problems/kamacoder/0094.城市间货物运输I.md
index 2afc014b..9edde8ac 100644
--- a/problems/kamacoder/0094.城市间货物运输I.md
+++ b/problems/kamacoder/0094.城市间货物运输I.md
@@ -46,7 +46,7 @@
1 3 5
```
-
+
## 思路
@@ -78,7 +78,7 @@
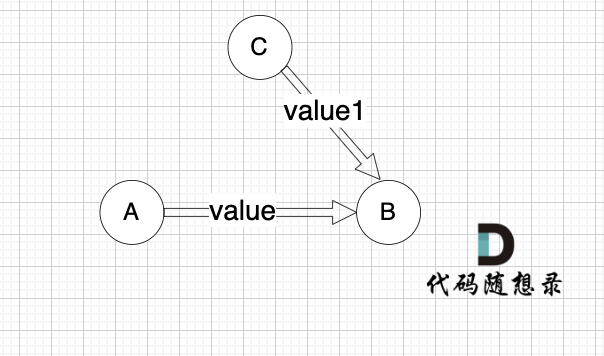
这里我给大家举一个例子,每条边有起点、终点和边的权值。例如一条边,节点A 到 节点B 权值为value,如图:
-
+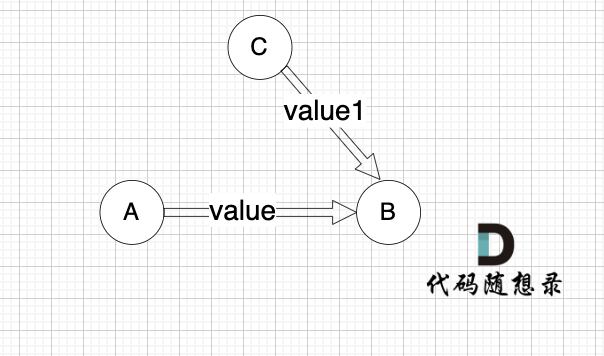
minDist[B] 表示 到达B节点 最小权值,minDist[B] 有哪些状态可以推出来?
@@ -127,7 +127,7 @@ if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
如图:
-
+
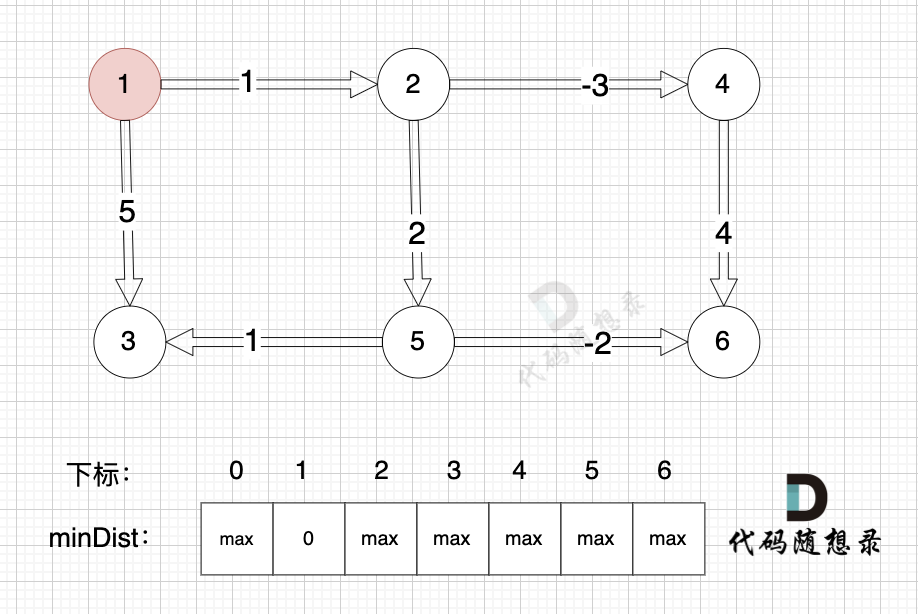
其他节点对应的minDist初始化为max,因为我们要求最小距离,那么还没有计算过的节点 默认是一个最大数,这样才能更新最小距离。
@@ -150,36 +150,36 @@ if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
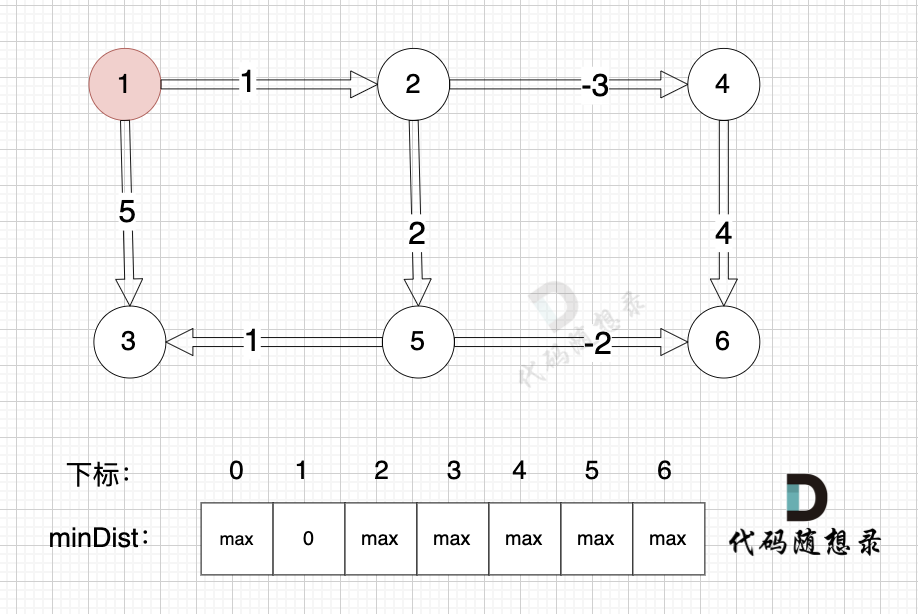
边:节点5 -> 节点6,权值为-2 ,minDist[5] 还是默认数值max,所以不能基于 节点5 去更新节点6,如图:
-
+
(在复习一下,minDist[5] 表示起点到节点5的最短距离)
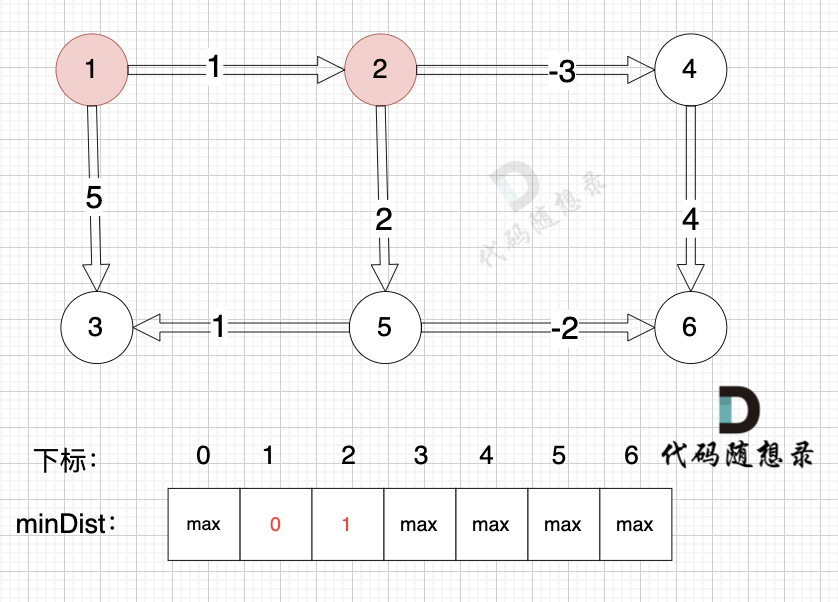
边:节点1 -> 节点2,权值为1 ,minDist[2] > minDist[1] + 1 ,更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1 ,如图:
-
+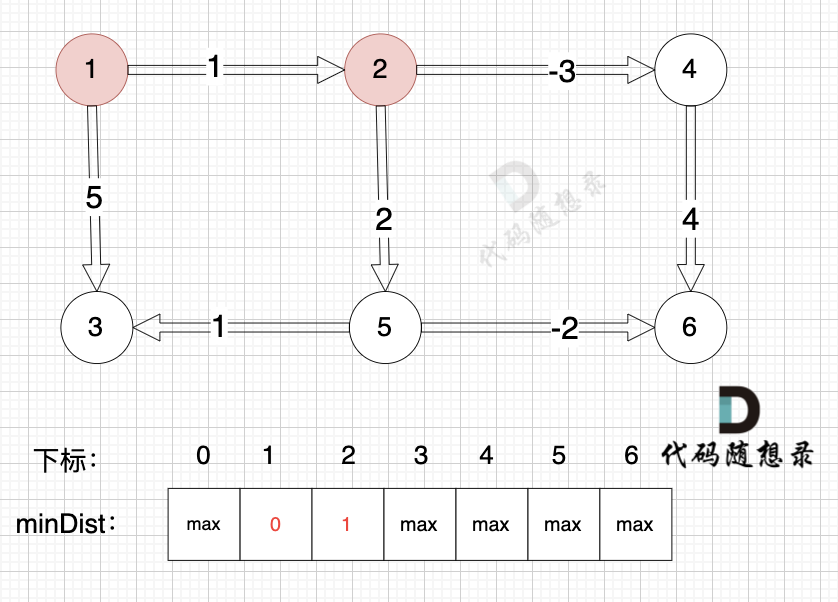
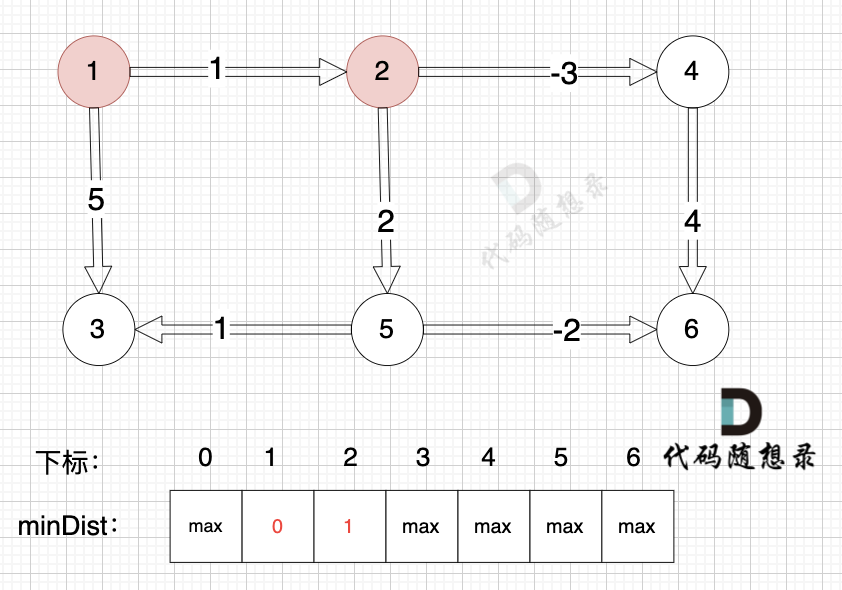
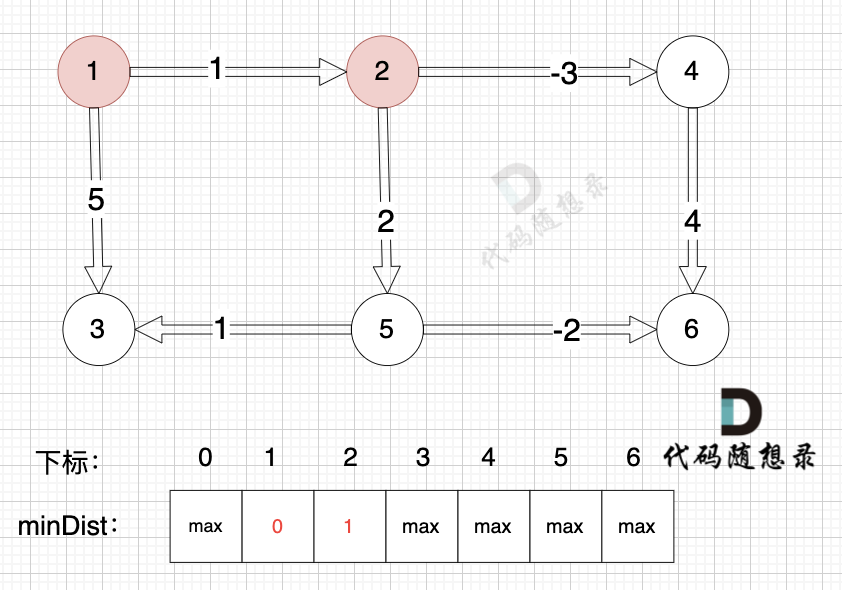
边:节点5 -> 节点3,权值为1 ,minDist[5] 还是默认数值max,所以不能基于节点5去更新节点3 如图:
-
+
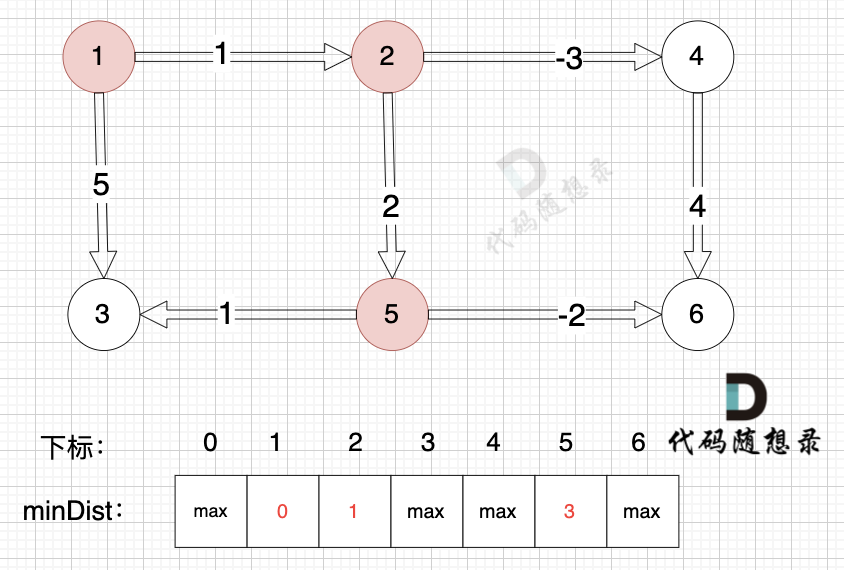
边:节点2 -> 节点5,权值为2 ,minDist[5] > minDist[2] + 2 (经过上面的计算minDist[2]已经不是默认值,而是 1),更新 minDist[5] = minDist[2] + 2 = 1 + 2 = 3 ,如图:
-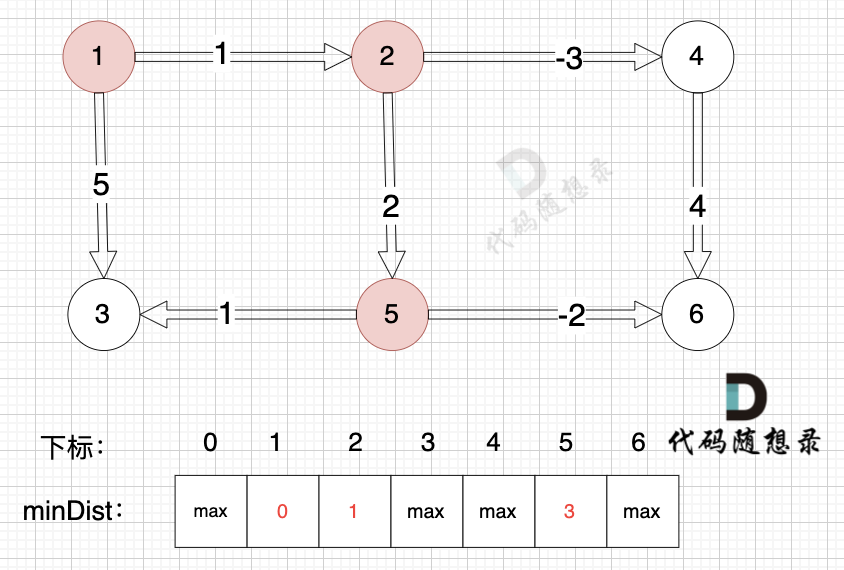
+
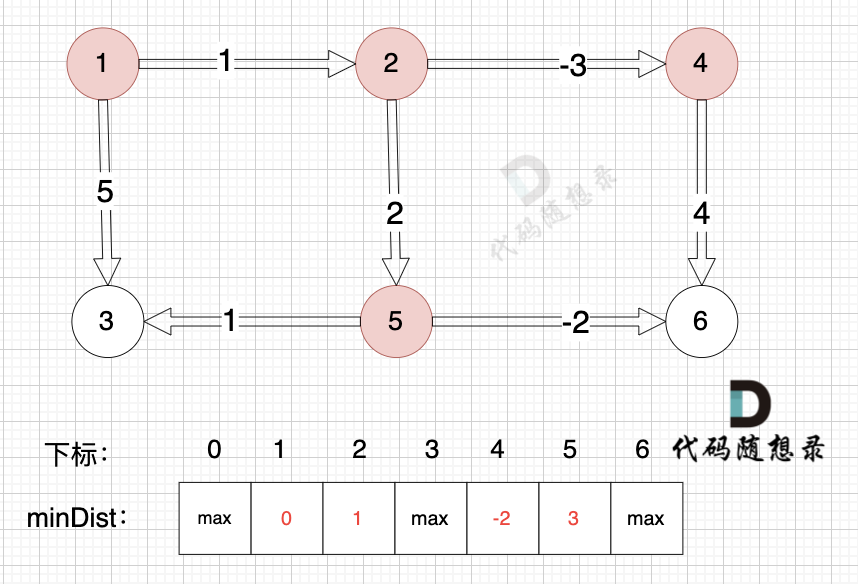
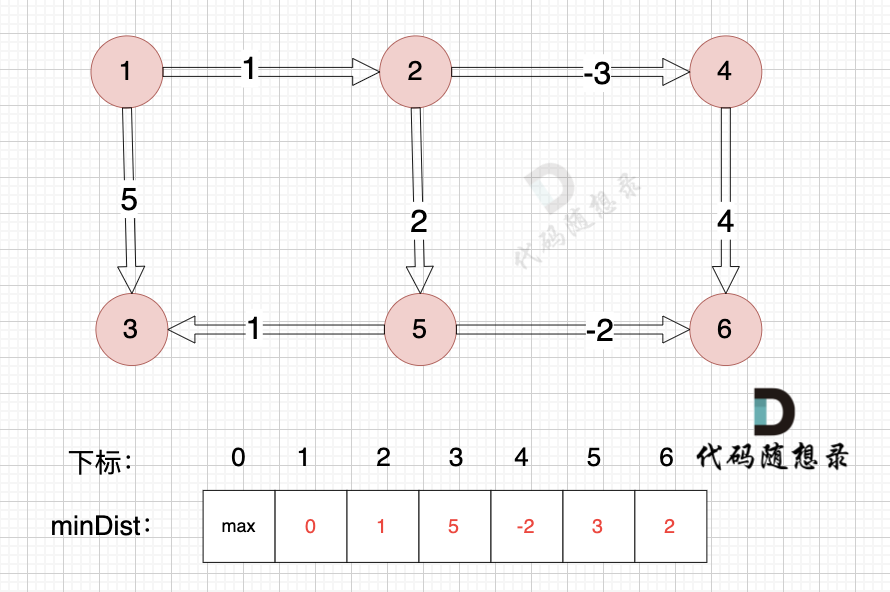
边:节点2 -> 节点4,权值为-3 ,minDist[4] > minDist[2] + (-3),更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 ,如图:
-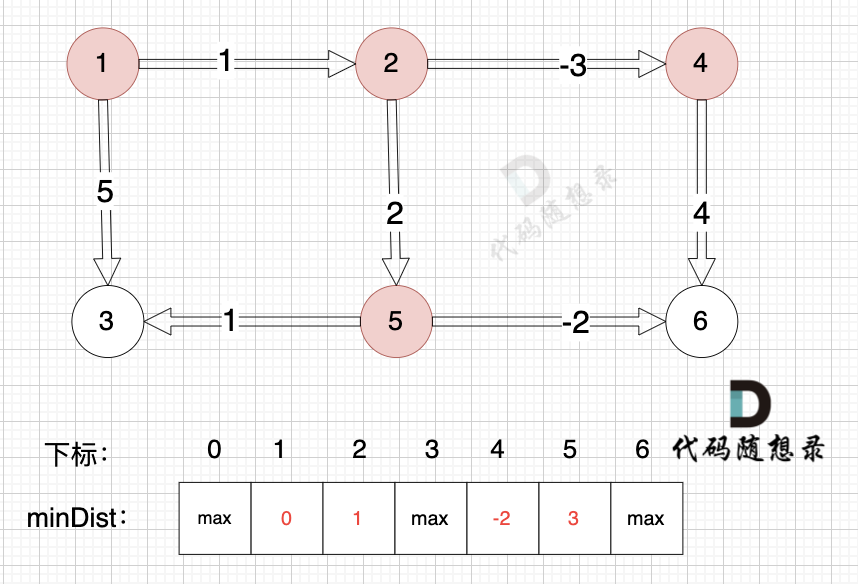
+
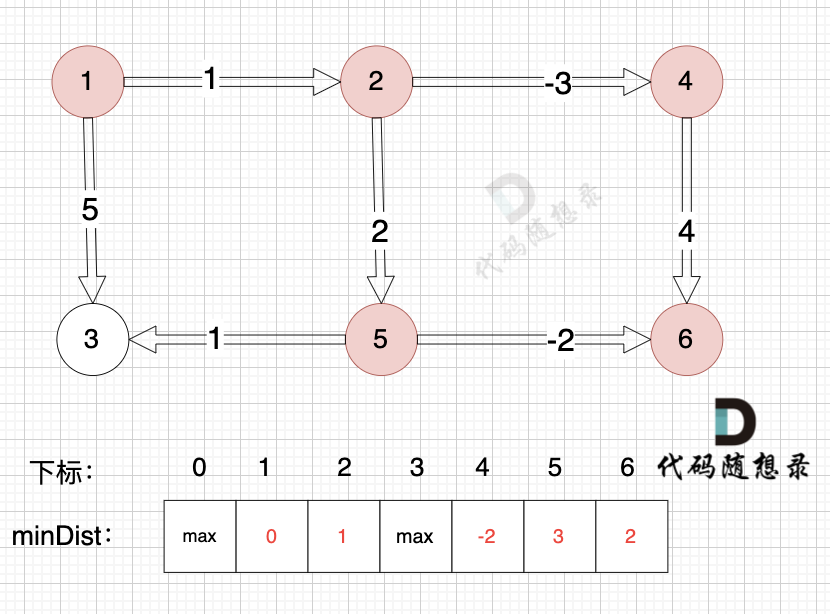
边:节点4 -> 节点6,权值为4 ,minDist[6] > minDist[4] + 4,更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2
-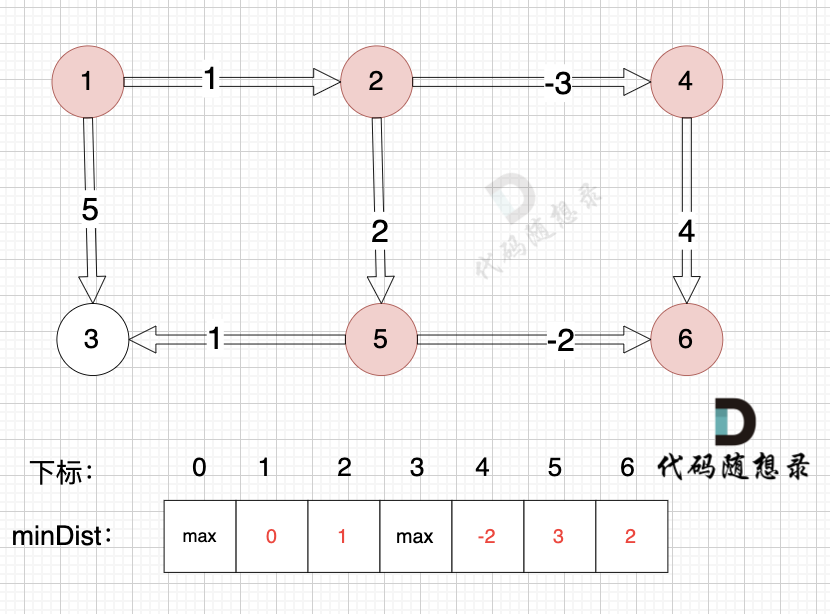
+
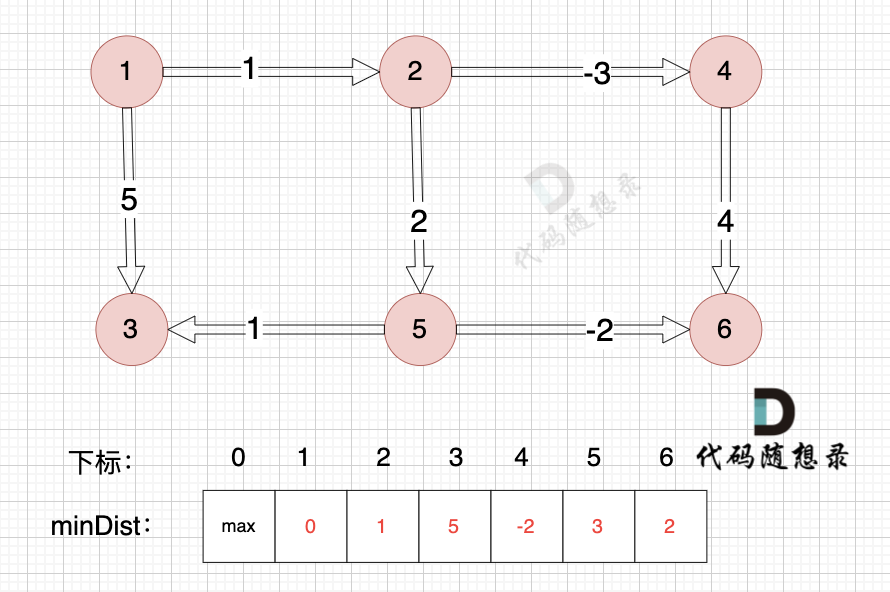
边:节点1 -> 节点3,权值为5 ,minDist[3] > minDist[1] + 5,更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5 ,如图:
-
+
--------
diff --git a/problems/kamacoder/0095.城市间货物运输II.md b/problems/kamacoder/0095.城市间货物运输II.md
index a3896b88..5dddf450 100644
--- a/problems/kamacoder/0095.城市间货物运输II.md
+++ b/problems/kamacoder/0095.城市间货物运输II.md
@@ -78,7 +78,7 @@ circle
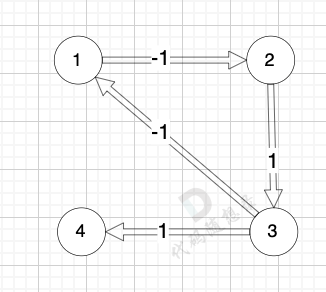
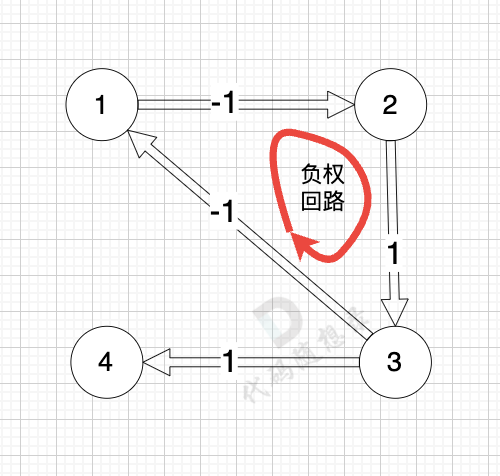
我们拿题目中示例来画一个图:
-
+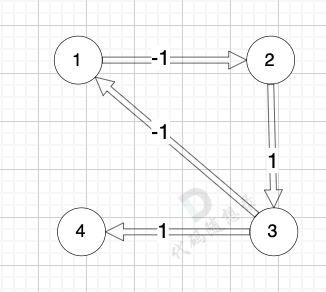
图中 节点1 到 节点4 的最短路径是多少(题目中的最低运输成本) (注意边可以为负数的)
@@ -86,7 +86,7 @@ circle
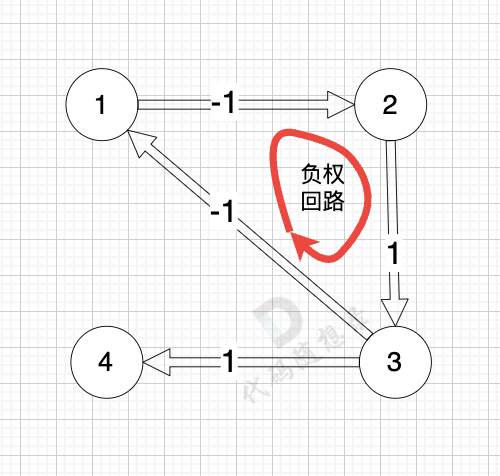
而图中有负权回路:
-
+
那么我们在负权回路中多绕一圈,我们的最短路径 是不是就更小了 (也就是更低的运输成本)
diff --git a/problems/kamacoder/0096.城市间货物运输III.md b/problems/kamacoder/0096.城市间货物运输III.md
index eb80e048..37cfaee0 100644
--- a/problems/kamacoder/0096.城市间货物运输III.md
+++ b/problems/kamacoder/0096.城市间货物运输III.md
@@ -63,7 +63,7 @@
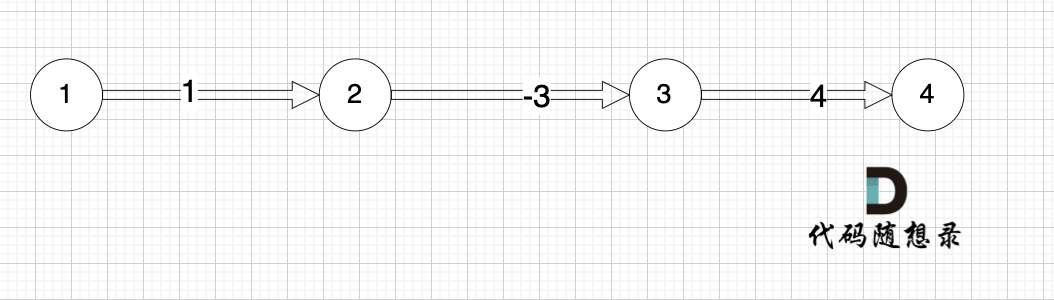
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
-
+
图中,节点1 最多已经经过2个节点 到达节点4,那么中间是有多少条边呢,是 3 条边对吧。
@@ -195,7 +195,7 @@ int main() {
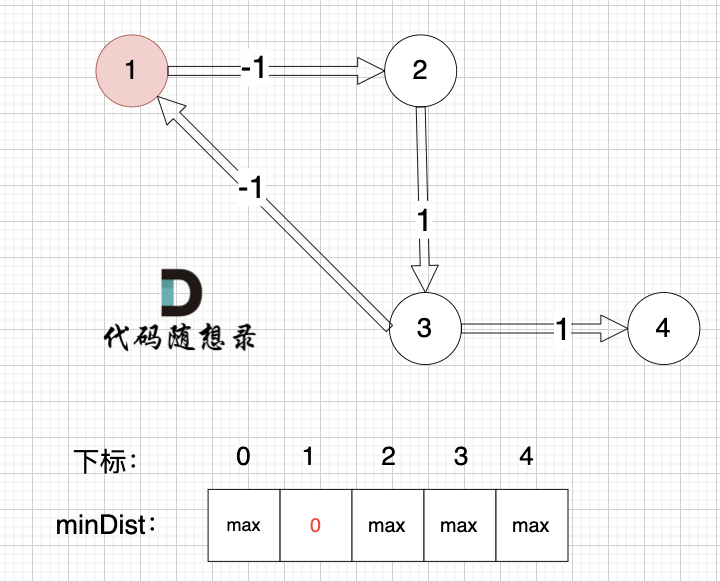
起点为节点1, 起点到起点的距离为0,所以 minDist[1] 初始化为0 ,如图:
-
+
其他节点对应的minDist初始化为max,因为我们要求最小距离,那么还没有计算过的节点 默认是一个最大数,这样才能更新最小距离。
@@ -203,21 +203,21 @@ int main() {
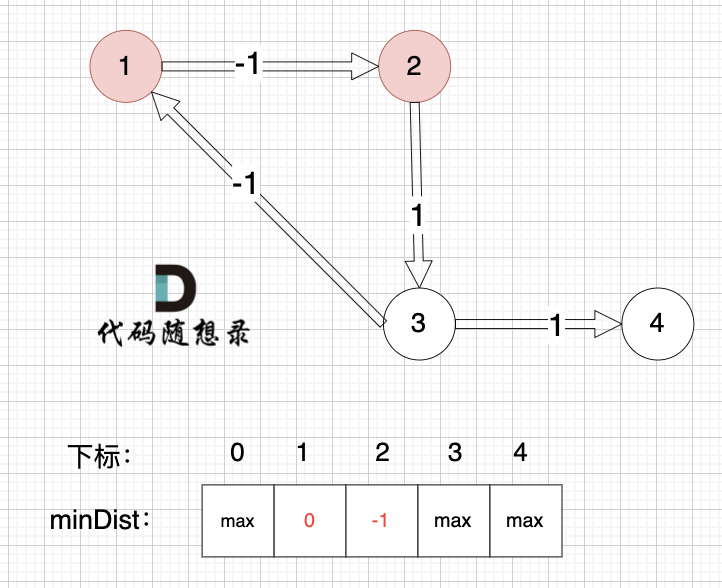
边:节点1 -> 节点2,权值为-1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = minDist[1] + (-1) = 0 - 1 = -1 ,如图:
-
+
边:节点2 -> 节点3,权值为1 ,minDist[3] > minDist[2] + 1 ,更新 minDist[3] = minDist[2] + 1 = -1 + 1 = 0 ,如图:
-
+
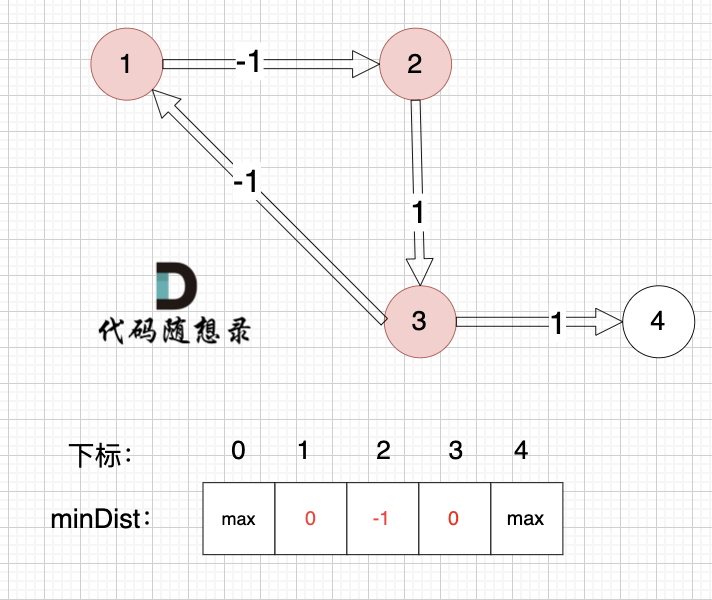
边:节点3 -> 节点1,权值为-1 ,minDist[1] > minDist[3] + (-1),更新 minDist[1] = 0 + (-1) = -1 ,如图:
-
+
边:节点3 -> 节点4,权值为1 ,minDist[4] > minDist[3] + 1,更新 minDist[4] = 0 + 1 = 1 ,如图:
-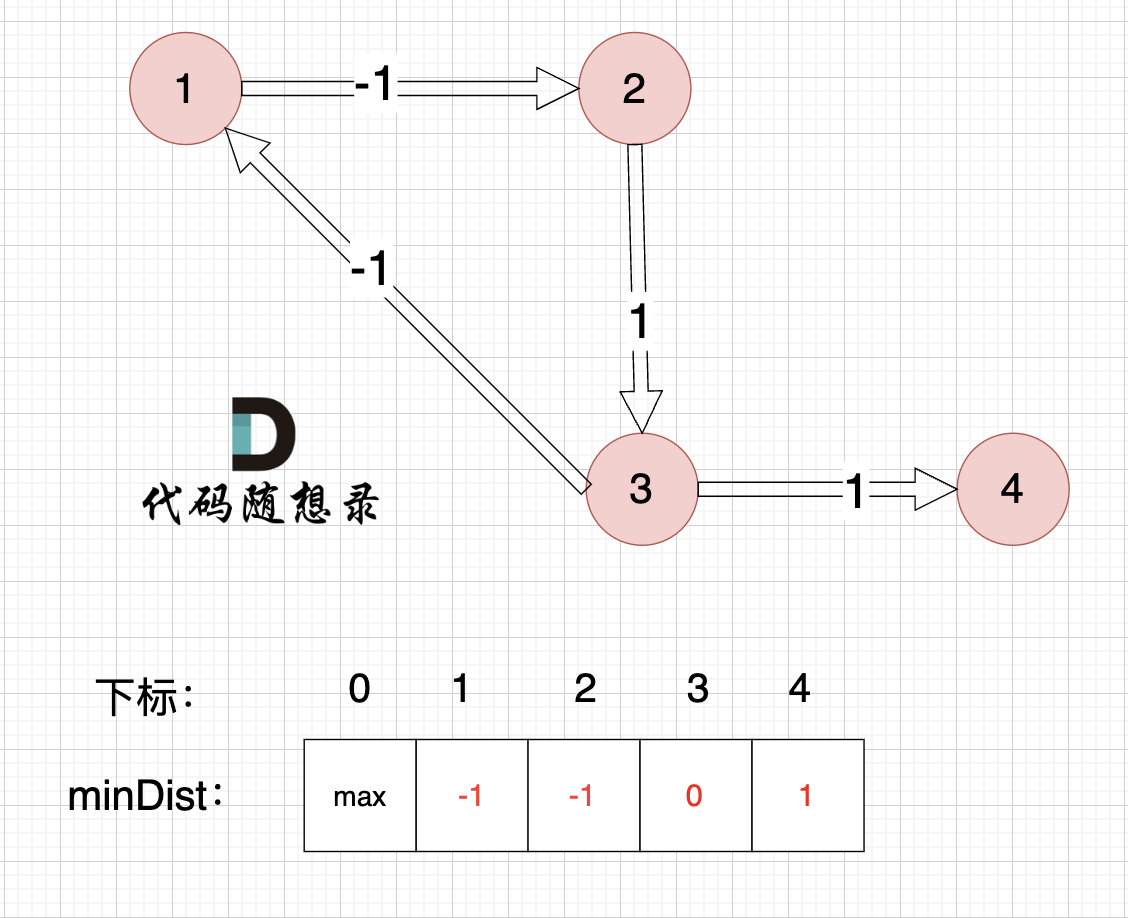
+
以上是对所有边进行的第一次松弛,最后 minDist数组为 :-1 -1 0 1 ,(从下标1算起)
@@ -244,7 +244,7 @@ int main() {
在上面画图距离中,对所有边进行第一次松弛,在计算 边(节点2 -> 节点3) 的时候,更新了 节点3。
-
+
理论上来说节点3 应该在对所有边第二次松弛的时候才更新。 这因为当时是基于已经计算好的 节点2(minDist[2])来做计算了。
@@ -331,11 +331,11 @@ int main() {
所构成是图是一样的,都是如下的这个图,但给出的边的顺序是不一样的。
-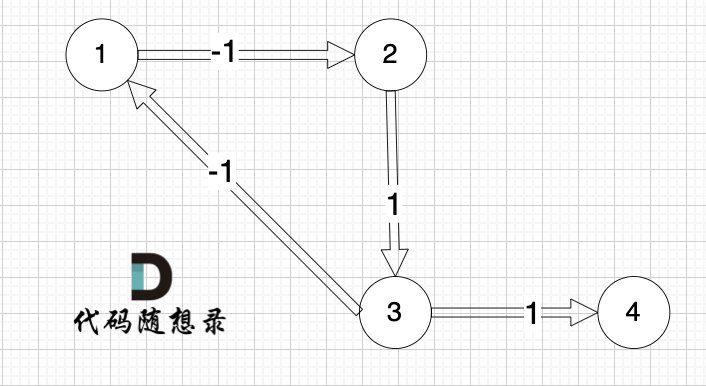
+
再用版本一的代码是运行一下,发现结果输出是 1, 是对的。
-
+
分明刚刚输出的结果是 -2,是错误的,怎么 一样的图,这次输出的结果就对了呢?
@@ -345,7 +345,7 @@ int main() {
初始化:
-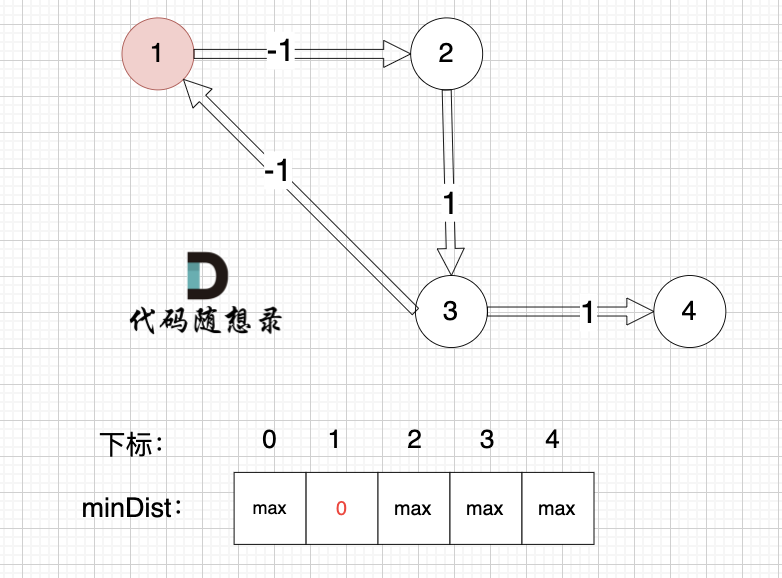
+
边:节点3 -> 节点1,权值为-1 ,节点3还没有被计算过,节点1 不更新。
@@ -355,7 +355,7 @@ int main() {
边:节点1 -> 节点2,权值为 -1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = 0 + (-1) = -1 ,如图:
-
+
以上是对所有边 松弛一次的状态。
@@ -472,7 +472,7 @@ int main() {
但大家会发现,以上代码大家提交后,怎么耗时这么多?
-
+
理论上,SPFA的时间复杂度不是要比 bellman_ford 更优吗?
@@ -554,7 +554,7 @@ int main() {
以上代码提交后,耗时情况:
-
+
大家发现 依然远比 bellman_ford 的代码版本 耗时高。
@@ -579,11 +579,11 @@ dijkstra 是贪心的思路 每一次搜索都只会找距离源点最近的非
在以下这个图中,求节点1 到 节点7 最多经过2个节点 的最短路是多少呢?
-
+
最短路显然是:
-
+
最多经过2个节点,也就是3条边相连的路线:节点1 -> 节点2 -> 节点6-> 节点7
@@ -591,24 +591,24 @@ dijkstra 是贪心的思路 每一次搜索都只会找距离源点最近的非
初始化如图所示:
-
+
找距离源点最近且没有被访问过的节点,先找节点1
-
+
距离源点最近且没有被访问过的节点,找节点2:
-
+
距离源点最近且没有被访问过的节点,找到节点3:
-
+
距离源点最近且没有被访问过的节点,找到节点4:
-
+
此时最多经过2个节点的搜索就完毕了,但结果中minDist[7] (即节点7的结果)并没有被更。
diff --git a/problems/kamacoder/0097.小明逛公园.md b/problems/kamacoder/0097.小明逛公园.md
index dfbd6aa9..97765ebc 100644
--- a/problems/kamacoder/0097.小明逛公园.md
+++ b/problems/kamacoder/0097.小明逛公园.md
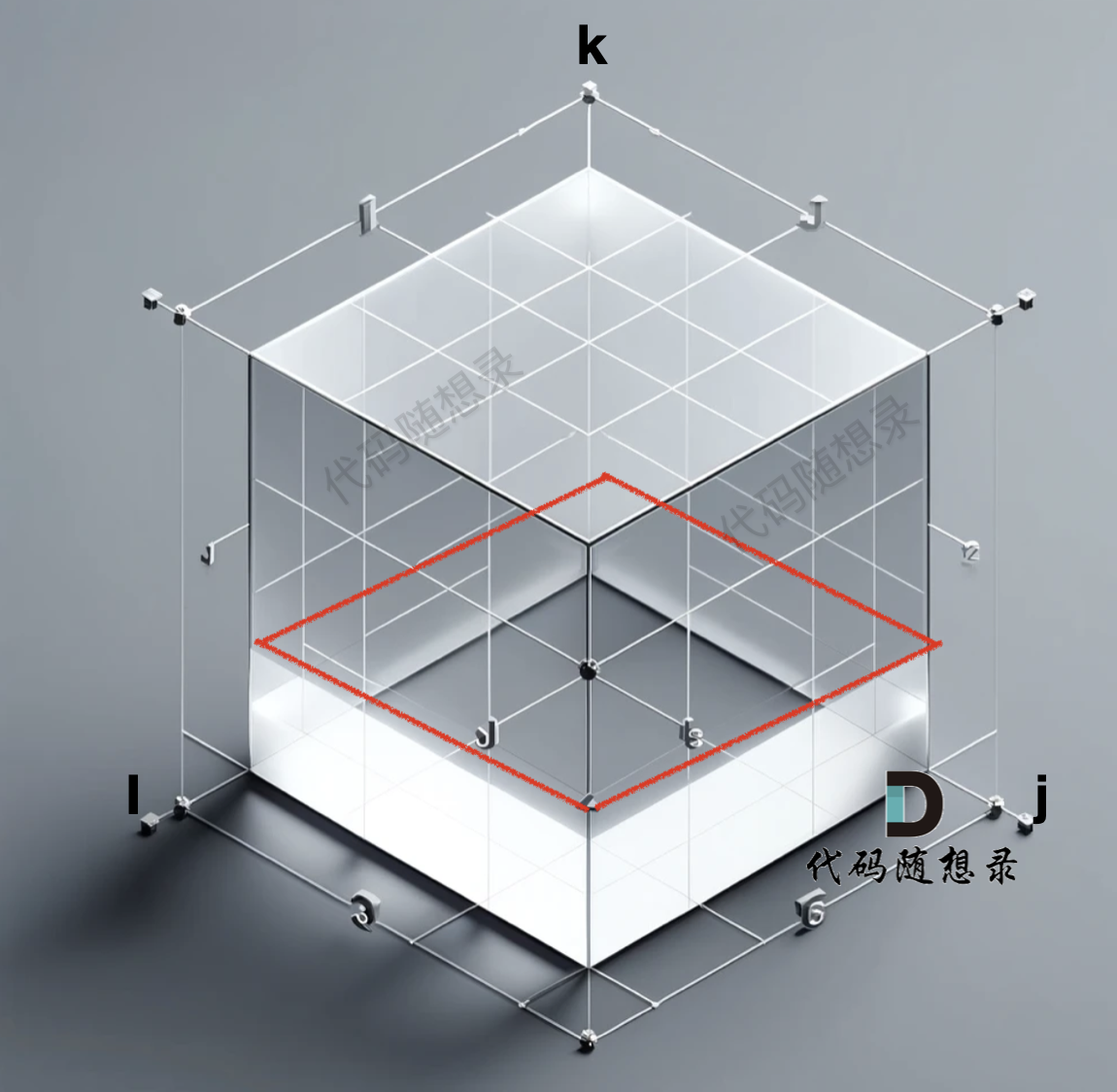
@@ -155,7 +155,7 @@ grid[i][j][k] = m,表示 节点i 到 节点j 以[1...k] 集合为中间节点
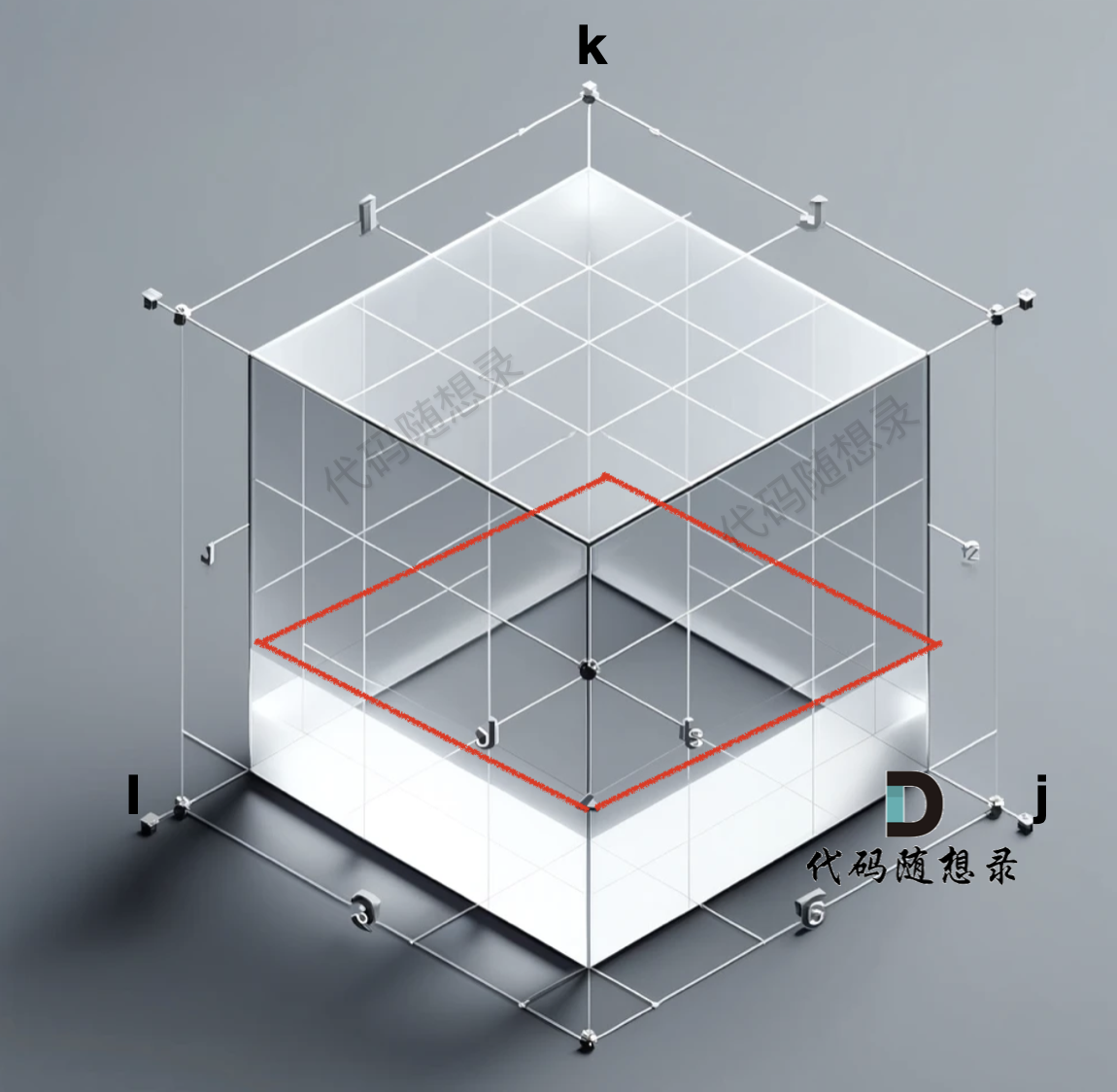
grid数组是一个三维数组,那么我们初始化的数据在 i 与 j 构成的平层,如图:
-
+
红色的 底部一层是我们初始化好的数据,注意:从三维角度去看初始化的数据很重要,下面我们在聊遍历顺序的时候还会再讲。
@@ -202,7 +202,7 @@ vector>> grid(n + 1, vector>(n + 1, vector(n
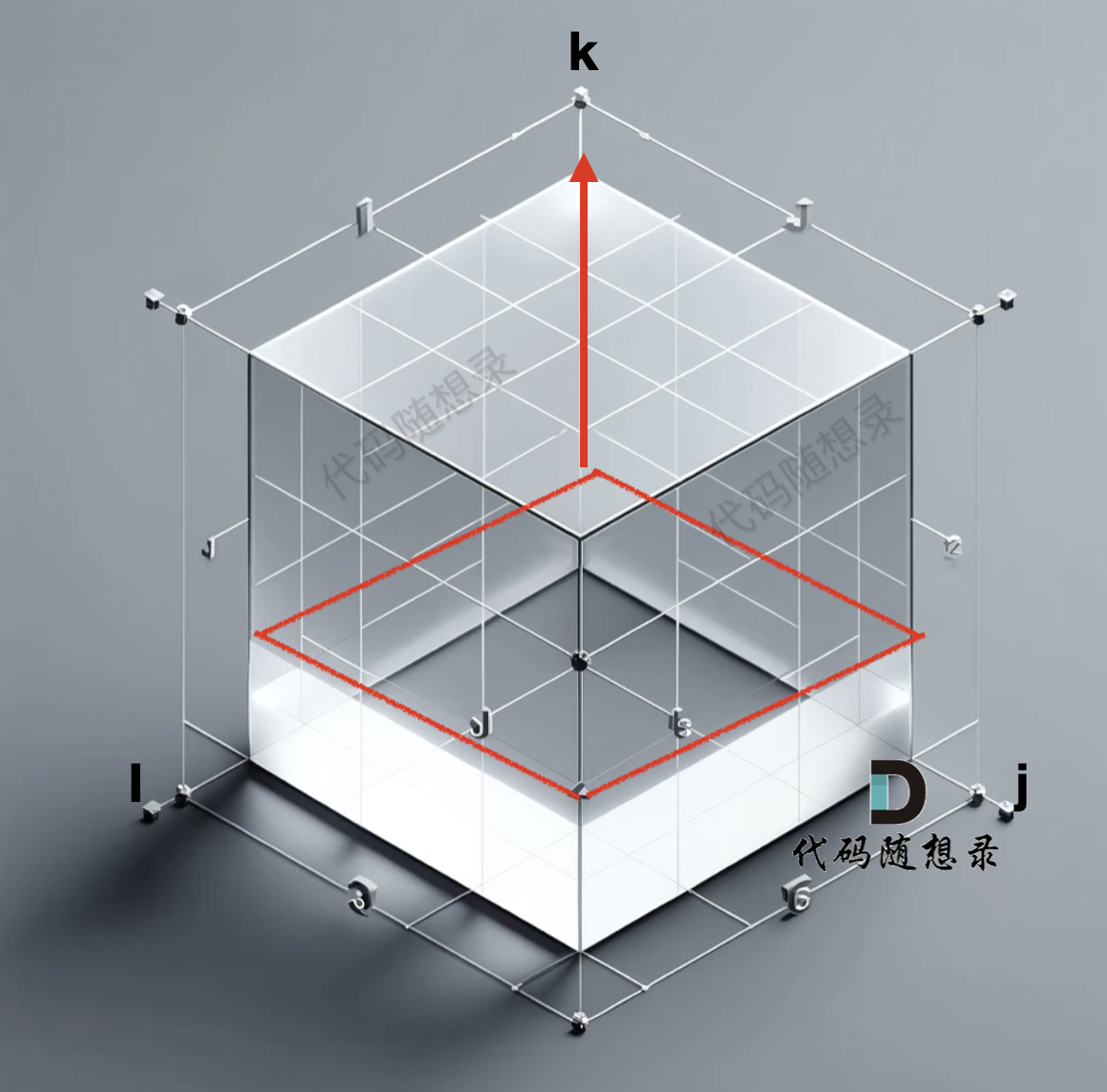
所以遍历k 的for循环一定是在最外面,这样才能一层一层去遍历。如图:
-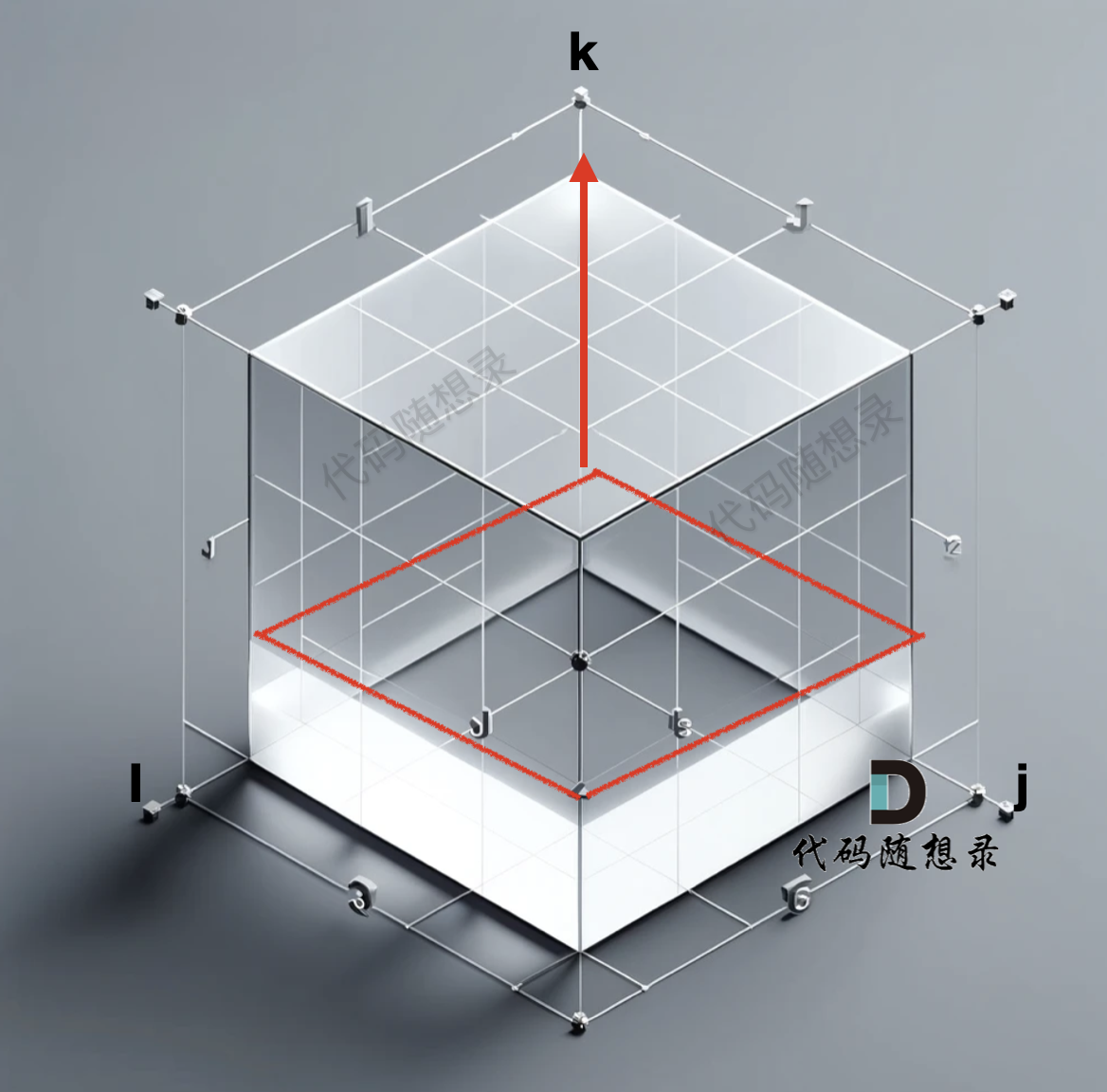
+
至于遍历 i 和 j 的话,for 循环的先后顺序无所谓。
@@ -234,7 +234,7 @@ for (int i = 1; i <= n; i++) {
此时就遍历了 j 与 k 形成一个平面,i 则是纵面,那遍历 就是这样的:
-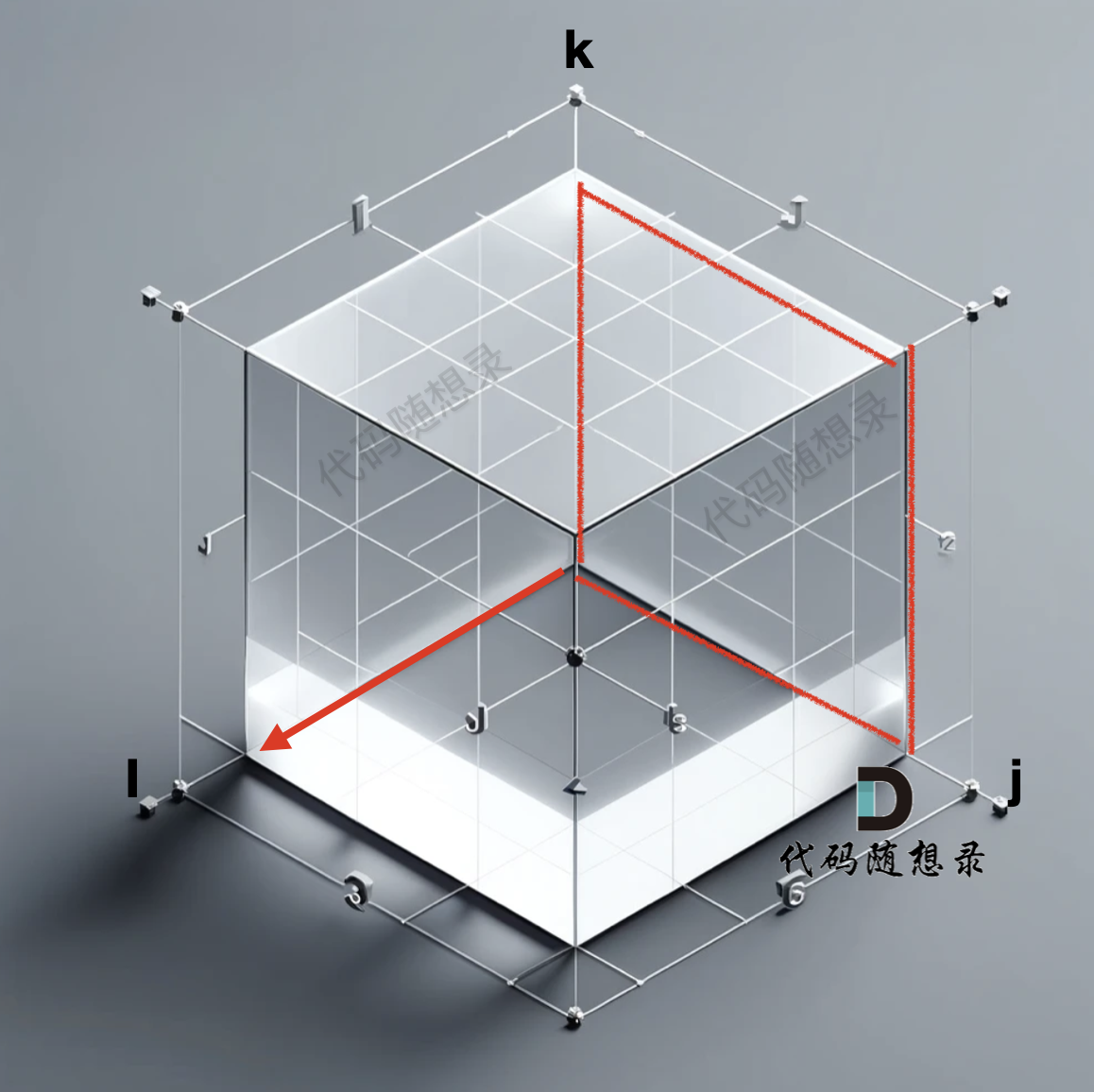
+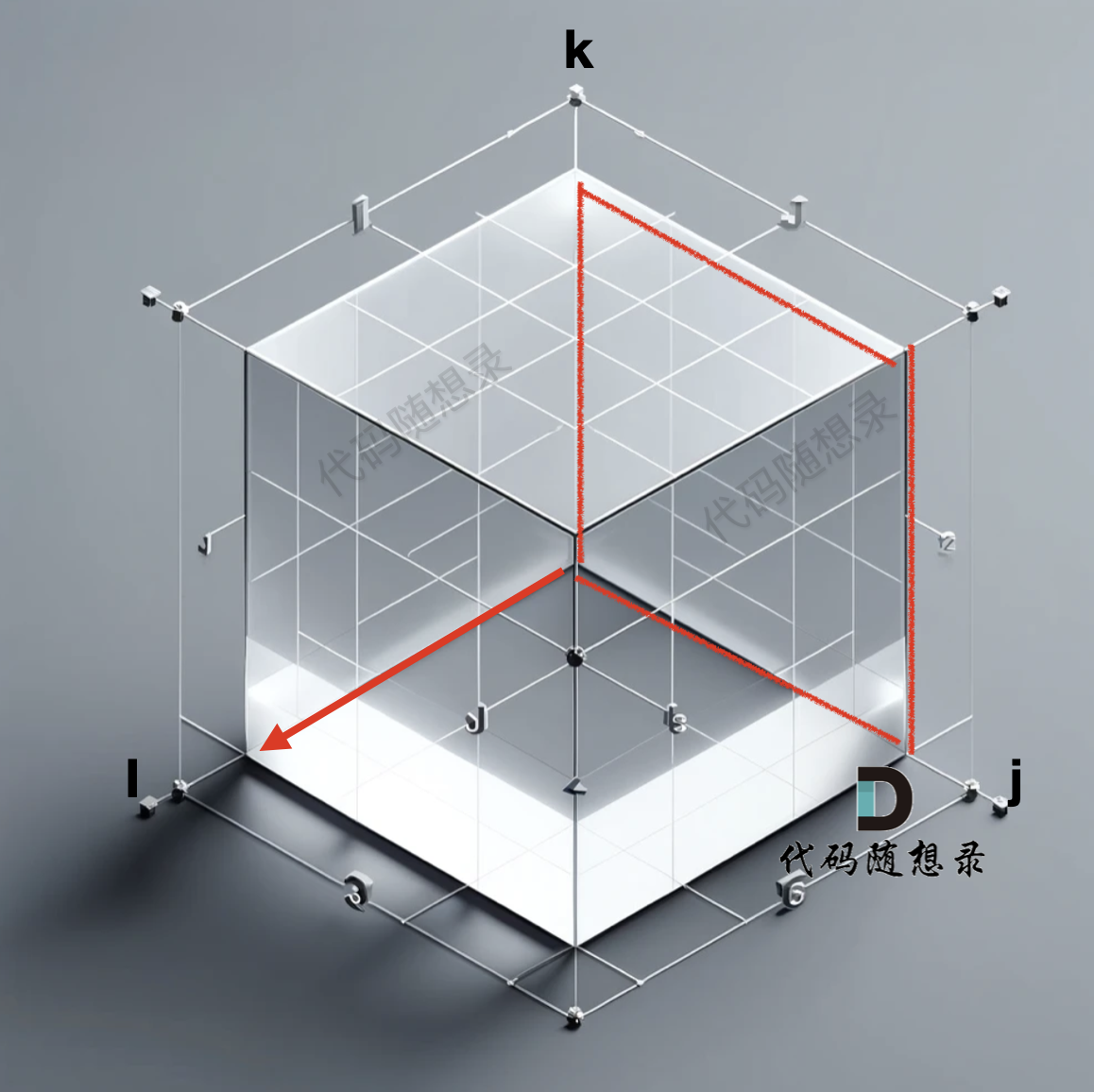
而我们初始化的数据 是 k 为0, i 和 j 形成的平面做初始化,如果以 k 和 j 形成的平面去一层一层遍历,就造成了 递推公式 用不上上一轮计算的结果,从而导致结果不对(初始化的部分是 i 与j 形成的平面,在初始部分有讲过)。
@@ -253,7 +253,7 @@ for (int i = 1; i <= n; i++) {
就是图:
-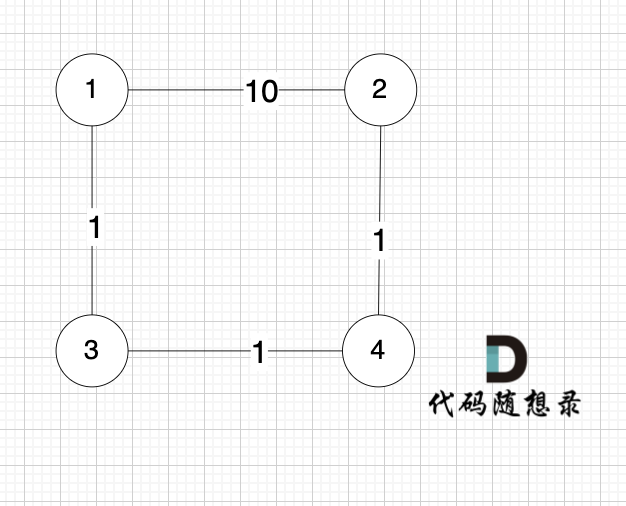
+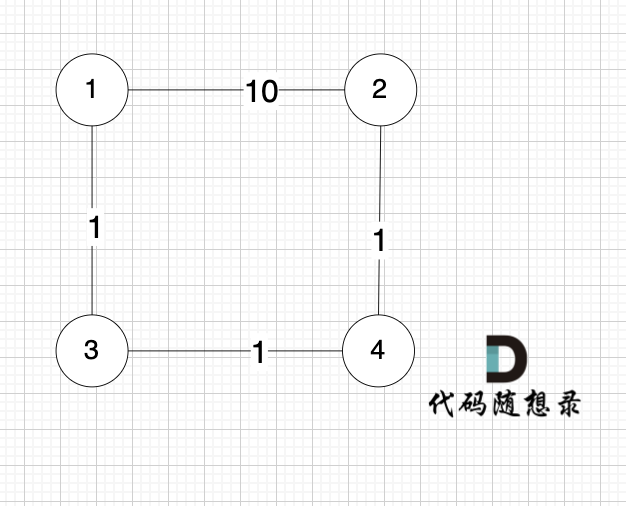
求节点1 到 节点 2 的最短距离,运行结果是 10 ,但正确的结果很明显是3。
@@ -267,7 +267,7 @@ for (int i = 1; i <= n; i++) {
而遍历k 的for循环如果放在中间呢,同样是 j 与k 行程一个平面,i 是纵面,遍历的也是这样:
-
+
同样不能完全用上初始化 和 上一层计算的结果。
@@ -283,7 +283,7 @@ for (int i = 1; i <= n; i++) {
图:
-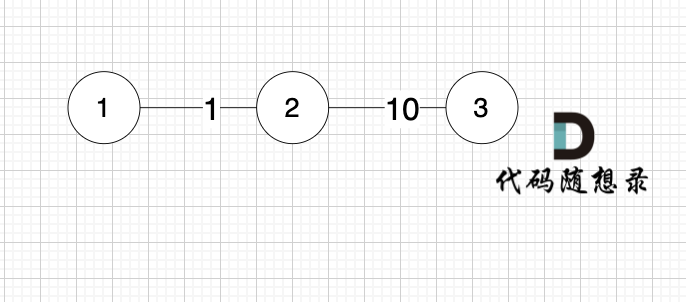
+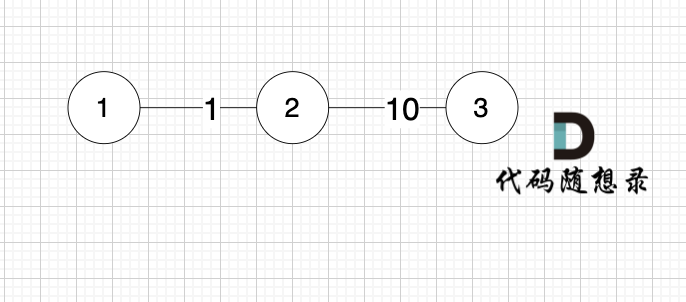
求 节点1 到节点3 的最短距离,如果k循环放中间,程序的运行结果是 -1,也就是不能到达节点3。
diff --git a/problems/kamacoder/0098.所有可达路径.md b/problems/kamacoder/0098.所有可达路径.md
index 4df53b44..2f0dcdcc 100644
--- a/problems/kamacoder/0098.所有可达路径.md
+++ b/problems/kamacoder/0098.所有可达路径.md
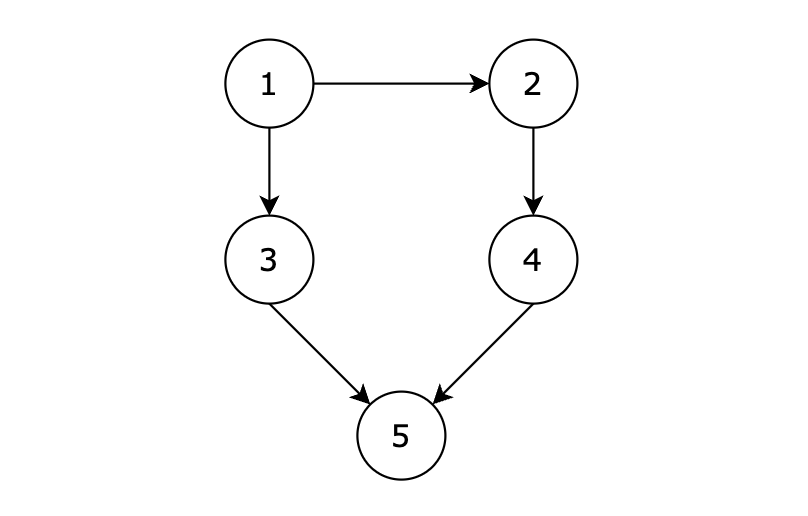
@@ -43,7 +43,7 @@
提示信息
-
+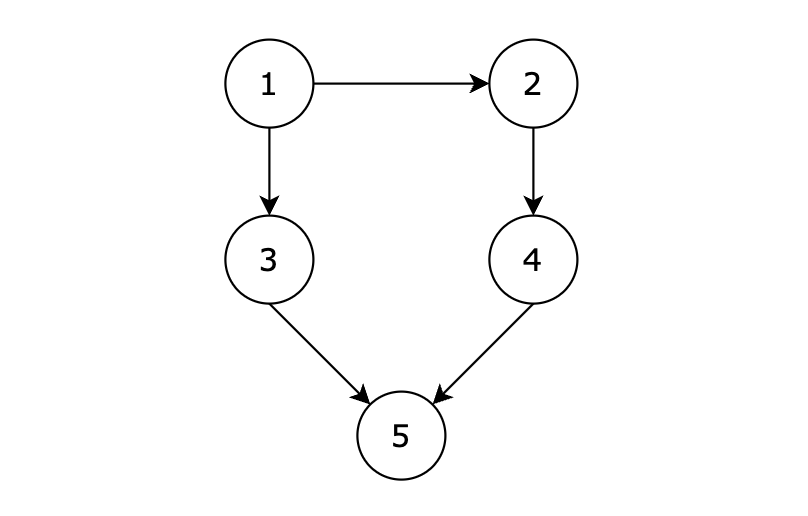
用例解释:
@@ -141,7 +141,7 @@ while (m--) {
我在 [图论理论基础篇](./图论理论基础.md) 举了一个例子:
-
+
这里表达的图是:
diff --git a/problems/kamacoder/0099.岛屿的数量广搜.md b/problems/kamacoder/0099.岛屿的数量广搜.md
index f8c36a00..0da2f315 100644
--- a/problems/kamacoder/0099.岛屿的数量广搜.md
+++ b/problems/kamacoder/0099.岛屿的数量广搜.md
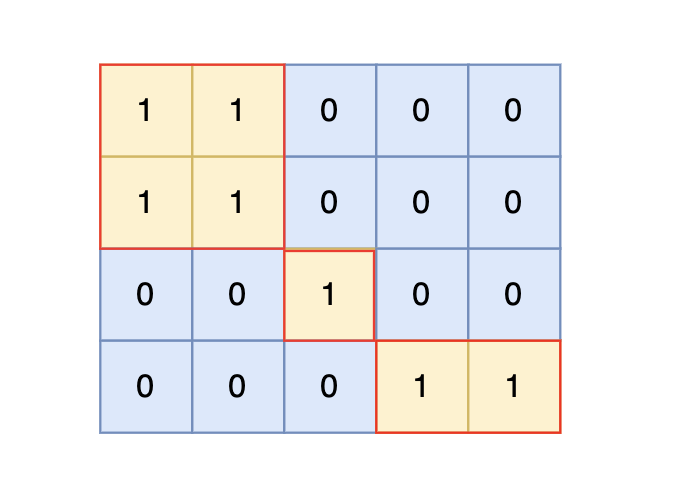
@@ -35,7 +35,7 @@
提示信息
-
+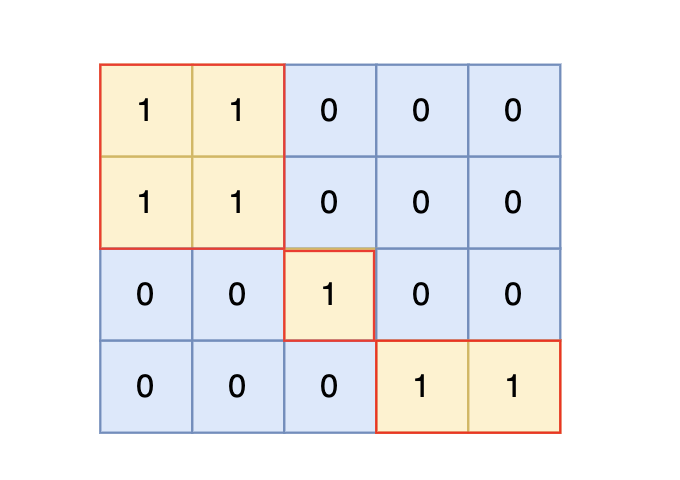
根据测试案例中所展示,岛屿数量共有 3 个,所以输出 3。
@@ -50,7 +50,7 @@
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
-
+
这道题题目是 DFS,BFS,并查集,基础题目。
@@ -72,7 +72,7 @@
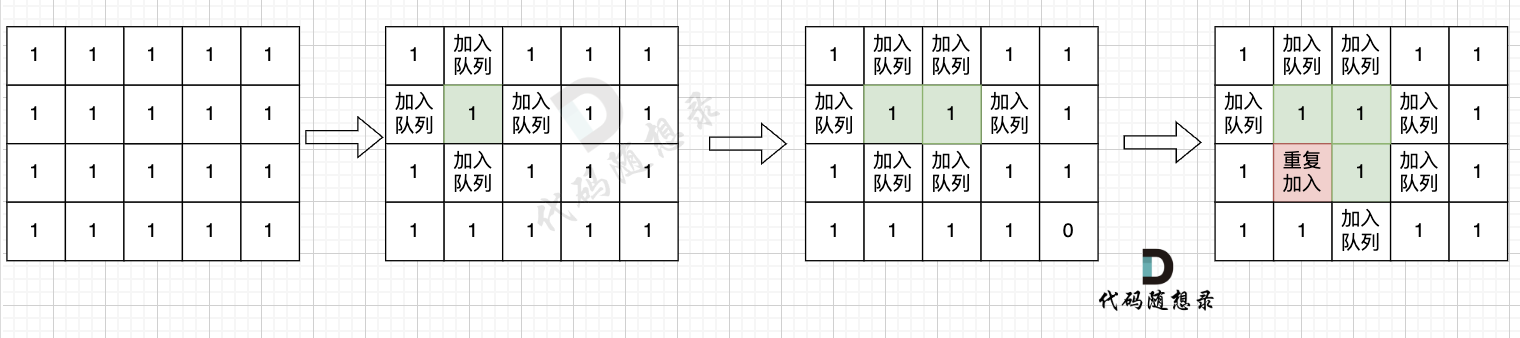
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。
-
+
超时写法 (从队列中取出节点再标记,注意代码注释的地方)
diff --git a/problems/kamacoder/0099.岛屿的数量深搜.md b/problems/kamacoder/0099.岛屿的数量深搜.md
index 5a21f387..06be9268 100644
--- a/problems/kamacoder/0099.岛屿的数量深搜.md
+++ b/problems/kamacoder/0099.岛屿的数量深搜.md
@@ -36,7 +36,7 @@
提示信息
-
+
根据测试案例中所展示,岛屿数量共有 3 个,所以输出 3。
@@ -50,7 +50,7 @@
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
-
+
这道题题目是 DFS,BFS,并查集,基础题目。
diff --git a/problems/kamacoder/0100.岛屿的最大面积.md b/problems/kamacoder/0100.岛屿的最大面积.md
index 170c0917..f2b9b901 100644
--- a/problems/kamacoder/0100.岛屿的最大面积.md
+++ b/problems/kamacoder/0100.岛屿的最大面积.md
@@ -33,7 +33,7 @@
提示信息
-
+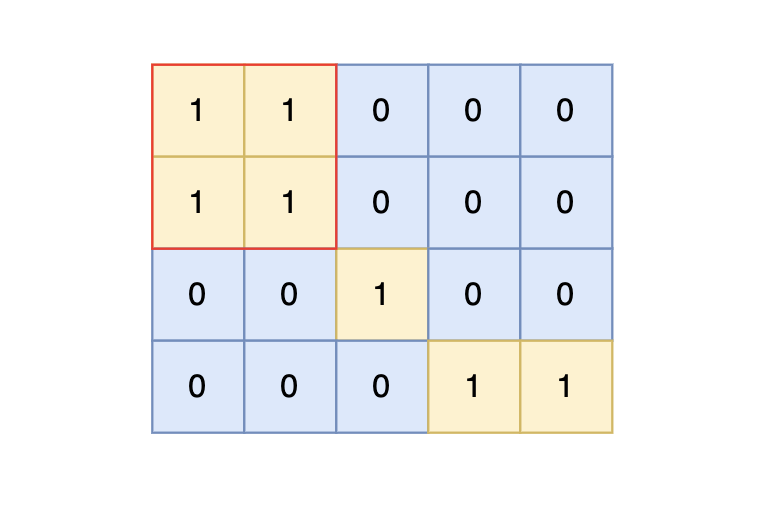
样例输入中,岛屿的最大面积为 4。
@@ -48,7 +48,7 @@
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
-
+
这道题目也是 dfs bfs基础类题目,就是搜索每个岛屿上“1”的数量,然后取一个最大的。
diff --git a/problems/kamacoder/0101.孤岛的总面积.md b/problems/kamacoder/0101.孤岛的总面积.md
index 43ac8ec9..c8fe372c 100644
--- a/problems/kamacoder/0101.孤岛的总面积.md
+++ b/problems/kamacoder/0101.孤岛的总面积.md
@@ -37,7 +37,7 @@
提示信息:
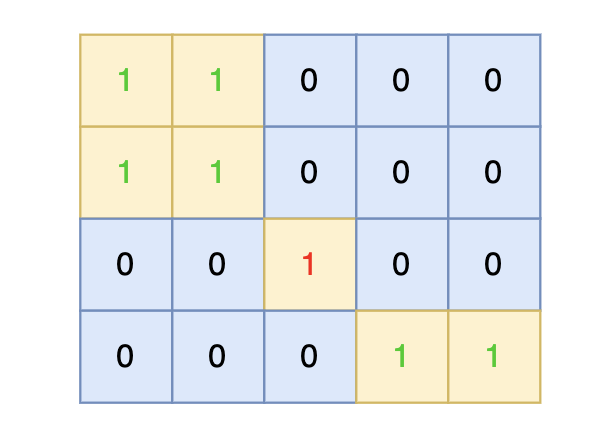
-
+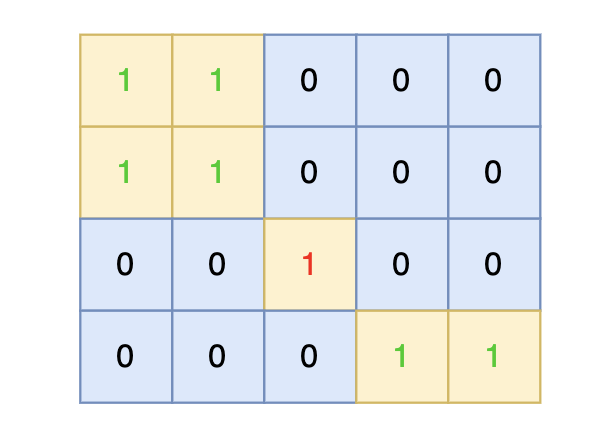
在矩阵中心部分的岛屿,因为没有任何一个单元格接触到矩阵边缘,所以该岛屿属于孤岛,总面积为 1。
@@ -54,11 +54,11 @@
如图,在遍历地图周围四个边,靠地图四边的陆地,都为绿色,
-
+
在遇到地图周边陆地的时候,将1都变为0,此时地图为这样:
-
+
然后我们再去遍历这个地图,遇到有陆地的地方,去采用深搜或者广搜,边统计所有陆地。
diff --git a/problems/kamacoder/0102.沉没孤岛.md b/problems/kamacoder/0102.沉没孤岛.md
index 5e211cd0..265ec31f 100644
--- a/problems/kamacoder/0102.沉没孤岛.md
+++ b/problems/kamacoder/0102.沉没孤岛.md
@@ -43,11 +43,11 @@
提示信息:
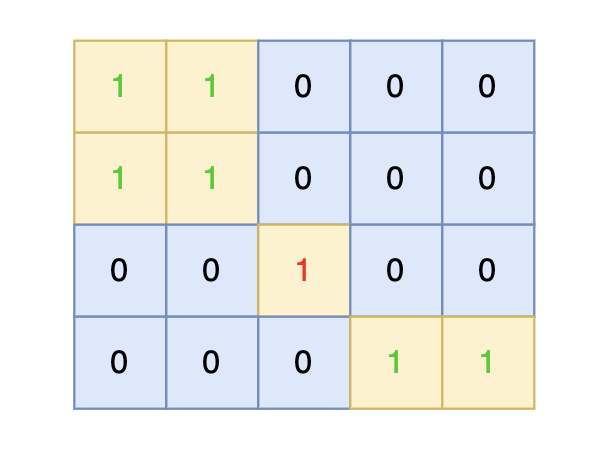
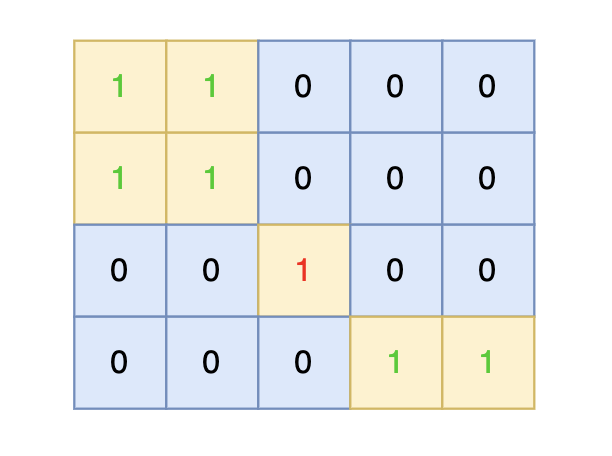
-
+
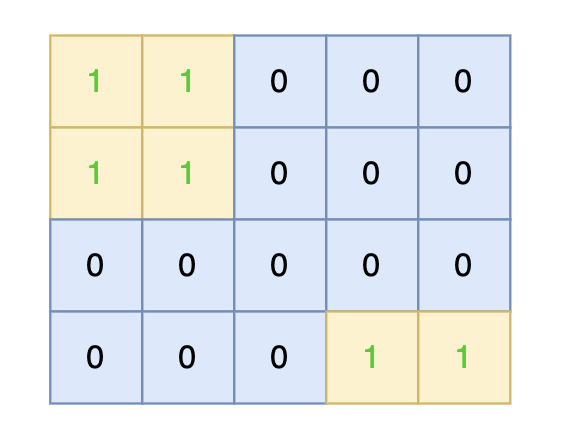
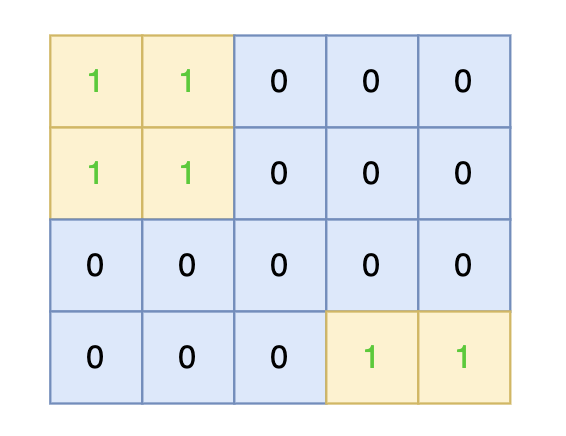
将孤岛沉没:
-
+
数据范围:
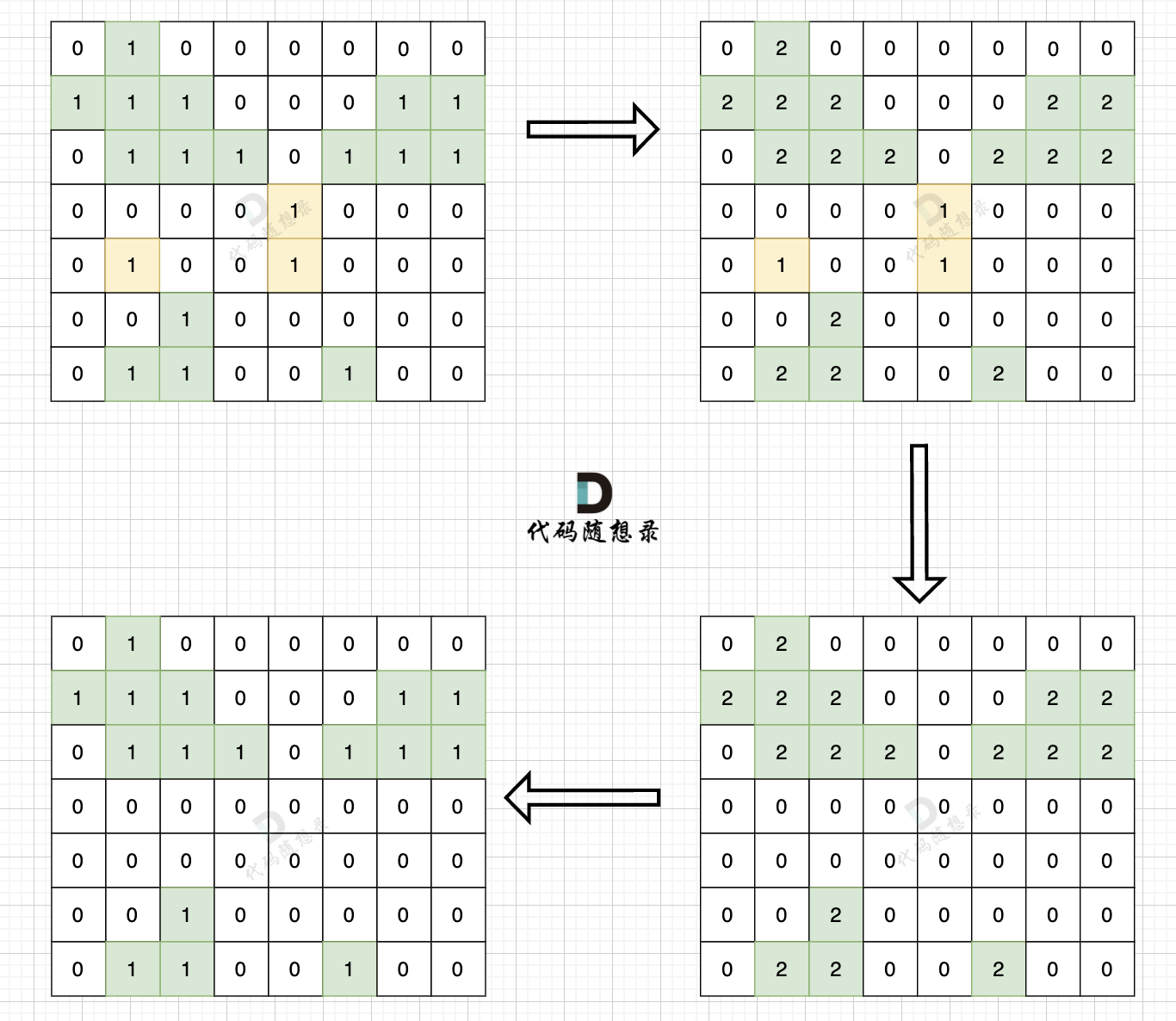
@@ -73,7 +73,7 @@
如图:
-
+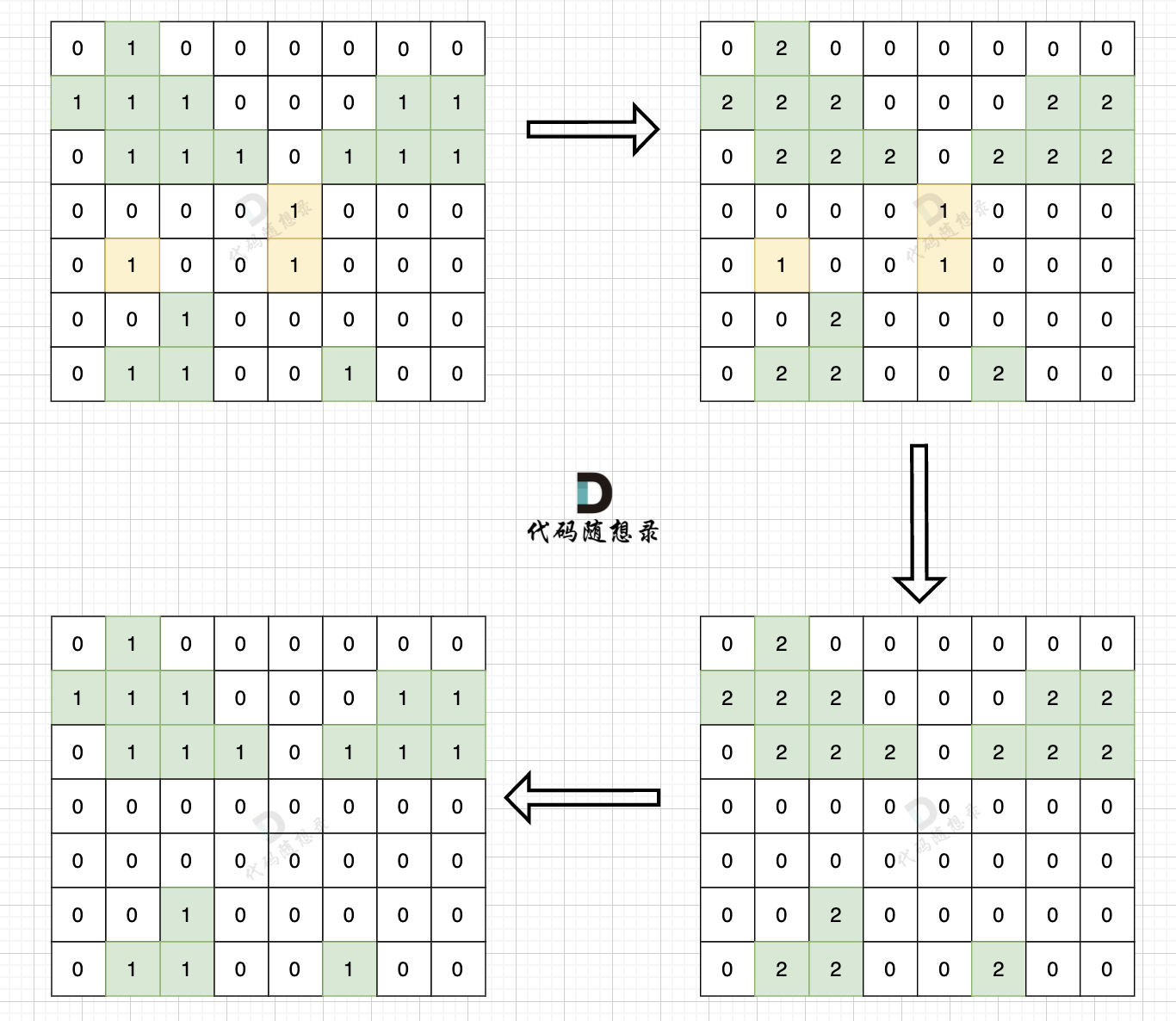
整体C++代码如下,以下使用dfs实现,其实遍历方式dfs,bfs都是可以的。
diff --git a/problems/kamacoder/0103.水流问题.md b/problems/kamacoder/0103.水流问题.md
index 1c646b1c..5924cb18 100644
--- a/problems/kamacoder/0103.水流问题.md
+++ b/problems/kamacoder/0103.水流问题.md
@@ -48,7 +48,7 @@
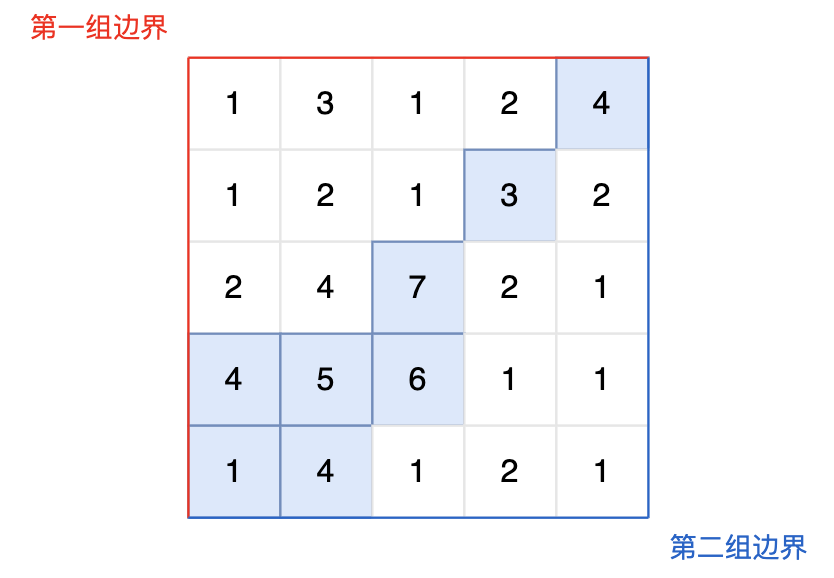
提示信息:
-
+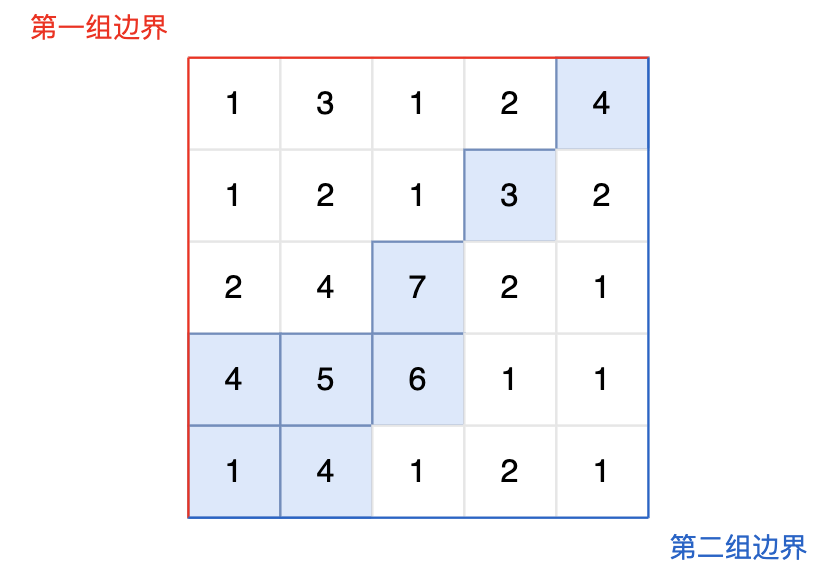
图中的蓝色方块上的雨水既能流向第一组边界,也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。
@@ -166,11 +166,11 @@ int main() {
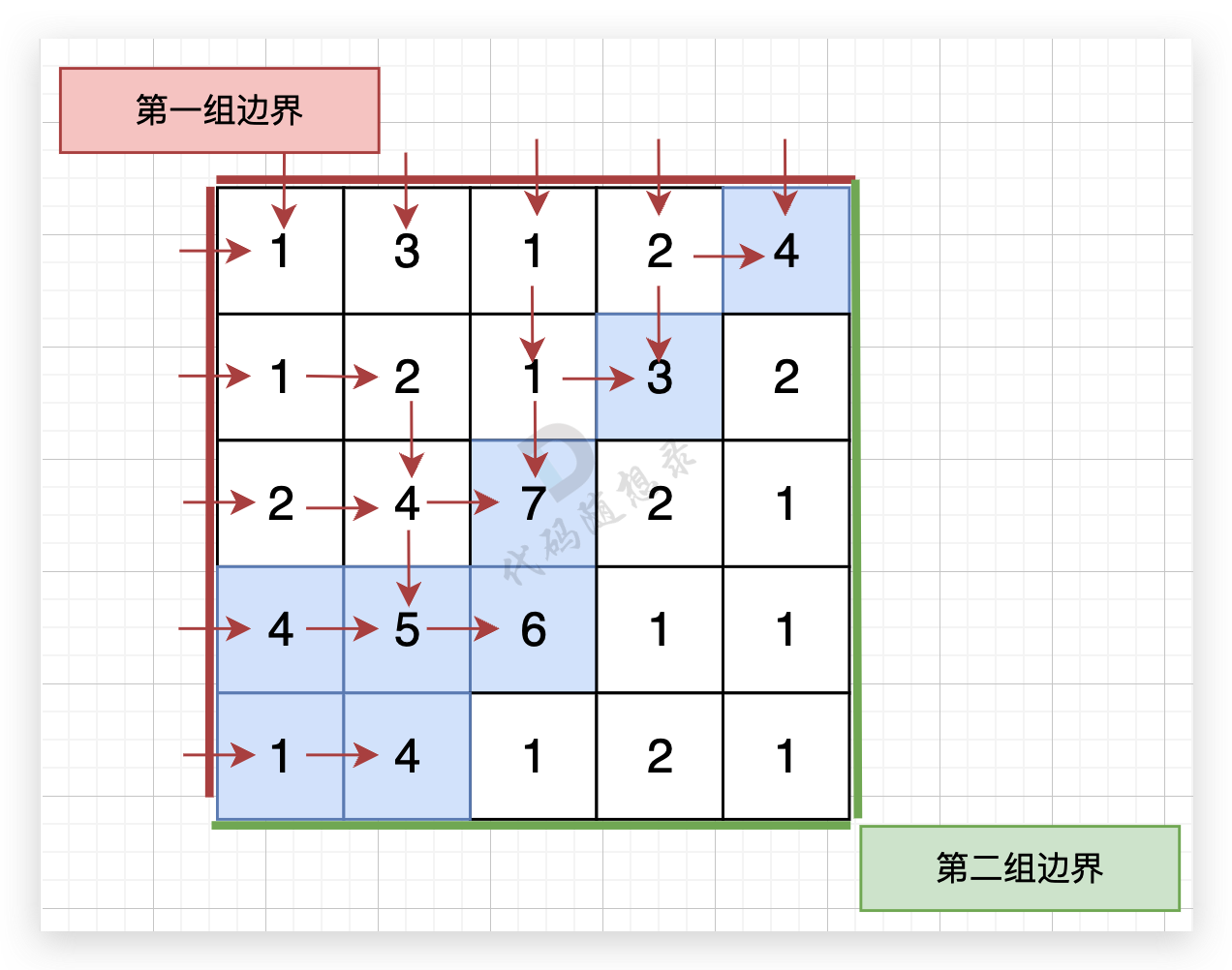
从第一组边界边上节点出发,如图: (图中并没有把所有遍历的方向都画出来,只画关键部分)
-
+
从第二组边界上节点出发,如图: (图中并没有把所有遍历的方向都画出来,只画关键部分)
-
+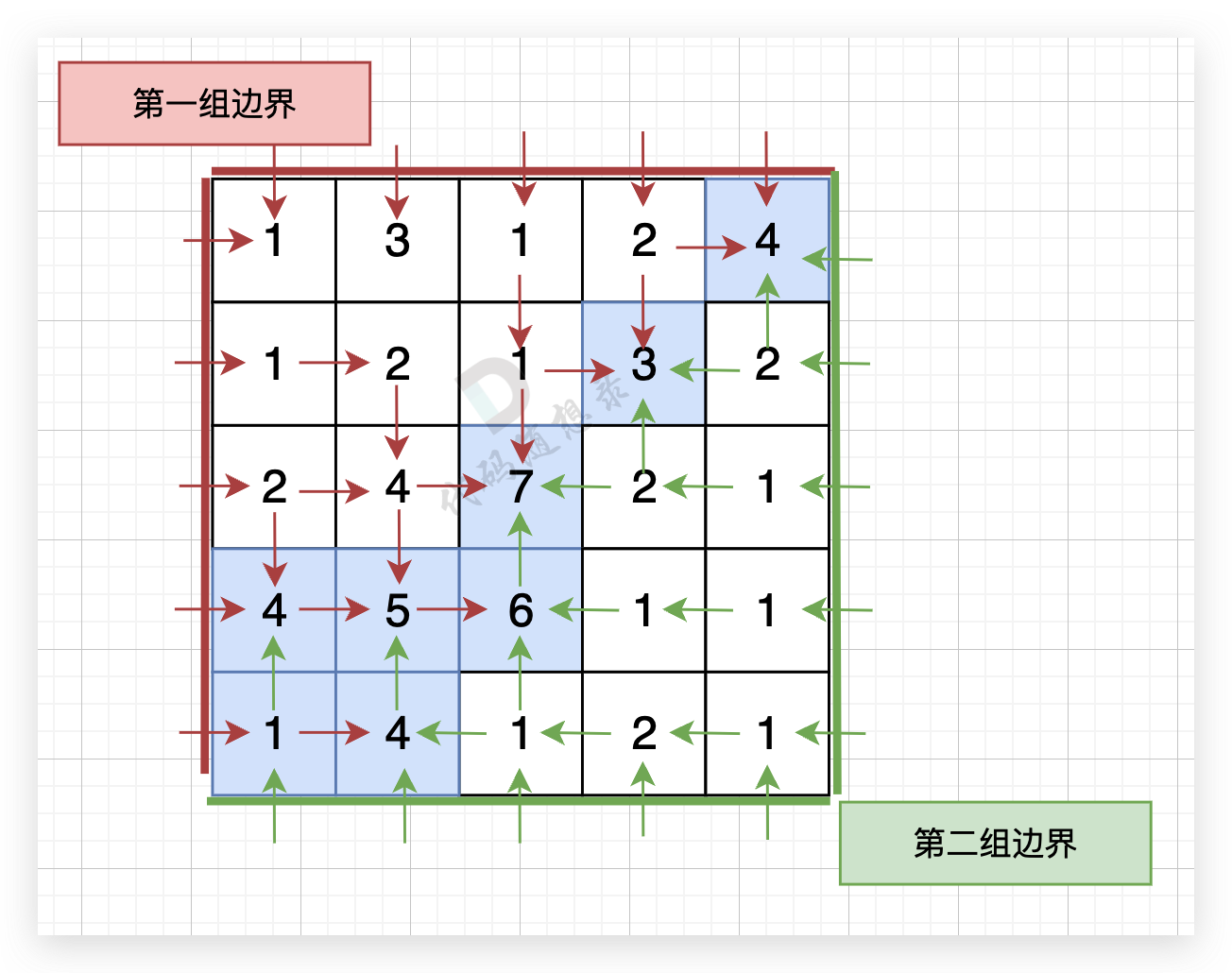
最后,我们得到两个方向交界的这些节点,就是我们最后要求的节点。
diff --git a/problems/kamacoder/0104.建造最大岛屿.md b/problems/kamacoder/0104.建造最大岛屿.md
index 5f091779..483d7772 100644
--- a/problems/kamacoder/0104.建造最大岛屿.md
+++ b/problems/kamacoder/0104.建造最大岛屿.md
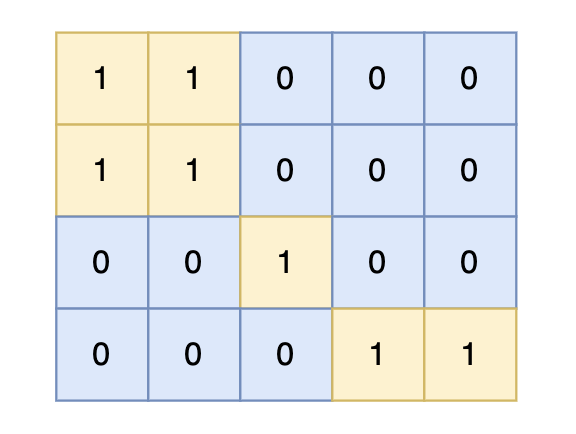
@@ -35,12 +35,12 @@
提示信息
-
+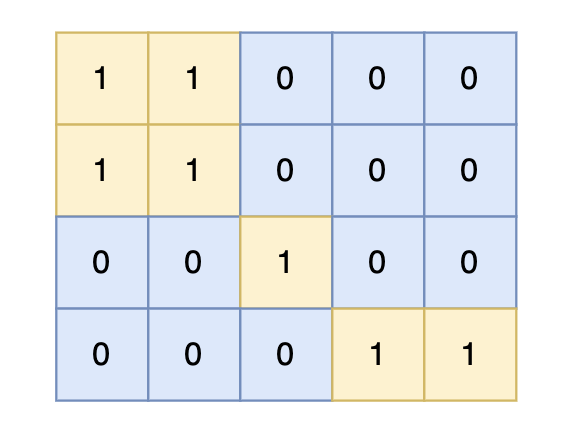
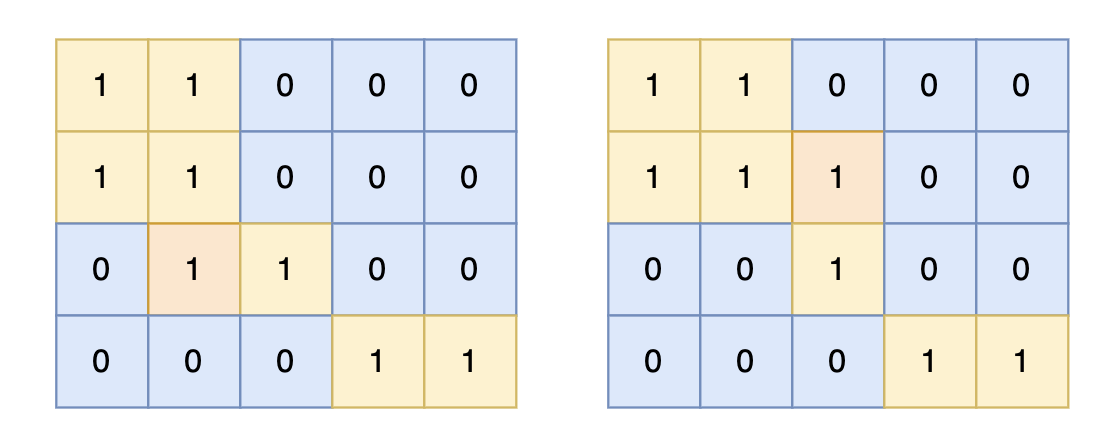
对于上面的案例,有两个位置可将 0 变成 1,使得岛屿的面积最大,即 6。
-
+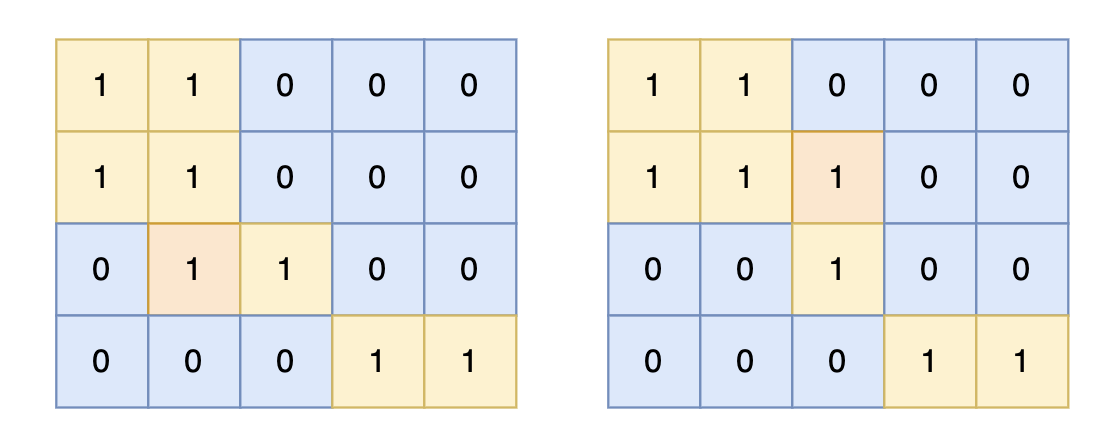
数据范围:
@@ -70,11 +70,11 @@
拿如下地图的岛屿情况来举例: (1为陆地)
-
+
第一步,则遍历地图,并将岛屿的编号和面积都统计好,过程如图所示:
-
+
本过程代码如下:
@@ -121,7 +121,7 @@ int largestIsland(vector>& grid) {
第二步过程如图所示:
-
+
也就是遍历每一个0的方格,并统计其相邻岛屿面积,最后取一个最大值。
diff --git a/problems/kamacoder/0105.有向图的完全可达性.md b/problems/kamacoder/0105.有向图的完全可达性.md
index 6901c655..cfe77c0d 100644
--- a/problems/kamacoder/0105.有向图的完全可达性.md
+++ b/problems/kamacoder/0105.有向图的完全可达性.md
@@ -33,7 +33,7 @@
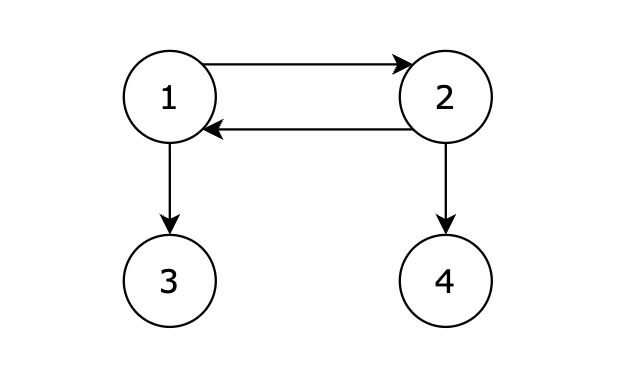
【提示信息】
-
+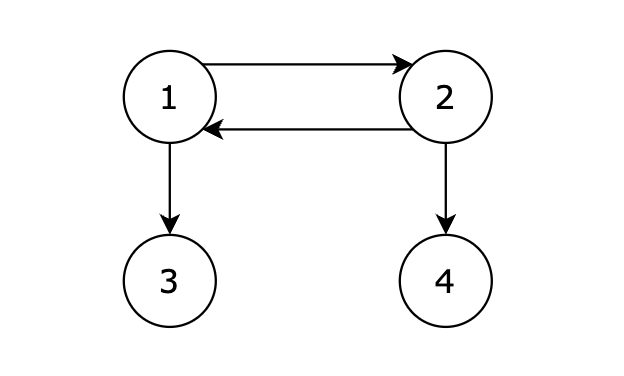
从 1 号节点可以到达任意节点,输出 1。
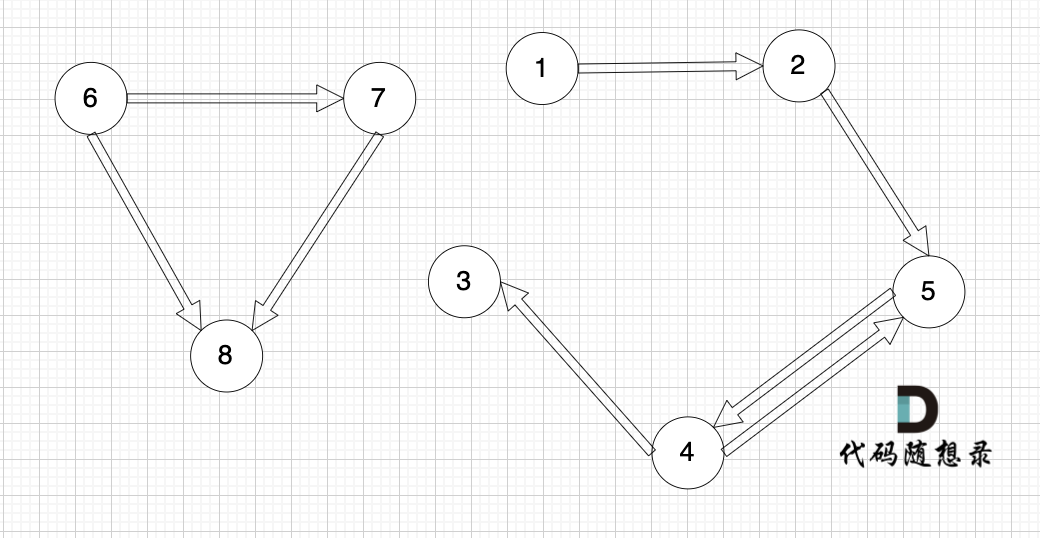
@@ -48,7 +48,7 @@
接下来我们再画一个图,从图里可以直观看出来,节点6 是 不能到达节点1 的
-
+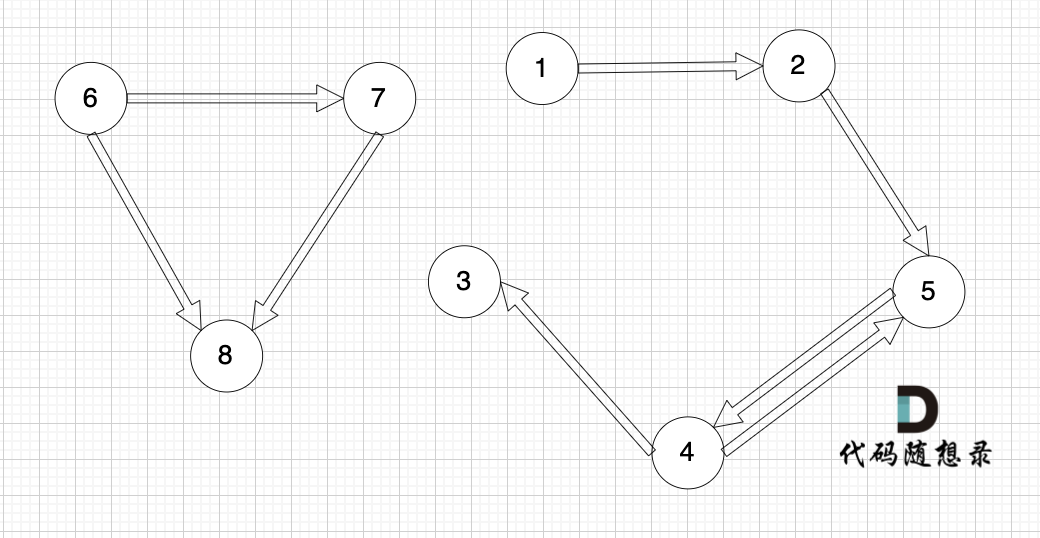
这就很容易让我们想起岛屿问题,只要发现独立的岛,就是不可到达的。
diff --git a/problems/kamacoder/0106.岛屿的周长.md b/problems/kamacoder/0106.岛屿的周长.md
index 91a1a438..a1ef2a76 100644
--- a/problems/kamacoder/0106.岛屿的周长.md
+++ b/problems/kamacoder/0106.岛屿的周长.md
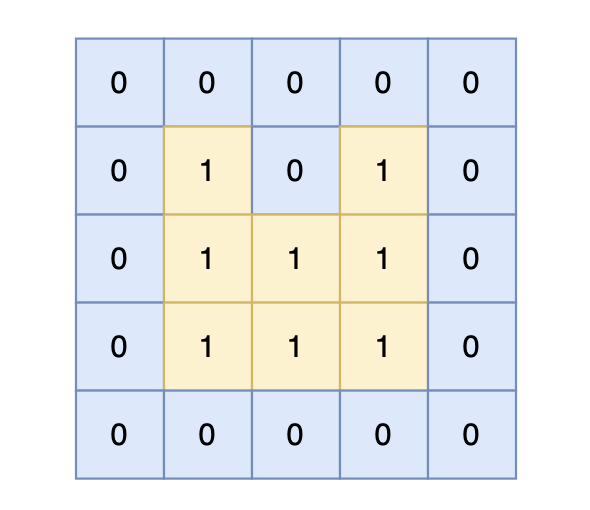
@@ -37,7 +37,7 @@
提示信息
-
+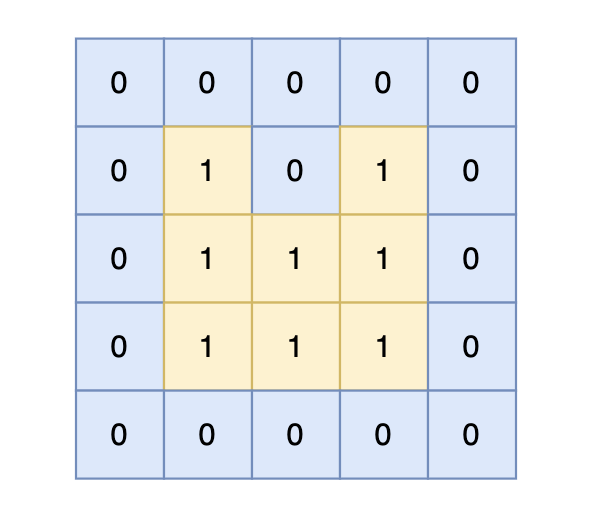
岛屿的周长为 14。
@@ -57,14 +57,14 @@
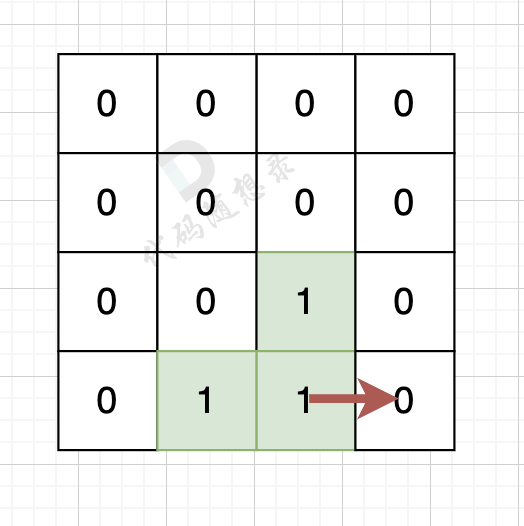
如果该陆地上下左右的空格是有水域,则说明是一条边,如图:
-
+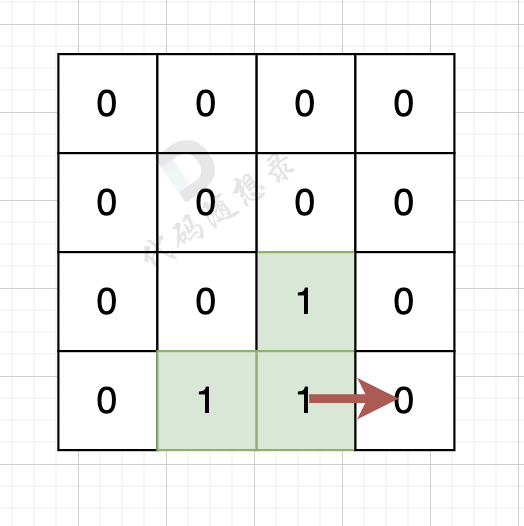
陆地的右边空格是水域,则说明找到一条边。
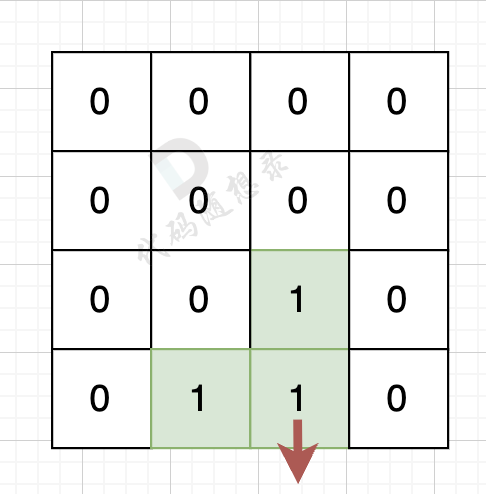
如果该陆地上下左右的空格出界了,则说明是一条边,如图:
-
+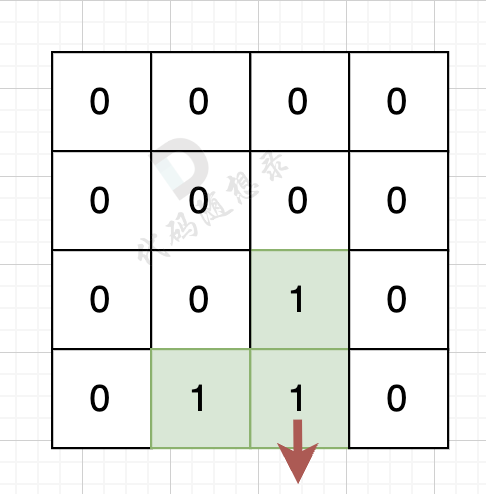
该陆地的下边空格出界了,则说明找到一条边。
@@ -114,7 +114,7 @@ int main() {
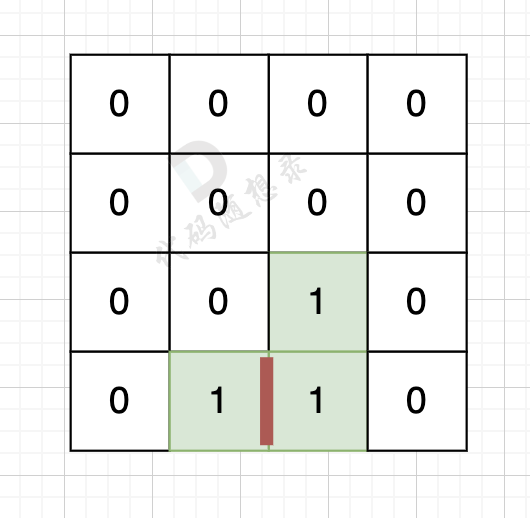
因为有一对相邻两个陆地,边的总数就要减2,如图红线部分,有两个陆地相邻,总边数就要减2
-
+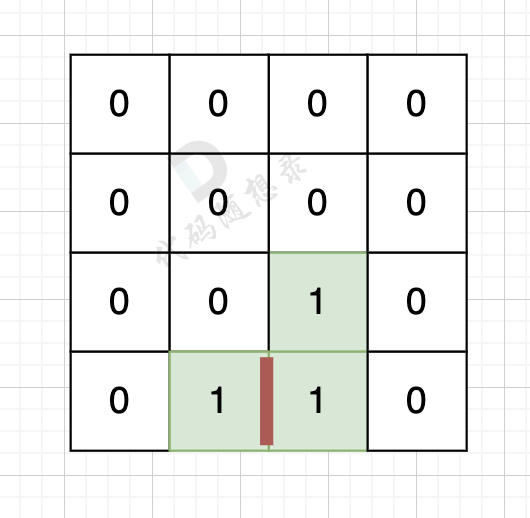
那么只需要在计算出相邻岛屿的数量就可以了,相邻岛屿数量为cover。
diff --git a/problems/kamacoder/0107.寻找存在的路径.md b/problems/kamacoder/0107.寻找存在的路径.md
index 779907c8..363a1884 100644
--- a/problems/kamacoder/0107.寻找存在的路径.md
+++ b/problems/kamacoder/0107.寻找存在的路径.md
@@ -40,7 +40,7 @@
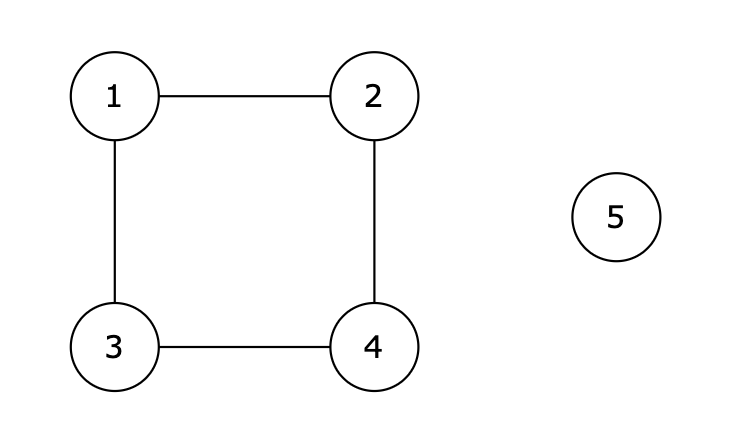
提示信息
-
+
数据范围:
diff --git a/problems/kamacoder/0108.冗余连接.md b/problems/kamacoder/0108.冗余连接.md
index ae247ac0..fe641f53 100644
--- a/problems/kamacoder/0108.冗余连接.md
+++ b/problems/kamacoder/0108.冗余连接.md
@@ -9,11 +9,11 @@
有一个图,它是一棵树,他是拥有 n 个节点(节点编号1到n)和 n - 1 条边的连通无环无向图(其实就是一个线形图),如图:
-
+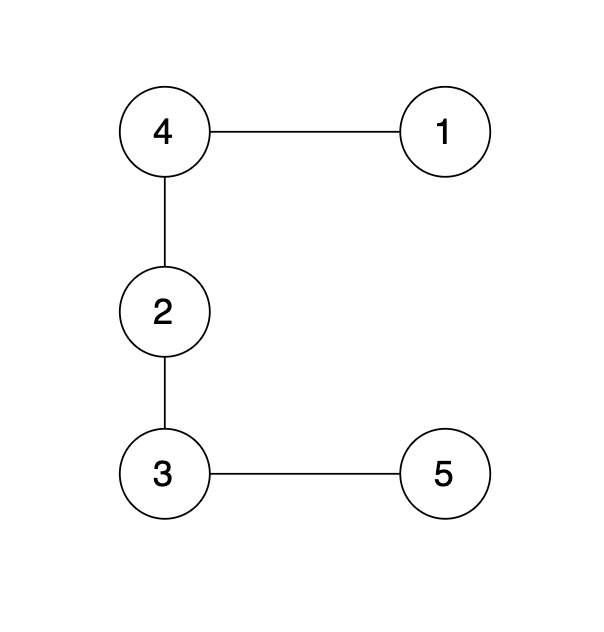
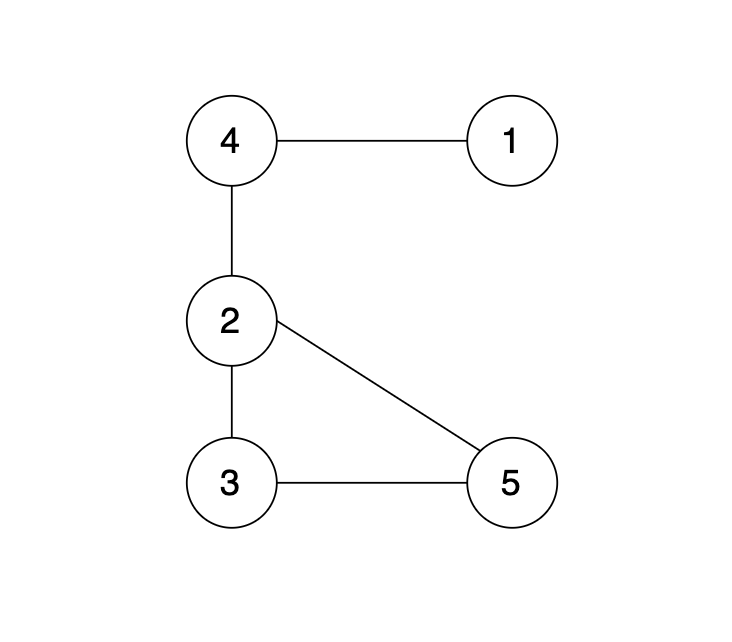
现在在这棵树上的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,如图
-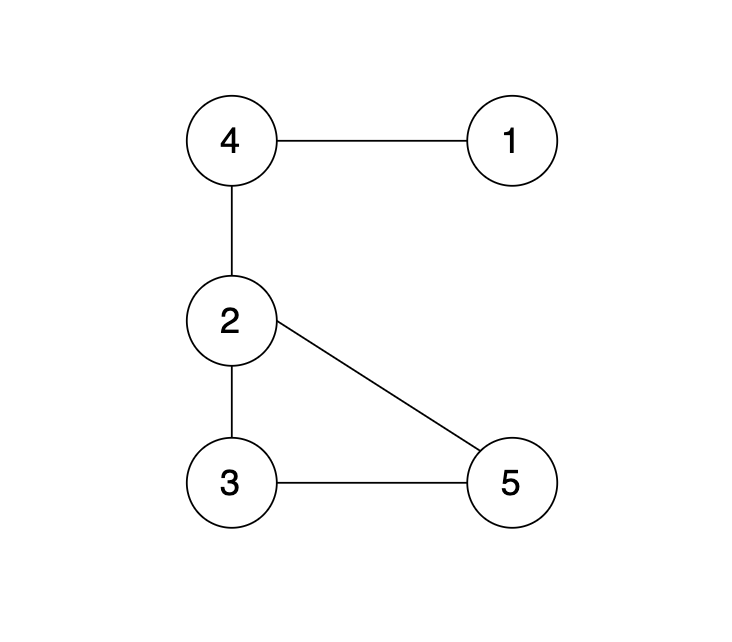
+
先请你找出冗余边,删除后,使该图可以重新变成一棵树。
@@ -42,7 +42,7 @@
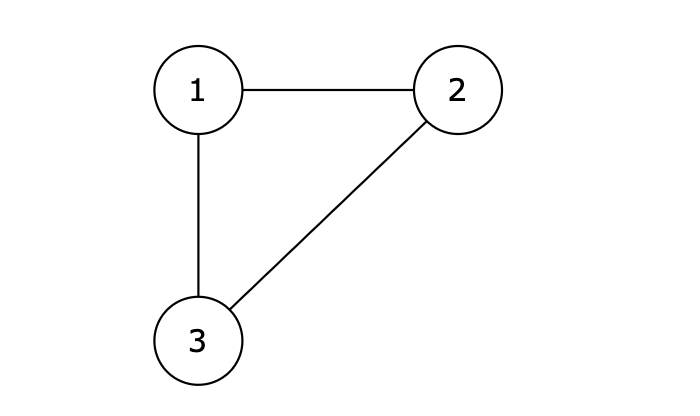
提示信息
-
+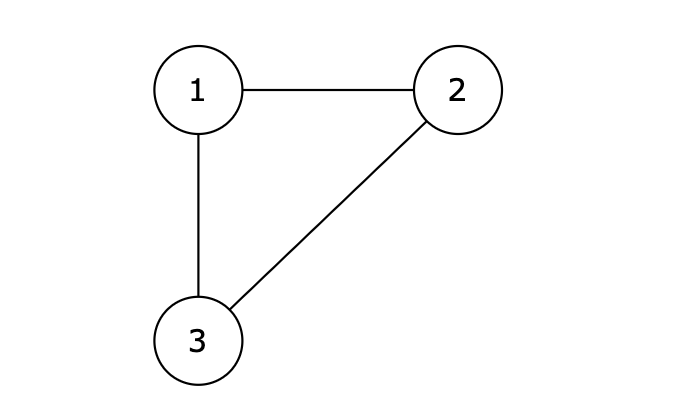
图中的 1 2,2 3,1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输入里最后出现的那条边,所以输出结果为 1 3
@@ -69,13 +69,13 @@
如图所示,节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
-
+
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
如图所示:
-
+
已经判断 节点A 和 节点B 在在同一个集合(同一个根),如果将 节点A 和 节点B 连在一起就一定会出现环。
@@ -157,7 +157,7 @@ int main() {
图:
-
+
输出示例
diff --git a/problems/kamacoder/0109.冗余连接II.md b/problems/kamacoder/0109.冗余连接II.md
index 070bc685..78132a32 100644
--- a/problems/kamacoder/0109.冗余连接II.md
+++ b/problems/kamacoder/0109.冗余连接II.md
@@ -9,11 +9,11 @@
有一种有向树,该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图:
-
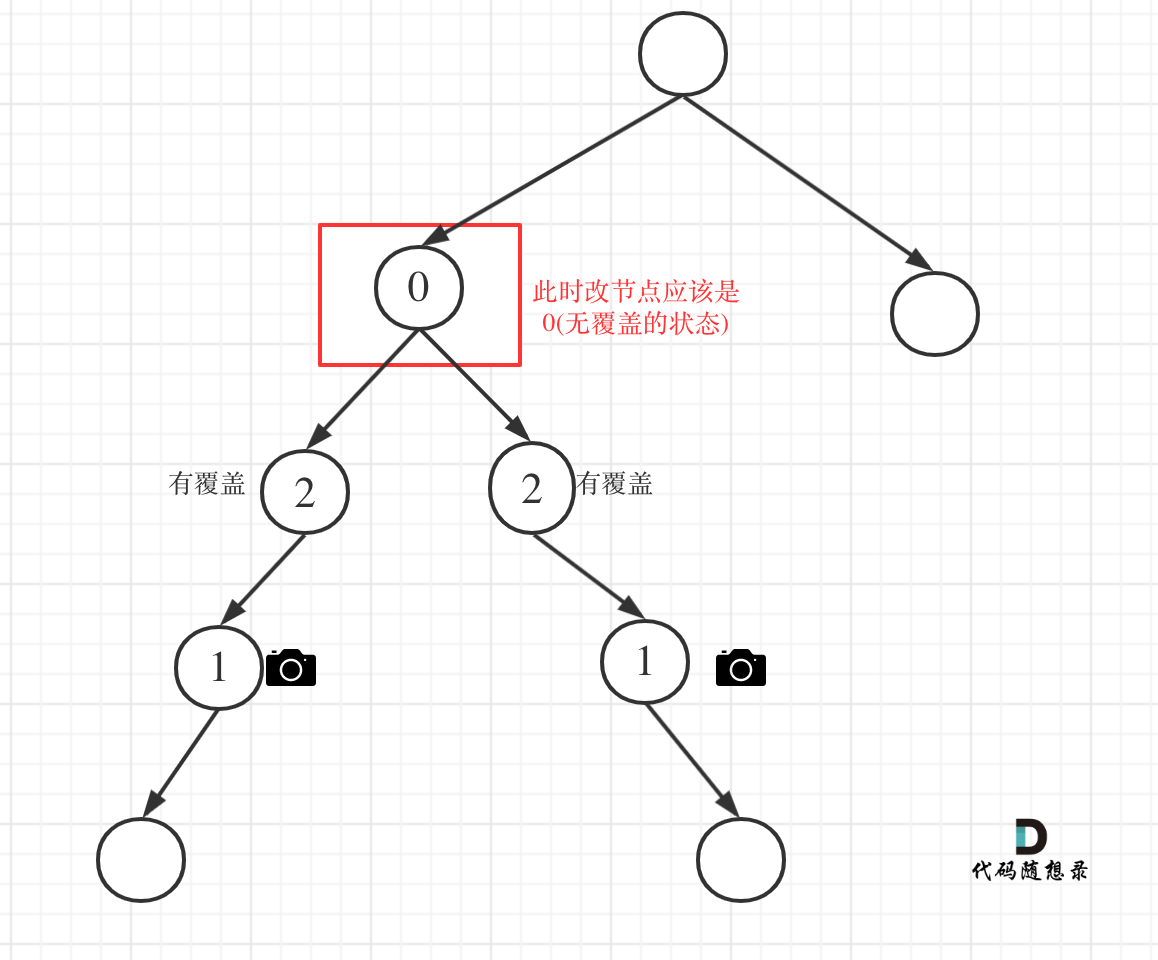
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
@@ -162,10 +162,10 @@ public:
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
完全二叉树(一)如图:
-
+
完全二叉树(二)如图:
-
+
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
@@ -173,15 +173,15 @@ public:
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
-
+
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
-
+
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
-
+
如果这么想,大家就是对 完全二叉树理解有误区了,**以上这棵二叉树,它根本就不是一个完全二叉树**!
diff --git a/problems/0226.翻转二叉树.md b/problems/0226.翻转二叉树.md
index 0980e600..248a28a4 100644
--- a/problems/0226.翻转二叉树.md
+++ b/problems/0226.翻转二叉树.md
@@ -10,7 +10,7 @@
翻转一棵二叉树。
-
+
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,全当一个乐子哈)
@@ -35,7 +35,7 @@
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
-
+
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
diff --git a/problems/0235.二叉搜索树的最近公共祖先.md b/problems/0235.二叉搜索树的最近公共祖先.md
index c5eb603a..98cc5b7d 100644
--- a/problems/0235.二叉搜索树的最近公共祖先.md
+++ b/problems/0235.二叉搜索树的最近公共祖先.md
@@ -14,7 +14,7 @@
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
-
+
示例 1:
@@ -52,7 +52,7 @@
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
-
+
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
@@ -64,7 +64,7 @@
如图所示:p为节点6,q为节点9
-
+
可以看出直接按照指定的方向,就可以找到节点8,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
diff --git a/problems/0236.二叉树的最近公共祖先.md b/problems/0236.二叉树的最近公共祖先.md
index f15d1cff..537d6240 100644
--- a/problems/0236.二叉树的最近公共祖先.md
+++ b/problems/0236.二叉树的最近公共祖先.md
@@ -16,7 +16,7 @@
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
-
+
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
@@ -51,7 +51,7 @@
**首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。** 即情况一:
-
+
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
@@ -61,7 +61,7 @@
**但是很多人容易忽略一个情况,就是节点本身p(q),它拥有一个子孙节点q(p)。** 情况二:
-
+
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
@@ -129,7 +129,7 @@ left与right的逻辑处理; // 中
如图:
-
+
就像图中一样直接返回7。
@@ -162,7 +162,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
如图:
-
+
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
@@ -183,7 +183,7 @@ else { // (left == NULL && right == NULL)
那么寻找最小公共祖先,完整流程图如下:
-
+
**从图中,大家可以看到,我们是如何回溯遍历整棵二叉树,将结果返回给头结点的!**
diff --git a/problems/0257.二叉树的所有路径.md b/problems/0257.二叉树的所有路径.md
index 287db209..5d713511 100644
--- a/problems/0257.二叉树的所有路径.md
+++ b/problems/0257.二叉树的所有路径.md
@@ -14,7 +14,7 @@
说明: 叶子节点是指没有子节点的节点。
示例:
-
+
## 算法公开课
@@ -28,7 +28,7 @@
前序遍历以及回溯的过程如图:
-
+
我们先使用递归的方式,来做前序遍历。**要知道递归和回溯就是一家的,本题也需要回溯。**
@@ -315,7 +315,7 @@ public:
其实关键还在于 参数,使用的是 `string path`,这里并没有加上引用`&` ,即本层递归中,path + 该节点数值,但该层递归结束,上一层path的数值并不会受到任何影响。 如图所示:
-
+
节点4 的path,在遍历到节点3,path+3,遍历节点3的递归结束之后,返回节点4(回溯的过程),path并不会把3加上。
diff --git a/problems/0279.完全平方数.md b/problems/0279.完全平方数.md
index c1077bd4..8171a409 100644
--- a/problems/0279.完全平方数.md
+++ b/problems/0279.完全平方数.md
@@ -93,7 +93,7 @@ for (int i = 0; i <= n; i++) { // 遍历背包
已输入n为5例,dp状态图如下:
-
+
dp[0] = 0
dp[1] = min(dp[0] + 1) = 1
diff --git a/problems/0300.最长上升子序列.md b/problems/0300.最长上升子序列.md
index 7d2e4886..de37ed5c 100644
--- a/problems/0300.最长上升子序列.md
+++ b/problems/0300.最长上升子序列.md
@@ -85,7 +85,7 @@ for (int i = 1; i < nums.size(); i++) {
输入:[0,1,0,3,2],dp数组的变化如下:
-
+
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
diff --git a/problems/0309.最佳买卖股票时机含冷冻期.md b/problems/0309.最佳买卖股票时机含冷冻期.md
index 6a819335..599a1f42 100644
--- a/problems/0309.最佳买卖股票时机含冷冻期.md
+++ b/problems/0309.最佳买卖股票时机含冷冻期.md
@@ -47,7 +47,7 @@ dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
* 状态三:今天卖出股票
* 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
-
+
j的状态为:
@@ -136,7 +136,7 @@ dp[i][3] = dp[i - 1][2];
以 [1,2,3,0,2] 为例,dp数组如下:
-
+
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
diff --git a/problems/0322.零钱兑换.md b/problems/0322.零钱兑换.md
index dea77a3d..7f3bc1e4 100644
--- a/problems/0322.零钱兑换.md
+++ b/problems/0322.零钱兑换.md
@@ -104,7 +104,7 @@ dp[0] = 0;
以输入:coins = [1, 2, 5], amount = 5为例
-
+
dp[amount]为最终结果。
diff --git a/problems/0332.重新安排行程.md b/problems/0332.重新安排行程.md
index f1df2522..fcdb6a33 100644
--- a/problems/0332.重新安排行程.md
+++ b/problems/0332.重新安排行程.md
@@ -57,7 +57,7 @@
对于死循环,我来举一个有重复机场的例子:
-
+
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
@@ -111,7 +111,7 @@ void backtracking(参数) {
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
-
+
开始回溯三部曲讲解:
@@ -137,7 +137,7 @@ bool backtracking(int ticketNum, vector& result) {
因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,如图:
-
+
所以找到了这个叶子节点了直接返回,这个递归函数的返回值问题我们在讲解二叉树的系列的时候,在这篇[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://programmercarl.com/0112.路径总和.html)详细介绍过。
diff --git a/problems/0337.打家劫舍III.md b/problems/0337.打家劫舍III.md
index 08728e4f..4916af4c 100644
--- a/problems/0337.打家劫舍III.md
+++ b/problems/0337.打家劫舍III.md
@@ -12,7 +12,7 @@
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
-
+
## 算法公开课
@@ -177,7 +177,7 @@ return {val2, val1};
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
-
+
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
diff --git a/problems/0343.整数拆分.md b/problems/0343.整数拆分.md
index 06549185..203c4228 100644
--- a/problems/0343.整数拆分.md
+++ b/problems/0343.整数拆分.md
@@ -127,7 +127,7 @@ for (int i = 3; i <= n ; i++) {
举例当n为10 的时候,dp数组里的数值,如下:
-
+
以上动规五部曲分析完毕,C++代码如下:
diff --git a/problems/0349.两个数组的交集.md b/problems/0349.两个数组的交集.md
index 5066bff1..65d22a80 100644
--- a/problems/0349.两个数组的交集.md
+++ b/problems/0349.两个数组的交集.md
@@ -14,7 +14,7 @@
题意:给定两个数组,编写一个函数来计算它们的交集。
-
+
**说明:**
输出结果中的每个元素一定是唯一的。
@@ -51,7 +51,7 @@ std::set和std::multiset底层实现都是红黑树,std::unordered_set的底
思路如图所示:
-
+
C++代码如下:
diff --git a/problems/0376.摆动序列.md b/problems/0376.摆动序列.md
index 886d86ae..50934981 100644
--- a/problems/0376.摆动序列.md
+++ b/problems/0376.摆动序列.md
@@ -46,7 +46,7 @@
用示例二来举例,如图所示:
-
+
**局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值**。
@@ -72,13 +72,13 @@
例如 [1,2,2,2,2,1]这样的数组,如图:
-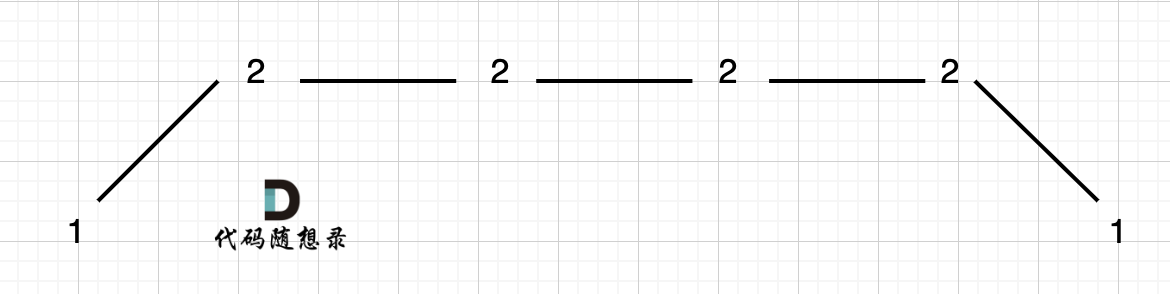
+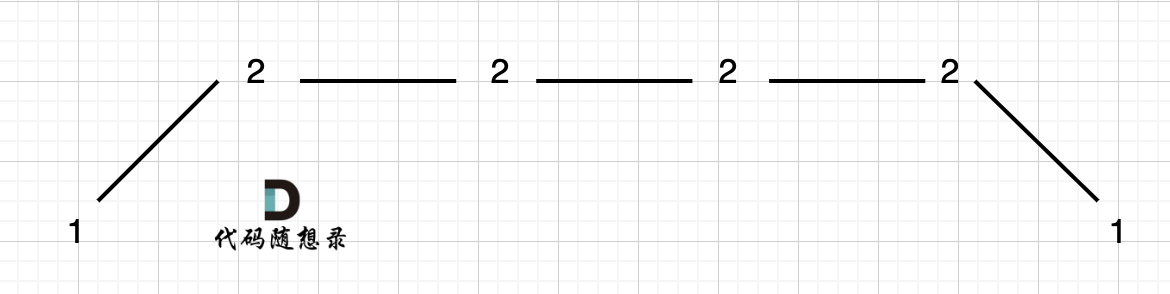
它的摇摆序列长度是多少呢? **其实是长度是 3**,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。
如图,可以统一规则,删除左边的三个 2:
-
+
在图中,当 i 指向第一个 2 的时候,`prediff > 0 && curdiff = 0` ,当 i 指向最后一个 2 的时候 `prediff = 0 && curdiff < 0`。
@@ -106,7 +106,7 @@
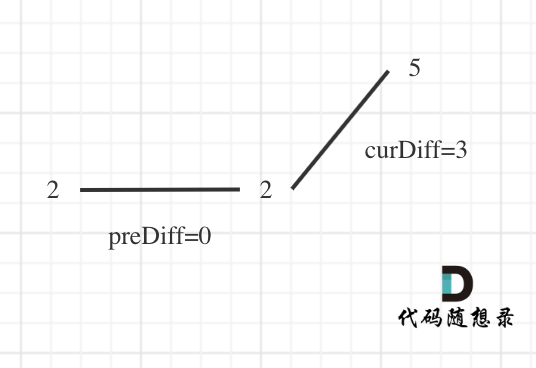
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0,如图:
-
+
针对以上情形,result 初始为 1(默认最右面有一个峰值),此时 curDiff > 0 && preDiff <= 0,那么 result++(计算了左面的峰值),最后得到的 result 就是 2(峰值个数为 2 即摆动序列长度为 2)
@@ -145,7 +145,7 @@ public:
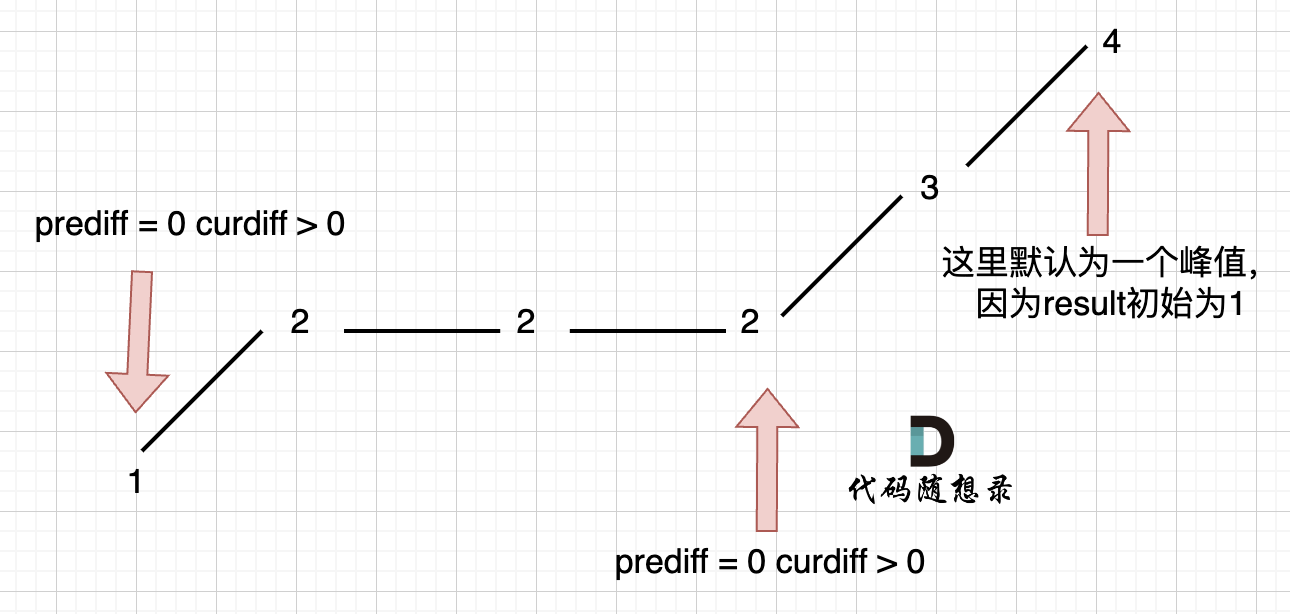
在版本一中,我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
-
+
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是 2,因为 单调中的平坡 不能算峰值(即摆动)。
@@ -184,7 +184,7 @@ public:
**本题异常情况的本质,就是要考虑平坡**, 平坡分两种,一个是 上下中间有平坡,一个是单调有平坡,如图:
-
+
### 思路 2(动态规划)
diff --git a/problems/0377.组合总和Ⅳ.md b/problems/0377.组合总和Ⅳ.md
index d2feb0c5..20a94331 100644
--- a/problems/0377.组合总和Ⅳ.md
+++ b/problems/0377.组合总和Ⅳ.md
@@ -103,7 +103,7 @@ dp[i](考虑nums[j])可以由 dp[i - nums[j]](不考虑nums[j]) 推导
我们再来用示例中的例子推导一下:
-
+
如果代码运行处的结果不是想要的结果,就把dp[i]都打出来,看看和我们推导的一不一样。
diff --git a/problems/0392.判断子序列.md b/problems/0392.判断子序列.md
index 2a5be51c..d59b7bc1 100644
--- a/problems/0392.判断子序列.md
+++ b/problems/0392.判断子序列.md
@@ -80,7 +80,7 @@ if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:
-
+
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
@@ -98,14 +98,14 @@ vector> dp(s.size() + 1, vector(t.size() + 1, 0));
如图所示:
-
+
5. 举例推导dp数组
以示例一为例,输入:s = "abc", t = "ahbgdc",dp状态转移图如下:
-
+
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
diff --git a/problems/0404.左叶子之和.md b/problems/0404.左叶子之和.md
index 0efdb6f6..69723815 100644
--- a/problems/0404.左叶子之和.md
+++ b/problems/0404.左叶子之和.md
@@ -12,7 +12,7 @@
示例:
-
+
## 算法公开课
@@ -26,12 +26,12 @@
大家思考一下如下图中二叉树,左叶子之和究竟是多少?
-
+
**其实是0,因为这棵树根本没有左叶子!**
但看这个图的左叶子之和是多少?
-
+
相信通过这两个图,大家对最左叶子的定义有明确理解了。
diff --git a/problems/0406.根据身高重建队列.md b/problems/0406.根据身高重建队列.md
index 11853e11..0d060ee8 100644
--- a/problems/0406.根据身高重建队列.md
+++ b/problems/0406.根据身高重建队列.md
@@ -61,7 +61,7 @@
以图中{5,2} 为例:
-
+
按照身高排序之后,优先按身高高的people的k来插入,后序插入节点也不会影响前面已经插入的节点,最终按照k的规则完成了队列。
diff --git a/problems/0416.分割等和子集.md b/problems/0416.分割等和子集.md
index 9cc6db0e..79b4d4f7 100644
--- a/problems/0416.分割等和子集.md
+++ b/problems/0416.分割等和子集.md
@@ -155,7 +155,7 @@ dp[j]的数值一定是小于等于j的。
用例1,输入[1,5,11,5] 为例,如图:
-
+
最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
diff --git a/problems/0417.太平洋大西洋水流问题.md b/problems/0417.太平洋大西洋水流问题.md
index ec87eb95..116cd08e 100644
--- a/problems/0417.太平洋大西洋水流问题.md
+++ b/problems/0417.太平洋大西洋水流问题.md
@@ -18,7 +18,7 @@
示例 1:
-
+
* 输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
* 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
@@ -130,11 +130,11 @@ public:
从太平洋边上节点出发,如图:
-
+
从大西洋边上节点出发,如图:
-
+
按照这样的逻辑,就可以写出如下遍历代码:(详细注释)
diff --git a/problems/0435.无重叠区间.md b/problems/0435.无重叠区间.md
index a37d1cad..04845ea7 100644
--- a/problems/0435.无重叠区间.md
+++ b/problems/0435.无重叠区间.md
@@ -44,7 +44,7 @@
这里记录非交叉区间的个数还是有技巧的,如图:
-
+
区间,1,2,3,4,5,6都按照右边界排好序。
diff --git a/problems/0450.删除二叉搜索树中的节点.md b/problems/0450.删除二叉搜索树中的节点.md
index 72809184..406116a3 100644
--- a/problems/0450.删除二叉搜索树中的节点.md
+++ b/problems/0450.删除二叉搜索树中的节点.md
@@ -20,7 +20,7 @@
示例:
-
+
## 算法公开课
diff --git a/problems/0452.用最少数量的箭引爆气球.md b/problems/0452.用最少数量的箭引爆气球.md
index 85449882..17d21cd1 100644
--- a/problems/0452.用最少数量的箭引爆气球.md
+++ b/problems/0452.用最少数量的箭引爆气球.md
@@ -76,7 +76,7 @@
以题目示例: [[10,16],[2,8],[1,6],[7,12]]为例,如图:(方便起见,已经排序)
-
+
可以看出首先第一组重叠气球,一定是需要一个箭,气球3,的左边界大于了 第一组重叠气球的最小右边界,所以再需要一支箭来射气球3了。
diff --git a/problems/0455.分发饼干.md b/problems/0455.分发饼干.md
index a2a1b1f3..2a6ade1b 100644
--- a/problems/0455.分发饼干.md
+++ b/problems/0455.分发饼干.md
@@ -46,7 +46,7 @@
如图:
-
+
这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
@@ -89,7 +89,7 @@ public:
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :
-
+
if 里的 index 指向 胃口 10, for 里的 i 指向饼干 9,因为 饼干 9 满足不了 胃口 10,所以 i 持续向前移动,而 index 走不到` s[index] >= g[i]` 的逻辑,所以 index 不会移动,那么当 i 持续向前移动,最后所有的饼干都匹配不上。
diff --git a/problems/0459.重复的子字符串.md b/problems/0459.重复的子字符串.md
index 78aad3e7..627a27a4 100644
--- a/problems/0459.重复的子字符串.md
+++ b/problems/0459.重复的子字符串.md
@@ -46,13 +46,13 @@
当一个字符串s:abcabc,内部由重复的子串组成,那么这个字符串的结构一定是这样的:
-
+
也就是由前后相同的子串组成。
那么既然前面有相同的子串,后面有相同的子串,用 s + s,这样组成的字符串中,后面的子串做前串,前面的子串做后串,就一定还能组成一个s,如图:
-
+
当然,我们在判断 s + s 拼接的字符串里是否出现一个s的的时候,**要刨除 s + s 的首字符和尾字符**,这样避免在s+s中搜索出原来的s,我们要搜索的是中间拼接出来的s。
@@ -64,11 +64,11 @@
如图,字符串s,图中数字为数组下标,在 s + s 拼接后, 不算首尾字符,中间凑成s字符串。 (图中数字为数组下标)
-
+
图中,因为中间拼接成了s,根据红色框 可以知道 s[4] = s[0], s[5] = s[1], s[0] = s[2], s[1] = s[3] s[2] = s[4] ,s[3] = s[5]
-
+
以上相等关系我们串联一下:
@@ -83,7 +83,7 @@ s[5] = s[1] = s[3]
这里可以有录友想,凭什么就是这样组成的s呢,我换一个方式组成s 行不行,如图:
-
+
s[3] = s[0],s[4] = s[1] ,s[5] = s[2],s[0] = s[3],s[1] = s[4],s[2] = s[5]
@@ -101,7 +101,7 @@ s[0] s[1] s[2] = s[3] s[4] s[5]
如果是这样的呢,如图:
-
+
s[1] = s[0],s[2] = s[1] ,s[3] = s[2],s[4] = s[3],s[5] = s[4],s[0] = s[5]
@@ -165,23 +165,23 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
那么相同前后缀可以是这样:
-
+
也可以是这样:
-
+
最长的相等前后缀,也就是这样:
-
+
这里有录友就想:如果字符串s 是由最小重复子串p组成,最长相等前后缀就不能更长一些? 例如这样:
-
+
如果这样的话,因为前后缀要相同,所以 p2 = p1,p3 = p2,如图:
-
+
p2 = p1,p3 = p2 即: p1 = p2 = p3
@@ -203,7 +203,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
情况一, 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大,那一定不是字符串s的重复子串,如图:
-
+
图中:前后缀不包含的子串的长度 大于 字符串s的长度的 二分之一
@@ -211,7 +211,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
情况二,最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,如图:
-
+
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,所以 s[0] 一定和 s[2]相同,s[1] 一定和 s[3]相同,即:,s[0]s[1]与s[2]s[3]相同 。
@@ -234,7 +234,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
那么它的最长相同前后缀,就不是上图中的前后缀,而是这样的的前后缀:
-
+
录友可能再问,由一个字符组成的字符串,最长相等前后缀凭什么就是这样的。
@@ -250,7 +250,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
**情况三,最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除得情况**,如图:
-
+
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,t[2] 与 k[2]相同。
diff --git a/problems/0463.岛屿的周长.md b/problems/0463.岛屿的周长.md
index bff619cc..40ddc57d 100644
--- a/problems/0463.岛屿的周长.md
+++ b/problems/0463.岛屿的周长.md
@@ -15,7 +15,7 @@
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
-
+
* 输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
* 输出:16
diff --git a/problems/0474.一和零.md b/problems/0474.一和零.md
index ca525ab2..8166b39a 100644
--- a/problems/0474.一和零.md
+++ b/problems/0474.一和零.md
@@ -51,7 +51,7 @@
其实本题并不是多重背包,再来看一下这个图,捋清几种背包的关系
-
+
多重背包是每个物品,数量不同的情况。
@@ -127,7 +127,7 @@ for (string str : strs) { // 遍历物品
最后dp数组的状态如下所示:
-
+
以上动规五部曲分析完毕,C++代码如下:
diff --git a/problems/0491.递增子序列.md b/problems/0491.递增子序列.md
index 1b927dd3..b3171c8a 100644
--- a/problems/0491.递增子序列.md
+++ b/problems/0491.递增子序列.md
@@ -45,7 +45,7 @@
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
-
+
@@ -79,7 +79,7 @@ if (path.size() > 1) {
* 单层搜索逻辑
-
+
在图中可以看出,**同一父节点下的同层上使用过的元素就不能再使用了**
那么单层搜索代码如下:
diff --git a/problems/0494.目标和.md b/problems/0494.目标和.md
index bde843ea..a23e1743 100644
--- a/problems/0494.目标和.md
+++ b/problems/0494.目标和.md
@@ -163,7 +163,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
先只考虑物品0,如图:
-
+
(这里的所有物品,都是题目中的数字1)。
@@ -177,7 +177,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
接下来 考虑 物品0 和 物品1,如图:
-
+
装满背包容量为0 的方法个数是1,即 放0件物品。
@@ -191,7 +191,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
接下来 考虑 物品0 、物品1 和 物品2 ,如图:
-
+
装满背包容量为0 的方法个数是1,即 放0件物品。
@@ -207,17 +207,17 @@ if (abs(target) > sum) return 0; // 此时没有方案
如图红色部分:
-
+
dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物品1 和 物品2, 如图所示,三种方法:
-
+
**容量为2 的背包,如果不放 物品2 有几种方法呢**?
有 dp[1][2] 种方法,即 背包容量为2,只考虑物品0 和 物品1 ,有 dp[1][2] 种方法,如图:
-
+
**容量为2 的背包, 如果放 物品2 有几种方法呢**?
@@ -229,7 +229,7 @@ dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物
如图:
-
+
有录友可能疑惑,这里计算的是放满 容量为2的背包 有几种方法,那物品2去哪了?
@@ -239,7 +239,7 @@ dp[2][2] = 容量为2的背包不放物品2有几种方法 + 容量为2的背包
所以 dp[2][2] = dp[1][2] + dp[1][1] ,如图:
-
+
以上过程,抽象化如下:
@@ -266,11 +266,11 @@ else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
先明确递推的方向,如图,求解 dp[2][2] 是由 上方和左上方推出。
-
+
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,如图红色部分:
-
+
关于dp[0][0]的值,在上面的递推公式讲解中已经讲过,装满背包容量为0 的方法数量是1,即 放0件物品。
@@ -323,7 +323,7 @@ for (int i = 0; i < nums.size(); i++) {
例如下图,如果上方没数值,左上方没数值,就无法推出 dp[2][2]。
-
+
那么是先 从上到下 ,再从左到右遍历,例如这样:
@@ -349,11 +349,11 @@ for (int j = 0; j <= bagSize; j++) { // 列,遍历背包
这里我再画图讲一下,以求dp[2][2]为例,当先从上到下,再从左到右遍历,矩阵是这样:
-
+
当先从左到右,再从上到下遍历,矩阵是这样:
-
+
这里大家可以看出,无论是以上哪种遍历,都不影响 dp[2][2]的求值,用来 推导 dp[2][2] 的数值都在。
@@ -366,7 +366,7 @@ bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
-
+
这么大的矩阵,我们是可以自己手动模拟出来的。
@@ -445,7 +445,7 @@ bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下:
-
+
大家可以和 二维dp数组的打印结果做一下对比。
diff --git a/problems/0501.二叉搜索树中的众数.md b/problems/0501.二叉搜索树中的众数.md
index 32a89e85..8cca8e65 100644
--- a/problems/0501.二叉搜索树中的众数.md
+++ b/problems/0501.二叉搜索树中的众数.md
@@ -23,7 +23,7 @@
给定 BST [1,null,2,2],
-
+
返回[2].
@@ -144,7 +144,7 @@ public:
如图:
-
+
中序遍历代码如下:
diff --git a/problems/0513.找树左下角的值.md b/problems/0513.找树左下角的值.md
index da373603..4098cb7b 100644
--- a/problems/0513.找树左下角的值.md
+++ b/problems/0513.找树左下角的值.md
@@ -12,11 +12,11 @@
示例 1:
-
+
示例 2:
-
+
## 算法公开课
diff --git a/problems/0516.最长回文子序列.md b/problems/0516.最长回文子序列.md
index f0ef2f53..5e456ac9 100644
--- a/problems/0516.最长回文子序列.md
+++ b/problems/0516.最长回文子序列.md
@@ -56,7 +56,7 @@
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
如图:
-
+
(如果这里看不懂,回忆一下dp[i][j]的定义)
@@ -68,7 +68,7 @@
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
-
+
代码如下:
@@ -97,7 +97,7 @@ for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],如图:
-
+
**所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的**。
@@ -121,7 +121,7 @@ for (int i = s.size() - 1; i >= 0; i--) {
输入s:"cbbd" 为例,dp数组状态如图:
-
+
红色框即:dp[0][s.size() - 1]; 为最终结果。
diff --git a/problems/0518.零钱兑换II.md b/problems/0518.零钱兑换II.md
index 1698db98..95122a7c 100644
--- a/problems/0518.零钱兑换II.md
+++ b/problems/0518.零钱兑换II.md
@@ -136,7 +136,7 @@
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,如图红色部分:
-
+
这里首先要关注的就是 dp[0][0] 应该是多少?
@@ -296,7 +296,7 @@ for (int j = 0; j <= amount; j++) { // 遍历背包容量
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
-
+
最后红色框dp[amount]为最终结果。
diff --git a/problems/0530.二叉搜索树的最小绝对差.md b/problems/0530.二叉搜索树的最小绝对差.md
index d7b0e056..466bd744 100644
--- a/problems/0530.二叉搜索树的最小绝对差.md
+++ b/problems/0530.二叉搜索树的最小绝对差.md
@@ -13,7 +13,7 @@
示例:
-
+
提示:树中至少有 2 个节点。
@@ -70,7 +70,7 @@ public:
如图:
-
+
一些同学不知道在递归中如何记录前一个节点的指针,其实实现起来是很简单的,大家只要看过一次,写过一次,就掌握了。
diff --git a/problems/0538.把二叉搜索树转换为累加树.md b/problems/0538.把二叉搜索树转换为累加树.md
index 1bbbdac7..45bf1f96 100644
--- a/problems/0538.把二叉搜索树转换为累加树.md
+++ b/problems/0538.把二叉搜索树转换为累加树.md
@@ -18,7 +18,7 @@
示例 1:
-
+
* 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
* 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
@@ -67,7 +67,7 @@
遍历顺序如图所示:
-
+
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
diff --git a/problems/0583.两个字符串的删除操作.md b/problems/0583.两个字符串的删除操作.md
index a86dfad1..7f7d30f6 100644
--- a/problems/0583.两个字符串的删除操作.md
+++ b/problems/0583.两个字符串的删除操作.md
@@ -81,7 +81,7 @@ for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
-
+
以上分析完毕,代码如下:
diff --git a/problems/0617.合并二叉树.md b/problems/0617.合并二叉树.md
index f180c4f3..755200fe 100644
--- a/problems/0617.合并二叉树.md
+++ b/problems/0617.合并二叉树.md
@@ -13,7 +13,7 @@
示例 1:
-
+
注意: 合并必须从两个树的根节点开始。
diff --git a/problems/0647.回文子串.md b/problems/0647.回文子串.md
index e2783027..72829535 100644
--- a/problems/0647.回文子串.md
+++ b/problems/0647.回文子串.md
@@ -48,7 +48,7 @@ dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
所以我们要看回文串的性质。 如图:
-
+
我们在判断字符串S是否是回文,那么如果我们知道 s[1],s[2],s[3] 这个子串是回文的,那么只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。
@@ -106,7 +106,7 @@ dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
-
+
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
@@ -136,7 +136,7 @@ for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
举例,输入:"aaa",dp[i][j]状态如下:
-
+
图中有6个true,所以就是有6个回文子串。
diff --git a/problems/0654.最大二叉树.md b/problems/0654.最大二叉树.md
index 9f897a75..b8841a8b 100644
--- a/problems/0654.最大二叉树.md
+++ b/problems/0654.最大二叉树.md
@@ -17,7 +17,7 @@
示例 :
-
+
提示:
diff --git a/problems/0669.修剪二叉搜索树.md b/problems/0669.修剪二叉搜索树.md
index 0a05360b..f4ded2c4 100644
--- a/problems/0669.修剪二叉搜索树.md
+++ b/problems/0669.修剪二叉搜索树.md
@@ -14,9 +14,9 @@
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
-
+
-
+
## 算法公开课
@@ -50,7 +50,7 @@ public:
我们在重新关注一下第二个示例,如图:
-
+
**所以以上的代码是不可行的!**
@@ -60,7 +60,7 @@ public:
在上图中我们发现节点0并不符合区间要求,那么将节点0的右孩子 节点2 直接赋给 节点3的左孩子就可以了(就是把节点0从二叉树中移除),如图:
-
+
理解了最关键部分了我们再递归三部曲:
@@ -127,7 +127,7 @@ return root;
在回顾一下上面的代码,针对下图中二叉树的情况:
-
+
如下代码相当于把节点0的右孩子(节点2)返回给上一层,
diff --git a/problems/0673.最长递增子序列的个数.md b/problems/0673.最长递增子序列的个数.md
index 9bfa91cc..92009f5b 100644
--- a/problems/0673.最长递增子序列的个数.md
+++ b/problems/0673.最长递增子序列的个数.md
@@ -178,7 +178,7 @@ for (int i = 0; i < nums.size(); i++) {
输入:[1,3,5,4,7]
-
+
**如果代码写出来了,怎么改都通过不了,那么把dp和count打印出来看看对不对!**
diff --git a/problems/0674.最长连续递增序列.md b/problems/0674.最长连续递增序列.md
index 2c490c0c..16bb2f18 100644
--- a/problems/0674.最长连续递增序列.md
+++ b/problems/0674.最长连续递增序列.md
@@ -85,7 +85,7 @@ for (int i = 1; i < nums.size(); i++) {
已输入nums = [1,3,5,4,7]为例,dp数组状态如下:
-
+
**注意这里要取dp[i]里的最大值,所以dp[2]才是结果!**
diff --git a/problems/0684.冗余连接.md b/problems/0684.冗余连接.md
index e6d2d8e5..8a7234df 100644
--- a/problems/0684.冗余连接.md
+++ b/problems/0684.冗余连接.md
@@ -12,7 +12,7 @@
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
-
+
提示:
* n == edges.length
@@ -85,7 +85,7 @@ void join(int u, int v) {
如图所示:
-
+
节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
@@ -95,7 +95,7 @@ void join(int u, int v) {
如图所示:
-
+
已经判断 节点A 和 节点B 在在同一个集合(同一个根),如果将 节点A 和 节点B 连在一起就一定会出现环。
diff --git a/problems/0685.冗余连接II.md b/problems/0685.冗余连接II.md
index 7b0e320c..66f7bfe1 100644
--- a/problems/0685.冗余连接II.md
+++ b/problems/0685.冗余连接II.md
@@ -16,9 +16,9 @@
返回一条能删除的边,使得剩下的图是有 n 个节点的有根树。若有多个答案,返回最后出现在给定二维数组的答案。
-
+
-
+
提示:
diff --git a/problems/0695.岛屿的最大面积.md b/problems/0695.岛屿的最大面积.md
index 0b84e651..972a9995 100644
--- a/problems/0695.岛屿的最大面积.md
+++ b/problems/0695.岛屿的最大面积.md
@@ -14,7 +14,7 @@
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
-
+
* 输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
* 输出:6
@@ -27,7 +27,7 @@
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
-
+
这道题目也是 dfs bfs基础类题目,就是搜索每个岛屿上“1”的数量,然后取一个最大的。
diff --git a/problems/0700.二叉搜索树中的搜索.md b/problems/0700.二叉搜索树中的搜索.md
index 4225b3fe..0c373f61 100644
--- a/problems/0700.二叉搜索树中的搜索.md
+++ b/problems/0700.二叉搜索树中的搜索.md
@@ -12,7 +12,7 @@
例如,
-
+
在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
@@ -124,7 +124,7 @@ public:
中间节点如果大于3就向左走,如果小于3就向右走,如图:
-
+
所以迭代法代码如下:
diff --git a/problems/0701.二叉搜索树中的插入操作.md b/problems/0701.二叉搜索树中的插入操作.md
index ef383faa..6ce9ef33 100644
--- a/problems/0701.二叉搜索树中的插入操作.md
+++ b/problems/0701.二叉搜索树中的插入操作.md
@@ -12,7 +12,7 @@
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。
-
+
提示:
diff --git a/problems/0704.二分查找.md b/problems/0704.二分查找.md
index 40501874..0ce2f3b8 100644
--- a/problems/0704.二分查找.md
+++ b/problems/0704.二分查找.md
@@ -59,7 +59,7 @@
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
-
+
代码如下:(详细注释)
@@ -102,7 +102,7 @@ public:
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(**注意和方法一的区别**)
-
+
代码如下:(详细注释)
diff --git a/problems/0707.设计链表.md b/problems/0707.设计链表.md
index 7023bd90..a2b2803b 100644
--- a/problems/0707.设计链表.md
+++ b/problems/0707.设计链表.md
@@ -20,7 +20,7 @@
* deleteAtIndex(index):如果索引 index 有效,则删除链表中的第 index 个节点。
-
+
## 算法公开课
@@ -35,10 +35,10 @@
如果对链表的虚拟头结点不清楚,可以看这篇文章:[链表:听说用虚拟头节点会方便很多?](https://programmercarl.com/0203.移除链表元素.html)
删除链表节点:
-
+
添加链表节点:
-
+
这道题目设计链表的五个接口:
* 获取链表第index个节点的数值
diff --git a/problems/0718.最长重复子数组.md b/problems/0718.最长重复子数组.md
index 0e4b346d..b371bd85 100644
--- a/problems/0718.最长重复子数组.md
+++ b/problems/0718.最长重复子数组.md
@@ -95,7 +95,7 @@ for (int i = 1; i <= nums1.size(); i++) {
拿示例1中,A: [1,2,3,2,1],B: [3,2,1,4,7]为例,画一个dp数组的状态变化,如下:
-
+
以上五部曲分析完毕,C++代码如下:
@@ -127,7 +127,7 @@ public:
在如下图中:
-
+
我们可以看出dp[i][j]都是由dp[i - 1][j - 1]推出。那么压缩为一维数组,也就是dp[j]都是由dp[j - 1]推出。
diff --git a/problems/0739.每日温度.md b/problems/0739.每日温度.md
index 542aad29..ed43cf14 100644
--- a/problems/0739.每日温度.md
+++ b/problems/0739.每日温度.md
@@ -69,7 +69,7 @@
首先先将第一个遍历元素加入单调栈
-
+
---------
@@ -77,65 +77,65 @@
我们要保持一个递增单调栈(从栈头到栈底),所以将T[0]弹出,T[1]加入,此时result数组可以记录了,result[0] = 1,即T[0]右面第一个比T[0]大的元素是T[1]。
-
+
-----------
加入T[2],同理,T[1]弹出
-
+
-------
加入T[3],T[3] < T[2] (当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况),加T[3]加入单调栈。
-
+
---------
加入T[4],T[4] == T[3] (当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况),此时依然要加入栈,不用计算距离,因为我们要求的是右面第一个大于本元素的位置,而不是大于等于!
-
+
---------
加入T[5],T[5] > T[4] (当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),将T[4]弹出,同时计算距离,更新result
-
+
----------
T[4]弹出之后, T[5] > T[3] (当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况),将T[3]继续弹出,同时计算距离,更新result
-
+
-------
直到发现T[5]小于T[st.top()],终止弹出,将T[5]加入单调栈
-
+
-------
加入T[6],同理,需要将栈里的T[5],T[2]弹出
-
+
-------
同理,继续弹出
-
+
------
此时栈里只剩下了T[6]
-
+
------------
加入T[7], T[7] < T[6] 直接入栈,这就是最后的情况,result数组也更新完了。
-
+
此时有同学可能就疑惑了,那result[6] , result[7]怎么没更新啊,元素也一直在栈里。
diff --git a/problems/0743.网络延迟时间.md b/problems/0743.网络延迟时间.md
index 6533a240..c8a87361 100644
--- a/problems/0743.网络延迟时间.md
+++ b/problems/0743.网络延迟时间.md
@@ -13,7 +13,7 @@ https://leetcode.cn/problems/network-delay-time/description/
现在,从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1 。
-
+
提示:
@@ -42,7 +42,7 @@ dijkstra算法:在有权图(权值非负数)中求从起点到其他节点
如本题示例中的图:
-
+
起点(节点1)到终点(节点7) 的最短路径是 图中 标记绿线的部分。
@@ -88,7 +88,7 @@ minDist数组数值初始化为int最大值。
这里在强点一下 **minDist数组的含义:记录所有节点到源点的最短路径**,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。
-
+
(图中,max 表示默认值,节点0 不做处理,统一从下标1 开始计算,这样下标和节点数值统一, 方便大家理解,避免搞混)
@@ -110,7 +110,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
@@ -136,7 +136,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点6 、 节点3 和 节点4的距离。
@@ -170,7 +170,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
@@ -190,7 +190,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点4的加入,那么源点可以链接到节点5 所以更新minDist数组:
@@ -210,7 +210,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点6的加入,那么源点可以链接到节点7 所以 更新minDist数组:
@@ -230,7 +230,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点5的加入,那么源点有新的路径可以链接到节点7 所以 更新minDist数组:
@@ -248,7 +248,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
节点7加入,但节点7到节点7的距离为0,所以 不用更新minDist数组
@@ -262,7 +262,7 @@ minDist数组数值初始化为int最大值。
路径如图:
-
+
在上面的讲解中,每一步 我都是按照 dijkstra 三部曲来讲解的,理解了这三部曲,代码也就好懂的。
@@ -431,7 +431,7 @@ select:4
看一下这个图: (有负权值)
-
+
节点1 到 节点5 的最短路径 应该是 节点1 -> 节点2 -> 节点3 -> 节点4 -> 节点5
@@ -441,7 +441,7 @@ select:4
初始化:
-
+
---------------
@@ -455,7 +455,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
@@ -474,7 +474,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
@@ -492,7 +492,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点4的加入,那么源点可以有新的路径链接到节点5 所以更新minDist数组:
@@ -510,7 +510,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
节点5的加入,而节点5 没有链接其他节点, 所以不用更新minDist数组,仅标记节点5被访问过了
@@ -526,7 +526,7 @@ select:4
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
--------------
@@ -654,7 +654,7 @@ for (int v = 1; v <= n; v++) {
如图:
-
+
在一个 n (节点数)为8 的图中,就需要申请 8 * 8 这么大的空间,有一条双向边,即:grid[2][5] = 6,grid[5][2] = 6
@@ -678,7 +678,7 @@ for (int v = 1; v <= n; v++) {
邻接表的构造如图:
-
+
这里表达的图是:
@@ -763,7 +763,7 @@ vector> grid(n + 1);
不少录友,不知道 如何定义的数据结构,怎么表示邻接表的,我来给大家画一个图:
-
+
图中邻接表表示:
@@ -784,7 +784,7 @@ vector>> grid(n + 1);
举例来给大家展示 该代码表达的数据 如下:
-
+
* 节点1 指向 节点3 权值为 1
* 节点1 指向 节点5 权值为 2
@@ -907,7 +907,7 @@ for (int v = 1; v <= n; v++) {
再回顾一下邻接表的构造(数组 + 链表):
-
+
假如 加入的cur 是节点 2, 那么 grid[2] 表示的就是图中第二行链表。 (grid数组的构造我们在 上面 「图的存储」中讲过)
diff --git a/problems/0746.使用最小花费爬楼梯.md b/problems/0746.使用最小花费爬楼梯.md
index 9145c7ed..147c7bfb 100644
--- a/problems/0746.使用最小花费爬楼梯.md
+++ b/problems/0746.使用最小花费爬楼梯.md
@@ -52,7 +52,7 @@
请你计算并返回达到楼梯顶部的最低花费。
-
+
## 思路
@@ -112,7 +112,7 @@ dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
-
+
如果大家代码写出来有问题,就把dp数组打印出来,看看和如上推导的是不是一样的。
diff --git a/problems/0763.划分字母区间.md b/problems/0763.划分字母区间.md
index 70ebfe4f..daf52bea 100644
--- a/problems/0763.划分字母区间.md
+++ b/problems/0763.划分字母区间.md
@@ -44,7 +44,7 @@
如图:
-
+
明白原理之后,代码并不复杂,如下:
diff --git a/problems/0787.K站中转内最便宜的航班.md b/problems/0787.K站中转内最便宜的航班.md
index 68d84215..6133ac77 100644
--- a/problems/0787.K站中转内最便宜的航班.md
+++ b/problems/0787.K站中转内最便宜的航班.md
@@ -9,11 +9,11 @@
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到出一条最多经过 k 站中转的路线,使得从 src 到 dst 的 价格最便宜 ,并返回该价格。 如果不存在这样的路线,则输出 -1。
-
+
-
+
-
+
## 思路
diff --git a/problems/0797.所有可能的路径.md b/problems/0797.所有可能的路径.md
index a37e5c3f..639b6b2b 100644
--- a/problems/0797.所有可能的路径.md
+++ b/problems/0797.所有可能的路径.md
@@ -11,7 +11,7 @@
graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
-
+
提示:
@@ -96,7 +96,7 @@ path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
一些录友可以疑惑这里如果找到x 链接的节点的,例如如果x目前是节点0,那么目前的过程就是这样的:
-
+
二维数组中,graph[x][i] 都是x链接的节点,当前遍历的节点就是 `graph[x][i]` 。
diff --git a/problems/0827.最大人工岛.md b/problems/0827.最大人工岛.md
index 0ebda252..e6aa4601 100644
--- a/problems/0827.最大人工岛.md
+++ b/problems/0827.最大人工岛.md
@@ -51,11 +51,11 @@
拿如下地图的岛屿情况来举例: (1为陆地)
-
+
第一步,则遍历题目,并将岛屿到编号和面积上的统计,过程如图所示:
-
+
本过程代码如下:
@@ -102,7 +102,7 @@ int largestIsland(vector>& grid) {
第二步过程如图所示:
-
+
也就是遍历每一个0的方格,并统计其相邻岛屿面积,最后取一个最大值。
diff --git a/problems/0841.钥匙和房间.md b/problems/0841.钥匙和房间.md
index 4076fce5..60180d27 100644
--- a/problems/0841.钥匙和房间.md
+++ b/problems/0841.钥匙和房间.md
@@ -35,7 +35,7 @@
图中给我的两个示例: `[[1],[2],[3],[]]` `[[1,3],[3,0,1],[2],[0]]`,画成对应的图如下:
-
+
我们可以看出图1的所有节点都是链接的,而图二中,节点2 是孤立的。
@@ -48,7 +48,7 @@
图3:[[5], [], [1, 3], [5]] ,如图:
-
+
在图3中,大家可以发现,节点0只能到节点5,然后就哪也去不了了。
diff --git a/problems/0941.有效的山脉数组.md b/problems/0941.有效的山脉数组.md
index 383f6aa5..d4165f36 100644
--- a/problems/0941.有效的山脉数组.md
+++ b/problems/0941.有效的山脉数组.md
@@ -16,7 +16,7 @@
* arr[0] < arr[1] < ... arr[i-1] < arr[i]
* arr[i] > arr[i+1] > ... > arr[arr.length - 1]
-
+
示例 1:
* 输入:arr = [2,1]
diff --git a/problems/0968.监控二叉树.md b/problems/0968.监控二叉树.md
index 0df2cc5b..d8c31ca9 100644
--- a/problems/0968.监控二叉树.md
+++ b/problems/0968.监控二叉树.md
@@ -17,7 +17,7 @@
示例 1:
-
+
* 输入:[0,0,null,0,0]
* 输出:1
@@ -25,7 +25,7 @@
示例 2:
-
+
* 输入:[0,0,null,0,null,0,null,null,0]
* 输出:2
@@ -143,7 +143,7 @@ if (cur == NULL) return 2;
如图:
-
+
代码如下:
@@ -191,7 +191,7 @@ if (left == 1 || right == 1) return 2;
**从这个代码中,可以看出,如果left == 1, right == 0 怎么办?其实这种条件在情况2中已经判断过了**,如图:
-
+
这种情况也是大多数同学容易迷惑的情况。
@@ -199,7 +199,7 @@ if (left == 1 || right == 1) return 2;
以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况,如图:
-
+
所以递归结束之后,还要判断根节点,如果没有覆盖,result++,代码如下:
diff --git a/problems/1020.飞地的数量.md b/problems/1020.飞地的数量.md
index 030d56a0..ae6b3895 100644
--- a/problems/1020.飞地的数量.md
+++ b/problems/1020.飞地的数量.md
@@ -12,13 +12,13 @@
返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。
-
+
* 输入:grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
* 输出:3
* 解释:有三个 1 被 0 包围。一个 1 没有被包围,因为它在边界上。
-
+
* 输入:grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
* 输出:0
@@ -32,11 +32,11 @@
如图,在遍历地图周围四个边,靠地图四边的陆地,都为绿色,
-
+
在遇到地图周边陆地的时候,将1都变为0,此时地图为这样:
-
+
然后我们再去遍历这个地图,遇到有陆地的地方,去采用深搜或者广搜,边统计所有陆地。
diff --git a/problems/1035.不相交的线.md b/problems/1035.不相交的线.md
index 53e0f370..0119df82 100644
--- a/problems/1035.不相交的线.md
+++ b/problems/1035.不相交的线.md
@@ -18,7 +18,7 @@
以这种方法绘制线条,并返回可以绘制的最大连线数。
-
+
## 算法公开课
@@ -36,7 +36,7 @@
拿示例一nums1 = [1,4,2], nums2 = [1,2,4]为例,相交情况如图:
-
+
其实也就是说nums1和nums2的最长公共子序列是[1,4],长度为2。 这个公共子序列指的是相对顺序不变(即数字4在字符串nums1中数字1的后面,那么数字4也应该在字符串nums2数字1的后面)
diff --git a/problems/1049.最后一块石头的重量II.md b/problems/1049.最后一块石头的重量II.md
index 62e7d9c5..6dfba4ed 100644
--- a/problems/1049.最后一块石头的重量II.md
+++ b/problems/1049.最后一块石头的重量II.md
@@ -114,7 +114,7 @@ for (int i = 0; i < stones.size(); i++) { // 遍历物品
举例,输入:[2,4,1,1],此时target = (2 + 4 + 1 + 1)/2 = 4 ,dp数组状态图如下:
-
+
最后dp[target]里是容量为target的背包所能背的最大重量。
diff --git a/problems/1143.最长公共子序列.md b/problems/1143.最长公共子序列.md
index 821f3c42..91c29b83 100644
--- a/problems/1143.最长公共子序列.md
+++ b/problems/1143.最长公共子序列.md
@@ -94,7 +94,7 @@ vector> dp(text1.size() + 1, vector(text2.size() + 1, 0));
从递推公式,可以看出,有三个方向可以推出dp[i][j],如图:
-
+
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵。
@@ -103,7 +103,7 @@ vector> dp(text1.size() + 1, vector(text2.size() + 1, 0));
以输入:text1 = "abcde", text2 = "ace" 为例,dp状态如图:
-
+
最后红框dp[text1.size()][text2.size()]为最终结果
diff --git a/problems/1254.统计封闭岛屿的数目.md b/problems/1254.统计封闭岛屿的数目.md
index 5d996709..ebea30e3 100644
--- a/problems/1254.统计封闭岛屿的数目.md
+++ b/problems/1254.统计封闭岛屿的数目.md
@@ -10,13 +10,13 @@
请返回 封闭岛屿 的数目。
-
+
* 输入:grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
* 输出:2
* 解释:灰色区域的岛屿是封闭岛屿,因为这座岛屿完全被水域包围(即被 1 区域包围)。
-
+
* 输入:grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
* 输出:1
diff --git a/problems/1382.将二叉搜索树变平衡.md b/problems/1382.将二叉搜索树变平衡.md
index 7a1a7f3c..7b0d3204 100644
--- a/problems/1382.将二叉搜索树变平衡.md
+++ b/problems/1382.将二叉搜索树变平衡.md
@@ -15,7 +15,7 @@
示例:
-
+
* 输入:root = [1,null,2,null,3,null,4,null,null]
* 输出:[2,1,3,null,null,null,4]
diff --git a/problems/1791.找出星型图的中心节点.md b/problems/1791.找出星型图的中心节点.md
index e9ea5f44..5dd56c65 100644
--- a/problems/1791.找出星型图的中心节点.md
+++ b/problems/1791.找出星型图的中心节点.md
@@ -10,7 +10,7 @@
什么是度,可以理解为,链接节点的边的数量。 题目中度如图所示:
-
+
至于出度和入度,那就是在有向图里的概念了,本题是无向图。
diff --git a/problems/1971.寻找图中是否存在路径.md b/problems/1971.寻找图中是否存在路径.md
index acb54415..33b48698 100644
--- a/problems/1971.寻找图中是否存在路径.md
+++ b/problems/1971.寻找图中是否存在路径.md
@@ -12,7 +12,7 @@
给你数组 edges 和整数 n、start 和 end,如果从 start 到 end 存在 有效路径 ,则返回 true,否则返回 false 。
-
+
diff --git a/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md b/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
index 7276af53..830bba7e 100644
--- a/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
+++ b/problems/O(n)的算法居然超时了,此时的n究竟是多大?.md
@@ -13,7 +13,7 @@
## 超时是怎么回事
-
+
大家在leetcode上练习算法的时候应该都遇到过一种错误是“超时”。
@@ -129,11 +129,11 @@ int main() {
来看一下运行的效果,如下图:
-
+
O(n)的算法,1s内大概计算机可以运行 5 * (10^8)次计算,可以推测一下O(n^2) 的算法应该1s可以处理的数量级的规模是 5 * (10^8)开根号,实验数据如下。
-
+
O(n^2)的算法,1s内大概计算机可以运行 22500次计算,验证了刚刚的推测。
@@ -141,7 +141,7 @@ O(n^2)的算法,1s内大概计算机可以运行 22500次计算,验证了刚
理论上应该是比 O(n)少一个数量级,因为logn的复杂度 其实是很快,看一下实验数据。
-
+
O(nlogn)的算法,1s内大概计算机可以运行 2 * (10^7)次计算,符合预期。
@@ -149,7 +149,7 @@ O(nlogn)的算法,1s内大概计算机可以运行 2 * (10^7)次计算,符
**整体测试数据整理如下:**
-
+
至于O(log n)和O(n^3) 等等这些时间复杂度在1s内可以处理的多大的数据规模,大家可以自己写一写代码去测一下了。
diff --git a/problems/kamacoder/0047.参会dijkstra堆.md b/problems/kamacoder/0047.参会dijkstra堆.md
index 75c12f8a..e361e8e0 100644
--- a/problems/kamacoder/0047.参会dijkstra堆.md
+++ b/problems/kamacoder/0047.参会dijkstra堆.md
@@ -46,13 +46,13 @@
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
-
+
不能到达的情况:
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
-
+
数据范围:
@@ -101,7 +101,7 @@
如图:
-
+
在一个 n (节点数)为8 的图中,就需要申请 8 * 8 这么大的空间,有一条双向边,即:grid[2][5] = 6,grid[5][2] = 6
@@ -125,7 +125,7 @@
邻接表的构造如图:
-
+
这里表达的图是:
@@ -210,7 +210,7 @@ vector> grid(n + 1);
不少录友,不知道 如何定义的数据结构,怎么表示邻接表的,我来给大家画一个图:
-
+
图中邻接表表示:
@@ -231,7 +231,7 @@ vector>> grid(n + 1);
举例来给大家展示 该代码表达的数据 如下:
-
+
* 节点1 指向 节点3 权值为 1
* 节点1 指向 节点5 权值为 2
@@ -354,7 +354,7 @@ for (int v = 1; v <= n; v++) {
再回顾一下邻接表的构造(数组 + 链表):
-
+
假如 加入的cur 是节点 2, 那么 grid[2] 表示的就是图中第二行链表。 (grid数组的构造我们在 上面 「图的存储」中讲过)
diff --git a/problems/kamacoder/0047.参会dijkstra朴素.md b/problems/kamacoder/0047.参会dijkstra朴素.md
index e71e9d53..1ff9f1a8 100644
--- a/problems/kamacoder/0047.参会dijkstra朴素.md
+++ b/problems/kamacoder/0047.参会dijkstra朴素.md
@@ -46,13 +46,13 @@
如下图所示,起始车站为 1 号车站,终点车站为 7 号车站,绿色路线为最短的路线,路线总长度为 12,则输出 12。
-
+
不能到达的情况:
如下图所示,当从起始车站不能到达终点车站时,则输出 -1。
-
+
数据范围:
@@ -76,7 +76,7 @@ dijkstra算法:在有权图(权值非负数)中求从起点到其他节点
如本题示例中的图:
-
+
起点(节点1)到终点(节点7) 的最短路径是 图中 标记绿线的部分。
@@ -122,7 +122,7 @@ minDist数组数值初始化为int最大值。
这里在强点一下 **minDist数组的含义:记录所有节点到源点的最短路径**,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。
-
+
(图中,max 表示默认值,节点0 不做处理,统一从下标1 开始计算,这样下标和节点数值统一, 方便大家理解,避免搞混)
@@ -144,7 +144,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
@@ -170,7 +170,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点6 、 节点3 和 节点4的距离。
@@ -204,7 +204,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
@@ -224,7 +224,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点4的加入,那么源点可以链接到节点5 所以更新minDist数组:
@@ -244,7 +244,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点6的加入,那么源点可以链接到节点7 所以 更新minDist数组:
@@ -264,7 +264,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点5的加入,那么源点有新的路径可以链接到节点7 所以 更新minDist数组:
@@ -282,7 +282,7 @@ minDist数组数值初始化为int最大值。
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
节点7加入,但节点7到节点7的距离为0,所以 不用更新minDist数组
@@ -296,7 +296,7 @@ minDist数组数值初始化为int最大值。
路径如图:
-
+
在上面的讲解中,每一步 我都是按照 dijkstra 三部曲来讲解的,理解了这三部曲,代码也就好懂的。
@@ -541,7 +541,7 @@ int main() {
对应如图:
-
+
### 出现负数
@@ -549,7 +549,7 @@ int main() {
看一下这个图: (有负权值)
-
+
节点1 到 节点5 的最短路径 应该是 节点1 -> 节点2 -> 节点3 -> 节点4 -> 节点5
@@ -559,7 +559,7 @@ int main() {
初始化:
-
+
---------------
@@ -573,7 +573,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
@@ -592,7 +592,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点3的加入,那么源点可以有新的路径链接到节点4 所以更新minDist数组:
@@ -610,7 +610,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
由于节点4的加入,那么源点可以有新的路径链接到节点5 所以更新minDist数组:
@@ -628,7 +628,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
节点5的加入,而节点5 没有链接其他节点, 所以不用更新minDist数组,仅标记节点5被访问过了
@@ -644,7 +644,7 @@ int main() {
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:
-
+
--------------
diff --git a/problems/kamacoder/0053.寻宝-Kruskal.md b/problems/kamacoder/0053.寻宝-Kruskal.md
index 861efe68..585fa476 100644
--- a/problems/kamacoder/0053.寻宝-Kruskal.md
+++ b/problems/kamacoder/0053.寻宝-Kruskal.md
@@ -63,7 +63,7 @@ kruscal的思路:
依然以示例中,如下这个图来举例。
-
+
将图中的边按照权值有小到大排序,这样从贪心的角度来说,优先选 权值小的边加入到 最小生成树中。
@@ -77,13 +77,13 @@ kruscal的思路:
选边(1,2),节点1 和 节点2 不在同一个集合,所以生成树可以添加边(1,2),并将 节点1,节点2 放在同一个集合。
-
+
--------
选边(4,5),节点4 和 节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5 放到同一个集合。
-
+
**大家判断两个节点是否在同一个集合,就看图中两个节点是否有绿色的粗线连着就行**
@@ -93,25 +93,25 @@ kruscal的思路:
选边(1,3),节点1 和 节点3 不在同一个集合,生成树添加边(1,3),并将节点1,节点3 放到同一个集合。
-
+
---------
选边(2,6),节点2 和 节点6 不在同一个集合,生成树添加边(2,6),并将节点2,节点6 放到同一个集合。
-
+
--------
选边(3,4),节点3 和 节点4 不在同一个集合,生成树添加边(3,4),并将节点3,节点4 放到同一个集合。
-
+
----------
选边(6,7),节点6 和 节点7 不在同一个集合,生成树添加边(6,7),并将 节点6,节点7 放到同一个集合。
-
+
-----------
@@ -126,7 +126,7 @@ kruscal的思路:
此时 我们就已经生成了一个最小生成树,即:
-
+
在上面的讲解中,看图的话 大家知道如何判断 两个节点 是否在同一个集合(是否有绿色的线连在一起),以及如何把两个节点加入集合(就在图中把两个节点连上)
@@ -346,7 +346,7 @@ int main() {
大家可能发现 怎么和我们 模拟画的图不一样,差别在于 代码生成的最小生成树中 节点5 和 节点7相连的。
-
+
其实造成这个差别 是对边排序的时候 权值相同的边先后顺序的问题导致的,无论相同权值边的顺序是什么样的,最后都能得出最小生成树。
@@ -366,7 +366,7 @@ Kruskal 与 prim 的关键区别在于,prim维护的是节点的集合,而 K
节点未必一定要连着边那, 例如 这个图,大家能明显感受到边没有那么多对吧,但节点数量 和 上述我们讲的例子是一样的。
-
+
为什么边少的话,使用 Kruskal 更优呢?
diff --git a/problems/kamacoder/0053.寻宝-prim.md b/problems/kamacoder/0053.寻宝-prim.md
index 8e26bea4..a7d35841 100644
--- a/problems/kamacoder/0053.寻宝-prim.md
+++ b/problems/kamacoder/0053.寻宝-prim.md
@@ -61,7 +61,7 @@
例如本题示例中的无向有权图为:
-
+
那么在这个图中,如何选取n-1条边使得图中所有节点连接到一起,并且边的权值和最小呢?
@@ -100,7 +100,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
如图:
-
+
开始构造最小生成树
@@ -118,7 +118,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
接下来,我们要更新所有节点距离最小生成树的距离,如图:
-
+
注意下标0,我们就不管它了,下标1与节点1对应,这样可以避免大家把节点搞混。
@@ -148,7 +148,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
接下来,我们要更新节点距离最小生成树的距离,如图:
-
+
此时所有非生成树的节点距离最小生成树(节点1、节点2)的距离都已经跟新了。
@@ -172,7 +172,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
接下来更新节点距离最小生成树的距离,如图:
-
+
所有非生成树的节点距离最小生成树(节点1、节点2、节点3)的距离都已经跟新了。
@@ -188,7 +188,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
继续选择一个距离最小生成树(节点1、节点2、节点3)最近的非生成树里的节点,为了巩固大家对minDist数组的理解,这里我再啰嗦一遍:
-
+
**minDist数组是记录了所有非生成树节点距离生成树的最小距离**,所以从数组里我们能看出来,非生成树节点4和节点6距离生成树最近。
@@ -209,7 +209,7 @@ minDist数组里的数值初始化为最大数,因为本题节点距离不会
接下来更新节点距离最小生成树的距离,如图:
-
+
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4)的距离。
@@ -232,7 +232,7 @@ minDist数组已经更新了所有非生成树的节点距离最小生成树(
接下来更新节点距离最小生成树的距离,如图:
-
+
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4、节点5)的距离。
@@ -253,11 +253,11 @@ minDist数组已经更新了所有非生成树的节点距离最小生成树(
节点1、节点2、节点3、节点4、节点5、节点6算是最小生成树的节点,接下来更新节点距离最小生成树的距离,如图:
-
+
这里就不在重复描述了,大家类推,最后,节点7加入生成树,如图:
-
+
### 最后
@@ -478,7 +478,7 @@ int main() {
大家可以和我们本题最后生成的最小生成树的图去对比一下边的链接情况:
-
+
绿色的边是最小生成树,和我们的输出完全一致。
diff --git a/problems/kamacoder/0054.替换数字.md b/problems/kamacoder/0054.替换数字.md
index f788d65b..665e8ecb 100644
--- a/problems/kamacoder/0054.替换数字.md
+++ b/problems/kamacoder/0054.替换数字.md
@@ -29,11 +29,11 @@
如图:
-
+
然后从后向前替换数字字符,也就是双指针法,过程如下:i指向新长度的末尾,j指向旧长度的末尾。
-
+
有同学问了,为什么要从后向前填充,从前向后填充不行么?
diff --git a/problems/kamacoder/0055.右旋字符串.md b/problems/kamacoder/0055.右旋字符串.md
index 2b32cb44..48150222 100644
--- a/problems/kamacoder/0055.右旋字符串.md
+++ b/problems/kamacoder/0055.右旋字符串.md
@@ -40,16 +40,16 @@ fgabcde
本题中,我们需要将字符串右移n位,字符串相当于分成了两个部分,如果n为2,符串相当于分成了两个部分,如图: (length为字符串长度)
-
+
右移n位, 就是将第二段放在前面,第一段放在后面,先不考虑里面字符的顺序,是不是整体倒叙不就行了。如图:
-
+
此时第一段和第二段的顺序是我们想要的,但里面的字符位置被我们倒叙,那么此时我们在把 第一段和第二段里面的字符再倒叙一把,这样字符顺序不就正确了。 如果:
-
+
其实,思路就是 通过 整体倒叙,把两段子串顺序颠倒,两个段子串里的的字符在倒叙一把,**负负得正**,这样就不影响子串里面字符的顺序了。
@@ -80,7 +80,7 @@ int main() {
可以的,不过,要记得 控制好 局部反转的长度,如果先局部反转,那么先反转的子串长度就是 len - n,如图:
-
+
代码如下:
diff --git a/problems/kamacoder/0058.区间和.md b/problems/kamacoder/0058.区间和.md
index 23e7189a..a6342ef8 100644
--- a/problems/kamacoder/0058.区间和.md
+++ b/problems/kamacoder/0058.区间和.md
@@ -93,7 +93,7 @@ int main() {
如图:
-
+
如果,我们想统计,在vec数组上 下标 2 到下标 5 之间的累加和,那是不是就用 p[5] - p[1] 就可以了。
@@ -109,7 +109,7 @@ int main() {
如图所示:
-
+
`p[5] - p[1]` 就是 红色部分的区间和。
diff --git a/problems/kamacoder/0094.城市间货物运输I-SPFA.md b/problems/kamacoder/0094.城市间货物运输I-SPFA.md
index 99986aaa..b5920292 100644
--- a/problems/kamacoder/0094.城市间货物运输I-SPFA.md
+++ b/problems/kamacoder/0094.城市间货物运输I-SPFA.md
@@ -62,7 +62,7 @@
给大家举一个例子:
-
+
本图中,对所有边进行松弛,真正有效的松弛,只有松弛 边(节点1->节点2) 和 边(节点1->节点3) 。
@@ -97,7 +97,7 @@
初始化,起点为节点1, 起点到起点的最短距离为0,所以minDist[1] 为 0。 将节点1 加入队列 (下次松弛从节点1开始)
-
+
------------
@@ -109,7 +109,7 @@
将节点2、节点3 加入队列,如图:
-
+
-----------------
@@ -124,7 +124,7 @@
将节点4,节点5 加入队列,如图:
-
+
--------------------
@@ -134,7 +134,7 @@
因为没有从节点3作为出发点的边,所以这里就从队列里取出节点3就好,不用做其他操作,如图:
-
+
------------
@@ -147,7 +147,7 @@
如图:
-
+
---------------
@@ -160,7 +160,7 @@
如图,将节点3加入队列,因为节点6已经在队列里,所以不用重复添加
-
+
所以我们在加入队列的过程可以有一个优化,**用visited数组记录已经在队列里的元素,已经在队列的元素不用重复加入**
@@ -174,7 +174,7 @@
所以直接从队列中取出,如图:
-
+
----------
@@ -264,7 +264,7 @@ int main() {
至于为什么 双向图且每一个节点和所有其他节点都相连的话,每个节点 都有 n-1 条指向该节点的边, 我再来举个例子,如图:
-[](https://code-thinking-1253855093.file.myqcloud.com/pics/20240416104138.png)
+[](https://file.kamacoder.com/pics/20240416104138.png)
图中 每个节点都与其他所有节点相连,节点数n 为 4,每个节点都有3条指向该节点的边,即入度为3。
@@ -329,7 +329,7 @@ SPFA(队列优化版Bellman_ford) 在理论上 时间复杂度更胜一筹
如图:
-
+
正权回路 就是有环,但环的总权值为正数。
diff --git a/problems/kamacoder/0094.城市间货物运输I.md b/problems/kamacoder/0094.城市间货物运输I.md
index 2afc014b..9edde8ac 100644
--- a/problems/kamacoder/0094.城市间货物运输I.md
+++ b/problems/kamacoder/0094.城市间货物运输I.md
@@ -46,7 +46,7 @@
1 3 5
```
-
+
## 思路
@@ -78,7 +78,7 @@
这里我给大家举一个例子,每条边有起点、终点和边的权值。例如一条边,节点A 到 节点B 权值为value,如图:
-
+
minDist[B] 表示 到达B节点 最小权值,minDist[B] 有哪些状态可以推出来?
@@ -127,7 +127,7 @@ if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
如图:
-
+
其他节点对应的minDist初始化为max,因为我们要求最小距离,那么还没有计算过的节点 默认是一个最大数,这样才能更新最小距离。
@@ -150,36 +150,36 @@ if (minDist[B] > minDist[A] + value) minDist[B] = minDist[A] + value
边:节点5 -> 节点6,权值为-2 ,minDist[5] 还是默认数值max,所以不能基于 节点5 去更新节点6,如图:
-
+
(在复习一下,minDist[5] 表示起点到节点5的最短距离)
边:节点1 -> 节点2,权值为1 ,minDist[2] > minDist[1] + 1 ,更新 minDist[2] = minDist[1] + 1 = 0 + 1 = 1 ,如图:
-
+
边:节点5 -> 节点3,权值为1 ,minDist[5] 还是默认数值max,所以不能基于节点5去更新节点3 如图:
-
+
边:节点2 -> 节点5,权值为2 ,minDist[5] > minDist[2] + 2 (经过上面的计算minDist[2]已经不是默认值,而是 1),更新 minDist[5] = minDist[2] + 2 = 1 + 2 = 3 ,如图:
-
+
边:节点2 -> 节点4,权值为-3 ,minDist[4] > minDist[2] + (-3),更新 minDist[4] = minDist[2] + (-3) = 1 + (-3) = -2 ,如图:
-
+
边:节点4 -> 节点6,权值为4 ,minDist[6] > minDist[4] + 4,更新 minDist[6] = minDist[4] + 4 = -2 + 4 = 2
-
+
边:节点1 -> 节点3,权值为5 ,minDist[3] > minDist[1] + 5,更新 minDist[3] = minDist[1] + 5 = 0 + 5 = 5 ,如图:
-
+
--------
diff --git a/problems/kamacoder/0095.城市间货物运输II.md b/problems/kamacoder/0095.城市间货物运输II.md
index a3896b88..5dddf450 100644
--- a/problems/kamacoder/0095.城市间货物运输II.md
+++ b/problems/kamacoder/0095.城市间货物运输II.md
@@ -78,7 +78,7 @@ circle
我们拿题目中示例来画一个图:
-
+
图中 节点1 到 节点4 的最短路径是多少(题目中的最低运输成本) (注意边可以为负数的)
@@ -86,7 +86,7 @@ circle
而图中有负权回路:
-
+
那么我们在负权回路中多绕一圈,我们的最短路径 是不是就更小了 (也就是更低的运输成本)
diff --git a/problems/kamacoder/0096.城市间货物运输III.md b/problems/kamacoder/0096.城市间货物运输III.md
index eb80e048..37cfaee0 100644
--- a/problems/kamacoder/0096.城市间货物运输III.md
+++ b/problems/kamacoder/0096.城市间货物运输III.md
@@ -63,7 +63,7 @@
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
-
+
图中,节点1 最多已经经过2个节点 到达节点4,那么中间是有多少条边呢,是 3 条边对吧。
@@ -195,7 +195,7 @@ int main() {
起点为节点1, 起点到起点的距离为0,所以 minDist[1] 初始化为0 ,如图:
-
+
其他节点对应的minDist初始化为max,因为我们要求最小距离,那么还没有计算过的节点 默认是一个最大数,这样才能更新最小距离。
@@ -203,21 +203,21 @@ int main() {
边:节点1 -> 节点2,权值为-1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = minDist[1] + (-1) = 0 - 1 = -1 ,如图:
-
+
边:节点2 -> 节点3,权值为1 ,minDist[3] > minDist[2] + 1 ,更新 minDist[3] = minDist[2] + 1 = -1 + 1 = 0 ,如图:
-
+
边:节点3 -> 节点1,权值为-1 ,minDist[1] > minDist[3] + (-1),更新 minDist[1] = 0 + (-1) = -1 ,如图:
-
+
边:节点3 -> 节点4,权值为1 ,minDist[4] > minDist[3] + 1,更新 minDist[4] = 0 + 1 = 1 ,如图:
-
+
以上是对所有边进行的第一次松弛,最后 minDist数组为 :-1 -1 0 1 ,(从下标1算起)
@@ -244,7 +244,7 @@ int main() {
在上面画图距离中,对所有边进行第一次松弛,在计算 边(节点2 -> 节点3) 的时候,更新了 节点3。
-
+
理论上来说节点3 应该在对所有边第二次松弛的时候才更新。 这因为当时是基于已经计算好的 节点2(minDist[2])来做计算了。
@@ -331,11 +331,11 @@ int main() {
所构成是图是一样的,都是如下的这个图,但给出的边的顺序是不一样的。
-
+
再用版本一的代码是运行一下,发现结果输出是 1, 是对的。
-
+
分明刚刚输出的结果是 -2,是错误的,怎么 一样的图,这次输出的结果就对了呢?
@@ -345,7 +345,7 @@ int main() {
初始化:
-
+
边:节点3 -> 节点1,权值为-1 ,节点3还没有被计算过,节点1 不更新。
@@ -355,7 +355,7 @@ int main() {
边:节点1 -> 节点2,权值为 -1 ,minDist[2] > minDist[1] + (-1),更新 minDist[2] = 0 + (-1) = -1 ,如图:
-
+
以上是对所有边 松弛一次的状态。
@@ -472,7 +472,7 @@ int main() {
但大家会发现,以上代码大家提交后,怎么耗时这么多?
-
+
理论上,SPFA的时间复杂度不是要比 bellman_ford 更优吗?
@@ -554,7 +554,7 @@ int main() {
以上代码提交后,耗时情况:
-
+
大家发现 依然远比 bellman_ford 的代码版本 耗时高。
@@ -579,11 +579,11 @@ dijkstra 是贪心的思路 每一次搜索都只会找距离源点最近的非
在以下这个图中,求节点1 到 节点7 最多经过2个节点 的最短路是多少呢?
-
+
最短路显然是:
-
+
最多经过2个节点,也就是3条边相连的路线:节点1 -> 节点2 -> 节点6-> 节点7
@@ -591,24 +591,24 @@ dijkstra 是贪心的思路 每一次搜索都只会找距离源点最近的非
初始化如图所示:
-
+
找距离源点最近且没有被访问过的节点,先找节点1
-
+
距离源点最近且没有被访问过的节点,找节点2:
-
+
距离源点最近且没有被访问过的节点,找到节点3:
-
+
距离源点最近且没有被访问过的节点,找到节点4:
-
+
此时最多经过2个节点的搜索就完毕了,但结果中minDist[7] (即节点7的结果)并没有被更。
diff --git a/problems/kamacoder/0097.小明逛公园.md b/problems/kamacoder/0097.小明逛公园.md
index dfbd6aa9..97765ebc 100644
--- a/problems/kamacoder/0097.小明逛公园.md
+++ b/problems/kamacoder/0097.小明逛公园.md
@@ -155,7 +155,7 @@ grid[i][j][k] = m,表示 节点i 到 节点j 以[1...k] 集合为中间节点
grid数组是一个三维数组,那么我们初始化的数据在 i 与 j 构成的平层,如图:
-
+
红色的 底部一层是我们初始化好的数据,注意:从三维角度去看初始化的数据很重要,下面我们在聊遍历顺序的时候还会再讲。
@@ -202,7 +202,7 @@ vector>> grid(n + 1, vector>(n + 1, vector(n
所以遍历k 的for循环一定是在最外面,这样才能一层一层去遍历。如图:
-
+
至于遍历 i 和 j 的话,for 循环的先后顺序无所谓。
@@ -234,7 +234,7 @@ for (int i = 1; i <= n; i++) {
此时就遍历了 j 与 k 形成一个平面,i 则是纵面,那遍历 就是这样的:
-
+
而我们初始化的数据 是 k 为0, i 和 j 形成的平面做初始化,如果以 k 和 j 形成的平面去一层一层遍历,就造成了 递推公式 用不上上一轮计算的结果,从而导致结果不对(初始化的部分是 i 与j 形成的平面,在初始部分有讲过)。
@@ -253,7 +253,7 @@ for (int i = 1; i <= n; i++) {
就是图:
-
+
求节点1 到 节点 2 的最短距离,运行结果是 10 ,但正确的结果很明显是3。
@@ -267,7 +267,7 @@ for (int i = 1; i <= n; i++) {
而遍历k 的for循环如果放在中间呢,同样是 j 与k 行程一个平面,i 是纵面,遍历的也是这样:
-
+
同样不能完全用上初始化 和 上一层计算的结果。
@@ -283,7 +283,7 @@ for (int i = 1; i <= n; i++) {
图:
-
+
求 节点1 到节点3 的最短距离,如果k循环放中间,程序的运行结果是 -1,也就是不能到达节点3。
diff --git a/problems/kamacoder/0098.所有可达路径.md b/problems/kamacoder/0098.所有可达路径.md
index 4df53b44..2f0dcdcc 100644
--- a/problems/kamacoder/0098.所有可达路径.md
+++ b/problems/kamacoder/0098.所有可达路径.md
@@ -43,7 +43,7 @@
提示信息
-
+
用例解释:
@@ -141,7 +141,7 @@ while (m--) {
我在 [图论理论基础篇](./图论理论基础.md) 举了一个例子:
-
+
这里表达的图是:
diff --git a/problems/kamacoder/0099.岛屿的数量广搜.md b/problems/kamacoder/0099.岛屿的数量广搜.md
index f8c36a00..0da2f315 100644
--- a/problems/kamacoder/0099.岛屿的数量广搜.md
+++ b/problems/kamacoder/0099.岛屿的数量广搜.md
@@ -35,7 +35,7 @@
提示信息
-
+
根据测试案例中所展示,岛屿数量共有 3 个,所以输出 3。
@@ -50,7 +50,7 @@
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
-
+
这道题题目是 DFS,BFS,并查集,基础题目。
@@ -72,7 +72,7 @@
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。
-
+
超时写法 (从队列中取出节点再标记,注意代码注释的地方)
diff --git a/problems/kamacoder/0099.岛屿的数量深搜.md b/problems/kamacoder/0099.岛屿的数量深搜.md
index 5a21f387..06be9268 100644
--- a/problems/kamacoder/0099.岛屿的数量深搜.md
+++ b/problems/kamacoder/0099.岛屿的数量深搜.md
@@ -36,7 +36,7 @@
提示信息
-
+
根据测试案例中所展示,岛屿数量共有 3 个,所以输出 3。
@@ -50,7 +50,7 @@
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
-
+
这道题题目是 DFS,BFS,并查集,基础题目。
diff --git a/problems/kamacoder/0100.岛屿的最大面积.md b/problems/kamacoder/0100.岛屿的最大面积.md
index 170c0917..f2b9b901 100644
--- a/problems/kamacoder/0100.岛屿的最大面积.md
+++ b/problems/kamacoder/0100.岛屿的最大面积.md
@@ -33,7 +33,7 @@
提示信息
-
+
样例输入中,岛屿的最大面积为 4。
@@ -48,7 +48,7 @@
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
-
+
这道题目也是 dfs bfs基础类题目,就是搜索每个岛屿上“1”的数量,然后取一个最大的。
diff --git a/problems/kamacoder/0101.孤岛的总面积.md b/problems/kamacoder/0101.孤岛的总面积.md
index 43ac8ec9..c8fe372c 100644
--- a/problems/kamacoder/0101.孤岛的总面积.md
+++ b/problems/kamacoder/0101.孤岛的总面积.md
@@ -37,7 +37,7 @@
提示信息:
-
+
在矩阵中心部分的岛屿,因为没有任何一个单元格接触到矩阵边缘,所以该岛屿属于孤岛,总面积为 1。
@@ -54,11 +54,11 @@
如图,在遍历地图周围四个边,靠地图四边的陆地,都为绿色,
-
+
在遇到地图周边陆地的时候,将1都变为0,此时地图为这样:
-
+
然后我们再去遍历这个地图,遇到有陆地的地方,去采用深搜或者广搜,边统计所有陆地。
diff --git a/problems/kamacoder/0102.沉没孤岛.md b/problems/kamacoder/0102.沉没孤岛.md
index 5e211cd0..265ec31f 100644
--- a/problems/kamacoder/0102.沉没孤岛.md
+++ b/problems/kamacoder/0102.沉没孤岛.md
@@ -43,11 +43,11 @@
提示信息:
-
+
将孤岛沉没:
-
+
数据范围:
@@ -73,7 +73,7 @@
如图:
-
+
整体C++代码如下,以下使用dfs实现,其实遍历方式dfs,bfs都是可以的。
diff --git a/problems/kamacoder/0103.水流问题.md b/problems/kamacoder/0103.水流问题.md
index 1c646b1c..5924cb18 100644
--- a/problems/kamacoder/0103.水流问题.md
+++ b/problems/kamacoder/0103.水流问题.md
@@ -48,7 +48,7 @@
提示信息:
-
+
图中的蓝色方块上的雨水既能流向第一组边界,也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。
@@ -166,11 +166,11 @@ int main() {
从第一组边界边上节点出发,如图: (图中并没有把所有遍历的方向都画出来,只画关键部分)
-
+
从第二组边界上节点出发,如图: (图中并没有把所有遍历的方向都画出来,只画关键部分)
-
+
最后,我们得到两个方向交界的这些节点,就是我们最后要求的节点。
diff --git a/problems/kamacoder/0104.建造最大岛屿.md b/problems/kamacoder/0104.建造最大岛屿.md
index 5f091779..483d7772 100644
--- a/problems/kamacoder/0104.建造最大岛屿.md
+++ b/problems/kamacoder/0104.建造最大岛屿.md
@@ -35,12 +35,12 @@
提示信息
-
+
对于上面的案例,有两个位置可将 0 变成 1,使得岛屿的面积最大,即 6。
-
+
数据范围:
@@ -70,11 +70,11 @@
拿如下地图的岛屿情况来举例: (1为陆地)
-
+
第一步,则遍历地图,并将岛屿的编号和面积都统计好,过程如图所示:
-
+
本过程代码如下:
@@ -121,7 +121,7 @@ int largestIsland(vector>& grid) {
第二步过程如图所示:
-
+
也就是遍历每一个0的方格,并统计其相邻岛屿面积,最后取一个最大值。
diff --git a/problems/kamacoder/0105.有向图的完全可达性.md b/problems/kamacoder/0105.有向图的完全可达性.md
index 6901c655..cfe77c0d 100644
--- a/problems/kamacoder/0105.有向图的完全可达性.md
+++ b/problems/kamacoder/0105.有向图的完全可达性.md
@@ -33,7 +33,7 @@
【提示信息】
-
+
从 1 号节点可以到达任意节点,输出 1。
@@ -48,7 +48,7 @@
接下来我们再画一个图,从图里可以直观看出来,节点6 是 不能到达节点1 的
-
+
这就很容易让我们想起岛屿问题,只要发现独立的岛,就是不可到达的。
diff --git a/problems/kamacoder/0106.岛屿的周长.md b/problems/kamacoder/0106.岛屿的周长.md
index 91a1a438..a1ef2a76 100644
--- a/problems/kamacoder/0106.岛屿的周长.md
+++ b/problems/kamacoder/0106.岛屿的周长.md
@@ -37,7 +37,7 @@
提示信息
-
+
岛屿的周长为 14。
@@ -57,14 +57,14 @@
如果该陆地上下左右的空格是有水域,则说明是一条边,如图:
-
+
陆地的右边空格是水域,则说明找到一条边。
如果该陆地上下左右的空格出界了,则说明是一条边,如图:
-
+
该陆地的下边空格出界了,则说明找到一条边。
@@ -114,7 +114,7 @@ int main() {
因为有一对相邻两个陆地,边的总数就要减2,如图红线部分,有两个陆地相邻,总边数就要减2
-
+
那么只需要在计算出相邻岛屿的数量就可以了,相邻岛屿数量为cover。
diff --git a/problems/kamacoder/0107.寻找存在的路径.md b/problems/kamacoder/0107.寻找存在的路径.md
index 779907c8..363a1884 100644
--- a/problems/kamacoder/0107.寻找存在的路径.md
+++ b/problems/kamacoder/0107.寻找存在的路径.md
@@ -40,7 +40,7 @@
提示信息
-
+
数据范围:
diff --git a/problems/kamacoder/0108.冗余连接.md b/problems/kamacoder/0108.冗余连接.md
index ae247ac0..fe641f53 100644
--- a/problems/kamacoder/0108.冗余连接.md
+++ b/problems/kamacoder/0108.冗余连接.md
@@ -9,11 +9,11 @@
有一个图,它是一棵树,他是拥有 n 个节点(节点编号1到n)和 n - 1 条边的连通无环无向图(其实就是一个线形图),如图:
-
+
现在在这棵树上的基础上,添加一条边(依然是n个节点,但有n条边),使这个图变成了有环图,如图
-
+
先请你找出冗余边,删除后,使该图可以重新变成一棵树。
@@ -42,7 +42,7 @@
提示信息
-
+
图中的 1 2,2 3,1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输入里最后出现的那条边,所以输出结果为 1 3
@@ -69,13 +69,13 @@
如图所示,节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
-
+
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
如图所示:
-
+
已经判断 节点A 和 节点B 在在同一个集合(同一个根),如果将 节点A 和 节点B 连在一起就一定会出现环。
@@ -157,7 +157,7 @@ int main() {
图:
-
+
输出示例
diff --git a/problems/kamacoder/0109.冗余连接II.md b/problems/kamacoder/0109.冗余连接II.md
index 070bc685..78132a32 100644
--- a/problems/kamacoder/0109.冗余连接II.md
+++ b/problems/kamacoder/0109.冗余连接II.md
@@ -9,11 +9,11 @@
有一种有向树,该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图:
-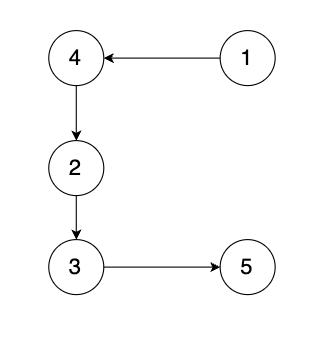 +
+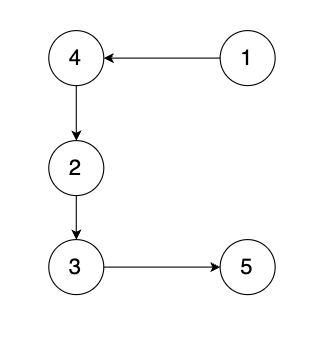 现在有一个有向图,有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图:
-
现在有一个有向图,有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图:
-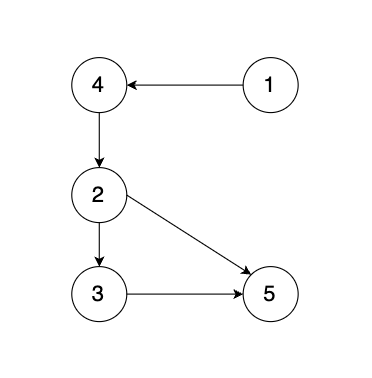 +
+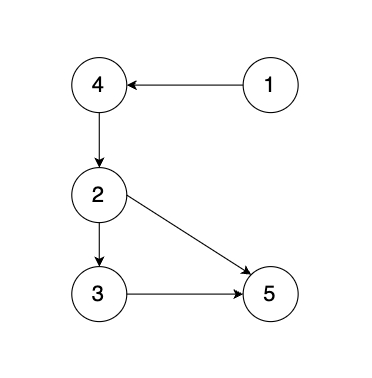 输入一个有向图,该图由一个有着 n 个节点(节点编号 从 1 到 n),n 条边,请返回一条可以删除的边,使得删除该条边之后该有向图可以被当作一颗有向树。
@@ -42,7 +42,7 @@
提示信息
-
输入一个有向图,该图由一个有着 n 个节点(节点编号 从 1 到 n),n 条边,请返回一条可以删除的边,使得删除该条边之后该有向图可以被当作一颗有向树。
@@ -42,7 +42,7 @@
提示信息
-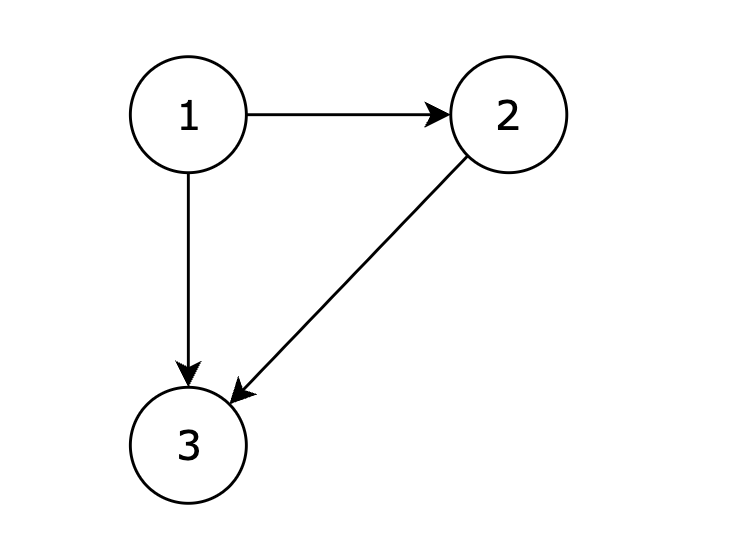 +
+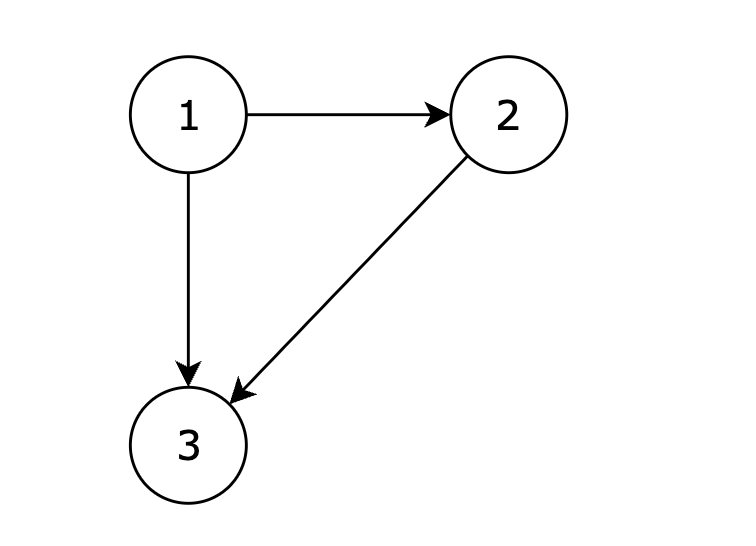 在删除 2 3 后有向图可以变为一棵合法的有向树,所以输出 2 3
@@ -64,13 +64,13 @@
如图:
-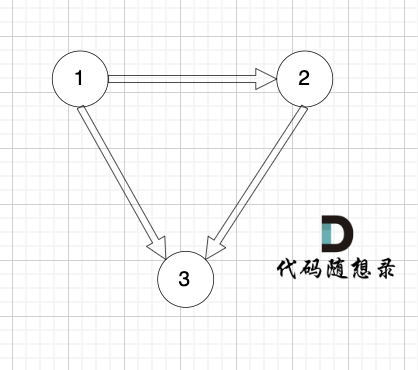
+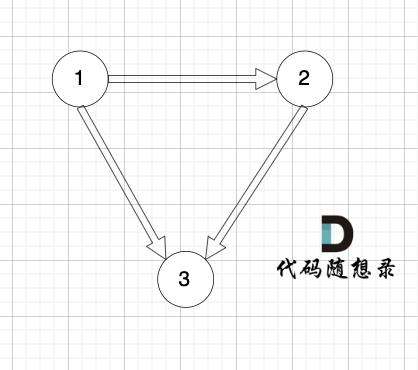
找到了节点3 的入度为2,删 1 -> 3 或者 2 -> 3 。选择删顺序靠后便可。
但 入度为2 还有一种情况,情况二,只能删特定的一条边,如图:
-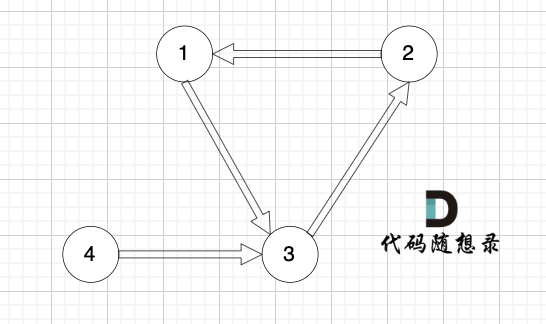
+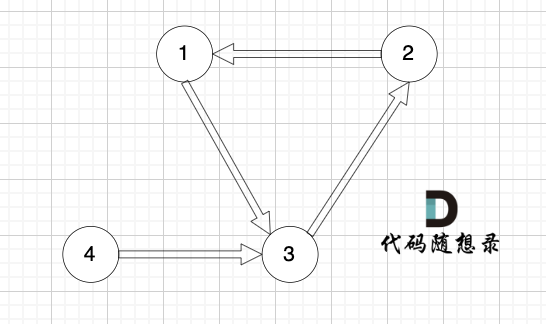
节点3 的入度为 2,但在删除边的时候,只能删 这条边(节点1 -> 节点3),如果删这条边(节点4 -> 节点3),那么删后本图也不是有向树了(因为找不到根节点)。
@@ -81,7 +81,7 @@
如图:
-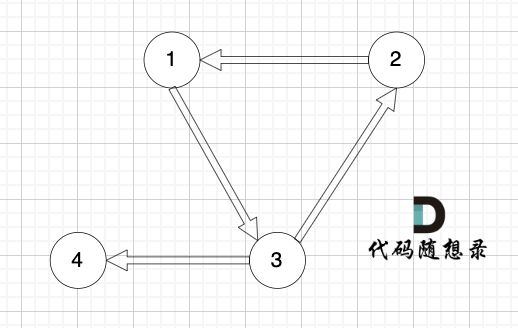
+
对于情况三,删掉构成环的边就可以了。
diff --git a/problems/kamacoder/0110.字符串接龙.md b/problems/kamacoder/0110.字符串接龙.md
index 8bae6280..af343690 100644
--- a/problems/kamacoder/0110.字符串接龙.md
+++ b/problems/kamacoder/0110.字符串接龙.md
@@ -57,7 +57,7 @@ yhn
2 <= N <= 500
在删除 2 3 后有向图可以变为一棵合法的有向树,所以输出 2 3
@@ -64,13 +64,13 @@
如图:
-
+
找到了节点3 的入度为2,删 1 -> 3 或者 2 -> 3 。选择删顺序靠后便可。
但 入度为2 还有一种情况,情况二,只能删特定的一条边,如图:
-
+
节点3 的入度为 2,但在删除边的时候,只能删 这条边(节点1 -> 节点3),如果删这条边(节点4 -> 节点3),那么删后本图也不是有向树了(因为找不到根节点)。
@@ -81,7 +81,7 @@
如图:
-
+
对于情况三,删掉构成环的边就可以了。
diff --git a/problems/kamacoder/0110.字符串接龙.md b/problems/kamacoder/0110.字符串接龙.md
index 8bae6280..af343690 100644
--- a/problems/kamacoder/0110.字符串接龙.md
+++ b/problems/kamacoder/0110.字符串接龙.md
@@ -57,7 +57,7 @@ yhn
2 <= N <= 500
-  +
+ 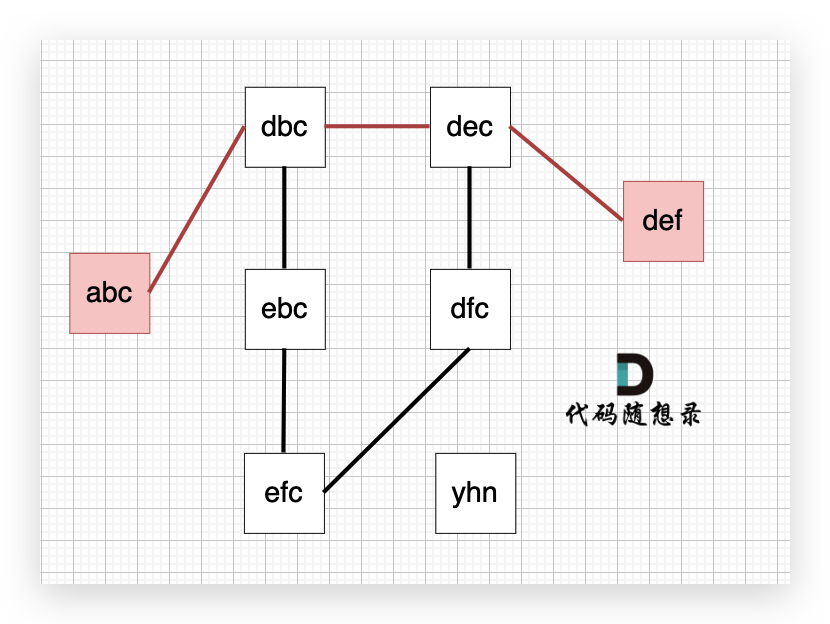
@@ -65,7 +65,7 @@ yhn
以示例1为例,从这个图中可以看出 abc 到 def的路线 不止一条,但最短的一条路径上是4个节点。
-
+
本题只需要求出最短路径的长度就可以了,不用找出具体路径。
diff --git a/problems/kamacoder/0117.软件构建.md b/problems/kamacoder/0117.软件构建.md
index 58c17763..18802765 100644
--- a/problems/kamacoder/0117.软件构建.md
+++ b/problems/kamacoder/0117.软件构建.md
@@ -39,7 +39,7 @@
文件依赖关系如下:
-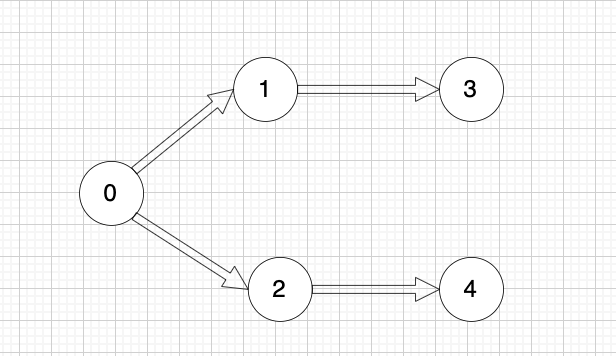
+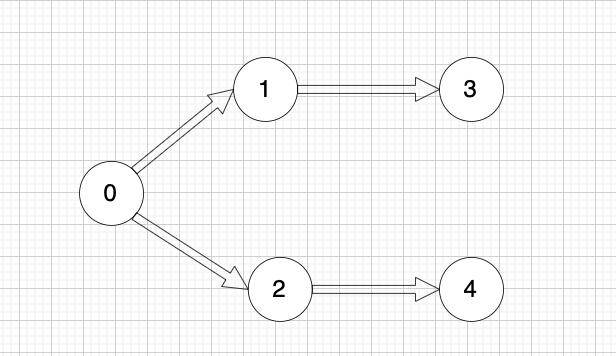
所以,文件处理的顺序除了示例中的顺序,还存在
@@ -104,7 +104,7 @@
以题目中示例为例如图:
-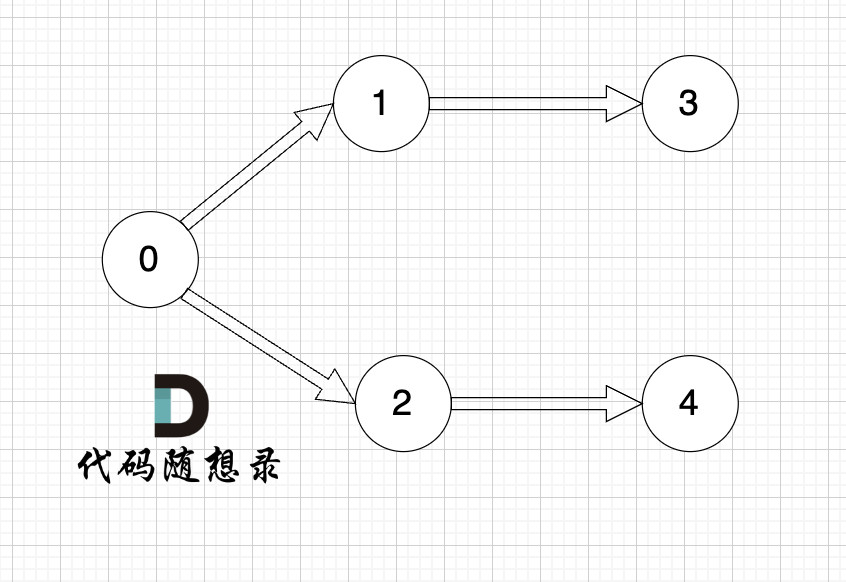
+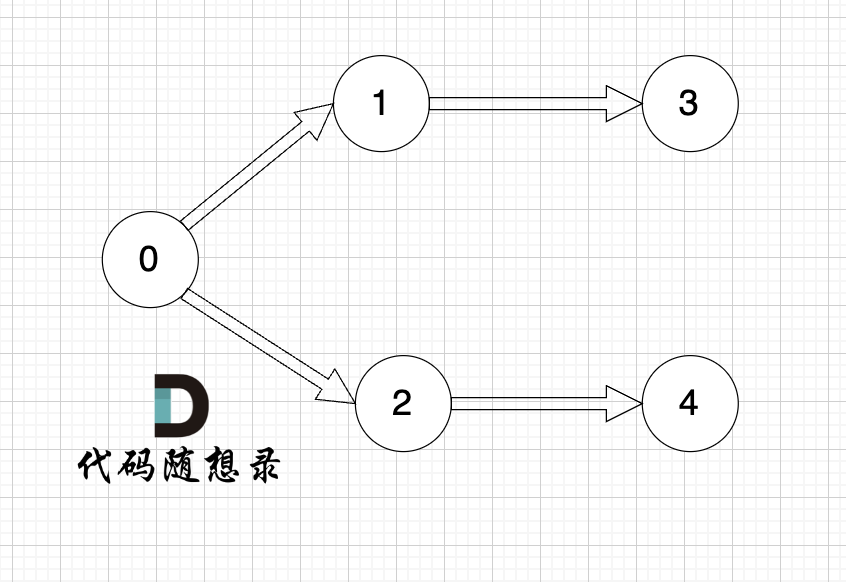
做拓扑排序的话,如果肉眼去找开头的节点,一定能找到 节点0 吧,都知道要从节点0 开始。
@@ -135,17 +135,17 @@
1、找到入度为0 的节点,加入结果集
-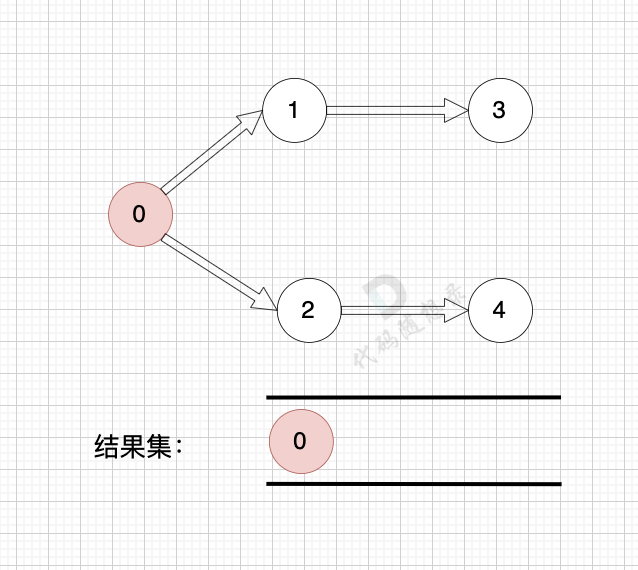
+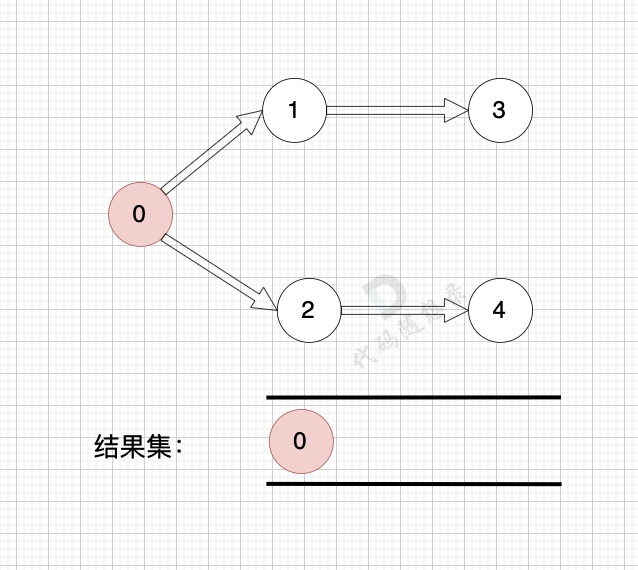
2、将该节点从图中移除
-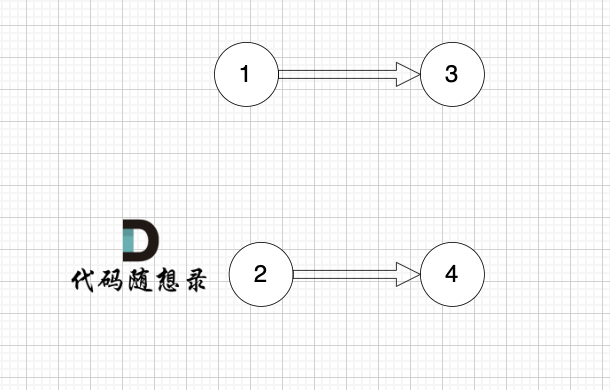
+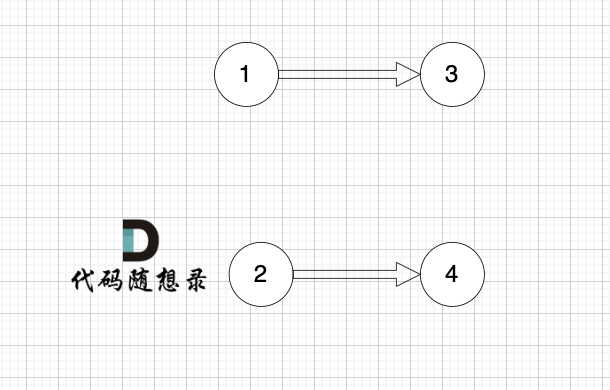
----------------
1、找到入度为0 的节点,加入结果集
-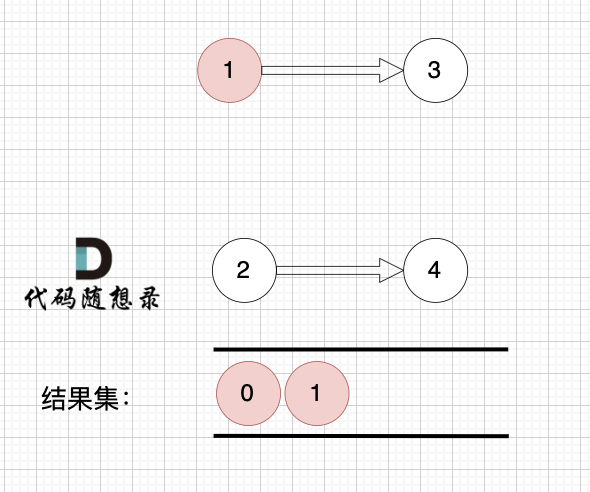
+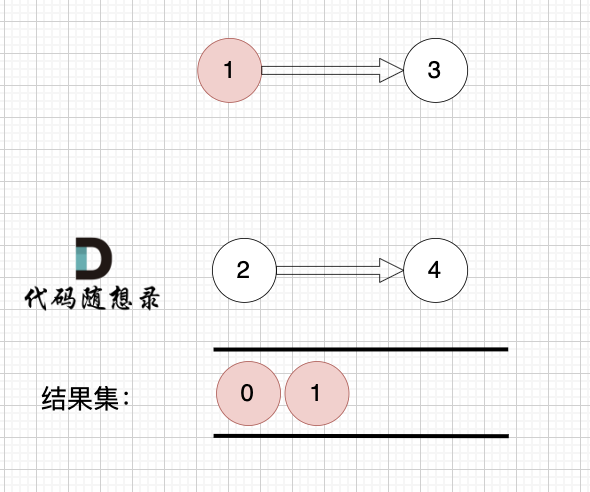
这里大家会发现,节点1 和 节点2 入度都为0, 选哪个呢?
@@ -153,19 +153,19 @@
2、将该节点从图中移除
-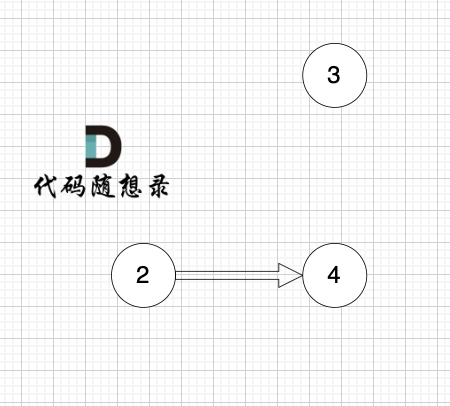
+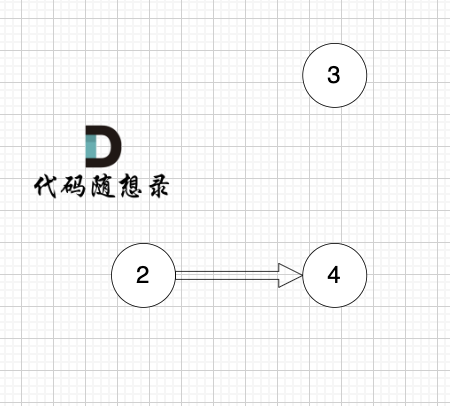
---------------
1、找到入度为0 的节点,加入结果集
-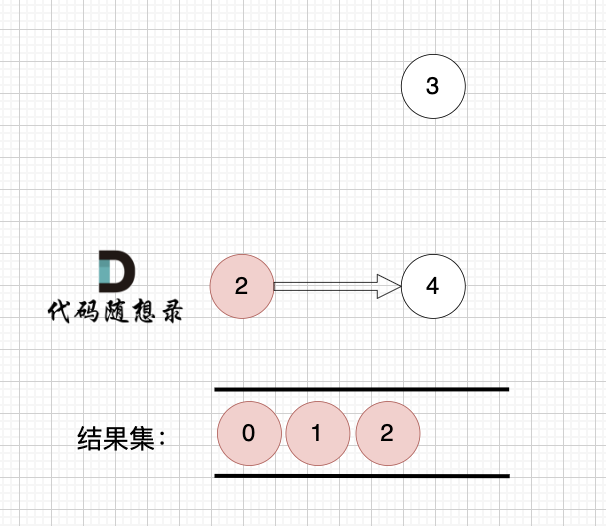
+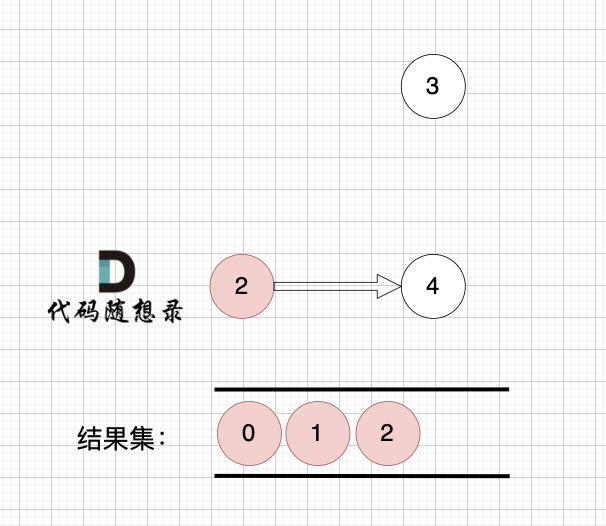
节点2 和 节点3 入度都为0,选哪个都行,这里选节点2
2、将该节点从图中移除
-
+
--------------
@@ -177,7 +177,7 @@
如果有 有向环怎么办呢?例如这个图:
-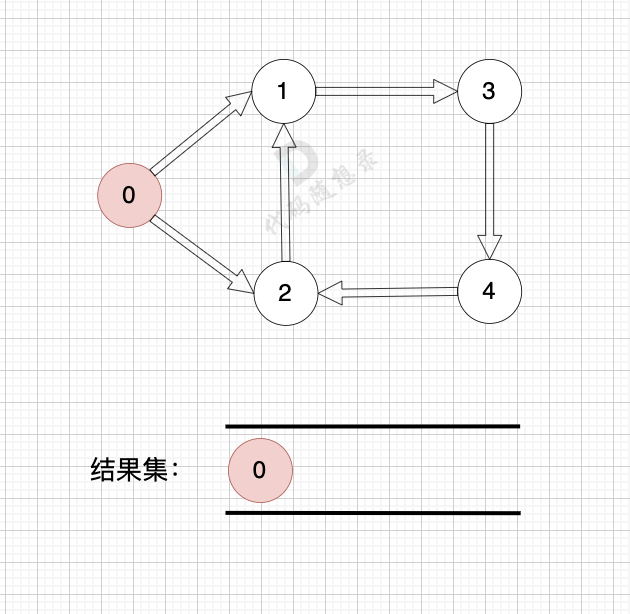
+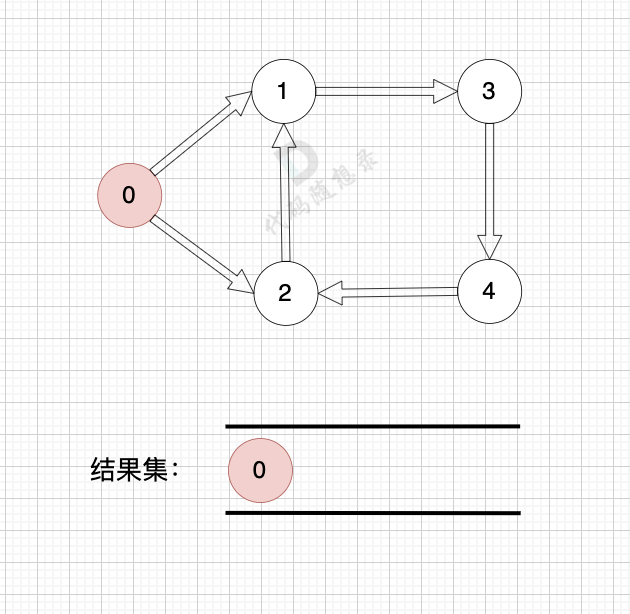
这个图,我们只能将入度为0 的节点0 接入结果集。
@@ -252,13 +252,13 @@ while (que.size()) {
如果这里不理解,看上面的模拟过程第一步:
-
+
这事节点1 和 节点2 的入度为 1。
将节点0删除后,图为这样:
-
+
那么 节点0 作为出发点 所连接的节点的入度 就都做了 减一 的操作。
diff --git a/problems/kamacoder/0126.骑士的攻击astar.md b/problems/kamacoder/0126.骑士的攻击astar.md
index 8ad32644..7d0096d5 100644
--- a/problems/kamacoder/0126.骑士的攻击astar.md
+++ b/problems/kamacoder/0126.骑士的攻击astar.md
@@ -9,7 +9,7 @@
骑士移动规则如图,红色是起始位置,黄色是骑士可以走的地方。
-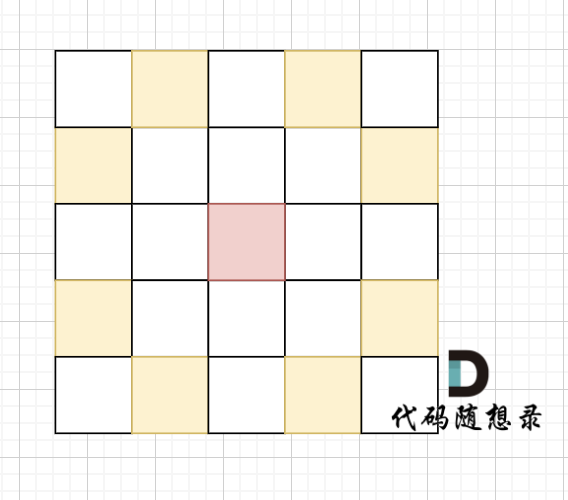
+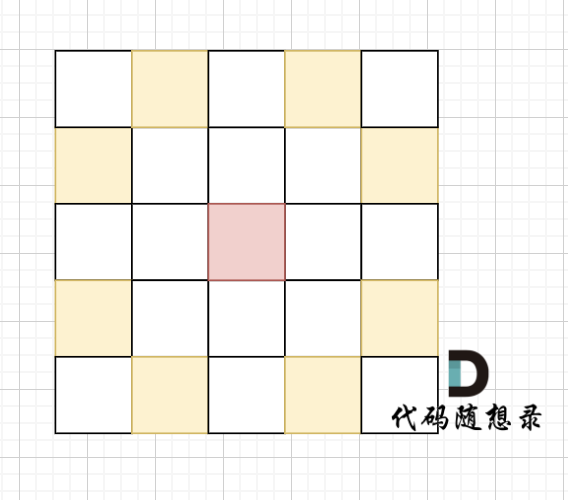
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
@@ -108,7 +108,7 @@ int main()
我们来看一下广搜的搜索过程,如图,红色是起点,绿色是终点,黄色是要遍历的点,最后从 起点 找到 达到终点的最短路径是棕色。
-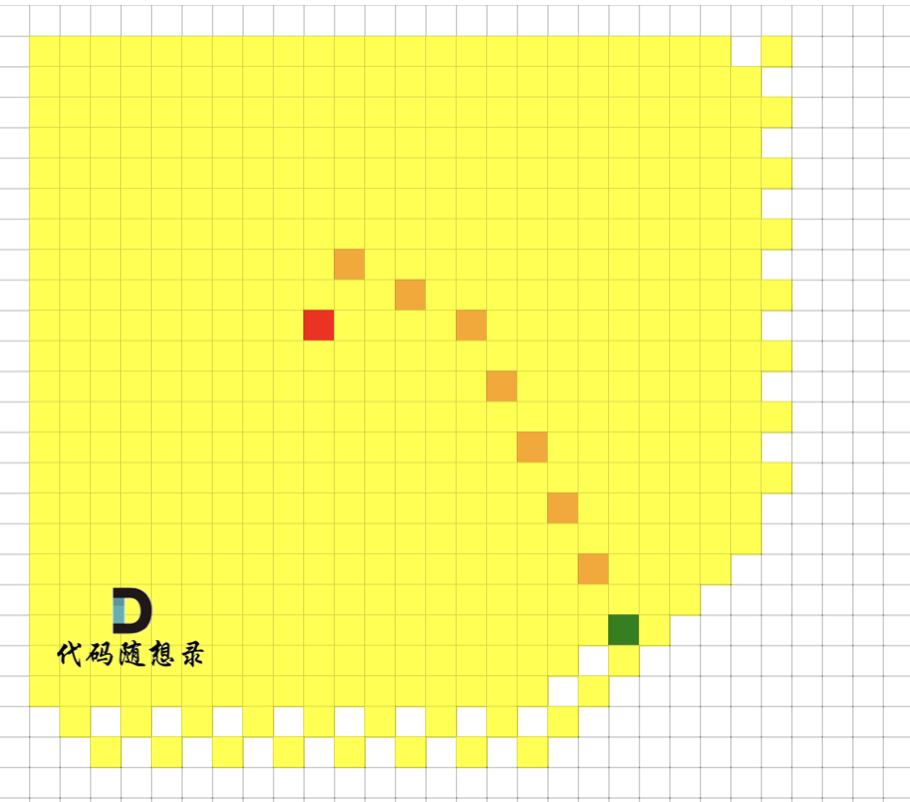
+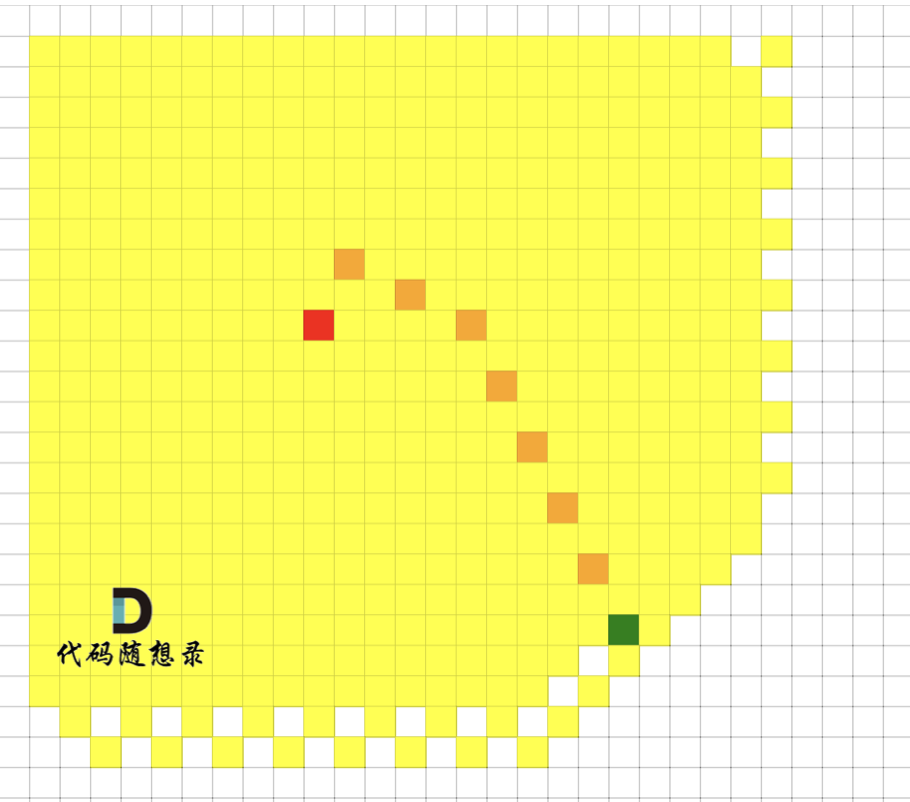
可以看出 广搜中,做了很多无用的遍历, 黄色的格子是广搜遍历到的点。
@@ -131,11 +131,11 @@ Astar 是一种 广搜的改良版。 有的是 Astar是 dijkstra 的改良版
在BFS中,我们想搜索,从起点到终点的最短路径,要一层一层去遍历。
-
+
如果 使用A * 的话,其搜索过程是这样的,如图,图中着色的都是我们要遍历的点。
-
+
(上面两图中 最短路长度都是8,只是走的方式不同而已)
diff --git a/problems/kamacoder/图论并查集理论基础.md b/problems/kamacoder/图论并查集理论基础.md
index e463b956..5eb5127a 100644
--- a/problems/kamacoder/图论并查集理论基础.md
+++ b/problems/kamacoder/图论并查集理论基础.md
@@ -105,13 +105,13 @@ bool isSame(int u, int v) {
搜索过程像是一个多叉树中从叶子到根节点的过程,如图:
-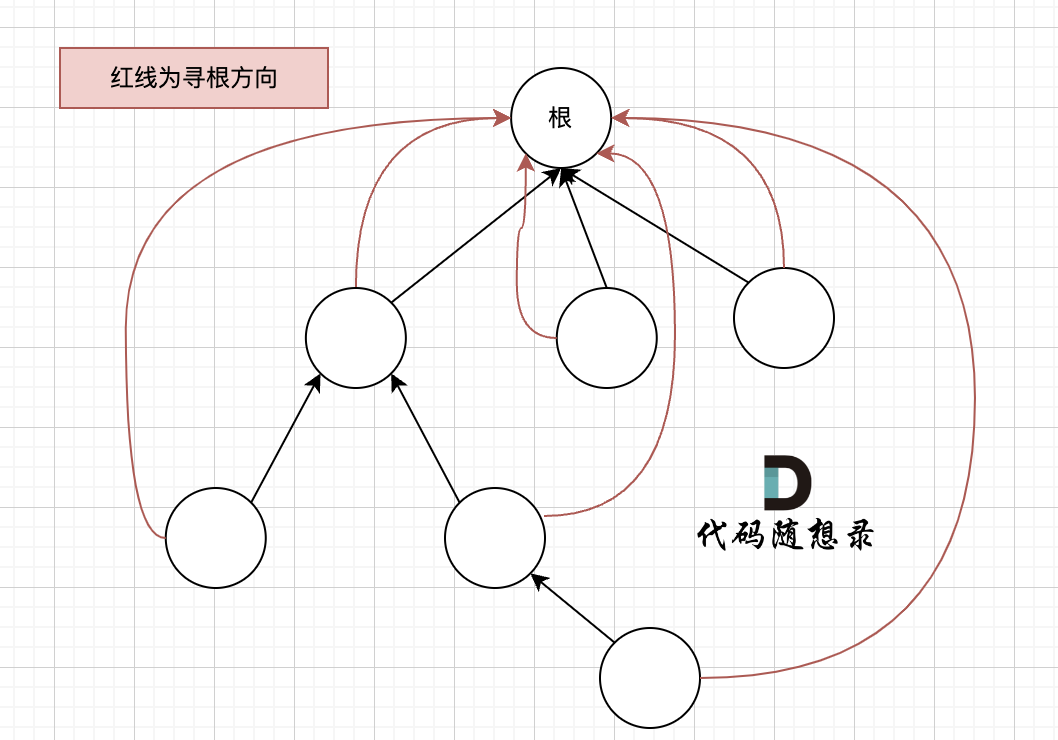
+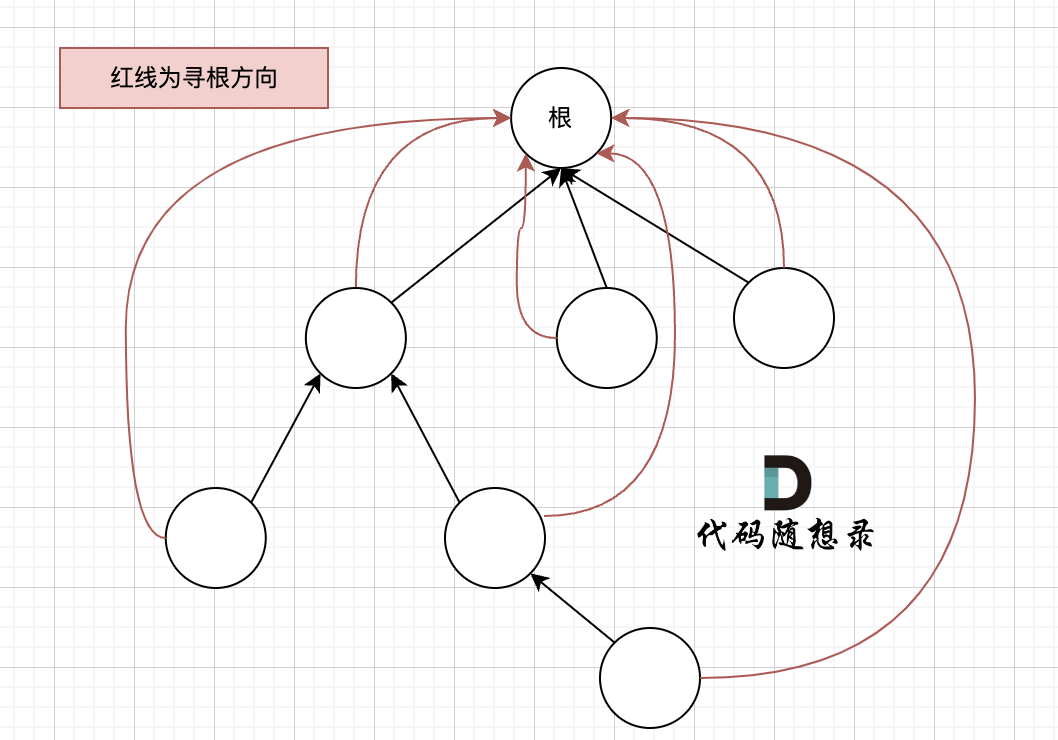
如果这棵多叉树高度很深的话,每次find函数 去寻找根的过程就要递归很多次。
我们的目的只需要知道这些节点在同一个根下就可以,所以对这棵多叉树的构造只需要这样就可以了,如图:
-
+
除了根节点其他所有节点都挂载根节点下,这样我们在寻根的时候就很快,只需要一步,
@@ -226,7 +226,7 @@ join(3, 2);
此时构成的图是这样的:
-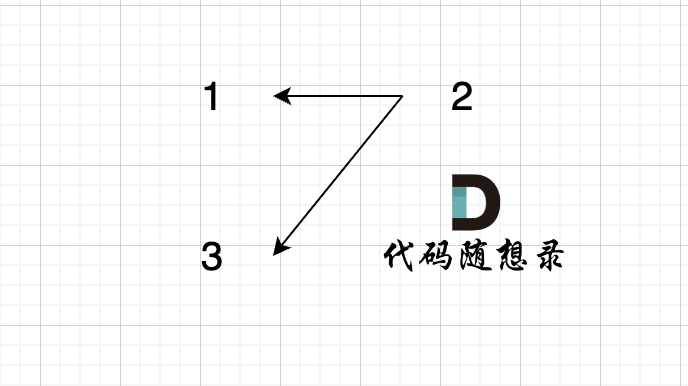
+
此时问 1,3是否在同一个集合,我们调用 `join(1, 2); join(3, 2);` 很明显本意要表示 1,3是在同一个集合。
@@ -256,7 +256,7 @@ join(3, 2);
构成的图是这样的:
-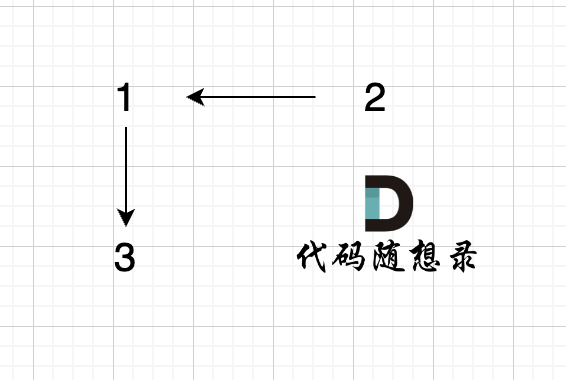
+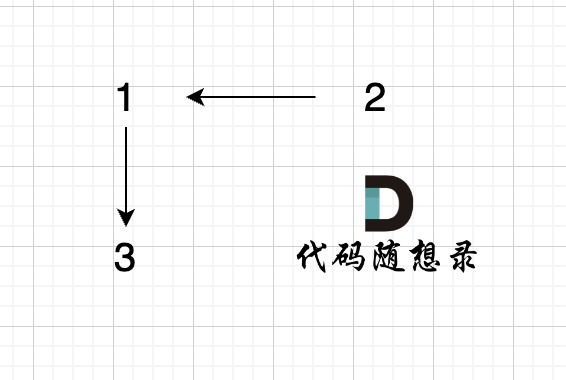
因为在join函数里,我们有find函数进行寻根的过程,这样就保证元素 1,2,3在这个有向图里是强连通的。
@@ -275,12 +275,12 @@ join(3, 2);
1、`join(1, 8);`
-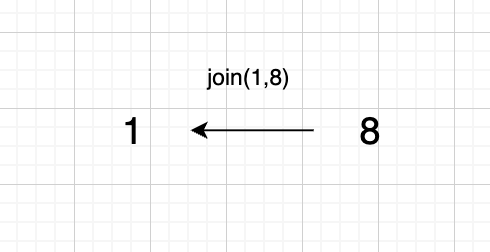
+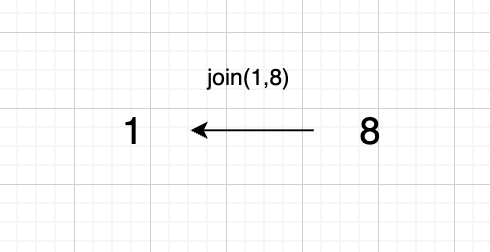
2、`join(3, 8);`
-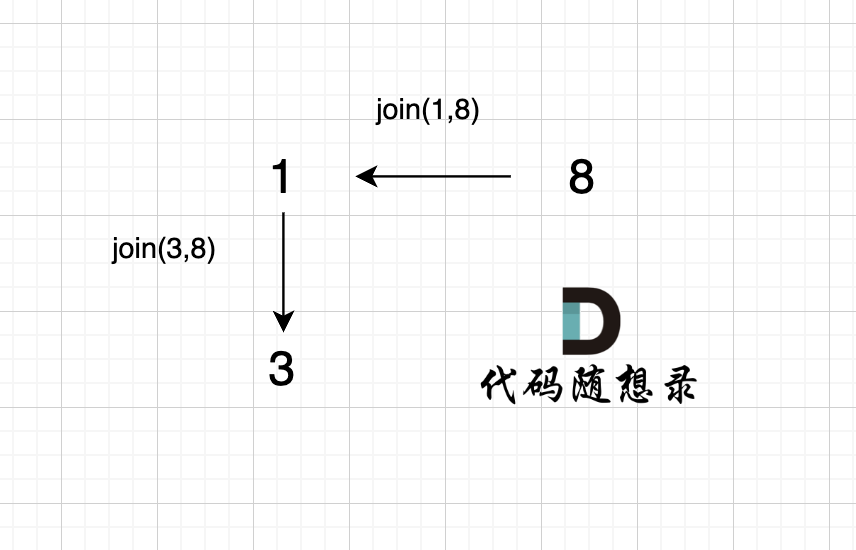
+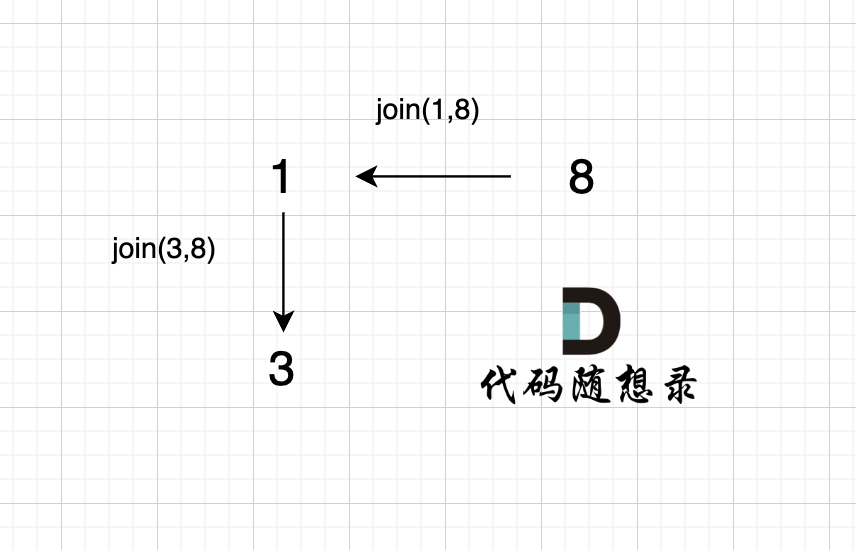
有录友可能想,`join(3, 8)` 在图中为什么 将 元素1 连向元素 3 而不是将 元素 8 连向 元素 3 呢?
@@ -288,12 +288,12 @@ join(3, 2);
3、`join(1, 7);`
-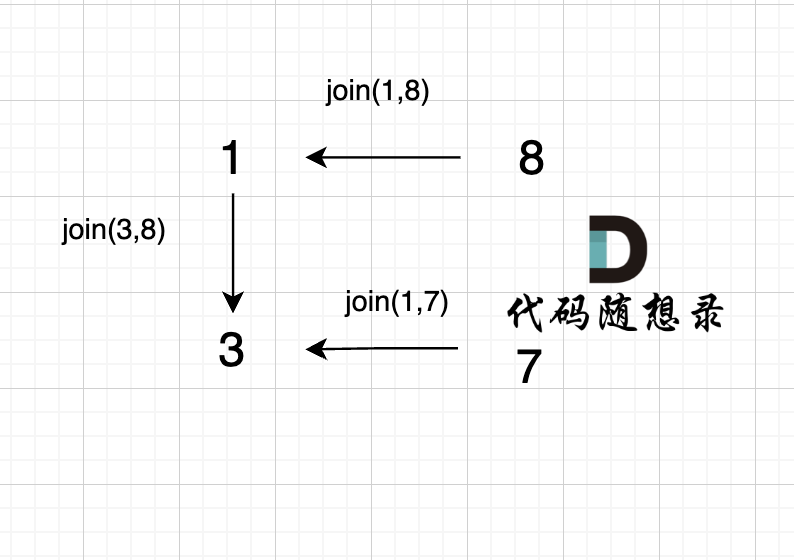
+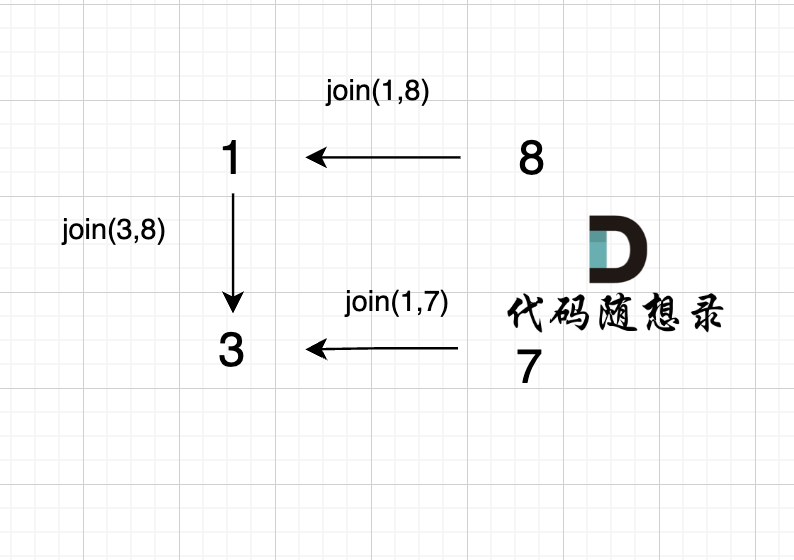
4、`join(8, 5);`
-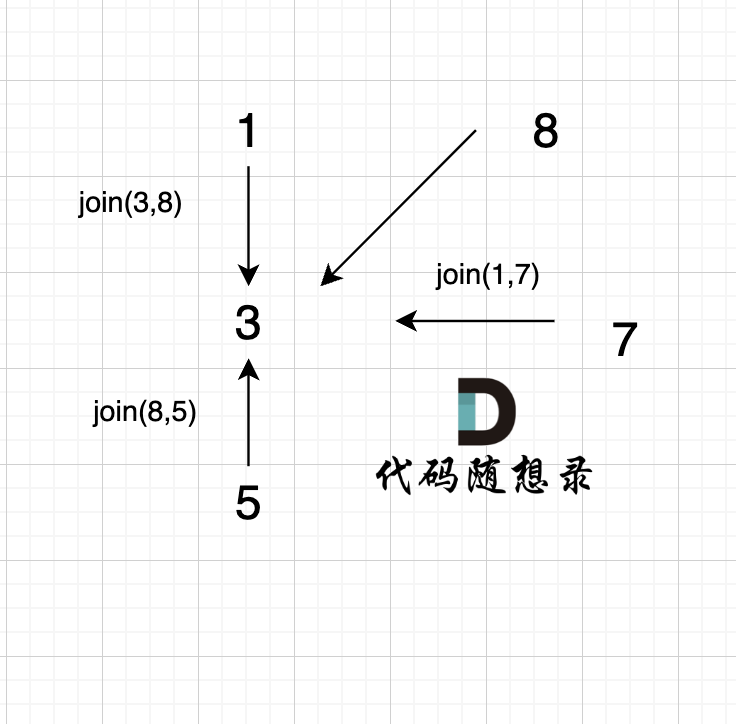
+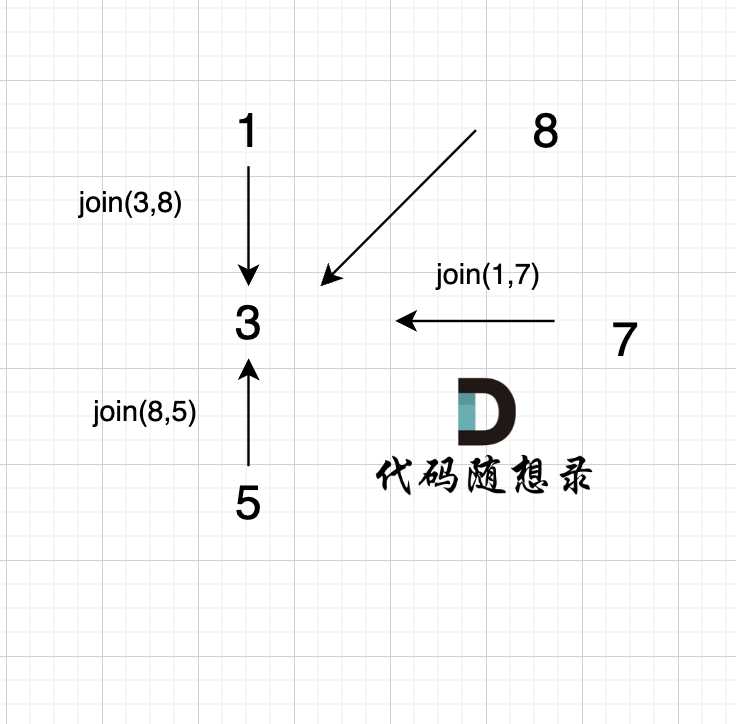
这里8的根是3,那么 5 应该指向 8 的根 3,这里的原因,我们在上面「常见误区」已经讲过了。 但 为什么 图中 8 又直接指向了 3 了呢?
@@ -310,11 +310,11 @@ int find(int u) {
5、`join(2, 9);`
-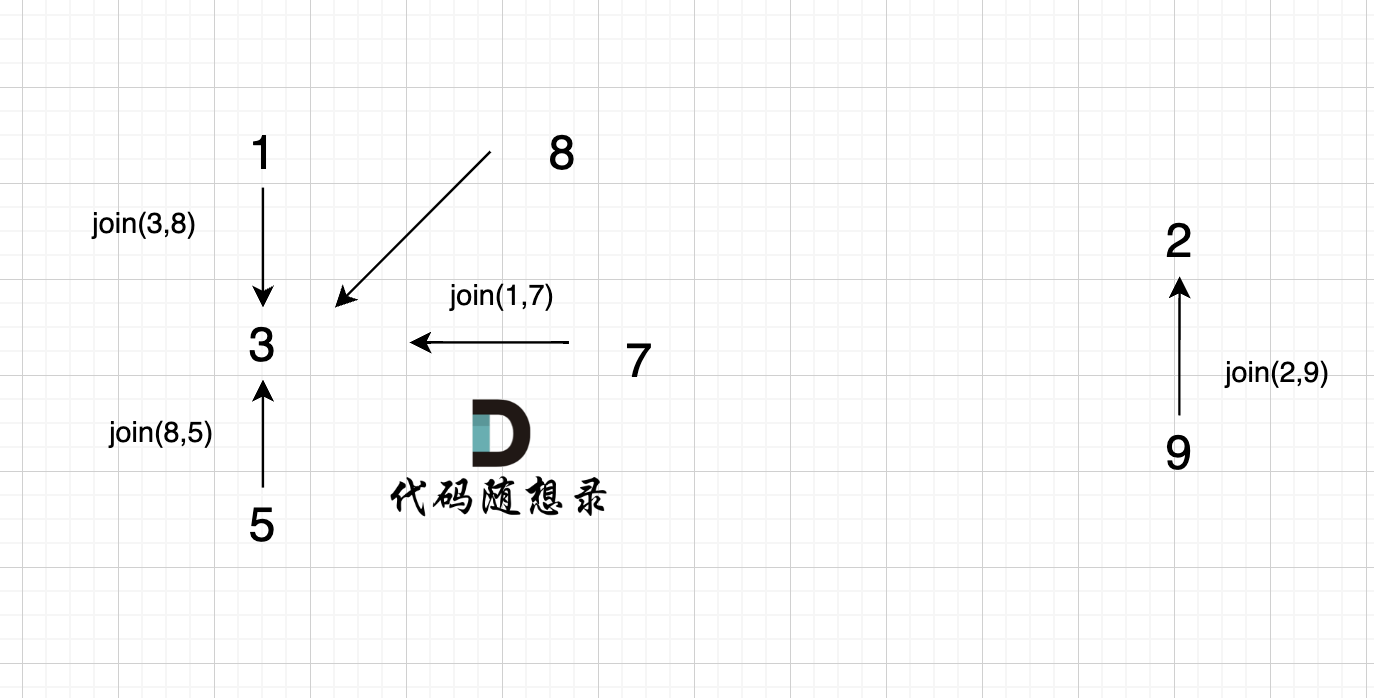
+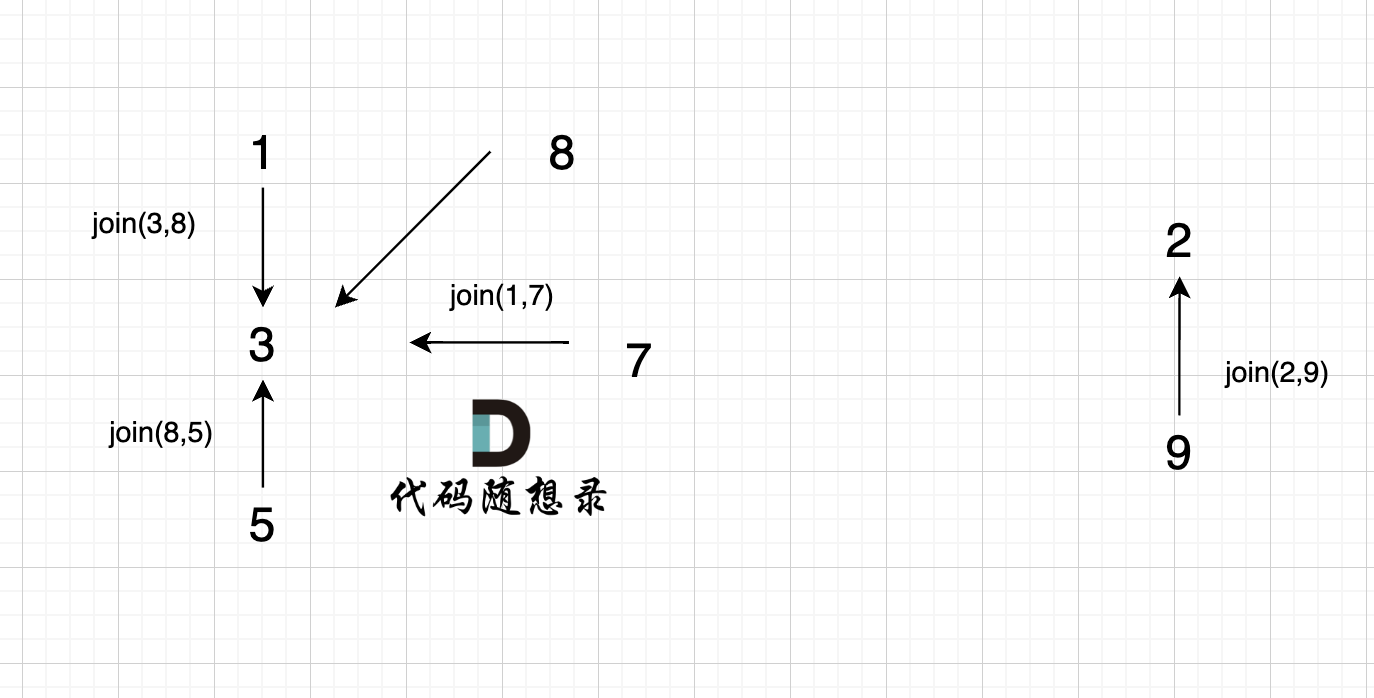
6、`join(6, 9);`
-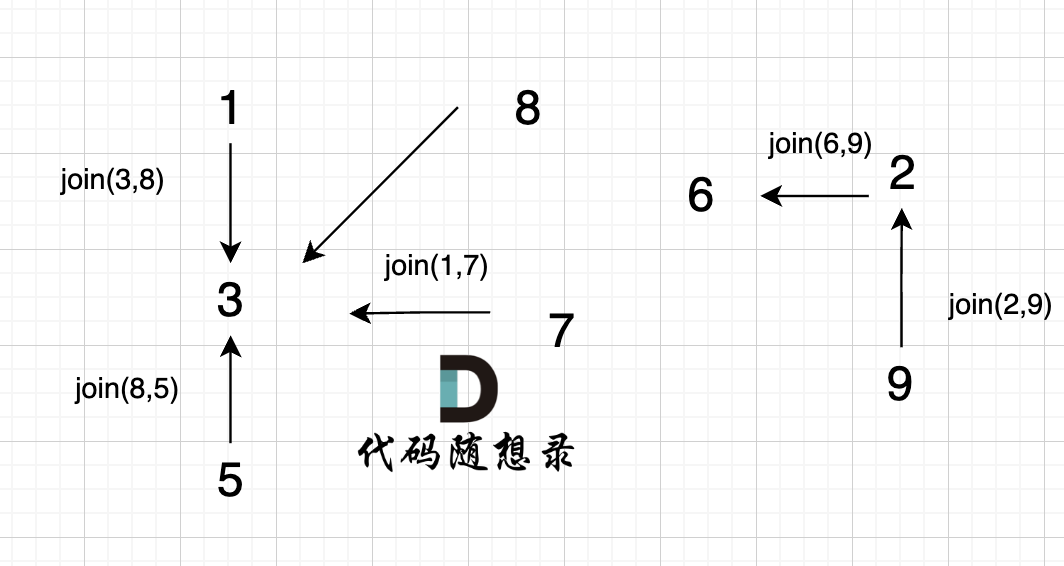
+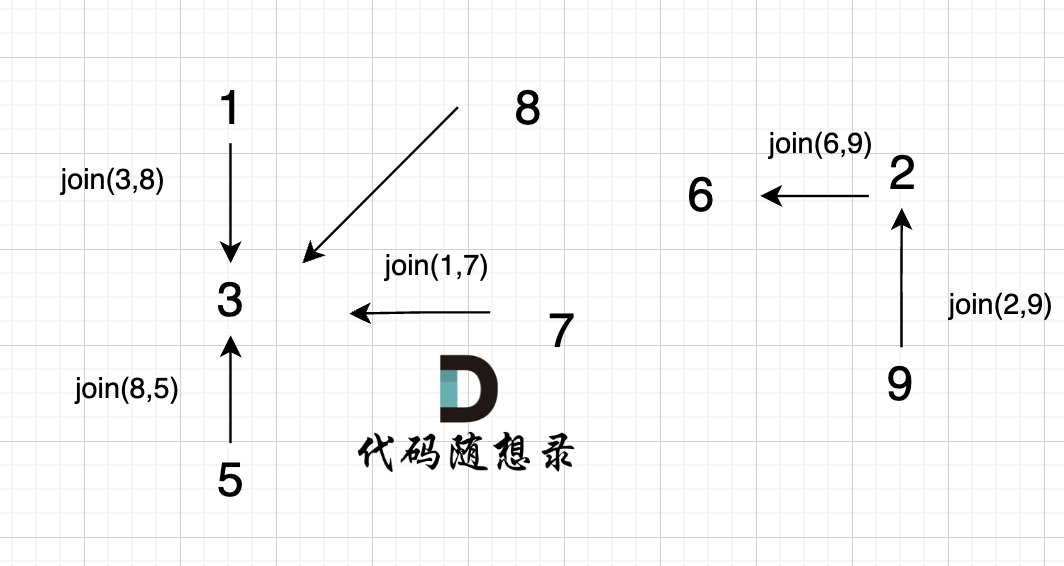
这里为什么是 2 指向了 6,因为 9的根为 2,所以用2指向6。
@@ -347,13 +347,13 @@ rank表示树的高度,即树中结点层次的最大值。
例如两个集合(多叉树)需要合并,如图所示:
-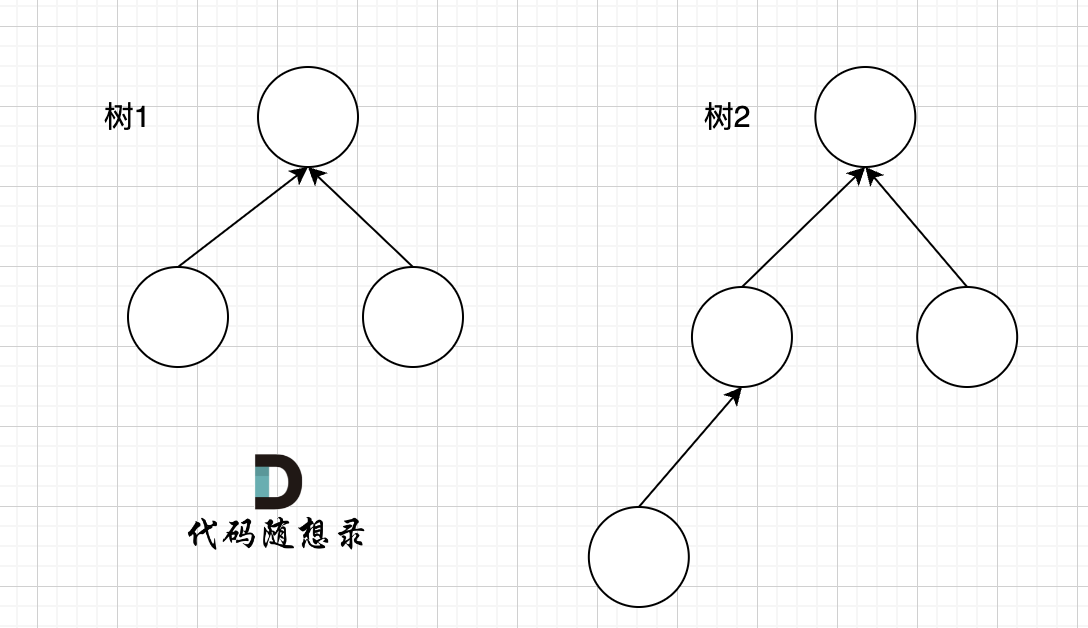
+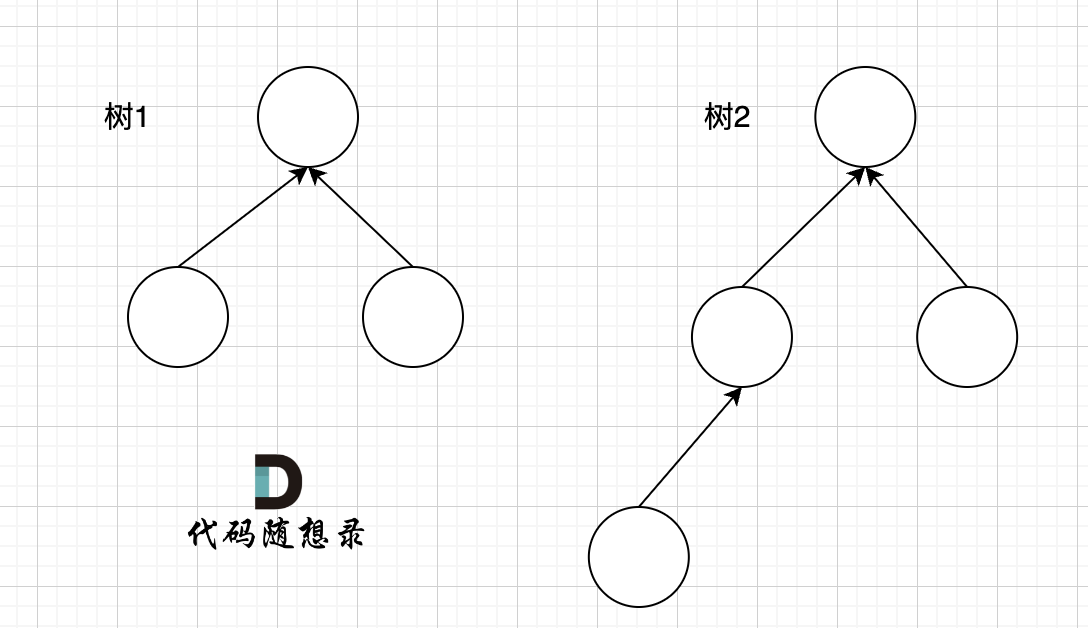
树1 rank 为2,树2 rank 为 3。那么合并两个集合,是 树1 合入 树2,还是 树2 合入 树1呢?
我们来看两个不同方式合入的效果。
-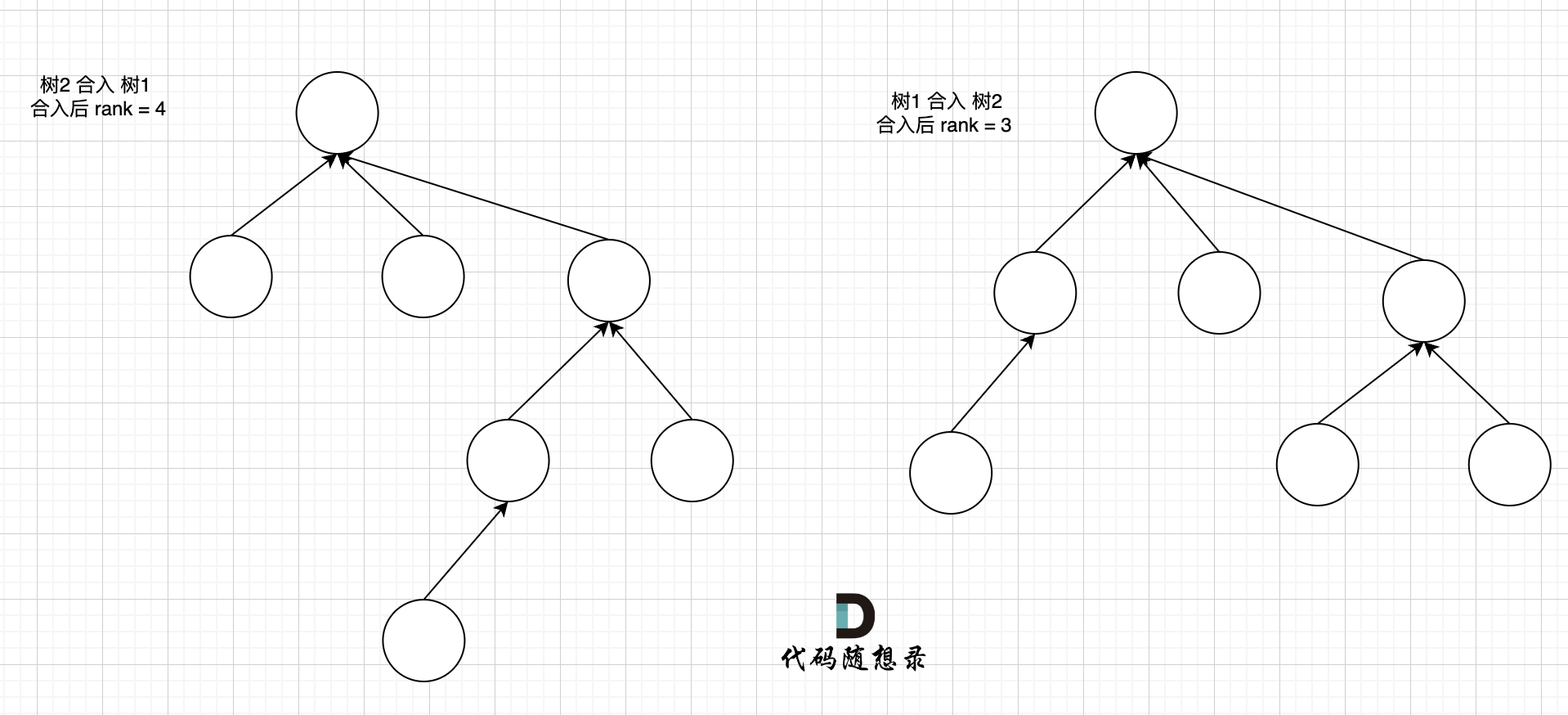
+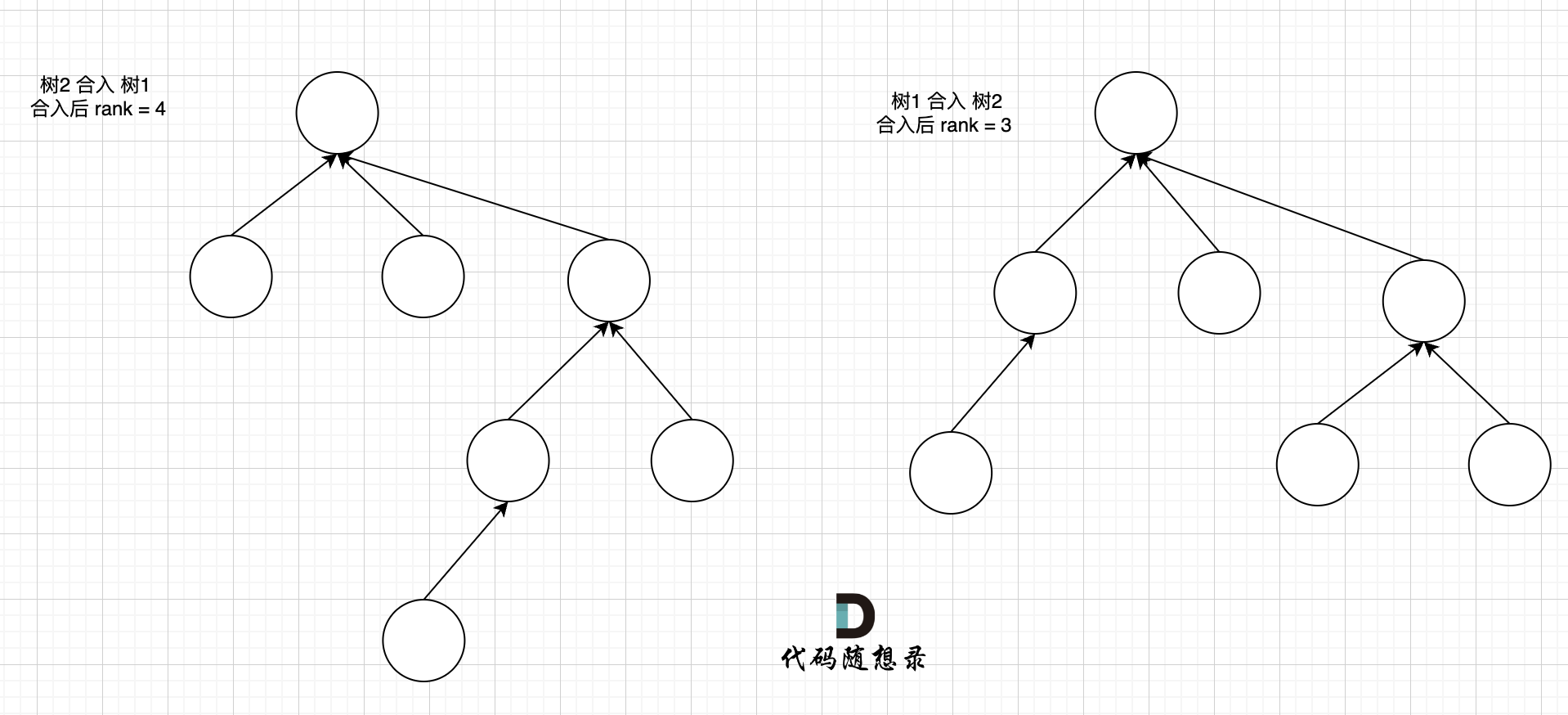
这里可以看出,树2 合入 树1 会导致整棵树的高度变的更高,而 树1 合入 树2 整棵树的高度 和 树2 保持一致。
diff --git a/problems/kamacoder/图论广搜理论基础.md b/problems/kamacoder/图论广搜理论基础.md
index d791d2c0..96e313fc 100644
--- a/problems/kamacoder/图论广搜理论基础.md
+++ b/problems/kamacoder/图论广搜理论基础.md
@@ -18,11 +18,11 @@
我们用一个方格地图,假如每次搜索的方向为 上下左右(不包含斜上方),那么给出一个start起始位置,那么BFS就是从四个方向走出第一步。
-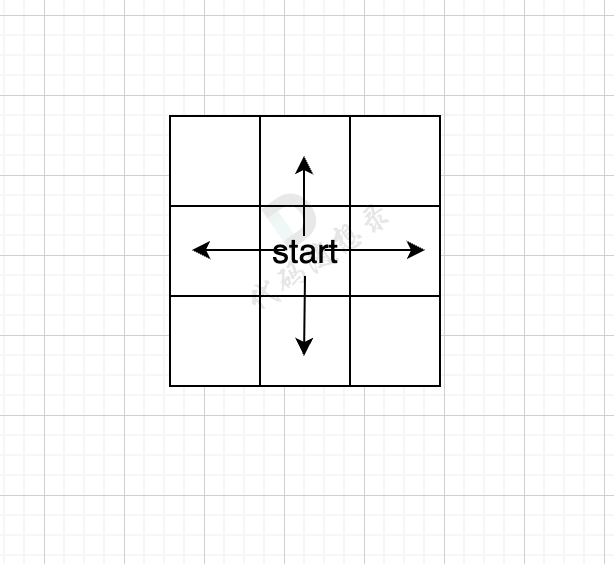
+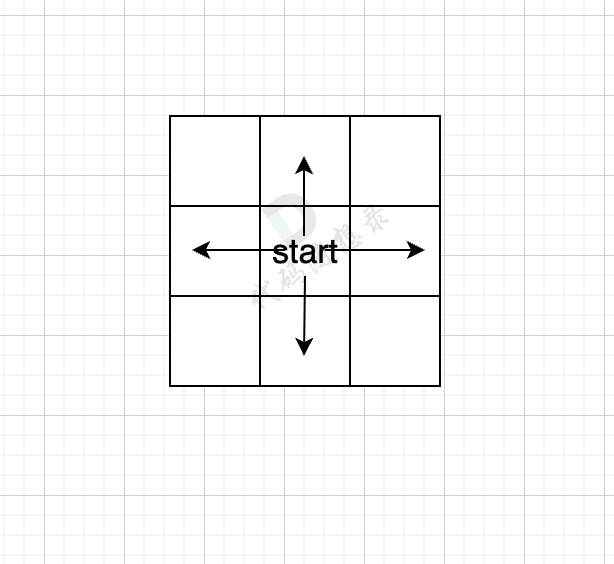
如果加上一个end终止位置,那么使用BFS的搜索过程如图所示:
-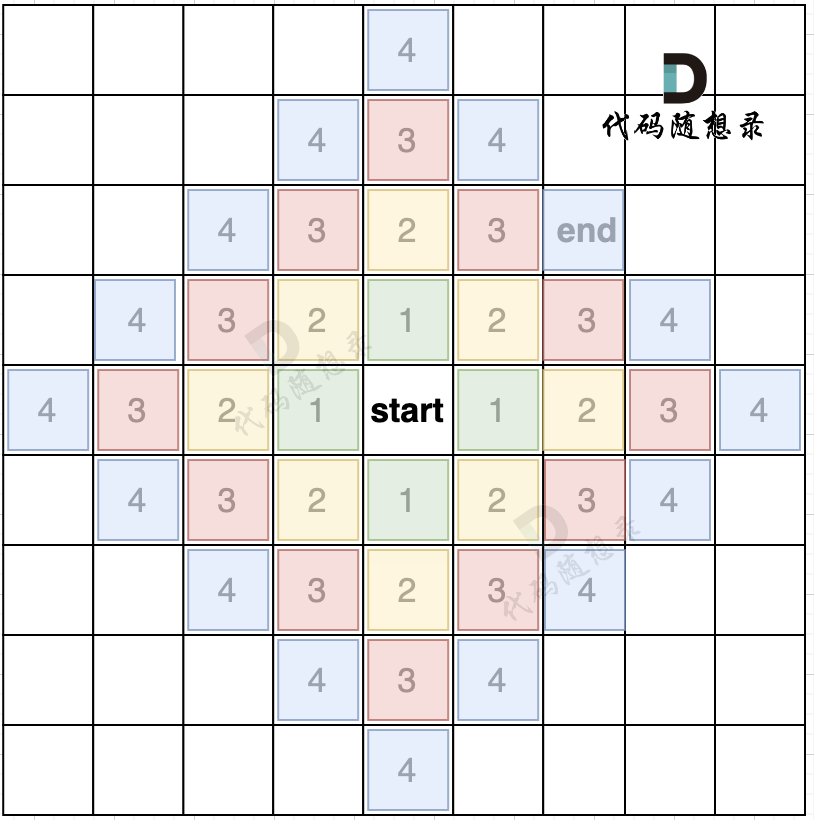
+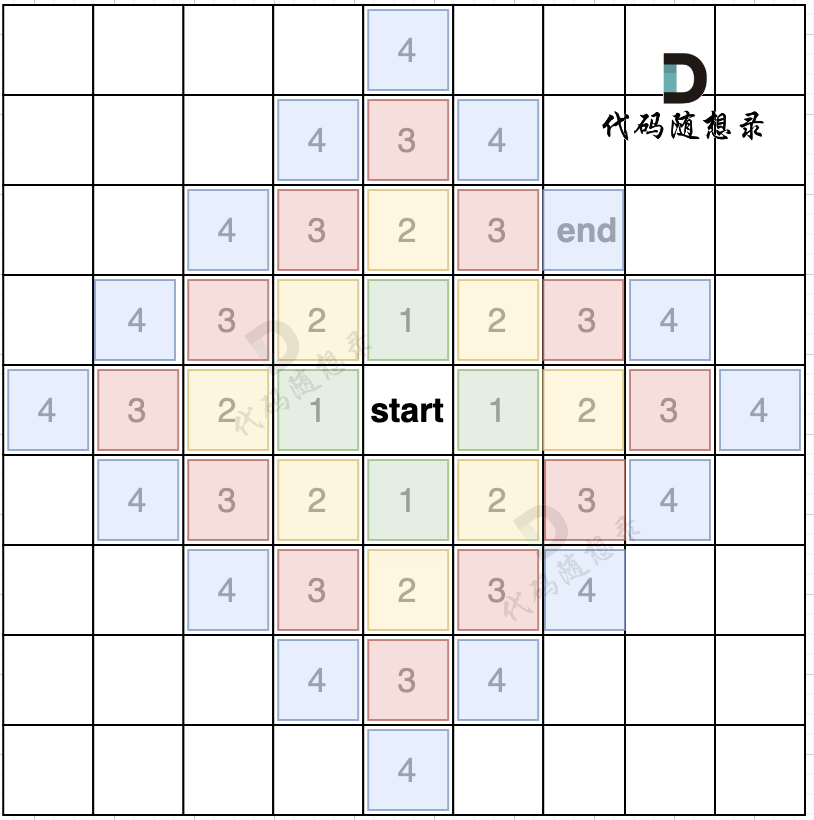
我们从图中可以看出,从start起点开始,是一圈一圈,向外搜索,方格编号1为第一步遍历的节点,方格编号2为第二步遍历的节点,第四步的时候我们找到终止点end。
@@ -30,7 +30,7 @@
而且地图还可以有障碍,如图所示:
-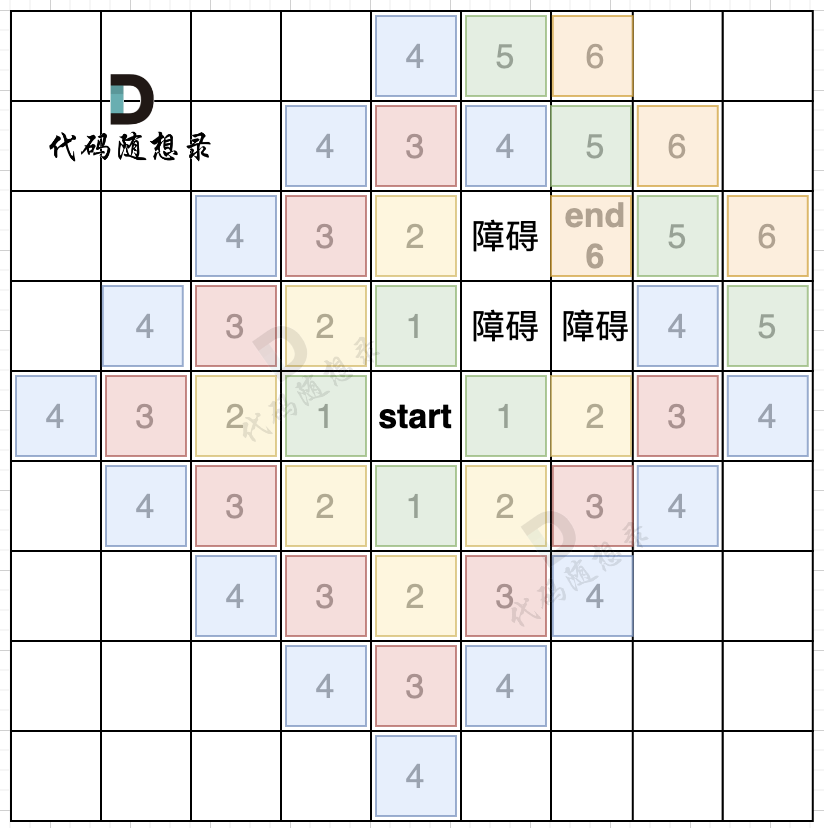
+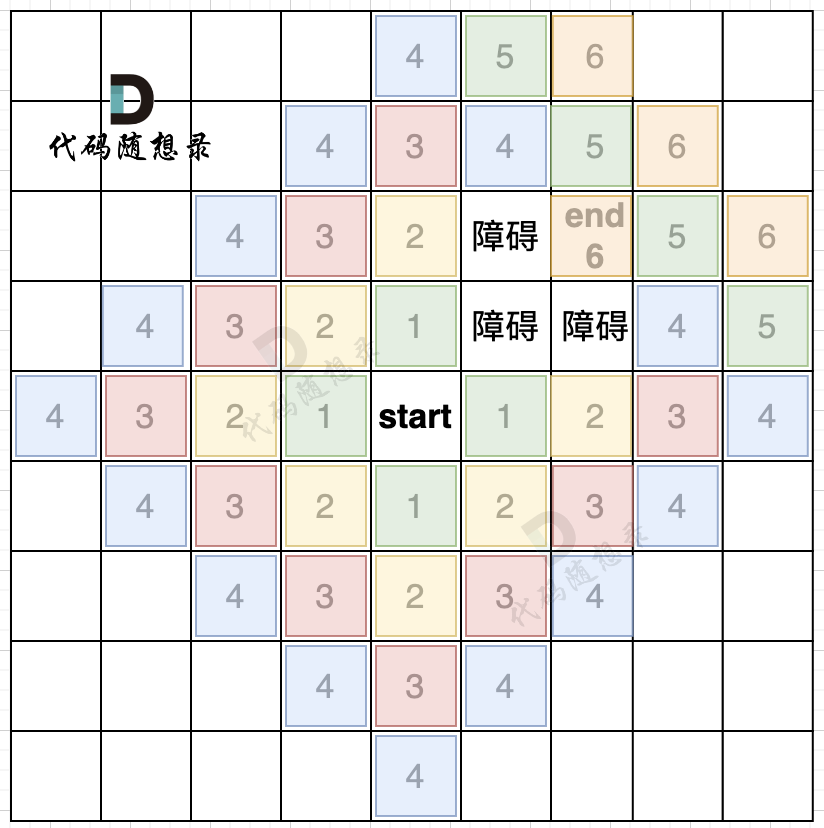
在第五步,第六步 我只把关键的节点染色了,其他方向周边没有去染色,大家只要关注关键地方染色的逻辑就可以。
diff --git a/problems/kamacoder/图论深搜理论基础.md b/problems/kamacoder/图论深搜理论基础.md
index ce3dbbdb..1611e00a 100644
--- a/problems/kamacoder/图论深搜理论基础.md
+++ b/problems/kamacoder/图论深搜理论基础.md
@@ -28,29 +28,29 @@
如图一,是一个无向图,我们要搜索从节点1到节点6的所有路径。
-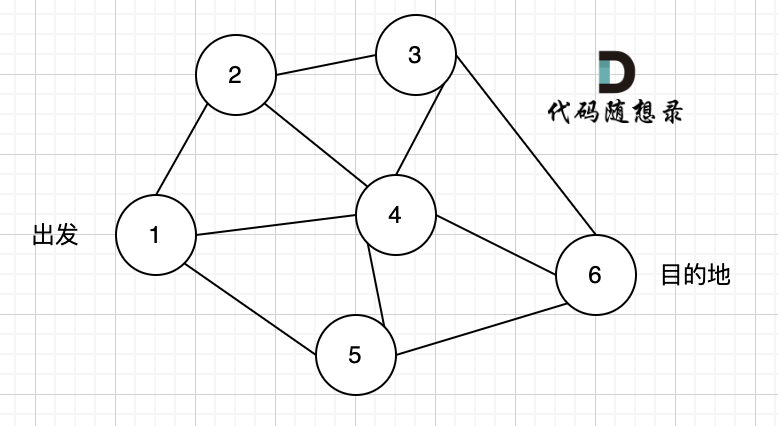
+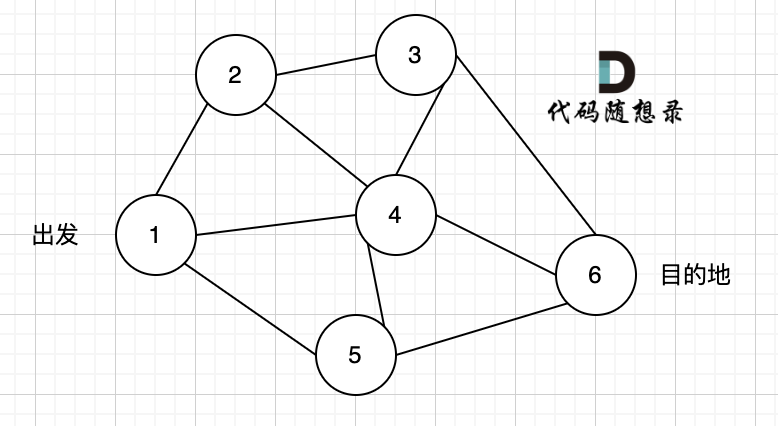
那么dfs搜索的第一条路径是这样的: (假设第一次延默认方向,就找到了节点6),图二
-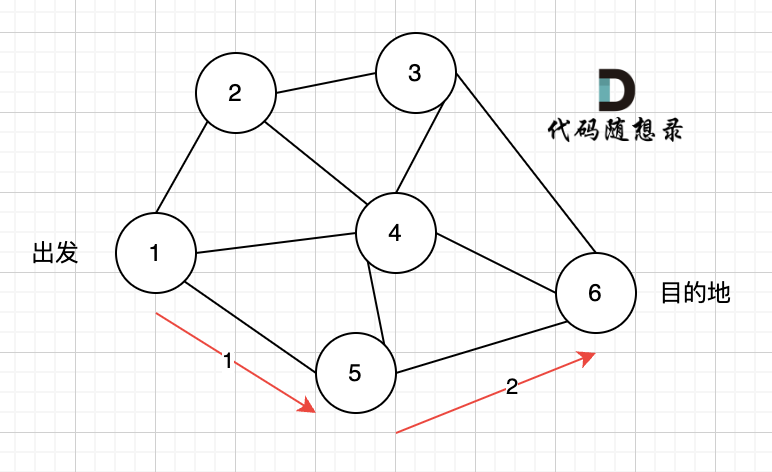
+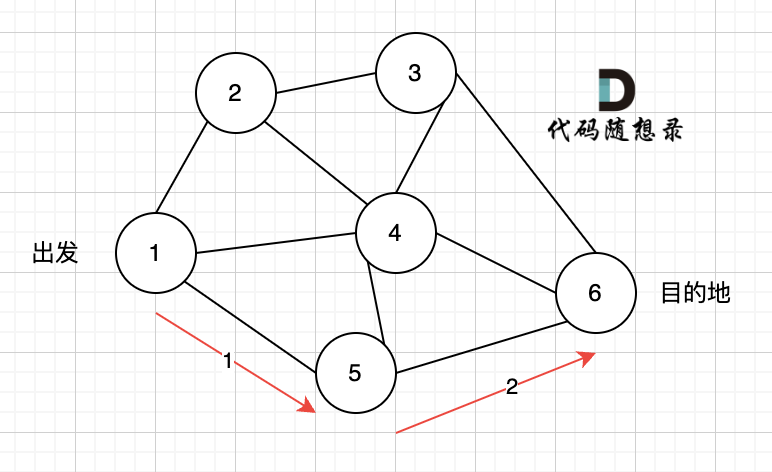
此时我们找到了节点6,(遇到黄河了,是不是应该回头了),那么应该再去搜索其他方向了。 如图三:
-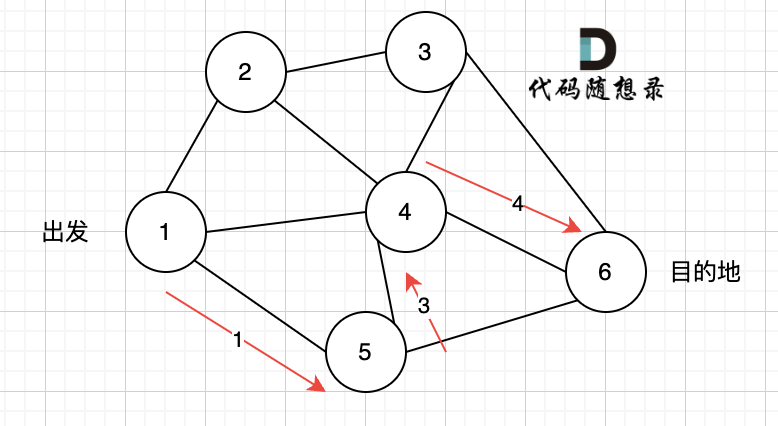
+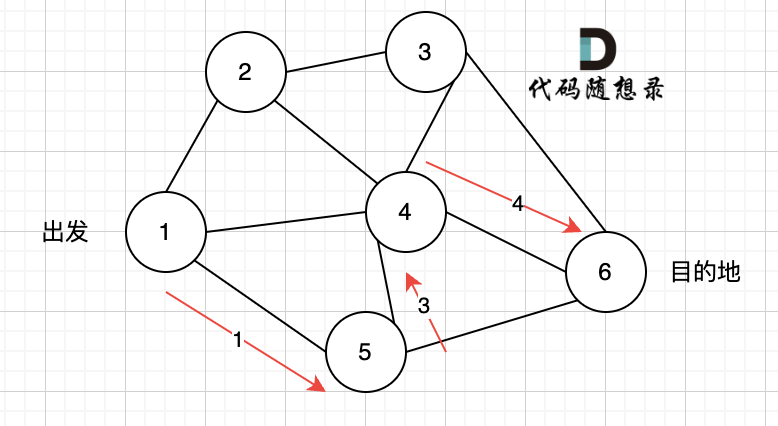
路径2撤销了,改变了方向,走路径3(红色线), 接着也找到终点6。 那么撤销路径2,改为路径3,在dfs中其实就是回溯的过程(这一点很重要,很多录友不理解dfs代码中回溯是用来干什么的)
又找到了一条从节点1到节点6的路径,又到黄河了,此时再回头,下图图四中,路径4撤销(回溯的过程),改为路径5。
-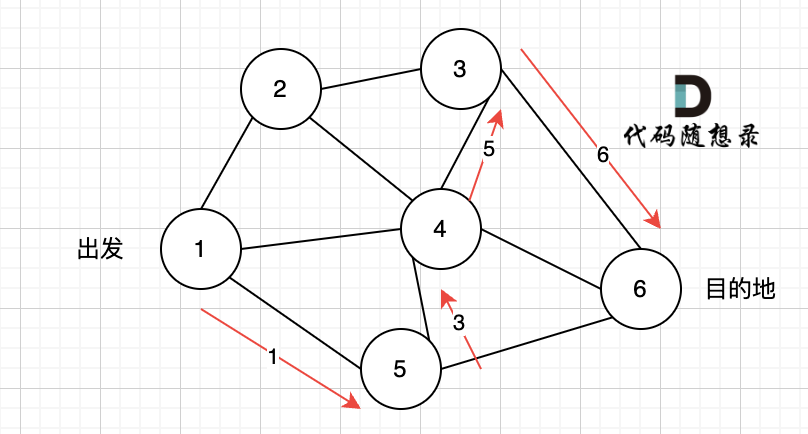
+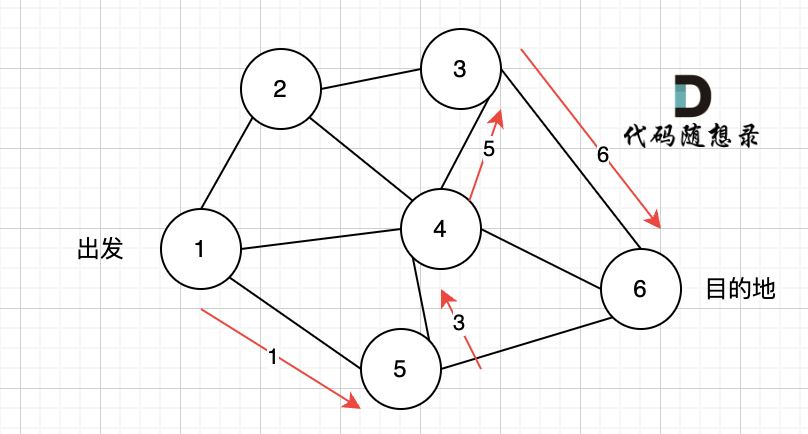
又找到了一条从节点1到节点6的路径,又到黄河了,此时再回头,下图图五,路径6撤销(回溯的过程),改为路径7,路径8 和 路径7,路径9, 结果发现死路一条,都走到了自己走过的节点。
-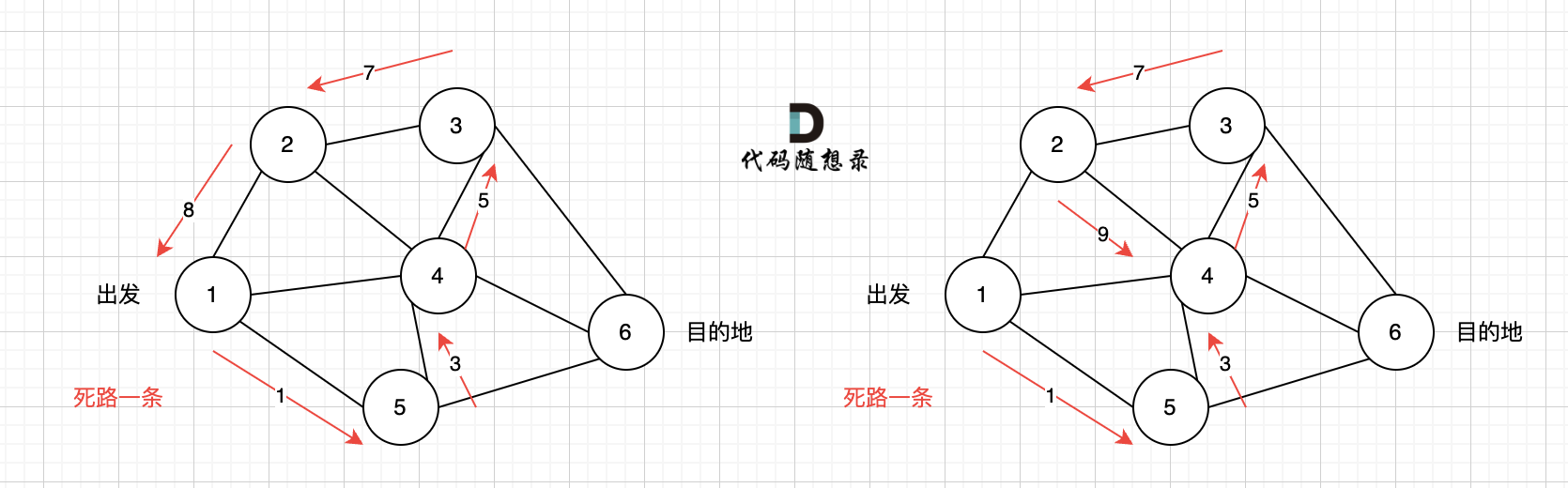
+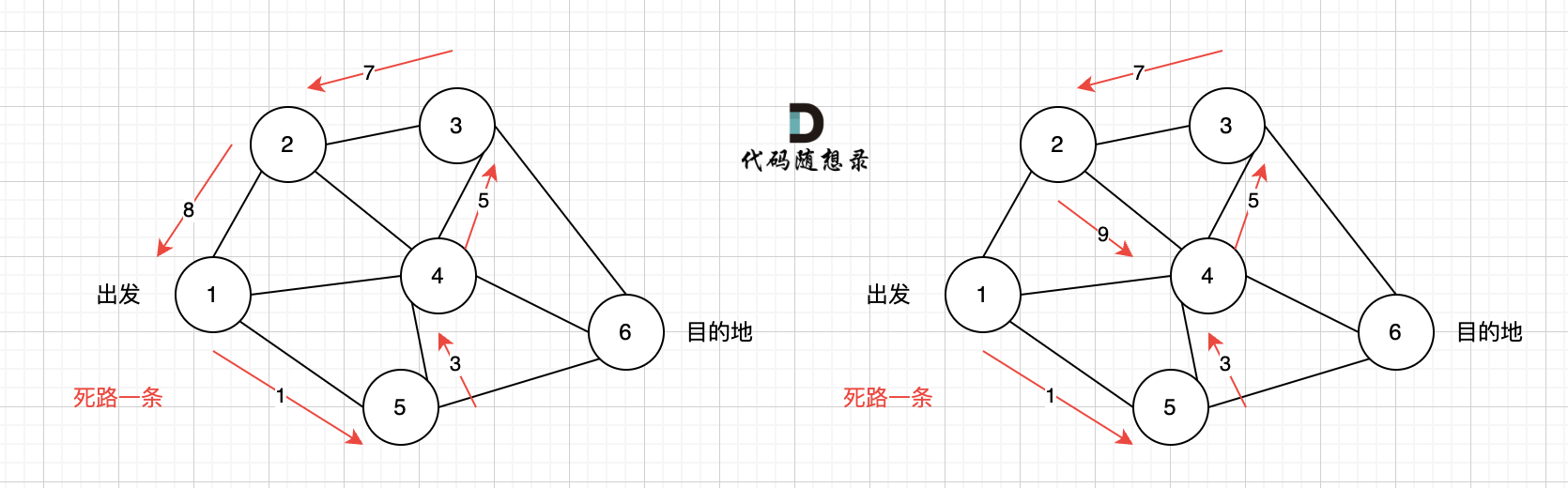
那么节点2所连接路径和节点3所链接的路径 都走过了,撤销路径只能向上回退,去选择撤销当初节点4的选择,也就是撤销路径5,改为路径10 。 如图图六:
-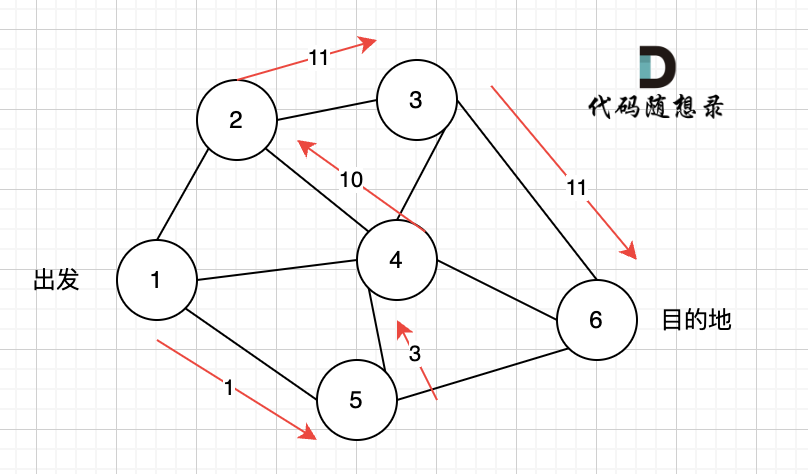
+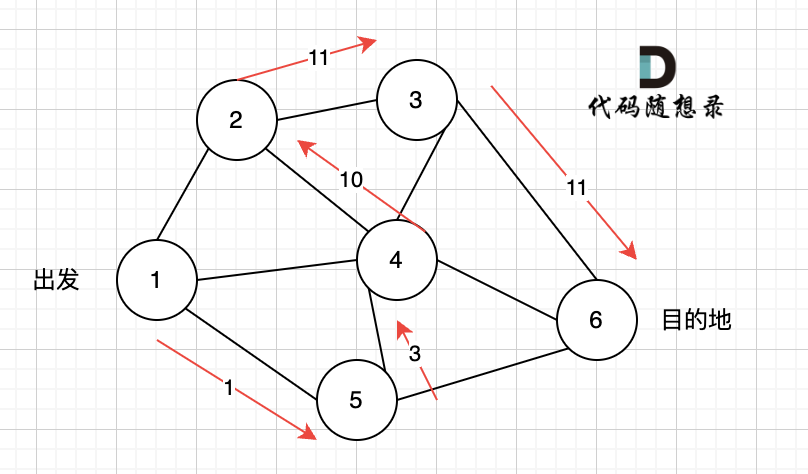
上图演示中,其实我并没有把 所有的 从节点1 到节点6的dfs(深度优先搜索)的过程都画出来,那样太冗余了,但 已经把dfs 关键的地方都涉及到了,关键就两点:
@@ -180,7 +180,7 @@ for (选择:本节点所连接的其他节点) {
如图七所示, 路径2 已经走到了 目的地节点6,那么 路径2 是如何撤销,然后改为 路径3呢? 其实这就是 回溯的过程,撤销路径2,走换下一个方向。
-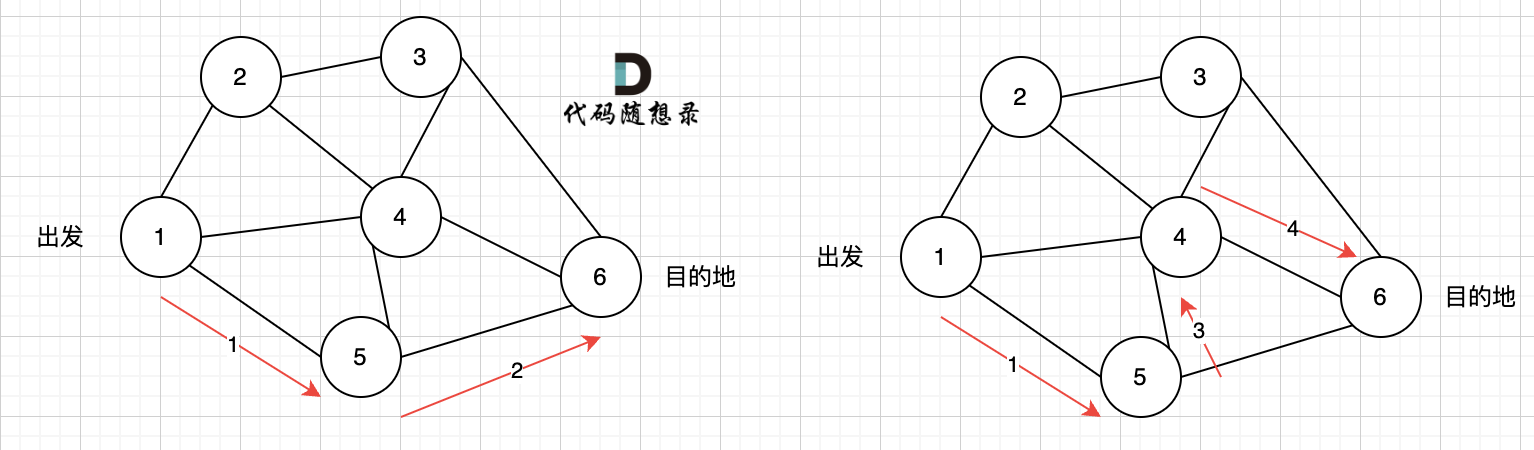
+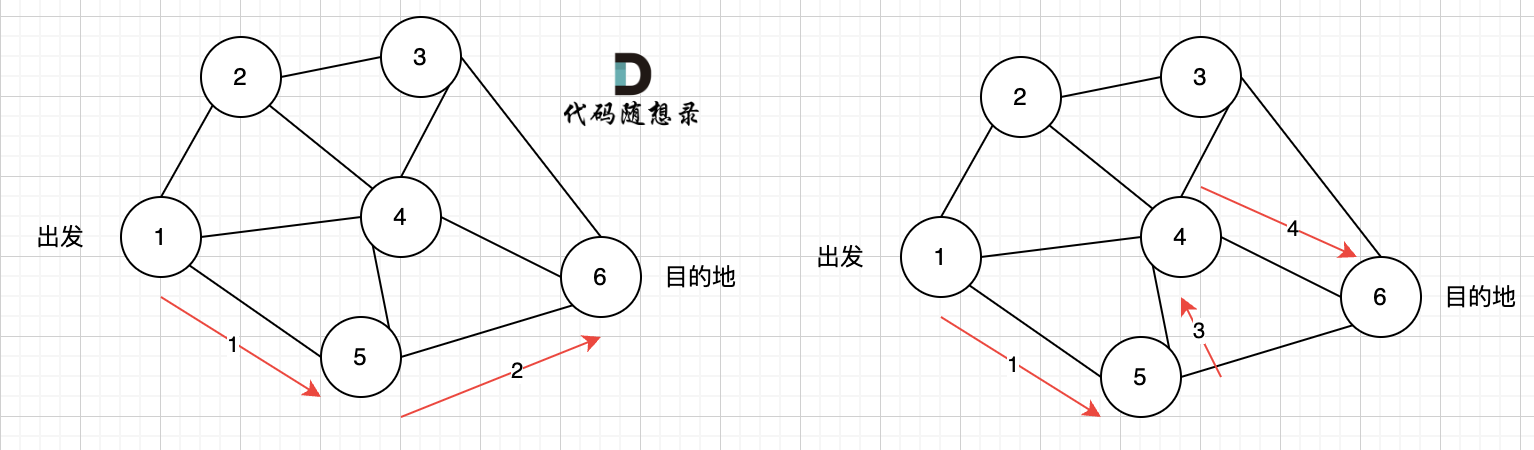
## 总结
diff --git a/problems/kamacoder/图论理论基础.md b/problems/kamacoder/图论理论基础.md
index 84f693a0..9bec3227 100644
--- a/problems/kamacoder/图论理论基础.md
+++ b/problems/kamacoder/图论理论基础.md
@@ -17,15 +17,15 @@
有向图是指 图中边是有方向的:
-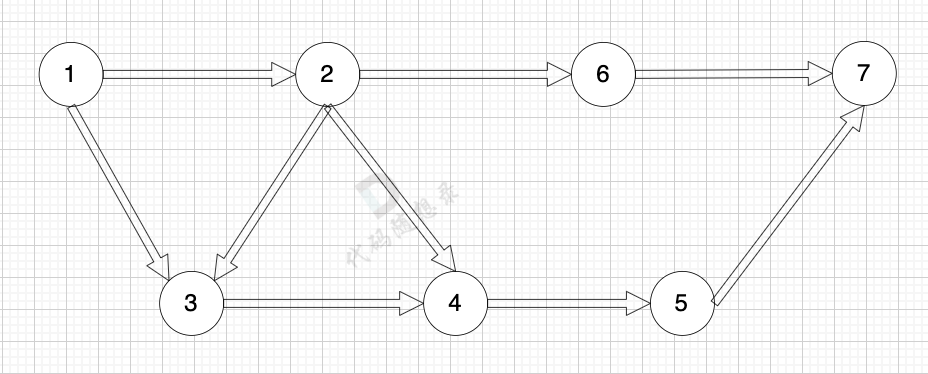
+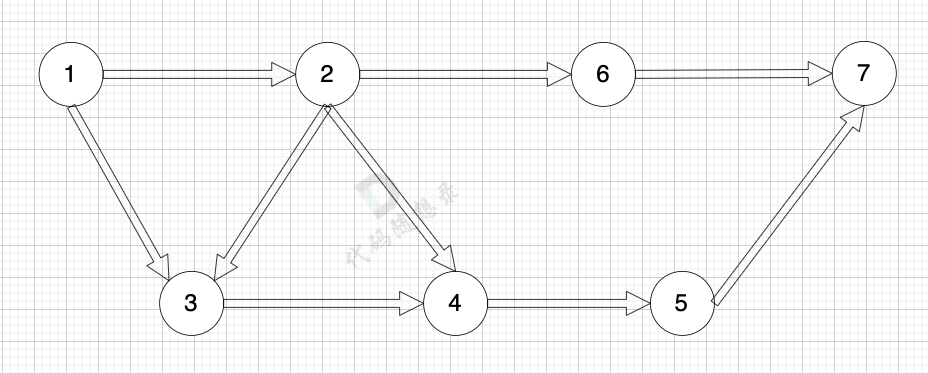
无向图是指 图中边没有方向:
-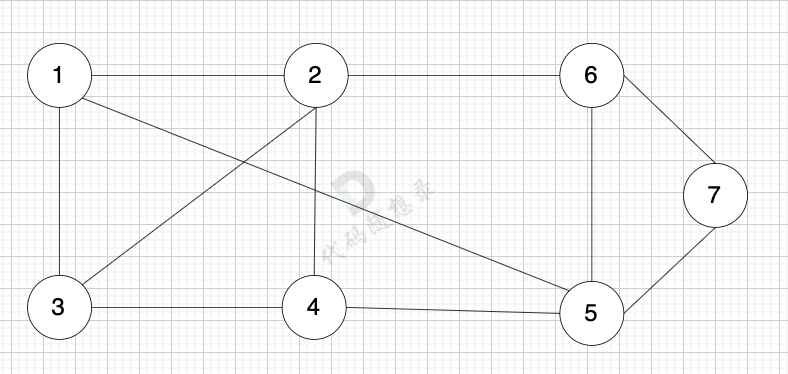
+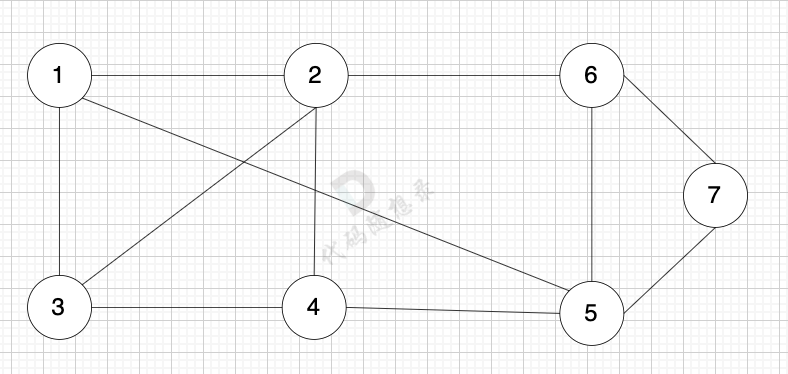
加权有向图,就是图中边是有权值的,例如:
-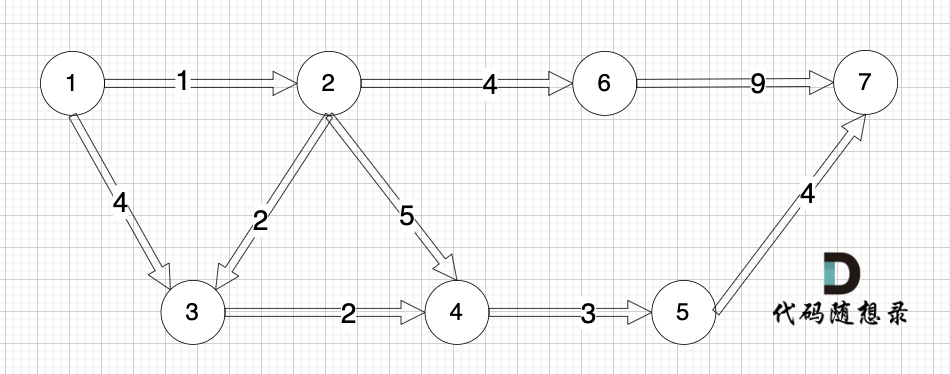
+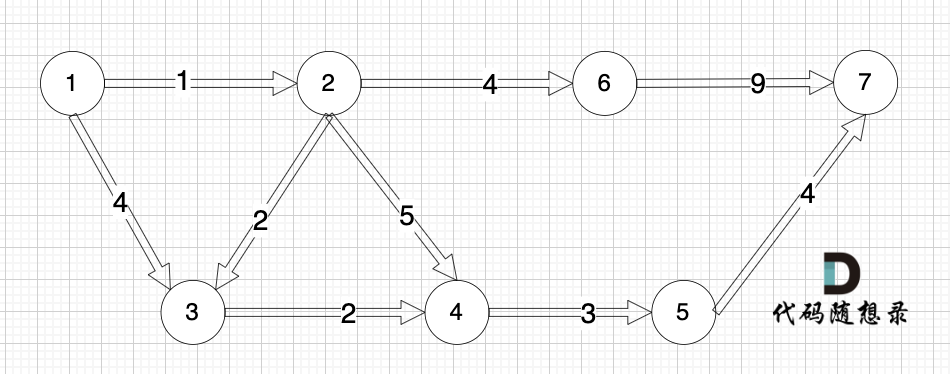
加权无向图也是同理。
@@ -35,7 +35,7 @@
例如,该无向图中,节点4的度为5,节点6的度为3。
-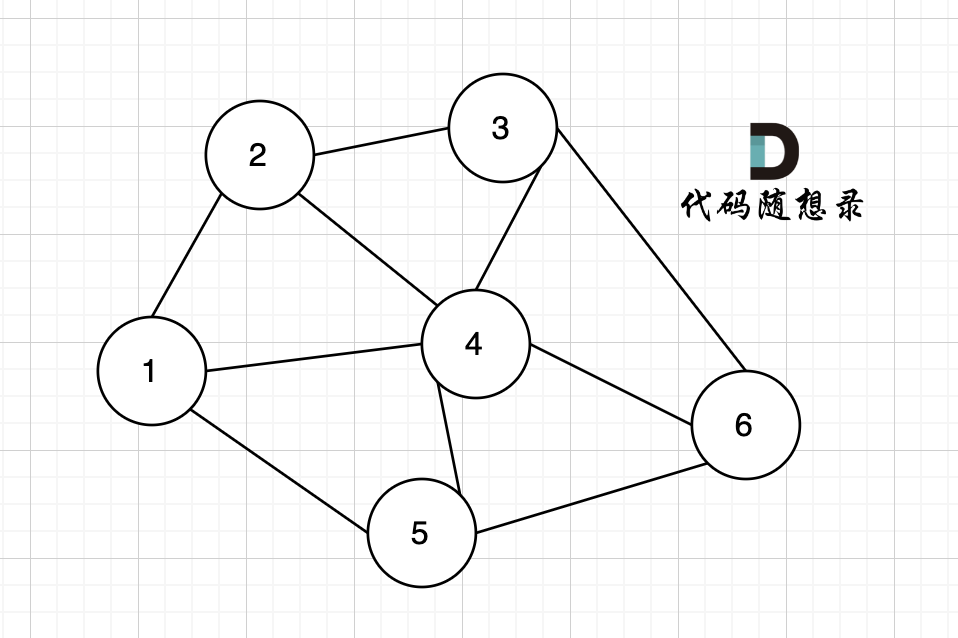
+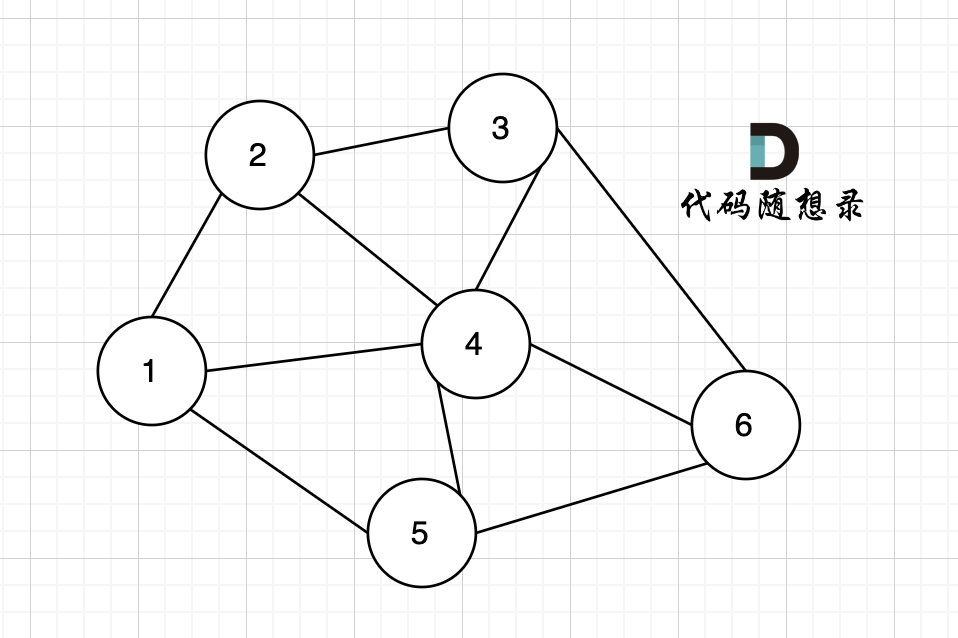
在有向图中,每个节点有出度和入度。
@@ -45,7 +45,7 @@
例如,该有向图中,节点3的入度为2,出度为1,节点1的入度为0,出度为2。
-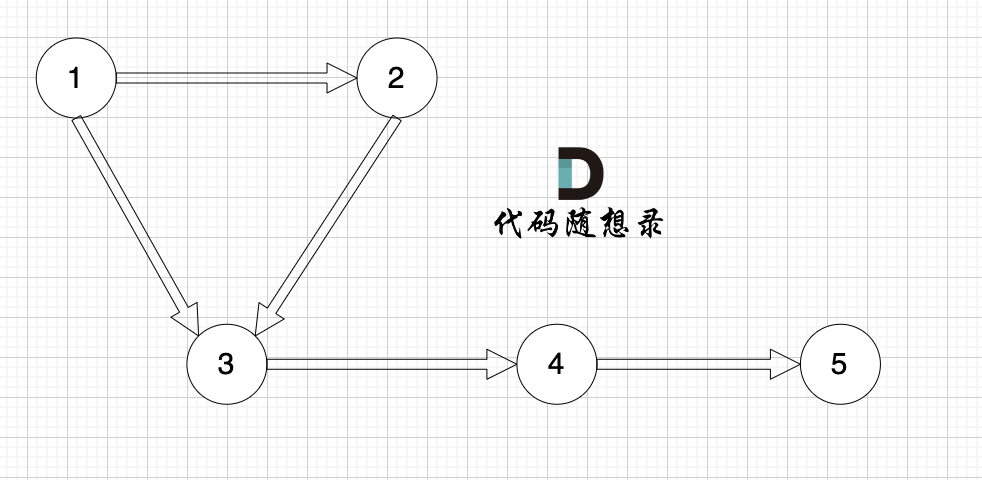
+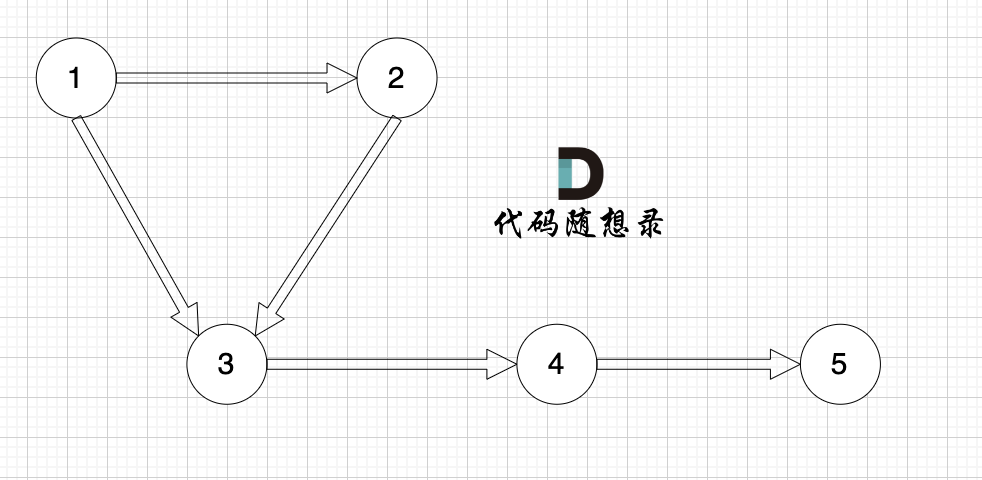
## 连通性
@@ -56,11 +56,11 @@
在无向图中,任何两个节点都是可以到达的,我们称之为连通图 ,如图:
-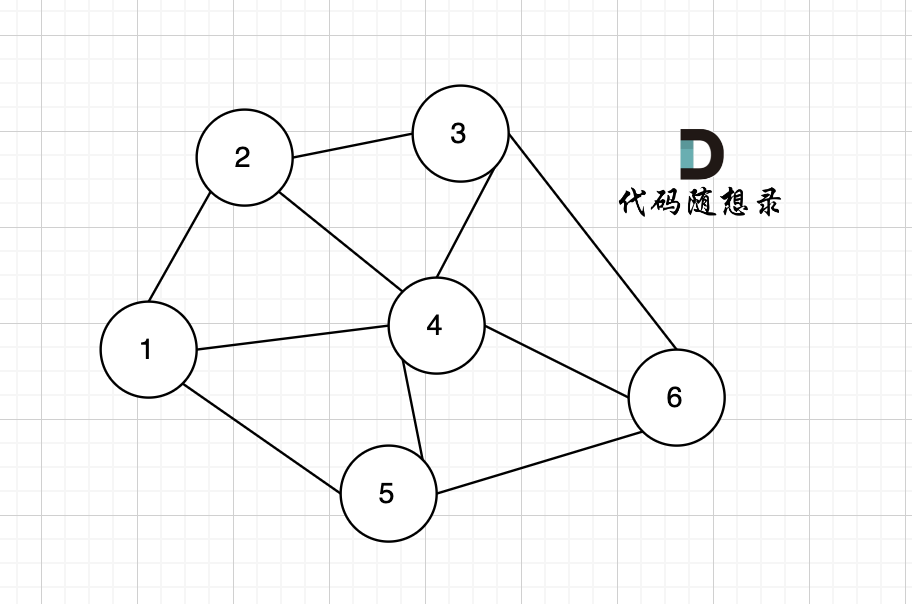
+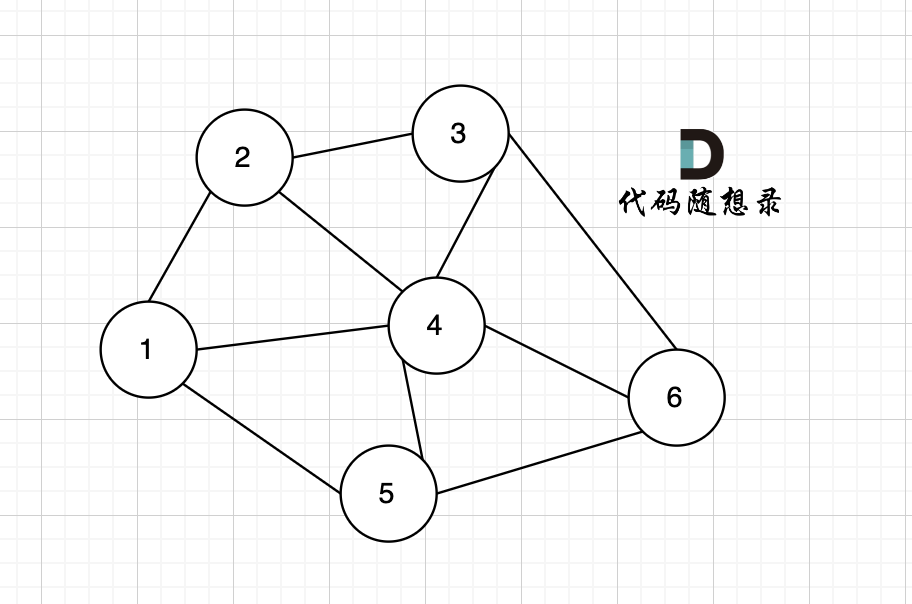
如果有节点不能到达其他节点,则为非连通图,如图:
-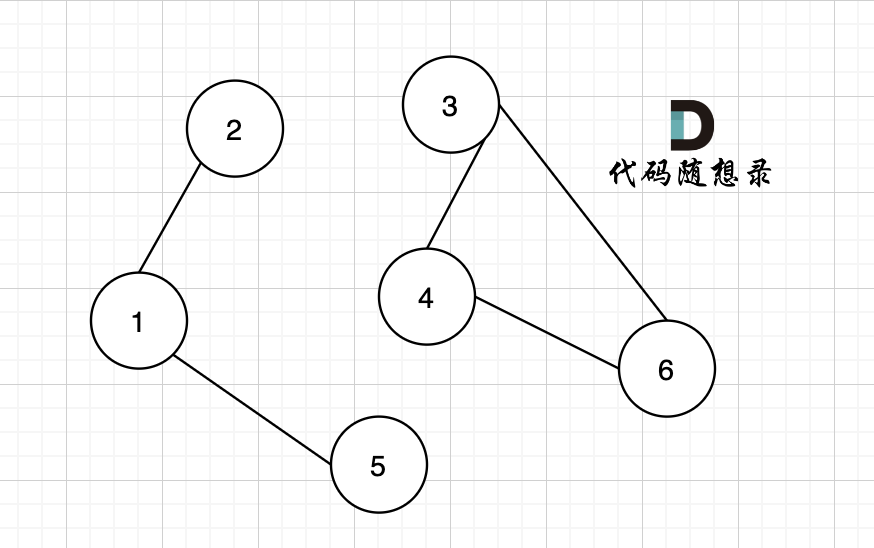
+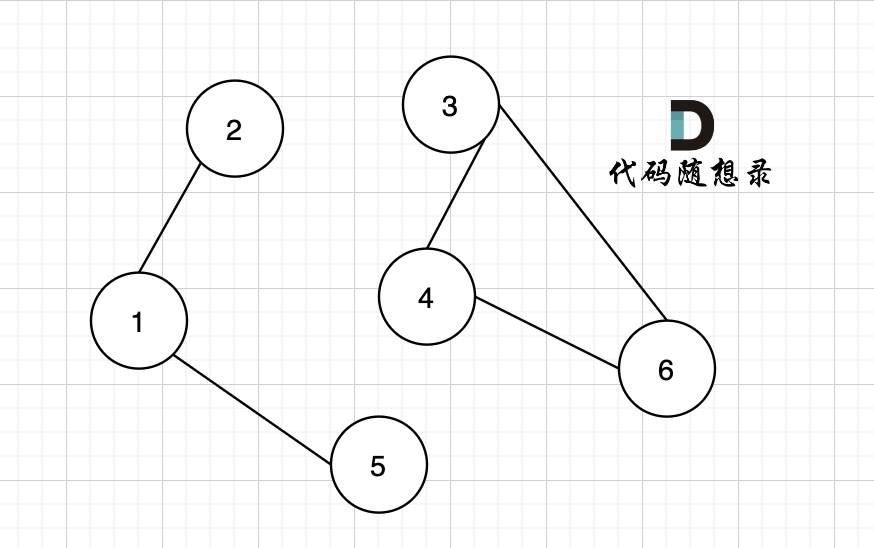
节点1 不能到达节点4。
@@ -72,7 +72,7 @@
我们来看这个有向图:
-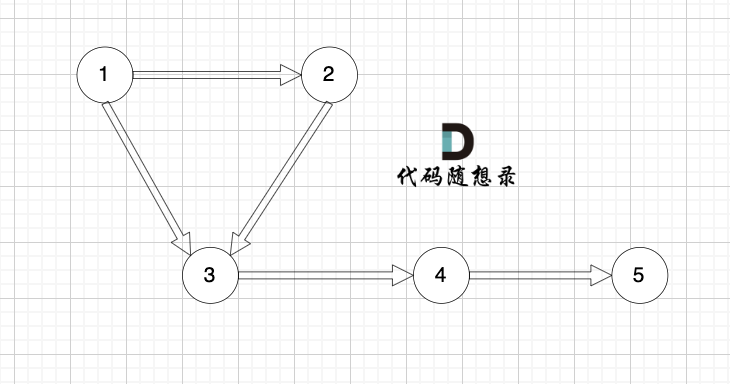
+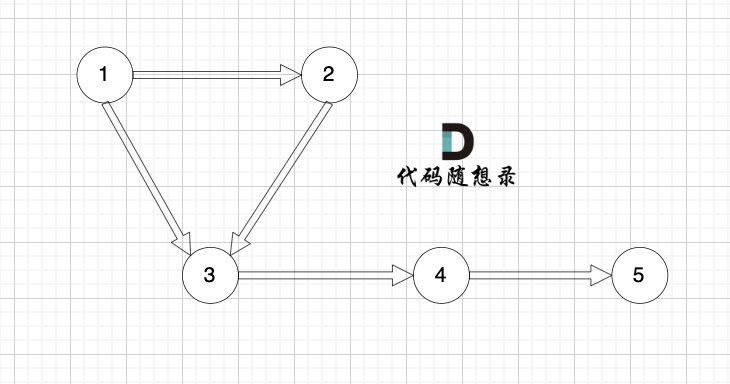
这个图是强连通图吗?
@@ -82,7 +82,7 @@
下面这个有向图才是强连通图:
-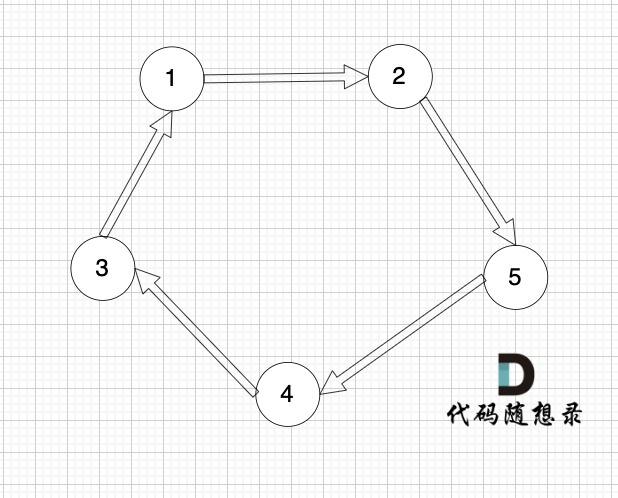
+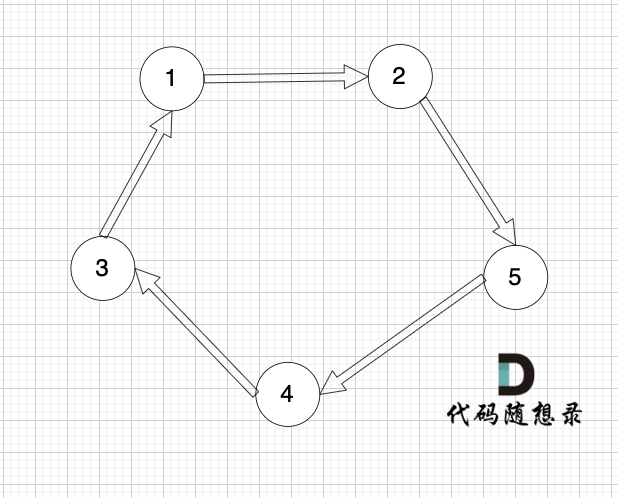
### 连通分量
@@ -91,7 +91,7 @@
只看概念大家可能不理解,我来画个图:
-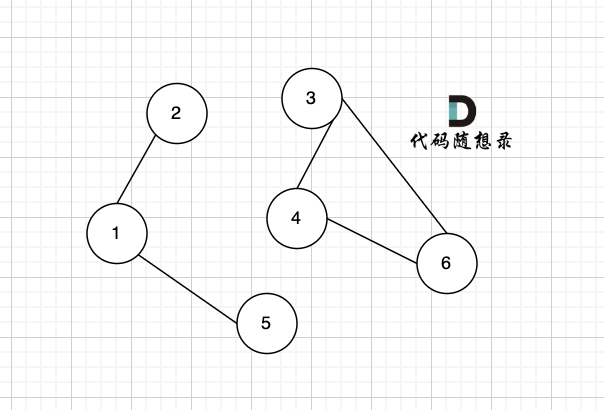
+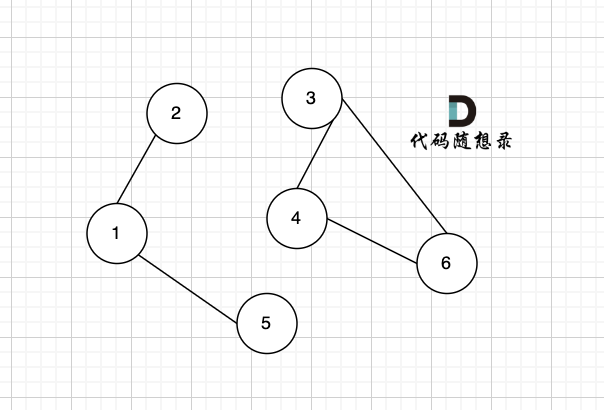
该无向图中 节点1、节点2、节点5 构成的子图就是 该无向图中的一个连通分量,该子图所有节点都是相互可达到的。
@@ -111,7 +111,7 @@
如图:
-
+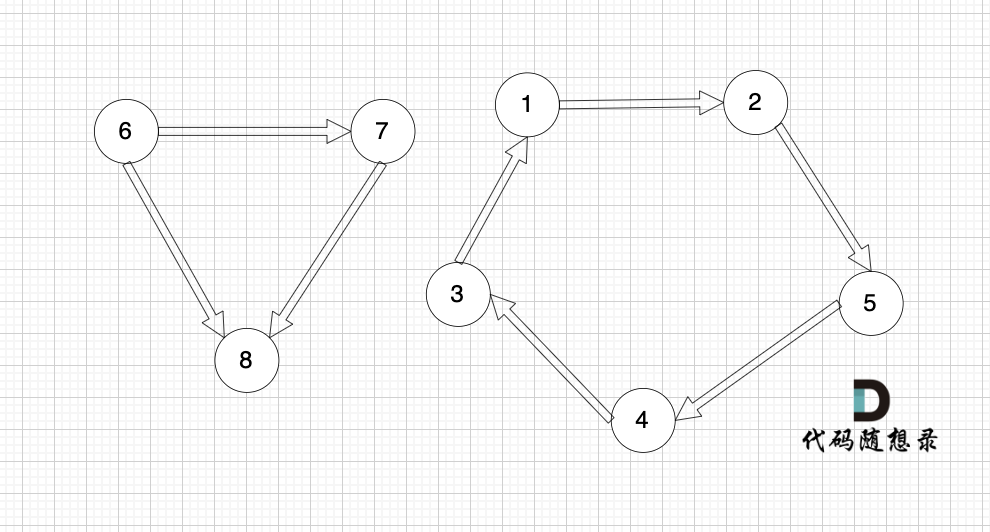
节点1、节点2、节点3、节点4、节点5 构成的子图是强连通分量,因为这是强连通图,也是极大图。
@@ -132,11 +132,11 @@
例如图:
-
+
图中有8条边,我们就定义 8 * 2的数组,即有n条边就申请n * 2,这么大的数组:
-
+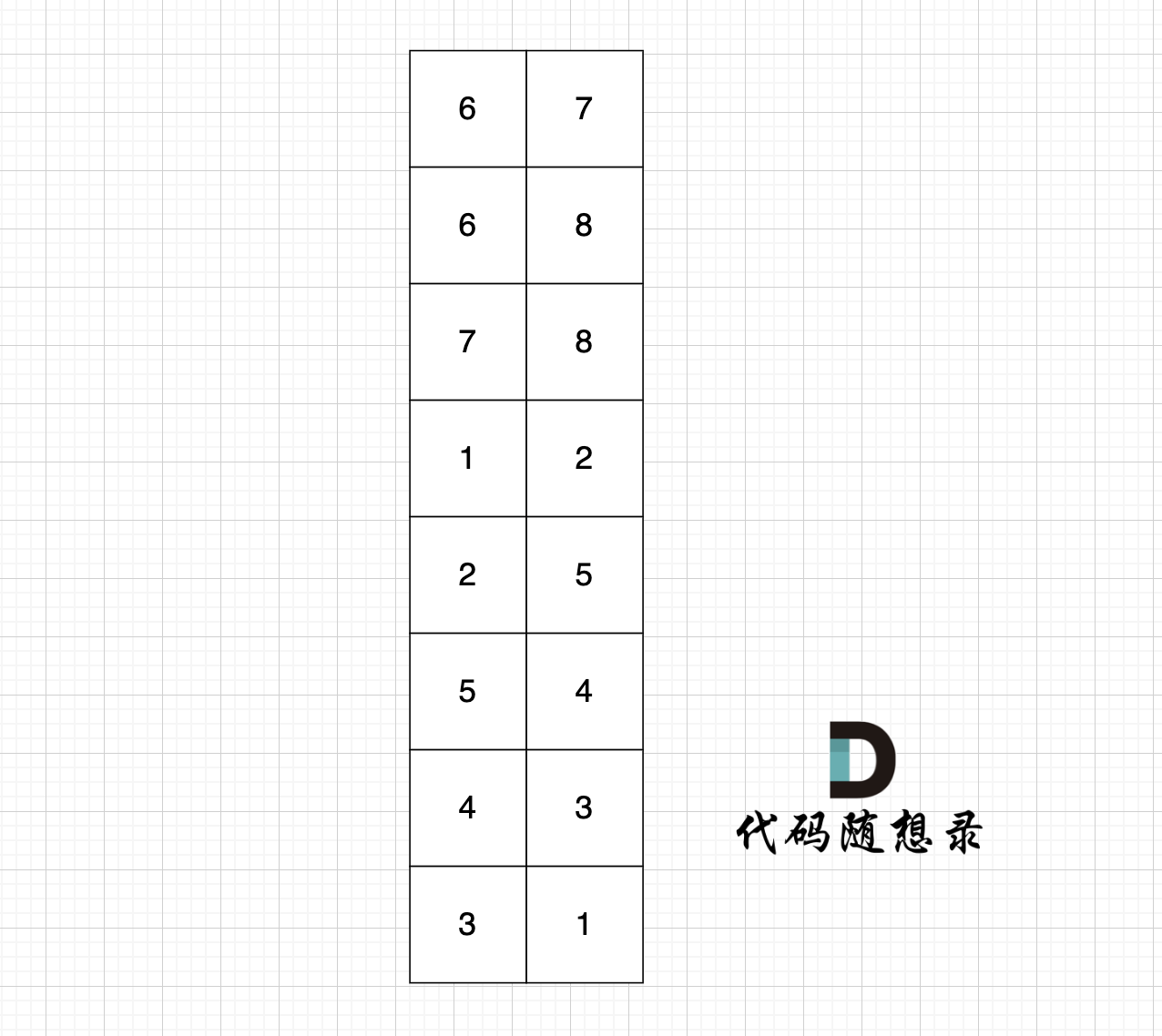
数组第一行:6 7,就表示节点6 指向 节点7,以此类推。
@@ -162,7 +162,7 @@
如图:
-
+
在一个 n (节点数)为8 的图中,就需要申请 8 * 8 这么大的空间。
@@ -188,7 +188,7 @@
邻接表的构造如图:
-
+
这里表达的图是:
diff --git a/problems/kamacoder/最短路问题总结篇.md b/problems/kamacoder/最短路问题总结篇.md
index 54f91539..e83880da 100644
--- a/problems/kamacoder/最短路问题总结篇.md
+++ b/problems/kamacoder/最短路问题总结篇.md
@@ -17,7 +17,7 @@
最短路算法比较复杂,而且各自有各自的应用场景,我来用一张表把讲过的最短路算法的使用场景都展现出来:
-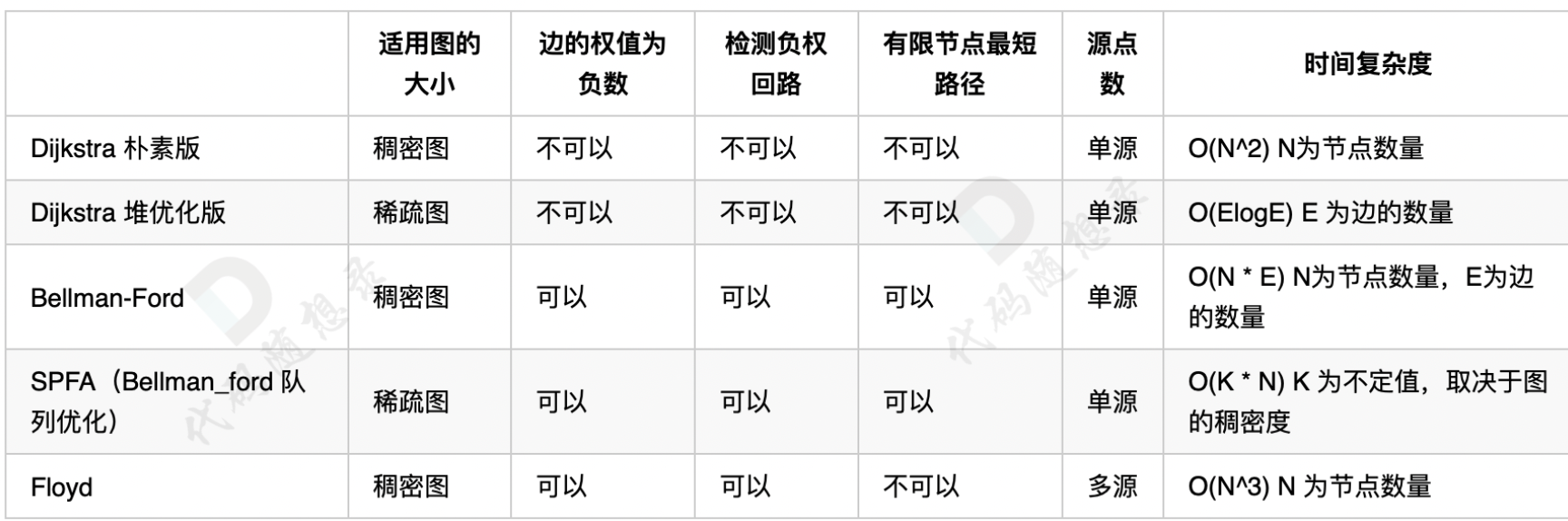
+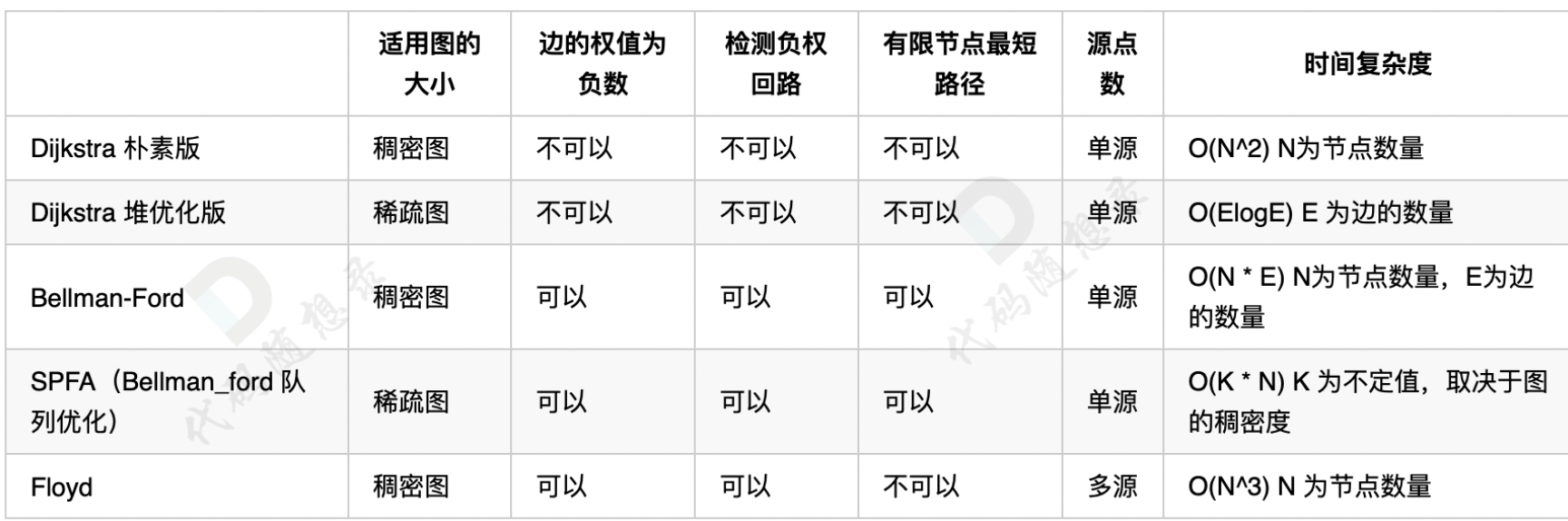
(因为A * 属于启发式搜索,和上面最短路算法并不是一类,不适合一起对比,所以没有放在一起)
diff --git a/problems/qita/acm.md b/problems/qita/acm.md
index 99928356..33dcd8a6 100644
--- a/problems/qita/acm.md
+++ b/problems/qita/acm.md
@@ -11,15 +11,15 @@
[知识星球](https://programmercarl.com/other/kstar.html)里很多录友的日常打卡中,都表示被 ACM模式折磨过:
-






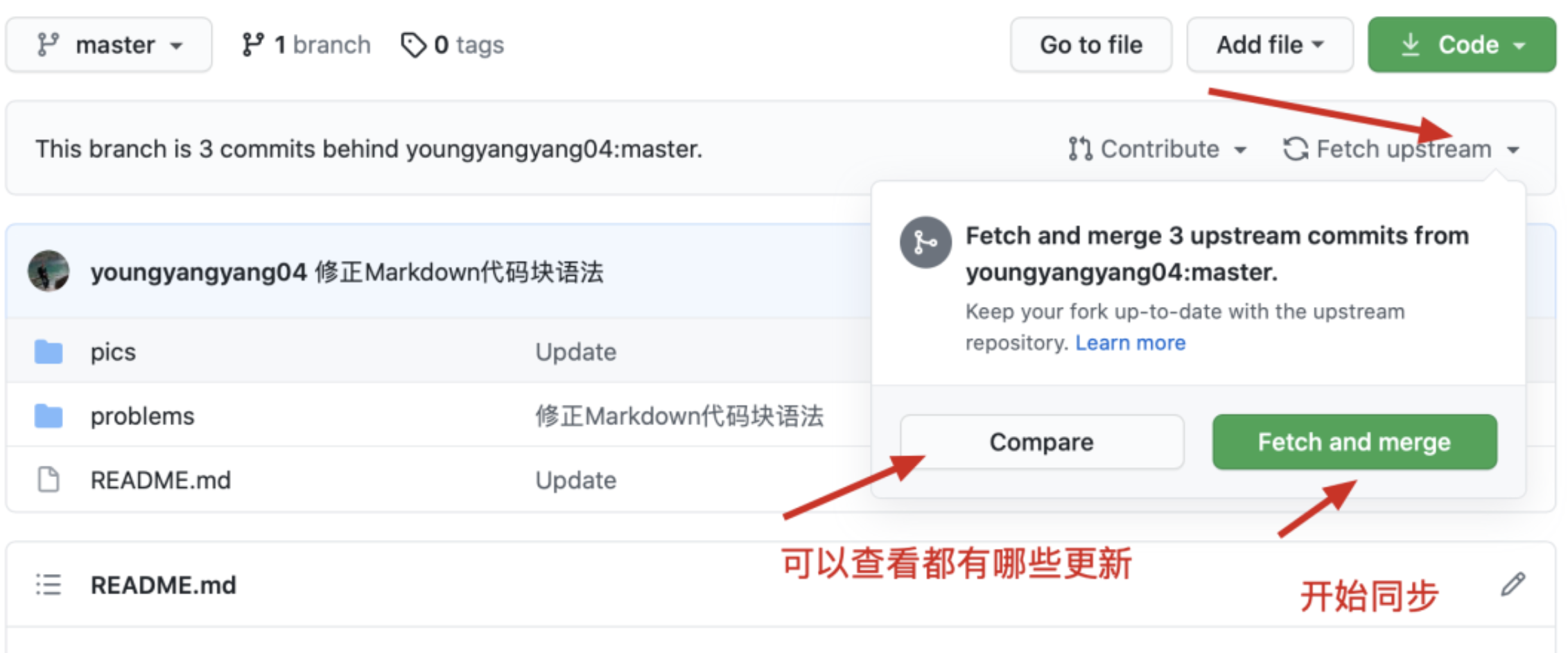
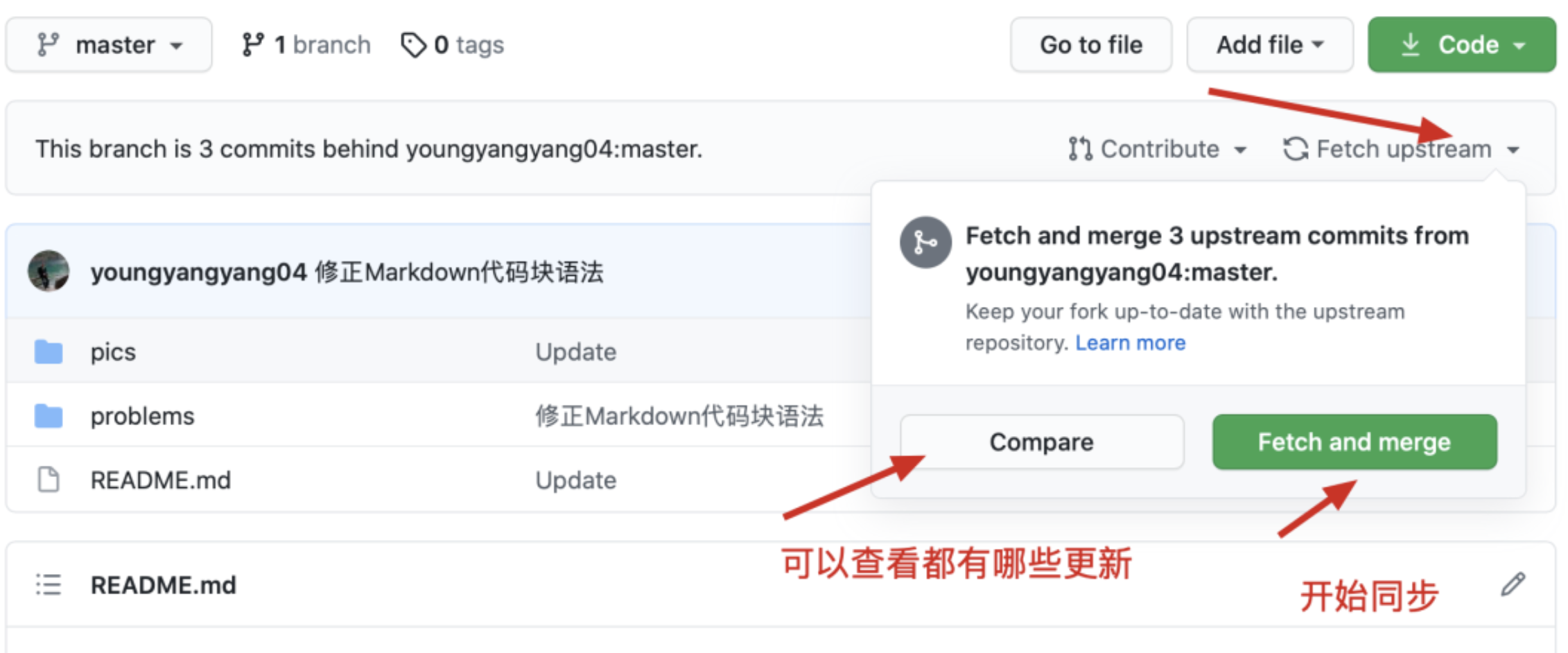
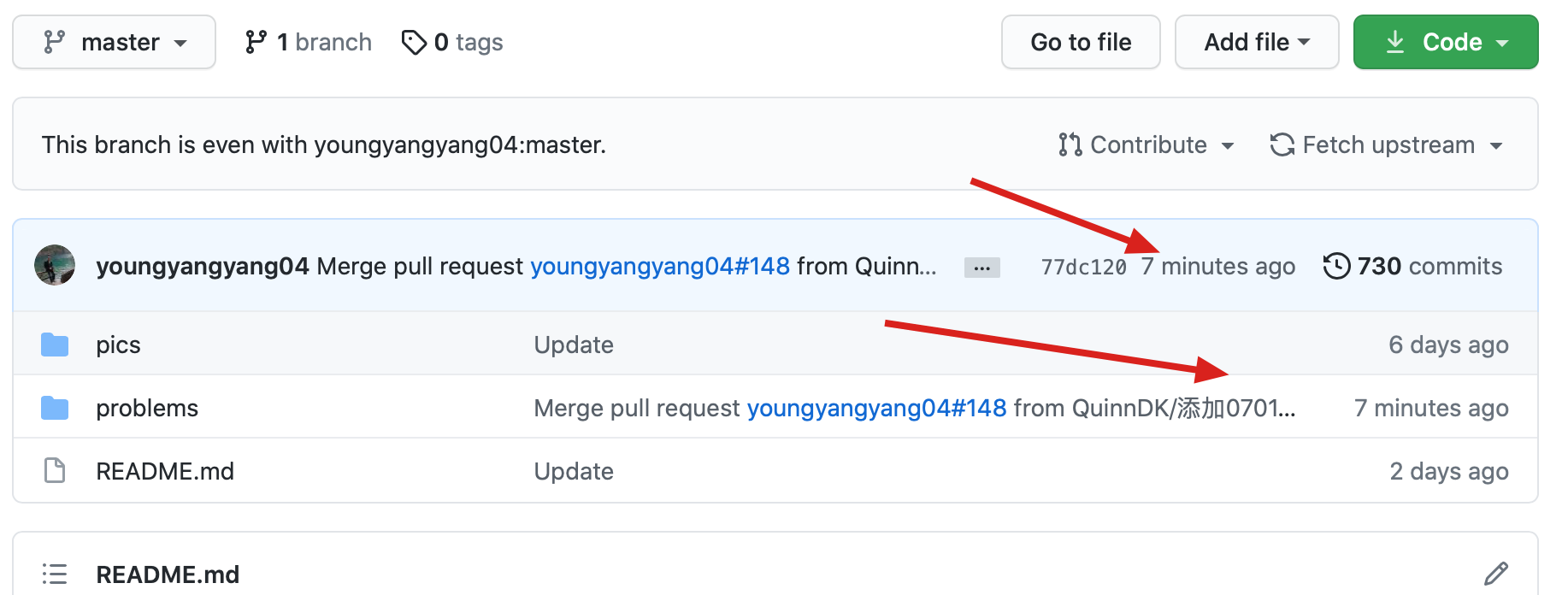
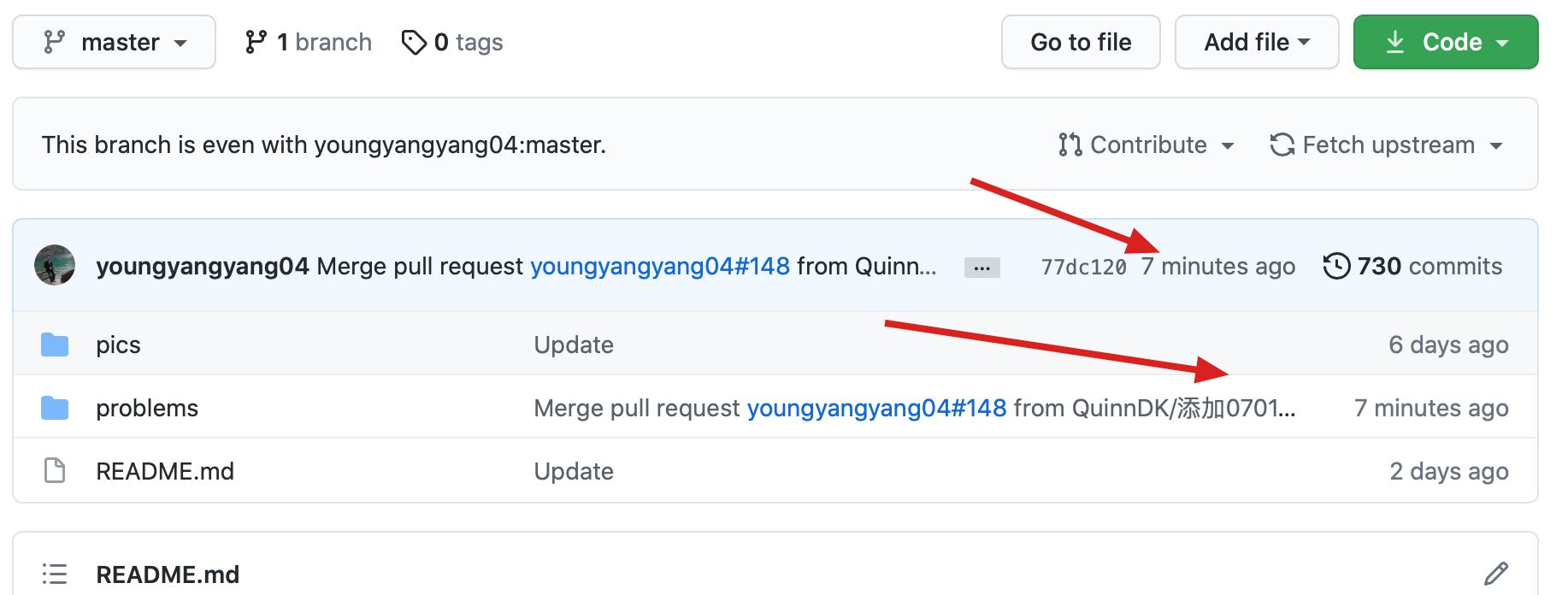
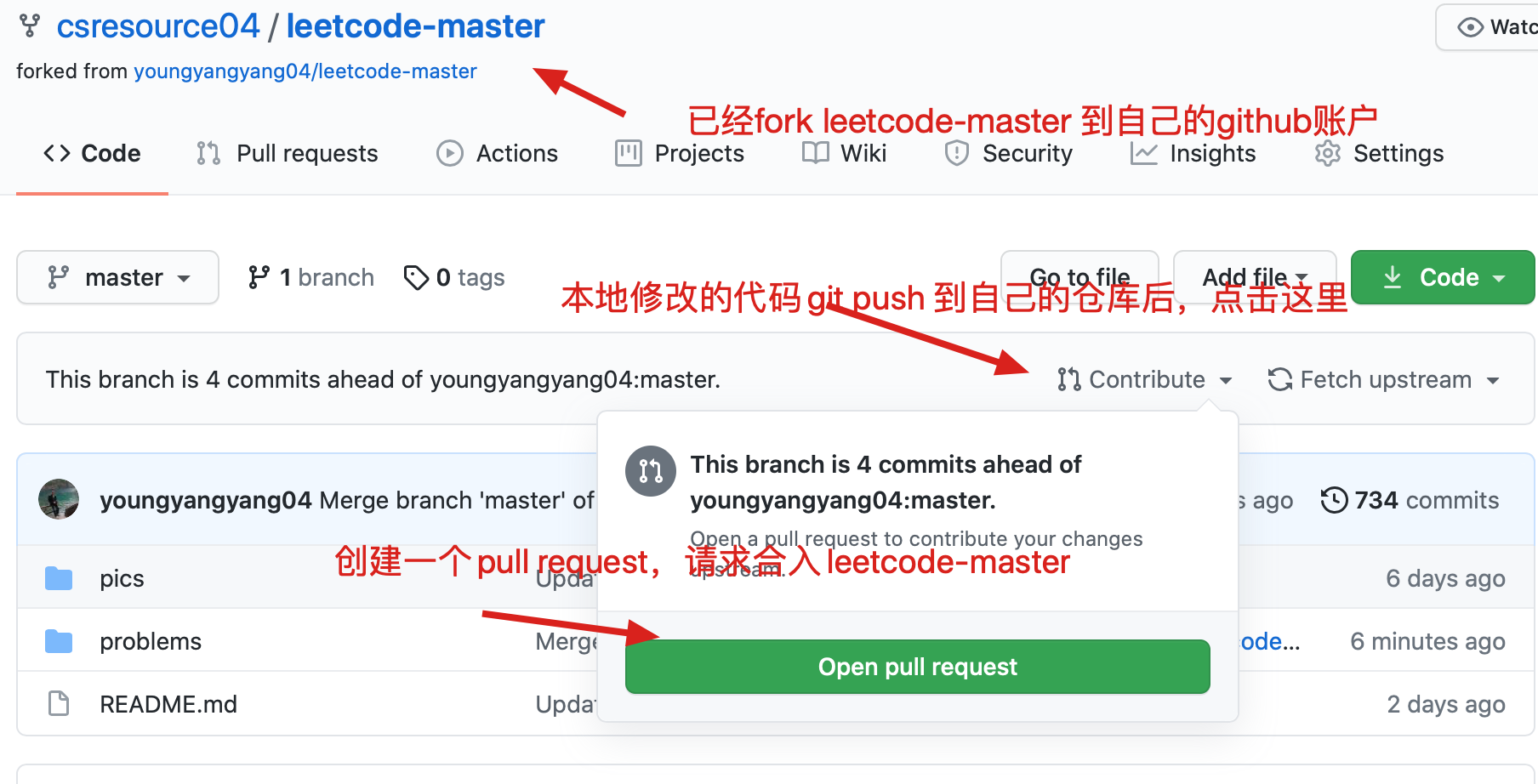
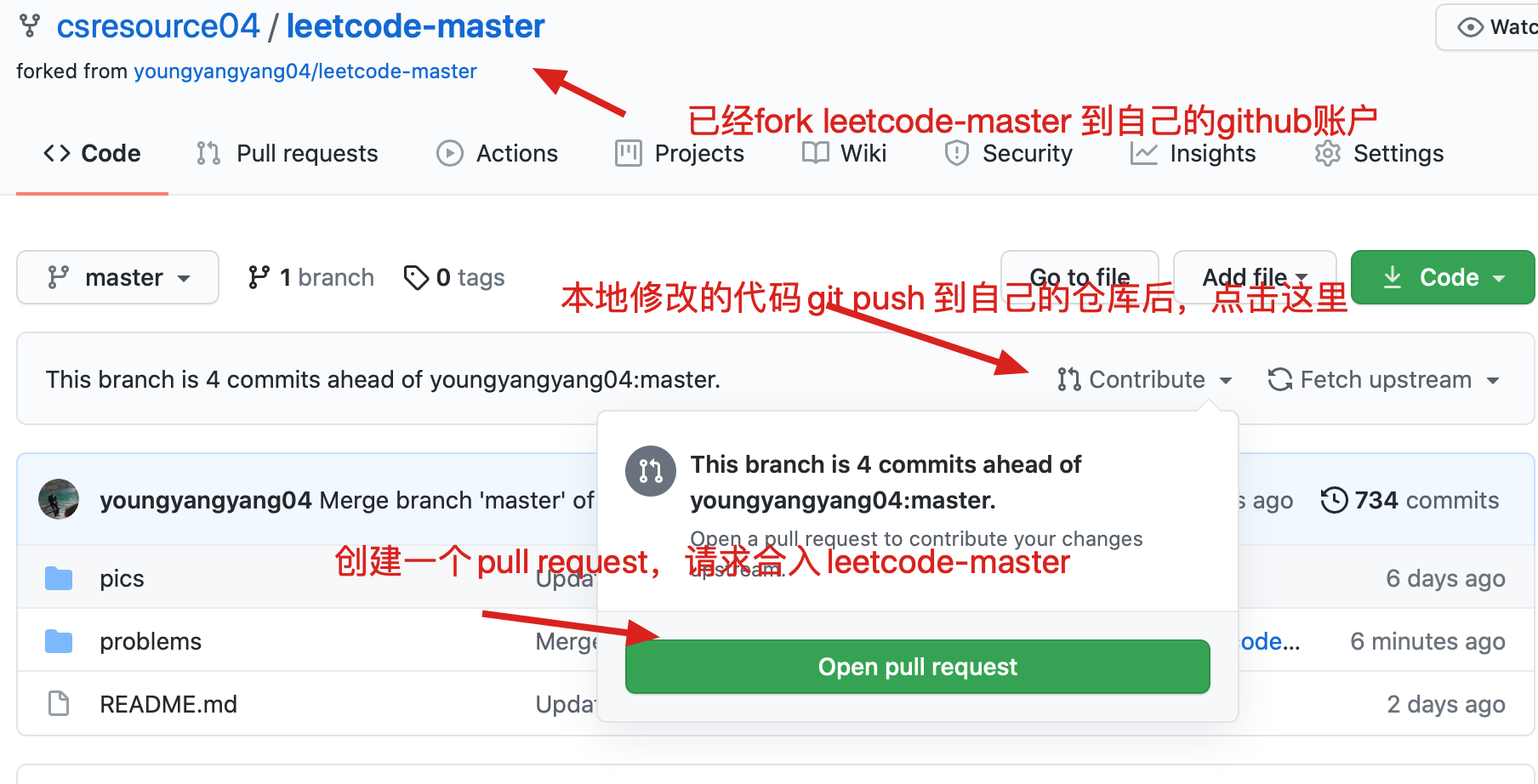
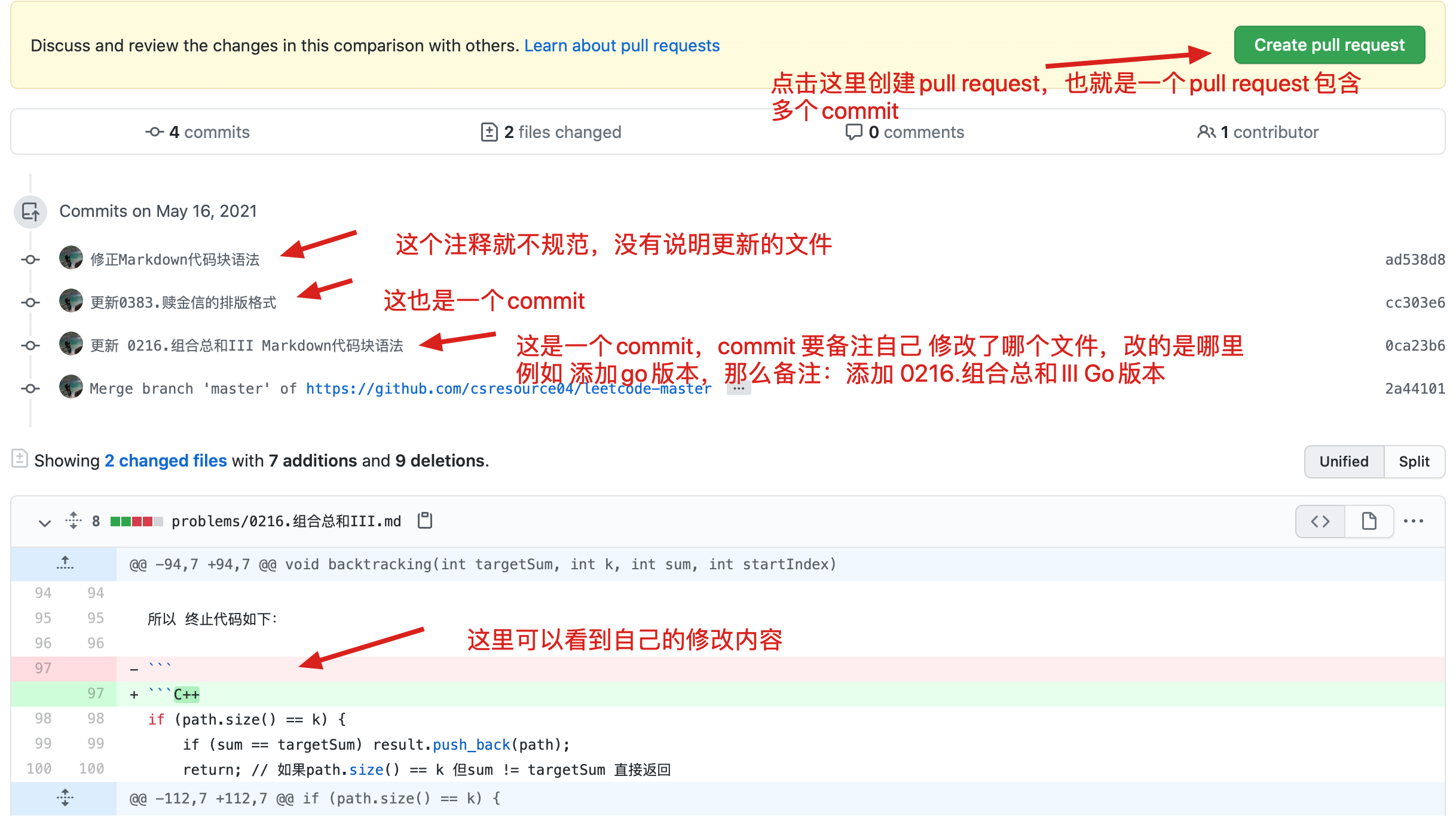
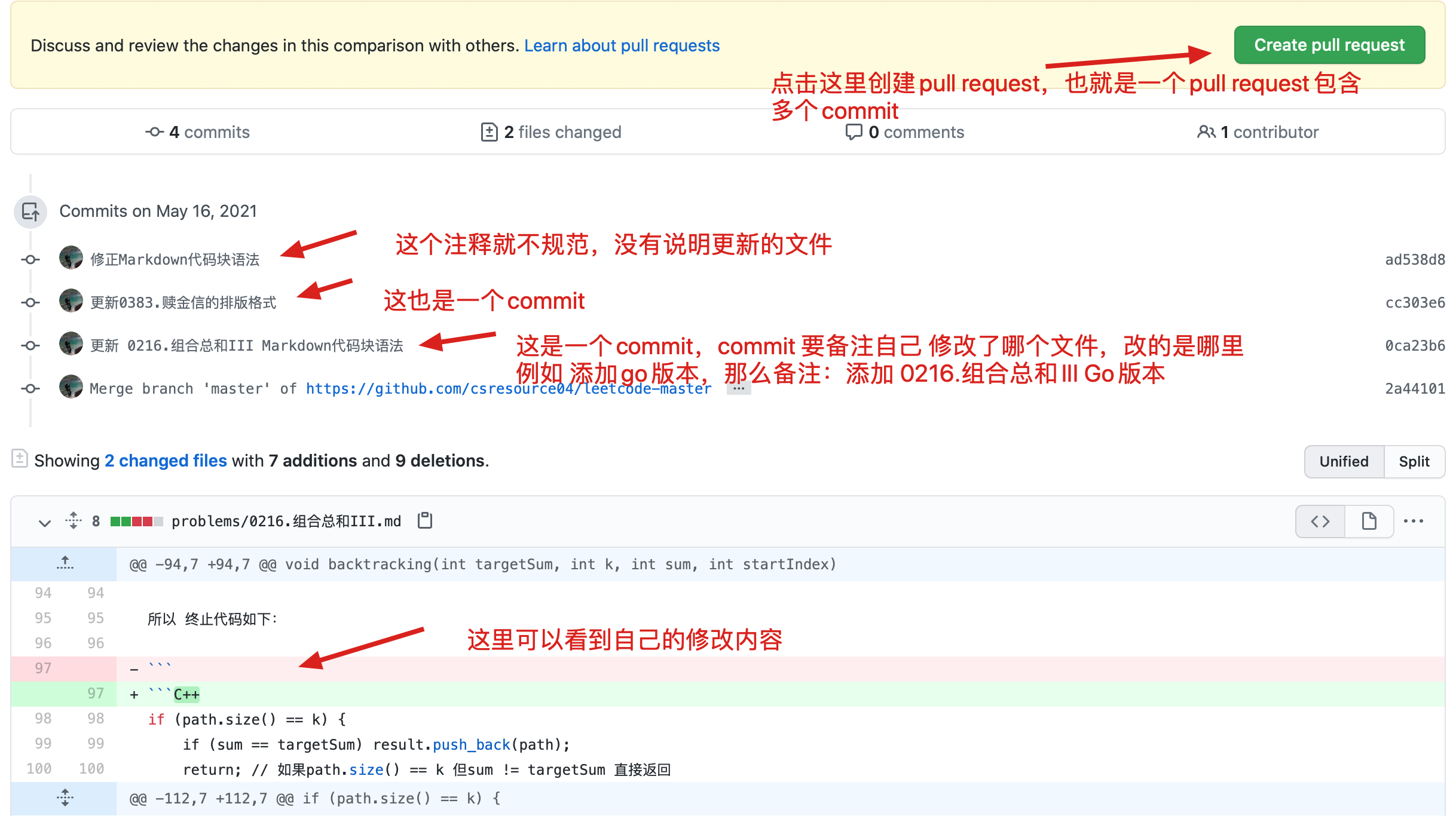
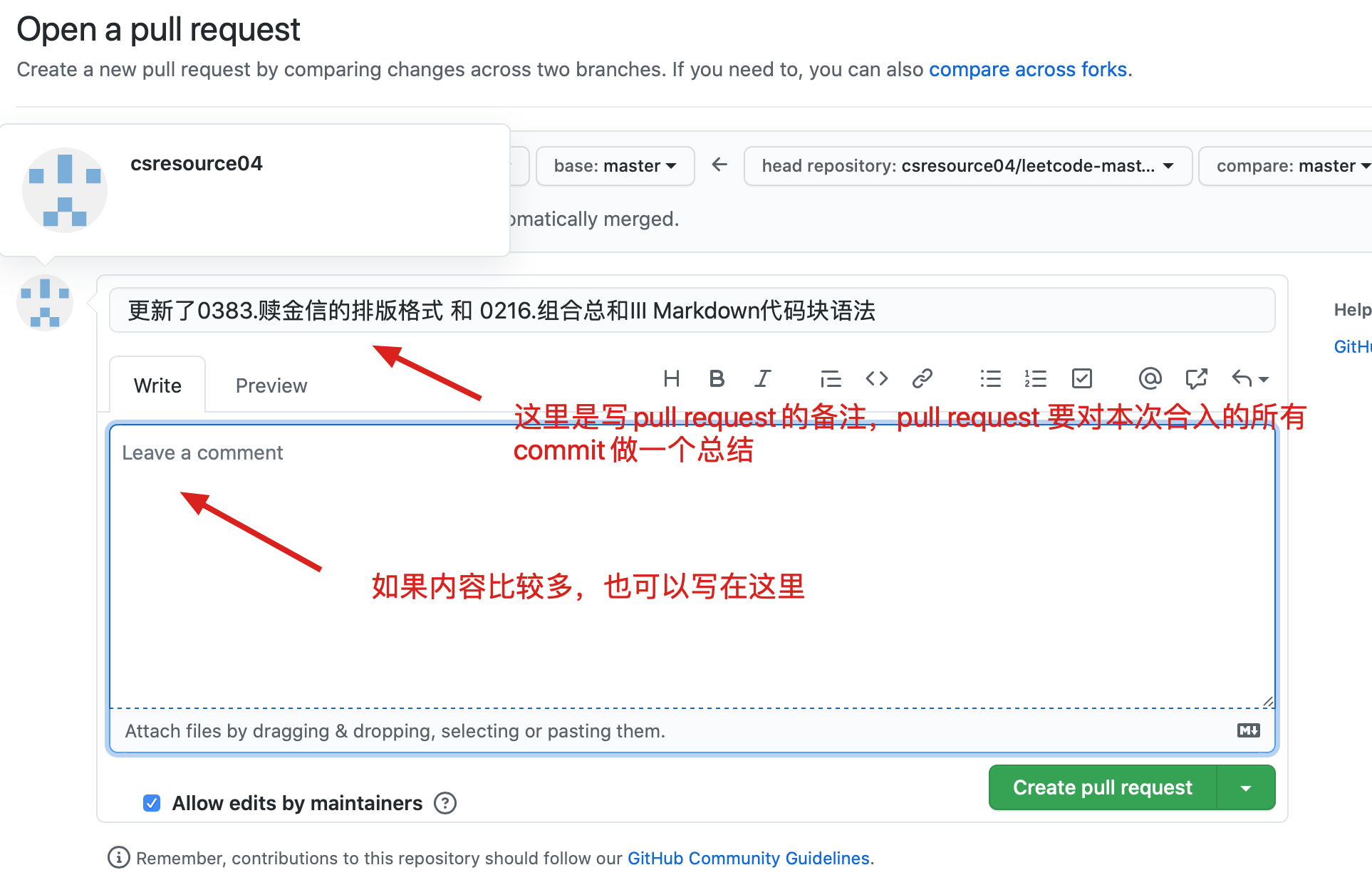
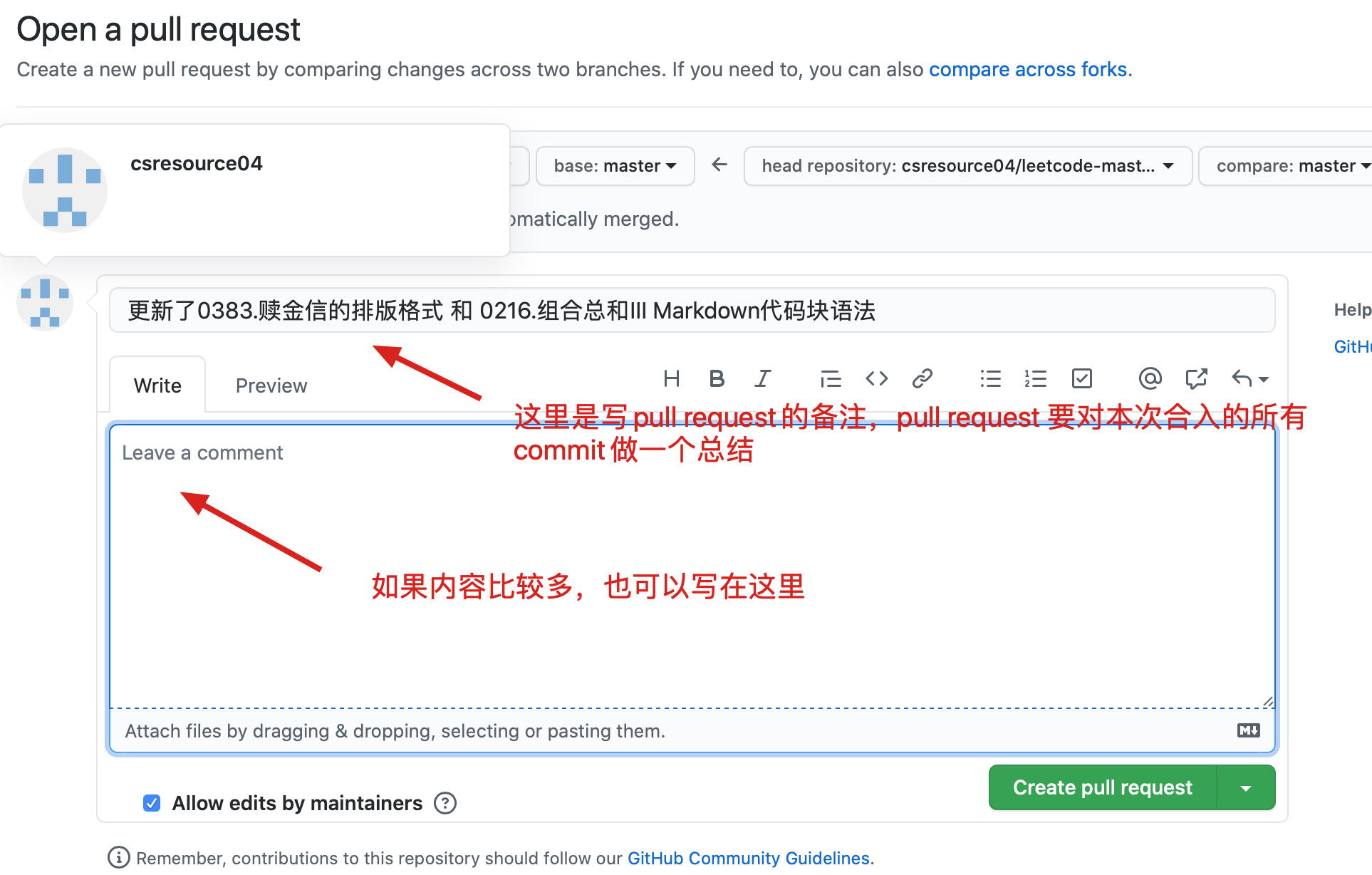
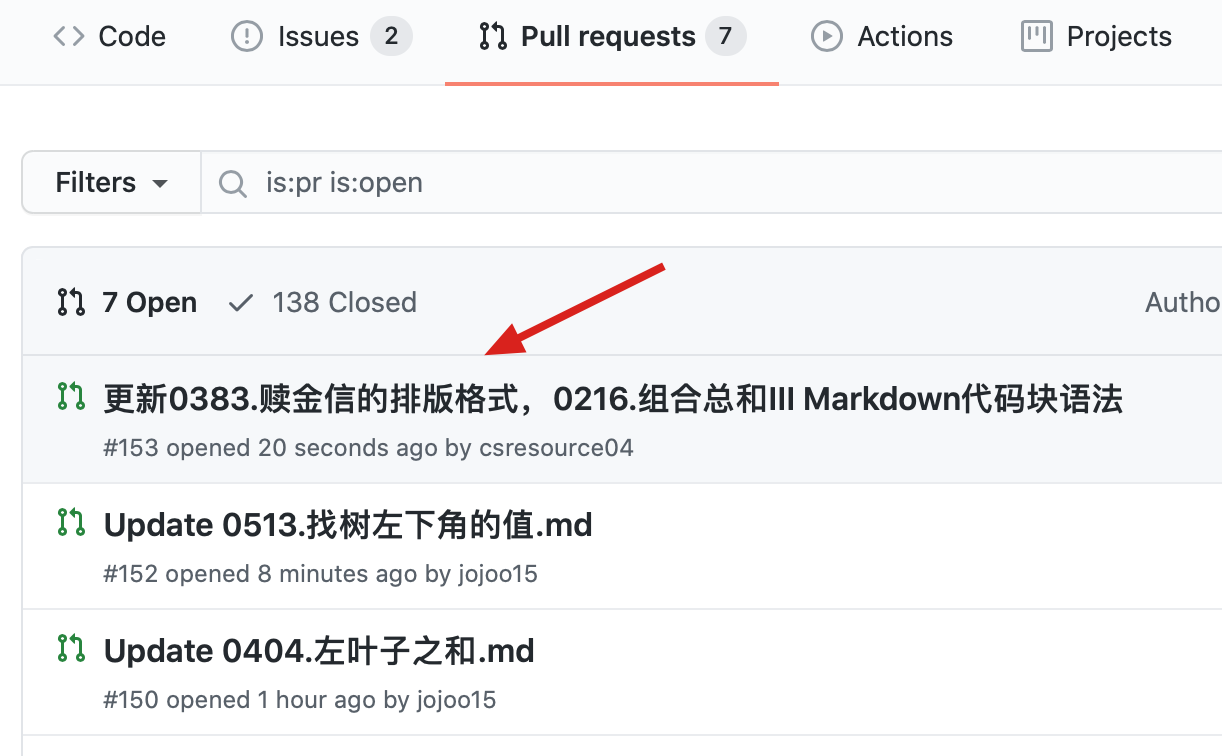




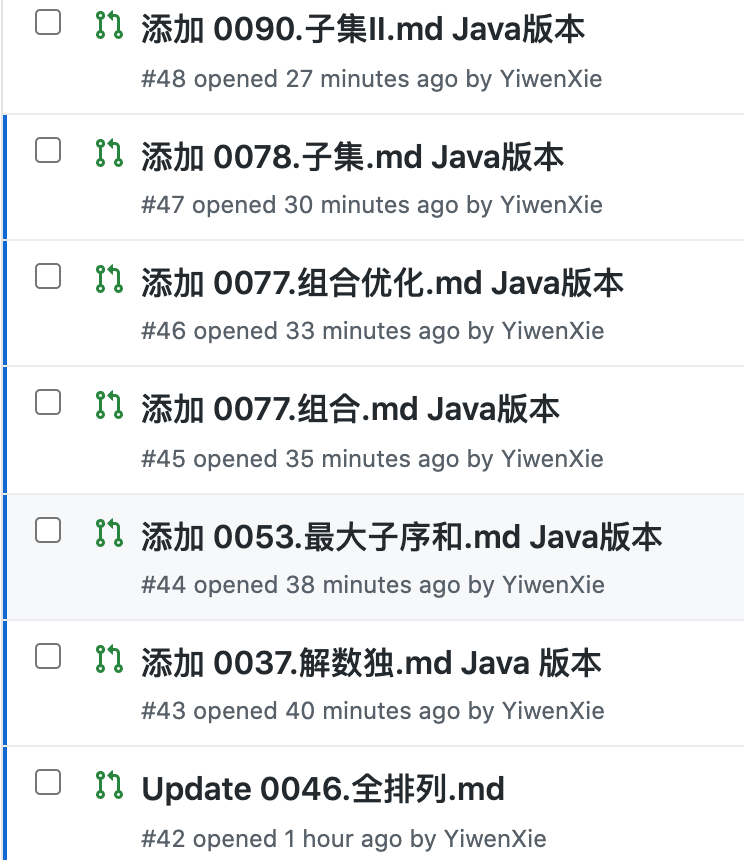
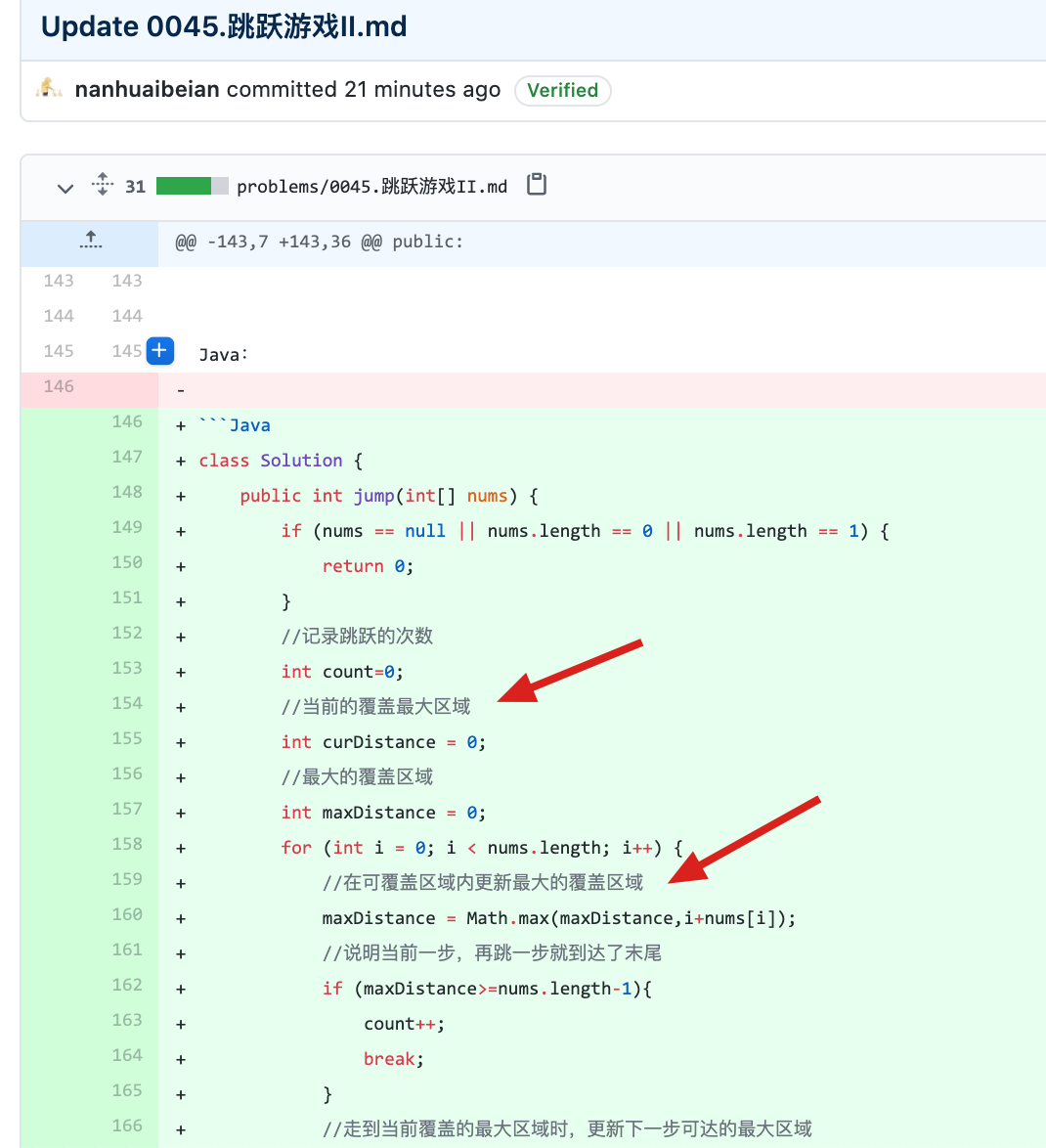
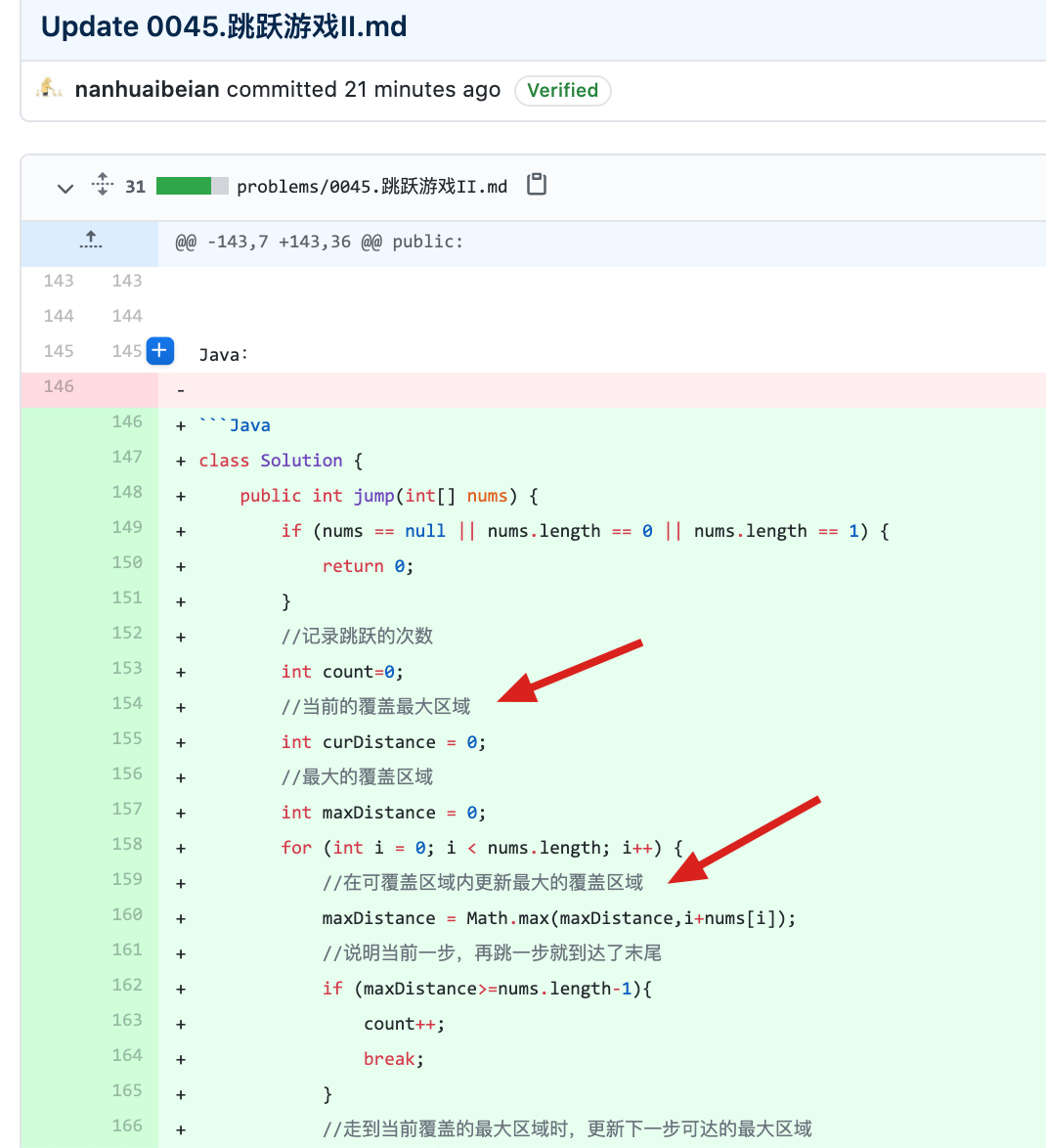
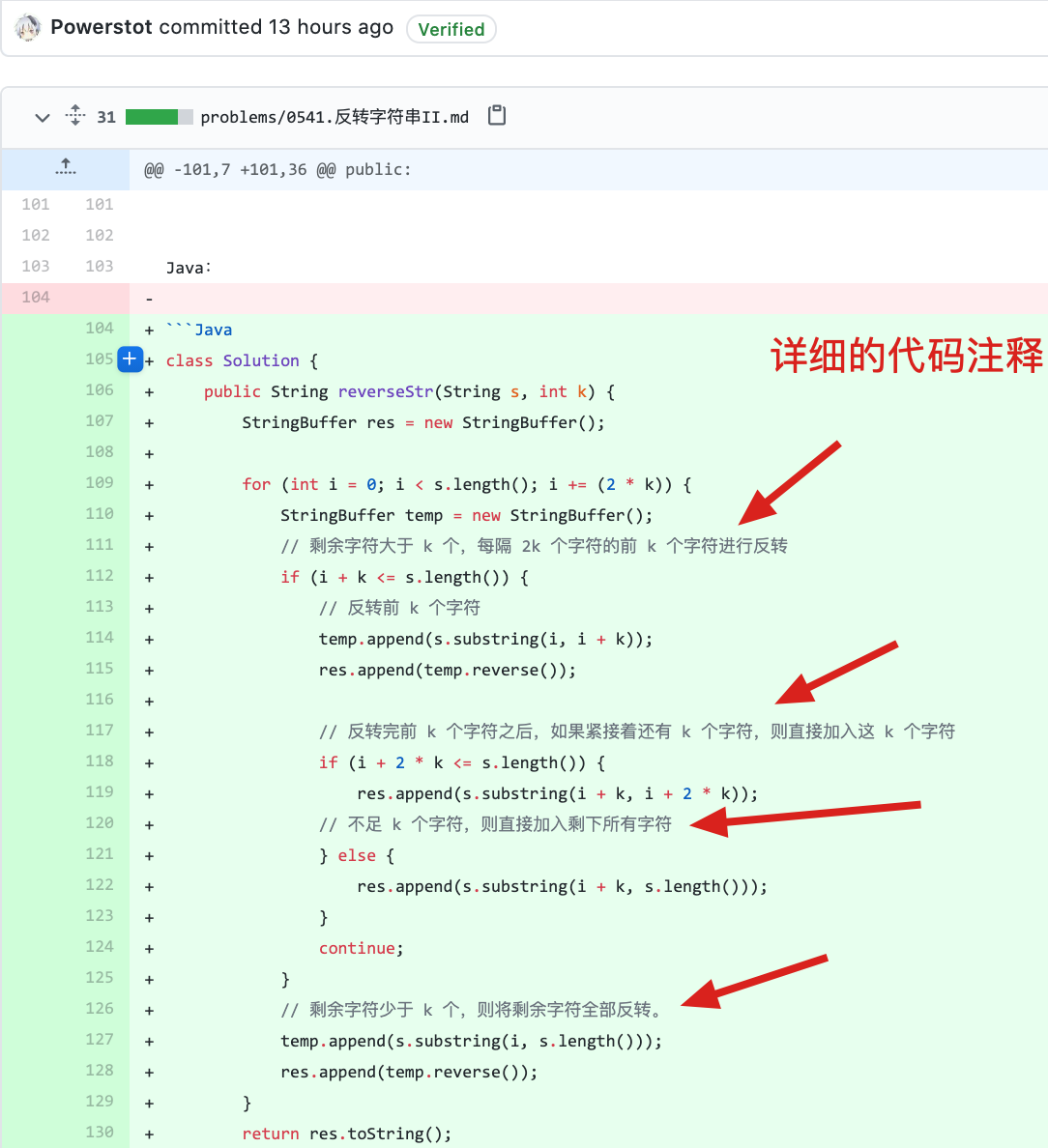
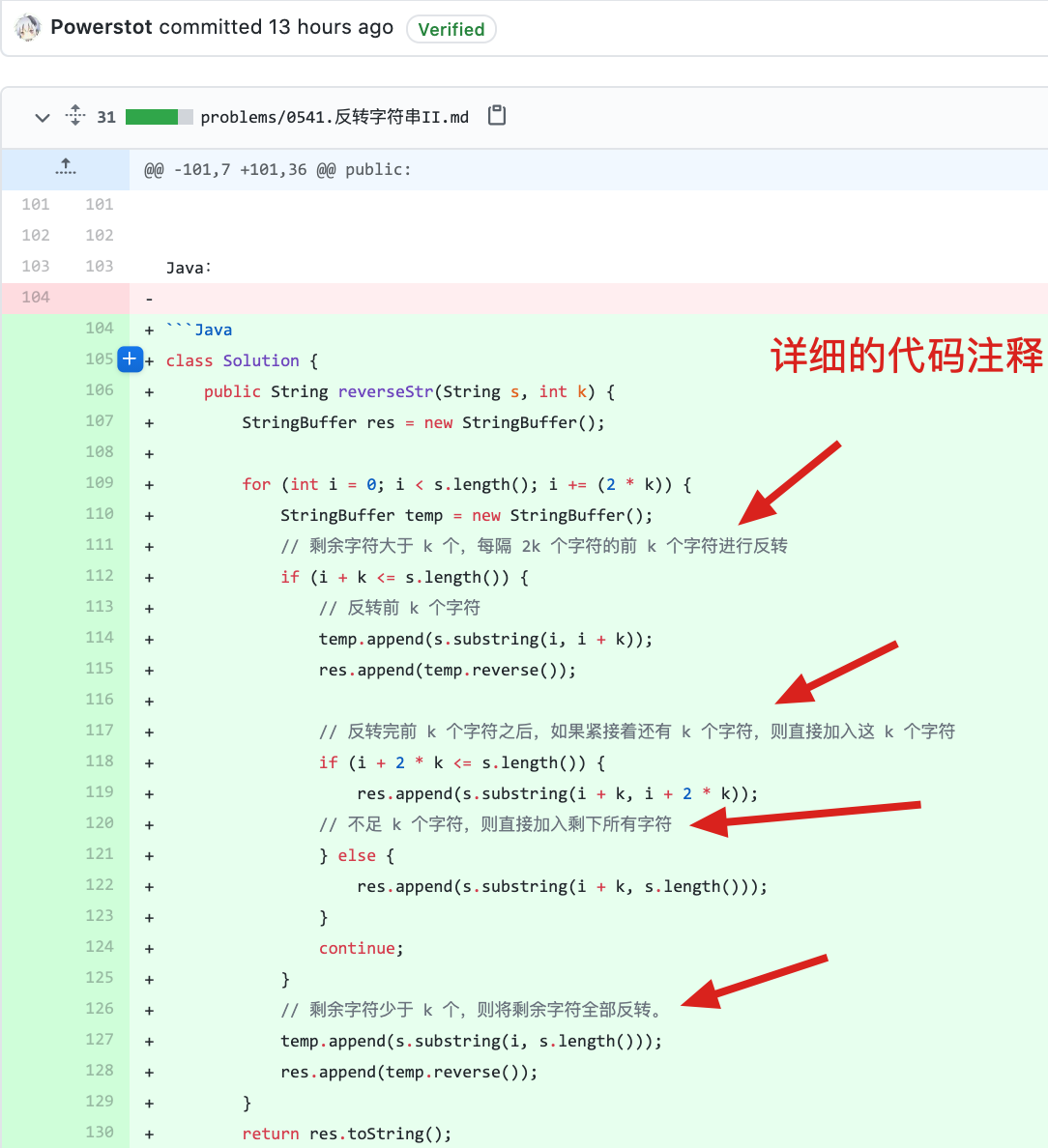
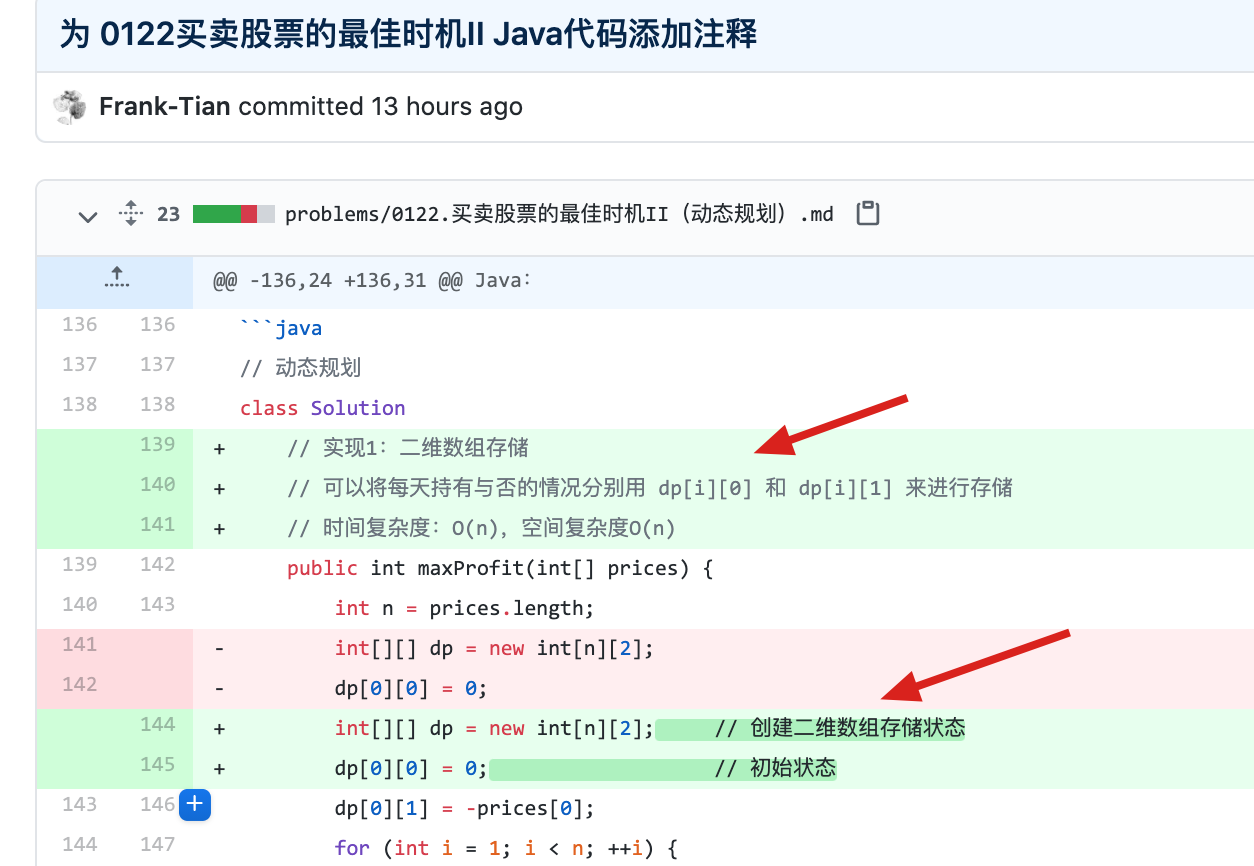
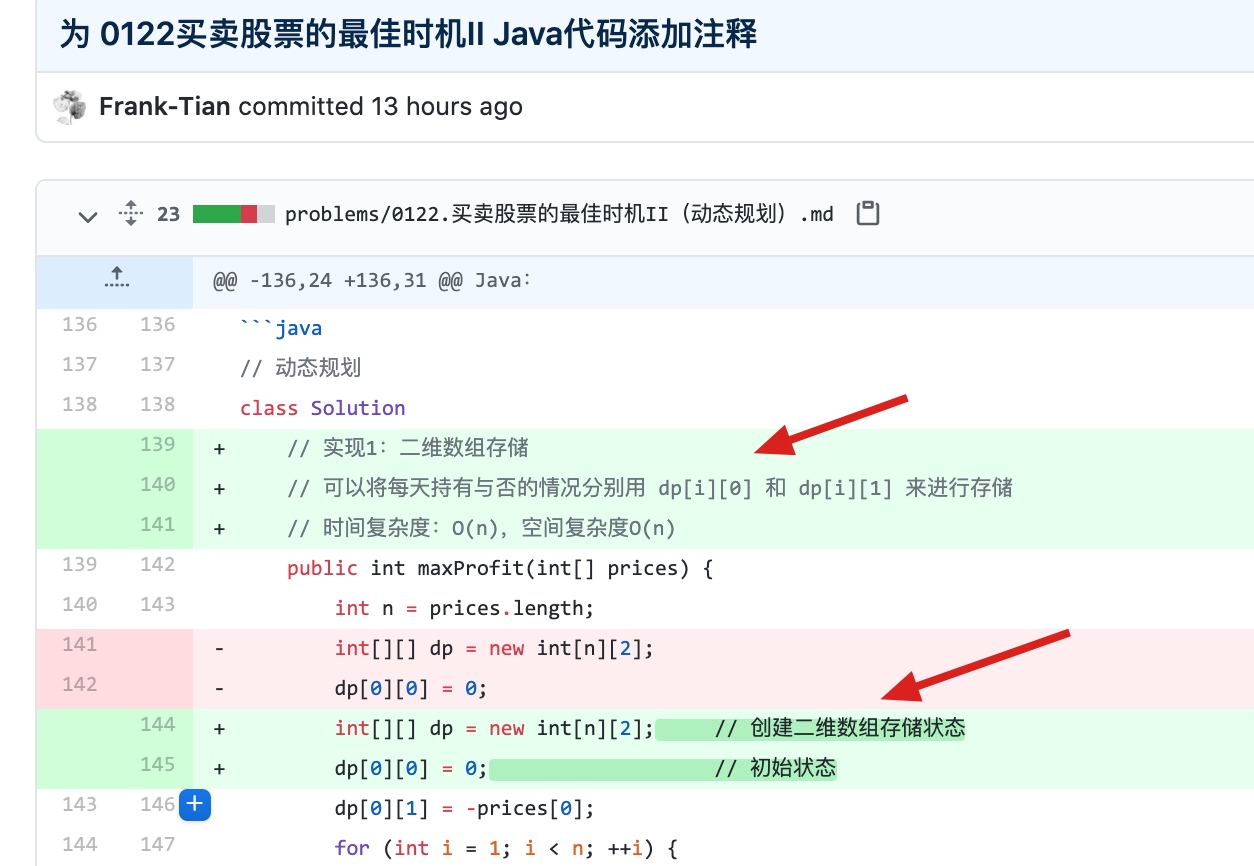
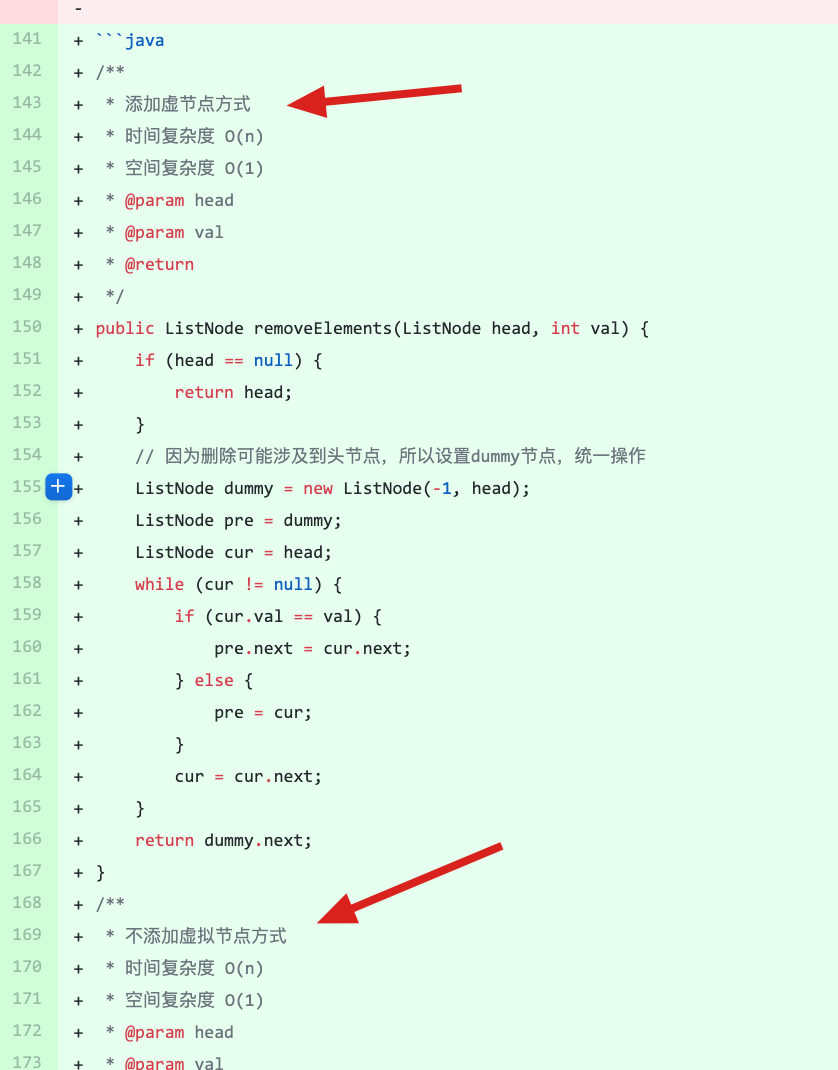
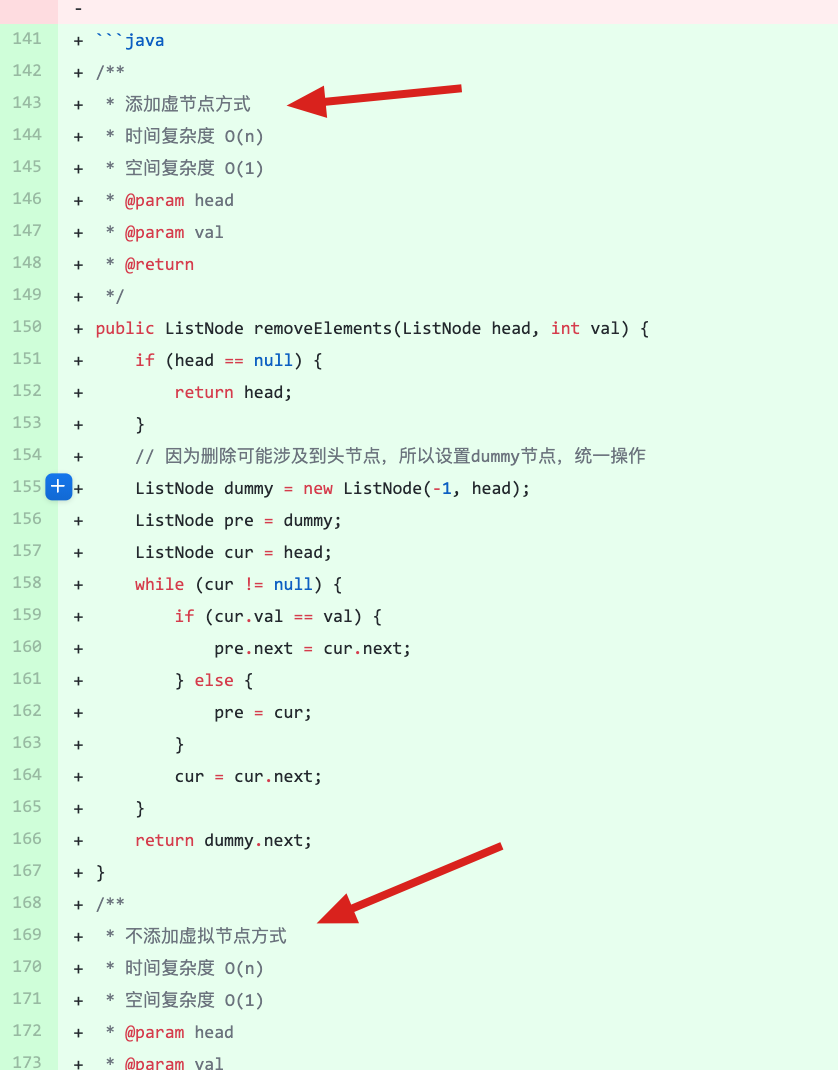
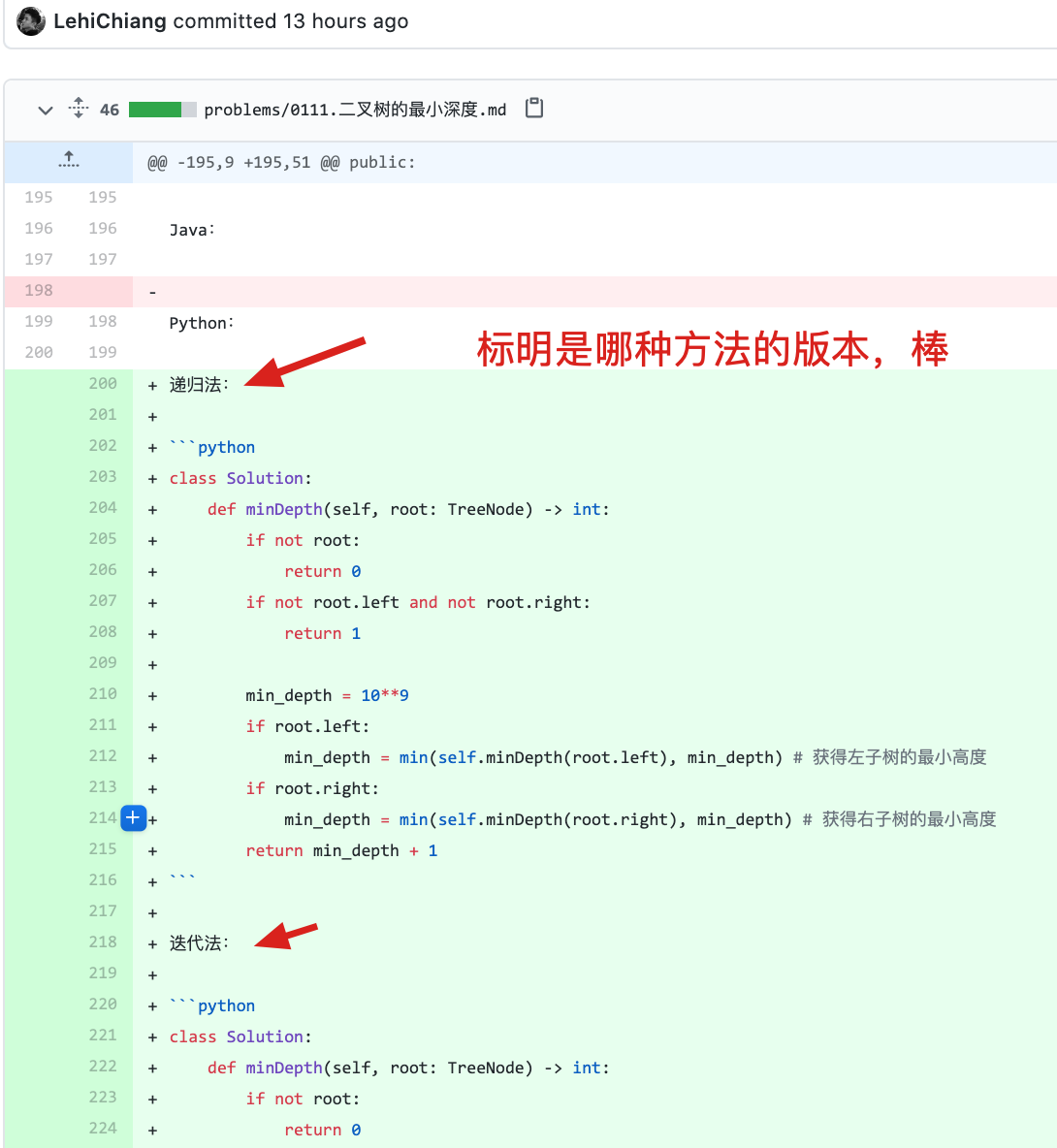
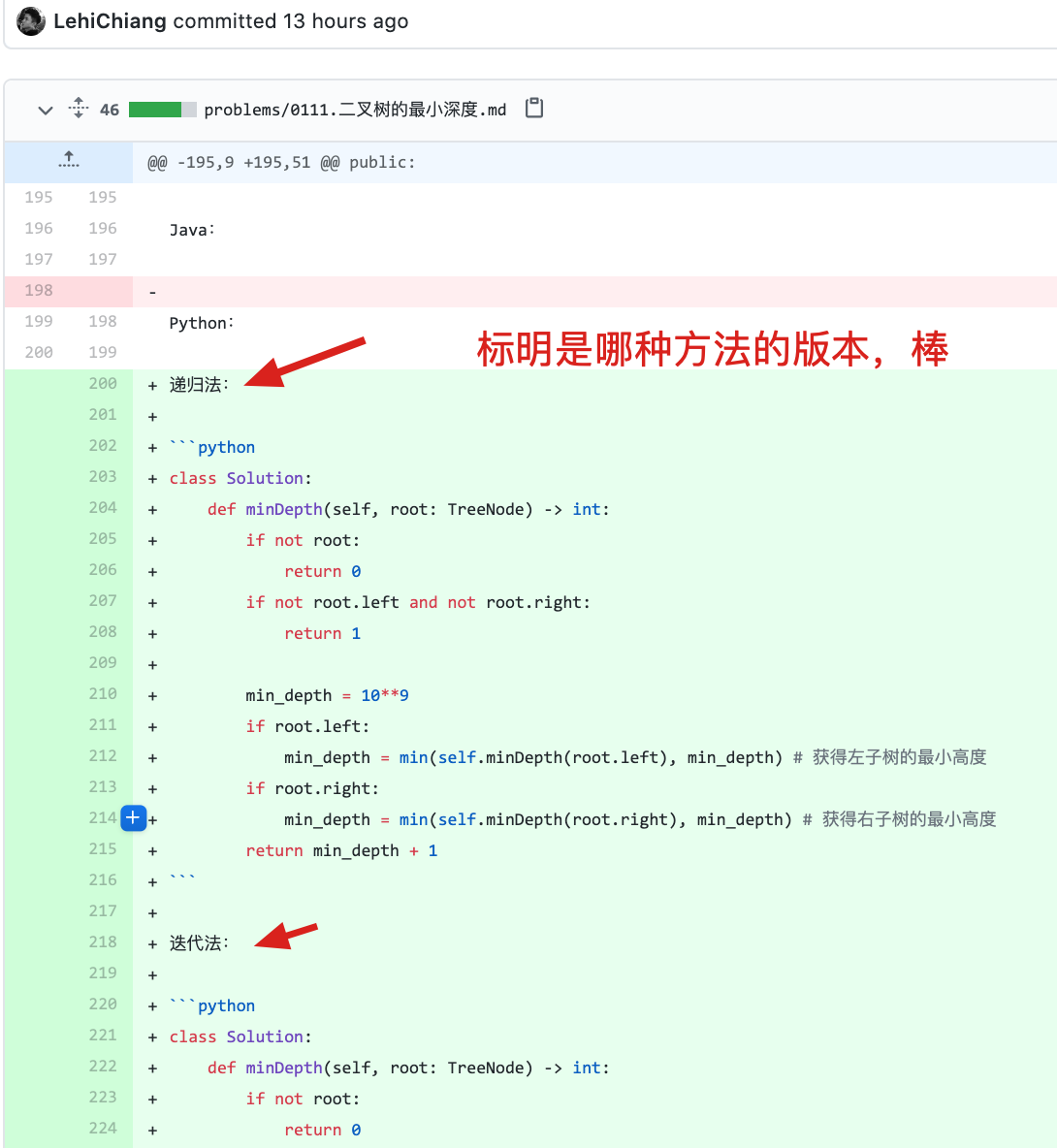




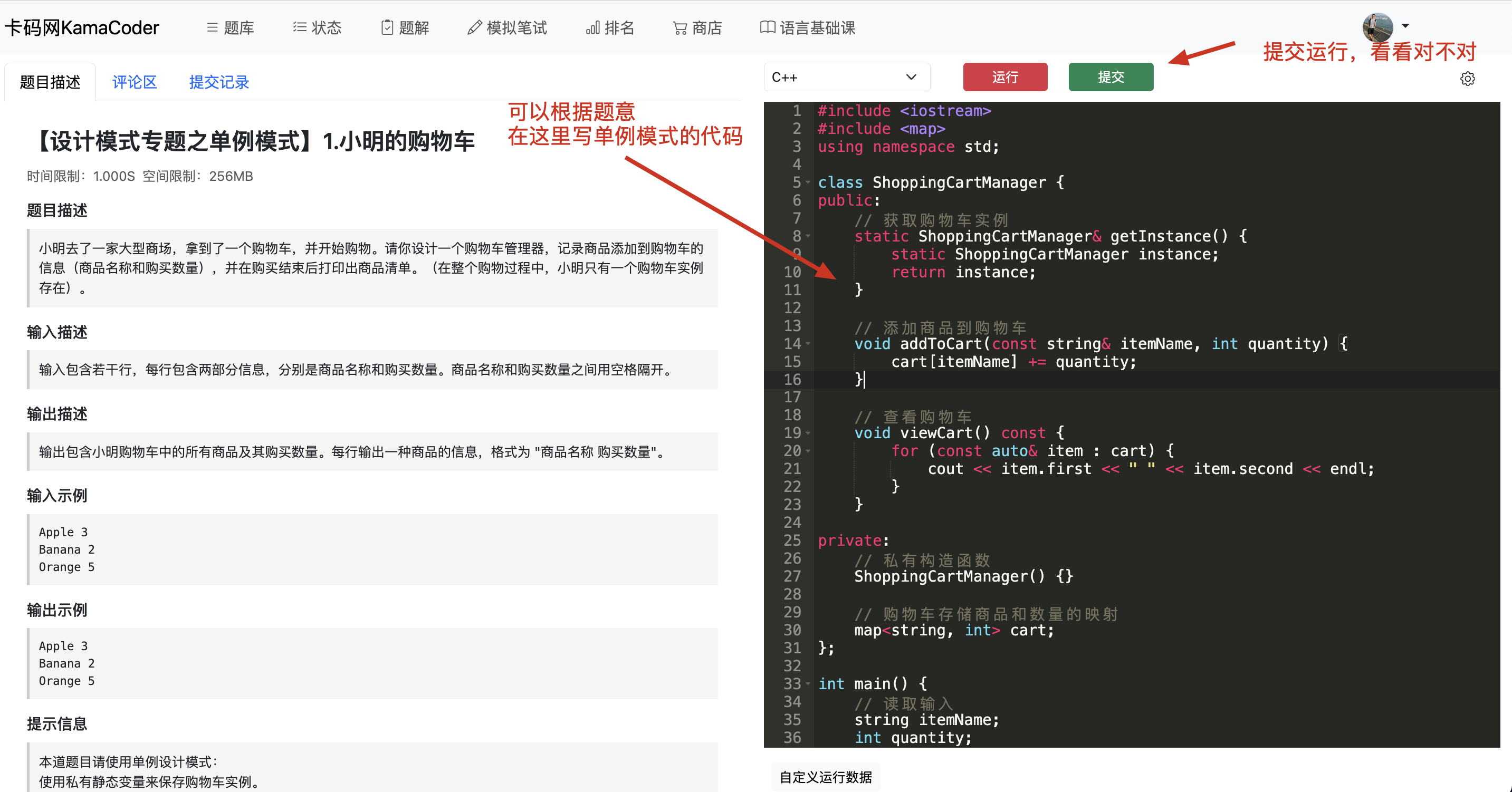









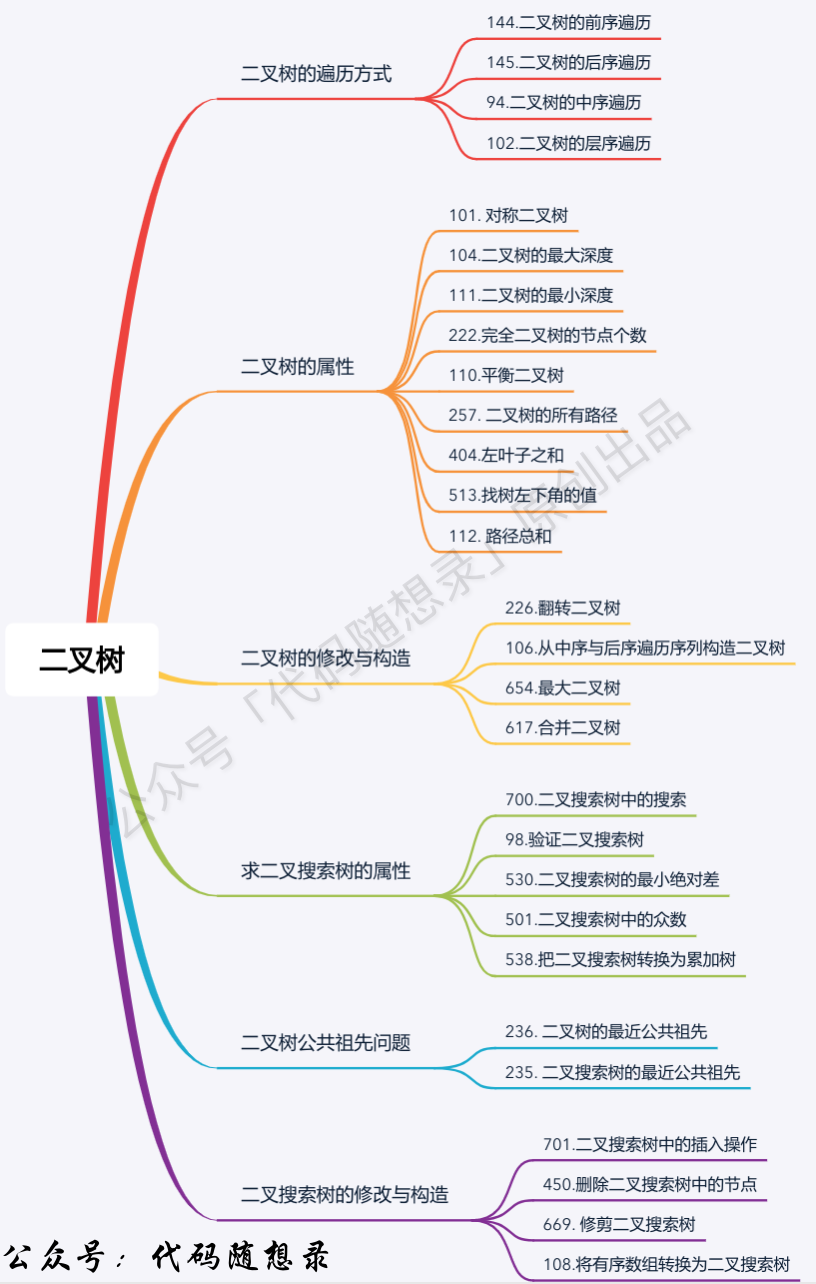 +
+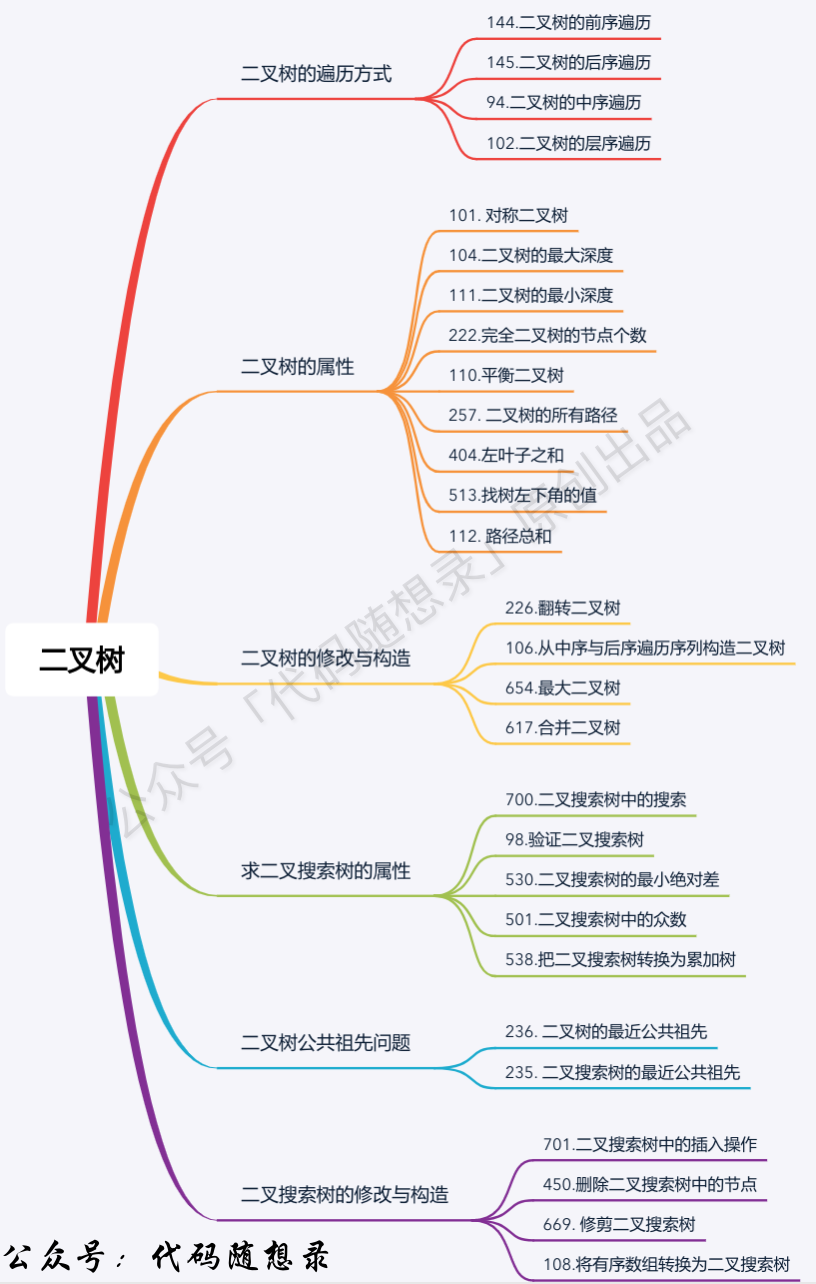 说到二叉树,大家对于二叉树其实都很熟悉了,本文呢我也不想教科书式的把二叉树的基础内容再啰嗦一遍,所以以下我讲的都是一些比较重点的内容。
@@ -31,7 +31,7 @@
如图所示:
-
说到二叉树,大家对于二叉树其实都很熟悉了,本文呢我也不想教科书式的把二叉树的基础内容再啰嗦一遍,所以以下我讲的都是一些比较重点的内容。
@@ -31,7 +31,7 @@
如图所示:
-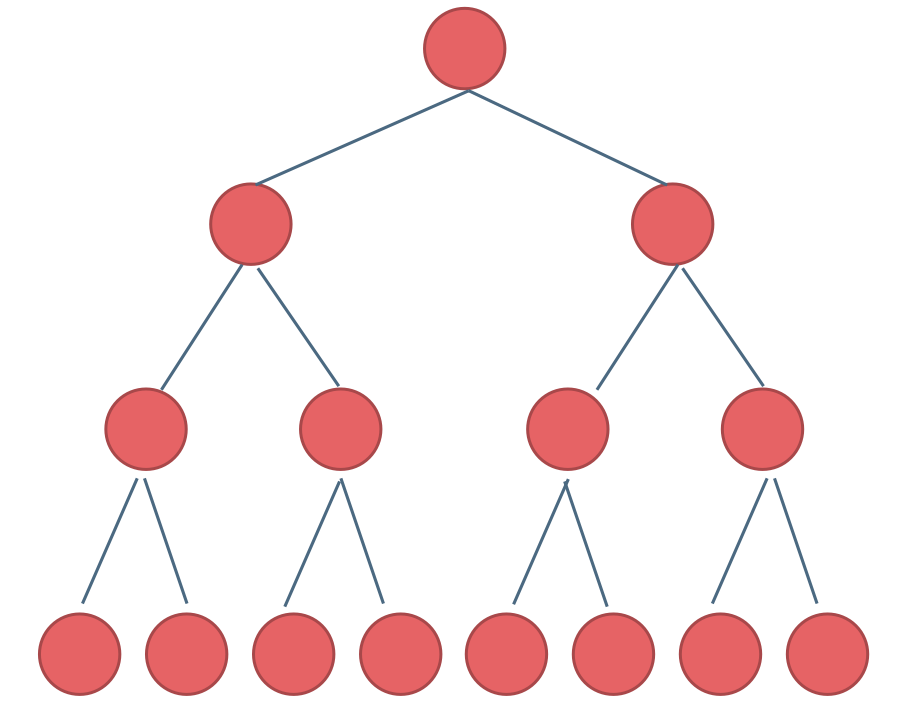 +
+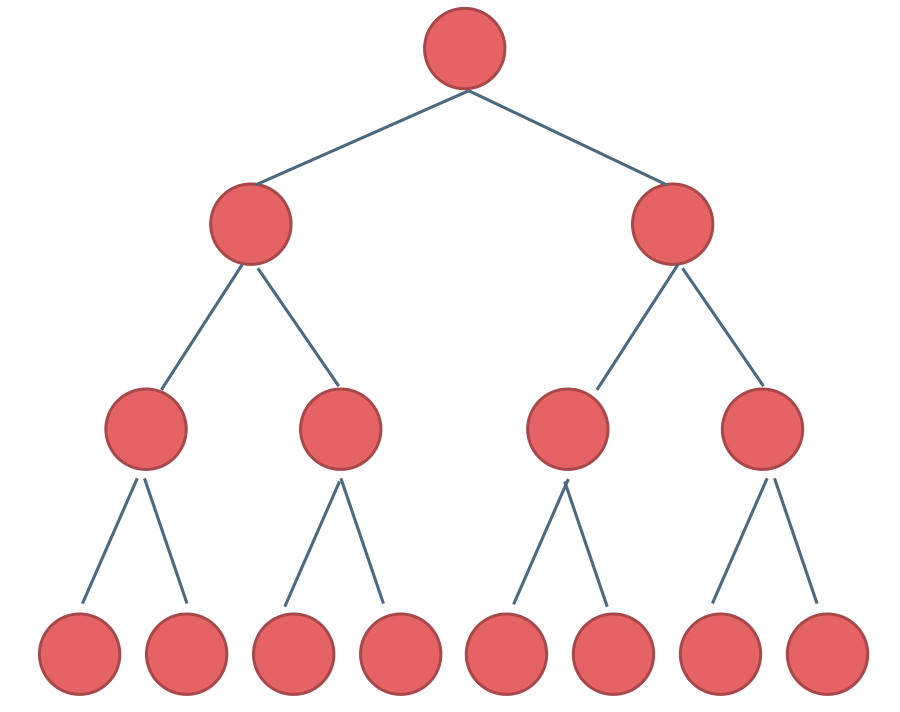 这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
@@ -46,7 +46,7 @@
我来举一个典型的例子如题:
-
这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
@@ -46,7 +46,7 @@
我来举一个典型的例子如题:
-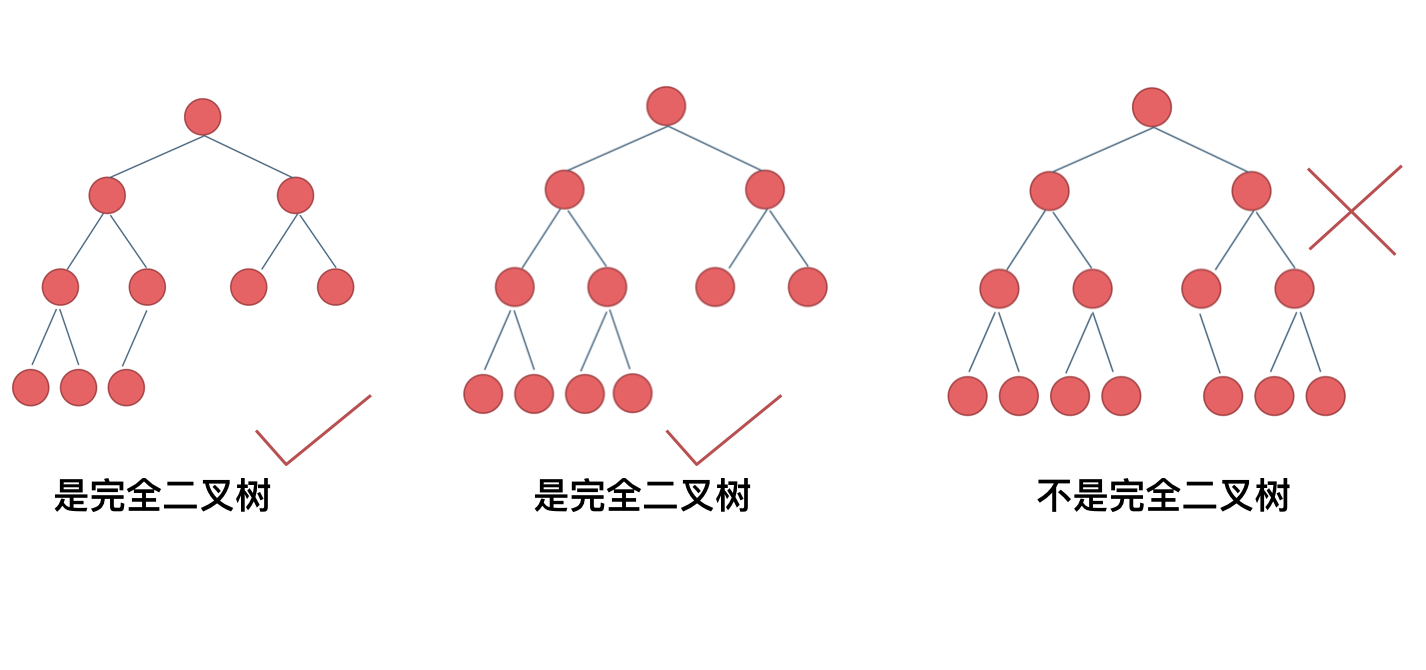 +
+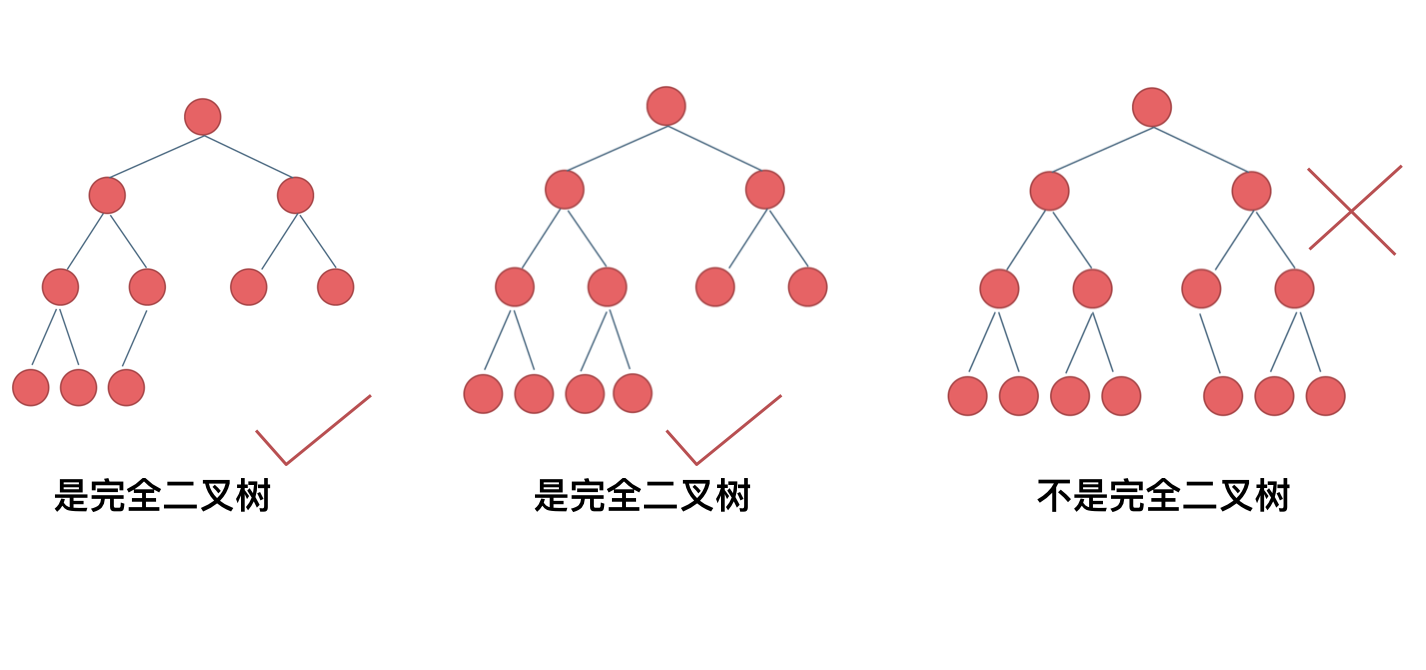 相信不少同学最后一个二叉树是不是完全二叉树都中招了。
@@ -63,7 +63,7 @@
下面这两棵树都是搜索树
-
相信不少同学最后一个二叉树是不是完全二叉树都中招了。
@@ -63,7 +63,7 @@
下面这两棵树都是搜索树
-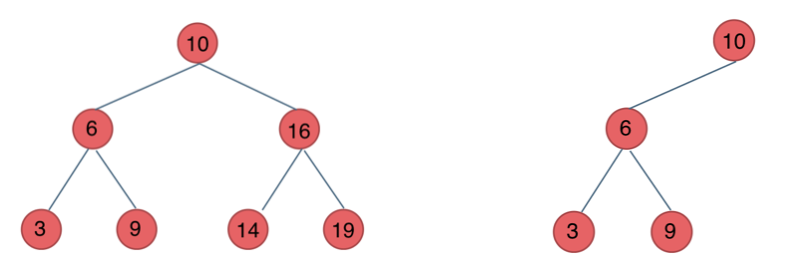 +
+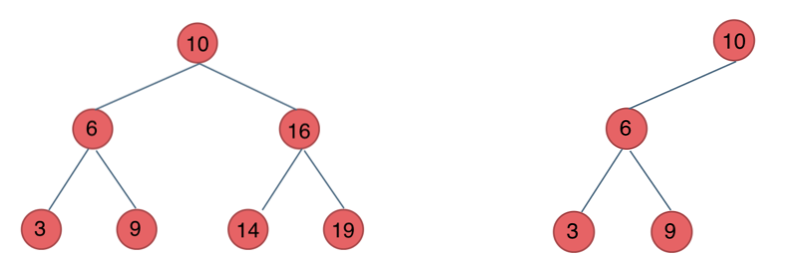 ### 平衡二叉搜索树
@@ -72,7 +72,7 @@
如图:
-
### 平衡二叉搜索树
@@ -72,7 +72,7 @@
如图:
-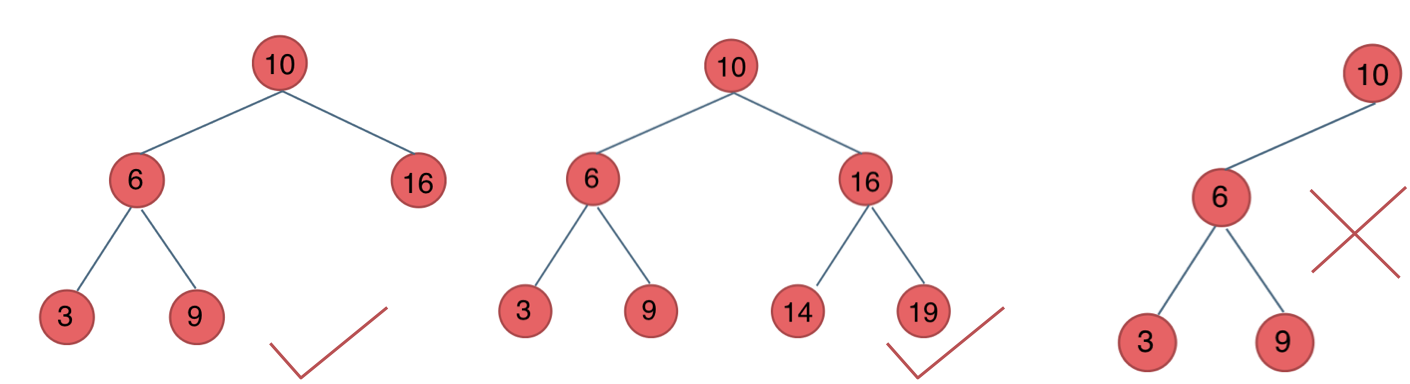 +
+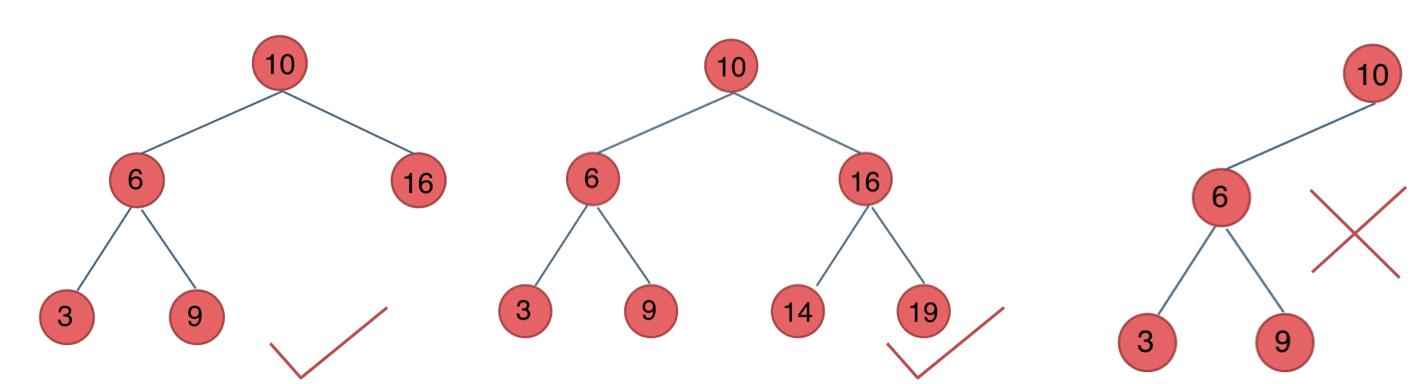 最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
@@ -91,13 +91,13 @@
链式存储如图:
-
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
@@ -91,13 +91,13 @@
链式存储如图:
-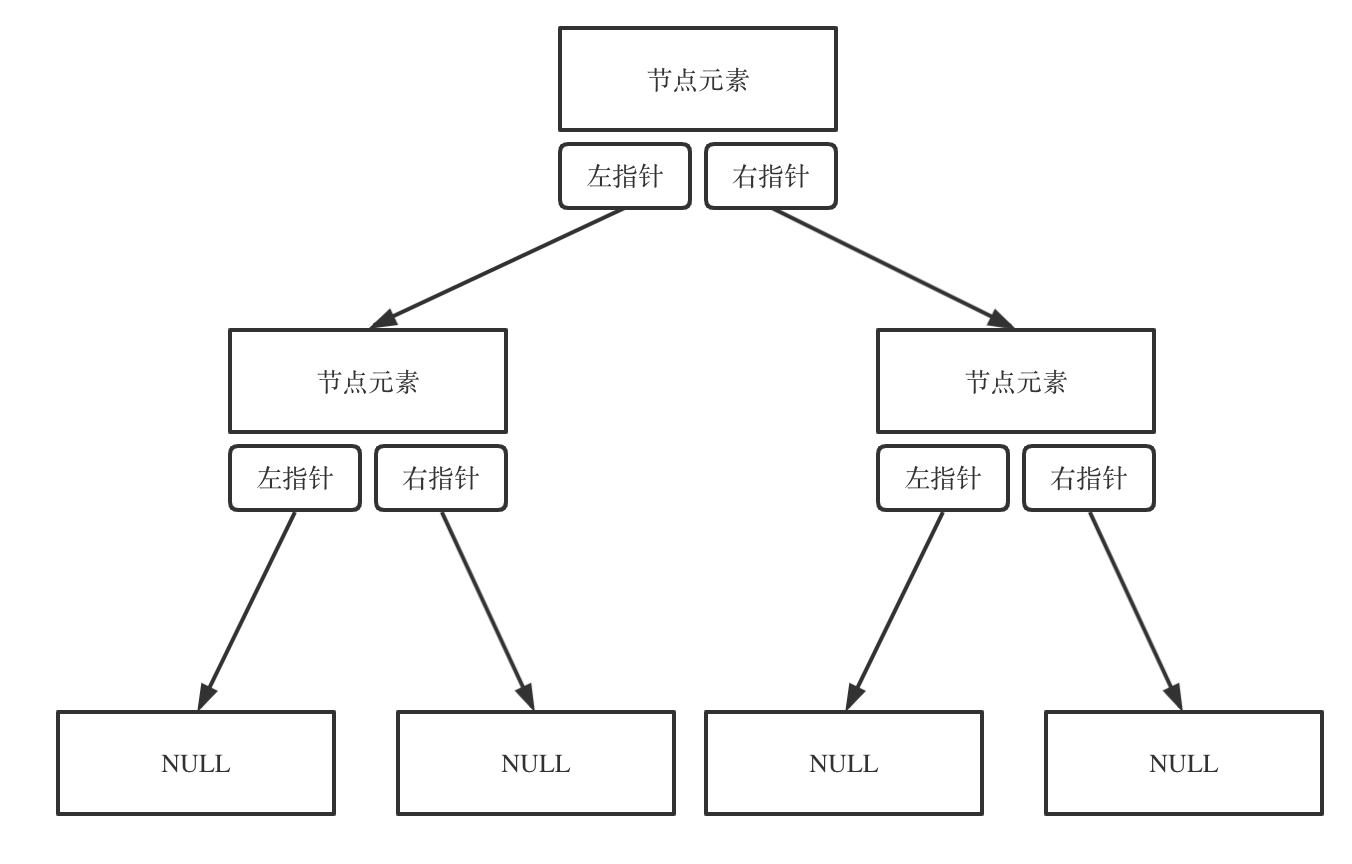 +
+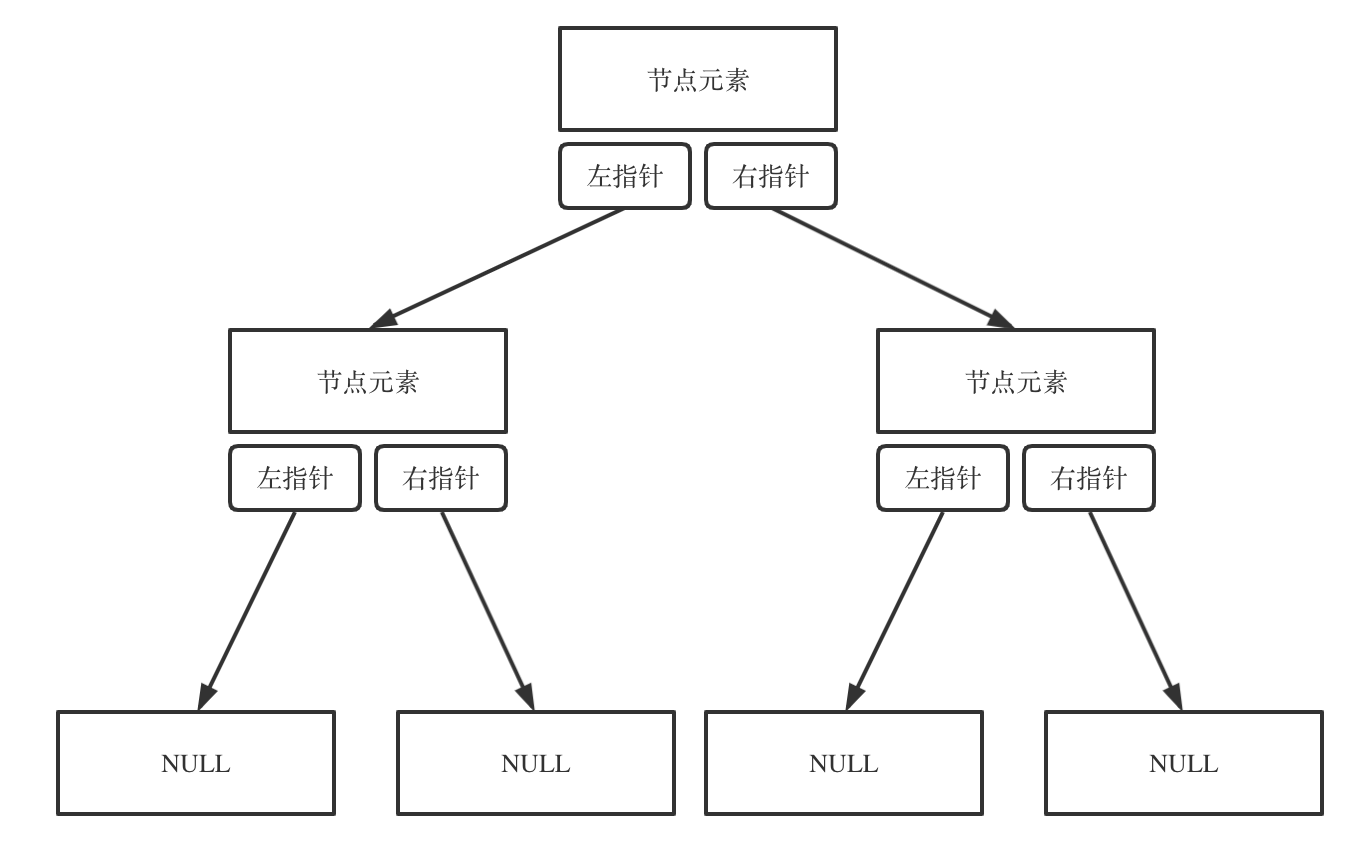 链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
-
链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
-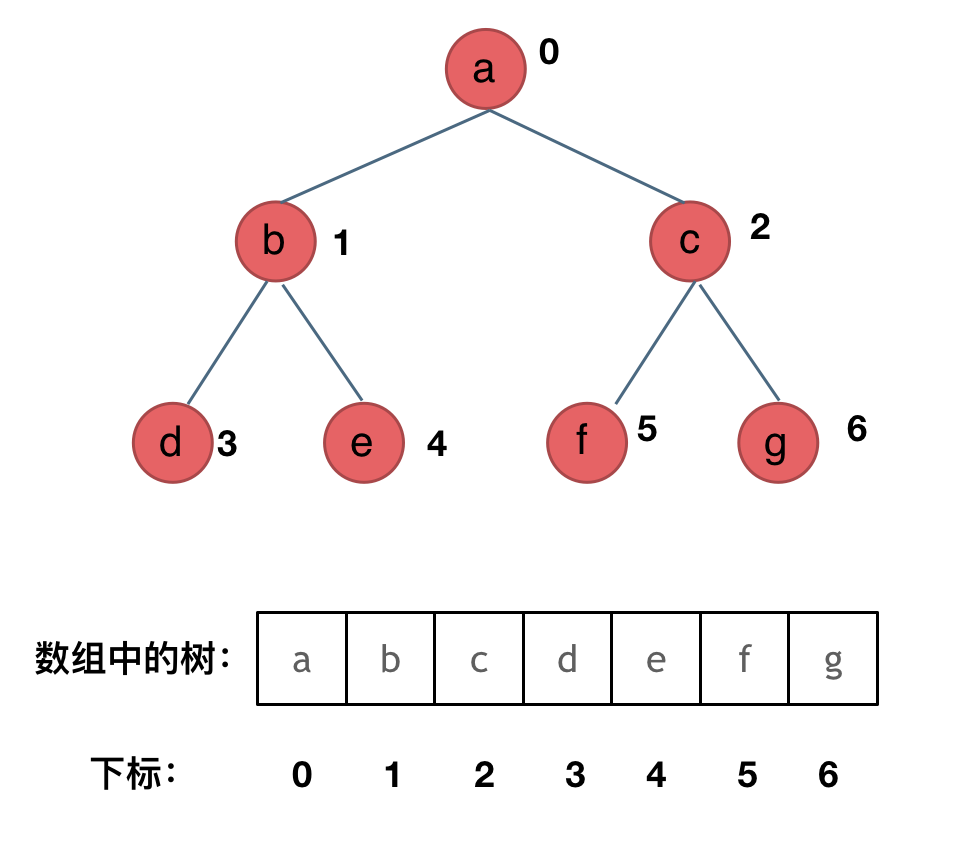 +
+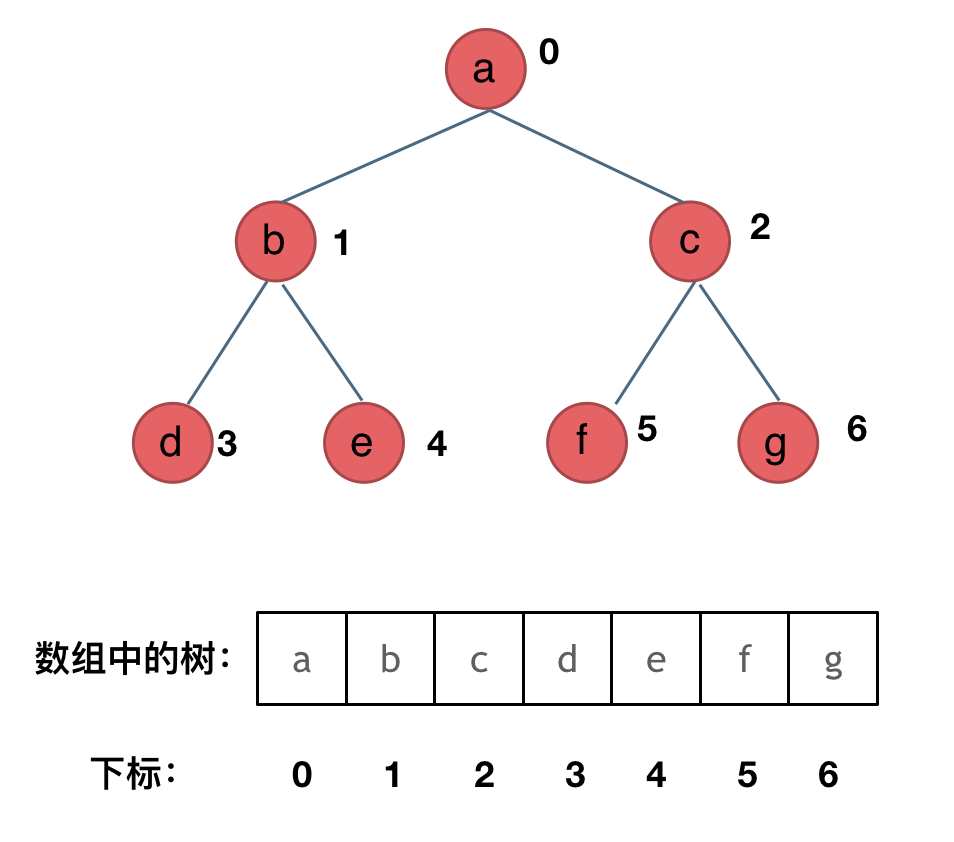 用数组来存储二叉树如何遍历的呢?
@@ -144,7 +144,7 @@
大家可以对着如下图,看看自己理解的前后中序有没有问题。
-
用数组来存储二叉树如何遍历的呢?
@@ -144,7 +144,7 @@
大家可以对着如下图,看看自己理解的前后中序有没有问题。
-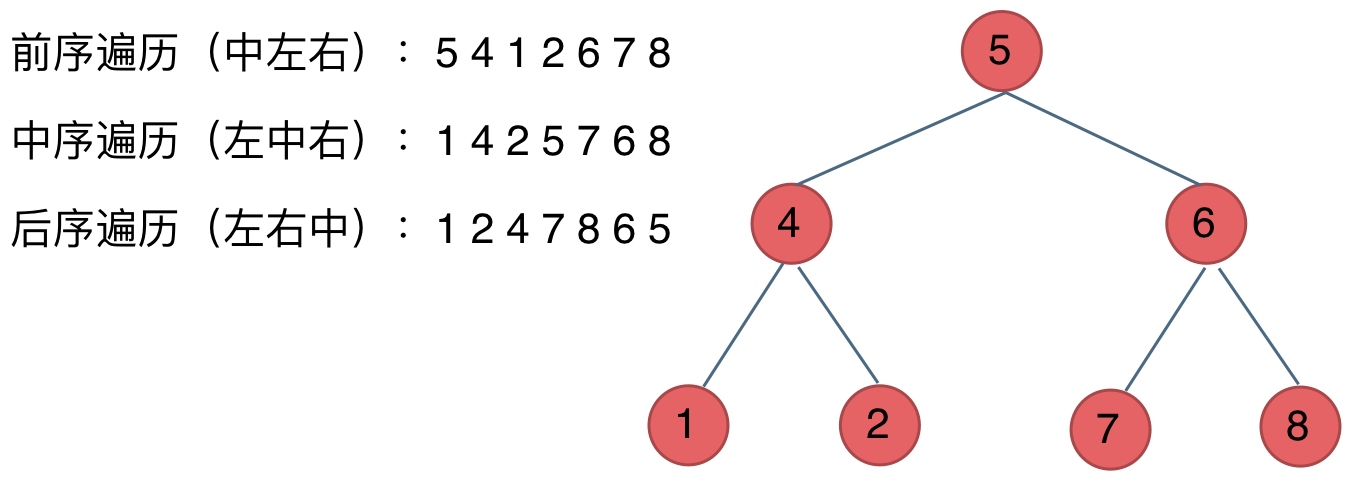 +
+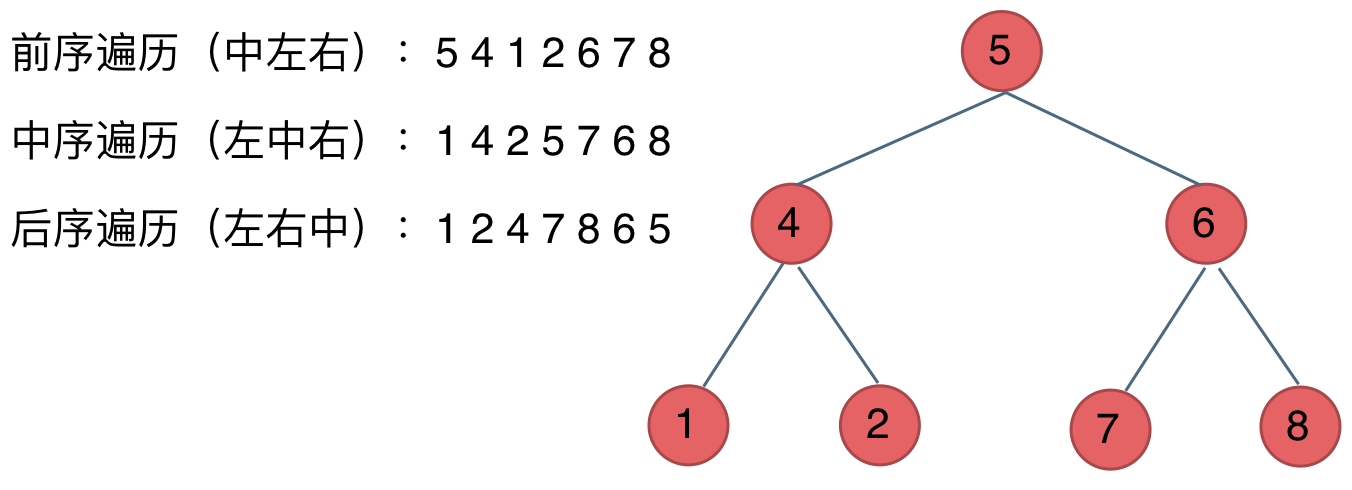 最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
diff --git a/problems/二叉树的迭代遍历.md b/problems/二叉树的迭代遍历.md
index 289c651b..e011612c 100644
--- a/problems/二叉树的迭代遍历.md
+++ b/problems/二叉树的迭代遍历.md
@@ -117,7 +117,7 @@ public:
再来看后序遍历,先序遍历是中左右,后序遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了,如下图:
-
+
**所以后序遍历只需要前序遍历的代码稍作修改就可以了,代码如下:**
diff --git a/problems/前序/ACM模式.md b/problems/前序/ACM模式.md
index 313264fb..f1ff3a5f 100644
--- a/problems/前序/ACM模式.md
+++ b/problems/前序/ACM模式.md
@@ -5,15 +5,15 @@
平时大家在力扣上刷题,就是 核心代码模式,即给你一个函数,直接写函数实现,例如这样:
-
+
而ACM模式,是程序头文件,main函数,数据的输入输出都要自己处理,例如这样:
-
+
大家可以发现 右边代码框什么都没有,程序从头到尾都需要自己实现,本题如果写完代码是这样的: (细心的录友可以发现和力扣上刷题是不一样的)
-
+
**如果大家从一开始学习算法就一直在力扣上的话,突然切到ACM模式会非常不适应**。
@@ -21,15 +21,15 @@
知识星球里也有很多录友,因为不熟悉ACM模式在面试的过程中吃了不少亏。
-
最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
diff --git a/problems/二叉树的迭代遍历.md b/problems/二叉树的迭代遍历.md
index 289c651b..e011612c 100644
--- a/problems/二叉树的迭代遍历.md
+++ b/problems/二叉树的迭代遍历.md
@@ -117,7 +117,7 @@ public:
再来看后序遍历,先序遍历是中左右,后序遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了,如下图:
-
+
**所以后序遍历只需要前序遍历的代码稍作修改就可以了,代码如下:**
diff --git a/problems/前序/ACM模式.md b/problems/前序/ACM模式.md
index 313264fb..f1ff3a5f 100644
--- a/problems/前序/ACM模式.md
+++ b/problems/前序/ACM模式.md
@@ -5,15 +5,15 @@
平时大家在力扣上刷题,就是 核心代码模式,即给你一个函数,直接写函数实现,例如这样:
-
+
而ACM模式,是程序头文件,main函数,数据的输入输出都要自己处理,例如这样:
-
+
大家可以发现 右边代码框什么都没有,程序从头到尾都需要自己实现,本题如果写完代码是这样的: (细心的录友可以发现和力扣上刷题是不一样的)
-
+
**如果大家从一开始学习算法就一直在力扣上的话,突然切到ACM模式会非常不适应**。
@@ -21,15 +21,15 @@
知识星球里也有很多录友,因为不熟悉ACM模式在面试的过程中吃了不少亏。
-












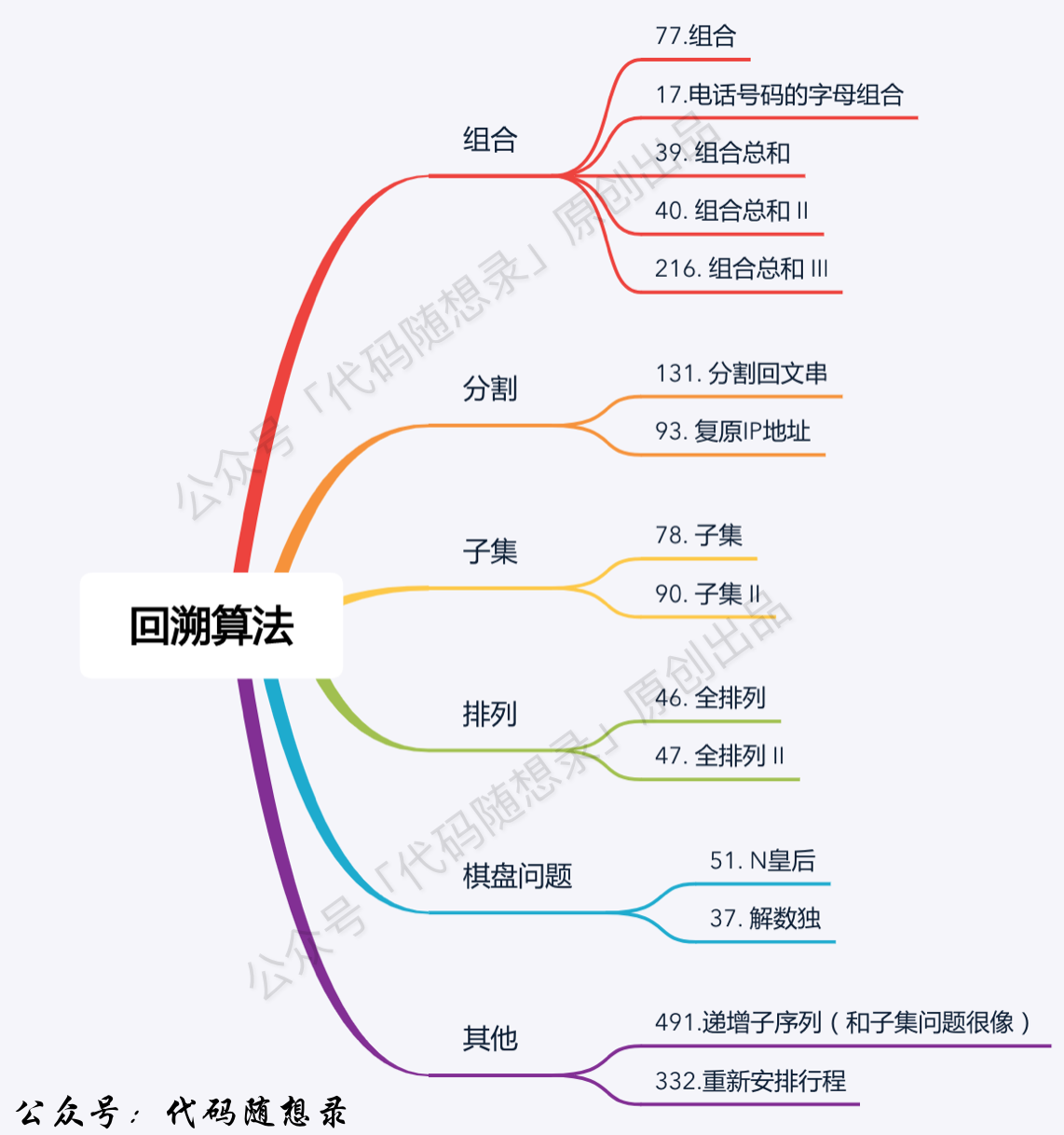 +
+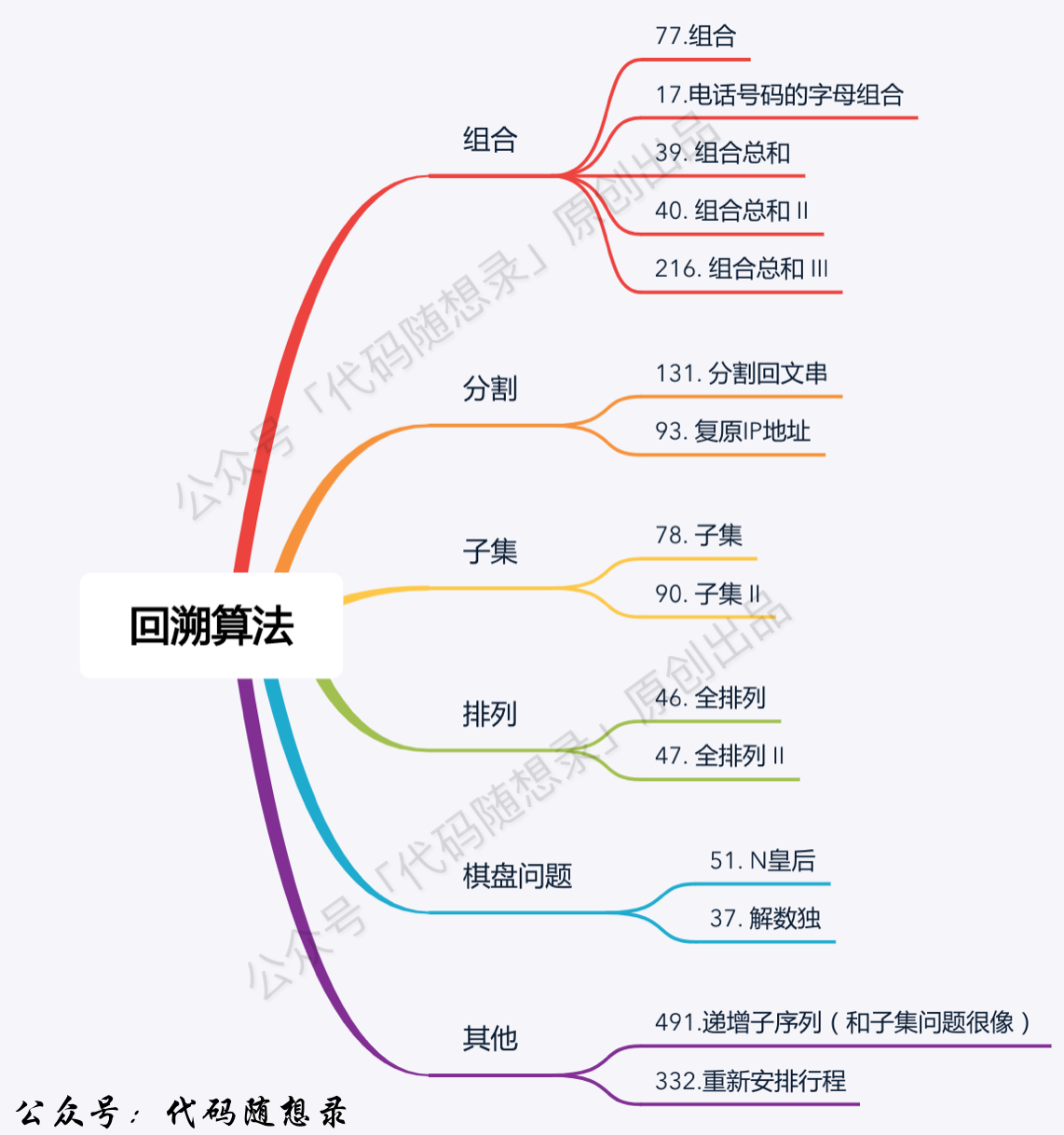 ## 算法公开课
@@ -114,7 +114,7 @@ if (终止条件) {
如图:
-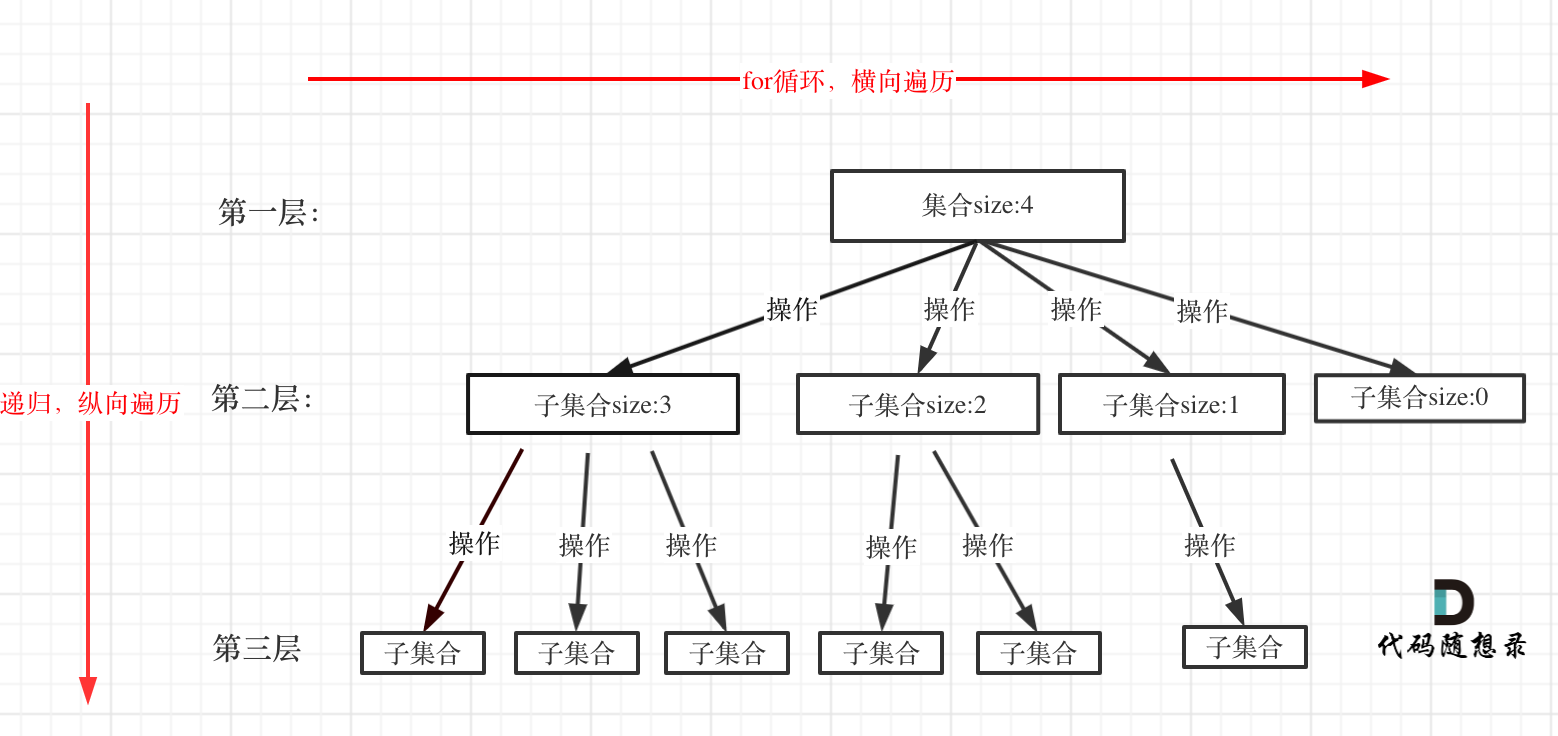
+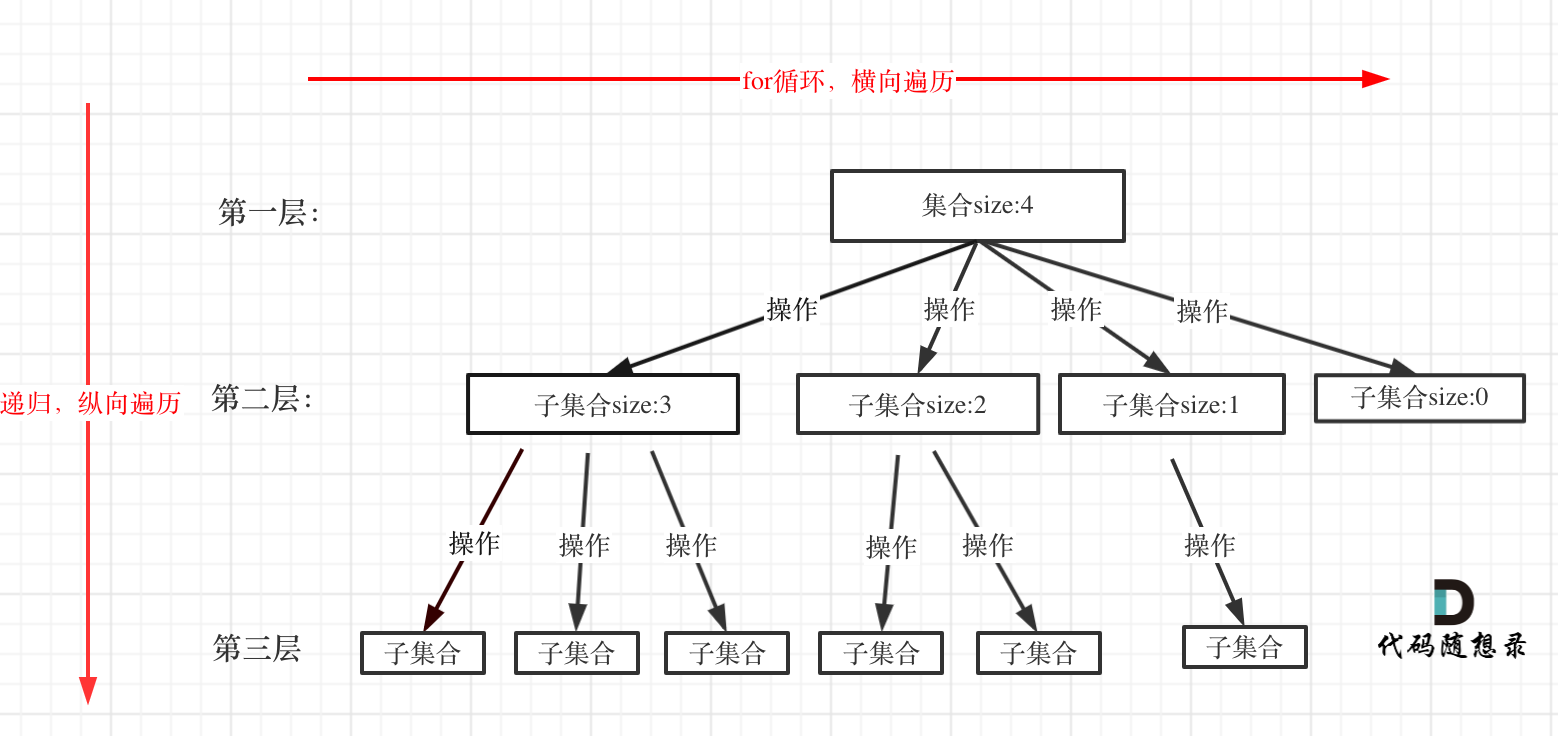
注意图中,我特意举例集合大小和孩子的数量是相等的!
diff --git a/problems/数组总结篇.md b/problems/数组总结篇.md
index e45165a6..e29a7bd3 100644
--- a/problems/数组总结篇.md
+++ b/problems/数组总结篇.md
@@ -125,7 +125,7 @@
## 总结
-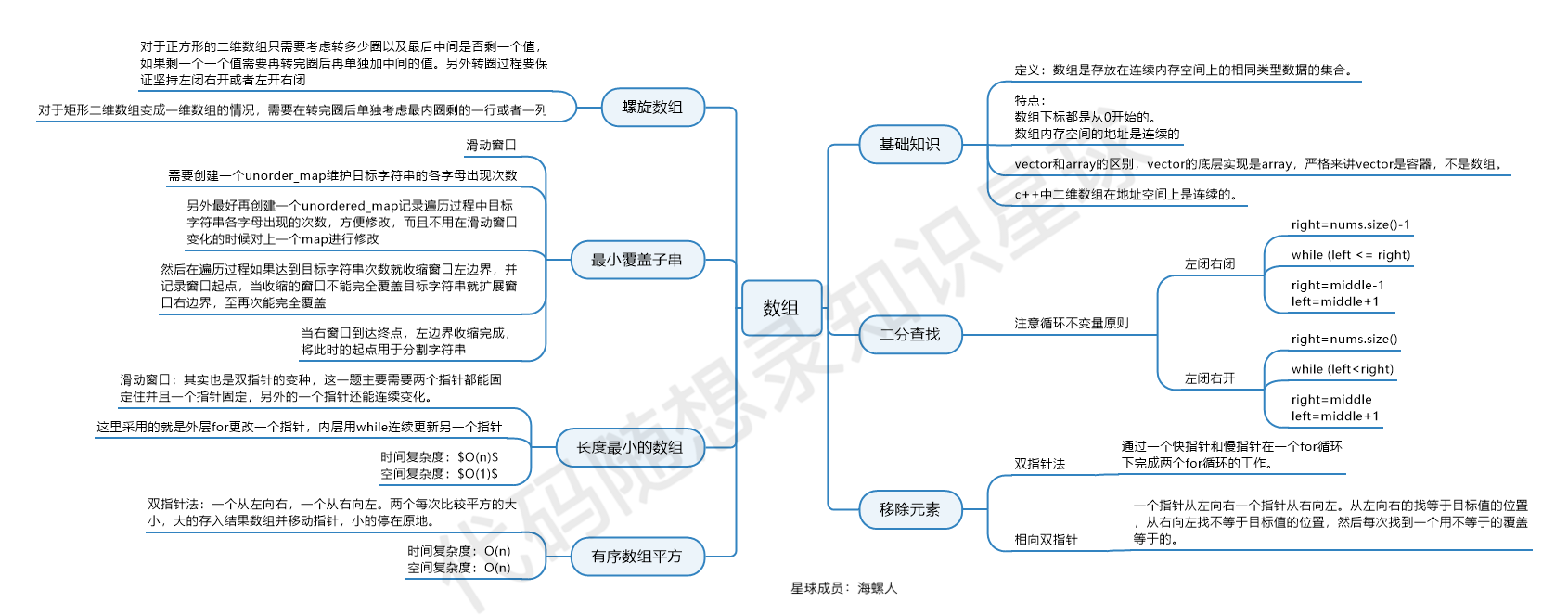
+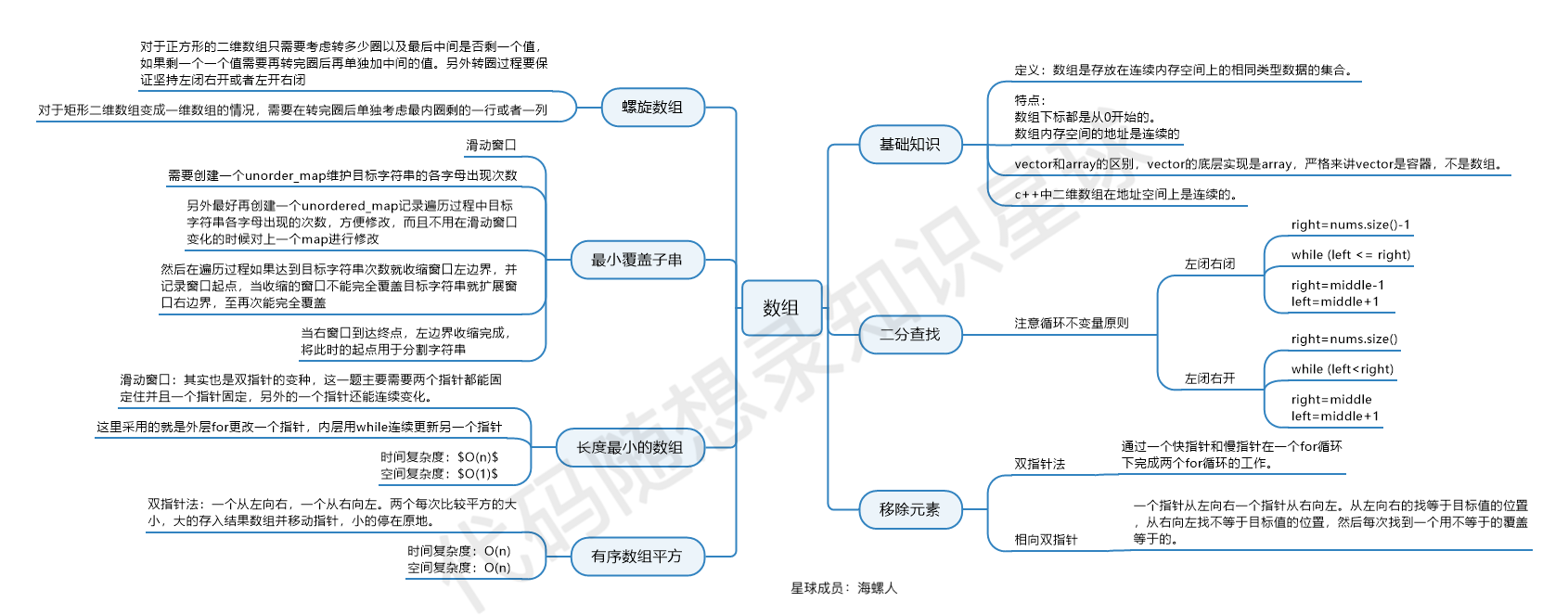
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画,总结的非常好,分享给大家。
diff --git a/problems/数组理论基础.md b/problems/数组理论基础.md
index c1ac287d..4000208a 100644
--- a/problems/数组理论基础.md
+++ b/problems/数组理论基础.md
@@ -40,7 +40,7 @@
那么二维数组直接上图,大家应该就知道怎么回事了
-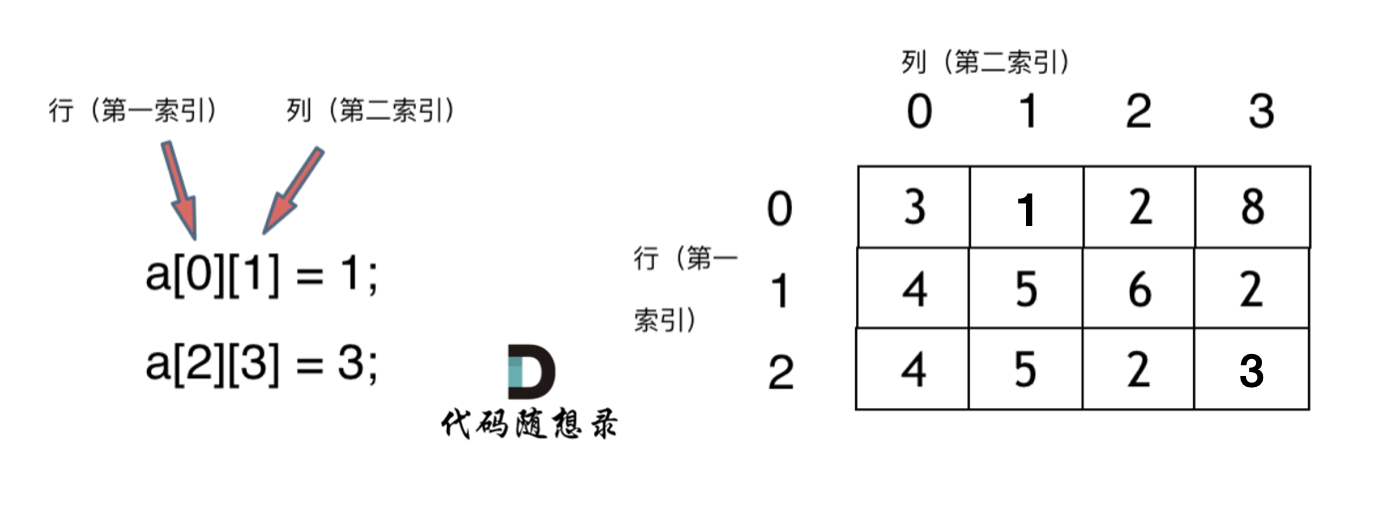
+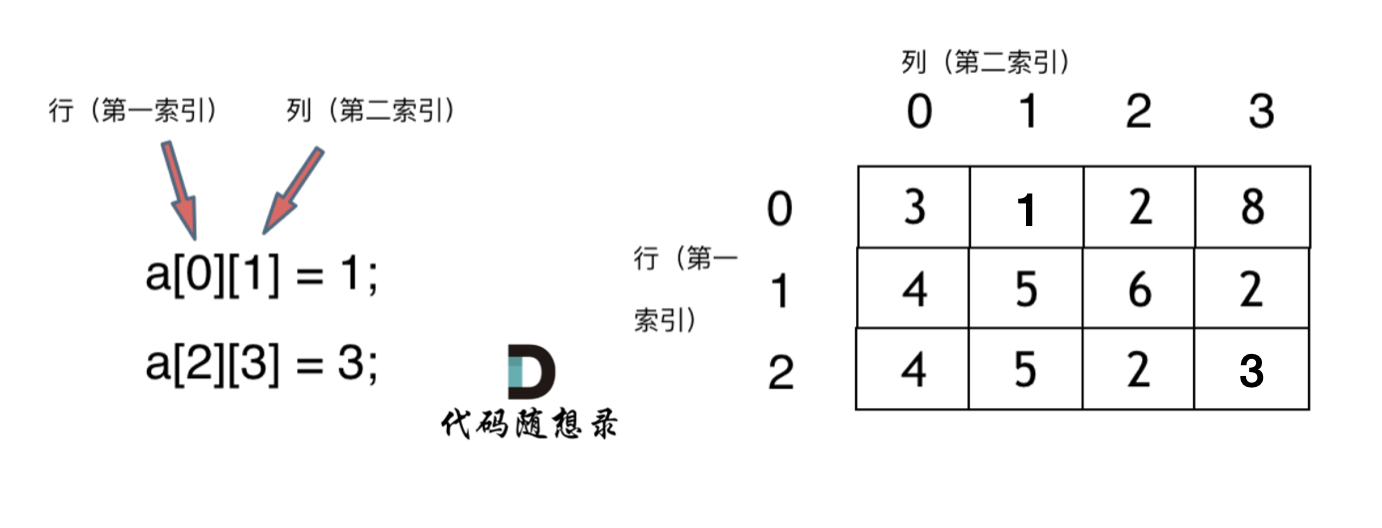
**那么二维数组在内存的空间地址是连续的么?**
@@ -80,7 +80,7 @@ int main() {
如图:
-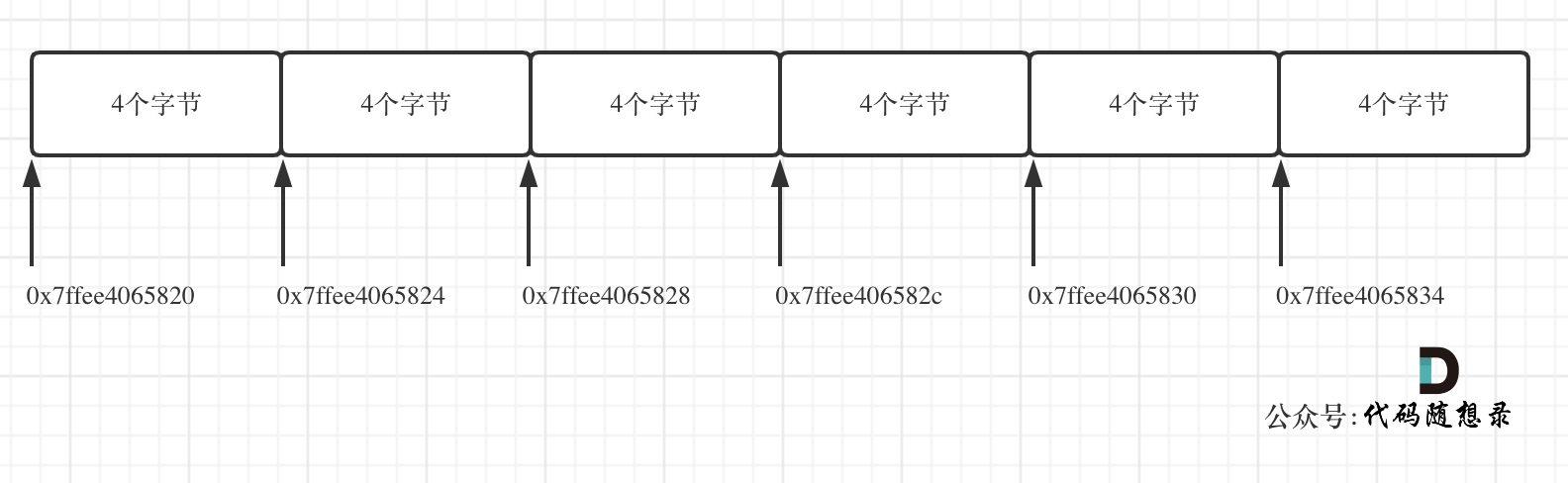
+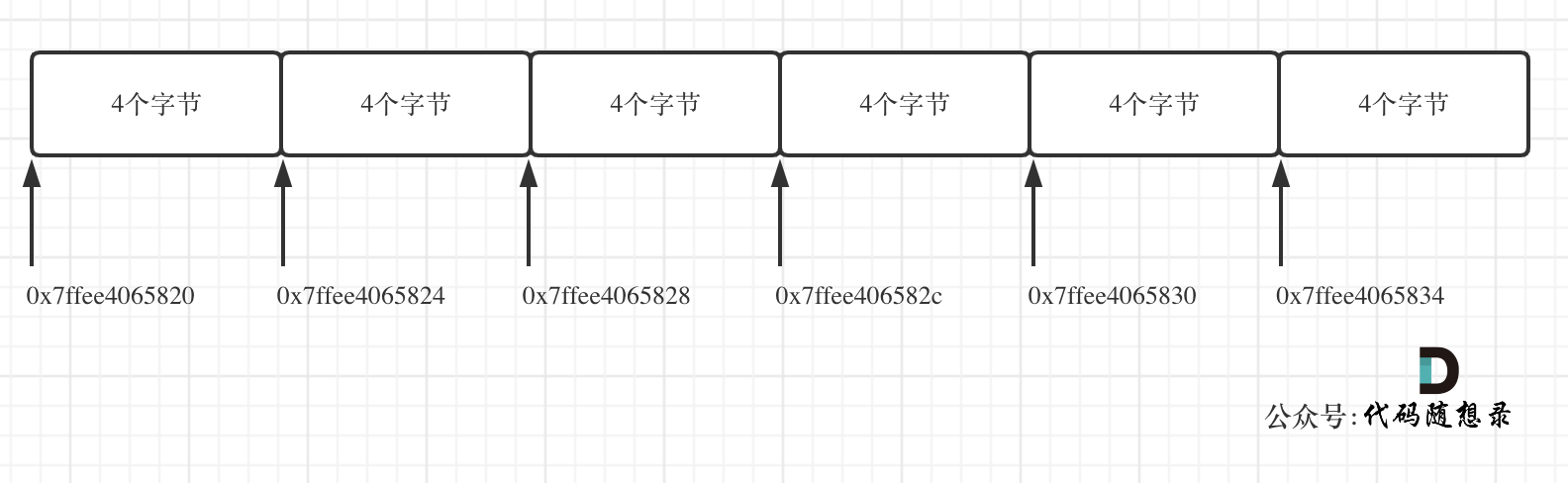
**所以可以看出在C++中二维数组在地址空间上是连续的**。
@@ -111,7 +111,7 @@ public static void test_arr() {
所以Java的二维数组可能是如下排列的方式:
-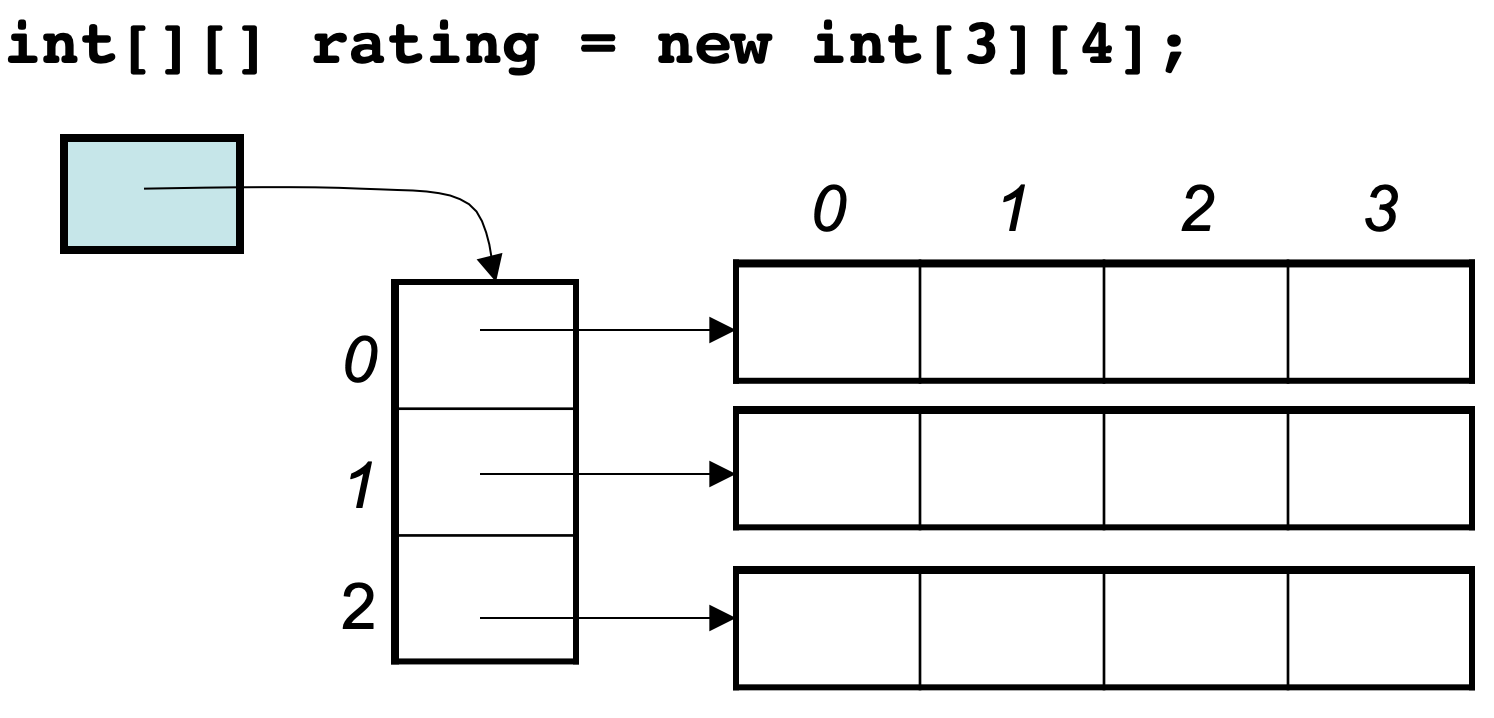
+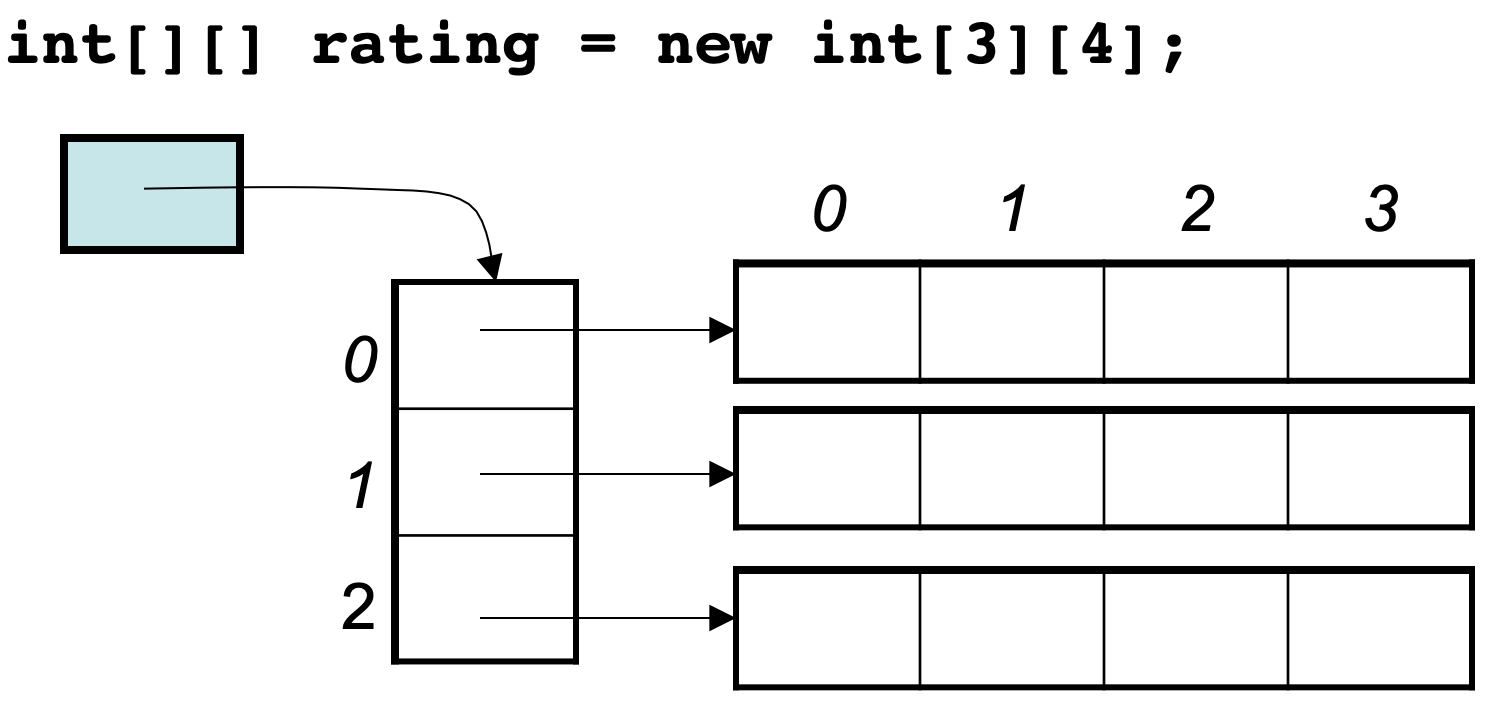
这里面试中数组相关的理论知识就介绍完了。
diff --git a/problems/栈与队列理论基础.md b/problems/栈与队列理论基础.md
index bff0ec63..912bfe1d 100644
--- a/problems/栈与队列理论基础.md
+++ b/problems/栈与队列理论基础.md
@@ -11,7 +11,7 @@
如图所示:
-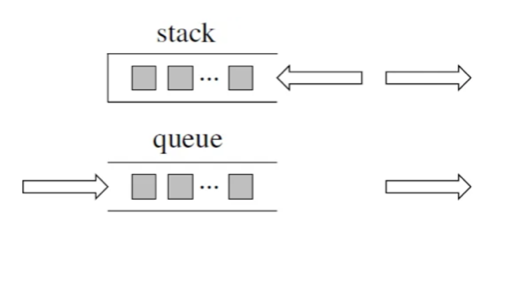
+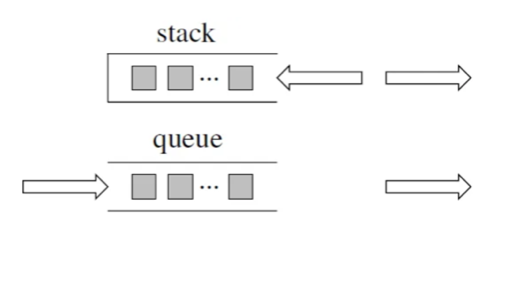
那么我这里再列出四个关于栈的问题,大家可以思考一下。以下是以C++为例,使用其他编程语言的同学也对应思考一下,自己使用的编程语言里栈和队列是什么样的。
@@ -46,7 +46,7 @@ C++标准库是有多个版本的,要知道我们使用的STL是哪个版本
来说一说栈,栈先进后出,如图所示:
-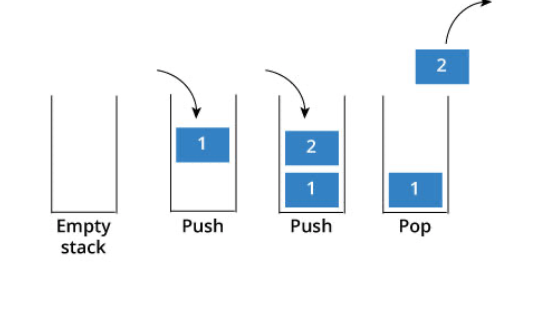
+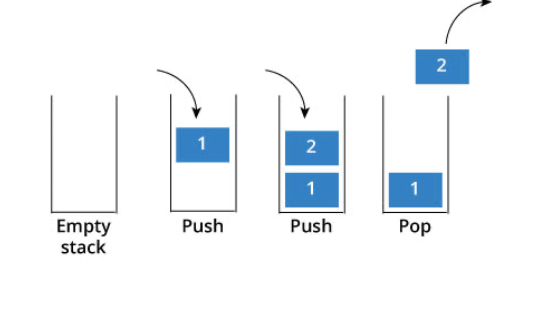
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
@@ -59,7 +59,7 @@ C++标准库是有多个版本的,要知道我们使用的STL是哪个版本
从下图中可以看出,栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
-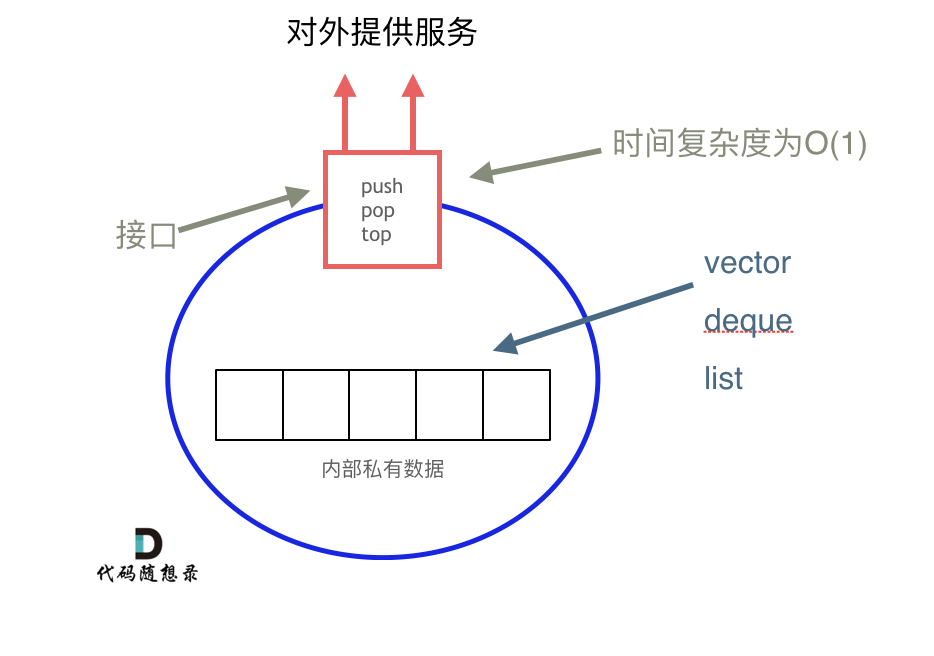
+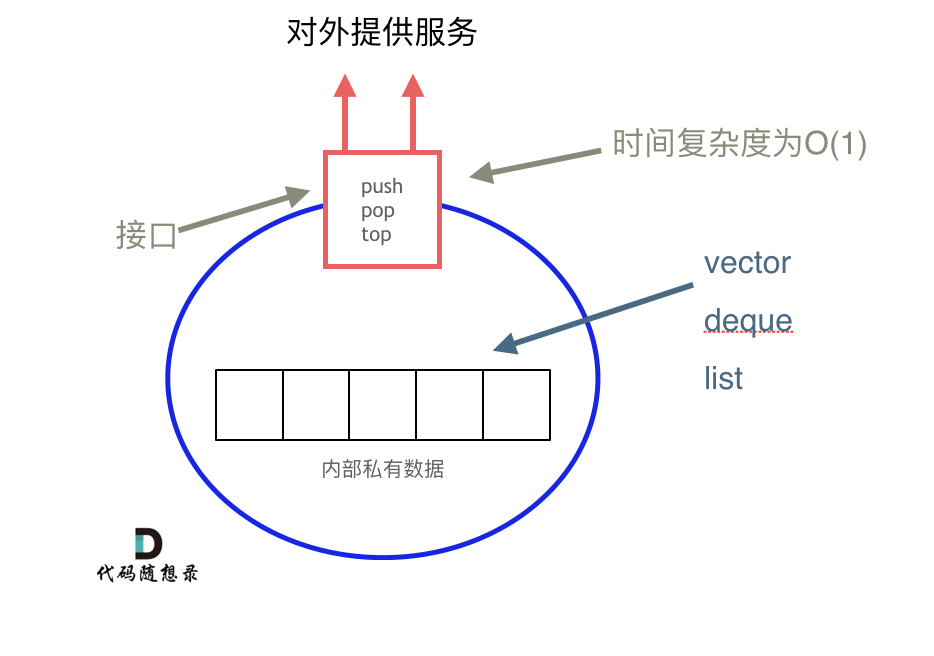
**我们常用的SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。**
diff --git a/problems/根据身高重建队列(vector原理讲解).md b/problems/根据身高重建队列(vector原理讲解).md
index a2350835..162ee273 100644
--- a/problems/根据身高重建队列(vector原理讲解).md
+++ b/problems/根据身高重建队列(vector原理讲解).md
@@ -35,7 +35,7 @@ public:
```
耗时如下:
-
+
其直观上来看数组的insert操作是O(n)的,整体代码的时间复杂度是O(n^2)。
@@ -68,7 +68,7 @@ public:
耗时如下:
-
+
大家都知道对于普通数组,一旦定义了大小就不能改变,例如int a[10];,这个数组a至多只能放10个元素,改不了的。
@@ -95,7 +95,7 @@ for (int i = 0; i < vec.size(); i++) {
就是重新申请一个二倍于原数组大小的数组,然后把数据都拷贝过去,并释放原数组内存。(对,就是这么原始粗暴的方法!)
举一个例子,如图:
-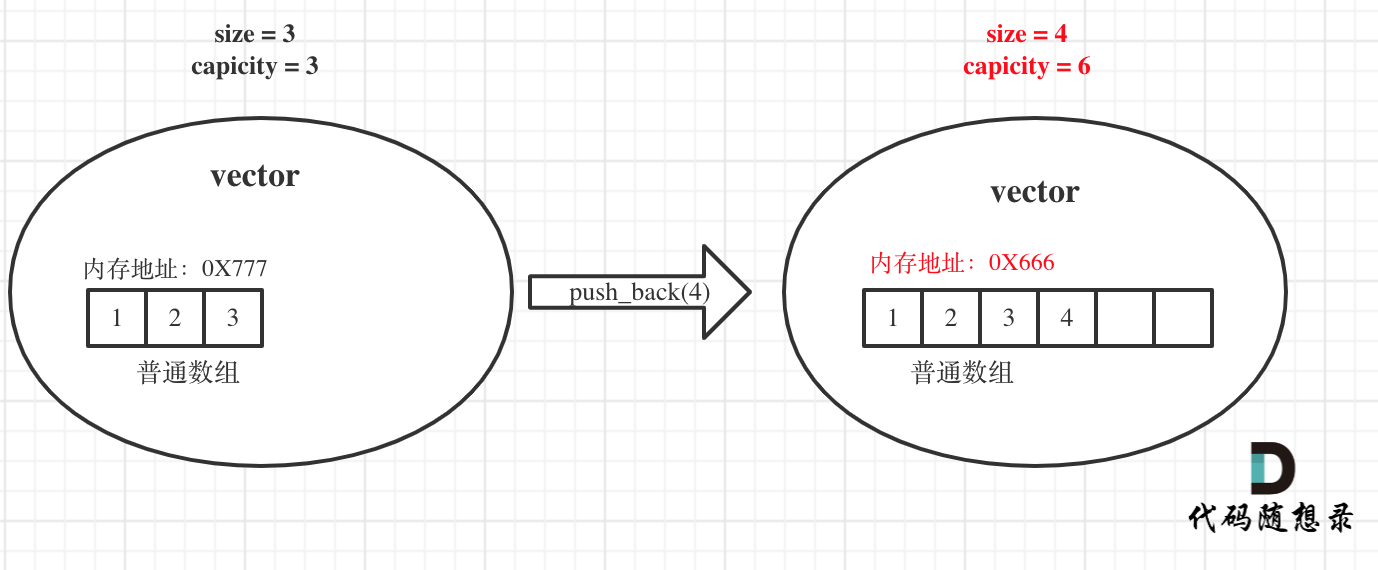
+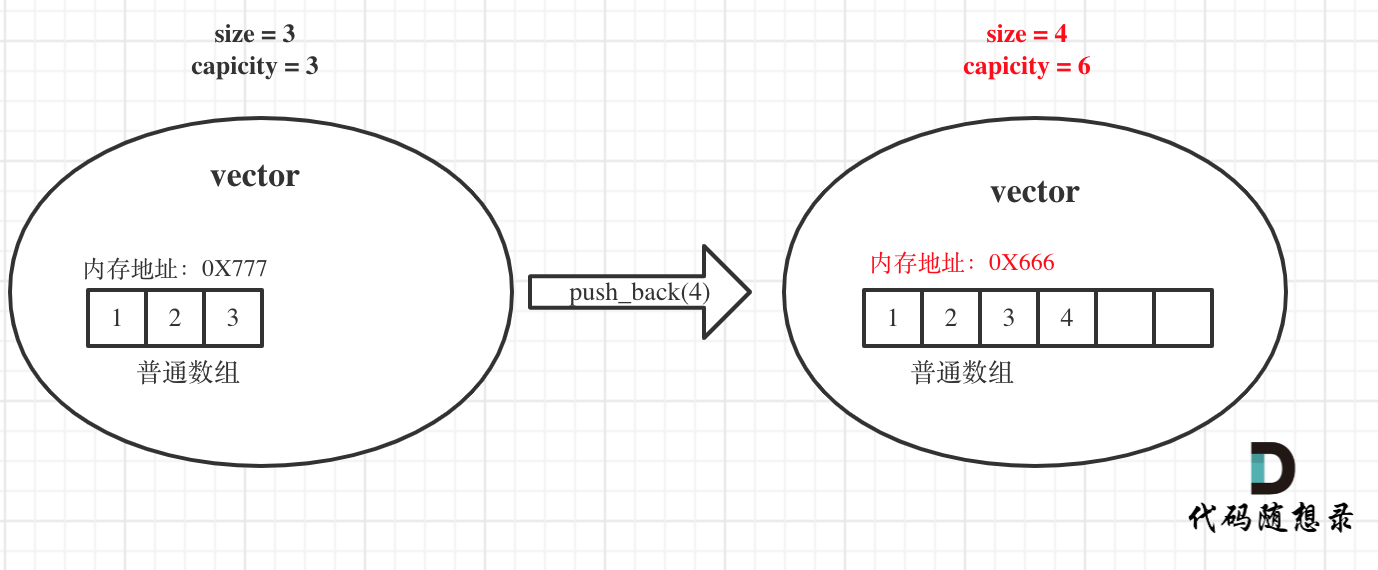
原vector中的size和capicity相同都是3,初始化为1 2 3,此时要push_back一个元素4。
@@ -138,7 +138,7 @@ public:
耗时如下:
-
+
这份代码就是不让vector动态扩容,全程我们自己模拟insert的操作,大家也可以直观的看出是一个O(n^2)的方法了。
diff --git a/problems/背包总结篇.md b/problems/背包总结篇.md
index 3c587b6d..9ce3fdda 100644
--- a/problems/背包总结篇.md
+++ b/problems/背包总结篇.md
@@ -11,7 +11,7 @@
关于这几种常见的背包,其关系如下:
-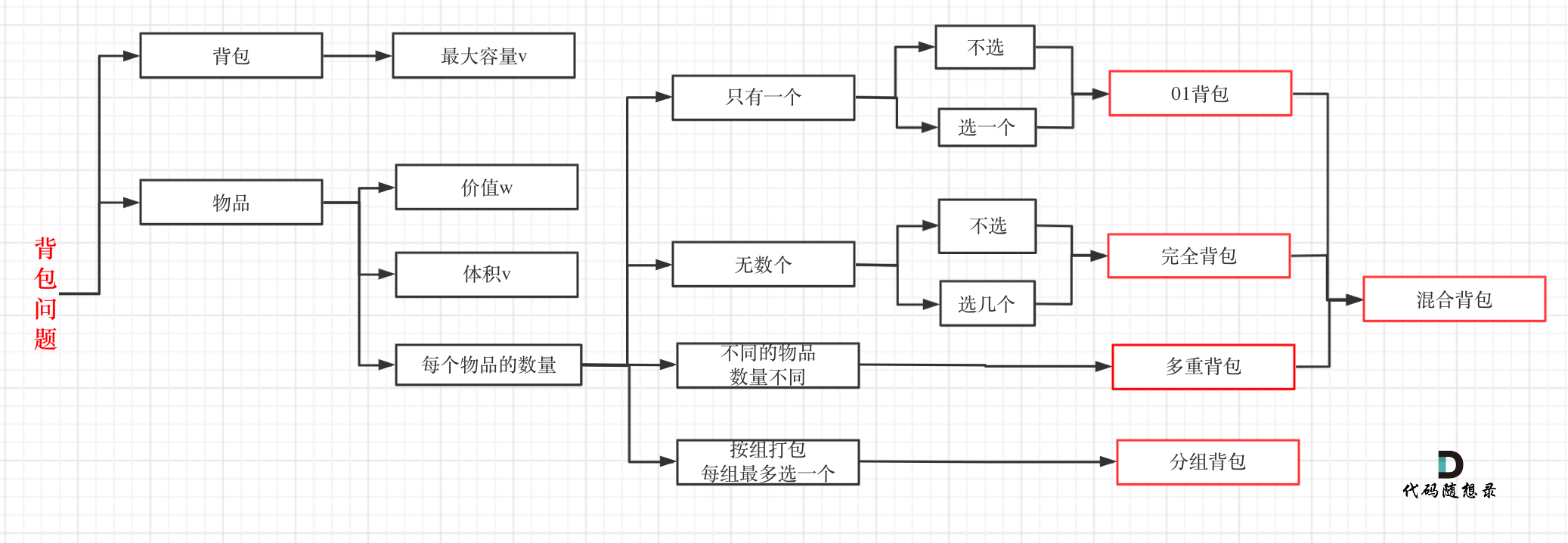
+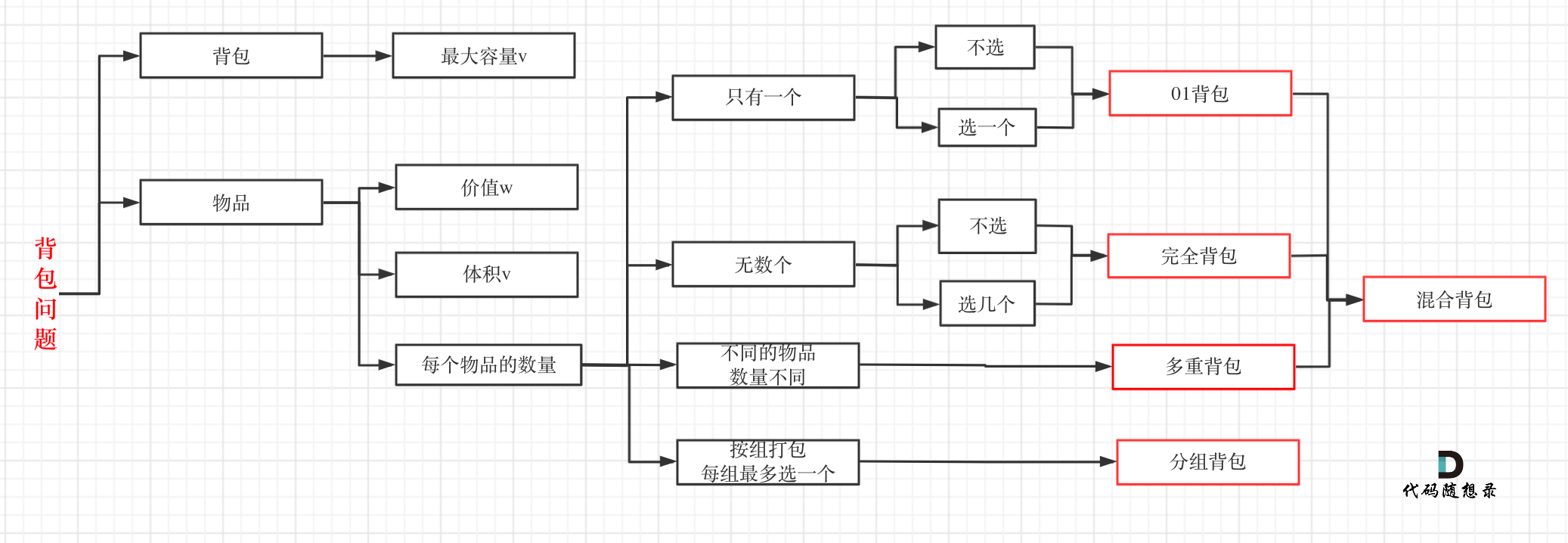
通过这个图,可以很清晰分清这几种常见背包之间的关系。
@@ -93,7 +93,7 @@
背包问题总结:
-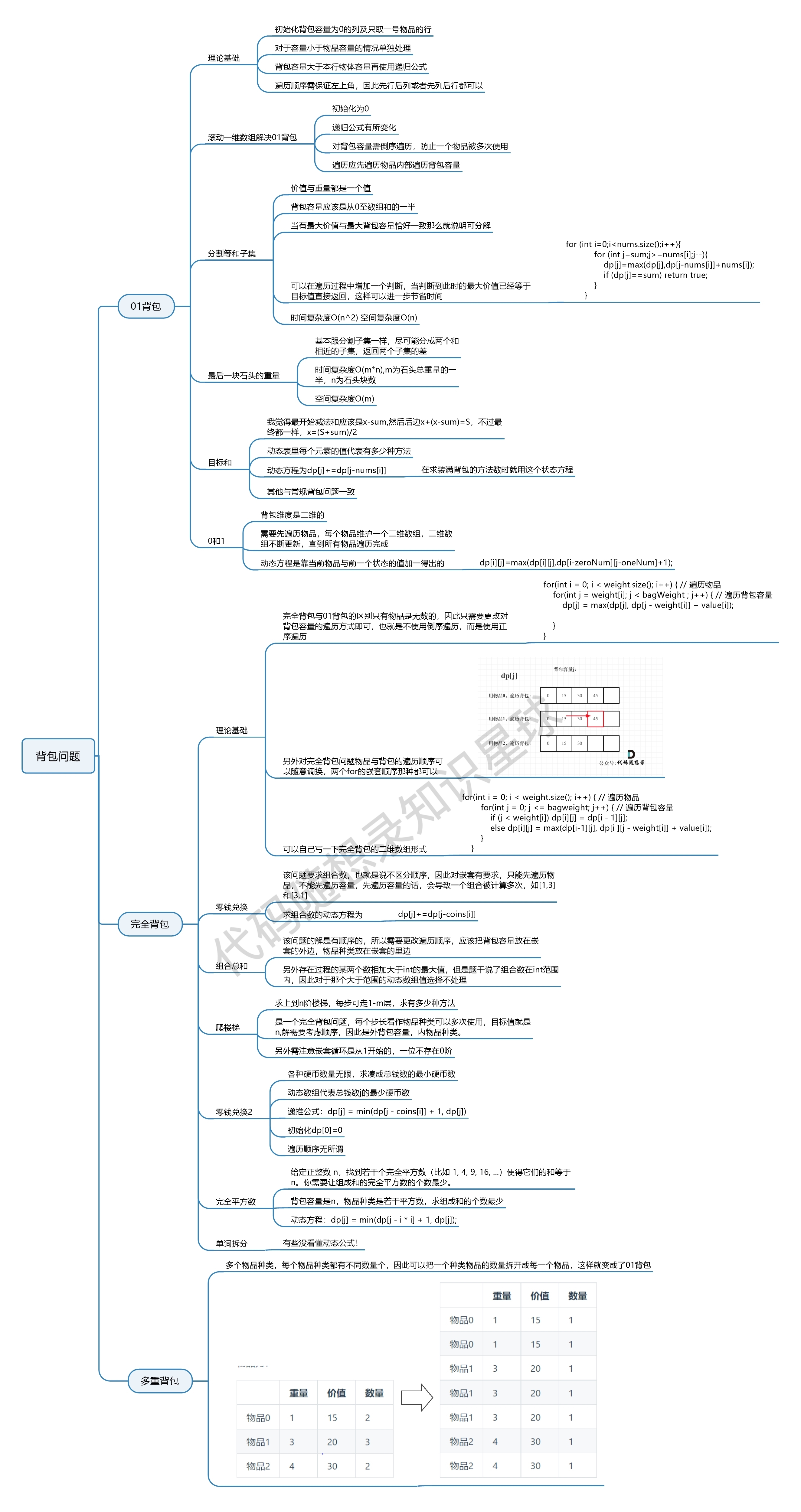
+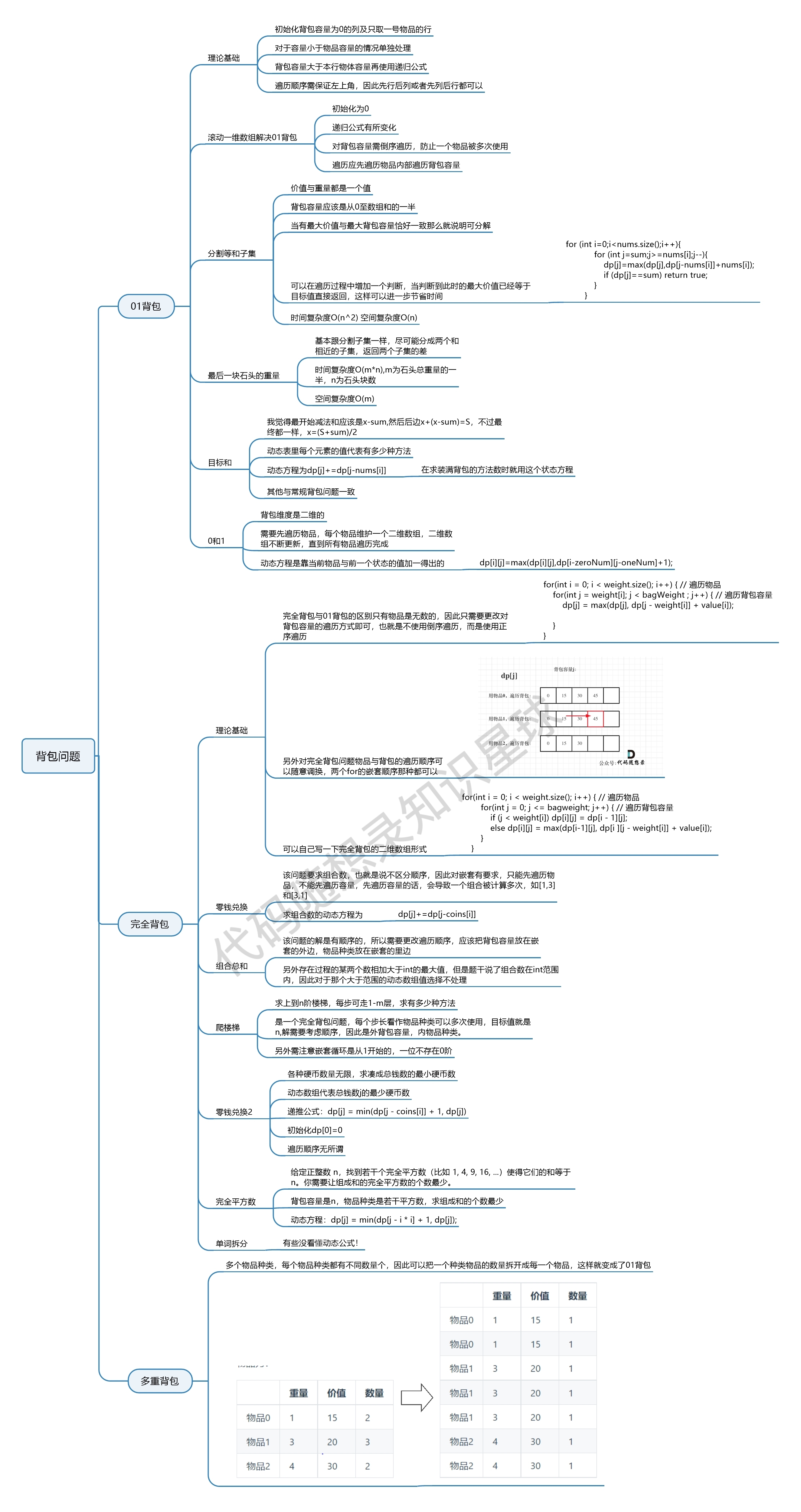
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画结的非常好,分享给大家。
diff --git a/problems/背包理论基础01背包-1.md b/problems/背包理论基础01背包-1.md
index c2598ec9..79751c89 100644
--- a/problems/背包理论基础01背包-1.md
+++ b/problems/背包理论基础01背包-1.md
@@ -21,7 +21,7 @@
如果这几种背包,分不清,我这里画了一个图,如下:
-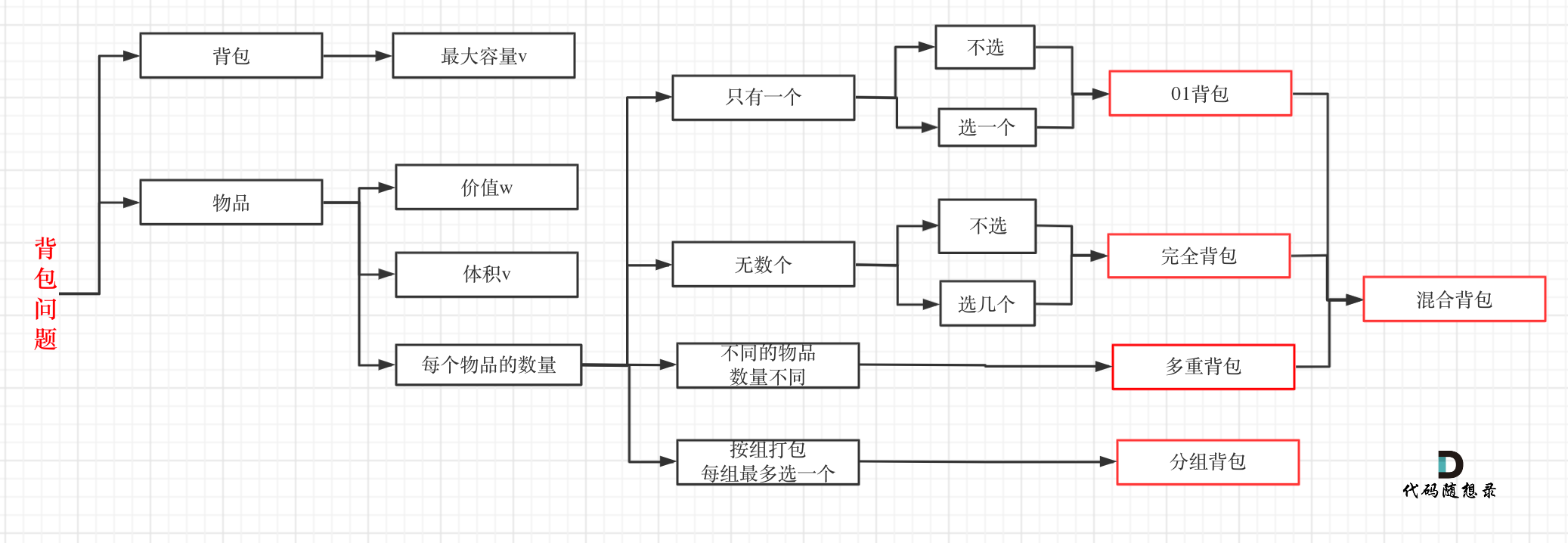
+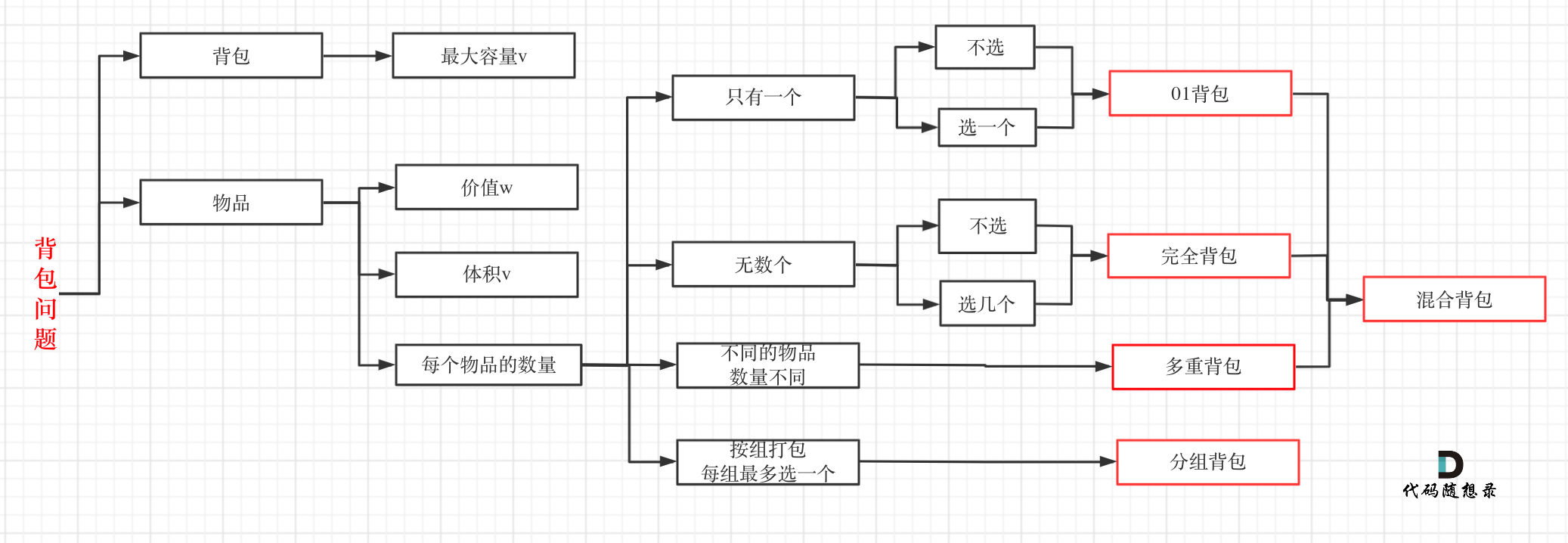
除此以外其他类型的背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
@@ -77,7 +77,7 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
如图,二维数组为 dp[i][j]。
-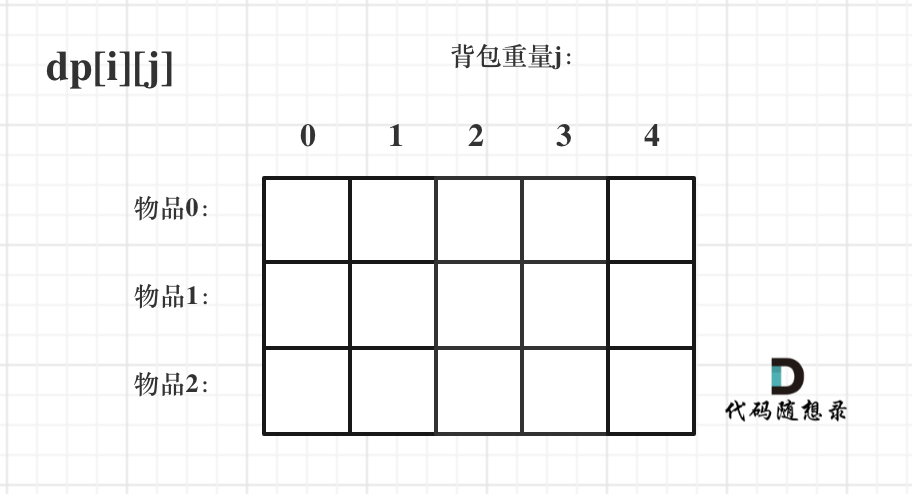
+
那么这里 i 、j、dp[i][j] 分别表示什么呢?
@@ -91,7 +91,7 @@ i 来表示物品、j表示背包容量。
我们先看把物品0 放入背包的情况:
-
+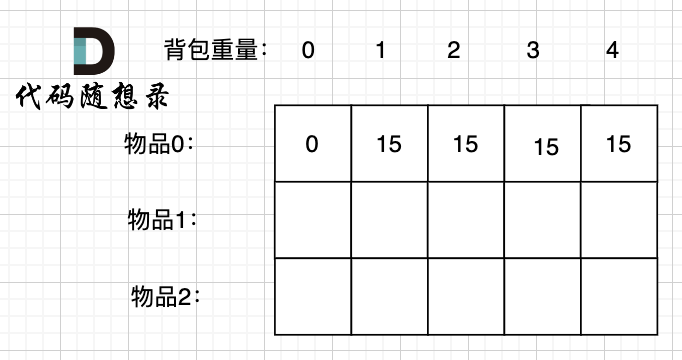
背包容量为0,放不下物品0,此时背包里的价值为0。
@@ -103,7 +103,7 @@ i 来表示物品、j表示背包容量。
再看把物品1 放入背包:
-
+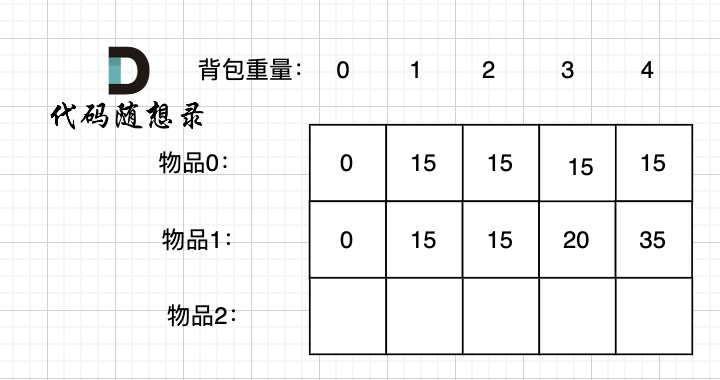
背包容量为 0,放不下物品0 或者物品1,此时背包里的价值为0。
@@ -150,7 +150,7 @@ i 来表示物品、j表示背包容量。
推导方向如图:
-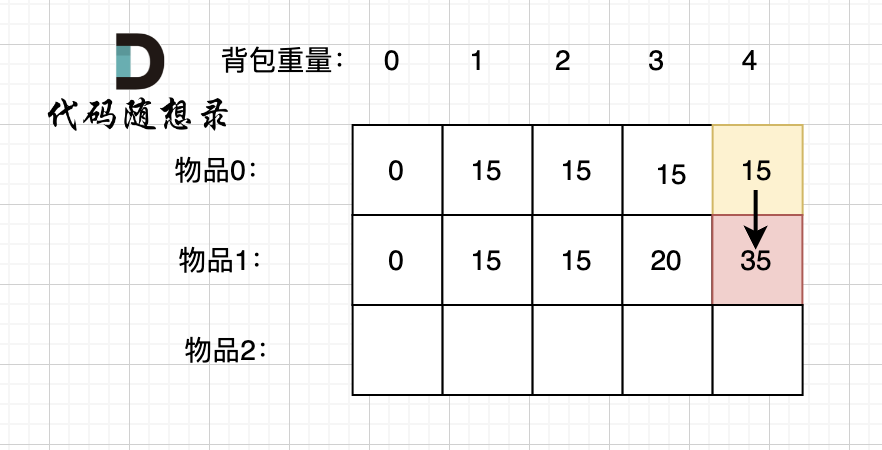
+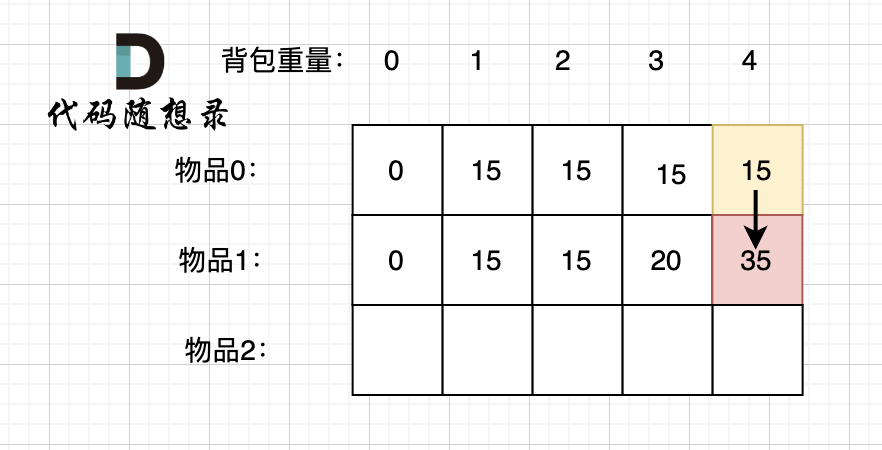
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 的容量(就是物品1的重量)为3,此时背包剩下容量为1。
@@ -158,7 +158,7 @@ i 来表示物品、j表示背包容量。
所以 放物品1 的情况 = dp[0][1] + 物品1 的价值,推导方向如图:
-
+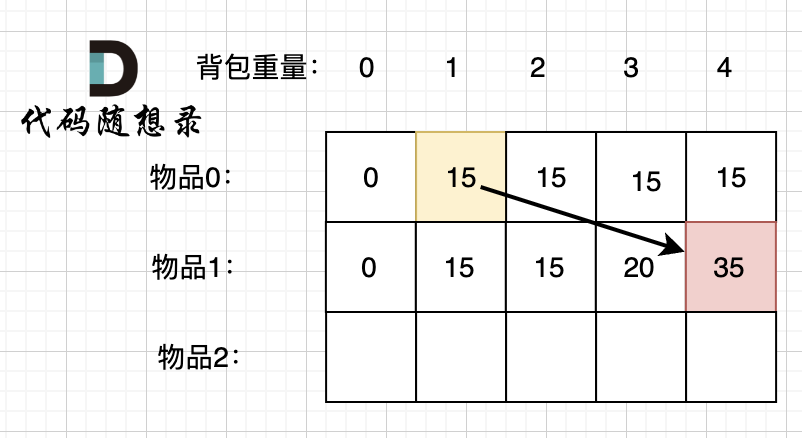
两种情况,分别是放物品1 和 不放物品1,我们要取最大值(毕竟求的是最大价值)
@@ -178,7 +178,7 @@ i 来表示物品、j表示背包容量。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
-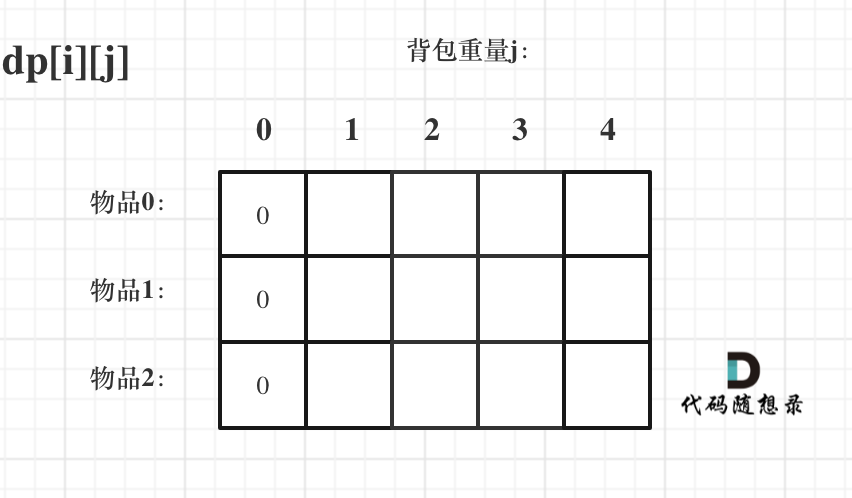
+
在看其他情况。
@@ -205,7 +205,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
此时dp数组初始化情况如图所示:
-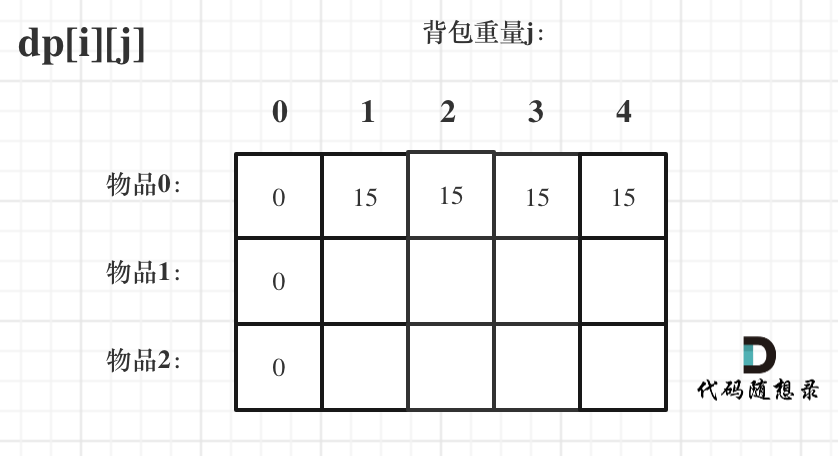
+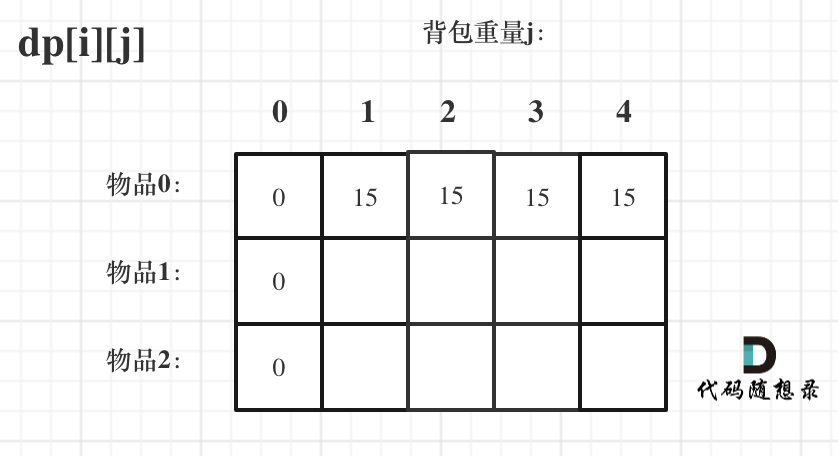
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
@@ -217,7 +217,7 @@ dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化
如图:
-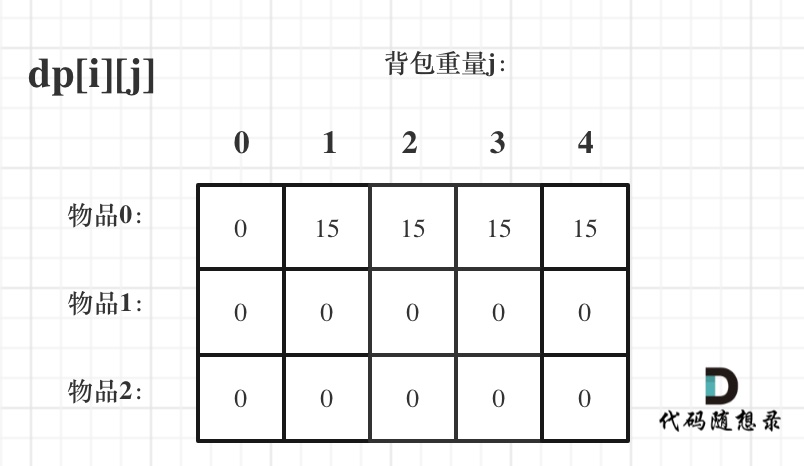
+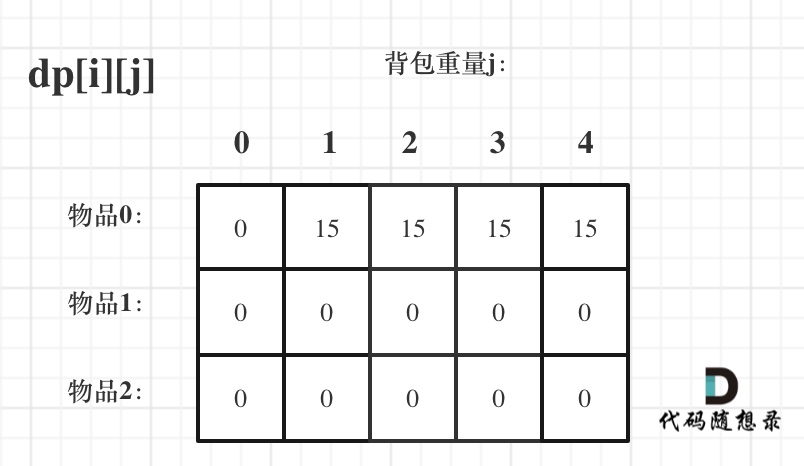
最后初始化代码如下:
@@ -236,7 +236,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
在如下图中,可以看出,有两个遍历的维度:物品与背包重量
-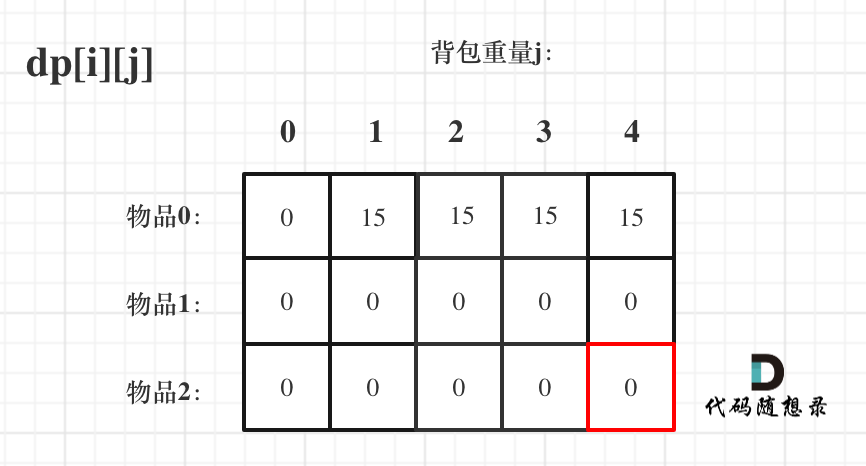
+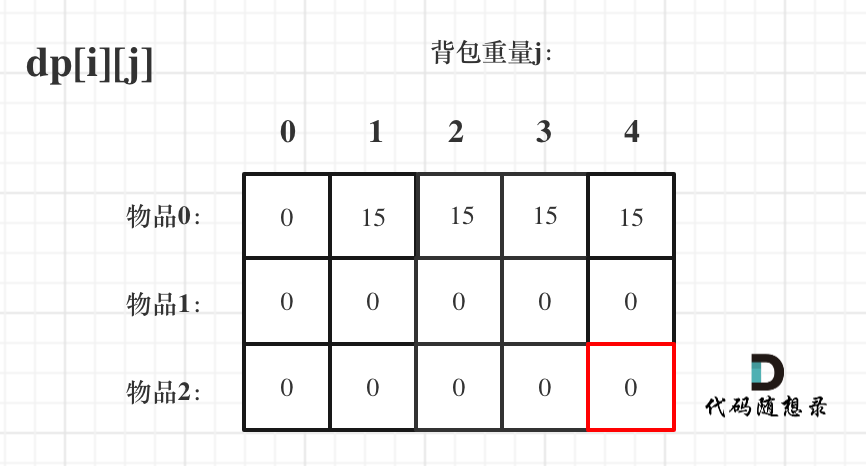
那么问题来了,**先遍历 物品还是先遍历背包重量呢?**
@@ -277,11 +277,11 @@ for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
-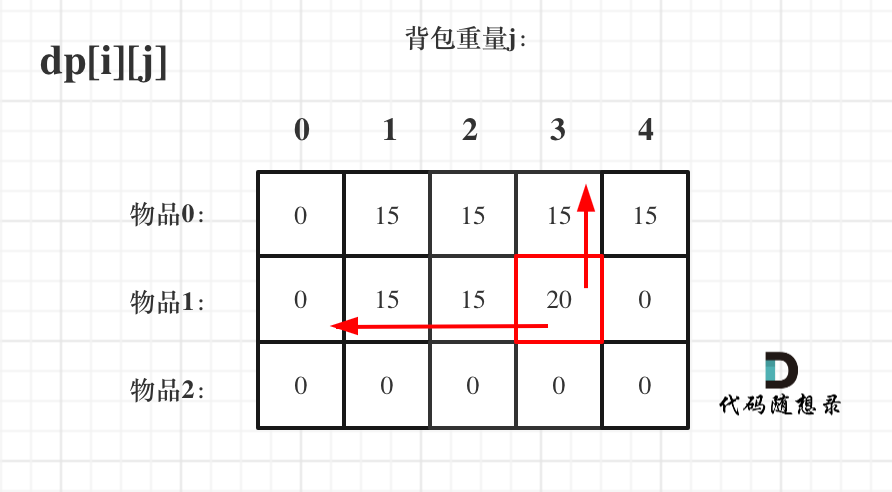
+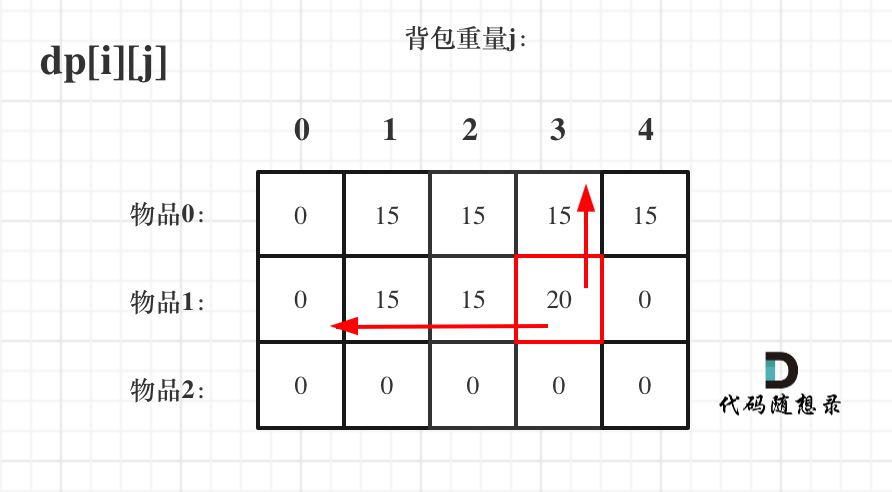
再来看看先遍历背包,再遍历物品呢,如图:
-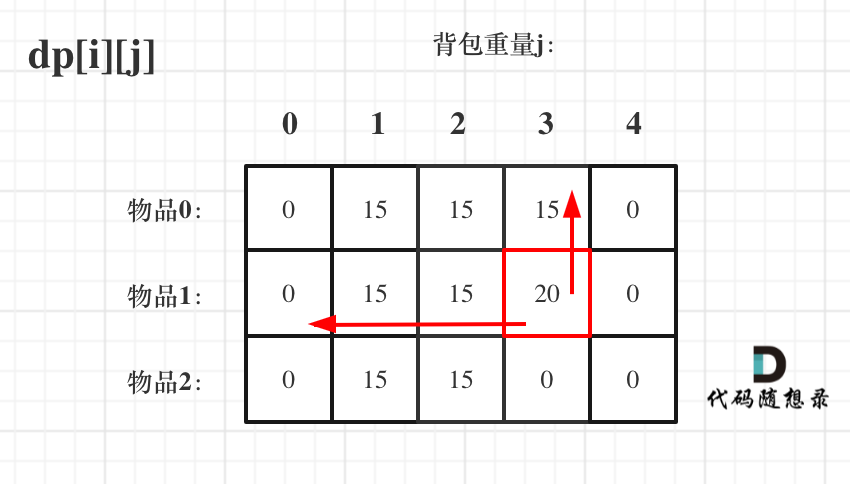
+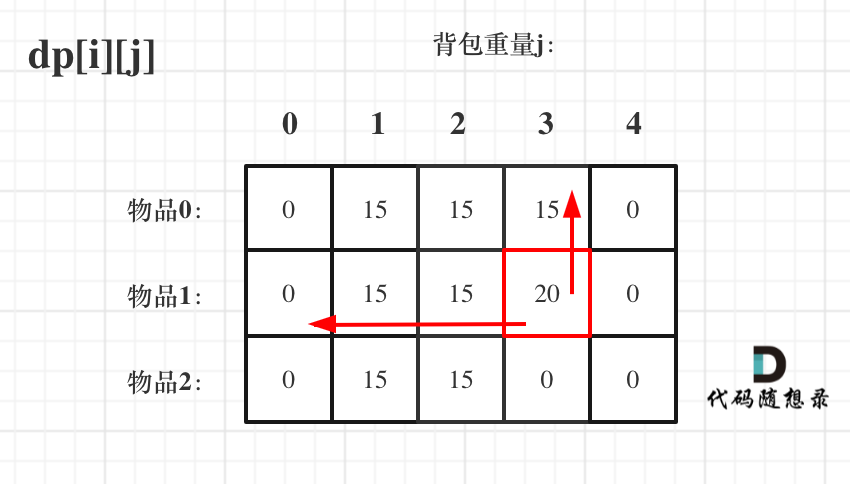
**大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!**
@@ -293,7 +293,7 @@ dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括
来看一下对应的dp数组的数值,如图:
-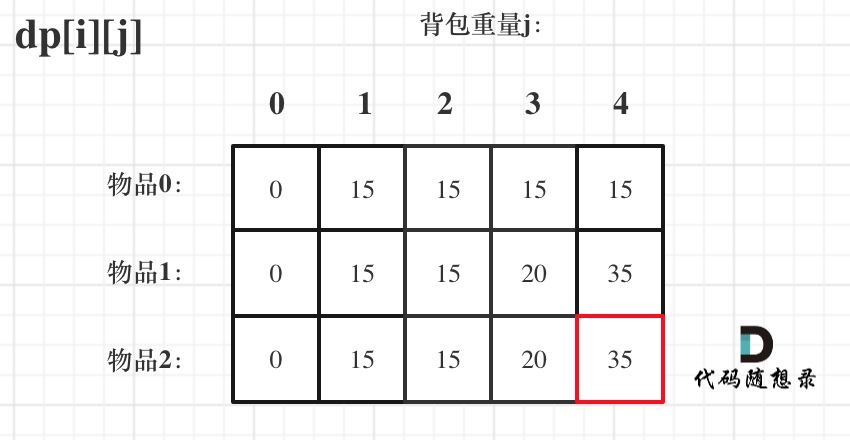
+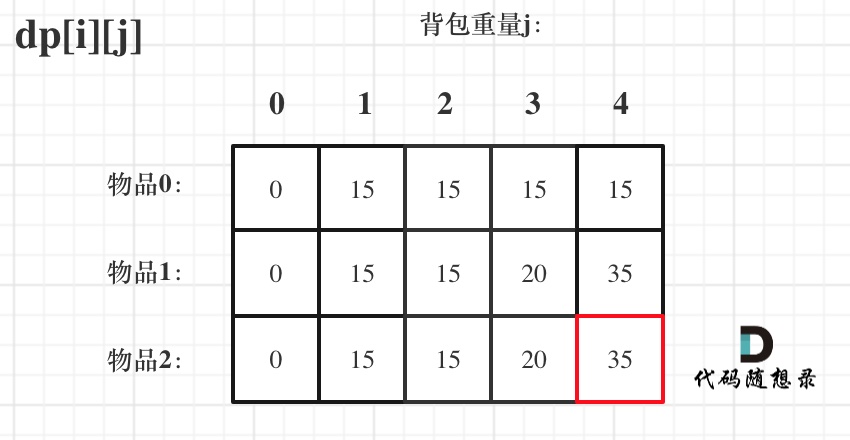
最终结果就是dp[2][4]。
diff --git a/problems/背包理论基础01背包-2.md b/problems/背包理论基础01背包-2.md
index 6caa4f63..b6a68960 100644
--- a/problems/背包理论基础01背包-2.md
+++ b/problems/背包理论基础01背包-2.md
@@ -163,7 +163,7 @@ dp[1] = dp[1 - weight[0]] + value[0] = 15
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
-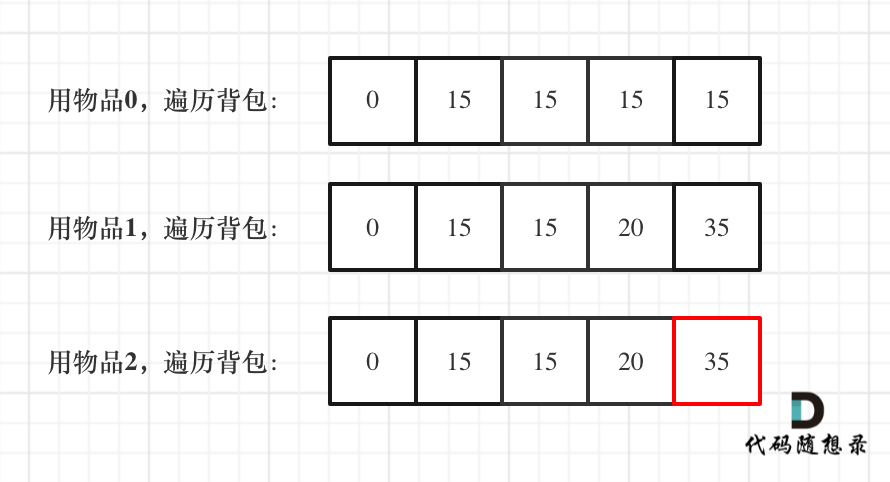
+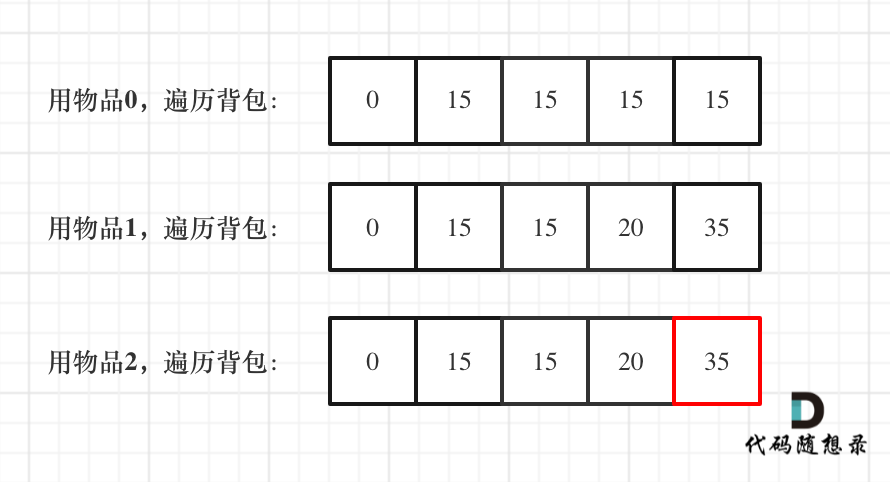
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problempage.php?pid=1046)去练习,题意是一样的,代码如下:
diff --git a/problems/背包问题完全背包一维.md b/problems/背包问题完全背包一维.md
index 5a23b67c..be7a5d54 100644
--- a/problems/背包问题完全背包一维.md
+++ b/problems/背包问题完全背包一维.md
@@ -54,11 +54,11 @@ for (int i = 1; i < n; i++) { // 遍历物品
遍历物品在外层循环,遍历背包容量在内层循环,状态如图:
-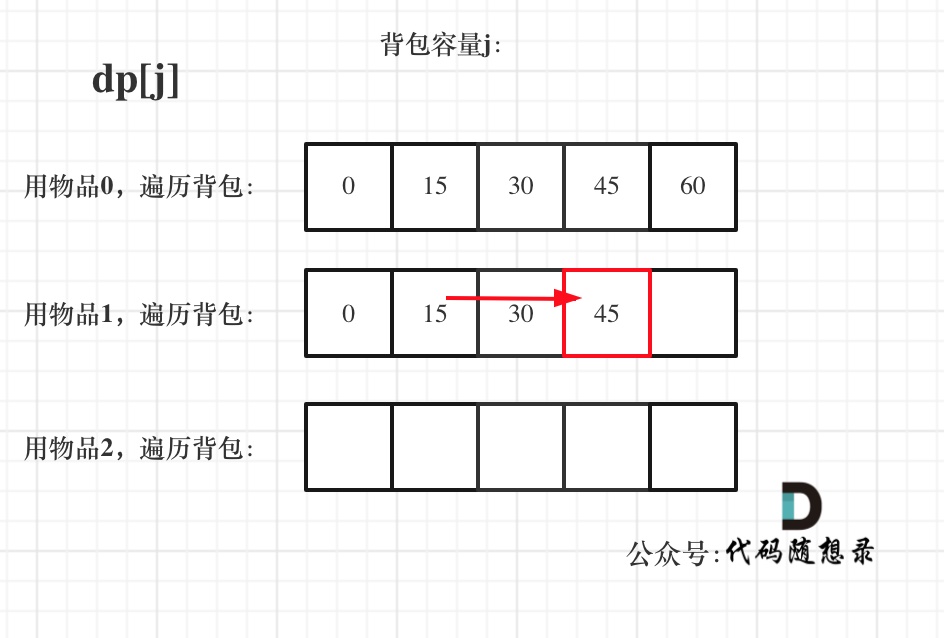
+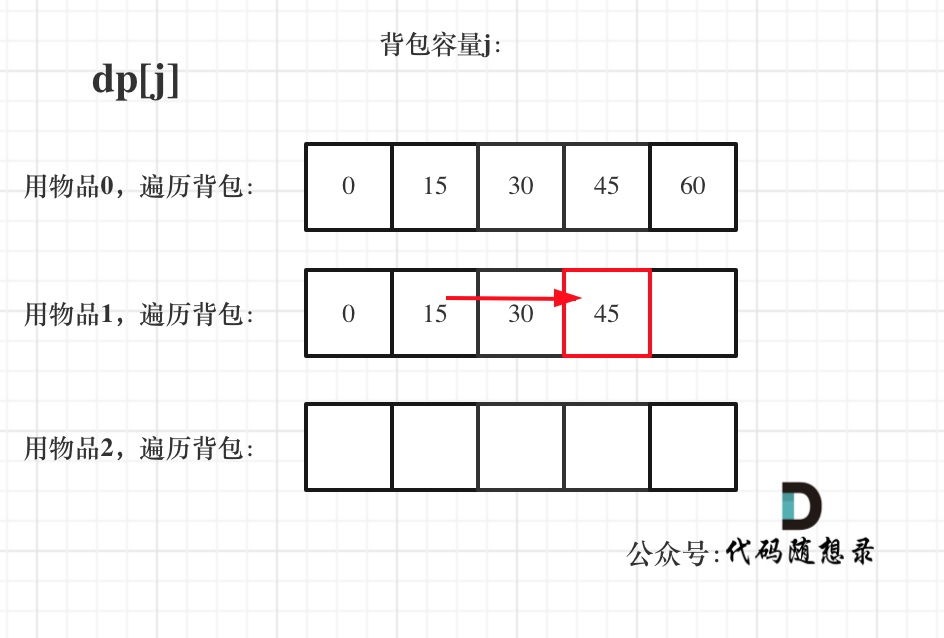
遍历背包容量在外层循环,遍历物品在内层循环,状态如图:
-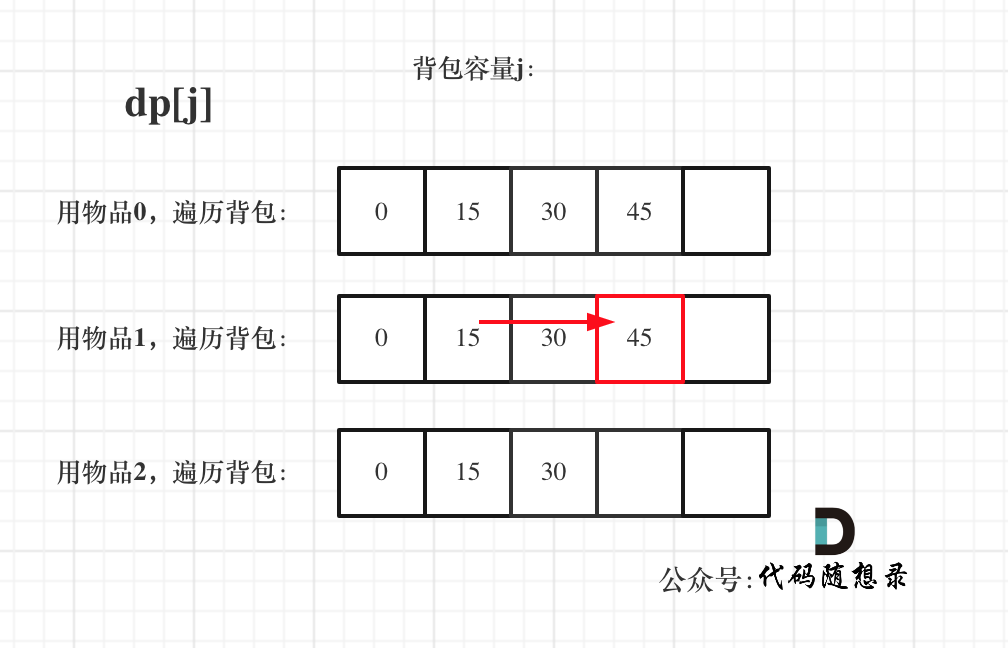
+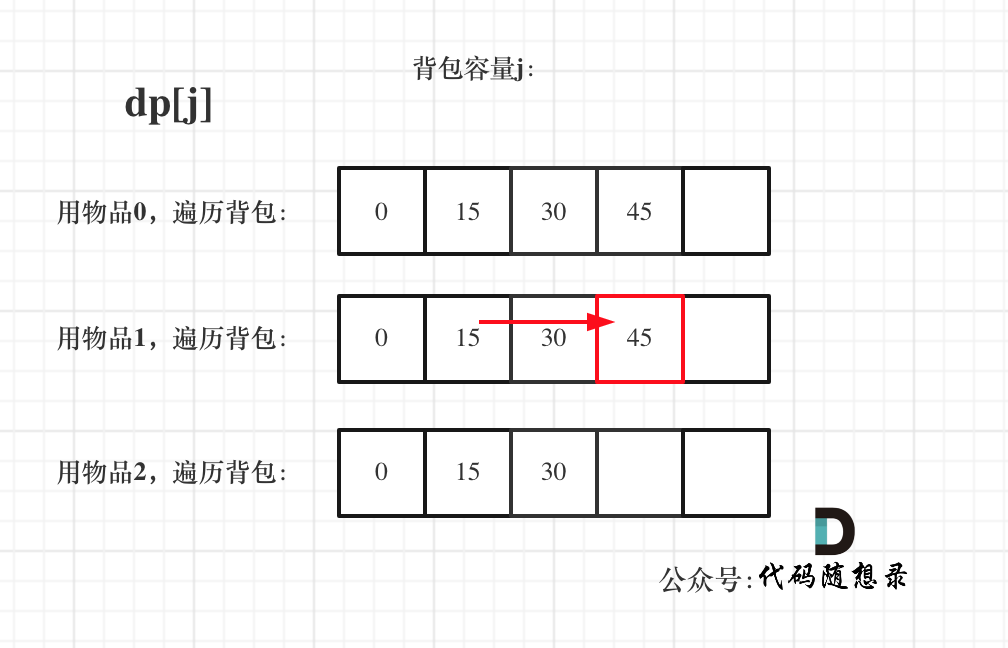
看了这两个图,大家就会理解,完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值(这个值就是下标j之前所对应的dp[j])。
diff --git a/problems/背包问题理论基础完全背包.md b/problems/背包问题理论基础完全背包.md
index d76ff196..cb8db1e0 100644
--- a/problems/背包问题理论基础完全背包.md
+++ b/problems/背包问题理论基础完全背包.md
@@ -66,7 +66,7 @@
推导方向如图:
-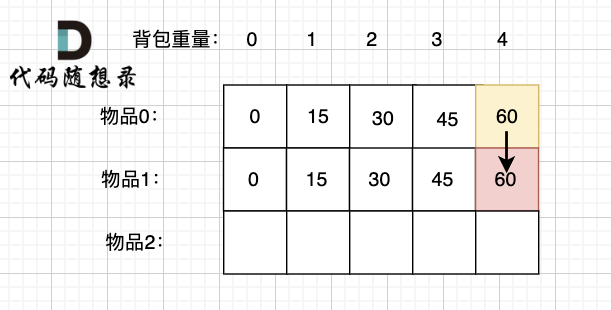
+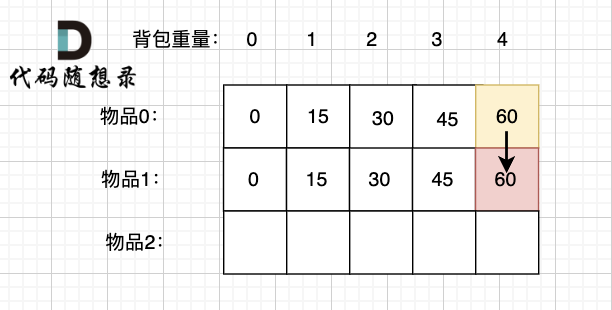
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 的容量(就是物品1的重量)为3,此时背包剩下容量为1。
@@ -78,7 +78,7 @@
所以 放物品1 的情况 = dp[1][1] + 物品1 的价值,推导方向如图:
-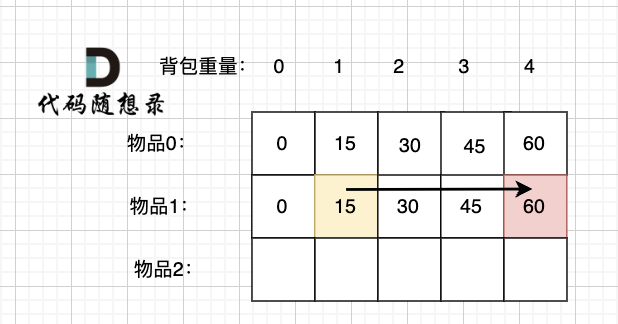
+
(**注意上图和 [01背包理论基础(二维数组)](https://programmercarl.com/背包理论基础01背包-1.html) 中的区别**,对于理解完全背包很重要)
@@ -103,7 +103,7 @@
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
-
+
在看其他情况。
@@ -132,7 +132,7 @@ for (int j = weight[0]; j <= bagWeight; j++)
此时dp数组初始化情况如图所示:
-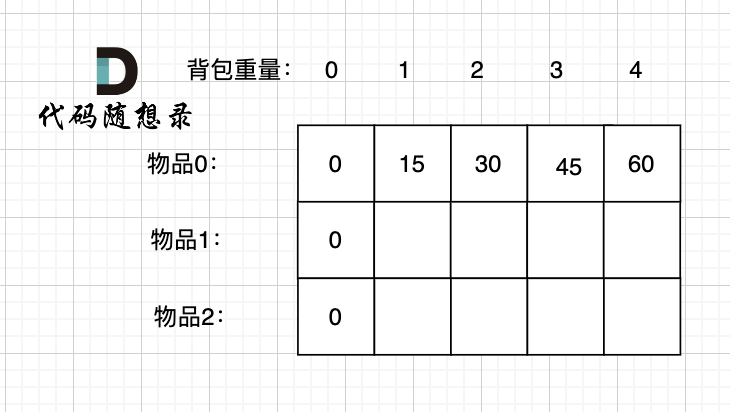
+
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
@@ -185,7 +185,7 @@ for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
以本篇举例数据为例,填满了dp二维数组如图:
-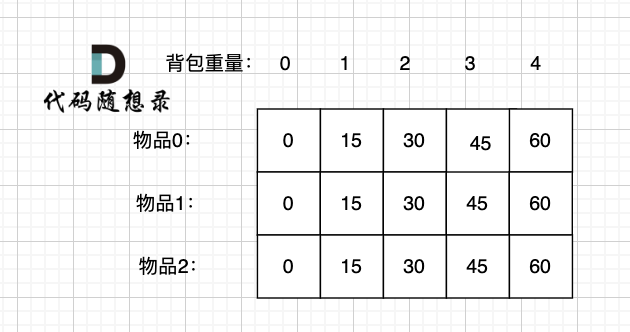
+
因为 物品0 的性价比是最高的,而且 在完全背包中,每一类物品都有无限个,所以有无限个物品0,既然物品0 性价比最高,当然是优先放物品0。
diff --git a/problems/贪心算法总结篇.md b/problems/贪心算法总结篇.md
index 7d4c57e8..4c67fb40 100644
--- a/problems/贪心算法总结篇.md
+++ b/problems/贪心算法总结篇.md
@@ -128,7 +128,7 @@ Carl个人认为:如果找出局部最优并可以推出全局最优,就是
贪心专题汇聚为一张图:
-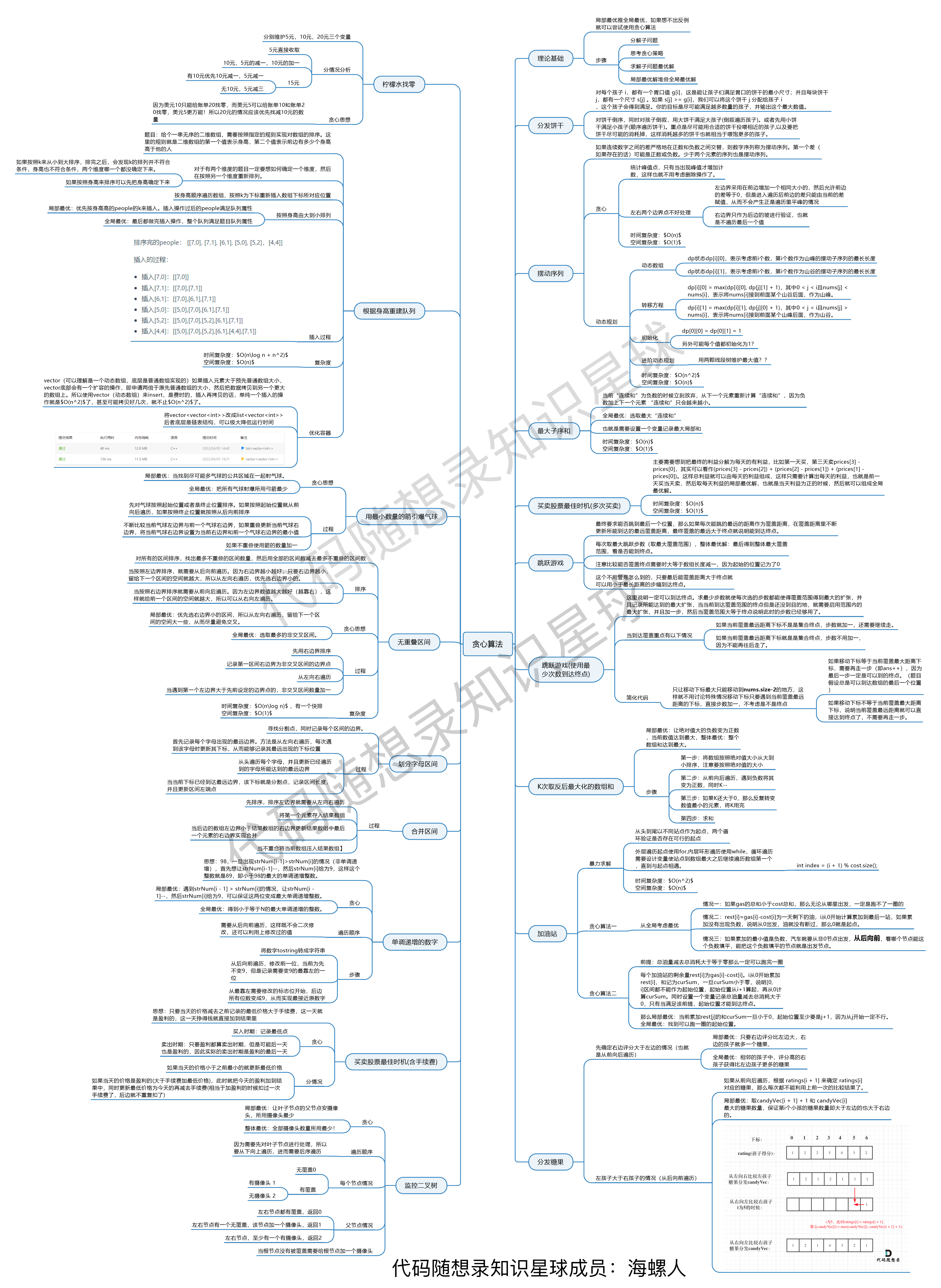
+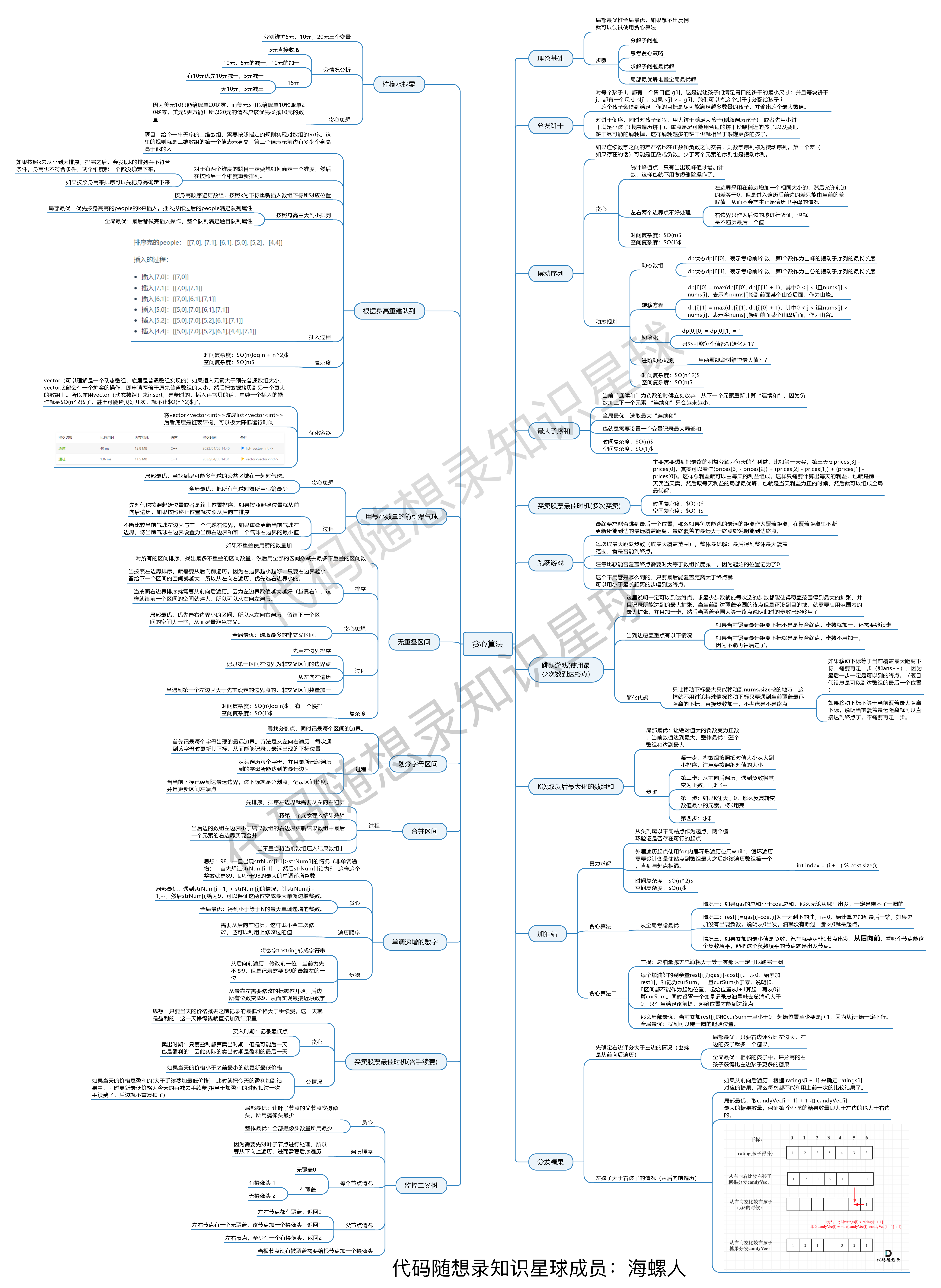
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412)所画,总结的非常好,分享给大家。
diff --git a/problems/贪心算法理论基础.md b/problems/贪心算法理论基础.md
index 14f39729..2d0af879 100644
--- a/problems/贪心算法理论基础.md
+++ b/problems/贪心算法理论基础.md
@@ -7,7 +7,7 @@
题目分类大纲如下:
-
## 算法公开课
@@ -114,7 +114,7 @@ if (终止条件) {
如图:
-
+
注意图中,我特意举例集合大小和孩子的数量是相等的!
diff --git a/problems/数组总结篇.md b/problems/数组总结篇.md
index e45165a6..e29a7bd3 100644
--- a/problems/数组总结篇.md
+++ b/problems/数组总结篇.md
@@ -125,7 +125,7 @@
## 总结
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画,总结的非常好,分享给大家。
diff --git a/problems/数组理论基础.md b/problems/数组理论基础.md
index c1ac287d..4000208a 100644
--- a/problems/数组理论基础.md
+++ b/problems/数组理论基础.md
@@ -40,7 +40,7 @@
那么二维数组直接上图,大家应该就知道怎么回事了
-
+
**那么二维数组在内存的空间地址是连续的么?**
@@ -80,7 +80,7 @@ int main() {
如图:
-
+
**所以可以看出在C++中二维数组在地址空间上是连续的**。
@@ -111,7 +111,7 @@ public static void test_arr() {
所以Java的二维数组可能是如下排列的方式:
-
+
这里面试中数组相关的理论知识就介绍完了。
diff --git a/problems/栈与队列理论基础.md b/problems/栈与队列理论基础.md
index bff0ec63..912bfe1d 100644
--- a/problems/栈与队列理论基础.md
+++ b/problems/栈与队列理论基础.md
@@ -11,7 +11,7 @@
如图所示:
-
+
那么我这里再列出四个关于栈的问题,大家可以思考一下。以下是以C++为例,使用其他编程语言的同学也对应思考一下,自己使用的编程语言里栈和队列是什么样的。
@@ -46,7 +46,7 @@ C++标准库是有多个版本的,要知道我们使用的STL是哪个版本
来说一说栈,栈先进后出,如图所示:
-
+
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
@@ -59,7 +59,7 @@ C++标准库是有多个版本的,要知道我们使用的STL是哪个版本
从下图中可以看出,栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
-
+
**我们常用的SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。**
diff --git a/problems/根据身高重建队列(vector原理讲解).md b/problems/根据身高重建队列(vector原理讲解).md
index a2350835..162ee273 100644
--- a/problems/根据身高重建队列(vector原理讲解).md
+++ b/problems/根据身高重建队列(vector原理讲解).md
@@ -35,7 +35,7 @@ public:
```
耗时如下:
-
+
其直观上来看数组的insert操作是O(n)的,整体代码的时间复杂度是O(n^2)。
@@ -68,7 +68,7 @@ public:
耗时如下:
-
+
大家都知道对于普通数组,一旦定义了大小就不能改变,例如int a[10];,这个数组a至多只能放10个元素,改不了的。
@@ -95,7 +95,7 @@ for (int i = 0; i < vec.size(); i++) {
就是重新申请一个二倍于原数组大小的数组,然后把数据都拷贝过去,并释放原数组内存。(对,就是这么原始粗暴的方法!)
举一个例子,如图:
-
+
原vector中的size和capicity相同都是3,初始化为1 2 3,此时要push_back一个元素4。
@@ -138,7 +138,7 @@ public:
耗时如下:
-
+
这份代码就是不让vector动态扩容,全程我们自己模拟insert的操作,大家也可以直观的看出是一个O(n^2)的方法了。
diff --git a/problems/背包总结篇.md b/problems/背包总结篇.md
index 3c587b6d..9ce3fdda 100644
--- a/problems/背包总结篇.md
+++ b/problems/背包总结篇.md
@@ -11,7 +11,7 @@
关于这几种常见的背包,其关系如下:
-
+
通过这个图,可以很清晰分清这几种常见背包之间的关系。
@@ -93,7 +93,7 @@
背包问题总结:
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画结的非常好,分享给大家。
diff --git a/problems/背包理论基础01背包-1.md b/problems/背包理论基础01背包-1.md
index c2598ec9..79751c89 100644
--- a/problems/背包理论基础01背包-1.md
+++ b/problems/背包理论基础01背包-1.md
@@ -21,7 +21,7 @@
如果这几种背包,分不清,我这里画了一个图,如下:
-
+
除此以外其他类型的背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
@@ -77,7 +77,7 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
如图,二维数组为 dp[i][j]。
-
+
那么这里 i 、j、dp[i][j] 分别表示什么呢?
@@ -91,7 +91,7 @@ i 来表示物品、j表示背包容量。
我们先看把物品0 放入背包的情况:
-
+
背包容量为0,放不下物品0,此时背包里的价值为0。
@@ -103,7 +103,7 @@ i 来表示物品、j表示背包容量。
再看把物品1 放入背包:
-
+
背包容量为 0,放不下物品0 或者物品1,此时背包里的价值为0。
@@ -150,7 +150,7 @@ i 来表示物品、j表示背包容量。
推导方向如图:
-
+
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 的容量(就是物品1的重量)为3,此时背包剩下容量为1。
@@ -158,7 +158,7 @@ i 来表示物品、j表示背包容量。
所以 放物品1 的情况 = dp[0][1] + 物品1 的价值,推导方向如图:
-
+
两种情况,分别是放物品1 和 不放物品1,我们要取最大值(毕竟求的是最大价值)
@@ -178,7 +178,7 @@ i 来表示物品、j表示背包容量。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
-
+
在看其他情况。
@@ -205,7 +205,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
此时dp数组初始化情况如图所示:
-
+
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
@@ -217,7 +217,7 @@ dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化
如图:
-
+
最后初始化代码如下:
@@ -236,7 +236,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
在如下图中,可以看出,有两个遍历的维度:物品与背包重量
-
+
那么问题来了,**先遍历 物品还是先遍历背包重量呢?**
@@ -277,11 +277,11 @@ for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
-
+
再来看看先遍历背包,再遍历物品呢,如图:
-
+
**大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!**
@@ -293,7 +293,7 @@ dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括
来看一下对应的dp数组的数值,如图:
-
+
最终结果就是dp[2][4]。
diff --git a/problems/背包理论基础01背包-2.md b/problems/背包理论基础01背包-2.md
index 6caa4f63..b6a68960 100644
--- a/problems/背包理论基础01背包-2.md
+++ b/problems/背包理论基础01背包-2.md
@@ -163,7 +163,7 @@ dp[1] = dp[1 - weight[0]] + value[0] = 15
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
-
+
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problempage.php?pid=1046)去练习,题意是一样的,代码如下:
diff --git a/problems/背包问题完全背包一维.md b/problems/背包问题完全背包一维.md
index 5a23b67c..be7a5d54 100644
--- a/problems/背包问题完全背包一维.md
+++ b/problems/背包问题完全背包一维.md
@@ -54,11 +54,11 @@ for (int i = 1; i < n; i++) { // 遍历物品
遍历物品在外层循环,遍历背包容量在内层循环,状态如图:
-
+
遍历背包容量在外层循环,遍历物品在内层循环,状态如图:
-
+
看了这两个图,大家就会理解,完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值(这个值就是下标j之前所对应的dp[j])。
diff --git a/problems/背包问题理论基础完全背包.md b/problems/背包问题理论基础完全背包.md
index d76ff196..cb8db1e0 100644
--- a/problems/背包问题理论基础完全背包.md
+++ b/problems/背包问题理论基础完全背包.md
@@ -66,7 +66,7 @@
推导方向如图:
-
+
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 的容量(就是物品1的重量)为3,此时背包剩下容量为1。
@@ -78,7 +78,7 @@
所以 放物品1 的情况 = dp[1][1] + 物品1 的价值,推导方向如图:
-
+
(**注意上图和 [01背包理论基础(二维数组)](https://programmercarl.com/背包理论基础01背包-1.html) 中的区别**,对于理解完全背包很重要)
@@ -103,7 +103,7 @@
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
-
+
在看其他情况。
@@ -132,7 +132,7 @@ for (int j = weight[0]; j <= bagWeight; j++)
此时dp数组初始化情况如图所示:
-
+
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
@@ -185,7 +185,7 @@ for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
以本篇举例数据为例,填满了dp二维数组如图:
-
+
因为 物品0 的性价比是最高的,而且 在完全背包中,每一类物品都有无限个,所以有无限个物品0,既然物品0 性价比最高,当然是优先放物品0。
diff --git a/problems/贪心算法总结篇.md b/problems/贪心算法总结篇.md
index 7d4c57e8..4c67fb40 100644
--- a/problems/贪心算法总结篇.md
+++ b/problems/贪心算法总结篇.md
@@ -128,7 +128,7 @@ Carl个人认为:如果找出局部最优并可以推出全局最优,就是
贪心专题汇聚为一张图:
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412)所画,总结的非常好,分享给大家。
diff --git a/problems/贪心算法理论基础.md b/problems/贪心算法理论基础.md
index 14f39729..2d0af879 100644
--- a/problems/贪心算法理论基础.md
+++ b/problems/贪心算法理论基础.md
@@ -7,7 +7,7 @@
题目分类大纲如下:
- +
+ ## 算法公开课
diff --git a/problems/链表总结篇.md b/problems/链表总结篇.md
index e29ba268..99bb2abc 100644
--- a/problems/链表总结篇.md
+++ b/problems/链表总结篇.md
@@ -75,7 +75,7 @@
## 总结
-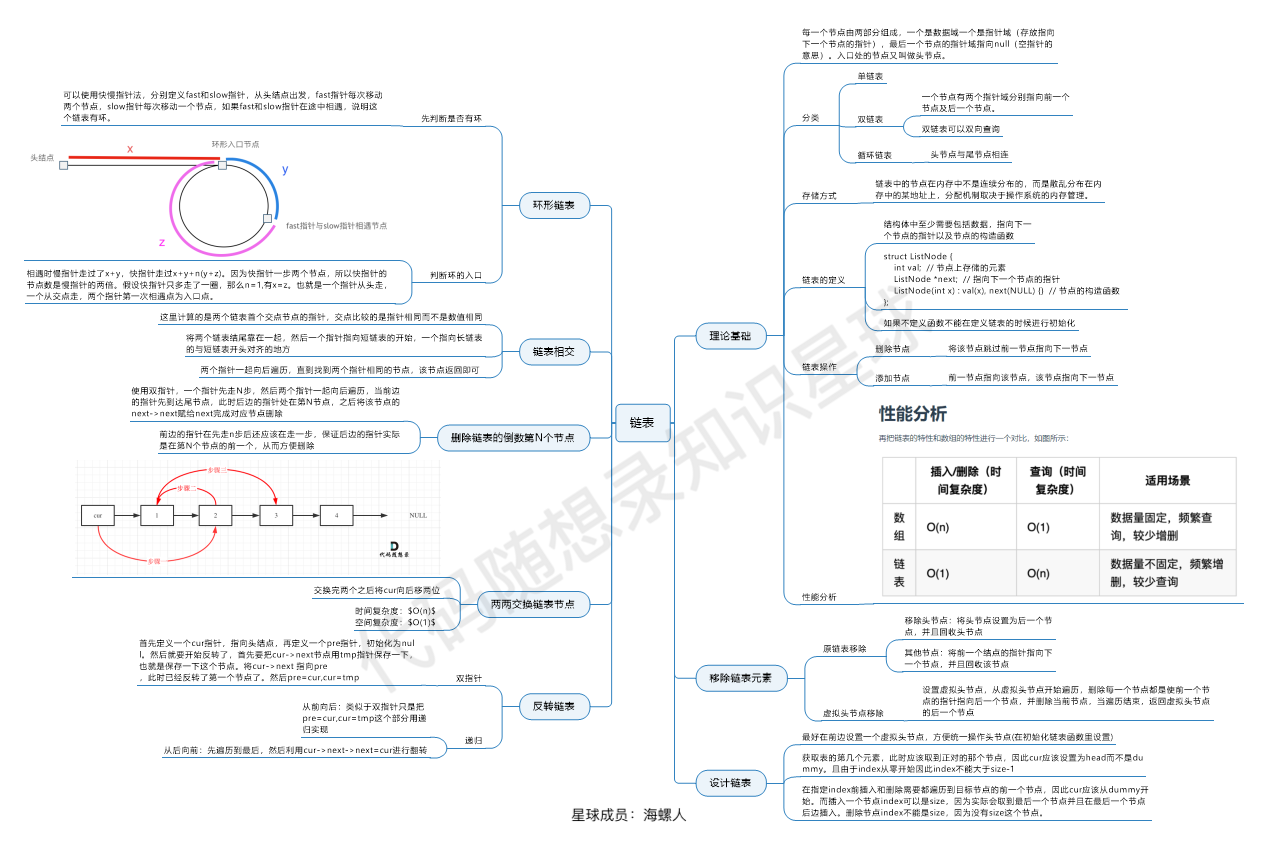
+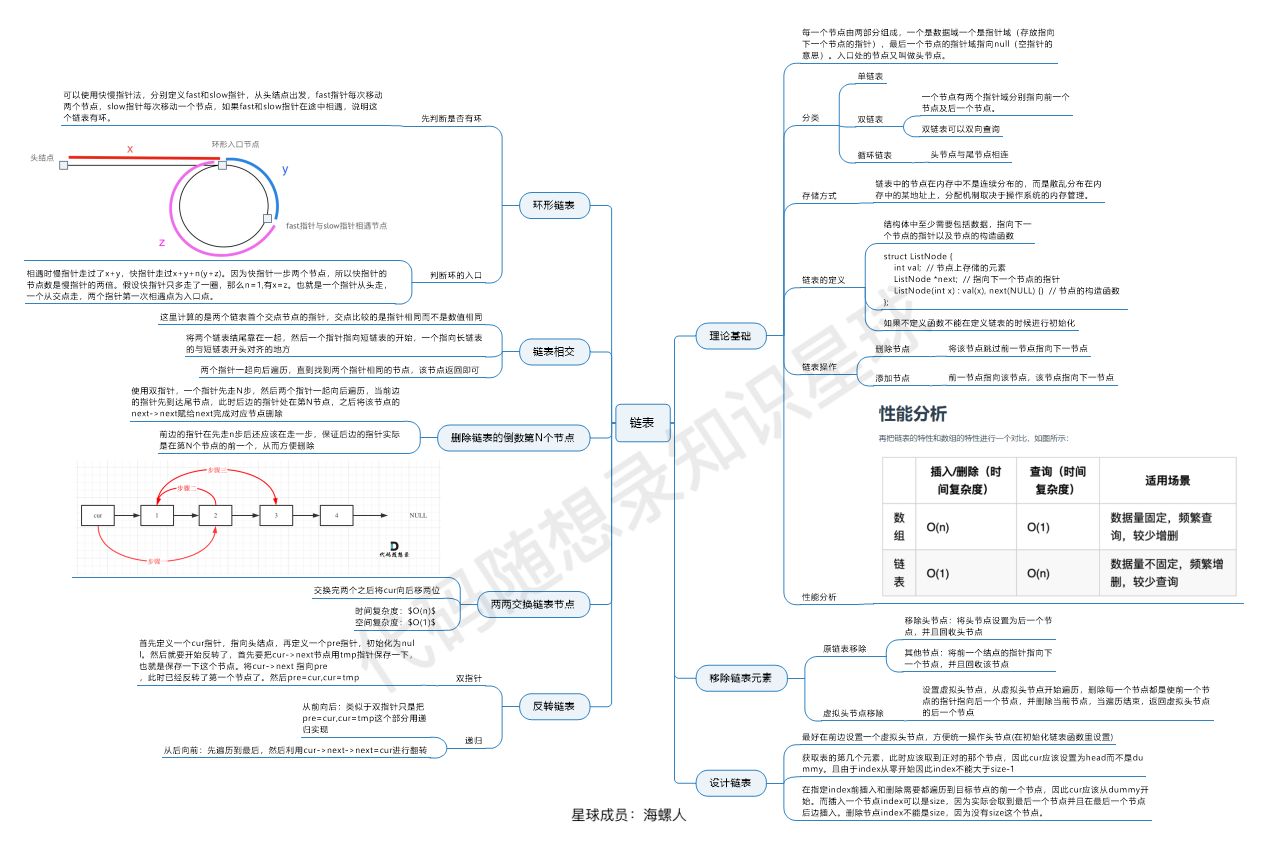
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画,总结的非常好,分享给大家。
diff --git a/problems/链表理论基础.md b/problems/链表理论基础.md
index 3637d05f..5305c9a9 100644
--- a/problems/链表理论基础.md
+++ b/problems/链表理论基础.md
@@ -12,7 +12,7 @@
链表的入口节点称为链表的头结点也就是head。
如图所示:
-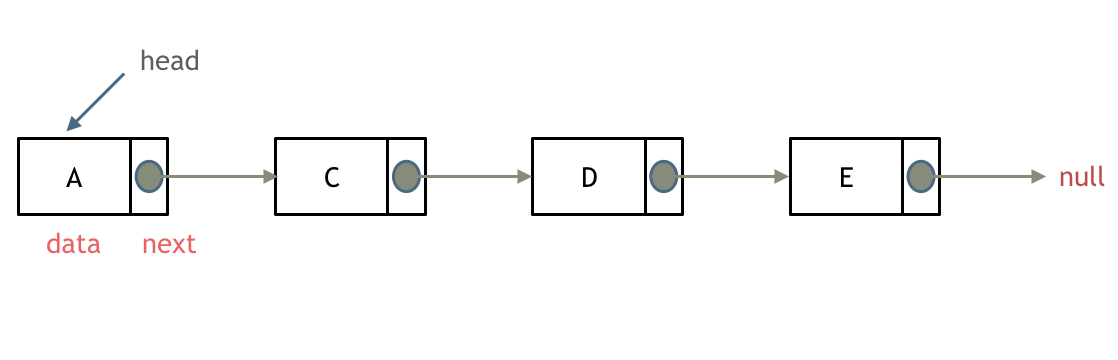
+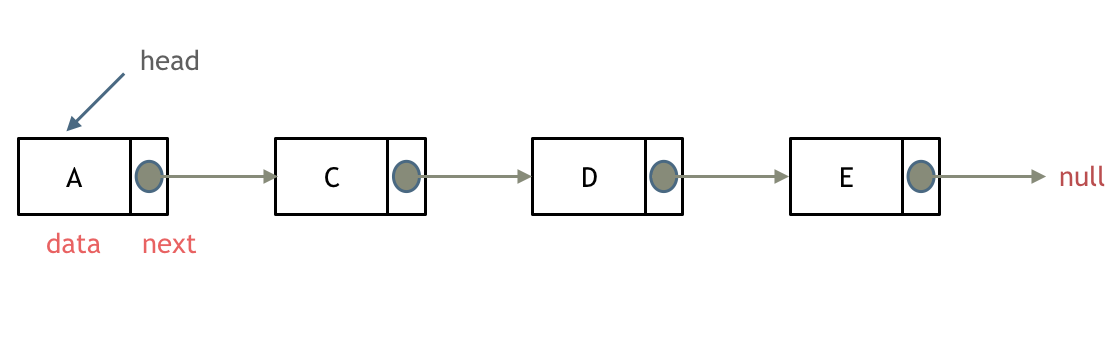
## 链表的类型
@@ -31,7 +31,7 @@
双链表 既可以向前查询也可以向后查询。
如图所示:
-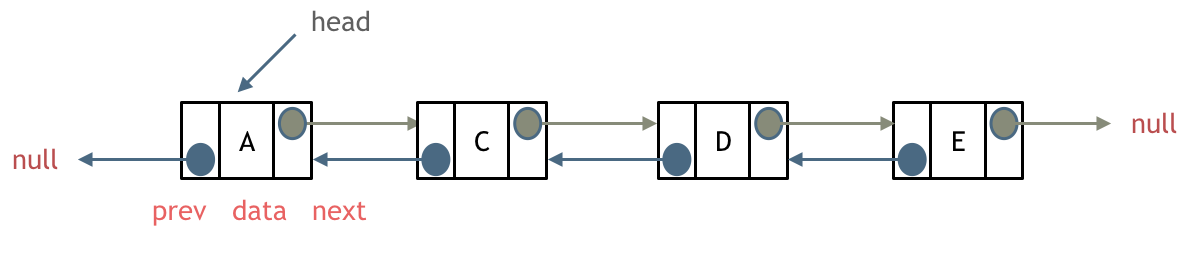
+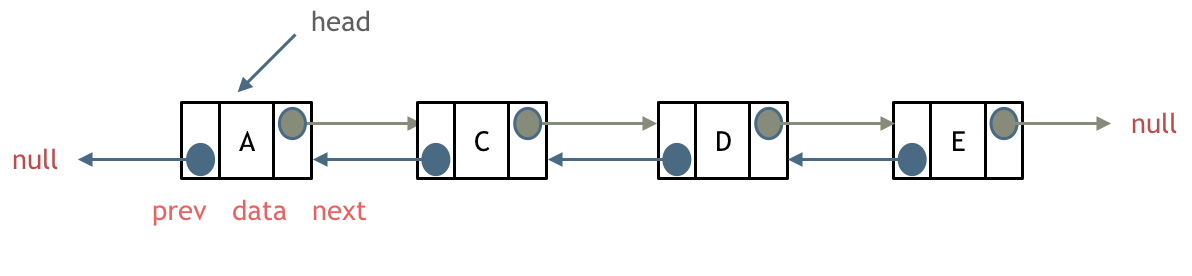
### 循环链表
@@ -39,7 +39,7 @@
循环链表可以用来解决约瑟夫环问题。
-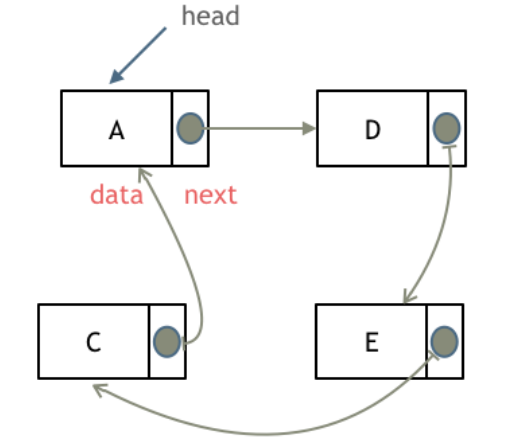
+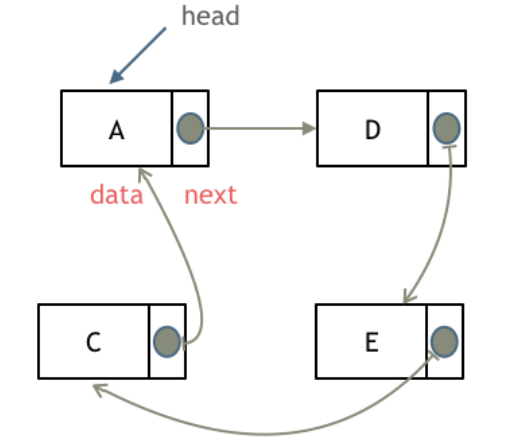
## 链表的存储方式
@@ -54,7 +54,7 @@
如图所示:
-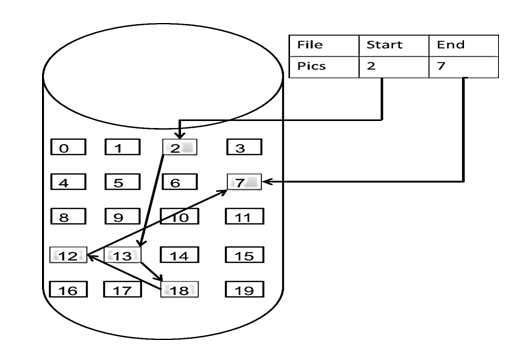
+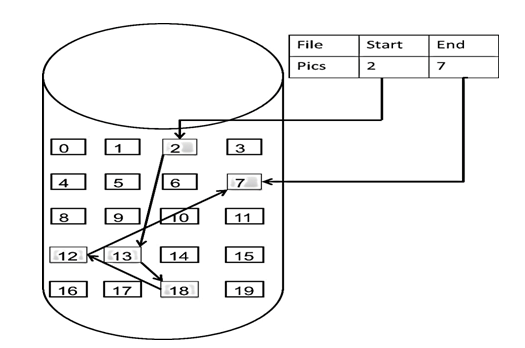
这个链表起始节点为2, 终止节点为7, 各个节点分布在内存的不同地址空间上,通过指针串联在一起。
@@ -104,7 +104,7 @@ head->val = 5;
删除D节点,如图所示:
-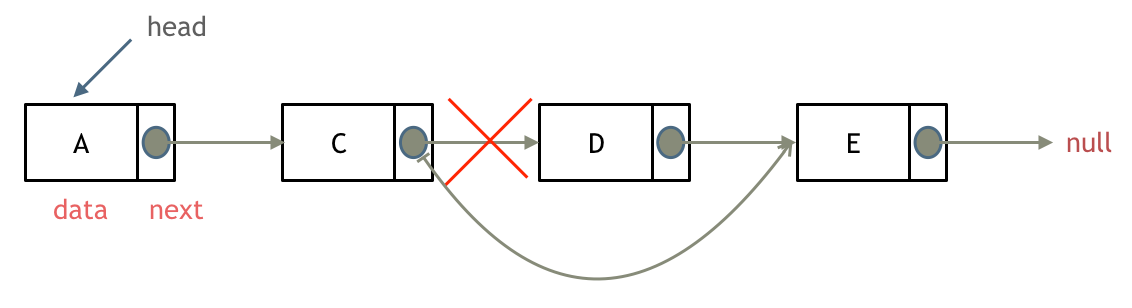
+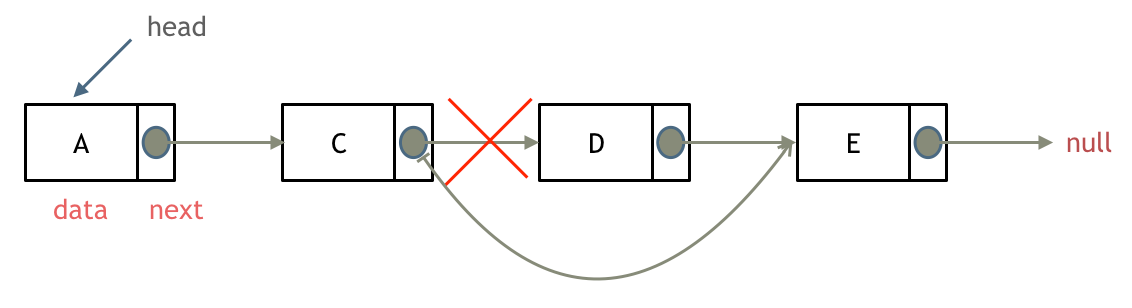
只要将C节点的next指针 指向E节点就可以了。
@@ -118,7 +118,7 @@ head->val = 5;
如图所示:
-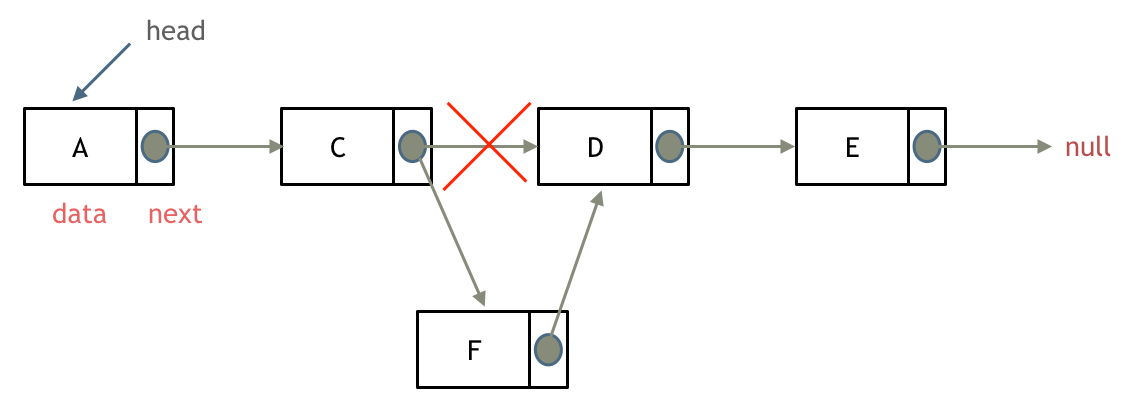
+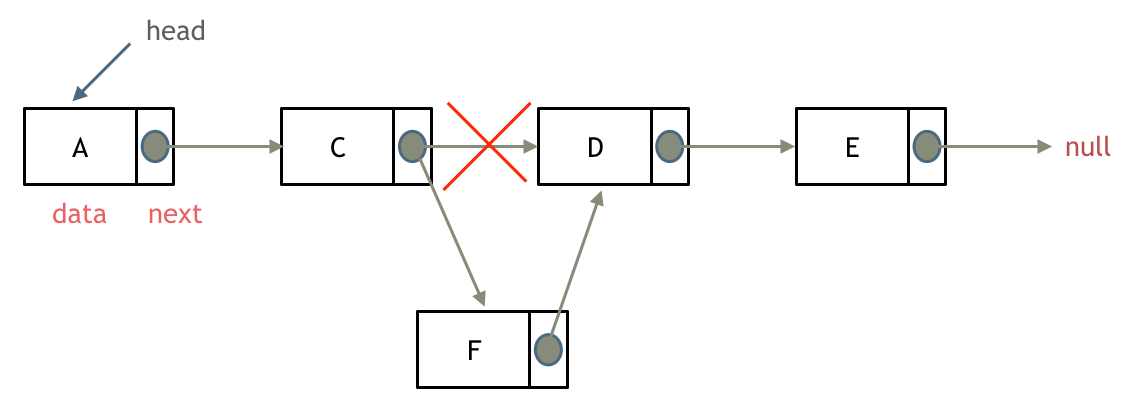
可以看出链表的增添和删除都是O(1)操作,也不会影响到其他节点。
@@ -128,7 +128,7 @@ head->val = 5;
再把链表的特性和数组的特性进行一个对比,如图所示:
-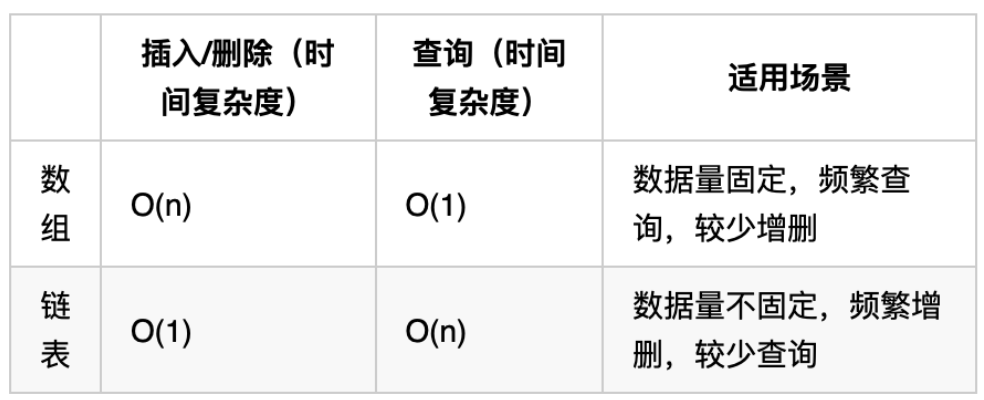
+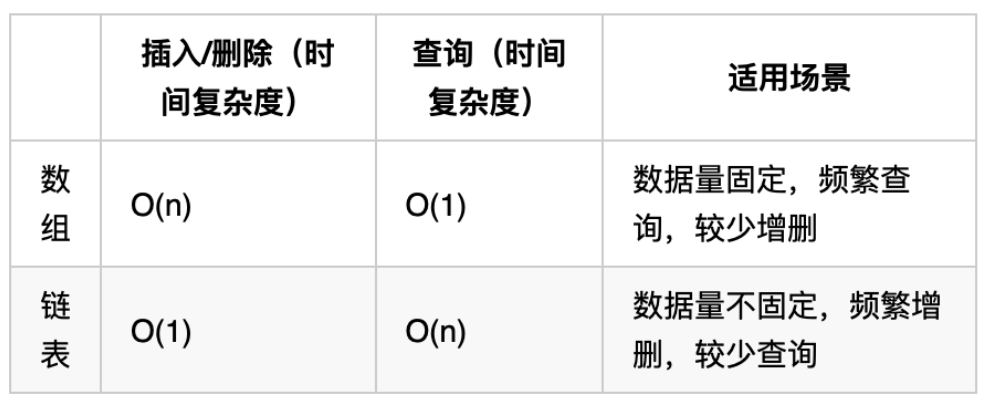
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
diff --git a/problems/面试题02.07.链表相交.md b/problems/面试题02.07.链表相交.md
index f8d9039a..0207b71e 100644
--- a/problems/面试题02.07.链表相交.md
+++ b/problems/面试题02.07.链表相交.md
@@ -13,7 +13,7 @@
图示两个链表在节点 c1 开始相交:
-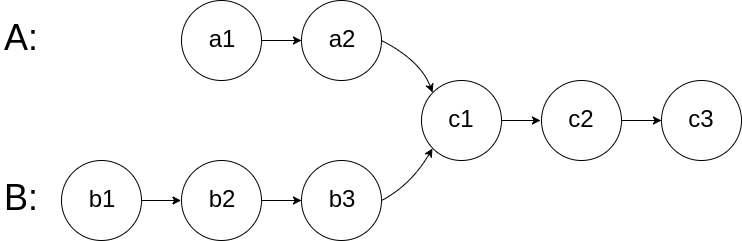
+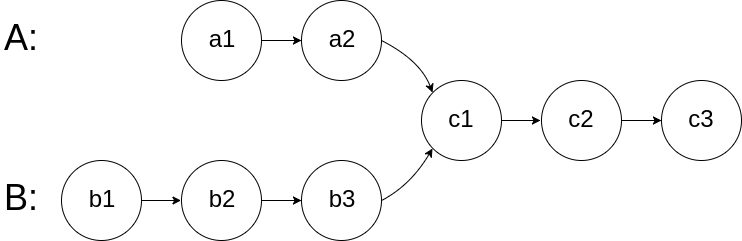
题目数据 保证 整个链式结构中不存在环。
@@ -21,15 +21,15 @@
示例 1:
-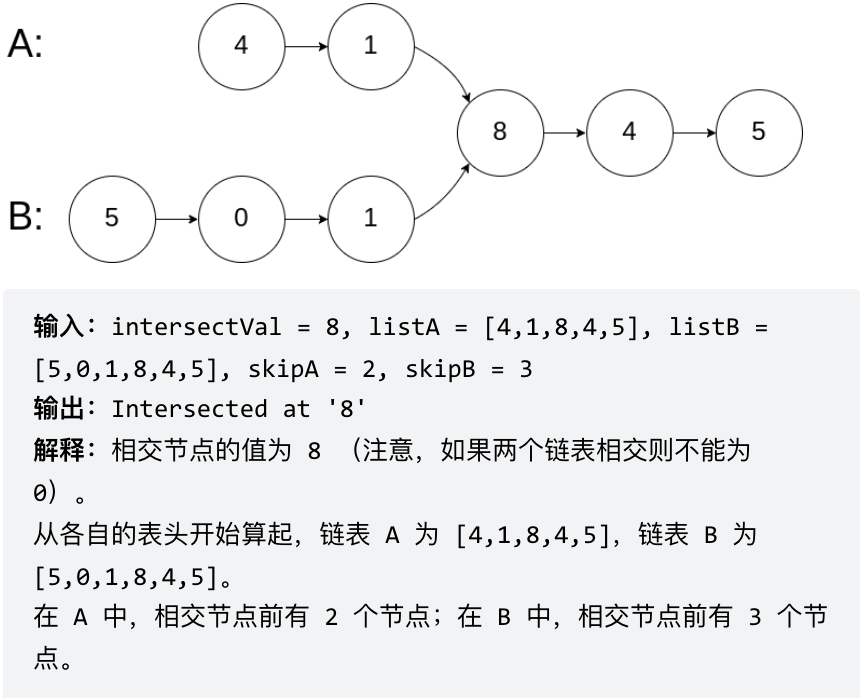
+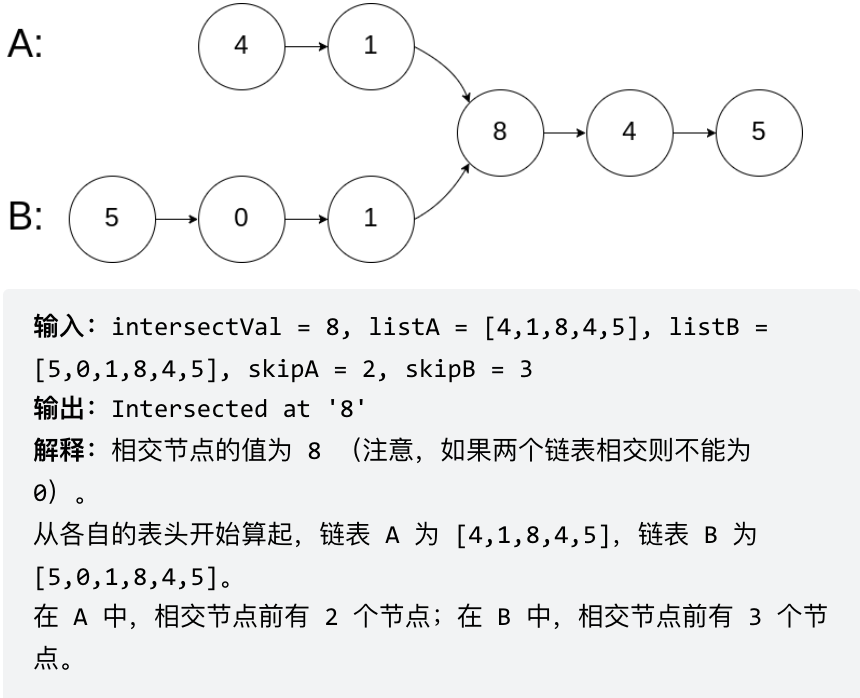
示例 2:
-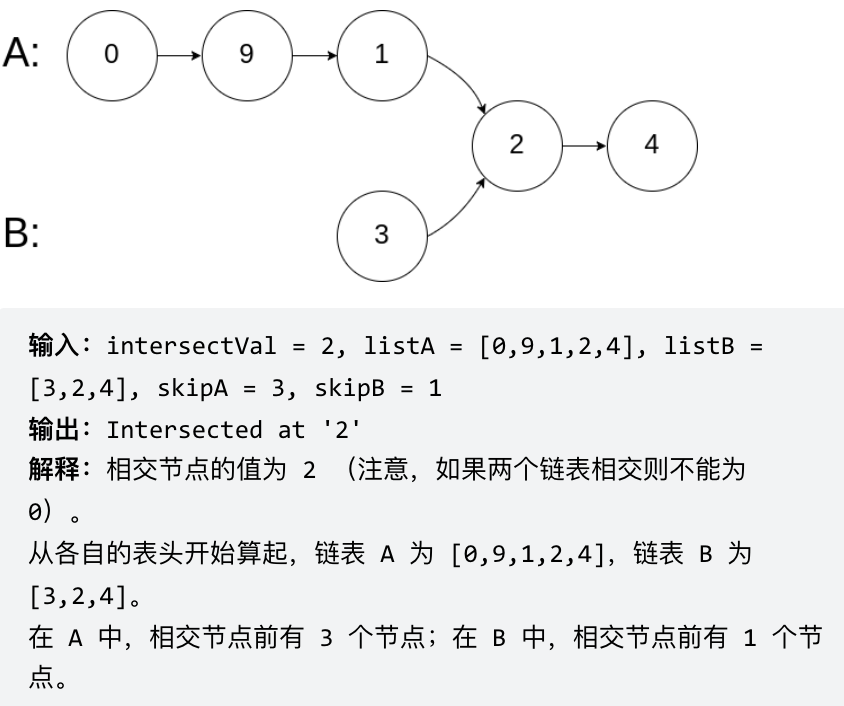
+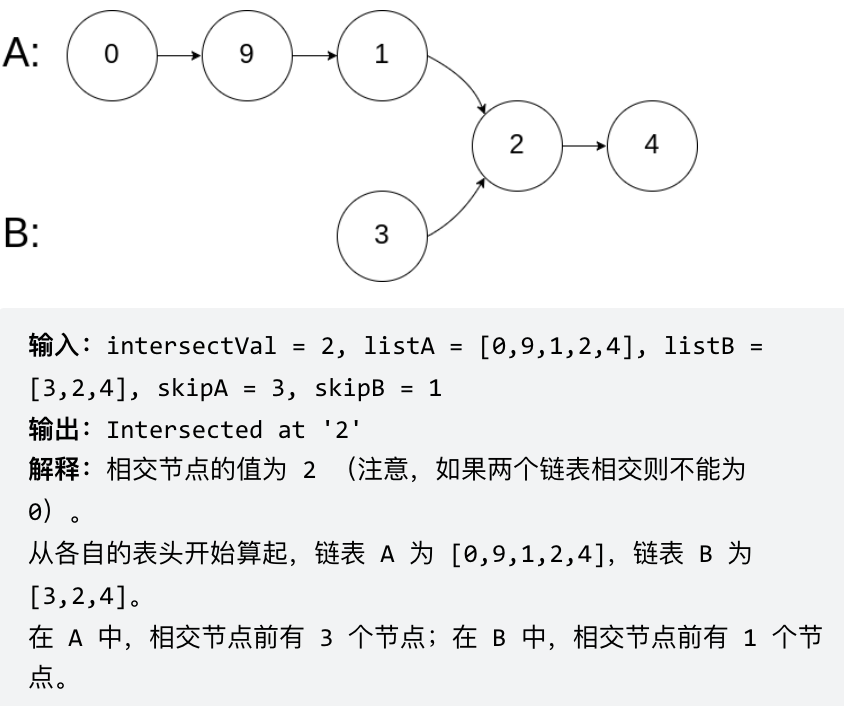
示例 3:
-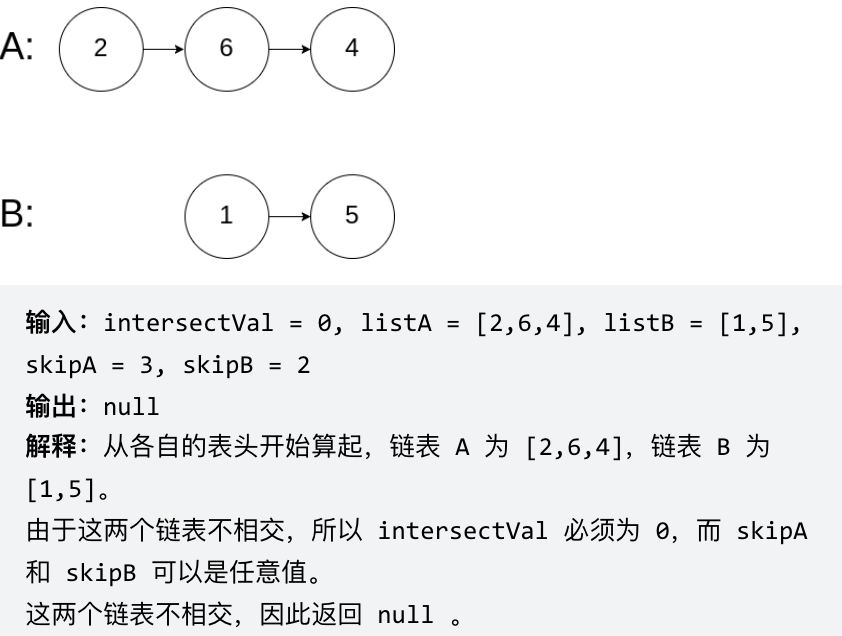
+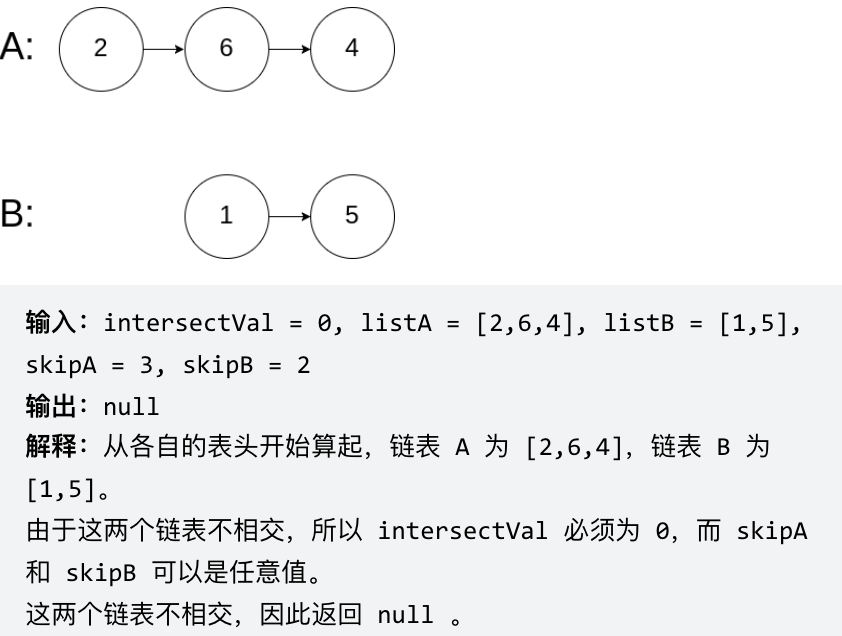
## 算法公开课
diff --git a/problems/链表总结篇.md b/problems/链表总结篇.md
index e29ba268..99bb2abc 100644
--- a/problems/链表总结篇.md
+++ b/problems/链表总结篇.md
@@ -75,7 +75,7 @@
## 总结
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画,总结的非常好,分享给大家。
diff --git a/problems/链表理论基础.md b/problems/链表理论基础.md
index 3637d05f..5305c9a9 100644
--- a/problems/链表理论基础.md
+++ b/problems/链表理论基础.md
@@ -12,7 +12,7 @@
链表的入口节点称为链表的头结点也就是head。
如图所示:
-
+
## 链表的类型
@@ -31,7 +31,7 @@
双链表 既可以向前查询也可以向后查询。
如图所示:
-
+
### 循环链表
@@ -39,7 +39,7 @@
循环链表可以用来解决约瑟夫环问题。
-
+
## 链表的存储方式
@@ -54,7 +54,7 @@
如图所示:
-
+
这个链表起始节点为2, 终止节点为7, 各个节点分布在内存的不同地址空间上,通过指针串联在一起。
@@ -104,7 +104,7 @@ head->val = 5;
删除D节点,如图所示:
-
+
只要将C节点的next指针 指向E节点就可以了。
@@ -118,7 +118,7 @@ head->val = 5;
如图所示:
-
+
可以看出链表的增添和删除都是O(1)操作,也不会影响到其他节点。
@@ -128,7 +128,7 @@ head->val = 5;
再把链表的特性和数组的特性进行一个对比,如图所示:
-
+
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
diff --git a/problems/面试题02.07.链表相交.md b/problems/面试题02.07.链表相交.md
index f8d9039a..0207b71e 100644
--- a/problems/面试题02.07.链表相交.md
+++ b/problems/面试题02.07.链表相交.md
@@ -13,7 +13,7 @@
图示两个链表在节点 c1 开始相交:
-
+
题目数据 保证 整个链式结构中不存在环。
@@ -21,15 +21,15 @@
示例 1:
-
+
示例 2:
-
+
示例 3:
-
+

 +
+ 1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
@@ -222,7 +222,7 @@
题目分类大纲如下:
-
1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
@@ -222,7 +222,7 @@
题目分类大纲如下:
- +
+ 1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
2. [回溯算法:77.组合](./problems/0077.组合.md)
@@ -252,7 +252,7 @@
题目分类大纲如下:
-
1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
2. [回溯算法:77.组合](./problems/0077.组合.md)
@@ -252,7 +252,7 @@
题目分类大纲如下:
- +
+ 1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
@@ -503,5 +503,5 @@
添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
-
1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
@@ -503,5 +503,5 @@
添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
-

 +
+ 完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
@@ -162,10 +162,10 @@ public:
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
完全二叉树(一)如图:
-
+
完全二叉树(二)如图:
-
+
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
@@ -173,15 +173,15 @@ public:
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
-
+
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
-
+
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
-
+
如果这么想,大家就是对 完全二叉树理解有误区了,**以上这棵二叉树,它根本就不是一个完全二叉树**!
diff --git a/problems/0226.翻转二叉树.md b/problems/0226.翻转二叉树.md
index 0980e600..248a28a4 100644
--- a/problems/0226.翻转二叉树.md
+++ b/problems/0226.翻转二叉树.md
@@ -10,7 +10,7 @@
翻转一棵二叉树。
-
+
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,全当一个乐子哈)
@@ -35,7 +35,7 @@
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
-
+
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
diff --git a/problems/0235.二叉搜索树的最近公共祖先.md b/problems/0235.二叉搜索树的最近公共祖先.md
index c5eb603a..98cc5b7d 100644
--- a/problems/0235.二叉搜索树的最近公共祖先.md
+++ b/problems/0235.二叉搜索树的最近公共祖先.md
@@ -14,7 +14,7 @@
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
-
+
示例 1:
@@ -52,7 +52,7 @@
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
-
+
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
@@ -64,7 +64,7 @@
如图所示:p为节点6,q为节点9
-
+
可以看出直接按照指定的方向,就可以找到节点8,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
diff --git a/problems/0236.二叉树的最近公共祖先.md b/problems/0236.二叉树的最近公共祖先.md
index f15d1cff..537d6240 100644
--- a/problems/0236.二叉树的最近公共祖先.md
+++ b/problems/0236.二叉树的最近公共祖先.md
@@ -16,7 +16,7 @@
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
-
+
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
@@ -51,7 +51,7 @@
**首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。** 即情况一:
-
+
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
@@ -61,7 +61,7 @@
**但是很多人容易忽略一个情况,就是节点本身p(q),它拥有一个子孙节点q(p)。** 情况二:
-
+
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
@@ -129,7 +129,7 @@ left与right的逻辑处理; // 中
如图:
-
+
就像图中一样直接返回7。
@@ -162,7 +162,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
如图:
-
+
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
@@ -183,7 +183,7 @@ else { // (left == NULL && right == NULL)
那么寻找最小公共祖先,完整流程图如下:
-
+
**从图中,大家可以看到,我们是如何回溯遍历整棵二叉树,将结果返回给头结点的!**
diff --git a/problems/0257.二叉树的所有路径.md b/problems/0257.二叉树的所有路径.md
index 287db209..5d713511 100644
--- a/problems/0257.二叉树的所有路径.md
+++ b/problems/0257.二叉树的所有路径.md
@@ -14,7 +14,7 @@
说明: 叶子节点是指没有子节点的节点。
示例:
-
+
## 算法公开课
@@ -28,7 +28,7 @@
前序遍历以及回溯的过程如图:
-
+
我们先使用递归的方式,来做前序遍历。**要知道递归和回溯就是一家的,本题也需要回溯。**
@@ -315,7 +315,7 @@ public:
其实关键还在于 参数,使用的是 `string path`,这里并没有加上引用`&` ,即本层递归中,path + 该节点数值,但该层递归结束,上一层path的数值并不会受到任何影响。 如图所示:
-
+
节点4 的path,在遍历到节点3,path+3,遍历节点3的递归结束之后,返回节点4(回溯的过程),path并不会把3加上。
diff --git a/problems/0279.完全平方数.md b/problems/0279.完全平方数.md
index c1077bd4..8171a409 100644
--- a/problems/0279.完全平方数.md
+++ b/problems/0279.完全平方数.md
@@ -93,7 +93,7 @@ for (int i = 0; i <= n; i++) { // 遍历背包
已输入n为5例,dp状态图如下:
-
+
dp[0] = 0
dp[1] = min(dp[0] + 1) = 1
diff --git a/problems/0300.最长上升子序列.md b/problems/0300.最长上升子序列.md
index 7d2e4886..de37ed5c 100644
--- a/problems/0300.最长上升子序列.md
+++ b/problems/0300.最长上升子序列.md
@@ -85,7 +85,7 @@ for (int i = 1; i < nums.size(); i++) {
输入:[0,1,0,3,2],dp数组的变化如下:
-
+
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
diff --git a/problems/0309.最佳买卖股票时机含冷冻期.md b/problems/0309.最佳买卖股票时机含冷冻期.md
index 6a819335..599a1f42 100644
--- a/problems/0309.最佳买卖股票时机含冷冻期.md
+++ b/problems/0309.最佳买卖股票时机含冷冻期.md
@@ -47,7 +47,7 @@ dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
* 状态三:今天卖出股票
* 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
-
+
j的状态为:
@@ -136,7 +136,7 @@ dp[i][3] = dp[i - 1][2];
以 [1,2,3,0,2] 为例,dp数组如下:
-
+
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
diff --git a/problems/0322.零钱兑换.md b/problems/0322.零钱兑换.md
index dea77a3d..7f3bc1e4 100644
--- a/problems/0322.零钱兑换.md
+++ b/problems/0322.零钱兑换.md
@@ -104,7 +104,7 @@ dp[0] = 0;
以输入:coins = [1, 2, 5], amount = 5为例
-
+
dp[amount]为最终结果。
diff --git a/problems/0332.重新安排行程.md b/problems/0332.重新安排行程.md
index f1df2522..fcdb6a33 100644
--- a/problems/0332.重新安排行程.md
+++ b/problems/0332.重新安排行程.md
@@ -57,7 +57,7 @@
对于死循环,我来举一个有重复机场的例子:
-
+
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
@@ -111,7 +111,7 @@ void backtracking(参数) {
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
-
+
开始回溯三部曲讲解:
@@ -137,7 +137,7 @@ bool backtracking(int ticketNum, vector
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
@@ -162,10 +162,10 @@ public:
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
完全二叉树(一)如图:
-
+
完全二叉树(二)如图:
-
+
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
@@ -173,15 +173,15 @@ public:
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
-
+
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
-
+
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
-
+
如果这么想,大家就是对 完全二叉树理解有误区了,**以上这棵二叉树,它根本就不是一个完全二叉树**!
diff --git a/problems/0226.翻转二叉树.md b/problems/0226.翻转二叉树.md
index 0980e600..248a28a4 100644
--- a/problems/0226.翻转二叉树.md
+++ b/problems/0226.翻转二叉树.md
@@ -10,7 +10,7 @@
翻转一棵二叉树。
-
+
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,全当一个乐子哈)
@@ -35,7 +35,7 @@
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
-
+
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
diff --git a/problems/0235.二叉搜索树的最近公共祖先.md b/problems/0235.二叉搜索树的最近公共祖先.md
index c5eb603a..98cc5b7d 100644
--- a/problems/0235.二叉搜索树的最近公共祖先.md
+++ b/problems/0235.二叉搜索树的最近公共祖先.md
@@ -14,7 +14,7 @@
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
-
+
示例 1:
@@ -52,7 +52,7 @@
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
-
+
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
@@ -64,7 +64,7 @@
如图所示:p为节点6,q为节点9
-
+
可以看出直接按照指定的方向,就可以找到节点8,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
diff --git a/problems/0236.二叉树的最近公共祖先.md b/problems/0236.二叉树的最近公共祖先.md
index f15d1cff..537d6240 100644
--- a/problems/0236.二叉树的最近公共祖先.md
+++ b/problems/0236.二叉树的最近公共祖先.md
@@ -16,7 +16,7 @@
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
-
+
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
@@ -51,7 +51,7 @@
**首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。** 即情况一:
-
+
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
@@ -61,7 +61,7 @@
**但是很多人容易忽略一个情况,就是节点本身p(q),它拥有一个子孙节点q(p)。** 情况二:
-
+
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
@@ -129,7 +129,7 @@ left与right的逻辑处理; // 中
如图:
-
+
就像图中一样直接返回7。
@@ -162,7 +162,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
如图:
-
+
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
@@ -183,7 +183,7 @@ else { // (left == NULL && right == NULL)
那么寻找最小公共祖先,完整流程图如下:
-
+
**从图中,大家可以看到,我们是如何回溯遍历整棵二叉树,将结果返回给头结点的!**
diff --git a/problems/0257.二叉树的所有路径.md b/problems/0257.二叉树的所有路径.md
index 287db209..5d713511 100644
--- a/problems/0257.二叉树的所有路径.md
+++ b/problems/0257.二叉树的所有路径.md
@@ -14,7 +14,7 @@
说明: 叶子节点是指没有子节点的节点。
示例:
-
+
## 算法公开课
@@ -28,7 +28,7 @@
前序遍历以及回溯的过程如图:
-
+
我们先使用递归的方式,来做前序遍历。**要知道递归和回溯就是一家的,本题也需要回溯。**
@@ -315,7 +315,7 @@ public:
其实关键还在于 参数,使用的是 `string path`,这里并没有加上引用`&` ,即本层递归中,path + 该节点数值,但该层递归结束,上一层path的数值并不会受到任何影响。 如图所示:
-
+
节点4 的path,在遍历到节点3,path+3,遍历节点3的递归结束之后,返回节点4(回溯的过程),path并不会把3加上。
diff --git a/problems/0279.完全平方数.md b/problems/0279.完全平方数.md
index c1077bd4..8171a409 100644
--- a/problems/0279.完全平方数.md
+++ b/problems/0279.完全平方数.md
@@ -93,7 +93,7 @@ for (int i = 0; i <= n; i++) { // 遍历背包
已输入n为5例,dp状态图如下:
-
+
dp[0] = 0
dp[1] = min(dp[0] + 1) = 1
diff --git a/problems/0300.最长上升子序列.md b/problems/0300.最长上升子序列.md
index 7d2e4886..de37ed5c 100644
--- a/problems/0300.最长上升子序列.md
+++ b/problems/0300.最长上升子序列.md
@@ -85,7 +85,7 @@ for (int i = 1; i < nums.size(); i++) {
输入:[0,1,0,3,2],dp数组的变化如下:
-
+
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
diff --git a/problems/0309.最佳买卖股票时机含冷冻期.md b/problems/0309.最佳买卖股票时机含冷冻期.md
index 6a819335..599a1f42 100644
--- a/problems/0309.最佳买卖股票时机含冷冻期.md
+++ b/problems/0309.最佳买卖股票时机含冷冻期.md
@@ -47,7 +47,7 @@ dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
* 状态三:今天卖出股票
* 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
-
+
j的状态为:
@@ -136,7 +136,7 @@ dp[i][3] = dp[i - 1][2];
以 [1,2,3,0,2] 为例,dp数组如下:
-
+
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
diff --git a/problems/0322.零钱兑换.md b/problems/0322.零钱兑换.md
index dea77a3d..7f3bc1e4 100644
--- a/problems/0322.零钱兑换.md
+++ b/problems/0322.零钱兑换.md
@@ -104,7 +104,7 @@ dp[0] = 0;
以输入:coins = [1, 2, 5], amount = 5为例
-
+
dp[amount]为最终结果。
diff --git a/problems/0332.重新安排行程.md b/problems/0332.重新安排行程.md
index f1df2522..fcdb6a33 100644
--- a/problems/0332.重新安排行程.md
+++ b/problems/0332.重新安排行程.md
@@ -57,7 +57,7 @@
对于死循环,我来举一个有重复机场的例子:
-
+
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
@@ -111,7 +111,7 @@ void backtracking(参数) {
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
-
+
开始回溯三部曲讲解:
@@ -137,7 +137,7 @@ bool backtracking(int ticketNum, vector +
+ 现在有一个有向图,有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图:
-
现在有一个有向图,有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图:
- +
+ 输入一个有向图,该图由一个有着 n 个节点(节点编号 从 1 到 n),n 条边,请返回一条可以删除的边,使得删除该条边之后该有向图可以被当作一颗有向树。
@@ -42,7 +42,7 @@
提示信息
-
输入一个有向图,该图由一个有着 n 个节点(节点编号 从 1 到 n),n 条边,请返回一条可以删除的边,使得删除该条边之后该有向图可以被当作一颗有向树。
@@ -42,7 +42,7 @@
提示信息
- +
+ 在删除 2 3 后有向图可以变为一棵合法的有向树,所以输出 2 3
@@ -64,13 +64,13 @@
如图:
-
+
找到了节点3 的入度为2,删 1 -> 3 或者 2 -> 3 。选择删顺序靠后便可。
但 入度为2 还有一种情况,情况二,只能删特定的一条边,如图:
-
+
节点3 的入度为 2,但在删除边的时候,只能删 这条边(节点1 -> 节点3),如果删这条边(节点4 -> 节点3),那么删后本图也不是有向树了(因为找不到根节点)。
@@ -81,7 +81,7 @@
如图:
-
+
对于情况三,删掉构成环的边就可以了。
diff --git a/problems/kamacoder/0110.字符串接龙.md b/problems/kamacoder/0110.字符串接龙.md
index 8bae6280..af343690 100644
--- a/problems/kamacoder/0110.字符串接龙.md
+++ b/problems/kamacoder/0110.字符串接龙.md
@@ -57,7 +57,7 @@ yhn
2 <= N <= 500
在删除 2 3 后有向图可以变为一棵合法的有向树,所以输出 2 3
@@ -64,13 +64,13 @@
如图:
-
+
找到了节点3 的入度为2,删 1 -> 3 或者 2 -> 3 。选择删顺序靠后便可。
但 入度为2 还有一种情况,情况二,只能删特定的一条边,如图:
-
+
节点3 的入度为 2,但在删除边的时候,只能删 这条边(节点1 -> 节点3),如果删这条边(节点4 -> 节点3),那么删后本图也不是有向树了(因为找不到根节点)。
@@ -81,7 +81,7 @@
如图:
-
+
对于情况三,删掉构成环的边就可以了。
diff --git a/problems/kamacoder/0110.字符串接龙.md b/problems/kamacoder/0110.字符串接龙.md
index 8bae6280..af343690 100644
--- a/problems/kamacoder/0110.字符串接龙.md
+++ b/problems/kamacoder/0110.字符串接龙.md
@@ -57,7 +57,7 @@ yhn
2 <= N <= 500
 +
+ 


















































































 +
+ 说到二叉树,大家对于二叉树其实都很熟悉了,本文呢我也不想教科书式的把二叉树的基础内容再啰嗦一遍,所以以下我讲的都是一些比较重点的内容。
@@ -31,7 +31,7 @@
如图所示:
-
说到二叉树,大家对于二叉树其实都很熟悉了,本文呢我也不想教科书式的把二叉树的基础内容再啰嗦一遍,所以以下我讲的都是一些比较重点的内容。
@@ -31,7 +31,7 @@
如图所示:
- +
+ 这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
@@ -46,7 +46,7 @@
我来举一个典型的例子如题:
-
这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。
@@ -46,7 +46,7 @@
我来举一个典型的例子如题:
- +
+ 相信不少同学最后一个二叉树是不是完全二叉树都中招了。
@@ -63,7 +63,7 @@
下面这两棵树都是搜索树
-
相信不少同学最后一个二叉树是不是完全二叉树都中招了。
@@ -63,7 +63,7 @@
下面这两棵树都是搜索树
- +
+ ### 平衡二叉搜索树
@@ -72,7 +72,7 @@
如图:
-
### 平衡二叉搜索树
@@ -72,7 +72,7 @@
如图:
- +
+ 最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
@@ -91,13 +91,13 @@
链式存储如图:
-
最后一棵 不是平衡二叉树,因为它的左右两个子树的高度差的绝对值超过了1。
@@ -91,13 +91,13 @@
链式存储如图:
- +
+ 链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
-
链式存储是大家很熟悉的一种方式,那么我们来看看如何顺序存储呢?
其实就是用数组来存储二叉树,顺序存储的方式如图:
- +
+ 用数组来存储二叉树如何遍历的呢?
@@ -144,7 +144,7 @@
大家可以对着如下图,看看自己理解的前后中序有没有问题。
-
用数组来存储二叉树如何遍历的呢?
@@ -144,7 +144,7 @@
大家可以对着如下图,看看自己理解的前后中序有没有问题。
- +
+ 最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
diff --git a/problems/二叉树的迭代遍历.md b/problems/二叉树的迭代遍历.md
index 289c651b..e011612c 100644
--- a/problems/二叉树的迭代遍历.md
+++ b/problems/二叉树的迭代遍历.md
@@ -117,7 +117,7 @@ public:
再来看后序遍历,先序遍历是中左右,后序遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了,如下图:
-
+
**所以后序遍历只需要前序遍历的代码稍作修改就可以了,代码如下:**
diff --git a/problems/前序/ACM模式.md b/problems/前序/ACM模式.md
index 313264fb..f1ff3a5f 100644
--- a/problems/前序/ACM模式.md
+++ b/problems/前序/ACM模式.md
@@ -5,15 +5,15 @@
平时大家在力扣上刷题,就是 核心代码模式,即给你一个函数,直接写函数实现,例如这样:
-
+
而ACM模式,是程序头文件,main函数,数据的输入输出都要自己处理,例如这样:
-
+
大家可以发现 右边代码框什么都没有,程序从头到尾都需要自己实现,本题如果写完代码是这样的: (细心的录友可以发现和力扣上刷题是不一样的)
-
+
**如果大家从一开始学习算法就一直在力扣上的话,突然切到ACM模式会非常不适应**。
@@ -21,15 +21,15 @@
知识星球里也有很多录友,因为不熟悉ACM模式在面试的过程中吃了不少亏。
-
最后再说一说二叉树中深度优先和广度优先遍历实现方式,我们做二叉树相关题目,经常会使用递归的方式来实现深度优先遍历,也就是实现前中后序遍历,使用递归是比较方便的。
diff --git a/problems/二叉树的迭代遍历.md b/problems/二叉树的迭代遍历.md
index 289c651b..e011612c 100644
--- a/problems/二叉树的迭代遍历.md
+++ b/problems/二叉树的迭代遍历.md
@@ -117,7 +117,7 @@ public:
再来看后序遍历,先序遍历是中左右,后序遍历是左右中,那么我们只需要调整一下先序遍历的代码顺序,就变成中右左的遍历顺序,然后在反转result数组,输出的结果顺序就是左右中了,如下图:
-
+
**所以后序遍历只需要前序遍历的代码稍作修改就可以了,代码如下:**
diff --git a/problems/前序/ACM模式.md b/problems/前序/ACM模式.md
index 313264fb..f1ff3a5f 100644
--- a/problems/前序/ACM模式.md
+++ b/problems/前序/ACM模式.md
@@ -5,15 +5,15 @@
平时大家在力扣上刷题,就是 核心代码模式,即给你一个函数,直接写函数实现,例如这样:
-
+
而ACM模式,是程序头文件,main函数,数据的输入输出都要自己处理,例如这样:
-
+
大家可以发现 右边代码框什么都没有,程序从头到尾都需要自己实现,本题如果写完代码是这样的: (细心的录友可以发现和力扣上刷题是不一样的)
-
+
**如果大家从一开始学习算法就一直在力扣上的话,突然切到ACM模式会非常不适应**。
@@ -21,15 +21,15 @@
知识星球里也有很多录友,因为不熟悉ACM模式在面试的过程中吃了不少亏。
-












 +
+ ## 算法公开课
@@ -114,7 +114,7 @@ if (终止条件) {
如图:
-
+
注意图中,我特意举例集合大小和孩子的数量是相等的!
diff --git a/problems/数组总结篇.md b/problems/数组总结篇.md
index e45165a6..e29a7bd3 100644
--- a/problems/数组总结篇.md
+++ b/problems/数组总结篇.md
@@ -125,7 +125,7 @@
## 总结
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画,总结的非常好,分享给大家。
diff --git a/problems/数组理论基础.md b/problems/数组理论基础.md
index c1ac287d..4000208a 100644
--- a/problems/数组理论基础.md
+++ b/problems/数组理论基础.md
@@ -40,7 +40,7 @@
那么二维数组直接上图,大家应该就知道怎么回事了
-
+
**那么二维数组在内存的空间地址是连续的么?**
@@ -80,7 +80,7 @@ int main() {
如图:
-
+
**所以可以看出在C++中二维数组在地址空间上是连续的**。
@@ -111,7 +111,7 @@ public static void test_arr() {
所以Java的二维数组可能是如下排列的方式:
-
+
这里面试中数组相关的理论知识就介绍完了。
diff --git a/problems/栈与队列理论基础.md b/problems/栈与队列理论基础.md
index bff0ec63..912bfe1d 100644
--- a/problems/栈与队列理论基础.md
+++ b/problems/栈与队列理论基础.md
@@ -11,7 +11,7 @@
如图所示:
-
+
那么我这里再列出四个关于栈的问题,大家可以思考一下。以下是以C++为例,使用其他编程语言的同学也对应思考一下,自己使用的编程语言里栈和队列是什么样的。
@@ -46,7 +46,7 @@ C++标准库是有多个版本的,要知道我们使用的STL是哪个版本
来说一说栈,栈先进后出,如图所示:
-
+
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
@@ -59,7 +59,7 @@ C++标准库是有多个版本的,要知道我们使用的STL是哪个版本
从下图中可以看出,栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
-
+
**我们常用的SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。**
diff --git a/problems/根据身高重建队列(vector原理讲解).md b/problems/根据身高重建队列(vector原理讲解).md
index a2350835..162ee273 100644
--- a/problems/根据身高重建队列(vector原理讲解).md
+++ b/problems/根据身高重建队列(vector原理讲解).md
@@ -35,7 +35,7 @@ public:
```
耗时如下:
-
+
其直观上来看数组的insert操作是O(n)的,整体代码的时间复杂度是O(n^2)。
@@ -68,7 +68,7 @@ public:
耗时如下:
-
+
大家都知道对于普通数组,一旦定义了大小就不能改变,例如int a[10];,这个数组a至多只能放10个元素,改不了的。
@@ -95,7 +95,7 @@ for (int i = 0; i < vec.size(); i++) {
就是重新申请一个二倍于原数组大小的数组,然后把数据都拷贝过去,并释放原数组内存。(对,就是这么原始粗暴的方法!)
举一个例子,如图:
-
+
原vector中的size和capicity相同都是3,初始化为1 2 3,此时要push_back一个元素4。
@@ -138,7 +138,7 @@ public:
耗时如下:
-
+
这份代码就是不让vector动态扩容,全程我们自己模拟insert的操作,大家也可以直观的看出是一个O(n^2)的方法了。
diff --git a/problems/背包总结篇.md b/problems/背包总结篇.md
index 3c587b6d..9ce3fdda 100644
--- a/problems/背包总结篇.md
+++ b/problems/背包总结篇.md
@@ -11,7 +11,7 @@
关于这几种常见的背包,其关系如下:
-
+
通过这个图,可以很清晰分清这几种常见背包之间的关系。
@@ -93,7 +93,7 @@
背包问题总结:
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画结的非常好,分享给大家。
diff --git a/problems/背包理论基础01背包-1.md b/problems/背包理论基础01背包-1.md
index c2598ec9..79751c89 100644
--- a/problems/背包理论基础01背包-1.md
+++ b/problems/背包理论基础01背包-1.md
@@ -21,7 +21,7 @@
如果这几种背包,分不清,我这里画了一个图,如下:
-
+
除此以外其他类型的背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
@@ -77,7 +77,7 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
如图,二维数组为 dp[i][j]。
-
+
那么这里 i 、j、dp[i][j] 分别表示什么呢?
@@ -91,7 +91,7 @@ i 来表示物品、j表示背包容量。
我们先看把物品0 放入背包的情况:
-
+
背包容量为0,放不下物品0,此时背包里的价值为0。
@@ -103,7 +103,7 @@ i 来表示物品、j表示背包容量。
再看把物品1 放入背包:
-
+
背包容量为 0,放不下物品0 或者物品1,此时背包里的价值为0。
@@ -150,7 +150,7 @@ i 来表示物品、j表示背包容量。
推导方向如图:
-
+
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 的容量(就是物品1的重量)为3,此时背包剩下容量为1。
@@ -158,7 +158,7 @@ i 来表示物品、j表示背包容量。
所以 放物品1 的情况 = dp[0][1] + 物品1 的价值,推导方向如图:
-
+
两种情况,分别是放物品1 和 不放物品1,我们要取最大值(毕竟求的是最大价值)
@@ -178,7 +178,7 @@ i 来表示物品、j表示背包容量。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
-
+
在看其他情况。
@@ -205,7 +205,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
此时dp数组初始化情况如图所示:
-
+
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
@@ -217,7 +217,7 @@ dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化
如图:
-
+
最后初始化代码如下:
@@ -236,7 +236,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
在如下图中,可以看出,有两个遍历的维度:物品与背包重量
-
+
那么问题来了,**先遍历 物品还是先遍历背包重量呢?**
@@ -277,11 +277,11 @@ for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
-
+
再来看看先遍历背包,再遍历物品呢,如图:
-
+
**大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!**
@@ -293,7 +293,7 @@ dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括
来看一下对应的dp数组的数值,如图:
-
+
最终结果就是dp[2][4]。
diff --git a/problems/背包理论基础01背包-2.md b/problems/背包理论基础01背包-2.md
index 6caa4f63..b6a68960 100644
--- a/problems/背包理论基础01背包-2.md
+++ b/problems/背包理论基础01背包-2.md
@@ -163,7 +163,7 @@ dp[1] = dp[1 - weight[0]] + value[0] = 15
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
-
+
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problempage.php?pid=1046)去练习,题意是一样的,代码如下:
diff --git a/problems/背包问题完全背包一维.md b/problems/背包问题完全背包一维.md
index 5a23b67c..be7a5d54 100644
--- a/problems/背包问题完全背包一维.md
+++ b/problems/背包问题完全背包一维.md
@@ -54,11 +54,11 @@ for (int i = 1; i < n; i++) { // 遍历物品
遍历物品在外层循环,遍历背包容量在内层循环,状态如图:
-
+
遍历背包容量在外层循环,遍历物品在内层循环,状态如图:
-
+
看了这两个图,大家就会理解,完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值(这个值就是下标j之前所对应的dp[j])。
diff --git a/problems/背包问题理论基础完全背包.md b/problems/背包问题理论基础完全背包.md
index d76ff196..cb8db1e0 100644
--- a/problems/背包问题理论基础完全背包.md
+++ b/problems/背包问题理论基础完全背包.md
@@ -66,7 +66,7 @@
推导方向如图:
-
+
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 的容量(就是物品1的重量)为3,此时背包剩下容量为1。
@@ -78,7 +78,7 @@
所以 放物品1 的情况 = dp[1][1] + 物品1 的价值,推导方向如图:
-
+
(**注意上图和 [01背包理论基础(二维数组)](https://programmercarl.com/背包理论基础01背包-1.html) 中的区别**,对于理解完全背包很重要)
@@ -103,7 +103,7 @@
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
-
+
在看其他情况。
@@ -132,7 +132,7 @@ for (int j = weight[0]; j <= bagWeight; j++)
此时dp数组初始化情况如图所示:
-
+
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
@@ -185,7 +185,7 @@ for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
以本篇举例数据为例,填满了dp二维数组如图:
-
+
因为 物品0 的性价比是最高的,而且 在完全背包中,每一类物品都有无限个,所以有无限个物品0,既然物品0 性价比最高,当然是优先放物品0。
diff --git a/problems/贪心算法总结篇.md b/problems/贪心算法总结篇.md
index 7d4c57e8..4c67fb40 100644
--- a/problems/贪心算法总结篇.md
+++ b/problems/贪心算法总结篇.md
@@ -128,7 +128,7 @@ Carl个人认为:如果找出局部最优并可以推出全局最优,就是
贪心专题汇聚为一张图:
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412)所画,总结的非常好,分享给大家。
diff --git a/problems/贪心算法理论基础.md b/problems/贪心算法理论基础.md
index 14f39729..2d0af879 100644
--- a/problems/贪心算法理论基础.md
+++ b/problems/贪心算法理论基础.md
@@ -7,7 +7,7 @@
题目分类大纲如下:
-
## 算法公开课
@@ -114,7 +114,7 @@ if (终止条件) {
如图:
-
+
注意图中,我特意举例集合大小和孩子的数量是相等的!
diff --git a/problems/数组总结篇.md b/problems/数组总结篇.md
index e45165a6..e29a7bd3 100644
--- a/problems/数组总结篇.md
+++ b/problems/数组总结篇.md
@@ -125,7 +125,7 @@
## 总结
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画,总结的非常好,分享给大家。
diff --git a/problems/数组理论基础.md b/problems/数组理论基础.md
index c1ac287d..4000208a 100644
--- a/problems/数组理论基础.md
+++ b/problems/数组理论基础.md
@@ -40,7 +40,7 @@
那么二维数组直接上图,大家应该就知道怎么回事了
-
+
**那么二维数组在内存的空间地址是连续的么?**
@@ -80,7 +80,7 @@ int main() {
如图:
-
+
**所以可以看出在C++中二维数组在地址空间上是连续的**。
@@ -111,7 +111,7 @@ public static void test_arr() {
所以Java的二维数组可能是如下排列的方式:
-
+
这里面试中数组相关的理论知识就介绍完了。
diff --git a/problems/栈与队列理论基础.md b/problems/栈与队列理论基础.md
index bff0ec63..912bfe1d 100644
--- a/problems/栈与队列理论基础.md
+++ b/problems/栈与队列理论基础.md
@@ -11,7 +11,7 @@
如图所示:
-
+
那么我这里再列出四个关于栈的问题,大家可以思考一下。以下是以C++为例,使用其他编程语言的同学也对应思考一下,自己使用的编程语言里栈和队列是什么样的。
@@ -46,7 +46,7 @@ C++标准库是有多个版本的,要知道我们使用的STL是哪个版本
来说一说栈,栈先进后出,如图所示:
-
+
栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。
@@ -59,7 +59,7 @@ C++标准库是有多个版本的,要知道我们使用的STL是哪个版本
从下图中可以看出,栈的内部结构,栈的底层实现可以是vector,deque,list 都是可以的, 主要就是数组和链表的底层实现。
-
+
**我们常用的SGI STL,如果没有指定底层实现的话,默认是以deque为缺省情况下栈的底层结构。**
diff --git a/problems/根据身高重建队列(vector原理讲解).md b/problems/根据身高重建队列(vector原理讲解).md
index a2350835..162ee273 100644
--- a/problems/根据身高重建队列(vector原理讲解).md
+++ b/problems/根据身高重建队列(vector原理讲解).md
@@ -35,7 +35,7 @@ public:
```
耗时如下:
-
+
其直观上来看数组的insert操作是O(n)的,整体代码的时间复杂度是O(n^2)。
@@ -68,7 +68,7 @@ public:
耗时如下:
-
+
大家都知道对于普通数组,一旦定义了大小就不能改变,例如int a[10];,这个数组a至多只能放10个元素,改不了的。
@@ -95,7 +95,7 @@ for (int i = 0; i < vec.size(); i++) {
就是重新申请一个二倍于原数组大小的数组,然后把数据都拷贝过去,并释放原数组内存。(对,就是这么原始粗暴的方法!)
举一个例子,如图:
-
+
原vector中的size和capicity相同都是3,初始化为1 2 3,此时要push_back一个元素4。
@@ -138,7 +138,7 @@ public:
耗时如下:
-
+
这份代码就是不让vector动态扩容,全程我们自己模拟insert的操作,大家也可以直观的看出是一个O(n^2)的方法了。
diff --git a/problems/背包总结篇.md b/problems/背包总结篇.md
index 3c587b6d..9ce3fdda 100644
--- a/problems/背包总结篇.md
+++ b/problems/背包总结篇.md
@@ -11,7 +11,7 @@
关于这几种常见的背包,其关系如下:
-
+
通过这个图,可以很清晰分清这几种常见背包之间的关系。
@@ -93,7 +93,7 @@
背包问题总结:
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画结的非常好,分享给大家。
diff --git a/problems/背包理论基础01背包-1.md b/problems/背包理论基础01背包-1.md
index c2598ec9..79751c89 100644
--- a/problems/背包理论基础01背包-1.md
+++ b/problems/背包理论基础01背包-1.md
@@ -21,7 +21,7 @@
如果这几种背包,分不清,我这里画了一个图,如下:
-
+
除此以外其他类型的背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
@@ -77,7 +77,7 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
如图,二维数组为 dp[i][j]。
-
+
那么这里 i 、j、dp[i][j] 分别表示什么呢?
@@ -91,7 +91,7 @@ i 来表示物品、j表示背包容量。
我们先看把物品0 放入背包的情况:
-
+
背包容量为0,放不下物品0,此时背包里的价值为0。
@@ -103,7 +103,7 @@ i 来表示物品、j表示背包容量。
再看把物品1 放入背包:
-
+
背包容量为 0,放不下物品0 或者物品1,此时背包里的价值为0。
@@ -150,7 +150,7 @@ i 来表示物品、j表示背包容量。
推导方向如图:
-
+
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 的容量(就是物品1的重量)为3,此时背包剩下容量为1。
@@ -158,7 +158,7 @@ i 来表示物品、j表示背包容量。
所以 放物品1 的情况 = dp[0][1] + 物品1 的价值,推导方向如图:
-
+
两种情况,分别是放物品1 和 不放物品1,我们要取最大值(毕竟求的是最大价值)
@@ -178,7 +178,7 @@ i 来表示物品、j表示背包容量。
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
-
+
在看其他情况。
@@ -205,7 +205,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
此时dp数组初始化情况如图所示:
-
+
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
@@ -217,7 +217,7 @@ dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化
如图:
-
+
最后初始化代码如下:
@@ -236,7 +236,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
在如下图中,可以看出,有两个遍历的维度:物品与背包重量
-
+
那么问题来了,**先遍历 物品还是先遍历背包重量呢?**
@@ -277,11 +277,11 @@ for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
-
+
再来看看先遍历背包,再遍历物品呢,如图:
-
+
**大家可以看出,虽然两个for循环遍历的次序不同,但是dp[i][j]所需要的数据就是左上角,根本不影响dp[i][j]公式的推导!**
@@ -293,7 +293,7 @@ dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括
来看一下对应的dp数组的数值,如图:
-
+
最终结果就是dp[2][4]。
diff --git a/problems/背包理论基础01背包-2.md b/problems/背包理论基础01背包-2.md
index 6caa4f63..b6a68960 100644
--- a/problems/背包理论基础01背包-2.md
+++ b/problems/背包理论基础01背包-2.md
@@ -163,7 +163,7 @@ dp[1] = dp[1 - weight[0]] + value[0] = 15
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
-
+
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problempage.php?pid=1046)去练习,题意是一样的,代码如下:
diff --git a/problems/背包问题完全背包一维.md b/problems/背包问题完全背包一维.md
index 5a23b67c..be7a5d54 100644
--- a/problems/背包问题完全背包一维.md
+++ b/problems/背包问题完全背包一维.md
@@ -54,11 +54,11 @@ for (int i = 1; i < n; i++) { // 遍历物品
遍历物品在外层循环,遍历背包容量在内层循环,状态如图:
-
+
遍历背包容量在外层循环,遍历物品在内层循环,状态如图:
-
+
看了这两个图,大家就会理解,完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值(这个值就是下标j之前所对应的dp[j])。
diff --git a/problems/背包问题理论基础完全背包.md b/problems/背包问题理论基础完全背包.md
index d76ff196..cb8db1e0 100644
--- a/problems/背包问题理论基础完全背包.md
+++ b/problems/背包问题理论基础完全背包.md
@@ -66,7 +66,7 @@
推导方向如图:
-
+
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 的容量(就是物品1的重量)为3,此时背包剩下容量为1。
@@ -78,7 +78,7 @@
所以 放物品1 的情况 = dp[1][1] + 物品1 的价值,推导方向如图:
-
+
(**注意上图和 [01背包理论基础(二维数组)](https://programmercarl.com/背包理论基础01背包-1.html) 中的区别**,对于理解完全背包很重要)
@@ -103,7 +103,7 @@
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
-
+
在看其他情况。
@@ -132,7 +132,7 @@ for (int j = weight[0]; j <= bagWeight; j++)
此时dp数组初始化情况如图所示:
-
+
dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化多少呢?
@@ -185,7 +185,7 @@ for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
以本篇举例数据为例,填满了dp二维数组如图:
-
+
因为 物品0 的性价比是最高的,而且 在完全背包中,每一类物品都有无限个,所以有无限个物品0,既然物品0 性价比最高,当然是优先放物品0。
diff --git a/problems/贪心算法总结篇.md b/problems/贪心算法总结篇.md
index 7d4c57e8..4c67fb40 100644
--- a/problems/贪心算法总结篇.md
+++ b/problems/贪心算法总结篇.md
@@ -128,7 +128,7 @@ Carl个人认为:如果找出局部最优并可以推出全局最优,就是
贪心专题汇聚为一张图:
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412)所画,总结的非常好,分享给大家。
diff --git a/problems/贪心算法理论基础.md b/problems/贪心算法理论基础.md
index 14f39729..2d0af879 100644
--- a/problems/贪心算法理论基础.md
+++ b/problems/贪心算法理论基础.md
@@ -7,7 +7,7 @@
题目分类大纲如下:
- +
+ ## 算法公开课
diff --git a/problems/链表总结篇.md b/problems/链表总结篇.md
index e29ba268..99bb2abc 100644
--- a/problems/链表总结篇.md
+++ b/problems/链表总结篇.md
@@ -75,7 +75,7 @@
## 总结
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画,总结的非常好,分享给大家。
diff --git a/problems/链表理论基础.md b/problems/链表理论基础.md
index 3637d05f..5305c9a9 100644
--- a/problems/链表理论基础.md
+++ b/problems/链表理论基础.md
@@ -12,7 +12,7 @@
链表的入口节点称为链表的头结点也就是head。
如图所示:
-
+
## 链表的类型
@@ -31,7 +31,7 @@
双链表 既可以向前查询也可以向后查询。
如图所示:
-
+
### 循环链表
@@ -39,7 +39,7 @@
循环链表可以用来解决约瑟夫环问题。
-
+
## 链表的存储方式
@@ -54,7 +54,7 @@
如图所示:
-
+
这个链表起始节点为2, 终止节点为7, 各个节点分布在内存的不同地址空间上,通过指针串联在一起。
@@ -104,7 +104,7 @@ head->val = 5;
删除D节点,如图所示:
-
+
只要将C节点的next指针 指向E节点就可以了。
@@ -118,7 +118,7 @@ head->val = 5;
如图所示:
-
+
可以看出链表的增添和删除都是O(1)操作,也不会影响到其他节点。
@@ -128,7 +128,7 @@ head->val = 5;
再把链表的特性和数组的特性进行一个对比,如图所示:
-
+
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
diff --git a/problems/面试题02.07.链表相交.md b/problems/面试题02.07.链表相交.md
index f8d9039a..0207b71e 100644
--- a/problems/面试题02.07.链表相交.md
+++ b/problems/面试题02.07.链表相交.md
@@ -13,7 +13,7 @@
图示两个链表在节点 c1 开始相交:
-
+
题目数据 保证 整个链式结构中不存在环。
@@ -21,15 +21,15 @@
示例 1:
-
+
示例 2:
-
+
示例 3:
-
+
## 算法公开课
diff --git a/problems/链表总结篇.md b/problems/链表总结篇.md
index e29ba268..99bb2abc 100644
--- a/problems/链表总结篇.md
+++ b/problems/链表总结篇.md
@@ -75,7 +75,7 @@
## 总结
-
+
这个图是 [代码随想录知识星球](https://programmercarl.com/other/kstar.html) 成员:[海螺人](https://wx.zsxq.com/dweb2/index/footprint/844412858822412),所画,总结的非常好,分享给大家。
diff --git a/problems/链表理论基础.md b/problems/链表理论基础.md
index 3637d05f..5305c9a9 100644
--- a/problems/链表理论基础.md
+++ b/problems/链表理论基础.md
@@ -12,7 +12,7 @@
链表的入口节点称为链表的头结点也就是head。
如图所示:
-
+
## 链表的类型
@@ -31,7 +31,7 @@
双链表 既可以向前查询也可以向后查询。
如图所示:
-
+
### 循环链表
@@ -39,7 +39,7 @@
循环链表可以用来解决约瑟夫环问题。
-
+
## 链表的存储方式
@@ -54,7 +54,7 @@
如图所示:
-
+
这个链表起始节点为2, 终止节点为7, 各个节点分布在内存的不同地址空间上,通过指针串联在一起。
@@ -104,7 +104,7 @@ head->val = 5;
删除D节点,如图所示:
-
+
只要将C节点的next指针 指向E节点就可以了。
@@ -118,7 +118,7 @@ head->val = 5;
如图所示:
-
+
可以看出链表的增添和删除都是O(1)操作,也不会影响到其他节点。
@@ -128,7 +128,7 @@ head->val = 5;
再把链表的特性和数组的特性进行一个对比,如图所示:
-
+
数组在定义的时候,长度就是固定的,如果想改动数组的长度,就需要重新定义一个新的数组。
diff --git a/problems/面试题02.07.链表相交.md b/problems/面试题02.07.链表相交.md
index f8d9039a..0207b71e 100644
--- a/problems/面试题02.07.链表相交.md
+++ b/problems/面试题02.07.链表相交.md
@@ -13,7 +13,7 @@
图示两个链表在节点 c1 开始相交:
-
+
题目数据 保证 整个链式结构中不存在环。
@@ -21,15 +21,15 @@
示例 1:
-
+
示例 2:
-
+
示例 3:
-
+