+ 
- 
+
-
+
1. [关于动态规划，你该了解这些！](./problems/动态规划理论基础.md)
2. [动态规划：斐波那契数](./problems/0509.斐波那契数.md)
3. [动态规划：爬楼梯](./problems/0070.爬楼梯.md)
diff --git a/problems/0018.四数之和.md b/problems/0018.四数之和.md
index a1591736..0caf12be 100644
--- a/problems/0018.四数之和.md
+++ b/problems/0018.四数之和.md
@@ -31,38 +31,39 @@ https://leetcode-cn.com/problems/4sum/
# 思路
-四数之和，和[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)是一个思路，都是使用双指针法, 基本解法就是在[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A) 的基础上再套一层for循环。
+四数之和，和[15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg)是一个思路，都是使用双指针法, 基本解法就是在[15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg) 的基础上再套一层for循环。
但是有一些细节需要注意，例如： 不要判断`nums[k] > target` 就返回了，三数之和 可以通过 `nums[i] > 0` 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。（大家亲自写代码就能感受出来）
-[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下表作为双指针，找到nums[i] + nums[left] + nums[right] == 0。
+[15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下表作为双指针，找到nums[i] + nums[left] + nums[right] == 0。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下表作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。
那么一样的道理，五数之和、六数之和等等都采用这种解法。
-对于[三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。
+对于[15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg)双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。
-之前我们讲过哈希表的经典题目：[四数相加II](https://mp.weixin.qq.com/s/Ue8pKKU5hw_m-jPgwlHcbA)，相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时四元组不能重复。
+之前我们讲过哈希表的经典题目：[454.四数相加II](https://mp.weixin.qq.com/s/12g_w6RzHuEpFts1pT6BWw)，相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时四元组不能重复。
-而[四数相加II](https://mp.weixin.qq.com/s/Ue8pKKU5hw_m-jPgwlHcbA)是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况，所以相对于本题还是简单了不少！
+而[454.四数相加II](https://mp.weixin.qq.com/s/12g_w6RzHuEpFts1pT6BWw)是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况，所以相对于本题还是简单了不少！
我们来回顾一下，几道题目使用了双指针法。
双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级，题目如下：
-* [0027.移除元素](https://mp.weixin.qq.com/s/wj0T-Xs88_FHJFwayElQlA)
-* [15.三数之和](https://mp.weixin.qq.com/s/r5cgZFu0tv4grBAexdcd8A)
+
+* [27.移除元素](https://mp.weixin.qq.com/s/RMkulE4NIb6XsSX83ra-Ww)
+* [15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg)
* [18.四数之和](https://mp.weixin.qq.com/s/nQrcco8AZJV1pAOVjeIU_g)
-双指针来记录前后指针实现链表反转：
-* [206.反转链表](https://mp.weixin.qq.com/s/pnvVP-0ZM7epB8y3w_Njwg)
+操作链表：
-使用双指针来确定有环：
+* [206.反转链表](https://mp.weixin.qq.com/s/ckEvIVGcNLfrz6OLOMoT0A)
+* [19.删除链表的倒数第N个节点](https://mp.weixin.qq.com/s/gxu65X1343xW_sBrkTz0Eg)
+* [面试题 02.07. 链表相交](https://mp.weixin.qq.com/s/BhfFfaGvt9Zs7UmH4YehZw)
+* [142题.环形链表II](https://mp.weixin.qq.com/s/gt_VH3hQTqNxyWcl1ECSbQ)
-* [142题.环形链表II](https://mp.weixin.qq.com/s/_QVP3IkRZWx9zIpQRgajzA)
-
-双指针法在数组和链表中还有很多应用，后面还会介绍到。
+双指针法在字符串题目中还有很多应用，后面还会介绍到。
C++代码
diff --git a/problems/0028.实现strStr.md b/problems/0028.实现strStr.md
index b8ebcaa1..6f257d5e 100644
--- a/problems/0028.实现strStr.md
+++ b/problems/0028.实现strStr.md
@@ -61,11 +61,6 @@ KMP的经典思想就是:**当出现字符串不匹配时，可以记录一部
读完本篇可以顺便，把leetcode上28.实现strStr()题目做了。
-如果文字实在看不下去，就看我在B站上的视频吧，如下：
-
-* [帮你把KMP算法学个通透！（理论篇）B站](https://www.bilibili.com/video/BV1PD4y1o7nd/)
-* [帮你把KMP算法学个通透！（求next数组代码篇）B站](https://www.bilibili.com/video/BV1M5411j7Xx/)
-
# 什么是KMP
diff --git a/problems/0454.四数相加II.md b/problems/0454.四数相加II.md
index 2c648f58..939ed20d 100644
--- a/problems/0454.四数相加II.md
+++ b/problems/0454.四数相加II.md
@@ -11,6 +11,7 @@
# 第454题.四数相加II
+
https://leetcode-cn.com/problems/4sum-ii/
给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ，使得 A[i] + B[j] + C[k] + D[l] = 0。
@@ -24,10 +25,8 @@ A = [ 1, 2]
B = [-2,-1]
C = [-1, 2]
D = [ 0, 2]
-
输出:
2
-
**解释:**
两个元组如下:
1. (0, 0, 0, 1) -> A[0] + B[0] + C[0] + D[1] = 1 + (-2) + (-1) + 2 = 0
diff --git a/problems/二叉树的理论基础.md b/problems/二叉树的理论基础.md
deleted file mode 100644
index 4b52e511..00000000
--- a/problems/二叉树的理论基础.md
+++ /dev/null
@@ -1,202 +0,0 @@
-
-
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
- -## 二叉树理论基础 - -我们要开启新的征程了，大家跟上！ - -说道二叉树，大家对于二叉树其实都很熟悉了，本文呢我也不想教科书式的把二叉树的基础内容再啰嗦一遍，所以一下我讲的都是一些比较重点的内容。 - -相信只要耐心看完，都会有所收获。 - -## 二叉树的种类 - -在我们解题过程中二叉树有两种主要的形式：满二叉树和完全二叉树。 - -### 满二叉树 - -满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。 - -如图所示： - -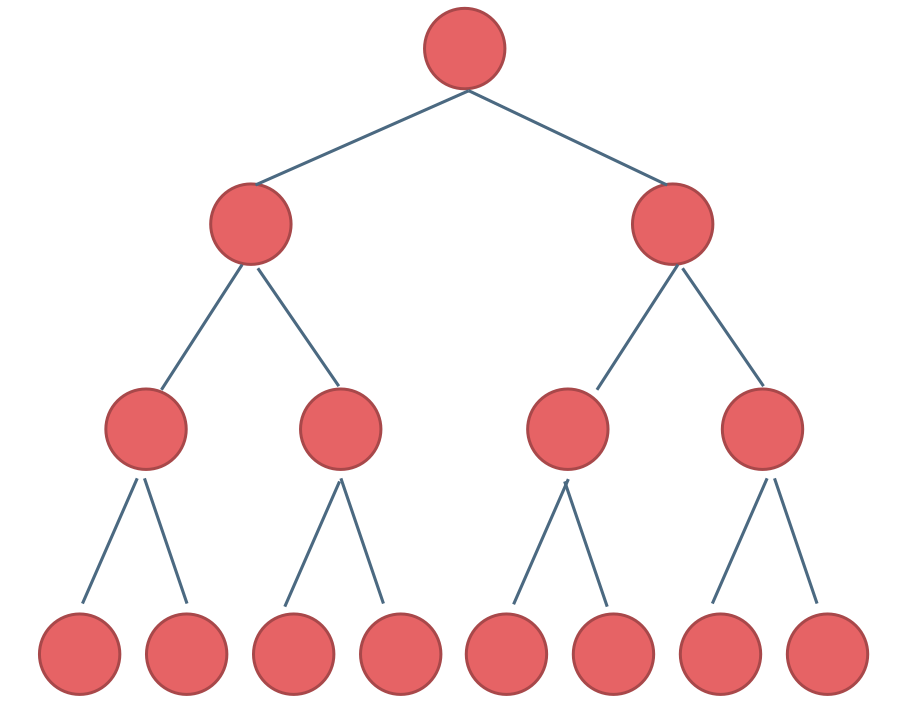
-
-这棵二叉树为满二叉树，也可以说深度为 k，有 $(2^k)-1$ 个节点的二叉树。
-
-
-### 完全二叉树
-
-什么是完全二叉树？
-
-完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1 ~ $2^{(h-1)}$ 个节点。
-
-**大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。**
-
-我来举一个典型的例子如题：
-
-
-
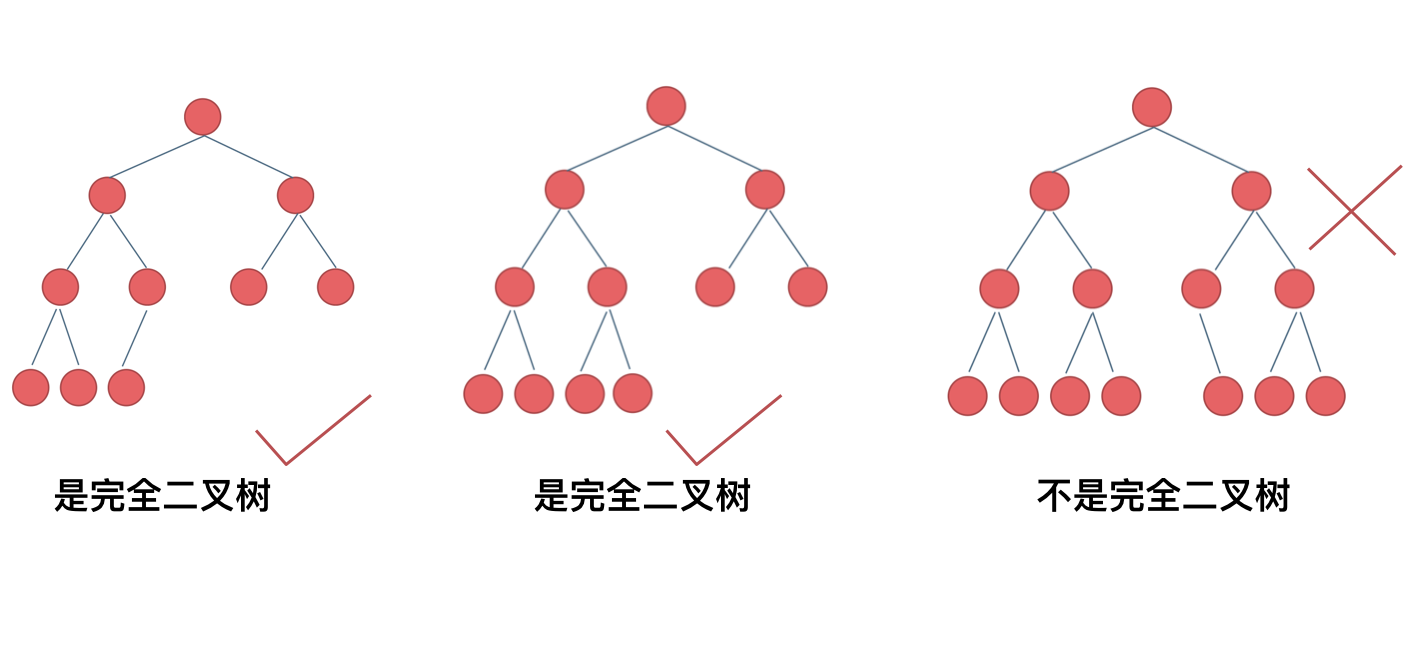-相信不少同学最后一个二叉树是不是完全二叉树都中招了。
-
-**之前我们刚刚讲过优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。**
-
-### 二叉搜索树
-
-前面介绍的书，都没有数值的，而二叉搜索树是有数值的了，**二叉搜索树是一个有序树**。
-
-
-* 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
-* 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
-* 它的左、右子树也分别为二叉排序树
-
-下面这两棵树都是搜索树
-
-
-
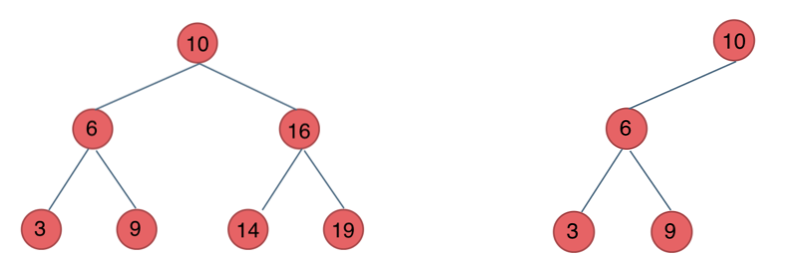-### 平衡二叉搜索树
-
-平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。
-
-如图：
-
-
-
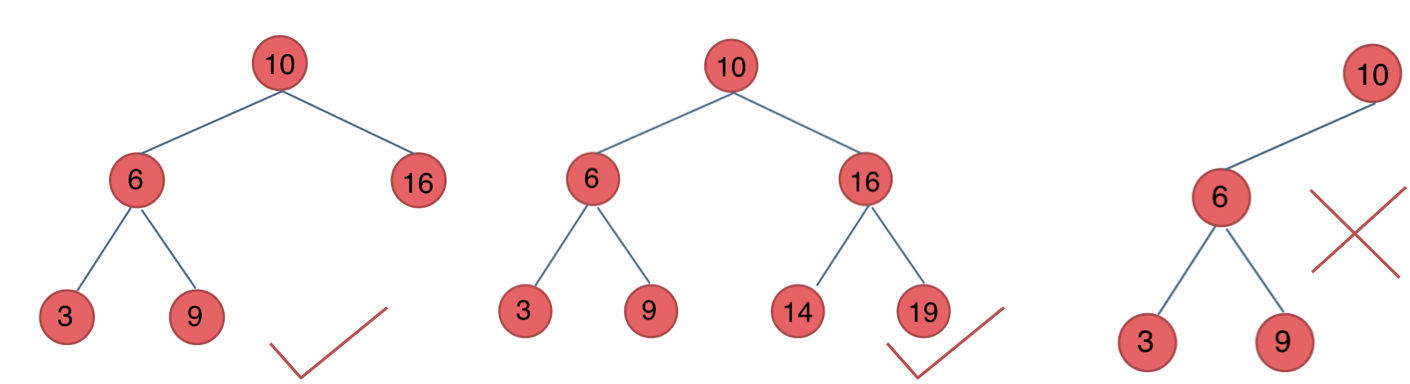-最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。
-
-**C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树**，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_map底层实现是哈希表。
-
-**所以大家使用自己熟悉的编程语言写算法，一定要知道常用的容器底层都是如何实现的，最基本的就是map、set等等，否则自己写的代码，自己对其性能分析都分析不清楚！**
-
-
-## 二叉树的存储方式
-
-**二叉树可以链式存储，也可以顺序存储。**
-
-那么链式存储方式就用指针， 顺序存储的方式就是用数组。
-
-顾名思义就是顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在散落在各个地址的节点串联一起。
-
-链式存储如图：
-
-
-
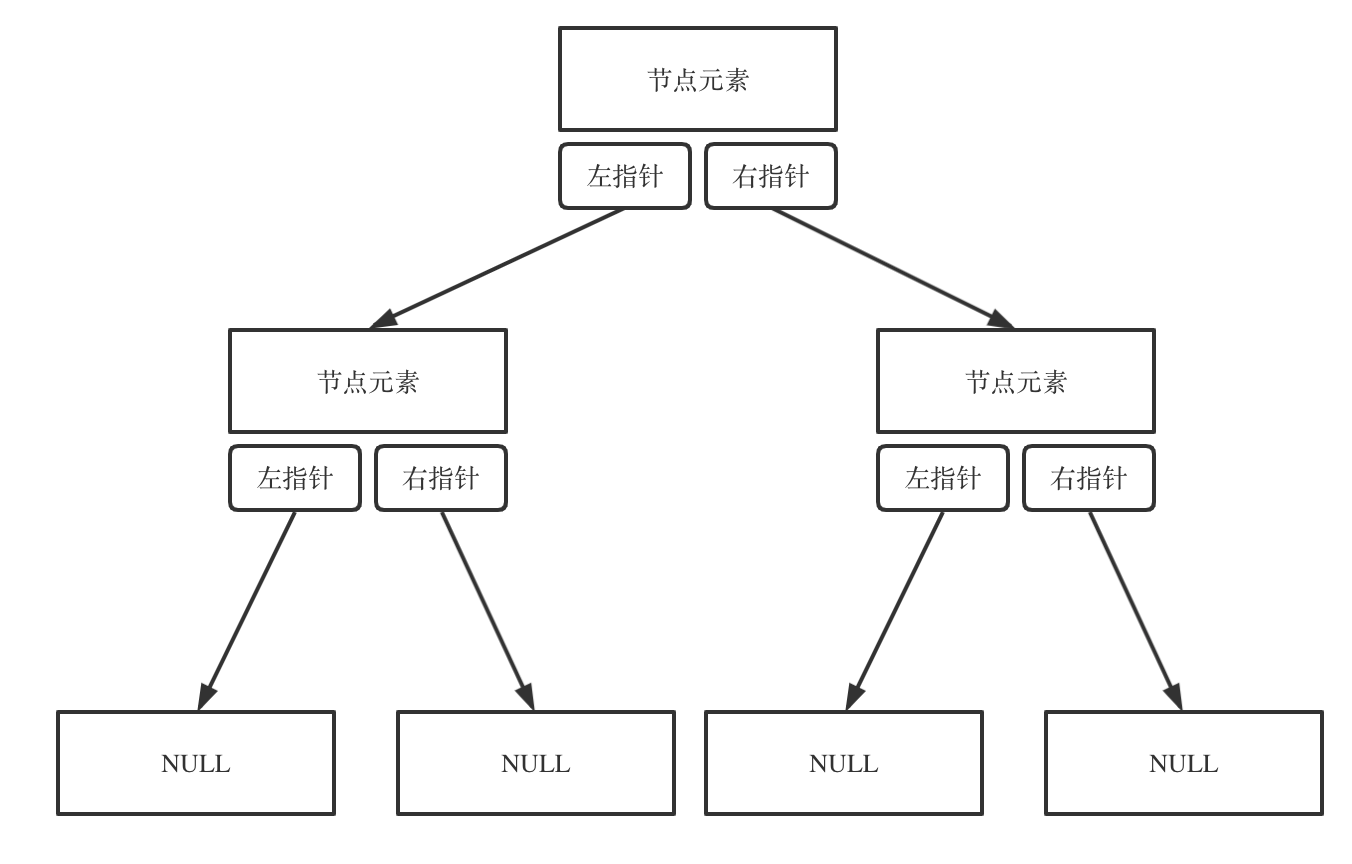-链式存储是大家很熟悉的一种方式，那么我们来看看如何顺序存储呢？
-
-其实就是用数组来存储二叉树，顺序存储的方式如图：
-
-
-
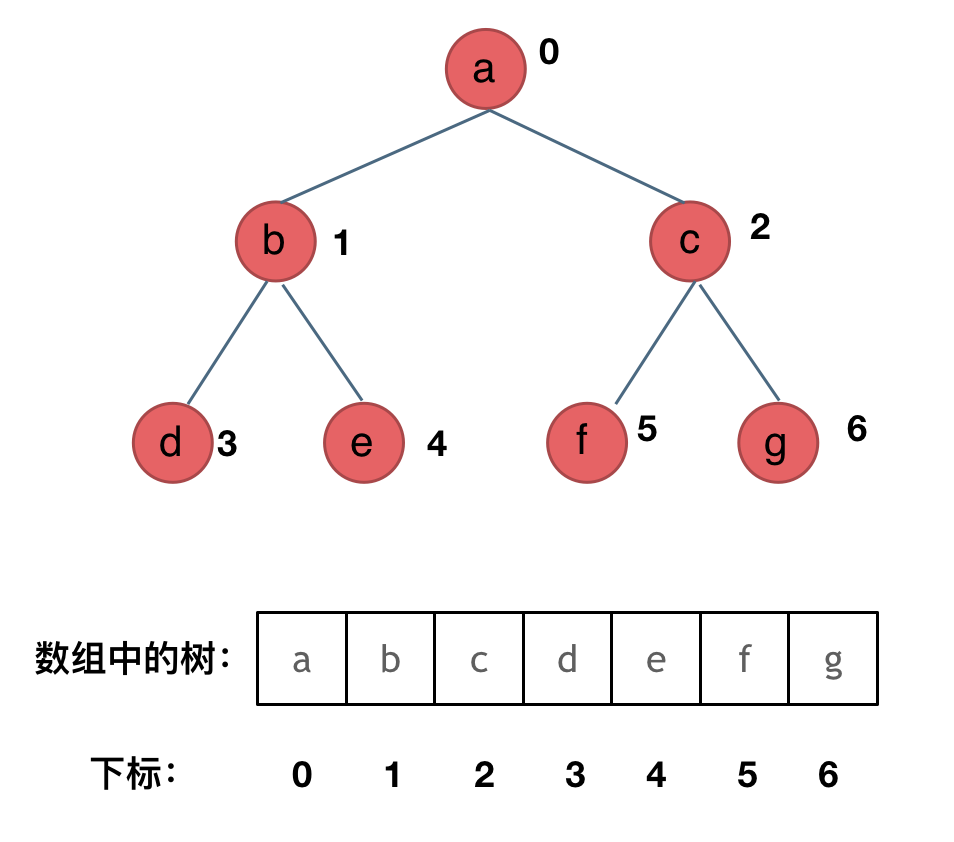-用数组来存储二叉树如何遍历的呢？
-
-**如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。**
-
-但是用链式表示的二叉树，更有利于我们理解，所以一般我们都是用链式存储二叉树。
-
-**所以大家要了解，用数组依然可以表示二叉树。**
-
-## 二叉树的遍历方式
-
-关于二叉树的遍历方式，要知道二叉树遍历的基本方式都有哪些。
-
-一些同学用做了很多二叉树的题目了，可能知道前序、中序、后序遍历，可能知道层序遍历，但是却没有框架。
-
-我这里把二叉树的几种遍历方式列出来，大家就可以一一串起来了。
-
-二叉树主要有两种遍历方式：
-1. 深度优先遍历：先往深走，遇到叶子节点再往回走。
-2. 广度优先遍历：一层一层的去遍历。
-
-**这两种遍历是图论中最基本的两种遍历方式**，后面在介绍图论的时候 还会介绍到。
-
-那么从深度优先遍历和广度优先遍历进一步拓展，才有如下遍历方式：
-
-* 深度优先遍历
- * 前序遍历（递归法，迭代法）
- * 中序遍历（递归法，迭代法）
- * 后序遍历（递归法，迭代法）
-* 广度优先遍历
- * 层次遍历（迭代法）
-
-
-在深度优先遍历中：有三个顺序，前序、中序、后序遍历， 有同学总分不清这三个顺序，经常搞混，我这里教大家一个技巧。
-
-**这里前、中、后，其实指的就是中间节点的遍历顺序**，只要大家记住 前序、中序、后序指的就是中间节点的位置就可以了。
-
-看如下中间节点的顺序，就可以发现，中间节点的顺序就是所谓的遍历方式
-
-* 前序遍历：中左右
-* 中序遍历：左中右
-* 后序遍历：左右中
-
-大家可以对着如下图，看看自己理解的前后中序有没有问题。
-
-
-
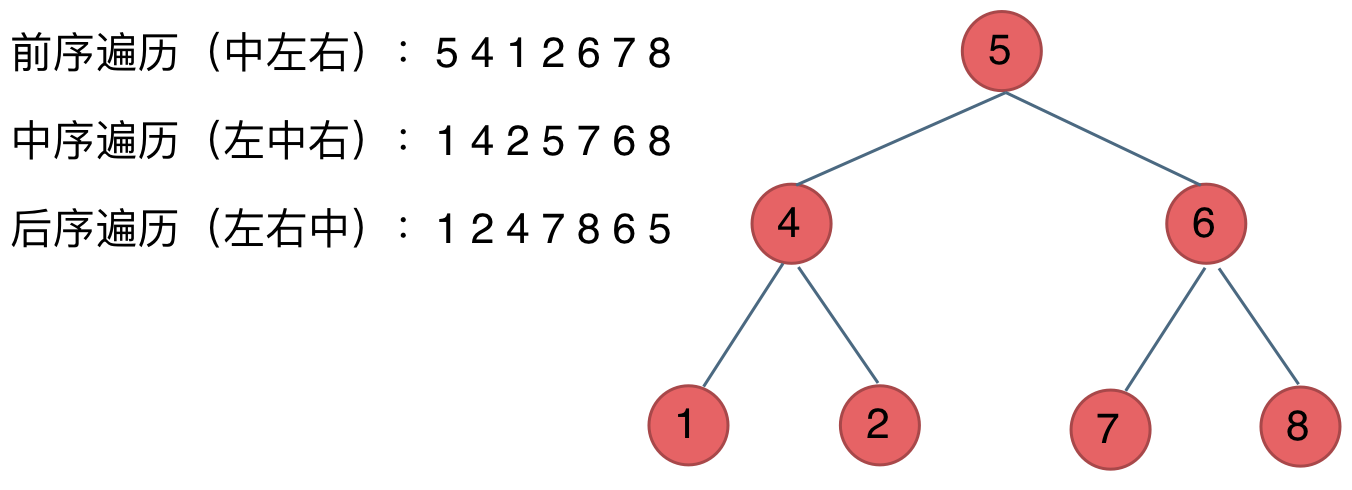-最后再说一说二叉树中深度优先和广度优先遍历实现方式，我们做二叉树相关题目，经常会使用递归的方式来实现深度优先遍历，也就是实现前序、中序、后序遍历，使用递归是比较方便的。
-
-**之前我们讲栈与队列的时候，就说过栈其实就是递归的一种是实现结构**，也就说前序、中序、后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现的。
-
-而广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。
-
-**这里其实我们又了解了栈与队列的一个应用场景了。**
-
-具体的实现我们后面都会讲的，这里大家先要清楚这些理论基础。
-
-## 二叉树的定义
-
-刚刚我们说过了二叉树有两种存储方式顺序存储，和链式存储，顺序存储就是用数组来存，这个定义没啥可说的，我们来看看链式存储的二叉树节点的定义方式。
-
-
-C++代码如下：
-
-```
-struct TreeNode {
- int val;
- TreeNode *left;
- TreeNode *right;
- TreeNode(int x) : val(x), left(NULL), right(NULL) {}
-};
-```
-
-大家会发现二叉树的定义 和链表是差不多的，相对于链表 ，二叉树的节点里多了一个指针， 有两个指针，指向左右孩子.
-
-这里要提醒大家要注意二叉树节点定义的书写方式。
-
-**在现场面试的时候 面试官可能要求手写代码，所以数据结构的定义以及简单逻辑的代码一定要锻炼白纸写出来。**
-
-因为我们在刷leetcode的时候，节点的定义默认都定义好了，真到面试的时候，需要自己写节点定义的时候，有时候会一脸懵逼！
-
-## 总结
-
-二叉树是一种基础数据结构，在算法面试中都是常客，也是众多数据结构的基石。
-
-本篇我们介绍了二叉树的种类、存储方式、遍历方式以及定义，比较全面的介绍了二叉树各个方面的重点，帮助大家扫一遍基础。
-
-**说道二叉树，就不得不说递归，很多同学对递归都是又熟悉又陌生，递归的代码一般很简短，但每次都是一看就会，一写就废。**
-
-
-
-## 其他语言版本
-
-
-Java：
-
-
-Python：
-
-
-Go：
-
-
-
-
------------------------
-* 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
-* B站视频：[代码随想录](https://space.bilibili.com/525438321)
-* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
-
-
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
- -# 动态规划：关于01背包问题，你该了解这些！（滚动数组） - -昨天[动态规划：关于01背包问题，你该了解这些！](https://mp.weixin.qq.com/s/FwIiPPmR18_AJO5eiidT6w)中是用二维dp数组来讲解01背包。 - -今天我们就来说一说滚动数组，其实在前面的题目中我们已经用到过滚动数组了，就是把二维dp降为一维dp，一些录友当时还表示比较困惑。 - -那么我们通过01背包，来彻底讲一讲滚动数组！ - -接下来还是用如下这个例子来进行讲解 - -背包最大重量为4。 - -物品为： - -| | 重量 | 价值 | -| --- | --- | --- | -| 物品0 | 1 | 15 | -| 物品1 | 3 | 20 | -| 物品2 | 4 | 30 | - -问背包能背的物品最大价值是多少？ - -## 一维dp数组（滚动数组） - -对于背包问题其实状态都是可以压缩的。 - -在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); - -**其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);** - -**于其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了**，只用dp[j]（一维数组，也可以理解是一个滚动数组）。 - -这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。 - -读到这里估计大家都忘了 dp[i][j]里的i和j表达的是什么了，i是物品，j是背包容量。 - -**dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少**。 - -一定要时刻记住这里i和j的含义，要不然很容易看懵了。 - -动规五部曲分析如下： - -1. 确定dp数组的定义 - -在一维dp数组中，dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。 - -2. 一维dp数组的递推公式 - -dp[j]为 容量为j的背包所背的最大价值，那么如何推导dp[j]呢？ - -dp[j]可以通过dp[j - weight[j]]推导出来，dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。 - -dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。（也就是容量为j的背包，放入物品i了之后的价值即：dp[j]） - -此时dp[j]有两个选择，一个是取自己dp[j]，一个是取dp[j - weight[i]] + value[i]，指定是取最大的，毕竟是求最大价值， - -所以递归公式为： - -``` -dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); -``` - -可以看出相对于二维dp数组的写法，就是把dp[i][j]中i的维度去掉了。 - -3. 一维dp数组如何初始化 - -**关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱**。 - -dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。 - -那么dp数组除了下标0的位置，初始为0，其他下标应该初始化多少呢？ - -看一下递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); - -dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了，如果题目给的价值有负数，那么非0下标就要初始化为负无穷。 - -**这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了**。 - -那么我假设物品价值都是大于0的，所以dp数组初始化的时候，都初始为0就可以了。 - -4. 一维dp数组遍历顺序 - -代码如下： - -``` -for(int i = 0; i < weight.size(); i++) { // 遍历物品 - for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量 - dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); - - } -} -``` - -**这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！** - -二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。 - -为什么呢？ - -**倒叙遍历是为了保证物品i只被放入一次！**，在[动态规划：关于01背包问题，你该了解这些！](https://mp.weixin.qq.com/s/FwIiPPmR18_AJO5eiidT6w)中讲解二维dp数组初始化dp[0][j]时候已经讲解到过一次。 - -举一个例子：物品0的重量weight[0] = 1，价值value[0] = 15 - -如果正序遍历 - -dp[1] = dp[1 - weight[0]] + value[0] = 15 - -dp[2] = dp[2 - weight[0]] + value[0] = 30 - -此时dp[2]就已经是30了，意味着物品0，被放入了两次，所以不能正序遍历。 - -为什么倒叙遍历，就可以保证物品只放入一次呢？ - -倒叙就是先算dp[2] - -dp[2] = dp[2 - weight[0]] + value[0] = 15 （dp数组已经都初始化为0） - -dp[1] = dp[1 - weight[0]] + value[0] = 15 - -所以从后往前循环，每次取得状态不会和之前取得状态重合，这样每种物品就只取一次了。 - -**那么问题又来了，为什么二维dp数组历的时候不用倒叙呢？** - -因为对于二维dp，dp[i][j]都是通过上一层即dp[i - 1][j]计算而来，本层的dp[i][j]并不会被覆盖！ - -（如何这里读不懂，大家就要动手试一试了，空想还是不靠谱的，实践出真知！） - -**再来看看两个嵌套for循环的顺序，代码中是先遍历物品嵌套遍历背包容量，那可不可以先遍历背包容量嵌套遍历物品呢？** - -不可以！ - -因为一维dp的写法，背包容量一定是要倒序遍历（原因上面已经讲了），如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品，即：背包里只放入了一个物品。 - -（这里如果读不懂，就在回想一下dp[j]的定义，或者就把两个for循环顺序颠倒一下试试！） - -**所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的！**，这一点大家一定要注意。 - -5. 举例推导dp数组 - -一维dp，分别用物品0，物品1，物品2 来遍历背包，最终得到结果如下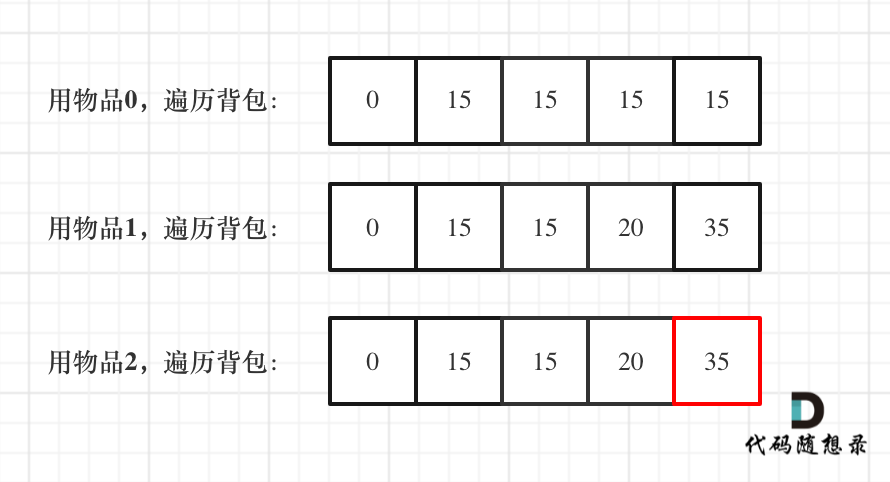： - - - - - -## 一维dp01背包完整C++测试代码 - -``` -void test_1_wei_bag_problem() { - vector
-
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
- -# 背包问题理论基础 - - -这周我们正式开始讲解背包问题！ - -背包问题的经典资料当然是：背包九讲。在公众号「代码随想录」后台回复：背包九讲，就可以获得背包九讲的PDF。 - -但说实话，背包九讲对于小白来说确实不太友好，看起来还是有点费劲的，而且都是伪代码理解起来也吃力。 - -对于面试的话，其实掌握01背包，和完全背包，就够用了，最多可以再来一个多重背包。 - -如果这几种背包，分不清，我这里画了一个图，如下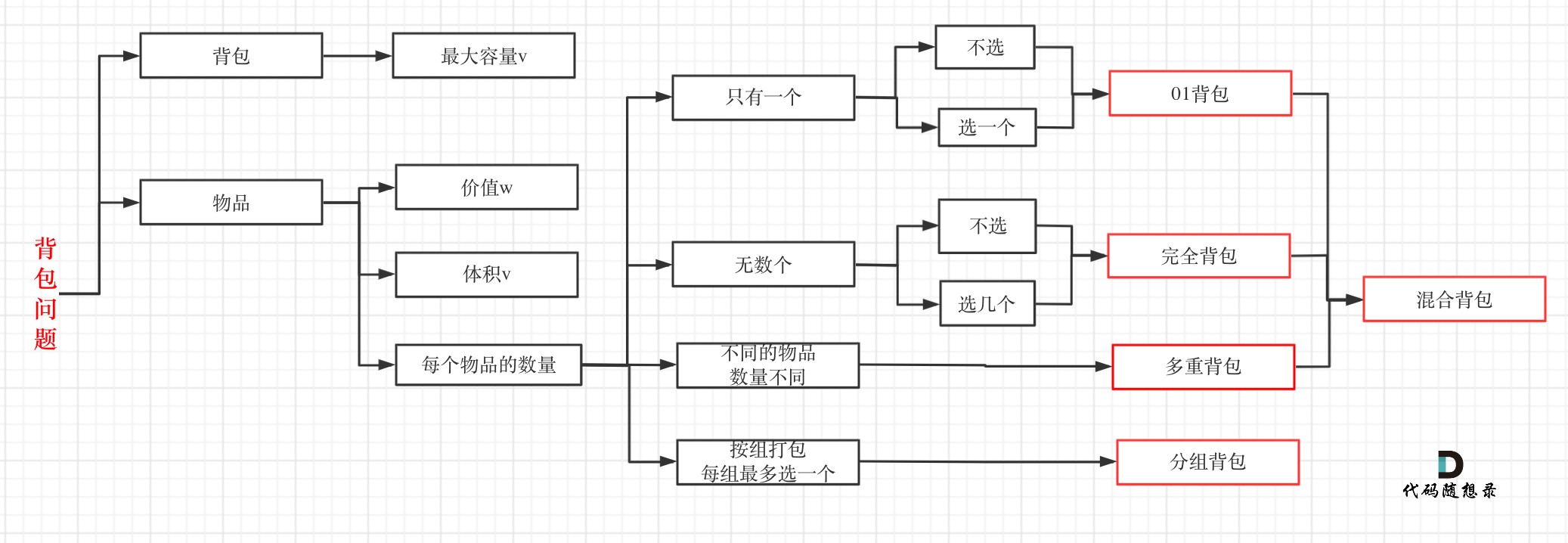： - - - -至于背包九讲其其他背包，面试几乎不会问，都是竞赛级别的了，leetcode上连多重背包的题目都没有，所以题库也告诉我们，01背包和完全背包就够用了。 - -而完全背包又是也是01背包稍作变化而来，即：完全背包的物品数量是无限的。 - -**所以背包问题的理论基础重中之重是01背包，一定要理解透！** - -leetcode上没有纯01背包的问题，都是01背包应用方面的题目，也就是需要转化为01背包问题。 - -**所以我先通过纯01背包问题，把01背包原理讲清楚，后续再讲解leetcode题目的时候，重点就是讲解如何转化为01背包问题了**。 - -之前可能有些录友已经可以熟练写出背包了，但只要把这个文章仔细看完，相信你会意外收获！ - -## 01 背包 - -有N件物品和一个最多能被重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。**每件物品只能用一次**，求解将哪些物品装入背包里物品价值总和最大。 - - - -这是标准的背包问题，以至于很多同学看了这个自然就会想到背包，甚至都不知道暴力的解法应该怎么解了。 - -这样其实是没有从底向上去思考，而是习惯性想到了背包，那么暴力的解法应该是怎么样的呢？ - -每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是O(2^n)，这里的n表示物品数量。 - -**所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！** - -在下面的讲解中，我举一个例子： - -背包最大重量为4。 - -物品为： - -| | 重量 | 价值 | -| --- | --- | --- | -| 物品0 | 1 | 15 | -| 物品1 | 3 | 20 | -| 物品2 | 4 | 30 | - -问背包能背的物品最大价值是多少？ - -以下讲解和图示中出现的数字都是以这个例子为例。 - -## 二维dp数组01背包 - -依然动规五部曲分析一波。 - -1. 确定dp数组以及下标的含义 - -对于背包问题，有一种写法， 是使用二维数组，即**dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少**。 - -只看这个二维数组的定义，大家一定会有点懵，看下面这个图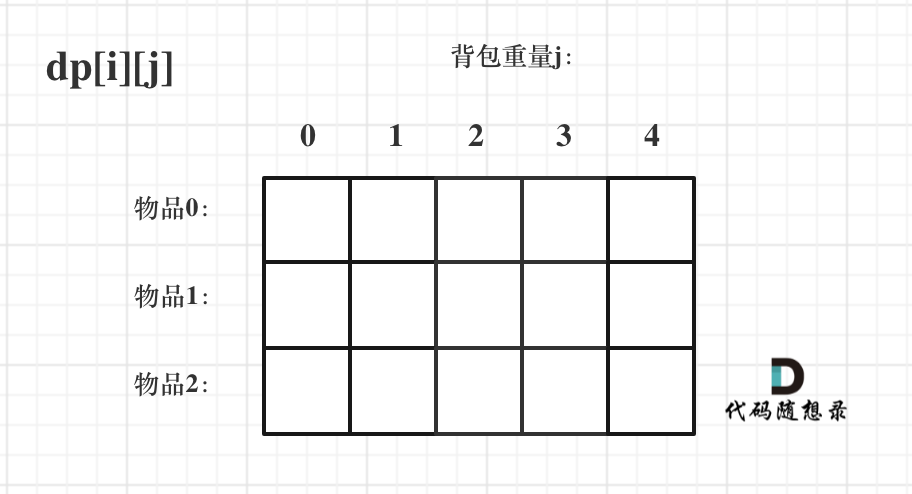： - - - -**要时刻记着这个dp数组的含义，下面的一些步骤都围绕这dp数组的含义进行的**，如果哪里看懵了，就来回顾一下i代表什么，j又代表什么。 - -2. 确定递推公式 - -再回顾一下dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。 - -那么可以有两个方向推出来dp[i][j]， - -* 由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j] -* 由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值 - -所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); - -3. dp数组如何初始化 - -**关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱**。 - -首先从dp[i][j]的定义触发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图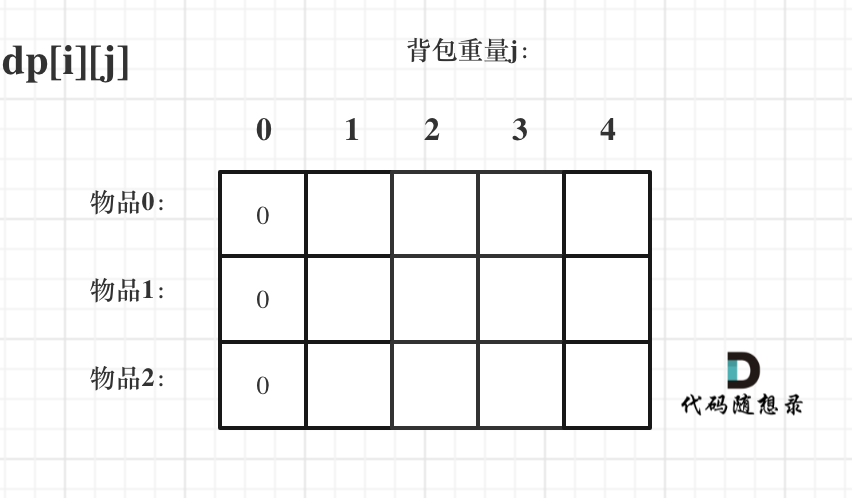： - - - -在看其他情况。 - -状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。 - -dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。 - -代码如下： - -``` -// 倒叙遍历 -for (int j = bagWeight; j >= weight[0]; j--) { - dp[0][j] = dp[0][j - weight[0]] + value[0]; // 初始化i为0时候的情况 -} -``` - -**大家应该发现，这个初始化为什么是倒叙的遍历的？正序遍历就不行么？** - -正序遍历还真就不行，dp[0][j]表示容量为j的背包存放物品0时候的最大价值，物品0的价值就是15，因为题目中说了**每个物品只有一个！**所以dp[0][j]如果不是初始值的话，就应该都是物品0的价值，也就是15。 - -但如果一旦正序遍历了，那么物品0就会被重复加入多次！ 例如代码如下： -``` -// 正序遍历 -for (int j = weight[0]; j <= bagWeight; j++) { - dp[0][j] = dp[0][j - weight[0]] + value[0]; -} -``` - -例如dp[0][1] 是15，到了dp[0][2] = dp[0][2 - 1] + 15; 也就是dp[0][2] = 30 了，那么就是物品0被重复放入了。 - -**所以一定要倒叙遍历，保证物品0只被放入一次！这一点对01背包很重要，后面在讲解滚动数组的时候，还会用到倒叙遍历来保证物品使用一次！** - - -此时dp数组初始化情况如图所示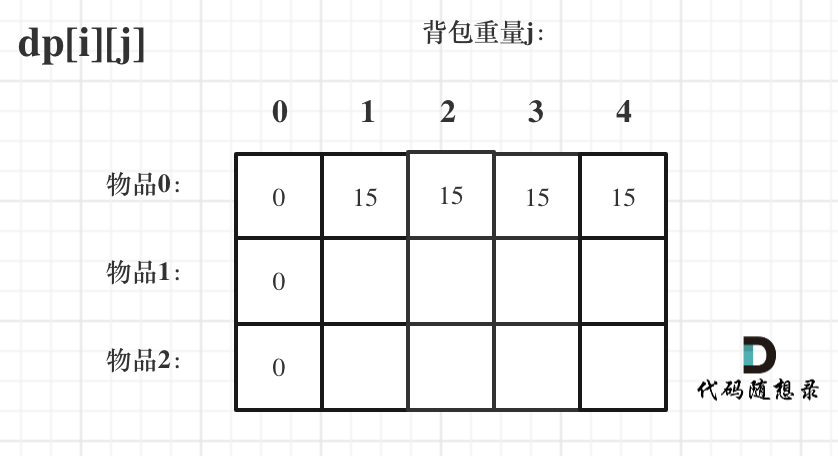： - - - -dp[0][j] 和 dp[i][0] 都已经初始化了，那么其他下标应该初始化多少呢？ - - -dp[i][j]在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了，因为0就是最小的了，不会影响取最大价值的结果。 - -如果题目给的价值有负数，那么非0下标就要初始化为负无穷了。例如：一个物品的价值是-2，但对应的位置依然初始化为0，那么取最大值的时候，就会取0而不是-2了，所以要初始化为负无穷。 - -**这样才能让dp数组在递归公式的过程中取最大的价值，而不是被初始值覆盖了**。 - -最后初始化代码如下： - -``` -// 初始化 dp -vector