更新图片链接
This commit is contained in:
parent
b489cb69b5
commit
ce6e658d14
16
README.md
16
README.md
|
|
@ -181,7 +181,7 @@
|
|||
|
||||
|
||||
题目分类大纲如下:
|
||||
<img src='https://file.kamacoder.com/pics/20240424172231.png' width=600 alt='二叉树大纲'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/20240424172231.png' width=600 alt='二叉树大纲'> </img></div>
|
||||
|
||||
1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
|
||||
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
|
||||
|
|
@ -222,7 +222,7 @@
|
|||
|
||||
题目分类大纲如下:
|
||||
|
||||
<img src='https://file.kamacoder.com/pics/20240424172311.png' width=600 alt='回溯算法大纲'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/20240424172311.png' width=600 alt='回溯算法大纲'> </img></div>
|
||||
|
||||
1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
|
||||
2. [回溯算法:77.组合](./problems/0077.组合.md)
|
||||
|
|
@ -252,7 +252,7 @@
|
|||
题目分类大纲如下:
|
||||
|
||||
|
||||
<img src='https://file.kamacoder.com/pics/20210917104315.png' width=600 alt='贪心算法大纲'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/20210917104315.png' width=600 alt='贪心算法大纲'> </img></div>
|
||||
|
||||
1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
|
||||
2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
|
||||
|
|
@ -283,7 +283,7 @@
|
|||
|
||||
动态规划专题已经开始啦,来不及解释了,小伙伴们上车别掉队!
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/动态规划-总结大纲1.jpg' width=500> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/动态规划-总结大纲1.jpg' width=500> </img></div>
|
||||
1. [关于动态规划,你该了解这些!](./problems/动态规划理论基础.md)
|
||||
2. [动态规划:509.斐波那契数](./problems/0509.斐波那契数.md)
|
||||
3. [动态规划:70.爬楼梯](./problems/0070.爬楼梯.md)
|
||||
|
|
@ -297,7 +297,7 @@
|
|||
|
||||
背包问题系列:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/动态规划-背包问题总结.png' width=500 alt='背包问题大纲'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/动态规划-背包问题总结.png' width=500 alt='背包问题大纲'> </img></div>
|
||||
|
||||
|
||||
11. [动态规划:01背包理论基础(二维dp数组)](./problems/背包理论基础01背包-1.md)
|
||||
|
|
@ -328,7 +328,7 @@
|
|||
|
||||
股票系列:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/股票问题总结.jpg' width=500 alt='股票问题总结'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/股票问题总结.jpg' width=500 alt='股票问题总结'> </img></div>
|
||||
|
||||
|
||||
32. [动态规划:121.买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
|
||||
|
|
@ -343,7 +343,7 @@
|
|||
|
||||
子序列系列:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/动态规划-子序列问题总结.jpg' width=500 alt=''> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/动态规划-子序列问题总结.jpg' width=500 alt=''> </img></div>
|
||||
|
||||
|
||||
41. [动态规划:300.最长递增子序列](./problems/0300.最长上升子序列.md)
|
||||
|
|
@ -503,5 +503,5 @@
|
|||
|
||||
添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
|
||||
|
||||
<div align="center"><img src="https://file.kamacoder.com/pics/第二企业刷题活码.png" data-img="1" width="200" height="200"></img></div>
|
||||
<div align="center"><img src="https://file1.kamacoder.com/i/algo/shuati20250519.jpg" data-img="1" width="200" height="200"></img></div>
|
||||
|
||||
|
|
|
|||
|
|
@ -83,10 +83,10 @@ map目的用来存放我们访问过的元素,因为遍历数组的时候,
|
|||
|
||||
过程如下:
|
||||
|
||||
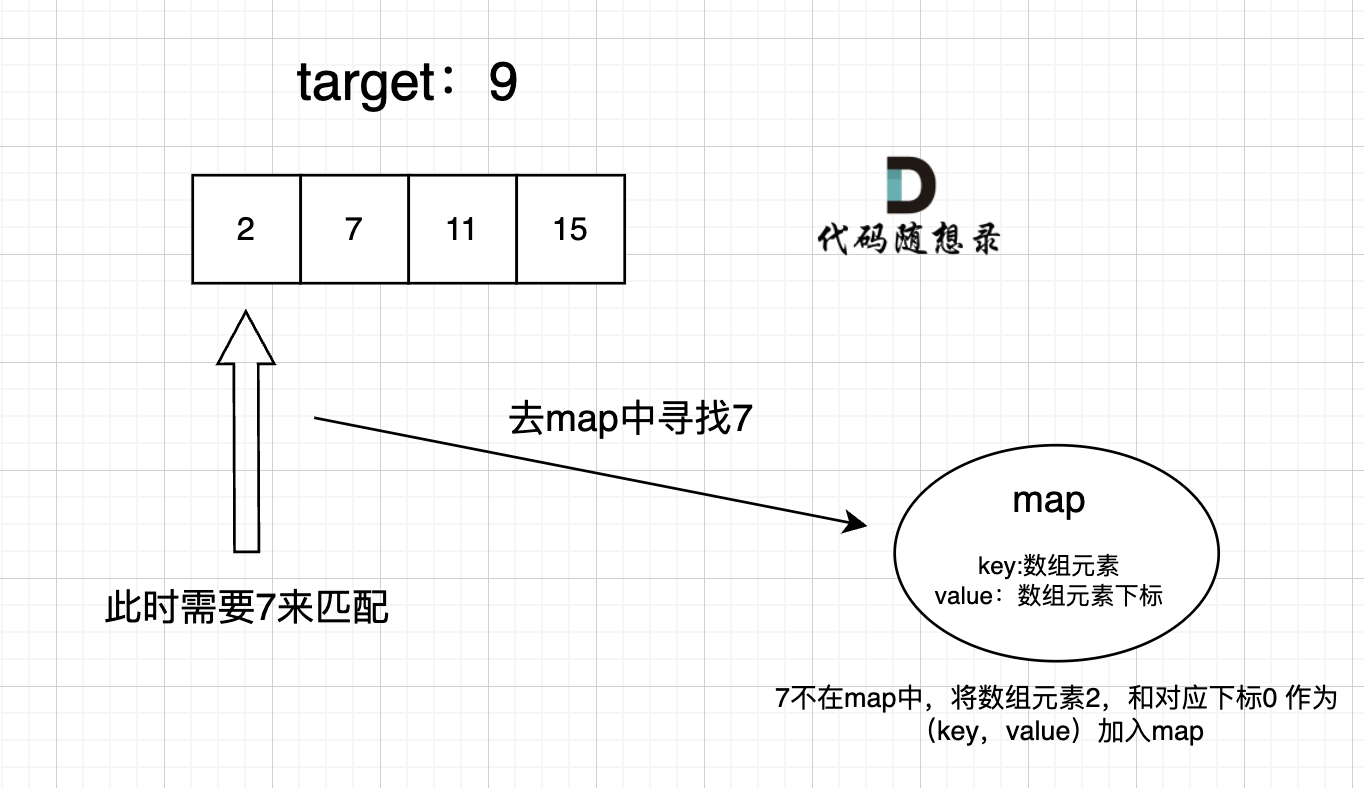
|
||||
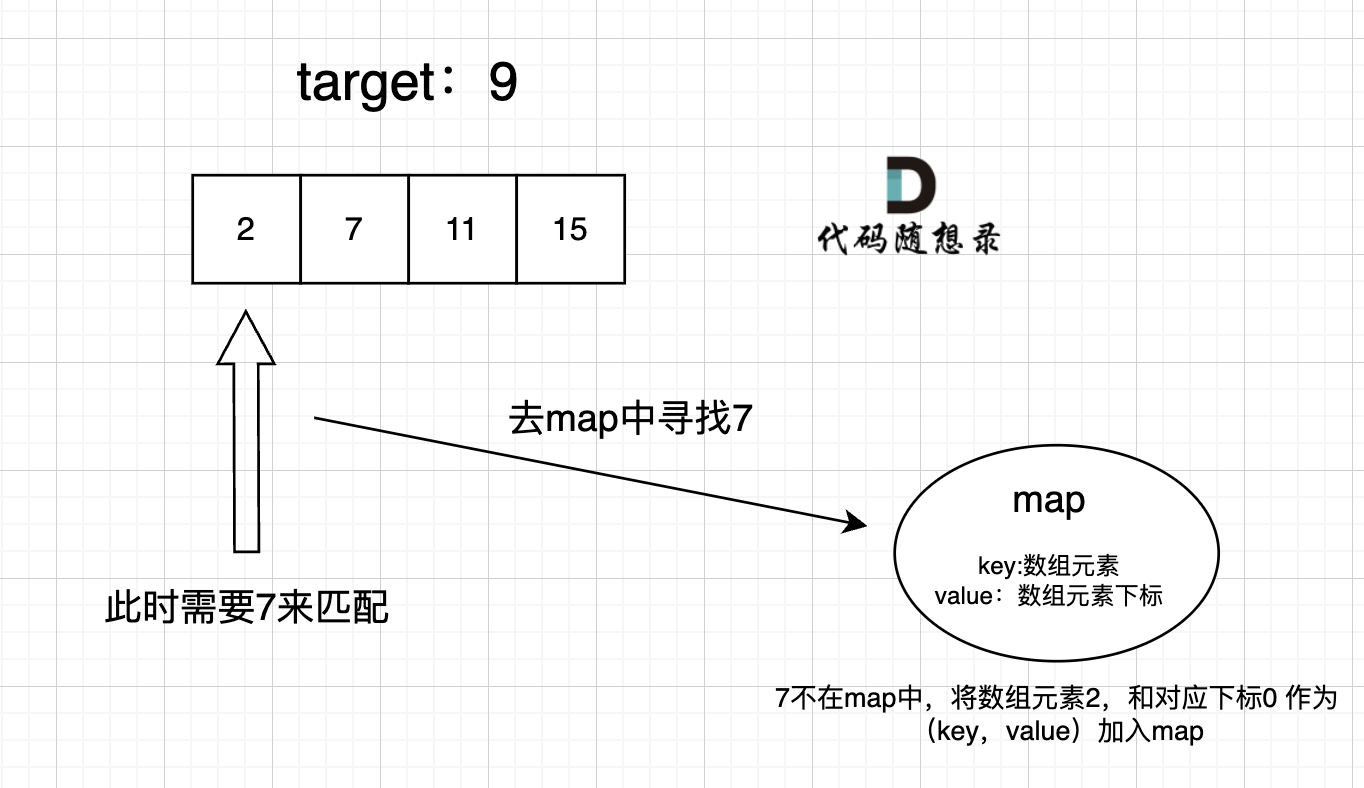
|
||||
|
||||
|
||||
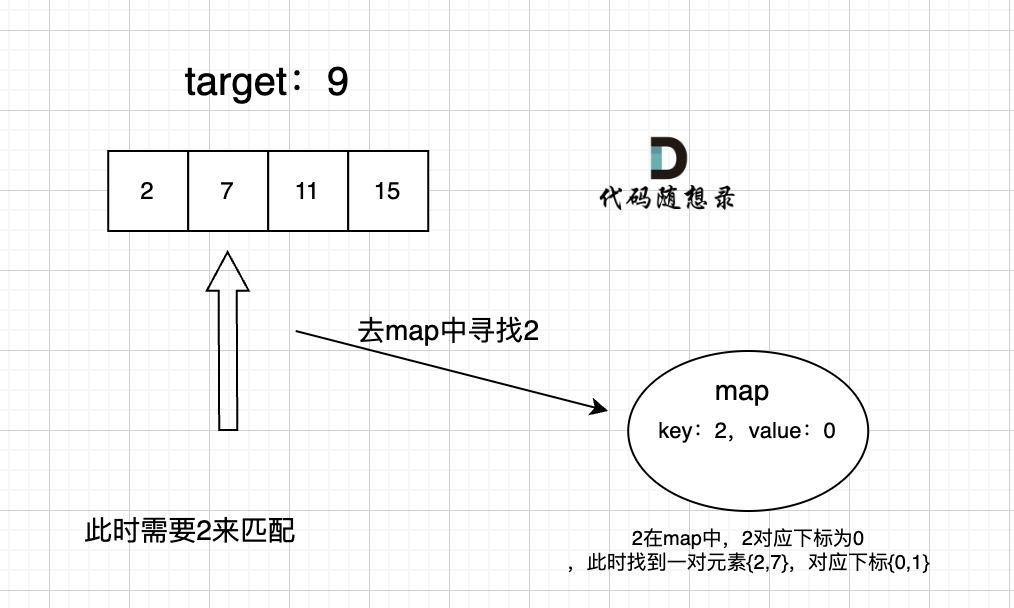
|
||||
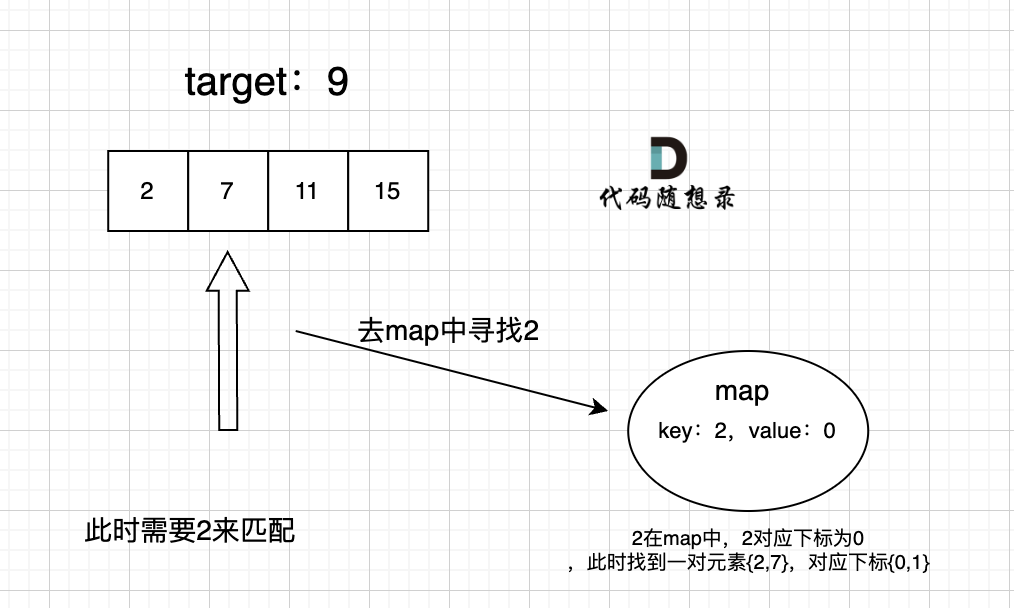
|
||||
|
||||
C++代码:
|
||||
|
||||
|
|
|
|||
|
|
@ -106,7 +106,7 @@ dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹
|
|||
|
||||
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
|
||||
|
||||

|
||||

|
||||
|
||||
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
|
||||
|
||||
|
|
@ -140,7 +140,7 @@ for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
|
|||
|
||||
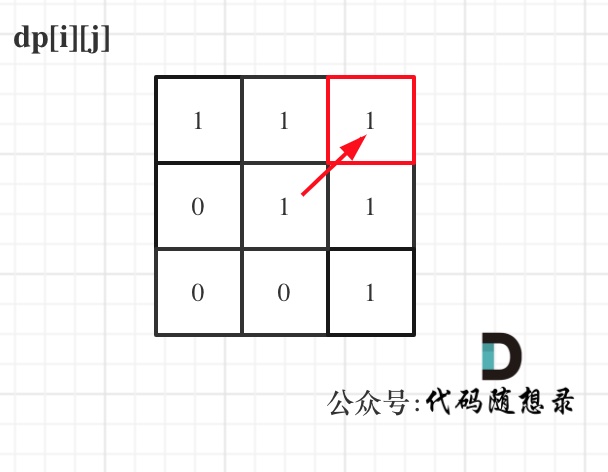
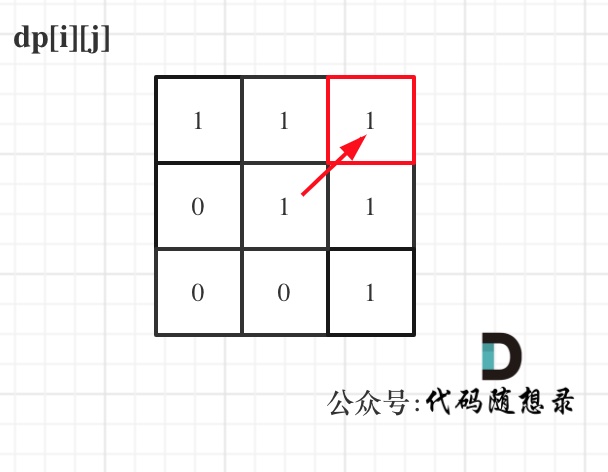
举例,输入:"aaa",dp[i][j]状态如下:
|
||||
|
||||
|
||||
|
||||
|
||||
**注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分**。
|
||||
|
||||
|
|
|
|||
|
|
@ -100,7 +100,7 @@ public:
|
|||
|
||||
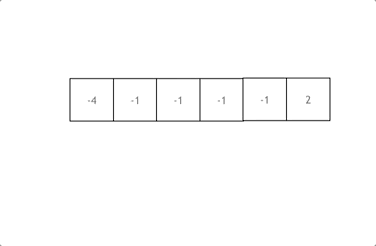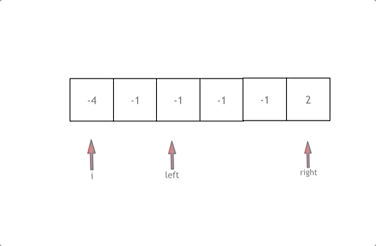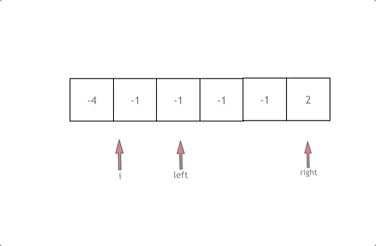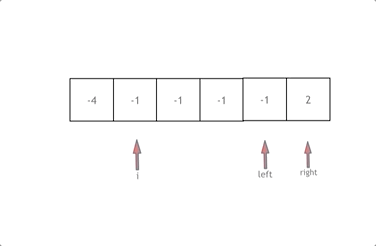
动画效果如下:
|
||||
|
||||

|
||||
|
||||
|
||||
拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
|
||||
|
||||
|
|
|
|||
|
|
@ -11,7 +11,7 @@
|
|||
|
||||
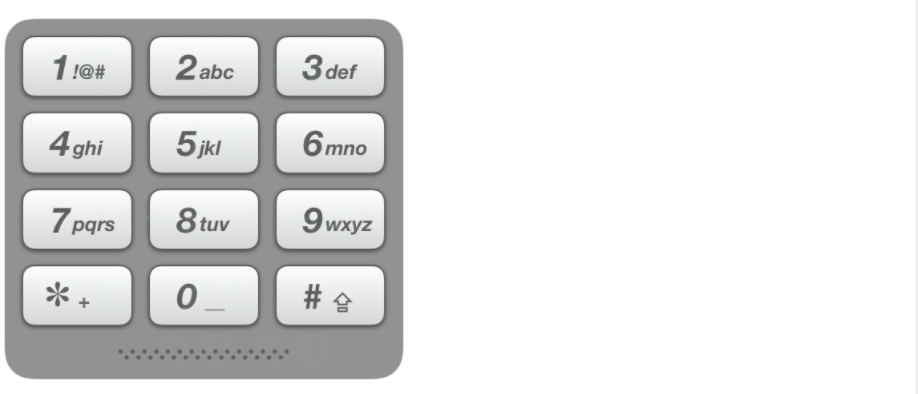
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
|
||||
|
||||

|
||||
|
||||
|
||||
示例:
|
||||
* 输入:"23"
|
||||
|
|
@ -64,7 +64,7 @@ const string letterMap[10] = {
|
|||
|
||||
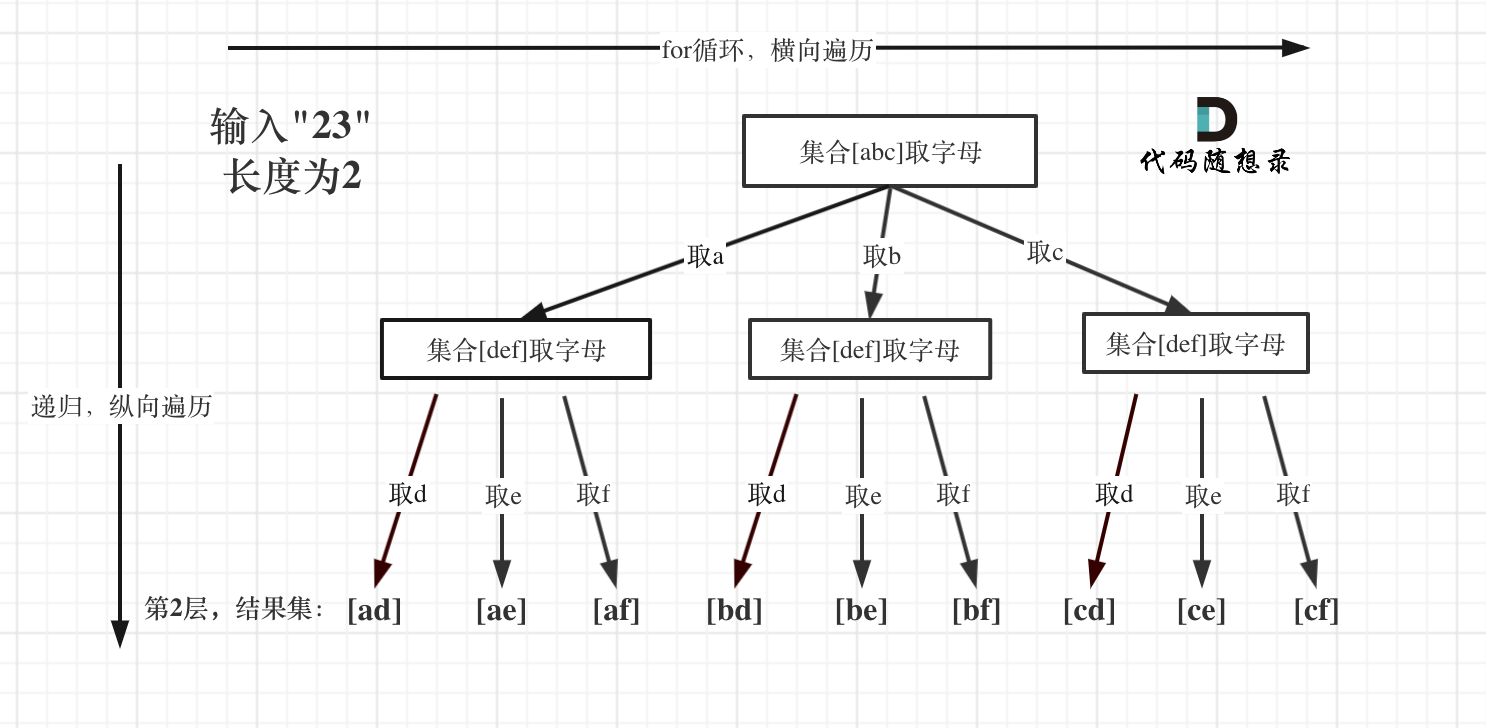
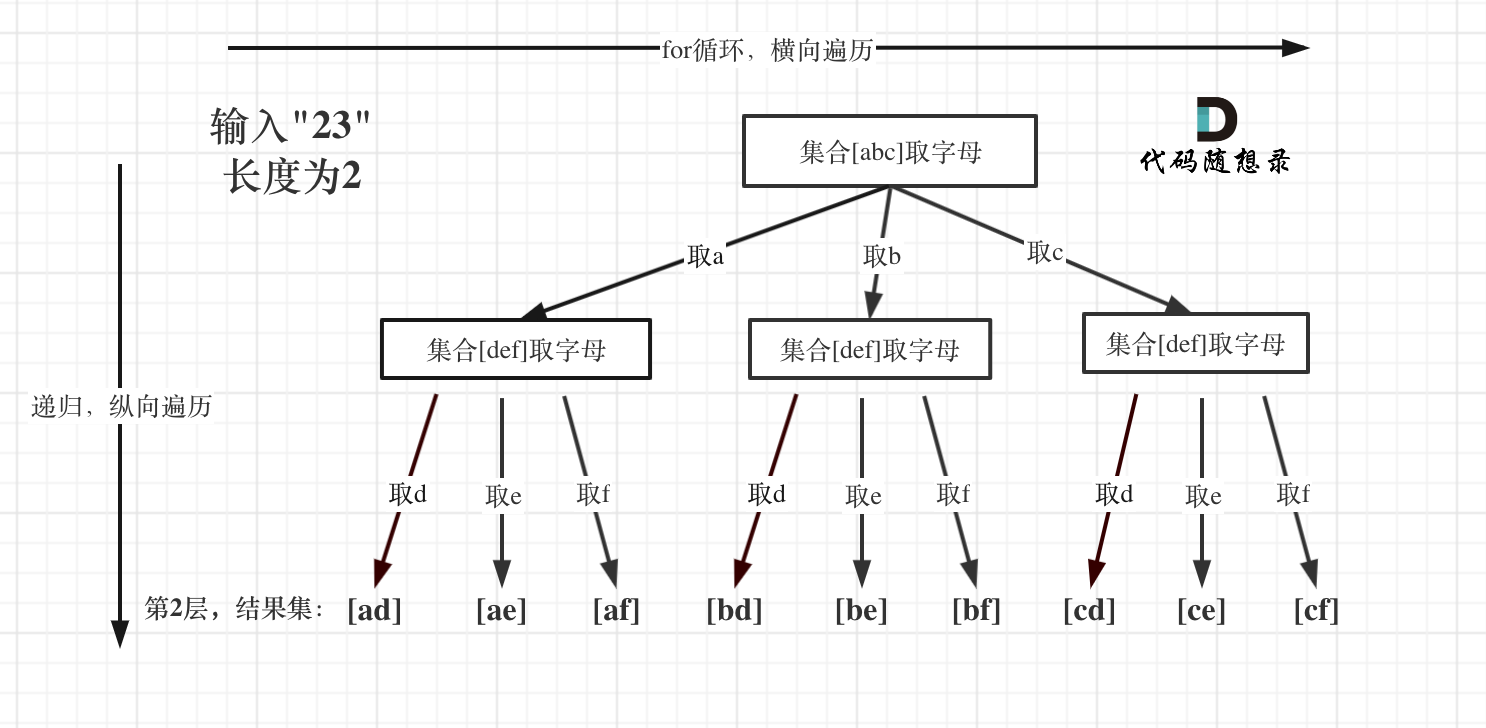
例如:输入:"23",抽象为树形结构,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
|
||||
|
||||
|
|
|
|||
|
|
@ -16,7 +16,7 @@
|
|||
示例 1:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
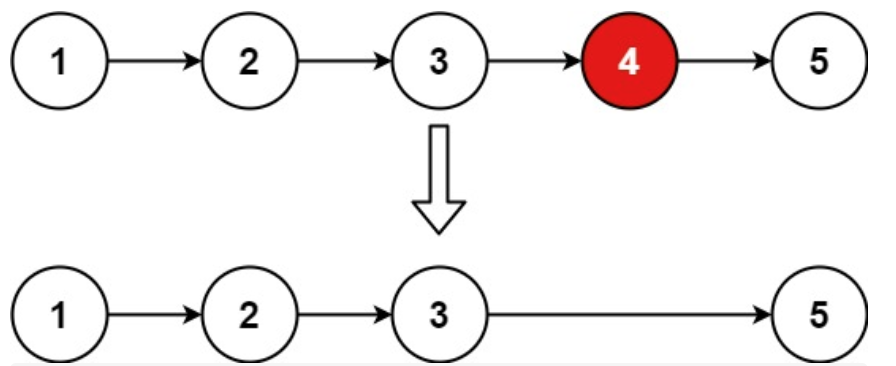
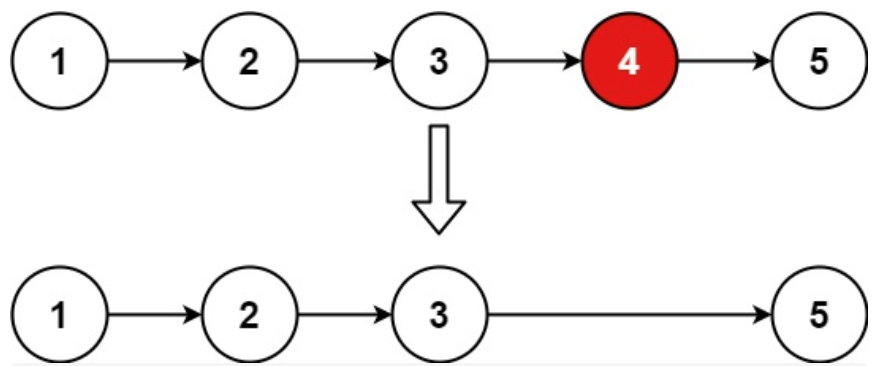
输入:head = [1,2,3,4,5], n = 2
|
||||
输出:[1,2,3,5]
|
||||
|
|
@ -49,16 +49,16 @@
|
|||
|
||||
* 定义fast指针和slow指针,初始值为虚拟头结点,如图:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B9.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B9.png' width=600> </img></div>
|
||||
|
||||
* fast首先走n + 1步 ,为什么是n+1呢,因为只有这样同时移动的时候slow才能指向删除节点的上一个节点(方便做删除操作),如图:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B91.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B91.png' width=600> </img></div>
|
||||
|
||||
* fast和slow同时移动,直到fast指向末尾,如题:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B92.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B92.png' width=600> </img></div>
|
||||
//图片中有错别词:应该将“只到”改为“直到”
|
||||
* 删除slow指向的下一个节点,如图:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B93.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/19.%E5%88%A0%E9%99%A4%E9%93%BE%E8%A1%A8%E7%9A%84%E5%80%92%E6%95%B0%E7%AC%ACN%E4%B8%AA%E8%8A%82%E7%82%B93.png' width=600> </img></div>
|
||||
|
||||
此时不难写出如下C++代码:
|
||||
|
||||
|
|
|
|||
|
|
@ -81,13 +81,13 @@ cd a/b/c/../../
|
|||
|
||||
|
||||
1. 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
|
||||
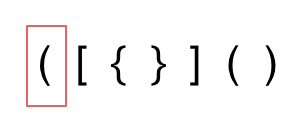
|
||||
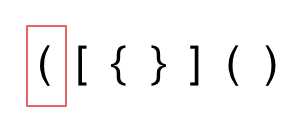
|
||||
|
||||
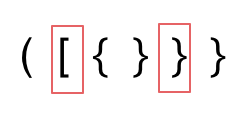
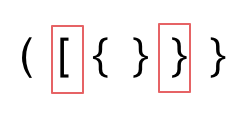
2. 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
|
||||
|
||||
|
||||
|
||||
3. 第三种情况,字符串里右方向的括号多余了,所以不匹配。
|
||||
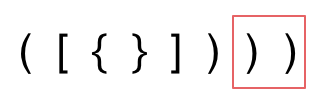
|
||||
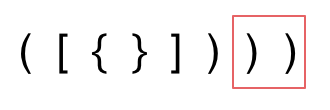
|
||||
|
||||
|
||||
|
||||
|
|
@ -95,7 +95,7 @@ cd a/b/c/../../
|
|||
|
||||
动画如下:
|
||||
|
||||

|
||||
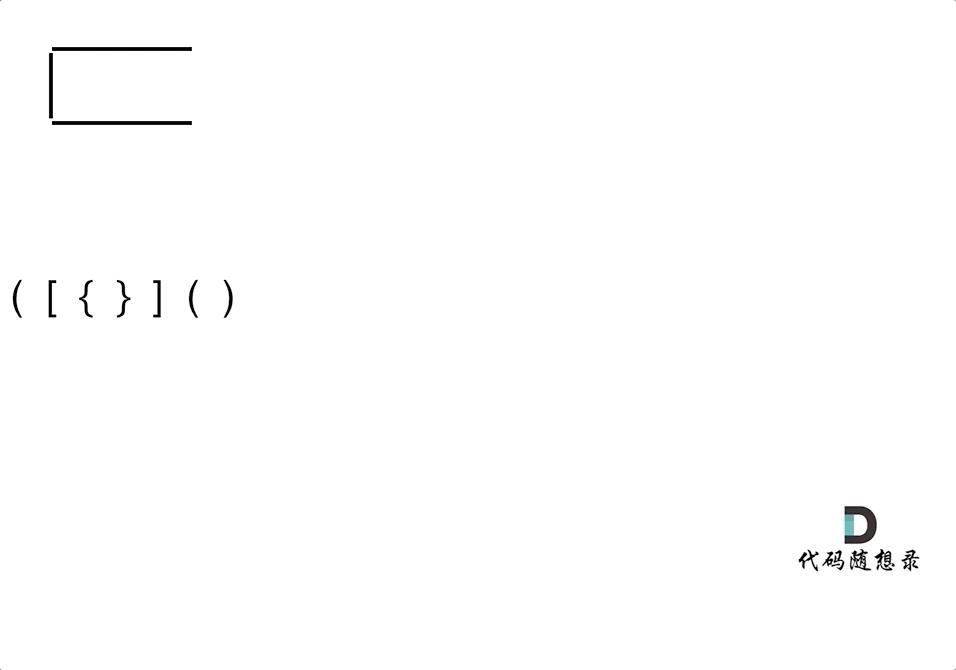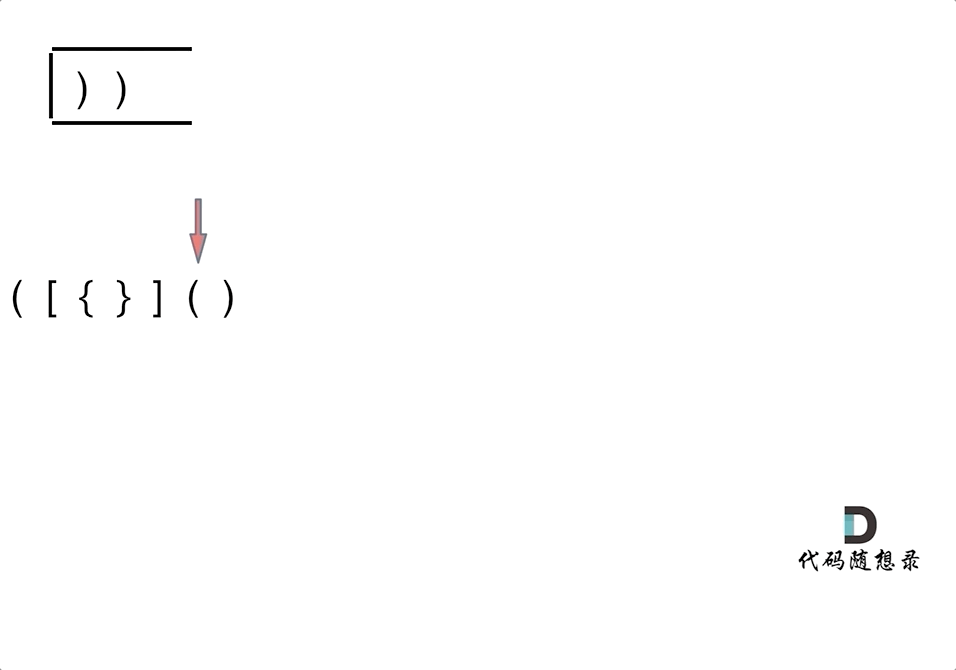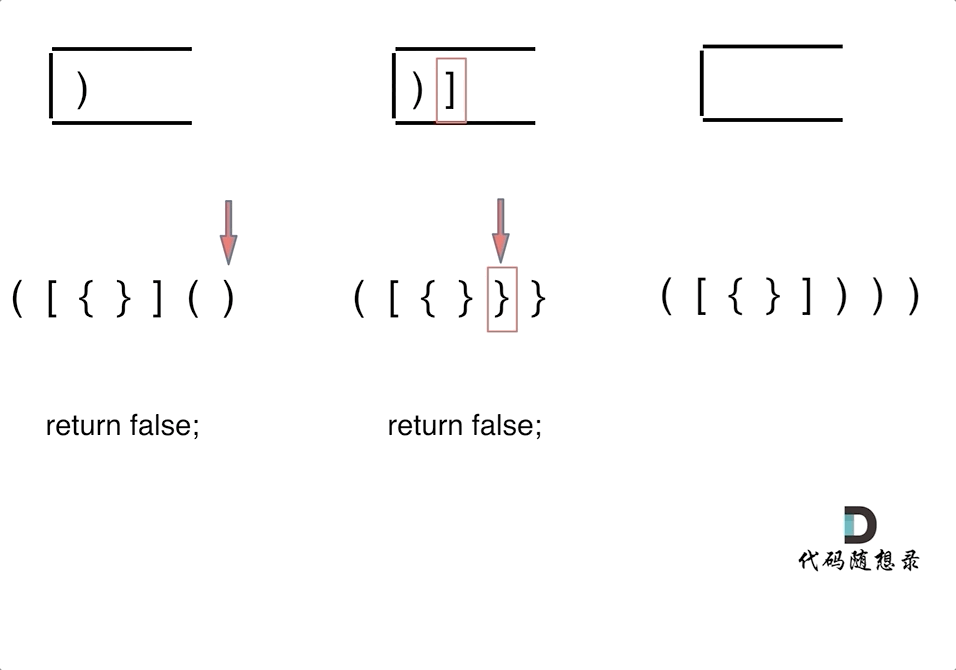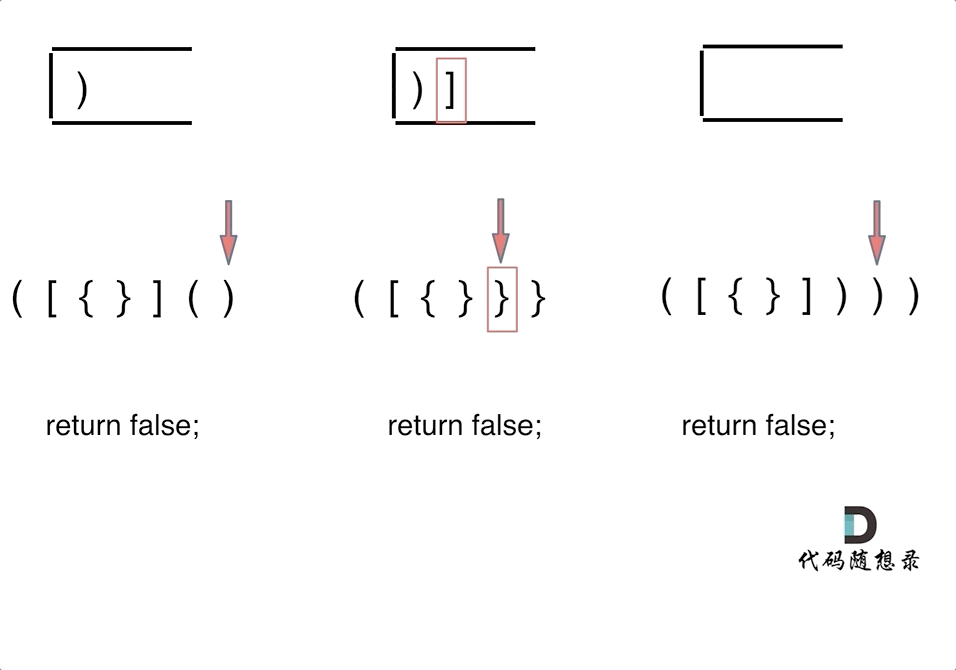
|
||||
|
||||
|
||||
第一种情况:已经遍历完了字符串,但是栈不为空,说明有相应的左括号没有右括号来匹配,所以return false
|
||||
|
|
|
|||
|
|
@ -12,7 +12,7 @@
|
|||
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
|
||||
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/24.%E4%B8%A4%E4%B8%A4%E4%BA%A4%E6%8D%A2%E9%93%BE%E8%A1%A8%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9-%E9%A2%98%E6%84%8F.jpg' width=600 alt='24.两两交换链表中的节点-题意'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/24.%E4%B8%A4%E4%B8%A4%E4%BA%A4%E6%8D%A2%E9%93%BE%E8%A1%A8%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9-%E9%A2%98%E6%84%8F.jpg' width=600 alt='24.两两交换链表中的节点-题意'> </img></div>
|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -31,16 +31,16 @@
|
|||
|
||||
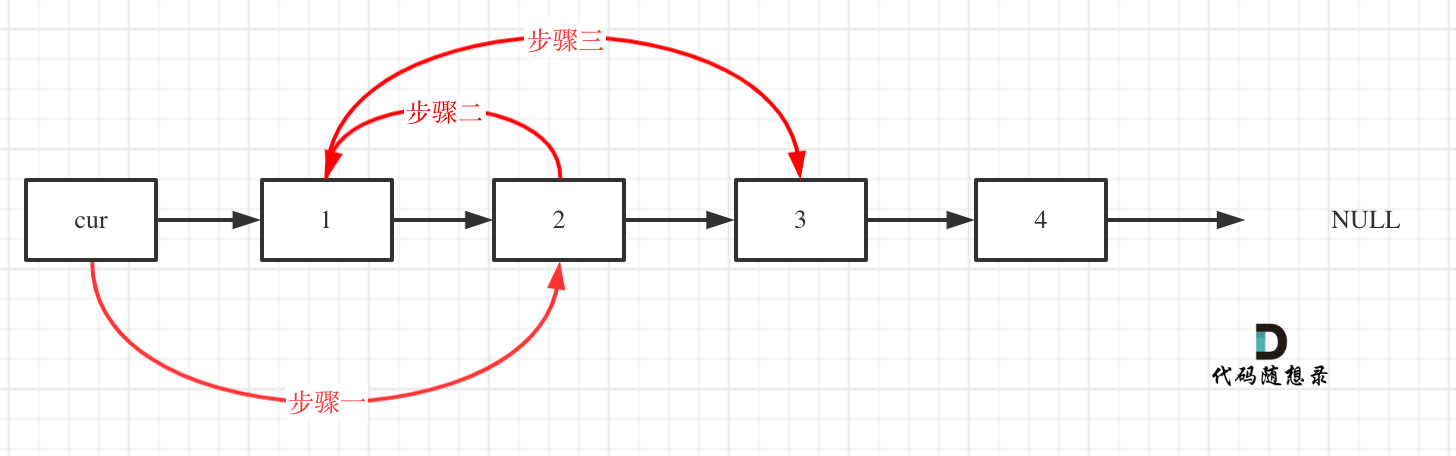
初始时,cur指向虚拟头结点,然后进行如下三步:
|
||||
|
||||

|
||||
|
||||
|
||||
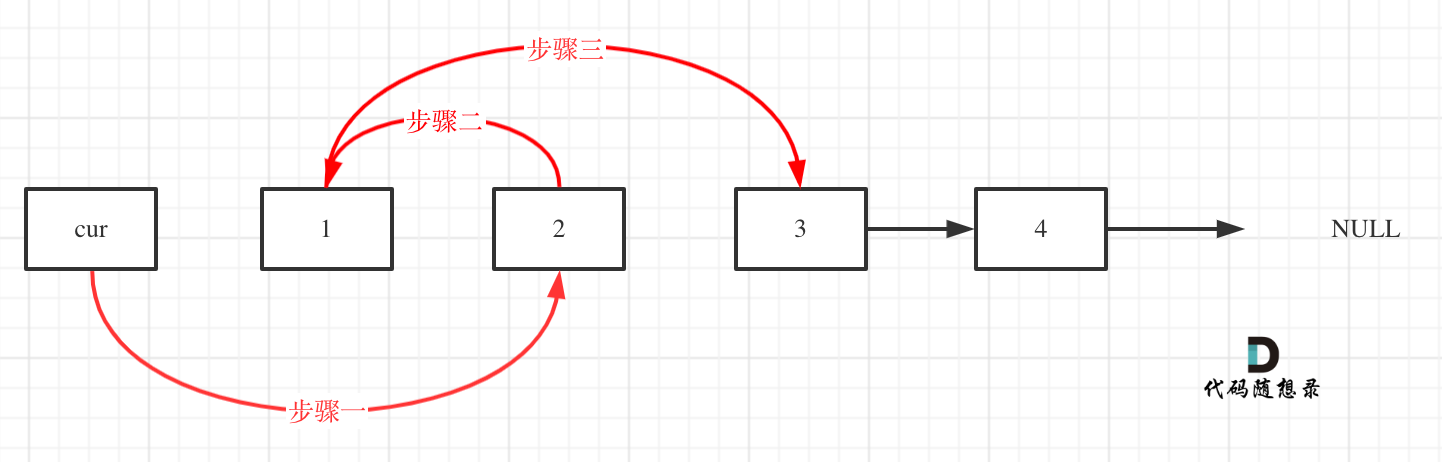
操作之后,链表如下:
|
||||
|
||||

|
||||
|
||||
|
||||
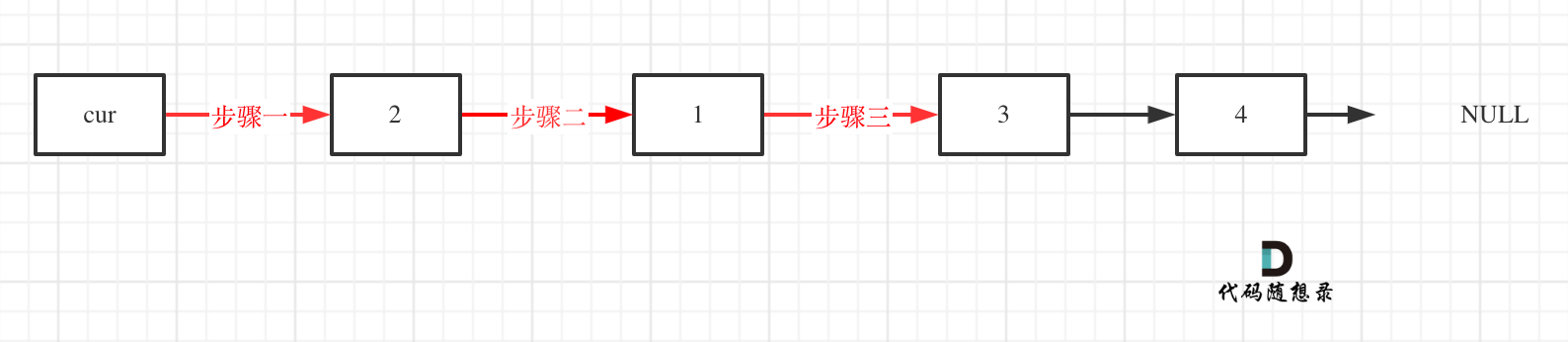
看这个可能就更直观一些了:
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
对应的C++代码实现如下: (注释中详细和如上图中的三步做对应)
|
||||
|
||||
|
|
@ -81,7 +81,7 @@ public:
|
|||
|
||||
心想应该没有更好的方法了吧,也就 $O(n)$ 的时间复杂度,重复提交几次,这样了:
|
||||
|
||||

|
||||

|
||||
|
||||
力扣上的统计如果两份代码是 100ms 和 300ms的耗时,其实是需要注意的。
|
||||
|
||||
|
|
|
|||
|
|
@ -43,7 +43,7 @@
|
|||
|
||||
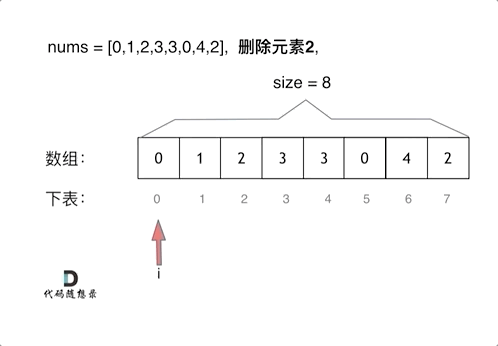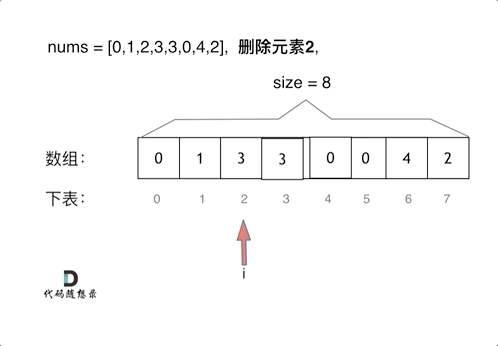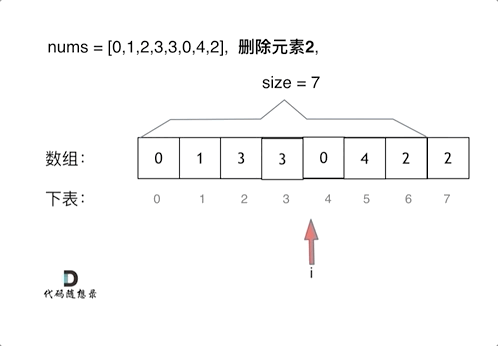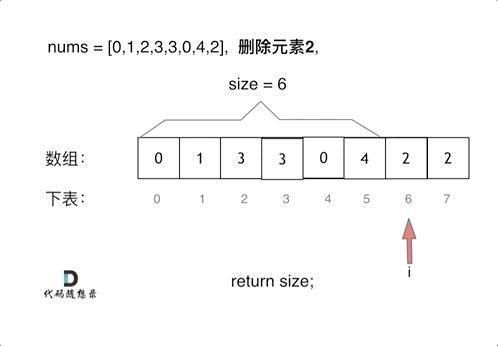
删除过程如下:
|
||||
|
||||

|
||||
|
||||
|
||||
很明显暴力解法的时间复杂度是O(n^2),这道题目暴力解法在leetcode上是可以过的。
|
||||
|
||||
|
|
@ -87,7 +87,7 @@ public:
|
|||
|
||||
删除过程如下:
|
||||
|
||||

|
||||
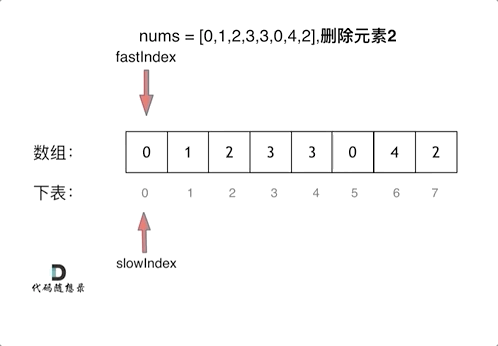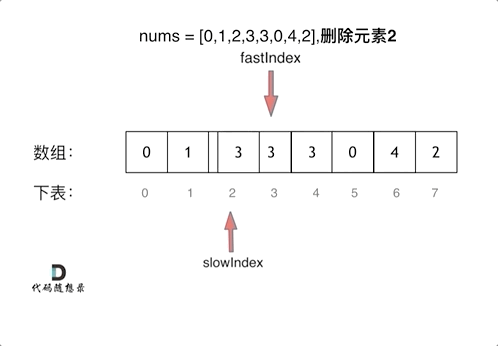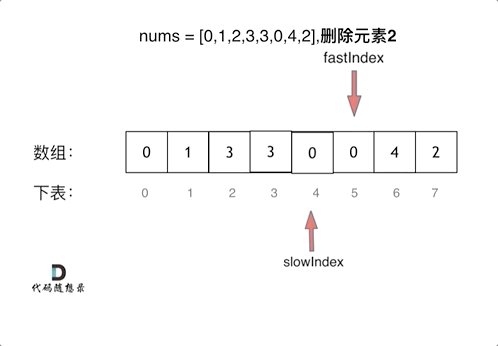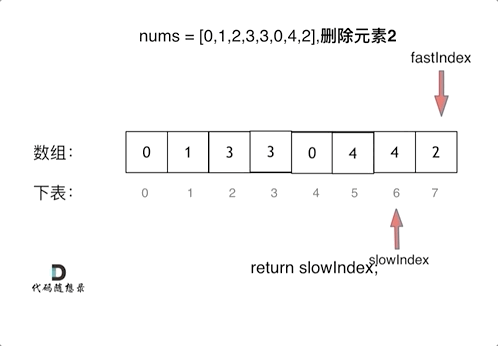
|
||||
|
||||
很多同学不了解
|
||||
|
||||
|
|
|
|||
|
|
@ -106,7 +106,7 @@ next数组就是一个前缀表(prefix table)。
|
|||
|
||||
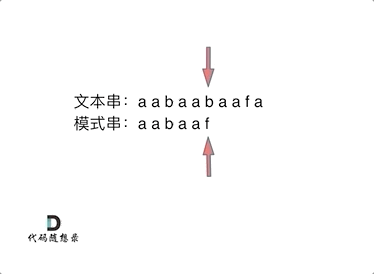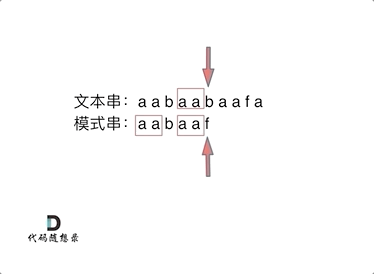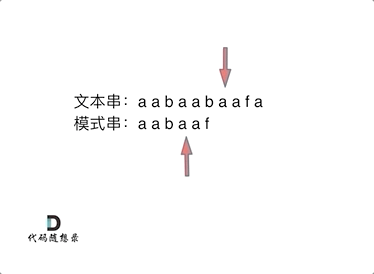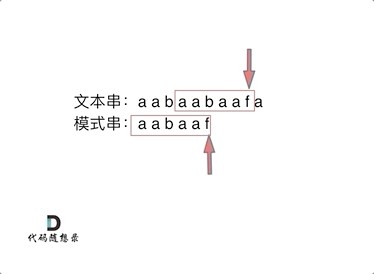
如动画所示:
|
||||
|
||||

|
||||
|
||||
|
||||
动画里,我特意把 子串`aa` 标记上了,这是有原因的,大家先注意一下,后面还会说到。
|
||||
|
||||
|
|
@ -147,11 +147,11 @@ next数组就是一个前缀表(prefix table)。
|
|||
这就是前缀表,那为啥就能告诉我们 上次匹配的位置,并跳过去呢?
|
||||
|
||||
回顾一下,刚刚匹配的过程在下标5的地方遇到不匹配,模式串是指向f,如图:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/KMP%E7%B2%BE%E8%AE%B21.png' width=600 alt='KMP精讲1'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/KMP%E7%B2%BE%E8%AE%B21.png' width=600 alt='KMP精讲1'> </img></div>
|
||||
|
||||
|
||||
然后就找到了下标2,指向b,继续匹配:如图:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/KMP%E7%B2%BE%E8%AE%B22.png' width=600 alt='KMP精讲2'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/KMP%E7%B2%BE%E8%AE%B22.png' width=600 alt='KMP精讲2'> </img></div>
|
||||
|
||||
以下这句话,对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要!
|
||||
|
||||
|
|
@ -167,15 +167,15 @@ next数组就是一个前缀表(prefix table)。
|
|||
|
||||
如图:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/KMP%E7%B2%BE%E8%AE%B25.png' width=600 alt='KMP精讲5'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/KMP%E7%B2%BE%E8%AE%B25.png' width=600 alt='KMP精讲5'> </img></div>
|
||||
|
||||
长度为前1个字符的子串`a`,最长相同前后缀的长度为0。(注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**;**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。)
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/KMP%E7%B2%BE%E8%AE%B26.png' width=600 alt='KMP精讲6'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/KMP%E7%B2%BE%E8%AE%B26.png' width=600 alt='KMP精讲6'> </img></div>
|
||||
|
||||
长度为前2个字符的子串`aa`,最长相同前后缀的长度为1。
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/KMP%E7%B2%BE%E8%AE%B27.png' width=600 alt='KMP精讲7'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/KMP%E7%B2%BE%E8%AE%B27.png' width=600 alt='KMP精讲7'> </img></div>
|
||||
|
||||
长度为前3个字符的子串`aab`,最长相同前后缀的长度为0。
|
||||
|
||||
|
|
@ -185,13 +185,13 @@ next数组就是一个前缀表(prefix table)。
|
|||
长度为前6个字符的子串`aabaaf`,最长相同前后缀的长度为0。
|
||||
|
||||
那么把求得的最长相同前后缀的长度就是对应前缀表的元素,如图:
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/KMP%E7%B2%BE%E8%AE%B28.png' width=600 alt='KMP精讲8'> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/KMP%E7%B2%BE%E8%AE%B28.png' width=600 alt='KMP精讲8'> </img></div>
|
||||
|
||||
可以看出模式串与前缀表对应位置的数字表示的就是:**下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。**
|
||||
|
||||
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:
|
||||
|
||||

|
||||
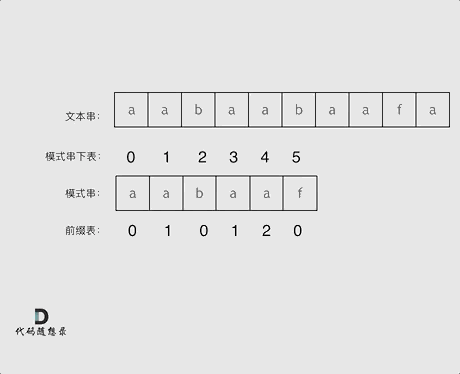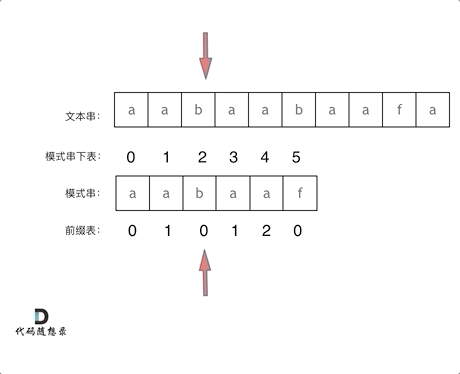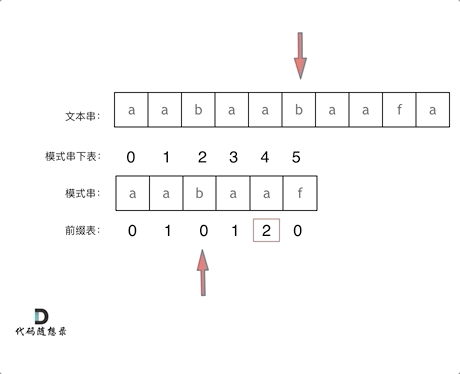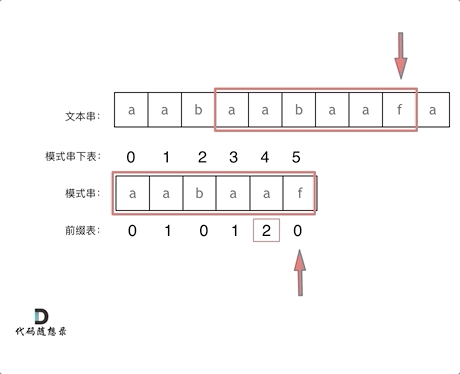
|
||||
|
||||
找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
|
||||
|
||||
|
|
@ -225,7 +225,7 @@ next数组就可以是前缀表,但是很多实现都是把前缀表统一减
|
|||
|
||||
匹配过程动画如下:
|
||||
|
||||

|
||||
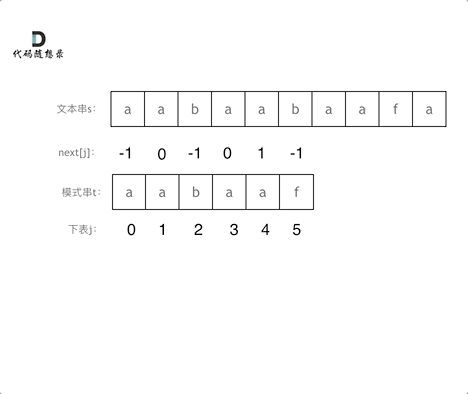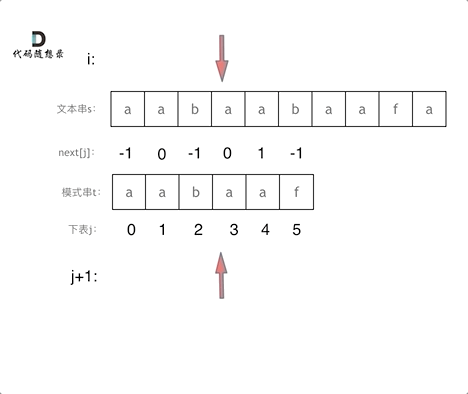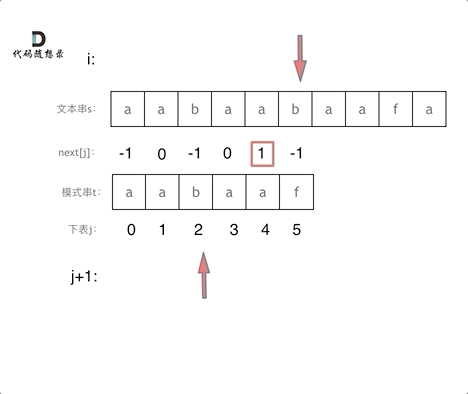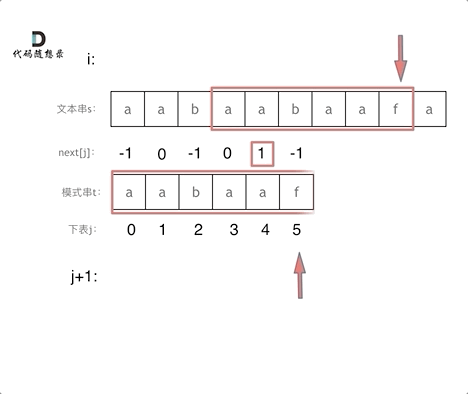
|
||||
|
||||
### 时间复杂度分析
|
||||
|
||||
|
|
@ -332,7 +332,7 @@ void getNext(int* next, const string& s){
|
|||
|
||||
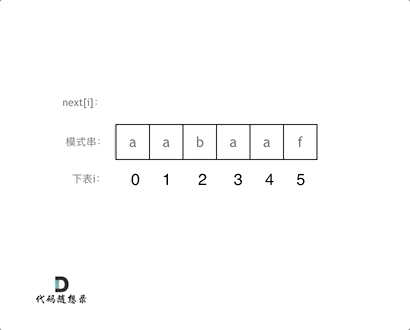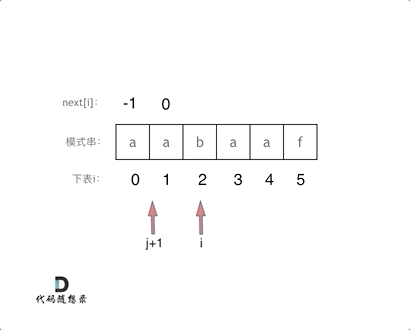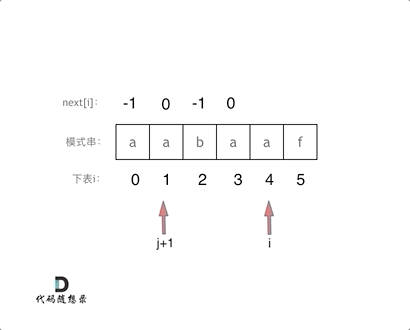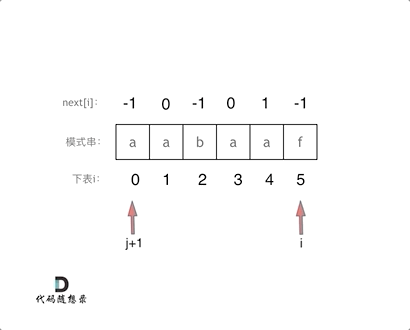
代码构造next数组的逻辑流程动画如下:
|
||||
|
||||

|
||||
|
||||
|
||||
得到了next数组之后,就要用这个来做匹配了。
|
||||
|
||||
|
|
|
|||
|
|
@ -67,7 +67,7 @@
|
|||
|
||||
以求1243为例,流程如图:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/31.下一个排列.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/31.下一个排列.png' width=600> </img></div>
|
||||
|
||||
对应的C++代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -41,7 +41,7 @@
|
|||
|
||||
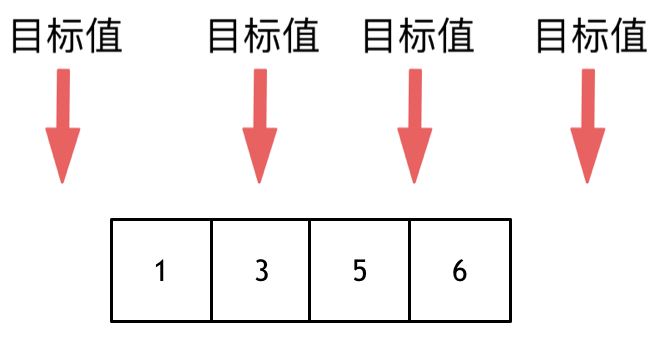
这道题目,要在数组中插入目标值,无非是这四种情况。
|
||||
|
||||

|
||||
|
||||
|
||||
* 目标值在数组所有元素之前
|
||||
* 目标值等于数组中某一个元素
|
||||
|
|
@ -82,14 +82,14 @@ public:
|
|||
|
||||
效率如下:
|
||||
|
||||

|
||||

|
||||
|
||||
### 二分法
|
||||
|
||||
既然暴力解法的时间复杂度是O(n),就要尝试一下使用二分查找法。
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
大家注意这道题目的前提是数组是有序数组,这也是使用二分查找的基础条件。
|
||||
|
||||
|
|
@ -99,7 +99,7 @@ public:
|
|||
|
||||
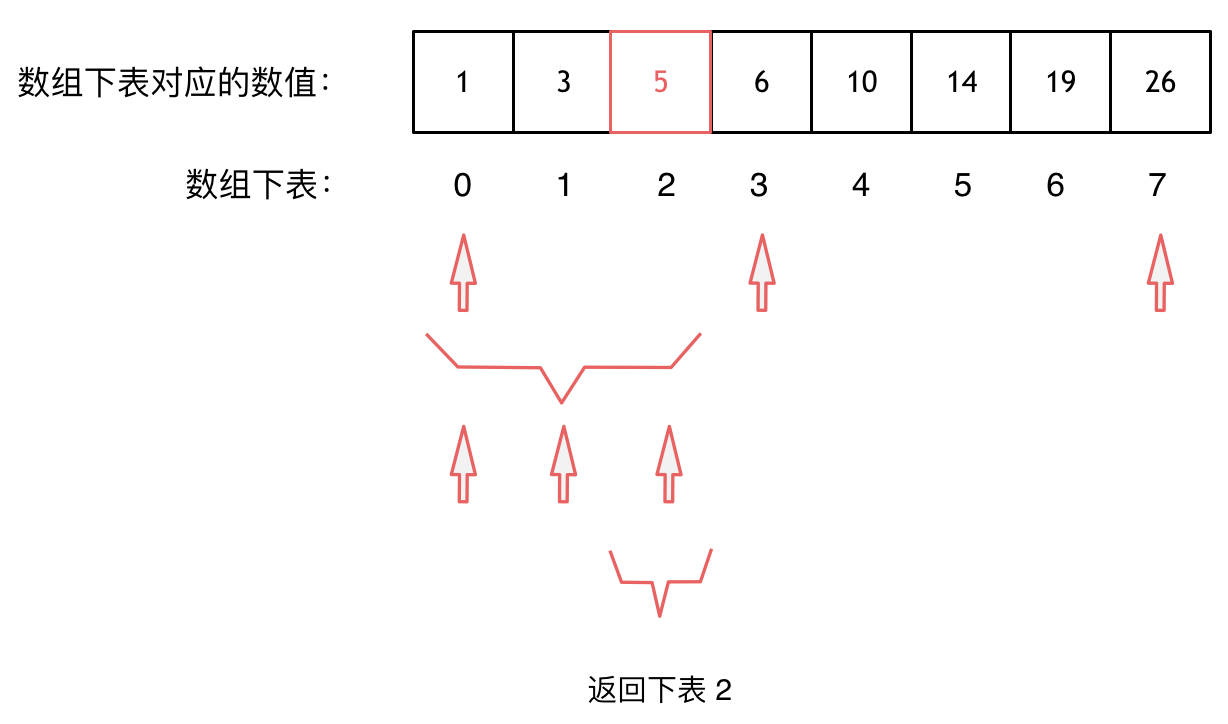
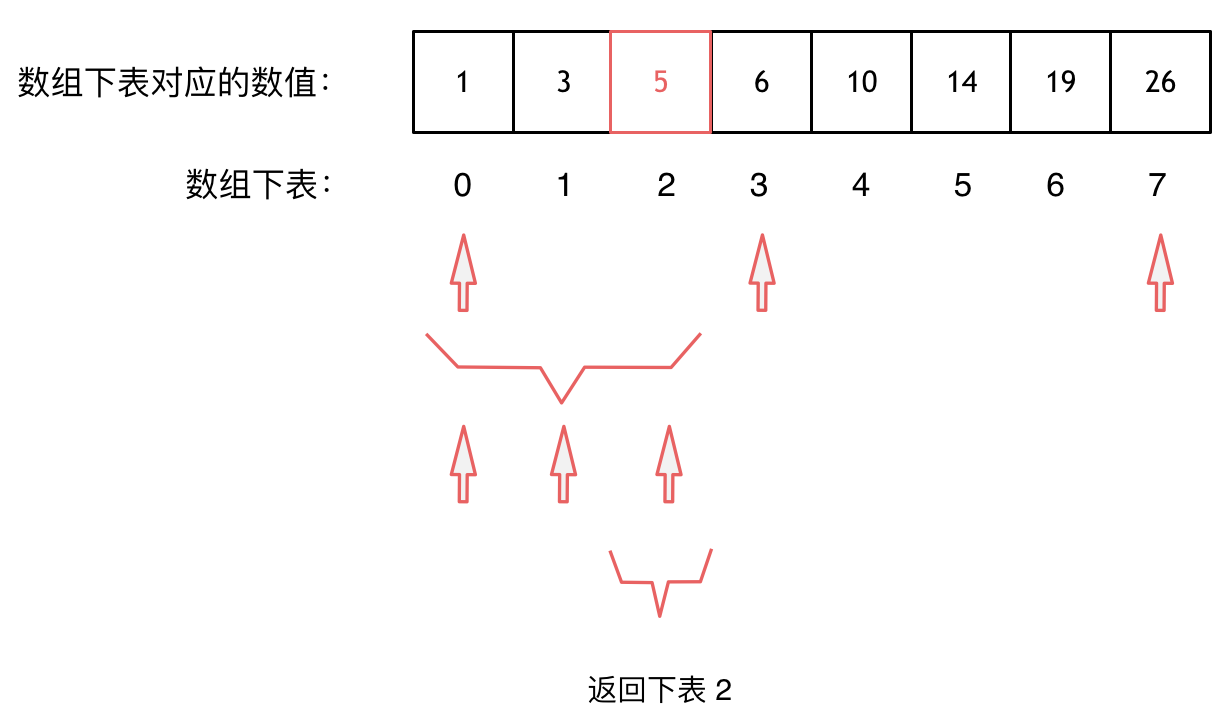
大体讲解一下二分法的思路,这里来举一个例子,例如在这个数组中,使用二分法寻找元素为5的位置,并返回其下标。
|
||||
|
||||
|
||||
|
||||
|
||||
二分查找涉及的很多的边界条件,逻辑比较简单,就是写不好。
|
||||
|
||||
|
|
@ -150,7 +150,7 @@ public:
|
|||
* 空间复杂度:O(1)
|
||||
|
||||
效率如下:
|
||||

|
||||

|
||||
|
||||
### 二分法第二种写法
|
||||
|
||||
|
|
|
|||
|
|
@ -18,11 +18,11 @@
|
|||
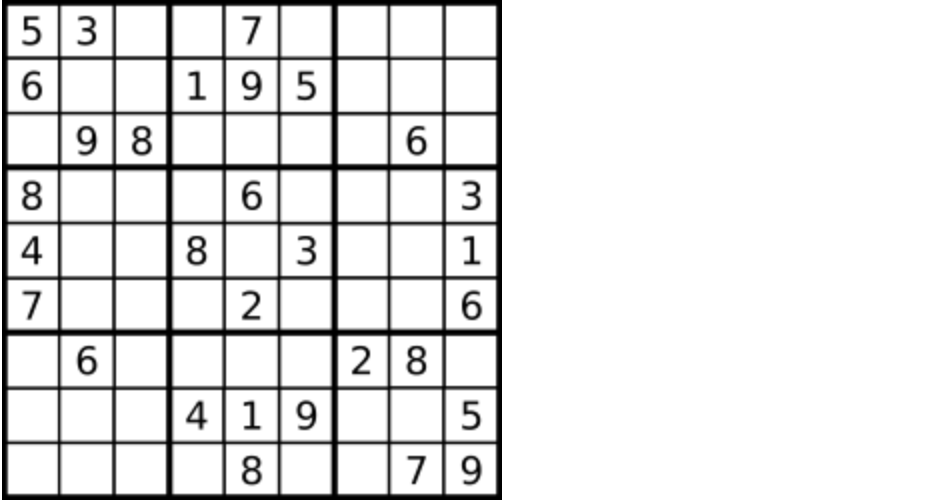
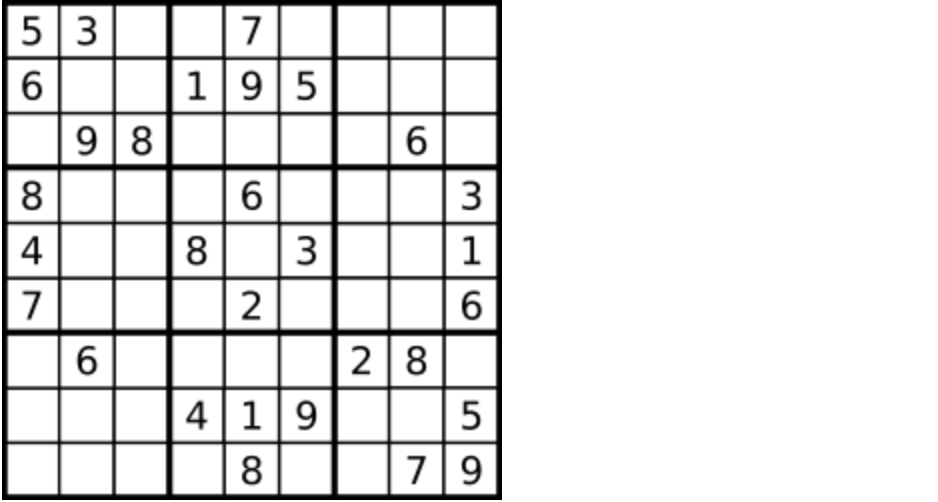
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
|
||||
空白格用 '.' 表示。
|
||||
|
||||
|
||||
|
||||
|
||||
一个数独。
|
||||
|
||||
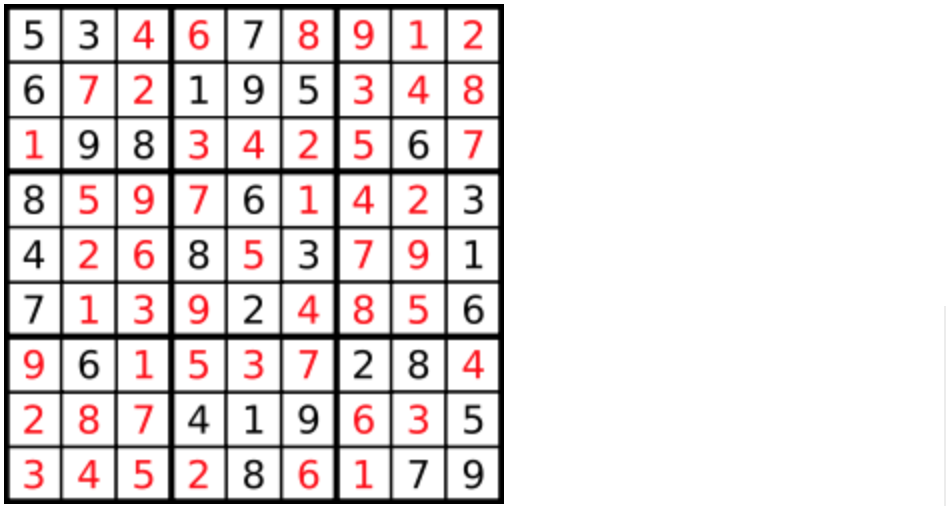
|
||||
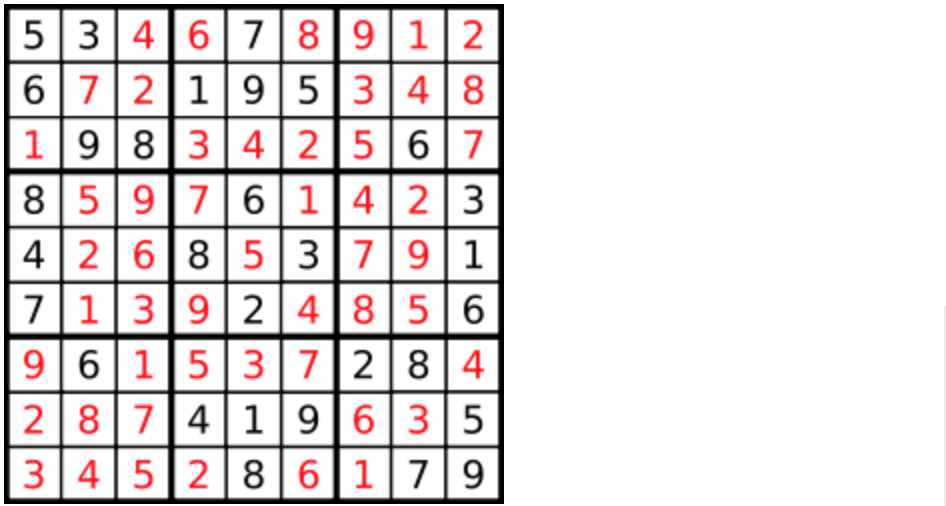
|
||||
|
||||
答案被标成红色。
|
||||
|
||||
|
|
@ -52,7 +52,7 @@
|
|||
|
||||
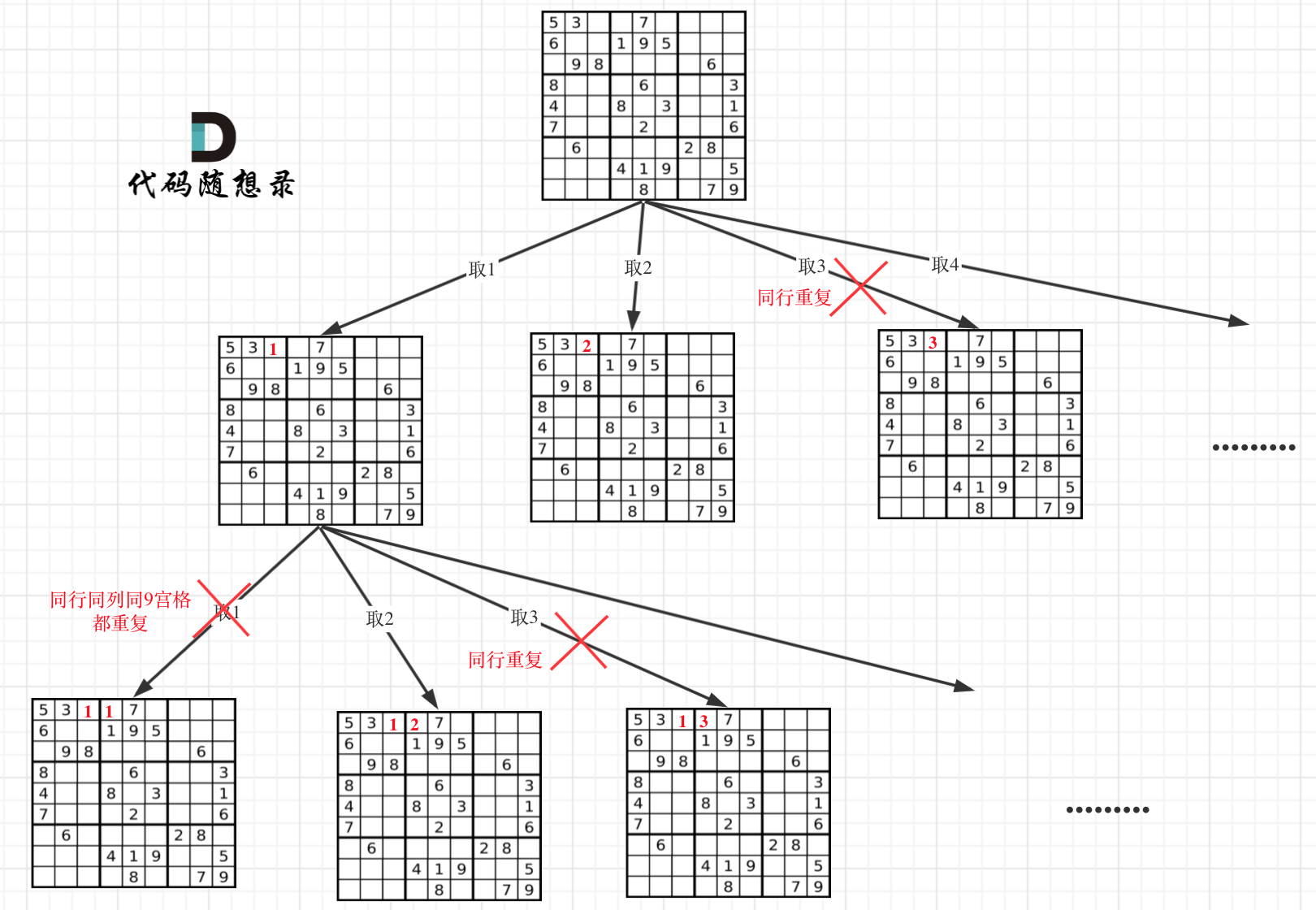
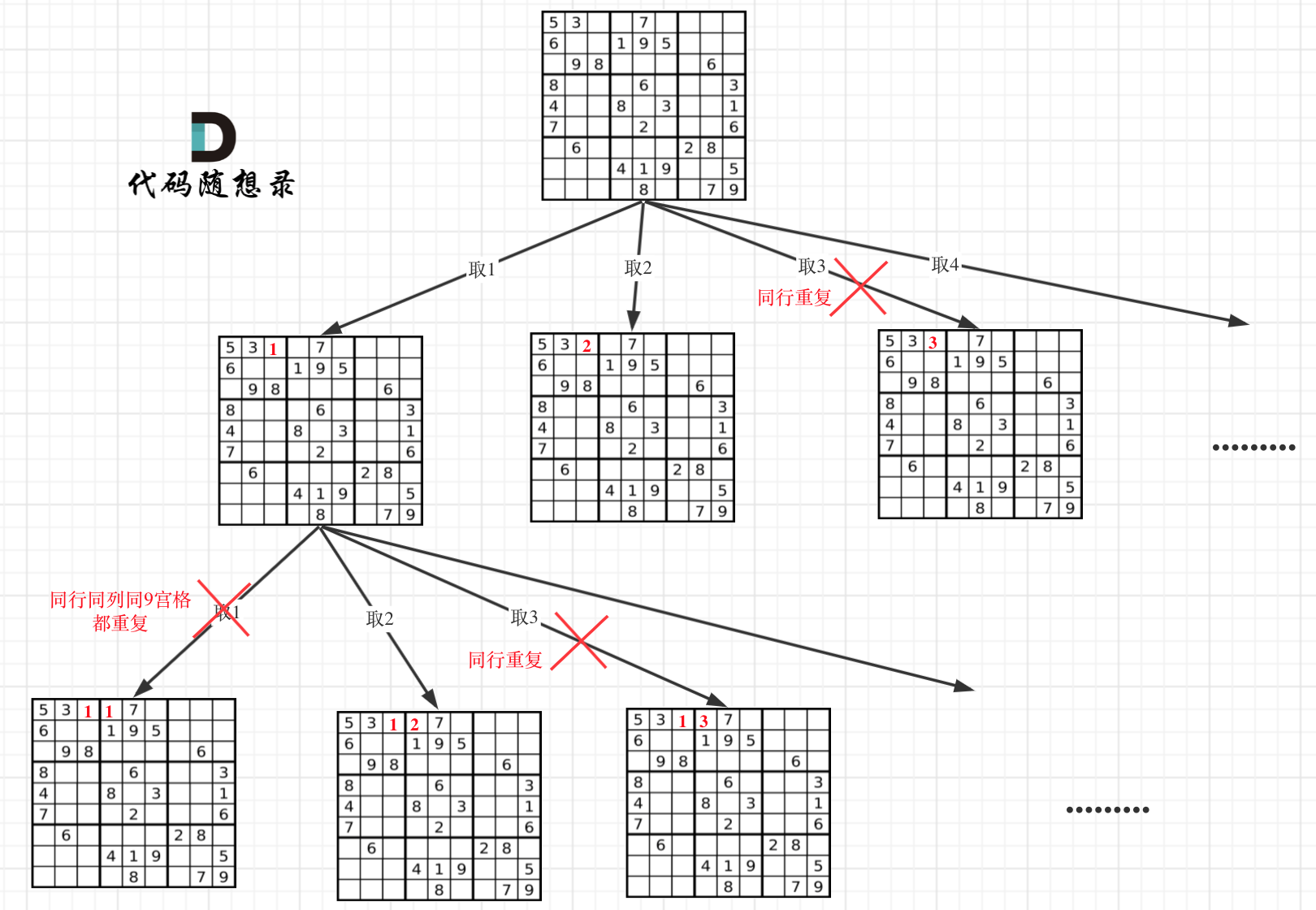
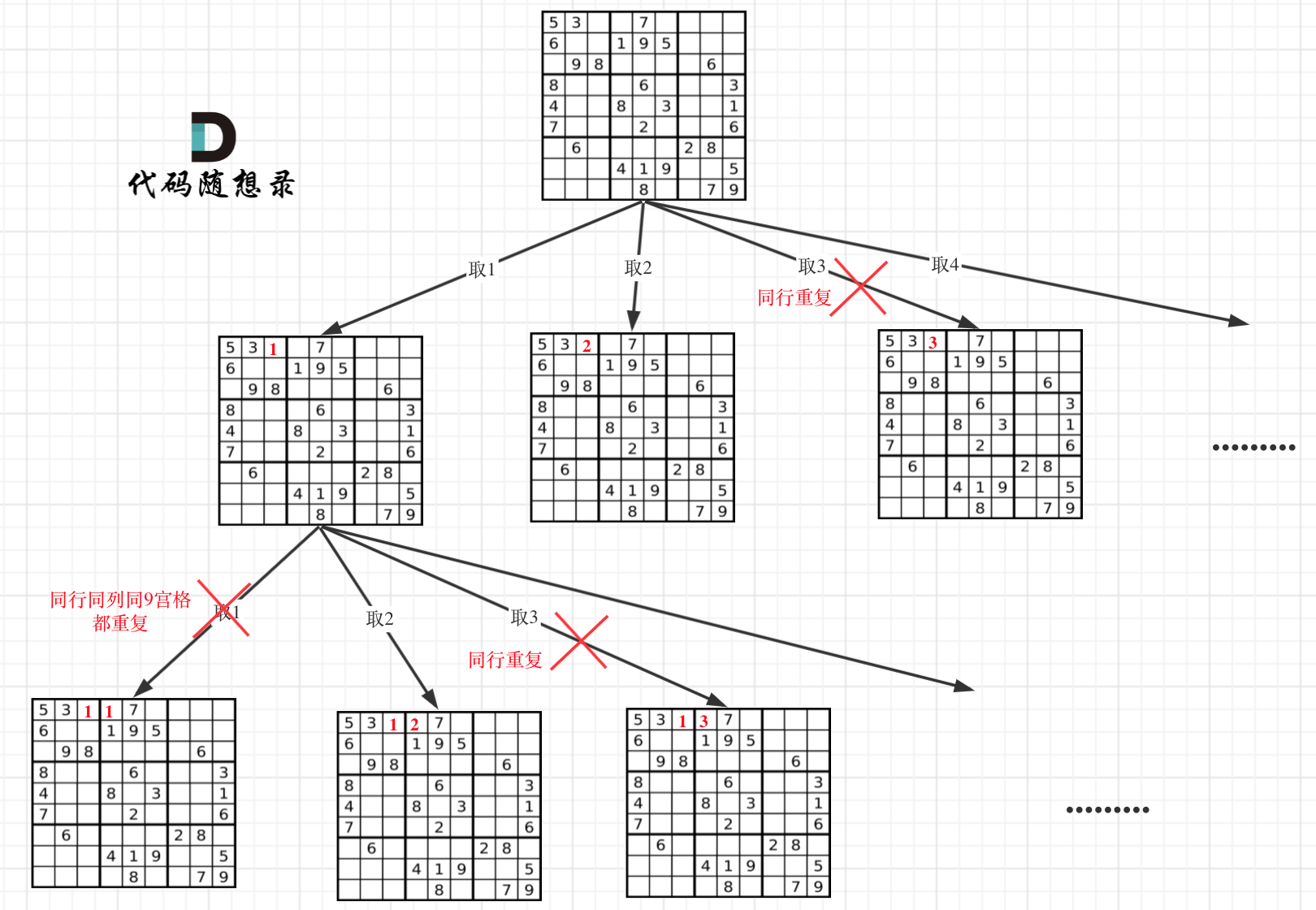
因为这个树形结构太大了,我抽取一部分,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 回溯三部曲
|
||||
|
|
@ -83,7 +83,7 @@ bool backtracking(vector<vector<char>>& board)
|
|||
|
||||
* 递归单层搜索逻辑
|
||||
|
||||

|
||||
|
||||
|
||||
在树形图中可以看出我们需要的是一个二维的递归 (一行一列)
|
||||
|
||||
|
|
|
|||
|
|
@ -50,7 +50,7 @@ candidates 中的数字可以无限制重复被选取。
|
|||
|
||||
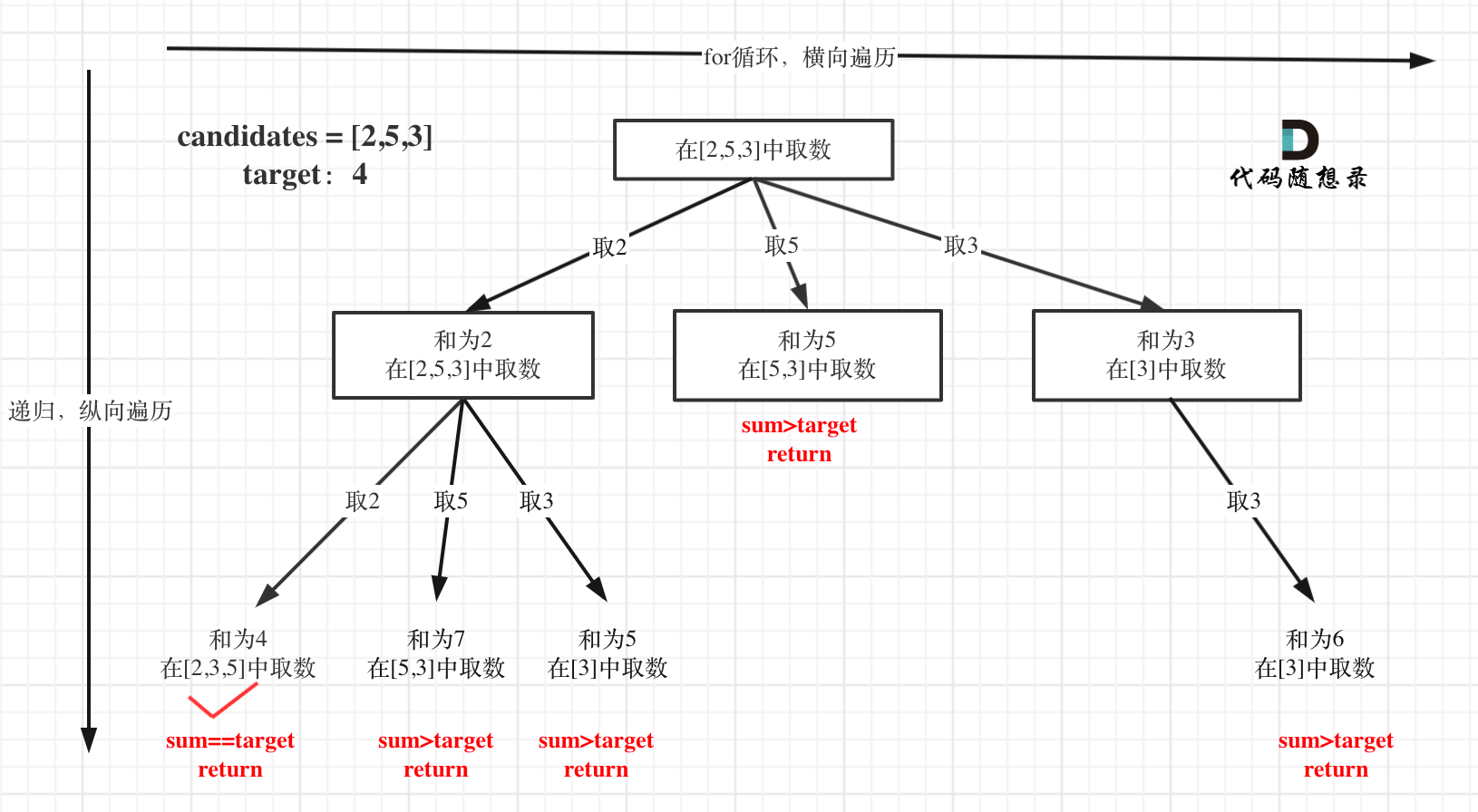
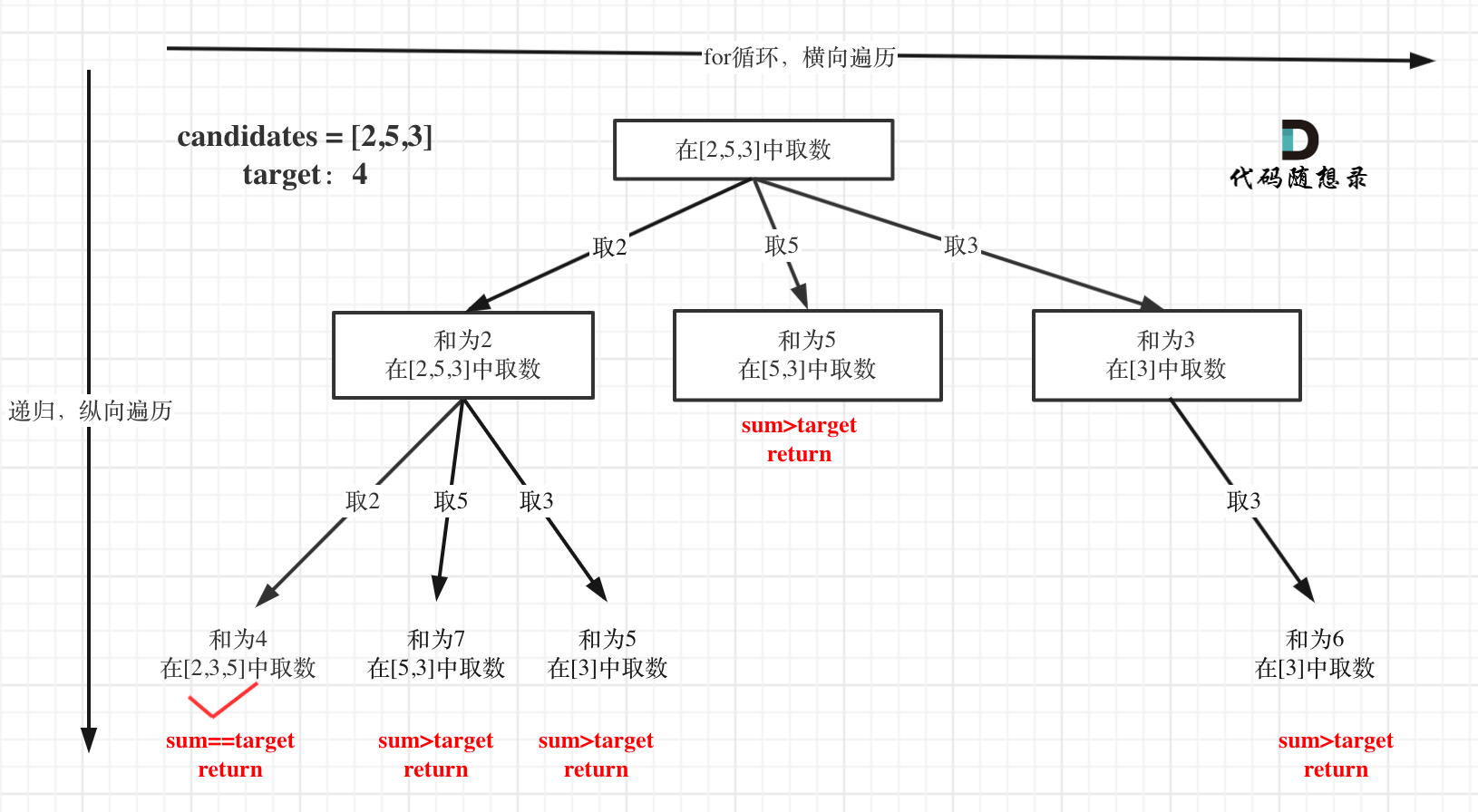
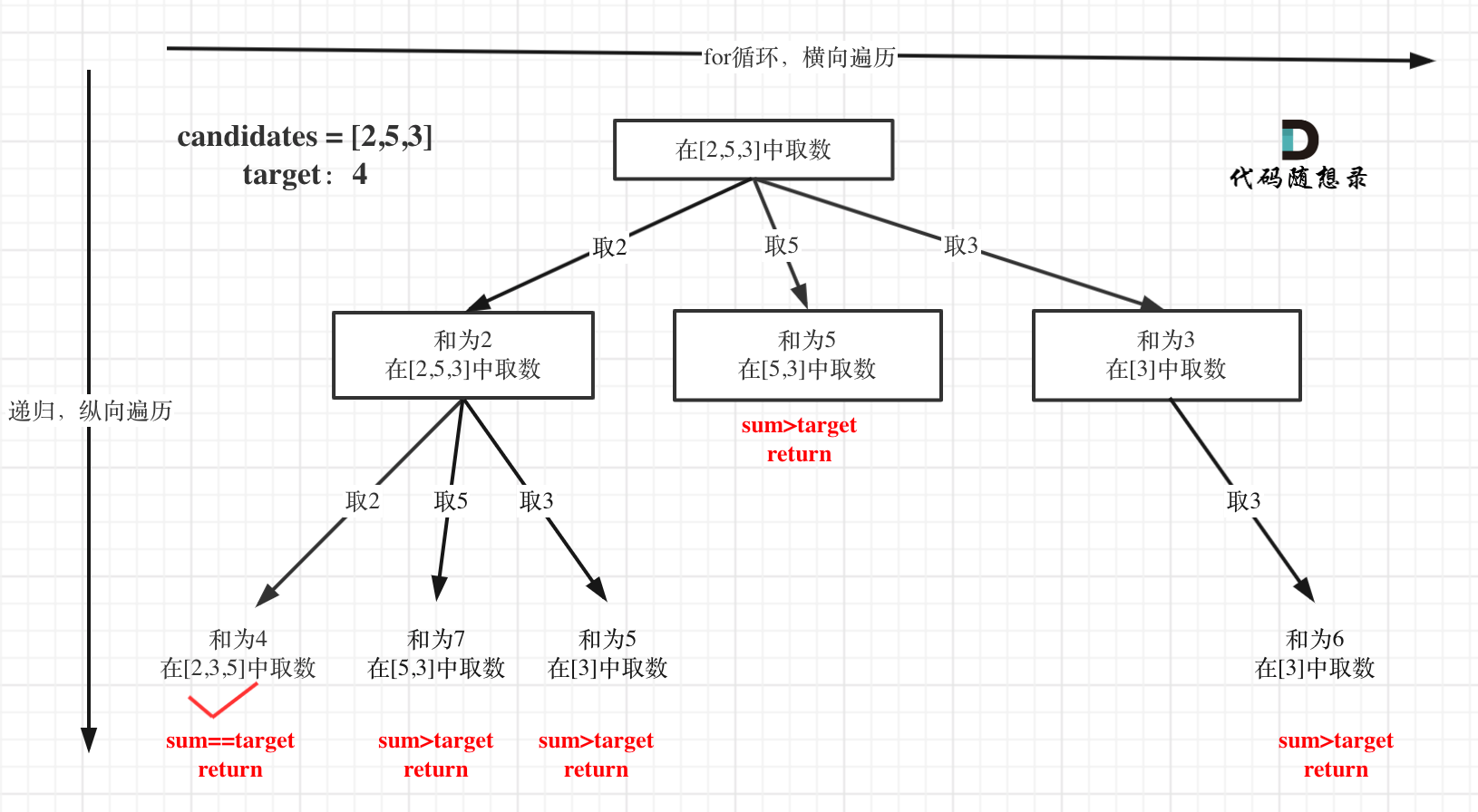
本题搜索的过程抽象成树形结构如下:
|
||||
|
||||
|
||||
|
||||
注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
|
||||
|
||||
而在[77.组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html) 中都可以知道要递归K层,因为要取k个元素的组合。
|
||||
|
|
@ -85,7 +85,7 @@ void backtracking(vector<int>& candidates, int target, int sum, int startIndex)
|
|||
|
||||
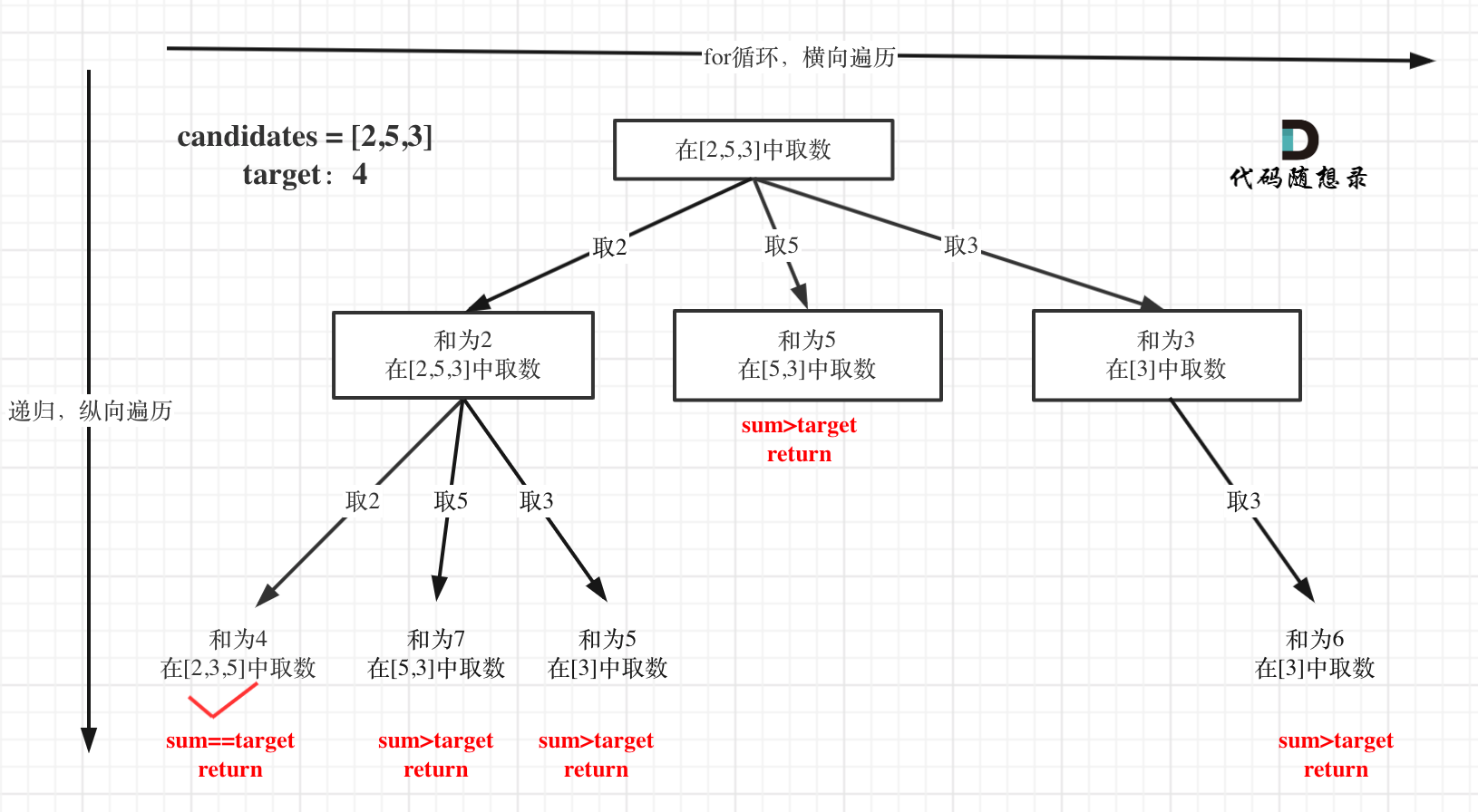
在如下树形结构中:
|
||||
|
||||
|
||||
|
||||
|
||||
从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。
|
||||
|
||||
|
|
@ -158,7 +158,7 @@ public:
|
|||
|
||||
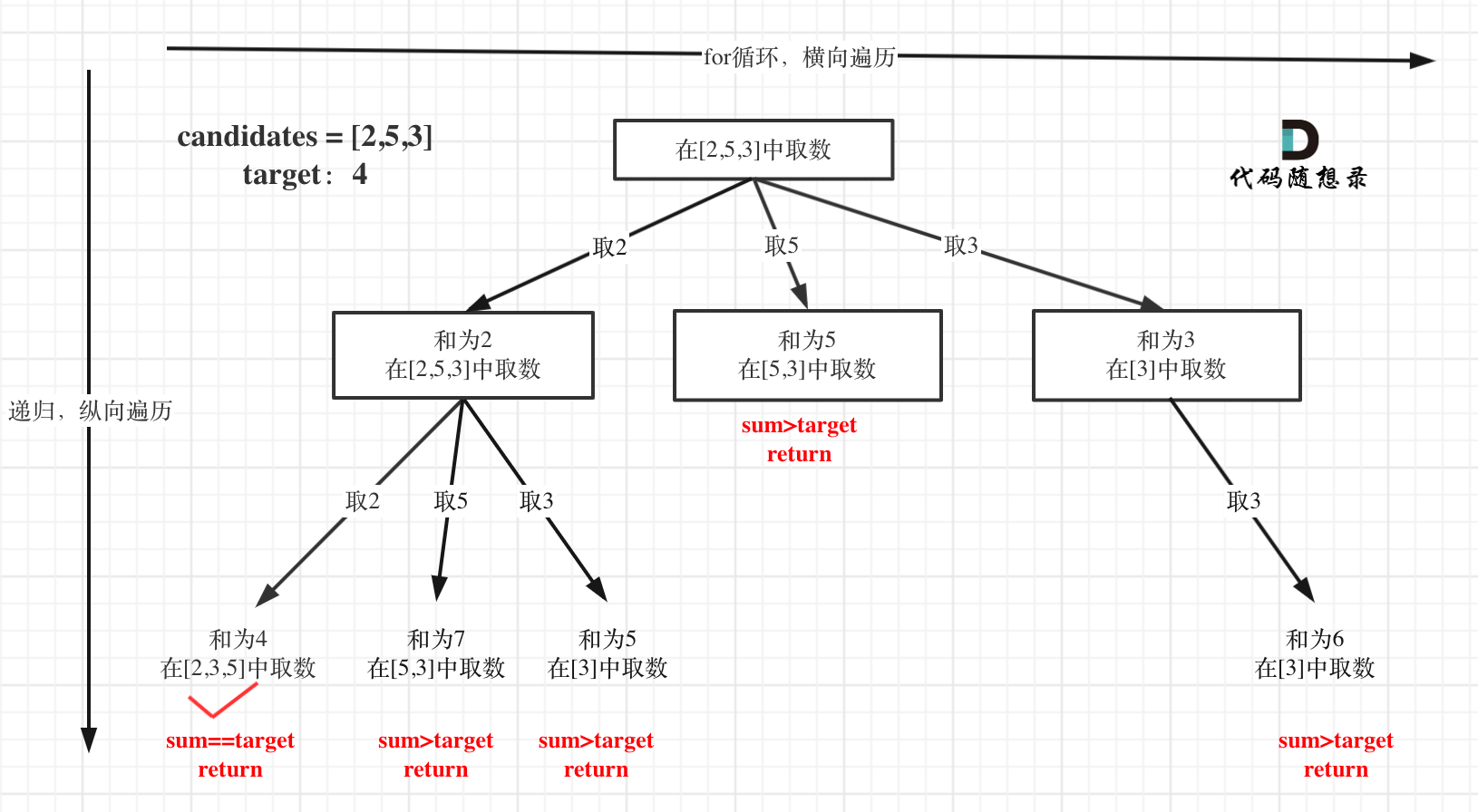
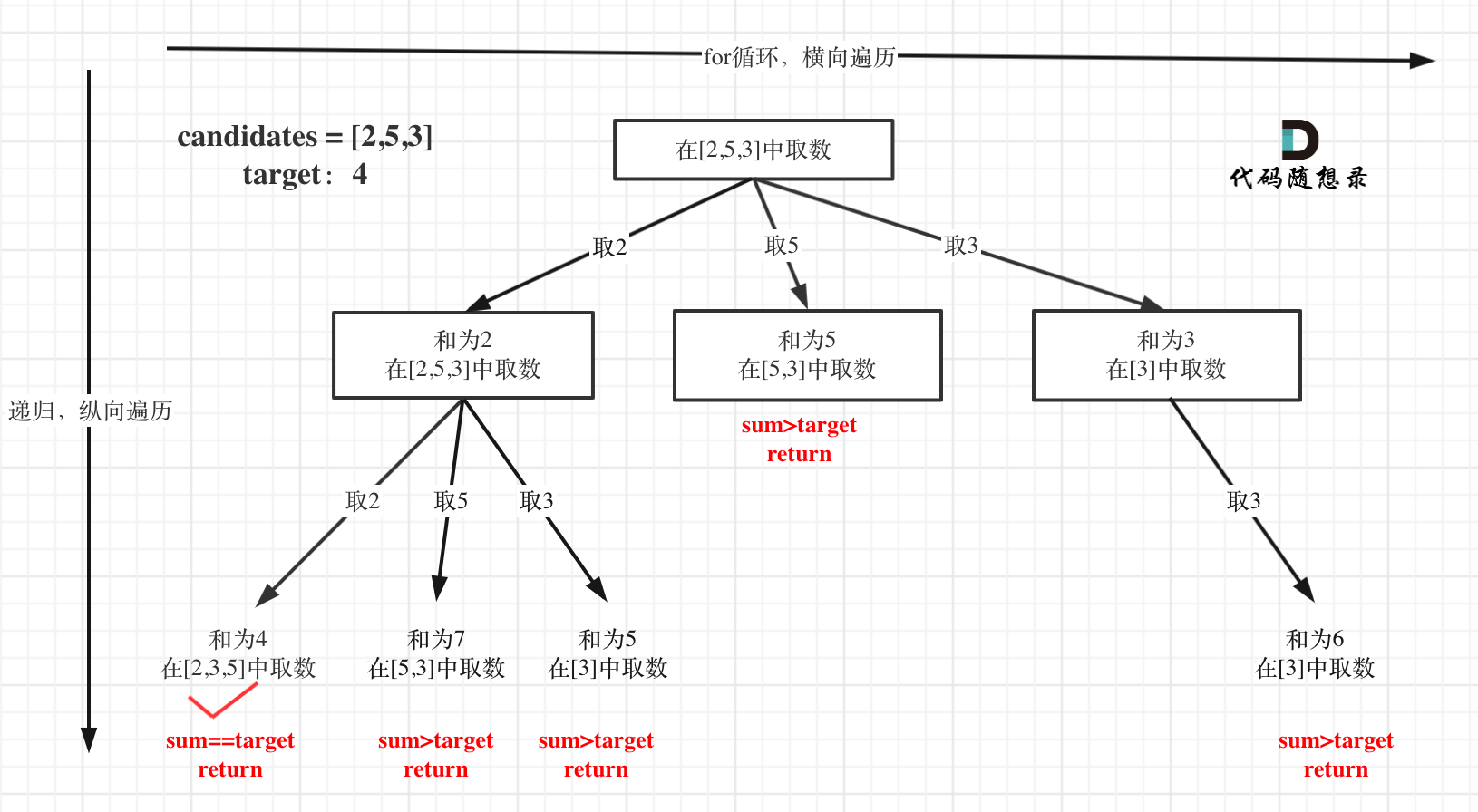
在这个树形结构中:
|
||||
|
||||
|
||||
|
||||
|
||||
以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
|
||||
|
||||
|
|
@ -171,7 +171,7 @@ public:
|
|||
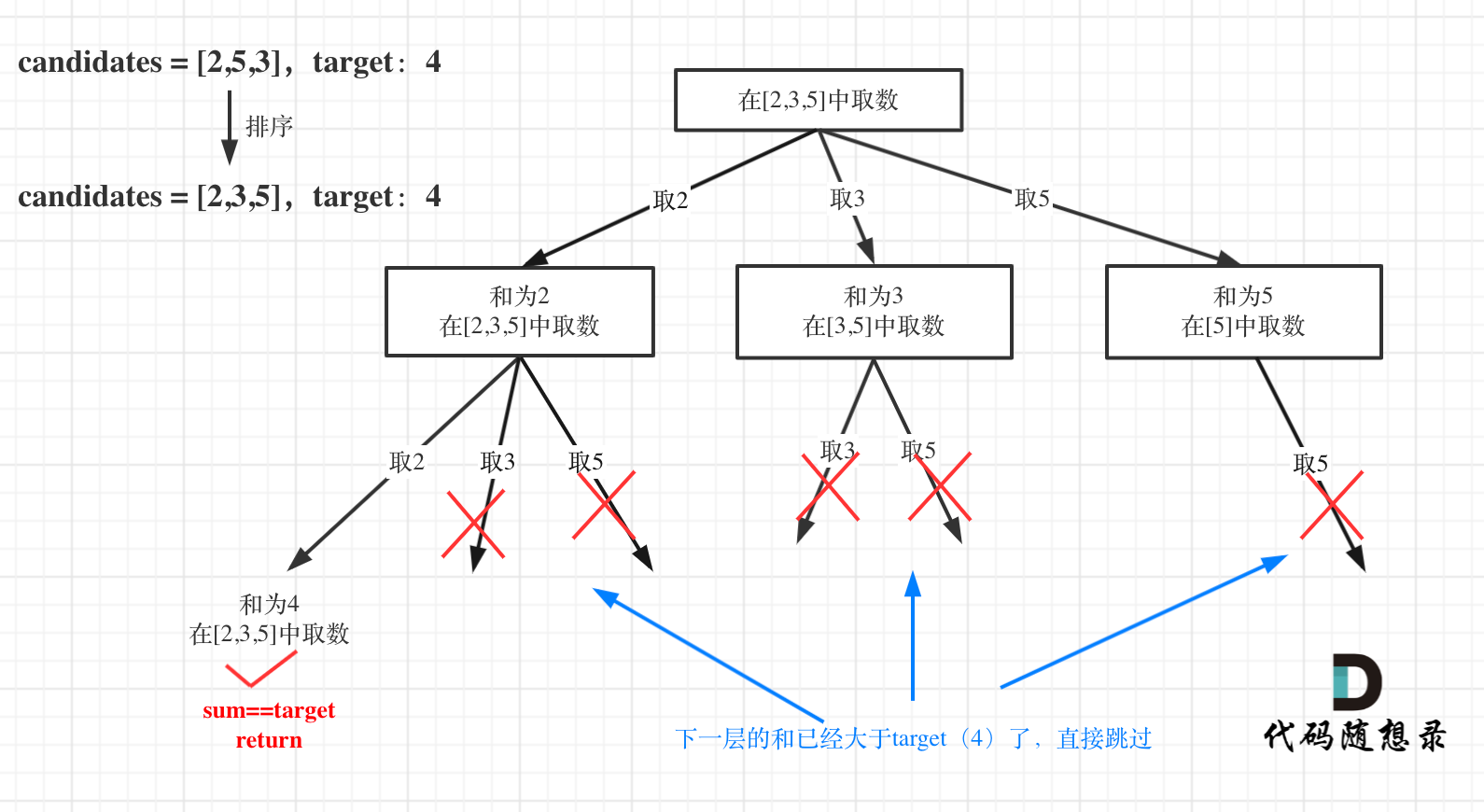
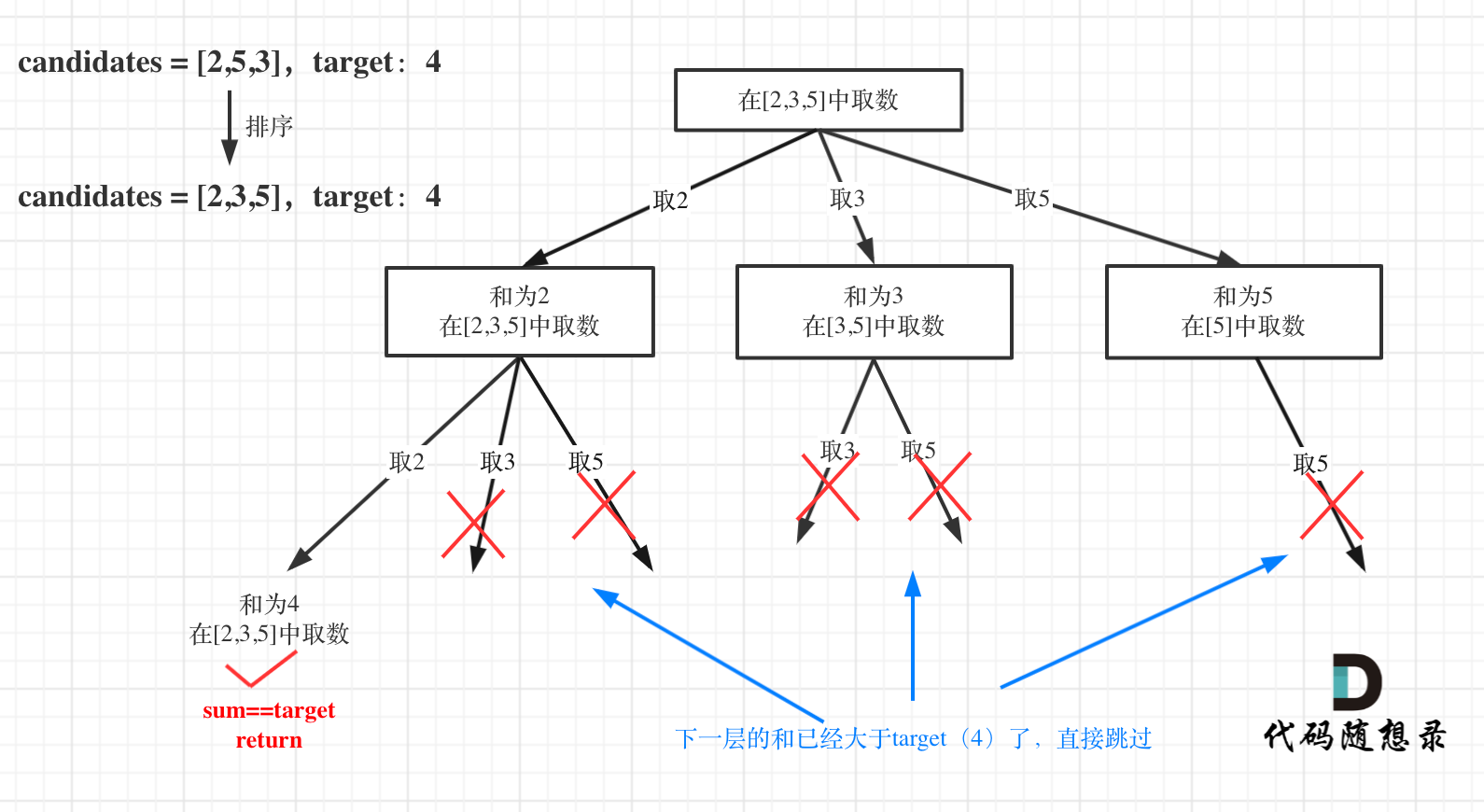
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
for循环剪枝代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -76,7 +76,7 @@ candidates 中的每个数字在每个组合中只能使用一次。
|
|||
|
||||
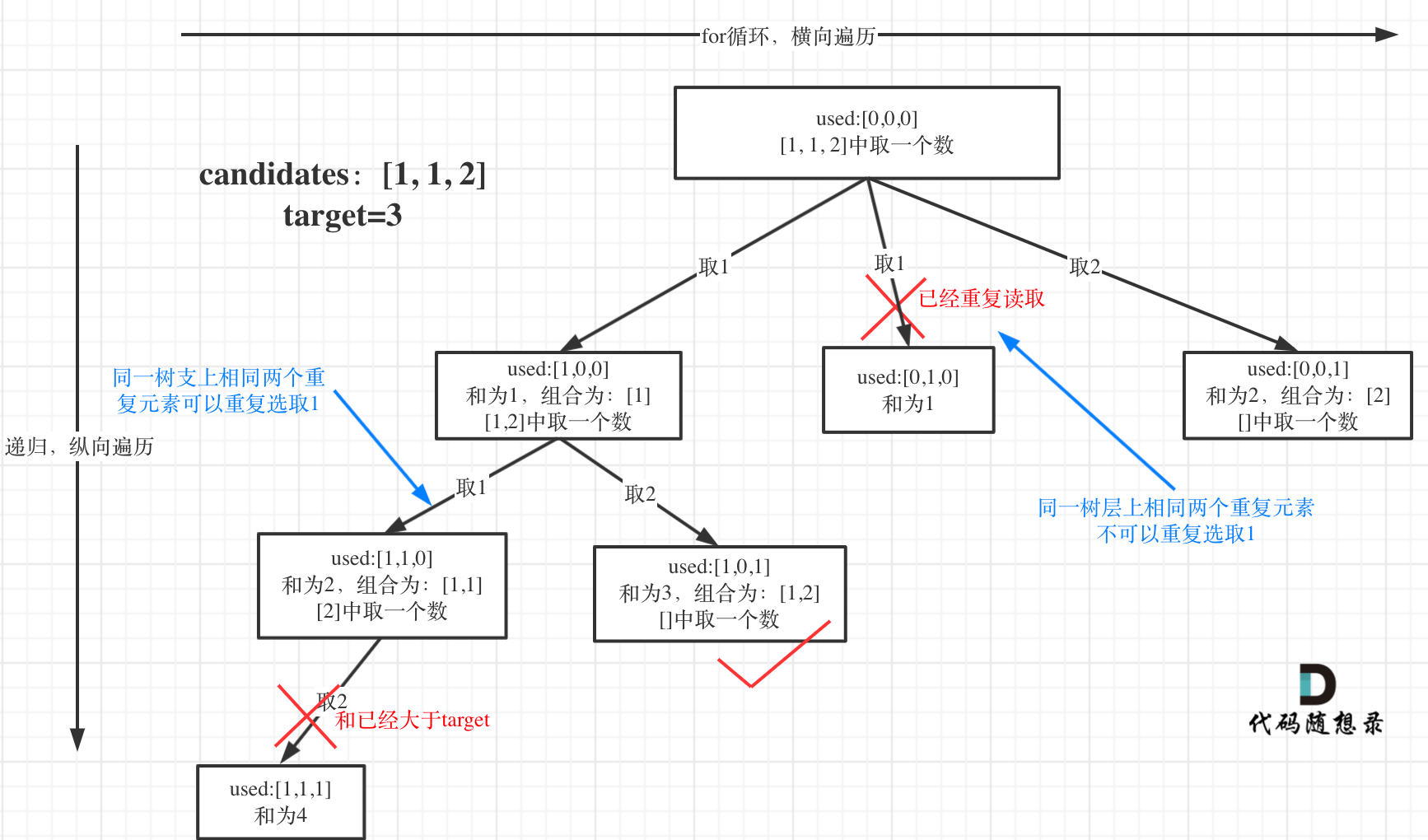
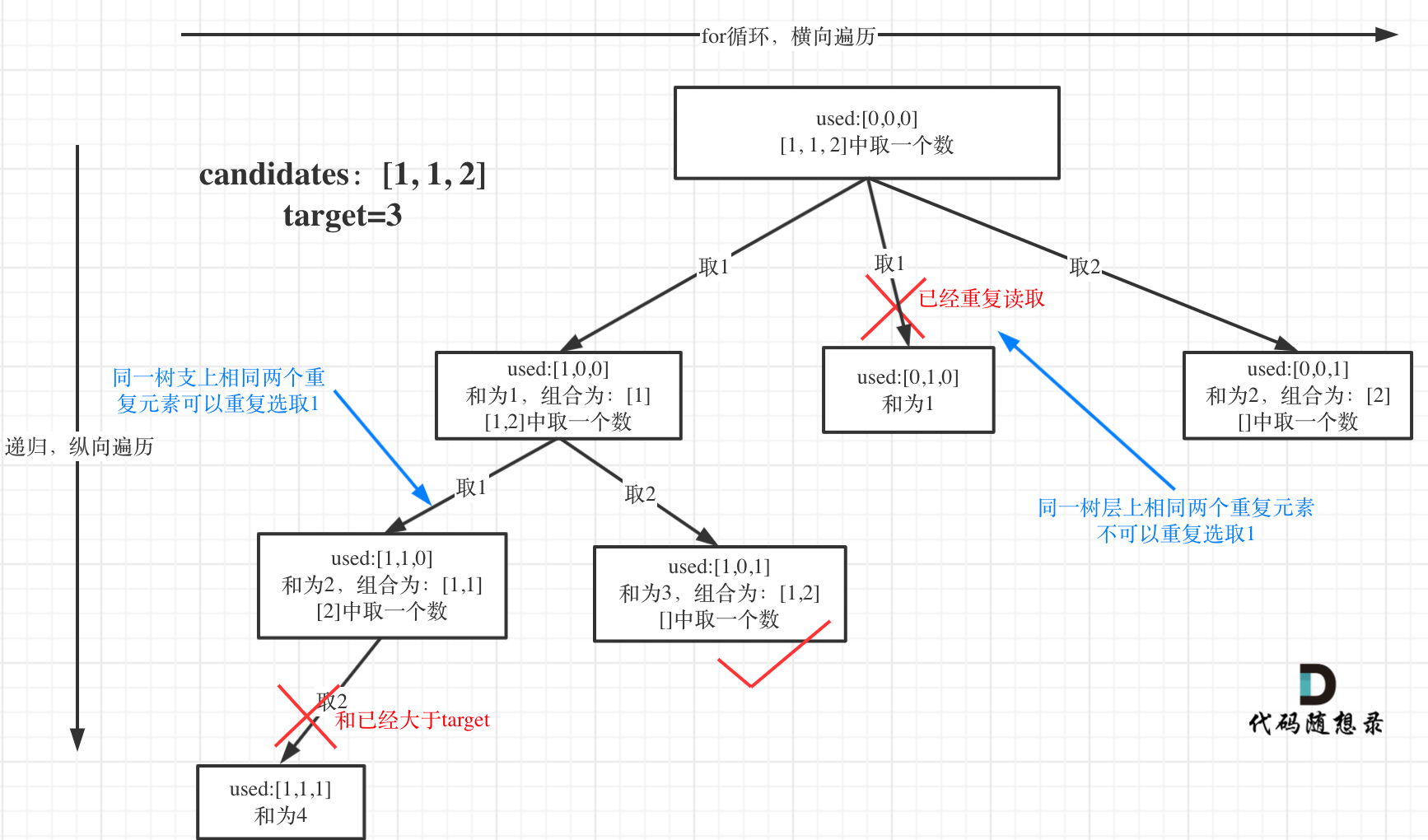
选择过程树形结构如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
可以看到图中,每个节点相对于 [39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)我多加了used数组,这个used数组下面会重点介绍。
|
||||
|
||||
|
|
@ -126,7 +126,7 @@ if (sum == target) {
|
|||
|
||||
这块比较抽象,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
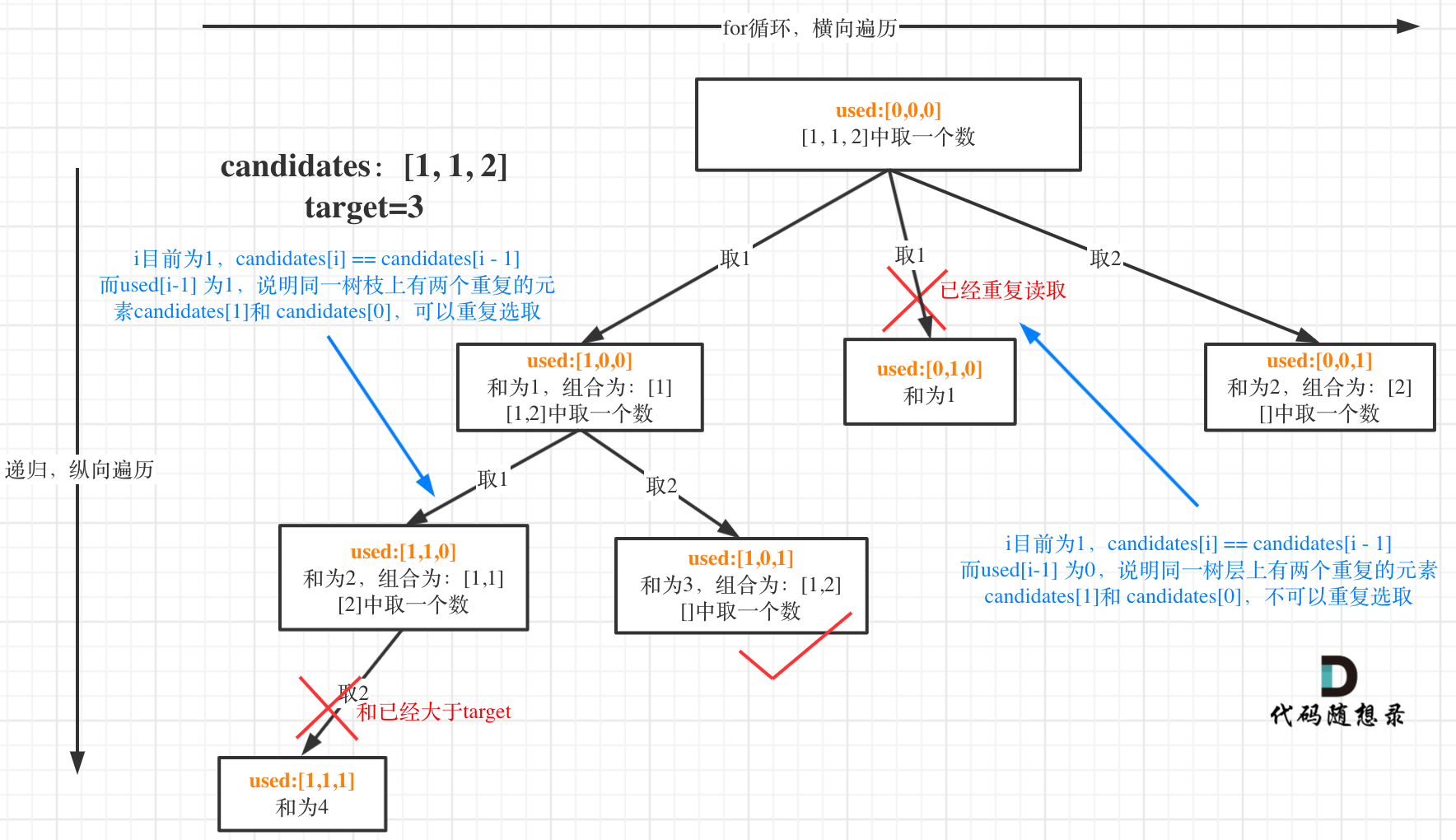
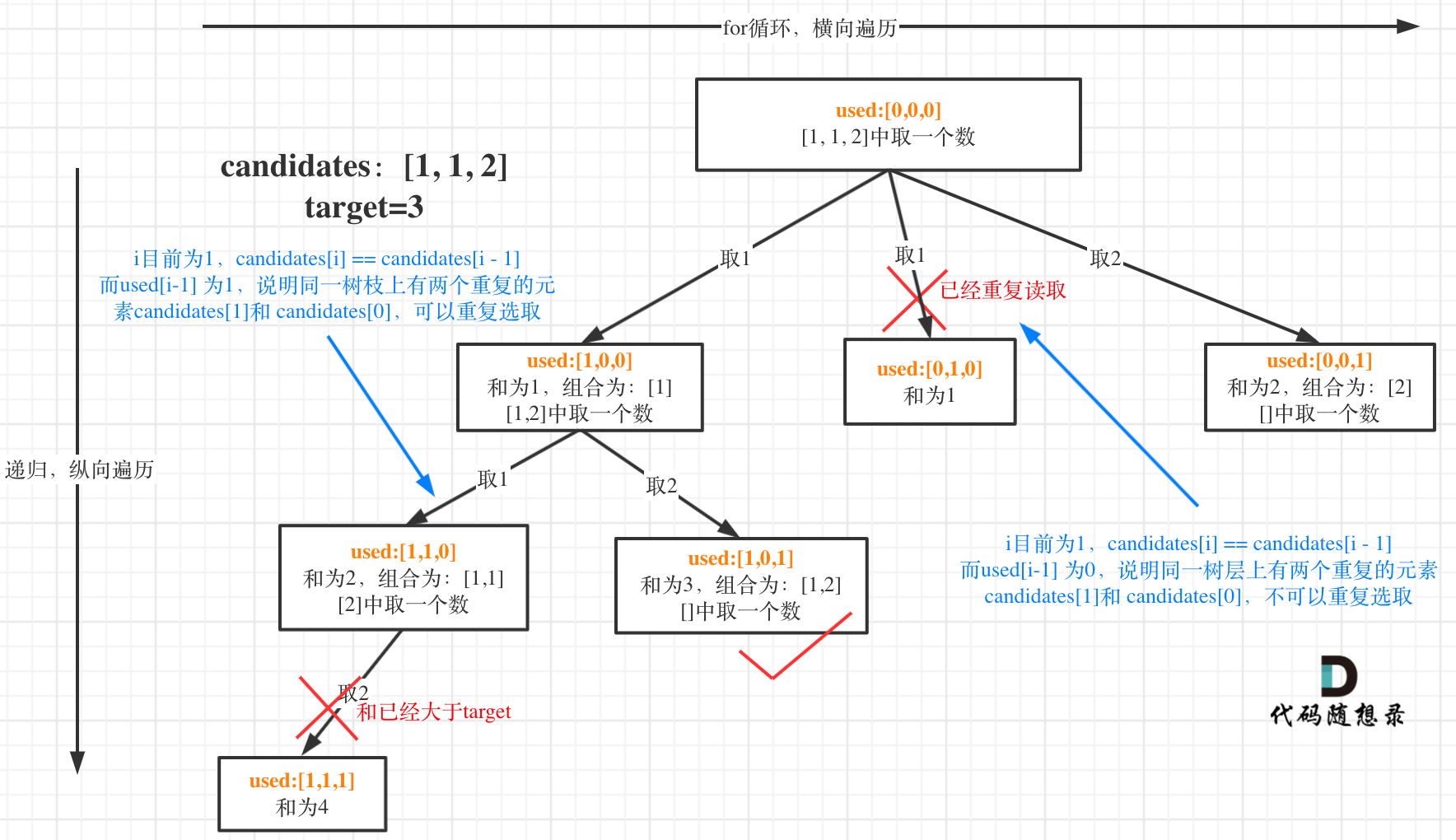
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
|
||||
|
||||
|
|
@ -137,7 +137,7 @@ if (sum == target) {
|
|||
|
||||
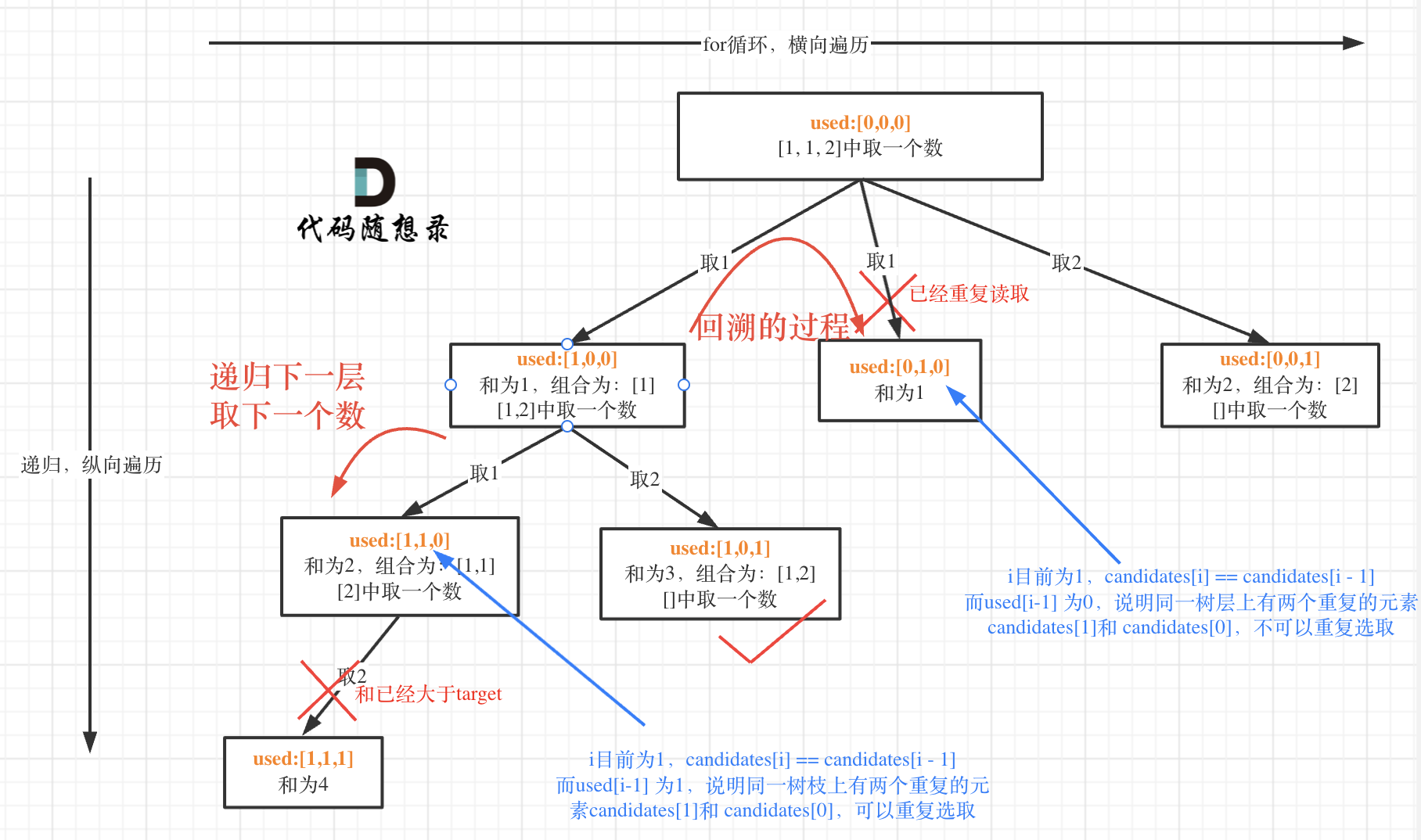
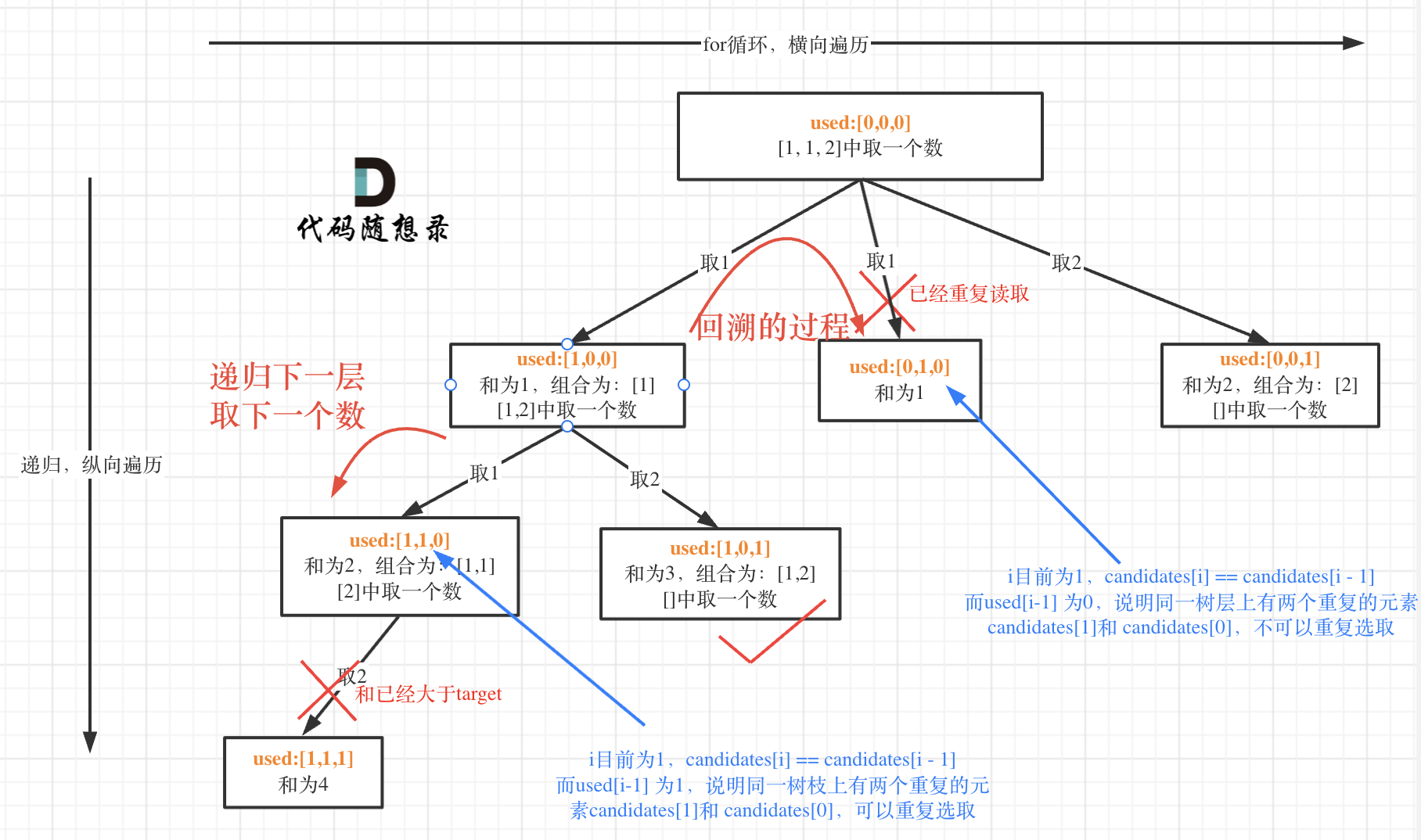
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!**
|
||||
|
|
|
|||
|
|
@ -47,10 +47,10 @@
|
|||
首先要明确,要按照行来计算,还是按照列来计算。
|
||||
|
||||
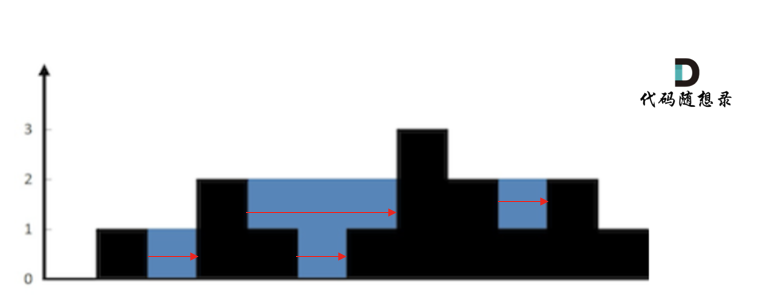
按照行来计算如图:
|
||||
|
||||

|
||||
|
||||
按照列来计算如图:
|
||||
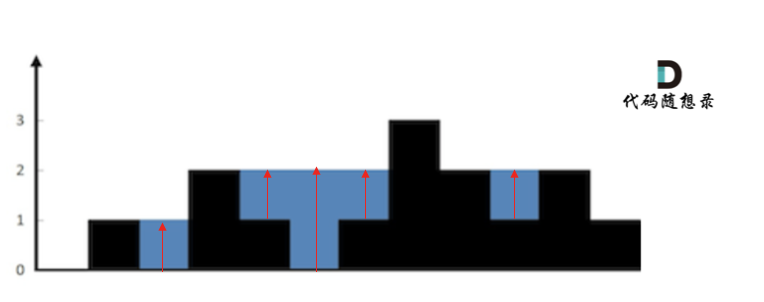
|
||||
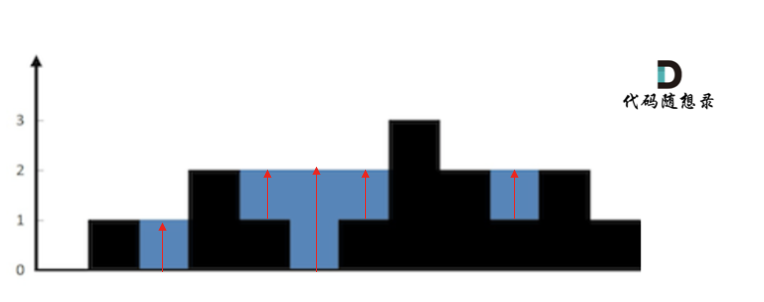
|
||||
|
||||
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
|
||||
|
||||
|
|
@ -62,7 +62,7 @@
|
|||
|
||||
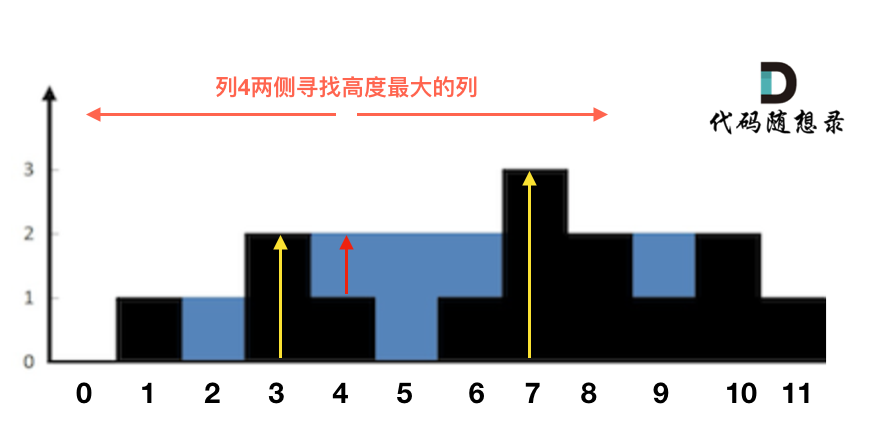
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
|
||||
|
||||
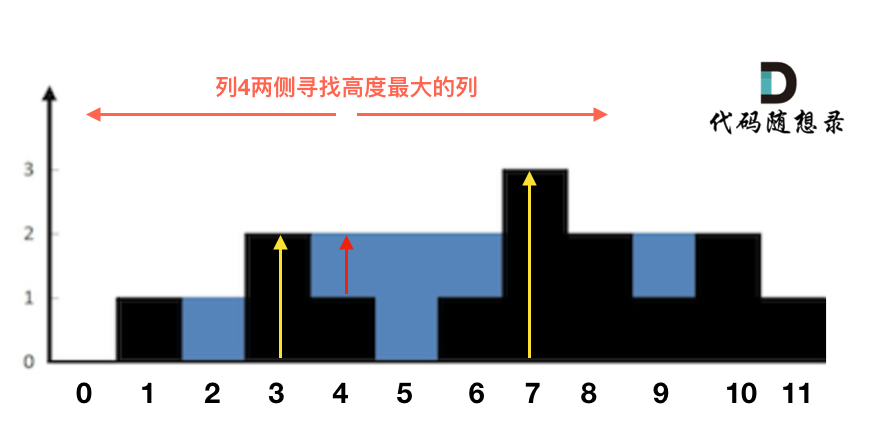
|
||||
|
||||
|
||||
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
|
||||
|
||||
|
|
@ -201,7 +201,7 @@ public:
|
|||
|
||||
1. 首先单调栈是按照行方向来计算雨水,如图:
|
||||
|
||||

|
||||

|
||||
|
||||
知道这一点,后面的就可以理解了。
|
||||
|
||||
|
|
@ -215,7 +215,7 @@ public:
|
|||
|
||||
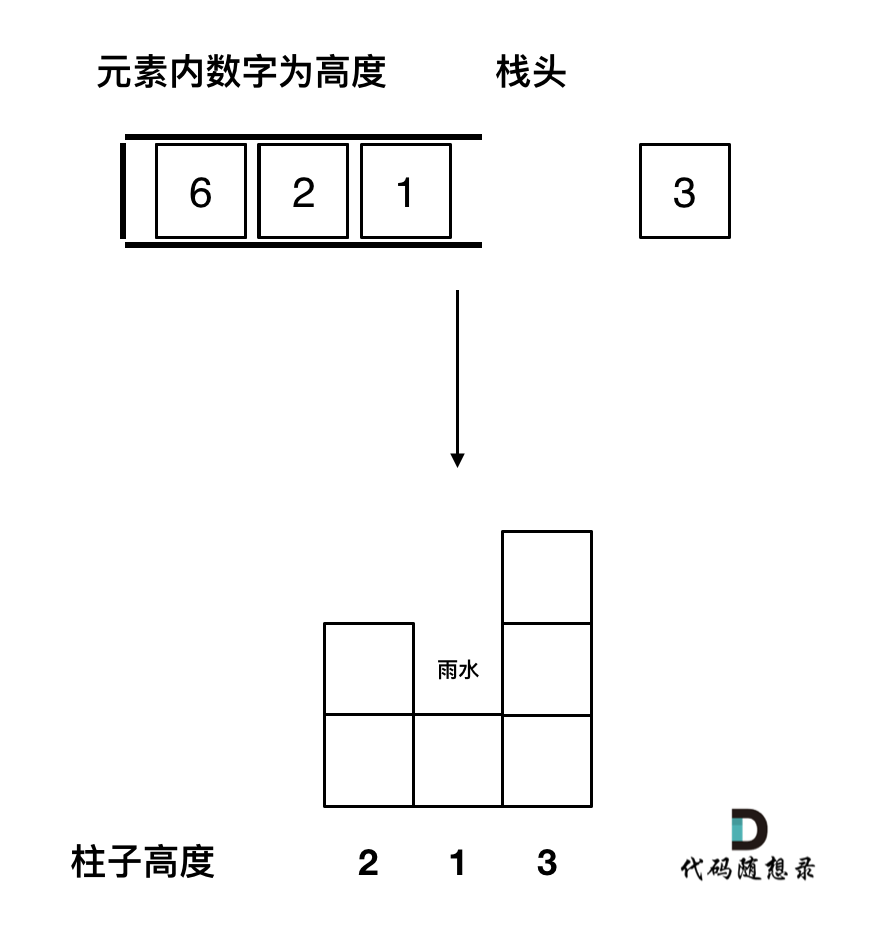
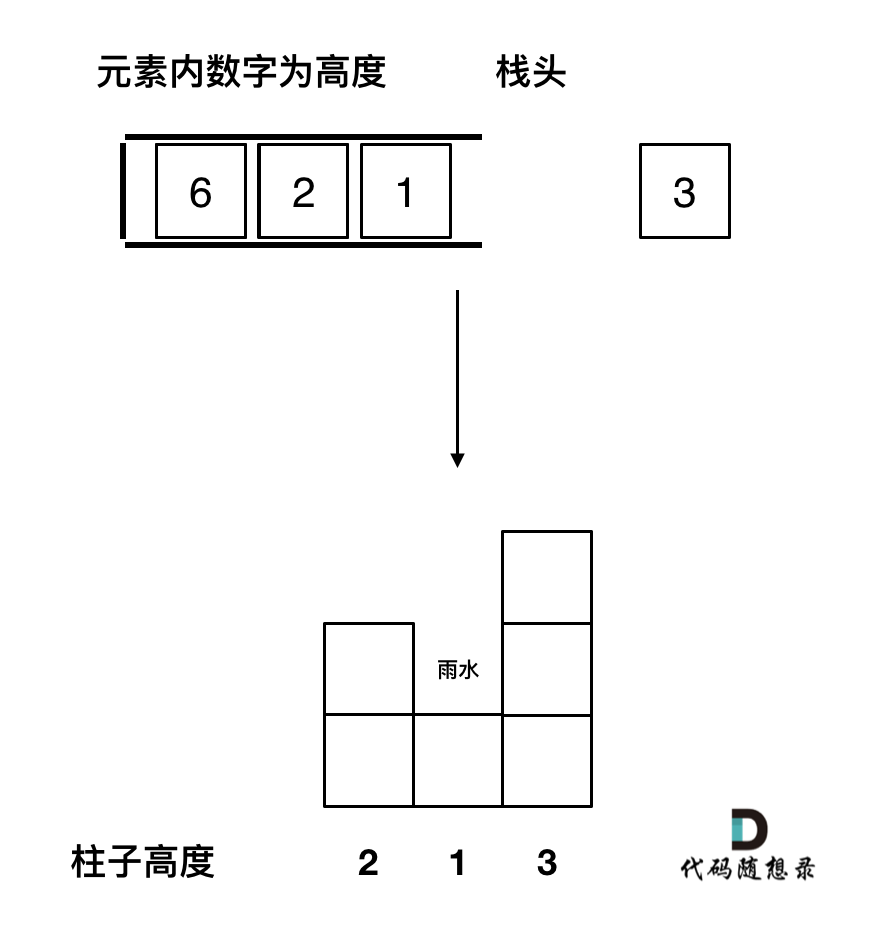
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
关于单调栈的顺序给大家一个总结: [739. 每日温度](https://programmercarl.com/0739.每日温度.html) 中求一个元素右边第一个更大元素,单调栈就是递增的,[84.柱状图中最大的矩形](https://programmercarl.com/0084.柱状图中最大的矩形.html)求一个元素右边第一个更小元素,单调栈就是递减的。
|
||||
|
||||
|
|
@ -229,7 +229,7 @@ public:
|
|||
|
||||
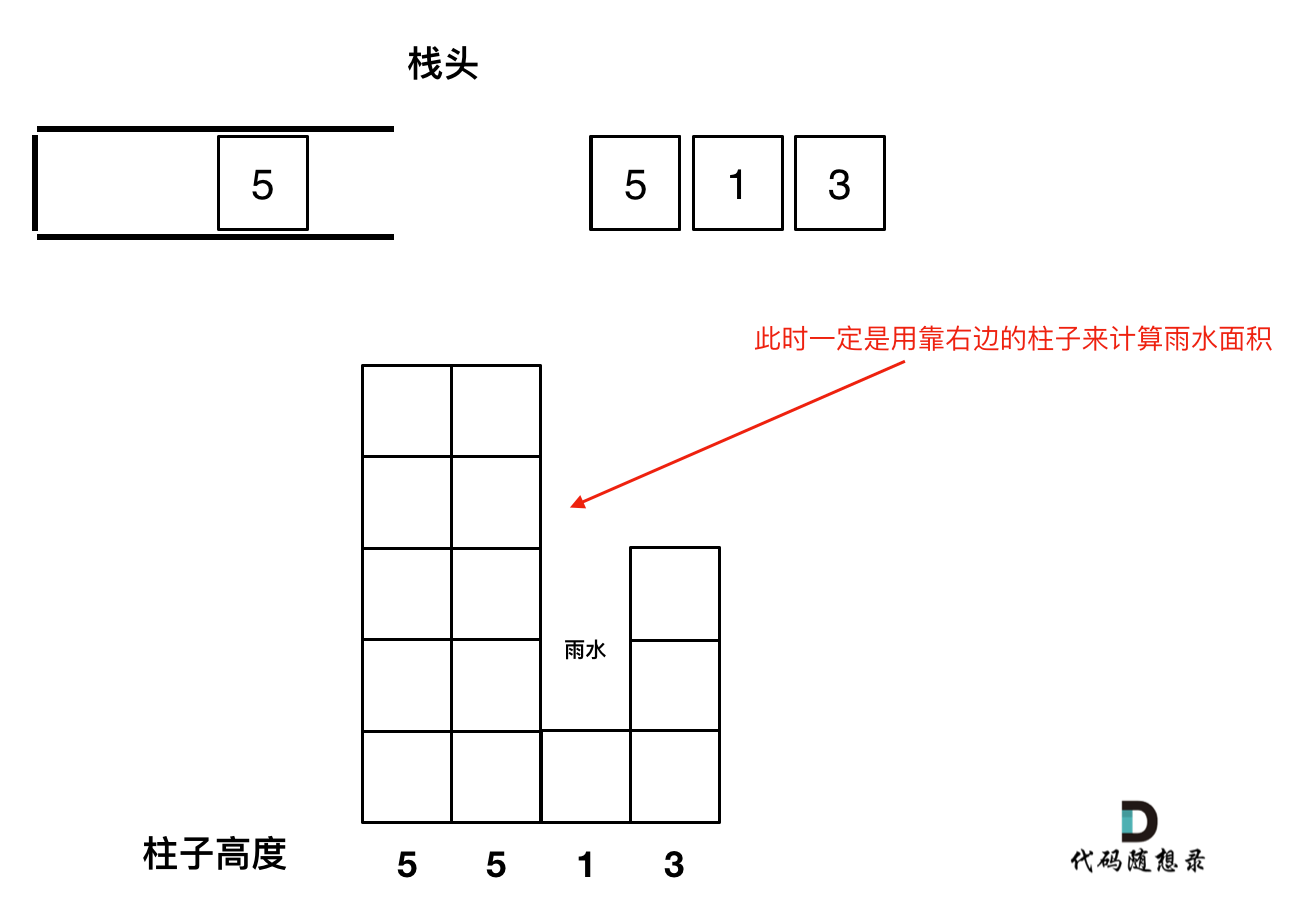
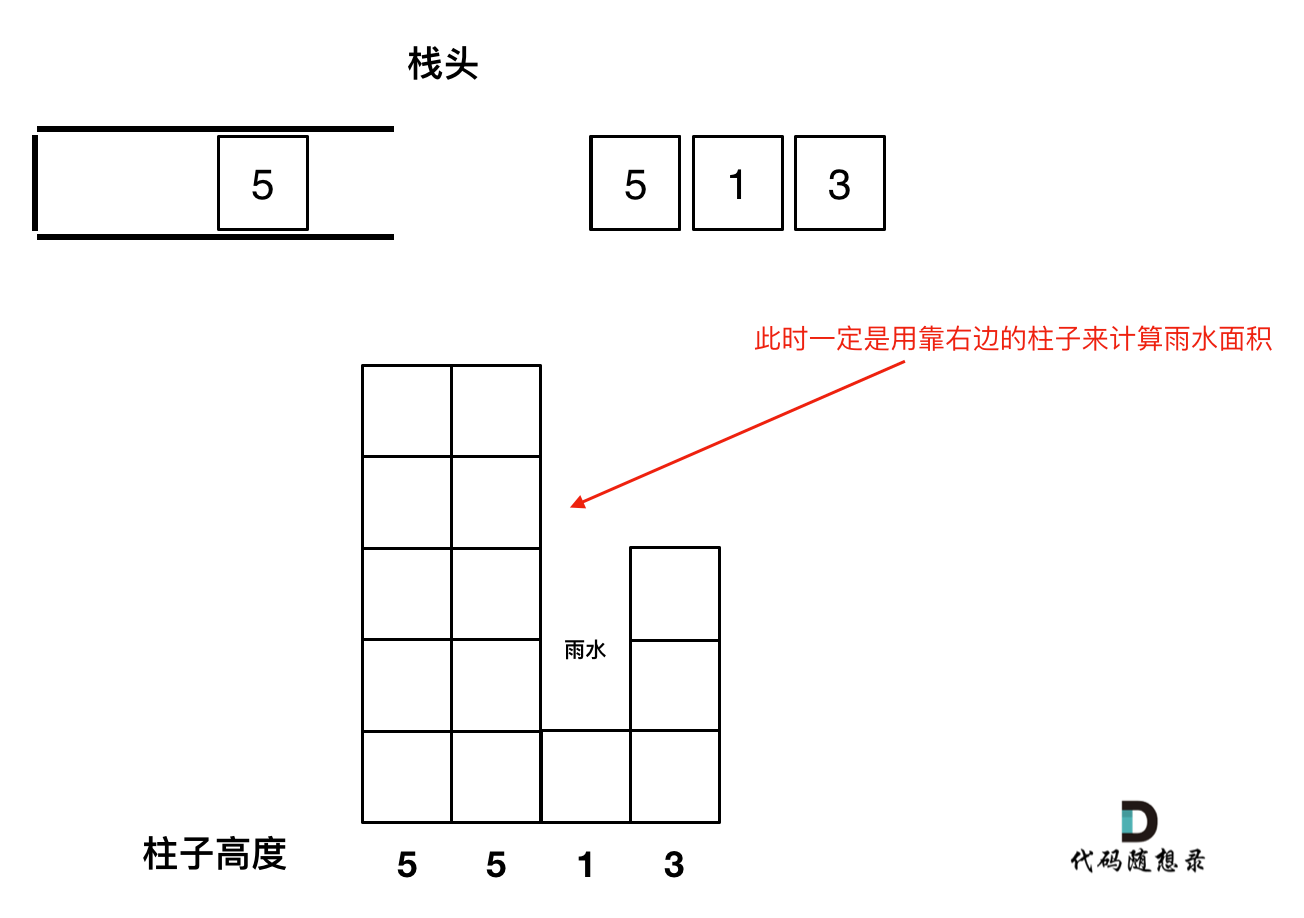
如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
4. 栈里要保存什么数值
|
||||
|
||||
|
|
@ -284,7 +284,7 @@ if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
|
|||
|
||||
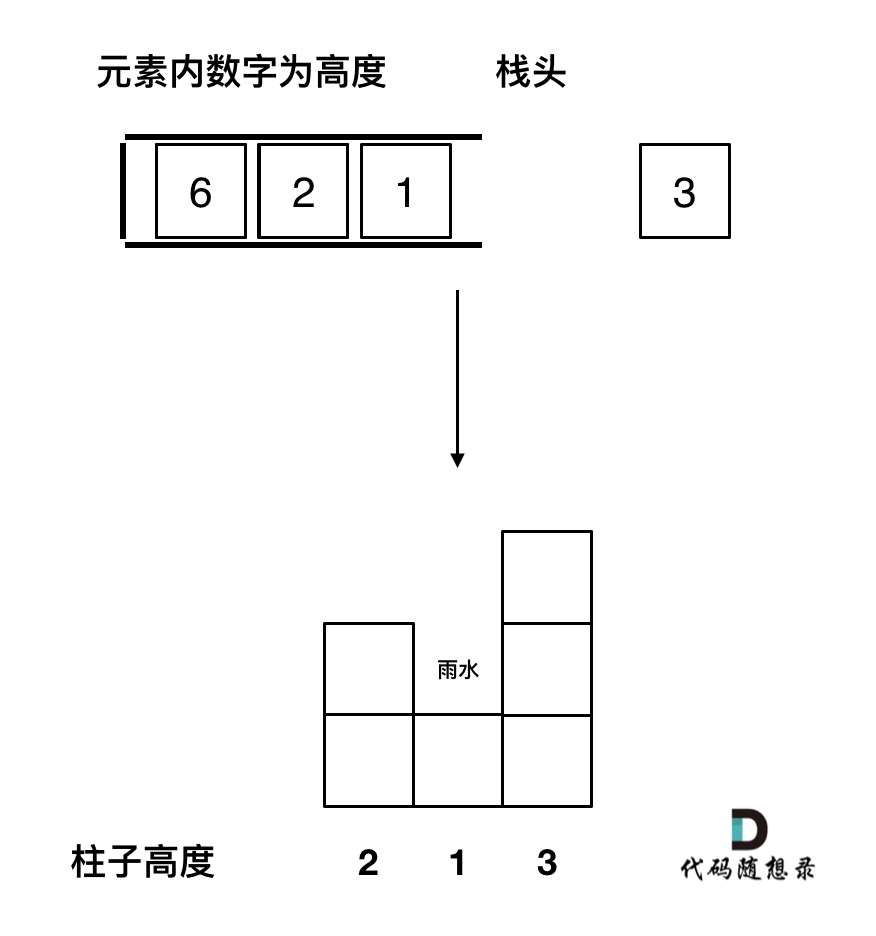
如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
|
||||
|
||||

|
||||
|
||||
|
||||
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
|
||||
|
||||
|
|
|
|||
|
|
@ -47,7 +47,7 @@
|
|||
|
||||
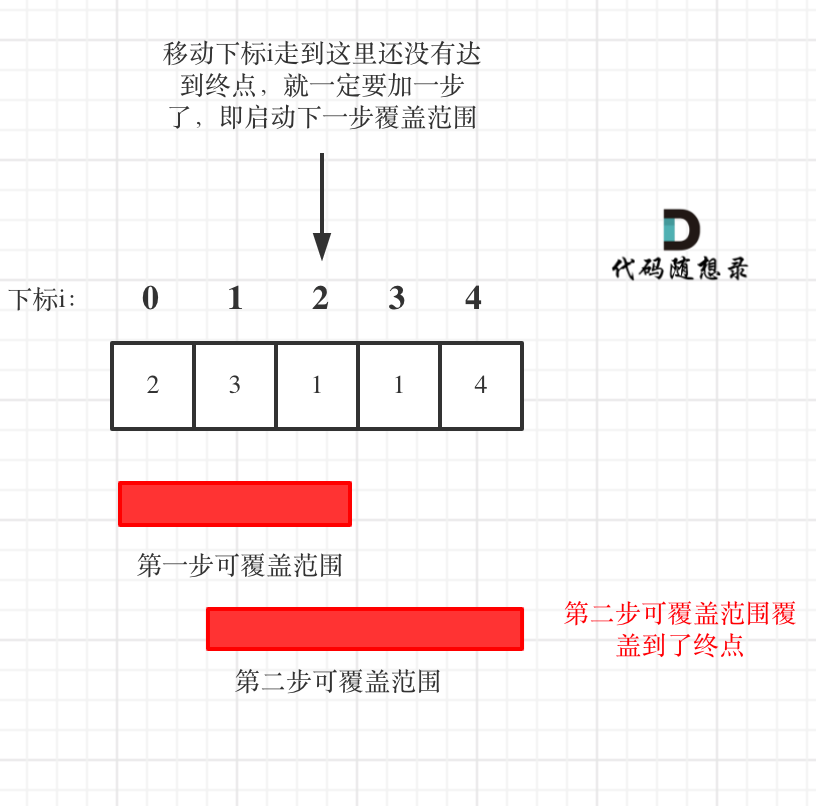
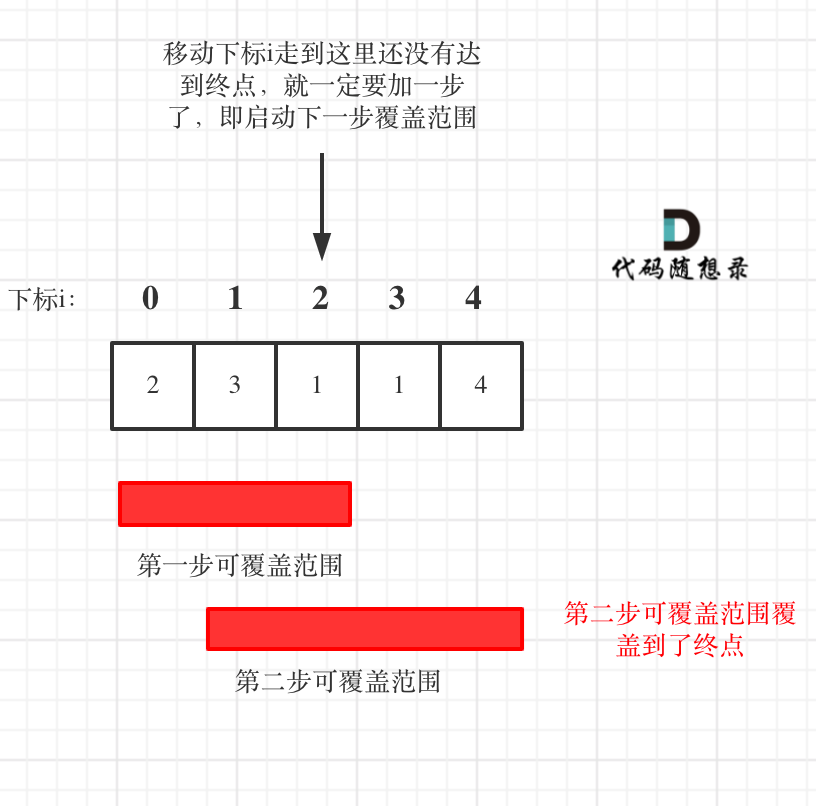
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
|
||||
|
||||
|
|
@ -99,11 +99,11 @@ public:
|
|||
因为当移动下标指向 nums.size - 2 时:
|
||||
|
||||
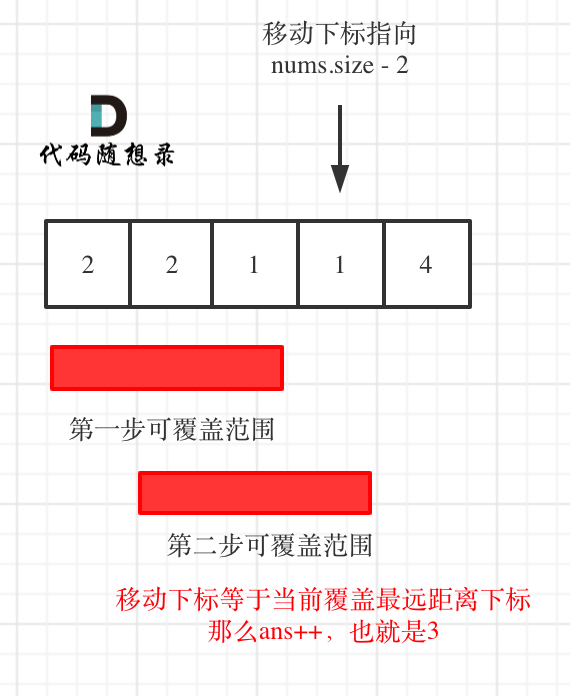
- 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即 ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
||||

|
||||
|
||||
|
||||
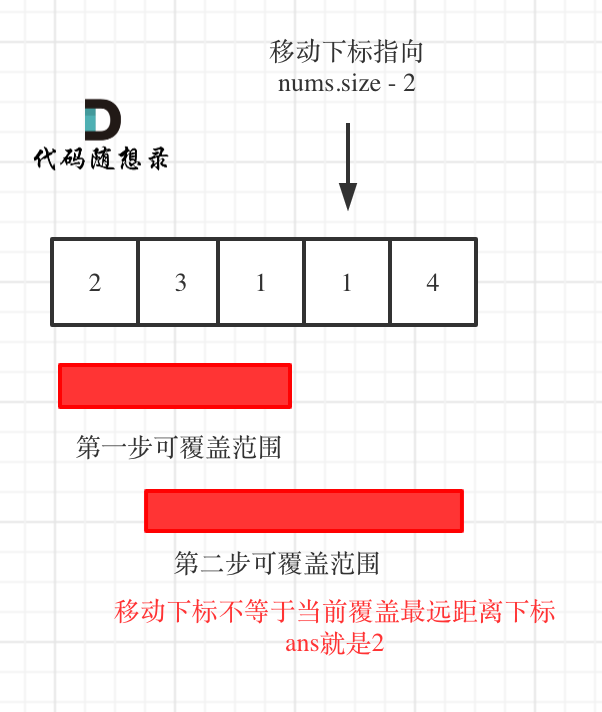
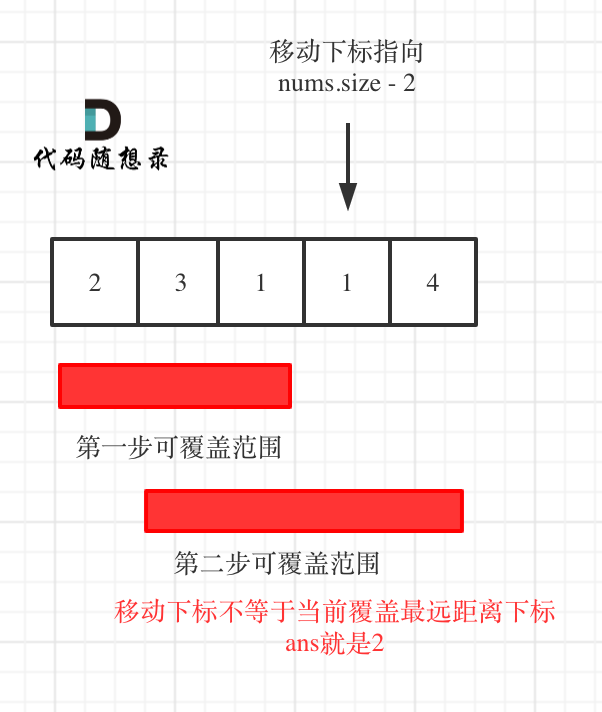
- 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
||||
|
||||
|
||||
|
||||
|
||||
代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -41,7 +41,7 @@
|
|||
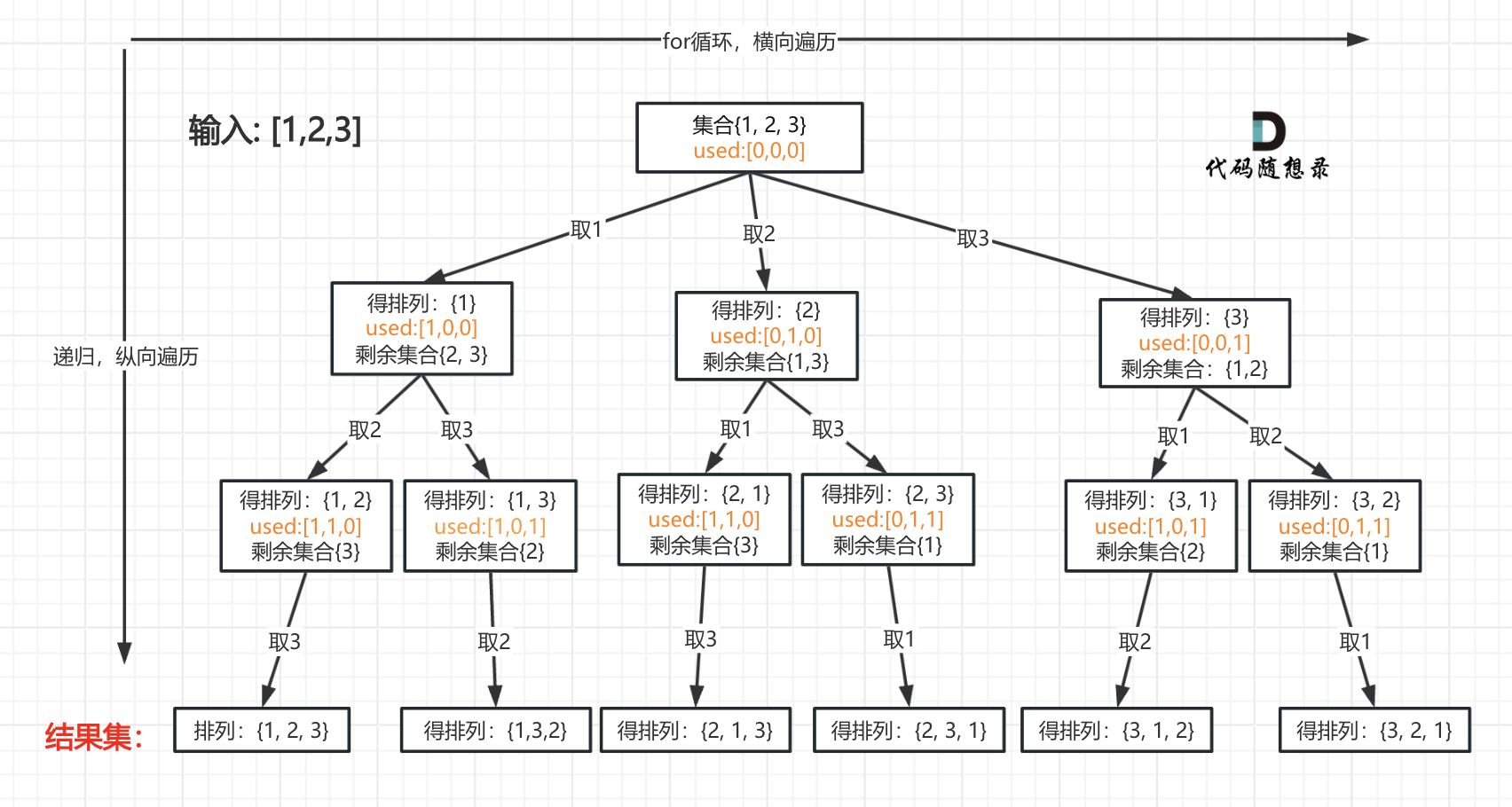
我以[1,2,3]为例,抽象成树形结构如下:
|
||||
|
||||
|
||||
|
||||
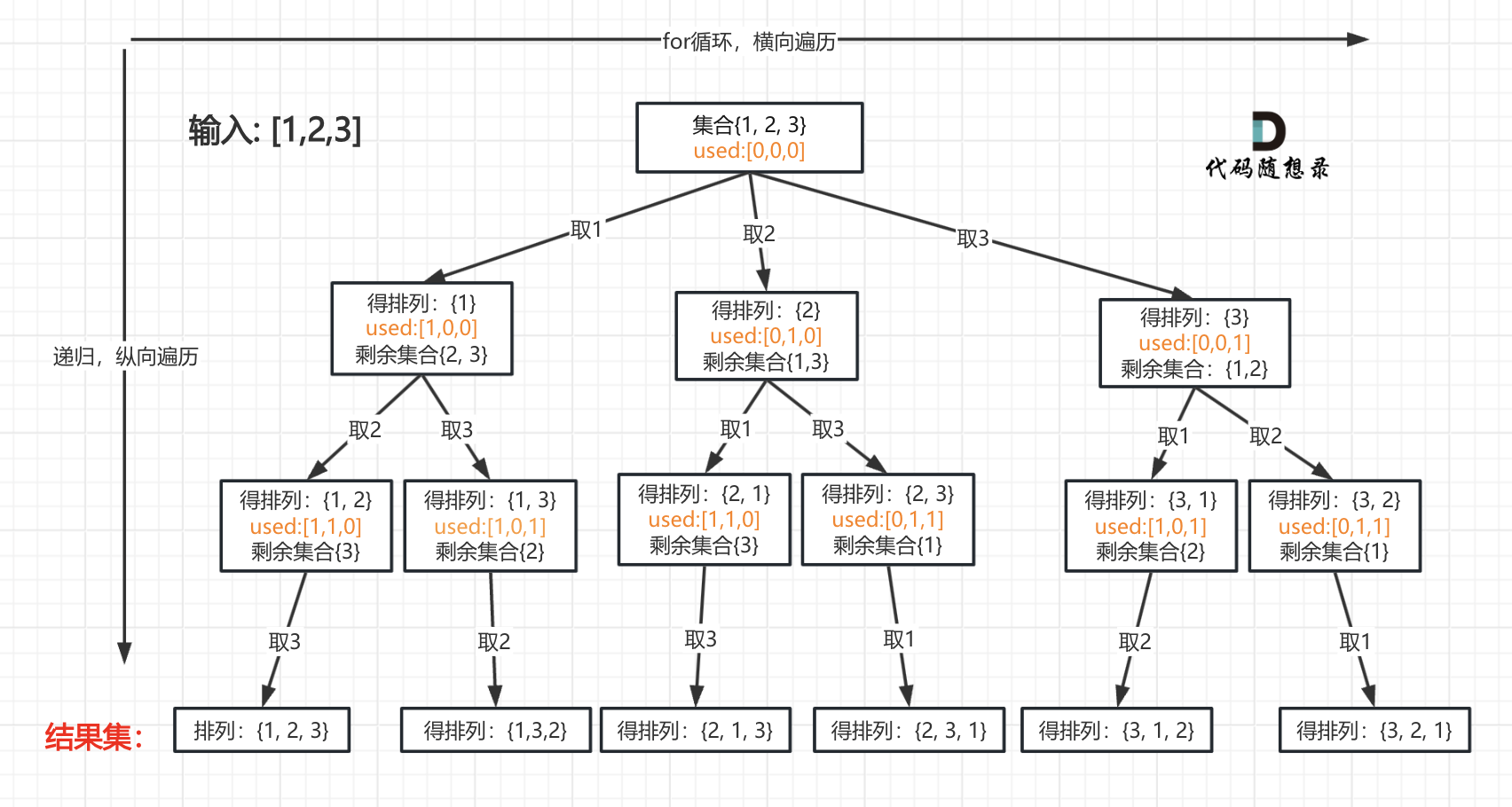
|
||||
|
||||
### 回溯三部曲
|
||||
|
||||
|
|
@ -53,7 +53,7 @@
|
|||
|
||||
但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
|
||||
|
||||

|
||||

|
||||
|
||||
代码如下:
|
||||
|
||||
|
|
@ -65,7 +65,7 @@ void backtracking (vector<int>& nums, vector<bool>& used)
|
|||
|
||||
* 递归终止条件
|
||||
|
||||

|
||||

|
||||
|
||||
可以看出叶子节点,就是收割结果的地方。
|
||||
|
||||
|
|
|
|||
|
|
@ -48,7 +48,7 @@
|
|||
|
||||
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
|
||||
|
||||
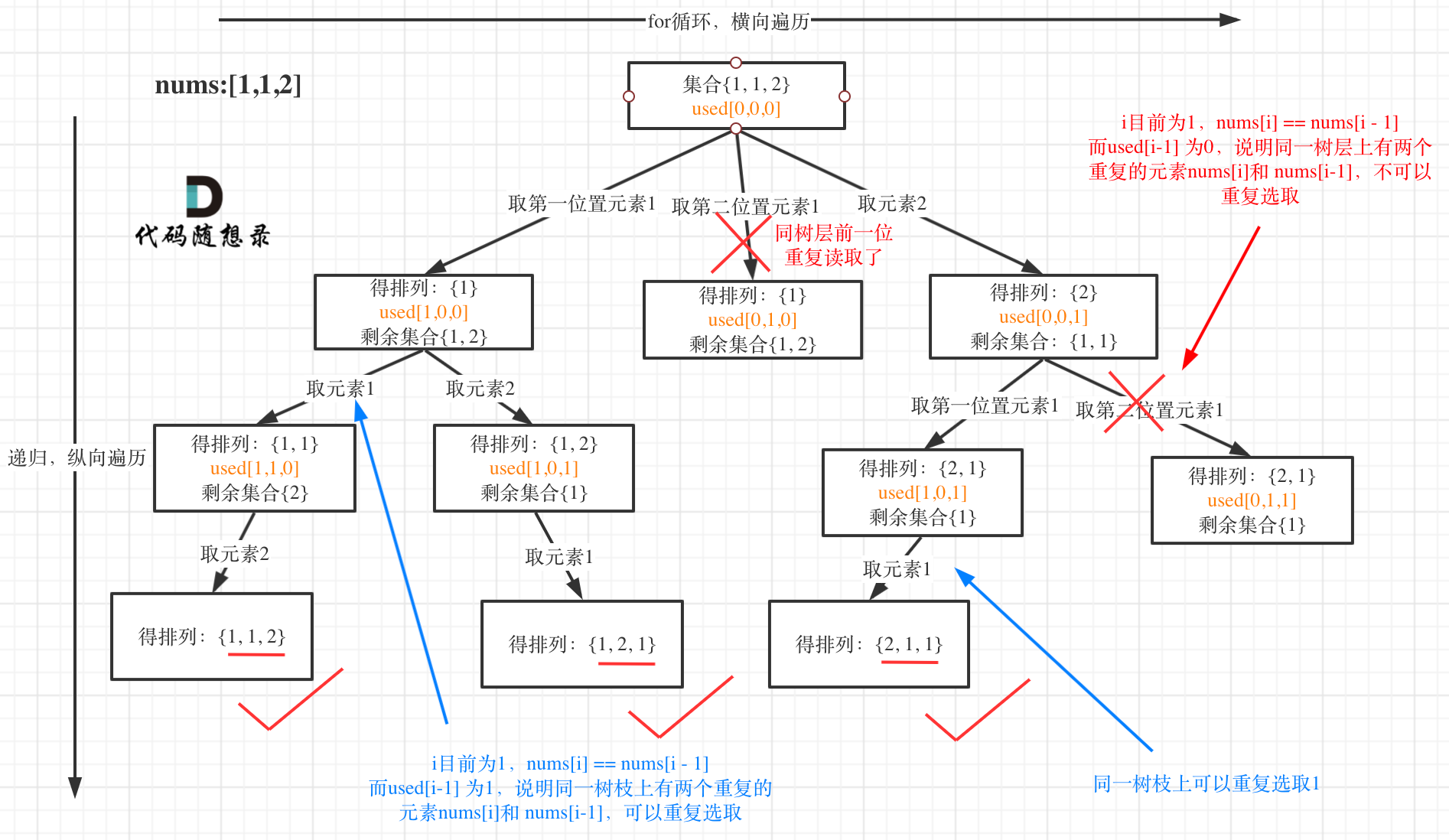
|
||||
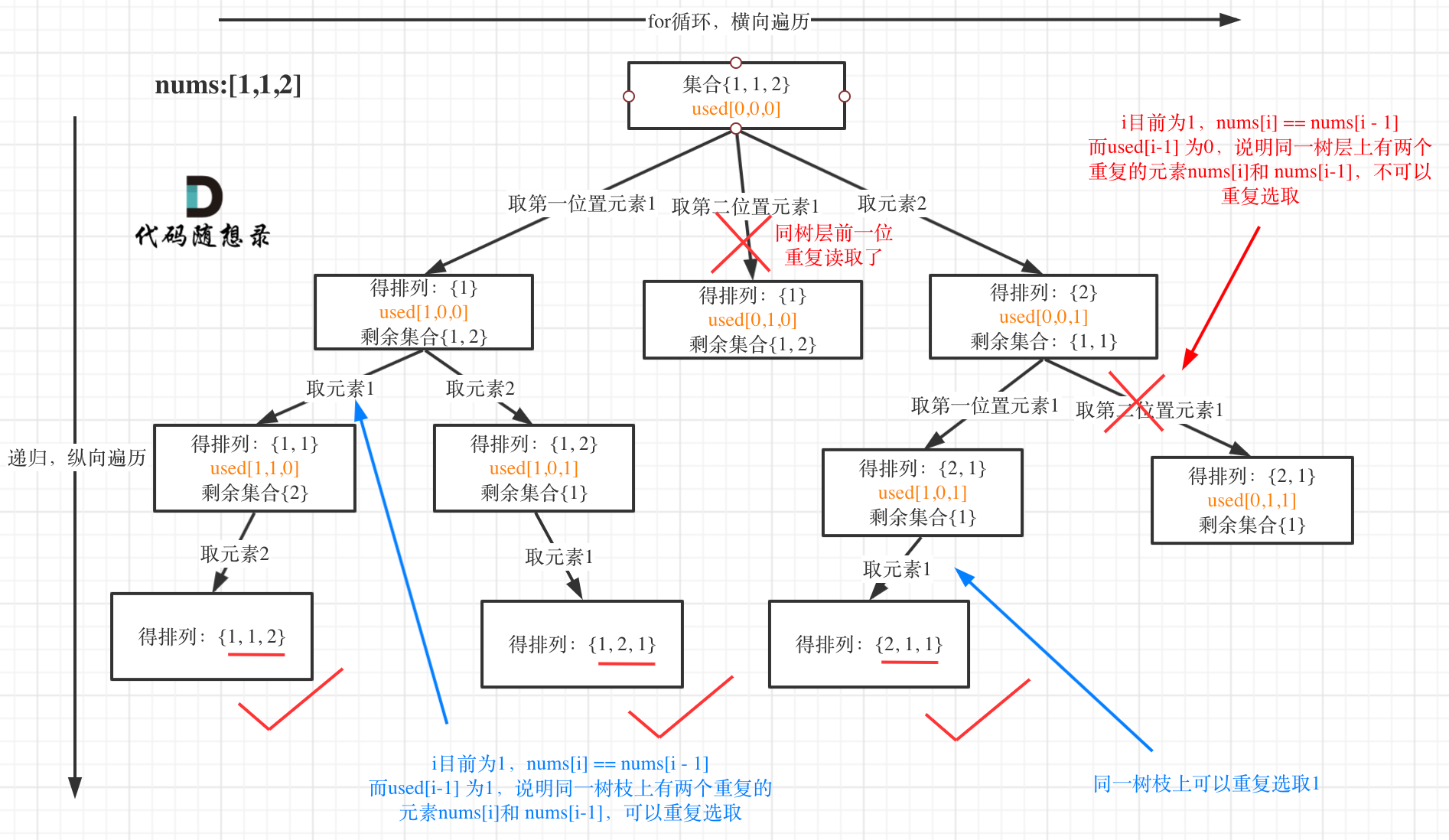
|
||||
|
||||
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
|
||||
|
||||
|
|
@ -130,11 +130,11 @@ if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
|||
|
||||
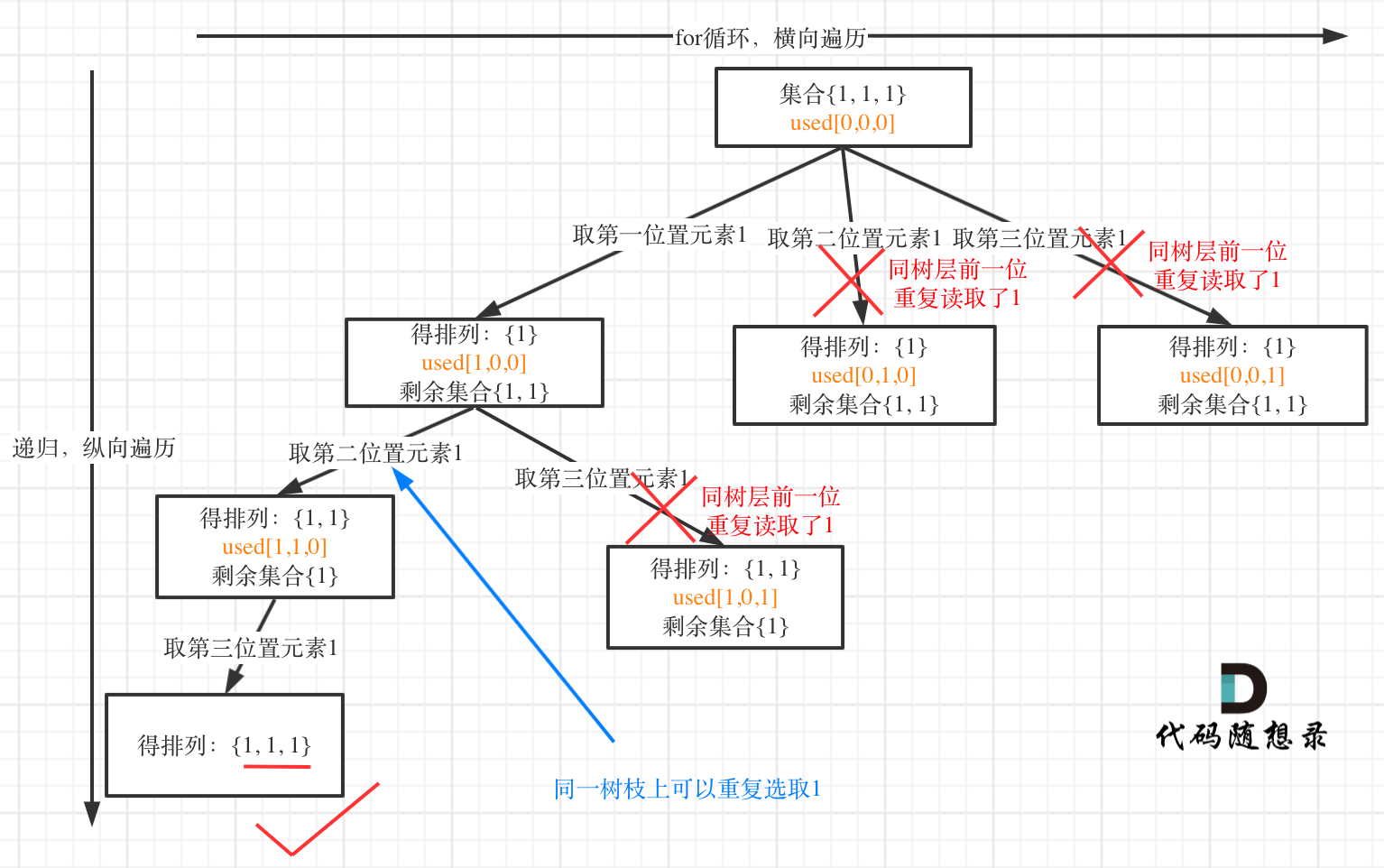
树层上去重(used[i - 1] == false),的树形结构如下:
|
||||
|
||||
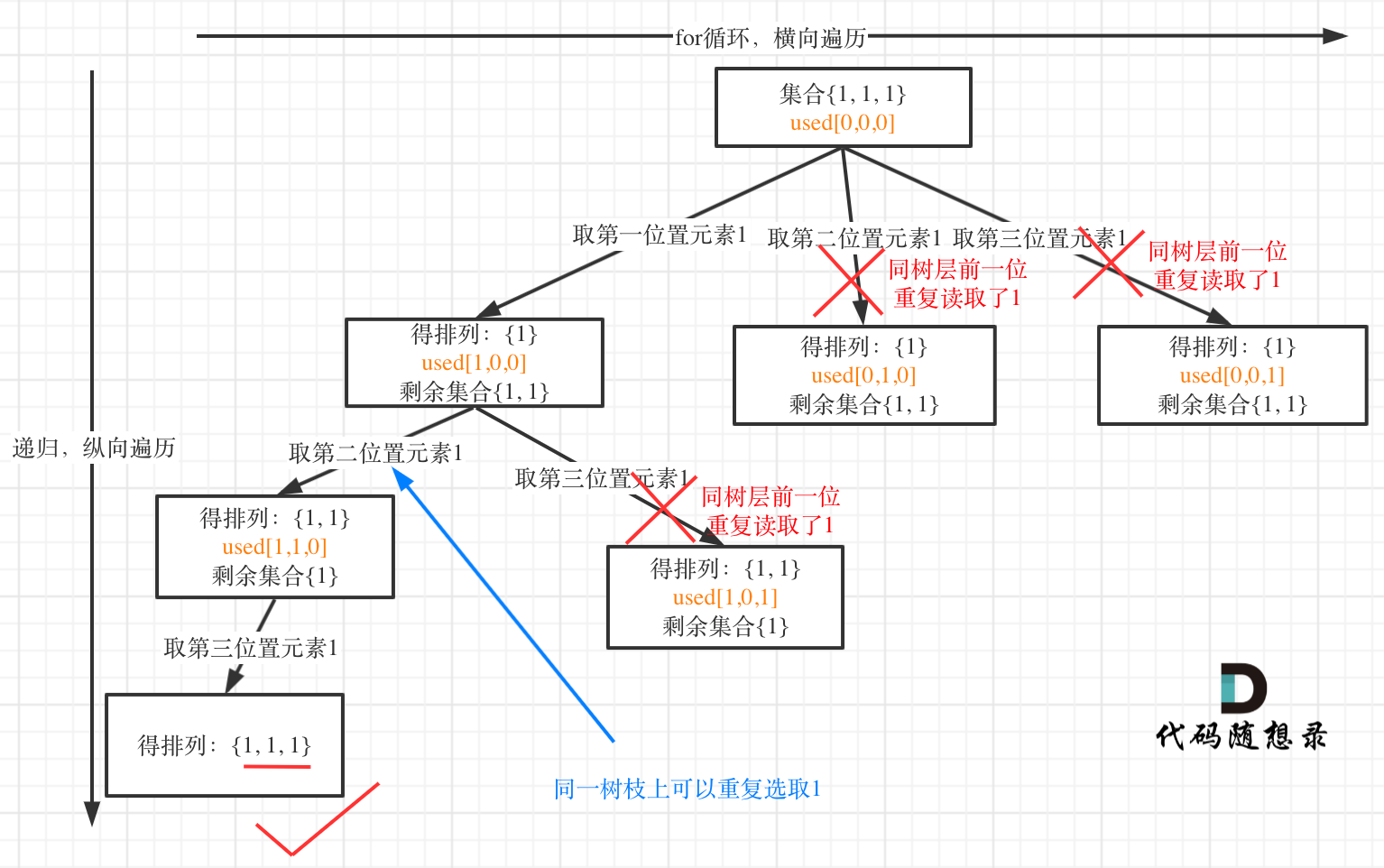
|
||||
|
||||
|
||||
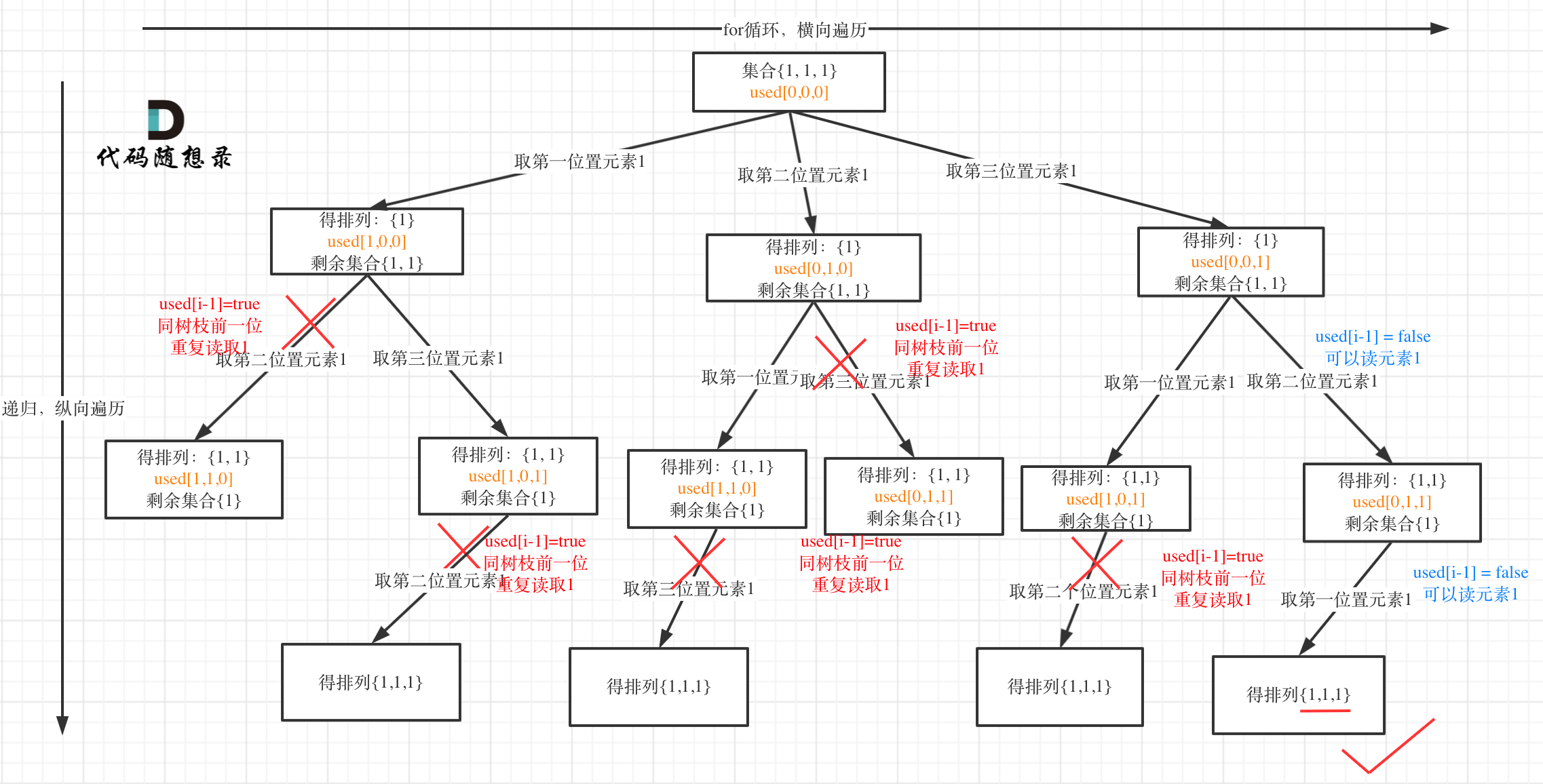
树枝上去重(used[i - 1] == true)的树型结构如下:
|
||||
|
||||
|
||||

|
||||
|
||||
大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
|
||||
|
||||
|
|
|
|||
|
|
@ -15,7 +15,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
|
|||
|
||||
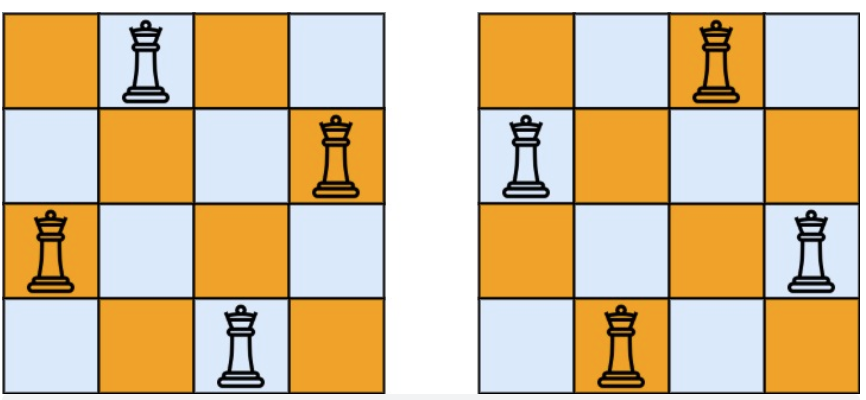
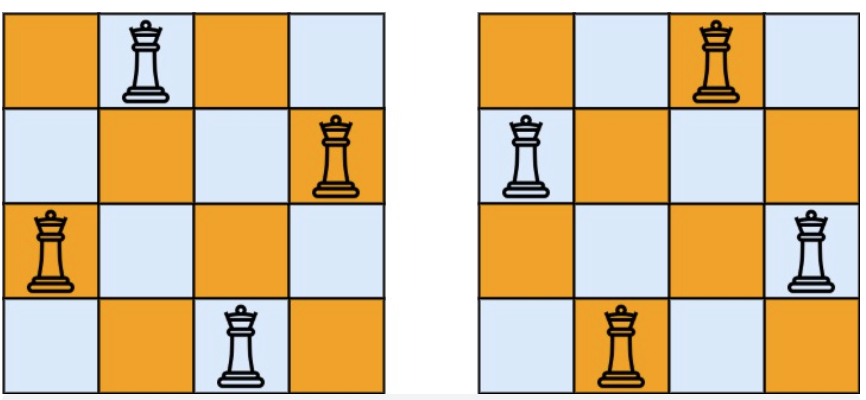
示例 1:
|
||||
|
||||
|
||||
|
||||
|
||||
* 输入:n = 4
|
||||
* 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
|
||||
|
|
@ -45,7 +45,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
|
|||
|
||||
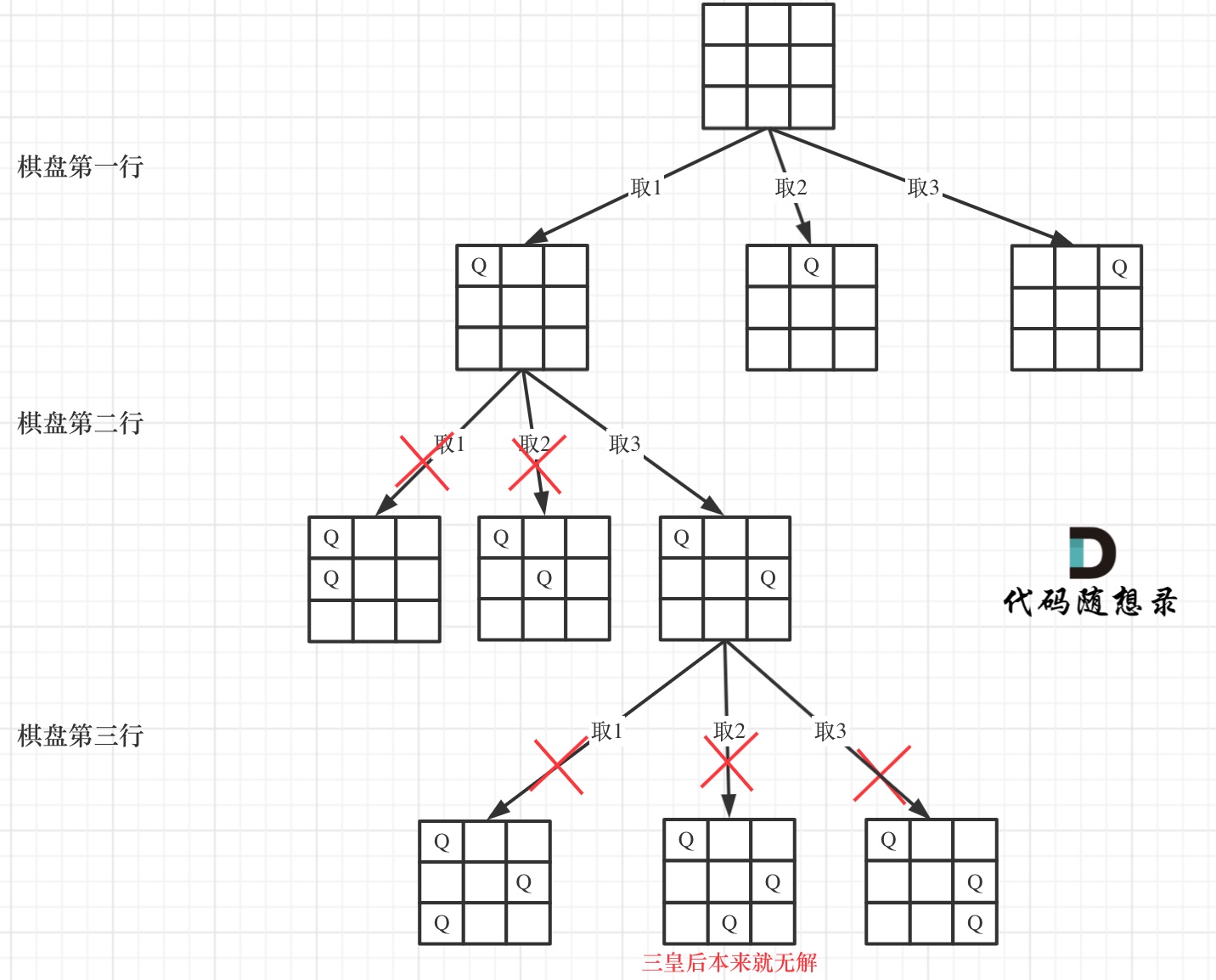
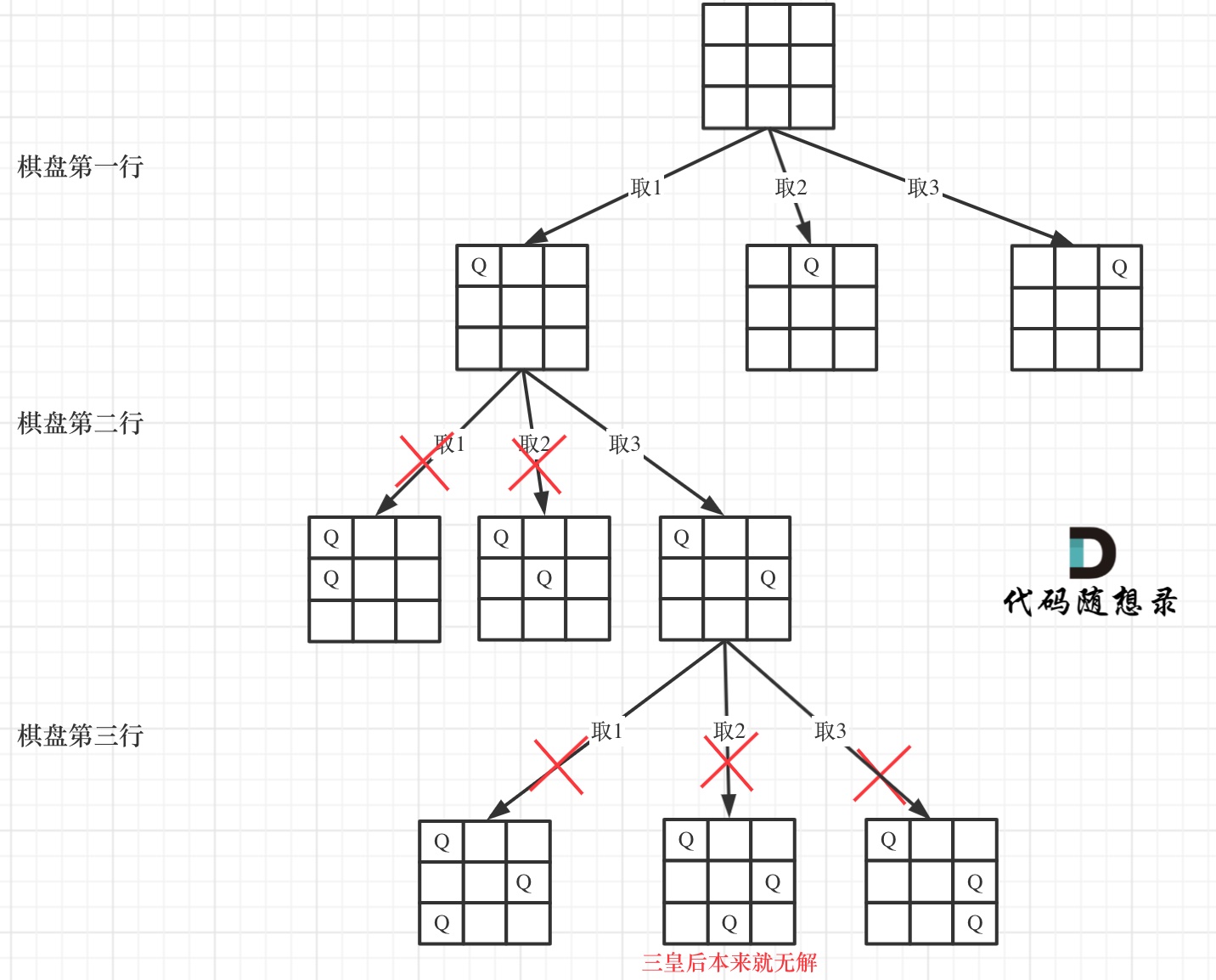
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
|
||||
|
||||
|
|
@ -85,7 +85,7 @@ void backtracking(int n, int row, vector<string>& chessboard) {
|
|||
* 递归终止条件
|
||||
|
||||
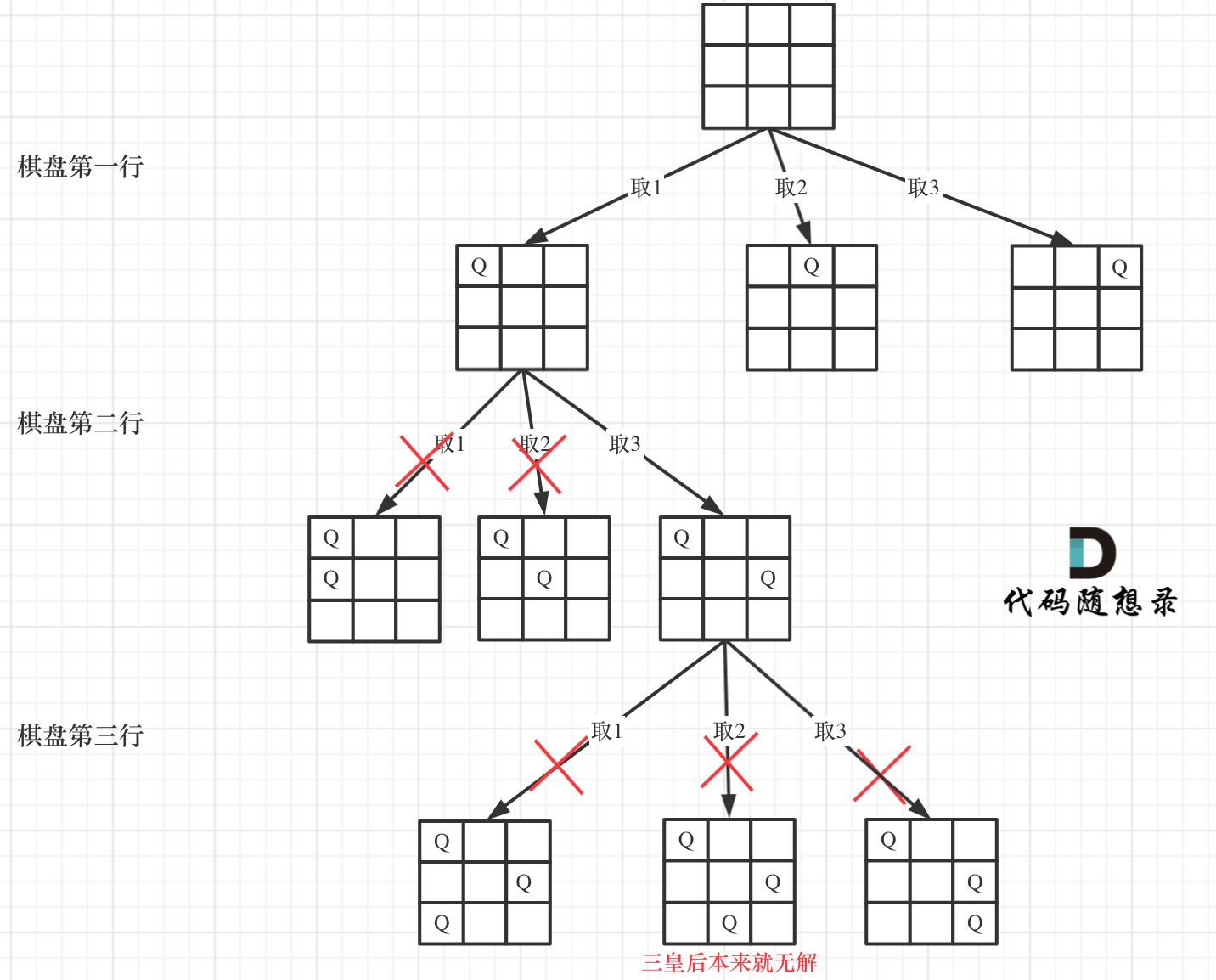
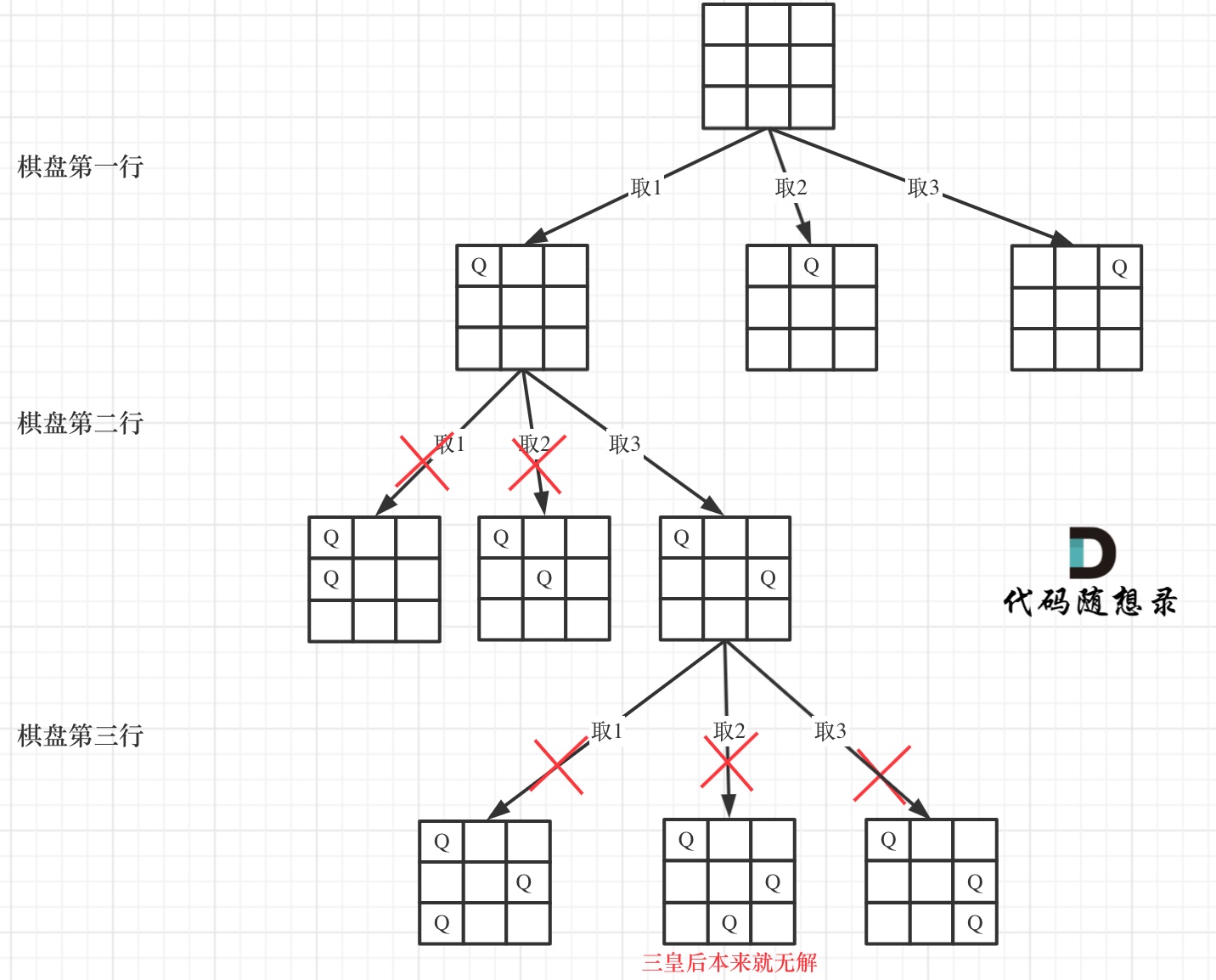
在如下树形结构中:
|
||||
|
||||
|
||||
|
||||
|
||||
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
|
||||
|
|
|
|||
|
|
@ -13,7 +13,7 @@ n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并
|
|||
上图为 8 皇后问题的一种解法。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
|
||||
|
||||
|
|
|
|||
|
|
@ -76,7 +76,7 @@ if (count > result) result = count;
|
|||
|
||||
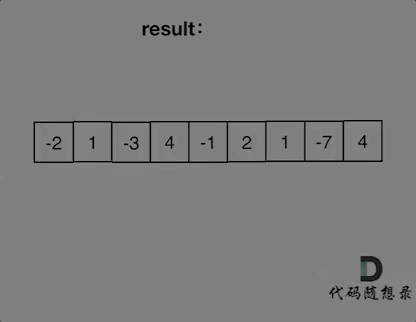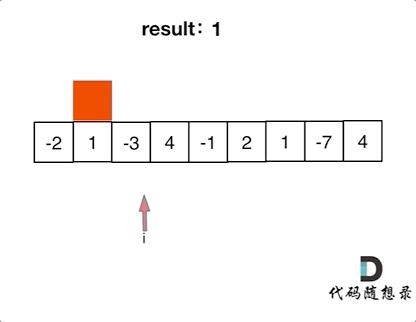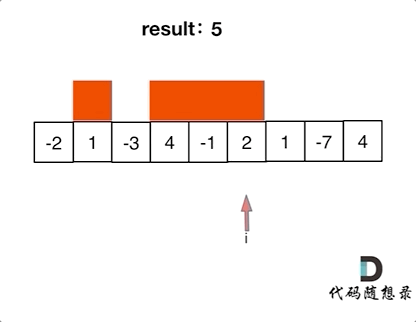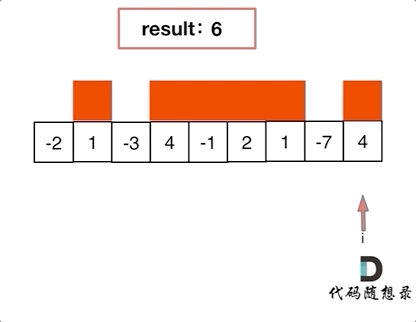
如动画所示:
|
||||
|
||||

|
||||
|
||||
|
||||
红色的起始位置就是贪心每次取 count 为正数的时候,开始一个区间的统计。
|
||||
|
||||
|
|
|
|||
|
|
@ -54,7 +54,7 @@ dp[0]应该是多少呢?
|
|||
5. 举例推导dp数组
|
||||
|
||||
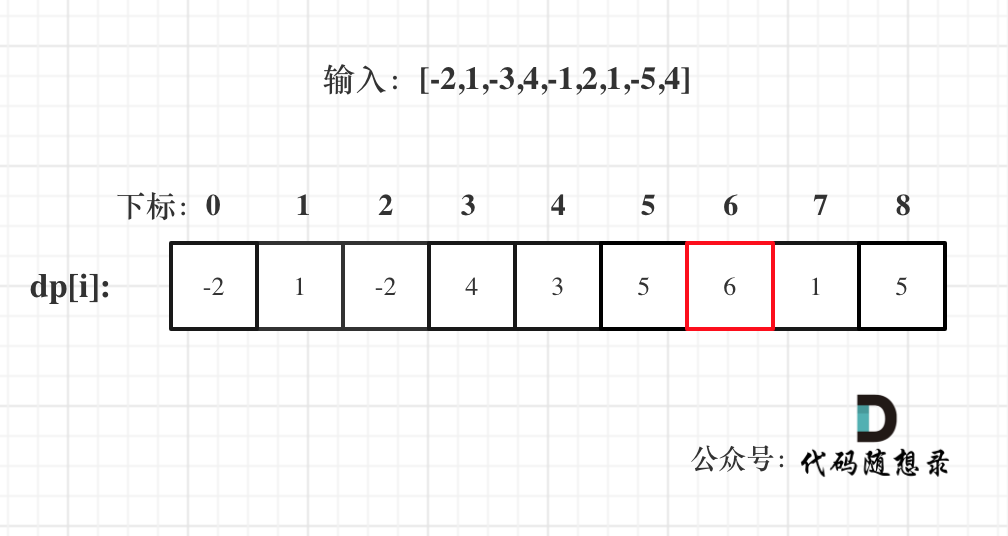
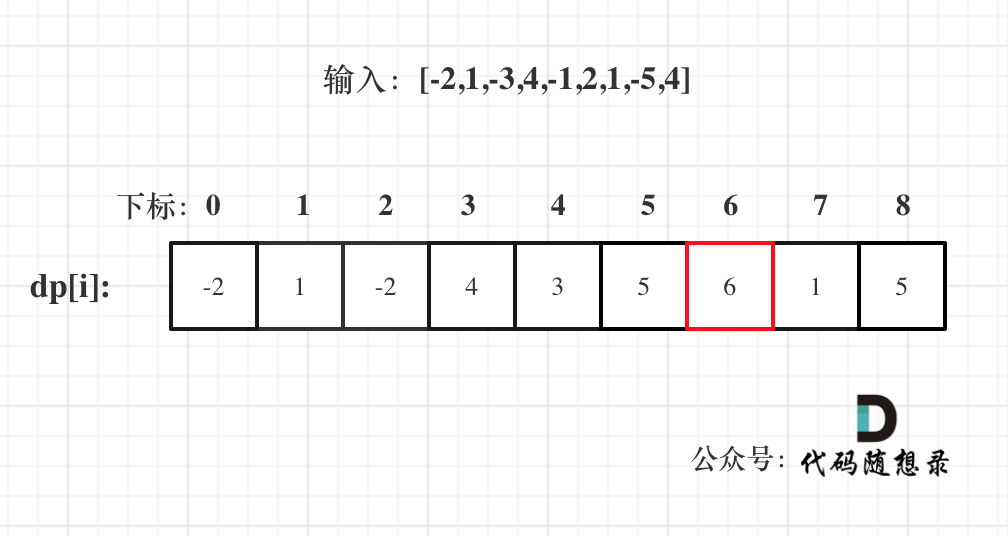
以示例一为例,输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的dp状态如下:
|
||||
|
||||
|
||||
|
||||
**注意最后的结果可不是dp[nums.size() - 1]!** ,而是dp[6]。
|
||||
|
||||
|
|
|
|||
|
|
@ -36,7 +36,7 @@
|
|||
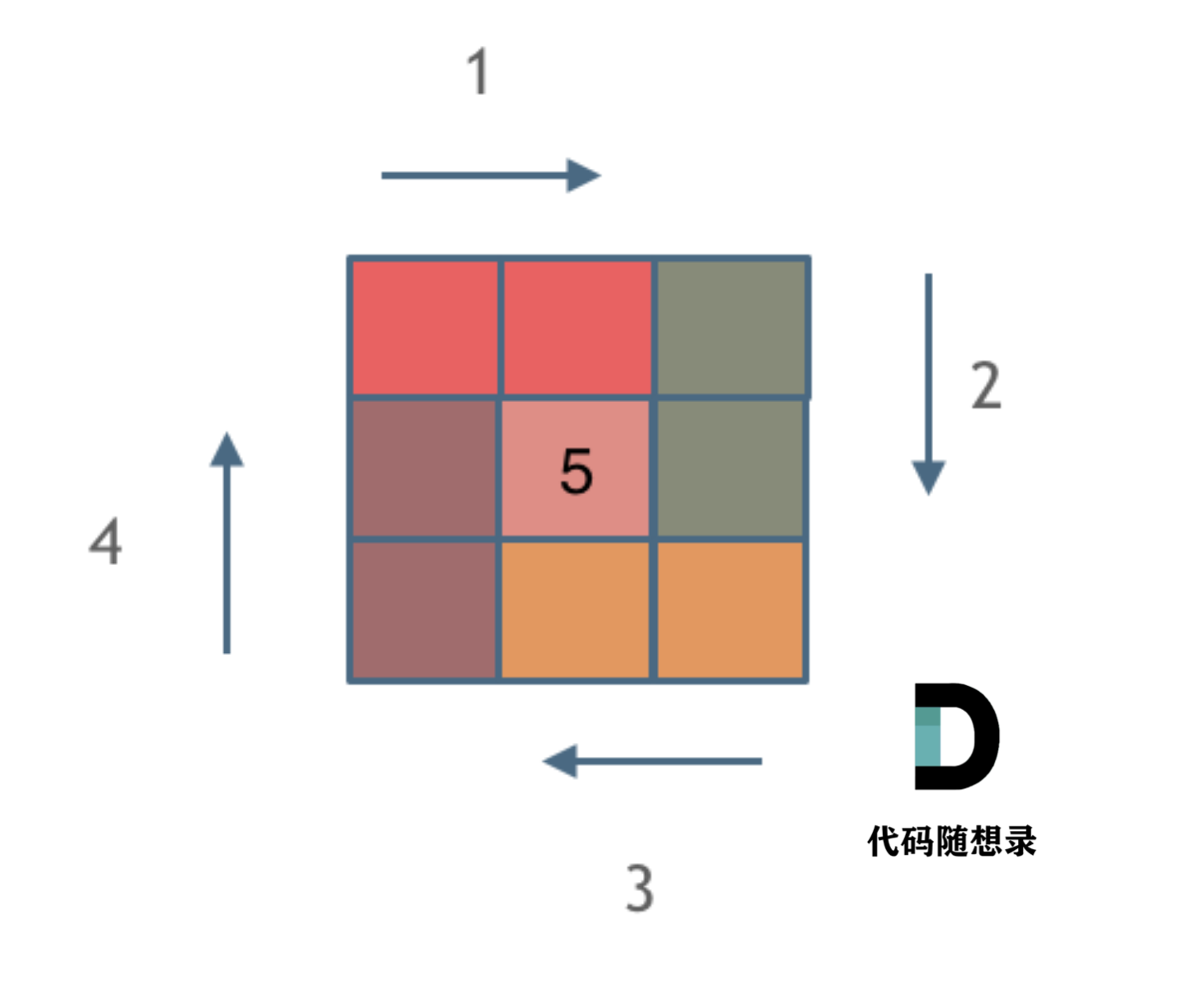
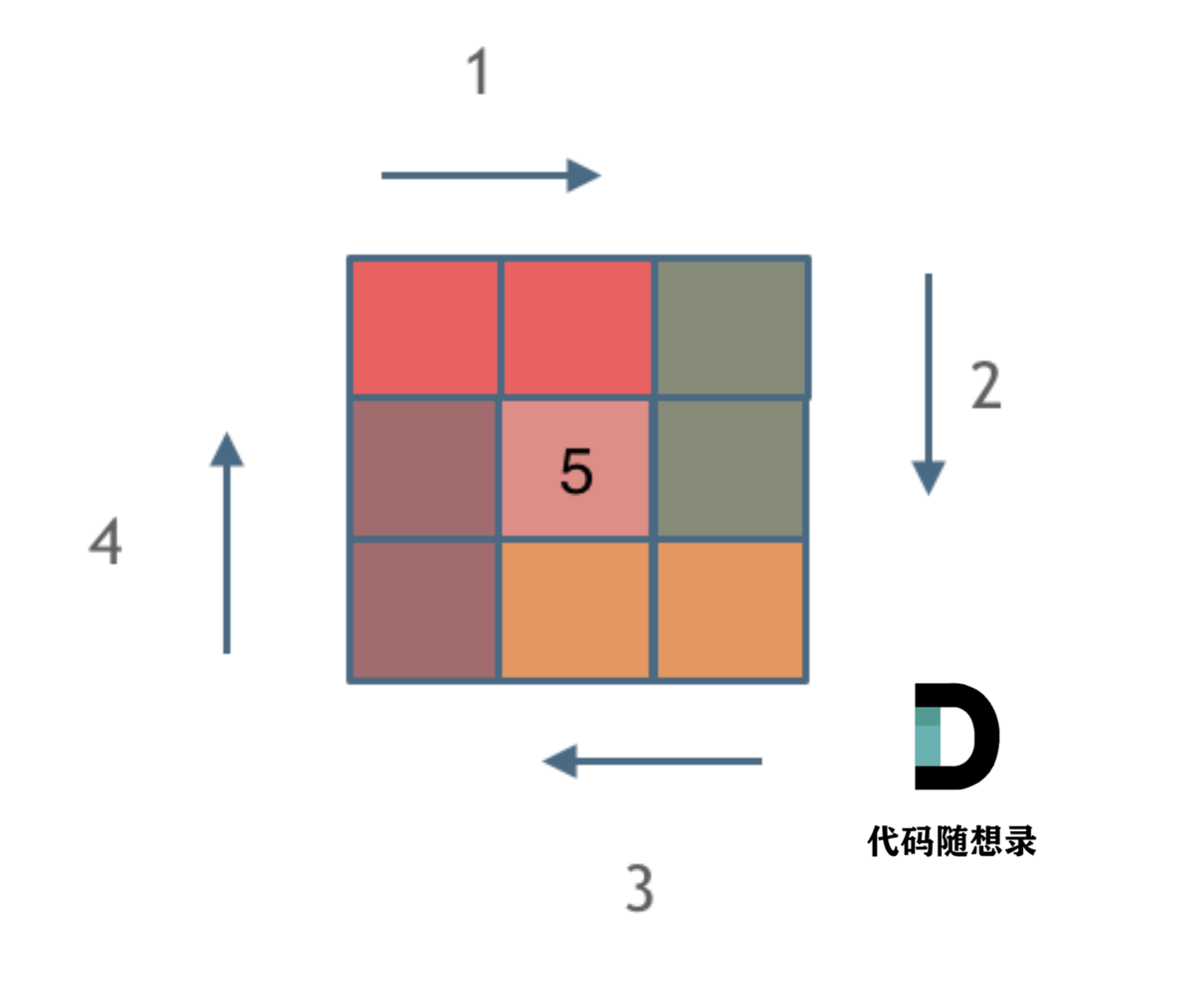
由外向内一圈一圈这么画下去,如下所示:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
|
||||
|
||||
|
|
|
|||
|
|
@ -48,7 +48,7 @@
|
|||
|
||||
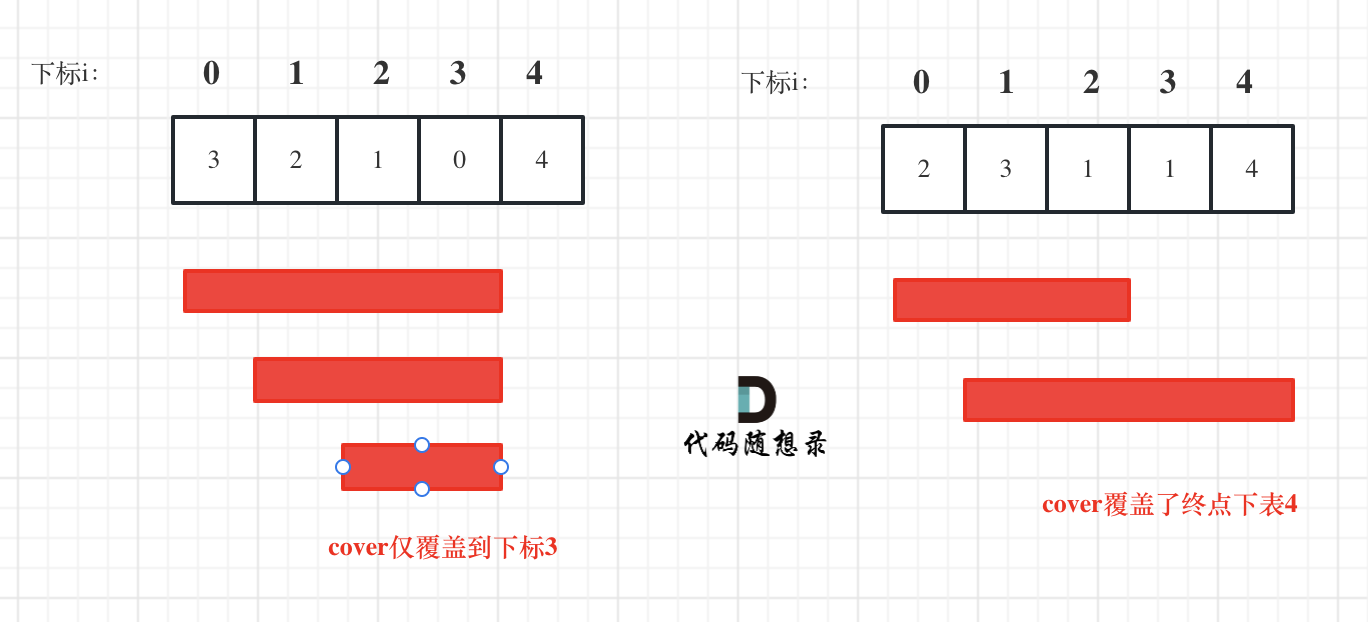
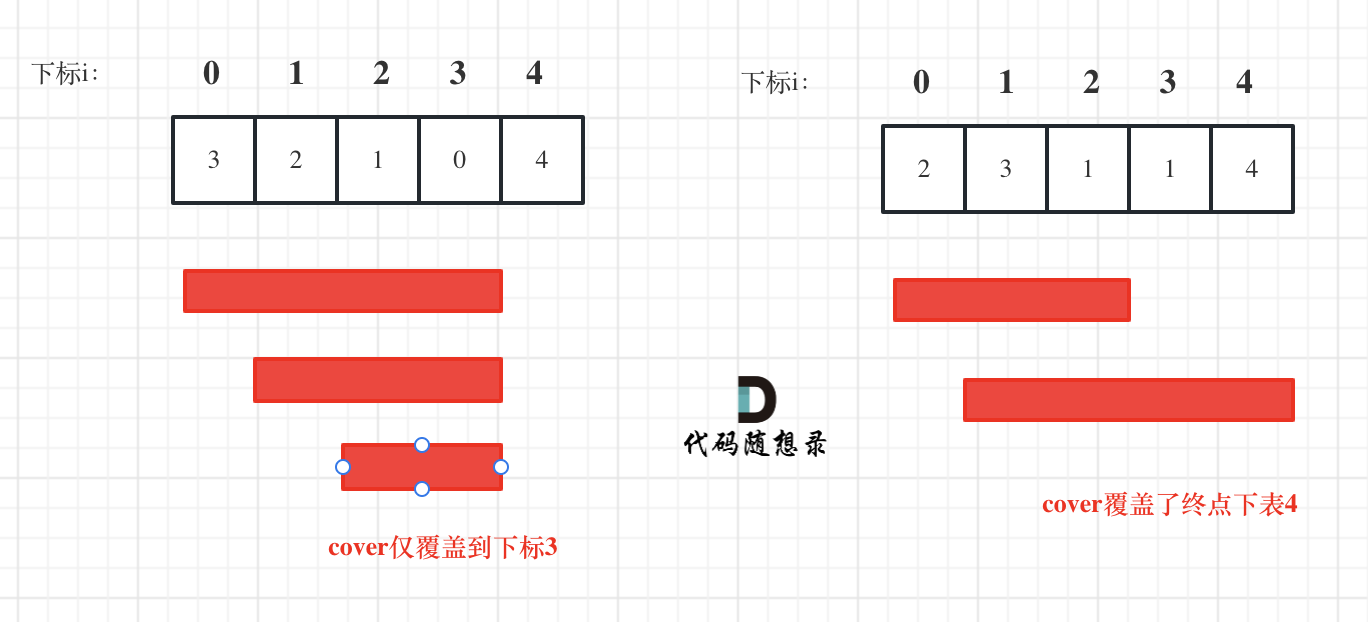
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
|
||||
|
|
|
|||
|
|
@ -38,7 +38,7 @@
|
|||
|
||||
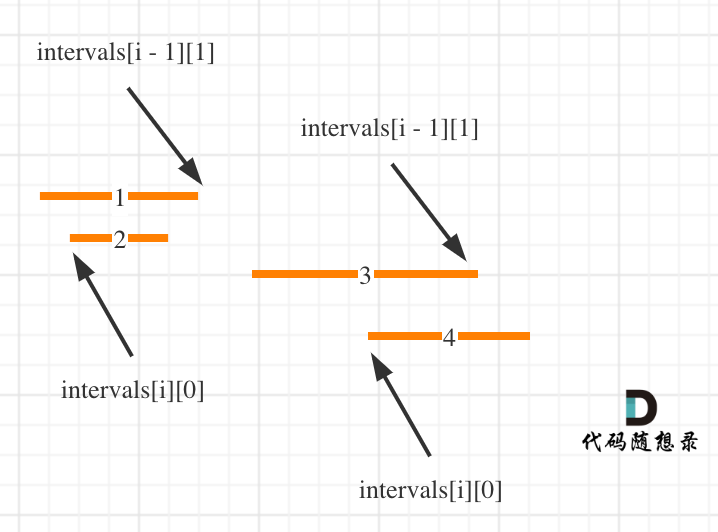
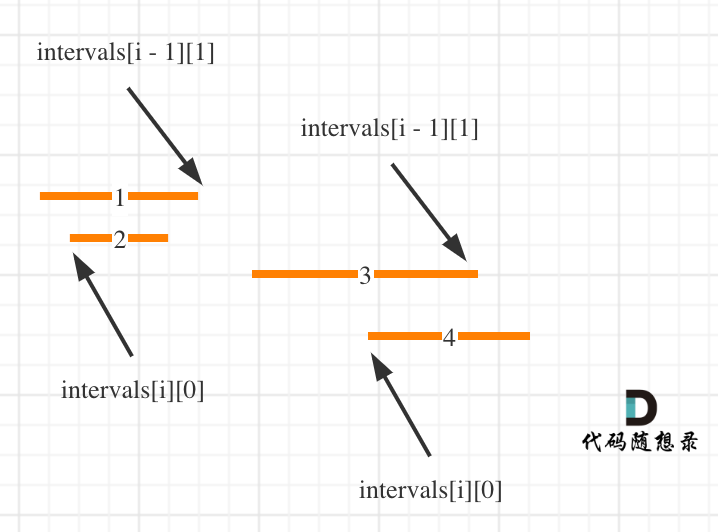
这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
|
||||
|
||||
|
||||
|
||||
|
||||
知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
|
||||
|
||||
|
|
|
|||
|
|
@ -54,7 +54,7 @@
|
|||
|
||||
那么我按照左闭右开的原则,来画一圈,大家看一下:
|
||||
|
||||

|
||||

|
||||
|
||||
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
|
||||
|
||||
|
|
|
|||
|
|
@ -16,7 +16,7 @@
|
|||
|
||||
示例 1:
|
||||
|
||||

|
||||

|
||||
|
||||
* 输入:m = 3, n = 7
|
||||
* 输出:28
|
||||
|
|
@ -62,7 +62,7 @@
|
|||
|
||||
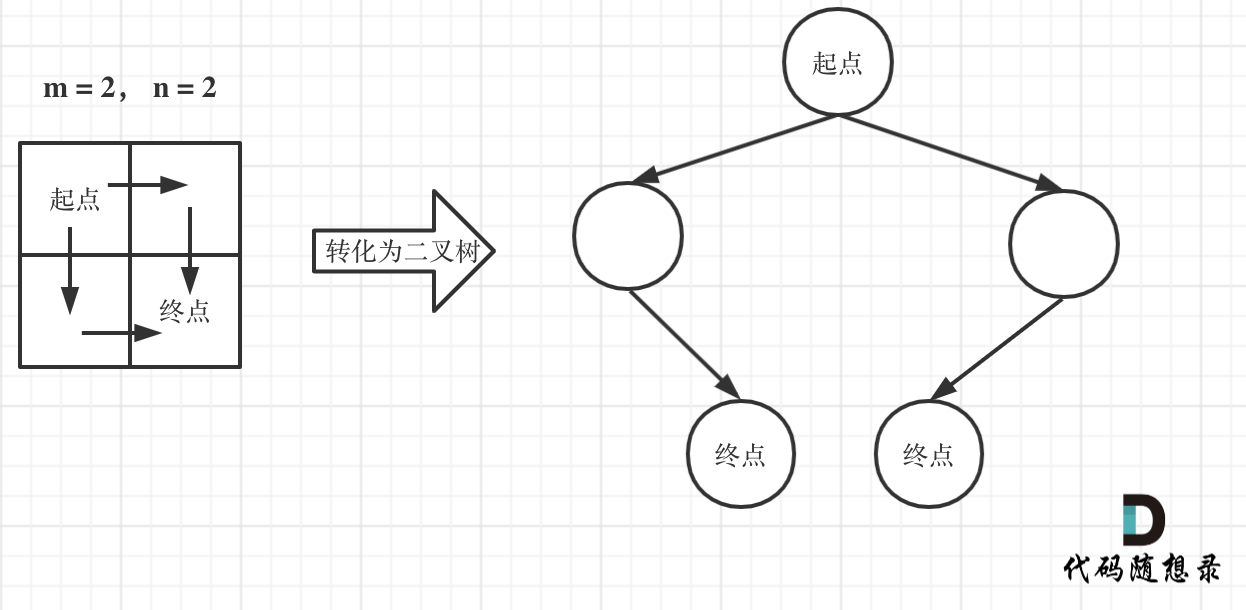
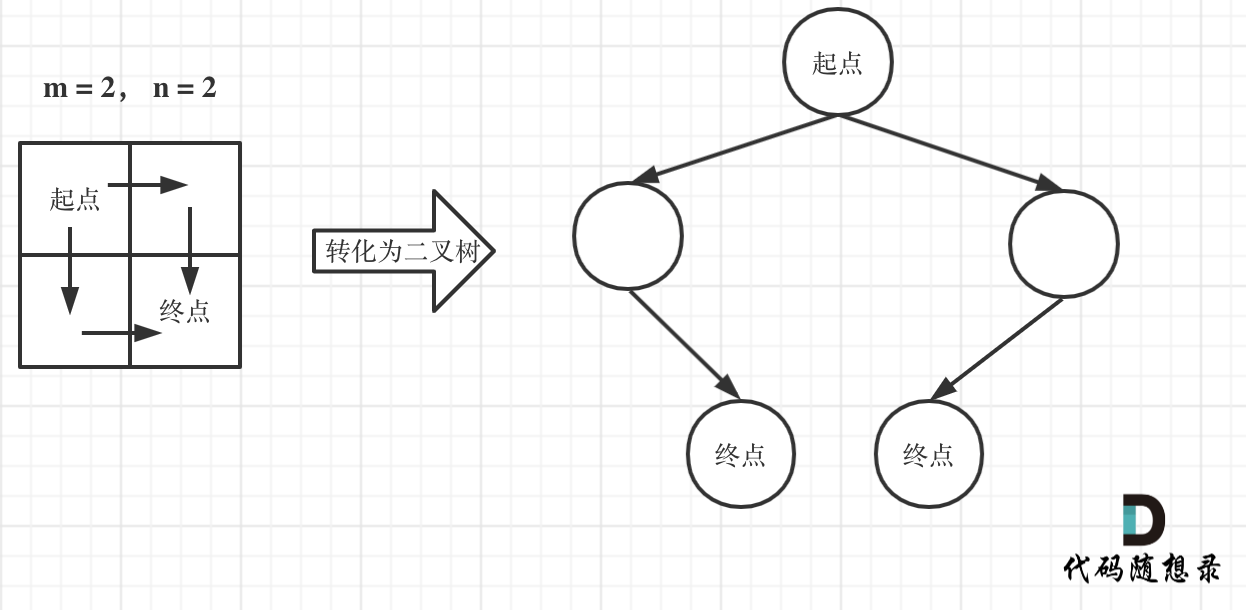
如图举例:
|
||||
|
||||
|
||||
|
||||
|
||||
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
|
||||
|
||||
|
|
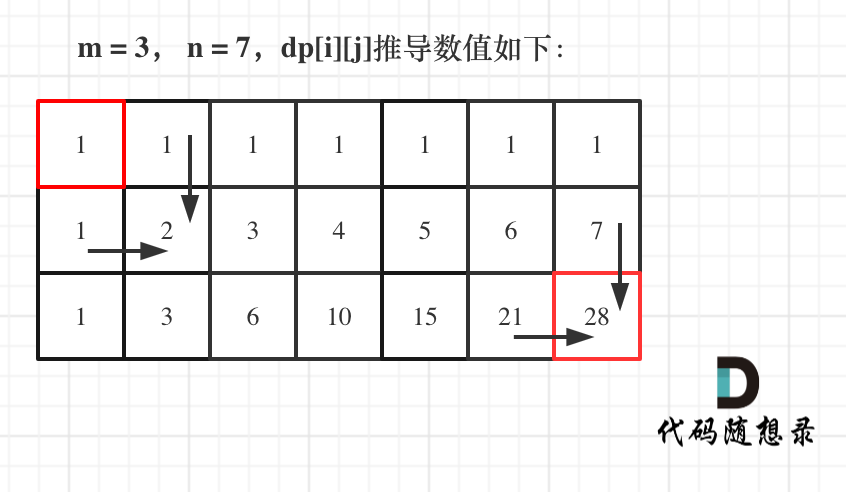
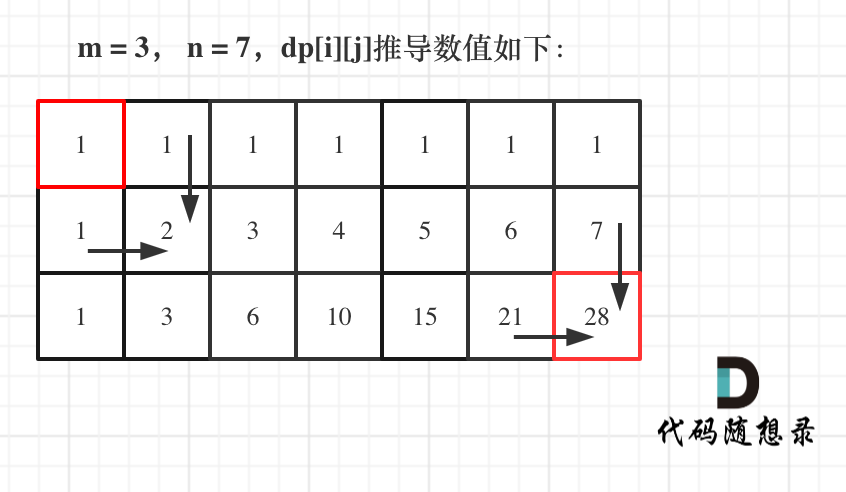
@ -131,7 +131,7 @@ for (int j = 0; j < n; j++) dp[0][j] = 1;
|
|||
|
||||
如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
以上动规五部曲分析完毕,C++代码如下:
|
||||
|
||||
|
|
@ -180,7 +180,7 @@ public:
|
|||
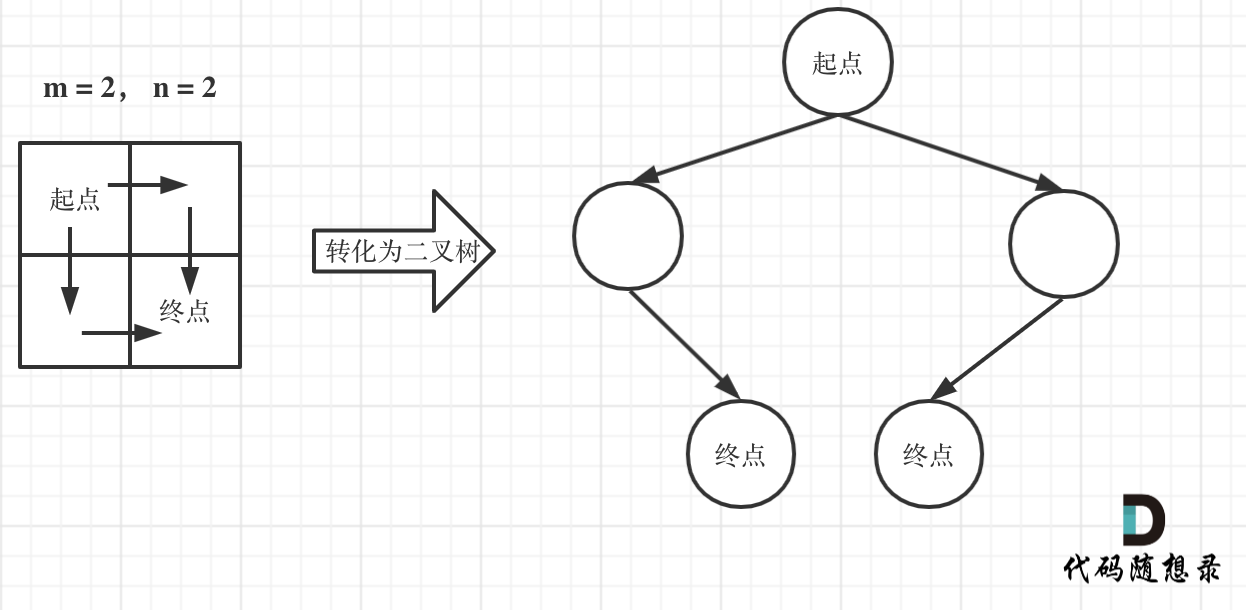
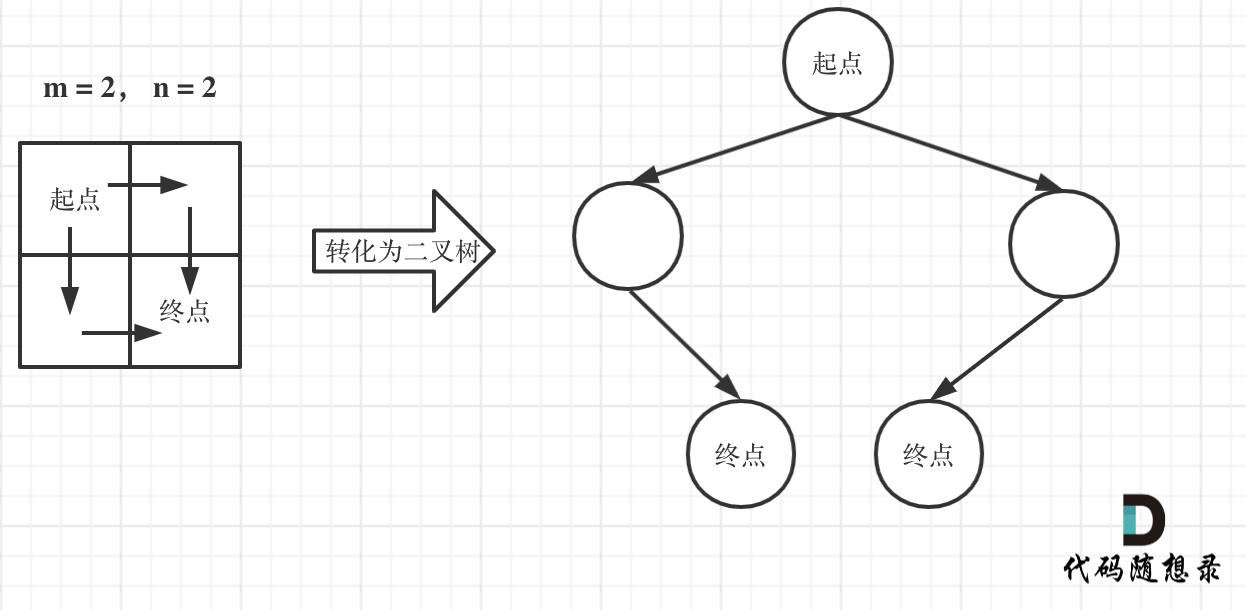
|
||||
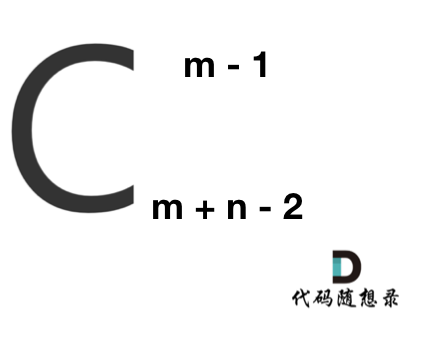
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
|
||||
|
||||
|
||||
|
||||
|
||||
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
|
||||
|
||||
|
|
@ -190,7 +190,7 @@ public:
|
|||
|
||||
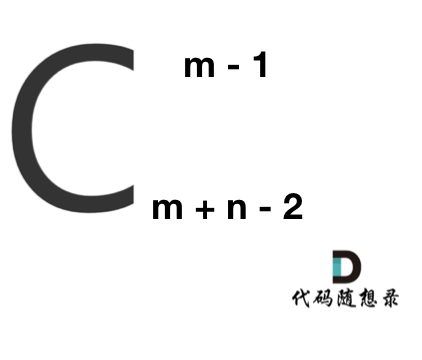
那么答案,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
**求组合的时候,要防止两个int相乘溢出!** 所以不能把算式的分子都算出来,分母都算出来再做除法。
|
||||
|
||||
|
|
|
|||
|
|
@ -14,13 +14,13 @@
|
|||
|
||||
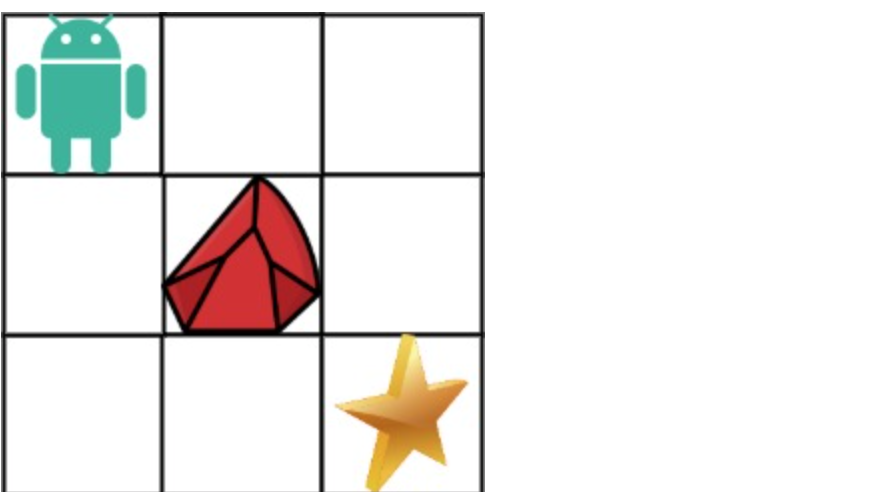
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
|
||||
|
||||

|
||||

|
||||
|
||||
网格中的障碍物和空位置分别用 1 和 0 来表示。
|
||||
|
||||
示例 1:
|
||||
|
||||
|
||||
|
||||
|
||||
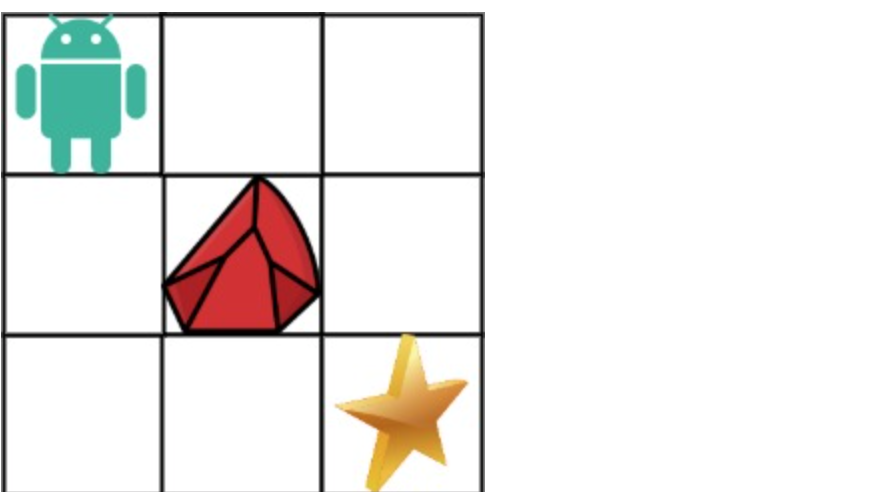
* 输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
|
||||
* 输出:2
|
||||
|
|
@ -32,7 +32,7 @@
|
|||
|
||||
示例 2:
|
||||
|
||||

|
||||

|
||||
|
||||
* 输入:obstacleGrid = [[0,1],[0,0]]
|
||||
* 输出:1
|
||||
|
|
@ -93,7 +93,7 @@ for (int j = 0; j < n; j++) dp[0][j] = 1;
|
|||
|
||||
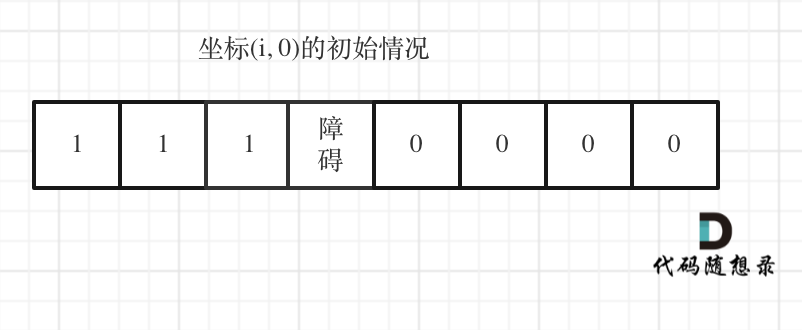
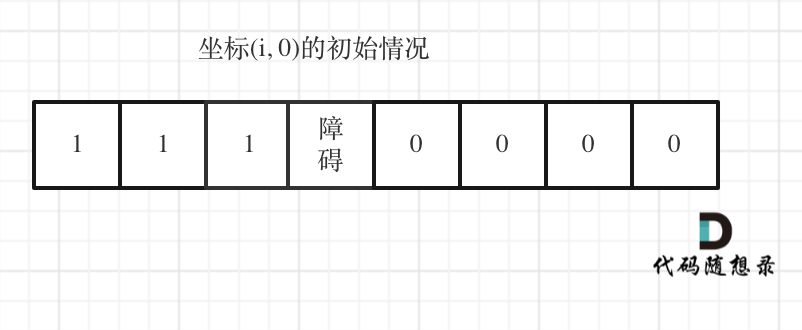
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
下标(0, j)的初始化情况同理。
|
||||
|
||||
|
|
@ -127,11 +127,11 @@ for (int i = 1; i < m; i++) {
|
|||
|
||||
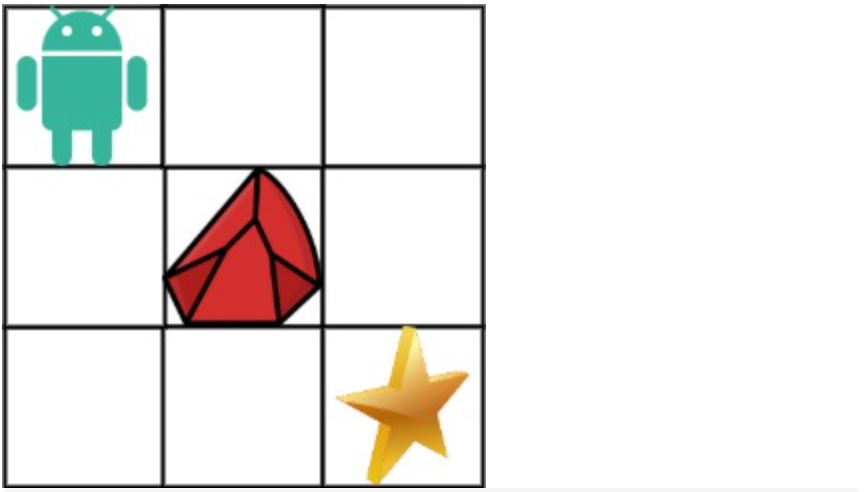
拿示例1来举例如题:
|
||||
|
||||
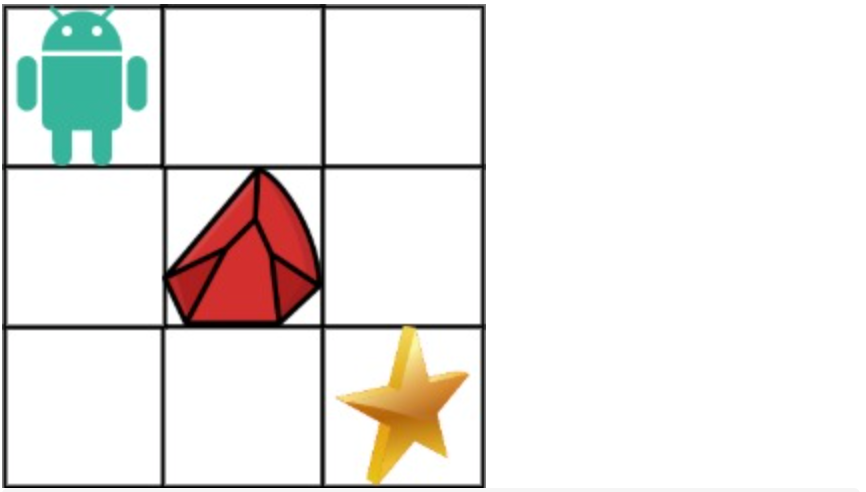
|
||||
|
||||
|
||||
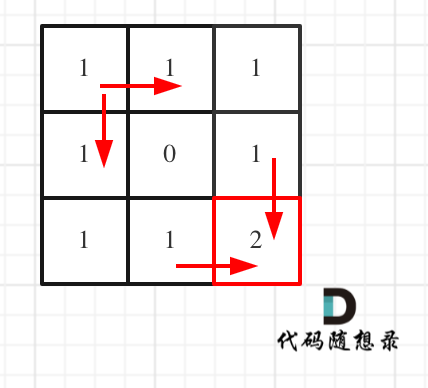
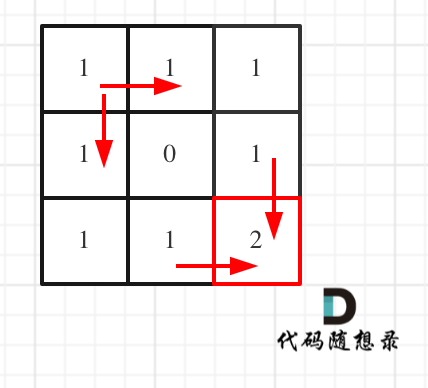
对应的dp table 如图:
|
||||
|
||||
|
||||
|
||||
|
||||
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
|
||||
|
||||
|
|
|
|||
|
|
@ -101,7 +101,7 @@ dp[i]: 爬到第i层楼梯,有dp[i]种方法
|
|||
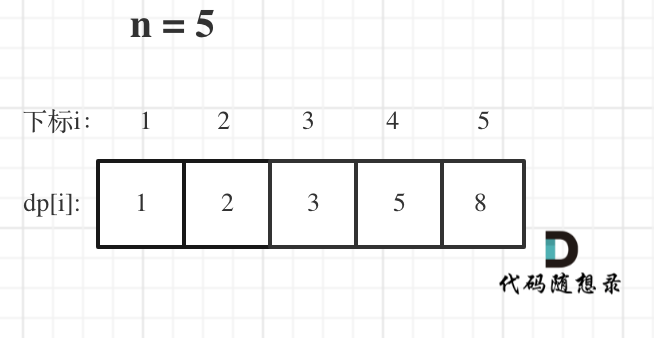
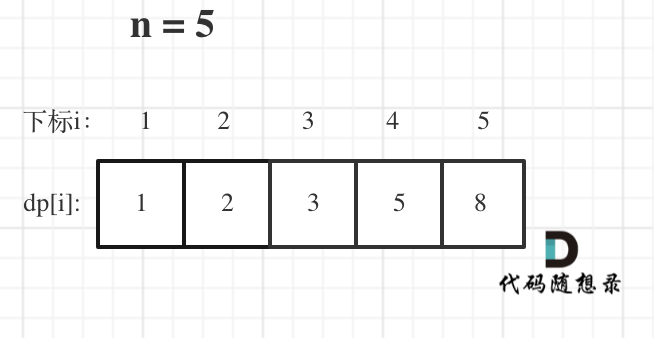
举例当n为5的时候,dp table(dp数组)应该是这样的
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
|
||||
|
||||
|
|
|
|||
|
|
@ -170,7 +170,7 @@ for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
|
|||
|
||||
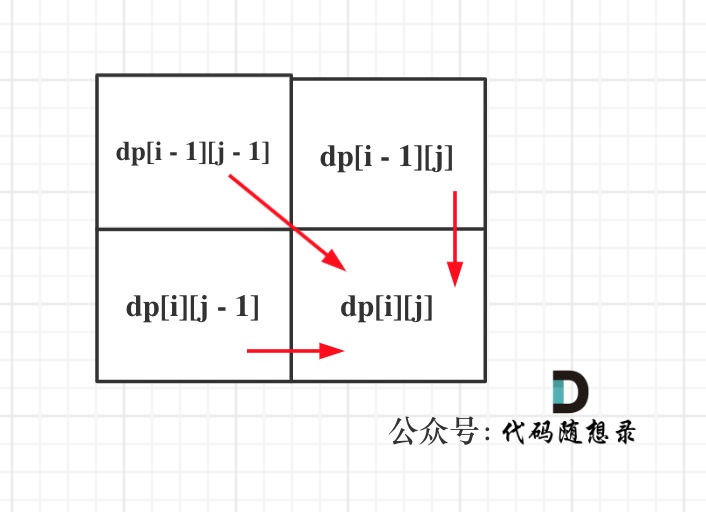
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:
|
||||
|
||||

|
||||
|
||||
|
||||
所以在dp矩阵中一定是从左到右从上到下去遍历。
|
||||
|
||||
|
|
@ -194,7 +194,7 @@ for (int i = 1; i <= word1.size(); i++) {
|
|||
|
||||
以示例1为例,输入:`word1 = "horse", word2 = "ros"`为例,dp矩阵状态图如下:
|
||||
|
||||
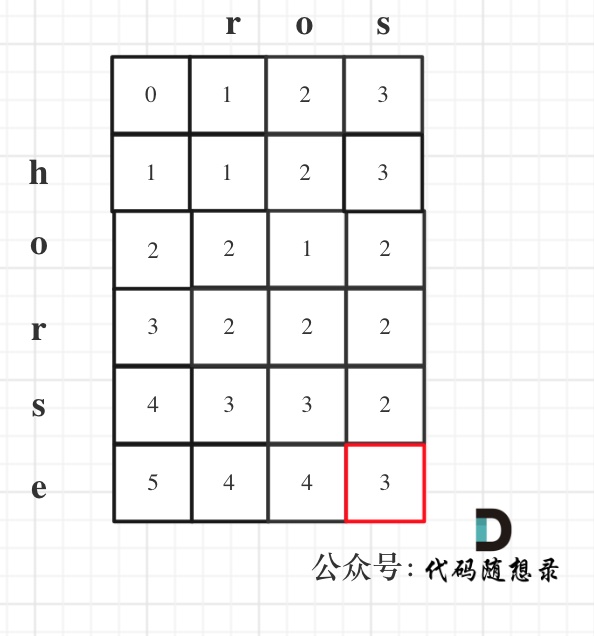
|
||||
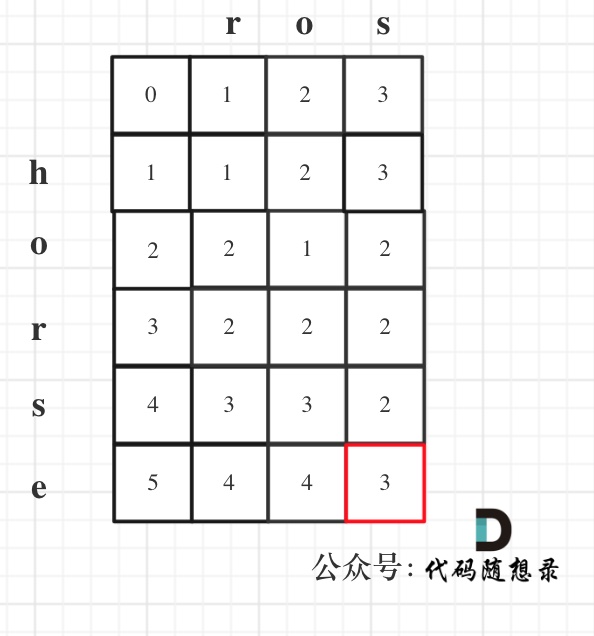
|
||||
|
||||
以上动规五部分析完毕,C++代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -82,7 +82,7 @@ for (int i = 1; i <= n; i++) {
|
|||
|
||||
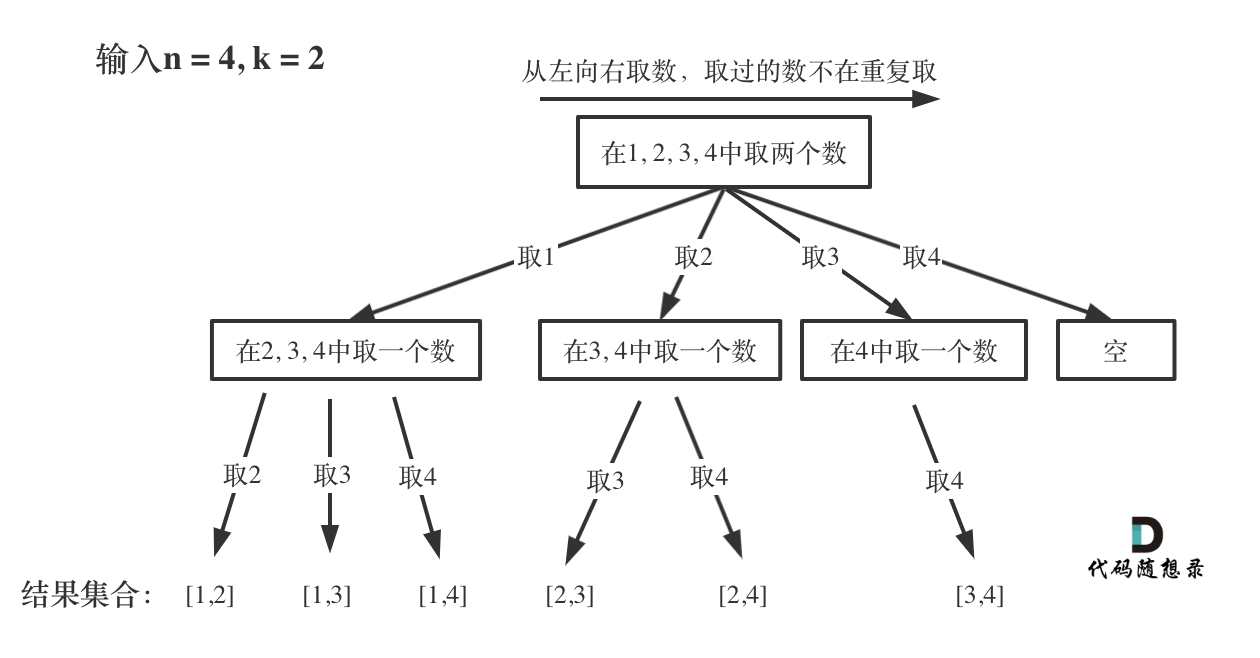
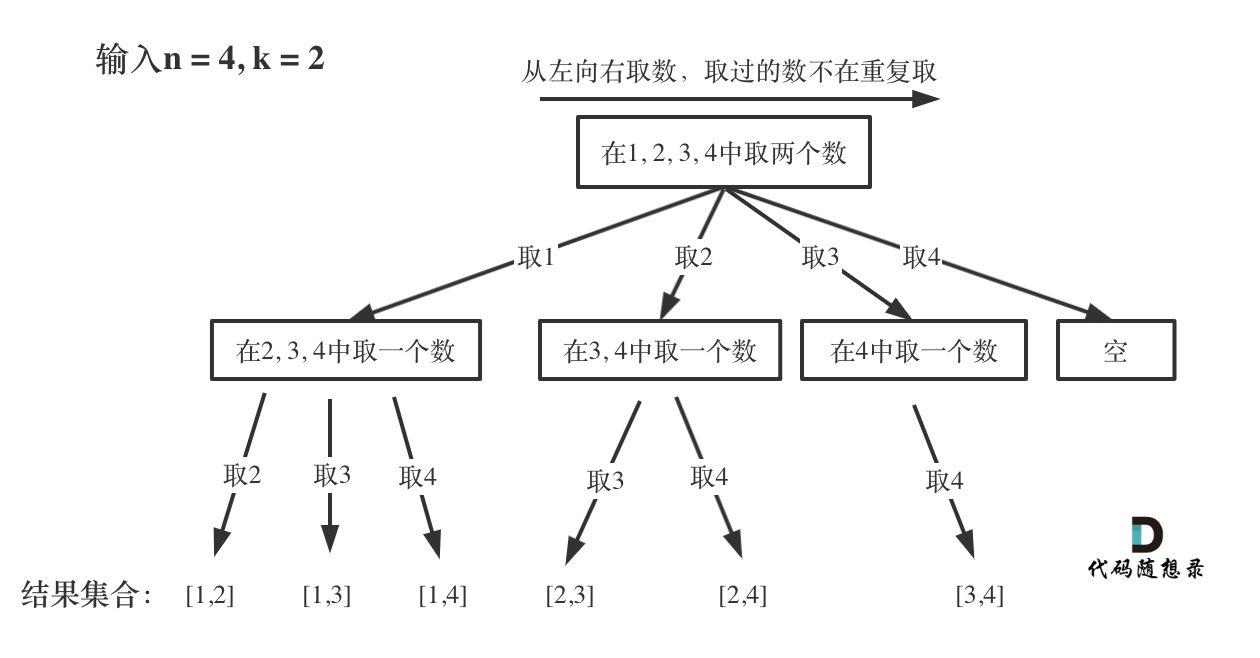
那么我把组合问题抽象为如下树形结构:
|
||||
|
||||
|
||||
|
||||
|
||||
可以看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
|
||||
|
||||
|
|
@ -126,7 +126,7 @@ vector<int> path; // 用来存放符合条件结果
|
|||
|
||||
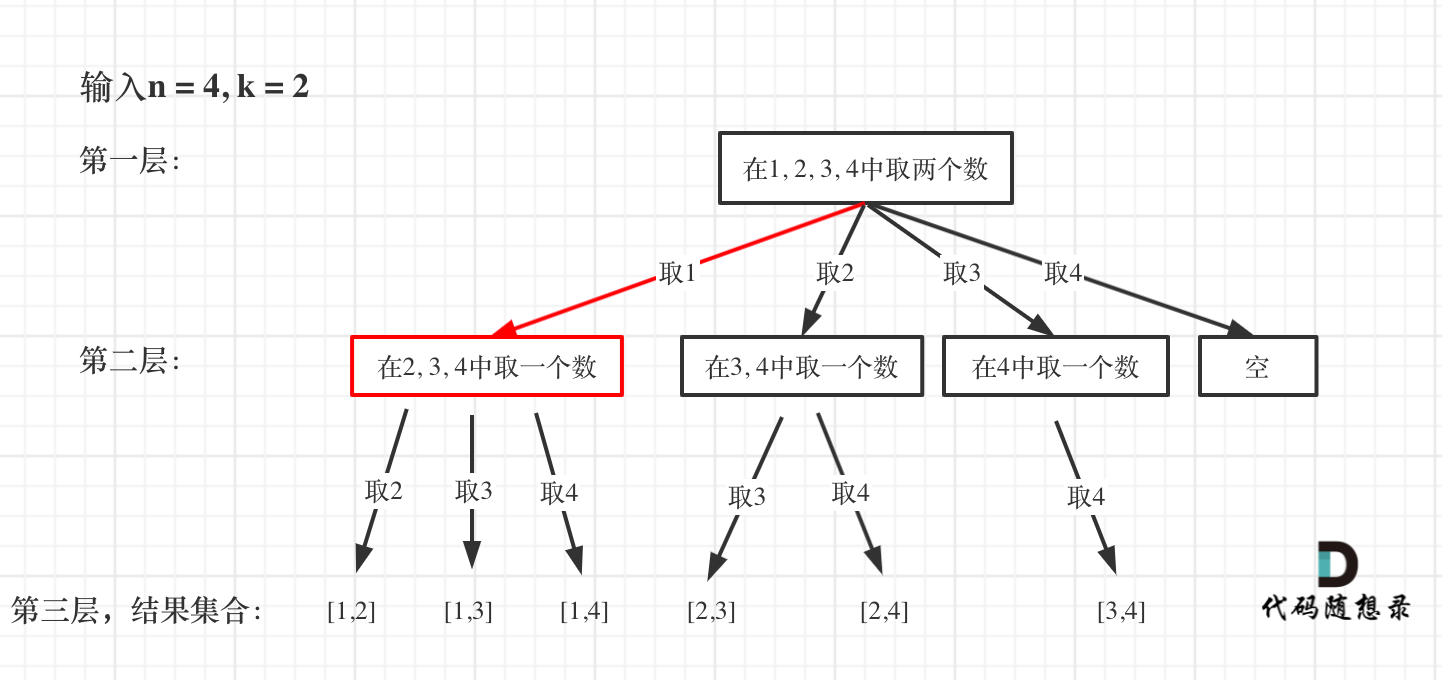
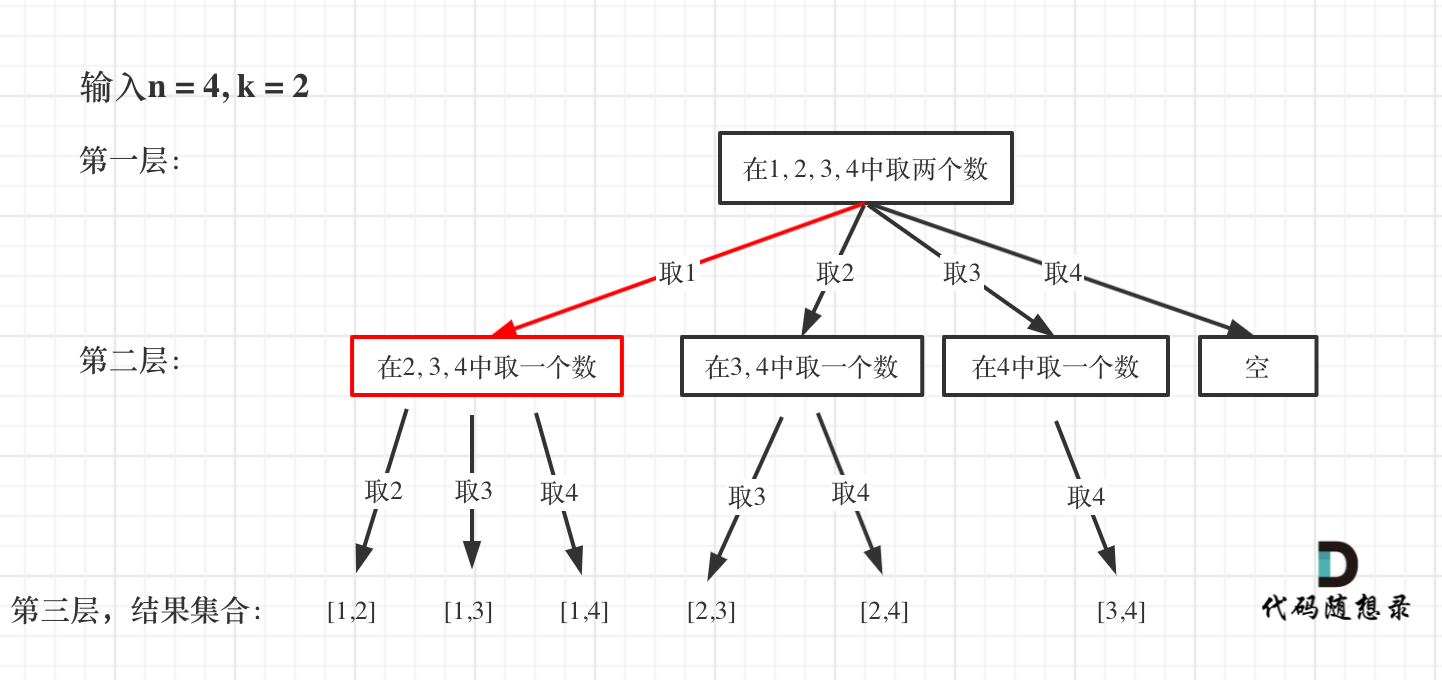
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。
|
||||
|
||||
|
||||
|
||||
|
||||
所以需要startIndex来记录下一层递归,搜索的起始位置。
|
||||
|
||||
|
|
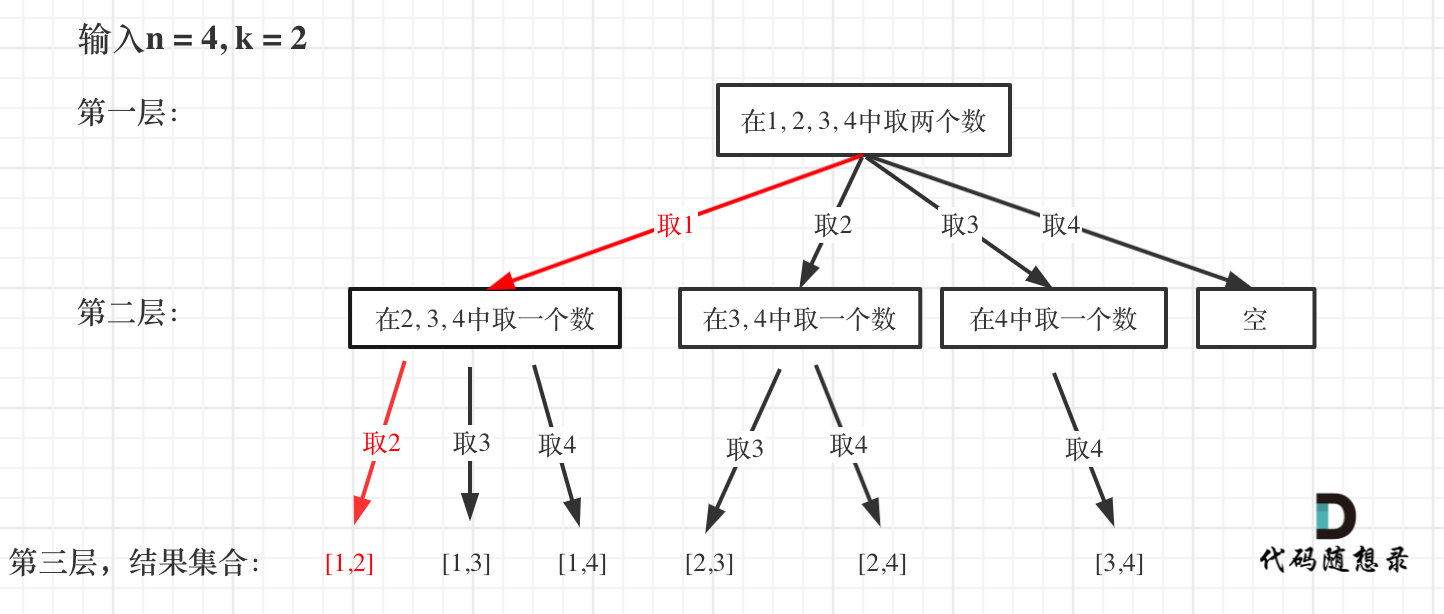
@ -146,7 +146,7 @@ path这个数组的大小如果达到k,说明我们找到了一个子集大小
|
|||
|
||||
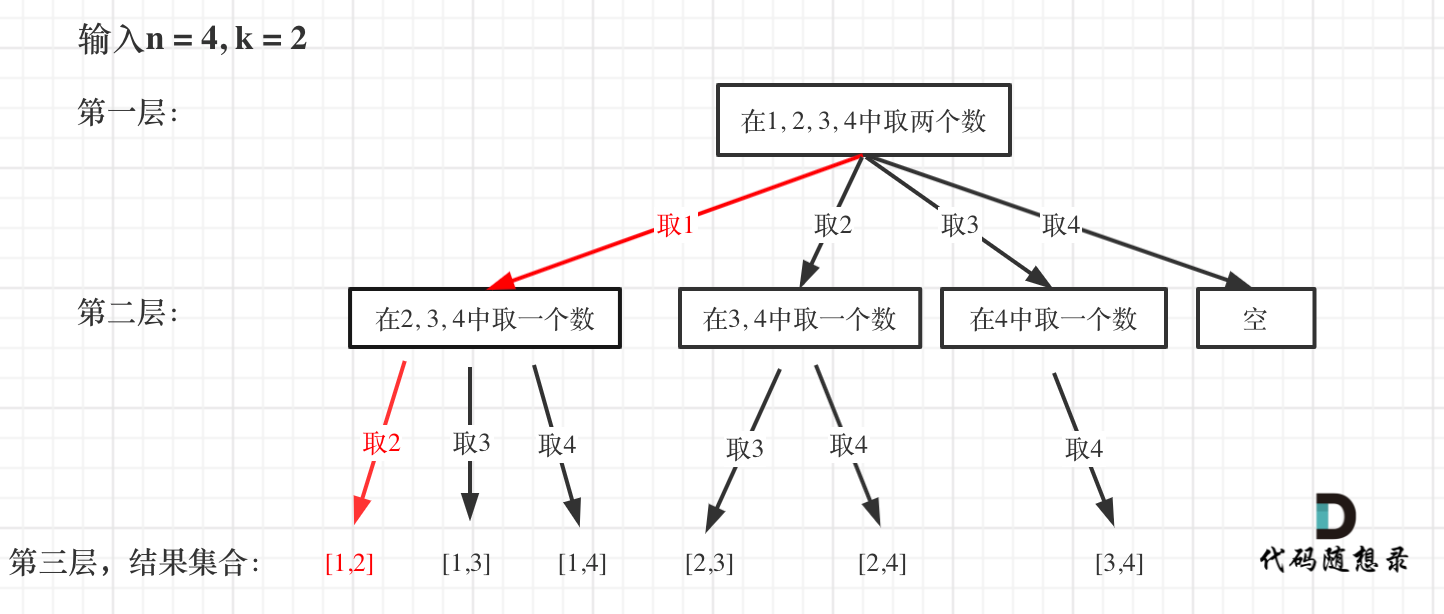
如图红色部分:
|
||||
|
||||
|
||||
|
||||
|
||||
此时用result二维数组,把path保存起来,并终止本层递归。
|
||||
|
||||
|
|
@ -163,7 +163,7 @@ if (path.size() == k) {
|
|||
|
||||
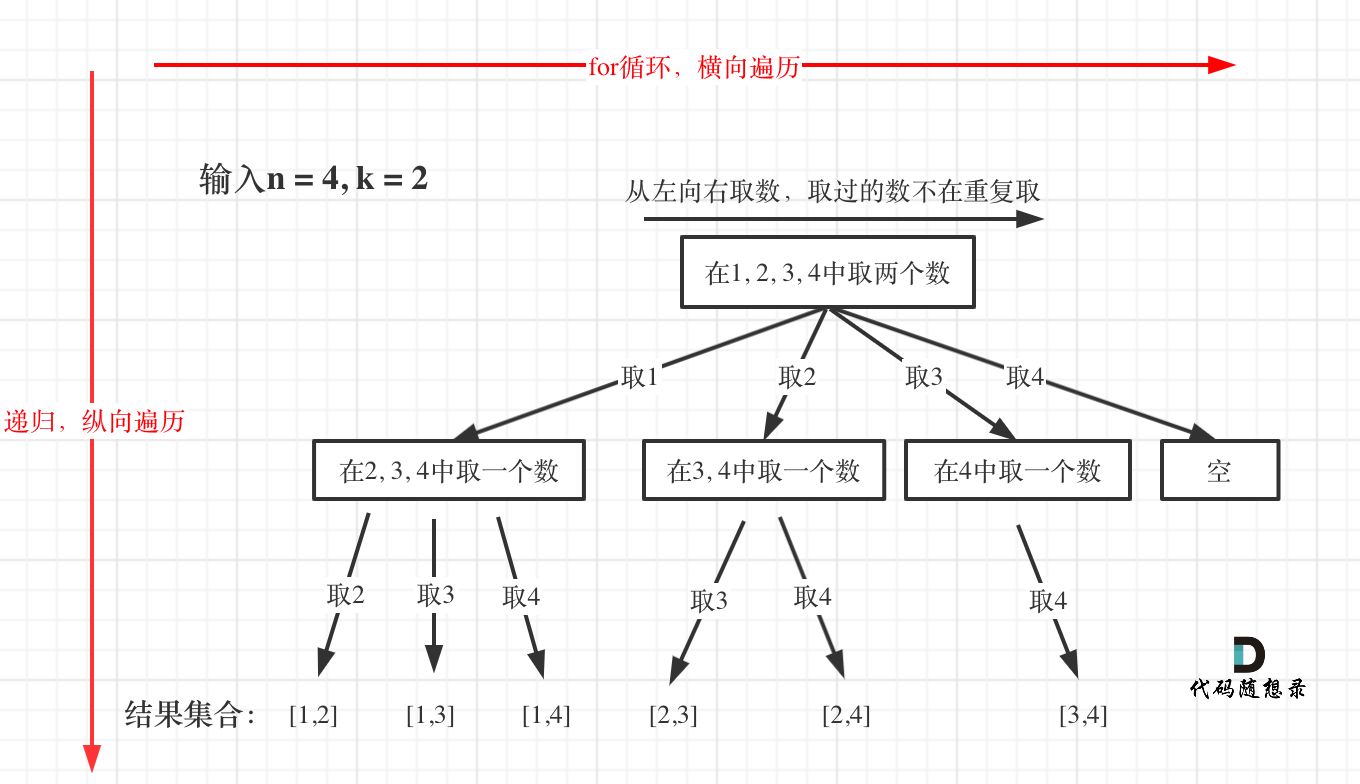
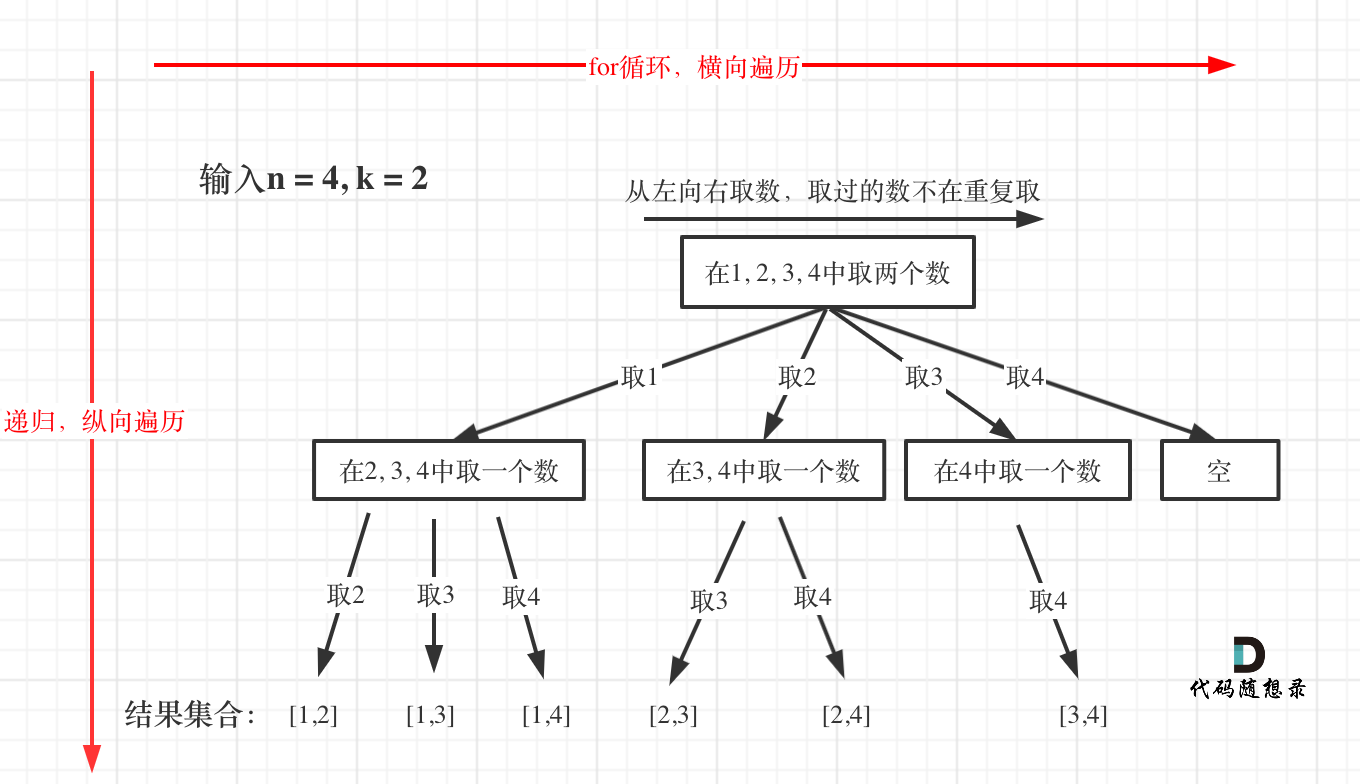
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。
|
||||
|
||||
|
||||
|
||||
|
||||
如此我们才遍历完图中的这棵树。
|
||||
|
||||
|
|
@ -267,7 +267,7 @@ for (int i = startIndex; i <= n; i++) {
|
|||
|
||||
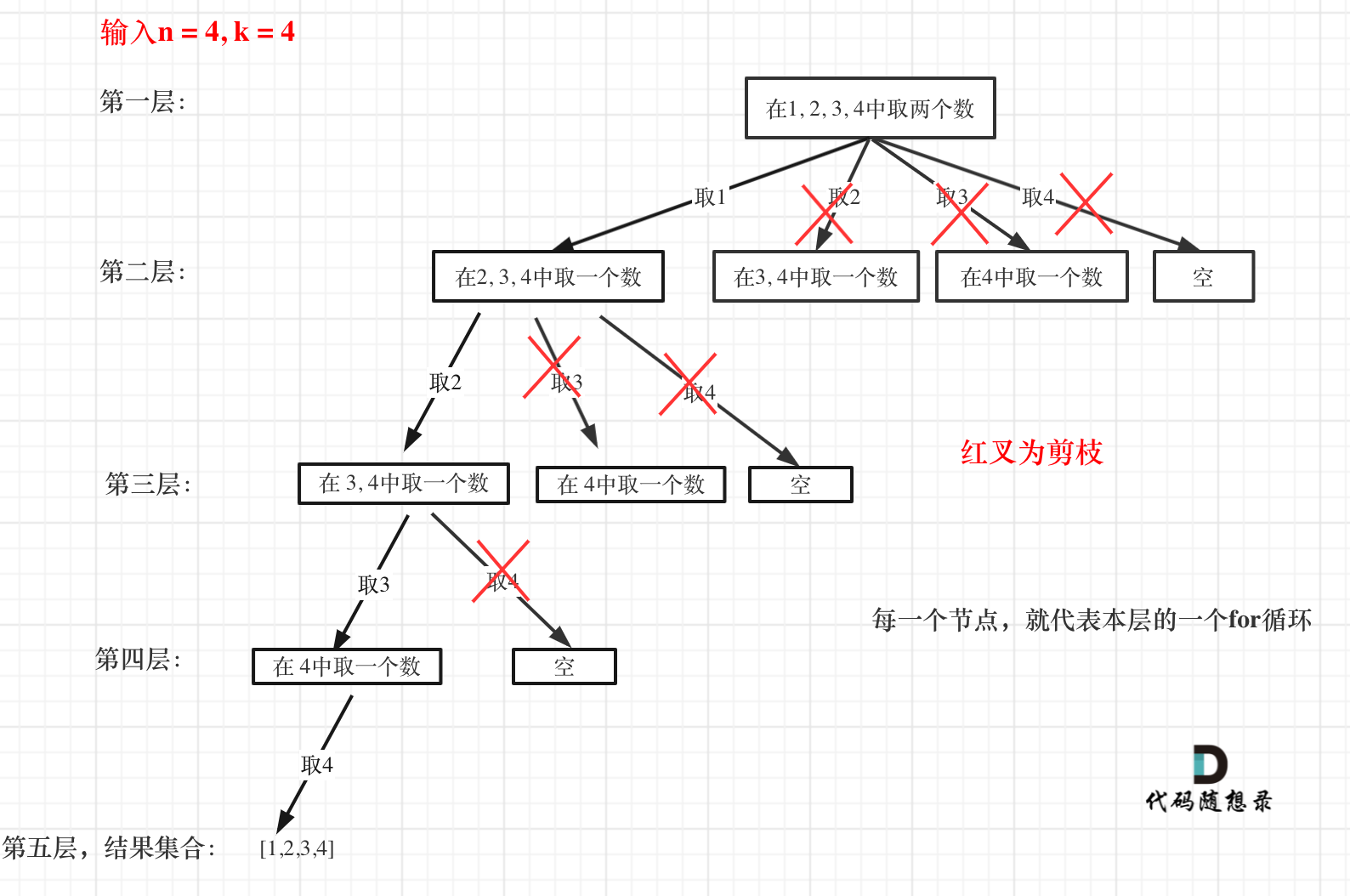
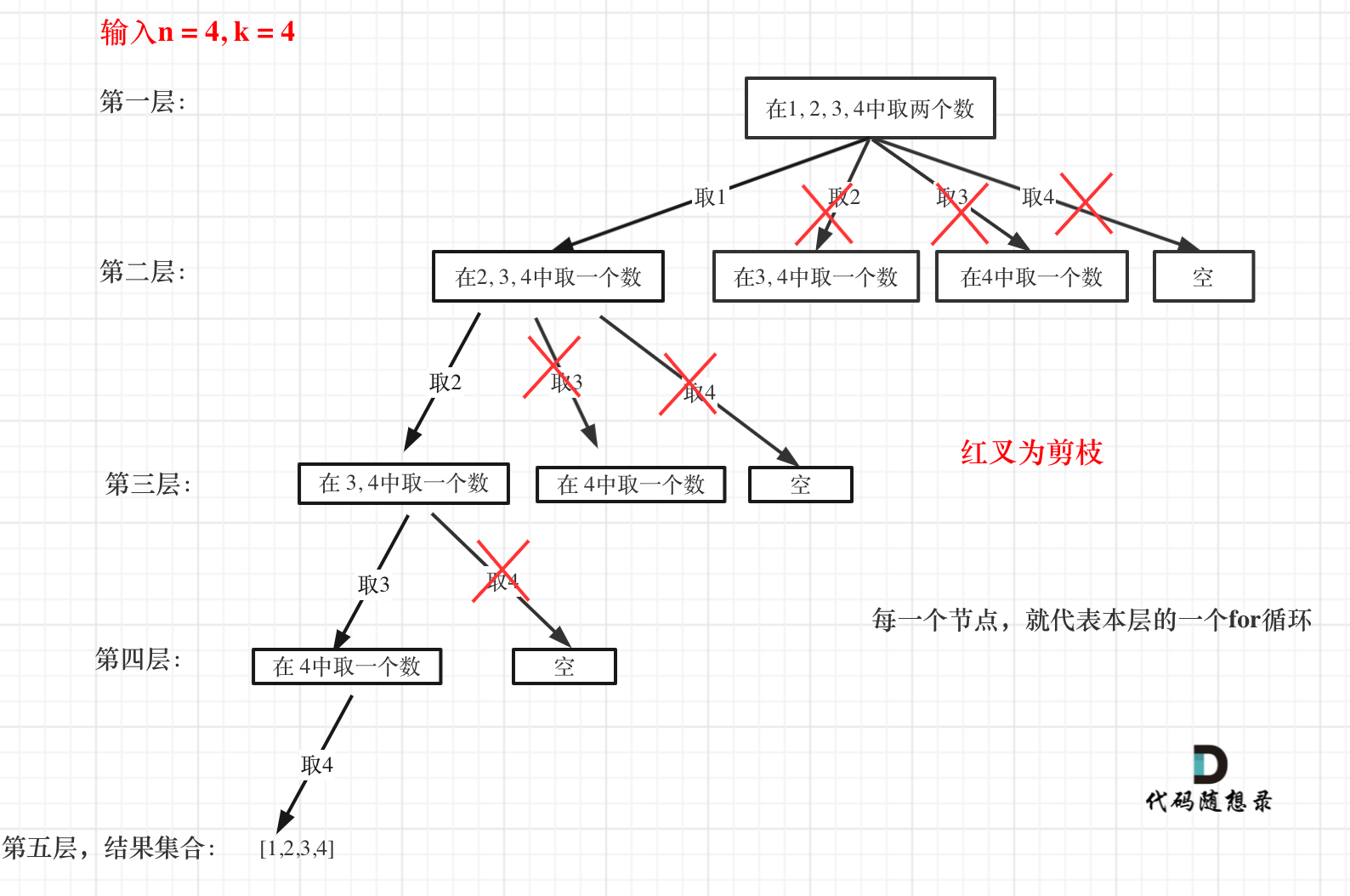
这么说有点抽象,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
|
||||
|
||||
|
|
|
|||
|
|
@ -67,7 +67,7 @@ for (int i = startIndex; i <= n; i++) {
|
|||
|
||||
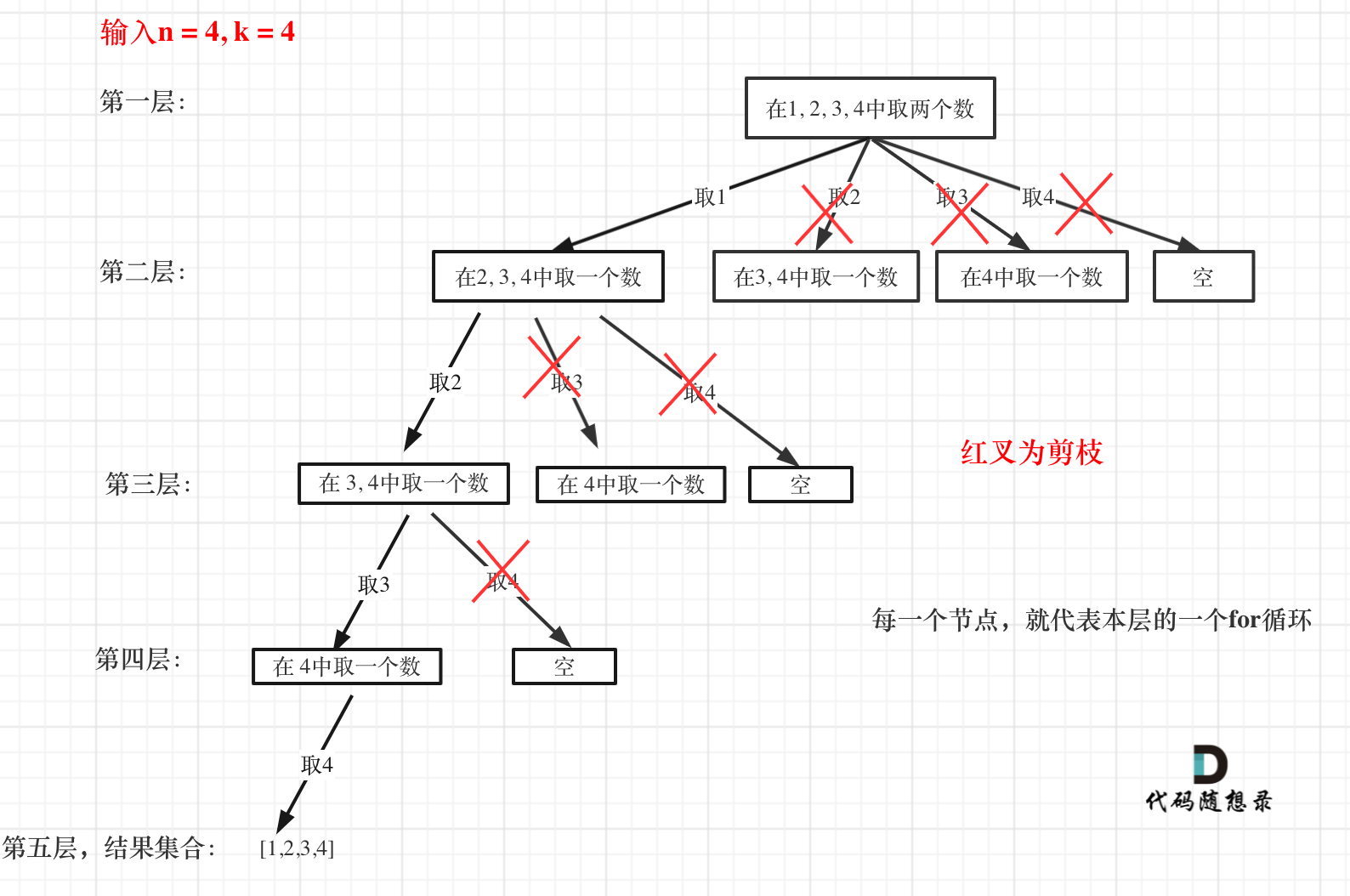
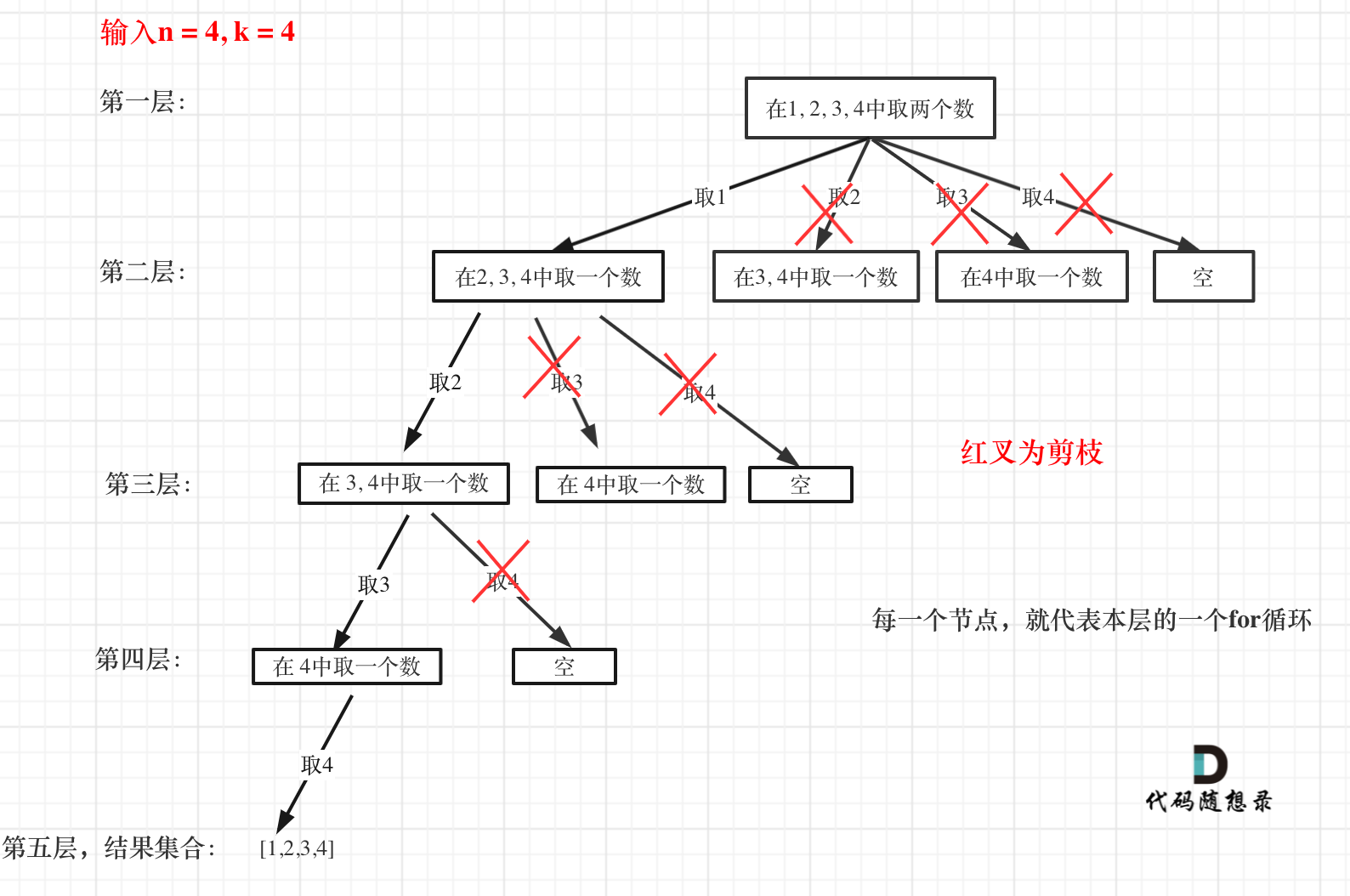
这么说有点抽象,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
|
||||
|
|
|
|||
|
|
@ -46,7 +46,7 @@
|
|||
|
||||
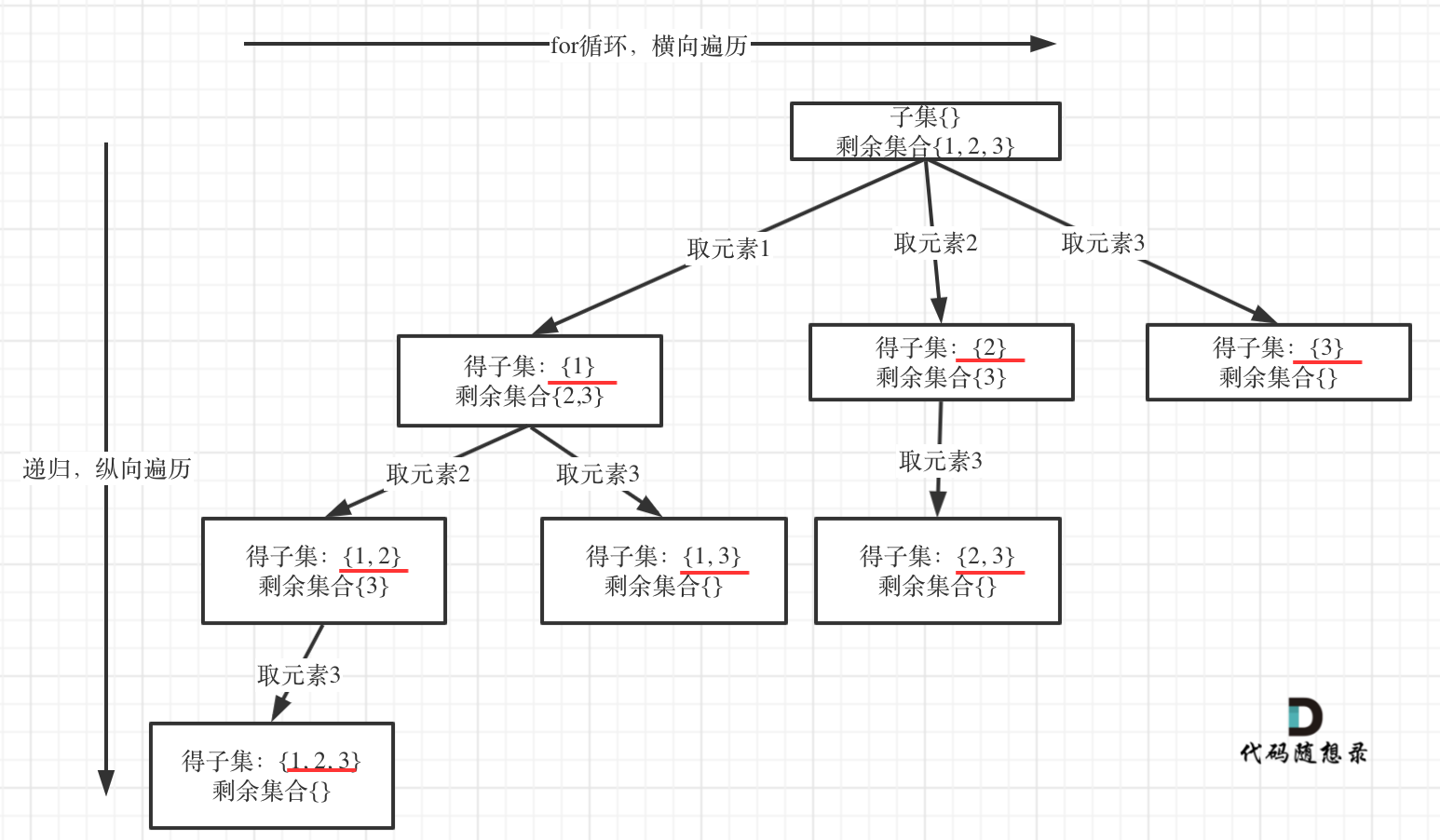
以示例中nums = [1,2,3]为例把求子集抽象为树型结构,如下:
|
||||
|
||||

|
||||
|
||||
|
||||
从图中红线部分,可以看出**遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合**。
|
||||
|
||||
|
|
@ -70,7 +70,7 @@ void backtracking(vector<int>& nums, int startIndex) {
|
|||
|
||||
从图中可以看出:
|
||||
|
||||

|
||||

|
||||
|
||||
剩余集合为空的时候,就是叶子节点。
|
||||
|
||||
|
|
|
|||
|
|
@ -11,9 +11,9 @@
|
|||
|
||||
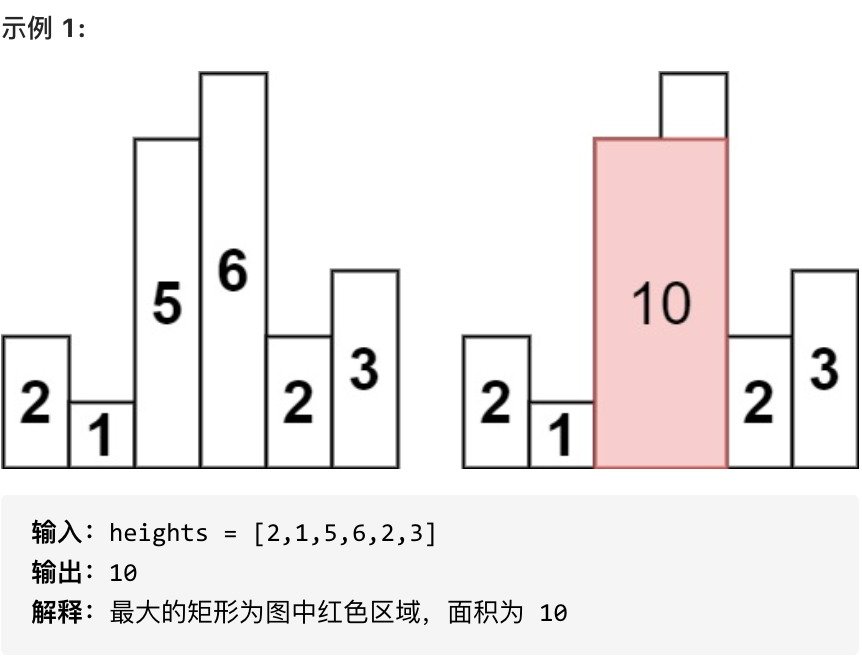
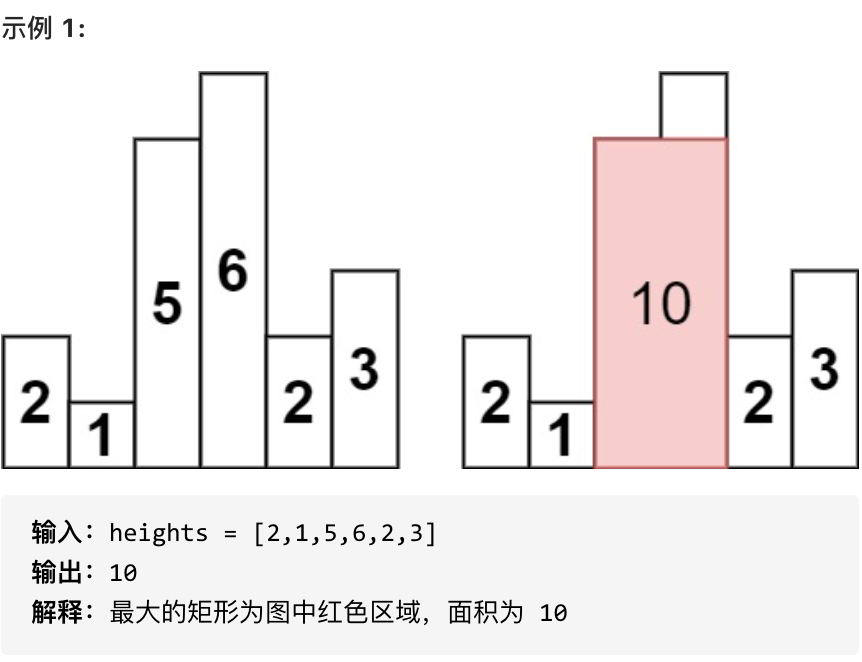
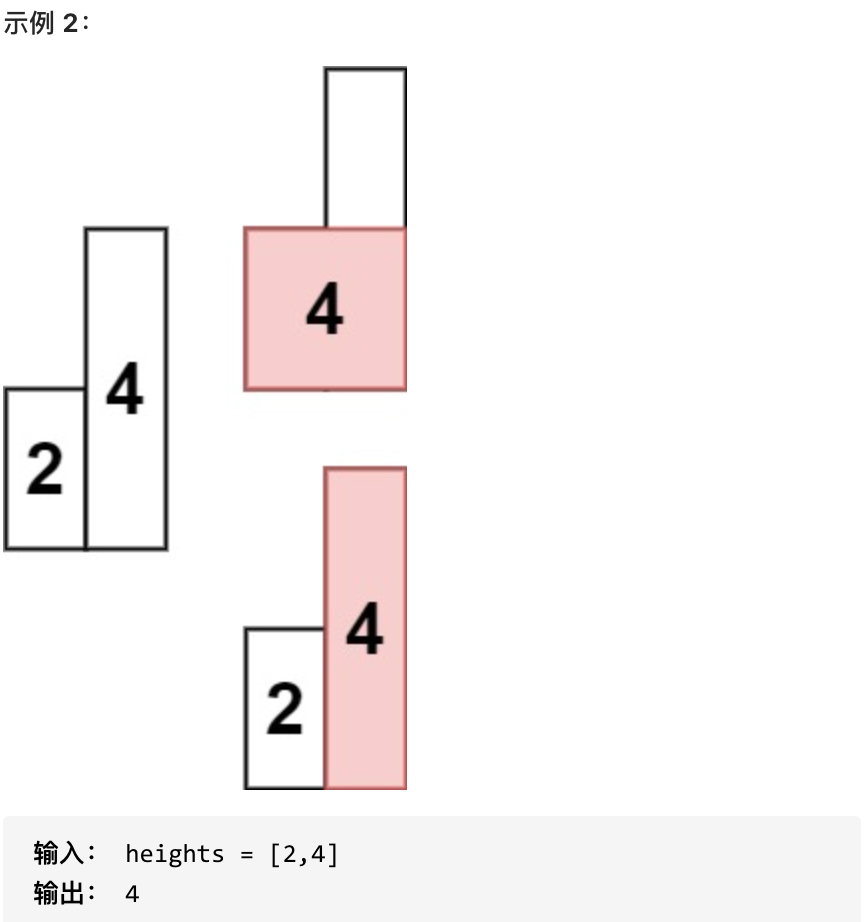
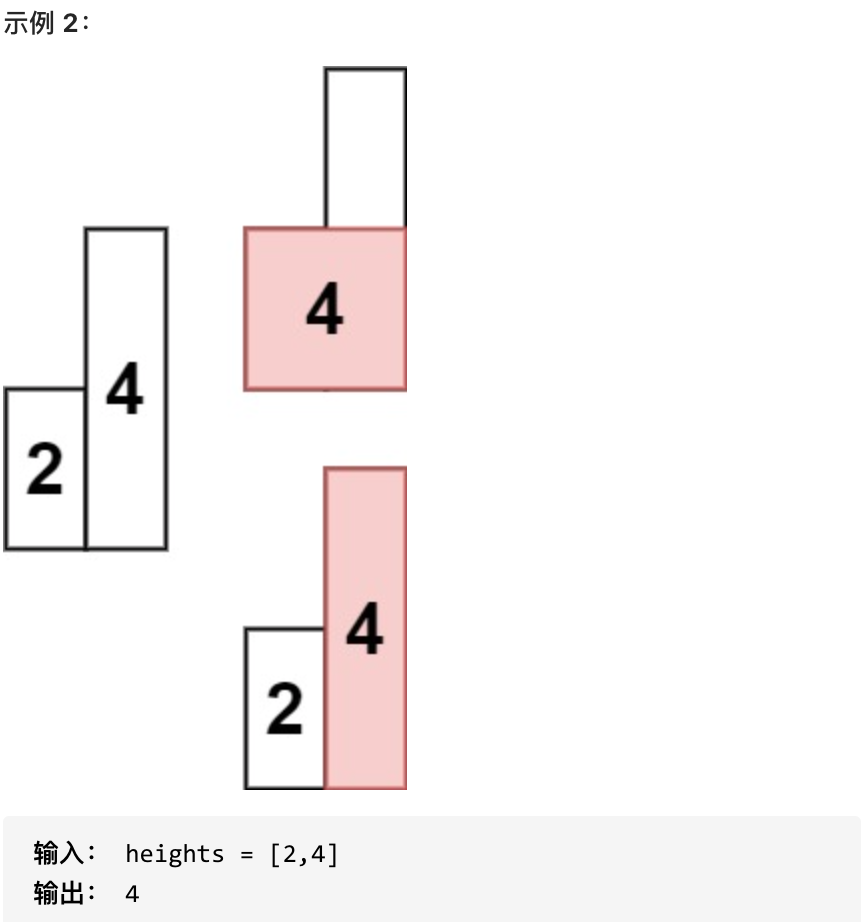
求在该柱状图中,能够勾勒出来的矩形的最大面积。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
* 1 <= heights.length <=10^5
|
||||
* 0 <= heights[i] <= 10^4
|
||||
|
|
@ -114,7 +114,7 @@ public:
|
|||
|
||||
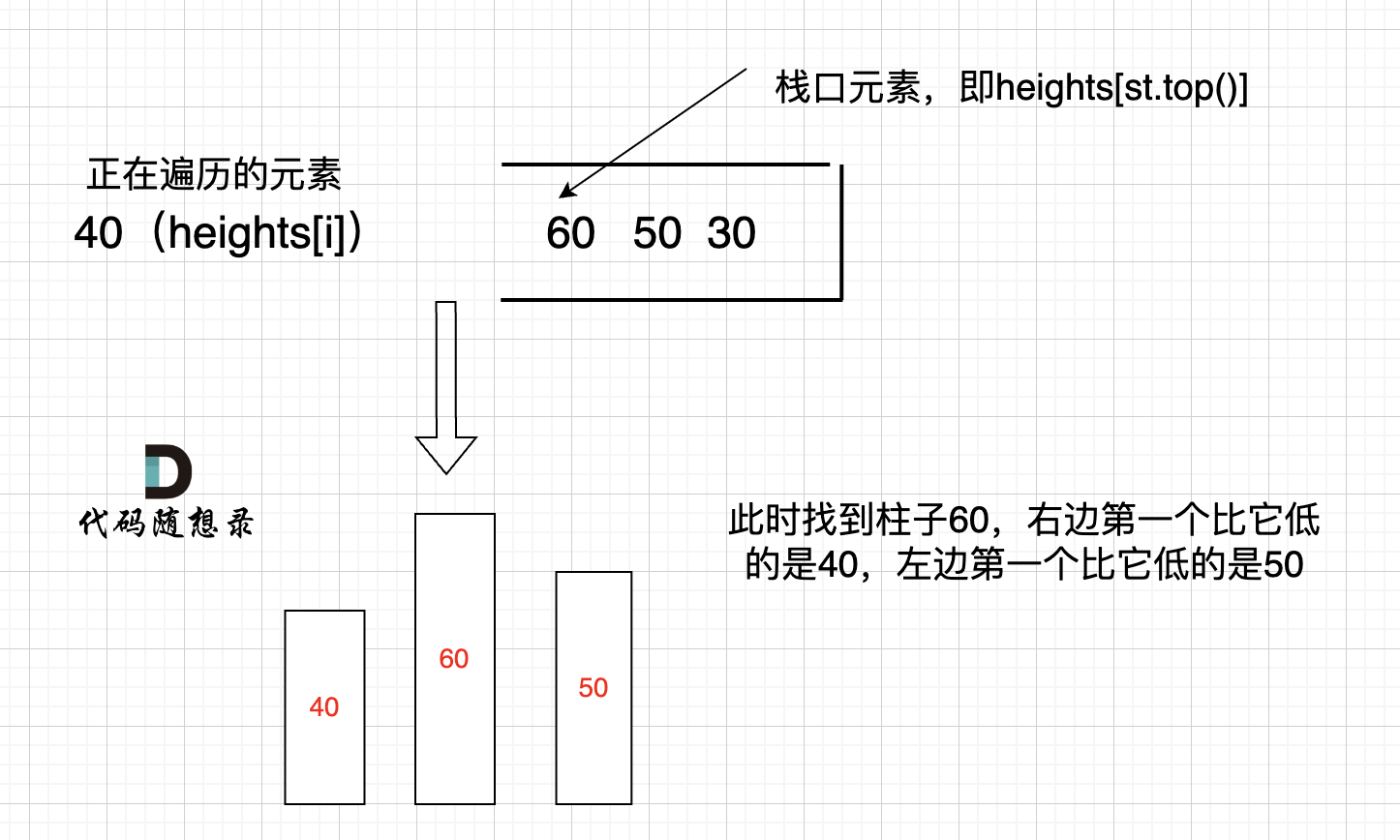
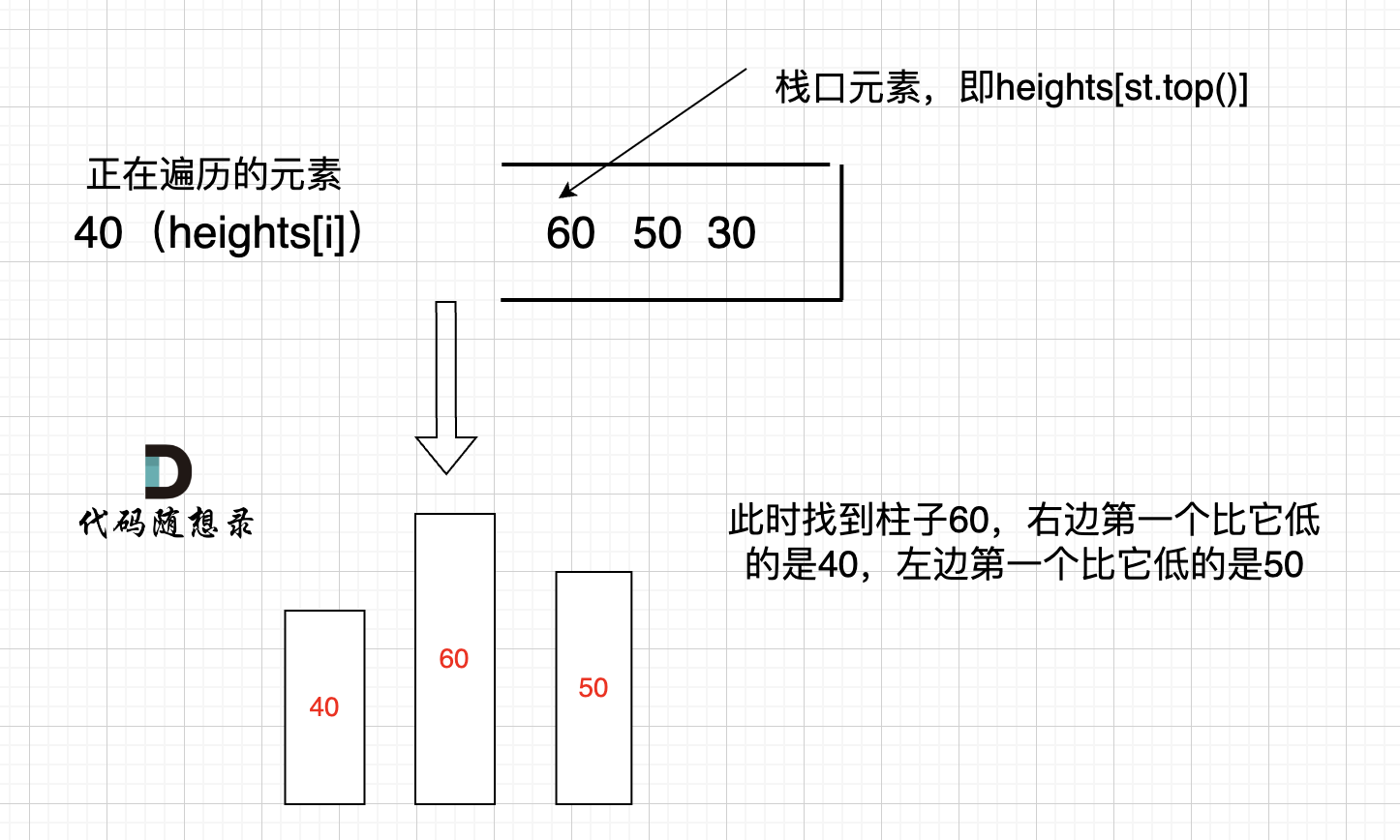
我来举一个例子,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
|
||||
|
||||
|
|
@ -179,7 +179,7 @@ public:
|
|||
|
||||
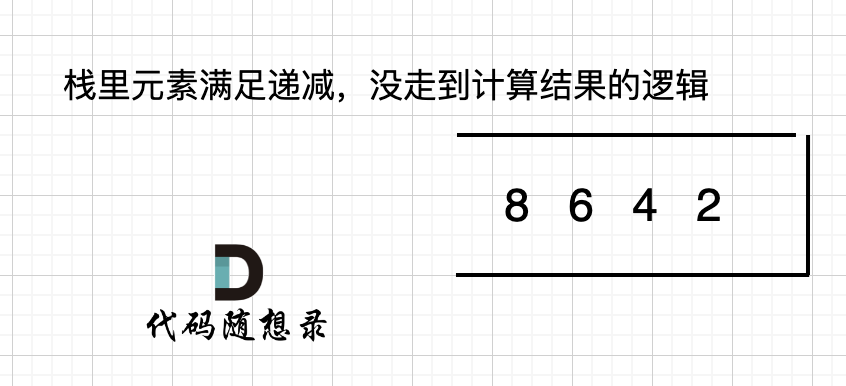
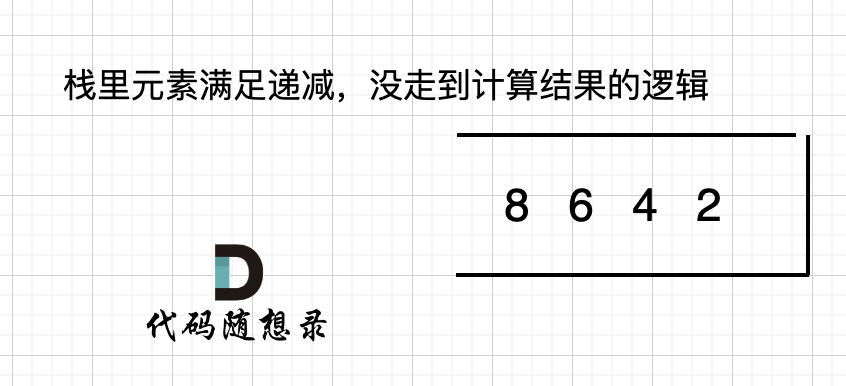
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图:
|
||||
|
||||
|
||||
|
||||
|
||||
那么结尾加一个0,就会让栈里的所有元素,走到情况三的逻辑。
|
||||
|
||||
|
|
@ -194,7 +194,7 @@ public:
|
|||
|
||||
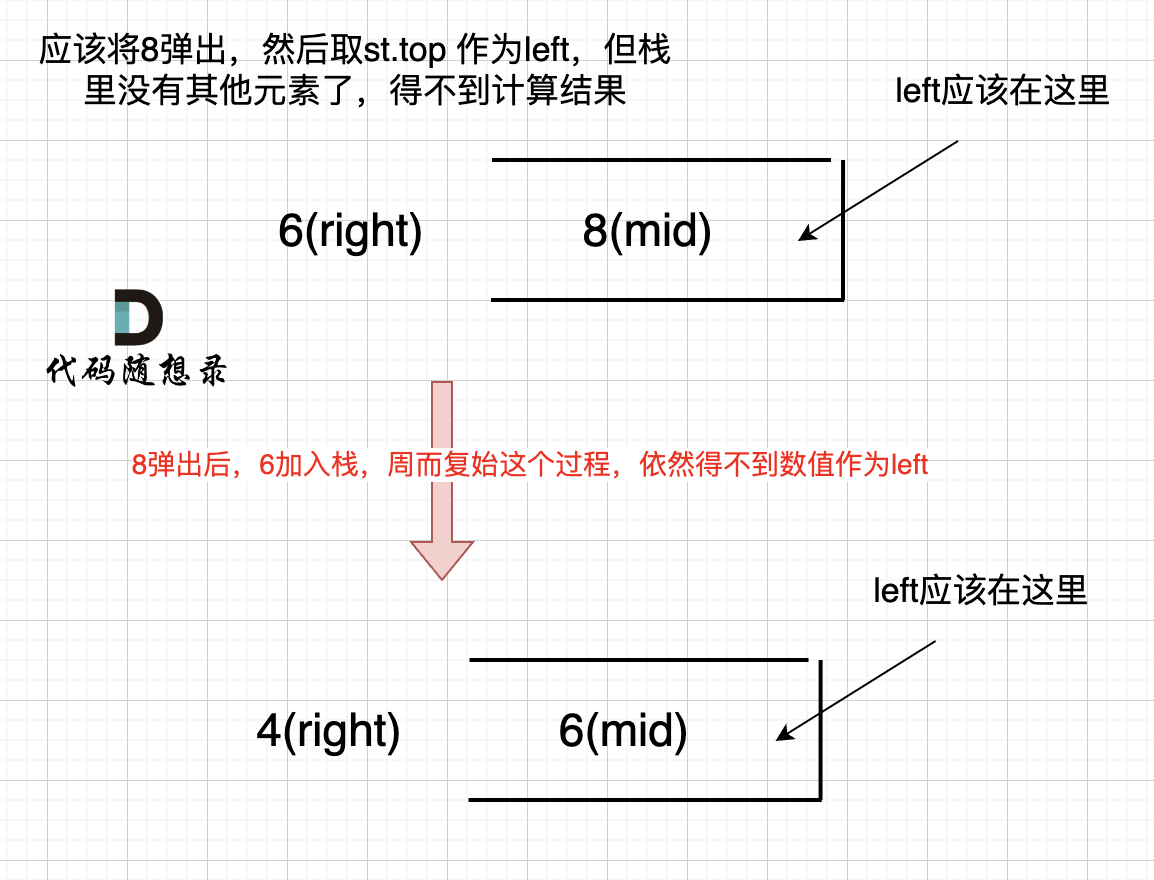
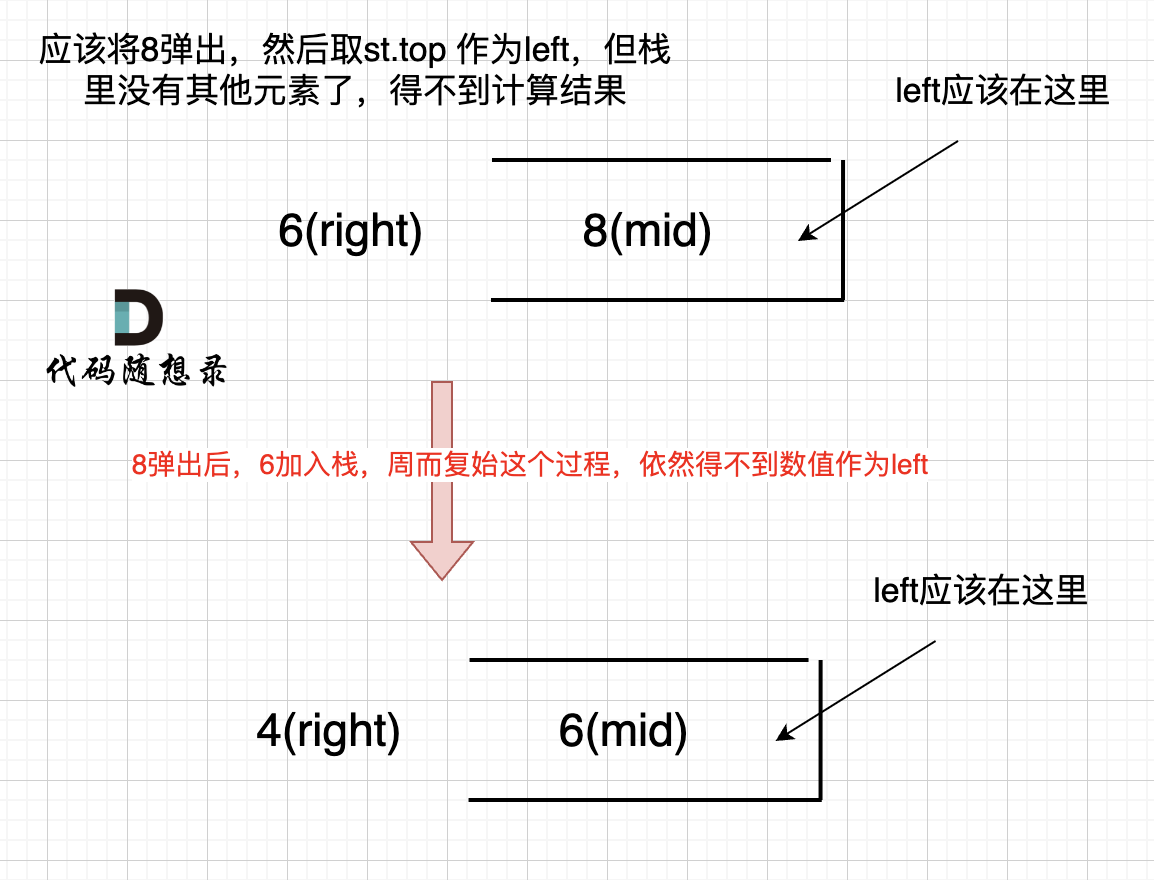
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 6 进行比较,周而复始,那么计算的最后结果result就是0。 如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
所以我们需要在 height数组前后各加一个元素0。
|
||||
|
||||
|
|
|
|||
|
|
@ -39,7 +39,7 @@
|
|||
|
||||
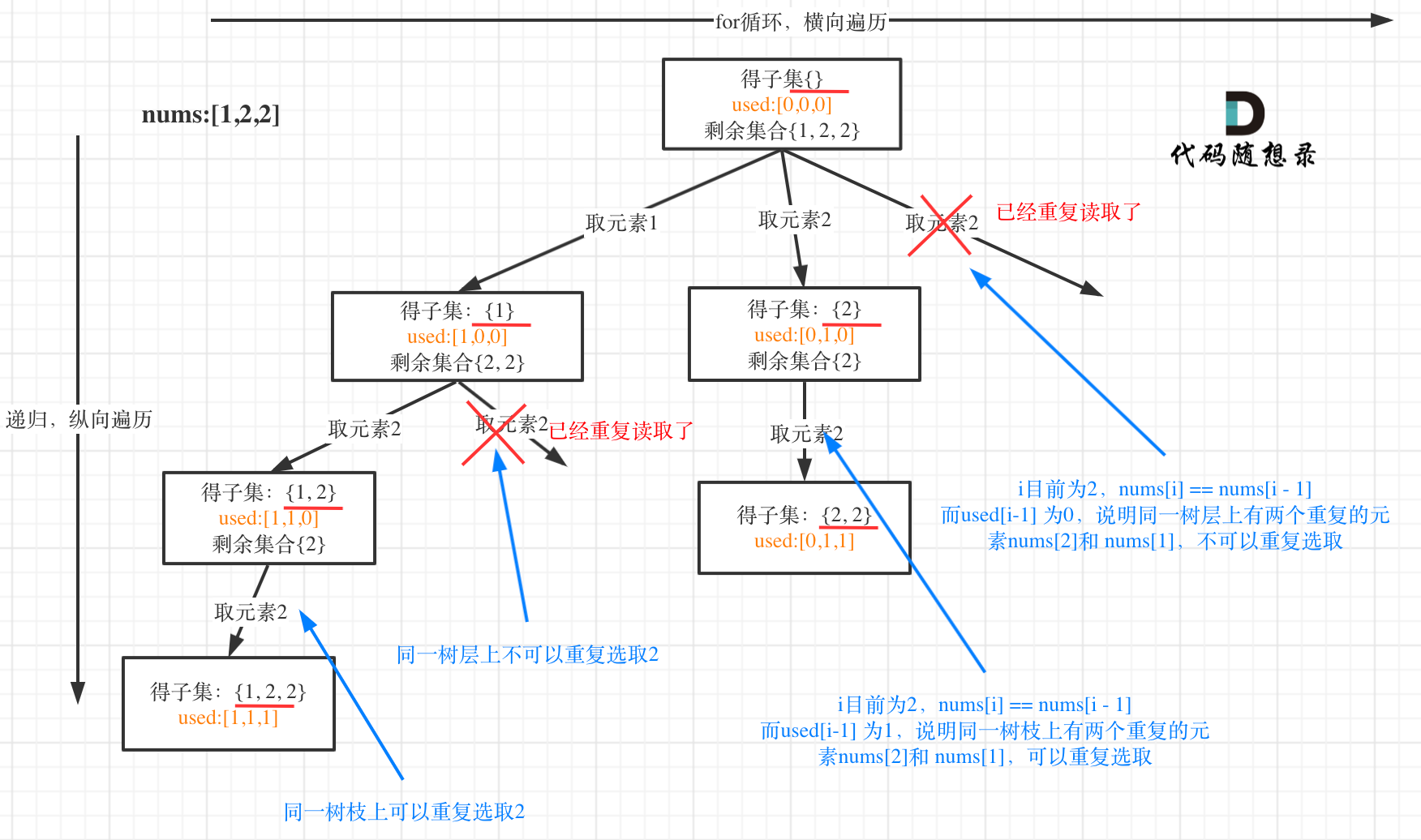
用示例中的[1, 2, 2] 来举例,如图所示: (**注意去重需要先对集合排序**)
|
||||
|
||||

|
||||
|
||||
|
||||
从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
|
||||
|
||||
|
|
|
|||
|
|
@ -54,7 +54,7 @@
|
|||
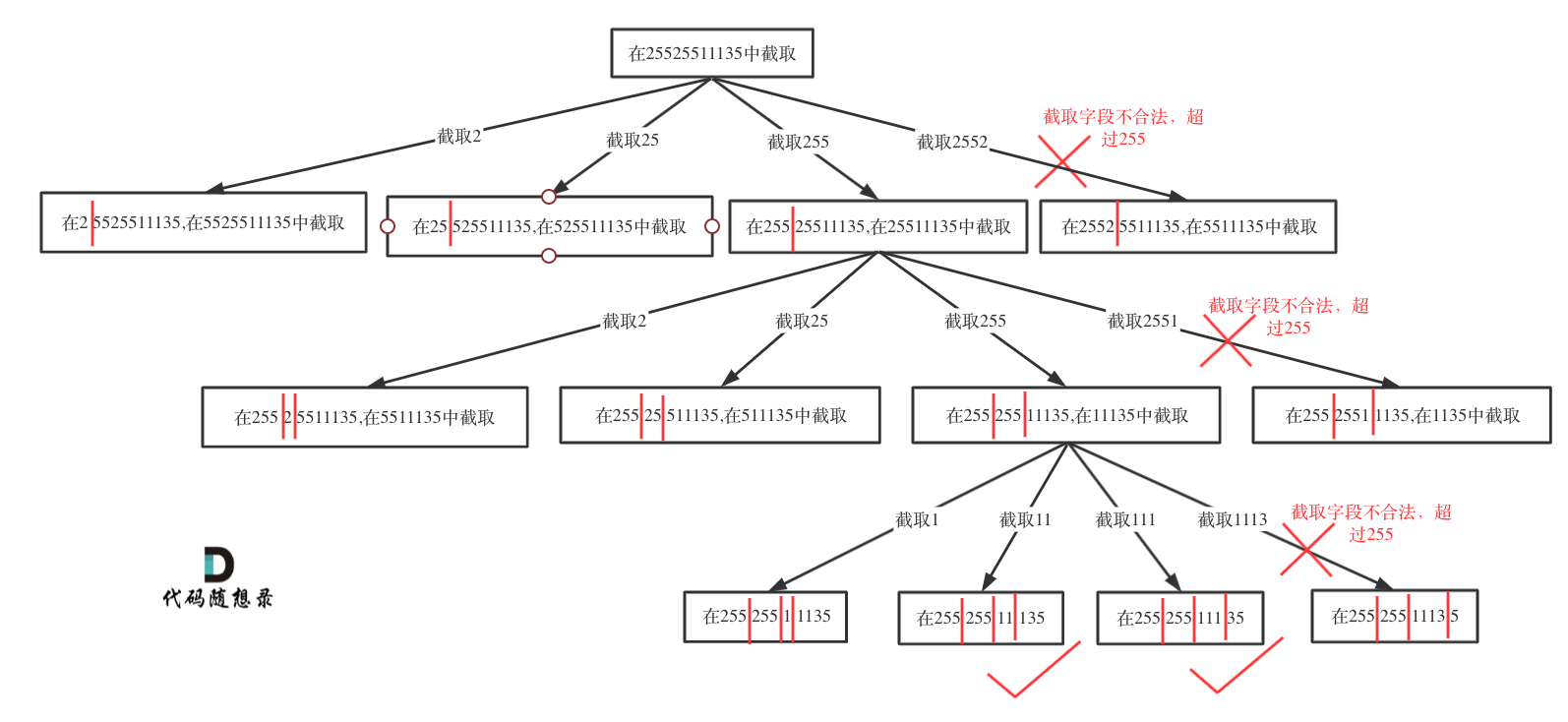
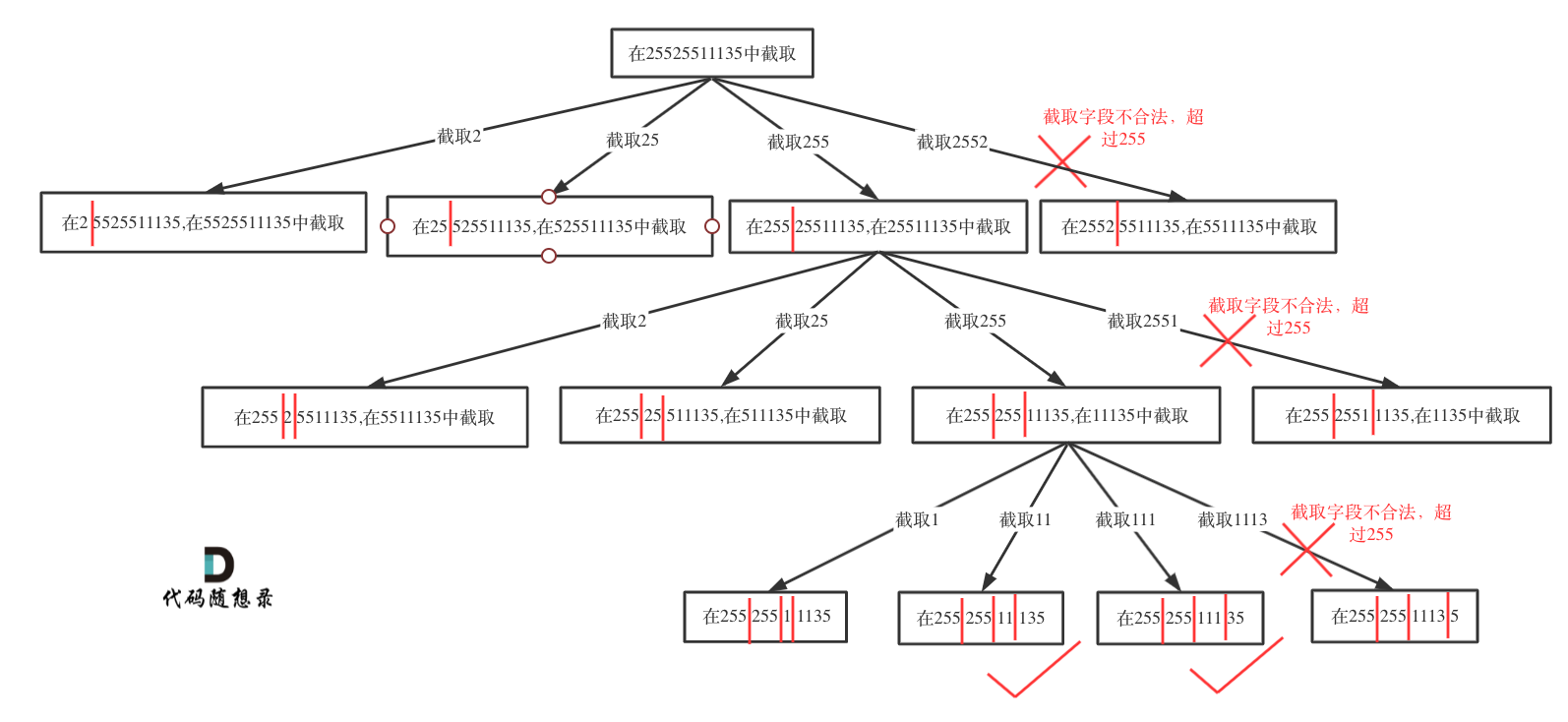
切割问题可以抽象为树型结构,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 回溯三部曲
|
||||
|
|
@ -106,7 +106,7 @@ if (pointNum == 3) { // 逗点数量为3时,分隔结束
|
|||
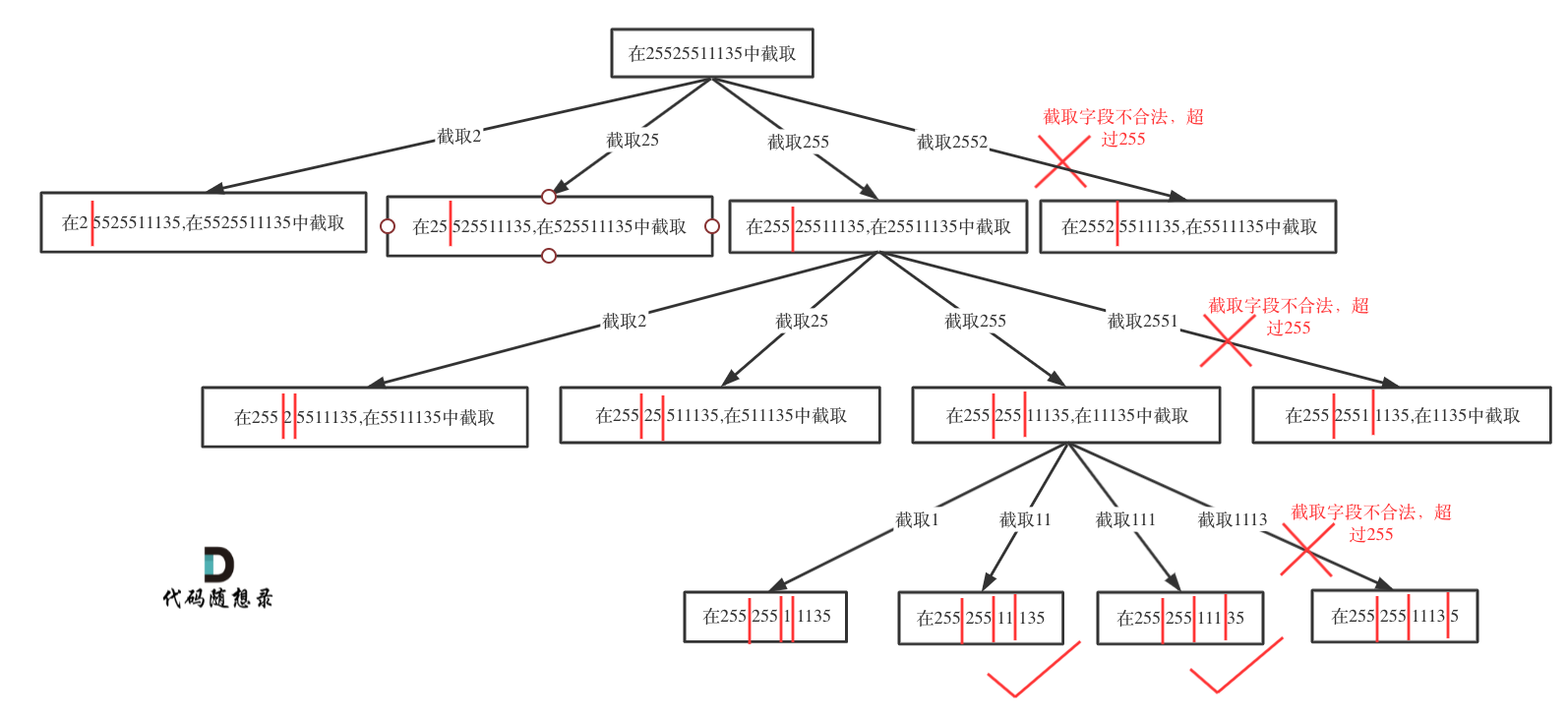
如果不合法就结束本层循环,如图中剪掉的分支:
|
||||
|
||||
|
||||
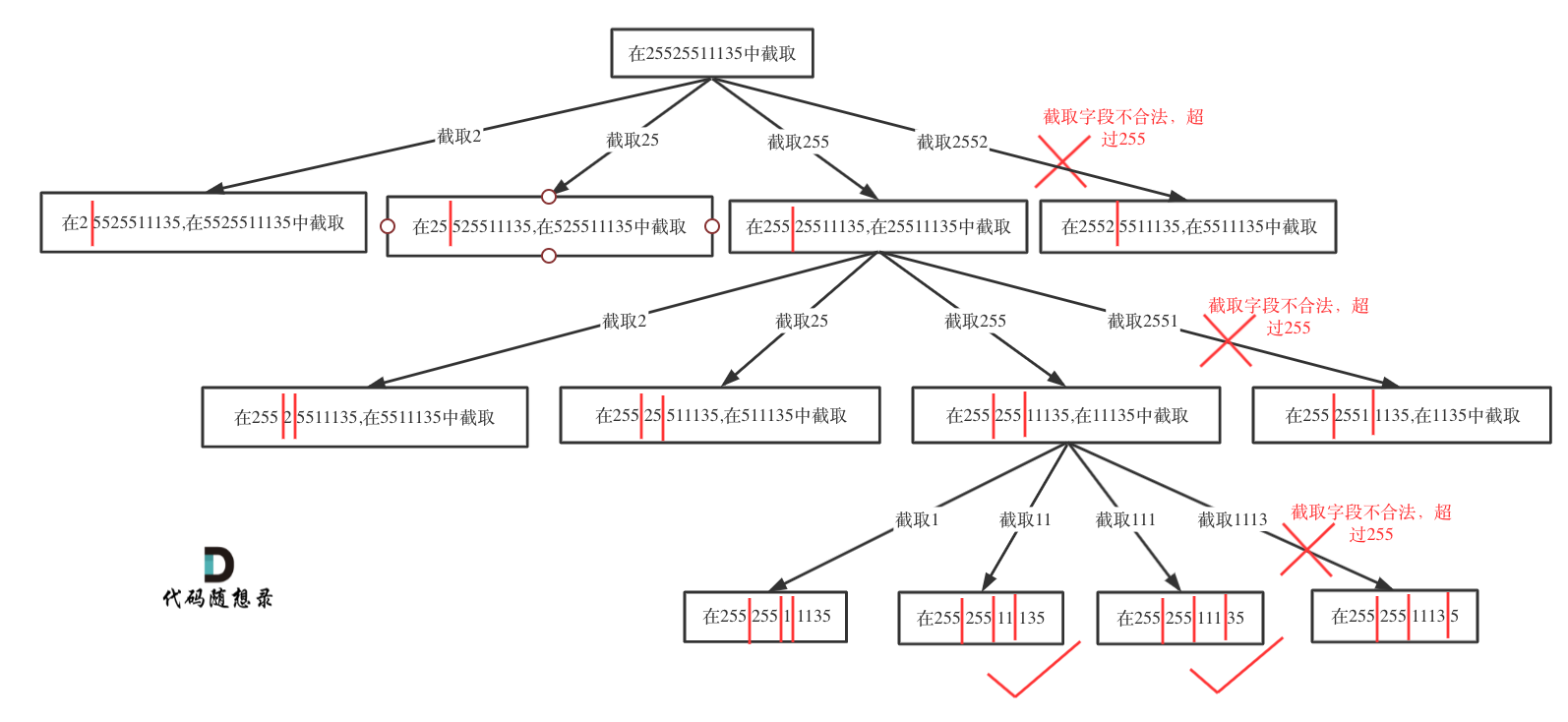
|
||||
|
||||
|
||||
然后就是递归和回溯的过程:
|
||||
|
||||
|
|
|
|||
|
|
@ -12,7 +12,7 @@
|
|||
|
||||
示例:
|
||||
|
||||

|
||||

|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -27,11 +27,11 @@
|
|||
|
||||
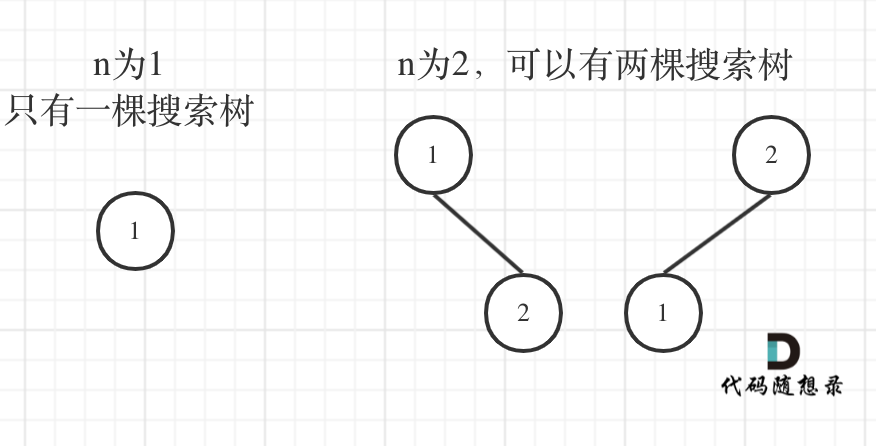
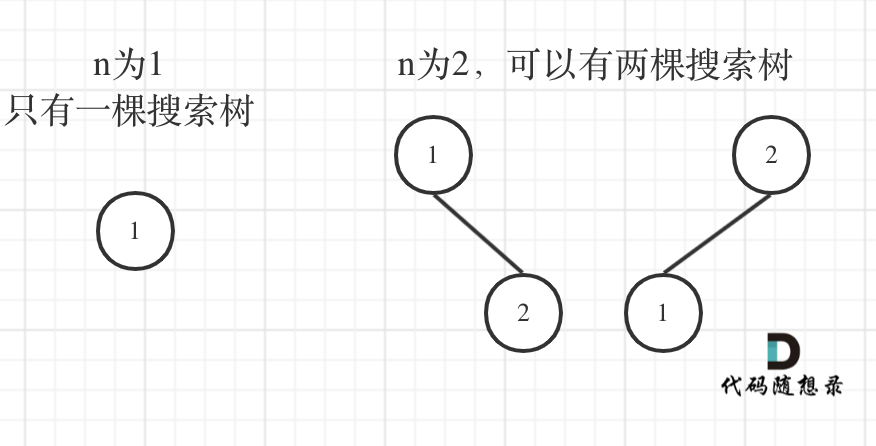
了解了二叉搜索树之后,我们应该先举几个例子,画画图,看看有没有什么规律,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
n为1的时候有一棵树,n为2有两棵树,这个是很直观的。
|
||||
|
||||
|
||||
|
||||
|
||||
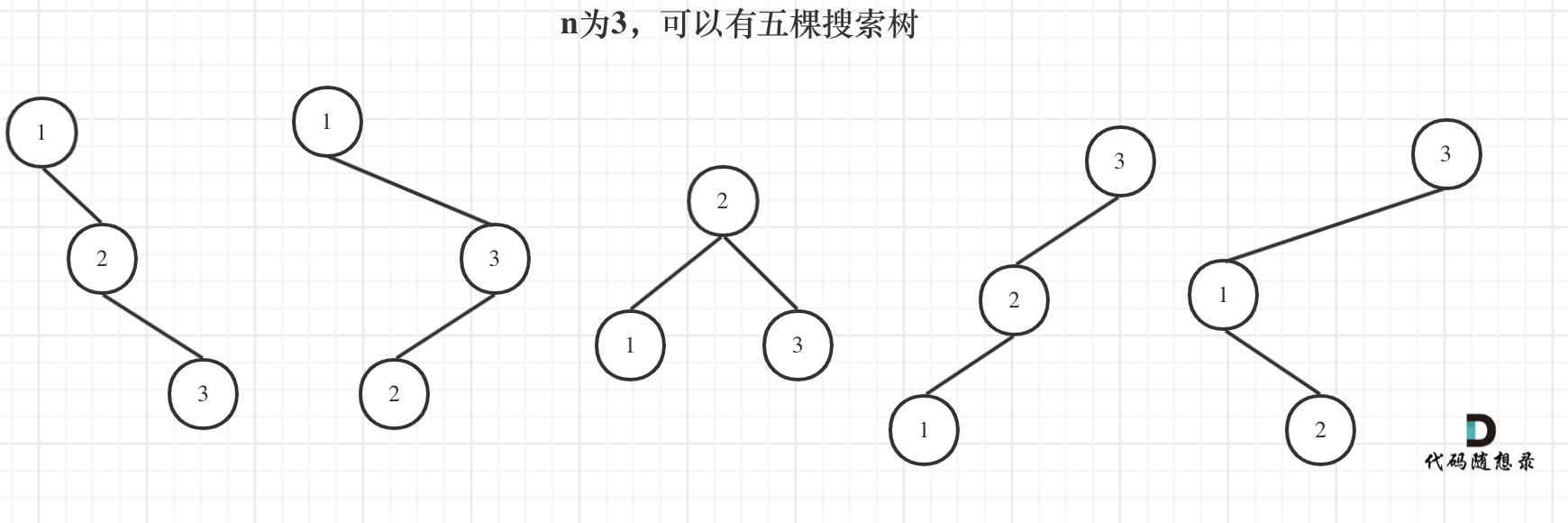
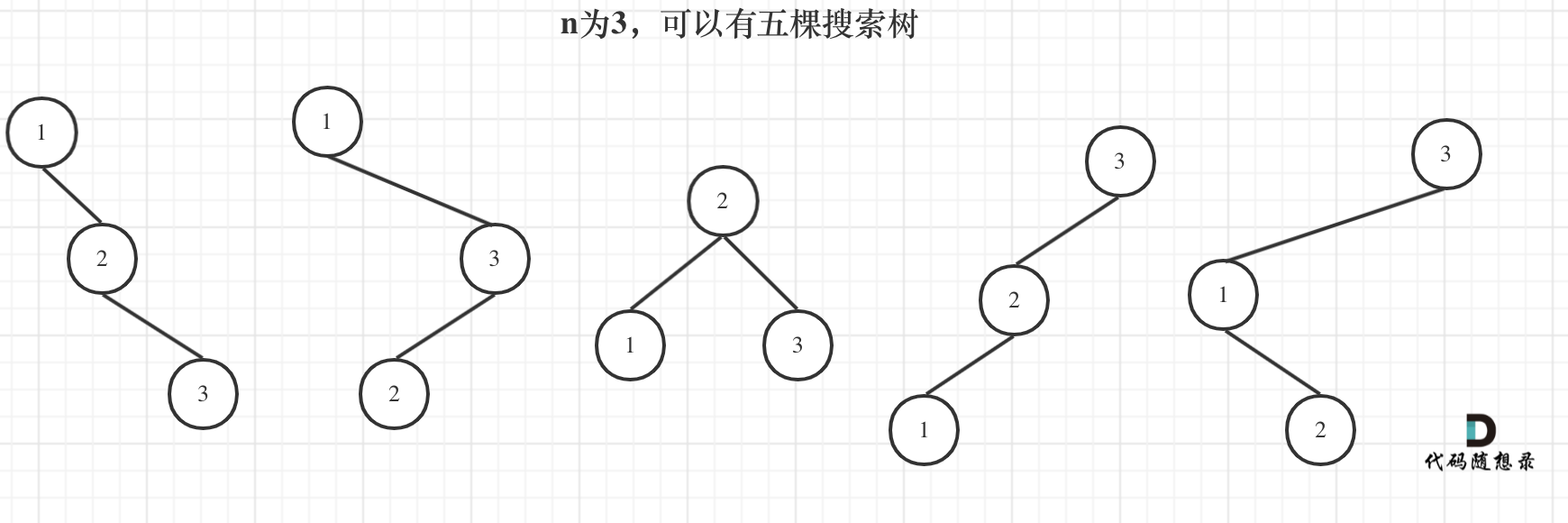
来看看n为3的时候,有哪几种情况。
|
||||
|
||||
|
|
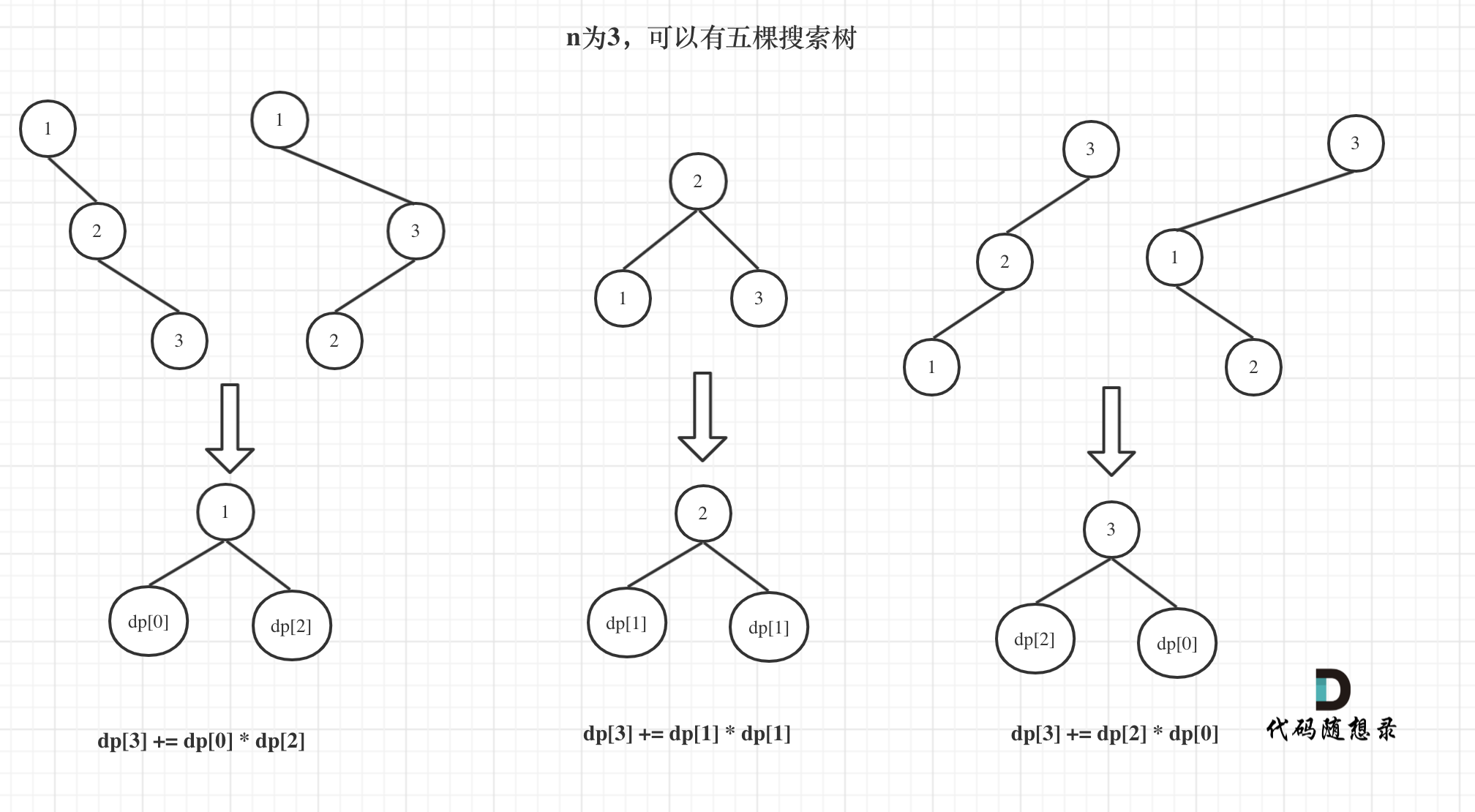
@ -65,7 +65,7 @@ dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索
|
|||
|
||||
如图所示:
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
此时我们已经找到递推关系了,那么可以用动规五部曲再系统分析一遍。
|
||||
|
|
@ -118,7 +118,7 @@ for (int i = 1; i <= n; i++) {
|
|||
|
||||
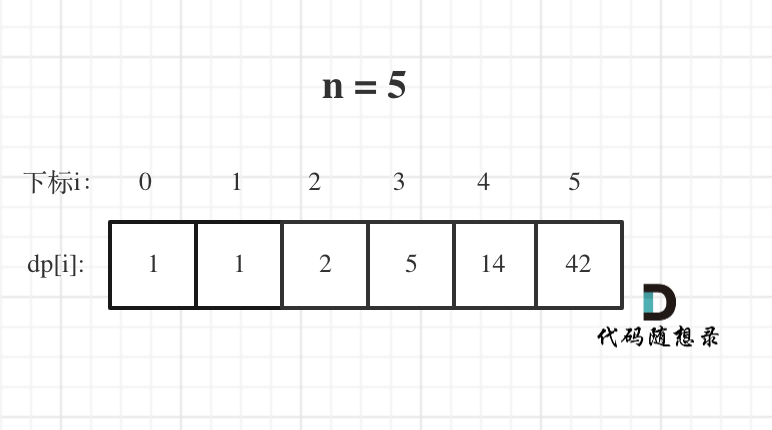
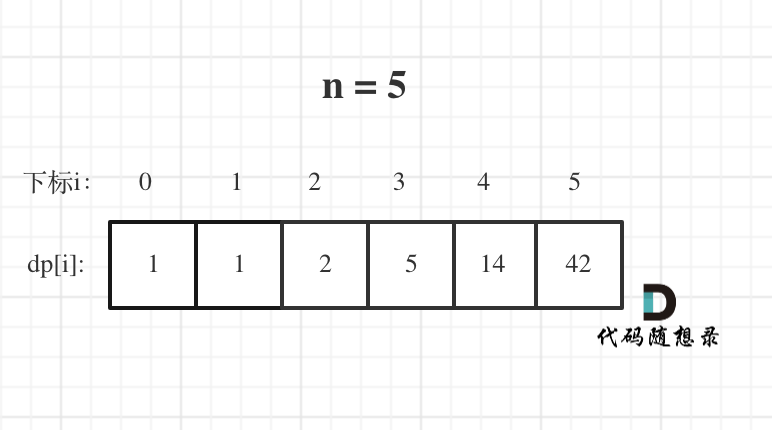
n为5时候的dp数组状态如图:
|
||||
|
||||
|
||||
|
||||
|
||||
当然如果自己画图举例的话,基本举例到n为3就可以了,n为4的时候,画图已经比较麻烦了。
|
||||
|
||||
|
|
|
|||
|
|
@ -16,7 +16,7 @@
|
|||
* 节点的右子树只包含大于当前节点的数。
|
||||
* 所有左子树和右子树自身必须也是二叉搜索树。
|
||||
|
||||

|
||||

|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -102,7 +102,7 @@ if (root->val > root->left->val && root->val < root->right->val) {
|
|||
|
||||
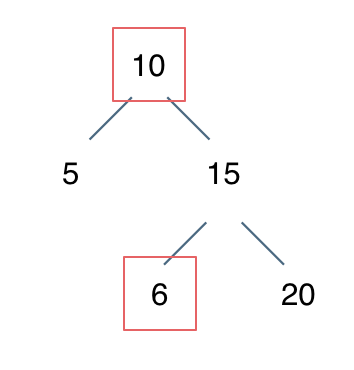
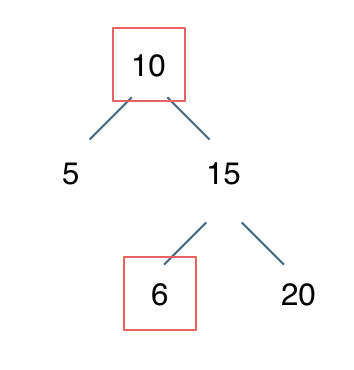
例如: [10,5,15,null,null,6,20] 这个case:
|
||||
|
||||
|
||||
|
||||
|
||||
节点10大于左节点5,小于右节点15,但右子树里出现了一个6 这就不符合了!
|
||||
|
||||
|
|
|
|||
|
|
@ -12,9 +12,9 @@
|
|||
|
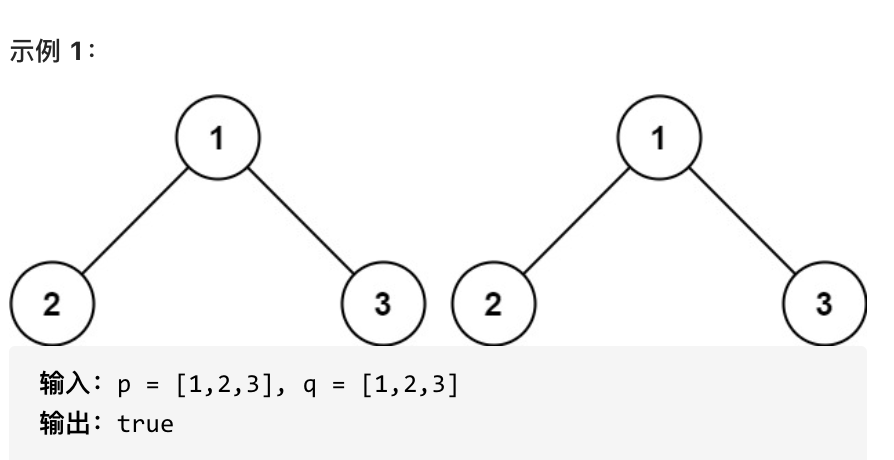
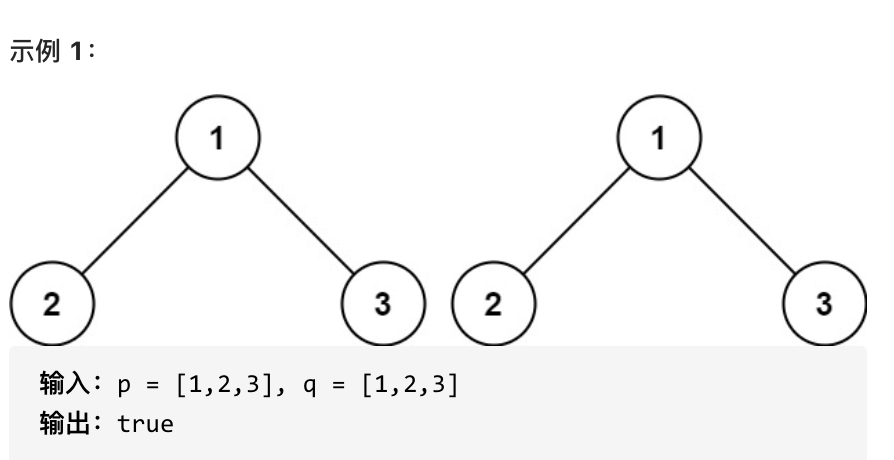
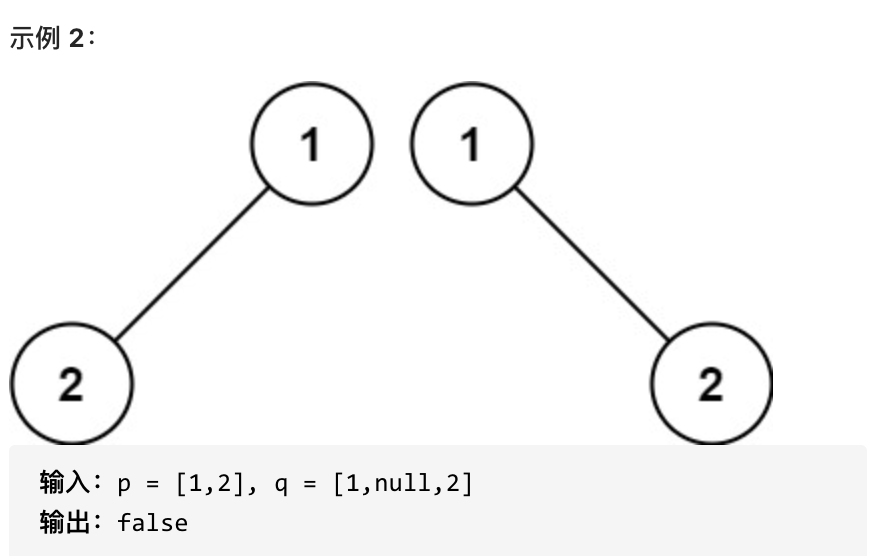
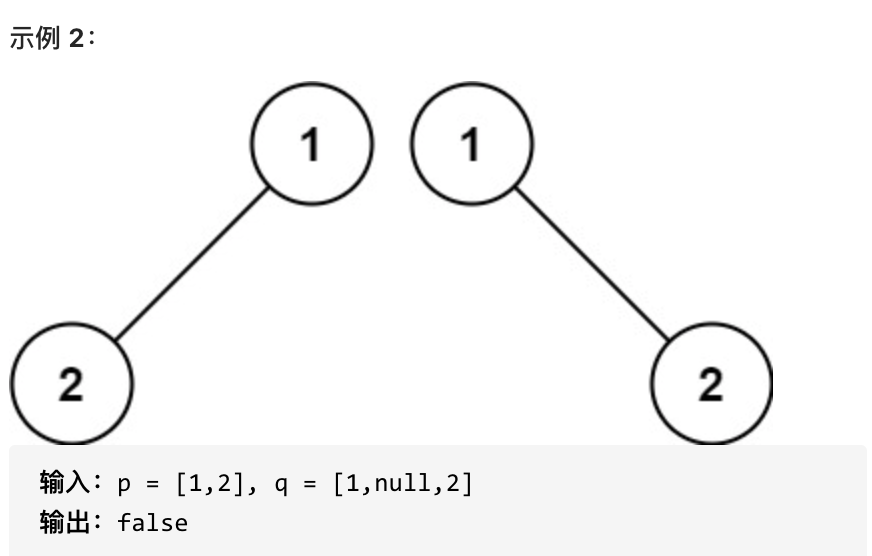
||||
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
## 思路
|
||||
|
|
|
|||
|
|
@ -9,7 +9,7 @@
|
|||
|
||||
给定一个二叉树,检查它是否是镜像对称的。
|
||||
|
||||

|
||||

|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -25,7 +25,7 @@
|
|||
|
||||
比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
|
||||
|
||||

|
||||
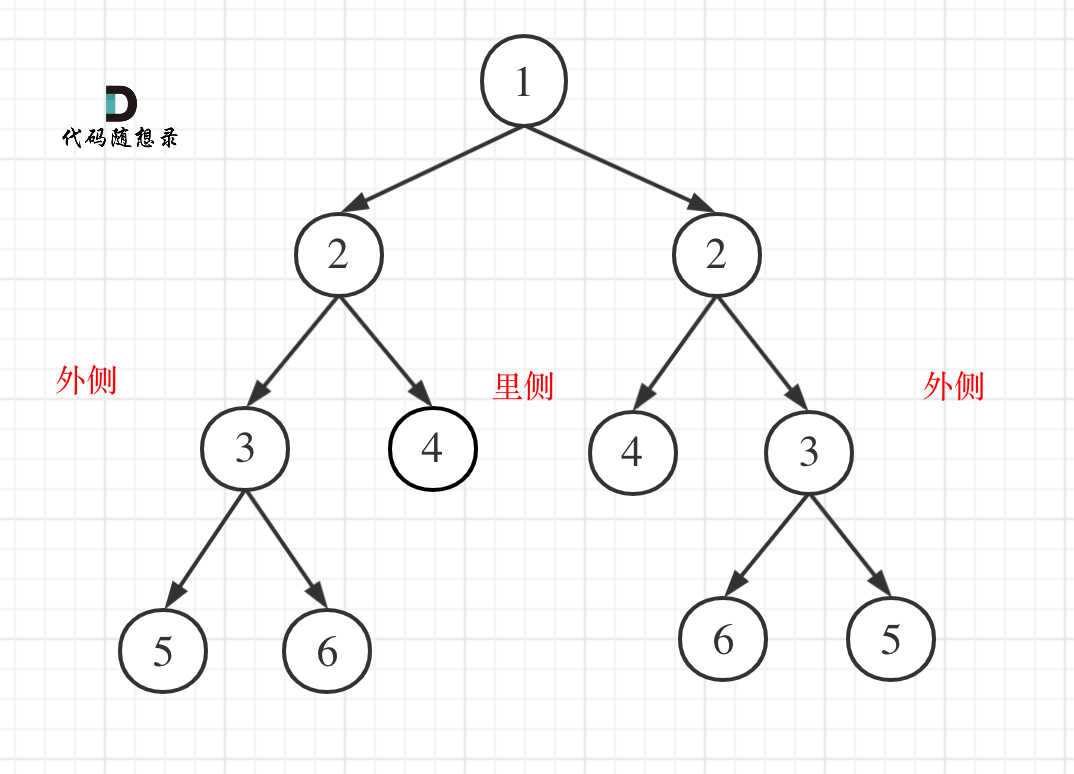
|
||||
|
||||
那么遍历的顺序应该是什么样的呢?
|
||||
|
||||
|
|
@ -169,7 +169,7 @@ public:
|
|||
|
||||
通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等,如动画所示:
|
||||
|
||||

|
||||
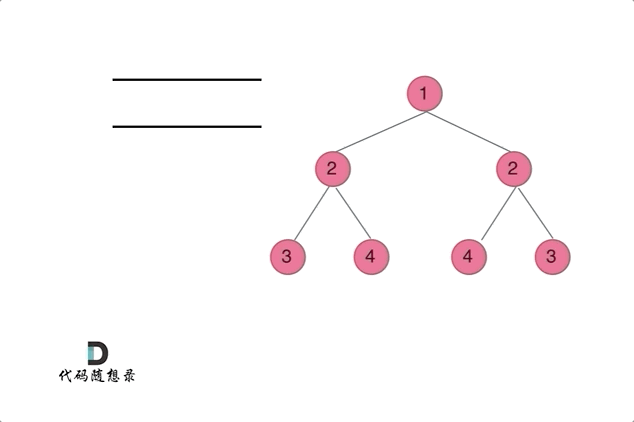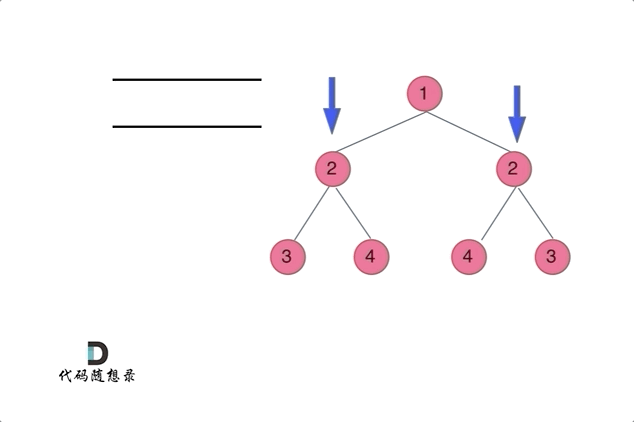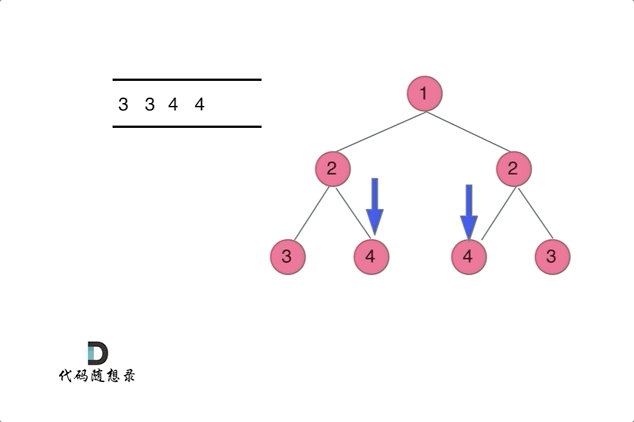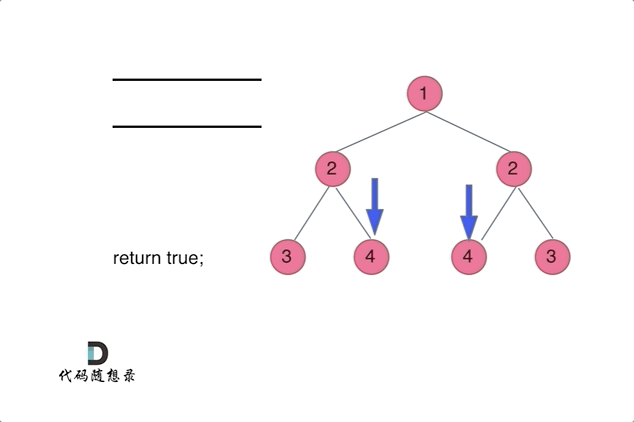
|
||||
|
||||
|
||||
|
||||
|
|
|
|||
|
|
@ -26,7 +26,7 @@
|
|||
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
|
||||
|
|
@ -37,7 +37,7 @@
|
|||
|
||||
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
|
||||
|
||||

|
||||

|
||||
|
||||
### 思路
|
||||
|
||||
|
|
@ -57,7 +57,7 @@
|
|||
|
||||
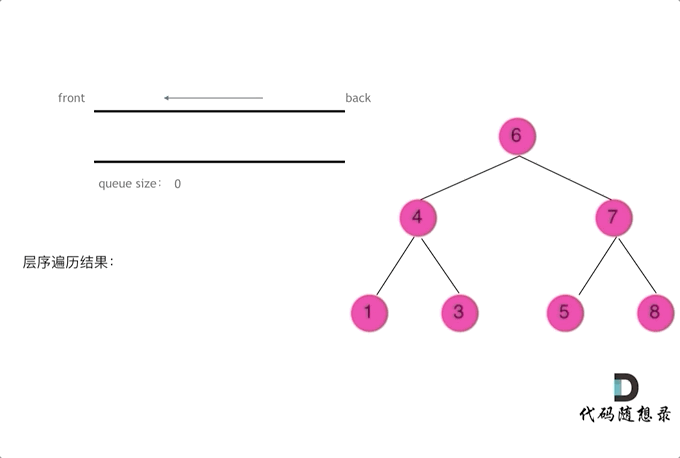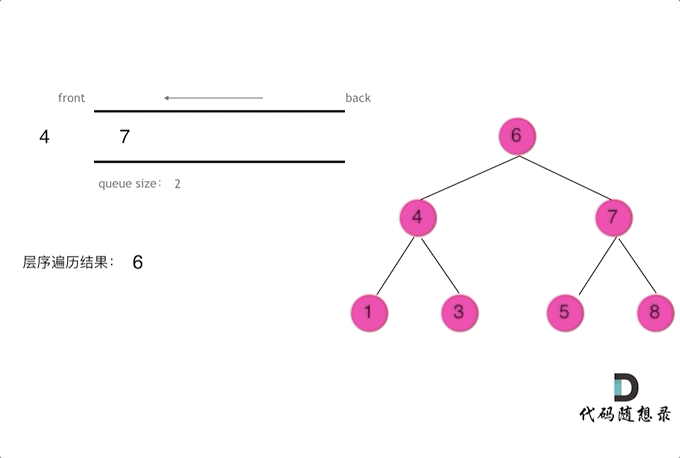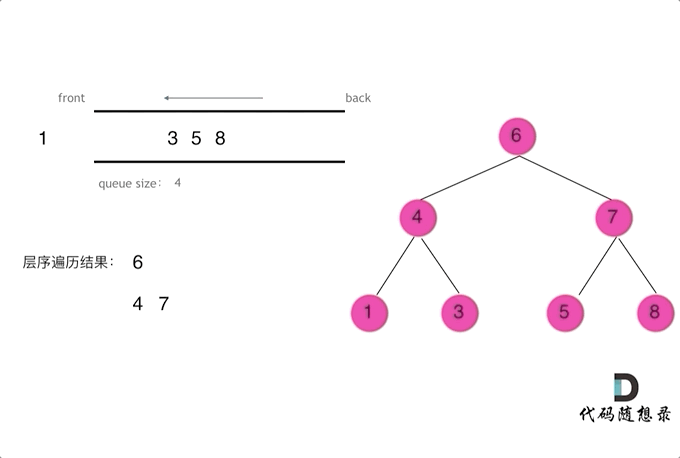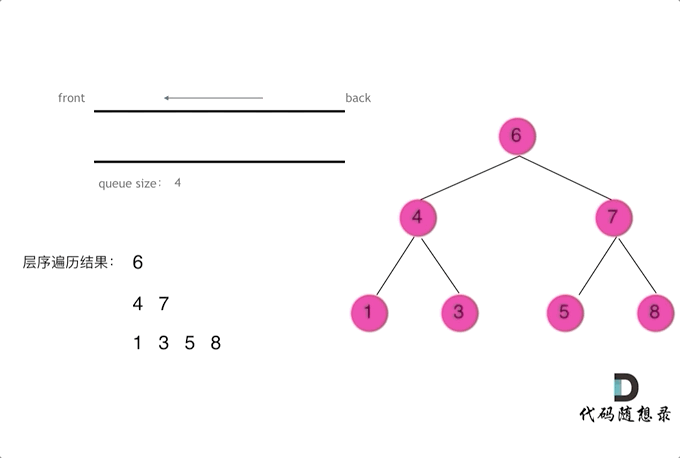
使用队列实现二叉树广度优先遍历,动画如下:
|
||||
|
||||

|
||||
|
||||
|
||||
这样就实现了层序从左到右遍历二叉树。
|
||||
|
||||
|
|
@ -532,7 +532,7 @@ public IList<IList<int>> LevelOrder(TreeNode root)
|
|||
|
||||
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
|
||||
|
||||

|
||||

|
||||
|
||||
### 思路
|
||||
|
||||
|
|
@ -926,7 +926,7 @@ public IList<IList<int>> LevelOrderBottom(TreeNode root)
|
|||
|
||||
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
|
||||
|
||||

|
||||

|
||||
|
||||
### 思路
|
||||
|
||||
|
|
@ -1276,7 +1276,7 @@ public class Solution
|
|||
|
||||
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
|
||||
|
||||

|
||||

|
||||
|
||||
### 思路
|
||||
|
||||
|
|
@ -1634,7 +1634,7 @@ public class Solution {
|
|||
|
||||
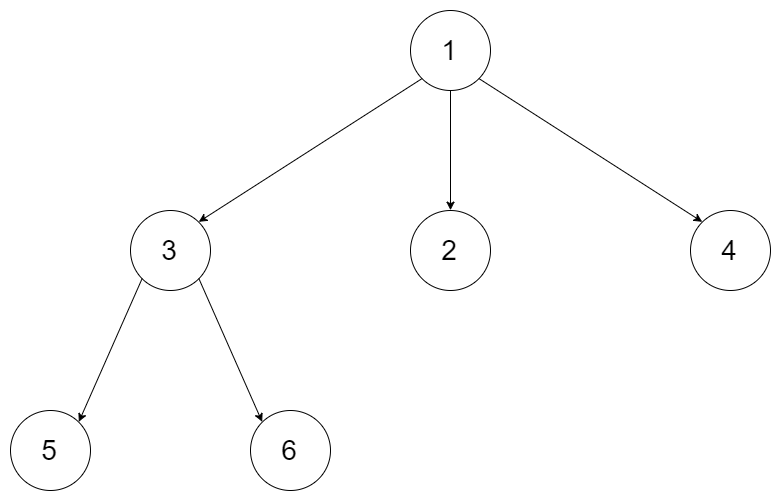
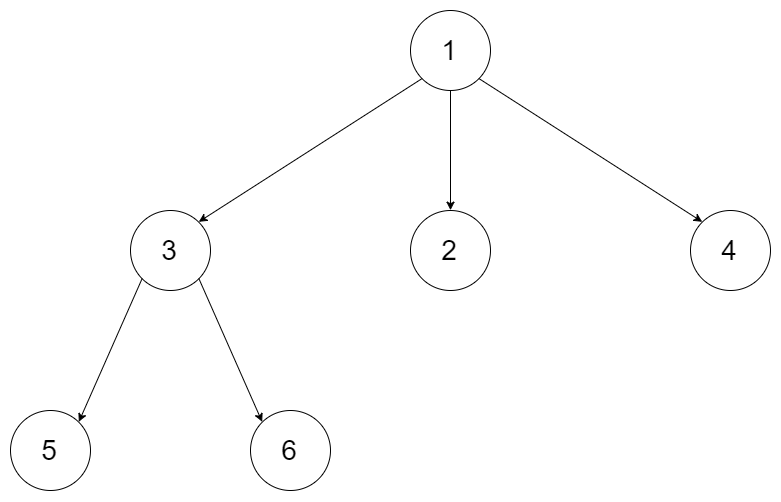
例如,给定一个 3叉树 :
|
||||
|
||||
|
||||
|
||||
|
||||
返回其层序遍历:
|
||||
|
||||
|
|
@ -2006,7 +2006,7 @@ impl Solution {
|
|||
|
||||
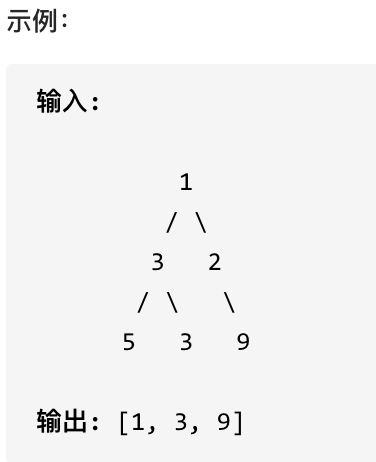
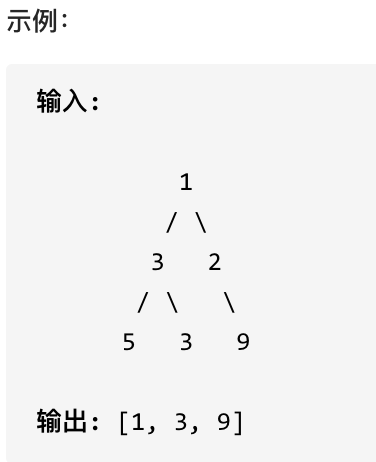
您需要在二叉树的每一行中找到最大的值。
|
||||
|
||||
|
||||
|
||||
|
||||
### 思路
|
||||
|
||||
|
|
@ -2337,7 +2337,7 @@ struct Node {
|
|||
|
||||
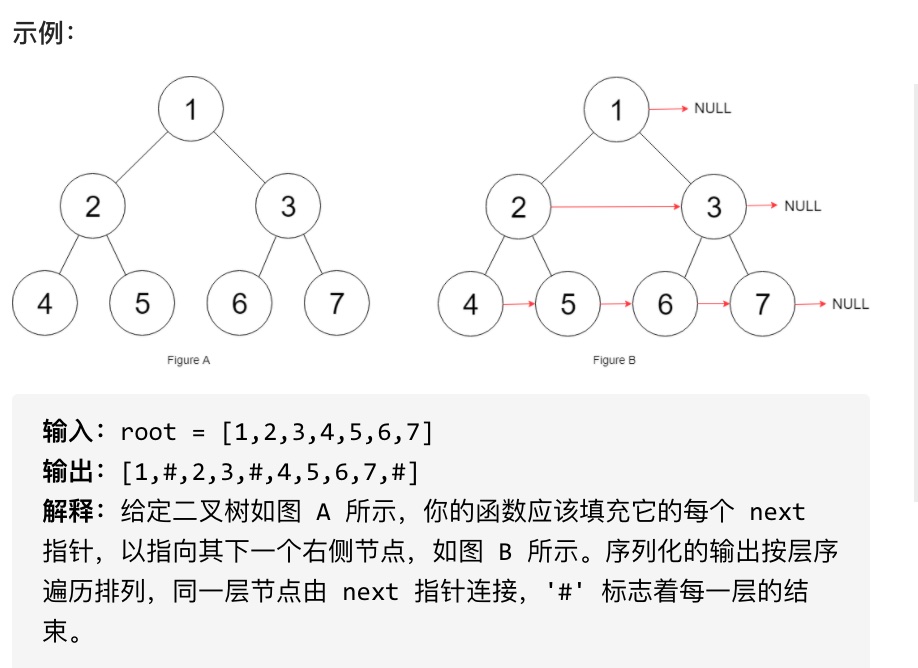
初始状态下,所有 next 指针都被设置为 NULL。
|
||||
|
||||
|
||||

|
||||
|
||||
### 思路
|
||||
|
||||
|
|
@ -2971,7 +2971,7 @@ object Solution {
|
|||
|
||||
给定二叉树 [3,9,20,null,null,15,7],
|
||||
|
||||

|
||||

|
||||
|
||||
返回它的最大深度 3 。
|
||||
|
||||
|
|
@ -2981,7 +2981,7 @@ object Solution {
|
|||
|
||||
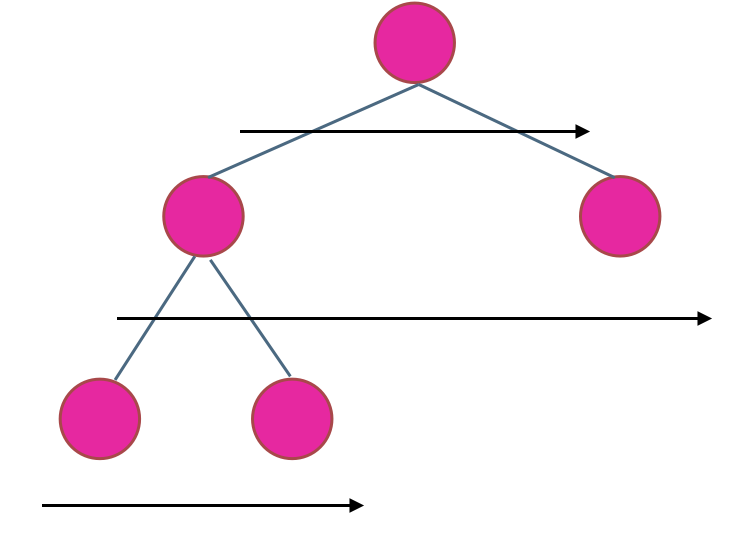
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
|
||||
|
||||
|
||||

|
||||
|
||||
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
|
||||
|
||||
|
|
|
|||
|
|
@ -18,7 +18,7 @@
|
|||
给定二叉树 [3,9,20,null,null,15,7],
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
返回它的最大深度 3 。
|
||||
|
||||
|
|
@ -172,7 +172,7 @@ public:
|
|||
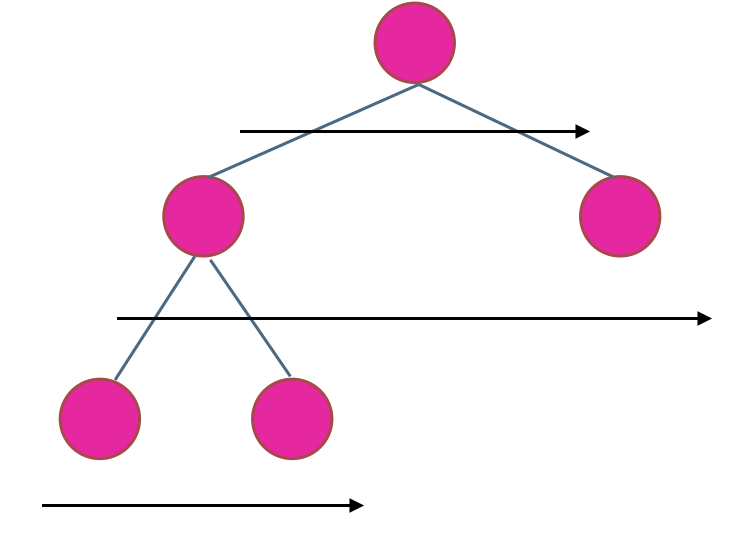
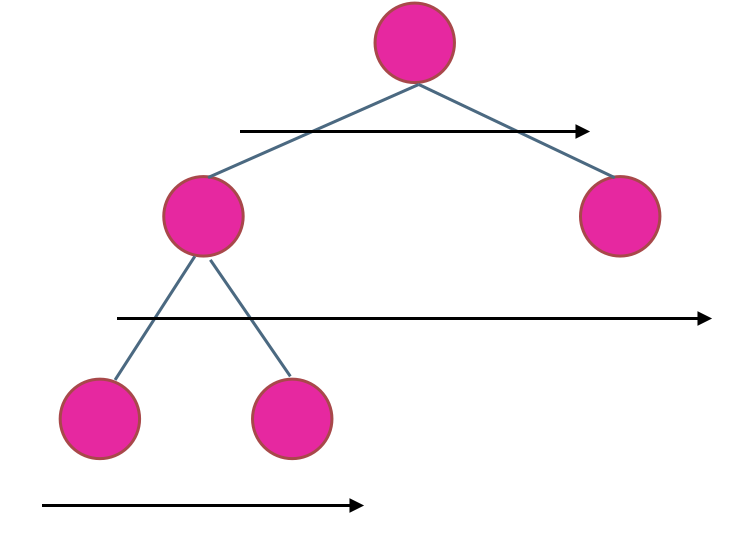
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
|
||||
|
||||
|
|
@ -217,7 +217,7 @@ public:
|
|||
|
||||
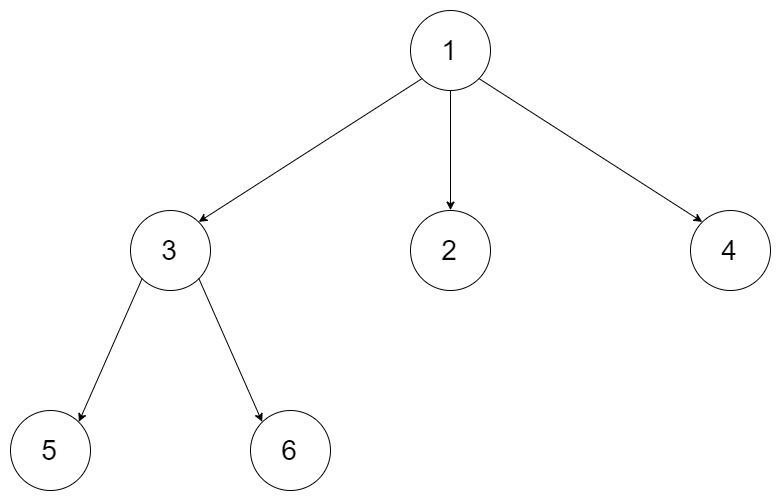
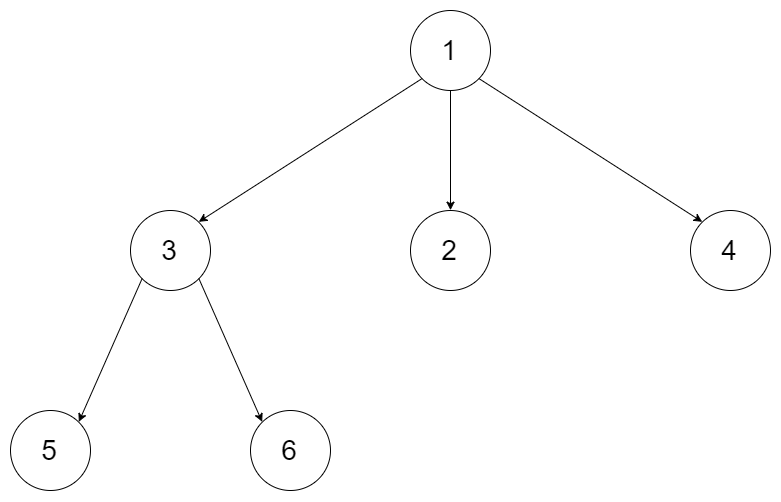
例如,给定一个 3叉树 :
|
||||
|
||||
|
||||
|
||||
|
||||
我们应返回其最大深度,3。
|
||||
|
||||
|
|
|
|||
|
|
@ -25,7 +25,7 @@
|
|||
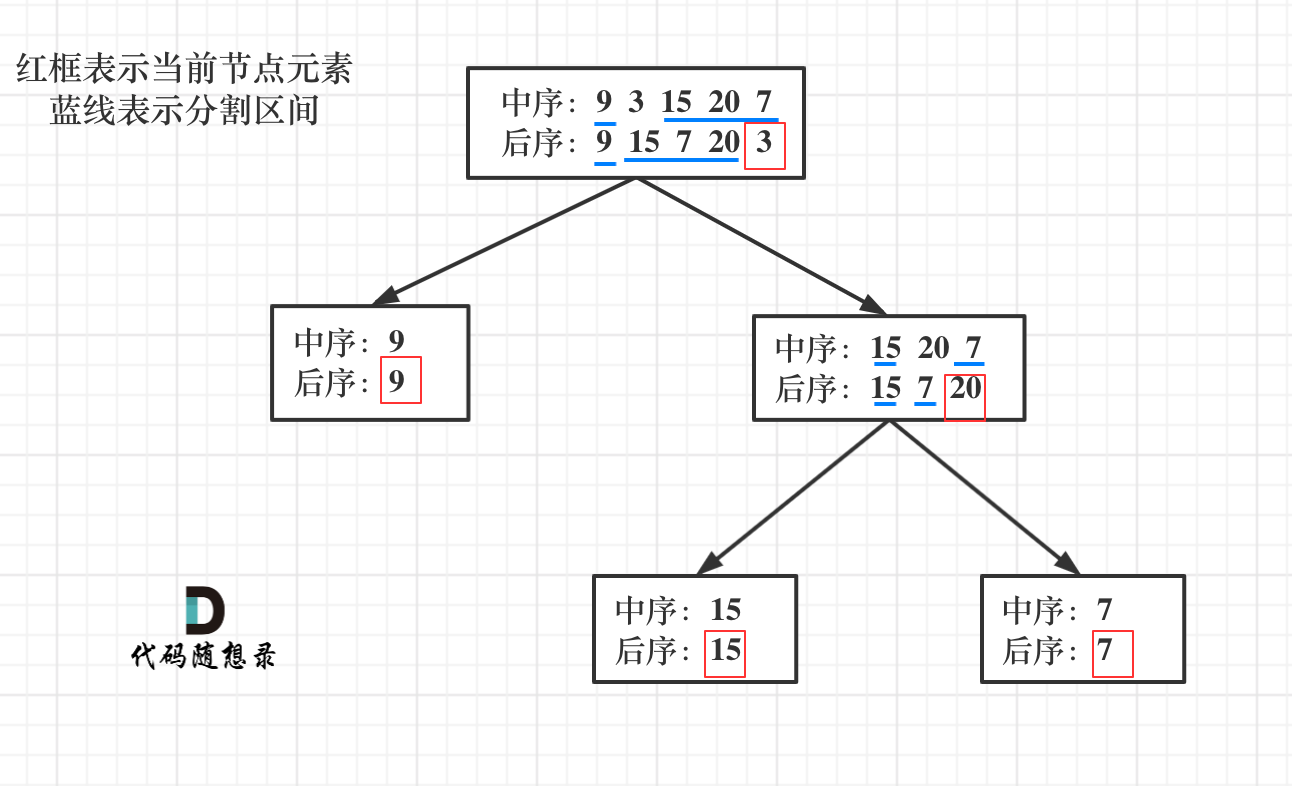
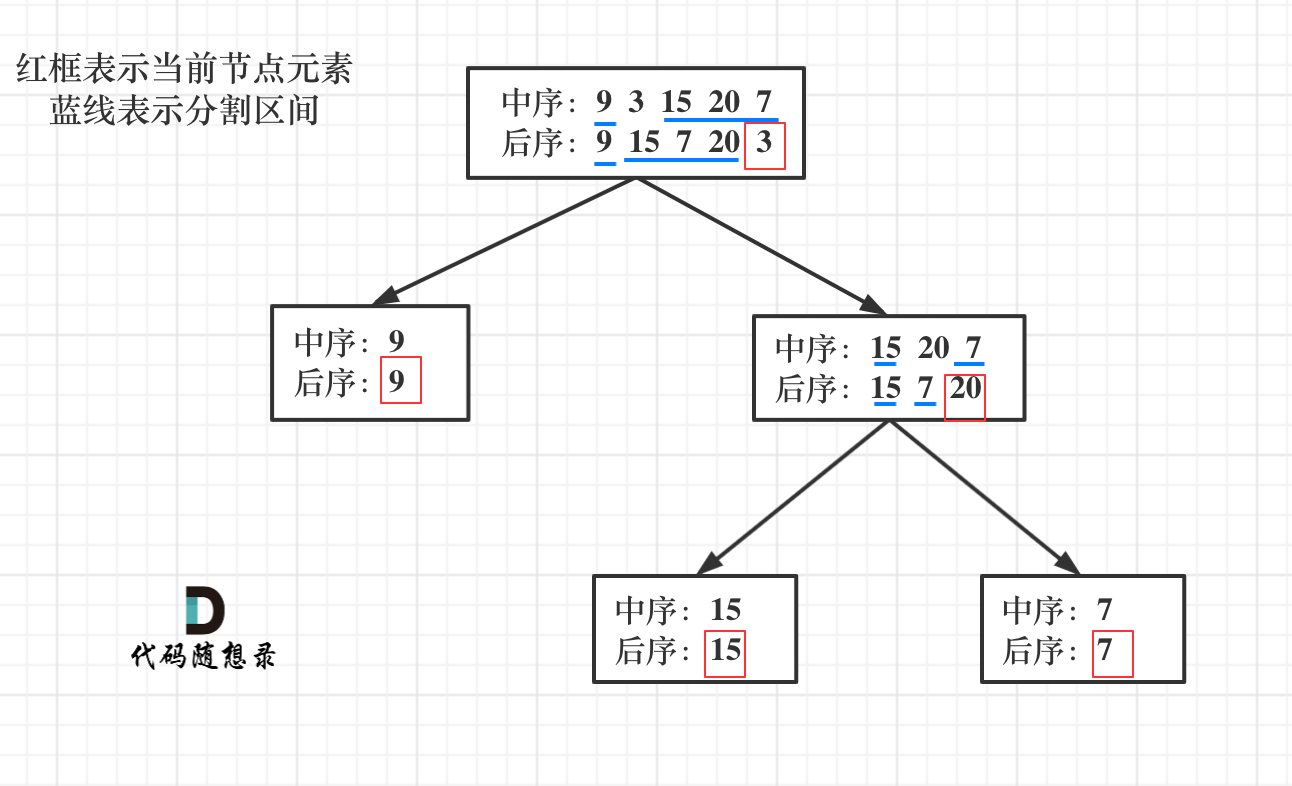
* 后序遍历 postorder = [9,15,7,20,3]
|
||||
返回如下的二叉树:
|
||||
|
||||

|
||||

|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -40,7 +40,7 @@
|
|||
|
||||
流程如图:
|
||||
|
||||
|
||||
|
||||
|
||||
那么代码应该怎么写呢?
|
||||
|
||||
|
|
@ -411,7 +411,7 @@ public:
|
|||
中序遍历 inorder = [9,3,15,20,7]
|
||||
返回如下的二叉树:
|
||||
|
||||

|
||||

|
||||
|
||||
### 思路
|
||||
|
||||
|
|
@ -554,7 +554,7 @@ public:
|
|||
|
||||
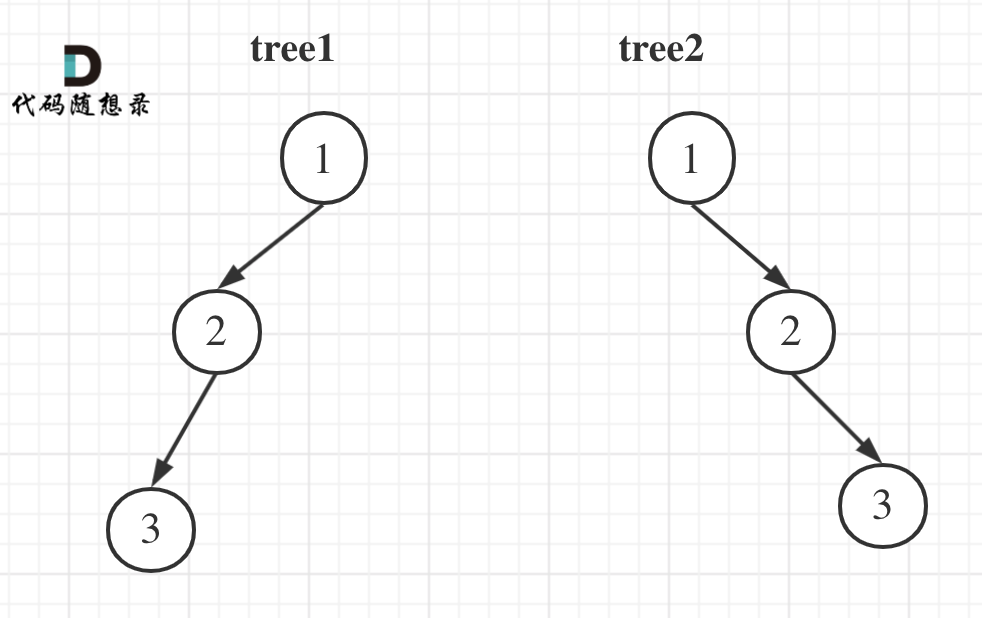
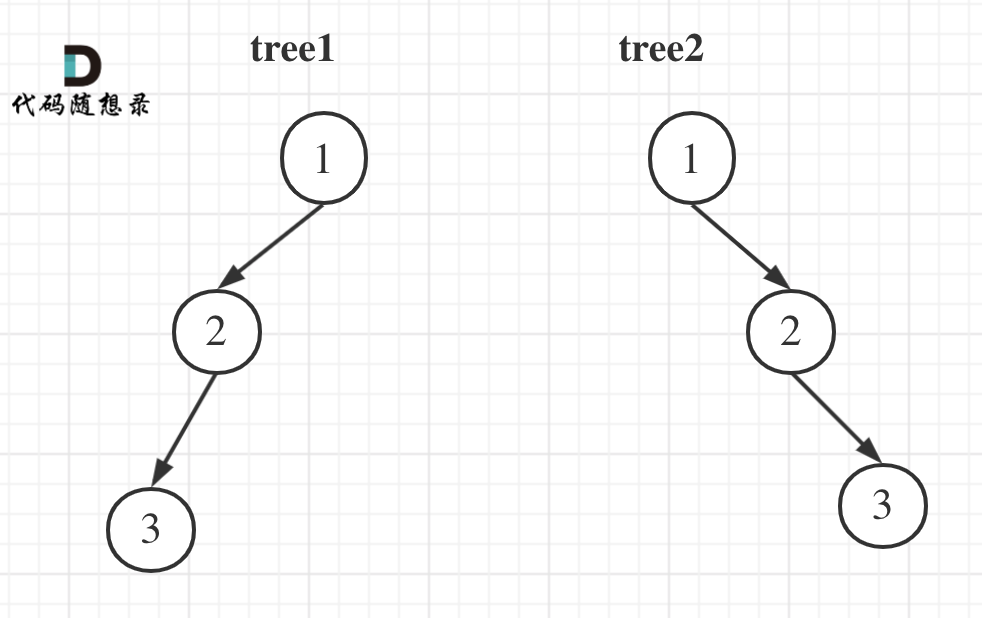
举一个例子:
|
||||
|
||||
|
||||
|
||||
|
||||
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
|
||||
|
||||
|
|
|
|||
|
|
@ -16,7 +16,7 @@
|
|||
示例:
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -40,7 +40,7 @@
|
|||
|
||||
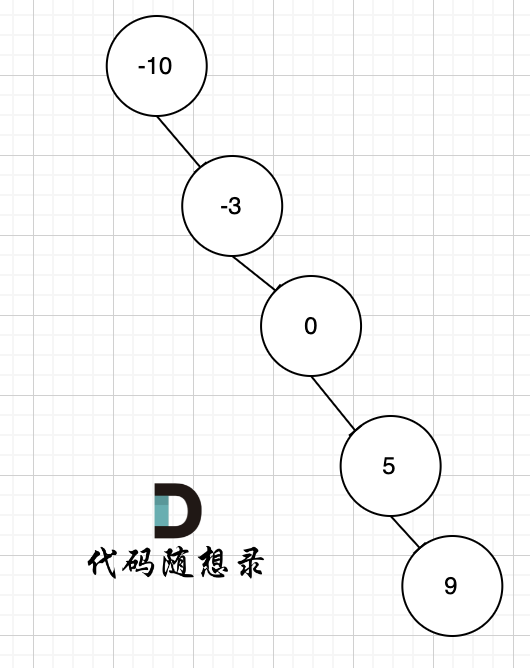
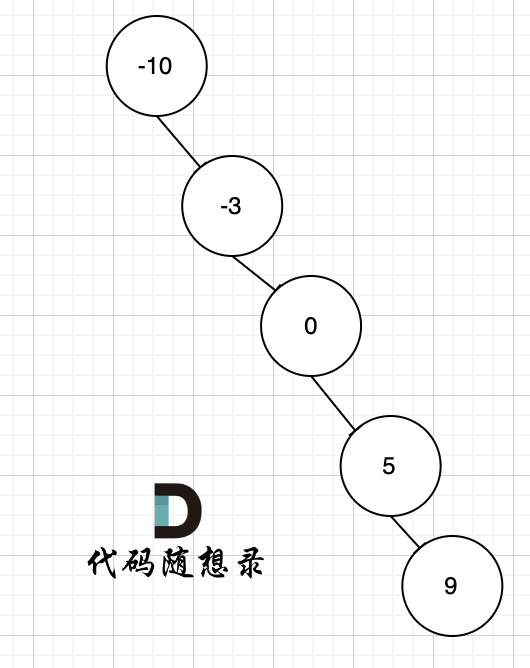
例如 有序数组[-10,-3,0,5,9] 就可以构造成这样的二叉搜索树,如图。
|
||||
|
||||
|
||||
|
||||
|
||||
上图中,是符合二叉搜索树的特性吧,如果要这么做的话,是不是本题意义就不大了,所以才强调是平衡二叉搜索树。
|
||||
|
||||
|
|
@ -63,7 +63,7 @@
|
|||
|
||||
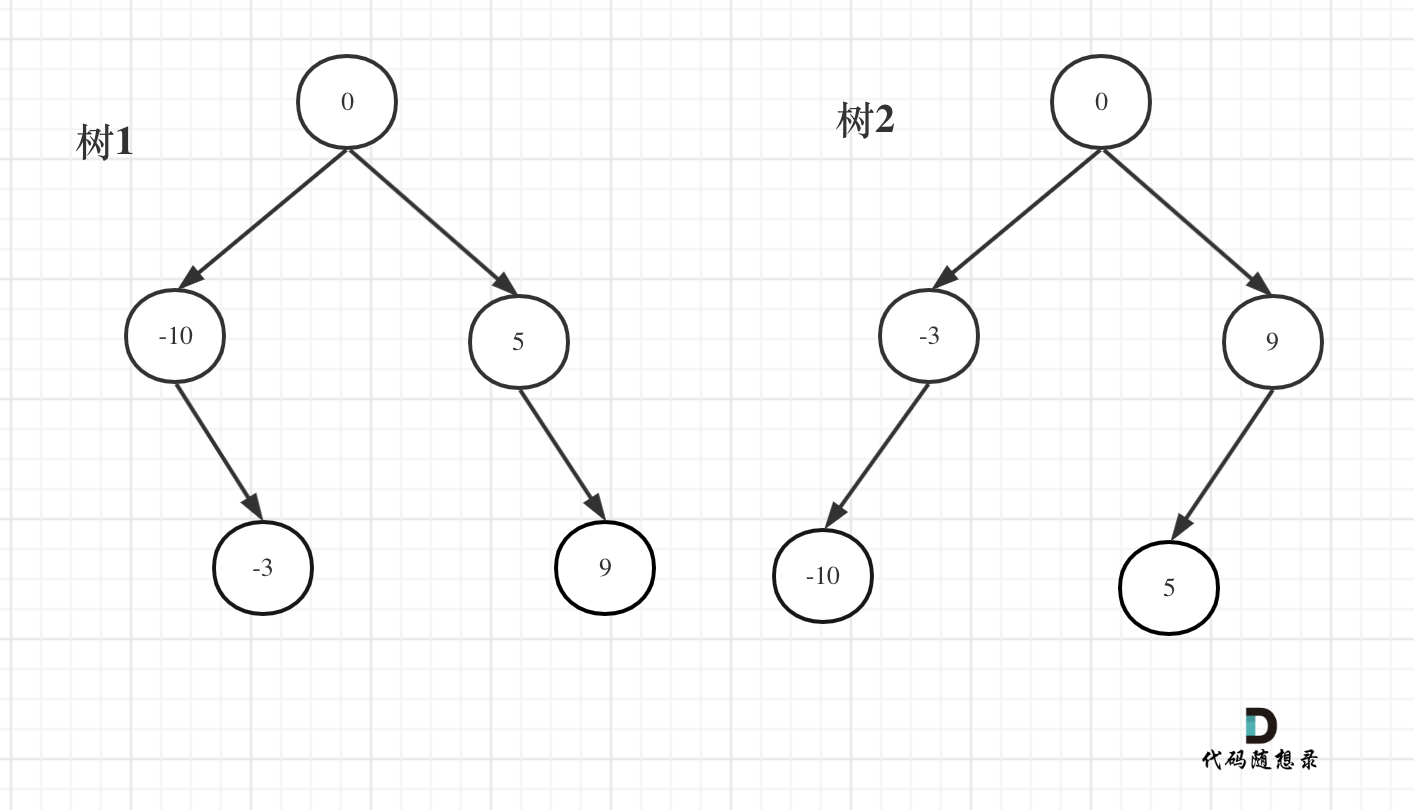
如下两棵树,都是这个数组的平衡二叉搜索树:
|
||||
|
||||

|
||||
|
||||
|
||||
如果要分割的数组长度为偶数的时候,中间元素为两个,是取左边元素 就是树1,取右边元素就是树2。
|
||||
|
||||
|
|
|
|||
|
|
@ -19,7 +19,7 @@
|
|||
|
||||
给定二叉树 [3,9,20,null,null,15,7]
|
||||
|
||||

|
||||

|
||||
|
||||
返回 true 。
|
||||
|
||||
|
|
@ -27,7 +27,7 @@
|
|||
|
||||
给定二叉树 [1,2,2,3,3,null,null,4,4]
|
||||
|
||||

|
||||

|
||||
|
||||
返回 false 。
|
||||
|
||||
|
|
@ -46,7 +46,7 @@
|
|||
|
||||
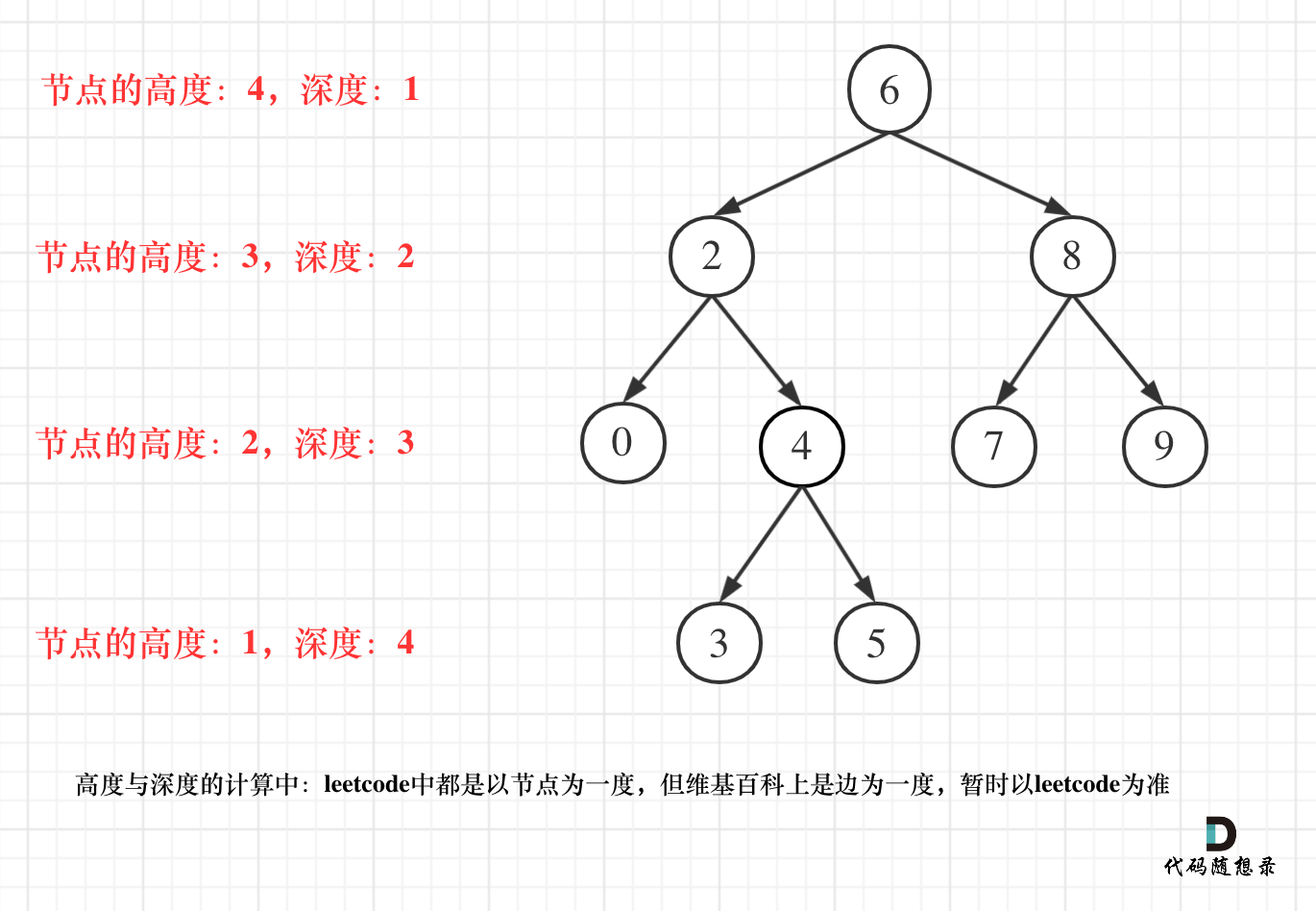
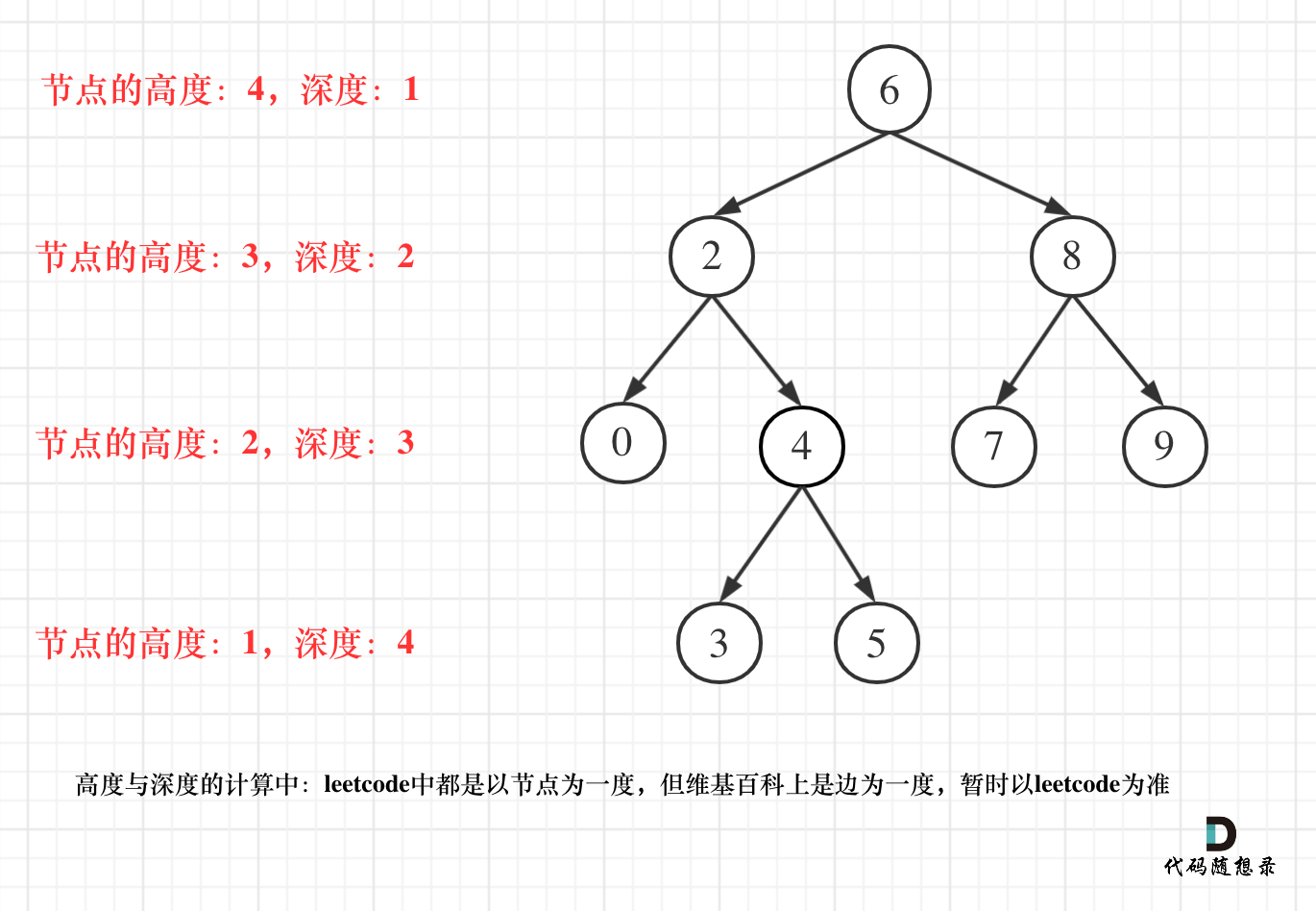
但leetcode中强调的深度和高度很明显是按照节点来计算的,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
关于根节点的深度究竟是1 还是 0,不同的地方有不一样的标准,leetcode的题目中都是以节点为一度,即根节点深度是1。但维基百科上定义用边为一度,即根节点的深度是0,我们暂时以leetcode为准(毕竟要在这上面刷题)。
|
||||
|
||||
|
|
|
|||
|
|
@ -20,7 +20,7 @@
|
|||
给定二叉树 [3,9,20,null,null,15,7],
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
返回它的最小深度 2.
|
||||
|
||||
|
|
@ -46,7 +46,7 @@
|
|||
|
||||
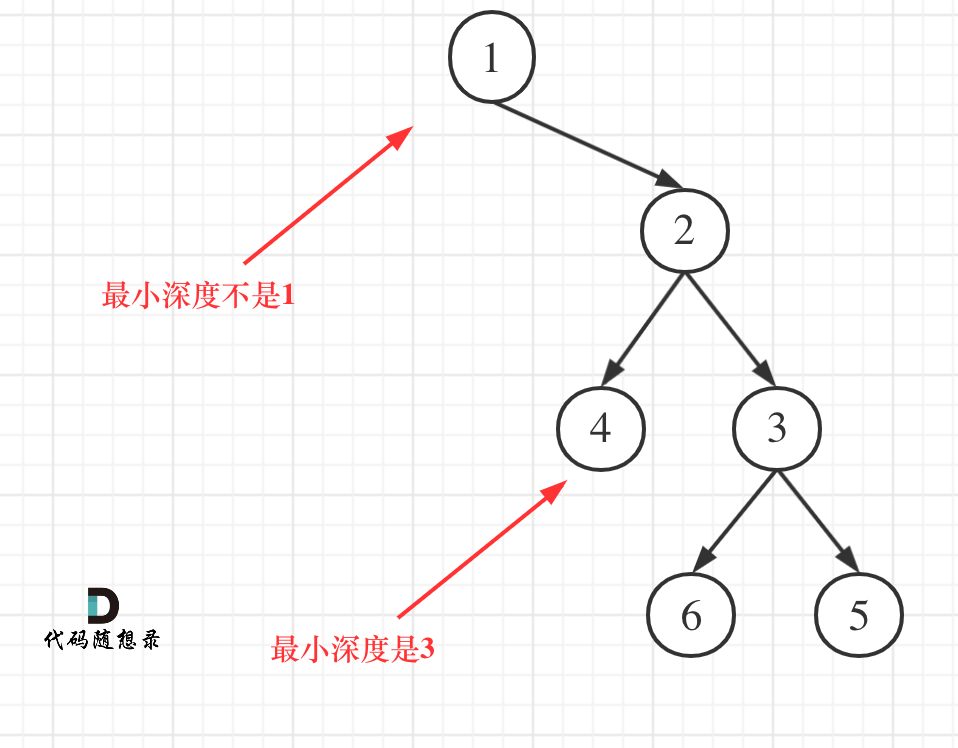
本题还有一个误区,在处理节点的过程中,最大深度很容易理解,最小深度就不那么好理解,如图:
|
||||
|
||||

|
||||
|
||||
|
||||
这就重新审题了,题目中说的是:**最小深度是从根节点到最近叶子节点的最短路径上的节点数量。**注意是**叶子节点**。
|
||||
|
||||
|
|
@ -88,7 +88,7 @@ return result;
|
|||
|
||||
这个代码就犯了此图中的误区:
|
||||
|
||||

|
||||

|
||||
|
||||
如果这么求的话,没有左孩子的分支会算为最短深度。
|
||||
|
||||
|
|
|
|||
|
|
@ -15,7 +15,7 @@
|
|||
示例:
|
||||
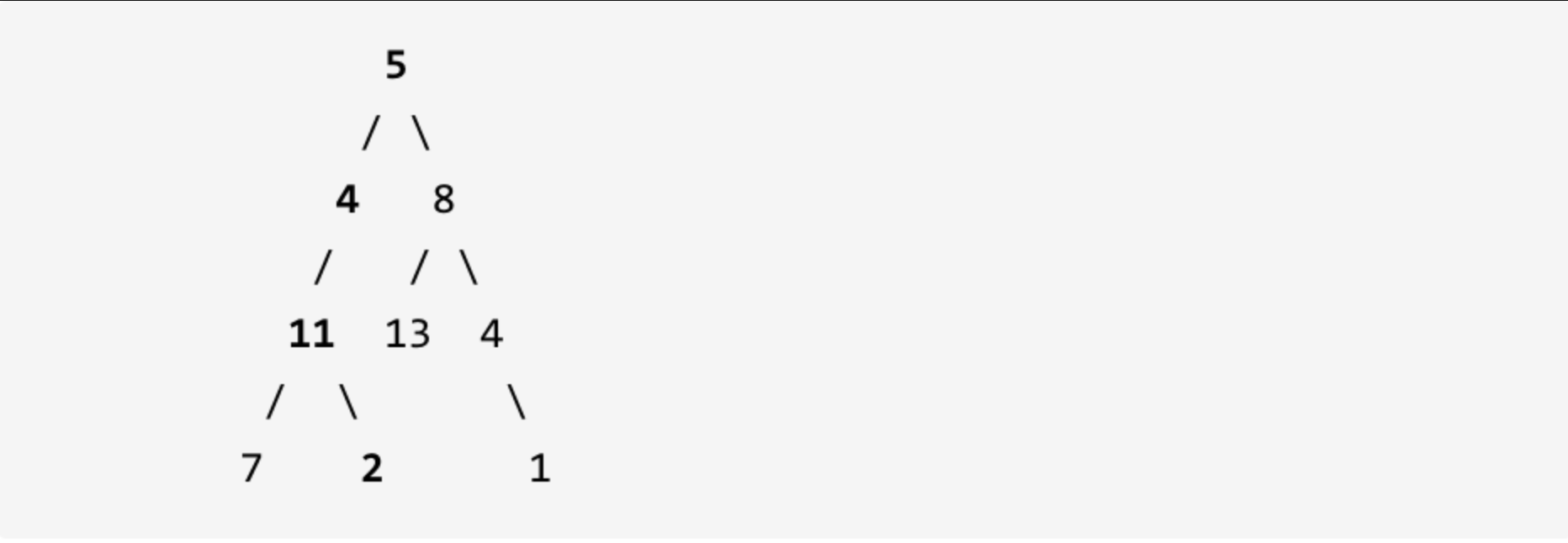
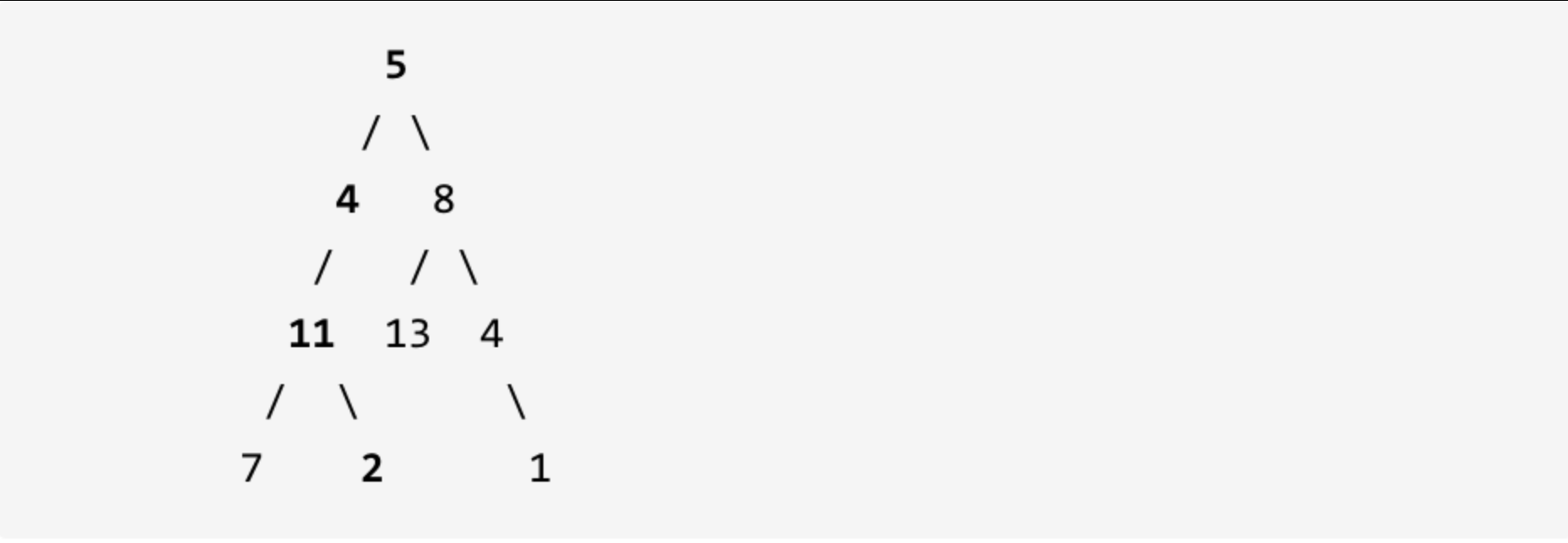
给定如下二叉树,以及目标和 sum = 22,
|
||||
|
||||
|
||||
|
||||
|
||||
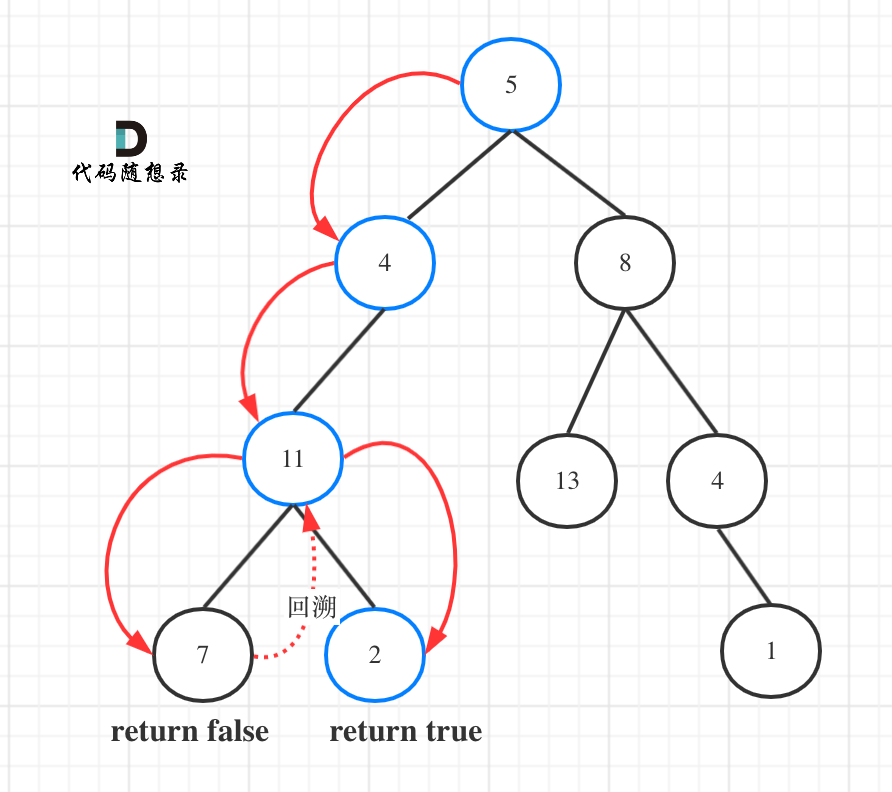
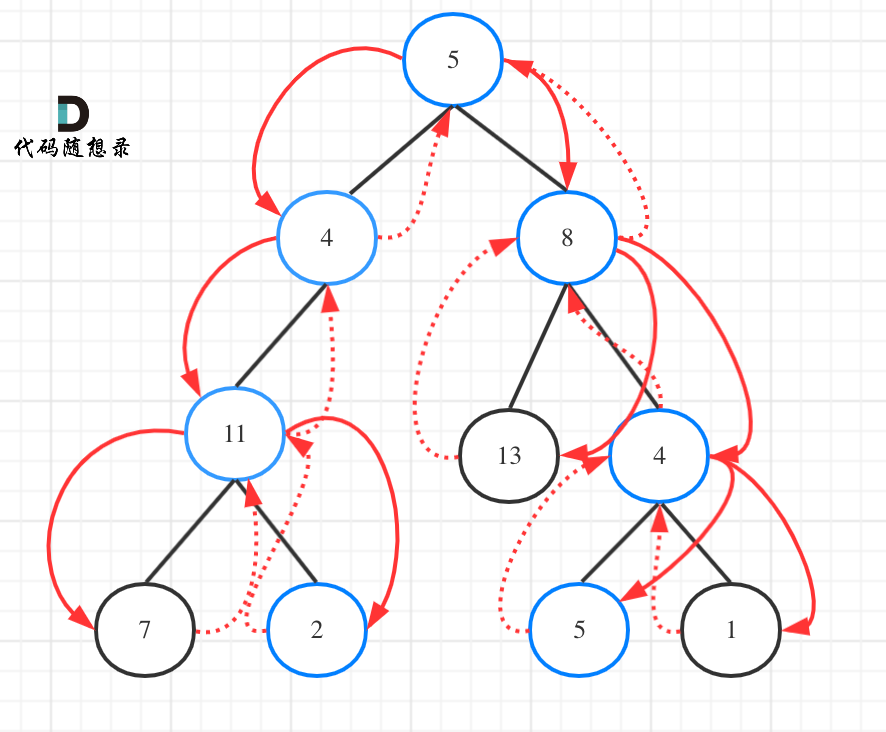
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
|
||||
|
||||
|
|
@ -53,7 +53,7 @@
|
|||
|
||||
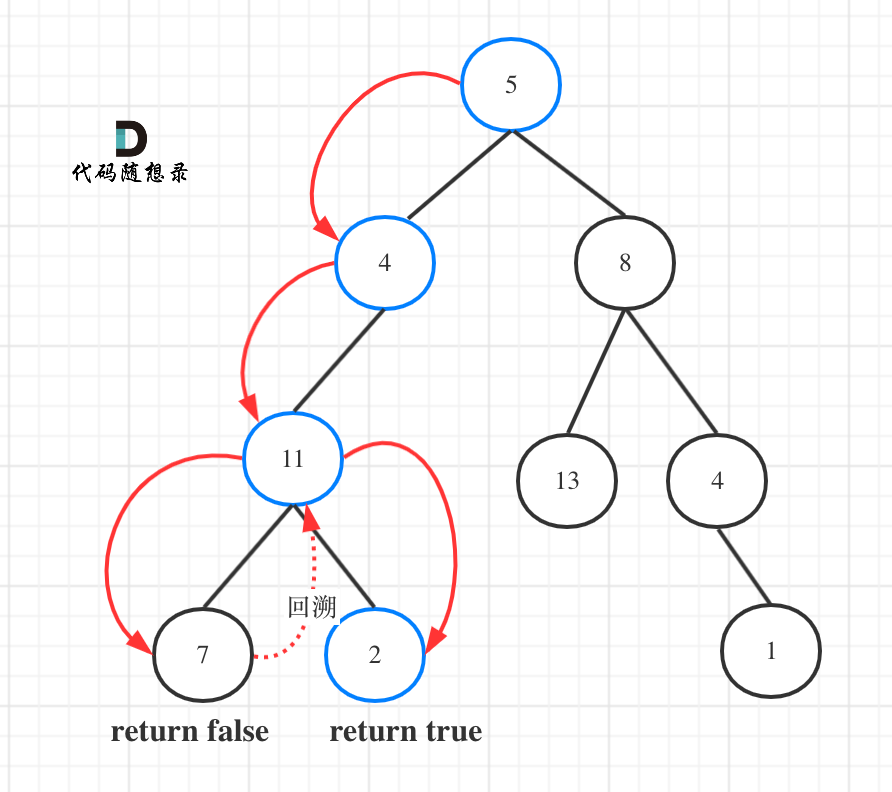
如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
图中可以看出,遍历的路线,并不要遍历整棵树,所以递归函数需要返回值,可以用bool类型表示。
|
||||
|
||||
|
|
@ -230,7 +230,7 @@ public:
|
|||
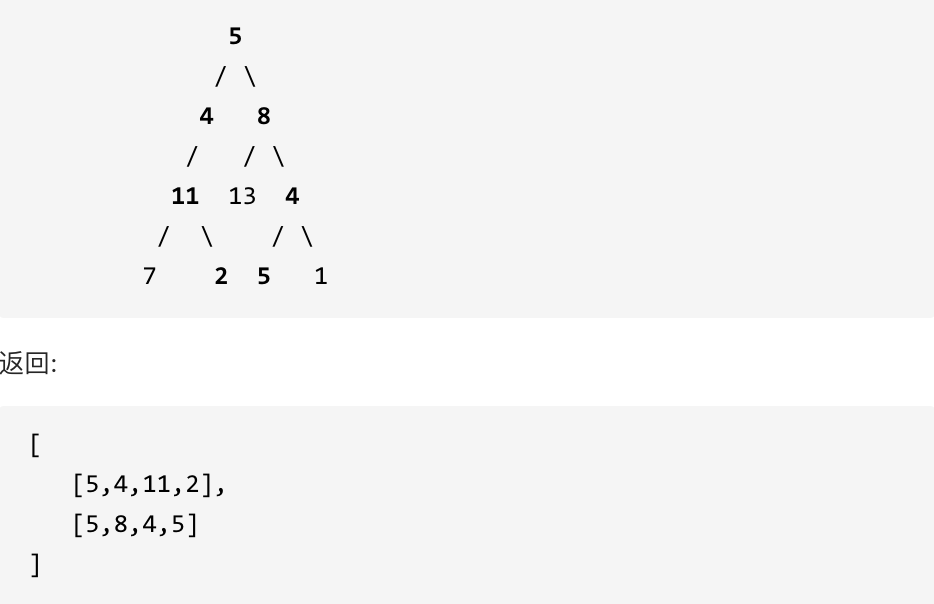
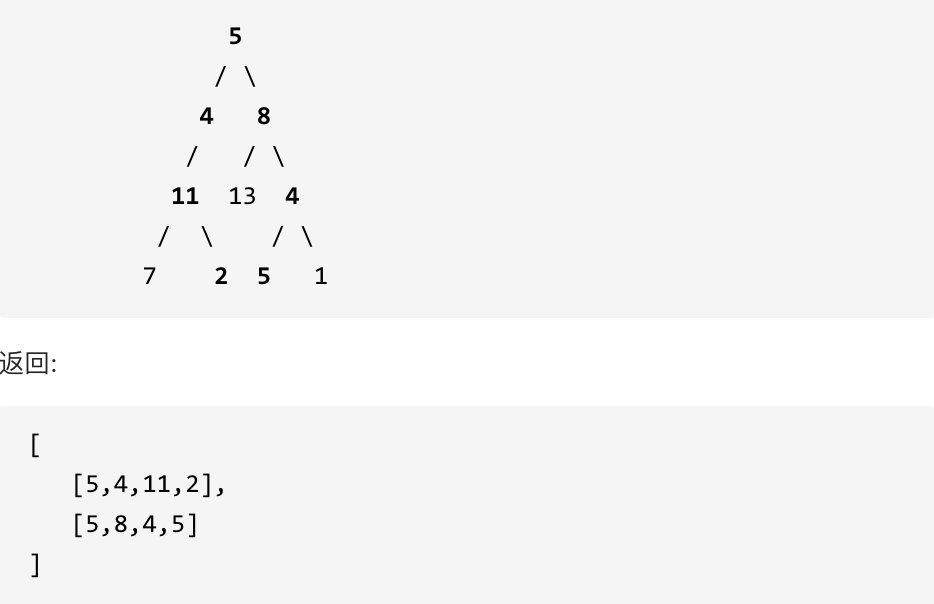
给定如下二叉树,以及目标和 sum = 22,
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
### 思路
|
||||
|
||||
|
|
@ -239,7 +239,7 @@ public:
|
|||
|
||||
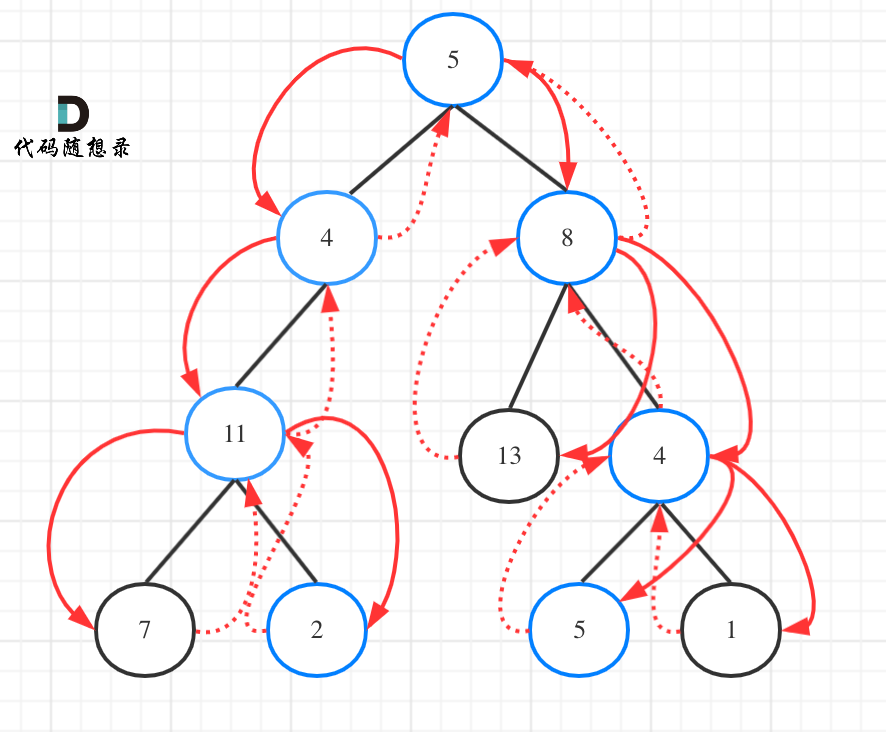
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
为了尽可能的把细节体现出来,我写出如下代码(**这份代码并不简洁,但是逻辑非常清晰**)
|
||||
|
|
|
|||
|
|
@ -12,7 +12,7 @@
|
|||
|
||||
题目数据保证答案符合 32 位带符号整数范围。
|
||||
|
||||

|
||||

|
||||
|
||||
提示:
|
||||
|
||||
|
|
@ -70,7 +70,7 @@ dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为d
|
|||
|
||||
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。
|
||||
|
||||
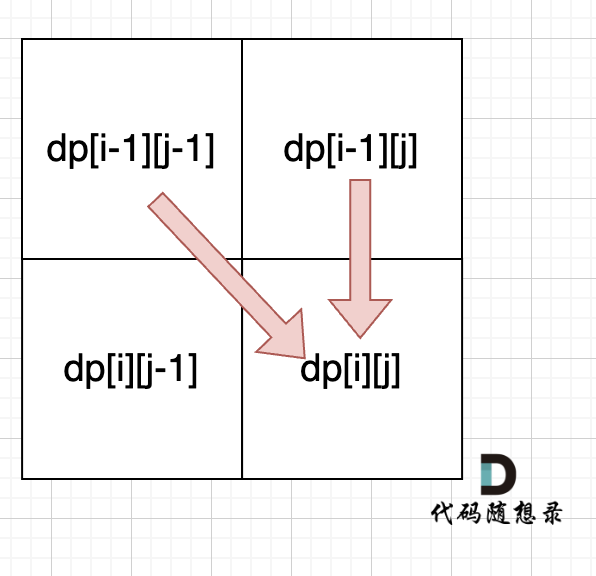
|
||||
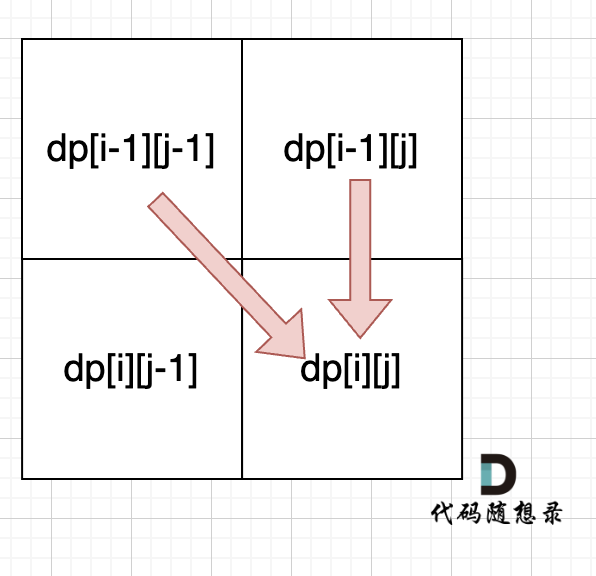
|
||||
|
||||
每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
|
||||
|
||||
|
|
@ -101,7 +101,7 @@ for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和
|
|||
|
||||
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。
|
||||
|
||||

|
||||

|
||||
|
||||
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
|
||||
|
||||
|
|
@ -123,7 +123,7 @@ for (int i = 1; i <= s.size(); i++) {
|
|||
|
||||
以s:"baegg",t:"bag"为例,推导dp数组状态如下:
|
||||
|
||||

|
||||
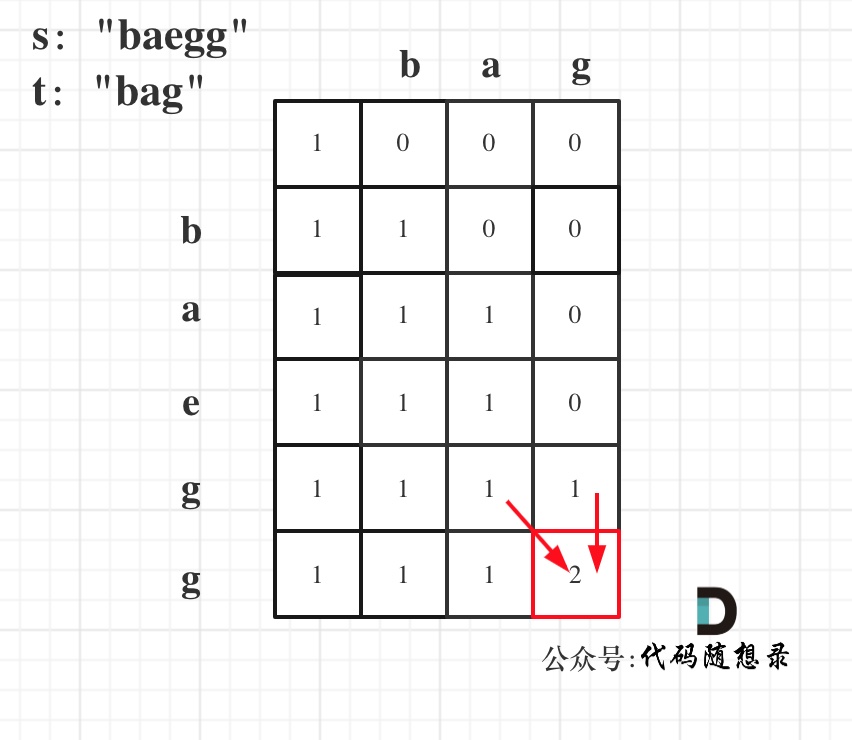
|
||||
|
||||
如果写出来的代码怎么改都通过不了,不妨把dp数组打印出来,看一看,是不是这样的。
|
||||
|
||||
|
|
|
|||
|
|
@ -26,7 +26,7 @@ struct Node {
|
|||
* 你只能使用常量级额外空间。
|
||||
* 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
|
||||
|
||||
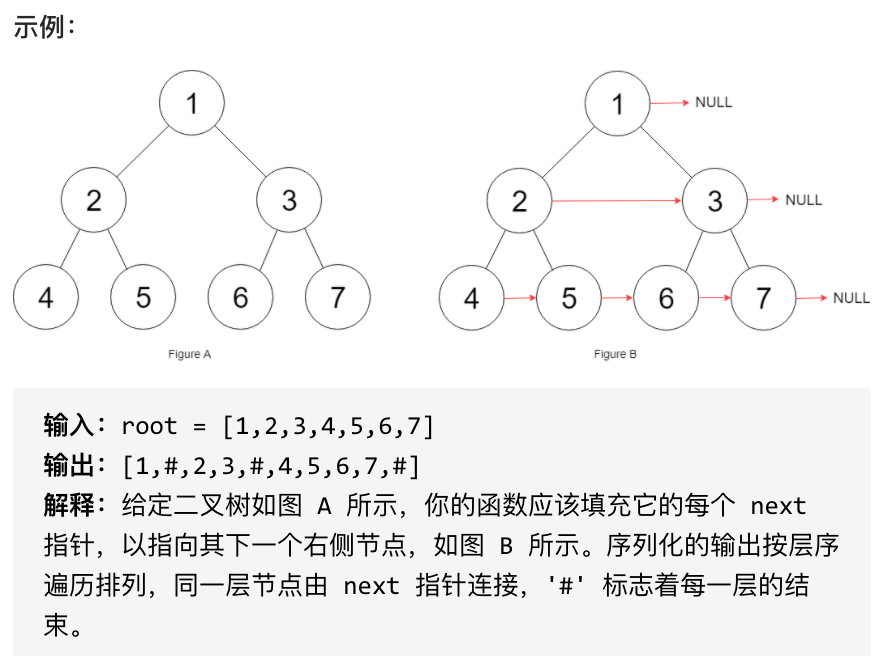
|
||||
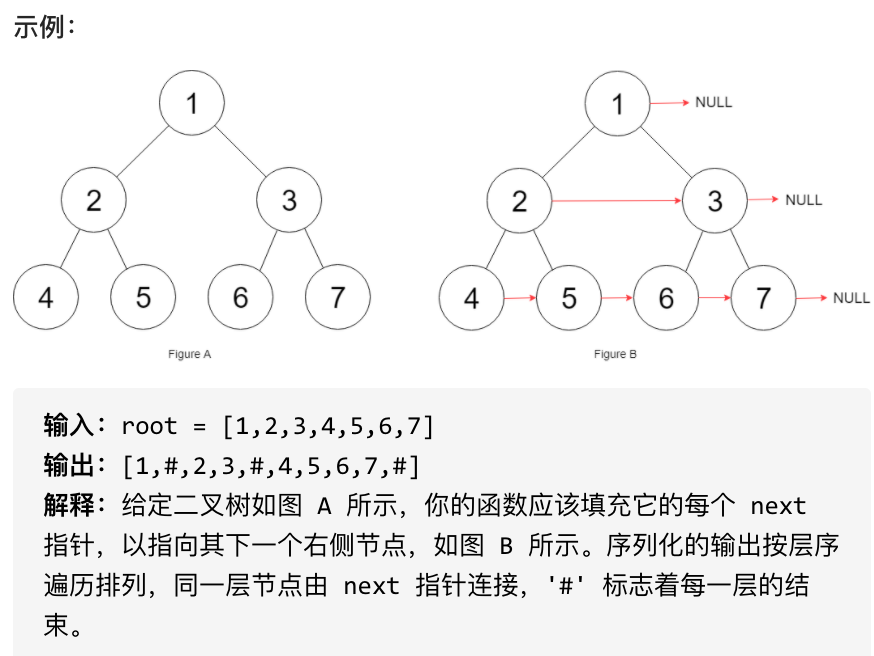
|
||||
|
||||
## 思路
|
||||
|
||||
|
|
@ -42,7 +42,7 @@ struct Node {
|
|||
|
||||
如图,假如当前操作的节点是cur:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/116.填充每个节点的下一个右侧节点指针1.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/116.填充每个节点的下一个右侧节点指针1.png' width=600> </img></div>
|
||||
|
||||
最关键的点是可以通过上一层递归 搭出来的线,进行本次搭线。
|
||||
|
||||
|
|
|
|||
|
|
@ -129,7 +129,7 @@ dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所
|
|||
以示例1,输入:[7,1,5,3,6,4]为例,dp数组状态如下:
|
||||
|
||||
|
||||
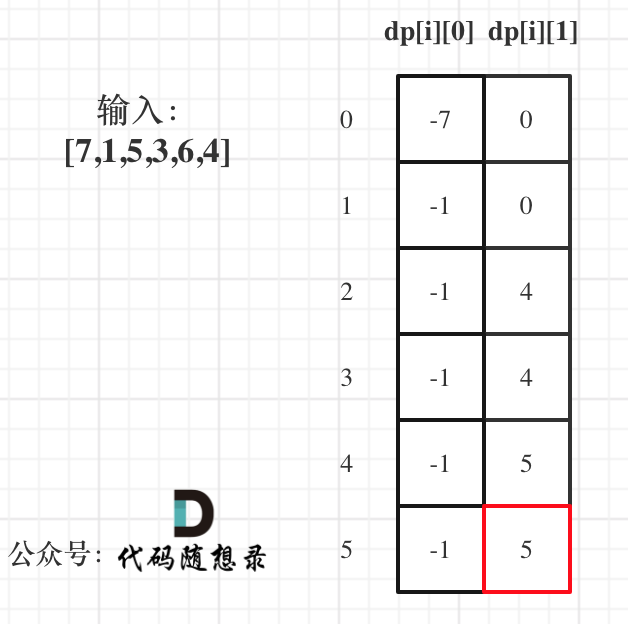
|
||||
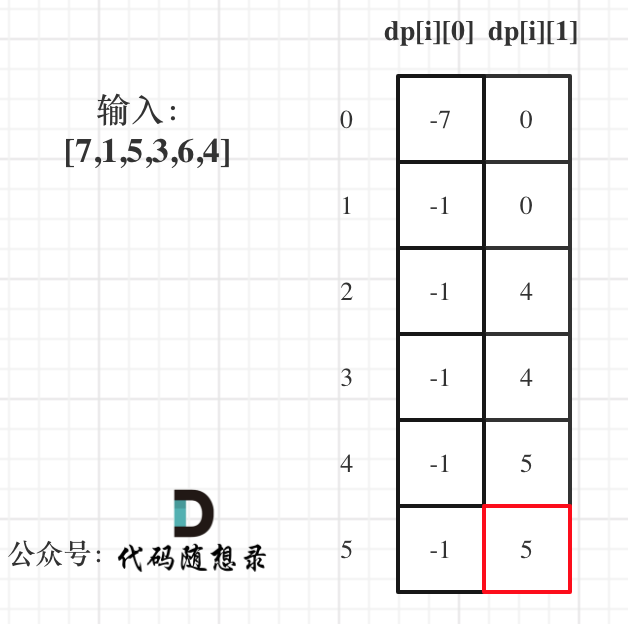
|
||||
|
||||
|
||||
dp[5][1]就是最终结果。
|
||||
|
|
|
|||
|
|
@ -66,7 +66,7 @@
|
|||
|
||||
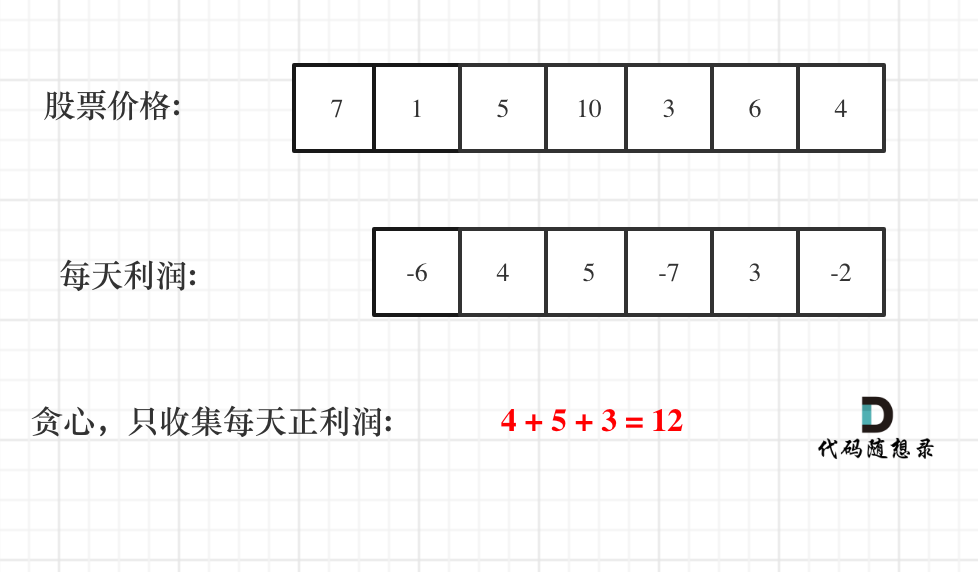
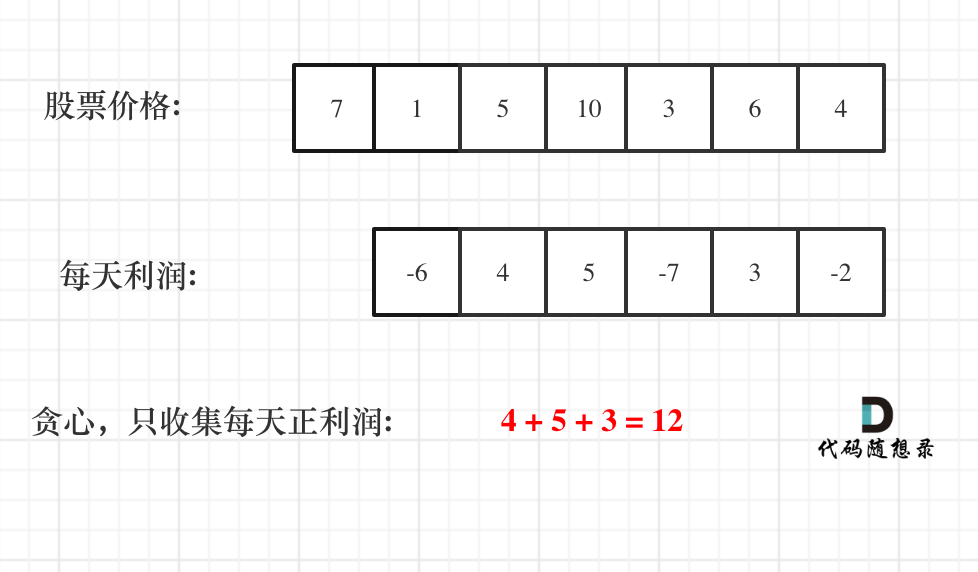
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
一些同学陷入:第一天怎么就没有利润呢,第一天到底算不算的困惑中。
|
||||
|
||||
|
|
|
|||
|
|
@ -120,7 +120,7 @@ dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
|
|||
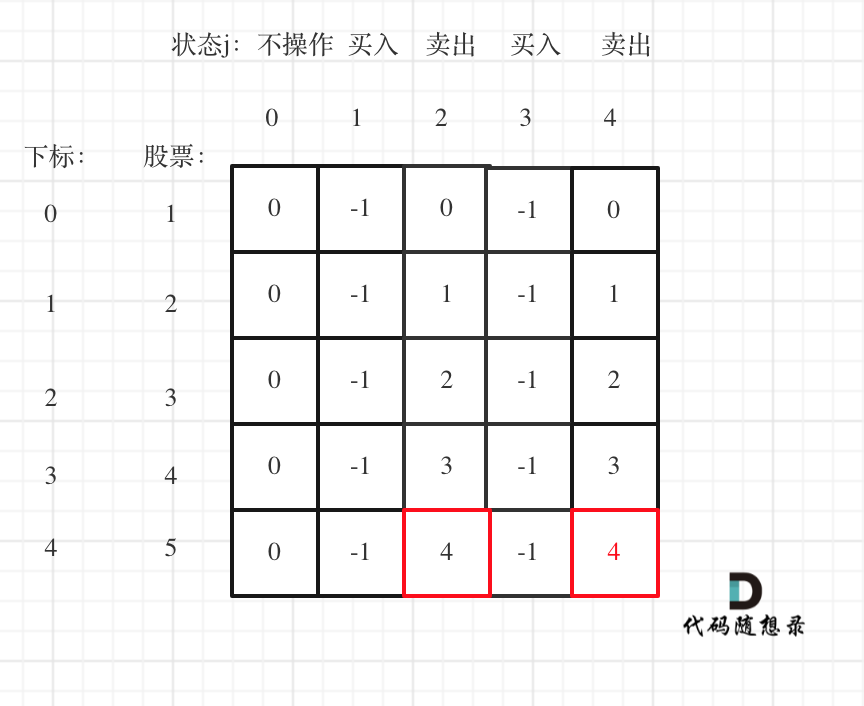
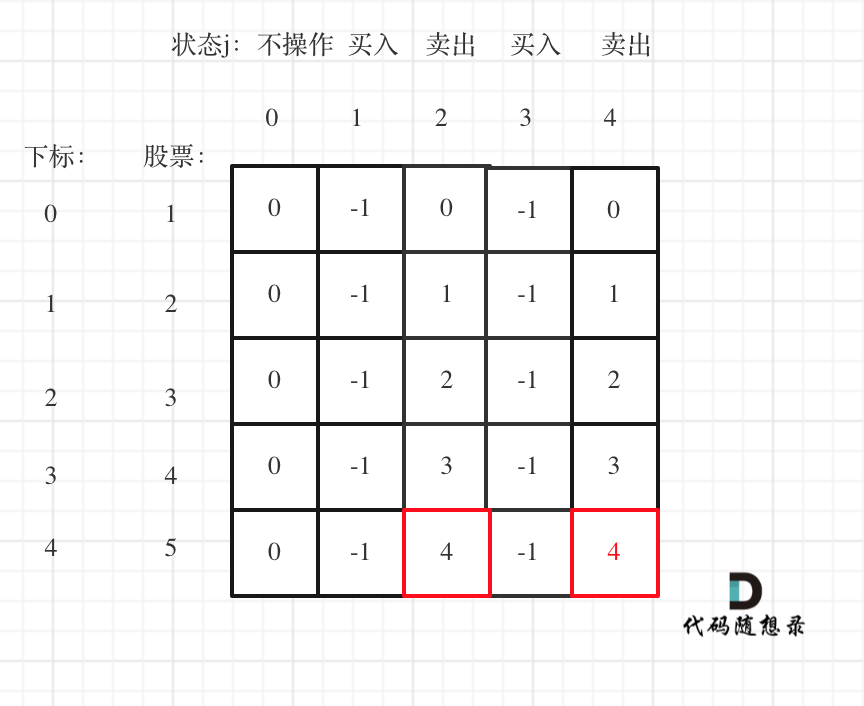
以输入[1,2,3,4,5]为例
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
大家可以看到红色框为最后两次卖出的状态。
|
||||
|
||||
|
|
|
|||
|
|
@ -31,7 +31,7 @@
|
|||
|
||||
以示例1为例,从这个图中可以看出 hit 到 cog的路线,不止一条,有三条,一条是最短的长度为5,两条长度为6。
|
||||
|
||||
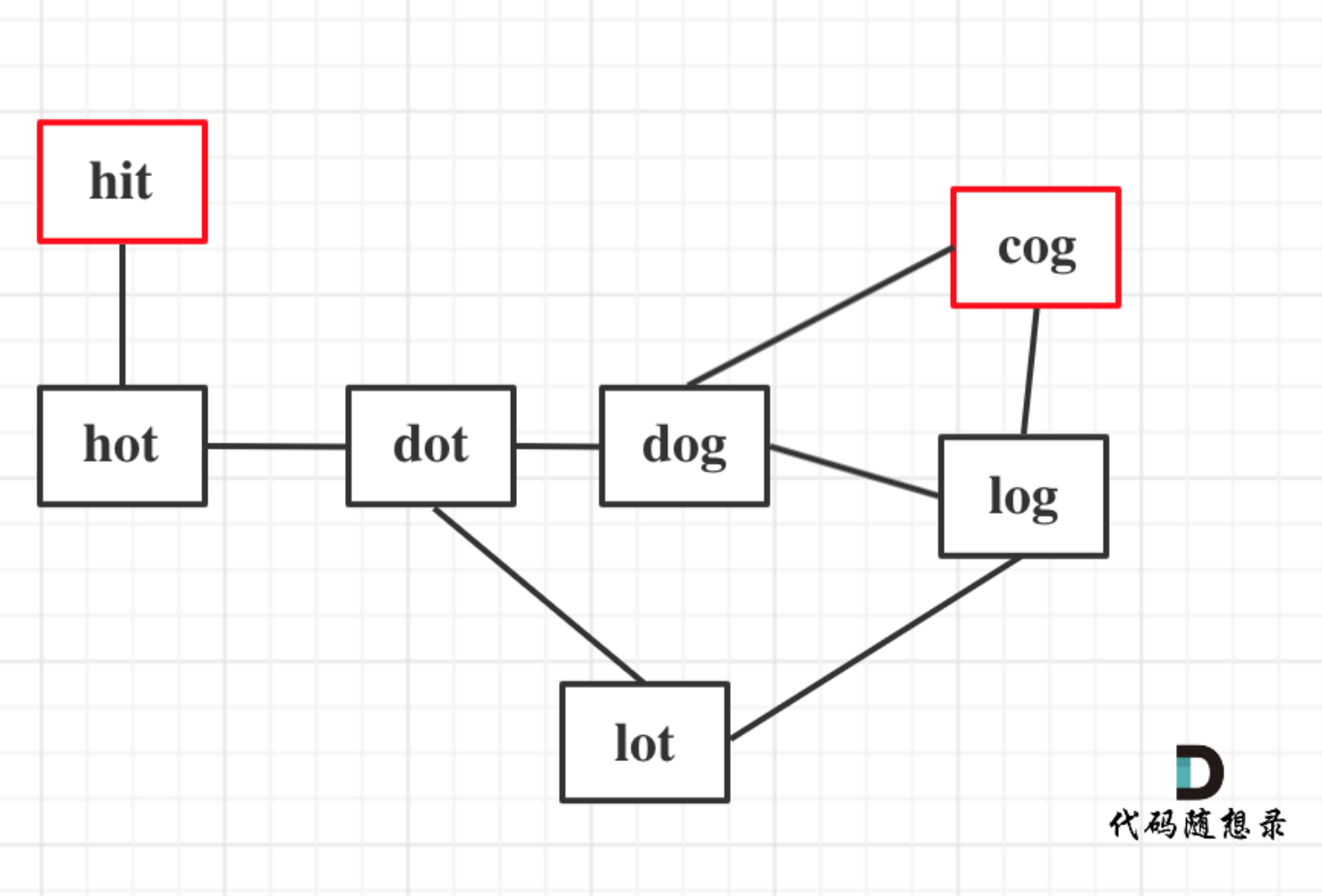
|
||||
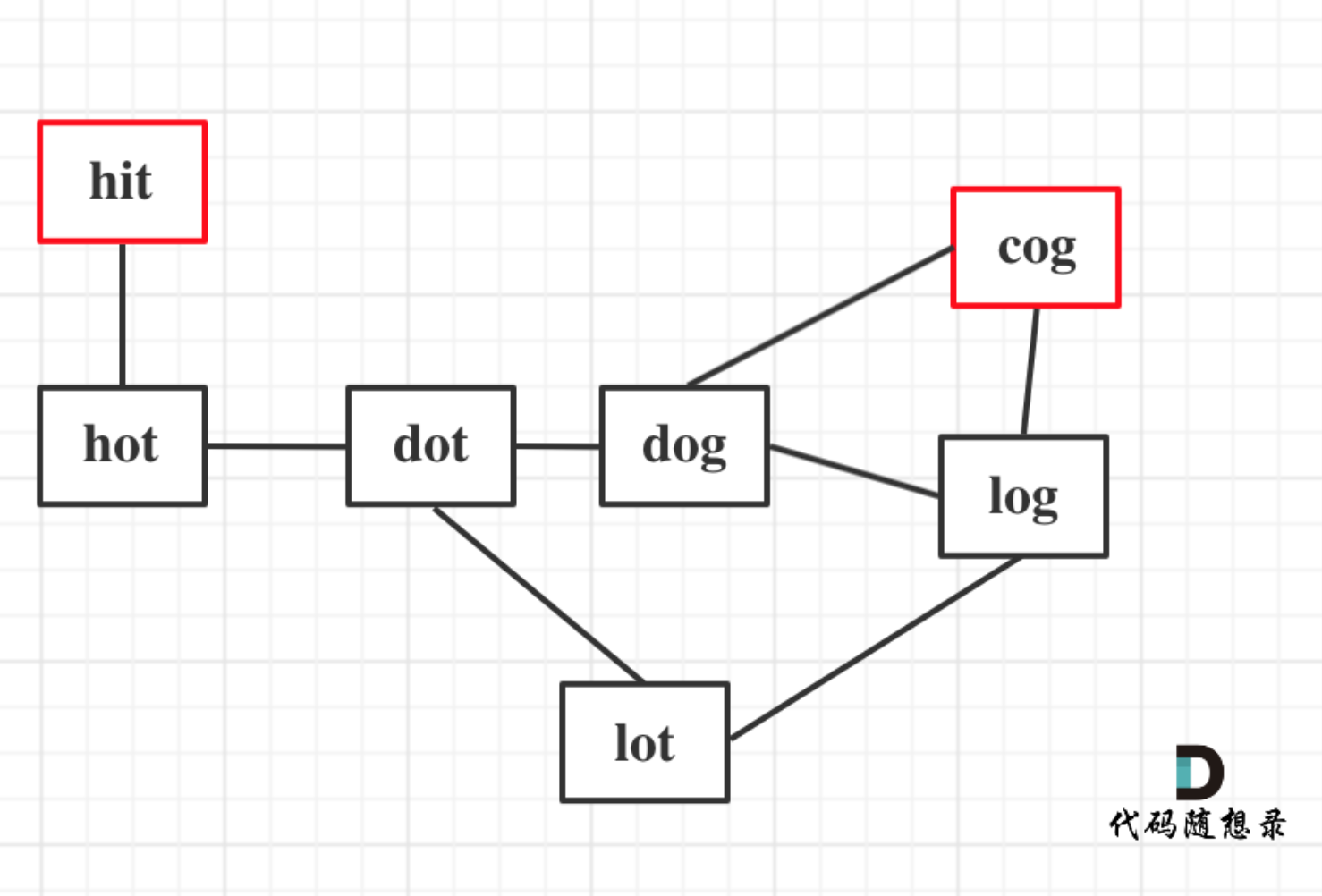
|
||||
|
||||
本题只需要求出最短路径的长度就可以了,不用找出路径。
|
||||
|
||||
|
|
|
|||
|
|
@ -81,7 +81,7 @@ int vectorToInt(const vector<int>& vec) {
|
|||
如图:
|
||||
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/129.求根到叶子节点数字之和.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/129.求根到叶子节点数字之和.png' width=600> </img></div>
|
||||
|
||||
代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -8,7 +8,7 @@
|
|||
|
||||
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
|
||||
|
||||
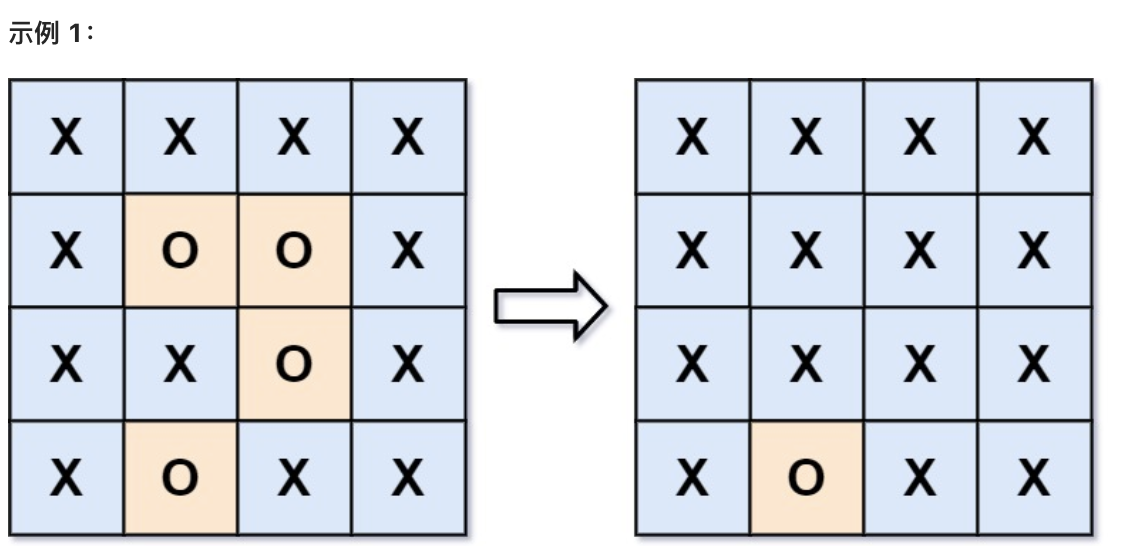
|
||||
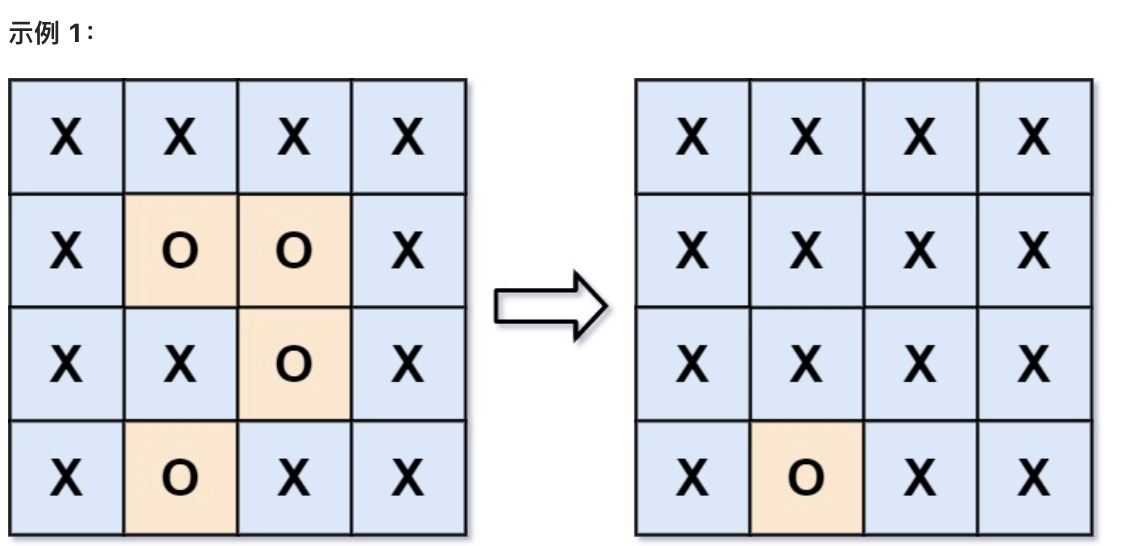
|
||||
|
||||
* 输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
|
||||
* 输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
|
||||
|
|
@ -28,11 +28,11 @@
|
|||
|
||||
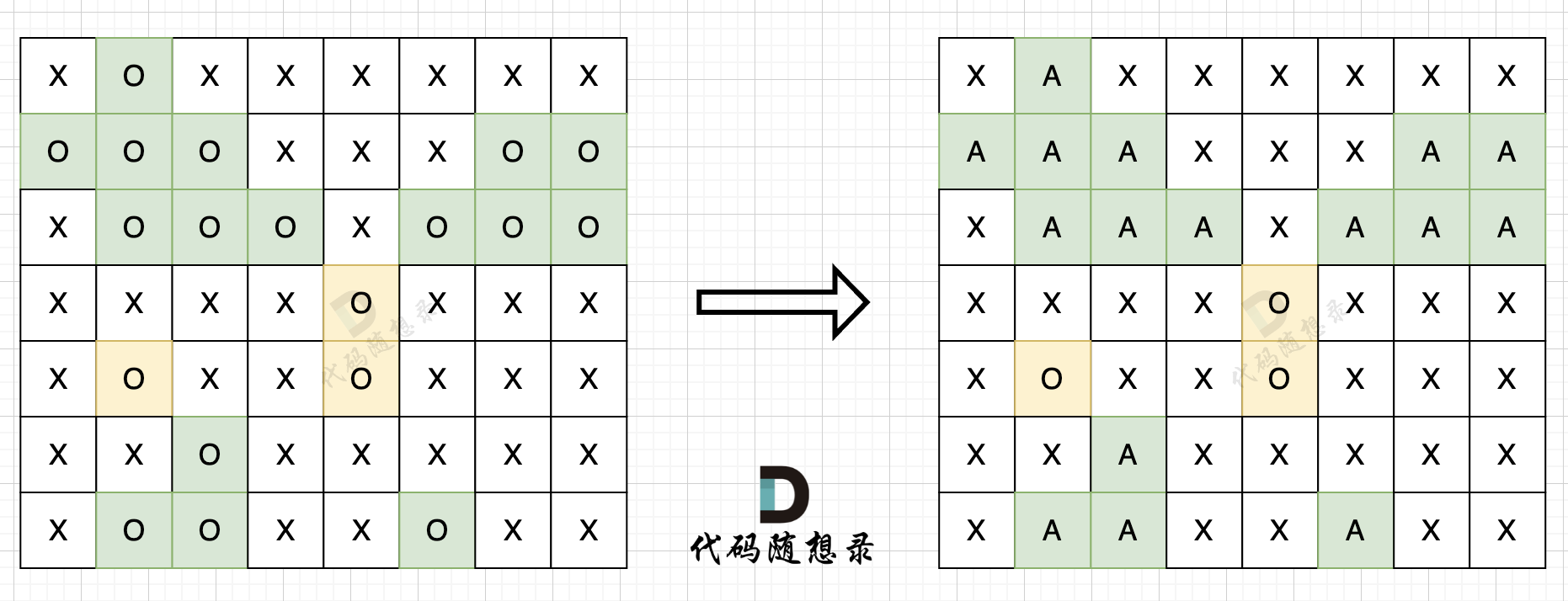
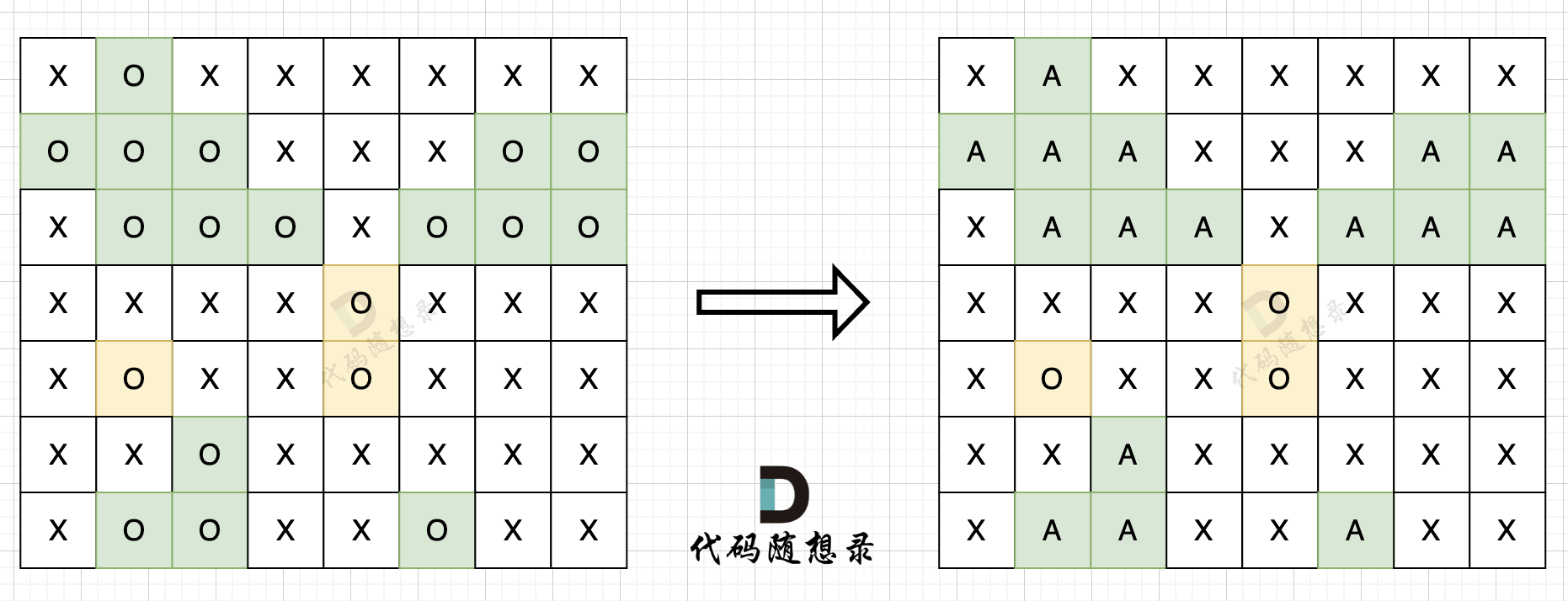
步骤一:深搜或者广搜将地图周边的'O'全部改成'A',如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
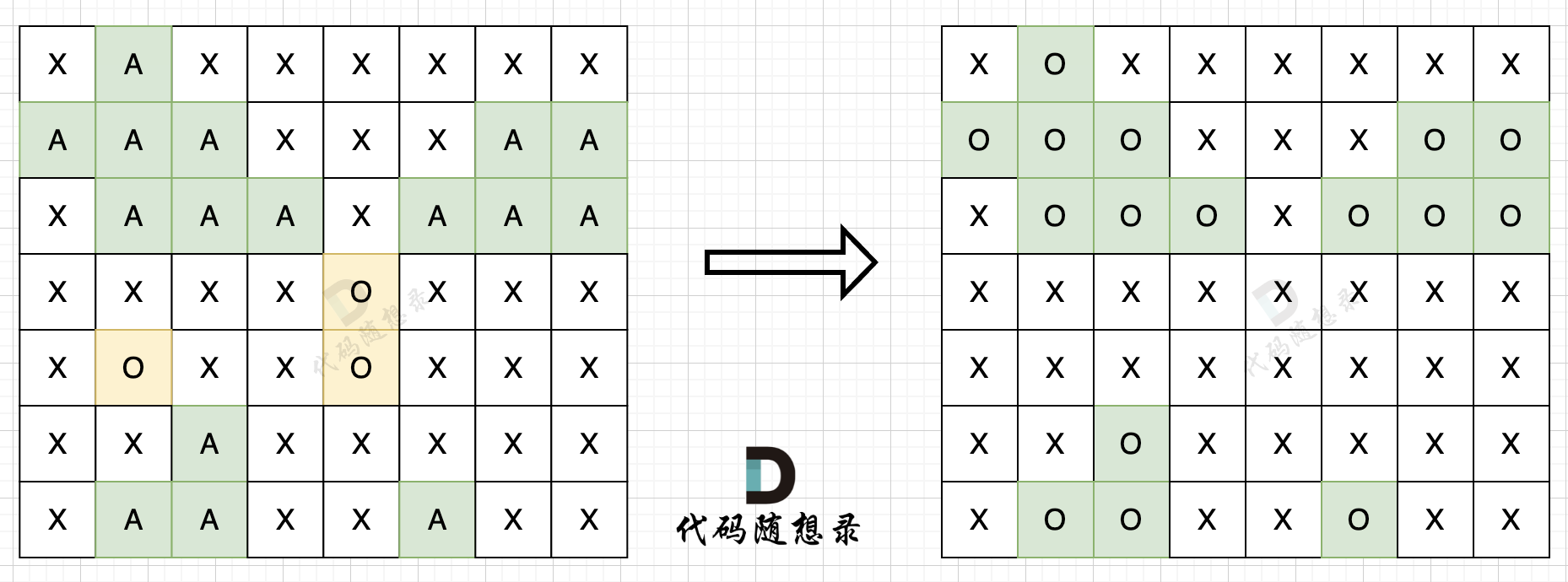
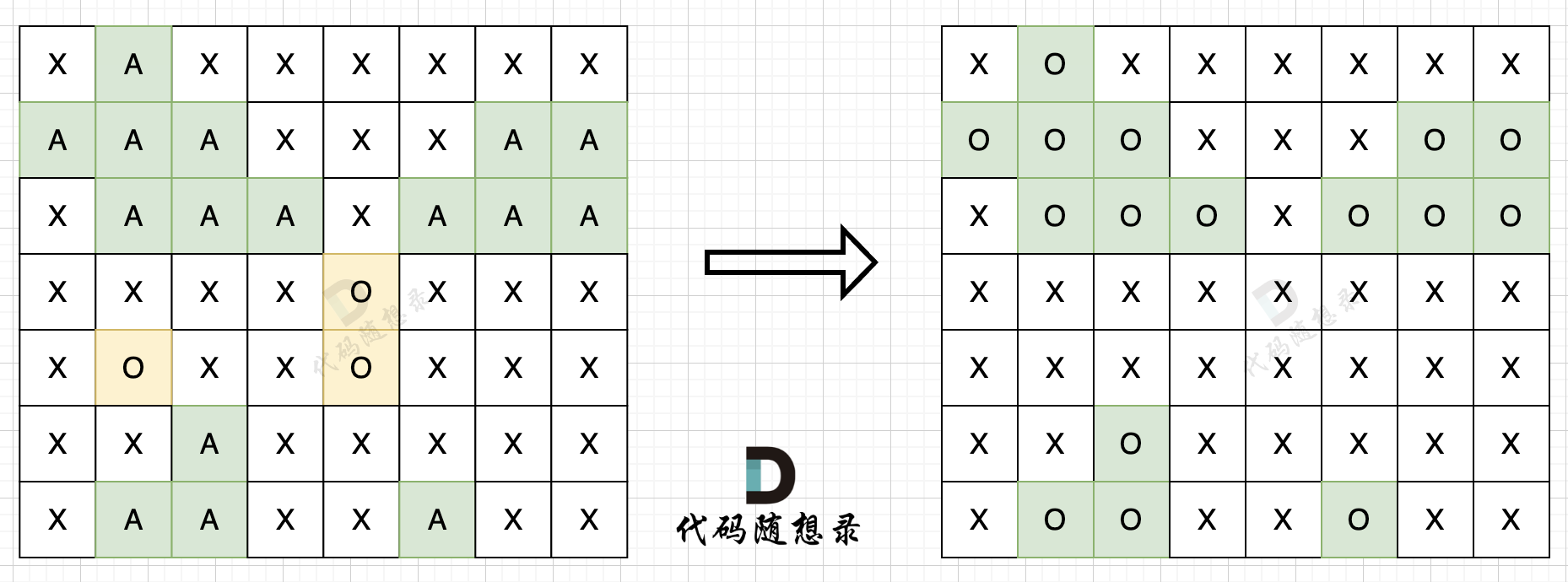
步骤二:在遍历地图,将'O'全部改成'X'(地图中间的'O'改成了'X'),将'A'改回'O'(保留的地图周边的'O'),如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
整体C++代码如下,以下使用dfs实现,其实遍历方式dfs,bfs都是可以的。
|
||||
|
||||
|
|
|
|||
|
|
@ -50,7 +50,7 @@
|
|||
|
||||
所以切割问题,也可以抽象为一棵树形结构,如图:
|
||||
|
||||

|
||||
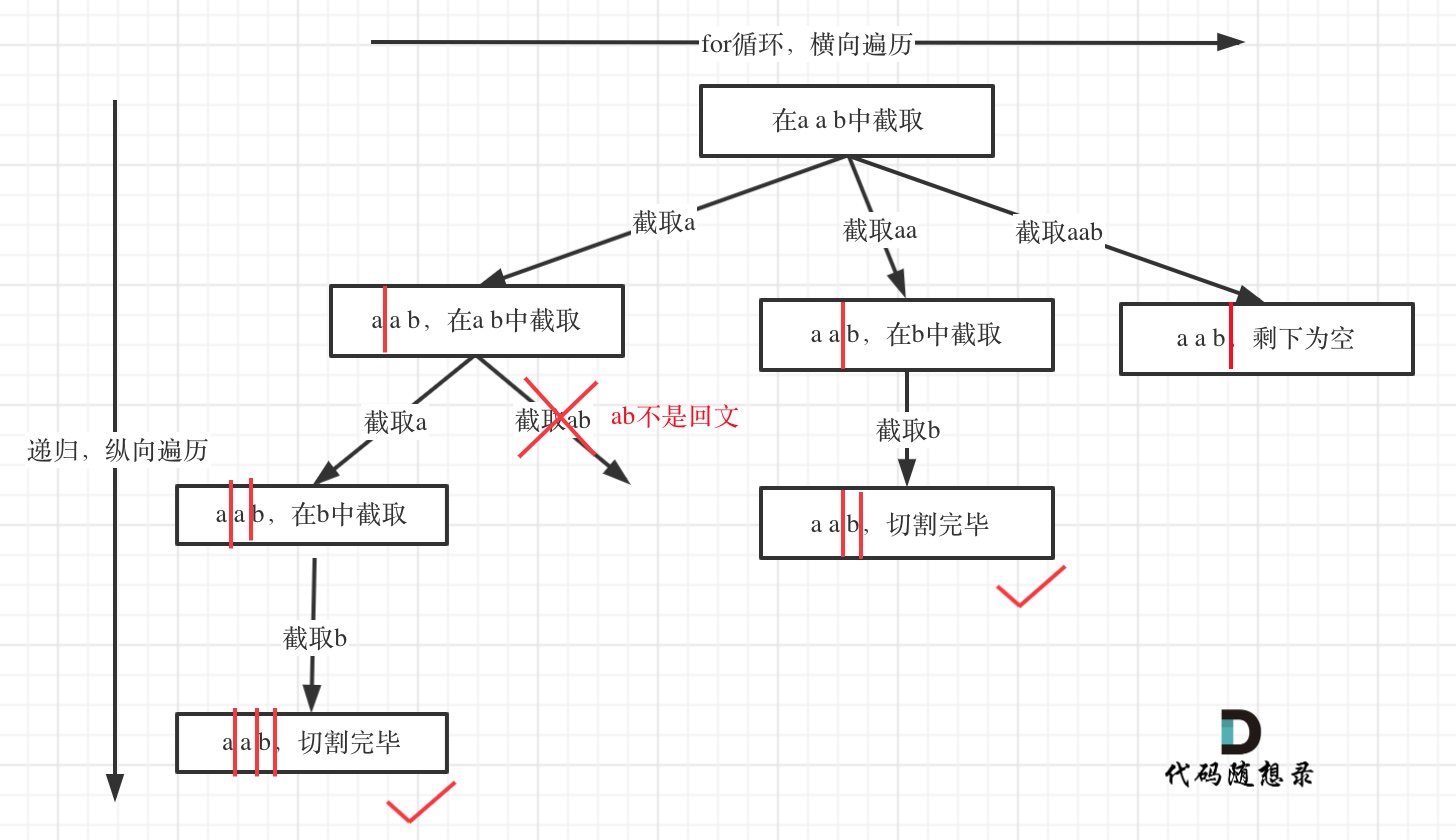
|
||||
|
||||
递归用来纵向遍历,for循环用来横向遍历,切割线(就是图中的红线)切割到字符串的结尾位置,说明找到了一个切割方法。
|
||||
|
||||
|
|
@ -76,7 +76,7 @@ void backtracking (const string& s, int startIndex) {
|
|||
|
||||
* 递归函数终止条件
|
||||
|
||||

|
||||

|
||||
|
||||
从树形结构的图中可以看出:切割线切到了字符串最后面,说明找到了一种切割方法,此时就是本层递归的终止条件。
|
||||
|
||||
|
|
|
|||
|
|
@ -161,7 +161,7 @@ for (int i = s.size() - 1; i >= 0; i--) {
|
|||
|
||||
以输入:"aabc" 为例:
|
||||
|
||||
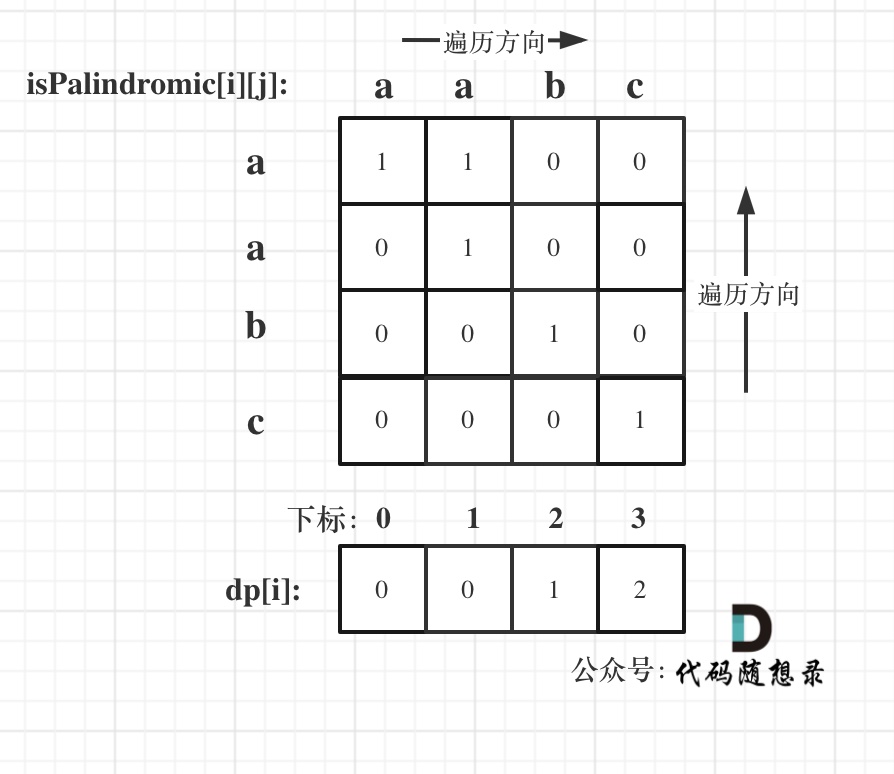
|
||||

|
||||
|
||||
以上分析完毕,代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -144,7 +144,7 @@ i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i
|
|||
|
||||
如图:
|
||||
|
||||
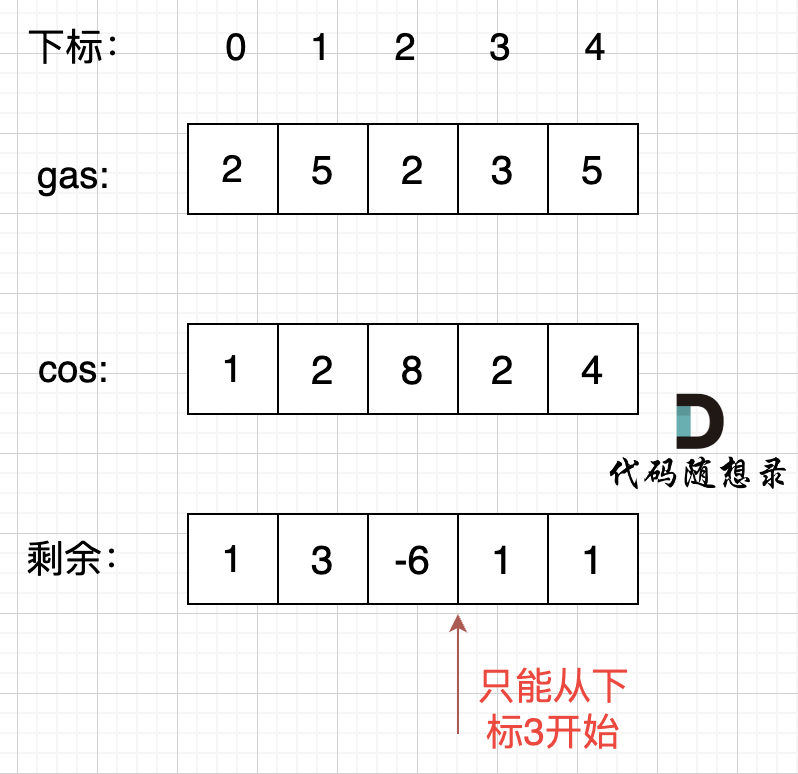
|
||||
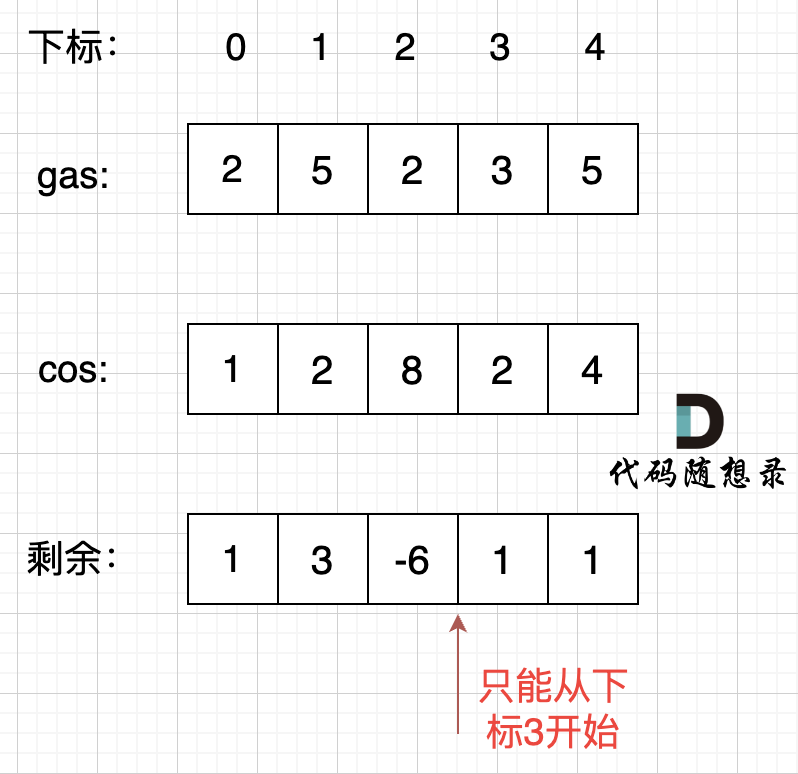
|
||||
|
||||
那么为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
|
||||
|
||||
|
|
@ -152,7 +152,7 @@ i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i
|
|||
|
||||
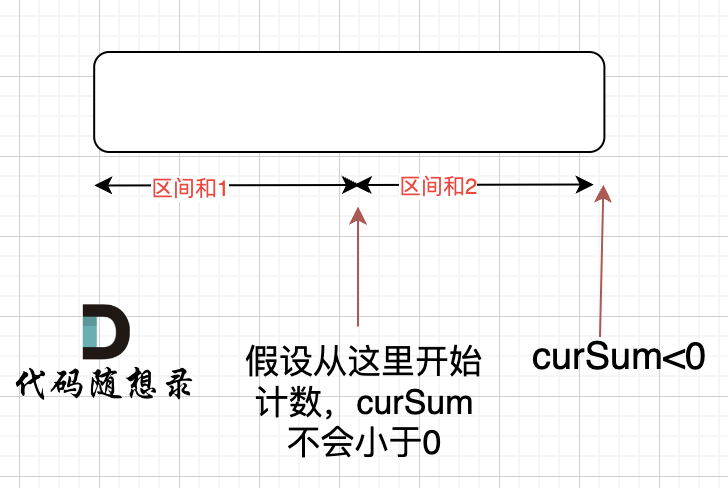
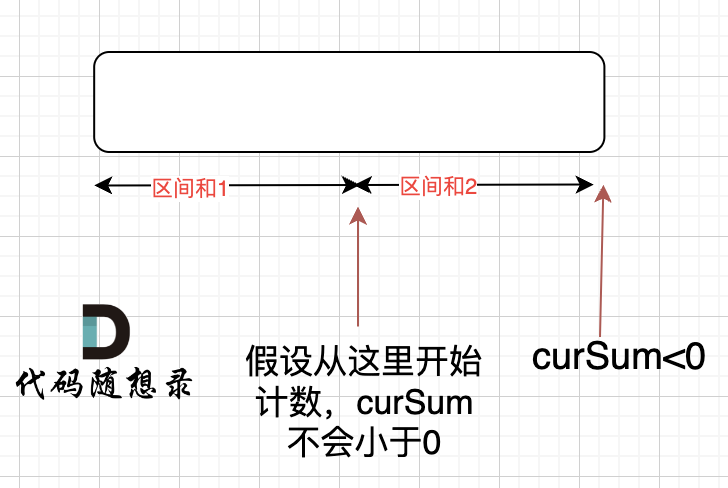
那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零呢? 如图:
|
||||
|
||||
|
||||
|
||||
|
||||
如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
|
||||
|
||||
|
|
|
|||
|
|
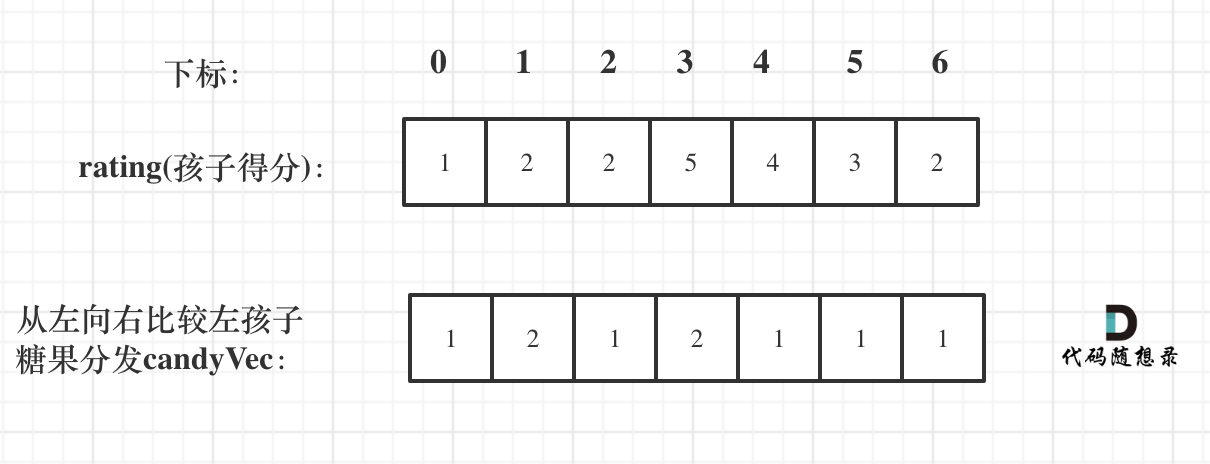
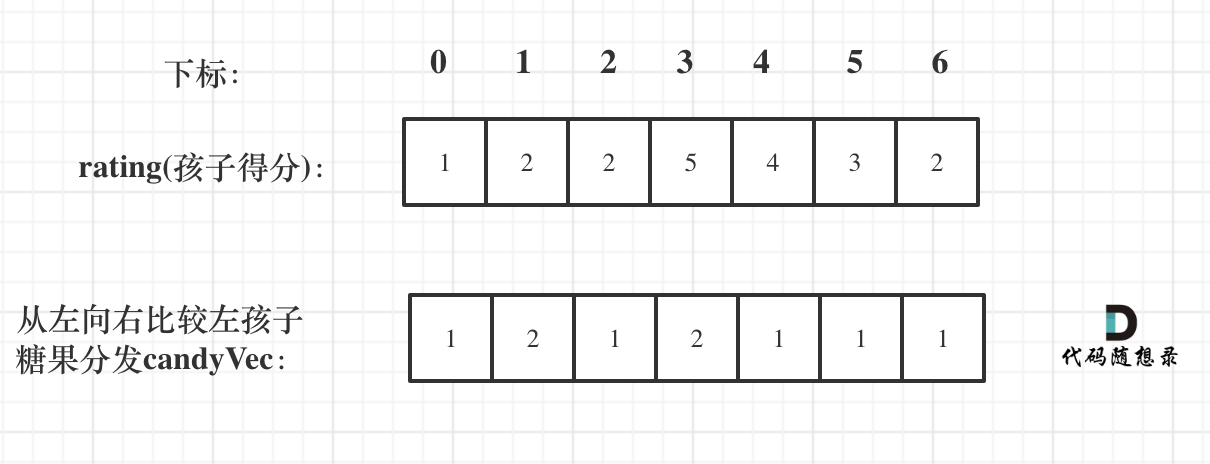
@ -56,7 +56,7 @@ for (int i = 1; i < ratings.size(); i++) {
|
|||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
再确定左孩子大于右孩子的情况(从后向前遍历)
|
||||
|
||||
|
|
@ -66,7 +66,7 @@ for (int i = 1; i < ratings.size(); i++) {
|
|||
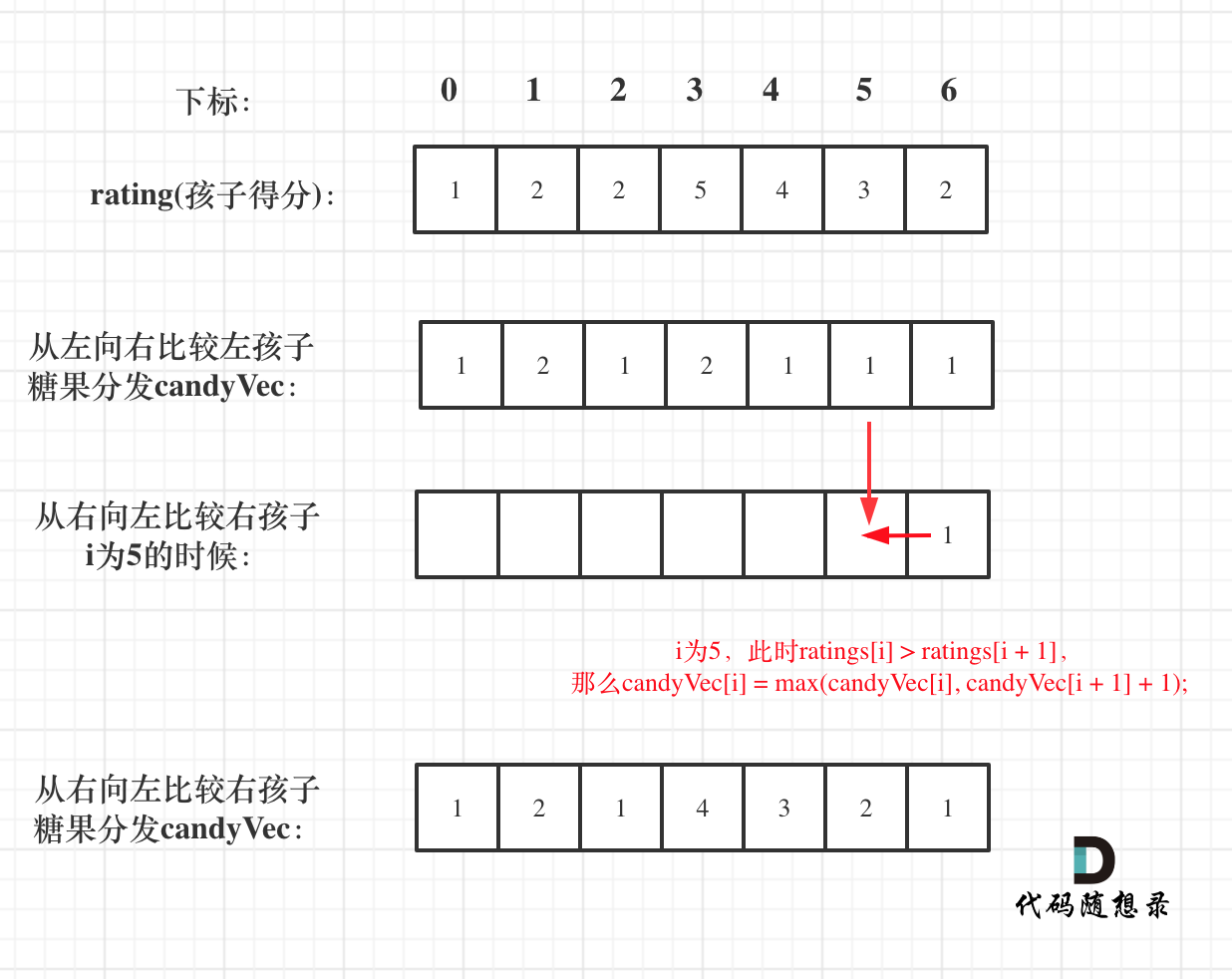
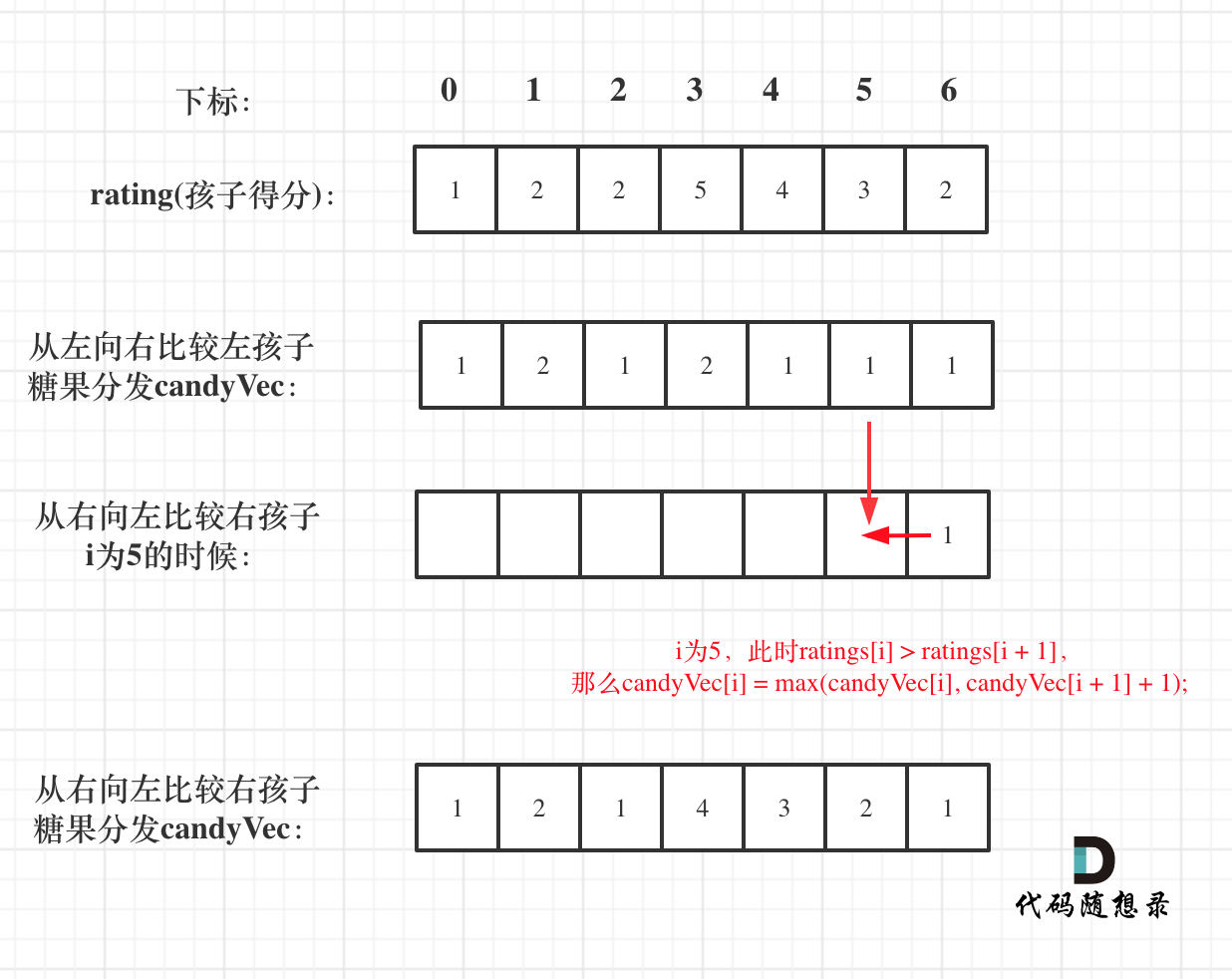
|
||||
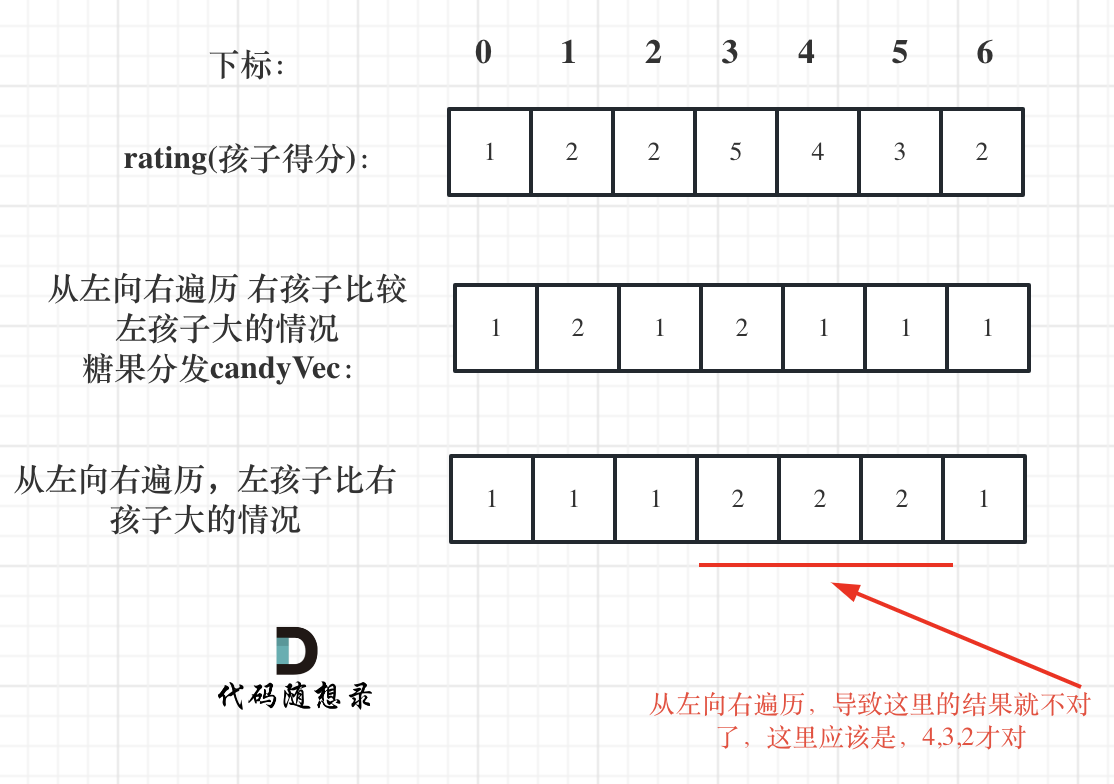
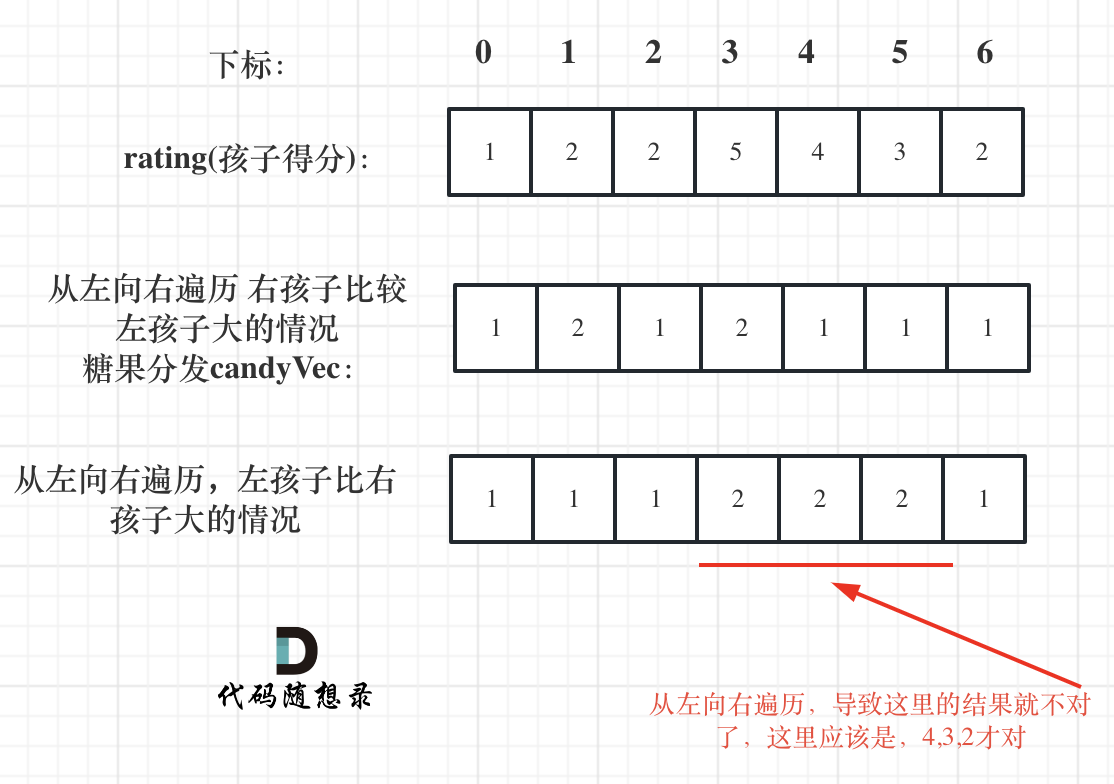
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图:
|
||||
|
||||
|
||||
|
||||
|
||||
**所以确定左孩子大于右孩子的情况一定要从后向前遍历!**
|
||||
|
||||
|
|
@ -82,7 +82,7 @@ for (int i = 1; i < ratings.size(); i++) {
|
|||
如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
所以该过程代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -180,7 +180,7 @@ dp[0]表示如果字符串为空的话,说明出现在字典里。
|
|||
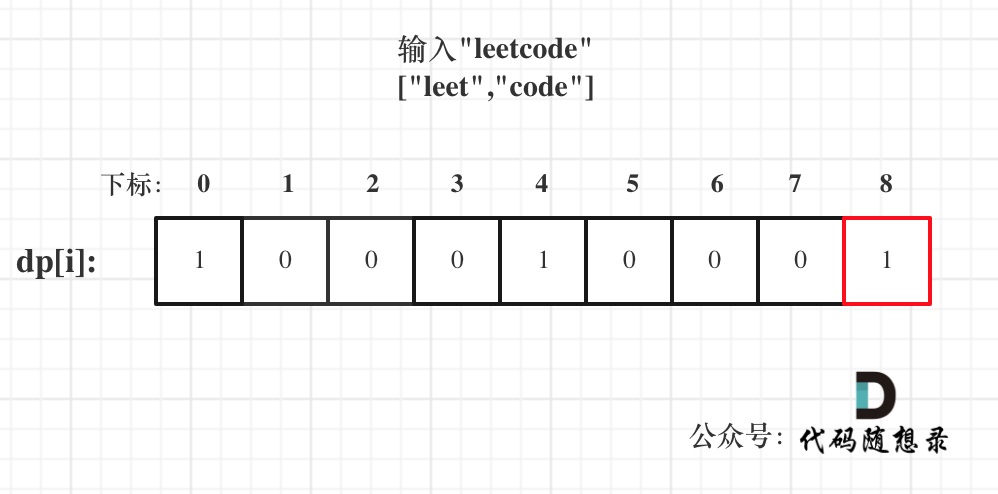
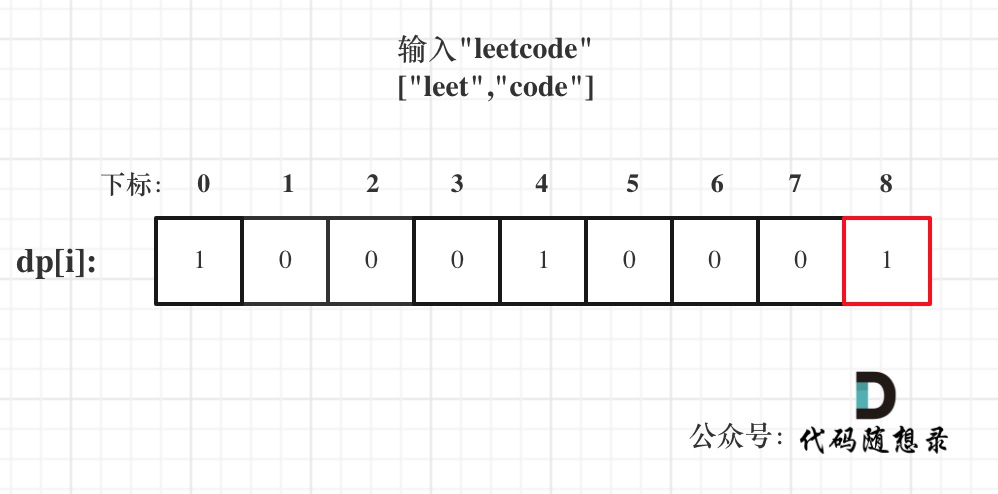
以输入: s = "leetcode", wordDict = ["leet", "code"]为例,dp状态如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
dp[s.size()]就是最终结果。
|
||||
|
||||
|
|
@ -241,7 +241,7 @@ public:
|
|||
|
||||
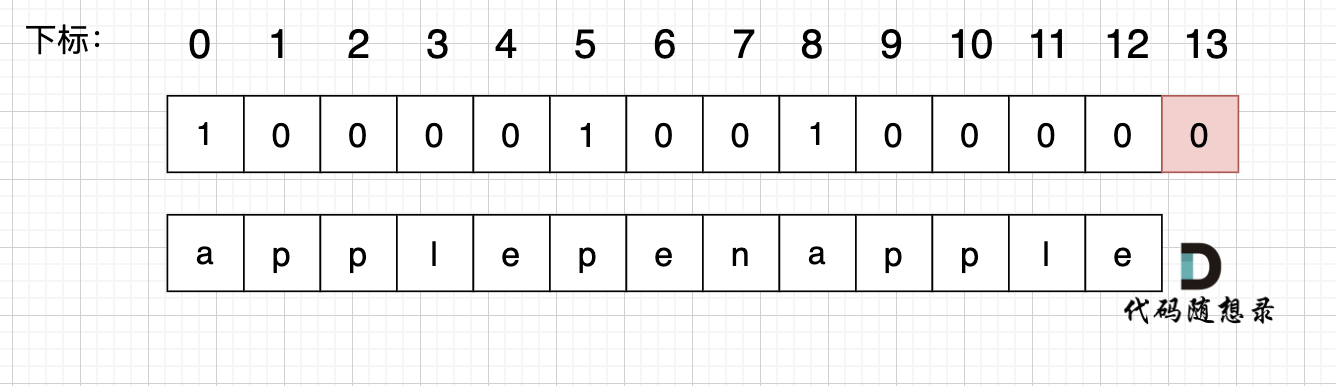
使用用例:s = "applepenapple", wordDict = ["apple", "pen"],对应的dp数组状态如下:
|
||||
|
||||

|
||||
|
||||
|
||||
最后dp[s.size()] = 0 即 dp[13] = 0 ,而不是1,因为先用 "apple" 去遍历的时候,dp[8]并没有被赋值为1 (还没用"pen"),所以 dp[13]也不能变成1。
|
||||
|
||||
|
|
|
|||
|
|
@ -13,7 +13,7 @@
|
|||
|
||||
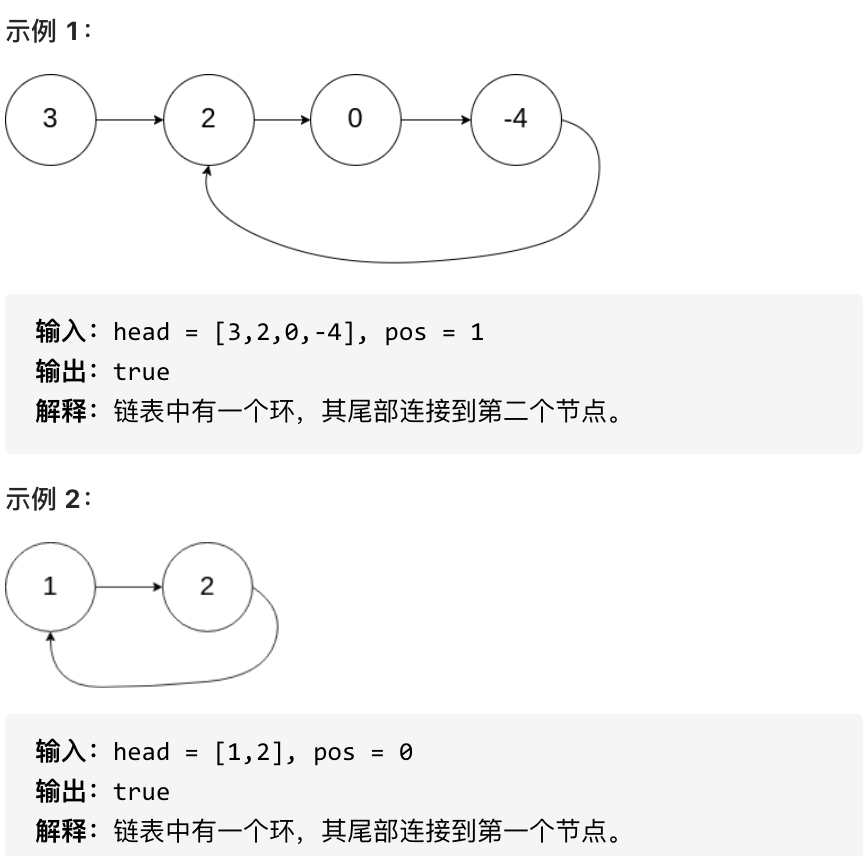
如果链表中存在环,则返回 true 。 否则,返回 false 。
|
||||
|
||||
|
||||
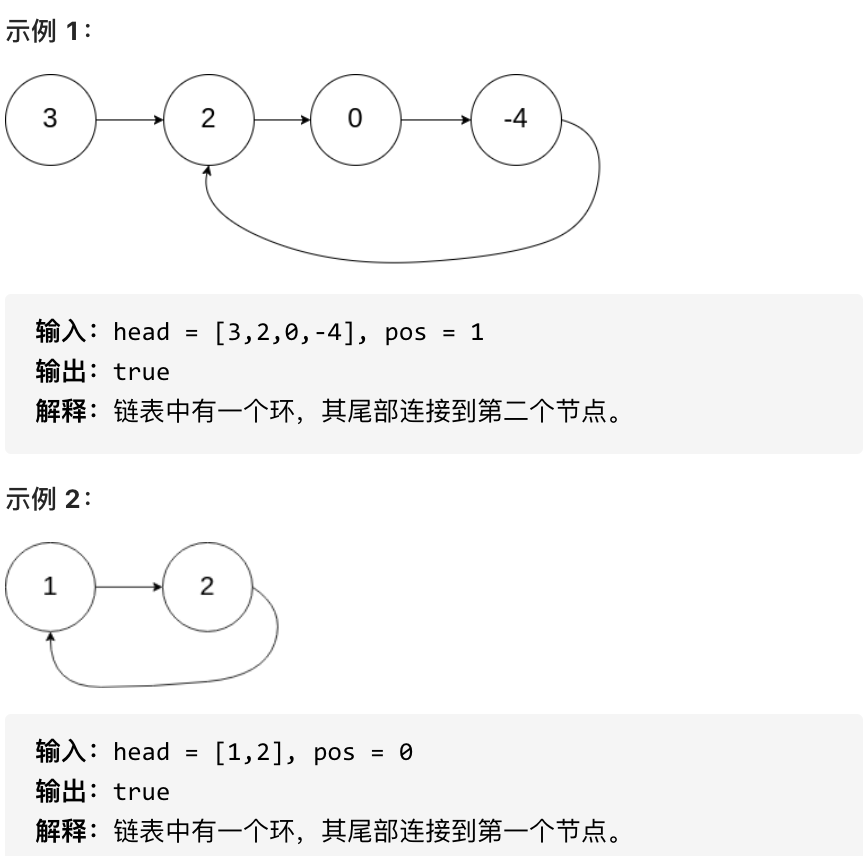
|
||||
|
||||
## 思路
|
||||
|
||||
|
|
@ -29,7 +29,7 @@
|
|||
|
||||
会发现最终都是这种情况, 如下图:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/142环形链表1.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/142环形链表1.png' width=600> </img></div>
|
||||
|
||||
fast和slow各自再走一步, fast和slow就相遇了
|
||||
|
||||
|
|
@ -38,7 +38,7 @@ fast和slow各自再走一步, fast和slow就相遇了
|
|||
动画如下:
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
C++代码如下
|
||||
|
|
|
|||
|
|
@ -20,7 +20,7 @@
|
|||
|
||||
**说明**:不允许修改给定的链表。
|
||||
|
||||
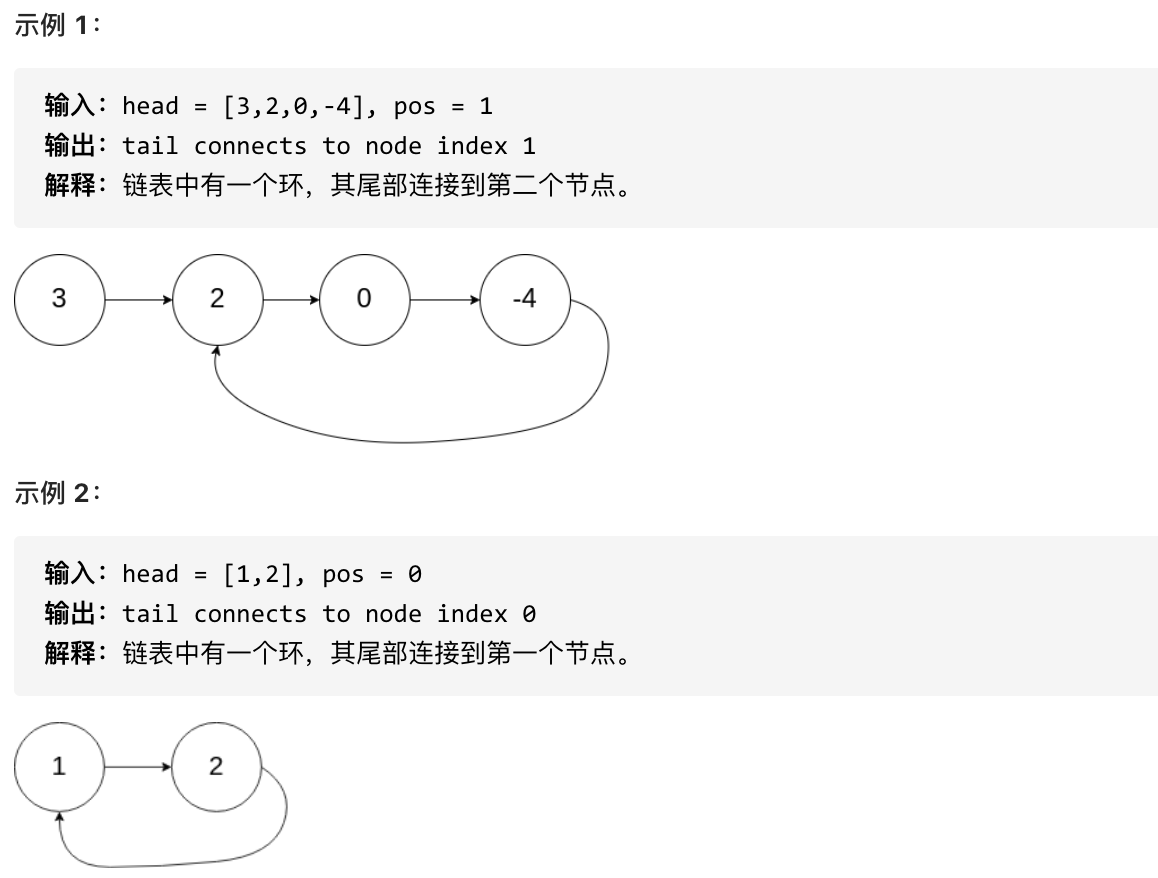
|
||||
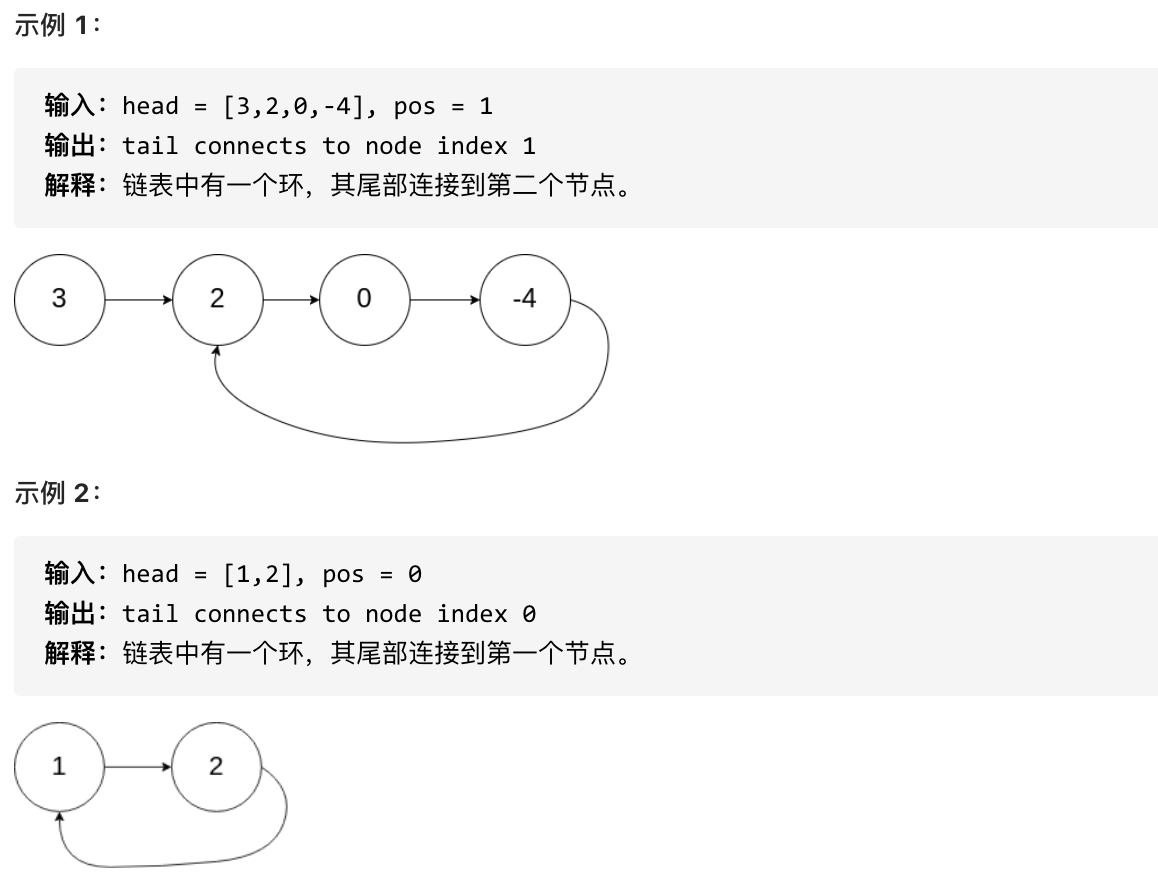
|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -50,7 +50,7 @@
|
|||
|
||||
会发现最终都是这种情况, 如下图:
|
||||
|
||||
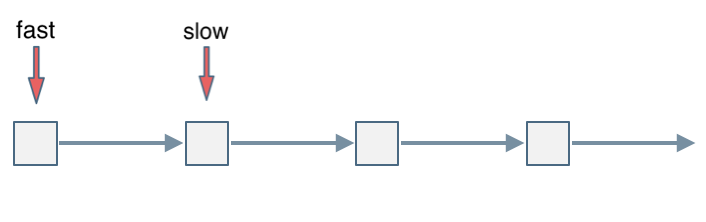
|
||||

|
||||
|
||||
|
||||
fast和slow各自再走一步, fast和slow就相遇了
|
||||
|
|
@ -59,7 +59,7 @@ fast和slow各自再走一步, fast和slow就相遇了
|
|||
|
||||
动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
### 如果有环,如何找到这个环的入口
|
||||
|
|
@ -70,7 +70,7 @@ fast和slow各自再走一步, fast和slow就相遇了
|
|||
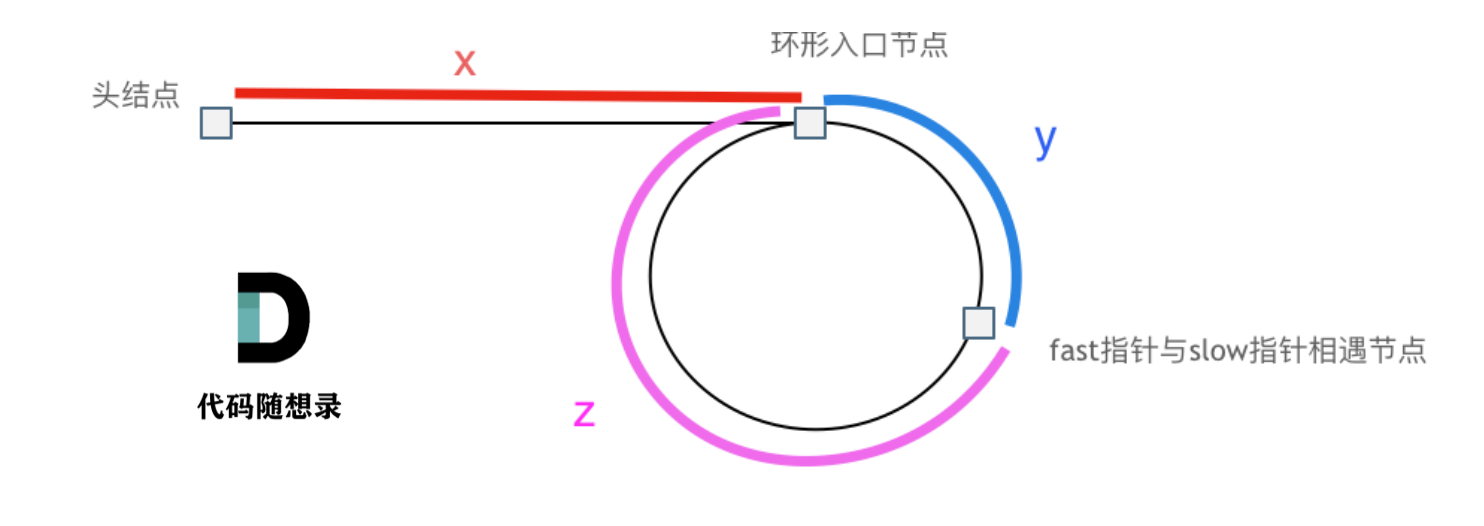
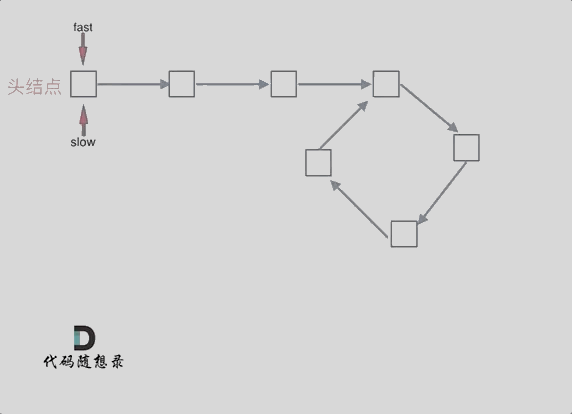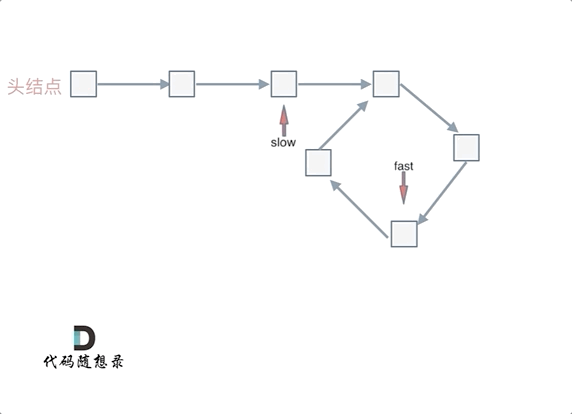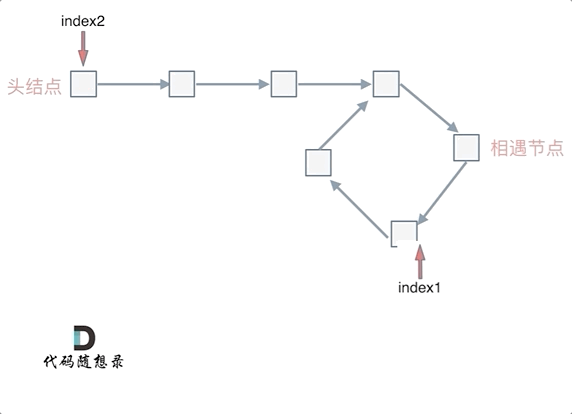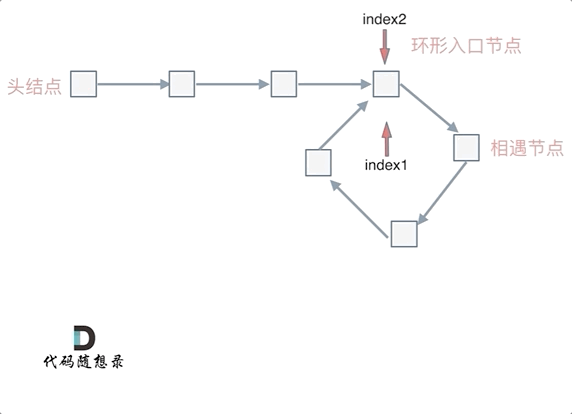
环形入口节点到 fast指针与slow指针相遇节点 节点数为y。
|
||||
从相遇节点 再到环形入口节点节点数为 z。 如图所示:
|
||||
|
||||
|
||||

|
||||
|
||||
那么相遇时:
|
||||
slow指针走过的节点数为: `x + y`,
|
||||
|
|
@ -103,7 +103,7 @@ fast指针走过的节点数:` x + y + n (y + z)`,n为fast指针在环内走
|
|||
|
||||
动画如下:
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
那么 n如果大于1是什么情况呢,就是fast指针在环形转n圈之后才遇到 slow指针。
|
||||
|
|
@ -154,20 +154,20 @@ public:
|
|||
|
||||
即文章[链表:环找到了,那入口呢?](https://programmercarl.com/0142.环形链表II.html)中如下的地方:
|
||||
|
||||
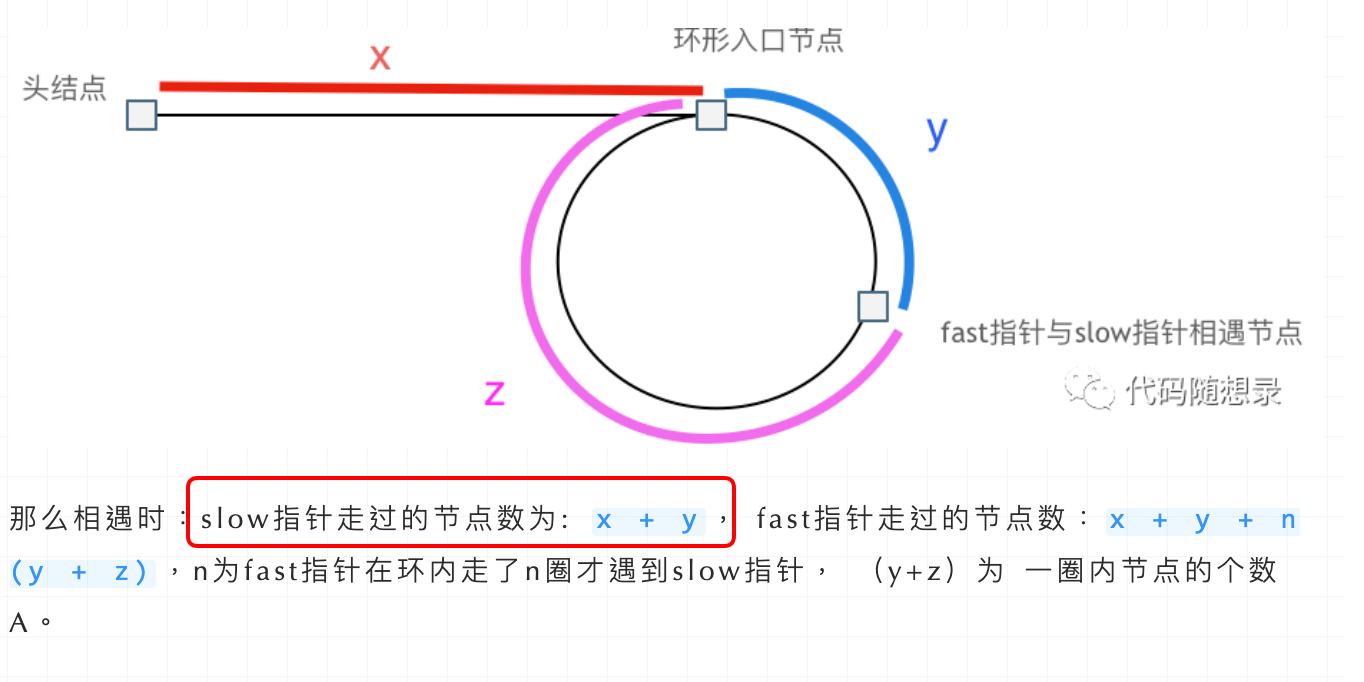
|
||||

|
||||
|
||||
|
||||
首先slow进环的时候,fast一定是先进环来了。
|
||||
|
||||
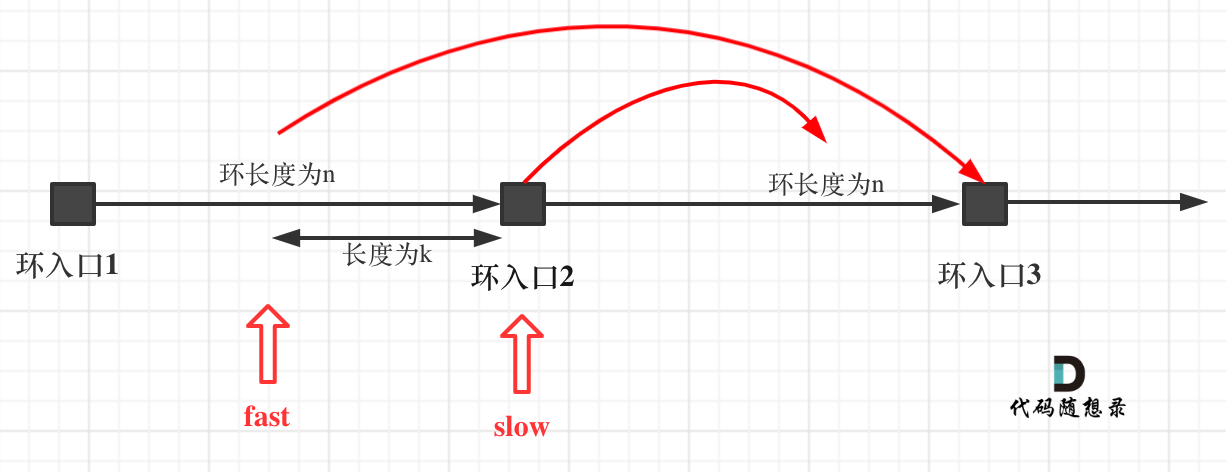
如果slow进环入口,fast也在环入口,那么把这个环展开成直线,就是如下图的样子:
|
||||
|
||||
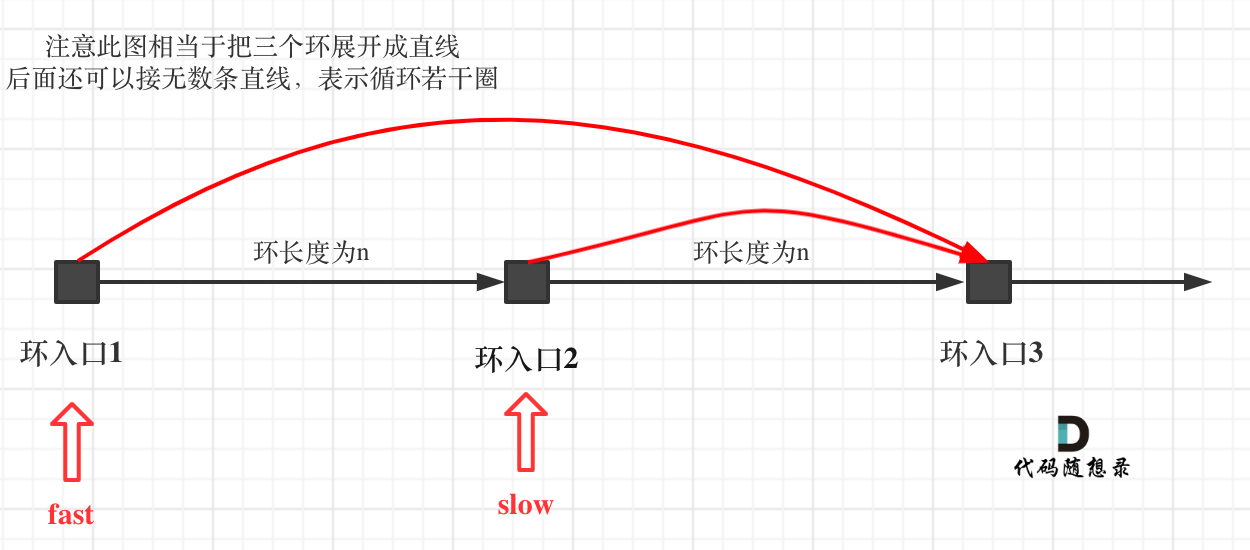
|
||||
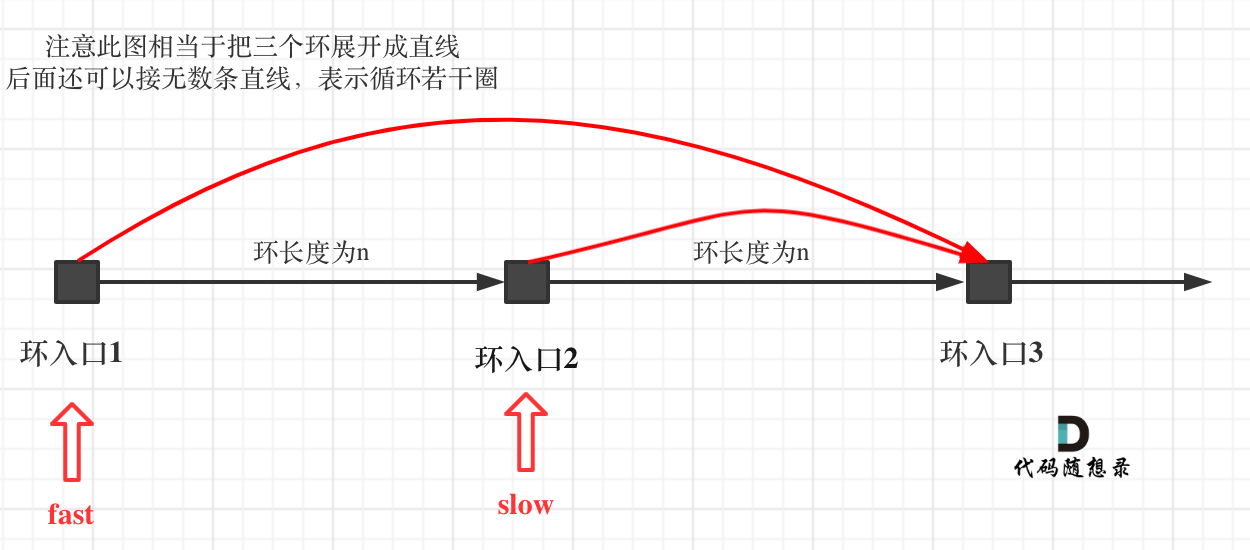
|
||||
|
||||
可以看出如果slow 和 fast同时在环入口开始走,一定会在环入口3相遇,slow走了一圈,fast走了两圈。
|
||||
|
||||
重点来了,slow进环的时候,fast一定是在环的任意一个位置,如图:
|
||||
|
||||
|
||||

|
||||
|
||||
那么fast指针走到环入口3的时候,已经走了k + n 个节点,slow相应的应该走了(k + n) / 2 个节点。
|
||||
|
||||
|
|
|
|||
|
|
@ -6,7 +6,7 @@
|
|||
|
||||
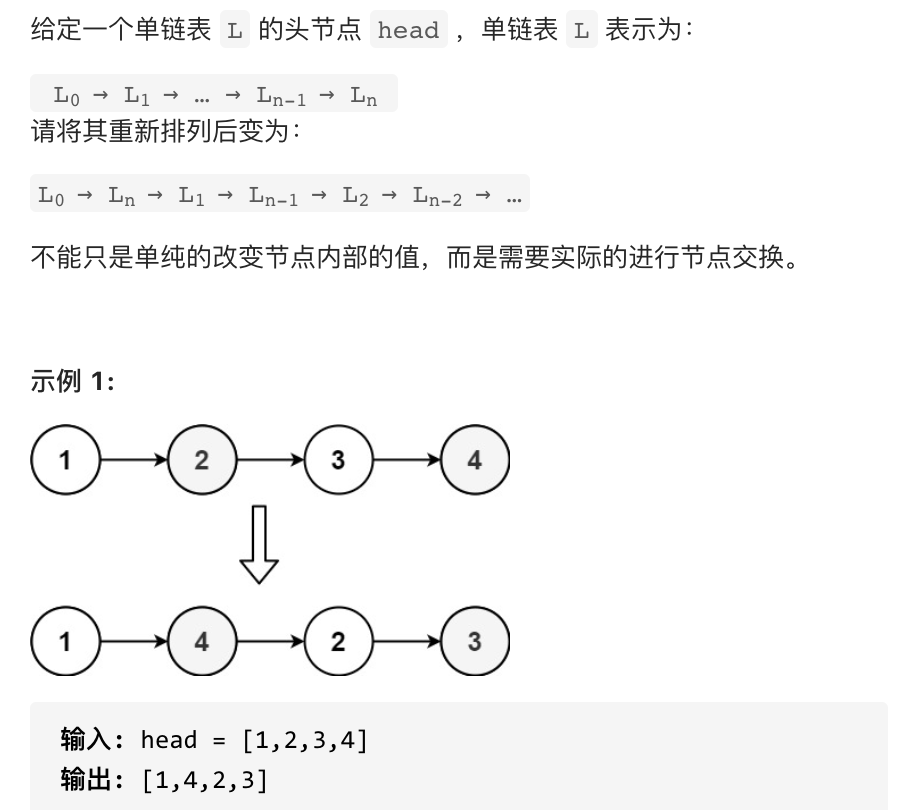
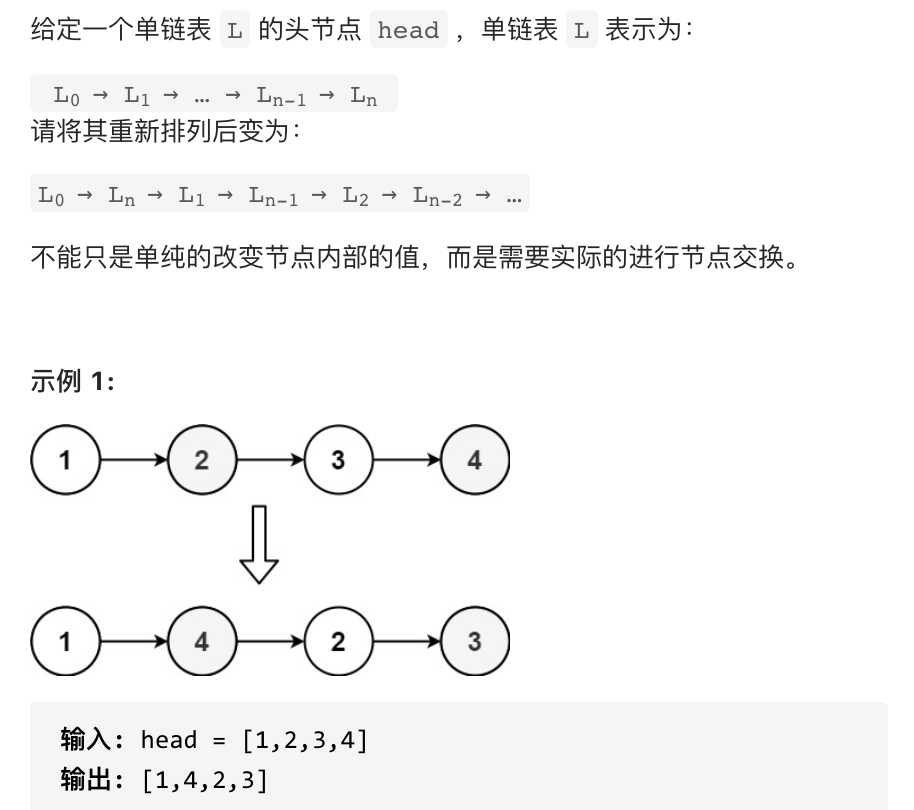
[力扣题目链接](https://leetcode.cn/problems/reorder-list/submissions/)
|
||||
|
||||
|
||||
|
||||
|
||||
## 思路
|
||||
|
||||
|
|
@ -96,7 +96,7 @@ public:
|
|||
|
||||
如图:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/143.重排链表.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/143.重排链表.png' width=600> </img></div>
|
||||
|
||||
这种方法,比较难,平均切割链表,看上去很简单,真正代码写的时候有很多细节,同时两个链表最后拼装整一个新的链表也有一些细节需要注意!
|
||||
|
||||
|
|
|
|||
|
|
@ -78,7 +78,7 @@
|
|||
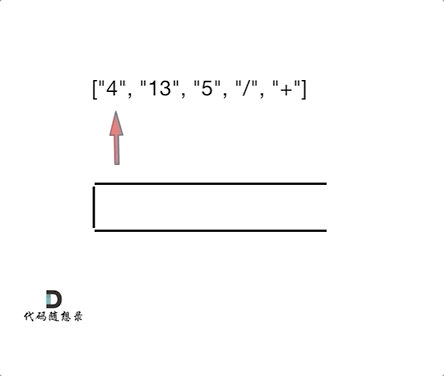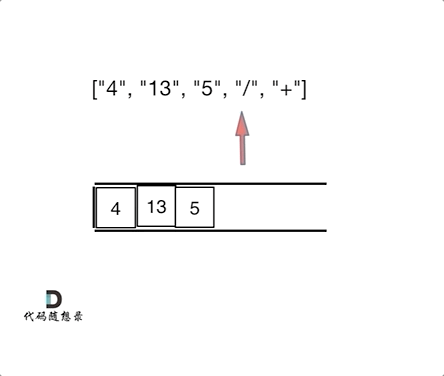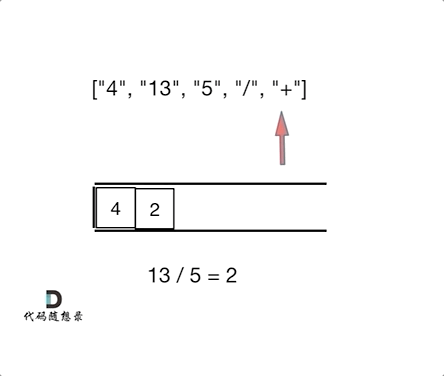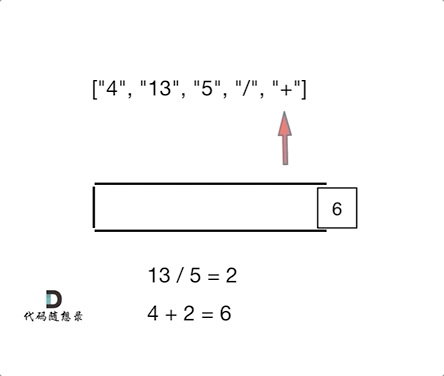
在进一步看,本题中每一个子表达式要得出一个结果,然后拿这个结果再进行运算,那么**这岂不就是一个相邻字符串消除的过程,和[1047.删除字符串中的所有相邻重复项](https://programmercarl.com/1047.删除字符串中的所有相邻重复项.html)中的对对碰游戏是不是就非常像了。**
|
||||
|
||||
如动画所示:
|
||||

|
||||
|
||||
|
||||
相信看完动画大家应该知道,这和[1047. 删除字符串中的所有相邻重复项](https://programmercarl.com/1047.删除字符串中的所有相邻重复项.html)是差不多的,只不过本题不要相邻元素做消除了,而是做运算!
|
||||
|
||||
|
|
|
|||
|
|
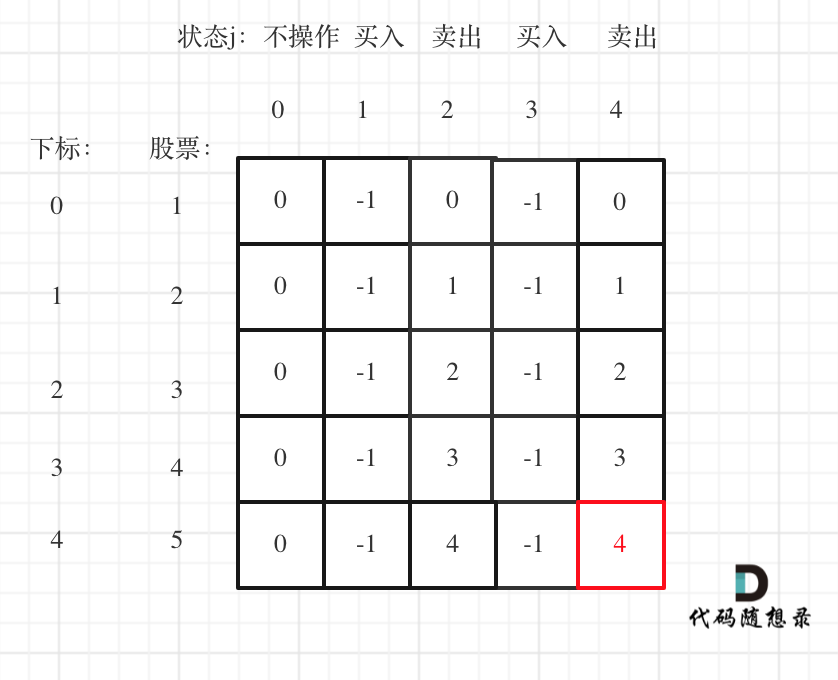
@ -132,7 +132,7 @@ for (int j = 1; j < 2 * k; j += 2) {
|
|||
|
||||
以输入[1,2,3,4,5],k=2为例。
|
||||
|
||||
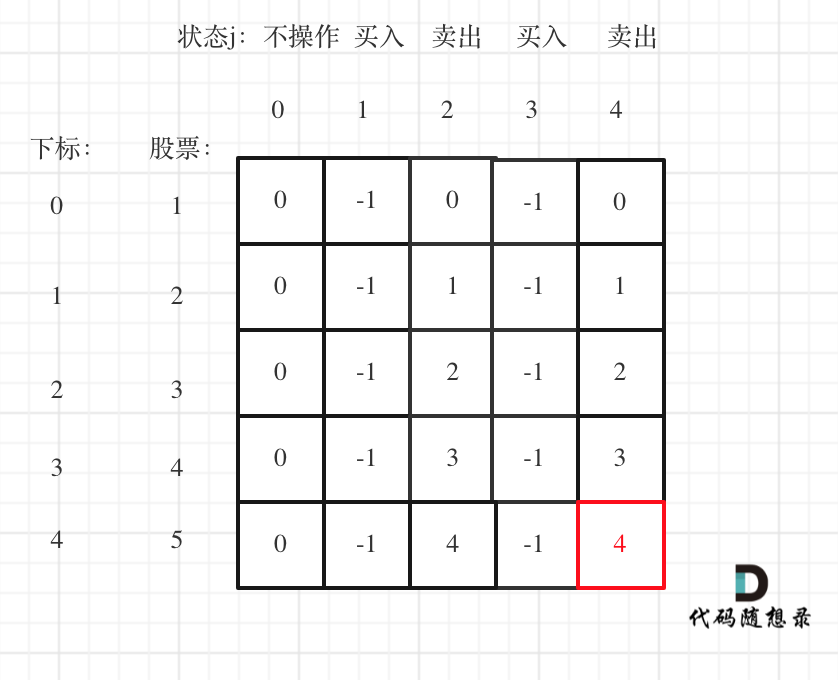
|
||||
|
||||
|
||||
最后一次卖出,一定是利润最大的,dp[prices.size() - 1][2 * k]即红色部分就是最后求解。
|
||||
|
||||
|
|
|
|||
|
|
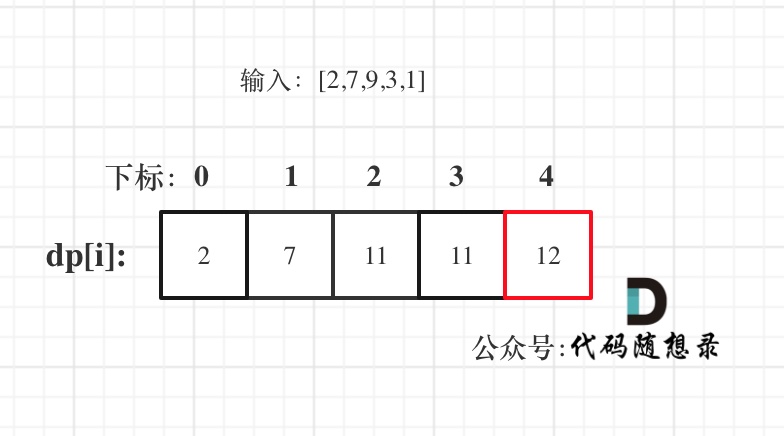
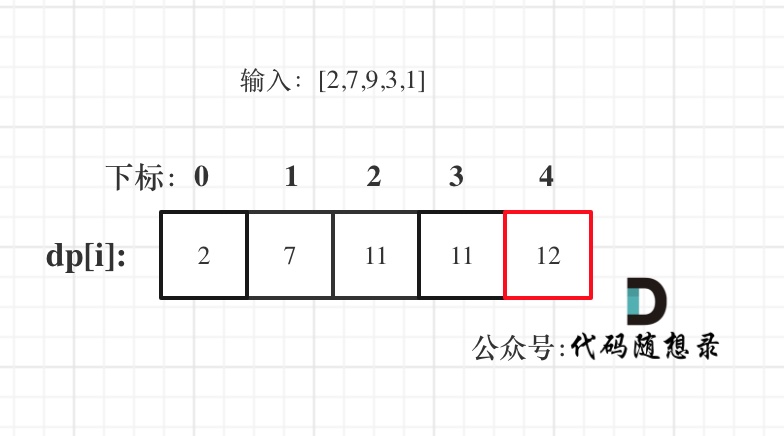
@ -87,7 +87,7 @@ for (int i = 2; i < nums.size(); i++) {
|
|||
|
||||
以示例二,输入[2,7,9,3,1]为例。
|
||||
|
||||
|
||||
|
||||
|
||||
红框dp[nums.size() - 1]为结果。
|
||||
|
||||
|
|
|
|||
|
|
@ -13,7 +13,7 @@
|
|||
|
||||
此外,你可以假设该网格的四条边均被水包围。
|
||||
|
||||

|
||||

|
||||
|
||||
提示:
|
||||
|
||||
|
|
@ -28,7 +28,7 @@
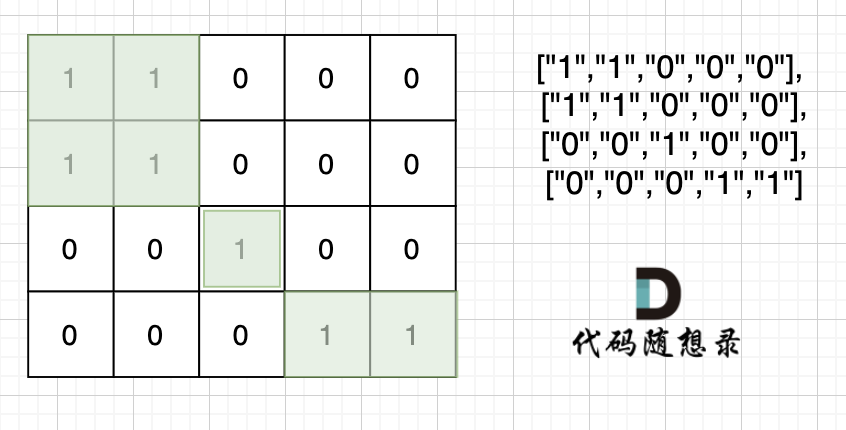
|
|||
|
||||
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
||||
|
||||
|
||||
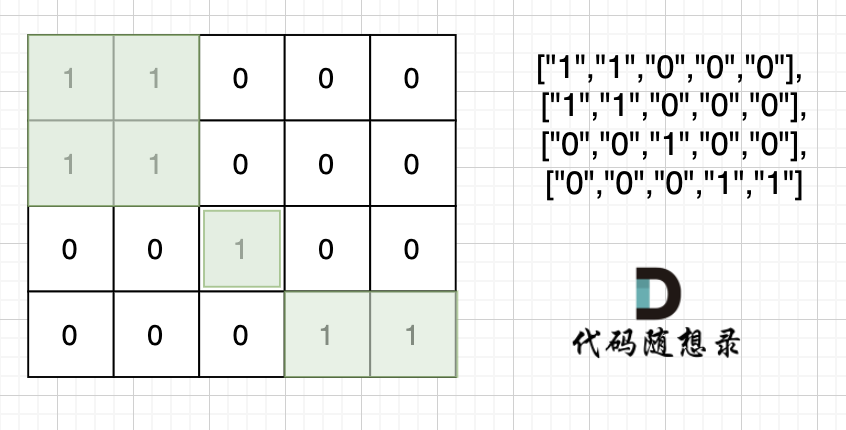
|
||||
|
||||
这道题题目是 DFS,BFS,并查集,基础题目。
|
||||
|
||||
|
|
@ -48,7 +48,7 @@
|
|||
|
||||
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。
|
||||
|
||||
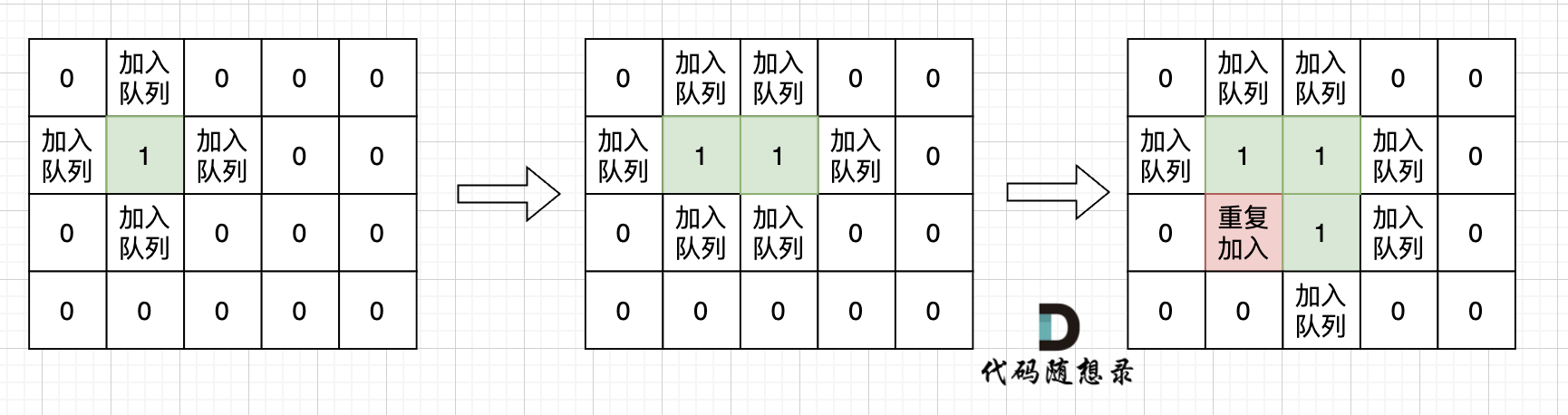
|
||||
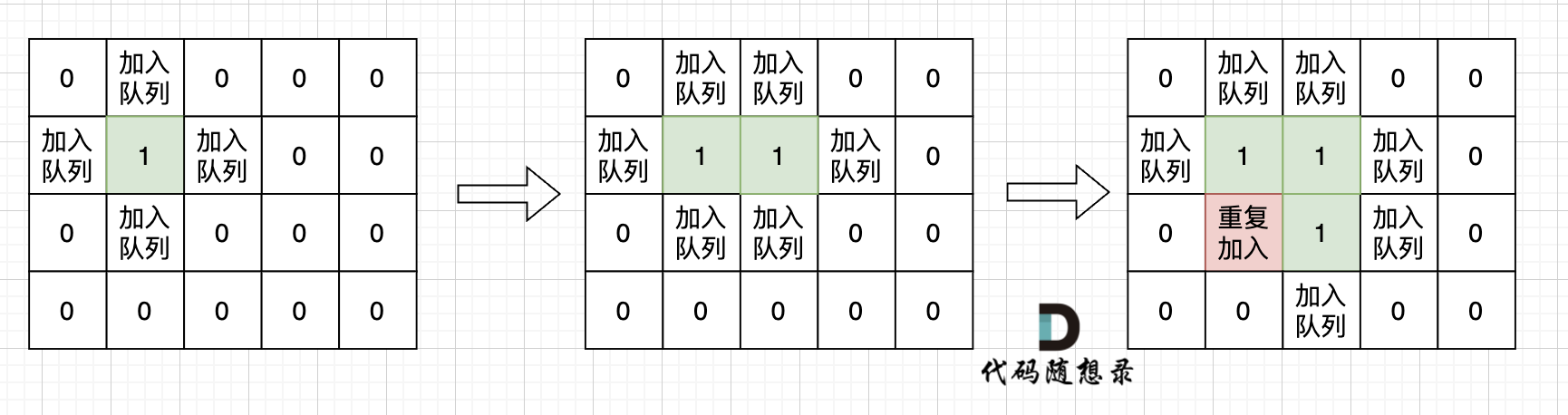
|
||||
|
||||
超时写法 (从队列中取出节点再标记)
|
||||
|
||||
|
|
|
|||
|
|
@ -12,7 +12,7 @@
|
|||
|
||||
此外,你可以假设该网格的四条边均被水包围。
|
||||
|
||||

|
||||

|
||||
|
||||
提示:
|
||||
|
||||
|
|
@ -27,7 +27,7 @@
|
|||
|
||||
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
||||
|
||||

|
||||

|
||||
|
||||
这道题题目是 DFS,BFS,并查集,基础题目。
|
||||
|
||||
|
|
|
|||
|
|
@ -34,11 +34,11 @@
|
|||
|
||||
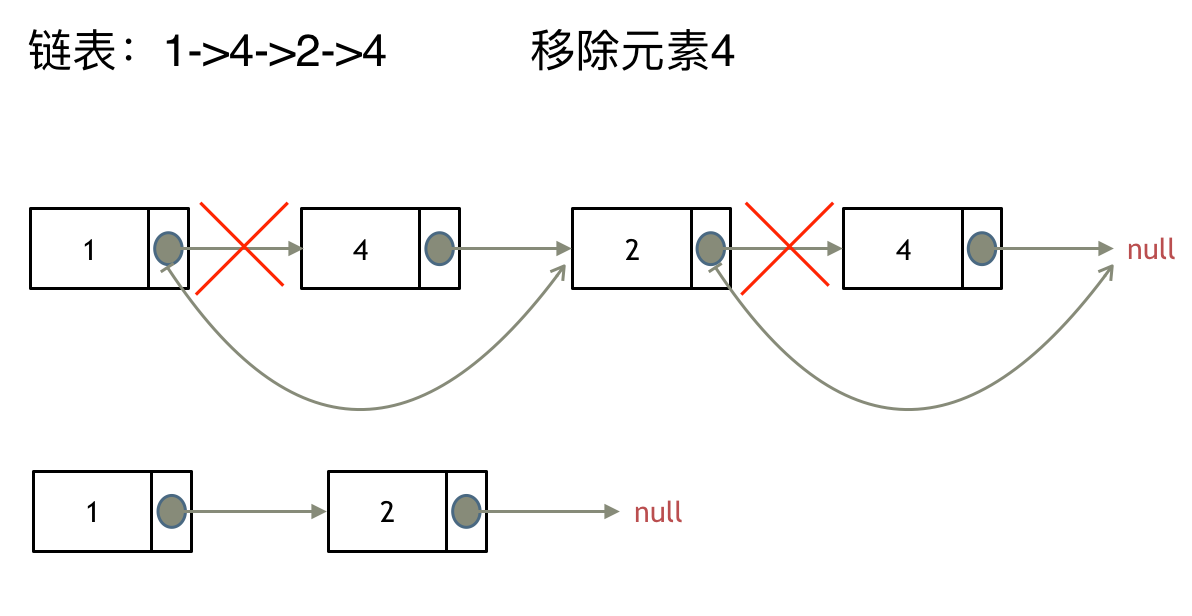
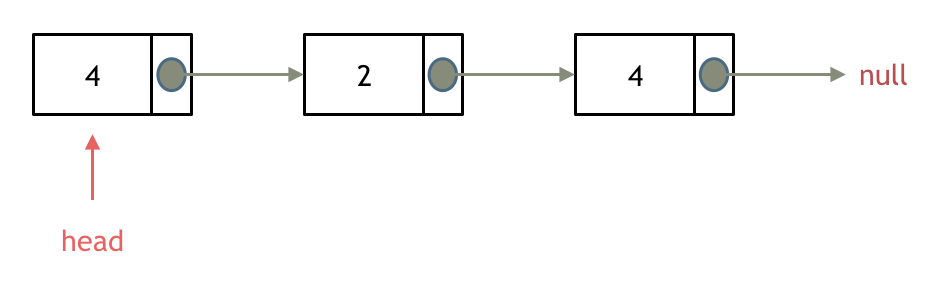
这里以链表 1 4 2 4 来举例,移除元素4。
|
||||
|
||||
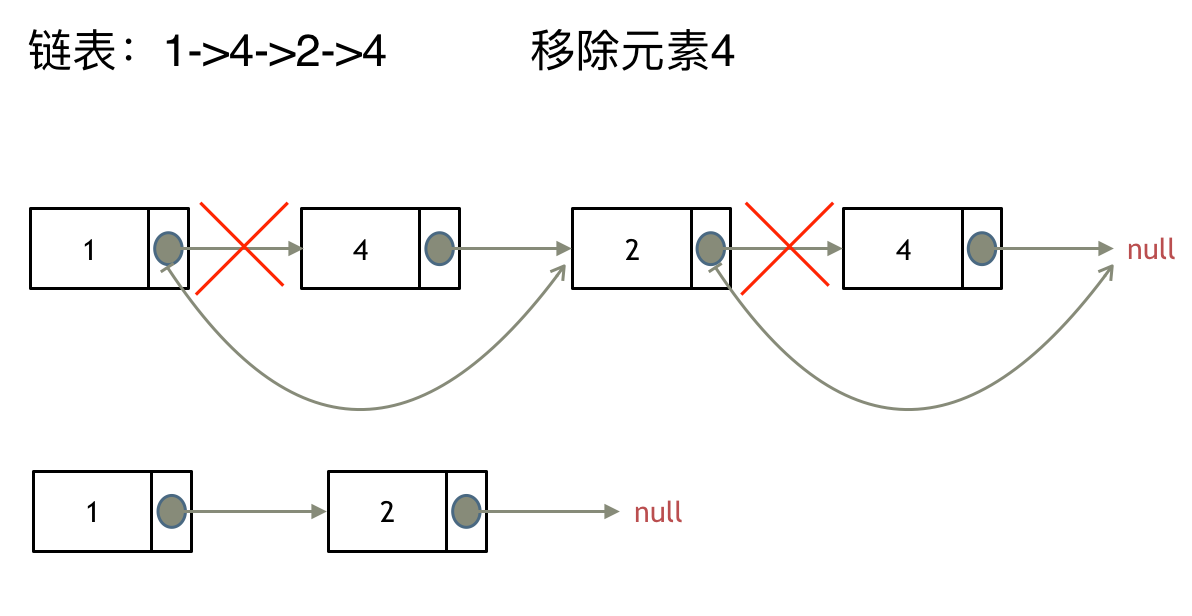
|
||||
|
||||
|
||||
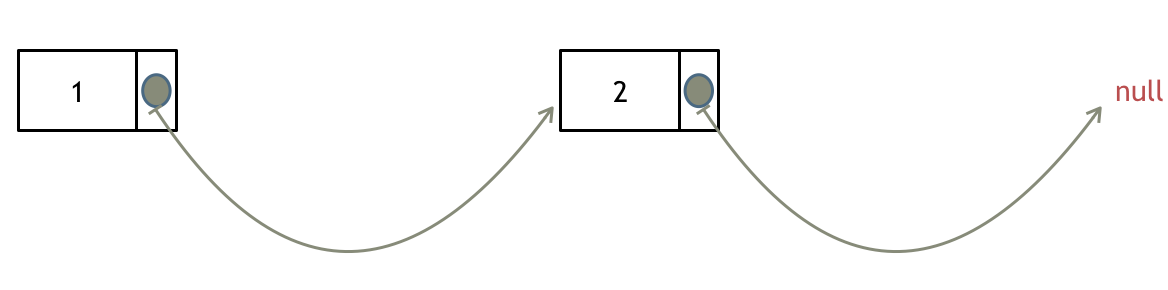
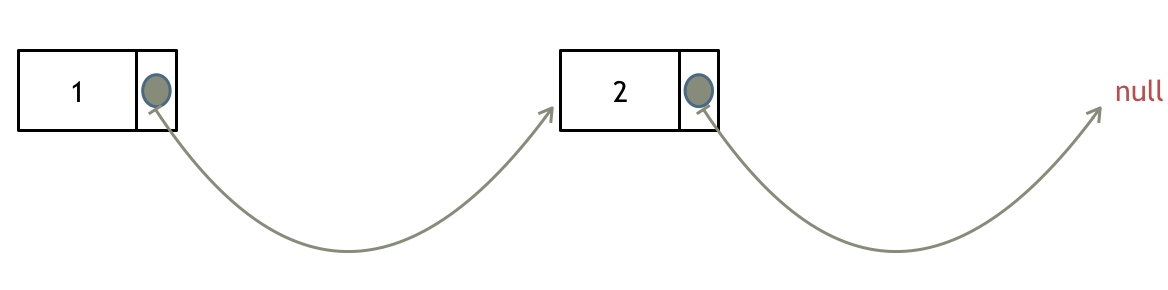
如果使用C,C++编程语言的话,不要忘了还要从内存中删除这两个移除的节点, 清理节点内存之后如图:
|
||||
|
||||
|
||||
|
||||
|
||||
**当然如果使用java ,python的话就不用手动管理内存了。**
|
||||
|
||||
|
|
@ -56,16 +56,16 @@
|
|||
|
||||
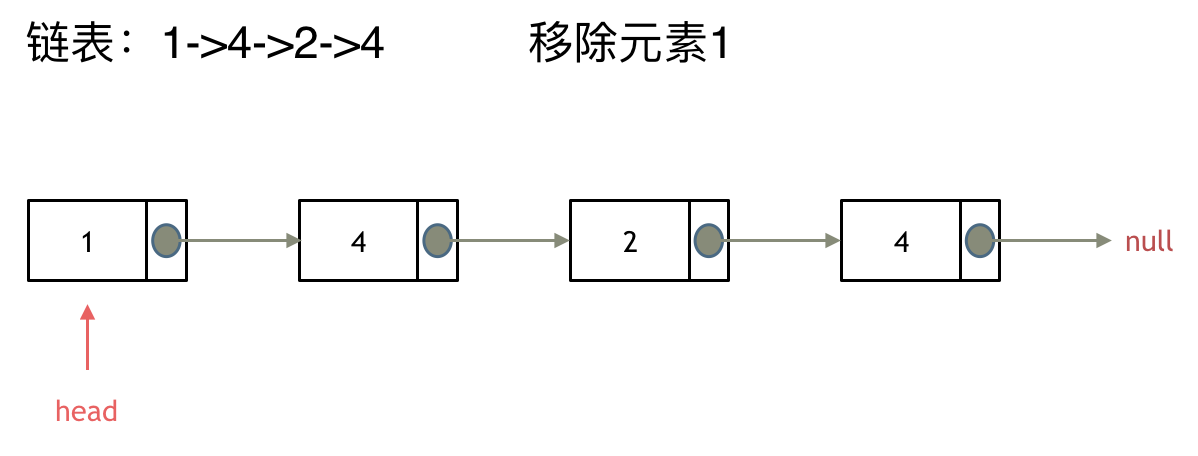
来看第一种操作:直接使用原来的链表来进行移除。
|
||||
|
||||
|
||||
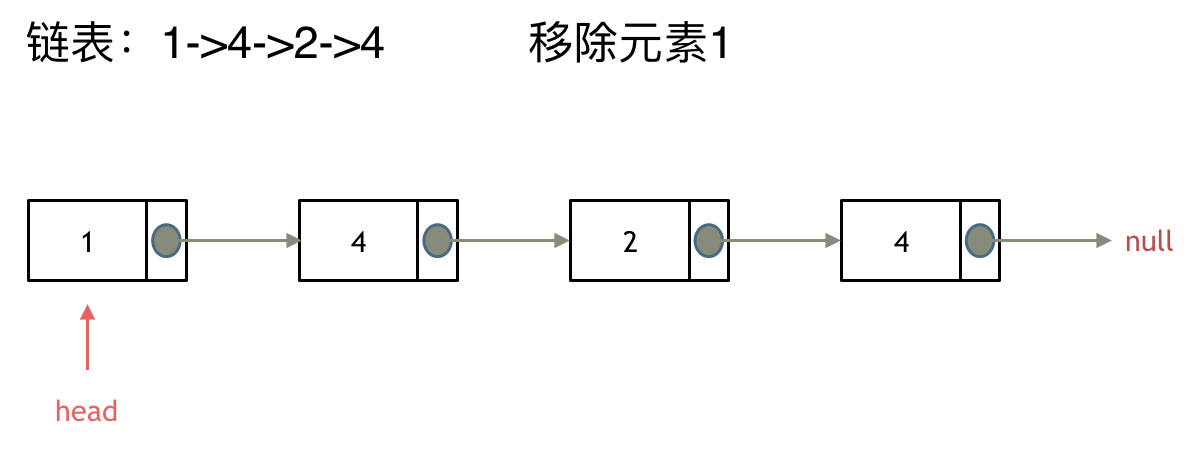
|
||||
|
||||
移除头结点和移除其他节点的操作是不一样的,因为链表的其他节点都是通过前一个节点来移除当前节点,而头结点没有前一个节点。
|
||||
|
||||
所以头结点如何移除呢,其实只要将头结点向后移动一位就可以,这样就从链表中移除了一个头结点。
|
||||
|
||||
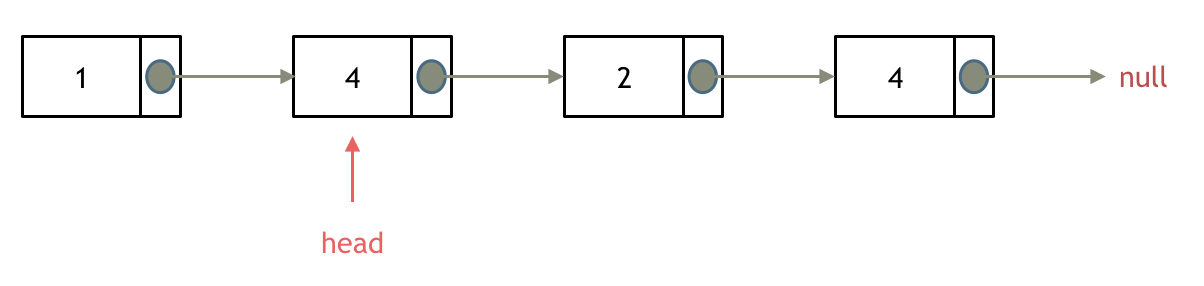
|
||||
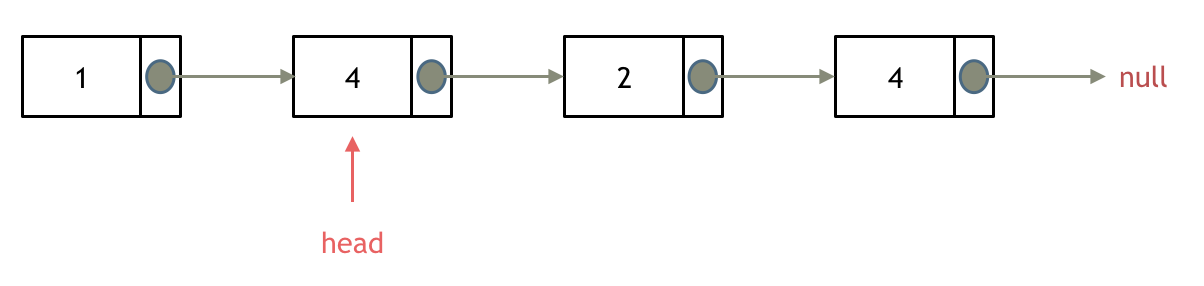
|
||||
|
||||
依然别忘将原头结点从内存中删掉。
|
||||
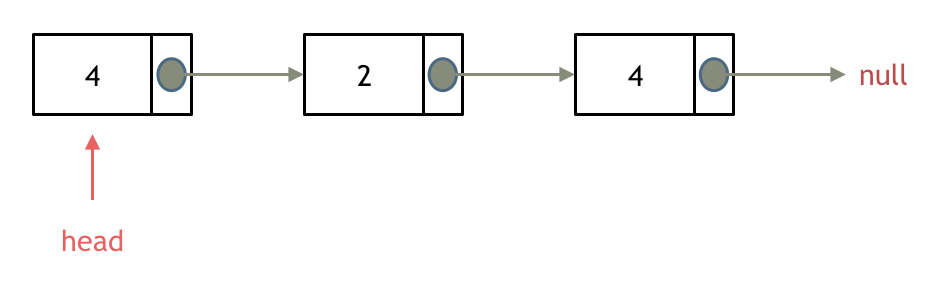
|
||||
|
||||
|
||||
|
||||
这样移除了一个头结点,是不是发现,在单链表中移除头结点 和 移除其他节点的操作方式是不一样,其实在写代码的时候也会发现,需要单独写一段逻辑来处理移除头结点的情况。
|
||||
|
|
@ -76,7 +76,7 @@
|
|||
|
||||
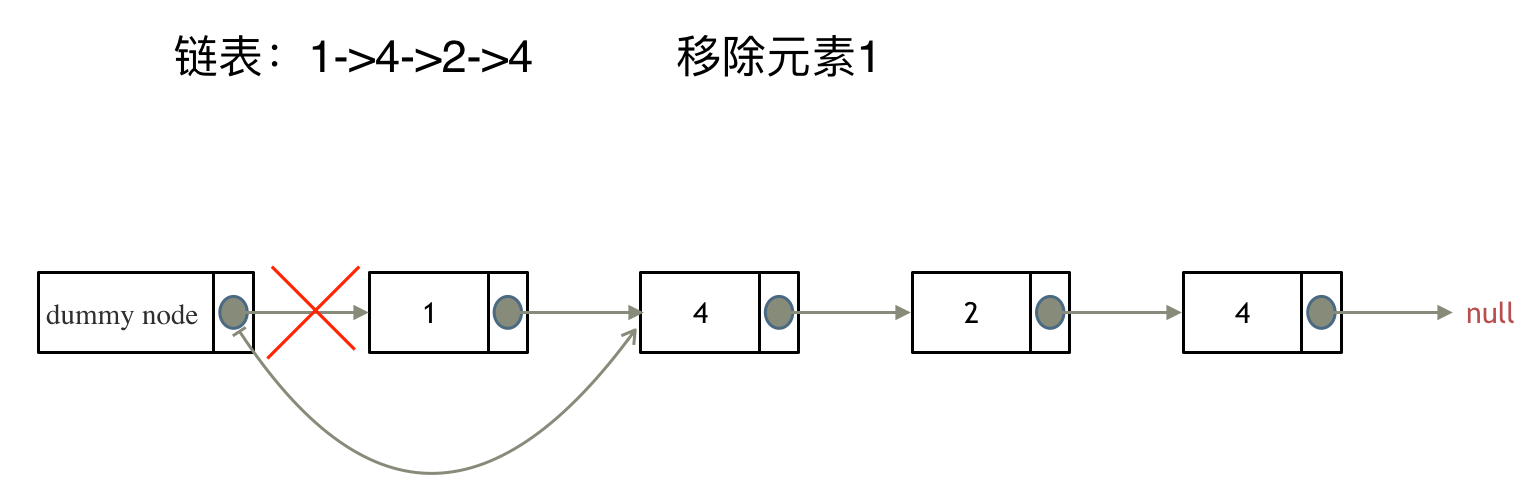
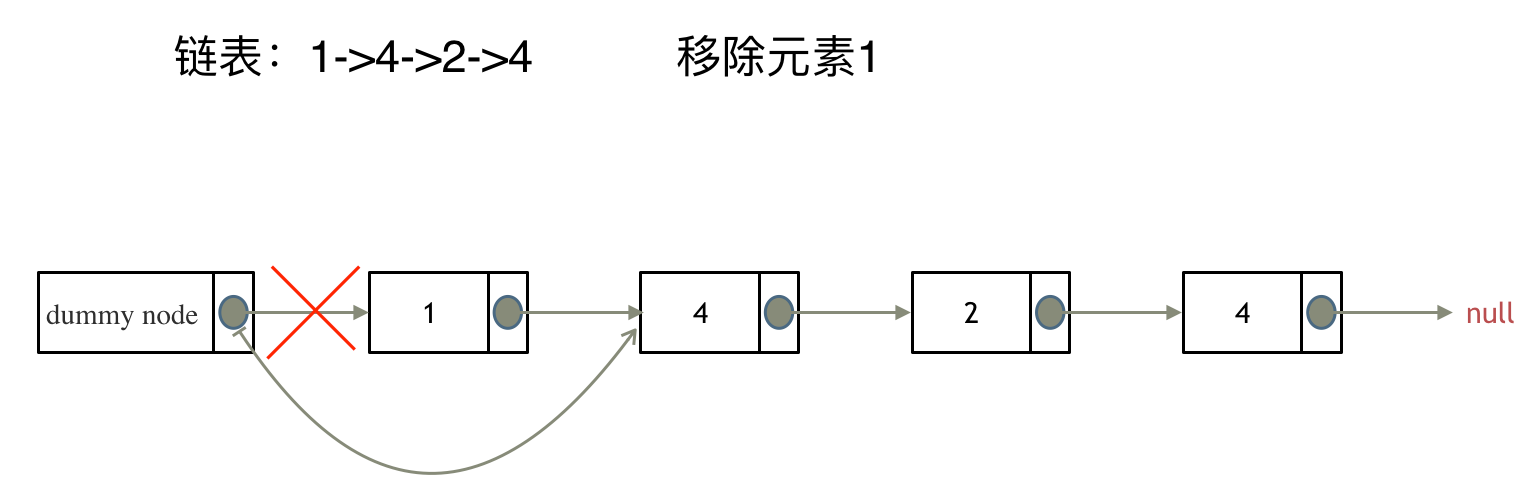
来看看如何设置一个虚拟头。依然还是在这个链表中,移除元素1。
|
||||
|
||||
|
||||
|
||||
|
||||
这里来给链表添加一个虚拟头结点为新的头结点,此时要移除这个旧头结点元素1。
|
||||
|
||||
|
|
|
|||
|
|
@ -27,7 +27,7 @@
|
|||
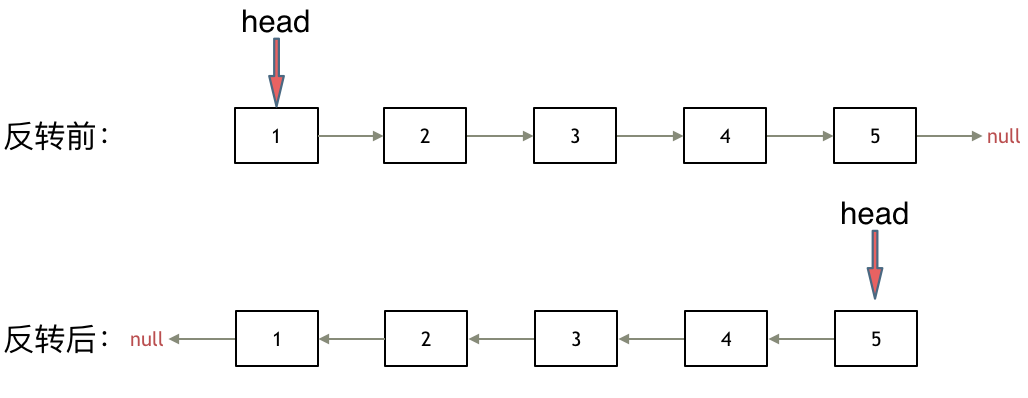
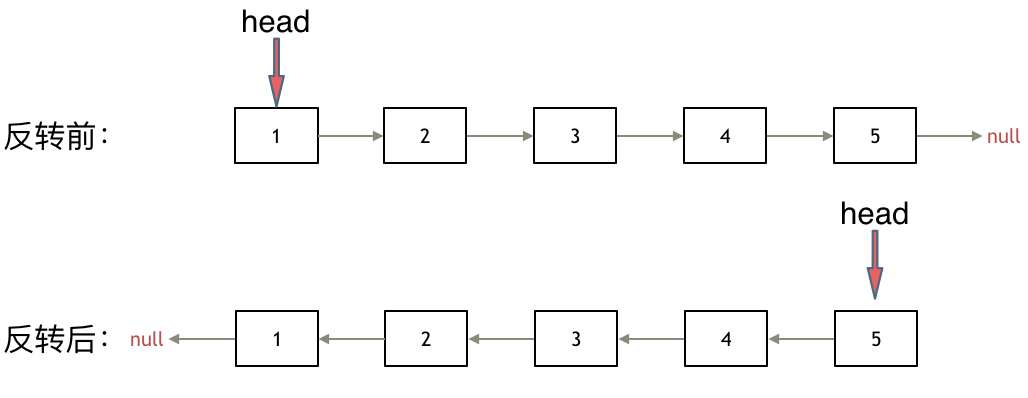
其实只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表,如图所示:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改变next指针的方向。
|
||||
|
||||
|
|
@ -35,7 +35,7 @@
|
|||
|
||||
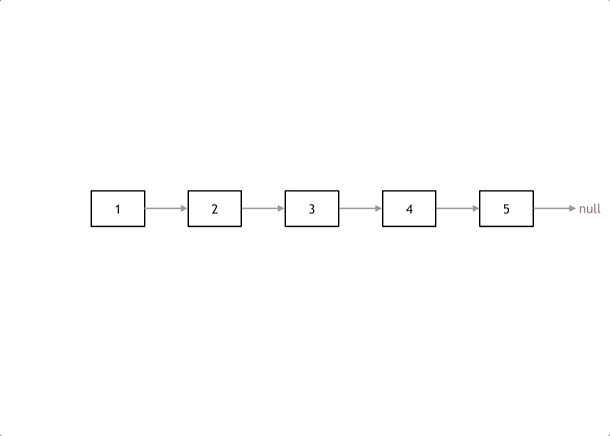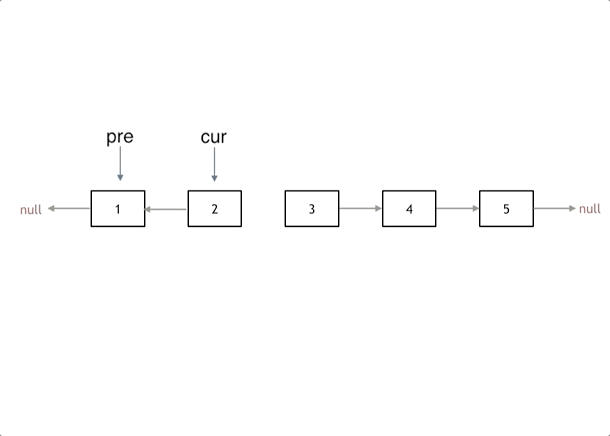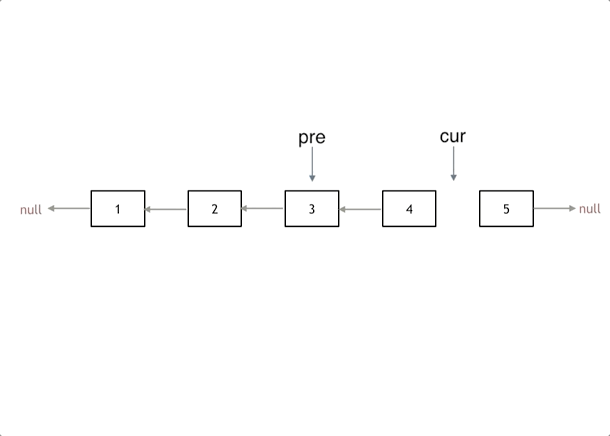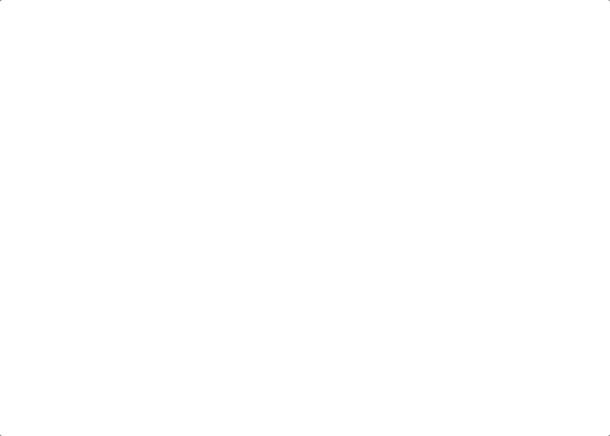
我们拿有示例中的链表来举例,如动画所示:(纠正:动画应该是先移动pre,在移动cur)
|
||||
|
||||

|
||||
|
||||
|
||||
首先定义一个cur指针,指向头结点,再定义一个pre指针,初始化为null。
|
||||
|
||||
|
|
|
|||
|
|
@ -84,7 +84,7 @@ public:
|
|||
|
||||
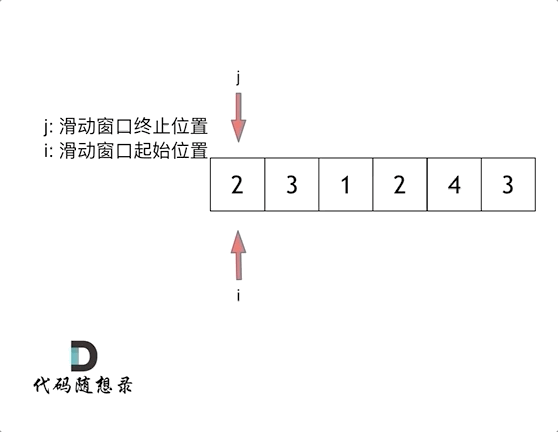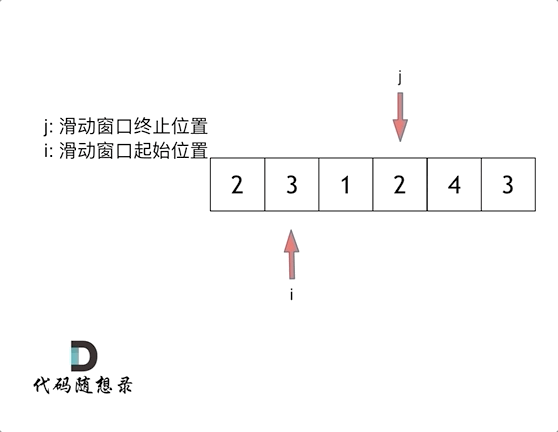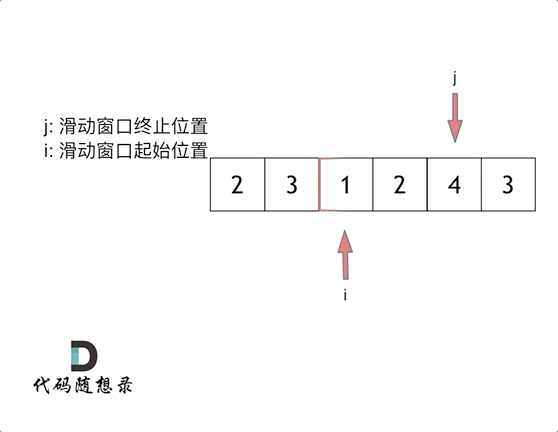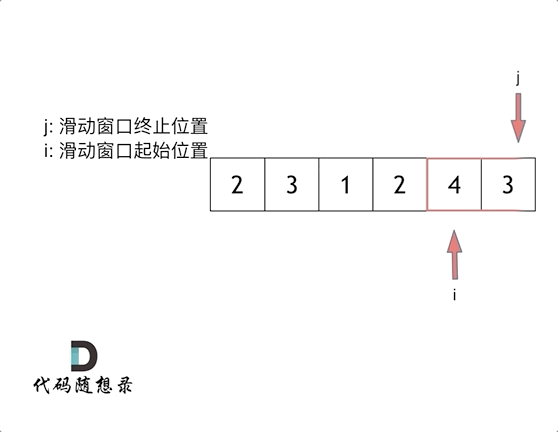
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
|
||||
|
||||

|
||||
|
||||
|
||||
最后找到 4,3 是最短距离。
|
||||
|
||||
|
|
@ -104,7 +104,7 @@ public:
|
|||
|
||||
解题的关键在于 窗口的起始位置如何移动,如图所示:
|
||||
|
||||
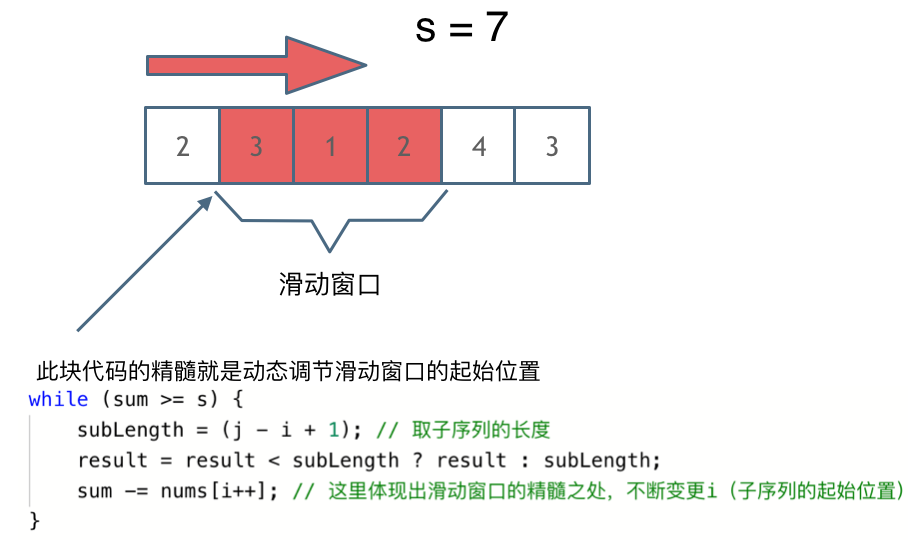
|
||||
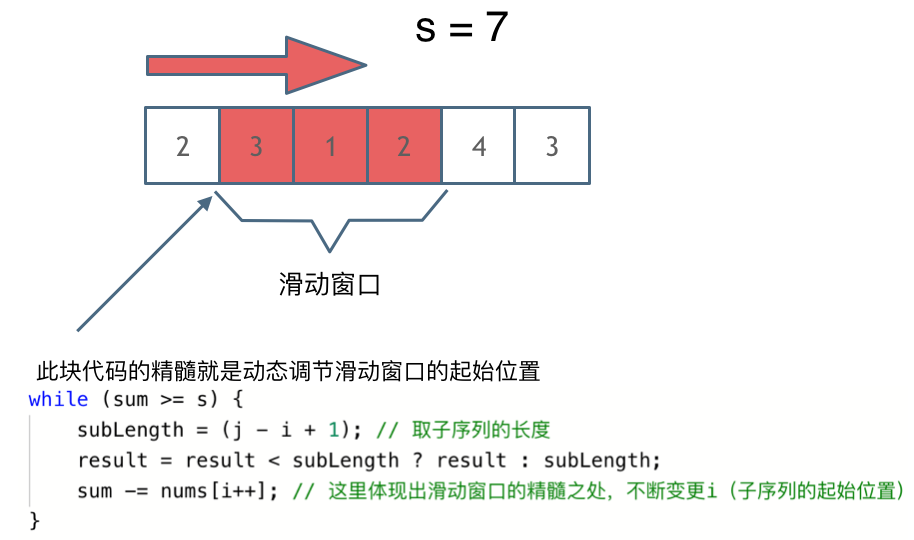
|
||||
|
||||
可以发现**滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。**
|
||||
|
||||
|
|
|
|||
|
|
@ -42,15 +42,15 @@
|
|||
|
||||
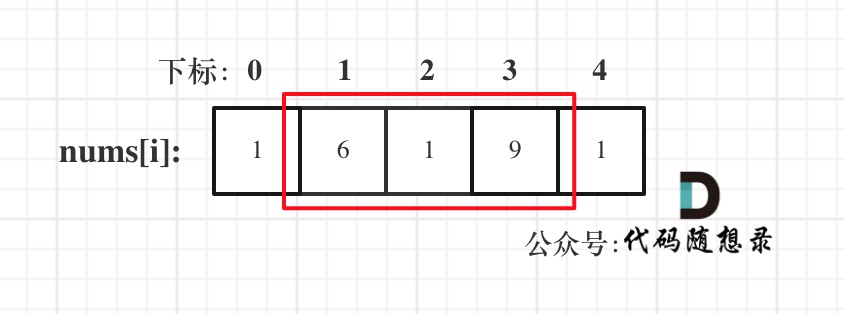
* 情况一:考虑不包含首尾元素
|
||||
|
||||
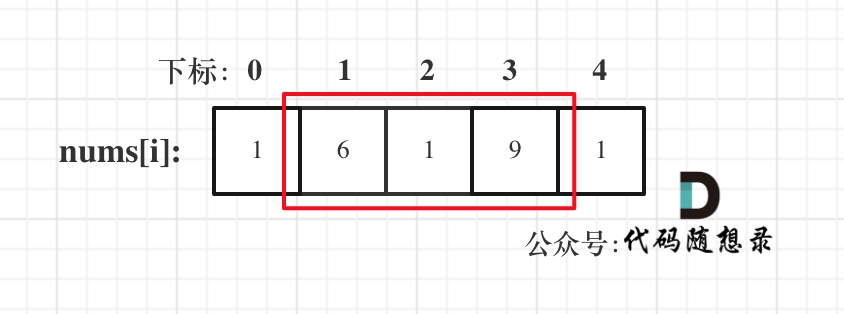
|
||||
|
||||
|
||||
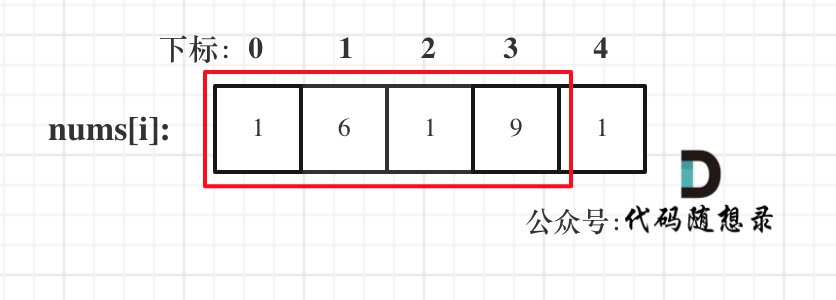
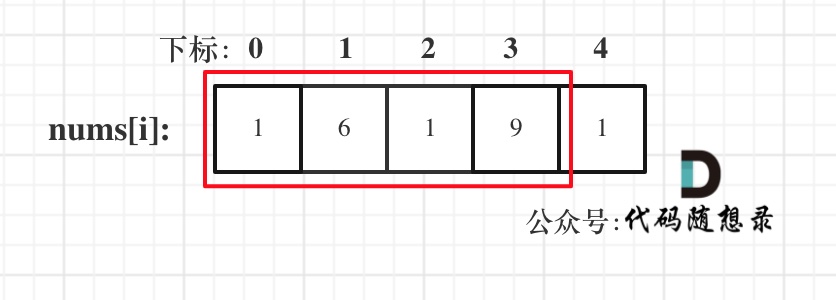
* 情况二:考虑包含首元素,不包含尾元素
|
||||
|
||||
|
||||
|
||||
|
||||
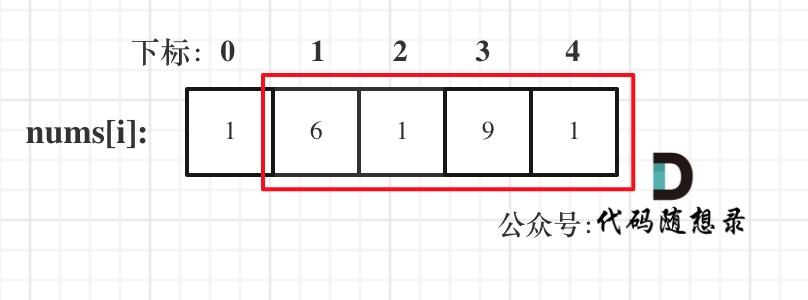
* 情况三:考虑包含尾元素,不包含首元素
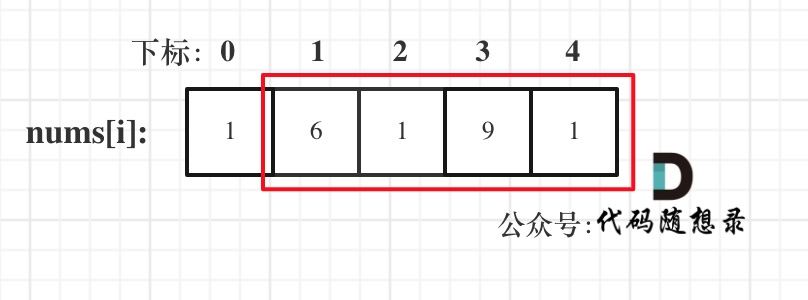
|
||||
|
||||
|
||||
|
||||
|
||||
**注意我这里用的是"考虑"**,例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
|
||||
|
||||
|
|
|
|||
|
|
@ -45,7 +45,7 @@
|
|||
|
||||
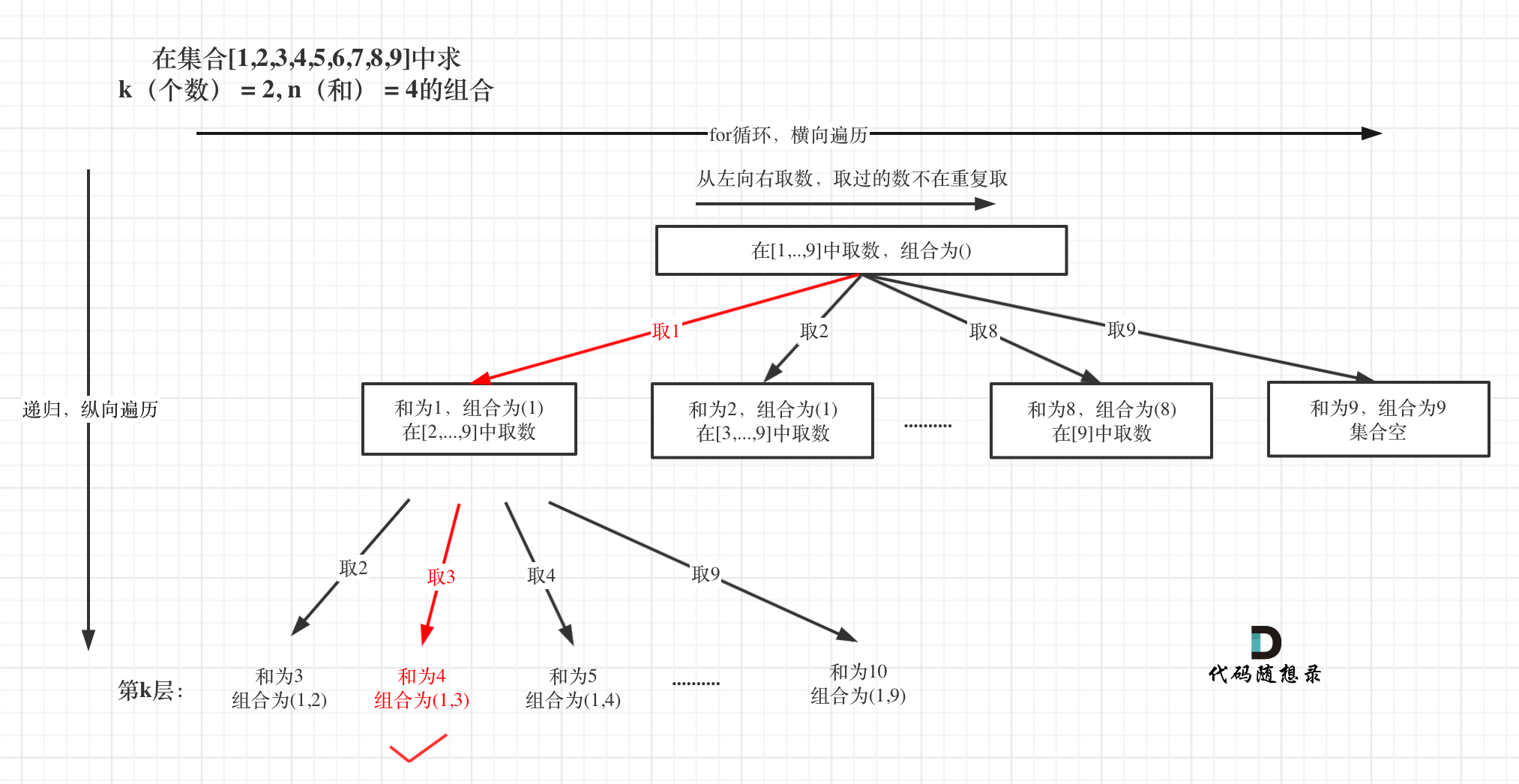
选取过程如图:
|
||||
|
||||

|
||||
|
||||
|
||||
图中,可以看出,只有最后取到集合(1,3)和为4 符合条件。
|
||||
|
||||
|
|
@ -108,7 +108,7 @@ if (path.size() == k) {
|
|||
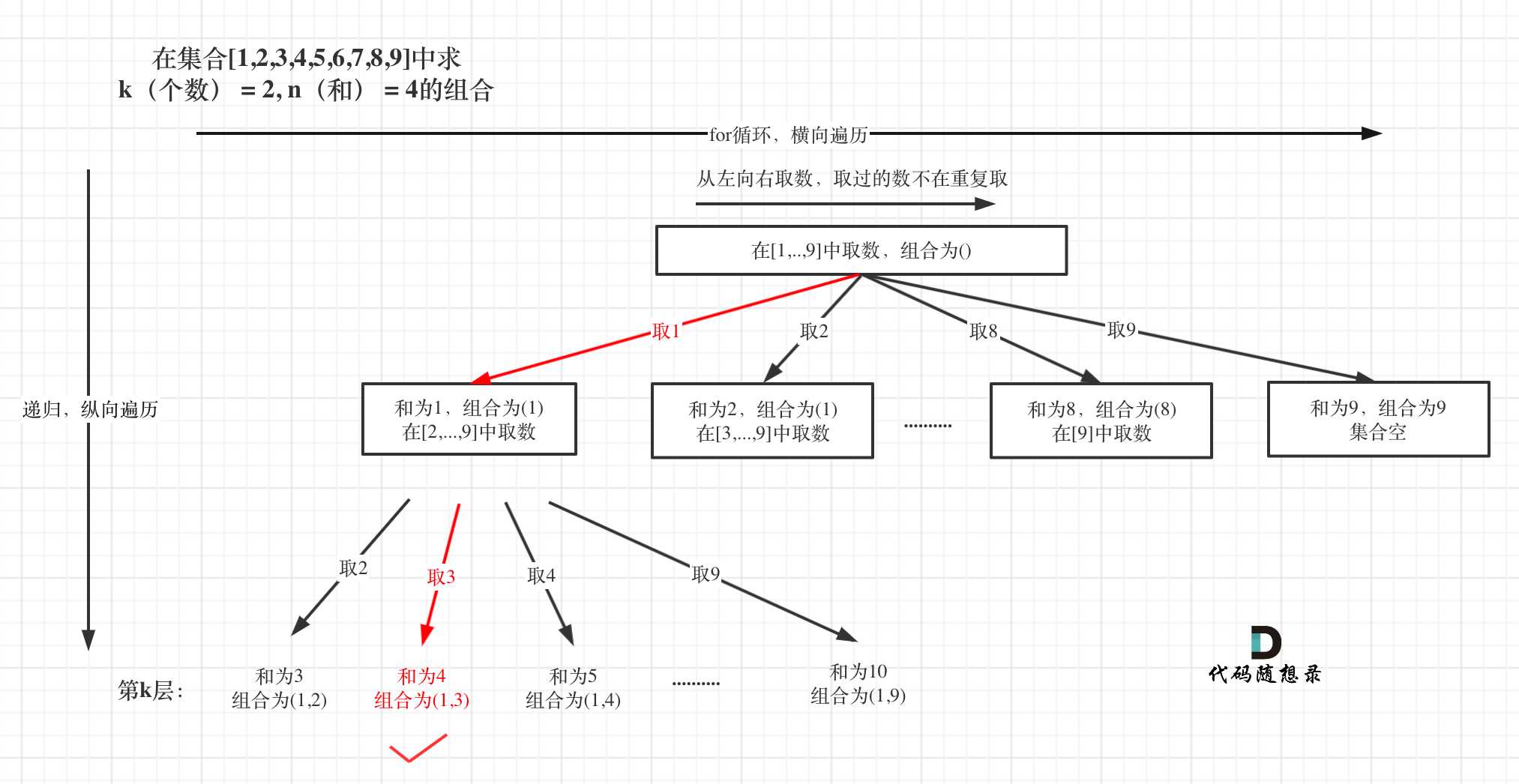
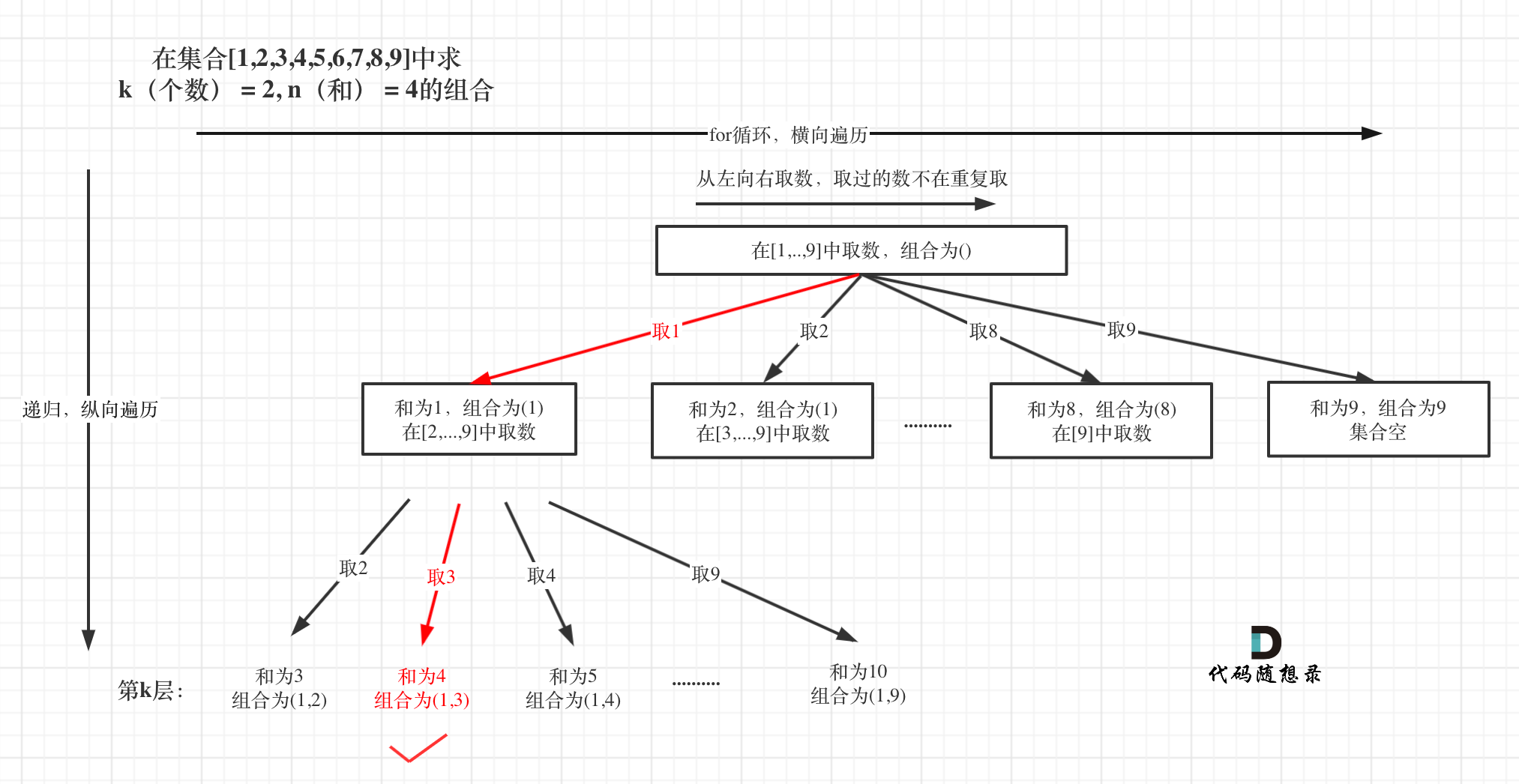
本题和[77. 组合](https://programmercarl.com/0077.组合.html)区别之一就是集合固定的就是9个数[1,...,9],所以for循环固定i<=9
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
处理过程就是 path收集每次选取的元素,相当于树型结构里的边,sum来统计path里元素的总和。
|
||||
|
||||
|
|
@ -166,7 +166,7 @@ public:
|
|||
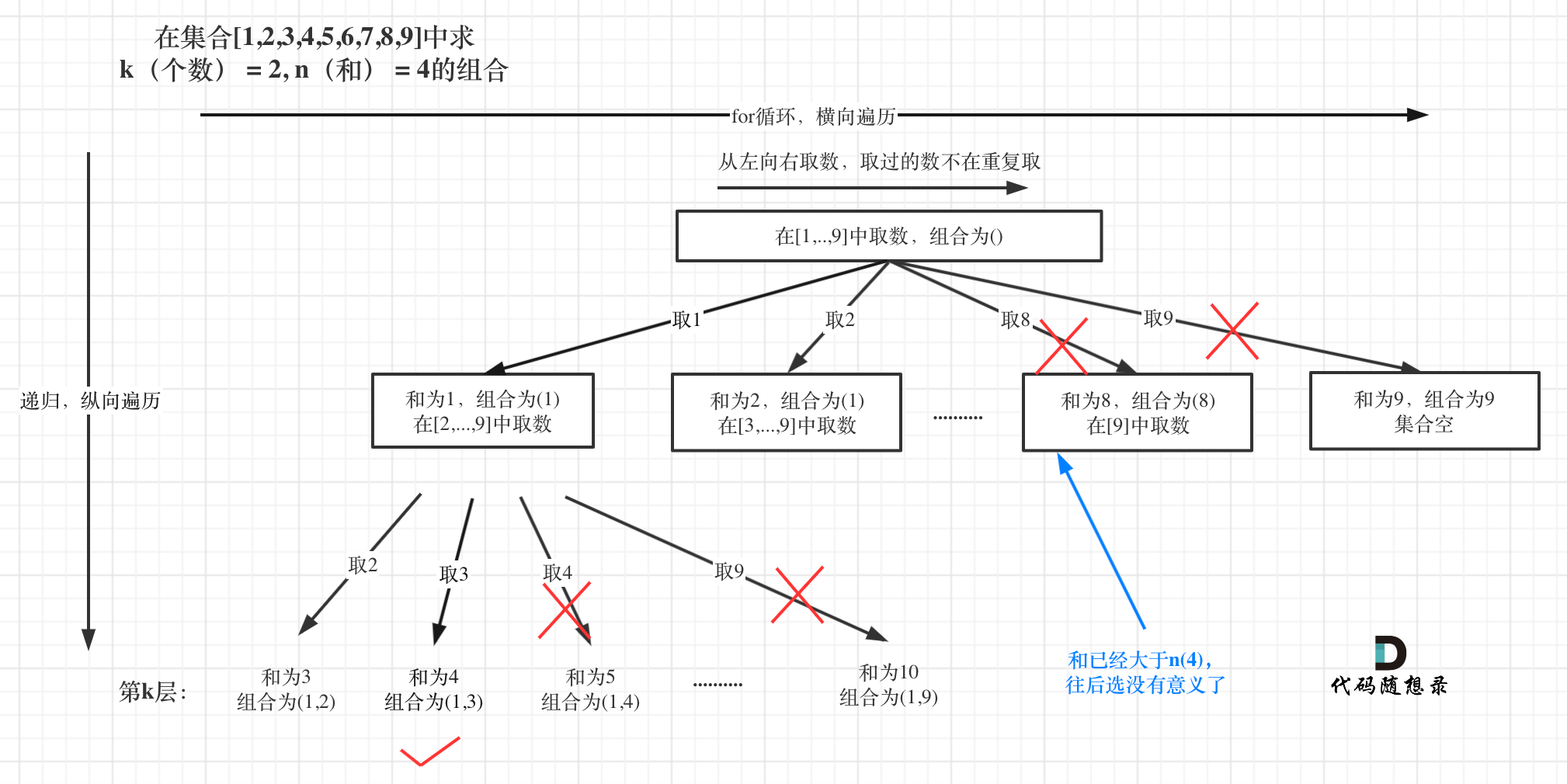
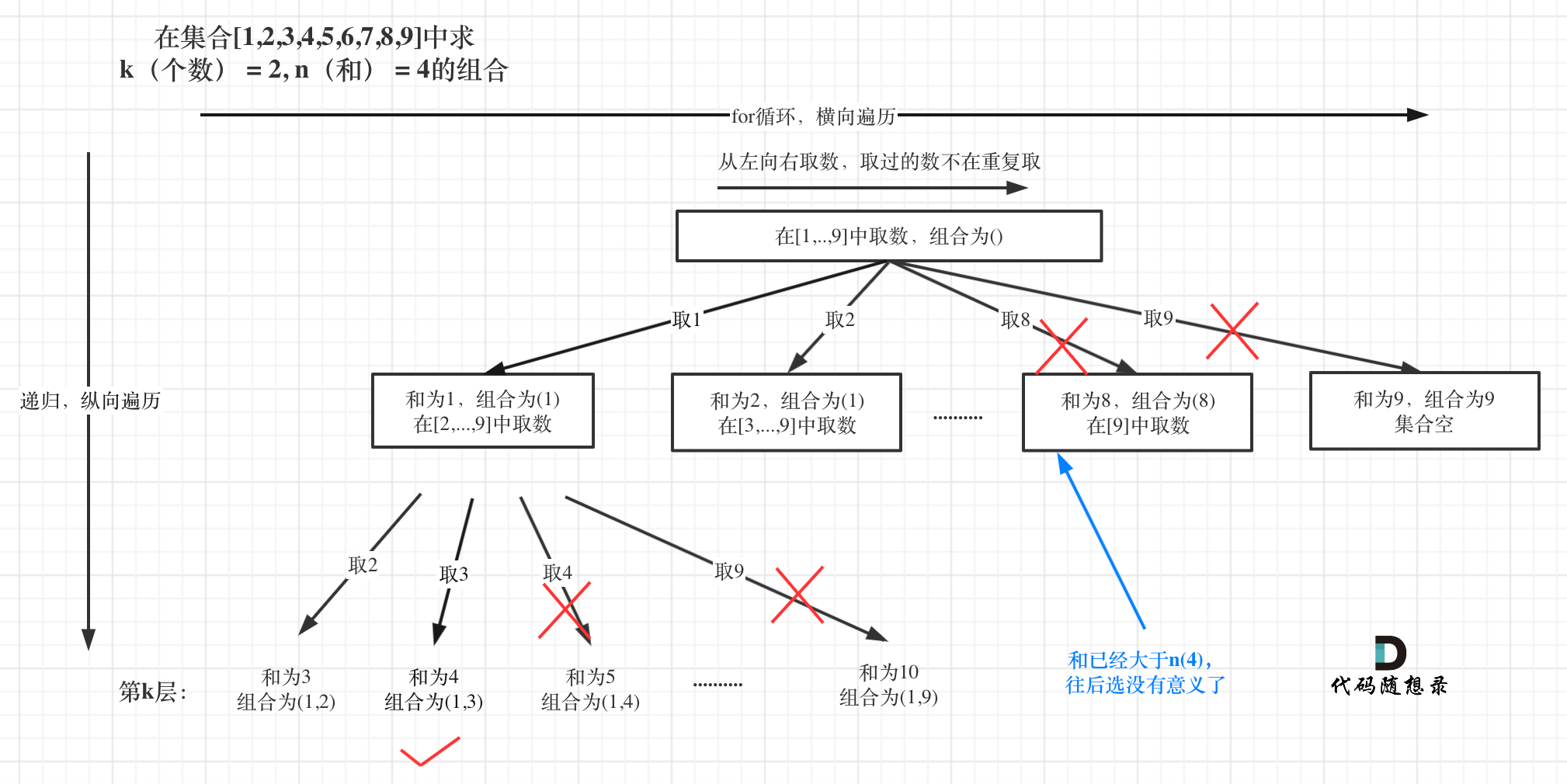
这道题目,剪枝操作其实是很容易想到了,想必大家看上面的树形图的时候已经想到了。
|
||||
|
||||
如图:
|
||||
|
||||
|
||||
|
||||
已选元素总和如果已经大于n(图中数值为4)了,那么往后遍历就没有意义了,直接剪掉。
|
||||
|
||||
|
|
|
|||
|
|
@ -153,7 +153,7 @@ public:
|
|||
|
||||
我来举一个典型的例子如题:
|
||||
|
||||
<img src='https://file.kamacoder.com/pics/20200920221638903-20230310123444151.png' width=600> </img>
|
||||
<img src='https://file1.kamacoder.com/i/algo/20200920221638903-20230310123444151.png' width=600> </img>
|
||||
|
||||
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
|
||||
|
||||
|
|
@ -162,10 +162,10 @@ public:
|
|||
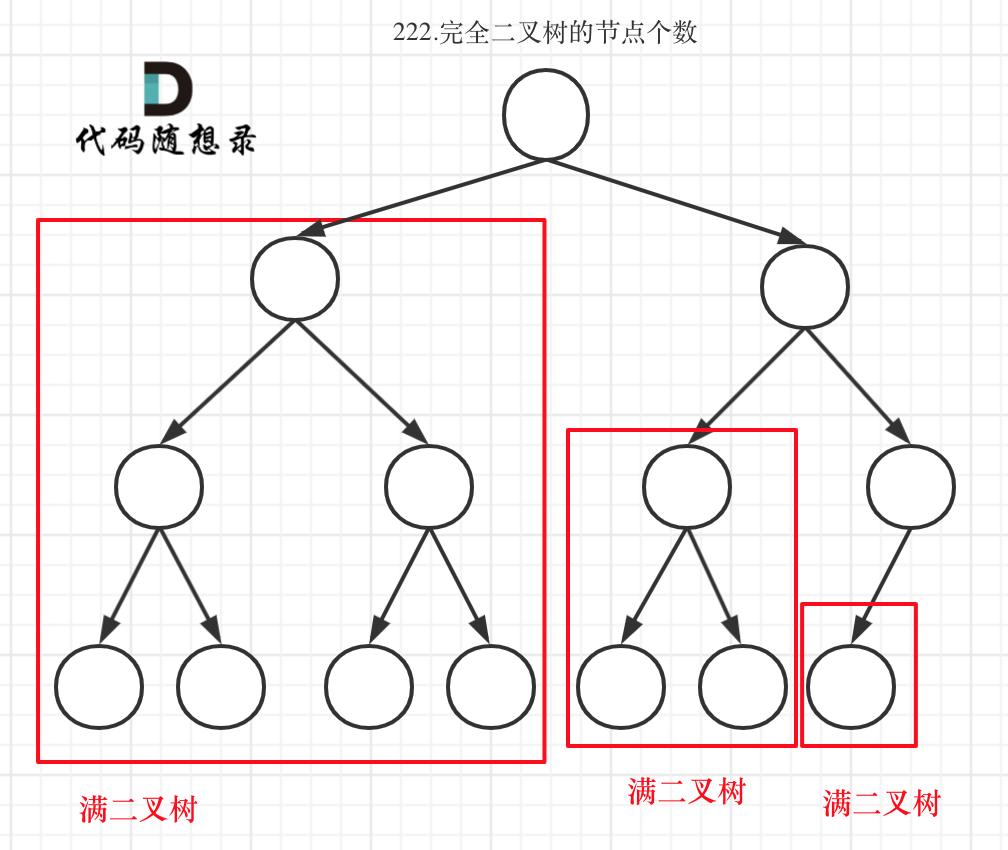
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
|
||||
|
||||
完全二叉树(一)如图:
|
||||

|
||||
|
||||
|
||||
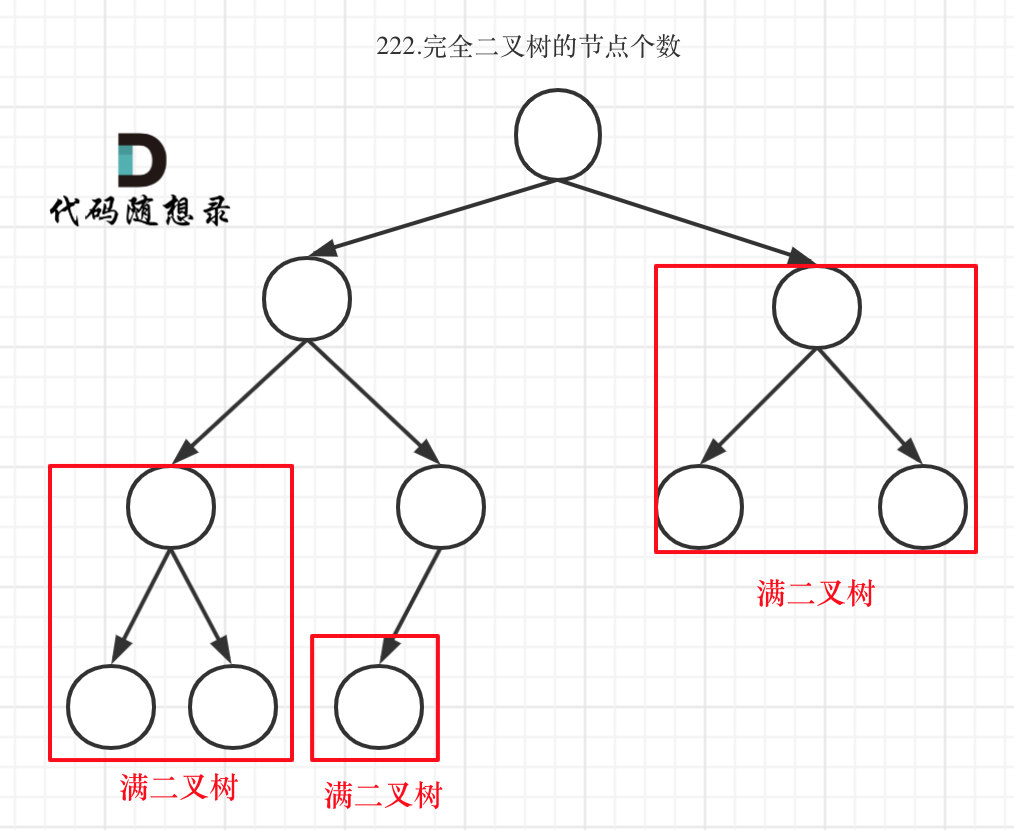
完全二叉树(二)如图:
|
||||
|
||||
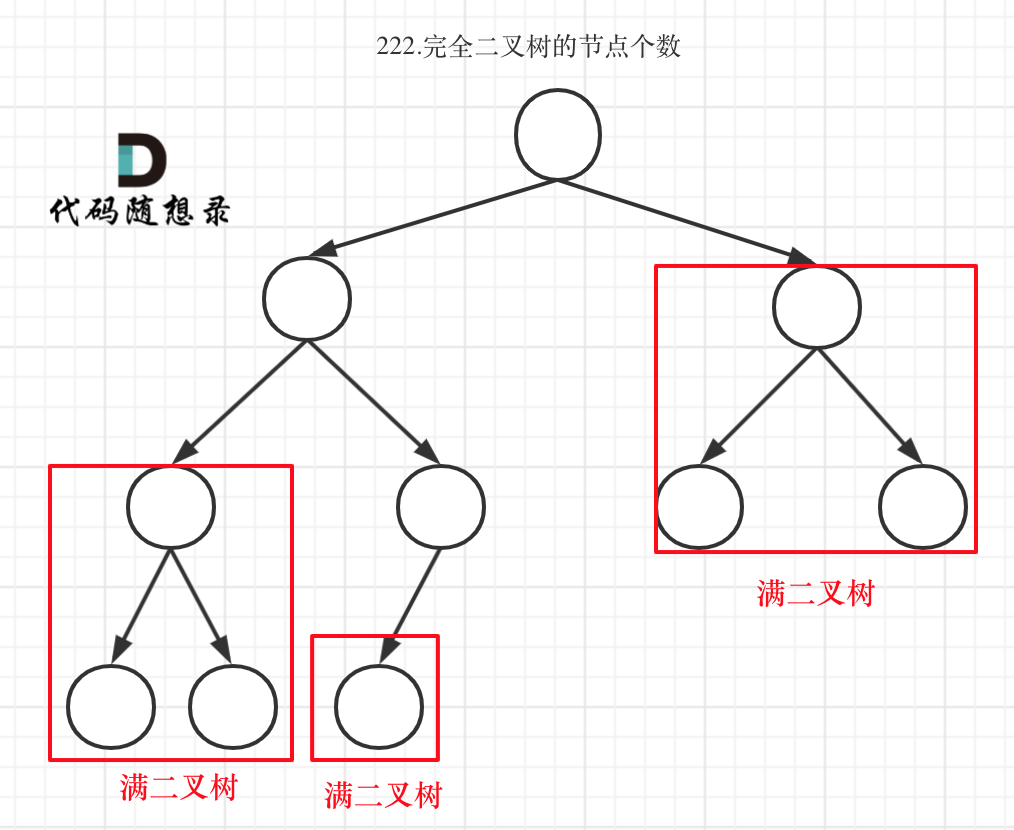
|
||||
|
||||
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
|
||||
|
||||
|
|
@ -173,15 +173,15 @@ public:
|
|||
|
||||
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
|
||||
|
||||
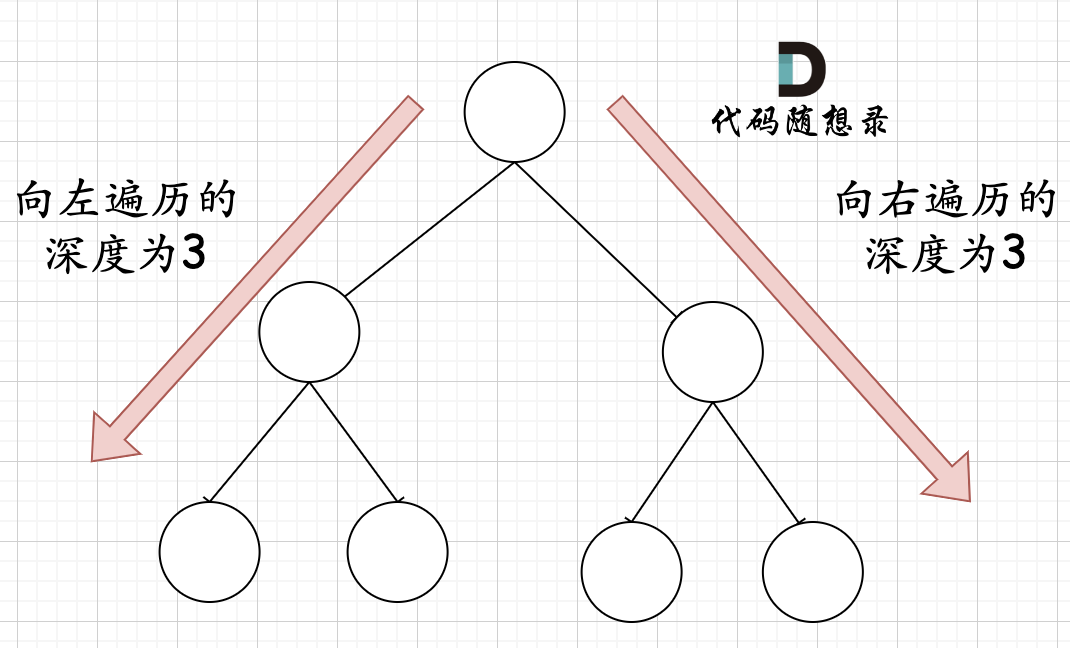
|
||||
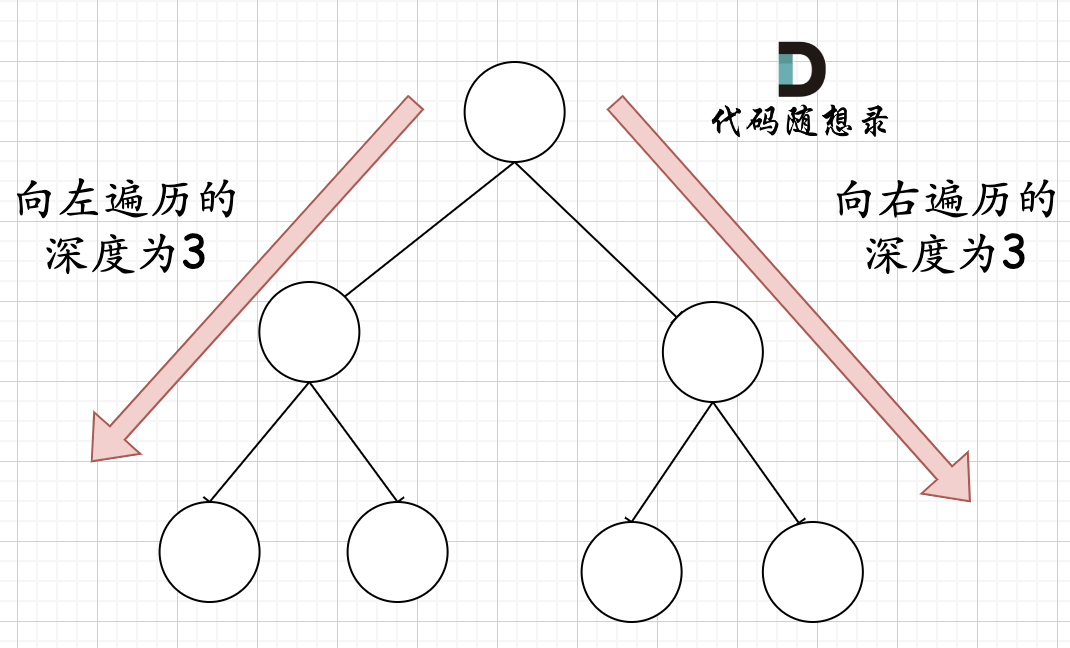
|
||||
|
||||
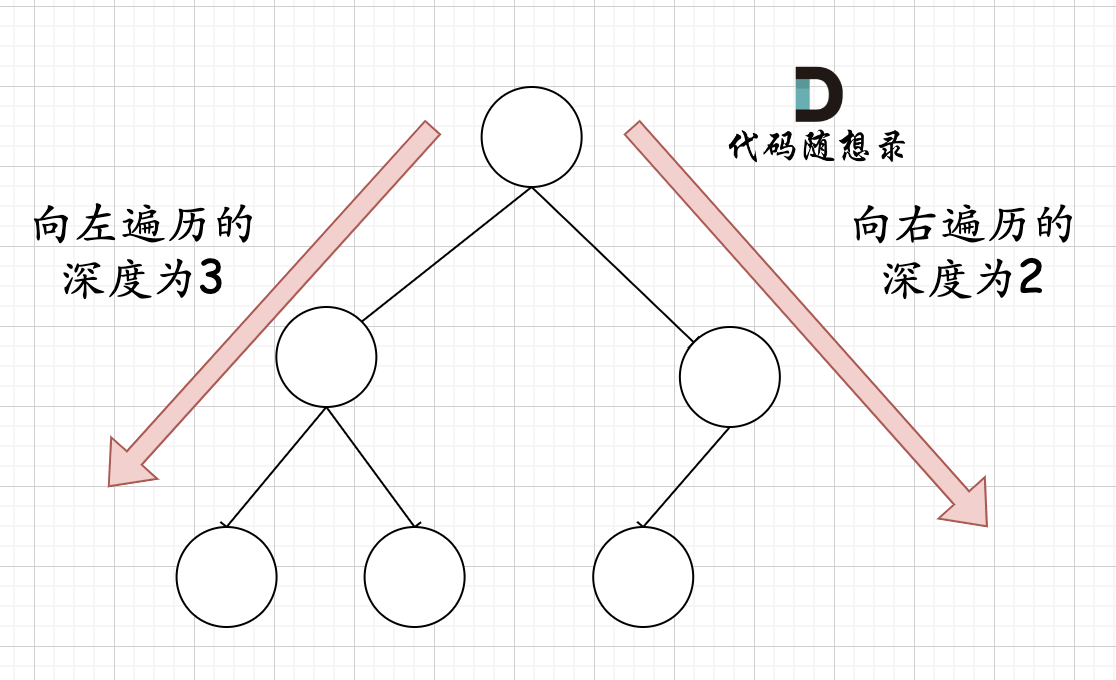
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
|
||||
|
||||
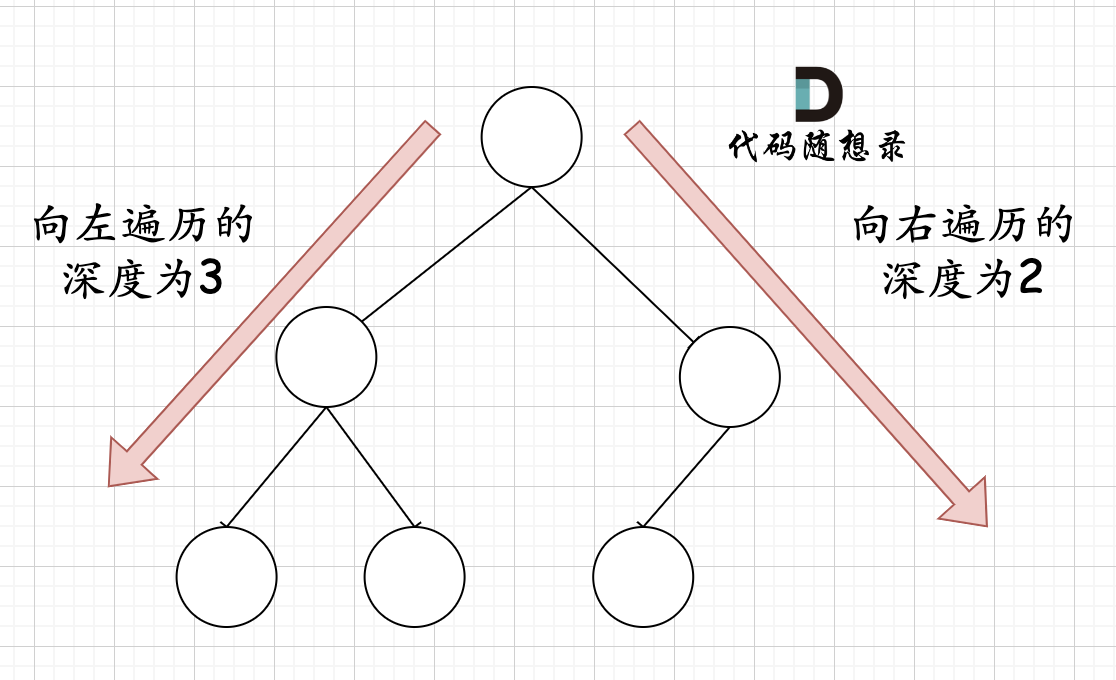
|
||||
|
||||
|
||||
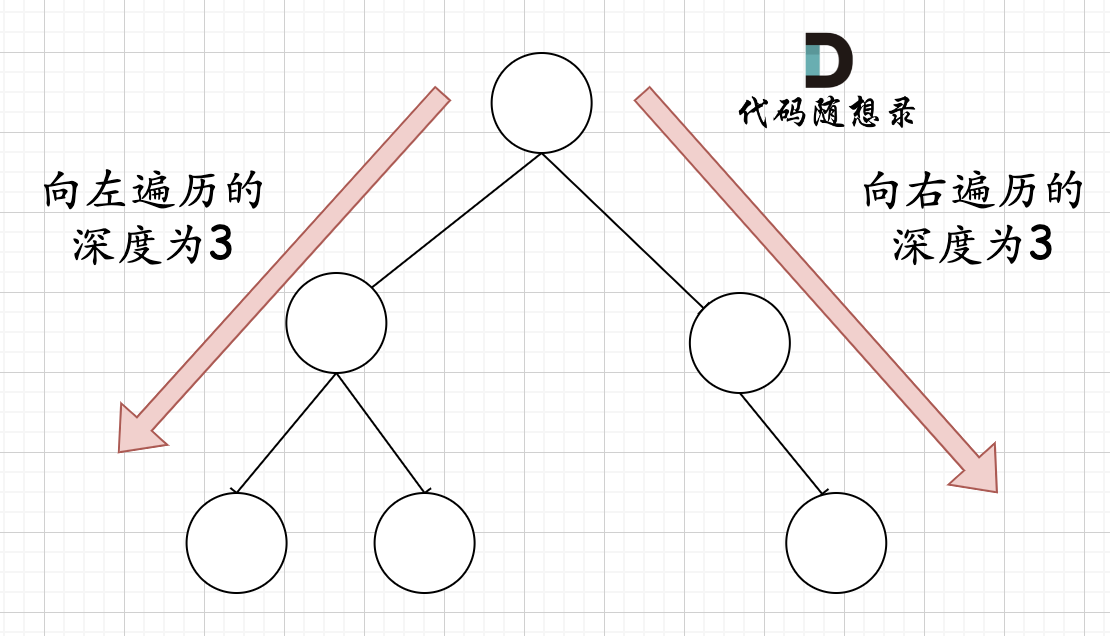
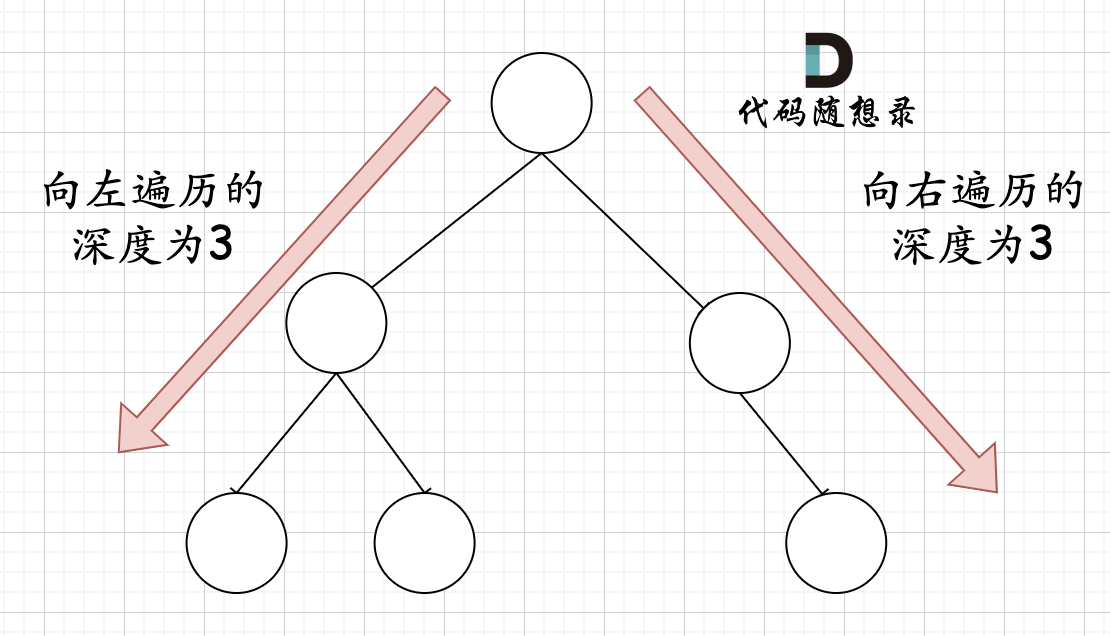
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
|
||||
|
||||
|
||||
|
||||
|
||||
如果这么想,大家就是对 完全二叉树理解有误区了,**以上这棵二叉树,它根本就不是一个完全二叉树**!
|
||||
|
||||
|
|
|
|||
|
|
@ -60,7 +60,7 @@ queue.pop();
|
|||
queue.empty();
|
||||
```
|
||||
|
||||

|
||||
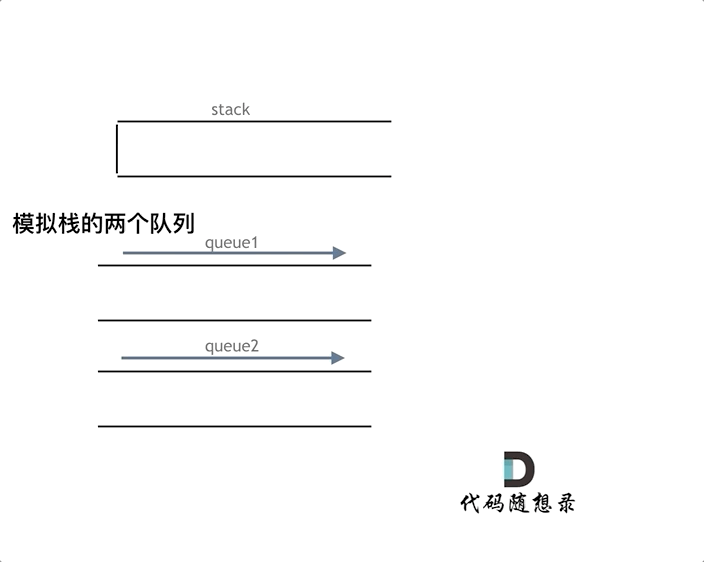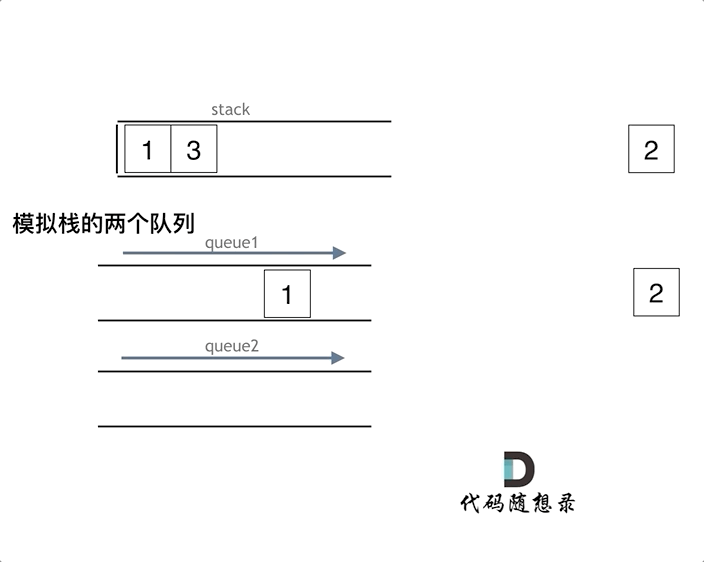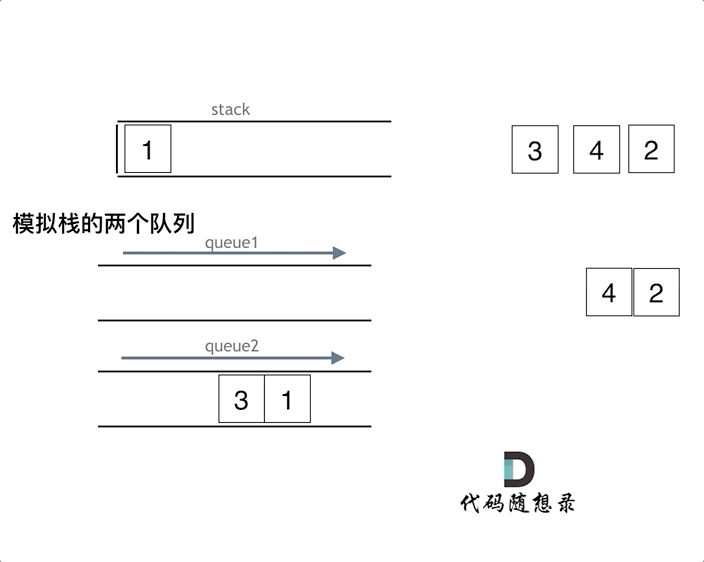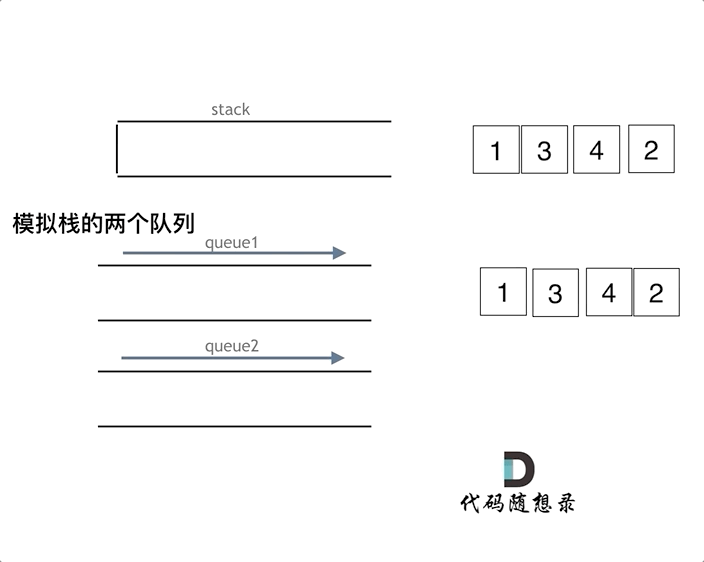
|
||||
|
||||
详细如代码注释所示:
|
||||
|
||||
|
|
|
|||
|
|
@ -10,7 +10,7 @@
|
|||
翻转一棵二叉树。
|
||||
|
||||
|
||||
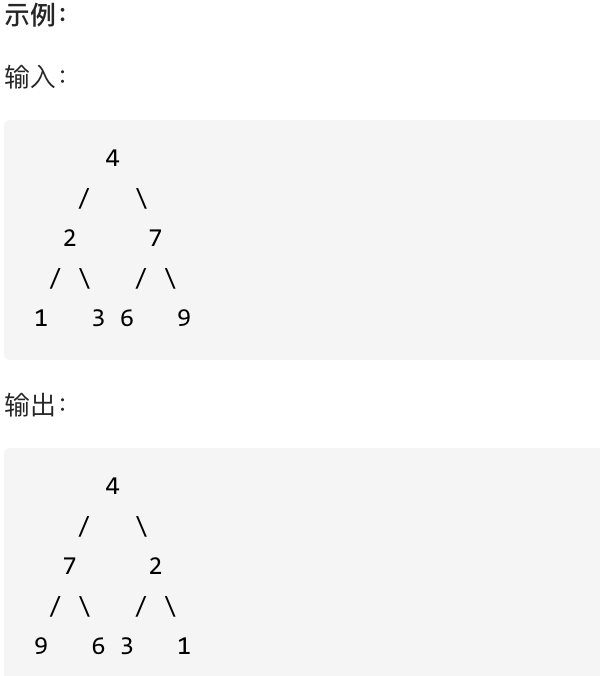
|
||||

|
||||
|
||||
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,全当一个乐子哈)
|
||||
|
||||
|
|
@ -35,7 +35,7 @@
|
|||
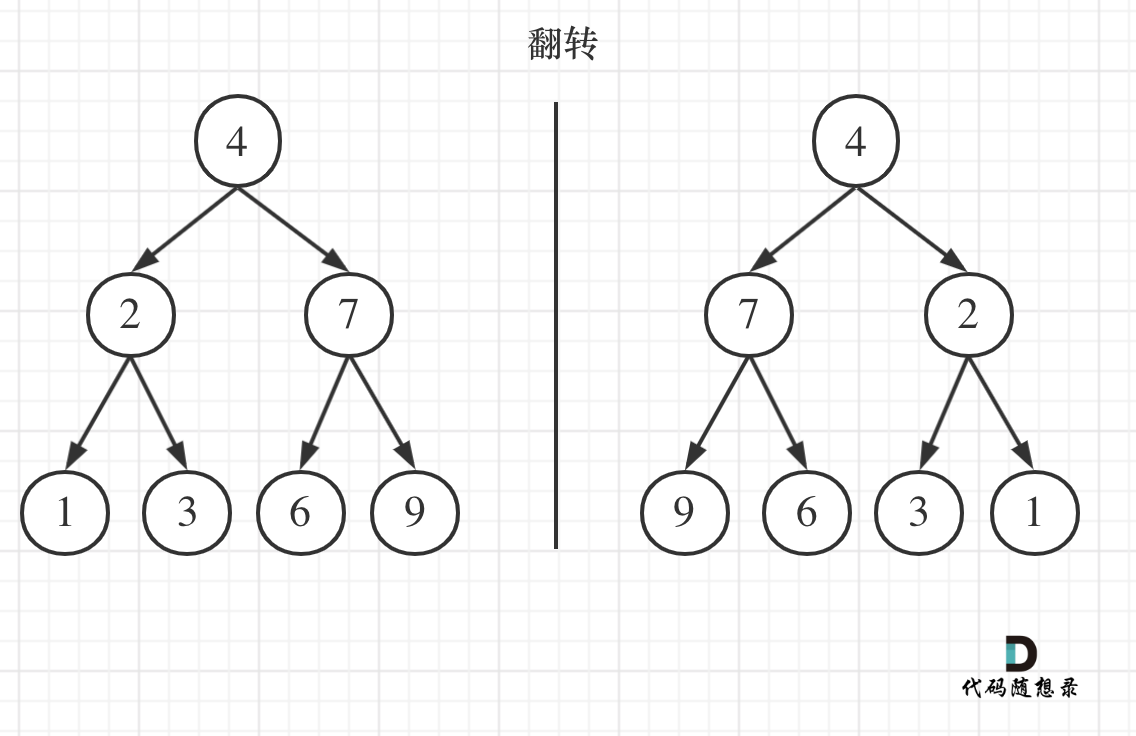
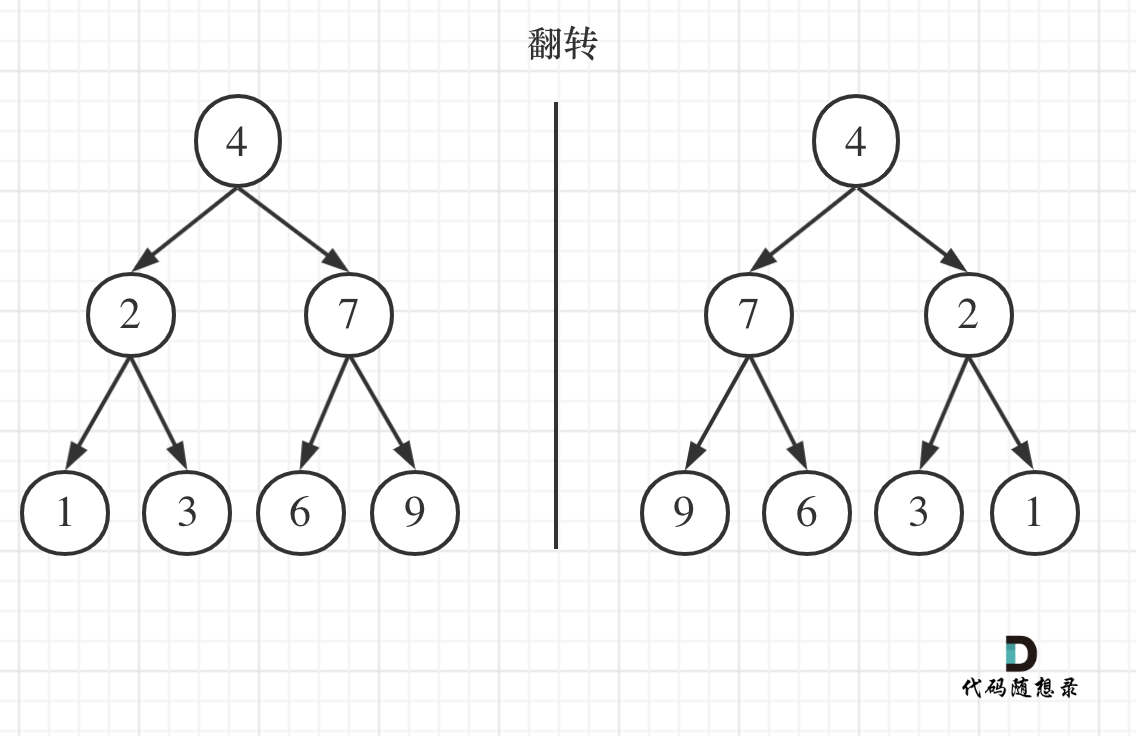
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
|
||||
|
||||
|
|
@ -55,7 +55,7 @@
|
|||
|
||||
我们下文以前序遍历为例,通过动画来看一下翻转的过程:
|
||||
|
||||

|
||||

|
||||
|
||||
我们来看一下递归三部曲:
|
||||
|
||||
|
|
|
|||
|
|
@ -57,7 +57,7 @@ queue.pop();**注意此时的输出栈的操作**
|
|||
queue.pop();
|
||||
queue.empty();
|
||||
|
||||

|
||||
|
||||
|
||||
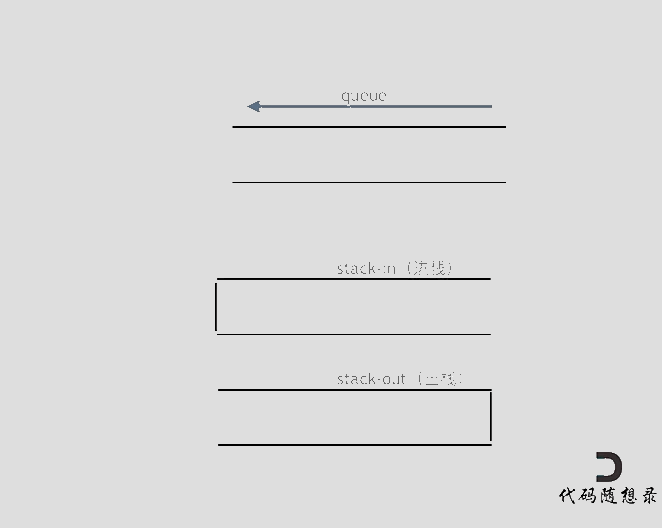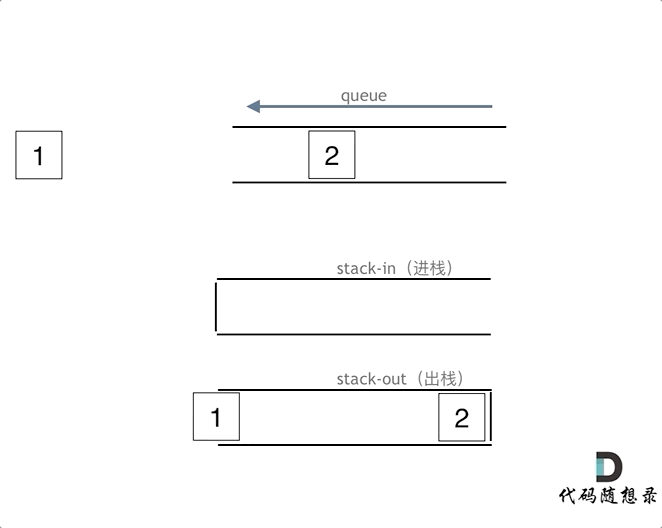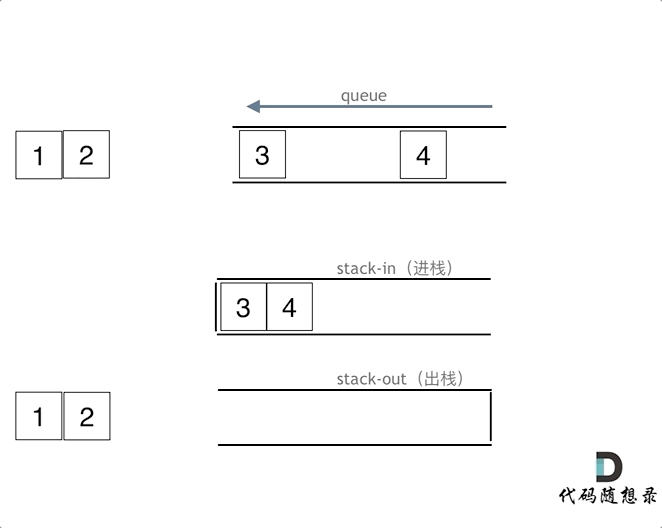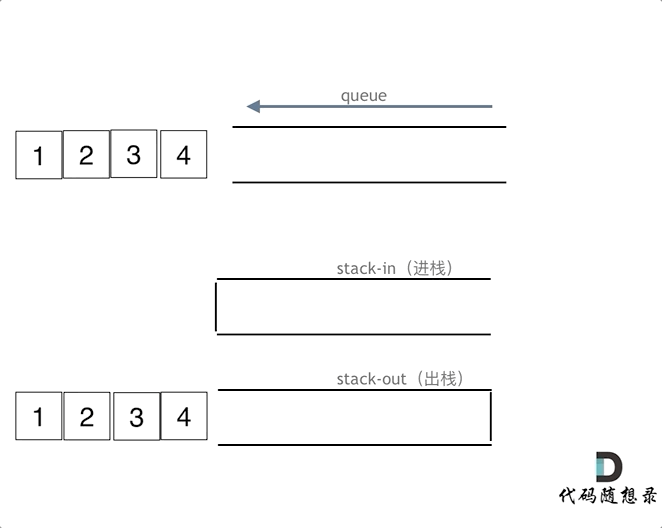
在push数据的时候,只要数据放进输入栈就好,**但在pop的时候,操作就复杂一些,输出栈如果为空,就把进栈数据全部导入进来(注意是全部导入)**,再从出栈弹出数据,如果输出栈不为空,则直接从出栈弹出数据就可以了。
|
||||
|
||||
|
|
|
|||
|
|
@ -87,7 +87,7 @@ public:
|
|||
|
||||
如图所示:
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/234.回文链表.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/234.回文链表.png' width=600> </img></div>
|
||||
|
||||
代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -14,7 +14,7 @@
|
|||
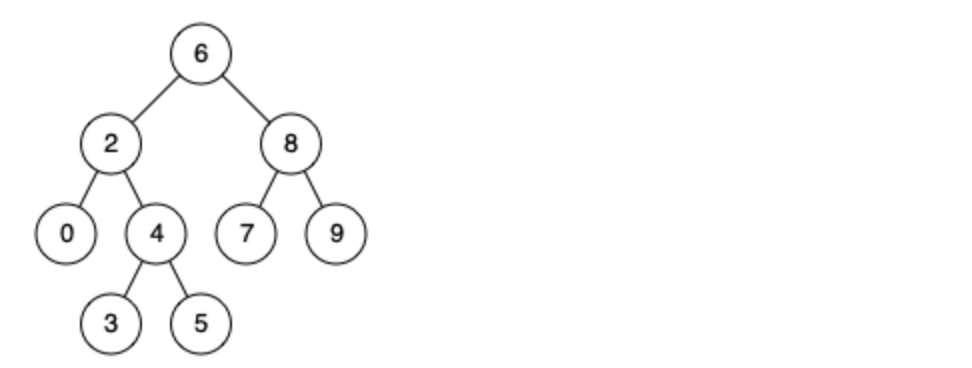
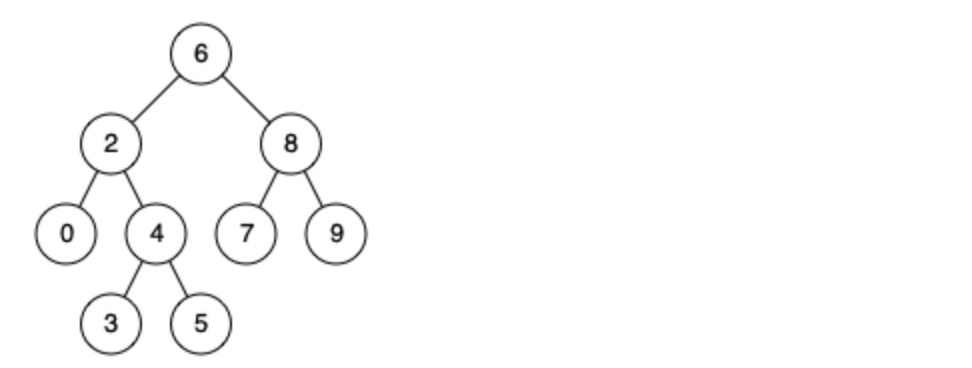
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
示例 1:
|
||||
|
||||
|
|
@ -52,7 +52,7 @@
|
|||
|
||||
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
|
||||
|
||||
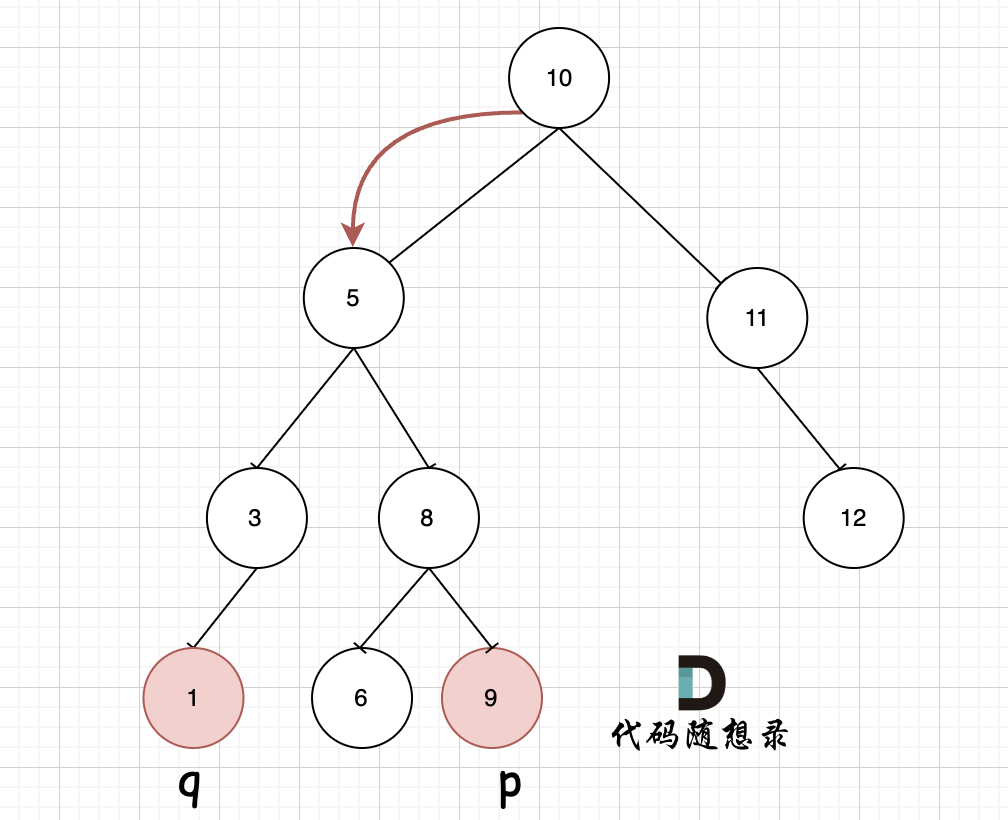
|
||||
|
||||
|
||||
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
|
||||
|
||||
|
|
@ -64,7 +64,7 @@
|
|||
|
||||
如图所示:p为节点6,q为节点9
|
||||
|
||||
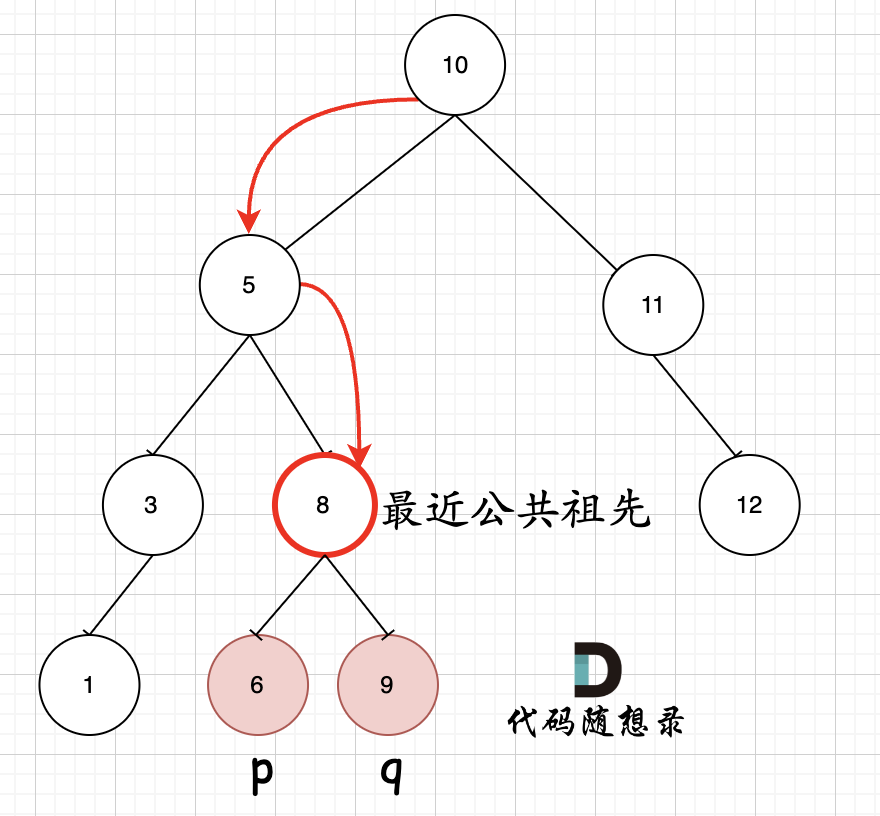
|
||||
|
||||
|
||||
|
||||
可以看出直接按照指定的方向,就可以找到节点8,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
|
||||
|
|
|
|||
|
|
@ -16,7 +16,7 @@
|
|||
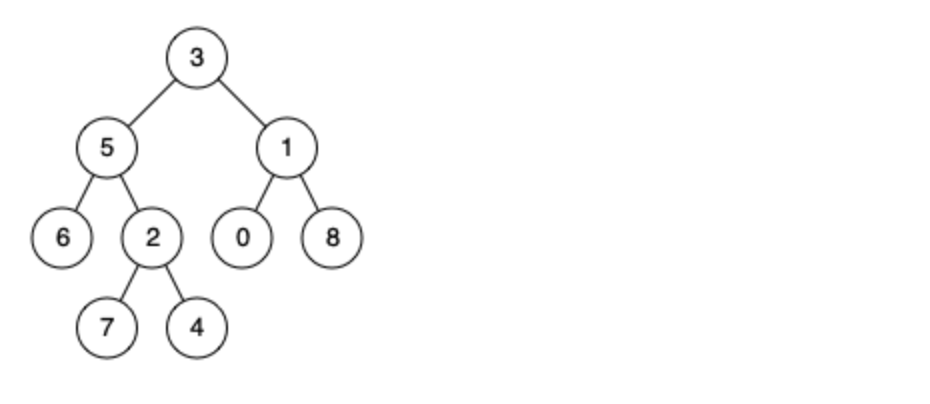
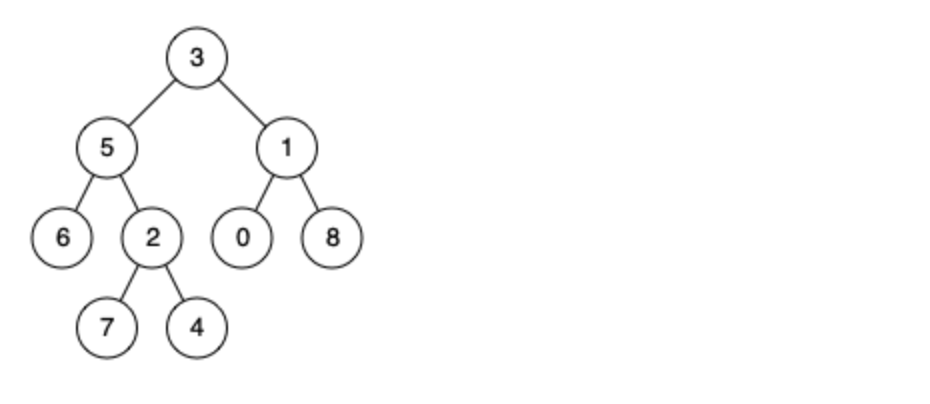
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
示例 1:
|
||||
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
|
||||
|
|
@ -51,7 +51,7 @@
|
|||
|
||||
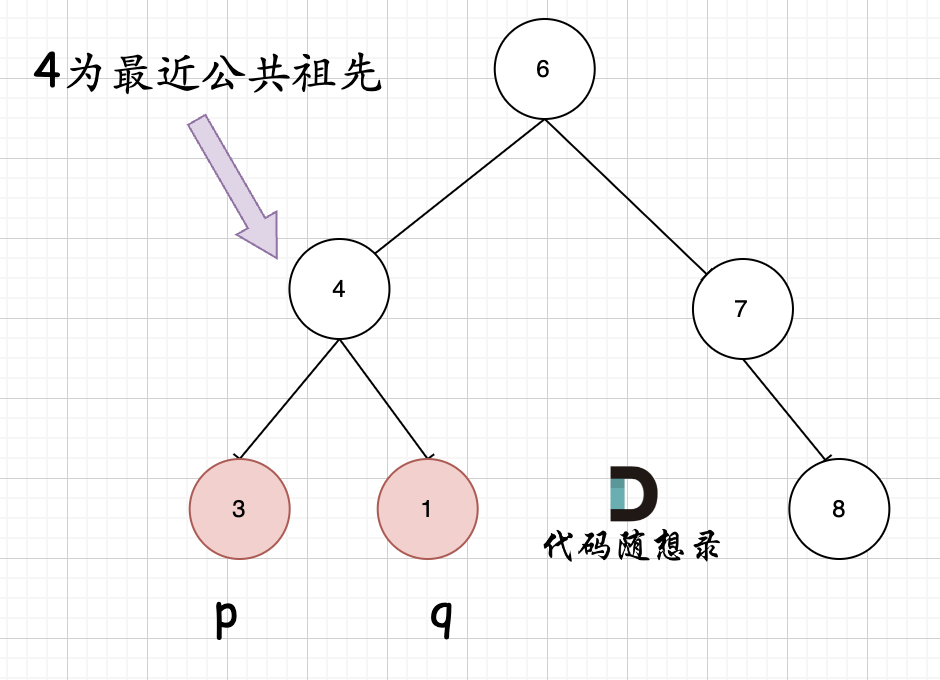
**首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。** 即情况一:
|
||||
|
||||
|
||||
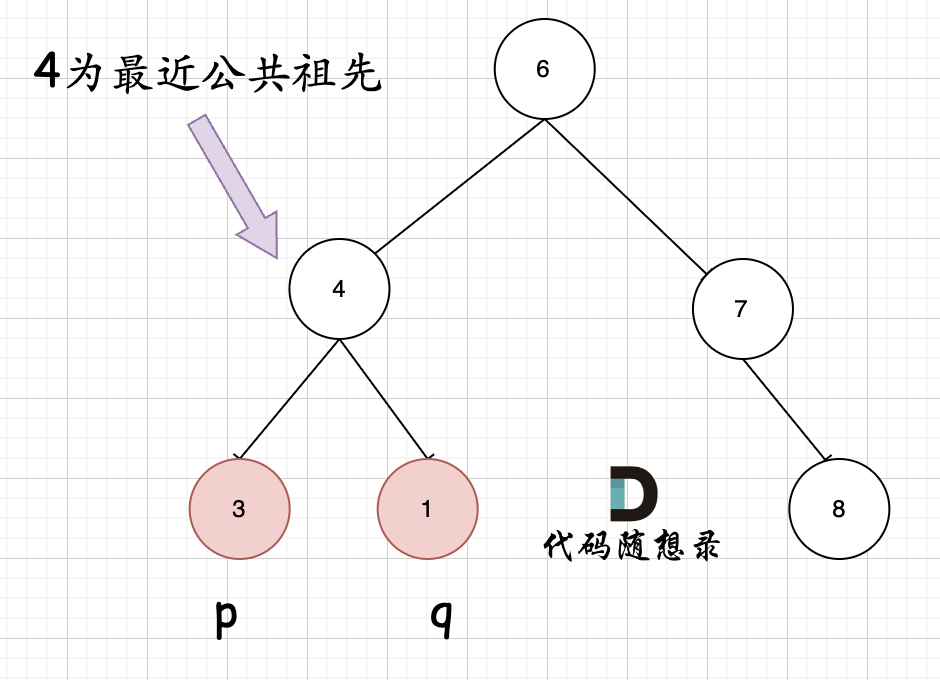
|
||||
|
||||
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
|
||||
|
||||
|
|
@ -61,7 +61,7 @@
|
|||
|
||||
**但是很多人容易忽略一个情况,就是节点本身p(q),它拥有一个子孙节点q(p)。** 情况二:
|
||||
|
||||
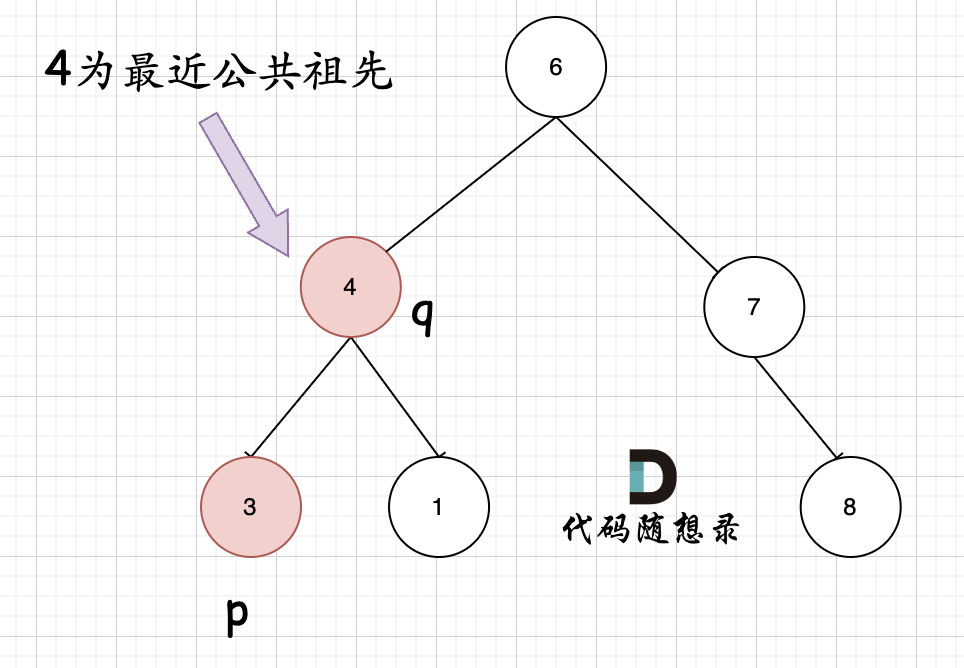
|
||||
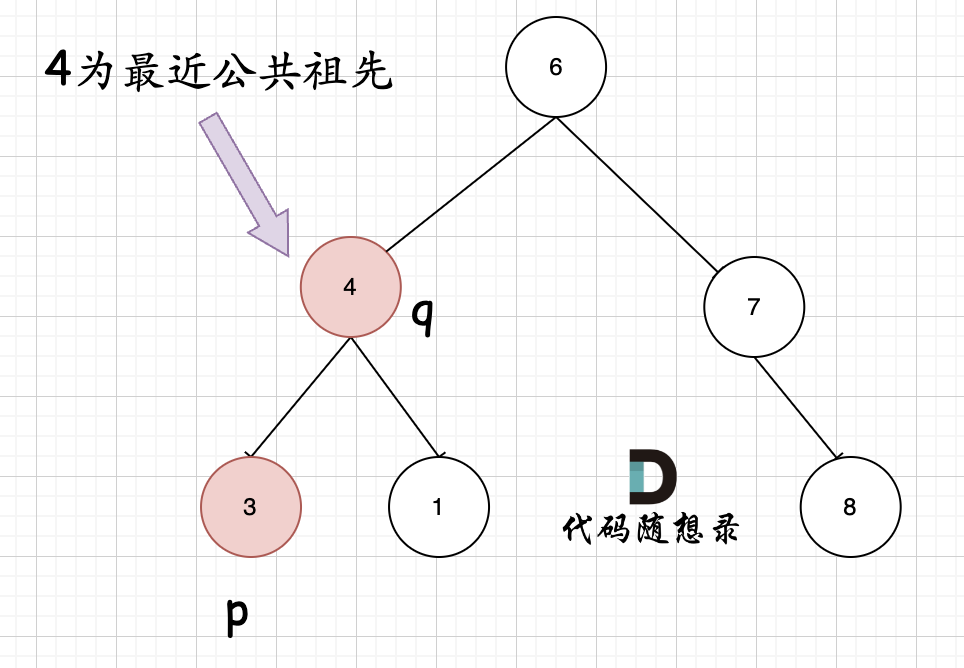
|
||||
|
||||
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
|
||||
|
||||
|
|
@ -129,7 +129,7 @@ left与right的逻辑处理; // 中
|
|||
|
||||
如图:
|
||||
|
||||
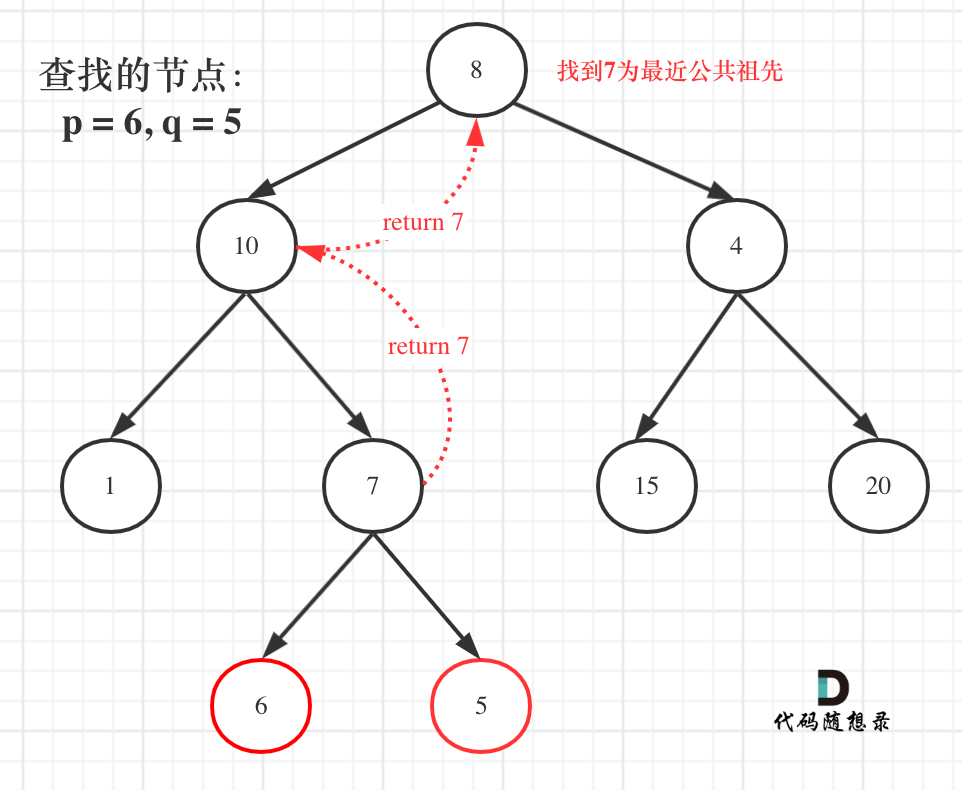
|
||||
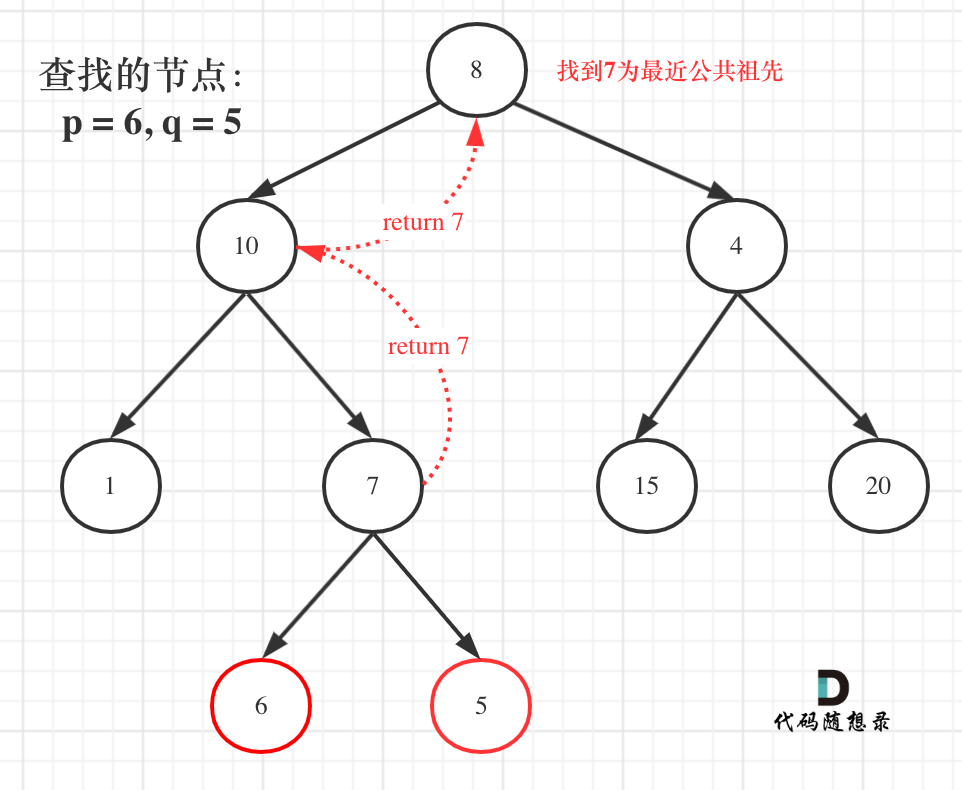
|
||||
|
||||
就像图中一样直接返回7。
|
||||
|
||||
|
|
@ -162,7 +162,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
|
|||
|
||||
如图:
|
||||
|
||||
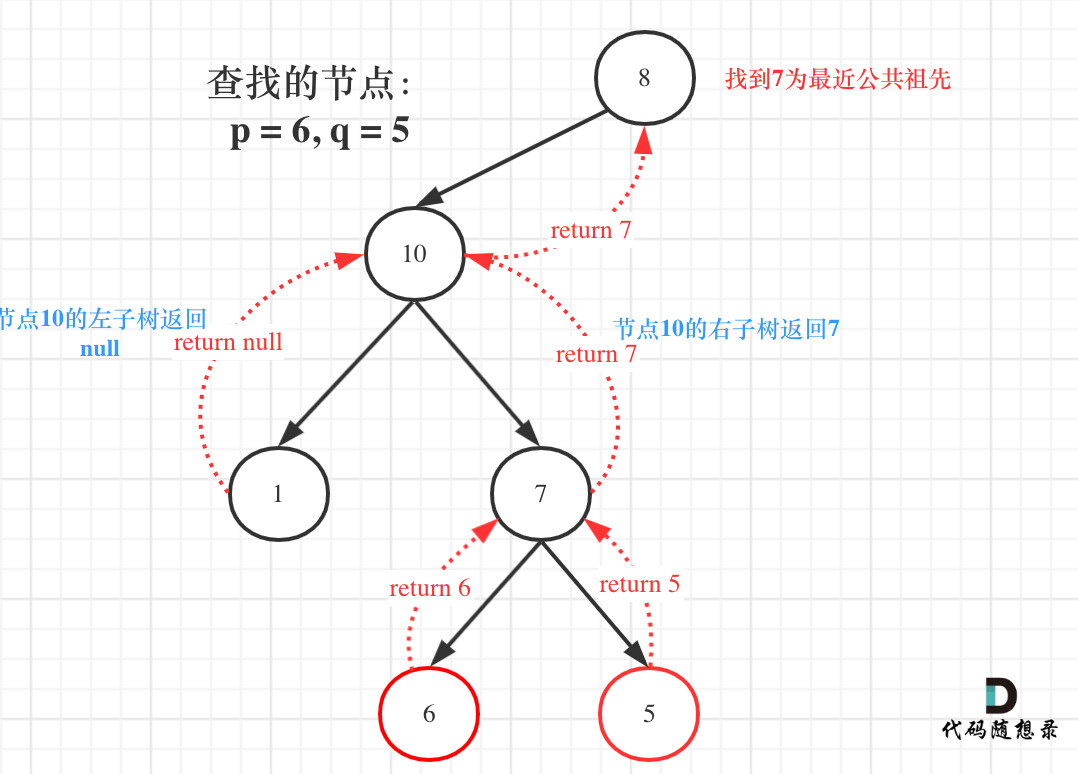
|
||||
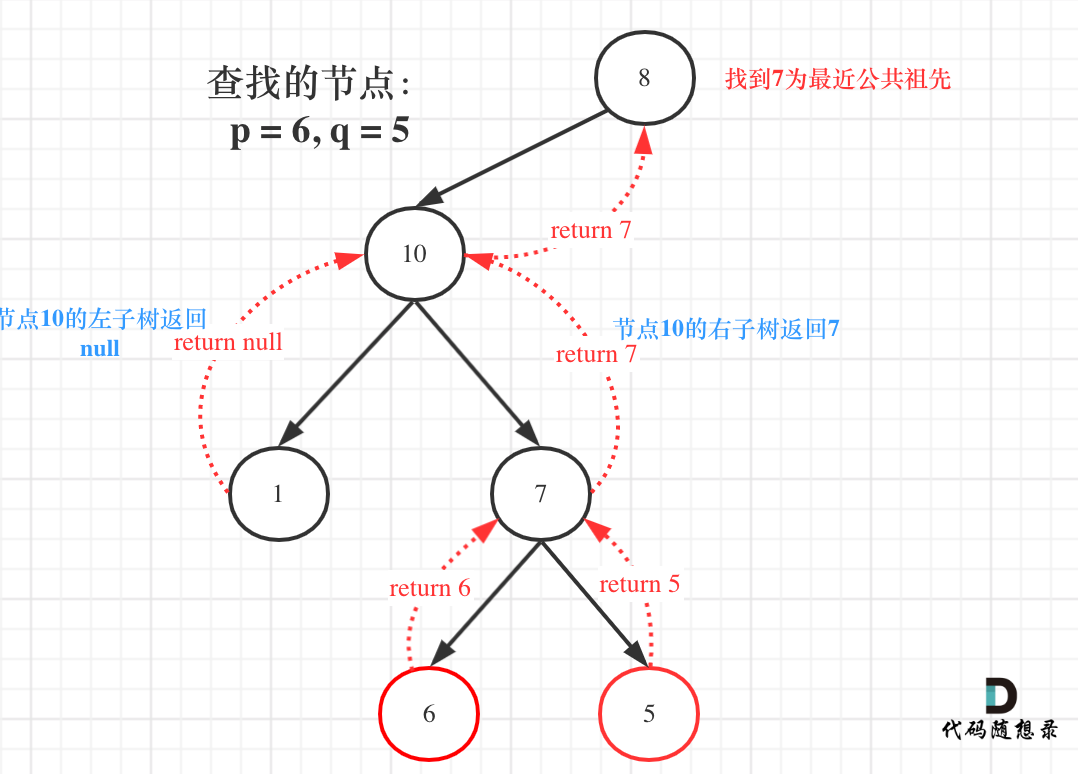
|
||||
|
||||
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
|
||||
|
||||
|
|
@ -183,7 +183,7 @@ else { // (left == NULL && right == NULL)
|
|||
|
||||
那么寻找最小公共祖先,完整流程图如下:
|
||||
|
||||
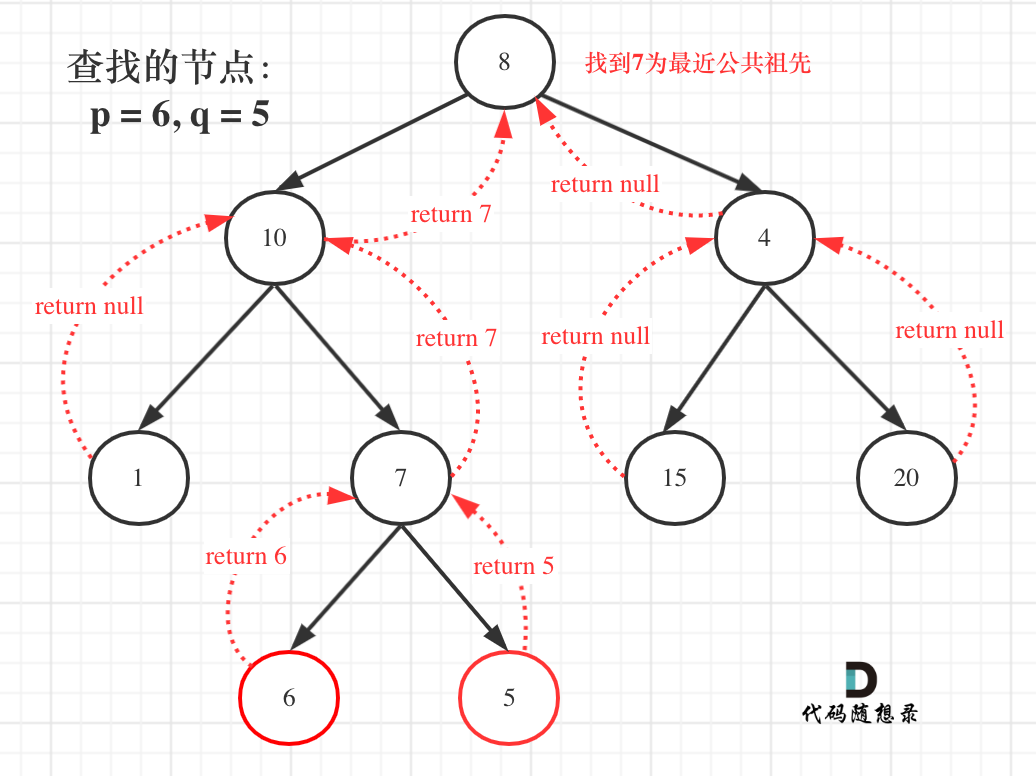
|
||||
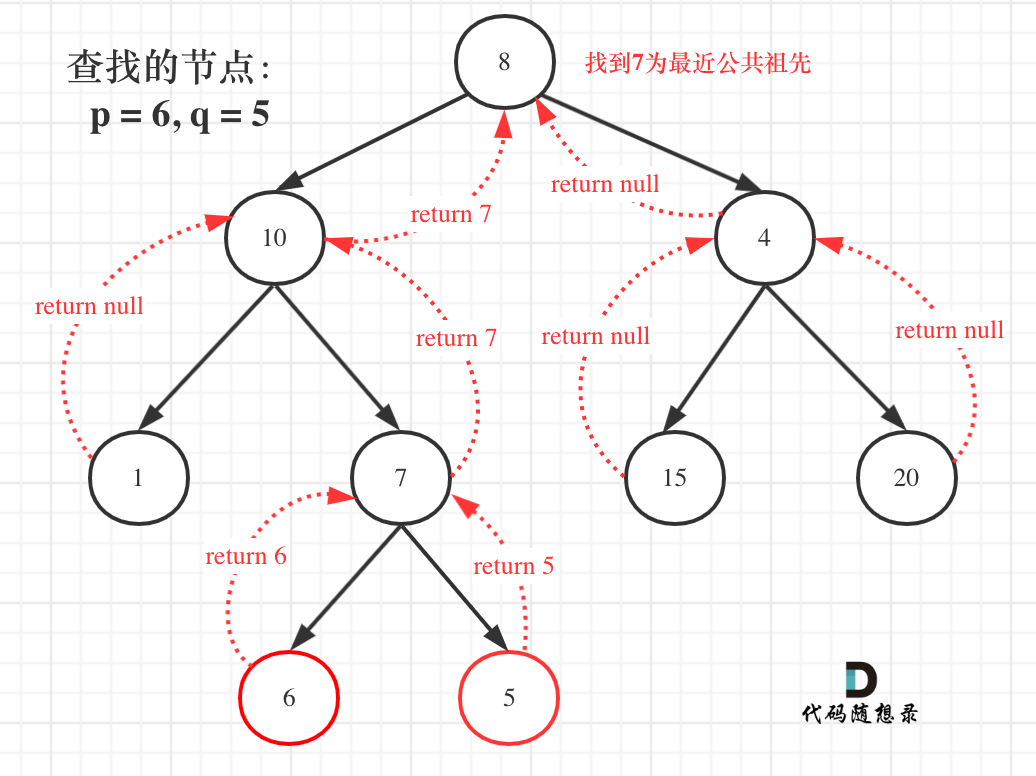
|
||||
|
||||
**从图中,大家可以看到,我们是如何回溯遍历整棵二叉树,将结果返回给头结点的!**
|
||||
|
||||
|
|
|
|||
|
|
@ -18,7 +18,7 @@
|
|||
|
||||
你能在线性时间复杂度内解决此题吗?
|
||||
|
||||
<img src='https://code-thinking.cdn.bcebos.com/pics/239.滑动窗口最大值.png' width=600> </img></div>
|
||||
<img src='https://file1.kamacoder.com/i/algo/239.滑动窗口最大值.png' width=600> </img></div>
|
||||
|
||||
提示:
|
||||
|
||||
|
|
@ -82,7 +82,7 @@ public:
|
|||
|
||||
动画如下:
|
||||
|
||||

|
||||
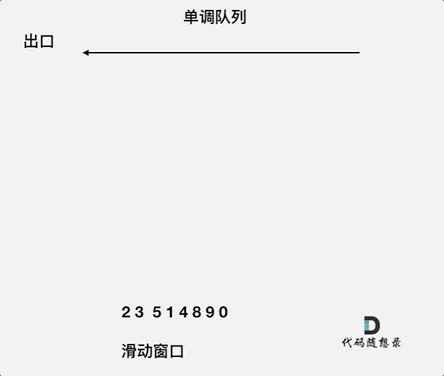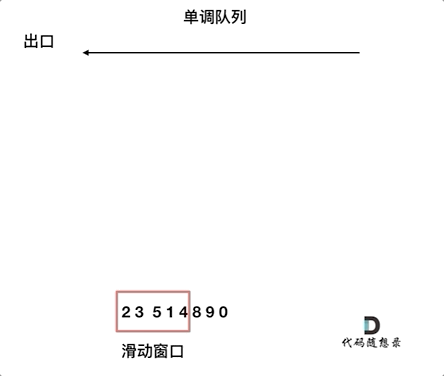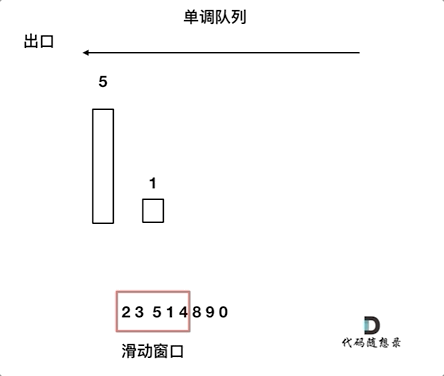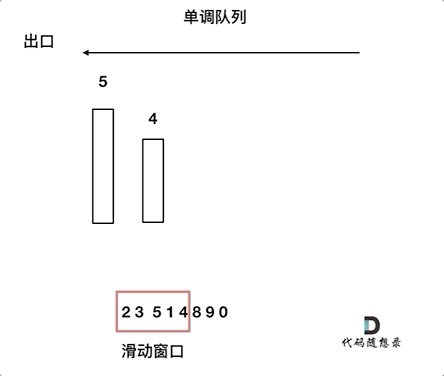
|
||||
|
||||
对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
|
||||
|
||||
|
|
@ -98,7 +98,7 @@ public:
|
|||
为了更直观的感受到单调队列的工作过程,以题目示例为例,输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
那么我们用什么数据结构来实现这个单调队列呢?
|
||||
|
||||
|
|
|
|||
|
|
@ -42,7 +42,7 @@
|
|||
|
||||
操作动画如下:
|
||||
|
||||

|
||||

|
||||
|
||||
定义一个数组叫做record用来上记录字符串s里字符出现的次数。
|
||||
|
||||
|
|
|
|||
|
|
@ -14,7 +14,7 @@
|
|||
说明: 叶子节点是指没有子节点的节点。
|
||||
|
||||
示例:
|
||||

|
||||

|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -28,7 +28,7 @@
|
|||
|
||||
前序遍历以及回溯的过程如图:
|
||||
|
||||
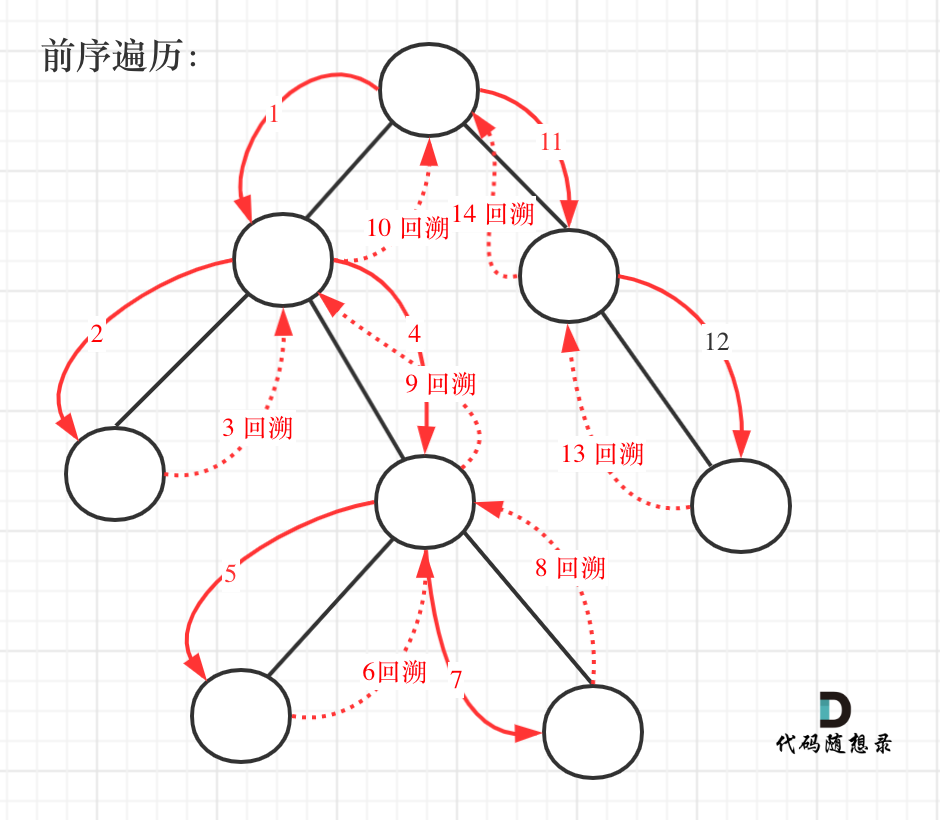
|
||||
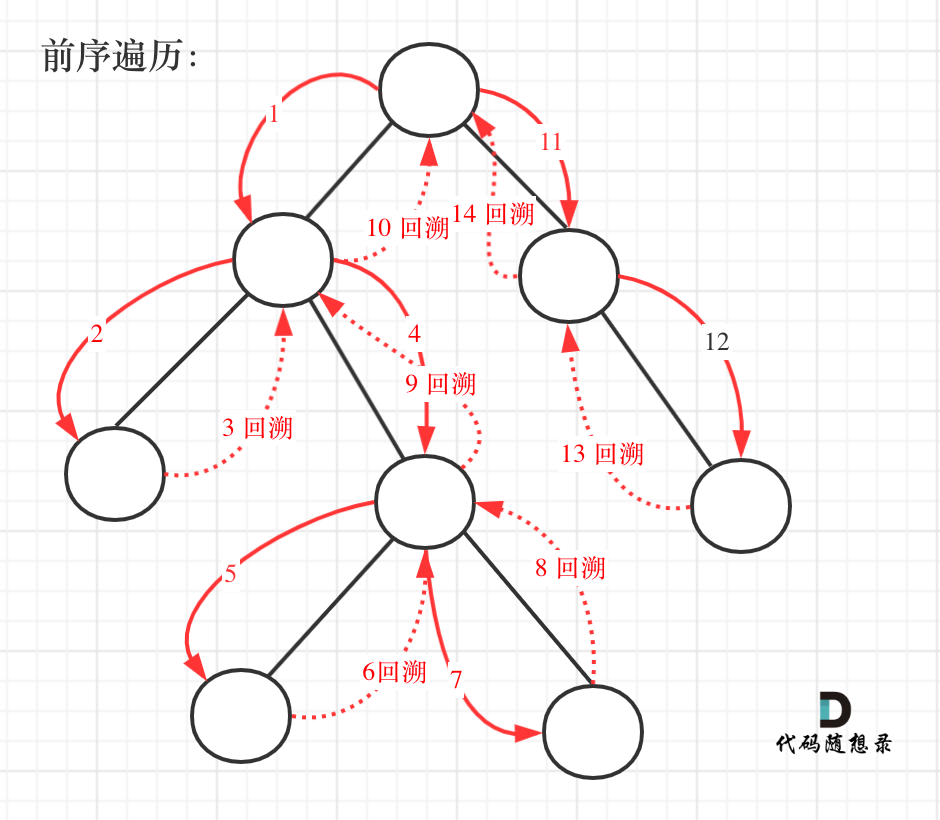
|
||||
|
||||
我们先使用递归的方式,来做前序遍历。**要知道递归和回溯就是一家的,本题也需要回溯。**
|
||||
|
||||
|
|
@ -315,7 +315,7 @@ public:
|
|||
|
||||
其实关键还在于 参数,使用的是 `string path`,这里并没有加上引用`&` ,即本层递归中,path + 该节点数值,但该层递归结束,上一层path的数值并不会受到任何影响。 如图所示:
|
||||
|
||||
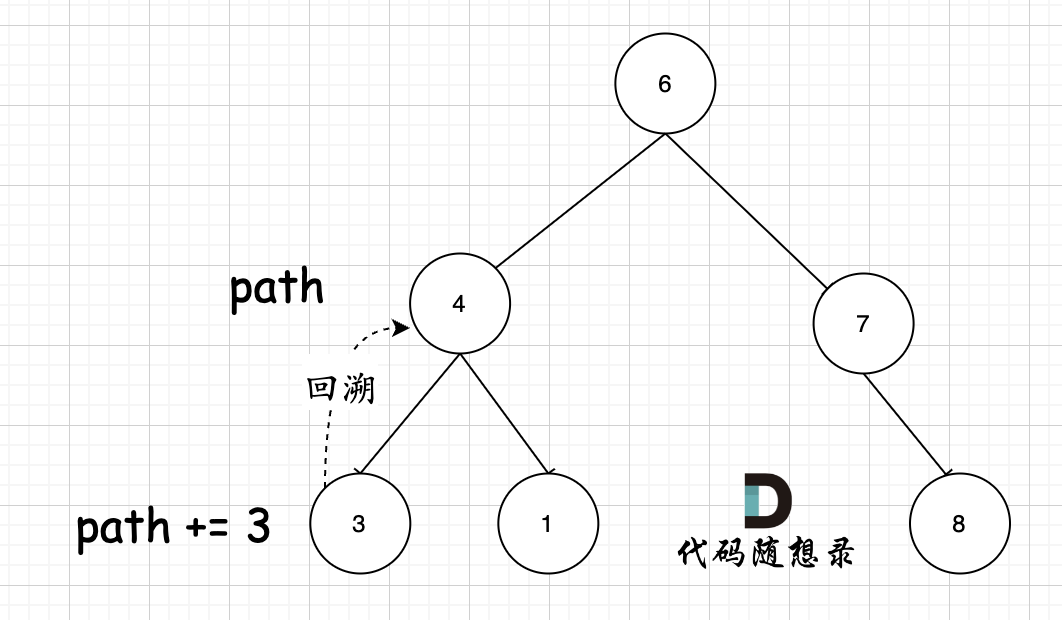
|
||||
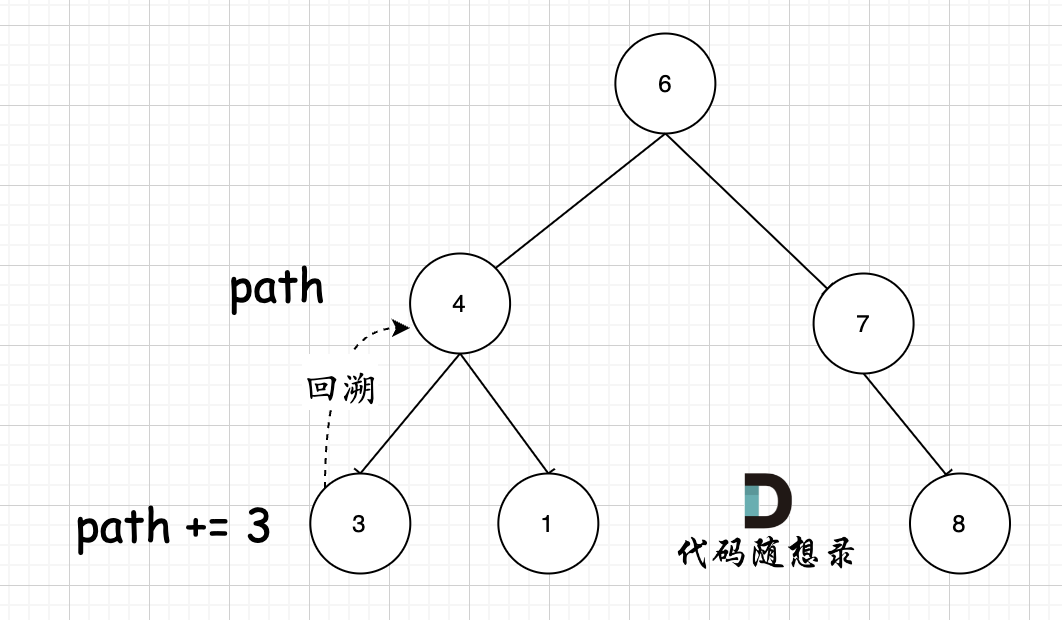
|
||||
|
||||
节点4 的path,在遍历到节点3,path+3,遍历节点3的递归结束之后,返回节点4(回溯的过程),path并不会把3加上。
|
||||
|
||||
|
|
|
|||
|
|
@ -93,7 +93,7 @@ for (int i = 0; i <= n; i++) { // 遍历背包
|
|||
已输入n为5例,dp状态图如下:
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
dp[0] = 0
|
||||
dp[1] = min(dp[0] + 1) = 1
|
||||
|
|
|
|||
|
|
@ -32,7 +32,7 @@
|
|||
|
||||
如动画所示:
|
||||
|
||||

|
||||
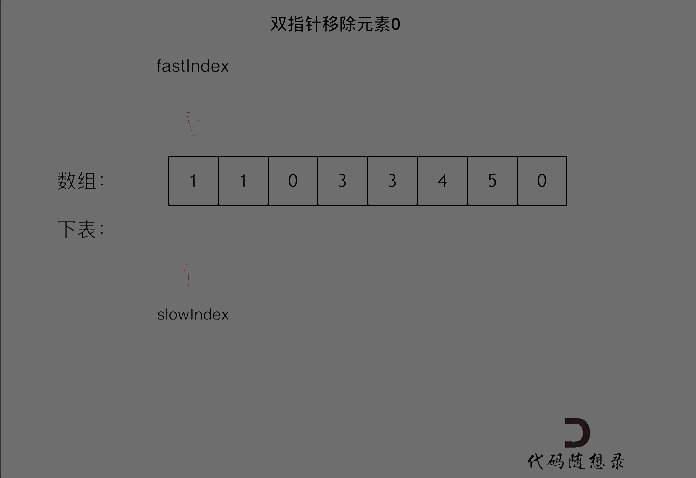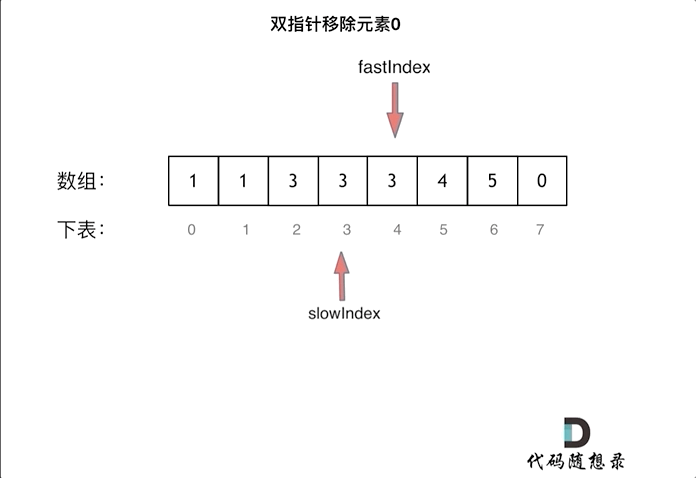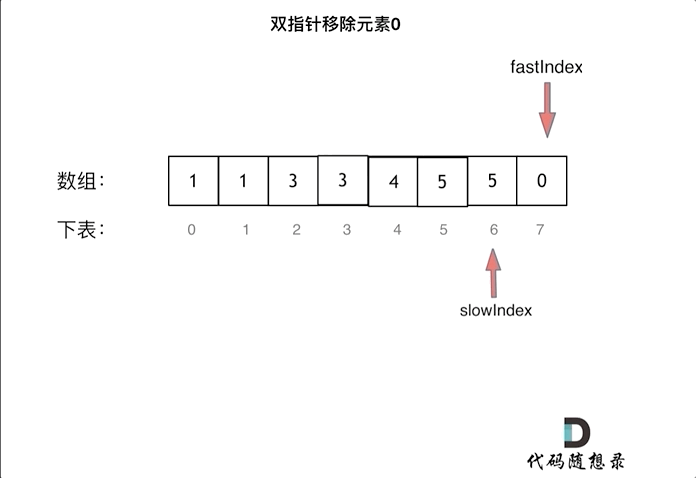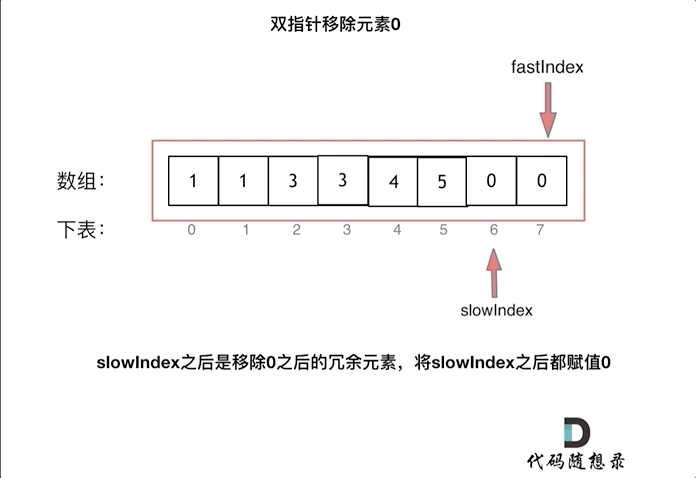
|
||||
|
||||
C++代码如下:
|
||||
|
||||
|
|
|
|||
|
|
@ -85,7 +85,7 @@ for (int i = 1; i < nums.size(); i++) {
|
|||
|
||||
输入:[0,1,0,3,2],dp数组的变化如下:
|
||||
|
||||
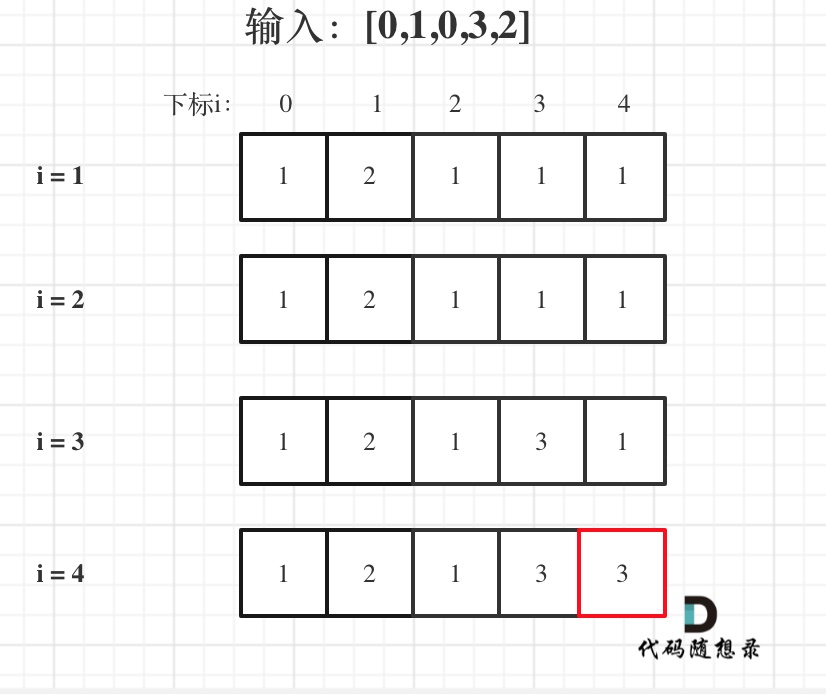
|
||||
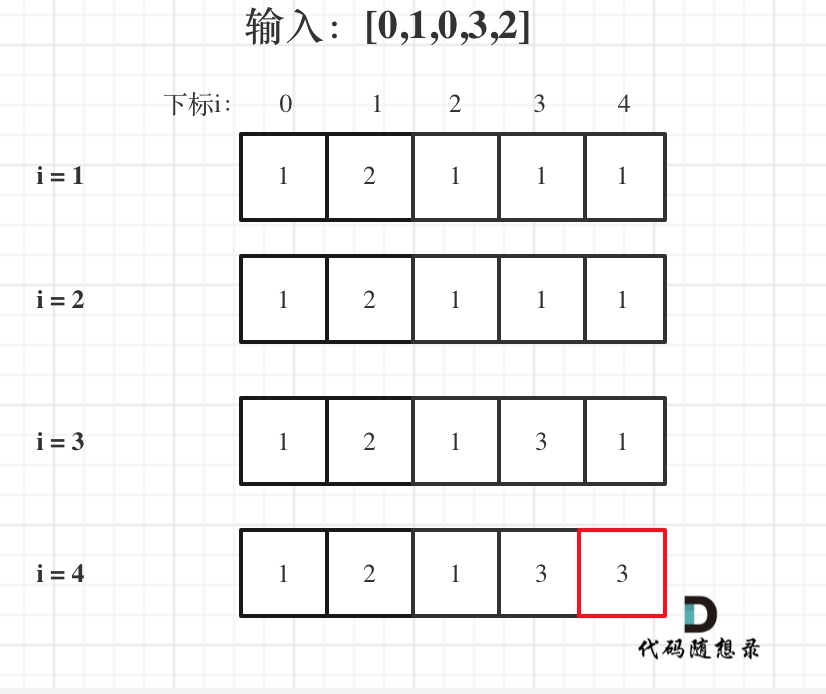
|
||||
|
||||
|
||||
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
|
||||
|
|
|
|||
|
|
@ -47,7 +47,7 @@ dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
|
|||
* 状态三:今天卖出股票
|
||||
* 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
|
||||
|
||||
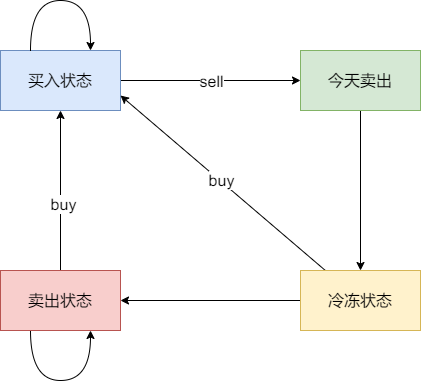
|
||||
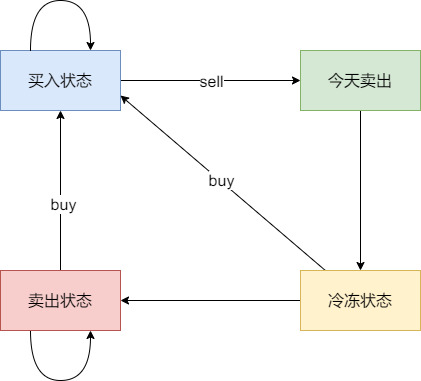
|
||||
|
||||
j的状态为:
|
||||
|
||||
|
|
@ -136,7 +136,7 @@ dp[i][3] = dp[i - 1][2];
|
|||
以 [1,2,3,0,2] 为例,dp数组如下:
|
||||
|
||||
|
||||
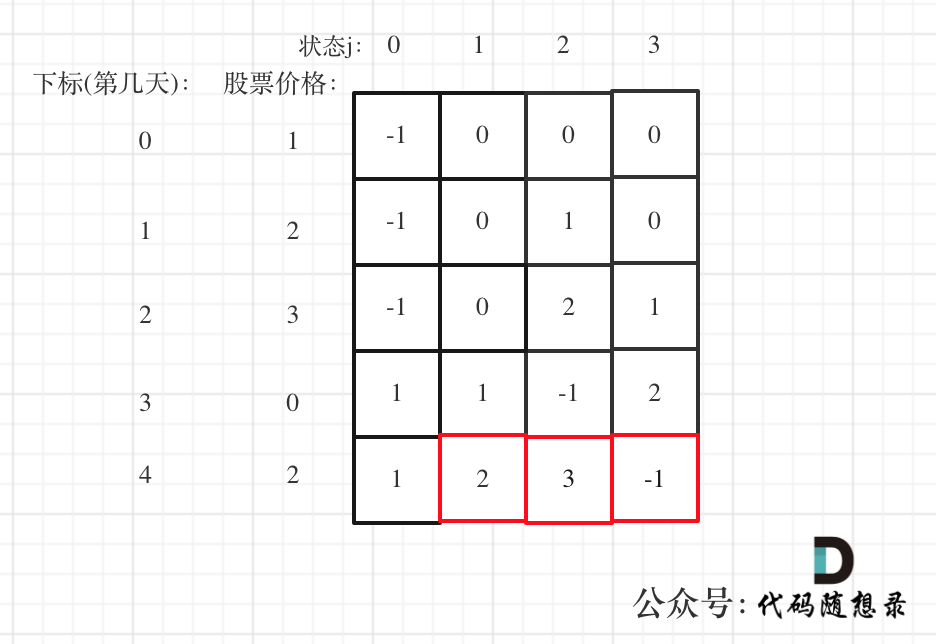
|
||||
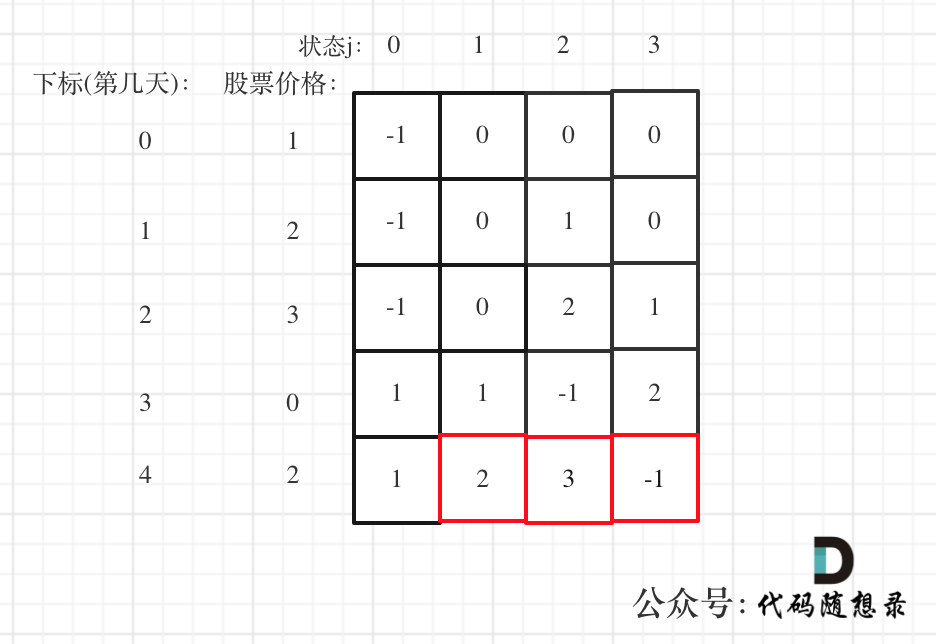
|
||||
|
||||
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
|
||||
|
||||
|
|
|
|||
|
|
@ -104,7 +104,7 @@ dp[0] = 0;
|
|||
|
||||
以输入:coins = [1, 2, 5], amount = 5为例
|
||||
|
||||
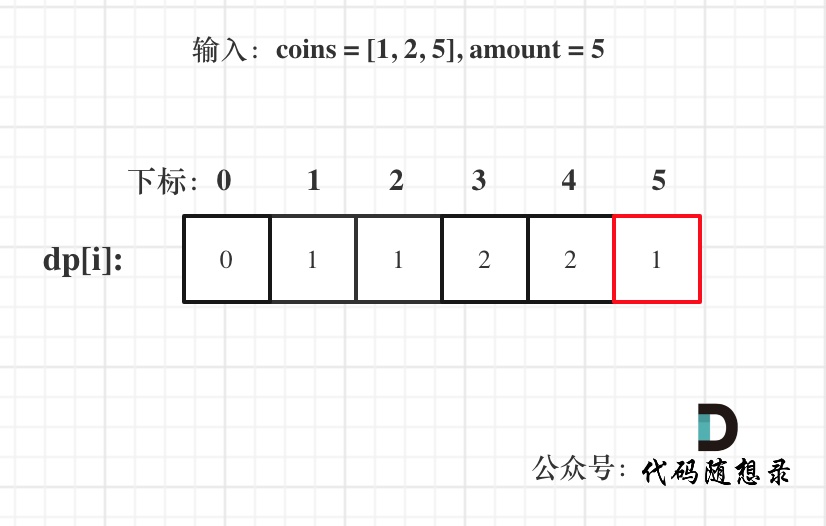
|
||||
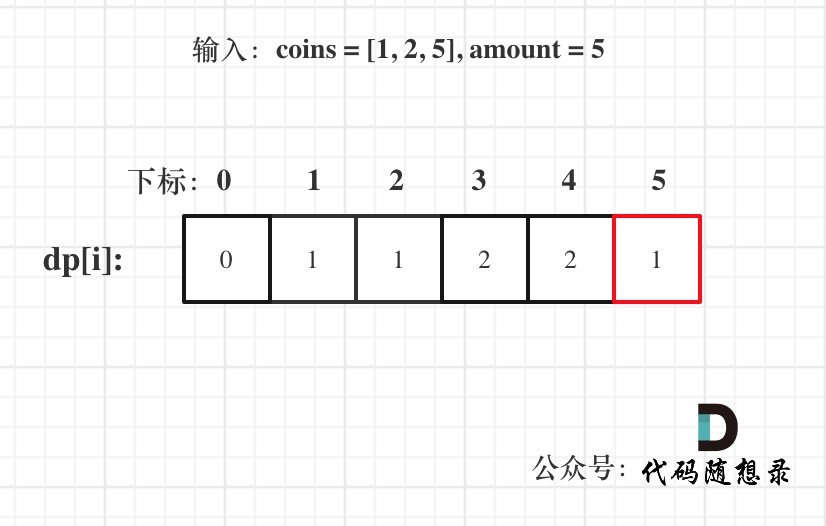
|
||||
|
||||
dp[amount]为最终结果。
|
||||
|
||||
|
|
|
|||
|
|
@ -57,7 +57,7 @@
|
|||
|
||||
对于死循环,我来举一个有重复机场的例子:
|
||||
|
||||

|
||||
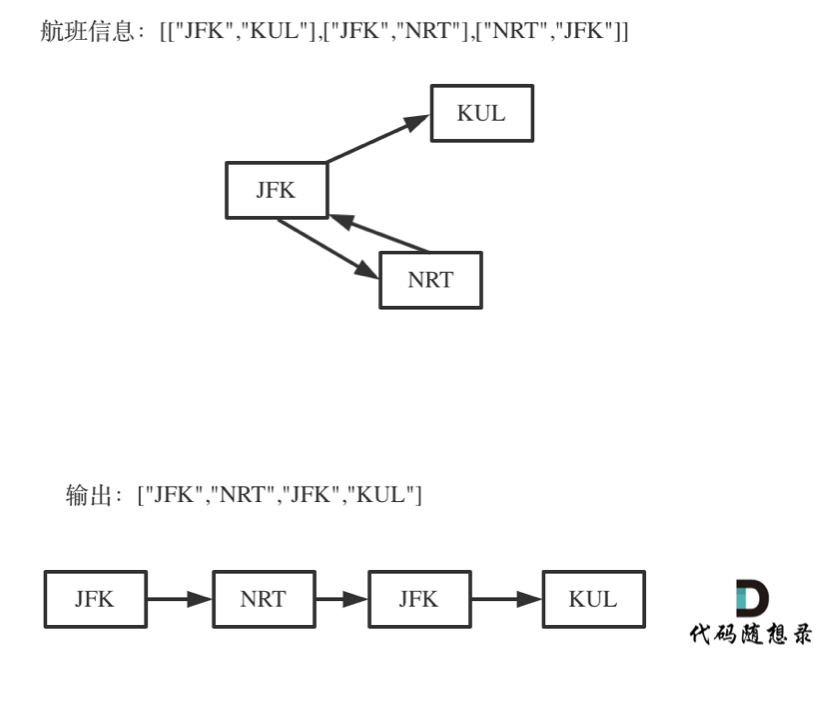
|
||||
|
||||
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
|
||||
|
||||
|
|
@ -111,7 +111,7 @@ void backtracking(参数) {
|
|||
|
||||
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
|
||||
|
||||
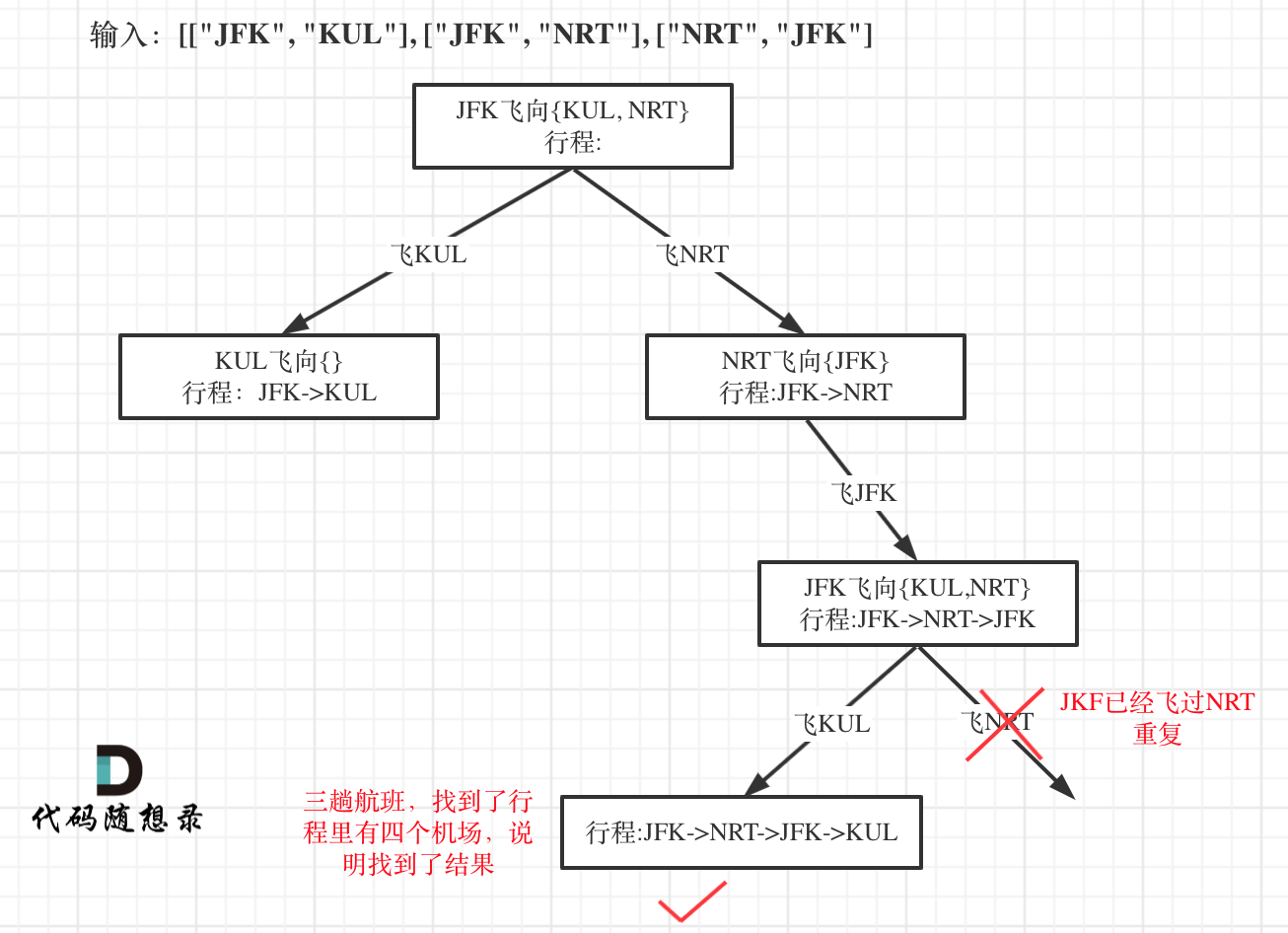
|
||||
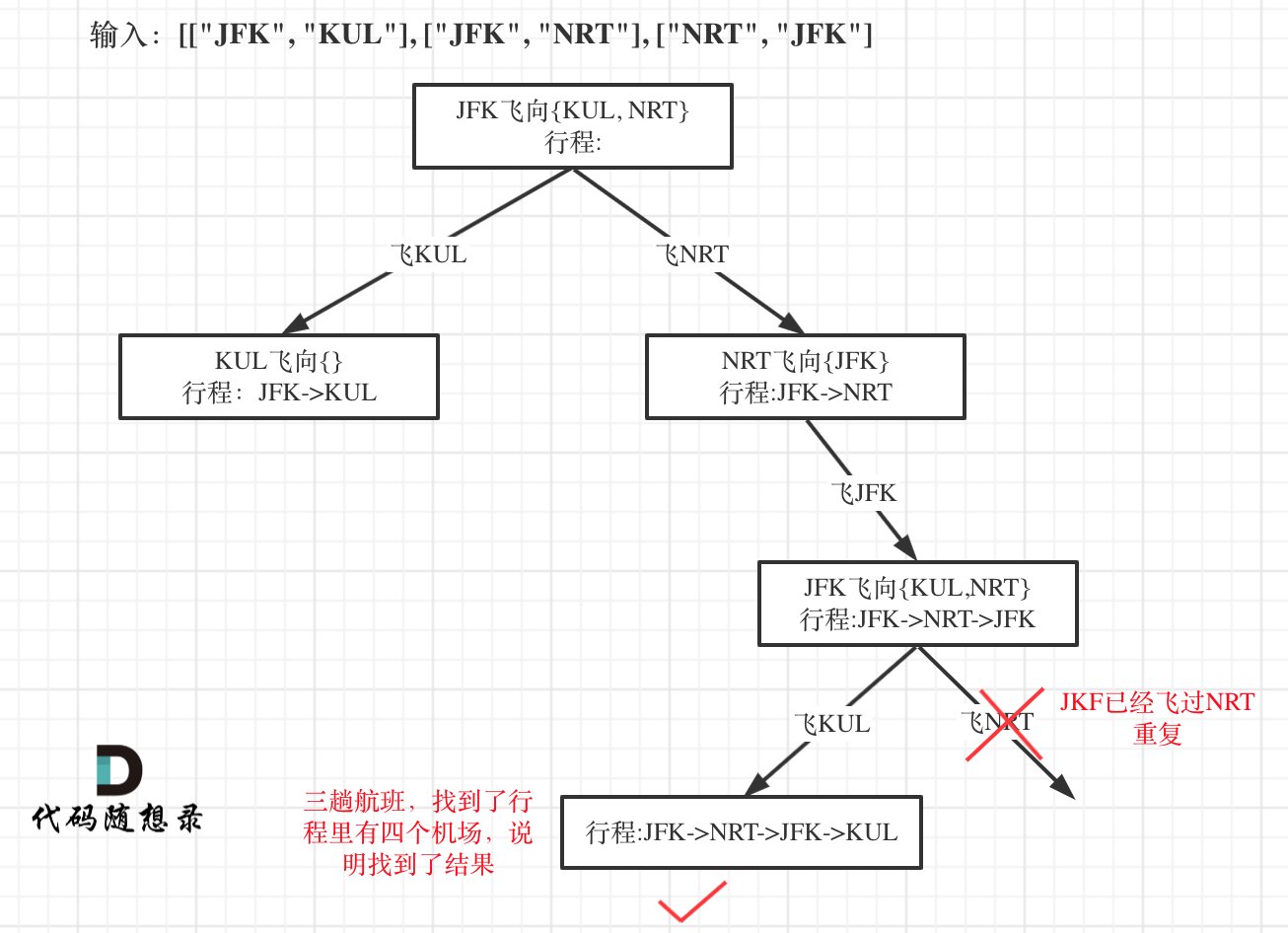
|
||||
|
||||
开始回溯三部曲讲解:
|
||||
|
||||
|
|
@ -137,7 +137,7 @@ bool backtracking(int ticketNum, vector<string>& result) {
|
|||
|
||||
因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,如图:
|
||||
|
||||
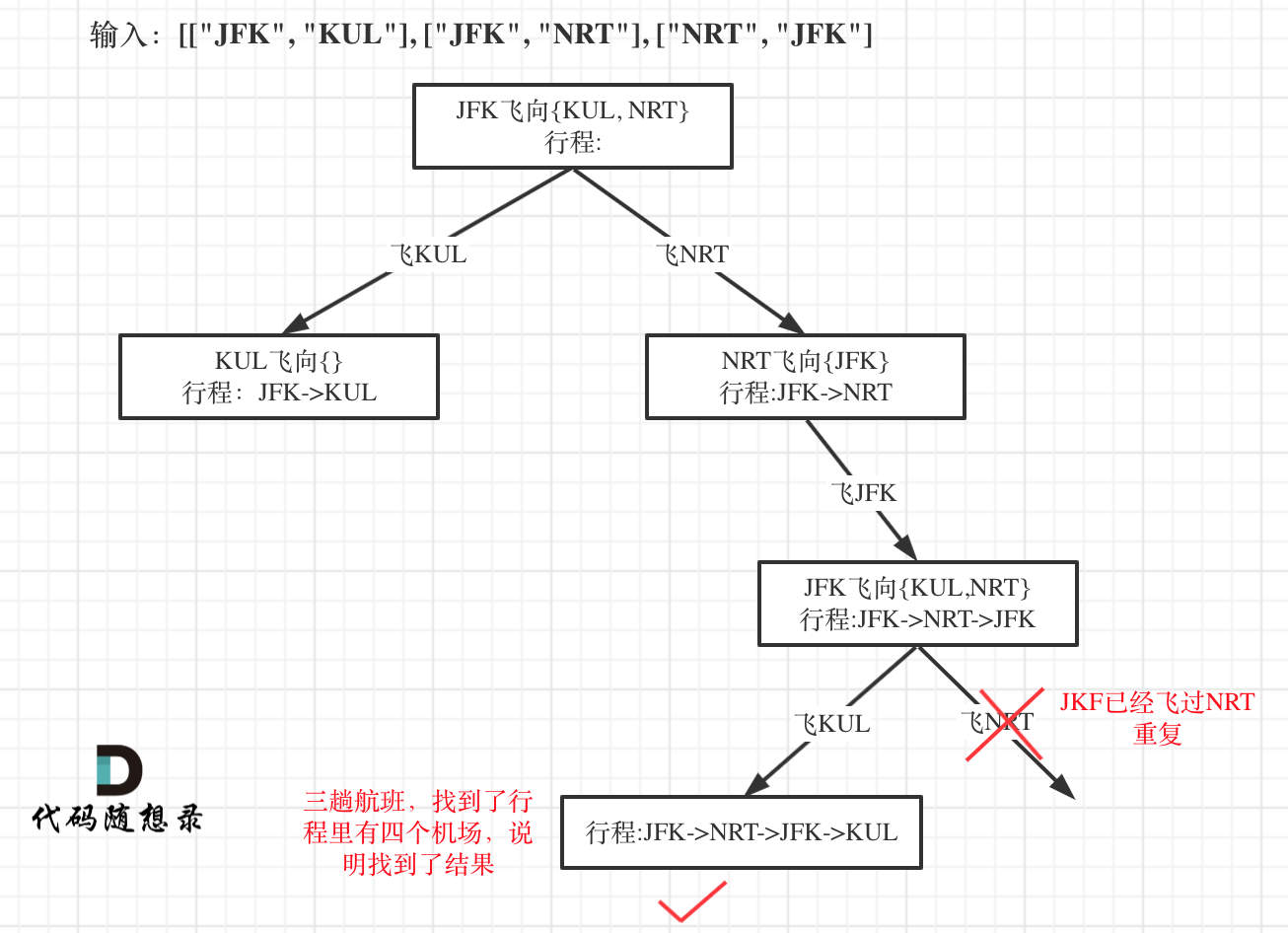
|
||||
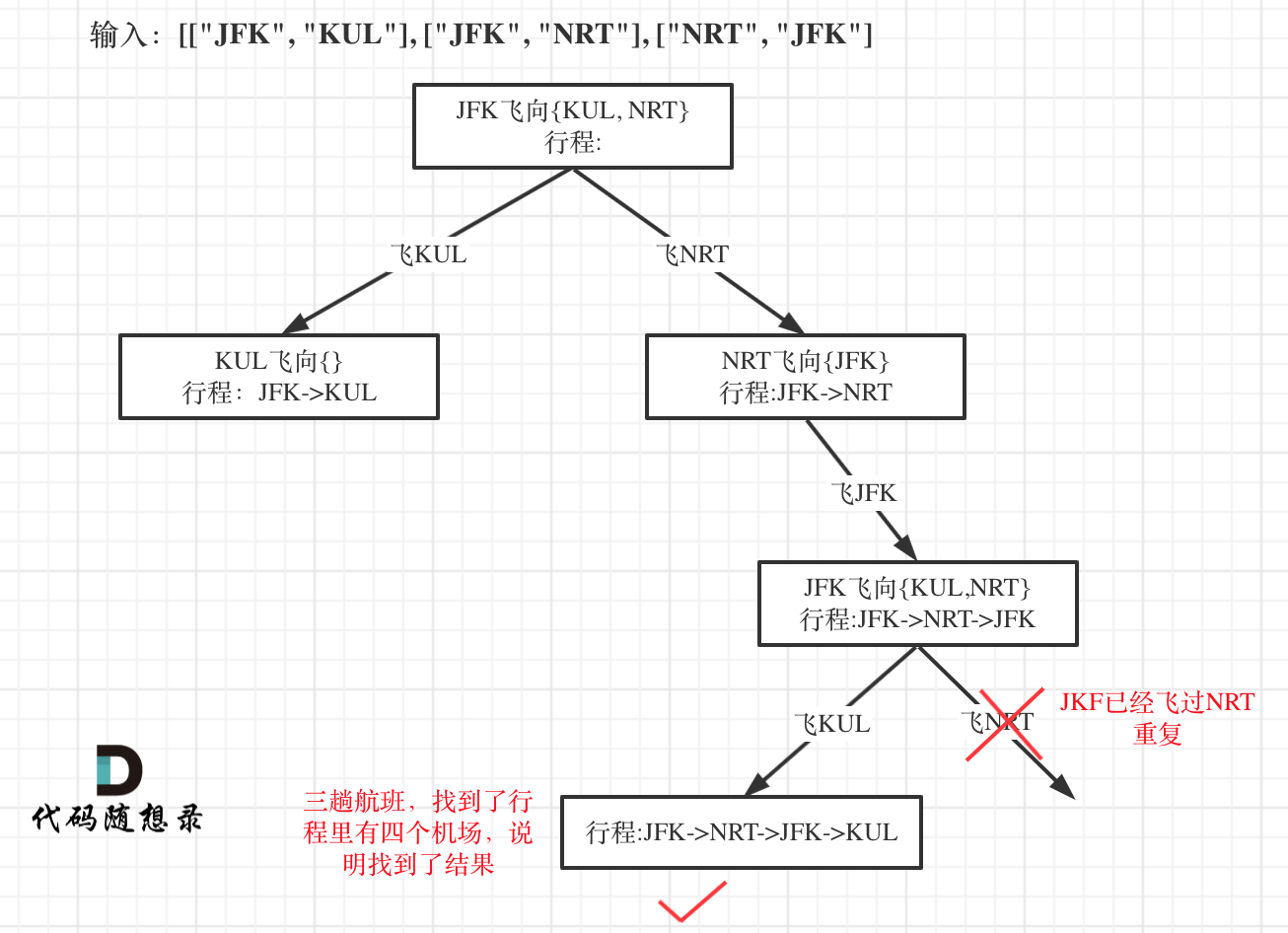
|
||||
|
||||
所以找到了这个叶子节点了直接返回,这个递归函数的返回值问题我们在讲解二叉树的系列的时候,在这篇[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://programmercarl.com/0112.路径总和.html)详细介绍过。
|
||||
|
||||
|
|
|
|||
|
|
@ -12,7 +12,7 @@
|
|||
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
|
||||
|
||||
|
||||

|
||||

|
||||
|
||||
## 算法公开课
|
||||
|
||||
|
|
@ -177,7 +177,7 @@ return {val2, val1};
|
|||
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
|
||||
|
||||
|
||||
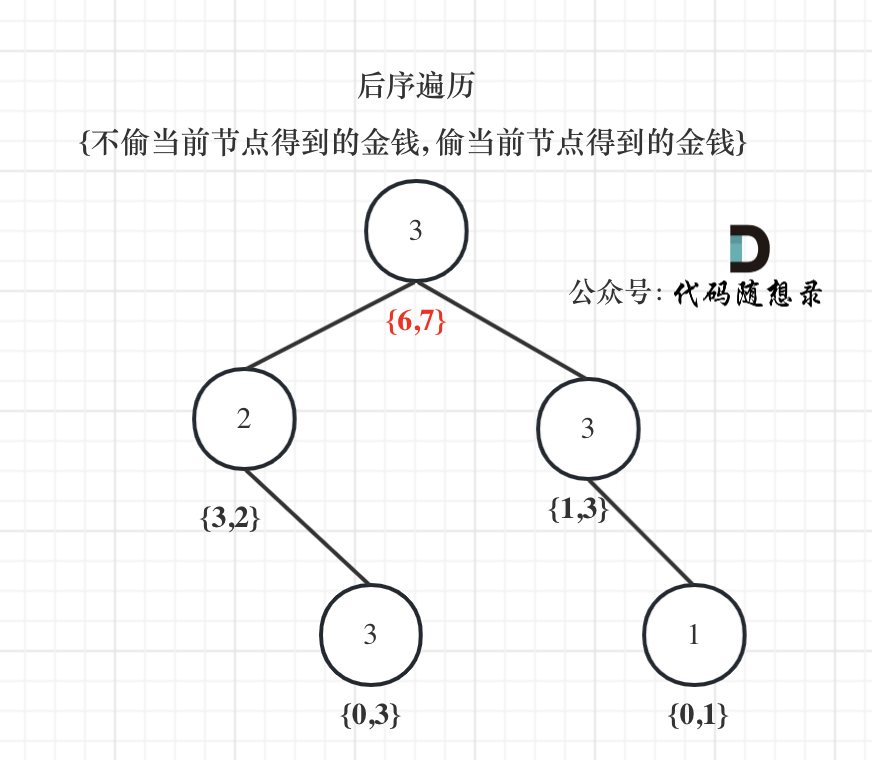
|
||||
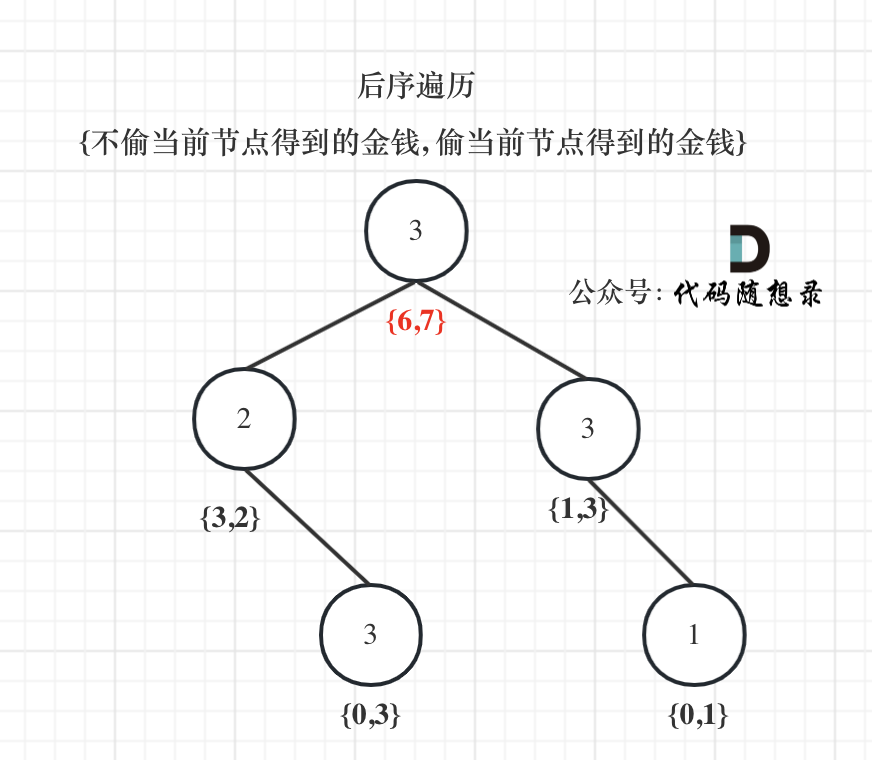
|
||||
|
||||
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
|
||||
|
||||
|
|
|
|||
Some files were not shown because too many files have changed in this diff Show More
Loading…
Reference in New Issue