欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

# 404.左叶子之和 [力扣题目链接](https://leetcode-cn.com/problems/sum-of-left-leaves/) 计算给定二叉树的所有左叶子之和。示例： ![404.左叶子之和1](https://img-blog.csdnimg.cn/20210204151927654.png) # 思路 **首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。** 因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：**如果左节点不为空，且左节点没有左右孩子，那么这个节点就是左叶子** 大家思考一下如下图中二叉树，左叶子之和究竟是多少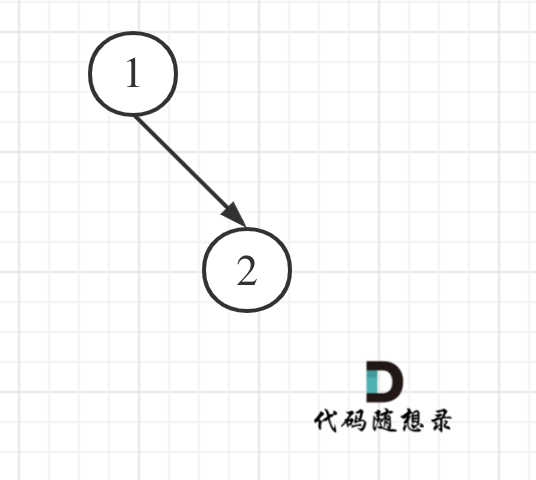？ ![404.左叶子之和](https://img-blog.csdnimg.cn/20210204151949672.png) **其实是0，因为这棵树根本没有左叶子！** 那么**判断当前节点是不是左叶子是无法判断的，必须要通过节点的父节点来判断其左孩子是不是左叶子。** 如果该节点的左节点不为空，该节点的左节点的左节点为空，该节点的左节点的右节点为空，则找到了一个左叶子，判断代码如下： ``` if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) { 左叶子节点处理逻辑 } ``` ## 递归法递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。。递归三部曲： 1. 确定递归函数的参数和返回值判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int 使用题目中给出的函数就可以了。 2. 确定终止条件依然是 ``` if (root == NULL) return 0; ``` 3. 确定单层递归的逻辑当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和右子树左叶子之和，相加便是整个树的左叶子之和。代码如下： ```CPP int leftValue = sumOfLeftLeaves(root->left); // 左 int rightValue = sumOfLeftLeaves(root->right); // 右 // 中 int midValue = 0; if (root->left && !root->left->left && !root->left->right) { midValue = root->left->val; } int sum = midValue + leftValue + rightValue; return sum; ``` 整体递归代码如下： ```CPP class Solution { public: int sumOfLeftLeaves(TreeNode* root) { if (root == NULL) return 0; int leftValue = sumOfLeftLeaves(root->left); // 左 int rightValue = sumOfLeftLeaves(root->right); // 右 // 中 int midValue = 0; if (root->left && !root->left->left && !root->left->right) { // 中 midValue = root->left->val; } int sum = midValue + leftValue + rightValue; return sum; } }; ``` 以上代码精简之后如下： ```CPP class Solution { public: int sumOfLeftLeaves(TreeNode* root) { if (root == NULL) return 0; int midValue = 0; if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) { midValue = root->left->val; } return midValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right); } }; ``` ## 迭代法本题迭代法使用前中后序都是可以的，只要把左叶子节点统计出来，就可以了，那么参考文章 [二叉树：听说递归能做的，栈也能做！](https://programmercarl.com/二叉树的迭代遍历.html)和[二叉树：迭代法统一写法](https://programmercarl.com/二叉树的统一迭代法.html)中的写法，可以写出一个前序遍历的迭代法。判断条件都是一样的，代码如下： ```CPP class Solution { public: int sumOfLeftLeaves(TreeNode* root) { stack st; if (root == NULL) return 0; st.push(root); int result = 0; while (!st.empty()) { TreeNode* node = st.top(); st.pop(); if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) { result += node->left->val; } if (node->right) st.push(node->right); if (node->left) st.push(node->left); } return result; } }; ``` # 总结这道题目要求左叶子之和，其实是比较绕的，因为不能判断本节点是不是左叶子节点。此时就要通过节点的父节点来判断其左孩子是不是左叶子了。 **平时我们解二叉树的题目时，已经习惯了通过节点的左右孩子判断本节点的属性，而本题我们要通过节点的父节点判断本节点的属性。** 希望通过这道题目，可以扩展大家对二叉树的解题思路。 # 其他语言版本 ## Java **递归** ```java class Solution { public int sumOfLeftLeaves(TreeNode root) { if (root == null) return 0; int leftValue = sumOfLeftLeaves(root.left); // 左 int rightValue = sumOfLeftLeaves(root.right); // 右 int midValue = 0; if (root.left != null && root.left.left == null && root.left.right == null) { midValue = root.left.val; } int sum = midValue + leftValue + rightValue; // 中 return sum; } } ``` **迭代** ```java class Solution { public int sumOfLeftLeaves(TreeNode root) { if (root == null) return 0; Stack stack = new Stack<> (); stack.add(root); int result = 0; while (!stack.isEmpty()) { TreeNode node = stack.pop(); if (node.left != null && node.left.left == null && node.left.right == null) { result += node.left.val; } if (node.right != null) stack.add(node.right); if (node.left != null) stack.add(node.left); } return result; } } ``` ```java // 层序遍历迭代法 class Solution { public int sumOfLeftLeaves(TreeNode root) { int sum = 0; if (root == null) return 0; Queue queue = new LinkedList<>(); queue.offer(root); while (!queue.isEmpty()) { int size = queue.size(); while (size -- > 0) { TreeNode node = queue.poll(); if (node.left != null) { // 左节点不为空 queue.offer(node.left); if (node.left.left == null && node.left.right == null){ // 左叶子节点 sum += node.left.val; } } if (node.right != null) queue.offer(node.right); } } return sum; } } ``` ## Python **递归后序遍历** ```python3 class Solution: def sumOfLeftLeaves(self, root: TreeNode) -> int: if not root: return 0 left_left_leaves_sum = self.sumOfLeftLeaves(root.left) # 左 right_left_leaves_sum = self.sumOfLeftLeaves(root.right) # 右 cur_left_leaf_val = 0 if root.left and not root.left.left and not root.left.right: cur_left_leaf_val = root.left.val return cur_left_leaf_val + left_left_leaves_sum + right_left_leaves_sum # 中 ``` **迭代** ```python3 class Solution: def sumOfLeftLeaves(self, root: TreeNode) -> int: """ Idea: Each time check current node's left node. If current node don't have one, skip it. """ stack = [] if root: stack.append(root) res = 0 while stack: # 每次都把当前节点的左节点加进去. cur_node = stack.pop() if cur_node.left and not cur_node.left.left and not cur_node.left.right: res += cur_node.left.val if cur_node.left: stack.append(cur_node.left) if cur_node.right: stack.append(cur_node.right) return res ``` ## Go **递归法** ```go func sumOfLeftLeaves(root *TreeNode) int { var res int findLeft(root,&res) return res } func findLeft(root *TreeNode,res *int){ //左节点 if root.Left!=nil&&root.Left.Left==nil&&root.Left.Right==nil{ *res=*res+root.Left.Val } if root.Left!=nil{ findLeft(root.Left,res) } if root.Right!=nil{ findLeft(root.Right,res) } } ``` **迭代法** ```go func sumOfLeftLeaves(root *TreeNode) int { var res int queue:=list.New() queue.PushBack(root) for queue.Len()>0{ length:=queue.Len() for i:=0;i