
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
> 这个图就是大厂面试经典题目,接雨水! 最常青藤的一道题,面试官百出不厌!
# 42. 接雨水
[力扣题目链接](https://leetcode-cn.com/problems/trapping-rain-water/)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

* 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
* 输出:6
* 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
* 输入:height = [4,2,0,3,2,5]
* 输出:9
# 思路
接雨水问题在面试中还是常见题目的,有必要好好讲一讲。
本文深度讲解如下三种方法:
* 双指针法
* 动态规划
* 单调栈
## 双指针解法
这道题目使用双指针法并不简单,我们来看一下思路。
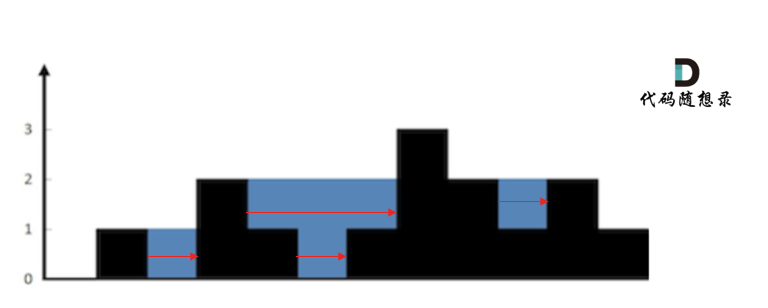
首先要明确,要按照行来计算,还是按照列来计算。
按照行来计算如图:
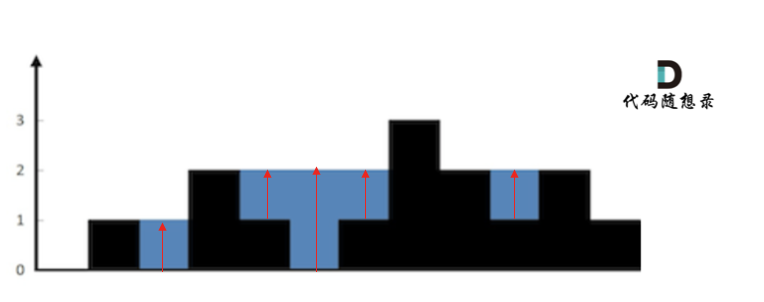
按照列来计算如图:
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
我个人倾向于按照列来计算,比较容易理解,接下来看一下按照列如何计算。
首先,**如果按照列来计算的话,宽度一定是1了,我们再把每一列的雨水的高度求出来就可以了。**
可以看出每一列雨水的高度,取决于,该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度。
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
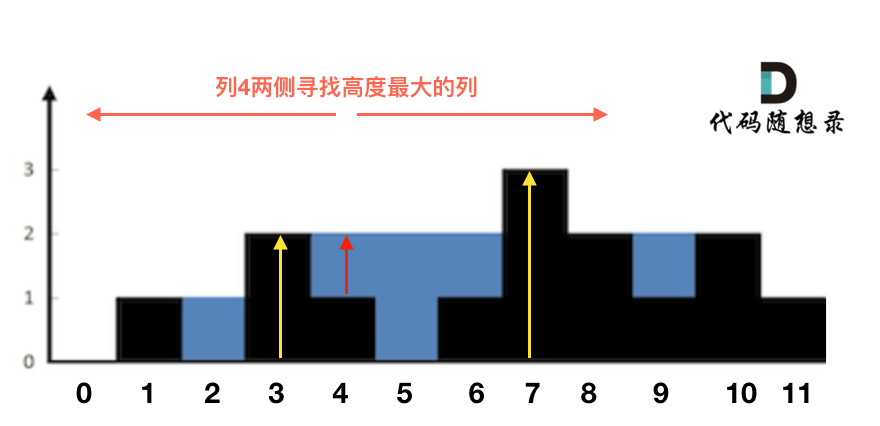
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
列4 右侧最高的柱子是列7,高度为3(以下用rHeight表示)。
列4 柱子的高度为1(以下用height表示)
那么列4的雨水高度为 列3和列7的高度最小值减列4高度,即: min(lHeight, rHeight) - height。
列4的雨水高度求出来了,宽度为1,相乘就是列4的雨水体积了。
此时求出了列4的雨水体积。
一样的方法,只要从头遍历一遍所有的列,然后求出每一列雨水的体积,相加之后就是总雨水的体积了。
首先从头遍历所有的列,并且**要注意第一个柱子和最后一个柱子不接雨水**,代码如下:
```CPP
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
}
```
在for循环中求左右两边最高柱子,代码如下:
```CPP
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
```
最后,计算该列的雨水高度,代码如下:
```CPP
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h; // 注意只有h大于零的时候,在统计到总和中
```
整体代码如下:
```CPP
class Solution {
public:
int trap(vector& height) {
int sum = 0;
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
};
```
因为每次遍历列的时候,还要向两边寻找最高的列,所以时间复杂度为$O(n^2)$。
空间复杂度为$O(1)$。
## 动态规划解法
在上一节的双指针解法中,我们可以看到只要记录左边柱子的最高高度 和 右边柱子的最高高度,就可以计算当前位置的雨水面积,这就是通过列来计算。
当前列雨水面积:min(左边柱子的最高高度,记录右边柱子的最高高度) - 当前柱子高度。
为了得到两边的最高高度,使用了双指针来遍历,每到一个柱子都向两边遍历一遍,这其实是有重复计算的。我们把每一个位置的左边最高高度记录在一个数组上(maxLeft),右边最高高度记录在一个数组上(maxRight)。这样就避免了重复计算,这就用到了动态规划。
当前位置,左边的最高高度是前一个位置的左边最高高度和本高度的最大值。
即从左向右遍历:maxLeft[i] = max(height[i], maxLeft[i - 1]);
从右向左遍历:maxRight[i] = max(height[i], maxRight[i + 1]);
这样就找到递推公式。
代码如下:
```CPP
class Solution {
public:
int trap(vector& height) {
if (height.size() <= 2) return 0;
vector maxLeft(height.size(), 0);
vector maxRight(height.size(), 0);
int size = maxRight.size();
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i < size; i++) {
maxLeft[i] = max(height[i], maxLeft[i - 1]);
}
// 记录每个柱子右边柱子最大高度
maxRight[size - 1] = height[size - 1];
for (int i = size - 2; i >= 0; i--) {
maxRight[i] = max(height[i], maxRight[i + 1]);
}
// 求和
int sum = 0;
for (int i = 0; i < size; i++) {
int count = min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;
}
return sum;
}
};
```
## 单调栈解法
这个解法可以说是最不好理解的了,所以下面我花了大量的篇幅来介绍这种方法。
单调栈就是保持栈内元素有序。和[栈与队列:单调队列](https://programmercarl.com/0239.滑动窗口最大值.html)一样,需要我们自己维持顺序,没有现成的容器可以用。
### 准备工作
那么本题使用单调栈有如下几个问题:
1. 首先单调栈是按照行方向来计算雨水,如图:

知道这一点,后面的就可以理解了。
2. 使用单调栈内元素的顺序
从大到小还是从小到大呢?
从栈头(元素从栈头弹出)到栈底的顺序应该是从小到大的顺序。
因为一旦发现添加的柱子高度大于栈头元素了,此时就出现凹槽了,栈头元素就是凹槽底部的柱子,栈头第二个元素就是凹槽左边的柱子,而添加的元素就是凹槽右边的柱子。
如图:

3. 遇到相同高度的柱子怎么办。
遇到相同的元素,更新栈内下标,就是将栈里元素(旧下标)弹出,将新元素(新下标)加入栈中。
例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出,把第二个5添加到栈中。
**因为我们要求宽度的时候 如果遇到相同高度的柱子,需要使用最右边的柱子来计算宽度**。
如图所示:

4. 栈里要保存什么数值
是用单调栈,其实是通过 长 * 宽 来计算雨水面积的。
长就是通过柱子的高度来计算,宽是通过柱子之间的下标来计算,
那么栈里有没有必要存一个pair类型的元素,保存柱子的高度和下标呢。
其实不用,栈里就存放int类型的元素就行了,表示下标,想要知道对应的高度,通过height[stack.top()] 就知道弹出的下标对应的高度了。
所以栈的定义如下:
```
stack st; // 存着下标,计算的时候用下标对应的柱子高度
```
明确了如上几点,我们再来看处理逻辑。
### 单调栈处理逻辑
先将下标0的柱子加入到栈中,`st.push(0);`。
然后开始从下标1开始遍历所有的柱子,`for (int i = 1; i < height.size(); i++)`。
如果当前遍历的元素(柱子)高度小于栈顶元素的高度,就把这个元素加入栈中,因为栈里本来就要保持从小到大的顺序(从栈头到栈底)。
代码如下:
```
if (height[i] < height[st.top()]) st.push(i);
```
如果当前遍历的元素(柱子)高度等于栈顶元素的高度,要跟更新栈顶元素,因为遇到相相同高度的柱子,需要使用最右边的柱子来计算宽度。
代码如下:
```
if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
st.pop();
st.push(i);
}
```
如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:

取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
此时的栈顶元素st.top(),就是凹槽的左边位置,下标为st.top(),对应的高度为height[st.top()](就是图中的高度2)。
当前遍历的元素i,就是凹槽右边的位置,下标为i,对应的高度为height[i](就是图中的高度3)。
此时大家应该可以发现其实就是**栈顶和栈顶的下一个元素以及要入栈的三个元素来接水!**
那么雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度,代码为:`int h = min(height[st.top()], height[i]) - height[mid];`
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度),代码为:`int w = i - st.top() - 1 ;`
当前凹槽雨水的体积就是:`h * w`。
求当前凹槽雨水的体积代码如下:
```CPP
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while,持续跟新栈顶元素
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
```
关键部分讲完了,整体代码如下:
```CPP
class Solution {
public:
int trap(vector& height) {
if (height.size() <= 2) return 0; // 可以不加
stack st; // 存着下标,计算的时候用下标对应的柱子高度
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
if (height[i] < height[st.top()]) { // 情况一
st.push(i);
} if (height[i] == height[st.top()]) { // 情况二
st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
st.push(i);
} else { // 情况三
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
};
```
以上代码冗余了一些,但是思路是清晰的,下面我将代码精简一下,如下:
```CPP
class Solution {
public:
int trap(vector& height) {
stack st;
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
while (!st.empty() && height[i] > height[st.top()]) {
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1;
sum += h * w;
}
}
st.push(i);
}
return sum;
}
};
```
精简之后的代码,大家就看不出去三种情况的处理了,貌似好像只处理的情况三,其实是把情况一和情况二融合了。 这样的代码不太利于理解。
## 其他语言版本
Java:
双指针法
```java
class Solution {
public int trap(int[] height) {
int sum = 0;
for (int i = 0; i < height.length; i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i==0 || i== height.length - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i+1; r < height.length; r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i-1; l >= 0; l--) {
if(height[l] > lHeight) lHeight = height[l];
}
int h = Math.min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
}
```
动态规划法
```java
class Solution {
public int trap(int[] height) {
int length = height.length;
if (length <= 2) return 0;
int[] maxLeft = new int[length];
int[] maxRight = new int[length];
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i< length; i++) maxLeft[i] = Math.max(height[i], maxLeft[i-1]);
// 记录每个柱子右边柱子最大高度
maxRight[length - 1] = height[length - 1];
for(int i = length - 2; i >= 0; i--) maxRight[i] = Math.max(height[i], maxRight[i+1]);
// 求和
int sum = 0;
for (int i = 0; i < length; i++) {
int count = Math.min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;
}
return sum;
}
}
```
单调栈法
```java
class Solution {
public int trap(int[] height){
int size = height.length;
if (size <= 2) return 0;
// in the stack, we push the index of array
// using height[] to access the real height
Stack stack = new Stack();
stack.push(0);
int sum = 0;
for (int index = 1; index < size; index++){
int stackTop = stack.peek();
if (height[index] < height[stackTop]){
stack.push(index);
}else if (height[index] == height[stackTop]){
// 因为相等的相邻墙,左边一个是不可能存放雨水的,所以pop左边的index, push当前的index
stack.pop();
stack.push(index);
}else{
//pop up all lower value
int heightAtIdx = height[index];
while (!stack.isEmpty() && (heightAtIdx > height[stackTop])){
int mid = stack.pop();
if (!stack.isEmpty()){
int left = stack.peek();
int h = Math.min(height[left], height[index]) - height[mid];
int w = index - left - 1;
int hold = h * w;
if (hold > 0) sum += hold;
stackTop = stack.peek();
}
}
stack.push(index);
}
}
return sum;
}
}
```
Python:
双指针法
```python3
class Solution:
def trap(self, height: List[int]) -> int:
res = 0
for i in range(len(height)):
if i == 0 or i == len(height)-1: continue
lHight = height[i-1]
rHight = height[i+1]
for j in range(i-1):
if height[j] > lHight:
lHight = height[j]
for k in range(i+2,len(height)):
if height[k] > rHight:
rHight = height[k]
res1 = min(lHight,rHight) - height[i]
if res1 > 0:
res += res1
return res
```
动态规划
```python3
class Solution:
def trap(self, height: List[int]) -> int:
leftheight, rightheight = [0]*len(height), [0]*len(height)
leftheight[0]=height[0]
for i in range(1,len(height)):
leftheight[i]=max(leftheight[i-1],height[i])
rightheight[-1]=height[-1]
for i in range(len(height)-2,-1,-1):
rightheight[i]=max(rightheight[i+1],height[i])
result = 0
for i in range(0,len(height)):
summ = min(leftheight[i],rightheight[i])-height[i]
result += summ
return result
```
单调栈
```python3
class Solution:
def trap(self, height: List[int]) -> int:
# 单调栈
'''
单调栈是按照 行 的方向来计算雨水
从栈顶到栈底的顺序:从小到大
通过三个元素来接水:栈顶,栈顶的下一个元素,以及即将入栈的元素
雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度
雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1(因为只求中间宽度)
'''
# stack储存index,用于计算对应的柱子高度
stack = [0]
result = 0
for i in range(1, len(height)):
# 情况一
if height[i] < height[stack[-1]]:
stack.append(i)
# 情况二
# 当当前柱子高度和栈顶一致时,左边的一个是不可能存放雨水的,所以保留右侧新柱子
# 需要使用最右边的柱子来计算宽度
elif height[i] == height[stack[-1]]:
stack.pop()
stack.append(i)
# 情况三
else:
# 抛出所有较低的柱子
while stack and height[i] > height[stack[-1]]:
# 栈顶就是中间的柱子:储水槽,就是凹槽的地步
mid_height = height[stack[-1]]
stack.pop()
if stack:
right_height = height[i]
left_height = height[stack[-1]]
# 两侧的较矮一方的高度 - 凹槽底部高度
h = min(right_height, left_height) - mid_height
# 凹槽右侧下标 - 凹槽左侧下标 - 1: 只求中间宽度
w = i - stack[-1] - 1
# 体积:高乘宽
result += h * w
stack.append(i)
return result
# 单调栈压缩版
class Solution:
def trap(self, height: List[int]) -> int:
stack = [0]
result = 0
for i in range(1, len(height)):
while stack and height[i] > height[stack[-1]]:
mid_height = stack.pop()
if stack:
# 雨水高度是 min(凹槽左侧高度, 凹槽右侧高度) - 凹槽底部高度
h = min(height[stack[-1]], height[i]) - height[mid_height]
# 雨水宽度是 凹槽右侧的下标 - 凹槽左侧的下标 - 1
w = i - stack[-1] - 1
# 累计总雨水体积
result += h * w
stack.append(i)
return result
```
Go:
```go
func trap(height []int) int {
var left, right, leftMax, rightMax, res int
right = len(height) - 1
for left < right {
if height[left] < height[right] {
if height[left] >= leftMax {
leftMax = height[left] // 设置左边最高柱子
} else {
res += leftMax - height[left] // //右边必定有柱子挡水,所以遇到所有值小于等于leftMax的,全部加入水池中
}
left++
} else {
if height[right] > rightMax {
rightMax = height[right] // //设置右边最高柱子
} else {
res += rightMax - height[right] // //左边必定有柱子挡水,所以,遇到所有值小于等于rightMax的,全部加入水池
}
right--
}
}
return res
}
```
动态规划解法:
```go
func trap(height []int) int {
sum:=0
n:=len(height)
lh:=make([]int,n)
rh:=make([]int,n)
lh[0]=height[0]
rh[n-1]=height[n-1]
for i:=1;i=0;i--{
rh[i]=max(rh[i+1],height[i])
}
for i:=1;i0{
sum+=h
}
}
return sum
}
func max(a,b int)int{
if a>b{
return a
}
return b
}
func min(a,b int)int{
if a rHeight) rHeight = height[r];
}
for(let l = i - 1; l >= 0; l--){
if(height[l] > lHeight) lHeight = height[l];
}
let h = Math.min(lHeight, rHeight) - height[i];
if(h > 0) sum += h;
}
return sum;
};
//动态规划
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0;
const maxLeft = new Array(len).fill(0);
const maxRight = new Array(len).fill(0);
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for(let i = 1; i < len; i++){
maxLeft[i] = Math.max(height[i], maxLeft[i - 1]);
}
// 记录每个柱子右边柱子最大高度
maxRight[len - 1] = height[len - 1];
for(let i = len - 2; i >= 0; i--){
maxRight[i] = Math.max(height[i], maxRight[i + 1]);
}
// 求和
let sum = 0;
for(let i = 0; i < len; i++){
let count = Math.min(maxLeft[i], maxRight[i]) - height[i];
if(count > 0) sum += count;
}
return sum;
};
//单调栈 js数组作为栈
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0; // 可以不加
const st = [];// 存着下标,计算的时候用下标对应的柱子高度
st.push(0);
let sum = 0;
for(let i = 1; i < len; i++){
if(height[i] < height[st[st.length - 1]]){ // 情况一
st.push(i);
}
if (height[i] == height[st[st.length - 1]]) { // 情况二
st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
st.push(i);
} else { // 情况三
while (st.length !== 0 && height[i] > height[st[st.length - 1]]) { // 注意这里是while
let mid = st[st.length - 1];
st.pop();
if (st.length !== 0) {
let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
let w = i - st[st.length - 1] - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
st.push(i);
}
}
return sum;
};
//单调栈 简洁版本 只处理情况三
var trap = function(height) {
const len = height.length;
if(len <= 2) return 0; // 可以不加
const st = [];// 存着下标,计算的时候用下标对应的柱子高度
st.push(0);
let sum = 0;
for(let i = 1; i < len; i++){ // 只处理的情况三,其实是把情况一和情况二融合了
while (st.length !== 0 && height[i] > height[st[st.length - 1]]) { // 注意这里是while
let mid = st[st.length - 1];
st.pop();
if (st.length !== 0) {
let h = Math.min(height[st[st.length - 1]], height[i]) - height[mid];
let w = i - st[st.length - 1] - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
st.push(i);
}
return sum;
};
```
C:
一种更简便的双指针方法:
之前的双指针方法的原理是固定“底”的位置,往两边找比它高的“壁”,循环若干次求和。
我们逆向思维,把“壁”用两个初始位置在数组首末位置的指针表示,“壁”往中间推,同样可以让每个“底”都能找到最高的“壁”
本质上就是改变了运算方向,从而减少了重复运算
代码如下:
```C
int trap(int* height, int heightSize) {
int ans = 0;
int left = 0, right = heightSize - 1; //初始化两个指针到左右两边
int leftMax = 0, rightMax = 0; //这两个值用来记录左右的“壁”的最高值
while (left < right) { //两个指针重合就结束
leftMax = fmax(leftMax, height[left]);
rightMax = fmax(rightMax, height[right]);
if (leftMax < rightMax) {
ans += leftMax - height[left]; //这里考虑的是下标为left的“底”能装多少水
++left;//指针的移动次序是这个方法的关键
//这里左指针右移是因为左“墙”较矮,左边这一片实际情况下的盛水量是受制于这个矮的左“墙”的
//而较高的右边在实际情况下的限制条件可能不是当前的左“墙”,比如限制条件可能是右“墙”,就能装更高的水,
}
else {
ans += rightMax - height[right]; //同理,考虑下标为right的元素
--right;
}
}
return ans;
}
```
* 时间复杂度 $O(n)$
* 空间复杂度 $O(1)$
-----------------------

