欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

> 求高度还是求深度，你搞懂了不？ ## 110.平衡二叉树题目地址：https://leetcode-cn.com/problems/balanced-binary-tree/ 给定一个二叉树，判断它是否是高度平衡的二叉树。本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。示例 1: 给定二叉树 [3,9,20,null,null,15,7] ![110.平衡二叉树](https://img-blog.csdnimg.cn/2021020315542230.png) 返回 true 。示例 2: 给定二叉树 [1,2,2,3,3,null,null,4,4] ![110.平衡二叉树1](https://img-blog.csdnimg.cn/20210203155447919.png) 返回 false 。 ## 题外话咋眼一看这道题目和[二叉树：看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)很像，其实有很大区别。这里强调一波概念： * 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数。 * 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数。但leetcode中强调的深度和高度很明显是按照节点来计算的，如图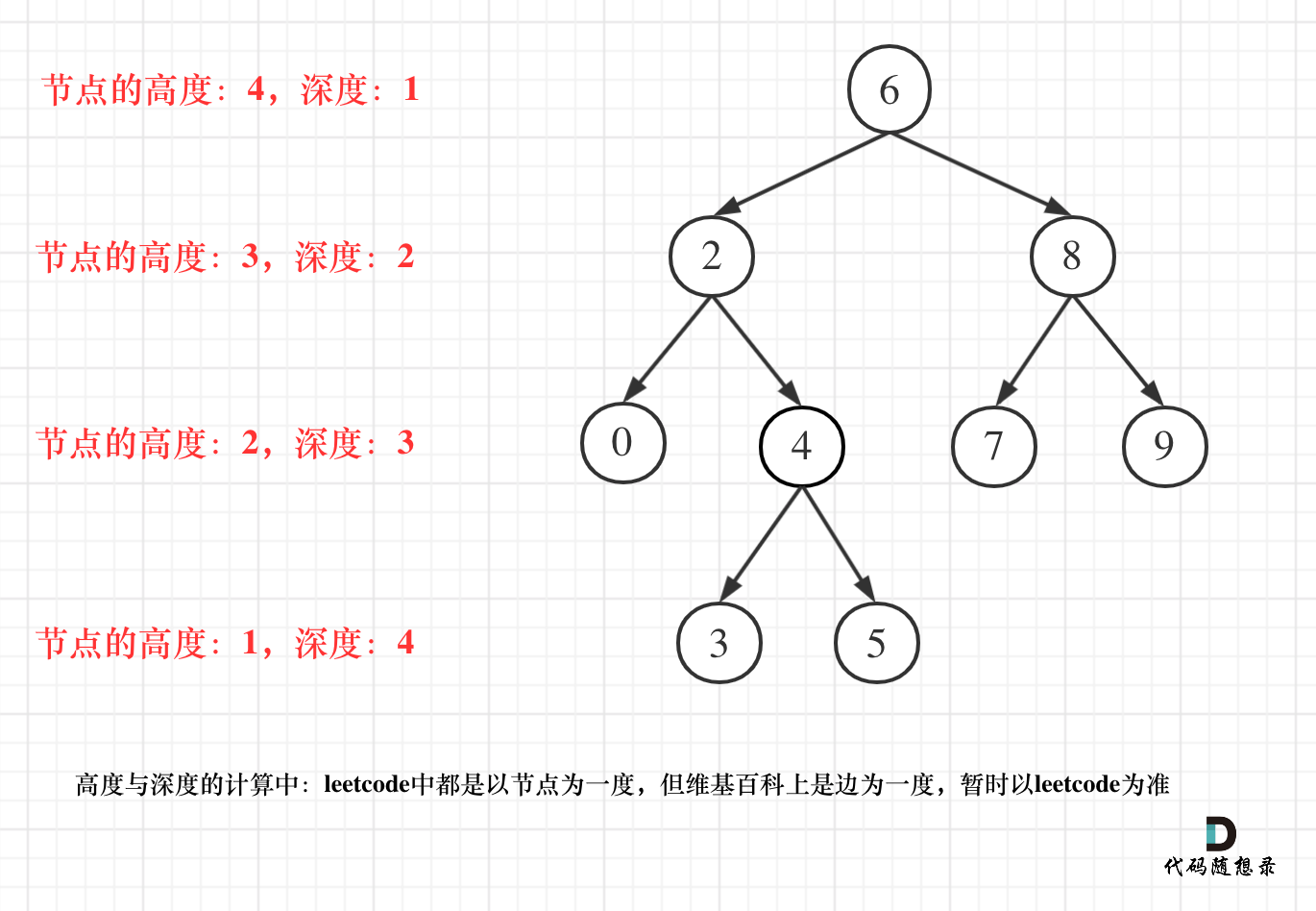： ![110.平衡二叉树2](https://img-blog.csdnimg.cn/20210203155515650.png) 关于根节点的深度究竟是1 还是 0，不同的地方有不一样的标准，leetcode的题目中都是以节点为一度，即根节点深度是1。但维基百科上定义用边为一度，即根节点的深度是0，我们暂时以leetcode为准（毕竟要在这上面刷题）。因为求深度可以从上到下去查所以需要前序遍历（中左右），而高度只能从下到上去查，所以只能后序遍历（左右中）有的同学一定疑惑，为什么[二叉树：看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中求的是二叉树的最大深度，也用的是后序遍历。 **那是因为代码的逻辑其实是求的根节点的高度，而根节点的高度就是这颗树的最大深度，所以才可以使用后序遍历。** 在[二叉树：看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中，如果真正求取二叉树的最大深度，代码应该写成如下：（前序遍历） ```C++ class Solution { public: int result; void getDepth(TreeNode* node, int depth) { result = depth > result ? depth : result; // 中 if (node->left == NULL && node->right == NULL) return ; if (node->left) { // 左 depth++; // 深度+1 getDepth(node->left, depth); depth--; // 回溯，深度-1 } if (node->right) { // 右 depth++; // 深度+1 getDepth(node->right, depth); depth--; // 回溯，深度-1 } return ; } int maxDepth(TreeNode* root) { result = 0; if (root == 0) return result; getDepth(root, 1); return result; } }; ``` **可以看出使用了前序（中左右）的遍历顺序，这才是真正求深度的逻辑！** 注意以上代码是为了把细节体现出来，简化一下代码如下： ```C++ class Solution { public: int result; void getDepth(TreeNode* node, int depth) { result = depth > result ? depth : result; // 中 if (node->left == NULL && node->right == NULL) return ; if (node->left) { // 左 getDepth(node->left, depth + 1); } if (node->right) { // 右 getDepth(node->right, depth + 1); } return ; } int maxDepth(TreeNode* root) { result = 0; if (root == 0) return result; getDepth(root, 1); return result; } }; ``` ## 本题思路 ### 递归此时大家应该明白了既然要求比较高度，必然是要后序遍历。递归三步曲分析： 1. 明确递归函数的参数和返回值参数的话为传入的节点指针，就没有其他参数需要传递了，返回值要返回传入节点为根节点树的深度。那么如何标记左右子树是否差值大于1呢。如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。所以如果已经不是二叉平衡树了，可以返回-1 来标记已经不符合平衡树的规则了。代码如下： ``` // -1 表示已经不是平衡二叉树了，否则返回值是以该节点为根节点树的高度 int getDepth(TreeNode* node) ``` 2. 明确终止条件递归的过程中依然是遇到空节点了为终止，返回0，表示当前节点为根节点的书高度为0 代码如下： ``` if (node == NULL) { return 0; } ``` 3. 明确单层递归的逻辑如何判断当前传入节点为根节点的二叉树是否是平衡二叉树呢，当然是左子树高度和右子树高度相差。分别求出左右子树的高度，然后如果差值小于等于1，则返回当前二叉树的高度，否则则返回-1，表示已经不是二叉树了。代码如下： ``` int leftDepth = depth(node->left); // 左 if (leftDepth == -1) return -1; int rightDepth = depth(node->right); // 右 if (rightDepth == -1) return -1; int result; if (abs(leftDepth - rightDepth) > 1) { // 中 result = -1; } else { result = 1 + max(leftDepth, rightDepth); // 以当前节点为根节点的最大高度 } return result; ``` 代码精简之后如下： ``` int leftDepth = getDepth(node->left); if (leftDepth == -1) return -1; int rightDepth = getDepth(node->right); if (rightDepth == -1) return -1; return abs(leftDepth - rightDepth) > 1 ? -1 : 1 + max(leftDepth, rightDepth); ``` 此时递归的函数就已经写出来了，这个递归的函数传入节点指针，返回以该节点为根节点的二叉树的高度，如果不是二叉平衡树，则返回-1。 getDepth整体代码如下： ```C++ int getDepth(TreeNode* node) { if (node == NULL) { return 0; } int leftDepth = getDepth(node->left); if (leftDepth == -1) return -1; int rightDepth = getDepth(node->right); if (rightDepth == -1) return -1; return abs(leftDepth - rightDepth) > 1 ? -1 : 1 + max(leftDepth, rightDepth); } ``` 最后本题整体递归代码如下： ```C++ class Solution { public: // 返回以该节点为根节点的二叉树的高度，如果不是二叉搜索树了则返回-1 int getDepth(TreeNode* node) { if (node == NULL) { return 0; } int leftDepth = getDepth(node->left); if (leftDepth == -1) return -1; // 说明左子树已经不是二叉平衡树 int rightDepth = getDepth(node->right); if (rightDepth == -1) return -1; // 说明右子树已经不是二叉平衡树 return abs(leftDepth - rightDepth) > 1 ? -1 : 1 + max(leftDepth, rightDepth); } bool isBalanced(TreeNode* root) { return getDepth(root) == -1 ? false : true; } }; ``` ### 迭代在[二叉树：看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)中我们可以使用层序遍历来求深度，但是就不能直接用层序遍历来求高度了，这就体现出求高度和求深度的不同。本题的迭代方式可以先定义一个函数，专门用来求高度。这个函数通过栈模拟的后序遍历找每一个节点的高度（其实是通过求传入节点为根节点的最大深度来求的高度）代码如下： ```C++ // cur节点的最大深度，就是cur的高度 int getDepth(TreeNode* cur) { stack st; if (cur != NULL) st.push(cur); int depth = 0; // 记录深度 int result = 0; while (!st.empty()) { TreeNode* node = st.top(); if (node != NULL) { st.pop(); st.push(node); // 中 st.push(NULL); depth++; if (node->right) st.push(node->right); // 右 if (node->left) st.push(node->left); // 左 } else { st.pop(); node = st.top(); st.pop(); depth--; } result = result > depth ? result : depth; } return result; } ``` 然后再用栈来模拟前序遍历，遍历每一个节点的时候，再去判断左右孩子的高度是否符合，代码如下： ``` bool isBalanced(TreeNode* root) { stack st; if (root == NULL) return true; st.push(root); while (!st.empty()) { TreeNode* node = st.top(); // 中 st.pop(); if (abs(getDepth(node->left) - getDepth(node->right)) > 1) { // 判断左右孩子高度是否符合 return false; } if (node->right) st.push(node->right); // 右（空节点不入栈） if (node->left) st.push(node->left); // 左（空节点不入栈） } return true; } ``` 整体代码如下： ``` class Solution { private: int getDepth(TreeNode* cur) { stack st; if (cur != NULL) st.push(cur); int depth = 0; // 记录深度 int result = 0; while (!st.empty()) { TreeNode* node = st.top(); if (node != NULL) { st.pop(); st.push(node); // 中 st.push(NULL); depth++; if (node->right) st.push(node->right); // 右 if (node->left) st.push(node->left); // 左 } else { st.pop(); node = st.top(); st.pop(); depth--; } result = result > depth ? result : depth; } return result; } public: bool isBalanced(TreeNode* root) { stack st; if (root == NULL) return true; st.push(root); while (!st.empty()) { TreeNode* node = st.top(); // 中 st.pop(); if (abs(getDepth(node->left) - getDepth(node->right)) > 1) { return false; } if (node->right) st.push(node->right); // 右（空节点不入栈） if (node->left) st.push(node->left); // 左（空节点不入栈） } return true; } }; ``` 当然此题用迭代法，其实效率很低，因为没有很好的模拟回溯的过程，所以迭代法有很多重复的计算。虽然理论上所有的递归都可以用迭代来实现，但是有的场景难度可能比较大。 **例如：都知道回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法！** 因为对于回溯算法已经是非常复杂的递归了，如果在用迭代的话，就是自己给自己找麻烦，效率也并不一定高。 ## 总结通过本题可以了解求二叉树深度和二叉树高度的差异，求深度适合用前序遍历，而求高度适合用后序遍历。本题迭代法其实有点复杂，大家可以有一个思路，也不一定说非要写出来。但是递归方式是一定要掌握的！ ## 其他语言版本 Java： ```Java class Solution { /** * 递归法 */ public boolean isBalanced(TreeNode root) { return getHeight(root) != -1; } private int getHeight(TreeNode root) { if (root == null) { return 0; } int leftHeight = getHeight(root.left); if (leftHeight == -1) { return -1; } int rightHeight = getHeight(root.right); if (rightHeight == -1) { return -1; } // 左右子树高度差大于1，return -1表示已经不是平衡树了 if (Math.abs(leftHeight - rightHeight) > 1) { return -1; } return Math.max(leftHeight, rightHeight) + 1; } } class Solution { /** * 迭代法，效率较低，计算高度时会重复遍历 * 时间复杂度：O(n^2) */ public boolean isBalanced(TreeNode root) { if (root == null) { return true; } Stack stack = new Stack<>(); TreeNode pre = null; while (root!= null || !stack.isEmpty()) { while (root != null) { stack.push(root); root = root.left; } TreeNode inNode = stack.peek(); // 右结点为null或已经遍历过 if (inNode.right == null || inNode.right == pre) { // 比较左右子树的高度差，输出 if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) { return false; } stack.pop(); pre = inNode; root = null;// 当前结点下，没有要遍历的结点了 } else { root = inNode.right;// 右结点还没遍历，遍历右结点 } } return true; } /** * 层序遍历，求结点的高度 */ public int getHeight(TreeNode root) { if (root == null) { return 0; } Deque deque = new LinkedList<>(); deque.offer(root); int depth = 0; while (!deque.isEmpty()) { int size = deque.size(); depth++; for (int i = 0; i < size; i++) { TreeNode poll = deque.poll(); if (poll.left != null) { deque.offer(poll.left); } if (poll.right != null) { deque.offer(poll.right); } } } return depth; } } class Solution { /** * 优化迭代法，针对暴力迭代法的getHeight方法做优化，利用TreeNode.val来保存当前结点的高度，这样就不会有重复遍历 * 获取高度算法时间复杂度可以降到O(1)，总的时间复杂度降为O(n)。 *

* 时间复杂度：O(n) */ public boolean isBalanced(TreeNode root) { if (root == null) { return true; } Stack stack = new Stack<>(); TreeNode pre = null; while (root != null || !stack.isEmpty()) { while (root != null) { stack.push(root); root = root.left; } TreeNode inNode = stack.peek(); // 右结点为null或已经遍历过 if (inNode.right == null || inNode.right == pre) { // 输出 if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) { return false; } stack.pop(); pre = inNode; root = null;// 当前结点下，没有要遍历的结点了 } else { root = inNode.right;// 右结点还没遍历，遍历右结点 } } return true; } /** * 求结点的高度 */ public int getHeight(TreeNode root) { if (root == null) { return 0; } int leftHeight = root.left != null ? root.left.val : 0; int rightHeight = root.right != null ? root.right.val : 0; int height = Math.max(leftHeight, rightHeight) + 1; root.val = height;// 用TreeNode.val来保存当前结点的高度 return height; } } // LeetCode题解链接：https://leetcode-cn.com/problems/balanced-binary-tree/solution/110-ping-heng-er-cha-shu-di-gui-fa-bao-l-yqr3/ ``` Python： Go： ```Go func isBalanced(root *TreeNode) bool { if root==nil{ return true } if !isBalanced(root.Left) || !isBalanced(root.Right){ return false } LeftH:=maxdepth(root.Left)+1 RightH:=maxdepth(root.Right)+1 if abs(LeftH-RightH)>1{ return false } return true } func maxdepth(root *TreeNode)int{ if root==nil{ return 0 } return max(maxdepth(root.Left),maxdepth(root.Right))+1 } func max(a,b int)int{ if a>b{ return a } return b } func abs(a int)int{ if a<0{ return -a } return a } ``` ----------------------- * 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw) * B站视频：[代码随想录](https://space.bilibili.com/525438321) * 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)