参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

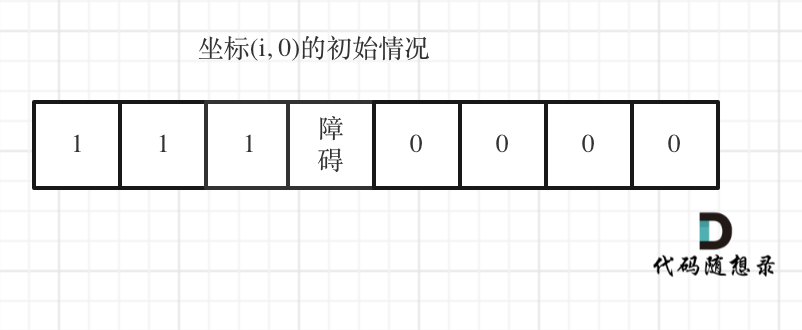
> dp(m, vector(n, 0)); // 初始值为0 for (int i = 0; i < m; i++) dp[i][0] = 1; for (int j = 0; j < n; j++) dp[0][j] = 1; ``` 因为从(0, 0)的位置到(i, 0)的路径只有一条，所以dp[i][0]一定为1，dp[0][j]也同理。 但如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。 如图：  下标(0, j)的初始化情况同理。 所以本题初始化代码为： ```CPP vector> dp(m, vector(n, 0)); for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1; for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1; ``` **注意代码里for循环的终止条件，一旦遇到obstacleGrid[i][0] == 1的情况就停止dp[i][0]的赋值1的操作，dp[0][j]同理** 4. 确定遍历顺序 从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出，一定是从左到右一层一层遍历，这样保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。 代码如下： ```CPP for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { if (obstacleGrid[i][j] == 1) continue; dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } } ``` 5. 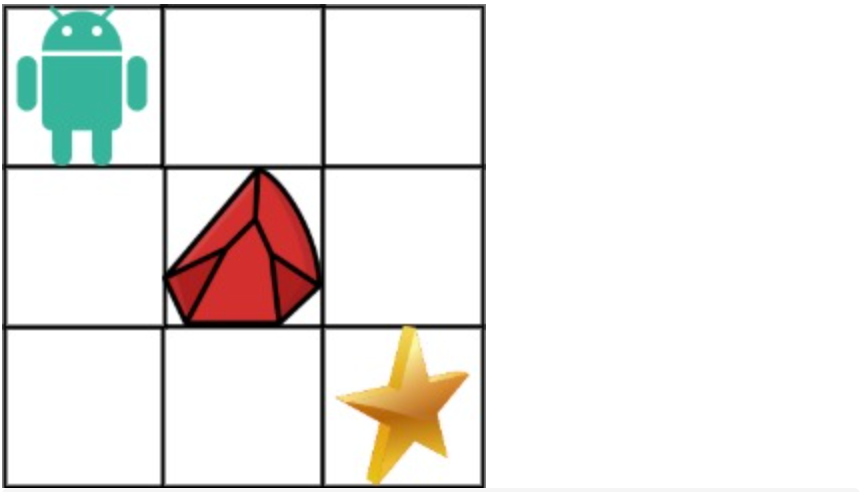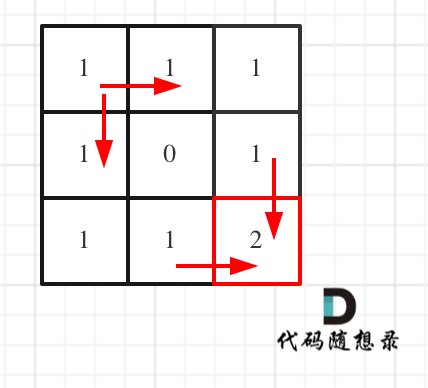举例推导dp数组 拿示例1来举例如题：  对应的dp table 如图：  如果这个图看不同，建议在理解一下递归公式，然后照着文章中说的遍历顺序，自己推导一下​！​ 动规五部分分析完毕，对应C++代码如下： ```CPP class Solution { public: int uniquePathsWithObstacles(vector>& obstacleGrid) { int m = obstacleGrid.size(); int n = obstacleGrid[0].size(); vector> dp(m, vector(n, 0)); for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1; for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1; for (int i = 1; i < m; i++) { for (int j = 1; j < n; j++) { if (obstacleGrid[i][j] == 1) continue; dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } } return dp[m - 1][n - 1]; } }; ``` * 时间复杂度：$O(n × m)$，n、m 分别为obstacleGrid 长度和宽度 * 空间复杂度：$O(n × m)$ ## 总结 本题是[62.不同路径](https://programmercarl.com/0062.不同路径.html)的障碍版，整体思路大体一致。 但就算是做过62.不同路径，在做本题也会有感觉遇到障碍无从下手。 其实只要考虑到，遇到障碍dp[i][j]保持0就可以了。 也有一些小细节，例如：初始化的部分，很容易忽略了障碍之后应该都是0的情况。 就酱，「代码随想录」值得推荐给身边学算法的同学朋友们，关注后都会发现相见恨晚！ ## 其他语言版本 ### Java ```java class Solution { public int uniquePathsWithObstacles(int[][] obstacleGrid) { int n = obstacleGrid.length, m = obstacleGrid[0].length; int[][] dp = new int[n][m]; for (int i = 0; i < m; i++) { if (obstacleGrid[0][i] == 1) break; //一旦遇到障碍，后续都到不了 dp[0][i] = 1; } for (int i = 0; i < n; i++) { if (obstacleGrid[i][0] == 1) break; ////一旦遇到障碍，后续都到不了 dp[i][0] = 1; } for (int i = 1; i < n; i++) { for (int j = 1; j < m; j++) { if (obstacleGrid[i][j] == 1) continue; dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; } } return dp[n - 1][m - 1]; } } ``` ### Python ```python class Solution: def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int: # 构造一个DP table row = len(obstacleGrid) col = len(obstacleGrid[0]) dp = [[0 for _ in range(col)] for _ in range(row)] dp[0][0] = 1 if obstacleGrid[0][0] != 1 else 0 if dp[0][0] == 0: return 0 # 如果第一个格子就是障碍，return 0 # 第一行 for i in range(1, col): if obstacleGrid[0][i] != 1: dp[0][i] = dp[0][i-1] # 第一列 for i in range(1, row): if obstacleGrid[i][0] != 1: dp[i][0] = dp[i-1][0] print(dp) for i in range(1, row): for j in range(1, col): if obstacleGrid[i][j] != 1: dp[i][j] = dp[i-1][j] + dp[i][j-1] return dp[-1][-1] ``` ```python class Solution: """ 使用一维dp数组 """ def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int: m, n = len(obstacleGrid), len(obstacleGrid[0]) # 初始化dp数组 # 该数组缓存当前行 curr = [0] * n for j in range(n): if obstacleGrid[0][j] == 1: break curr[j] = 1 for i in range(1, m): # 从第二行开始 for j in range(n): # 从第一列开始，因为第一列可能有障碍物 # 有障碍物处无法通行，状态就设成0 if obstacleGrid[i][j] == 1: curr[j] = 0 elif j > 0: # 等价于 # dp[i][j] = dp[i - 1][j] + dp[i][j - 1] curr[j] = curr[j] + curr[j - 1] # 隐含的状态更新 # dp[i][0] = dp[i - 1][0] return curr[n - 1] ``` ### Go ```go func uniquePathsWithObstacles(obstacleGrid [][]int) int { m, n := len(obstacleGrid), len(obstacleGrid[0]) // 定义一个dp数组 dp := make([][]int, m) for i, _ := range dp { dp[i] = make([]int, n) } // 初始化, 如果是障碍物, 后面的就都是0, 不用循环了 for i := 0; i < m && obstacleGrid[i][0] == 0; i++ { dp[i][0] = 1 } for i := 0; i < n && obstacleGrid[0][i] == 0; i++ { dp[0][i] = 1 } // dp数组推导过程 for i := 1; i < m; i++ { for j := 1; j < n; j++ { // 如果obstacleGrid[i][j]这个点是障碍物, 那么dp[i][j]保持为0 if obstacleGrid[i][j] != 1 { // 否则我们需要计算当前点可以到达的路径数 dp[i][j] = dp[i-1][j] + dp[i][j-1] } } } return dp[m-1][n-1] } ``` ### Javascript ```Javascript var uniquePathsWithObstacles = function(obstacleGrid) { const m = obstacleGrid.length const n = obstacleGrid[0].length const dp = Array(m).fill().map(item => Array(n).fill(0)) for (let i = 0; i < m && obstacleGrid[i][0] === 0; ++i) { dp[i][0] = 1 } for (let i = 0; i < n && obstacleGrid[0][i] === 0; ++i) { dp[0][i] = 1 } for (let i = 1; i < m; ++i) { for (let j = 1; j < n; ++j) { dp[i][j] = obstacleGrid[i][j] === 1 ? 0 : dp[i - 1][j] + dp[i][j - 1] } } return dp[m - 1][n - 1] }; ``` C ```c //初始化dp数组 int **initDP(int m, int n, int** obstacleGrid) { int **dp = (int**)malloc(sizeof(int*) * m); int i, j; //初始化每一行数组 for(i = 0; i < m; ++i) { dp[i] = (int*)malloc(sizeof(int) * n); } //先将第一行第一列设为0 for(i = 0; i < m; ++i) { dp[i][0] = 0; } for(j = 0; j < n; ++j) { dp[0][j] = 0; } //若碰到障碍，之后的都走不了。退出循环 for(i = 0; i < m; ++i) { if(obstacleGrid[i][0]) { break; } dp[i][0] = 1; } for(j = 0; j < n; ++j) { if(obstacleGrid[0][j]) break; dp[0][j] = 1; } return dp; } int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize){ int m = obstacleGridSize, n = *obstacleGridColSize; //初始化dp数组 int **dp = initDP(m, n, obstacleGrid); int i, j; for(i = 1; i < m; ++i) { for(j = 1; j < n; ++j) { //若当前i,j位置有障碍 if(obstacleGrid[i][j]) //路线不同 dp[i][j] = 0; else dp[i][j] = dp[i-1][j] + dp[i][j-1]; } } //返回最后终点的路径个数 return dp[m-1][n-1]; } ``` -----------------------