参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# kruskal算法精讲
[卡码网:53. 寻宝](https://kamacoder.com/problempage.php?pid=1053)
题目描述:
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将 所有岛屿联通起来。
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
输入描述:
第一行包含两个整数V 和 E,V代表顶点数,E代表边数 。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
接下来共有 E 行,每行三个整数 v1,v2 和 val,v1 和 v2 为边的起点和终点,val代表边的权值。
输出描述:
输出联通所有岛屿的最小路径总距离
输入示例:
```
7 11
1 2 1
1 3 1
1 5 2
2 6 1
2 4 2
2 3 2
3 4 1
4 5 1
5 6 2
5 7 1
6 7 1
```
输出示例:
6
## 解题思路
在上一篇 我们讲解了 prim算法求解 最小生成树,本篇我们来讲解另一个算法:Kruskal,同样可以求最小生成树。
**prim 算法是维护节点的集合,而 Kruskal 是维护边的集合**。
上来就这么说,大家应该看不太懂,这里是先让大家有这么个印象,带着这个印象在看下文,理解的会更到位一些。
kruscal的思路:
* 边的权值排序,因为要优先选最小的边加入到生成树里
* 遍历排序后的边
* 如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环
* 如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合
下面我们画图举例说明kruscal的工作过程。
依然以示例中,如下这个图来举例。
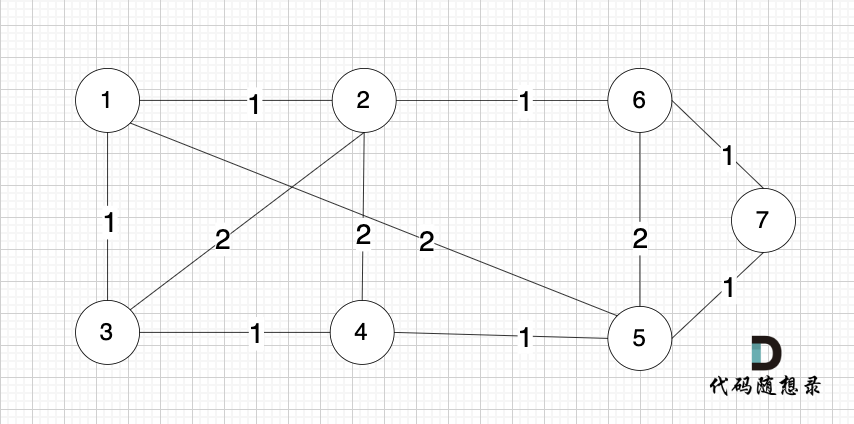
将图中的边按照权值有小到大排序,这样从贪心的角度来说,优先选 权值小的边加入到 最小生成树中。
排序后的边顺序为[(1,2) (4,5) (1,3) (2,6) (3,4) (6,7) (5,7) (1,5) (3,2) (2,4) (5,6)]
> (1,2) 表示节点1 与 节点2 之间的边。权值相同的边,先后顺序无所谓。
**开始从头遍历排序后的边**。
--------
选边(1,2),节点1 和 节点2 不在同一个集合,所以生成树可以添加边(1,2),并将 节点1,节点2 放在同一个集合。
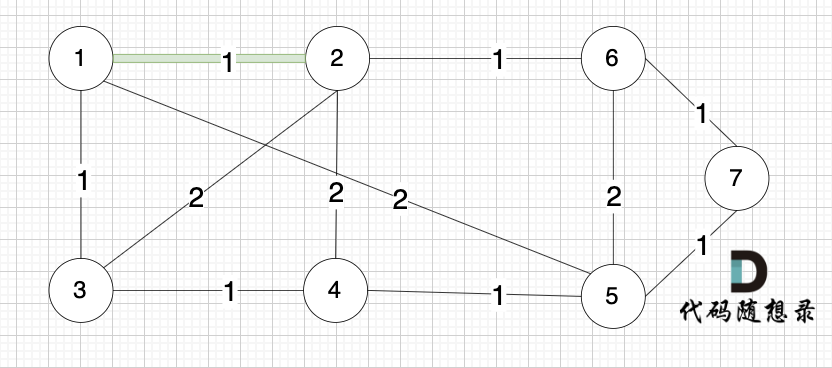
--------
选边(4,5),节点4 和 节点 5 不在同一个集合,生成树可以添加边(4,5) ,并将节点4,节点5 放到同一个集合。
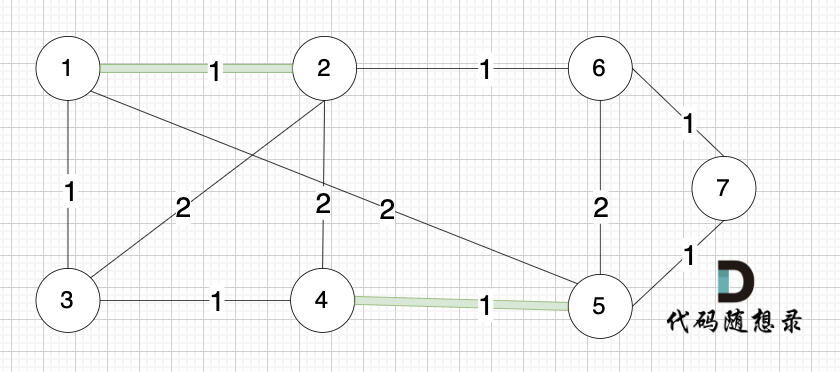
**大家判断两个节点是否在同一个集合,就看图中两个节点是否有绿色的粗线连着就行**
------
(这里在强调一下,以下选边是按照上面排序好的边的数组来选择的)
选边(1,3),节点1 和 节点3 不在同一个集合,生成树添加边(1,3),并将节点1,节点3 放到同一个集合。
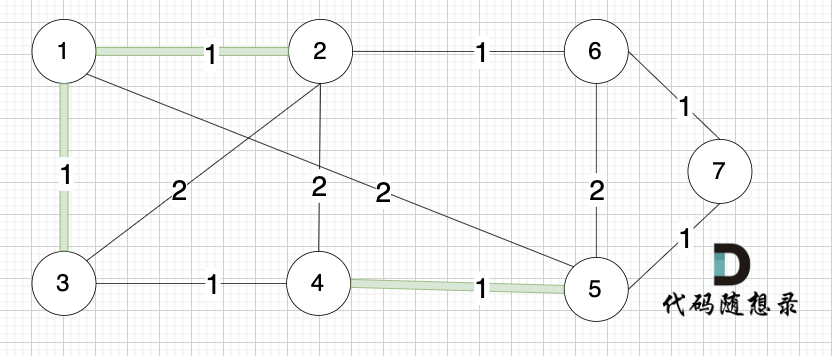
---------
选边(2,6),节点2 和 节点6 不在同一个集合,生成树添加边(2,6),并将节点2,节点6 放到同一个集合。
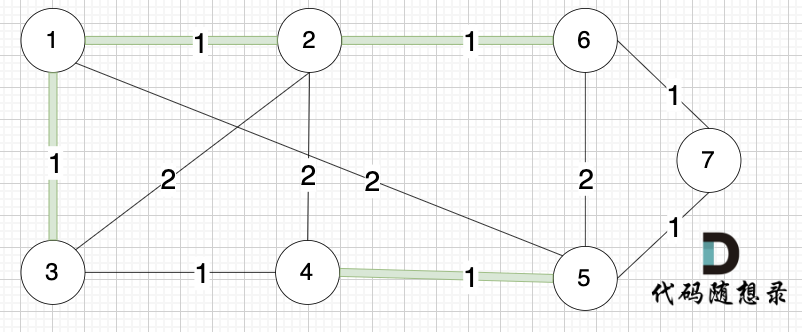
--------
选边(3,4),节点3 和 节点4 不在同一个集合,生成树添加边(3,4),并将节点3,节点4 放到同一个集合。
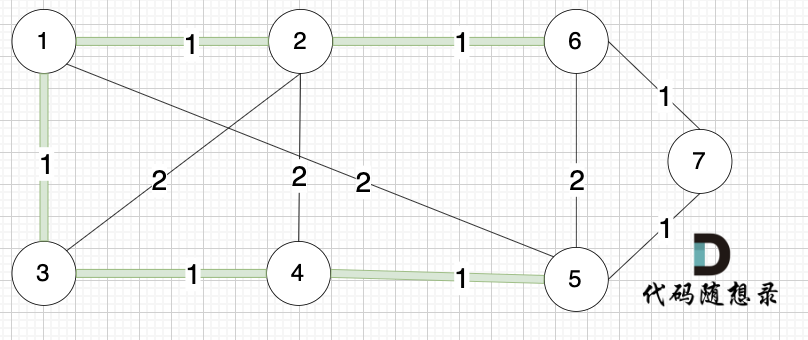
----------
选边(6,7),节点6 和 节点7 不在同一个集合,生成树添加边(6,7),并将 节点6,节点7 放到同一个集合。
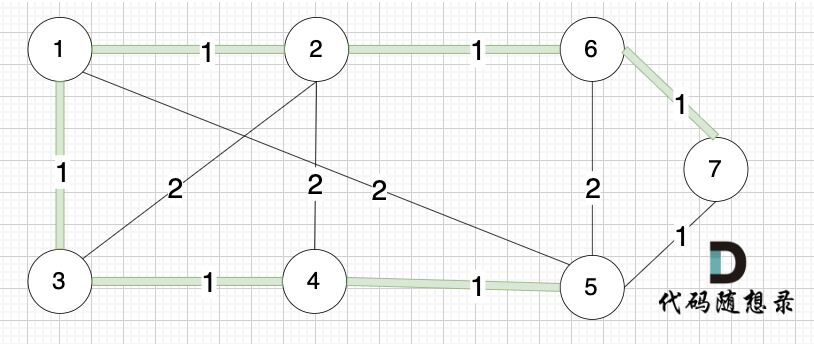
-----------
选边(5,7),节点5 和 节点7 在同一个集合,不做计算。
选边(1,5),两个节点在同一个集合,不做计算。
后面遍历 边(3,2),(2,4),(5,6) 同理,都因两个节点已经在同一集合,不做计算。
-------
此时 我们就已经生成了一个最小生成树,即:

在上面的讲解中,看图的话 大家知道如何判断 两个节点 是否在同一个集合(是否有绿色的线连在一起),以及如何把两个节点加入集合(就在图中把两个节点连上)
**但在代码中,如果将两个节点加入同一个集合,又如何判断两个节点是否在同一个集合呢**?
这里就涉及到我们之前讲解的[并查集](./图论并查集理论基础.md)。
我们在并查集开篇的时候就讲了,并查集主要就两个功能:
* 将两个元素添加到一个集合中
* 判断两个元素在不在同一个集合
大家发现这正好符合 Kruskal算法的需求,这也是为什么 **我要先讲并查集,再讲 Kruskal**。
关于 并查集,我已经在[并查集精讲](./图论并查集理论基础.md) 详细讲解过了,所以这里不再赘述,我们直接用。
本题代码如下,已经详细注释:
```CPP
#include
#include
#include
using namespace std;
// l,r为 边两边的节点,val为边的数值
struct Edge {
int l, r, val;
};
// 节点数量
int n = 10001;
// 并查集标记节点关系的数组
vector father(n, -1); // 节点编号是从1开始的,n要大一些
// 并查集初始化
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
// 并查集的查找操作
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}
// 并查集的加入集合
void join(int u, int v) {
u = find(u); // 寻找u的根
v = find(v); // 寻找v的根
if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[v] = u;
}
int main() {
int v, e;
int v1, v2, val;
vector edges;
int result_val = 0;
cin >> v >> e;
while (e--) {
cin >> v1 >> v2 >> val;
edges.push_back({v1, v2, val});
}
// 执行Kruskal算法
// 按边的权值对边进行从小到大排序
sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) {
return a.val < b.val;
});
// 并查集初始化
init();
// 从头开始遍历边
for (Edge edge : edges) {
// 并查集,搜出两个节点的祖先
int x = find(edge.l);
int y = find(edge.r);
// 如果祖先不同,则不在同一个集合
if (x != y) {
result_val += edge.val; // 这条边可以作为生成树的边
join(x, y); // 两个节点加入到同一个集合
}
}
cout << result_val << endl;
return 0;
}
```
时间复杂度:nlogn (快排) + logn (并查集) ,所以最后依然是 nlogn 。n为边的数量。
关于并查集时间复杂度,可以看我在 [并查集理论基础](https://programmercarl.com/%E5%9B%BE%E8%AE%BA%E5%B9%B6%E6%9F%A5%E9%9B%86%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html) 的讲解。
## 拓展一
如果题目要求将最小生成树的边输出的话,应该怎么办呢?
Kruskal 算法 输出边的话,相对prim 要容易很多,因为 Kruskal 本来就是直接操作边,边的结构自然清晰,不用像 prim一样 需要再将节点连成线输出边 (因为prim是对节点操作,而 Kruskal是对边操作,这是本质区别)
本题中,边的结构为:
```CPP
struct Edge {
int l, r, val;
};
```
那么我们只需要找到 在哪里把生成树的边保存下来就可以了。
当判断两个节点不在同一个集合的时候,这两个节点的边就加入到最小生成树, 所以添加边的操作在这里:
```CPP
vector result; // 存储最小生成树的边
// 如果祖先不同,则不在同一个集合
if (x != y) {
result.push_back(edge); // 记录最小生成树的边
result_val += edge.val; // 这条边可以作为生成树的边
join(x, y); // 两个节点加入到同一个集合
}
```
整体代码如下,为了突出重点,我仅仅将 打印最小生成树的部分代码注释了,大家更容易看到哪些改动。
```CPP
#include
#include
#include
using namespace std;
struct Edge {
int l, r, val;
};
int n = 10001;
vector father(n, -1);
void init() {
for (int i = 0; i < n; ++i) {
father[i] = i;
}
}
int find(int u) {
return u == father[u] ? u : father[u] = find(father[u]);
}
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return ;
father[v] = u;
}
int main() {
int v, e;
int v1, v2, val;
vector edges;
int result_val = 0;
cin >> v >> e;
while (e--) {
cin >> v1 >> v2 >> val;
edges.push_back({v1, v2, val});
}
sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) {
return a.val < b.val;
});
vector result; // 存储最小生成树的边
init();
for (Edge edge : edges) {
int x = find(edge.l);
int y = find(edge.r);
if (x != y) {
result.push_back(edge); // 保存最小生成树的边
result_val += edge.val;
join(x, y);
}
}
// 打印最小生成树的边
for (Edge edge : result) {
cout << edge.l << " - " << edge.r << " : " << edge.val << endl;
}
return 0;
}
```
按照题目中的示例,打印边的输出为:
```
1 - 2 : 1
1 - 3 : 1
2 - 6 : 1
3 - 4 : 1
4 - 5 : 1
5 - 7 : 1
```
大家可能发现 怎么和我们 模拟画的图不一样,差别在于 代码生成的最小生成树中 节点5 和 节点7相连的。
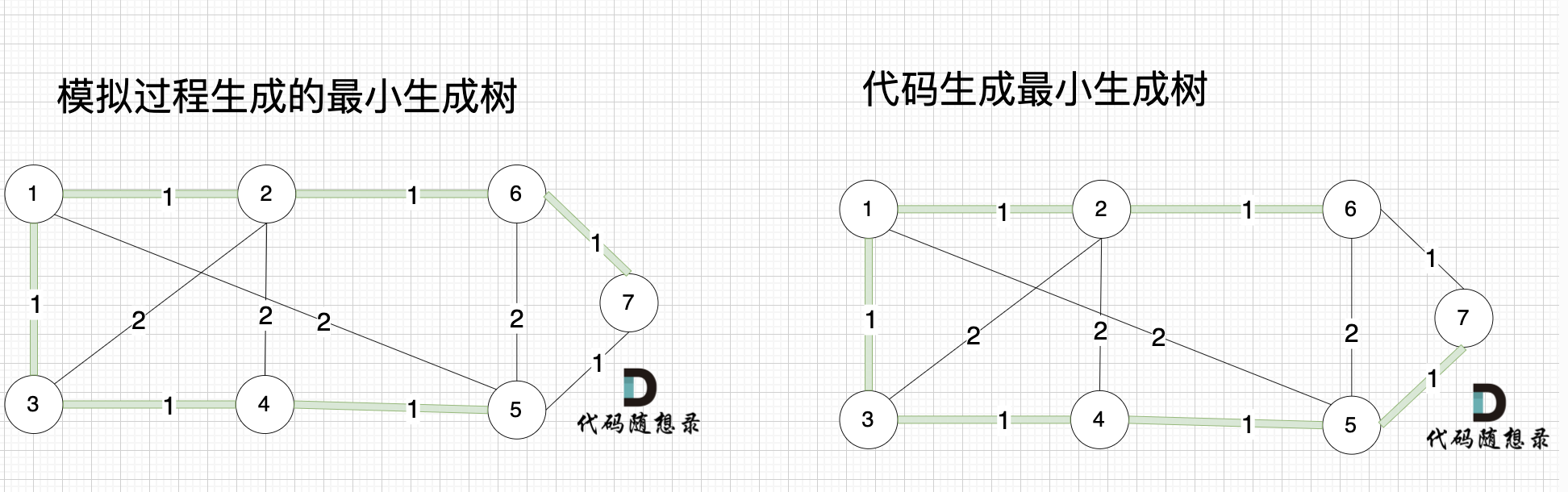
其实造成这个差别 是对边排序的时候 权值相同的边先后顺序的问题导致的,无论相同权值边的顺序是什么样的,最后都能得出最小生成树。
## 拓展二
此时我们已经讲完了 Kruskal 和 prim 两个解法来求最小生成树。
什么情况用哪个算法更合适呢。
Kruskal 与 prim 的关键区别在于,prim维护的是节点的集合,而 Kruskal 维护的是边的集合。
如果 一个图中,节点多,但边相对较少,那么使用Kruskal 更优。
有录友可能疑惑,一个图里怎么可能节点多,边却少呢?
节点未必一定要连着边那, 例如 这个图,大家能明显感受到边没有那么多对吧,但节点数量 和 上述我们讲的例子是一样的。
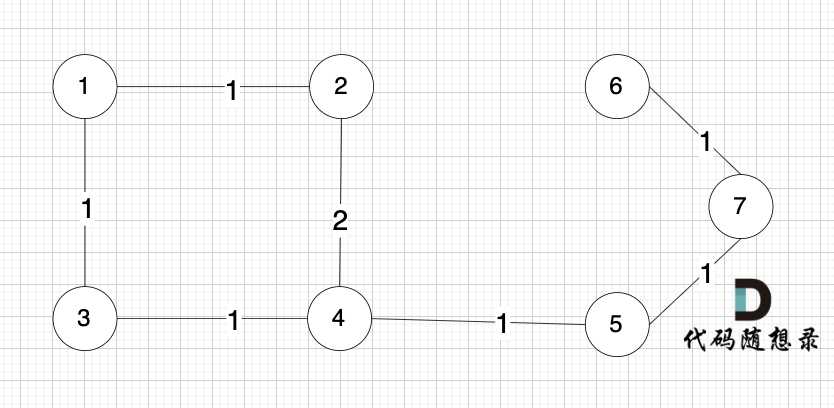
为什么边少的话,使用 Kruskal 更优呢?
因为 Kruskal 是对边进行排序的后 进行操作是否加入到最小生成树。
边如果少,那么遍历操作的次数就少。
在节点数量固定的情况下,图中的边越少,Kruskal 需要遍历的边也就越少。
而 prim 算法是对节点进行操作的,节点数量越少,prim算法效率就越优。
所以在 稀疏图中,用Kruskal更优。 在稠密图中,用prim算法更优。
> 边数量较少为稀疏图,接近或等于完全图(所有节点皆相连)为稠密图
Prim 算法 时间复杂度为 O(n^2),其中 n 为节点数量,它的运行效率和图中边树无关,适用稠密图。
Kruskal算法 时间复杂度 为 nlogn,其中n 为边的数量,适用稀疏图。
## 总结
如果学过了并查集,其实 kruskal 比 prim更好理解一些。
本篇,我们依然通过模拟 Kruskal 算法的过程,来带大家一步步了解其工作过程。
在 拓展一 中讲解了 如何输出最小生成树的边。
在拓展二 中讲解了 prim 和 Kruskal的区别。
录友们可以细细体会。
## 其他语言版本
### Java
```Java
import java.util.*;
class Edge {
int l, r, val;
Edge(int l, int r, int val) {
this.l = l;
this.r = r;
this.val = val;
}
}
public class Main {
private static int n = 10001;
private static int[] father = new int[n];
// 并查集初始化
public static void init() {
for (int i = 0; i < n; i++) {
father[i] = i;
}
}
// 并查集的查找操作
public static int find(int u) {
if (u == father[u]) return u;
return father[u] = find(father[u]);
}
// 并查集的加入集合
public static void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return;
father[v] = u;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int v = scanner.nextInt();
int e = scanner.nextInt();
List edges = new ArrayList<>();
int result_val = 0;
for (int i = 0; i < e; i++) {
int v1 = scanner.nextInt();
int v2 = scanner.nextInt();
int val = scanner.nextInt();
edges.add(new Edge(v1, v2, val));
}
// 执行Kruskal算法
edges.sort(Comparator.comparingInt(edge -> edge.val));
// 并查集初始化
init();
// 从头开始遍历边
for (Edge edge : edges) {
int x = find(edge.l);
int y = find(edge.r);
if (x != y) {
result_val += edge.val;
join(x, y);
}
}
System.out.println(result_val);
scanner.close();
}
}
```
### Python
```python
class Edge:
def __init__(self, l, r, val):
self.l = l
self.r = r
self.val = val
n = 10001
father = list(range(n))
def init():
global father
father = list(range(n))
def find(u):
if u != father[u]:
father[u] = find(father[u])
return father[u]
def join(u, v):
u = find(u)
v = find(v)
if u != v:
father[v] = u
def kruskal(v, edges):
edges.sort(key=lambda edge: edge.val)
init()
result_val = 0
for edge in edges:
x = find(edge.l)
y = find(edge.r)
if x != y:
result_val += edge.val
join(x, y)
return result_val
if __name__ == "__main__":
import sys
input = sys.stdin.read
data = input().split()
v = int(data[0])
e = int(data[1])
edges = []
index = 2
for _ in range(e):
v1 = int(data[index])
v2 = int(data[index + 1])
val = int(data[index + 2])
edges.append(Edge(v1, v2, val))
index += 3
result_val = kruskal(v, edges)
print(result_val)
```
### Go
### Rust
### Javascript
### TypeScript
### PhP
### Swift
### Scala
### C#
### Dart
### C
并查集方法一
```c
#include
#include
// 定义边结构体,包含两个顶点vex1和vex2以及它们之间的权重val
struct Edge
{
int vex1, vex2, val;
};
// 冒泡排序函数,用于按边的权重val不减序排序边数组
void bubblesort(struct Edge *a, int numsize)
{
for (int i = 0; i < numsize - 1; ++i)
{
for (int j = 0; j < numsize - i - 1; ++j)
{
if (a[j].val > a[j + 1].val)
{
struct Edge temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}
int main()
{
int v, e;
int v1, v2, val;
int ret = 0;
scanf("%d%d", &v, &e);
struct Edge *edg = (struct Edge *)malloc(sizeof(struct Edge) * e);
int *conne_gra = (int *)malloc(sizeof(int) * (v + 1));
// 初始化连通图数组,每个顶点初始时只与自己相连通
for (int i = 0; i <= v; ++i)
{
conne_gra[i] = i;
}
// 读取所有边的信息并存储到edg(存储所有边的)数组中
for (int i = 0; i < e; ++i)
{
scanf("%d%d%d", &v1, &v2, &val);
edg[i].vex1 = v1;
edg[i].vex2 = v2;
edg[i].val = val;
}
bubblesort(edg, e); // 调用冒泡排序函数对边进行排序
// 遍历所有边,执行Kruskal算法来找到最小生成树
for (int i = 0; i < e; ++i)
{
if (conne_gra[edg[i].vex1] != conne_gra[edg[i].vex2])
{ // 如果当前边的两个顶点不在同一个连通分量中
int tmp1 = conne_gra[edg[i].vex1], tmp2 = conne_gra[edg[i].vex2];
for (int k = 1; k <= v; ++k)
{ // 将所有属于tmp2的顶点合并到tmp1的连通分量中
if (conne_gra[k] == tmp2)
conne_gra[k] = tmp1;
}
ret += edg[i].val; // 将当前边的权重加到最小生成树的权重中
}
}
printf("%d", ret);
return 0;
}
```
并查集方法二
```c
#include
#include
// 定义边结构体,包含两个顶点vex1和vex2以及它们之间的权重val (略,同上)
// 冒泡排序函数,用于按边的权重val不减序排序边数组(略,同上)
// 并查集的查找操作
int find(int m, int *father)
{ // 如果当前节点是其自身的父节点,则直接返回该节点
// 否则递归查找其父节点的根,并将当前节点直接连接到根节点
return (m == father[m]) ? m : (father[m] = find(father[m], father)); // 路径压缩
}
// 并查集的加入集合
void Union(int m, int n, int *father)
{
int x = find(m, father);
int y = find(n, father);
if (x == y)
return; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
father[y] = x;
}
int main()
{
int v, e;
int v1, v2, val;
int ret = 0;
scanf("%d%d", &v, &e);
struct Edge *edg = (struct Edge *)malloc(sizeof(struct Edge) * e);
int *conne_gra = (int *)malloc(sizeof(int) * (v + 1));
// 初始化连通图数组,每个顶点初始时只与自己相连通
for (int i = 0; i <= v; ++i)
{
conne_gra[i] = i;
}
// 读取所有边的信息并存储到edg(存储所有边的)数组中
for (int i = 0; i < e; ++i)
{
scanf("%d%d%d", &v1, &v2, &val);
edg[i].vex1 = v1;
edg[i].vex2 = v2;
edg[i].val = val;
}
bubblesort(edg, e); // 调用冒泡排序函数对边进行排序
// Kruskal算法的实现,通过边数组构建最小生成树
int j = 0, count = 0;
while (v > 1)
{
if (find(edg[j].vex1, conne_gra) != find(edg[j].vex2, conne_gra))
{
ret += edg[j].val; // 将当前边的权重加到最小生成树的权重中
Union(edg[j].vex1, edg[j].vex2, conne_gra);
v--;
}
j++;
}
printf("%d", ret);
return 0;
}
```