
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 198.打家劫舍
[力扣题目链接](https://leetcode.cn/problems/house-robber/)
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
* 示例 1:
* 输入:[1,2,3,1]
* 输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
* 示例 2:
* 输入:[2,7,9,3,1]
* 输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
* 0 <= nums.length <= 100
* 0 <= nums[i] <= 400
## 算法公开课
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[动态规划,偷不偷这个房间呢?| LeetCode:198.打家劫舍](https://www.bilibili.com/video/BV1Te411N7SX),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
大家如果刚接触这样的题目,会有点困惑,当前的状态我是偷还是不偷呢?
仔细一想,当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。
所以这里就更感觉到,当前状态和前面状态会有一种依赖关系,那么这种依赖关系都是动规的递推公式。
当然以上是大概思路,打家劫舍是dp解决的经典问题,接下来我们来动规五部曲分析如下:
1. 确定dp数组(dp table)以及下标的含义
**dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]**。
2. 确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷。
如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。
如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房,(**注意这里是考虑,并不是一定要偷i-1房,这是很多同学容易混淆的点**)
然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
3. dp数组如何初始化
从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出,递推公式的基础就是dp[0] 和 dp[1]
从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1]);
代码如下:
```CPP
vector dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
```
4. 确定遍历顺序
dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历!
代码如下:
```CPP
for (int i = 2; i < nums.size(); i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
```
5. 举例推导dp数组
以示例二,输入[2,7,9,3,1]为例。
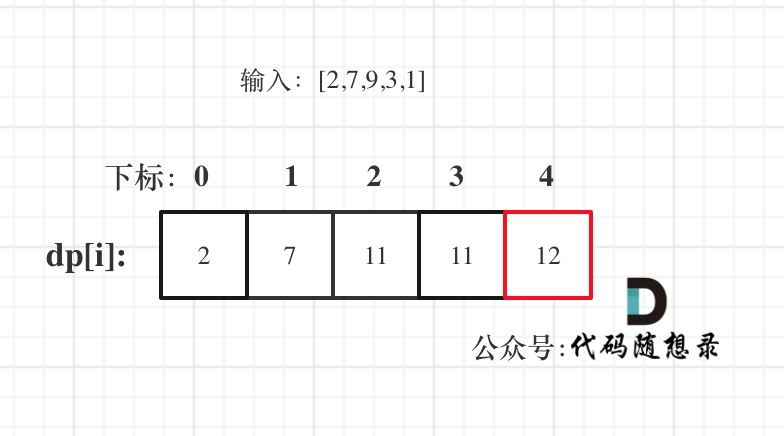
红框dp[nums.size() - 1]为结果。
以上分析完毕,C++代码如下:
```CPP
class Solution {
public:
int rob(vector& nums) {
if (nums.size() == 0) return 0;
if (nums.size() == 1) return nums[0];
vector dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i < nums.size(); i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[nums.size() - 1];
}
};
```
* 时间复杂度: O(n)
* 空间复杂度: O(n)
## 总结
打家劫舍是DP解决的经典题目,这道题也是打家劫舍入门级题目,后面我们还会变种方式来打劫的。
## 其他语言版本
### Java:
```Java
// 动态规划
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0) return 0;
if (nums.length == 1) return nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
dp[1] = Math.max(dp[0], nums[1]);
for (int i = 2; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[nums.length - 1];
}
}
// 使用滚动数组思想,优化空间
// 分析本题可以发现,所求结果仅依赖于前两种状态,此时可以使用滚动数组思想将空间复杂度降低为3个空间
class Solution {
public int rob(int[] nums) {
int len = nums.length;
if (len == 0) return 0;
else if (len == 1) return nums[0];
else if (len == 2) return Math.max(nums[0],nums[1]);
int[] result = new int[3]; //存放选择的结果
result[0] = nums[0];
result[1] = Math.max(nums[0],nums[1]);
for(int i=2;i int:
if len(nums) == 0: # 如果没有房屋,返回0
return 0
if len(nums) == 1: # 如果只有一个房屋,返回其金额
return nums[0]
# 创建一个动态规划数组,用于存储最大金额
dp = [0] * len(nums)
dp[0] = nums[0] # 将dp的第一个元素设置为第一个房屋的金额
dp[1] = max(nums[0], nums[1]) # 将dp的第二个元素设置为第一二个房屋中的金额较大者
# 遍历剩余的房屋
for i in range(2, len(nums)):
# 对于每个房屋,选择抢劫当前房屋和抢劫前一个房屋的最大金额
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])
return dp[-1] # 返回最后一个房屋中可抢劫的最大金额
```
2维DP
```python
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums: # 如果没有房屋,返回0
return 0
n = len(nums)
dp = [[0, 0] for _ in range(n)] # 创建二维动态规划数组,dp[i][0]表示不抢劫第i个房屋的最大金额,dp[i][1]表示抢劫第i个房屋的最大金额
dp[0][1] = nums[0] # 抢劫第一个房屋的最大金额为第一个房屋的金额
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1]) # 不抢劫第i个房屋,最大金额为前一个房屋抢劫和不抢劫的最大值
dp[i][1] = dp[i-1][0] + nums[i] # 抢劫第i个房屋,最大金额为前一个房屋不抢劫的最大金额加上当前房屋的金额
return max(dp[n-1][0], dp[n-1][1]) # 返回最后一个房屋中可抢劫的最大金额
```
优化版
```python
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums: # 如果没有房屋,返回0
return 0
prev_max = 0 # 上一个房屋的最大金额
curr_max = 0 # 当前房屋的最大金额
for num in nums:
temp = curr_max # 临时变量保存当前房屋的最大金额
curr_max = max(prev_max + num, curr_max) # 更新当前房屋的最大金额
prev_max = temp # 更新上一个房屋的最大金额
return curr_max # 返回最后一个房屋中可抢劫的最大金额
```
### Go:
```Go
func rob(nums []int) int {
n := len(nums)
dp := make([]int, n+1) // dp[i]表示偷到第i家能够偷得的最大金额
dp[1] = nums[0]
for i := 2; i <= n; i++ {
dp[i] = max(dp[i-1], dp[i-2] + nums[i-1])
}
return dp[n]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
```
### JavaScript:
```javascript
const rob = nums => {
// 数组长度
const len = nums.length;
// dp数组初始化
const dp = [nums[0], Math.max(nums[0], nums[1])];
// 从下标2开始遍历
for (let i = 2; i < len; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[len - 1];
};
```
### TypeScript:
```typescript
function rob(nums: number[]): number {
/**
dp[i]: 前i个房屋能偷到的最大金额
dp[0]: nums[0];
dp[1]: max(nums[0], nums[1]);
...
dp[i]: max(dp[i-1], dp[i-2]+nums[i]);
*/
const length: number = nums.length;
if (length === 1) return nums[0];
const dp: number[] = [];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (let i = 2; i < length; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[length - 1];
};
```
### C
```c
#define max(a, b) ((a) > (b) ? (a) : (b))
int rob(int* nums, int numsSize) {
if(numsSize == 0){
return 0;
}
if(numsSize == 1){
return nums[0];
}
// dp初始化
int dp[numsSize];
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for(int i = 2; i < numsSize; i++){
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[numsSize - 1];
}
```
### Rust:
```rust
impl Solution {
pub fn rob(nums: Vec) -> i32 {
if nums.len() == 1 {
return nums[0];
}
let mut dp = vec![0; nums.len()];
dp[0] = nums[0];
dp[1] = nums[0].max(nums[1]);
for i in 2..nums.len() {
dp[i] = (dp[i - 2] + nums[i]).max(dp[i - 1]);
}
dp[nums.len() - 1]
}
}
```

