
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
## 392.判断子序列
[力扣题目链接](https://leetcode-cn.com/problems/is-subsequence/)
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true
示例 2:
输入:s = "axc", t = "ahbgdc"
输出:false
提示:
* 0 <= s.length <= 100
* 0 <= t.length <= 10^4
两个字符串都只由小写字符组成。
## 思路
(这道题可以用双指针的思路来实现,时间复杂度就是$O(n)$)
这道题应该算是编辑距离的入门题目,因为从题意中我们也可以发现,只需要计算删除的情况,不用考虑增加和替换的情况。
**所以掌握本题也是对后面要讲解的编辑距离的题目打下基础**。
动态规划五部曲分析如下:
1. 确定dp数组(dp table)以及下标的含义
**dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]**。
注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。
有同学问了,为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
用i来表示也可以!
但我统一以下标i-1为结尾的字符串来计算,这样在下面的递归公式中会容易理解一些,如果还有疑惑,可以继续往下看。
2. 确定递推公式
在确定递推公式的时候,首先要考虑如下两种操作,整理如下:
* if (s[i - 1] == t[j - 1])
* t中找到了一个字符在s中也出现了
* if (s[i - 1] != t[j - 1])
* 相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(**如果不理解,在回看一下dp[i][j]的定义**)
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
3. dp数组如何初始化
从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],所以dp[0][0]和dp[i][0]是一定要初始化的。
这里大家已经可以发现,在定义dp[i][j]含义的时候为什么要**表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]**。
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:
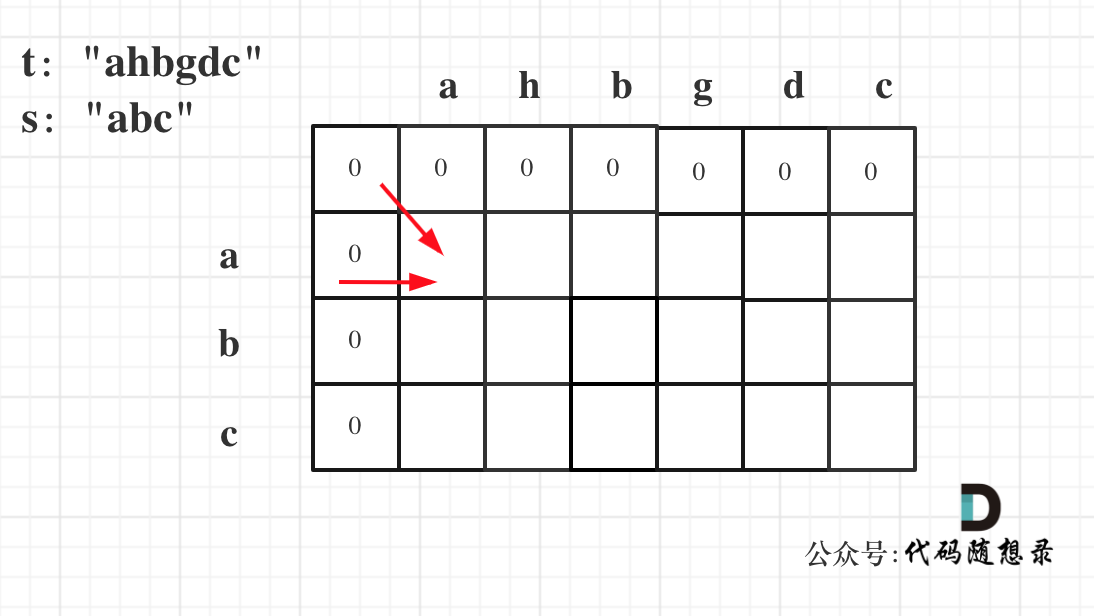
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
这里dp[i][0]和dp[0][j]是没有含义的,仅仅是为了给递推公式做前期铺垫,所以初始化为0。
**其实这里只初始化dp[i][0]就够了,但一起初始化也方便,所以就一起操作了**,代码如下:
```CPP
vector> dp(s.size() + 1, vector(t.size() + 1, 0));
```
4. 确定遍历顺序
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],那么遍历顺序也应该是从上到下,从左到右
如图所示:
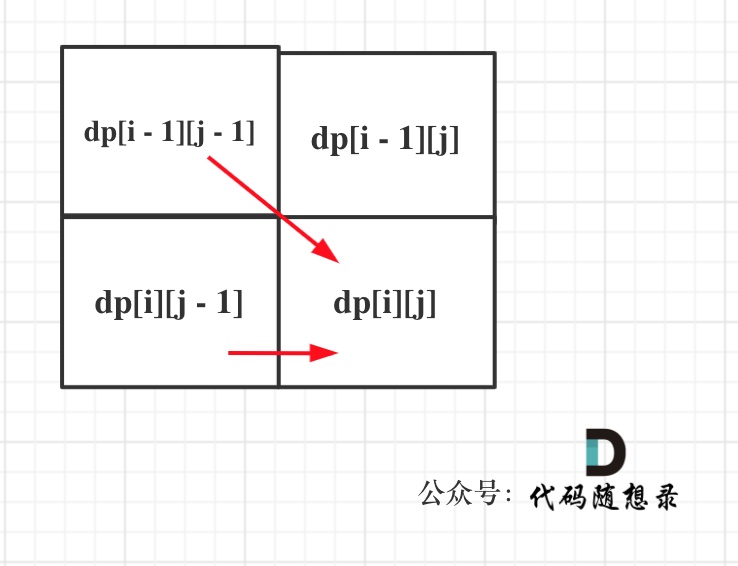
5. 举例推导dp数组
以示例一为例,输入:s = "abc", t = "ahbgdc",dp状态转移图如下:
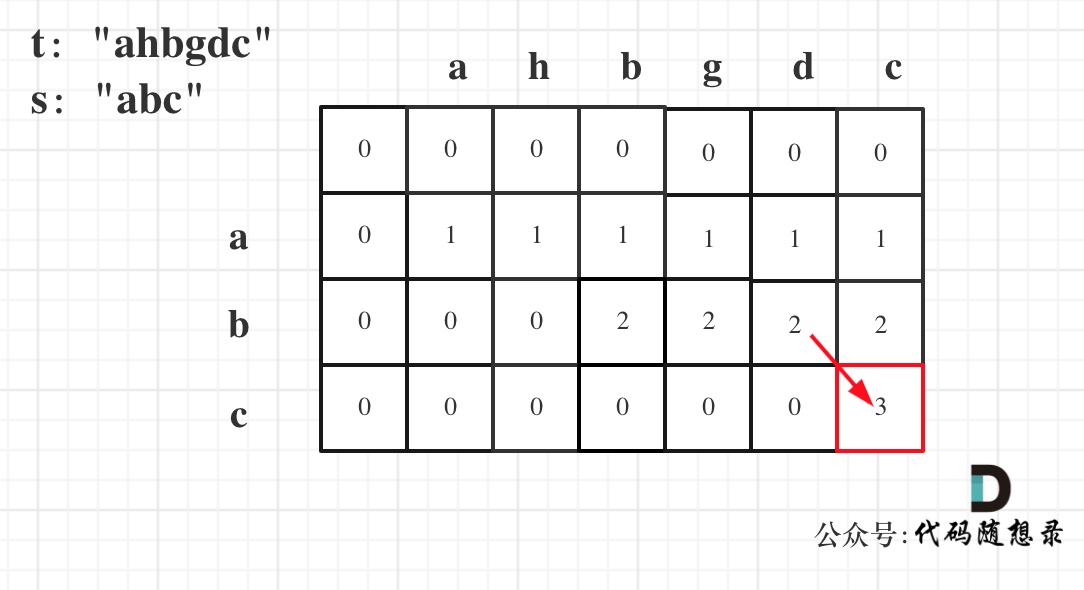
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
图中dp[s.size()][t.size()] = 3, 而s.size() 也为3。所以s是t 的子序列,返回true。
动规五部曲分析完毕,C++代码如下:
```CPP
class Solution {
public:
bool isSubsequence(string s, string t) {
vector> dp(s.size() + 1, vector(t.size() + 1, 0));
for (int i = 1; i <= s.size(); i++) {
for (int j = 1; j <= t.size(); j++) {
if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = dp[i][j - 1];
}
}
if (dp[s.size()][t.size()] == s.size()) return true;
return false;
}
};
```
* 时间复杂度:$O(n × m)$
* 空间复杂度:$O(n × m)$
## 总结
这道题目算是编辑距离的入门题目(毕竟这里只是涉及到减法),也是动态规划解决的经典题型。
这一类题都是题目读上去感觉很复杂,模拟一下也发现很复杂,用动规分析完了也感觉很复杂,但是最终代码却很简短。
编辑距离的题目最能体现出动规精髓和巧妙之处,大家可以好好体会一下。
## 其他语言版本
Java:
```java
class Solution {
public boolean isSubsequence(String s, String t) {
int length1 = s.length(); int length2 = t.length();
int[][] dp = new int[length1+1][length2+1];
for(int i = 1; i <= length1; i++){
for(int j = 1; j <= length2; j++){
if(s.charAt(i-1) == t.charAt(j-1)){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = dp[i][j-1];
}
}
}
if(dp[length1][length2] == length1){
return true;
}else{
return false;
}
}
}
```
Python:
```python
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]
for i in range(1, len(s)+1):
for j in range(1, len(t)+1):
if s[i-1] == t[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = dp[i][j-1]
if dp[-1][-1] == len(s):
return True
return False
```
JavaScript:
```javascript
const isSubsequence = (s, t) => {
// s、t的长度
const [m, n] = [s.length, t.length];
// dp全初始化为0
const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// 更新dp[i][j],两种情况
if (s[i - 1] === t[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = dp[i][j - 1];
}
}
}
// 遍历结束,判断dp右下角的数是否等于s的长度
return dp[m][n] === m ? true : false;
};
```
Go:
```go
func isSubsequence(s string, t string) bool {
dp := make([][]int,len(s)+1)
for i:=0;i

