
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
> 这也可以用回溯法? 其实深搜和回溯也是相辅相成的,毕竟都用递归。
# 332.重新安排行程
[力扣题目链接](https://leetcode.cn/problems/reconstruct-itinerary/)
给定一个机票的字符串二维数组 [from, to],子数组中的两个成员分别表示飞机出发和降落的机场地点,对该行程进行重新规划排序。所有这些机票都属于一个从 JFK(肯尼迪国际机场)出发的先生,所以该行程必须从 JFK 开始。
提示:
* 如果存在多种有效的行程,请你按字符自然排序返回最小的行程组合。例如,行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前
* 所有的机场都用三个大写字母表示(机场代码)。
* 假定所有机票至少存在一种合理的行程。
* 所有的机票必须都用一次 且 只能用一次。
示例 1:
* 输入:[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
* 输出:["JFK", "MUC", "LHR", "SFO", "SJC"]
示例 2:
* 输入:[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
* 输出:["JFK","ATL","JFK","SFO","ATL","SFO"]
* 解释:另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。
## 算法公开课
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[带你学透回溯算法(理论篇)](https://www.bilibili.com/video/BV1cy4y167mM/) ,相信结合视频再看本篇题解,更有助于大家对本题的理解。**
## 思路
这道题目还是很难的,之前我们用回溯法解决了如下问题:[组合问题](https://programmercarl.com/0077.组合.html),[分割问题](https://programmercarl.com/0093.复原IP地址.html),[子集问题](https://programmercarl.com/0078.子集.html),[排列问题](https://programmercarl.com/0046.全排列.html)。
直觉上来看 这道题和回溯法没有什么关系,更像是图论中的深度优先搜索。
实际上确实是深搜,但这是深搜中使用了回溯的例子,在查找路径的时候,如果不回溯,怎么能查到目标路径呢。
所以我倾向于说本题应该使用回溯法,那么我也用回溯法的思路来讲解本题,其实深搜一般都使用了回溯法的思路,在图论系列中我会再详细讲解深搜。
**这里就是先给大家拓展一下,原来回溯法还可以这么玩!**
**这道题目有几个难点:**
1. 一个行程中,如果航班处理不好容易变成一个圈,成为死循环
2. 有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
3. 使用回溯法(也可以说深搜) 的话,那么终止条件是什么呢?
4. 搜索的过程中,如何遍历一个机场所对应的所有机场。
针对以上问题我来逐一解答!
### 如何理解死循环
对于死循环,我来举一个有重复机场的例子:
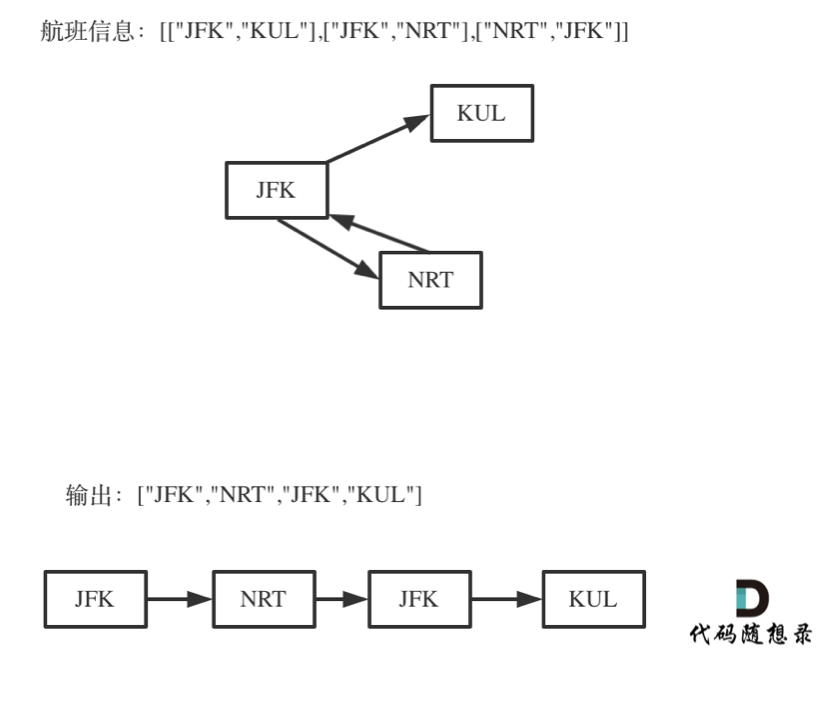
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
### 该记录映射关系
有多种解法,字母序靠前排在前面,让很多同学望而退步,如何该记录映射关系呢 ?
一个机场映射多个机场,机场之间要靠字母序排列,一个机场映射多个机场,可以使用std::unordered_map,如果让多个机场之间再有顺序的话,就是用std::map 或者std::multimap 或者 std::multiset。
如果对map 和 set 的实现机制不太了解,也不清楚为什么 map、multimap就是有序的同学,可以看这篇文章[关于哈希表,你该了解这些!](https://programmercarl.com/哈希表理论基础.html)。
这样存放映射关系可以定义为 `unordered_map> targets` 或者 `unordered_map> targets`。
含义如下:
unordered_map> targets:unordered_map<出发机场, 到达机场的集合> targets
unordered_map> targets:unordered_map<出发机场, map<到达机场, 航班次数>> targets
这两个结构,我选择了后者,因为如果使用`unordered_map> targets` 遍历multiset的时候,不能删除元素,一旦删除元素,迭代器就失效了。
**再说一下为什么一定要增删元素呢,正如开篇我给出的图中所示,出发机场和到达机场是会重复的,搜索的过程没及时删除目的机场就会死循环。**
所以搜索的过程中就是要不断的删multiset里的元素,那么推荐使用`unordered_map> targets`。
在遍历 `unordered_map<出发机场, map<到达机场, 航班次数>> targets`的过程中,**可以使用"航班次数"这个字段的数字做相应的增减,来标记到达机场是否使用过了。**
如果“航班次数”大于零,说明目的地还可以飞,如果“航班次数”等于零说明目的地不能飞了,而不用对集合做删除元素或者增加元素的操作。
**相当于说我不删,我就做一个标记!**
### 回溯法
这道题目我使用回溯法,那么下面按照我总结的回溯模板来:
```
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
```
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
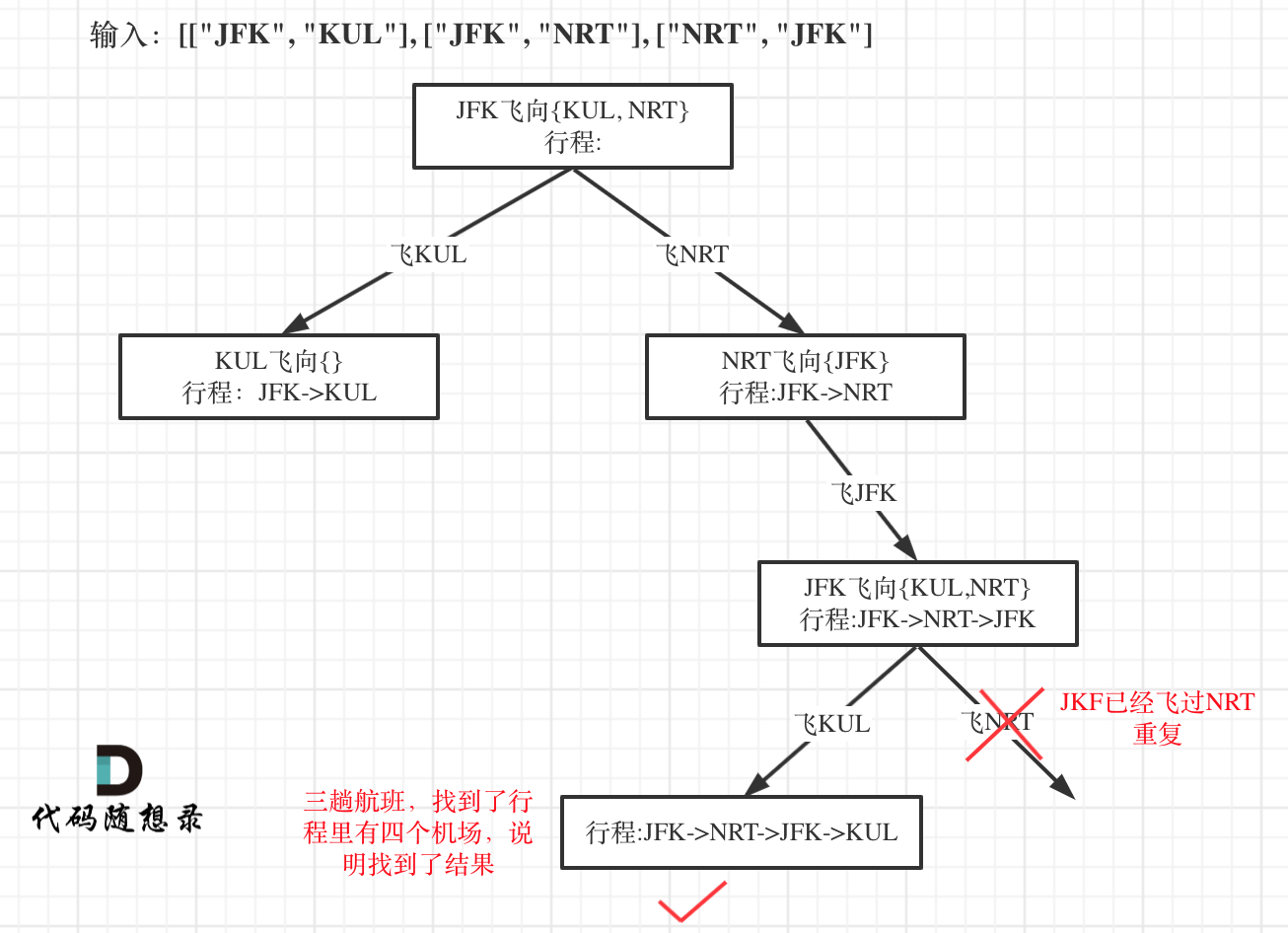
开始回溯三部曲讲解:
* 递归函数参数
在讲解映射关系的时候,已经讲过了,使用`unordered_map> targets;` 来记录航班的映射关系,我定义为全局变量。
当然把参数放进函数里传进去也是可以的,我是尽量控制函数里参数的长度。
参数里还需要ticketNum,表示有多少个航班(终止条件会用上)。
代码如下:
```cpp
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map> targets;
bool backtracking(int ticketNum, vector& result) {
```
**注意函数返回值我用的是bool!**
我们之前讲解回溯算法的时候,一般函数返回值都是void,这次为什么是bool呢?
因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,如图:
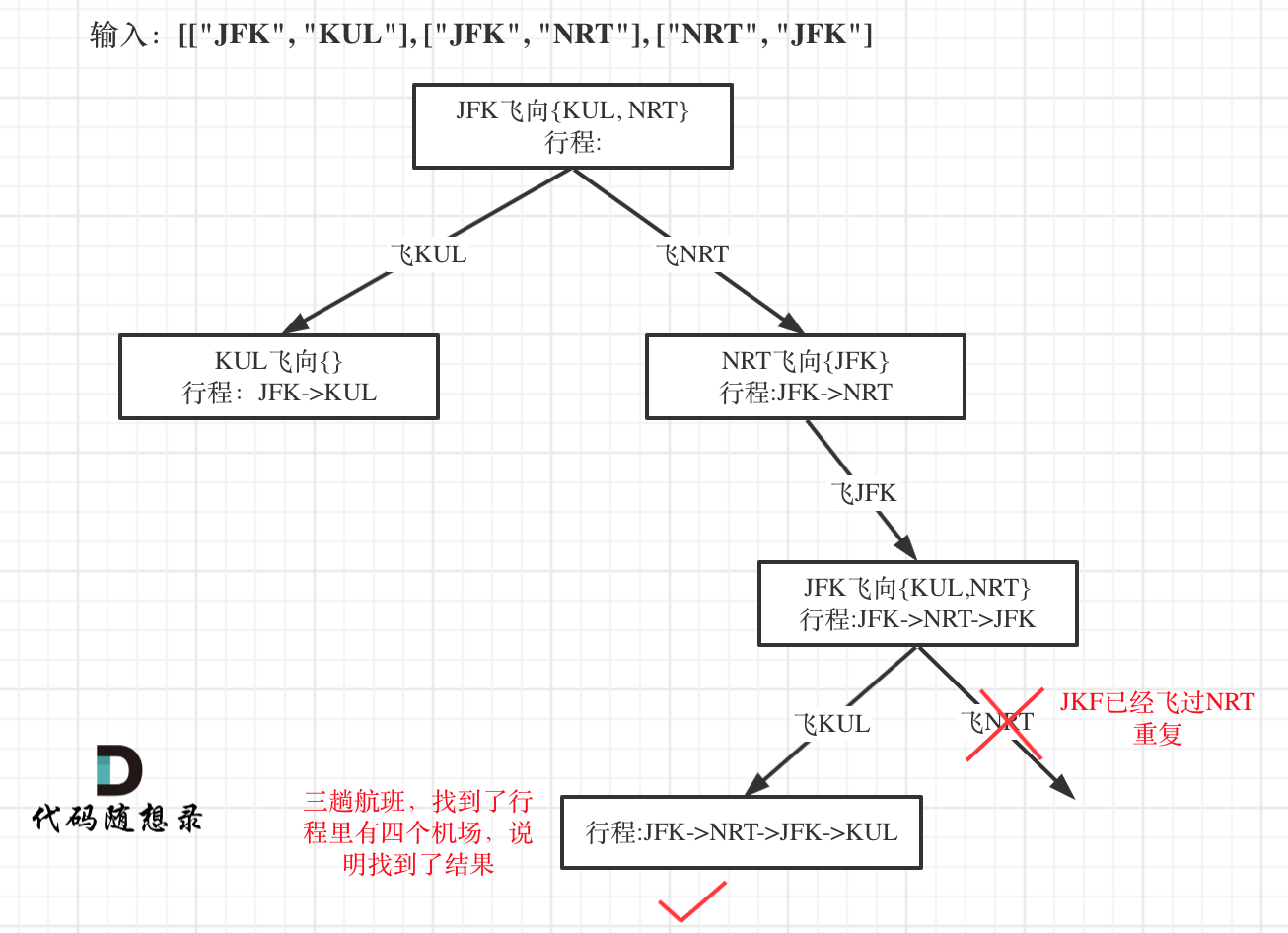
所以找到了这个叶子节点了直接返回,这个递归函数的返回值问题我们在讲解二叉树的系列的时候,在这篇[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://programmercarl.com/0112.路径总和.html)详细介绍过。
当然本题的targets和result都需要初始化,代码如下:
```cpp
for (const vector& vec : tickets) {
targets[vec[0]][vec[1]]++; // 记录映射关系
}
result.push_back("JFK"); // 起始机场
```
* 递归终止条件
拿题目中的示例为例,输入: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]] ,这是有4个航班,那么只要找出一种行程,行程里的机场个数是5就可以了。
所以终止条件是:我们回溯遍历的过程中,遇到的机场个数,如果达到了(航班数量+1),那么我们就找到了一个行程,把所有航班串在一起了。
代码如下:
```cpp
if (result.size() == ticketNum + 1) {
return true;
}
```
已经看习惯回溯法代码的同学,到叶子节点了习惯性的想要收集结果,但发现并不需要,本题的result相当于 [回溯算法:求组合总和!](https://programmercarl.com/0216.组合总和III.html)中的path,也就是本题的result就是记录路径的(就一条),在如下单层搜索的逻辑中result就添加元素了。
* 单层搜索的逻辑
回溯的过程中,如何遍历一个机场所对应的所有机场呢?
这里刚刚说过,在选择映射函数的时候,不能选择`unordered_map> targets`, 因为一旦有元素增删multiset的迭代器就会失效,当然可能有牛逼的容器删除元素迭代器不会失效,这里就不在讨论了。
**可以说本题既要找到一个对数据进行排序的容器,而且还要容易增删元素,迭代器还不能失效**。
所以我选择了`unordered_map> targets` 来做机场之间的映射。
遍历过程如下:
```CPP
for (pair& target : targets[result[result.size() - 1]]) {
if (target.second > 0 ) { // 记录到达机场是否飞过了
result.push_back(target.first);
target.second--;
if (backtracking(ticketNum, result)) return true;
result.pop_back();
target.second++;
}
}
```
可以看出 通过`unordered_map> targets`里的int字段来判断 这个集合里的机场是否使用过,这样避免了直接去删元素。
分析完毕,此时完整C++代码如下:
```CPP
class Solution {
private:
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map> targets;
bool backtracking(int ticketNum, vector& result) {
if (result.size() == ticketNum + 1) {
return true;
}
for (pair& target : targets[result[result.size() - 1]]) {
if (target.second > 0 ) { // 记录到达机场是否飞过了
result.push_back(target.first);
target.second--;
if (backtracking(ticketNum, result)) return true;
result.pop_back();
target.second++;
}
}
return false;
}
public:
vector findItinerary(vector>& tickets) {
targets.clear();
vector result;
for (const vector& vec : tickets) {
targets[vec[0]][vec[1]]++; // 记录映射关系
}
result.push_back("JFK"); // 起始机场
backtracking(tickets.size(), result);
return result;
}
};
```
一波分析之后,可以看出我就是按照回溯算法的模板来的。
代码中
```cpp
for (pair& target : targets[result[result.size() - 1]])
```
一定要加上引用即 `& target`,因为后面有对 target.second 做减减操作,如果没有引用,单纯复制,这个结果就没记录下来,那最后的结果就不对了。
加上引用之后,就必须在 string 前面加上 const,因为map中的key 是不可修改了,这就是语法规定了。
## 总结
本题其实可以算是一道hard的题目了,关于本题的难点我在文中已经列出了。
**如果单纯的回溯搜索(深搜)并不难,难还难在容器的选择和使用上**。
本题其实是一道深度优先搜索的题目,但是我完全使用回溯法的思路来讲解这道题题目,**算是给大家拓展一下思维方式,其实深搜和回溯也是分不开的,毕竟最终都是用递归**。
如果最终代码,发现照着回溯法模板画的话好像也能画出来,但难就难如何知道可以使用回溯,以及如果套进去,所以我再写了这么长的一篇来详细讲解。
就酱,很多录友表示和「代码随想录」相见恨晚,那么帮Carl宣传一波吧,让更多同学知道这里!
## 其他语言版本
### Java
```java
class Solution {
private LinkedList res;
private LinkedList path = new LinkedList<>();
public List findItinerary(List> tickets) {
Collections.sort(tickets, (a, b) -> a.get(1).compareTo(b.get(1)));
path.add("JFK");
boolean[] used = new boolean[tickets.size()];
backTracking((ArrayList) tickets, used);
return res;
}
public boolean backTracking(ArrayList> tickets, boolean[] used) {
if (path.size() == tickets.size() + 1) {
res = new LinkedList(path);
return true;
}
for (int i = 0; i < tickets.size(); i++) {
if (!used[i] && tickets.get(i).get(0).equals(path.getLast())) {
path.add(tickets.get(i).get(1));
used[i] = true;
if (backTracking(tickets, used)) {
return true;
}
used[i] = false;
path.removeLast();
}
}
return false;
}
}
```
```java
class Solution {
private Deque res;
private Map> map;
private boolean backTracking(int ticketNum){
if(res.size() == ticketNum + 1){
return true;
}
String last = res.getLast();
if(map.containsKey(last)){//防止出现null
for(Map.Entry target : map.get(last).entrySet()){
int count = target.getValue();
if(count > 0){
res.add(target.getKey());
target.setValue(count - 1);
if(backTracking(ticketNum)) return true;
res.removeLast();
target.setValue(count);
}
}
}
return false;
}
public List findItinerary(List> tickets) {
map = new HashMap>();
res = new LinkedList<>();
for(List t : tickets){
Map temp;
if(map.containsKey(t.get(0))){
temp = map.get(t.get(0));
temp.put(t.get(1), temp.getOrDefault(t.get(1), 0) + 1);
}else{
temp = new TreeMap<>();//升序Map
temp.put(t.get(1), 1);
}
map.put(t.get(0), temp);
}
res.add("JFK");
backTracking(tickets.size());
return new ArrayList<>(res);
}
}
```
```java
/* 该方法是对第二个方法的改进,主要变化在于将某点的所有终点变更为链表的形式,优点在于
1.添加终点时直接在对应位置添加节点,避免了TreeMap增元素时的频繁调整
2.同时每次对终点进行增加删除查找时直接通过下标操作,避免hashMap反复计算hash*/
class Solution {
//key为起点,value是有序的终点的列表
Map> ticketMap = new HashMap<>();
LinkedList result = new LinkedList<>();
int total;
public List findItinerary(List> tickets) {
total = tickets.size() + 1;
//遍历tickets,存入ticketMap中
for (List ticket : tickets) {
addNew(ticket.get(0), ticket.get(1));
}
deal("JFK");
return result;
}
boolean deal(String currentLocation) {
result.add(currentLocation);
//机票全部用完,找到最小字符路径
if (result.size() == total) {
return true;
}
//当前位置的终点列表
LinkedList targetLocations = ticketMap.get(currentLocation);
//没有从当前位置出发的机票了,说明这条路走不通
if (targetLocations != null && !targetLocations.isEmpty()) {
//终点列表中遍历到的终点
String targetLocation;
//遍历从当前位置出发的机票
for (int i = 0; i < targetLocations.size(); i++) {
targetLocation = targetLocations.get(i);
//删除终点列表中当前的终点
targetLocations.remove(i);
//递归
if (deal(targetLocation)) {
return true;
}
//路线走不通,将机票重新加回去
targetLocations.add(i, targetLocation);
result.removeLast();
}
}
return false;
}
/**
* 在map中按照字典顺序添加新元素
*
* @param start 起点
* @param end 终点
*/
void addNew(String start, String end) {
LinkedList startAllEnd = ticketMap.getOrDefault(start, new LinkedList<>());
if (!startAllEnd.isEmpty()) {
for (int i = 0; i < startAllEnd.size(); i++) {
if (end.compareTo(startAllEnd.get(i)) < 0) {
startAllEnd.add(i, end);
return;
}
}
startAllEnd.add(startAllEnd.size(), end);
} else {
startAllEnd.add(end);
ticketMap.put(start, startAllEnd);
}
}
}
```
### Python
回溯 使用used数组
```python
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
tickets.sort() # 先排序,这样一旦找到第一个可行路径,一定是字母排序最小的
used = [0] * len(tickets)
path = ['JFK']
results = []
self.backtracking(tickets, used, path, 'JFK', results)
return results[0]
def backtracking(self, tickets, used, path, cur, results):
if len(path) == len(tickets) + 1: # 终止条件:路径长度等于机票数量+1
results.append(path[:]) # 将当前路径添加到结果列表
return True
for i, ticket in enumerate(tickets): # 遍历机票列表
if ticket[0] == cur and used[i] == 0: # 找到起始机场为cur且未使用过的机票
used[i] = 1 # 标记该机票为已使用
path.append(ticket[1]) # 将到达机场添加到路径中
state = self.backtracking(tickets, used, path, ticket[1], results) # 递归搜索
path.pop() # 回溯,移除最后添加的到达机场
used[i] = 0 # 标记该机票为未使用
if state:
return True # 只要找到一个可行路径就返回,不继续搜索
```
回溯 使用字典
```python
class Solution:
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
self.adj = {}
# sort by the destination alphabetically
# 根据航班每一站的重点字母顺序排序
tickets.sort(key=lambda x:x[1])
# get all possible connection for each destination
# 罗列每一站的下一个可选项
for u,v in tickets:
if u in self.adj: self.adj[u].append(v)
else: self.adj[u] = [v]
# 从JFK出发
self.result = []
self.dfs("JFK") # start with JFK
return self.result[::-1] # reverse to get the result
def dfs(self, s):
# if depart city has flight and the flight can go to another city
while s in self.adj and len(self.adj[s]) > 0:
# 找到s能到哪里,选能到的第一个机场
v = self.adj[s][0] # we go to the 1 choice of the city
# 在之后的可选项机场中去掉这个机场
self.adj[s].pop(0) # get rid of this choice since we used it
# 从当前的新出发点开始
self.dfs(v) # we start from the new airport
self.result.append(s) # after append, it will back track to last node, thus the result list is in reversed order
```
回溯 使用字典 逆序
```python
from collections import defaultdict
class Solution:
def findItinerary(self, tickets):
targets = defaultdict(list) # 创建默认字典,用于存储机场映射关系
for ticket in tickets:
targets[ticket[0]].append(ticket[1]) # 将机票输入到字典中
for key in targets:
targets[key].sort(reverse=True) # 对到达机场列表进行字母逆序排序
result = []
self.backtracking("JFK", targets, result) # 调用回溯函数开始搜索路径
return result[::-1] # 返回逆序的行程路径
def backtracking(self, airport, targets, result):
while targets[airport]: # 当机场还有可到达的机场时
next_airport = targets[airport].pop() # 弹出下一个机场
self.backtracking(next_airport, targets, result) # 递归调用回溯函数进行深度优先搜索
result.append(airport) # 将当前机场添加到行程路径中
```
### Go
```go
type pair struct {
target string
visited bool
}
type pairs []*pair
func (p pairs) Len() int {
return len(p)
}
func (p pairs) Swap(i, j int) {
p[i], p[j] = p[j], p[i]
}
func (p pairs) Less(i, j int) bool {
return p[i].target < p[j].target
}
func findItinerary(tickets [][]string) []string {
result := []string{}
// map[出发机场] pair{目的地,是否被访问过}
targets := make(map[string]pairs)
for _, ticket := range tickets {
if targets[ticket[0]] == nil {
targets[ticket[0]] = make(pairs, 0)
}
targets[ticket[0]] = append(targets[ticket[0]], &pair{target: ticket[1], visited: false})
}
for k, _ := range targets {
sort.Sort(targets[k])
}
result = append(result, "JFK")
var backtracking func() bool
backtracking = func() bool {
if len(tickets)+1 == len(result) {
return true
}
// 取出起飞航班对应的目的地
for _, pair := range targets[result[len(result)-1]] {
if pair.visited == false {
result = append(result, pair.target)
pair.visited = true
if backtracking() {
return true
}
result = result[:len(result)-1]
pair.visited = false
}
}
return false
}
backtracking()
return result
}
```
### Javascript
```Javascript
var findItinerary = function(tickets) {
let result = ['JFK']
let map = {}
for (const tickt of tickets) {
const [from, to] = tickt
if (!map[from]) {
map[from] = []
}
map[from].push(to)
}
for (const city in map) {
// 对到达城市列表排序
map[city].sort()
}
function backtracing() {
if (result.length === tickets.length + 1) {
return true
}
if (!map[result[result.length - 1]] || !map[result[result.length - 1]].length) {
return false
}
for(let i = 0 ; i < map[result[result.length - 1]].length; i++) {
let city = map[result[result.length - 1]][i]
// 删除已走过航线,防止死循环
map[result[result.length - 1]].splice(i, 1)
result.push(city)
if (backtracing()) {
return true
}
result.pop()
map[result[result.length - 1]].splice(i, 0, city)
}
}
backtracing()
return result
};
```
**javascript版本二 处理对象key无序问题**
```javascript
/**
* @param {string[][]} tickets
* @return {string[]}
*/
var findItinerary = function (tickets) {
const ans = ["JFK"];
let map = {};
// 整理每个站点的终点站信息
tickets.forEach((t) => {
let targets = map[t[0]];
if (!targets) {
targets = { [t[1]]: 0 };
map[t[0]] = targets;
}
targets[t[1]] = (targets[t[1]] || 0) + 1;
});
// 按照key字典序排序对象
const sortObject = (obj) => {
const newObj = {};
const keys = Object.keys(obj);
keys.sort((k1, k2) => (k1 < k2 ? -1 : 1));
keys.forEach((key) => {
if (obj[key] !== null && typeof obj[key] === "object") {
newObj[key] = sortObject(obj[key]);
} else {
newObj[key] = obj[key];
}
});
return newObj;
};
const backtrack = (tickets, targets) => {
if (ans.length === tickets.length + 1) {
return true;
}
const target = targets[ans[ans.length - 1]];
// 没有下一站
if (!target) {
return false;
}
// 或者在这里排序
// const keyList = Object.keys(target).sort((k1, k2) => (k1 < k2 ? -1 : 1));
const keyList = Object.keys(target);
for (const key of keyList) {
// 判断当前站是否还能飞
if (target[key] > 0) {
target[key]--;
ans.push(key);
// 对象key有序 此时的行程就是字典序最小的 直接跳出
if (backtrack(tickets, targets)) {
return true;
}
target[key]++;
ans.pop();
}
}
return false;
};
map = sortObject(map);
backtrack(tickets, map);
return ans;
};
```
### TypeScript
```typescript
function findItinerary(tickets: string[][]): string[] {
/**
TicketsMap 实例:
{ NRT: Map(1) { 'JFK' => 1 }, JFK: Map(2) { 'KUL' => 1, 'NRT' => 1 } }
这里选择Map数据结构的原因是:与Object类型的一个主要差异是,Map实例会维护键值对的插入顺序。
*/
type TicketsMap = {
[index: string]: Map
};
tickets.sort((a, b) => {
return a[1] < b[1] ? -1 : 1;
});
const ticketMap: TicketsMap = {};
for (const [from, to] of tickets) {
if (ticketMap[from] === undefined) {
ticketMap[from] = new Map();
}
ticketMap[from].set(to, (ticketMap[from].get(to) || 0) + 1);
}
const resRoute = ['JFK'];
backTracking(tickets.length, ticketMap, resRoute);
return resRoute;
function backTracking(ticketNum: number, ticketMap: TicketsMap, route: string[]): boolean {
if (route.length === ticketNum + 1) return true;
const targetMap = ticketMap[route[route.length - 1]];
if (targetMap !== undefined) {
for (const [to, count] of targetMap.entries()) {
if (count > 0) {
route.push(to);
targetMap.set(to, count - 1);
if (backTracking(ticketNum, ticketMap, route) === true) return true;
targetMap.set(to, count);
route.pop();
}
}
}
return false;
}
};
```
### C
```C
typedef struct {
char *name; /* key */
int cnt; /* 记录到达机场是否飞过了 */
UT_hash_handle hh; /* makes this structure hashable */
} to_airport_t;
typedef struct {
char *name; /* key */
to_airport_t *to_airports;
UT_hash_handle hh; /* makes this structure hashable */
} from_airport_t;
void to_airport_destroy(to_airport_t *airports) {
to_airport_t *airport, *tmp;
HASH_ITER(hh, airports, airport, tmp) {
HASH_DEL(airports, airport);
free(airport);
}
}
void from_airport_destroy(from_airport_t *airports) {
from_airport_t *airport, *tmp;
HASH_ITER(hh, airports, airport, tmp) {
to_airport_destroy(airport->to_airports);
HASH_DEL(airports, airport);
free(airport);
}
}
int name_sort(to_airport_t *a, to_airport_t *b) {
return strcmp(a->name, b->name);
}
bool backtracking(from_airport_t *airports, int target_path_len, char **path,
int path_len) {
if (path_len == target_path_len) return true;
from_airport_t *from_airport = NULL;
HASH_FIND_STR(airports, path[path_len - 1], from_airport);
if (!from_airport) return false;
for (to_airport_t *to_airport = from_airport->to_airports;
to_airport != NULL; to_airport = to_airport->hh.next) {
if (to_airport->cnt == 0) continue;
to_airport->cnt--;
path[path_len] = to_airport->name;
if (backtracking(airports, target_path_len, path, path_len + 1))
return true;
to_airport->cnt++;
}
return false;
}
char **findItinerary(char ***tickets, int ticketsSize, int *ticketsColSize,
int *returnSize) {
from_airport_t *airports = NULL;
// 记录映射关系
for (int i = 0; i < ticketsSize; i++) {
from_airport_t *from_airport = NULL;
to_airport_t *to_airport = NULL;
HASH_FIND_STR(airports, tickets[i][0], from_airport);
if (!from_airport) {
from_airport = malloc(sizeof(from_airport_t));
from_airport->name = tickets[i][0];
from_airport->to_airports = NULL;
HASH_ADD_KEYPTR(hh, airports, from_airport->name,
strlen(from_airport->name), from_airport);
}
HASH_FIND_STR(from_airport->to_airports, tickets[i][1], to_airport);
if (!to_airport) {
to_airport = malloc(sizeof(to_airport_t));
to_airport->name = tickets[i][1];
to_airport->cnt = 0;
HASH_ADD_KEYPTR(hh, from_airport->to_airports, to_airport->name,
strlen(to_airport->name), to_airport);
}
to_airport->cnt++;
}
// 机场排序
for (from_airport *from_airport = airports; from_airport != NULL;
from_airport = from_airport->hh.next) {
HASH_SRT(hh, from_airport->to_airports, name_sort);
}
char **path = malloc(sizeof(char *) * (ticketsSize + 1));
path[0] = "JFK"; // 起始机场
backtracking(airports, ticketsSize + 1, path, 1);
from_airport_destroy(airports);
*returnSize = ticketsSize + 1;
return path;
}
```
### Swift
直接迭代tickets数组:
```swift
func findItinerary(_ tickets: [[String]]) -> [String] {
// 先对路线进行排序
let tickets = tickets.sorted { (arr1, arr2) -> Bool in
if arr1[0] < arr2[0] {
return true
} else if arr1[0] > arr2[0] {
return false
}
if arr1[1] < arr2[1] {
return true
} else if arr1[1] > arr2[1] {
return false
}
return true
}
var path = ["JFK"]
var used = [Bool](repeating: false, count: tickets.count)
@discardableResult
func backtracking() -> Bool {
// 结束条件:满足一条路径的数量
if path.count == tickets.count + 1 { return true }
for i in 0 ..< tickets.count {
// 巧妙之处!跳过处理过或出发站不是path末尾站的线路,即筛选出未处理的又可以衔接path的线路
guard !used[i], tickets[i][0] == path.last! else { continue }
// 处理
used[i] = true
path.append(tickets[i][1])
// 递归
if backtracking() { return true }
// 回溯
path.removeLast()
used[i] = false
}
return false
}
backtracking()
return path
}
```
使用字典优化迭代遍历:
```swift
func findItinerary(_ tickets: [[String]]) -> [String] {
// 建立出发站和目的站的一对多关系,要对目的地进行排序
typealias Destination = (name: String, used: Bool)
var targets = [String: [Destination]]()
for line in tickets {
let src = line[0], des = line[1]
var value = targets[src] ?? []
value.append((des, false))
targets[src] = value
}
for (k, v) in targets {
targets[k] = v.sorted { $0.name < $1.name }
}
var path = ["JFK"]
let pathCount = tickets.count + 1
@discardableResult
func backtracking() -> Bool {
if path.count == pathCount { return true }
let startPoint = path.last!
guard let end = targets[startPoint]?.count, end > 0 else { return false }
for i in 0 ..< end {
// 排除处理过的线路
guard !targets[startPoint]![i].used else { continue }
// 处理
targets[startPoint]![i].used = true
path.append(targets[startPoint]![i].name)
// 递归
if backtracking() { return true }
// 回溯
path.removeLast()
targets[startPoint]![i].used = false
}
return false
}
backtracking()
return path
}
```
使用插入时排序优化targets字典的构造:
```swift
// 建立出发站和目的站的一对多关系,在构建的时候进行插入排序
typealias Destination = (name: String, used: Bool)
var targets = [String: [Destination]]()
func sortedInsert(_ element: Destination, to array: inout [Destination]) {
var left = 0, right = array.count - 1
while left <= right {
let mid = left + (right - left) / 2
if array[mid].name < element.name {
left = mid + 1
} else if array[mid].name > element.name {
right = mid - 1
} else {
left = mid
break
}
}
array.insert(element, at: left)
}
for line in tickets {
let src = line[0], des = line[1]
var value = targets[src] ?? []
sortedInsert((des, false), to: &value)
targets[src] = value
}
```
### Rust
** 文中的Hashmap嵌套Hashmap的方法因为Rust的所有权问题暂时无法实现,此方法为删除哈希表中元素法 **
```Rust
use std::collections::HashMap;
impl Solution {
fn backtracking(airport: String, targets: &mut HashMap<&String, Vec<&String>>, result: &mut Vec) {
while let Some(next_airport) = targets.get_mut(&airport).unwrap_or(&mut vec![]).pop() {
Self::backtracking(next_airport.clone(), targets, result);
}
result.push(airport.clone());
}
pub fn find_itinerary(tickets: Vec>) -> Vec {
let mut targets: HashMap<&String, Vec<&String>> = HashMap::new();
let mut result = Vec::new();
for t in 0..tickets.len() {
targets.entry(&tickets[t][0]).or_default().push(&tickets[t][1]);
}
for (_, target) in targets.iter_mut() {
target.sort_by(|a, b| b.cmp(a));
}
Self::backtracking("JFK".to_string(), &mut targets, &mut result);
result.reverse();
result
}
}
```

