



欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备! ## 45.跳跃游戏II 题目地址:https://leetcode-cn.com/problems/jump-game-ii/ 给定一个非负整数数组,你最初位于数组的第一个位置。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 你的目标是使用最少的跳跃次数到达数组的最后一个位置。 示例: 输入: [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。 说明: 假设你总是可以到达数组的最后一个位置。 ## 思路 本题相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)还是难了不少。 但思路是相似的,还是要看最大覆盖范围。 本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢? 贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。 思路虽然是这样,但在写代码的时候还不能真的就能跳多远跳远,那样就不知道下一步最远能跳到哪里了。 **所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!** **这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖**。 如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。 如图: 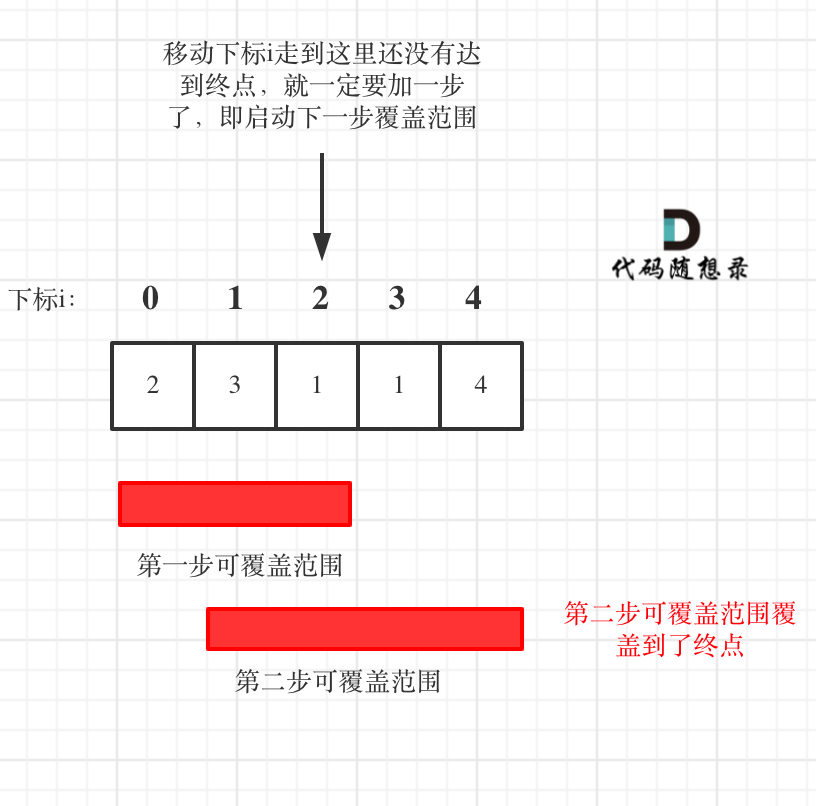 **图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)** ## 方法一 从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。 这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时 * 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。 * 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。 C++代码如下:(详细注释) ```C++ // 版本一 class Solution { public: int jump(vector