
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 17.电话号码的字母组合
[力扣题目链接](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
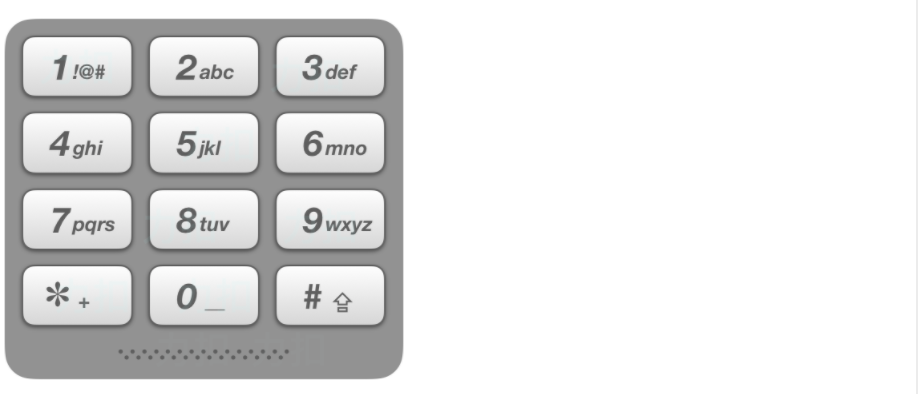
示例:
* 输入:"23"
* 输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
# 算法公开课
**《代码随想录》算法视频公开课:[还得用回溯算法!| LeetCode:17.电话号码的字母组合](https://www.bilibili.com/video/BV1yV4y1V7Ug),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
# 思路
从示例上来说,输入"23",最直接的想法就是两层for循环遍历了吧,正好把组合的情况都输出了。
如果输入"233"呢,那么就三层for循环,如果"2333"呢,就四层for循环.......
大家应该感觉出和[77.组合](https://programmercarl.com/0077.组合.html)遇到的一样的问题,就是这for循环的层数如何写出来,此时又是回溯法登场的时候了。
理解本题后,要解决如下三个问题:
1. 数字和字母如何映射
2. 两个字母就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来
3. 输入1 * #按键等等异常情况
## 数字和字母如何映射
可以使用map或者定义一个二维数组,例如:string letterMap[10],来做映射,我这里定义一个二维数组,代码如下:
```cpp
const string letterMap[10] = {
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz", // 9
};
```
## 回溯法来解决n个for循环的问题
对于回溯法还不了解的同学看这篇:[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)
例如:输入:"23",抽象为树形结构,如图所示:
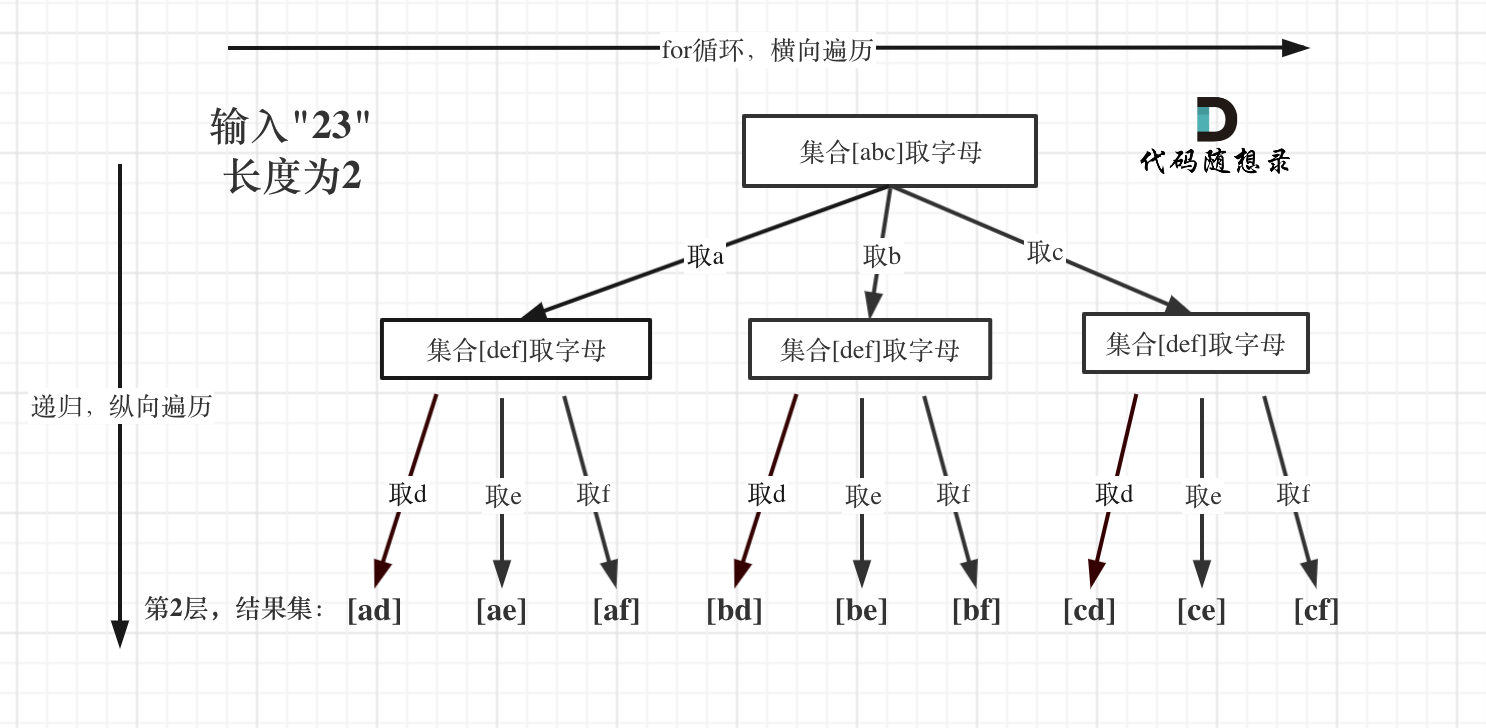
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
回溯三部曲:
* 确定回溯函数参数
首先需要一个字符串s来收集叶子节点的结果,然后用一个字符串数组result保存起来,这两个变量我依然定义为全局。
再来看参数,参数指定是有题目中给的string digits,然后还要有一个参数就是int型的index。
注意这个index可不是 [77.组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)中的startIndex了。
这个index是记录遍历第几个数字了,就是用来遍历digits的(题目中给出数字字符串),同时index也表示树的深度。
代码如下:
```cpp
vector result;
string s;
void backtracking(const string& digits, int index)
```
* 确定终止条件
例如输入用例"23",两个数字,那么根节点往下递归两层就可以了,叶子节点就是要收集的结果集。
那么终止条件就是如果index 等于 输入的数字个数(digits.size)了(本来index就是用来遍历digits的)。
然后收集结果,结束本层递归。
代码如下:
```cpp
if (index == digits.size()) {
result.push_back(s);
return;
}
```
* 确定单层遍历逻辑
首先要取index指向的数字,并找到对应的字符集(手机键盘的字符集)。
然后for循环来处理这个字符集,代码如下:
```CPP
int digit = digits[index] - '0'; // 将index指向的数字转为int
string letters = letterMap[digit]; // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {
s.push_back(letters[i]); // 处理
backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了
s.pop_back(); // 回溯
}
```
**注意这里for循环,可不像是在[回溯算法:求组合问题!](https://programmercarl.com/0077.组合.html)和[回溯算法:求组合总和!](https://programmercarl.com/0216.组合总和III.html)中从startIndex开始遍历的**。
**因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合,而[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)都是求同一个集合中的组合!**
注意:输入1 * #按键等等异常情况
代码中最好考虑这些异常情况,但题目的测试数据中应该没有异常情况的数据,所以我就没有加了。
**但是要知道会有这些异常,如果是现场面试中,一定要考虑到!**
## C++代码
关键地方都讲完了,按照[关于回溯算法,你该了解这些!](https://programmercarl.com/回溯算法理论基础.html)中的回溯法模板,不难写出如下C++代码:
```CPP
// 版本一
class Solution {
private:
const string letterMap[10] = {
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz", // 9
};
public:
vector result;
string s;
void backtracking(const string& digits, int index) {
if (index == digits.size()) {
result.push_back(s);
return;
}
int digit = digits[index] - '0'; // 将index指向的数字转为int
string letters = letterMap[digit]; // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {
s.push_back(letters[i]); // 处理
backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了
s.pop_back(); // 回溯
}
}
vector letterCombinations(string digits) {
s.clear();
result.clear();
if (digits.size() == 0) {
return result;
}
backtracking(digits, 0);
return result;
}
};
```
* 时间复杂度: O(3^m * 4^n),其中 m 是对应四个字母的数字个数,n 是对应三个字母的数字个数
* 空间复杂度: O(3^m * 4^n)
一些写法,是把回溯的过程放在递归函数里了,例如如下代码,我可以写成这样:(注意注释中不一样的地方)
```CPP
// 版本二
class Solution {
private:
const string letterMap[10] = {
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz", // 9
};
public:
vector result;
void getCombinations(const string& digits, int index, const string& s) { // 注意参数的不同
if (index == digits.size()) {
result.push_back(s);
return;
}
int digit = digits[index] - '0';
string letters = letterMap[digit];
for (int i = 0; i < letters.size(); i++) {
getCombinations(digits, index + 1, s + letters[i]); // 注意这里的不同
}
}
vector letterCombinations(string digits) {
result.clear();
if (digits.size() == 0) {
return result;
}
getCombinations(digits, 0, "");
return result;
}
};
```
我不建议把回溯藏在递归的参数里这种写法,很不直观,我在[二叉树:以为使用了递归,其实还隐藏着回溯](https://programmercarl.com/二叉树中递归带着回溯.html)这篇文章中也深度分析了,回溯隐藏在了哪里。
所以大家可以按照版本一来写就可以了。
# 总结
本篇将题目的三个要点一一列出,并重点强调了和前面讲解过的[77. 组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html)的区别,本题是多个集合求组合,所以在回溯的搜索过程中,都有一些细节需要注意的。
其实本题不算难,但也处处是细节,大家还要自己亲自动手写一写。
# 其他语言版本
## Java
```Java
class Solution {
//设置全局列表存储最后的结果
List list = new ArrayList<>();
public List letterCombinations(String digits) {
if (digits == null || digits.length() == 0) {
return list;
}
//初始对应所有的数字,为了直接对应2-9,新增了两个无效的字符串""
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
//迭代处理
backTracking(digits, numString, 0);
return list;
}
//每次迭代获取一个字符串,所以会设计大量的字符串拼接,所以这里选择更为高效的 StringBuild
StringBuilder temp = new StringBuilder();
//比如digits如果为"23",num 为0,则str表示2对应的 abc
public void backTracking(String digits, String[] numString, int num) {
//遍历全部一次记录一次得到的字符串
if (num == digits.length()) {
list.add(temp.toString());
return;
}
//str 表示当前num对应的字符串
String str = numString[digits.charAt(num) - '0'];
for (int i = 0; i < str.length(); i++) {
temp.append(str.charAt(i));
//c
backTracking(digits, numString, num + 1);
//剔除末尾的继续尝试
temp.deleteCharAt(temp.length() - 1);
}
}
}
```
## Python
回溯
```python
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
self.result = []
self.s = ""
def backtracking(self, digits, index):
if index == len(digits):
self.result.append(self.s)
return
digit = int(digits[index]) # 将索引处的数字转换为整数
letters = self.letterMap[digit] # 获取对应的字符集
for i in range(len(letters)):
self.s += letters[i] # 处理字符
self.backtracking(digits, index + 1) # 递归调用,注意索引加1,处理下一个数字
self.s = self.s[:-1] # 回溯,删除最后添加的字符
def letterCombinations(self, digits):
if len(digits) == 0:
return self.result
self.backtracking(digits, 0)
return self.result
```
回溯精简(版本一)
```python
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
self.result = []
def getCombinations(self, digits, index, s):
if index == len(digits):
self.result.append(s)
return
digit = int(digits[index])
letters = self.letterMap[digit]
for letter in letters:
self.getCombinations(digits, index + 1, s + letter)
def letterCombinations(self, digits):
if len(digits) == 0:
return self.result
self.getCombinations(digits, 0, "")
return self.result
```
回溯精简(版本二)
```python
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
def getCombinations(self, digits, index, s, result):
if index == len(digits):
result.append(s)
return
digit = int(digits[index])
letters = self.letterMap[digit]
for letter in letters:
self.getCombinations(digits, index + 1, s + letter, result)
def letterCombinations(self, digits):
result = []
if len(digits) == 0:
return result
self.getCombinations(digits, 0, "", result)
return result
```
回溯优化使用列表
```python
class Solution:
def __init__(self):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz" # 9
]
def getCombinations(self, digits, index, path, result):
if index == len(digits):
result.append(''.join(path))
return
digit = int(digits[index])
letters = self.letterMap[digit]
for letter in letters:
path.append(letter)
self.getCombinations(digits, index + 1, path, result)
path.pop()
def letterCombinations(self, digits):
result = []
if len(digits) == 0:
return result
self.getCombinations(digits, 0, [], result)
return result
```
## Go
主要在于递归中传递下一个数字
```go
var (
m []string
path []byte
res []string
)
func letterCombinations(digits string) []string {
m = []string{"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}
path, res = make([]byte, 0), make([]string, 0)
if digits == "" {
return res
}
dfs(digits, 0)
return res
}
func dfs(digits string, start int) {
if len(path) == len(digits) { //终止条件,字符串长度等于digits的长度
tmp := string(path)
res = append(res, tmp)
return
}
digit := int(digits[start] - '0') // 将index指向的数字转为int(确定下一个数字)
str := m[digit-2] // 取数字对应的字符集(注意和map中的对应)
for j := 0; j < len(str); j++ {
path = append(path, str[j])
dfs(digits, start+1)
path = path[:len(path)-1]
}
}
```
## javaScript
```js
var letterCombinations = function(digits) {
const k = digits.length;
const map = ["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"];
if(!k) return [];
if(k === 1) return map[digits].split("");
const res = [], path = [];
backtracking(digits, k, 0);
return res;
function backtracking(n, k, a) {
if(path.length === k) {
res.push(path.join(""));
return;
}
for(const v of map[n[a]]) {
path.push(v);
backtracking(n, k, a + 1);
path.pop();
}
}
};
```
## TypeScript
```typescript
function letterCombinations(digits: string): string[] {
if (digits === '') return [];
const strMap: { [index: string]: string[] } = {
1: [],
2: ['a', 'b', 'c'],
3: ['d', 'e', 'f'],
4: ['g', 'h', 'i'],
5: ['j', 'k', 'l'],
6: ['m', 'n', 'o'],
7: ['p', 'q', 'r', 's'],
8: ['t', 'u', 'v'],
9: ['w', 'x', 'y', 'z'],
}
const resArr: string[] = [];
function backTracking(digits: string, curIndex: number, route: string[]): void {
if (curIndex === digits.length) {
resArr.push(route.join(''));
return;
}
let tempArr: string[] = strMap[digits[curIndex]];
for (let i = 0, length = tempArr.length; i < length; i++) {
route.push(tempArr[i]);
backTracking(digits, curIndex + 1, route);
route.pop();
}
}
backTracking(digits, 0, []);
return resArr;
};
```
## Rust
```Rust
const map: [&str; 10] = [
"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz",
];
impl Solution {
fn back_trace(result: &mut Vec, s: &mut String, digits: &String, index: usize) {
let len = digits.len();
if len == index {
result.push(s.to_string());
return;
}
let digit = (digits.as_bytes()[index] - b'0') as usize;
for i in map[digit].chars() {
s.push(i);
Self::back_trace(result, s, digits, index + 1);
s.pop();
}
}
pub fn letter_combinations(digits: String) -> Vec {
if digits.is_empty() {
return vec![];
}
let mut res = vec![];
let mut s = String::new();
Self::back_trace(&mut res, &mut s, &digits, 0);
res
}
}
```
## C
```c
char* path;
int pathTop;
char** result;
int resultTop;
char* letterMap[10] = {"", //0
"", //1
"abc", //2
"def", //3
"ghi", //4
"jkl", //5
"mno", //6
"pqrs", //7
"tuv", //8
"wxyz", //9
};
void backTracking(char* digits, int index) {
//若当前下标等于digits数组长度
if(index == strlen(digits)) {
//复制digits数组,因为最后要多存储一个0,所以数组长度要+1
char* tempString = (char*)malloc(sizeof(char) * strlen(digits) + 1);
int j;
for(j = 0; j < strlen(digits); j++) {
tempString[j] = path[j];
}
//char数组最后要以0结尾
tempString[strlen(digits)] = 0;
result[resultTop++] = tempString;
return ;
}
//将字符数字转换为真的数字
int digit = digits[index] - '0';
//找到letterMap中对应的字符串
char* letters = letterMap[digit];
int i;
for(i = 0; i < strlen(letters); i++) {
path[pathTop++] = letters[i];
//递归,处理下一层数字
backTracking(digits, index+1);
pathTop--;
}
}
char ** letterCombinations(char * digits, int* returnSize){
//初始化path和result
path = (char*)malloc(sizeof(char) * strlen(digits));
result = (char**)malloc(sizeof(char*) * 300);
*returnSize = 0;
//若digits数组中元素个数为0,返回空集
if(strlen(digits) == 0)
return result;
pathTop = resultTop = 0;
backTracking(digits, 0);
*returnSize = resultTop;
return result;
}
```
## Swift
```swift
func letterCombinations(_ digits: String) -> [String] {
// 按键与字母串映射
let letterMap = [
"",
"", "abc", "def",
"ghi", "jkl", "mno",
"pqrs", "tuv", "wxyz"
]
// 把输入的按键字符串转成Int数组
let baseCode = ("0" as Character).asciiValue!
let digits = digits.map { c in
guard let code = c.asciiValue else { return -1 }
return Int(code - baseCode)
}.filter { $0 >= 0 && $0 <= 9 }
guard !digits.isEmpty else { return [] }
var result = [String]()
var s = ""
func backtracking(index: Int) {
// 结束条件:收集结果
if index == digits.count {
result.append(s)
return
}
// 遍历当前按键对应的字母串
let letters = letterMap[digits[index]]
for letter in letters {
s.append(letter) // 处理
backtracking(index: index + 1) // 递归,记得+1
s.removeLast() // 回溯
}
}
backtracking(index: 0)
return result
}
```
## Scala:
```scala
object Solution {
import scala.collection.mutable
def letterCombinations(digits: String): List[String] = {
var result = mutable.ListBuffer[String]()
if(digits == "") return result.toList // 如果参数为空,返回空结果集的List形式
var path = mutable.ListBuffer[Char]()
// 数字和字符的映射关系
val map = Array[String]("", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz")
def backtracking(index: Int): Unit = {
if (index == digits.size) {
result.append(path.mkString) // mkString语法:将数组类型直接转换为字符串
return
}
var digit = digits(index) - '0' // 这里使用toInt会报错!必须 -'0'
for (i <- 0 until map(digit).size) {
path.append(map(digit)(i))
backtracking(index + 1)
path = path.take(path.size - 1)
}
}
backtracking(0)
result.toList
}
}
```

