



欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 动态规划: 给我个机会,我再兑换一次零钱
## 322. 零钱兑换
题目链接:https://leetcode-cn.com/problems/coin-change/
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
示例 4:
输入:coins = [1], amount = 1
输出:1
示例 5:
输入:coins = [1], amount = 2
输出:2
提示:
* 1 <= coins.length <= 12
* 1 <= coins[i] <= 2^31 - 1
* 0 <= amount <= 10^4
## 思路
在[动态规划:518.零钱兑换II](https://mp.weixin.qq.com/s/PlowDsI4WMBOzf3q80AksQ)中我们已经兑换一次零钱了,这次又要兑换,套路不一样!
题目中说每种硬币的数量是无限的,可以看出是典型的完全背包问题。
动规五部曲分析如下:
1. 确定dp数组以及下标的含义
**dp[j]:凑足总额为j所需钱币的最少个数为dp[j]**
2. 确定递推公式
得到dp[j](考虑coins[i]),只有一个来源,dp[j - coins[i]](没有考虑coins[i])。
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
3. dp数组如何初始化
首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
其他下标对应的数值呢?
考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
所以下标非0的元素都是应该是最大值。
代码如下:
```
vector dp(amount + 1, INT_MAX);
dp[0] = 0;
```
4. 确定遍历顺序
本题求钱币最小个数,**那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。**。
所以本题并不强调集合是组合还是排列。
**如果求组合数就是外层for循环遍历物品,内层for遍历背包**。
**如果求排列数就是外层for遍历背包,内层for循环遍历物品**。
在动态规划专题我们讲过了求组合数是[动态规划:518.零钱兑换II](https://mp.weixin.qq.com/s/PlowDsI4WMBOzf3q80AksQ),求排列数是[动态规划:377. 组合总和 Ⅳ](https://mp.weixin.qq.com/s/Iixw0nahJWQgbqVNk8k6gA)。
**所以本题的两个for循环的关系是:外层for循环遍历物品,内层for遍历背包或者外层for遍历背包,内层for循环遍历物品都是可以的!**
那么我采用coins放在外循环,target在内循环的方式。
本题钱币数量可以无限使用,那么是完全背包。所以遍历的内循环是正序
综上所述,遍历顺序为:coins(物品)放在外循环,target(背包)在内循环。且内循环正序。
5. 举例推导dp数组
以输入:coins = [1, 2, 5], amount = 5为例
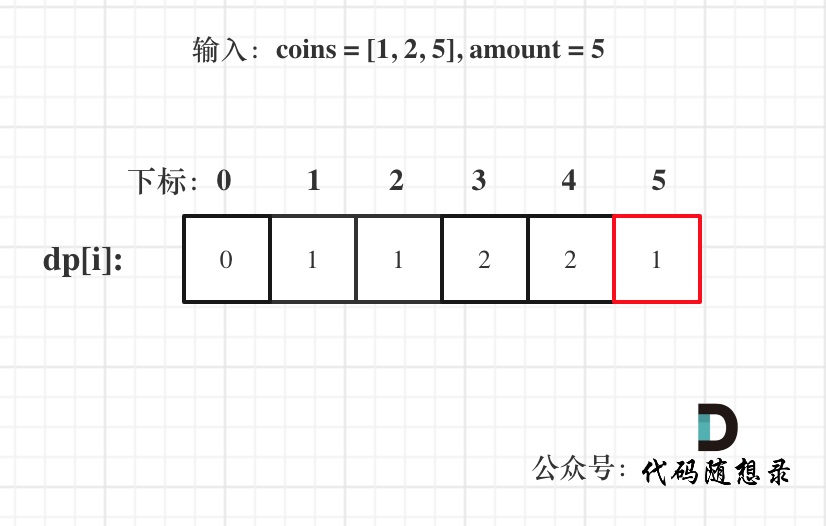
dp[amount]为最终结果。
## C++代码
以上分析完毕,C++ 代码如下:
```C++
// 版本一
class Solution {
public:
int coinChange(vector& coins, int amount) {
vector dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包
if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
}
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};
```
对于遍历方式遍历背包放在外循环,遍历物品放在内循环也是可以的,我就直接给出代码了
```C++
// 版本二
class Solution {
public:
int coinChange(vector& coins, int amount) {
vector dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i <= amount; i++) { // 遍历背包
for (int j = 0; j < coins.size(); j++) { // 遍历物品
if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX ) {
dp[i] = min(dp[i - coins[j]] + 1, dp[i]);
}
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};
```
## 总结
细心的同学看网上的题解,**可能看一篇是遍历背包的for循环放外面,看一篇又是遍历背包的for循环放里面,看多了都看晕了**,到底两个for循环应该是什么先后关系。
能把遍历顺序讲明白的文章几乎找不到!
这也是大多数同学学习动态规划的苦恼所在,有的时候递推公式很简单,难在遍历顺序上!
但最终又可以稀里糊涂的把题目过了,也不知道为什么这样可以过,反正就是过了,哈哈
那么这篇文章就把遍历顺序分析的清清楚楚。
[动态规划:518.零钱兑换II](https://mp.weixin.qq.com/s/PlowDsI4WMBOzf3q80AksQ)中求的是组合数,[动态规划:377. 组合总和 Ⅳ](https://mp.weixin.qq.com/s/Iixw0nahJWQgbqVNk8k6gA)中求的是排列数。
**而本题是要求最少硬币数量,硬币是组合数还是排列数都无所谓!所以两个for循环先后顺序怎样都可以!**
这也是我为什么要先讲518.零钱兑换II 然后再讲本题即:322.零钱兑换,这是Carl的良苦用心那。
相信大家看完之后,对背包问题中的遍历顺序又了更深的理解了。
## 其他语言版本
Java:
```Java
class Solution {
public int coinChange(int[] coins, int amount) {
int max = Integer.MAX_VALUE;
int[] dp = new int[amount + 1];
//初始化dp数组为最大值
for (int j = 0; j < dp.length; j++) {
dp[j] = max;
}
//当金额为0时需要的硬币数目为0
dp[0] = 0;
for (int i = 0; i < coins.length; i++) {
//正序遍历:完全背包每个硬币可以选择多次
for (int j = coins[i]; j <= amount; j++) {
//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要
if (dp[j - coins[i]] != max) {
//选择硬币数目最小的情况
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount] == max ? -1 : dp[amount];
}
}
```
Python:
Go:
-----------------------
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)




