



欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
## 746. 使用最小花费爬楼梯
题目链接:https://leetcode-cn.com/problems/min-cost-climbing-stairs/
数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
示例 1:
输入:cost = [10, 15, 20]
输出:15
解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。
示例 2:
输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出:6
解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。
提示:
* cost 的长度范围是 [2, 1000]。
* cost[i] 将会是一个整型数据,范围为 [0, 999] 。
## 思路
这道题目可以说是昨天[动态规划:爬楼梯](https://mp.weixin.qq.com/s/Ohop0jApSII9xxOMiFhGIw)的花费版本。
**注意题目描述:每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯**
所以示例1中只花费一个15 就可以到阶梯顶,最后一步可以理解为 不用花费。
读完题大家应该知道指定需要动态规划的,贪心是不可能了。
1. 确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
**dp[i]的定义:到达第i个台阶所花费的最少体力为dp[i]**。(注意这里认为是第一步一定是要花费)
**对于dp数组的定义,大家一定要清晰!**
2. 确定递推公式
**可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]**。
那么究竟是选dp[i-1]还是dp[i-2]呢?
一定是选最小的,所以dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
**注意这里为什么是加cost[i],而不是cost[i-1],cost[i-2]之类的**,因为题目中说了:每当你爬上一个阶梯你都要花费对应的体力值
3. dp数组如何初始化
根据dp数组的定义,dp数组初始化其实是比较难的,因为不可能初始化为第i台阶所花费的最少体力。
那么看一下递归公式,dp[i]由dp[i-1],dp[i-2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
所以初始化代码为:
```
vector dp(cost.size());
dp[0] = cost[0];
dp[1] = cost[1];
```
4. 确定遍历顺序
最后一步,递归公式有了,初始化有了,如何遍历呢?
本题的遍历顺序其实比较简单,简单到很多同学都忽略了思考这一步直接就把代码写出来了。
因为是模拟台阶,而且dp[i]又dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
**但是稍稍有点难度的动态规划,其遍历顺序并不容易确定下来**。
例如:01背包,都知道两个for循环,一个for遍历物品嵌套一个for遍历背包容量,那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢? 以及在使用一维dp数组的时候遍历背包容量为什么要倒叙呢?
**这些都是遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的!**
5. 举例推导dp数组
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
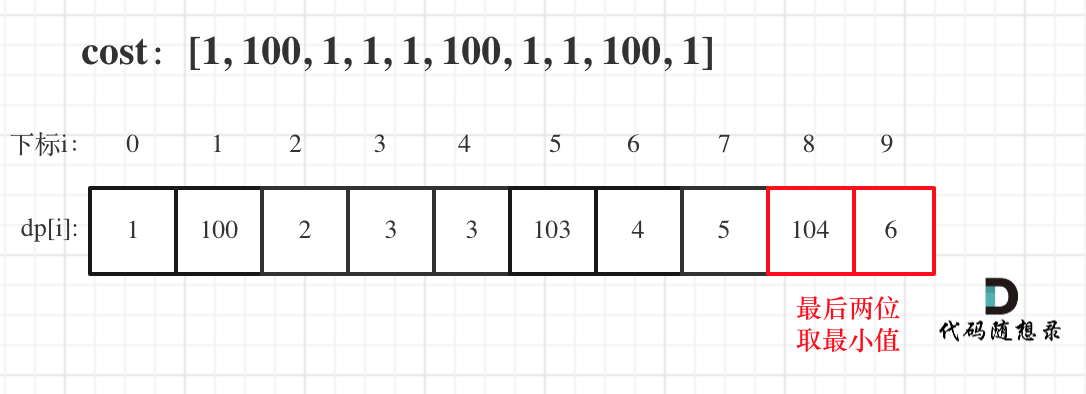
如果大家代码写出来有问题,就把dp数组打印出来,看看和如上推导的是不是一样的。
以上分析完毕,整体C++代码如下:
```C++
// 版本一
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
vector dp(cost.size());
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < cost.size(); i++) {
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
}
// 注意最后一步可以理解为不用花费,所以取倒数第一步,第二步的最少值
return min(dp[cost.size() - 1], dp[cost.size() - 2]);
}
};
```
* 时间复杂度:O(n)
* 空间复杂度:O(n)
还可以优化空间复杂度,因为dp[i]就是由前两位推出来的,那么也不用dp数组了,C++代码如下:
```C++
// 版本二
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
int dp0 = cost[0];
int dp1 = cost[1];
for (int i = 2; i < cost.size(); i++) {
int dpi = min(dp0, dp1) + cost[i];
dp0 = dp1; // 记录一下前两位
dp1 = dpi;
}
return min(dp0, dp1);
}
};
```
* 时间复杂度:O(n)
* 空间复杂度:O(1)
**当然我不建议这么写,能写出版本一就可以了,直观简洁!**
在后序的讲解中,可能我会忽略这种版本二的写法,大家只要知道有这么个写法就可以了哈。
## 拓展
这道题描述也确实有点魔幻。
题目描述为:每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
示例1:
输入:cost = [10, 15, 20]
输出:15
**从题目描述可以看出:要不是第一步不需要花费体力,要不就是第最后一步不需要花费体力,我个人理解:题意说的其实是第一步是要支付费用的!**。因为是当你爬上一个台阶就要花费对应的体力值!
所以我定义的dp[i]意思是也是第一步是要花费体力的,最后一步不用花费体力了,因为已经支付了。
当然也可以样,定义dp[i]为:第一步是不花费体力,最后一步是花费体力的。
所以代码这么写:
```C++
class Solution {
public:
int minCostClimbingStairs(vector& cost) {
vector dp(cost.size() + 1);
dp[0] = 0; // 默认第一步都是不花费体力的
dp[1] = 0;
for (int i = 2; i <= cost.size(); i++) {
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.size()];
}
};
```
这么写看上去比较顺,但是就是感觉和题目描述的不太符。哈哈,也没有必要这么细扣题意了,大家只要知道,题目的意思反正就是要不是第一步不花费,要不是最后一步不花费,都可以。
# 总结
大家可以发现这道题目相对于 昨天的[动态规划:爬楼梯](https://mp.weixin.qq.com/s/Ohop0jApSII9xxOMiFhGIw)有难了一点,但整体思路是一样。
从[动态规划:斐波那契数](https://mp.weixin.qq.com/s/ko0zLJplF7n_4TysnPOa_w)到 [动态规划:爬楼梯](https://mp.weixin.qq.com/s/Ohop0jApSII9xxOMiFhGIw)再到今天这道题目,录友们感受到循序渐进的梯度了嘛。
每个系列开始的时候,都有录友和我反馈说题目太简单了,赶紧上难度,但也有录友和我说有点难了,快跟不上了。
其实我选的题目都是有目的性的,就算是简单题,也是为了练习方法论,然后难度都是梯度上来的,一环扣一环。
但我也可以随便选来一道难题讲呗,这其实是最省事的,不用管什么题目顺序,看心情找一道就讲。
难的是把题目按梯度排好,循序渐进,再按照统一方法论把这些都串起来,哈哈,所以大家不要催我哈,按照我的节奏一步一步来就行啦。
学算法,认准「代码随想录」,没毛病!
## 其他语言版本
Java:
```Java
class Solution {
public int minCostClimbingStairs(int[] cost) {
if (cost == null || cost.length == 0) {
return 0;
}
if (cost.length == 1) {
return cost[0];
}
int[] dp = new int[cost.length];
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < cost.length; i++) {
dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
}
//最后一步,如果是由倒数第二步爬,则最后一步的体力花费可以不用算
return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
}
}
```
Python:
```python
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp = [0] * (len(cost))
dp[0] = cost[0]
dp[1] = cost[1]
for i in range(2, len(cost)):
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]
return min(dp[len(cost) - 1], dp[len(cost) - 2])
```
Go:
```Go
func minCostClimbingStairs(cost []int) int {
dp := make([]int, len(cost))
dp[0], dp[1] = cost[0], cost[1]
for i := 2; i < len(cost); i++ {
dp[i] = min(dp[i-1], dp[i-2]) + cost[i]
}
return min(dp[len(cost)-1], dp[len(cost)-2])
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
```
-----------------------
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)




