
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# 56. 合并区间
[力扣题目链接](https://leetcode.cn/problems/merge-intervals/)
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
* 输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
* 输出: [[1,6],[8,10],[15,18]]
* 解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
* 输入: intervals = [[1,4],[4,5]]
* 输出: [[1,5]]
* 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
* 注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
## 算法公开课
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[贪心算法,合并区间有细节!LeetCode:56.合并区间](https://www.bilibili.com/video/BV1wx4y157nD),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
## 思路
本题的本质其实还是判断重叠区间问题。
大家如果认真做题的话,话发现和我们刚刚讲过的[452. 用最少数量的箭引爆气球](https://programmercarl.com/0452.用最少数量的箭引爆气球.html) 和 [435. 无重叠区间](https://programmercarl.com/0435.无重叠区间.html) 都是一个套路。
这几道题都是判断区间重叠,区别就是判断区间重叠后的逻辑,本题是判断区间重贴后要进行区间合并。
所以一样的套路,先排序,让所有的相邻区间尽可能的重叠在一起,按左边界,或者右边界排序都可以,处理逻辑稍有不同。
按照左边界从小到大排序之后,如果 `intervals[i][0] <= intervals[i - 1][1]` 即intervals[i]的左边界 <= intervals[i - 1]的右边界,则一定有重叠。(本题相邻区间也算重贴,所以是<=)
这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
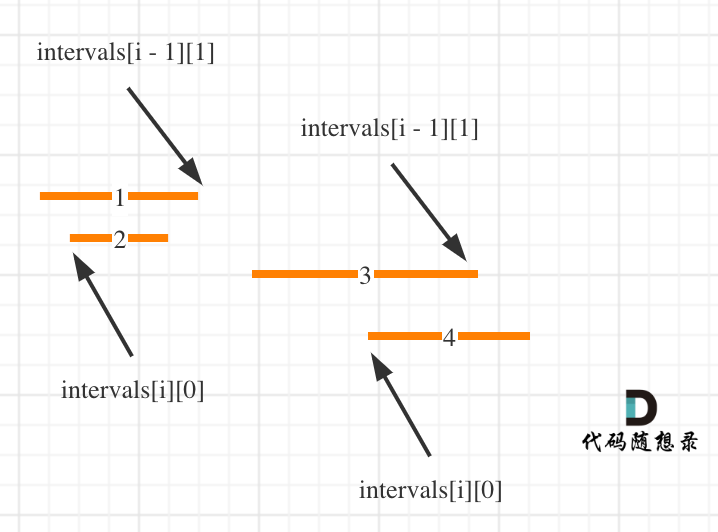
知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
其实就是用合并区间后左边界和右边界,作为一个新的区间,加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。
C++代码如下:
```CPP
class Solution {
public:
vector> merge(vector>& intervals) {
vector> result;
if (intervals.size() == 0) return result; // 区间集合为空直接返回
// 排序的参数使用了lambda表达式
sort(intervals.begin(), intervals.end(), [](const vector& a, const vector& b){return a[0] < b[0];});
// 第一个区间就可以放进结果集里,后面如果重叠,在result上直接合并
result.push_back(intervals[0]);
for (int i = 1; i < intervals.size(); i++) {
if (result.back()[1] >= intervals[i][0]) { // 发现重叠区间
// 合并区间,只更新右边界就好,因为result.back()的左边界一定是最小值,因为我们按照左边界排序的
result.back()[1] = max(result.back()[1], intervals[i][1]);
} else {
result.push_back(intervals[i]); // 区间不重叠
}
}
return result;
}
};
```
* 时间复杂度: O(nlogn)
* 空间复杂度: O(logn),排序需要的空间开销
## 其他语言版本
### Java
```java
/**
时间复杂度 : O(NlogN) 排序需要O(NlogN)
空间复杂度 : O(logN) java 的内置排序是快速排序 需要 O(logN)空间
*/
class Solution {
public int[][] merge(int[][] intervals) {
List res = new LinkedList<>();
//按照左边界排序
Arrays.sort(intervals, (x, y) -> Integer.compare(x[0], y[0]));
//initial start 是最小左边界
int start = intervals[0][0];
int rightmostRightBound = intervals[0][1];
for (int i = 1; i < intervals.length; i++) {
//如果左边界大于最大右边界
if (intervals[i][0] > rightmostRightBound) {
//加入区间 并且更新start
res.add(new int[]{start, rightmostRightBound});
start = intervals[i][0];
rightmostRightBound = intervals[i][1];
} else {
//更新最大右边界
rightmostRightBound = Math.max(rightmostRightBound, intervals[i][1]);
}
}
res.add(new int[]{start, rightmostRightBound});
return res.toArray(new int[res.size()][]);
}
}
```
```java
// 版本2
class Solution {
public int[][] merge(int[][] intervals) {
LinkedList res = new LinkedList<>();
Arrays.sort(intervals, (o1, o2) -> Integer.compare(o1[0], o2[0]));
res.add(intervals[0]);
for (int i = 1; i < intervals.length; i++) {
if (intervals[i][0] <= res.getLast()[1]) {
int start = res.getLast()[0];
int end = Math.max(intervals[i][1], res.getLast()[1]);
res.removeLast();
res.add(new int[]{start, end});
}
else {
res.add(intervals[i]);
}
}
return res.toArray(new int[res.size()][]);
}
}
```
### Python
```python
class Solution:
def merge(self, intervals):
result = []
if len(intervals) == 0:
return result # 区间集合为空直接返回
intervals.sort(key=lambda x: x[0]) # 按照区间的左边界进行排序
result.append(intervals[0]) # 第一个区间可以直接放入结果集中
for i in range(1, len(intervals)):
if result[-1][1] >= intervals[i][0]: # 发现重叠区间
# 合并区间,只需要更新结果集最后一个区间的右边界,因为根据排序,左边界已经是最小的
result[-1][1] = max(result[-1][1], intervals[i][1])
else:
result.append(intervals[i]) # 区间不重叠
return result
```
### Go
```go
func merge(intervals [][]int) [][]int {
sort.Slice(intervals, func(i, j int) bool {
return intervals[i][0] < intervals[j][0]
})
res := make([][]int, 0, len(intervals))
left, right := intervals[0][0], intervals[0][1]
for i := 1; i < len(intervals); i++ {
if right < intervals[i][0] {
res = append(res, []int{left, right})
left, right = intervals[i][0], intervals[i][1]
} else {
right = max(right, intervals[i][1])
}
}
res = append(res, []int{left, right}) // 将最后一个区间放入
return res
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
```
```go
// 版本2
func merge(intervals [][]int) [][]int {
if len(intervals) == 1 {
return intervals
}
sort.Slice(intervals, func(i, j int) bool {
return intervals[i][0] < intervals[j][0]
})
res := make([][]int, 0)
res = append(res, intervals[0])
for i := 1; i < len(intervals); i++ {
if intervals[i][0] <= res[len(res)-1][1]{
res[len(res)-1][1] = max56(res[len(res)-1][1],intervals[i][1])
} else {
res = append(res, intervals[i])
}
}
return res
}
func max56(a, b int) int {
if a > b {
return a
}
return b
}
```
### Javascript
```javascript
var merge = function (intervals) {
intervals.sort((a, b) => a[0] - b[0]);
let prev = intervals[0]
let result = []
for(let i =0; i prev[1]){
result.push(prev)
prev = cur
}else{
prev[1] = Math.max(cur[1],prev[1])
}
}
result.push(prev)
return result
};
```
版本二:左右区间
```javascript
/**
* @param {number[][]} intervals
* @return {number[][]}
*/
var merge = function(intervals) {
let n = intervals.length;
if ( n < 2) return intervals;
intervals.sort((a, b) => a[0]- b[0]);
let res = [],
left = intervals[0][0],
right = intervals[0][1];
for (let i = 1; i < n; i++) {
if (intervals[i][0] > right) {
res.push([left, right]);
left = intervals[i][0];
right = intervals[i][1];
} else {
right = Math.max(intervals[i][1], right);
}
}
res.push([left, right]);
return res;
};
```
### TypeScript
```typescript
function merge(intervals: number[][]): number[][] {
const resArr: number[][] = [];
intervals.sort((a, b) => a[0] - b[0]);
resArr[0] = [...intervals[0]]; // 避免修改原intervals
for (let i = 1, length = intervals.length; i < length; i++) {
let interval: number[] = intervals[i];
let last: number[] = resArr[resArr.length - 1];
if (interval[0] <= last[1]) {
last[1] = Math.max(interval[1], last[1]);
} else {
resArr.push([...intervals[i]]);
}
}
return resArr;
};
```
### Scala
```scala
object Solution {
import scala.collection.mutable
def merge(intervals: Array[Array[Int]]): Array[Array[Int]] = {
var res = mutable.ArrayBuffer[Array[Int]]()
// 排序
var interval = intervals.sortWith((a, b) => {
a(0) < b(0)
})
var left = interval(0)(0)
var right = interval(0)(1)
for (i <- 1 until interval.length) {
if (interval(i)(0) <= right) {
left = math.min(left, interval(i)(0))
right = math.max(right, interval(i)(1))
} else {
res.append(Array[Int](left, right))
left = interval(i)(0)
right = interval(i)(1)
}
}
res.append(Array[Int](left, right))
res.toArray // 返回res的Array形式
}
}
```
### Rust
```Rust
impl Solution {
pub fn merge(mut intervals: Vec>) -> Vec> {
let mut res = vec![];
if intervals.is_empty() {
return res;
}
intervals.sort_by_key(|a| a[0]);
res.push(intervals[0].clone());
for interval in intervals.into_iter().skip(1) {
let res_last_ele = res.last_mut().unwrap();
if res_last_ele[1] >= interval[0] {
res_last_ele[1] = interval[1].max(res_last_ele[1]);
} else {
res.push(interval);
}
}
res
}
}
```
### C
```c
#define max(a, b) ((a) > (b) ? (a) : (b))
// 根据左边界进行排序
int cmp(const void * var1, const void * var2){
int *v1 = *(int **) var1;
int *v2 = *(int **) var2;
return v1[0] - v2[0];
}
int** merge(int** intervals, int intervalsSize, int* intervalsColSize, int* returnSize, int** returnColumnSizes) {
int ** result = malloc(sizeof (int *) * intervalsSize);
* returnColumnSizes = malloc(sizeof (int ) * intervalsSize);
for(int i = 0; i < intervalsSize; i++){
result[i] = malloc(sizeof (int ) * 2);
}
qsort(intervals, intervalsSize, sizeof (int *), cmp);
int count = 0;
for(int i = 0; i < intervalsSize; i++){
// 记录区间的左右边界
int L = intervals[i][0], R = intervals[i][1];
// 如果count为0或者前一区间的右区间小于此时的左边,加入结果中
if (count == 0 || result[count - 1][1] < L) {
returnColumnSizes[0][count] = 2;
result[count][0] = L;
result[count][1] = R;
count++;
}
else{ // 更新右边界的值
result[count - 1][1] = max(R, result[count - 1][1]);
}
}
*returnSize = count;
return result;
}
```
### C#
```csharp
public class Solution
{
public int[][] Merge(int[][] intervals)
{
if (intervals.Length == 0)
return intervals;
Array.Sort(intervals, (a, b) => a[0] - b[0]);
List> res = new List>();
res.Add(intervals[0].ToList());
for (int i = 1; i < intervals.Length; i++)
{
if (res[res.Count - 1][1] >= intervals[i][0])
{
res[res.Count - 1][1] = Math.Max(res[res.Count - 1][1], intervals[i][1]);
}
else
{
res.Add(intervals[i].ToList());
}
}
return res.Select(x => x.ToArray()).ToArray();
}
}
```

