欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

## 674. 最长连续递增序列题目链接：https://leetcode-cn.com/problems/longest-continuous-increasing-subsequence/ 给定一个未经排序的整数数组，找到最长且连续递增的子序列，并返回该序列的长度。连续递增的子序列可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。示例 1：输入：nums = [1,3,5,4,7] 输出：3 解释：最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。示例 2：输入：nums = [2,2,2,2,2] 输出：1 解释：最长连续递增序列是 [2], 长度为1。提示： * 0 <= nums.length <= 10^4 * -10^9 <= nums[i] <= 10^9 ## 思路本题相对于昨天的[动态规划：300.最长递增子序列](https://mp.weixin.qq.com/s/f8nLO3JGfgriXep_gJQpqQ)最大的区别在于“连续”。本题要求的是最长**连续**递增序列 ### 动态规划动规五部曲分析如下： 1. 确定dp数组（dp table）以及下标的含义 **dp[i]：以下标i为结尾的数组的连续递增的子序列长度为dp[i]**。注意这里的定义，一定是以下标i为结尾，并不是说一定以下标0为起始位置。 2. 确定递推公式如果 nums[i + 1] > nums[i]，那么以 i+1 为结尾的数组的连续递增的子序列长度一定等于以i为结尾的数组的连续递增的子序列长度 + 1 。即：dp[i + 1] = dp[i] + 1; **注意这里就体现出和[动态规划：300.最长递增子序列](https://mp.weixin.qq.com/s/f8nLO3JGfgriXep_gJQpqQ)的区别！** 因为本题要求连续递增子序列，所以就必要比较nums[i + 1]与nums[i]，而不用去比较nums[j]与nums[i] （j是在0到i之间遍历）。既然不用j了，那么也不用两层for循环，本题一层for循环就行，比较nums[i + 1] 和 nums[i]。这里大家要好好体会一下！ 3. dp数组如何初始化以下标i为结尾的数组的连续递增的子序列长度最少也应该是1，即就是nums[i]这一个元素。所以dp[i]应该初始1; 4. 确定遍历顺序从递推公式上可以看出， dp[i + 1]依赖dp[i]，所以一定是从前向后遍历。本文在确定递推公式的时候也说明了为什么本题只需要一层for循环，代码如下： ```C++ for (int i = 0; i < nums.size() - 1; i++) { if (nums[i + 1] > nums[i]) { // 连续记录 dp[i + 1] = dp[i] + 1; // 递推公式 } } ``` 5. 举例推导dp数组已输入nums = [1,3,5,4,7]为例，dp数组状态如下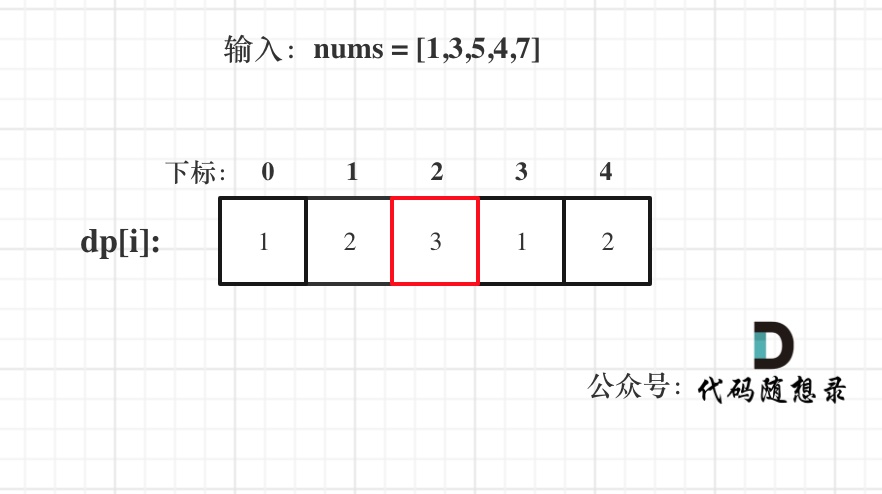： ![674.最长连续递增序列](https://img-blog.csdnimg.cn/20210204103529742.jpg) **注意这里要取dp[i]里的最大值，所以dp[2]才是结果！** 以上分析完毕，C++代码如下： ```C++ class Solution { public: int findLengthOfLCIS(vector& nums) { if (nums.size() == 0) return 0; int result = 1; vector dp(nums.size() ,1); for (int i = 0; i < nums.size() - 1; i++) { if (nums[i + 1] > nums[i]) { // 连续记录 dp[i + 1] = dp[i] + 1; } if (dp[i + 1] > result) result = dp[i + 1]; } return result; } }; ``` * 时间复杂度：O(n) * 空间复杂度：O(n) ### 贪心这道题目也可以用贪心来做，也就是遇到nums[i + 1] > nums[i]的情况，count就++，否则count为1，记录count的最大值就可以了。代码如下： ```C++ class Solution { public: int findLengthOfLCIS(vector& nums) { if (nums.size() == 0) return 0; int result = 1; // 连续子序列最少也是1 int count = 1; for (int i = 0; i < nums.size() - 1; i++) { if (nums[i + 1] > nums[i]) { // 连续记录 count++; } else { // 不连续，count从头开始 count = 1; } if (count > result) result = count; } return result; } }; ``` * 时间复杂度：O(n) * 空间复杂度：O(1) ## 总结本题也是动规里子序列问题的经典题目，但也可以用贪心来做，大家也会发现贪心好像更简单一点，而且空间复杂度仅是O(1)。在动规分析中，关键是要理解和[动态规划：300.最长递增子序列](https://mp.weixin.qq.com/s/f8nLO3JGfgriXep_gJQpqQ)的区别。 **要联动起来，才能理解递增子序列怎么求，递增连续子序列又要怎么求**。概括来说：不连续递增子序列的跟前0-i 个状态有关，连续递增的子序列只跟前一个状态有关本篇我也把区别所在之处重点介绍了，关键在递推公式和遍历方法上，大家可以仔细体会一波！ ## 其他语言版本 Java： Python： Go： ----------------------- * 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw) * B站视频：[代码随想录](https://space.bilibili.com/525438321) * 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)