
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 968.监控二叉树 [力扣题目链接](https://leetcode.cn/problems/binary-tree-cameras/) 给定一个二叉树,我们在树的节点上安装摄像头。 节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。 计算监控树的所有节点所需的最小摄像头数量。 示例 1:  * 输入:[0,0,null,0,0] * 输出:1 * 解释:如图所示,一台摄像头足以监控所有节点。 示例 2: 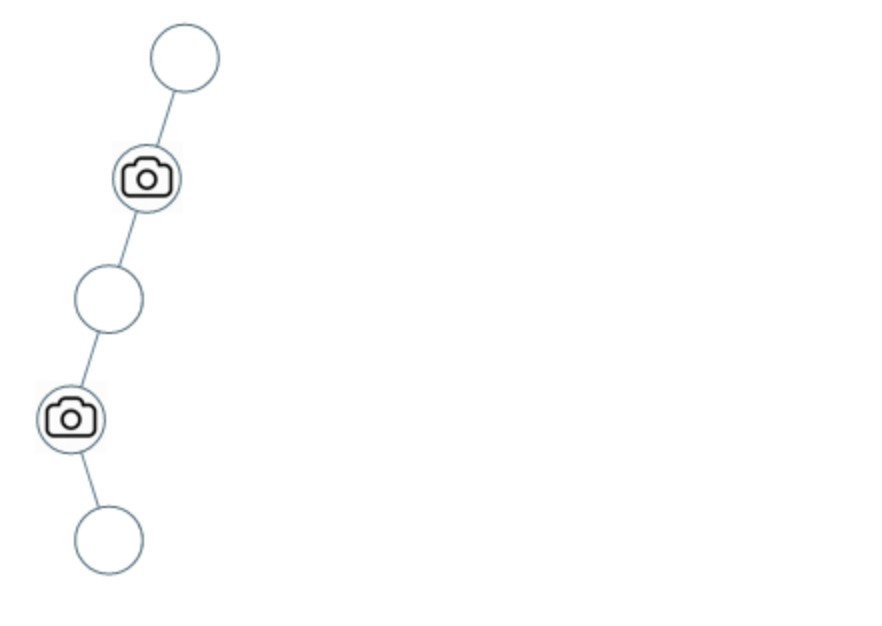 * 输入:[0,0,null,0,null,0,null,null,0] * 输出:2 * 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。 提示: * 给定树的节点数的范围是 [1, 1000]。 * 每个节点的值都是 0。 # 视频讲解 **《代码随想录》算法视频公开课:[贪心算法,二叉树与贪心的结合,有点难...... LeetCode:968.监督二叉树](https://www.bilibili.com/video/BV1SA411U75i),相信结合视频在看本篇题解,更有助于大家对本题的理解**。 ## 思路 这道题目首先要想,如何放置,才能让摄像头最小的呢? 从题目中示例,其实可以得到启发,**我们发现题目示例中的摄像头都没有放在叶子节点上!** 这是很重要的一个线索,摄像头可以覆盖上中下三层,如果把摄像头放在叶子节点上,就浪费的一层的覆盖。 所以把摄像头放在叶子节点的父节点位置,才能充分利用摄像头的覆盖面积。 那么有同学可能问了,为什么不从头结点开始看起呢,为啥要从叶子节点看呢? 因为头结点放不放摄像头也就省下一个摄像头, 叶子节点放不放摄像头省下了的摄像头数量是指数阶别的。 **所以我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!** 局部最优推出全局最优,找不出反例,那么就按照贪心来! 此时,大体思路就是从低到上,先给叶子节点父节点放个摄像头,然后隔两个节点放一个摄像头,直至到二叉树头结点。 此时这道题目还有两个难点: 1. 二叉树的遍历 2. 如何隔两个节点放一个摄像头 ### 确定遍历顺序 在二叉树中如何从低向上推导呢? 可以使用后序遍历也就是左右中的顺序,这样就可以在回溯的过程中从下到上进行推导了。 后序遍历代码如下: ```CPP int traversal(TreeNode* cur) { // 空节点,该节点有覆盖 if (终止条件) return ; int left = traversal(cur->left); // 左 int right = traversal(cur->right); // 右 逻辑处理 // 中 return ; } ``` **注意在以上代码中我们取了左孩子的返回值,右孩子的返回值,即left 和 right, 以后推导中间节点的状态** ### 如何隔两个节点放一个摄像头 此时需要状态转移的公式,大家不要和动态的状态转移公式混到一起,本题状态转移没有择优的过程,就是单纯的状态转移! 来看看这个状态应该如何转移,先来看看每个节点可能有几种状态: 有如下三种: * 该节点无覆盖 * 本节点有摄像头 * 本节点有覆盖 我们分别有三个数字来表示: * 0:该节点无覆盖 * 1:本节点有摄像头 * 2:本节点有覆盖 大家应该找不出第四个节点的状态了。 **一些同学可能会想有没有第四种状态:本节点无摄像头,其实无摄像头就是 无覆盖 或者 有覆盖的状态,所以一共还是三个状态。** **因为在遍历树的过程中,就会遇到空节点,那么问题来了,空节点究竟是哪一种状态呢? 空节点表示无覆盖? 表示有摄像头?还是有覆盖呢?** 回归本质,为了让摄像头数量最少,我们要尽量让叶子节点的父节点安装摄像头,这样才能摄像头的数量最少。 那么空节点不能是无覆盖的状态,这样叶子节点就要放摄像头了,空节点也不能是有摄像头的状态,这样叶子节点的父节点就没有必要放摄像头了,而是可以把摄像头放在叶子节点的爷爷节点上。 **所以空节点的状态只能是有覆盖,这样就可以在叶子节点的父节点放摄像头了** 接下来就是递推关系。 那么递归的终止条件应该是遇到了空节点,此时应该返回2(有覆盖),原因上面已经解释过了。 代码如下: ```CPP // 空节点,该节点有覆盖 if (cur == NULL) return 2; ``` 递归的函数,以及终止条件已经确定了,再来看单层逻辑处理。 主要有如下四类情况: * 情况1:左右节点都有覆盖 左孩子有覆盖,右孩子有覆盖,那么此时中间节点应该就是无覆盖的状态了。 如图: 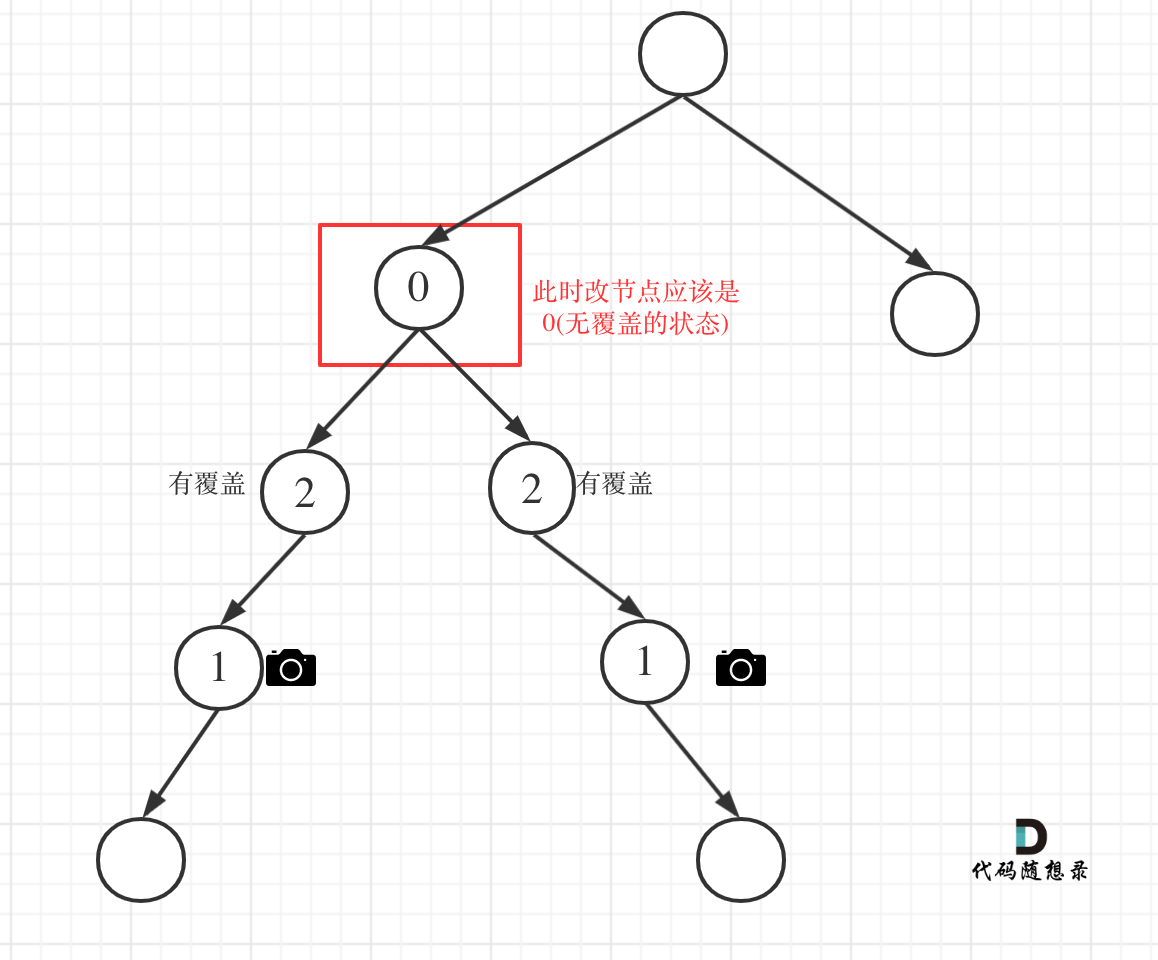 代码如下: ```CPP // 左右节点都有覆盖 if (left == 2 && right == 2) return 0; ``` * 情况2:左右节点至少有一个无覆盖的情况 如果是以下情况,则中间节点(父节点)应该放摄像头: * left == 0 && right == 0 左右节点无覆盖 * left == 1 && right == 0 左节点有摄像头,右节点无覆盖 * left == 0 && right == 1 左节点有无覆盖,右节点摄像头 * left == 0 && right == 2 左节点无覆盖,右节点覆盖 * left == 2 && right == 0 左节点覆盖,右节点无覆盖 这个不难理解,毕竟有一个孩子没有覆盖,父节点就应该放摄像头。 此时摄像头的数量要加一,并且return 1,代表中间节点放摄像头。 代码如下: ```CPP if (left == 0 || right == 0) { result++; return 1; } ``` * 情况3:左右节点至少有一个有摄像头 如果是以下情况,其实就是 左右孩子节点有一个有摄像头了,那么其父节点就应该是2(覆盖的状态) * left == 1 && right == 2 左节点有摄像头,右节点有覆盖 * left == 2 && right == 1 左节点有覆盖,右节点有摄像头 * left == 1 && right == 1 左右节点都有摄像头 代码如下: ```CPP if (left == 1 || right == 1) return 2; ``` **从这个代码中,可以看出,如果left == 1, right == 0 怎么办?其实这种条件在情况2中已经判断过了**,如图: 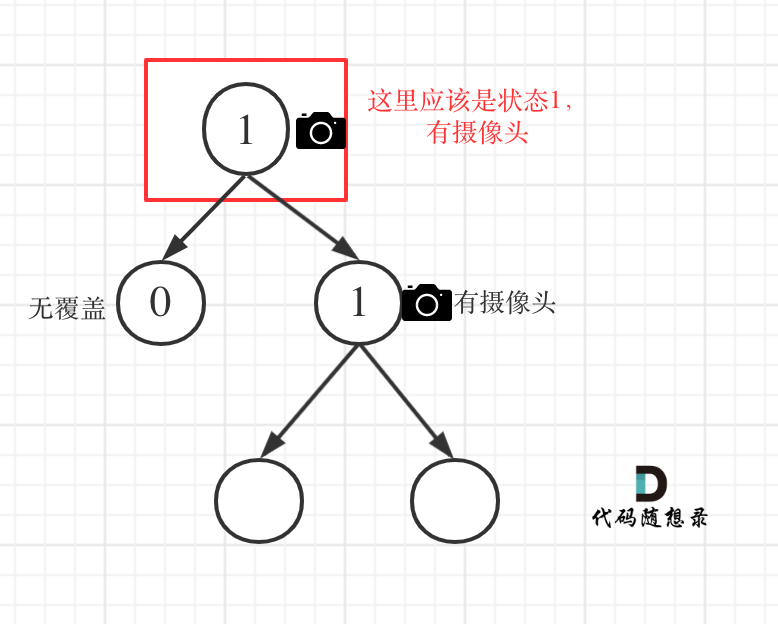 这种情况也是大多数同学容易迷惑的情况。 4. 情况4:头结点没有覆盖 以上都处理完了,递归结束之后,可能头结点 还有一个无覆盖的情况,如图: 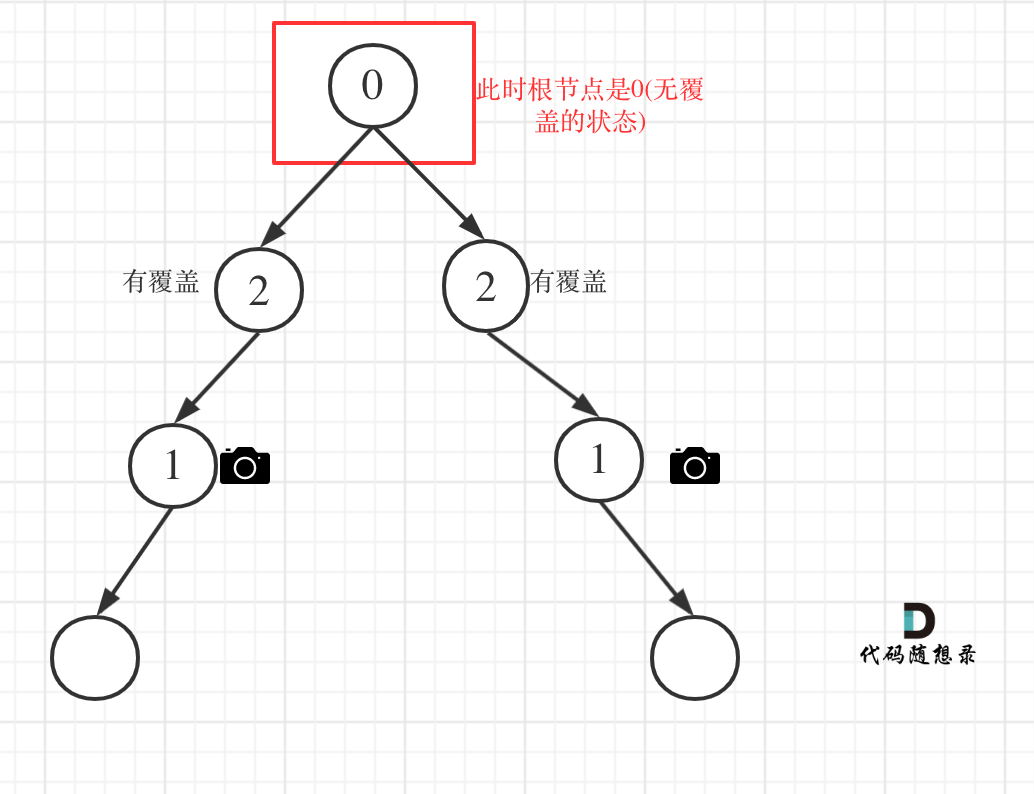 所以递归结束之后,还要判断根节点,如果没有覆盖,result++,代码如下: ```CPP int minCameraCover(TreeNode* root) { result = 0; if (traversal(root) == 0) { // root 无覆盖 result++; } return result; } ``` 以上四种情况我们分析完了,代码也差不多了,整体代码如下: (**以下我的代码注释很详细,为了把情况说清楚,特别把每种情况列出来。**) C++代码如下: ```CPP // 版本一 class Solution { private: int result; int traversal(TreeNode* cur) { // 空节点,该节点有覆盖 if (cur == NULL) return 2; int left = traversal(cur->left); // 左 int right = traversal(cur->right); // 右 // 情况1 // 左右节点都有覆盖 if (left == 2 && right == 2) return 0; // 情况2 // left == 0 && right == 0 左右节点无覆盖 // left == 1 && right == 0 左节点有摄像头,右节点无覆盖 // left == 0 && right == 1 左节点有无覆盖,右节点摄像头 // left == 0 && right == 2 左节点无覆盖,右节点覆盖 // left == 2 && right == 0 左节点覆盖,右节点无覆盖 if (left == 0 || right == 0) { result++; return 1; } // 情况3 // left == 1 && right == 2 左节点有摄像头,右节点有覆盖 // left == 2 && right == 1 左节点有覆盖,右节点有摄像头 // left == 1 && right == 1 左右节点都有摄像头 // 其他情况前段代码均已覆盖 if (left == 1 || right == 1) return 2; // 以上代码我没有使用else,主要是为了把各个分支条件展现出来,这样代码有助于读者理解 // 这个 return -1 逻辑不会走到这里。 return -1; } public: int minCameraCover(TreeNode* root) { result = 0; // 情况4 if (traversal(root) == 0) { // root 无覆盖 result++; } return result; } }; ``` 在以上代码的基础上,再进行精简,代码如下: ```CPP // 版本二 class Solution { private: int result; int traversal(TreeNode* cur) { if (cur == NULL) return 2; int left = traversal(cur->left); // 左 int right = traversal(cur->right); // 右 if (left == 2 && right == 2) return 0; else if (left == 0 || right == 0) { result++; return 1; } else return 2; } public: int minCameraCover(TreeNode* root) { result = 0; if (traversal(root) == 0) { // root 无覆盖 result++; } return result; } }; ``` 大家可能会惊讶,居然可以这么简短,**其实就是在版本一的基础上,使用else把一些情况直接覆盖掉了**。 在网上关于这道题解可以搜到很多这种神级别的代码,但都没讲不清楚,如果直接看代码的话,指定越看越晕,**所以建议大家对着版本一的代码一步一步来,版本二中看不中用!**。 ## 总结 本题的难点首先是要想到贪心的思路,然后就是遍历和状态推导。 在二叉树上进行状态推导,其实难度就上了一个台阶了,需要对二叉树的操作非常娴熟。 这道题目是名副其实的hard,大家感受感受。 ## 其他语言版本 ### Java ```java class Solution { int res=0; public int minCameraCover(TreeNode root) { // 对根节点的状态做检验,防止根节点是无覆盖状态 . if(minCame(root)==0){ res++; } return res; } /** 节点的状态值: 0 表示无覆盖 1 表示 有摄像头 2 表示有覆盖 后序遍历,根据左右节点的情况,来判读 自己的状态 */ public int minCame(TreeNode root){ if(root==null){ // 空节点默认为 有覆盖状态,避免在叶子节点上放摄像头 return 2; } int left=minCame(root.left); int right=minCame(root.right); // 如果左右节点都覆盖了的话, 那么本节点的状态就应该是无覆盖,没有摄像头 if(left==2&&right==2){ //(2,2) return 0; }else if(left==0||right==0){ // 左右节点都是无覆盖状态,那 根节点此时应该放一个摄像头 // (0,0) (0,1) (0,2) (1,0) (2,0) // 状态值为 1 摄像头数 ++; res++; return 1; }else{ // 左右节点的 状态为 (1,1) (1,2) (2,1) 也就是左右节点至少存在 1个摄像头, // 那么本节点就是处于被覆盖状态 return 2; } } } ``` ### Python ```python class Solution: def minCameraCover(self, root: TreeNode) -> int: # Greedy Algo: # 从下往上安装摄像头:跳过leaves这样安装数量最少,局部最优 -> 全局最优 # 先给leaves的父节点安装,然后每隔两层节点安装一个摄像头,直到Head # 0: 该节点未覆盖 # 1: 该节点有摄像头 # 2: 该节点有覆盖 result = 0 # 从下往上遍历:后序(左右中) def traversal(curr: TreeNode) -> int: nonlocal result if not curr: return 2 left = traversal(curr.left) right = traversal(curr.right) # Case 1: # 左右节点都有覆盖 if left == 2 and right == 2: return 0 # Case 2: # left == 0 && right == 0 左右节点无覆盖 # left == 1 && right == 0 左节点有摄像头,右节点无覆盖 # left == 0 && right == 1 左节点有无覆盖,右节点摄像头 # left == 0 && right == 2 左节点无覆盖,右节点覆盖 # left == 2 && right == 0 左节点覆盖,右节点无覆盖 elif left == 0 or right == 0: result += 1 return 1 # Case 3: # left == 1 && right == 2 左节点有摄像头,右节点有覆盖 # left == 2 && right == 1 左节点有覆盖,右节点有摄像头 # left == 1 && right == 1 左右节点都有摄像头 elif left == 1 or right == 1: return 2 # 其他情况前段代码均已覆盖 if traversal(root) == 0: result += 1 return result ``` ### Go ```go const inf = math.MaxInt64 / 2 func minCameraCover(root *TreeNode) int { var dfs func(*TreeNode) (a, b, c int) dfs = func(node *TreeNode) (a, b, c int) { if node == nil { return inf, 0, 0 } lefta, leftb, leftc := dfs(node.Left) righta, rightb, rightc := dfs(node.Right) a = leftc + rightc + 1 b = min(a, min(lefta+rightb, righta+leftb)) c = min(a, leftb+rightb) return } _, ans, _ := dfs(root) return ans } func min(a, b int) int { if a <= b { return a } return b } ``` ### Javascript ```Javascript var minCameraCover = function(root) { let result = 0 function traversal(cur) { if(cur === null) { return 2 } let left = traversal(cur.left) let right = traversal(cur.right) if(left === 2 && right === 2) { return 0 } if(left === 0 || right === 0) { result++ return 1 } if(left === 1 || right === 1) { return 2 } return -1 } if(traversal(root) === 0) { result++ } return result }; ``` ### TypeScript ```typescript function minCameraCover(root: TreeNode | null): number { /** 0-无覆盖, 1-有摄像头, 2-有覆盖 */ type statusCode = 0 | 1 | 2; let resCount: number = 0; if (recur(root) === 0) resCount++; return resCount; function recur(node: TreeNode | null): statusCode { if (node === null) return 2; const left: statusCode = recur(node.left), right: statusCode = recur(node.right); let resStatus: statusCode = 0; if (left === 0 || right === 0) { resStatus = 1; resCount++; } else if (left === 1 || right === 1) { resStatus = 2; } else { resStatus = 0; } return resStatus; } }; ``` ### C ```c /* **函数后序遍历二叉树。判断一个结点状态时,根据其左右孩子结点的状态进行判断 **状态:0为没有被摄像头覆盖到。1为此结点处应设置摄像头。2为此结点已被摄像头覆盖 */ int traversal(struct TreeNode* node, int* ans) { //递归结束条件:传入结点为NULL,假设此结点能被摄像头覆盖。这样方便与对叶子结点的判断,将叶子结点设为0 if(!node) return 2; //后序遍历二叉树,记录左右孩子的状态。根据左右孩子状态更新结点自身状态 int left = traversal(node->left, ans); int right = traversal(node->right, ans); //若左右孩子都可以被摄像头覆盖,将父亲结点状态设为0 if(left == 2 && right == 2) { return 0; } //若左右孩子有一个结点状态为没有被覆盖(0),则将父亲结点状态设置为摄像头 if(left == 0 || right == 0) { (*ans)++; return 1; } //若左右孩子有一个为摄像头,证明父亲结点可以被覆盖。将父亲结点状态变为2 if(left == 1 || right == 1) return 2; //逻辑不会走到-1,语句不会执行 return -1; } int minCameraCover(struct TreeNode* root){ int ans = 0; //在对整个二叉树遍历后。头结点可能未被覆盖,这时候如果函数返回值为0,证明头结点未被覆盖。说明头结点也需要添置摄像头,ans++ if(traversal(root, &ans) == 0) ans++; return ans; } ``` ### Scala ```scala object Solution { def minCameraCover(root: TreeNode): Int = { var result = 0 def traversal(cur: TreeNode): Int = { // 空节点,该节点有覆盖 if (cur == null) return 2 var left = traversal(cur.left) var right = traversal(cur.right) // 情况1,左右节点都有覆盖 if (left == 2 && right == 2) { return 0 } // 情况2 if (left == 0 || right == 0) { result += 1 return 1 } // 情况3 if (left == 1 || right == 1) { return 2 } -1 } if (traversal(root) == 0) { result += 1 } result } } ``` ### Rust ```Rust /// 版本一 impl Solution { pub fn min_camera_cover(root: Option