欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

## 72. 编辑距离 https://leetcode-cn.com/problems/edit-distance/ 给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数。你可以对一个单词进行如下三种操作： * 插入一个字符 * 删除一个字符 * 替换一个字符示例 1：输入：word1 = "horse", word2 = "ros" 输出：3 解释： horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e') 示例 2：输入：word1 = "intention", word2 = "execution" 输出：5 解释： intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u') 提示： * 0 <= word1.length, word2.length <= 500 * word1 和 word2 由小写英文字母组成 ## 思路编辑距离终于来了，这道题目如果大家没有了解动态规划的话，会感觉超级复杂。编辑距离是用动规来解决的经典题目，这道题目看上去好像很复杂，但用动规可以很巧妙的算出最少编辑距离。接下来我依然使用动规五部曲，对本题做一个详细的分析： ----------------------- ### 1. 确定dp数组（dp table）以及下标的含义 **dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]**。这里在强调一下：为啥要表示下标i-1为结尾的字符串呢，为啥不表示下标i为结尾的字符串呢？用i来表示也可以！但我统一以下标i-1为结尾的字符串，在下面的递归公式中会容易理解一点。 ----------------------- ### 2. 确定递推公式在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下： ``` if (word1[i - 1] == word2[j - 1]) 不操作 if (word1[i - 1] != word2[j - 1]) 增删换 ``` 也就是如上4种情况。 `if (word1[i - 1] == word2[j - 1])` 那么说明不用任何编辑，`dp[i][j]` 就应该是 `dp[i - 1][j - 1]`，即`dp[i][j] = dp[i - 1][j - 1];` 此时可能有同学有点不明白，为啥要即`dp[i][j] = dp[i - 1][j - 1]`呢？那么就在回顾上面讲过的`dp[i][j]`的定义，`word1[i - 1]` 与 `word2[j - 1]`相等了，那么就不用编辑了，以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串`word2`的最近编辑距离`dp[i - 1][j - 1]`就是 `dp[i][j]`了。在下面的讲解中，如果哪里看不懂，就回想一下`dp[i][j]`的定义，就明白了。 **在整个动规的过程中，最为关键就是正确理解`dp[i][j]`的定义！** `if (word1[i - 1] != word2[j - 1])`，此时就需要编辑了，如何编辑呢？操作一：word1增加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-2为结尾的word1 与 j-1为结尾的word2的最近编辑距离加上一个增加元素的操作。即 `dp[i][j] = dp[i - 1][j] + 1;` 操作二：word2添加一个元素，使其word1[i - 1]与word2[j - 1]相同，那么就是以下标i-1为结尾的word1 与 j-2为结尾的word2的最近编辑距离加上一个增加元素的操作。即 `dp[i][j] = dp[i][j - 1] + 1;` 这里有同学发现了，怎么都是添加元素，删除元素去哪了。 **word2添加一个元素，相当于word1删除一个元素**，例如 `word1 = "ad" ，word2 = "a"`，`word1`删除元素`'d'`，`word2`添加一个元素`'d'`，变成`word1="a", word2="ad"`，最终的操作数是一样！ dp数组如下图所示意的： ``` a a d +-----+-----+ +-----+-----+-----+ | 0 | 1 | | 0 | 1 | 2 | +-----+-----+ ===> +-----+-----+-----+ a | 1 | 0 | a | 1 | 0 | 1 | +-----+-----+ +-----+-----+-----+ d | 2 | 1 | +-----+-----+ ``` 操作三：替换元素，`word1`替换`word1[i - 1]`，使其与`word2[j - 1]`相同，此时不用增加元素，那么以下标`i-2`为结尾的`word1` 与 `j-2`为结尾的`word2`的最近编辑距离加上一个替换元素的操作。即 `dp[i][j] = dp[i - 1][j - 1] + 1;` 综上，当 `if (word1[i - 1] != word2[j - 1])` 时取最小的，即：`dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;` 递归公式代码如下： ```C++ if (word1[i - 1] == word2[j - 1]) { dp[i][j] = dp[i - 1][j - 1]; } else { dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1; } ``` --- ### 3. dp数组如何初始化再回顾一下dp[i][j]的定义： **dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]**。那么dp[i][0] 和 dp[0][j] 表示什么呢？ dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i; 同理dp[0][j] = j; 所以C++代码如下： ```C++ for (int i = 0; i <= word1.size(); i++) dp[i][0] = i; for (int j = 0; j <= word2.size(); j++) dp[0][j] = j; ``` ----------------------- ### 4. 确定遍历顺序从如下四个递推公式： * `dp[i][j] = dp[i - 1][j - 1]` * `dp[i][j] = dp[i - 1][j - 1] + 1` * `dp[i][j] = dp[i][j - 1] + 1` * `dp[i][j] = dp[i - 1][j] + 1` 可以看出dp[i][j]是依赖左方，上方和左上方元素的，如图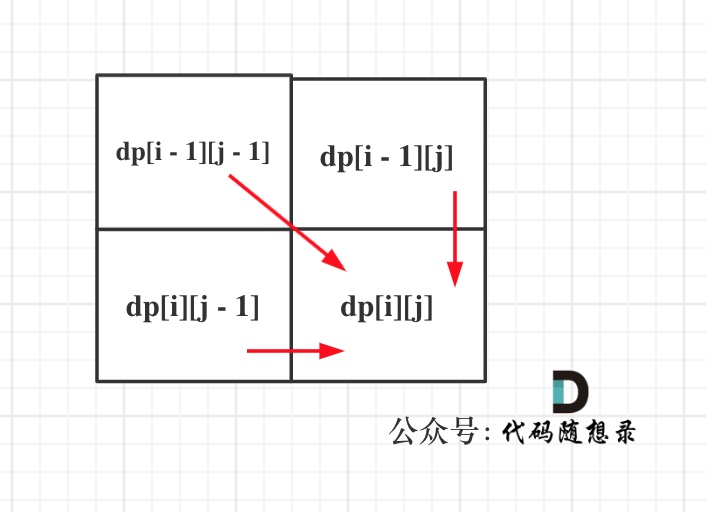： ![72.编辑距离](https://img-blog.csdnimg.cn/20210114162113131.jpg) 所以在dp矩阵中一定是从左到右从上到下去遍历。代码如下： ```C++ for (int i = 1; i <= word1.size(); i++) { for (int j = 1; j <= word2.size(); j++) { if (word1[i - 1] == word2[j - 1]) { dp[i][j] = dp[i - 1][j - 1]; } else { dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1; } } } ``` ----------------------- ### 5. 举例推导dp数组以示例1为例，输入：`word1 = "horse", word2 = "ros"`为例，dp矩阵状态图如下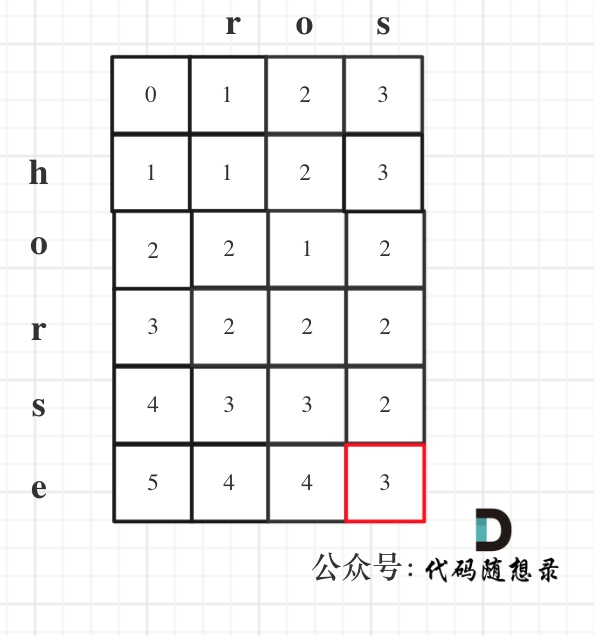： ![72.编辑距离1](https://img-blog.csdnimg.cn/20210114162132300.jpg) 以上动规五部分析完毕，C++代码如下： ```C++ class Solution { public: int minDistance(string word1, string word2) { vector> dp(word1.size() + 1, vector(word2.size() + 1, 0)); for (int i = 0; i <= word1.size(); i++) dp[i][0] = i; for (int j = 0; j <= word2.size(); j++) dp[0][j] = j; for (int i = 1; i <= word1.size(); i++) { for (int j = 1; j <= word2.size(); j++) { if (word1[i - 1] == word2[j - 1]) { dp[i][j] = dp[i - 1][j - 1]; } else { dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1; } } } return dp[word1.size()][word2.size()]; } }; ``` ----------------------- ## 其他语言版本 Java： ```java public int minDistance(String word1, String word2) { int m = word1.length(); int n = word2.length(); int[][] dp = new int[m + 1][n + 1]; // 初始化 for (int i = 1; i <= m; i++) { dp[i][0] = i; } for (int j = 1; j <= n; j++) { dp[0][j] = j; } for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { // 因为dp数组有效位从1开始 // 所以当前遍历到的字符串的位置为i-1 | j-1 if (word1.charAt(i - 1) == word2.charAt(j - 1)) { dp[i][j] = dp[i - 1][j - 1]; } else { dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1; } } } return dp[m][n]; } ``` Python： ```python class Solution: def minDistance(self, word1: str, word2: str) -> int: dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)] for i in range(len(word1)+1): dp[i][0] = i for j in range(len(word2)+1): dp[0][j] = j for i in range(1, len(word1)+1): for j in range(1, len(word2)+1): if word1[i-1] == word2[j-1]: dp[i][j] = dp[i-1][j-1] else: dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1 return dp[-1][-1] ``` Go： ```Go func minDistance(word1 string, word2 string) int { m, n := len(word1), len(word2) dp := make([][]int, m+1) for i := range dp { dp[i] = make([]int, n+1) } for i := 0; i < m+1; i++ { dp[i][0] = i // word1[i] 变成 word2[0], 删掉 word1[i], 需要 i 部操作 } for j := 0; j < n+1; j++ { dp[0][j] = j // word1[0] 变成 word2[j], 插入 word1[j]，需要 j 部操作 } for i := 1; i < m+1; i++ { for j := 1; j < n+1; j++ { if word1[i-1] == word2[j-1] { dp[i][j] = dp[i-1][j-1] } else { // Min(插入，删除，替换) dp[i][j] = Min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1 } } } return dp[m][n] } func Min(args ...int) int { min := args[0] for _, item := range args { if item < min { min = item } } return min } ``` ----------------------- * 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw) * B站视频：[代码随想录](https://space.bilibili.com/525438321) * 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)