



欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
## 209.长度最小的子数组
题目链接: https://leetcode-cn.com/problems/minimum-size-subarray-sum/
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
示例:
输入:s = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
## 暴力解法
这道题目暴力解法当然是 两个for循环,然后不断的寻找符合条件的子序列,时间复杂度很明显是O(n^2) 。
代码如下:
```C++
class Solution {
public:
int minSubArrayLen(int s, vector& nums) {
int result = INT32_MAX; // 最终的结果
int sum = 0; // 子序列的数值之和
int subLength = 0; // 子序列的长度
for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
sum = 0;
for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
sum += nums[j];
if (sum >= s) { // 一旦发现子序列和超过了s,更新result
subLength = j - i + 1; // 取子序列的长度
result = result < subLength ? result : subLength;
break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break
}
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
```
时间复杂度:$O(n^2)$
空间复杂度:$O(1)$
## 滑动窗口
接下来就开始介绍数组操作中另一个重要的方法:**滑动窗口**。
所谓滑动窗口,**就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果**。
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:

最后找到 4,3 是最短距离。
其实从动画中可以发现滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
在本题中实现滑动窗口,主要确定如下三点:
* 窗口内是什么?
* 如何移动窗口的起始位置?
* 如何移动窗口的结束位置?
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,窗口的起始位置设置为数组的起始位置就可以了。
解题的关键在于 窗口的起始位置如何移动,如图所示:
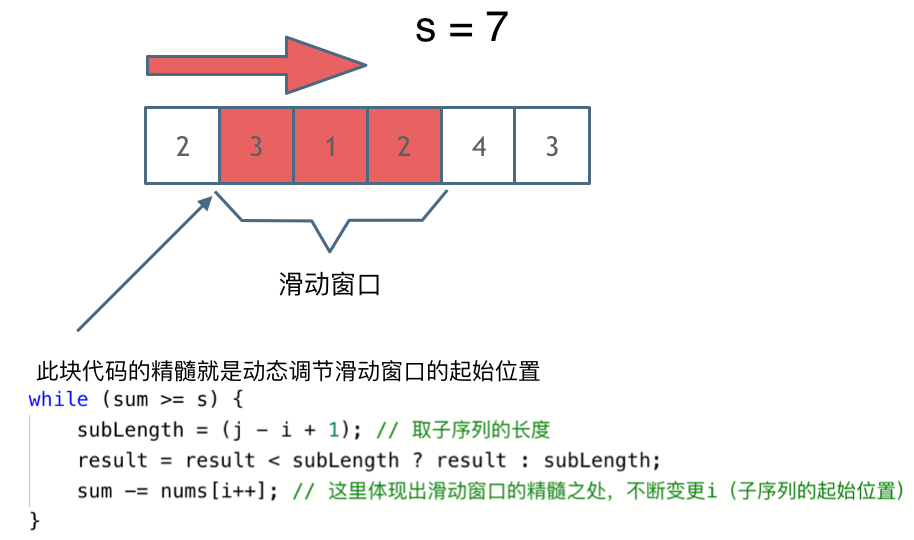
可以发现**滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)的暴力解法降为O(n)。**
C++代码如下:
```C++
class Solution {
public:
int minSubArrayLen(int s, vector& nums) {
int result = INT32_MAX;
int sum = 0; // 滑动窗口数值之和
int i = 0; // 滑动窗口起始位置
int subLength = 0; // 滑动窗口的长度
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件
while (sum >= s) {
subLength = (j - i + 1); // 取子序列的长度
result = result < subLength ? result : subLength;
sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
```
时间复杂度:$O(n)$
空间复杂度:$O(1)$
**一些录友会疑惑为什么时间复杂度是O(n)**。
不要以为for里放一个while就以为是$O(n^2)$啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被被操作两次,所以时间复杂度是2 * n 也就是$O(n)$。
## 其他语言补充
python:
```python
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
# 定义一个无限大的数
res = float("inf")
Sum = 0
index = 0
for i in range(len(nums)):
Sum += nums[i]
while Sum >= s:
res = min(res, i-index+1)
Sum -= nums[index]
index += 1
return 0 if res==float("inf") else res
```
## 相关题目推荐
* 904.水果成篮
* 76.最小覆盖子串
## 其他语言版本
Java:
Python:
Go:
JavaScript:
```
var minSubArrayLen = (target, nums) => {
let left = 0, right = 0,win = Infinity,sum = 0;
while(right < nums.length){
sum += nums[right];
while(sum >= target){
win = right - left + 1 < win? right - left + 1 : win;
sum -= nums[left];
left++;
}
right++;
}
return win === Infinity? 0:win;
};
```
-----------------------
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)




