|
|
||
|---|---|---|
| .. | ||
| images | ||
| README.md | ||
| README_EN.md | ||
| Solution.cpp | ||
| Solution.cs | ||
| Solution.go | ||
| Solution.java | ||
| Solution.js | ||
| Solution.py | ||
| Solution.ts | ||
README_EN.md
| comments | difficulty | edit_url | tags | ||||
|---|---|---|---|---|---|---|---|
| true | Medium | https://github.com/doocs/leetcode/edit/main/solution/0100-0199/0133.Clone%20Graph/README_EN.md |
|
133. Clone Graph
Description
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
class Node {
public int val;
public List<Node> neighbors;
}
Test case format:
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
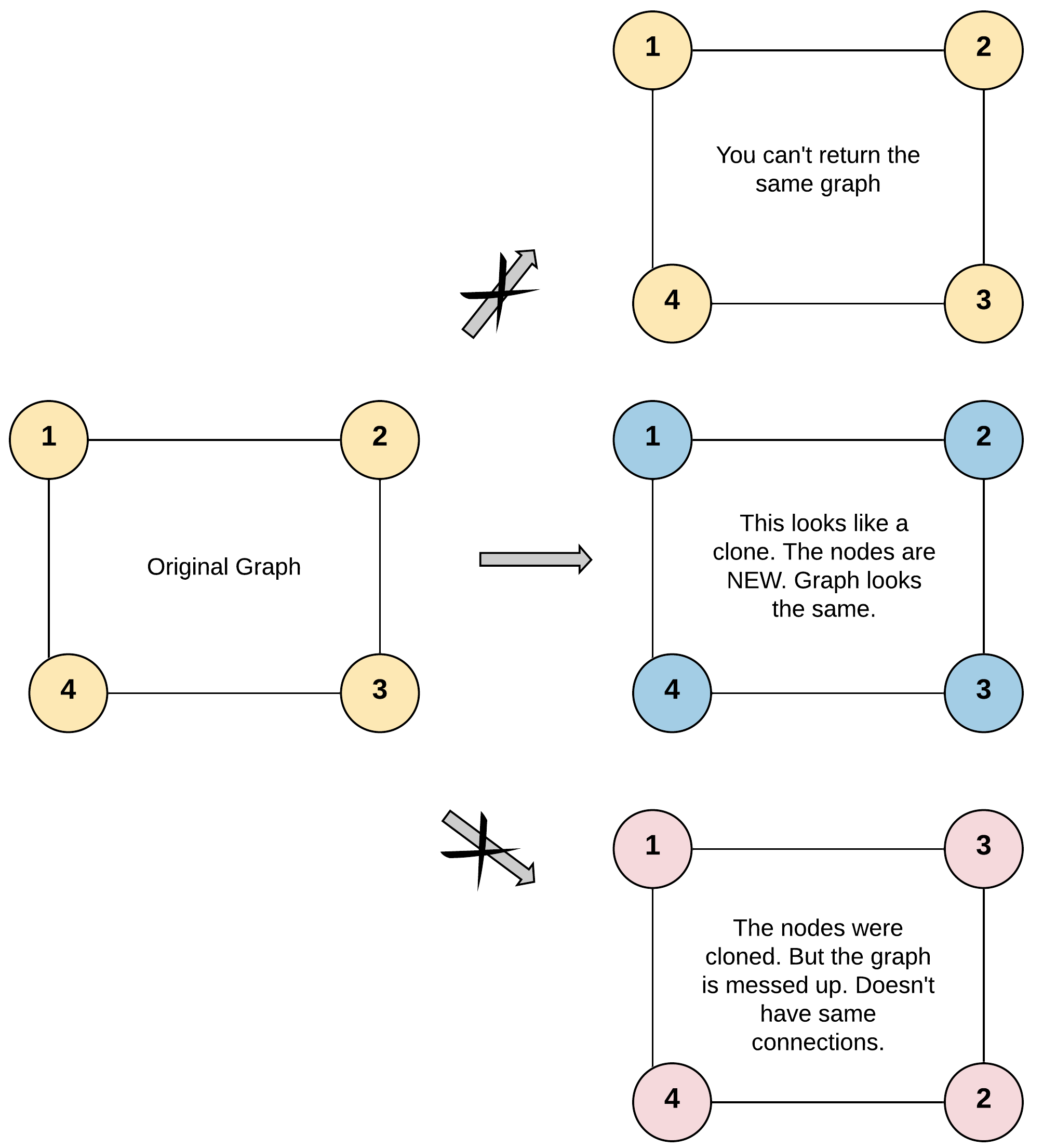
Input: adjList = [[2,4],[1,3],[2,4],[1,3]] Output: [[2,4],[1,3],[2,4],[1,3]] Explanation: There are 4 nodes in the graph. 1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3). 3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4). 4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
Example 2:
Input: adjList = [[]] Output: [[]] Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.
Example 3:
Input: adjList = [] Output: [] Explanation: This an empty graph, it does not have any nodes.
Constraints:
- The number of nodes in the graph is in the range
[0, 100]. 1 <= Node.val <= 100Node.valis unique for each node.- There are no repeated edges and no self-loops in the graph.
- The Graph is connected and all nodes can be visited starting from the given node.
Solutions
Solution 1: Hash Table + DFS
We use a hash table \textit{g} to record the correspondence between each node in the original graph and its copy, and then perform depth-first search.
We define the function \text{dfs}(node), which returns the copy of the \textit{node}. The process of \text{dfs}(node) is as follows:
- If
\textit{node}is\text{null}, then the return value of\text{dfs}(node)is\text{null}. - If
\textit{node}is in\textit{g}, then the return value of\text{dfs}(node)is\textit{g}[node]. - Otherwise, we create a new node
\textit{cloned}and set the value of\textit{g}[node]to\textit{cloned}. Then, we traverse all the neighbor nodes\textit{nxt}of\textit{node}and add\text{dfs}(nxt)to the neighbor list of\textit{cloned}. - Finally, return
\textit{cloned}.
In the main function, we return \text{dfs}(node).
The time complexity is O(n), and the space complexity is O(n). Here, n is the number of nodes.
Python3
"""
# Definition for a Node.
class Node:
def __init__(self, val = 0, neighbors = None):
self.val = val
self.neighbors = neighbors if neighbors is not None else []
"""
from typing import Optional
class Solution:
def cloneGraph(self, node: Optional["Node"]) -> Optional["Node"]:
def dfs(node):
if node is None:
return None
if node in g:
return g[node]
cloned = Node(node.val)
g[node] = cloned
for nxt in node.neighbors:
cloned.neighbors.append(dfs(nxt))
return cloned
g = defaultdict()
return dfs(node)
Java
/*
// Definition for a Node.
class Node {
public int val;
public List<Node> neighbors;
public Node() {
val = 0;
neighbors = new ArrayList<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new ArrayList<Node>();
}
public Node(int _val, ArrayList<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
}
*/
class Solution {
private Map<Node, Node> g = new HashMap<>();
public Node cloneGraph(Node node) {
return dfs(node);
}
private Node dfs(Node node) {
if (node == null) {
return null;
}
Node cloned = g.get(node);
if (cloned == null) {
cloned = new Node(node.val);
g.put(node, cloned);
for (Node nxt : node.neighbors) {
cloned.neighbors.add(dfs(nxt));
}
}
return cloned;
}
}
C++
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> neighbors;
Node() {
val = 0;
neighbors = vector<Node*>();
}
Node(int _val) {
val = _val;
neighbors = vector<Node*>();
}
Node(int _val, vector<Node*> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
public:
Node* cloneGraph(Node* node) {
unordered_map<Node*, Node*> g;
auto dfs = [&](this auto&& dfs, Node* node) -> Node* {
if (!node) {
return nullptr;
}
if (g.contains(node)) {
return g[node];
}
Node* cloned = new Node(node->val);
g[node] = cloned;
for (auto& nxt : node->neighbors) {
cloned->neighbors.push_back(dfs(nxt));
}
return cloned;
};
return dfs(node);
}
};
Go
/**
* Definition for a Node.
* type Node struct {
* Val int
* Neighbors []*Node
* }
*/
func cloneGraph(node *Node) *Node {
g := map[*Node]*Node{}
var dfs func(node *Node) *Node
dfs = func(node *Node) *Node {
if node == nil {
return nil
}
if n, ok := g[node]; ok {
return n
}
cloned := &Node{node.Val, []*Node{}}
g[node] = cloned
for _, nxt := range node.Neighbors {
cloned.Neighbors = append(cloned.Neighbors, dfs(nxt))
}
return cloned
}
return dfs(node)
}
TypeScript
/**
* Definition for _Node.
* class _Node {
* val: number
* neighbors: _Node[]
*
* constructor(val?: number, neighbors?: _Node[]) {
* this.val = (val===undefined ? 0 : val)
* this.neighbors = (neighbors===undefined ? [] : neighbors)
* }
* }
*
*/
function cloneGraph(node: _Node | null): _Node | null {
const g: Map<_Node, _Node> = new Map();
const dfs = (node: _Node | null): _Node | null => {
if (!node) {
return null;
}
if (g.has(node)) {
return g.get(node);
}
const cloned = new _Node(node.val);
g.set(node, cloned);
for (const nxt of node.neighbors) {
cloned.neighbors.push(dfs(nxt));
}
return cloned;
};
return dfs(node);
}
JavaScript
/**
* // Definition for a _Node.
* function _Node(val, neighbors) {
* this.val = val === undefined ? 0 : val;
* this.neighbors = neighbors === undefined ? [] : neighbors;
* };
*/
/**
* @param {_Node} node
* @return {_Node}
*/
var cloneGraph = function (node) {
const g = new Map();
const dfs = node => {
if (!node) {
return null;
}
if (g.has(node)) {
return g.get(node);
}
const cloned = new _Node(node.val);
g.set(node, cloned);
for (const nxt of node.neighbors) {
cloned.neighbors.push(dfs(nxt));
}
return cloned;
};
return dfs(node);
};
C#
/*
// Definition for a Node.
public class Node {
public int val;
public IList<Node> neighbors;
public Node() {
val = 0;
neighbors = new List<Node>();
}
public Node(int _val) {
val = _val;
neighbors = new List<Node>();
}
public Node(int _val, List<Node> _neighbors) {
val = _val;
neighbors = _neighbors;
}
}
*/
public class Solution {
public Node CloneGraph(Node node) {
var g = new Dictionary<Node, Node>();
Node Dfs(Node n) {
if (n == null) {
return null;
}
if (g.ContainsKey(n)) {
return g[n];
}
var cloned = new Node(n.val);
g[n] = cloned;
foreach (var neighbor in n.neighbors) {
cloned.neighbors.Add(Dfs(neighbor));
}
return cloned;
}
return Dfs(node);
}
}