|
…
|
||
|---|---|---|
| .. | ||
| images | ||
| README.md | ||
| README_EN.md | ||
| Solution.cpp | ||
| Solution.cs | ||
| Solution.go | ||
| Solution.java | ||
| Solution.py | ||
| Solution.rs | ||
| Solution.ts | ||
README_EN.md
| comments | difficulty | edit_url | tags | ||
|---|---|---|---|---|---|
| true | Medium | https://github.com/doocs/leetcode/edit/main/solution/0500-0599/0573.Squirrel%20Simulation/README_EN.md |
|
573. Squirrel Simulation 🔒
Description
You are given two integers height and width representing a garden of size height x width. You are also given:
- an array
treewheretree = [treer, treec]is the position of the tree in the garden, - an array
squirrelwheresquirrel = [squirrelr, squirrelc]is the position of the squirrel in the garden, - and an array
nutswherenuts[i] = [nutir, nutic]is the position of theithnut in the garden.
The squirrel can only take at most one nut at one time and can move in four directions: up, down, left, and right, to the adjacent cell.
Return the minimal distance for the squirrel to collect all the nuts and put them under the tree one by one.
The distance is the number of moves.
Example 1:
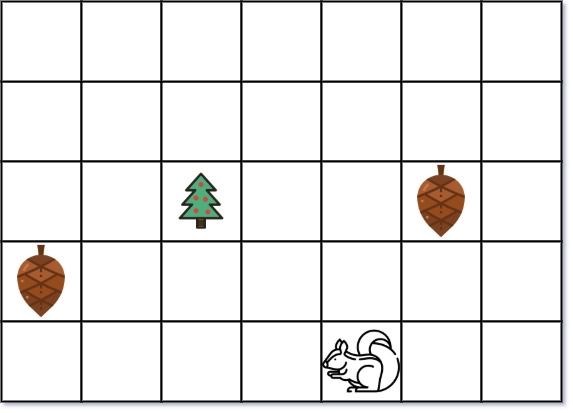
Input: height = 5, width = 7, tree = [2,2], squirrel = [4,4], nuts = [[3,0], [2,5]] Output: 12 Explanation: The squirrel should go to the nut at [2, 5] first to achieve a minimal distance.
Example 2:

Input: height = 1, width = 3, tree = [0,1], squirrel = [0,0], nuts = [[0,2]] Output: 3
Constraints:
1 <= height, width <= 100tree.length == 2squirrel.length == 21 <= nuts.length <= 5000nuts[i].length == 20 <= treer, squirrelr, nutir <= height0 <= treec, squirrelc, nutic <= width
Solutions
Solution 1: Mathematics
Observing the squirrel's movement path, we can see that the squirrel will first move to the position of a nut, then move to the position of the tree. After that, the total movement path of the squirrel is equal to "the sum of the distances from the remaining nuts to the tree" multiplied by 2.
Therefore, we only need to select a nut as the squirrel's first target, such that the sum of its distance to the tree is minimized, to obtain the shortest path.
The time complexity is O(n), where n is the number of nuts. The space complexity is O(1).
Python3
class Solution:
def minDistance(
self,
height: int,
width: int,
tree: List[int],
squirrel: List[int],
nuts: List[List[int]],
) -> int:
tr, tc = tree
sr, sc = squirrel
s = sum(abs(r - tr) + abs(c - tc) for r, c in nuts) * 2
ans = inf
for r, c in nuts:
a = abs(r - tr) + abs(c - tc)
b = abs(r - sr) + abs(c - sc)
ans = min(ans, s - a + b)
return ans
Java
import static java.lang.Math.*;
class Solution {
public int minDistance(int height, int width, int[] tree, int[] squirrel, int[][] nuts) {
int tr = tree[0], tc = tree[1];
int sr = squirrel[0], sc = squirrel[1];
int s = 0;
for (var e : nuts) {
s += abs(e[0] - tr) + abs(e[1] - tc);
}
s <<= 1;
int ans = Integer.MAX_VALUE;
for (var e : nuts) {
int a = abs(e[0] - tr) + abs(e[1] - tc);
int b = abs(e[0] - sr) + abs(e[1] - sc);
ans = min(ans, s - a + b);
}
return ans;
}
}
C++
class Solution {
public:
int minDistance(int height, int width, vector<int>& tree, vector<int>& squirrel, vector<vector<int>>& nuts) {
int tr = tree[0], tc = tree[1];
int sr = squirrel[0], sc = squirrel[1];
int s = 0;
for (const auto& e : nuts) {
s += abs(e[0] - tr) + abs(e[1] - tc);
}
s <<= 1;
int ans = INT_MAX;
for (const auto& e : nuts) {
int a = abs(e[0] - tr) + abs(e[1] - tc);
int b = abs(e[0] - sr) + abs(e[1] - sc);
ans = min(ans, s - a + b);
}
return ans;
}
};
Go
func minDistance(height int, width int, tree []int, squirrel []int, nuts [][]int) int {
tr, tc := tree[0], tree[1]
sr, sc := squirrel[0], squirrel[1]
s := 0
for _, e := range nuts {
s += abs(e[0]-tr) + abs(e[1]-tc)
}
s <<= 1
ans := math.MaxInt32
for _, e := range nuts {
a := abs(e[0]-tr) + abs(e[1]-tc)
b := abs(e[0]-sr) + abs(e[1]-sc)
ans = min(ans, s-a+b)
}
return ans
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
TypeScript
function minDistance(
height: number,
width: number,
tree: number[],
squirrel: number[],
nuts: number[][],
): number {
const [tr, tc] = tree;
const [sr, sc] = squirrel;
const s = nuts.reduce((acc, [r, c]) => acc + (Math.abs(tr - r) + Math.abs(tc - c)) * 2, 0);
let ans = Infinity;
for (const [r, c] of nuts) {
const a = Math.abs(tr - r) + Math.abs(tc - c);
const b = Math.abs(sr - r) + Math.abs(sc - c);
ans = Math.min(ans, s - a + b);
}
return ans;
}
Rust
impl Solution {
pub fn min_distance(
height: i32,
width: i32,
tree: Vec<i32>,
squirrel: Vec<i32>,
nuts: Vec<Vec<i32>>,
) -> i32 {
let (tr, tc) = (tree[0], tree[1]);
let (sr, sc) = (squirrel[0], squirrel[1]);
let s: i32 = nuts
.iter()
.map(|nut| (nut[0] - tr).abs() + (nut[1] - tc).abs())
.sum::<i32>()
* 2;
let mut ans = i32::MAX;
for nut in &nuts {
let a = (nut[0] - tr).abs() + (nut[1] - tc).abs();
let b = (nut[0] - sr).abs() + (nut[1] - sc).abs();
ans = ans.min(s - a + b);
}
ans
}
}
C#
public class Solution {
public int MinDistance(int height, int width, int[] tree, int[] squirrel, int[][] nuts) {
int tr = tree[0], tc = tree[1];
int sr = squirrel[0], sc = squirrel[1];
int s = 0;
foreach (var e in nuts) {
s += Math.Abs(e[0] - tr) + Math.Abs(e[1] - tc);
}
s <<= 1;
int ans = int.MaxValue;
foreach (var e in nuts) {
int a = Math.Abs(e[0] - tr) + Math.Abs(e[1] - tc);
int b = Math.Abs(e[0] - sr) + Math.Abs(e[1] - sc);
ans = Math.Min(ans, s - a + b);
}
return ans;
}
}