History

…
..
images	…
README.md	…
README_EN.md	…
Solution.cpp	…
Solution.go	…
Solution.java	…
Solution.py	…
Solution.ts	…

README_EN.md

comments

difficulty

edit_url

rating

source

1330. Reverse Subarray To Maximize Array Value

中文文档

Description

You are given an integer array nums. The value of this array is defined as the sum of |nums[i] - nums[i + 1]| for all 0 <= i < nums.length - 1.

You are allowed to select any subarray of the given array and reverse it. You can perform this operation only once.

Find maximum possible value of the final array.

Example 1:

Input: nums = [2,3,1,5,4]
Output: 10
Explanation: By reversing the subarray [3,1,5] the array becomes [2,5,1,3,4] whose value is 10.

Example 2:

Input: nums = [2,4,9,24,2,1,10]
Output: 68

Constraints:

2 <= nums.length <= 3 * 10⁴
-10⁵ <= nums[i] <= 10⁵
The answer is guaranteed to fit in a 32-bit integer.

Solutions

Solution 1: Classification Discussion + Enumeration

According to the problem description, we need to find the maximum value of the array \sum_{i=0}^{n-2} |a_i - a_{i+1}| when reversing a subarray once.

Next, we discuss the following cases:

Do not reverse the subarray.
Reverse the subarray, and the subarray "includes" the first element.
Reverse the subarray, and the subarray "includes" the last element.
Reverse the subarray, and the subarray "does not include" the first and last elements.

Let s be the array value when the subarray is not reversed, then s = \sum_{i=0}^{n-2} |a_i - a_{i+1}|. We can initialize the answer ans to s.

If we reverse the subarray and the subarray includes the first element, we can enumerate the last element a_i of the reversed subarray, where 0 \leq i < n-1. In this case, ans = \max(ans, s + |a_0 - a_{i+1}| - |a_i - a_{i+1}|).

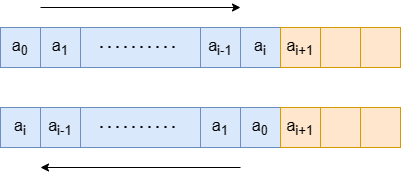
Similarly, if we reverse the subarray and the subarray includes the last element, we can enumerate the first element a_{i+1} of the reversed subarray, where 0 \leq i < n-1. In this case, ans = \max(ans, s + |a_{n-1} - a_i| - |a_i - a_{i+1}|).

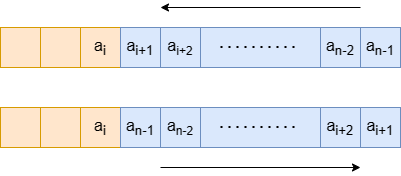
If we reverse the subarray and the subarray does not include the first and last elements, we consider any two adjacent elements in the array as a point pair (x, y). Let the first element of the reversed subarray be y_1, and its left adjacent element be x_1; let the last element of the reversed subarray be x_2, and its right adjacent element be y_2.

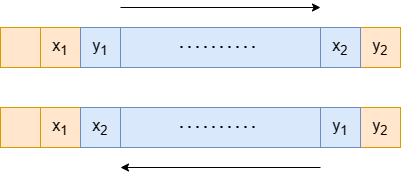
At this time, compared to not reversing the subarray, the change in the array value is |x_1 - x_2| + |y_1 - y_2| - |x_1 - y_1| - |x_2 - y_2|, where the first two terms can be expressed as:


\left | x_1 - x_2 \right |  + \left | y_1 - y_2 \right | = \max \begin{cases} (x_1 + y_1) - (x_2 + y_2) \\ (x_1 - y_1) - (x_2 - y_2) \\ (-x_1 + y_1) - (-x_2 + y_2) \\ (-x_1 - y_1) - (-x_2 - y_2) \end{cases}

Then the change in the array value is:


\left | x_1 - x_2 \right |  + \left | y_1 - y_2 \right | - \left | x_1 - y_1 \right | - \left | x_2 - y_2 \right |  = \max \begin{cases} (x_1 + y_1) - \left |x_1 - y_1 \right | - \left ( (x_2 + y_2) + \left |x_2 - y_2 \right | \right ) \\ (x_1 - y_1) - \left |x_1 - y_1 \right | - \left ( (x_2 - y_2) + \left |x_2 - y_2 \right | \right ) \\ (-x_1 + y_1) - \left |x_1 - y_1 \right | - \left ( (-x_2 + y_2) + \left |x_2 - y_2 \right | \right ) \\ (-x_1 - y_1) - \left |x_1 - y_1 \right | - \left ( (-x_2 - y_2) + \left |x_2 - y_2 \right | \right ) \end{cases}

Therefore, we only need to find the maximum value mx of k_1 \times x + k_2 \times y, where k_1, k_2 \in \{-1, 1\}, and the corresponding minimum value mi of |x - y|. Then the maximum change in the array value is mx - mi. The answer is ans = \max(ans, s + \max(0, mx - mi)).

In the code implementation, we define an array of length 5, dirs=[1, -1, -1, 1, 1]. Each time we take two adjacent elements of the array as the values of k_1 and k_2, which can cover all cases of k_1, k_2 \in \{-1, 1\}.

The time complexity is O(n), where n is the length of the array nums. The space complexity is O(1).

Python3

class Solution:
    def maxValueAfterReverse(self, nums: List[int]) -> int:
        ans = s = sum(abs(x - y) for x, y in pairwise(nums))
        for x, y in pairwise(nums):
            ans = max(ans, s + abs(nums[0] - y) - abs(x - y))
            ans = max(ans, s + abs(nums[-1] - x) - abs(x - y))
        for k1, k2 in pairwise((1, -1, -1, 1, 1)):
            mx, mi = -inf, inf
            for x, y in pairwise(nums):
                a = k1 * x + k2 * y
                b = abs(x - y)
                mx = max(mx, a - b)
                mi = min(mi, a + b)
            ans = max(ans, s + max(mx - mi, 0))
        return ans

Java

class Solution {
    public int maxValueAfterReverse(int[] nums) {
        int n = nums.length;
        int s = 0;
        for (int i = 0; i < n - 1; ++i) {
            s += Math.abs(nums[i] - nums[i + 1]);
        }
        int ans = s;
        for (int i = 0; i < n - 1; ++i) {
            ans = Math.max(
                ans, s + Math.abs(nums[0] - nums[i + 1]) - Math.abs(nums[i] - nums[i + 1]));
            ans = Math.max(
                ans, s + Math.abs(nums[n - 1] - nums[i]) - Math.abs(nums[i] - nums[i + 1]));
        }
        int[] dirs = {1, -1, -1, 1, 1};
        final int inf = 1 << 30;
        for (int k = 0; k < 4; ++k) {
            int k1 = dirs[k], k2 = dirs[k + 1];
            int mx = -inf, mi = inf;
            for (int i = 0; i < n - 1; ++i) {
                int a = k1 * nums[i] + k2 * nums[i + 1];
                int b = Math.abs(nums[i] - nums[i + 1]);
                mx = Math.max(mx, a - b);
                mi = Math.min(mi, a + b);
            }
            ans = Math.max(ans, s + Math.max(0, mx - mi));
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maxValueAfterReverse(vector<int>& nums) {
        int n = nums.size();
        int s = 0;
        for (int i = 0; i < n - 1; ++i) {
            s += abs(nums[i] - nums[i + 1]);
        }
        int ans = s;
        for (int i = 0; i < n - 1; ++i) {
            ans = max(ans, s + abs(nums[0] - nums[i + 1]) - abs(nums[i] - nums[i + 1]));
            ans = max(ans, s + abs(nums[n - 1] - nums[i]) - abs(nums[i] - nums[i + 1]));
        }
        int dirs[5] = {1, -1, -1, 1, 1};
        const int inf = 1 << 30;
        for (int k = 0; k < 4; ++k) {
            int k1 = dirs[k], k2 = dirs[k + 1];
            int mx = -inf, mi = inf;
            for (int i = 0; i < n - 1; ++i) {
                int a = k1 * nums[i] + k2 * nums[i + 1];
                int b = abs(nums[i] - nums[i + 1]);
                mx = max(mx, a - b);
                mi = min(mi, a + b);
            }
            ans = max(ans, s + max(0, mx - mi));
        }
        return ans;
    }
};

Go

func maxValueAfterReverse(nums []int) int {
	s, n := 0, len(nums)
	for i, x := range nums[:n-1] {
		y := nums[i+1]
		s += abs(x - y)
	}
	ans := s
	for i, x := range nums[:n-1] {
		y := nums[i+1]
		ans = max(ans, s+abs(nums[0]-y)-abs(x-y))
		ans = max(ans, s+abs(nums[n-1]-x)-abs(x-y))
	}
	dirs := [5]int{1, -1, -1, 1, 1}
	const inf = 1 << 30
	for k := 0; k < 4; k++ {
		k1, k2 := dirs[k], dirs[k+1]
		mx, mi := -inf, inf
		for i, x := range nums[:n-1] {
			y := nums[i+1]
			a := k1*x + k2*y
			b := abs(x - y)
			mx = max(mx, a-b)
			mi = min(mi, a+b)
		}
		ans = max(ans, s+max(mx-mi, 0))
	}
	return ans
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

TypeScript

function maxValueAfterReverse(nums: number[]): number {
    const n = nums.length;
    let s = 0;
    for (let i = 0; i < n - 1; ++i) {
        s += Math.abs(nums[i] - nums[i + 1]);
    }
    let ans = s;
    for (let i = 0; i < n - 1; ++i) {
        const d = Math.abs(nums[i] - nums[i + 1]);
        ans = Math.max(ans, s + Math.abs(nums[0] - nums[i + 1]) - d);
        ans = Math.max(ans, s + Math.abs(nums[n - 1] - nums[i]) - d);
    }
    const dirs = [1, -1, -1, 1, 1];
    const inf = 1 << 30;
    for (let k = 0; k < 4; ++k) {
        let mx = -inf;
        let mi = inf;
        for (let i = 0; i < n - 1; ++i) {
            const a = dirs[k] * nums[i] + dirs[k + 1] * nums[i + 1];
            const b = Math.abs(nums[i] - nums[i + 1]);
            mx = Math.max(mx, a - b);
            mi = Math.min(mi, a + b);
        }
        ans = Math.max(ans, s + Math.max(0, mx - mi));
    }
    return ans;
}