替换图片链接
This commit is contained in:
parent
91e7dab72c
commit
86a0208485
|
|
@ -181,7 +181,7 @@
|
||||||
|
|
||||||
|
|
||||||
题目分类大纲如下:
|
题目分类大纲如下:
|
||||||
<img src='https://code-thinking-1253855093.file.myqcloud.com/pics/20240424172231.png' width=600 alt='二叉树大纲'> </img></div>
|
<img src='https://file.kamacoder.com/pics/20240424172231.png' width=600 alt='二叉树大纲'> </img></div>
|
||||||
|
|
||||||
1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
|
1. [关于二叉树,你该了解这些!](./problems/二叉树理论基础.md)
|
||||||
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
|
2. [二叉树:二叉树的递归遍历](./problems/二叉树的递归遍历.md)
|
||||||
|
|
@ -222,7 +222,7 @@
|
||||||
|
|
||||||
题目分类大纲如下:
|
题目分类大纲如下:
|
||||||
|
|
||||||
<img src='https://code-thinking-1253855093.file.myqcloud.com/pics/20240424172311.png' width=600 alt='回溯算法大纲'> </img></div>
|
<img src='https://file.kamacoder.com/pics/20240424172311.png' width=600 alt='回溯算法大纲'> </img></div>
|
||||||
|
|
||||||
1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
|
1. [关于回溯算法,你该了解这些!](./problems/回溯算法理论基础.md)
|
||||||
2. [回溯算法:77.组合](./problems/0077.组合.md)
|
2. [回溯算法:77.组合](./problems/0077.组合.md)
|
||||||
|
|
@ -252,7 +252,7 @@
|
||||||
题目分类大纲如下:
|
题目分类大纲如下:
|
||||||
|
|
||||||
|
|
||||||
<img src='https://code-thinking-1253855093.file.myqcloud.com/pics/20210917104315.png' width=600 alt='贪心算法大纲'> </img></div>
|
<img src='https://file.kamacoder.com/pics/20210917104315.png' width=600 alt='贪心算法大纲'> </img></div>
|
||||||
|
|
||||||
1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
|
1. [关于贪心算法,你该了解这些!](./problems/贪心算法理论基础.md)
|
||||||
2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
|
2. [贪心算法:455.分发饼干](./problems/0455.分发饼干.md)
|
||||||
|
|
@ -503,5 +503,5 @@
|
||||||
|
|
||||||
添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
|
添加微信记得备注,如果是已工作,备注:姓名-城市-岗位。如果学生,备注:姓名-学校-年级。**备注没有自我介绍不通过哦**
|
||||||
|
|
||||||
<div align="center"><img src="https://code-thinking-1253855093.file.myqcloud.com/pics/第二企业刷题活码.png" data-img="1" width="200" height="200"></img></div>
|
<div align="center"><img src="https://file.kamacoder.com/pics/第二企业刷题活码.png" data-img="1" width="200" height="200"></img></div>
|
||||||
|
|
||||||
|
|
|
||||||
|
|
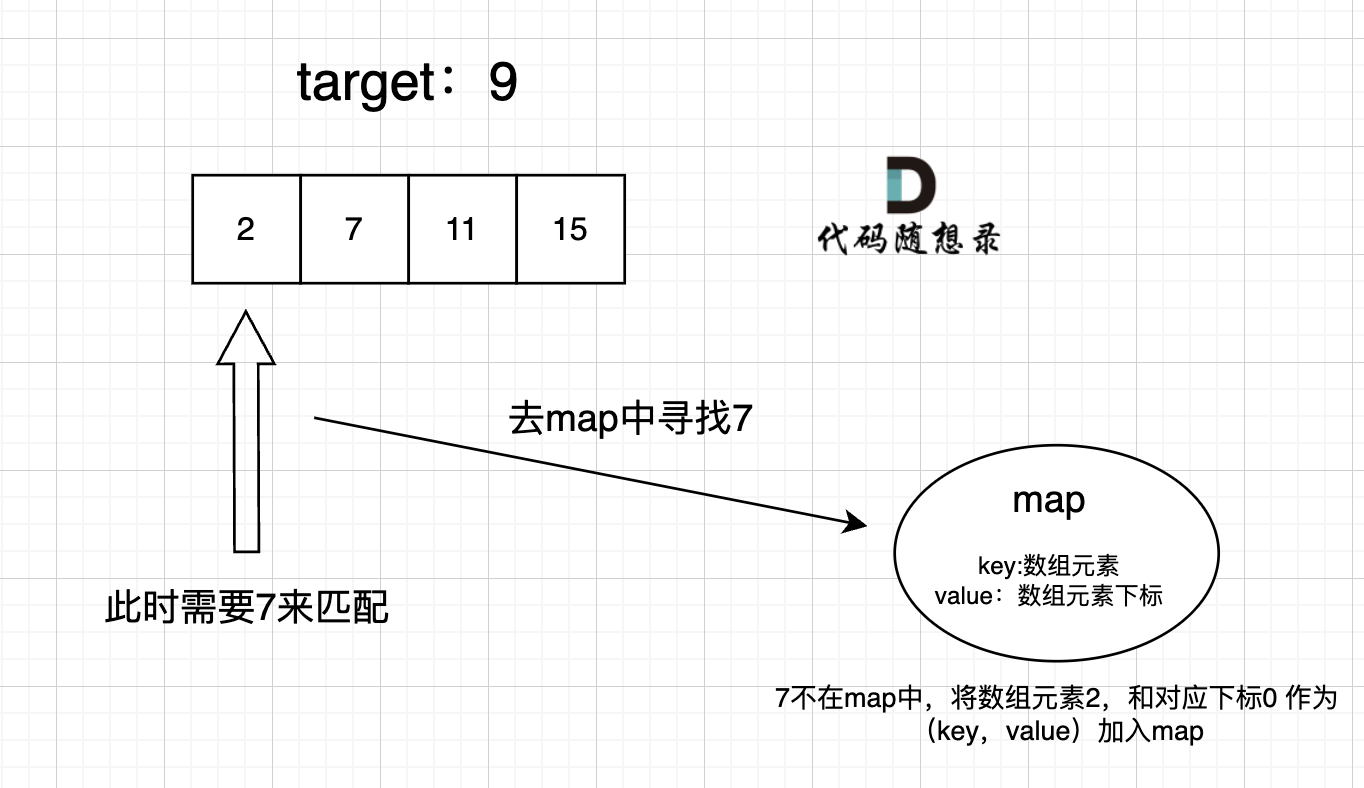
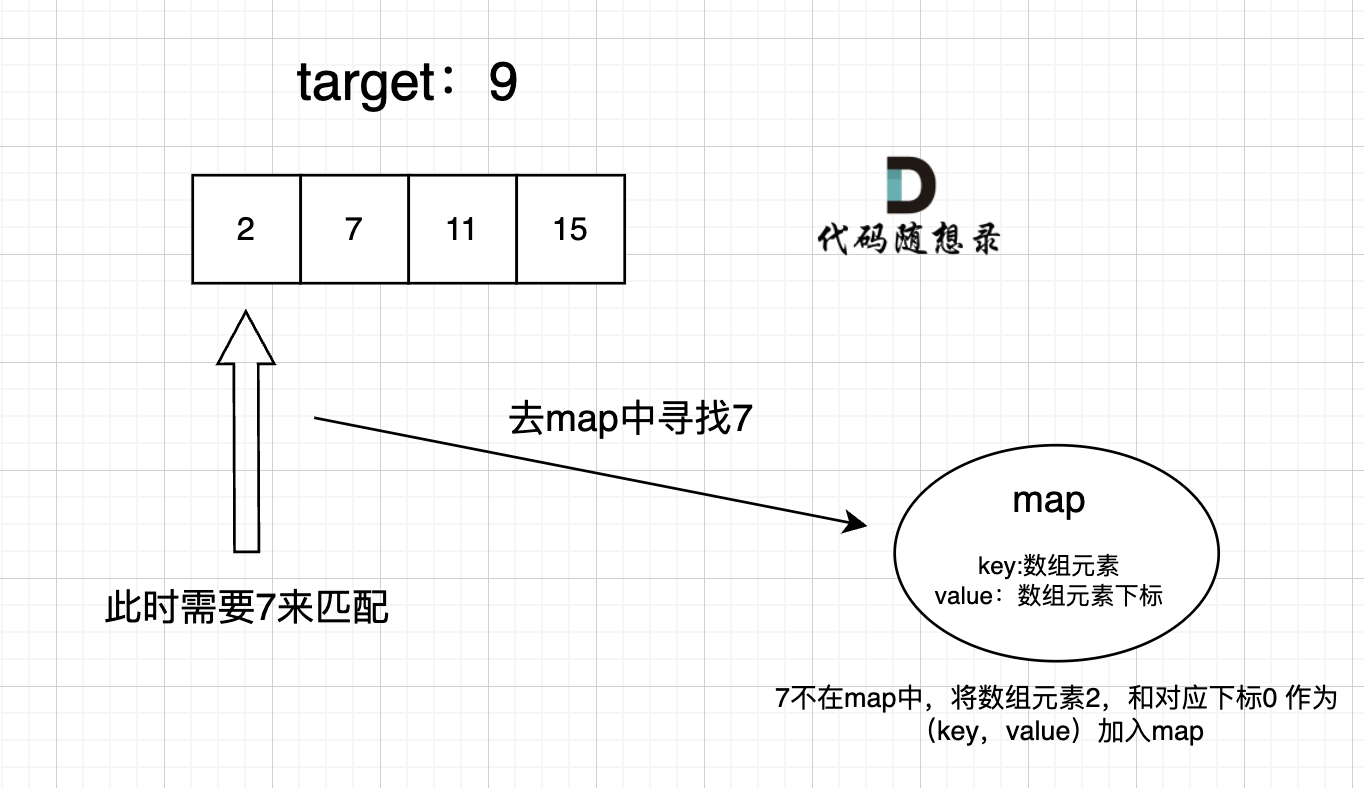
@ -83,10 +83,10 @@ map目的用来存放我们访问过的元素,因为遍历数组的时候,
|
||||||
|
|
||||||
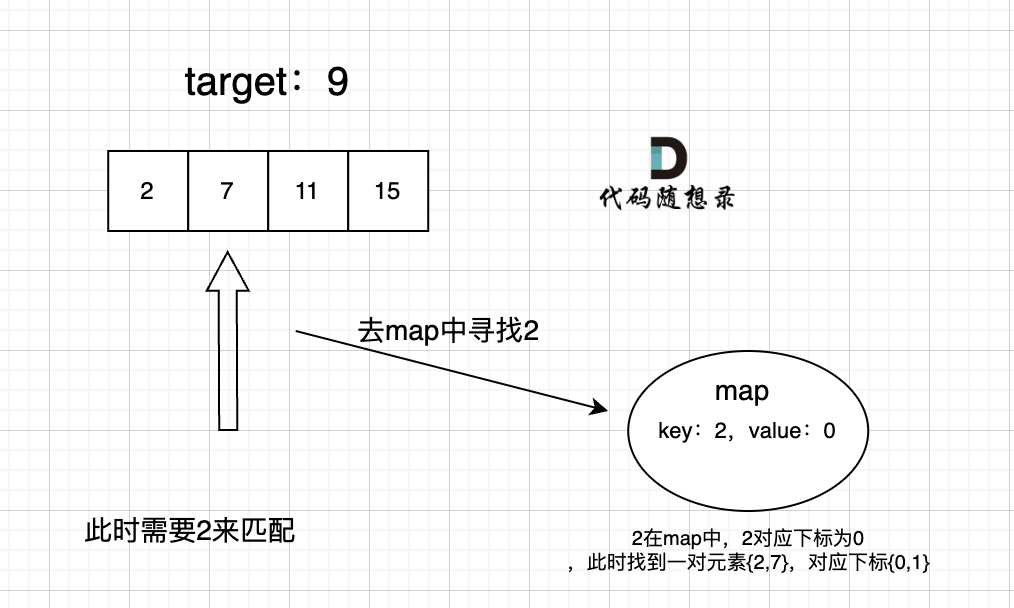
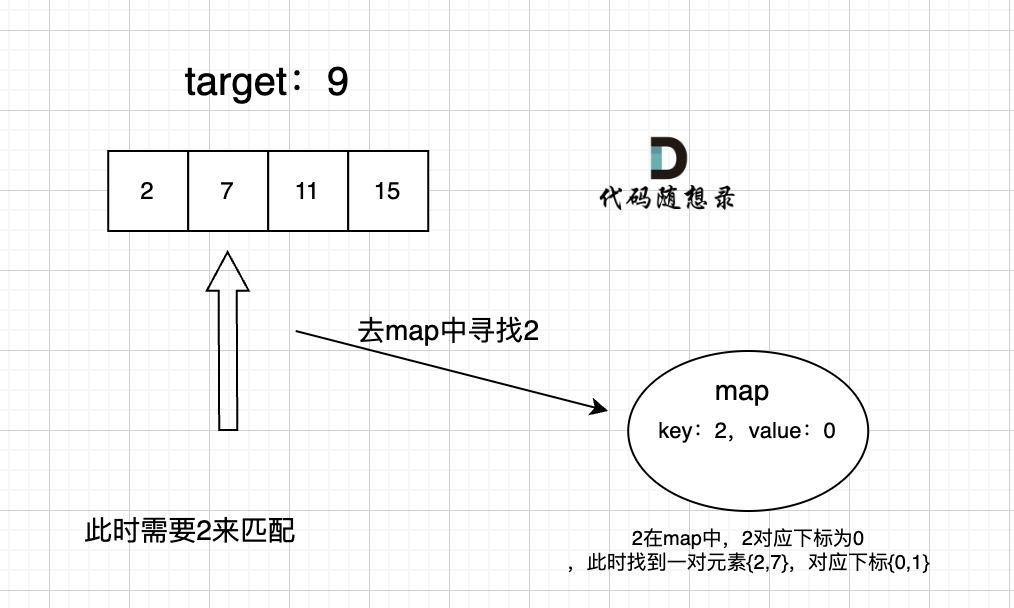
过程如下:
|
过程如下:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
C++代码:
|
C++代码:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -106,7 +106,7 @@ dp[i][j]可以初始化为true么? 当然不行,怎能刚开始就全都匹
|
||||||
|
|
||||||
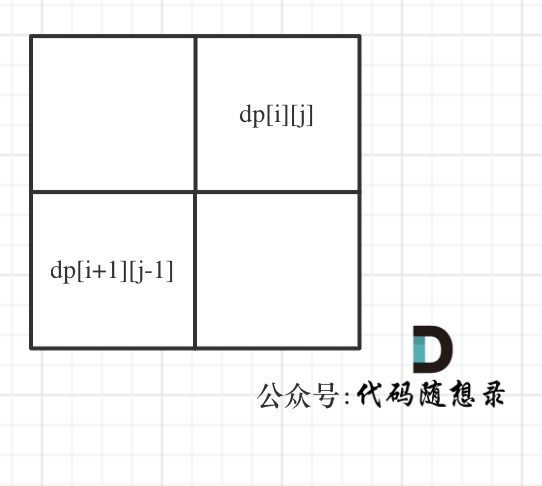
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
|
dp[i + 1][j - 1] 在 dp[i][j]的左下角,如图:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
|
如果这矩阵是从上到下,从左到右遍历,那么会用到没有计算过的dp[i + 1][j - 1],也就是根据不确定是不是回文的区间[i+1,j-1],来判断了[i,j]是不是回文,那结果一定是不对的。
|
||||||
|
|
||||||
|
|
@ -140,7 +140,7 @@ for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
|
||||||
|
|
||||||
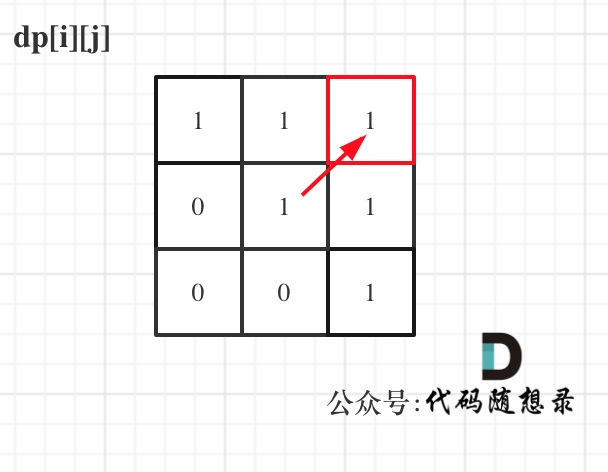
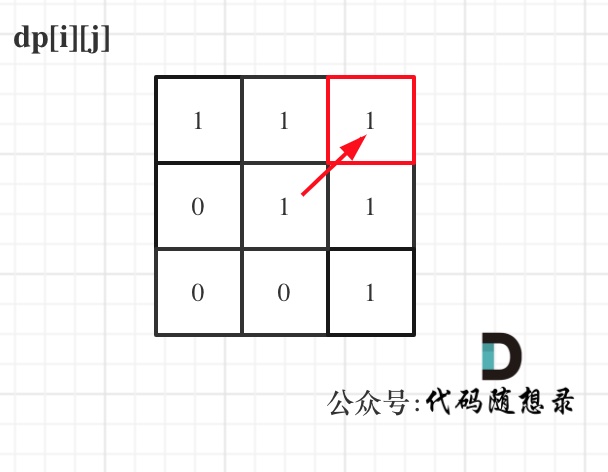
举例,输入:"aaa",dp[i][j]状态如下:
|
举例,输入:"aaa",dp[i][j]状态如下:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分**。
|
**注意因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分**。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -11,7 +11,7 @@
|
||||||
|
|
||||||
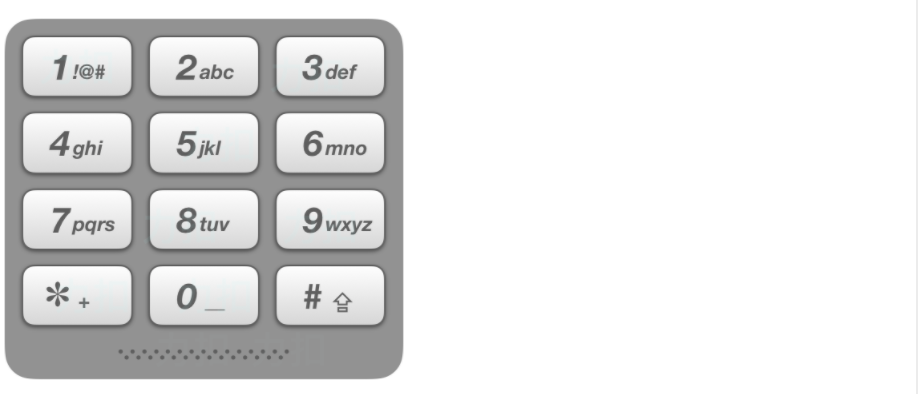
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
|
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
示例:
|
示例:
|
||||||
* 输入:"23"
|
* 输入:"23"
|
||||||
|
|
@ -64,7 +64,7 @@ const string letterMap[10] = {
|
||||||
|
|
||||||
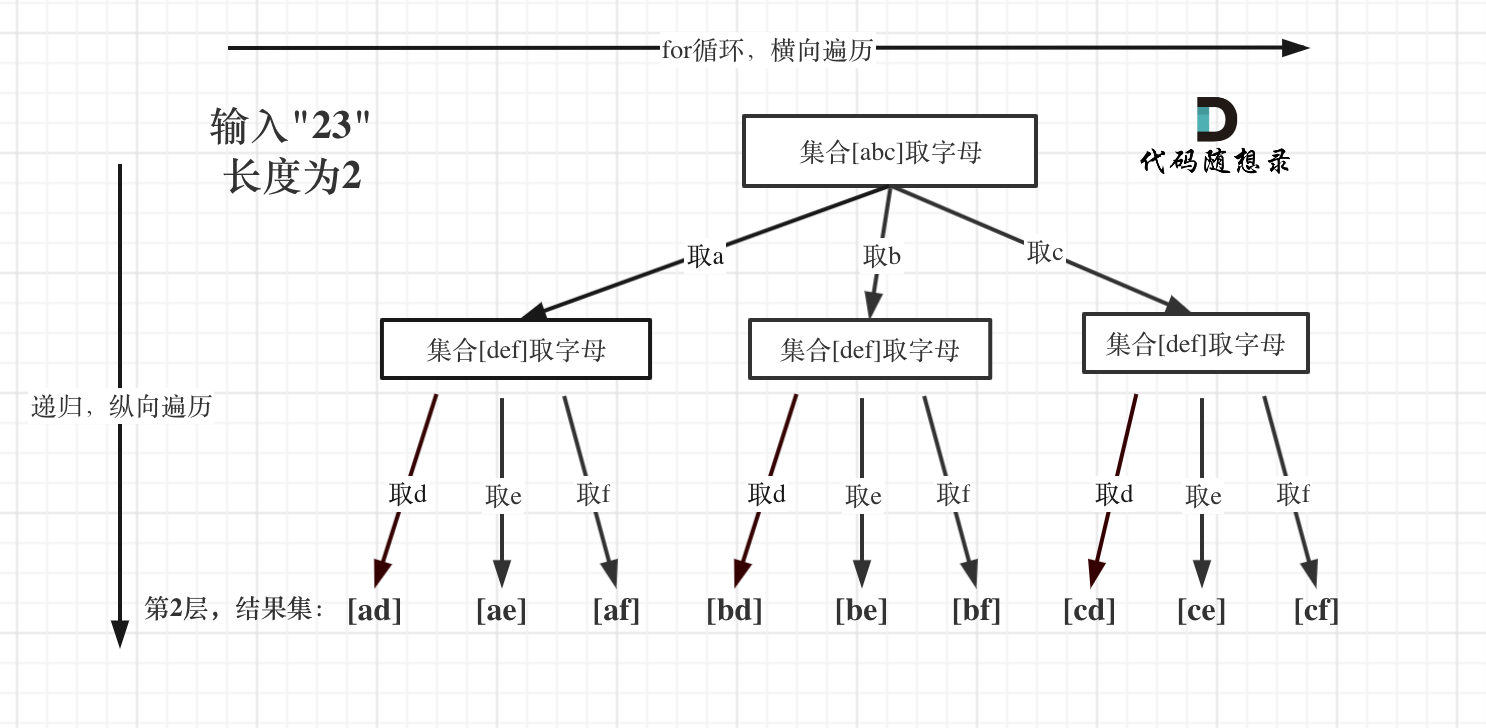
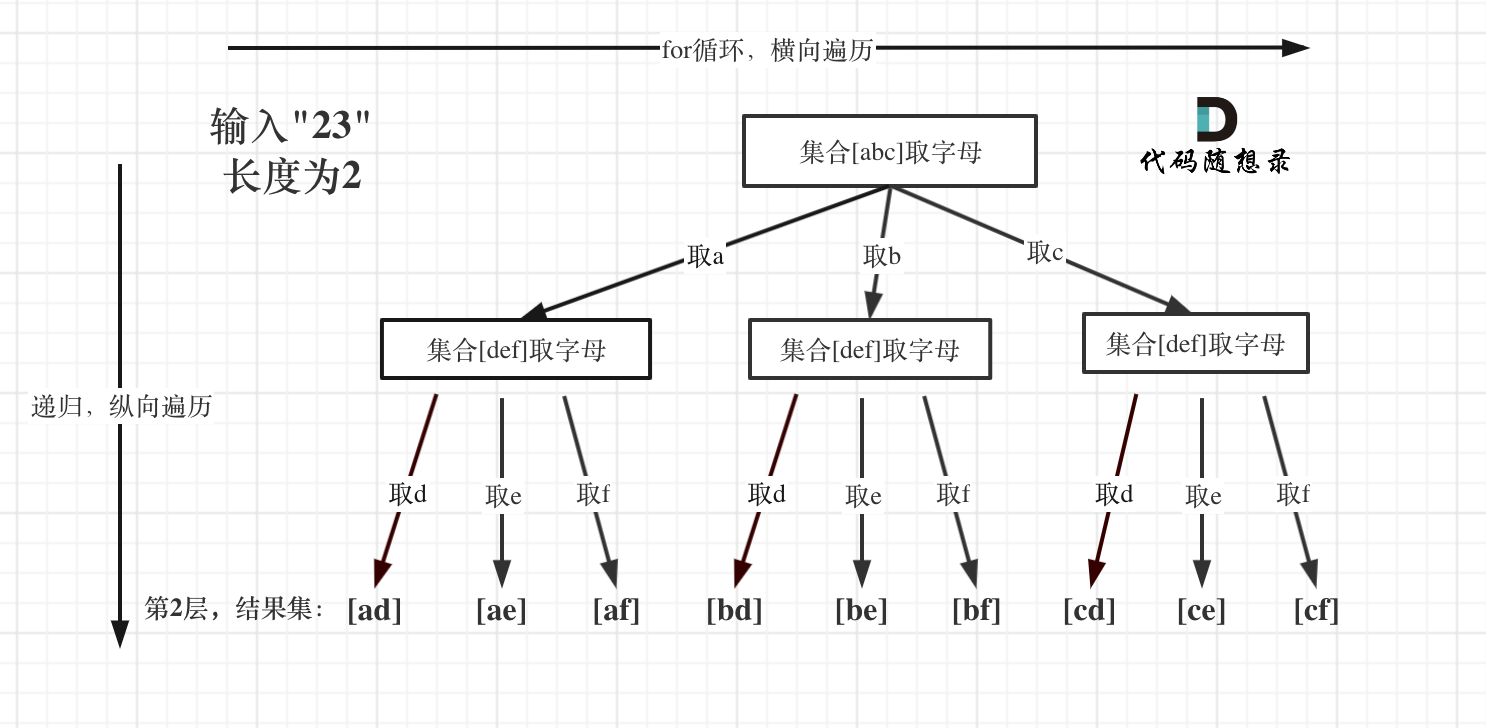
例如:输入:"23",抽象为树形结构,如图所示:
|
例如:输入:"23",抽象为树形结构,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
|
图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -16,7 +16,7 @@
|
||||||
示例 1:
|
示例 1:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
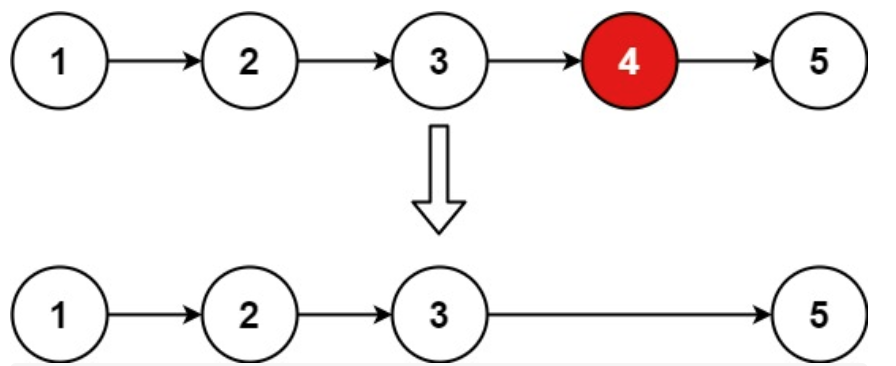
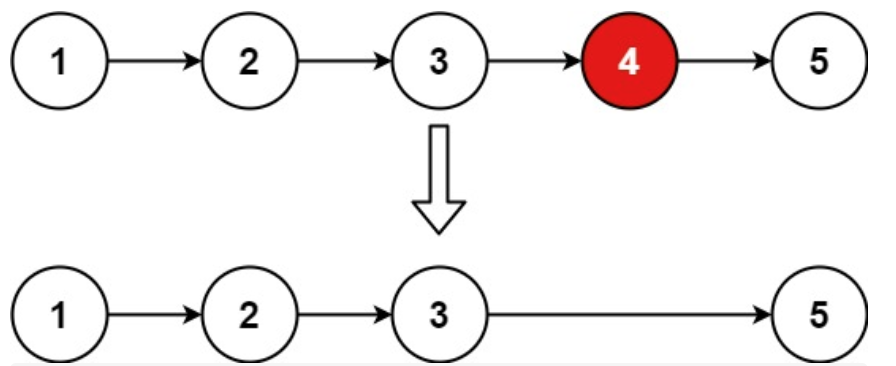
输入:head = [1,2,3,4,5], n = 2
|
输入:head = [1,2,3,4,5], n = 2
|
||||||
输出:[1,2,3,5]
|
输出:[1,2,3,5]
|
||||||
|
|
|
||||||
|
|
@ -81,13 +81,13 @@ cd a/b/c/../../
|
||||||
|
|
||||||
|
|
||||||
1. 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
|
1. 第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
|
||||||
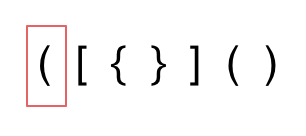
|
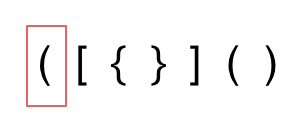
|
||||||
|
|
||||||
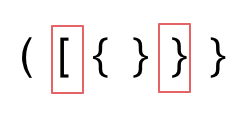
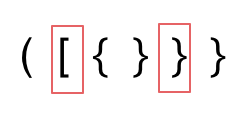
2. 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
|
2. 第二种情况,括号没有多余,但是 括号的类型没有匹配上。
|
||||||
|
|
||||||
|
|
||||||
3. 第三种情况,字符串里右方向的括号多余了,所以不匹配。
|
3. 第三种情况,字符串里右方向的括号多余了,所以不匹配。
|
||||||
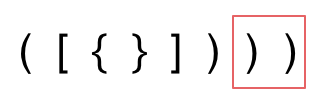
|
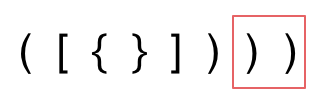
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -41,7 +41,7 @@
|
||||||
|
|
||||||
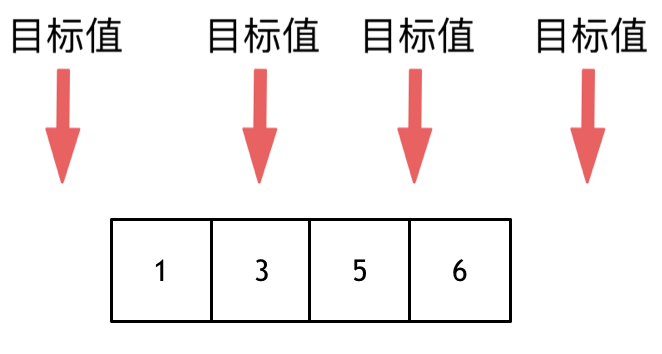
这道题目,要在数组中插入目标值,无非是这四种情况。
|
这道题目,要在数组中插入目标值,无非是这四种情况。
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
* 目标值在数组所有元素之前
|
* 目标值在数组所有元素之前
|
||||||
* 目标值等于数组中某一个元素
|
* 目标值等于数组中某一个元素
|
||||||
|
|
@ -82,14 +82,14 @@ public:
|
||||||
|
|
||||||
效率如下:
|
效率如下:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
### 二分法
|
### 二分法
|
||||||
|
|
||||||
既然暴力解法的时间复杂度是O(n),就要尝试一下使用二分查找法。
|
既然暴力解法的时间复杂度是O(n),就要尝试一下使用二分查找法。
|
||||||
|
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
大家注意这道题目的前提是数组是有序数组,这也是使用二分查找的基础条件。
|
大家注意这道题目的前提是数组是有序数组,这也是使用二分查找的基础条件。
|
||||||
|
|
||||||
|
|
@ -99,7 +99,7 @@ public:
|
||||||
|
|
||||||
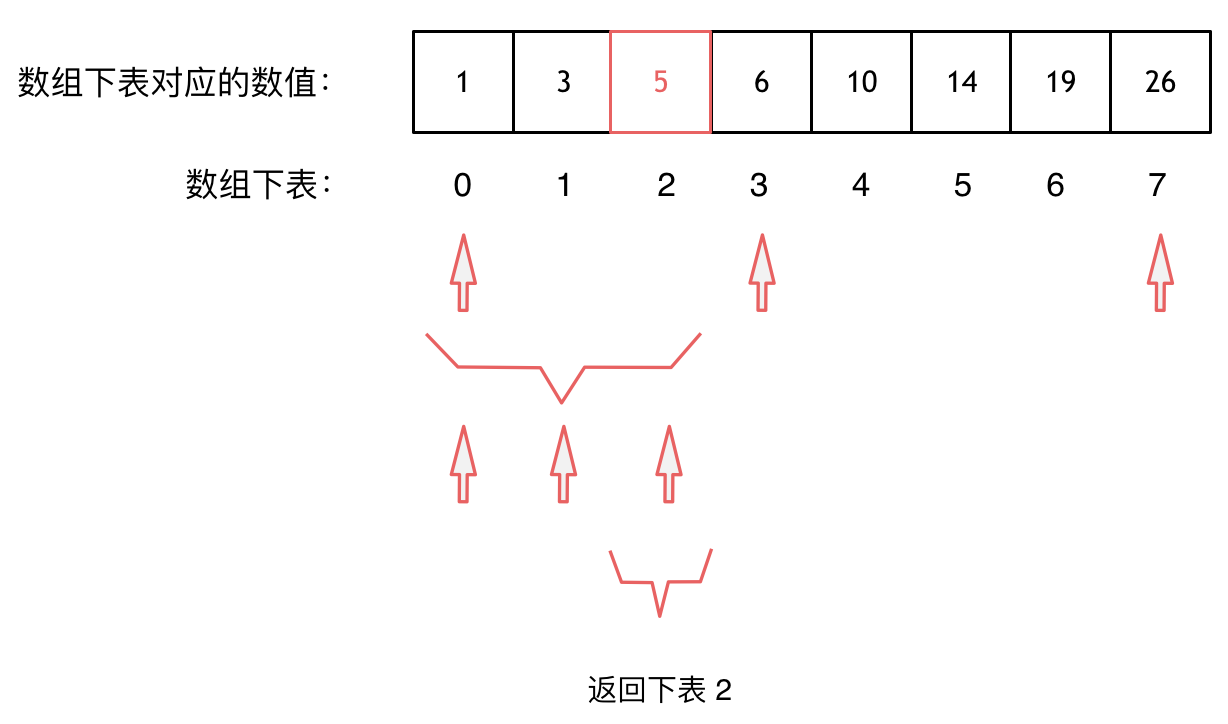
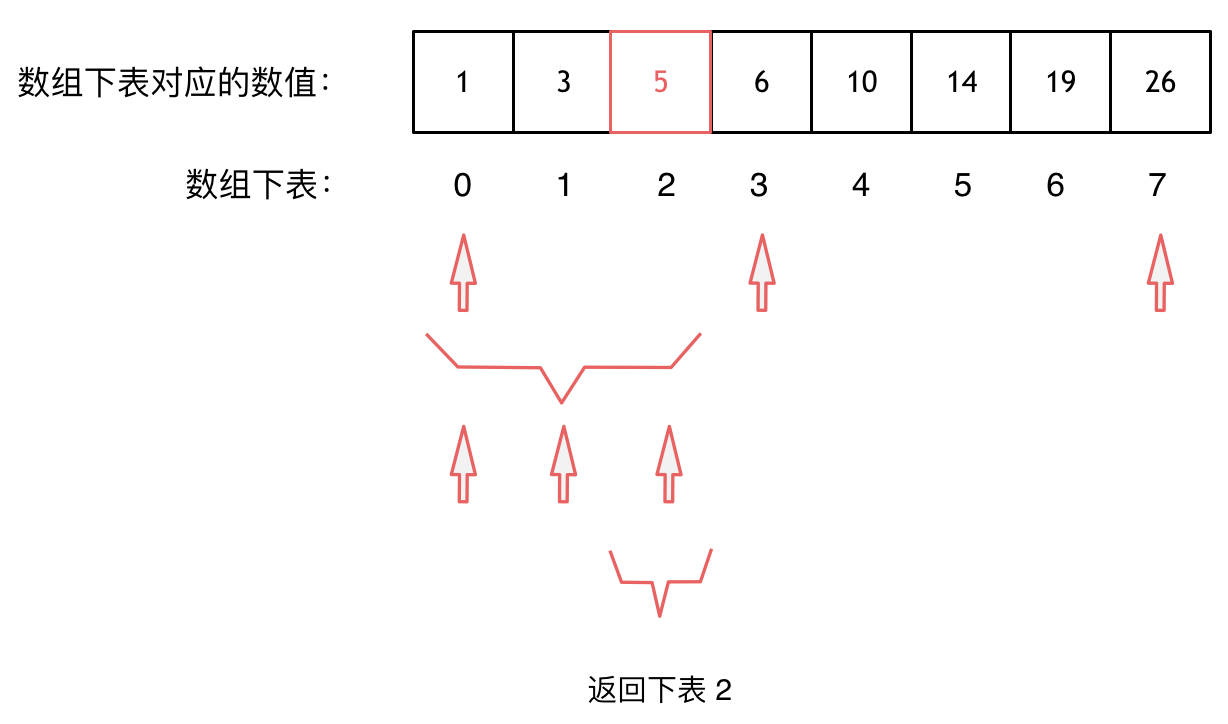
大体讲解一下二分法的思路,这里来举一个例子,例如在这个数组中,使用二分法寻找元素为5的位置,并返回其下标。
|
大体讲解一下二分法的思路,这里来举一个例子,例如在这个数组中,使用二分法寻找元素为5的位置,并返回其下标。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
二分查找涉及的很多的边界条件,逻辑比较简单,就是写不好。
|
二分查找涉及的很多的边界条件,逻辑比较简单,就是写不好。
|
||||||
|
|
||||||
|
|
@ -150,7 +150,7 @@ public:
|
||||||
* 空间复杂度:O(1)
|
* 空间复杂度:O(1)
|
||||||
|
|
||||||
效率如下:
|
效率如下:
|
||||||

|

|
||||||
|
|
||||||
### 二分法第二种写法
|
### 二分法第二种写法
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -18,11 +18,11 @@
|
||||||
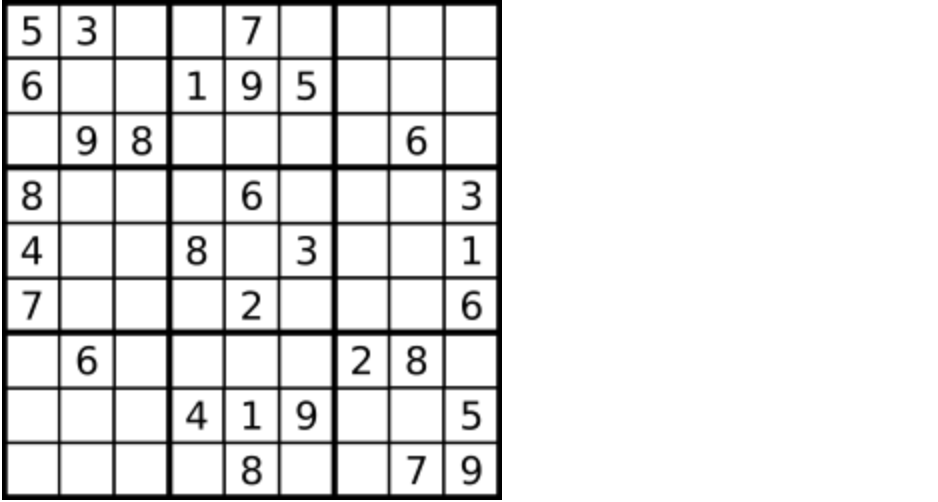
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
|
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。
|
||||||
空白格用 '.' 表示。
|
空白格用 '.' 表示。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
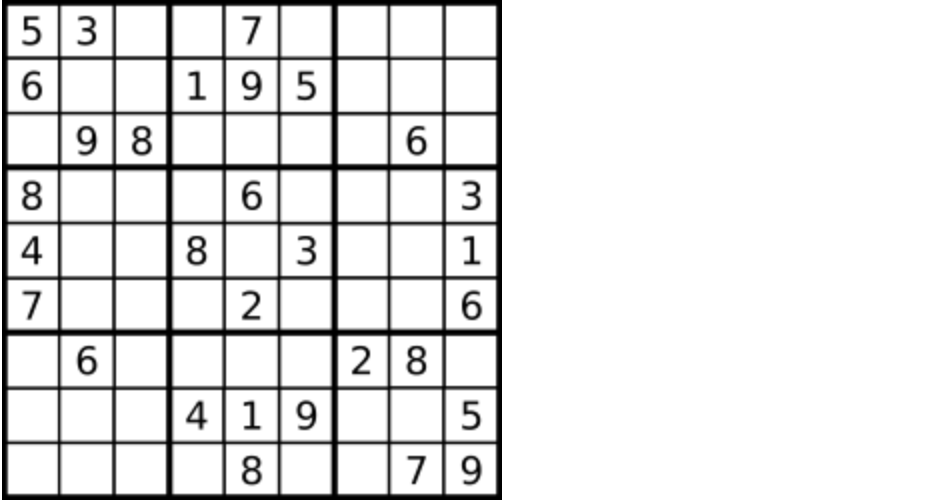
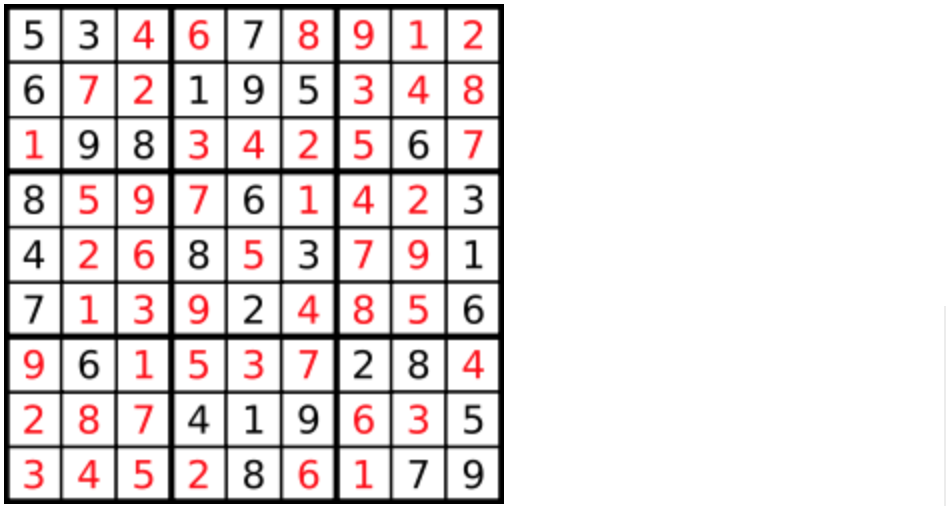
一个数独。
|
一个数独。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
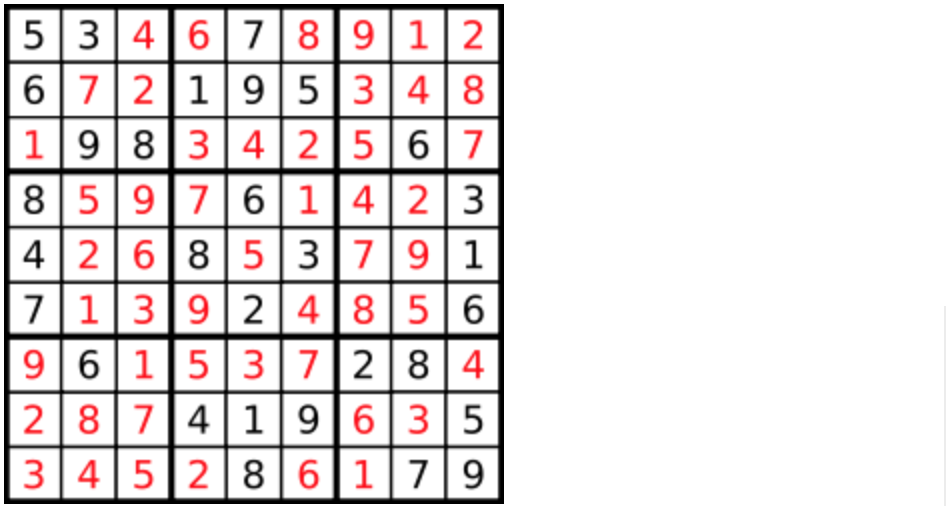
答案被标成红色。
|
答案被标成红色。
|
||||||
|
|
||||||
|
|
@ -52,7 +52,7 @@
|
||||||
|
|
||||||
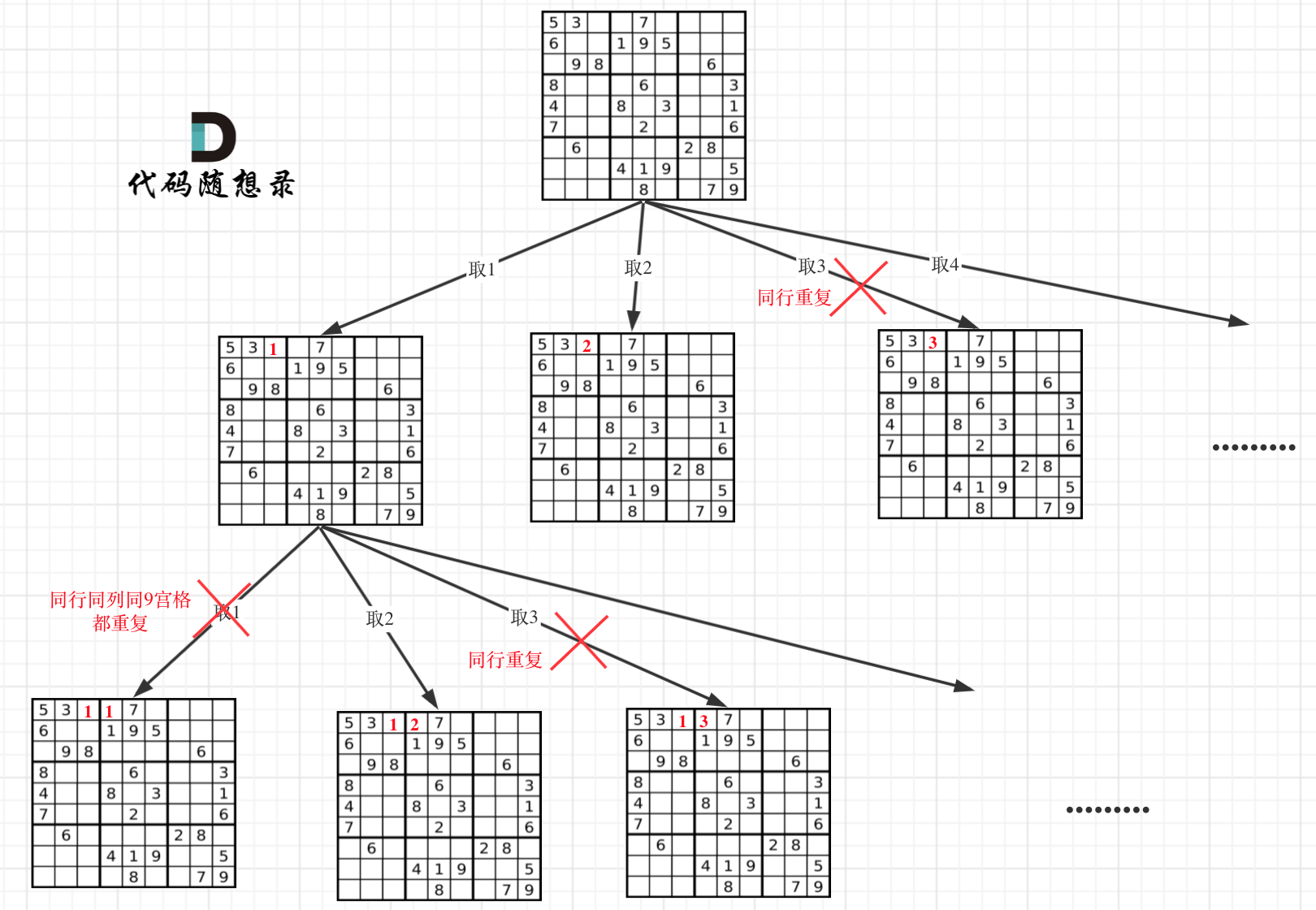
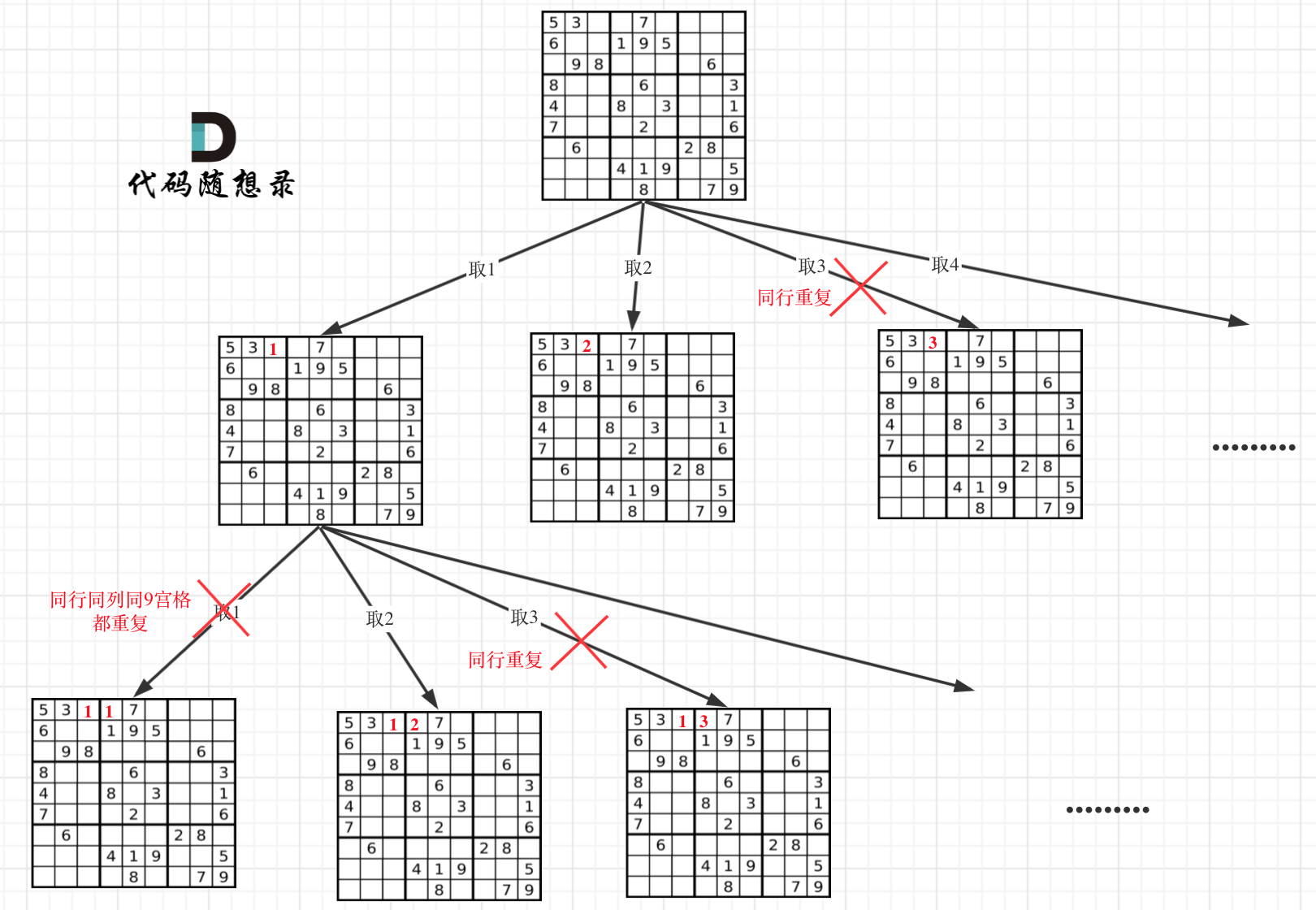
因为这个树形结构太大了,我抽取一部分,如图所示:
|
因为这个树形结构太大了,我抽取一部分,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 回溯三部曲
|
### 回溯三部曲
|
||||||
|
|
@ -83,7 +83,7 @@ bool backtracking(vector<vector<char>>& board)
|
||||||
|
|
||||||
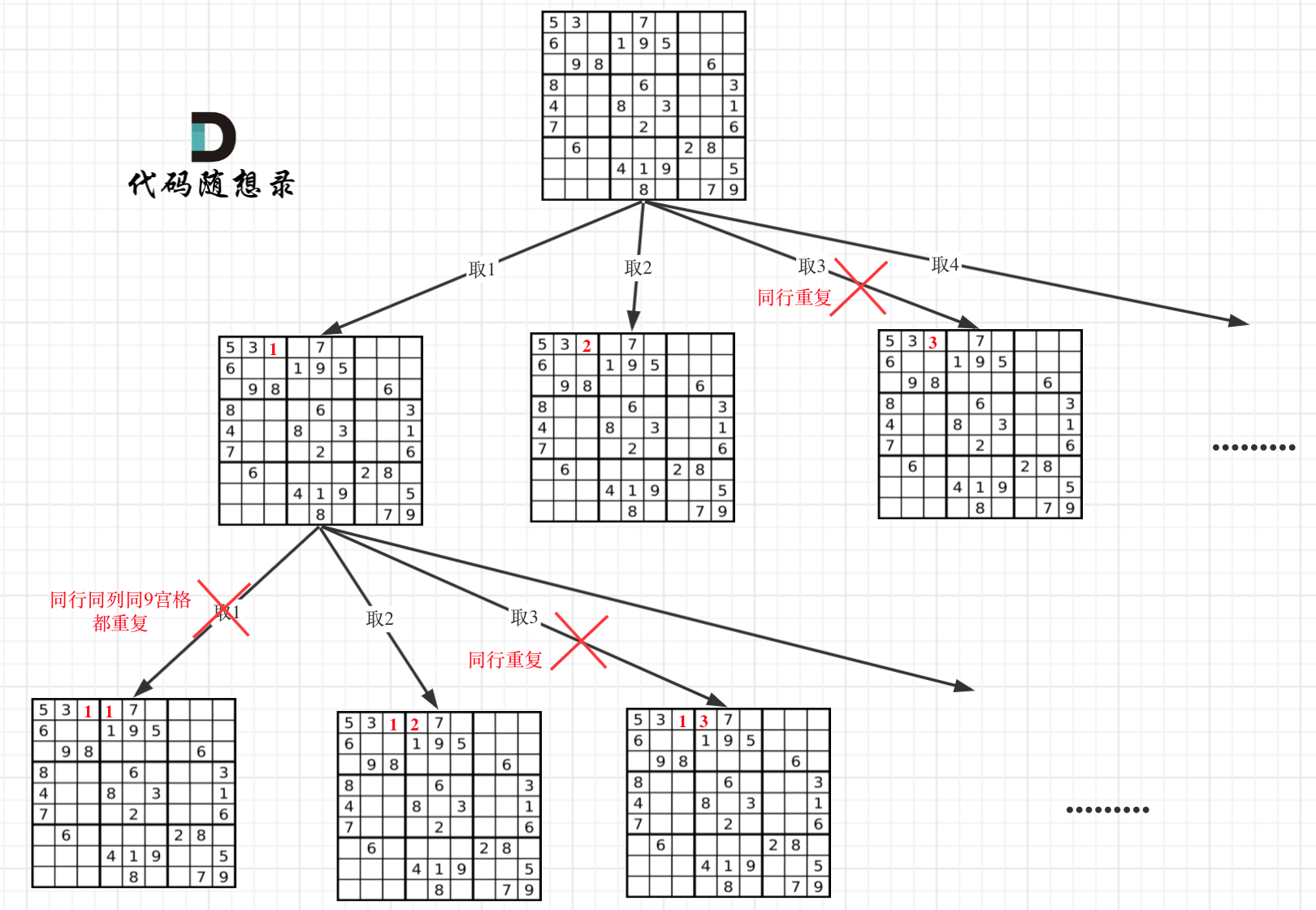
* 递归单层搜索逻辑
|
* 递归单层搜索逻辑
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
在树形图中可以看出我们需要的是一个二维的递归 (一行一列)
|
在树形图中可以看出我们需要的是一个二维的递归 (一行一列)
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -50,7 +50,7 @@ candidates 中的数字可以无限制重复被选取。
|
||||||
|
|
||||||
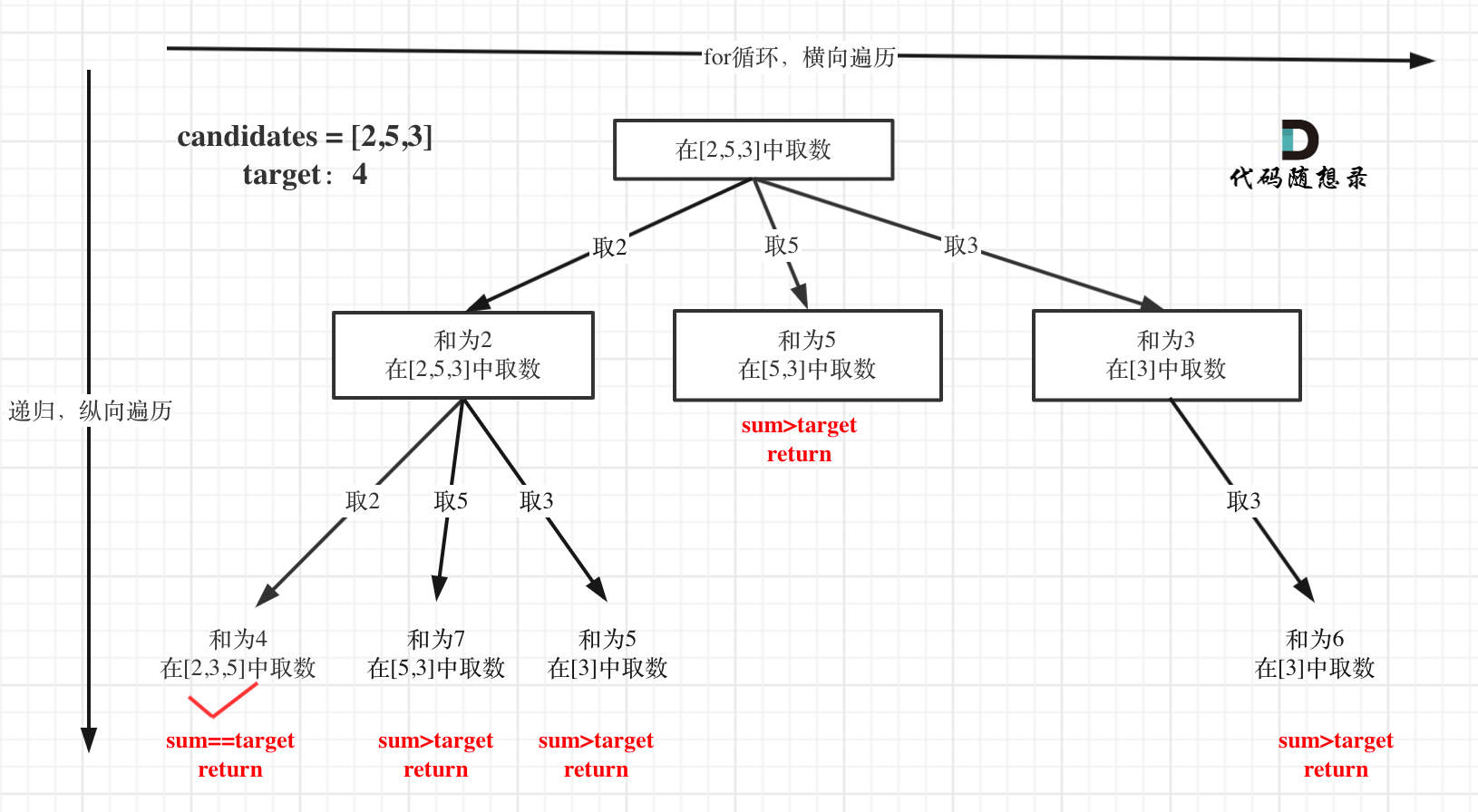
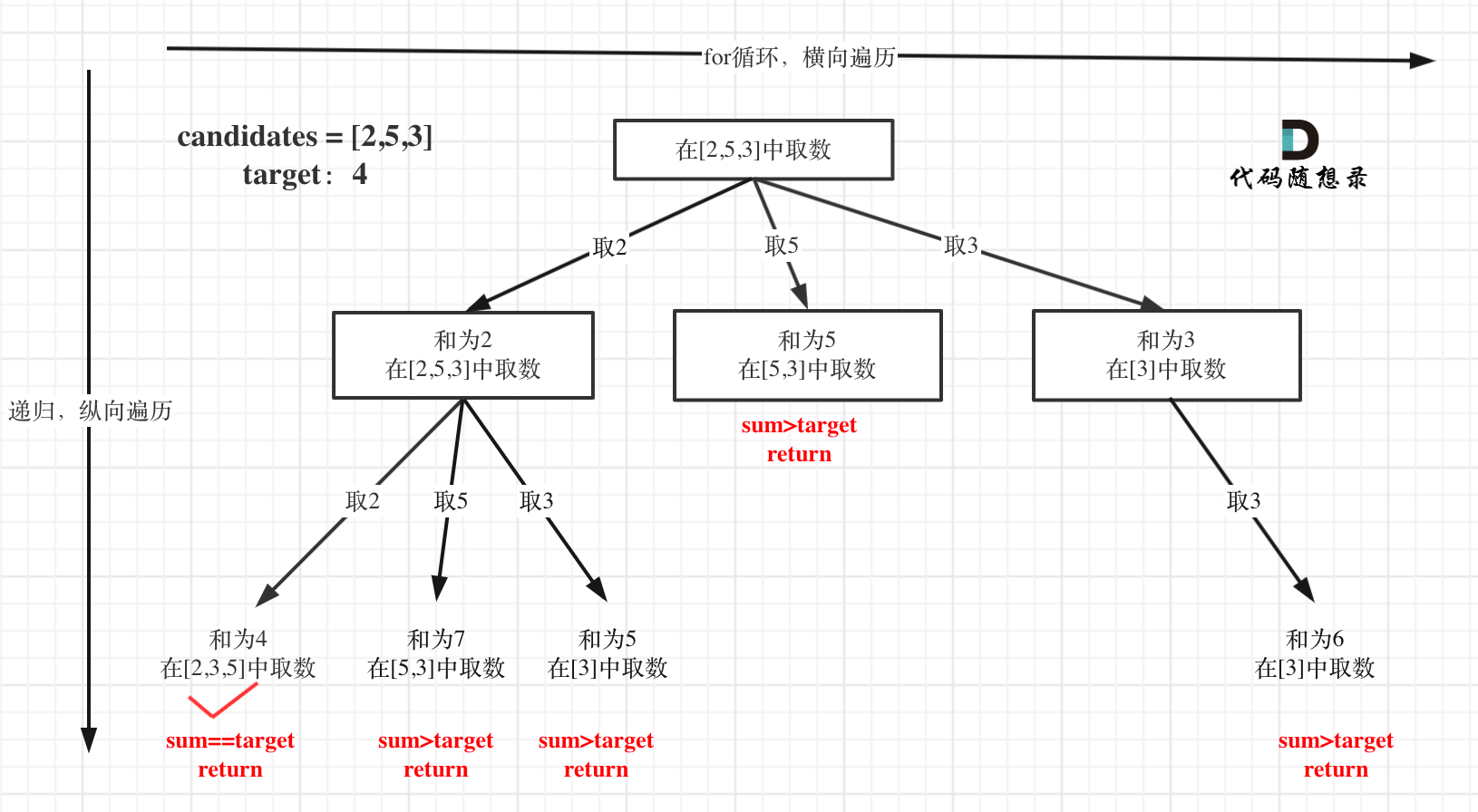
本题搜索的过程抽象成树形结构如下:
|
本题搜索的过程抽象成树形结构如下:
|
||||||
|
|
||||||
|
|
||||||
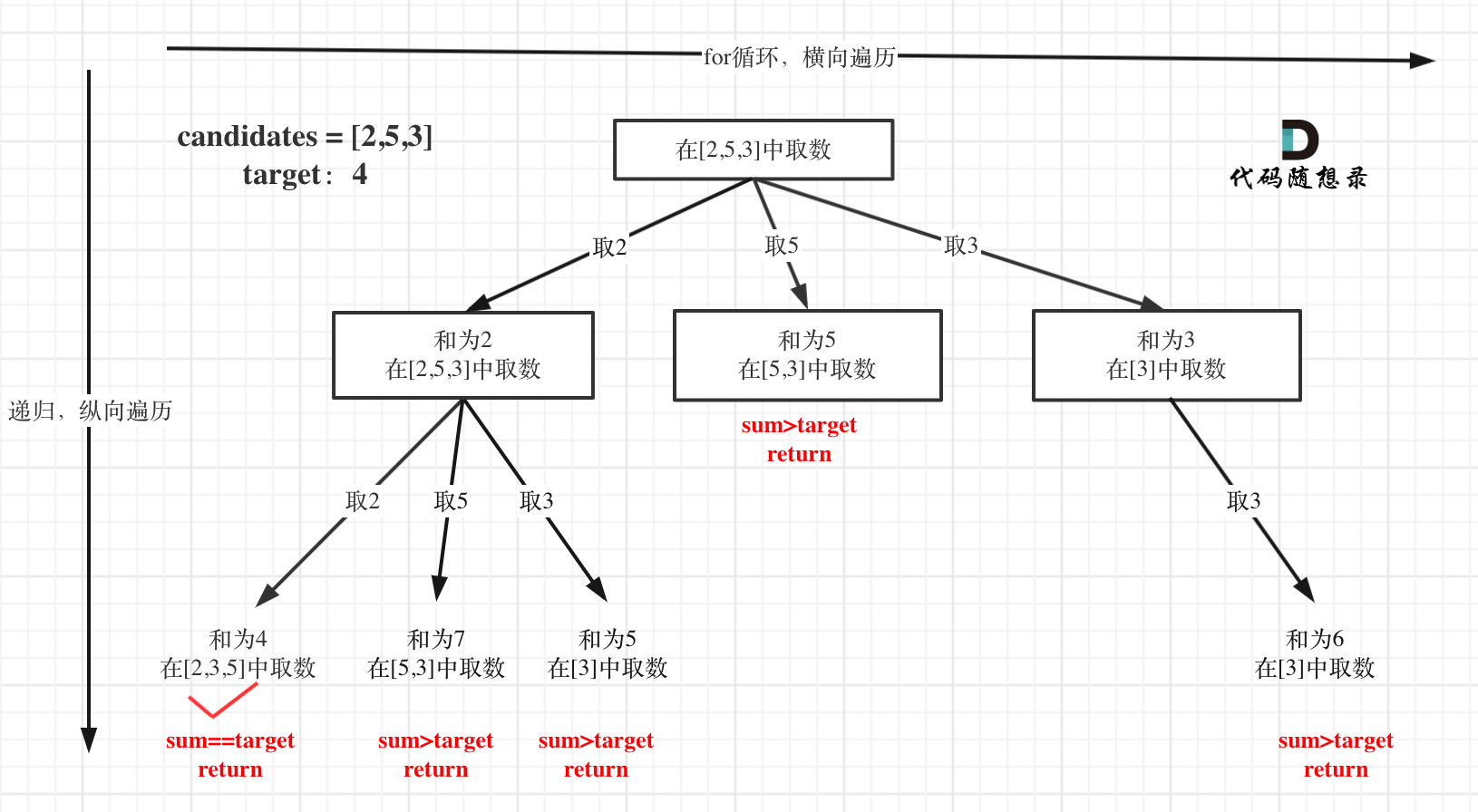
注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
|
注意图中叶子节点的返回条件,因为本题没有组合数量要求,仅仅是总和的限制,所以递归没有层数的限制,只要选取的元素总和超过target,就返回!
|
||||||
|
|
||||||
而在[77.组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html) 中都可以知道要递归K层,因为要取k个元素的组合。
|
而在[77.组合](https://programmercarl.com/0077.组合.html)和[216.组合总和III](https://programmercarl.com/0216.组合总和III.html) 中都可以知道要递归K层,因为要取k个元素的组合。
|
||||||
|
|
@ -85,7 +85,7 @@ void backtracking(vector<int>& candidates, int target, int sum, int startIndex)
|
||||||
|
|
||||||
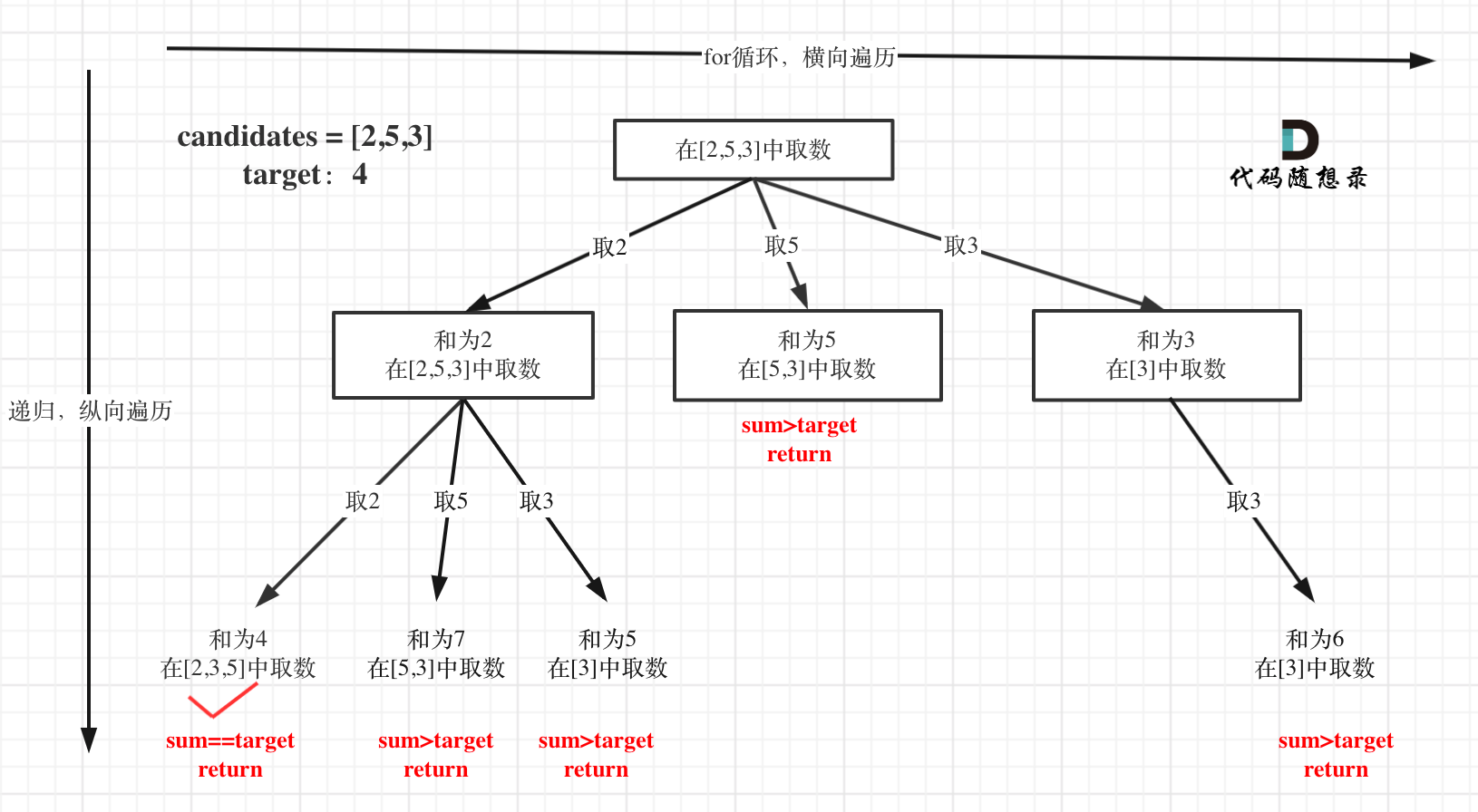
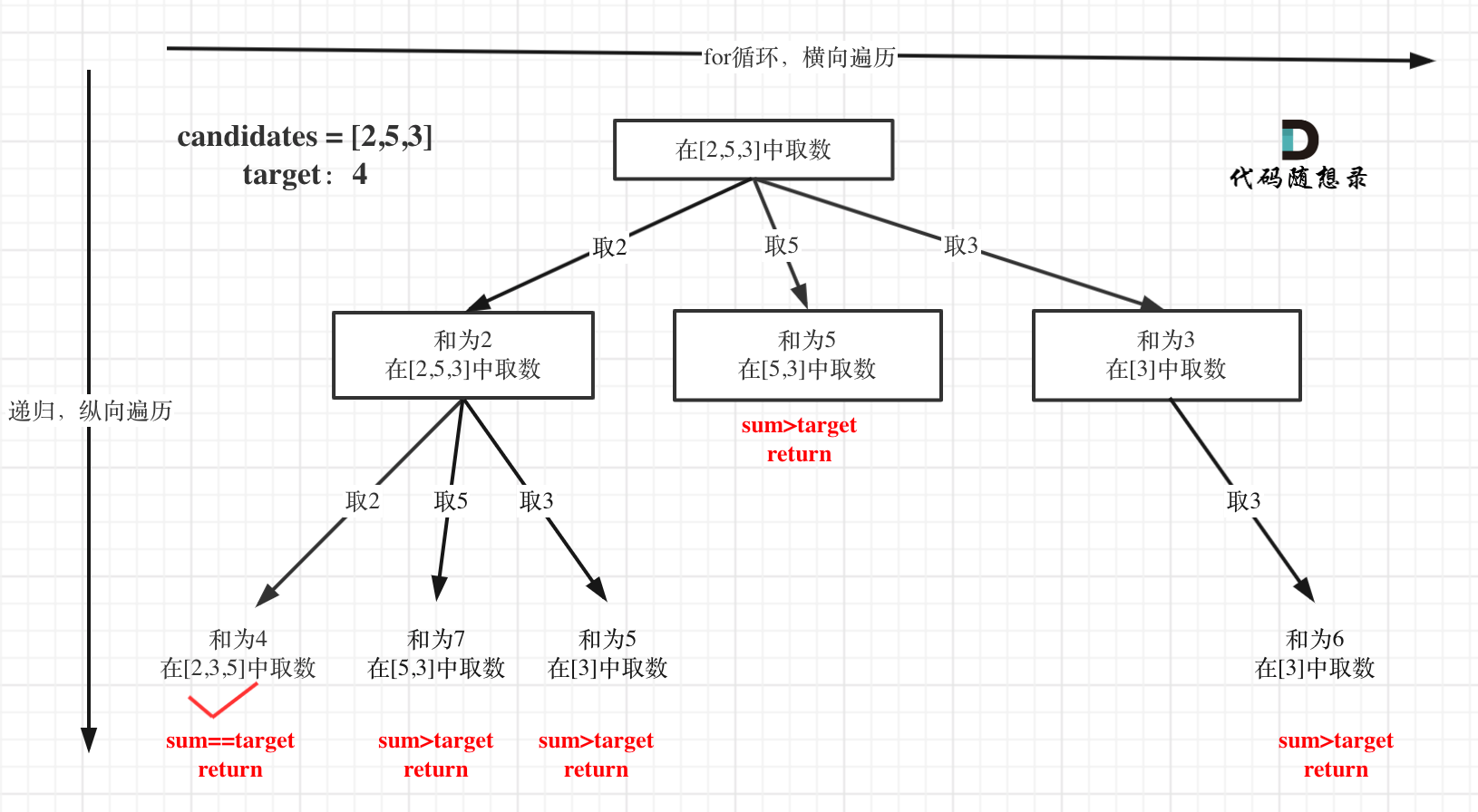
在如下树形结构中:
|
在如下树形结构中:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。
|
从叶子节点可以清晰看到,终止只有两种情况,sum大于target和sum等于target。
|
||||||
|
|
||||||
|
|
@ -158,7 +158,7 @@ public:
|
||||||
|
|
||||||
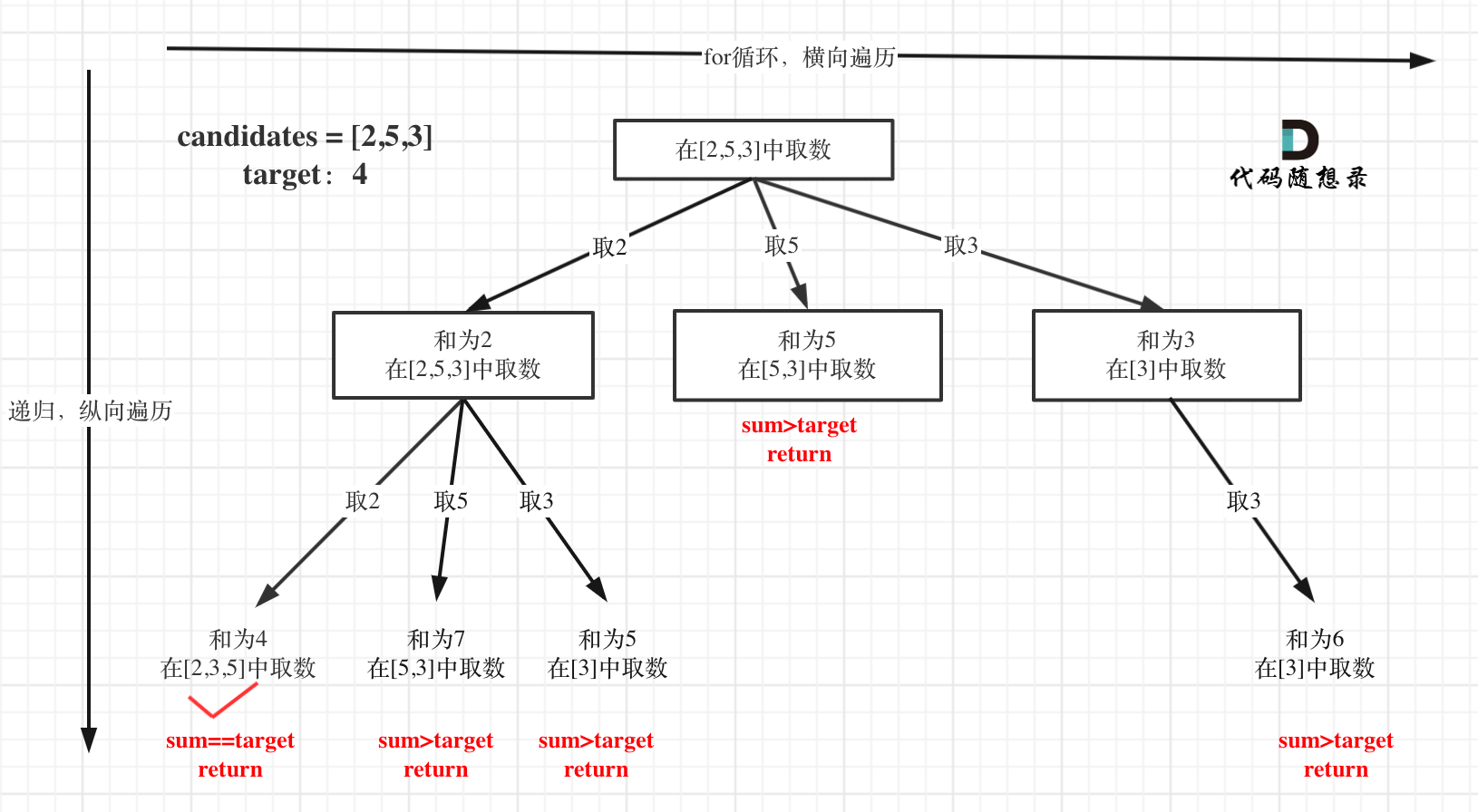
在这个树形结构中:
|
在这个树形结构中:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
|
以及上面的版本一的代码大家可以看到,对于sum已经大于target的情况,其实是依然进入了下一层递归,只是下一层递归结束判断的时候,会判断sum > target的话就返回。
|
||||||
|
|
||||||
|
|
@ -171,7 +171,7 @@ public:
|
||||||
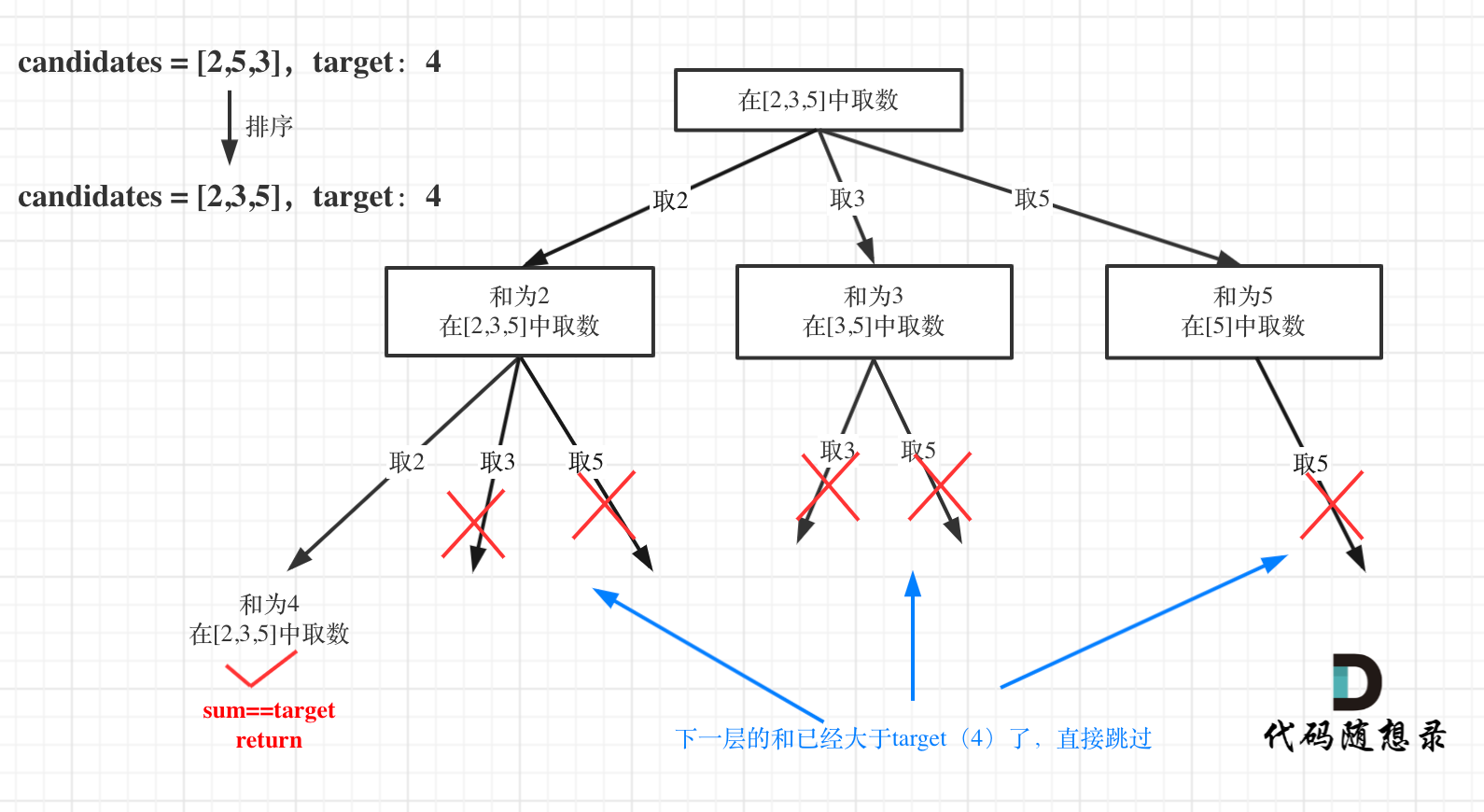
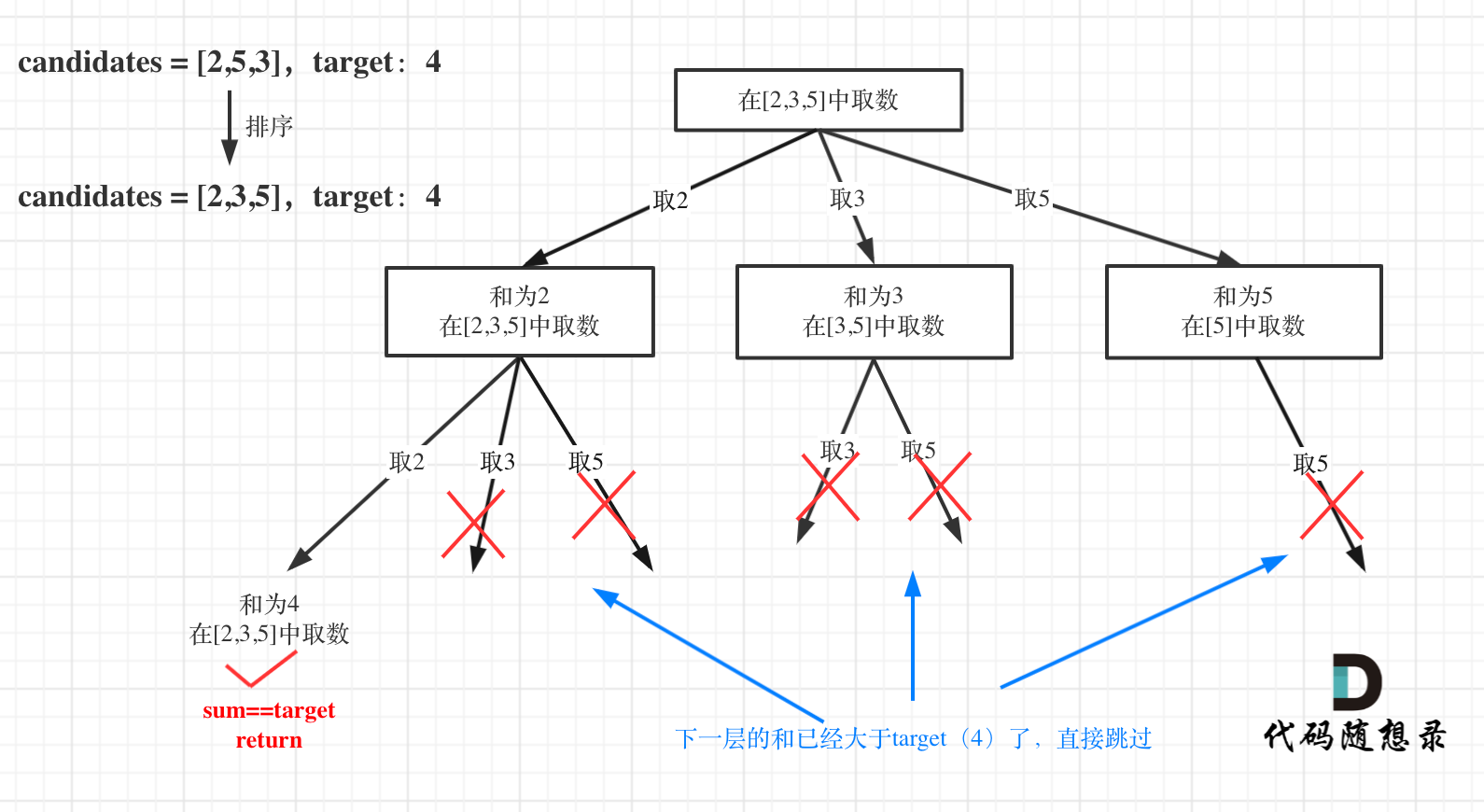
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
for循环剪枝代码如下:
|
for循环剪枝代码如下:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -76,7 +76,7 @@ candidates 中的每个数字在每个组合中只能使用一次。
|
||||||
|
|
||||||
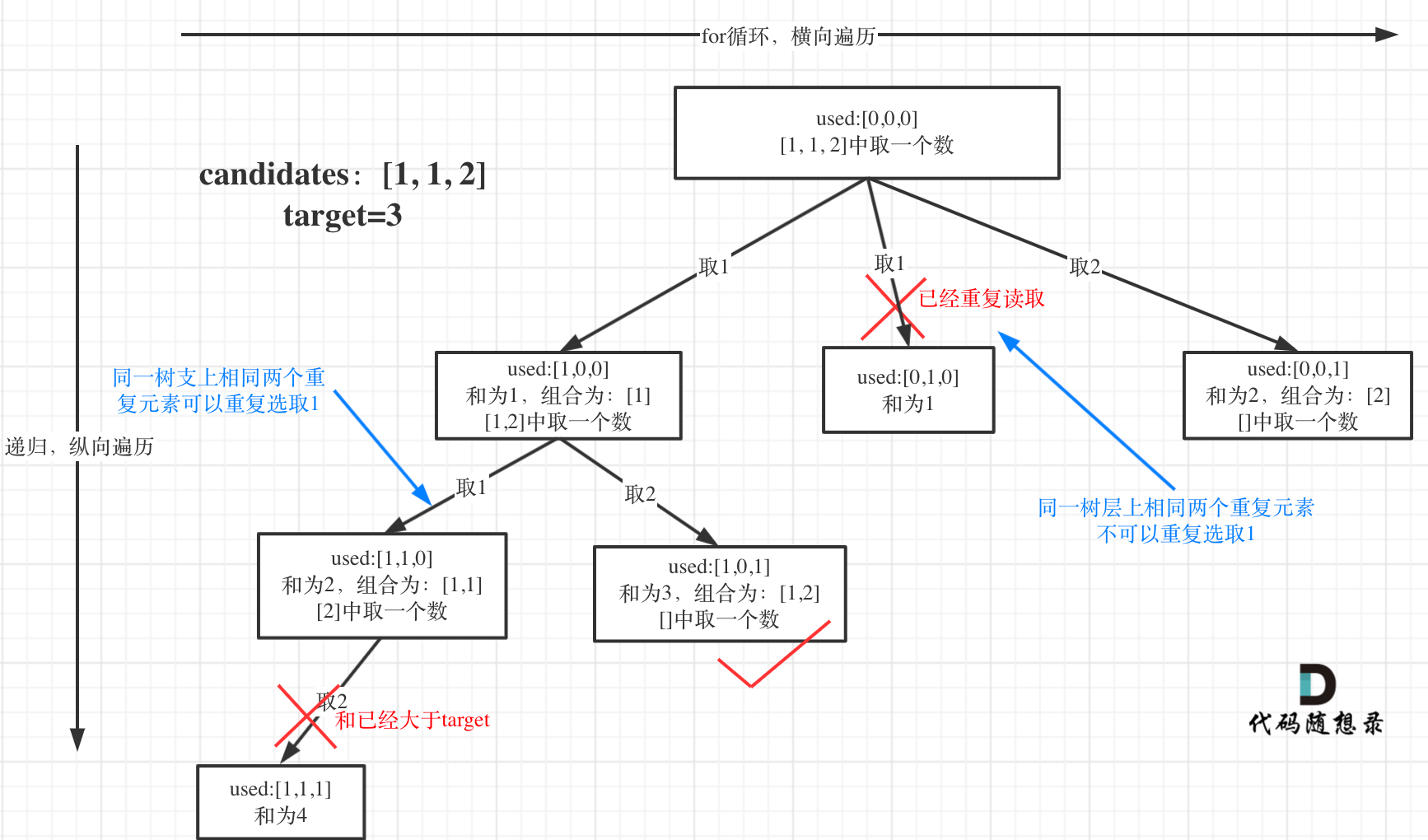
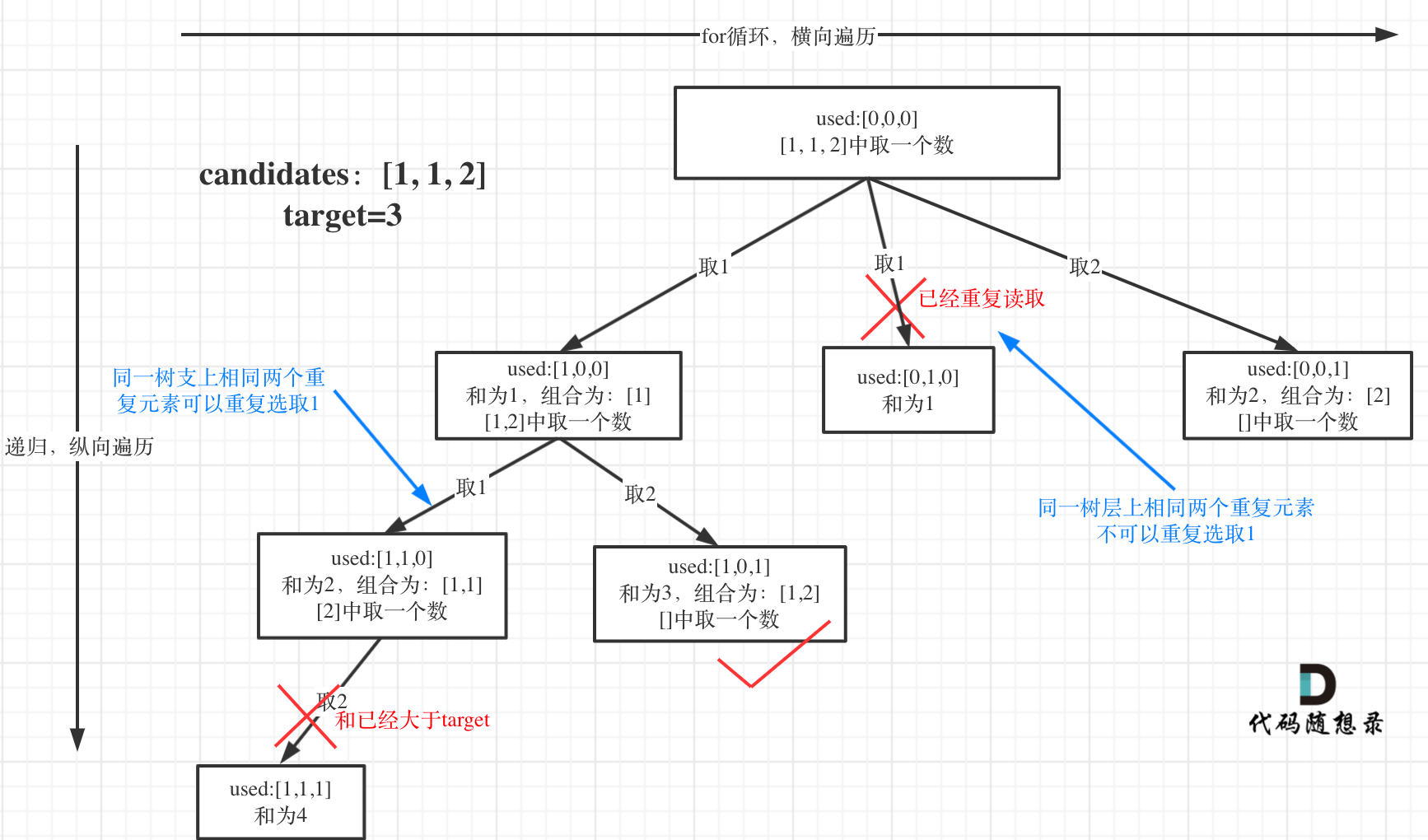
选择过程树形结构如图所示:
|
选择过程树形结构如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
可以看到图中,每个节点相对于 [39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)我多加了used数组,这个used数组下面会重点介绍。
|
可以看到图中,每个节点相对于 [39.组合总和](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)我多加了used数组,这个used数组下面会重点介绍。
|
||||||
|
|
||||||
|
|
@ -126,7 +126,7 @@ if (sum == target) {
|
||||||
|
|
||||||
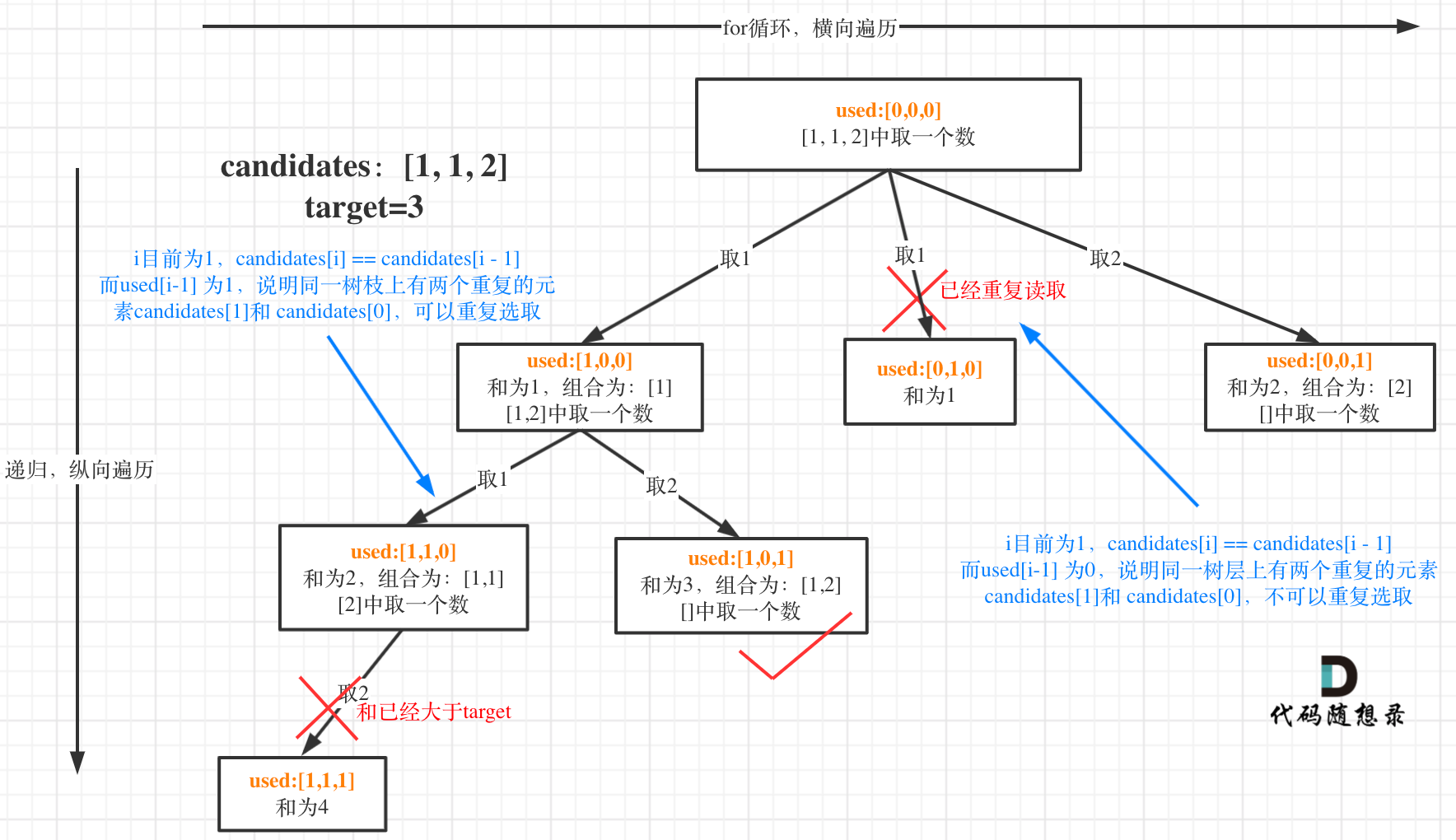
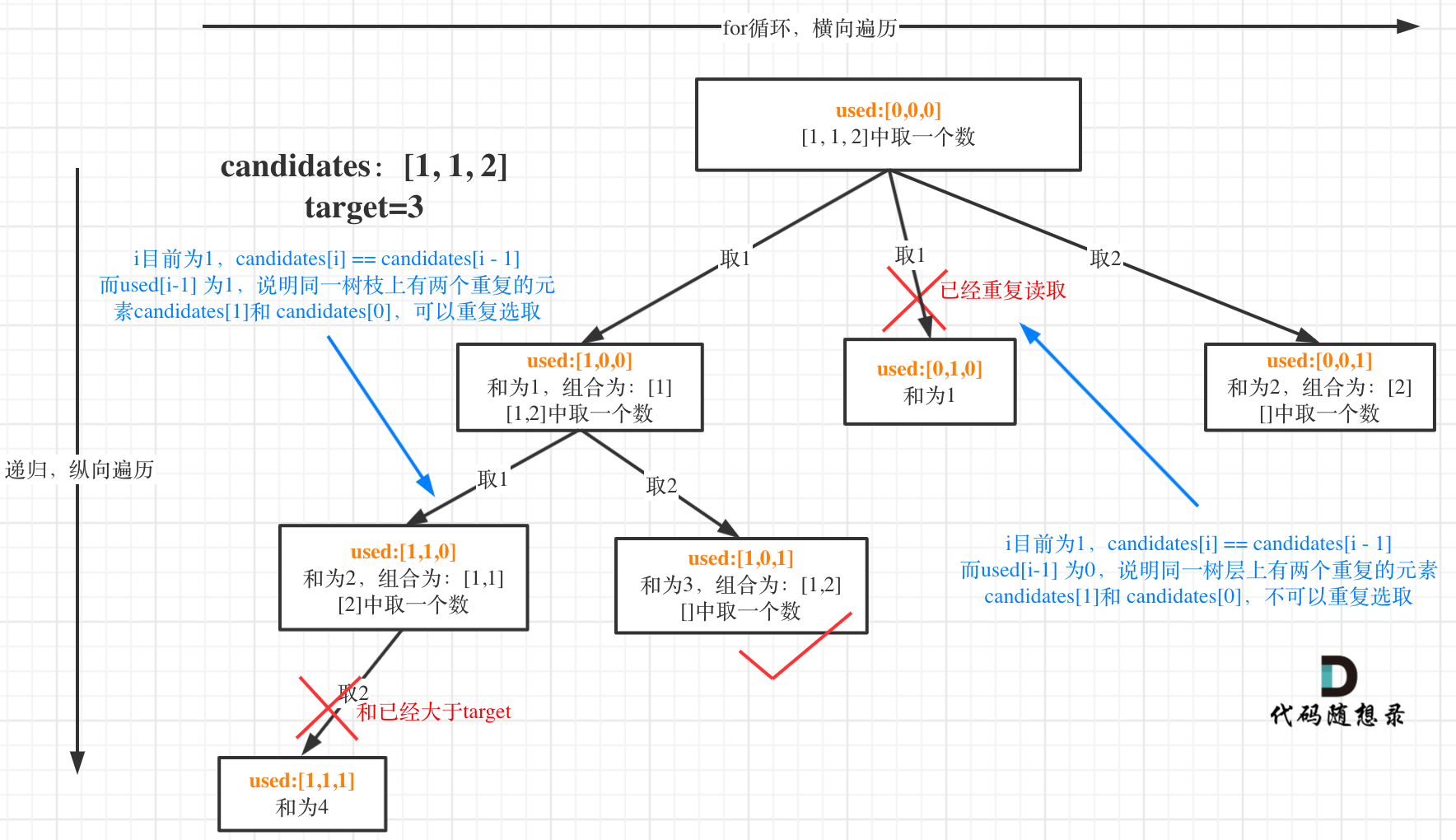
这块比较抽象,如图:
|
这块比较抽象,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
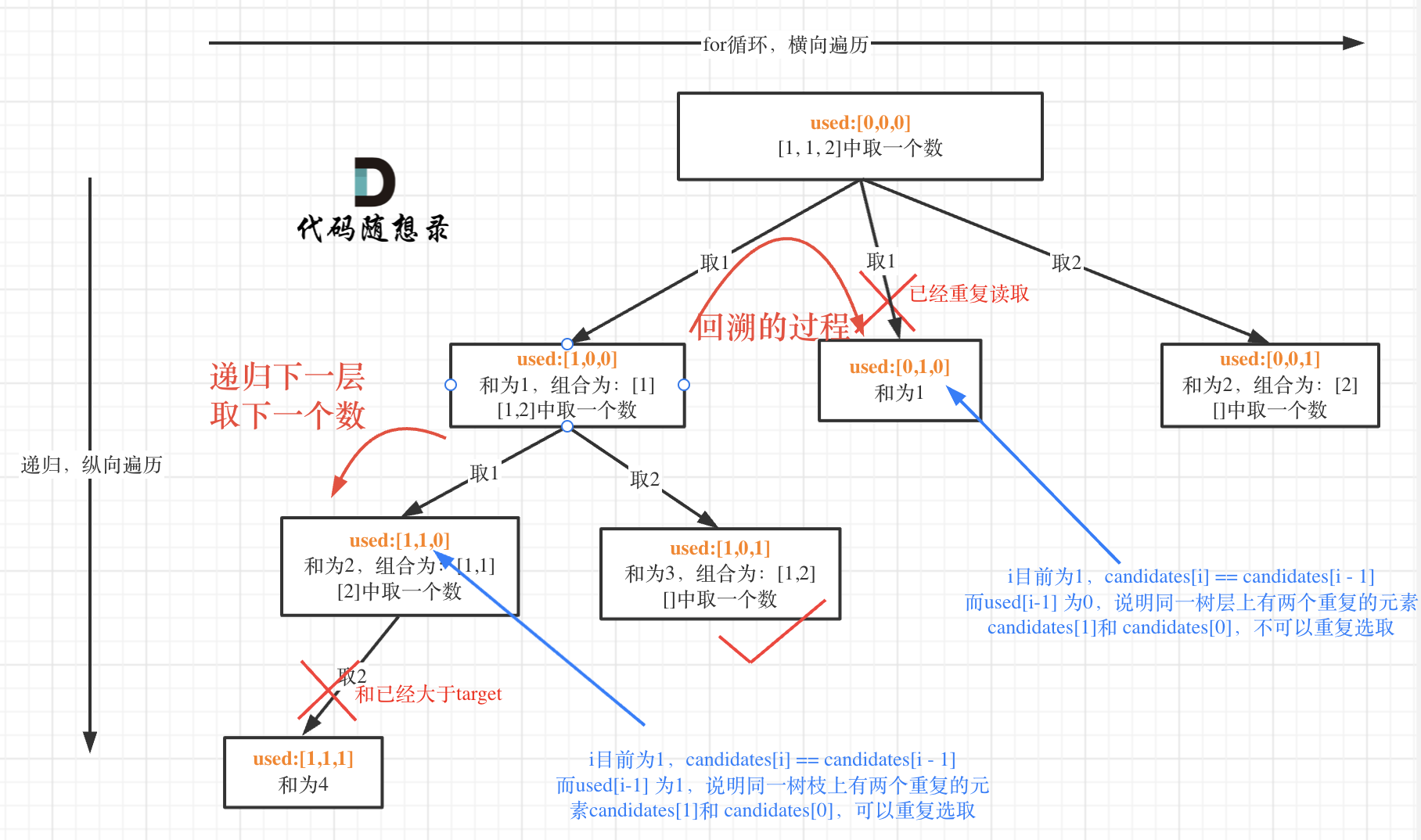
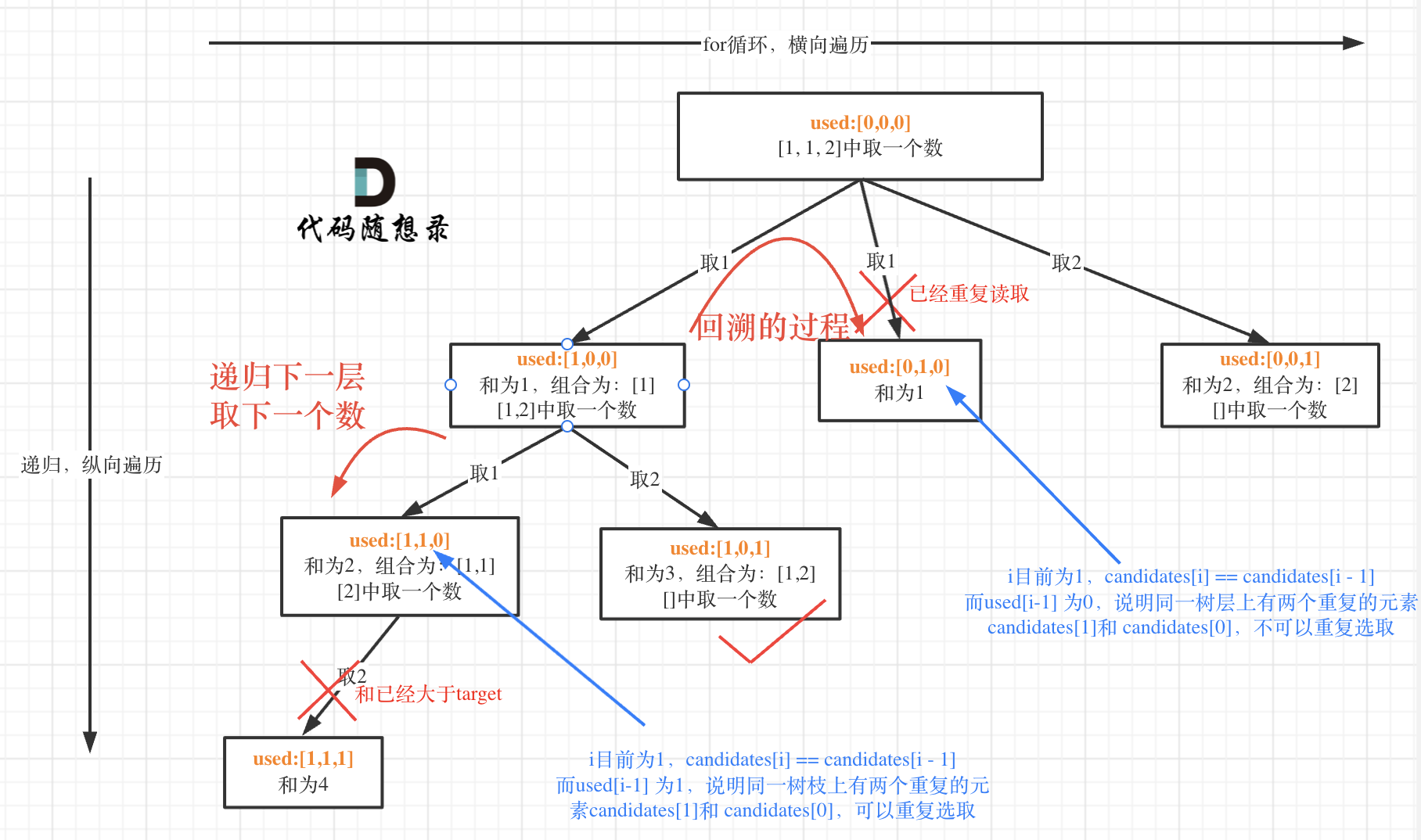
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
|
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
|
||||||
|
|
||||||
|
|
@ -137,7 +137,7 @@ if (sum == target) {
|
||||||
|
|
||||||
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
|
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!**
|
**这块去重的逻辑很抽象,网上搜的题解基本没有能讲清楚的,如果大家之前思考过这个问题或者刷过这道题目,看到这里一定会感觉通透了很多!**
|
||||||
|
|
|
||||||
|
|
@ -47,10 +47,10 @@
|
||||||
首先要明确,要按照行来计算,还是按照列来计算。
|
首先要明确,要按照行来计算,还是按照列来计算。
|
||||||
|
|
||||||
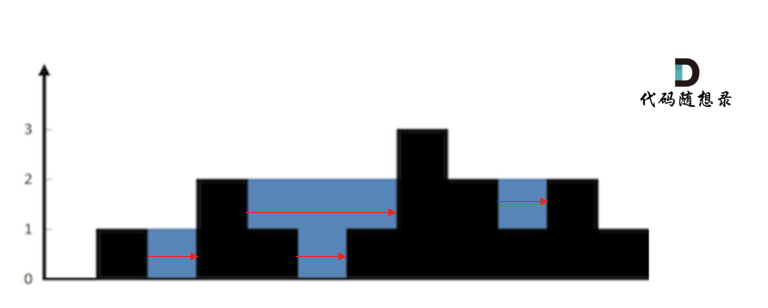
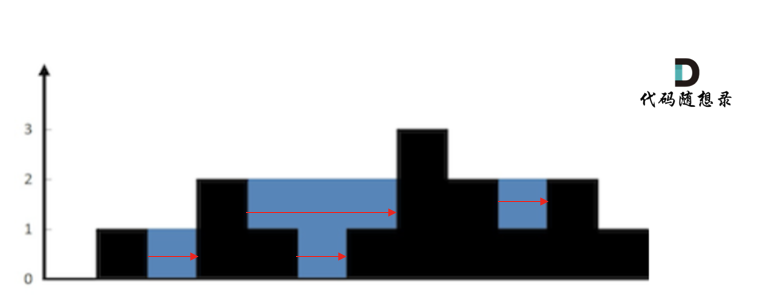
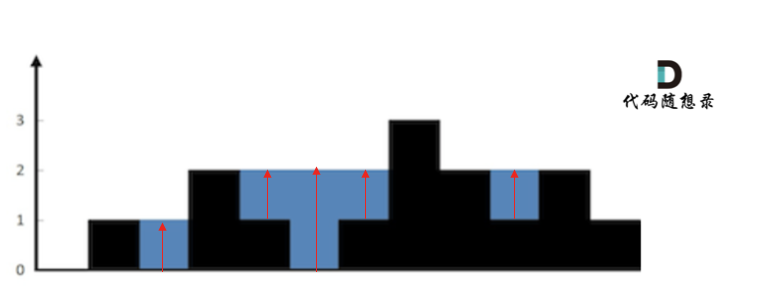
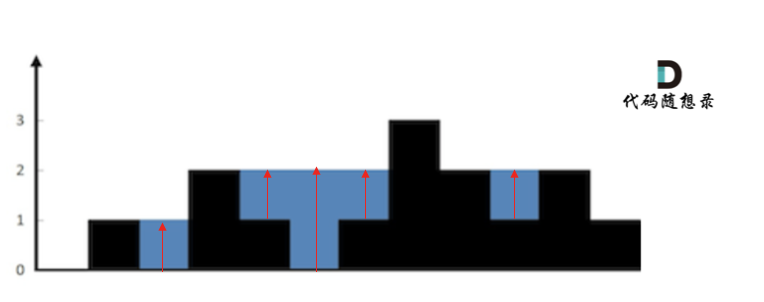
按照行来计算如图:
|
按照行来计算如图:
|
||||||
|
|
||||||
|
|
||||||
按照列来计算如图:
|
按照列来计算如图:
|
||||||
|
|
||||||
|
|
||||||
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
|
一些同学在实现的时候,很容易一会按照行来计算一会按照列来计算,这样就会越写越乱。
|
||||||
|
|
||||||
|
|
@ -62,7 +62,7 @@
|
||||||
|
|
||||||
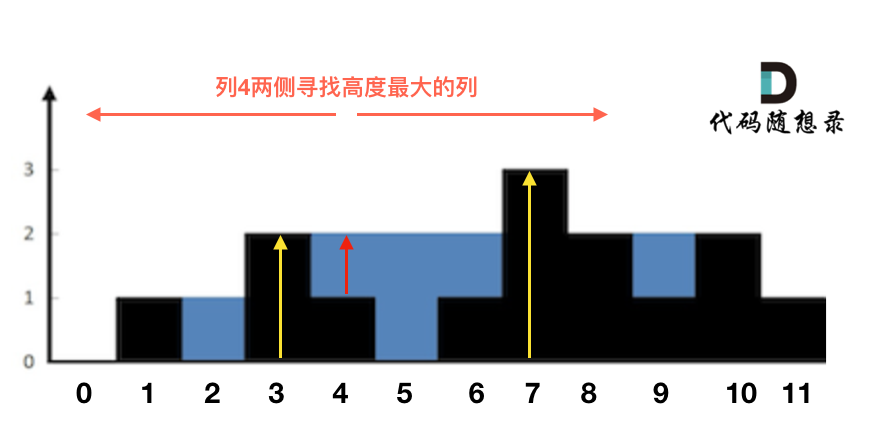
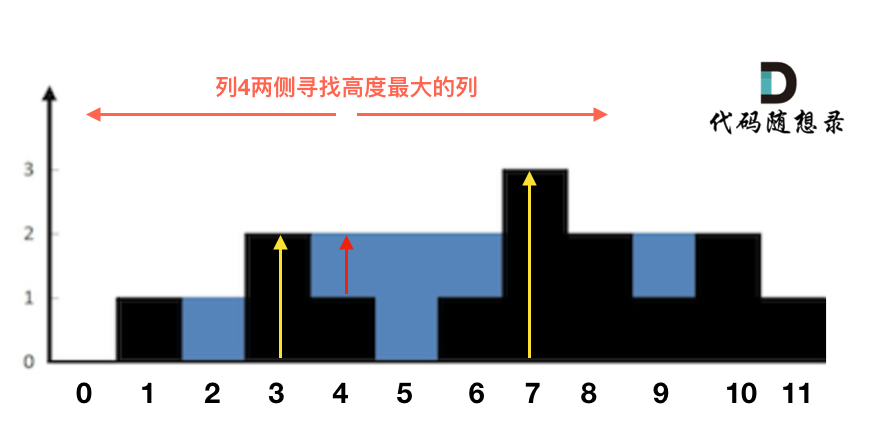
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
|
这句话可以有点绕,来举一个理解,例如求列4的雨水高度,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
|
列4 左侧最高的柱子是列3,高度为2(以下用lHeight表示)。
|
||||||
|
|
||||||
|
|
@ -201,7 +201,7 @@ public:
|
||||||
|
|
||||||
1. 首先单调栈是按照行方向来计算雨水,如图:
|
1. 首先单调栈是按照行方向来计算雨水,如图:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
知道这一点,后面的就可以理解了。
|
知道这一点,后面的就可以理解了。
|
||||||
|
|
||||||
|
|
@ -215,7 +215,7 @@ public:
|
||||||
|
|
||||||
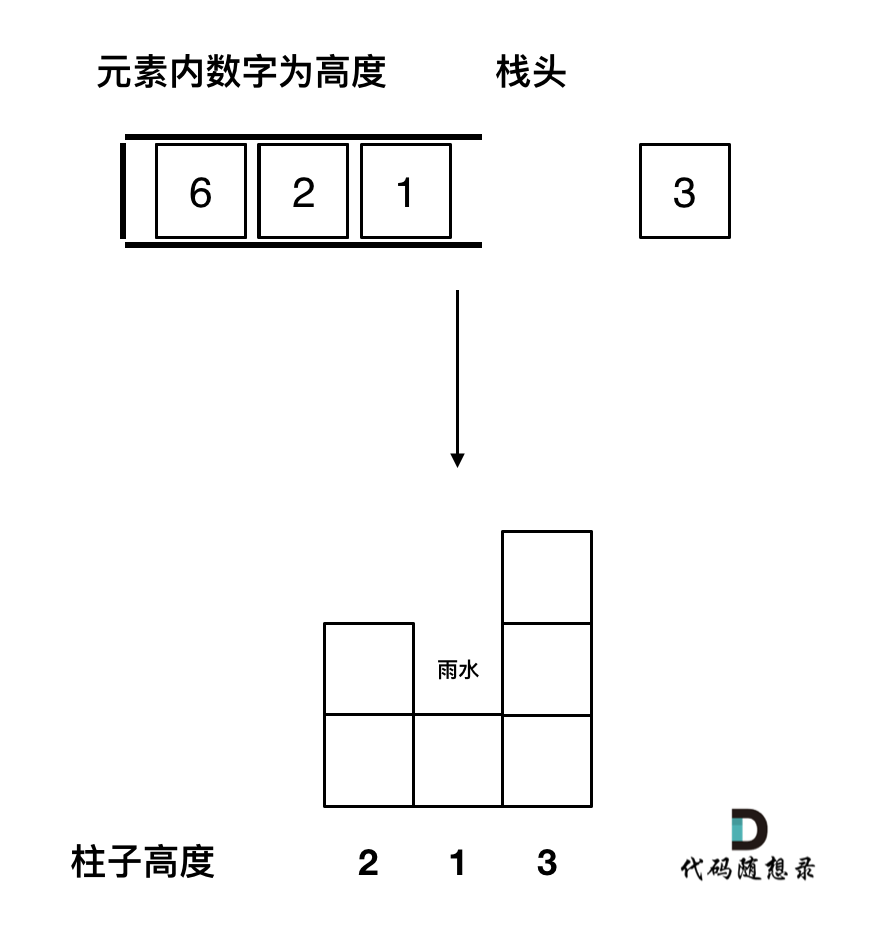
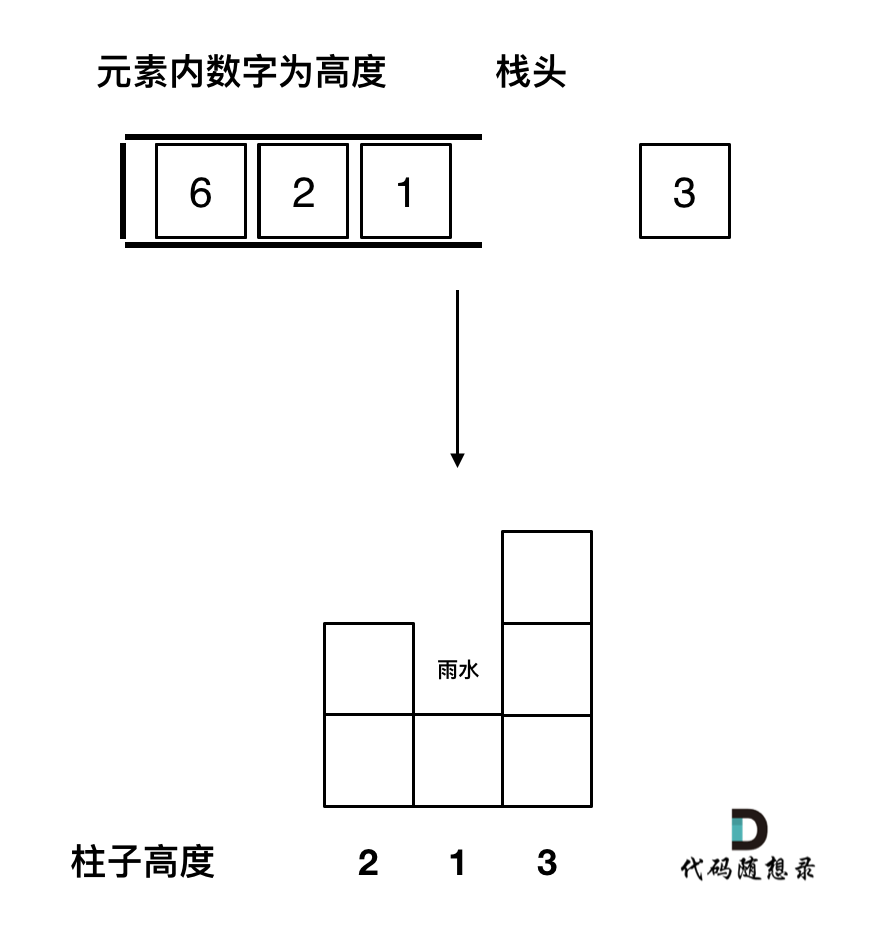
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
关于单调栈的顺序给大家一个总结: [739. 每日温度](https://programmercarl.com/0739.每日温度.html) 中求一个元素右边第一个更大元素,单调栈就是递增的,[84.柱状图中最大的矩形](https://programmercarl.com/0084.柱状图中最大的矩形.html)求一个元素右边第一个更小元素,单调栈就是递减的。
|
关于单调栈的顺序给大家一个总结: [739. 每日温度](https://programmercarl.com/0739.每日温度.html) 中求一个元素右边第一个更大元素,单调栈就是递增的,[84.柱状图中最大的矩形](https://programmercarl.com/0084.柱状图中最大的矩形.html)求一个元素右边第一个更小元素,单调栈就是递减的。
|
||||||
|
|
||||||
|
|
@ -229,7 +229,7 @@ public:
|
||||||
|
|
||||||
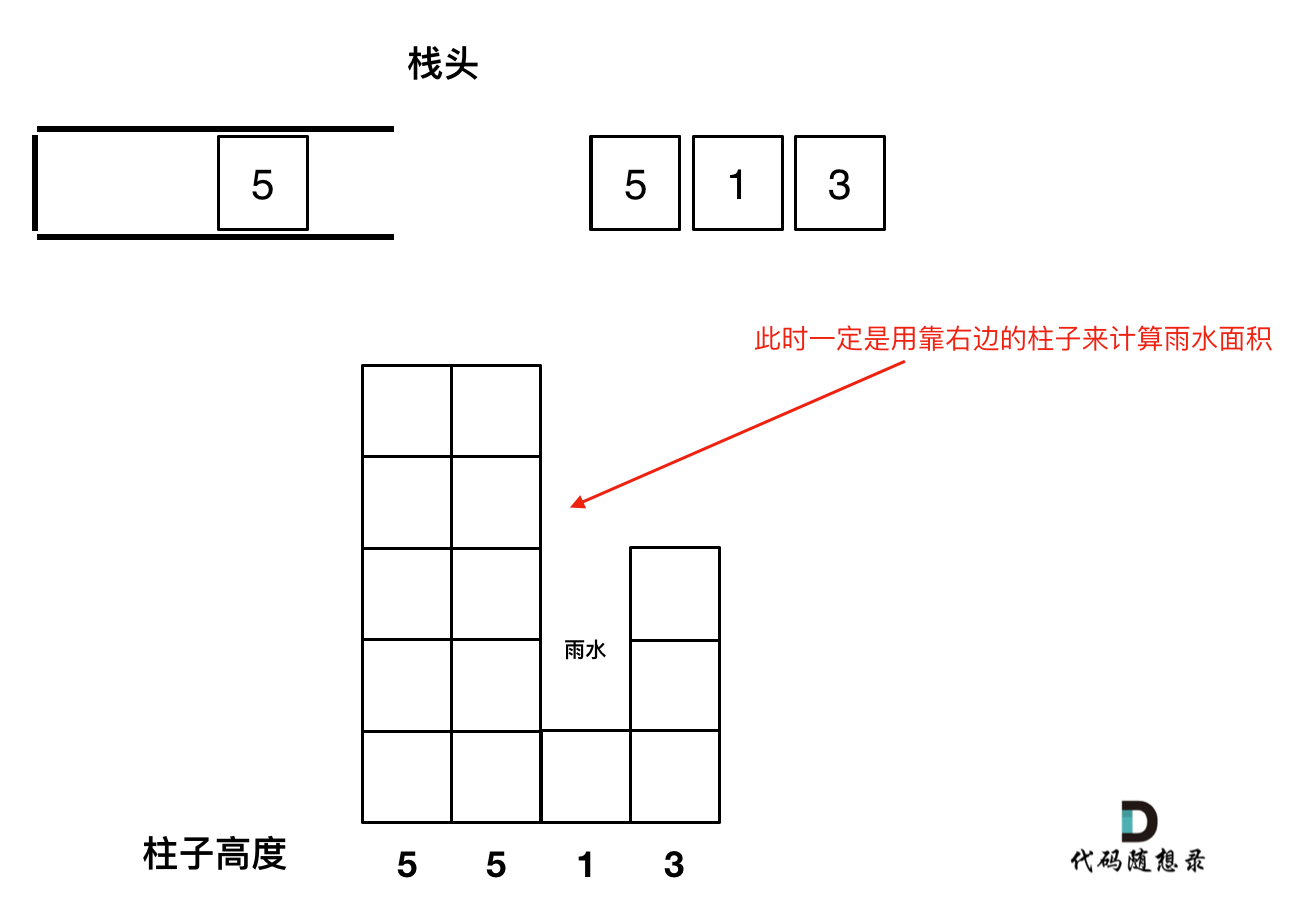
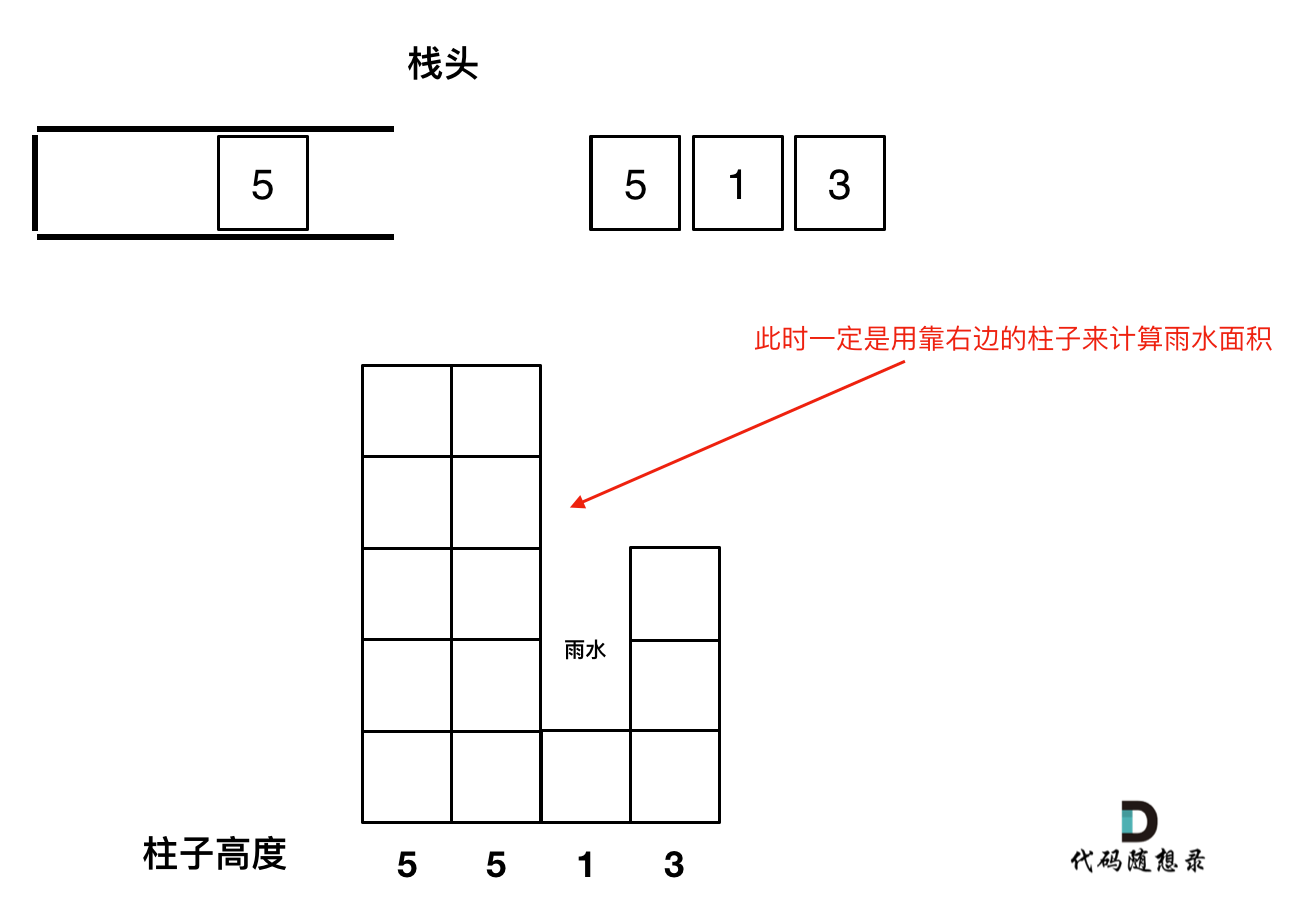
如图所示:
|
如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
4. 栈里要保存什么数值
|
4. 栈里要保存什么数值
|
||||||
|
|
||||||
|
|
@ -284,7 +284,7 @@ if (height[i] == height[st.top()]) { // 例如 5 5 1 7 这种情况
|
||||||
|
|
||||||
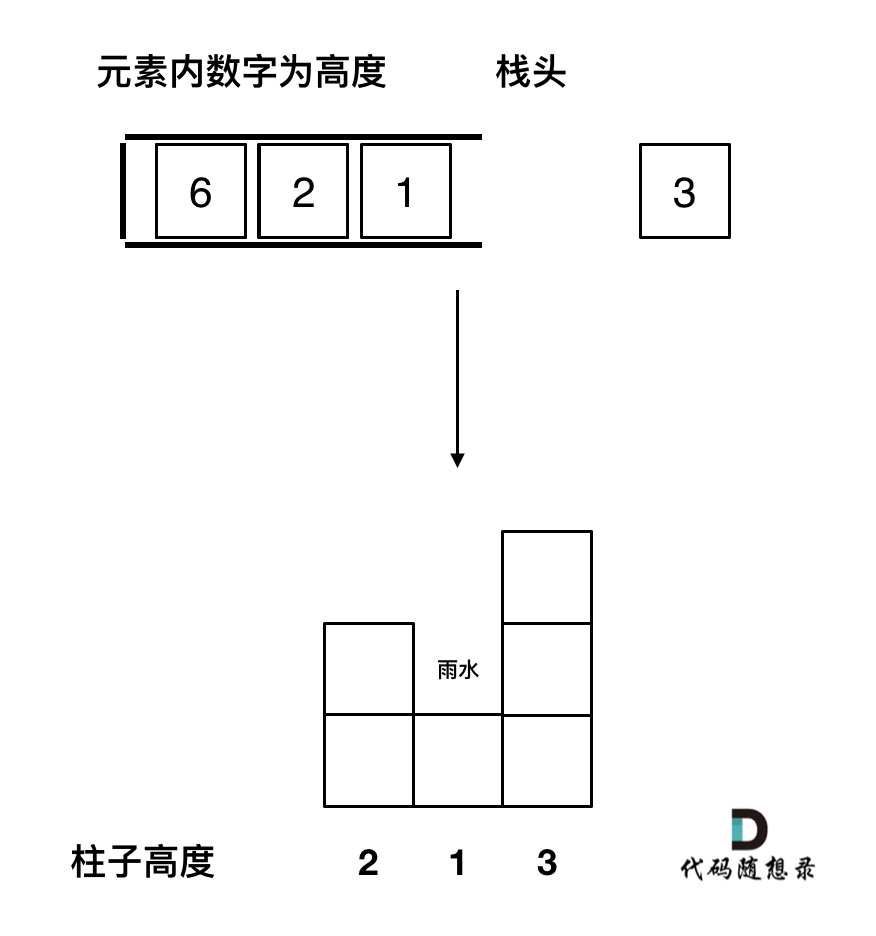
如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
|
如果当前遍历的元素(柱子)高度大于栈顶元素的高度,此时就出现凹槽了,如图所示:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
|
取栈顶元素,将栈顶元素弹出,这个就是凹槽的底部,也就是中间位置,下标记为mid,对应的高度为height[mid](就是图中的高度1)。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -47,7 +47,7 @@
|
||||||
|
|
||||||
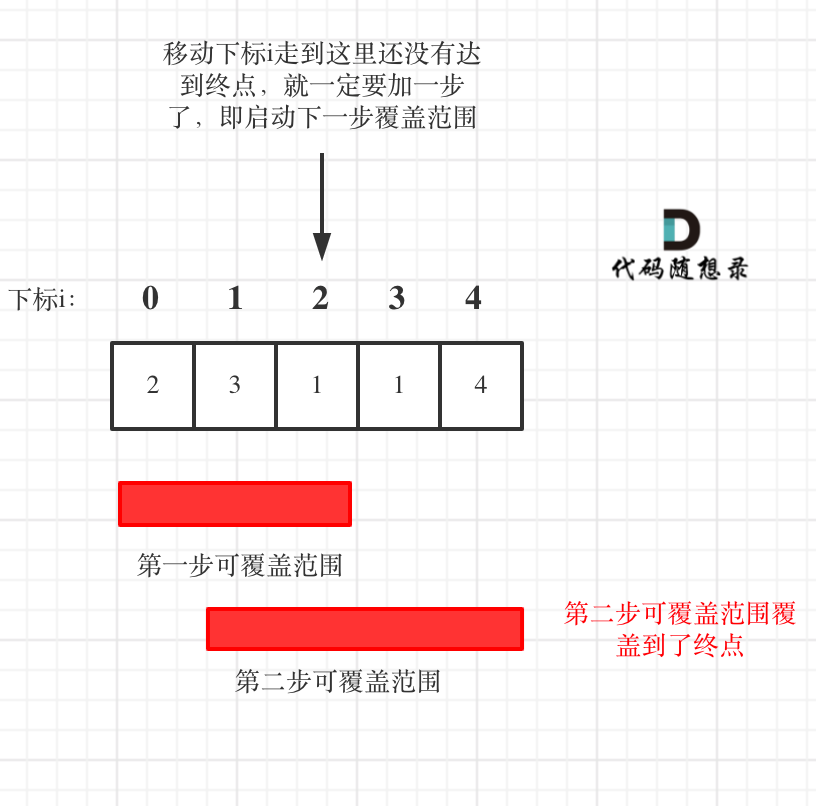
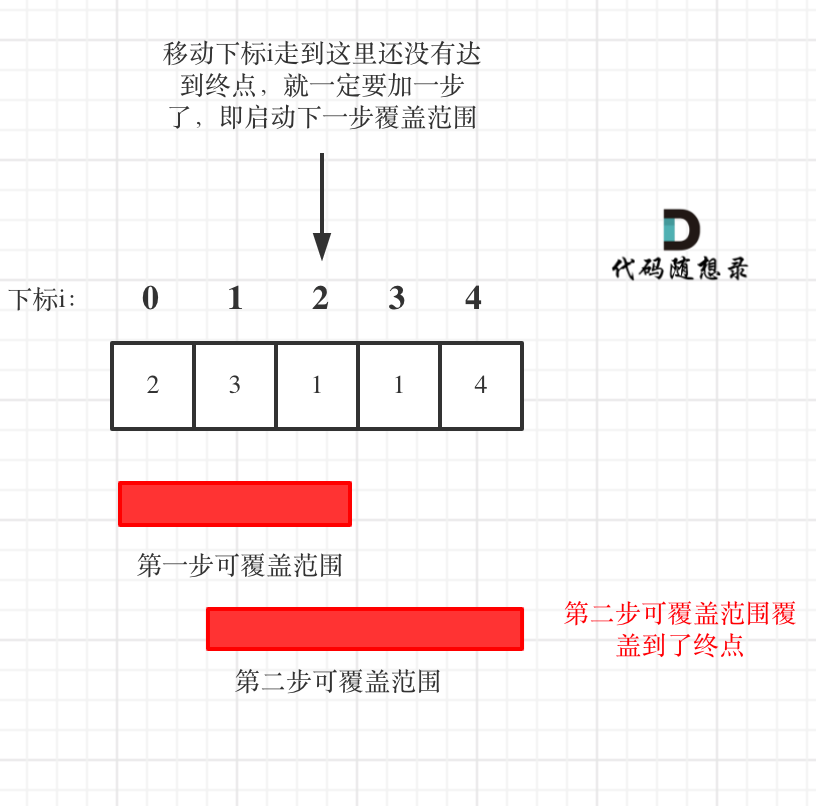
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
|
**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
|
||||||
|
|
||||||
|
|
@ -99,11 +99,11 @@ public:
|
||||||
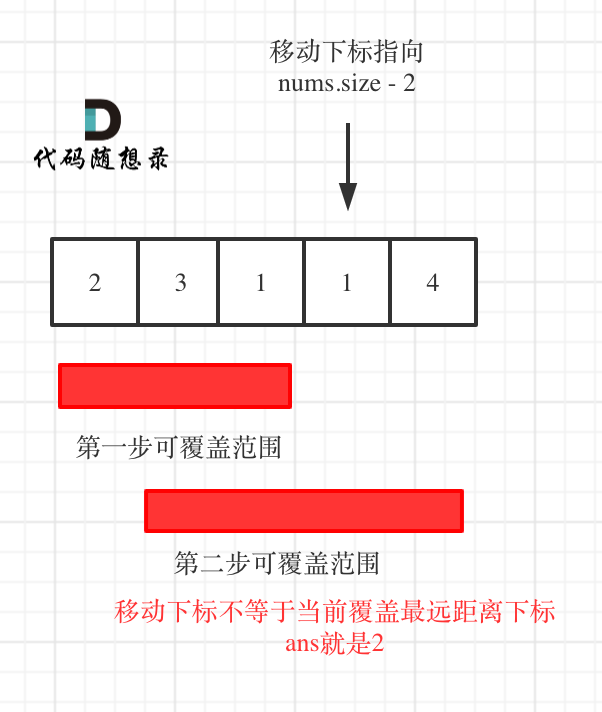
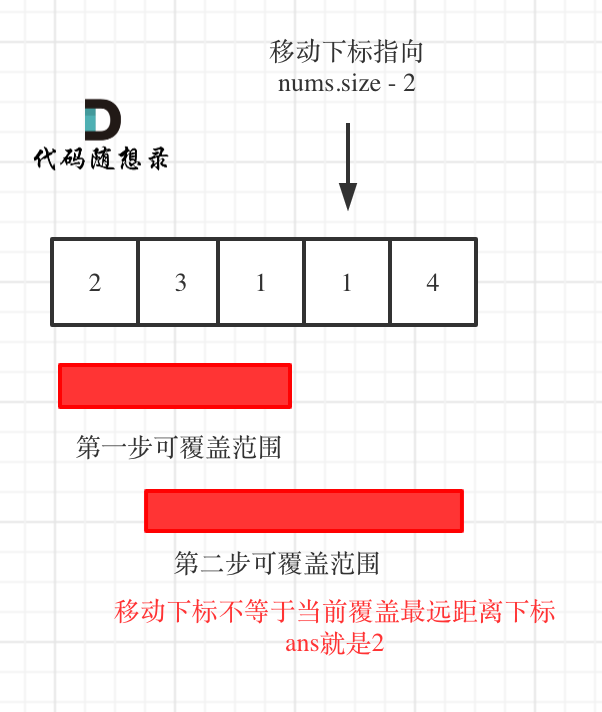
因为当移动下标指向 nums.size - 2 时:
|
因为当移动下标指向 nums.size - 2 时:
|
||||||
|
|
||||||
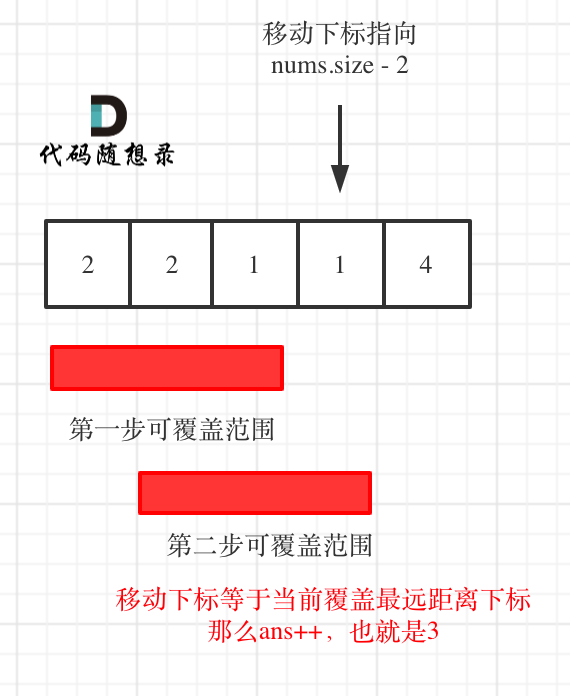
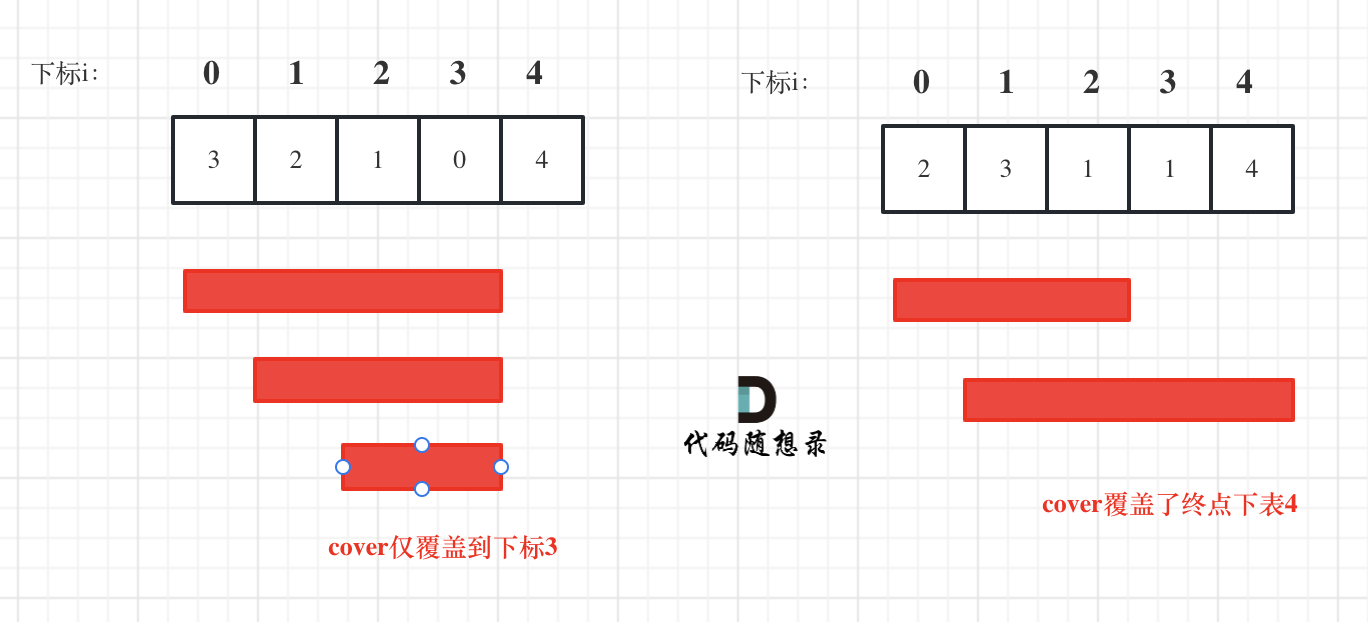
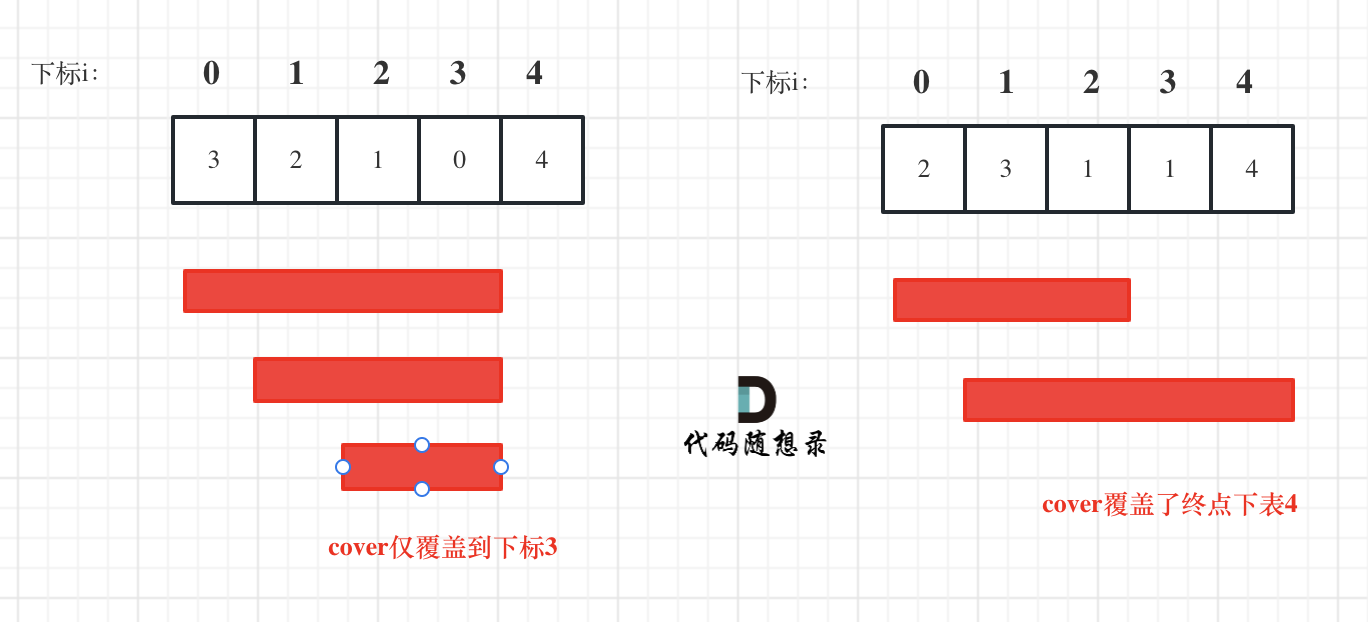
- 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即 ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
- 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即 ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
||||||
|

|
||||||
|
|
||||||
- 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
- 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -41,7 +41,7 @@
|
||||||
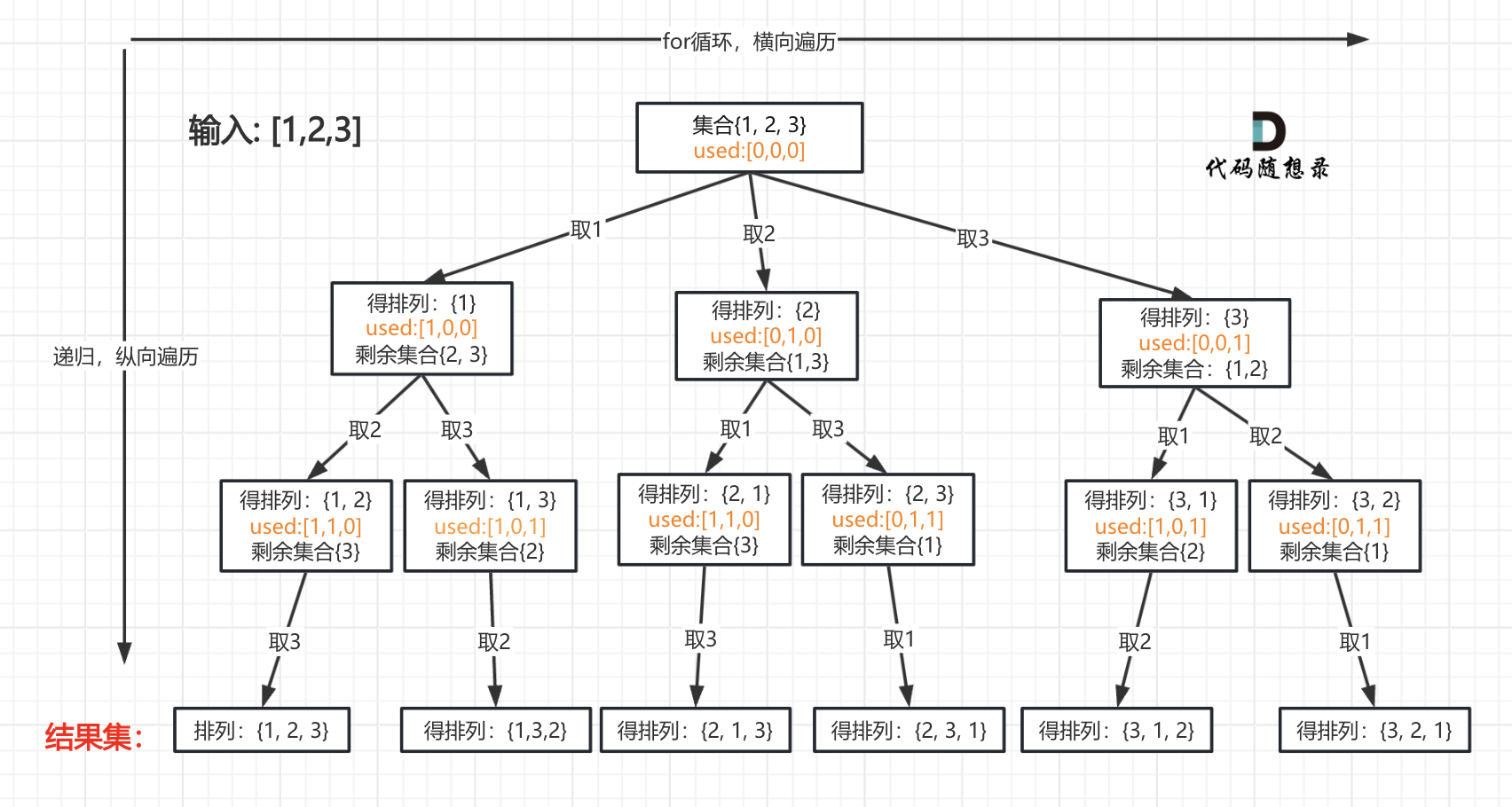
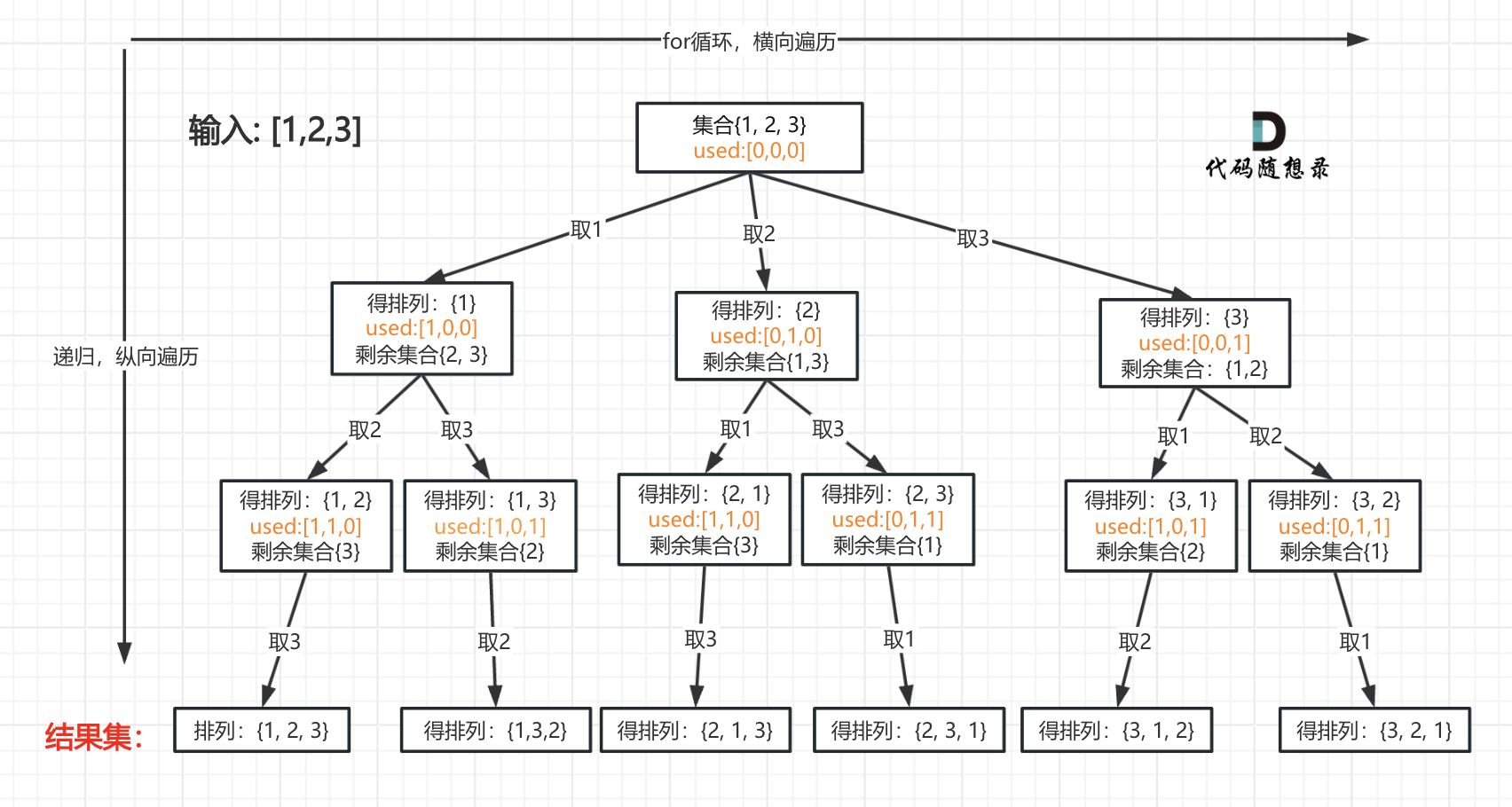
我以[1,2,3]为例,抽象成树形结构如下:
|
我以[1,2,3]为例,抽象成树形结构如下:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 回溯三部曲
|
### 回溯三部曲
|
||||||
|
|
||||||
|
|
@ -53,7 +53,7 @@
|
||||||
|
|
||||||
但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
|
但排列问题需要一个used数组,标记已经选择的元素,如图橘黄色部分所示:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
|
|
@ -65,7 +65,7 @@ void backtracking (vector<int>& nums, vector<bool>& used)
|
||||||
|
|
||||||
* 递归终止条件
|
* 递归终止条件
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
可以看出叶子节点,就是收割结果的地方。
|
可以看出叶子节点,就是收割结果的地方。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -48,7 +48,7 @@
|
||||||
|
|
||||||
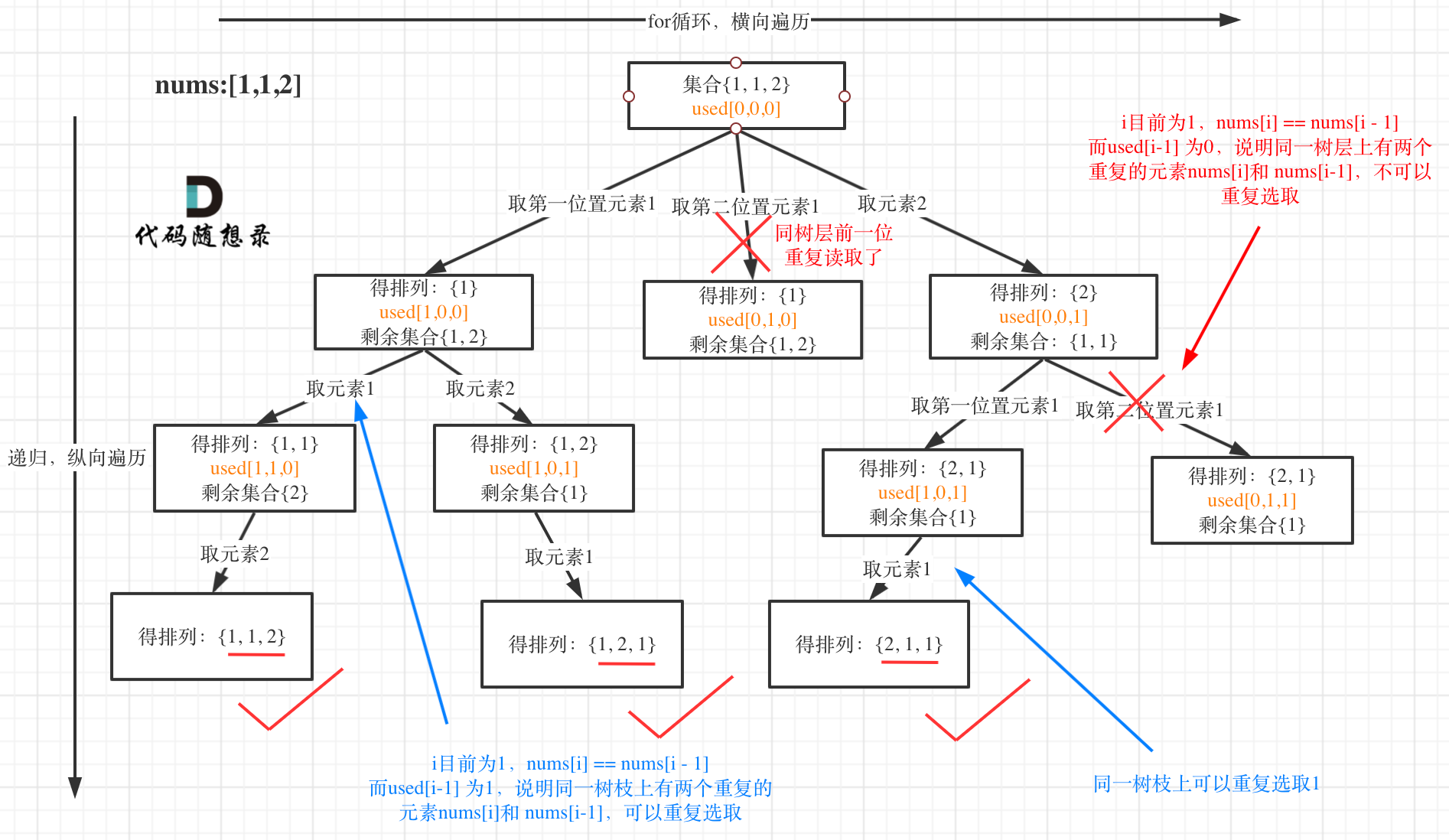
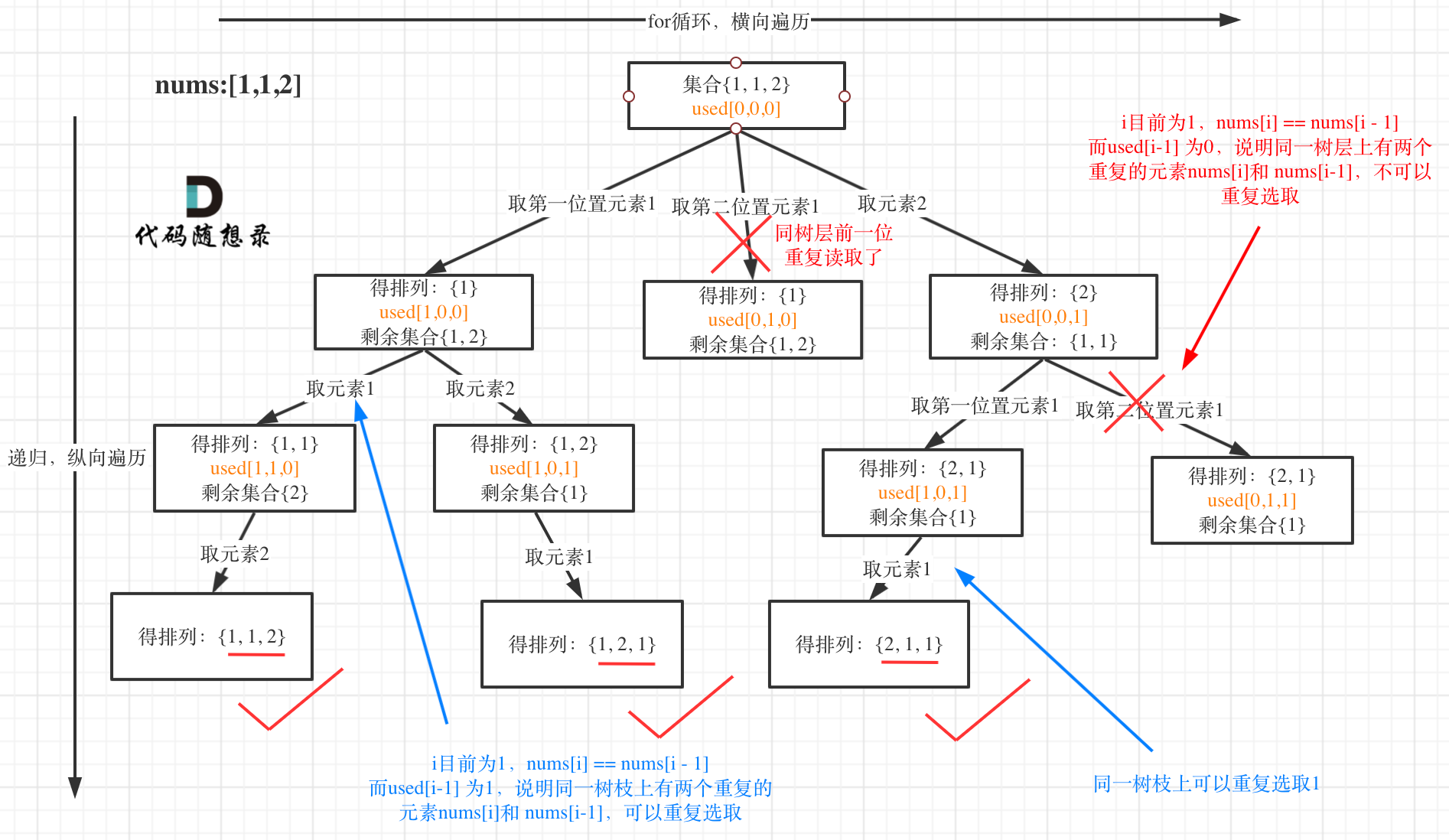
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
|
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
|
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
|
||||||
|
|
||||||
|
|
@ -130,11 +130,11 @@ if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
|
||||||
|
|
||||||
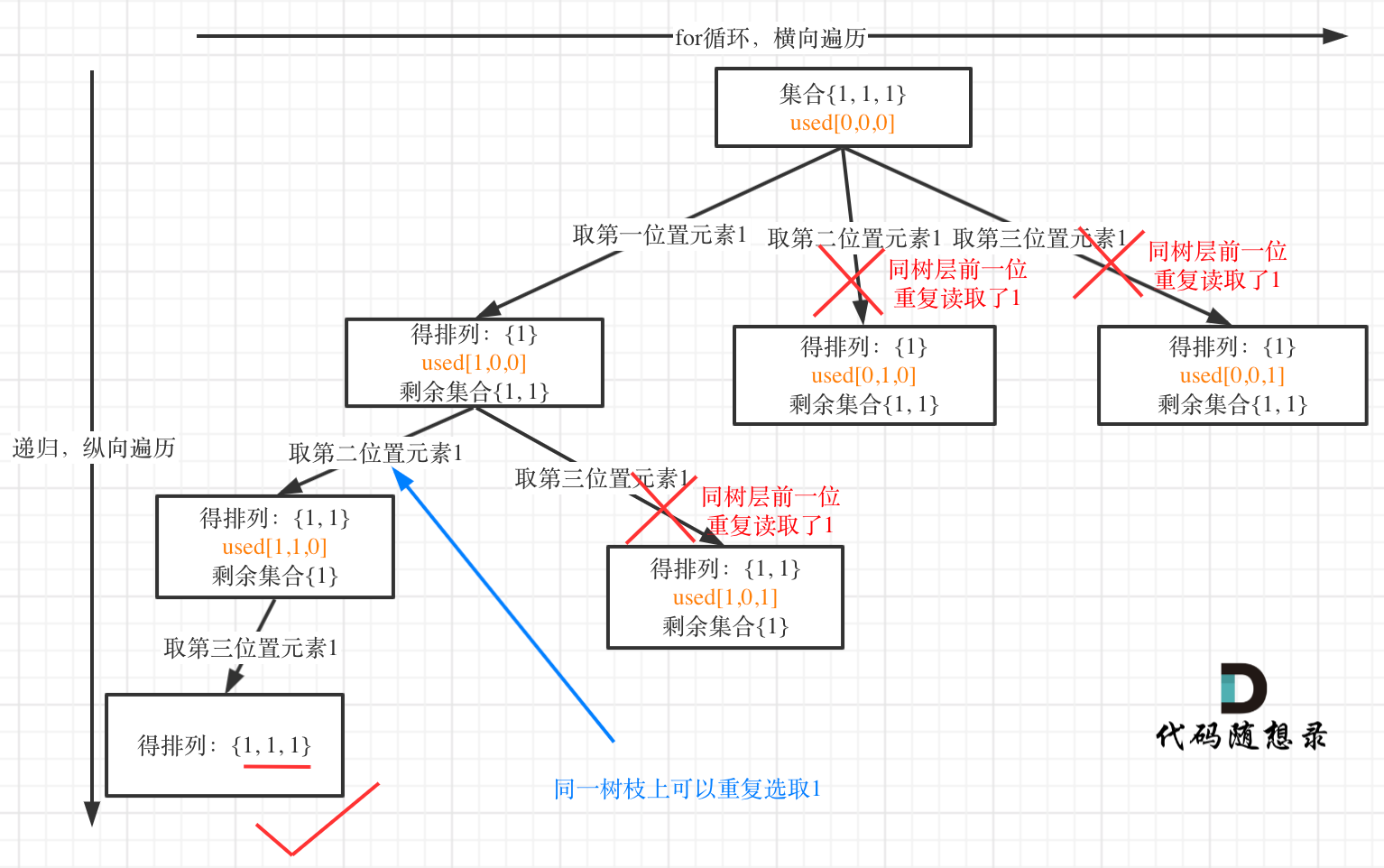
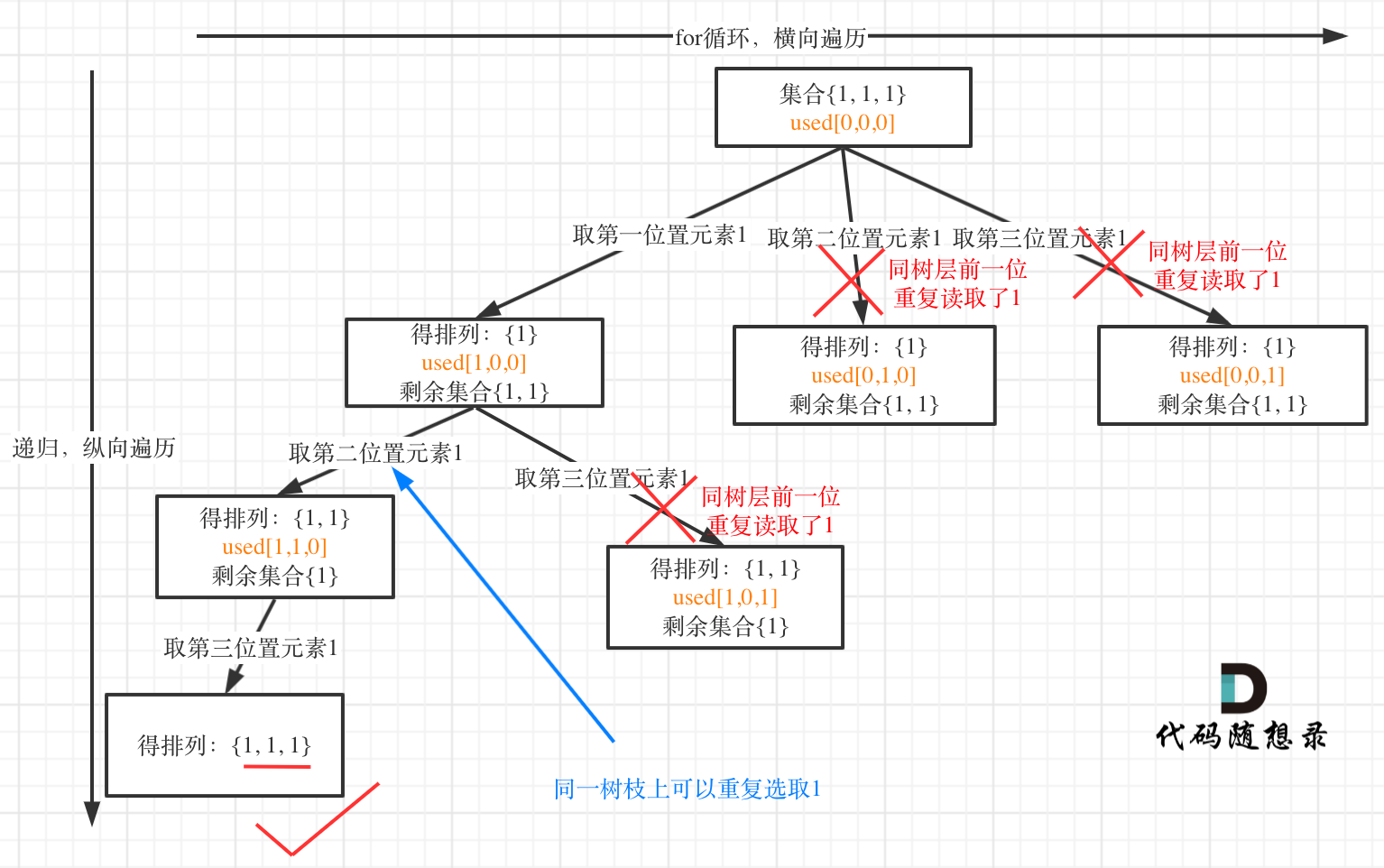
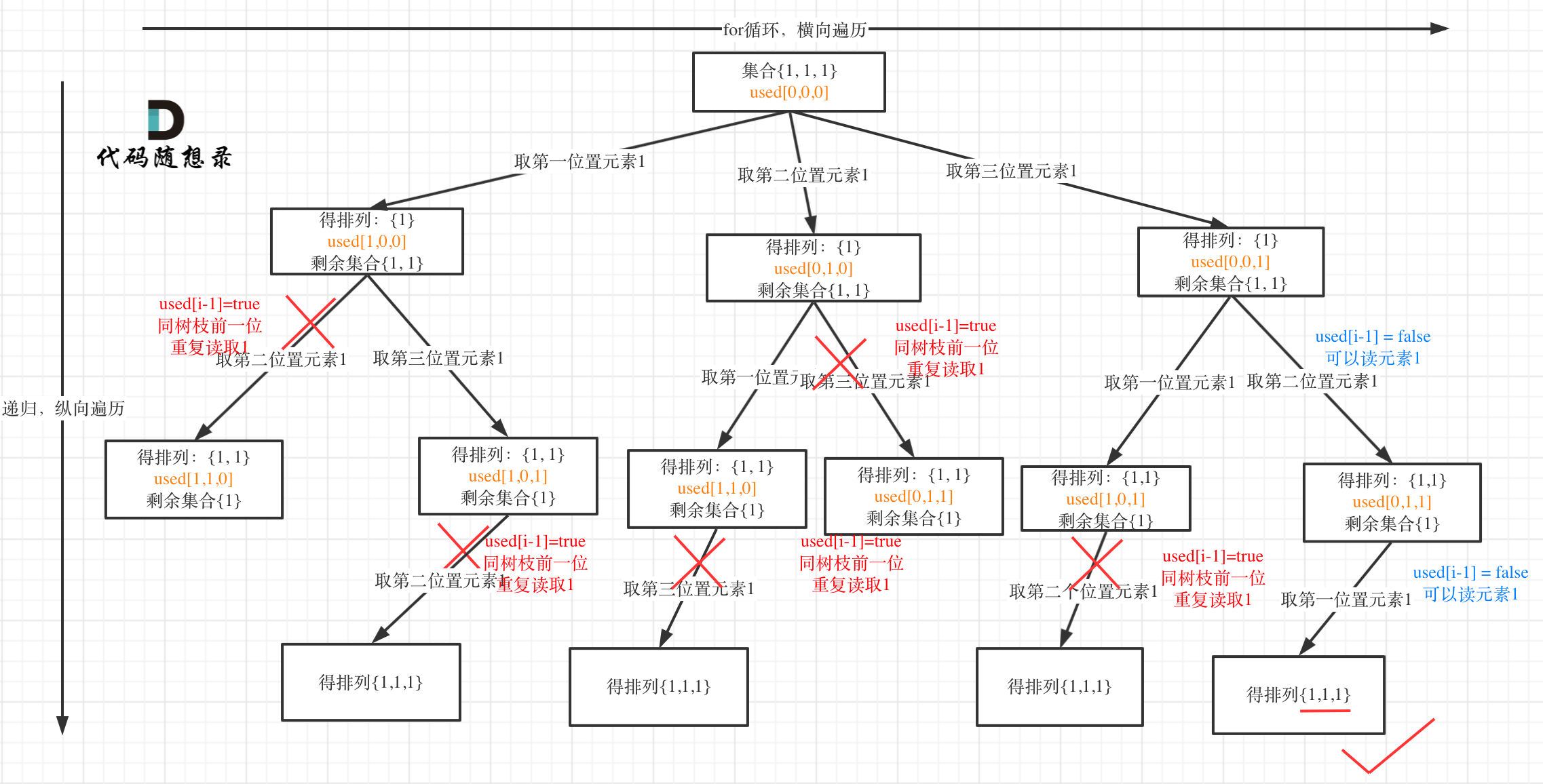
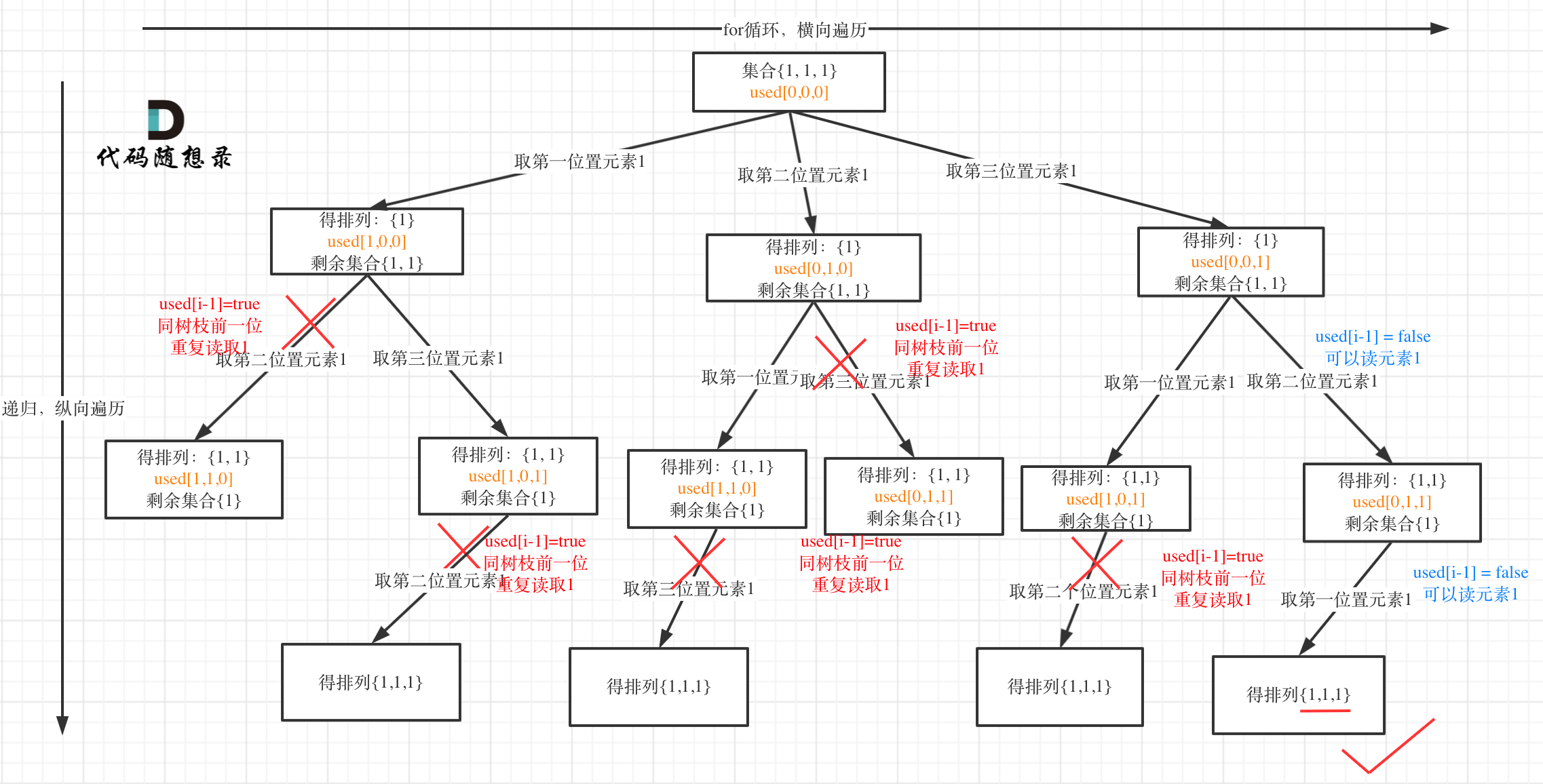
树层上去重(used[i - 1] == false),的树形结构如下:
|
树层上去重(used[i - 1] == false),的树形结构如下:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
树枝上去重(used[i - 1] == true)的树型结构如下:
|
树枝上去重(used[i - 1] == true)的树型结构如下:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
|
大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -15,7 +15,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
|
||||||
|
|
||||||
示例 1:
|
示例 1:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
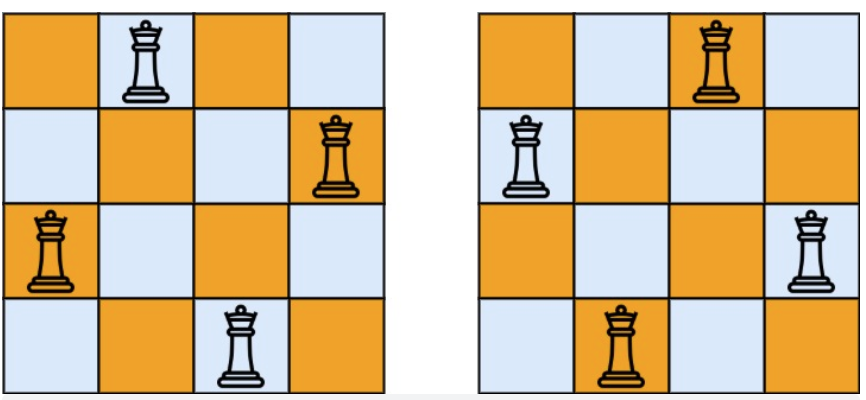
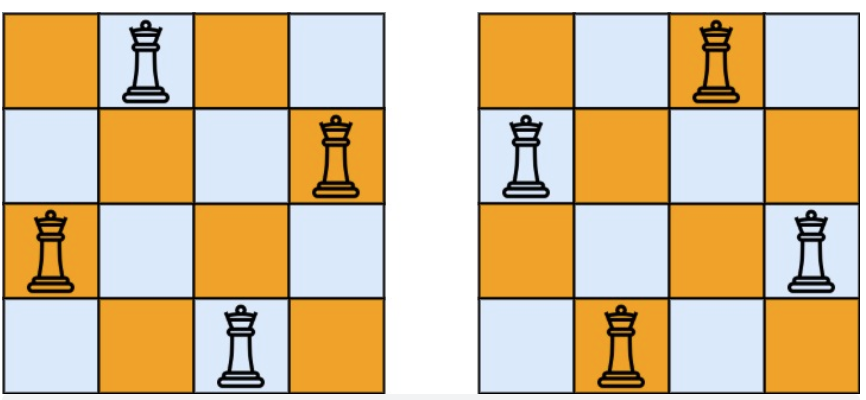
* 输入:n = 4
|
* 输入:n = 4
|
||||||
* 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
|
* 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
|
||||||
|
|
@ -45,7 +45,7 @@ n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,
|
||||||
|
|
||||||
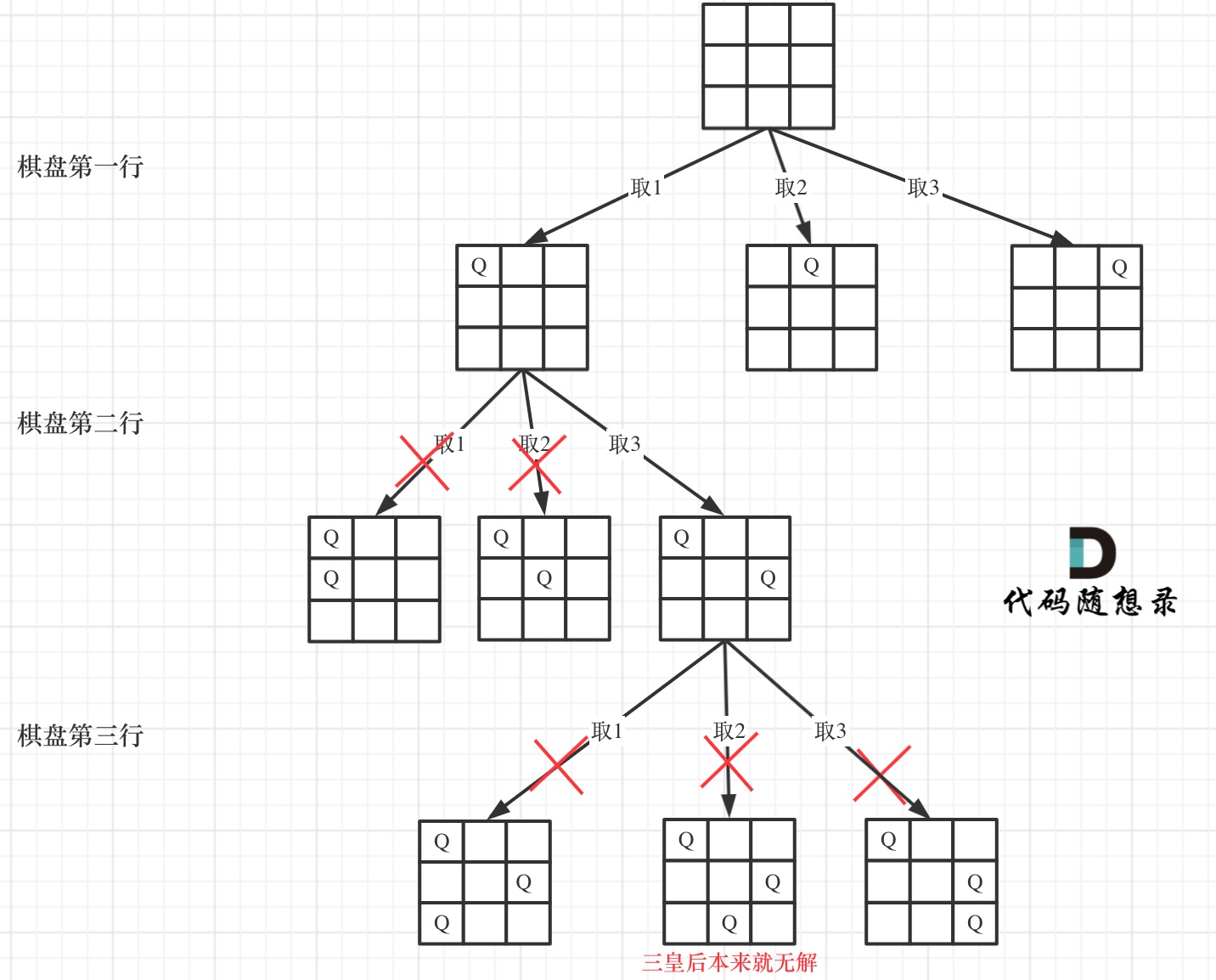
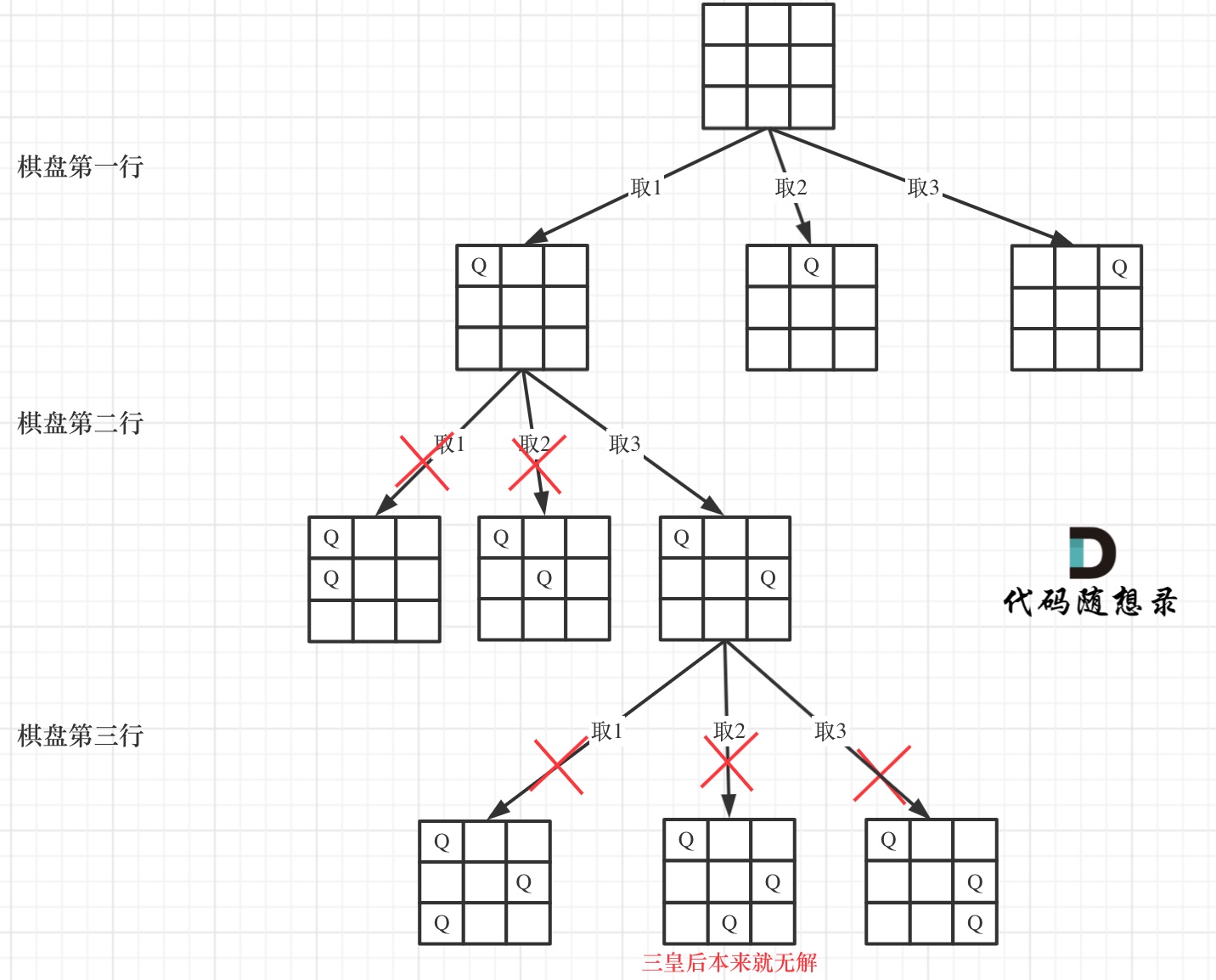
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
|
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
|
从图中,可以看出,二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。
|
||||||
|
|
||||||
|
|
@ -85,7 +85,7 @@ void backtracking(int n, int row, vector<string>& chessboard) {
|
||||||
* 递归终止条件
|
* 递归终止条件
|
||||||
|
|
||||||
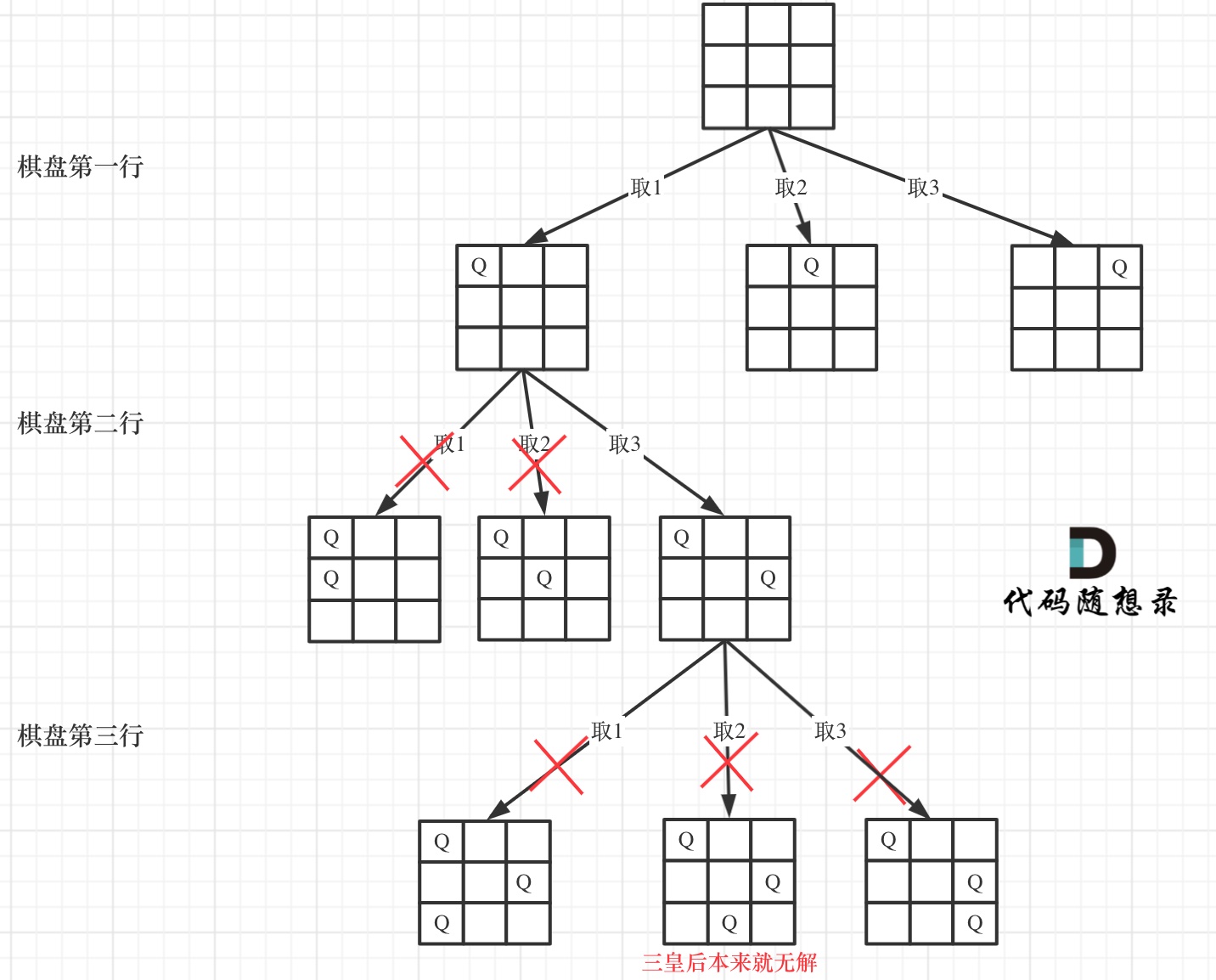
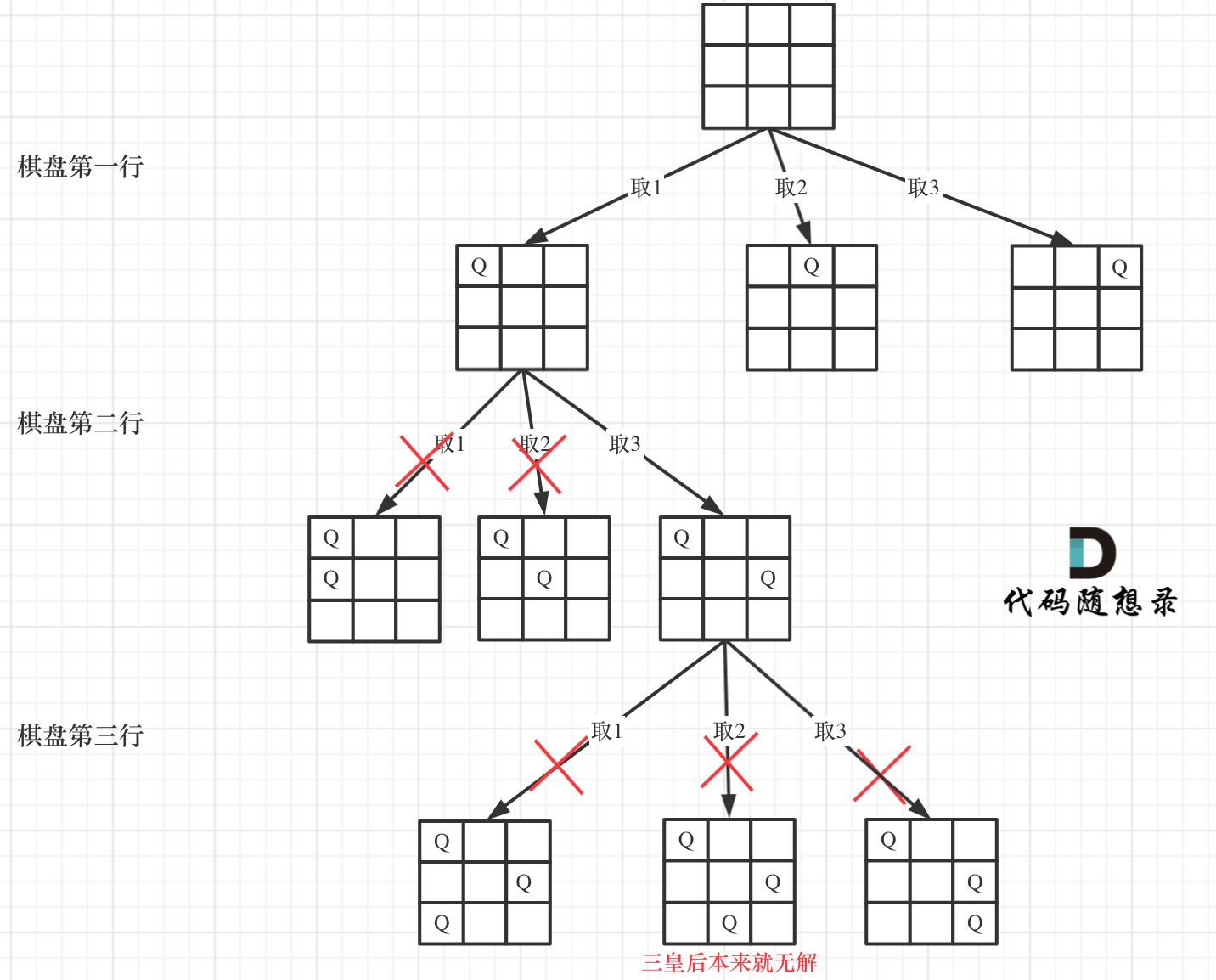
在如下树形结构中:
|
在如下树形结构中:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
|
可以看出,当递归到棋盘最底层(也就是叶子节点)的时候,就可以收集结果并返回了。
|
||||||
|
|
|
||||||
|
|
@ -13,7 +13,7 @@ n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并
|
||||||
上图为 8 皇后问题的一种解法。
|
上图为 8 皇后问题的一种解法。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
|
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -54,7 +54,7 @@ dp[0]应该是多少呢?
|
||||||
5. 举例推导dp数组
|
5. 举例推导dp数组
|
||||||
|
|
||||||
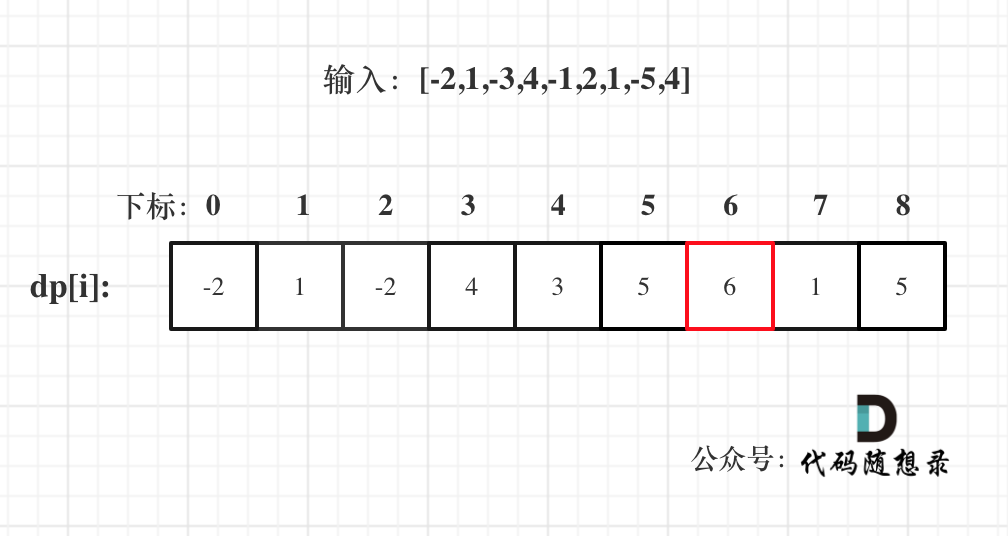
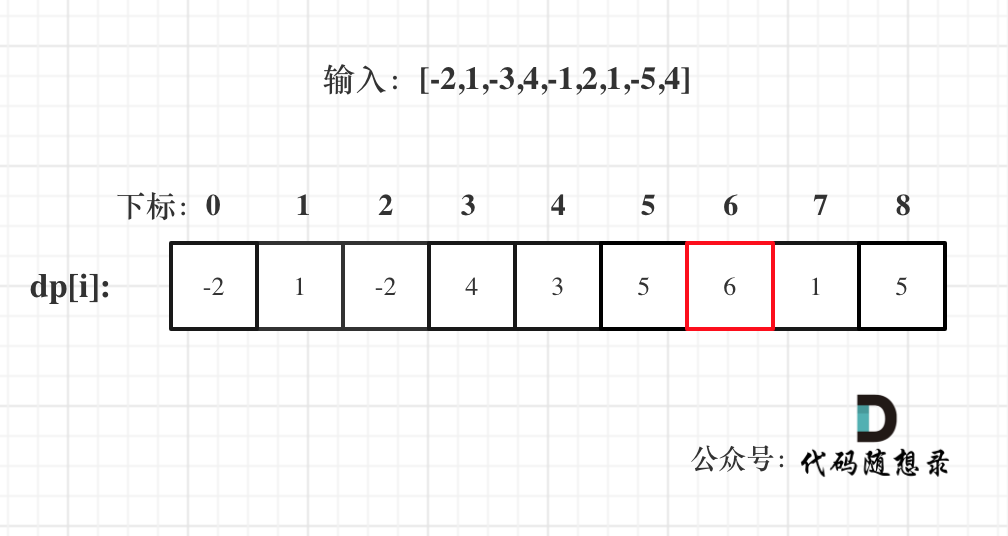
以示例一为例,输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的dp状态如下:
|
以示例一为例,输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的dp状态如下:
|
||||||
|
|
||||||
|
|
||||||
**注意最后的结果可不是dp[nums.size() - 1]!** ,而是dp[6]。
|
**注意最后的结果可不是dp[nums.size() - 1]!** ,而是dp[6]。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -36,7 +36,7 @@
|
||||||
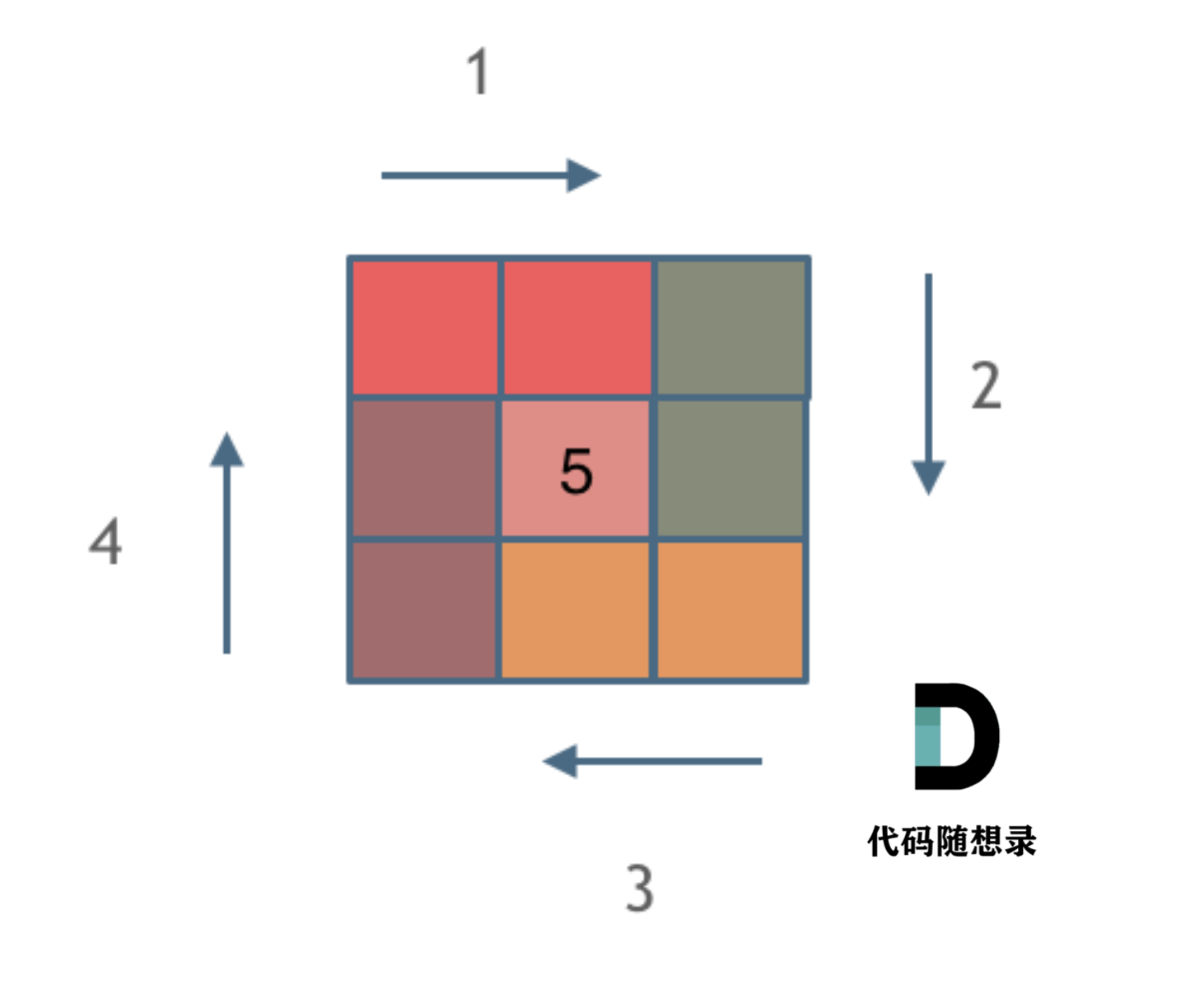
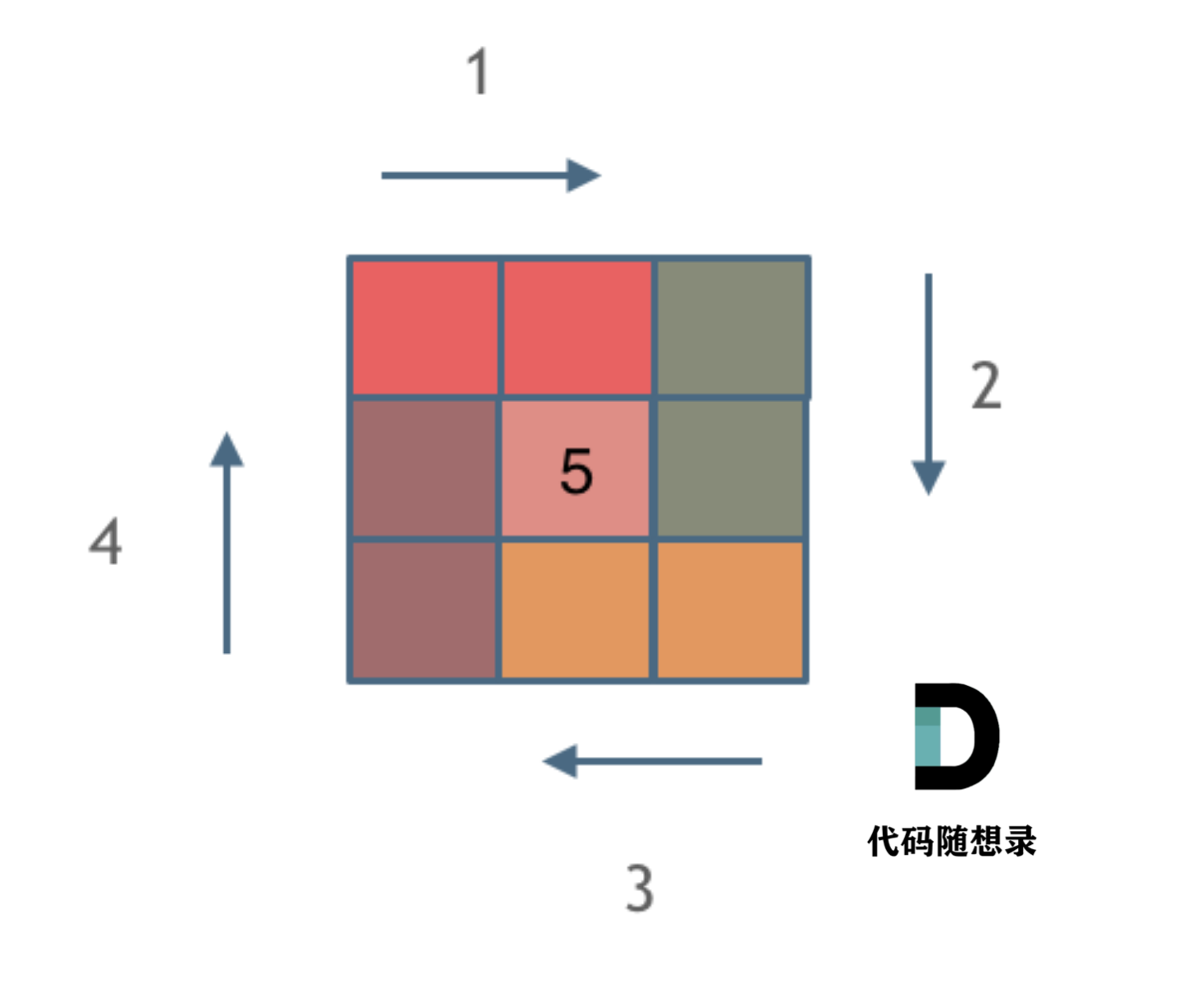
由外向内一圈一圈这么画下去,如下所示:
|
由外向内一圈一圈这么画下去,如下所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
|
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -48,7 +48,7 @@
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
|
i 每次移动只能在 cover 的范围内移动,每移动一个元素,cover 得到该元素数值(新的覆盖范围)的补充,让 i 继续移动下去。
|
||||||
|
|
|
||||||
|
|
@ -38,7 +38,7 @@
|
||||||
|
|
||||||
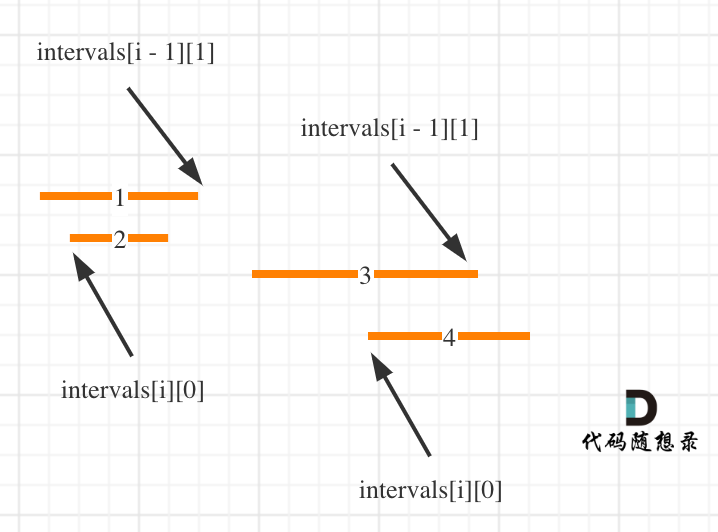
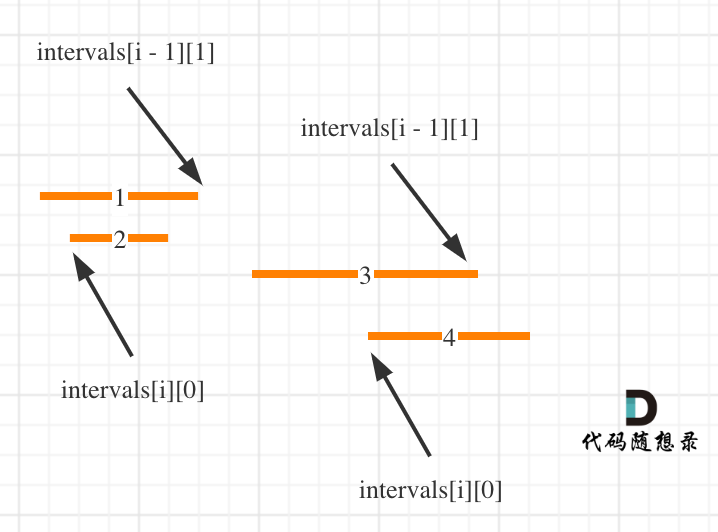
这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
|
这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
|
知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -54,7 +54,7 @@
|
||||||
|
|
||||||
那么我按照左闭右开的原则,来画一圈,大家看一下:
|
那么我按照左闭右开的原则,来画一圈,大家看一下:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
|
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -16,7 +16,7 @@
|
||||||
|
|
||||||
示例 1:
|
示例 1:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
* 输入:m = 3, n = 7
|
* 输入:m = 3, n = 7
|
||||||
* 输出:28
|
* 输出:28
|
||||||
|
|
@ -62,7 +62,7 @@
|
||||||
|
|
||||||
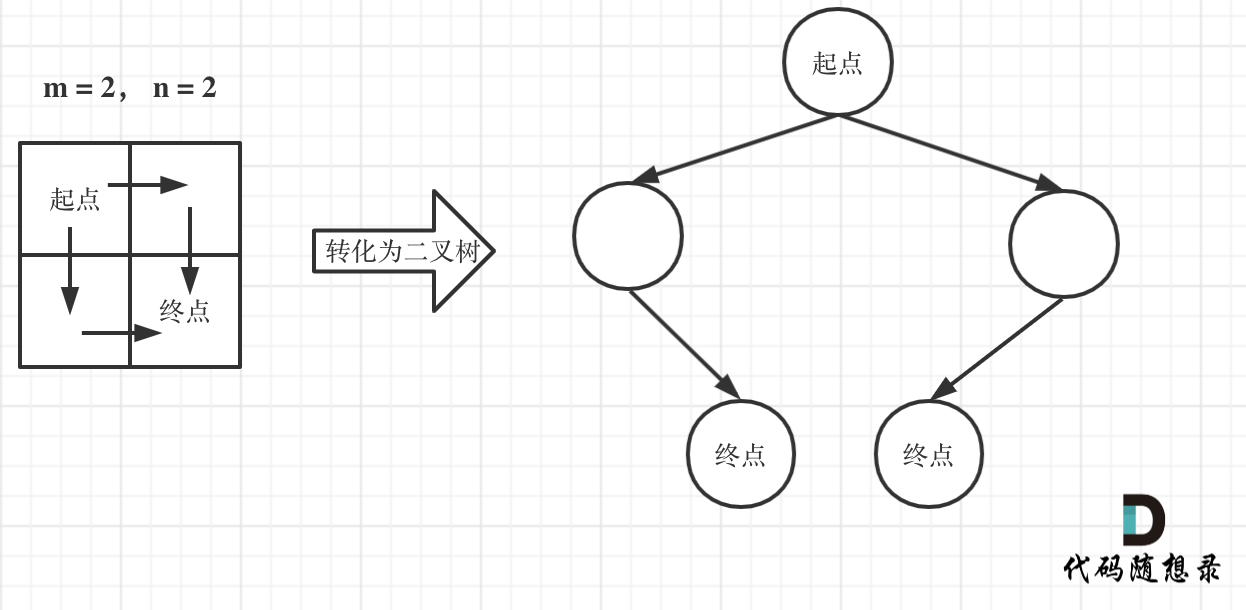
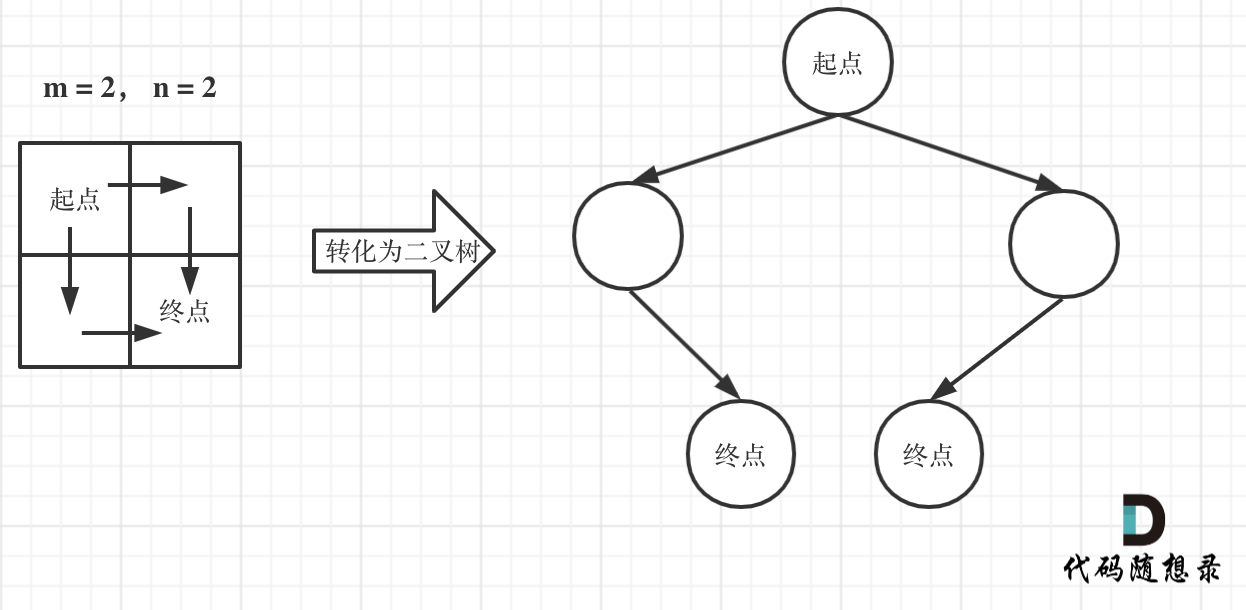
如图举例:
|
如图举例:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
|
此时问题就可以转化为求二叉树叶子节点的个数,代码如下:
|
||||||
|
|
||||||
|
|
@ -131,7 +131,7 @@ for (int j = 0; j < n; j++) dp[0][j] = 1;
|
||||||
|
|
||||||
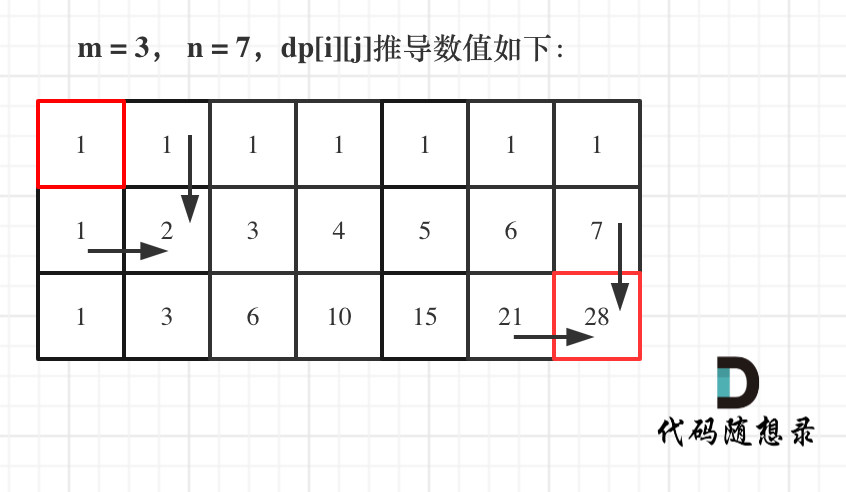
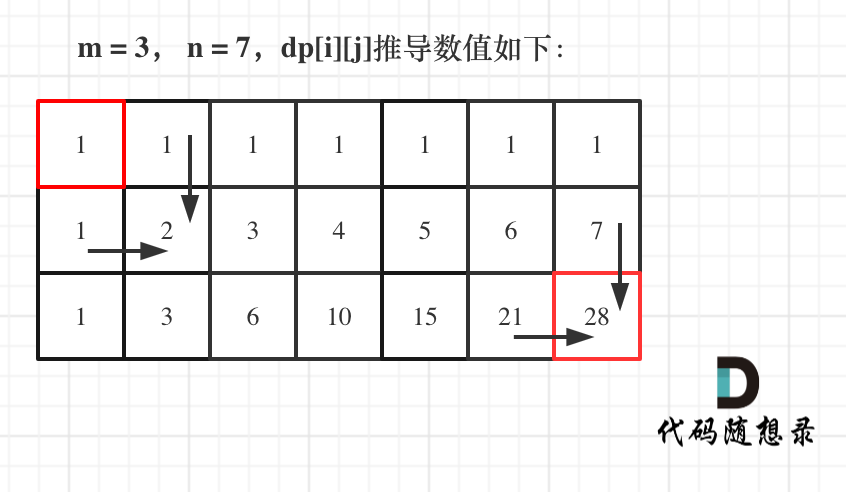
如图所示:
|
如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
以上动规五部曲分析完毕,C++代码如下:
|
以上动规五部曲分析完毕,C++代码如下:
|
||||||
|
|
||||||
|
|
@ -180,7 +180,7 @@ public:
|
||||||
|
|
||||||
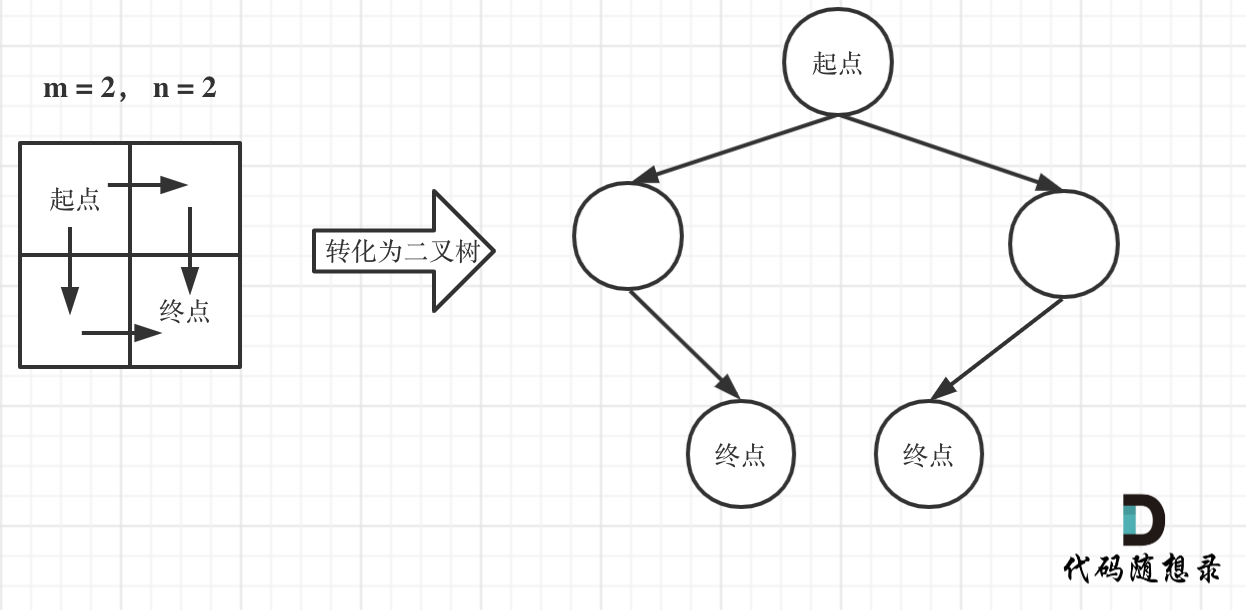
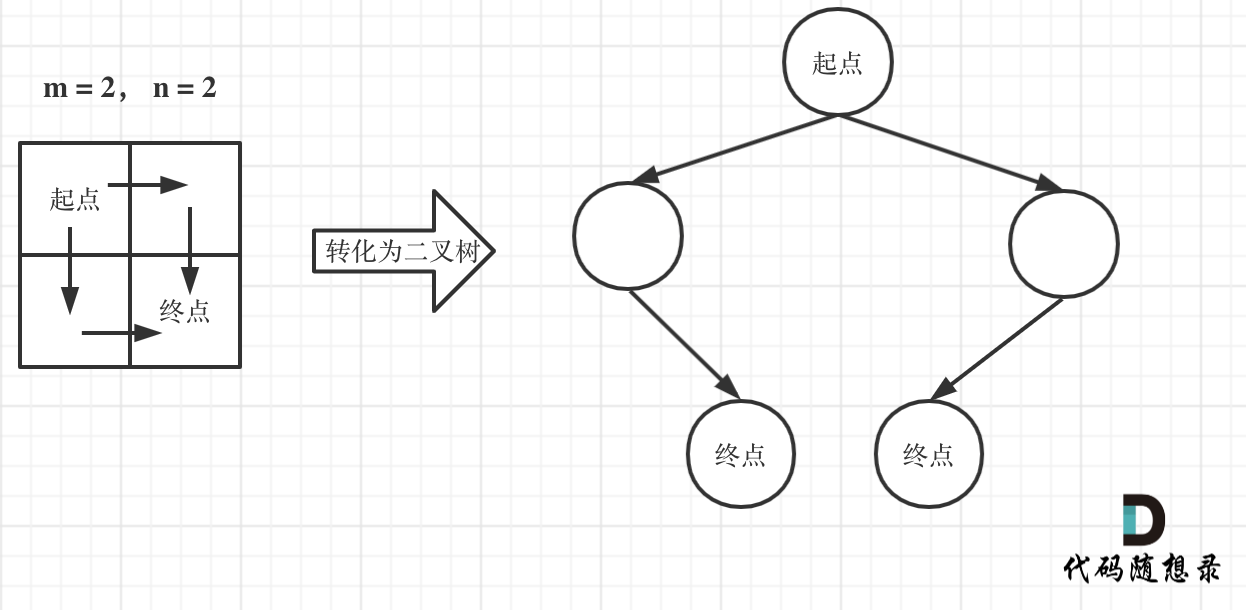
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
|
在这个图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
|
在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
|
||||||
|
|
||||||
|
|
@ -190,7 +190,7 @@ public:
|
||||||
|
|
||||||
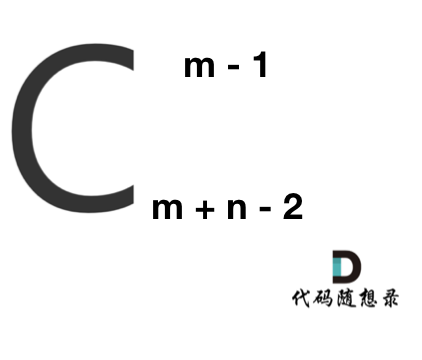
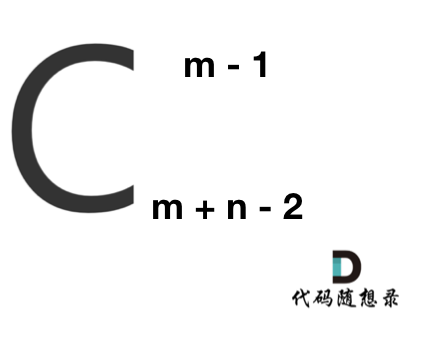
那么答案,如图所示:
|
那么答案,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**求组合的时候,要防止两个int相乘溢出!** 所以不能把算式的分子都算出来,分母都算出来再做除法。
|
**求组合的时候,要防止两个int相乘溢出!** 所以不能把算式的分子都算出来,分母都算出来再做除法。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -14,13 +14,13 @@
|
||||||
|
|
||||||
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
|
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
网格中的障碍物和空位置分别用 1 和 0 来表示。
|
网格中的障碍物和空位置分别用 1 和 0 来表示。
|
||||||
|
|
||||||
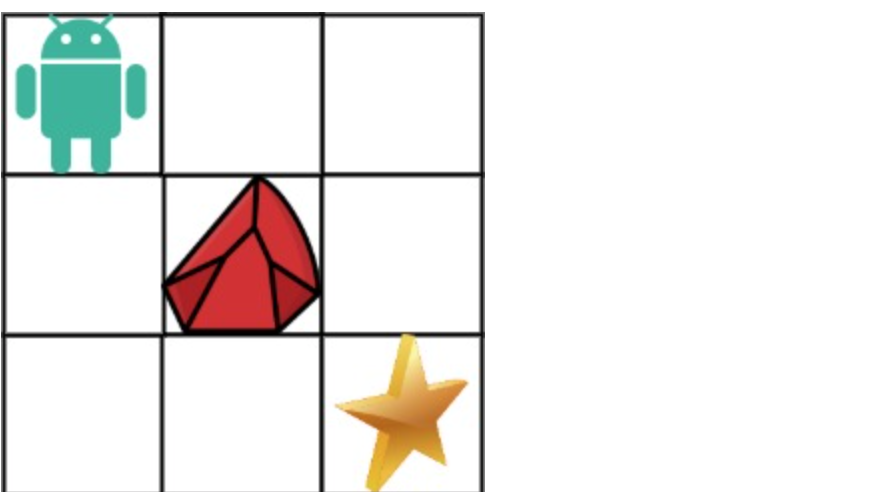
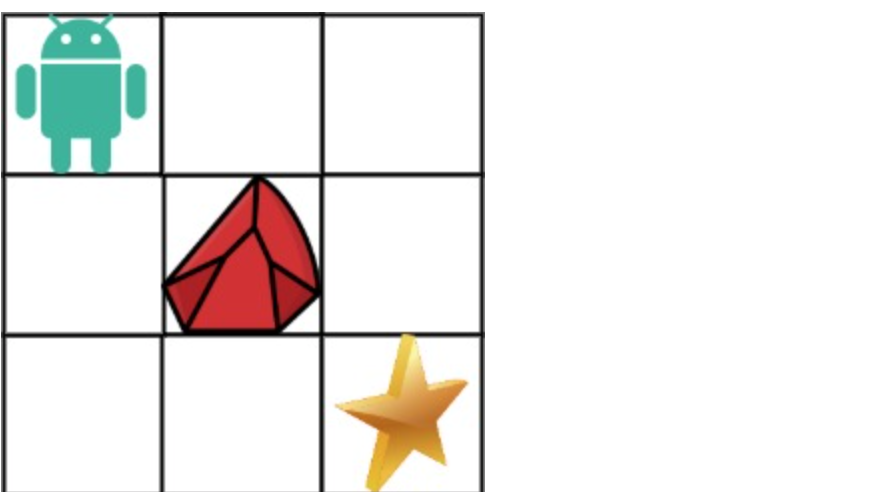
示例 1:
|
示例 1:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
* 输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
|
* 输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
|
||||||
* 输出:2
|
* 输出:2
|
||||||
|
|
@ -32,7 +32,7 @@
|
||||||
|
|
||||||
示例 2:
|
示例 2:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
* 输入:obstacleGrid = [[0,1],[0,0]]
|
* 输入:obstacleGrid = [[0,1],[0,0]]
|
||||||
* 输出:1
|
* 输出:1
|
||||||
|
|
@ -93,7 +93,7 @@ for (int j = 0; j < n; j++) dp[0][j] = 1;
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
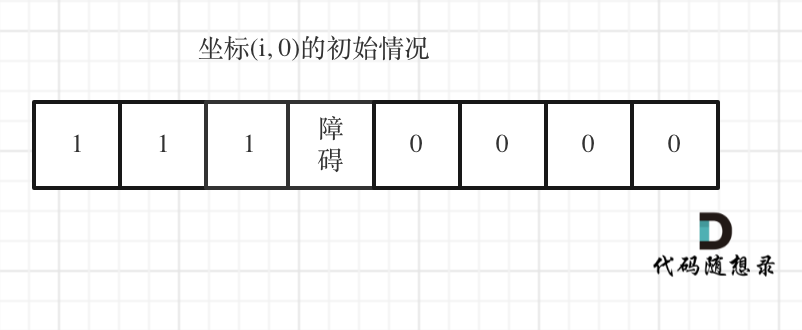
|
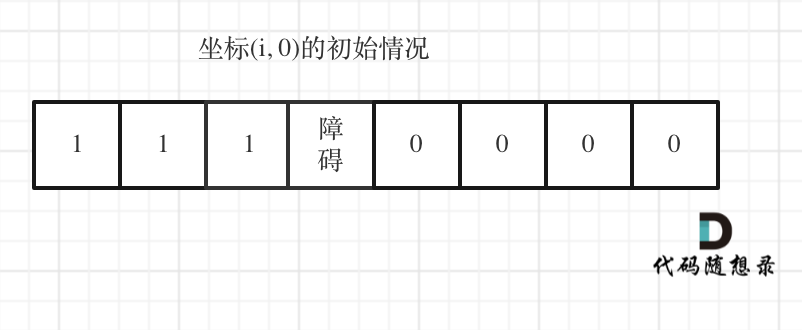
|
||||||
|
|
||||||
下标(0, j)的初始化情况同理。
|
下标(0, j)的初始化情况同理。
|
||||||
|
|
||||||
|
|
@ -127,11 +127,11 @@ for (int i = 1; i < m; i++) {
|
||||||
|
|
||||||
拿示例1来举例如题:
|
拿示例1来举例如题:
|
||||||
|
|
||||||
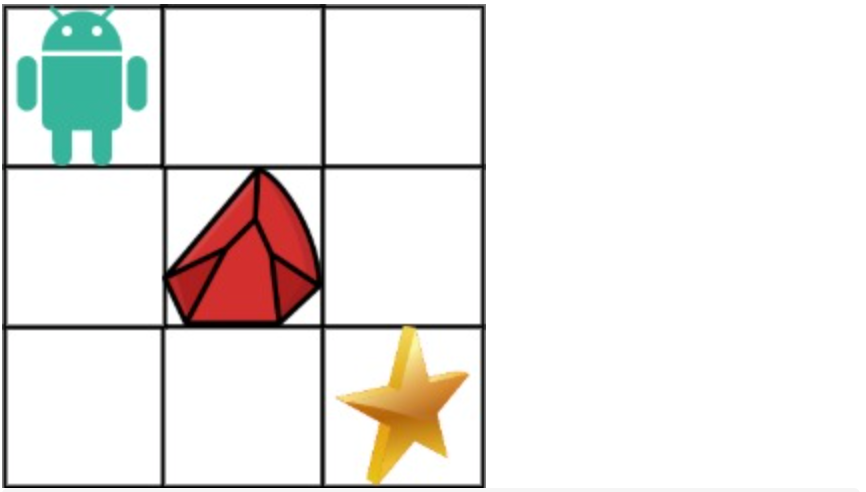
|
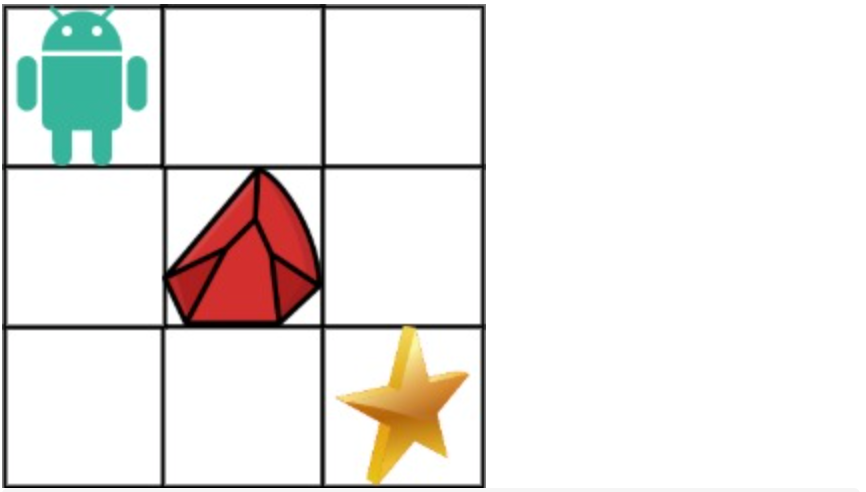
|
||||||
|
|
||||||
对应的dp table 如图:
|
对应的dp table 如图:
|
||||||
|
|
||||||
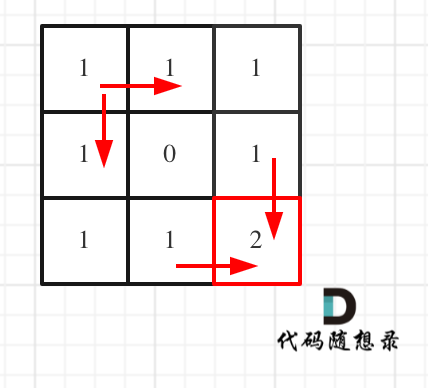
|
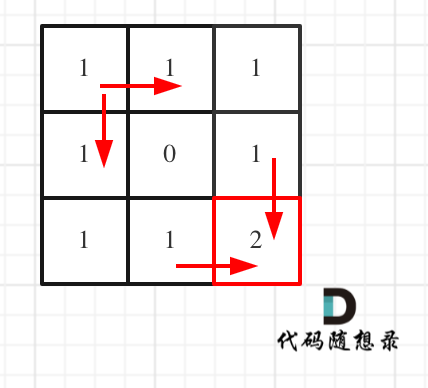
|
||||||
|
|
||||||
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
|
如果这个图看不懂,建议再理解一下递归公式,然后照着文章中说的遍历顺序,自己推导一下!
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -101,7 +101,7 @@ dp[i]: 爬到第i层楼梯,有dp[i]种方法
|
||||||
举例当n为5的时候,dp table(dp数组)应该是这样的
|
举例当n为5的时候,dp table(dp数组)应该是这样的
|
||||||
|
|
||||||
|
|
||||||
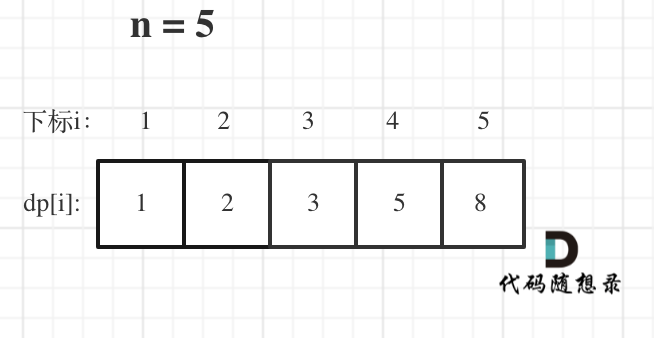
|
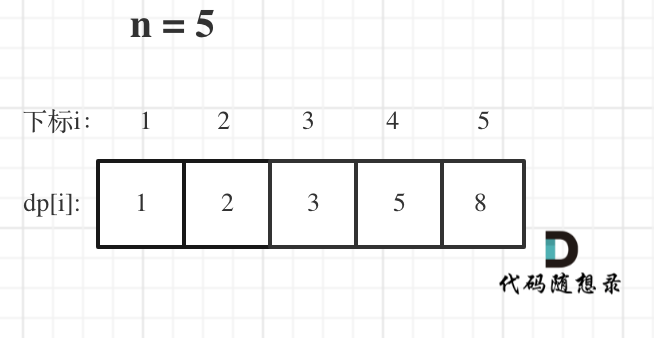
|
||||||
|
|
||||||
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
|
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -170,7 +170,7 @@ for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
|
||||||
|
|
||||||
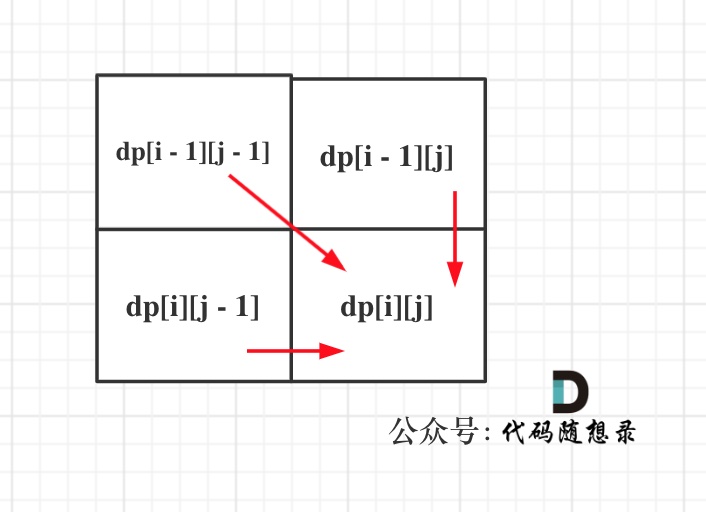
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:
|
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
所以在dp矩阵中一定是从左到右从上到下去遍历。
|
所以在dp矩阵中一定是从左到右从上到下去遍历。
|
||||||
|
|
||||||
|
|
@ -194,7 +194,7 @@ for (int i = 1; i <= word1.size(); i++) {
|
||||||
|
|
||||||
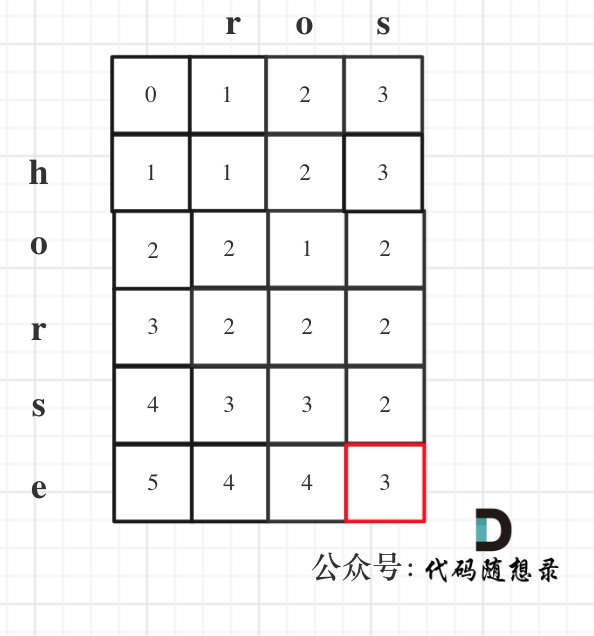
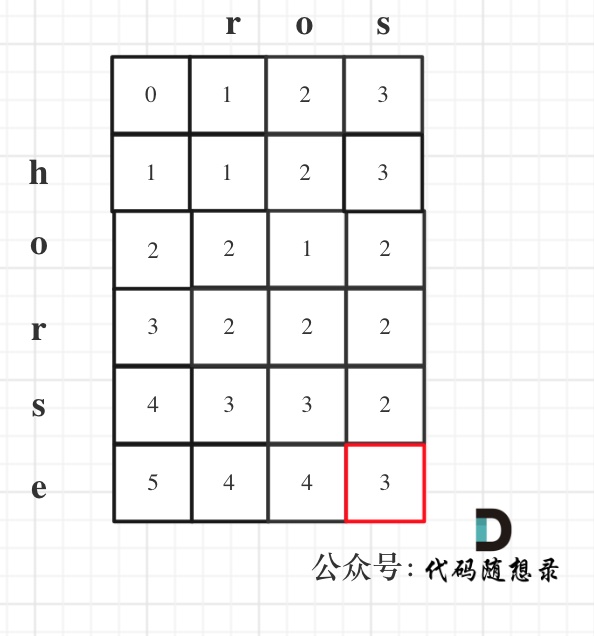
以示例1为例,输入:`word1 = "horse", word2 = "ros"`为例,dp矩阵状态图如下:
|
以示例1为例,输入:`word1 = "horse", word2 = "ros"`为例,dp矩阵状态图如下:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
以上动规五部分析完毕,C++代码如下:
|
以上动规五部分析完毕,C++代码如下:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -82,7 +82,7 @@ for (int i = 1; i <= n; i++) {
|
||||||
|
|
||||||
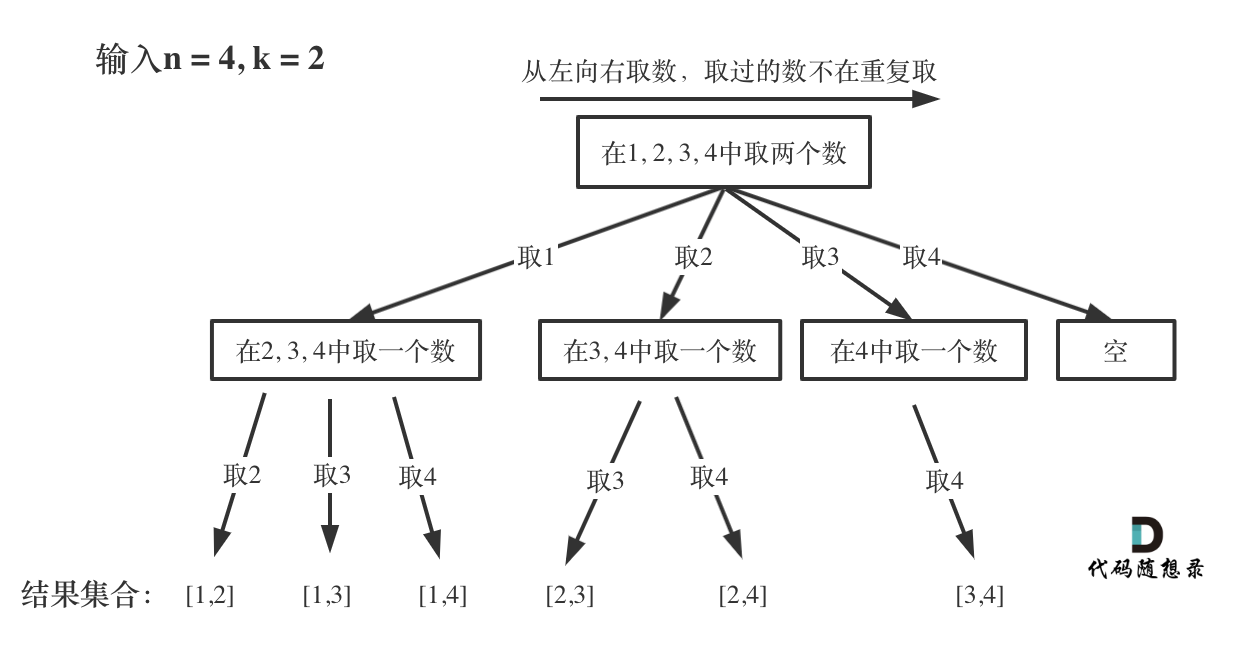
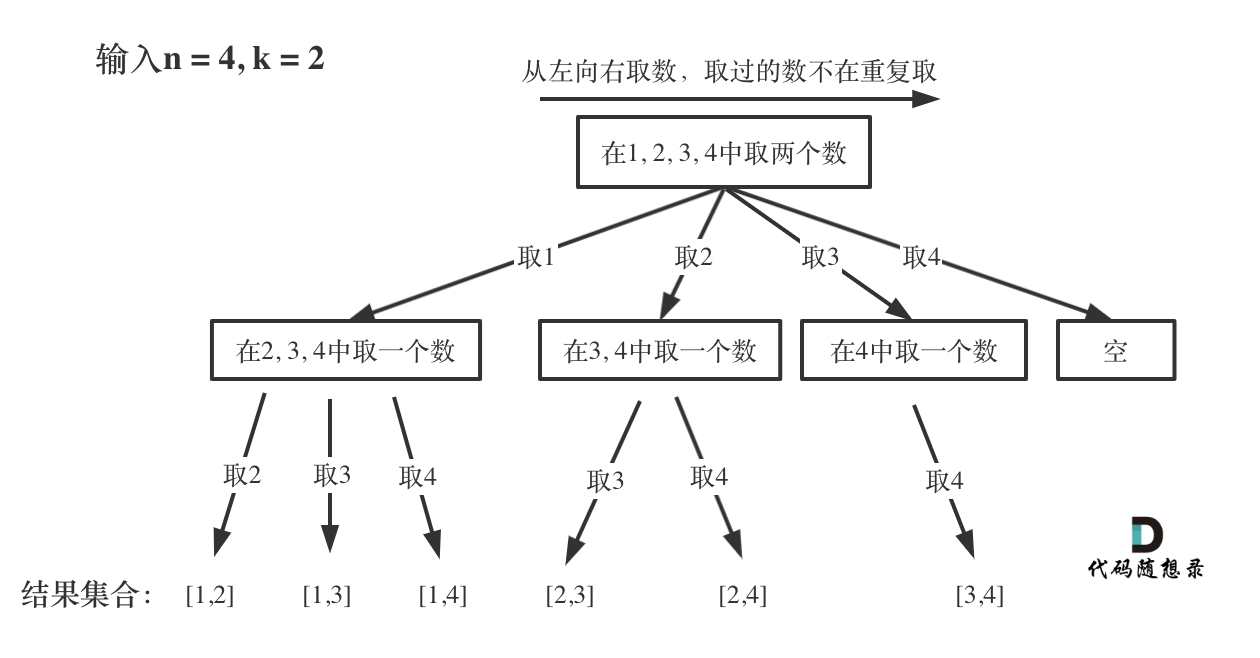
那么我把组合问题抽象为如下树形结构:
|
那么我把组合问题抽象为如下树形结构:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
可以看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
|
可以看出这棵树,一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。
|
||||||
|
|
||||||
|
|
@ -126,7 +126,7 @@ vector<int> path; // 用来存放符合条件结果
|
||||||
|
|
||||||
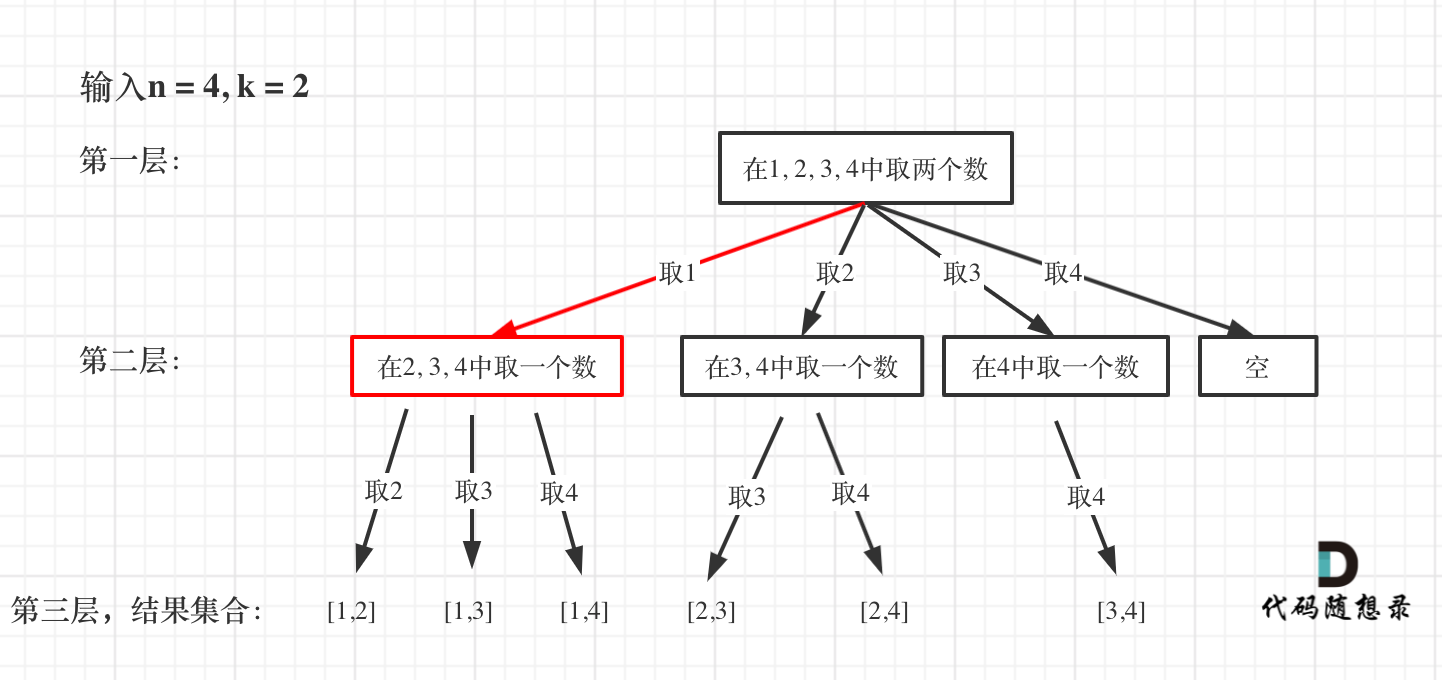
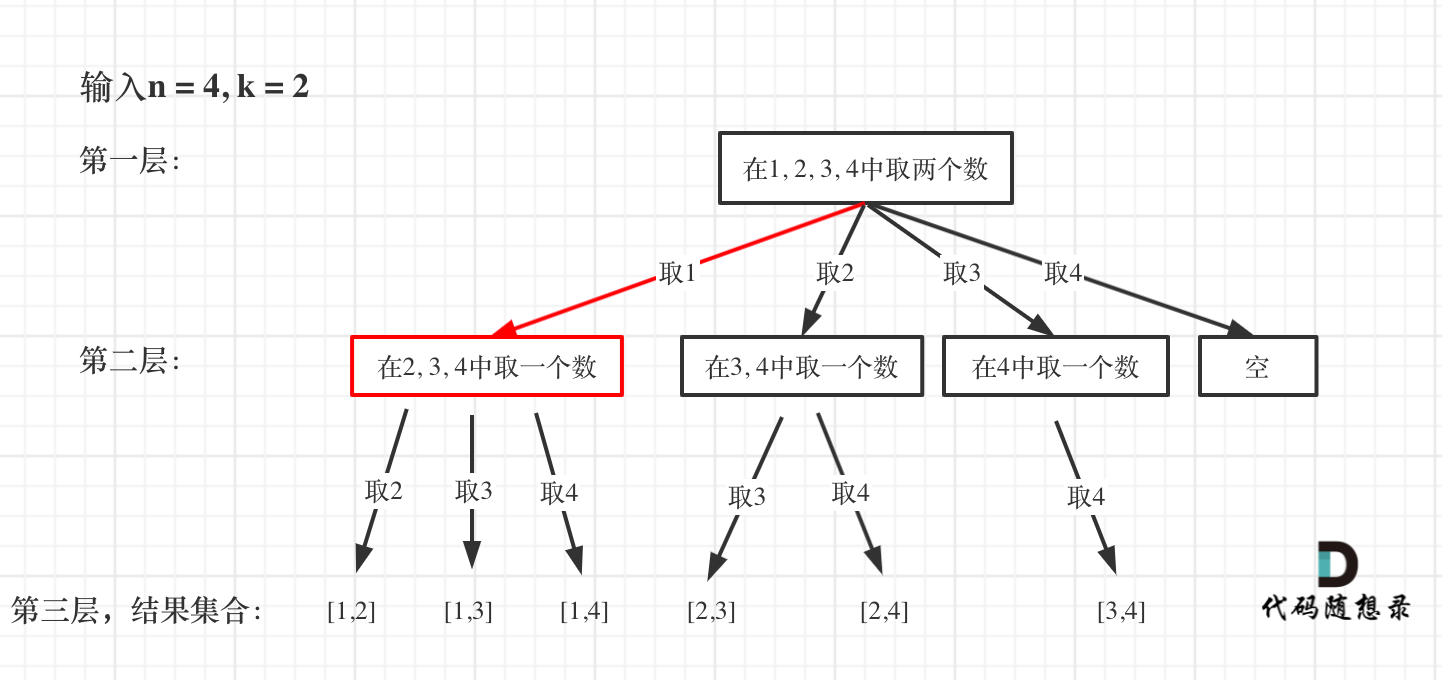
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。
|
从下图中红线部分可以看出,在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
所以需要startIndex来记录下一层递归,搜索的起始位置。
|
所以需要startIndex来记录下一层递归,搜索的起始位置。
|
||||||
|
|
||||||
|
|
@ -146,7 +146,7 @@ path这个数组的大小如果达到k,说明我们找到了一个子集大小
|
||||||
|
|
||||||
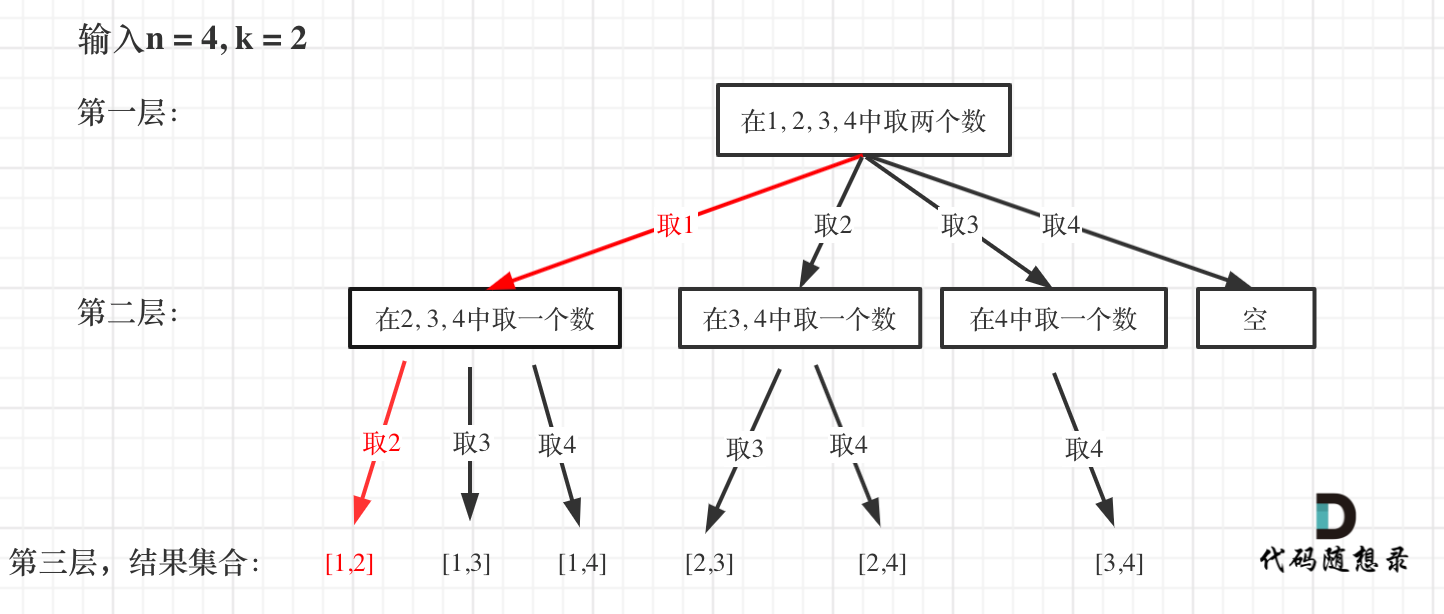
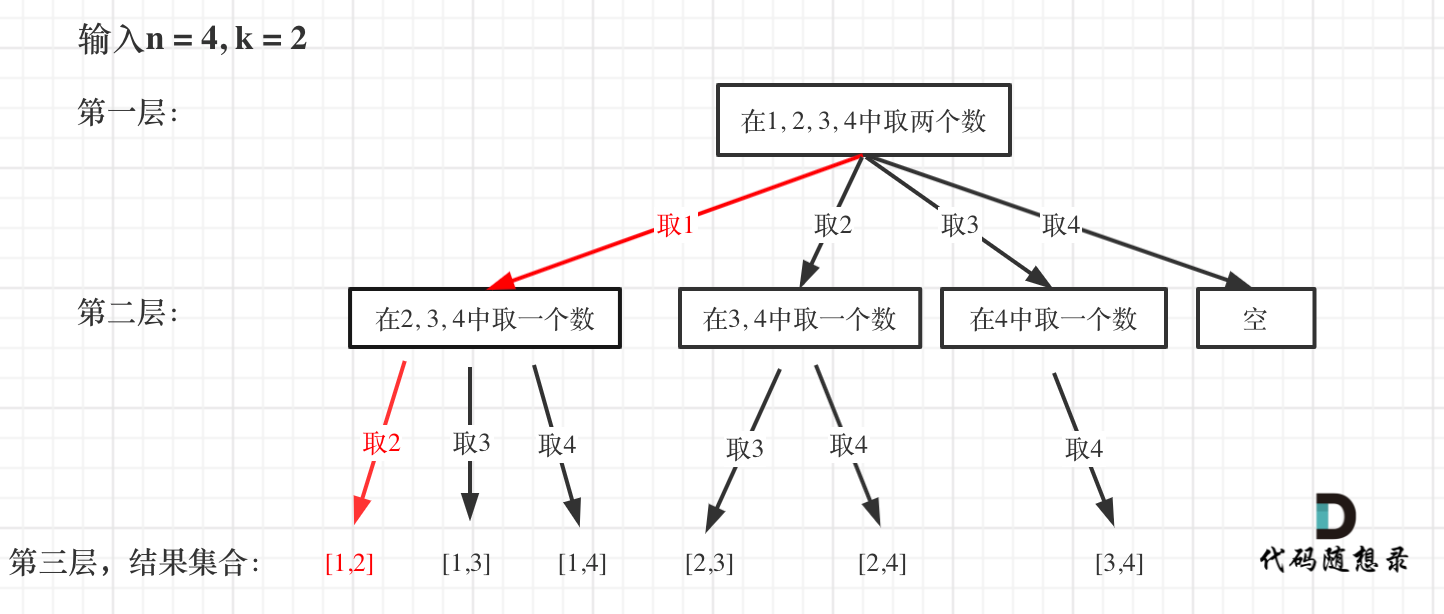
如图红色部分:
|
如图红色部分:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
此时用result二维数组,把path保存起来,并终止本层递归。
|
此时用result二维数组,把path保存起来,并终止本层递归。
|
||||||
|
|
||||||
|
|
@ -163,7 +163,7 @@ if (path.size() == k) {
|
||||||
|
|
||||||
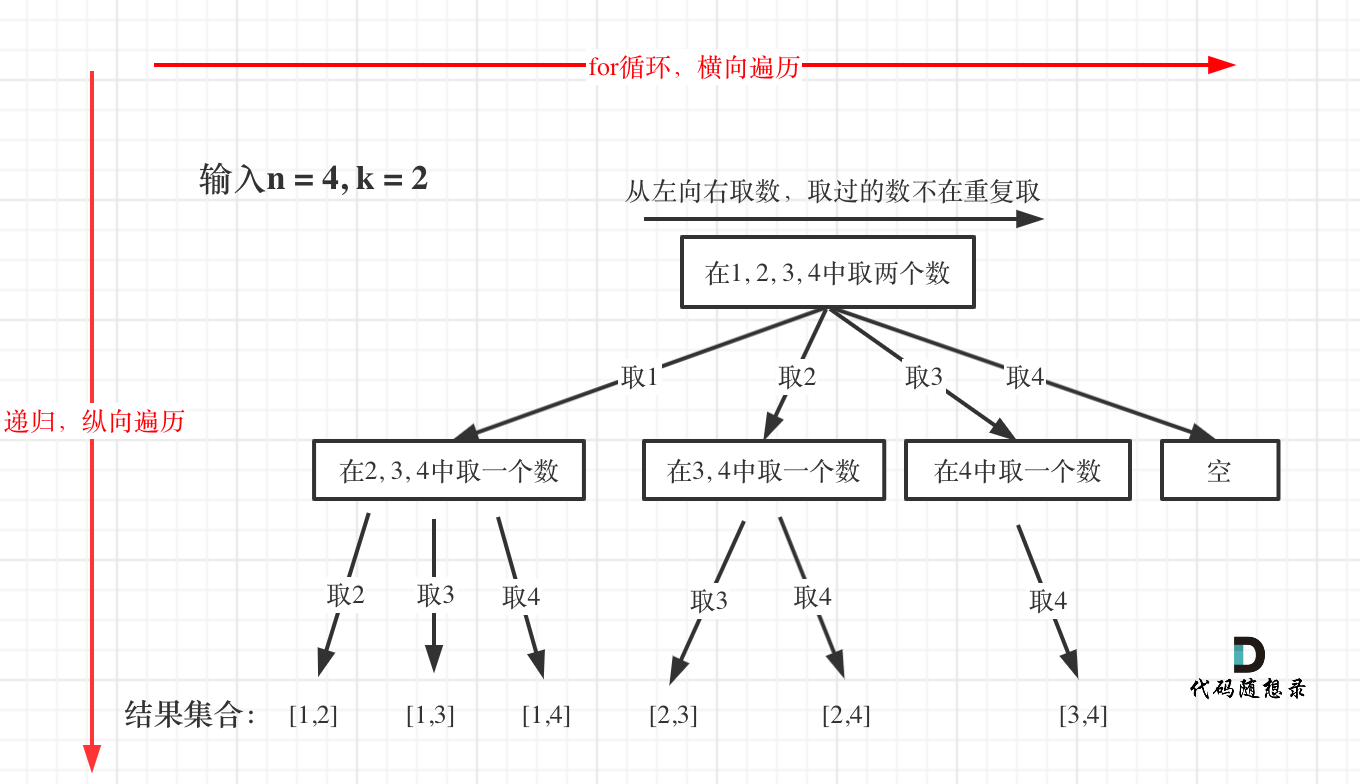
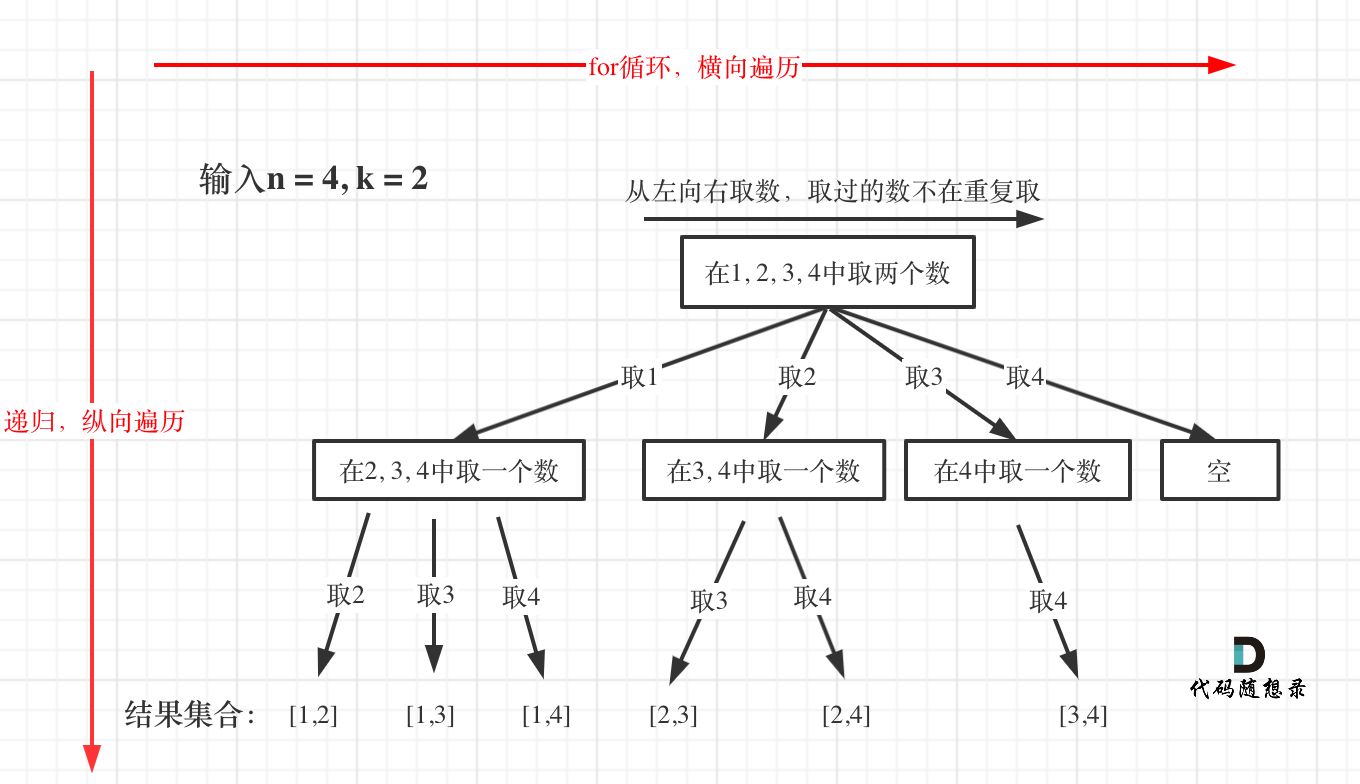
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。
|
回溯法的搜索过程就是一个树型结构的遍历过程,在如下图中,可以看出for循环用来横向遍历,递归的过程是纵向遍历。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
如此我们才遍历完图中的这棵树。
|
如此我们才遍历完图中的这棵树。
|
||||||
|
|
||||||
|
|
@ -267,7 +267,7 @@ for (int i = startIndex; i <= n; i++) {
|
||||||
|
|
||||||
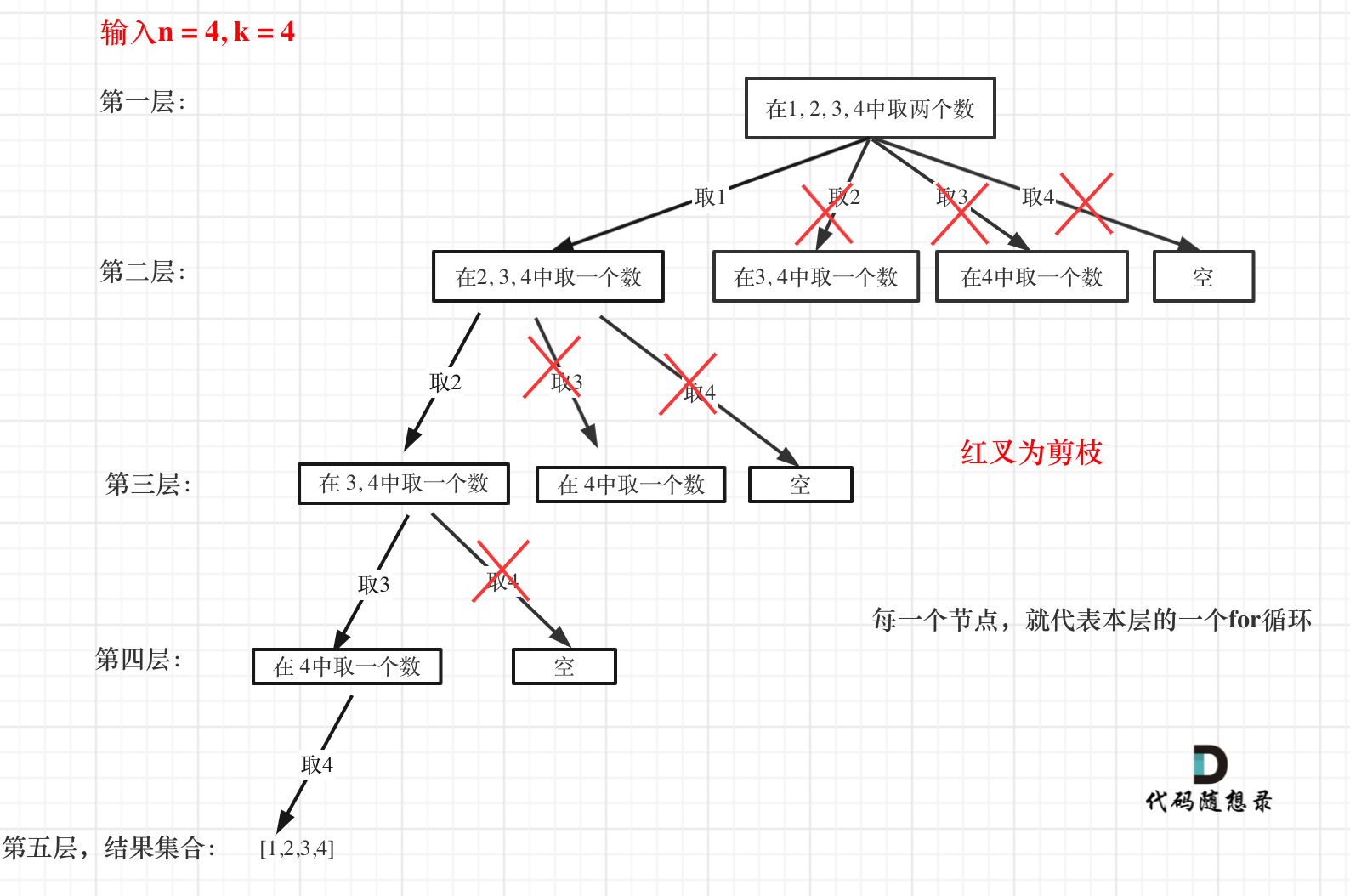
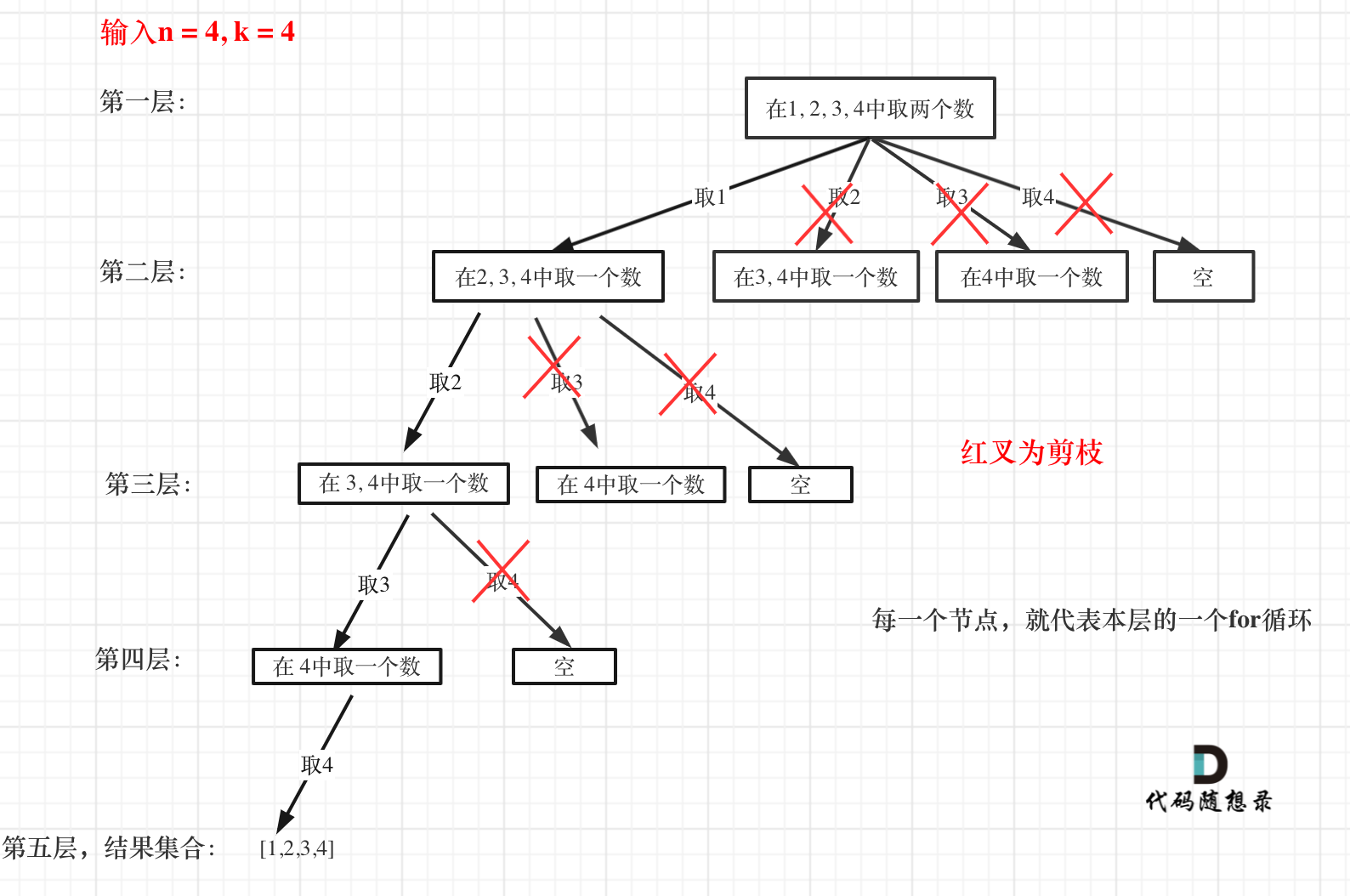
这么说有点抽象,如图所示:
|
这么说有点抽象,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
|
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -67,7 +67,7 @@ for (int i = startIndex; i <= n; i++) {
|
||||||
|
|
||||||
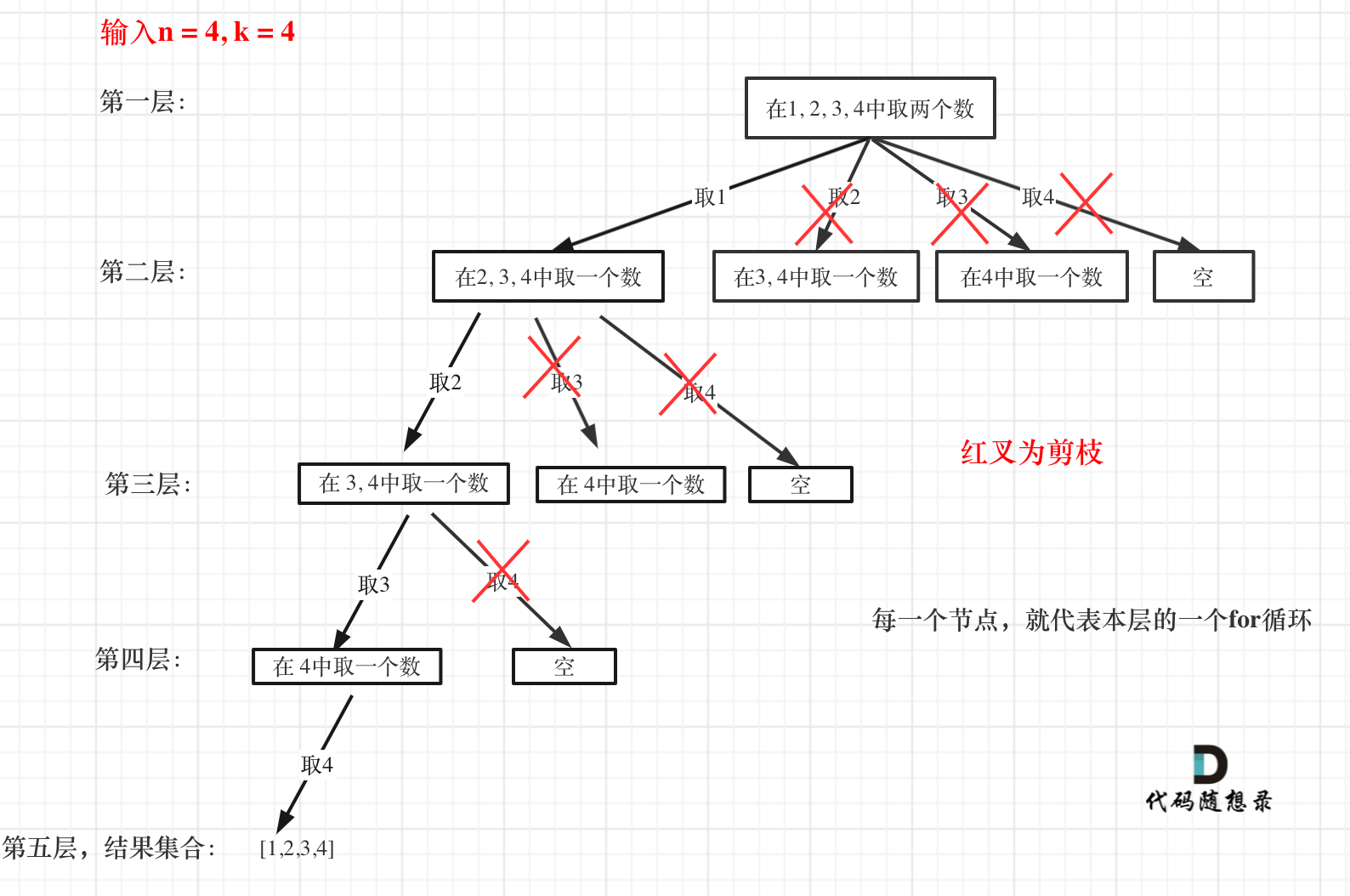
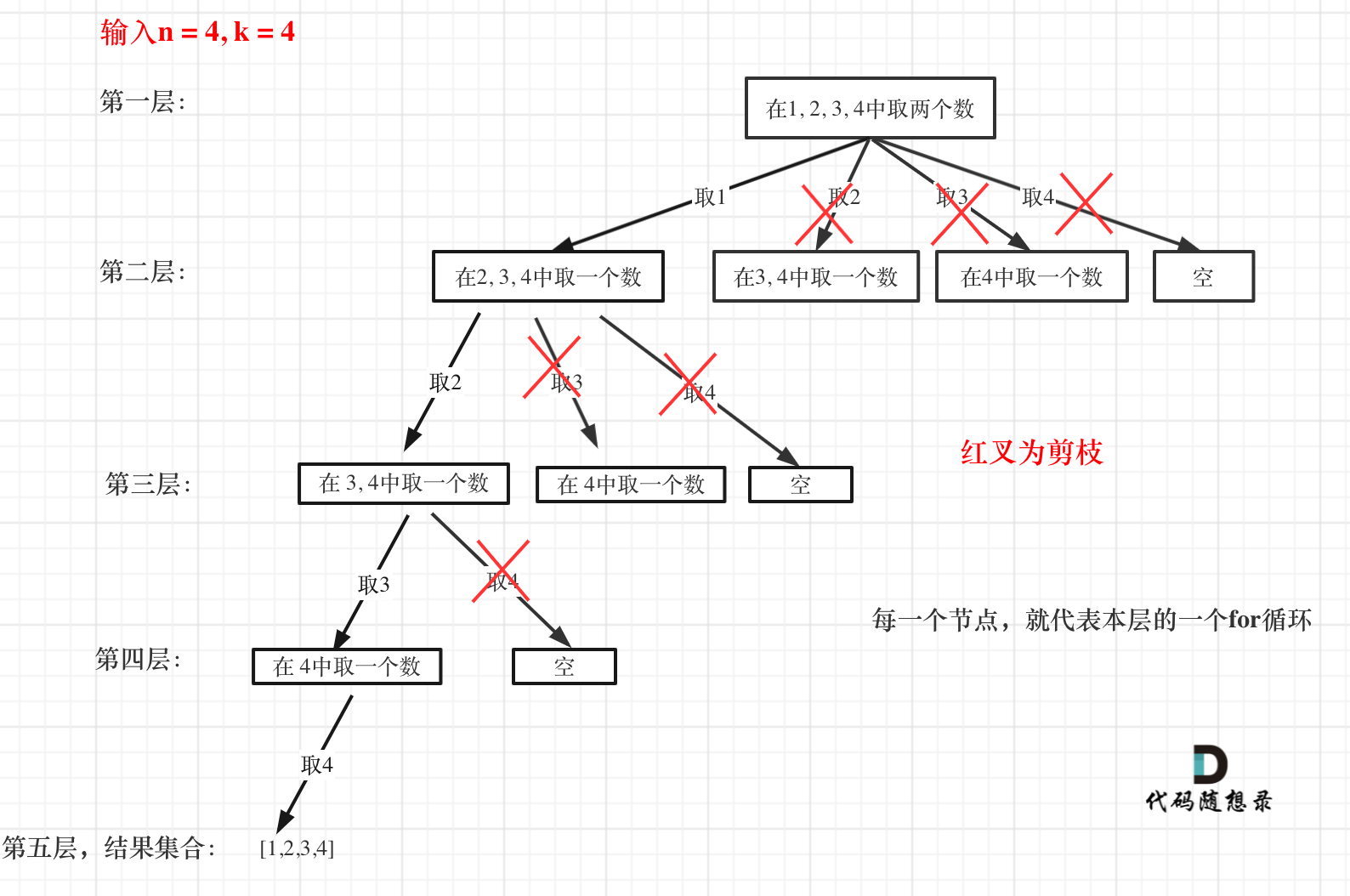
这么说有点抽象,如图所示:
|
这么说有点抽象,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
|
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
|
||||||
|
|
|
||||||
|
|
@ -11,9 +11,9 @@
|
||||||
|
|
||||||
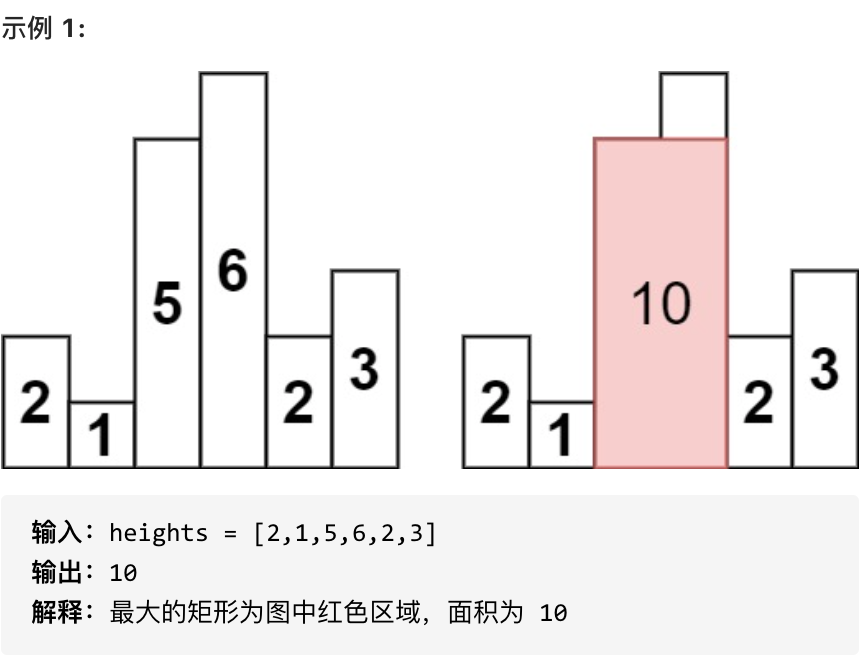
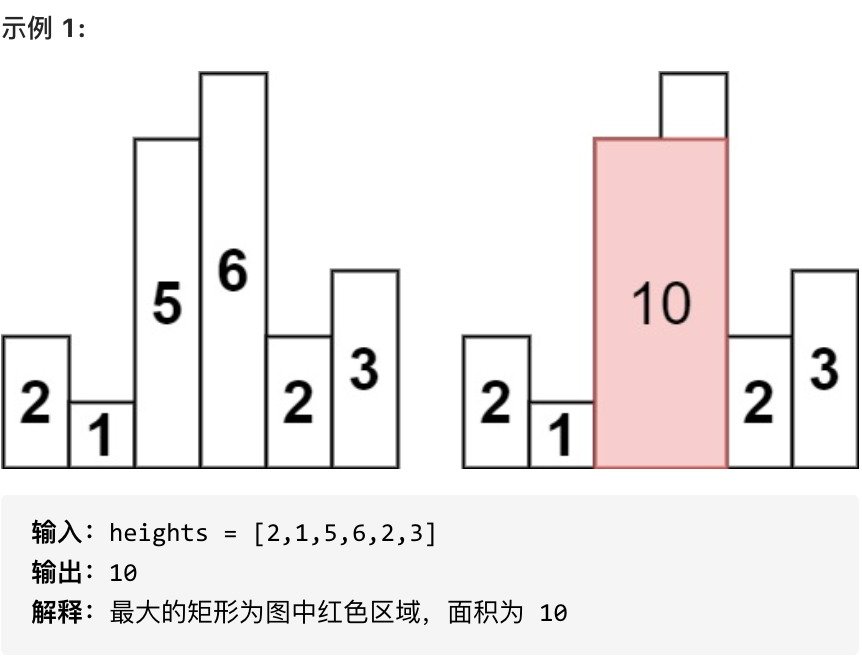
求在该柱状图中,能够勾勒出来的矩形的最大面积。
|
求在该柱状图中,能够勾勒出来的矩形的最大面积。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
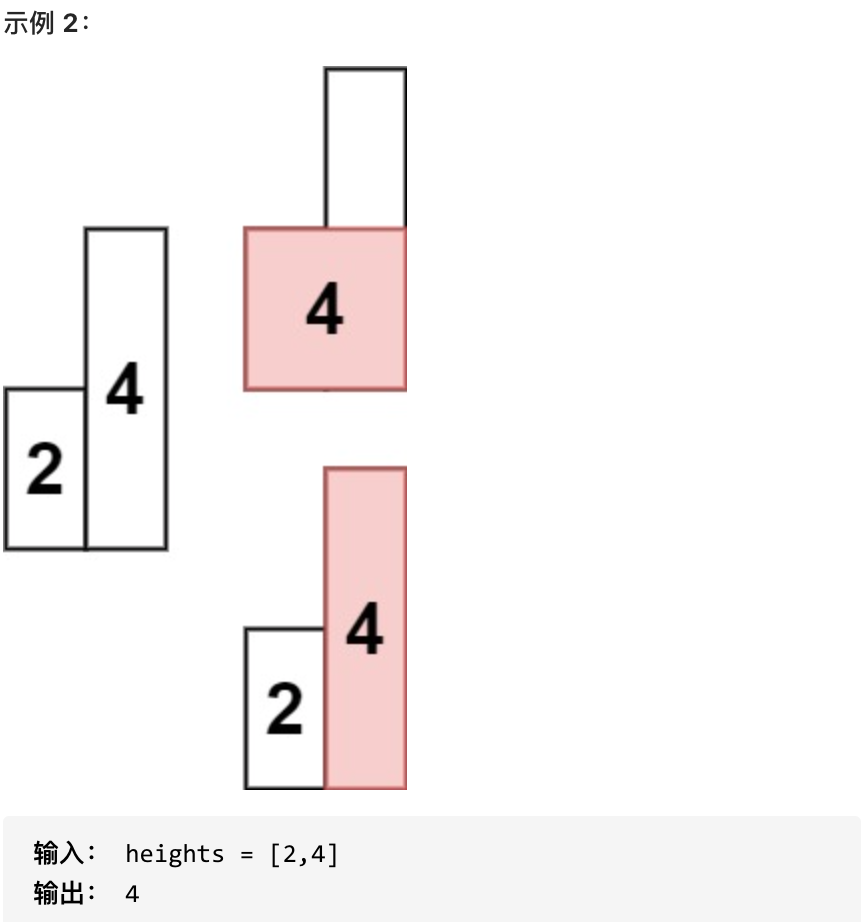
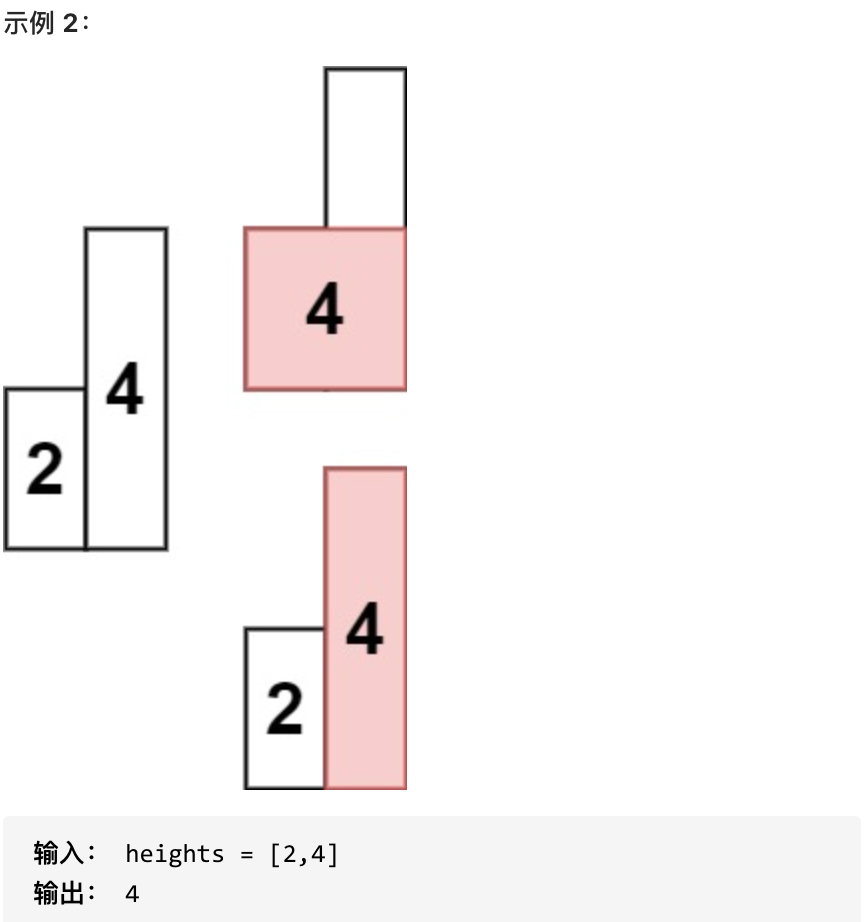
* 1 <= heights.length <=10^5
|
* 1 <= heights.length <=10^5
|
||||||
* 0 <= heights[i] <= 10^4
|
* 0 <= heights[i] <= 10^4
|
||||||
|
|
@ -114,7 +114,7 @@ public:
|
||||||
|
|
||||||
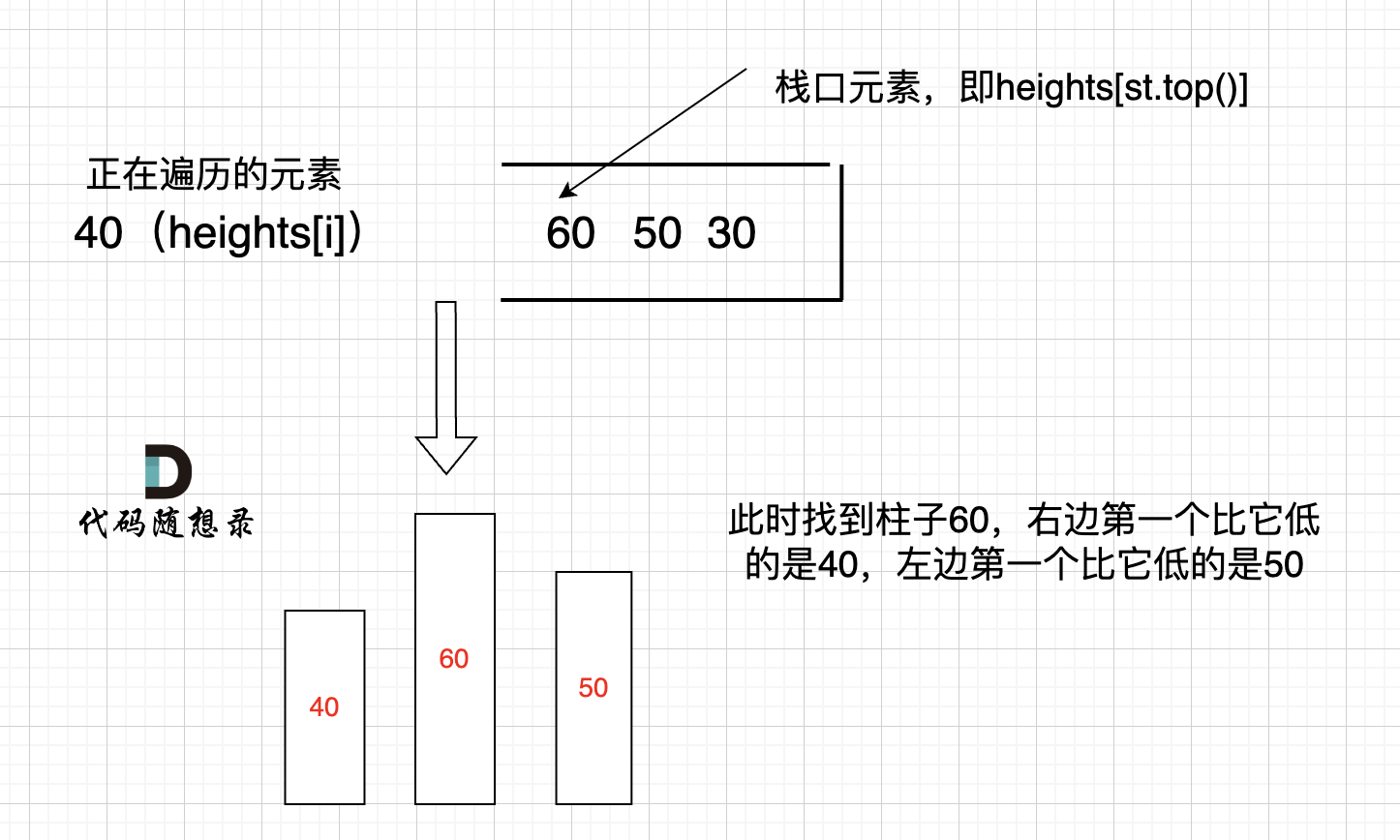
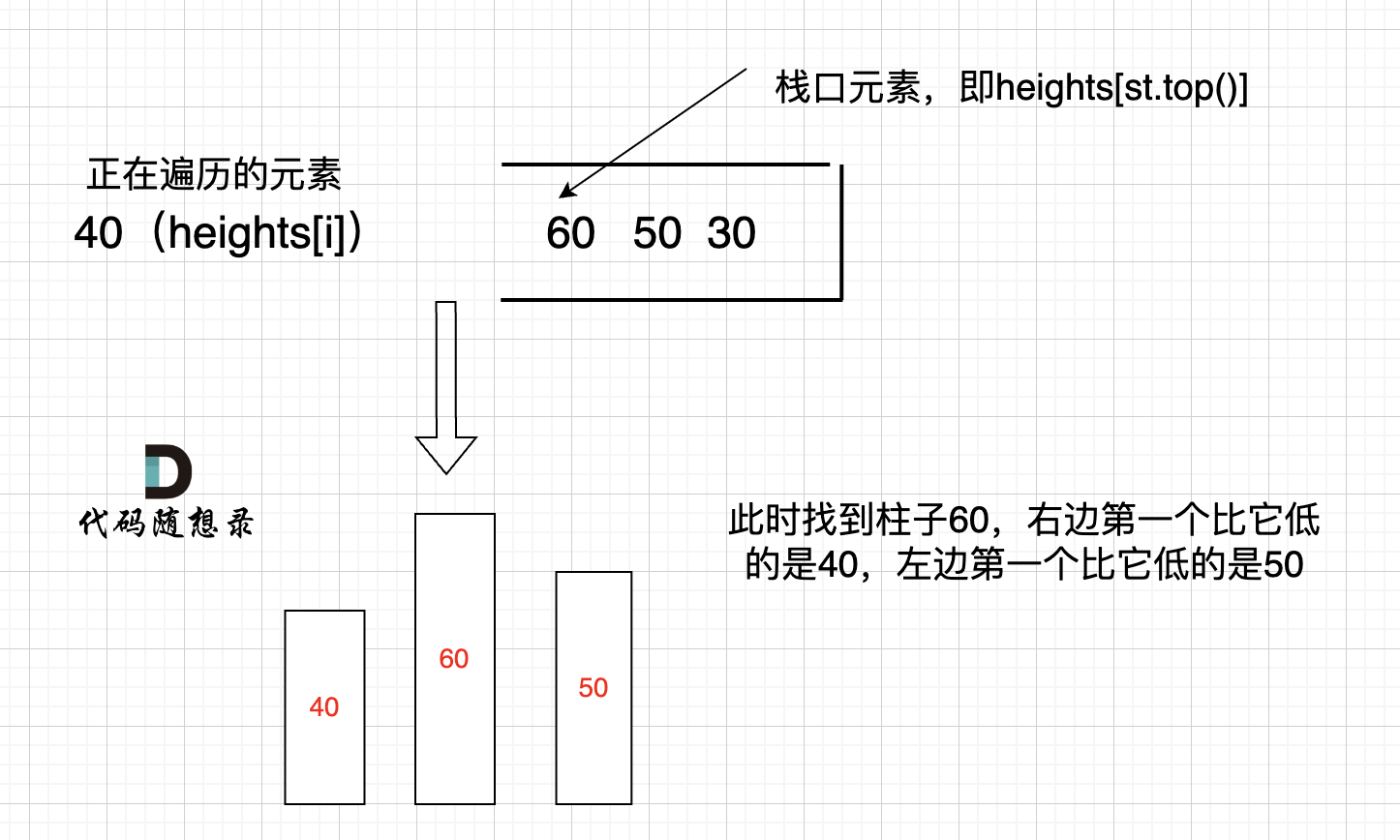
我来举一个例子,如图:
|
我来举一个例子,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
|
只有栈里从大到小的顺序,才能保证栈顶元素找到左右两边第一个小于栈顶元素的柱子。
|
||||||
|
|
||||||
|
|
@ -179,7 +179,7 @@ public:
|
||||||
|
|
||||||
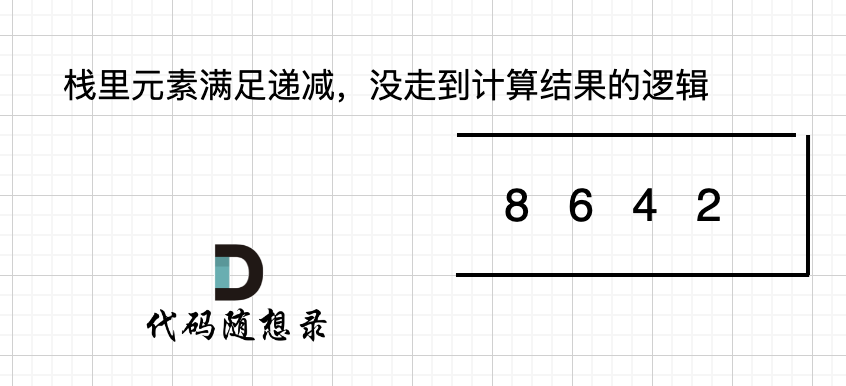
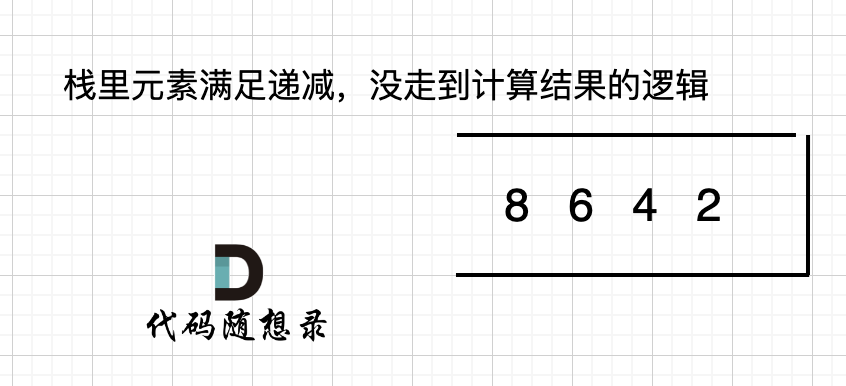
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图:
|
如果数组本身就是升序的,例如[2,4,6,8],那么入栈之后 都是单调递减,一直都没有走 情况三 计算结果的哪一步,所以最后输出的就是0了。 如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
那么结尾加一个0,就会让栈里的所有元素,走到情况三的逻辑。
|
那么结尾加一个0,就会让栈里的所有元素,走到情况三的逻辑。
|
||||||
|
|
||||||
|
|
@ -194,7 +194,7 @@ public:
|
||||||
|
|
||||||
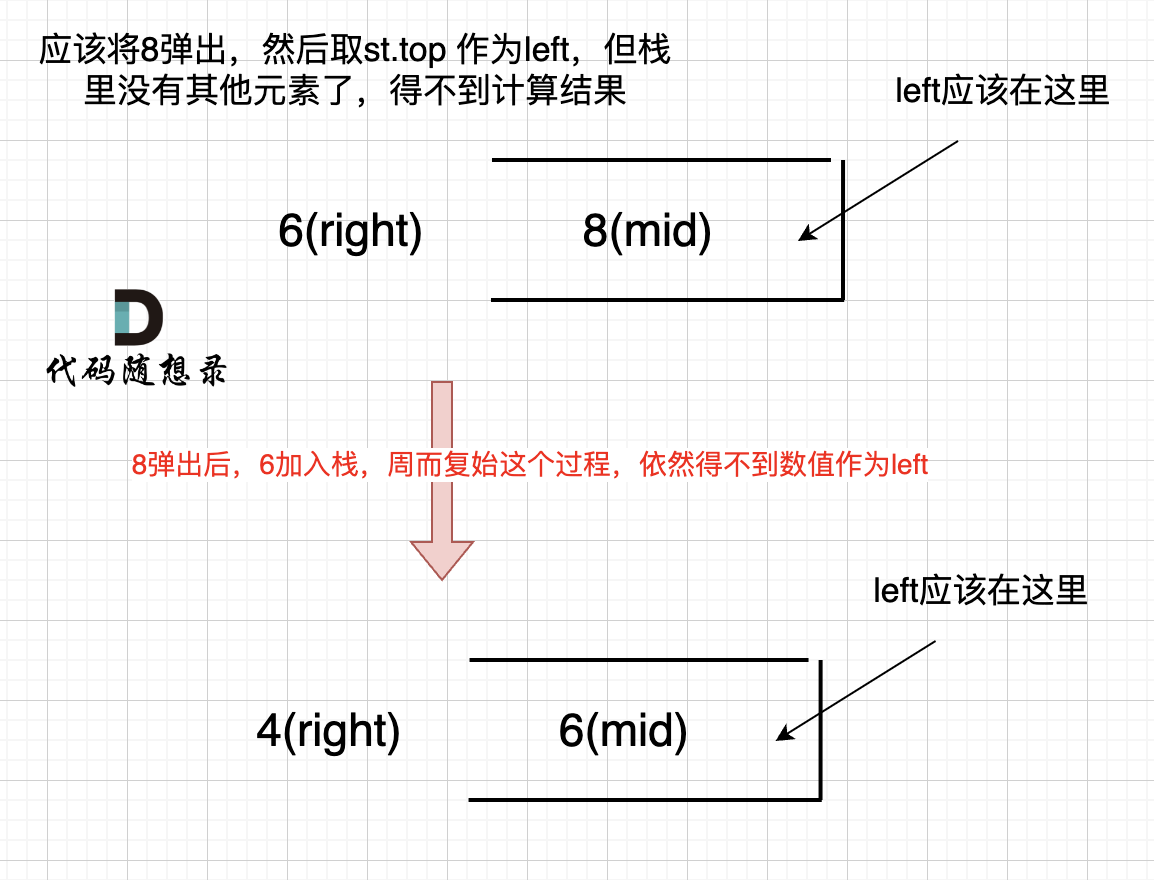
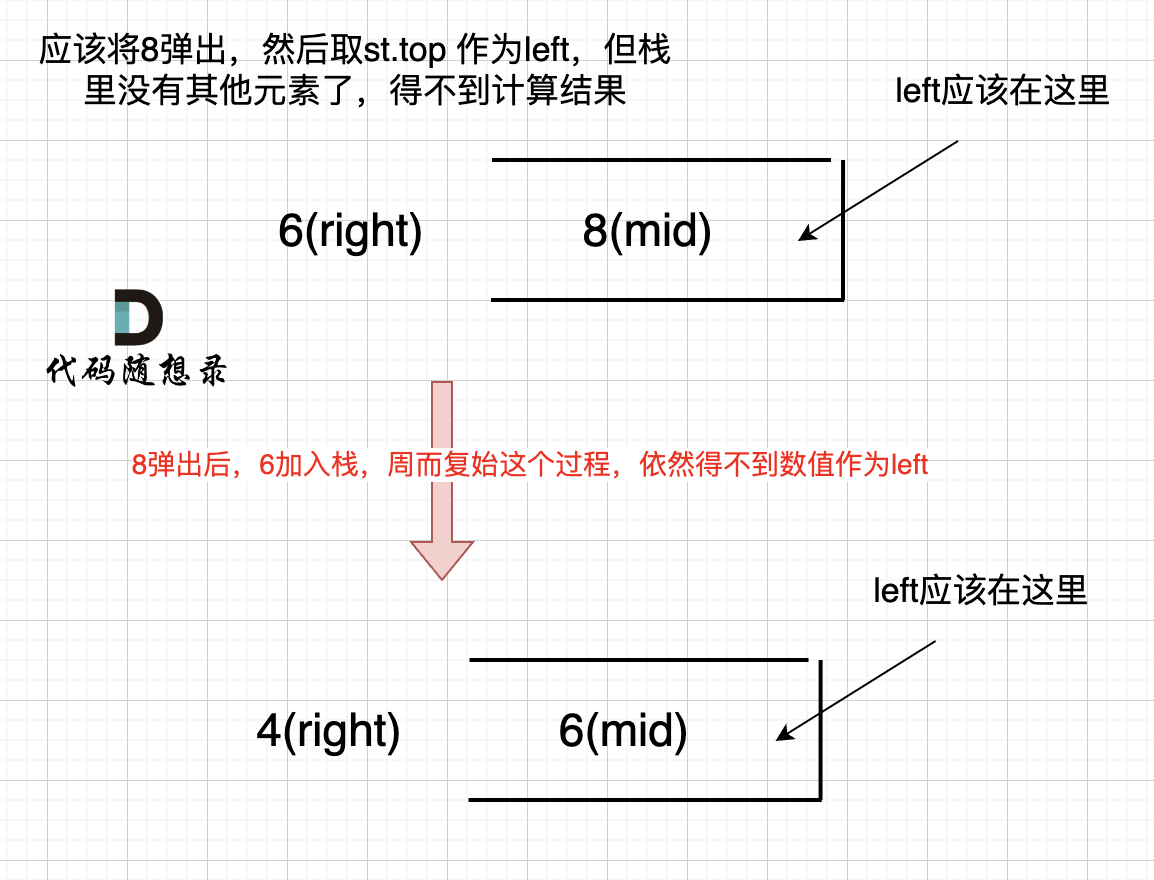
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 6 进行比较,周而复始,那么计算的最后结果result就是0。 如图所示:
|
之后又将6 加入栈(此时8已经弹出了),然后 就是 4 与 栈口元素 6 进行比较,周而复始,那么计算的最后结果result就是0。 如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
所以我们需要在 height数组前后各加一个元素0。
|
所以我们需要在 height数组前后各加一个元素0。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -39,7 +39,7 @@
|
||||||
|
|
||||||
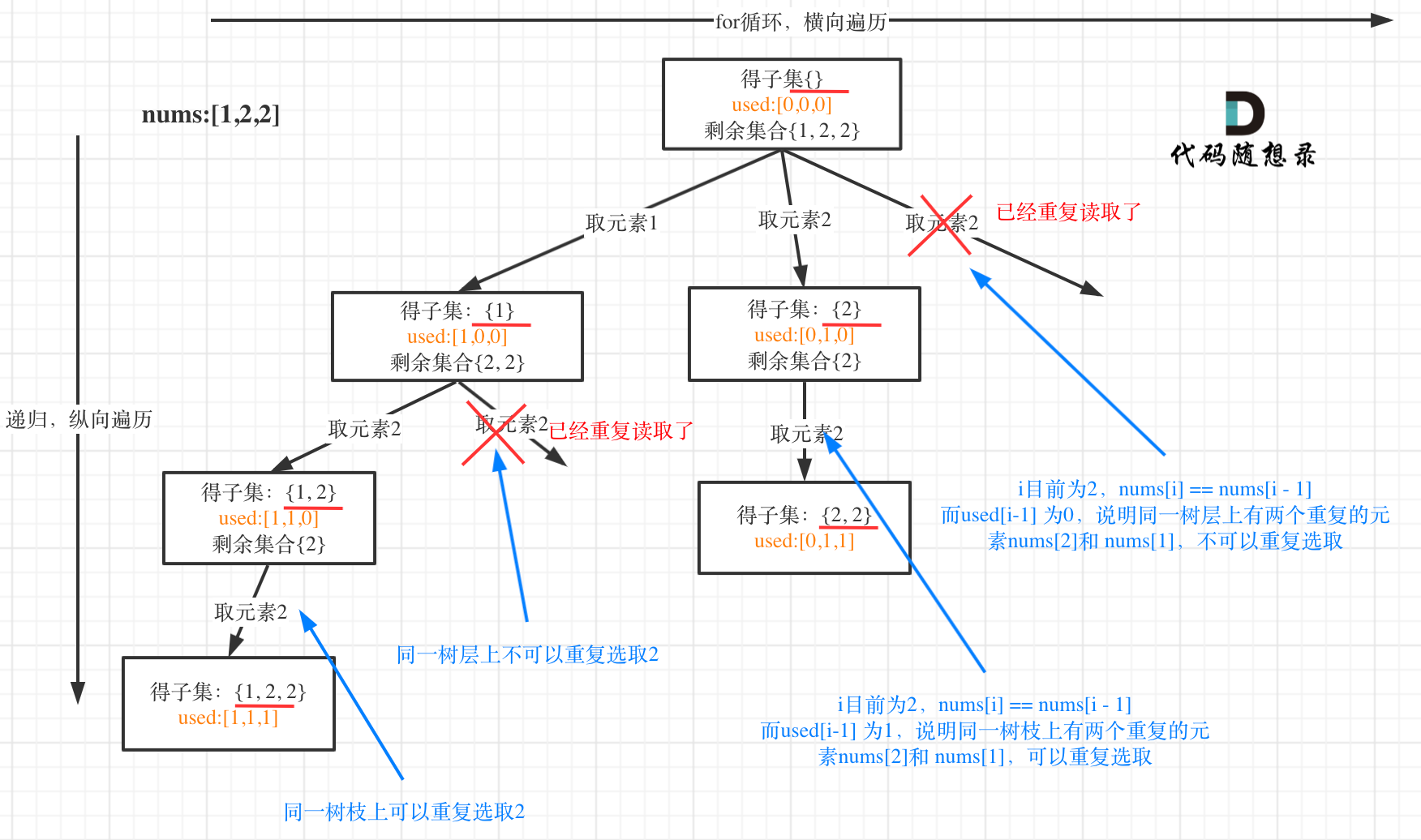
用示例中的[1, 2, 2] 来举例,如图所示: (**注意去重需要先对集合排序**)
|
用示例中的[1, 2, 2] 来举例,如图所示: (**注意去重需要先对集合排序**)
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
|
从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -54,7 +54,7 @@
|
||||||
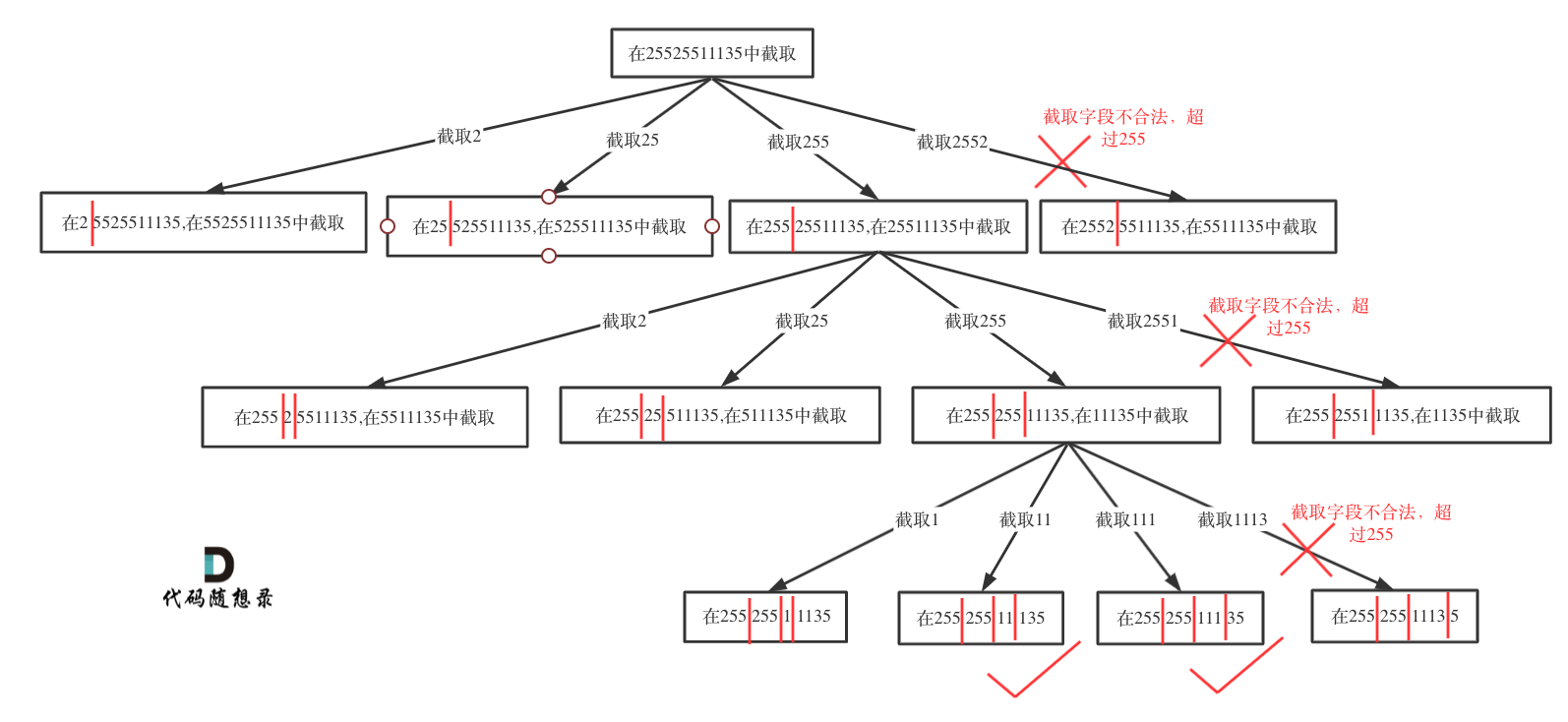
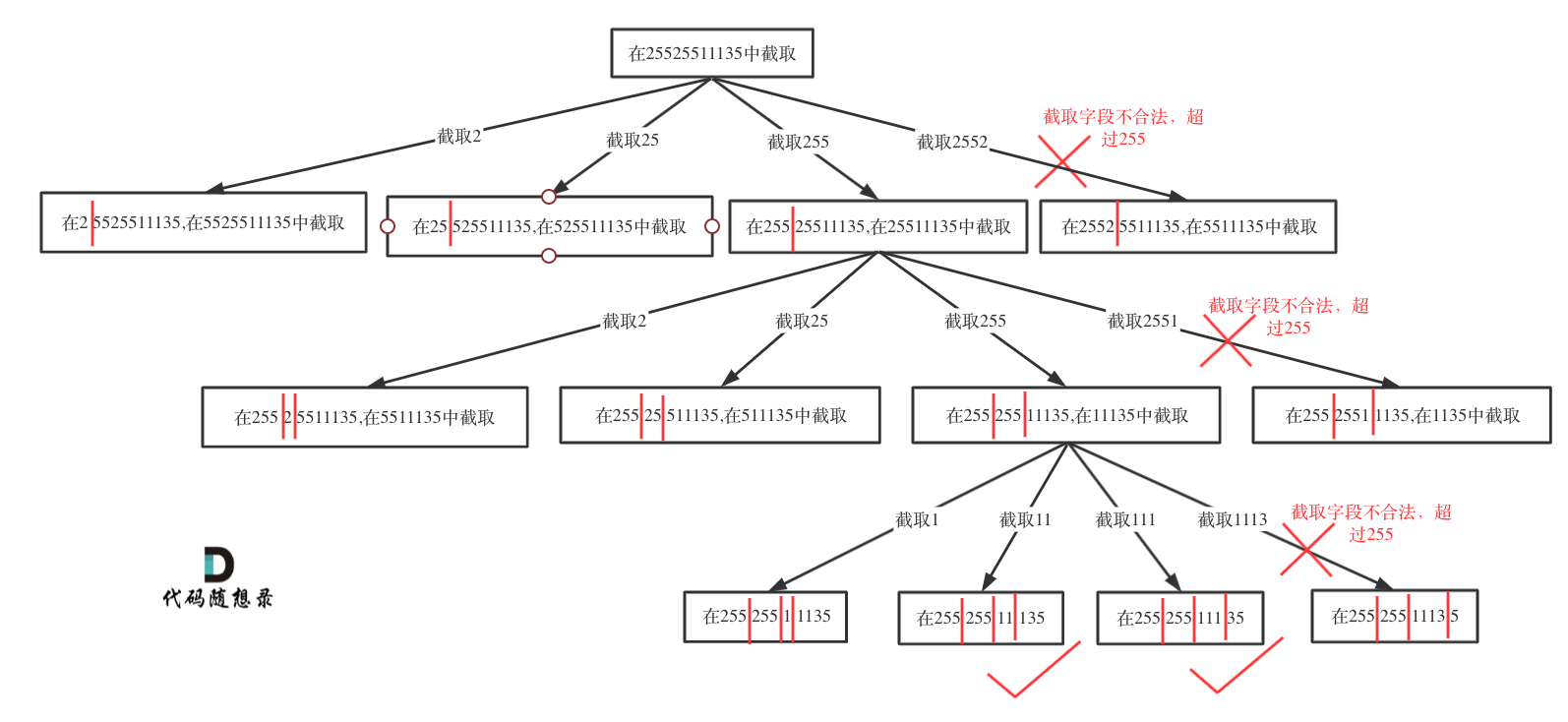
切割问题可以抽象为树型结构,如图:
|
切割问题可以抽象为树型结构,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 回溯三部曲
|
### 回溯三部曲
|
||||||
|
|
@ -106,7 +106,7 @@ if (pointNum == 3) { // 逗点数量为3时,分隔结束
|
||||||
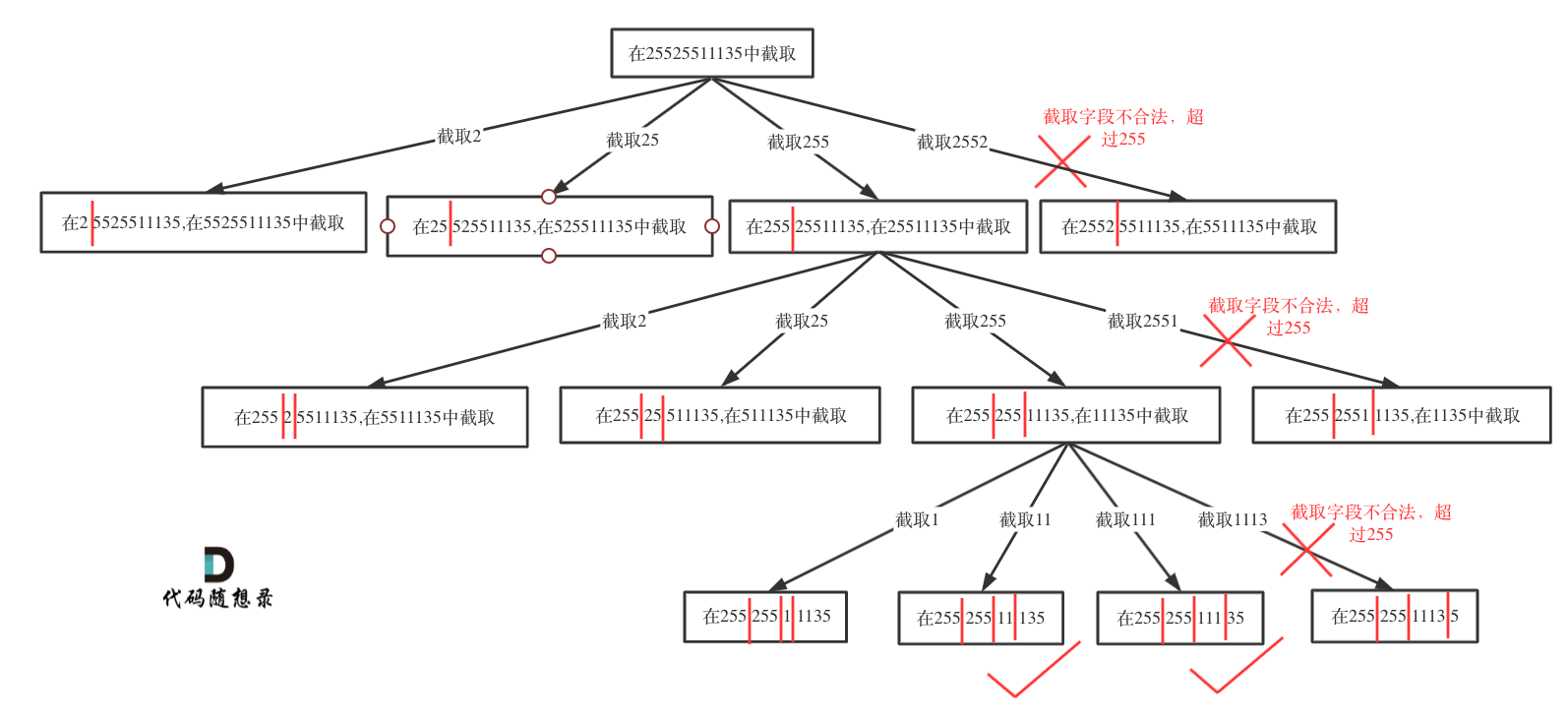
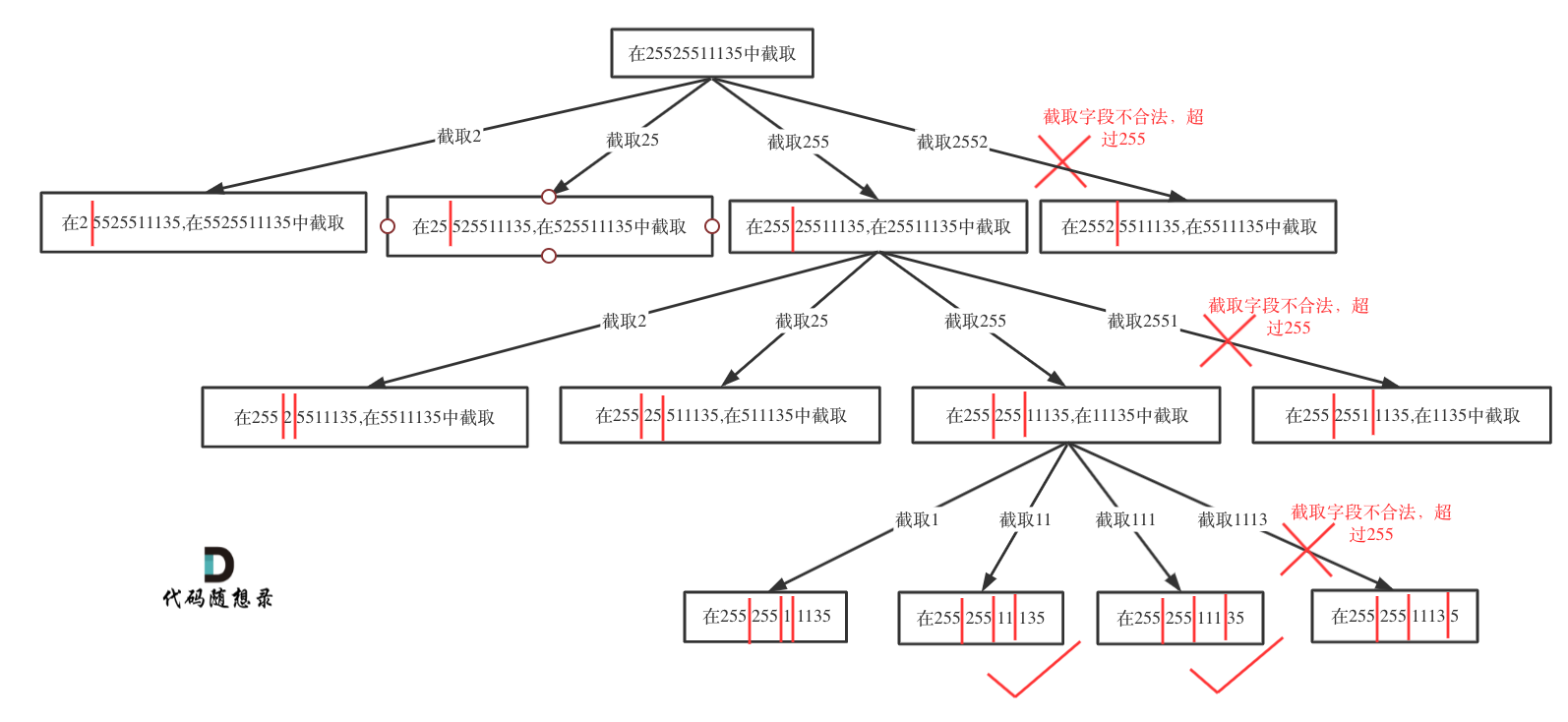
如果不合法就结束本层循环,如图中剪掉的分支:
|
如果不合法就结束本层循环,如图中剪掉的分支:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
然后就是递归和回溯的过程:
|
然后就是递归和回溯的过程:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -12,7 +12,7 @@
|
||||||
|
|
||||||
示例:
|
示例:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -27,11 +27,11 @@
|
||||||
|
|
||||||
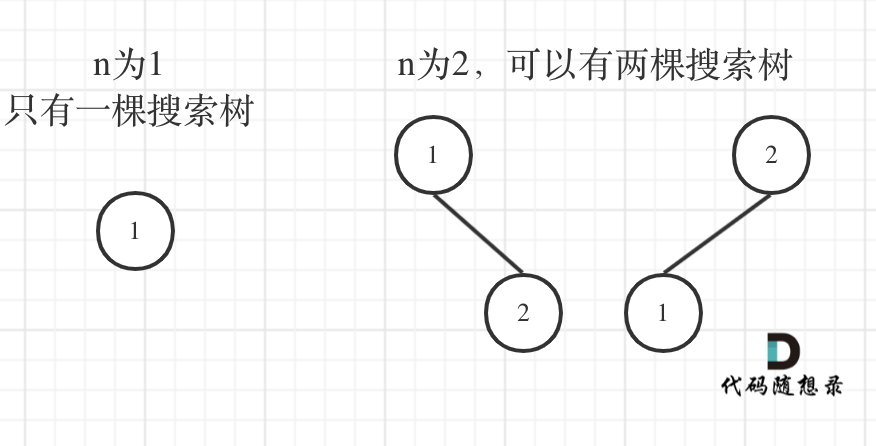
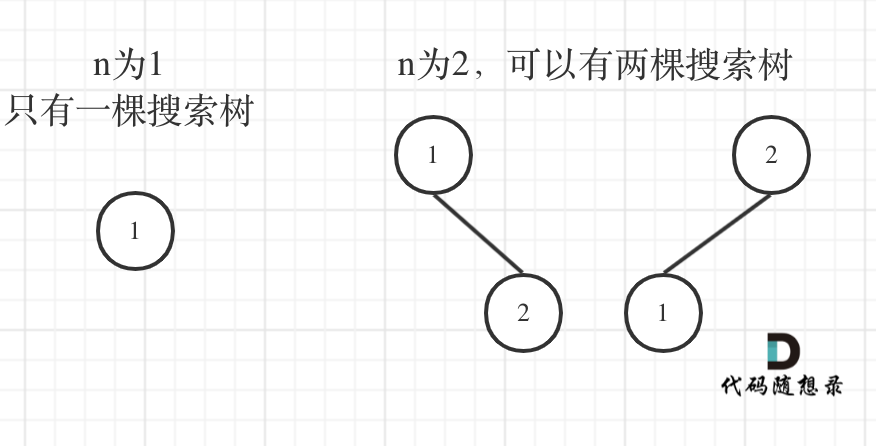
了解了二叉搜索树之后,我们应该先举几个例子,画画图,看看有没有什么规律,如图:
|
了解了二叉搜索树之后,我们应该先举几个例子,画画图,看看有没有什么规律,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
n为1的时候有一棵树,n为2有两棵树,这个是很直观的。
|
n为1的时候有一棵树,n为2有两棵树,这个是很直观的。
|
||||||
|
|
||||||
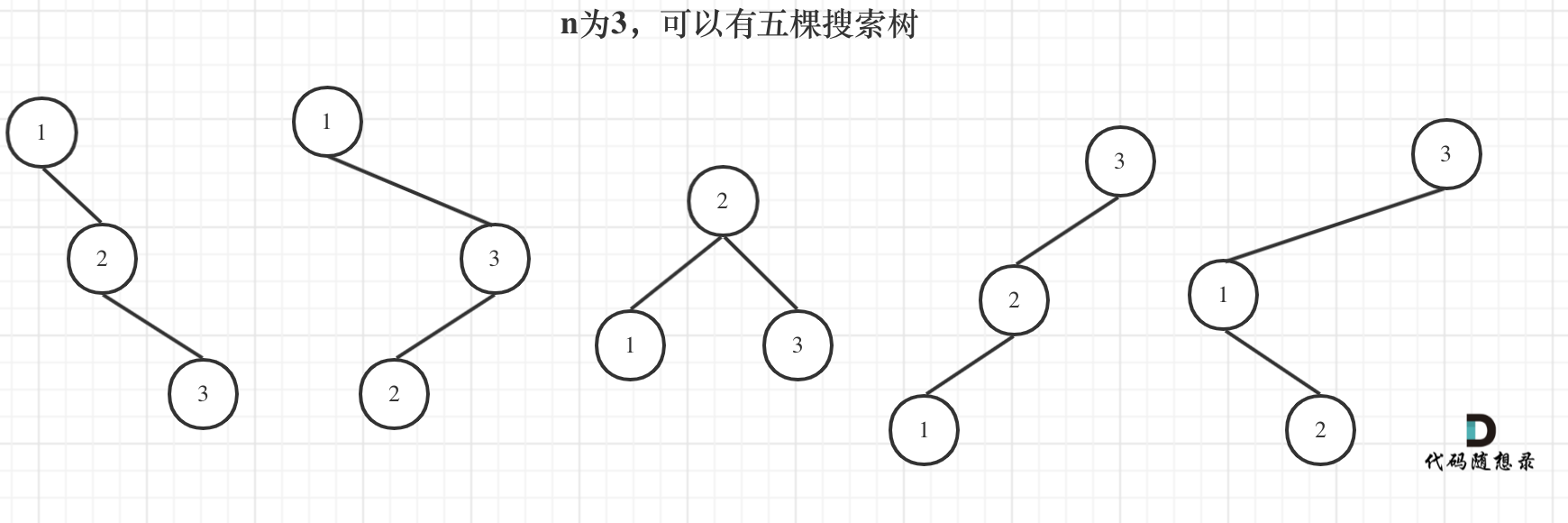
|
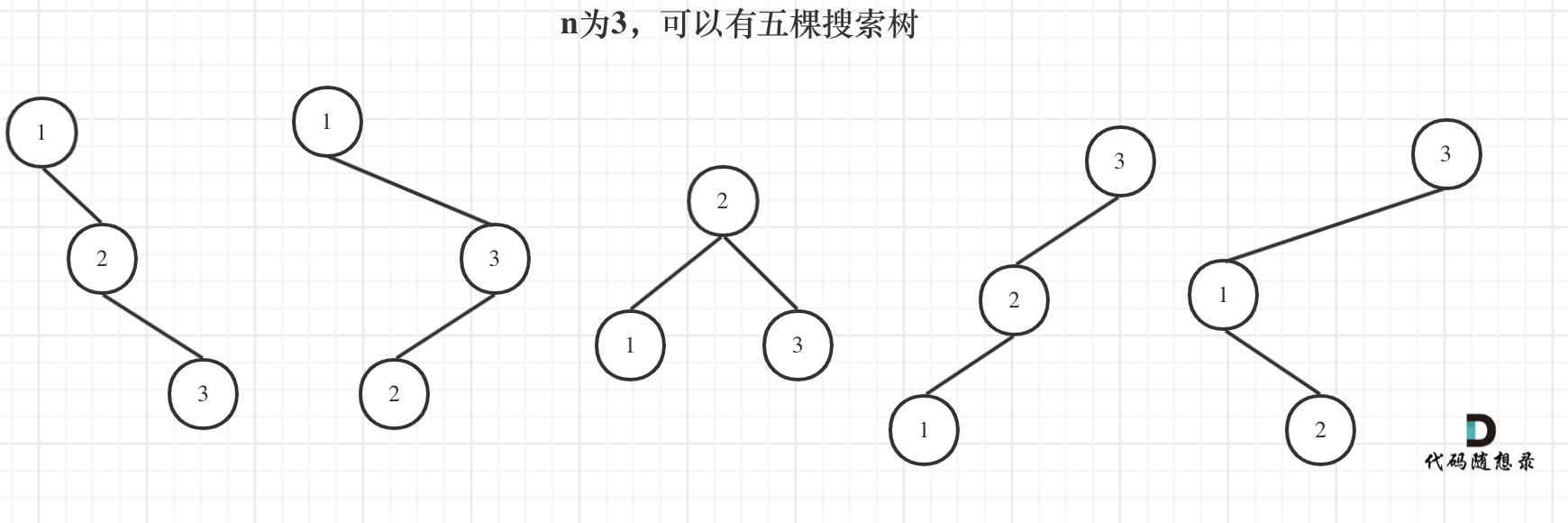
|
||||||
|
|
||||||
来看看n为3的时候,有哪几种情况。
|
来看看n为3的时候,有哪几种情况。
|
||||||
|
|
||||||
|
|
@ -65,7 +65,7 @@ dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索
|
||||||
|
|
||||||
如图所示:
|
如图所示:
|
||||||
|
|
||||||
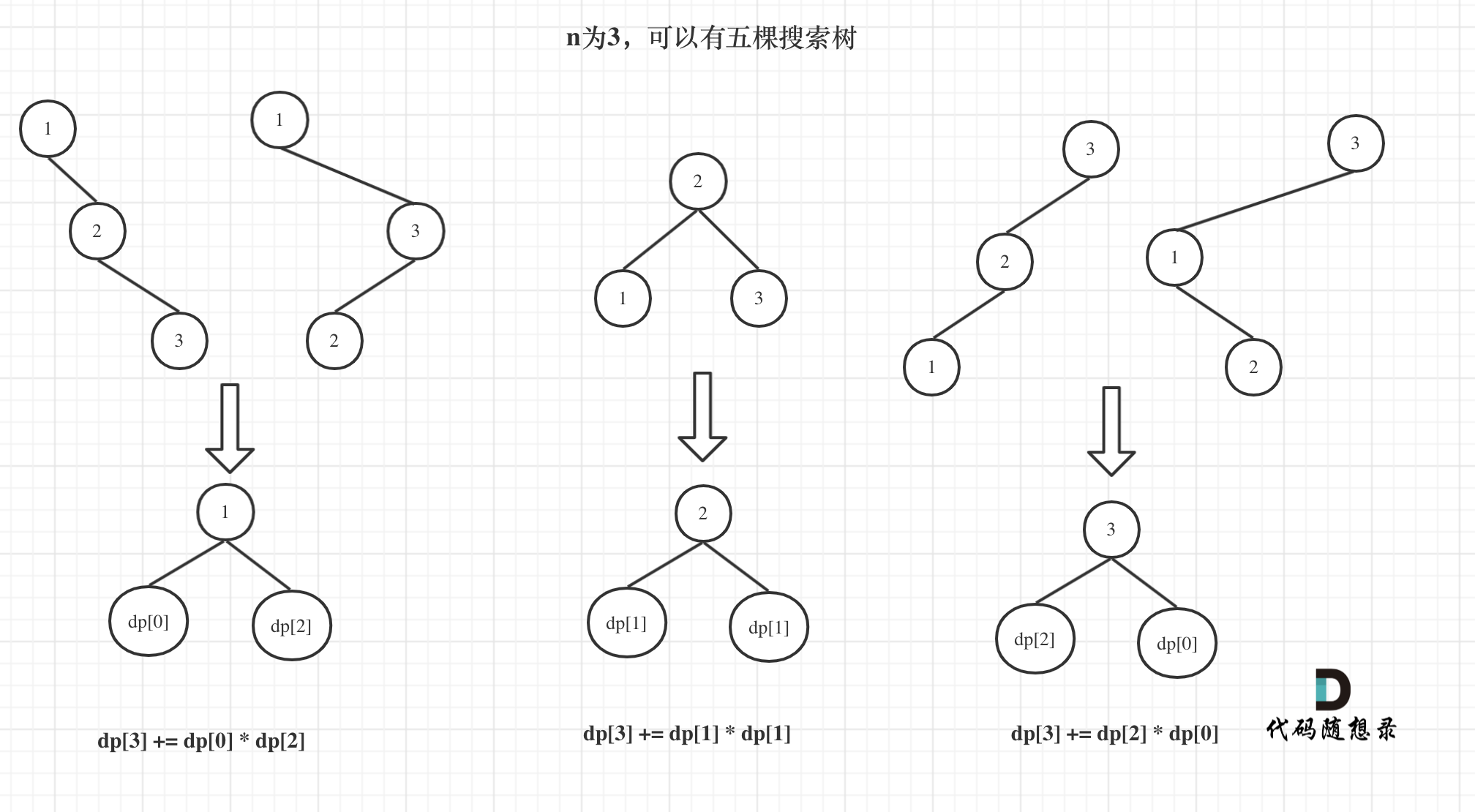
|
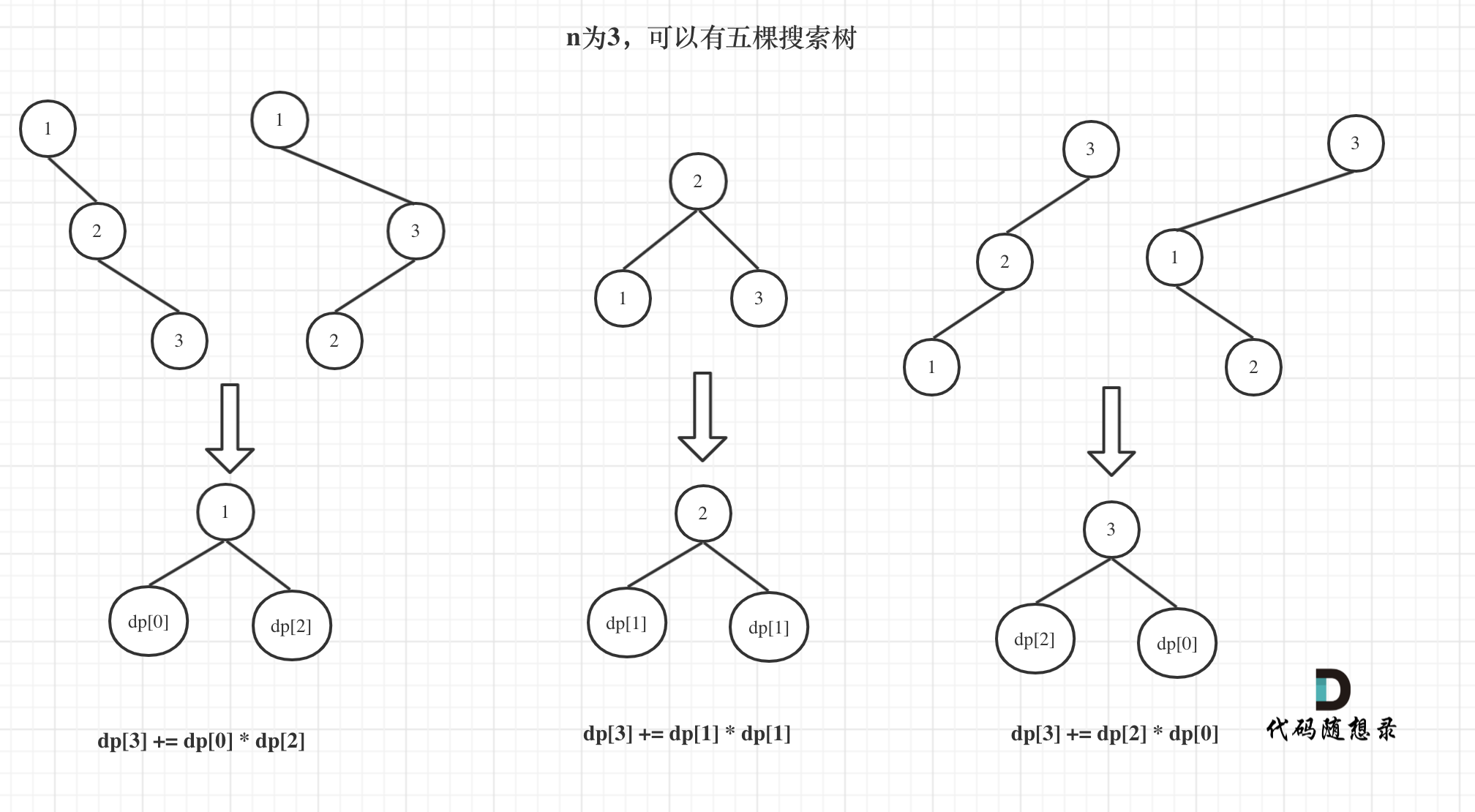
|
||||||
|
|
||||||
|
|
||||||
此时我们已经找到递推关系了,那么可以用动规五部曲再系统分析一遍。
|
此时我们已经找到递推关系了,那么可以用动规五部曲再系统分析一遍。
|
||||||
|
|
@ -118,7 +118,7 @@ for (int i = 1; i <= n; i++) {
|
||||||
|
|
||||||
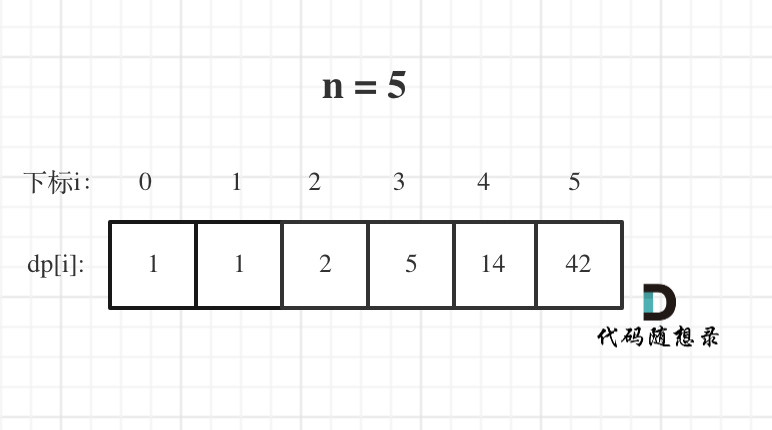
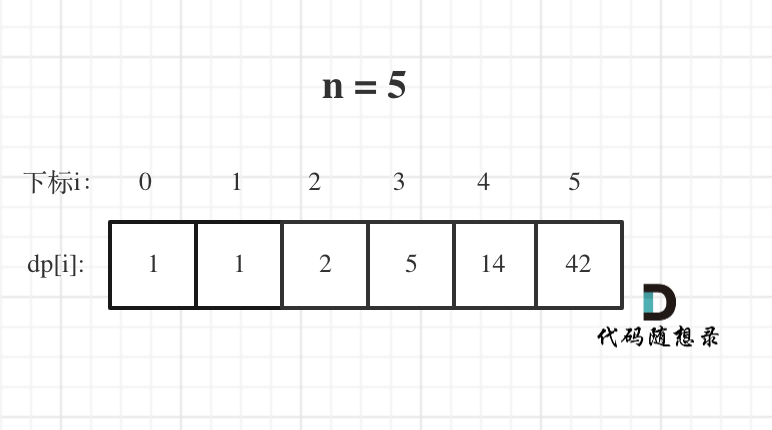
n为5时候的dp数组状态如图:
|
n为5时候的dp数组状态如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
当然如果自己画图举例的话,基本举例到n为3就可以了,n为4的时候,画图已经比较麻烦了。
|
当然如果自己画图举例的话,基本举例到n为3就可以了,n为4的时候,画图已经比较麻烦了。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -16,7 +16,7 @@
|
||||||
* 节点的右子树只包含大于当前节点的数。
|
* 节点的右子树只包含大于当前节点的数。
|
||||||
* 所有左子树和右子树自身必须也是二叉搜索树。
|
* 所有左子树和右子树自身必须也是二叉搜索树。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -102,7 +102,7 @@ if (root->val > root->left->val && root->val < root->right->val) {
|
||||||
|
|
||||||
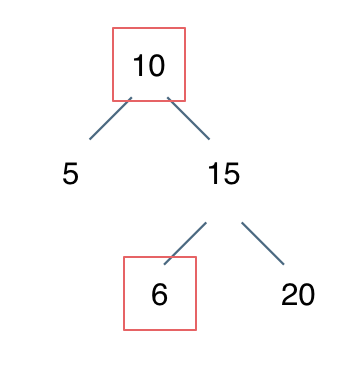
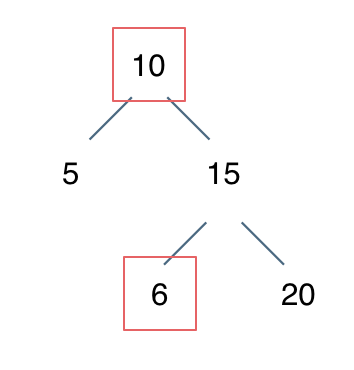
例如: [10,5,15,null,null,6,20] 这个case:
|
例如: [10,5,15,null,null,6,20] 这个case:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
节点10大于左节点5,小于右节点15,但右子树里出现了一个6 这就不符合了!
|
节点10大于左节点5,小于右节点15,但右子树里出现了一个6 这就不符合了!
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -12,9 +12,9 @@
|
||||||
|
|
||||||
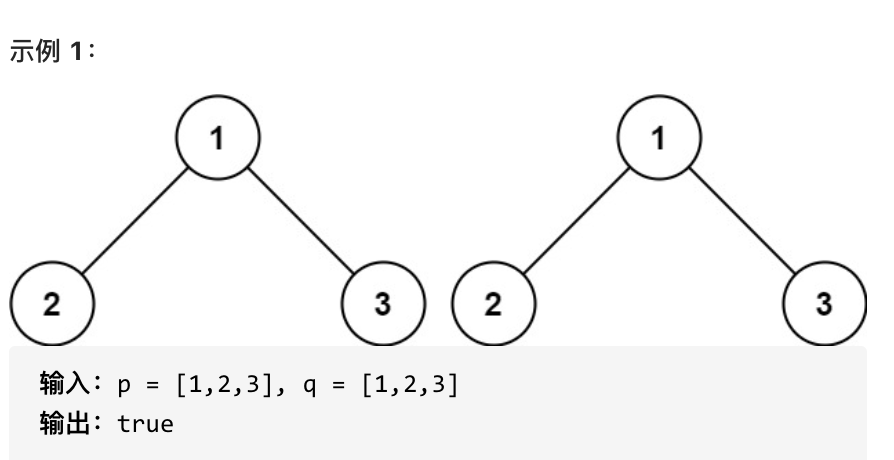
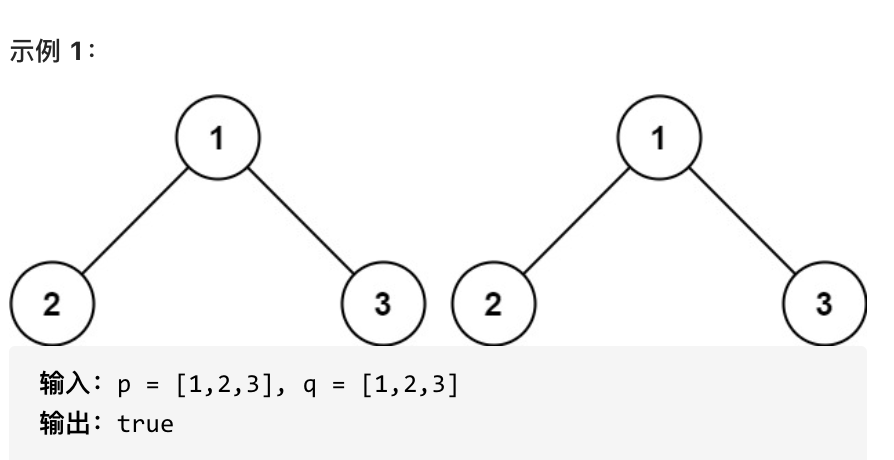
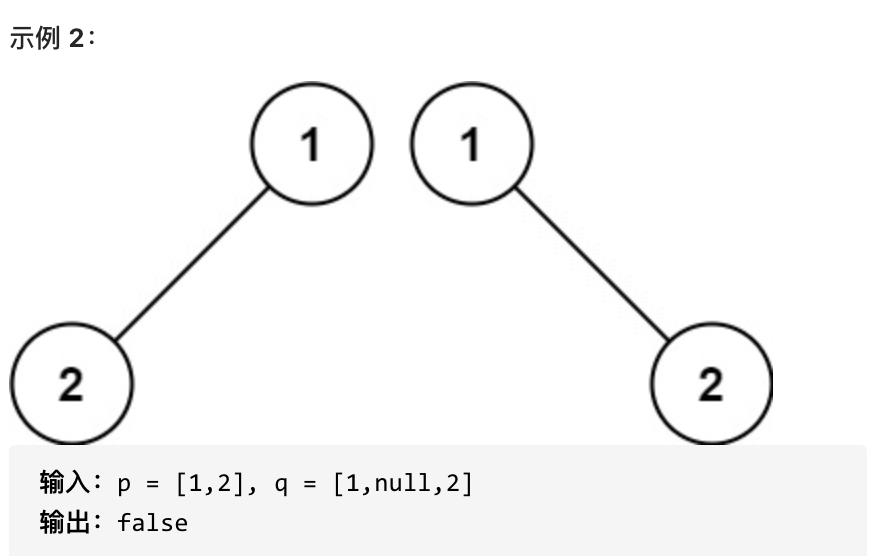
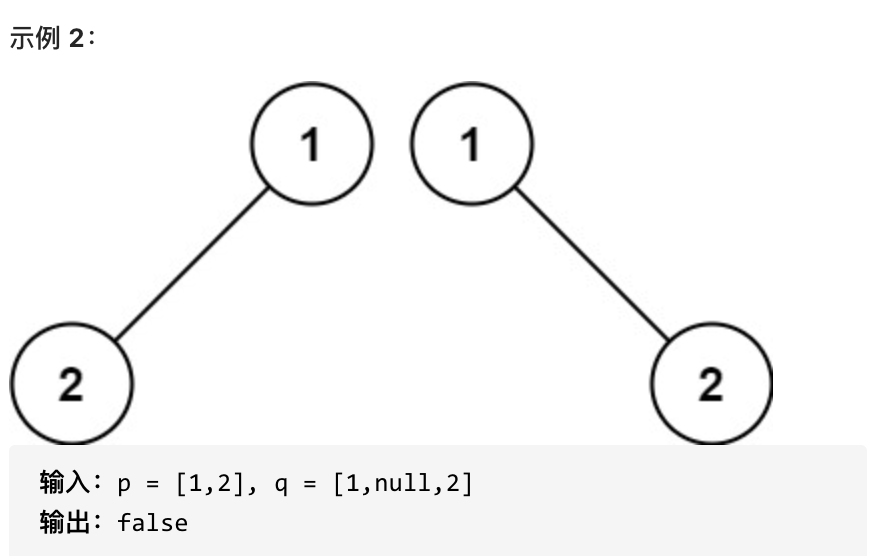
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
|
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
## 思路
|
## 思路
|
||||||
|
|
|
||||||
|
|
@ -9,7 +9,7 @@
|
||||||
|
|
||||||
给定一个二叉树,检查它是否是镜像对称的。
|
给定一个二叉树,检查它是否是镜像对称的。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -25,7 +25,7 @@
|
||||||
|
|
||||||
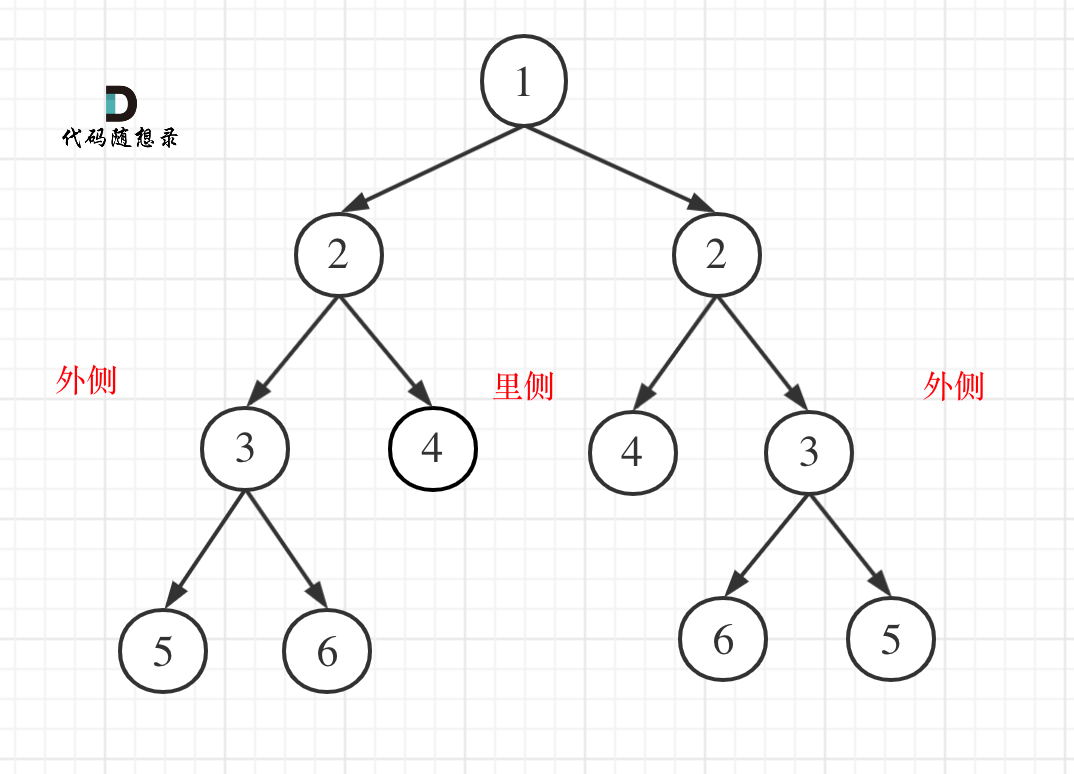
比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
|
比较的是两个子树的里侧和外侧的元素是否相等。如图所示:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
那么遍历的顺序应该是什么样的呢?
|
那么遍历的顺序应该是什么样的呢?
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -37,7 +37,7 @@
|
||||||
|
|
||||||
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
|
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
### 思路
|
### 思路
|
||||||
|
|
||||||
|
|
@ -532,7 +532,7 @@ public IList<IList<int>> LevelOrder(TreeNode root)
|
||||||
|
|
||||||
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
|
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
### 思路
|
### 思路
|
||||||
|
|
||||||
|
|
@ -926,7 +926,7 @@ public IList<IList<int>> LevelOrderBottom(TreeNode root)
|
||||||
|
|
||||||
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
|
给定一棵二叉树,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
### 思路
|
### 思路
|
||||||
|
|
||||||
|
|
@ -1276,7 +1276,7 @@ public class Solution
|
||||||
|
|
||||||
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
|
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
### 思路
|
### 思路
|
||||||
|
|
||||||
|
|
@ -1634,7 +1634,7 @@ public class Solution {
|
||||||
|
|
||||||
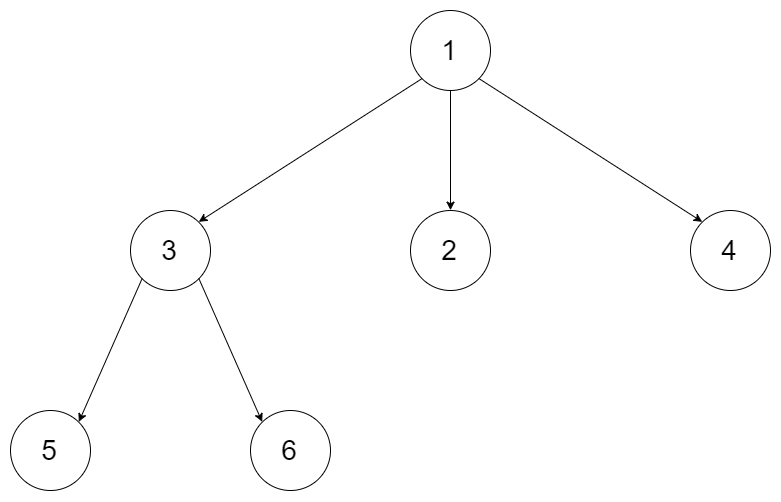
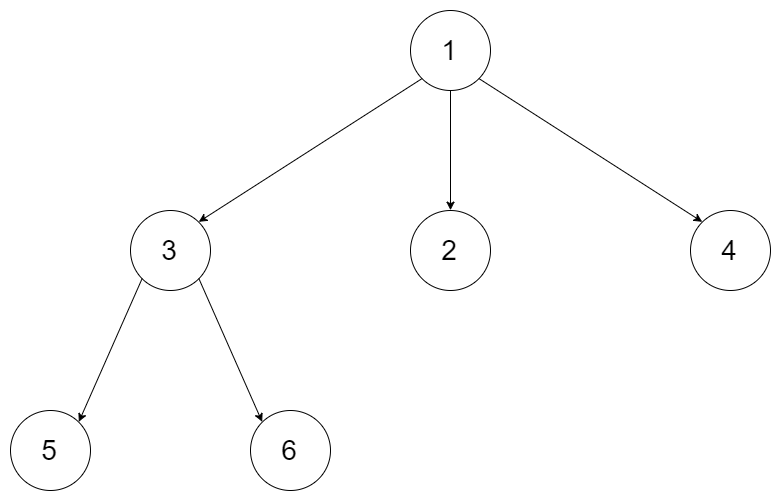
例如,给定一个 3叉树 :
|
例如,给定一个 3叉树 :
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
返回其层序遍历:
|
返回其层序遍历:
|
||||||
|
|
||||||
|
|
@ -2006,7 +2006,7 @@ impl Solution {
|
||||||
|
|
||||||
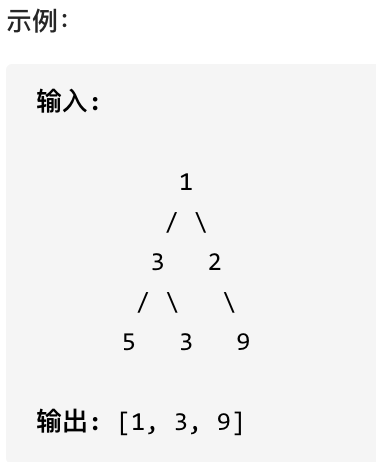
您需要在二叉树的每一行中找到最大的值。
|
您需要在二叉树的每一行中找到最大的值。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 思路
|
### 思路
|
||||||
|
|
||||||
|
|
@ -2337,7 +2337,7 @@ struct Node {
|
||||||
|
|
||||||
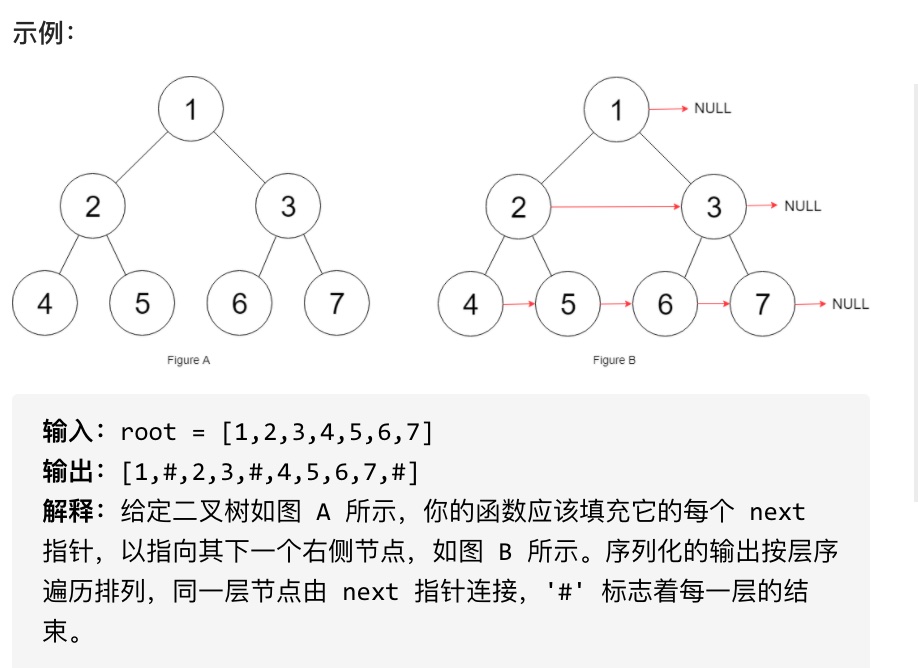
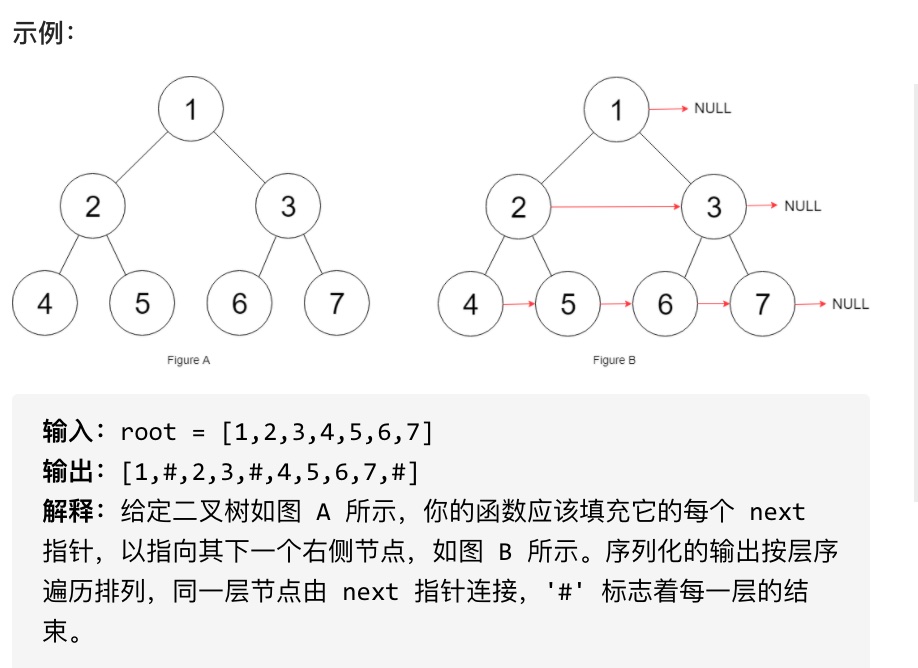
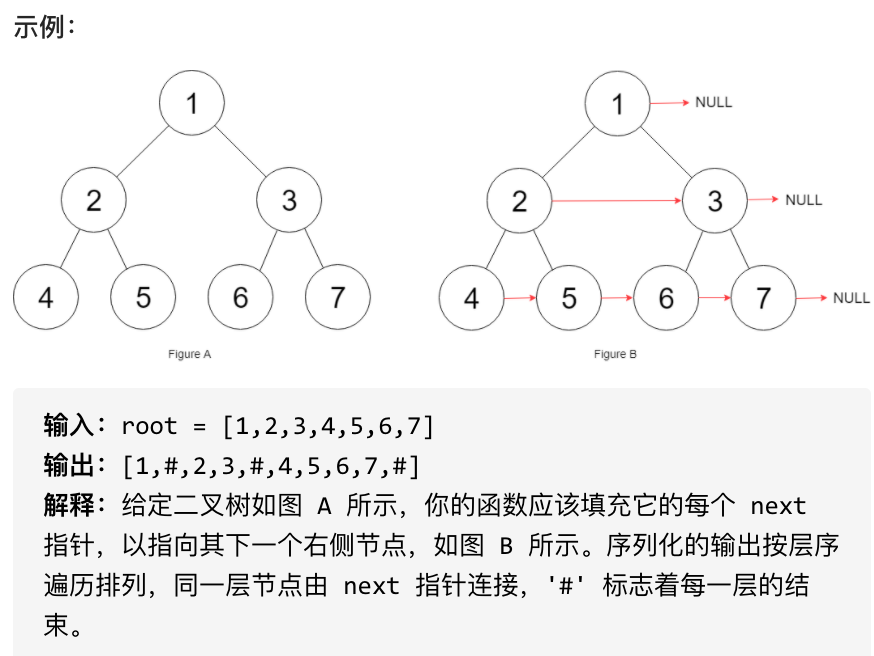
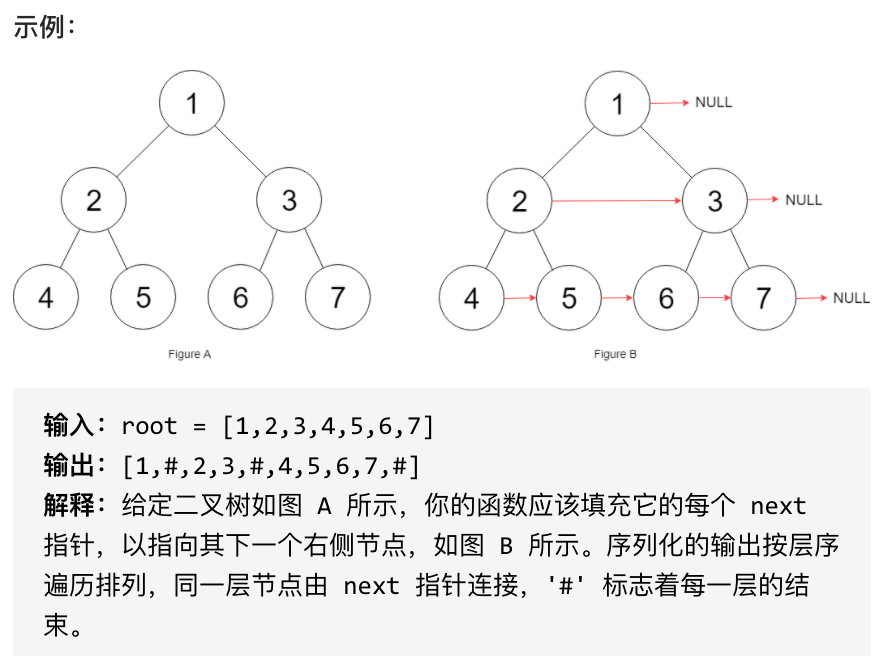
初始状态下,所有 next 指针都被设置为 NULL。
|
初始状态下,所有 next 指针都被设置为 NULL。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 思路
|
### 思路
|
||||||
|
|
||||||
|
|
@ -2971,7 +2971,7 @@ object Solution {
|
||||||
|
|
||||||
给定二叉树 [3,9,20,null,null,15,7],
|
给定二叉树 [3,9,20,null,null,15,7],
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
返回它的最大深度 3 。
|
返回它的最大深度 3 。
|
||||||
|
|
||||||
|
|
@ -2981,7 +2981,7 @@ object Solution {
|
||||||
|
|
||||||
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
|
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
|
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -18,7 +18,7 @@
|
||||||
给定二叉树 [3,9,20,null,null,15,7],
|
给定二叉树 [3,9,20,null,null,15,7],
|
||||||
|
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
返回它的最大深度 3 。
|
返回它的最大深度 3 。
|
||||||
|
|
||||||
|
|
@ -172,7 +172,7 @@ public:
|
||||||
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
|
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
|
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
|
||||||
|
|
||||||
|
|
@ -217,7 +217,7 @@ public:
|
||||||
|
|
||||||
例如,给定一个 3叉树 :
|
例如,给定一个 3叉树 :
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
我们应返回其最大深度,3。
|
我们应返回其最大深度,3。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -25,7 +25,7 @@
|
||||||
* 后序遍历 postorder = [9,15,7,20,3]
|
* 后序遍历 postorder = [9,15,7,20,3]
|
||||||
返回如下的二叉树:
|
返回如下的二叉树:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -40,7 +40,7 @@
|
||||||
|
|
||||||
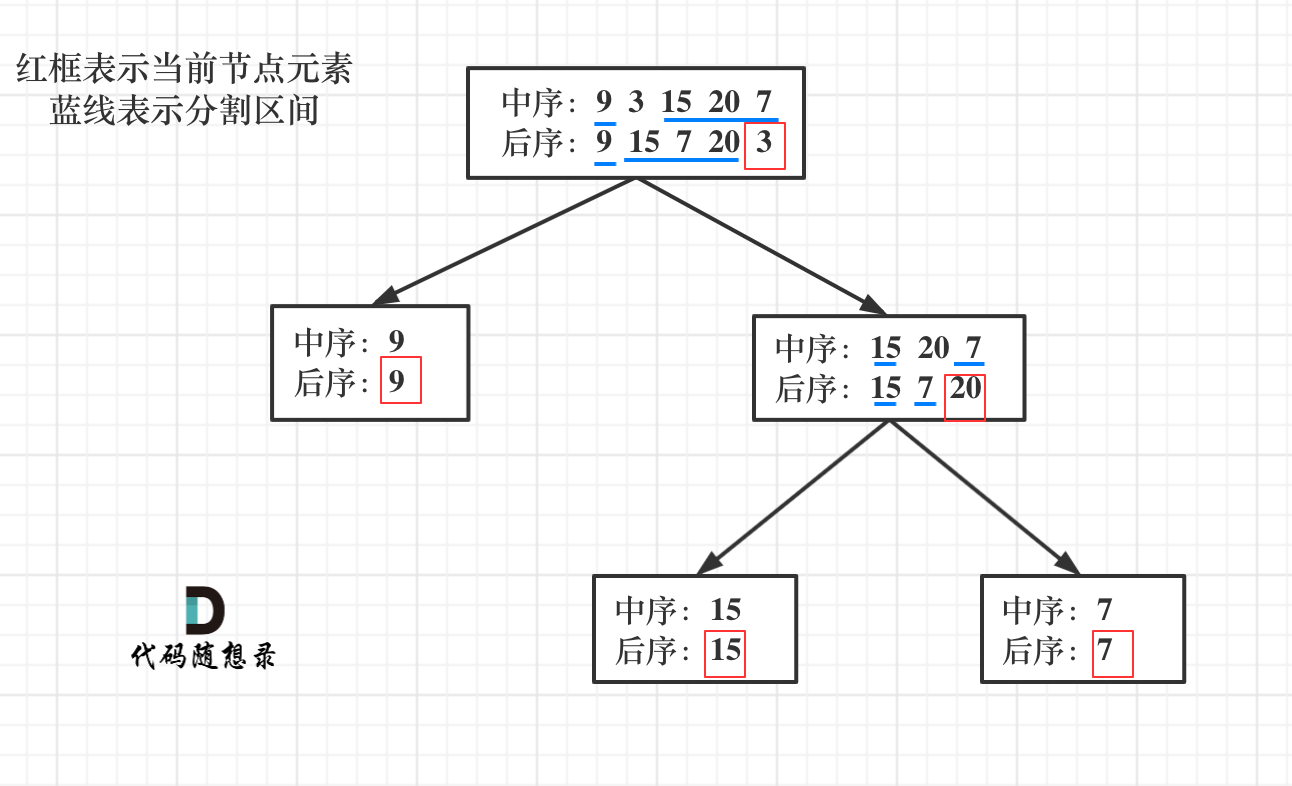
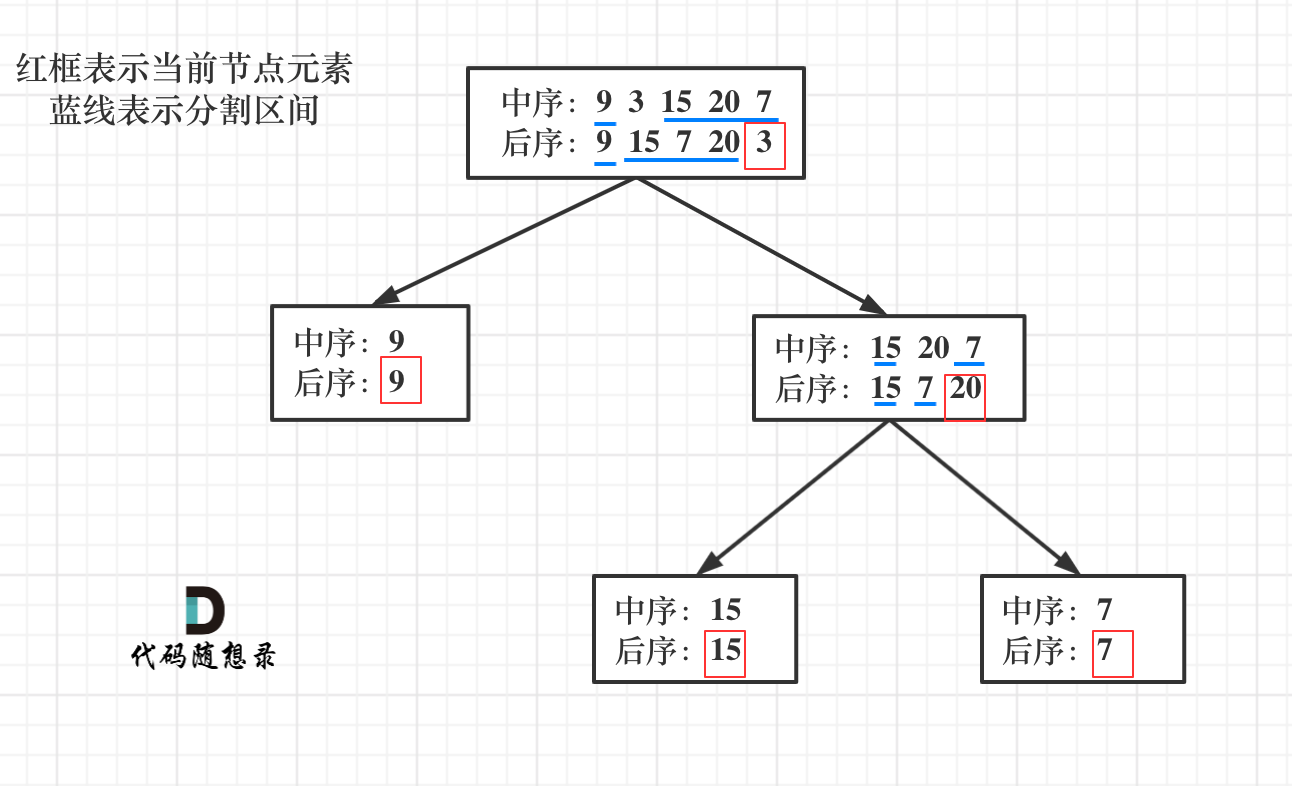
流程如图:
|
流程如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
那么代码应该怎么写呢?
|
那么代码应该怎么写呢?
|
||||||
|
|
||||||
|
|
@ -411,7 +411,7 @@ public:
|
||||||
中序遍历 inorder = [9,3,15,20,7]
|
中序遍历 inorder = [9,3,15,20,7]
|
||||||
返回如下的二叉树:
|
返回如下的二叉树:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
### 思路
|
### 思路
|
||||||
|
|
||||||
|
|
@ -554,7 +554,7 @@ public:
|
||||||
|
|
||||||
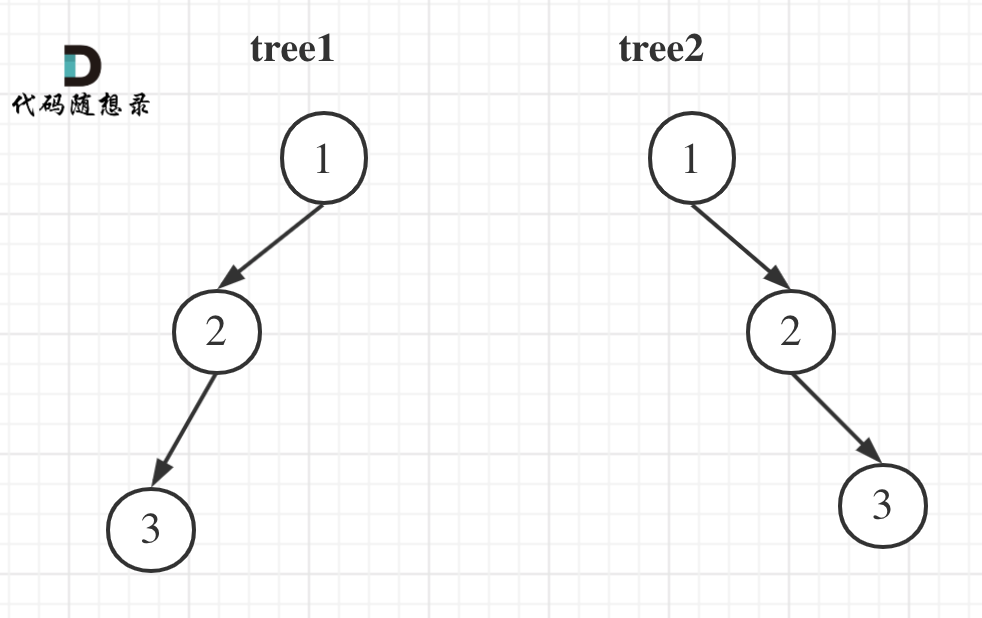
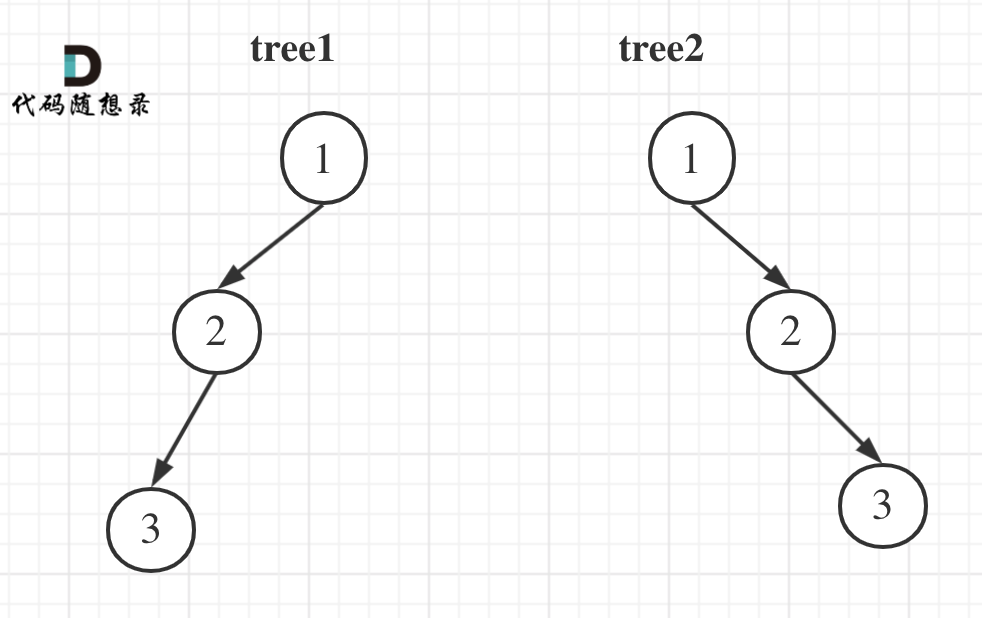
举一个例子:
|
举一个例子:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
|
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -16,7 +16,7 @@
|
||||||
示例:
|
示例:
|
||||||
|
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -40,7 +40,7 @@
|
||||||
|
|
||||||
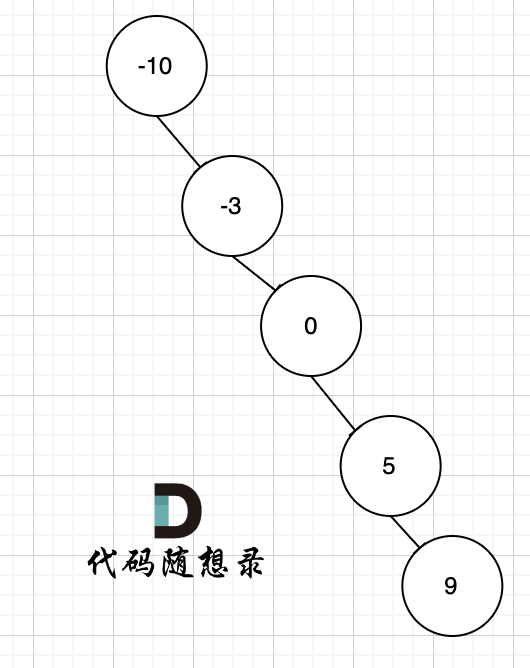
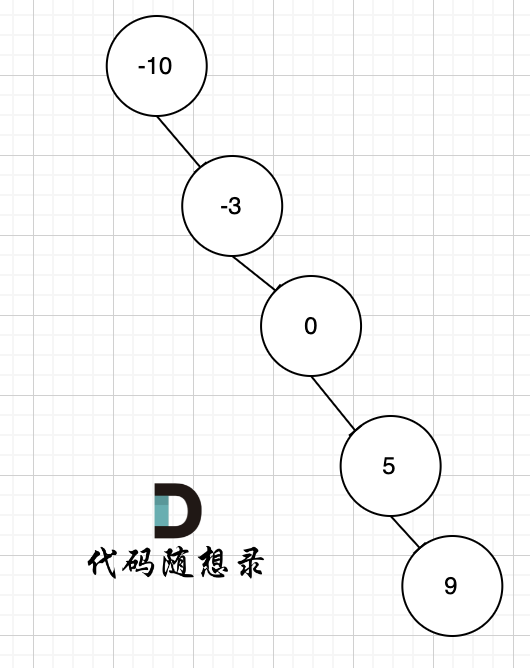
例如 有序数组[-10,-3,0,5,9] 就可以构造成这样的二叉搜索树,如图。
|
例如 有序数组[-10,-3,0,5,9] 就可以构造成这样的二叉搜索树,如图。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
上图中,是符合二叉搜索树的特性吧,如果要这么做的话,是不是本题意义就不大了,所以才强调是平衡二叉搜索树。
|
上图中,是符合二叉搜索树的特性吧,如果要这么做的话,是不是本题意义就不大了,所以才强调是平衡二叉搜索树。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -19,7 +19,7 @@
|
||||||
|
|
||||||
给定二叉树 [3,9,20,null,null,15,7]
|
给定二叉树 [3,9,20,null,null,15,7]
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
返回 true 。
|
返回 true 。
|
||||||
|
|
||||||
|
|
@ -27,7 +27,7 @@
|
||||||
|
|
||||||
给定二叉树 [1,2,2,3,3,null,null,4,4]
|
给定二叉树 [1,2,2,3,3,null,null,4,4]
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
返回 false 。
|
返回 false 。
|
||||||
|
|
||||||
|
|
@ -46,7 +46,7 @@
|
||||||
|
|
||||||
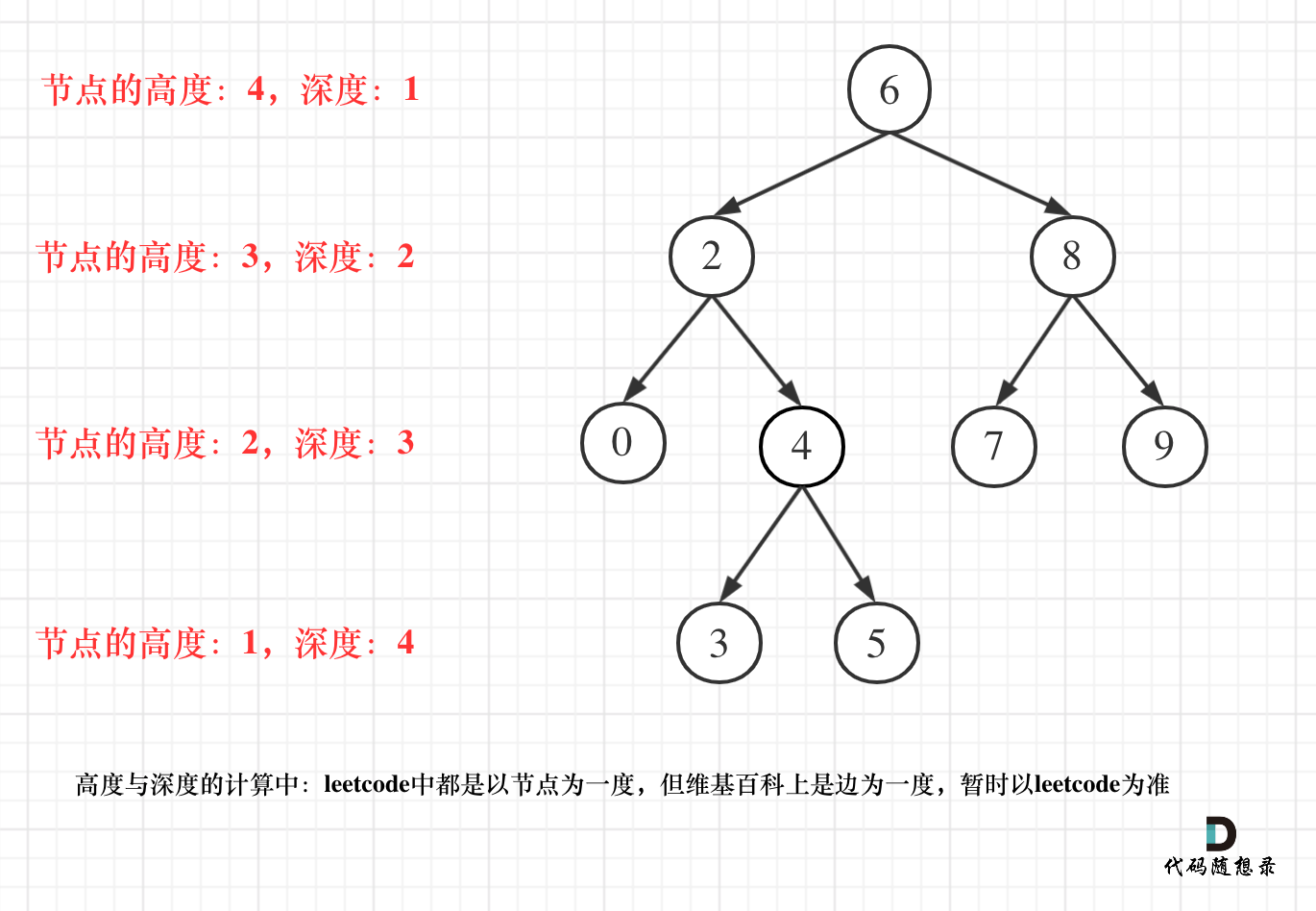
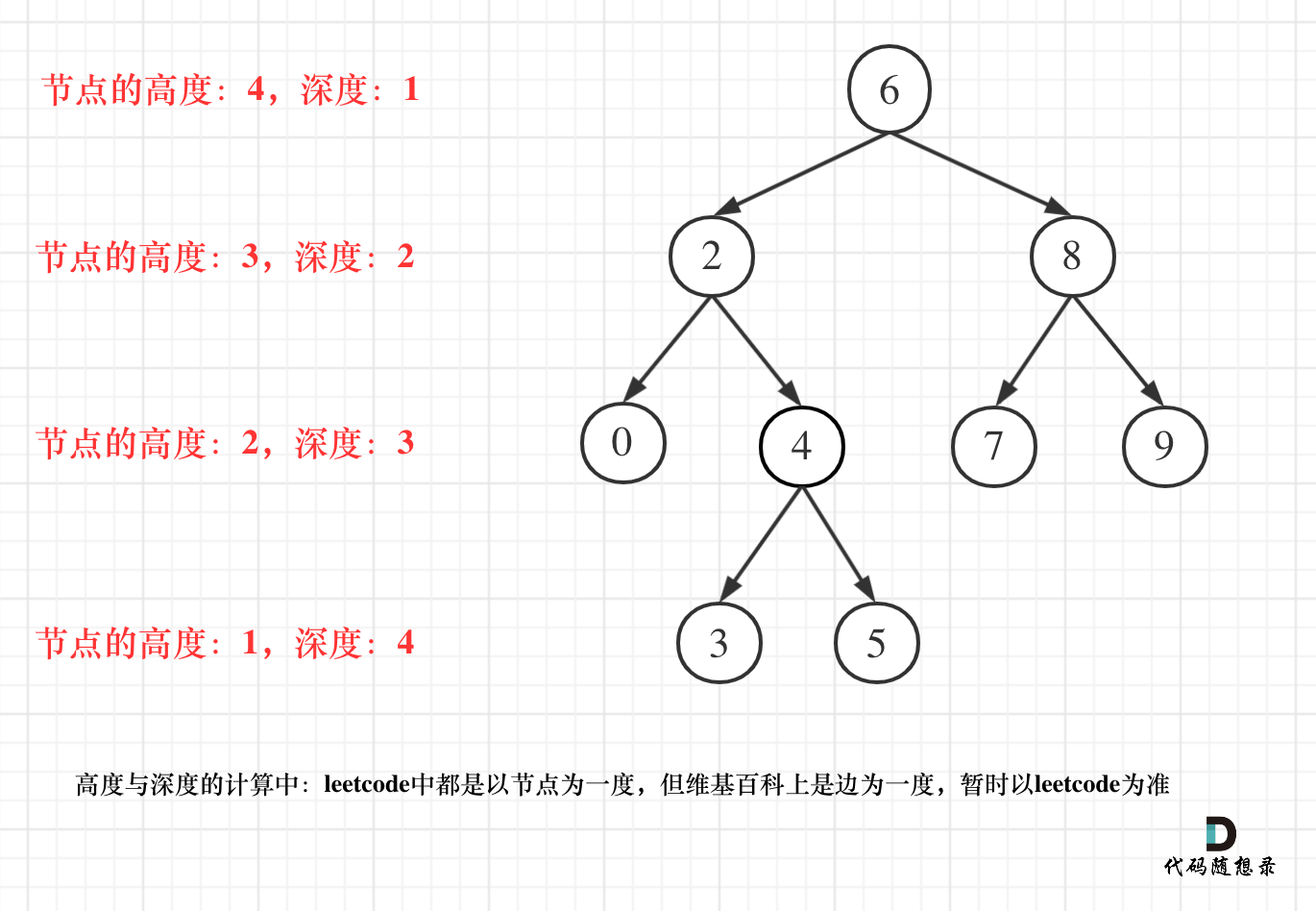
但leetcode中强调的深度和高度很明显是按照节点来计算的,如图:
|
但leetcode中强调的深度和高度很明显是按照节点来计算的,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
关于根节点的深度究竟是1 还是 0,不同的地方有不一样的标准,leetcode的题目中都是以节点为一度,即根节点深度是1。但维基百科上定义用边为一度,即根节点的深度是0,我们暂时以leetcode为准(毕竟要在这上面刷题)。
|
关于根节点的深度究竟是1 还是 0,不同的地方有不一样的标准,leetcode的题目中都是以节点为一度,即根节点深度是1。但维基百科上定义用边为一度,即根节点的深度是0,我们暂时以leetcode为准(毕竟要在这上面刷题)。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -20,7 +20,7 @@
|
||||||
给定二叉树 [3,9,20,null,null,15,7],
|
给定二叉树 [3,9,20,null,null,15,7],
|
||||||
|
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
返回它的最小深度 2.
|
返回它的最小深度 2.
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -15,7 +15,7 @@
|
||||||
示例:
|
示例:
|
||||||
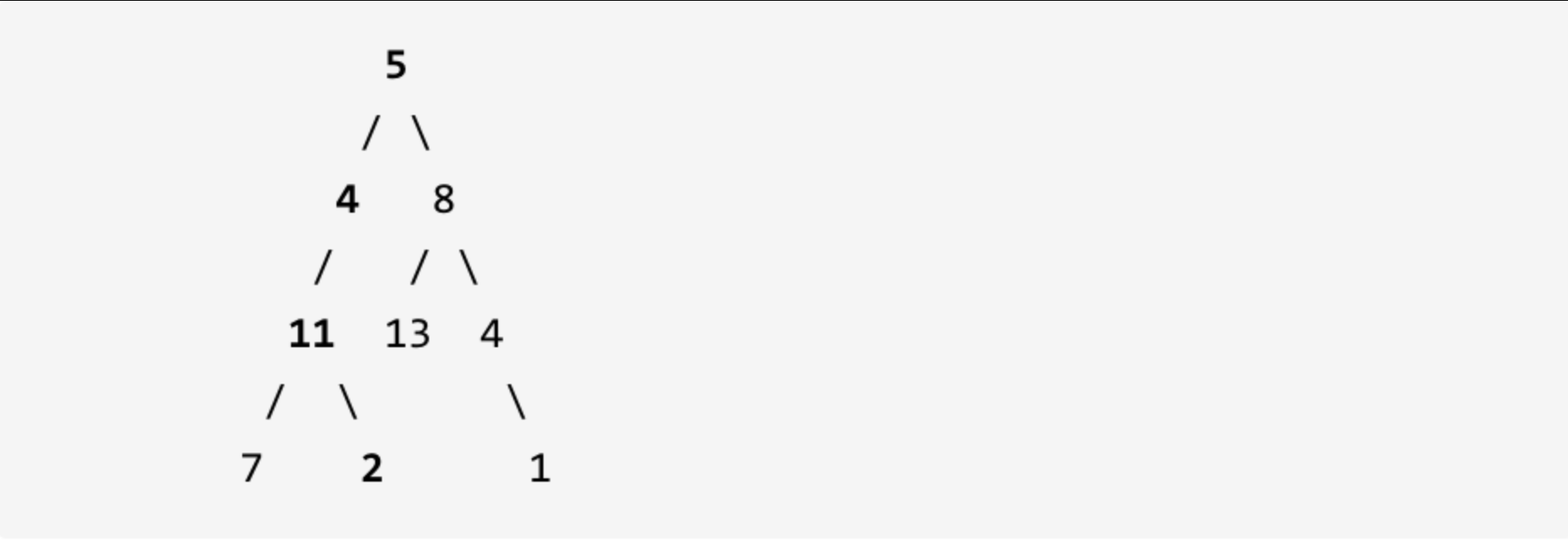
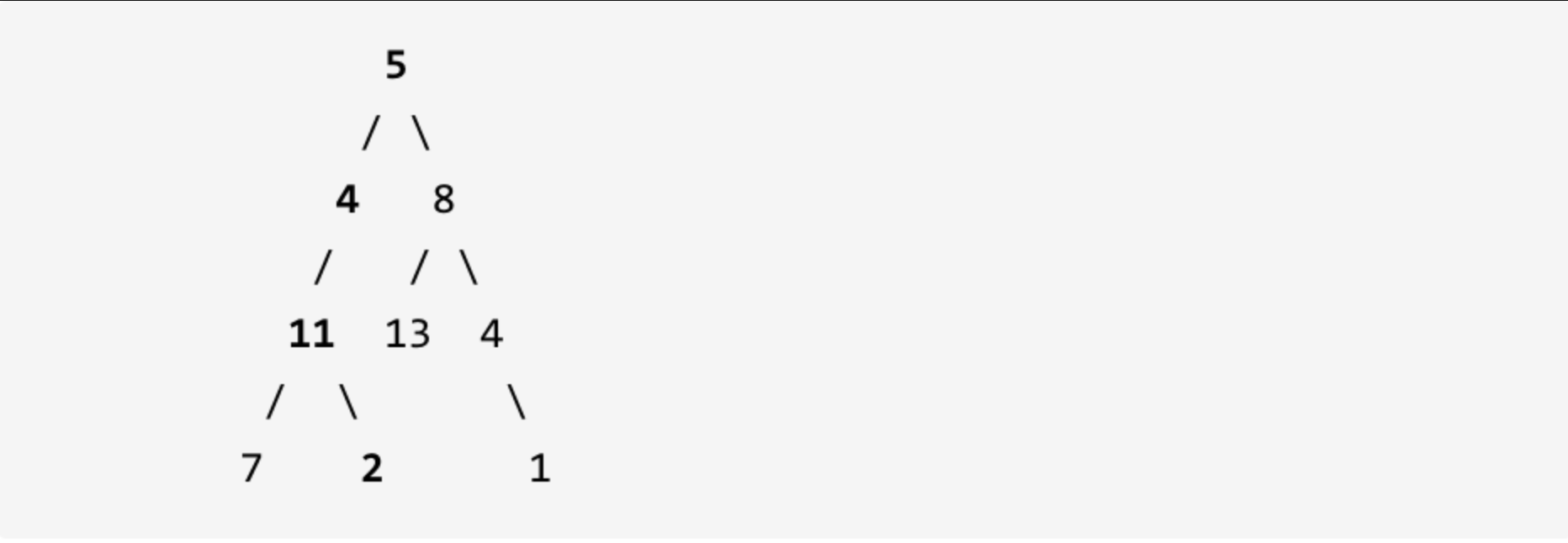
给定如下二叉树,以及目标和 sum = 22,
|
给定如下二叉树,以及目标和 sum = 22,
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
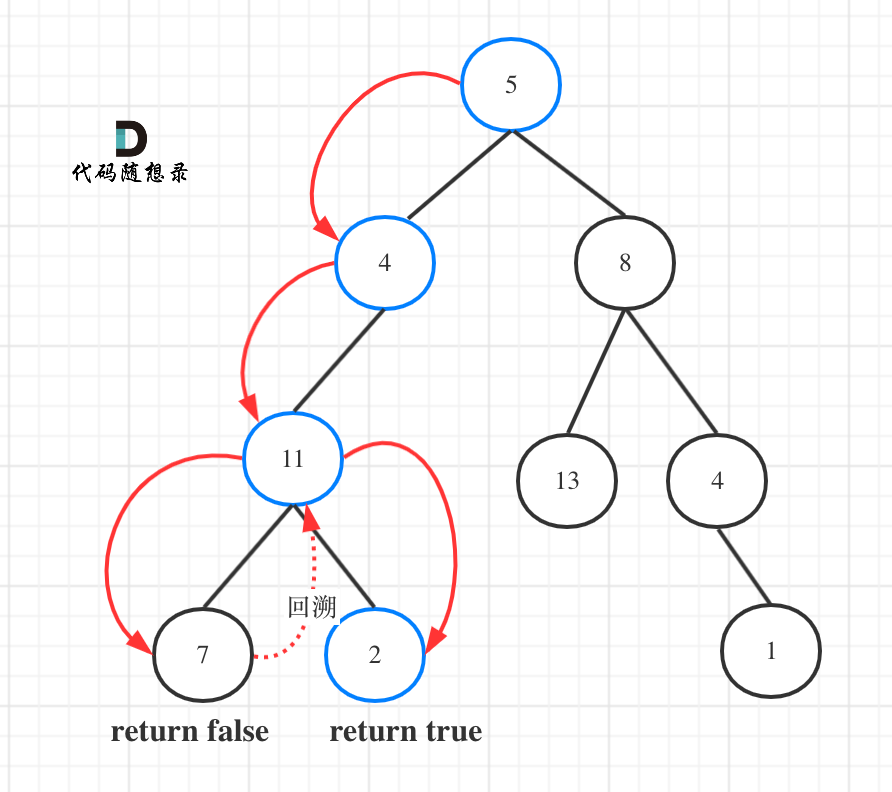
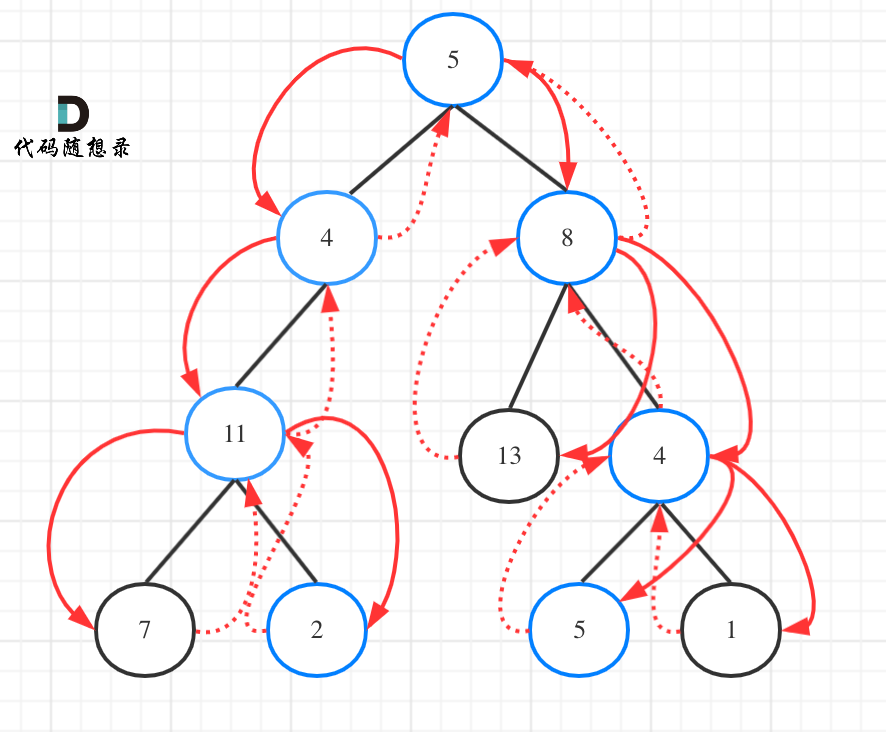
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
|
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
|
||||||
|
|
||||||
|
|
@ -53,7 +53,7 @@
|
||||||
|
|
||||||
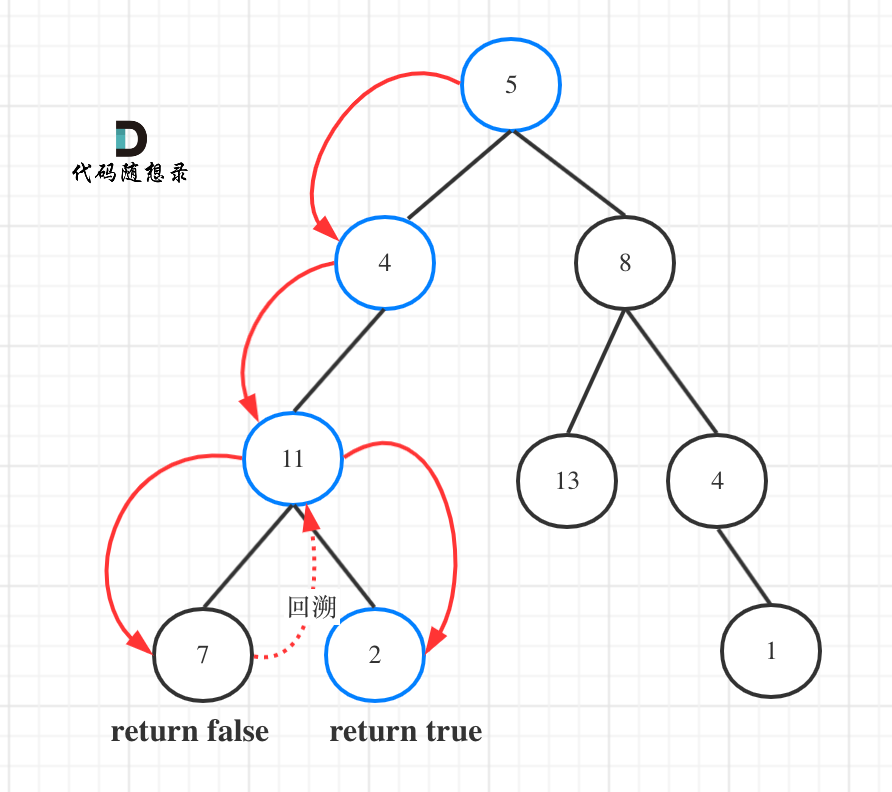
如图所示:
|
如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
图中可以看出,遍历的路线,并不要遍历整棵树,所以递归函数需要返回值,可以用bool类型表示。
|
图中可以看出,遍历的路线,并不要遍历整棵树,所以递归函数需要返回值,可以用bool类型表示。
|
||||||
|
|
||||||
|
|
@ -230,7 +230,7 @@ public:
|
||||||
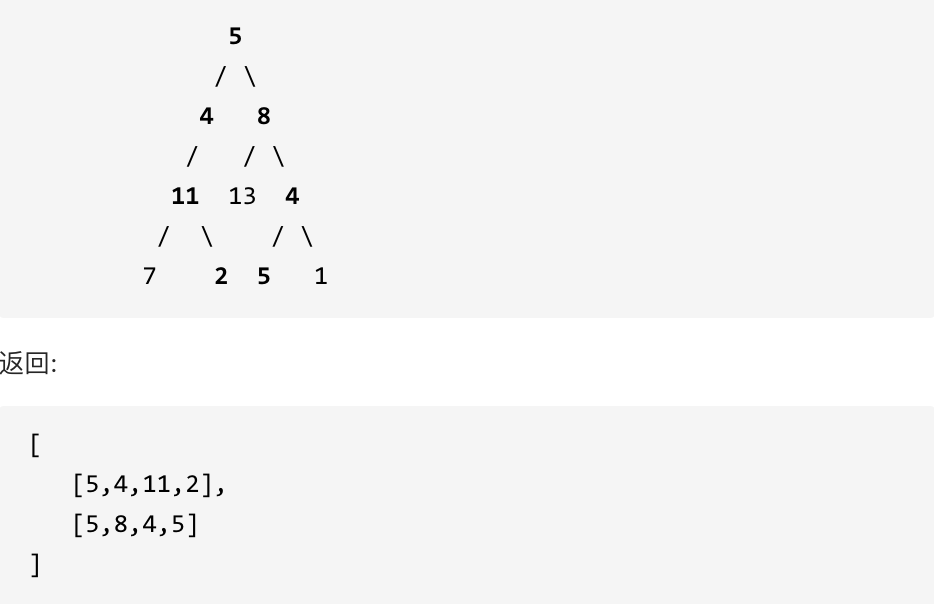
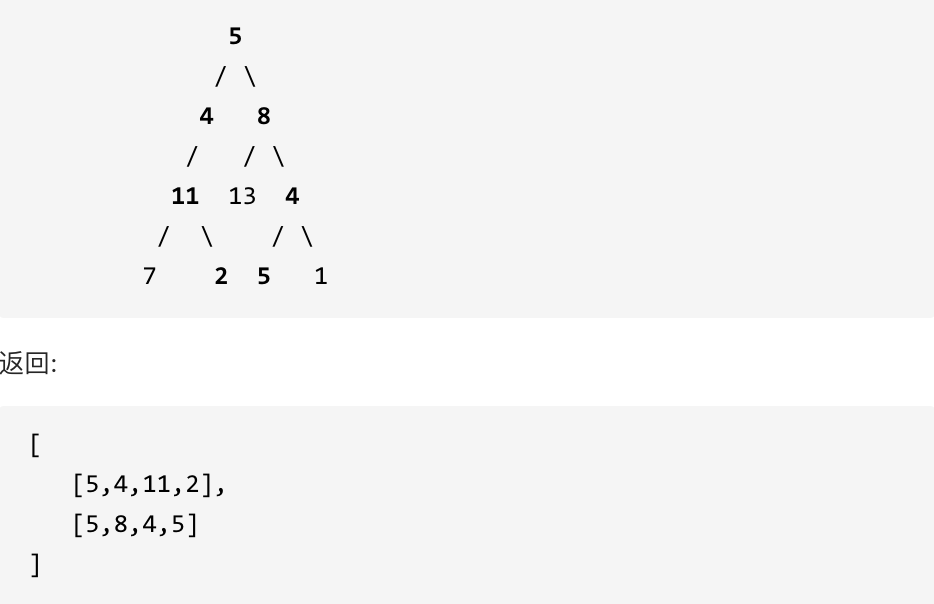
给定如下二叉树,以及目标和 sum = 22,
|
给定如下二叉树,以及目标和 sum = 22,
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
### 思路
|
### 思路
|
||||||
|
|
||||||
|
|
@ -239,7 +239,7 @@ public:
|
||||||
|
|
||||||
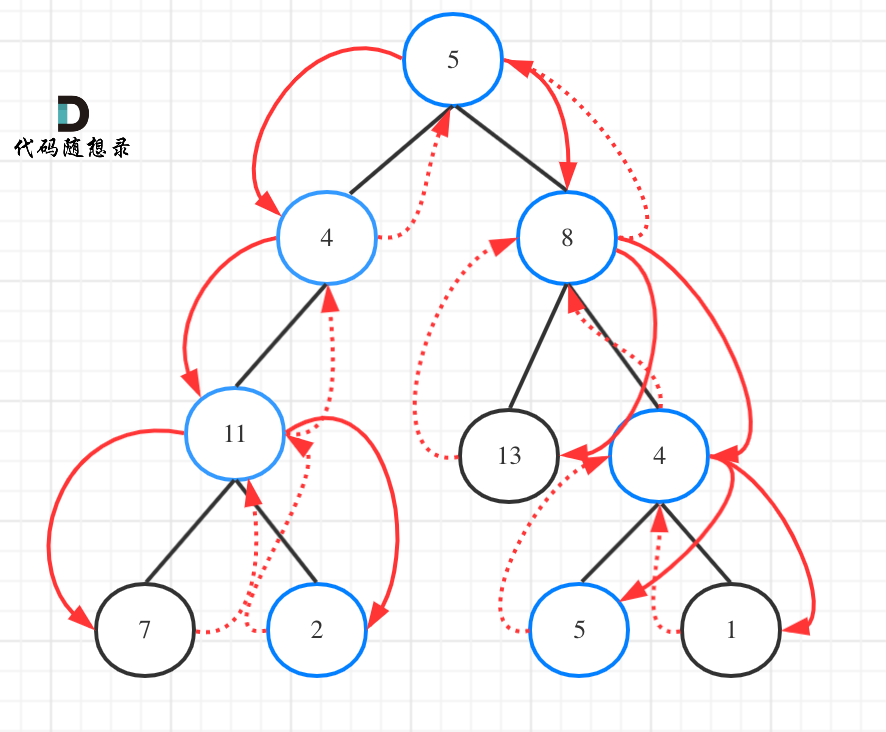
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
为了尽可能的把细节体现出来,我写出如下代码(**这份代码并不简洁,但是逻辑非常清晰**)
|
为了尽可能的把细节体现出来,我写出如下代码(**这份代码并不简洁,但是逻辑非常清晰**)
|
||||||
|
|
|
||||||
|
|
@ -70,7 +70,7 @@ dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为d
|
||||||
|
|
||||||
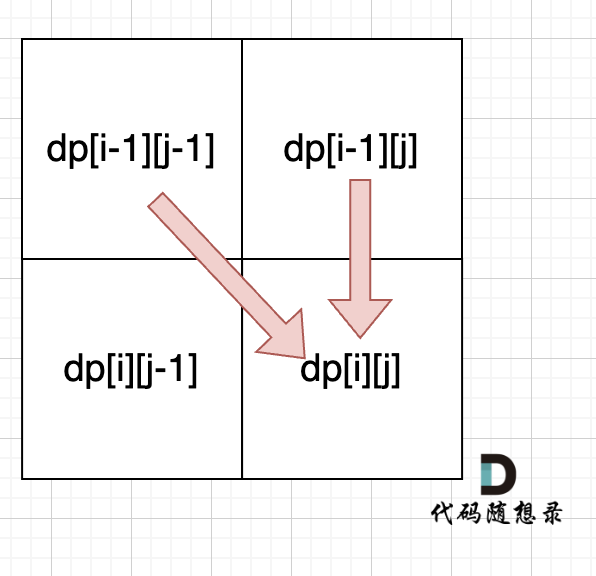
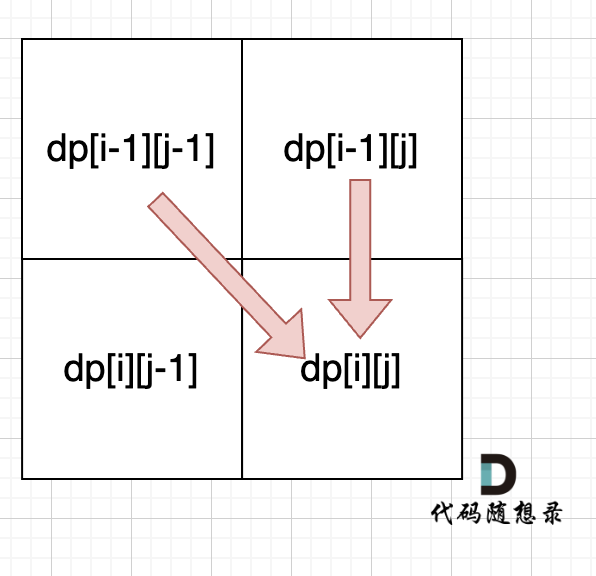
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。
|
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
|
每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
|
||||||
|
|
||||||
|
|
@ -101,7 +101,7 @@ for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和
|
||||||
|
|
||||||
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。
|
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
|
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -26,7 +26,7 @@ struct Node {
|
||||||
* 你只能使用常量级额外空间。
|
* 你只能使用常量级额外空间。
|
||||||
* 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
|
* 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
## 思路
|
## 思路
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -129,7 +129,7 @@ dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所
|
||||||
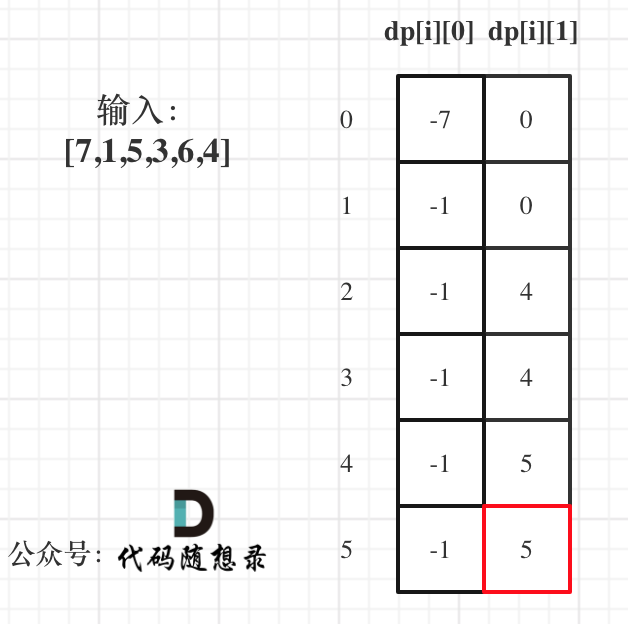
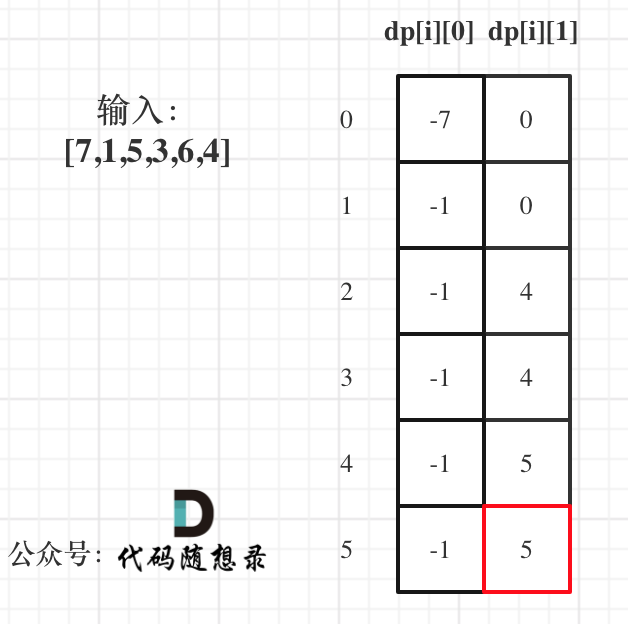
以示例1,输入:[7,1,5,3,6,4]为例,dp数组状态如下:
|
以示例1,输入:[7,1,5,3,6,4]为例,dp数组状态如下:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
dp[5][1]就是最终结果。
|
dp[5][1]就是最终结果。
|
||||||
|
|
|
||||||
|
|
@ -66,7 +66,7 @@
|
||||||
|
|
||||||
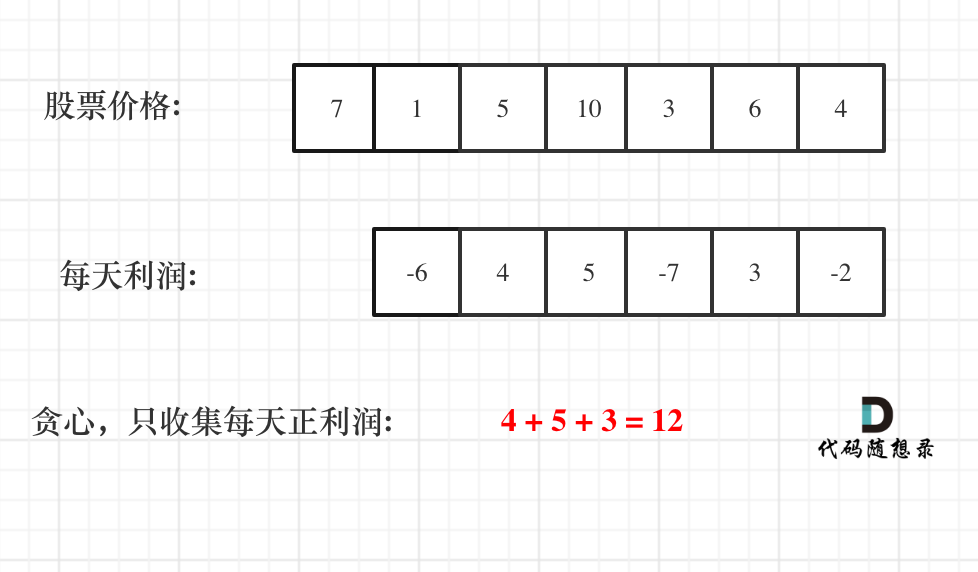
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
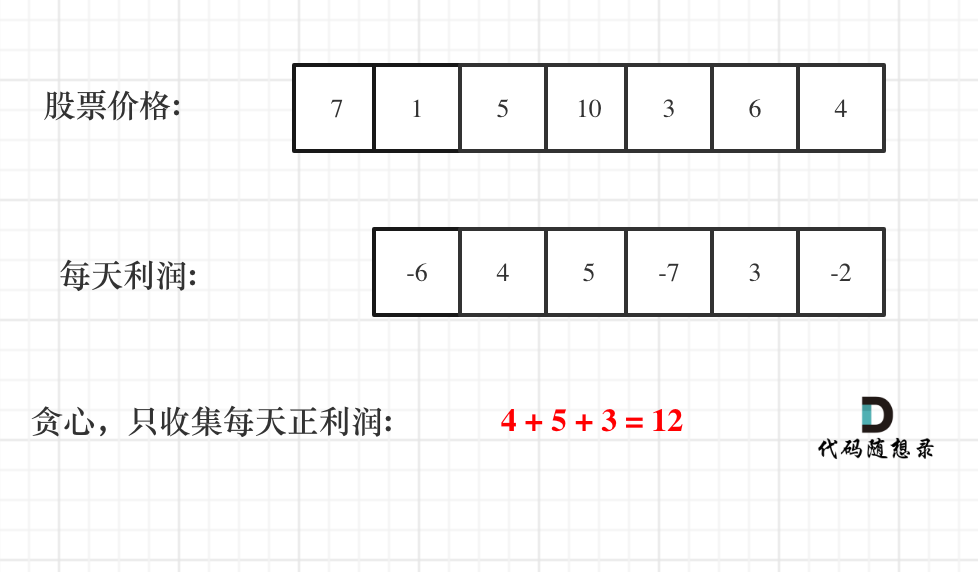
||||||
一些同学陷入:第一天怎么就没有利润呢,第一天到底算不算的困惑中。
|
一些同学陷入:第一天怎么就没有利润呢,第一天到底算不算的困惑中。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -120,7 +120,7 @@ dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
|
||||||
以输入[1,2,3,4,5]为例
|
以输入[1,2,3,4,5]为例
|
||||||
|
|
||||||
|
|
||||||
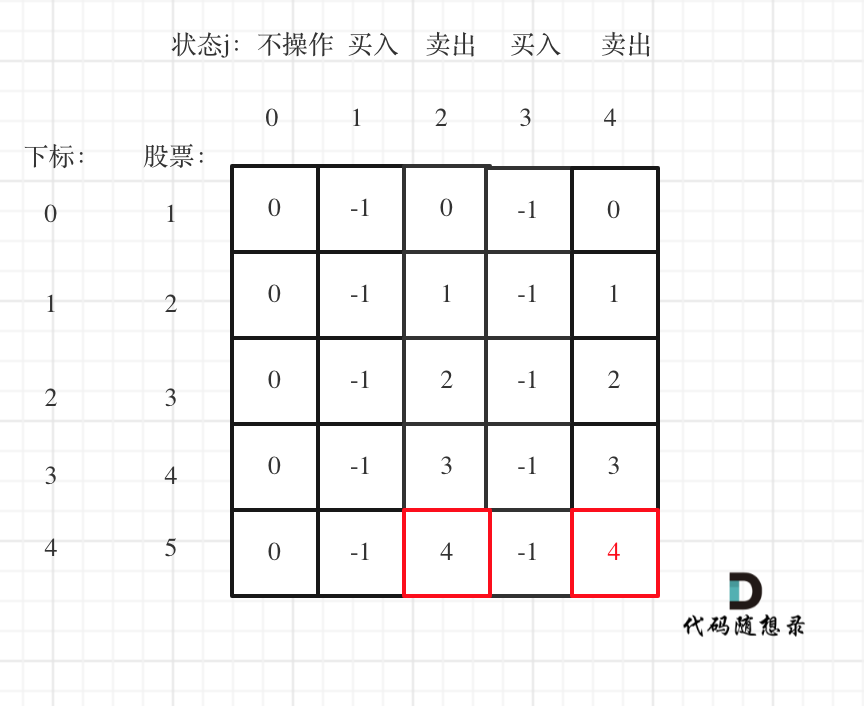
|
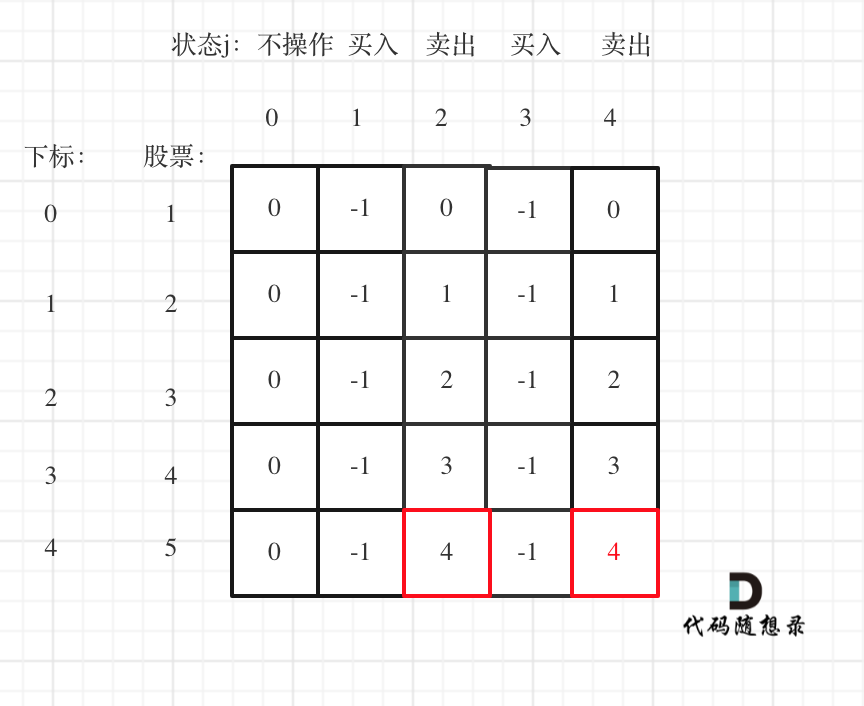
|
||||||
|
|
||||||
大家可以看到红色框为最后两次卖出的状态。
|
大家可以看到红色框为最后两次卖出的状态。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -31,7 +31,7 @@
|
||||||
|
|
||||||
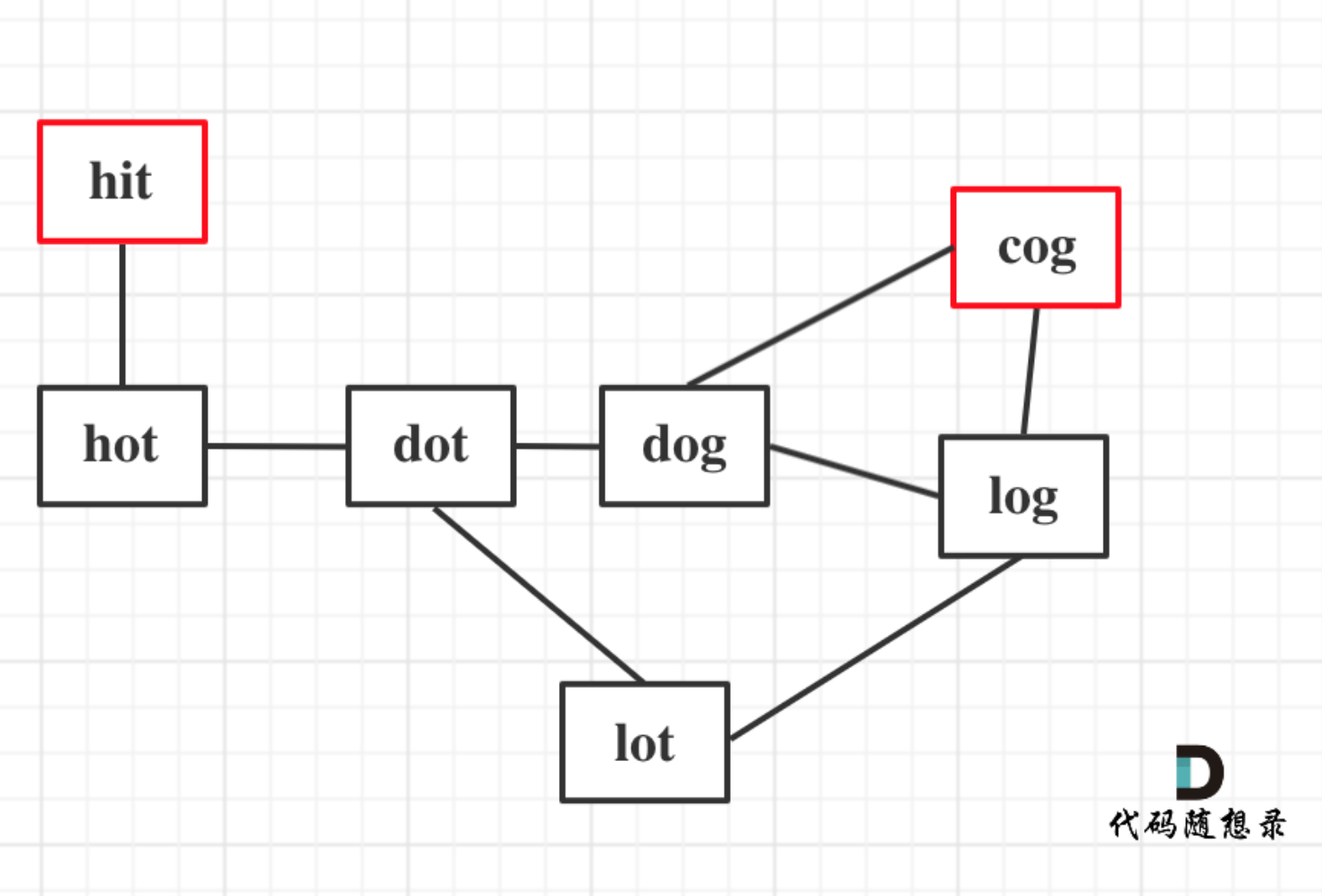
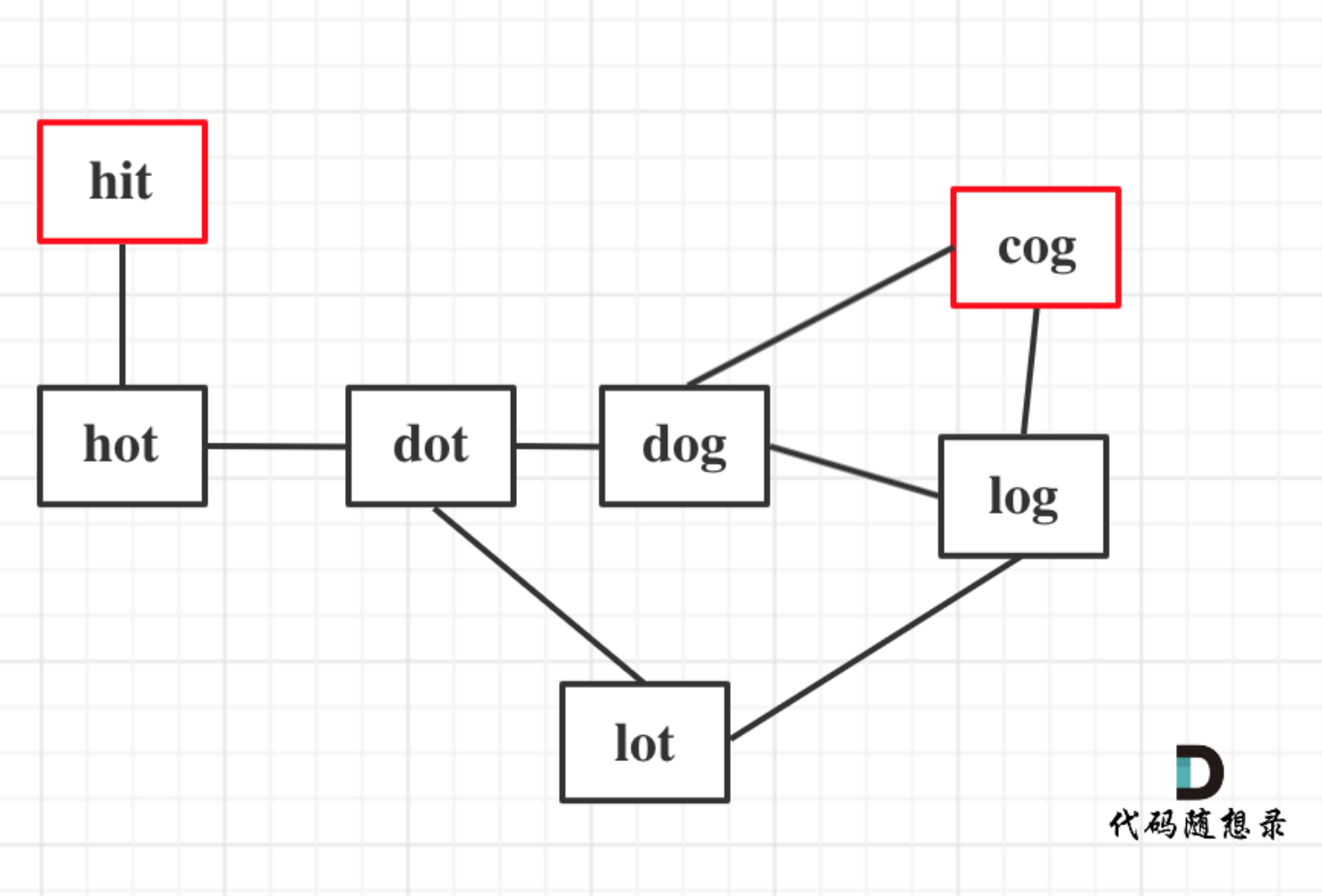
以示例1为例,从这个图中可以看出 hit 到 cog的路线,不止一条,有三条,一条是最短的长度为5,两条长度为6。
|
以示例1为例,从这个图中可以看出 hit 到 cog的路线,不止一条,有三条,一条是最短的长度为5,两条长度为6。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
本题只需要求出最短路径的长度就可以了,不用找出路径。
|
本题只需要求出最短路径的长度就可以了,不用找出路径。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -8,7 +8,7 @@
|
||||||
|
|
||||||
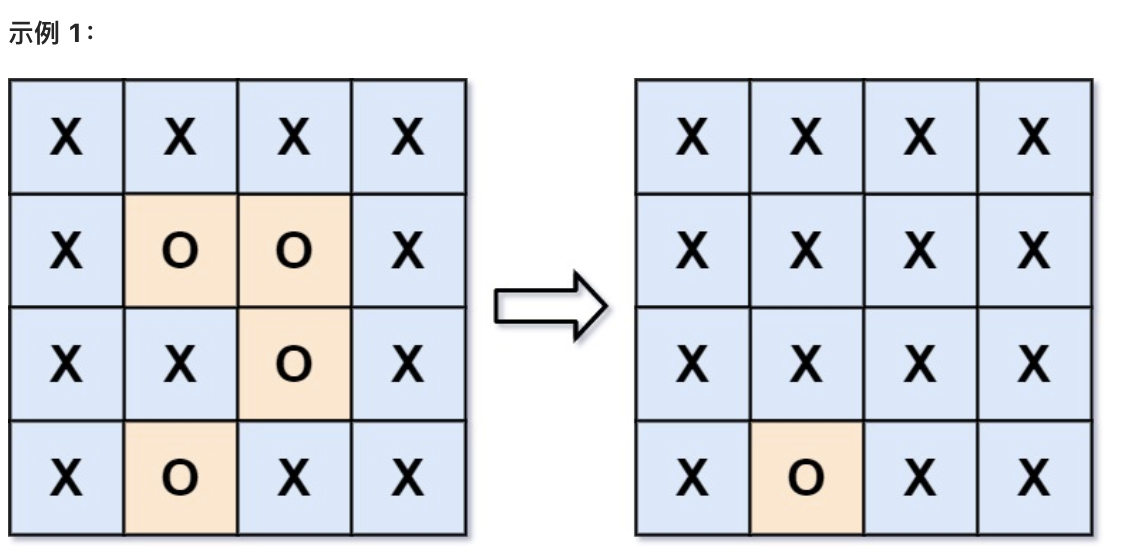
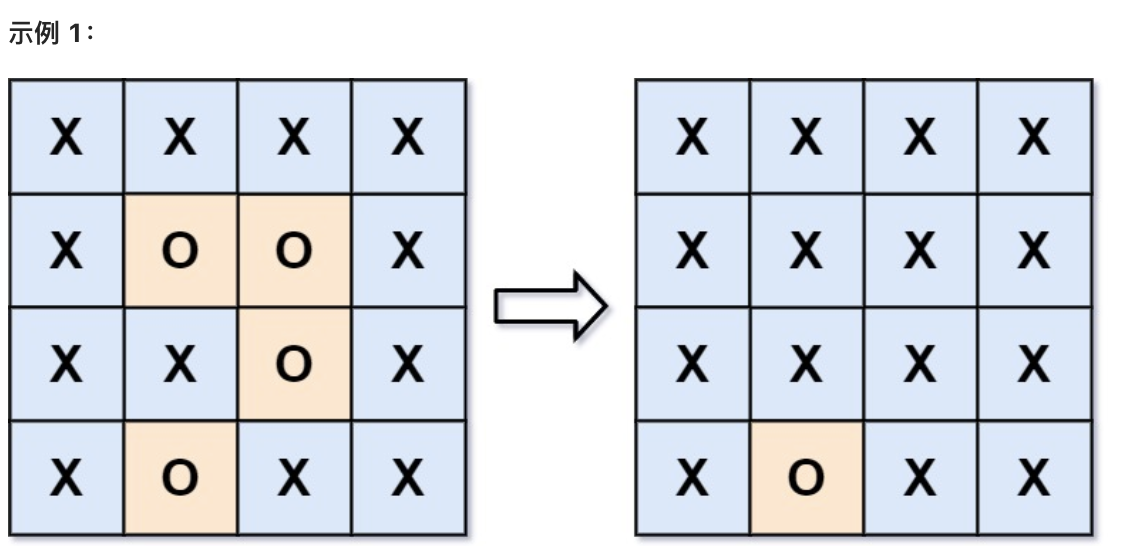
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
|
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
* 输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
|
* 输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
|
||||||
* 输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
|
* 输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
|
||||||
|
|
@ -28,11 +28,11 @@
|
||||||
|
|
||||||
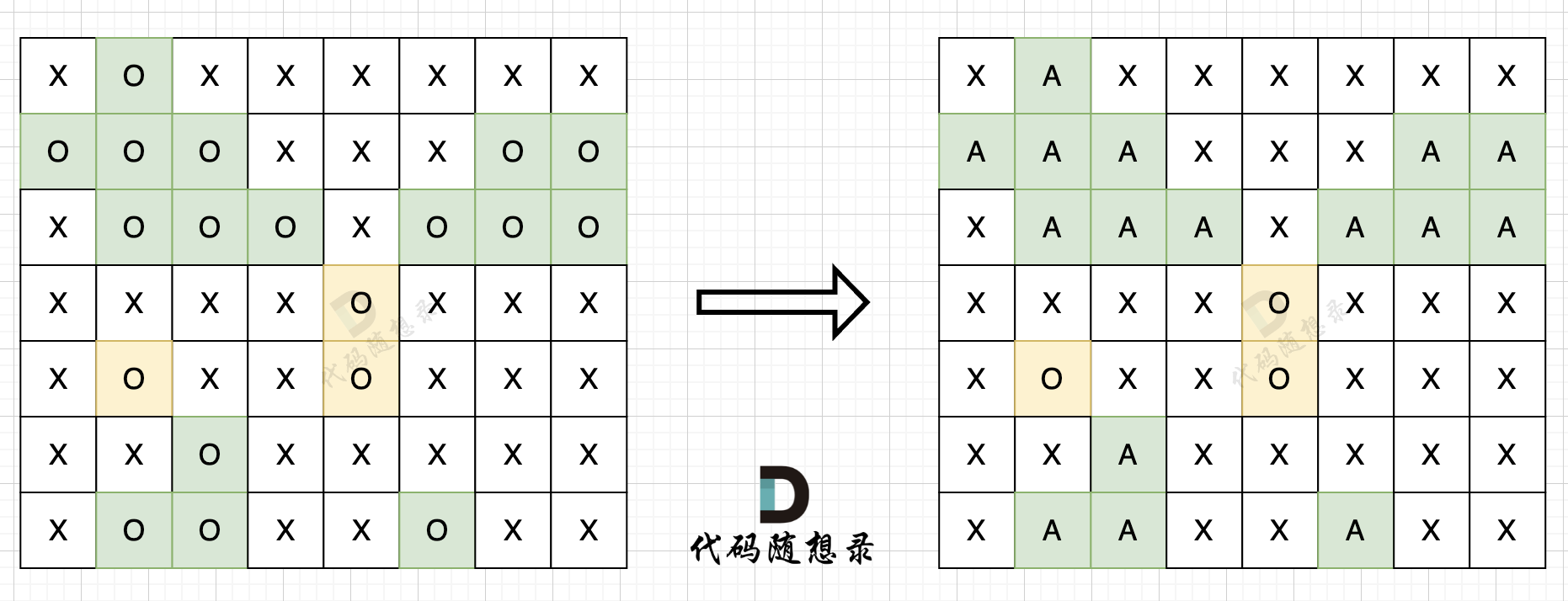
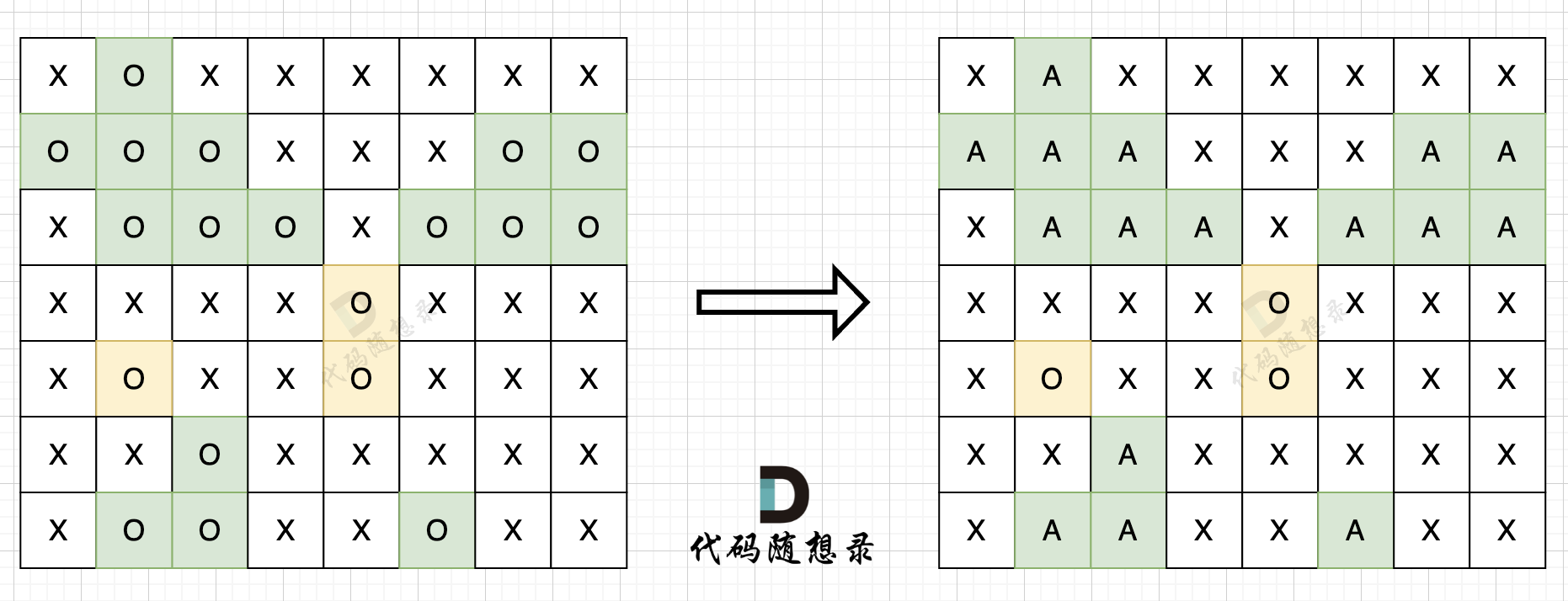
步骤一:深搜或者广搜将地图周边的'O'全部改成'A',如图所示:
|
步骤一:深搜或者广搜将地图周边的'O'全部改成'A',如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
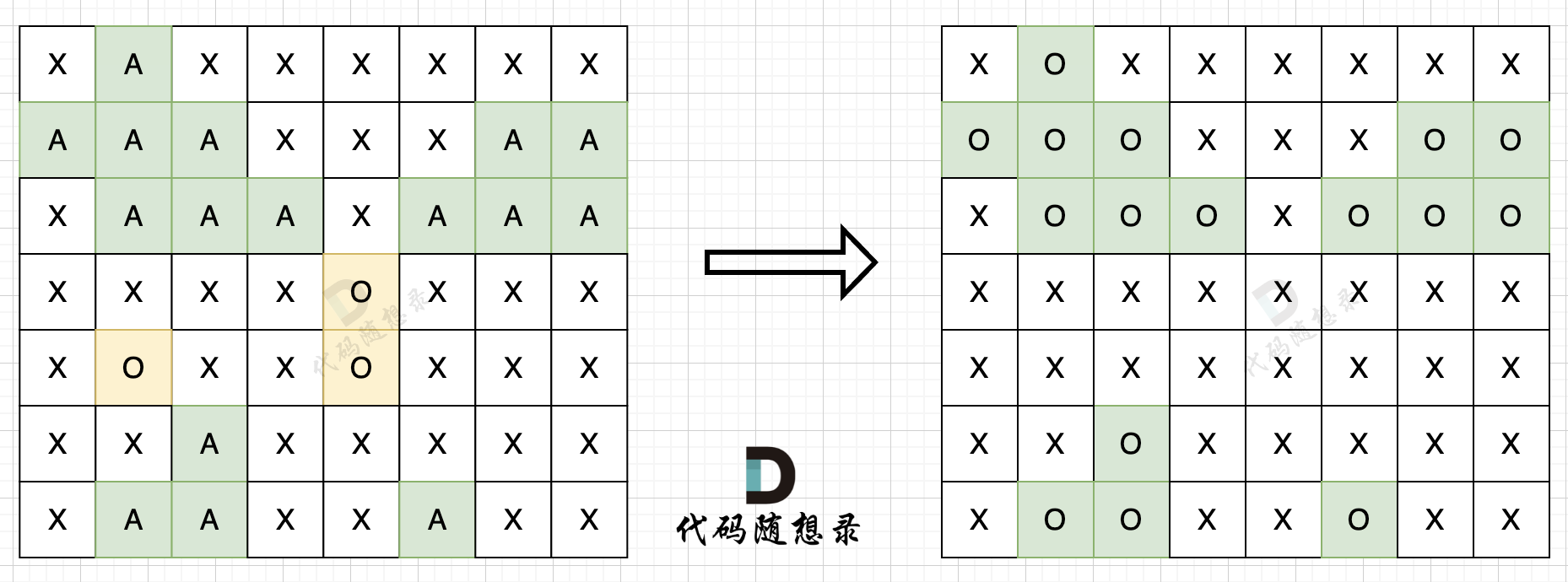
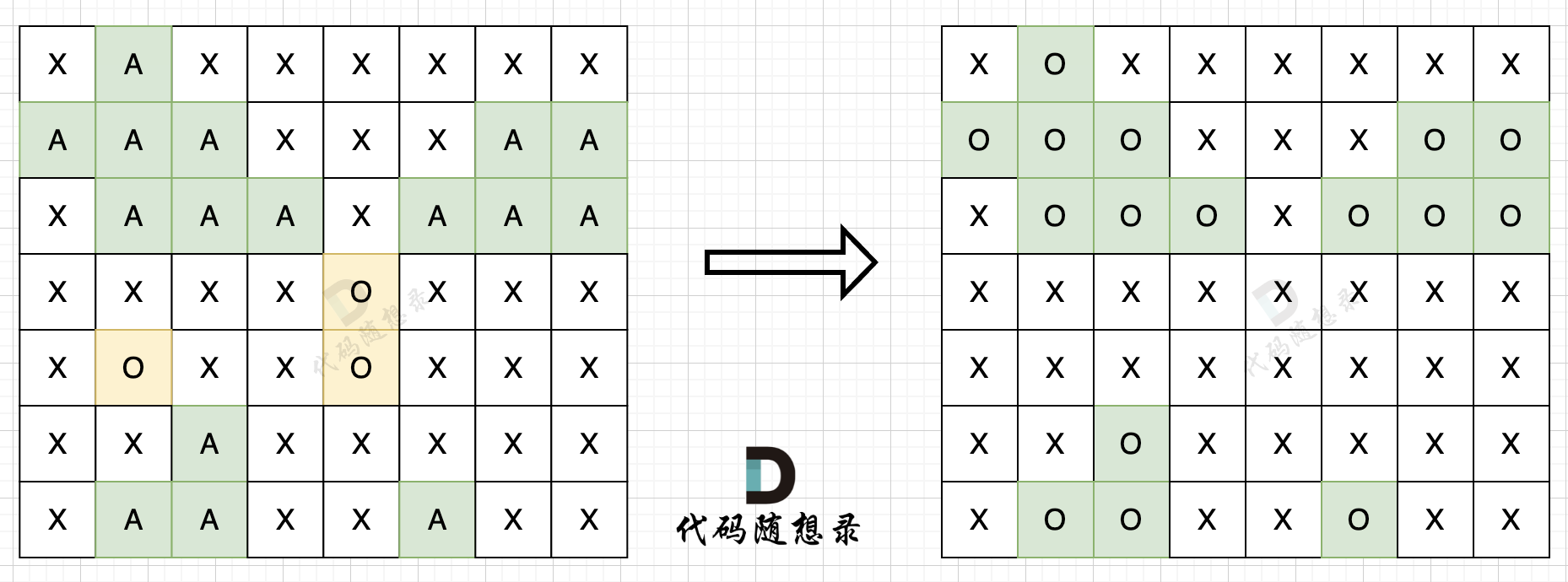
步骤二:在遍历地图,将'O'全部改成'X'(地图中间的'O'改成了'X'),将'A'改回'O'(保留的地图周边的'O'),如图所示:
|
步骤二:在遍历地图,将'O'全部改成'X'(地图中间的'O'改成了'X'),将'A'改回'O'(保留的地图周边的'O'),如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
整体C++代码如下,以下使用dfs实现,其实遍历方式dfs,bfs都是可以的。
|
整体C++代码如下,以下使用dfs实现,其实遍历方式dfs,bfs都是可以的。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -161,7 +161,7 @@ for (int i = s.size() - 1; i >= 0; i--) {
|
||||||
|
|
||||||
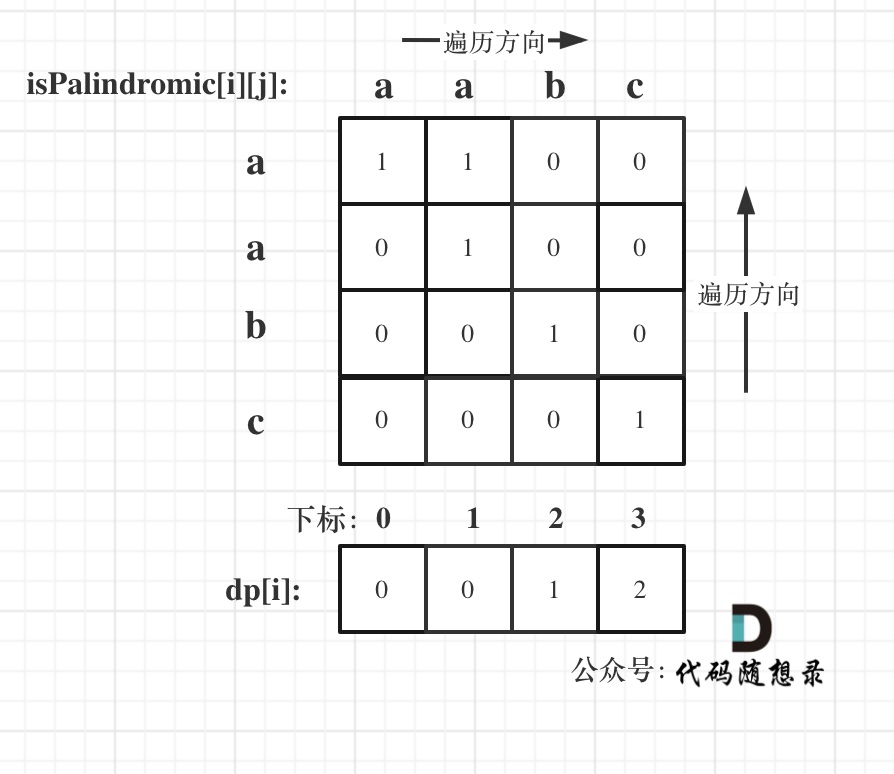
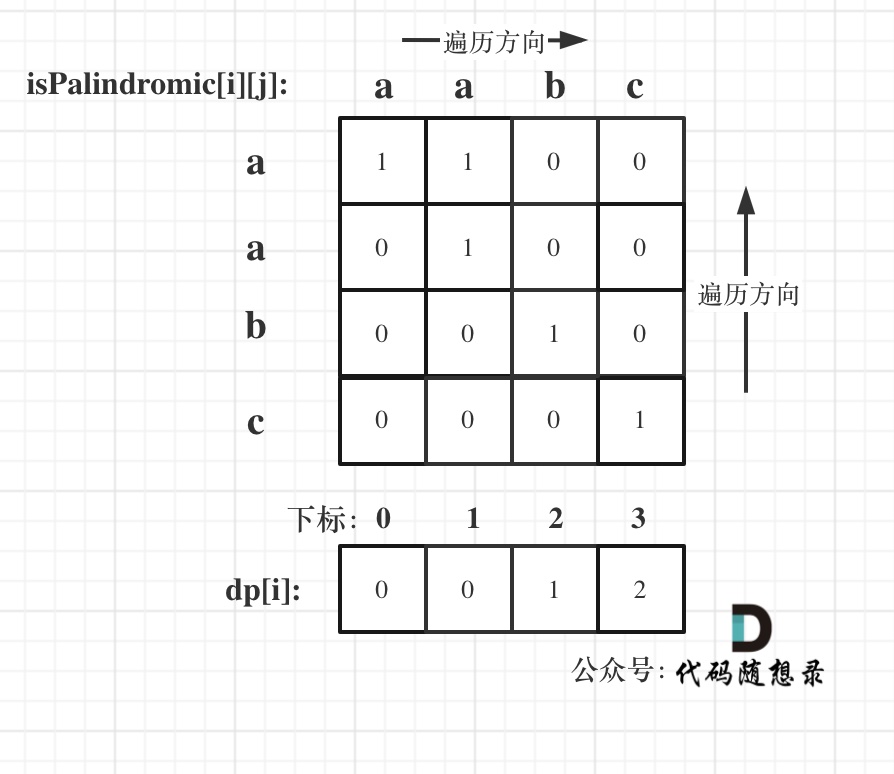
以输入:"aabc" 为例:
|
以输入:"aabc" 为例:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
以上分析完毕,代码如下:
|
以上分析完毕,代码如下:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -144,7 +144,7 @@ i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i
|
||||||
|
|
||||||
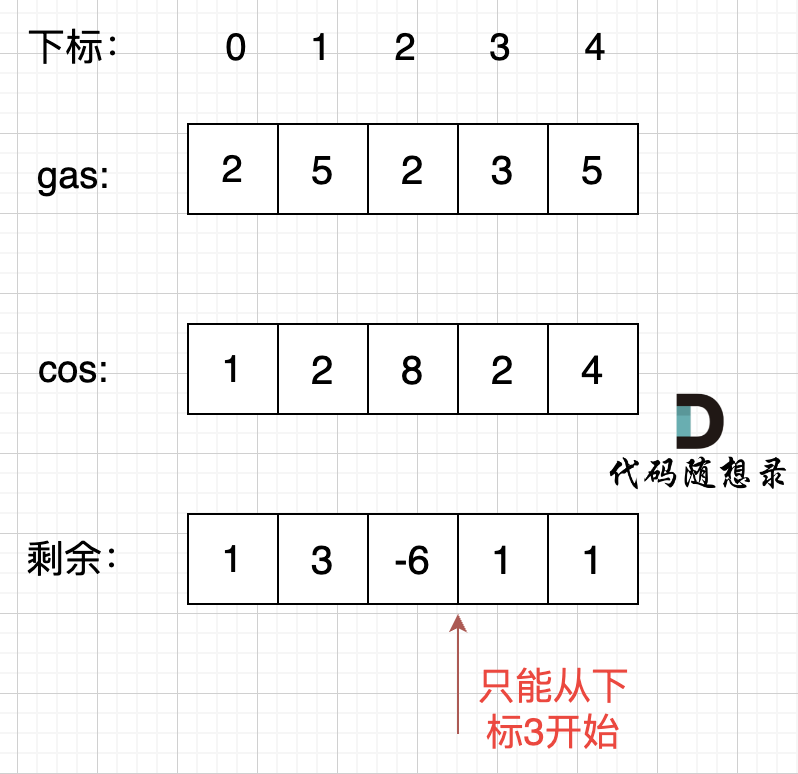
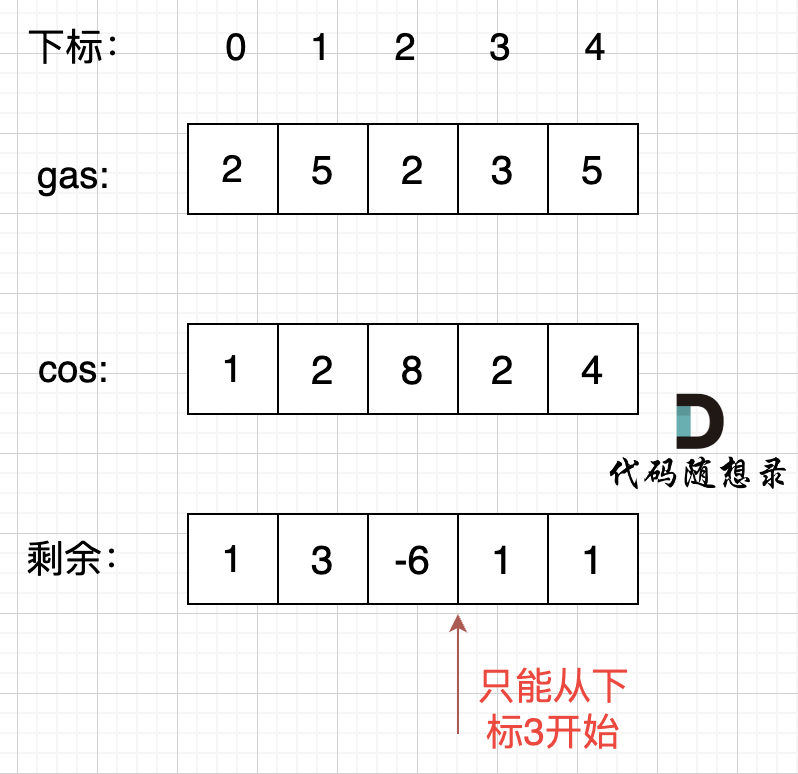
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
那么为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
|
那么为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
|
||||||
|
|
||||||
|
|
@ -152,7 +152,7 @@ i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i
|
||||||
|
|
||||||
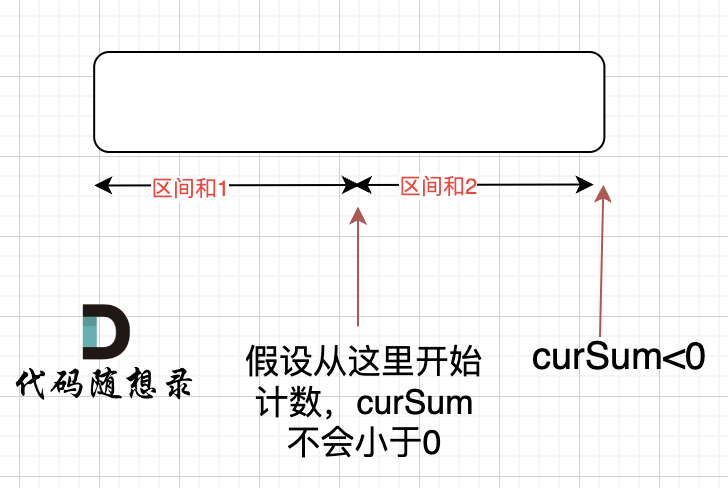
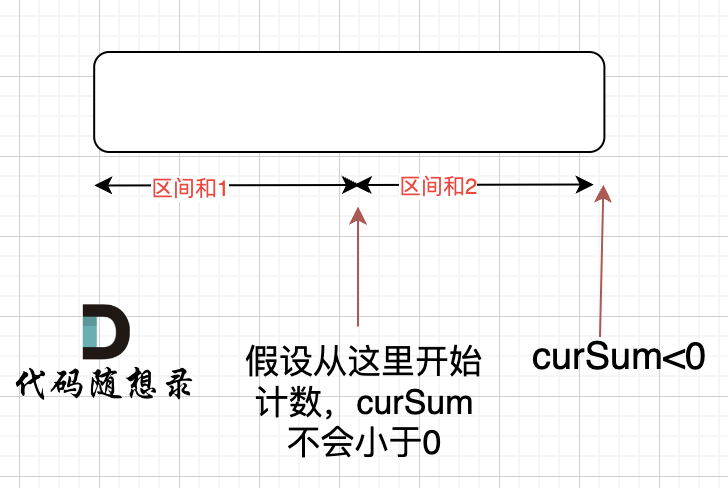
那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零呢? 如图:
|
那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零呢? 如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
|
如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -56,7 +56,7 @@ for (int i = 1; i < ratings.size(); i++) {
|
||||||
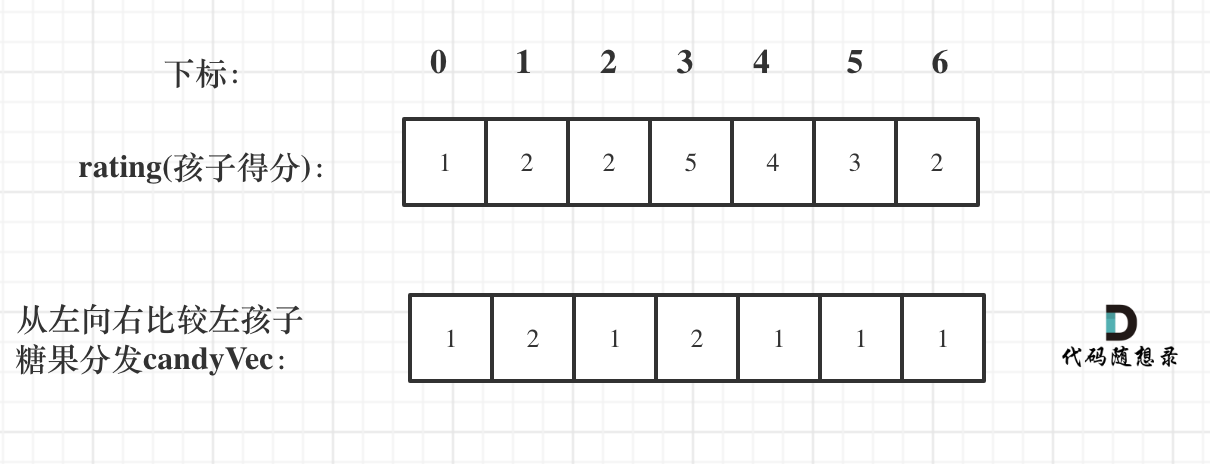
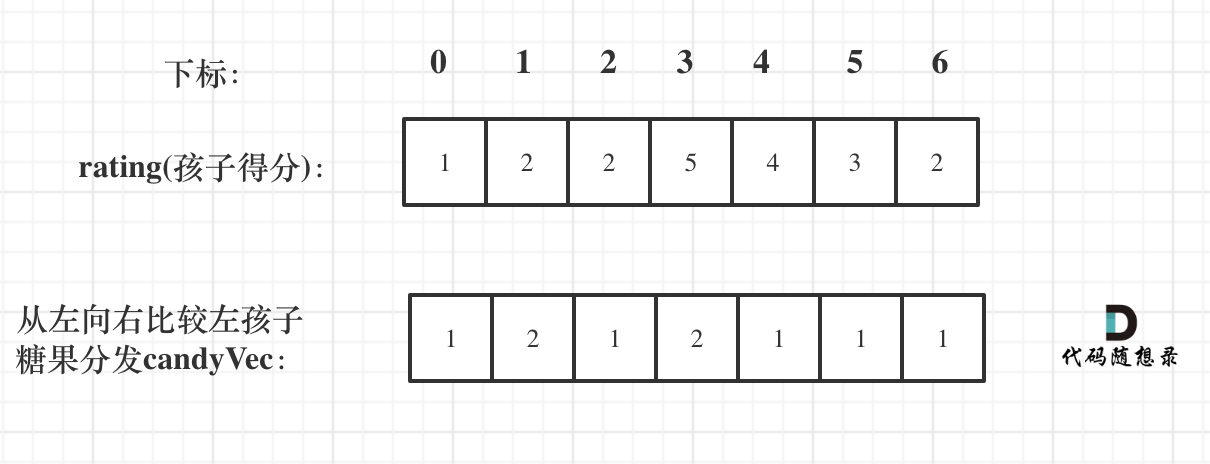
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
再确定左孩子大于右孩子的情况(从后向前遍历)
|
再确定左孩子大于右孩子的情况(从后向前遍历)
|
||||||
|
|
||||||
|
|
@ -66,7 +66,7 @@ for (int i = 1; i < ratings.size(); i++) {
|
||||||
|
|
||||||
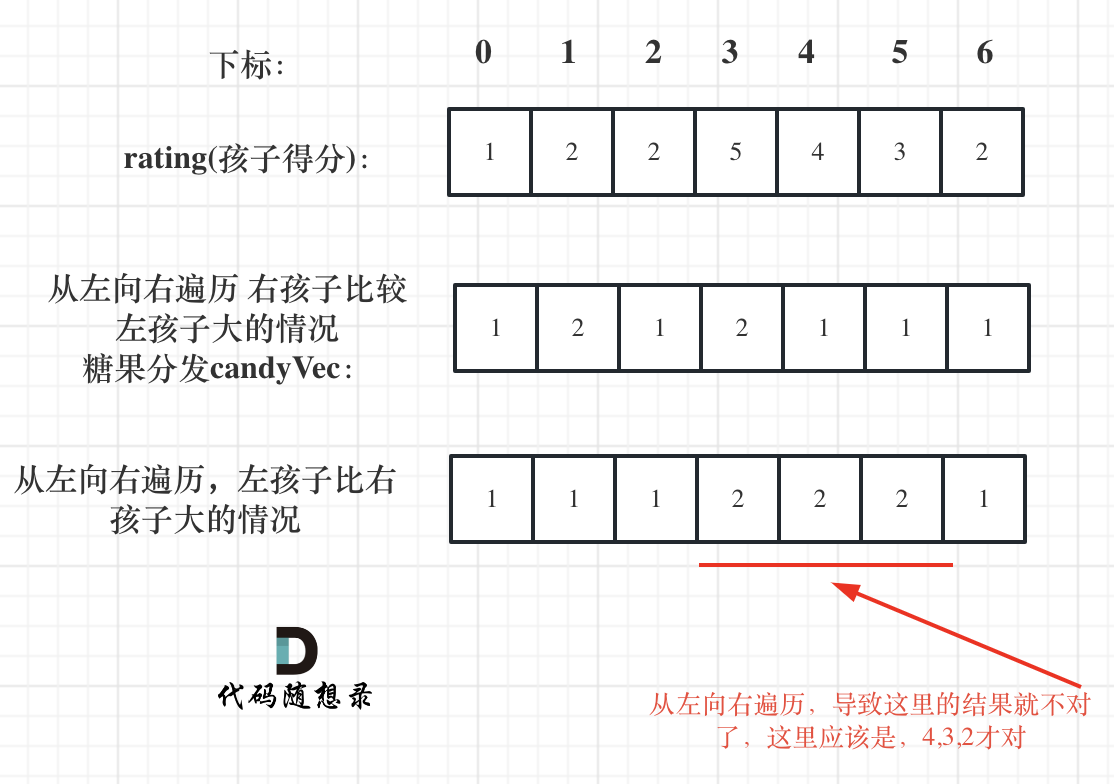
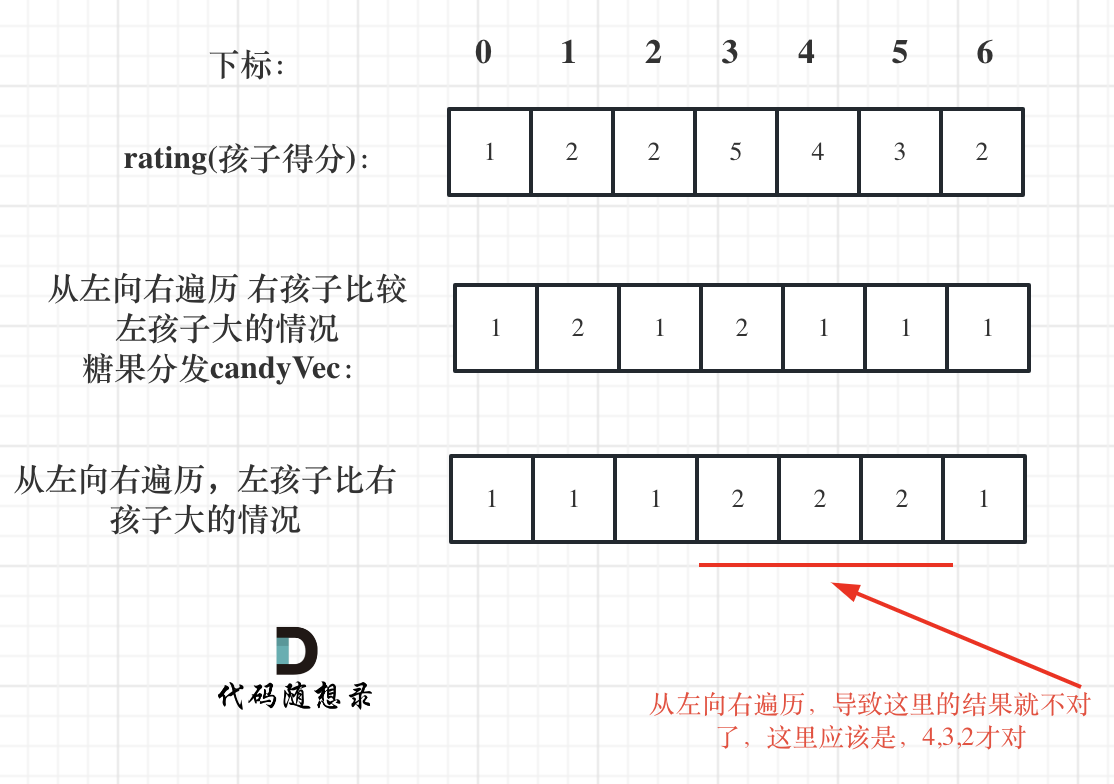
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图:
|
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**所以确定左孩子大于右孩子的情况一定要从后向前遍历!**
|
**所以确定左孩子大于右孩子的情况一定要从后向前遍历!**
|
||||||
|
|
||||||
|
|
@ -82,7 +82,7 @@ for (int i = 1; i < ratings.size(); i++) {
|
||||||
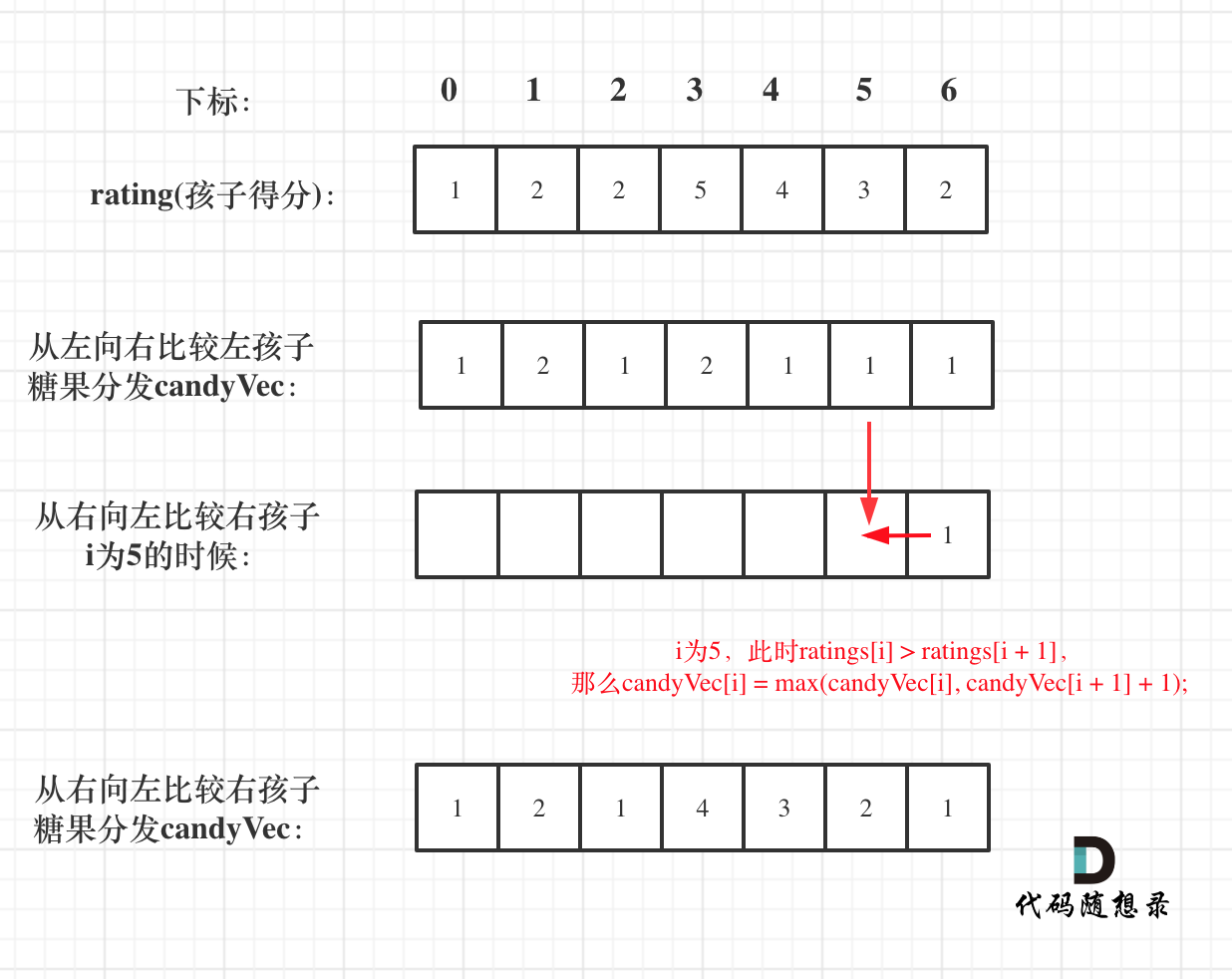
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
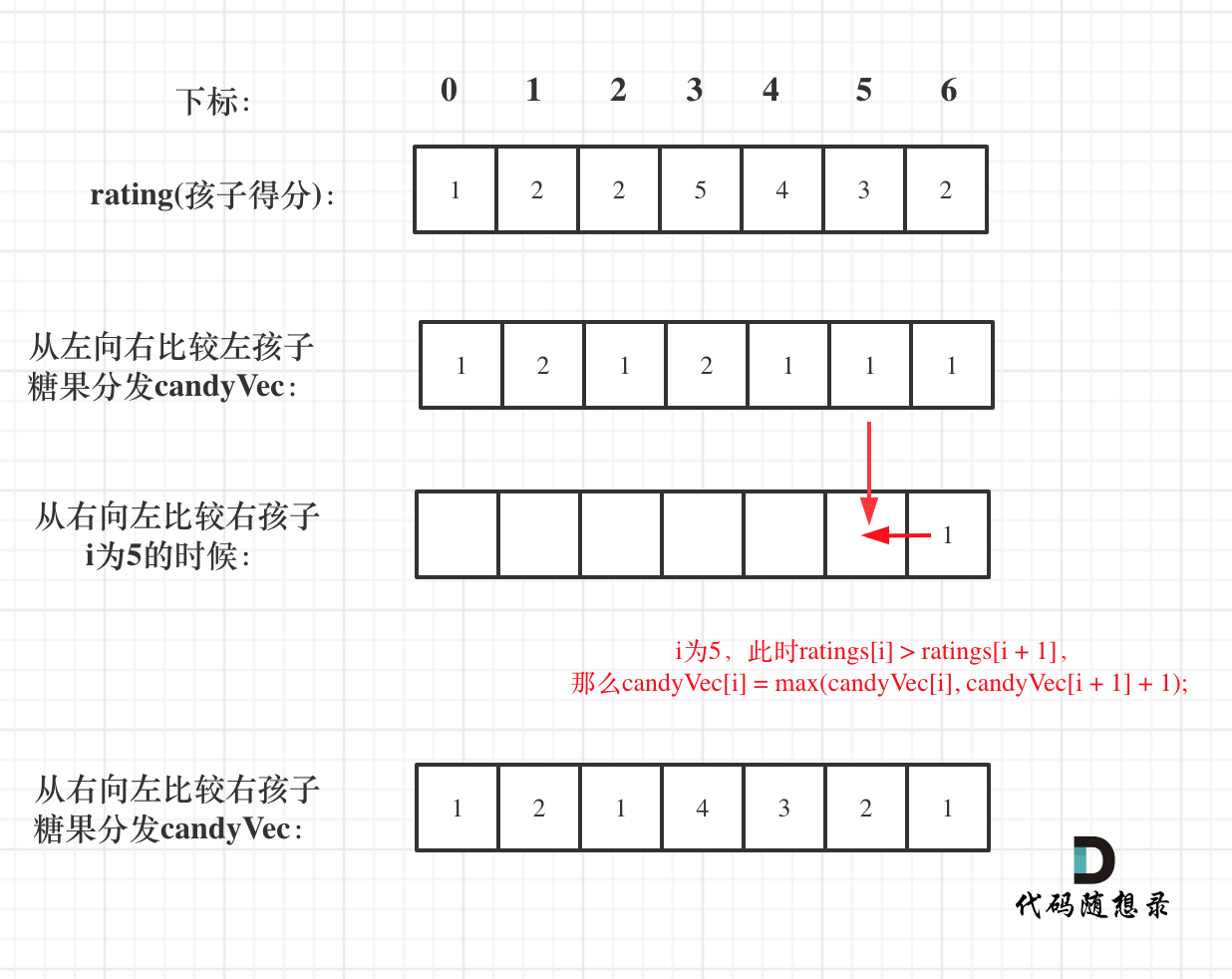
|
|
||||||
|
|
||||||
所以该过程代码如下:
|
所以该过程代码如下:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -180,7 +180,7 @@ dp[0]表示如果字符串为空的话,说明出现在字典里。
|
||||||
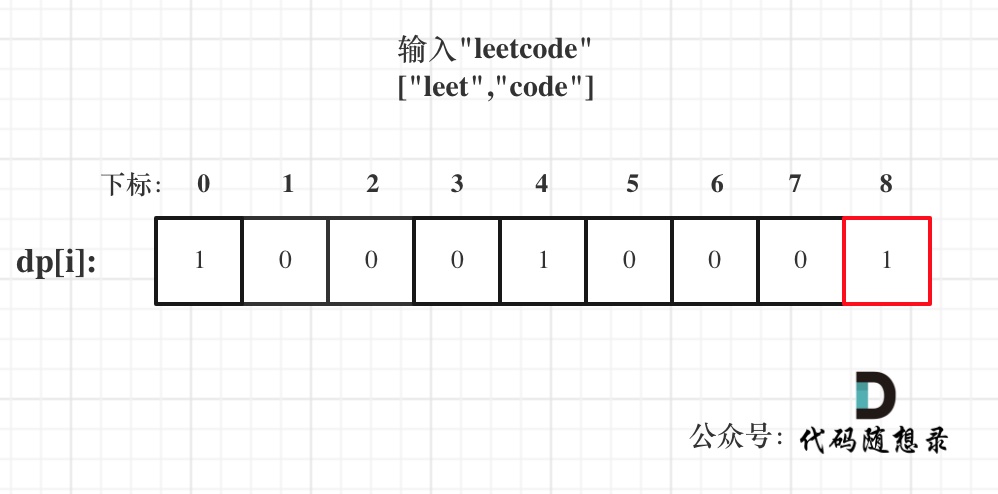
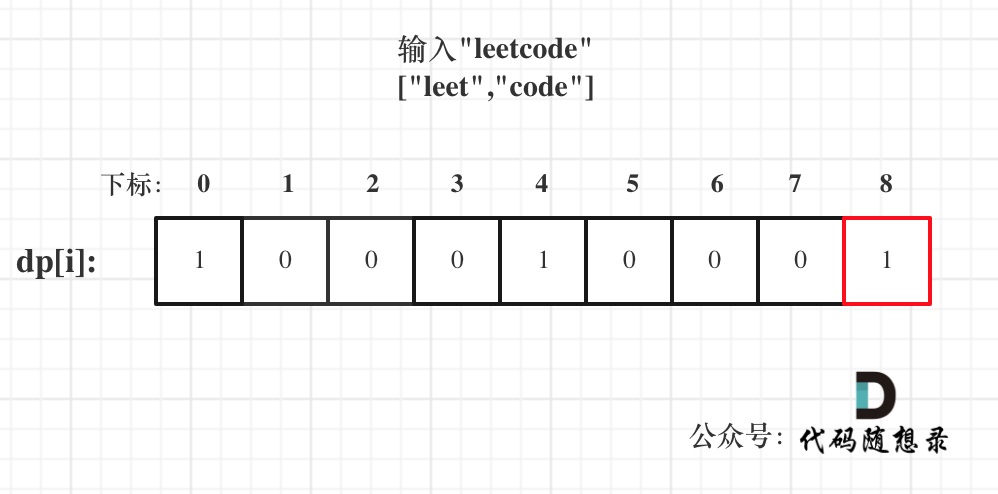
以输入: s = "leetcode", wordDict = ["leet", "code"]为例,dp状态如图:
|
以输入: s = "leetcode", wordDict = ["leet", "code"]为例,dp状态如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
dp[s.size()]就是最终结果。
|
dp[s.size()]就是最终结果。
|
||||||
|
|
||||||
|
|
@ -241,7 +241,7 @@ public:
|
||||||
|
|
||||||
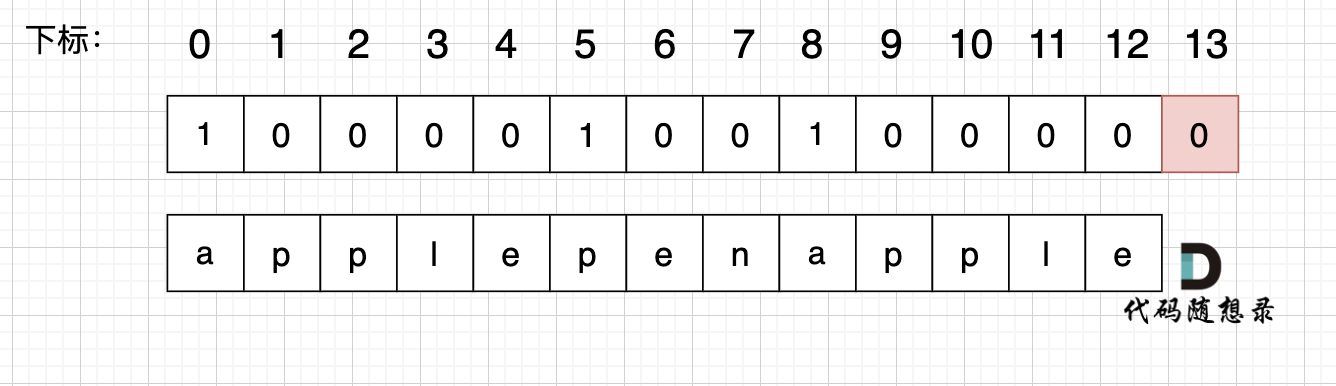
使用用例:s = "applepenapple", wordDict = ["apple", "pen"],对应的dp数组状态如下:
|
使用用例:s = "applepenapple", wordDict = ["apple", "pen"],对应的dp数组状态如下:
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
最后dp[s.size()] = 0 即 dp[13] = 0 ,而不是1,因为先用 "apple" 去遍历的时候,dp[8]并没有被赋值为1 (还没用"pen"),所以 dp[13]也不能变成1。
|
最后dp[s.size()] = 0 即 dp[13] = 0 ,而不是1,因为先用 "apple" 去遍历的时候,dp[8]并没有被赋值为1 (还没用"pen"),所以 dp[13]也不能变成1。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -13,7 +13,7 @@
|
||||||
|
|
||||||
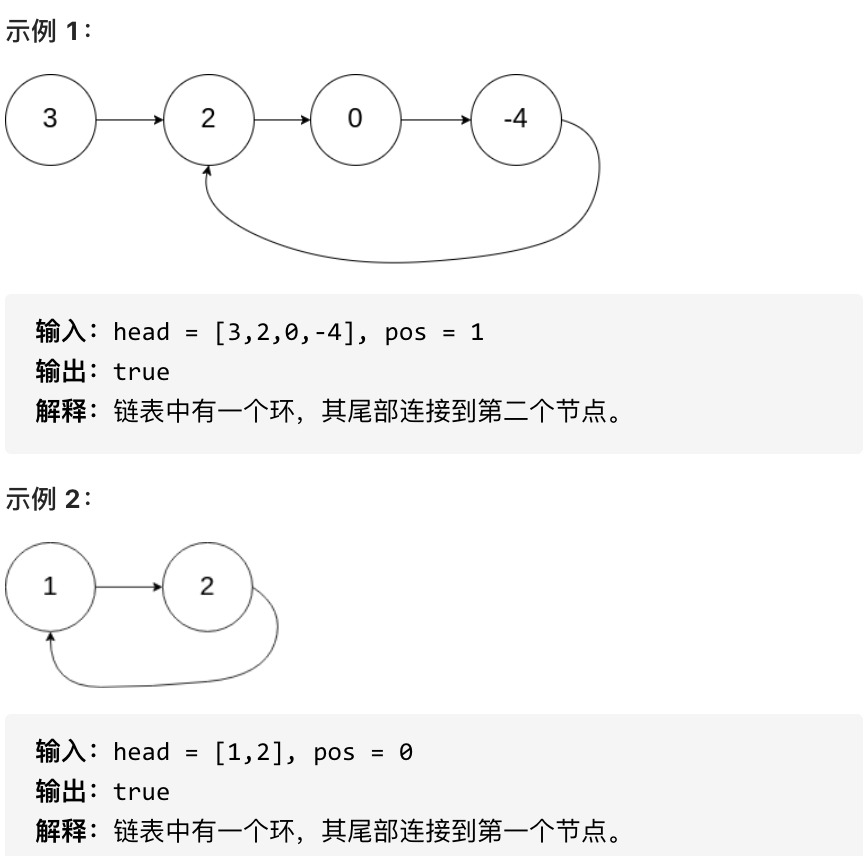
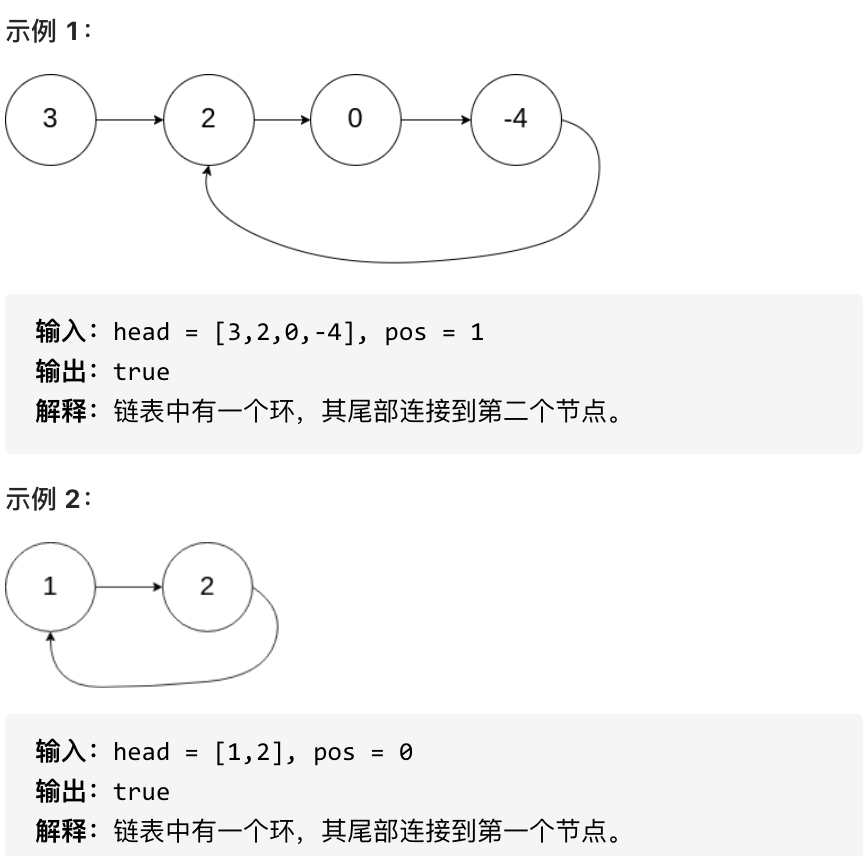
如果链表中存在环,则返回 true 。 否则,返回 false 。
|
如果链表中存在环,则返回 true 。 否则,返回 false 。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
## 思路
|
## 思路
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -20,7 +20,7 @@
|
||||||
|
|
||||||
**说明**:不允许修改给定的链表。
|
**说明**:不允许修改给定的链表。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -50,7 +50,7 @@
|
||||||
|
|
||||||
会发现最终都是这种情况, 如下图:
|
会发现最终都是这种情况, 如下图:
|
||||||
|
|
||||||
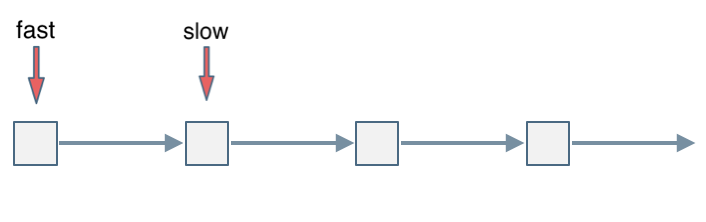
|
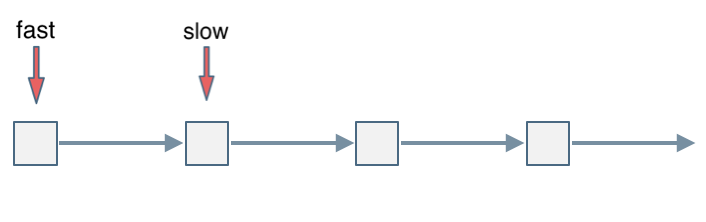
|
||||||
|
|
||||||
|
|
||||||
fast和slow各自再走一步, fast和slow就相遇了
|
fast和slow各自再走一步, fast和slow就相遇了
|
||||||
|
|
@ -70,7 +70,7 @@ fast和slow各自再走一步, fast和slow就相遇了
|
||||||
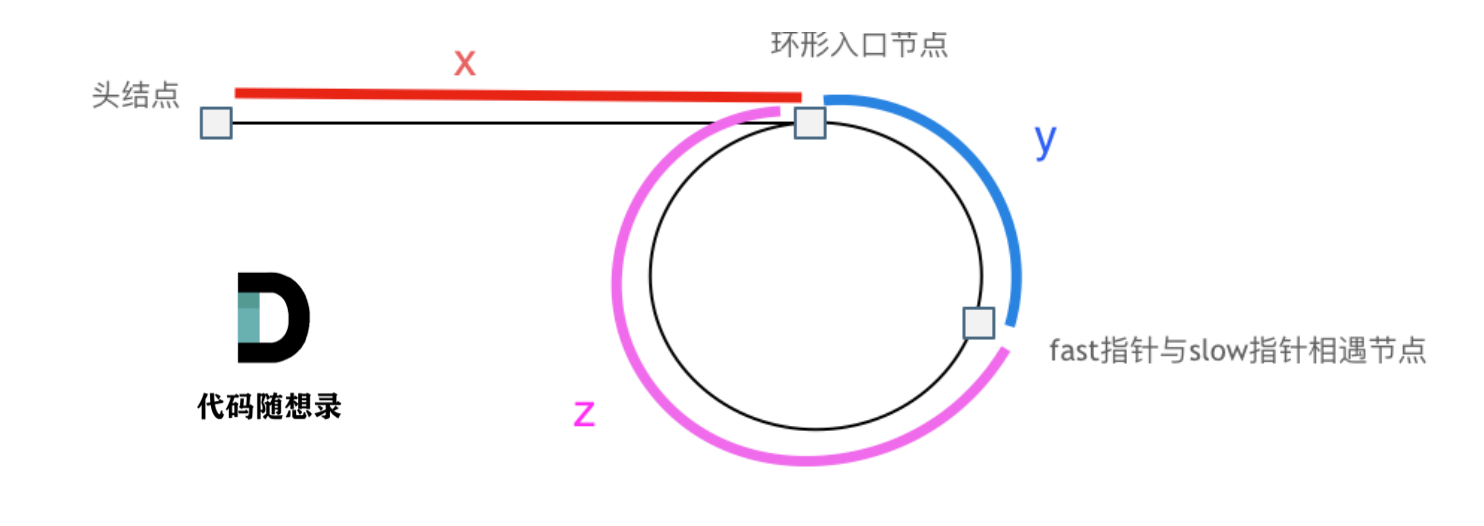
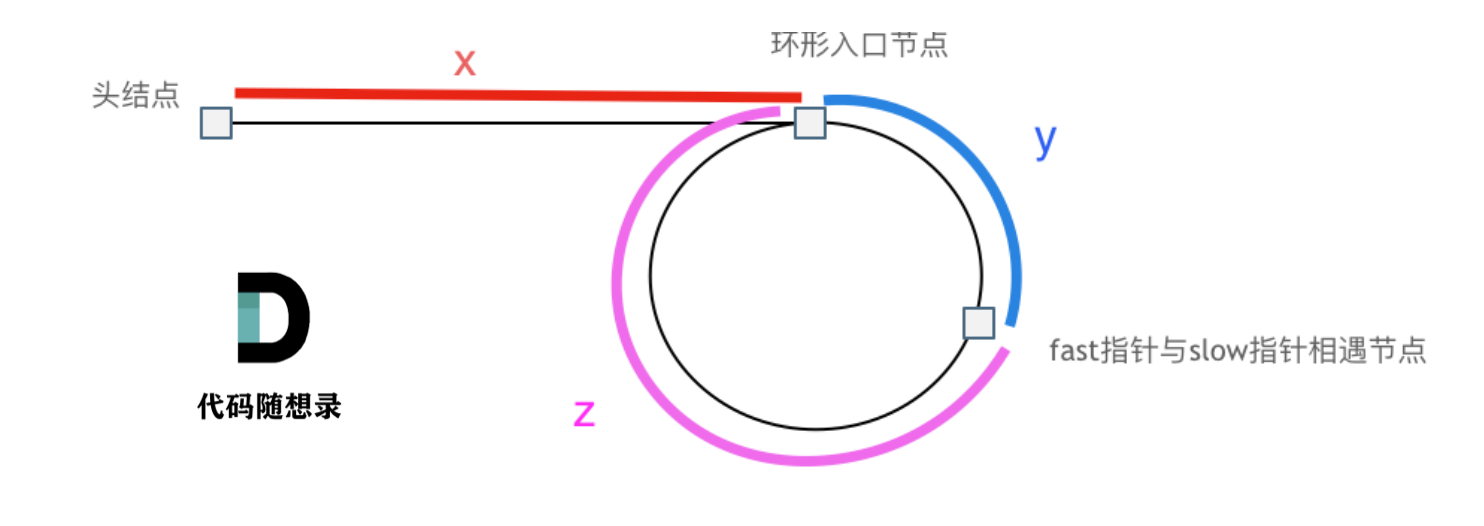
环形入口节点到 fast指针与slow指针相遇节点 节点数为y。
|
环形入口节点到 fast指针与slow指针相遇节点 节点数为y。
|
||||||
从相遇节点 再到环形入口节点节点数为 z。 如图所示:
|
从相遇节点 再到环形入口节点节点数为 z。 如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
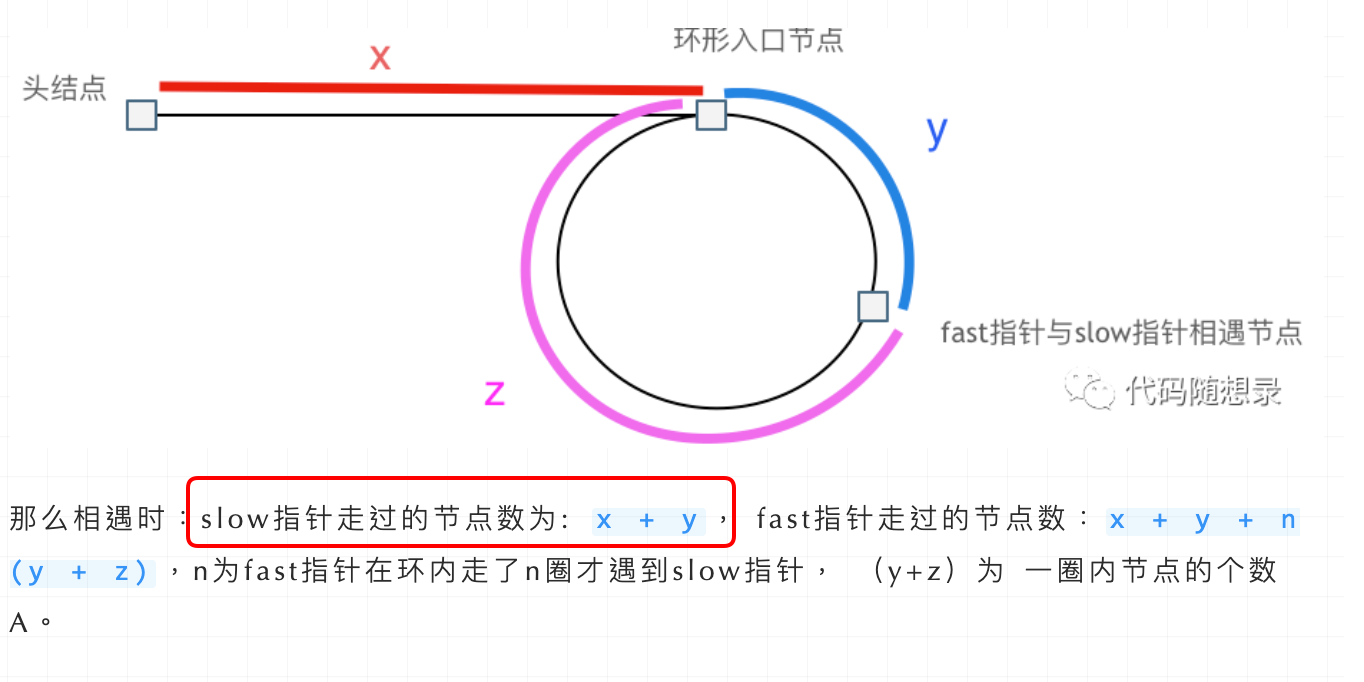
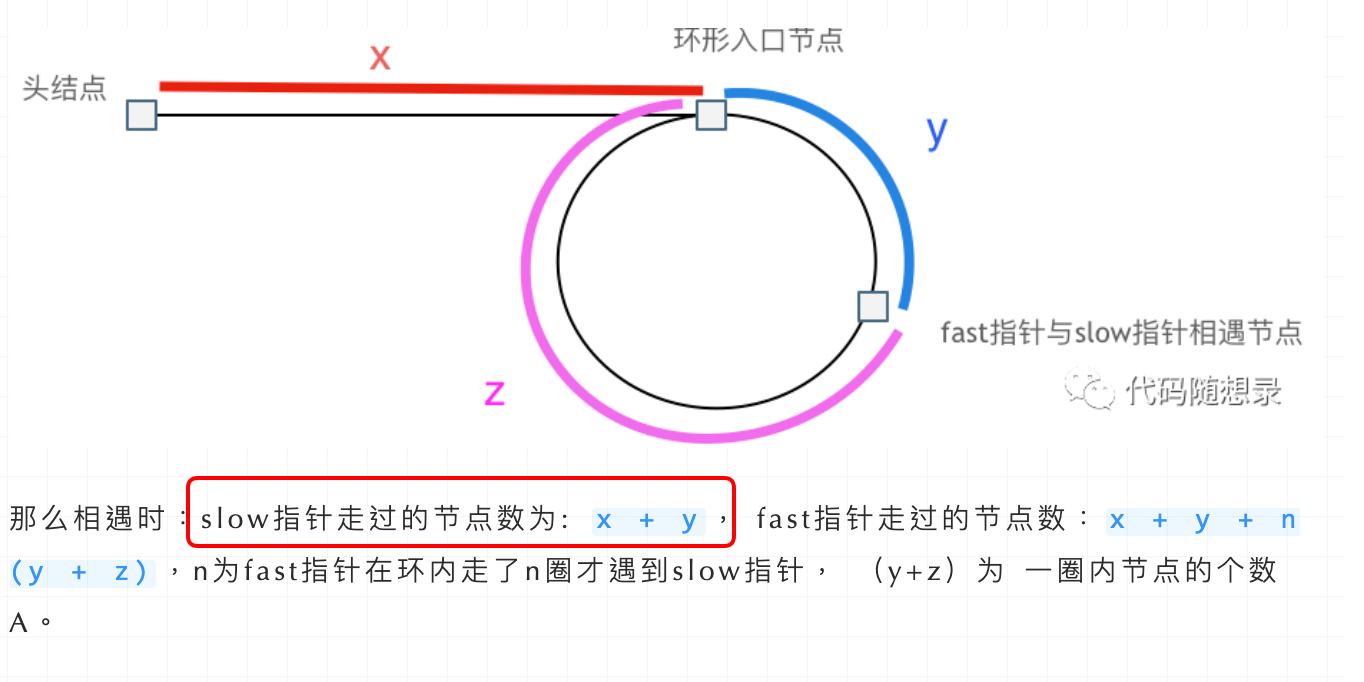
那么相遇时:
|
那么相遇时:
|
||||||
slow指针走过的节点数为: `x + y`,
|
slow指针走过的节点数为: `x + y`,
|
||||||
|
|
@ -154,20 +154,20 @@ public:
|
||||||
|
|
||||||
即文章[链表:环找到了,那入口呢?](https://programmercarl.com/0142.环形链表II.html)中如下的地方:
|
即文章[链表:环找到了,那入口呢?](https://programmercarl.com/0142.环形链表II.html)中如下的地方:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
首先slow进环的时候,fast一定是先进环来了。
|
首先slow进环的时候,fast一定是先进环来了。
|
||||||
|
|
||||||
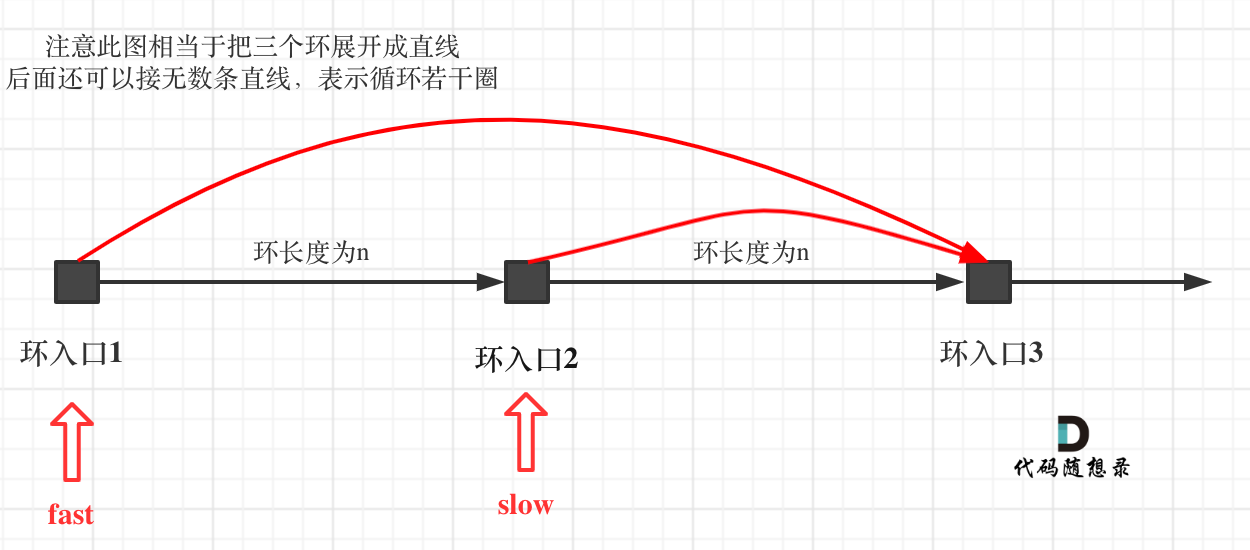
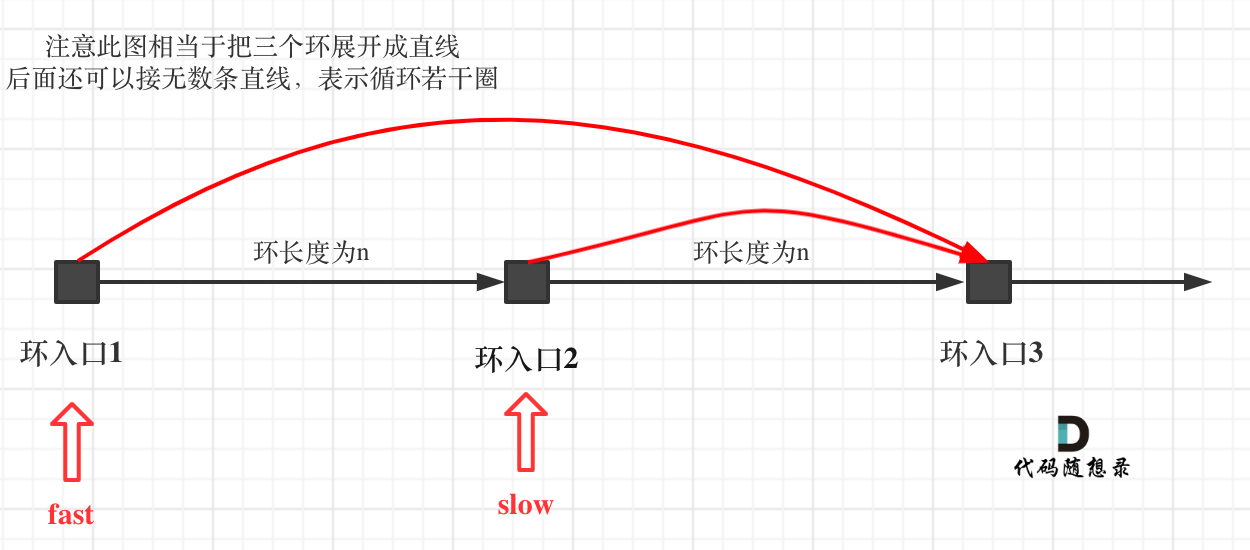
如果slow进环入口,fast也在环入口,那么把这个环展开成直线,就是如下图的样子:
|
如果slow进环入口,fast也在环入口,那么把这个环展开成直线,就是如下图的样子:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
可以看出如果slow 和 fast同时在环入口开始走,一定会在环入口3相遇,slow走了一圈,fast走了两圈。
|
可以看出如果slow 和 fast同时在环入口开始走,一定会在环入口3相遇,slow走了一圈,fast走了两圈。
|
||||||
|
|
||||||
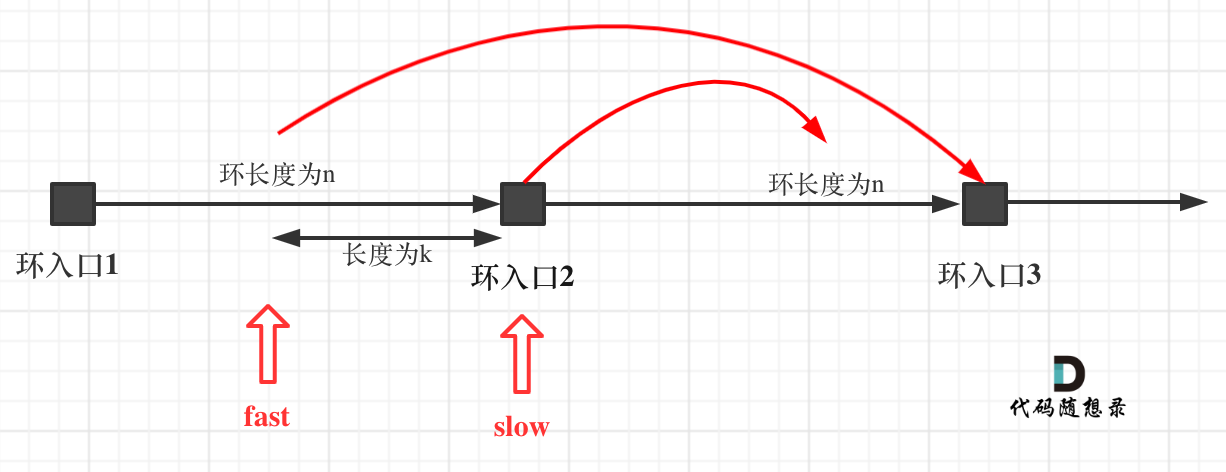
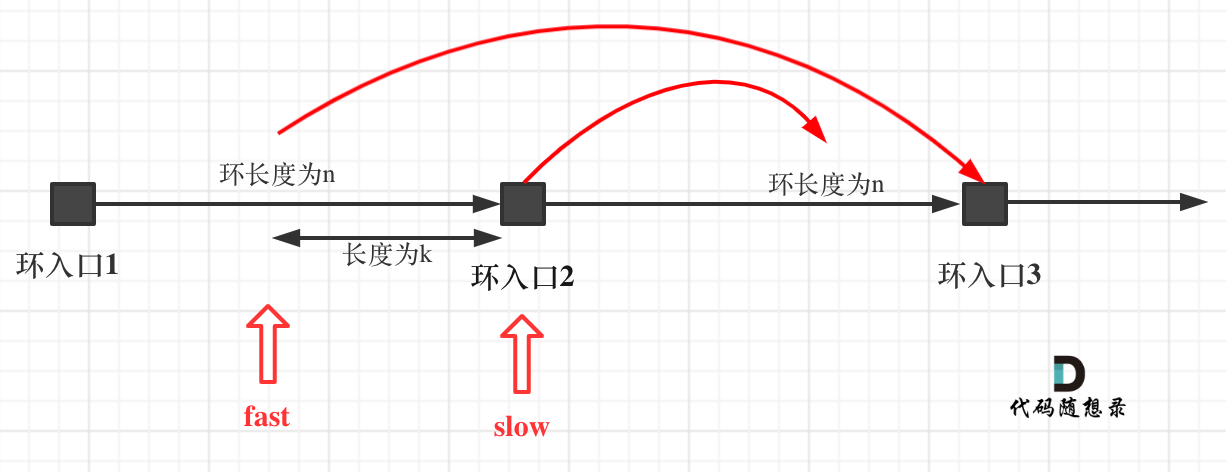
重点来了,slow进环的时候,fast一定是在环的任意一个位置,如图:
|
重点来了,slow进环的时候,fast一定是在环的任意一个位置,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
那么fast指针走到环入口3的时候,已经走了k + n 个节点,slow相应的应该走了(k + n) / 2 个节点。
|
那么fast指针走到环入口3的时候,已经走了k + n 个节点,slow相应的应该走了(k + n) / 2 个节点。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -6,7 +6,7 @@
|
||||||
|
|
||||||
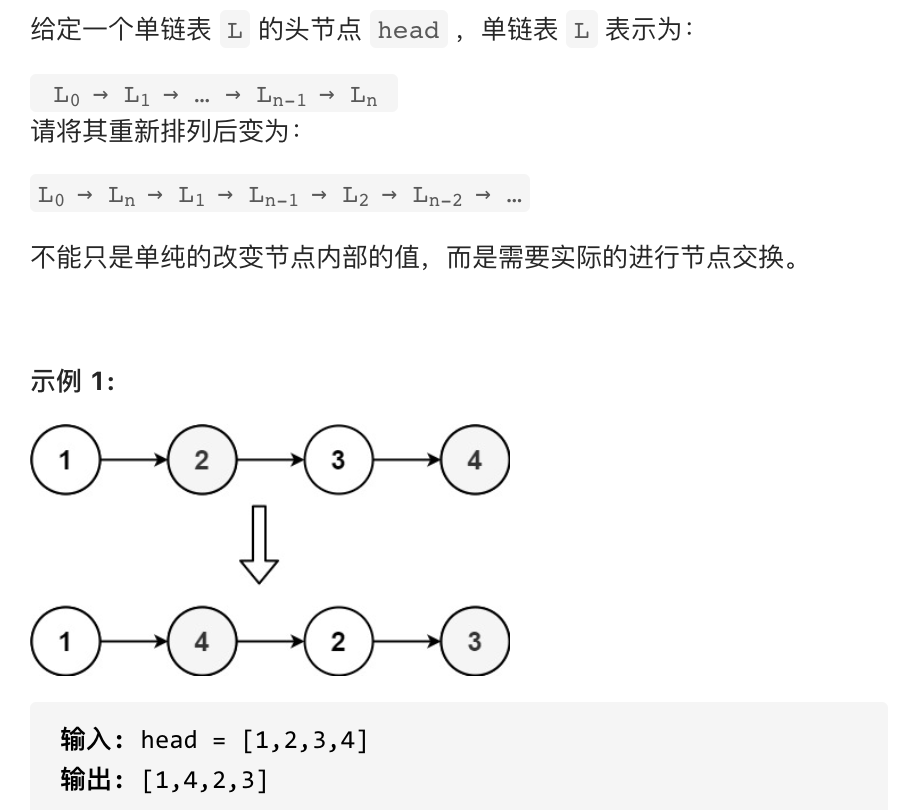
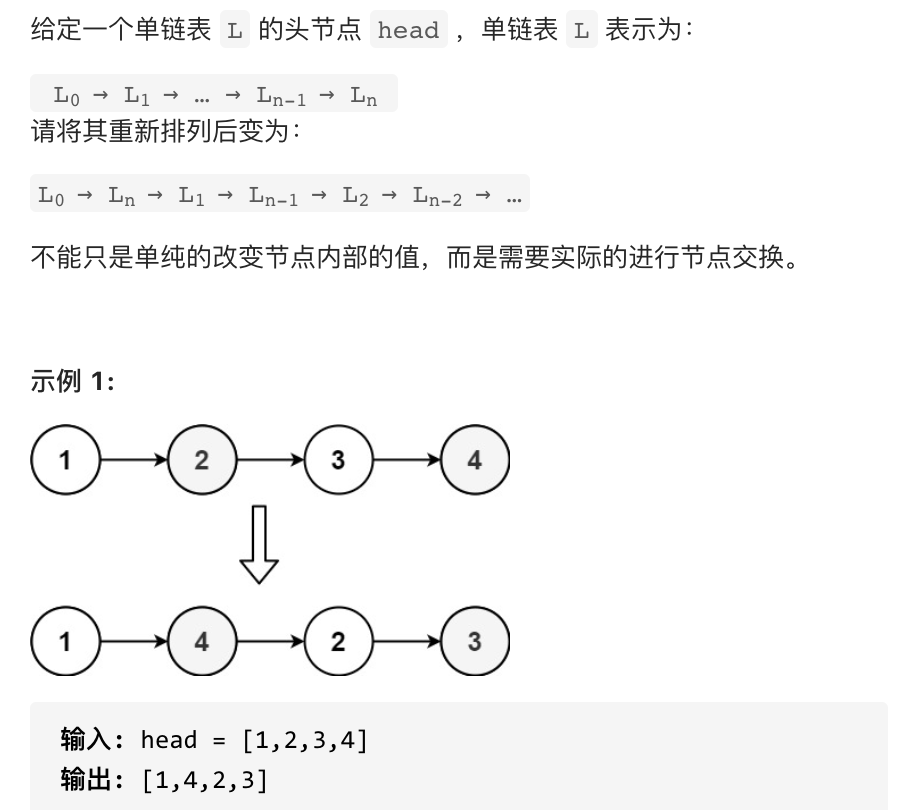
[力扣题目链接](https://leetcode.cn/problems/reorder-list/submissions/)
|
[力扣题目链接](https://leetcode.cn/problems/reorder-list/submissions/)
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
## 思路
|
## 思路
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -132,7 +132,7 @@ for (int j = 1; j < 2 * k; j += 2) {
|
||||||
|
|
||||||
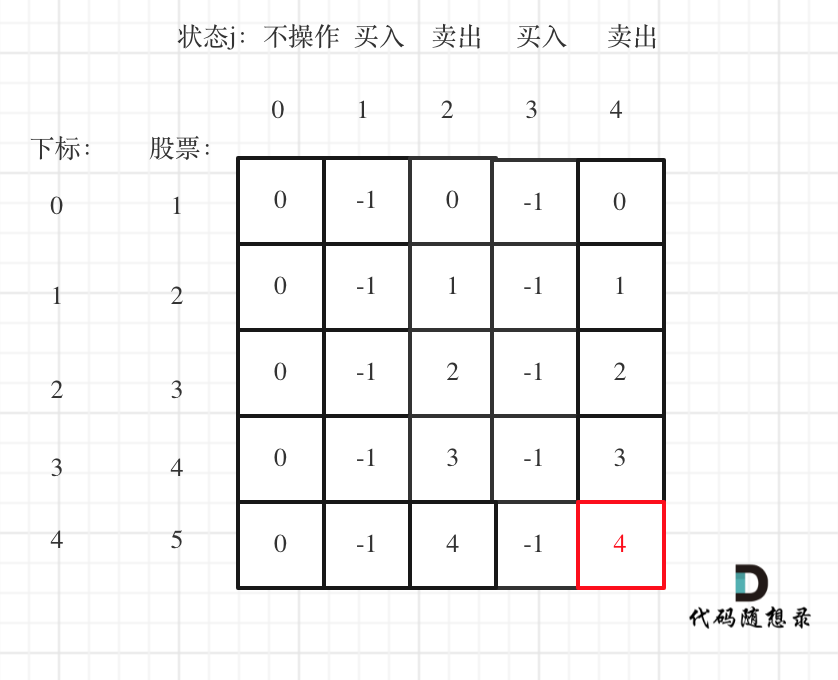
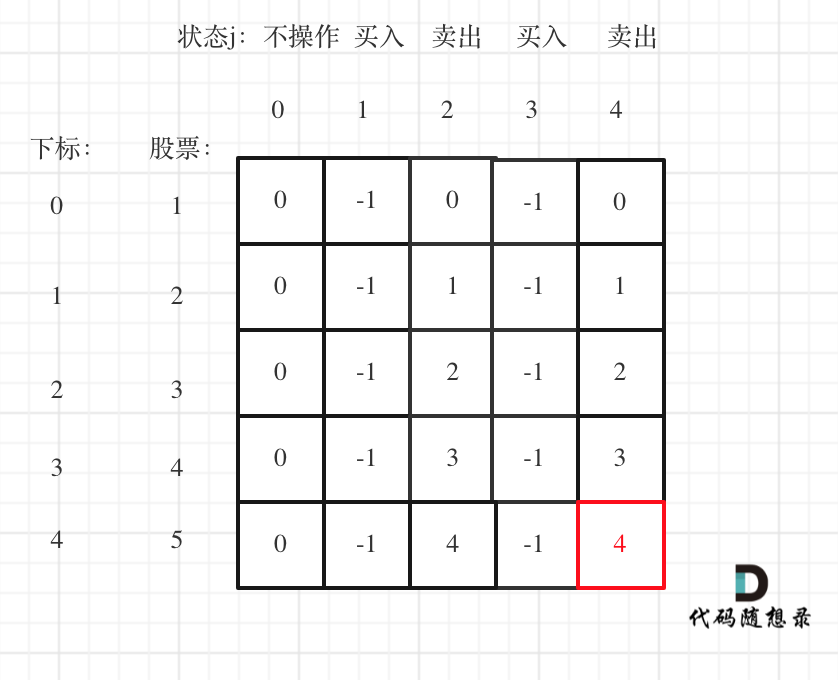
以输入[1,2,3,4,5],k=2为例。
|
以输入[1,2,3,4,5],k=2为例。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
最后一次卖出,一定是利润最大的,dp[prices.size() - 1][2 * k]即红色部分就是最后求解。
|
最后一次卖出,一定是利润最大的,dp[prices.size() - 1][2 * k]即红色部分就是最后求解。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -87,7 +87,7 @@ for (int i = 2; i < nums.size(); i++) {
|
||||||
|
|
||||||
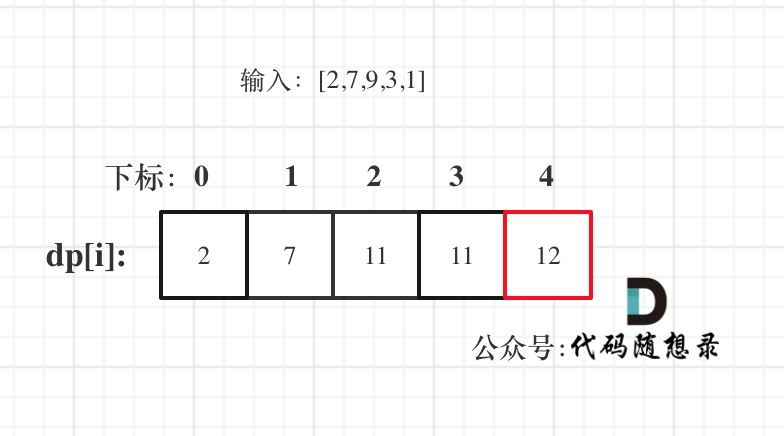
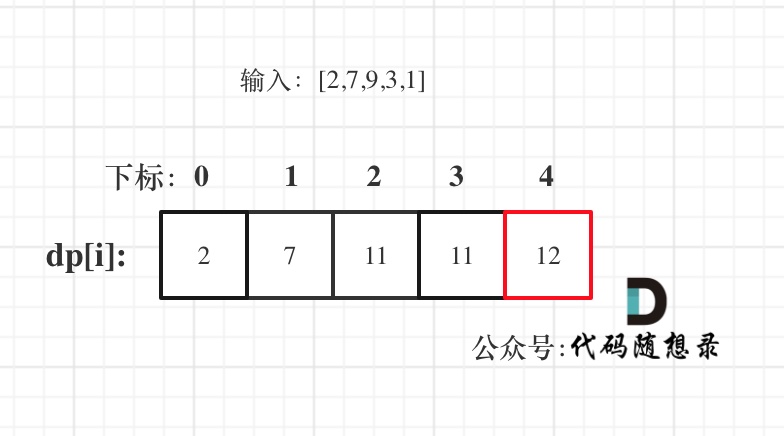
以示例二,输入[2,7,9,3,1]为例。
|
以示例二,输入[2,7,9,3,1]为例。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
红框dp[nums.size() - 1]为结果。
|
红框dp[nums.size() - 1]为结果。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -13,7 +13,7 @@
|
||||||
|
|
||||||
此外,你可以假设该网格的四条边均被水包围。
|
此外,你可以假设该网格的四条边均被水包围。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
提示:
|
提示:
|
||||||
|
|
||||||
|
|
@ -28,7 +28,7 @@
|
||||||
|
|
||||||
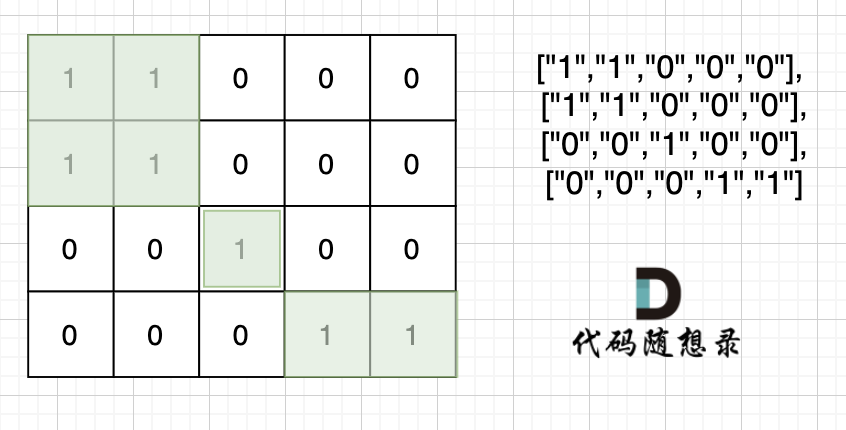
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
||||||
|
|
||||||

|
|
||||||
|
|
||||||
这道题题目是 DFS,BFS,并查集,基础题目。
|
这道题题目是 DFS,BFS,并查集,基础题目。
|
||||||
|
|
||||||
|
|
@ -48,7 +48,7 @@
|
||||||
|
|
||||||
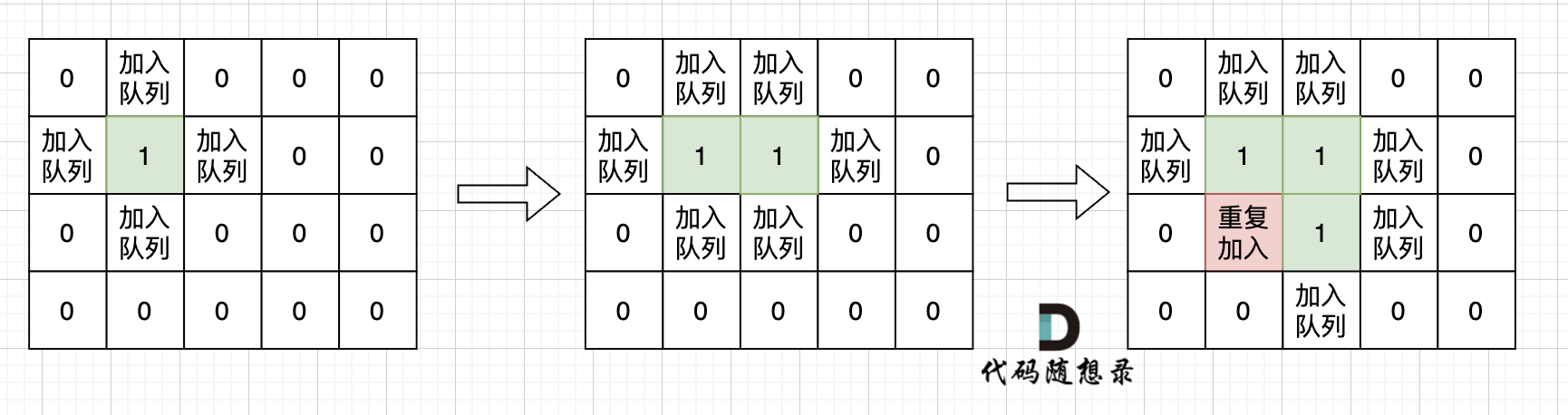
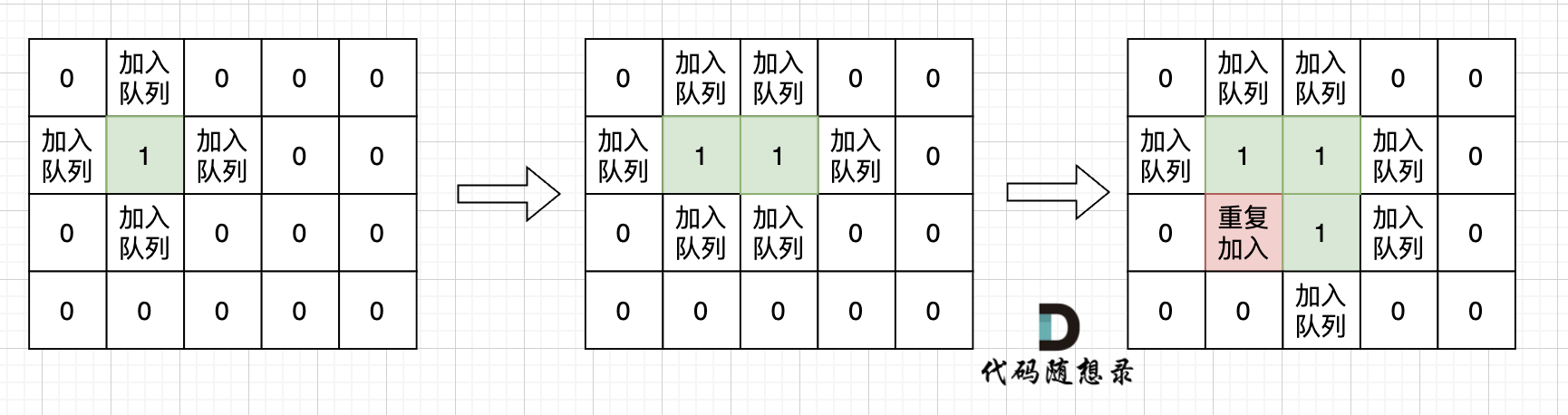
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。
|
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
超时写法 (从队列中取出节点再标记)
|
超时写法 (从队列中取出节点再标记)
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -12,7 +12,7 @@
|
||||||
|
|
||||||
此外,你可以假设该网格的四条边均被水包围。
|
此外,你可以假设该网格的四条边均被水包围。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
提示:
|
提示:
|
||||||
|
|
||||||
|
|
@ -27,7 +27,7 @@
|
||||||
|
|
||||||
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
这道题题目是 DFS,BFS,并查集,基础题目。
|
这道题题目是 DFS,BFS,并查集,基础题目。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -34,11 +34,11 @@
|
||||||
|
|
||||||
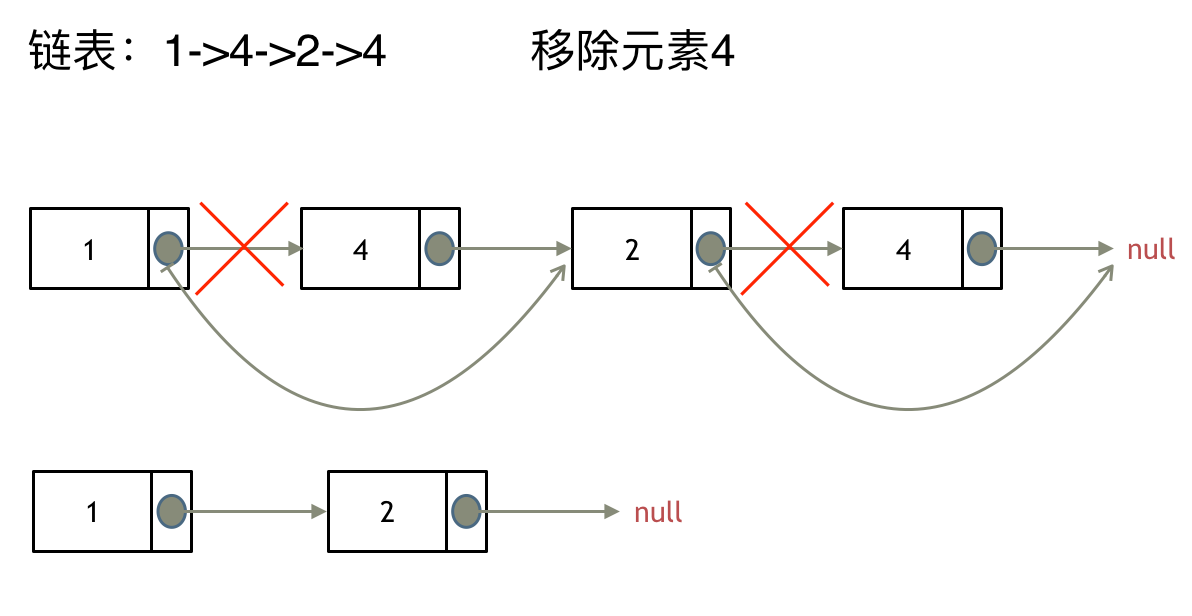
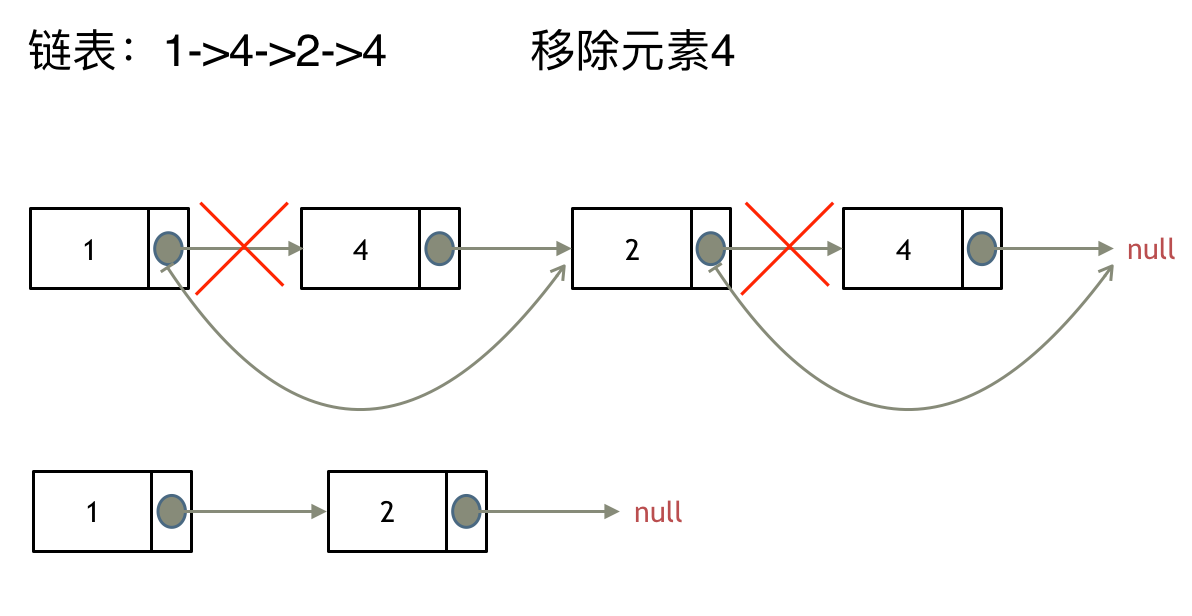
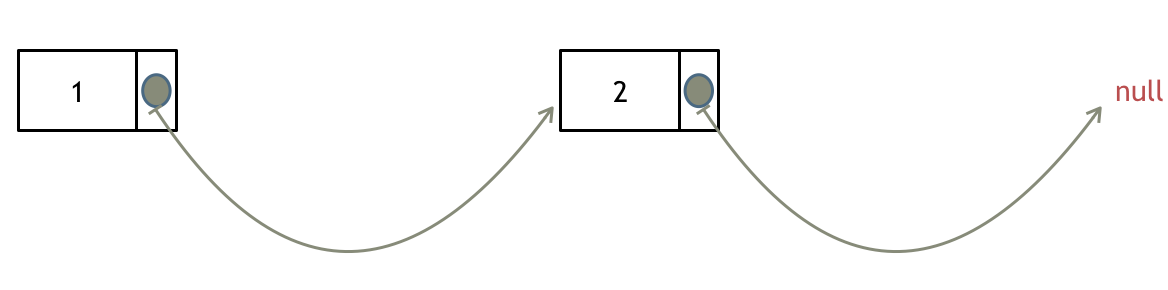
这里以链表 1 4 2 4 来举例,移除元素4。
|
这里以链表 1 4 2 4 来举例,移除元素4。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
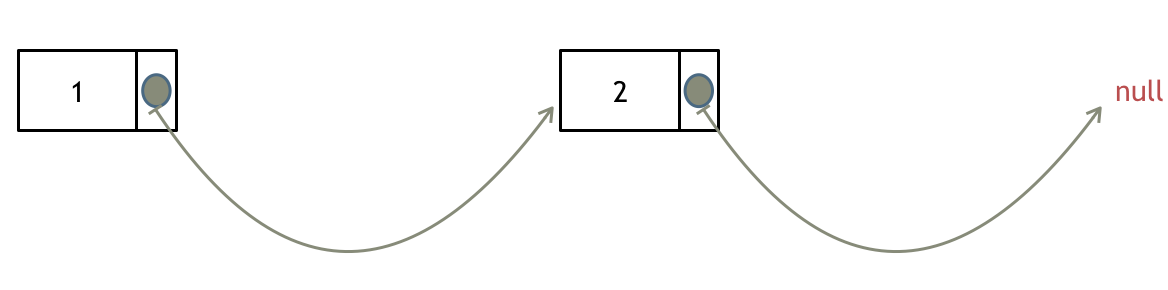
如果使用C,C++编程语言的话,不要忘了还要从内存中删除这两个移除的节点, 清理节点内存之后如图:
|
如果使用C,C++编程语言的话,不要忘了还要从内存中删除这两个移除的节点, 清理节点内存之后如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
**当然如果使用java ,python的话就不用手动管理内存了。**
|
**当然如果使用java ,python的话就不用手动管理内存了。**
|
||||||
|
|
||||||
|
|
@ -56,16 +56,16 @@
|
||||||
|
|
||||||
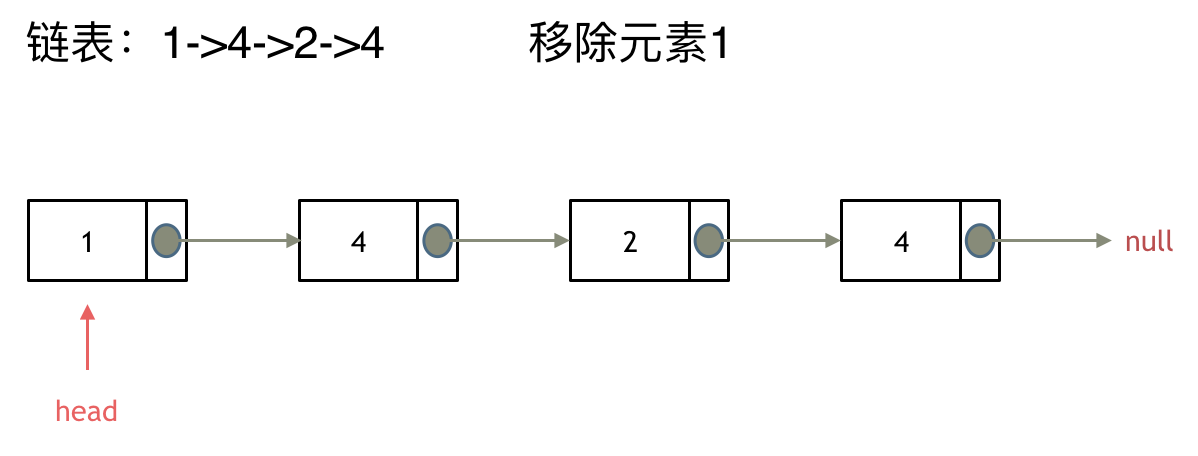
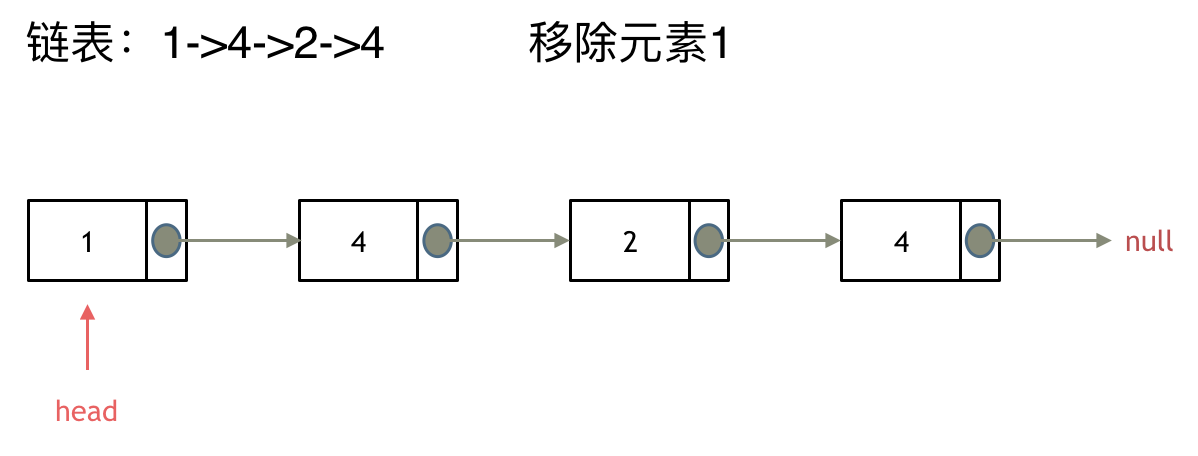
来看第一种操作:直接使用原来的链表来进行移除。
|
来看第一种操作:直接使用原来的链表来进行移除。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
移除头结点和移除其他节点的操作是不一样的,因为链表的其他节点都是通过前一个节点来移除当前节点,而头结点没有前一个节点。
|
移除头结点和移除其他节点的操作是不一样的,因为链表的其他节点都是通过前一个节点来移除当前节点,而头结点没有前一个节点。
|
||||||
|
|
||||||
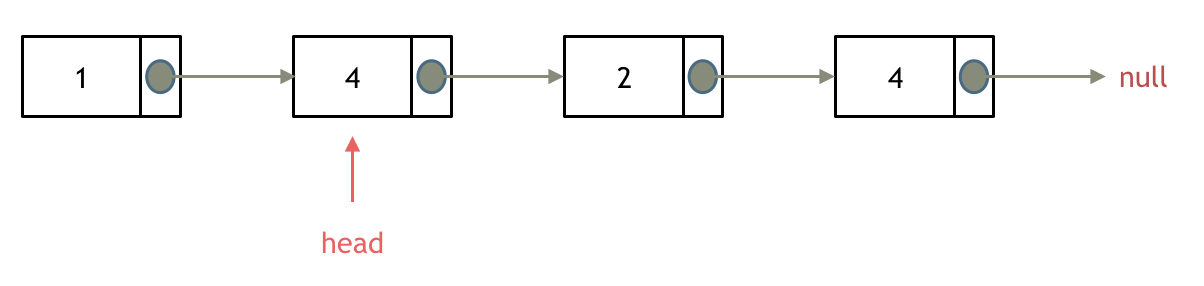
所以头结点如何移除呢,其实只要将头结点向后移动一位就可以,这样就从链表中移除了一个头结点。
|
所以头结点如何移除呢,其实只要将头结点向后移动一位就可以,这样就从链表中移除了一个头结点。
|
||||||
|
|
||||||
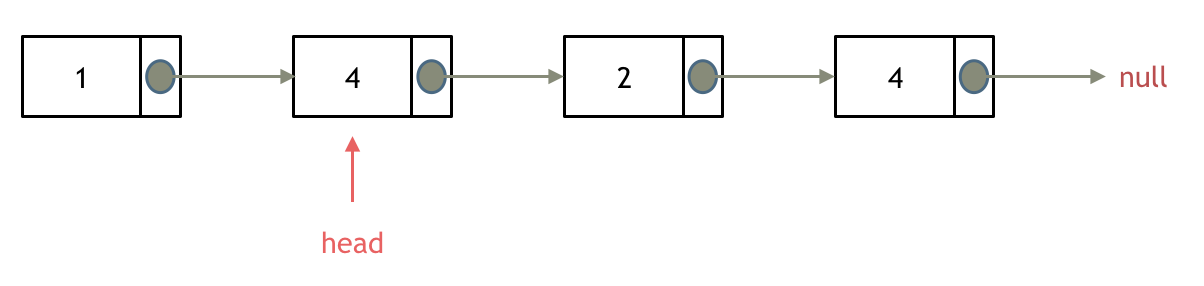
|
|
||||||
|
|
||||||
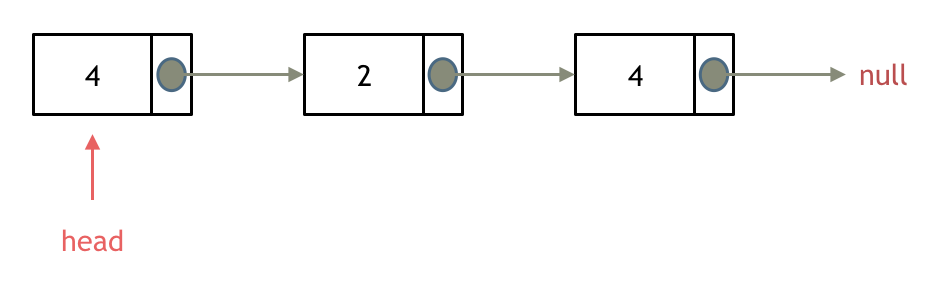
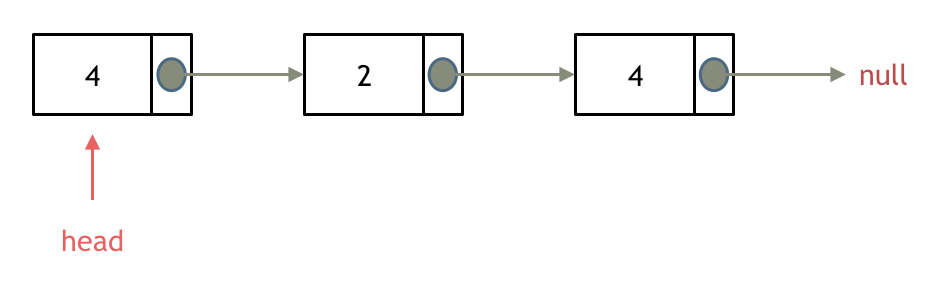
依然别忘将原头结点从内存中删掉。
|
依然别忘将原头结点从内存中删掉。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
这样移除了一个头结点,是不是发现,在单链表中移除头结点 和 移除其他节点的操作方式是不一样,其实在写代码的时候也会发现,需要单独写一段逻辑来处理移除头结点的情况。
|
这样移除了一个头结点,是不是发现,在单链表中移除头结点 和 移除其他节点的操作方式是不一样,其实在写代码的时候也会发现,需要单独写一段逻辑来处理移除头结点的情况。
|
||||||
|
|
@ -76,7 +76,7 @@
|
||||||
|
|
||||||
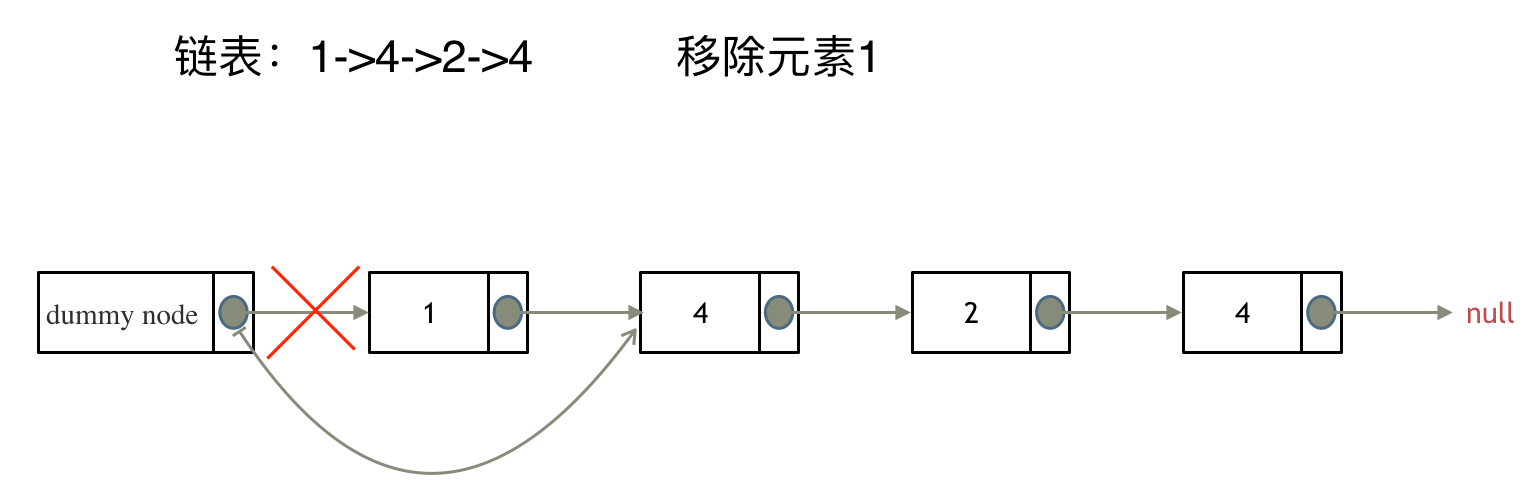
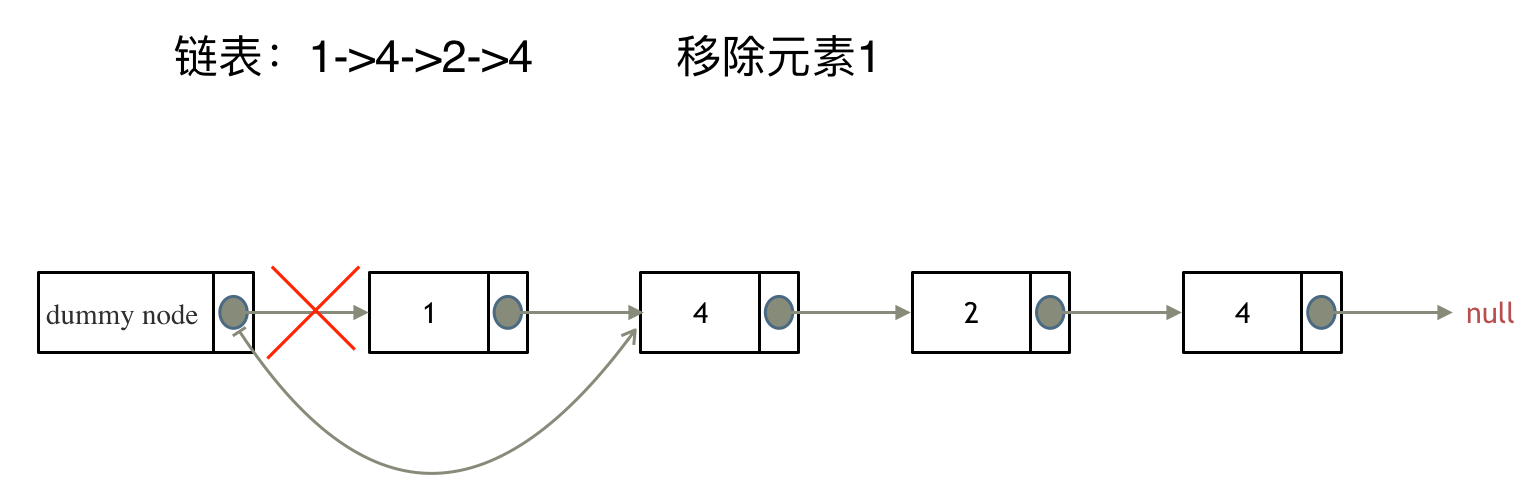
来看看如何设置一个虚拟头。依然还是在这个链表中,移除元素1。
|
来看看如何设置一个虚拟头。依然还是在这个链表中,移除元素1。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
这里来给链表添加一个虚拟头结点为新的头结点,此时要移除这个旧头结点元素1。
|
这里来给链表添加一个虚拟头结点为新的头结点,此时要移除这个旧头结点元素1。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -27,7 +27,7 @@
|
||||||
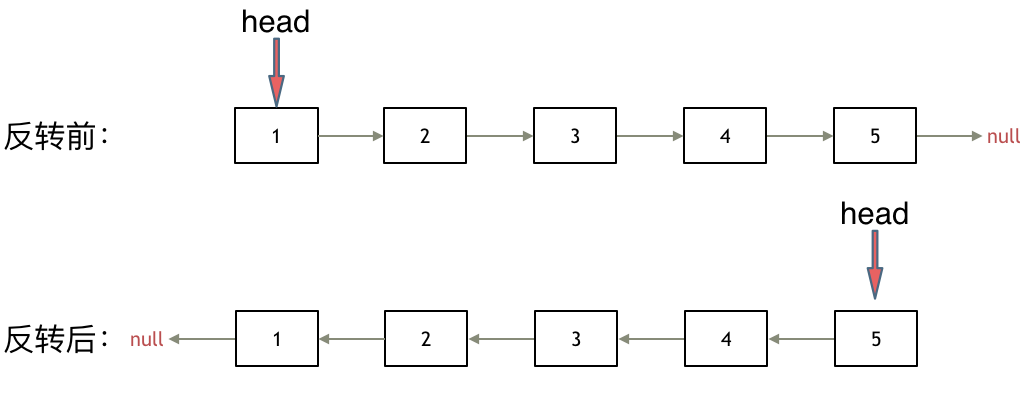
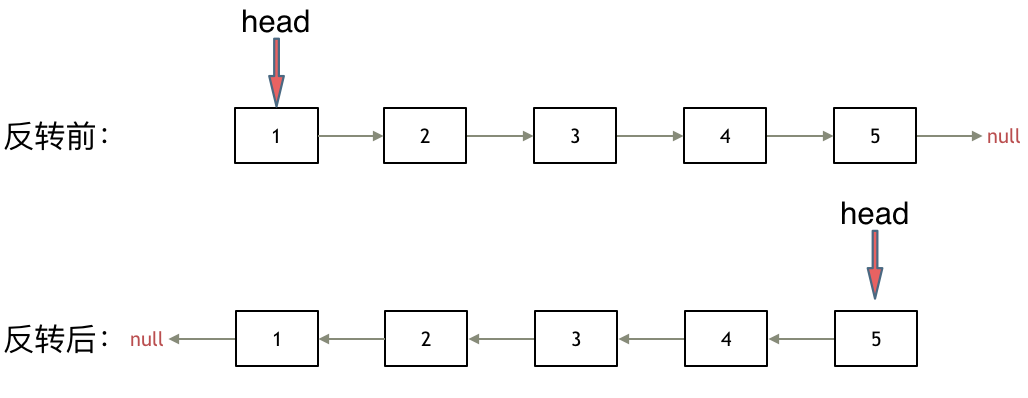
其实只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表,如图所示:
|
其实只需要改变链表的next指针的指向,直接将链表反转 ,而不用重新定义一个新的链表,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改变next指针的方向。
|
之前链表的头节点是元素1, 反转之后头结点就是元素5 ,这里并没有添加或者删除节点,仅仅是改变next指针的方向。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -104,7 +104,7 @@ public:
|
||||||
|
|
||||||
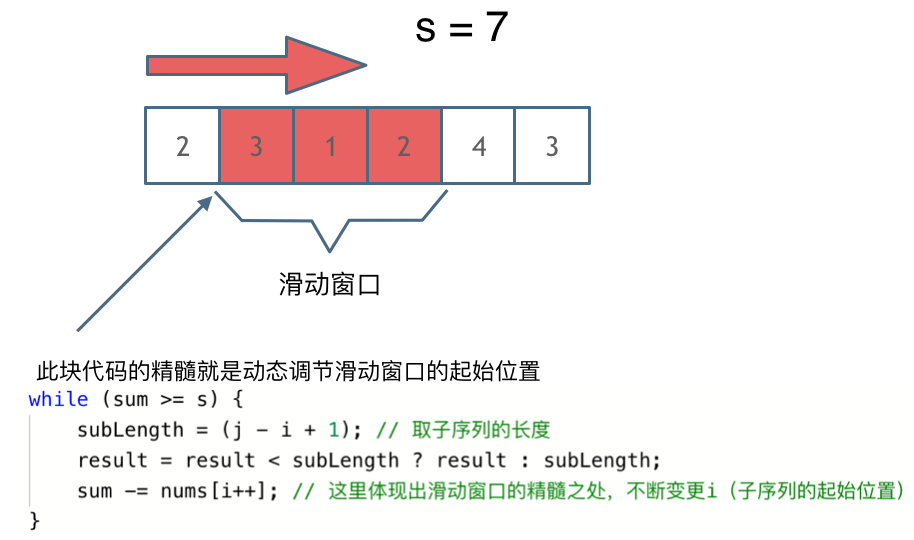
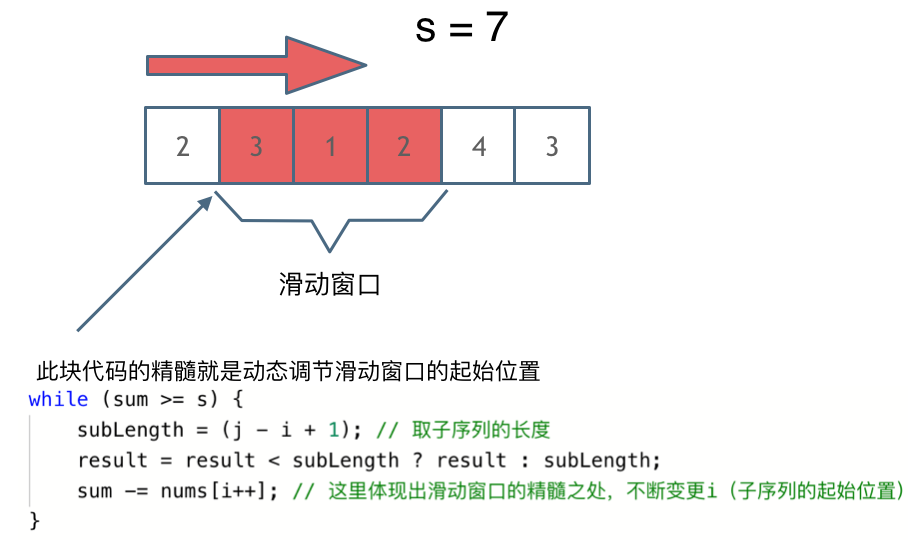
解题的关键在于 窗口的起始位置如何移动,如图所示:
|
解题的关键在于 窗口的起始位置如何移动,如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
可以发现**滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。**
|
可以发现**滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。**
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -42,15 +42,15 @@
|
||||||
|
|
||||||
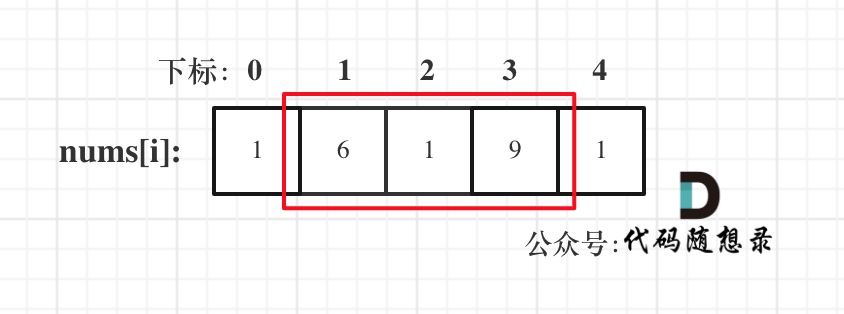
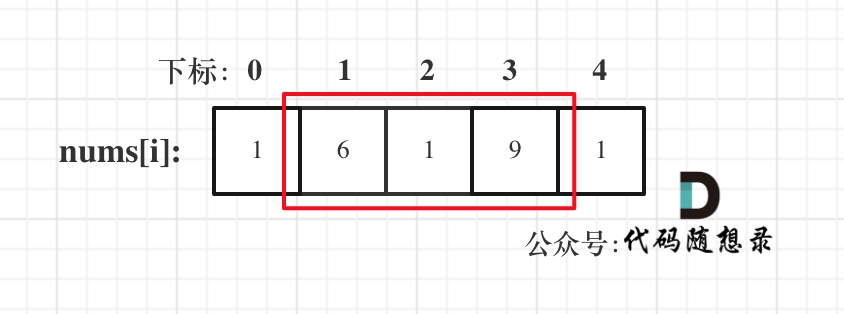
* 情况一:考虑不包含首尾元素
|
* 情况一:考虑不包含首尾元素
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
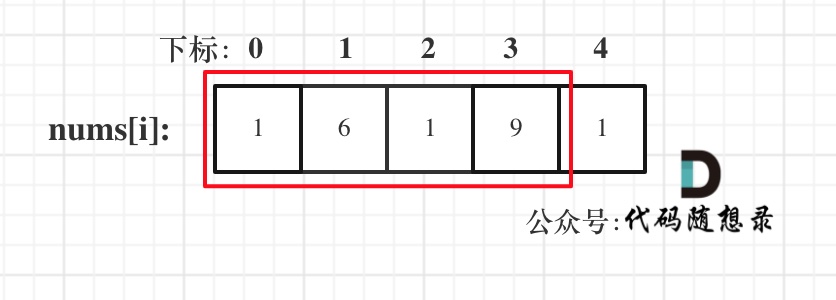
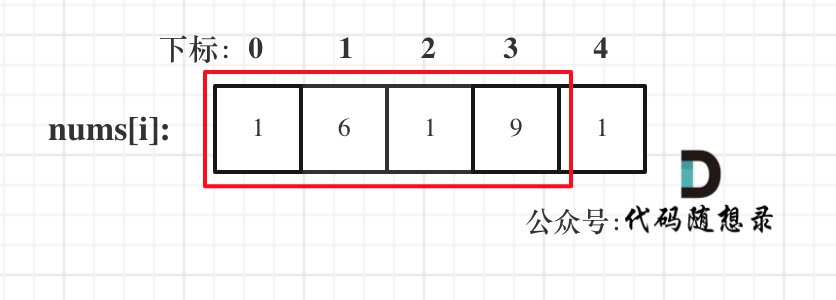
* 情况二:考虑包含首元素,不包含尾元素
|
* 情况二:考虑包含首元素,不包含尾元素
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
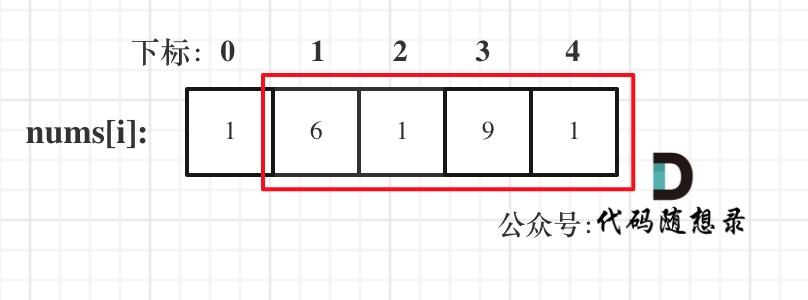
* 情况三:考虑包含尾元素,不包含首元素
|
* 情况三:考虑包含尾元素,不包含首元素
|
||||||
|
|
||||||
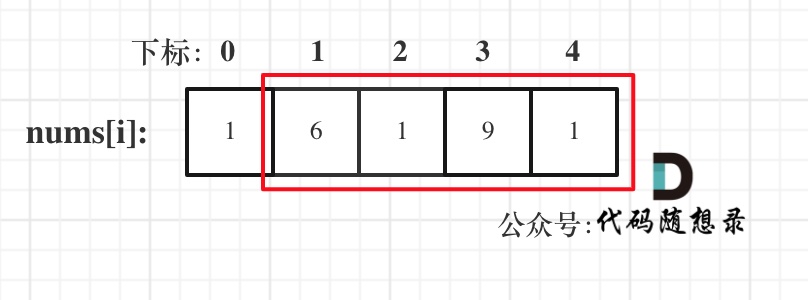
|
|
||||||
|
|
||||||
**注意我这里用的是"考虑"**,例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
|
**注意我这里用的是"考虑"**,例如情况三,虽然是考虑包含尾元素,但不一定要选尾部元素! 对于情况三,取nums[1] 和 nums[3]就是最大的。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -45,7 +45,7 @@
|
||||||
|
|
||||||
选取过程如图:
|
选取过程如图:
|
||||||
|
|
||||||
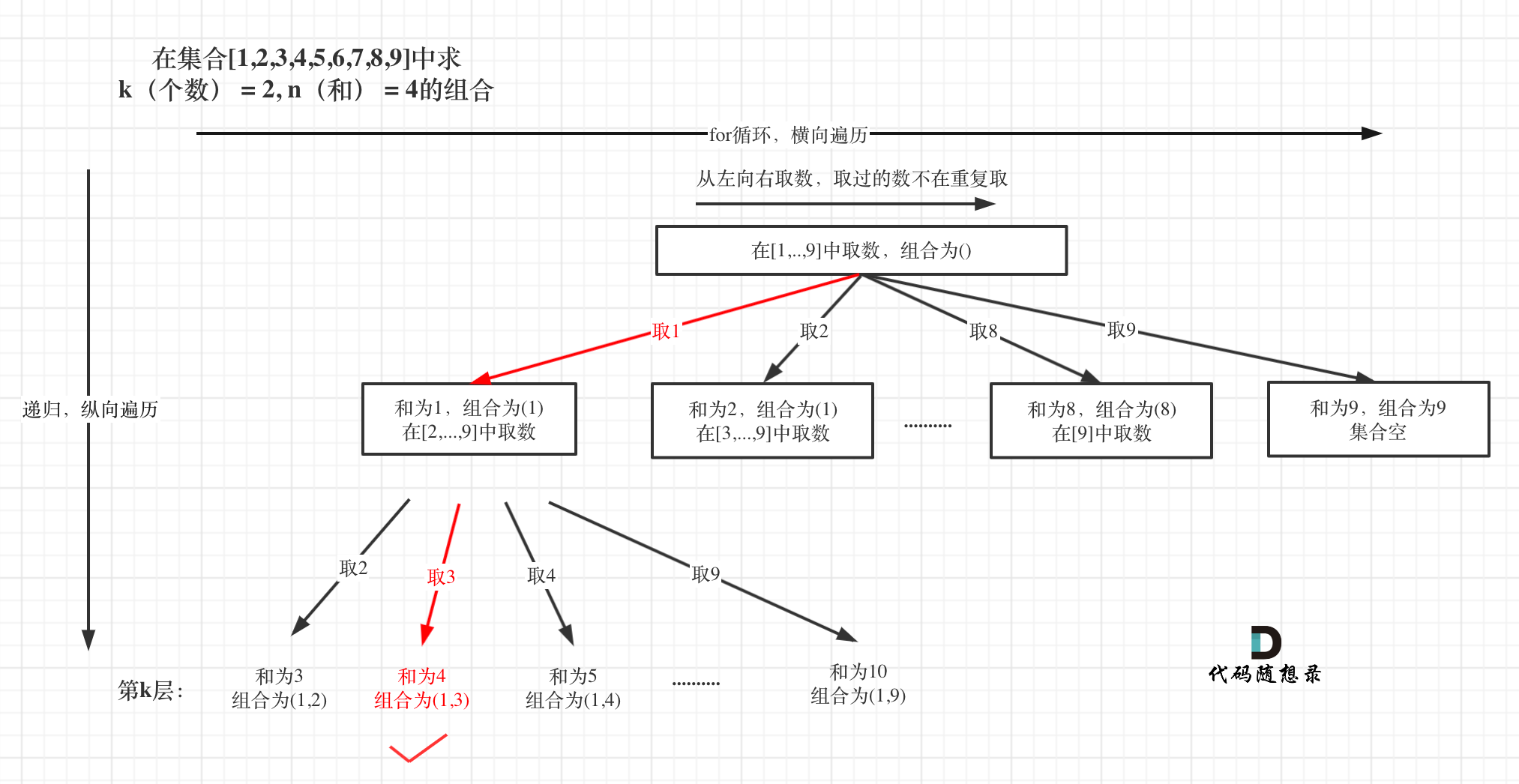
|

|
||||||
|
|
||||||
图中,可以看出,只有最后取到集合(1,3)和为4 符合条件。
|
图中,可以看出,只有最后取到集合(1,3)和为4 符合条件。
|
||||||
|
|
||||||
|
|
@ -108,7 +108,7 @@ if (path.size() == k) {
|
||||||
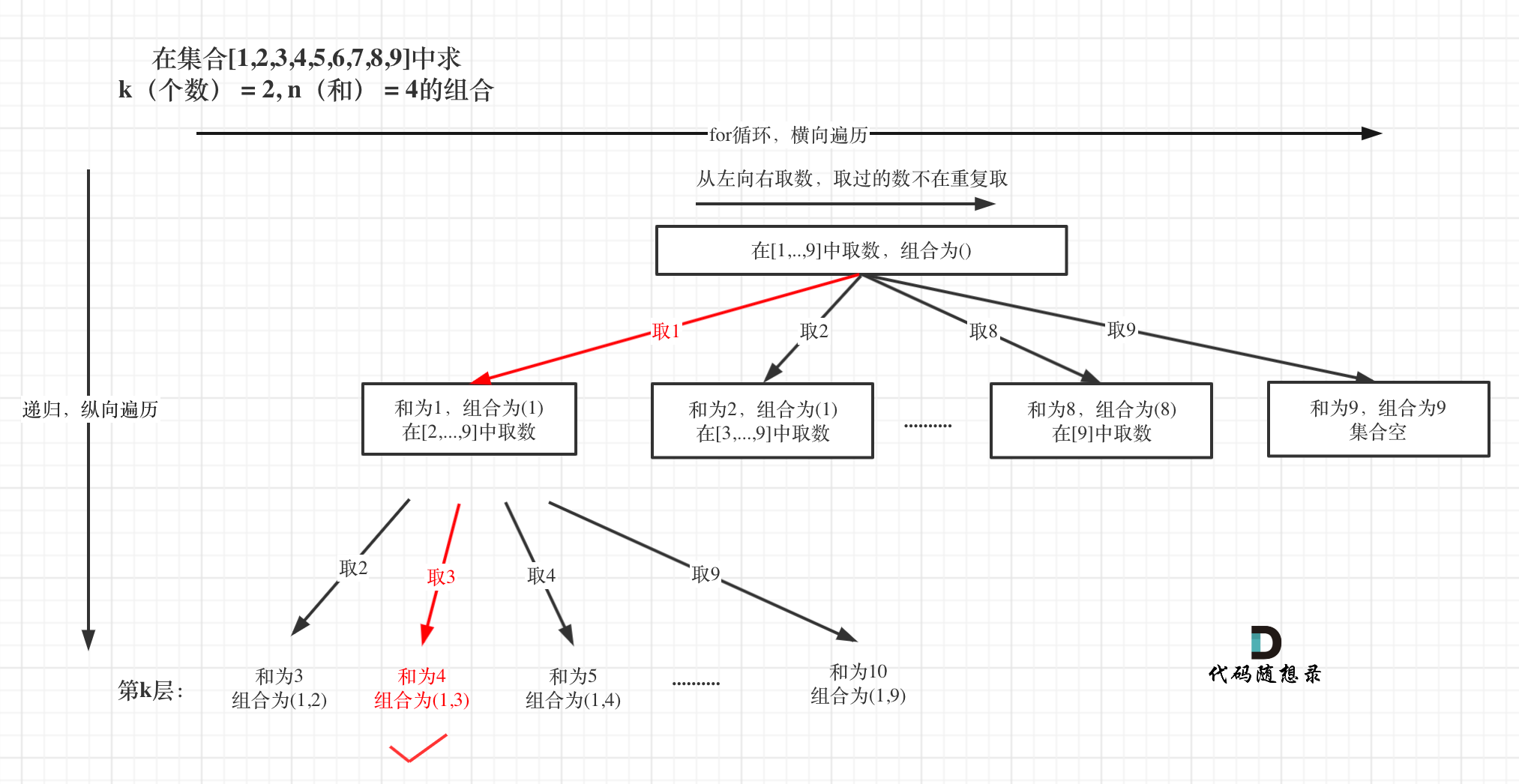
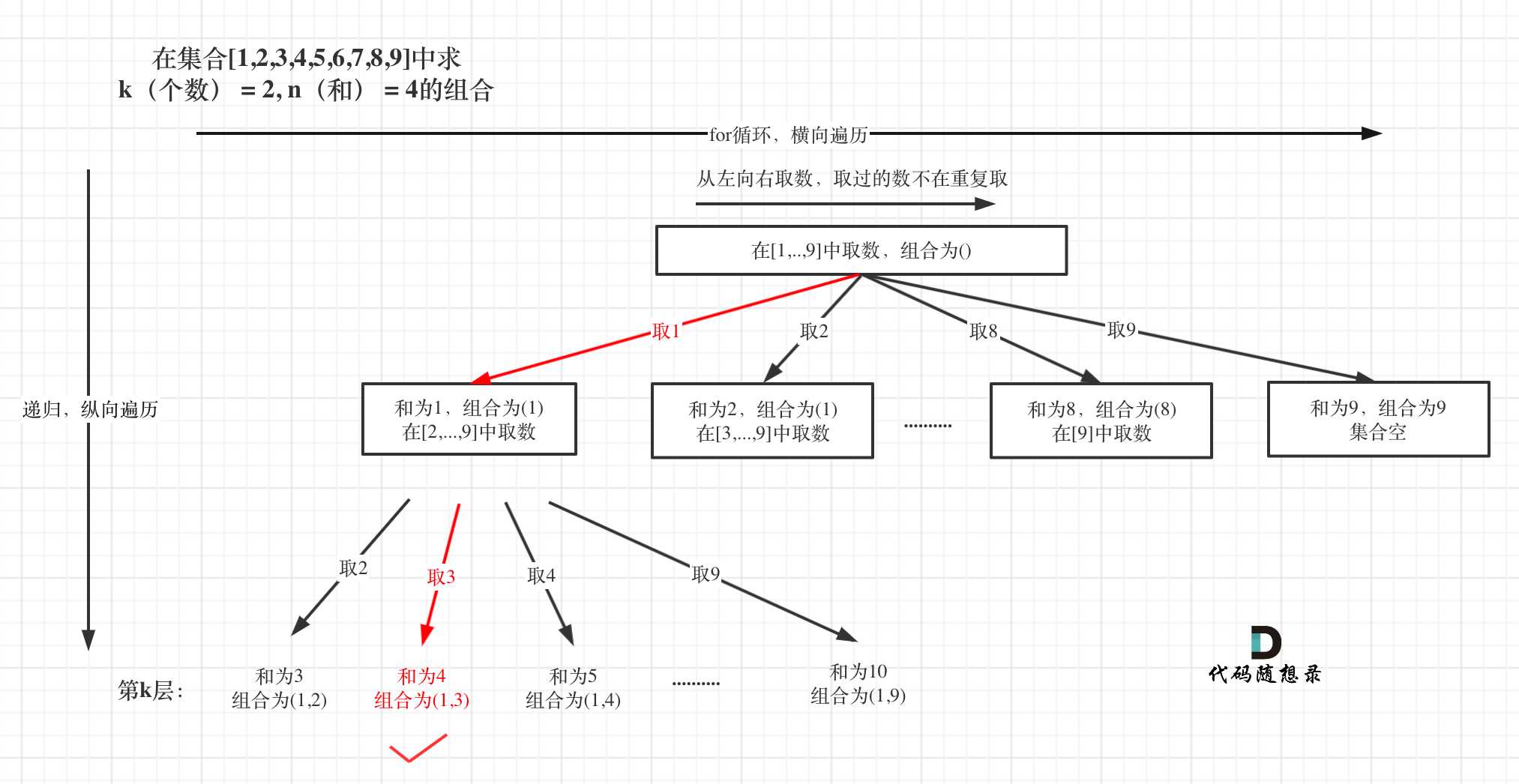
本题和[77. 组合](https://programmercarl.com/0077.组合.html)区别之一就是集合固定的就是9个数[1,...,9],所以for循环固定i<=9
|
本题和[77. 组合](https://programmercarl.com/0077.组合.html)区别之一就是集合固定的就是9个数[1,...,9],所以for循环固定i<=9
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
处理过程就是 path收集每次选取的元素,相当于树型结构里的边,sum来统计path里元素的总和。
|
处理过程就是 path收集每次选取的元素,相当于树型结构里的边,sum来统计path里元素的总和。
|
||||||
|
|
||||||
|
|
@ -166,7 +166,7 @@ public:
|
||||||
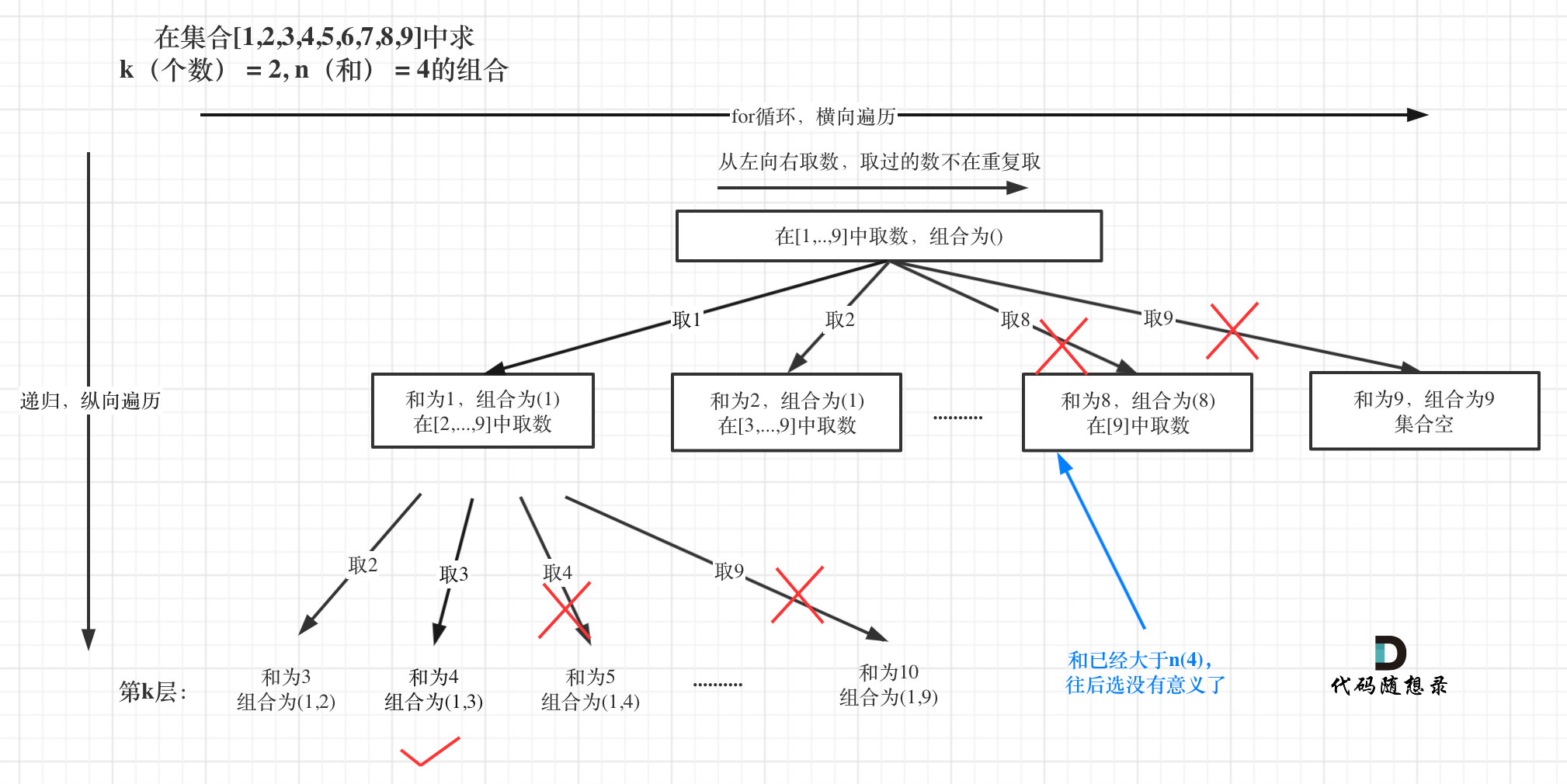
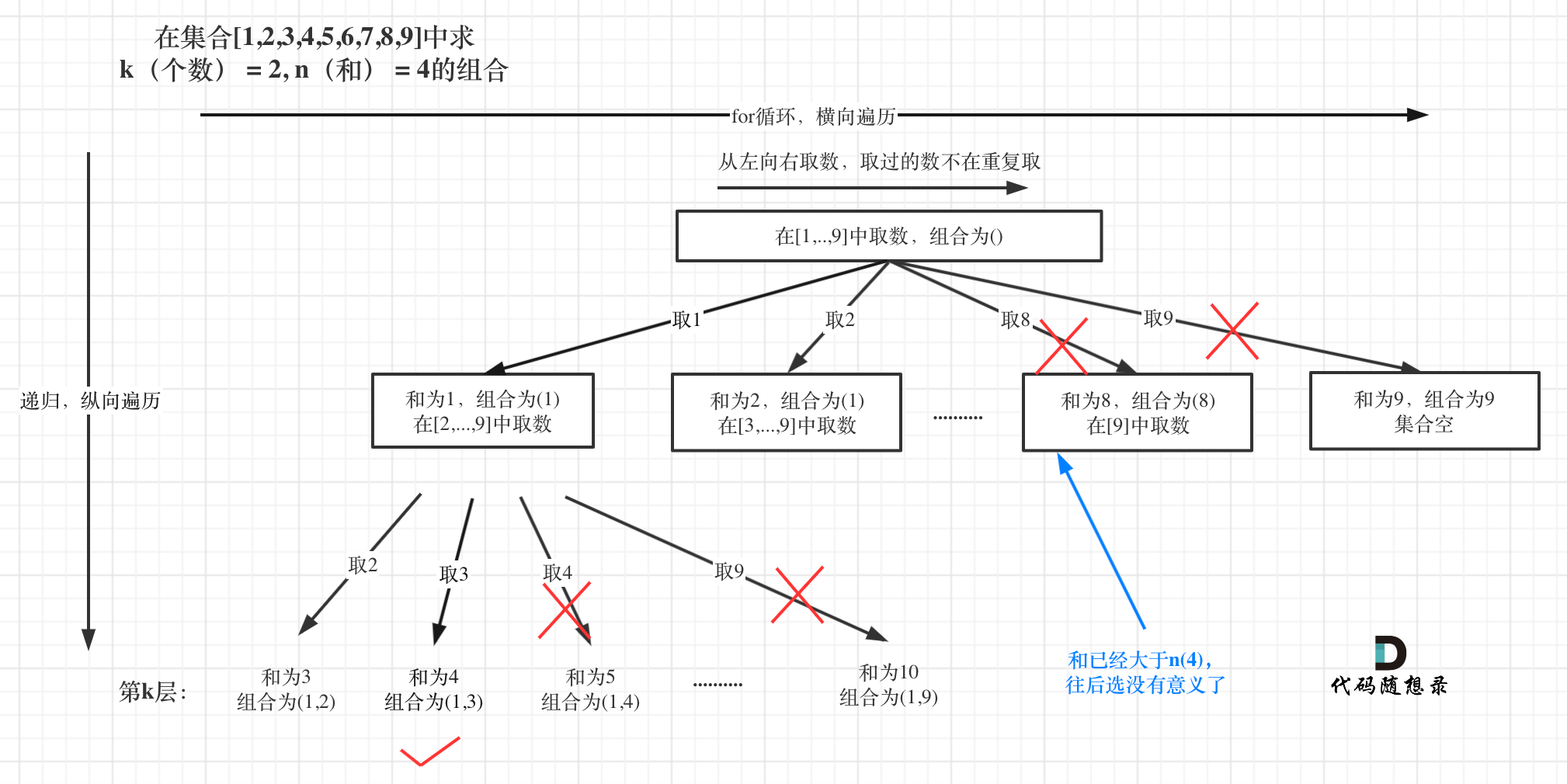
这道题目,剪枝操作其实是很容易想到了,想必大家看上面的树形图的时候已经想到了。
|
这道题目,剪枝操作其实是很容易想到了,想必大家看上面的树形图的时候已经想到了。
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
|
|
||||||
已选元素总和如果已经大于n(图中数值为4)了,那么往后遍历就没有意义了,直接剪掉。
|
已选元素总和如果已经大于n(图中数值为4)了,那么往后遍历就没有意义了,直接剪掉。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -153,7 +153,7 @@ public:
|
||||||
|
|
||||||
我来举一个典型的例子如题:
|
我来举一个典型的例子如题:
|
||||||
|
|
||||||
<img src='https://code-thinking-1253855093.file.myqcloud.com/pics/20200920221638903-20230310123444151.png' width=600> </img>
|
<img src='https://file.kamacoder.com/pics/20200920221638903-20230310123444151.png' width=600> </img>
|
||||||
|
|
||||||
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
|
完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
|
||||||
|
|
||||||
|
|
@ -162,10 +162,10 @@ public:
|
||||||
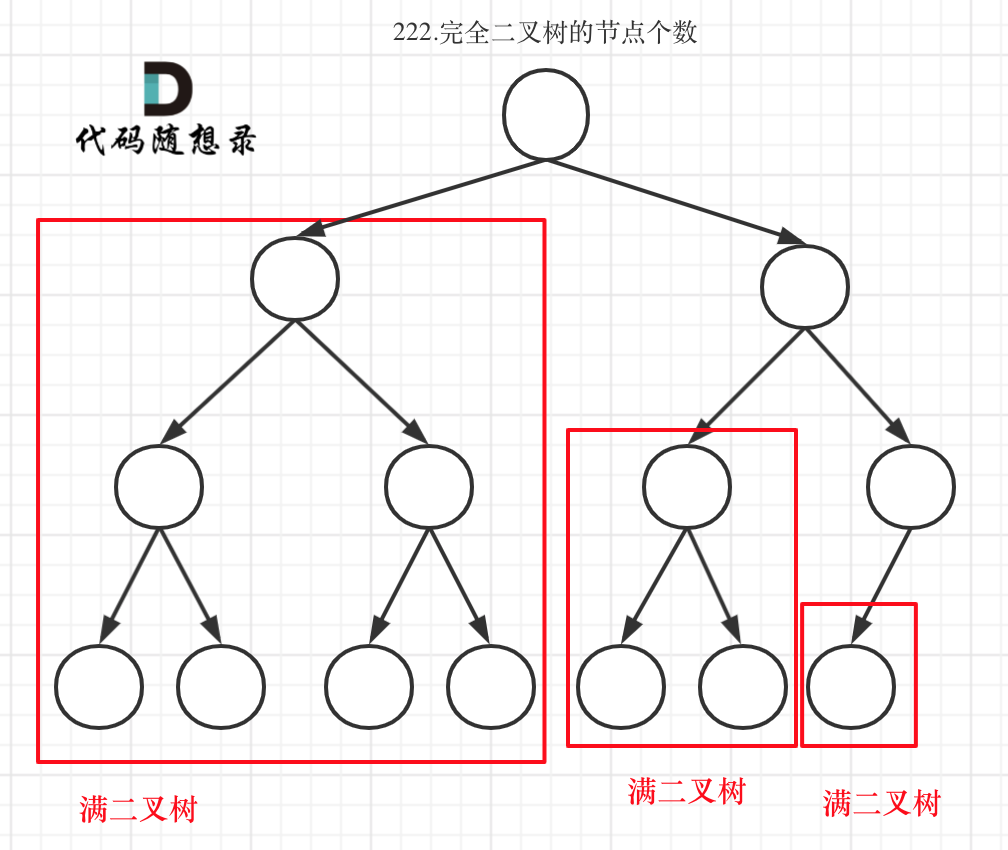
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
|
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
|
||||||
|
|
||||||
完全二叉树(一)如图:
|
完全二叉树(一)如图:
|
||||||
|

|
||||||
|
|
||||||
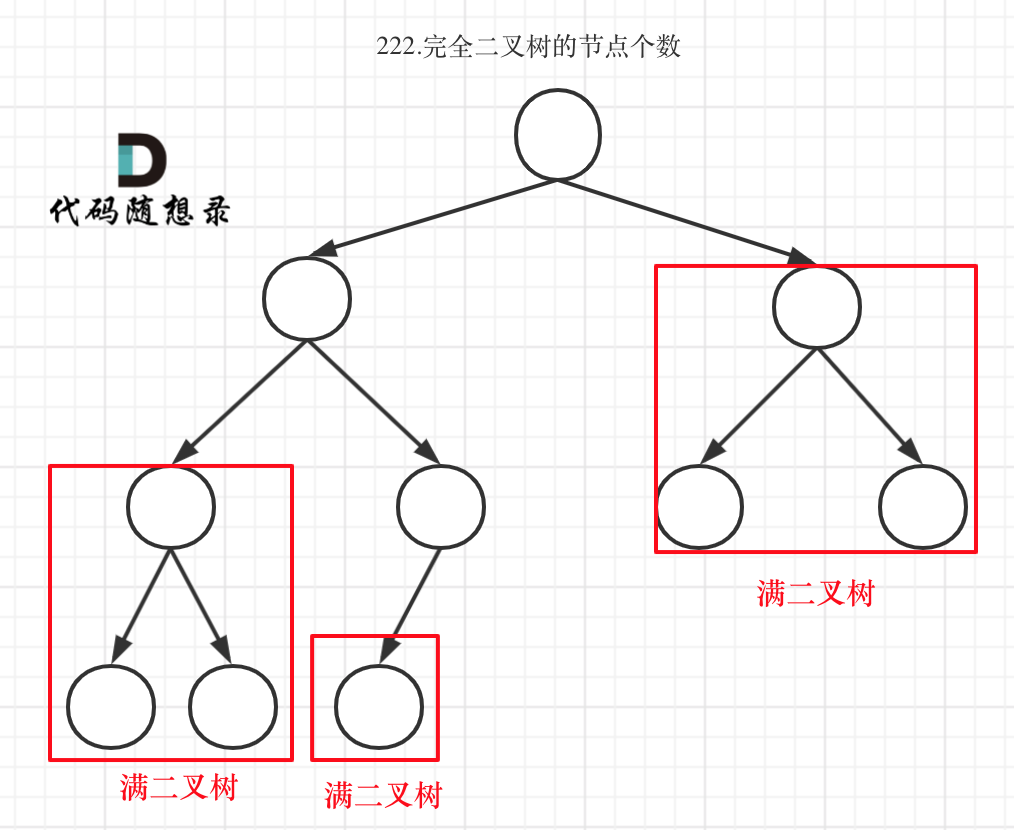
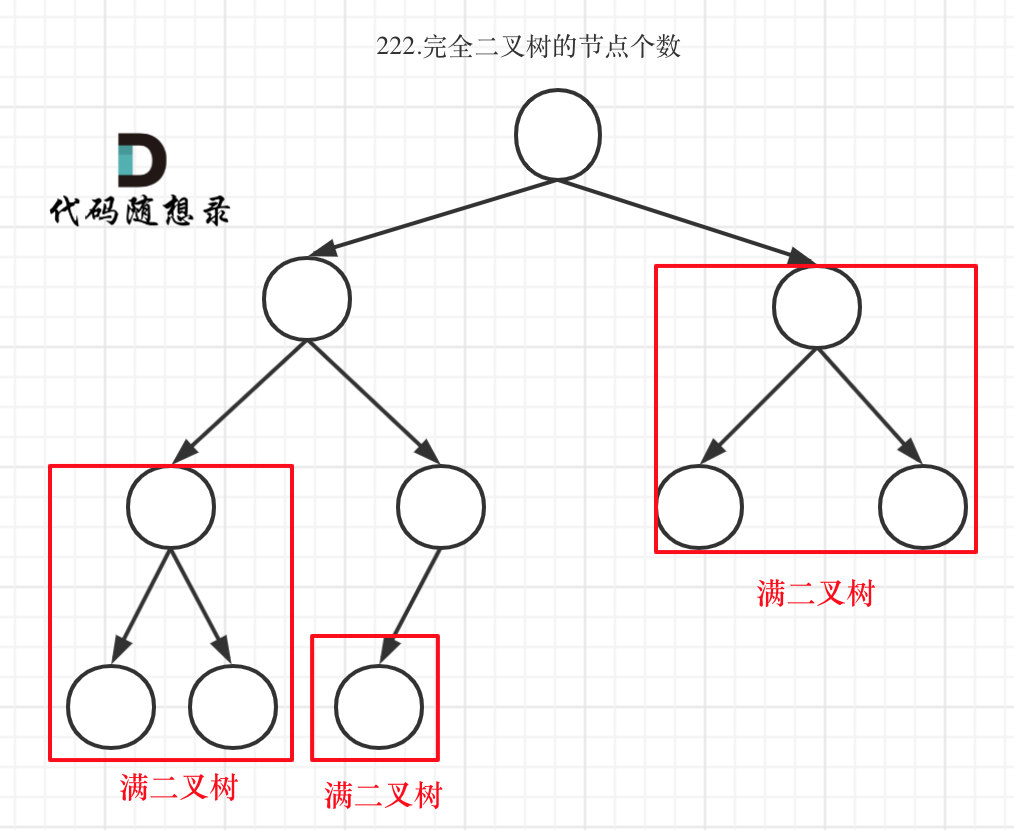
完全二叉树(二)如图:
|
完全二叉树(二)如图:
|
||||||
|
|
||||||
|
|
||||||
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
|
可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
|
||||||
|
|
||||||
|
|
@ -173,15 +173,15 @@ public:
|
||||||
|
|
||||||
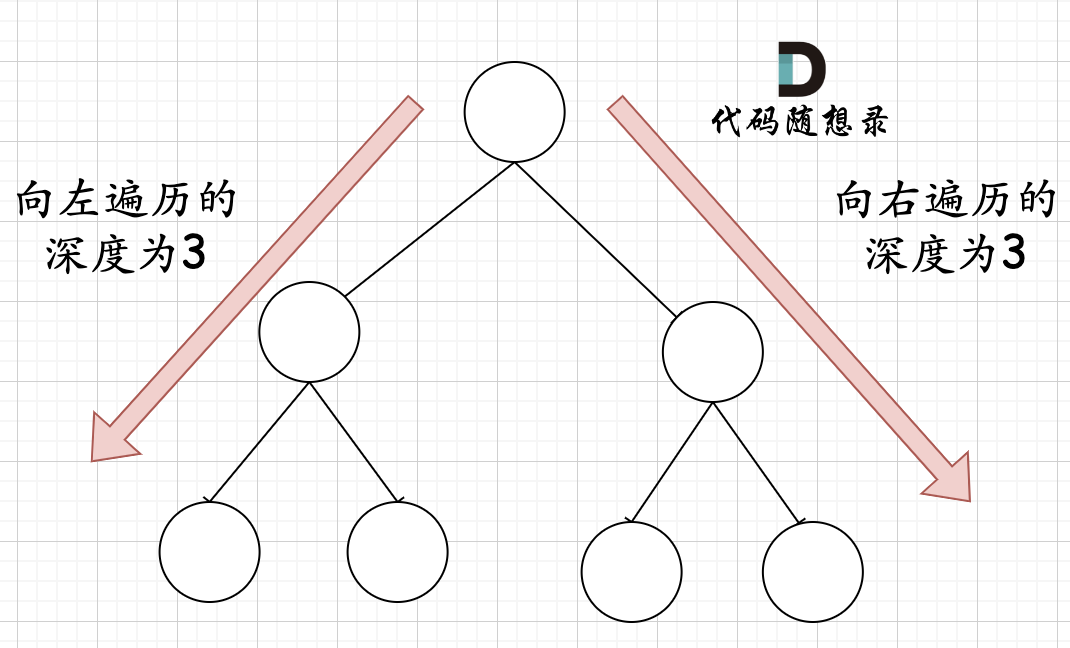
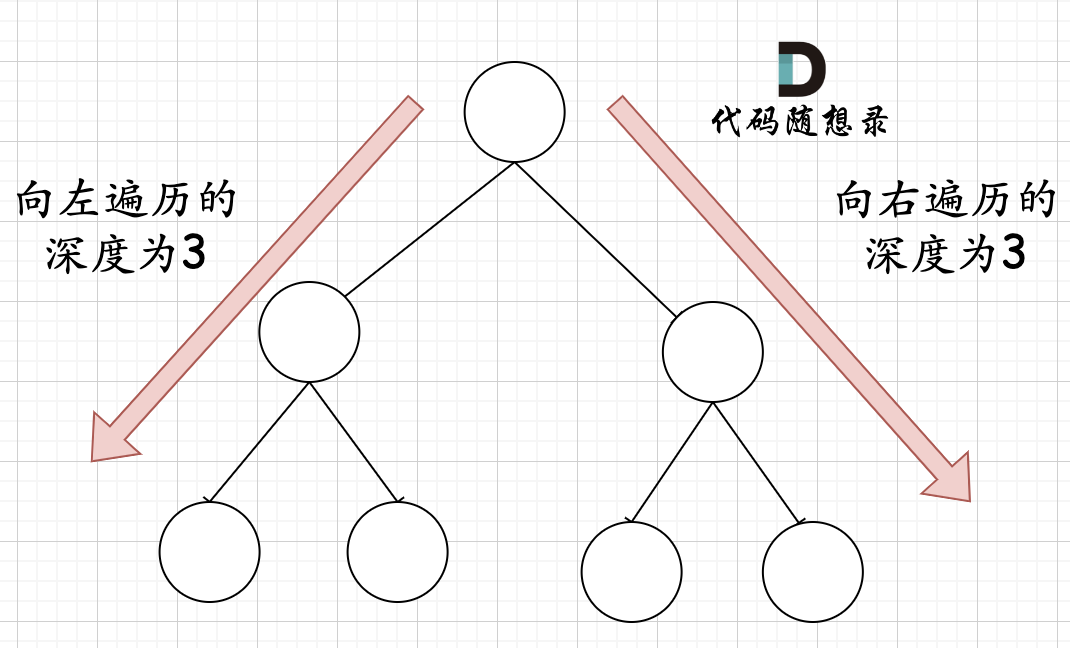
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
|
在完全二叉树中,如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树。如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
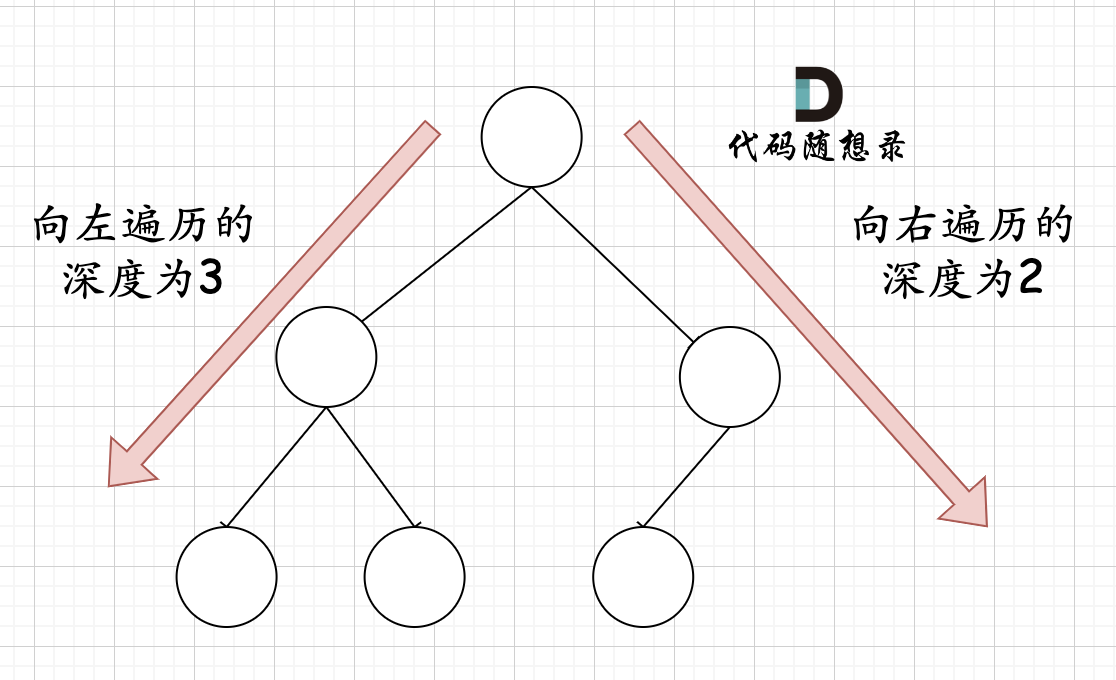
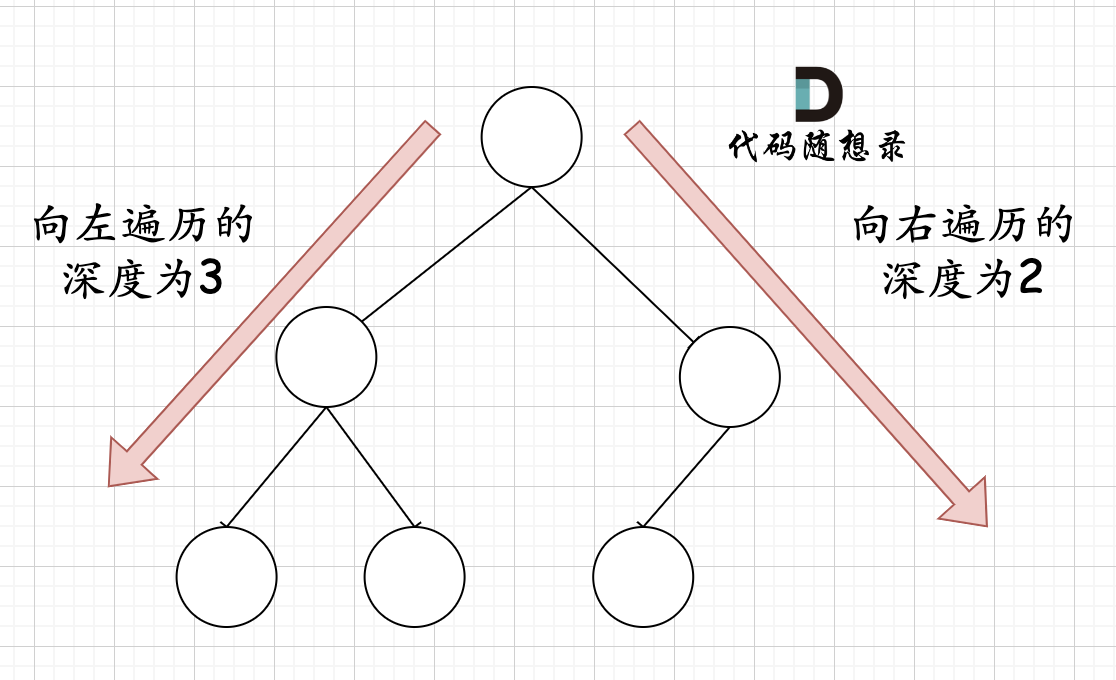
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
|
在完全二叉树中,如果递归向左遍历的深度不等于递归向右遍历的深度,则说明不是满二叉树,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
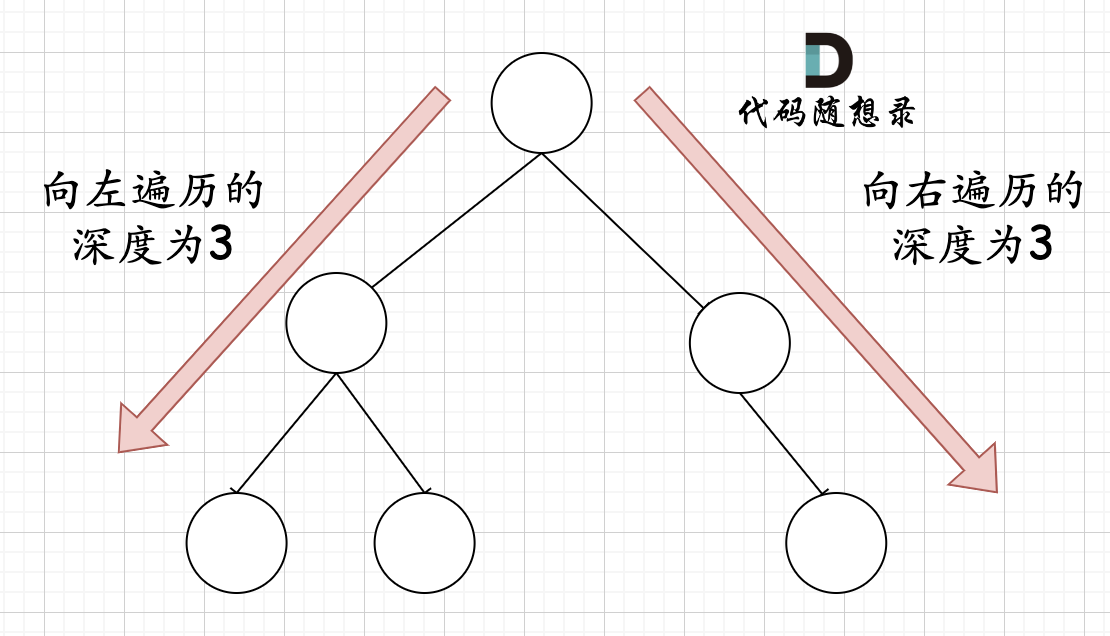
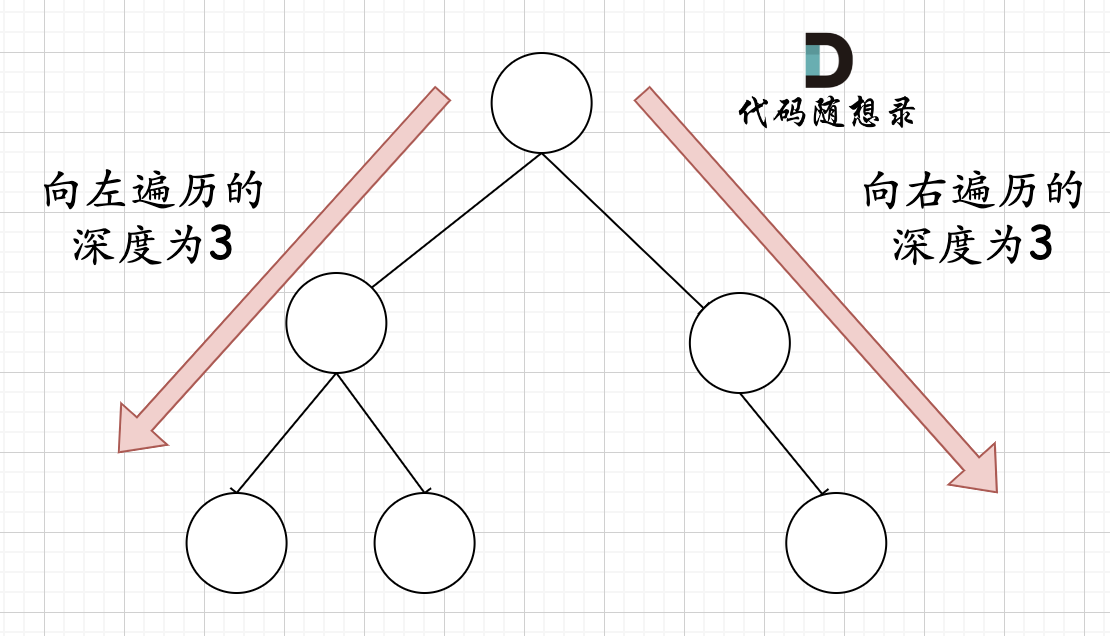
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
|
那有录友说了,这种情况,递归向左遍历的深度等于递归向右遍历的深度,但也不是满二叉树,如题:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
如果这么想,大家就是对 完全二叉树理解有误区了,**以上这棵二叉树,它根本就不是一个完全二叉树**!
|
如果这么想,大家就是对 完全二叉树理解有误区了,**以上这棵二叉树,它根本就不是一个完全二叉树**!
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -10,7 +10,7 @@
|
||||||
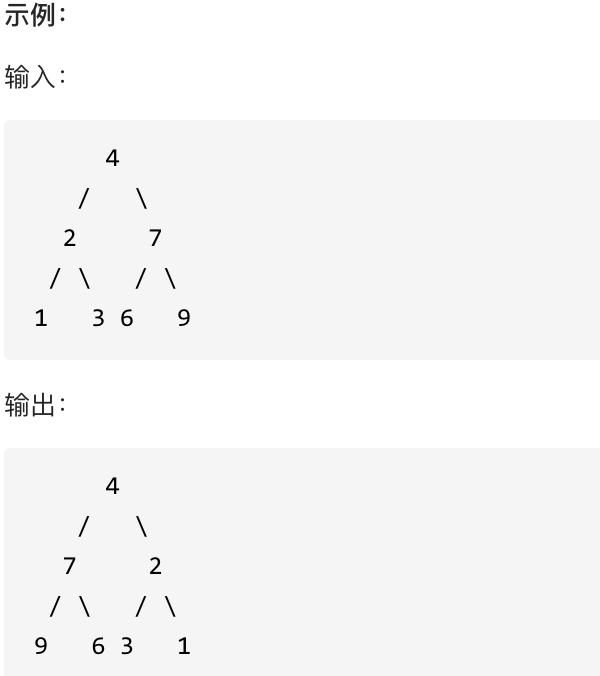
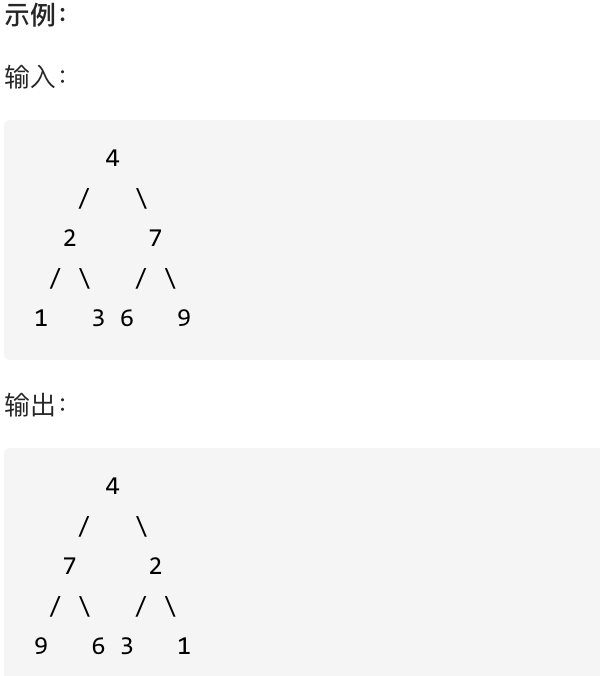
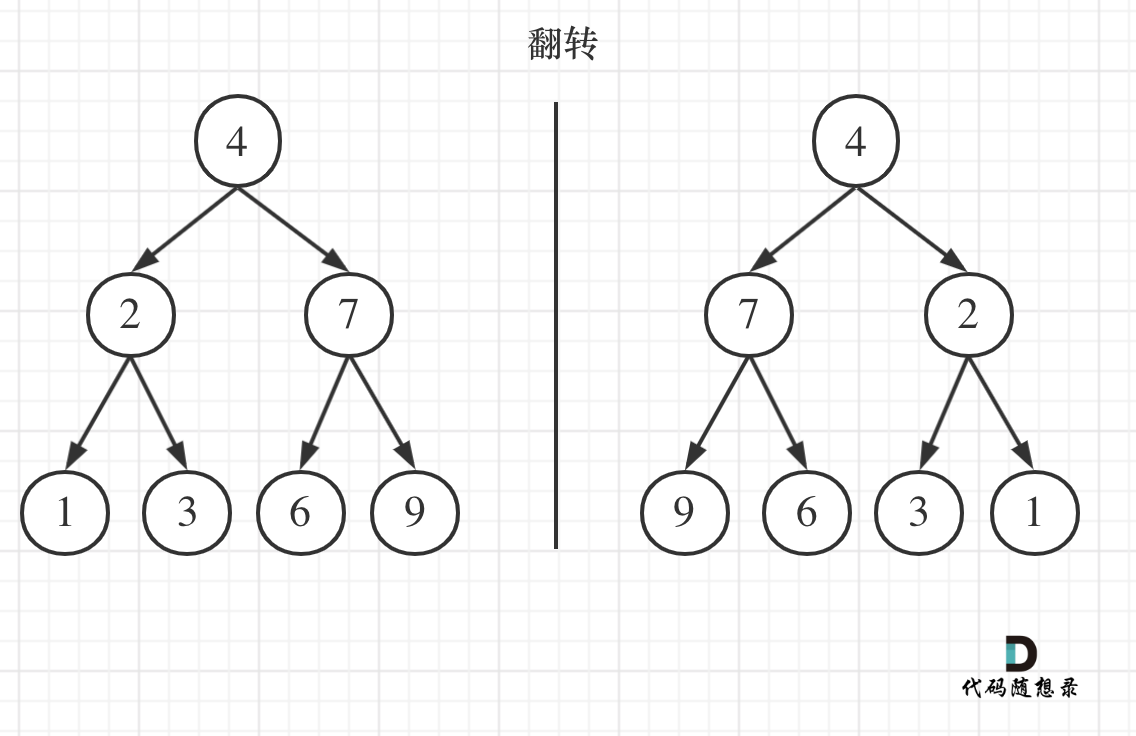
翻转一棵二叉树。
|
翻转一棵二叉树。
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,全当一个乐子哈)
|
这道题目背后有一个让程序员心酸的故事,听说 Homebrew的作者Max Howell,就是因为没在白板上写出翻转二叉树,最后被Google拒绝了。(真假不做判断,全当一个乐子哈)
|
||||||
|
|
||||||
|
|
@ -35,7 +35,7 @@
|
||||||
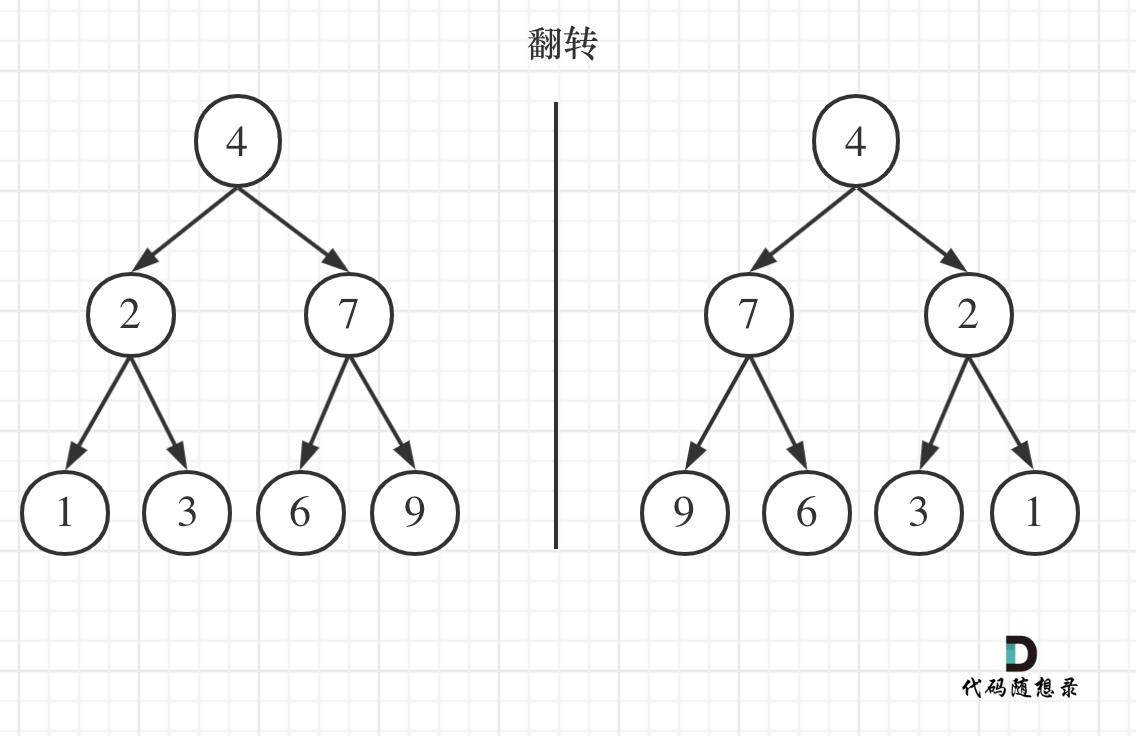
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
|
如果要从整个树来看,翻转还真的挺复杂,整个树以中间分割线进行翻转,如图:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
|
可以发现想要翻转它,其实就把每一个节点的左右孩子交换一下就可以了。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -14,7 +14,7 @@
|
||||||
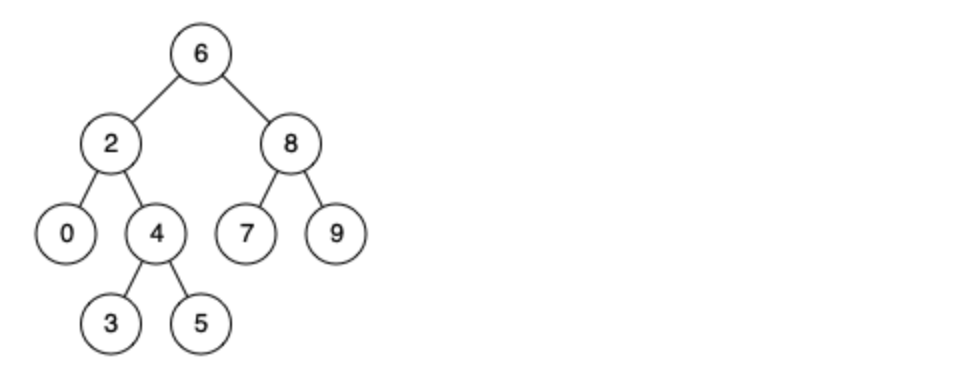
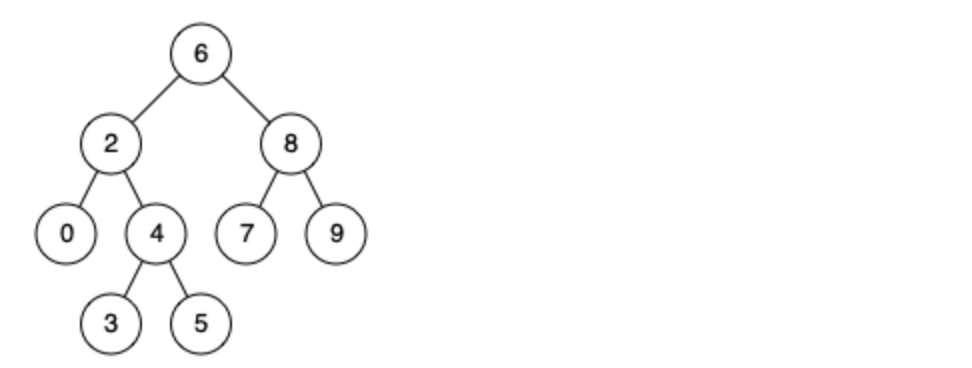
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
|
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
示例 1:
|
示例 1:
|
||||||
|
|
||||||
|
|
@ -52,7 +52,7 @@
|
||||||
|
|
||||||
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
|
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
|
||||||
|
|
||||||
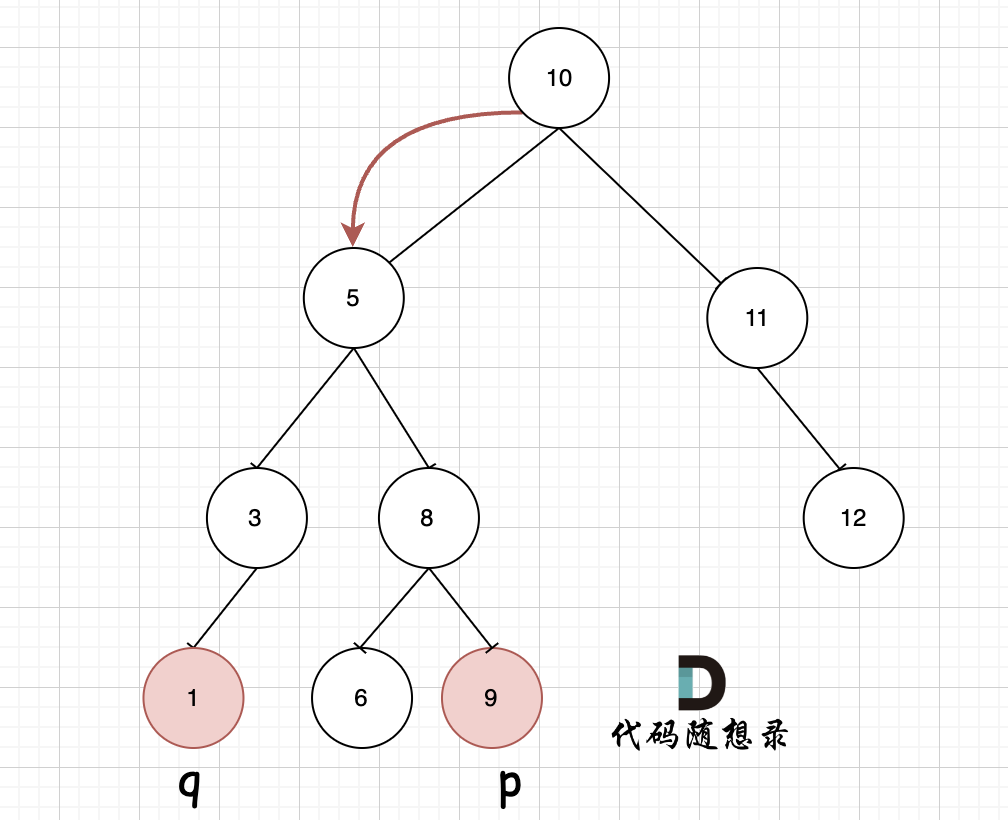
|
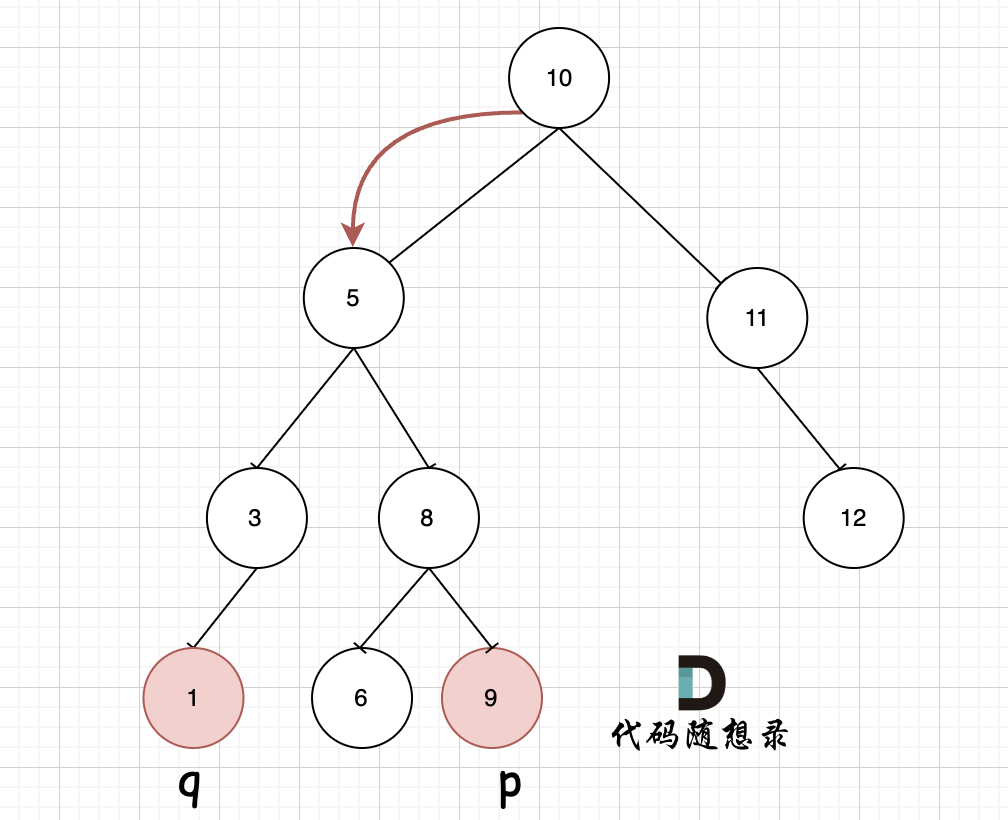
|
||||||
|
|
||||||
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
|
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
|
||||||
|
|
||||||
|
|
@ -64,7 +64,7 @@
|
||||||
|
|
||||||
如图所示:p为节点6,q为节点9
|
如图所示:p为节点6,q为节点9
|
||||||
|
|
||||||
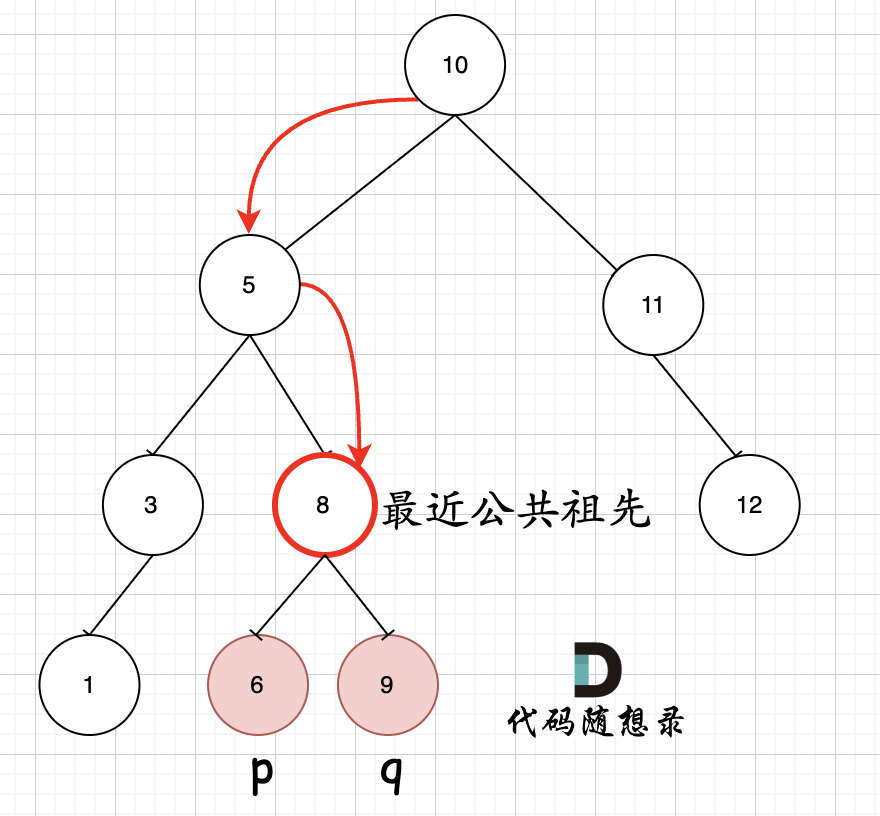
|
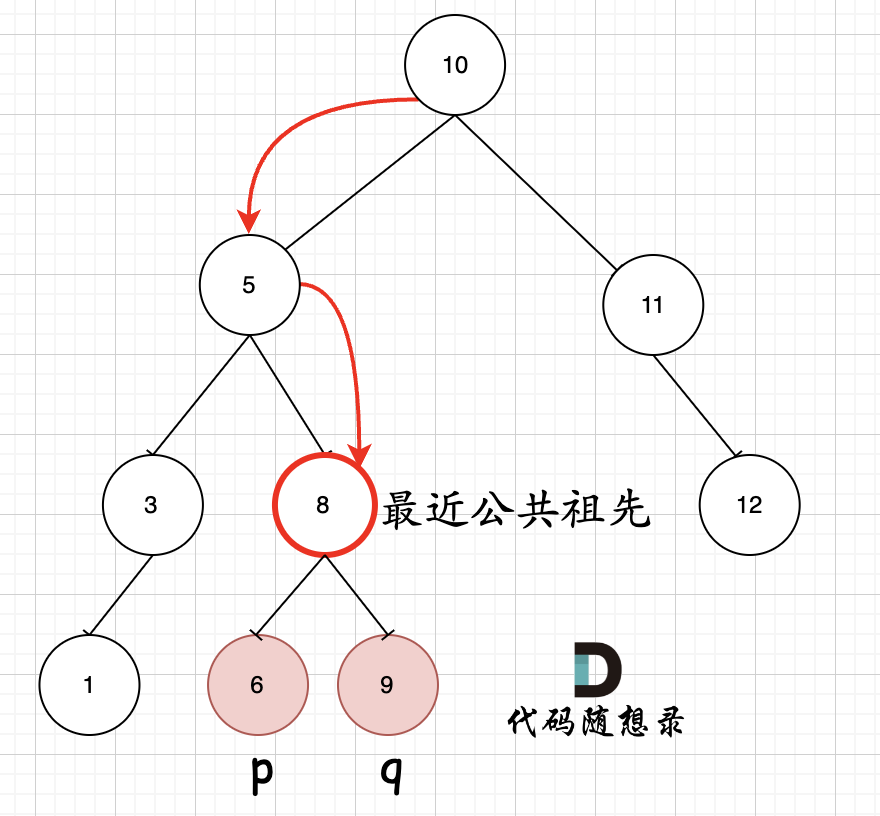
|
||||||
|
|
||||||
|
|
||||||
可以看出直接按照指定的方向,就可以找到节点8,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
|
可以看出直接按照指定的方向,就可以找到节点8,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
|
||||||
|
|
|
||||||
|
|
@ -16,7 +16,7 @@
|
||||||
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
|
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
|
||||||
|
|
||||||
|
|
||||||
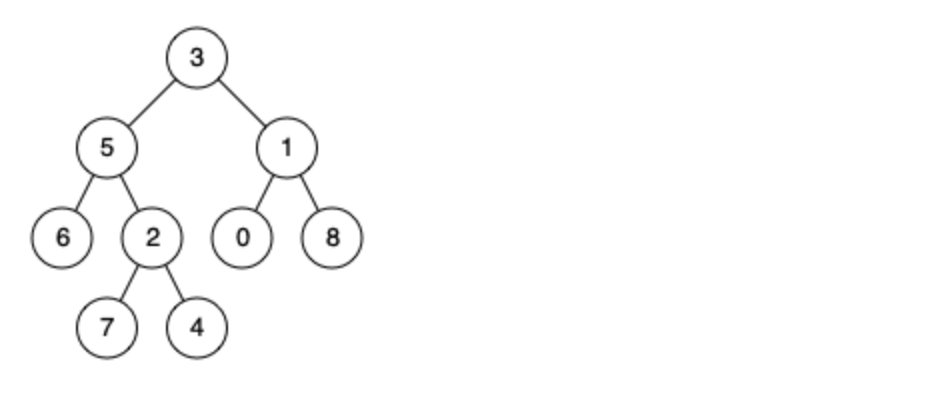
|
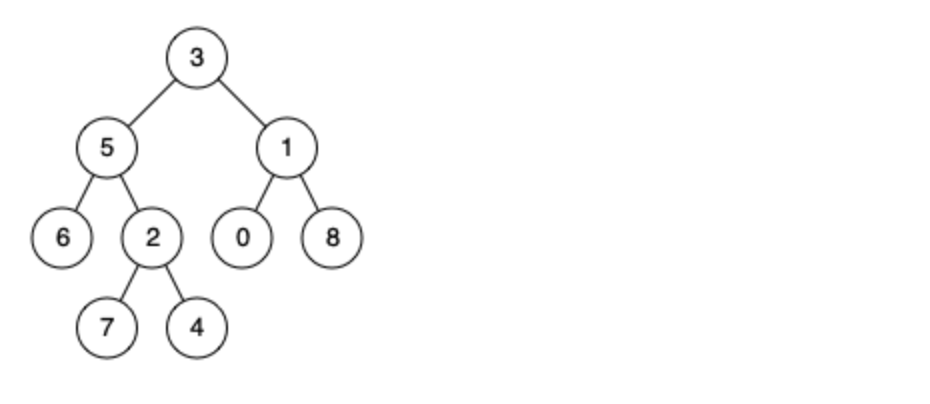
|
||||||
|
|
||||||
示例 1:
|
示例 1:
|
||||||
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
|
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
|
||||||
|
|
@ -51,7 +51,7 @@
|
||||||
|
|
||||||
**首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。** 即情况一:
|
**首先最容易想到的一个情况:如果找到一个节点,发现左子树出现结点p,右子树出现节点q,或者 左子树出现结点q,右子树出现节点p,那么该节点就是节点p和q的最近公共祖先。** 即情况一:
|
||||||
|
|
||||||
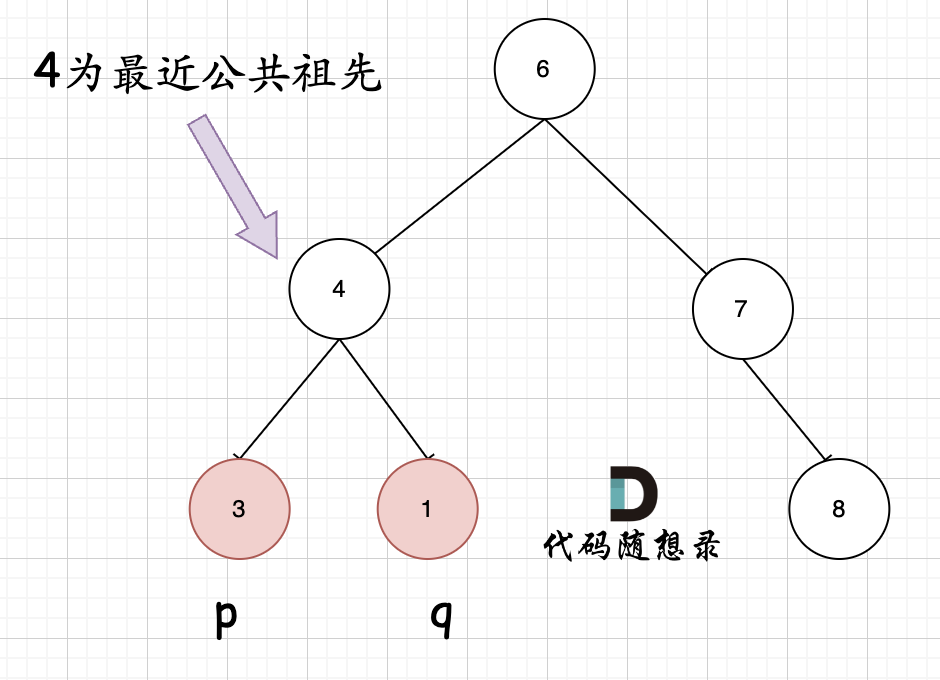
|
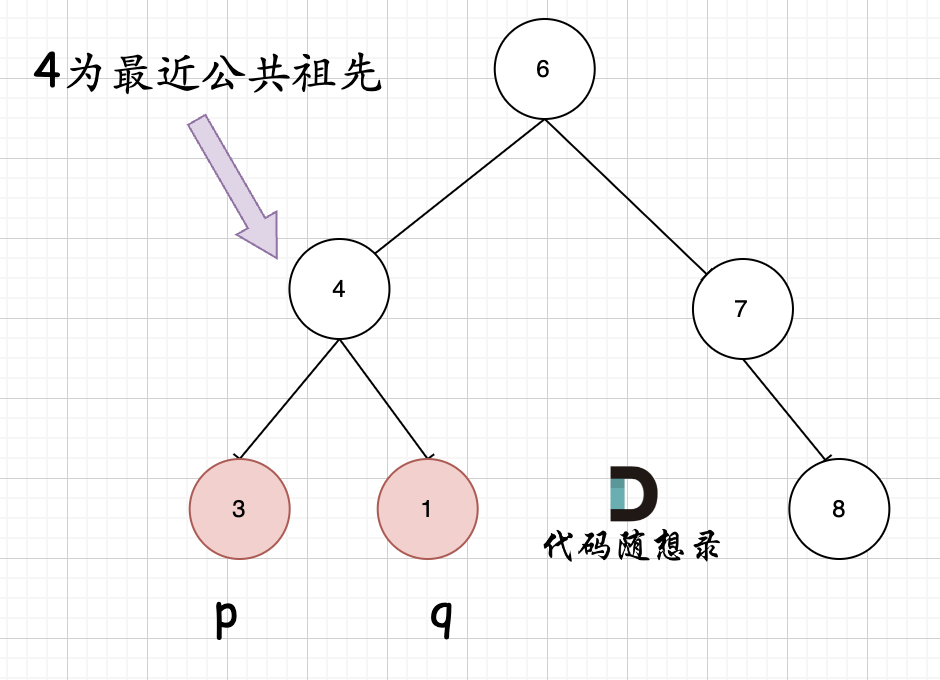
|
||||||
|
|
||||||
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
|
判断逻辑是 如果递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果 左右子树的返回值都不为空,说明此时的中节点,一定是q 和p 的最近祖先。
|
||||||
|
|
||||||
|
|
@ -61,7 +61,7 @@
|
||||||
|
|
||||||
**但是很多人容易忽略一个情况,就是节点本身p(q),它拥有一个子孙节点q(p)。** 情况二:
|
**但是很多人容易忽略一个情况,就是节点本身p(q),它拥有一个子孙节点q(p)。** 情况二:
|
||||||
|
|
||||||
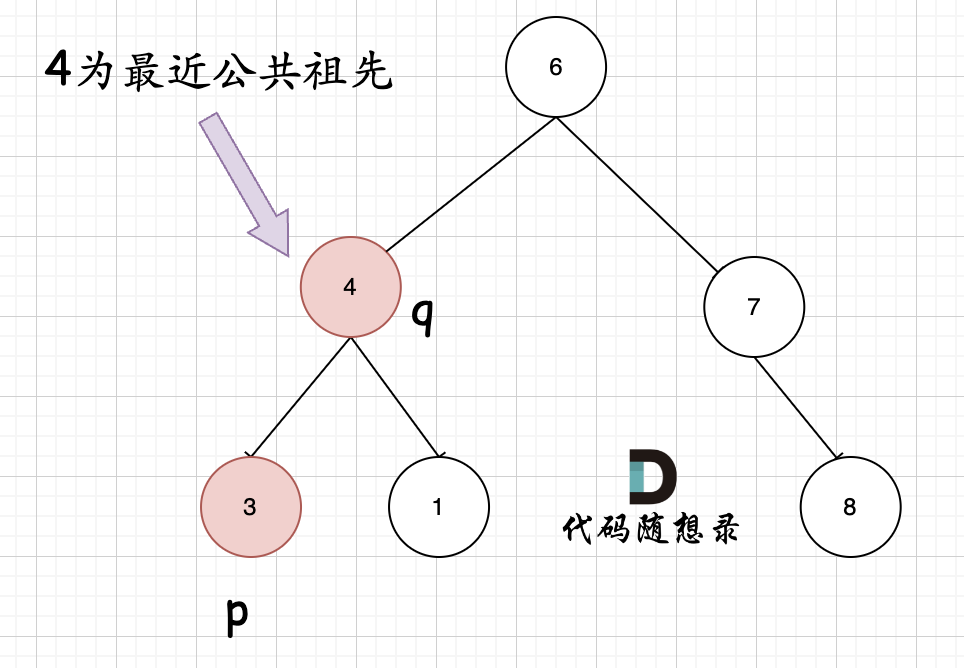
|
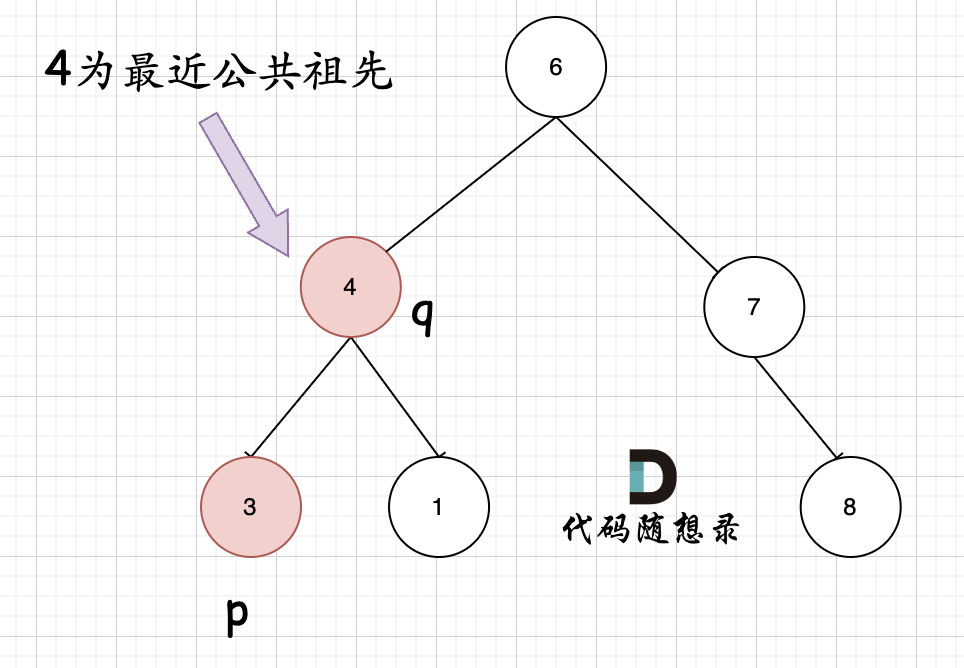
|
||||||
|
|
||||||
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
|
其实情况一 和 情况二 代码实现过程都是一样的,也可以说,实现情况一的逻辑,顺便包含了情况二。
|
||||||
|
|
||||||
|
|
@ -129,7 +129,7 @@ left与right的逻辑处理; // 中
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
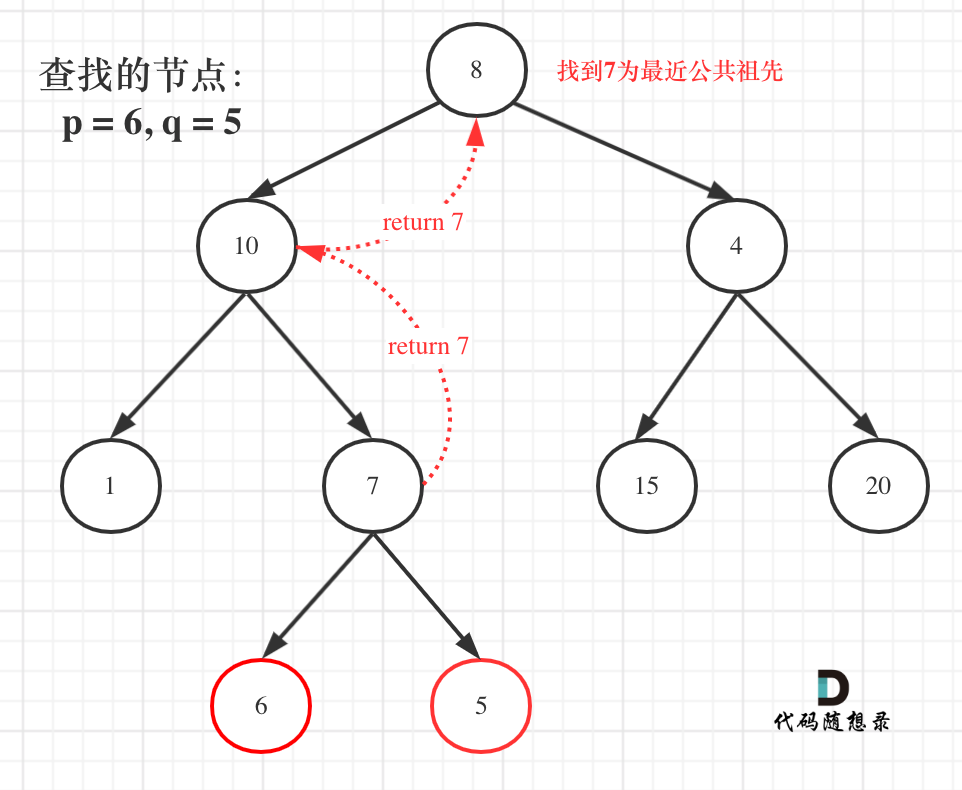
|
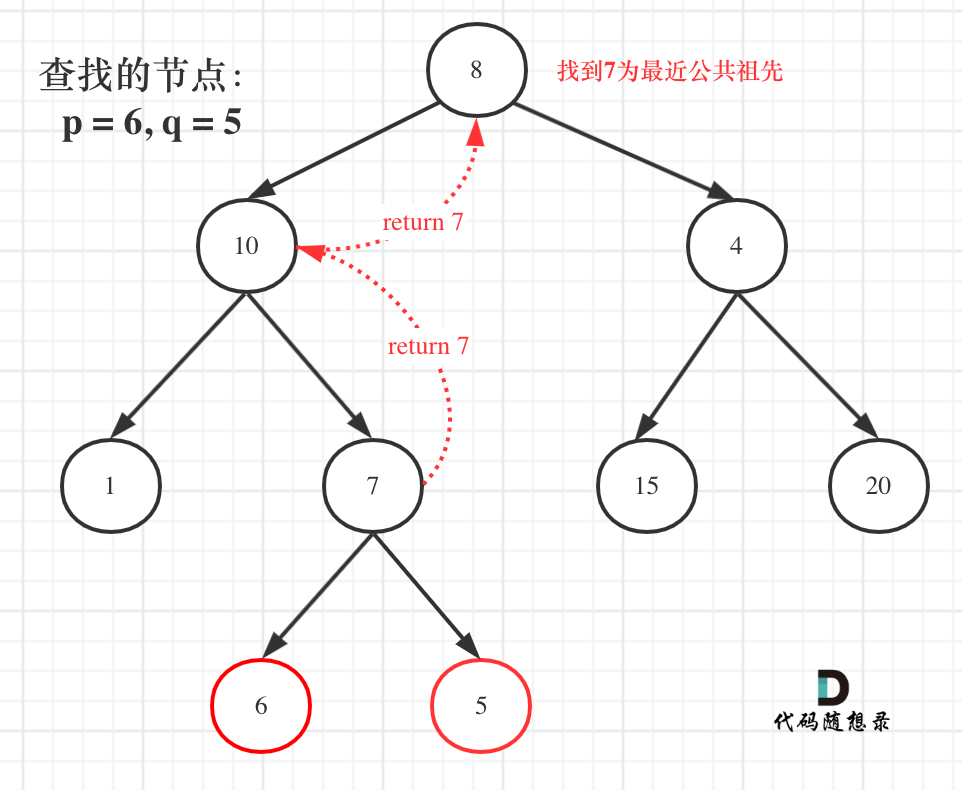
|
||||||
|
|
||||||
就像图中一样直接返回7。
|
就像图中一样直接返回7。
|
||||||
|
|
||||||
|
|
@ -162,7 +162,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
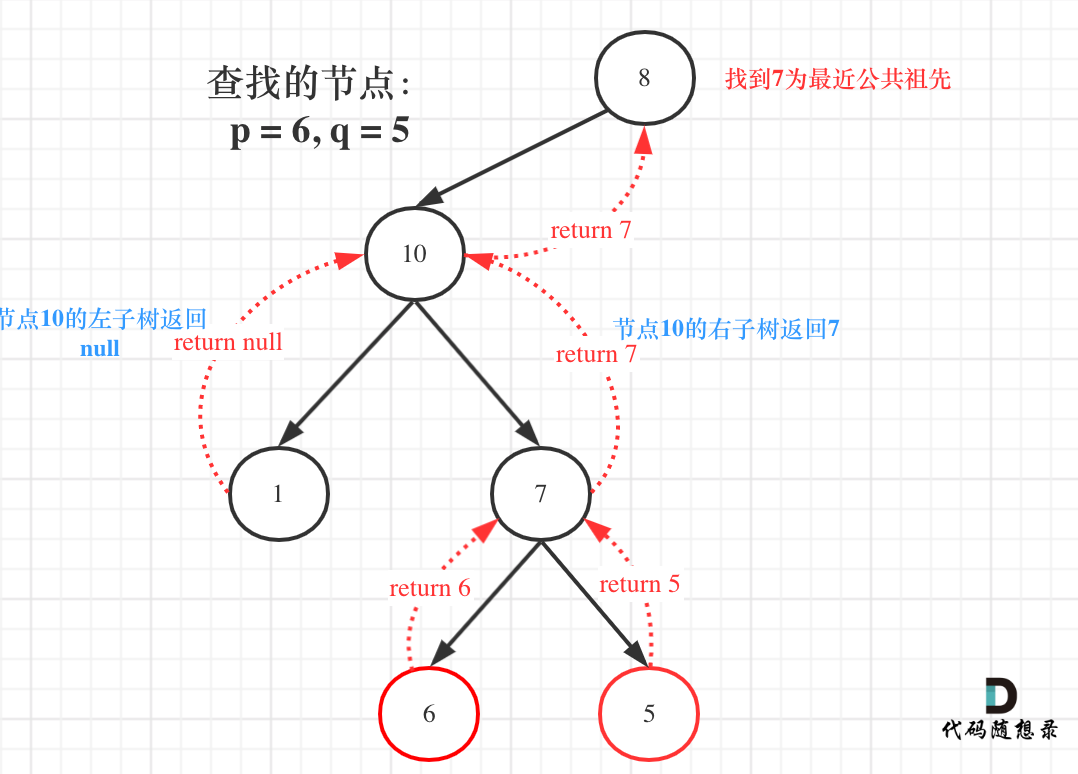
|
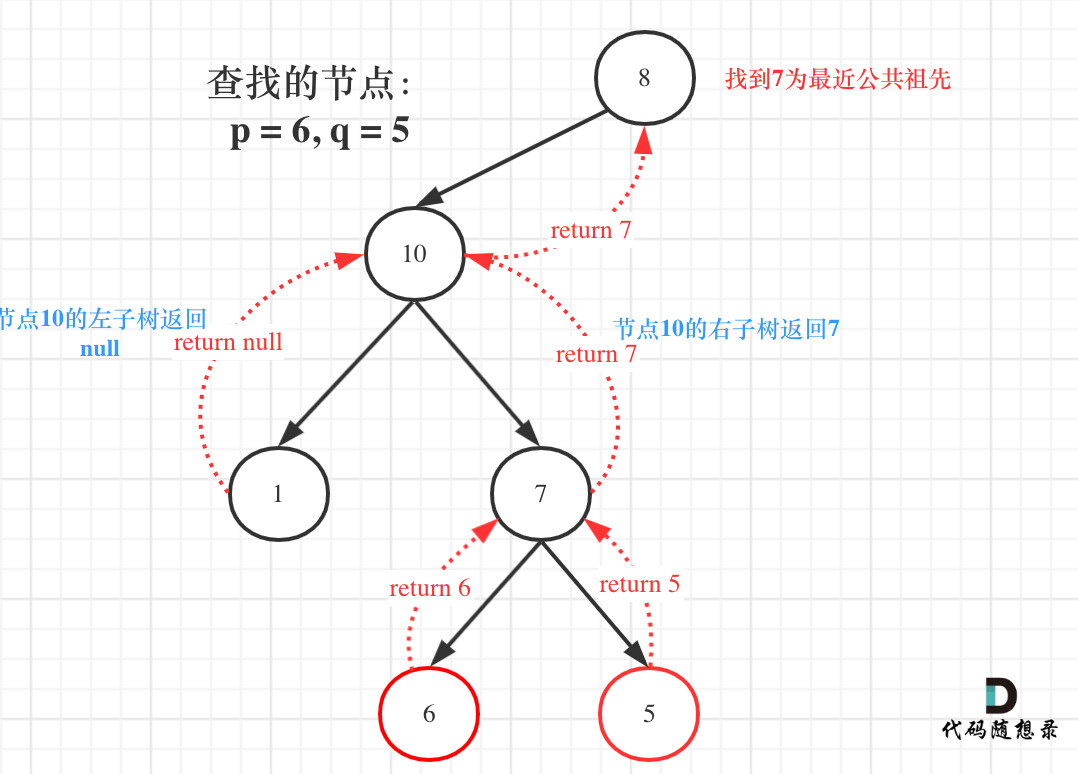
|
||||||
|
|
||||||
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
|
图中节点10的左子树返回null,右子树返回目标值7,那么此时节点10的处理逻辑就是把右子树的返回值(最近公共祖先7)返回上去!
|
||||||
|
|
||||||
|
|
@ -183,7 +183,7 @@ else { // (left == NULL && right == NULL)
|
||||||
|
|
||||||
那么寻找最小公共祖先,完整流程图如下:
|
那么寻找最小公共祖先,完整流程图如下:
|
||||||
|
|
||||||
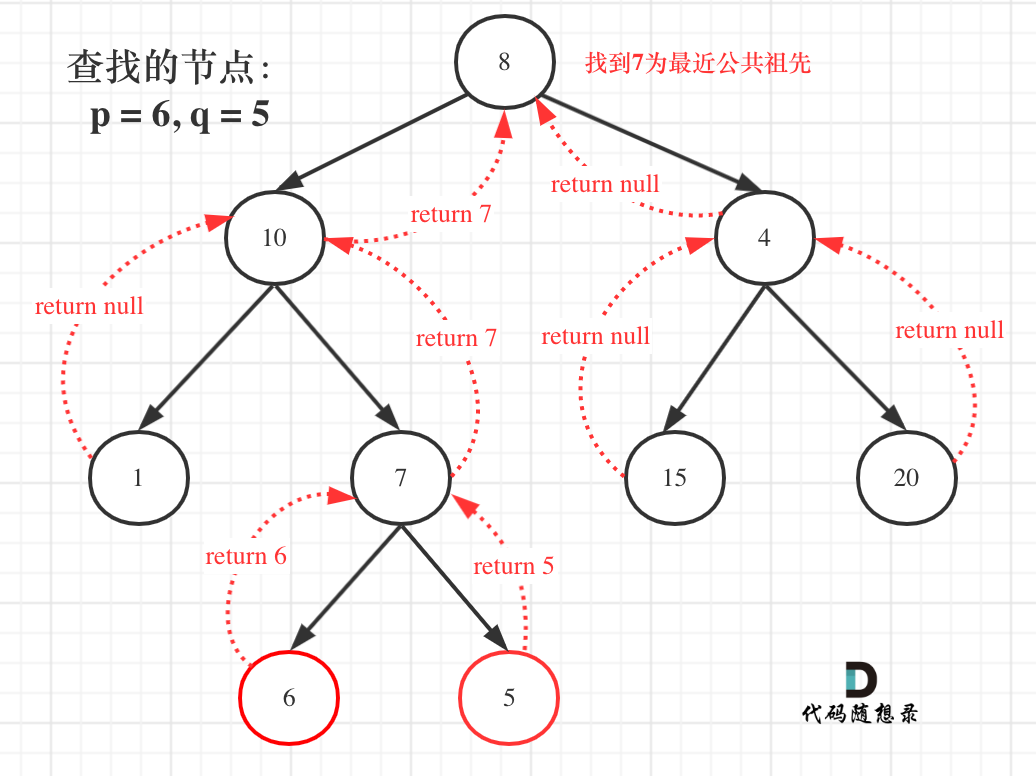
|
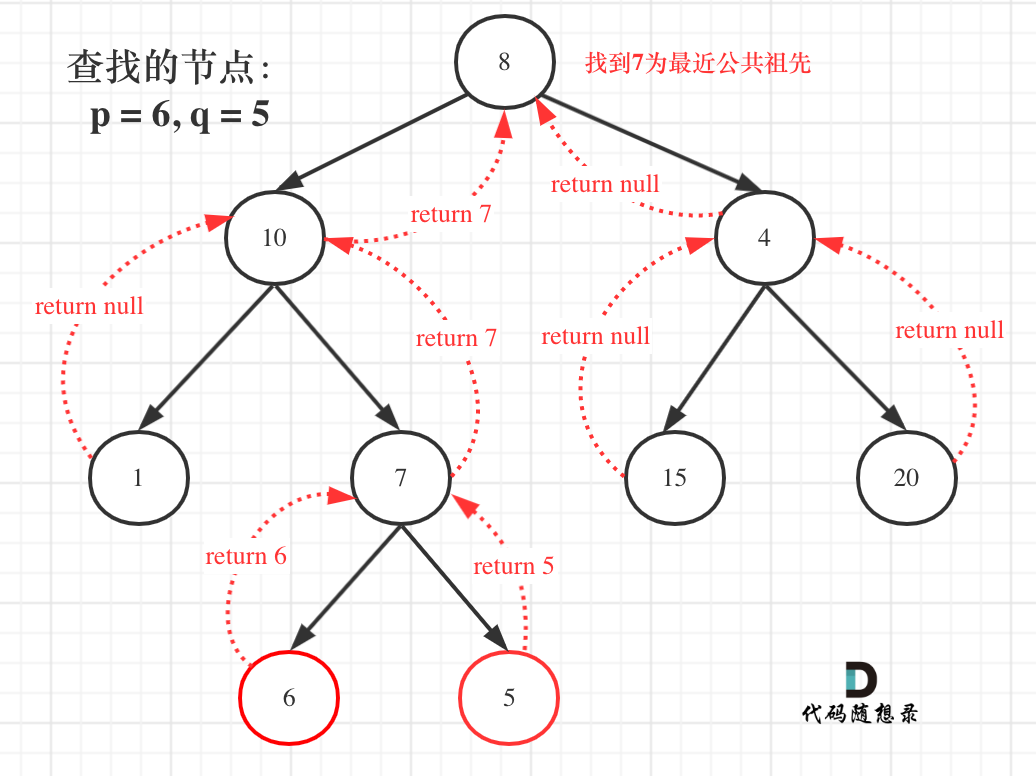
|
||||||
|
|
||||||
**从图中,大家可以看到,我们是如何回溯遍历整棵二叉树,将结果返回给头结点的!**
|
**从图中,大家可以看到,我们是如何回溯遍历整棵二叉树,将结果返回给头结点的!**
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -14,7 +14,7 @@
|
||||||
说明: 叶子节点是指没有子节点的节点。
|
说明: 叶子节点是指没有子节点的节点。
|
||||||
|
|
||||||
示例:
|
示例:
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -28,7 +28,7 @@
|
||||||
|
|
||||||
前序遍历以及回溯的过程如图:
|
前序遍历以及回溯的过程如图:
|
||||||
|
|
||||||
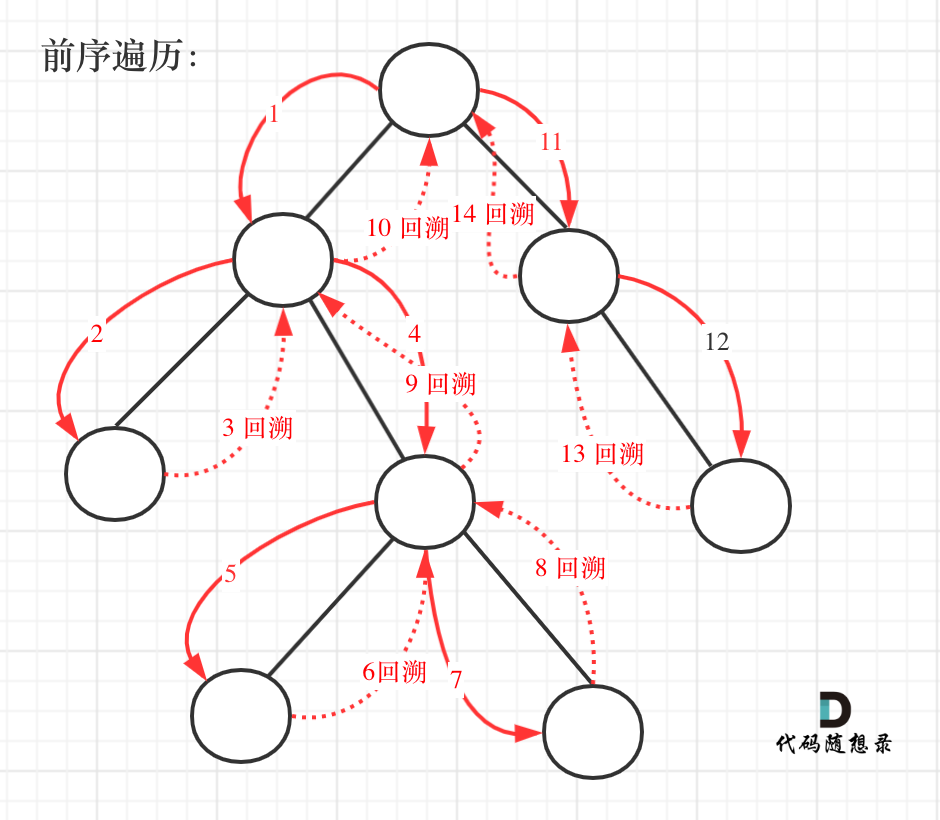
|
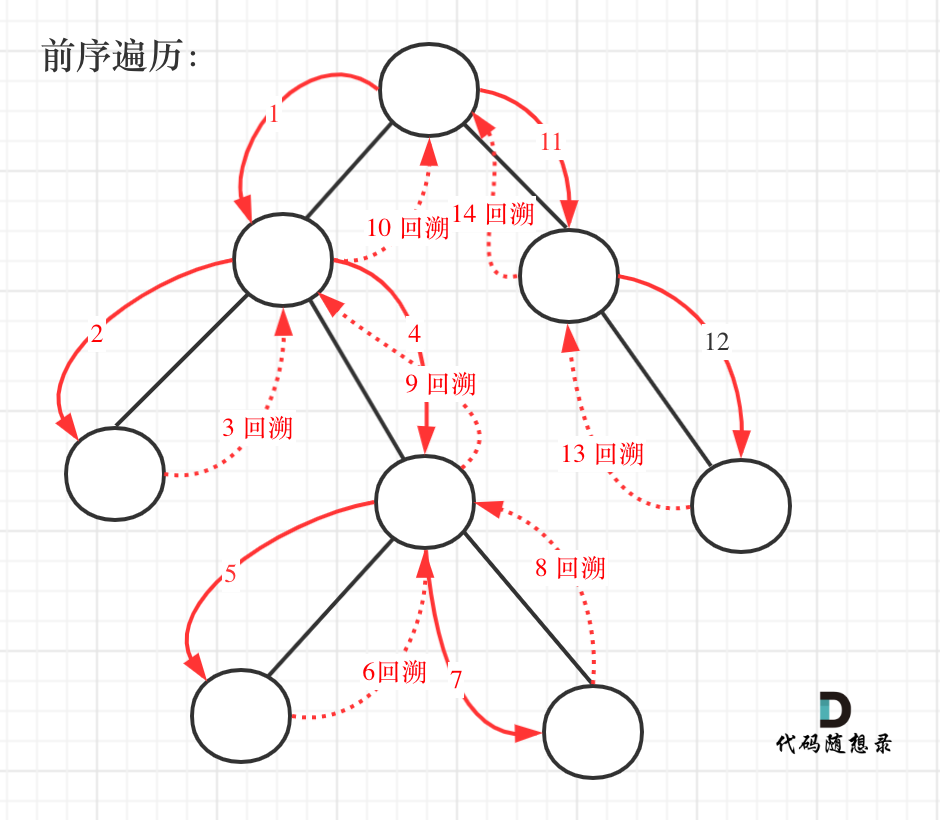
|
||||||
|
|
||||||
我们先使用递归的方式,来做前序遍历。**要知道递归和回溯就是一家的,本题也需要回溯。**
|
我们先使用递归的方式,来做前序遍历。**要知道递归和回溯就是一家的,本题也需要回溯。**
|
||||||
|
|
||||||
|
|
@ -315,7 +315,7 @@ public:
|
||||||
|
|
||||||
其实关键还在于 参数,使用的是 `string path`,这里并没有加上引用`&` ,即本层递归中,path + 该节点数值,但该层递归结束,上一层path的数值并不会受到任何影响。 如图所示:
|
其实关键还在于 参数,使用的是 `string path`,这里并没有加上引用`&` ,即本层递归中,path + 该节点数值,但该层递归结束,上一层path的数值并不会受到任何影响。 如图所示:
|
||||||
|
|
||||||
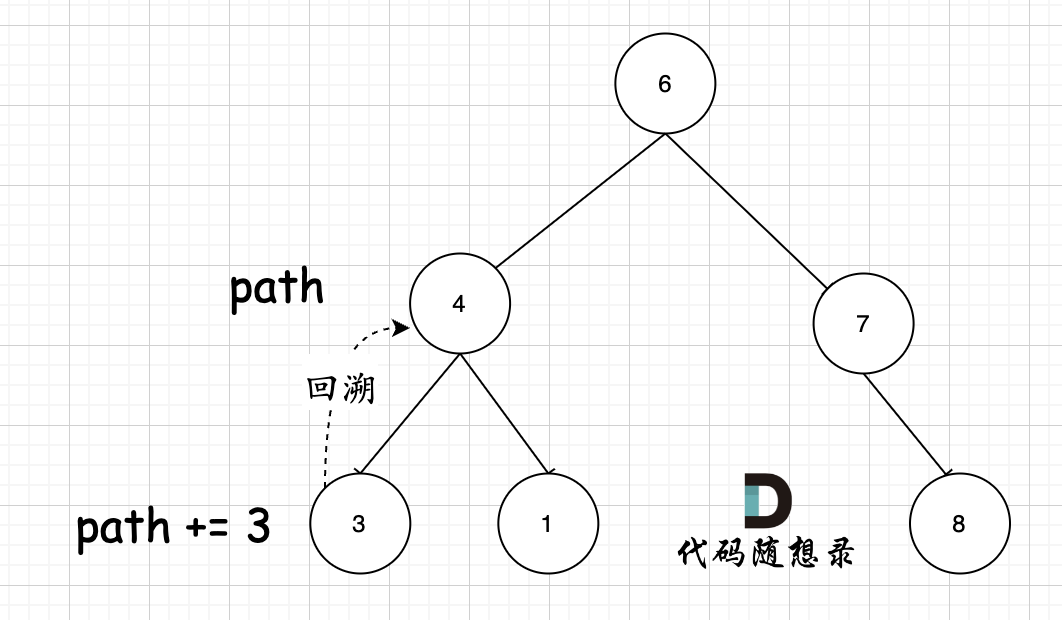
|
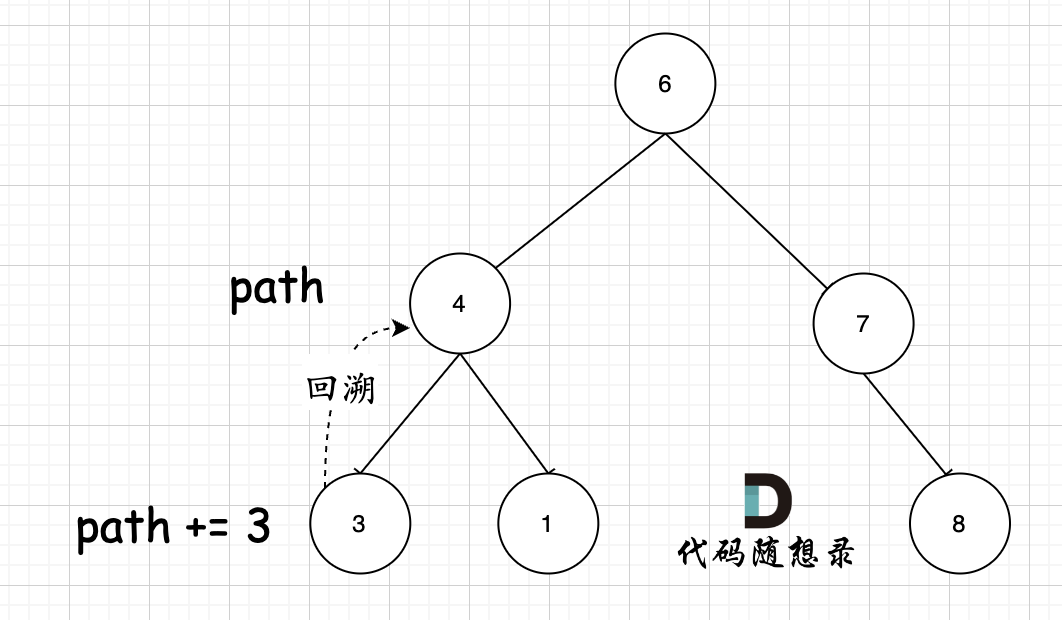
|
||||||
|
|
||||||
节点4 的path,在遍历到节点3,path+3,遍历节点3的递归结束之后,返回节点4(回溯的过程),path并不会把3加上。
|
节点4 的path,在遍历到节点3,path+3,遍历节点3的递归结束之后,返回节点4(回溯的过程),path并不会把3加上。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -93,7 +93,7 @@ for (int i = 0; i <= n; i++) { // 遍历背包
|
||||||
已输入n为5例,dp状态图如下:
|
已输入n为5例,dp状态图如下:
|
||||||
|
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
dp[0] = 0
|
dp[0] = 0
|
||||||
dp[1] = min(dp[0] + 1) = 1
|
dp[1] = min(dp[0] + 1) = 1
|
||||||
|
|
|
||||||
|
|
@ -85,7 +85,7 @@ for (int i = 1; i < nums.size(); i++) {
|
||||||
|
|
||||||
输入:[0,1,0,3,2],dp数组的变化如下:
|
输入:[0,1,0,3,2],dp数组的变化如下:
|
||||||
|
|
||||||
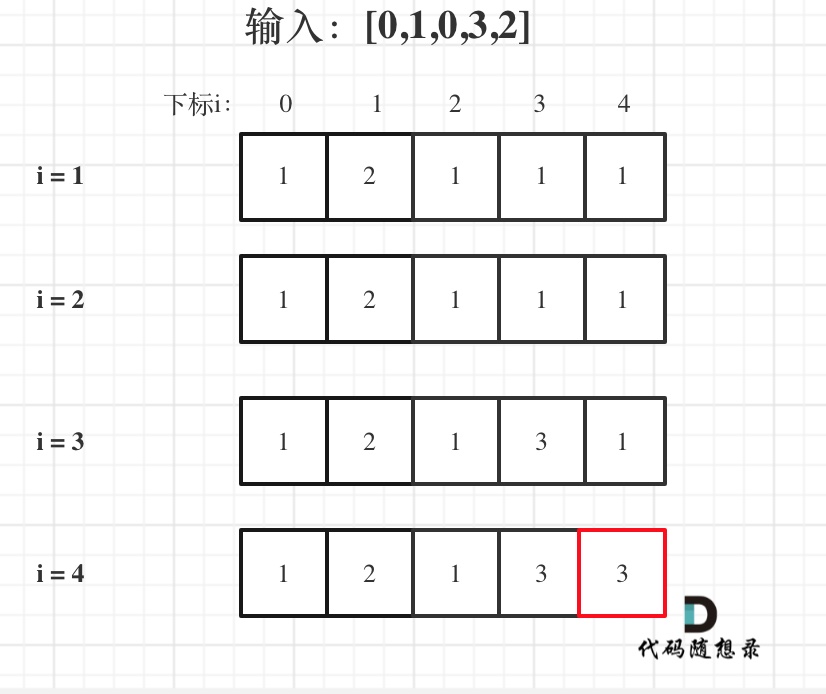
|
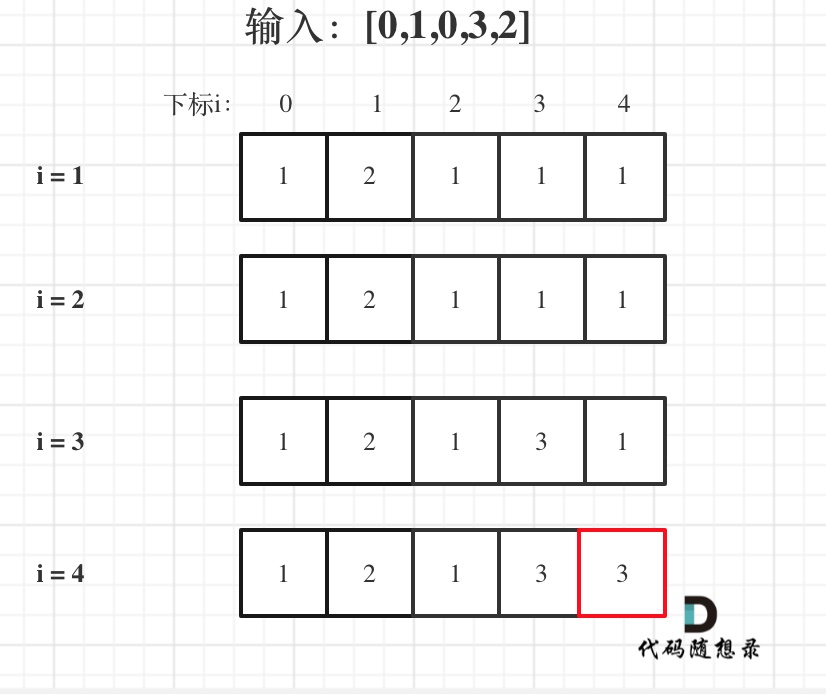
|
||||||
|
|
||||||
|
|
||||||
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
|
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
|
||||||
|
|
|
||||||
|
|
@ -47,7 +47,7 @@ dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
|
||||||
* 状态三:今天卖出股票
|
* 状态三:今天卖出股票
|
||||||
* 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
|
* 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
|
||||||
|
|
||||||
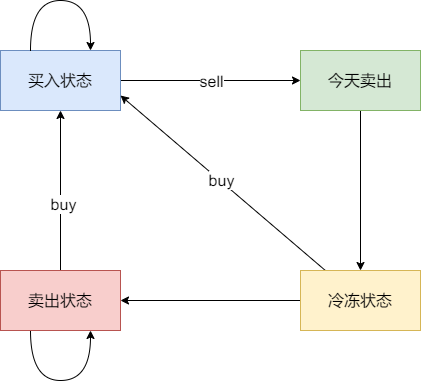
|
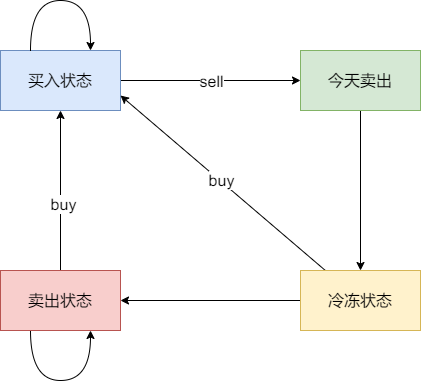
|
||||||
|
|
||||||
j的状态为:
|
j的状态为:
|
||||||
|
|
||||||
|
|
@ -136,7 +136,7 @@ dp[i][3] = dp[i - 1][2];
|
||||||
以 [1,2,3,0,2] 为例,dp数组如下:
|
以 [1,2,3,0,2] 为例,dp数组如下:
|
||||||
|
|
||||||
|
|
||||||
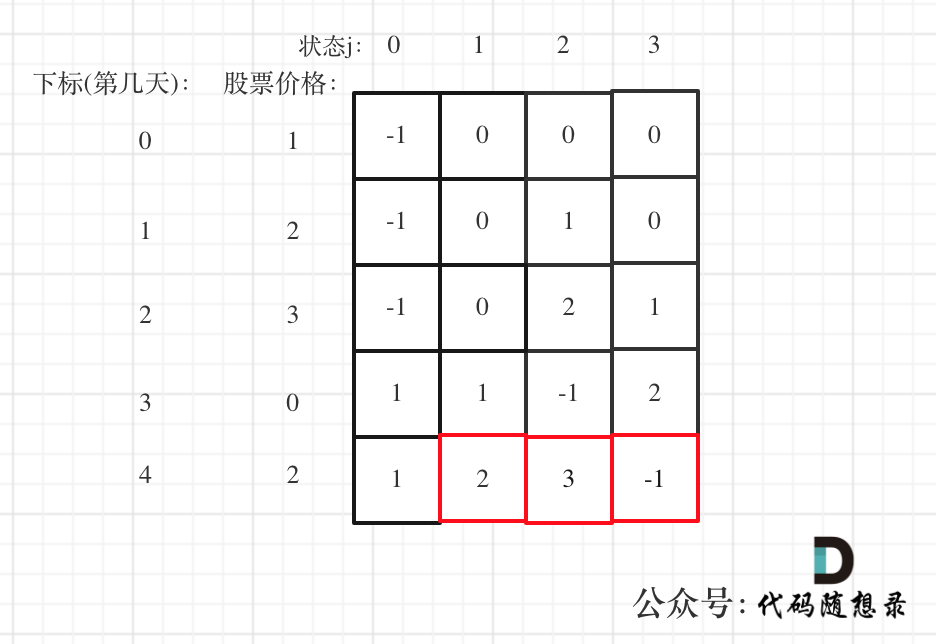
|
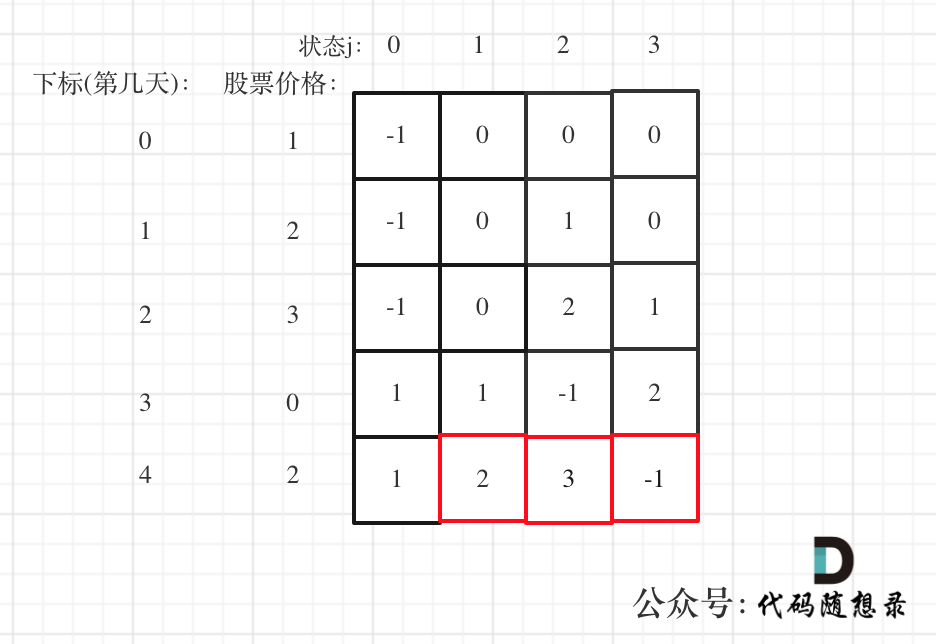
|
||||||
|
|
||||||
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
|
最后结果是取 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -104,7 +104,7 @@ dp[0] = 0;
|
||||||
|
|
||||||
以输入:coins = [1, 2, 5], amount = 5为例
|
以输入:coins = [1, 2, 5], amount = 5为例
|
||||||
|
|
||||||
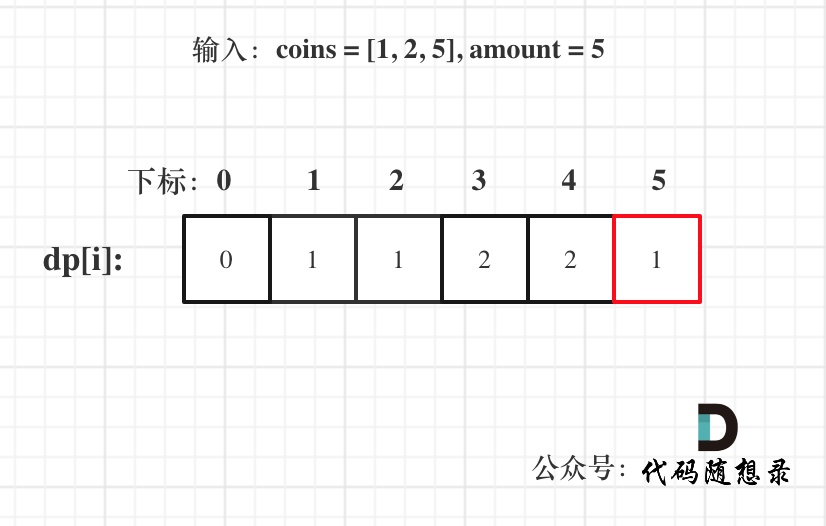
|
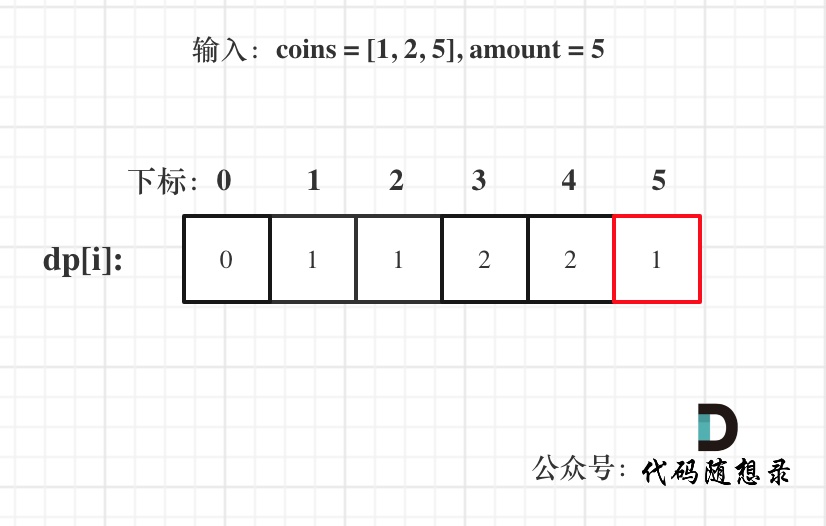
|
||||||
|
|
||||||
dp[amount]为最终结果。
|
dp[amount]为最终结果。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -57,7 +57,7 @@
|
||||||
|
|
||||||
对于死循环,我来举一个有重复机场的例子:
|
对于死循环,我来举一个有重复机场的例子:
|
||||||
|
|
||||||
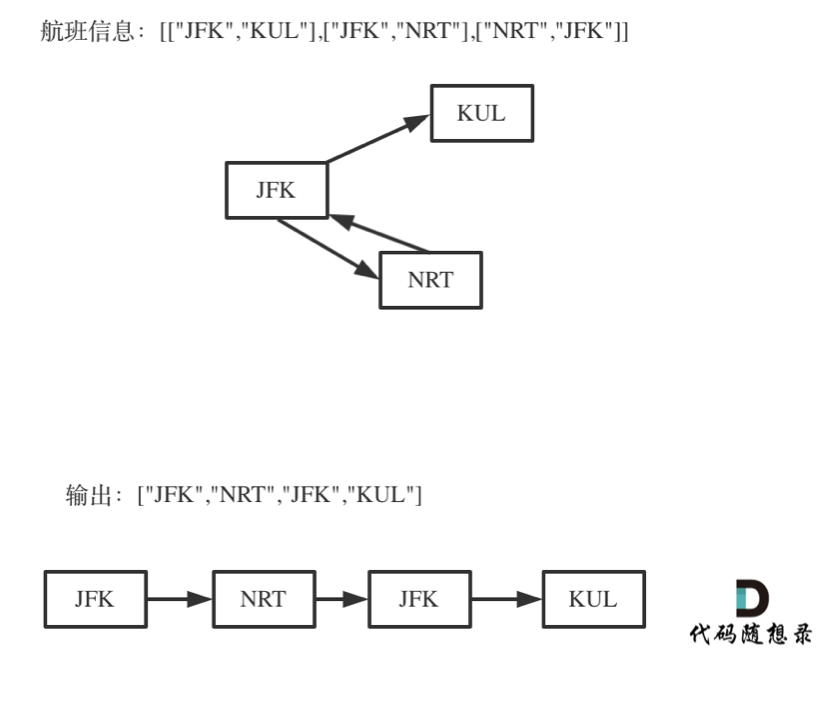
|

|
||||||
|
|
||||||
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
|
为什么要举这个例子呢,就是告诉大家,出发机场和到达机场也会重复的,**如果在解题的过程中没有对集合元素处理好,就会死循环。**
|
||||||
|
|
||||||
|
|
@ -111,7 +111,7 @@ void backtracking(参数) {
|
||||||
|
|
||||||
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
|
本题以输入:[["JFK", "KUL"], ["JFK", "NRT"], ["NRT", "JFK"]为例,抽象为树形结构如下:
|
||||||
|
|
||||||
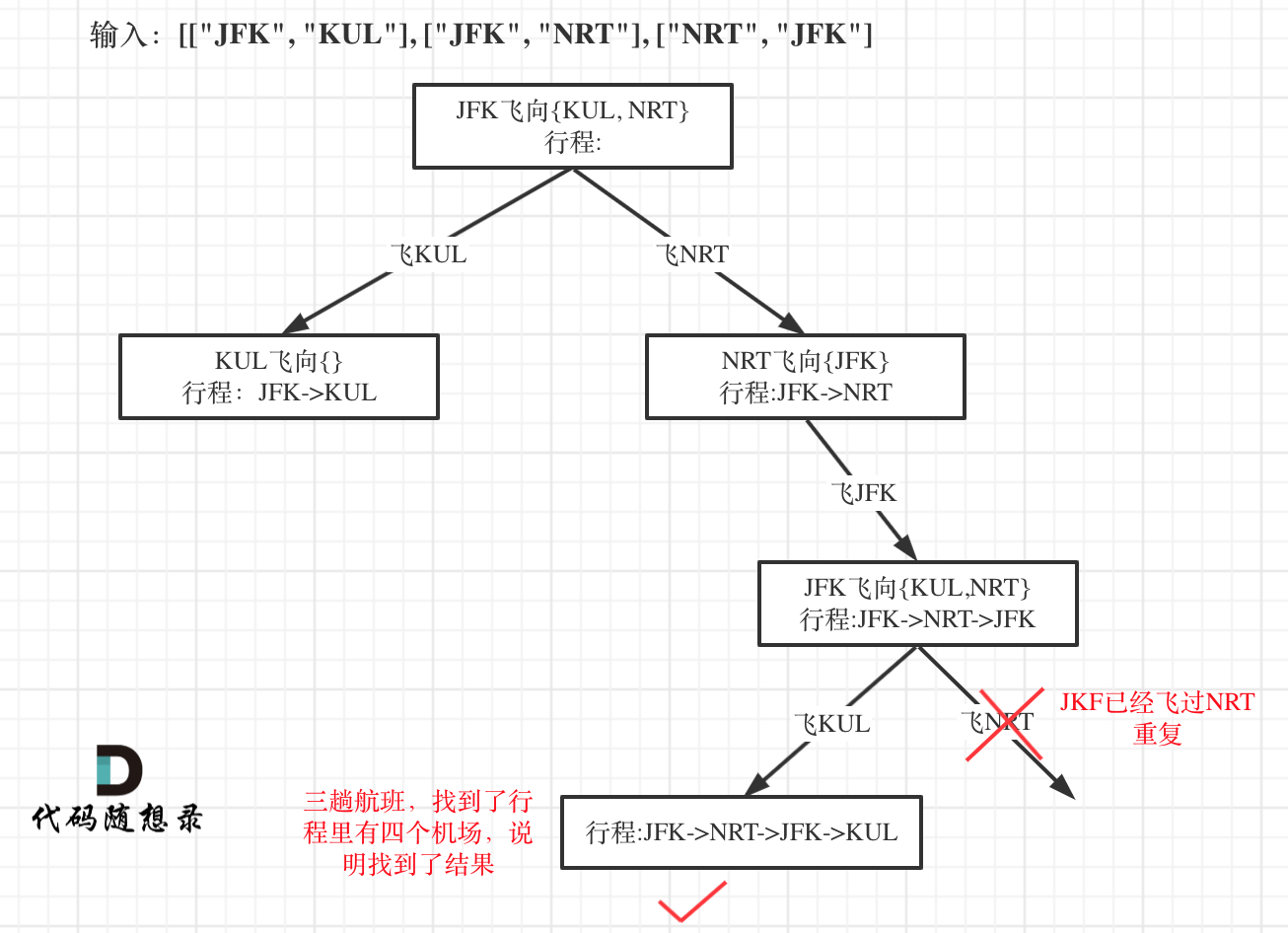
|
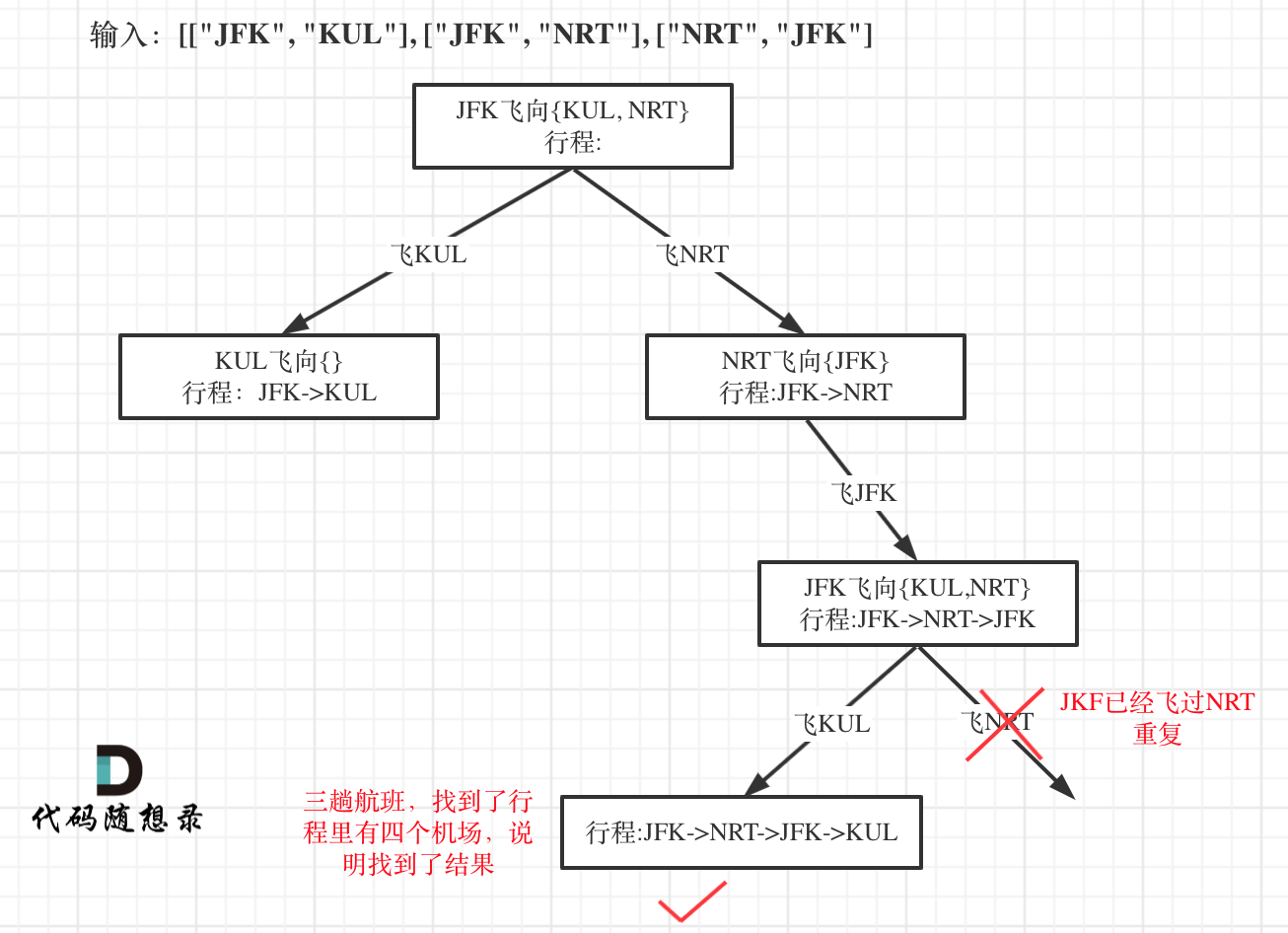
|
||||||
|
|
||||||
开始回溯三部曲讲解:
|
开始回溯三部曲讲解:
|
||||||
|
|
||||||
|
|
@ -137,7 +137,7 @@ bool backtracking(int ticketNum, vector<string>& result) {
|
||||||
|
|
||||||
因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,如图:
|
因为我们只需要找到一个行程,就是在树形结构中唯一的一条通向叶子节点的路线,如图:
|
||||||
|
|
||||||
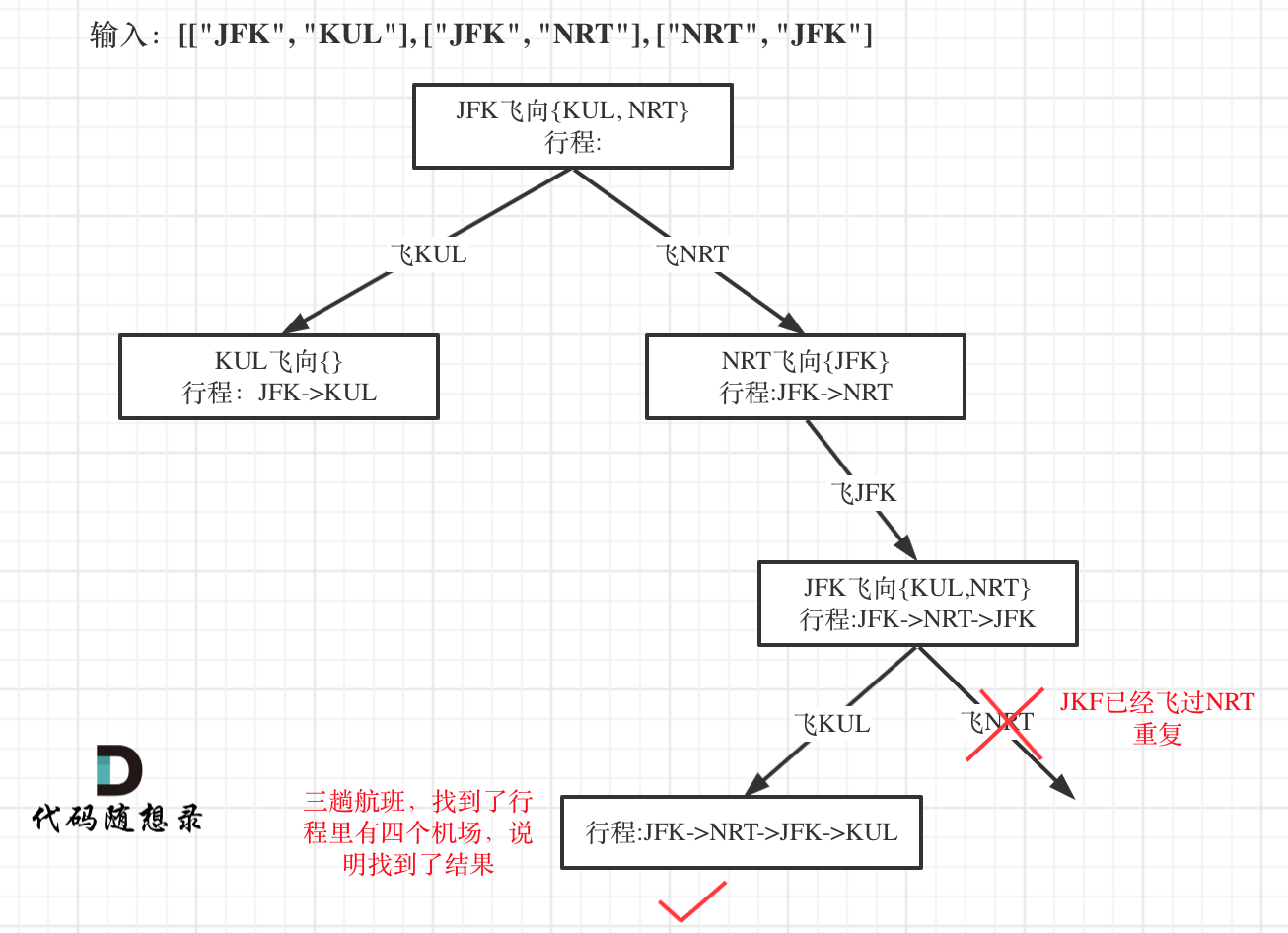
|
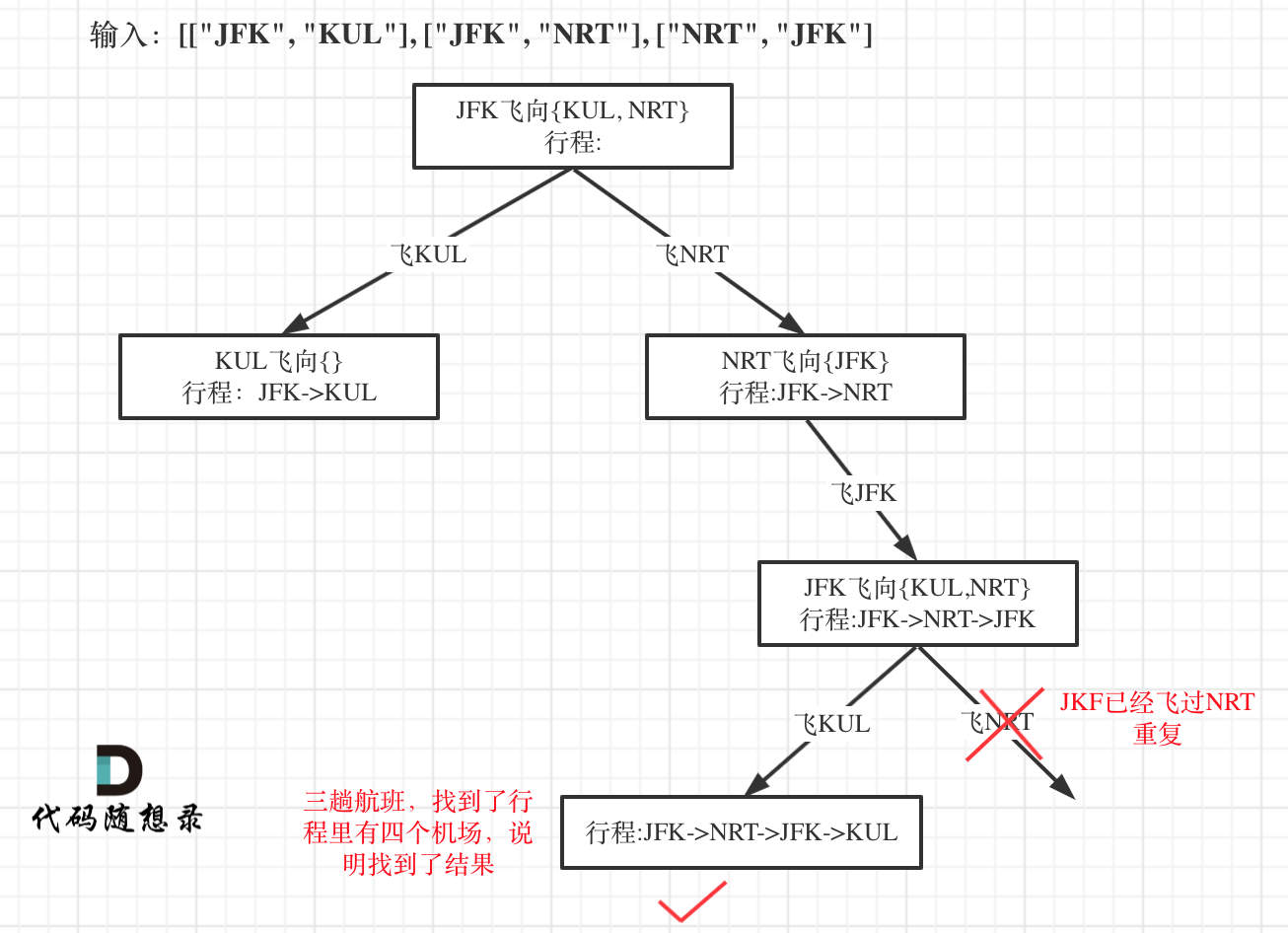
|
||||||
|
|
||||||
所以找到了这个叶子节点了直接返回,这个递归函数的返回值问题我们在讲解二叉树的系列的时候,在这篇[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://programmercarl.com/0112.路径总和.html)详细介绍过。
|
所以找到了这个叶子节点了直接返回,这个递归函数的返回值问题我们在讲解二叉树的系列的时候,在这篇[二叉树:递归函数究竟什么时候需要返回值,什么时候不要返回值?](https://programmercarl.com/0112.路径总和.html)详细介绍过。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -12,7 +12,7 @@
|
||||||
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
|
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
|
||||||
|
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -177,7 +177,7 @@ return {val2, val1};
|
||||||
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
|
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
|
||||||
|
|
||||||
|
|
||||||
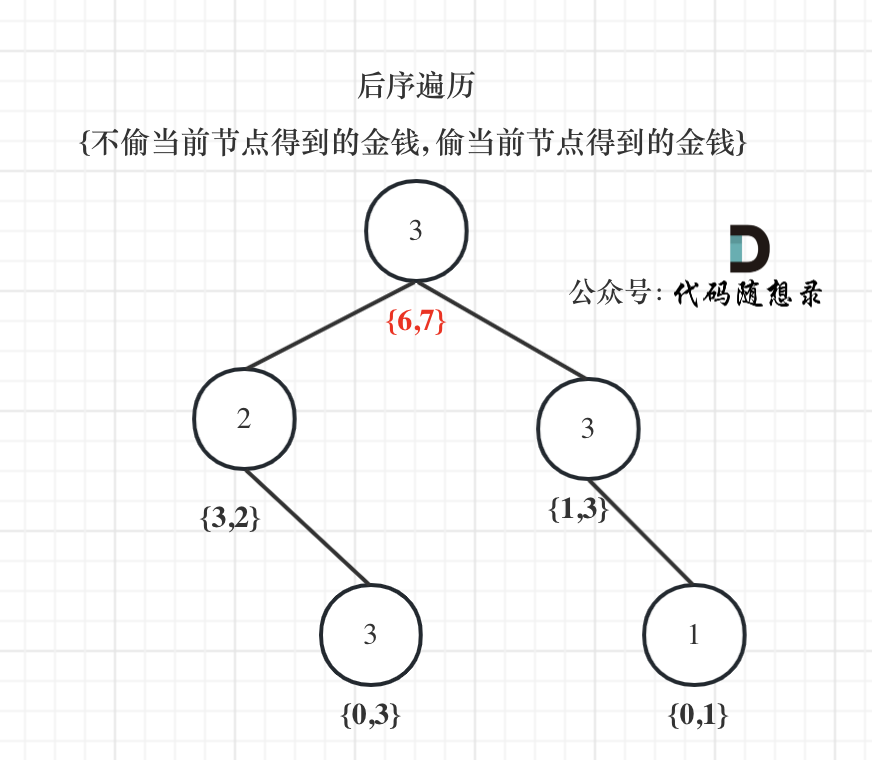
|
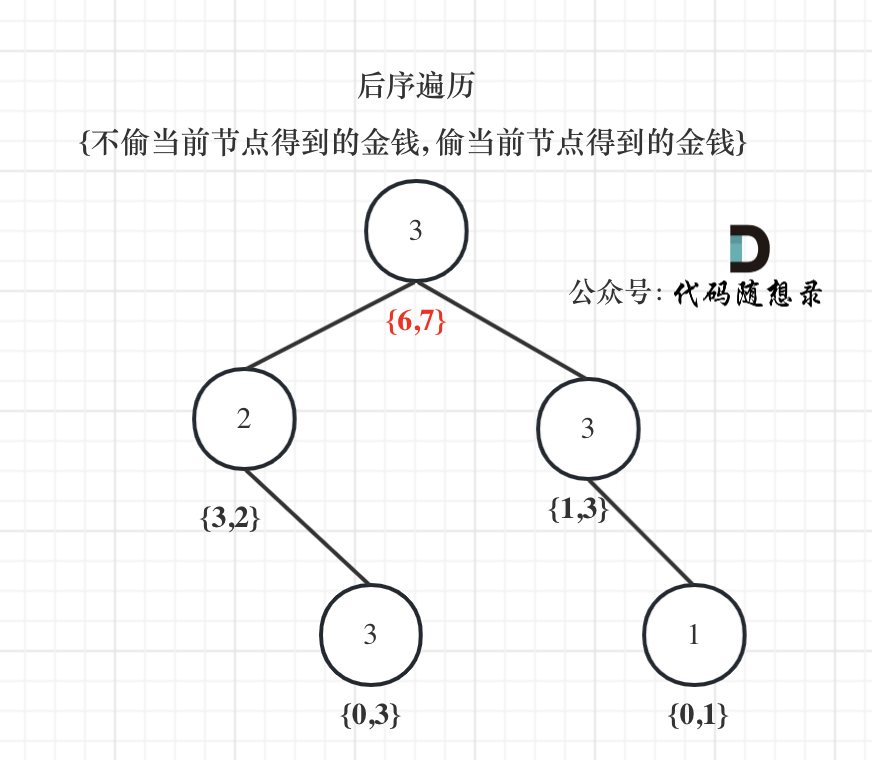
|
||||||
|
|
||||||
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
|
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -127,7 +127,7 @@ for (int i = 3; i <= n ; i++) {
|
||||||
|
|
||||||
举例当n为10 的时候,dp数组里的数值,如下:
|
举例当n为10 的时候,dp数组里的数值,如下:
|
||||||
|
|
||||||
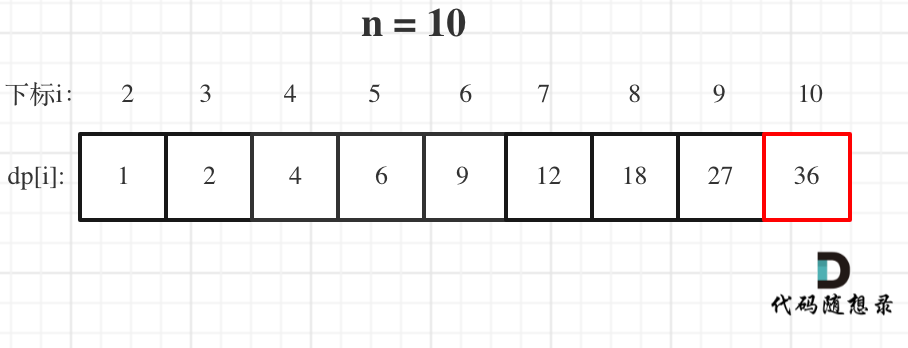
|
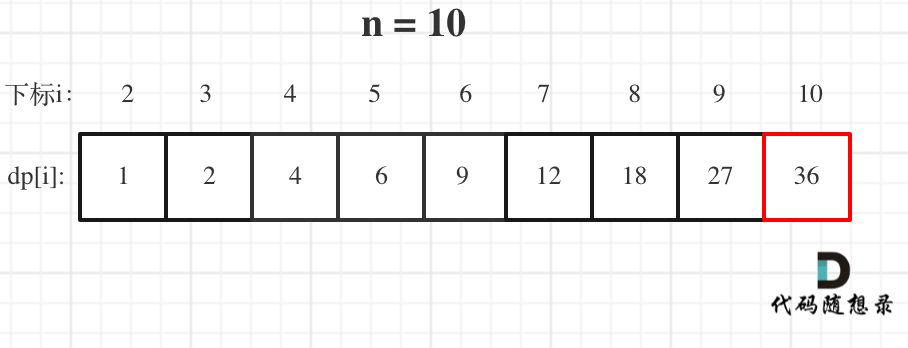
|
||||||
|
|
||||||
以上动规五部曲分析完毕,C++代码如下:
|
以上动规五部曲分析完毕,C++代码如下:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -14,7 +14,7 @@
|
||||||
|
|
||||||
题意:给定两个数组,编写一个函数来计算它们的交集。
|
题意:给定两个数组,编写一个函数来计算它们的交集。
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
**说明:**
|
**说明:**
|
||||||
输出结果中的每个元素一定是唯一的。
|
输出结果中的每个元素一定是唯一的。
|
||||||
|
|
@ -51,7 +51,7 @@ std::set和std::multiset底层实现都是红黑树,std::unordered_set的底
|
||||||
思路如图所示:
|
思路如图所示:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
C++代码如下:
|
C++代码如下:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -46,7 +46,7 @@
|
||||||
|
|
||||||
用示例二来举例,如图所示:
|
用示例二来举例,如图所示:
|
||||||
|
|
||||||
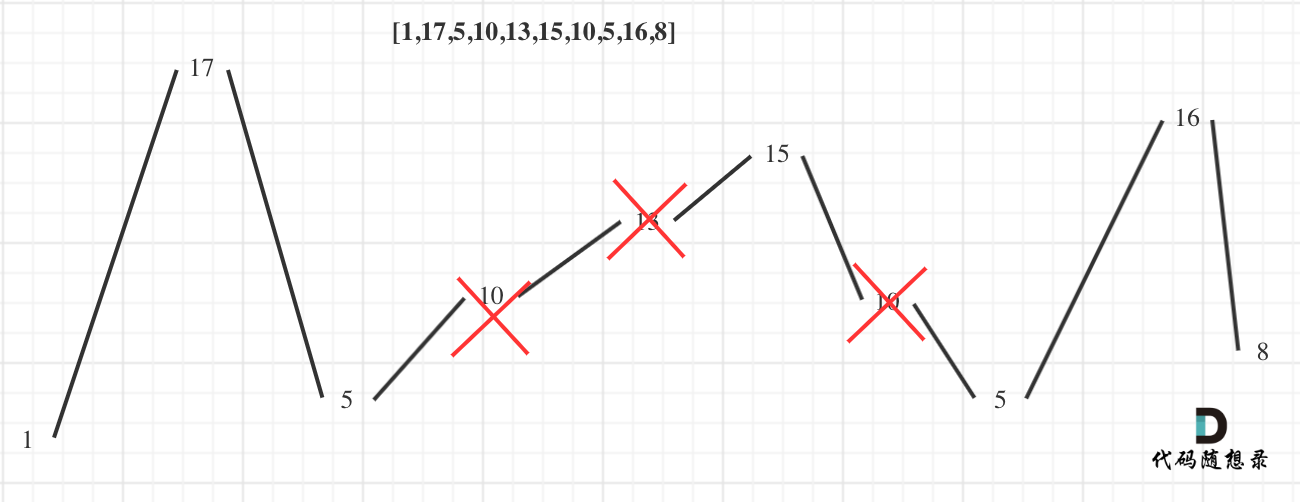
|
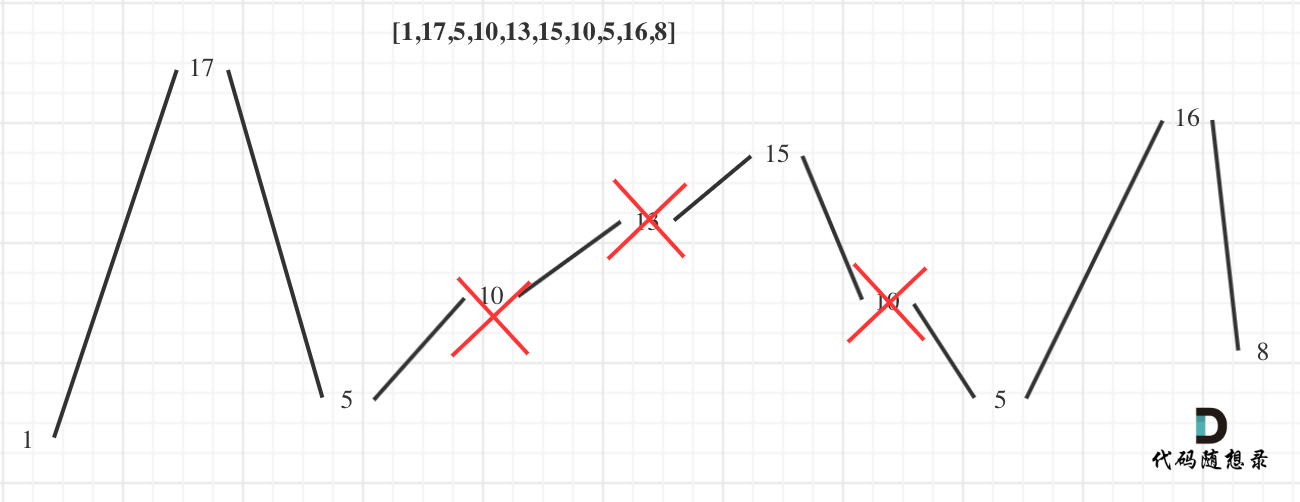
|
||||||
|
|
||||||
**局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值**。
|
**局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值**。
|
||||||
|
|
||||||
|
|
@ -72,13 +72,13 @@
|
||||||
|
|
||||||
例如 [1,2,2,2,2,1]这样的数组,如图:
|
例如 [1,2,2,2,2,1]这样的数组,如图:
|
||||||
|
|
||||||
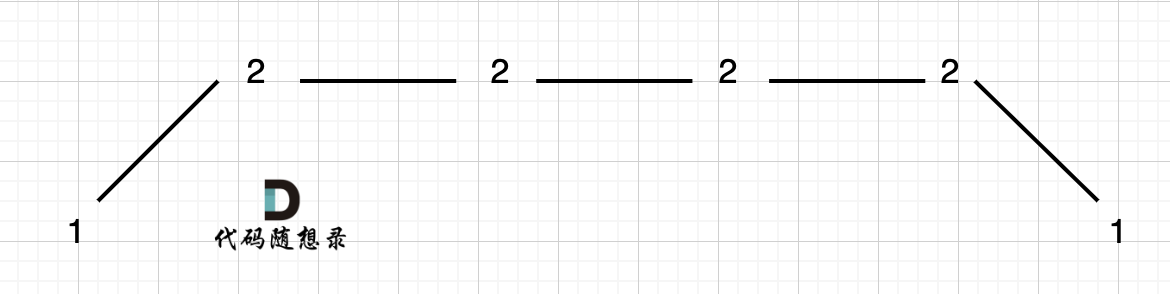
|
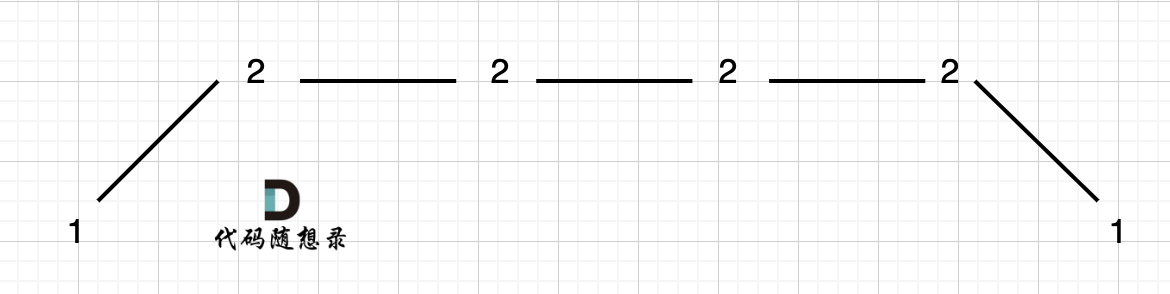
|
||||||
|
|
||||||
它的摇摆序列长度是多少呢? **其实是长度是 3**,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。
|
它的摇摆序列长度是多少呢? **其实是长度是 3**,也就是我们在删除的时候 要不删除左面的三个 2,要不就删除右边的三个 2。
|
||||||
|
|
||||||
如图,可以统一规则,删除左边的三个 2:
|
如图,可以统一规则,删除左边的三个 2:
|
||||||
|
|
||||||
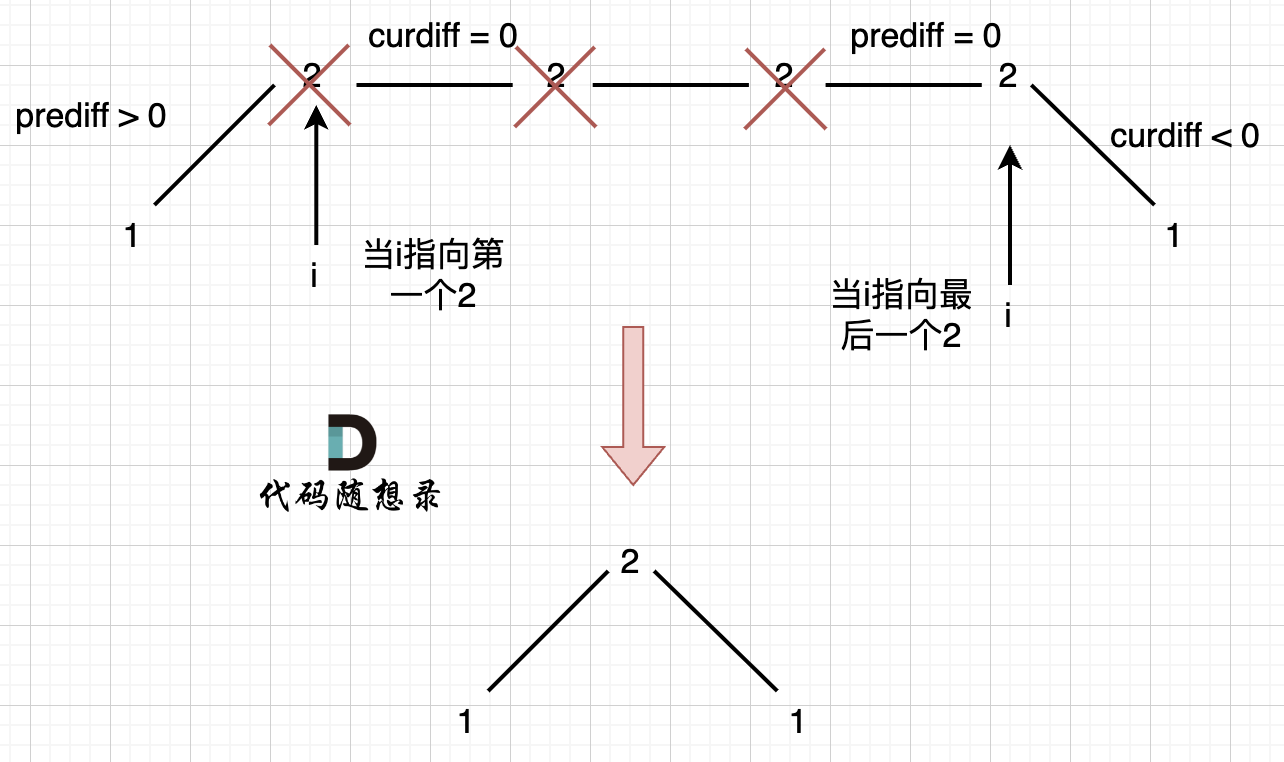
|
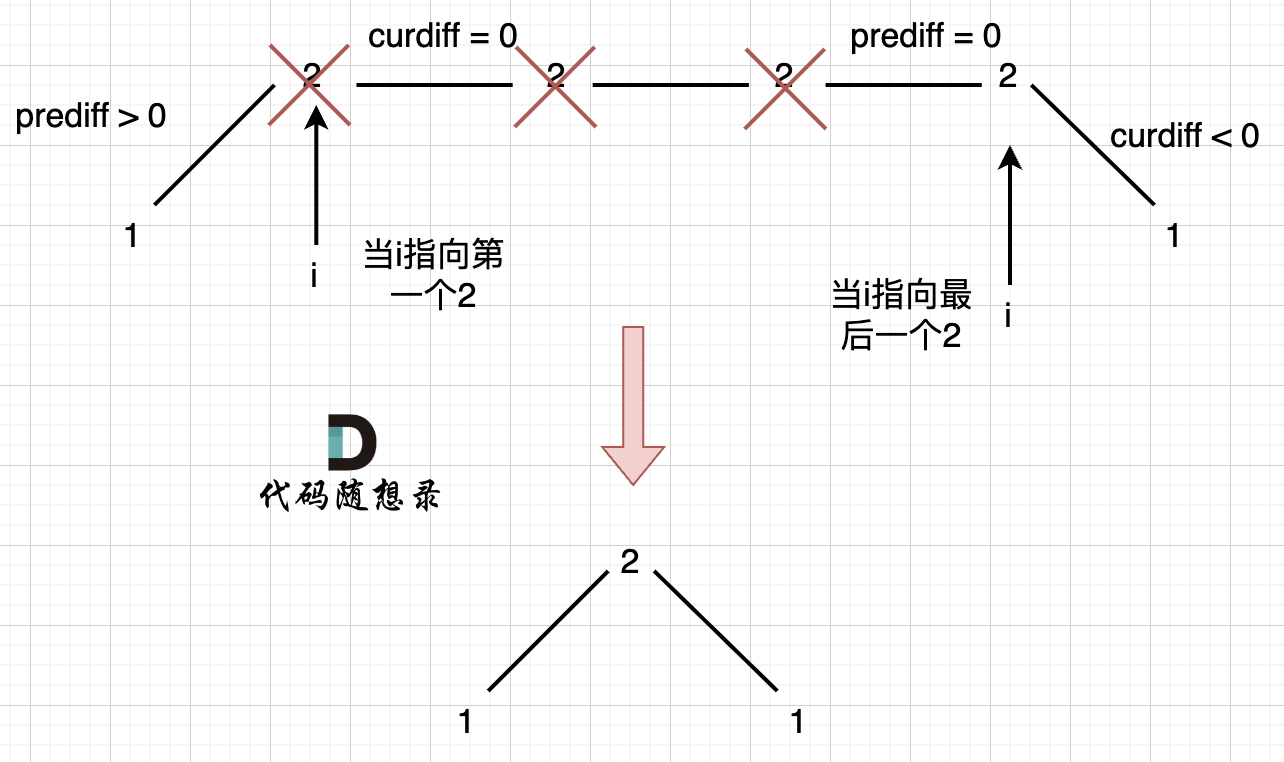
|
||||||
|
|
||||||
在图中,当 i 指向第一个 2 的时候,`prediff > 0 && curdiff = 0` ,当 i 指向最后一个 2 的时候 `prediff = 0 && curdiff < 0`。
|
在图中,当 i 指向第一个 2 的时候,`prediff > 0 && curdiff = 0` ,当 i 指向最后一个 2 的时候 `prediff = 0 && curdiff < 0`。
|
||||||
|
|
||||||
|
|
@ -106,7 +106,7 @@
|
||||||
|
|
||||||
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0,如图:
|
那么为了规则统一,针对序列[2,5],可以假设为[2,2,5],这样它就有坡度了即 preDiff = 0,如图:
|
||||||
|
|
||||||
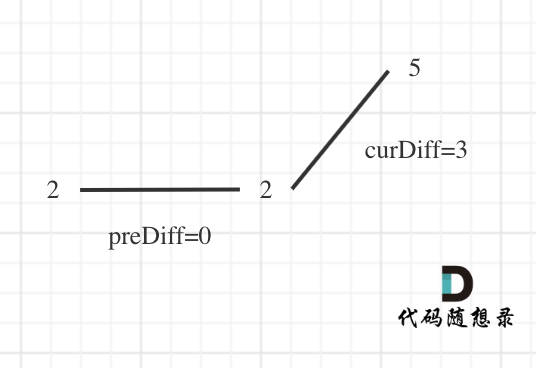
|
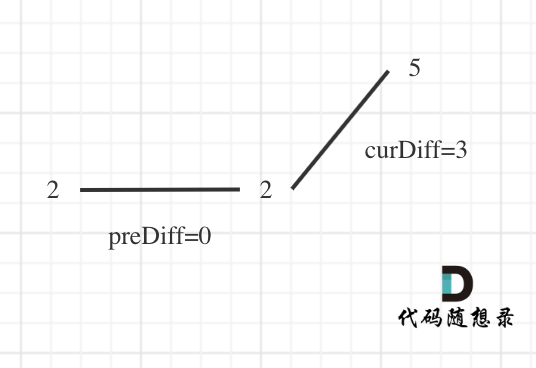
|
||||||
|
|
||||||
针对以上情形,result 初始为 1(默认最右面有一个峰值),此时 curDiff > 0 && preDiff <= 0,那么 result++(计算了左面的峰值),最后得到的 result 就是 2(峰值个数为 2 即摆动序列长度为 2)
|
针对以上情形,result 初始为 1(默认最右面有一个峰值),此时 curDiff > 0 && preDiff <= 0,那么 result++(计算了左面的峰值),最后得到的 result 就是 2(峰值个数为 2 即摆动序列长度为 2)
|
||||||
|
|
||||||
|
|
@ -145,7 +145,7 @@ public:
|
||||||
|
|
||||||
在版本一中,我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
|
在版本一中,我们忽略了一种情况,即 如果在一个单调坡度上有平坡,例如[1,2,2,2,3,4],如图:
|
||||||
|
|
||||||
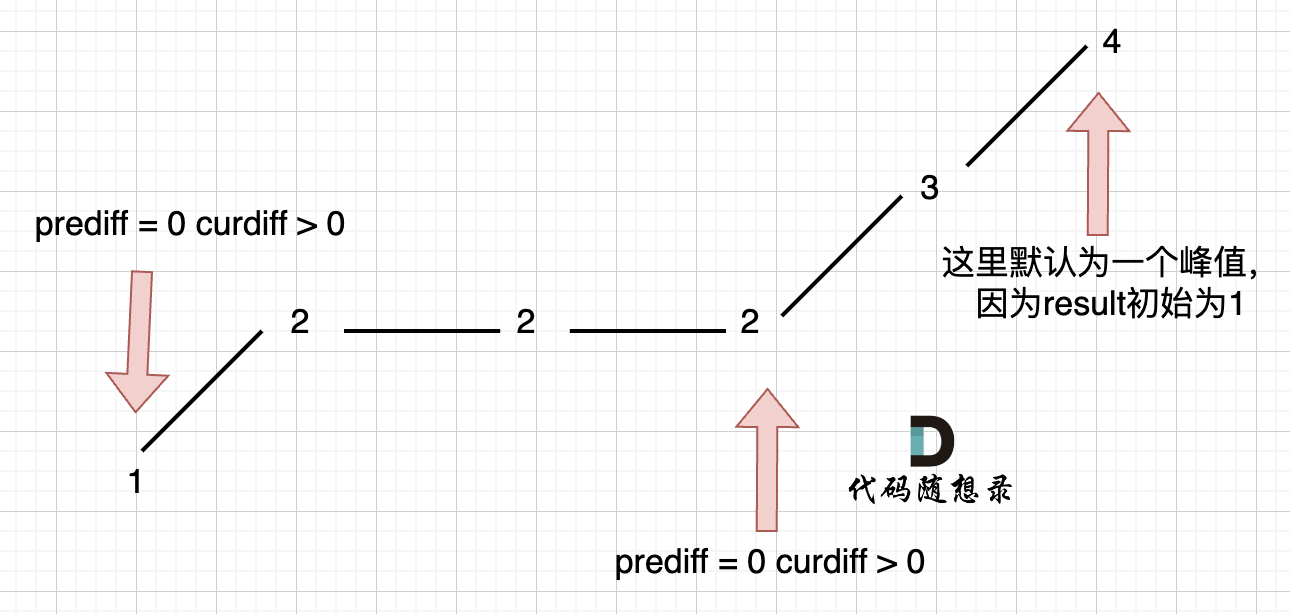
|
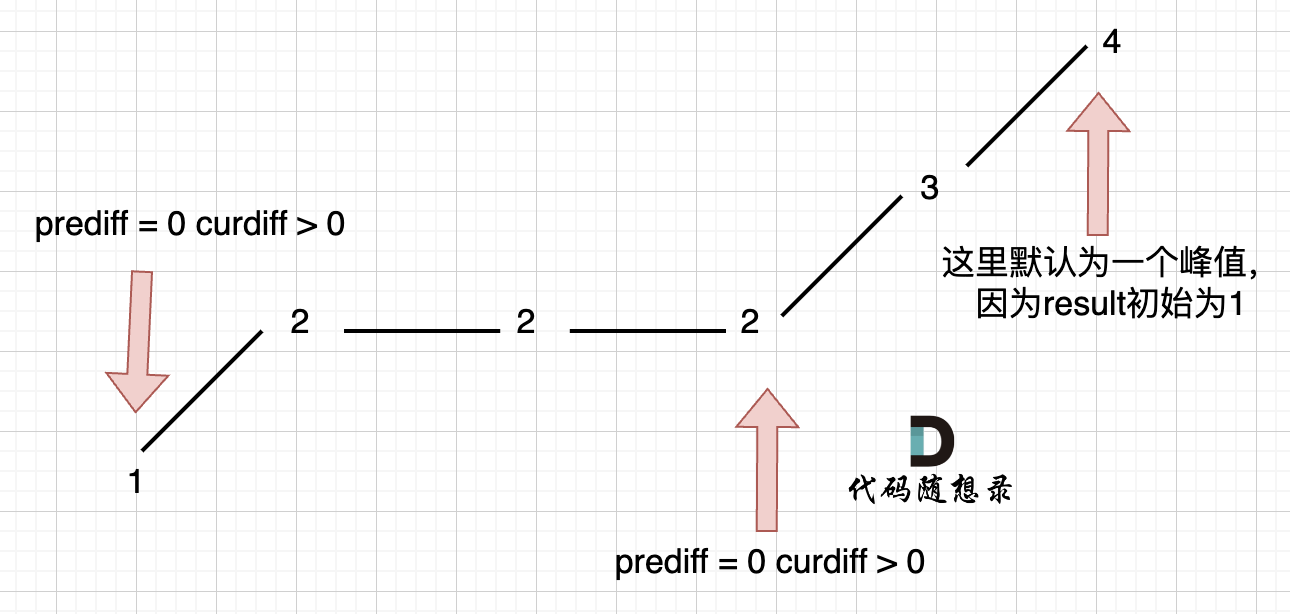
|
||||||
|
|
||||||
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是 2,因为 单调中的平坡 不能算峰值(即摆动)。
|
图中,我们可以看出,版本一的代码在三个地方记录峰值,但其实结果因为是 2,因为 单调中的平坡 不能算峰值(即摆动)。
|
||||||
|
|
||||||
|
|
@ -184,7 +184,7 @@ public:
|
||||||
|
|
||||||
**本题异常情况的本质,就是要考虑平坡**, 平坡分两种,一个是 上下中间有平坡,一个是单调有平坡,如图:
|
**本题异常情况的本质,就是要考虑平坡**, 平坡分两种,一个是 上下中间有平坡,一个是单调有平坡,如图:
|
||||||
|
|
||||||
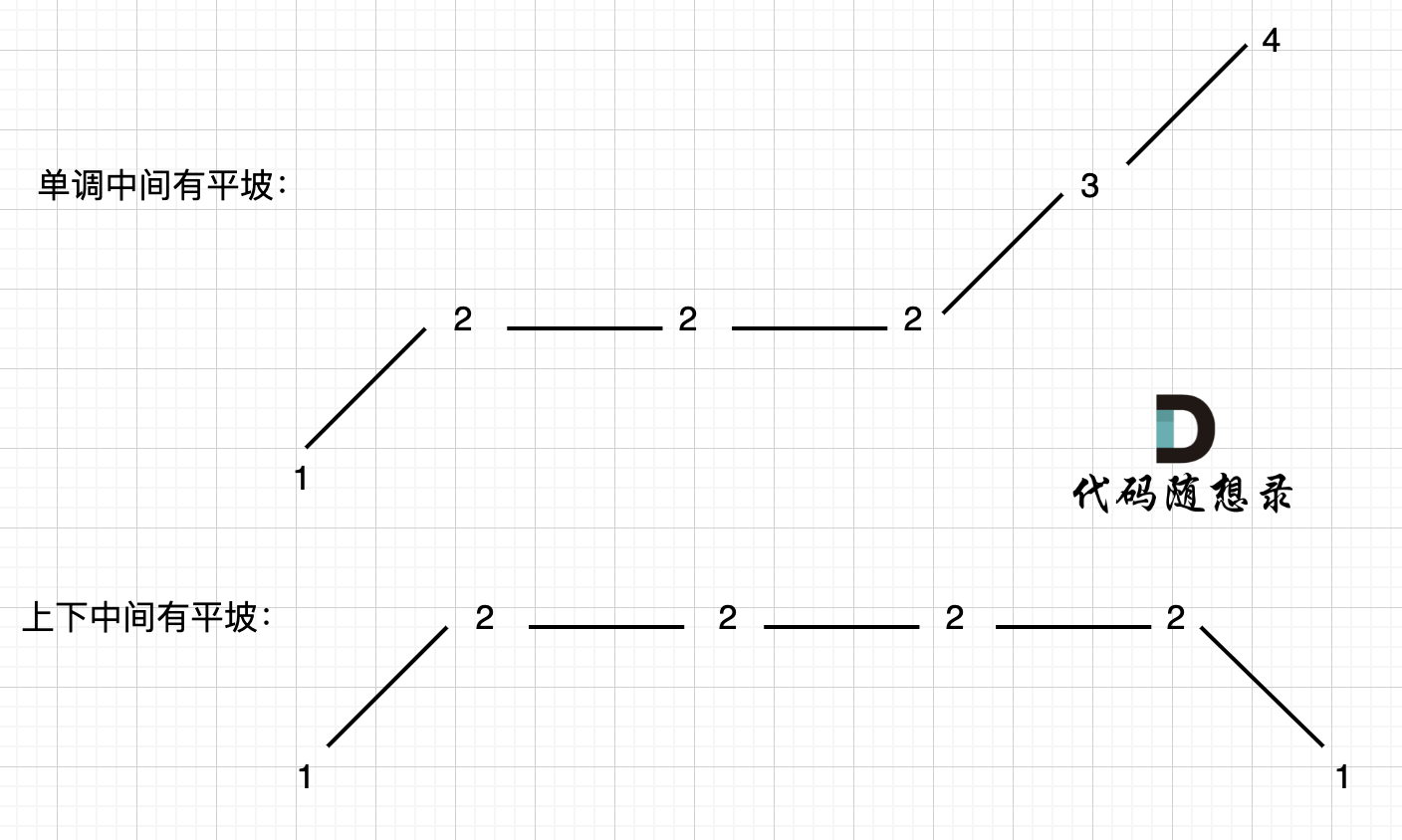
|
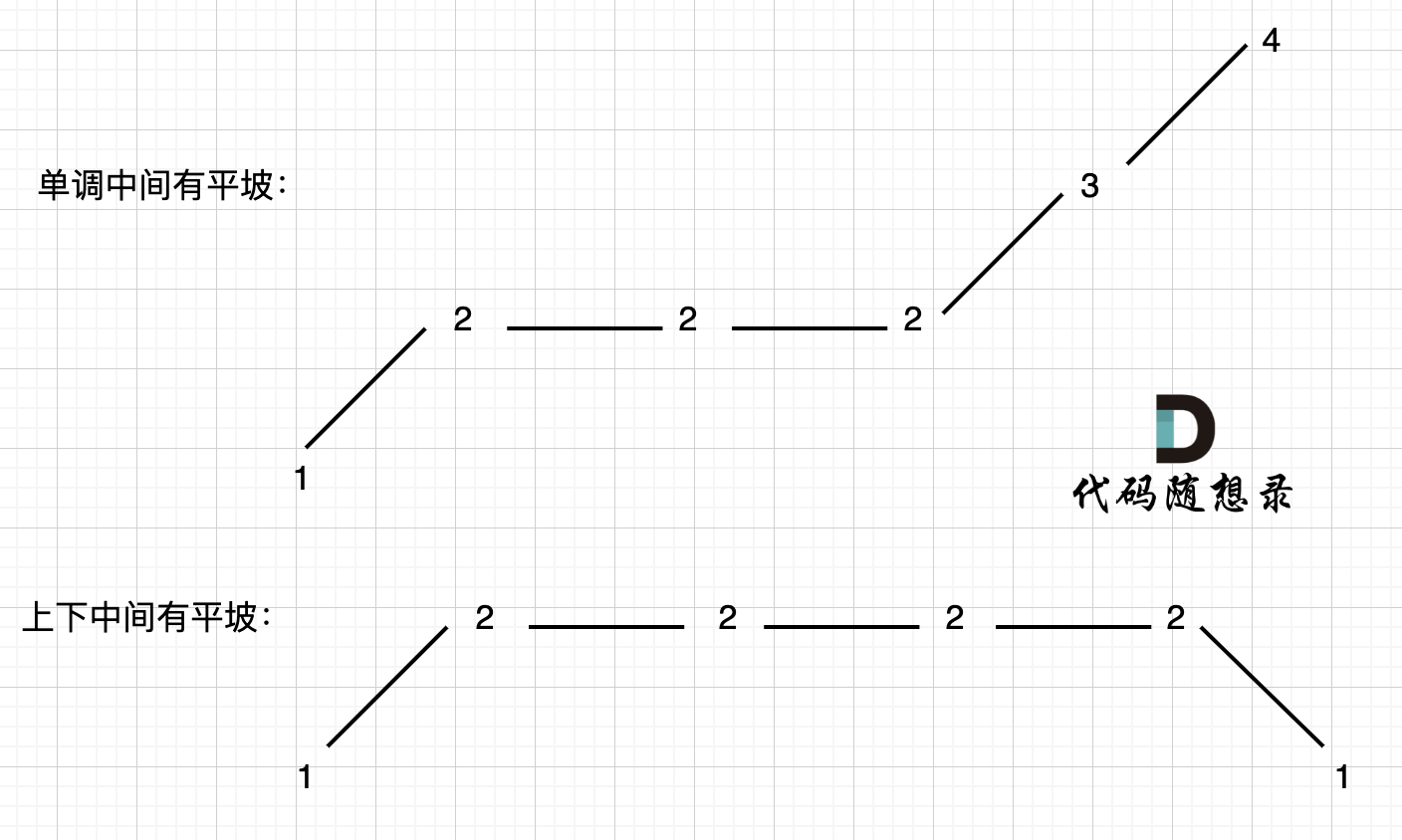
|
||||||
|
|
||||||
### 思路 2(动态规划)
|
### 思路 2(动态规划)
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -103,7 +103,7 @@ dp[i](考虑nums[j])可以由 dp[i - nums[j]](不考虑nums[j]) 推导
|
||||||
|
|
||||||
我们再来用示例中的例子推导一下:
|
我们再来用示例中的例子推导一下:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
如果代码运行处的结果不是想要的结果,就把dp[i]都打出来,看看和我们推导的一不一样。
|
如果代码运行处的结果不是想要的结果,就把dp[i]都打出来,看看和我们推导的一不一样。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -80,7 +80,7 @@ if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前
|
||||||
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:
|
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:
|
||||||
|
|
||||||
|
|
||||||
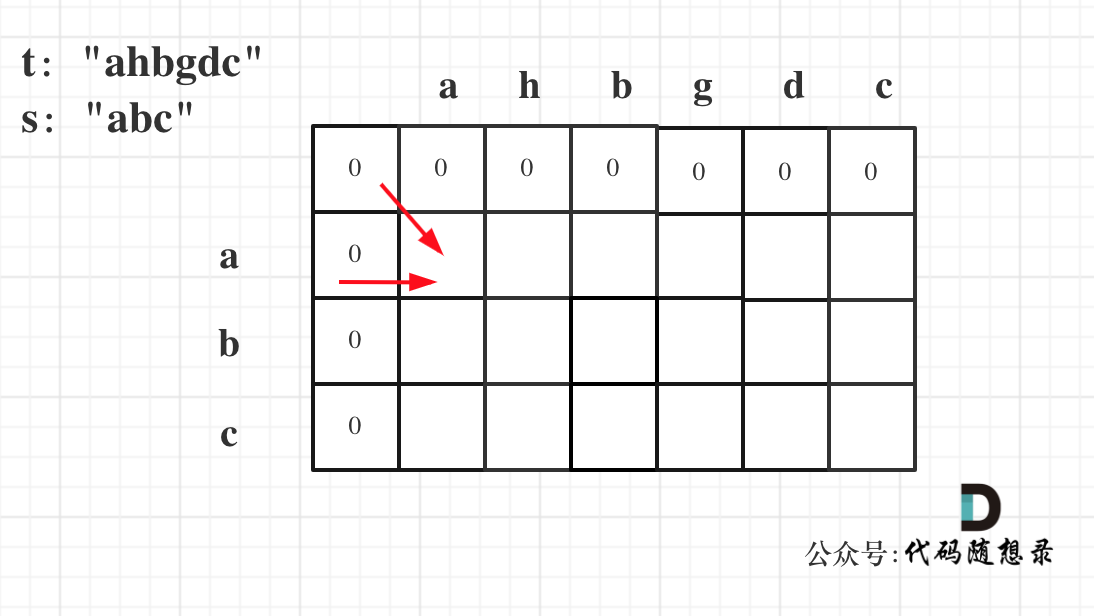
|
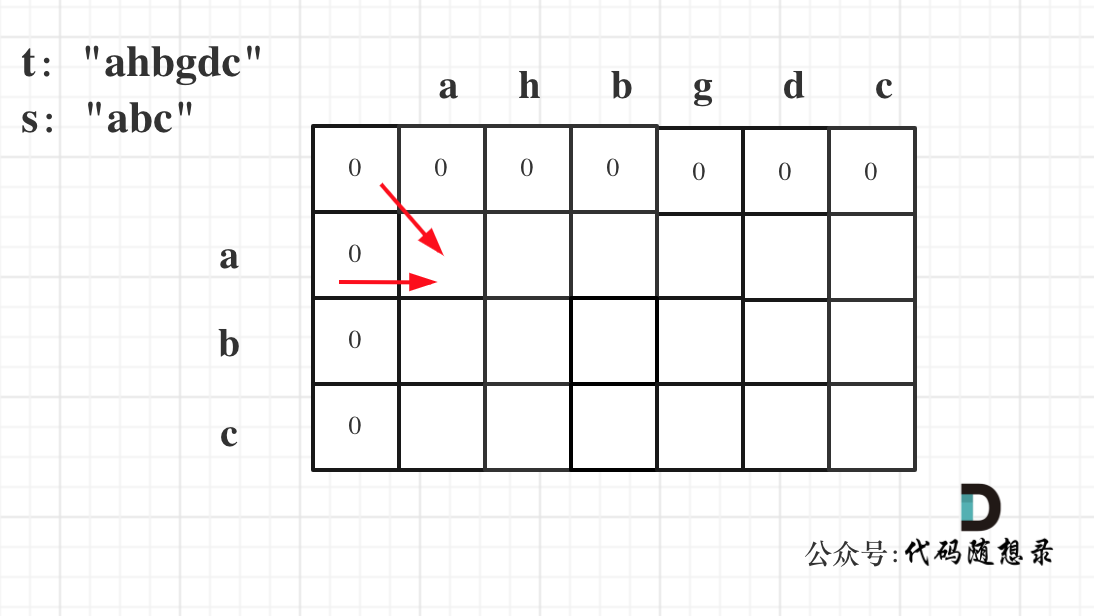
|
||||||
|
|
||||||
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
|
如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
|
||||||
|
|
||||||
|
|
@ -98,14 +98,14 @@ vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
|
||||||
如图所示:
|
如图所示:
|
||||||
|
|
||||||
|
|
||||||
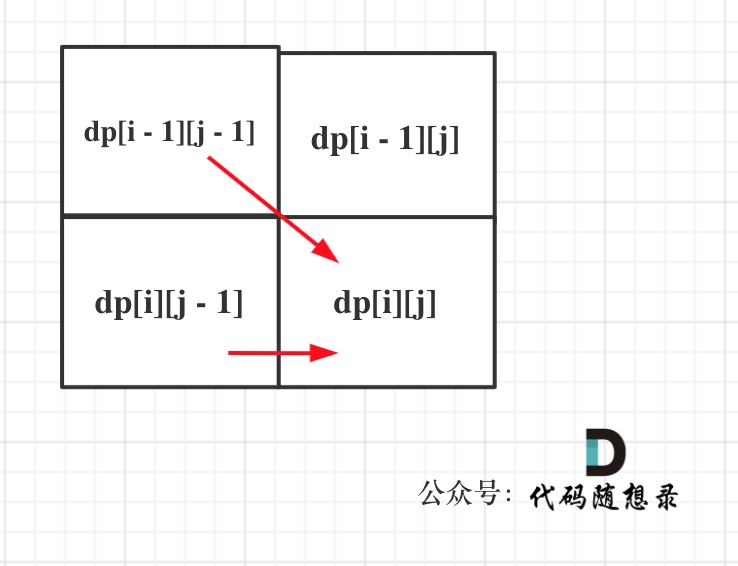
|

|
||||||
|
|
||||||
5. 举例推导dp数组
|
5. 举例推导dp数组
|
||||||
|
|
||||||
以示例一为例,输入:s = "abc", t = "ahbgdc",dp状态转移图如下:
|
以示例一为例,输入:s = "abc", t = "ahbgdc",dp状态转移图如下:
|
||||||
|
|
||||||
|
|
||||||
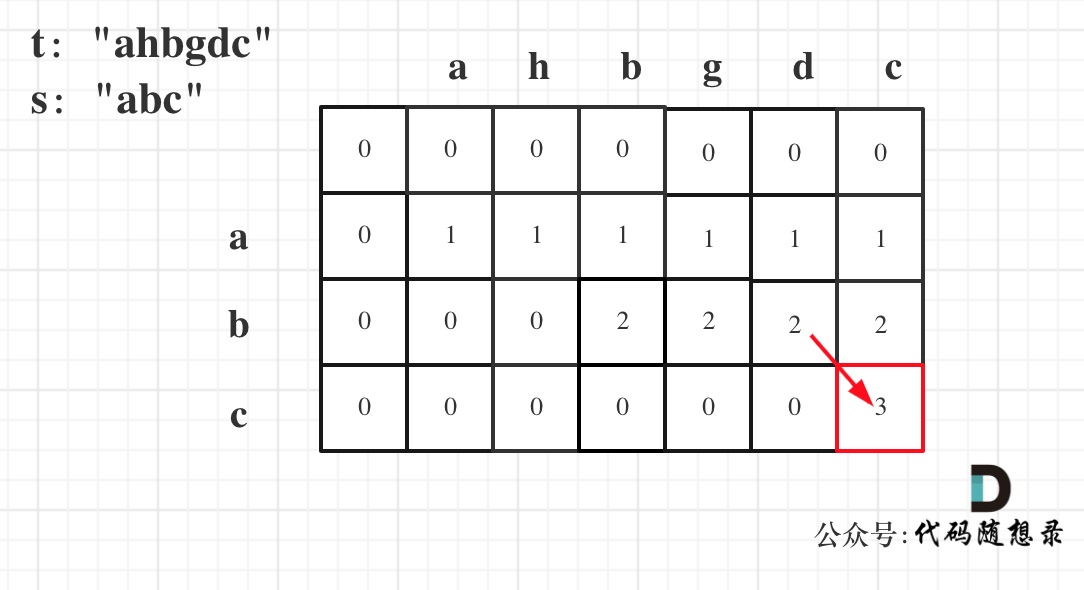
|
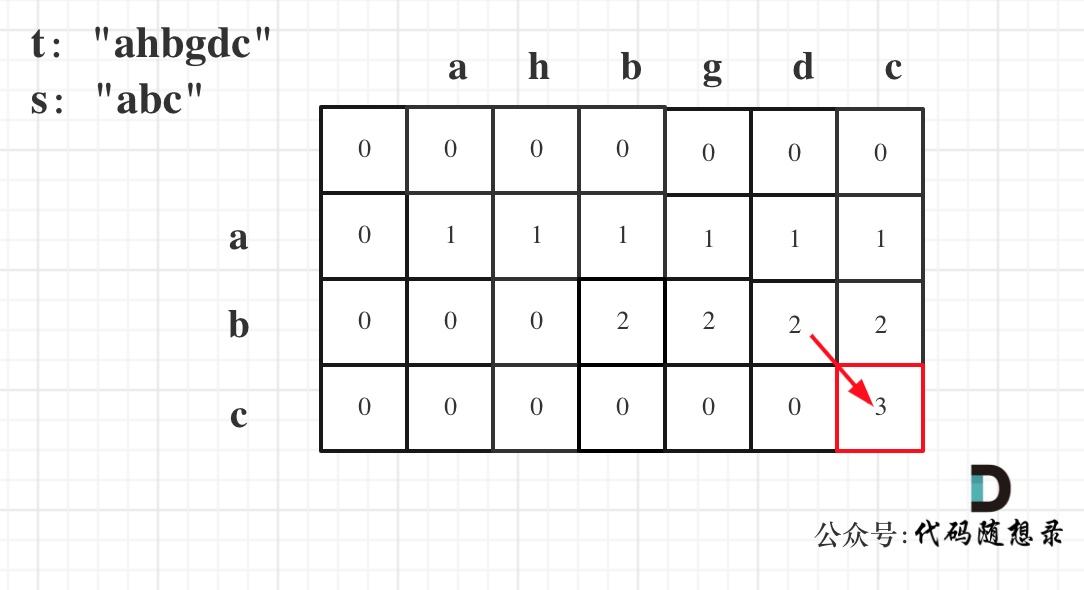
|
||||||
|
|
||||||
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
|
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -12,7 +12,7 @@
|
||||||
示例:
|
示例:
|
||||||
|
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
@ -26,12 +26,12 @@
|
||||||
|
|
||||||
大家思考一下如下图中二叉树,左叶子之和究竟是多少?
|
大家思考一下如下图中二叉树,左叶子之和究竟是多少?
|
||||||
|
|
||||||
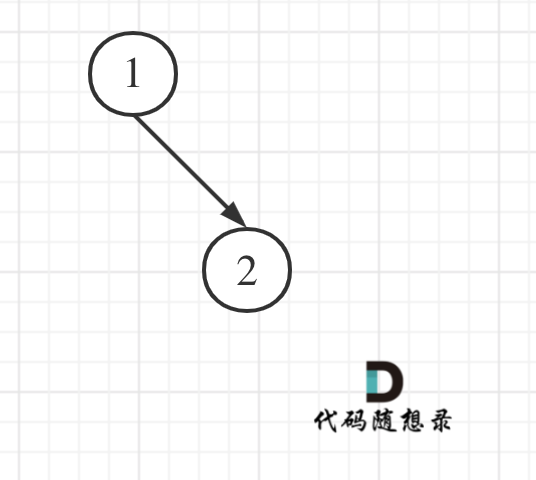
|
|
||||||
**其实是0,因为这棵树根本没有左叶子!**
|
**其实是0,因为这棵树根本没有左叶子!**
|
||||||
|
|
||||||
但看这个图的左叶子之和是多少?
|
但看这个图的左叶子之和是多少?
|
||||||
|
|
||||||
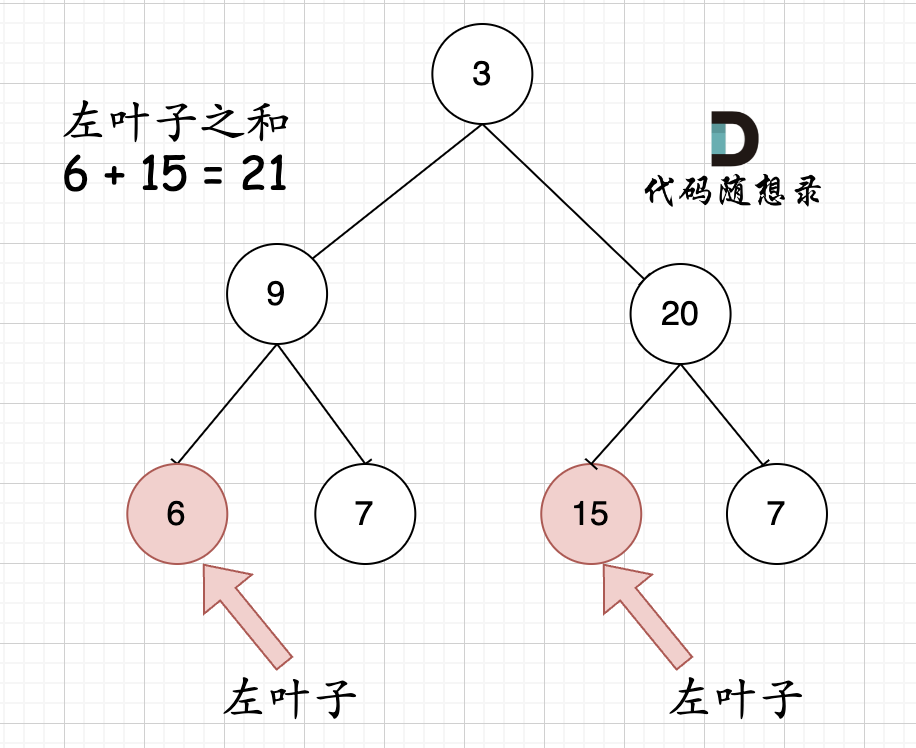
|
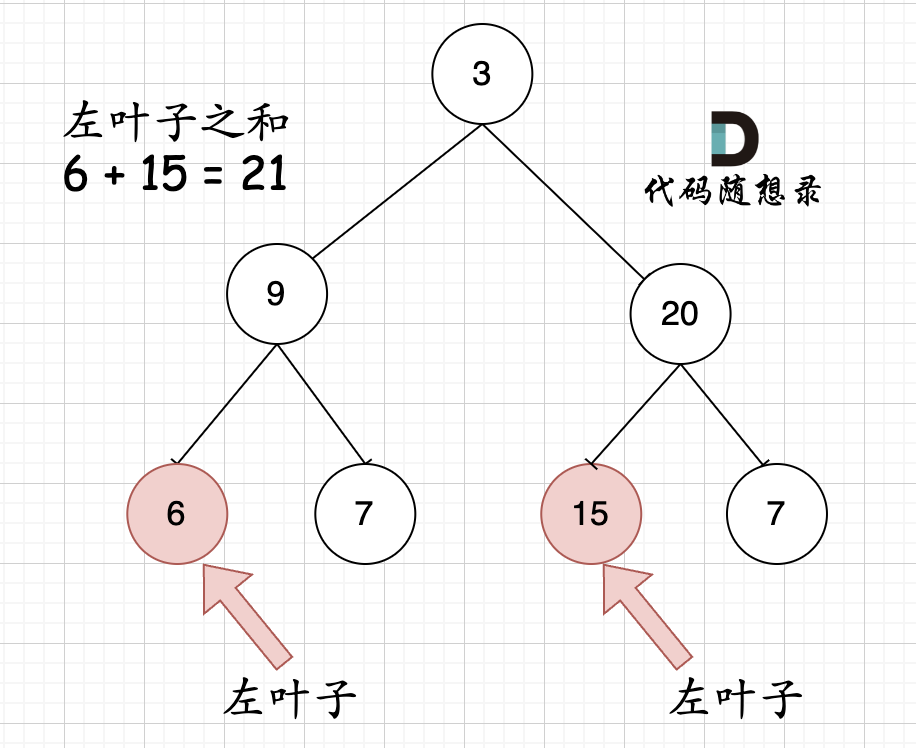
|
||||||
|
|
||||||
相信通过这两个图,大家对最左叶子的定义有明确理解了。
|
相信通过这两个图,大家对最左叶子的定义有明确理解了。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -61,7 +61,7 @@
|
||||||
|
|
||||||
以图中{5,2} 为例:
|
以图中{5,2} 为例:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
|
|
||||||
按照身高排序之后,优先按身高高的people的k来插入,后序插入节点也不会影响前面已经插入的节点,最终按照k的规则完成了队列。
|
按照身高排序之后,优先按身高高的people的k来插入,后序插入节点也不会影响前面已经插入的节点,最终按照k的规则完成了队列。
|
||||||
|
|
|
||||||
|
|
@ -155,7 +155,7 @@ dp[j]的数值一定是小于等于j的。
|
||||||
用例1,输入[1,5,11,5] 为例,如图:
|
用例1,输入[1,5,11,5] 为例,如图:
|
||||||
|
|
||||||
|
|
||||||
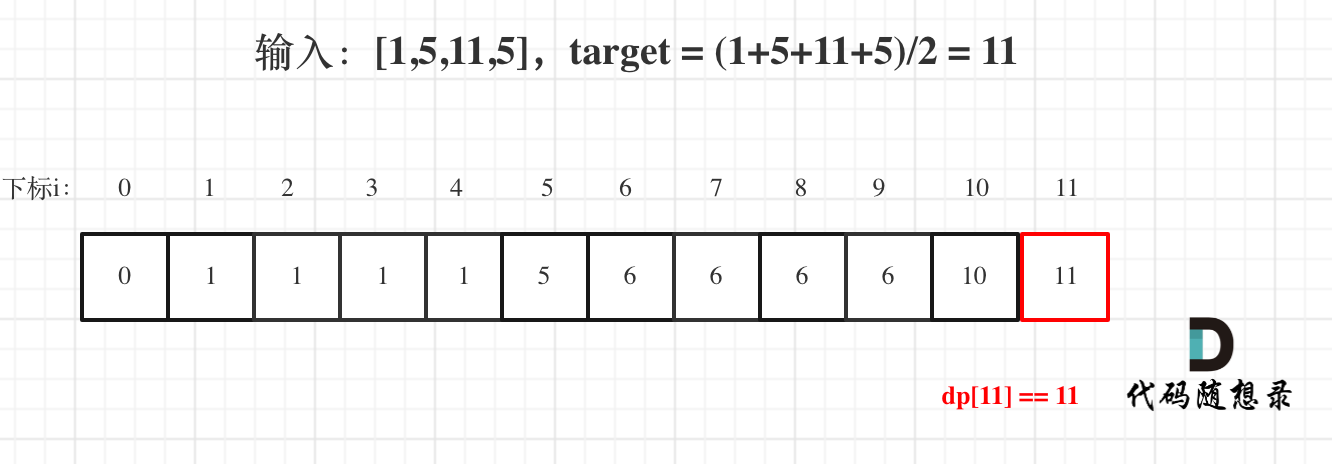
|
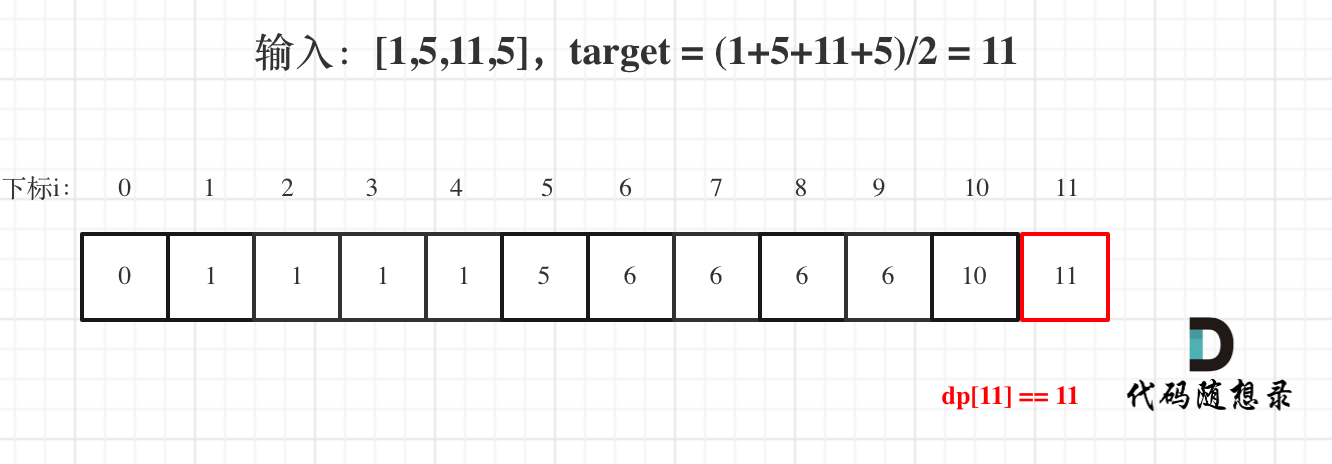
|
||||||
|
|
||||||
最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
|
最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -18,7 +18,7 @@
|
||||||
|
|
||||||
示例 1:
|
示例 1:
|
||||||
|
|
||||||
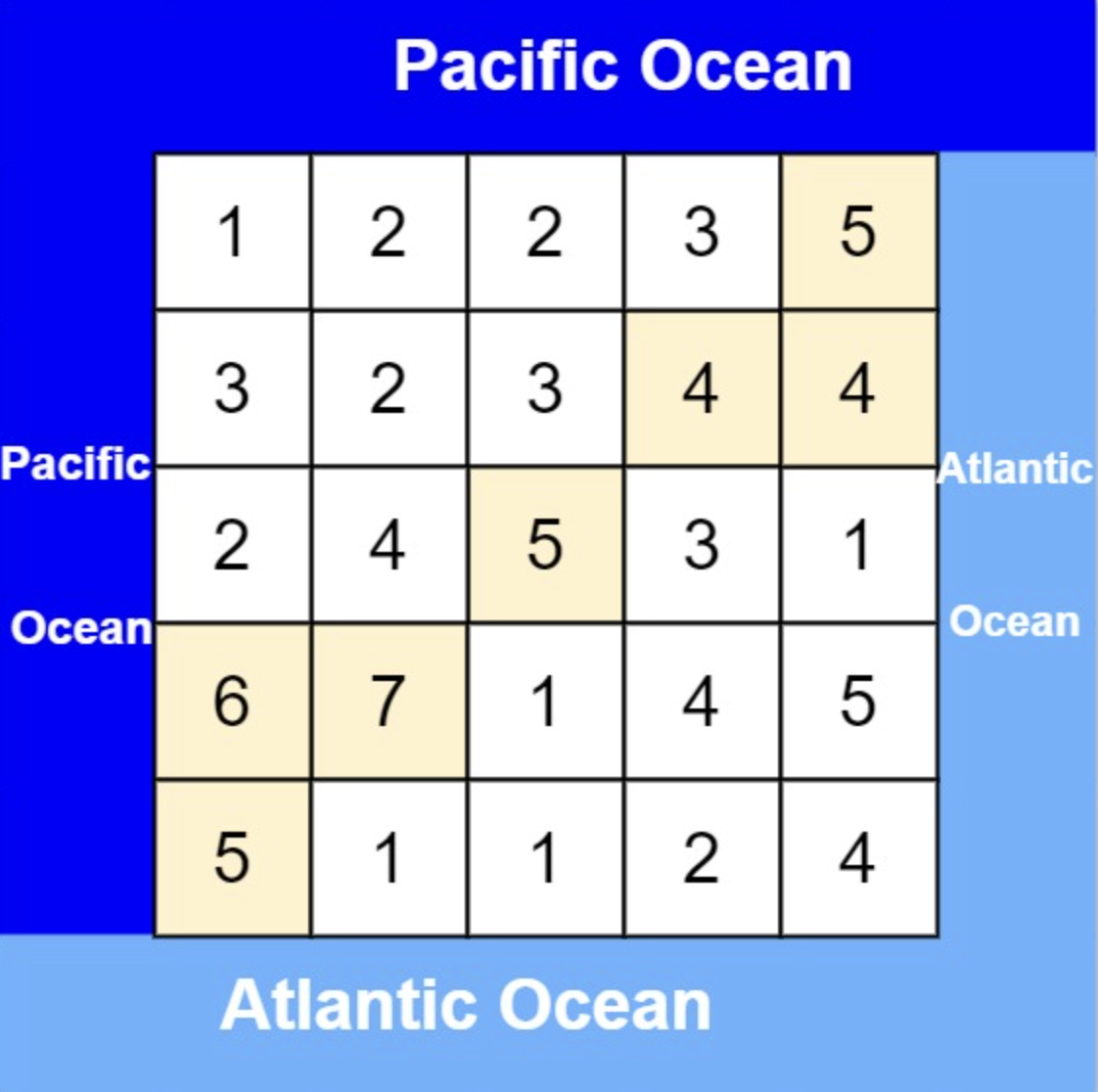
|
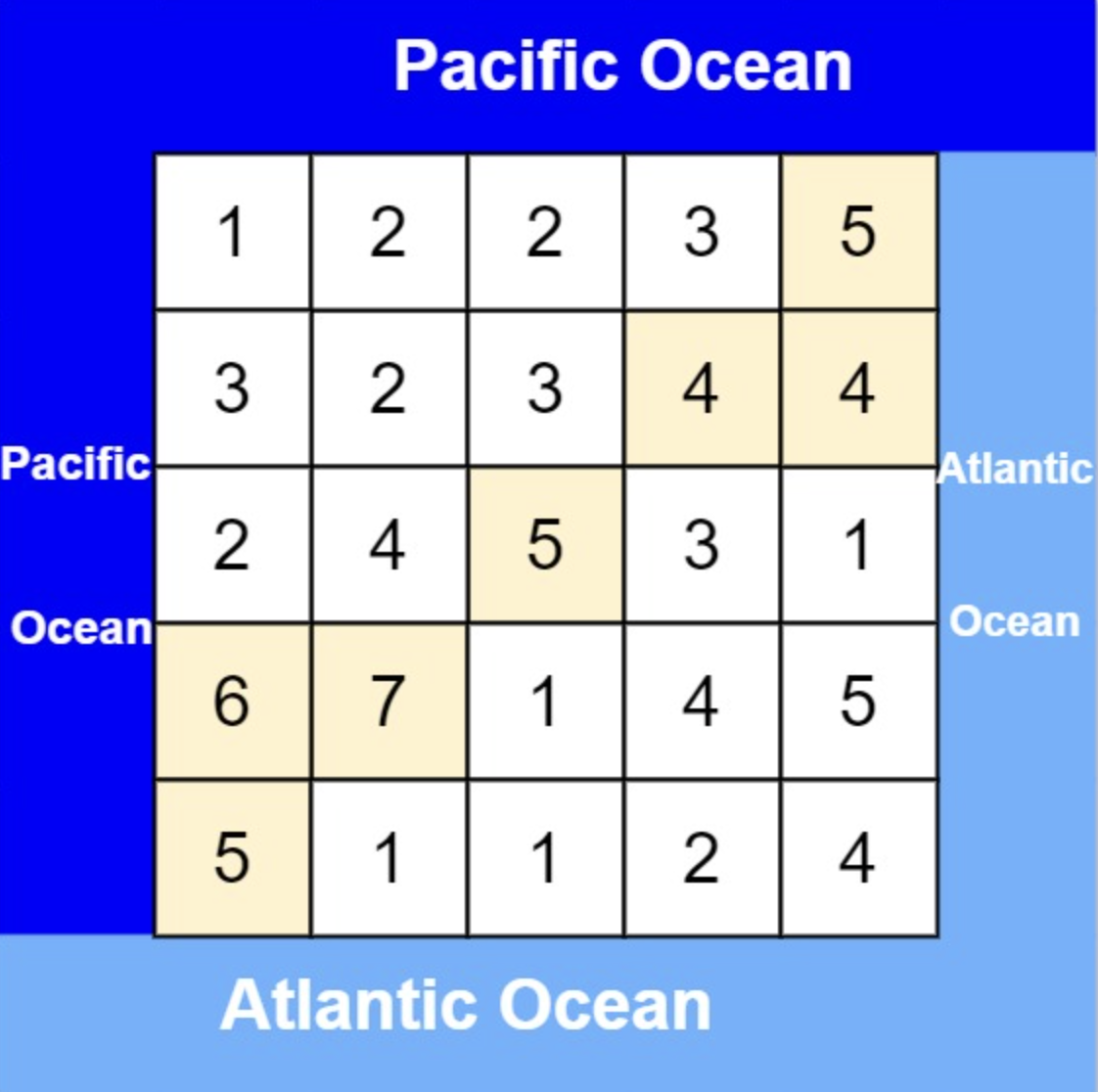
|
||||||
|
|
||||||
* 输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
|
* 输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
|
||||||
* 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
|
* 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
|
||||||
|
|
@ -130,11 +130,11 @@ public:
|
||||||
|
|
||||||
从太平洋边上节点出发,如图:
|
从太平洋边上节点出发,如图:
|
||||||
|
|
||||||
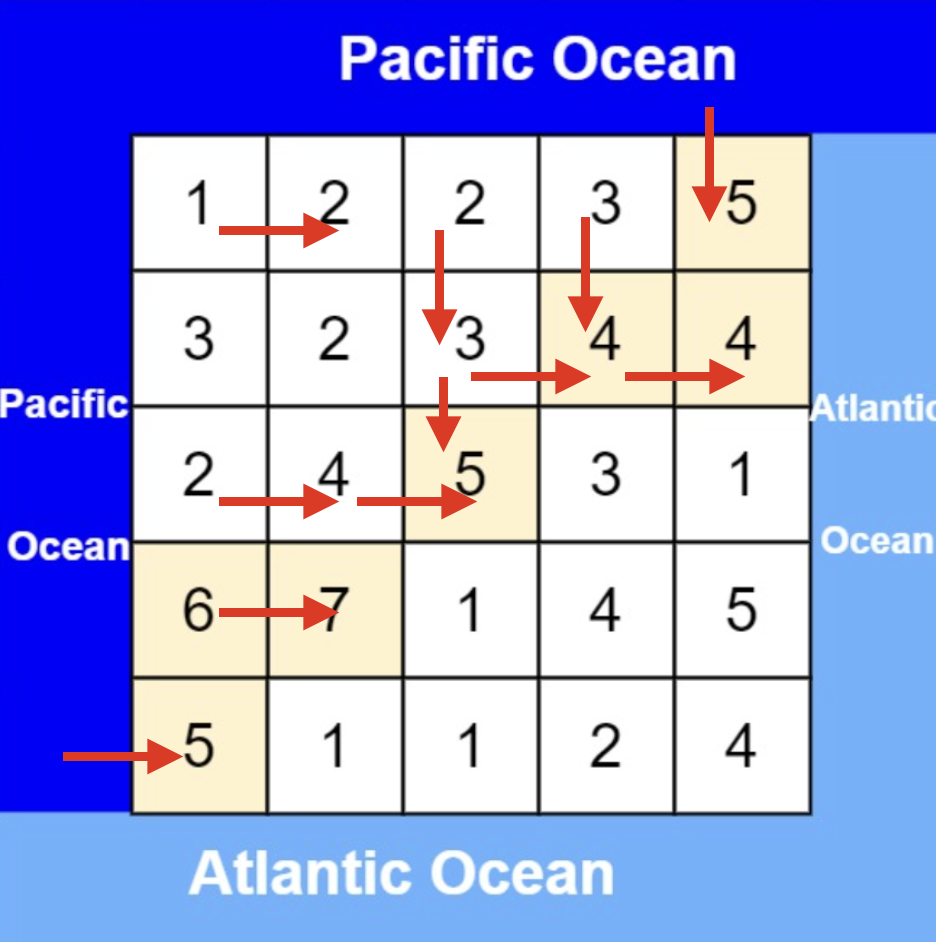
|
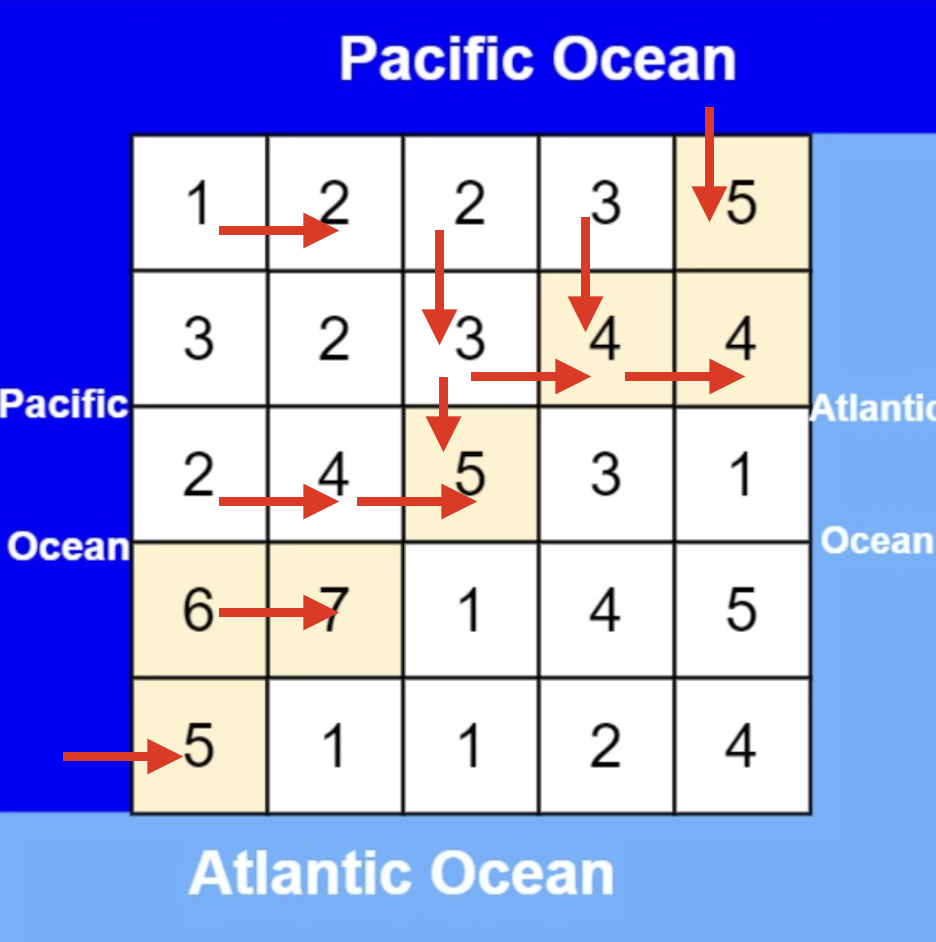
|
||||||
|
|
||||||
从大西洋边上节点出发,如图:
|
从大西洋边上节点出发,如图:
|
||||||
|
|
||||||
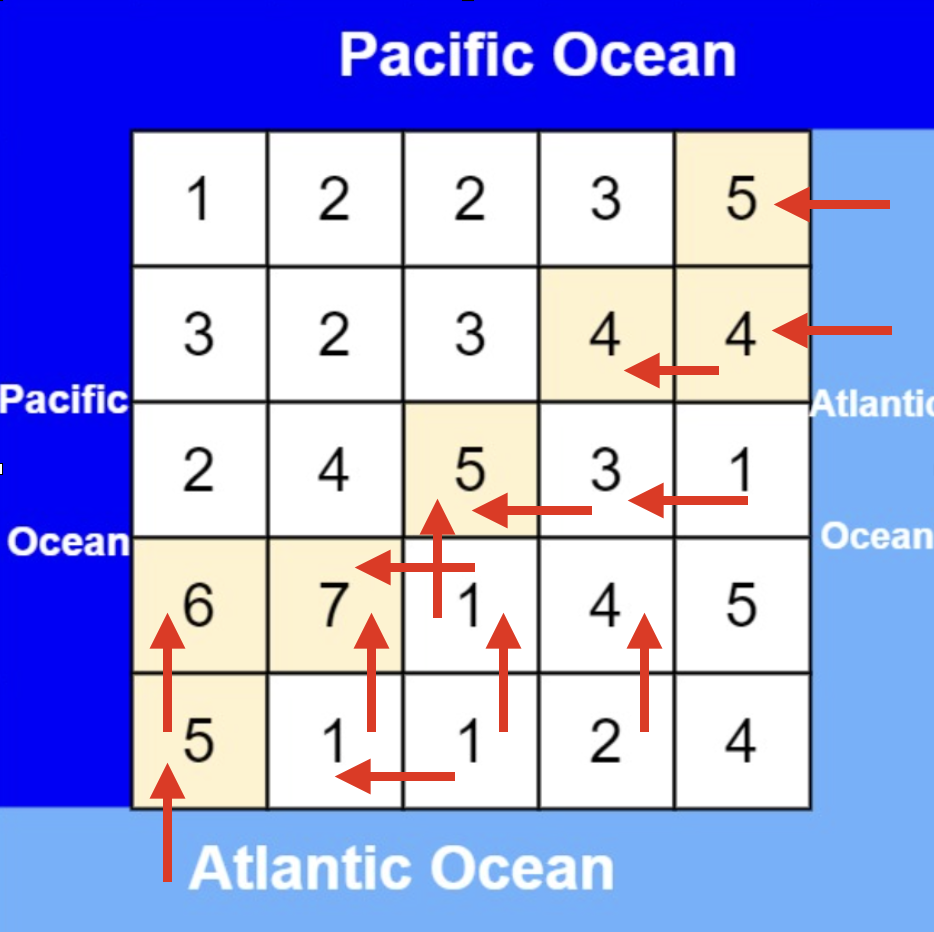
|
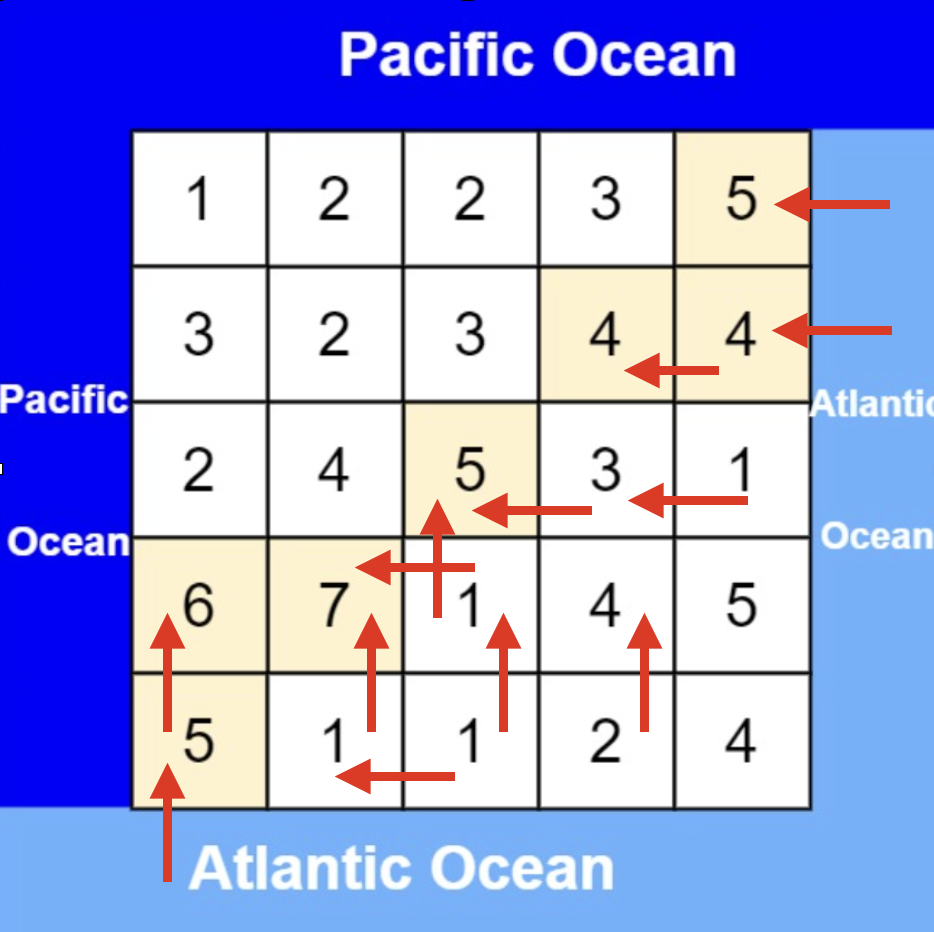
|
||||||
|
|
||||||
按照这样的逻辑,就可以写出如下遍历代码:(详细注释)
|
按照这样的逻辑,就可以写出如下遍历代码:(详细注释)
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -44,7 +44,7 @@
|
||||||
|
|
||||||
这里记录非交叉区间的个数还是有技巧的,如图:
|
这里记录非交叉区间的个数还是有技巧的,如图:
|
||||||
|
|
||||||

|
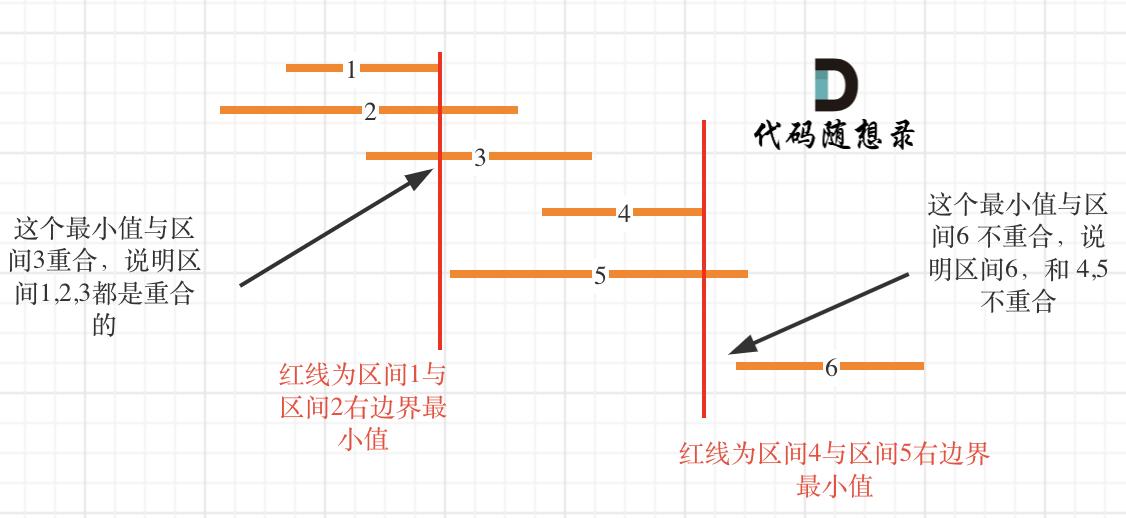
|
||||||
|
|
||||||
区间,1,2,3,4,5,6都按照右边界排好序。
|
区间,1,2,3,4,5,6都按照右边界排好序。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -20,7 +20,7 @@
|
||||||
示例:
|
示例:
|
||||||
|
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -76,7 +76,7 @@
|
||||||
|
|
||||||
以题目示例: [[10,16],[2,8],[1,6],[7,12]]为例,如图:(方便起见,已经排序)
|
以题目示例: [[10,16],[2,8],[1,6],[7,12]]为例,如图:(方便起见,已经排序)
|
||||||
|
|
||||||
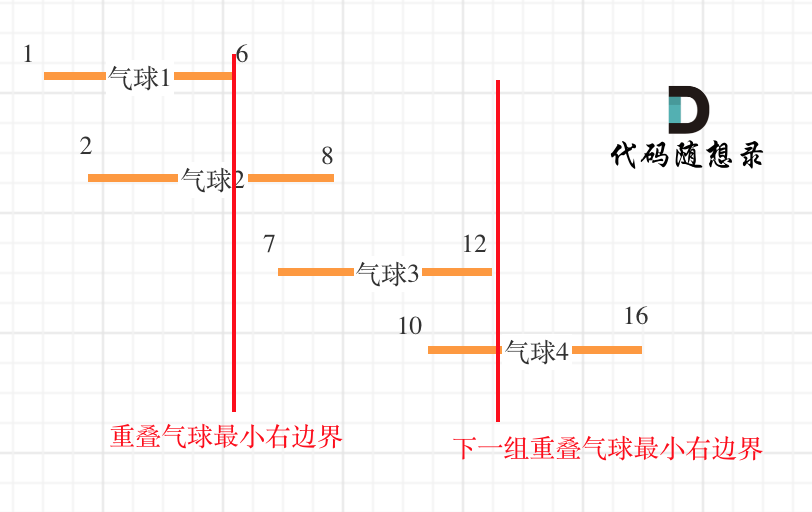
|
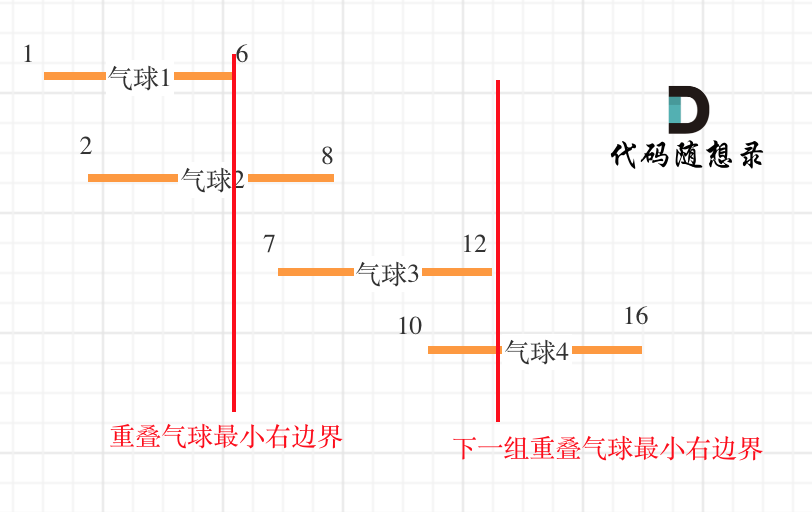
|
||||||
|
|
||||||
可以看出首先第一组重叠气球,一定是需要一个箭,气球3,的左边界大于了 第一组重叠气球的最小右边界,所以再需要一支箭来射气球3了。
|
可以看出首先第一组重叠气球,一定是需要一个箭,气球3,的左边界大于了 第一组重叠气球的最小右边界,所以再需要一支箭来射气球3了。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -46,7 +46,7 @@
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
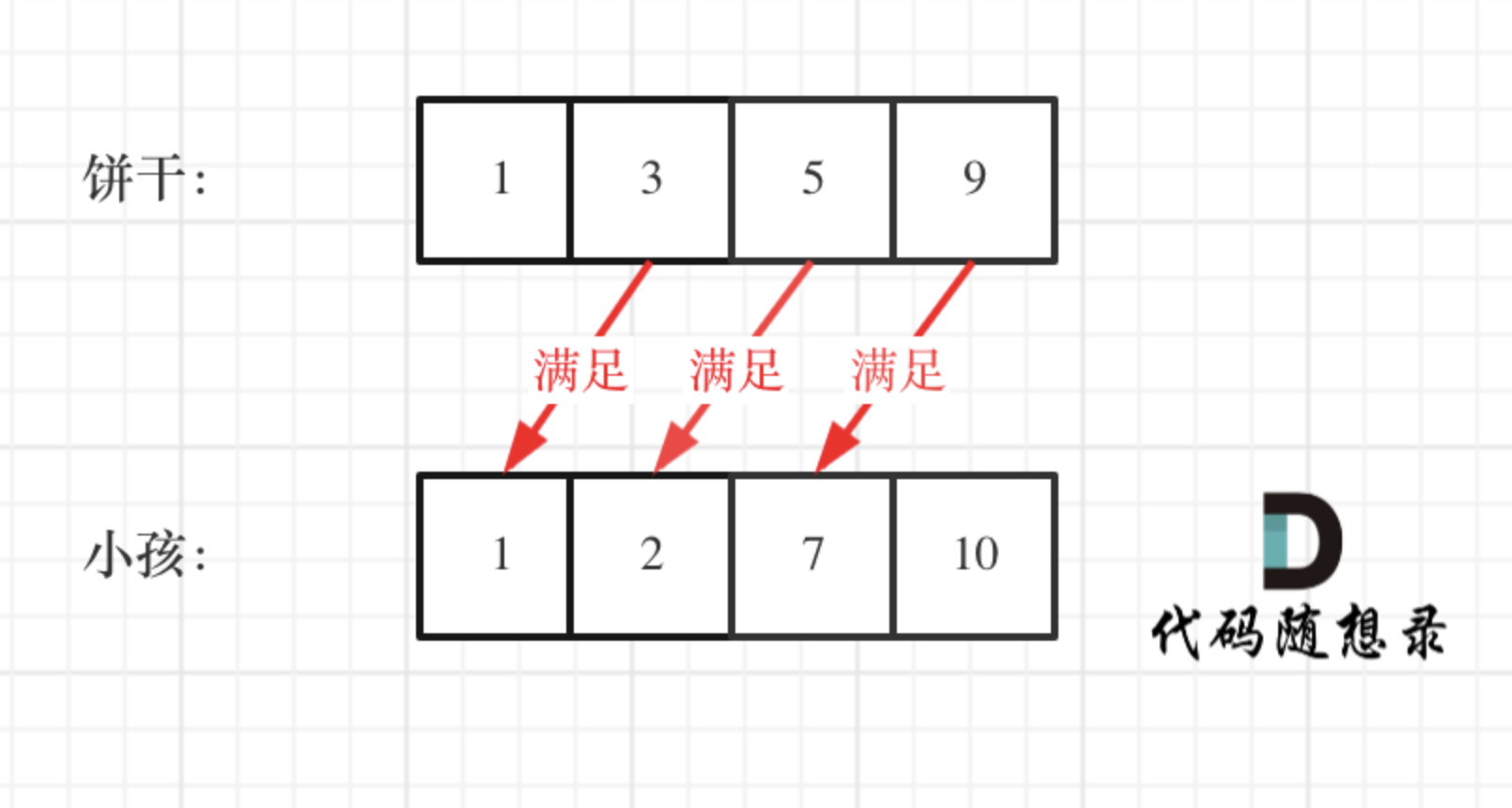
|
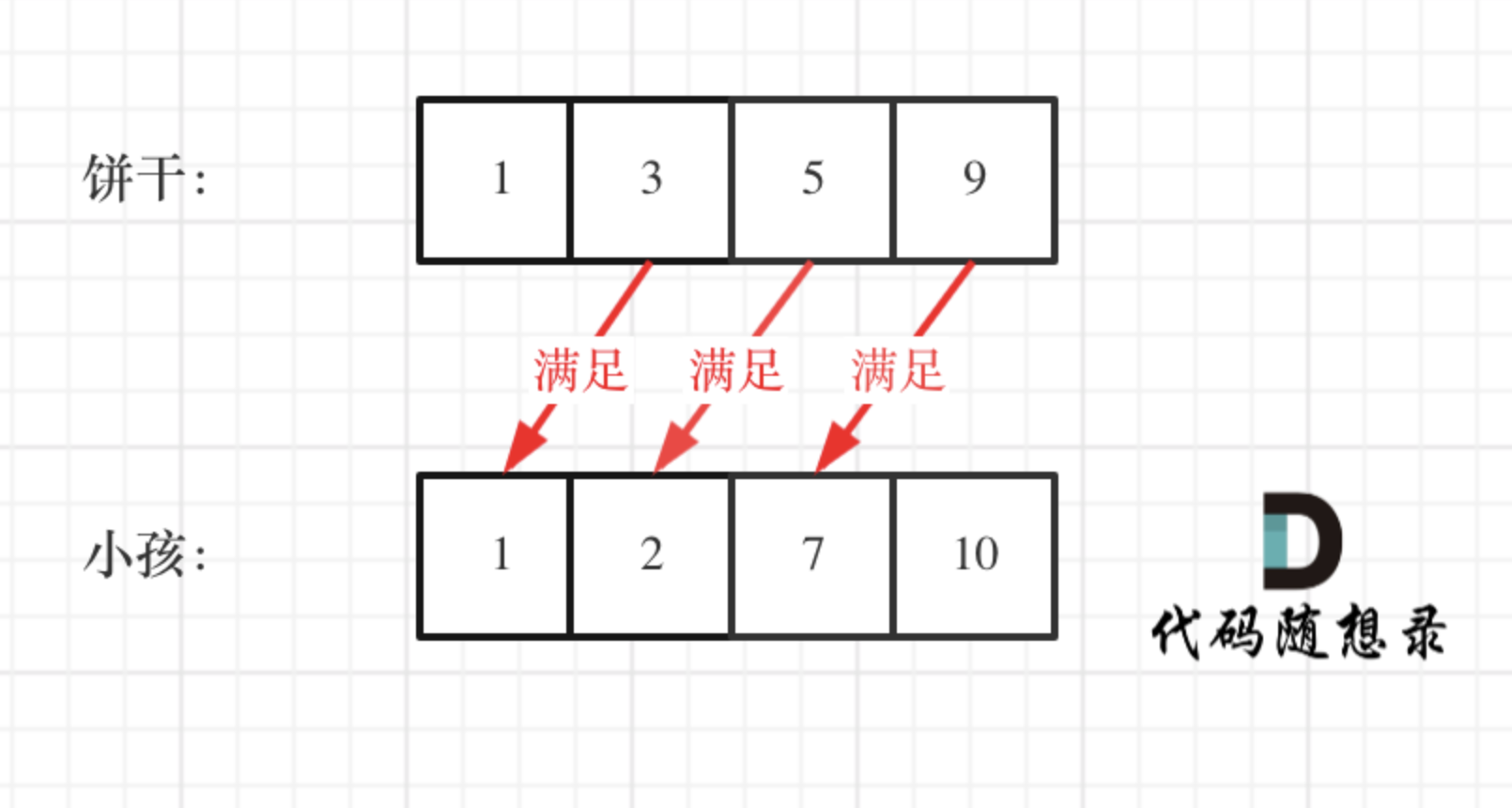
|
||||||
|
|
||||||
这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
|
这个例子可以看出饼干 9 只有喂给胃口为 7 的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
|
||||||
|
|
||||||
|
|
@ -89,7 +89,7 @@ public:
|
||||||
|
|
||||||
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :
|
如果 for 控制的是饼干, if 控制胃口,就是出现如下情况 :
|
||||||
|
|
||||||
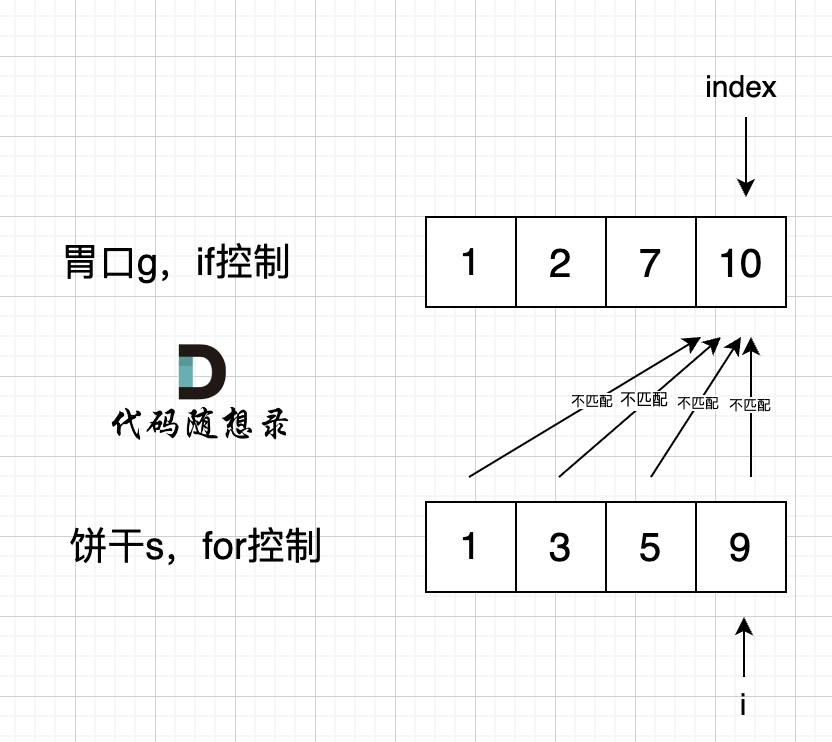
|
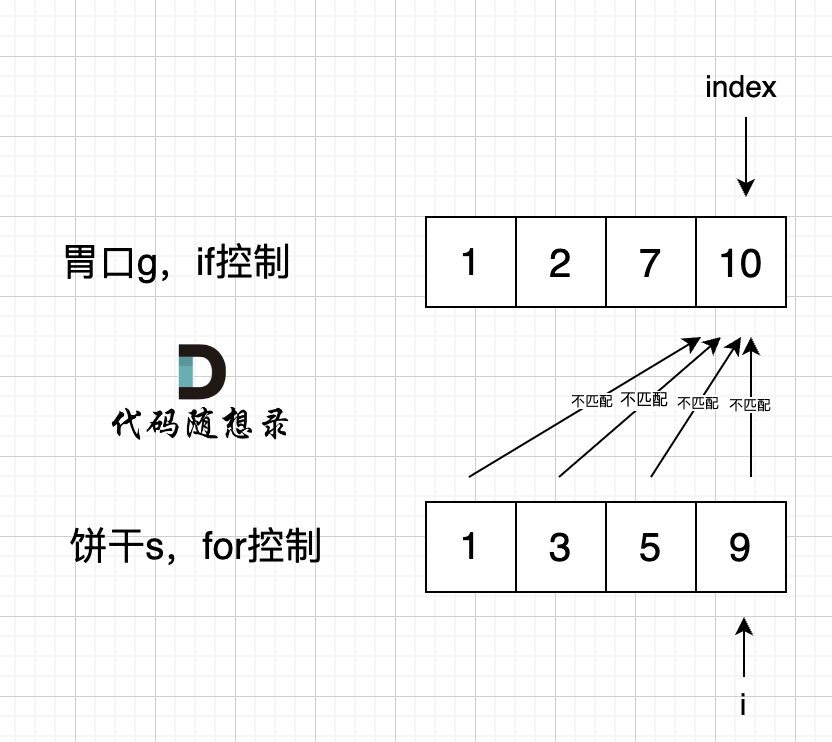
|
||||||
|
|
||||||
if 里的 index 指向 胃口 10, for 里的 i 指向饼干 9,因为 饼干 9 满足不了 胃口 10,所以 i 持续向前移动,而 index 走不到` s[index] >= g[i]` 的逻辑,所以 index 不会移动,那么当 i 持续向前移动,最后所有的饼干都匹配不上。
|
if 里的 index 指向 胃口 10, for 里的 i 指向饼干 9,因为 饼干 9 满足不了 胃口 10,所以 i 持续向前移动,而 index 走不到` s[index] >= g[i]` 的逻辑,所以 index 不会移动,那么当 i 持续向前移动,最后所有的饼干都匹配不上。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -46,13 +46,13 @@
|
||||||
|
|
||||||
当一个字符串s:abcabc,内部由重复的子串组成,那么这个字符串的结构一定是这样的:
|
当一个字符串s:abcabc,内部由重复的子串组成,那么这个字符串的结构一定是这样的:
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
也就是由前后相同的子串组成。
|
也就是由前后相同的子串组成。
|
||||||
|
|
||||||
那么既然前面有相同的子串,后面有相同的子串,用 s + s,这样组成的字符串中,后面的子串做前串,前面的子串做后串,就一定还能组成一个s,如图:
|
那么既然前面有相同的子串,后面有相同的子串,用 s + s,这样组成的字符串中,后面的子串做前串,前面的子串做后串,就一定还能组成一个s,如图:
|
||||||
|
|
||||||
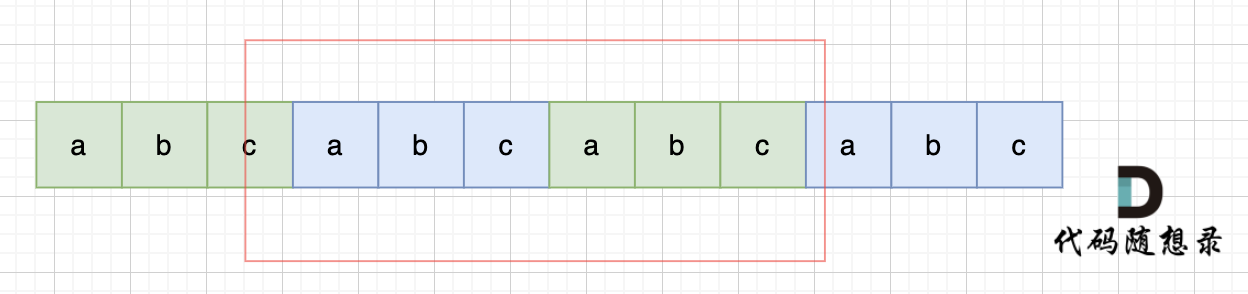
|
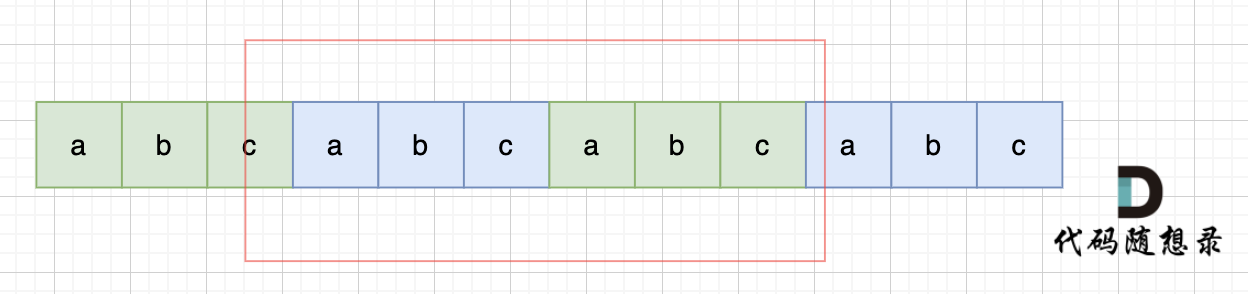
|
||||||
|
|
||||||
|
|
||||||
当然,我们在判断 s + s 拼接的字符串里是否出现一个s的的时候,**要刨除 s + s 的首字符和尾字符**,这样避免在s+s中搜索出原来的s,我们要搜索的是中间拼接出来的s。
|
当然,我们在判断 s + s 拼接的字符串里是否出现一个s的的时候,**要刨除 s + s 的首字符和尾字符**,这样避免在s+s中搜索出原来的s,我们要搜索的是中间拼接出来的s。
|
||||||
|
|
@ -64,11 +64,11 @@
|
||||||
|
|
||||||
如图,字符串s,图中数字为数组下标,在 s + s 拼接后, 不算首尾字符,中间凑成s字符串。 (图中数字为数组下标)
|
如图,字符串s,图中数字为数组下标,在 s + s 拼接后, 不算首尾字符,中间凑成s字符串。 (图中数字为数组下标)
|
||||||
|
|
||||||
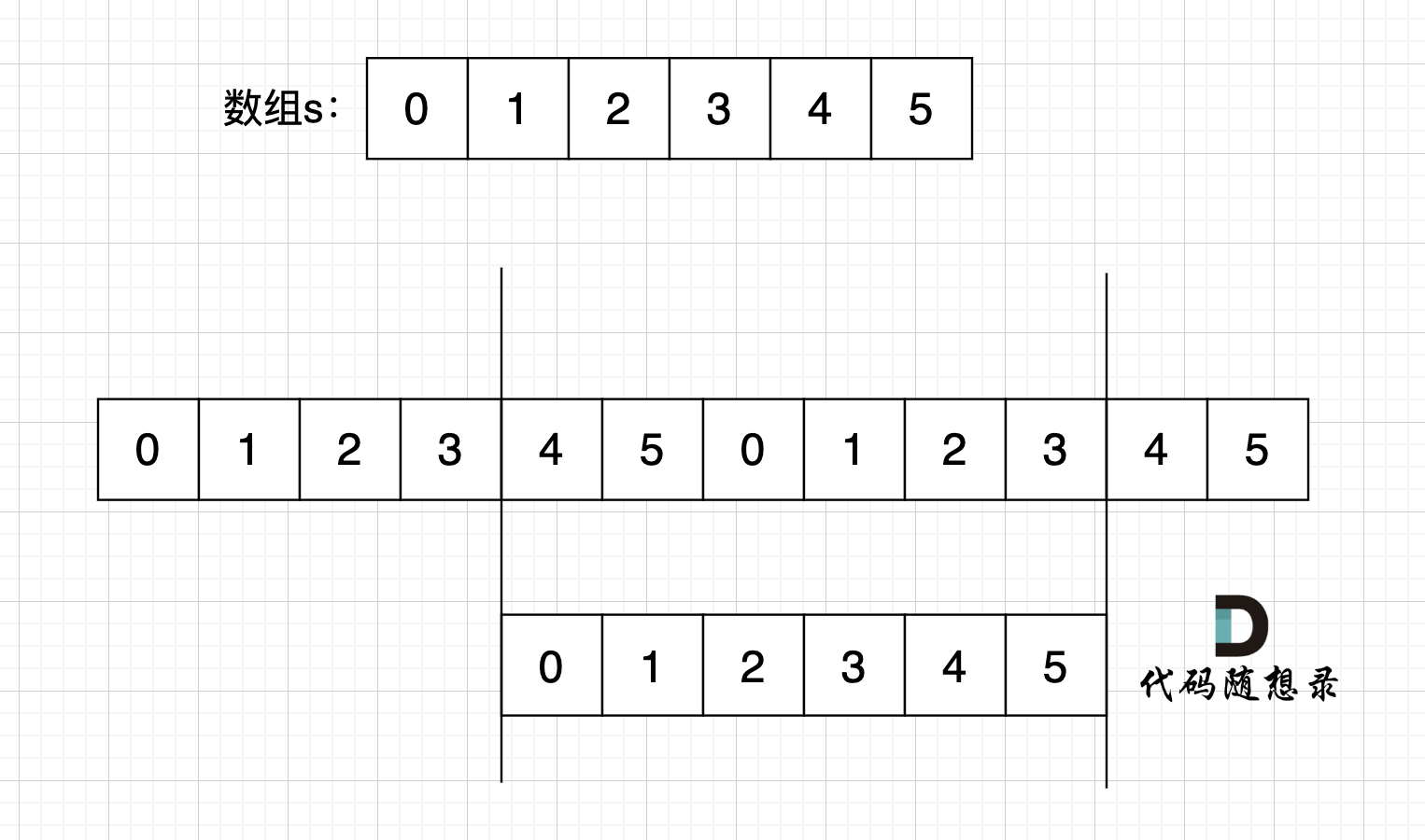
|
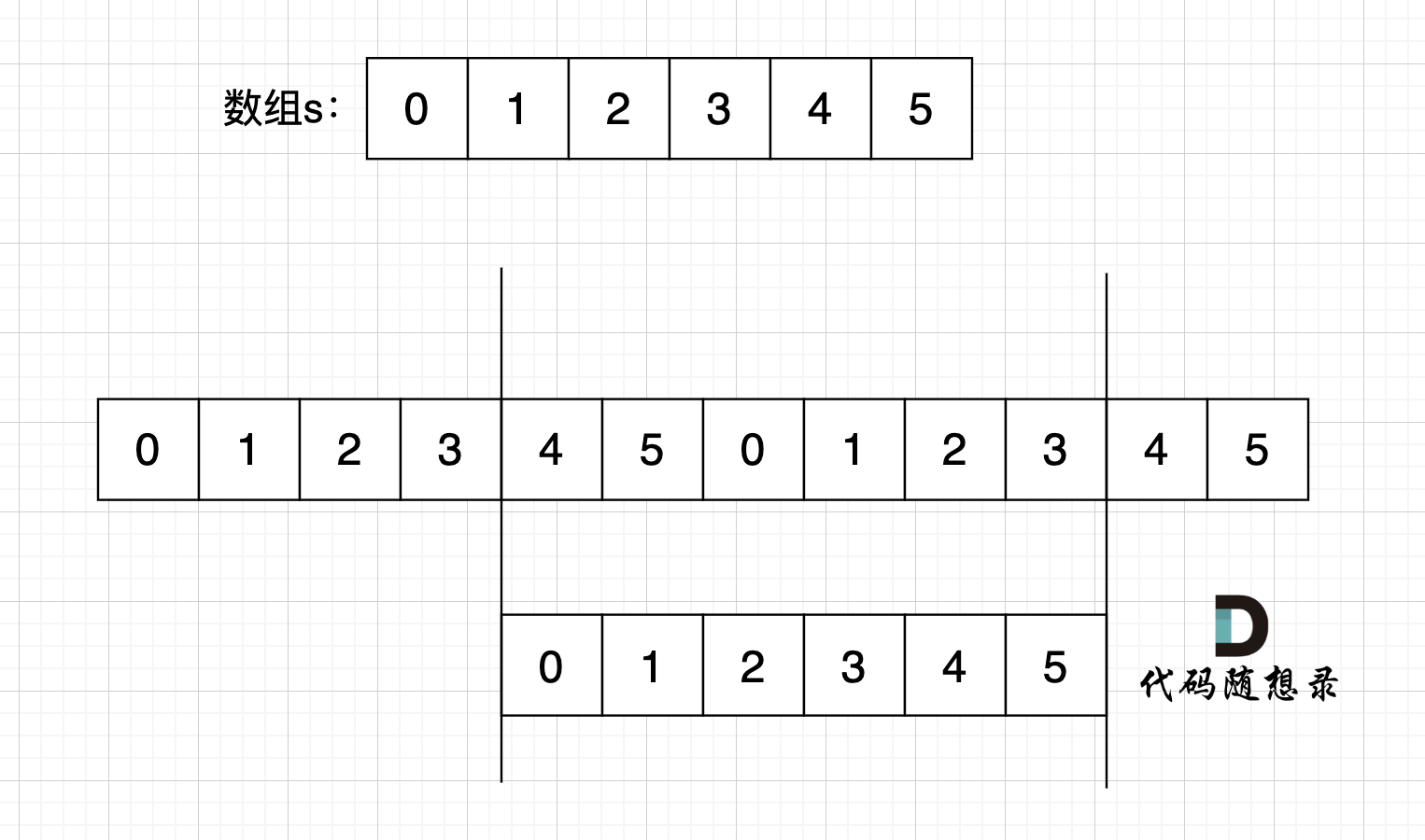
|
||||||
|
|
||||||
图中,因为中间拼接成了s,根据红色框 可以知道 s[4] = s[0], s[5] = s[1], s[0] = s[2], s[1] = s[3] s[2] = s[4] ,s[3] = s[5]
|
图中,因为中间拼接成了s,根据红色框 可以知道 s[4] = s[0], s[5] = s[1], s[0] = s[2], s[1] = s[3] s[2] = s[4] ,s[3] = s[5]
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
以上相等关系我们串联一下:
|
以上相等关系我们串联一下:
|
||||||
|
|
||||||
|
|
@ -83,7 +83,7 @@ s[5] = s[1] = s[3]
|
||||||
|
|
||||||
这里可以有录友想,凭什么就是这样组成的s呢,我换一个方式组成s 行不行,如图:
|
这里可以有录友想,凭什么就是这样组成的s呢,我换一个方式组成s 行不行,如图:
|
||||||
|
|
||||||

|
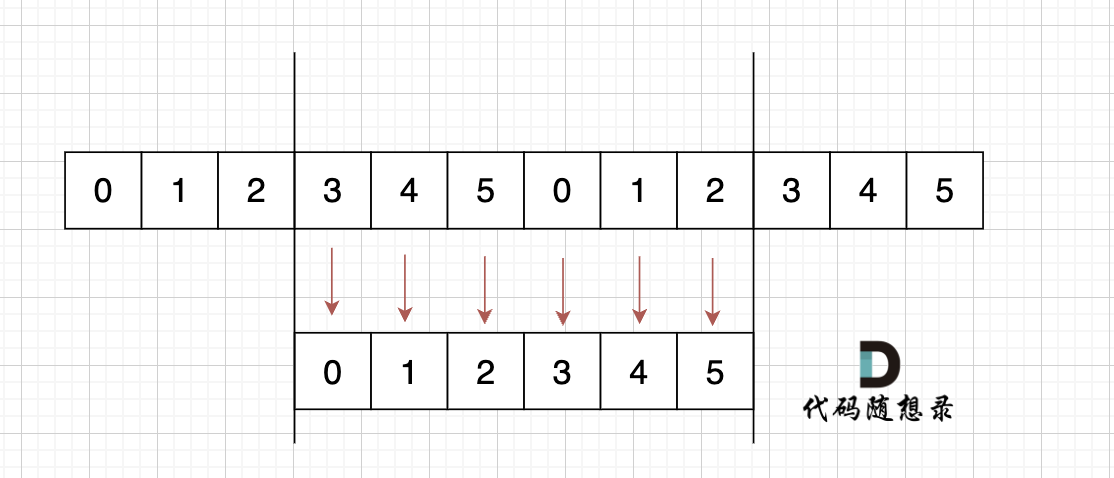
|
||||||
|
|
||||||
s[3] = s[0],s[4] = s[1] ,s[5] = s[2],s[0] = s[3],s[1] = s[4],s[2] = s[5]
|
s[3] = s[0],s[4] = s[1] ,s[5] = s[2],s[0] = s[3],s[1] = s[4],s[2] = s[5]
|
||||||
|
|
||||||
|
|
@ -101,7 +101,7 @@ s[0] s[1] s[2] = s[3] s[4] s[5]
|
||||||
|
|
||||||
如果是这样的呢,如图:
|
如果是这样的呢,如图:
|
||||||
|
|
||||||
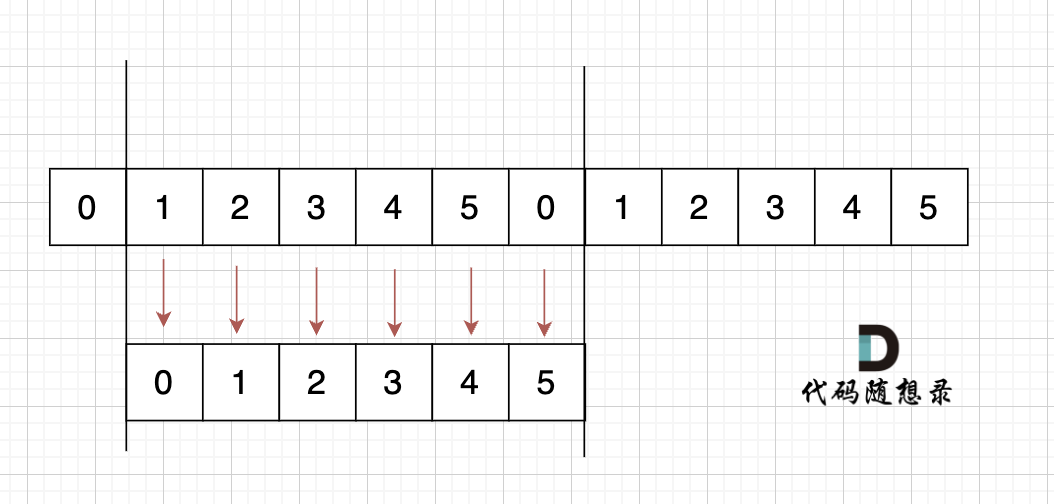
|
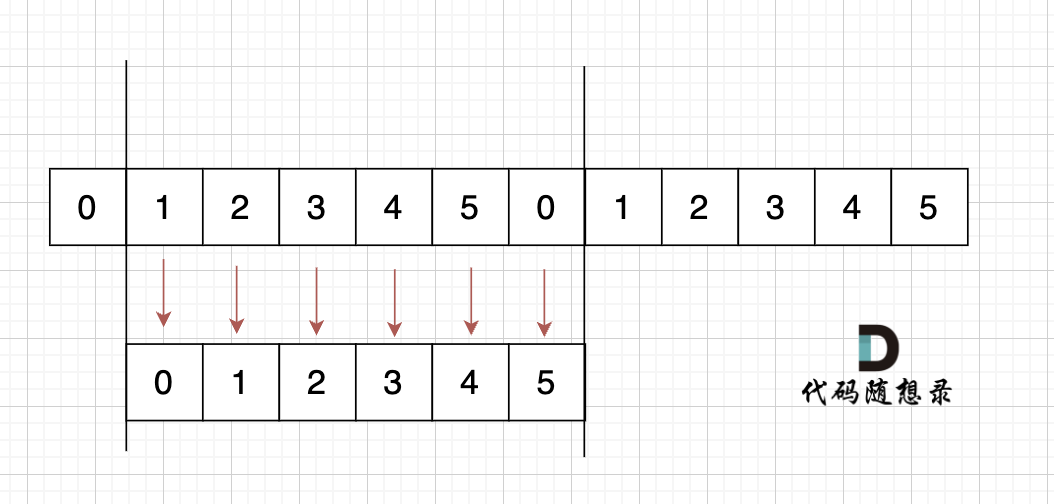
|
||||||
|
|
||||||
s[1] = s[0],s[2] = s[1] ,s[3] = s[2],s[4] = s[3],s[5] = s[4],s[0] = s[5]
|
s[1] = s[0],s[2] = s[1] ,s[3] = s[2],s[4] = s[3],s[5] = s[4],s[0] = s[5]
|
||||||
|
|
||||||
|
|
@ -165,23 +165,23 @@ KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一
|
||||||
|
|
||||||
那么相同前后缀可以是这样:
|
那么相同前后缀可以是这样:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
也可以是这样:
|
也可以是这样:
|
||||||
|
|
||||||

|
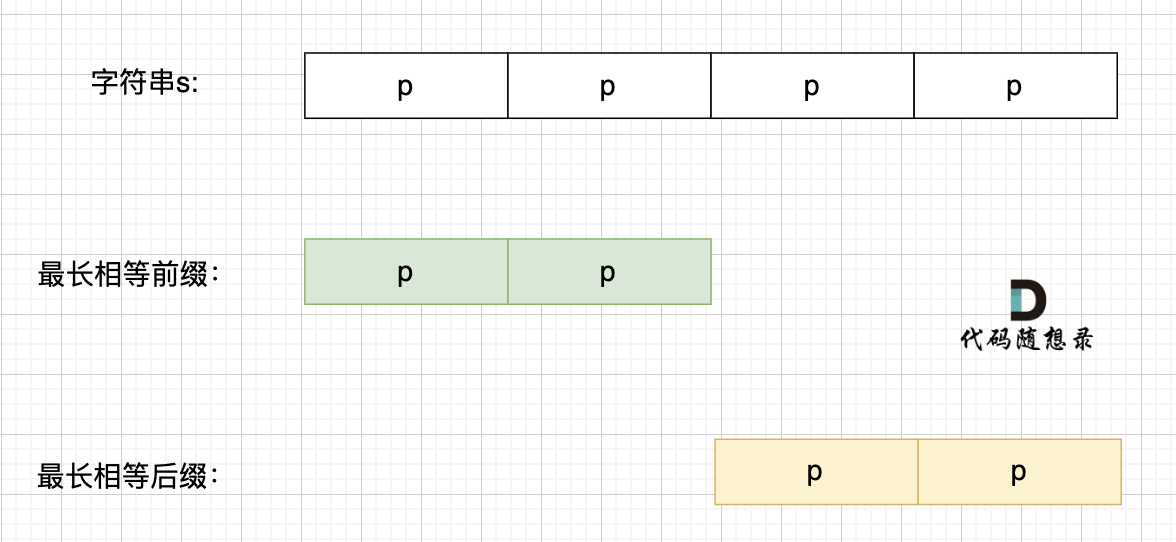
|
||||||
|
|
||||||
最长的相等前后缀,也就是这样:
|
最长的相等前后缀,也就是这样:
|
||||||
|
|
||||||

|
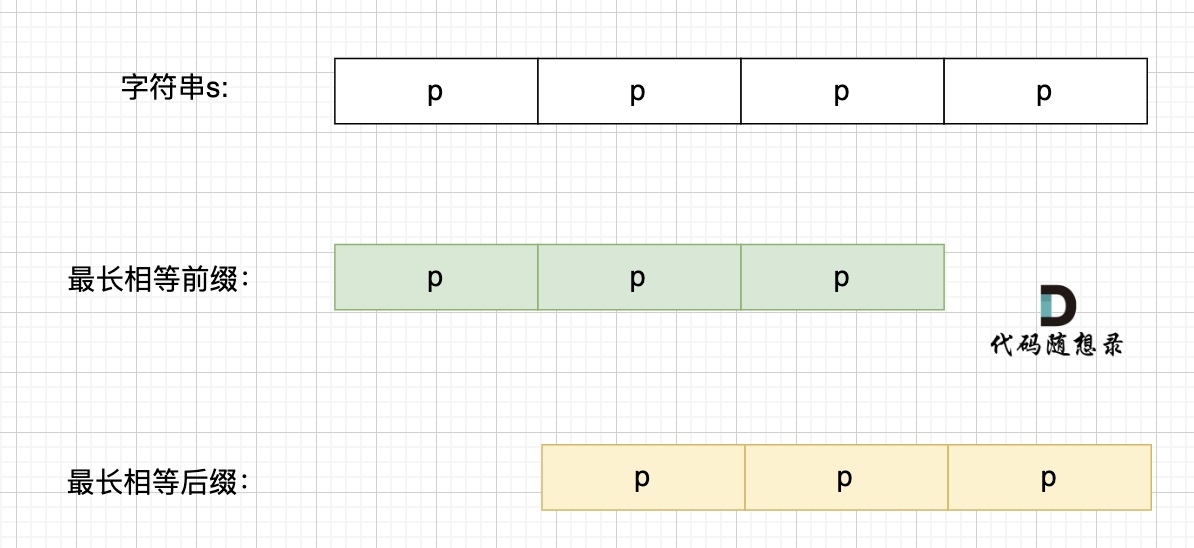
|
||||||
|
|
||||||
这里有录友就想:如果字符串s 是由最小重复子串p组成,最长相等前后缀就不能更长一些? 例如这样:
|
这里有录友就想:如果字符串s 是由最小重复子串p组成,最长相等前后缀就不能更长一些? 例如这样:
|
||||||
|
|
||||||
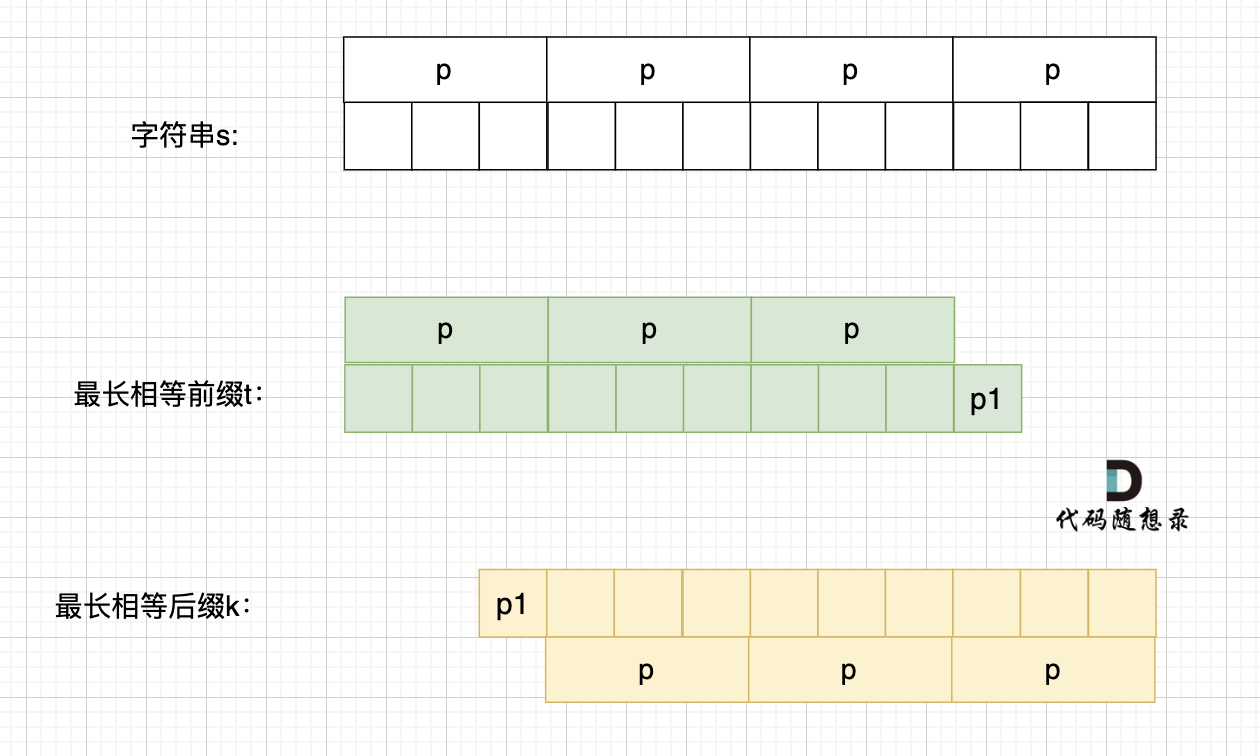
|
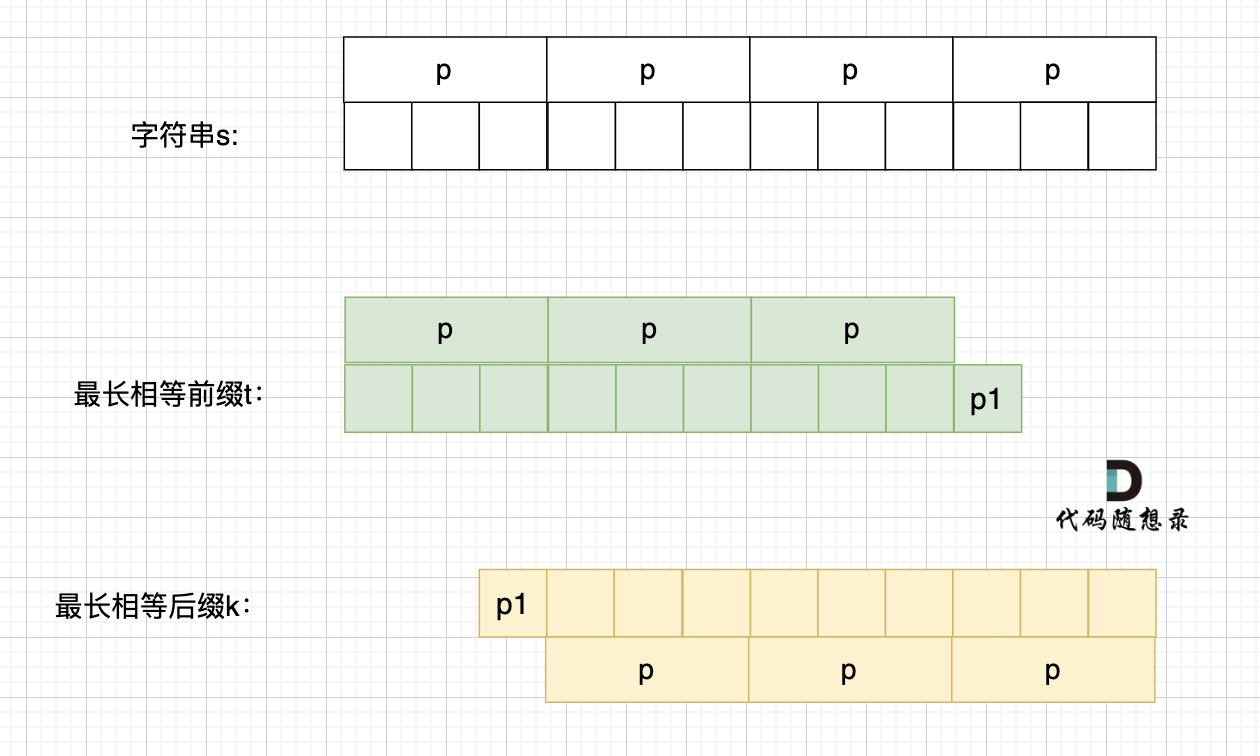
|
||||||
|
|
||||||
如果这样的话,因为前后缀要相同,所以 p2 = p1,p3 = p2,如图:
|
如果这样的话,因为前后缀要相同,所以 p2 = p1,p3 = p2,如图:
|
||||||
|
|
||||||
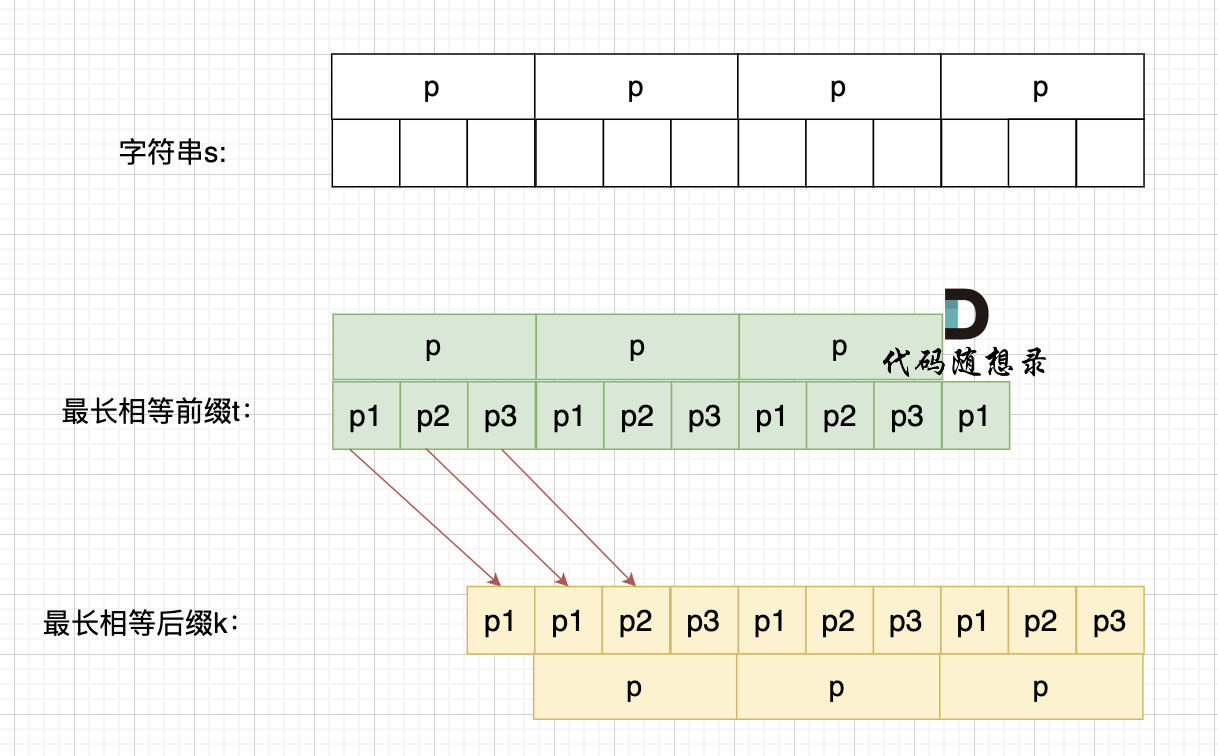
|
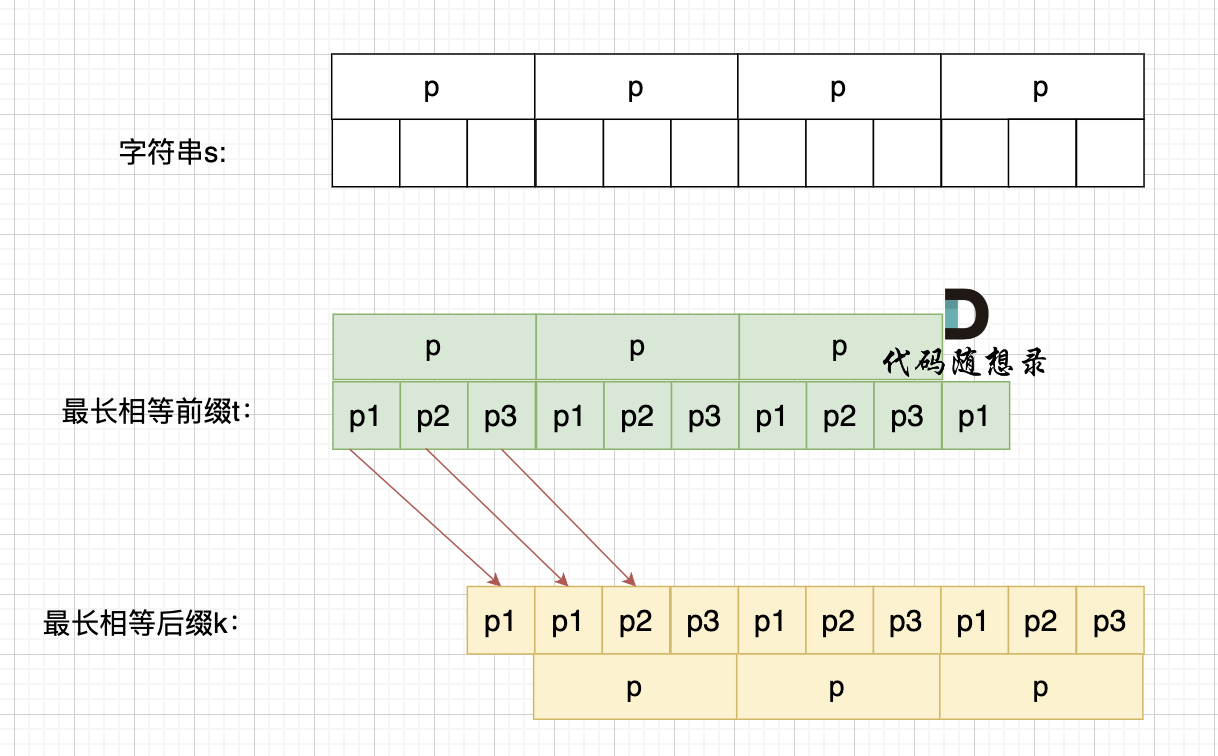
|
||||||
|
|
||||||
p2 = p1,p3 = p2 即: p1 = p2 = p3
|
p2 = p1,p3 = p2 即: p1 = p2 = p3
|
||||||
|
|
||||||
|
|
@ -203,7 +203,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
|
||||||
|
|
||||||
情况一, 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大,那一定不是字符串s的重复子串,如图:
|
情况一, 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大,那一定不是字符串s的重复子串,如图:
|
||||||
|
|
||||||
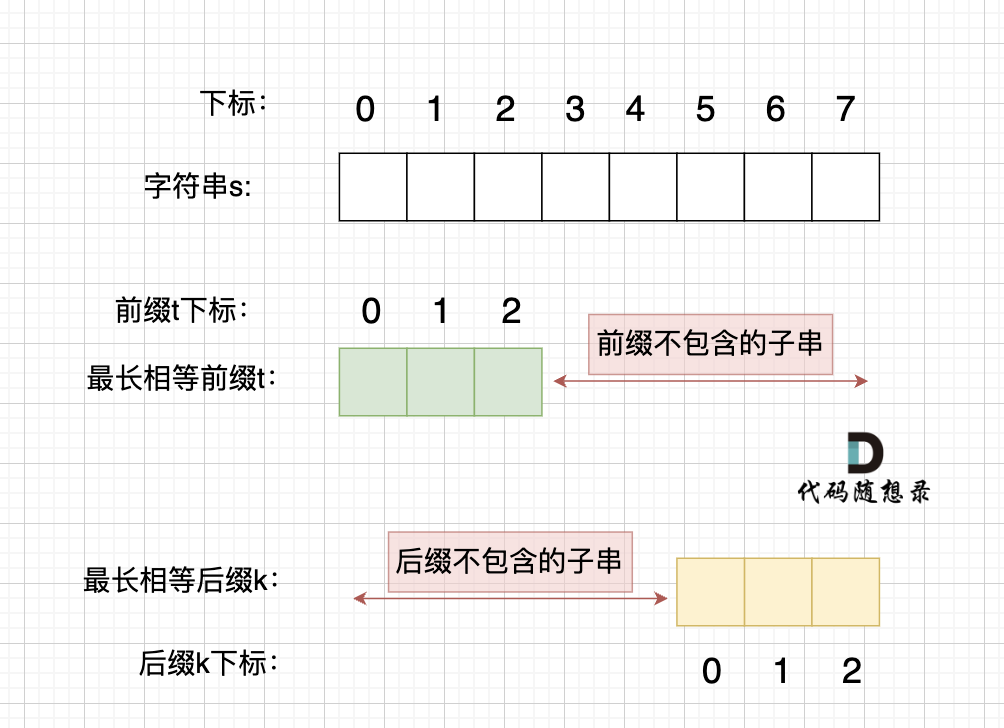
|
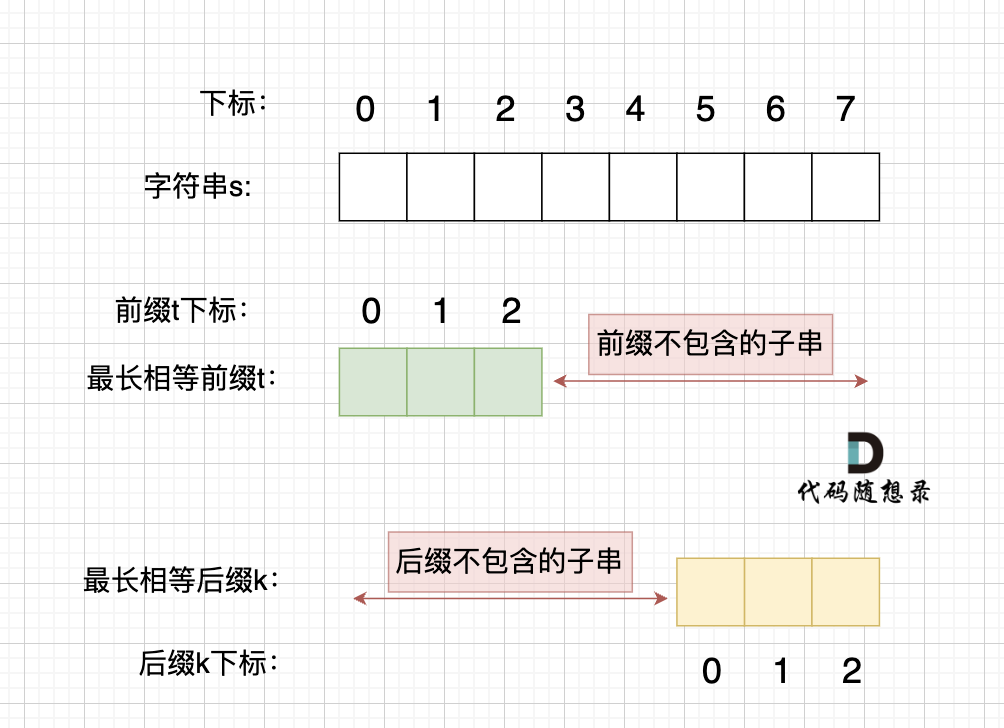
|
||||||
|
|
||||||
图中:前后缀不包含的子串的长度 大于 字符串s的长度的 二分之一
|
图中:前后缀不包含的子串的长度 大于 字符串s的长度的 二分之一
|
||||||
|
|
||||||
|
|
@ -211,7 +211,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
|
||||||
|
|
||||||
情况二,最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,如图:
|
情况二,最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除,如图:
|
||||||
|
|
||||||
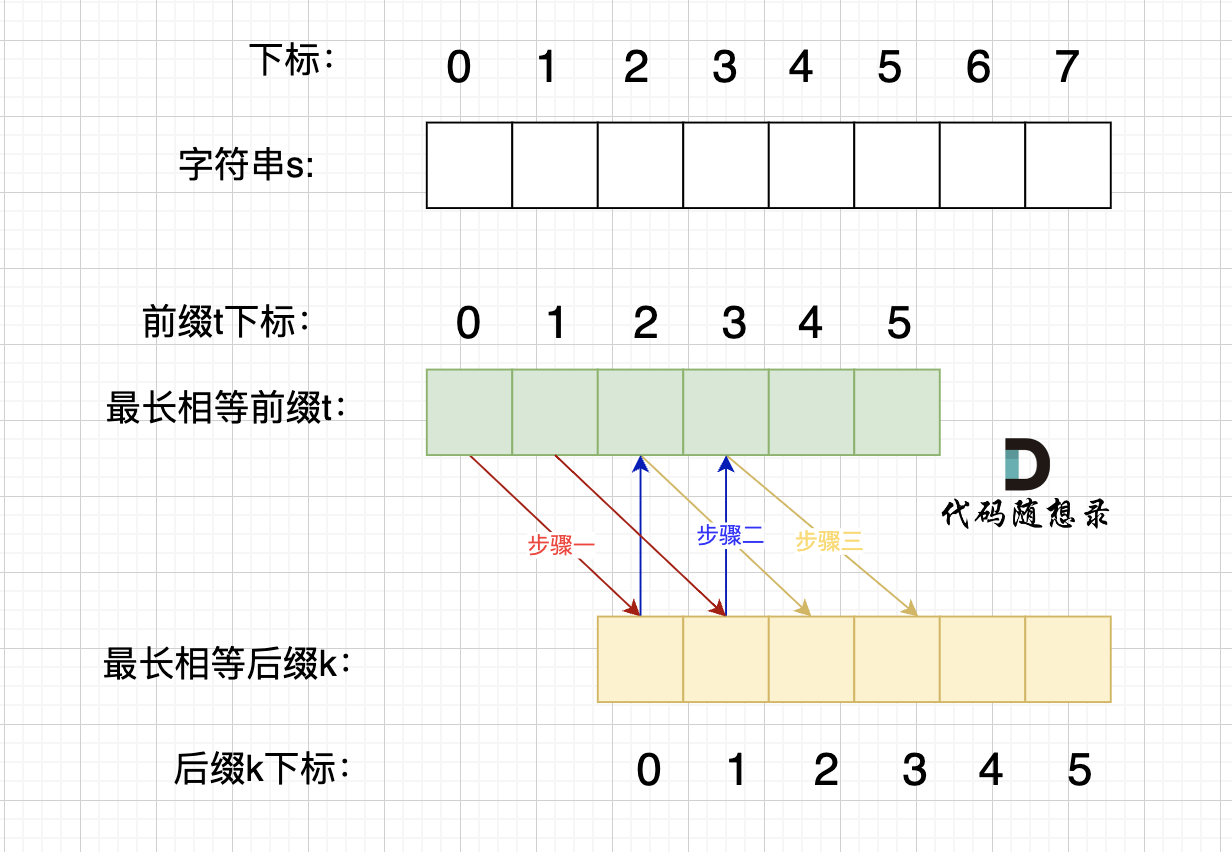
|
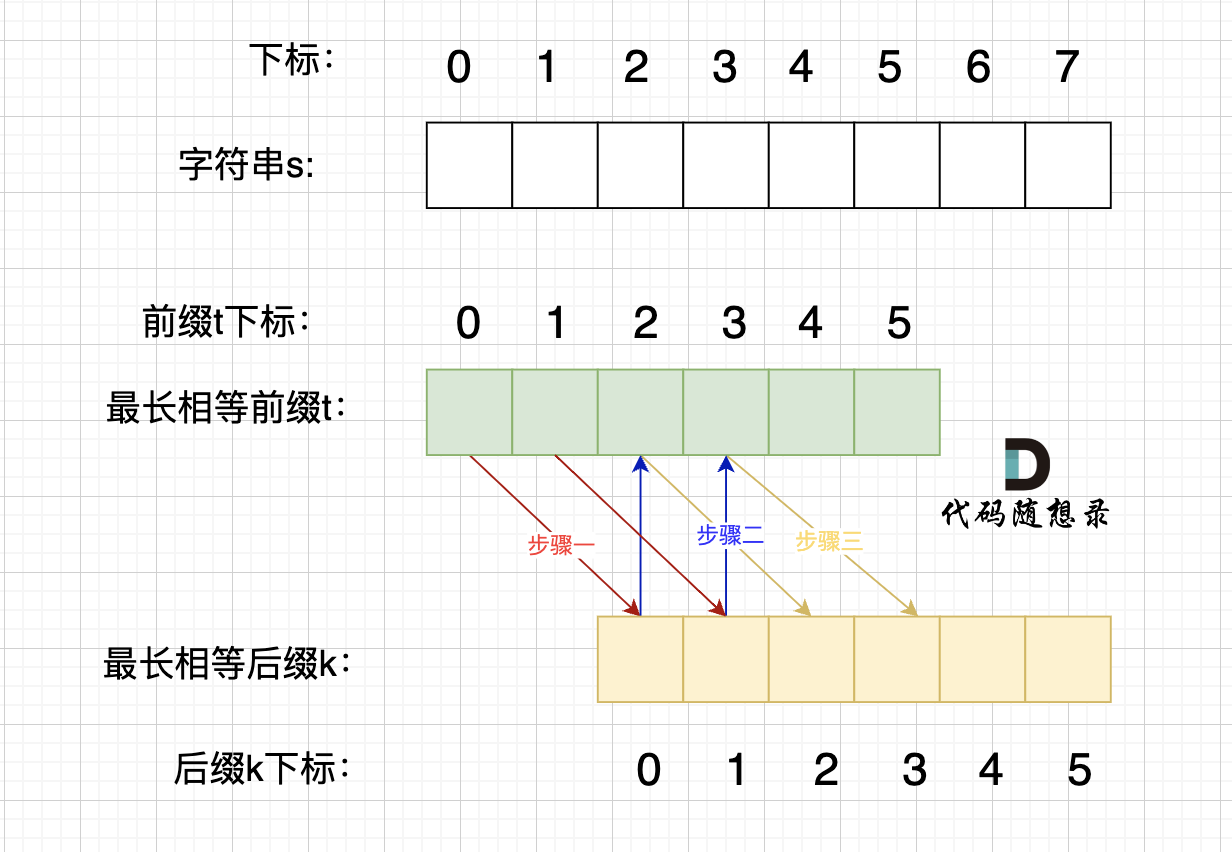
|
||||||
|
|
||||||
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,所以 s[0] 一定和 s[2]相同,s[1] 一定和 s[3]相同,即:,s[0]s[1]与s[2]s[3]相同 。
|
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,所以 s[0] 一定和 s[2]相同,s[1] 一定和 s[3]相同,即:,s[0]s[1]与s[2]s[3]相同 。
|
||||||
|
|
||||||
|
|
@ -234,7 +234,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
|
||||||
|
|
||||||
那么它的最长相同前后缀,就不是上图中的前后缀,而是这样的的前后缀:
|
那么它的最长相同前后缀,就不是上图中的前后缀,而是这样的的前后缀:
|
||||||
|
|
||||||
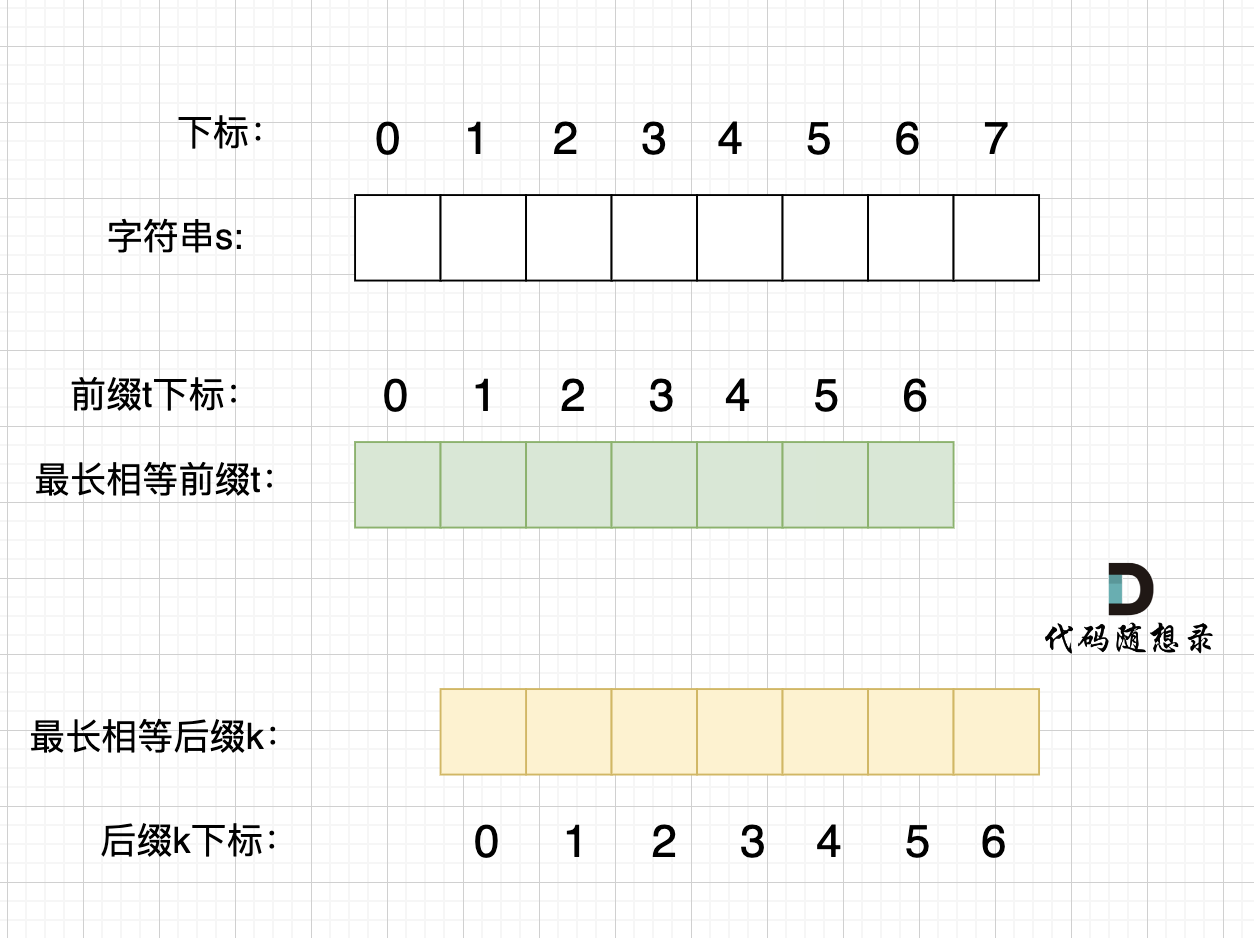
|
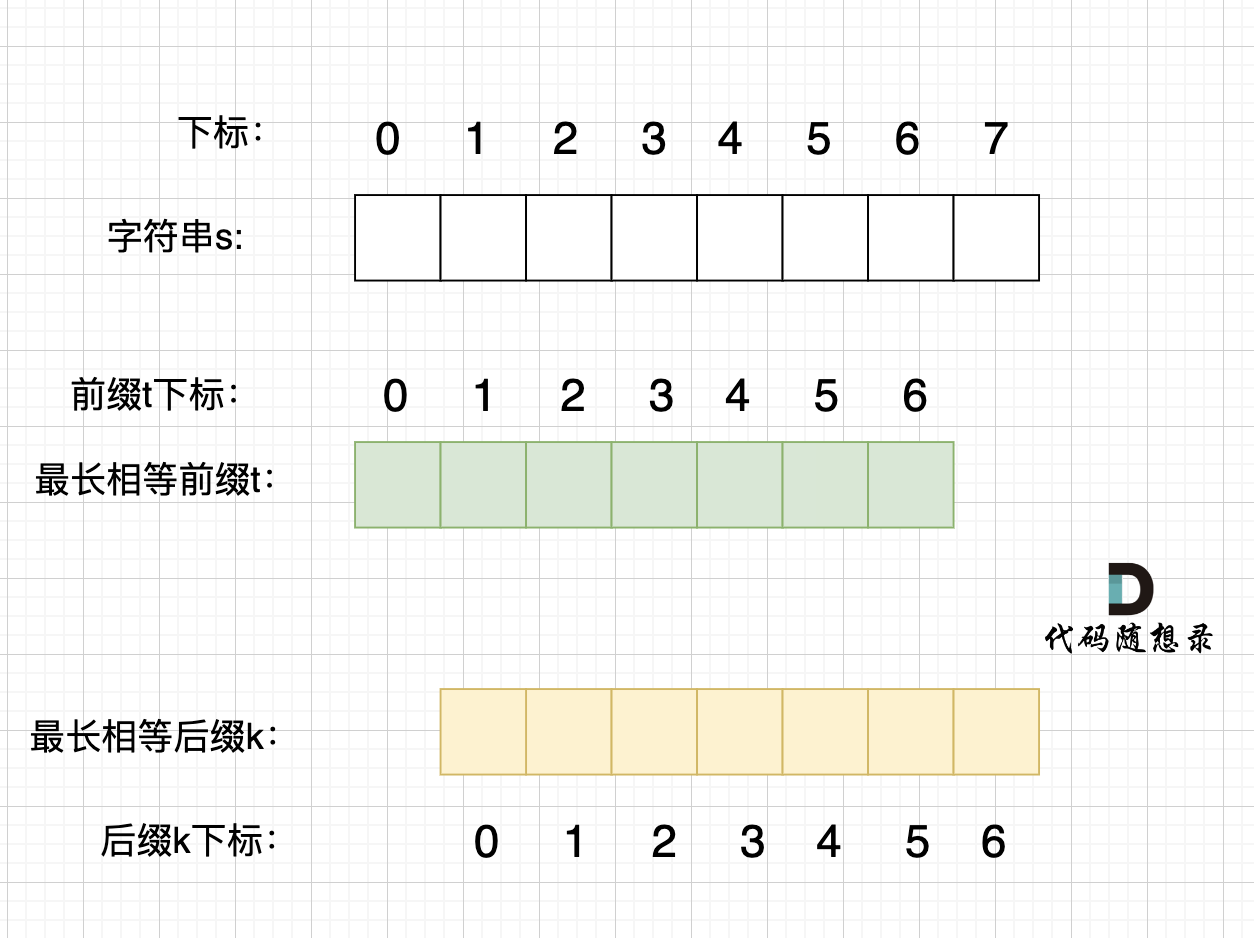
|
||||||
|
|
||||||
录友可能再问,由一个字符组成的字符串,最长相等前后缀凭什么就是这样的。
|
录友可能再问,由一个字符组成的字符串,最长相等前后缀凭什么就是这样的。
|
||||||
|
|
||||||
|
|
@ -250,7 +250,7 @@ p2 = p1,p3 = p2 即: p1 = p2 = p3
|
||||||
|
|
||||||
**情况三,最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除得情况**,如图:
|
**情况三,最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除得情况**,如图:
|
||||||
|
|
||||||
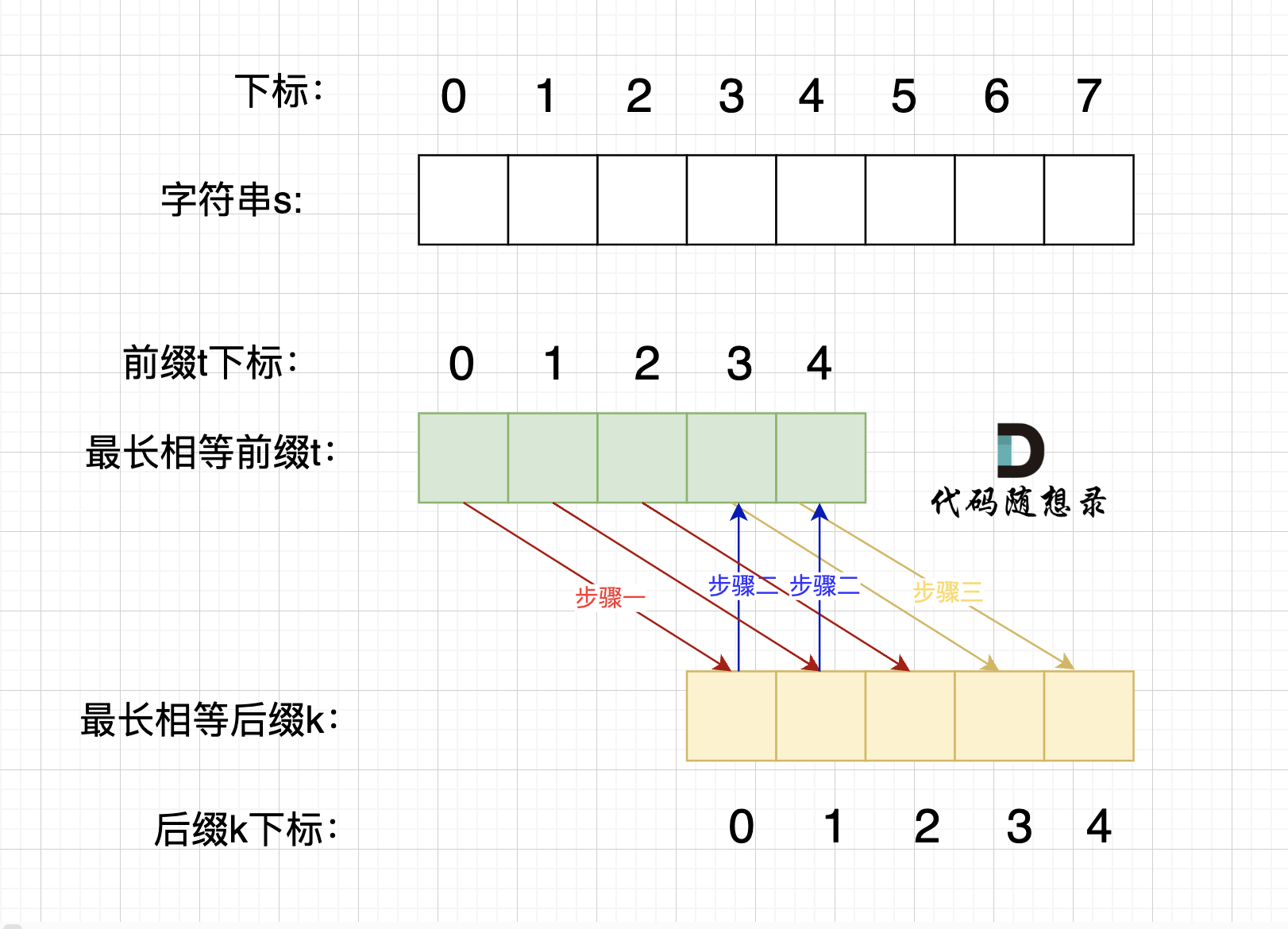
|
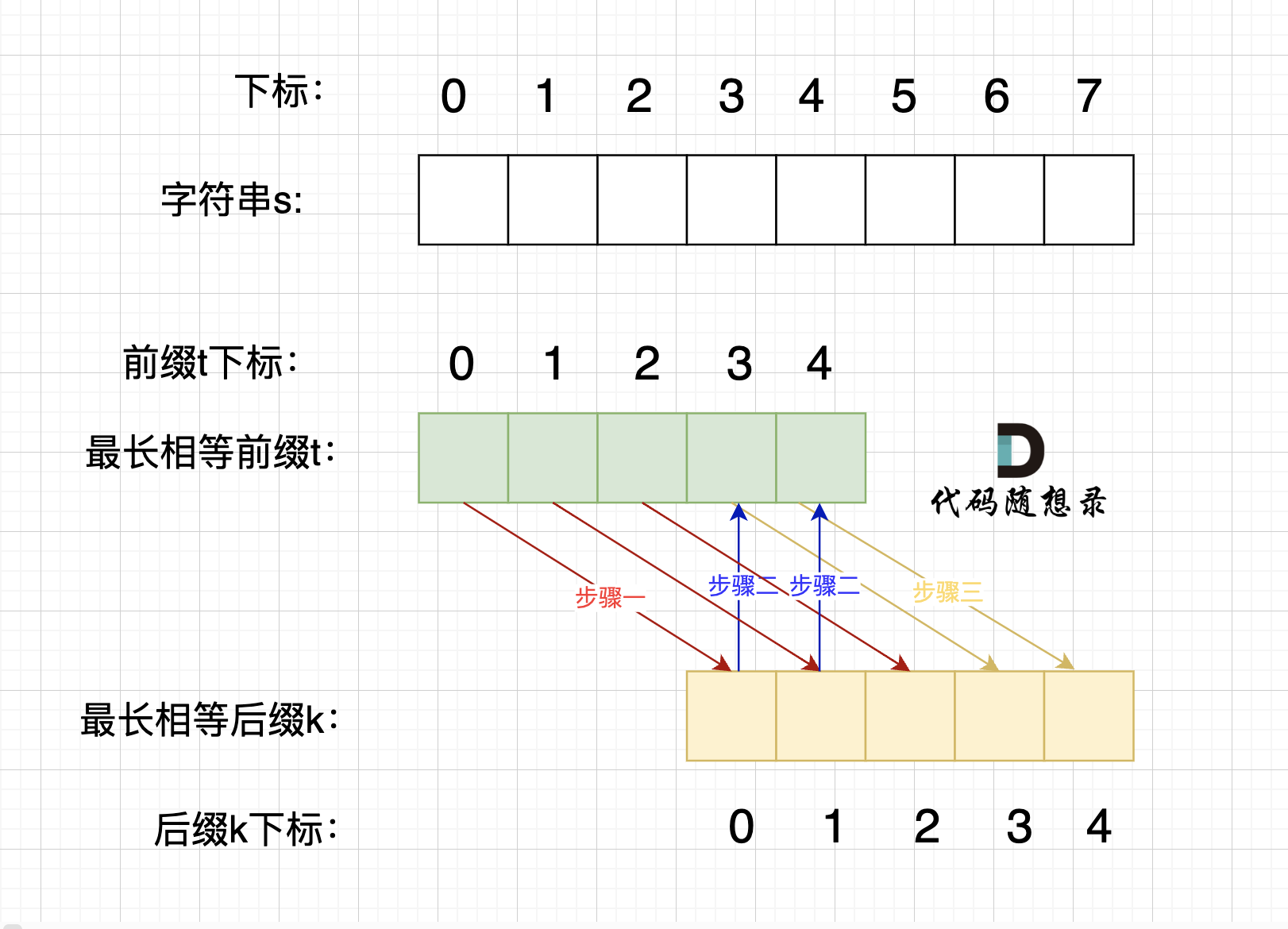
|
||||||
|
|
||||||
|
|
||||||
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,t[2] 与 k[2]相同。
|
步骤一:因为 这是相等的前缀和后缀,t[0] 与 k[0]相同, t[1] 与 k[1]相同,t[2] 与 k[2]相同。
|
||||||
|
|
|
||||||
|
|
@ -15,7 +15,7 @@
|
||||||
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
|
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
|
||||||
|
|
||||||
|
|
||||||
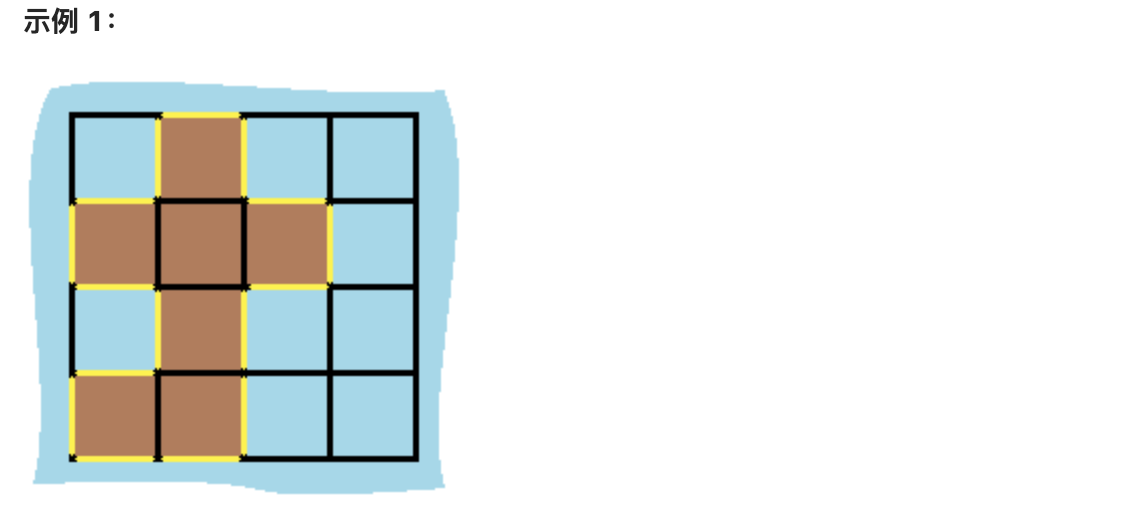
|
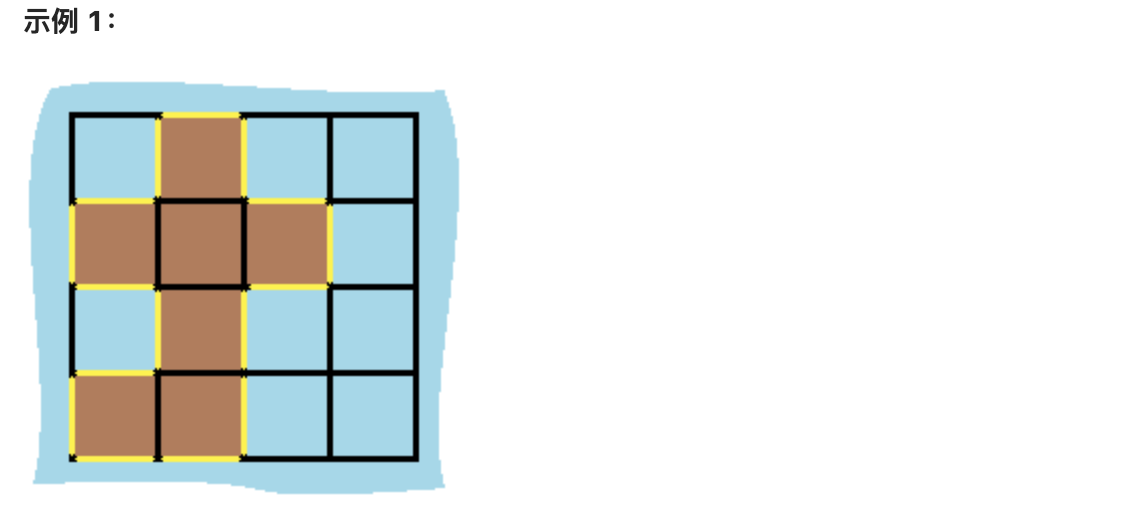
|
||||||
|
|
||||||
* 输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
|
* 输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
|
||||||
* 输出:16
|
* 输出:16
|
||||||
|
|
|
||||||
|
|
@ -51,7 +51,7 @@
|
||||||
其实本题并不是多重背包,再来看一下这个图,捋清几种背包的关系
|
其实本题并不是多重背包,再来看一下这个图,捋清几种背包的关系
|
||||||
|
|
||||||
|
|
||||||
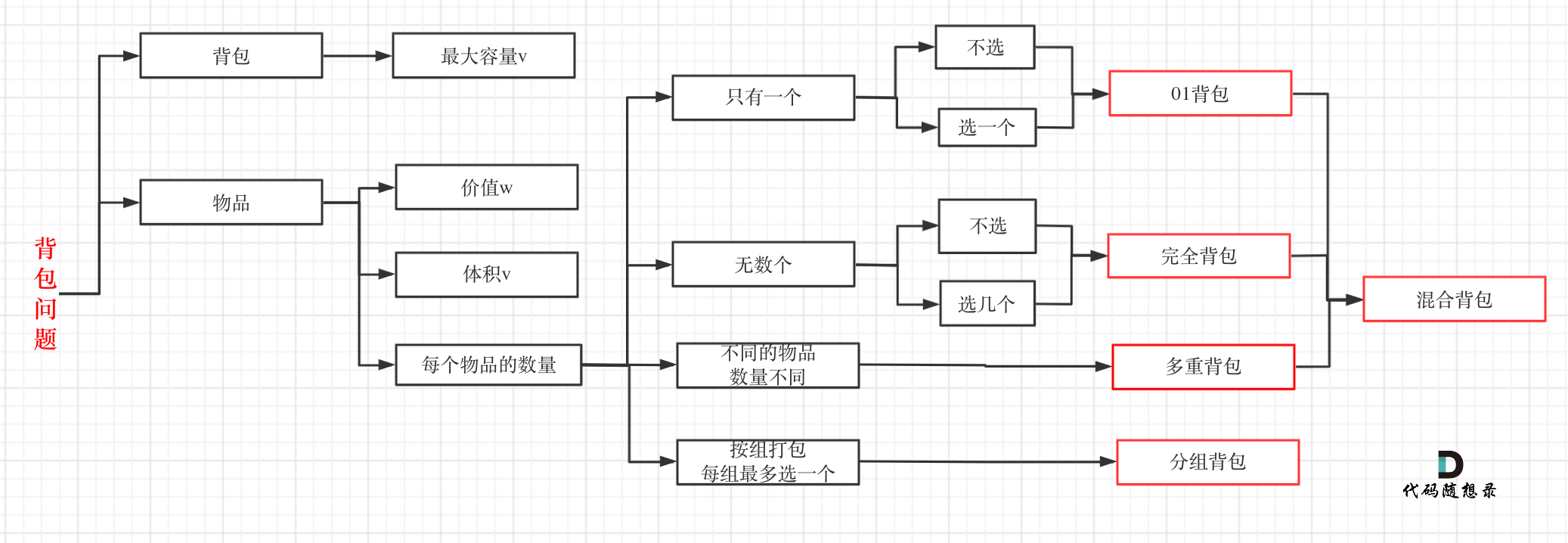
|
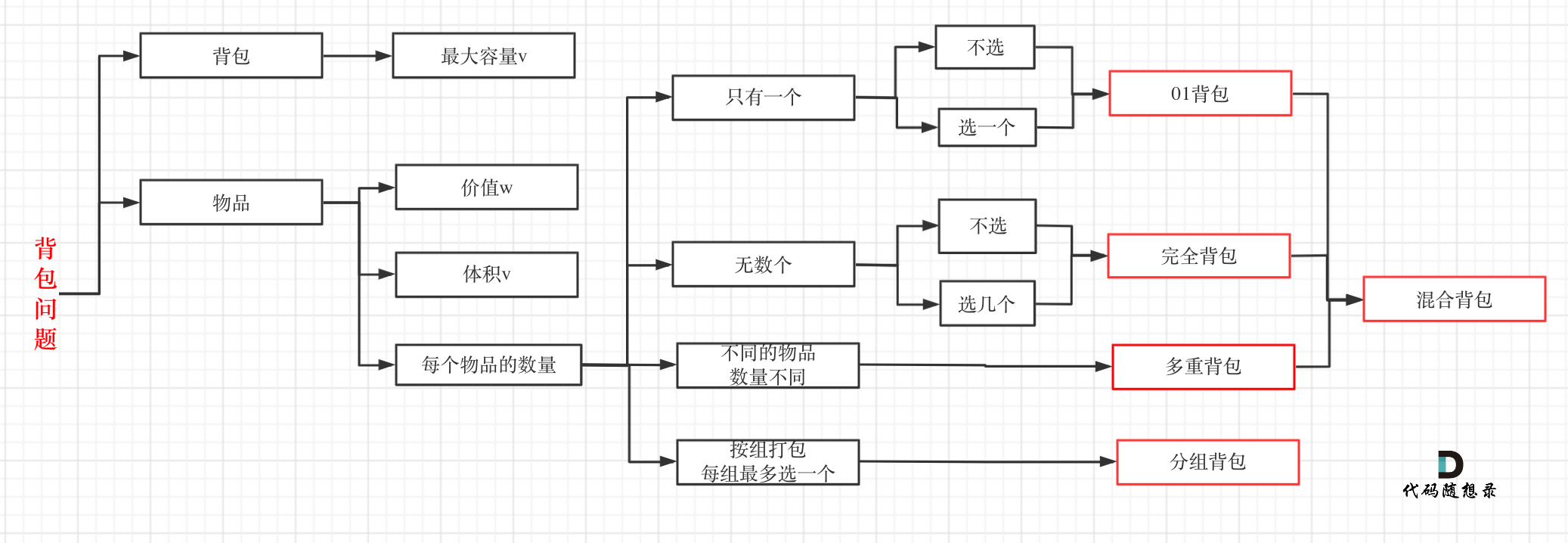
|
||||||
|
|
||||||
多重背包是每个物品,数量不同的情况。
|
多重背包是每个物品,数量不同的情况。
|
||||||
|
|
||||||
|
|
@ -127,7 +127,7 @@ for (string str : strs) { // 遍历物品
|
||||||
最后dp数组的状态如下所示:
|
最后dp数组的状态如下所示:
|
||||||
|
|
||||||
|
|
||||||
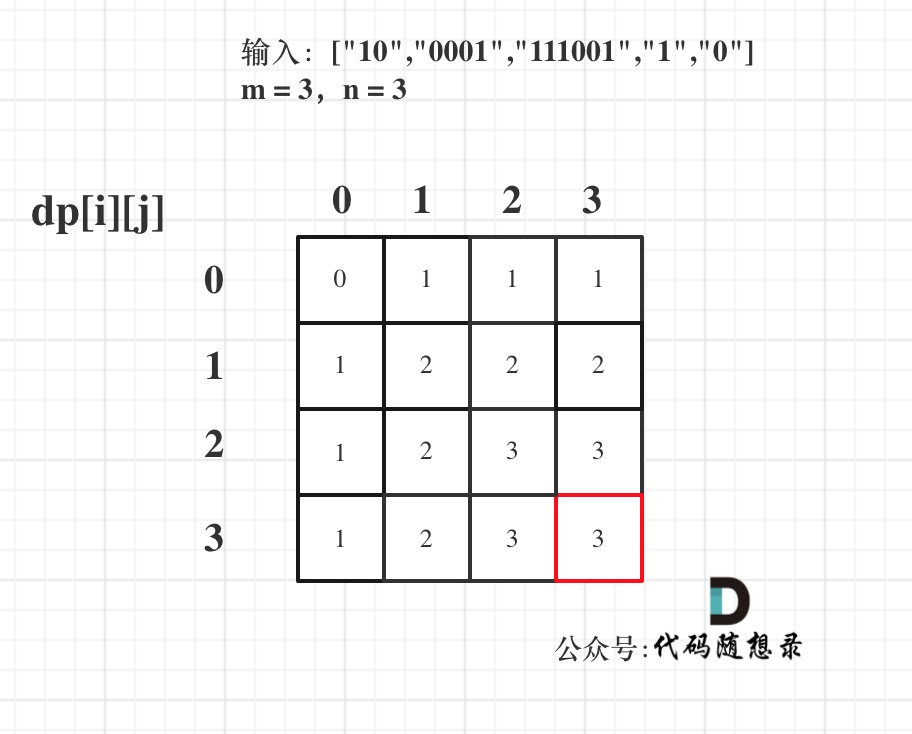
|
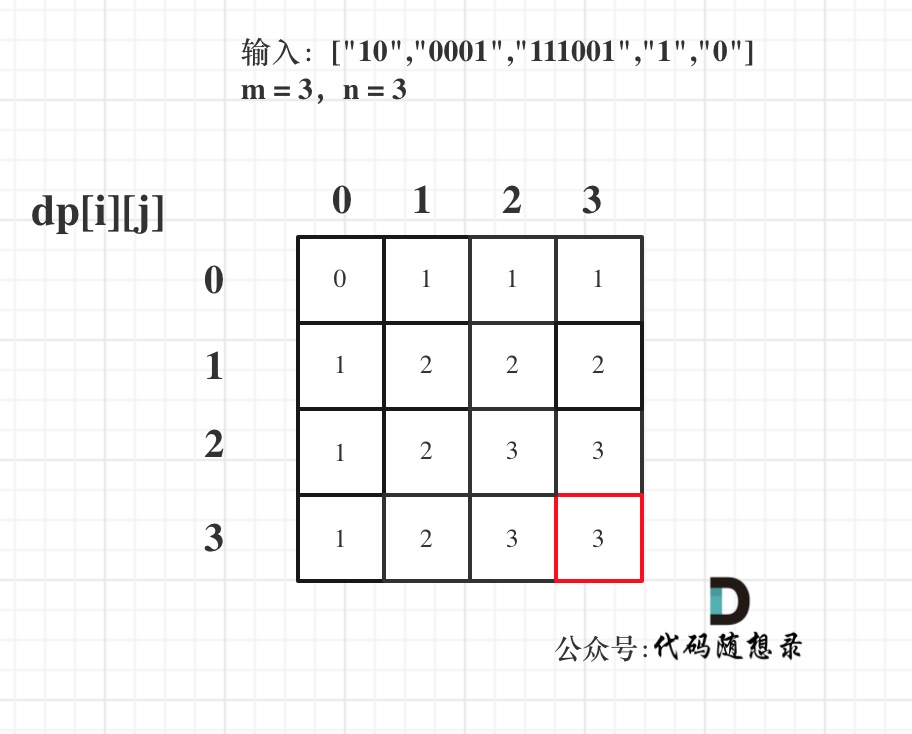
|
||||||
|
|
||||||
|
|
||||||
以上动规五部曲分析完毕,C++代码如下:
|
以上动规五部曲分析完毕,C++代码如下:
|
||||||
|
|
|
||||||
|
|
@ -45,7 +45,7 @@
|
||||||
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
|
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
|
||||||
|
|
||||||
|
|
||||||
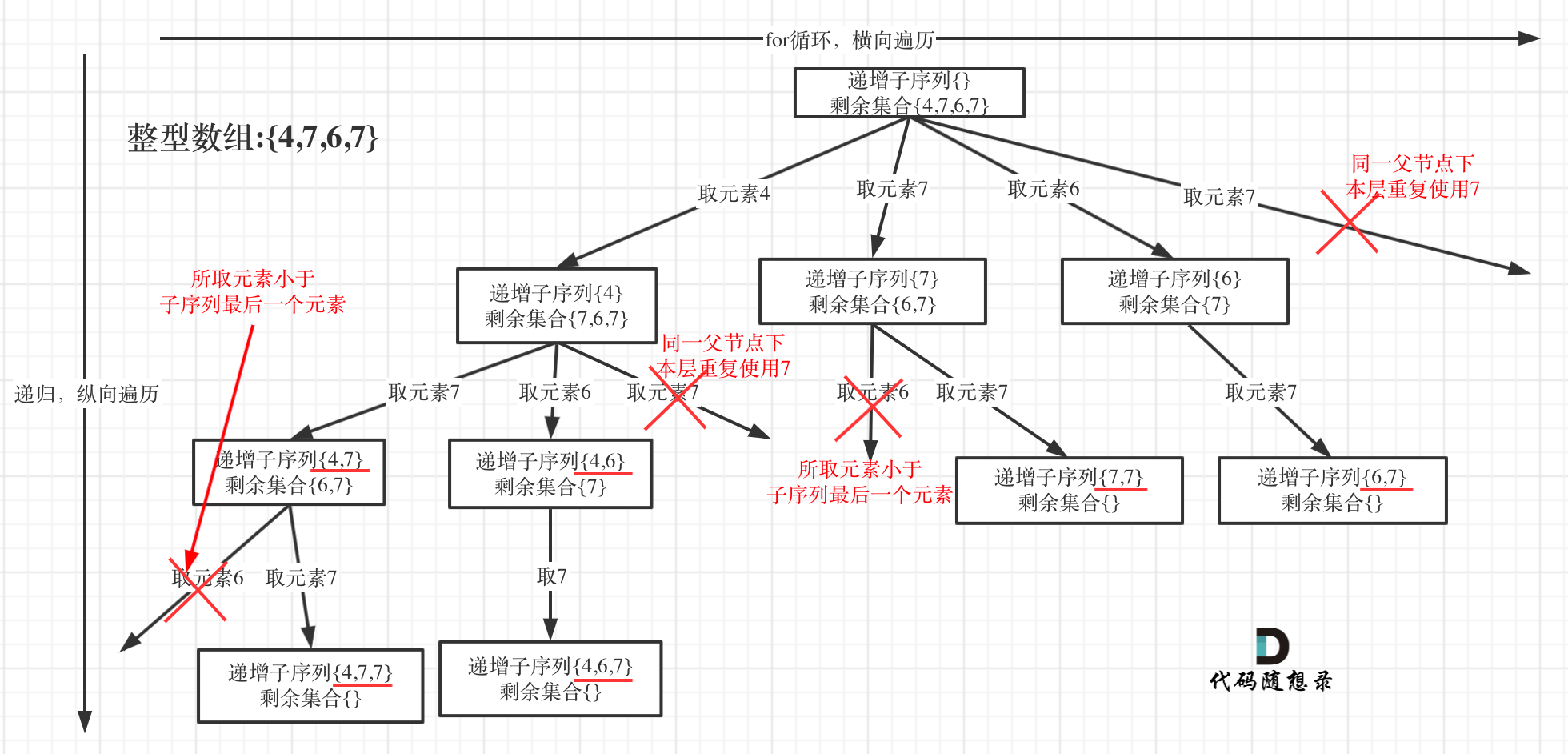
|
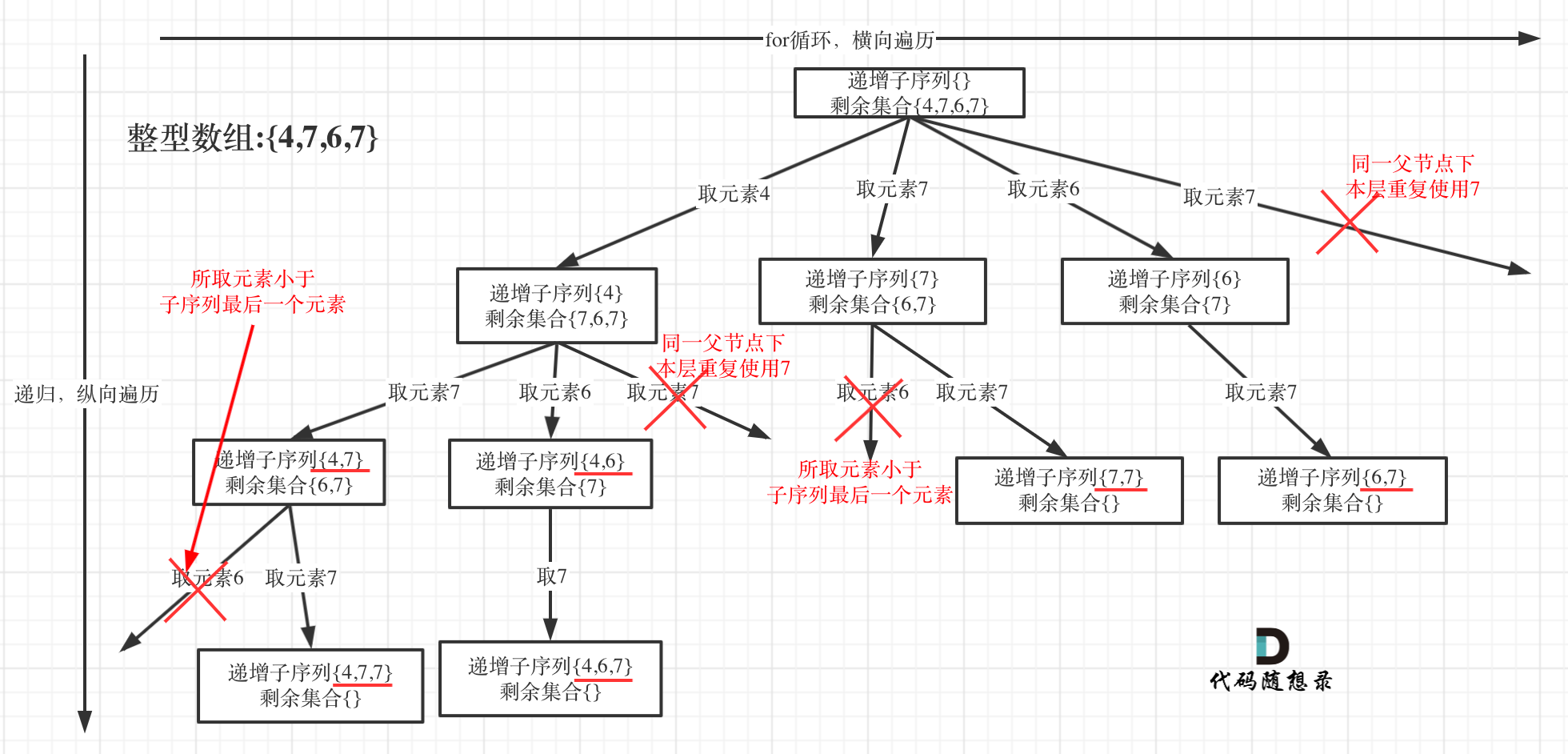
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
@ -79,7 +79,7 @@ if (path.size() > 1) {
|
||||||
|
|
||||||
* 单层搜索逻辑
|
* 单层搜索逻辑
|
||||||
|
|
||||||
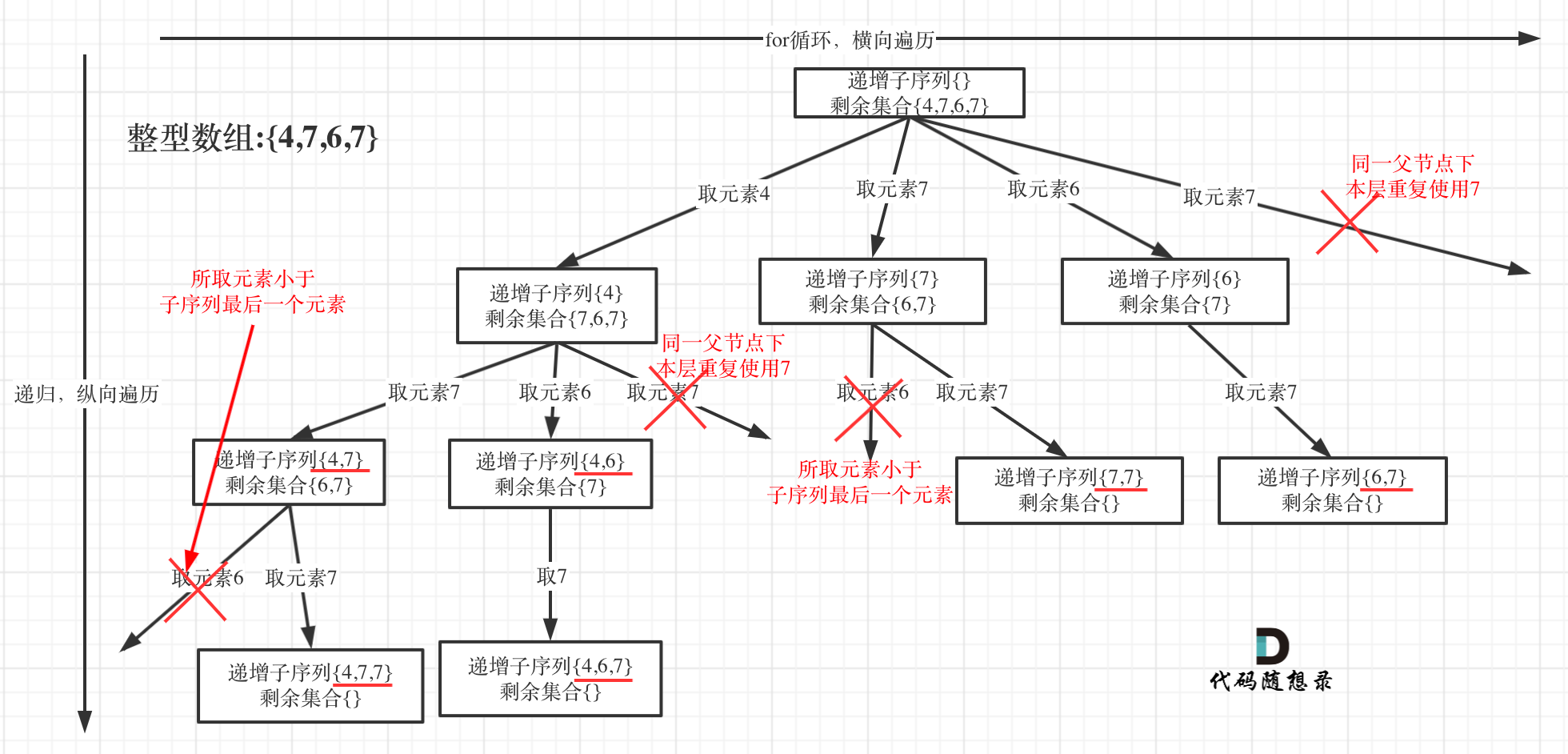
|
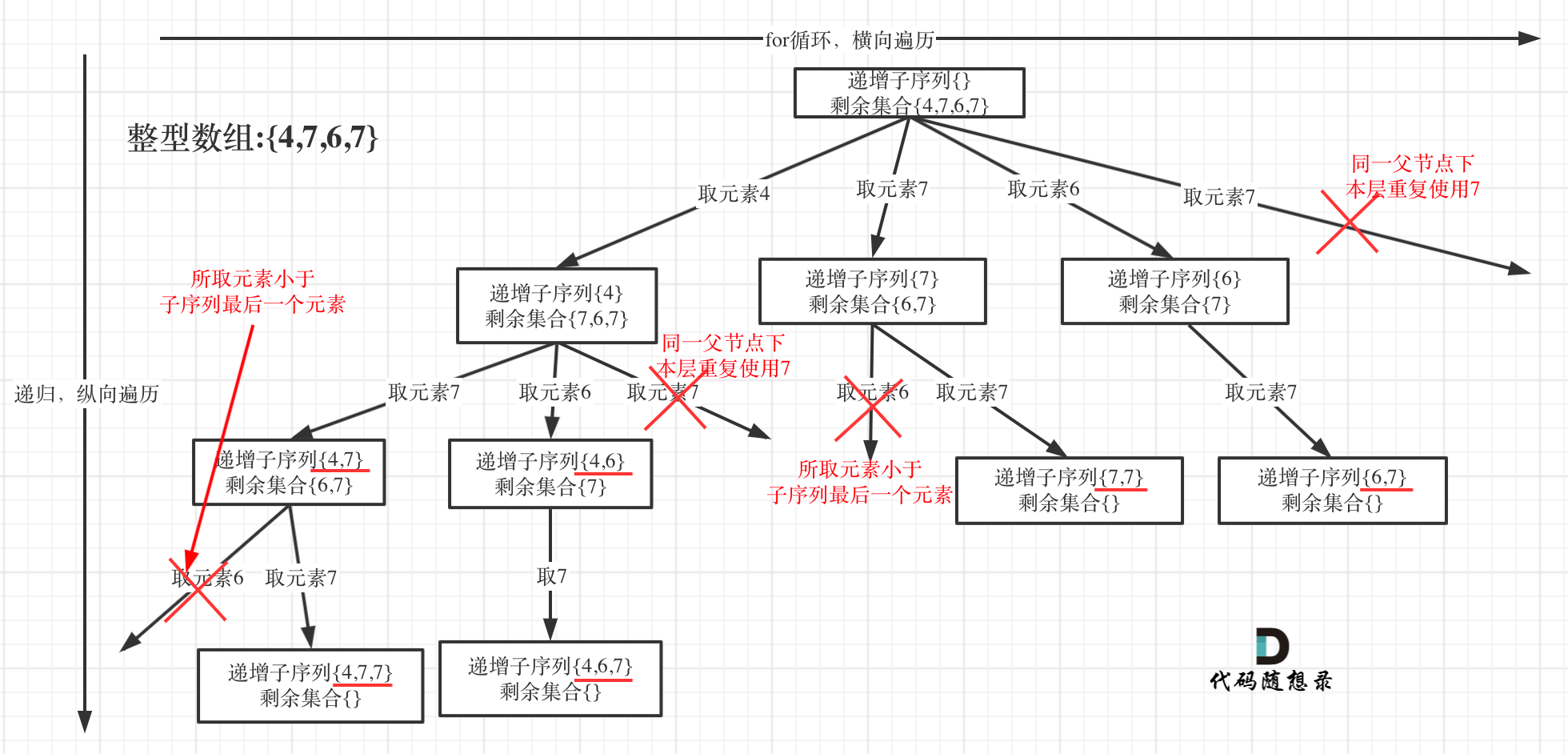
|
||||||
在图中可以看出,**同一父节点下的同层上使用过的元素就不能再使用了**
|
在图中可以看出,**同一父节点下的同层上使用过的元素就不能再使用了**
|
||||||
|
|
||||||
那么单层搜索代码如下:
|
那么单层搜索代码如下:
|
||||||
|
|
|
||||||
|
|
@ -163,7 +163,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||||
|
|
||||||
先只考虑物品0,如图:
|
先只考虑物品0,如图:
|
||||||
|
|
||||||

|
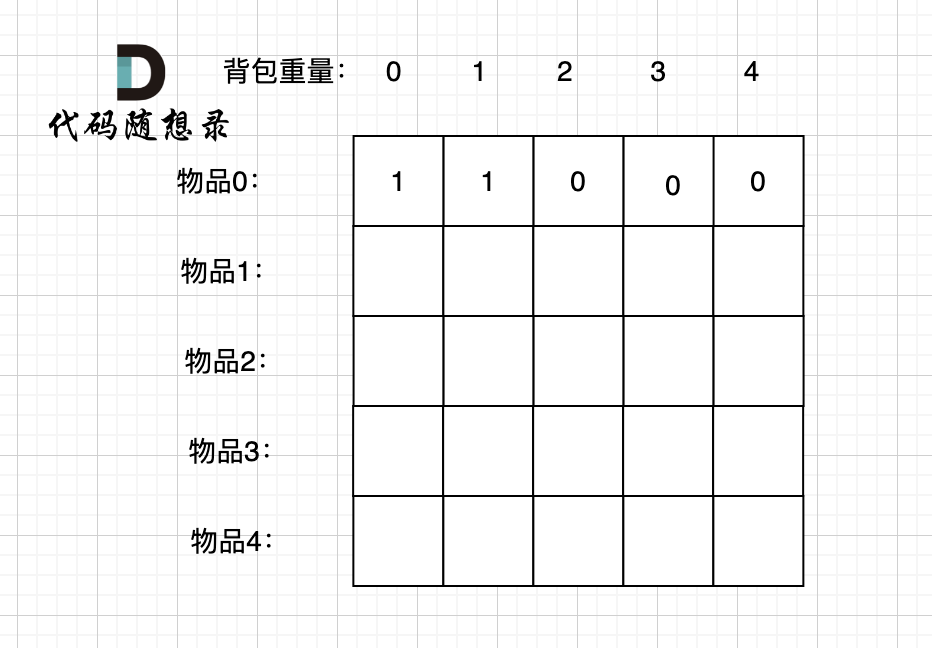
|
||||||
|
|
||||||
(这里的所有物品,都是题目中的数字1)。
|
(这里的所有物品,都是题目中的数字1)。
|
||||||
|
|
||||||
|
|
@ -177,7 +177,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||||
|
|
||||||
接下来 考虑 物品0 和 物品1,如图:
|
接下来 考虑 物品0 和 物品1,如图:
|
||||||
|
|
||||||
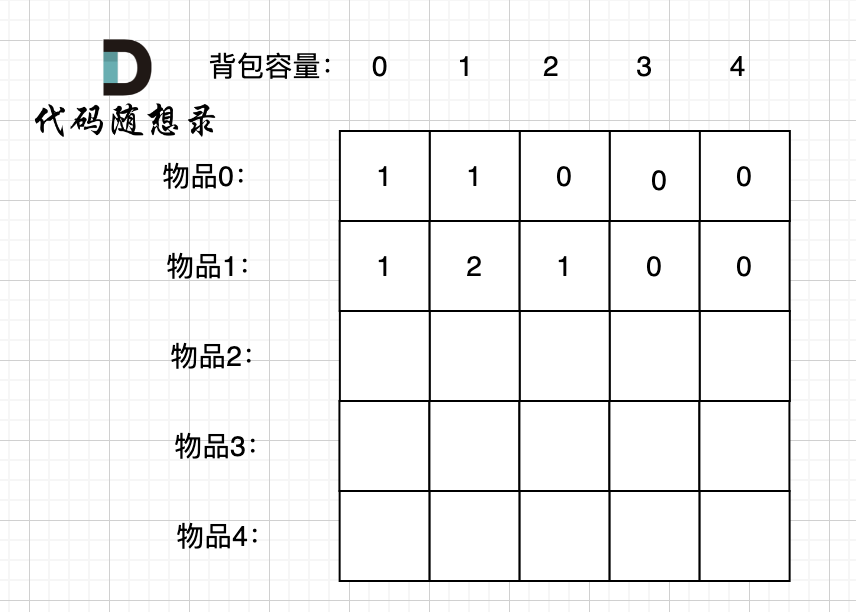
|
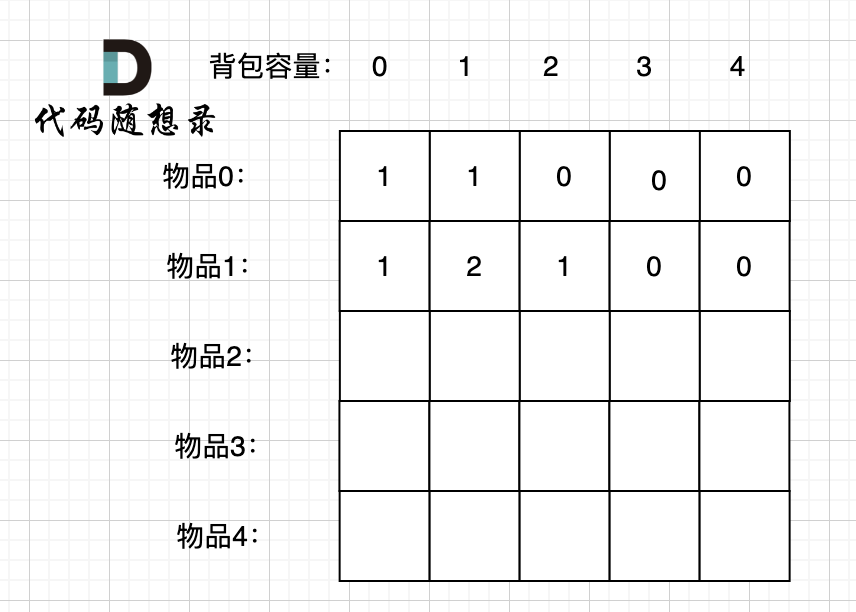
|
||||||
|
|
||||||
装满背包容量为0 的方法个数是1,即 放0件物品。
|
装满背包容量为0 的方法个数是1,即 放0件物品。
|
||||||
|
|
||||||
|
|
@ -191,7 +191,7 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||||
|
|
||||||
接下来 考虑 物品0 、物品1 和 物品2 ,如图:
|
接下来 考虑 物品0 、物品1 和 物品2 ,如图:
|
||||||
|
|
||||||
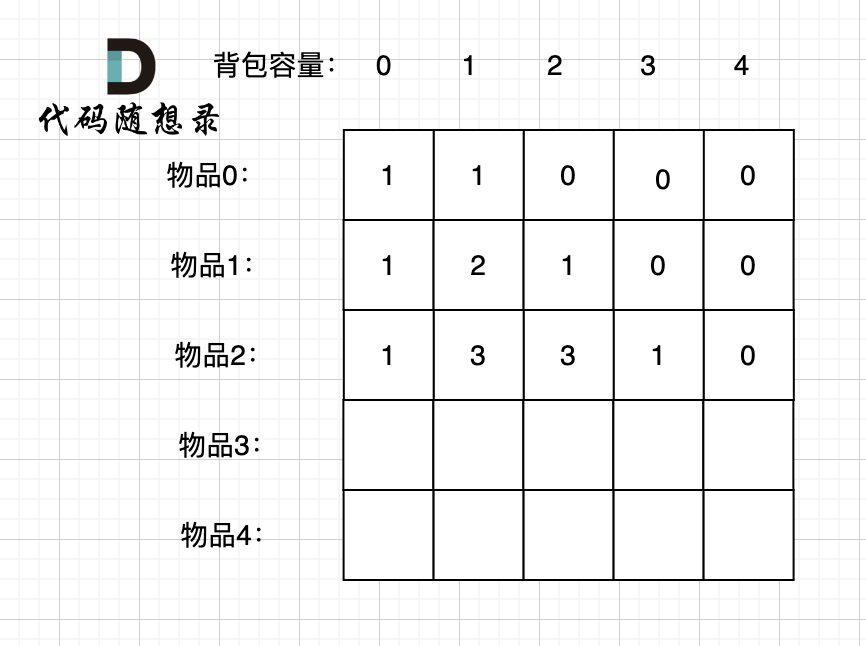
|
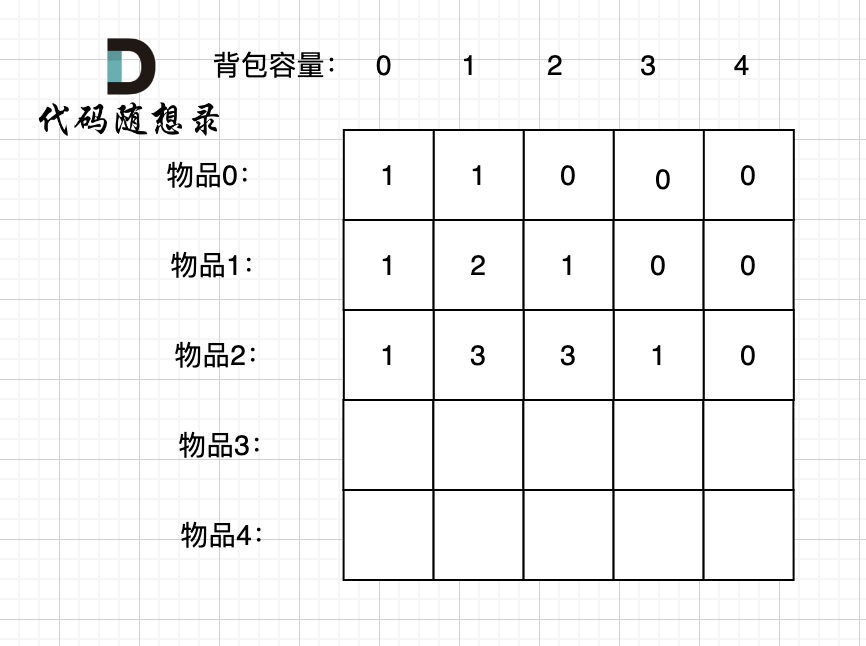
|
||||||
|
|
||||||
装满背包容量为0 的方法个数是1,即 放0件物品。
|
装满背包容量为0 的方法个数是1,即 放0件物品。
|
||||||
|
|
||||||
|
|
@ -207,17 +207,17 @@ if (abs(target) > sum) return 0; // 此时没有方案
|
||||||
|
|
||||||
如图红色部分:
|
如图红色部分:
|
||||||
|
|
||||||
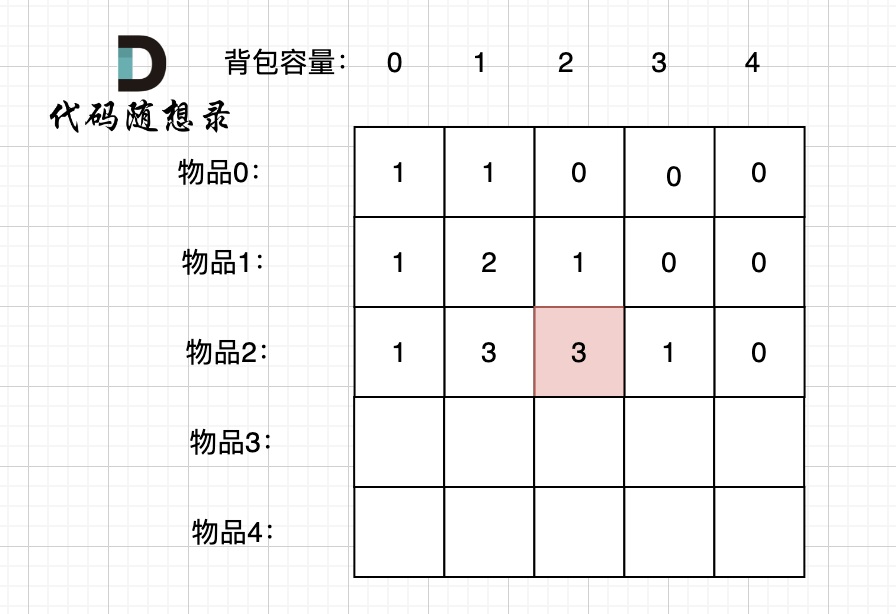
|
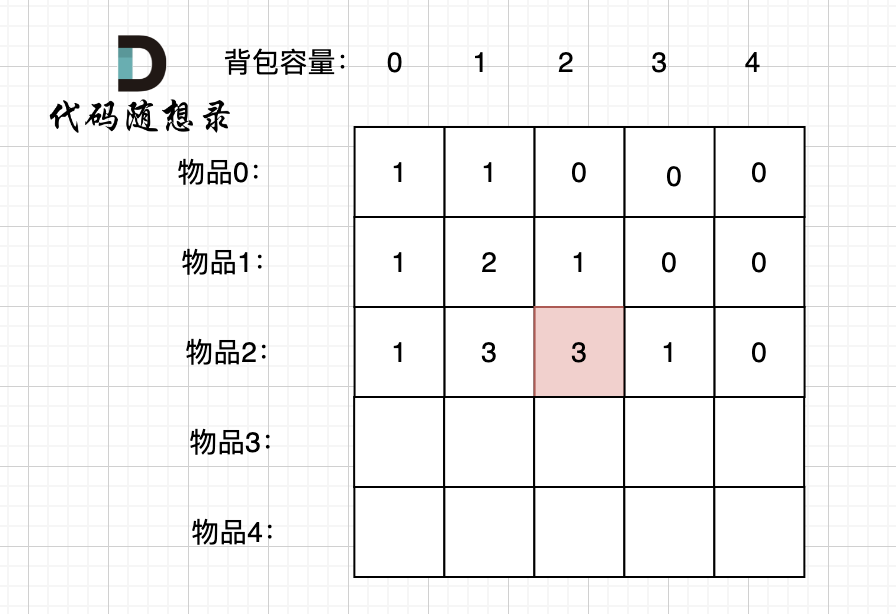
|
||||||
|
|
||||||
dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物品1 和 物品2, 如图所示,三种方法:
|
dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物品1 和 物品2, 如图所示,三种方法:
|
||||||
|
|
||||||
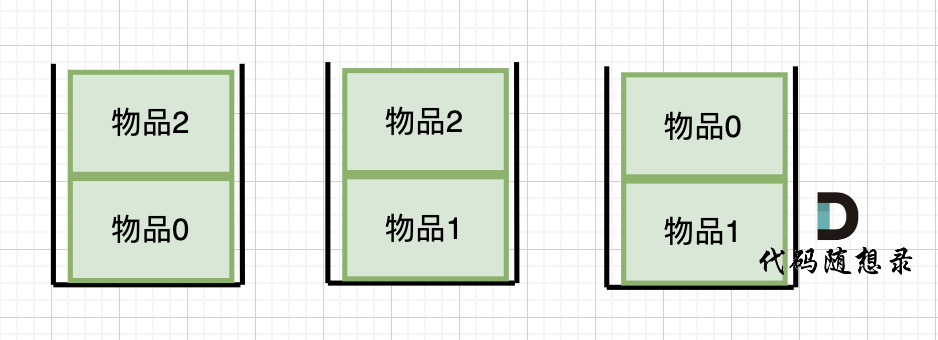
|
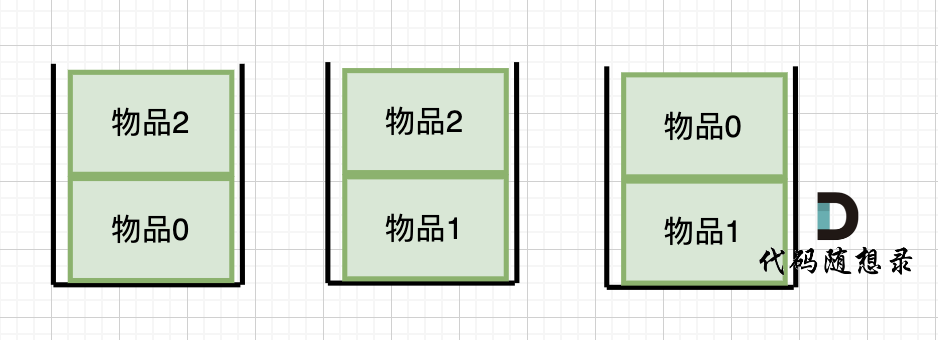
|
||||||
|
|
||||||
**容量为2 的背包,如果不放 物品2 有几种方法呢**?
|
**容量为2 的背包,如果不放 物品2 有几种方法呢**?
|
||||||
|
|
||||||
有 dp[1][2] 种方法,即 背包容量为2,只考虑物品0 和 物品1 ,有 dp[1][2] 种方法,如图:
|
有 dp[1][2] 种方法,即 背包容量为2,只考虑物品0 和 物品1 ,有 dp[1][2] 种方法,如图:
|
||||||
|
|
||||||
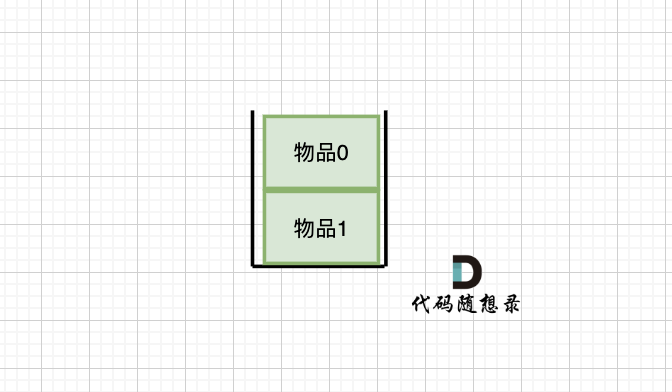
|
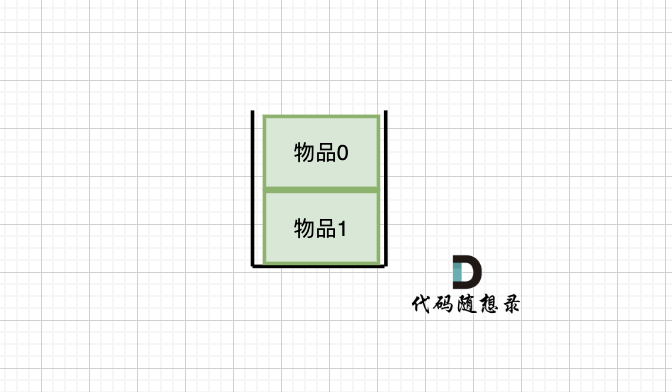
|
||||||
|
|
||||||
**容量为2 的背包, 如果放 物品2 有几种方法呢**?
|
**容量为2 的背包, 如果放 物品2 有几种方法呢**?
|
||||||
|
|
||||||
|
|
@ -229,7 +229,7 @@ dp[2][2] = 3,即 放物品0 和 放物品1、放物品0 和 物品 2、放物
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||

|
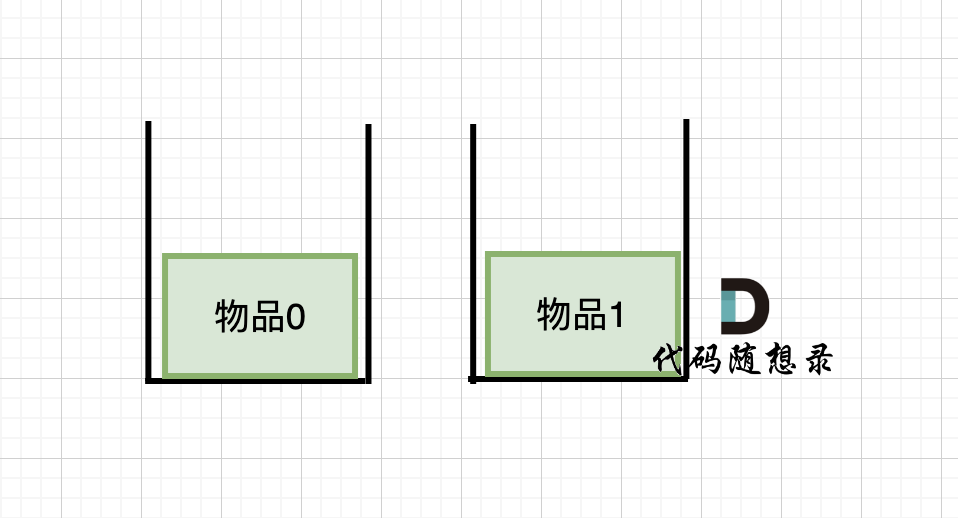
|
||||||
|
|
||||||
有录友可能疑惑,这里计算的是放满 容量为2的背包 有几种方法,那物品2去哪了?
|
有录友可能疑惑,这里计算的是放满 容量为2的背包 有几种方法,那物品2去哪了?
|
||||||
|
|
||||||
|
|
@ -239,7 +239,7 @@ dp[2][2] = 容量为2的背包不放物品2有几种方法 + 容量为2的背包
|
||||||
|
|
||||||
所以 dp[2][2] = dp[1][2] + dp[1][1] ,如图:
|
所以 dp[2][2] = dp[1][2] + dp[1][1] ,如图:
|
||||||
|
|
||||||

|
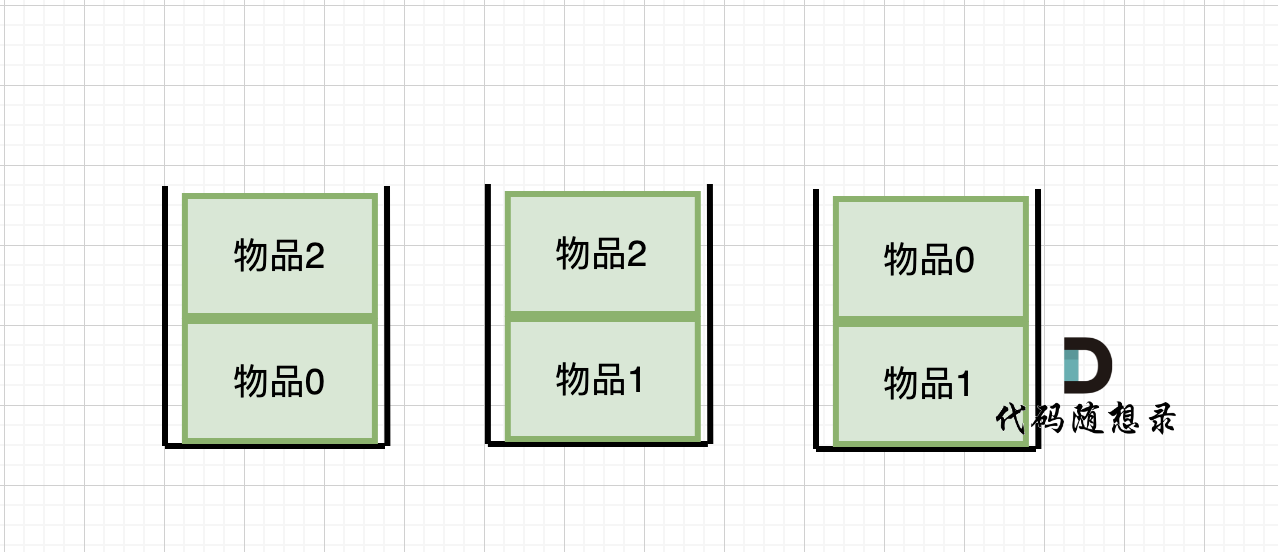
|
||||||
|
|
||||||
以上过程,抽象化如下:
|
以上过程,抽象化如下:
|
||||||
|
|
||||||
|
|
@ -266,11 +266,11 @@ else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
|
||||||
|
|
||||||
先明确递推的方向,如图,求解 dp[2][2] 是由 上方和左上方推出。
|
先明确递推的方向,如图,求解 dp[2][2] 是由 上方和左上方推出。
|
||||||
|
|
||||||
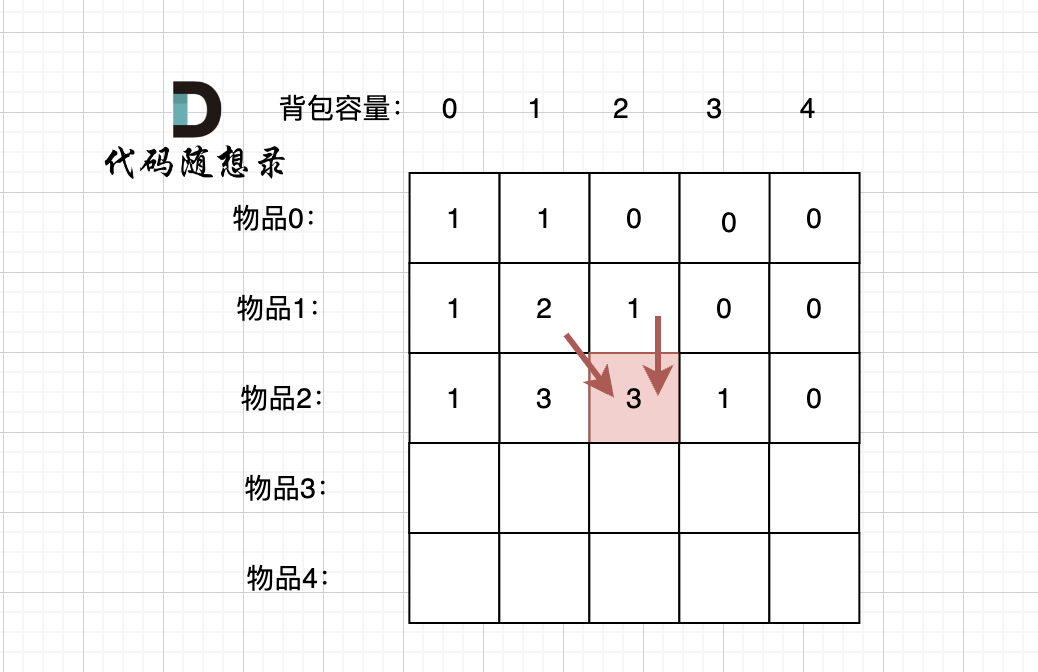
|
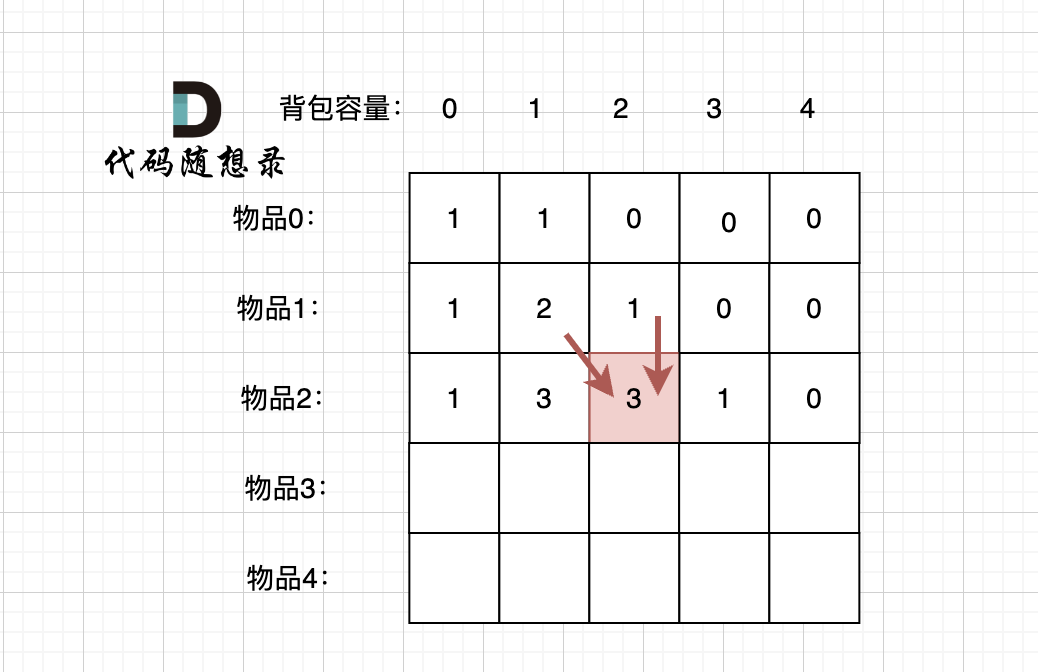
|
||||||
|
|
||||||
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,如图红色部分:
|
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,如图红色部分:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
关于dp[0][0]的值,在上面的递推公式讲解中已经讲过,装满背包容量为0 的方法数量是1,即 放0件物品。
|
关于dp[0][0]的值,在上面的递推公式讲解中已经讲过,装满背包容量为0 的方法数量是1,即 放0件物品。
|
||||||
|
|
||||||
|
|
@ -323,7 +323,7 @@ for (int i = 0; i < nums.size(); i++) {
|
||||||
|
|
||||||
例如下图,如果上方没数值,左上方没数值,就无法推出 dp[2][2]。
|
例如下图,如果上方没数值,左上方没数值,就无法推出 dp[2][2]。
|
||||||
|
|
||||||
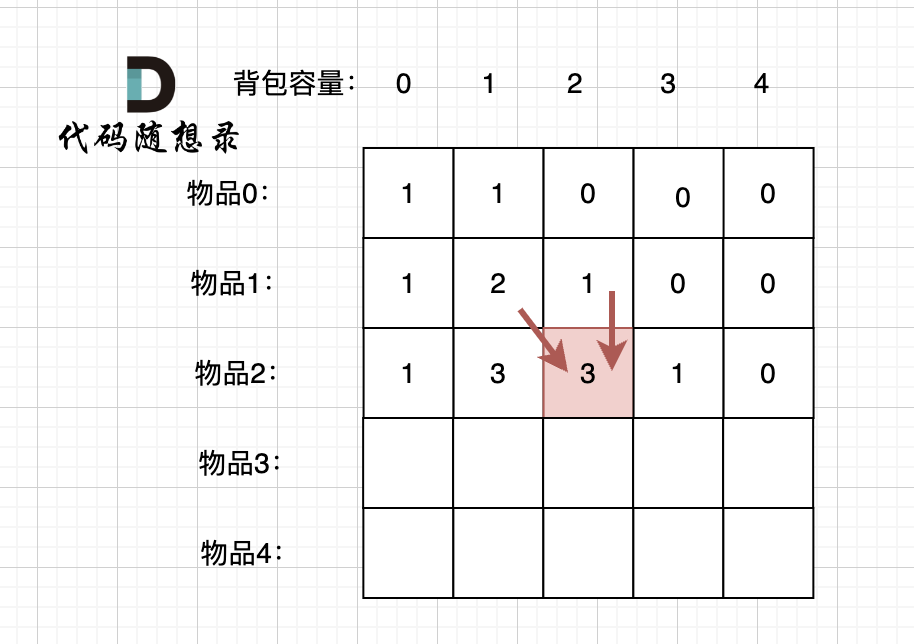
|
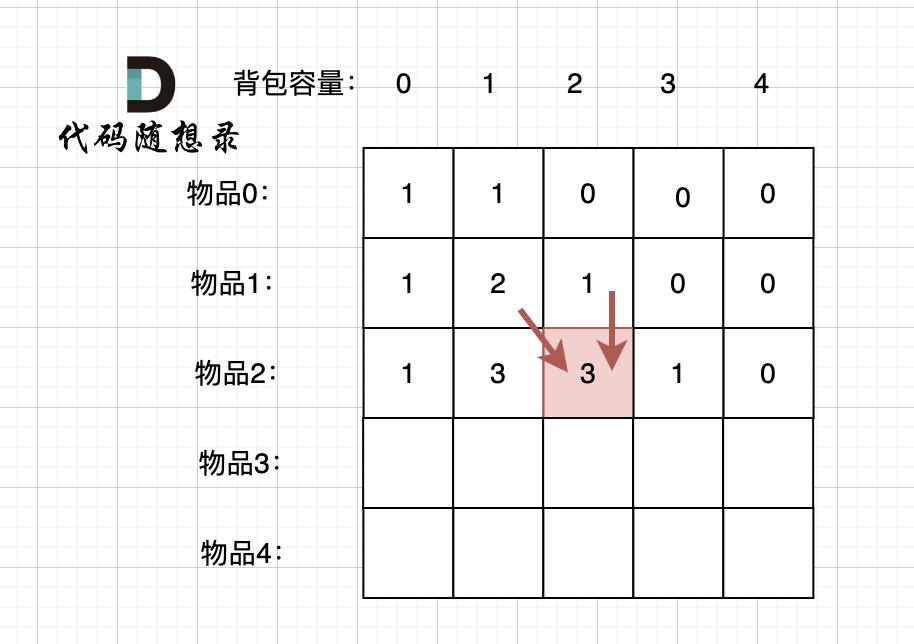
|
||||||
|
|
||||||
那么是先 从上到下 ,再从左到右遍历,例如这样:
|
那么是先 从上到下 ,再从左到右遍历,例如这样:
|
||||||
|
|
||||||
|
|
@ -349,11 +349,11 @@ for (int j = 0; j <= bagSize; j++) { // 列,遍历背包
|
||||||
|
|
||||||
这里我再画图讲一下,以求dp[2][2]为例,当先从上到下,再从左到右遍历,矩阵是这样:
|
这里我再画图讲一下,以求dp[2][2]为例,当先从上到下,再从左到右遍历,矩阵是这样:
|
||||||
|
|
||||||
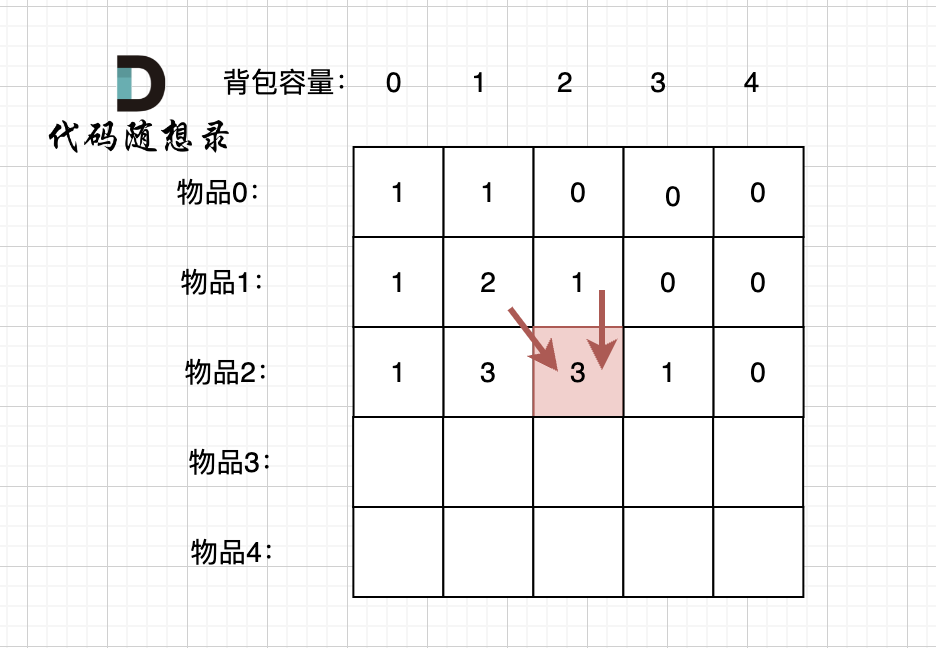
|
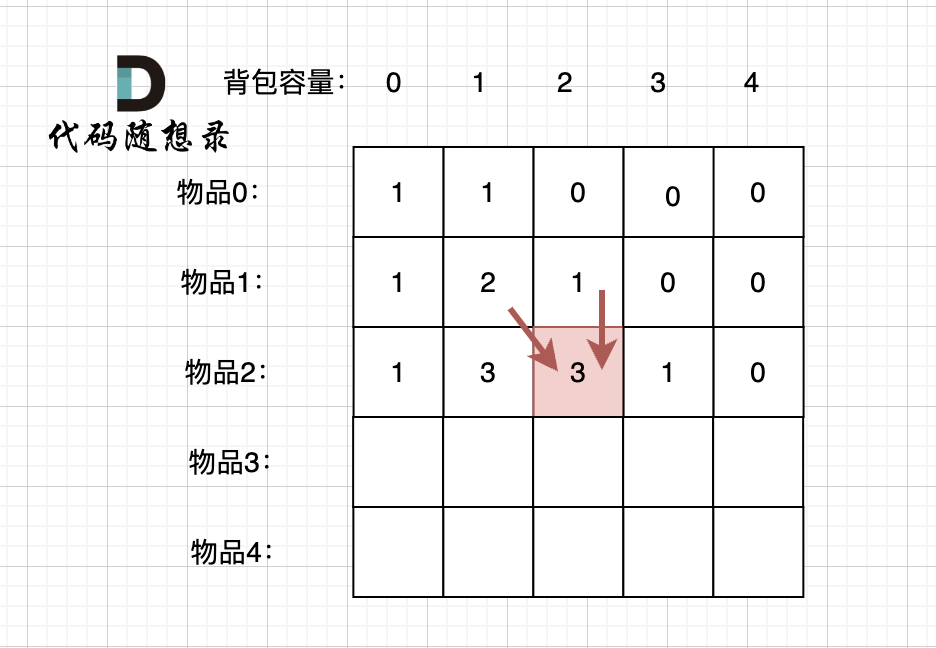
|
||||||
|
|
||||||
当先从左到右,再从上到下遍历,矩阵是这样:
|
当先从左到右,再从上到下遍历,矩阵是这样:
|
||||||
|
|
||||||
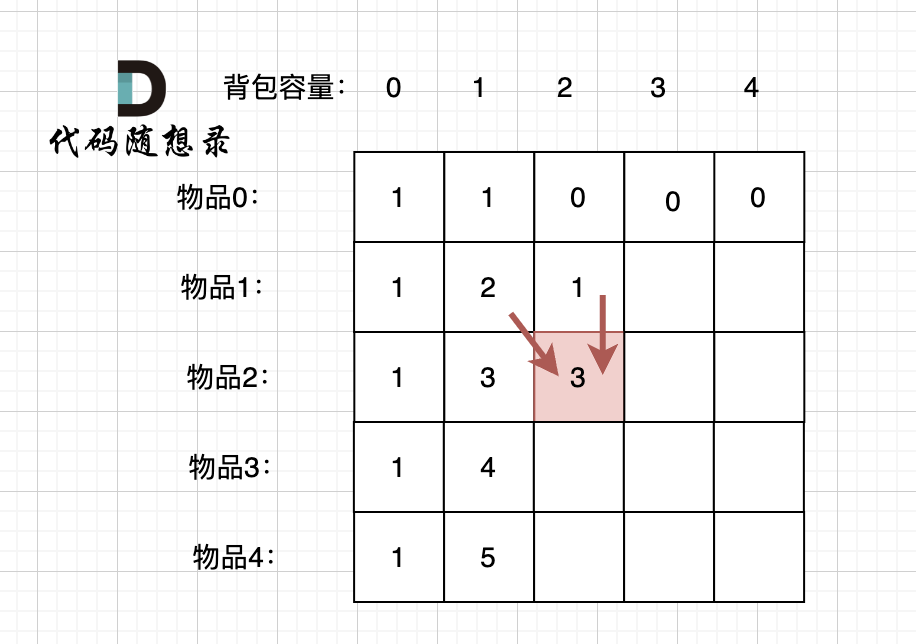
|
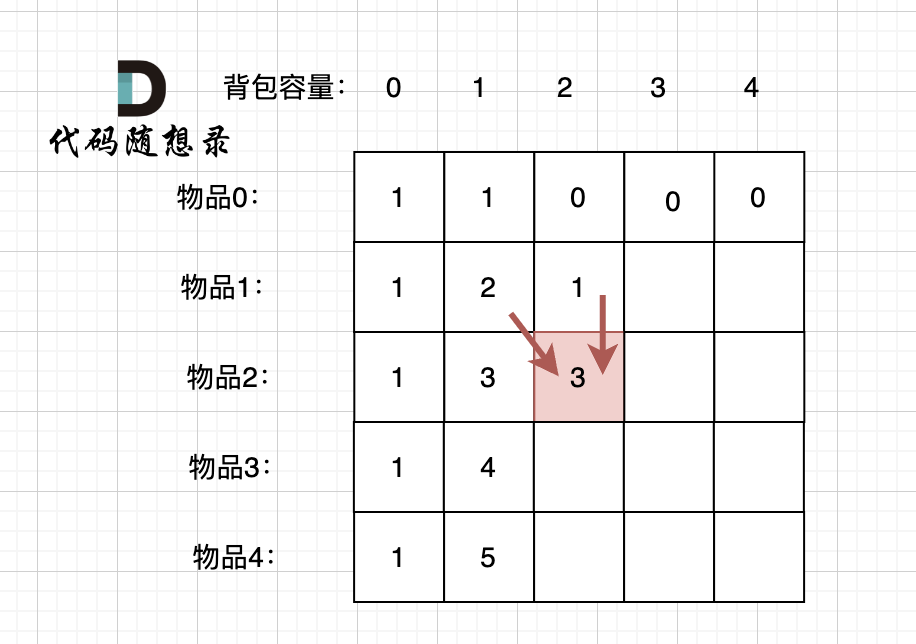
|
||||||
|
|
||||||
这里大家可以看出,无论是以上哪种遍历,都不影响 dp[2][2]的求值,用来 推导 dp[2][2] 的数值都在。
|
这里大家可以看出,无论是以上哪种遍历,都不影响 dp[2][2]的求值,用来 推导 dp[2][2] 的数值都在。
|
||||||
|
|
||||||
|
|
@ -366,7 +366,7 @@ bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
|
||||||
|
|
||||||
dp数组状态变化如下:
|
dp数组状态变化如下:
|
||||||
|
|
||||||

|
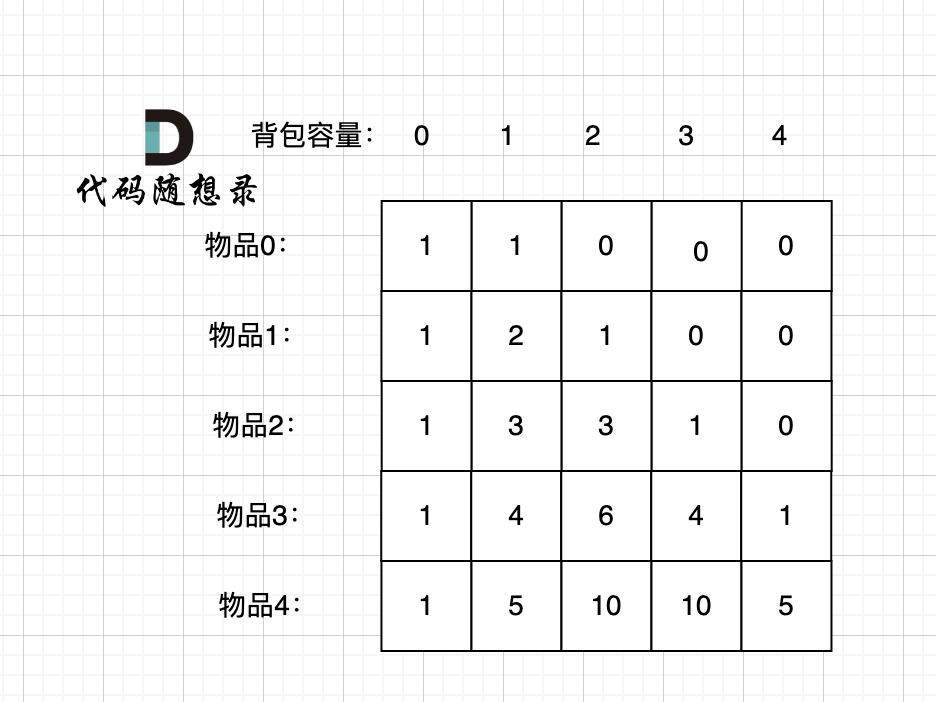
|
||||||
|
|
||||||
这么大的矩阵,我们是可以自己手动模拟出来的。
|
这么大的矩阵,我们是可以自己手动模拟出来的。
|
||||||
|
|
||||||
|
|
@ -445,7 +445,7 @@ bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
|
||||||
|
|
||||||
dp数组状态变化如下:
|
dp数组状态变化如下:
|
||||||
|
|
||||||
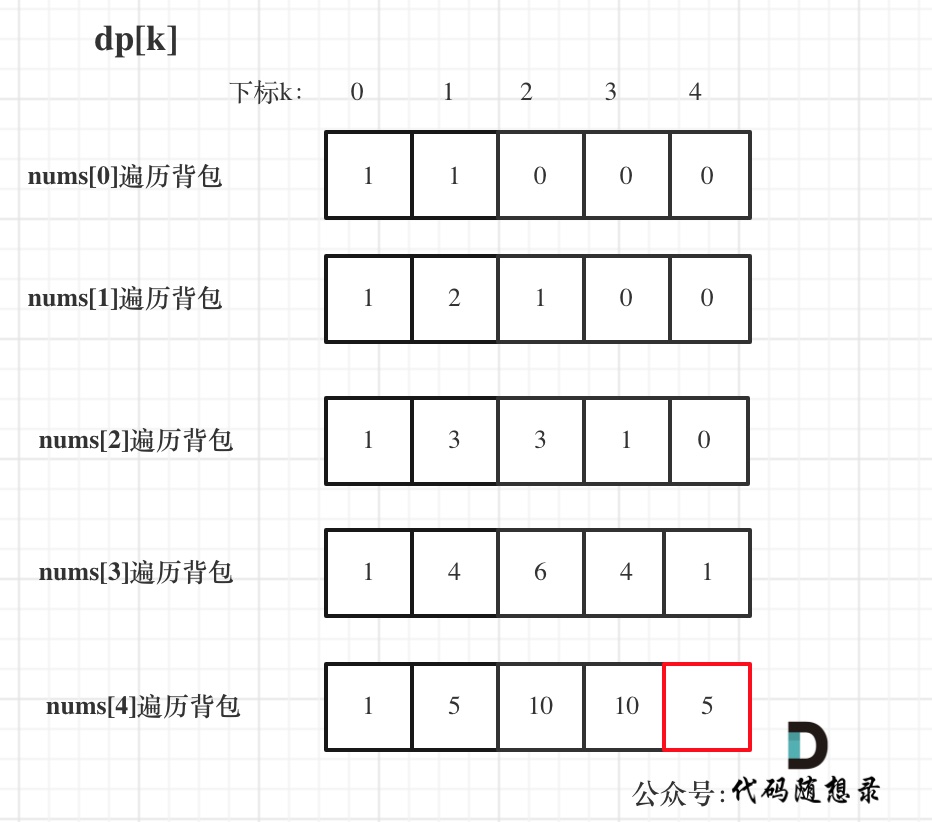
|
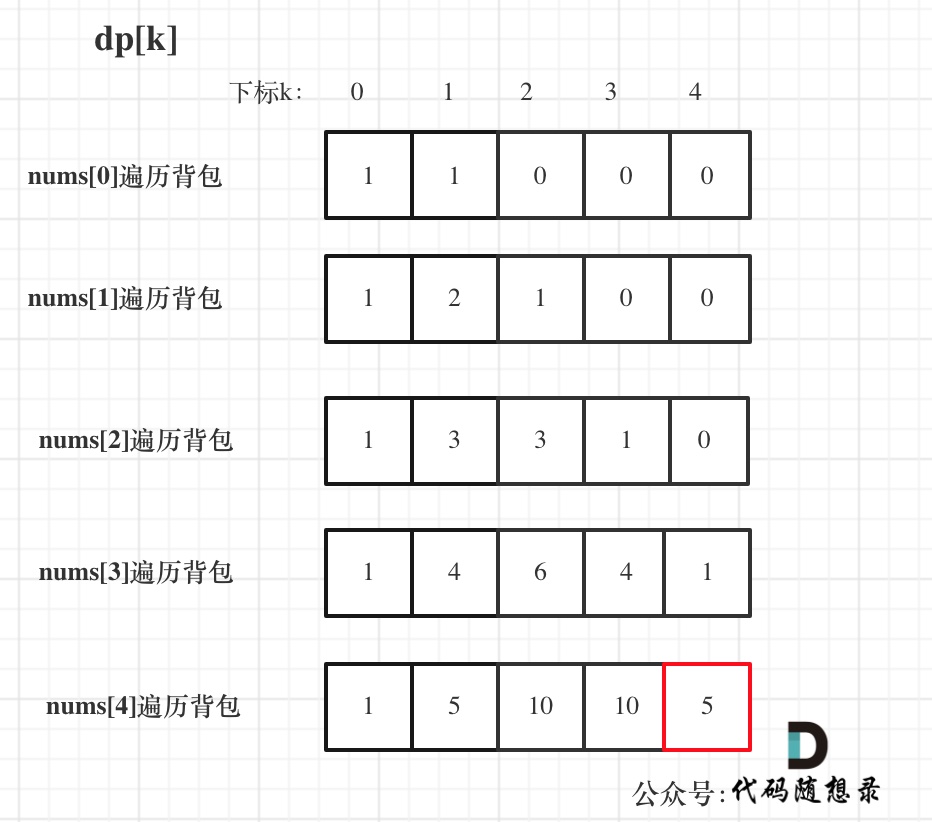
|
||||||
|
|
||||||
大家可以和 二维dp数组的打印结果做一下对比。
|
大家可以和 二维dp数组的打印结果做一下对比。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -23,7 +23,7 @@
|
||||||
|
|
||||||
给定 BST [1,null,2,2],
|
给定 BST [1,null,2,2],
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
返回[2].
|
返回[2].
|
||||||
|
|
||||||
|
|
@ -144,7 +144,7 @@ public:
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
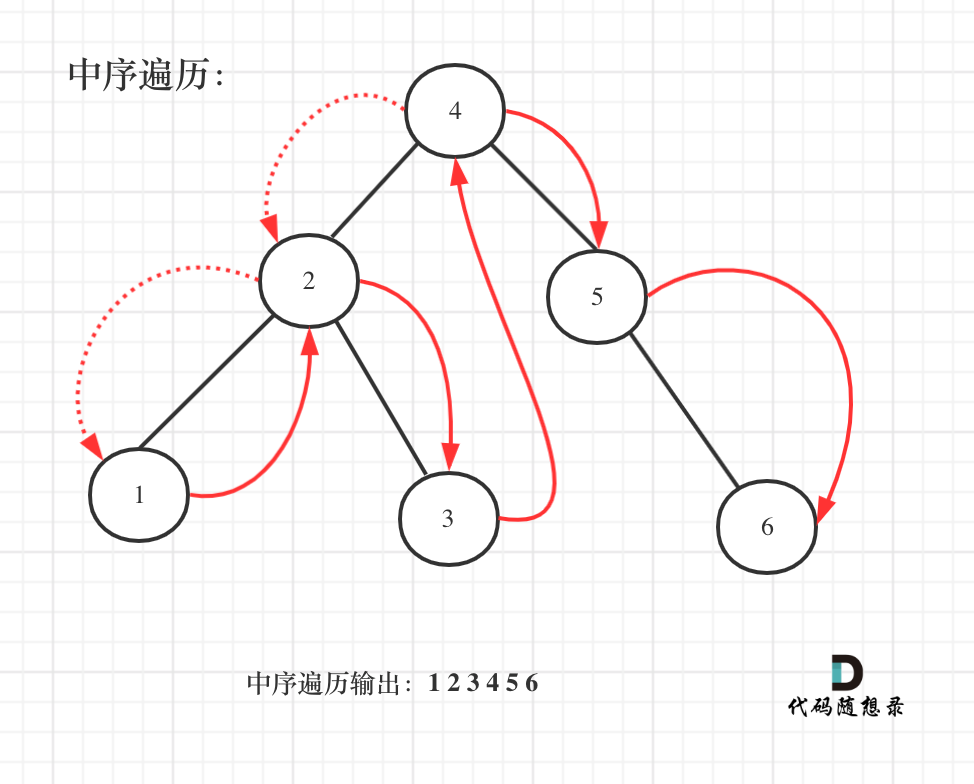
|
|
||||||
|
|
||||||
中序遍历代码如下:
|
中序遍历代码如下:
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -12,11 +12,11 @@
|
||||||
|
|
||||||
示例 1:
|
示例 1:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
示例 2:
|
示例 2:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
## 算法公开课
|
## 算法公开课
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -56,7 +56,7 @@
|
||||||
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
|
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
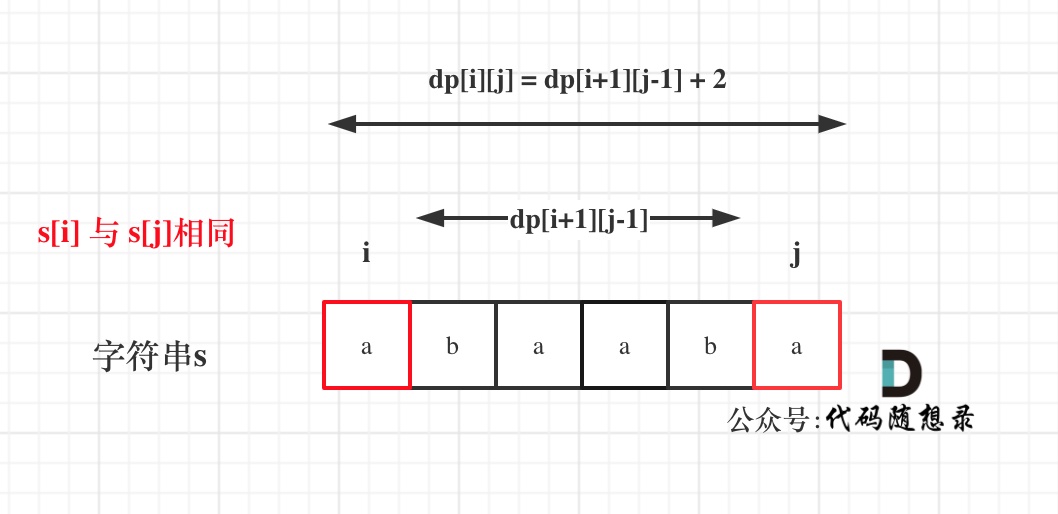
|
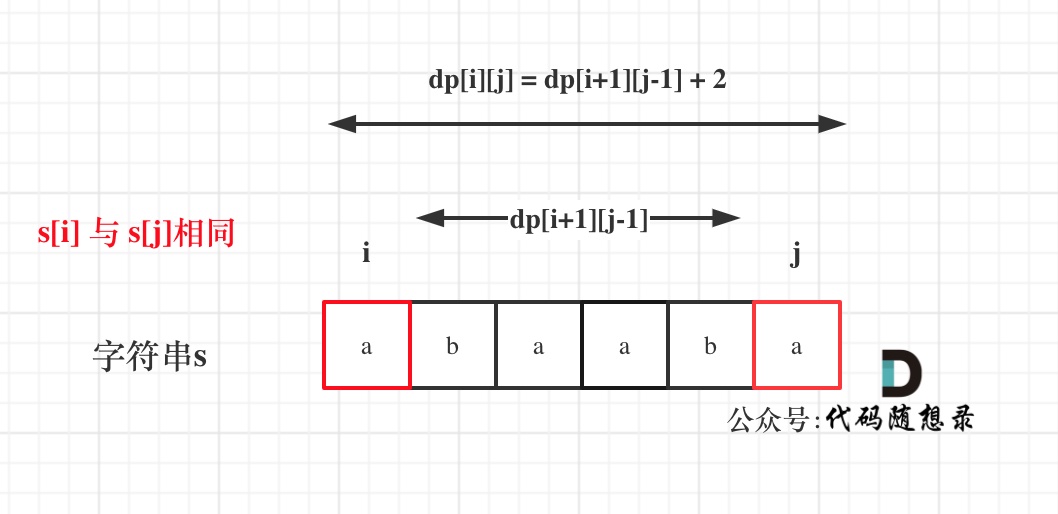
|
||||||
|
|
||||||
(如果这里看不懂,回忆一下dp[i][j]的定义)
|
(如果这里看不懂,回忆一下dp[i][j]的定义)
|
||||||
|
|
||||||
|
|
@ -68,7 +68,7 @@
|
||||||
|
|
||||||
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
|
那么dp[i][j]一定是取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
|
||||||
|
|
||||||
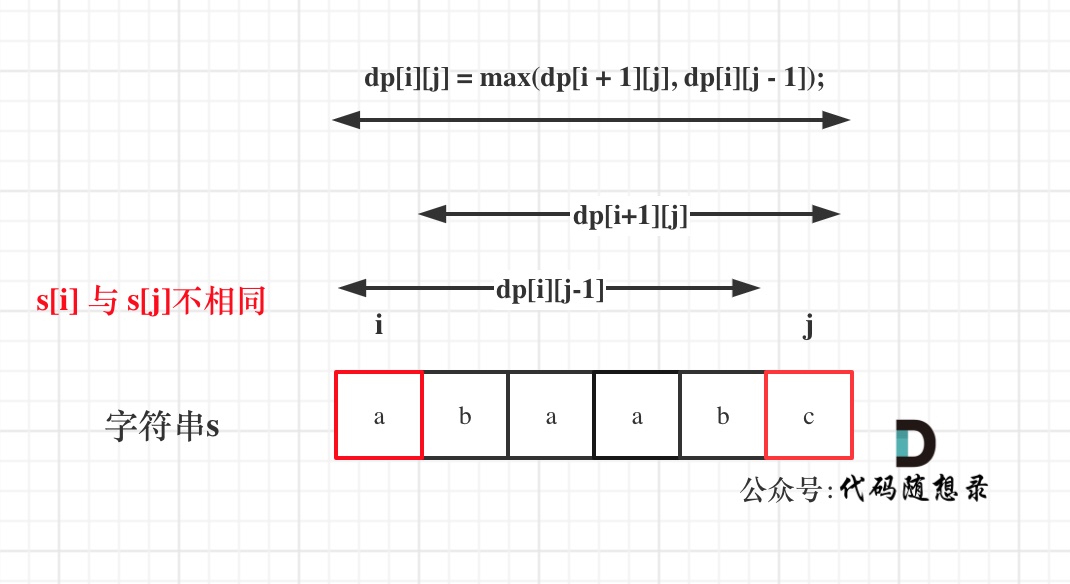
|
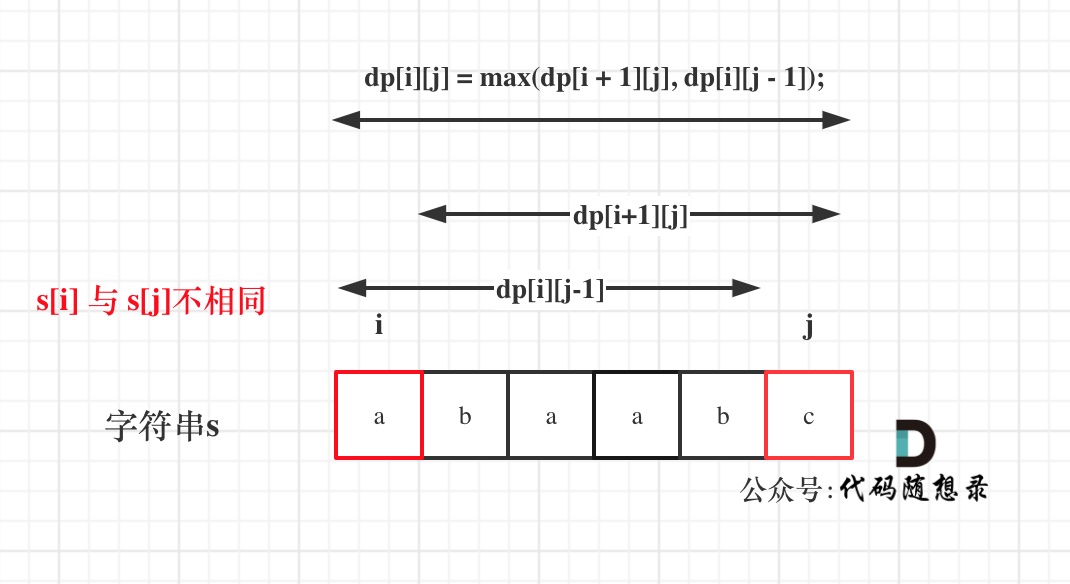
|
||||||
|
|
||||||
代码如下:
|
代码如下:
|
||||||
|
|
||||||
|
|
@ -97,7 +97,7 @@ for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
|
||||||
|
|
||||||
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],如图:
|
从递归公式中,可以看出,dp[i][j] 依赖于 dp[i + 1][j - 1] ,dp[i + 1][j] 和 dp[i][j - 1],如图:
|
||||||
|
|
||||||
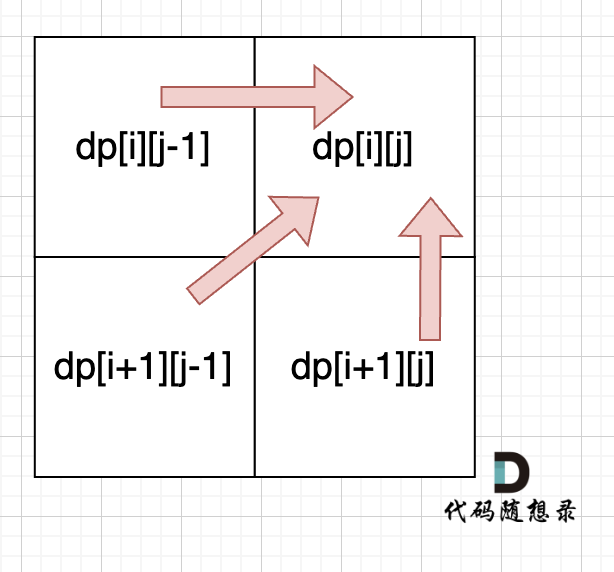
|
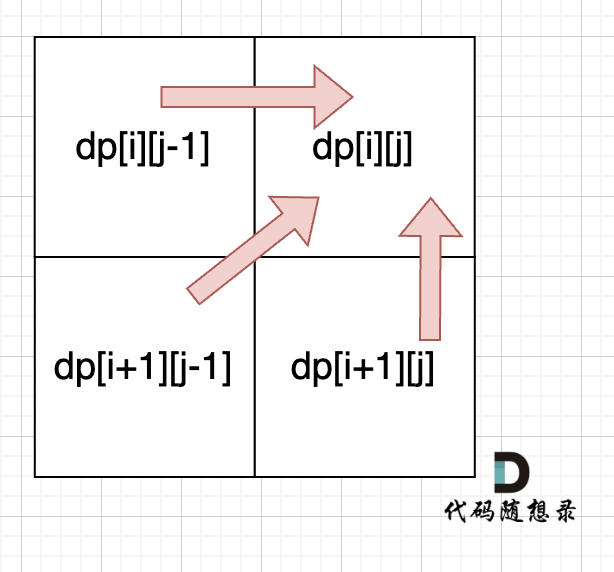
|
||||||
|
|
||||||
**所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的**。
|
**所以遍历i的时候一定要从下到上遍历,这样才能保证下一行的数据是经过计算的**。
|
||||||
|
|
||||||
|
|
@ -121,7 +121,7 @@ for (int i = s.size() - 1; i >= 0; i--) {
|
||||||
|
|
||||||
输入s:"cbbd" 为例,dp数组状态如图:
|
输入s:"cbbd" 为例,dp数组状态如图:
|
||||||
|
|
||||||
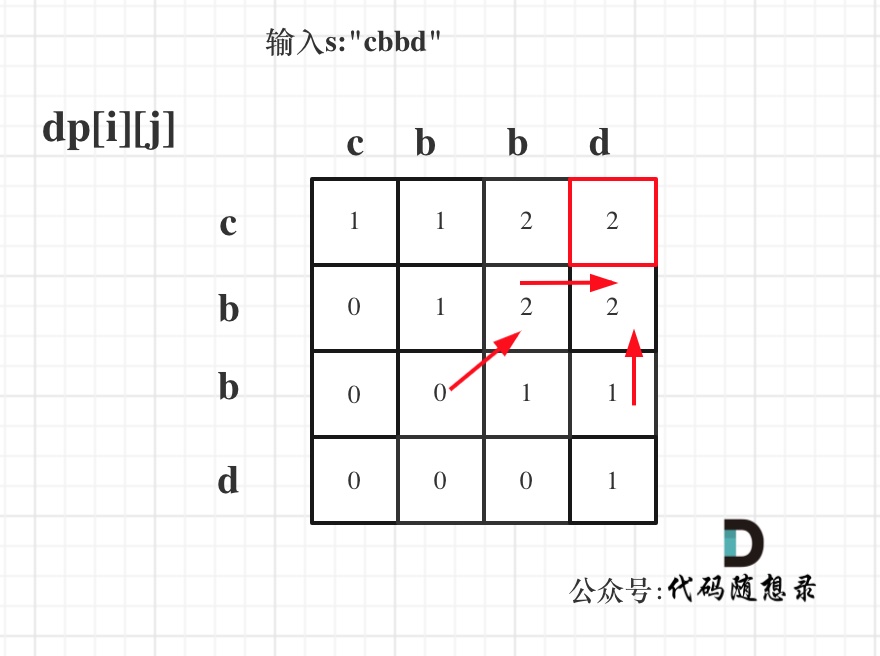
|
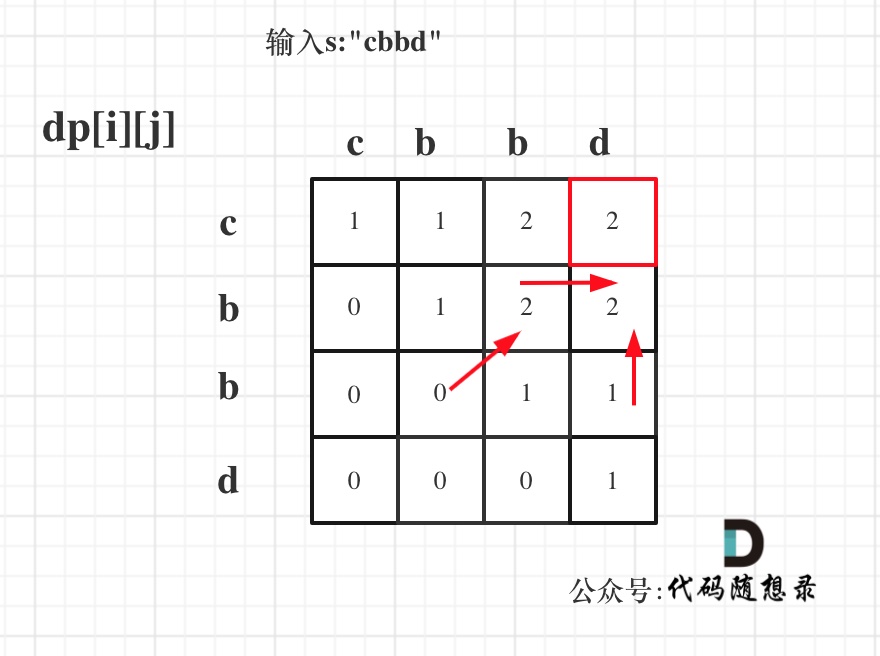
|
||||||
|
|
||||||
红色框即:dp[0][s.size() - 1]; 为最终结果。
|
红色框即:dp[0][s.size() - 1]; 为最终结果。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -136,7 +136,7 @@
|
||||||
|
|
||||||
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,如图红色部分:
|
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,如图红色部分:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
|
|
||||||
这里首先要关注的就是 dp[0][0] 应该是多少?
|
这里首先要关注的就是 dp[0][0] 应该是多少?
|
||||||
|
|
@ -296,7 +296,7 @@ for (int j = 0; j <= amount; j++) { // 遍历背包容量
|
||||||
|
|
||||||
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
|
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:
|
||||||
|
|
||||||
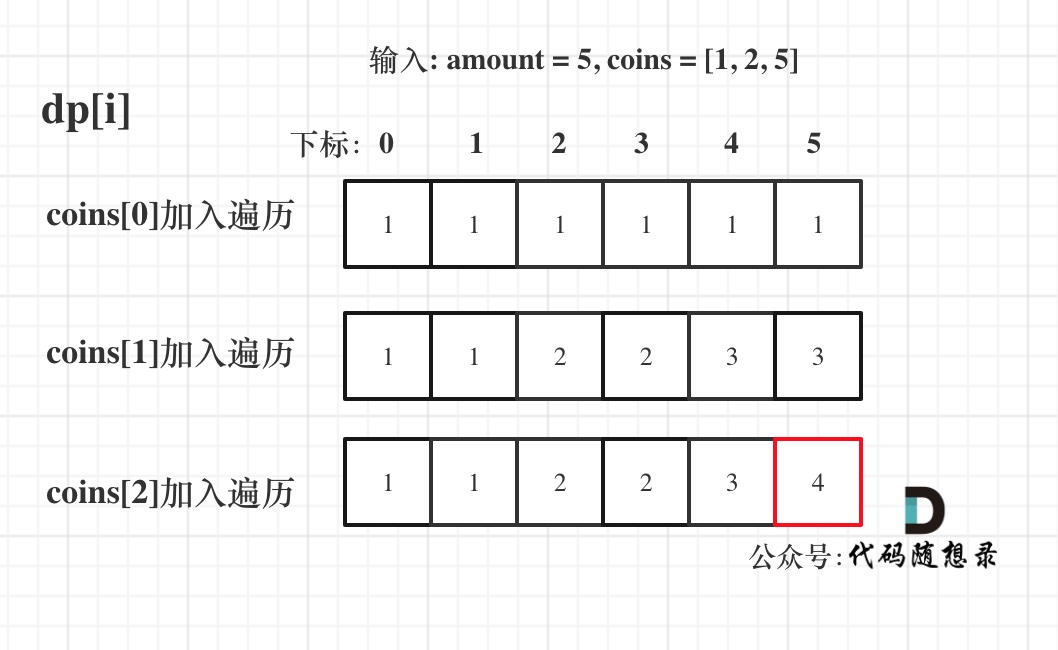
|
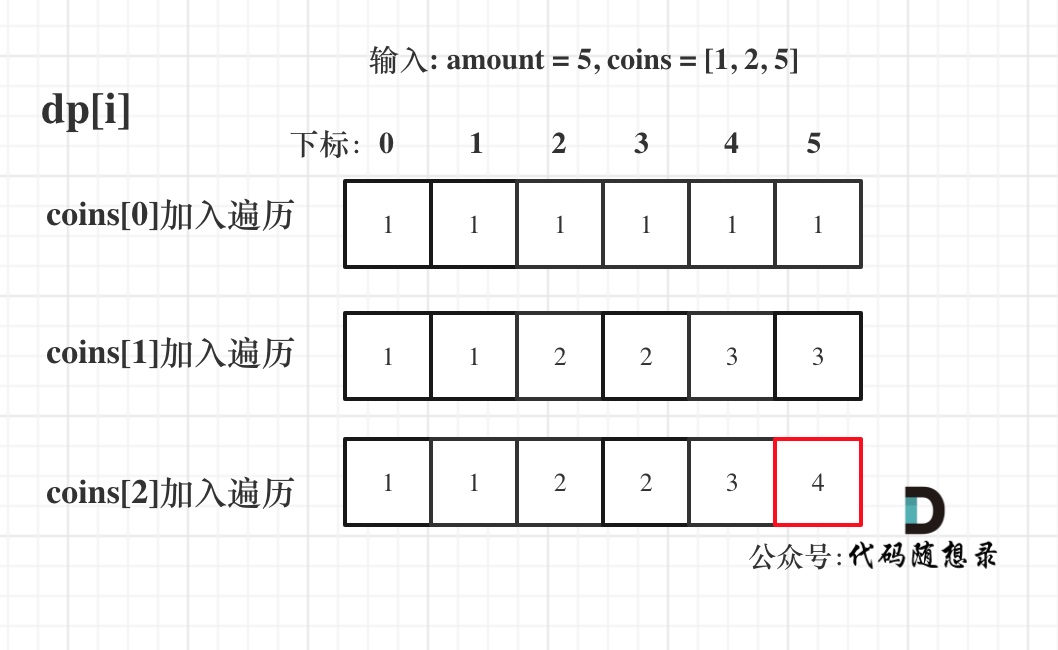
|
||||||
|
|
||||||
最后红色框dp[amount]为最终结果。
|
最后红色框dp[amount]为最终结果。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -13,7 +13,7 @@
|
||||||
|
|
||||||
示例:
|
示例:
|
||||||
|
|
||||||

|

|
||||||
|
|
||||||
提示:树中至少有 2 个节点。
|
提示:树中至少有 2 个节点。
|
||||||
|
|
||||||
|
|
@ -70,7 +70,7 @@ public:
|
||||||
|
|
||||||
如图:
|
如图:
|
||||||
|
|
||||||
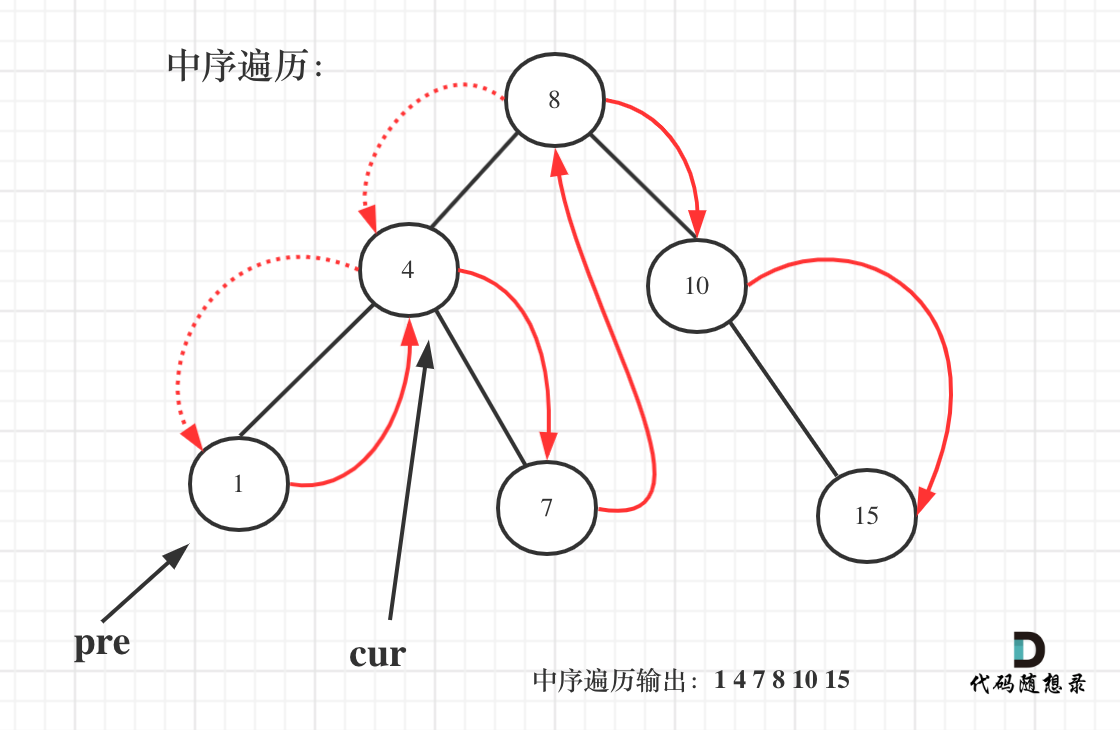
|
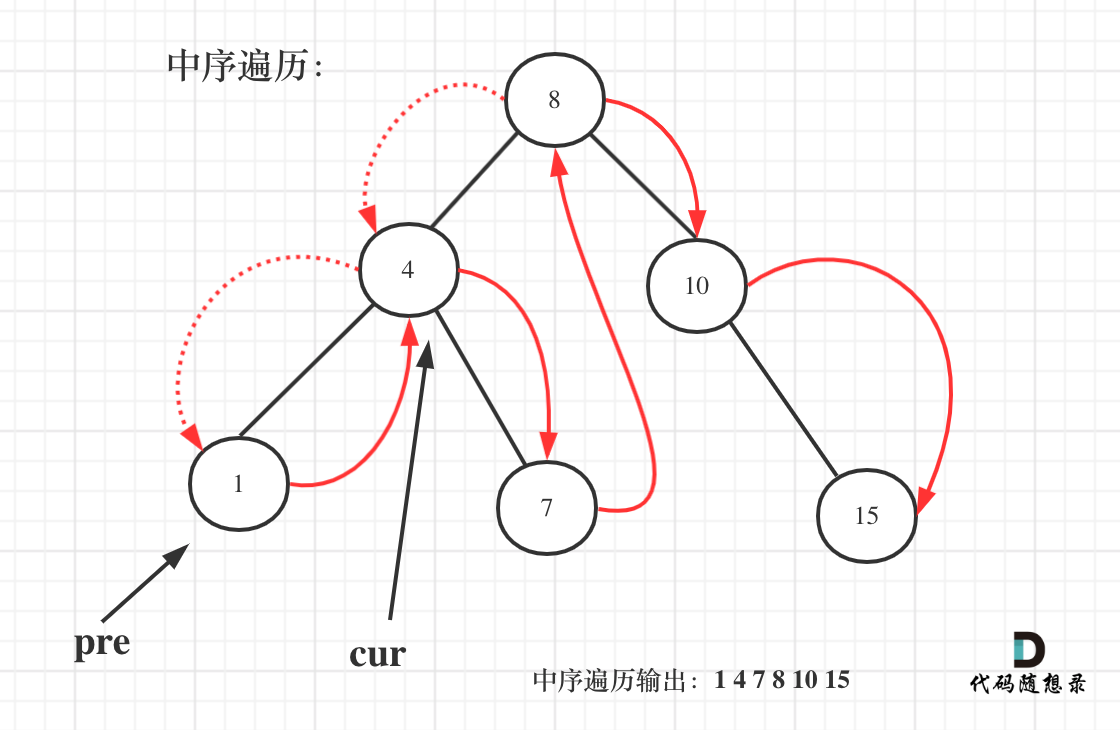
|
||||||
|
|
||||||
一些同学不知道在递归中如何记录前一个节点的指针,其实实现起来是很简单的,大家只要看过一次,写过一次,就掌握了。
|
一些同学不知道在递归中如何记录前一个节点的指针,其实实现起来是很简单的,大家只要看过一次,写过一次,就掌握了。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -18,7 +18,7 @@
|
||||||
示例 1:
|
示例 1:
|
||||||
|
|
||||||
|
|
||||||
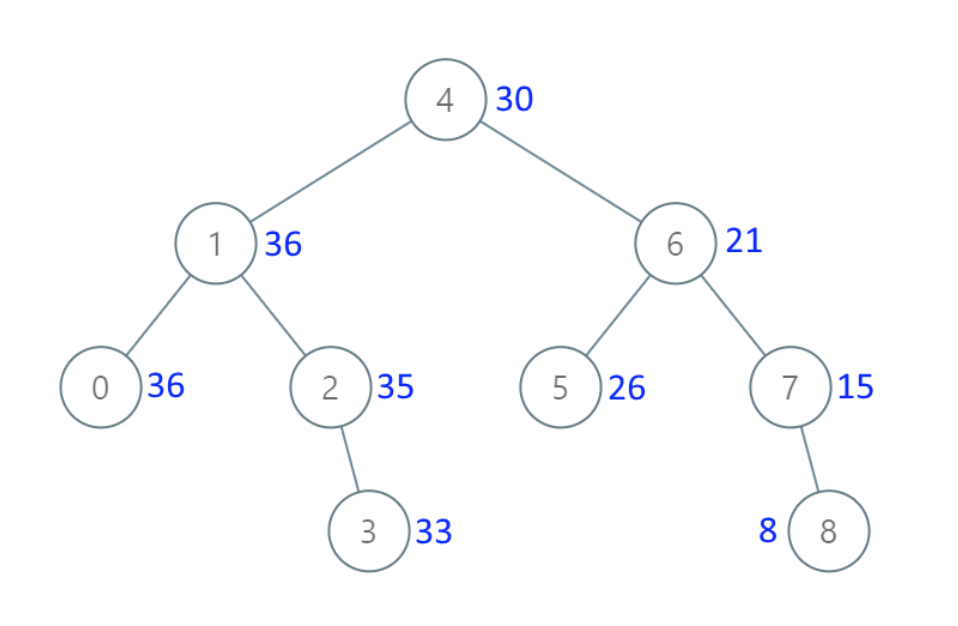
|
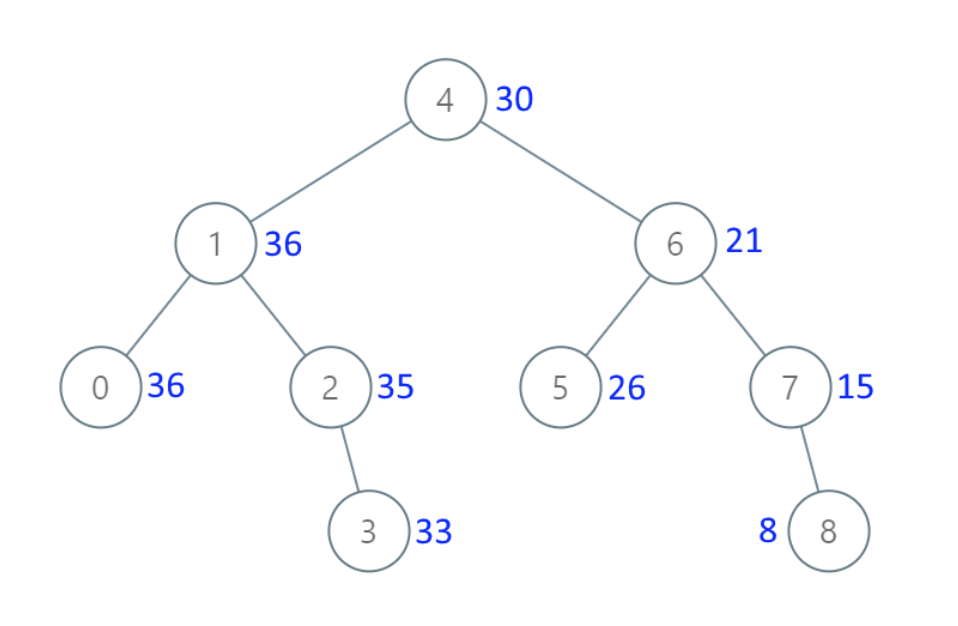
|
||||||
|
|
||||||
* 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
|
* 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
|
||||||
* 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
|
* 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
|
||||||
|
|
@ -67,7 +67,7 @@
|
||||||
遍历顺序如图所示:
|
遍历顺序如图所示:
|
||||||
|
|
||||||
|
|
||||||
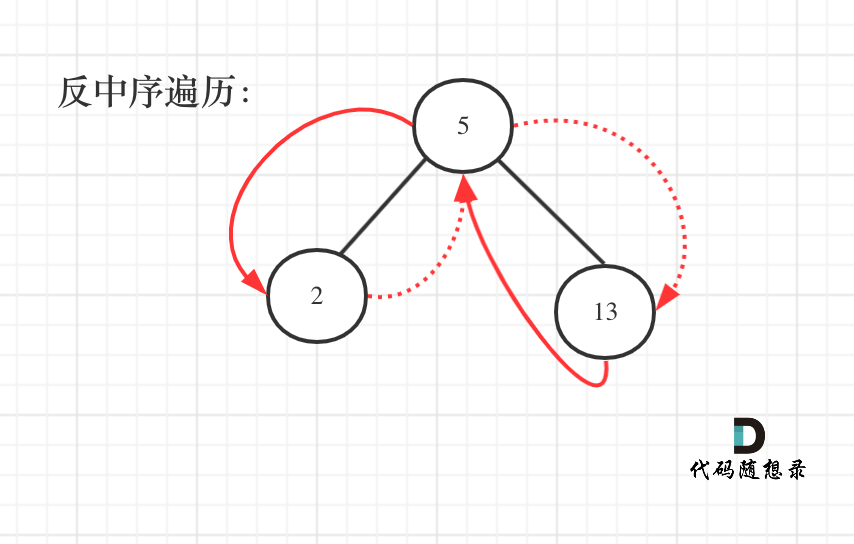
|
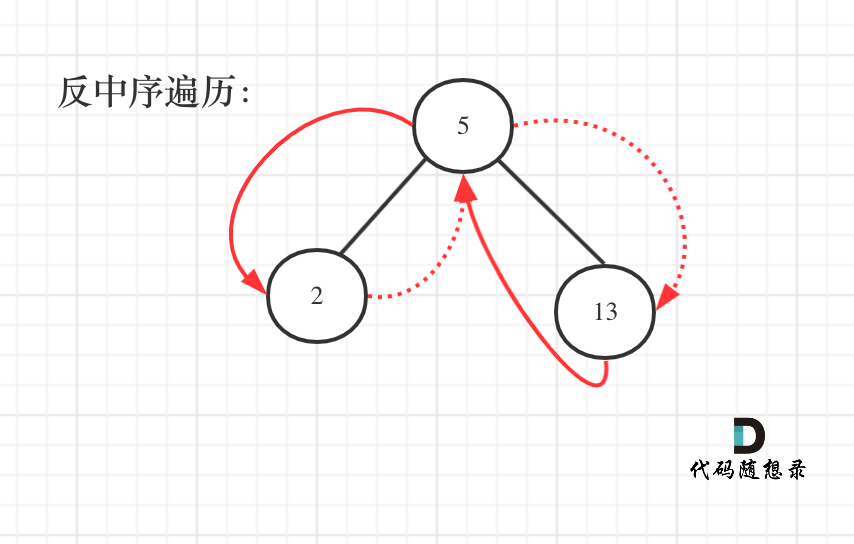
|
||||||
|
|
||||||
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
|
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
|
||||||
|
|
||||||
|
|
|
||||||
|
|
@ -81,7 +81,7 @@ for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
|
||||||
|
|
||||||
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
|
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
|
||||||
|
|
||||||
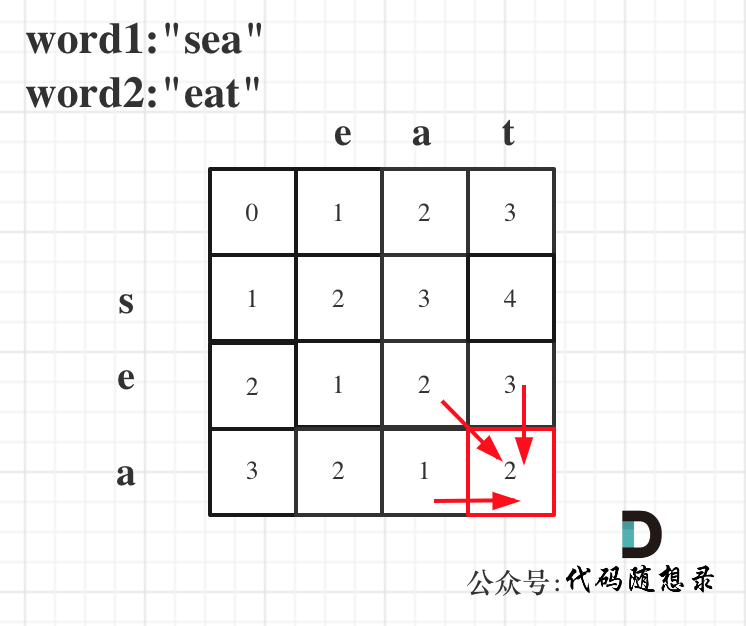
|
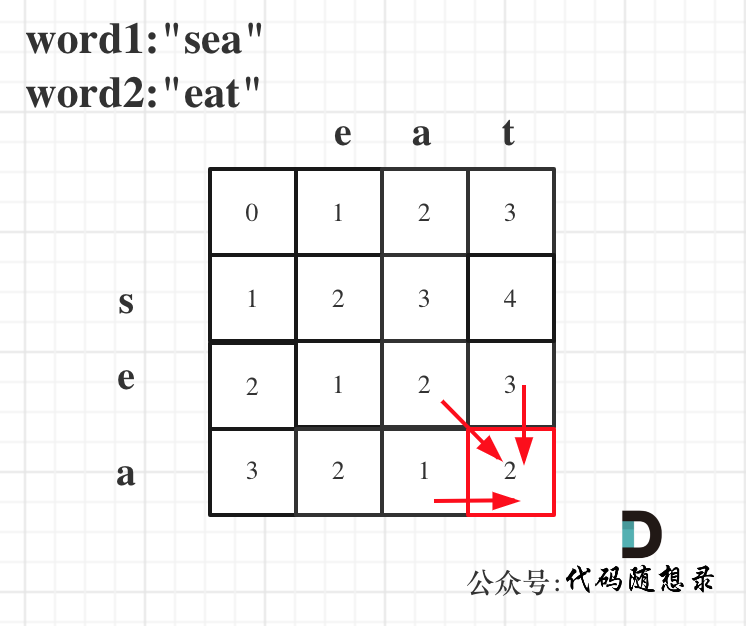
|
||||||
|
|
||||||
|
|
||||||
以上分析完毕,代码如下:
|
以上分析完毕,代码如下:
|
||||||
|
|
|
||||||
Some files were not shown because too many files have changed in this diff Show More
Loading…
Reference in New Issue