231 lines
7.4 KiB
Markdown
231 lines
7.4 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/RsdcQ9umo09R6cfnwXZlrQ"><img src="https://img.shields.io/badge/PDF下载-代码随想录-blueviolet" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||
</p>
|
||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
|
||
|
||
|
||
|
||
在[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)中,我们通过回溯搜索法,解决了n个数中求k个数的组合问题。
|
||
|
||
> 可以直接看我的B栈视频讲解:[带你学透回溯算法-组合问题的剪枝操作](https://www.bilibili.com/video/BV1wi4y157er)
|
||
|
||
文中的回溯法是可以剪枝优化的,本篇我们继续来看一下题目77. 组合。
|
||
|
||
链接:https://leetcode-cn.com/problems/combinations/
|
||
|
||
**看本篇之前,需要先看[回溯算法:求组合问题!](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)**。
|
||
|
||
大家先回忆一下[77. 组合]给出的回溯法的代码:
|
||
|
||
```
|
||
class Solution {
|
||
private:
|
||
vector<vector<int>> result; // 存放符合条件结果的集合
|
||
vector<int> path; // 用来存放符合条件结果
|
||
void backtracking(int n, int k, int startIndex) {
|
||
if (path.size() == k) {
|
||
result.push_back(path);
|
||
return;
|
||
}
|
||
for (int i = startIndex; i <= n; i++) {
|
||
path.push_back(i); // 处理节点
|
||
backtracking(n, k, i + 1); // 递归
|
||
path.pop_back(); // 回溯,撤销处理的节点
|
||
}
|
||
}
|
||
public:
|
||
vector<vector<int>> combine(int n, int k) {
|
||
result.clear(); // 可以不写
|
||
path.clear(); // 可以不写
|
||
backtracking(n, k, 1);
|
||
return result;
|
||
}
|
||
};
|
||
```
|
||
|
||
# 剪枝优化
|
||
|
||
我们说过,回溯法虽然是暴力搜索,但也有时候可以有点剪枝优化一下的。
|
||
|
||
在遍历的过程中有如下代码:
|
||
|
||
```
|
||
for (int i = startIndex; i <= n; i++) {
|
||
path.push_back(i);
|
||
backtracking(n, k, i + 1);
|
||
path.pop_back();
|
||
}
|
||
```
|
||
|
||
这个遍历的范围是可以剪枝优化的,怎么优化呢?
|
||
|
||
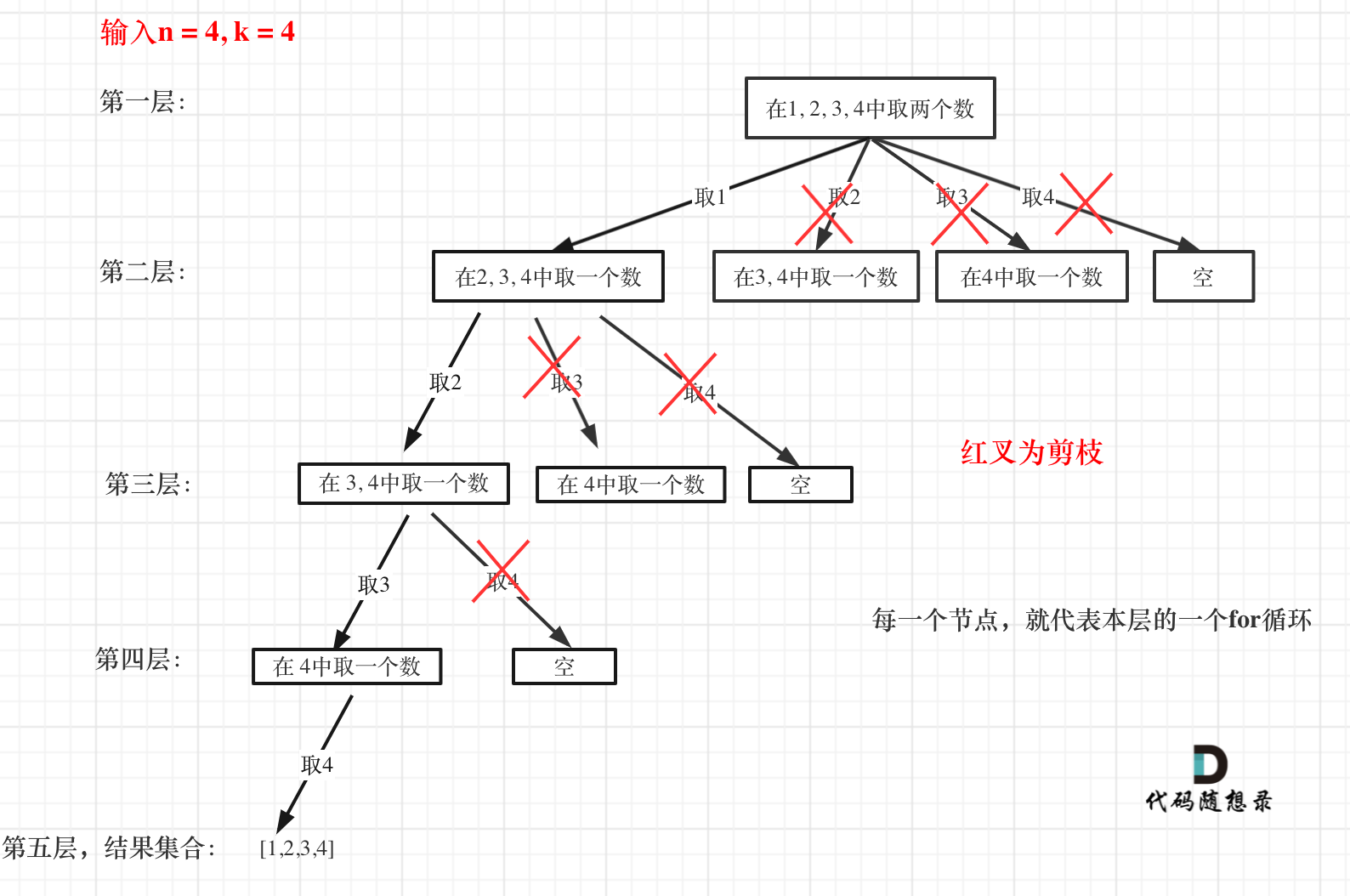
来举一个例子,n = 4,k = 4的话,那么第一层for循环的时候,从元素2开始的遍历都没有意义了。 在第二层for循环,从元素3开始的遍历都没有意义了。
|
||
|
||
这么说有点抽象,如图所示:
|
||
|
||
|
||
|
||
|
||
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
|
||
|
||
**所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置**。
|
||
|
||
**如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了**。
|
||
|
||
注意代码中i,就是for循环里选择的起始位置。
|
||
```
|
||
for (int i = startIndex; i <= n; i++) {
|
||
```
|
||
|
||
接下来看一下优化过程如下:
|
||
|
||
1. 已经选择的元素个数:path.size();
|
||
|
||
2. 还需要的元素个数为: k - path.size();
|
||
|
||
3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
|
||
|
||
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
|
||
|
||
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
|
||
|
||
从2开始搜索都是合理的,可以是组合[2, 3, 4]。
|
||
|
||
这里大家想不懂的话,建议也举一个例子,就知道是不是要+1了。
|
||
|
||
所以优化之后的for循环是:
|
||
|
||
```
|
||
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
|
||
```
|
||
|
||
优化后整体代码如下:
|
||
|
||
```
|
||
class Solution {
|
||
private:
|
||
vector<vector<int>> result;
|
||
vector<int> path;
|
||
void backtracking(int n, int k, int startIndex) {
|
||
if (path.size() == k) {
|
||
result.push_back(path);
|
||
return;
|
||
}
|
||
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
|
||
path.push_back(i); // 处理节点
|
||
backtracking(n, k, i + 1);
|
||
path.pop_back(); // 回溯,撤销处理的节点
|
||
}
|
||
}
|
||
public:
|
||
|
||
vector<vector<int>> combine(int n, int k) {
|
||
backtracking(n, k, 1);
|
||
return result;
|
||
}
|
||
};
|
||
```
|
||
|
||
# 总结
|
||
|
||
本篇我们准对求组合问题的回溯法代码做了剪枝优化,这个优化如果不画图的话,其实不好理解,也不好讲清楚。
|
||
|
||
所以我依然是把整个回溯过程抽象为一颗树形结构,然后可以直观的看出,剪枝究竟是剪的哪里。
|
||
|
||
**就酱,学到了就帮Carl转发一下吧,让更多的同学知道这里!**
|
||
|
||
|
||
|
||
|
||
|
||
## 其他语言版本
|
||
|
||
|
||
Java:
|
||
```
|
||
class Solution {
|
||
List<List<Integer>> result = new ArrayList<>();
|
||
LinkedList<Integer> path = new LinkedList<>();
|
||
public List<List<Integer>> combine(int n, int k) {
|
||
combineHelper(n, k, 1);
|
||
return result;
|
||
}
|
||
|
||
/**
|
||
* 每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围,就是要靠startIndex
|
||
* @param startIndex 用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。
|
||
*/
|
||
private void combineHelper(int n, int k, int startIndex){
|
||
//终止条件
|
||
if (path.size() == k){
|
||
result.add(new ArrayList<>(path));
|
||
return;
|
||
}
|
||
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){
|
||
path.add(i);
|
||
combineHelper(n, k, i + 1);
|
||
path.removeLast();
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
Python:
|
||
```python3
|
||
class Solution:
|
||
def combine(self, n: int, k: int) -> List[List[int]]:
|
||
res=[] #存放符合条件结果的集合
|
||
path=[] #用来存放符合条件结果
|
||
def backtrack(n,k,startIndex):
|
||
if len(path) == k:
|
||
res.append(path[:])
|
||
return
|
||
for i in range(startIndex,n-(k-len(path))+2): #优化的地方
|
||
path.append(i) #处理节点
|
||
backtrack(n,k,i+1) #递归
|
||
path.pop() #回溯,撤销处理的节点
|
||
backtrack(n,k,1)
|
||
return res
|
||
```
|
||
Go:
|
||
```Go
|
||
var res [][]int
|
||
func combine(n int, k int) [][]int {
|
||
res=[][]int{}
|
||
if n <= 0 || k <= 0 || k > n {
|
||
return res
|
||
}
|
||
backtrack(n, k, 1, []int{})
|
||
return res
|
||
}
|
||
func backtrack(n,k,start int,track []int){
|
||
if len(track)==k{
|
||
temp:=make([]int,k)
|
||
copy(temp,track)
|
||
res=append(res,temp)
|
||
}
|
||
if len(track)+n-start+1 < k {
|
||
return
|
||
}
|
||
for i:=start;i<=n;i++{
|
||
track=append(track,i)
|
||
backtrack(n,k,i+1,track)
|
||
track=track[:len(track)-1]
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
|
||
-----------------------
|
||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||
<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div>
|