335 lines
9.8 KiB
Markdown
335 lines
9.8 KiB
Markdown
<p align="center">
|
||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||
<img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20210924105952.png" width="1000"/>
|
||
</a>
|
||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
|
||
## 209.长度最小的子数组
|
||
|
||
[力扣题目链接](https://leetcode-cn.com/problems/minimum-size-subarray-sum/)
|
||
|
||
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。
|
||
|
||
示例:
|
||
|
||
输入:s = 7, nums = [2,3,1,2,4,3]
|
||
输出:2
|
||
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
|
||
|
||
|
||
## 暴力解法
|
||
|
||
这道题目暴力解法当然是 两个for循环,然后不断的寻找符合条件的子序列,时间复杂度很明显是$O(n^2)$。
|
||
|
||
代码如下:
|
||
|
||
```CPP
|
||
class Solution {
|
||
public:
|
||
int minSubArrayLen(int s, vector<int>& nums) {
|
||
int result = INT32_MAX; // 最终的结果
|
||
int sum = 0; // 子序列的数值之和
|
||
int subLength = 0; // 子序列的长度
|
||
for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
|
||
sum = 0;
|
||
for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
|
||
sum += nums[j];
|
||
if (sum >= s) { // 一旦发现子序列和超过了s,更新result
|
||
subLength = j - i + 1; // 取子序列的长度
|
||
result = result < subLength ? result : subLength;
|
||
break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break
|
||
}
|
||
}
|
||
}
|
||
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
|
||
return result == INT32_MAX ? 0 : result;
|
||
}
|
||
};
|
||
```
|
||
时间复杂度:$O(n^2)$
|
||
空间复杂度:$O(1)$
|
||
|
||
## 滑动窗口
|
||
|
||
接下来就开始介绍数组操作中另一个重要的方法:**滑动窗口**。
|
||
|
||
所谓滑动窗口,**就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果**。
|
||
|
||
这里还是以题目中的示例来举例,s=7, 数组是 2,3,1,2,4,3,来看一下查找的过程:
|
||
|
||

|
||
|
||
最后找到 4,3 是最短距离。
|
||
|
||
其实从动画中可以发现滑动窗口也可以理解为双指针法的一种!只不过这种解法更像是一个窗口的移动,所以叫做滑动窗口更适合一些。
|
||
|
||
在本题中实现滑动窗口,主要确定如下三点:
|
||
|
||
* 窗口内是什么?
|
||
* 如何移动窗口的起始位置?
|
||
* 如何移动窗口的结束位置?
|
||
|
||
窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。
|
||
|
||
窗口的起始位置如何移动:如果当前窗口的值大于s了,窗口就要向前移动了(也就是该缩小了)。
|
||
|
||
窗口的结束位置如何移动:窗口的结束位置就是遍历数组的指针,窗口的起始位置设置为数组的起始位置就可以了。
|
||
|
||
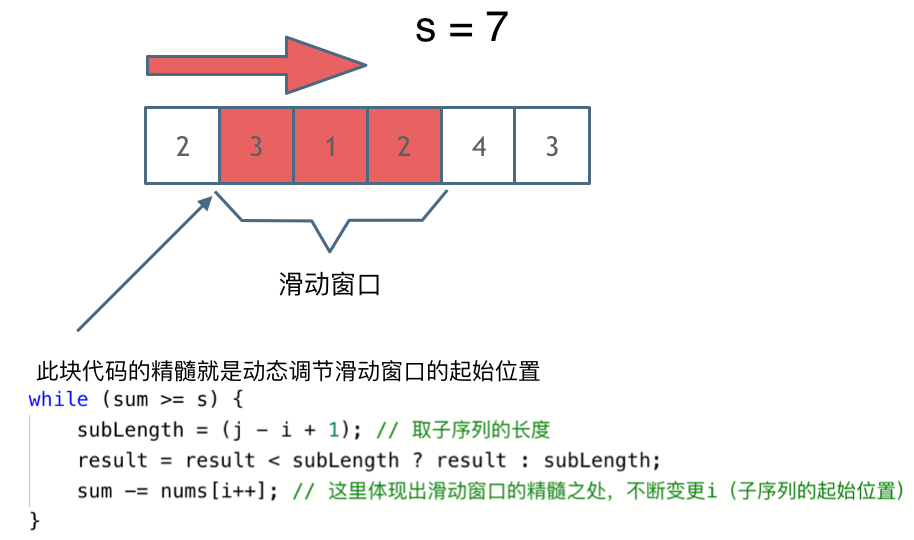
解题的关键在于 窗口的起始位置如何移动,如图所示:
|
||
|
||
|
||
|
||
可以发现**滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将$O(n^2)$的暴力解法降为$O(n)$。**
|
||
|
||
C++代码如下:
|
||
|
||
```CPP
|
||
class Solution {
|
||
public:
|
||
int minSubArrayLen(int s, vector<int>& nums) {
|
||
int result = INT32_MAX;
|
||
int sum = 0; // 滑动窗口数值之和
|
||
int i = 0; // 滑动窗口起始位置
|
||
int subLength = 0; // 滑动窗口的长度
|
||
for (int j = 0; j < nums.size(); j++) {
|
||
sum += nums[j];
|
||
// 注意这里使用while,每次更新 i(起始位置),并不断比较子序列是否符合条件
|
||
while (sum >= s) {
|
||
subLength = (j - i + 1); // 取子序列的长度
|
||
result = result < subLength ? result : subLength;
|
||
sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)
|
||
}
|
||
}
|
||
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
|
||
return result == INT32_MAX ? 0 : result;
|
||
}
|
||
};
|
||
```
|
||
|
||
时间复杂度:$O(n)$
|
||
空间复杂度:$O(1)$
|
||
|
||
**一些录友会疑惑为什么时间复杂度是$O(n)$**。
|
||
|
||
不要以为for里放一个while就以为是$O(n^2)$啊, 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被被操作两次,所以时间复杂度是 2 × n 也就是$O(n)$。
|
||
|
||
## 相关题目推荐
|
||
|
||
* [904.水果成篮](https://leetcode-cn.com/problems/fruit-into-baskets/)
|
||
* [76.最小覆盖子串](https://leetcode-cn.com/problems/minimum-window-substring/)
|
||
|
||
|
||
|
||
## 其他语言版本
|
||
|
||
|
||
Java:
|
||
```java
|
||
class Solution {
|
||
|
||
// 滑动窗口
|
||
public int minSubArrayLen(int s, int[] nums) {
|
||
int left = 0;
|
||
int sum = 0;
|
||
int result = Integer.MAX_VALUE;
|
||
for (int right = 0; right < nums.length; right++) {
|
||
sum += nums[right];
|
||
while (sum >= s) {
|
||
result = Math.min(result, right - left + 1);
|
||
sum -= nums[left++];
|
||
}
|
||
}
|
||
return result == Integer.MAX_VALUE ? 0 : result;
|
||
}
|
||
}
|
||
```
|
||
|
||
Python:
|
||
|
||
```python
|
||
class Solution:
|
||
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
|
||
# 定义一个无限大的数
|
||
res = float("inf")
|
||
Sum = 0
|
||
index = 0
|
||
for i in range(len(nums)):
|
||
Sum += nums[i]
|
||
while Sum >= s:
|
||
res = min(res, i-index+1)
|
||
Sum -= nums[index]
|
||
index += 1
|
||
return 0 if res==float("inf") else res
|
||
```
|
||
|
||
|
||
Go:
|
||
```go
|
||
func minSubArrayLen(target int, nums []int) int {
|
||
i := 0
|
||
l := len(nums) // 数组长度
|
||
sum := 0 // 子数组之和
|
||
result := l + 1 // 初始化返回长度为l+1,目的是为了判断“不存在符合条件的子数组,返回0”的情况
|
||
for j := 0; j < l; j++ {
|
||
sum += nums[j]
|
||
for sum >= target {
|
||
subLength := j - i + 1
|
||
if subLength < result {
|
||
result = subLength
|
||
}
|
||
sum -= nums[i]
|
||
i++
|
||
}
|
||
}
|
||
if result == l+1 {
|
||
return 0
|
||
} else {
|
||
return result
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
JavaScript:
|
||
|
||
```js
|
||
|
||
var minSubArrayLen = function(target, nums) {
|
||
// 长度计算一次
|
||
const len = nums.length;
|
||
let l = r = sum = 0,
|
||
res = len + 1; // 子数组最大不会超过自身
|
||
while(r < len) {
|
||
sum += nums[r++];
|
||
// 窗口滑动
|
||
while(sum >= target) {
|
||
// r始终为开区间 [l, r)
|
||
res = res < r - l ? res : r - l;
|
||
sum-=nums[l++];
|
||
}
|
||
}
|
||
return res > len ? 0 : res;
|
||
};
|
||
```
|
||
|
||
Typescript:
|
||
|
||
```typescript
|
||
function minSubArrayLen(target: number, nums: number[]): number {
|
||
let left: number = 0, right: number = 0;
|
||
let res: number = nums.length + 1;
|
||
let sum: number = 0;
|
||
while (right < nums.length) {
|
||
sum += nums[right];
|
||
if (sum >= target) {
|
||
// 不断移动左指针,直到不能再缩小为止
|
||
while (sum - nums[left] >= target) {
|
||
sum -= nums[left++];
|
||
}
|
||
res = Math.min(res, right - left + 1);
|
||
}
|
||
right++;
|
||
}
|
||
return res === nums.length + 1 ? 0 : res;
|
||
};
|
||
```
|
||
|
||
Swift:
|
||
|
||
```swift
|
||
func minSubArrayLen(_ target: Int, _ nums: [Int]) -> Int {
|
||
var result = Int.max
|
||
var sum = 0
|
||
var starIndex = 0
|
||
for endIndex in 0..<nums.count {
|
||
sum += nums[endIndex]
|
||
|
||
while sum >= target {
|
||
result = min(result, endIndex - starIndex + 1)
|
||
sum -= nums[starIndex]
|
||
starIndex += 1
|
||
}
|
||
}
|
||
|
||
return result == Int.max ? 0 : result
|
||
}
|
||
```
|
||
|
||
Rust:
|
||
|
||
```rust
|
||
impl Solution {
|
||
pub fn min_sub_array_len(target: i32, nums: Vec<i32>) -> i32 {
|
||
let (mut result, mut subLength): (i32, i32) = (i32::MAX, 0);
|
||
let (mut sum, mut i) = (0, 0);
|
||
|
||
for (pos, val) in nums.iter().enumerate() {
|
||
sum += val;
|
||
while sum >= target {
|
||
subLength = (pos - i + 1) as i32;
|
||
if result > subLength {
|
||
result = subLength;
|
||
}
|
||
sum -= nums[i];
|
||
i += 1;
|
||
}
|
||
}
|
||
if result == i32::MAX {
|
||
return 0;
|
||
}
|
||
result
|
||
}
|
||
}
|
||
```
|
||
|
||
PHP:
|
||
```php
|
||
// 双指针 - 滑动窗口
|
||
class Solution {
|
||
/**
|
||
* @param Integer $target
|
||
* @param Integer[] $nums
|
||
* @return Integer
|
||
*/
|
||
function minSubArrayLen($target, $nums) {
|
||
if (count($nums) < 1) {
|
||
return 0;
|
||
}
|
||
$sum = 0;
|
||
$res = PHP_INT_MAX;
|
||
$left = 0;
|
||
for ($right = 0; $right < count($nums); $right++) {
|
||
$sum += $nums[$right];
|
||
while ($sum >= $target) {
|
||
$res = min($res, $right - $left + 1);
|
||
$sum -= $nums[$left];
|
||
$left++;
|
||
}
|
||
}
|
||
return $res == PHP_INT_MAX ? 0 : $res;
|
||
}
|
||
}
|
||
```
|
||
|
||
Ruby:
|
||
|
||
```ruby
|
||
def min_sub_array_len(target, nums)
|
||
res = Float::INFINITY # 无穷大
|
||
i, sum = 0, 0
|
||
nums.length.times do |j|
|
||
sum += nums[j]
|
||
while sum >= target
|
||
res = [res, j - i + 1].min
|
||
sum -= nums[i]
|
||
i += 1
|
||
end
|
||
end
|
||
res == Float::INFINITY ? 0 : res
|
||
end
|
||
```
|
||
|
||
-----------------------
|
||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|