148 lines
4.9 KiB
Markdown
148 lines
4.9 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||
<a href="https://img-blog.csdnimg.cn/20201210231711160.png"><img src="https://img.shields.io/badge/公众号-代码随想录-brightgreen" alt=""></a>
|
||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||
</p>
|
||
<p align="center"><strong>欢迎大家参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
|
||
## 455.分发饼干
|
||
|
||
题目链接:https://leetcode-cn.com/problems/assign-cookies/
|
||
|
||
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
|
||
|
||
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
|
||
|
||
示例 1:
|
||
输入: g = [1,2,3], s = [1,1]
|
||
输出: 1
|
||
解释:
|
||
你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。
|
||
虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。
|
||
所以你应该输出1。
|
||
|
||
示例 2:
|
||
输入: g = [1,2], s = [1,2,3]
|
||
输出: 2
|
||
解释:
|
||
你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。
|
||
你拥有的饼干数量和尺寸都足以让所有孩子满足。
|
||
所以你应该输出2.
|
||
|
||
|
||
提示:
|
||
* 1 <= g.length <= 3 * 10^4
|
||
* 0 <= s.length <= 3 * 10^4
|
||
* 1 <= g[i], s[j] <= 2^31 - 1
|
||
|
||
|
||
## 思路
|
||
|
||
为了了满足更多的小孩,就不要造成饼干尺寸的浪费。
|
||
|
||
大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子,那么就应该优先满足胃口大的。
|
||
|
||
**这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩**。
|
||
|
||
可以尝试使用贪心策略,先将饼干数组和小孩数组排序。
|
||
|
||
然后从后向前遍历小孩数组,用大饼干优先满足胃口大的,并统计满足小孩数量。
|
||
|
||
如图:
|
||
|
||
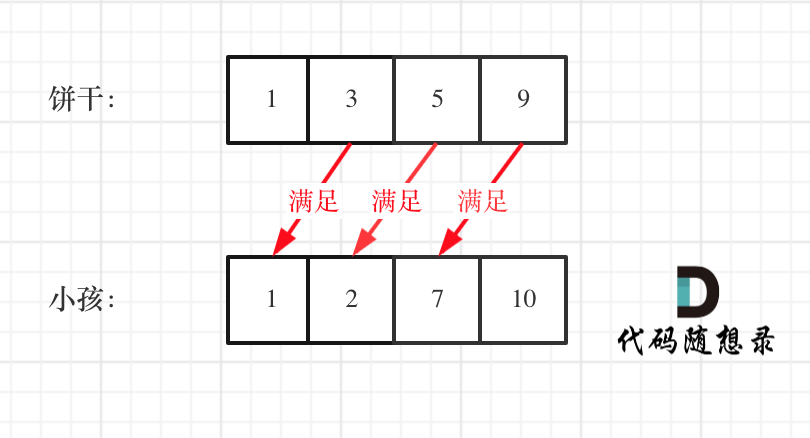
|
||
|
||
这个例子可以看出饼干9只有喂给胃口为7的小孩,这样才是整体最优解,并想不出反例,那么就可以撸代码了。
|
||
|
||
|
||
C++代码整体如下:
|
||
|
||
```C++
|
||
// 时间复杂度:O(nlogn)
|
||
// 空间复杂度:O(1)
|
||
class Solution {
|
||
public:
|
||
int findContentChildren(vector<int>& g, vector<int>& s) {
|
||
sort(g.begin(), g.end());
|
||
sort(s.begin(), s.end());
|
||
int index = s.size() - 1; // 饼干数组的下表
|
||
int result = 0;
|
||
for (int i = g.size() - 1; i >= 0; i--) {
|
||
if (index >= 0 && s[index] >= g[i]) {
|
||
result++;
|
||
index--;
|
||
}
|
||
}
|
||
return result;
|
||
}
|
||
};
|
||
```
|
||
|
||
从代码中可以看出我用了一个index来控制饼干数组的遍历,遍历饼干并没有再起一个for循环,而是采用自减的方式,这也是常用的技巧。
|
||
|
||
有的同学看到要遍历两个数组,就想到用两个for循环,那样逻辑其实就复杂了。
|
||
|
||
**也可以换一个思路,小饼干先喂饱小胃口**
|
||
|
||
代码如下:
|
||
|
||
```C++
|
||
class Solution {
|
||
public:
|
||
int findContentChildren(vector<int>& g, vector<int>& s) {
|
||
sort(g.begin(),g.end());
|
||
sort(s.begin(),s.end());
|
||
int index = 0;
|
||
for(int i = 0;i < s.size();++i){
|
||
if(index < g.size() && g[index] <= s[i]){
|
||
index++;
|
||
}
|
||
}
|
||
return index;
|
||
}
|
||
};
|
||
```
|
||
|
||
## 总结
|
||
|
||
这道题是贪心很好的一道入门题目,思路还是比较容易想到的。
|
||
|
||
文中详细介绍了思考的过程,**想清楚局部最优,想清楚全局最优,感觉局部最优是可以推出全局最优,并想不出反例,那么就试一试贪心**。
|
||
|
||
## 其他语言版本
|
||
|
||
|
||
Java:
|
||
```java
|
||
class Solution {
|
||
public int findContentChildren(int[] g, int[] s) {
|
||
Arrays.sort(g);
|
||
Arrays.sort(s);
|
||
int start = 0;
|
||
int count = 0;
|
||
for (int i = 0; i < s.length && start < g.length; i++) {
|
||
if (s[i] >= g[start]) {
|
||
start++;
|
||
count++;
|
||
}
|
||
}
|
||
return count;
|
||
}
|
||
}
|
||
```
|
||
|
||
Python:
|
||
|
||
|
||
Go:
|
||
|
||
|
||
|
||
|
||
-----------------------
|
||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||
<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div> |