325 lines
11 KiB
Markdown
325 lines
11 KiB
Markdown
|
||
看一下 算法4,深搜是怎么讲的
|
||
|
||
# 797.所有可能的路径
|
||
|
||
本题是一道 原汁原味的 深度优先搜索(dfs)模板题,那么用这道题目 来讲解 深搜最合适不过了。
|
||
|
||
接下来给大家详细讲解dfs:
|
||
|
||
## dfs 与 bfs 区别
|
||
|
||
先来了解dfs的过程,很多录友可能对dfs(深度优先搜索),bfs(广度优先搜索)分不清。
|
||
|
||
先给大家说一下两者大概的区别:
|
||
|
||
* dfs是可一个方向去搜,不到黄河不回头,直到遇到绝境了,搜不下去了,在换方向(换方向的过程就涉及到了回溯)。
|
||
* bfs是先把本节点所连接的所有节点遍历一遍,走到下一个节点的时候,再把连接节点的所有节点遍历一遍,搜索方向更像是广度,四面八方的搜索过程。
|
||
|
||
当然以上讲的是,大体可以这么理解,接下来 我们详细讲解dfs,(bfs在用单独一篇文章详细讲解)
|
||
|
||
## dfs 搜索过程
|
||
|
||
上面说道dfs是可一个方向搜,不到黄河不回头。 那么我们来举一个例子。
|
||
|
||
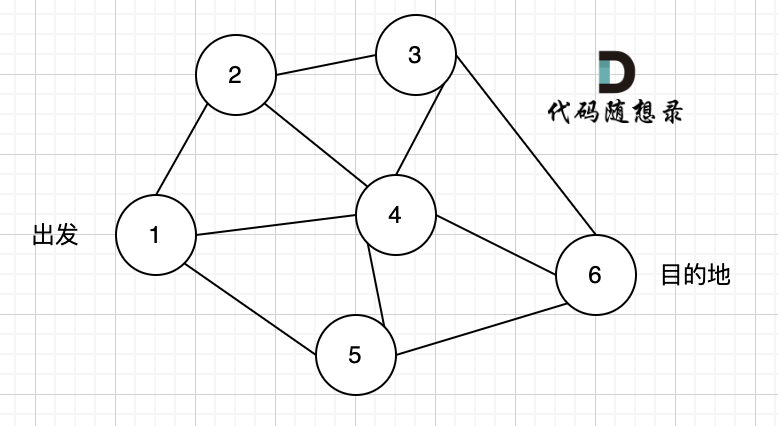
如图一,是一个无向图,我们要搜索从节点1到节点6的所有路径。
|
||
|
||
|
||
|
||
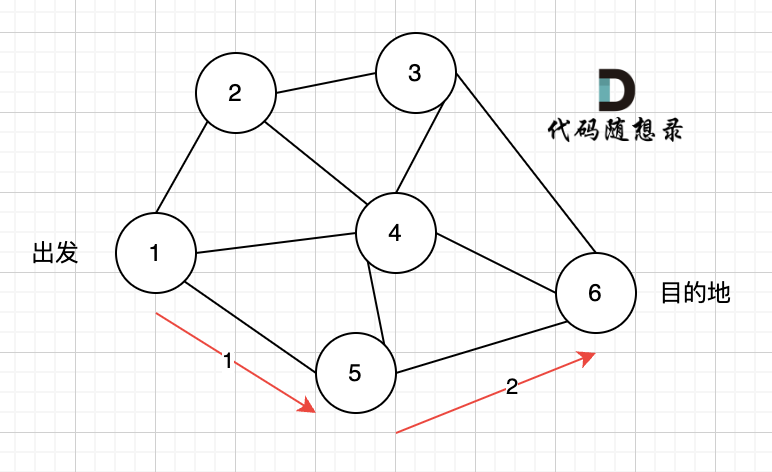
那么dfs搜索的第一条路径是这样的: (假设第一次延默认方向,就找到了节点6),图二
|
||
|
||
|
||
|
||
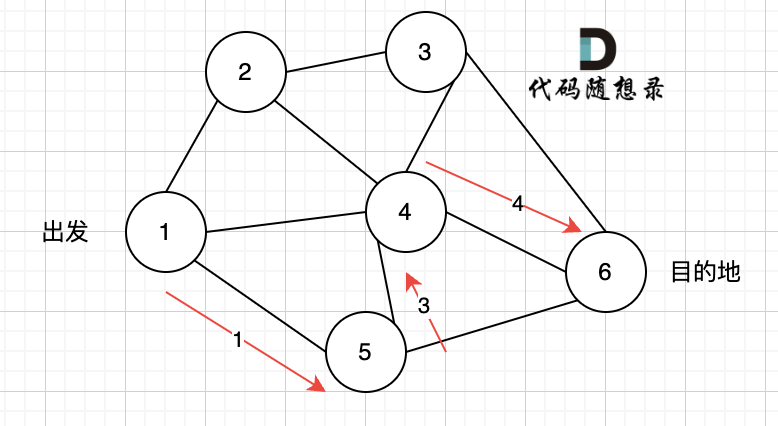
此时我们找到了节点6,(遇到黄河了,是不是应该回头了),那么应该再去搜索其他方向了。 如图三:
|
||
|
||
|
||
|
||
路径2撤销了,改变了方向,走路径3(红色线), 接着也找到终点6。 那么撤销路径2,改为路径3,在dfs中其实就是回溯的过程(这一点很重要,很多录友,都不理解dfs代码中回溯是用来干什么的)
|
||
|
||
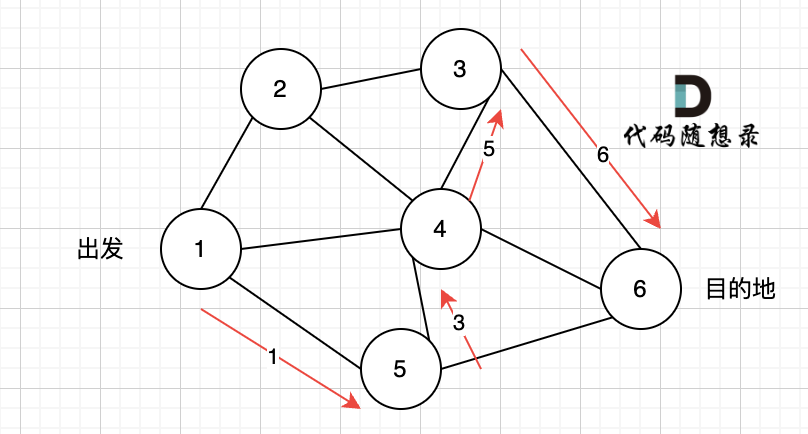
又找到了一条从节点1到节点6的路径,又到黄河了,此时再回头,下图图四中,路径4撤销(回溯的过程),改为路径5。
|
||
|
||
|
||
|
||
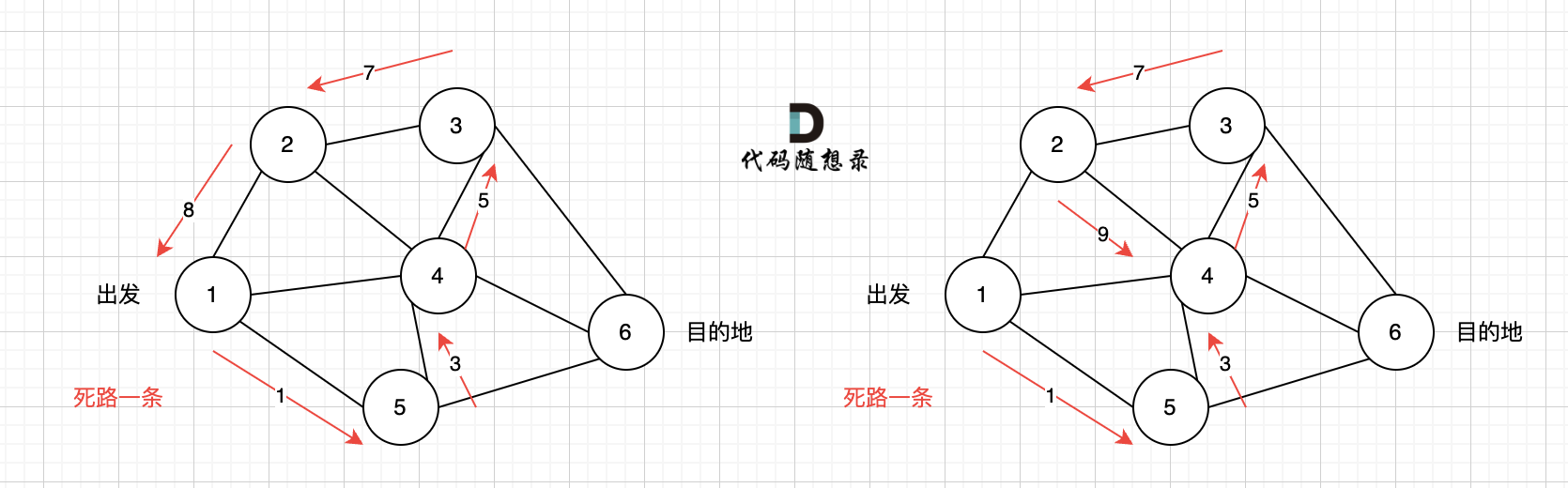
又找到了一条从节点1到节点6的路径,又到黄河了,此时再回头,下图图五,路径6撤销(回溯的过程),改为路径7,路径8 和 路径7,路径9, 结果发现死路一条,都走到了自己走过的节点。
|
||
|
||
|
||
|
||
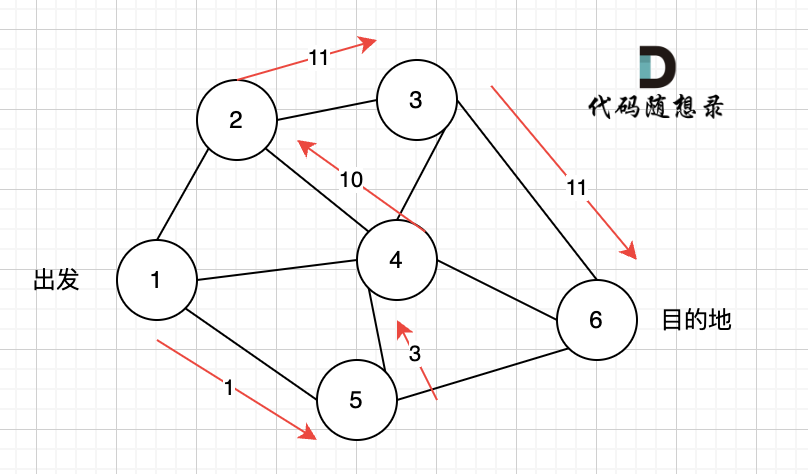
那么节点2所连接路径和节点3所链接的路径 都走过了,撤销路径只能向上回退,去选择撤销当初节点4的选择,也就是撤销路径5,改为路径10 。 如图图六:
|
||
|
||
|
||
|
||
|
||
上图演示中,其实我并没有把 所有的 从节点1 到节点6的dfs(深度优先搜索)的过程都画出来,那样太冗余了,但 已经把dfs 关键的地方都涉及到了,关键就两点:
|
||
|
||
* 搜索方向,是认准一个方向搜,直到碰壁之后在换方向
|
||
* 换方向是撤销原路径,改为节点链接的下一个路径,回溯的过程。
|
||
|
||
|
||
## 代码框架
|
||
|
||
正式因为dfs搜索可一个方向,并需要回溯,所以用递归的方式来实现是最方便的。
|
||
|
||
很多录友对回溯很陌生,建议先看看码随想录,[回溯算法章节](https://programmercarl.com/回溯算法理论基础.html)。
|
||
|
||
有递归的地方就有回溯,那么回溯在哪里呢?
|
||
|
||
就地递归函数的下面,例如如下代码:
|
||
```
|
||
void dfs(参数) {
|
||
处理节点
|
||
dfs(图,选择的节点); // 递归
|
||
回溯,撤销处理结果
|
||
}
|
||
```
|
||
|
||
可以看到回溯操作就在递归函数的下面,递归和回溯是相辅相成的。
|
||
|
||
在讲解[二叉树章节](https://programmercarl.com/二叉树理论基础.html)的时候,二叉树的递归法其实就是dfs,而二叉树的迭代法,就是bfs(广度优先搜索)
|
||
|
||
所以**dfs,bfs其实是基础搜索算法,也广泛应用与其他数据结构与算法中**。
|
||
|
||
我们在回顾一下[回溯法](https://programmercarl.com/回溯算法理论基础.html)的代码框架:
|
||
|
||
```
|
||
void backtracking(参数) {
|
||
if (终止条件) {
|
||
存放结果;
|
||
return;
|
||
}
|
||
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
|
||
处理节点;
|
||
backtracking(路径,选择列表); // 递归
|
||
回溯,撤销处理结果
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
回溯算法,其实就是dfs的过程,这里给出dfs的代码框架:
|
||
|
||
```
|
||
void dfs(参数) {
|
||
if (终止条件) {
|
||
存放结果;
|
||
return;
|
||
}
|
||
|
||
for (选择:本节点所连接的其他节点) {
|
||
处理节点;
|
||
dfs(图,选择的节点); // 递归
|
||
回溯,撤销处理结果
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
可以发现dfs的代码框架和回溯算法的代码框架是差不多的。
|
||
|
||
下面我在用 深搜三部曲,来解读 dfs的代码框架。
|
||
|
||
## 深搜三部曲
|
||
|
||
在 [二叉树递归讲解](https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E9%80%92%E5%BD%92%E9%81%8D%E5%8E%86.html)中,给出了递归三部曲。
|
||
|
||
[回溯算法](https://programmercarl.com/回溯算法理论基础.html)讲解中,给出了 回溯三部曲。
|
||
|
||
其实深搜也是一样的,深搜三部曲如下:
|
||
|
||
1. 确认递归函数,参数
|
||
|
||
```
|
||
void dfs(参数)
|
||
```
|
||
|
||
通常我们递归的时候,我们递归搜索需要了解哪些参数,其实也可以在写递归函数的时候,发现需要什么参数,再去补充就可以。
|
||
|
||
一般情况,深搜需要 二维数组数组结构保存所有路径,需要一维数组保存单一路径,这种保存结果的数组,我们可以定义一个全局遍历,避免让我们的函数参数过多。
|
||
|
||
例如这样:
|
||
|
||
```
|
||
vector<vector<int>> result; // 保存符合条件的所有路径
|
||
vector<int> path; // 起点到终点的路径
|
||
void dfs (图,目前搜索的节点)
|
||
```
|
||
|
||
但这种写法看个人习惯,不强求。
|
||
|
||
2. 确认终止条件
|
||
|
||
终止条件很重要,很多同学写dfs的时候,之所以容易死循环,栈溢出等等这些问题,都是因为终止条件没有想清楚。
|
||
|
||
```
|
||
if (终止条件) {
|
||
存放结果;
|
||
return;
|
||
}
|
||
```
|
||
|
||
终止添加不仅是结束本层递归,同时也是我们收获结果的时候。
|
||
|
||
另外,其实很多dfs写法,没有写终止条件,其实终止条件写在了, 下面dfs递归的逻辑里了,也就是不符合条件,直接不会向下递归。这里如果大家不理解的话,没关系,后面会有具体题目来讲解。
|
||
* 841.钥匙和房间
|
||
* 200. 岛屿数量
|
||
|
||
3. 处理目前搜索节点出发的路径
|
||
|
||
一般这里就是一个for循环的操作,去遍历 目前搜索节点 所能到的所有节点。
|
||
|
||
```
|
||
for (选择:本节点所连接的其他节点) {
|
||
处理节点;
|
||
dfs(图,选择的节点); // 递归
|
||
回溯,撤销处理结果
|
||
}
|
||
```
|
||
|
||
不少录友疑惑的地方,都是 dfs代码框架中for循环里分明已经处理节点了,那么 dfs函数下面 为什么还要撤销的呢。
|
||
|
||
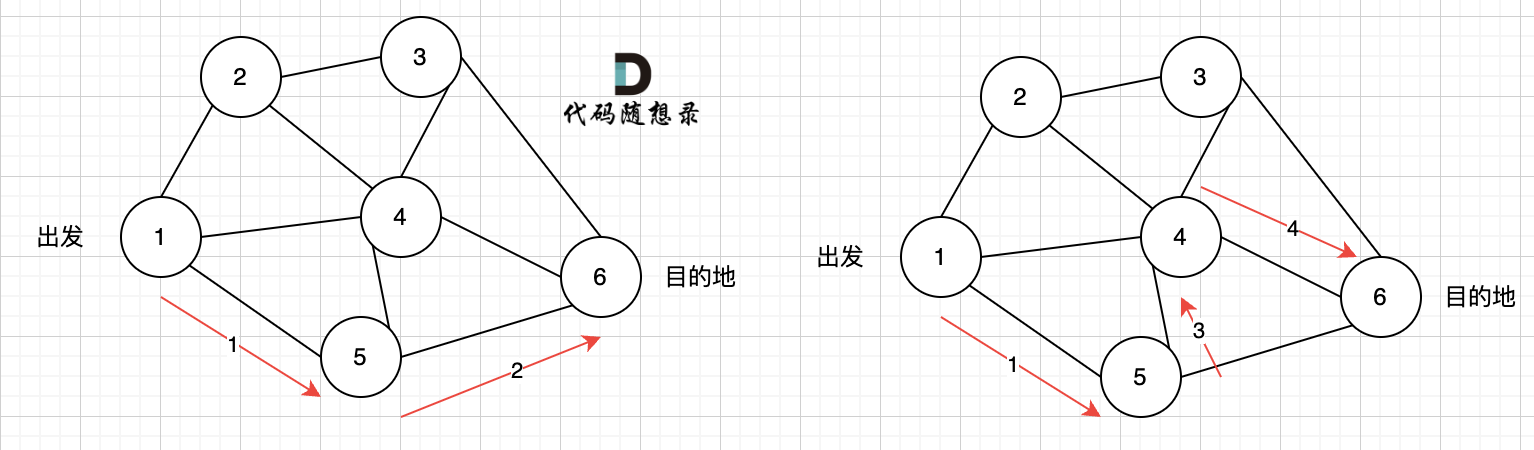
如图七所示, 路径2 已经走到了 目的地节点6,那么 路径2 是如何撤销,然后改为 路径3呢? 其实这就是 回溯的过程,撤销路径2,走换下一个方向。
|
||
|
||
|
||
|
||
|
||
## 总结
|
||
|
||
我们讲解了,dfs 和 bfs的大体区别(bfs详细过程下篇来讲),dfs的搜索过程以及代码框架。
|
||
|
||
最后还有 深搜三部曲来解读这份代码框架。
|
||
|
||
以上如果大家都能理解了,其实搜索的代码就很好写,具体题目套用具体场景就可以了。
|
||
|
||
## 797. 所有可能的路径
|
||
|
||
### 思路
|
||
|
||
1. 确认递归函数,参数
|
||
|
||
首先我们dfs函数一定要存一个图,用来遍历的,还要存一个目前我们遍历的节点,定义为x
|
||
|
||
至于 单一路径,和路径集合可以放在全局变量,那么代码是这样的:
|
||
|
||
```c++
|
||
vector<vector<int>> result; // 收集符合条件的路径
|
||
vector<int> path; // 0节点到终点的路径
|
||
// x:目前遍历的节点
|
||
// graph:存当前的图
|
||
void dfs (vector<vector<int>>& graph, int x)
|
||
```
|
||
|
||
2. 确认终止条件
|
||
|
||
什么时候我们就找到一条路径了?
|
||
|
||
当目前遍历的节点 为 最后一个节点的时候,就找到了一条,从 出发点到终止点的路径。
|
||
|
||
当前遍历的节点,我们定义为x,最后一点节点,就是 graph.size() - 1。
|
||
|
||
所以 但 x 等于 graph.size() - 1 的时候就找到一条有效路径。 代码如下:
|
||
|
||
|
||
```c++
|
||
// 要求从节点 0 到节点 n-1 的路径并输出,所以是 graph.size() - 1
|
||
if (x == graph.size() - 1) { // 找到符合条件的一条路径
|
||
result.push_back(path); // 收集有效路径
|
||
return;
|
||
}
|
||
```
|
||
|
||
3. 处理目前搜索节点出发的路径
|
||
|
||
接下来是走 当前遍历节点x的下一个节点。
|
||
|
||
首先是要找到 x节点链接了哪些节点呢? 遍历方式是这样的:
|
||
|
||
```c++
|
||
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
|
||
```
|
||
|
||
接下来就是将 选中的x所连接的节点,加入到 单一路劲来。
|
||
|
||
```C++
|
||
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
|
||
|
||
```
|
||
|
||
当前遍历的节点就是 `graph[x][i]` 了,所以进入下一层递归
|
||
|
||
```C++
|
||
dfs(graph, graph[x][i]); // 进入下一层递归
|
||
```
|
||
|
||
最后就是回溯的过程,撤销本次添加节点的操作。 该过程整体代码:
|
||
|
||
```C++
|
||
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
|
||
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
|
||
dfs(graph, graph[x][i]); // 进入下一层递归
|
||
path.pop_back(); // 回溯,撤销本节点
|
||
}
|
||
```
|
||
|
||
|
||
### 本题代码
|
||
|
||
```c++
|
||
class Solution {
|
||
private:
|
||
vector<vector<int>> result; // 收集符合条件的路径
|
||
vector<int> path; // 0节点到终点的路径
|
||
// x:目前遍历的节点
|
||
// graph:存当前的图
|
||
void dfs (vector<vector<int>>& graph, int x) {
|
||
// 要求从节点 0 到节点 n-1 的路径并输出,所以是 graph.size() - 1
|
||
if (x == graph.size() - 1) { // 找到符合条件的一条路径
|
||
result.push_back(path);
|
||
return;
|
||
}
|
||
for (int i = 0; i < graph[x].size(); i++) { // 遍历节点n链接的所有节点
|
||
path.push_back(graph[x][i]); // 遍历到的节点加入到路径中来
|
||
dfs(graph, graph[x][i]); // 进入下一层递归
|
||
path.pop_back(); // 回溯,撤销本节点
|
||
}
|
||
}
|
||
public:
|
||
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
|
||
path.push_back(0); // 无论什么路径已经是从0节点出发
|
||
dfs(graph, 0); // 开始遍历
|
||
return result;
|
||
}
|
||
};
|
||
|
||
```
|
||
|
||
## 其他语言版本
|
||
|
||
### Java
|
||
|
||
### Python
|
||
```python
|
||
class Solution:
|
||
def __init__(self):
|
||
self.result = []
|
||
self.path = [0]
|
||
|
||
def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
|
||
if not graph: return []
|
||
|
||
self.dfs(graph, 0)
|
||
return self.result
|
||
|
||
def dfs(self, graph, root: int):
|
||
if root == len(graph) - 1: # 成功找到一条路径时
|
||
# ***Python的list是mutable类型***
|
||
# ***回溯中必须使用Deep Copy***
|
||
self.result.append(self.path[:])
|
||
return
|
||
|
||
for node in graph[root]: # 遍历节点n的所有后序节点
|
||
self.path.append(node)
|
||
self.dfs(graph, node)
|
||
self.path.pop() # 回溯
|
||
```
|
||
|
||
### Go
|