98 lines
4.9 KiB
Markdown
98 lines
4.9 KiB
Markdown
|
||
|
||
# 本周小结!(回溯算法系列三)
|
||
|
||
## 周一
|
||
|
||
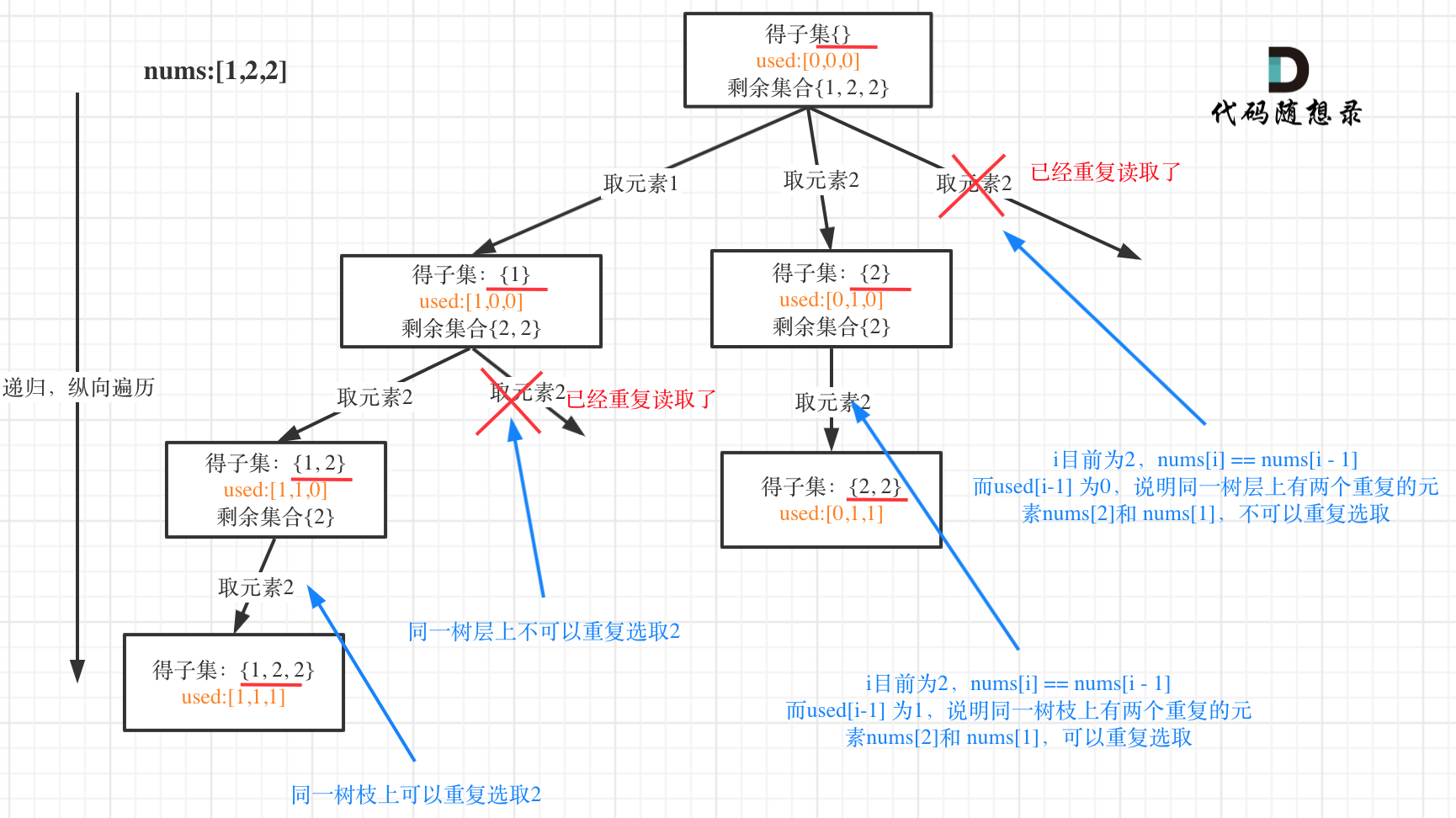
在[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)中,开始针对子集问题进行去重。
|
||
|
||
本题就是[回溯算法:求子集问题!](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)的基础上加上了去重,去重我们在[回溯算法:求组合总和(三)](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)也讲过了。
|
||
|
||
所以本题对大家应该并不难。
|
||
|
||
树形结构如下:
|
||
|
||
|
||
|
||
## 周二
|
||
|
||
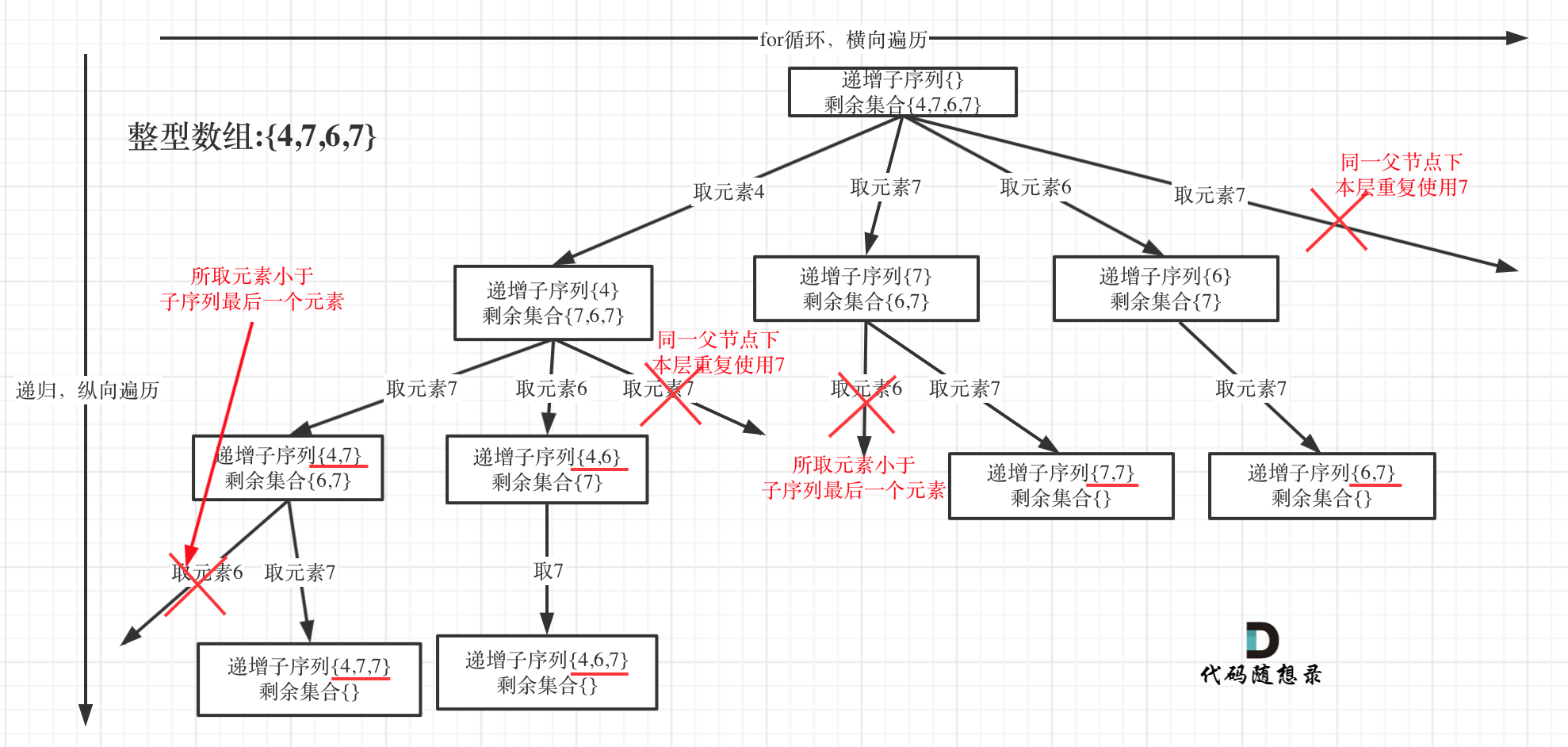
在[回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)中,处处都能看到子集的身影,但处处是陷阱,值得好好琢磨琢磨!
|
||
|
||
树形结构如下:
|
||
|
||
|
||
[回溯算法:递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)留言区大家有很多疑问,主要还是和[回溯算法:求子集问题(二)](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)混合在了一起。
|
||
|
||
详细在[本周小结!(回溯算法系列三)续集](https://mp.weixin.qq.com/s/kSMGHc_YpsqL2j-jb_E_Ag)中给出了介绍!
|
||
|
||
## 周三
|
||
|
||
我们已经分析了组合问题,分割问题,子集问题,那么[回溯算法:排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw) 又不一样了。
|
||
|
||
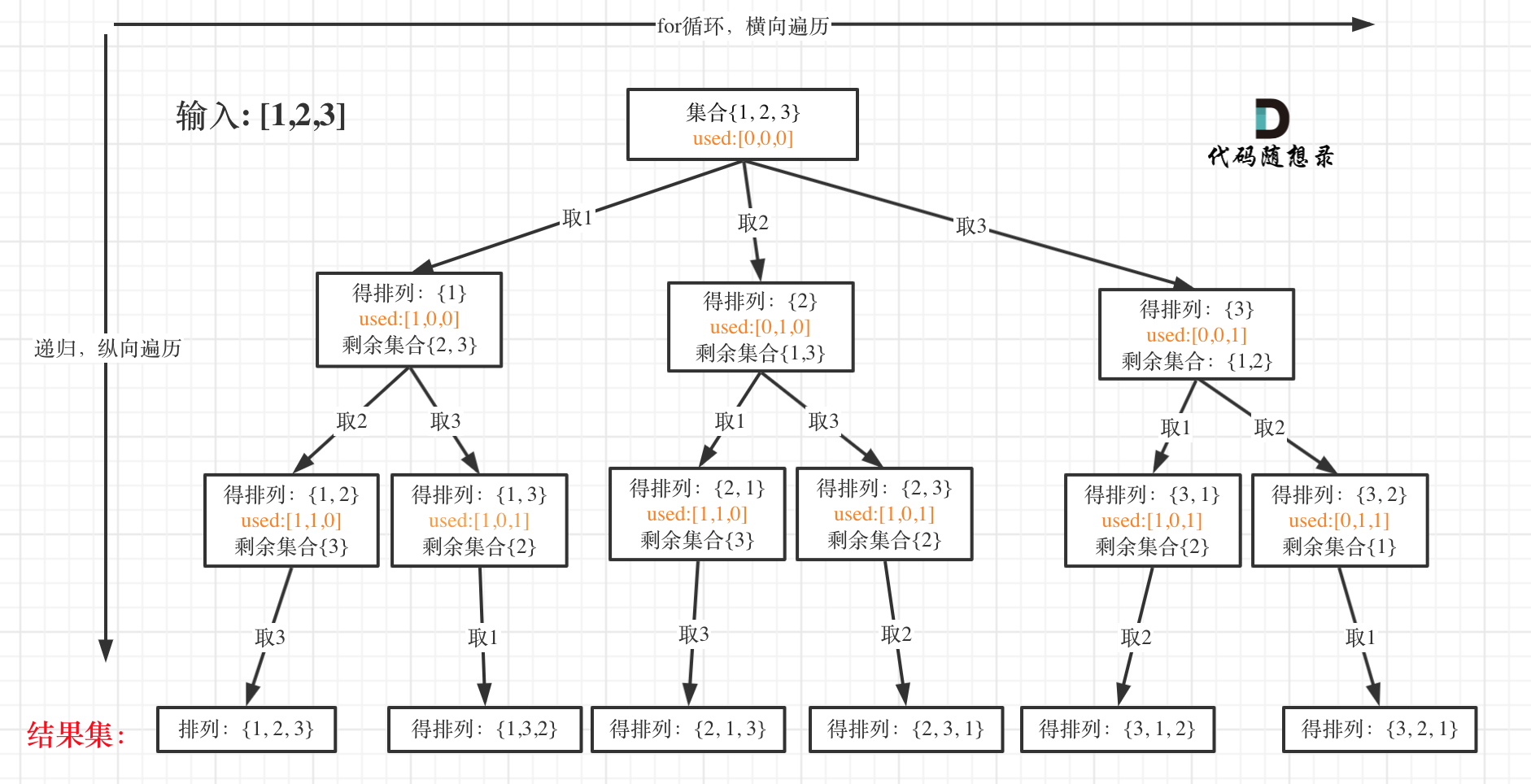
排列是有序的,也就是说[1,2] 和[2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方。
|
||
|
||
可以看出元素1在[1,2]中已经使用过了,但是在[2,1]中还要在使用一次1,所以处理排列问题就不用使用startIndex了。
|
||
|
||
如图:
|
||
|
||
|
||
**大家此时可以感受出排列问题的不同:**
|
||
|
||
* 每层都是从0开始搜索而不是startIndex
|
||
* 需要used数组记录path里都放了哪些元素了
|
||
|
||
## 周四
|
||
|
||
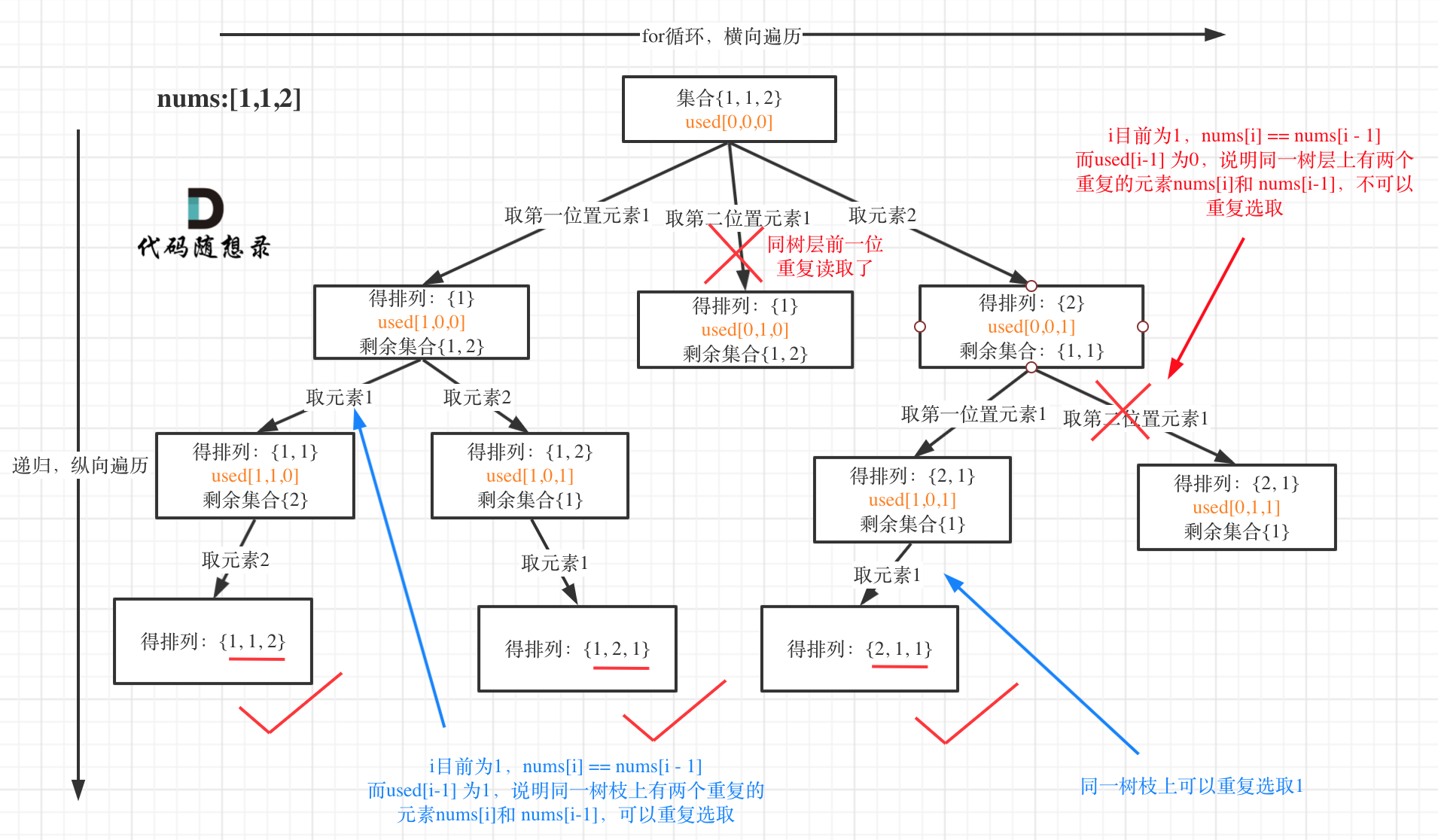
排列问题也要去重了,在[回溯算法:排列问题(二)](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)中又一次强调了“树层去重”和“树枝去重”。
|
||
|
||
树形结构如下:
|
||
|
||
|
||
|
||
**这道题目神奇的地方就是used[i - 1] == false也可以,used[i - 1] == true也可以!**
|
||
|
||
我就用输入: [1,1,1] 来举一个例子。
|
||
|
||
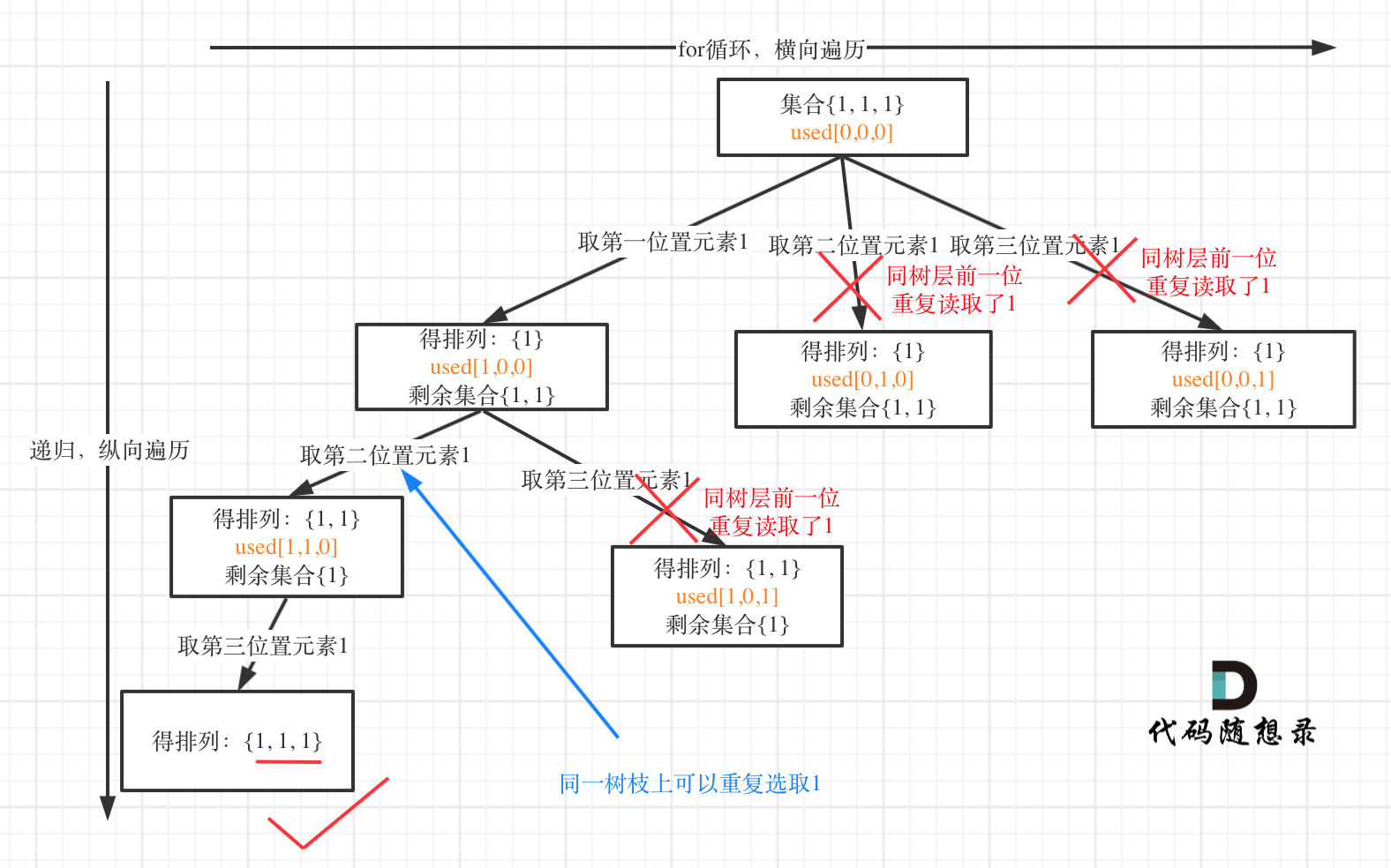
树层上去重(used[i - 1] == false),的树形结构如下:
|
||
|
||
|
||
|
||
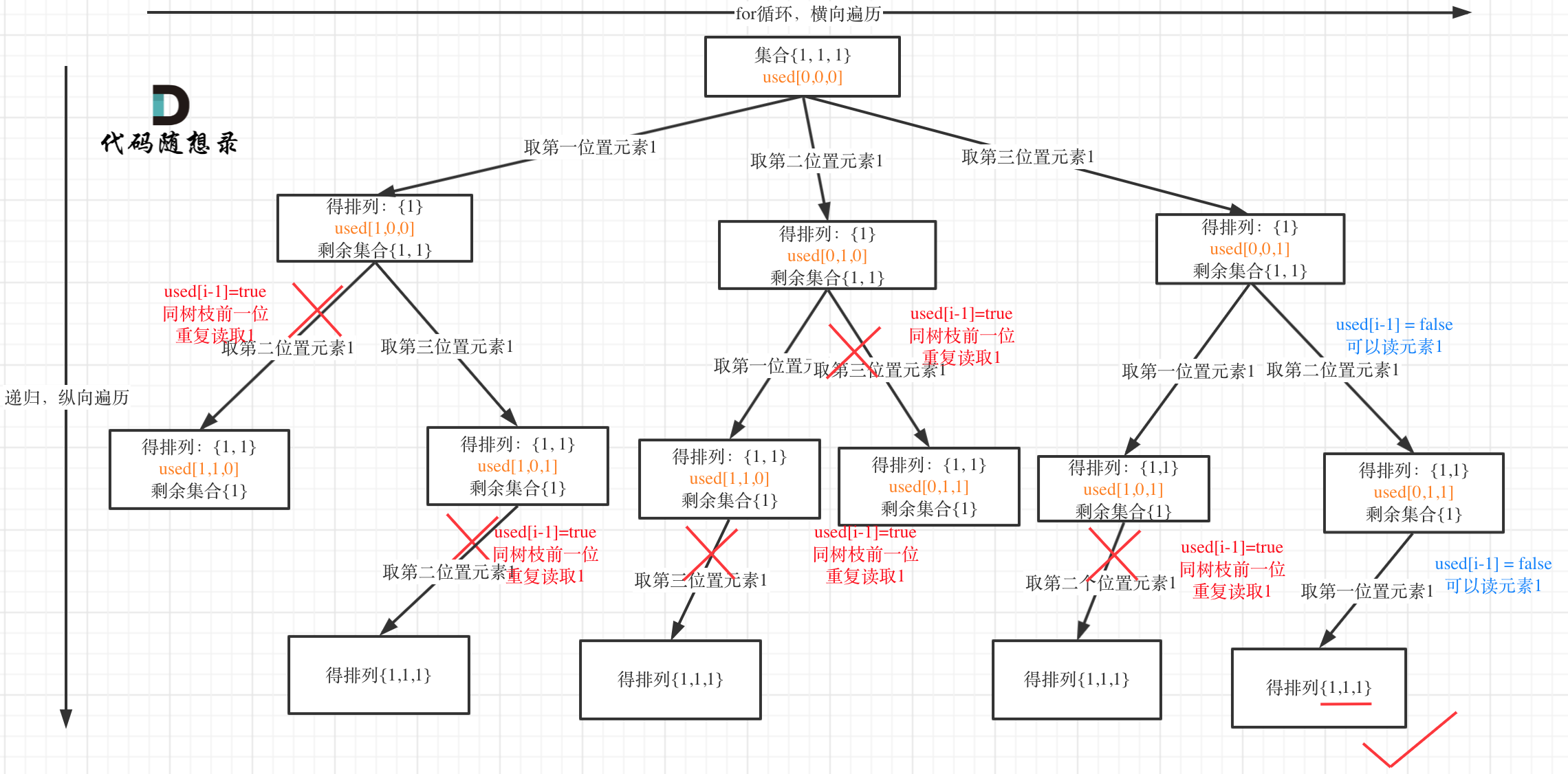
树枝上去重(used[i - 1] == true)的树型结构如下:
|
||
|
||
|
||
|
||
**可以清晰的看到使用(used[i - 1] == false),即树层去重,效率更高!**
|
||
|
||
## 性能分析
|
||
|
||
之前并没有分析各个问题的时间复杂度和空间复杂度,这次来说一说。
|
||
|
||
这块网上的资料鱼龙混杂,一些所谓的经典面试书籍根本不讲回溯算法,算法书籍对这块也避而不谈,感觉就像是算法里模糊的边界。
|
||
|
||
**所以这块就说一说我个人理解,对内容持开放态度,集思广益,欢迎大家来讨论!**
|
||
|
||
子集问题分析:
|
||
* 时间复杂度:O(n * 2^n),因为每一个元素的状态无外乎取与不取,所以时间复杂度为O(2^n),构造每一组子集都需要填进数组,又有需要O(n),最终时间复杂度:O(n * 2^n)
|
||
* 空间复杂度:O(n),递归深度为n,所以系统栈所用空间为O(n),每一层递归所用的空间都是常数级别,注意代码里的result和path都是全局变量,就算是放在参数里,传的也是引用,并不会新申请内存空间,最终空间复杂度为O(n)
|
||
|
||
排列问题分析:
|
||
* 时间复杂度:O(n!),这个可以从排列的树形图中很明显发现,每一层节点为n,第二层每一个分支都延伸了n-1个分支,再往下又是n-2个分支,所以一直到叶子节点一共就是 n * n-1 * n-2 * ..... 1 = n!。
|
||
* 空间复杂度:O(n),和子集问题同理。
|
||
|
||
组合问题分析:
|
||
* 时间复杂度:O(n * 2^n),组合问题其实就是一种子集的问题,所以组合问题最坏的情况,也不会超过子集问题的时间复杂度。
|
||
* 空间复杂度:O(n),和子集问题同理。
|
||
|
||
**一般说道回溯算法的复杂度,都说是指数级别的时间复杂度,这也算是一个概括吧!**
|
||
|
||
## 总结
|
||
|
||
本周我们对[子集问题进行了去重](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ),然后介绍了和子集问题非常像的[递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ),如果还保持惯性思维,这道题就可以掉坑里。
|
||
|
||
接着介绍了[排列问题!](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw),以及对[排列问题如何进行去重](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)。
|
||
|
||
最后我补充了子集问题,排列问题和组合问题的性能分析,给大家提供了回溯算法复杂度的分析思路。
|
||
|
||
|
||
|