202 lines
6.1 KiB
Markdown
202 lines
6.1 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/RsdcQ9umo09R6cfnwXZlrQ"><img src="https://img.shields.io/badge/PDF下载-代码随想录-blueviolet" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||
</p>
|
||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
## 300.最长递增子序列
|
||
|
||
题目链接:https://leetcode-cn.com/problems/longest-increasing-subsequence/
|
||
|
||
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
|
||
|
||
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
|
||
|
||
|
||
示例 1:
|
||
输入:nums = [10,9,2,5,3,7,101,18]
|
||
输出:4
|
||
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
|
||
|
||
示例 2:
|
||
输入:nums = [0,1,0,3,2,3]
|
||
输出:4
|
||
|
||
示例 3:
|
||
输入:nums = [7,7,7,7,7,7,7]
|
||
输出:1
|
||
|
||
提示:
|
||
|
||
* 1 <= nums.length <= 2500
|
||
* -10^4 <= nums[i] <= 104
|
||
|
||
|
||
## 思路
|
||
|
||
最长上升子序列是动规的经典题目,这里dp[i]是可以根据dp[j] (j < i)推导出来的,那么依然用动规五部曲来分析详细一波:
|
||
|
||
1. dp[i]的定义
|
||
|
||
**dp[i]表示i之前包括i的最长上升子序列**。
|
||
|
||
2. 状态转移方程
|
||
|
||
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
|
||
|
||
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
|
||
|
||
**注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值**。
|
||
|
||
3. dp[i]的初始化
|
||
|
||
每一个i,对应的dp[i](即最长上升子序列)起始大小至少都是是1.
|
||
|
||
4. 确定遍历顺序
|
||
|
||
dp[i] 是有0到i-1各个位置的最长升序子序列 推导而来,那么遍历i一定是从前向后遍历。
|
||
|
||
j其实就是0到i-1,遍历i的循环里外层,遍历j则在内层,代码如下:
|
||
|
||
```C++
|
||
for (int i = 1; i < nums.size(); i++) {
|
||
for (int j = 0; j < i; j++) {
|
||
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
|
||
}
|
||
if (dp[i] > result) result = dp[i]; // 取长的子序列
|
||
}
|
||
```
|
||
|
||
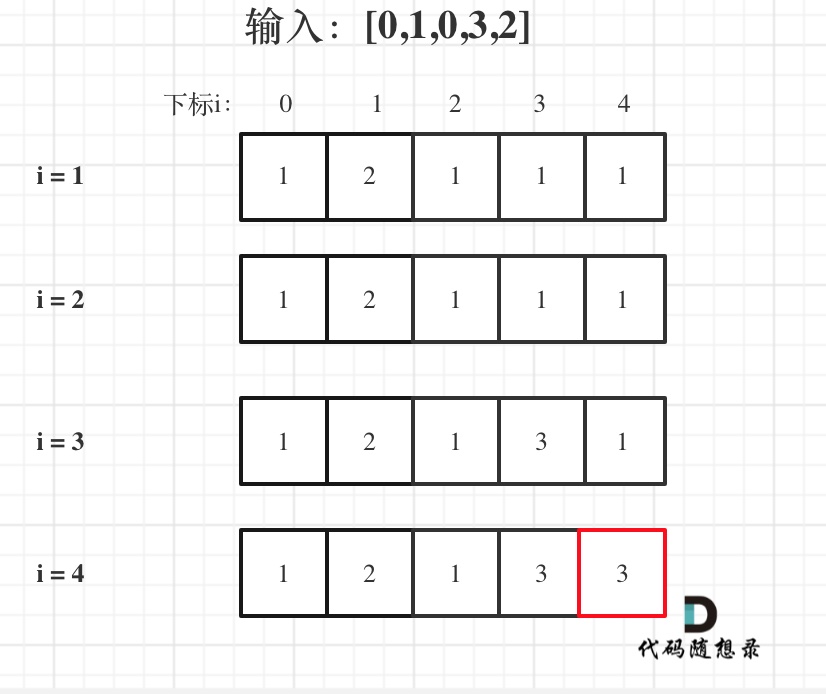
5. 举例推导dp数组
|
||
|
||
输入:[0,1,0,3,2],dp数组的变化如下:
|
||
|
||
|
||
|
||
|
||
如果代码写出来,但一直AC不了,那么就把dp数组打印出来,看看对不对!
|
||
|
||
以上五部分析完毕,C++代码如下:
|
||
|
||
```C++
|
||
class Solution {
|
||
public:
|
||
int lengthOfLIS(vector<int>& nums) {
|
||
if (nums.size() <= 1) return nums.size();
|
||
vector<int> dp(nums.size(), 1);
|
||
int result = 0;
|
||
for (int i = 1; i < nums.size(); i++) {
|
||
for (int j = 0; j < i; j++) {
|
||
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
|
||
}
|
||
if (dp[i] > result) result = dp[i]; // 取长的子序列
|
||
}
|
||
return result;
|
||
}
|
||
};
|
||
```
|
||
|
||
## 总结
|
||
|
||
本题最关键的是要想到dp[i]由哪些状态可以推出来,并取最大值,那么很自然就能想到递推公式:dp[i] = max(dp[i], dp[j] + 1);
|
||
|
||
子序列问题是动态规划的一个重要系列,本题算是入门题目,好戏刚刚开始!
|
||
|
||
## 其他语言版本
|
||
|
||
|
||
Java:
|
||
```Java
|
||
class Solution {
|
||
public int lengthOfLIS(int[] nums) {
|
||
int[] dp = new int[nums.length];
|
||
Arrays.fill(dp, 1);
|
||
for (int i = 0; i < dp.length; i++) {
|
||
for (int j = 0; j < i; j++) {
|
||
if (nums[i] > nums[j]) {
|
||
dp[i] = Math.max(dp[i], dp[j] + 1);
|
||
}
|
||
}
|
||
}
|
||
int res = 0;
|
||
for (int i = 0; i < dp.length; i++) {
|
||
res = Math.max(res, dp[i]);
|
||
}
|
||
return res;
|
||
}
|
||
}
|
||
```
|
||
|
||
Python:
|
||
```python
|
||
class Solution:
|
||
def lengthOfLIS(self, nums: List[int]) -> int:
|
||
if len(nums) <= 1:
|
||
return len(nums)
|
||
dp = [1] * len(nums)
|
||
result = 0
|
||
for i in range(1, len(nums)):
|
||
for j in range(0, i):
|
||
if nums[i] > nums[j]:
|
||
dp[i] = max(dp[i], dp[j] + 1)
|
||
result = max(result, dp[i]) #取长的子序列
|
||
return result
|
||
```
|
||
|
||
Go:
|
||
```go
|
||
func lengthOfLIS(nums []int ) int {
|
||
dp := []int{}
|
||
for _, num := range nums {
|
||
if len(dp) ==0 || dp[len(dp) - 1] < num {
|
||
dp = append(dp, num)
|
||
} else {
|
||
l, r := 0, len(dp) - 1
|
||
pos := r
|
||
for l <= r {
|
||
mid := (l + r) >> 1
|
||
if dp[mid] >= num {
|
||
pos = mid;
|
||
r = mid - 1
|
||
} else {
|
||
l = mid + 1
|
||
}
|
||
}
|
||
dp[pos] = num
|
||
}//二分查找
|
||
}
|
||
return len(dp)
|
||
}
|
||
```
|
||
|
||
Javascript
|
||
```javascript
|
||
const lengthOfLIS = (nums) => {
|
||
let dp = Array(nums.length).fill(1);
|
||
let result = 1;
|
||
|
||
for(let i = 1; i < nums.length; i++) {
|
||
for(let j = 0; j < i; j++) {
|
||
if(nums[i] > nums[j]) {
|
||
dp[i] = Math.max(dp[i], dp[j]+1);
|
||
}
|
||
}
|
||
result = Math.max(result, dp[i]);
|
||
}
|
||
|
||
return result;
|
||
};
|
||
```
|
||
*复杂度分析*
|
||
- 时间复杂度:O(nlogn)。数组 nums 的长度为 n,我们依次用数组中的元素去更新 dp 数组,相当于插入最后递增的元素,而更新 dp 数组时需要进行 O(logn) 的二分搜索,所以总时间复杂度为 O(nlogn)。
|
||
- 空间复杂度:O(n),需要额外使用长度为 n 的 dp 数组。
|
||
|
||
|
||
-----------------------
|
||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||
<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div>
|