408 lines
13 KiB
Markdown
408 lines
13 KiB
Markdown
<p align="center">
|
||
<a href="https://www.programmercarl.com/xunlian/xunlianying.html" target="_blank">
|
||
<img src="../pics/训练营.png" width="1000"/>
|
||
</a>
|
||
<p align="center"><strong><a href="./qita/join.md">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!</strong></p>
|
||
|
||
# 1143.最长公共子序列
|
||
|
||
[力扣题目链接](https://leetcode.cn/problems/longest-common-subsequence/)
|
||
|
||
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
|
||
|
||
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
|
||
|
||
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
|
||
|
||
若这两个字符串没有公共子序列,则返回 0。
|
||
|
||
示例 1:
|
||
|
||
* 输入:text1 = "abcde", text2 = "ace"
|
||
* 输出:3
|
||
* 解释:最长公共子序列是 "ace",它的长度为 3。
|
||
|
||
示例 2:
|
||
* 输入:text1 = "abc", text2 = "abc"
|
||
* 输出:3
|
||
* 解释:最长公共子序列是 "abc",它的长度为 3。
|
||
|
||
示例 3:
|
||
* 输入:text1 = "abc", text2 = "def"
|
||
* 输出:0
|
||
* 解释:两个字符串没有公共子序列,返回 0。
|
||
|
||
提示:
|
||
* 1 <= text1.length <= 1000
|
||
* 1 <= text2.length <= 1000
|
||
输入的字符串只含有小写英文字符。
|
||
|
||
## 算法公开课
|
||
|
||
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[动态规划子序列问题经典题目 | LeetCode:1143.最长公共子序列](https://www.bilibili.com/video/BV1ye4y1L7CQ),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||
|
||
|
||
## 思路
|
||
|
||
本题和[动态规划:718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html)区别在于这里不要求是连续的了,但要有相对顺序,即:"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。
|
||
|
||
继续动规五部曲分析如下:
|
||
|
||
1. 确定dp数组(dp table)以及下标的含义
|
||
|
||
dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]
|
||
|
||
有同学会问:为什么要定义长度为[0, i - 1]的字符串text1,定义为长度为[0, i]的字符串text1不香么?
|
||
|
||
这样定义是为了后面代码实现方便,如果非要定义为长度为[0, i]的字符串text1也可以,我在 [动态规划:718. 最长重复子数组](https://programmercarl.com/0718.最长重复子数组.html) 中的「拓展」里 详细讲解了区别所在,其实就是简化了dp数组第一行和第一列的初始化逻辑。
|
||
|
||
2. 确定递推公式
|
||
|
||
主要就是两大情况: text1[i - 1] 与 text2[j - 1]相同,text1[i - 1] 与 text2[j - 1]不相同
|
||
|
||
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;
|
||
|
||
如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。
|
||
|
||
即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
|
||
|
||
代码如下:
|
||
|
||
```CPP
|
||
if (text1[i - 1] == text2[j - 1]) {
|
||
dp[i][j] = dp[i - 1][j - 1] + 1;
|
||
} else {
|
||
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
|
||
}
|
||
```
|
||
|
||
3. dp数组如何初始化
|
||
|
||
先看看dp[i][0]应该是多少呢?
|
||
|
||
test1[0, i-1]和空串的最长公共子序列自然是0,所以dp[i][0] = 0;
|
||
|
||
同理dp[0][j]也是0。
|
||
|
||
其他下标都是随着递推公式逐步覆盖,初始为多少都可以,那么就统一初始为0。
|
||
|
||
代码:
|
||
|
||
```
|
||
vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
|
||
```
|
||
|
||
4. 确定遍历顺序
|
||
|
||
从递推公式,可以看出,有三个方向可以推出dp[i][j],如图:
|
||
|
||
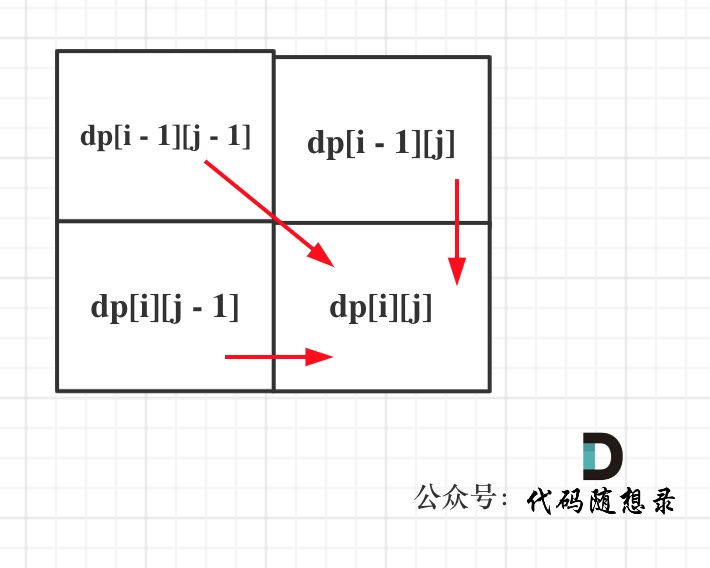
|
||
|
||
那么为了在递推的过程中,这三个方向都是经过计算的数值,所以要从前向后,从上到下来遍历这个矩阵。
|
||
|
||
5. 举例推导dp数组
|
||
|
||
以输入:text1 = "abcde", text2 = "ace" 为例,dp状态如图:
|
||
|
||
|
||
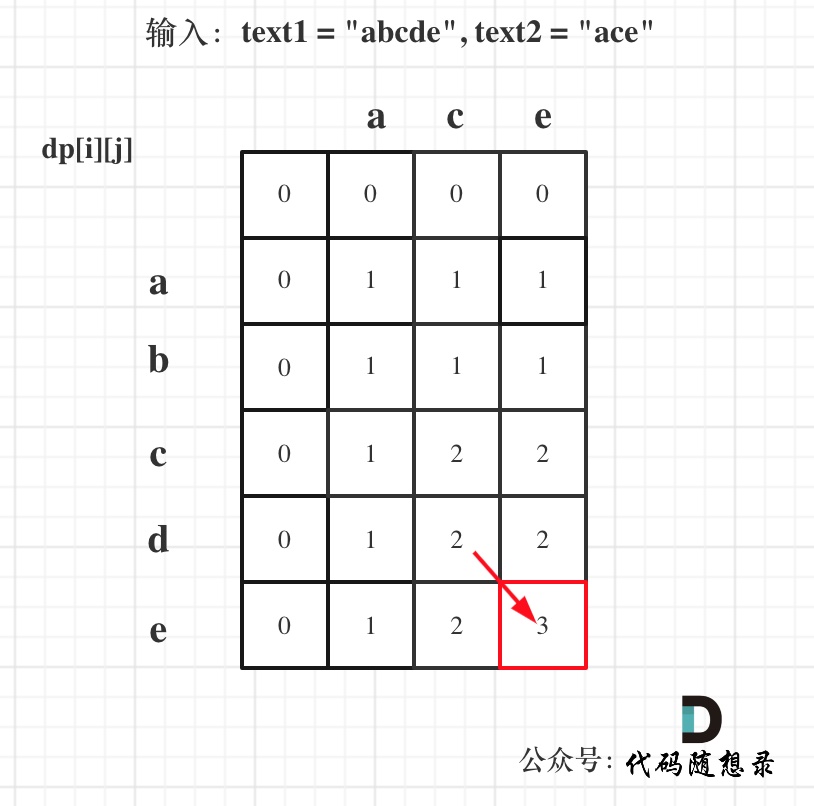
|
||
|
||
最后红框dp[text1.size()][text2.size()]为最终结果
|
||
|
||
以上分析完毕,C++代码如下:
|
||
|
||
```CPP
|
||
class Solution {
|
||
public:
|
||
int longestCommonSubsequence(string text1, string text2) {
|
||
vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
|
||
for (int i = 1; i <= text1.size(); i++) {
|
||
for (int j = 1; j <= text2.size(); j++) {
|
||
if (text1[i - 1] == text2[j - 1]) {
|
||
dp[i][j] = dp[i - 1][j - 1] + 1;
|
||
} else {
|
||
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
|
||
}
|
||
}
|
||
}
|
||
return dp[text1.size()][text2.size()];
|
||
}
|
||
};
|
||
```
|
||
* 时间复杂度: O(n * m),其中 n 和 m 分别为 text1 和 text2 的长度
|
||
* 空间复杂度: O(n * m)
|
||
|
||
|
||
|
||
## 其他语言版本
|
||
|
||
### Java:
|
||
|
||
```java
|
||
/*
|
||
二维dp数组
|
||
*/
|
||
class Solution {
|
||
public int longestCommonSubsequence(String text1, String text2) {
|
||
// char[] char1 = text1.toCharArray();
|
||
// char[] char2 = text2.toCharArray();
|
||
// 可以在一開始的時候就先把text1, text2 轉成char[],之後就不需要有這麼多爲了處理字串的調整
|
||
// 就可以和卡哥的code更一致
|
||
|
||
int[][] dp = new int[text1.length() + 1][text2.length() + 1]; // 先对dp数组做初始化操作
|
||
for (int i = 1 ; i <= text1.length() ; i++) {
|
||
char char1 = text1.charAt(i - 1);
|
||
for (int j = 1; j <= text2.length(); j++) {
|
||
char char2 = text2.charAt(j - 1);
|
||
if (char1 == char2) { // 开始列出状态转移方程
|
||
dp[i][j] = dp[i - 1][j - 1] + 1;
|
||
} else {
|
||
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
|
||
}
|
||
}
|
||
}
|
||
return dp[text1.length()][text2.length()];
|
||
}
|
||
}
|
||
|
||
|
||
|
||
/**
|
||
一维dp数组
|
||
*/
|
||
class Solution {
|
||
public int longestCommonSubsequence(String text1, String text2) {
|
||
int n1 = text1.length();
|
||
int n2 = text2.length();
|
||
|
||
// 多从二维dp数组过程分析
|
||
// 关键在于 如果记录 dp[i - 1][j - 1]
|
||
// 因为 dp[i - 1][j - 1] <!=> dp[j - 1] <=> dp[i][j - 1]
|
||
int [] dp = new int[n2 + 1];
|
||
|
||
for(int i = 1; i <= n1; i++){
|
||
|
||
// 这里pre相当于 dp[i - 1][j - 1]
|
||
int pre = dp[0];
|
||
for(int j = 1; j <= n2; j++){
|
||
|
||
//用于给pre赋值
|
||
int cur = dp[j];
|
||
if(text1.charAt(i - 1) == text2.charAt(j - 1)){
|
||
//这里pre相当于dp[i - 1][j - 1] 千万不能用dp[j - 1] !!
|
||
dp[j] = pre + 1;
|
||
} else{
|
||
// dp[j] 相当于 dp[i - 1][j]
|
||
// dp[j - 1] 相当于 dp[i][j - 1]
|
||
dp[j] = Math.max(dp[j], dp[j - 1]);
|
||
}
|
||
|
||
//更新dp[i - 1][j - 1], 为下次使用做准备
|
||
pre = cur;
|
||
}
|
||
}
|
||
|
||
return dp[n2];
|
||
}
|
||
}
|
||
```
|
||
|
||
### Python:
|
||
2维DP
|
||
|
||
```python
|
||
class Solution:
|
||
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
|
||
# 创建一个二维数组 dp,用于存储最长公共子序列的长度
|
||
dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]
|
||
|
||
# 遍历 text1 和 text2,填充 dp 数组
|
||
for i in range(1, len(text1) + 1):
|
||
for j in range(1, len(text2) + 1):
|
||
if text1[i - 1] == text2[j - 1]:
|
||
# 如果 text1[i-1] 和 text2[j-1] 相等,则当前位置的最长公共子序列长度为左上角位置的值加一
|
||
dp[i][j] = dp[i - 1][j - 1] + 1
|
||
else:
|
||
# 如果 text1[i-1] 和 text2[j-1] 不相等,则当前位置的最长公共子序列长度为上方或左方的较大值
|
||
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
|
||
|
||
# 返回最长公共子序列的长度
|
||
return dp[len(text1)][len(text2)]
|
||
|
||
```
|
||
1维DP
|
||
```python
|
||
class Solution:
|
||
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
|
||
m, n = len(text1), len(text2)
|
||
dp = [0] * (n + 1) # 初始化一维DP数组
|
||
|
||
for i in range(1, m + 1):
|
||
prev = 0 # 保存上一个位置的最长公共子序列长度
|
||
for j in range(1, n + 1):
|
||
curr = dp[j] # 保存当前位置的最长公共子序列长度
|
||
if text1[i - 1] == text2[j - 1]:
|
||
# 如果当前字符相等,则最长公共子序列长度加一
|
||
dp[j] = prev + 1
|
||
else:
|
||
# 如果当前字符不相等,则选择保留前一个位置的最长公共子序列长度中的较大值
|
||
dp[j] = max(dp[j], dp[j - 1])
|
||
prev = curr # 更新上一个位置的最长公共子序列长度
|
||
|
||
return dp[n] # 返回最后一个位置的最长公共子序列长度作为结果
|
||
|
||
```
|
||
|
||
### Go:
|
||
|
||
```Go
|
||
func longestCommonSubsequence(text1 string, text2 string) int {
|
||
t1 := len(text1)
|
||
t2 := len(text2)
|
||
dp:=make([][]int,t1+1)
|
||
for i:=range dp{
|
||
dp[i]=make([]int,t2+1)
|
||
}
|
||
|
||
for i := 1; i <= t1; i++ {
|
||
for j := 1; j <=t2; j++ {
|
||
if text1[i-1]==text2[j-1]{
|
||
dp[i][j]=dp[i-1][j-1]+1
|
||
}else{
|
||
dp[i][j]=max(dp[i-1][j],dp[i][j-1])
|
||
}
|
||
}
|
||
}
|
||
return dp[t1][t2]
|
||
}
|
||
|
||
func max(a,b int)int {
|
||
if a>b{
|
||
return a
|
||
}
|
||
return b
|
||
}
|
||
|
||
```
|
||
|
||
### JavaScript:
|
||
|
||
```javascript
|
||
const longestCommonSubsequence = (text1, text2) => {
|
||
let dp = Array.from(Array(text1.length+1), () => Array(text2.length+1).fill(0));
|
||
|
||
for(let i = 1; i <= text1.length; i++) {
|
||
for(let j = 1; j <= text2.length; j++) {
|
||
if(text1[i-1] === text2[j-1]) {
|
||
dp[i][j] = dp[i-1][j-1] +1;;
|
||
} else {
|
||
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1])
|
||
}
|
||
}
|
||
}
|
||
|
||
return dp[text1.length][text2.length];
|
||
};
|
||
```
|
||
|
||
### TypeScript:
|
||
|
||
```typescript
|
||
function longestCommonSubsequence(text1: string, text2: string): number {
|
||
/**
|
||
dp[i][j]: text1中前i-1个和text2中前j-1个,最长公共子序列的长度
|
||
*/
|
||
const length1: number = text1.length,
|
||
length2: number = text2.length;
|
||
const dp: number[][] = new Array(length1 + 1).fill(0)
|
||
.map(_ => new Array(length2 + 1).fill(0));
|
||
for (let i = 1; i <= length1; i++) {
|
||
for (let j = 1; j <= length2; j++) {
|
||
if (text1[i - 1] === text2[j - 1]) {
|
||
dp[i][j] = dp[i - 1][j - 1] + 1;
|
||
} else {
|
||
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
|
||
}
|
||
}
|
||
}
|
||
return dp[length1][length2];
|
||
};
|
||
```
|
||
|
||
### Rust
|
||
|
||
```rust
|
||
impl Solution {
|
||
pub fn longest_common_subsequence(text1: String, text2: String) -> i32 {
|
||
let mut dp = vec![vec![0; text2.len() + 1]; text1.len() + 1];
|
||
for (i, c1) in text1.chars().enumerate() {
|
||
for (j, c2) in text2.chars().enumerate() {
|
||
if c1 == c2 {
|
||
dp[i + 1][j + 1] = dp[i][j] + 1;
|
||
} else {
|
||
dp[i + 1][j + 1] = dp[i][j + 1].max(dp[i + 1][j]);
|
||
}
|
||
}
|
||
}
|
||
dp[text1.len()][text2.len()]
|
||
}
|
||
}
|
||
```
|
||
|
||
一维:
|
||
|
||
```rust
|
||
impl Solution {
|
||
pub fn longest_common_subsequence(text1: String, text2: String) -> i32 {
|
||
let mut dp = vec![0; text2.len() + 1];
|
||
for c1 in text1.chars() {
|
||
// 初始化 prev
|
||
let mut prev = 0;
|
||
|
||
for (j, c2) in text2.chars().enumerate() {
|
||
let temp = dp[j + 1];
|
||
if c1 == c2 {
|
||
// 使用上一次的状态,防止重复计算
|
||
dp[j + 1] = prev + 1;
|
||
} else {
|
||
dp[j + 1] = dp[j + 1].max(dp[j]);
|
||
}
|
||
// 使用上一次的状态更新 prev
|
||
prev = temp;
|
||
}
|
||
}
|
||
dp[text2.len()]
|
||
}
|
||
}
|
||
```
|
||
|
||
### C:
|
||
|
||
```c
|
||
#define max(a, b) ((a) > (b) ? (a) : (b))
|
||
|
||
int longestCommonSubsequence(char* text1, char* text2) {
|
||
int text1Len = strlen(text1);
|
||
int text2Len = strlen(text2);
|
||
int dp[text1Len + 1][text2Len + 1];
|
||
memset(dp, 0, sizeof (dp));
|
||
for (int i = 1; i <= text1Len; ++i) {
|
||
for (int j = 1; j <= text2Len; ++j) {
|
||
if(text1[i - 1] == text2[j - 1]){
|
||
dp[i][j] = dp[i - 1][j - 1] + 1;
|
||
} else{
|
||
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
|
||
}
|
||
}
|
||
}
|
||
return dp[text1Len][text2Len];
|
||
}
|
||
```
|
||
|
||
|
||
|
||
<p align="center">
|
||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||
</a>
|