781 lines
21 KiB
Markdown
781 lines
21 KiB
Markdown
|
||
<p align="center"><strong><a href="./qita/join.md">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!</strong></p>
|
||
|
||
# 103. 水流问题
|
||
|
||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1175)
|
||
|
||
题目描述:
|
||
|
||
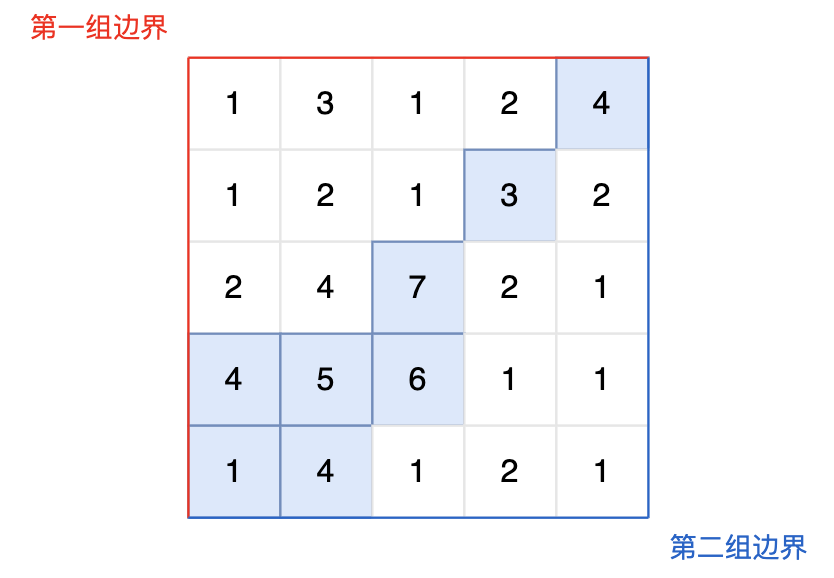
现有一个 N × M 的矩阵,每个单元格包含一个数值,这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界,而矩阵的右边界和下边界被视为第二组边界。
|
||
|
||
|
||
矩阵模拟了一个地形,当雨水落在上面时,水会根据地形的倾斜向低处流动,但只能从较高或等高的地点流向较低或等高并且相邻(上下左右方向)的地点。我们的目标是确定那些单元格,从这些单元格出发的水可以达到第一组边界和第二组边界。
|
||
|
||
输入描述:
|
||
|
||
第一行包含两个整数 N 和 M,分别表示矩阵的行数和列数。
|
||
|
||
后续 N 行,每行包含 M 个整数,表示矩阵中的每个单元格的高度。
|
||
|
||
输出描述:
|
||
|
||
输出共有多行,每行输出两个整数,用一个空格隔开,表示可达第一组边界和第二组边界的单元格的坐标,输出顺序任意。
|
||
|
||
输入示例:
|
||
|
||
```
|
||
5 5
|
||
1 3 1 2 4
|
||
1 2 1 3 2
|
||
2 4 7 2 1
|
||
4 5 6 1 1
|
||
1 4 1 2 1
|
||
```
|
||
|
||
输出示例:
|
||
|
||
```
|
||
0 4
|
||
1 3
|
||
2 2
|
||
3 0
|
||
3 1
|
||
3 2
|
||
4 0
|
||
4 1
|
||
```
|
||
|
||
提示信息:
|
||
|
||
|
||
|
||
图中的蓝色方块上的雨水既能流向第一组边界,也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。
|
||
|
||
|
||
数据范围:
|
||
|
||
1 <= M, N <= 50
|
||
|
||
## 思路
|
||
|
||
一个比较直白的想法,其实就是 遍历每个点,然后看这个点 能不能同时到达第一组边界和第二组边界。
|
||
|
||
至于遍历方式,可以用dfs,也可以用bfs,以下用dfs来举例。
|
||
|
||
那么这种思路的实现代码如下:
|
||
|
||
```CPP
|
||
#include <iostream>
|
||
#include <vector>
|
||
using namespace std;
|
||
int n, m;
|
||
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
|
||
|
||
// 从 x,y 出发 把可以走的地方都标记上
|
||
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||
if (visited[x][y]) return;
|
||
|
||
visited[x][y] = true;
|
||
|
||
for (int i = 0; i < 4; i++) {
|
||
int nextx = x + dir[i][0];
|
||
int nexty = y + dir[i][1];
|
||
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
|
||
if (grid[x][y] < grid[nextx][nexty]) continue; // 高度不合适
|
||
|
||
dfs (grid, visited, nextx, nexty);
|
||
}
|
||
return;
|
||
}
|
||
bool isResult(vector<vector<int>>& grid, int x, int y) {
|
||
vector<vector<bool>> visited(n, vector<bool>(m, false));
|
||
|
||
// 深搜,将x,y出发 能到的节点都标记上。
|
||
dfs(grid, visited, x, y);
|
||
bool isFirst = false;
|
||
bool isSecond = false;
|
||
|
||
// 以下就是判断x,y出发,是否到达第一组边界和第二组边界
|
||
// 第一边界的上边
|
||
for (int j = 0; j < m; j++) {
|
||
if (visited[0][j]) {
|
||
isFirst = true;
|
||
break;
|
||
}
|
||
}
|
||
// 第一边界的左边
|
||
for (int i = 0; i < n; i++) {
|
||
if (visited[i][0]) {
|
||
isFirst = true;
|
||
break;
|
||
}
|
||
}
|
||
// 第二边界右边
|
||
for (int j = 0; j < m; j++) {
|
||
if (visited[n - 1][j]) {
|
||
isSecond = true;
|
||
break;
|
||
}
|
||
}
|
||
// 第二边界下边
|
||
for (int i = 0; i < n; i++) {
|
||
if (visited[i][m - 1]) {
|
||
isSecond = true;
|
||
break;
|
||
}
|
||
}
|
||
if (isFirst && isSecond) return true;
|
||
return false;
|
||
}
|
||
|
||
|
||
int main() {
|
||
cin >> n >> m;
|
||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||
for (int i = 0; i < n; i++) {
|
||
for (int j = 0; j < m; j++) {
|
||
cin >> grid[i][j];
|
||
}
|
||
}
|
||
// 遍历每一个点,看是否能同时到达第一组边界和第二组边界
|
||
for (int i = 0; i < n; i++) {
|
||
for (int j = 0; j < m; j++) {
|
||
if (isResult(grid, i, j)) {
|
||
cout << i << " " << j << endl;
|
||
}
|
||
}
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
这种思路很直白,但很明显,以上代码超时了。 来看看时间复杂度。
|
||
|
||
遍历每一个节点,是 m * n,遍历每一个节点的时候,都要做深搜,深搜的时间复杂度是: m * n
|
||
|
||
那么整体时间复杂度 就是 O(m^2 * n^2) ,这是一个四次方的时间复杂度。
|
||
|
||
## 优化
|
||
|
||
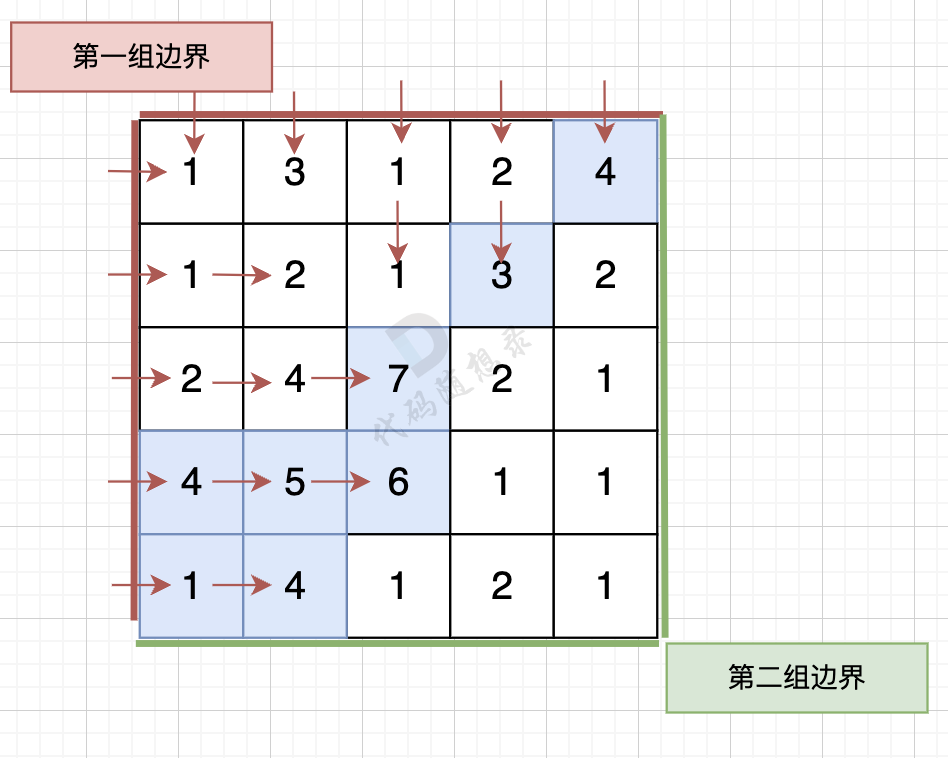
那么我们可以 反过来想,从第一组边界上的节点 逆流而上,将遍历过的节点都标记上。
|
||
|
||
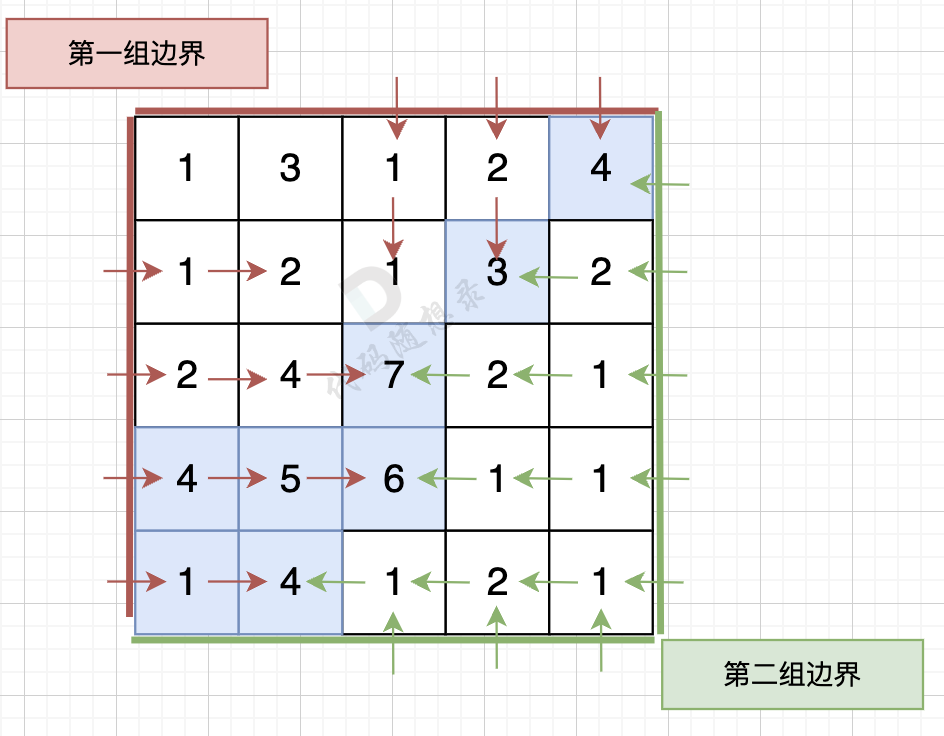
同样从第二组边界的边上节点 逆流而上,将遍历过的节点也标记上。
|
||
|
||
然后**两方都标记过的节点就是既可以流太平洋也可以流大西洋的节点**。
|
||
|
||
从第一组边界边上节点出发,如图:
|
||
|
||
|
||
|
||
|
||
从第二组边界上节点出发,如图:
|
||
|
||
|
||
|
||
按照这样的逻辑,就可以写出如下遍历代码:(详细注释)
|
||
|
||
|
||
```CPP
|
||
#include <iostream>
|
||
#include <vector>
|
||
using namespace std;
|
||
int n, m;
|
||
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
|
||
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
|
||
if (visited[x][y]) return;
|
||
|
||
visited[x][y] = true;
|
||
|
||
for (int i = 0; i < 4; i++) {
|
||
int nextx = x + dir[i][0];
|
||
int nexty = y + dir[i][1];
|
||
if (nextx < 0 || nextx >= n || nexty < 0 || nexty >= m) continue;
|
||
if (grid[x][y] > grid[nextx][nexty]) continue; // 注意:这里是从低向高遍历
|
||
|
||
dfs (grid, visited, nextx, nexty);
|
||
}
|
||
return;
|
||
}
|
||
|
||
|
||
|
||
int main() {
|
||
|
||
cin >> n >> m;
|
||
vector<vector<int>> grid(n, vector<int>(m, 0));
|
||
|
||
for (int i = 0; i < n; i++) {
|
||
for (int j = 0; j < m; j++) {
|
||
cin >> grid[i][j];
|
||
}
|
||
}
|
||
// 标记从第一组边界上的节点出发,可以遍历的节点
|
||
vector<vector<bool>> firstBorder(n, vector<bool>(m, false));
|
||
|
||
// 标记从第一组边界上的节点出发,可以遍历的节点
|
||
vector<vector<bool>> secondBorder(n, vector<bool>(m, false));
|
||
|
||
// 从最上和最下行的节点出发,向高处遍历
|
||
for (int i = 0; i < n; i++) {
|
||
dfs (grid, firstBorder, i, 0); // 遍历最左列,接触第一组边界
|
||
dfs (grid, secondBorder, i, m - 1); // 遍历最右列,接触第二组边界
|
||
}
|
||
|
||
// 从最左和最右列的节点出发,向高处遍历
|
||
for (int j = 0; j < m; j++) {
|
||
dfs (grid, firstBorder, 0, j); // 遍历最上行,接触第一组边界
|
||
dfs (grid, secondBorder, n - 1, j); // 遍历最下行,接触第二组边界
|
||
}
|
||
for (int i = 0; i < n; i++) {
|
||
for (int j = 0; j < m; j++) {
|
||
// 如果这个节点,从第一组边界和第二组边界出发都遍历过,就是结果
|
||
if (firstBorder[i][j] && secondBorder[i][j]) cout << i << " " << j << endl;;
|
||
}
|
||
}
|
||
|
||
|
||
}
|
||
|
||
```
|
||
|
||
|
||
时间复杂度分析, 关于dfs函数搜索的过程 时间复杂度是 O(n * m),这个大家比较容易想。
|
||
|
||
关键看主函数,那么每次dfs的时候,上面还是有for循环的。
|
||
|
||
第一个for循环,时间复杂度是:n * (n * m) 。
|
||
|
||
第二个for循环,时间复杂度是:m * (n * m)。
|
||
|
||
所以本题看起来 时间复杂度好像是 : n * (n * m) + m * (n * m) = (m * n) * (m + n) 。
|
||
|
||
其实这是一个误区,大家再自己看 dfs函数的实现,其实 有visited函数记录 走过的节点,而走过的节点是不会再走第二次的。
|
||
|
||
所以 调用dfs函数,**只要参数传入的是 数组 firstBorder,那么地图中 每一个节点其实就遍历一次,无论你调用多少次**。
|
||
|
||
同理,调用dfs函数,只要 参数传入的是 数组 secondBorder,地图中每个节点也只会遍历一次。
|
||
|
||
所以,以下这段代码的时间复杂度是 2 * n * m。 地图用每个节点就遍历了两次,参数传入 firstBorder 的时候遍历一次,参数传入 secondBorder 的时候遍历一次。
|
||
|
||
```CPP
|
||
// 从最上和最下行的节点出发,向高处遍历
|
||
for (int i = 0; i < n; i++) {
|
||
dfs (grid, firstBorder, i, 0); // 遍历最左列,接触第一组边界
|
||
dfs (grid, secondBorder, i, m - 1); // 遍历最右列,接触第二组边界
|
||
}
|
||
|
||
// 从最左和最右列的节点出发,向高处遍历
|
||
for (int j = 0; j < m; j++) {
|
||
dfs (grid, firstBorder, 0, j); // 遍历最上行,接触第一组边界
|
||
dfs (grid, secondBorder, n - 1, j); // 遍历最下行,接触第二组边界
|
||
}
|
||
```
|
||
|
||
那么本题整体的时间复杂度其实是: 2 * n * m + n * m ,所以最终时间复杂度为 O(n * m) 。
|
||
|
||
空间复杂度为:O(n * m) 这个就不难理解了。开了几个 n * m 的数组。
|
||
|
||
|
||
|
||
## 其他语言版本
|
||
|
||
### Java
|
||
```Java
|
||
public class Main {
|
||
|
||
// 采用 DFS 进行搜索
|
||
public static void dfs(int[][] heights, int x, int y, boolean[][] visited, int preH) {
|
||
// 遇到边界或者访问过的点,直接返回
|
||
if (x < 0 || x >= heights.length || y < 0 || y >= heights[0].length || visited[x][y]) return;
|
||
// 不满足水流入条件的直接返回
|
||
if (heights[x][y] < preH) return;
|
||
// 满足条件,设置为true,表示可以从边界到达此位置
|
||
visited[x][y] = true;
|
||
|
||
// 向下一层继续搜索
|
||
dfs(heights, x + 1, y, visited, heights[x][y]);
|
||
dfs(heights, x - 1, y, visited, heights[x][y]);
|
||
dfs(heights, x, y + 1, visited, heights[x][y]);
|
||
dfs(heights, x, y - 1, visited, heights[x][y]);
|
||
}
|
||
|
||
public static void main(String[] args) {
|
||
Scanner sc = new Scanner(System.in);
|
||
int m = sc.nextInt();
|
||
int n = sc.nextInt();
|
||
|
||
int[][] heights = new int[m][n];
|
||
for (int i = 0; i < m; i++) {
|
||
for (int j = 0; j < n; j++) {
|
||
heights[i][j] = sc.nextInt();
|
||
}
|
||
}
|
||
|
||
// 初始化两个二位boolean数组,代表两个边界
|
||
boolean[][] pacific = new boolean[m][n];
|
||
boolean[][] atlantic = new boolean[m][n];
|
||
|
||
// 从左右边界出发进行DFS
|
||
for (int i = 0; i < m; i++) {
|
||
dfs(heights, i, 0, pacific, Integer.MIN_VALUE);
|
||
dfs(heights, i, n - 1, atlantic, Integer.MIN_VALUE);
|
||
}
|
||
|
||
// 从上下边界出发进行DFS
|
||
for (int j = 0; j < n; j++) {
|
||
dfs(heights, 0, j, pacific, Integer.MIN_VALUE);
|
||
dfs(heights, m - 1, j, atlantic, Integer.MIN_VALUE);
|
||
}
|
||
|
||
// 当两个边界二维数组在某个位置都为true时,符合题目要求
|
||
List<List<Integer>> res = new ArrayList<>();
|
||
for (int i = 0; i < m; i++) {
|
||
for (int j = 0; j < n; j++) {
|
||
if (pacific[i][j] && atlantic[i][j]) {
|
||
res.add(Arrays.asList(i, j));
|
||
}
|
||
}
|
||
}
|
||
|
||
// 打印结果
|
||
for (List<Integer> list : res) {
|
||
for (int k = 0; k < list.size(); k++) {
|
||
if (k == 0) {
|
||
System.out.print(list.get(k) + " ");
|
||
} else {
|
||
System.out.print(list.get(k));
|
||
}
|
||
}
|
||
System.out.println();
|
||
}
|
||
}
|
||
}
|
||
|
||
```
|
||
|
||
### Python
|
||
```Python
|
||
first = set()
|
||
second = set()
|
||
directions = [[-1, 0], [0, 1], [1, 0], [0, -1]]
|
||
|
||
def dfs(i, j, graph, visited, side):
|
||
if visited[i][j]:
|
||
return
|
||
|
||
visited[i][j] = True
|
||
side.add((i, j))
|
||
|
||
for x, y in directions:
|
||
new_x = i + x
|
||
new_y = j + y
|
||
if (
|
||
0 <= new_x < len(graph)
|
||
and 0 <= new_y < len(graph[0])
|
||
and int(graph[new_x][new_y]) >= int(graph[i][j])
|
||
):
|
||
dfs(new_x, new_y, graph, visited, side)
|
||
|
||
def main():
|
||
global first
|
||
global second
|
||
|
||
N, M = map(int, input().strip().split())
|
||
graph = []
|
||
for _ in range(N):
|
||
row = input().strip().split()
|
||
graph.append(row)
|
||
|
||
# 是否可到达第一边界
|
||
visited = [[False] * M for _ in range(N)]
|
||
for i in range(M):
|
||
dfs(0, i, graph, visited, first)
|
||
for i in range(N):
|
||
dfs(i, 0, graph, visited, first)
|
||
|
||
# 是否可到达第二边界
|
||
visited = [[False] * M for _ in range(N)]
|
||
for i in range(M):
|
||
dfs(N - 1, i, graph, visited, second)
|
||
for i in range(N):
|
||
dfs(i, M - 1, graph, visited, second)
|
||
|
||
# 可到达第一边界和第二边界
|
||
res = first & second
|
||
|
||
for x, y in res:
|
||
print(f"{x} {y}")
|
||
|
||
|
||
if __name__ == "__main__":
|
||
main()
|
||
```
|
||
|
||
### Go
|
||
|
||
### Rust
|
||
|
||
### Javascript
|
||
|
||
#### 深搜
|
||
|
||
```javascript
|
||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||
// 创建readline接口
|
||
let iter = r1[Symbol.asyncIterator]();
|
||
// 创建异步迭代器
|
||
const readline = async () => (await iter.next()).value;
|
||
|
||
let graph // 地图
|
||
let N, M // 地图大小
|
||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||
|
||
|
||
// 读取输入,初始化地图
|
||
const initGraph = async () => {
|
||
let line = await readline();
|
||
[N, M] = line.split(' ').map(Number);
|
||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||
|
||
for (let i = 0; i < N; i++) {
|
||
line = await readline()
|
||
line = line.split(' ').map(Number)
|
||
for (let j = 0; j < M; j++) {
|
||
graph[i][j] = line[j]
|
||
}
|
||
}
|
||
}
|
||
|
||
|
||
/**
|
||
* @description: 从(x,y)开始深度优先遍历地图
|
||
* @param {*} graph 地图
|
||
* @param {*} visited 可访问节点
|
||
* @param {*} x 开始搜索节点的下标
|
||
* @param {*} y 开始搜索节点的下标
|
||
* @return {*}
|
||
*/
|
||
const dfs = (graph, visited, x, y) => {
|
||
if (visited[x][y]) return
|
||
visited[x][y] = true // 标记为可访问
|
||
|
||
for (let i = 0; i < 4; i++) {
|
||
let nextx = x + dir[i][0]
|
||
let nexty = y + dir[i][1]
|
||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界,跳过
|
||
if (graph[x][y] < graph[nextx][nexty]) continue //不能流过.跳过
|
||
dfs(graph, visited, nextx, nexty)
|
||
}
|
||
}
|
||
|
||
|
||
/**
|
||
* @description: 判断地图上的(x, y)是否可以到达第一组边界和第二组边界
|
||
* @param {*} x 坐标
|
||
* @param {*} y 坐标
|
||
* @return {*} true可以到达,false不可以到达
|
||
*/
|
||
const isResult = (x, y) => {
|
||
let visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||
|
||
let isFirst = false //是否可到达第一边界
|
||
let isSecond = false //是否可到达第二边界
|
||
|
||
// 深搜,将(x, y)可到达的所有节点做标记
|
||
dfs(graph, visited, x, y)
|
||
|
||
// 判断能否到第一边界左边
|
||
for (let i = 0; i < N; i++) {
|
||
if (visited[i][0]) {
|
||
isFirst = true
|
||
break
|
||
}
|
||
}
|
||
|
||
// 判断能否到第一边界上边
|
||
for (let j = 0; j < M; j++) {
|
||
if (visited[0][j]) {
|
||
isFirst = true
|
||
break
|
||
}
|
||
}
|
||
|
||
// 判断能否到第二边界右边
|
||
for (let i = 0; i < N; i++) {
|
||
if (visited[i][M - 1]) {
|
||
isSecond = true
|
||
break
|
||
}
|
||
}
|
||
|
||
// 判断能否到第二边界下边
|
||
for (let j = 0; j < M; j++) {
|
||
if (visited[N - 1][j]) {
|
||
isSecond = true
|
||
break
|
||
}
|
||
}
|
||
|
||
return isFirst && isSecond
|
||
}
|
||
|
||
(async function () {
|
||
|
||
// 读取输入,初始化地图
|
||
await initGraph()
|
||
|
||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||
for (let i = 0; i < N; i++) {
|
||
for (let j = 0; j < M; j++) {
|
||
if (isResult(i, j)) console.log(i + ' ' + j);
|
||
}
|
||
}
|
||
})()
|
||
```
|
||
|
||
|
||
|
||
#### 广搜-解法一
|
||
|
||
```java
|
||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||
// 创建readline接口
|
||
let iter = r1[Symbol.asyncIterator]();
|
||
// 创建异步迭代器
|
||
const readline = async () => (await iter.next()).value;
|
||
|
||
let graph // 地图
|
||
let N, M // 地图大小
|
||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||
|
||
|
||
// 读取输入,初始化地图
|
||
const initGraph = async () => {
|
||
let line = await readline();
|
||
[N, M] = line.split(' ').map(Number);
|
||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||
|
||
for (let i = 0; i < N; i++) {
|
||
line = await readline()
|
||
line = line.split(' ').map(Number)
|
||
for (let j = 0; j < M; j++) {
|
||
graph[i][j] = line[j]
|
||
}
|
||
}
|
||
}
|
||
|
||
|
||
/**
|
||
* @description: 从(x,y)开始广度优先遍历地图
|
||
* @param {*} graph 地图
|
||
* @param {*} visited 可访问节点
|
||
* @param {*} x 开始搜索节点的下标
|
||
* @param {*} y 开始搜索节点的下标
|
||
* @return {*}
|
||
*/
|
||
const bfs = (graph, visited, x, y) => {
|
||
let queue = []
|
||
queue.push([x, y])
|
||
visited[x][y] = true
|
||
|
||
while (queue.length) {
|
||
const [xx, yy] = queue.shift()
|
||
for (let i = 0; i < 4; i++) {
|
||
let nextx = xx + dir[i][0]
|
||
let nexty = yy + dir[i][1]
|
||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
|
||
|
||
// 可访问或者不能流过, 跳过 (注意这里是graph[xx][yy] < graph[nextx][nexty], 不是graph[x][y] < graph[nextx][nexty])
|
||
if (visited[nextx][nexty] || graph[xx][yy] < graph[nextx][nexty]) continue
|
||
|
||
queue.push([nextx, nexty])
|
||
visited[nextx][nexty] = true
|
||
|
||
}
|
||
}
|
||
}
|
||
|
||
|
||
/**
|
||
* @description: 判断地图上的(x, y)是否可以到达第一组边界和第二组边界
|
||
* @param {*} x 坐标
|
||
* @param {*} y 坐标
|
||
* @return {*} true可以到达,false不可以到达
|
||
*/
|
||
const isResult = (x, y) => {
|
||
let visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||
|
||
let isFirst = false //是否可到达第一边界
|
||
let isSecond = false //是否可到达第二边界
|
||
|
||
// 深搜,将(x, y)可到达的所有节点做标记
|
||
bfs(graph, visited, x, y)
|
||
|
||
// console.log(visited);
|
||
|
||
// 判断能否到第一边界左边
|
||
for (let i = 0; i < N; i++) {
|
||
if (visited[i][0]) {
|
||
isFirst = true
|
||
break
|
||
}
|
||
}
|
||
|
||
// 判断能否到第一边界上边
|
||
for (let j = 0; j < M; j++) {
|
||
if (visited[0][j]) {
|
||
isFirst = true
|
||
break
|
||
}
|
||
}
|
||
|
||
// 判断能否到第二边界右边
|
||
for (let i = 0; i < N; i++) {
|
||
if (visited[i][M - 1]) {
|
||
isSecond = true
|
||
break
|
||
}
|
||
}
|
||
|
||
// 判断能否到第二边界下边
|
||
for (let j = 0; j < M; j++) {
|
||
if (visited[N - 1][j]) {
|
||
isSecond = true
|
||
break
|
||
}
|
||
}
|
||
|
||
return isFirst && isSecond
|
||
}
|
||
|
||
(async function () {
|
||
|
||
// 读取输入,初始化地图
|
||
await initGraph()
|
||
|
||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||
for (let i = 0; i < N; i++) {
|
||
for (let j = 0; j < M; j++) {
|
||
if (isResult(i, j)) console.log(i + ' ' + j);
|
||
}
|
||
}
|
||
})()
|
||
```
|
||
|
||
|
||
|
||
#### 广搜-解法二
|
||
|
||
从第一边界和第二边界开始向高处流, 标记可以流到的位置, 两个边界都能到达的位置就是所求结果
|
||
|
||
```javascript
|
||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||
// 创建readline接口
|
||
let iter = r1[Symbol.asyncIterator]();
|
||
// 创建异步迭代器
|
||
const readline = async () => (await iter.next()).value;
|
||
|
||
let graph // 地图
|
||
let N, M // 地图大小
|
||
const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
|
||
|
||
|
||
// 读取输入,初始化地图
|
||
const initGraph = async () => {
|
||
let line = await readline();
|
||
[N, M] = line.split(' ').map(Number);
|
||
graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
|
||
|
||
for (let i = 0; i < N; i++) {
|
||
line = await readline()
|
||
line = line.split(' ').map(Number)
|
||
for (let j = 0; j < M; j++) {
|
||
graph[i][j] = line[j]
|
||
}
|
||
}
|
||
}
|
||
|
||
|
||
/**
|
||
* @description: 从(x,y)开始广度优先遍历地图
|
||
* @param {*} graph 地图
|
||
* @param {*} visited 可访问节点
|
||
* @param {*} x 开始搜索节点的下标
|
||
* @param {*} y 开始搜索节点的下标
|
||
* @return {*}
|
||
*/
|
||
const bfs = (graph, visited, x, y) => {
|
||
if(visited[x][y]) return
|
||
|
||
let queue = []
|
||
queue.push([x, y])
|
||
visited[x][y] = true
|
||
|
||
while (queue.length) {
|
||
const [xx, yy] = queue.shift()
|
||
for (let i = 0; i < 4; i++) {
|
||
let nextx = xx + dir[i][0]
|
||
let nexty = yy + dir[i][1]
|
||
if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
|
||
|
||
// 可访问或者不能流过, 跳过 (注意因为是从边界往高处流, 所以这里是graph[xx][yy] >= graph[nextx][nexty], 还要注意不是graph[xx][yy] >= graph[nextx][nexty])
|
||
if (visited[nextx][nexty] || graph[xx][yy] >= graph[nextx][nexty]) continue
|
||
|
||
queue.push([nextx, nexty])
|
||
visited[nextx][nexty] = true
|
||
}
|
||
}
|
||
}
|
||
|
||
(async function () {
|
||
|
||
// 读取输入,初始化地图
|
||
await initGraph()
|
||
|
||
// 记录第一边界可到达的节点
|
||
let firstBorder = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||
|
||
// 记录第二边界可到达的节点
|
||
let secondBorder = new Array(N).fill(false).map(() => new Array(M).fill(false))
|
||
|
||
// 第一边界左边和第二边界右边
|
||
for (let i = 0; i < N; i++) {
|
||
bfs(graph, firstBorder, i, 0)
|
||
bfs(graph, secondBorder, i, M - 1)
|
||
}
|
||
|
||
// 第一边界上边和第二边界下边
|
||
for (let j = 0; j < M; j++) {
|
||
bfs(graph, firstBorder, 0, j)
|
||
bfs(graph, secondBorder, N - 1, j)
|
||
}
|
||
|
||
// 遍历地图,判断是否能到达第一组边界和第二组边界
|
||
for (let i = 0; i < N; i++) {
|
||
for (let j = 0; j < M; j++) {
|
||
if (firstBorder[i][j] && secondBorder[i][j]) console.log(i + ' ' + j);
|
||
}
|
||
}
|
||
})()
|
||
```
|
||
|
||
|
||
|
||
### TypeScript
|
||
|
||
### PhP
|
||
|
||
### Swift
|
||
|
||
### Scala
|
||
|
||
### C#
|
||
|
||
### Dart
|
||
|
||
### C
|
||
|
||
|
||
|