222 lines
5.1 KiB
Markdown
222 lines
5.1 KiB
Markdown
|
||
<p align="center"><strong><a href="./qita/join.md">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!</strong></p>
|
||
|
||
# 108. 冗余连接
|
||
|
||
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1181)
|
||
|
||
题目描述
|
||
|
||
树可以看成是一个图(拥有 n 个节点和 n - 1 条边的连通无环无向图)。
|
||
|
||
现给定一个拥有 n 个节点(节点编号从 1 到 n)和 n 条边的连通无向图,请找出一条可以删除的边,删除后图可以变成一棵树。
|
||
|
||
输入描述
|
||
|
||
第一行包含一个整数 N,表示图的节点个数和边的个数。
|
||
|
||
后续 N 行,每行包含两个整数 s 和 t,表示图中 s 和 t 之间有一条边。
|
||
|
||
输出描述
|
||
|
||
输出一条可以删除的边。如果有多个答案,请删除标准输入中最后出现的那条边。
|
||
|
||
输入示例
|
||
|
||
```
|
||
3
|
||
1 2
|
||
2 3
|
||
1 3
|
||
```
|
||
|
||
输出示例
|
||
|
||
1 3
|
||
|
||
提示信息
|
||
|
||
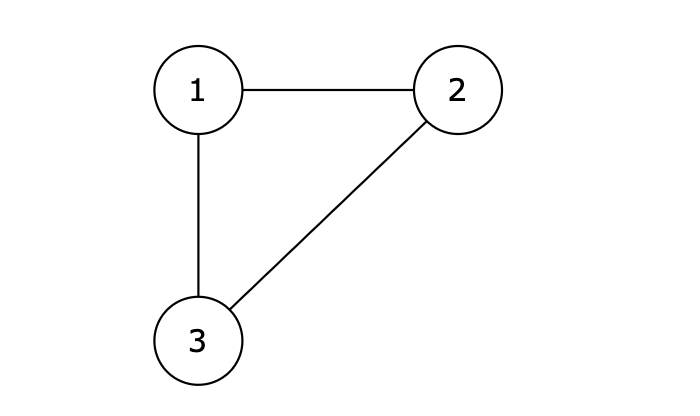
|
||
|
||
图中的 1 2,2 3,1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边,所以输出结果为 1 3
|
||
|
||
数据范围:
|
||
|
||
1 <= N <= 1000.
|
||
|
||
## 思路
|
||
|
||
这道题目也是并查集基础题目。
|
||
|
||
这里我依然降调一下,并查集可以解决什么问题:两个节点是否在一个集合,也可以将两个节点添加到一个集合中。
|
||
|
||
如果还不了解并查集,可以看这里:[并查集理论基础](./图论并查集理论基础.md)
|
||
|
||
我们再来看一下这道题目。
|
||
|
||
题目说是无向图,返回一条可以删去的边,使得结果图是一个有着N个节点的树(即:只有一个根节点)。
|
||
|
||
如果有多个答案,则返回二维数组中最后出现的边。
|
||
|
||
那么我们就可以从前向后遍历每一条边(因为优先让前面的边连上),边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
|
||
|
||
如图所示:
|
||
|
||
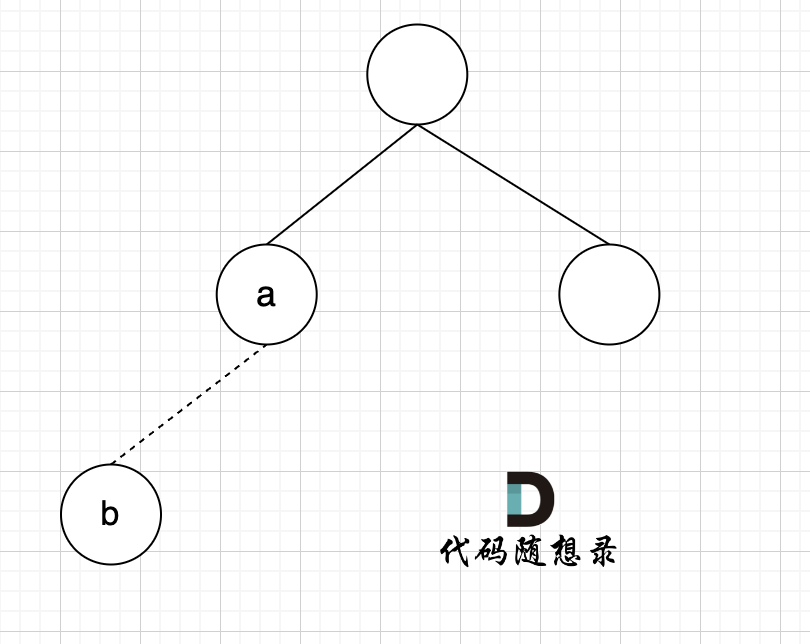
|
||
|
||
节点A 和节点 B 不在同一个集合,那么就可以将两个 节点连在一起。
|
||
|
||
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
|
||
|
||
如图所示:
|
||
|
||
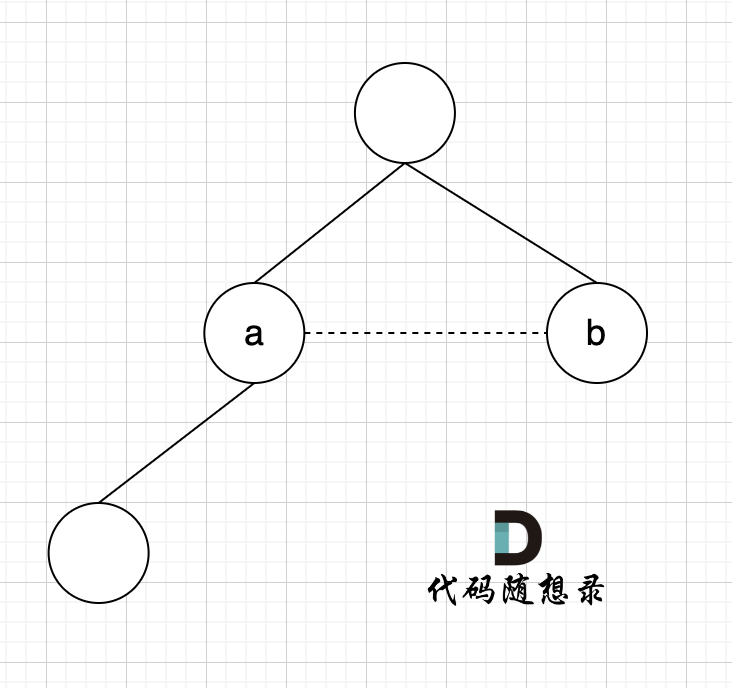
|
||
|
||
已经判断 节点A 和 节点B 在在同一个集合(同一个根),如果将 节点A 和 节点B 连在一起就一定会出现环。
|
||
|
||
这个思路清晰之后,代码就很好写了。
|
||
|
||
并查集C++代码如下:
|
||
|
||
```CPP
|
||
#include <iostream>
|
||
#include <vector>
|
||
using namespace std;
|
||
int n; // 节点数量
|
||
vector<int> father(1001, 0); // 按照节点大小范围定义数组
|
||
|
||
// 并查集初始化
|
||
void init() {
|
||
for (int i = 0; i <= n; ++i) {
|
||
father[i] = i;
|
||
}
|
||
}
|
||
// 并查集里寻根的过程
|
||
int find(int u) {
|
||
return u == father[u] ? u : father[u] = find(father[u]);
|
||
}
|
||
// 判断 u 和 v是否找到同一个根
|
||
bool isSame(int u, int v) {
|
||
u = find(u);
|
||
v = find(v);
|
||
return u == v;
|
||
}
|
||
// 将v->u 这条边加入并查集
|
||
void join(int u, int v) {
|
||
u = find(u); // 寻找u的根
|
||
v = find(v); // 寻找v的根
|
||
if (u == v) return ; // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
|
||
father[v] = u;
|
||
}
|
||
|
||
int main() {
|
||
int s, t;
|
||
cin >> n;
|
||
init();
|
||
for (int i = 0; i < n; i++) {
|
||
cin >> s >> t;
|
||
if (isSame(s, t)) {
|
||
cout << s << " " << t << endl;
|
||
return 0;
|
||
} else {
|
||
join(s, t);
|
||
}
|
||
}
|
||
}
|
||
```
|
||
|
||
可以看出,主函数的代码很少,就判断一下边的两个节点在不在同一个集合就可以了。
|
||
|
||
|
||
|
||
## 其他语言版本
|
||
|
||
### Java
|
||
|
||
### Python
|
||
|
||
### Go
|
||
|
||
### Rust
|
||
|
||
### Javascript
|
||
|
||
```javascript
|
||
const r1 = require('readline').createInterface({ input: process.stdin });
|
||
// 创建readline接口
|
||
let iter = r1[Symbol.asyncIterator]();
|
||
// 创建异步迭代器
|
||
const readline = async () => (await iter.next()).value;
|
||
|
||
|
||
let N // 节点数和边数
|
||
let father = [] // 并查集
|
||
|
||
|
||
// 并查集初始化
|
||
const init = () => {
|
||
for (let i = 1; i <= N; i++) father[i] = i;
|
||
}
|
||
|
||
// 并查集里寻根的过程
|
||
const find = (u) => {
|
||
return u == father[u] ? u : father[u] = find(father[u])
|
||
}
|
||
|
||
// 将v->u 这条边加入并查集
|
||
const join = (u, v) => {
|
||
u = find(u)
|
||
v = find(v)
|
||
if (u == v) return // 如果发现根相同,则说明在一个集合,不用两个节点相连直接返回
|
||
father[v] = u
|
||
}
|
||
|
||
// 判断 u 和 v是否找到同一个根
|
||
const isSame = (u, v) => {
|
||
u = find(u)
|
||
v = find(v)
|
||
return u == v
|
||
}
|
||
|
||
|
||
(async function () {
|
||
// 读取第一行输入
|
||
let line = await readline();
|
||
N = Number(line);
|
||
|
||
// 初始化并查集
|
||
father = new Array(N)
|
||
init()
|
||
|
||
// 读取边信息, 加入并查集
|
||
for (let i = 0; i < N; i++) {
|
||
line = await readline()
|
||
line = line.split(' ').map(Number)
|
||
|
||
if (!isSame(line[0], line[1])) {
|
||
join(line[0], line[1])
|
||
}else{
|
||
console.log(line[0], line[1]);
|
||
break
|
||
}
|
||
}
|
||
})()
|
||
```
|
||
|
||
|
||
|
||
### TypeScript
|
||
|
||
### PhP
|
||
|
||
### Swift
|
||
|
||
### Scala
|
||
|
||
### C#
|
||
|
||
### Dart
|
||
|
||
### C
|
||
|