802 lines
24 KiB
Markdown
802 lines
24 KiB
Markdown
* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
|
||
* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
|
||
* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
|
||
|
||
|
||
# 416. 分割等和子集
|
||
|
||
[力扣题目链接](https://leetcode.cn/problems/partition-equal-subset-sum/)
|
||
|
||
题目难易:中等
|
||
|
||
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
|
||
|
||
注意:
|
||
每个数组中的元素不会超过 100
|
||
数组的大小不会超过 200
|
||
|
||
示例 1:
|
||
* 输入: [1, 5, 11, 5]
|
||
* 输出: true
|
||
* 解释: 数组可以分割成 [1, 5, 5] 和 [11].
|
||
|
||
示例 2:
|
||
* 输入: [1, 2, 3, 5]
|
||
* 输出: false
|
||
* 解释: 数组不能分割成两个元素和相等的子集.
|
||
|
||
提示:
|
||
* 1 <= nums.length <= 200
|
||
* 1 <= nums[i] <= 100
|
||
|
||
## 算法公开课
|
||
|
||
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[动态规划之背包问题,这个包能装满吗?| LeetCode:416.分割等和子集](https://www.bilibili.com/video/BV1rt4y1N7jE/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||
|
||
|
||
## 思路
|
||
|
||
这道题目初步看,和如下两题几乎是一样的,大家可以用回溯法,解决如下两题
|
||
|
||
* 698.划分为k个相等的子集
|
||
* 473.火柴拼正方形
|
||
|
||
这道题目是要找是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
|
||
|
||
那么只要找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了。
|
||
|
||
本题是可以用回溯暴力搜索出所有答案的,但最后超时了,也不想再优化了,放弃回溯。
|
||
|
||
是否有其他解法可以解决此题。
|
||
|
||
本题的本质是,能否把容量为 sum / 2的背包装满。
|
||
|
||
**这是 背包算法可以解决的经典类型题目**。
|
||
|
||
如果对01背包不够了解,建议仔细看完如下两篇:
|
||
|
||
* [动态规划:关于01背包问题,你该了解这些!](https://programmercarl.com/背包理论基础01背包-1.html)
|
||
* [动态规划:关于01背包问题,你该了解这些!(滚动数组)](https://programmercarl.com/背包理论基础01背包-2.html)
|
||
|
||
## 01背包问题
|
||
|
||
01背包问题,大家都知道,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
|
||
|
||
**背包问题有多种背包方式,常见的有:01背包、完全背包、多重背包、分组背包和混合背包等等。**
|
||
|
||
要注意题目描述中商品是不是可以重复放入。
|
||
|
||
**即一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包,写法还是不一样的。**
|
||
|
||
**元素我们只能用一次,如果使用背包,那么也是01背包**
|
||
|
||
回归主题:首先,本题要求集合里能否出现总和为 sum / 2 的子集。
|
||
|
||
既有一个 只能装重量为 sum / 2 的背包,商品为数字,这些数字能不能把 这个背包装满。
|
||
|
||
那每一件商品是数字的话,对应的重量 和 价值是多少呢?
|
||
|
||
一个数字只有一个维度,即 重量等于价值。
|
||
|
||
当数字 可以装满 承载重量为 sum / 2 的背包的背包时,这个背包的价值也是 sum / 2。
|
||
|
||
那么这道题就是 装满 承载重量为 sum / 2 的背包,价值最大是多少?
|
||
|
||
如果最大价值是 sum / 2,说明正好被商品装满了。
|
||
|
||
因为商品是数字,重量和对应的价值是相同的。
|
||
|
||
以上分析完,我们就可以直接用01背包 来解决这个问题了。
|
||
|
||
动规五部曲分析如下:
|
||
|
||
### 1. 确定dp数组以及下标的含义
|
||
|
||
01背包中,dp[j] 表示: 容量(所能装的重量)为j的背包,所背的物品价值最大可以为dp[j]。
|
||
|
||
如果背包所载重量为target, dp[target]就是装满 背包之后的总价值,因为 本题中每一个元素的数值既是重量,也是价值,所以,当 dp[target] == target 的时候,背包就装满了。
|
||
|
||
有录友可能想,那还有装不满的时候?
|
||
|
||
拿输入数组 [1, 5, 11, 5],举例, dp[7] 只能等于 6,因为 只能放进 1 和 5。
|
||
|
||
而dp[6] 就可以等于6了,放进1 和 5,那么dp[6] == 6,说明背包装满了。
|
||
|
||
### 2. 确定递推公式
|
||
|
||
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
|
||
|
||
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
|
||
|
||
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
|
||
|
||
|
||
### 3. dp数组如何初始化
|
||
|
||
在01背包,一维dp如何初始化,已经讲过,
|
||
|
||
从dp[j]的定义来看,首先dp[0]一定是0。
|
||
|
||
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
|
||
|
||
**这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了**。
|
||
|
||
本题题目中 只包含正整数的非空数组,所以非0下标的元素初始化为0就可以了。
|
||
|
||
代码如下:
|
||
|
||
```CPP
|
||
// 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200
|
||
// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了
|
||
vector<int> dp(10001, 0);
|
||
```
|
||
|
||
### 4. 确定遍历顺序
|
||
|
||
在[动态规划:关于01背包问题,你该了解这些!(滚动数组)](https://programmercarl.com/背包理论基础01背包-2.html)中就已经说明:如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
|
||
|
||
代码如下:
|
||
|
||
```CPP
|
||
// 开始 01背包
|
||
for(int i = 0; i < nums.size(); i++) {
|
||
for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历
|
||
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
|
||
}
|
||
}
|
||
```
|
||
|
||
### 5. 举例推导dp数组
|
||
|
||
dp[j]的数值一定是小于等于j的。
|
||
|
||
**如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j,理解这一点很重要。**
|
||
|
||
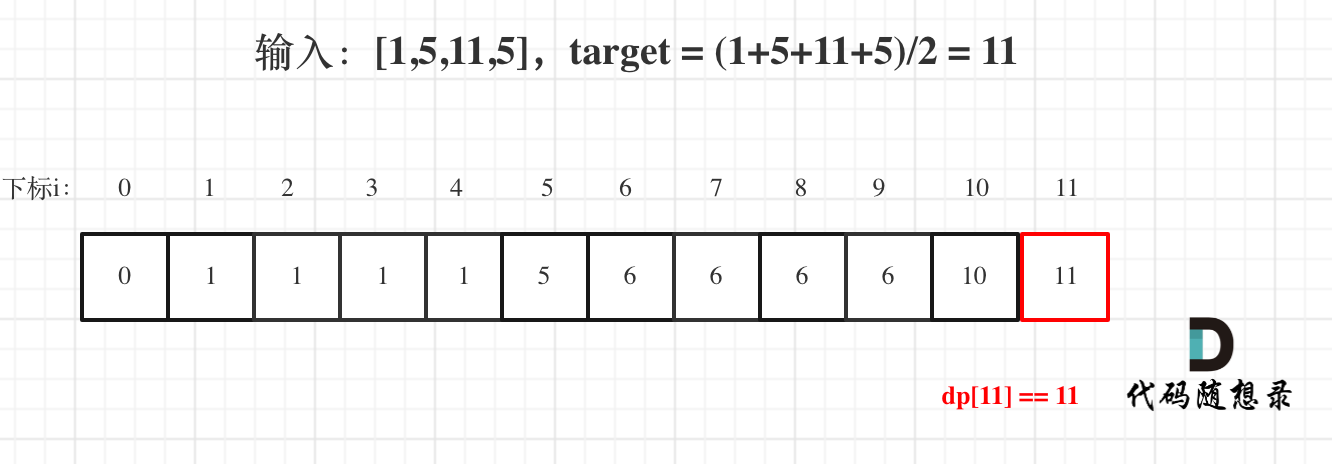
用例1,输入[1,5,11,5] 为例,如图:
|
||
|
||
|
||
|
||
|
||
最后dp[11] == 11,说明可以将这个数组分割成两个子集,使得两个子集的元素和相等。
|
||
|
||
综上分析完毕,C++代码如下:
|
||
|
||
```CPP
|
||
class Solution {
|
||
public:
|
||
bool canPartition(vector<int>& nums) {
|
||
int sum = 0;
|
||
|
||
// dp[i]中的i表示背包内总和
|
||
// 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200
|
||
// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了
|
||
vector<int> dp(10001, 0);
|
||
for (int i = 0; i < nums.size(); i++) {
|
||
sum += nums[i];
|
||
}
|
||
// 也可以使用库函数一步求和
|
||
// int sum = accumulate(nums.begin(), nums.end(), 0);
|
||
if (sum % 2 == 1) return false;
|
||
int target = sum / 2;
|
||
|
||
// 开始 01背包
|
||
for(int i = 0; i < nums.size(); i++) {
|
||
for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历
|
||
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
|
||
}
|
||
}
|
||
// 集合中的元素正好可以凑成总和target
|
||
if (dp[target] == target) return true;
|
||
return false;
|
||
}
|
||
};
|
||
```
|
||
|
||
* 时间复杂度:O(n^2)
|
||
* 空间复杂度:O(n),虽然dp数组大小为一个常数,但是大常数
|
||
|
||
## 总结
|
||
|
||
这道题目就是一道01背包经典应用类的题目,需要我们拆解题目,然后才能发现可以使用01背包。
|
||
|
||
01背包相对于本题,主要要理解,题目中物品是nums[i],重量是nums[i],价值也是nums[i],背包体积是sum/2。
|
||
|
||
做完本题后,需要大家清晰:背包问题,不仅可以求 背包能被的最大价值,还可以求这个背包是否可以装满。
|
||
|
||
## 其他语言版本
|
||
|
||
|
||
### Java:
|
||
```Java
|
||
class Solution {
|
||
public boolean canPartition(int[] nums) {
|
||
if(nums == null || nums.length == 0) return false;
|
||
int n = nums.length;
|
||
int sum = 0;
|
||
for(int num : nums) {
|
||
sum += num;
|
||
}
|
||
//总和为奇数,不能平分
|
||
if(sum % 2 != 0) return false;
|
||
int target = sum / 2;
|
||
int[] dp = new int[target + 1];
|
||
for(int i = 0; i < n; i++) {
|
||
for(int j = target; j >= nums[i]; j--) {
|
||
//物品 i 的重量是 nums[i],其价值也是 nums[i]
|
||
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
|
||
}
|
||
|
||
//剪枝一下,每一次完成內層的for-loop,立即檢查是否dp[target] == target,優化時間複雜度(26ms -> 20ms)
|
||
if(dp[target] == target)
|
||
return true;
|
||
}
|
||
return dp[target] == target;
|
||
}
|
||
}
|
||
```
|
||
|
||
二维数组版本(易于理解):
|
||
```java
|
||
public class Solution {
|
||
public static void main(String[] args) {
|
||
int num[] = {1,5,11,5};
|
||
canPartition(num);
|
||
|
||
}
|
||
public static boolean canPartition(int[] nums) {
|
||
int len = nums.length;
|
||
// 题目已经说非空数组,可以不做非空判断
|
||
int sum = 0;
|
||
for (int num : nums) {
|
||
sum += num;
|
||
}
|
||
// 特判:如果是奇数,就不符合要求
|
||
if ((sum %2 ) != 0) {
|
||
return false;
|
||
}
|
||
|
||
int target = sum / 2; //目标背包容量
|
||
// 创建二维状态数组,行:物品索引,列:容量(包括 0)
|
||
/*
|
||
dp[i][j]表示从数组的 [0, i] 这个子区间内挑选一些正整数
|
||
每个数只能用一次,使得这些数的和恰好等于 j。
|
||
*/
|
||
boolean[][] dp = new boolean[len][target + 1];
|
||
|
||
// 先填表格第 0 行,第 1 个数只能让容积为它自己的背包恰好装满 (这里的dp[][]数组的含义就是“恰好”,所以就算容积比它大的也不要)
|
||
if (nums[0] <= target) {
|
||
dp[0][nums[0]] = true;
|
||
}
|
||
// 再填表格后面几行
|
||
//外层遍历物品
|
||
for (int i = 1; i < len; i++) {
|
||
//内层遍历背包
|
||
for (int j = 0; j <= target; j++) {
|
||
// 直接从上一行先把结果抄下来,然后再修正
|
||
dp[i][j] = dp[i - 1][j];
|
||
|
||
//如果某个物品单独的重量恰好就等于背包的重量,那么也是满足dp数组的定义的
|
||
if (nums[i] == j) {
|
||
dp[i][j] = true;
|
||
continue;
|
||
}
|
||
//如果某个物品的重量小于j,那就可以看该物品是否放入背包
|
||
//dp[i - 1][j]表示该物品不放入背包,如果在 [0, i - 1] 这个子区间内已经有一部分元素,使得它们的和为 j ,那么 dp[i][j] = true;
|
||
//dp[i - 1][j - nums[i]]表示该物品放入背包。如果在 [0, i - 1] 这个子区间内就得找到一部分元素,使得它们的和为 j - nums[i]。
|
||
if (nums[i] < j) {
|
||
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
|
||
}
|
||
}
|
||
}
|
||
for (int i = 0; i < len; i++) {
|
||
for (int j = 0; j <= target; j++) {
|
||
System.out.print(dp[i][j]+" ");
|
||
}
|
||
System.out.println();
|
||
}
|
||
return dp[len - 1][target];
|
||
}
|
||
}
|
||
//dp数组的打印结果
|
||
false true false false false false false false false false false false
|
||
false true false false false true true false false false false false
|
||
false true false false false true true false false false false true
|
||
false true false false false true true false false false true true
|
||
```
|
||
二維數組整數版本
|
||
```Java
|
||
class Solution {
|
||
public boolean canPartition(int[] nums) {
|
||
//using 2-D DP array.
|
||
int len = nums.length;
|
||
//check edge cases;
|
||
if(len == 0)
|
||
return false;
|
||
|
||
int sum = 0;
|
||
for (int num : nums)
|
||
sum += num;
|
||
//we only deal with even numbers. If sum is odd, return false;
|
||
if(sum % 2 == 1)
|
||
return false;
|
||
|
||
int target = sum / 2;
|
||
int[][] dp = new int[nums.length][target + 1];
|
||
|
||
// for(int j = 0; j <= target; j++){
|
||
// if(j < nums[0])
|
||
// dp[0][j] = 0;
|
||
// else
|
||
// dp[0][j] = nums[0];
|
||
// }
|
||
|
||
//initialize dp array
|
||
for(int j = nums[0]; j <= target; j++){
|
||
dp[0][j] = nums[0];
|
||
}
|
||
|
||
for(int i = 1; i < len; i++){
|
||
for(int j = 0; j <= target; j++){
|
||
if (j < nums[i])
|
||
dp[i][j] = dp[i - 1][j];
|
||
else
|
||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
|
||
}
|
||
}
|
||
|
||
//print out DP array
|
||
// for(int x : dp){
|
||
// System.out.print(x + ",");
|
||
// }
|
||
// System.out.print(" "+i+" row"+"\n");
|
||
return dp[len - 1][target] == target;
|
||
}
|
||
}
|
||
//dp数组的打印结果 for test case 1.
|
||
0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
|
||
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 6, 6,
|
||
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 6, 11,
|
||
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 10, 11,
|
||
```
|
||
|
||
### Python:
|
||
卡哥版
|
||
```python
|
||
class Solution:
|
||
def canPartition(self, nums: List[int]) -> bool:
|
||
_sum = 0
|
||
|
||
# dp[i]中的i表示背包内总和
|
||
# 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200
|
||
# 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了
|
||
dp = [0] * 10001
|
||
for num in nums:
|
||
_sum += num
|
||
# 也可以使用内置函数一步求和
|
||
# _sum = sum(nums)
|
||
if _sum % 2 == 1:
|
||
return False
|
||
target = _sum // 2
|
||
|
||
# 开始 0-1背包
|
||
for num in nums:
|
||
for j in range(target, num - 1, -1): # 每一个元素一定是不可重复放入,所以从大到小遍历
|
||
dp[j] = max(dp[j], dp[j - num] + num)
|
||
|
||
# 集合中的元素正好可以凑成总和target
|
||
if dp[target] == target:
|
||
return True
|
||
return False
|
||
|
||
```
|
||
|
||
卡哥版(简化版)
|
||
```python
|
||
class Solution:
|
||
def canPartition(self, nums: List[int]) -> bool:
|
||
if sum(nums) % 2 != 0:
|
||
return False
|
||
target = sum(nums) // 2
|
||
dp = [0] * (target + 1)
|
||
for num in nums:
|
||
for j in range(target, num-1, -1):
|
||
dp[j] = max(dp[j], dp[j-num] + num)
|
||
return dp[-1] == target
|
||
|
||
```
|
||
二维DP版
|
||
```python
|
||
class Solution:
|
||
def canPartition(self, nums: List[int]) -> bool:
|
||
|
||
total_sum = sum(nums)
|
||
|
||
if total_sum % 2 != 0:
|
||
return False
|
||
|
||
target_sum = total_sum // 2
|
||
dp = [[False] * (target_sum + 1) for _ in range(len(nums) + 1)]
|
||
|
||
# 初始化第一行(空子集可以得到和为0)
|
||
for i in range(len(nums) + 1):
|
||
dp[i][0] = True
|
||
|
||
for i in range(1, len(nums) + 1):
|
||
for j in range(1, target_sum + 1):
|
||
if j < nums[i - 1]:
|
||
# 当前数字大于目标和时,无法使用该数字
|
||
dp[i][j] = dp[i - 1][j]
|
||
else:
|
||
# 当前数字小于等于目标和时,可以选择使用或不使用该数字
|
||
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]]
|
||
|
||
return dp[len(nums)][target_sum]
|
||
|
||
```
|
||
一维DP版
|
||
```python
|
||
class Solution:
|
||
def canPartition(self, nums: List[int]) -> bool:
|
||
|
||
total_sum = sum(nums)
|
||
|
||
if total_sum % 2 != 0:
|
||
return False
|
||
|
||
target_sum = total_sum // 2
|
||
dp = [False] * (target_sum + 1)
|
||
dp[0] = True
|
||
|
||
for num in nums:
|
||
# 从target_sum逆序迭代到num,步长为-1
|
||
for i in range(target_sum, num - 1, -1):
|
||
dp[i] = dp[i] or dp[i - num]
|
||
return dp[target_sum]
|
||
|
||
|
||
```
|
||
|
||
### Go:
|
||
一维dp
|
||
```go
|
||
// 分割等和子集 动态规划
|
||
// 时间复杂度O(n^2) 空间复杂度O(n)
|
||
func canPartition(nums []int) bool {
|
||
sum := 0
|
||
for _, num := range nums {
|
||
sum += num
|
||
}
|
||
// 如果 nums 的总和为奇数则不可能平分成两个子集
|
||
if sum % 2 == 1 {
|
||
return false
|
||
}
|
||
|
||
target := sum / 2
|
||
dp := make([]int, target + 1)
|
||
|
||
for _, num := range nums {
|
||
for j := target; j >= num; j-- {
|
||
if dp[j] < dp[j - num] + num {
|
||
dp[j] = dp[j - num] + num
|
||
}
|
||
}
|
||
}
|
||
return dp[target] == target
|
||
}
|
||
```
|
||
|
||
二维dp
|
||
```go
|
||
func canPartition(nums []int) bool {
|
||
sum := 0
|
||
for _, val := range nums {
|
||
sum += val
|
||
}
|
||
if sum % 2 == 1 {
|
||
return false
|
||
}
|
||
target := sum / 2
|
||
dp := make([][]int, len(nums))
|
||
for i := range dp {
|
||
dp[i] = make([]int, target + 1)
|
||
}
|
||
for j := nums[0]; j <= target; j++ {
|
||
dp[0][j] = nums[0]
|
||
}
|
||
for i := 1; i < len(nums); i++ {
|
||
for j := 0; j <= target; j++ {
|
||
if j < nums[i] {
|
||
dp[i][j] = dp[i-1][j]
|
||
} else {
|
||
dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i])
|
||
}
|
||
}
|
||
}
|
||
return dp[len(nums)-1][target] == target
|
||
}
|
||
|
||
func max(x, y int) int {
|
||
if x > y {
|
||
return x
|
||
}
|
||
return y
|
||
}
|
||
```
|
||
|
||
### JavaScript:
|
||
|
||
```js
|
||
var canPartition = function(nums) {
|
||
const sum = (nums.reduce((p, v) => p + v));
|
||
if (sum & 1) return false;
|
||
const dp = Array(sum / 2 + 1).fill(0);
|
||
for(let i = 0; i < nums.length; i++) {
|
||
for(let j = sum / 2; j >= nums[i]; j--) {
|
||
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
|
||
if (dp[j] === sum / 2) {
|
||
return true;
|
||
}
|
||
}
|
||
}
|
||
return dp[sum / 2] === sum / 2;
|
||
};
|
||
```
|
||
|
||
|
||
### Rust:
|
||
|
||
```Rust
|
||
impl Solution {
|
||
pub fn can_partition(nums: Vec<i32>) -> bool {
|
||
let sum = nums.iter().sum::<i32>() as usize;
|
||
if sum % 2 == 1 {
|
||
return false;
|
||
}
|
||
let target = sum / 2;
|
||
let mut dp = vec![0; target + 1];
|
||
for n in nums {
|
||
for j in (n as usize..=target).rev() {
|
||
dp[j] = dp[j].max(dp[j - n as usize] + n)
|
||
}
|
||
}
|
||
if dp[target] == target as i32 {
|
||
return true;
|
||
}
|
||
false
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
### C:
|
||
|
||
二维dp:
|
||
```c
|
||
/**
|
||
1. dp数组含义:dp[i][j]为背包重量为j时,从[0-i]元素和最大值
|
||
2. 递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i])
|
||
3. 初始化:dp[i][0]初始化为0。因为背包重量为0时,不可能放入元素。dp[0][j] = nums[0],当j >= nums[0] && j < target时
|
||
4. 遍历顺序:先遍历物品,再遍历背包
|
||
*/
|
||
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
|
||
|
||
int getSum(int* nums, int numsSize) {
|
||
int sum = 0;
|
||
|
||
int i;
|
||
for(i = 0; i < numsSize; ++i) {
|
||
sum += nums[i];
|
||
}
|
||
return sum;
|
||
}
|
||
|
||
bool canPartition(int* nums, int numsSize){
|
||
// 求出元素总和
|
||
int sum = getSum(nums, numsSize);
|
||
// 若元素总和为奇数,则不可能得到两个和相等的子数组
|
||
if(sum % 2)
|
||
return false;
|
||
|
||
// 若子数组的和等于target,则nums可以被分割
|
||
int target = sum / 2;
|
||
// 初始化dp数组
|
||
int dp[numsSize][target + 1];
|
||
// dp[j][0]都应被设置为0。因为当背包重量为0时,不可放入元素
|
||
memset(dp, 0, sizeof(int) * numsSize * (target + 1));
|
||
|
||
int i, j;
|
||
// 当背包重量j大于nums[0]时,可以在dp[0][j]中放入元素nums[0]
|
||
for(j = nums[0]; j <= target; ++j) {
|
||
dp[0][j] = nums[0];
|
||
}
|
||
|
||
for(i = 1; i < numsSize; ++i) {
|
||
for(j = 1; j <= target; ++j) {
|
||
// 若当前背包重量j小于nums[i],则其值等于只考虑0到i-1物品时的值
|
||
if(j < nums[i])
|
||
dp[i][j] = dp[i - 1][j];
|
||
// 否则,背包重量等于在背包中放入num[i]/不放入nums[i]的较大值
|
||
else
|
||
dp[i][j] = MAX(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
|
||
}
|
||
}
|
||
// 判断背包重量为target,且考虑到所有物品时,放入的元素和是否等于target
|
||
return dp[numsSize - 1][target] == target;
|
||
}
|
||
```
|
||
滚动数组:
|
||
```c
|
||
/**
|
||
1. dp数组含义:dp[j]为背包重量为j时,其中可放入元素的最大值
|
||
2. 递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
|
||
3. 初始化:均初始化为0即可
|
||
4. 遍历顺序:先遍历物品,再后序遍历背包
|
||
*/
|
||
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
|
||
|
||
int getSum(int* nums, int numsSize) {
|
||
int sum = 0;
|
||
|
||
int i;
|
||
for(i = 0; i < numsSize; ++i) {
|
||
sum += nums[i];
|
||
}
|
||
return sum;
|
||
}
|
||
|
||
bool canPartition(int* nums, int numsSize){
|
||
// 求出元素总和
|
||
int sum = getSum(nums, numsSize);
|
||
// 若元素总和为奇数,则不可能得到两个和相等的子数组
|
||
if(sum % 2)
|
||
return false;
|
||
// 背包容量
|
||
int target = sum / 2;
|
||
|
||
// 初始化dp数组,元素均为0
|
||
int dp[target + 1];
|
||
memset(dp, 0, sizeof(int) * (target + 1));
|
||
|
||
int i, j;
|
||
// 先遍历物品,后遍历背包
|
||
for(i = 0; i < numsSize; ++i) {
|
||
for(j = target; j >= nums[i]; --j) {
|
||
dp[j] = MAX(dp[j], dp[j - nums[i]] + nums[i]);
|
||
}
|
||
}
|
||
|
||
// 查看背包容量为target时,元素总和是否等于target
|
||
return dp[target] == target;
|
||
}
|
||
```
|
||
|
||
### TypeScript:
|
||
|
||
> 一维数组,简洁
|
||
|
||
```typescript
|
||
function canPartition(nums: number[]): boolean {
|
||
const sum: number = nums.reduce((pre, cur) => pre + cur);
|
||
if (sum % 2 === 1) return false;
|
||
const bagSize: number = sum / 2;
|
||
const goodsNum: number = nums.length;
|
||
const dp: number[] = new Array(bagSize + 1).fill(0);
|
||
for (let i = 0; i < goodsNum; i++) {
|
||
for (let j = bagSize; j >= nums[i]; j--) {
|
||
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
|
||
}
|
||
}
|
||
return dp[bagSize] === bagSize;
|
||
};
|
||
```
|
||
|
||
> 二维数组,易懂
|
||
|
||
```typescript
|
||
function canPartition(nums: number[]): boolean {
|
||
/**
|
||
weightArr = nums;
|
||
valueArr = nums;
|
||
bagSize = sum / 2; (sum为nums各元素总和);
|
||
按照0-1背包处理
|
||
*/
|
||
const sum: number = nums.reduce((pre, cur) => pre + cur);
|
||
if (sum % 2 === 1) return false;
|
||
const bagSize: number = sum / 2;
|
||
const weightArr: number[] = nums;
|
||
const valueArr: number[] = nums;
|
||
const goodsNum: number = weightArr.length;
|
||
const dp: number[][] = new Array(goodsNum)
|
||
.fill(0)
|
||
.map(_ => new Array(bagSize + 1).fill(0));
|
||
for (let i = weightArr[0]; i <= bagSize; i++) {
|
||
dp[0][i] = valueArr[0];
|
||
}
|
||
for (let i = 1; i < goodsNum; i++) {
|
||
for (let j = 0; j <= bagSize; j++) {
|
||
if (j < weightArr[i]) {
|
||
dp[i][j] = dp[i - 1][j];
|
||
} else {
|
||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weightArr[i]] + valueArr[i]);
|
||
}
|
||
}
|
||
}
|
||
return dp[goodsNum - 1][bagSize] === bagSize;
|
||
};
|
||
```
|
||
|
||
### Scala:
|
||
|
||
滚动数组:
|
||
```scala
|
||
object Solution {
|
||
def canPartition(nums: Array[Int]): Boolean = {
|
||
var sum = nums.sum
|
||
if (sum % 2 != 0) return false
|
||
var half = sum / 2
|
||
var dp = new Array[Int](half + 1)
|
||
|
||
// 遍历
|
||
for (i <- 0 until nums.length; j <- half to nums(i) by -1) {
|
||
dp(j) = math.max(dp(j), dp(j - nums(i)) + nums(i))
|
||
}
|
||
|
||
if (dp(half) == half) true else false
|
||
}
|
||
}
|
||
```
|
||
|
||
二维数组:
|
||
```scala
|
||
object Solution {
|
||
def canPartition(nums: Array[Int]): Boolean = {
|
||
var sum = nums.sum
|
||
if (sum % 2 != 0) return false
|
||
var half = sum / 2
|
||
var dp = Array.ofDim[Int](nums.length, half + 1)
|
||
|
||
// 初始化
|
||
for (j <- nums(0) to half) dp(0)(j) = nums(0)
|
||
|
||
// 遍历
|
||
for (i <- 1 until nums.length; j <- 1 to half) {
|
||
if (j - nums(i) >= 0) dp(i)(j) = nums(i) + dp(i - 1)(j - nums(i))
|
||
dp(i)(j) = math.max(dp(i)(j), dp(i - 1)(j))
|
||
}
|
||
|
||
// 如果等于half就返回ture,否则返回false
|
||
if (dp(nums.length - 1)(half) == half) true else false
|
||
}
|
||
}
|
||
```
|
||
### C#
|
||
```csharp
|
||
public class Solution
|
||
{
|
||
public bool CanPartition(int[] nums)
|
||
{
|
||
int sum = 0;
|
||
int[] dp = new int[10001];
|
||
foreach (int num in nums)
|
||
{
|
||
sum += num;
|
||
}
|
||
if (sum % 2 == 1) return false;
|
||
int tartget = sum / 2;
|
||
for (int i = 0; i < nums.Length; i++)
|
||
{
|
||
for (int j = tartget; j >= nums[i]; j--)
|
||
{
|
||
dp[j] = Math.Max(dp[j], dp[j - nums[i]] + nums[i]);
|
||
}
|
||
}
|
||
if (dp[tartget] == tartget)
|
||
return true;
|
||
|
||
return false;
|
||
|
||
}
|
||
}
|
||
```
|
||
|