301 lines
12 KiB
Markdown
301 lines
12 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/RsdcQ9umo09R6cfnwXZlrQ"><img src="https://img.shields.io/badge/PDF下载-代码随想录-blueviolet" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||
</p>
|
||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
|
||
## 337.打家劫舍 III
|
||
|
||
题目链接:https://leetcode-cn.com/problems/house-robber-iii/
|
||
|
||
在上次打劫完一条街道之后和一圈房屋后,小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为“根”。 除了“根”之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果两个直接相连的房子在同一天晚上被打劫,房屋将自动报警。
|
||
|
||
计算在不触动警报的情况下,小偷一晚能够盗取的最高金额。
|
||
|
||

|
||
|
||
## 思路
|
||
|
||
这道题目和 [198.打家劫舍](https://mp.weixin.qq.com/s/UZ31WdLEEFmBegdgLkJ8Dw),[213.打家劫舍II](https://mp.weixin.qq.com/s/kKPx4HpH3RArbRcxAVHbeQ)也是如出一辙,只不过这个换成了树。
|
||
|
||
如果对树的遍历不够熟悉的话,那本题就有难度了。
|
||
|
||
对于树的话,首先就要想到遍历方式,前中后序(深度优先搜索)还是层序遍历(广度优先搜索)。
|
||
|
||
**本题一定是要后序遍历,因为通过递归函数的返回值来做下一步计算**。
|
||
|
||
与198.打家劫舍,213.打家劫舍II一样,关键是要讨论当前节点抢还是不抢。
|
||
|
||
如果抢了当前节点,两个孩子就不是动,如果没抢当前节点,就可以考虑抢左右孩子(**注意这里说的是“考虑”**)
|
||
|
||
### 暴力递归
|
||
|
||
代码如下:
|
||
|
||
```C++
|
||
class Solution {
|
||
public:
|
||
int rob(TreeNode* root) {
|
||
if (root == NULL) return 0;
|
||
if (root->left == NULL && root->right == NULL) return root->val;
|
||
// 偷父节点
|
||
int val1 = root->val;
|
||
if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 跳过root->left,相当于不考虑左孩子了
|
||
if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 跳过root->right,相当于不考虑右孩子了
|
||
// 不偷父节点
|
||
int val2 = rob(root->left) + rob(root->right); // 考虑root的左右孩子
|
||
return max(val1, val2);
|
||
}
|
||
};
|
||
```
|
||
|
||
* 时间复杂度:O(n^2) 这个时间复杂度不太标准,也不容易准确化,例如越往下的节点重复计算次数就越多
|
||
* 空间复杂度:O(logn) 算上递推系统栈的空间
|
||
|
||
当然以上代码超时了,这个递归的过程中其实是有重复计算了。
|
||
|
||
我们计算了root的四个孙子(左右孩子的孩子)为头结点的子树的情况,又计算了root的左右孩子为头结点的子树的情况,计算左右孩子的时候其实又把孙子计算了一遍。
|
||
|
||
### 记忆化递推
|
||
|
||
所以可以使用一个map把计算过的结果保存一下,这样如果计算过孙子了,那么计算孩子的时候可以复用孙子节点的结果。
|
||
|
||
代码如下:
|
||
|
||
```C++
|
||
class Solution {
|
||
public:
|
||
unordered_map<TreeNode* , int> umap; // 记录计算过的结果
|
||
int rob(TreeNode* root) {
|
||
if (root == NULL) return 0;
|
||
if (root->left == NULL && root->right == NULL) return root->val;
|
||
if (umap[root]) return umap[root]; // 如果umap里已经有记录则直接返回
|
||
// 偷父节点
|
||
int val1 = root->val;
|
||
if (root->left) val1 += rob(root->left->left) + rob(root->left->right); // 跳过root->left
|
||
if (root->right) val1 += rob(root->right->left) + rob(root->right->right); // 跳过root->right
|
||
// 不偷父节点
|
||
int val2 = rob(root->left) + rob(root->right); // 考虑root的左右孩子
|
||
umap[root] = max(val1, val2); // umap记录一下结果
|
||
return max(val1, val2);
|
||
}
|
||
};
|
||
|
||
```
|
||
* 时间复杂度:O(n)
|
||
* 空间复杂度:O(logn) 算上递推系统栈的空间
|
||
|
||
|
||
### 动态规划
|
||
|
||
在上面两种方法,其实对一个节点 投与不投得到的最大金钱都没有做记录,而是需要实时计算。
|
||
|
||
而动态规划其实就是使用状态转移容器来记录状态的变化,这里可以使用一个长度为2的数组,记录当前节点偷与不偷所得到的的最大金钱。
|
||
|
||
**这道题目算是树形dp的入门题目,因为是在树上进行状态转移,我们在讲解二叉树的时候说过递归三部曲,那么下面我以递归三部曲为框架,其中融合动规五部曲的内容来进行讲解**。
|
||
|
||
1. 确定递归函数的参数和返回值
|
||
|
||
这里我们要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。
|
||
|
||
参数为当前节点,代码如下:
|
||
|
||
```C++
|
||
vector<int> robTree(TreeNode* cur) {
|
||
```
|
||
|
||
其实这里的返回数组就是dp数组。
|
||
|
||
所以dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
|
||
|
||
**所以本题dp数组就是一个长度为2的数组!**
|
||
|
||
那么有同学可能疑惑,长度为2的数组怎么标记树中每个节点的状态呢?
|
||
|
||
**别忘了在递归的过程中,系统栈会保存每一层递归的参数**。
|
||
|
||
如果还不理解的话,就接着往下看,看到代码就理解了哈。
|
||
|
||
2. 确定终止条件
|
||
|
||
在遍历的过程中,如果遇到空间点的话,很明显,无论偷还是不偷都是0,所以就返回
|
||
```
|
||
if (cur == NULL) return vector<int>{0, 0};
|
||
```
|
||
这也相当于dp数组的初始化
|
||
|
||
|
||
3. 确定遍历顺序
|
||
|
||
首先明确的是使用后序遍历。 因为通过递归函数的返回值来做下一步计算。
|
||
|
||
通过递归左节点,得到左节点偷与不偷的金钱。
|
||
|
||
通过递归右节点,得到右节点偷与不偷的金钱。
|
||
|
||
代码如下:
|
||
|
||
```C++
|
||
// 下标0:不偷,下标1:偷
|
||
vector<int> left = robTree(cur->left); // 左
|
||
vector<int> right = robTree(cur->right); // 右
|
||
// 中
|
||
|
||
```
|
||
|
||
4. 确定单层递归的逻辑
|
||
|
||
如果是偷当前节点,那么左右孩子就不能偷,val1 = cur->val + left[0] + right[0]; (**如果对下标含义不理解就在回顾一下dp数组的含义**)
|
||
|
||
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
|
||
|
||
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
|
||
|
||
代码如下:
|
||
|
||
```C++
|
||
vector<int> left = robTree(cur->left); // 左
|
||
vector<int> right = robTree(cur->right); // 右
|
||
|
||
// 偷cur
|
||
int val1 = cur->val + left[0] + right[0];
|
||
// 不偷cur
|
||
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
|
||
return {val2, val1};
|
||
```
|
||
|
||
|
||
|
||
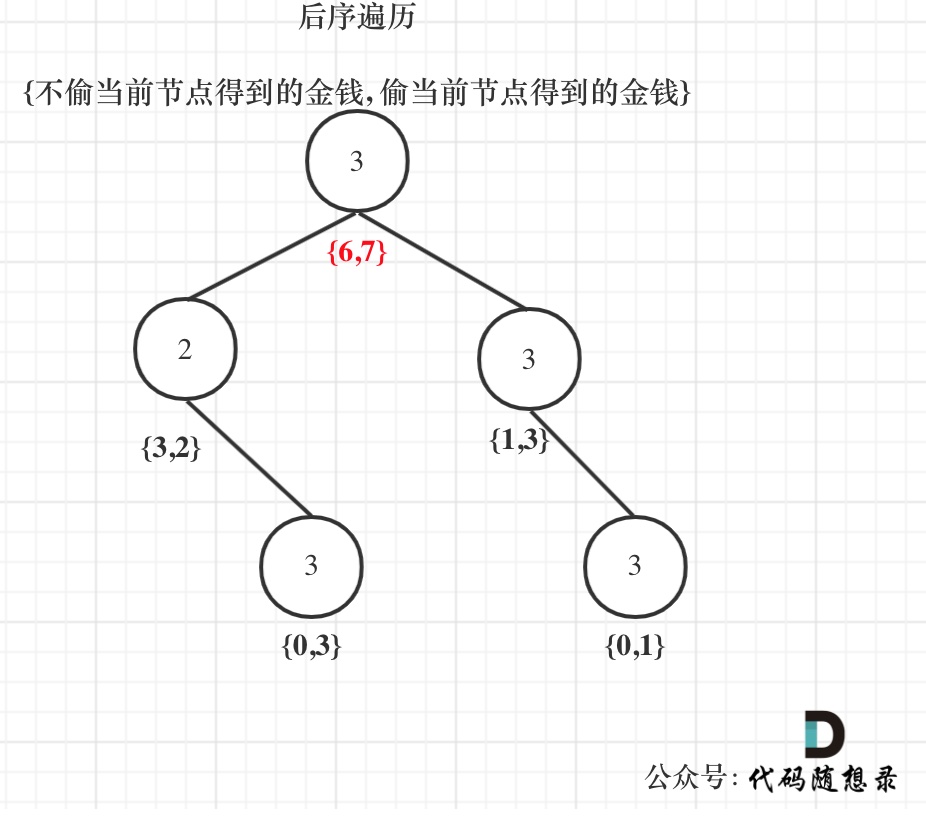
5. 举例推导dp数组
|
||
|
||
以示例1为例,dp数组状态如下:(**注意用后序遍历的方式推导**)
|
||
|
||
|
||
|
||
**最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱**。
|
||
|
||
递归三部曲与动规五部曲分析完毕,C++代码如下:
|
||
|
||
```C++
|
||
class Solution {
|
||
public:
|
||
int rob(TreeNode* root) {
|
||
vector<int> result = robTree(root);
|
||
return max(result[0], result[1]);
|
||
}
|
||
// 长度为2的数组,0:不偷,1:偷
|
||
vector<int> robTree(TreeNode* cur) {
|
||
if (cur == NULL) return vector<int>{0, 0};
|
||
vector<int> left = robTree(cur->left);
|
||
vector<int> right = robTree(cur->right);
|
||
// 偷cur
|
||
int val1 = cur->val + left[0] + right[0];
|
||
// 不偷cur
|
||
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
|
||
return {val2, val1};
|
||
}
|
||
};
|
||
```
|
||
* 时间复杂度:O(n) 每个节点只遍历了一次
|
||
* 空间复杂度:O(logn) 算上递推系统栈的空间
|
||
|
||
## 总结
|
||
|
||
这道题是树形DP的入门题目,通过这道题目大家应该也了解了,所谓树形DP就是在树上进行递归公式的推导。
|
||
|
||
**所以树形DP也没有那么神秘!**
|
||
|
||
只不过平时我们习惯了在一维数组或者二维数组上推导公式,一下子换成了树,就需要对树的遍历方式足够了解!
|
||
|
||
大家还记不记得我在讲解贪心专题的时候,讲到这道题目:[贪心算法:我要监控二叉树!](https://mp.weixin.qq.com/s/kCxlLLjWKaE6nifHC3UL2Q),这也是贪心算法在树上的应用。**那我也可以把这个算法起一个名字,叫做树形贪心**,哈哈哈
|
||
|
||
“树形贪心”词汇从此诞生,来自「代码随想录」
|
||
|
||
## 其他语言版本
|
||
|
||
|
||
Java:
|
||
```Java
|
||
class Solution {
|
||
// 1.递归去偷,超时
|
||
public int rob(TreeNode root) {
|
||
if (root == null)
|
||
return 0;
|
||
int money = root.val;
|
||
if (root.left != null) {
|
||
money += rob(root.left.left) + rob(root.left.right);
|
||
}
|
||
if (root.right != null) {
|
||
money += rob(root.right.left) + rob(root.right.right);
|
||
}
|
||
return Math.max(money, rob(root.left) + rob(root.right));
|
||
}
|
||
|
||
// 2.递归去偷,记录状态
|
||
// 执行用时:3 ms , 在所有 Java 提交中击败了 56.24% 的用户
|
||
public int rob1(TreeNode root) {
|
||
Map<TreeNode, Integer> memo = new HashMap<>();
|
||
return robAction(root, memo);
|
||
}
|
||
|
||
int robAction(TreeNode root, Map<TreeNode, Integer> memo) {
|
||
if (root == null)
|
||
return 0;
|
||
if (memo.containsKey(root))
|
||
return memo.get(root);
|
||
int money = root.val;
|
||
if (root.left != null) {
|
||
money += robAction(root.left.left, memo) + robAction(root.left.right, memo);
|
||
}
|
||
if (root.right != null) {
|
||
money += robAction(root.right.left, memo) + robAction(root.right.right, memo);
|
||
}
|
||
int res = Math.max(money, robAction(root.left, memo) + robAction(root.right, memo));
|
||
memo.put(root, res);
|
||
return res;
|
||
}
|
||
|
||
// 3.状态标记递归
|
||
// 执行用时:0 ms , 在所有 Java 提交中击败了 100% 的用户
|
||
// 不偷:Max(左孩子不偷,左孩子偷) + Max(又孩子不偷,右孩子偷)
|
||
// root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) +
|
||
// Math.max(rob(root.right)[0], rob(root.right)[1])
|
||
// 偷:左孩子不偷+ 右孩子不偷 + 当前节点偷
|
||
// root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;
|
||
public int rob3(TreeNode root) {
|
||
int[] res = robAction1(root);
|
||
return Math.max(res[0], res[1]);
|
||
}
|
||
|
||
int[] robAction1(TreeNode root) {
|
||
int res[] = new int[2];
|
||
if (root == null)
|
||
return res;
|
||
|
||
int[] left = robAction1(root.left);
|
||
int[] right = robAction1(root.right);
|
||
|
||
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
|
||
res[1] = root.val + left[0] + right[0];
|
||
return res;
|
||
}
|
||
}
|
||
```
|
||
|
||
Python:
|
||
|
||
|
||
Go:
|
||
|
||
|
||
|
||
|
||
-----------------------
|
||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||
<div align="center"><img src=../pics/公众号.png width=450 alt=> </img></div>
|