135 lines
5.5 KiB
Markdown
135 lines
5.5 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||
<a href="https://img-blog.csdnimg.cn/20201210231711160.png"><img src="https://img.shields.io/badge/公众号-代码随想录-brightgreen" alt=""></a>
|
||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||
</p>
|
||
|
||
|
||
## 56. 合并区间
|
||
|
||
题目链接:https://leetcode-cn.com/problems/merge-intervals/
|
||
|
||
给出一个区间的集合,请合并所有重叠的区间。
|
||
|
||
示例 1:
|
||
输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
|
||
输出: [[1,6],[8,10],[15,18]]
|
||
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
|
||
|
||
示例 2:
|
||
输入: intervals = [[1,4],[4,5]]
|
||
输出: [[1,5]]
|
||
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
|
||
注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
|
||
|
||
提示:
|
||
|
||
* intervals[i][0] <= intervals[i][1]
|
||
|
||
## 思路
|
||
|
||
大家应该都感觉到了,此题一定要排序,那么按照左边界排序,还是右边界排序呢?
|
||
|
||
都可以!
|
||
|
||
那么我按照左边界排序,排序之后局部最优:每次合并都取最大的右边界,这样就可以合并更多的区间了,整体最优:合并所有重叠的区间。
|
||
|
||
局部最优可以推出全局最优,找不出反例,试试贪心。
|
||
|
||
那有同学问了,本来不就应该合并最大右边界么,这和贪心有啥关系?
|
||
|
||
有时候贪心就是常识!哈哈
|
||
|
||
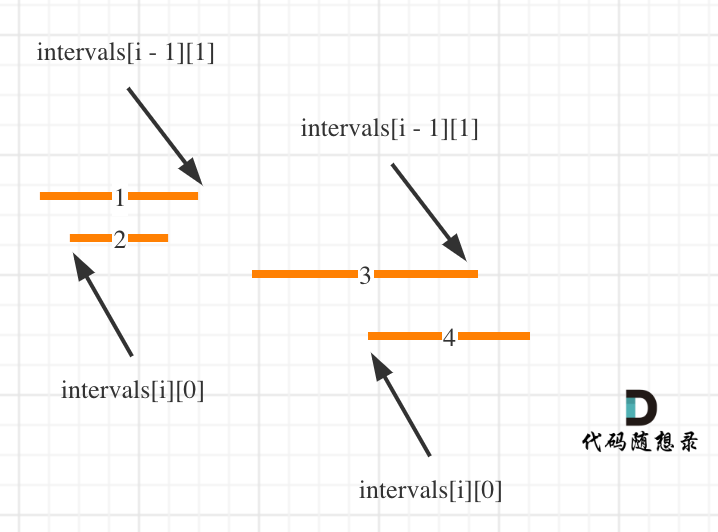
按照左边界从小到大排序之后,如果 `intervals[i][0] < intervals[i - 1][1]` 即intervals[i]左边界 < intervals[i - 1]右边界,则一定有重复,因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。
|
||
|
||
即:intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内,那么一定有重复!
|
||
|
||
这么说有点抽象,看图:(**注意图中区间都是按照左边界排序之后了**)
|
||
|
||
|
||
|
||
知道如何判断重复之后,剩下的就是合并了,如何去模拟合并区间呢?
|
||
|
||
其实就是用合并区间后左边界和右边界,作为一个新的区间,加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。
|
||
|
||
C++代码如下:
|
||
|
||
```C++
|
||
class Solution {
|
||
public:
|
||
// 按照区间左边界从小到大排序
|
||
static bool cmp (const vector<int>& a, const vector<int>& b) {
|
||
return a[0] < b[0];
|
||
}
|
||
vector<vector<int>> merge(vector<vector<int>>& intervals) {
|
||
vector<vector<int>> result;
|
||
if (intervals.size() == 0) return result;
|
||
sort(intervals.begin(), intervals.end(), cmp);
|
||
bool flag = false; // 标记最后一个区间有没有合并
|
||
int length = intervals.size();
|
||
|
||
for (int i = 1; i < length; i++) {
|
||
int start = intervals[i - 1][0]; // 初始为i-1区间的左边界
|
||
int end = intervals[i - 1][1]; // 初始i-1区间的右边界
|
||
while (i < length && intervals[i][0] <= end) { // 合并区间
|
||
end = max(end, intervals[i][1]); // 不断更新右区间
|
||
if (i == length - 1) flag = true; // 最后一个区间也合并了
|
||
i++; // 继续合并下一个区间
|
||
}
|
||
// start和end是表示intervals[i - 1]的左边界右边界,所以最优intervals[i]区间是否合并了要标记一下
|
||
result.push_back({start, end});
|
||
}
|
||
// 如果最后一个区间没有合并,将其加入result
|
||
if (flag == false) {
|
||
result.push_back({intervals[length - 1][0], intervals[length - 1][1]});
|
||
}
|
||
return result;
|
||
}
|
||
};
|
||
```
|
||
|
||
当然以上代码有冗余一些,可以优化一下,如下:(思路是一样的)
|
||
|
||
```C++
|
||
class Solution {
|
||
public:
|
||
vector<vector<int>> merge(vector<vector<int>>& intervals) {
|
||
vector<vector<int>> result;
|
||
if (intervals.size() == 0) return result;
|
||
// 排序的参数使用了lamda表达式
|
||
sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b){return a[0] < b[0];});
|
||
|
||
result.push_back(intervals[0]);
|
||
for (int i = 1; i < intervals.size(); i++) {
|
||
if (result.back()[1] >= intervals[i][0]) { // 合并区间
|
||
result.back()[1] = max(result.back()[1], intervals[i][1]);
|
||
} else {
|
||
result.push_back(intervals[i]);
|
||
}
|
||
}
|
||
return result;
|
||
}
|
||
};
|
||
```
|
||
|
||
* 时间复杂度:O(nlogn) ,有一个快排
|
||
* 空间复杂度:O(1),我没有算result数组(返回值所需容器占的空间)
|
||
|
||
|
||
## 总结
|
||
|
||
对于贪心算法,很多同学都是:**如果能凭常识直接做出来,就会感觉不到自己用了贪心, 一旦第一直觉想不出来, 可能就一直想不出来了**。
|
||
|
||
跟着「代码随想录」刷题的录友应该感受过,贪心难起来,真的难。
|
||
|
||
那应该怎么办呢?
|
||
|
||
正如我贪心系列开篇词[关于贪心算法,你该了解这些!](https://mp.weixin.qq.com/s/O935TaoHE9Eexwe_vSbRAg)中讲解的一样,贪心本来就没有套路,也没有框架,所以各种常规解法需要多接触多练习,自然而然才会想到。
|
||
|
||
「代码随想录」会把贪心常见的经典题目覆盖到,大家只要认真学习打卡就可以了。
|
||
|
||
|
||
|
||
|