157 lines
5.8 KiB
Markdown
157 lines
5.8 KiB
Markdown
# 本周小结!(动态规划系列二)
|
||
|
||
## 周一
|
||
|
||
[动态规划:不同路径](https://programmercarl.com/0062.不同路径.html)中求从出发点到终点有几种路径,只能向下或者向右移动一步。
|
||
|
||
我们提供了三种方法,但重点讲解的还是动规,也是需要重点掌握的。
|
||
|
||
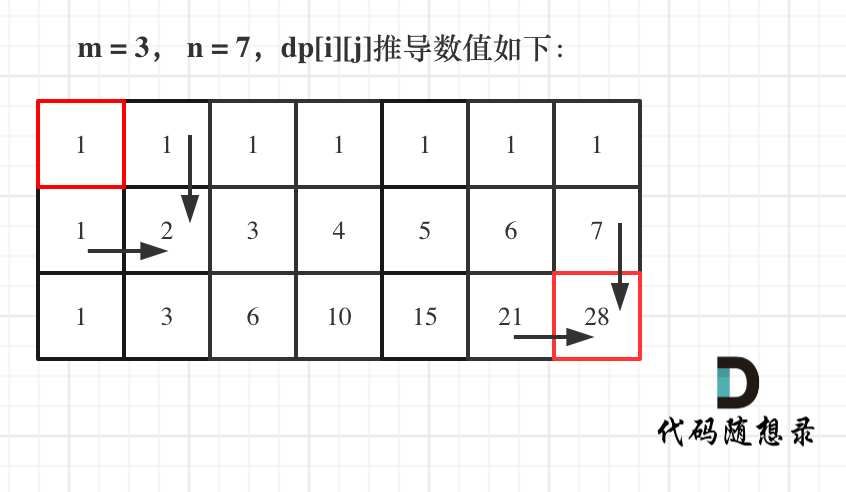
**dp[i][j]定义 :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径**。
|
||
|
||
本题在初始化的时候需要点思考了,即:
|
||
|
||
dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
|
||
|
||
所以初始化为:
|
||
|
||
```
|
||
for (int i = 0; i < m; i++) dp[i][0] = 1;
|
||
for (int j = 0; j < n; j++) dp[0][j] = 1;
|
||
```
|
||
|
||
这里已经不像之前做过的题目,随便赋个0就行的。
|
||
|
||
遍历顺序以及递推公式:
|
||
|
||
```
|
||
for (int i = 1; i < m; i++) {
|
||
for (int j = 1; j < n; j++) {
|
||
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
|
||
## 周二
|
||
|
||
[动态规划:不同路径还不够,要有障碍!](https://programmercarl.com/0063.不同路径II.html)相对于[动态规划:不同路径](https://programmercarl.com/0062.不同路径.html)添加了障碍。
|
||
|
||
dp[i][j]定义依然是:表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
|
||
|
||
|
||
本题难点在于初始化,如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。
|
||
|
||
如图:
|
||
|
||

|
||
|
||
|
||
这里难住了不少同学,代码如下:
|
||
|
||
```
|
||
vector<vector<int>> dp(m, vector<int>(n, 0));
|
||
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
|
||
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
|
||
```
|
||
|
||
|
||
递推公式只要考虑一下障碍,就不赋值了就可以了,如下:
|
||
|
||
```
|
||
for (int i = 1; i < m; i++) {
|
||
for (int j = 1; j < n; j++) {
|
||
if (obstacleGrid[i][j] == 1) continue;
|
||
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
|
||
}
|
||
}
|
||
```
|
||
|
||
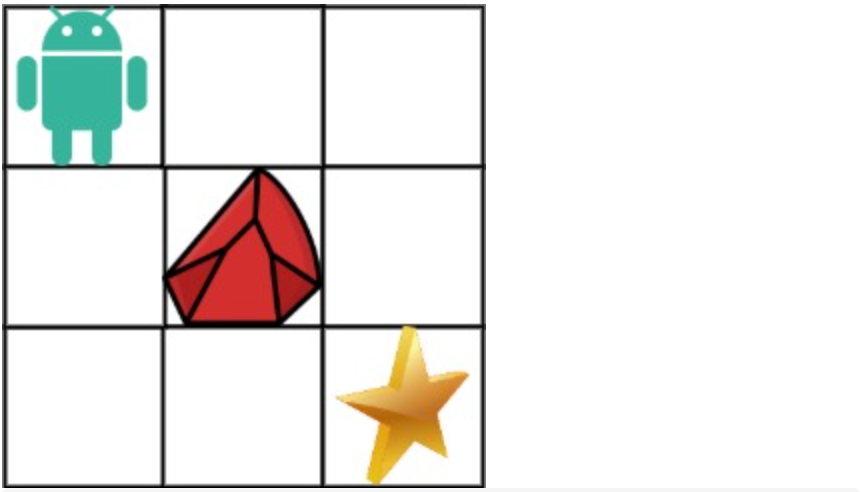
拿示例1来举例如题:
|
||
|
||
|
||
|
||
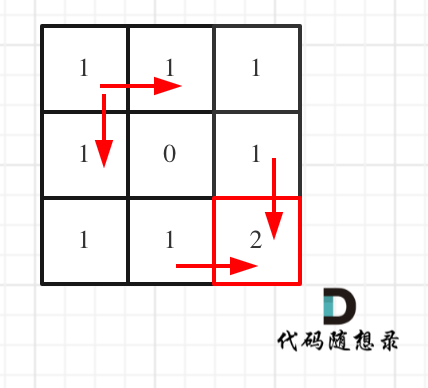
对应的dp table 如图:
|
||
|
||
|
||
|
||
|
||
## 周三
|
||
|
||
[动态规划:整数拆分,你要怎么拆?](https://programmercarl.com/0343.整数拆分.html)给出一个整数,问有多少种拆分的方法。
|
||
|
||
这道题目就有点难度了,题目中dp我也给出了两种方法,但通过两种方法的比较可以看出,对dp数组定义的理解,以及dp数组初始化的重要性。
|
||
|
||
|
||
**dp[i]定义:分拆数字i,可以得到的最大乘积为dp[i]**。
|
||
|
||
本题中dp[i]的初始化其实也很有考究,严格从dp[i]的定义来说,dp[0] dp[1] 就不应该初始化,也就是没有意义的数值。
|
||
|
||
拆分0和拆分1的最大乘积是多少?
|
||
|
||
这是无解的。
|
||
|
||
所以题解里我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1,这个没有任何异议!
|
||
|
||
```
|
||
vector<int> dp(n + 1);
|
||
dp[2] = 1;
|
||
```
|
||
|
||
遍历顺序以及递推公式:
|
||
|
||
```
|
||
for (int i = 3; i <= n ; i++) {
|
||
for (int j = 1; j < i - 1; j++) {
|
||
dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
|
||
}
|
||
}
|
||
```
|
||
|
||
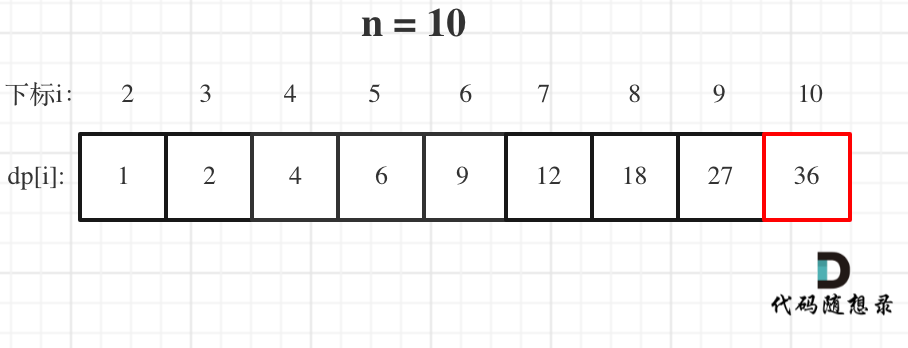
举例当n为10 的时候,dp数组里的数值,如下:
|
||
|
||
|
||
|
||
|
||
|
||
一些录友可能对为什么没有拆分j没有想清楚。
|
||
|
||
其实可以模拟一下哈,拆分j的情况,在遍历j的过程中dp[i - j]其实都计算过了。
|
||
|
||
例如 i= 10,j = 5,i-j = 5,如果把j拆分为 2 和 3,其实在j = 2 的时候,i-j= 8 ,拆分i-j的时候就可以拆出来一个3了。
|
||
|
||
**或者也可以理解j是拆分i的第一个整数**。
|
||
|
||
[动态规划:整数拆分,你要怎么拆?](https://programmercarl.com/0343.整数拆分.html)总结里,我也给出了递推公式dp[i] = max(dp[i], dp[i - j] * dp[j])这种写法。
|
||
|
||
对于这种写法,一位录友总结的很好,意思就是:如果递推公式是dp[i-j] * dp[j],这样就相当于强制把一个数至少拆分成四份。
|
||
|
||
dp[i-j]至少是两个数的乘积,dp[j]又至少是两个数的乘积,但其实3以下的数,数的本身比任何它的拆分乘积都要大了,所以文章中初始化的时候才要特殊处理。
|
||
|
||
## 周四
|
||
|
||
[动态规划:不同的二叉搜索树](https://programmercarl.com/0096.不同的二叉搜索树.html)给出n个不同的节点求能组成多少个不同二叉搜索树。
|
||
|
||
这道题目还是比较难的,想到用动态规划的方法就很不容易了!
|
||
|
||
**dp[i]定义 :1到i为节点组成的二叉搜索树的个数为dp[i]**。
|
||
|
||
递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
|
||
|
||
dp数组如何初始化:只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。
|
||
|
||
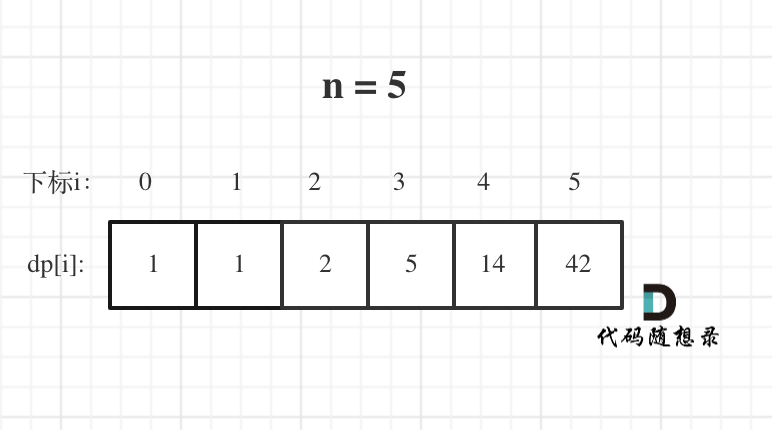
n为5时候的dp数组状态如图:
|
||
|
||
|
||
|
||
## 总结
|
||
|
||
本周题目已经开始点难度了,特别是[动态规划:不同的二叉搜索树](https://programmercarl.com/0096.不同的二叉搜索树.html)这道题目,明显感觉阅读量很低,可能是因为确实有点难吧。
|
||
|
||
我现在也陷入了纠结,题目一简单,就会有录友和我反馈说题目太简单了,题目一难,阅读量就特别低。
|
||
|
||
**但我还会坚持规划好的路线,难度循序渐进,并以面试经典题目为准,该简单的时候就是简单,同时也不会因为阅读量低就放弃有难度的题目!**。
|
||
|
||
<div align="center"><img src='https://file1.kamacoder.com/i/algo/01二维码.jpg' width=450> </img></div>
|