486 lines
15 KiB
Markdown
486 lines
15 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/RsdcQ9umo09R6cfnwXZlrQ"><img src="https://img.shields.io/badge/PDF下载-代码随想录-blueviolet" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||
</p>
|
||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
|
||
## 704. 二分查找
|
||
|
||
[力扣题目链接](https://leetcode-cn.com/problems/binary-search/)
|
||
|
||
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
|
||
|
||
示例 1:
|
||
|
||
```
|
||
输入: nums = [-1,0,3,5,9,12], target = 9
|
||
输出: 4
|
||
解释: 9 出现在 nums 中并且下标为 4
|
||
```
|
||
|
||
示例 2:
|
||
|
||
```
|
||
输入: nums = [-1,0,3,5,9,12], target = 2
|
||
输出: -1
|
||
解释: 2 不存在 nums 中因此返回 -1
|
||
```
|
||
|
||
提示:
|
||
|
||
* 你可以假设 nums 中的所有元素是不重复的。
|
||
* n 将在 [1, 10000]之间。
|
||
* nums 的每个元素都将在 [-9999, 9999]之间。
|
||
|
||
|
||
## 思路
|
||
|
||
**这道题目的前提是数组为有序数组**,同时题目还强调**数组中无重复元素**,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件,当大家看到题目描述满足如上条件的时候,可要想一想是不是可以用二分法了。
|
||
|
||
二分查找涉及的很多的边界条件,逻辑比较简单,但就是写不好。例如到底是 `while(left < right)` 还是 `while(left <= right)`,到底是`right = middle`呢,还是要`right = middle - 1`呢?
|
||
|
||
大家写二分法经常写乱,主要是因为**对区间的定义没有想清楚,区间的定义就是不变量**。要在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,这就是**循环不变量**规则。
|
||
|
||
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
|
||
|
||
下面我用这两种区间的定义分别讲解两种不同的二分写法。
|
||
|
||
### 二分法第一种写法
|
||
|
||
第一种写法,我们定义 target 是在一个在左闭右闭的区间里,**也就是[left, right] (这个很重要非常重要)**。
|
||
|
||
区间的定义这就决定了二分法的代码应该如何写,**因为定义target在[left, right]区间,所以有如下两点:**
|
||
|
||
* while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
|
||
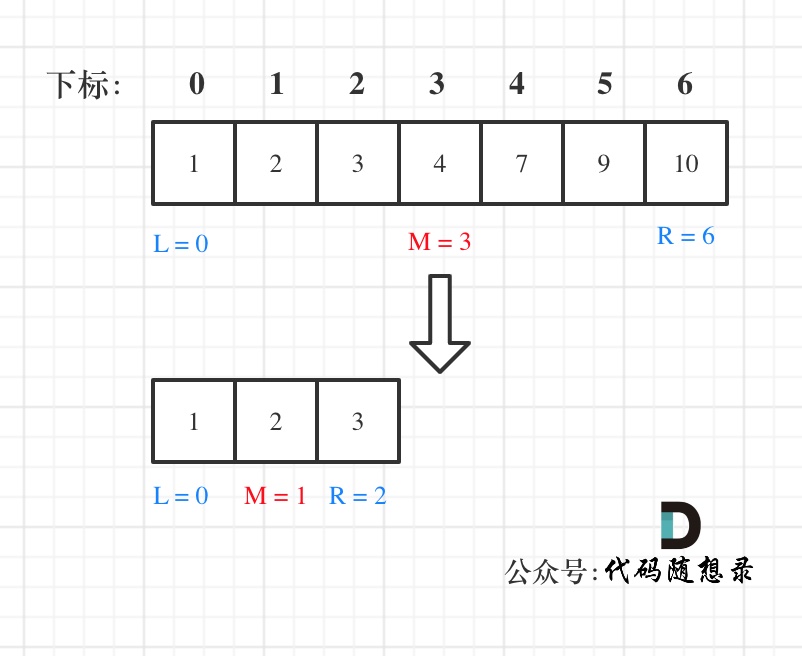
* if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
|
||
|
||
例如在数组:1,2,3,4,7,9,10中查找元素2,如图所示:
|
||
|
||
|
||
|
||
代码如下:(详细注释)
|
||
|
||
```CPP
|
||
// 版本一
|
||
class Solution {
|
||
public:
|
||
int search(vector<int>& nums, int target) {
|
||
int left = 0;
|
||
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
|
||
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
|
||
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
|
||
if (nums[middle] > target) {
|
||
right = middle - 1; // target 在左区间,所以[left, middle - 1]
|
||
} else if (nums[middle] < target) {
|
||
left = middle + 1; // target 在右区间,所以[middle + 1, right]
|
||
} else { // nums[middle] == target
|
||
return middle; // 数组中找到目标值,直接返回下标
|
||
}
|
||
}
|
||
// 未找到目标值
|
||
return -1;
|
||
}
|
||
};
|
||
|
||
```
|
||
|
||
### 二分法第二种写法
|
||
|
||
如果说定义 target 是在一个在左闭右开的区间里,也就是[left, right) ,那么二分法的边界处理方式则截然不同。
|
||
|
||
有如下两点:
|
||
|
||
* while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
|
||
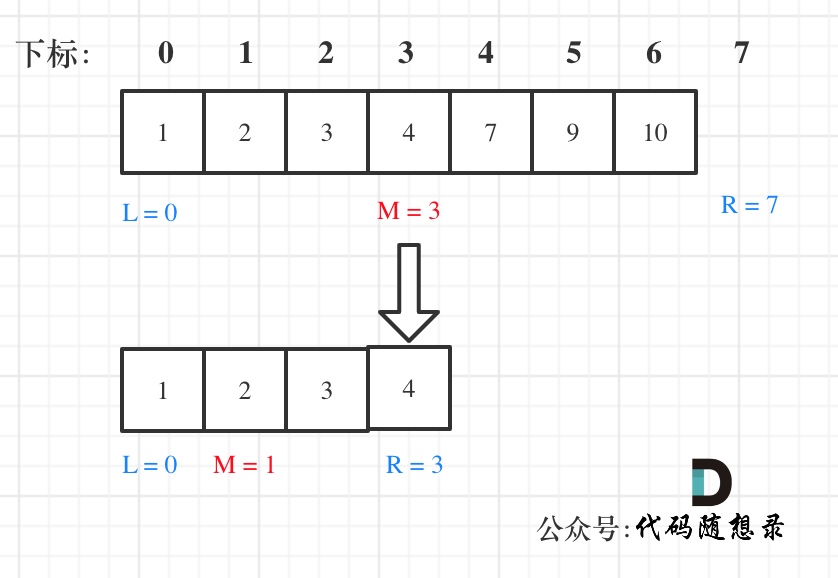
* if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
|
||
|
||
在数组:1,2,3,4,7,9,10中查找元素2,如图所示:(**注意和方法一的区别**)
|
||
|
||
|
||
|
||
代码如下:(详细注释)
|
||
|
||
```CPP
|
||
// 版本二
|
||
class Solution {
|
||
public:
|
||
int search(vector<int>& nums, int target) {
|
||
int left = 0;
|
||
int right = nums.size(); // 定义target在左闭右开的区间里,即:[left, right)
|
||
while (left < right) { // 因为left == right的时候,在[left, right)是无效的空间,所以使用 <
|
||
int middle = left + ((right - left) >> 1);
|
||
if (nums[middle] > target) {
|
||
right = middle; // target 在左区间,在[left, middle)中
|
||
} else if (nums[middle] < target) {
|
||
left = middle + 1; // target 在右区间,在[middle + 1, right)中
|
||
} else { // nums[middle] == target
|
||
return middle; // 数组中找到目标值,直接返回下标
|
||
}
|
||
}
|
||
// 未找到目标值
|
||
return -1;
|
||
}
|
||
};
|
||
```
|
||
|
||
## 总结
|
||
|
||
二分法是非常重要的基础算法,为什么很多同学对于二分法都是**一看就会,一写就废**?
|
||
|
||
其实主要就是对区间的定义没有理解清楚,在循环中没有始终坚持根据查找区间的定义来做边界处理。
|
||
|
||
区间的定义就是不变量,那么在循环中坚持根据查找区间的定义来做边界处理,就是循环不变量规则。
|
||
|
||
本篇根据两种常见的区间定义,给出了两种二分法的写法,每一个边界为什么这么处理,都根据区间的定义做了详细介绍。
|
||
|
||
相信看完本篇应该对二分法有更深刻的理解了。
|
||
|
||
## 相关题目推荐
|
||
|
||
* [35.搜索插入位置](https://programmercarl.com/0035.搜索插入位置.html)
|
||
* 34.在排序数组中查找元素的第一个和最后一个位置
|
||
* 69.x 的平方根
|
||
* 367.有效的完全平方数
|
||
|
||
|
||
|
||
|
||
|
||
|
||
## 其他语言版本
|
||
|
||
**Java:**
|
||
|
||
(版本一)左闭右闭区间
|
||
|
||
```java
|
||
class Solution {
|
||
public int search(int[] nums, int target) {
|
||
// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
|
||
if (target < nums[0] || target > nums[nums.length - 1]) {
|
||
return -1;
|
||
}
|
||
int left = 0, right = nums.length - 1;
|
||
while (left <= right) {
|
||
int mid = left + ((right - left) >> 1);
|
||
if (nums[mid] == target)
|
||
return mid;
|
||
else if (nums[mid] < target)
|
||
left = mid + 1;
|
||
else if (nums[mid] > target)
|
||
right = mid - 1;
|
||
}
|
||
return -1;
|
||
}
|
||
}
|
||
```
|
||
|
||
(版本二)左闭右开区间
|
||
|
||
```java
|
||
class Solution {
|
||
public int search(int[] nums, int target) {
|
||
int left = 0, right = nums.length;
|
||
while (left < right) {
|
||
int mid = left + ((right - left) >> 1);
|
||
if (nums[mid] == target)
|
||
return mid;
|
||
else if (nums[mid] < target)
|
||
left = mid + 1;
|
||
else if (nums[mid] > target)
|
||
right = mid;
|
||
}
|
||
return -1;
|
||
}
|
||
}
|
||
```
|
||
|
||
**Python:**
|
||
|
||
(版本一)左闭右闭区间
|
||
|
||
```python
|
||
class Solution:
|
||
def search(self, nums: List[int], target: int) -> int:
|
||
left, right = 0, len(nums) - 1
|
||
|
||
while left <= right:
|
||
middle = (left + right) // 2
|
||
|
||
if nums[middle] < target:
|
||
left = middle + 1
|
||
elif nums[middle] > target:
|
||
right = middle - 1
|
||
else:
|
||
return middle
|
||
return -1
|
||
```
|
||
|
||
(版本二)左闭右开区间
|
||
|
||
```python
|
||
class Solution:
|
||
def search(self, nums: List[int], target: int) -> int:
|
||
left,right =0, len(nums)
|
||
while left < right:
|
||
mid = (left + right) // 2
|
||
if nums[mid] < target:
|
||
left = mid+1
|
||
elif nums[mid] > target:
|
||
right = mid
|
||
else:
|
||
return mid
|
||
return -1
|
||
```
|
||
|
||
**Go:**
|
||
|
||
(版本一)左闭右闭区间
|
||
|
||
```go
|
||
func search(nums []int, target int) int {
|
||
high := len(nums)-1
|
||
low := 0
|
||
for low <= high {
|
||
mid := low + (high-low)/2
|
||
if nums[mid] == target {
|
||
return mid
|
||
} else if nums[mid] > target {
|
||
high = mid-1
|
||
} else {
|
||
low = mid+1
|
||
}
|
||
}
|
||
return -1
|
||
}
|
||
```
|
||
|
||
(版本二)左闭右开区间
|
||
|
||
```go
|
||
func search(nums []int, target int) int {
|
||
high := len(nums)
|
||
low := 0
|
||
for low < high {
|
||
mid := low + (high-low)/2
|
||
if nums[mid] == target {
|
||
return mid
|
||
} else if nums[mid] > target {
|
||
high = mid
|
||
} else {
|
||
low = mid+1
|
||
}
|
||
}
|
||
return -1
|
||
}
|
||
```
|
||
|
||
**JavaScript:**
|
||
|
||
```js
|
||
|
||
// (版本一)左闭右闭区间
|
||
|
||
var search = function(nums, target) {
|
||
let l = 0, r = nums.length - 1;
|
||
// 区间 [l, r]
|
||
while(l <= r) {
|
||
let mid = (l + r) >> 1;
|
||
if(nums[mid] === target) return mid;
|
||
let isSmall = nums[mid] < target;
|
||
l = isSmall ? mid + 1 : l;
|
||
r = isSmall ? r : mid - 1;
|
||
}
|
||
return -1;
|
||
};
|
||
|
||
// (版本二)左闭右开区间
|
||
|
||
var search = function(nums, target) {
|
||
let l = 0, r = nums.length;
|
||
// 区间 [l, r)
|
||
while(l < r) {
|
||
let mid = (l + r) >> 1;
|
||
if(nums[mid] === target) return mid;
|
||
let isSmall = nums[mid] < target;
|
||
l = isSmall ? mid + 1 : l;
|
||
// 所以 mid 不会被取到
|
||
r = isSmall ? r : mid;
|
||
}
|
||
return -1;
|
||
};
|
||
|
||
```
|
||
|
||
**Ruby:**
|
||
|
||
```ruby
|
||
# (版本一)左闭右闭区间
|
||
|
||
def search(nums, target)
|
||
left, right = 0, nums.length - 1
|
||
while left <= right # 由于定义target在一个在左闭右闭的区间里,因此极限情况下存在left==right
|
||
middle = (left + right) / 2
|
||
if nums[middle] > target
|
||
right = middle - 1
|
||
elsif nums[middle] < target
|
||
left = middle + 1
|
||
else
|
||
return middle # return兼具返回与跳出循环的作用
|
||
end
|
||
end
|
||
-1
|
||
end
|
||
|
||
# (版本二)左闭右开区间
|
||
|
||
def search(nums, target)
|
||
left, right = 0, nums.length
|
||
while left < right # 由于定义target在一个在左闭右开的区间里,因此极限情况下right=left+1
|
||
middle = (left + right) / 2
|
||
if nums[middle] > target
|
||
right = middle
|
||
elsif nums[middle] < target
|
||
left = middle + 1
|
||
else
|
||
return middle
|
||
end
|
||
end
|
||
-1
|
||
end
|
||
```
|
||
|
||
**Swift:**
|
||
|
||
```swift
|
||
// (版本一)左闭右闭区间
|
||
func search(nums: [Int], target: Int) -> Int {
|
||
// 1. 先定义区间。这里的区间是[left, right]
|
||
var left = 0
|
||
var right = nums.count - 1
|
||
|
||
while left <= right {// 因为taeget是在[left, right]中,包括两个边界值,所以这里的left == right是有意义的
|
||
// 2. 计算区间中间的下标(如果left、right都比较大的情况下,left + right就有可能会溢出)
|
||
// let middle = (left + right) / 2
|
||
// 防溢出:
|
||
let middle = left + (right - left) / 2
|
||
|
||
// 3. 判断
|
||
if target < nums[middle] {
|
||
// 当目标在区间左侧,就需要更新右边的边界值,新区间为[left, middle - 1]
|
||
right = middle - 1
|
||
} else if target > nums[middle] {
|
||
// 当目标在区间右侧,就需要更新左边的边界值,新区间为[middle + 1, right]
|
||
left = middle + 1
|
||
} else {
|
||
// 当目标就是在中间,则返回中间值的下标
|
||
return middle
|
||
}
|
||
}
|
||
|
||
// 如果找不到目标,则返回-1
|
||
return -1
|
||
}
|
||
|
||
// (版本二)左闭右开区间
|
||
func search(nums: [Int], target: Int) -> Int {
|
||
var left = 0
|
||
var right = nums.count
|
||
|
||
while left < right {
|
||
let middle = left + ((right - left) >> 1)
|
||
|
||
if target < nums[middle] {
|
||
right = middle
|
||
} else if target > nums[middle] {
|
||
left = middle + 1
|
||
} else {
|
||
return middle
|
||
}
|
||
}
|
||
|
||
return -1
|
||
}
|
||
|
||
```
|
||
|
||
**Rust:**
|
||
|
||
```rust
|
||
# (版本一)左闭右闭区间
|
||
|
||
impl Solution {
|
||
pub fn search(nums: Vec<i32>, target: i32) -> i32 {
|
||
let mut left:usize = 0;
|
||
let mut right:usize = nums.len() - 1;
|
||
while left as i32 <= right as i32{
|
||
let mid = (left + right) / 2;
|
||
if nums[mid] < target {
|
||
left = mid + 1;
|
||
} else if nums[mid] > target {
|
||
right = mid - 1;
|
||
} else {
|
||
return mid as i32;
|
||
}
|
||
}
|
||
-1
|
||
}
|
||
}
|
||
|
||
# (版本二)左闭右开区间
|
||
|
||
impl Solution {
|
||
pub fn search(nums: Vec<i32>, target: i32) -> i32 {
|
||
let mut left:usize = 0;
|
||
let mut right:usize = nums.len();
|
||
while left < right {
|
||
let mid = (left + right) / 2;
|
||
if nums[mid] < target {
|
||
left = mid + 1;
|
||
} else if nums[mid] > target {
|
||
right = mid;
|
||
} else {
|
||
return mid as i32;
|
||
}
|
||
}
|
||
-1
|
||
}
|
||
}
|
||
```
|
||
|
||
**C:**
|
||
```c
|
||
int search(int* nums, int numsSize, int target){
|
||
int left = 0;
|
||
int right = numsSize-1;
|
||
int middle = 0;
|
||
//若left小于等于right,说明区间中元素不为0
|
||
while(left<=right) {
|
||
//更新查找下标middle的值
|
||
middle = (left+right)/2;
|
||
//此时target可能会在[left,middle-1]区间中
|
||
if(nums[middle] > target) {
|
||
right = middle-1;
|
||
}
|
||
//此时target可能会在[middle+1,right]区间中
|
||
else if(nums[middle] < target) {
|
||
left = middle+1;
|
||
}
|
||
//当前下标元素等于target值时,返回middle
|
||
else if(nums[middle] == target){
|
||
return middle;
|
||
}
|
||
}
|
||
//若未找到target元素,返回-1
|
||
return -1;
|
||
}
|
||
```
|
||
|
||
-----------------------
|
||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码.jpg width=450> </img></div>
|