473 lines
15 KiB
Markdown
473 lines
15 KiB
Markdown
<p align="center">
|
||
<a href="https://programmercarl.com/other/xunlianying.html" target="_blank">
|
||
<img src="../pics/训练营.png" width="1000"/>
|
||
</a>
|
||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
> 相对于[贪心算法:跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)难了不少,做好心里准备!
|
||
|
||
# 45.跳跃游戏 II
|
||
|
||
[力扣题目链接](https://leetcode.cn/problems/jump-game-ii/)
|
||
|
||
给定一个非负整数数组,你最初位于数组的第一个位置。
|
||
|
||
数组中的每个元素代表你在该位置可以跳跃的最大长度。
|
||
|
||
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
|
||
|
||
示例:
|
||
|
||
- 输入: [2,3,1,1,4]
|
||
- 输出: 2
|
||
- 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
|
||
|
||
说明:
|
||
假设你总是可以到达数组的最后一个位置。
|
||
|
||
## 算法公开课
|
||
|
||
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[贪心算法,最少跳几步还得看覆盖范围 | LeetCode: 45.跳跃游戏 II](https://www.bilibili.com/video/BV1Y24y1r7XZ),相信结合视频在看本篇题解,更有助于大家对本题的理解**。
|
||
|
||
## 思路
|
||
|
||
本题相对于[55.跳跃游戏](https://programmercarl.com/0055.跳跃游戏.html)还是难了不少。
|
||
|
||
但思路是相似的,还是要看最大覆盖范围。
|
||
|
||
本题要计算最小步数,那么就要想清楚什么时候步数才一定要加一呢?
|
||
|
||
贪心的思路,局部最优:当前可移动距离尽可能多走,如果还没到终点,步数再加一。整体最优:一步尽可能多走,从而达到最小步数。
|
||
|
||
思路虽然是这样,但在写代码的时候还不能真的能跳多远就跳多远,那样就不知道下一步最远能跳到哪里了。
|
||
|
||
**所以真正解题的时候,要从覆盖范围出发,不管怎么跳,覆盖范围内一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了终点,得到的就是最小步数!**
|
||
|
||
**这里需要统计两个覆盖范围,当前这一步的最大覆盖和下一步最大覆盖**。
|
||
|
||
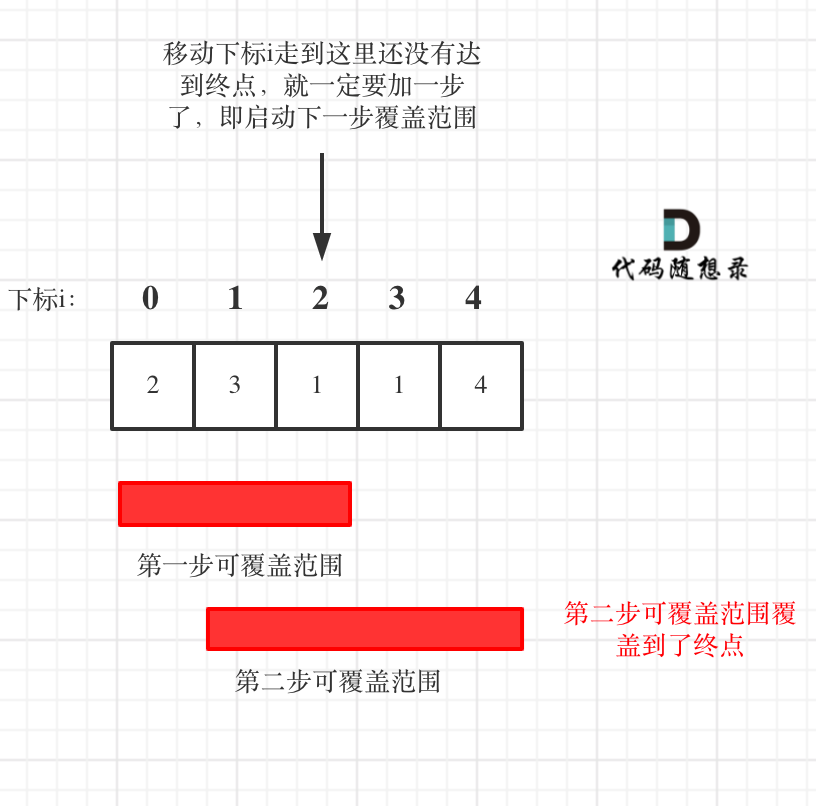
如果移动下标达到了当前这一步的最大覆盖最远距离了,还没有到终点的话,那么就必须再走一步来增加覆盖范围,直到覆盖范围覆盖了终点。
|
||
|
||
如图:
|
||
|
||
|
||
|
||
**图中覆盖范围的意义在于,只要红色的区域,最多两步一定可以到!(不用管具体怎么跳,反正一定可以跳到)**
|
||
|
||
### 方法一
|
||
|
||
从图中可以看出来,就是移动下标达到了当前覆盖的最远距离下标时,步数就要加一,来增加覆盖距离。最后的步数就是最少步数。
|
||
|
||
这里还是有个特殊情况需要考虑,当移动下标达到了当前覆盖的最远距离下标时
|
||
|
||
- 如果当前覆盖最远距离下标不是是集合终点,步数就加一,还需要继续走。
|
||
- 如果当前覆盖最远距离下标就是是集合终点,步数不用加一,因为不能再往后走了。
|
||
|
||
C++代码如下:(详细注释)
|
||
|
||
```CPP
|
||
// 版本一
|
||
class Solution {
|
||
public:
|
||
int jump(vector<int>& nums) {
|
||
if (nums.size() == 1) return 0;
|
||
int curDistance = 0; // 当前覆盖最远距离下标
|
||
int ans = 0; // 记录走的最大步数
|
||
int nextDistance = 0; // 下一步覆盖最远距离下标
|
||
for (int i = 0; i < nums.size(); i++) {
|
||
nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖最远距离下标
|
||
if (i == curDistance) { // 遇到当前覆盖最远距离下标
|
||
ans++; // 需要走下一步
|
||
curDistance = nextDistance; // 更新当前覆盖最远距离下标(相当于加油了)
|
||
if (nextDistance >= nums.size() - 1) break; // 当前覆盖最远距到达集合终点,不用做ans++操作了,直接结束
|
||
}
|
||
}
|
||
return ans;
|
||
}
|
||
};
|
||
```
|
||
|
||
* 时间复杂度: O(n)
|
||
* 空间复杂度: O(1)
|
||
|
||
|
||
### 方法二
|
||
|
||
依然是贪心,思路和方法一差不多,代码可以简洁一些。
|
||
|
||
**针对于方法一的特殊情况,可以统一处理**,即:移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不考虑是不是终点的情况。
|
||
|
||
想要达到这样的效果,只要让移动下标,最大只能移动到 nums.size - 2 的地方就可以了。
|
||
|
||
因为当移动下标指向 nums.size - 2 时:
|
||
|
||
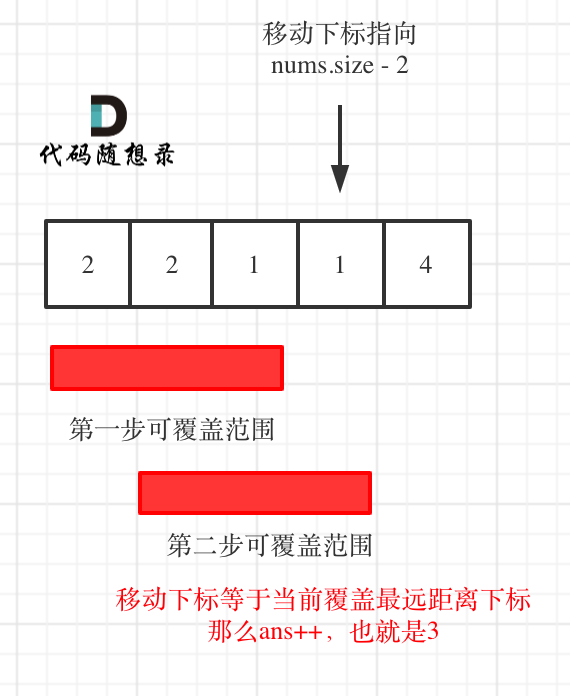
- 如果移动下标等于当前覆盖最大距离下标, 需要再走一步(即 ans++),因为最后一步一定是可以到的终点。(题目假设总是可以到达数组的最后一个位置),如图:
|
||
|
||
|
||
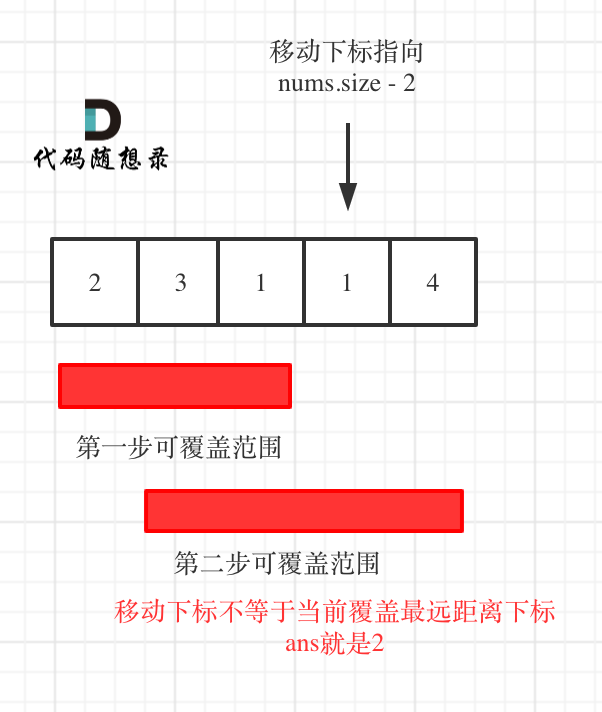
- 如果移动下标不等于当前覆盖最大距离下标,说明当前覆盖最远距离就可以直接达到终点了,不需要再走一步。如图:
|
||
|
||
|
||
|
||
代码如下:
|
||
|
||
```CPP
|
||
// 版本二
|
||
class Solution {
|
||
public:
|
||
int jump(vector<int>& nums) {
|
||
int curDistance = 0; // 当前覆盖的最远距离下标
|
||
int ans = 0; // 记录走的最大步数
|
||
int nextDistance = 0; // 下一步覆盖的最远距离下标
|
||
for (int i = 0; i < nums.size() - 1; i++) { // 注意这里是小于nums.size() - 1,这是关键所在
|
||
nextDistance = max(nums[i] + i, nextDistance); // 更新下一步覆盖的最远距离下标
|
||
if (i == curDistance) { // 遇到当前覆盖的最远距离下标
|
||
curDistance = nextDistance; // 更新当前覆盖的最远距离下标
|
||
ans++;
|
||
}
|
||
}
|
||
return ans;
|
||
}
|
||
};
|
||
```
|
||
|
||
* 时间复杂度: O(n)
|
||
* 空间复杂度: O(1)
|
||
|
||
|
||
|
||
可以看出版本二的代码相对于版本一简化了不少!
|
||
|
||
**其精髓在于控制移动下标 i 只移动到 nums.size() - 2 的位置**,所以移动下标只要遇到当前覆盖最远距离的下标,直接步数加一,不用考虑别的了。
|
||
|
||
## 总结
|
||
|
||
相信大家可以发现,这道题目相当于[55.跳跃游戏](https://programmercarl.com/0055.跳跃游戏.html)难了不止一点。
|
||
|
||
但代码又十分简单,贪心就是这么巧妙。
|
||
|
||
理解本题的关键在于:**以最小的步数增加最大的覆盖范围,直到覆盖范围覆盖了终点**,这个范围内最小步数一定可以跳到,不用管具体是怎么跳的,不纠结于一步究竟跳一个单位还是两个单位。
|
||
|
||
## 其他语言版本
|
||
|
||
### Java
|
||
|
||
```Java
|
||
// 版本一
|
||
class Solution {
|
||
public int jump(int[] nums) {
|
||
if (nums == null || nums.length == 0 || nums.length == 1) {
|
||
return 0;
|
||
}
|
||
//记录跳跃的次数
|
||
int count=0;
|
||
//当前的覆盖最大区域
|
||
int curDistance = 0;
|
||
//最大的覆盖区域
|
||
int maxDistance = 0;
|
||
for (int i = 0; i < nums.length; i++) {
|
||
//在可覆盖区域内更新最大的覆盖区域
|
||
maxDistance = Math.max(maxDistance,i+nums[i]);
|
||
//说明当前一步,再跳一步就到达了末尾
|
||
if (maxDistance>=nums.length-1){
|
||
count++;
|
||
break;
|
||
}
|
||
//走到当前覆盖的最大区域时,更新下一步可达的最大区域
|
||
if (i==curDistance){
|
||
curDistance = maxDistance;
|
||
count++;
|
||
}
|
||
}
|
||
return count;
|
||
}
|
||
}
|
||
```
|
||
|
||
```java
|
||
// 版本二
|
||
class Solution {
|
||
public int jump(int[] nums) {
|
||
int result = 0;
|
||
// 当前覆盖的最远距离下标
|
||
int end = 0;
|
||
// 下一步覆盖的最远距离下标
|
||
int temp = 0;
|
||
for (int i = 0; i <= end && end < nums.length - 1; ++i) {
|
||
temp = Math.max(temp, i + nums[i]);
|
||
// 可达位置的改变次数就是跳跃次数
|
||
if (i == end) {
|
||
end = temp;
|
||
result++;
|
||
}
|
||
}
|
||
return result;
|
||
}
|
||
}
|
||
```
|
||
|
||
### Python
|
||
贪心(版本一)
|
||
```python
|
||
class Solution:
|
||
def jump(self, nums):
|
||
if len(nums) == 1:
|
||
return 0
|
||
|
||
cur_distance = 0 # 当前覆盖最远距离下标
|
||
ans = 0 # 记录走的最大步数
|
||
next_distance = 0 # 下一步覆盖最远距离下标
|
||
|
||
for i in range(len(nums)):
|
||
next_distance = max(nums[i] + i, next_distance) # 更新下一步覆盖最远距离下标
|
||
if i == cur_distance: # 遇到当前覆盖最远距离下标
|
||
ans += 1 # 需要走下一步
|
||
cur_distance = next_distance # 更新当前覆盖最远距离下标(相当于加油了)
|
||
if next_distance >= len(nums) - 1: # 当前覆盖最远距离达到数组末尾,不用再做ans++操作,直接结束
|
||
break
|
||
|
||
return ans
|
||
|
||
```
|
||
贪心(版本二)
|
||
|
||
```python
|
||
class Solution:
|
||
def jump(self, nums):
|
||
cur_distance = 0 # 当前覆盖的最远距离下标
|
||
ans = 0 # 记录走的最大步数
|
||
next_distance = 0 # 下一步覆盖的最远距离下标
|
||
|
||
for i in range(len(nums) - 1): # 注意这里是小于len(nums) - 1,这是关键所在
|
||
next_distance = max(nums[i] + i, next_distance) # 更新下一步覆盖的最远距离下标
|
||
if i == cur_distance: # 遇到当前覆盖的最远距离下标
|
||
cur_distance = next_distance # 更新当前覆盖的最远距离下标
|
||
ans += 1
|
||
|
||
return ans
|
||
|
||
```
|
||
贪心(版本三) 类似‘55-跳跃游戏’写法
|
||
|
||
```python
|
||
class Solution:
|
||
def jump(self, nums) -> int:
|
||
if len(nums)==1: # 如果数组只有一个元素,不需要跳跃,步数为0
|
||
return 0
|
||
|
||
i = 0 # 当前位置
|
||
count = 0 # 步数计数器
|
||
cover = 0 # 当前能够覆盖的最远距离
|
||
|
||
while i <= cover: # 当前位置小于等于当前能够覆盖的最远距离时循环
|
||
for i in range(i, cover+1): # 遍历从当前位置到当前能够覆盖的最远距离之间的所有位置
|
||
cover = max(nums[i]+i, cover) # 更新当前能够覆盖的最远距离
|
||
if cover >= len(nums)-1: # 如果当前能够覆盖的最远距离达到或超过数组的最后一个位置,直接返回步数+1
|
||
return count+1
|
||
count += 1 # 每一轮遍历结束后,步数+1
|
||
|
||
|
||
```
|
||
动态规划
|
||
```python
|
||
class Solution:
|
||
def jump(self, nums: List[int]) -> int:
|
||
result = [10**4+1] * len(nums) # 初始化结果数组,初始值为一个较大的数
|
||
result[0] = 0 # 起始位置的步数为0
|
||
|
||
for i in range(len(nums)): # 遍历数组
|
||
for j in range(nums[i] + 1): # 在当前位置能够跳跃的范围内遍历
|
||
if i + j < len(nums): # 确保下一跳的位置不超过数组范围
|
||
result[i + j] = min(result[i + j], result[i] + 1) # 更新到达下一跳位置的最小步数
|
||
|
||
return result[-1] # 返回到达最后一个位置的最小步数
|
||
|
||
|
||
```
|
||
|
||
### Go
|
||
|
||
```go
|
||
// 贪心版本一
|
||
func jump(nums []int) int {
|
||
n := len(nums)
|
||
if n == 1 {
|
||
return 0
|
||
}
|
||
cur, next := 0, 0
|
||
step := 0
|
||
for i := 0; i < n; i++ {
|
||
next = max(nums[i]+i, next)
|
||
if i == cur {
|
||
if cur != n-1 {
|
||
step++
|
||
cur = next
|
||
if cur >= n-1 {
|
||
return step
|
||
}
|
||
} else {
|
||
return step
|
||
}
|
||
}
|
||
}
|
||
return step
|
||
}
|
||
|
||
func max(a, b int) int {
|
||
if a > b {
|
||
return a
|
||
}
|
||
return b
|
||
}
|
||
```
|
||
|
||
```go
|
||
// 贪心版本二
|
||
func jump(nums []int) int {
|
||
n := len(nums)
|
||
if n == 1 {
|
||
return 0
|
||
}
|
||
cur, next := 0, 0
|
||
step := 0
|
||
for i := 0; i < n-1; i++ {
|
||
next = max(nums[i]+i, next)
|
||
if i == cur {
|
||
cur = next
|
||
step++
|
||
}
|
||
}
|
||
return step
|
||
}
|
||
|
||
func max(a, b int) int {
|
||
if a > b {
|
||
return a
|
||
}
|
||
return b
|
||
}
|
||
```
|
||
|
||
### Javascript
|
||
|
||
```Javascript
|
||
var jump = function(nums) {
|
||
let curIndex = 0
|
||
let nextIndex = 0
|
||
let steps = 0
|
||
for(let i = 0; i < nums.length - 1; i++) {
|
||
nextIndex = Math.max(nums[i] + i, nextIndex)
|
||
if(i === curIndex) {
|
||
curIndex = nextIndex
|
||
steps++
|
||
}
|
||
}
|
||
|
||
return steps
|
||
};
|
||
```
|
||
|
||
### TypeScript
|
||
|
||
```typescript
|
||
function jump(nums: number[]): number {
|
||
const length: number = nums.length;
|
||
let curFarthestIndex: number = 0,
|
||
nextFarthestIndex: number = 0;
|
||
let curIndex: number = 0;
|
||
let stepNum: number = 0;
|
||
while (curIndex < length - 1) {
|
||
nextFarthestIndex = Math.max(nextFarthestIndex, curIndex + nums[curIndex]);
|
||
if (curIndex === curFarthestIndex) {
|
||
curFarthestIndex = nextFarthestIndex;
|
||
stepNum++;
|
||
}
|
||
curIndex++;
|
||
}
|
||
return stepNum;
|
||
}
|
||
```
|
||
|
||
### Scala
|
||
|
||
```scala
|
||
object Solution {
|
||
def jump(nums: Array[Int]): Int = {
|
||
if (nums.length == 0) return 0
|
||
var result = 0 // 记录走的最大步数
|
||
var curDistance = 0 // 当前覆盖最远距离下标
|
||
var nextDistance = 0 // 下一步覆盖最远距离下标
|
||
for (i <- nums.indices) {
|
||
nextDistance = math.max(nums(i) + i, nextDistance) // 更新下一步覆盖最远距离下标
|
||
if (i == curDistance) {
|
||
if (curDistance != nums.length - 1) {
|
||
result += 1
|
||
curDistance = nextDistance
|
||
if (nextDistance >= nums.length - 1) return result
|
||
} else {
|
||
return result
|
||
}
|
||
}
|
||
}
|
||
result
|
||
}
|
||
}
|
||
```
|
||
|
||
### Rust
|
||
|
||
```Rust
|
||
//版本一
|
||
impl Solution {
|
||
pub fn jump(nums: Vec<i32>) -> i32 {
|
||
if nums.len() == 1 {
|
||
return 0;
|
||
}
|
||
let mut cur_distance = 0;
|
||
let mut ans = 0;
|
||
let mut next_distance = 0;
|
||
for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
|
||
next_distance = (n as usize + i).max(next_distance);
|
||
if i == cur_distance {
|
||
if cur_distance < nums.len() - 1 {
|
||
ans += 1;
|
||
cur_distance = next_distance;
|
||
if next_distance >= nums.len() - 1 {
|
||
break;
|
||
};
|
||
} else {
|
||
break;
|
||
}
|
||
}
|
||
}
|
||
ans
|
||
}
|
||
}
|
||
```
|
||
|
||
```Rust
|
||
//版本二
|
||
impl Solution {
|
||
pub fn jump(nums: Vec<i32>) -> i32 {
|
||
if nums.len() == 1 {
|
||
return 0;
|
||
}
|
||
let mut cur_distance = 0;
|
||
let mut ans = 0;
|
||
let mut next_distance = 0;
|
||
for (i, &n) in nums.iter().enumerate().take(nums.len() - 1) {
|
||
next_distance = (n as usize + i).max(next_distance);
|
||
if i == cur_distance {
|
||
cur_distance = next_distance;
|
||
ans += 1;
|
||
}
|
||
}
|
||
ans
|
||
}
|
||
}
|
||
```
|
||
|
||
<p align="center">
|
||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||
</a>
|
||
|